Abstract
In this paper we consider a steady phase change problem for non-isothermal incompressible viscous flow in porous media with an enthalpy-porosity-viscosity coupling mechanism, and introduce and analyze a Banach spaces-based variational formulation yielding a new mixed-primal finite element method for its numerical solution. The momentum and mass conservation equations are formulated in terms of velocity and the tensors of strain rate, vorticity, and stress; and the incompressibility constraint is used to eliminate the pressure, which is computed afterwards by a postprocessing formula depending on the stress and the velocity. The resulting continuous formulation for the flow becomes a nonlinear perturbation of a perturbed saddle point linear system. The energy conservation equation is written as a nonlinear primal formulation that incorporates the additional unknown of boundary heat flux. The whole mixed-primal formulation is regarded as a fixed-point operator equation, so that its well-posedness hinges on Banach’s theorem, along with smallness assumptions on the data. In turn, the solvability analysis of the uncoupled problem in the fluid employs the Babuška–Brezzi theory, a recently obtained result for perturbed saddle-point problems, and the Banach–Nečas–Babuška Theorem, all them in Banach spaces, whereas the one for the uncoupled energy equation applies a nonlinear version of the Babuška–Brezzi theory in Hilbert spaces. An analogue fixed-point strategy is employed for the analysis of the associated Galerkin scheme, using in this case Brouwer’s theorem and assuming suitable conditions on the respective discrete subspaces. The error analysis is conducted under appropriate assumptions, and selecting specific finite element families that fit the theory. We finally report on the verification of theoretical convergence rates with the help of numerical examples.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
1 Introduction
1.1 Scope
Heat driven flow is a class of physical phenomena that has been extensively studied and it has practical applications in many branches of science and engineering. Specific mechanisms such as natural convection lay the foundation for other—more involved—processes including heat and mass transfer, phase change such as melting and solidification [28, 45], the design of energy storage devices [30], the description of ocean and atmosphere dynamics [29], and crystallization in magma chambers [44].
Throughout the literature, phase change is incorporated into the Boussinesq approximation by means of enthalpy-porosity methods [43] or enthalpy-viscosity models [28]. Numerical methods proposed for the former include a class of stabilised discontinuous Galerkin [43] and finite volume methods [45], whereas a primal finite element scheme [28] is employed for the latter. Other techniques used for either case include primal formulations with Taylor–Hood discretization, projection schemes, variational multiscale stabilization, and other variants [3, 31, 40, 41, 47]. Here we consider the general case where viscosity, enthalpy and porosity all depend on temperature. In turn, in the recent work [46] the authors introduced a phase change model for natural convection in porous media, where the problem is modeled as a viscous Newtonian fluid and the change of phase is encoded in the viscosity itself, and using a Brinkman–Boussinesq approximation where the solidification process influences the drag directly. A fully-primal formulation for the non-stationary case was analyzed in [46, Section 4.2], while rigorous mathematical and numerical analyses for mixed-primal and fully-mixed methods for the stationary case were provided in [7]. These numerical methods, as well as the related weak formulations, have been analyzed in Hilbert spaces-based frameworks.
The numerical analysis of Banach spaces formulations for linear, nonlinear, and coupled problems in continuum mechanics has been carried out in the very recent contributions [11, 15, 18, 21, 23, 25, 27, 34, 35] (see also the references therein), which consider Poisson, Brinkman–Forchheimer, Darcy–Forchheimer, Navier–Stokes, chemotaxis/Navier–Stokes, Boussinesq, coupled flow–transport, and fluidized beds, among others models. Using the more general approach of working with Banach spaces framework permits us to avoid augmentation techniques, maintaining a structure much closer to the initial physical model in mixed form. This type of formalisms has other benefits such as enforcing strongly (momentum and mass and energy) conservative schemes. Here we also illustrate numerically this advantage taking as an example the momentum conservation and comparing with the results produced with the methods from [7]. The purpose of the present manuscript is to extend and adapt the analysis developed in [34] for the Navier–Stokes–Brinkman equations, to accommodate the analysis of the coupling with phase change models such as that of [7]. We recall that in [7] it is necessary to augment the formulation for sake of the analysis (since one cannot complete the norms and conveniently control the terms that appear naturally in the formulation due to the use of a functional structure based only on Hilbert spaces) and currently we are not aware of non-augmented formulations specifically aimed for such a system. We also stress that the fixed-point strategy used herein differs substantially from that used in [7].
1.2 Outline
We have laid out the remainder of the paper in the following manner. Before the end of this section we introduce some notations and recall some auxiliary results to be employed throughout the paper. In Sect. 2 we introduce the model problem, define auxiliary variables to be employed in the setting of the mixed-primal formulation, and eliminate the pressure unknown. In Sect. 3 we derive the continuous formulation, and adopt a fixed-point strategy to analyze the corresponding solvability. Recent results on perturbed saddle-point problems, as well as the Babuška–Brezzi theory, both in Banach spaces, are employed to study the corresponding uncoupled problems, and then the classical Banach theorem is applied to conclude the existence of a unique solution. The associated Galerkin scheme is introduced in Sect. 4, where, under suitable assumptions on finite element subspaces, the discrete analogue of the methodology from Sect. 3, along with the Brouwer theorem instead of the Banach one, are utilized to prove existence of solution. In addition, ad-hoc Strang-type lemmas in Banach spaces are applied to derive a priori error estimates, specific finite element subspaces satisfying the aforementioned assumptions are introduced, and corresponding rates of convergence are established. The performance of the method is illustrated in Sect. 5 with several numerical examples, and we close with a summary of our findings and some concluding remarks in Sect. 6.
1.3 Background and Preliminary Notation
Throughout the paper, \(\Omega \) is a given bounded Lipschitz-continuous domain of \(\textrm{R}^n\), \(n \in \{2,3\}\), whose outward unit normal at its boundary \(\Gamma \) is denoted \({\varvec{\nu }}\). Standard notations will be adopted for Lebesgue spaces \(\textrm{L}^r(\Omega )\), with \(r\in (1,\infty )\), and Sobolev spaces \(\textrm{W}^{s,r}(\Omega )\), with \(s \ge 0\), endowed with the norms \(\Vert \cdot \Vert _{0,r;\Omega }\) and \(\Vert \cdot \Vert _{s,r;\Omega }\), respectively, whose vector and tensor versions are denoted in the same way. In particular, note that \(\textrm{W}^{0,r}(\Omega ) = \textrm{L}^r(\Omega )\), and that when \(r=2\) we simply write \(\textrm{H}^s(\Omega )\) in place of \(\textrm{W}^{s,2}(\Omega )\), with the corresponding Lebesgue and Sobolev norms denoted by \(\Vert \cdot \Vert _{0;\Omega }\) and \(\Vert \cdot \Vert _{s;\Omega }\), respectively. We also set \(|\cdot |_{s;\Omega }\) for the seminorm of \(\textrm{H}^s(\Omega )\). In turn, \(\textrm{H}^{1/2}(\Gamma )\) is the space of traces of functions of \(\textrm{H}^1(\Omega )\), \(\textrm{H}^{-1/2}(\Gamma )\) is its dual, and \(\langle \cdot ,\cdot \rangle \) denotes the duality pairing between them. On the other hand, by \({\textbf{S}}\) and \({\mathbb {S}}\) we mean the corresponding vector and tensor counterparts, respectively, of a generic scalar functional space \(\textrm{S}\). Furthermore, for any vector fields \({{\textbf{v}}}=(v_i)_{i=1,n}\) and \({{\textbf{w}}}=(w_i)_{i=1,n}\), we set the gradient, symmetric part of the gradient (also named strain rate tensor), divergence, and tensor product operators, as
where the superscript \((\cdot )^\texttt{t}\) stands for the matrix transposition. In addition, for any tensor fields \({\varvec{\tau }}=(\tau _{ij})_{i,j=1,n}\) and \({\varvec{\zeta }}=(\zeta _{ij})_{i,j=1,n}\), we let \({\textbf{div}}({\varvec{\tau }})\) be the divergence operator \({\textrm{div}}\) acting along the rows of \({\varvec{\tau }}\), and define the trace, the tensor inner product, and the deviatoric tensor, respectively, as
where \(\mathbb {I}\) is the identity matrix in \({\mathbb {R}}:= \textrm{R}^{n \times n}\). On the other hand, for each \(r\in [1,+\infty ]\) we introduce the Banach space
which is endowed with the natural norm
and recall that, proceeding as in [33, eq. (1.43), Sect. 1.3.4] one can prove that for each \(r\ge \frac{2 n}{n+2}\) there holds
where \(\langle \cdot , \cdot \rangle \) stands as well for the duality pairing between \({{\textbf{H}}}^{-1/2}(\Gamma )\) and \({{\textbf{H}}}^{1/2}(\Gamma )\). Finally, bear in mind that when \(r = 2\), the Hilbert space \(\mathbb H({\textbf{div}}_2;\Omega )\) and its norm \(\Vert \cdot \Vert _{{\textbf{div}}_2;\Omega }\) are simply denoted \({\mathbb {H}}({\textbf{div}};\Omega )\) and \(\Vert \cdot \Vert _{{\textbf{div}};\Omega }\), respectively.
Finally, the symbol \([\,\cdot ,\cdot \,]\) will denote a duality pairing induced by an appropriately defined operator.
2 The Model Problem
Let us consider the following Navier–Stokes–Brinkman equations coupled with a generalized energy equation, describing phase change mechanisms involving viscous fluids within porous media:
with \(\lambda :={\textrm{Re}}^{-1}\), \(\rho :={(C\,{\textrm{Pr}})}^{-1}\), where \({\textrm{Re}}\) and \({\textrm{Pr}}\) are the Reynolds and Prandtl numbers, respectively, \(\kappa \) and C are the non-dimensional heat conductivity tensor (here assumed isotropic) and specific heat, respectively, \({{\textbf{k}}}\) stands for the unit vector pointing oppositely to gravity, and \({{\textbf{u}}}: \Omega \rightarrow {\textrm{R}}^{n},\,\,p: \Omega \rightarrow {\textrm{R}}\) and \(\varphi : \Omega \rightarrow {\textrm{R}}\), correspond to the velocity, pressure, and the temperature of the fluid flow, respectively. Finally, \(\mu ,\, \eta ,\, s\) and f are the nonlinear viscosity, porosity, enthalpy and buoyancy terms, respectively, which depend on the temperature. Here \(s(\varphi )\) denotes an enthalpy function that accounts for the latent heat of fusion, i.e., the energy needed to change the phase of a material (cf. [46]).
Typical constitutive forms for the permeability-viscosity-enthalpy functions include, for example, the well-known Carman–Kozeny, exponential, and polynomial laws
respectively, where \(\phi (\varphi )= {\hat{\epsilon }}_1 + {\hat{\epsilon }}_2(1+ \tanh [\varphi -\varphi _\epsilon ])\) is a sharp liquid fraction field (porosity). For the subsequent analysis we assume a regular porosity-enthalpy hypothesis. In particular, this implies that the functions \(\mu ,\,\eta ,\, s\) are uniformly bounded and Lipschitz continuous, which means that there exist positive constants \(\mu _0,\,\mu _1,\,\eta _0,\,\eta _1,\,s_0,\,s_1,\,L_\mu ,\,L_\eta \) and \(L_s\), such that
Similar assumptions are placed on the buoyancy f: there exist positive constants \(C_f\) and \(L_f\) such that
On the other hand, we will suppose that for every \(\psi \in {\textrm{H}}^1(\Omega )\), we have \(s(\psi )\in {\textrm{H}}^1(\Omega )\), and that there exist positive constants \(s_3\) and \(L_{\widehat{s}}\) such that
Finally, we suppose that \(\kappa \) and \(\kappa ^{-1}\) are uniformly bounded and uniformly positive definite tensors, meaning that there exist positive constants \(\kappa _0,\,\kappa _1,\,{\widetilde{\kappa }}_0\) and \({\widetilde{\kappa }}_1\) such that
In turn, note that the incompressibility constraint imposes on \({{\textbf{u}}}_D\) the compatibility condition
and we also recall (see, e.g., [39]) that uniqueness of pressure is ensured in the space
We now proceed as in [7] (see also [6, 17, 24, 34]), and transform (2.1) into an equivalent first-order system without pressure. We introduce the strain rate \({{\textbf{t}}}\), vorticity \({\varvec{\gamma }}\), and stress \({\varvec{\sigma }}\) as auxiliary tensor unknowns
so that, thanks to the incompressibility of the fluid, the first equation of (2.1) is rewritten as
Moreover, the second equation of (2.1) (written in the form \({\textrm{tr}}({{\textbf{t}}}) \,=\, 0\)) together with (2.6), are equivalent to the pair of equations given by
In summary, (2.1) can be equivalently reformulated as
3 Continuous Weak Formulation
In this section we use a Banach framework for the continuous weak formulation of (2.8) and analyze its solvability by means of a fixed-point approach. More precisely, we follow [34] and introduce a mixed method for the Navier–Stokes–Brinkman equations, whereas for the energy equation we propose a primal method, which, differently from [7, 46], is formulated in a nonlinear version.
3.1 Mixed-Primal Approach
Note that the uncoupled Navier–Stokes–Brinkman problem—described by the first three equations of (2.8) and the respective boundary condition for the velocity—has been analyzed in detail in [34] by using the abstract results for perturbed saddle-point problems derived in [26], along with the Banach–Nečas–Babuška theorem. Following [34], we recall the definitions
and the decomposition
where
In particular, the unknown \({\varvec{\sigma }}\) can be uniquely decomposed as \({\varvec{\sigma }}\,=\, {\varvec{\sigma }}_0\,+\, c_0\,{{\mathbb {I}}}\), where \({\varvec{\sigma }}_0 \in {{\mathbb {H}}}_0({\textbf{div}}_{4/3};\Omega )\), and, from the last equation of (2.8), we have
Consequently, we can re-denote from now on \({\varvec{\sigma }}_0\) as simply \({\varvec{\sigma }}\in {{\mathbb {H}}}_0({\textbf{div}}_{4/3};\Omega )\). This implies in particular that the expression \(-\,({{\textbf{u}}}\otimes {{\textbf{u}}})^\texttt{d}- {\varvec{\sigma }}^\texttt{d}\) in the constitutive equation of (3.1) becomes \(-\,({{\textbf{u}}}\otimes {{\textbf{u}}})^\texttt{d} - {\varvec{\sigma }}\). In addition, the fact that the aforementioned equation is tested later on against \({{\textbf{s}}}\in {{\mathbb {L}}}^2_{\textrm{tr}}(\Omega )\) explains that the expression \(\int _\Omega ({{\textbf{u}}}\otimes {{\textbf{u}}})^\texttt{d}: {{\textbf{s}}}\) will then reduce to \(\int _\Omega ({{\textbf{u}}}\otimes {{\textbf{u}}}): {{\textbf{s}}}\) (see below definition of the bilinear form \(b({{\textbf{w}}};\cdot ,\cdot )\)). Next we proceed to introduce the spaces
and to set the notations
equipping \({{\textbf{H}}}\) and \({{\textbf{Q}}}\) with the norms
We refer to [34, Section 3.1] for a detailed explanation of the need of seeking \({{\textbf{u}}}\) in \({\textbf{L}}^4(\Omega )\) and \({\varvec{\sigma }}\) in \({\mathbb {H}}({\textbf{div}}_{4/3};\Omega )\). Thus, following [34], and assuming that the temperature dependency of \(\mu , \eta , f\) does not affect the aforementioned analysis, we arrive at the following formulation: Find \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\in {{\textbf{H}}}\times {{\textbf{Q}}}\) such that
for all \((\vec {{\textbf{s}}},\vec {{\textbf{v}}}) \in {{\textbf{H}}}\times {{\textbf{Q}}}\), where the bilinear forms \(a_\phi : {{\mathbb {L}}}^2_{{\textrm{tr}}}(\Omega ) \times {{\mathbb {L}}}^2_{{\textrm{tr}}}(\Omega ) \rightarrow {\textrm{R}}\), \(b_i: {{\mathbb {L}}}^2_{{\textrm{tr}}}(\Omega ) \times {{\mathbb {H}}}_0({\textbf{div}}_{4/3};\Omega ) \rightarrow {\textrm{R}}\), \(i \in \big \{1,2\big \}\), \({{\textbf{b}}}: {{\textbf{H}}}\times {{\textbf{Q}}}\rightarrow {\textrm{R}}\), and \({{\textbf{c}}}_\phi : {{\textbf{Q}}}\times {{\textbf{Q}}}\rightarrow {\textrm{R}}\), with \(\phi \in \textrm{H}^1(\Omega )\), are defined, respectively, as
whereas for each \({{\textbf{w}}}\in {{\textbf{L}}}^4(\Omega )\), \(b({{\textbf{w}}};\cdot ,\cdot ): {{\textbf{L}}}^4(\Omega ) \times {{\mathbb {L}}}^2_{{\textrm{tr}}}(\Omega ) \rightarrow {\textrm{R}}\) is the bilinear form given by
We stress here that the symmetry of the stress \({\varvec{\sigma }}\) is imposed weakly through the equation \(\int _\Omega {\varvec{\delta }}: {\varvec{\sigma }}= 0\) \(\,\forall \,{\varvec{\delta }}\in {{\mathbb {L}}}^2_\texttt{skew}(\Omega )\), which explains the first term of the bilinear form \({{\textbf{b}}}\). See further details in, e.g., [46] or [34].
Next, and letting, for each \(\phi \in {\textrm{H}}^1(\Omega )\), \({{\textbf{a}}}_\phi : {{\textbf{H}}}\times {{\textbf{H}}}\rightarrow {\textrm{R}}\) be the bilinear form that arises from the block \(\left( \begin{array}{ll} a_\phi &{} b_1 \\ b_2 &{} \end{array}\right) \) by adding the first two equations of (3.1), that is
we find that (3.1) can be rewritten as: Find \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\in {{\textbf{H}}}\times {{\textbf{Q}}}\) such that
Moreover, letting now \({{\textbf{A}}}_\phi : \big ({{\textbf{H}}}\times {{\textbf{Q}}}\big ) \times \big ({{\textbf{H}}}\times {{\textbf{Q}}}\big ) \rightarrow {\textrm{R}}\) be the bilinear form that arises from the block \(\left( \begin{array}{lc} {{\textbf{a}}}_\phi &{} {{\textbf{b}}}\\ {{\textbf{b}}}&{} -{{\textbf{c}}}_\phi \end{array}\right) \), for each \(\phi \in {\textrm{H}}^1(\Omega )\), by adding both equations of (3.2), that is
we deduce that (3.2) (and hence (3.1)) can be stated equivalently as: Find \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\in {{\textbf{H}}}\times {{\textbf{Q}}}\) such that
where, for each \(\phi \in \textrm{H}^1(\Omega )\), the functional \({{\textbf{F}}}_\phi \in \big ( {{\textbf{H}}}\times {{\textbf{Q}}}\big )'\) is defined by
On the other hand, in order to derive a weak form for the energy equation, we recall that the injection \(\textrm{i}_4:\,\textrm{H}^1(\Omega )\rightarrow \textrm{L}^4(\Omega )\) is continuous (cf. [39, Theorem 1.3.4]), which is valid in \({\textrm{R}}^n\), \(n\in \{2,3\}\):
Proceeding as in [7, Section 3.1], we test the fourth equation of (2.8) against \(\psi \in {\textrm{H}}^{1}(\Omega )\), integrate by parts, introduce the normal heat flux \(\chi :=\,-\rho \kappa \nabla \varphi \cdot {\varvec{\nu }}\in \textrm{H}^{-1/2}(\Gamma )\) as a new unknown, and impose the Dirichlet boundary condition for \(\varphi \) in a weak sense, so that we get
Here we readily note that, in order for the second term in the first equation of (3.5) to be well-defined, and thanks to the continuous injection \(\textrm{i}_4\) (cf. (3.4)) and the assumption on s (cf. Section 2), we require that \(({{\textbf{u}}},\varphi )\) lies in \({{\textbf{L}}}^{4}(\Omega )\times {\textrm{H}}^{1}(\Omega )\). Then, given \({{\textbf{u}}}\in {{\textbf{L}}}^{4}(\Omega )\), we now consider the following primal formulation for the energy equation: Find \((\varphi ,\chi )\in {\textrm{H}}^{1}(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\) such that
where given \({{\textbf{z}}}\in {{\textbf{L}}}^{4}(\Omega )\), the nonlinear operator \({\mathcal {A}}_{{{\textbf{z}}}}:{\textrm{H}}^{1}(\Omega )\rightarrow {\textrm{H}}^{1}(\Omega )'\) and the linear operator \({\mathcal {B}}:{\textrm{H}}^{1}(\Omega ) \rightarrow {\textrm{H}}^{-1/2}(\Gamma )'\) are defined by
and
whereas \({\mathcal {G}}\in \textrm{H}^{-1/2}(\Gamma )'\) is the functional given by
Summarizing, the non-augmented mixed-primal formulation for (2.8) reduces to (3.3) and (3.6), that is: Find \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\in {{\textbf{H}}}\times {{\textbf{Q}}}\) and \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\) such that
3.2 Fixed-Point Strategy
Let \({\textbf{S}}:{{\textbf{L}}}^4(\Omega )\times {\textrm{H}}^1(\Omega )\rightarrow \textbf{L}^4(\Omega )\) be defined by
where \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})=\big (({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }})\big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) is the unique solution (to be confirmed below) of
In turn, we let \({\widetilde{\textbf{S}}}:{{\textbf{L}}}^4(\Omega )\rightarrow {\textrm{H}}^1(\Omega )\) be the operator given by
where \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\) is the unique solution (to be confirmed below) of
Then, we define the operator \({{\textbf{T}}}:{{\textbf{L}}}^4(\Omega )\rightarrow {{\textbf{L}}}^4(\Omega )\) by
Solving (3.8) is equivalent to seeking a fixed point of \({{\textbf{T}}}\), that is, finding \({{\textbf{z}}}\in {{\textbf{L}}}^4(\Omega )\) such that
3.3 Well-Posedness of the Uncoupled Problems
We now show that the uncoupled problems (3.3) and (3.6) are well-posed. We remark again that the only difference between (3.3) and the formulation in [34] is that \(\mu , \eta ,f\) are temperature-dependent, but in virtue of assumptions (2.2) and (2.3), we can simply state the following result (with an almost verbatim proof).
Lemma 3.1
For any \(({{\textbf{z}}},\phi )\in \textrm{L}^4(\Omega )\times \textrm{H}^1(\Omega )\) such that \(\Vert {{\textbf{z}}}\Vert _{0,4;\Omega }\le \frac{\alpha _{{\textbf{A}}}}{2}\), problem (3.9) has a unique solution \((\vec {{\textbf{t}}},\vec {{\textbf{u}}}):=\big (({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }})\big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\), and hence \({\textbf{S}}({{\textbf{z}}},\phi ):={{\textbf{u}}}\in {\textbf{L}}^4(\Omega )\) is well-defined. Moreover, there exists \(C_{\textbf{S}}>0\), depending only on \(\alpha _{{{\textbf{A}}}}\), \(C_f\) (cf. (2.3)), \(|\Omega |\) and \(\Vert {{\textbf{k}}}\Vert _\infty \), such that
Proof
It follows directly from [34, Lemma 3.5], with the exception that now there holds
where \(C_{{\textbf{F}}}\,:=\,\max \big \{1,\, C_f|\Omega |^{1/4}\Vert {{\textbf{k}}}\Vert _{\infty }\big \}\). \(\square \)
The previous lemma suggests to consider the ball (which will be employed below in Sect. 3.4)
It remains to prove that \({\widetilde{\textbf{S}}}\) is well-defined. To this end, and in order to proceed similarly to [12], we state next an abstract result that will be utilized to establish the well-posedness of problem (3.10), and which can be viewed as a nonlinear version of the Babuška–Brezzi theory. We notice in advance that, while the above is valid within a Banach spaces framework, its application below is just for a particular Hilbertian case.
Theorem 3.2
Let \({\textrm{H}}\) and \({\textrm{Q}}\) be separable and reflexive Banach spaces, with \({\textrm{H}}\) uniformly convex, and let \(a:{\textrm{H}}\rightarrow {\textrm{H}}'\) be a nonlinear operator and \(b\in \mathcal {L}({\textrm{H}},{\textrm{Q}}')\). Let \({\textrm{V}}\) be the null space of b, and assume that
-
(i)
a is Lipschitz-continuous, that is there exists \(L>0\) such that
$$\begin{aligned} \Vert a(u)-a(v)\Vert _{{\textrm{H}}'} \le L\Vert u-v\Vert _{{\textrm{H}}}\quad \forall \, u,v\in {\textrm{H}}\,. \end{aligned}$$ -
(ii)
The family of operators \(a(\cdot +t):{\textrm{V}}\rightarrow {\textrm{V}}'\), with \(t\in {\textrm{H}}\), is uniformly strongly monotone, that is there exists a positive constant \(\alpha \) such that
$$\begin{aligned} {[}a(u+t)-a(v+t),u-v]\ge \alpha \Vert u-v\Vert _{{\textrm{H}}}^2\quad \forall \, t\in {\textrm{H}},\,\forall \, u,v\in {\textrm{V}}\,. \end{aligned}$$(3.15) -
(iii)
There exists a positive constant \(\beta \) such that
$$\begin{aligned} \sup _{{\mathop {v\not = 0}\limits ^{v\in {\textrm{H}}}}} \dfrac{[b(v),\tau ]}{\Vert v\Vert _{\textrm{H}}} \ge \beta \Vert \tau \Vert _{\textrm{Q}}\quad \forall \,\tau \in {\textrm{Q}}\,. \end{aligned}$$
Then, for each \((F,G)\in {\textrm{H}}'\times {\textrm{Q}}'\) there exists a unique \((u,\sigma )\in {\textrm{H}}\times {\textrm{Q}}\) such that
Furthermore, there hold
Proof
It follows from a slight adaptation of [42, Proposition 2.3] with \(p=2\) (see also [19, Theorem 3.1] with \(p_1=p_2=2\)). \(\square \)
Next, in order to apply Theorem 3.2 to problem (3.10), we first observe, thanks to the duality between \({\textrm{H}}^{-1/2}(\Gamma )\) and \({\textrm{H}}^{1/2}(\Gamma )\), that the linear operator \({\mathcal {B}}\) and the functional \({\mathcal {G}}\) are bounded, that is
We continue our analysis by proving that for each \({{\textbf{z}}}\in {{\textbf{L}}}^4(\Omega )\), \({\mathcal {A}}_{{{\textbf{z}}}}\) is Lipschitz continuous.
Lemma 3.3
There exists a positive constant \(L_{\mathcal {A}}\), depending only on \(\rho \), \(\kappa _1\), \(L_{\widehat{s}}\) and \(\Vert \textrm{i}_4\Vert \), such that
for all \({{\textbf{z}}}\in {{\textbf{L}}}^4(\Omega )\), and for all \(\phi _1,\phi _2\in {\textrm{H}}^1(\Omega )\).
Proof
Given \({{\textbf{z}}}\in {{\textbf{L}}}^4(\Omega )\) and \(\phi _1,\phi _2,\psi \in {\textrm{H}}^1(\Omega )\), using (3.7), the upper bounds (2.4) and (2.5), the Cauchy–Schwarz and triangle inequalities, and the continuous injection \(\textrm{i}_4\) (cf. (3.4)), we deduce that
which confirms the mentioned property on \({\mathcal {A}}_{{\textbf{z}}}\) with \(L_{\mathcal {A}}\,:=\,\max \big \{\rho \kappa _1,\,(1+L_{\widehat{s}})\Vert \textrm{i}_4\Vert \big \}\). \(\square \)
Now, aiming to prove that \({\mathcal {A}}_{{\textbf{z}}}\) satisfies (3.15), we require the Friedrichs–Poincaré inequality, which establishes the existence of a positive constant \(c_{_\textrm{P}}\), depending only on \(\Omega \), such that
In addition, we note that the kernel \({{\widetilde{{\textrm{V}}}}}\) of the operator \({\mathcal {B}}\) is given by
and introduce the ball
Then, the following result states that \({\mathcal {A}}_{{\textbf{z}}}\) satisfies hypothesis ii) of Theorem 3.2.
Lemma 3.4
There exists a positive constant \(\alpha _{\mathcal {A}}\), depending only on \(\rho \), \(\kappa _0\) and \(c_{_\textrm{P}}\), such that for each \({{\textbf{z}}}\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}}}\), the family of operators \({\mathcal {A}}_{{{\textbf{z}}}}(\,\cdot +\phi )\) with \(\phi \in {\textrm{H}}^1(\Omega )\), is uniformly strongly monotone in \({{\widetilde{{\textrm{V}}}}}\):
Proof
Given \({{\textbf{z}}}\in {{\textbf{L}}}^4(\Omega )\), \(\phi \in {\textrm{H}}^1(\Omega )\) and \(\theta _1,\theta _2\in {{\widetilde{{\textrm{V}}}}}\), using (3.7), (2.5), (2.4), Friedrichs–Poincaré inequality (3.19), the continuous injection (3.4), and the Cauchy–Schwarz inequality, it follows that
In this way, defining \( \alpha _{\mathcal {A}}\,:=\, \dfrac{\rho \kappa _0c_{_\textrm{P}}}{2}\,\), we obtain
from which, using that \({{\textbf{z}}}\in {{\textbf{W}}}_{\widetilde{\textbf{S}}}\), we readily conclude the proof. \(\square \)
We observe here that, instead of imposing \(\Vert {{\textbf{z}}}\Vert _{0,4;\Omega }\le \alpha _{\mathcal {A}}/\big ((1+L_{\widehat{s}})\Vert \textrm{i}_4\Vert \big )\), we could have assumed that \(\Vert {{\textbf{z}}}\Vert _{0,4;\Omega }\le 2\delta \alpha _{\mathcal {A}}/\big ((1+L_{\widehat{s}})\Vert \textrm{i}_4\Vert \big )\), with \(\delta \in (0,1)\). Then choosing \(\delta \) closer to 1, the larger the resulting range of \(\Vert {{\textbf{z}}}\Vert _{0,4;\Omega }\), but then the strong monotonicity constant approaches 0. Conversely, the closer \(\delta \) to 0, the smaller the range for \(\Vert {{\textbf{z}}}\Vert _{0,4;\Omega }\), but then the strong monotonicity constant approaches \(2\alpha _{\mathcal {A}}\). Hence the choice \(\delta =\frac{1}{2}\) aims to balance both aspects.
We complete the verification of the hypotheses of Theorem 3.2 with the inf-sup condition for \({\mathcal {B}}\), which can be found in [33, section 2.4.4].
Lemma 3.5
The following inf-sup condition holds with inf-sup constant equal to 1
Now, we are in position to establish the unique solvability of the nonlinear problem (3.10).
Lemma 3.6
For each \({{\textbf{z}}}\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}}}\), the problem (3.10) has a unique solution \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\), and hence \({\widetilde{\textbf{S}}}({{\textbf{z}}}):=\,\varphi \in \textrm{H}^1(\Omega )\) is well-defined. Moreover, there exist positive constants \(C_{{\widetilde{\textbf{S}}}}\) and \(\widetilde{C}_{{\widetilde{\textbf{S}}}}\), depending only on \(L_{\mathcal {A}}\) (cf. proof of Lemma (3.3)) and \(\alpha _{\mathcal {A}}\) (cf. proof of Lemma 3.4), such that
Proof
We first recall from (3.17a) to (3.17b) that \({\mathcal {B}}\) and \({\mathcal {G}}\) are linear and bounded. Thus, using Lemmas 3.3, 3.4 and 3.5, and applying Theorem 3.2 to problem (3.9) implies the well-definedness of the operator \({\widetilde{\textbf{S}}}\) for each \({{\textbf{z}}}\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}}}\). Moreover, noting that \({\mathcal {A}}_{{\textbf{z}}}(0)\in {\textrm{H}}^1(\Omega )'\) is the null functional, recalling from Lemma 3.5 that the inf-sup constant is 1, and denoting \(\widetilde{L}_{\mathcal {A}}:= L_{\mathcal {A}}(1+\alpha _{\mathcal {A}})\), the a priori estimate (3.16) yields
which, along with the upper bound of \(\Vert {\mathcal {G}}\Vert \) (cf. (3.17b)), implies (3.22). \(\square \)
3.4 Solvability Analysis
Consider now the ball
We proceed to prove that, under sufficiently small data, \({{\textbf{T}}}\) maps \({{\textbf{W}}}\) into itself.
Lemma 3.7
Assume that the data satisfy
where \(C_{{\textbf{T}}}:=\,C_{\textbf{S}}\max \big \{1,C_{\widetilde{\textbf{S}}}\big \}\), and \(C_{\textbf{S}}\) and \(C_{\widetilde{\textbf{S}}}\) are the constants specified in Lemmas 3.1 and 3.6. Then, there holds \({{\textbf{T}}}({{\textbf{W}}})\subseteq {{\textbf{W}}}\).
Proof
Given \({{\textbf{z}}}\in {{\textbf{W}}}\), we have that \({{\textbf{z}}}\) satisfies the well-defined conditions for \({\textbf{S}}\) and \({\widetilde{\textbf{S}}}\), and hence for \({{\textbf{T}}}\). Moreover, the corresponding estimate (3.13) yields
Then, bounding \(\Vert {\widetilde{\textbf{S}}}({{\textbf{z}}})\Vert _{1;\Omega }\) in the foregoing inequality according to the estimate (3.22) and using the assumption (3.24), we get \(\Vert {{\textbf{T}}}({{\textbf{z}}})\Vert _{0,4;\Omega }\,\le \,\varrho \), which completes the proof. \(\square \)
We now prove that \({{\textbf{T}}}\) is Lipschitz continuous (it suffices to show that \({\textbf{S}}\) and \({\widetilde{\textbf{S}}}\) satisfy this property). For \({\textbf{S}}\) we assume the further regularity \({{\textbf{u}}}_D\in {{\textbf{H}}}^{1/2+\epsilon }(\Gamma )\) for some \(\epsilon \in [1/2,1)\) (when \(n=2\)) or \(\epsilon \in [3/4,1)\) (when \(n=3\)), and that for each \(({{\textbf{z}}},\phi )\in {{\textbf{W}}}_{{\textbf{S}}}\times {\textrm{H}}^1(\Omega )\) there holds \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\,=\,\big (({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }})\big )\in \big (\big ({{\mathbb {L}}}_{{\textrm{tr}}}^2(\Omega )\cap {{\mathbb {H}}}^\epsilon (\Omega )\big )\times \big ({{\mathbb {H}}}_0({\textbf{div}}_{4/3};\Omega )\cap {{\mathbb {H}}}^\epsilon (\Omega )\big )\big )\times \big (\big ({{\textbf{L}}}^4(\Omega )\cap {{\textbf{W}}}^{\epsilon ,4}(\Omega )\big )\times \big ({{\mathbb {L}}}_\texttt{skew}^2(\Omega )\cap {{\mathbb {H}}}^\epsilon (\Omega )\big )\big )\) with \({\textbf{S}}({{\textbf{z}}},\phi ):=\,{{\textbf{u}}}\) and
with a positive constant \(c_{{\textbf{S}}}\) independent of the given \(({{\textbf{z}}},\phi )\). The chosen range for \(\epsilon \) will be clarified in the proof of the following lemma.
Lemma 3.8
There exists a positive constant \(L_{\textbf{S}}\), depending on \(|\Omega |\), \(\Vert {{\textbf{k}}}\Vert _{\infty }\), \(L_\mu \), \(L_\eta \), \(\Vert \textrm{i}_4\Vert \), \(\alpha _{{\textbf{A}}}\) and \(\epsilon \), such that
for all \(({{\textbf{z}}}_1,\phi _1),({{\textbf{z}}}_2,\phi _2)\in {{\textbf{W}}}_{\textbf{S}}\times {\textrm{H}}^1(\Omega )\).
Proof
Given \(({{\textbf{z}}}_i,\phi _i)\in {{\textbf{W}}}_{\textbf{S}}\times {\textrm{H}}^1(\Omega )\), for each \(i\in \big \{1,2\big \}\), we let \({\textbf{S}}({{\textbf{z}}}_i,\phi _i):=\,{{\textbf{u}}}_i\), where \((\vec {{\textbf{t}}}_i,\vec {{\textbf{u}}}_i)\,:=\,\big ( ({{\textbf{t}}}_i,{\varvec{\sigma }}_i),({{\textbf{u}}}_i,{\varvec{\gamma }}_i) \big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) is the unique solution of (3.9) with \(({{\textbf{z}}},\phi ):=\,({{\textbf{z}}}_i,\phi _i)\), that is
Now, applying the inf-sup condition for the bilinear form in the left hand side of the foregoing equation (cf. [34, eq. (3.64)]) with \(({{\textbf{z}}},\phi )=({{\textbf{z}}}_1,\phi _1)\) to \((\vec {{\textbf{r}}},\vec {{\textbf{w}}}) \,:=\, (\vec {{\textbf{t}}}_1,\vec {{\textbf{u}}}_1) - (\vec {{\textbf{t}}}_2,\vec {{\textbf{u}}}_2)\), we obtain
from which, adding and subtracting \(b({{\textbf{z}}}_2;{{\textbf{u}}}_2,{{\textbf{s}}})\), and then employing (3.27), we obtain
We now estimate the right-hand side of (3.28) by separating its numerator into three suitable terms. Indeed, we first observe that
where \(p,q\in [1,\infty )\) are such that \(\frac{1}{p}+\frac{1}{q}=1\). In this way, bearing in mind the further regularity (3.25), we recall that the Sobolev embedding Theorem [1, Theorem 4.12] establishes the continuous injection \(\textrm{i}_\epsilon :{{\mathbb {H}}}^\epsilon (\Omega )\rightarrow {{\mathbb {L}}}^{\epsilon ^*}(\Omega )\), where \(\epsilon ^*\,=\,\left\{ \begin{array}{ll} \frac{2}{1-\epsilon } &{}\quad \hbox {if } n=2\,,\\ \frac{6}{3-2\epsilon } &{}\quad \hbox {if } n=3 \end{array}\right. .\) Thus, choosing q such that \(2q = \epsilon ^*\), there holds \({{\textbf{t}}}_2\in {{\mathbb {L}}}^{2q}(\Omega )\) and
In turn, with that choice of 2q, we obtain that \(2p\,=\,n/\epsilon \) and hence, using now that for the specified ranges of \(\epsilon \) the injection \(\widetilde{\textrm{i}}_\epsilon \) of \(\textrm{L}^4(\Omega )\) into \(\textrm{L}^{n/\epsilon }(\Omega )\) is continuous, and applying that \({\textrm{H}}^1(\Omega )\) is continuously embedded into \(\textrm{L}^4(\Omega )\) (cf. (3.4)), there holds
Then, putting (3.30) and (3.31) back into (3.29), and denoting \(L_{{\textbf{A}}}\,{:=}\,\max \big \{ \lambda \,L_\mu \, \Vert \widetilde{\textrm{i}}_\epsilon \Vert \,\Vert \textrm{i}_4\Vert \,\Vert i_\epsilon \Vert , L_\eta \big \}\), gives
Next, it is easy to see that
Now, thanks to the properties of f (cf. (2.3)) together with the Cauchy–Schwarz inequality, we have
with \(L_{{\textbf{F}}}:=\, |\Omega |^{1/4}\Vert {{\textbf{k}}}\Vert _\infty \). Finally, replacing (3.32), (3.33) and (3.34) back into (3.28), and then simplifying by \(\Vert (\vec {{\textbf{s}}},\vec {{\textbf{v}}})\Vert _{{{\textbf{H}}}\times {{\textbf{Q}}}}\), we obtain (3.26) with
\(\square \)
We now focus on proving the Lipschitz-continuity of \({\widetilde{\textbf{S}}}\).
Lemma 3.9
There exists a positive constant \(L_{{\widetilde{\textbf{S}}}}\), depending only on \(s_3\), \(\Vert \textrm{i}_4\Vert \) and \(\alpha _{\mathcal {A}}\) (cf. proof of Lemma 3.4), such that for all \({{\textbf{z}}}_1,{{\textbf{z}}}_2\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}}}\), there holds
Proof
Given \({{\textbf{z}}}_i\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}}}\), \(i\in \big \{1,2\big \}\), we let \({\widetilde{\textbf{S}}}({{\textbf{z}}}_i)\,=\,\varphi _i\), where \((\varphi _i,\chi _i)\in {\textrm{H}}^{1}(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\) is the unique solution of (3.10) with \({{\textbf{z}}}:=\,{{\textbf{z}}}_i\), that is
Then, subtracting the two problems, we obtain
It follows from the second equation of (3.36) that \(\varphi _1-\varphi _2\in {{\widetilde{{\textrm{V}}}}}\) (cf. (3.20)), and hence, using that \({\mathcal {A}}_{{{\textbf{z}}}_1}\) is uniformly strongly monotone on \({{\widetilde{{\textrm{V}}}}}\) (cf. (3.21)), with \(\varphi _2\in {\textrm{H}}^1(\Omega )\) and \(0,\varphi _1-\varphi _2\in {{\widetilde{{\textrm{V}}}}}\), we get
Now, using (3.7), adding and subtracting \({\mathcal {A}}_{{{\textbf{z}}}_2}(\varphi _2)\) in the first term on the right-hand side of (3.37), using the first equation of (3.36) and Cauchy–Schwarz and Hölder inequalities, we have
Then, using the triangle inequality, the upper bound for the gradient of s (cf. (2.4)) and (3.4), we get
which yields (3.35) and ends the proof. \(\square \)
As a consequence of the previous lemmas, we establish now the Lipschitz-continuity of \({{\textbf{T}}}\).
Lemma 3.10
There exists a positive constant \(L_{{\textbf{T}}}\), depending only on \(C_{\widetilde{\textbf{S}}}\), \(C_{{\textbf{T}}}\), \(c_{\textbf{S}}\), \(L_{\textbf{S}}\), and \(L_{\widetilde{\textbf{S}}}\), such that for all \({{\textbf{z}}}_1,{{\textbf{z}}}_2\in {{\textbf{W}}}\), there holds
where
Proof
Given \({{\textbf{z}}}_1,{{\textbf{z}}}_2\in {{\textbf{W}}}\), and according to (3.11) and (3.26), we first obtain
where for each \(i\in \{1,2\}\), \((\vec {{\textbf{t}}}_i,\vec {{\textbf{u}}}_i):=\,\big (({{\textbf{t}}}_i,{\varvec{\sigma }}_i),({{\textbf{u}}}_i,{\varvec{\gamma }}_i)\big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) is the unique solution of (3.9) with \(\big ({{\textbf{z}}}_i,{\widetilde{\textbf{S}}}({{\textbf{z}}}_i)\big )\) instead of \(({{\textbf{z}}},\phi )\). In turn, the a priori estimate for \({\widetilde{\textbf{S}}}\) (cf. (3.22)) holds
whereas the Lipschitz-continuity of \({\widetilde{\textbf{S}}}\) (cf. (3.35)) with (3.41), gives
and the a priori estimates for \({{\textbf{T}}}\) (cf. Lemma 3.7) yields
and finally, replacing (3.41) on the regularity assumption (3.25) for \({{\textbf{t}}}_2\), we find that
In this way, replacing (3.42), (3.43) and (3.44) in (3.40), and performing several algebraic manipulations aiming to simplify the whole writing, we are lead to (3.38) with
\(\square \)
The main result of this section is given as follows.
Theorem 3.11
Assume the data satisfies (3.24), that is
and
Then \({{\textbf{T}}}\) has a unique fixed point \({{\textbf{u}}}\in {{\textbf{W}}}\). Equivalently, the coupled problem (3.8) has a unique solution \((\vec {{\textbf{t}}},\vec {{\textbf{u}}}):=\,\big (({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }})\big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) and \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\), with \({{\textbf{u}}}\in {{\textbf{W}}}\). Moreover, there holds
Proof
It is clear, thanks to assumption (3.45) and Lemma 3.10, that \({{\textbf{T}}}\) is a contraction, which together with Lemma 3.7, proves that the fixed point operator \({{\textbf{T}}}\) satisfies the hypotheses of Banach’s fixed-point theorem, which implies the solvability of the problem (3.12), equivalently, the solvability of (3.8). Consequently, the a priori estimates (3.46a) and (3.46b) follow from (3.13) to (3.22), respectively. \(\square \)
4 The Galerkin Scheme
In this section, we introduce and analyze the Galerkin scheme associated with (3.8). The solvability of this scheme is addressed following basically the same techniques employed throughout Sect. 3. To this end, we let \({{\mathbb {H}}}_h^{{{\textbf{t}}}}\), \({\widetilde{{{\mathbb {H}}}}}_h^{{\varvec{\sigma }}}\), \({{\textbf{H}}}_h^{{{\textbf{u}}}}\), \({{\mathbb {H}}}_h^{{\varvec{\gamma }}}\), \({\textrm{H}}_h^{\varphi }\) and \({\textrm{H}}_h^{\chi }\) be arbitrary finite element subspaces of \({{\mathbb {L}}}_{{\textrm{tr}}}^2(\Omega )\), \({{\mathbb {H}}}({\textbf{div}}_{4/3};\Omega )\), \({{\textbf{L}}}^4(\Omega )\), \({{\mathbb {L}}}_\texttt{skew}^{2}(\Omega )\), \({\textrm{H}}^1(\Omega )\) and \({\textrm{H}}^{-1/2}(\Gamma )\), respectively. Hereafter, \(h\,:=\,\max \big \{ h_{K}:\quad K\in \mathcal {T}_h\big \}\) stands for the size of a regular triangulation \({\mathcal {T}}_h\) of \({\bar{\Omega }}\). Specific finite element subspaces satisfying suitable hypotheses to be introduced along the analysis will be provided later on in Sect. 4.5. Then, letting
defining the product spaces
and setting the notations
the Galerkin scheme associated with (3.8) reads as follows: Find \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h)\,:=\,\big (({{\textbf{t}}}_h,{\varvec{\sigma }}_h),({{\textbf{u}}}_h,{\varvec{\gamma }}_h) \big )\in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\) and \((\varphi _h,\chi _h)\in {\textrm{H}}_h^{\varphi }\times {\textrm{H}}_h^{\chi }\) such that
4.1 The Discrete Fixed Point Strategy
We adopt the discrete analogue of Sect. 3.2 to analyze (4.3). Let \({\textbf{S}}_h:{{\textbf{H}}}_h^{{{\textbf{u}}}}\times {\textrm{H}}_h^{\varphi }\rightarrow {{\textbf{H}}}_h^{{{\textbf{u}}}}\) be the operator given by
where \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h):=\big (({{\textbf{t}}}_h,{\varvec{\sigma }}_h),({{\textbf{u}}}_h,{\varvec{\gamma }}_h)\big )\in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\) is the unique solution (to be confirmed below) of the linear problem given by
In turn, we let \({\widetilde{\textbf{S}}}_h:{{\textbf{H}}}_h^{{{\textbf{u}}}}\rightarrow {\textrm{H}}_h^{\varphi }\) be the operator defined by
where \((\varphi _h,\chi _h)\in {\textrm{H}}_h^{\varphi }\times {\textrm{H}}_h^{\chi }\) is the unique solution (to be confirmed below) of
Then, we define the operator \({{\textbf{T}}}_h:{{\textbf{H}}}_h^{{{\textbf{u}}}}\rightarrow {{\textbf{H}}}_h^{{{\textbf{u}}}}\) by
and realize that solving (4.3) is equivalent to seeking a fixed point of \({{\textbf{T}}}_h\): Find \({{\textbf{z}}}_h\in {{\textbf{H}}}_h^{{{\textbf{u}}}}\) such that
4.2 Well-Definedness of the Discrete Problems
In this section we apply the discrete versions of the solvability result for perturbed saddle-point problems and the nonlinear version of the Babuška–Brezzi theory employed in Sect. 3.3, to prove that the operators \({\textbf{S}}_h\), \({\widetilde{\textbf{S}}}_h\), and hence \({{\textbf{T}}}_h\), are well-defined. As observed in the previous section, these goals reduce, equivalently, to establishing that the uncoupled problems (4.4) and (4.5) are well-posed. To this end, we begin by remarking, as in the continuous counterpart, that the solvability of the discrete problem (4.4) is addressed in [34, Section 4.2], and for this reason we just state the following result.
Lemma 4.1
For each \(({{\textbf{z}}}_h,\phi _h)\in {{\textbf{H}}}_h^{{\textbf{u}}}\times \textrm{H}_h^\varphi \) such that \(\Vert {{\textbf{z}}}_h\Vert _{0,4;\Omega }\le \dfrac{\alpha _{{{\textbf{A}}},\mathtt d}}{2}\) (cf. [34, eq. 4.23]), problem (4.4) has a unique solution \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h):=\,\big (({{\textbf{t}}}_h,{\varvec{\sigma }}_h),({{\textbf{u}}}_h,{\varvec{\gamma }}_h)\big )\in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\), and hence \({\textbf{S}}_h({{\textbf{z}}}_h,\phi _h):=\,{{\textbf{u}}}_h\in {{\textbf{H}}}_h^{{\textbf{u}}}\) is well-defined. Moreover, there exists a positive constant \(C_{{\textbf{S}},\mathtt d}\), depending only on \(\alpha _{{{\textbf{A}}},\mathtt d}\), \(C_f\), \(|\Omega |\) and \(\Vert {{\textbf{k}}}\Vert _\infty \), and hence independent of h, such that
Proof
It follows directly from [34, Lemma 4.2] to (3.14). \(\square \)
The following assumptions, specified in [34, Section 4.2], are necessary to apply Lemma 4.1.
(H.0) \({\widetilde{{{\mathbb {H}}}}}_{h}^{{\varvec{\sigma }}}\) contains the multiplies of the identity tensor \({\mathbb {I}}\).
(H.1) \({\textbf{div}}({\widetilde{{{\mathbb {H}}}}}_{h}^{{\varvec{\sigma }}})\,\subseteq \, {{\textbf{H}}}_h^{{{\textbf{u}}}}\).
(H.2) \(\big ( {\textrm{V}}_{0,h} \big )^\texttt{d}\,\subseteq \,{{\mathbb {H}}}_{h}^{{{\textbf{t}}}} \), where \({{\textbf{V}}}_{h}\,:=\,\mathbb H_h^{{{\textbf{t}}}}\times {\textrm{V}}_{0,h}\) is the kernel of \({{\textbf{b}}}\vert _{{{\textbf{H}}}_h\times {{\textbf{Q}}}_h}\), with
(H.3) There exists a positive constant \(\beta _{{{\textbf{b}}},\mathtt d}\), independent of h, such that
In addition, the previous lemma suggests to consider the ball
which will be employed below in Sect. 4.3.
Next, aiming to prove the solvability of (4.5), we require a consequence of the generalized Poincaré inequality, which establishes the existence of a positive constant \(\widehat{c}_{_\textrm{P}}\) such that
where \({\widehat{{\textrm{V}}}}\,:=\,\big \{\phi \in {\textrm{H}}^1(\Omega )\,:\ \int _\Gamma \phi \,=\,0\big \}\,\). Then, in order to apply Theorem 3.2, we introduce appropriate hypotheses on the discrete spaces \({\textrm{H}}_h^\varphi \) and \({\textrm{H}}_h^\chi \):
(H.4) \(\textrm{P}_0(\Gamma )\,\subseteq \,{\textrm{H}}_h^\chi \).
(H.5) There exists a positive constant \(\beta _{{\mathcal {B}},\mathtt d}\), independent of h, such that
We highlight here that each one of the above hypotheses has a clear purpose regarding the solvability of (4.4) and (4.5), and hence of (4.3). In fact, (H.0) allows to employ the discrete version of the decomposition \({\mathbb {H}}({\textbf{div}}_{4/3};\Omega ) \,=\, \mathbb {H}_0({\textbf{div}}_{4/3};\Omega ) \,\oplus \,{\textrm{R}}\,{{\mathbb {I}}}\), namely \(\widetilde{{\mathbb {H}}}^{\varvec{\sigma }}_h \,=\, {\mathbb {H}}^{\varvec{\sigma }}_h \,\oplus \, {\textrm{R}}\,{{\mathbb {I}}}\), thanks to which \({\mathbb {H}}^{\varvec{\sigma }}_h\) can be used as the subspace where the unknown \({\varvec{\sigma }}_h\) is sought. In turn, (H.1) is utilized to conclude that the tensors of the subspace \(\textrm{V}_{0,h}\) are divergence free, so that \(\Vert \cdot \Vert _{0,\Omega }\) and \(\Vert \cdot \Vert _{{\textbf{div}}_{4/3};\Omega }\) become equivalent there. On the other hand, (H.2) plays a key role in the proof of the discrete inf-sup conditions for \(b_1\) and \(b_2\), whereas (H.3) and (H.5) constitute inf-sup conditions required to be able to apply the discrete versions of the solvability result for perturbed saddle point problems in Banach spaces, and the Babuška-Brezzi theory in Hilbert spaces, respectively. Finally, the need of (H.4) is explained below in the proof of Lemma 4.2.
Taking the above assumptions into account, and defining
we can prove that the operator \({\widetilde{\textbf{S}}}_h\) is well-posed, which is abridged in the following lemma.
Lemma 4.2
For each \({{\textbf{z}}}_h\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}},h}\), problem (4.5) has a unique solution \((\varphi _h,\chi _h)\in {\textrm{H}}_h^{\varphi }\times {\textrm{H}}_h^{\chi }\), and hence \({\widetilde{\textbf{S}}}_h({{\textbf{z}}}_h):=\,\varphi _h\in {\textrm{H}}^{\varphi }_h\) is well-defined. Moreover, there exist positive constants \(C_{{\widetilde{\textbf{S}}},\texttt{d}}\) and \({\widetilde{C}}_{{\widetilde{\textbf{S}}},\mathtt d}\), depending on \(\rho \), \(\kappa _0\), \({\widehat{c}}_{_\textrm{P}}\) (cf. (4.9)) and \(\kappa _1\), \(\beta _{{\mathcal {B}},\mathtt d}\) (cf. (4.10)), such that
Proof
We begin by introducing the discrete kernel of \({\mathcal {B}}\), namely
which, as a consequence of (H.4), is clearly contained in \({\widehat{{\textrm{V}}}}\), and thus, (4.9) is certainly valid in \({{\widetilde{{\textrm{V}}}}}_h\). On the other hand, given \({{\textbf{z}}}_h\in {{\textbf{H}}}_h^{{{\textbf{u}}}}\), \(\phi _h\in {\textrm{H}}_h^{\varphi }\) and \(\theta _{1,h},\theta _{2,h}\in {{\widetilde{{\textrm{V}}}}}_h\), and proceeding as in Lemma 3.4, using in this case (4.9) instead of (3.19), we obtain
from which, defining \(\alpha _{{\mathcal {A}},\mathtt d}\,:=\,\rho \,\kappa _0\,{\widehat{c}}_{_\textrm{P}}/2\) and using that \({{\textbf{z}}}_h\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}},h}\), we readily conclude that the family of operators \({\mathcal {A}}_{{{\textbf{z}}}_h}(\cdot +\phi _h)\), with \(\phi _h\in {\textrm{H}}_h^{\varphi }\), is uniformly strongly monotone in \({{\widetilde{{\textrm{V}}}}}_h\) with constant \(\alpha _{{\mathcal {A}},\mathtt d}\). In addition, (3.18) and the specified bound on \(\Vert {{\textbf{z}}}_h\Vert _{0,4;\Omega }\) imply the Lipschitz-continuity of \({\mathcal {A}}_{{{\textbf{z}}}_h}\) with constant \(L_{{\mathcal {A}},\mathtt d}\,=\,\rho \kappa _1+\alpha _{{\mathcal {A}},\mathtt d}\). Moreover, thanks to assumption (H.5) (cf (4.10)), a straightforward application of Theorem 3.2 and the upper bound for \({\mathcal {G}}\) (cf. (3.17b)), we obtain (4.11) with
\(\square \)
4.3 Solvability Analysis of the Discrete Fixed Point
Having proved that \({{\textbf{T}}}_h\) is well-defined, we now apply the following version of Brouwer’s theorem (cf. [22, Theorem 9.9-2]) needed to show the solvability of (4.7).
Theorem 4.3
Let \(\textrm{W}\) be a compact and convex subset of a finite dimensional Banach space \(\textrm{X}\) and \(T:\textrm{W}\rightarrow \textrm{W}\) be a continuous mapping. Then T has at least one fixed-point.
Similarly to Sect. 3.4, we introduce the ball
which is a compact and convex subset of the finite dimensional space \({{\textbf{H}}}_{h}^{{{\textbf{u}}}}\). Then, the discrete analogue of Lemma 3.7 is stated as follows.
Lemma 4.4
Assume that
where \(C_{{{\textbf{T}}},\mathtt d}:=\,C_{{\textbf{S}},\mathtt d}\max \{1,C_{{\widetilde{\textbf{S}}},\mathtt d}\}\), and \(C_{{\textbf{S}},\mathtt d}\) and \(C_{{\widetilde{\textbf{S}}},\mathtt d}\) are the constants specified in Lemmas 4.1 and 4.2, respectively. Then, there holds \({{\textbf{T}}}_h({{\textbf{W}}}_{h})\subseteq {{\textbf{W}}}_h\).
Proof
Similarly to the proof of Lemma 3.7, it is a direct consequence of the assumption (4.13) and Lemmas 4.1 and 4.2, particularly of the respective a priori bounds (4.8) and (4.11). \(\square \)
We now aim to prove that \({{\textbf{T}}}_h\) is continuous, for which we previously address the same property for \({\textbf{S}}_h\) and \({\widetilde{\textbf{S}}}_h\). Indeed, in what follows we state the discrete analogues of Lemmas 3.8 and 3.9.
Lemma 4.5
There exists a positive constant \(L_{{\textbf{S}},\mathtt d}\), independent of h, depending only on \(\alpha _{{{\textbf{A}}},\mathtt d}\), \(L_\mu \), \(L_\eta \), \(\Vert \textrm{i}_4\Vert \), \(|\Omega |\) and \(\Vert {{\textbf{k}}}\Vert _\infty \), such that for all \(({{\textbf{z}}}_{1,h},\phi _{1,h}),({{\textbf{z}}}_{2,h},\phi _{2.h})\in {{\textbf{W}}}_{{\textbf{S}},h}\times {\textrm{H}}_h^{\varphi }\), there holds
Proof
Given \(({{\textbf{z}}}_{1,h},\phi _{1,h}),({{\textbf{z}}}_{2,h},\phi _{2.h})\in {{\textbf{W}}}_{{\textbf{S}},h}\times {\textrm{H}}_h^{\varphi }\), we let \({\textbf{S}}_h({{\textbf{z}}}_{i,h},\phi _{i,h}):=\,{{\textbf{u}}}_{i,h}\), for each \(i\in \{1,2\}\), where \((\vec {{\textbf{t}}}_{i,h},\vec {{\textbf{u}}}_{i,h})\,=\,\big (({{\textbf{t}}}_{i,h},{\varvec{\sigma }}_{i,h}),({{\textbf{u}}}_{i,h},{\varvec{\gamma }}_{i,h})\big )\) is the unique solution of (4.4) with \(({{\textbf{z}}}_{i,h},\phi _{i,h})\) instead of \(({{\textbf{z}}}_h,\phi _h)\). Then the proof of (4.14), starting now from the discrete global inf-sup condition [34, eq. (4.24)], is very similar to the one for Lemma 3.8. However, since a regularity assumption such as (3.25) is not available in the present discrete settings, we estimate \({{\textbf{a}}}_{\phi _{2,h}}-{{\textbf{a}}}_{\phi _{1,h}}\) by using an \(\textrm{L}^4(\Omega )-{{\mathbb {L}}}^4(\Omega )-{{\mathbb {L}}}^2(\Omega )\) argument along with (3.4). In this way, we obtain
The rest of the estimates are similar to those in the proof of Lemma 3.8, and are therefore omitted. \(\square \)
Lemma 4.6
There exists a positive constant \(L_{{\widetilde{\textbf{S}}},\mathtt d}\), independent of h, depending only on \(s_3\), \(\Vert \textrm{i}_4\Vert \) and \(\alpha _{{\mathcal {A}},\mathtt d}\) (cf. proof of Lemma 4.2), such that for all \({{\textbf{z}}}_{1,h},{{\textbf{z}}}_{2,h}\in {{\textbf{W}}}_{{\widetilde{\textbf{S}}},h}\), there holds
Proof
It follows very closely the arguments from the proof of Lemma 3.9. \(\square \)
As a consequence of the previous two lemmas, we have the continuity of the operator \({{\textbf{T}}}_h\).
Lemma 4.7
There exists a positive constant \(L_{{{\textbf{T}}},\mathtt d}\), independent of h, depending only on \(C_{{\widetilde{\textbf{S}}},\mathtt d}\), \(C_{{{\textbf{T}}},\mathtt d}\), \(L_{{\textbf{S}},\mathtt d}\) and \(L_{{\widetilde{\textbf{S}}},\mathtt d}\), such that for all \({{\textbf{z}}}_{1,h},{{\textbf{z}}}_{2,h}\in {{\textbf{W}}}_h\), there holds
where
Proof
Given \({{\textbf{z}}}_{1,h},{{\textbf{z}}}_{2,h}\in {{\textbf{W}}}_h\), and proceeding as in the proof of Lemma 3.10, but now using the definition of \({{\textbf{T}}}_h\) (cf. (4.6)) and the continuity of \({\textbf{S}}_h\) (cf (4.5)), we readily find that
Then, thanks to the a priori estimate (4.8), the Lipschitz-continuity of \({\widetilde{\textbf{S}}}_h\) (cf (4.15)) yields
In addition, using the a priori estimates for \({\textbf{S}}_h\) and \({\widetilde{\textbf{S}}}_h\) (cf. (4.8) and (4.11)), we have
Finally, replacing (4.18) and (4.19) in (4.17), and performing some minor algebraic manipulations, we obtain (4.16) with the constant
\(\square \)
We remark that, while the inequality (4.16) establishes the continuity of \({{\textbf{T}}}_h\), the lack of control of the term \(\Vert {{\textbf{t}}}_{2,h}\Vert _{0,4;\Omega }\) prevents us from deducing Lipschitz-continuity and hence contractivity of \({{\textbf{T}}}_h\). Consequently, we are only able to establish existence of a fixed point.
Theorem 4.8
Assume that the data satisfy (4.13). Then, the Galerkin scheme (4.3) has at least a solution \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h):=\,\big (({{\textbf{t}}}_h,{\varvec{\sigma }}_h),({{\textbf{u}}}_h,{\varvec{\gamma }}_h)\big )\in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\) and \((\varphi _h,\chi _h)\in {\textrm{H}}_h^{\varphi }\times {\textrm{H}}_h^{\chi }\), with \({{\textbf{u}}}_h\in {{\textbf{W}}}_h\). Moreover,
Proof
Since \({{\textbf{W}}}_h\) is compact and convex, and \({{\textbf{T}}}_h\) maps \({{\textbf{W}}}_h\) into itself (cf. Lemma 4.4), then Brouwer’s theorem yields the existence of solution for (4.3). In turn, since \({{\textbf{u}}}_h\,=\,{{\textbf{T}}}_h({{\textbf{u}}}_h)\,=\,{\textbf{S}}_{h}\big ({{\textbf{u}}}_h,{\widetilde{\textbf{S}}}_h({{\textbf{u}}}_h)\big )\) and \(\varphi _h\,=\,{\widetilde{\textbf{S}}}_h({{\textbf{u}}}_h)\), then (4.8) and (4.11) imply the continuous dependence on data of the solutions. \(\square \)
4.4 A Priori Error Analysis
In this section we derive a priori error estimates for the Galerkin scheme (4.3) with arbitrary finite element spaces satisfying the hypotheses (H.0)–(H.5) from Sect. 4.2. We focus on the global error
where \((\vec {{\textbf{t}}},\vec {{\textbf{u}}})\,:=\,\big ( ({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }}) \big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) and \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\), with \({{\textbf{u}}}\in {{\textbf{W}}}\) (cf. (3.23)), is the unique solution of (3.8), and \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h)\,:=\,\big ( ({{\textbf{t}}}_h,{\varvec{\sigma }}_h),\) \(({{\textbf{u}}}_h,{\varvec{\gamma }}_h) \big )\in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\) and \((\varphi _h,\chi _h)\in {\textrm{H}}_h^{\varphi }\times {\textrm{H}}_h^\chi \), with \({{\textbf{u}}}_h\in {{\textbf{W}}}_h\) (cf. (4.12)), is a solution of the discrete coupled problem (4.3). To this end, we establish next two ad-hoc Strang-type estimates. Hereafter, given a subspace \(\textrm{X}_h\) of a generic Banach space \((\textrm{X},\Vert \cdot \Vert _{\textrm{X}})\), we set as usual \(\displaystyle {\text {dist}}(x,\textrm{X}_h):=\inf _{x_h\in \textrm{X}_h}\Vert x-x_h\Vert _{\textrm{X}}\) for all \(x\in \textrm{X}\).
Lemma 4.9
Let \({\textrm{H}}\) be a reflexive Banach space, and let \(a:{\textrm{H}}\times {\textrm{H}}\) be a bounded bilinear form inducing the operator \({\mathcal {A}}\in \mathcal {L}({\textrm{H}},{\textrm{H}}')\), such that a satisfies the hypothesis of the Banach–Nečas–Babuška theorem (cf. [32, Theorem 2.6]). Furthermore, let \(\{{\textrm{H}}_h\}_{h>0}\) be a sequence of finite dimensional subspaces of \({\textrm{H}}\), and for each \(h>0\), consider a bounded bilinear form \(a_h:{\textrm{H}}_h\times {\textrm{H}}_h\rightarrow {\textrm{R}}\) inducing \({\mathcal {A}}_h\in \mathcal {L}({\textrm{H}}_h,{\textrm{H}}_h')\), such that \(a_h\vert _{{\textrm{H}}_h\times {\textrm{H}}_h}\) satisfies the hypotheses of Banach–Nečas–Babuška theorem as well, with constant \({\widetilde{\alpha }}\) independent of h. In turn, given \(F\in {\textrm{H}}'\), and a sequence of functionals \(\{F_h\}_{h>0}\), with \(F_h\in {\textrm{H}}_h'\) for each \(h>0\), we let \(u\in {\textrm{H}}\) and \(u_h\in {\textrm{H}}_h\) be the unique solutions to problems
and
respectively. Then, there holds
where \(C_{S,1}\) and \(C_{S,2}\) are the positive constants given by
Proof
See [20, Lemma 5.1]. \(\square \)
Lemma 4.10
Let \({\textrm{H}}\) and \({\textrm{Q}}\) be separable and reflexive Banach spaces, with \({\textrm{H}}\) uniformly convex, and let \(a:{\textrm{H}}\rightarrow {\textrm{H}}'\) be a nonlinear operator and \(b\in \mathcal {L}({\textrm{H}},{\textrm{Q}}')\) satisfying the hypotheses of Theorem 3.2 with constants L, \(\alpha \) and \(\beta \). Furthermore, let \(\{{\textrm{H}}_h \}_{h>0}\) and \(\{{\textrm{Q}}_h \}_{h>0}\) be sequences of finite dimensional subspaces of \({\textrm{H}}\) and \({\textrm{Q}}\), respectively, and for each \(h>0\) consider a nonlinear operator \(a_h:{\textrm{H}}\rightarrow {\textrm{H}}'\), such that \(a\vert _{{\textrm{H}}_h}:{\textrm{H}}_h\rightarrow {\textrm{H}}_h'\) and \(b\vert _{{\textrm{H}}_h}:{\textrm{H}}_h\rightarrow {\textrm{Q}}_h'\) satisfy the hypothesis of Theorem 3.2 with constants \(L_\texttt{d}\), \(\alpha _\texttt{d}\), and \(\beta _\texttt{d}\), all independent of h. In turn, given \(F\in {\textrm{H}}'\), \(G\in {\textrm{Q}}'\), and sequences of functionals \(\{F_h\}_{h>0}\) and \(\{G_h\}_{h>0}\), with \(F_h\in {\textrm{H}}_h'\) and \(G_h\in {\textrm{Q}}_h'\) for each \(h>0\), we let \((\sigma ,u)\in {\textrm{H}}\times {\textrm{Q}}\) and \((\sigma _h,u_h)\in {\textrm{H}}_h\times {\textrm{Q}}_h\) be the unique solutions to problems
and
respectively. Then, there exists a positive constants \(C_{S,i}\), depending only on L, \(\alpha _\texttt{d}\), \(\beta _\texttt{d}\), and \(\Vert b\Vert \), such that
Proof
See [12, Lemma 5.1]. \(\square \)
In order to apply Lemmas 4.9 and 4.10, we now observe that (3.8) and (4.3) can be rewritten as two pairs of continuous and discrete formulations as (4.20)–(4.21) and (4.24)–(4.25), respectively, namely
and
The following lemma provides a preliminary estimate for the error \(\Vert \vec {{\textbf{t}}}-\vec {{\textbf{t}}}_h\Vert _{{\textbf{H}}}\,+\,\Vert \vec {{\textbf{u}}}-\vec {{\textbf{u}}}_h\Vert _{{\textbf{Q}}}\).
Lemma 4.11
There exists a positive constant \(C_{ST}\), independent of h, such that
where \(C({{\textbf{u}}}_D,\varphi _D)\) is given by (3.39).
Proof
We recall from Sects. 3.4 to 4.2 that \({{\textbf{A}}}_{\varphi }+b({{\textbf{u}}};\cdot ,\cdot )\) and \({{\textbf{A}}}_{\varphi _h}+b({{\textbf{u}}}_h;\cdot ,\cdot )\), with \({{\textbf{u}}}\in {{\textbf{W}}}\) and \({{\textbf{u}}}_h\in {{\textbf{W}}}_h\), satisfy the hypotheses of Banach–Nečas–Babuška theorem on \({{\textbf{H}}}\times {{\textbf{Q}}}\) and \({{\textbf{H}}}_h\times {{\textbf{Q}}}_h\), respectively, the latter with constant \(\alpha _{{{\textbf{A}}},\mathtt d}/2\) (cf. [34, eq. (4.23)]). Then, applying Lemma 4.9 to (4.27), and according to (4.23), the estimates [34, eqs. (3.41a) and (3.43)], and the bounds (3.23) and (3.23), we conclude the existence of \(C_{S,1}>0\), independent of h, depending only on \(\lambda \), \(\mu _1\), \(\eta _1\), \(|\Omega |\), \(\alpha _{{{\textbf{A}}},\mathtt d}\), \(\varrho \) and \(\varrho _\texttt{d}\), such that
Then, proceeding exactly as in Lemma 3.8, particularly from Eqs. (3.32), (3.33) to (3.34), yields
In this way, replacing (4.31) back into (4.30), using (3.25) and the bounds for \(\Vert {{\textbf{u}}}\Vert _{0,4;\Omega }\) and \(\Vert \varphi \Vert _{1;\Omega }\) from Theorem 3.11, and performing algebraic manipulations, we obtain (4.29). \(\square \)
Next, we have the following result concerning \(\Vert \varphi -\varphi _h\Vert _{1;\Omega }\,+\,\Vert \chi -\chi _h\Vert _{-1/2;\Omega }\).
Lemma 4.12
There exists a positive constant \({\widetilde{C}}_{ST}\), independent of h, depending only on \(s_3\), \(\Vert \textrm{i}_4\Vert \), L, \(\alpha _{{\mathcal {A}},\mathtt d}\), \(\beta _{{\mathcal {B}},\mathtt d}\) and \(C_{\widetilde{\textbf{S}}}\), such that
Proof
With \({{\textbf{u}}}\in {{\textbf{W}}}\) and \({{\textbf{u}}}_h\in {{\textbf{W}}}_h\) given, the continuous and discrete systems associated with (4.28) satisfy the hypothesis of Theorem 3.2, with constants \(L_{\mathcal {A}}\), \(\alpha _{\mathcal {A}}\), \(\beta _{\mathcal {B}}=1\), \(L_{{\mathcal {A}},\mathtt d}\), \(\alpha _{{\mathcal {A}},\mathtt d}\) and \(\beta _{{\mathcal {B}},\mathtt d}\) (cf. Lemmas 3.3, 3.4, 3.5 and 4.2). Therefore, applying Lemma 4.10 to (4.28), we deduce the existence of a constant \({\widehat{C}}_{ST}>0\), depending on \(L_{{\mathcal {A}}}\), \(\alpha _{{\mathcal {A}},\mathtt d}\) and \(\beta _{{\mathcal {B}},\mathtt d}\), and hence independent of h, such that
Then, employing (2.4), (3.4) and Hölder inequality, we find that for each \(\psi _h\in {\textrm{H}}_h^{\varphi }\) there holds
which yields
Then from (4.34), (4.33) to (3.22), we obtain (4.32) with \({\widetilde{C}}_{ST} \,:=\,{\widehat{C}}_{ST}\max \big \{1,(1+s_3)\Vert \textrm{i}_4\Vert C_{\widetilde{\textbf{S}}}\big \}\). \(\square \)
The required Céa estimate will follow from Lemmas 4.10 to 4.11. Incorporating (4.32) into (4.29), and performing some algebraic manipulations, we find that there exist \({\widetilde{C}}_1, C_1>0\), independent of h, such that
Thus, imposing the constant multiplying \(\Vert {{\textbf{u}}}-{{\textbf{u}}}_h\Vert _{0,4;\Omega }\) in (4.35) to be sufficient small, say less than or equal to 1/2, provides the a priori error estimate for \(\Vert \vec {{\textbf{t}}}-\vec {{\textbf{t}}}_h\Vert _{{\textbf{H}}}\,+\,\Vert \vec {{\textbf{u}}}-\vec {{\textbf{u}}}_h\Vert _{{\textbf{Q}}}\), which, employed then to bound the third term on the right-hand side of (4.32), provides an upper bound for \(\Vert \varphi -\varphi _h\Vert _{1;\Omega }\,+\,\Vert \chi -\chi _h\Vert _{-1/2;\Gamma }\). More precisely, we have proved the following result.
Theorem 4.13
Assume that the data \({{\textbf{u}}}_D\) and \(\varphi _D\) satisfy
Then, there exists a positive constant \(C_\texttt{d}\), independent of h, such that
Finally, regarding the pressure error \(\Vert p-p_h\Vert _{0;\Omega }\), where \(p_h\) is the discrete pressure computed by the postprocessing formula suggested by the second identity in (2.7), that is
we readily deduce from (4.37), similarly as in [16, Section 4] (see also [34, eq. (4.39)]), the existence of a positive constant \({\widehat{C}}\), independent of h, such that
Thus, combining (4.37) and (4.39), we conclude the existence of \({\widehat{C}}_\texttt{d}>0\), independent of h, such that
4.5 Specific Finite Element Spaces
We refer to [34, Section 4.4] and [7, Section 3.5] to specify two examples of finite element subspaces \({\mathbb {H}}^{{\textbf{t}}}_h\), \(\widetilde{{\mathbb {H}}}^{\varvec{\sigma }}_h\), \({\textbf{H}}^{{\textbf{u}}}_h\), \({\mathbb {H}}^{\varvec{\gamma }}_h\), \({\textrm{H}}_h^{\varphi }\) and \({\textrm{H}}_h^\chi \) satisfying the hypotheses (H.0), (H.1), (H.2), (H.3), (H.4) and (H.5) from Sect. 4.2, and establish the associated rates of convergence for the Galerkin scheme (4.3).
4.5.1 Preliminaries
Given an integer \(\ell \ge 0\) and \(K\in {{\mathcal {T}}}_h\), let \(\textrm{P}_\ell (K)\) denote the space of polynomials of degree \(\le \ell \) defined on K with vector and tensorial versions denoted by \({{\textbf{P}}}_\ell (K)\,:=\, [{\textrm{P}}_\ell (K)]^{n}\) and \({{\mathbb {P}}}_\ell (K)\,:=\, [{\textrm{P}}_\ell (K)]^{n\times n}\), respectively. By \({\textbf{RT}}_\ell (K):=\,{{\textbf{P}}}_\ell (K) \,+\, {\textrm{P}}_\ell (K) {{\textbf{x}}}\) we denote the local Raviart–Thomas space of order \(\ell \) defined on K, where \({{\textbf{x}}}\) stands for a generic vector in \({\textrm{R}}^n\). Furthermore, denoting by \(b_K\) the bubble function on K (the product of its \(n+1\) barycentric coordinates), we set the local bubble space of order \(\ell \) as
where \({\textrm{curl}}(v):= \big (\frac{\partial v}{\partial x_2}, -\frac{\partial v}{\partial x_1}\big )\) if \(n = 2\) and \(v: K \rightarrow {\textrm{R}}\), and \({\textrm{curl}}({{\textbf{v}}}):= \nabla \times {{\textbf{v}}}\) if \(n = 3\) and \({{\textbf{v}}}: K \rightarrow {\textrm{R}}^3\). In addition, we need to set the global spaces
where \({\varvec{\tau }}_{h,i}\) stands for the ith-row of \({\varvec{\tau }}_h\). As noticed in [35], it is easily seen that \({{\textbf{P}}}_\ell (\Omega )\) and \({{\mathbb {P}}}_\ell (\Omega )\) are also subspaces of \({\textbf{L}}^4(\Omega )\) and \({\mathbb {L}}^4(\Omega )\), respectively, and that \(\mathbb{R}\mathbb{T}_\ell (\Omega )\) and \(\mathbb {B}_\ell (\Omega )\) are both subspaces of \({\mathbb {H}}({\textbf{div}}_{4/3};\Omega )\) as well. Actually, since \({\mathbb {H}}({\textbf{div}};\Omega )\) is clearly contained in \({\mathbb {H}}({\textbf{div}}_{4/3};\Omega )\), any subspace of the former is also subspace of the latter.
4.5.2 Two Specific Examples
Similarly to [34, Section 4.4], we employ the stable triplets for linear elasticity proposed in [35, Section 4.4] to describe two examples of finite element subspaces \(\widetilde{{\mathbb {H}}}_h^{\varvec{\sigma }}\), \({\textbf{H}}_h^{{\textbf{u}}}\) and \({\mathbb {H}}_h^{\varvec{\gamma }}\) and \({\mathbb {H}}_h^{{\textbf{t}}}\) satisfying (H.0)-(H.3).
First, we consider \(\hbox {PEERS}_\ell \) (plane elasticity element with reduced symmetry of order \(\ell \ge 0\), [8, 38]), and the subspace \({{\mathbb {H}}}_h^{{\textbf{t}}}\) introduced in [34, Section 4.4.2]. Letting \({\mathbb {C}}({\bar{\Omega }}):= [C({\bar{\Omega }})]^{n\times n}\), we have
Secondly, \(\hbox {AFW}_\ell \) (Arnold–Falk–Winther elements of order \(\ell \ge 0\), [9]), and \({{\mathbb {H}}}_h^{{\textbf{t}}}\) as in [34, Section 4.4.3]:
In addition, and similarly to [7, Section 3.5] (see also [5, Section 4.3]), the approximation space for temperature will consist of continuous piecewise polynomials of degree \(\le \ell +1\)
and for the normal heat flux, we let \(\big \{ {{\widetilde{\Gamma }}}_1,{{\widetilde{\Gamma }}}_2,\ldots ,{{\widetilde{\Gamma }}}_m\big \}\) be an independent triangulation of \(\Gamma \) (made of straight segments in \({\textrm{R}}^2\), or triangles in \({\textrm{R}}^3\)), and hence \(\displaystyle \widetilde{h}:=\,\max _{j\in \{1,\ldots ,m\}}|{{\widetilde{\Gamma }}}_j|\). Then, we approximate \(\chi \) by piecewise polynomials of degree \(\le \ell \) over this new mesh, that is
Assumption (H.4) is trivially satisfied, whereas it can be proved (cf. [10, Section III], [24, Lemma 4.10], [33, Lemma 4.7]) that there exists a positive constant \({\widetilde{c}}_0 \in (0,1]\) such that, provided that \(h \,\le \, {\widetilde{c}}_0 \, \widetilde{h}\), \({\textrm{H}}_{{\widetilde{h}}}^\chi \) satisfies (H.5) as well.
4.5.3 The Rates of Convergence
According to [34, 35], and denoting \(\ell ^*:= \left\{ \begin{array}{ll} \ell + n &{} \,\, \hbox {for PEERS-based} \\ \ell + 1 &{} \,\,\hbox {for AFW-based} \end{array}\right. \), the approximation properties of \({\mathbb {H}}_h^{{\textbf{t}}}\), \({\mathbb {H}}^{\varvec{\sigma }}_h\), \({\textbf{H}}^{{\textbf{u}}}_h\), and \({\mathbb {H}}^{\varvec{\gamma }}_h\), for PEERS (cf. (4.41)) as well as for AFW (cf. (4.42)), are given as follows:
\(\big (\textbf{AP}^{{\textbf{t}}}_h\big )\) there exists a positive constant C, independent of h, such that for each \(r \in [0, \ell ^* + 1]\), and for each \({{\textbf{s}}}\in {\mathbb {H}}^r(\Omega ) \cap {{\mathbb {L}}}^2_{\textrm{tr}}(\Omega )\), there holds
\(\big (\textbf{AP}^{\varvec{\sigma }}_h\big )\) there exists a positive constant C, independent of h, such that for each \(r \in [0, \ell + 1]\), and for each \({\varvec{\tau }}\in {\mathbb {H}}^r(\Omega ) \cap {\mathbb {H}}_0({\textbf{div}}_{4/3};\Omega )\) with \({\textbf{div}}({\varvec{\tau }}) \in {{\textbf{W}}}^{r,4/3}(\Omega )\), there holds
\(\big (\textbf{AP}^{{\textbf{u}}}_h\big )\) there exists a positive constant C, independent of h, such that for each \(r \in [0, \ell + 1]\), and for each \({{\textbf{v}}}\in {{\textbf{W}}}^{r,4}(\Omega )\), there holds
and
\(\big (\textbf{AP}^{\varvec{\gamma }}_h\big )\) there exists a positive constant C, independent of h, such that for each \(r \in [0, \ell + 1]\), and for each \({\varvec{\delta }}\in {\mathbb {H}}^r(\Omega ) \cap {{\mathbb {L}}}^2_\texttt{skew}(\Omega )\), there holds
Aditionally, the approximation properties for the subpaces \({\textrm{H}}_h^\varphi \) and \({\textrm{H}}_{{\widetilde{h}}}^\chi \) (cf. [13] and [33]), are the following:
\(\big (\textbf{AP}^\varphi _h\big )\) there exists a positive constant C, independent of h, such that for each \(r \in [0, \ell + 1]\), and for each \(\psi \in {\textrm{H}}^{1+r}(\Omega )\), there holds
\(\big (\textbf{AP}^\chi _h\big )\) there exists a positive constant C, independent of \({\widetilde{h}}\), such that for each \(r \in [0, \ell + 1]\), and for each \(\xi \in {\textrm{H}}^{-1/2+r}(\Gamma ) \), there holds
We are now in position to specify the rates of convergence of (4.3) with the spaces from Sect. 4.5.2.
Theorem 4.14
Assume that the data satisfy (4.36), and let \((\vec {{\textbf{t}}},\vec {{\textbf{u}}}):= \big (({{\textbf{t}}},{\varvec{\sigma }}),({{\textbf{u}}},{\varvec{\gamma }})\big )\in {{\textbf{H}}}\times {{\textbf{Q}}}\) and \((\varphi ,\chi )\in {\textrm{H}}^1(\Omega )\times {\textrm{H}}^{-1/2}(\Gamma )\), and \((\vec {{\textbf{t}}}_h,\vec {{\textbf{u}}}_h):= \big (({{\textbf{t}}}_h,{\varvec{\sigma }}_h),({{\textbf{u}}}_h,{\varvec{\gamma }}_h)\big ) \in {{\textbf{H}}}_h\times {{\textbf{Q}}}_h\) and \((\varphi _h,\chi _h)\in {\textrm{H}}_h^\varphi \times {\textrm{H}}_h^\chi \), be solutions of (3.8) and (4.3), respectively, with \({{\textbf{u}}}\in {{\textbf{W}}}\) (cf. (3.23)) and \({{\textbf{u}}}_h\in {{\textbf{W}}}_h\) (cf. (4.12)), whose existences are guaranteed by Theorems 3.11 and 4.8, respectively. In turn, let p and \(p_h\) be the exact and approximate pressure defined by the second identity in (2.7) and (4.38), respectively. Furthermore, given an integer \(\ell \ge 0\), assume that there exists \(r \in [0,\ell + 1]\) such that \({{\textbf{t}}}\in {\mathbb {H}}^r(\Omega ) \cap {{\mathbb {L}}}^2_{\textrm{tr}}(\Omega )\), \({\varvec{\sigma }}\in {\mathbb {H}}^r(\Omega ) \cap {\mathbb {H}}_0({\textbf{div}}_{4/3};\Omega )\), \({\textbf{div}}({\varvec{\sigma }}) \in {{\textbf{W}}}^{r,4/3}(\Omega )\), \({{\textbf{u}}}\in {{\textbf{W}}}^{r,4}(\Omega )\), \({\varvec{\gamma }}\in {\mathbb {H}}^r(\Omega ) \cap {{\mathbb {L}}}^2_\texttt{skew}(\Omega )\), \(\varphi \in {\textrm{H}}^{1+r}(\Omega )\), and \(\chi \in {\textrm{H}}^{-1/2+r}(\Gamma )\). Then, there exist constants \({\widetilde{c}}_0 \in (0,1]\) and \(C > 0\), independent of h and \(\widetilde{h}\), such that for all \(h \,\le \, {\widetilde{c}}_0 \, \widetilde{h}\), there holds
Proof
It follows straightforwardly from Céa’s estimate (4.40) and the approximation properties \(\big (\textbf{AP}^{{\textbf{t}}}_h\big )\), \(\big (\textbf{AP}^{\varvec{\sigma }}_h\big )\), \(\big (\textbf{AP}^{{\textbf{u}}}_h\big )\), \(\big (\textbf{AP}^{\varvec{\gamma }}_h\big )\), \(\big (\textbf{AP}^\varphi _h\big )\) and \(\big (\textbf{AP}^\chi _h\big )\). \(\square \)
5 Illustrative Numerical Examples
In this section we demonstrate properties of the proposed family of methods. Mesh generation, discretization, and solvers were implemented using the automated finite element library FEniCS [4] and, in particular, the specialized module \(\hbox {FEniCS}_{{ii}}\) [36] required for the treatment of mixed-dimensional meshes of non-conforming type (and also instrumental to numerically realize the \(H^{-1/2}(\Gamma )\) norm). The nonlinear algebraic equations were solved using a Newton–Raphson method with exact Jacobian, and the iterations were terminated once the \(\ell ^2\)-norm of either the relative or absolute residual drops below the prescribed tolerance \(10^{-7}\). The numerical tests are divided into three parts: a verification of convergence, the simulation of stationary phase change in 2D, and the extension to the 3D case.
Example 1
Let the square domain \(\Omega = (0,1)^2\) meshed by successively refined regular triangles. We use this simple test case to assess the convergence of the finite element discretization, and consider the following smooth closed-form primary variables for an adaptation of the Burggraf flow [14] (a regularization of the well-known lid-driven cavity flow but here there is no velocity singularity at the top corners) to the case of thermally driven problems (see, e.g., [40])
with \( C_0>0\) a scaling parameter and
These solutions are used to set boundary velocity and temperature to be imposed on the boundary. Also, as typically done when using manufactured solutions, after inserting these closed-form functions into the governing momentum and energy equations, additional source terms appear that constitute an augmented problem [48] (the mass conservation is satisfied as the manufactured velocity is divergence-free).
We consider the strong form (2.8) with the following constitutive equations and adimensional model parameters
This choice of parameter regime is simply exemplary and similar in magnitude to the experiments considered in [40]. The null mean value for the trace of the stress is enforced through a real Lagrange multiplier method. Note that, as requested by the constraint \(h \,\le \, {\widetilde{c}}_0 \, {\widetilde{h}}\) (cf. remark on the verification of (H.5) at the end of Sect. 4.5.2), the mesh for the heat flux approximation is simply taken as two levels lower than a conforming mesh to the boundary of the bulk mesh (the former is constructed with \(2^{j+2}+4\) segments per side and the latter with \(2^j+1\) segments per side, giving \(\widetilde{h}\approx 4 h\)).
Absolute errors are measured in the norms suggested by the analysis (where the exact solutions are evaluated at the quadrature points), which we denote – together with the experimental rates of convergence – as usual
with % \(\in \{{{\textbf{t}}},{\varvec{\sigma }},{{\textbf{u}}},p,{\varvec{\gamma }},\varphi \}\), and where \(\texttt {e},\texttt {e}'\) stand for errors generated on two consecutive meshes of sizes \(h,h'\) (\(\widetilde{h}\) and \(\widetilde{h}'\) for \(\chi \)), respectively.
To compute \(\Vert \chi -\chi _{\widetilde{h}}\Vert _{-1/2,\Gamma }\) we use the characterization of \({\textrm{H}}^{-1/2}(\Gamma )\) in terms of the spectral decomposition of the Laplacian operator (see, e.g., [37, Sect. 2]). More precisely, let \(S: {\textrm{H}}^1_0(\Gamma ) \longrightarrow {\textrm{H}}^1_0(\Gamma )\) be the bounded linear operator defined by
where \((\cdot , \cdot )_{1,\Gamma }\) and \((\cdot , \cdot )_{0,\Gamma }\) denote the inner products of \({\textrm{H}}^1_0(\Gamma )\) and \(\textrm{L}^2(\Gamma )\), respectively. Then, one can find a basis \(\{z_i\}_{i=1}^\infty \) of eigenfunctions of S with a non-increasing sequence of positive eigenvalues \(\lambda _i\), and for any \(u = \sum _{i=1}^\infty c_i z_i\) there holds
so that \({\textrm{H}}^{-1/2}(\Gamma )\) becomes the closure of the span of the basis \(\{z_i\}_{i=1}^\infty \) in this norm. Certainly, for the practical computation of \(\Vert u\Vert _{-1/2,\Gamma }^2\) one utilizes a discrete approximation of the aforementioned spectral decomposition.
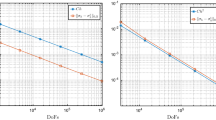
We take \(\ell =0,1\) in the \(\hbox {PEERS}_\ell \)- and \(\hbox {AFW}_\ell \)-based families of finite elements (4.41) and (4.42), respectively; with (4.43), (4.44). We show the results of the convergence verification analysis in Table 1. There we depict the errors and decay rate and observe, for all field variables, the optimal convergence order \(h^{\ell +1}\) predicted by (4.51). Sample approximate solutions are provided in Fig. 1, which are confirmed to follow the flow patterns obtained in [40]. With the aim of illustrating the performance of the method in a higher Re regime we repeat the experiments of accuracy verification using \(\textrm{Re}=1000\), and we only take the lowest-order cases. The results displayed in Table 2 (using also a different ratio between the bulk and surface meshes \(\widetilde{h}\approx 2 h\)) confirm that the method exhibits optimal convergence in this regime as well.
We further demonstrate the momentum conservation property by computing the norm of the momentum residual (considering the last case of \(\textrm{Re}=1000\)). More precisely, we project the forcing term on \({\textbf{H}}^{{\textbf{u}}}_h\) and compute the \(\ell ^\infty \)-norm of the residual vector
We use as an example the \(\hbox {AFW}_\ell \)-based discretization with \(\ell =0\) and for sake of comparison we also tabulate the obtained loss in momentum conservation obtained with the similar method in [7]. The results are presented in Table 3 confirming the machine precision momentum conservation of the proposed family of methods.
Example 2
Next we consider the steady regime of the phase change of a material adopting a 2D slice of a shell-and-tube geometry configuration, which is commonly used in thermal energy storage systems [2, 41]. We construct a unit disk-shaped geometry with four circular inclusions of radius \(\frac{1}{8}\). The inner tubes are kept hot with \(\varphi _{\textrm{hot}} =1\) and the outer shell is kept cold \(\varphi _{\textrm{cold}} =-0.01\) (which differs from the mixed Dirichlet–Neumann conditions used in [41]). For the flow equations, all boundaries are equipped with no-slip velocity conditions. The meshes are unstructured, and the mesh sizes selected for the bulk and for the boundary are \(h \approx 0.022\) and \(\widetilde{h} \approx 0.051\), respectively.
Similarly as in [40, 46], we use a porosity-enthalpy model, which means that the viscosity is taken constant. The temperature-dependent buoyancy, porosity and enthalpy functions are chosen as follows
respectively, where the denominator in the argument of the hyperbolic tangent regularization indicates the size of the mushy zone (the region that approximates a sharp phase fraction jump). The remaining coefficients assume the following values
where Ste denotes the Stefan number.
In Fig. 2 we have portrayed the approximate solutions, generated with the second-order \(\hbox {PEERS}_{\ell }\)-based finite element family (4.41). In particular, the bottom-right panel of the figure shows the approximate heat flux on the (coarser) boundary mesh, and the top-right panel shows the typical counter rotating flow patterns expected in differentially heated enclosures. No closed-form solution is available for this problem but all fields exhibit a well resolved behavior, even on relative coarse meshes.
Example 3
Our last test, adapted from [7], simulates the phase change occurring in the melting of N–octadecane. The domain consists of the cuboid \(\Omega = (0,1.5,0.3,1.5)\) \(\hbox {cm}^3\). For the thermal energy conservation, the boundary is split into two regions: \(\Gamma _{\textrm{hot}} \cup \Gamma _{\textrm{cold}}\) (left and right ends) and \(\Gamma _{\textrm{flux}}\) (remainder of the boundary) where temperature and heat flux are prescribed, respectively. The molten material is on the “left" of the domain (towards the wall at \(x=0\) where we prescribe \(\varphi _{\textrm{hot}} =1\)). The low temperature imposed on the right wall \(x=1.5\) cm, \(\varphi _{\textrm{cold}} = -0.01\) is lower than the phase change temperature \(\varphi = 0\), in order to allow the phase change to occur. The remaining boundaries are insulated (zero temperature flux), and on the whole boundary we impose no-slip conditions (\({{\textbf{u}}}= \varvec{0}\) everywhere on \(\Gamma \)). For this test we use a space resolution of \(h \approx 0.07\) cm and for the boundary sub-mesh we use a triangulation with \(\widetilde{h} \approx 0.12\) cm.
Example 1. Primal variables (velocity line integral convolution colored according to velocity magnitude, and temperature distribution) and mixed unknowns (velocity gradient magnitude, stress magnitude, vorticity magnitude, and heat flux on the coarser boundary mesh) for the Burggraf stationary flow with thermal effects obtained after 4 steps of uniform refinement
Example 2. Phase change on a differentially heated shell-tube system. Approximate solutions (velocity gradient magnitude, total stress magnitude, velocity streamlines, vorticity magnitude, dimensionless temperature, and heat flux) computed with the second-order \(\hbox {PEERS}_\ell \)-based mixed-primal method
As in example 2, here we use a porosity-enthalpy model together with the following constitutive relations and parameter scalings
Given the strong nonlinearity of the non-isothermal coupling, it was necessary to use a continuation approach (the initial guess at each Newton–Raphson iteration is improved by solving intermediate problems with an increased value of a given parameter) and as continuation parameter we use the Rayleigh number starting from Ra\(=10^3\). Nine iterations are required in this case to reach the prescribed tolerance.
The thermal and fluid flow characteristics of the system are shown in Fig. 3 where we plot temperature iso-surfaces, velocity streamlines, and all other computed quantities using the lowest-order method based on the \(\hbox {AFW}_{\ell }\) family of finite elements. The obtained flow structures are qualitatively similar to the expected behaviour for a stationary coupling (that is, a buoyancy-driven recirculation with a relatively large solid–liquid interface and the typical temperature distribution on the xz-plane).
6 Summary and Concluding Remarks
The purpose of this paper has been to extend and adapt the analysis developed in previous works for the Navier–Stokes–Brinkman equations to include the coupling with phase change models. We have introduced a model problem and derived the continuous formulation, adopting a fixed-point strategy to analyze the corresponding solvability. We have utilized recent results on perturbed saddle-point problems and the Babuška–Brezzi theory, both in Banach spaces, to study the corresponding uncoupled problems and then applied the classical Banach theorem to conclude the existence of a unique solution. We have also introduced a Galerkin scheme and used the Brouwer theorem to prove the existence of a solution, while deriving a priori error estimates and establishing corresponding rates of convergence using specific finite element subspaces satisfying suitable assumptions.
Overall, our results contribute to the understanding and analysis of coupled problems in heat-driven flow, specifically in the context of phase change models, using Banach spaces-based frameworks. The use of a Banach spaces-based framework has allowed for a more general approach, avoiding augmentation techniques and maintaining a closer structure to the physical model in mixed form. The techniques and methodologies presented in this paper can be applied to other models and problems in continuum mechanics and related fields, further advancing our understanding and ability to simulate and predict various physical phenomena.
Data Availability
Enquiries about data availability should be directed to the authors.
References
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces. Academic Press, Elsevier Ltd (2003)
Agyenim, F., Hewitt, N., Eames, P., Smyth, M.: A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS). Renew. Sustain. Energy Rev. 14(2), 615–628 (2010)
Aldbaissy, R., Hecht, F., Mansour, G., Sayah, T.: A full discretisation of the time-dependent Boussinesq (buoyancy) model with nonlinear viscosity. Calcolo 55, 1–49 (2018)
Alnæs, M.S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E., Wells, G.N.: The FEniCS project version 1.5. Arch. Numer. Softw. 3(100), 9–23 (2015)
Almonacid, J.A., Gatica, G.N., Oyarzúa, R.: A mixed-primal finite element method for the Boussinesq problem with temperature-dependent viscosity. Calcolo 55(3), 1–42 (2018)
Almonacid, J.A., Gatica, G.N., Oyarzúa, R., Ruiz-Baier, R.: A new mixed finite element method for the n-dimensional Boussinesq problem with temperature-dependent viscosity. Netw. Heterog. Media 15(2), 215–245 (2020)
Alvarez, M., Gatica, G.N., Gómez-Vargas, B., Ruiz-Baier, R.: New mixed finite element methods for natural convection with phase-change in porous media. J. Sci. Comput. 80(1), 141–174 (2019)
Arnold, D.N., Brezzi, F., Douglas, J.: PEERS: A new mixed finite element method for plane elasticity. Jpn. J. Appl. Math. 1, 347–367 (1984)
Arnold, D.N., Falk, R.S., Winther, R.: Mixed finite element methods for linear elasticity with weakly imposed symmetry. Math. Comp. 76(260), 1699–1723 (2007)
Babuška, I., Gatica, G.N.: On the mixed finite element method with Lagrange multipliers. Numer. Methods Partial Differ. Equ. 19(2), 192–210 (2003)
Benavides, G.A., Caucao, S., Gatica, G.N., Hopper, A.A.: A Banach spaces-based analysis of a new mixed-primal finite element method for a coupled flow-transport problem. Comput. Methods Appl. Mech. Eng. 371, 113285 (2020)
Benavides, G.A., Caucao, S., Gatica, G.N., Hopper, A.A.: A new non-augmented and momentum-conserving fully-mixed finite element method for a coupled flow-transport problem. Calcolo 59(1), 6 (2022)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer-Verlag (1991)
Burggraf, O.R.: Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24, 113–151 (1966)
Camaño, J., García, C., Oyarzúa, R.: Analysis of a momentum conservative mixed-FEM for the stationary Navier-Stokes problem. Numer. Methods Partial Differ. Equ. 37(5), 2895–2923 (2021)
Camaño, J., Gatica, G.N., Oyarzúa, R., Ruiz-Baier, R.: An augmented stress-based mixed finite element method for the steady state Navier-Stokes equations with nonlinear viscosity. Numer. Methods Partial Differ. Equ. 33(5), 1692–1725 (2017)
Camaño, J., Oyarzúa, R., Ruiz-Baier, R., Tierra, G.: Error analysis of an augmented mixed method for the Navier-Stokes problem with mixed boundary conditions. IMA J. Numer. Anal. 38(3), 1452–1484 (2018)
Caucao, S., Colmenares, E., Gatica, G.N., Inzunza, C.: A Banach spaces-based fully mixed finite element method for the stationary chemotaxis-Navier-Stokes problem. Preprint 2022-16, Centro de Investigación en Ingeniería Matemática (\(\text{CI}^2\)MA), Universidad de Concepción, (2022)
Caucao, S., Discacciati, M., Gatica, G.N., Oyarzúa, R.: A conforming mixed finite element method for the Navier–Stokes/Darcy–Forchheimer coupled problem. ESAIM Math. Model. Numer. Anal. 54(5), 1689–1723 (2020)
Caucao, S., Gatica, G.N., Oyarzúa, R., Sánchez, N.: A fully-mixed formulation for the steady double-diffusive convection system based upon Brinkman–Forchheimer equations. J. Sci. Comput. 85(2), 44 (2020)
Caucao, S., Oyarzúa, R., Villa-Fuentes, S.: A new mixed-FEM for steady-state natural convection models allowing conservation of momentum and thermal energy. Calcolo 57(4), 36 (2020)
Ciarlet, P.: Linear and Nonlinear Functional Analysis with Applications. Society for Industrial and Applied Mathematics. Philadelphia, PA (2013)
Colmenares, E., Gatica, G.N., Moraga, S.: A Banach spaces-based analysis of a new fully-mixed finite element method for the Boussinesq problem. ESAIM Math. Model. Numer. Anal. 54(5), 1525–1568 (2020)
Colmenares, E., Gatica, G.N., Oyarzúa, R.: Analysis of an augmented mixed-primal formulation for the stationary Boussinesq problem. Numer. Methods Partial Differ. Equ. 32(2), 445–478 (2016)
Colmenares, E., Neilan, M.: Dual-mixed finite element methods for the stationary Boussinesq problem. Comp. Math. Appl. 72(7), 1828–1850 (2016)
Correa, C.I., Gatica, G.N.: On the continuous and discrete well-posedness of perturbed saddle-point formulations in Banach spaces. Comput. Math. Appl. 117, 14–23 (2022)
Correa, C.I., Gatica, G.N., Ruiz-Baier, R.: New mixed finite element methods for the coupled Stokes and Poisson-Nernst-Planck equations in Banach spaces. ESAIM Math. Model. Numer. Anal., https://doi.org/10.1051/m2an/2023024
Danaila, I., Moglan, R., Hecht, F., Le Masson, S.: A Newton method with adaptive finite elements for solving phase-change problems with natural convection. J. Comput. Phys. 274, 826–840 (2014)
Dinniman, M.S., Asay-Davis, X.S., Galton-Fenzi, B.K., Holland, P.R., Jenkins, A., Timmermann, R.: Modeling ice shelf/ocean interaction in antarctica: a review. Oceanography 29(4), 144–153 (2016)
Dutil, Y., Rousse, D.R., Salah, N.B., Lassue, S., Zalewski, L.: A review on phase-change materials: mathematical modeling and simulations. Renew. Sustain. Energy Rev. 15(1), 112–130 (2011)
El-Hadda, M., Belhamadia, Y., Deteix, J., Yakoubi, D.: A projection scheme for phase change problems with convection. Comput. Math. Appl. 108, 109–122 (2022)
Ern, A., Guermond, J.-L.: Theory and Practice of Finite Elements. Applied Mathematical Sciences, 159. Springer-Verlag, New York (2004)
Gatica, G.N.: A Simple Introduction to the Mixed Finite Element Method. Theory and Applications. Springer-Briefs in Mathematics. Springer, Cham (2014)
Gatica, G.N., Núñez, N., Ruiz-Baier, R.: New non-augmented mixed finite element methods for the Navier–Stokes–Brinkman equations using Banach spaces. J. Numer. Math., https://doi.org/10.1515/jnma-2022-0073
Gatica, G.N., Oyarzúa, R., Ruiz-Baier, R., Sobral, Y.D.: Banach spaces-based analysis of a fully-mixed finite element method for the steady-state model of fluidized beds. Comput. Math. Appl. 84, 244–276 (2021)
Kuchta, M.: Assembly of multiscale linear PDE operators. In: Vermolen, F.J., Vuik, C. (eds.) Numerical Mathematics and Advanced Applications ENUMATH 2019, pp. 641–650 (2021)
Kuchta, M., Nordaas, M., Verschaeve, J.C., Mortensen, M., Mardal, K.-A.: Preconditioners for saddle point systems with trace constraints coupling 2d and 1d domains. SIAM J. Sci. Comput. 38, B962–B987 (2016)
Lonsing, M., Verfürth, R.: On the stability of BDMS and PEERS elements. Numer. Math. 99(1), 131–140 (2004)
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations. Springer Series in Computational Mathematics, 23. Springer-Verlag, Berlin (1994)
Rakotondrandisa, A., Sadaka, G., Danaila, I.: A finite-element toolbox for the simulation of solid-liquid phase-change systems with natural convection. Comput. Phys. Commun. 253, 107188 (2020)
Sadaka, G., Rakotondrandisa, A., Tournier, P.H., Luddens, F., Lothodé, C., Danaila, I.: Parallel finite-element codes for the simulation of two-dimensional and three-dimensional solid-liquid phase-change systems with natural convection. Comput. Phys. Commun. 257, 107492 (2020)
Scheurer, B.: Existence et approximation de points selles pour certains problémes non linéaires. RAIRO Anal. Numér. 11(4), 369–400 (1977)
Schroeder, P.W., Lube, G.: Stabilised dG-FEM for incompressible natural convection flows with boundary and moving interior layers on non-adapted meshes. J. Comput. Phys. 335, 760–779 (2017)
Ulvrová, M., Labrosse, S., Coltice, N., Røaback, P., Tackley, P.J.: Numerical modelling of convection interacting with a melting and solidification front: application to the thermal evolution of the basal magma ocean. Phys. Earth Planet. Inter. 206–207, 51–66 (2012)
Wang, S., Faghri, A., Bergman, T.L.: A comprehensive numerical model for melting with natural convection. Int. J. Heat Mass Transf. 53(9–10), 1986–2000 (2010)
Woodfield, J., Alvarez, M., Gómez-Vargas, B., Ruiz-Baier, R.: Stability and finite element approximation of phase change models for natural convection in porous media. J. Comput. Appl. Math. 360, 117–137 (2019)
Zhang, Y., Hou, Y., Zhao, J.: Error analysis of a fully discrete finite element variational multiscale method for the natural convection problem. Comput. Math. Appl. 68(4), 543–567 (2014)
Zimmerman, A.G., Kowalski, J.: Mixed finite elements for convection-coupled phase-change in enthalpy form: open software verified and applied to 2D benchmarks. Comput. Math. Appl. 84, 77–96 (2021)
Acknowledgements
The authors express their gratitude to Miroslav Kuchta for his invaluable assistance in the extension of the \(\hbox {FEniCS}_{{ii}}\) library to accommodate tensor-valued spaces and fractional norms on non-conforming trace meshes.
Funding
This work was partially supported by ANID-Chile through the projects Centro de Modelamiento Matemático (FB210005), and Anillo of Computational Mathematics for Desalination Processes (ACT210087); by Centro de Investigación en Ingeniería Matemática (\(\hbox {CI}^2\)MA); by the Monash Mathematics Research Fund S05802-3,951,284; and by the Australian Research Council through the Discovery Project grant DP220103160 and the Future Fellowship grant FT220100496.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gatica, G.N., Núñez, N. & Ruiz-Baier, R. Mixed-Primal Methods for Natural Convection Driven Phase Change with Navier–Stokes–Brinkman Equations. J Sci Comput 95, 79 (2023). https://doi.org/10.1007/s10915-023-02202-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02202-9