Global-in-Time $H^1$-Stability of L2-1$_\sigma$ Method on General Nonuniform Meshes for Subdiffusion Equation

Abstract

In this work the L2-1$_\sigma$ method on general nonuniform meshes is studied for the subdiffusion equation. When the time step ratio is no less than 0.475329, a bilinear form associated with the L2-1$_\sigma$ fractional-derivative operator is proved to be positive semidefinite and a new global-in-time $H^1$-stability of L2-1$_\sigma$ schemes is then derived under simple assumptions on the initial condition and the source term. In addition, the sharp $L^2$-norm convergence is proved under the constraint that the time step ratio is no less than 0.475329.

1 Introduction

In the past decade, many numerical methods have been proposed to solve the time-fractional diffusion equations [6, 21]. If the solution is sufficiently smooth (which requires the initial value to be smooth and satisfying some compatibility conditions), it has been proved that the L2-1$_\sigma$ scheme has second order accuracy [2] and the L2-type methods can achieve $(3-\alpha )$-order accuracy [5, 20].

However, simple examples show that for given smooth data, the solutions to time-fractional problems typically have weak singularities. Some works start to focus on the numerical solution of more typical fractional problems whose solutions exhibit weak singularities. In particular, the L1, L2-1$_\sigma$, and L2 methods on the graded meshes have been developed. Stynes-Riordan-Gracia [25] prove the sharp error analysis of L1 scheme on graded meshes. Kopteva provides a different analysis framework of the L1 scheme on graded meshes in two and three spatial dimensions in [10]. Chen-Stynes [3] prove the second-order convergence of the L2-1$_\sigma$ scheme on fitted meshes combining the graded meshes and quasiuniform meshes. Kopteva-Meng [12] provide sharp pointwise-in-time error bounds for quasi-graded termporal meshes with arbitrary degree of grading for the L1 and L2-1$_\sigma$ schemes. Later Kopteva generalize this sharp pointwise error analysis to an L2-type scheme on quasi-graded meshes [11]. Liao-Li-Zhang establish the sharp error analysis for the L1 scheme of subdiffusion equation on general nonuniform meshes in [13] and then Liao-Mclean-Zhang study the L2-1$_\sigma$ scheme in [14, 15], where a discrete Grönwall inequality is introduced. This analysis for general nonuniform meshes can be used to design adaptive strategies of time steps.

Taking into account the singularity of exact solution, Mustapha-Abdallah-Furati [22] analyze the global high-order convergence of the discontinuous Galerkin method for subdiffusion equation on graded mesh. Jin-Li-Zhou [7, 8] combine BDF (backward differentiation formula) CQ methods with corrections to achieve higher (more than two) order convergence which can also overcome the weak singularity problem for time-fractional diffusion equation.

In this work, we first study the $H^1$-stability of the L2-1$_\sigma$ method proposed initially in [2] on general nonuniform meshes for subdiffusion equation with homogeneous Dirichlet boundary condition:

$$\begin{aligned} \begin{aligned} \partial _t^\alpha u(t,x) =\varDelta u(t,x)+f(t,x),{} & {} (t,x)\in (0,\infty )\times \varOmega , \end{aligned} \end{aligned}$$

(1.1)

where $\varOmega$ is a bounded Lipschitz domain in ${\mathbb {R}}^d$. For the L2-1$_\sigma$ fractional-derivative operator denoted by $L_k^{\alpha ,*}$, we prove that the following bilinear form

$$\begin{aligned} {\mathscr {B}}_n(v,w) = \sum _{k=1}^{n}\langle L_k^{\alpha ,*} v, \delta _k w\rangle ,\quad \delta _k w :=w^k-w^{k-1},~n\ge 1, \end{aligned}$$

(1.2)

is positive semidefinite under the restrictions (3.2) on time step ratios $\rho _k :=\tau _k/\tau _{k-1}$ with $\tau _k$ the kth time step and $k\ge 2$. In fact, the positive semidefiniteness of ${\mathscr {B}}_n$ on general nonuniform meshes is an open problem as stated in the conclusion of [16], where the maximum principle and convergence analysis are provided for L2-1$_\sigma$ scheme of the time-fractional Allen–Cahn equation but not the positive definiteness of L2-1$_\sigma$ operator. On the positive definiteness, Karaa presents in [1, 9] a general criteria ensuring the positivity of quadratic forms that can be applied to the time-fractional operators such as the L1 formula. In [17], Liao-Tang-Zhou proves the positive definiteness of a new L1-type operator.

Based on the positive semidefiniteness of ${\mathscr {B}}_n$ associated with L2-1$_\sigma$ operator, we propose a new global-in-time $H^1$-stability result in Theorem 2 for the L2-1$_\sigma$ scheme. In particular, when $\rho _k\ge 0.475329$ for $k\ge 2$, the restrictions (3.2) hold and the $H^1$-stability can be ensured for all time.

Besides the global-in-time $H^1$-stability of the L2-1$_\sigma$ scheme in Theorem 2, we revisit the sharp convergence analysis in [15] by Liao-Mclean-Zhang. We provide a proof of sharp $L^2$-norm convergence based on new properties of the L2-1$_\sigma$ coefficients, where the restriction on time step ratios is relaxed from $\rho _k\ge 4/7$ in [15] to $\rho _k\ge 0.475329$.

In the numerical implementations, we compare the L2-1$_\sigma$ schemes on the standard graded meshes [25] and the r-variable graded meshes (with varying grading parameter). According to our stability analysis, these methods are all $H^1$-stable. In our example, it can be observed that choosing proper r-variable graded meshes can lead to better numerical performance.

This work is organized as follows. In Sect. 2, the derivation, explicit expression and reformulation of L2-1$_\sigma$ fractional-derivative operator are provided. In Sect. 3, we prove the positive semidefiniteness of the bilinear form ${\mathscr {B}}_n$ under some mild restrictions on the time step ratios. In Sect. 4, we establish a new global-in-time $H^1$-stability of the L2-1$_\sigma$ scheme for the subdiffusion equation, based on the positive semidefiniteness result. Moreover we show the global error estimate when $\rho _k\ge 0.475329$ under low regularity assumptions on the exact solution. In Sect. 5, we do some first numerical tests.

2 Discrete Fractional-Derivative Operator

In this part we show the derivation, explicit expression and reformulation of L2-1$_\sigma$ operator on an arbitrary nonuniform mesh.

We consider the L2-1$_\sigma$ approximation of the fractional-derivative operator defined by

$$\begin{aligned} \partial _t^\alpha u = \frac{1}{\varGamma (1-\alpha )} \int _0^t \frac{u'(s)}{(t-s)^\alpha } \, \mathrm ds. \end{aligned}$$

Take a nonuniform time mesh $0 = t_0<t_1<\ldots<t_{k-1}<t_k<\ldots$ with $k\ge 1$. Let $\tau _j = t_j-t_{j-1}$ and $\sigma =1-\alpha /2$ (c.f. [2] for this setting of $\sigma$). The fractional derivative $\partial _t^\alpha u(t)$ at $t = t_k^*:=t_{k-1}+\sigma \tau _k$ could be approximated by the following L2-1$_\sigma$ fractional-derivative operator

$$\begin{aligned} L_k^{\alpha ,*} u&= \frac{1}{\varGamma (1-\alpha )} \left( \sum _{j=1}^{k-1}\int _{t_{j-1}}^{t_j} \frac{\partial _s H_2^j(s)}{(t_k^*-s)^\alpha }\,\mathrm ds+ \int _{t_{k-1}}^{t_k^*} \frac{\partial _s H_1^{k}(s)}{(t_k^*-s)^\alpha }\,\mathrm ds\right) \nonumber \\&= \frac{1}{\varGamma (1-\alpha )}\left( \sum _{j=1}^{k-1} (a_{j}^{(k)} u^{j-1} + b_{j}^{(k)} u^j + c_{j}^{(k)} u^{j+1} ) \right) +\frac{\sigma ^{1-\alpha }(u^k-u^{k-1})}{\varGamma (2-\alpha )\tau _k^{\alpha }}, \end{aligned}$$

(2.1)

where for $1\le j\le k-1$,

$$\begin{aligned} H_2^j (t) =&\frac{(t-t_j)(t-t_{j+1})}{(t_{j-1}-t_j)(t_{j-1}-t_{j+1})} u^{j-1} + \frac{(t-t_{j-1})(t-t_{j+1})}{(t_{j}-t_{j-1})(t_{j}-t_{j+1})} u^{j} \\&+ \frac{(t-t_{j-1})(t-t_{j})}{(t_{j+1}-t_{j-1})(t_{j+1}-t_{j})} u^{j+1},\\ H_1^k (t) =&\frac{t-t_k}{t_{k-1}-t_k} u^{k-1} + \frac{t-t_{k-1}}{t_{k}-t_{k-1}} u^k, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} a_{j}^{(k)}&= \int _{t_{j-1}}^{t_j} \frac{2s -t_j-t_{j+1}}{\tau _{j}(\tau _{j}+\tau _{j+1})} \frac{1}{(t_k^*-s)^\alpha }\,\mathrm ds= \int _0^1 \frac{-2 \tau _j(1-\theta )-\tau _{j+1}}{(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+\theta \tau _j))^\alpha }\,\mathrm d\theta ,\\ b_{j}^{(k)}&= -\int _{t_{j-1}}^{t_j} \frac{2s -t_{j-1}-t_{j+1}}{\tau _{j}\tau _{j+1}} \frac{1}{(t_k^*-s)^\alpha }\,\mathrm ds= -\int _0^1 \frac{2 \tau _j\theta -\tau _j-\tau _{j+1}}{\tau _{j+1}(t_k^*-(t_{j-1}+\theta \tau _j))^\alpha }\,\mathrm d\theta , \\ c_{j}^{(k)}&= \int _{t_{j-1}}^{t_j} \frac{2s -t_{j-1}-t_{j}}{\tau _{j+1}(\tau _{j}+\tau _{j+1})} \frac{1}{(t_k^*-s)^\alpha }\,\mathrm ds= \int _0^1 \frac{\tau _j^2(2\theta -1)}{\tau _{j+1}(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+\theta \tau _j))^\alpha }\,\mathrm d\theta . \end{aligned} \end{aligned}$$

(2.2)

It can be verified that $a_{j}^{(k)}<0$, $b_{j}^{(k)}>0$, $c_{j}^{(k)}>0$, and $a_{j}^{(k)}+b_{j}^{(k)}+c_{j}^{(k)} =0$ for $1\le j\le k-1$.

Specifically speaking, we can figure out the explicit expressions of $a_j^{(k)}$ and $c_j^{(k)}$ as follows (note that $b_j^{(k)} = -a_j^{(k)}-c_j^{(k)}$): for $1\le j\le k-1$,

$$\begin{aligned} a_j^{(k)}&= \frac{\tau _{j+1}}{(1-\alpha )\tau _j(\tau _j+\tau _{j+1})}(t_k^*-t_j)^{1-\alpha }-\frac{2\tau _{j}+\tau _{j+1}}{(1-\alpha )\tau _j(\tau _j+\tau _{j+1})}(t_k^*-t_{j-1})^{1-\alpha }\\&\quad +\frac{2}{(2-\alpha )(1-\alpha )\tau _j(\tau _j+\tau _{j+1})}\left[ (t_k^*-t_{j-1})^{2-\alpha }-(t_k^*-t_j)^{2-\alpha }\right] ,\\ c_j^{(k)}&= \frac{1}{(1-\alpha )\tau _{j+1}(\tau _j+\tau _{j+1})} \Big [-\tau _j( (t_k^*-t_{j-1})^{1-\alpha }+ (t_k^*-t_{j})^{1-\alpha })\\&\quad +2(2-\alpha )^{-1} ( (t_k^*-t_{j-1})^{2-\alpha }- (t_k^*-t_{j})^{2-\alpha }) \Big ]. \end{aligned}$$

We reformulate the discrete fractional derivative $L_k^{\alpha ,*}$ in (2.1) as

$$\begin{aligned} \begin{aligned} L_k^{\alpha ,*} u&=\frac{1}{\varGamma (1-\alpha )}\left( c_{k-1}^{(k)} \delta _k u -a_1^k\delta _1 u +\sum _{j=2}^{k-1} d^{(k)}_{j} \delta _j u \right) +\frac{\sigma ^{1-\alpha }}{\varGamma (2-\alpha )\tau _k^{\alpha }}\delta _k u, \end{aligned} \end{aligned}$$

(2.3)

where $\delta _j u= u^j-u^{j-1},$ $d^{(k)}_j:=c^{(k)}_{j-1}-a^{(k)}_{j}.$ Here we make a convention that $a_1^1=0$ and $c_0^1=0$.

To establish the global-in-time $H^1$-stability of L2-1$_\sigma$ method for fractional-order parabolic problem, we shall prove the positive semidefiniteness of ${\mathscr {B}}_n$ defined in (1.2).

3 Positive Semidefiniteness of Bilinear Form ${\mathscr {B}}_n$

In this section, we first propose some properties of the L2-1$_\sigma$ coefficients $a^{(k)}_j$, $c^{(k)}_j$ and $d^{(k)}_j$ in (2.3), which will be useful to establish the positive semidefiniteness of bilinear form ${\mathscr {B}}_n$. Then we prove rigorously the positive semidefiniteness of bilinear form $\mathscr {B}_n$ under some constraints of $\rho _k$, $k\ge 2$.

Lemma 1

(Properties of $a^{(k)}_j$, $c^{(k)}_j$ and $d^{(k)}_j$) For the L2-1$_\sigma$ coefficients given in (2.3), given a nonuniform mesh $\{\tau _j\}_{j\ge 1}$, the following properties hold:

• (P1) $a^{(k)}_j<0,~1\le j\le k-1,~k\ge 2$;

• (P2) $a^{(k+1)}_{j}-a^{(k)}_{j}>0,~1\le j\le k-1,~k\ge 2$;

• (P3) $a^{(k)}_{j+1}-a^{(k)}_{j}<0,~1\le j\le k-2,~k\ge 3$;

• (P4) $a_{j+1}^{(k)}-a_{j}^{(k)}<a_{j+1}^{(k+1)}-a_{j}^{(k+1)},~1\le j\le k-2,~k\ge 3$;

• (P5) $c^{(k)}_j>0,~1\le j\le k-1,~k\ge 2$;

• (P6) $c^{(k+1)}_{j}-c^{(k)}_{j}<0,~1\le j\le k-1,~k\ge 2$;

• (P7) $d^{(k)}_j>0,~2\le j\le k-1,~k\ge 3$;

• (P8) $d^{(k+1)}_{j}-d^{(k)}_j<0,~2\le j\le k-1,~k\ge 3$.

Furthermore, if the nonuniform mesh $\{\tau _j\}_{j\ge 1}$, with $\rho _j :=\tau _j/\tau _{j-1}$ satisfies

$$\begin{aligned} \frac{1}{\rho _{j+1}}\ge \frac{1}{\rho _{j}^2(1+\rho _{j})}-3,\quad \forall j\ge 2, \end{aligned}$$

(3.1)

then the following properties of $d_j^{(k)}$ hold:

• (P9) $d^{(k)}_{j+1}-d^{(k)}_j>0,~2\le j\le k-2,~k\ge 4$;

• (P10) $d_{j+1}^{(k)}-d_{j}^{(k)}>d_{j+1}^{(k+1)}-d_{j}^{(k+1)},~2\le j\le k-2,~k\ge 4$.

Proof

The proof is the same as the proof of [24, Lemma 3.1] except replacing $t_k$ with $t_k^*$. We omit it here. $\square$

Theorem 1

Consider a nonuniform mesh $\{\tau _k\}_{k\ge 1}$ satisfying that $k\ge 2$,

$$\begin{aligned} \left\{ \begin{aligned}&\rho _*<\rho _{k+1} \le \frac{\rho _k^2(1+\rho _k)}{1-3\rho _k^2(1+\rho _k)},{} & {} \rho _*<\rho _k< \eta ,\\&\rho _*<\rho _{k+1},{} & {} \eta \le \rho _k, \end{aligned} \right. \end{aligned}$$

(3.2)

where $\rho _*\approx 0.356341$, and $\eta \approx 0.475329$. Then the for any function u defined on $[0,\infty )\times \varOmega$ and $n\ge 1$,

$$\begin{aligned} {\mathscr {B}}_n(u,u) = \sum _{k=1}^{n}\langle L_k^{\alpha ,*} u, \delta _k u\rangle \ge \sum _{k=1}^{n} \frac{g_k(\alpha )}{2\varGamma (2-\alpha )} \Vert \delta _k u\Vert ^2_{L^2(\varOmega )}\ge 0, \end{aligned}$$

(3.3)

where

$$\begin{aligned} g_k(\alpha )= \left\{ \begin{array}{ll} \frac{1}{(\sigma \tau _1)^\alpha }\left( 2\sigma -\frac{1-\alpha }{\rho _2^\alpha }\right) , &{}k=1,\\ (1-\alpha )c_{k-1}^{(k)}+ \frac{1}{(\sigma \tau _k)^{\alpha }}\left( 2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha } \int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds\right) , &{}2\le k\le n-1,\\ (1-\alpha )c_{n-1}^{(n)}+ \frac{1}{(\sigma \tau _n)^{\alpha }}(2\sigma -(1-\alpha )),&{}k=n\ne 2, \end{array} \right. \end{aligned}$$

(3.4)

are always positive for $\alpha \in (0,1)$.

Proof

According to (2.3), we can rewrite ${\mathscr {B}}_n(u,u)$ in the following matrix form

$$\begin{aligned} {\mathscr {B}}_n(u,u) = \sum _{k=1}^{n}\langle L_k^{\alpha ,*} u, \delta _k u\rangle =\frac{1}{\varGamma (1-\alpha )}\int _{\varOmega }\psi {\textbf{M}} \psi ^{\textrm{T}}\mathrm dx, \end{aligned}$$

where $\psi =[\delta _{1} u,\delta _2 u,\cdots ,\delta _n u],$ and

$$\begin{aligned} {\textbf{M}}= \begin{pmatrix} \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _1^{\alpha }}&{} \\ -a_1^{(2)}&{} c^{(2)}_1+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }} \\ -a_1^{(3)} &{} d_2^{(3)}&{} c^{(3)}_2+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _3^{\alpha }} \\ \vdots &{} \vdots &{}\ddots &{} \ddots \\ -a_1^{(n)}&{} d_2^{(n)}&{}\cdots &{} d^{(n)}_{n-1}&{} c_{n-1}^{(n)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _n^{\alpha }} \end{pmatrix}, \end{aligned}$$

(3.5)

We split ${\textbf{M}}$ as ${\textbf{M}} = {\textbf{A}}+{\textbf{B}}$, where

$$\begin{aligned} \small {\textbf{A}}= \begin{pmatrix} \beta _1 &{} \\ -a_1^{(2)}&{} \beta _2 \\ -a_1^{(3)} &{} d_2^{(3)}&{} \beta _3 \\ \vdots &{} \vdots &{}\ddots &{} \ddots \\ -a_1^{(n)}&{} d_2^{(n)}&{}\cdots &{} d^{(n)}_{n-1}&{} \beta _n \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} {\textbf{B}}={\textrm{diag}}\left( \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _1^{\alpha }}-\beta _1,~c_1^{(2)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }}-\beta _2,~\cdots ,~c_{n-1}^{(n)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _n^{\alpha }}-\beta _n\right) , \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&2\beta _1= -a^{(2)}_1,\quad 2\beta _2 -d^{(3)}_2=a^{(3)}_1-a^{(2)}_1,\\&2\beta _k -d^{(k+1)}_k=d^{(k)}_{k-1}-d^{(k+1)}_{k-1},\quad 3\le k\le n-1,\\&2\beta _n=d^{(n)}_{n-1},\quad n\ge 3. \end{aligned} \end{aligned}$$

(3.6)

Consider the following symmetric matrix ${\textbf{S}} = \textbf{A}+{\textbf{A}}^{\mathrm T}+\varepsilon {\textbf{e}}_n^{\textrm{T}}{\textbf{e}}_n$ with small constant $\varepsilon >0$ and ${\textbf{e}}_n = (0,\cdots ,0,1)\in {\mathbb {R}}^{1\times n}$. According to Lemma 1, if the condition (3.1) holds, ${\textbf{S}}$ satisfies the following three properties:

• (1) $\forall \; 1\le j < i \le n$, $\left[ {\textbf{S}} \right] _{i-1,j}\ge \left[ {\textbf{S}} \right] _{i, j}$;

• (2) $\forall \; 1 < j \le i \le n$, $\left[ {\textbf{S}} \right] _{i, j-1}< \left[ {\textbf{S}} \right] _{i, j}$;

• (3) $\forall \;1< j < i \le n$, $\left[ {\textbf{S}} \right] _{i-1, j-1} - \left[ {\textbf{S}} \right] _{i, j-1}\le \left[ {\textbf{S}} \right] _{i-1, j} - \left[ {\textbf{S}} \right] _{i, j}$.

From [23, Lemma 2.1], ${\textbf{S}}$ is positive definite. Let $\varepsilon \rightarrow 0$. We can claim that ${\textbf{A}}+{\textbf{A}}^{\mathrm T}$ is positive semidefinite.

In the following we will prove $[{\textbf{B}}]_{kk}\ge 0$, $k\ge 1$, under some constraints on $\rho _k$. We first provide two equivalent forms of $a_j^{(k)}$ according to (2.2): $\forall 1\le j\le k-1$,

$$\begin{aligned} \begin{aligned} a_{j}^{(k)}&=\int _0^1 \frac{-2 \tau _j(1-s)-\tau _{j+1}}{(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+s\tau _j))^\alpha }\,\mathrm ds\\&=\frac{1}{\tau _{j}+\tau _{j+1}}\int _0^1 (t_k^*-(t_{j-1}+s \tau _j))^{-\alpha }\,\textrm{d}( \tau _j s^2-(2\tau _j+\tau _{j+1})s)\\&=-(t_k^*-t_j)^{-\alpha }+\frac{\alpha \tau _j}{\tau _j+\tau _{j+1}} \int _0^{1} (\tau _j+\tau _{j+1}+s\tau _j) (1-s)(t_k^*-t_{j}+s\tau _j)^{-\alpha -1}\,\mathrm ds\end{aligned} \end{aligned}$$

(3.7)

and

$$\begin{aligned} \begin{aligned} a_{j}^{(k)}&=\int _0^1 \frac{-2 \tau _j(1-s)-\tau _{j+1}}{(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+s\tau _j))^\alpha }\,\mathrm ds=\int _0^1 \frac{-2 \tau _j s-\tau _{j+1}}{(\tau _{j}+\tau _{j+1})(t_k^*-t_{j}+s \tau _j)^\alpha }\,\mathrm ds\\&=\frac{1}{\tau _{j}+\tau _{j+1}}\int _0^1 (t_k^*-t_{j}+s \tau _j)^{-\alpha }\,\textrm{d}( - \tau _j s^2-\tau _{j+1}s)\\&=-(t_k^*-t_{j-1})^{-\alpha }-\frac{\alpha \tau _j}{\tau _j+\tau _{j+1}} \int _0^{1} (\tau _j+\tau _{j+1}-s\tau _j)(1-s) (t_k^*-t_{j-1}-s\tau _j)^{-\alpha -1}\,\mathrm ds. \end{aligned} \end{aligned}$$

(3.8)

Furthermore, we also reformulate $c_j^{(k)}$ in (2.2) as: $\forall 1\le j\le k-1$,

$$\begin{aligned} \begin{aligned} c_j^{(k)}&= \int _0^1 \frac{\tau _j^2(2s-1)}{\tau _{j+1}(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+s \tau _j))^\alpha }\,\mathrm ds\\&=\frac{\tau _j^2}{\tau _{j+1}(\tau _{j}+\tau _{j+1})}\int _0^1(t_k^*-(t_{j-1}+s \tau _j))^{-\alpha } \textrm{d}(s^2-s)\\&=\frac{\alpha \tau _{j}^3}{\tau _{j+1}(\tau _{j}+\tau _{j+1})}\int _0^{1} s(1-s)(t_k^*-t_j+s\tau _{j})^{-\alpha -1}\ \mathrm ds. \end{aligned} \end{aligned}$$

(3.9)

In the following content, we consider four cases: $k=1$, $k=2$, $3\le k\le n-1$, and $k=n$.

Case 1 When $k=1$, from (2.2) and $2\beta _1= -a^{(2)}_1$ in (3.6), we have

$$\begin{aligned}{}[{\textbf{B}}]_{11}&=\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _1^{\alpha }}-\frac{1}{2}\int _0^1 \frac{2 \tau _1(1-\theta )+\tau _{2}}{(\tau _{1}+\tau _{2})(t_2^*-(t_{0}+\theta \tau _1))^\alpha }\,\mathrm d\theta \\&=\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _1^{\alpha }}-\frac{1}{2\tau _1^\alpha }\int _0^1\frac{2s+\rho _2}{(1+\rho _2)(\sigma \rho _2+s)^\alpha }\mathrm ds\\&> \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _1^{\alpha }}-\frac{1}{2\tau _1^\alpha (\sigma \rho _2)^\alpha }\int _0^1\frac{2s+\rho _2}{(1+\rho _2)}\mathrm ds=\frac{1}{2(1-\alpha )(\sigma \tau _1)^\alpha }\left( 2\sigma -\frac{1-\alpha }{\rho _2^\alpha }\right) . \end{aligned}$$

To ensure $[{\textbf{B}}]_{11}\ge 0$, we impose

$$\begin{aligned} 2\sigma -\frac{1-\alpha }{\rho _2^\alpha }\ge 0. \end{aligned}$$

(3.10)

Case 2 When $k=2$, combining $2\beta _2 -d^{(3)}_2=a^{(3)}_1-a^{(2)}_1$ in (3.6) and the property (P6) in Lemma (1) gives

$$\begin{aligned} \begin{aligned}{}[{\textbf{B}}]_{22}&=c^{(2)}_1+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }}-\frac{1}{2}(d^{(3)}_2+a^{(3)}_1-a^{(2)}_1)\\&=\frac{1}{2}c^{(2)}_1+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }}+\frac{1}{2}(a^{(2)}_1-a^{(3)}_1+a^{(3)}_2)+\frac{1}{2}(c^{(2)}_1-c^{(3)}_1)\\&\ge \frac{1}{2}c^{(2)}_1+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }}+\frac{1}{2}(a^{(2)}_1-a^{(3)}_1+a^{(3)}_2). \end{aligned} \end{aligned}$$

(3.11)

Using the forms (3.7) for $a^{(2)}_1,~a^{(3)}_1$ and (3.8) for $a^{(3)}_2$, we can derive

$$\begin{aligned} a^{(2)}_1-a^{(3)}_1+a^{(3)}_2&=-(\sigma \tau _2)^{-\alpha }+\frac{\alpha \tau _1}{\tau _1+\tau _2} \int _0^{1} (\tau _1+\tau _{2}+s\tau _1) (1-s)(t_2^*-t_{1}+s\tau _1)^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad -\frac{\alpha \tau _1}{\tau _1+\tau _{2}} \int _0^{1} (\tau _1+\tau _{2}+s\tau _1) (1-s)(t_3^*-t_{1}+s\tau _1)^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad -\frac{\alpha \tau _{2}}{\tau _{2}+\tau _{3}} \int _0^{1}(\tau _{2}+\tau _{3}-s\tau _{2}) (1-s)(t_3^*-t_{1}-s\tau _2)^{-\alpha -1}\,\mathrm ds>\nonumber \\&\quad -(\sigma \tau _2)^{-\alpha }-\frac{\alpha \tau _{2}}{\tau _{2}+\tau _{3}} \int _0^{1}(\tau _{2}+\tau _{3}-s\tau _{2}) (1-s)(\tau _2+\sigma \tau _3-s\tau _2)^{-\alpha -1}\,\mathrm ds\nonumber \\&=-(\sigma \tau _2)^{-\alpha }-\frac{\alpha }{(1+\rho _{3})\tau _2^\alpha } \int _0^{1} s(\rho _{3}+s)(\sigma \rho _{3}+s)^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad -(\sigma \tau _2)^{-\alpha }-\frac{\alpha }{(1+\rho _{3})(\sigma \tau _2)^\alpha \rho _{3}^\alpha } \int _0^{1}\frac{s(\rho _{3}+s)}{\sigma \rho _{3}+s} \,\mathrm ds. \end{aligned}$$

(3.12)

Substituting (3.12) into (3.11) yields

$$\begin{aligned} \begin{aligned}{}[{\textbf{B}}]_{22} \ge&\frac{1}{2}c^{(2)}_1+\frac{1}{2(1-\alpha )(\sigma \tau _2)^{\alpha }}\left( 2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{3})\rho _{3}^\alpha } \int _0^{1}\frac{s(\rho _{3}+s)}{\sigma \rho _{3}+s} \,\mathrm ds\right) . \end{aligned} \end{aligned}$$

To make sure $[{\textbf{B}}]_{22}\ge 0$, we impose

$$\begin{aligned} 2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _3)\rho _{3}^\alpha } \int _0^{1}\frac{s(\rho _{3}+s)}{\sigma \rho _{3}+s} \,\mathrm ds\ge 0. \end{aligned}$$

(3.13)

Case 3 When $3\le k \le n-1$, using $2\beta _k=d^{(k+1)}_k+d^{(k)}_{k-1}-d^{(k+1)}_{k-1}$ in (3.6) and $d^{(k)}_j=c^{(k)}_{j-1}-a^{(k)}_j$, we have

$$\begin{aligned}{}[{\textbf{B}}]_{kk}&=\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^{\alpha }}+\frac{1}{2}c_{k-1}^{(k)}+\frac{1}{2}(c_{k-1}^{(k)}-d^{(k+1)}_k-d^{(k)}_{k-1}+d^{(k+1)}_{k-1})\nonumber \\&= \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^{\alpha }}+\frac{1}{2}c_{k-1}^{(k)}+\frac{1}{2}[(c^{(k)}_{k-1}-c^{(k+1)}_{k-1})-(c^{(k)}_{k-2}-c^{(k+1)}_{k-2})\nonumber \\&\quad +(-a_{k-1}^{(k+1)}+a^{(k+1)}_{k}+a^{(k)}_{k-1})]. \end{aligned}$$

(3.14)

From (3.7) – (3.9), if (3.1) holds for $j=k-1$, we have

$$\begin{aligned}&(c^{(k)}_{k-1}-c^{(k+1)}_{k-1})-(c^{(k)}_{k-2}-c^{(k+1)}_{k-2} )+(-a_{k-1}^{(k+1)}+a^{(k+1)}_{k}+a^{(k)}_{k-1})\nonumber \\&\quad =\frac{\alpha \tau _{k-1}^3}{\tau _{k}(\tau _{k-1}+\tau _{k})}\int _0^{1} s(1-s)\bigg [(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\nonumber \\&\qquad -(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\bigg ]\ \mathrm ds-\frac{\alpha \tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\int _0^{1} s(1-s)\nonumber \\&\qquad \bigg [(t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1} -(t_{k+1}^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}\bigg ]\ \mathrm ds\nonumber \\&\qquad +\frac{\alpha \tau _{k-1}}{\tau _{k-1}+\tau _{k}} \int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)\bigg [(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\nonumber \\&\qquad -(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\bigg ]\,\mathrm ds\nonumber \\&\qquad -(\sigma \tau _k)^{-\alpha }-\frac{\alpha \tau _{k}}{\tau _{k}+\tau _{k+1}} \int _0^{1}(\tau _{k}+\tau _{k+1}-s\tau _{k}) (1-s)(t_{k+1}^*-t_{k-1}-s\tau _{k})^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad> -(\sigma \tau _k)^{-\alpha }-\frac{\alpha \tau _{k}}{\tau _{k}+\tau _{k+1}} \int _0^{1}s(\tau _{k+1}+s\tau _{k}) (\sigma \tau _{k+1}+s\tau _{k})^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad =-(\sigma \tau _k)^{-\alpha }-\frac{\alpha }{(1+\rho _{k+1})\tau _k^\alpha } \int _0^{1} s(\rho _{k+1}+s)(\sigma \rho _{k+1}+s)^{-\alpha -1}\,\mathrm ds>\nonumber \\&\qquad -(\sigma \tau _k)^{-\alpha }-\frac{\alpha }{(1+\rho _{k+1})(\sigma \tau _k)^\alpha \rho _{k+1}^\alpha } \int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds, \end{aligned}$$

(3.15)

where we use the forms (3.7) for $a_{k-1}^{(k)},~a_{k-1}^{(k+1)}$ and (3.8) for $a_k^{(k+1)}$. The first inequality in (3.15) can be derived as follows. For fixed j, it is easy to see that

$$\begin{aligned} (t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}-(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}>0 \end{aligned}$$

decreases w.r.t. s and $\int _0^1(1-3s)(1-s)\ \mathrm ds= 0,$ thus

$$\begin{aligned} \begin{aligned}&\int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)[(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}-(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}]\,\mathrm ds\\&\quad \ge \int _0^{1} (4\tau _{k-1}+3\tau _{k})s (1-s)[(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}-(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}]\,\mathrm ds. \end{aligned} \end{aligned}$$

Moreover the convexity of the function $t^{-1-\alpha }$ gives

$$\begin{aligned} \begin{aligned}&(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}-(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\\&\quad >(t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}-(t_{k+1}^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}, \end{aligned} \end{aligned}$$

Then we can get the following result:

$$\begin{aligned}&\frac{\alpha \tau _{k-1}^3}{\tau _{k}(\tau _{k-1}+\tau _{k})}\int _0^{1} s(1-s)\bigg [(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\\&\quad -(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\bigg ]\ \mathrm ds-\frac{\alpha \tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\int _0^{1} s(1-s)\\&\quad \bigg [(t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}-(t_{k+1}^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}\bigg ]\ \mathrm ds\\&\quad +\frac{\alpha \tau _{k-1}}{\tau _{k-1}+\tau _{k}} \int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)\bigg [(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\\&\quad -(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\bigg ]\,\mathrm ds\\&\quad >\alpha \left( \frac{\tau _{k-1}^3}{\tau _{k}(\tau _{k-1}+\tau _{k})}-\frac{\tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}+\frac{(4\tau _{k-1}+3\tau _{k})\tau _{k-1}}{\tau _{k-1}+\tau _{k}}\right) \int _0^{1} s(1-s)\\&\quad \bigg [(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1} -(t_{k+1}^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\bigg ]\, \mathrm ds\ge 0, \end{aligned}$$

as (3.1) for $j=k-1$ gives

$$\begin{aligned} \frac{\tau _{k-1}^3}{\tau _{k}(\tau _{k-1}+\tau _{k})}-\frac{\tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}+\frac{(4\tau _{k-1}+3\tau _{k})\tau _{k-1}}{\tau _{k-1}+\tau _{k}}\ge 0. \end{aligned}$$

Combining (3.15) with (3.14) yields

$$\begin{aligned} \begin{aligned}{}[{\textbf{B}}]_{kk} \ge&\frac{1}{2}c_{k-1}^{(k)}+\frac{1}{2(1-\alpha )(\sigma \tau _k)^{\alpha }}\left( 2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha } \int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds\right) . \end{aligned} \end{aligned}$$

Thus, to ensure $[{\textbf{B}}]_{kk} \ge 0$ for $3\le k \le n-1$, it is sufficient to impose

$$\begin{aligned}&\frac{1}{\rho _{k}}\ge \frac{1}{\rho _{k-1}^2(1+\rho _{k-1})}-3,\nonumber \\&2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha }\int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds\ge 0. \end{aligned}$$

(3.16)

Case 4 When $k=n$, we show $[{\textbf{B}}]_{nn}\ge 0$ under some constraints on $\rho _n$. From (3.6), (3.7) and (3.9), we can derive

$$\begin{aligned}{}[{\textbf{B}}]_{nn}&= c_{n-1}^{(n)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _n^{\alpha }}-\frac{1}{2}(c^{(n)}_{n-2}-a^{(n)}_{n-1})\nonumber \\&=\frac{1}{2}c_{n-1}^{(n)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _n^{\alpha }}+\frac{1}{2}(c_{n-1}^{(n)}-c^{(n)}_{n-2}+a^{(n)}_{n-1})\nonumber \\&=\frac{1}{2}c_{n-1}^{(n)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _n^{\alpha }} +\frac{1}{2}\bigg (\frac{\alpha \tau _{n-1}^3}{\tau _{n}(\tau _{n-1}+\tau _{n})}\int _0^{1} s(1-s)(t_n^*-t_{n-1}+s\tau _{n-1})^{-\alpha -1}\ \mathrm ds\nonumber \\&\quad -\frac{\alpha \tau _{n-2}^3}{\tau _{n-1}(\tau _{n-2}+\tau _{n-1})}\int _0^{1} s(1-s)(t_n^*-t_{n-2}+s\tau _{n-2})^{-\alpha -1}\ \mathrm ds\nonumber \\&\quad -(\sigma \tau _n)^{-\alpha }+\frac{\alpha \tau _{n-1}}{\tau _{n-1}+\tau _{n}} \int _0^{1} (\tau _{n-1}+\tau _{n}+s\tau _{n-1}) (1-s)(t_n^*-t_{n-1}+s\tau _{n-1})^{-\alpha -1}\,\mathrm ds\bigg )\nonumber \\&>\frac{1}{2}c_{n-1}^{(n)}+\frac{1}{2(1-\alpha )(\sigma \tau _{n})^{\alpha }}\left( 2\sigma -(1-\alpha )\right) , \end{aligned}$$

(3.17)

if (3.1) holds for $j=n-1$. The proof of the last inequality in (3.17) is similar to the previous proof of (3.15), where we use the facts

$$\begin{aligned} \begin{aligned}&\int _0^{1} (\tau _{n-1}+\tau _{n}+s\tau _{n-1}) (1-s)(t_n^*-t_{n-1}+s\tau _{n-1})^{-\alpha -1}\,\mathrm ds\\&\quad \ge \int _0^{1} (4\tau _{n-1}+3\tau _{n})s (1-s)(t_n^*-t_{n-1}+s\tau _{n-1})^{-\alpha -1}\,\mathrm ds, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} (t_n^*-t_{n-1}+s\tau _{n-1})^{-\alpha -1} >(t_n^*-t_{n-2}+s\tau _{n-2})^{-\alpha -1}. \end{aligned} \end{aligned}$$

We omit the details here. To ensure $[{\textbf{B}}]_{nn}\ge 0,$ it is sufficient to impose

$$\begin{aligned} \begin{aligned}&\frac{1}{\rho _{n}}\ge \frac{1}{\rho _{n-1}^2(1+\rho _{n-1})}-3,\quad 2\sigma -(1-\alpha )\ge 0. \end{aligned} \end{aligned}$$

(3.18)

Combining (3.10), (3.13), (3.16) and (3.18), we can conclude that if the condition (3.1) holds for $2\le k\le n-1$ and

$$\begin{aligned} \begin{aligned}&2\sigma -\frac{1-\alpha }{\rho _2^\alpha }\ge 0,\\&2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha }\int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds\ge 0,\quad 2\le k\le n-1,\\&2\sigma -(1-\alpha )\ge 0, \end{aligned} \end{aligned}$$

(3.19)

then $[{\textbf{B}}]_{kk}\ge 0$, $k\ge 1$. We have proved the following results:

• Positive semidefiniteness of ${\textbf{A}}+{\textbf{A}}^{\textrm{T}}$: (3.1) holds;

• Positive definiteness of ${\textbf{B}}$: (3.19) holds and (3.1) holds for $2\le k\le n-1$;

which ensure

$$\begin{aligned} {\textbf{M}}+{\textbf{M}}^{\textrm{T}}&= ({\textbf{A}}+{\textbf{A}}^{\textrm{T}})+2{\textbf{B}}\ge 2{\textbf{B}} \ge (1-\alpha )^{-1} {\textrm{diag}}\left( g_1(\alpha ),g_2(\alpha ),\ldots ,g_{n}(\alpha )\right) \ge 0, \end{aligned}$$

where $g_k(\alpha )$ is given in (3.4). In the following content, we just simplify the above constraints for the positive semidefiniteness of ${\textbf{M}}+{\textbf{M}}^{\textrm{T}}$.

The condition (3.1) actually says that $(\rho _j,\rho _{j+1})$ lies on the right-hand side of the blue solid curve in Fig. . Let $\rho _*\approx 0.356341$ be the root of $\rho (1+\rho )=1-3\rho ^2(1+\rho ).$ It can be found that if $\rho _{j}\le \rho _*$ for some j, then $\rho _*\ge \rho _j\ge \rho _{j+1}\ge \rho _{j+2}\ge \ldots$ and $\tau _j$ will shrink to 0 quickly as j increases. This doesn’t make sense in practice. We shall impose $\rho _{j}>\rho _*,~ \forall j\ge 2.$ As a consequence, we have the following constraints: for $j\ge 2$,

$$\begin{aligned} \left\{ \begin{aligned}&\rho _*<\rho _{j+1} \le \frac{\rho _j^2(1+\rho _j)}{1-3\rho _j^2(1+\rho _j)},{} & {} \rho _*<\rho _j< \eta ,\\&\rho _*<\rho _{j+1},{} & {} \eta \le \rho _j, \end{aligned} \right. \end{aligned}$$

(3.20)

where $\eta \approx 0.475329$ be the unique positive root of $1-3\rho ^2(1+\rho )=0.$

Fig. 1

Feasible region of $(\rho _j,\rho _{j+1})$, on the right-hand side of the blue solid curve and above the blue dashed line, obtained from the constraint (3.20) for $j\ge 2$. The blue star marker denotes $(\rho _*,\rho _*)$

We now prove that (3.20) leads to (3.19) when $\sigma = 1-\alpha /2\ge 1/2$. In fact, it is easy to check that

$$\begin{aligned} 2\sigma -\frac{1-\alpha }{\rho _2^\alpha }\ge 2-\alpha -\frac{1-\alpha }{\rho _*^\alpha }\ge 0,\quad 2\sigma -(1-\alpha )=1, \end{aligned}$$

and for $2\le k\le n-1$, we have

$$\begin{aligned}&2\sigma -(1-\alpha )-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha }\int _0^{1}\frac{s(\rho _{k+1}+s)}{\sigma \rho _{k+1}+s} \,\mathrm ds\\&\quad \ge 1-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha }\int _0^{1}\frac{s(\rho _{k+1}+s)}{\frac{1}{2}\rho _{k+1}+s} \,\mathrm ds\\&\quad \ge 1-\frac{\alpha (1-\alpha )}{(1+\rho _{k+1})\rho _{k+1}^\alpha }\ge 1-\frac{\alpha (1-\alpha )}{(1+\rho _*)\rho _*^\alpha }\ge 1-\frac{1}{4(1+\rho _*)\rho _*}\ge 0. \end{aligned}$$

In summary, if (3.20) holds, then

$$\begin{aligned} {\mathscr {B}}_n(u,u) = \sum _{k=1}^{n}\langle L_k^{\alpha ,*} u, \delta _k u\rangle \ge \sum _{k=1}^{n} \frac{g_k(\alpha )}{2\varGamma (2-\alpha )} \Vert \delta _k u\Vert ^2_{L^2(\varOmega )}\ge 0, \end{aligned}$$

with $g_k(\alpha )$ given in (3.4). $\square$

Remark 1

If $\rho _k\ge \eta \approx 0.475329$ for all $k\ge 2$, then the condition (3.2) holds, for which the positive semidefiniteness of bilinear form ${\mathscr {B}}_n(u,u)$ (3.3) can be guaranteed.

4 Stability and Convergence of L2-1$_\sigma$ Method for Subdiffusion Equation

We consider the following subdiffusion equation:

$$\begin{aligned} \begin{aligned} \partial _t^\alpha u(t,x)&= \varDelta u(t,x)+f(t,x),{} & {} (t,x)\in (0,\infty )\times \varOmega ,\\ u(t,x)&= 0,{} & {} (t,x)\in (0,\infty )\times \partial \varOmega ,\\ u(0,x)&= u^0(x),{} & {} x\in \varOmega , \end{aligned} \end{aligned}$$

(4.1)

where $\varOmega$ is a bounded Lipschitz domain in ${\mathbb {R}}^d$. Given an arbitrary nonuniform mesh $\{\tau _k\}_{k\ge 1}$, the L2-$1_\sigma$ scheme of this subdiffusion equation is written as

$$\begin{aligned} \begin{aligned} L_k^{\alpha ,*} u&= (1-\alpha /2)\varDelta u^k+\alpha /2\varDelta u^{k-1}+f^k,{} & {} \text {in}~ \varOmega ,\\ u^k&=0,{} & {} \text {on} ~\partial \varOmega , \end{aligned} \end{aligned}$$

(4.2)

where $f^k=f(t_k^*,\cdot )$.

4.1 Global-in-Time $H^1$-Stability of L2-1$_\sigma$ Scheme for Subdiffusion Equation

Theorem 2

Assume that $f(t,x) \in L^\infty ([0,\infty );L^2(\varOmega )) \cap BV([0,\infty ); L^2(\varOmega ))$ is a bounded variation function in time and $u^0\in H_0^1(\varOmega )$. If the nonuniform mesh $\{\tau _k\}_{k\ge 1}$ satisfies (3.2) (for example $\rho _k\ge \eta \approx 0.475329$ for $k\ge 2$), then the numerical solution $u^n$ of the L2-1$_\sigma$ scheme (4.2) satisfies the following global-in-time $H^1$-stability

$$\begin{aligned} \begin{aligned} \Vert \nabla u^n\Vert _{L^2(\varOmega )}&\le \Vert \nabla u^0\Vert _{L^2(\varOmega )} +2C_{f}C_{\varOmega }, \end{aligned} \end{aligned}$$

where $C_{f}= 2\Vert f\Vert _{L^\infty ([0,\infty );L^2(\varOmega ))}+\Vert f\Vert _{BV([0,\infty ); L^2(\varOmega ))}$, $C_\varOmega$ is the Sobolev embedding constant depending on $\varOmega$ and the spatial dimension d.

Proof

Multiplying (4.2) with $\delta _k u$, integrating over $\varOmega$, and summing up the derived equations over k yield

$$\begin{aligned} \begin{aligned} \sum _{k=1}^{n}\langle L_k^{\alpha ,*} u, \delta _k u\rangle =&\sum _{k=1}^{n}\langle (1-\alpha /2)\varDelta u^k+\alpha /2\varDelta u^{k-1}, \delta _k u\rangle +\sum _{k=1}^{n}\langle f^k, \delta _k u \rangle \\ =&-\frac{1}{2} \Vert \nabla u^n\Vert _{L^2(\varOmega )}^2 + \frac{1}{2} \Vert \nabla u^0\Vert _{L^2(\varOmega )}^2 - \frac{1-\alpha }{2} \sum _{k=1}^{n} \Vert \nabla \delta _k u\Vert _{L^2(\varOmega )}^2\\&+\langle f^n, u^n\rangle -\langle f^1, u^0\rangle -\sum _{k=2}^{n}\langle \delta _k f, u^{k-1}\rangle .\end{aligned} \end{aligned}$$

Applying the Cauchy–Schwarz inequality yields

$$\begin{aligned} \begin{aligned}&\langle f^n, u^n\rangle -\langle f^1, u^0\rangle +\sum _{k=2}^{n}\langle \delta _k f, u^{k-1}\rangle \\&\quad \le \left( 2\Vert f\Vert _{L^\infty ([0,\infty );L^2(\varOmega ))}+\Vert f\Vert _{BV([0,\infty ); L^2(\varOmega ))}\right) \max _{0\le k\le n} {\Vert u^k\Vert _{L^2(\varOmega )}}\\&\quad \le C_{f}C_{\varOmega } \max _{0\le k\le n} {\Vert \nabla u^k\Vert _{L^2(\varOmega )}}, \end{aligned} \end{aligned}$$

where $C_{f}= 2\Vert f\Vert _{L^\infty ([0,\infty );L^2(\varOmega ))}+\Vert f\Vert _{BV([0,\infty ); L^2(\varOmega ))}$, and $C_{\varOmega }$ is the Sobolev embedding constant depending on $\varOmega$ and the spatial dimension. From Theorem 1, we then have for $n\ge 1$,

$$\begin{aligned} \begin{aligned}&\Vert \nabla u^n\Vert _{L^2(\varOmega )}^2 \le \Vert \nabla u^0\Vert _{L^2(\varOmega )}^2 - (1-\alpha )\sum _{k=1}^{n} \Vert \nabla \delta _k u\Vert _{L^2(\varOmega )}^2-\sum _{k=1}^{n}\frac{g_k(\alpha )}{\varGamma (2-\alpha )}\Vert \delta _k u\Vert ^2_{L^2(\varOmega )}\\&\quad +2C_{f} C_{\varOmega } \max _{0\le k\le n} {\Vert \nabla u^k\Vert _{L^2(\varOmega )}}\\ \le&\Vert \nabla u^0\Vert _{L^2(\varOmega )}^2+2C_{f}C_{\varOmega } \max _{0\le k\le n} {\Vert \nabla u^k\Vert _{L^2(\varOmega )}}. \end{aligned} \end{aligned}$$

(4.3)

For any $N \ge 1$, we take $\max _{0\le n\le N}$ on both sides of (4.3), to obtain

$$\begin{aligned} \begin{aligned} \max _{0\le n\le N}\Vert \nabla u^n\Vert _{L^2(\varOmega )}^2 \le \Vert \nabla u^0\Vert _{L^2(\varOmega )}^2+2C_{f}C_{\varOmega } \max _{0\le n\le N} {\Vert \nabla u^n\Vert _{L^2(\varOmega )}}, \end{aligned} \end{aligned}$$

which indicates

$$\begin{aligned} \begin{aligned} \max _{0\le n\le N}\Vert \nabla u^n\Vert _{L^2(\varOmega )}&\le \Vert \nabla u^0\Vert _{L^2(\varOmega )} +2C_{f}C_{\varOmega }. \end{aligned} \end{aligned}$$

The proof is completed. $\square$

Remark 2

Assume that the solution of subdiffusion equation satisfies $u(t,x)\in C([0,\infty );H_0^1(\varOmega )\cap C^1((0,\infty );H_0^1(\varOmega ))$ and the source term satisfies $f(t,x) \in C([0,\infty );L^2(\varOmega )),~ \partial _t f(t,x)\in L^1([0,\infty );L^2(\varOmega ))$. For any fixed $T>0$, multiplying the first equation of (4.1) with $\partial _t u(t,x)$ and integrating over $(0,T)\times \varOmega$ yield

$$\begin{aligned} \begin{aligned} \int _0^T\int _\varOmega \partial _t^\alpha u(t,x) \partial _t u(t,x)\ \mathrm dx\mathrm dt= \frac{1}{2}\int _0^T \int _\varOmega \partial _t|\nabla u(t,x)|^2\ \mathrm dx\mathrm dt+\int _0^T\int _\varOmega f(t,x)\partial _t u(t,x)\ \mathrm dx\mathrm dt. \end{aligned} \end{aligned}$$

According to [26],

$$\begin{aligned} \int _0^T\int _\varOmega \partial _t^\alpha u(t,x) \partial _t u(t,x)\ \mathrm dx\mathrm dt\ge 0, \end{aligned}$$

and moreover,

$$\begin{aligned}&\int _0^T\int _\varOmega f(t,x) \partial _t u(t,x)\ \mathrm dx\mathrm dt\\&\quad =\left( \int _\varOmega f(t,x)u(t,x)\ \mathrm dx\right) \bigg |_0^T-\int _0^T\int _\varOmega \partial _t f(t,x)u(t,x)\ \mathrm dx\mathrm dt\\&\quad \le \left( 2\Vert f\Vert _{L^\infty ([0,\infty );L^2(\varOmega ))}+\int _0^\infty \Vert \partial _t f(t,x)\Vert _{L^2(\varOmega )}\,\mathrm dt\right) C_\varOmega \Vert \nabla u\Vert _{L^\infty ([0,T];L^2(\varOmega ))}\\&\quad =: C_f^{\text {cont}}C_\varOmega \Vert \nabla u\Vert _{L^\infty ([0,T];L^2(\varOmega ))}. \end{aligned}$$

Thus we derive the $H^1$-stability at the continuous level

$$\begin{aligned} \begin{aligned} \Vert \nabla u(T,x)\Vert _{L^2(\varOmega )}\le \Vert \nabla u(0,x)\Vert _{L^2(\varOmega )}+2C_f^{\text {cont}}C_\varOmega , \quad \forall \ T>0, \end{aligned} \end{aligned}$$

which corresponds to our $H^1$-stability result in Theorem 2 for the L2-1$_\sigma$ scheme of the subdiffusion equation (4.1).

Remark 3

In the case of $\alpha =1$, i.e., the standard diffusion equation, the energy stability (or $H^1$-stability) has been established for the second order BDF2 schemes in [19, Theorem 2.1] and for the third order BDF3 schemes in [18, Theorem 3.1] on general nonuniform meshes.

4.2 Sharp Convergence of L2-1$_\sigma$ Scheme for Subdiffusion Equation

We show the error estimate of the L2-1$_\sigma$ scheme (4.2) for the subdiffusion equation (4.1), that is different from the one in [14, 15]. To be precise we will reduce the restriction on time step ratios from $\rho _k\ge 4/7$ in [15] to $\rho _k\ge 0.475329$. We first reformulate the discrete fractional operator (2.3):

$$\begin{aligned} L^{\alpha ,*}_k u=\frac{1}{\varGamma (1-\alpha )}\left( [{\textbf{M}}]_{k,k} u^k - \sum _{j=2}^{k}([{\textbf{M}}]_{k,j}-[{\textbf{M}}]_{k,j-1}) u^{j-1}-[{\textbf{M}}]_{k,1}u^0\right) , \end{aligned}$$

where ${\textbf{M}}$ is given by (3.5). We now give some properties on $[{\textbf{M}}]_{k,j}$.

Lemma 2

Under the condition (3.2), the following properties of $[{\textbf{M}}]_{k,j}$ given by (3.5) hold:

• (Q1)
  $$\begin{aligned}{}[{\textbf{M}}]_{k,j}\ge \frac{\rho _*}{(1+\rho _*) \tau _j}\int _{t_{j-1}}^{\min \{t_j,t_k^*\}}(t_k^*-s)^{-\alpha }\,\mathrm ds,\quad 1\le j\le k. \end{aligned}$$

  (4.4)

• (Q2) For all $2\le j\le k-1$,

  $$\begin{aligned}{}[{\textbf{M}}]_{k,j}-[{\textbf{M}}]_{k,j-1}\ge \frac{\alpha \tau _j}{\tau _j+\tau _{j+1}} \int _0^{1} (\tau _j+\tau _{j+1}-s\tau _j)(1-s) (t_k^*-t_{j-1}-s\tau _j)^{-\alpha -1}\,\mathrm ds, \end{aligned}$$

  and

  $$\begin{aligned}{}[{\textbf{M}}]_{k,k}-[\textbf{M}]_{k,k-1}\ge \frac{\alpha }{2(1-\alpha )(\sigma \tau _{k})^{\alpha }}. \end{aligned}$$

• (Q3) Moreover, if $\rho _k\ge \eta \approx 0.475329$ for all $k\ge 2$, then

  $$\begin{aligned} \frac{1-\alpha }{\sigma }[{\textbf{M}}]_{k,k}-[{\textbf{M}}]_{k,k-1}\ge 0. \end{aligned}$$

  Here $\eta$ is the real root of $1-3\rho ^2(1+\rho ) = 0$.

Proof

From (3.5), for $1\le j\le k-1$,

$$\begin{aligned} \begin{aligned}{}[{\textbf{M}}]_{k,j}&\ge - a_j^{(k)}=\int _0^1 \frac{2 \tau _j(1-\theta )+\tau _{j+1}}{(\tau _{j}+\tau _{j+1})(t_k^*-(t_{j-1}+\theta \tau _j))^\alpha }\,\mathrm d\theta \\&\ge \frac{\rho _{j+1}}{1+\rho _{j+1}}\int _0^1 \frac{1}{(t_k^*-(t_{j-1}+\theta \tau _j))^\alpha }\,\mathrm d\theta \ge \frac{\rho _*}{(1+\rho _*)\tau _j}\int _{t_{j-1}}^{t_j}(t_k^*-s)^{-\alpha }\mathrm ds, \end{aligned} \end{aligned}$$

(4.5)

and for $j=k$,

$$\begin{aligned}{}[\textbf{M}]_{k,k}=c^{(k)}_{k-1}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^\alpha }\ge \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^\alpha }=\frac{1}{\tau _k}\int _{t_{k-1}}^{t_k^*}(t_k^*-s)^{-\alpha }\mathrm ds. \end{aligned}$$

The inequality (4.4) holds.

For $2\le j\le k-1$, according to (3.7) – (3.9),

$$\begin{aligned}&[{\textbf{M}}]_{k,j}-[{\textbf{M}}]_{k,j-1}\\&\quad =\frac{\alpha \tau _{j-1}^3}{\tau _{j}(\tau _{j-1}+\tau _{j})}\int _0^{1} s(1-s)(t_k^*-t_{j-1}+s\tau _{j-1})^{-\alpha -1}\ \mathrm ds\\&\quad -\frac{\alpha \tau _{j-2}^3}{\tau _{j-1}(\tau _{j-2}+\tau _{j-1})}\int _0^{1} s(1-s)(t_k^*-t_{j-2}+s\tau _{j-2})^{-\alpha -1}\ \mathrm ds\\&\quad +\frac{\alpha \tau _{j-1}}{\tau _{j-1}+\tau _{j}} \int _0^{1} (\tau _{j-1}+\tau _{j}+s\tau _{j-1}) (1-s)(t_k^*-t_{j-1}+s\tau _{j-1})^{-\alpha -1}\,\mathrm ds\\&\quad +\frac{\alpha \tau _{j}}{\tau _{j}+\tau _{j+1}} \int _0^{1}(\tau _{j}+\tau _{j+1}-s\tau _{j}) (1-s)(t_k^*-t_{j-1}-s\tau _{j})^{-\alpha -1}\,\mathrm ds\\&\quad \ge \frac{\alpha \tau _j}{\tau _j+\tau _{j+1}} \int _0^{1} (\tau _j+\tau _{j+1}-s\tau _j)(1-s) (t_k^*-t_{j-1}-s\tau _j)^{-\alpha -1}\,\mathrm ds, \end{aligned}$$

under the condition (3.2) (for simplicity we make a convention that $\tau _0 =0$). Note that (3.2) indicates the sum of first three terms is positive, using the techniques in (3.17). When $j=k=2$, we obtain from (3.7)

$$\begin{aligned}{}[{\textbf{M}}]_{2,2}-[\textbf{M}]_{2,1}=c^{(2)}_1+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }}+a^{(2)}_1 \ge \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _2^{\alpha }} - \frac{1}{(\sigma \tau _2)^\alpha } =\frac{\alpha }{2(1-\alpha )(\sigma \tau _{2})^{\alpha }}, \end{aligned}$$

where we use the fact $\sigma = 1-\alpha /2$. Moreover when $j=k\ge 3$, we have

$$\begin{aligned}&[{\textbf{M}}]_{k,k}-[{\textbf{M}}]_{k,k-1}\nonumber \\&\quad =\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^{\alpha }}+(c_{k-1}^{(k)}-c^{(k)}_{k-2}+a^{(k)}_{k-1})\nonumber \\&\quad =\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^{\alpha }} +\bigg (\frac{\alpha \tau _{k-1}^3}{\tau _{k}(\tau _{k-1}+\tau _{k})}\int _0^{1} s(1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\ \mathrm ds\nonumber \\&\quad -\frac{\alpha \tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\int _0^{1} s(1-s)(t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}\ \mathrm ds\nonumber \\&\quad -(\sigma \tau _k)^{-\alpha }+\frac{\alpha \tau _{k-1}}{\tau _{k-1}+\tau _{k}} \int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\,\mathrm ds\bigg )>\nonumber \\&\quad \frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _k^{\alpha }} - \frac{1}{(\sigma \tau _k)^\alpha }= \frac{\alpha }{2(1-\alpha )(\sigma \tau _{k})^{\alpha }}, \end{aligned}$$

when the condition (3.2) holds. This inequality coincide with (3.17) by replacing n with k.

For the property (Q3), the case of $k=2$ is trivial. In the case of $k\ge 3$, we have

$$\begin{aligned}&\frac{1-\alpha }{\sigma }[{\textbf{M}}]_{k,k}-[{\textbf{M}}]_{k,k-1}\\&\quad \ge (\sigma \tau _k)^{-\alpha }-c^{(k)}_{k-2}+a^{(k)}_{k-1} \\&\quad =(\sigma \tau _k)^{-\alpha }-\frac{\alpha \tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\int _0^{1} s(1-s)(t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}\ \mathrm ds\\&\quad -(\sigma \tau _k)^{-\alpha }+\frac{\alpha \tau _{k-1}}{\tau _{k-1}+\tau _{k}} \int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\,\mathrm ds>\\&\quad \alpha \left( \frac{\tau _{k-1}(4\tau _{k-1}+3\tau _{k})}{\tau _{k-1}+\tau _{k}}-\frac{\tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\right) \int _0^{1} s(1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\ \mathrm ds\\&\quad \ge 0, \end{aligned}$$

where we use the facts

$$\begin{aligned}&\int _0^{1} (\tau _{k-1}+\tau _{k}+s\tau _{k-1}) (1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\,\mathrm ds\\&\quad \ge (4\tau _{k-1}+3\tau _{k})\int _0^{1} s(1-s)(t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\ \mathrm ds,\\&\quad (t_k^*-t_{k-1}+s\tau _{k-1})^{-\alpha -1}\ge (t_k^*-t_{k-2}+s\tau _{k-2})^{-\alpha -1}, \end{aligned}$$

and

$$\begin{aligned} \frac{\tau _{k-1}(4\tau _{k-1}+3\tau _{k})}{\tau _{k-1}+\tau _{k}}-\frac{\tau _{k-2}^3}{\tau _{k-1}(\tau _{k-2}+\tau _{k-1})}\ge 0, \end{aligned}$$

when $\rho _k\ge \eta \approx 0.475329$ for all $k\ge 2$. $\square$

Consider the following three standard Lagrange interpolation operators with the following interpolation points:

$$\begin{aligned} \varPi _{1,j}:{t_{j-1},t_j},\quad \varPi _{2,j}:{t_{j-1},t_j,t_{j+1}},\quad \varPi ^*_{2,j}:{t_{j-1},t^*_j,t_j}. \end{aligned}$$

As stated in [12], when $\sigma =1-\alpha /2$,

$$\begin{aligned} \int _{t_k-1}^{t_k^*}(\varPi _{1,k}v-\varPi ^*_{2,k}v)'(s)(t_k^*-s)^{-\alpha }\,\mathrm ds=0. \end{aligned}$$

We now analyze the approximation error of the discrete fractional operator in the following lemma.

Lemma 3

Given a function u satisfying $|\partial _t^{m} u(t)|\le C_m(1+t^{\alpha -m})$ for $m=1,3$ and nonuniform mesh $\{\tau _k\}_{k\ge 1}$ satisfying condition (3.2), the approximation error is given by

$$\begin{aligned} r_k :=\frac{1}{\varGamma (1-\alpha )}\int _0^{t_k^*}(t_k^*-s)^{-\alpha }\partial _s[u(s)-I_2u(s)]\,\mathrm ds,\quad k\ge 1, \end{aligned}$$

(4.6)

where $I_2 u=\varPi _{2,j}u$ on $(t_{j-1},t_j)$ for $j<k$ and $I_2 u=\varPi ^*_{2,k}u$ on $(t_{k-1},t_k^*)$. Then for $k\ge 1$,

$$\begin{aligned} | r_k|\le \frac{C}{\varGamma (1-\alpha )}\bigg ( [\textbf{M}]_{k,1}\big (t_2^\alpha /\alpha +t_2\big )+\sum _{j=2}^{k}([\textbf{M}]_{k,j}-[\textbf{M}]_{k,j-1})(1+\rho _{j+1})(1+t_{j-1}^{\alpha -3})\tau _j^3\bigg ), \end{aligned}$$

(4.7)

where C is a constant depending on $C_m$ for $m=1,3$.

Proof

The case of $k=1$ is not difficult to prove. We now consider the case of $k\ge 2$. Let $\chi (s) :=u-I_2u$. Three subcases are discussed in the following content.

Subcase 1 On the interval $(t_0,t_1)$, we have

$$\begin{aligned} \partial _s I_2u (s) = \frac{2s -t_1-t_{2}}{\tau _{1}(\tau _{1}+\tau _{2})} u(t_0) - \frac{2s -t_{2}}{\tau _{1}\tau _{2} }u(t_1) + \frac{2s -t_{1}}{\tau _{2}(\tau _{1}+\tau _{2})} u(t_2) \end{aligned}$$

that is linear w.r.t. s. Then we have

$$\begin{aligned} |\partial _s I_2u (s)|&\le \max \{|\partial _s I_2u (t_0)|,|\partial _s I_2u (t_1)|\} \le C_1\frac{ 1+\rho _2}{\tau _1\rho _{2}}(t_2+t_2^\alpha /\alpha ), \end{aligned}$$

where we use the facts

$$\begin{aligned} \partial _s I_2u (t_0)&= - \frac{ 2\tau _1+\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})} u(t_0) + \frac{ \tau _1+\tau _2}{\tau _{1}\tau _{2} }u(t_1) - \frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})} u(t_2) \\&\quad =-\frac{ 2\tau _1+\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})} (u(t_0)-u(t_1) ) +\frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})} (u(t_1)-u(t_2)) \\&\quad \le \left( \frac{ 2\tau _1+\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})}+\frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})} \right) \max \{|u(t_0)-u(t_1)|,|u(t_1)-u(t_2)|\}\\&\quad =\frac{ \tau _1+\tau _2}{\tau _{1}\tau _{2}} \max \{|u(t_0)-u(t_1)|,|u(t_1)-u(t_2)|\},\\&\quad \partial _s I_2u (t_1)=-\frac{\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})} u(t_0) - \frac{\tau _1-\tau _2}{\tau _{1}\tau _{2} }u(t_1) + \frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})} u(t_2)\\&\quad =-\frac{\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})} (u(t_0) -u(t_1)) - \frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})}( u(t_1)-u(t_2))\\&\quad \le \left( \frac{\tau _2}{\tau _{1}(\tau _{1}+\tau _{2})}+\frac{\tau _1}{\tau _{2}(\tau _{1}+\tau _{2})}\right) \max \{|u(t_0)-u(t_1)|,|u(t_1)-u(t_2)|\}\\&\quad =\frac{\tau _1^2+\tau _2^2}{\tau _{1}\tau _2(\tau _{1}+\tau _{2})}\max \{|u(t_0)-u(t_1)|,|u(t_1)-u(t_2)|\},\\ |u(t_0)-u(t_1)|&\quad =|\int _0^{t_1}\partial _s u(s)\,\mathrm ds|\le C_1(\tau _1+\tau _1^\alpha /\alpha ),\\ |u(t_1)-u(t_2)|&\quad =|\int _{t_1}^{t_2}\partial _s u(s)\,\mathrm ds|\le C_1(\tau _2+(t_2^\alpha -t_1^\alpha )/\alpha ). \end{aligned}$$

Therefore, we have

$$\begin{aligned} |\partial _s\chi (s)|\le |\partial _s u|+|\partial _s I_2u| \le C_1\left( s^{\alpha -1}+ 1+\frac{ 1+\rho _2}{\tau _1\rho _{2}}(t_2+t_2^\alpha /\alpha )\right) , \end{aligned}$$

which yields

$$\begin{aligned} \begin{aligned}&| \frac{1}{\varGamma (1-\alpha )}\int _0^{t_1}(t^*_k-s)^{-\alpha }\partial _s\chi (s)\,\mathrm ds|\\&\quad \le \frac{C_1}{\varGamma (1-\alpha )}\left( \int _0^{t_1}s^{\alpha -1}(t_k^*-s)^{-\alpha }\,\mathrm ds+\frac{\tau _1+(1+\rho _2)/\rho _2(t_2+t_2^\alpha /\alpha )}{\tau _1}\int _0^{t_1}(t_k^*-s)^{-\alpha }\,\mathrm ds\right) \\&\quad \le \frac{C_1}{\varGamma (1-\alpha )}\left( \frac{\tau _1^\alpha }{\alpha (t_k^*-\tau _1)^\alpha }+\frac{\tau _1+(1+\rho _2)/\rho _2(t_2+t_2^\alpha /\alpha )}{\tau _1}\int _0^{t_1}(t_k^*-s)^{-\alpha }\,\mathrm ds\right) \\&\quad \le \frac{C(t_2^\alpha /\alpha +t_2)}{\varGamma (1-\alpha )}[\textbf{M}]_{k,1}, \end{aligned} \end{aligned}$$

(4.8)

where C is an absolute constant only depending on $C_1$. In the last inequality of (4.8), we use the fact

$$\begin{aligned}&[{\textbf{M}}]_{k,1}\ge \frac{\rho _2}{(1+\rho _2)\tau _1}\int _0^{t_1}(t_k^*-s)^{-\alpha }\,\mathrm ds\ge \frac{\rho _2}{(1+\rho _2)(t_k^*)^\alpha }\\&\quad \ge \frac{\rho _2^{1+\alpha }}{(1+\rho _2)(2+\rho _2)^\alpha (t_k^*-\tau _1)^\alpha }\ge \frac{\rho _*^{1+\alpha }}{(1+\rho _*)(2+\rho _*)^\alpha (t_k^*-\tau _1)^\alpha } \end{aligned}$$

obtained from the inequality (4.5).

Subcase 2 On the interval $(t_{j-1},t_j)$, $2\le j\le k-1$,

$$\begin{aligned} \begin{aligned} |\chi (s)|&=|\frac{u^{(3)}(\xi )}{6}(s-t_{j-1})(s-t_{j})(s-t_{j+1})|\ \le C_3(1+t_{j-1}^{\alpha -3})(s-t_{j-1})(s-t_{j})(s-t_{j+1}), \end{aligned} \end{aligned}$$

where $\xi \in (t_{j-1},t_{j+1})$. Then we have

$$\begin{aligned}&| \frac{1}{\varGamma (1-\alpha )}\int _{t_{j-1}}^{t_j}(t_k^*-s)^{-\alpha }\partial _s\chi (s)\,\mathrm ds|= |\frac{-\alpha }{\varGamma (1-\alpha )}\int _{t_{j-1}}^{t_j}(t_k^*-s)^{-\alpha -1}\chi (s)\,\mathrm ds|\nonumber \\&\quad \le \frac{C_3\alpha (1+t_{j-1}^{\alpha -3})}{\varGamma (1-\alpha )}\int _{t_{j-1}}^{t_j}(t_k^*-s)^{-\alpha -1}(s-t_{j-1})(s-t_{j})(s-t_{j+1})\,\mathrm ds\nonumber \\&\quad =\frac{C_3\alpha (1+t_{j-1}^{\alpha -3})\tau ^3_j}{\varGamma (1-\alpha )}\int _0^1s(\tau _j+\tau _{j+1}-s\tau _j)(1-s)(t_k^*-t_{j-1}-s\tau _j)^{-\alpha -1}\,\mathrm ds\nonumber \\&\quad \le \frac{C_3(1+\rho _{j+1}) (1+t_{j-1}^{\alpha -3})\tau ^3_j}{\varGamma (1-\alpha )} ([\textbf{M}]_{k,j}-[{\textbf{M}}]_{k,j-1}), \end{aligned}$$

(4.9)

from (Q2) in Lemma 2.

Subcase 3 On the interval $(t_{k-1},t_k^*)$,

$$\begin{aligned} |\chi (s)|\le&C_3(1+t_{k-1}^{\alpha -3})(s-t_{k-1})(t_k^*-s) (t_k-s) \le C_3(1+t_{k-1}^{\alpha -3})\tau _k^2(t_k^*-s), \end{aligned}$$

which yields

$$\begin{aligned}{} & {} | \frac{1}{\varGamma (1-\alpha )}\int _{t_{k-1}}^{t_k^*}(t_k^*-s)^{-\alpha }\partial _s\chi (s)\,\mathrm ds|=|\frac{-\alpha }{\varGamma (1-\alpha )}\int _{t_{k-1}}^{t_k^*}(t_k^*-s)^{-\alpha -1}\chi (s)\,\mathrm ds|\nonumber \\{} & {} \quad \le \frac{C_3\alpha (1+ t_{k-1}^{\alpha -3})\tau _k^2}{\varGamma (1-\alpha )}\int _{t_{k-1}}^{t_k^*}(t_k^*-s)^{-\alpha }\,\mathrm ds=\frac{2C_3\sigma (1+ t_{k-1}^{\alpha -3})\tau ^3_k }{\varGamma (1-\alpha )} \frac{\alpha }{2(1-\alpha )(\sigma \tau _k)^\alpha }\nonumber \\{} & {} \quad \le \frac{2 C_3\sigma (1+t_{k-1}^{\alpha -3})\tau ^3_k}{\varGamma (1-\alpha )} ([\textbf{M}]_{k,k}-[{\textbf{M}}]_{k,k-1}) \end{aligned}$$

(4.10)

from (Q2) in Lemma 2.

Combining (4.8), (4.9) and (4.10) we obtain the estimation (4.7) of approximation error. $\square$

Theorem 3

Assume that $u\in C^3((0,T],H^1_0(\varOmega ))$ and $|\partial _t^{m} u(t)|\le C_m(1+t^{\alpha -m})$, for $m=1,2,3$ for $0< t\le T$. If the nonuniform mesh satisfies $\rho _k\ge \eta \approx 0.475329$, then the numerical solutions of L2-1$_\sigma$ scheme (4.2) have the following global error estimate

$$\begin{aligned}&\max _{1\le k\le n} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}\\ \le&C\bigg (t_2^\alpha /\alpha +t_2+\frac{1}{1-\alpha }\max _{2\le k\le n}(1+\rho _{k+1}) (1+t_{k-1}^{\alpha -3})(t_{k-1}^*)^\alpha \tau _k^3\tau _{k-1}^{-\alpha }\\&\quad +(\tau _1^\alpha /\alpha +\tau _1)\tau _1^{\alpha /2}+\sqrt{\varGamma (1-\alpha )}\max _{2\le k\le n}(t_k^*)^{\alpha /2}(1+ t_{k-1}^{\alpha -2})\tau _k^2\bigg ), \end{aligned}$$

where C is a constant depending only on $C_m$, $m=1,2,3$ and $\varOmega$.

Proof

Let $e^k:=u(t_k)-u^k$. We have

$$\begin{aligned} L_k^{\alpha ,*} e = \varDelta e_k^*-r_k+\varDelta R_k^*, \end{aligned}$$

(4.11)

where $e_k^*:=(1-\alpha /2)e^k+\alpha /2 e^{k-1}$, $r_k$ is given in (4.6), and $R_k^* :=u(t_k^*)-((1-\alpha /2)u(t_k)+\alpha /2 u(t_{k-1}))$. Multiplying (4.11) with $e_k^*$ and integrating over $\varOmega$ yield

$$\begin{aligned} \begin{aligned} \langle L_k^{\alpha ,*} e,e_k^*\rangle&= -\Vert \nabla e_k^*\Vert _{L^2(\varOmega )}^2-\langle r_k,e_k^*\rangle -\langle \nabla R_k^*,\nabla e_k^*\rangle . \end{aligned} \end{aligned}$$

(4.12)

According to [2, Lemma 1] as well as Lemma 2, we can derive

$$\begin{aligned} \begin{aligned} \langle L_k^{\alpha ,*} e,e_k^*\rangle&= \frac{1}{\varGamma (1-\alpha )}\sum _{j=1}^{k} [{\textbf{M}}]_{k,j}\langle (e^j-e^{j-1}), (1-\alpha /2)e^k+\alpha /2 e^{k-1} \rangle \\&\ge \frac{1}{2\varGamma (1-\alpha )}\sum _{j=1}^k [\textbf{M}]_{k,j}\left( \Vert e^j\Vert _{L^2(\varOmega )}^2-\Vert e^{j-1}\Vert _{L^2(\varOmega )}^2\right) . \end{aligned} \end{aligned}$$

Applying Cauchy-Schwarz inequality in (4.12) yields

$$\begin{aligned}&\sum _{j=1}^k [\textbf{M}]_{k,j}\left( \Vert e^j\Vert _{L^2(\varOmega )}^2-\Vert e^{j-1}\Vert _{L^2(\varOmega )}^2\right) \le 2\varGamma (1-\alpha )\Vert r_k\Vert _{L^2(\varOmega )}\Vert e_k^*\Vert _{L^2(\varOmega )}\nonumber \\&\quad +\varGamma (1-\alpha )\Vert R_k^*\Vert _{H^1(\varOmega )}^2. \end{aligned}$$

(4.13)

We define a lower triangular ${\textbf{P}}$ matrix such that

$$\begin{aligned} {\textbf{P}} {\textbf{M}} = {\textbf{E}}_{\mathrm L} \end{aligned}$$

where

$$\begin{aligned} {\textbf{E}}_{\textrm{L}}= \begin{pmatrix} 1 &{} \\ 1&{}1 \\ \vdots &{} \vdots &{} \ddots \\ 1&{} 1&{}\cdots &{} 1 \end{pmatrix}. \end{aligned}$$

In other words,

$$\begin{aligned} \sum _{l=j}^k[{\textbf{P}}]_{k,l} [{\textbf{M}}]_{l,j}=1,\quad \forall 1\le j\le k\le n. \end{aligned}$$

Here ${\textbf{P}}$ is called complementary discrete convolution kernel in the work [14]. It can be easily checked that $[{\textbf{P}}]_{k,l}\ge 0$ due to the monotonicity properties of ${\textbf{M}}$. From (4.13) we can derive that $\forall 1\le k\le n,$

$$\begin{aligned} \begin{aligned} \Vert e^k\Vert _{L^2(\varOmega )}^2&\le 2 \varGamma (1-\alpha )\sum _{l=1}^k [{\textbf{P}}]_{k,l}\Vert r_l\Vert _{L^2(\varOmega )}\Vert e_l^*\Vert _{L^2(\varOmega )} +\varGamma (1-\alpha )\sum _{l=1}^k [{\textbf{P}}]_{k,l}\Vert R_l^*\Vert _{H^1(\varOmega )}^2\\&\le 2 \varGamma (1-\alpha ) \left( \max _{1\le l\le k} \Vert e_l^*\Vert _{L^2(\varOmega )}\right) \sum _{l=1}^k [\textbf{P}]_{k,l}\Vert r_l\Vert _{L^2(\varOmega )} +\varGamma (1-\alpha )\sum _{l=1}^k [\textbf{P}]_{k,l}\Vert R_l^*\Vert _{H^1(\varOmega )}^2, \end{aligned} \end{aligned}$$

(4.14)

where we use

$$\begin{aligned}{} & {} \sum _{l=1}^k [{\textbf{P}}]_{k,l}\sum _{j=1}^l[\textbf{M}]_{l,j}\left( \Vert e^j\Vert _{L^2(\varOmega )}^2-\Vert e^{j-1}\Vert _{L^2(\varOmega )}^2\right) \\{} & {} \quad =\sum _{j=1}^k\left( \Vert e^j\Vert _{L^2(\varOmega )}^2-\Vert e^{j-1}\Vert _{L^2(\varOmega )}^2\right) \sum _{l=j}^k [{\textbf{P}}]_{k,l}[\textbf{M}]_{l,j}\\{} & {} \quad =\sum _{j=1}^k\left( \Vert e^j\Vert _{L^2(\varOmega )}^2-\Vert e^{j-1}\Vert _{L^2(\varOmega )}^2\right) =\Vert e^k\Vert _{L^2(\varOmega )}^2. \end{aligned}$$

According to Lemma 3,

$$\begin{aligned}&\varGamma (1-\alpha )\sum _{l=1}^k[{\textbf{P}}]_{k,l}\Vert r_l\Vert \\&\quad \le C |\varOmega |\sum _{l=1}^k[{\textbf{P}}]_{k,l}\bigg ([{\textbf{M}}]_{l,1}(t_2^\alpha /\alpha +t_2)+\sum _{j=2}^l([{\textbf{M}}]_{l,j}-[{\textbf{M}}]_{l,j-1})(1+\rho _{j+1})(1+t_{j-1}^{\alpha -3})\tau _j^3\bigg )\\&\quad =C |\varOmega | \left( (t_2^\alpha /\alpha +t_2)+\sum _{j=2}^k(1+\rho _{j+1})(1+ t_{j-1}^{\alpha -3})\tau _j^3\sum _{l=j}^k [{\textbf{P}}]_{k,l}([{\textbf{M}}]_{l,j}-[{\textbf{M}}]_{l,j-1})\right) \\&\quad =C|\varOmega |\left( (t_2^\alpha /\alpha +t_2)+\sum _{j=2}^k (1+\rho _{j+1})(1+ t_{j-1}^{\alpha -3})\tau _j^3[{\textbf{P}}]_{k,j-1}[{\textbf{M}}]_{j-1,j-1}\right) \\&\quad =C|\varOmega |\left( (t_2^\alpha /\alpha +t_2)+ \sum _{j=2}^{k}[{\textbf{P}}]_{k,j-1}[{\textbf{M}}]_{j-1,1}\frac{[{\textbf{M}}]_{j-1,j-1}}{[{\textbf{M}}]_{j-1,1}}(1+\rho _{j+1})(1+ t_{j-1}^{\alpha -3})\tau _{j}^3\right) \\&\quad \le C|\varOmega |\left( (t_2^\alpha /\alpha +t_2)+ \max _{2\le j\le k}\frac{[{\textbf{M}}]_{j-1,j-1}}{[{\textbf{M}}]_{j-1,1}}(1+\rho _{j+1})(1+ t_{j-1}^{\alpha -3})\tau _{j}^3\right) \\&\quad \le C|\varOmega |\left( (t_2^\alpha /\alpha +t_2)+\frac{1}{1-\alpha }\max _{2\le j\le k}(1+\rho _{j+1}) (1+t_{j-1}^{\alpha -3})(t_{j-1}^*)^\alpha \tau _j^3\tau _{j-1}^{-\alpha }\right) , \end{aligned}$$

where C is a constant only depending on $C_m$. The last inequality is obtained by the following upper bound of $[{\textbf{M}}]_{j,j}$ and lower bound of $[{\textbf{M}}]_{j,1}$:

$$\begin{aligned} \begin{aligned}{}[{\textbf{M}}]_{j,j}&=c_{j-1}^{(j)}+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _j^\alpha }\\&\quad =\int _0^1 \frac{\tau _{j-1}^2(2\theta -1)}{\tau _{j}(\tau _{j-1}+\tau _{j})(t_j^*-(t_{j-2}+\theta \tau _{j-1}))^\alpha }\,\mathrm d\theta +\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _j^\alpha }\\&\quad \le \frac{1}{\rho _j(1+\rho _j)(\sigma \tau _j)^\alpha }+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _j^\alpha }\le \frac{1}{\eta (1+\eta )(\sigma \tau _j)^\alpha }+\frac{\sigma ^{1-\alpha }}{(1-\alpha )\tau _j^\alpha },\\ [{\textbf{M}}]_{j,1}&\ge \frac{\eta }{(1+\eta )\tau _1}\int _0^{t_1}(t_j^*-s)^{-\alpha }\mathrm ds\ge \frac{\eta }{(1+\eta )(t_j^*)^\alpha }, \end{aligned} \end{aligned}$$

(4.15)

where we use (Q1) in Lemma 2 for the inequality of $[{\textbf{M}}]_{j,1}$.

Using the Taylor formula with integral remainder for $R_j^*$ gives

$$\begin{aligned} R_j^*=-\alpha /2\int _{t_{j-1}}^{t_j^*}(s-t_{j-1})u''(s)\,\mathrm ds-(1-\alpha /2)\int _{t_j^*}^{t_j}(t_j-s)u''(s)\,\mathrm ds,\quad 1\le j\le k. \end{aligned}$$

Under the regularity assumption, we have

$$\begin{aligned} \Vert R_1^*\Vert _{H^1(\varOmega )}\le C(\tau _1^\alpha /\alpha +\tau _1), \quad \Vert R_j^*\Vert _{H^1(\varOmega )}\le C(1+ t_{j-1}^{\alpha -2})\tau _j^2, \,\quad 2\le j\le k. \end{aligned}$$

Then we have

$$\begin{aligned}&\sum _{l=1}^k [{\textbf{P}}]_{k,l}\Vert R_l^*\Vert _{H^1(\varOmega )}^2\\&\quad \le C\left( [{\textbf{P}}]_{k,1}[{\textbf{M}}]_{1,1}\frac{1}{[{\textbf{M}}]_{1,1}}(\tau _1^\alpha /\alpha +\tau _1)^2+\sum _{l=2}^k [{\textbf{P}}]_{k,l}[{\textbf{M}}]_{l,2}\frac{1}{[{\textbf{M}}]_{l,2}}\left( (1+ t_{l-1}^{\alpha -2})\tau _l^2\right) ^2\right) \\&\quad \le C\left( \frac{1}{[{\textbf{M}}]_{1,1}}(\tau _1^\alpha /\alpha +\tau _1)^2+\max _{2\le l\le k}\frac{1}{[{\textbf{M}}]_{l,2}}\left( (1+ t_{l-1}^{\alpha -2})\tau _l^2\right) ^2\right) \\&\quad \le C\left( (1-\alpha )\tau _1^\alpha (\tau _1^\alpha /\alpha +\tau _1)^2+\max _{2\le l\le k}(t_l^*)^\alpha ((1+ t_{l-1}^{\alpha -2})\tau _l^2)^2\right) , \end{aligned}$$

where we use $[{\textbf{M}}]_{l,2}\ge [{\textbf{M}}]_{l,1}$ and (4.15).

Taking the max for $1\le k \le n$ on both sides of (4.14), we can derive

$$\begin{aligned} \max _{1\le k\le n} \Vert e_k\Vert _{L^2(\varOmega )}\le & {} C\bigg ((t_2^\alpha /\alpha +t_2)+\frac{1}{1-\alpha }\max _{2\le k\le n}(1+\rho _{k+1}) (1+t_{k-1}^{\alpha -3})(t_{k-1}^*)^\alpha \tau _k^3\tau _{k-1}^{-\alpha }\nonumber \\{} & {} +(\tau _1^\alpha /\alpha +\tau _1)\tau _1^{\alpha /2}+\sqrt{\varGamma (1-\alpha )}\max _{2\le k\le n}(t_k^*)^{\alpha /2}(1+ t_{k-1}^{\alpha -2})\tau _k^2\bigg ).\nonumber \\ \end{aligned}$$

(4.16)

The proof is completed. $\square$

In the case of graded mesh with grading parameter r,

$$\begin{aligned} \begin{aligned} t_j = \left( \frac{j}{K}\right) ^r T, \quad \tau _j = t_j -t_{j-1} = \left[ \left( \frac{j}{K}\right) ^r-\left( \frac{j-1}{K}\right) ^r\right] T, \end{aligned} \end{aligned}$$

(4.17)

where K is the total time step number, $1\le j\le K,~t_K = T$. As a consequence, the two terms after $\max$ operations in (4.16) can be estimated as follows:

$$\begin{aligned} \begin{aligned}&(1+\rho _{k+1}) (1+t_{k-1}^{\alpha -3})(t_{k-1}^*)^\alpha \tau _k^3\tau _{k-1}^{-\alpha } \le C t_{k-1}^{2\alpha -3}\tau _k^{3-\alpha }\\&\quad = C t_{k-1}^{2\alpha -3}(t_k-t_{k-1})^{3-\alpha }= C(t_{k-1})^\alpha (t_k/t_{k-1}-1)^{3-\alpha }\\&\quad =Ct_{k-1}^\alpha ((1+1/(k-1))^r-1)^{3-\alpha }\\&\quad \le C\, r^{3-\alpha }T^\alpha \frac{(k-1)^{r\alpha -(3-\alpha )}}{K^{r\alpha }} = \frac{C_{T,1}}{K^{\min \{r\alpha ,3-\alpha \}}} \end{aligned} \end{aligned}$$

(4.18)

and

$$\begin{aligned}{} & {} (t_k^*)^{\alpha /2}(1+ t_{k-1}^{\alpha -2})\tau _k^2 \le C t_{k-1}^{\alpha -2}\tau _k^2= C t_{k-1}^{\alpha -2}(t_k-t_{k-1})^2 = C t_{k-1}^\alpha (t_k/t_{k-1}-1)^2\nonumber \\{} & {} \quad =C T^\alpha \left( \frac{k-1}{K}\right) ^{r\alpha }((1+1/(k-1))^r-1)^2 \le C\, r^{2}T^\alpha \frac{(k-1)^{r\alpha -2}}{K^{r\alpha }} = \frac{C_{T,2}}{K^{\min \{r\alpha ,2\}}}.\nonumber \\ \end{aligned}$$

(4.19)

In (4.18) and (4.19), $C_{T,1}$ and $C_{T,2}$ only depend on T. Therefore, if u satisfies the regularity assumptions in Theorem 3, then we have the following error estimate of numerical solutions of the L2-1$_\sigma$ scheme on the graded mesh with grading parameter r:

$$\begin{aligned} \max _{1\le k\le K} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}\le \frac{\tilde{C}}{K^{\min \{r\alpha ,2\}}}. \end{aligned}$$

(4.20)

where ${\tilde{C}}$ depends on $C_m$ with $m=1,2,3$, $\alpha$ and $\varOmega$.

Remark 4

When $\alpha \rightarrow 1^{-}$, the constant ${\tilde{C}}$ in (4.20) will tend to infinity. However, using the technique by Chen-Stynes in [4], one can obtain $\alpha$-robust error estimate in the sense that ${\tilde{C}}$ won’t tend to infinity when $\alpha \rightarrow 1^{-}$.

5 Numerical Tests

In this section, we provide some numerical tests on the L2-1$_\sigma$ scheme (4.2) of the subdiffusion equation (4.1).

As in [3, 15], the discrete coefficients $a_j^{(k)}$ and $c_j^{(k)}$ in (2.2) are computed by adaptive Gauss-Kronrod quadrature, to avoid roundoff error problems.

5.1 1D Example

We first test the convergence rate of an 1D example, where $\varOmega =[0,2\pi ]$, $T=1$, $u^0(x)\equiv 0$, and $f(t,x)=\left( \varGamma (1+\alpha )+ t^\alpha \right) \sin (x)$. It can be checked that the exact solution is $u(t,x)=t^\alpha \sin (x)$.

The graded mesh (4.17) with grading parameter r and time step number K is adopted in time. We use the central finite difference method in space with grid spacing $h=2\pi /10000$. The maximum $L_2$-error is computed by $\max _{1\le k\le K} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}$. Tables , and present the maximum $L_2$-errors for $\alpha =0.3,\ 0.5,\ 0.7$ and $r = 1,\ 2,\ 2/\alpha ,\ 3/\alpha$ respectively. It can be observed that the convergence rates are consistent with (4.20) derived from Theorem 3.

Table 1 $\max _{1\le k\le K} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}$ for the graded meshes with different grading parameters and time step numbers where $\alpha =0.3$

Table 2 $\max _{1\le k\le K} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}$ for the graded meshes with different grading parameters and time step numbers where $\alpha =0.5$

Table 3 $\max _{1\le k\le K} \Vert u(t_k)-u^k\Vert _{L^2(\varOmega )}$ for the graded meshes with different grading parameters and time step numbers where $\alpha =0.7$

In [10, 25], the authors state that the large value of r in the graded mesh increases the temporal mesh width near the final time $t = T$ which can lead to large errors. Indeed, when $r= 3/\alpha$, the errors seem larger than the case of $r=2/\alpha$, as observed in Tables 1, 2 and 3. We then propose to use the graded mesh with varying grading parameter $r_j$ (dependent on the time), called r-variable graded mesh. In particular, for this example, we use the following r-variable graded mesh

$$\begin{aligned} \begin{aligned} r_j&=2/\alpha +1.5-\frac{3(j-1)}{K-1},\\ t_j&= \left( \frac{j}{K}\right) ^{r_j} T, \quad \tau _j = t_j -t_{j-1} = \left[ \left( \frac{j}{K}\right) ^{r_j}-\left( \frac{j-1}{K}\right) ^{r_{j-1}}\right] T. \end{aligned} \end{aligned}$$

(5.1)

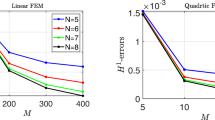
In Fig. , we compare the time steps, the pointwise $L^2$-errors, and the maximum $L^2$-errors of the r-variable graded mesh (5.1) and the standard graded meshes (4.17) with $r=2/\alpha ,~3/\alpha$. Here we set $\alpha =0.7$ and for the left and middle subfigures $K=640$. From the middle of Fig. 2, the maximum $L^2$-error for the r-variable graded mesh is smaller than the standard graded meshes with $r =2/\alpha ,~3/\alpha$.

Fig. 2

Time steps (left), pointwise $L^2$-errors (middle), and maximum $L^2$-errors (right) of the L2-1$_\sigma$ scheme in 1D on the r-variable graded mesh (5.1) and the graded meshes (4.17) with $r=2/\alpha ,\ 3/\alpha$ ($\alpha =0.7$)

5.2 2D Example

In the 2D case, we set $f(t,x,y)=\left( \varGamma (1+\alpha )+2 t^\alpha \right) \sin (x)\sin (y)$ and then the exact solution $u(t,x,y)=t^\alpha \sin (x)\sin (y)$. In this example, we set periodic boundary condition for the subdiffusion equation. We take $T=1$ and $\alpha =0.7$. Here we use Fourier spectral method in the domain $\varOmega =[0,2\pi ]^2$ with $256\times 256$ Fourier modes. In Fig. , we show the pointwise $L^2$-errors (with $K=640$) and the maximum $L^2$-errors of the L2-1$_\sigma$ schemes on the standard graded meshes (4.17) with $r=2/\alpha$ and the r-variable graded mesh (5.1). One can observe that the r-variable graded mesh performs better than the graded mesh for this example.

Fig. 3

Pointwise $L^2$-errors (left) with $K=640$ and maximum $L^2$-errors (right) of L2-1$_\sigma$ scheme in 2D on the r-variable graded mesh (5.1) and the graded mesh (4.17) with $r=2/\alpha$ ($\alpha =0.7$)