Parallel Numerical Picard Iteration Methods

Abstract

In this work, we propose a new class of parallel time integrators for initial-value problems based on the well-known Picard iteration. To this end, we first investigate a class of sequential integrators, known as numerical Picard iteration methods, which falls into the general framework of deferred correction methods. We show that the numerical Picard iteration methods admit a $\min (J,M+1)$-order rate of convergence, where J denotes the number of Picard iterations and $M+1$ is the number of collocation points. We then propose a class of parallel solvers so that J Picard iterations can be proceeded simultaneously and nearly constantly. We show that the parallel solvers yield the same convergence rate as that of the numerical Picard iteration methods. The main features of the proposed parallelized approach are as follows. (1) Instead of computing the solution point by point [as in revisionist integral deferred correction (RIDC) methods], the proposed methods proceed segment by segment. (2) The proposed approach leads to a higher speedup; the speedup is shown to be $J(M+1)$ (while the speedup of the Jth order RIDC is, at most, J). (3) The approach is applicable for non-uniform points, such as Chebyshev points. The stability region of the proposed methods is analyzed in detail, and we present numerical examples to verify the theoretical findings.

1 Introduction

Numerical methods are of significant importance in science and engineering for initial-value problems (IVPs). In the past several decades, great efforts have been focused on the construction of efficient, stable, high-order, and easily parallelized time integrators for solving IVPs [3,4,5, 15,16,17]. While Runge–Kutta and linear multi-step methods are popular approaches used to obtain a high-order rate of convergence, alternative approaches, such as enhancing the convergence of low-order schemes through deferred correction (DC) methods [12, 21], have also been proposed. Two important variants of DC methods, the spectral deferred correction (SDC) method [12] and the integral deferred correction (IDC) method [6], have also been proposed in recent years. To further enhance efficiency, parallel-in-time computations have begun to receive great attention. In fact, early studies along this line date back to more than 50 years ago [20]. Since then, there have been several interesting approaches for parallel-in-time computations; the reader is referred to [13, 14, 19, 22] and references therein for more detailed information.

In this paper, we propose a novel parallel-in-time integrator based on Picard iterations: parallel numerical Picard iteration. The main reason for choosing the Picard iteration as our starting point is that it is one of the simplest approaches and has been successfully applied to the propagations of perturbed orbits in astrodynamics [26, 27]. The original efforts were made by Clenshaw and collaborators [9,10,11], who developed the Picard iteration numerically with Chebyshev polynomials. The Picard iteration has also been adopted in [24, 25] to improve the convergence of SDCs and low-order methods. Nevertheless, the convergence of the numerical Picard method has not been well studied. To this end, our first contribution in this work is to present detailed convergence analysis of a class of numerical Picard iteration methods. In particular, we show a super-convergence property of the numerical Picard iteration methods by using the Legendre–Gauss points. More precisely, we demonstrate that the numerical Picard iteration methods admit a $\min (J,M+1)$-order rate of convergence, where J denotes the number of Picard iterations and $M+1$ is the number of collocation points.

In addition, we propose a class of parallel solvers by rearranging the order of numerical Picard iterations in different sub-intervals so that J Picard iterations can be proceeded simultaneously and nearly constantly. Furthermore, we demonstrate that the parallel solvers yield the same convergence rate as that of the numerical Picard iteration methods. We remark that our approach is analogous to that of the revisionist integral deferred correction (RIDC) methods in [7, 8]. However, compared to RIDC, the approaches proposed herein yield the following main features.

• Instead of computing the solution point by point (as in RIDC methods), the proposed methods proceed segment by segment.

• The proposed approach leads to a higher speedup: the speedup is shown to be $J(M+1)$ (while the speedup of the Jth order RIDC is, at most, J).

• The approach is applicable for non-uniform points, such as Chebyshev points.

The stability region of the proposed methods is analyzed in detail; we also present numerical examples to verify the theoretical findings.

The rest of this paper is organized as follows. In Sect. 2, we review the numerical Picard iteration methods and present our convergence analysis results. The parallel numerical Picard iteration methods are presented in Sect. 3, followed by stability analysis in Sect. 4. Numerical examples are presented in Sect. 5 to verify the theoretical results. We finally give concluding remarks in Sect. 6.

2 Numerical Picard Iteration Methods

In this section, we present the basic ideas of the numerical Picard iteration methods. First, we consider the following problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} y'(t) = f(t,y(t)), t\in [a,b],\\ y(0) = y_a, \end{array}\right. } \end{aligned}$$

(1)

where $y_a, y(t)\in \mathbb {C}^m$ and $f:\mathbb {R}\times \mathbb {C}^m \rightarrow \mathbb {C}^m$. We assume that the function f satisfies the Lipschitz continuous condition

$$\begin{aligned} \Vert f(\cdot ,y_1)-f(\cdot ,y_2)\Vert \le L \Vert y_1-y_2\Vert , \end{aligned}$$

(2)

where L is the Lipschitz constant and $\Vert \cdot \Vert$ denotes the Euclidean norm. Integrating Eq. (1) with respect to t, we obtain

$$\begin{aligned} y(t)=y(a)+\int _{a}^t f(\tau ,y(\tau ))d\tau . \end{aligned}$$

(3)

The well-known form of the Picard iteration is given by [16]

$$\begin{aligned} y_{i+1}(t)=y(a)+\int _{a}^t f(\tau ,y_i(\tau ))d\tau , \quad i=0,1,\ldots , \end{aligned}$$

(4)

where $y_0$ is an initial guess. It has been shown that the above Picard iteration yields a super-linear convergence rate when t is close enough to a [18]. Consequently, for a large time domain, one can split the interval [a, b] into small sub-intervals and conduct the Picard iteration on each sub-interval.

Note that, in the above iterations, repeated evaluations of integrals are needed. To alleviate this computational issue, a numerical version of the Picard iterations is proposed. To illustrate its main idea, we consider a standard interval $I=[-1,1]$ and let $\{c_i:i=0,1,\ldots ,M\}$ be a set of collocation points on I such that $-1\le c_0<c _1<\cdots <c_M\le 1$. For a given vector $\varvec{\varphi }=[\varphi _0,\varphi _1,\ldots ,\varphi _M]^\top$, we introduce the standard Lagrange interpolation operator $\mathcal {I}_M: \mathbb {C}^{M+1}\times I\rightarrow \mathbb {C}$:

$$\begin{aligned} \mathcal {I}_M( \varvec{\varphi },t)=\sum _{j=0}^M\varphi _j\ell _j(t), t\in I, \end{aligned}$$

where the functions $\ell _j(t)$ are given by

$$\begin{aligned} \ell _j(t):=\prod _{\begin{array}{c} i\ne j \\ i=0,1,\ldots ,M \end{array}} \frac{t-c_i}{c_j-c_i}, \quad j= 0, \ldots , M. \end{aligned}$$

We set $Y^{[0]}(t)\equiv y(-1), t\in I$, and once the ith approximation $Y^{[i]}$ is obtained, the numerical Picard iteration solves the $(i+1)$th approximation $Y^{[i+1]}$ by

$$\begin{aligned} Y^{[i+1]}(t)=y(-1)+\int _{-1}^{t} \mathcal {I}_M(f(\textbf{Y}^{[i]}),s) ds, \quad i=0,1,\ldots , \end{aligned}$$

(5)

where

$$\begin{aligned}{} & {} \textbf{Y}^{[i]}:=[Y^{[i]}(c_0),Y^{[i]}(c_1),\ldots , Y^{[i]}(c_M)]^\top ,\\{} & {} f(\textbf{Y}^{[i]}):=[f(c_0,Y^{[i]}(c_0)),f(c_1,Y^{[i]}(c_1)),\ldots ,f(c_M,Y^{[i]}(c_M))]^\top . \end{aligned}$$

For easily presenting our analysis results, we next define a numerical-Picard-iteration-based integrator for Eq. (1). To this end, we first discretize [a, b] into sub-intervals

$$\begin{aligned} \mathcal {M}_h:=\{t_n:a=t_0<t_1<\cdots <t_N=b\}. \end{aligned}$$

Then, we set

$$I_n:=(t_n,t_{n+1}],\,\, \bar{I}_n:=\{t_n\} \cup I_n,\,\, h_n:=t_{n+1}-t_n,\,\, n=0,1,\ldots ,N-1.$$

We also define the size of the mesh $\mathcal {M}_h$ as

$$\begin{aligned} h:=\max \{h_n: 0\le n\le N-1\}. \end{aligned}$$

We now denote $S_{M+1}(\mathcal {M}_h)$ as the space of the piecewise polynomial space

$$\begin{aligned} S_{M+1}(\mathcal {M}_h):=\big \{v\in C([a,b]): v|_{I_n}\in \pi _{M+1}, 0\le n \le N-1 \big \}, \end{aligned}$$

where $\pi _{M+1}$ denotes the space of all polynomials of degree $M+1$. We assume that $Y_n$ is the initial condition for the interval $I_n$, i.e., $y(t_n)=Y_n$, which is obtained by the previous step or initial condition, and set an initial guess as $Y_{n}^{[0]}(t)\equiv Y_n$. We then make a transform from $I_n$ to I and adopt the numerical Picard iteration (5) to obtain

$$\begin{aligned} Y_{n}^{[i+1]}(t)=Y_n+\frac{h_n}{2}\int _{-1}^{\frac{2}{h_n}(t-t_n)-1} \mathcal {I}_M(f(\textbf{Y}_{n}^{[i]}),s) ds, \quad i=0,1,\ldots , \end{aligned}$$

(6)

where

$$\begin{aligned}{} & {} t_{n,i}:=t_n+\frac{h_n}{2}(c_i+1), \quad i=0,1,\ldots ,M.\\{} & {} \textbf{Y}_n^{[i]}:=[Y_{n}^{[i]}(t_{n,0}),Y_{n}^{[i]}(t_{n,1}),\ldots , Y_{n}^{[i]}(t_{n,M})]^\top ,\\{} & {} f(\textbf{Y}_{n}^{[i]}):=[f(t_{n,0},Y_{n}^{[i]}(t_{n,0})),f(t_{n,1},Y_{n}^{[i]}(t_{n,1})),\ldots ,f(t_{n,M},Y_{n}^{[i]}(t_{n,M}))]^\top . \end{aligned}$$

We are now ready to define the numerical Picard iteration solution on the entire domain: for a given positive number J, the element $\eta _h^{[J]}\in S_{M+1}(\mathcal {M}_h)$ is called the J-Picard solution of Eq. (1) if it satisfies

$$\begin{aligned} \eta _h^{[J]}|_{I_n}=Y_n^{[J]}, n=0,1,\ldots ,N-1, \end{aligned}$$

where $Y_n^{[J]}$ is generated by Eq. (6).

Remark 1

Different kinds of collocation points have been proposed in the numerical Picard iteration methods. For the special case in which Chebyshev points are used, i.e.,

$$\begin{aligned} c_i=\cos \frac{i\pi }{M}, \quad i=0,1,\ldots ,M, \end{aligned}$$

the method is called the modified Chebyshev-Picard iteration method [2].

To easily present the numerical Picard iteration method, we next introduce the integration matrix associated with the points $\{c_i:i=0,1,\ldots ,M\}:$ given a vector $\varvec{\varphi }\in \mathbb {C}^{M+1}$ and $\varvec{\phi }=[\phi _0,\phi _1,\ldots ,\phi _M]^\top$ that is given by

$$\begin{aligned} \phi _i=\int _{-1}^{c_i} \mathcal {I}_M(\varvec{\varphi },s)ds, \quad i=0,1,\ldots ,M, \end{aligned}$$

we define the linear mapping $\mathcal {S}_M: \mathbb {C}^{M+1}\rightarrow \mathbb {C}^{M+1}$ by

$$\begin{aligned} \varvec{\phi }=\mathcal {S}_M(\varvec{\varphi }). \end{aligned}$$

With these notations, we summarize the numerical Picard iteration method as follows.

According to (7) in the numerical Picard iteration method, it is clear that the values $\varvec{Y}_n^{[j]}$ at different nodes in $I_n$ depend only on the values $\varvec{Y}_n^{[j-1]}$ in the previous iteration; hence, the numerical Picard iteration method refreshes the state values segment by segment, which means that the values $\varvec{Y}_n^{[j]}$ can be obtained simultaneously. This is quite different from the SDC methods, in which the values at different nodes must be computed point by point. This property has the merit that the matrix–vector product and the evaluations of the forcing function f are easily computed in parallel in one numerical Picard iteration.

We next present the convergence analysis of the above numerical Picard method. For this purpose, we recall the following interpolation error in terms of the Peano kernel theorem [23].

Lemma 1

If $\varphi \in C^d(\bar{I}_n)$, $1\le d\le M+1,$ then the Lagrange interpolant defined on the set $\{t_{n,j}\}$ satisfies

$$\begin{aligned} \varphi \left( t_n+\frac{h_n}{2}(s+1)\right) - \mathcal {I}_M(\varvec{\varphi },s) = \left( \frac{h_n}{2}\right) ^d \int _{-1}^1 K_d(s,z)\varphi ^{(d)}\left( t_n+\frac{h_n}{2}(z+1)\right) dz, \end{aligned}$$

where $\varvec{\varphi }:=[\varphi (t_{n,0}),\varphi (t_{n,1}),\ldots ,\varphi (t_{n,M})]^\top$ and

$$\begin{aligned} K_d(s,z):=\frac{1}{(d-1)!} \left\{ (s-z)^{d-1}_+ -\sum _{j=0}^M \ell _j(s) (c_j-z)^{d-1}_+ \right\} , \end{aligned}$$

with $(s-z)^p_+:=0$ for $s<z$ and $(s-z)^p_+:=(s-z)^p$ for $s\ge z$.

We also have the following lemma.

Lemma 2

Suppose that N and m are non-negative integers and h is a positive real number such that Nh is a constant independent of N and h. If the sequence $\{\epsilon _n: 0\le n\le N\}$ satisfies $\epsilon _0=0$ and

$$\begin{aligned} \epsilon _{n+1} \le c_0 h^m+ (1+c_1 h)\epsilon _n, 1\le n\le N-1, \end{aligned}$$

where $c_0$ and $c_1$ are positive numbers independent of h, then there exists a positive number c independent of h such that

$$\begin{aligned} \epsilon _n \le c h^{m-1}, n\le N. \end{aligned}$$

Proof

It is obtained through iteration that

$$\begin{aligned} \begin{aligned} \epsilon _{n}&\le c_0 h^m\sum _{i=0}^{n-1} (1+c_1h)^i=\frac{c_0 h^{m-1}}{c_1} \left( (1+c_1h)^n-1\right) \\&\le \frac{c_0}{c_1}\left( e^{c_1nh}-1\right) h^{m-1}, 1\le n\le N, \end{aligned} \end{aligned}$$

where we use the inequality $1+x\le e^x$. Since Nh is a constant independent of h, the conclusion follows directly. $\square$

We are now ready to present the following convergence analysis.

Theorem 1

Assume that the solution y(t) of Eq. (1) is $(M+2)$-times continuously differentiable and $\eta _h^{[J]}$ is the J-Picard solution. For sufficiently small h,  the following error estimate holds:

$$\begin{aligned} \left\| y-\eta _h^{[J]}\right\| _\infty =\max _{t\in [a,b]} \left| y(t)-\eta _h^{[J]}(t) \right| \le C h^{\min (J,M+1)}, \end{aligned}$$

(8)

where the constant C is independent of h.

Proof

We denote $\textbf{y}_n=[y(t_{n,0}),y(t_{n,1}),\ldots ,y(t_{n,M})]^\top$. By Lemma 1, there exists

$$\begin{aligned} y'\left( t_n+\frac{h_n}{2}(s+1)\right) =f\left( t_n+\frac{h_n}{2}(s+1),y\left( t_n+\frac{h_n}{2}(s+1)\right) \right) =\mathcal {I}_M(f(\textbf{y}_n),s)+\left( \frac{h_n}{2}\right) ^{M+1} H_{n}(s), \end{aligned}$$

(9)

where

$$\begin{aligned} H_n(s)=\int _{-1}^1 K_{J}(s,z)y^{(M+2)}\left( t_n+\frac{h_n}{2}(z+1)\right) dz. \end{aligned}$$

Integration of Eq. (9) leads to

$$\begin{aligned} y\left( t_{n}+\frac{h_n}{2}(s+1)\right) =y(t_n)+\frac{h_n}{2} \int _{-1}^{s} \mathcal {I}_M(f(\textbf{y}_n),z) dz + \left( \frac{h_n}{2}\right) ^{M+2}\int _{-1}^{s}H_{n}(z)dz. \end{aligned}$$

(10)

Recalling the formula for $Y_n^{[J]}$ in the Picard iteration, we rewrite $e_{h}(t):=y(t)-\eta _h^{[J]}(t)$ as

$$\begin{aligned} e_{h}\left( t_{n}+\frac{h_n}{2}(s+1)\right) =e_h(t_n)+\frac{h_n}{2} \int _{-1}^{s} \mathcal {I}_M(f(\textbf{y}_n)-f(\textbf{Y}_n^{[J-1]}),z) dz + \left( \frac{h_n}{2}\right) ^{M+2}\int _{-1}^{s}H_{n}(z)dz. \end{aligned}$$

Using the Lipschitz condition, we have

$$\begin{aligned} |e_{h}\left( t_{n}+\frac{h_n}{2}(s+1)\right) | \le |e_h(t_n)|+ch_n \left\| \textbf{y}_n-\textbf{Y}_n^{[J-1]}\right\| \sum _{i=0}^M |\beta _i(s)| + c h_n^{M+2}, \end{aligned}$$

(11)

where $\beta _i(s)=\int _{-1}^s \ell _i(z)dz$ and c is a generic constant independent of h. In particular, setting $s=1$, the following is obtained:

$$\begin{aligned} |e_h(t_{n+1})| \le |e_h(t_n)|+c h_n \left\| \textbf{y}_n-\textbf{Y}_n^{[J-1]}\right\| + c h_n^{M+2}. \end{aligned}$$

(12)

We next analyze the bounds of $e_h(t_n)$ and $\left\| \textbf{y}_n-\textbf{Y}_n^{[J-1]}\right\|$. Combining Eqs. (6) and (10), we have

$$\begin{aligned} \left\| \textbf{y}_n-\textbf{Y}_{n}^{[j+1]}\right\| \le |e_h(t_n)|+c h_n\left\| \textbf{y}_n-\textbf{Y}_n^{[j]}\right\| +c h_n^{M+2}, j=0,1,\ldots ,J-2. \end{aligned}$$

Note that we also have

$$\begin{aligned} \left\| \textbf{y}_n-\textbf{Y}_{n}^{[0]}\right\| \le |e_h(t_n)|+ \max _{i=0,1,\ldots ,M}|y(t_{n,i})-y(t_n)|\le |e_h(t_n)|+c h_n. \end{aligned}$$

It then follows that

$$\begin{aligned} \begin{aligned} \left\| \textbf{y}_n-\textbf{Y}_{n}^{[J-1]}\right\|&\le \left( |e_h(t_n)|+c h_n^{M+2}\right) \sum _{j=0}^{J-2}(c h_n)^j +(c h_n)^{J-1}\left\| \textbf{y}_n-\textbf{Y}_{n}^{[0]}\right\| \\&\le |e_h(t_n)|\sum _{j=0}^{J-1}(c h_n)^j +c h_n^{\min (J,M+2)}. \end{aligned} \end{aligned}$$

(13)

By substituting (13) into Eq. (12), we obtain

$$\begin{aligned} |e_h(t_{n+1})|\le |e_h(t_n)|\sum _{j=0}^{J}(c h_n)^j+c h_n^{\min (J+1,M+2)} \le |e_h(t_n)|\sum _{j=0}^{J}(c h)^j+c h^{\min (J+1,M+2)}. \end{aligned}$$

(14)

For a sufficiently small h, there exists a constant $c_1$ independent of h such that

$$\sum _{j=0}^{J}(c h)^j\le 1+c_1h.$$

Moreover, we have that $e_h(t_0)=0$. By Lemma 2, we have that

$$\begin{aligned} e_h(t_n)\le c h^{\min (J,M+1)}, \quad n=1,2,\ldots ,N. \end{aligned}$$

It then follows directly from (13) that

$$\begin{aligned} \left\| \textbf{y}_n-\textbf{Y}_{n}^{[J-1]}\right\| \le c h^{\min (J,M+1)}. \end{aligned}$$

Then, the desired error bound (8) follows by using the bounds of $e_h(t_n),$ $\left\| \textbf{y}_n-\textbf{Y}_{n}^{[J-1]}\right\| ,$ and the equality (11). $\square$

Next, we show that the J-Picard solution yields a super-convergence property when the Gaussian quadrature points are adopted. For this purpose, let

$$\begin{aligned} \delta _h^{[J]}(t):=-\eta _h^{[J]}{'}(t)+f(t,\eta _h^{[J]}(t)), \quad t\in [a,b] \end{aligned}$$

be the defect associated with the J-Picard solution. We first present the following lemma.

Lemma 3

If f is bounded and satisfies the Lipschitz condition, then there exists a constant C independent of h such that

$$\begin{aligned} \max _{\begin{array}{c} i=0,1,\ldots ,M\\ n=0,1,\ldots ,N-1 \end{array}}\left| \delta _h^{[J]}(t_{n,i})\right| \le C h^{J}. \end{aligned}$$

Proof

Let $\eta _h^{[J]}(t)=Y_n^{[J]}(t), t\in I_n$ and $\{Y_n^{[j]}: j=0,1,\ldots ,J\}$ be the sequences generated by the Picard iteration on $I_n$. For $t\in \{t_{n,i}: i=0,1,\ldots ,M\}$, $\delta _h^{[J]}$ can be represented by

$$\begin{aligned} \delta _h^{[J]}(t)=f (t,Y_n^{[J]}(t)) -f(t,Y_n^{[J-1]}(t)). \end{aligned}$$

Using the Lipschitz condition of f, there exists a constant independent of h such that

$$\begin{aligned} \left| \delta _h^{[J]}(t_{n,i})\right| \le C \left| Y_n^{[J]}(t_{n,i})-Y_n^{[J-1]}(t_{n,i}) \right| , \quad i=0,1,2\cdots , M. \end{aligned}$$

(15)

Let $\textbf{Y}_n^{[j]}$ be the vector of the function $Y_n^{[j]}$ evaluated at the points $\{t_{n,i}: i=0,1,\ldots ,M\}$. It is noted from the Picard iteration that $Y_n^{[0]}(t_{n,i})=\eta _h^{[J]}(t_n)$ and

$$\begin{aligned} Y_n^{[j+1]}(t_{n,i})=\eta _h^{[J]}(t_n) + \frac{h_n}{2} \int _{-1}^{c_i} \mathcal {I}_M(f(\textbf{Y}_n^{[j]}),s) ds, \quad j=0,1,\ldots , J-1. \end{aligned}$$

Hence, there exists a constant C independent of h such that

$$\begin{aligned} \left\| \textbf{Y}_n^{[j+1]} -\textbf{Y}_n^{[j]} \right\| \le Ch_n\left\| \textbf{Y}_n^{[j]} -\textbf{Y}_n^{[j-1]} \right\| ,\quad j=1,2,\ldots , J-1, \end{aligned}$$

and $\left\| \textbf{Y}_n^{[1]} -\textbf{Y}_n^{[0]} \right\| \le Ch_n$. It follows directly that

$$\begin{aligned} \left\| \textbf{Y}_n^{[J]} -\textbf{Y}_n^{[J-1]} \right\| \le Ch_n^J. \end{aligned}$$

(16)

The desired inequality follows directly from (15) and (16). The proof is completed. $\square$

We also recall the following standard lemma for the Gauss quadrature error [1].

Lemma 4

If $\varphi \in C^{2M+2}(\bar{I}_n)$, and the points $\{c_j:j=0,1,\ldots ,M\}$ are chosen to be Legendre–Gauss points, then the error

$$\begin{aligned} E_M(\varphi ) =\int _{t_n}^{t_{n+1}}\varphi (t)dt- \frac{h_n}{2}\sum _{j=0}^M \omega _j \varphi (t_{n,j}) \end{aligned}$$

satisfies

$$\begin{aligned} |E_M(\varphi )|\le C h_n^{2M+3}, \end{aligned}$$

where C is a constant independent of $h_n$.

We are now ready to present the super-convergence result.

Theorem 2

Assume that the solution y(t) of (1) is $(2M+3)$-times continuously differentiable and $\eta _h^{[J]}$ is a J-Picard solution. If the step size h is sufficiently small and the points $\{c_j\}_{j=0}^M$ are chosen to be Legendre–Gauss points, then the following error estimate holds:

$$\begin{aligned} \max _{t\in \mathcal {M}_h} |y(t)-\eta _h^{[J]}(t)| \le C h^{\min (J,2M+2)}, \end{aligned}$$

(17)

where the constant C is independent of h.

Proof

By Theorem 1, it holds that $\Vert e_h\Vert :=\Vert y(t)-\eta _h^{[J]}(t)\Vert \le Ch^{\min (J,M+1)}$. Moreover, we have

$$\begin{aligned} e_h'(t)=f(t,y(t))-f(t,\eta _h^{[J]}(t))+\delta _h^{[J]}(t)=f_y(t,y(t))e_h(t)+\delta _h^{[J]}(t)+R_h(t), \,\, t\in [a,b] \end{aligned}$$

(18)

with $e_h(a)=0$ and $\Vert R_h\Vert \le Ch^{\min (2J,2M+2)}$. We then have

$$\begin{aligned} e_h(t)=\int _a^t r(t,s)(\delta _h^{[J]}(s)+R_h(s))ds, t\in [a,b], \end{aligned}$$

where r(t, s) denotes the resolvent of the ODE (18):

$$\begin{aligned} r(t,s):=exp\left( \int _s^t f_y(z,y(z))dz\right) ,\; \text {with}\;\; r\in C^{2M+2}(D), \end{aligned}$$

where $D:=\{(t,s):a\le s\le t\le b\}$. The error $e_h(t_n)$ can be written as

$$\begin{aligned} e_h(t_n)=\sum _{j=0}^{n} \int _{t_{j}}^{t_{j+1}} r(t_n,s) \delta _h^{[J]}(s) ds. \end{aligned}$$

Supposing that each of the integrals is approximated by the Gaussian quadrature based on the Legendre Gauss points, we have

$$\begin{aligned} \int _{t_{j}}^{t_{j+1}} r(t_n,s) \delta _h^{[J]}(s) ds= \frac{h_j}{2} \sum _{k=0}^M \omega _k r(t_n,t_{n,k})\delta _h^{[J]}(t_{n,k}) + E_{M,n}, \end{aligned}$$

where the term $E_{M,n}$ denotes the quadrature error. Then, Lemma 4 indicates that $E_{M,n}$ is bounded by $Ch^{2M+3},$. Furthermore, Lemma 3 shows that

$$\begin{aligned} \frac{h_j}{2} \sum _{k=0}^M \omega _k r(t_n,t_{n,k})\delta _h^{[J]}(t_{n,k}) \le C h^{J+1}, \end{aligned}$$

where C is a generic constant independent of h. Hence, the integral $\int _{t_{j}}^{t_{j+1}} r(t_n,s) \delta _h^{[J]}(s) ds$ is bounded by $C h^{\min (J+1,2M+3)}$, which completes the proof. $\square$

3 Parallel Numerical Picard Iteration Methods

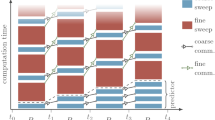
In addition to the parallelization in one Picard iteration due to the property of computation segment by segment, we further investigate the parallelization between the numerical Picard iterations on different sub-intervals. We propose a new parallel method called the parallel numerical Picard iteration (PNPI) method. Note that in the traditional numerical Picard iteration method one must complete the Picard iterations on the current interval before moving on to the next one. Instead, the proposed PNPI method allows one to perform Picard iterations simultaneously on different sub-intervals, once rough initial conditions and approximations are obtained.

We first illustrate one parallelization idea by considering a case with $N=4$ and $J=3$. We denote by $\eta _n^{[j]}$ the jth approximation value at $t_n$ for all $n=0,1,\ldots , N$, $j=0,1,\ldots ,J-1,$, and set

$$\eta _0^{[j]}=y_a, \quad j=0,1,\ldots ,J-1.$$

The notation $Y_n^{[j]}$ denotes the jth approximation of solution on the sub-interval $I_n$. The computation consists of the following steps (See Fig. ):

• On the first sub-interval $I_0$, the initial-state value $\eta _0^{[0]}$ is known and a rough approximation $Y_0^{[0]}$ is obtained by setting $Y_0^{[0]}(t)\equiv \eta _0^{[0]}, t\in I_0$. One numerical Picard iteration can be performed to obtain a more accurate solution $Y_0^{[1]}$ on $I_0$ and an initial-state value $\eta _1^{[0]}$ for the second sub-interval $I_1$.

• The second numerical Picard iteration can proceed on $I_0$ with $\eta _0^{[1]}$ and $Y_0^{[1]}$ to obtain a more accurate solution $Y_0^{[2]}$ for $I_0$ and a more accurate initial-state value $\eta _1^{[1]}$ for $I_1$. Meanwhile, another numerical Picard iteration can be conducted on $I_1$ with $\eta _1^{[0]}$ and $Y_1^{[0]}\equiv \eta _1^{[0]}$ to obtain a more accurate approximation $Y_1^{[1]}$ for $I_1$ and an initial-state value $\eta _2^{[0]}$ for $I_2$.

• We can next conduct three numerical Picard iterations on $I_0$, $I_1$, and $I_2$ simultaneously to obtain a more accurate approximation for the current sub-interval and provide a more accurate initial-state value for the next sub-interval.

• The procedure can continue until the computations are finished.

Fig. 1

Diagrams of parallel algorithm

We note that there are J numerical Picard iterations that can be computed in parallel all the time, except at the beginning and last $J-1$ steps.

However, the parallelization of the numerical Picard iterations shown in Fig. 1 leads to bad convergence of the iteration. To explain this, we focus on the second Picard iteration on $I_1$ with the initial-state condition $\eta _1^{[1]}$ and a rough approximation $Y_1^{[1]}$. Although $\eta _1^{[1]}$ is more accurate than $\eta _1^{[0]}$, it is easily found that the accuracy of $Y_1^{[1]}$ is of the same level as that of $\eta _1^{[0]}$ according to (6); that is,

$$\begin{aligned} Y_1^{[1]}(t)=\eta _1^{[0]}+\frac{h_1}{2}\int _{-1}^{\frac{2}{h_1}(t-t_1)-1} \mathcal {I}_M(f(\textbf{Y}_{1}^{[0]}),s) ds. \end{aligned}$$

Then, the accuracy of $\eta _2^{[1]}$ and $Y_1^{[2]}$ obtained from the numerical Picard iteration will be limited by the accuracy of $Y_1^{[1]}$, i.e., that of $\eta _1^{[0]}$. In fact, it can also be proved that the convergence of the numerical Picard iteration method with the above parallelization is only of one order. To overcome bad convergence, we make a slight modification for $Y_1^{[1]}$ by adding the difference between $\eta _1^{[0]}$ and $\eta _1^{[1]}$,

$$\begin{aligned} \tilde{Y}_1^{[1]}= Y_1^{[1]}+\eta _1^{[1]}-\eta _1^{[0]}, \end{aligned}$$

and then conduct the numerical Picard iteration with $\eta _1^{[1]}$ and $\tilde{Y}_1^{[1]}$ to derive $\eta _2^{[1]}$ and $Y_1^{[2]}$. It will be shown in Theorem 3 that the convergence order stays the same as that of the serial numerical Picard iteration methods.

We are now ready to present parallel numerical Picard iteration methods that make use of both the merits of the parallelization and the high-order convergence.

Definition 1

For a given positive number J, the element $\eta _h^{[J]}\in S_{M+1}(\mathcal {M}_h)$ is called the parallel J-Picard solution of Eq. (1) if it satisfies

$$\begin{aligned} \left. \eta _h^{[J]} \right| _{I_n}=Y_n^{[J]},\quad n=0,1,\ldots ,N-1, \end{aligned}$$

where $Y_n^{[J]}$ is generated by the iteration

$$\begin{aligned} \tilde{Y}_n^{[i]}(t)= & {} {\left\{ \begin{array}{ll}Y_n^{[i]}(t), i=0,\\ Y_n^{[i]}(t)+\eta _{n}^{[i]}-\eta _{n}^{[i-1]},\quad i=1,2,\ldots ,J-1, \end{array}\right. } \end{aligned}$$

(19)

$$\begin{aligned} Y_n^{[i+1]}(t)= & {} \eta _{n}^{[i]}+ \frac{h_n}{2}\int _{-1}^{\frac{2}{h_n}(t-t_n)-1} \mathcal {I}_M(f(\tilde{\textbf{Y}}_{n}^{[i]}),s) ds, i=0,1,\ldots ,J-1, \end{aligned}$$

(20)

with $\eta _0^{[j]}=y_a$, $j=0,1,\ldots ,J-1$, $\eta _{k}^{[j]}=Y_{k-1}^{[j+1]}(t_k)$, $k=1,\ldots ,N-1, j=0,1,\ldots ,J-1$, and $Y_k^{[0]}(t)\equiv \eta _{k}^{[0]}$, $t\in I_k, k=0,1,\ldots ,N-1$.

With the above definition, the PNPI method is presented in Algorithm 2. It is clear from Algorithm 2 that there is no restriction on the selection of points in each subinterval for the PNPI method. It is more flexible for the PNPI method than the RICD method [8] which requires the uniform nodes for easily conducting the parallelization.

The convergence analysis of the PNPI method is given in Theorem 3.

Theorem 3

Assuming that the solution y(t) of (1) is $(M+2)$-times continuously differentiable and that $\eta _h^{[J]}$ is a parallel J-Picard solution, if the step size h is sufficiently small, then the following error estimate holds:

$$\begin{aligned} \left\| y-\eta _h^{[J]}\right\| _\infty =\max _{t\in [a,b]} \left| y(t)-\eta _h^{[J]}(t) \right| \le c h^{\min \{J,M+1\}}, \end{aligned}$$

(21)

where the constant c is independent of h.

Proof

Denoting the error $e_n^{[i]}(t):=y(t)-Y_n^{[i]}(t)$ and $\xi _n^{[i]}:=y(t_n)-\eta _n^{[i]}$, $n=0,1,\ldots ,N-1$, $i=0,1,\ldots J-1$, it is obtained that

$$\begin{aligned} e_{n}^{[i+1]}\left( t_{n}+\frac{h_n}{2}(s+1)\right) =\xi _{n}^{[i]}+\frac{h_n}{2} \int _{-1}^{s} \mathcal {I}_M(f(\textbf{y}_n)-f(\tilde{\textbf{Y}}_n^{[i]}),z) dz + \left( \frac{h_n}{2}\right) ^{M+2}\int _{-1}^{s}H_{n}(z)dz, \end{aligned}$$

with $i=0,1,\ldots ,J-1,$ $n=0,1,\ldots ,N-1$ and $s\in [-1,1]$. Using the Lipschitz condition, we have

$$\begin{aligned} \left| e_{n}^{[i+1]}\left( t_{n}+\frac{h_n}{2}(s+1)\right) \right| \le \left| \xi _{n}^{[i]}\right| +c h \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i]}\right\| + c h^{M+2}, \end{aligned}$$

(22)

where c is a generic constant independent of h. In particular, we have from Eq. (22) that

$$\begin{aligned} \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i+1]}\right\| \le \left| \xi _{n}^{[i+1]}\right| +c h \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i]}\right\| + c h^{M+2}. \end{aligned}$$

(23)

Noting that $\xi _{n+1}^{[i]}=e_{n}^{[i+1]}(t_{n+1}), n=0,1,2,\ldots ,N-1$, $i=0,1,\ldots , J-1$, it follows from Eq. (22) that

$$\begin{aligned} \left| \xi _{n+1}^{[i]}\right| \le \left| \xi _{n}^{[i]}\right| +c h \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i]}\right\| + c h^{M+2}. \end{aligned}$$

(24)

We next present the bounds for $\xi _n^{[0]}$ and $\left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]}\right\|$. Since

$$\begin{aligned} \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]}\right\| \le \left\| \textbf{y}_n-y(t_n)\right\| +\left| \xi _{n}^{[0]}\right| \le ch + \left| \xi _{n}^{[0]}\right| , \end{aligned}$$

we obtain from Eq. (24) that

$$\begin{aligned} \left| \xi _{n+1}^{[0]}\right| \le (1+ch)\left| \xi _{n}^{[0]}\right| +c h^2 + c h^{M+2}, n=0,1,\ldots ,N-1. \end{aligned}$$

(25)

Since $\xi _0^{[0]}=0$, Lemma 2 shows that

$$\begin{aligned} \max _{n=0,1,\ldots ,N-1}\left| \xi _{n}^{[0]}\right| \le ch, \; \text {and} \; \max _{n=0,1,\ldots ,N-1}\left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]}\right\| \le ch. \end{aligned}$$

(26)

We then turn to the bound of $\left| \xi _{n+1}^{[i]}\right|$, $i\ge 1$. With the combination of Eqs. (23) and (24), it is obtained by induction that

$$\begin{aligned} \begin{aligned} \left| \xi _{n+1}^{[i]}\right|&\le \left| \xi _{n}^{[i]}\right| +\sum _{j=1}^{i} (ch)^{i+1-j} \left( \left| \xi _{n}^{[j]}\right| + (ch)^{M+2}\right) + (ch)^{i+1} \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]} \right\| +(ch)^{M+2}. \end{aligned} \end{aligned}$$

(27)

Combining the bound (26) for $\left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]} \right\|$ and Eq. (27), we have, for a small enough h, that

$$\begin{aligned} \begin{aligned} \left| \xi _{n+1}^{[i]}\right|&\le (1+ch)\left| \xi _{n}^{[i]}\right| +\sum _{j=1}^{i-1} (ch)^{i+1-j} \left| \xi _{n}^{[j]}\right| +c h^{\min \{i+2,M+2\}}. \end{aligned} \end{aligned}$$

(28)

Combining the inequality (28) and the fact that $\xi _0^{[j]}=0, j=0,1,\ldots ,J-1$, it can be verified by induction on i with the help of Lemma 2 that

$$\begin{aligned} \max _{n=1,2,\ldots ,N-1}\left| \xi _n^{[i]}\right| \le c h^{\min \{i+1,M+1\}},\; i=0,1,\ldots ,J-1. \end{aligned}$$

(29)

Combining Eqs. (23) and (29), we have

$$\begin{aligned} \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i+1]}\right\| \le c h \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i]}\right\| + c h^{\min \{i+2,M+1\}}. \end{aligned}$$

By induction on i, it is obtained from $\left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[0]}\right\| <ch$ that

$$\begin{aligned} \max _{n=1,2,\ldots ,N-1} \left\| \textbf{y}_n-\tilde{\textbf{Y}}_n^{[i]}\right\| \le c h^{\min \{i+1,M+1\}},\; i=0,1,\ldots ,J. \end{aligned}$$

(30)

It follows directly from Eqs. (22), (29), and (30) that

$$\begin{aligned} \left\| y-\eta _h^{[J]}\right\| _\infty =\max _{n=0,1,\ldots ,N-1} \left| e_n^{[J]} \right| \le ch^{\min \{J,M+1\}}, \end{aligned}$$

which finishes the proof. $\square$

We remark that the PNPI methods also possess the super-convergence property. We present this property as the following theorem, the proof of which is similar to that of Theorem 2.

Theorem 4

Assuming that the solution y(t) of (1) is $(2M+3)$-times continuously differentiable and $\eta _h^{[J]}$ is a parallel J-Picard solution, if the step size h is sufficiently small and the points $\{c_j:j=0,1,\ldots ,M\}$ are chosen to be Legendre–Gauss points, then the following error estimate holds:

$$\begin{aligned} \max _{t\in \mathcal {M}_h} |y(t)-\eta _h^{[J]}(t)| \le C h^{\min (J,2M+2)}, \end{aligned}$$

(31)

where the constant C is independent of h.

We end this section by presenting the speedup property of PNPI. To this end, we define the following index for speedup:

$$\begin{aligned} \text {Speedup}=\frac{T_{\text {serial}}}{T_{\text {parallel}}}, \end{aligned}$$

where $T_{\text {serial}}$ and $T_{\text {parallel}}$ are the computational times for the traditional method and PNPI method, respectively. We denote by $\textbf{u}_0$ one unit time to evaluate one force function and by $\textbf{u}_1$ one unit time to compute a dot product of two vectors of size $(M+1)$. To implement one numerical Picard iteration to obtain one $\textbf{Y}_n^{[j]}$ and $\eta _{n}^{[j]}$, $(M+1)$ functions and $m(M+1)$ dot products must be evaluated, as shown in Algorithm 2. Since NJ Picard iterations in total are needed, it is clear that

$$\begin{aligned} T_{\text {serial}}=NJ(M+1)(\textbf{u}_0+m\textbf{u}_1). \end{aligned}$$

Supposing that P cores are adopted in Algorithm 2, for simplicity we assume that there are J numerical Picard iterations in each outer iteration. In each outer iteration, there are $(M+1)J$ functions and $m(M+1)J$ dot products to be evaluated independently, which can be computed in parallel. It then follows that

$$\begin{aligned} T_{\text {parallel}}\approx \frac{1}{P}(N+J-1)(M+1)J(\textbf{u}_0+m\textbf{u}_1). \end{aligned}$$

Thus, the speedup of the parallel numerical Picard method is given by

$$\begin{aligned} \text {Speedup}=\frac{PN}{N+J-1}. \end{aligned}$$

Owing to the combination of parallelizations inside one numerical Picard iteration and between numerical Picard iterations on different sub-intervals, the parallel numerical Picard iteration method yields a larger speedup compared to the RIDC method [8]. In fact, the speedup of a Jth-order RIDC is at most J, while that for PNPI with the speedup can be $J(M+1)$, at least in theory.

4 Stability Analysis

We now investigate the numerical stability region for the numerical Picard iteration method. First, we recall the following definitions.

Definition 2

The amplification factor for a numerical method, $Am(\lambda )$, can be interpreted as the numerical solution to Dalhquist’s test equation,

$$\begin{aligned} y'(t)=\lambda y(t),\; y(0)=1, \end{aligned}$$

(32)

after one time step of size 1 for $\lambda \in \mathbb {C}$, i.e., $Am(\lambda )=y(1)$.

Definition 3

The stability region S for a numerical method is the subset of the complex plane $\mathbb {C}$ consisting of all $\lambda$ such that $Am(\lambda )\le 1$,

$$\begin{aligned} S=\{\lambda : Am(\lambda )\le 1\}. \end{aligned}$$

Fig. 2

Stability regions for numerical Picard iteration methods. Dependence of stability on a orders, b number of points, c iteration, and d type of points

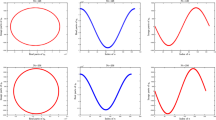
The stability regions for the numerical Picard iteration methods with different settings are computed numerically and presented in Fig. . In Fig. a–c, we explore the dependence of the stability on the convergence order, number M of points, and iteration number J with Chebyshev points. One observes a circle of radius 1 for the stability region after one Picard iteration, which is the same as the forward Euler integrator used. This is shown clearly in Fig. 2a, i.e., the area of the stability regions increases with increasing convergence order of the numerical Picard iteration methods. When the convergence order is unchanged, Fig. 2b shows that the stability regions would not increase with increasing number M of points, while Fig. 2c shows that the stability regions still increase with increasing iteration number J before the value J attaches $2(M+1)$. We also study the dependence of the stability regions on the choice of points. We chose three different types of points: Chebyshev, Legendre–Gauss, and uniform points. Interestingly, FIg. 2d shows that the stability regions almost do not depend on the choice of the points.

Fig. 3

Stability regions for parallel numerical Picard iteration methods. Dependence of stability on a orders, b number of points, c iteration, and d type of points

To study the stability regions of the PNPI methods, we introduce another definition of the stability region based on a uniform mesh.

Definition 4

The stability region S for a numerical method with a uniform mesh that has a size of $\Delta t$ is the subset of the complex plane $\mathbb {C}$ consisting of all $\lambda \Delta t$ such that $Am(\lambda )\le 1$,

$$\begin{aligned} S=\{\lambda \Delta t: Am(\lambda )\le 1\}. \end{aligned}$$

The stability regions for the parallel numerical Picard iteration methods with different settings are displayed in Fig. . In the first three Fig. 3a–c, we explore the dependence of the stability of the methods on the number M of points and the iteration number J while using Chebyshev points. One can also observe a circle of radius 1 for the stability region after one Picard iteration. Figure 3a shows that the area of the stability regions decreases with the convergence order of the numerical Picard iteration methods, but they encompass an increasing amount of the imaginary axis. This result is consistent with the stability regions of the RIDC [8]. We also note in Fig. 3b that the stability regions do not nearly depend on the number M of points, which is quite different from that for the numerical Picard iteration methods. The stability regions in Fig. 3c are nearly the same as those in Fig. 3a, which indicates that the stability regions depend mainly on the number of the iterations. Similarly, Fig. 3d shows that the stability regions do not nearly depend on the choice of points.

5 Numerical Examples

In this section, we illustrate the performance of numerical Picard iteration (NPI) and PNPI methods by numerical examples.

Fig. 4

Absolute error as function of number of intervals for different numbers of iterations, J,. NPM with J iterations adopts a five Chebyshev-Gauss nodes per interval and b three Legendre–Gauss nodes per interval. Expected orders of accuracy are observed

Example 1

Our first example is taken from [21]

$$\begin{aligned} {\left\{ \begin{array}{ll} y_1'(t)=ty_2(t)+y_1(t),\\ y_2'(t)=-ty_1(t)+y_2(t),\\ y(0)=(1,1)^\top , t\in [0,T]. \end{array}\right. } \end{aligned}$$

(33)

The analytic solution is $y(t)=(e^t(\cos \frac{t^2}{2}+\sin \frac{t^2}{2}), e^t(\cos \frac{t^2}{2}-\sin \frac{t^2}{2}))^\top$. We use this example to show the convergence rate of NPI methods.

Table 1 Rate of convergence of NPI methods with five different nodes ($J=5$, $T=1$)

Table 2 Rate of convergence of NPI methods with 10 nodes ($J=10$, $T=6$)

We set $T=1$ and adopt five Chebyshev–Gauss points, i.e., $\{\cos \frac{i\pi }{n-1}: i=0,1,\ldots ,n-1.\}$ in the NPI methods. The numerical errors with respect to the number of intervals is presented in Fig. a for different numbers of iterations. It is noted that the rates of convergence confirm the theoretical results. The super-convergence property with the Legendre–Gauss points is also presented in Fig. 4b, where three Legendre–Gauss nodes are used. It is clearly shown in Fig. 4b that the order increases as the number of iterations increases before it reaches two times the number of nodes.

The NPI methods with different choice of collocation points were also tested. More precisely, we compared three different types of nodes: Chebyshev–Gauss points, uniformly spaced nodes, and irregularly spaced nodes. Table shows the numerical errors and rates of convergence for the NPI methods $M,J=5$, while Table shows similar results with $M,J=10.$ Here, the uniform points are chosen as

$$\begin{aligned} \Big \{-1+\frac{2i}{n-1}: i=0,1,\ldots ,n-1.\Big \}, \end{aligned}$$

while the irregular points are selected as $[-0.9\; -0.6\; -0.5 \;0.2 \;0.25]$ in Table 1 and as $[-0.9 \;-0.8\; -0.6\; -0.55\; -0.5\; -0.15\; 0.2\; 0.225 \; 0.25\; 0.4 ]$ in Table 2. It is noted that, when the numbers of nodes and iterations are not too large (Table 1), the NPI methods steadily yield a fifth-order rate of convergence of no matter what kinds of nodes are adopted. However, when the numbers of nodes and iterations are relatively large (Table 2), the NPI methods with irregular points and uniform points demonstrate a reduction of the convergence order, while the NPI methods with Chebyshev points behave more stably.

Example 2

We next consider the following nonlinear ODE system [8]

$$\begin{aligned} {\left\{ \begin{array}{ll} y_1'(t)=-y_2(t)+y_1(t)(1-y_1^2(t)-y_2^2(t)),\\ y_2'(t)=y_1(t)+3y_2(t)(1-y_1^2(t)-y_2^2(t)),\\ y(0)=(1,0)^\top , t\in [0,T]. \end{array}\right. } \end{aligned}$$

(34)

The analytic solution is given by $y(t)=(\cos t, \sin t)^\top$. We use this example to validate the order of accuracy of PNPI methods. Figure a shows the error with respect to the number of intervals for different numbers of iterations. The desired order of accuracy is observed and the super-convergence of the PNPI methods is also observed in Fig. 5b when the Legendre–Gauss points are used. Comparison of the performance between the NPI and PNPI methods is presented in Table . The numerical result shows that the PNPI methods can preserve the convergence order of the NPI methods. As seen in Table , the PNPI methods exhibit similar behaviors as the NPI methods.

Fig. 5

Absolute error as function of number of intervals for different number of iterations, J. PNPI methods with J iterations adopting a five Chebyshev-Gauss nodes per interval and b three Legendre–Gauss nodes per interval. Expected orders of accuracy are observed

Table 3 Comparison of convergence of PNPI and NPI methods with five Chebyshev points and $J=5$

Table 4 Rate of convergence of PNPI methods with 10 nodes ($J=10$, $T=5$)

Example 3

The last example is the one-dimensional N-body problem [8]. Supposing that $N_+$ ions are uniformly spaced on the interval [0, 1] and that $N_-$ electrons are also uniformly spaced on the interval [0, 1], the motion of particles is then dominated by the equations

$$\begin{aligned}{} & {} \begin{bmatrix} x_i^+\\ v_i^+ \end{bmatrix}_t = \begin{bmatrix} v_i^+\\ \frac{q_+}{m_+} \left( \sum _{j=1}^{N_+} \frac{q_+ (x_i^+-x_j^+)}{\sqrt{(x_i^+ -x_j^+)^2+d^2}} + \sum _{j=1}^{N_-} \frac{q_- (x_i^+-x_j^-)}{\sqrt{(x_i^+ -x_j^-)^2+d^2}} \right) \end{bmatrix}, \; i=1,\ldots ,N_+,\\{} & {} \begin{bmatrix} x_i^-\\ v_i^- \end{bmatrix}_t = \begin{bmatrix} v_i^-\\ \frac{q_-}{m_-} \left( \sum _{j=1}^{N_+} \frac{q_+ (x_i^--x_j^+)}{\sqrt{(x_i^- -x_j^+)^2+d^2}} + \sum _{j=1}^{N_-} \frac{q_- (x_i^--x_j^-)}{\sqrt{(x_i^- -x_j^-)^2+d^2}} \right) \end{bmatrix}, \; i=1,\ldots ,N_-, \end{aligned}$$

where $t\in [0,T]$, $\{x_i^+,v_i^+\}_{i=1}^{N_+}$ and $\{x_i^-,v_i^-\}_{i=1}^{N_-}$ denote the locations and velocities of the ions and the electrons, respectively. The charge of each ion and electron is set to $q_+=\frac{1}{N_+}$ and $q_-=-\frac{1}{N_-}$, respectively. The mass of each ion and electron is set to $m_+=\frac{1000}{N_+}$ and $m_-=\frac{1}{N_-}$, respectively, which are physically reasonable mass ratios to work with. d is a regularization constant, which is set to 0.05 in this simulation. The initial conditions are set to

$$\begin{aligned}{} & {} x_i^+(0) = \frac{i-0.5}{N_+},\quad v_i^+(0)=0,\; i=1,\ldots ,N_+,\\{} & {} x_i^-(0) = \frac{i-0.5}{N_-},\quad v_i^-(0)=\sin (6\pi x_i^-(0)),\; i=1,\ldots ,N_-. \end{aligned}$$

In this example, we set $T=20$ and $N_+=N_-=200$, and the reference solution is obtained using the built-in solver ode45 in MatLab (MathWorks, Natick, MA, USA). We consider the maximum norm errors at the terminal time. For a fixed number of intervals, $N=1000$, and a fixed number of collocation points, $M+1=12$, in each interval, we tested the efficiency of the PNPI methods with different iterations J on different numbers of cores ranging from 2 to 12. The associated numerical results are presented in Table . It is noted that the error decays rapidly when the number of iterations, J, increases. To show the efficiency, we present both the CPU time of sequential computation (denoted ST) and of parallel computation (denoted PT) with different cores. We also introduce two indexes, speedup and efficiency, which are defined, respectively, by

The results are listed in Table 5. It is noted that the speedup well matches that of theory and that the parallel efficiency is approximately 69% when 12 cores are used. According to theory, the CPU time is expected to decrease if one increases the number of cores until up to 12J. We also adopted different cores to implement the PNPI methods with $J=12$ and $M+1=12$ in parallel, and the resulting computation times are listed in Table . Speedup in this table is defined by

$$\begin{aligned} \text {Speedup}=\frac{\text {CPU time of one core}}{\text {CPU time of multiple cores}}. \end{aligned}$$

Again, the results match the theoretical results very well and the efficiency can be maintained above 69%. As a comparison, we present the computation time of the built-in function ode45 in MatLab. It is noted that that the PNPI methods with more than six cores outperform the ode45 solver.

Table 5 Performance of PNPI methods with different numbers of iterations and of cores for fixed numbers of intervals, $N=1000$, and of points, $M+1=12$, on each interval

Table 6 Performance of PNPI methods with different numbers of cores for fixed numbers of intervals, $N=1000$; of iterations, $J=12$; and of points, $M+1=12$, on each interval

We also performed a parallel performance comparison between the PNPI methods and the eighth-order RIDC method (denoted RIDC8). We set $J=M+1=8$ and $N=1000$ for the PNPI methods. To achieve similar accuracy, the number of intervals was set as $N=6000$ for RIDC8. The numerical results are shown in Table , from which it can be seen that the PNPI methods take less time to achieve comparable accuracy and exhibit better speedup and efficiency.

Table 7 Performance comparison between PNPI methods with $J=M+1=8$ and RIDC8 based on forward Euler method with different cores

6 Concluding Remarks

In this paper, we propose a new class of parallel time integrators for initial-value problems based on Picard iterations. We demonstrate that the parallel solvers yield the same convergence rate as the traditional numerical Picard iteration methods. The main features of our approach are as follows. (1) Instead of computing the solution point by point (as in RIDC methods), the proposed methods proceed segment by segment. (2) The proposed approach leads to a higher speedup: the speedup is shown to be $J(M+1)$ (while the speedup of the Jth-order RIDC is, at most, J). (3) The proposed approach is applicable to non-uniform points, such as Chebyshev points. We also present a stability analysis and numerical examples to verify the theoretical findings. In future work, we plan to apply the proposed PNPI method to more challenging engineering problems.