An Efficient Quadrature Rule for the Oscillatory Infinite Generalized Bessel Transform with a General Oscillator and Its Error Analysis

Abstract

Our recent work (Kang and Wang in J Sci Comput 82:1–33, 2020) performed a complete asymptotic analysis and proposed a modified Filon-type method for a class of oscillatory infinite Bessel transform with a general oscillator. In this paper, we present and analyze a different method by converting the integration path to the complex plane for this class of oscillatory infinite Bessel transform. In particular, we establish a series of new quadrature rules for this transform and carry out rigorous analysis, including the cases that the oscillator g(x) has either zeros or stationary points. The error analysis shows the advantages that this approach exhibits high asymptotic order, and the accuracy improves significantly as either the frequency $\omega$ or the number of nodes n increases. Furthermore, the constructed method shows higher accuracy and error order by comparing with the existing modified Filon-type method in our recent work (Kang and Wang 2020) at the same computational cost. Some numerical experiments are provided to verify the theoretical results and demonstrate the efficiency of the proposed method.

1 Introduction

It is generally known that highly oscillatory Bessel transforms arise frequently in many areas such as astronomy, electromagnetic acoustics, scattering problems, physical optics, electrodynamics, seismology image processing and applied mathematics [3, 4, 6, 7, 13, 18]. In this work, we focus on the evaluation and analysis of the highly oscillatory infinite Bessel transforms with general oscillators

$$\begin{aligned} I[f]=\int _a^{+\infty } x^\alpha f(x)J_m(\omega g(x))dx, \end{aligned}$$

(1.1)

where f and g are analytic in a simply connected and sufficiently (infinitely) large complex domain D containing the interval $[a, +\infty ]$, $J_m(z)$ is the Bessel function of the first kind and of order m with $m\ge 0$, the frequency parameter $\omega$ is large, $\alpha <0$, and $a>0$. These highly oscillatory infinite integrals cannot be computed analytically and one has to resort to numerical methods. When the integrand becomes highly oscillatory, it presents serious difficulties in obtaining numerical convergence of the integration.

Here, we introduce some related articles for computing infinite oscillatory integrals. In 1976, Blakemore, Evans and Hyslop [5] made comparison of some numerical methods for computing infinite oscillatory integrals. However, those methods presented in [5] converge slowly, and have to use an extrapolation technique to accelerate convergence. The asymptotics and fast computation of one-sided oscillatory infinite Hilbert transforms was studied in [28] by Wang, Zhang and Huybrechs. Xu, Xiang and He developed the fast computation of a class of oscillatory infinite Bessel Hilbert transform in [37]. An asymptotic Filon-type method for calculating the infinite oscillatory integral $\int _a^{+\infty } f(x)e^{i\omega g(x)}dx$ was established by Hascelik in [16]. Based on the idea of [16], in [9, 10], Chen presented the efficient numerical methods for approximating the integral $\int _a^{+\infty }f(x)J_m(\omega x)dx$. Moreover, numerical methods for calculating the oscillatory infinite integrals of the form $\int _{1}^{+\infty }x^\alpha f(x)K(\omega x)dx$ were investigated in [21, 22], where $K(\omega x)$ denote different oscillatory kernel functions, such as $e^{i\omega x}$, $J_m(\omega x)$, $Y_m(\omega x)$, $H_m^{(1)}(\omega x)$, $H_m^{(2)}(\omega x)$, $Ai(-\omega x)$, respectively. Recently, Chen in [11] developed an asymptotic rule for approximating the infinite Bessel transform $\int _0^{+\infty }f(x)J_m(\omega x)dx$. Additionally, there has been tremendous interest in constructing numerical methods for finite oscillatory Bessel transforms (including singular or nonsingular cases) in articles [8, 19, 20, 24, 25, 27, 29, 33,34,35,36, 38]. Recently, new Levin methods were presented for calculating a class of the Fourier-type integral with algebraic and/or logarithmic singularities in [30]. Moreover, the numerical steepest descent method for the Fourier-type integral $\int _a^bf(x)e^{i\omega g(x)}dx$ proposed by Huybrechs and Vandewalle [17] in 2006 restricts that f is analytic in a sufficiently large complex region that contains [a, b]. Thanks to analytic continuation, the problem can be solved by using the Gauss–Laguerre quadrature rule. It is noteworthy that Kang and Wang in [23] provided asymptotic analysis and gave a modified Filon-type method for computing the considered integral (1.1). It can achieve the higher accuracy by either adding derivatives at the critical points (including zeros, end points and stationary points) or increasing the number of interpolation nodes. However, its derivatives are sometimes difficult to obtain for the complicated function f(x). Moreover, only increasing the number of interpolation points cannot improve the error order. This motivates us to explore a more efficient methods such that the obtained error order can be improved greatly by adding the node points.

The aim of this paper is to construct a numerical approach with higher error order for calculating the infinite integrals (1.1) with general oscillators. We propose a complex integration method for the Bessel transform (1.1) by converting the original integration path to the complex plane. The proposed numerical scheme shows the advantages that the obtained error order can be improved by increasing the number of node points n. Thanks to the relation between Bessel function and Hankel function, the computation of (1.1) can be changed into the problem of calculating the Hankel transform. In particular, we remedy the problem that the corresponding Hankel functions of the first kind $H_m^{(1)}(\omega g(x))$ and the second kind $H_m^{(2)}(\omega g(x))$ have singularities as $g(x)\rightarrow 0$ when the oscillator g(x) has zeros on the integral interval. Moreover, the stationary points of g(x) play a crucial role in our theoretical analysis. Therefore, for the case of g(x) without stationary points, we consider the following two types:

Type I : g(x) has no zero points, i,e., $g(x)\not =0$ on $[a, +\infty )$;

Type II :g(x) has zeros, i,e., $\exists$ $\xi \in [a, +\infty )$, s.t. $g(\xi )=0$.

The case that g(x) has stationary points, can be also classified into the following two types:

Type I : g(x) has stationary points, which are also zeros, i,e., $\exists$ $\zeta \in [a, +\infty )$, s.t. $g(\zeta )=g'(\zeta )=\cdots =g^{(r)}(\zeta )=0$ and $g^{(r+1)}(\zeta )\not =0$ , $r\ge 1$;

Type II :g(x) has stationary points, which are not zeros, i,e., $\exists$ $\zeta \in [a, +\infty )$, s.t. $g'(\zeta )=g''(\zeta )=\cdots =g^{(r)}(\zeta )=0$, $g^{(r+1)}(\zeta )\not =0$ and $g(\zeta )\not =0$ , $r\ge 1$.

For the above four cases, we derive the corresponding efficient quadrature formulae and perform the rigorous error analysis.

The structure of this paper is as follows. In Sect. 2, we analyze in detail the above two cases that g(x) has no stationary point. We explore the quadrature rules and error analysis for the case that g(x) has stationary points in Sect. 3. Additionally, some numerical experiments are illustrated to verify the established method in Sect. 4. The comparison results between the established method and the modified Filon-type method [23] is also shown in this section. Section 5 exhibits some summaries of this paper.

2 The Case Without Stationary Points

In this section, let us focus on the case that g(x) has no stationary points on the integration interval $[a, +\infty )$, i.e., $g'(x)\not =0$ for $x\in [a, +\infty )$ and $\lim _{x\rightarrow +\infty }g'(x)\ne 0$. This case includes two types that

Type I: g(x) has no zero points, i,e., $g(x)\not =0$ on $[a, +\infty )$;

Type II: g(x) has zeros, i,e., $\exists$ $\xi \in [a, +\infty )$, s.t. $g(\xi )=0$.

We first introduce some preliminaries which will be used in the later sections. From [2, p. 358], the relation formulae between the Hankel functions and the Bessel functions are as follows,

$$\begin{aligned}{} & {} H_m^{(1)}(x)=J_m(x)+iY_m(x), \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} H_m^{(2)}(x)=J_m(x)-iY_m(x), \end{aligned}$$

(2.2)

where $H_m^{(1)}(x)$ and $H_m^{(2)}(x)$ denote the Hankel functions of the first and second kinds of order m, respectively, and $Y_m(x)$ denotes the Bessel function of the second kind of order m. Moreover, when m is fixed and $|x|\rightarrow \infty$, the Hankel functions have the following asymptotic properties [2, p. 364],

$$\begin{aligned}{} & {} H_m^{(1)}(x)\sim \sqrt{\frac{2}{\pi x}}e^{i(x-\frac{1}{2}m\pi -\frac{\pi }{4})}, \end{aligned}$$

(2.3)

$$\begin{aligned}{} & {} H_m^{(2)}(x)\sim \sqrt{\frac{2}{\pi x}}e^{-i(x-\frac{1}{2}m\pi -\frac{\pi }{4})}. \end{aligned}$$

(2.4)

The definition of the notation “ $\sim$ ” is as follows. If $f(x)/\varphi (x)$ tends to unity as $x\rightarrow x_0$, we write $f(x)\sim \varphi (x)\ \ \ (x\rightarrow x_0)$. In words, f is asymptotic to $\varphi$.

In the sequel, we commence our analysis for the case of the type I.

2.1 Type I: g(x) Without Zero Points

We begin this subsection with an useful theorem concerning the reconstruction of the integration path.

Theorem 2.1

Assume that both g and f are analytic in D, and $g(x)\not =0$, $g'(x)\not =0$ for $x\in [a, +\infty )$. And, $\lim _{x\rightarrow +\infty }g'(x)\ne 0$. Denote that $\varGamma _{2}(p)=g^{-1}(g(a)+ip), \varLambda _{2}(p)=g^{-1}(g(a)-ip)$. Suppose that $|\varGamma _{2}(p)|$, $|\varLambda _{2}(p)|$, $|g'(\varGamma _{2}(p))|, |g'(\varLambda _{2}(p))|\ge \varepsilon _0, p\in [0, +\infty )$, where $\varepsilon _0$ is a positive constant. For $\omega >(\alpha +\nu +1)\omega _1$ and $\alpha <0$, if the following conditions hold in D:

$$\begin{aligned}{} & {} (1)\ \ \exists v\in \mathbb {R}, \ \ \text {s.t.}\ \ | f^{(j)}(z)|=O(|z|^{v-j}), j=0,1,2,\ldots , \ \ \text {as} \ \ |z|\rightarrow \infty , \end{aligned}$$

(2.5)

$$\begin{aligned}{} & {} (2)\ \ |\Im (g(z))|\rightarrow +\infty ,\ \ \ \text {as} \ \ |z|\rightarrow \infty , \end{aligned}$$

(2.6)

$$\begin{aligned}{} & {} (3)\ \text {for}\ \ k=0,1,2,\ldots , \exists \omega _1\in \mathbb {R},\ \ \text {s.t.}\ \ |[g^{-1}(z)]^{(k)}|=O(e^{\omega _1|\Im (z)|}), \ \text {as} \ \ |z|\rightarrow \infty ,\nonumber \\ \end{aligned}$$

(2.7)

where the zero order derivative of the function is the function itself, then it is true that

$$\begin{aligned} I[f]= & {} \frac{1}{2}\left\{ e^{i\omega g(a)}\int _0^{+\infty } \varGamma ^\alpha _{2}(p)f[\varGamma _{2}(p)]H_m^{(1)}[\omega (g(a)+ip)]e^{-i\omega (g(a)+ip)}\varGamma '_{2}(p)e^{-\omega p}dp\right. \nonumber \\{} & {} \left. +e^{-i\omega g(a)}\int _0^{+\infty } \varLambda ^\alpha _{2}(p)f[\varLambda _{2}(p)]H_m^{(2)}[\omega (g(a)-ip)]e^{i\omega (g(a)-ip)}\varLambda '_{2}(p)e^{-\omega p}dp\right\} .\nonumber \\ \end{aligned}$$

(2.8)

Proof

Based on the important relations (2.1) and (2.2), the integral I[f] can be rewritten as

$$\begin{aligned} I[f]=\frac{1}{2}\left[ \int _a^{+\infty }x^\alpha f(x)H_m^{(1)}(\omega g(x))dx+\int _a^{+\infty }x^\alpha f(x)H_m^{(2)}(\omega g(x))dx\right] . \end{aligned}$$

(2.9)

Here we give a notation as

$$\begin{aligned} I_1[f]=\int _a^{+\infty }x^\alpha f(x)H_m^{(1)}(\omega g(x))dx, \end{aligned}$$

(2.10)

$$\begin{aligned} I_2[f]=\int _a^{+\infty }x^\alpha f(x)H_m^{(2)}(\omega g(x))dx. \end{aligned}$$

(2.11)

Therefore, the key point is to construct the quadrature rules for the integrals $I_1[f]$ and $I_2[f]$, respectively.

By using (2.3) and (2.4), as $|\omega g(x)| \rightarrow \infty$, we can get

$$\begin{aligned} H_m^{(1)}(\omega g(x))\sim \sqrt{\frac{2}{\pi \omega g(x)}}e^{i\omega (g(x)-\frac{1}{2}m\pi -\frac{\pi }{4})}, \end{aligned}$$

(2.12)

$$\begin{aligned} H_m^{(2)}(\omega g(x))\sim \sqrt{\frac{2}{\pi \omega g(x)}}e^{-i\omega (g(x)-\frac{1}{2}m\pi -\frac{\pi }{4})}. \end{aligned}$$

(2.13)

Then, the integrals $I_1[f]$ and $I_2[f]$ can be rewritten as

$$\begin{aligned} I_1[f]=\int _a^{+\infty }x^\alpha f(x)H_m^{(1)}(\omega g(x))e^{-i\omega g(x)}e^{i\omega g(x)}dx, \end{aligned}$$

(2.14)

$$\begin{aligned} I_2[f]=\int _a^{+\infty }x^\alpha f(x)H_m^{(2)}(\omega g(x))e^{i\omega g(x)}e^{-i\omega g(x)}dx, \end{aligned}$$

(2.15)

where it can be seen from the two asymptotic formulae (2.12) and (2.13) that $H_m^{(1)}(\omega g(x)) e^{-i\omega g(x)}$ and $H_m^{(2)}(\omega g(x))e^{i\omega g(x)}$ are not oscillatory as $|\omega g(x)| \rightarrow \infty$.

Fig. 1

The integration paths for the oscillator g(x) in $e^{i\omega g(x)}$ (left figure) and the oscillator g(x) in $e^{-i\omega g(x)}$ (right figure)

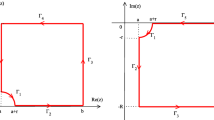
We shall construct the quadrature rules for $I_1[f]$ and $I_2[f]$ by the careful selection of the integration paths in the complex region, which are drawn in Fig. 1.

On the left panel of Fig. 1, $\varGamma _2(p)=g^{-1}(g(a)+ip), p\in [0, +\infty )$. Here, $\varGamma _2(p)$ has one intersection $\varGamma _2(p_{A})$ with the circle $a+(A-a)e^{i\theta }, \theta \in [0, 2\pi )$. The parametric form of $\varGamma _3$ is written as $\varGamma _3(\theta )=a+(A-a)e^{\text {sgn}(\theta _A)i\theta }, \theta \in \left[ 0, |\theta _A|\right]$, where $\theta _A=\arg \varGamma _2(p_{A})$.

Then, by Cauchy’s integral theorem [1, 15] in Fig. 1 (left figure), we have

$$\begin{aligned} \int _a^A x^\alpha f(x)H_m^{(1)}(\omega g(x))e^{-i\omega g(x)}e^{i\omega g(x)}dx= & {} \int _{\varGamma _2}z^\alpha f(z)H_m^{(1)}(\omega g(z))e^{-i\omega g(z)}e^{i\omega g(z)}dz\nonumber \\{} & {} +\int _{\varGamma _3}z^\alpha f(z)H_m^{(1)}(\omega g(z))e^{-i\omega g(z)}e^{i\omega g(z)}dz.\nonumber \\ \end{aligned}$$

(2.16)

From the asymptotic formula (2.3) of the Hankel function, we have

$$\begin{aligned} \bigg |H_m^{(1)}(x)e^{-ix}\bigg |\le M\frac{1}{\sqrt{|x|}}, \ \ \ \text {for} \ \ |x|\rightarrow +\infty , \end{aligned}$$

(2.17)

where M is some positive constant.

Furthermore, for $\alpha <0$, from (2.5), (2.6) and (2.17), it exists some positive number $M_1$, such that it follows that

$$\begin{aligned}{} & {} \bigg |\int _{\varGamma _3}z^\alpha f(z)H_m^{(1)}(\omega g(z))e^{-i\omega g(z)}e^{i\omega g(z)}dz \bigg |\\ \nonumber= & {} \bigg |\int _{|\theta _A|}^0 (A-a)\theta \text {sgn}(\theta _A)e^{\text {sgn}(\theta _A)i\theta } \\ {}{} & {} (a+(A-a)e^{\text {sgn}(\theta _A)i\theta })^\alpha f(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })H^{(1)}_m(\omega g(a+Ae^{\text {sgn}(\theta _A)i\theta }))\\{} & {} e^{-i\omega g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })}e^{i\omega g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })}d\theta \bigg |\\\le & {} \bigg |\theta _A\bigg |\max \limits _{\theta \in [0, |\theta _A|]}\bigg | (A-a)\theta (a+(A-a)e^{\text {sgn}(\theta _A)i\theta })^\alpha \\ {}{} & {} f(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })H^{(1)}_m(\omega g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta }))\\{} & {} e^{-i\omega g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })}e^{i\omega g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })}\bigg |\\\le & {} \bigg |\theta _A M_1 (A-a)\theta |A-2a|^{\frac{\alpha }{2}} (A-a)^v\\ {}{} & {} \frac{M}{\sqrt{\omega |g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })|}}e^{-(\omega |\Im {(g(z))}|)}\bigg |_{z=a+(A-a)e^{\text {sgn}(\theta _A)i\theta }}\\\rightarrow & {} 0, \end{aligned}$$

as $A\rightarrow +\infty$. Here, when $A\rightarrow +\infty$, it follows from (2.6) that $|\Im (g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta }))|\rightarrow +\infty$ and $|g(a+(A-a)e^{\text {sgn}(\theta _A)i\theta })|\rightarrow +\infty$.

Therefore, letting $A\rightarrow +\infty$ in (2.16), we have

$$\begin{aligned} I_1[f]=e^{i\omega g(a)}\int _0^{+\infty } \varGamma ^\alpha _{2}(p)f[\varGamma _{2}(p)]H_m^{(1)}[\omega (g(a)+ip)]e^{-i\omega (g(a)+ip)}\varGamma '_{2}(p)e^{-\omega p}dp.\nonumber \\ \end{aligned}$$

(2.18)

Similarly, by using the new path shown on the right panel of Fig. 1 with $\varLambda _2(p)=g^{-1}(g(a)-ip), p\in [0, +\infty )$, we have that

$$\begin{aligned} I_2[f]=e^{-i\omega g(a)}\int _0^{+\infty } \varLambda ^\alpha _{2}(p)f[\varLambda _{2}(p)]H_m^{(2)}[\omega (g(a)-ip)]e^{i\omega (g(a)-ip)}\varLambda '_{2}(p)e^{-\omega p}dp.\nonumber \\ \end{aligned}$$

(2.19)

The Eqs. (2.9), (2.18) and (2.19) yield the desired result (2.8). Thus, we complete this proof. $\square$

Letting $q=\omega p$ in (2.18) and (2.19), we have that

$$\begin{aligned} I_1[f]= & {} \frac{e^{i\omega g(a)}}{\omega }\int _0^{+\infty } \varGamma ^\alpha _{2}\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] H_m^{(1)}\left[ \omega \left( g(a)+i\frac{q}{\omega }\right) \right] \nonumber \\{} & {} \times e^{-i\omega \left( g(a)+i\frac{q}{\omega }\right) }\varGamma '_{2}\left( \frac{q}{\omega }\right) e^{-q}dq, \end{aligned}$$

(2.20)

and

$$\begin{aligned} I_2[f]= & {} \frac{e^{-i\omega g(a)}}{\omega }\int _0^{+\infty } \varLambda ^\alpha _{2}\left( \frac{q}{\omega }\right) f\left[ \varLambda _{2}\left( \frac{q}{\omega }\right) \right] H_m^{(2)}\left[ \omega \left( g(a)-i\frac{q}{\omega }\right) \right] \nonumber \\{} & {} \times e^{i\omega \left( g(a)-i\frac{q}{\omega }\right) }\varLambda '_{2}\left( \frac{q}{\omega }\right) e^{-q}dq. \end{aligned}$$

(2.21)

Then, by using the Gauss–Laguerre quadrature rule with the nodes $x_k$ and the weights $a_k, k=1, 2, \ldots , n$, we have the respective n-point quadrature formulae for $I_1[f]$ and $I_2[f]$, as follows,

$$\begin{aligned} Q_{n,1}[f]= & {} \frac{e^{i\omega g(a)}}{\omega }\sum \limits _{k=1}^n a_k \varGamma ^\alpha _{2}\left( \frac{x_k}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{x_k}{\omega }\right) \right] H_m^{(1)}\left[ \omega \left( g(a)+i\frac{x_k}{\omega }\right) \right] \nonumber \\{} & {} \times e^{-i\omega \left( g(a)+i\frac{x_k}{\omega }\right) }\varGamma '_{2}\left( \frac{x_k}{\omega }\right) , \end{aligned}$$

(2.22)

and

$$\begin{aligned} Q_{n,2}[f]= & {} \frac{e^{-i\omega g(a)}}{\omega }\sum \limits _{k=1}^n a_k \varLambda ^\alpha _{2}\left( \frac{x_k}{\omega }\right) f\left[ \varLambda _{2}\left( \frac{x_k}{\omega }\right) \right] H_m^{(2)}\left[ \omega \left( g(a)-i\frac{x_k}{\omega }\right) \right] \nonumber \\{} & {} \times e^{i\omega \left( g(a)-i\frac{x_k}{\omega }\right) }\varLambda '_{2}\left( \frac{x_k}{\omega }\right) . \end{aligned}$$

(2.23)

Then the considered integral (1.1) can be approximated by the quadrature formula

$$\begin{aligned} Q_n[f]= \frac{1}{2}(Q_{n,1}[f]+Q_{n,2}[f]). \end{aligned}$$

(2.24)

Now, we show the error analysis of the above presented numerical method.

Theorem 2.2

Under the assumption conditions of Theorem 2.1, the error of the quadrature formula (2.24) behaves asymptotically as

$$\begin{aligned} I[f]-Q_n[f]=O\left( \omega ^{-2n-\frac{3}{2}}\right) , \ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.25)

Proof

From [31], for large |z|, it follows that

$$\begin{aligned} H_m^{(1)}(z)e^{-iz}=\sqrt{\frac{2}{\pi z}}e^{-i(\frac{m\pi }{2}+\frac{\pi }{4})}\sum \limits _{j=0}^{2n+1}\frac{(\frac{1}{2}+m)_j(\frac{1}{2}-m)_j}{j!(2iz)^j}+O(|z|^{-2n-\frac{5}{2}}), \end{aligned}$$

(2.26)

where $(x)_j$ is defined by

$$\begin{aligned} (x)_j=\frac{\varGamma (x+j)}{\varGamma (x)}=\left\{ \begin{aligned}&1,&\ \ j=0,\\&x(x+1)(x+2)\cdots (x+j-1),&\ \ j\ge 1. \end{aligned}\right. \end{aligned}$$

Denote that $F_\omega (u)=\varGamma ^\alpha _{2}(u)f[\varGamma _{2}(u)]\varGamma '_{2}(u), u=\frac{q}{\omega }$ and $G_\omega (q)\!=\!\sum \limits _{j=0}^{2n+1}\frac{(\frac{1}{2}+m)_j(\frac{1}{2}-m)_j}{j!(2i)^j(\omega g(a)+iq)^{j+\frac{1}{2}}}$. Using Hermite interpolation for the function $F_\omega \left( \frac{q}{\omega }\right) G_\omega (q)$, we construct the interpolation polynomial $P_{2n-1}(\frac{q}{\omega })$, which satisfies that

$$\begin{aligned} P_{2n-1}\left( \frac{x_k}{\omega }\right)= & {} F_\omega \left( \frac{x_k}{\omega }\right) G_\omega (x_k),\\ P'_{2n-1}\left( \frac{x_k}{\omega }\right)= & {} \left[ F_\omega \left( \frac{q}{\omega }\right) G_\omega (q)\right] '|_{q=x_k}, \end{aligned}$$

where $x_k, k=1,2,\ldots ,n$ are Gauss–Laguerre nodes. Then, we have the following n-point Gauss–Laguerre quadrature formula

$$\begin{aligned} \int _0^{+\infty }P_{2n-1}\left( \frac{q}{\omega }\right) e^{-q}dq=\sum \limits _{k=1}^{n}a_kP_{2n-1}\left( \frac{x_k}{\omega }\right) =\sum \limits _{k=1}^{n}a_kF_\omega \left( \frac{x_k}{\omega }\right) G_\omega (x_k). \end{aligned}$$

The error formula is written as

$$\begin{aligned} E=\int _0^{+\infty }F_\omega \left( \frac{q}{\omega }\right) G_\omega \left( \frac{q}{\omega }\right) e^{-q}dq-\sum \limits _{k=1}^{n}a_kF_\omega \left( \frac{x_k}{\omega }\right) G_\omega (x_k). \end{aligned}$$

Thus, using the remainder formula of Hermite interpolation, we can obtain that

$$\begin{aligned} E= & {} \int _0^{+\infty }\left[ F_\omega \left( \frac{q}{\omega }\right) G_\omega (q)-P_{2n-1}\left( \frac{q}{\omega }\right) \right] e^{-q}dq\nonumber \\= & {} \int _0^{+\infty }\frac{[F_\omega (\frac{q}{\omega }) G_\omega (q)]^{(2n)}|_{q=\gamma }}{(2n)!}Ln^2(q)e^{-q}dq, \end{aligned}$$

(2.27)

where $Ln(x)=\prod _{j=1}^n(x-x_j), \gamma \in (0, \max (q,x_n)).$ Therefore, based on (2.26) and (2.27), the error can be expressed as

$$\begin{aligned}{} & {} I_1[f]-Q_{n,1}[f]\nonumber \\= & {} \frac{e^{i\omega g(a)}}{\omega }\int _0^{+\infty } \varGamma ^\alpha _{2}\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] H_m^{(1)}\left[ \omega \left( g(a)+i\frac{q}{\omega }\right) \right] e^{-i\omega \left( g(a)+i\frac{q}{\omega }\right) }\varGamma '_{2}\left( \frac{q}{\omega }\right) e^{-q}dq\nonumber \\{} & {} -\frac{e^{i\omega g(a)}}{\omega }\sum _{k=1}^na_k \varGamma ^\alpha _{2}\left( \frac{x_k}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{x_k}{\omega }\right) \right] H_m^{(1)}\left[ \omega \left( g(a)+i\frac{x_k}{\omega }\right) \right] e^{-i\omega \left( g(a)+i\frac{x_k}{\omega }\right) }\varGamma '_{2}\left( \frac{x_k}{\omega }\right) \nonumber \\= & {} \frac{e^{i\omega g(a)}}{\omega }\int _0^{+\infty } \varGamma ^\alpha _{2}\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \sqrt{\frac{2}{\pi }}e^{-i(\frac{m\pi }{2}+\frac{\pi }{4})} \nonumber \\{} & {} \times \sum \limits _{j=0}^{2n+1}\frac{(\frac{1}{2}+m)_j(\frac{1}{2}-m)_j}{j!(2i)^j(\omega g(a)+iq)^{j+\frac{1}{2}}}\varGamma '_{2}\left( \frac{q}{\omega }\right) e^{-q}dq \nonumber \\{} & {} +\frac{e^{i\omega g(a)}}{\omega }\int _0^\infty \varGamma _2^\alpha \left( \frac{q}{\omega }\right) f\left[ \varGamma _2\left( \frac{q}{\omega }\right) \right] \varGamma _2'\left( \frac{q}{\omega }\right) e^{-q}O(|\omega g(a)+iq|^{-2n-\frac{5}{2}})dq\nonumber \\{} & {} -\frac{e^{i\omega g(a)}}{\omega }\sum _{k=1}^na_k \varGamma ^\alpha _{2}\left( \frac{x_k}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{x_k}{\omega }\right) \right] \varGamma '_{2}\left( \frac{x_k}{\omega }\right) \sqrt{\frac{2}{\pi }}e^{-i(\frac{m\pi }{2}+\frac{\pi }{4})} \nonumber \\{} & {} \times \sum \limits _{j=0}^{2n+1}\frac{(\frac{1}{2}+m)_j(\frac{1}{2}-m)_j}{j!(2i)^j(\omega g(a)+ix_k)^{j+\frac{1}{2}}}+\frac{e^{i\omega g(a)}}{\omega }O\left( |\omega g(a)+ix_k|^{-2n-\frac{5}{2}}\right) \nonumber \\= & {} \frac{e^{i\omega g(a)}}{\omega }\sqrt{\frac{2}{\pi }}e^{-i\left( \frac{m\pi }{2}+\frac{\pi }{4}\right) }\int _0^{+\infty }\frac{\left[ F_\omega (\frac{q}{\omega }) G_\omega (q)\right] ^{(2n)}|_{q=\gamma }}{(2n)!}Ln^2(q)e^{-q}dq \nonumber \\{} & {} +\frac{e^{i\omega g(a)}}{\omega }\int _0^{+\infty } \varGamma _2^\alpha \left( \frac{q}{\omega }\right) f\left[ \varGamma _2\left( \frac{q}{\omega }\right) \right] \varGamma _2'\left( \frac{q}{\omega }\right) e^{-q}O(|\omega g(a)+iq|^{-2n-\frac{5}{2}})dq\nonumber \\{} & {} +\frac{e^{i\omega g(a)}}{\omega }O(|\omega g(a)+ix_k|^{-2n-\frac{5}{2}}), \end{aligned}$$

(2.28)

where $\gamma \in (0, \max (q,x_n))$.

Here, for the integral in the last line of (2.28), we have that

$$\begin{aligned}{} & {} \int _{0}^{+\infty } \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) e^{-q} O\left( \left| \omega g(a)+iq\right| ^{-2 n-\frac{5}{2}}\right) d q \nonumber \\ \le{} & {} \int _{0}^{+\infty }\left| \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) e^{-q}\right| O\left( \omega ^{-2 n-\frac{5}{2}}\right) \left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}dq\nonumber \\ \le{} & {} \omega ^{-2 n-\frac{5}{2}}M_2\int _0^\infty \left| \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) \right| e^{-q}\left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}dq\nonumber \\ ={} & {} \omega ^{-2 n-\frac{5}{2}}M_2\left\{ \int _0^1 \left| \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) \right| e^{-q}\left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}dq\right. \nonumber \\{} & {} \left. +\int _1^{+\infty } \left| \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) \right| e^{-q}\left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}dq\right\} , \end{aligned}$$

(2.29)

where $M_2$ is some positive constant. The integral in the fourth line of (2.29) is a definite integral, which must be convergent. In the following, it can be shown that the infinite integral in the last line of (2.29) is also convergent. Based on (2.5) and (2.7), we know that

$$\begin{aligned} \left| \varGamma ^\alpha _{2}\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma '_{2}\left( \frac{q}{\omega }\right) \right| =O\left( e^{\frac{(\alpha +\nu +1)\omega _1q}{\omega }}\right) , \ \ \ \text {as} \ \ q\rightarrow +\infty . \end{aligned}$$

If $\frac{(\alpha +\nu +1)\omega _1}{\omega }-1<0$, i.e. $\omega >(\alpha +\nu +1)\omega _1$, $|\varGamma _2(\frac{q}{\omega })|\ge \varepsilon _0>0$ and $|g'(\varGamma _2(\frac{q}{\omega }))|\ge \varepsilon _0>0$, there exists $\beta >1$ such that it follows from (2.5) and (2.7) that

$$\begin{aligned}{} & {} \lim _{q\rightarrow +\infty }q^\beta \cdot \left| \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) \right| e^{-q}\left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}\\= & {} \lim _{q\rightarrow +\infty }q^\beta \cdot O\left( e^{[\frac{(\alpha +\nu +1)\omega _1}{\omega }-1]q}\right) \left[ g^2(a)+\left( \frac{q}{\omega }\right) ^2\right] ^{-n-\frac{5}{4}}\\= & {} 0. \end{aligned}$$

Based on Cauchy’s test, the integral in the last line of (2.29) is also convergent. Therefore, for the integral in the last line of (2.28), we can deduce that

$$\begin{aligned} \int _0^{+\infty }{} & {} \varGamma _{2}^{\alpha }\left( \frac{q}{\omega }\right) f\left[ \varGamma _{2}\left( \frac{q}{\omega }\right) \right] \varGamma _{2}'\left( \frac{q}{\omega }\right) e^{-q} O\left( \left| \omega g(a)+iq\right| ^{-2 n-\frac{5}{2}}\right) d q\nonumber \\{} & {} \quad = O\left( \omega ^{-2 n-\frac{5}{2}}\right) , \ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.30)

Moreover, as $\omega \rightarrow +\infty$, it can be derived that

$$\begin{aligned} \frac{d}{dq} G_{\omega }(q)= & {} -i\sum \limits _{j=0}^{2n+1}\frac{(j+\frac{1}{2})(\frac{1}{2}+m)_j(\frac{1}{2}-m)_j}{j!(2i)^j(\omega g(a)+iq)^{j+\frac{3}{2}}}\\= & {} O(\omega ^{-\frac{3}{2}}). \end{aligned}$$

Similarly, we can obtain

$$\begin{aligned} \frac{d^k}{dq^k}G_\omega (q)=O(\omega ^{-k-\frac{1}{2}}), \ \ \text {as}\ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.31)

Letting $u=\frac{q}{\omega }$ in $F_\omega (\frac{q}{\omega })$, combining (2.5) and (2.7), we have that

$$\begin{aligned} F_\omega (u)= & {} \varGamma ^\alpha _{2}(u)f[\varGamma _{2}(u)]\varGamma '_{2}(u)=O(e^{\frac{(\alpha +\nu +1)\omega _1q}{\omega }}),\ \ \ \text {as} \ \ q\rightarrow +\infty ,\nonumber \\ F'_\omega (u)= & {} \alpha \varGamma _2^{\alpha -1}(u)[\varGamma '_2(u)]^2f(\varGamma _2(u))+\varGamma _2^{\alpha }(u)[\varGamma '_2(u)]^2f'(\varGamma _2(u))\nonumber \\{} & {} +\varGamma _2^{\alpha }(u)\varGamma ''_2(u)f(\varGamma _2(u))\nonumber \\= & {} O(e^{\frac{(\alpha +\nu +1)\omega _1q}{\omega }}),\ \ \ \text {as} \ \ q\rightarrow +\infty ,\nonumber \\ F''_\omega (u)= & {} \alpha (\alpha -1)\varGamma _2^{\alpha -2}(u)[\varGamma '_2(u)]^3f(\varGamma _2(u))+2\alpha \varGamma _2^{\alpha -1}(u)\varGamma '_2(u)\varGamma ''_2(u)f(\varGamma _2(u))\nonumber \\{} & {} +2\alpha \varGamma _2^{\alpha -1}(u)[\varGamma '_2(u)]^3f'(\varGamma _2(u))\nonumber \\{} & {} +\varGamma _2^{\alpha }(u)[\varGamma '_2(u)]^3f''(\varGamma _2(u))+2\varGamma _2^{\alpha }(u)\varGamma '_2(u)\varGamma ''_2(u)f'(\varGamma _2(u))\nonumber \\{} & {} +\alpha \varGamma _2^{\alpha -1}(u)\varGamma '_2(u)\varGamma ''_2(u)f(\varGamma _2(u))\nonumber \\{} & {} +\varGamma _2^{\alpha }(u)\varGamma '_2(u)\varGamma ''_2(u)f'(\varGamma _2(u))+\varGamma _2^{\alpha }(u)\varGamma '''_2(u)f(\varGamma _2(u))\nonumber \\= & {} O(e^{\frac{(\alpha +\nu +1)\omega _1q}{\omega }}),\ \ \ \text {as} \ \ q\rightarrow +\infty ,\nonumber \\ \vdots \nonumber \\ F^{(k)}_\omega (u)={} & {} O(e^{\frac{(\alpha +\nu +1)\omega _1q}{\omega }}),\ \ \ \text {as} \ \ q\rightarrow +\infty , \ \ k=0,1,2,\ldots . \end{aligned}$$

(2.32)

Based on (2.31) and (2.32), using Leibniz’s Theorem [2, p. 12], the integral in the seventh line of (2.28) can be written as

$$\begin{aligned} \int _0^{+\infty }\frac{[F_\omega (\frac{q}{\omega }) G_\omega (q)]^{(2n)}|_{q=\gamma }}{(2n)!}Ln^2(q)e^{-q}dq=\frac{1}{\omega ^{2n+\frac{1}{2}}}\int _0^{+\infty }\frac{R(\gamma )}{(2n)!}Ln^2(q)e^{-q}dq, \end{aligned}$$

where $[F_\omega (\frac{q}{\omega }) G_\omega (q)]^{(2n)}|_{q=\gamma }=\frac{1}{\omega ^{2n+\frac{1}{2}}}R(\gamma )$ and $R(\gamma )$ is a very long function expression of $\gamma$ and is omitted. Using a similar proof of (2.30) and by Cauchy’s test, under these conditions that $|\varGamma _2(\frac{q}{\omega })|\ge \varepsilon _0>0$ and $|g'(\varGamma _2(\frac{q}{\omega }))|\ge \varepsilon _0>0$, for $\omega >(\alpha +\nu +1)\omega _1$, it can be verified from (2.32) that the infinite integral $\int _0^{+\infty }\frac{R(\gamma )}{(2n)!}Ln^2(q)e^{-q}dq$ is also convergent. Hence, it follows that

$$\begin{aligned} \int _0^{+\infty }\frac{[F_\omega (\frac{q}{\omega }) G_\omega (q)]^{(2n)}|_{q=\gamma }}{(2n)!}Ln^2(q)e^{-q}dq=O\left( \frac{1}{\omega ^{2n+\frac{1}{2}}}\right) , \ \ \text {as}\ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.33)

Therefore, from (2.28), (2.30) and (2.33), we have

$$\begin{aligned} I_1[f]-Q_{n,1}[f]=O\left( \omega ^{-2n-\frac{3}{2}}\right) , \ \ \text {as}\ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.34)

In a similar way, we obtain

$$\begin{aligned} I_2[f]-Q_{n,2}[f]=O\left( \omega ^{-2n-\frac{3}{2}}\right) , \ \ \text {as}\ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.35)

Hence, we have the desired results that

$$\begin{aligned} I[f]-Q_n[f]= & {} \frac{1}{2}\left( I_1[f]-Q_{n,1}[f]+I_2[f]-Q_{n,2}[f]\right) \\= & {} O\left( \omega ^{-2n-\frac{3}{2}}\right) , \ \ \text {as}\ \ \omega \rightarrow +\infty . \end{aligned}$$

This completes the proof of (2.25). $\square$

In the following, we will devise a new method and perform its rigorous error analysis for the case that g(x) has zero points.

2.2 Type II: g(x) with Zero Points

In this subsection we are concerned with the case that g(x) has zeros on the integration interval $[a, +\infty )$. For convenience, we consider that g(x) has a single zero point on the interval $[a, +\infty )$, e.g., $g(\xi ) = 0$ where $\xi \in [a, +\infty )$. If g has a finite number of zeros on the interval $[a, +\infty )$, we can divide the whole interval into subintervals, such that the function g contains only a single zero point on each subinterval. The resulting subintervals may include the finite interval, and the integral on the finite interval can be computed in the similar way. Before proceeding, let us explain why the quadrature formula presented in the Sect. 2.1 fails when g has a zero point on $[a, +\infty )$. We see clearly that a simple pole at $x = \xi$ is introduced in the terms $H_m^{(1)}(\omega g(x))$ and $H_m^{(2)}(\omega g(x))$, and thus the complex integration methods in the Sect. 2.1 is no longer valid. To remedy this, we may make a series of transformations such that the resulting integrand has a removable singularity at $x = \xi$.

Here we only consider the case that the single zero point $\xi =a$, i.e., $g(a)=0$. If $\xi \not =a$, we divided the interval into $[a, \xi ]$ and $[\xi , +\infty )$ to ensure the zero point being the endpoint. Since g(x) has no stationary points on $[a, +\infty )$, g(x) is a monotonous function on $[a, +\infty )$. Thus, $t=g(x)$ is a bijection and then has an inverse function $x=g^{-1}(t)$. Assume that $g(x)\rightarrow +\infty$ as $x\rightarrow +\infty$. Setting $g(x)=t$, we rewrite I[f] as

$$\begin{aligned} I[f]=\int _{0}^{+\infty }G_1(t)J_m(\omega t)dt, \end{aligned}$$

(2.36)

where $G_1(t)=[g^{-1}(t)]^\alpha f[g^{-1}(t)][g^{-1}(t)]'$.

Furthermore, the function $G_1(t)$ can be expressed as

$$\begin{aligned} G_1(t)=G_1(t)-\sum ^{R_1}_{j=0}\frac{G_1^{(j)}(0)}{j!}t^j+\sum ^{R_1}_{j=0}\frac{G_1^{(j)}(0)}{j!}t^j, \end{aligned}$$

(2.37)

where

$$R_1 = {\left\{ \begin{array}{ll} [m]+2n-1, &{} m>0,\\ 2n, &{} m=0, \end{array}\right. }$$

and [m] denotes the smallest integer not less than m.

Combining (2.36) with (2.37), we have

$$\begin{aligned} I[f]=\int _{0}^{+\infty }L_1(t)J_m(\omega t)dt +\sum ^{R_1}_{j=0}\frac{G_1^{(j)}(0)}{j!}\int _{0}^{+\infty }t^jJ_m(\omega t)dt, \end{aligned}$$

(2.38)

where $L_1(t)=G_1(t)-\sum ^{R_1}_{j=0}\frac{G_1^{(j)}(0)}{j!}t^j$. And, suppose that $I_{R_1}=\sum ^{R_1}_{j=0}\frac{G_1^{(j)}(0)}{j!}\int _{0}^{+\infty }t^jJ_m (\omega t)dt.$

The integral $I_{R_1}$ can be exactly calculated by the explicit formula

$$\begin{aligned}{} & {} \int _0^{+\infty }t^jJ_m(\omega t)dt\nonumber \\= & {} \int _0^1t^jJ_m(\omega t)dt+\int _1^{+\infty }t^jJ_m(\omega t)dt\nonumber \\= & {} G(\omega ,m,j)+\frac{1}{2}G^{3,0}_{2,4}\left( \begin{array}{ccc}-\frac{j}{2},-\frac{j-1}{2}\\ frac{j+1}{2},-\frac{j}{2},\frac{1}{2}m,-\frac{1}{2}m\end{array}\biggl | \biggr .\frac{1}{4}\omega ^2\right) , \end{aligned}$$

(2.39)

where $G(\omega ,m,j)$ can be expressed by the following formulae (see [14, p. 676], [26, p. 44] and [2, p. 480]), for $\Re (j+m)>-1, \omega >0$,

$$\begin{aligned}{} & {} \int _{0}^{1}x^jJ_m(\omega x)dx =\frac{2^j\varGamma (\frac{m+j+1}{2})}{\nonumber }\\{} & {} {\omega ^{j+1}\varGamma (\frac{m-j+1}{2})} +\frac{1}{\omega ^j}[(j+m+1)J_m(\omega )S_{j-1, m-1}(\omega ) -J_{m-1}(\omega )S_{j, m}(\omega )] \nonumber \\ \end{aligned}$$

(2.40)

$$\begin{aligned}= & {} \frac{\omega ^m}{2^m(j+m+1)(\varGamma (m+1)} \ _1F_2\left( \frac{j+m+1}{2}; \frac{j+m+3}{2}, m+1; -\frac{\omega ^2}{4}\right) \end{aligned}$$

(2.41)

$$\begin{aligned}= & {} \frac{\varGamma (\frac{m+j+1}{2})}{\omega \varGamma (\frac{m-j+1}{2})}\sum ^\infty _{k=0}\frac{(m+2k+1)\varGamma (\frac{m-j+1}{2}+j)}{\varGamma (\frac{m+j+3}{2}+k)}J_{m+2k+1}(\omega ). \end{aligned}$$

(2.42)

Here, $S_{\mu ,\nu }(z),\varGamma (z),{_1F_2}(\mu ;\nu ,\lambda ;z), G^{m,n}_{p,q}$ denote the Lommel function of the second kind, the Gamma function, a class of generalized hypergeometric function, and the Meijer G-function, respectively. Moreover, ${_1F_2}(\mu ;\nu ,\lambda ;z)$ converges for all |z|. From [32, p. 346], $S_{\mu ,\nu }(z)$ can be expressed in terms of ${_1F_2}(\mu ;\nu ,\lambda ;z)$, namely,

$$\begin{aligned} S_{\mu ,\nu }(z)= & {} \frac{z^{\mu +1}}{(\mu +\nu +1)(\mu -\nu +1)}{_1F_2}(1;\frac{\mu -\nu +3}{2},\frac{\mu +\nu +3}{2};-\frac{z^2}{4})\nonumber \\{} & {} -\frac{2^{\mu -1}\varGamma (\frac{\mu +\nu +1}{2})}{\pi \varGamma (\frac{\nu -\mu }{2})}(J_\nu (z)-\cos (\pi (\mu -\nu )/2)Y_\nu (z)), \end{aligned}$$

(2.43)

where $Y_\nu (z)$ is a Bessel function of the second kind of order $\nu$. The efficient implementation of the moments is based on the fast computation of the above-mentioned special functions. Obviously, when programming the proposed algorithm in a language like Matlab, we can calculate the values of $\varGamma (z), J_m(z),Y_m(z)$, ${_1F_2}(\mu ;\nu ,\lambda ;z)$ and $G^{m,n}_{p,q}$ by invoking the built-in functions ‘gamma(z)’, ‘besselj(m, z)’,‘bessely(m, z)’, ‘hypergeom$(\mu , [\nu ,\lambda ], z)$’, ‘meijerG$([a_1,...,a_n],[a_{n+1},...,a_p],[b_1,...,b_m],[b_{m+1},..., b_q], z)$’, respectively.

In the following, we develop the numerical scheme for approximating the integral $I_{L_1}=\int _{0}^{+\infty }L_1(t)J_m(\omega t)dt$. We first give a key result, as follows.

Theorem 2.3

Assume that both g and f are analytic in D. Moreover, g and f satisfy those conditions (2.5)–(2.7). And, g has a single zero point at $x=a$ and $g'(x)\not =0$ on $[a, +\infty )$. Also, $\lim _{x\rightarrow +\infty }g'(x)\ne 0$. Then it is true that

$$\begin{aligned} I_{L_1}= & {} \frac{1}{2}\left[ i\int ^{+\infty }_0L_1(ip)H_m^{(1)}(\omega (ip))e^{-i\omega (ip)}e^{-\omega p}dp\right. \nonumber \\{} & {} \left. -i\int ^{+\infty }_0 L(-ip)H_m^{(2)}(i\omega (-ip))e^{i\omega (-ip)}e^{-\omega p}dp\right] . \end{aligned}$$

(2.44)

Proof

It follows immediately from (2.1) and (2.2) that

$$\begin{aligned} I_{L_1}=\frac{1}{2}\left[ \int _{0}^{+\infty }L_1(t)H_m^{(1)}(\omega t)dt+\int _{0}^{+\infty }L_1(t)H_m^{(2)}(\omega t)dt\right] . \end{aligned}$$

(2.45)

Here, assume that $I_{L_1,1}=\int _{0}^{+\infty }L_1(t)H_m^{(1)}(\omega t)dt$ and $I_{L_1,2}=\int _{0}^{+\infty }L_1(t)H_m^{(2)}(\omega t)dt$.

Moreover, the integral $I_{L_1,1}$ can be expressed as

$$\begin{aligned} I_{L_1,1}=\int _{0}^{+\infty }L_1(t)H_m^{(1)}(\omega t)e^{-i\omega t}e^{i\omega t}dt. \end{aligned}$$

(2.46)

For computing the integral in (2.46), we choose the new path in the complex plane, which is drawn on the left panel of Fig. 2.

Fig. 2

The integration paths for the oscillator $g(t)=t$ in $e^{i\omega t}$ (left figure) and the oscillator $g(t)=-t$ in $e^{-i\omega t}$ (right figure) on the interval $[0, +\infty )$

In Fig. 2, the integration paths are expressed by parametric forms: in the left figure: $\varGamma _2(p)=ip$, $\varGamma _3(\theta )=Ae^{i\theta }$, $p\in [0, A], \theta :\frac{\pi }{2}\rightarrow 0$; in the right figure: $\varLambda _2(p)=-ip$, $\varLambda _3(\theta )=Ae^{i\theta }$, $p\in [0, A], \theta :-\frac{\pi }{2}\rightarrow 0$.

First, we consider the integral $I_{L_1,1}$. By the Cauchy residue theorem (see Fig. 2 (left figure)), we obtain that

$$\begin{aligned} \int _{0}^AL_1(t)H_m^{(1)}(\omega t)e^{-i\omega t}e^{i\omega t}dt= & {} \int _{\varGamma _2}L_1(z)H_m^{(1)}(\omega z)e^{-i\omega z}e^{i\omega z}dz\nonumber \\{} & {} +\int _{\varGamma _3}L_1(z)H_m^{(1)}(\omega z)e^{-i\omega z}e^{i\omega z}dz. \end{aligned}$$

(2.47)

And, by the method which is similar to the proof of Theorem 2.1, we have that

$$\begin{aligned}{} & {} \bigg |\int _{\varGamma _3}L_1(z)H_m^{(1)}(\omega z)e^{-i\omega z}e^{i\omega z}dz\bigg |\\= & {} \bigg |\int ^0_{\frac{\pi }{2}}iAe^{i\theta }L_1(Ae^{i\theta })H_m^{(1)}(\omega (Ae^{i\theta }))e^{-i\omega (Ae^{i\theta }))}e^{i\omega (Ae^{i\theta }))}d\theta \bigg |\\\le & {} M\int _0^{\frac{\pi }{2}}\big |\sqrt{\frac{A}{\omega }} L_1(Ae^{i\theta })e^{-\omega A\sin \theta }\big |d\theta \\\rightarrow & {} 0, \ \ \text {as}\ \ A \rightarrow +\infty . \end{aligned}$$

Therefore, by letting $A \rightarrow +\infty$ in (2.47), we have

$$\begin{aligned} I_{L_1,1}=i\int ^{+\infty }_0L_1(ip)H_m^{(1)}(\omega (ip))e^{-i\omega (ip)}e^{-\omega p}dp. \end{aligned}$$

(2.48)

Similarly, from Fig. 2 (right figure), we can obtain

$$\begin{aligned} I_{L_1,2}=-i\int ^{+\infty }_0 L_1(-ip)H_m^{(2)}(i\omega (-ip))e^{i\omega (-ip)}e^{-\omega p}dp. \end{aligned}$$

(2.49)

Combining (2.45), (2.48) and (2.49), we can get the result (2.44). So we complete this proof. $\square$

Letting $q=\omega p$ in (2.48) and (2.49), we can get

$$\begin{aligned} I_{L_1,1}=\frac{i}{\omega }\int ^{+\infty }_0L_1\left( i\frac{q}{\omega }\right) H_m^{(1)}\left( \omega \left( i\frac{q}{\omega }\right) \right) e^{-i\omega \left( i\frac{q}{\omega }\right) }e^{-q}dq, \end{aligned}$$

(2.50)

and

$$\begin{aligned} I_{L_1,2}=-\frac{i}{\omega }\int ^{+\infty }_0 L_1\left( -i\frac{q}{\omega }\right) H_m^{(2)}\left( i\omega \left( -i\frac{q}{\omega }\right) \right) e^{i\omega \left( -i\frac{q}{\omega }\right) }e^{-q}dq. \end{aligned}$$

(2.51)

By using n-point Gauss–Laguerre quadrature rules for (2.50) and (2.51), together with the Eq. (2.45), the integral $I_{L_1}$ can be calculated by the following formula

$$\begin{aligned} Q_{L_1, n}= & {} \frac{1}{2}\left[ \frac{i}{\omega }\sum \limits _{k=1}^n a_k L\left( i\frac{x_k}{\omega }\right) H_m^{(1)}\left( \omega \left( i\frac{x_k}{\omega }\right) \right) e^{-i\omega \left( i\frac{x_k}{\omega }\right) }\right. \nonumber \\{} & {} -\left. \frac{i}{\omega } \sum \limits _{k=1}^n a_k L_1\left( -i\frac{x_k}{\omega }\right) H_m^{(2)}\left( i\omega \left( -i\frac{x_k}{\omega }\right) \right) e^{i\omega \left( -i\frac{x_k}{\omega }\right) }\right] . \end{aligned}$$

(2.52)

Thus, the integral (1.1) can be approximately evaluated by

$$\begin{aligned} Q_n[f]=Q_{L_1, n}+I_{R_1}. \end{aligned}$$

(2.53)

We shall give its error analysis as follows.

Theorem 2.4

Under the assumption conditions of Theorem 2.3, the error of the quadrature formula (2.53) behaves asymptotically as

$$\begin{aligned} I[f]-Q_n[f]=O\left( \omega ^{-2n-\frac{3}{2}}\right) , \ \ \ \omega \rightarrow +\infty . \end{aligned}$$

(2.54)

Proof

It follows that

$$\begin{aligned}{} & {} \bigg |I[f]-Q_n[f]\bigg |\\= & {} \bigg |I_{L_1,1}-Q_{L_1, n}\bigg |\\= & {} \Bigg |\frac{1}{2}\left[ \frac{i}{\omega }\int ^{+\infty }_0 L_1(i\frac{q}{\omega })H_m^{(1)}(\omega (i\frac{q}{\omega }))e^{-i\omega (i\frac{q}{\omega })}e^{-q}dq\right. \\{} & {} \left. -\frac{i}{\omega } \int ^{+\infty }_0 L_1(-i\frac{q}{\omega })H_m^{(2)}(i\omega (-i\frac{q}{\omega }))e^{i\omega (-i\frac{q}{\omega })}e^{-q}dq\right] \\{} & {} -\frac{1}{2}\left[ \frac{i}{\omega }\sum \limits _{k=1}^n a_k L_1(i\frac{x_k}{\omega })H_m^{(1)}(\omega (i\frac{x_k}{\omega }))e^{-i\omega (i\frac{x_k}{\omega })} \right. \\{} & {} \left. -\frac{i}{\omega } \sum \limits _{k=1}^n a_k L_1(-i\frac{x_k}{\omega })H_m^{(2)}(i\omega (-i\frac{x_k}{\omega }))e^{i\omega (-i\frac{x_k}{\omega })}\right] \Bigg |. \end{aligned}$$

It follows from [2, p. 360] that

$$\begin{aligned}{} & {} H_m^{(1)}(z) \sim {\left\{ \begin{array}{ll} z^{-m}, &{} m>0,\\ \ln (z) &{} m=0, \end{array}\right. } \end{aligned}$$

(2.55)

$$\begin{aligned}{} & {} H_m^{(2)}(z) \sim {\left\{ \begin{array}{ll} z^{-m}, &{} m>0,\\ \ln (z) &{} m=0, \end{array}\right. } \end{aligned}$$

(2.56)

as $|z|\rightarrow 0$.

Since $L_1(t)=O(t^{R_1+1})$, based on (2.55), (2.56), by using Leibniz’s Theorem [2, p. 12] and the similar proof of Theorem 2.2, we have

$$\bigg |I[f]-Q_n[f]\bigg |=O\left( \omega ^{-2n-\frac{3}{2}}\right) ,$$

as $\omega \rightarrow +\infty$. Hence, the desired results (2.54) can be obtained. $\square$

3 Numerical Evaluation for the Case of Stationary Points

When $g'(\zeta )=0$, $\zeta \in [a, +\infty )$, we call $x=\zeta$ as a stationary point. Further, we consider $x=\zeta$ as a stationary point of order r if $g^{(j)}(\zeta )=0, j = 1, 2, \ldots , r$ and $g^{(r+1)}(\zeta )\not = 0$, where $r \ge 1$. In this section, we put our attention to the case that g(x) has only one stationary point of order r at $x = \zeta \in [a, +\infty )$, i.e., $g'(x)\not = 0$ for $x \in [a, +\infty )\backslash \{\zeta \}$, and $\lim _{x\rightarrow +\infty }g'(x)\ne 0$. We also assume that $g(x)\not = 0$ for $x \in [a, +\infty )\backslash \{\zeta \}$. The stationary point can be classified into the following two types:

$$\begin{aligned}{} & {} \text {Type I}: g(\zeta ) = 0.\\{} & {} \text {Type II}: g(\zeta )\not = 0. \end{aligned}$$

3.1 $\text {Type I}: g(\zeta ) = 0$

Here we commence our analysis for the former case, i.e., $x = \zeta$ is a stationary point of $\text {Type I}$. If $\zeta \in (a, +\infty )$, we shall divide the integral interval into two subintervals $[a, \zeta ]$ and $[\zeta , +\infty )$ to ensure that the inverse function of g exists uniquely in any subinterval. And the integral on $[a, \zeta ]$ can be computed in a similar way. To simplify this procedure, without loss of generality, we assume that $\zeta =a$.

Assume that $g(x)\rightarrow +\infty$ as $x\rightarrow +\infty$. With the help of a diffeomorphic transformation $g(x)=(t-a)^{r+1}$, we rewrite (1.1) as

$$\begin{aligned} I[f]=\int _a^{+\infty } G_2(t)J_m(\omega (t-a)^{r+1})dt, \end{aligned}$$

(3.1)

where $G_2(t)=[g^{-1}((t-a)^{r+1})]^\alpha f[g^{-1}((t-a)^{r+1})][g^{-1}((t-a)^{r+1})]'$. And, the function $(t-a)^{r+1}$ is well-defined on $[a, +\infty )$.

Set

$$\begin{aligned} L_2(t)=G_2(t)-\sum ^{R_2}_{j=0}\frac{G_1^{(j)}(a)}{j!}(t-a)^j, \end{aligned}$$

where

$$\begin{aligned} R_2= {\left\{ \begin{array}{ll} [m(r+1)]+2n-1, &{} m>0,\\ 2n, &{} m=0, \end{array}\right. } \end{aligned}$$

and $[m(r+1)]$ denotes the smallest integer not less than $m(r+1)$. Furthermore, the expression (3.1) can be rewritten as

$$\begin{aligned} I[f]= & {} \int _a^{+\infty } L_2(t)J_m(\omega (t-a)^{r+1})dt\nonumber \\ {}{} & {} +\sum ^{R_2}_{j=0}\frac{G_2^{(j)}(a)}{j!}\int _{a}^{+\infty }(t-a)^jJ_m(\omega (t-a)^{r+1})dt. \end{aligned}$$

(3.2)

Suppose that $I_{R_2}=\sum ^{R_2}_{j=0}\frac{G_2^{(j)}(a)}{j!}\int _{a}^{+\infty }(t-a)^jJ_m(\omega (t-a)^{r+1})dt$. And the generalized moments $\int _{a}^{+\infty }(t-a)^jJ_m(\omega (t-a)^{r+1})dt$ can be transformed into the following form

$$\begin{aligned}{} & {} \int _{a}^{+\infty }(t-a)^jJ_m(\omega (t-a)^{r+1})dt\\= & {} \int _0^{+\infty } y^jJ_m(\omega y^{r+1})dy\\= & {} \frac{1}{r+1} \int _0^{+\infty } z^{\frac{j-r}{r+1}}J_m(\omega z)dz\\= & {} \frac{1}{r+1}\left[ \int _0^1 z^{\frac{j-r}{r+1}}J_m(\omega z)dz+\int _1^{+\infty } z^{\frac{j-r}{r+1}}J_m(\omega z)dz\right] , \end{aligned}$$

which can be exactly computed by (2.39)–(2.42).

Now we begin to develop the quadrature rule for the integral $I_{L_2}=\int _a^{+\infty } L_2(t)J_m(\omega (t-a)^{r+1})dt$. We first give an useful result, as follows.

Theorem 3.1

Suppose that both g and f are analytic in D, g and f satisfy those conditions (2.5)–(2.7), and g has a stationary point of Type I and of order r at $x=a$. Moreover, if we assume that $g(x)\not =0, g'(x)\not =0$ for $x\in (a, +\infty )$, and $\lim _{x\rightarrow +\infty }g'(x)\ne 0$, then it is true that

$$\begin{aligned} I_{L_2}= & {} \frac{1}{2}\left[ \int _0^{+\infty } L_2[\varGamma (p)]H_m^{(1)}[\omega (ip)]e^{-i\omega (ip)}\varGamma '(p)e^{-\omega p}dp\right. \nonumber \\{} & {} \left. +\int _0^{+\infty } L_2[\varLambda (p)]H_m^{(2)}[\omega (-ip)]e^{i\omega (-ip)}\varLambda '(p)e^{-\omega p}dp\right] , \end{aligned}$$

(3.3)

where $\varGamma (p)=a+\root r+1 \of {ip}$ and $\varLambda (p)=a+\root r+1 \of {-ip}$, $p\in [0, +\infty )$.

Proof

From (2.1) and (2.2), we have

$$\begin{aligned} I_{L_2}=\frac{1}{2}\left[ \int _a^{+\infty } L_2(t)H_m^{(1)}(\omega (t-a)^{r+1})dt+\int _a^{+\infty } L_2(t)H_m^{(2)}(\omega (t-a)^{r+1})dt\right] ,\nonumber \\ \end{aligned}$$

(3.4)

where we denote $I_{L_2,1}=\int _a^{+\infty } L_2(t)H_m^{(1)}(\omega (t-a)^{r+1})dt$ and $I_{L_2,2}=\int _a^{+\infty } L_2(t)H_m^{(2)}(\omega (t-a)^{r+1})dt$. Then we apply the method in Theorem 2.1 to $I_{L_2,1}$ and $I_{L_2,2}$, respectively.

For the computation of $I_{L_2,1}$, we choose the optimal integral path that

$$\begin{aligned} \varGamma (p)=a+\root r+1 \of {ip}, \ \ p\in [0, P]. \end{aligned}$$

From Theorem 2.1 and by letting $P\rightarrow \infty$, similarly, we have that

$$\begin{aligned} I_{L_2,1}=\int _0^{+\infty } L_2[\varGamma (p)]H_m^{(1)}[\omega (ip)]e^{-i\omega (ip)}\varGamma '(p)e^{-\omega p}dp. \end{aligned}$$

(3.5)

For the computation of $I_{L_2,2}$, we choose the optimal integral path that

$$\varLambda (p)=a+\root r+1 \of {-ip}, \ \ p\in [0, P].$$

Following Theorem 2.1 and by letting $P\rightarrow +\infty$, similarly, we obtain that

$$\begin{aligned} I_{L_2,2}=\int _0^{+\infty } L_2[\varLambda (p)]H_m^{(2)}[\omega (-ip)]e^{i\omega (-ip)}\varLambda '(p)e^{-\omega p}dp. \end{aligned}$$

(3.6)

Combining the Eqs. (3.4), (3.5) and (3.6), the desired result (3.3) can be obtained. Thus, we complete the proof. $\square$

By setting $q=\omega p$ in (3.5), it is not difficult to get

$$\begin{aligned} I_{L_2,1}=\frac{1}{\omega }\int _0^{+\infty } L_2[\varGamma (\frac{q}{\omega })]H_m^{(1)}[\omega (i\frac{q}{\omega })]e^{-i\omega (i\frac{q}{\omega })}\varGamma '(\frac{q}{\omega })e^{-q}dq. \end{aligned}$$

(3.7)

In (3.7), $\varGamma '(\frac{q}{\omega })$ has a singularity of the form $q^{\beta }$ as $q\rightarrow 0$, where $\beta =\frac{1}{r+1}-1$, since $\varGamma (p)=a+\root r+1 \of {ip}$. Fortunately, these types of singularities can be handled efficiently by the generalized Gauss–Laguerre quadrature. Generalized Laguerre polynomials are orthogonal with respect to the weight function $x^\beta e^{-x}, \beta > -1$ [12]. Then the integral (3.7) can be rewritten as

$$\begin{aligned} I_{L_2,1}=\frac{1}{\omega }\int _0^{+\infty } L_2[\varGamma (\frac{q}{\omega })]H_m^{(1)}[\omega (i\frac{q}{\omega })]e^{-i\omega (i\frac{q}{\omega })}\varGamma '(\frac{q}{\omega })q^{-\beta }q^{\beta }e^{-q}dq. \end{aligned}$$

(3.8)

Therefore, we can use the generalized Gauss–Laguerre quadrature rule with n points $t_k$ and weights $c_k, k=1, 2, \ldots , n$, for computing the integral (3.8). Then the desired quadrature formula of $I_{L_2,1}$ is as follows,

$$\begin{aligned} Q_{L_2, n, 1}=\frac{1}{\omega }\sum \limits _{k=1}^n c_k L_2[\varGamma (\frac{t_k}{\omega })]H_m^{(1)}[\omega (i\frac{t_k}{\omega })]e^{-i\omega (i\frac{t_k}{\omega })}\varGamma '(\frac{t_k}{\omega })t_k^{-\beta }. \end{aligned}$$

(3.9)

By setting $q=\omega p$ in (3.6), it follows immediately that

$$\begin{aligned} I_{L_2, 2}= & {} \frac{1}{\omega }\int _0^{+\infty } L_2[\varLambda (\frac{q}{\omega })]H_m^{(2)}[\omega (-i\frac{q}{\omega })]e^{i\omega (-i\frac{q}{\omega })}\varLambda '(\frac{q}{\omega })e^{-q}dq. \end{aligned}$$

(3.10)

By the similar process with the derivation of (3.8) and (3.9), we can get the quadrature formula for $I_{L_2,2}$,

$$\begin{aligned} Q_{L_2, n, 2}= & {} \frac{1}{\omega }\sum \limits _{k=1}^n c_k L_2[\varLambda (\frac{t_k}{\omega })]H_m^{(2)}[\omega (-i\frac{t_k}{\omega })]e^{i\omega (-i\frac{t_k}{\omega })}\varLambda '(\frac{t_k}{\omega })t_k^{-\beta }. \end{aligned}$$

(3.11)

Combining (3.2) and (3.4), we finally obtain the n-point quadrature formula for the integral (1.1),

$$\begin{aligned} Q_n[f]=\frac{1}{2}(Q_{L_2, n, 1}+Q_{L_2, n, 2})+I_{R_2}. \end{aligned}$$

(3.12)

In the following portion, we will show the error analysis for the quadrature formula (3.12).

Theorem 3.2

Under the assumption conditions of Theorem 3.1, the error of the quadrature formula (3.12) behaves asymptotically as

$$\begin{aligned} I[f]-Q_n[f]=O\left( \omega ^{-2n-\frac{3}{2}-\beta }\right) , \ \ \omega \rightarrow +\infty , \end{aligned}$$

(3.13)

where $\beta =\frac{1}{r+1}-1$.

Proof

It follows that

$$\begin{aligned}{} & {} I_{L_2, 1}-Q_{L_2, n,1}\nonumber \\= & {} \frac{1}{\omega }\int _0^{+\infty } L_2[\varGamma (\frac{q}{\omega })]H_m^{(1)}[\omega (i\frac{q}{\omega })]e^{-i\omega (i\frac{q}{\omega })}\varGamma '(\frac{q}{\omega })q^{-\beta }q^{\beta }e^{-q}dq\nonumber \\{} & {} -\frac{1}{\omega }\sum \limits _{k=1}^n c_k L_2[\varGamma (\frac{t_k}{\omega })]H_m^{(1)}[\omega (i\frac{t_k}{\omega })]e^{-i\omega (i\frac{t_k}{\omega })}\varGamma '(\frac{t_k}{\omega })t_k^{-\beta }. \end{aligned}$$

(3.14)

Since $L_2(t)=O(t^{R_2+1})$, by using the Leibniz’s Theorem [2, p. 12] and the similar proof of Theorem 2.2, it follows from (2.55), (2.56) and (3.14) that $I_{L_2, 1}-Q_{L_2, n,1}=O(\omega ^{-2n-\frac{3}{2}-\beta })$. We can also easily obtain that $I_{L_2, 2}-Q_{L_2, n, 2}=O(\omega ^{-2n-\frac{3}{2}-\beta })$ by using the same procedure. So we have

$$\begin{aligned} I[f]-Q_n[f]= & {} \frac{1}{2}(I_{L_2, 1}-Q_{L_2, n,1}+I_{L_2, 2}-Q_{L_2, n,2})\\= & {} O\left( \omega ^{-2n-\frac{3}{2}-\beta }\right) . \end{aligned}$$

Hence, the error is asymptotically of the order $O\left( \omega ^{-2n-\frac{3}{2}-\beta }\right)$. We complete this proof. $\square$

In the following, we shall present and analyze the numerical integration method of Type II, i.e., $g(\zeta ) \not = 0$.

3.2 $Type II: g(\zeta ) \not = 0$

Similarly, if $\zeta \in (a, +\infty )$, we shall divide the integral interval into two subintervals $[a, \zeta ]$ and $[\zeta , +\infty )$ to ensure that the inverse of g exists uniquely in any subinterval. In order to simplify our analysis process, without loss of generality, we assume that $\zeta =a$. Since $g(\zeta ) \not = 0$, i.e., g has no zero in $[a, +\infty )$, the function $H_m^{(1)}(\omega g(x))$ and $H_m^{(2)}(\omega g(x))$ always satisfy the conditions (2.12) and (2.13) on $[a, +\infty )$, respectively.

Based on (2.1) and (2.2), we have

$$\begin{aligned} I[f]=\frac{1}{2}\left[ \int _a^{+\infty } f(x)H_m^{(1)}(\omega g(x))dx+\int _a^{+\infty } f(x)H_m^{(2)}(\omega g(x))dx\right] . \end{aligned}$$

(3.15)

Here we give the notation that $I_1[f]=\int _a^{+\infty } f(x)H_m^{(1)}(\omega g(x))dx$ and $I_2[f]=\int _a^{+\infty } f(x)H_m^{(2)}(\omega g(x))dx$. By analogy with (2.20), we obtain that

$$\begin{aligned} I_1[f]= & {} \frac{e^{i\omega g(a)}}{\omega }\int _0^{+\infty } \varGamma ^\alpha _{2}(\frac{q}{\omega })f\left[ \varGamma _{2}(\frac{q}{\omega })\right] H_m^{(1)}\left[ \omega (g(a)+i\frac{q}{\omega })\right] \nonumber \\{} & {} \times \quad e^{-i\omega (g(a)+i\frac{q}{\omega })}\varGamma '_{2}(\frac{q}{\omega })e^{-q}dq. \end{aligned}$$

(3.16)

We now rewrite the Taylor series of g as

$$\begin{aligned} g(x)=g(a)+g^{(r+1)}(a)\frac{(x-a)^{r+1}}{(r+1)!}+O((x-a)^{r+2}), \end{aligned}$$

since $g^{(j)}(a)=0, j=1, 2, \ldots , r$. The path $\varGamma _2(p)=g^{-1}(g(a)+ip)$ solves $g(\varGamma _2(p))=g(a)+ip$, and thus it leads to the fact that

$$\begin{aligned} \varGamma _2(p)\sim a+\root r+1 \of {\frac{ip(r+1)!}{g^{(r+1)}(a)}}. \end{aligned}$$

(3.17)

This suggests immediately that

$$\begin{aligned} \varGamma '_2(p)=O(p^{\beta }), \beta =\frac{1}{r+1}-1, \ \ p\rightarrow 0. \end{aligned}$$

(3.18)

In (3.16), $\varGamma '_{2}(\frac{q}{\omega })=O(q^{\beta })$, identical to (3.8). Similarly, we can obtain the quadrature formula for the integral $I_1[f]$, as follows,

$$\begin{aligned} Q_{n,1}[f]= & {} \frac{e^{i\omega g(a)}}{\omega }\sum \limits _{k=1}^n c_k \varGamma ^\alpha _{2}(\frac{t_k}{\omega })f[\varGamma _{2}(\frac{t_k}{\omega })]\nonumber \\ {}{} & {} H_m^{(1)}\left[ \omega \left( g(a)+i\frac{t_k}{\omega }\right) \right] e^{-i\omega \left( g(a)+i\frac{t_k}{\omega }\right) }\varGamma '_{2}\left( \frac{t_k}{\omega }\right) t_k^{-\beta }. \end{aligned}$$

(3.19)

By the same process, we can derive the approximation of $I_2[f]$,

$$\begin{aligned} Q_{n,2}[f]= & {} \frac{e^{-i\omega g(a)}}{\omega }\sum _{k=1}^n c_k \varLambda ^\alpha _{2}f[\varLambda _{2}(\frac{t_k}{\omega })]H_m^{(2)}[\omega (g(a)-i\frac{t_k}{\omega })]\nonumber \\{} & {} \times \quad e^{i\omega (g(a)-i\frac{t_k}{\omega })}\varLambda '_{2}(\frac{t_k}{\omega })x_k^{-\beta }. \end{aligned}$$

(3.20)

Therefore, we get the n-point quadrature rule for the considered integral I[f] that

$$\begin{aligned} Q_n[f]=\frac{1}{2}(Q_{n,1}[f]+Q_{n,2}[f]). \end{aligned}$$

(3.21)

The error estimate of (3.21) will be given as follows.

Theorem 3.3

Suppose that both g and f are analytic in D, and g has a stationary point of Type II and of order r at $x=a$. Also, g and f satisfy those conditions (2.5)–(2.7). Moreover, if we suppose that $g'(x)\not =0$ for $x\in (a, +\infty ), \lim _{x\rightarrow +\infty }g'(x)\not =0$ and $g(x)\not =0$ on $[a, +\infty )$, then the error of the quadrature formula (3.21) behaves asymptotically as

$$\begin{aligned} I[f]-Q_n[f]=O\left( \omega ^{-2n-\frac{3}{2}-\beta }\right) , \ \ \omega \rightarrow +\infty , \end{aligned}$$

(3.22)

where $\beta =\frac{1}{r+1}-1$.

The proof is similar to that of Theorem 3.2 and hence it is omitted here.

4 Numerical Experiments

In this section, we test some numerical examples to demonstrate the quality of the evaluations obtained by the proposed quadrature rules. In the following figures, “ E ” denotes the absolute error produced by the numerical methods.

4.1 The Case Without Stationary Points: Type I: $g(x)\ne 0$ for $x\in [a,+\infty )$

Example 1

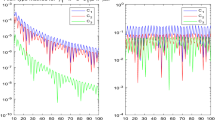
Let us consider the evaluation of $\int _1^{+\infty } x^{-4}\sin {\frac{1}{x}}J_2(\omega x)dx$ by $Q_n[f]$ derived in (2.24) and numerical results are shown in Fig. 3.

Fig. 3

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}}$ (right figure) of the integral $\int _1^{+\infty } x^{-4}\sin {\frac{1}{x}}J_2(\omega x)dx$ with $n=2, 3, 4$, respectively

Example 2

We focus on the computation of $\int _1^{+\infty } x^{-2}e^{-x}J_1(\omega x^2)dx$ by $Q_n[f]$ derived in (2.24) and numerical results are shown in Fig. 4.

Fig. 4

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}}$ (right figure) of the integral $\int _1^{+\infty } x^{-2}e^{-x}J_1(\omega x^2)dx$ with $n=2, 3, 4$, respectively

The numerical results of the quadrature rule (2.24) are illustrated in Figs. 3 and 4. On the left panel of the two figures, we can see that the presented method has the advantageous property that its accuracy improves when the frequency $\omega$ increases for fixed nodes n. At the same time, it is obvious that the precision can improve significantly by adding more nodes for fixed $\omega$. Particularly, only using a few nodes, such as $n=2, 3, 4$, the desired accuracy level can be achieved. On the right panel of the two figures, we illustrate the absolute error scaled by $\omega ^{2n+\frac{3}{2}}$, which can verify the asymptotic error order shown in Theorem 2.2.

4.2 The Case Without Stationary Points: Type II: g(x) Having Zeros on $x\in [a,+\infty )$

Example 3

We consider the computation of $\int _1^{+\infty } x^{-1}\sin {\frac{1}{x}}J_1(\omega (x-1))dx$ by $Q_n[f]$ derived in (2.53) and numerical results are shown in Fig. 5.

Fig. 5

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}}$ (right figure) of the integral $\int _1^{+\infty } x^{-1}\sin {\frac{1}{x}}J_1(\omega (x-1))dx$ with $R_1=2n+[m]-1, n=2, 3, 4$, respectively

Example 4

Let us focus on the approximation of $\int _1^{+\infty } x^{-\frac{1}{2}}\frac{1}{1+x}J_{\frac{1}{3}}(\omega (2x^2-2x))dx$ by $Q_n[f]$ derived in (2.53) and numerical results are shown in Fig. 6.

Fig. 6

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}}$ (right figure) of the integral $\int _1^{+\infty } x^{-\frac{1}{2}}\frac{1}{1+x}J_{\frac{1}{3}}(\omega (2x^2-2x))dx$ with $R_1=2n+[m]-1, n=2, 3, 4$, respectively

It is clear from Examples 3 and 4 that the presented method exhibits the fast convergence as shown on the left panel of Figs. 5 and 6. On one hand, the accuracy improves greatly as $\omega$ increases for fixed n. On the other hand, the accuracy improves as the number of nodes n increases for fixed $\omega$. Furthermore, the decay rate of the absolute error satisfies $O(\omega ^{-2n-\frac{3}{2}})$ while letting $R_1=2n+[m]-1$, which can confirm our error analysis shown in Theorem 2.4. As expected, for fixed nodes n, the precision of $Q_{n}[f]$ improves as $\omega$ increases.

4.3 The Case with Stationary Points: Type I: $g(\zeta )=0$

Example 5

We consider the calculation of $\int _1^{+\infty } x^{-3}\frac{1}{1+x^3}J_5(\omega (x-1)^2)dx$ by $Q_n[f]$ derived in (3.12) and numerical results are shown in Fig. 7.

Fig. 7

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}+\beta }$ (right figure) of the integral $\int _1^\infty x^{-3}\frac{1}{1+x^3}J_5(\omega (x-1)^2)dx$ for $n=2,3,4, r=1, R_2=2n+[m(r+1)]-1, \beta =-\frac{1}{2}$

Example 6

We focus on the computation of $\int _1^{+\infty } x^{-2}\sin {\frac{1}{x}}J_{\pi }(\omega (x-1)^3)dx$ by $Q_n[f]$ derived in (3.12) and numerical results are shown in Fig. 8.

Fig. 8

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}+\beta }$ (right figure) of the integral $\int _1^{+\infty } x^{-2}\sin {\frac{1}{x}}J_{\pi }(\omega (x-1)^3)dx$ with $n=1,2,3, r=2, R_2=2n+[m(r+1)]-1, \beta =-\frac{2}{3}$

The left figures of Figs. 7 and 8 show that the accuracy of the proposed method improves greatly by adding more node points for fixed frequency $\omega$. Meanwhile, the proposed method for the oscillatory integral of the case that g has zeros can lead to more accurate approximations for increasing $\omega$ with fixed n. Meanwhile, the decay rates of the absolute error shown in Figs. 7 and 8 are consistent with the error analysis in Theorem 3.2 when $R_2=2n+[m(r+1)]-1$.

4.4 The Case with Stationary Points: Type II: $g(\zeta )\not =0$

Example 7

Let us consider the evaluation of $\int _1^{+\infty } x^{-1}xJ_3(\omega ((x-1)^2+1))dx$ by $Q_n[f]$ derived in (3.21) and numerical results are shown in Fig. 9.

Fig. 9

The base-10 logarithm of the absolute error (left figure) and absolute error scaled by $\omega ^{2n+\frac{3}{2}+\beta }$ (right figure) of the integral $\int _1^{+\infty } x^{-1}xJ_3(\omega ((x-1)^2+1))dx$ with $n=2, 3, 4$, respectively and $\beta =-\frac{1}{2}$

Obviously, we can see from Fig. 9 that the absolute error improves greatly by either adding more nodes for fixed $\omega$ or increasing $\omega$ for fixed n. Moreover, the error order shown in the right figure of Fig. 9 is $\omega ^{2n+\frac{3}{2}+\beta }$, which is perfectly consistent with the error analysis in Theorem 3.3.

4.5 Comparison with the Modified Filon-Type Method

We make a comparison between the established method and the modified Filon-type method developed in [23] by three tables.

Table 1 Absolute errors of computing the integral $\int _1^{+\infty }x^{-1}\sin {\frac{1}{x^4}}J_{3}(\omega x)dx$ by the proposed quadrature formula (2.24) with $n=3$, and the modified Filon-type method with the nodes $\{-2/3, -1/3, 0, 1/3, 2/3, 1\}$ and multiplicities $\{1, 1, 1, 1, 1, 1\}$ for $\omega =20, 40, 80, 160$

Table 2 Absolute errors of evaluation the integral $\int _1^{+\infty }x^{-\frac{1}{2}}\frac{1}{1+x^3}J_{1}(\omega \ln {x})dx$ by the proposed quadrature formula (2.53) with $n=2, R_1=[m]+2n-1$, and the modified Filon-type method with the nodes $\{-1/3, 0, 1/3, 1\}$ and multiplicities $\{1, 1, 1, 1\}$ for $\omega =20, 40, 80, 160$

Table 3 Absolute errors of evaluation the integral $\int _1^{+\infty }x^{-2}e^{-x^2}J_{2}(\omega (x-1)^2)dx$ by the proposed quadrature formula (3.12) with $n=3, r=2, R_1=[m(r+1)]+2n-1$, and the modified Filon-type method with the nodes $\{-7/8, -1/2, 0, 1/2, 7/8, 1\}$ and multiplicities $\{1, 1, 1, 1, 1, 1\}$ for $\omega =20, 40, 80, 160$

We can see that from Tables 1, 2 and 3 that the accuracy level of the proposed method is far higher than that of the modified Filon-type method while using the same computational cost. However, the function f in the proposed method is required to be analytic in a simply connected complex region that contains the interval $[a, +\infty )$. The Filon-type method can relax the analytic condition and only requires the function f to be continuous on $[a, +\infty )$. Thus, the two different methods have their own advantages and disadvantages, and we can choose the appropriate approach in different situation.

5 Conclusion

In this work, we propose and analyze an efficient numerical approximation method for the oscillatory infinite Bessel transforms with general oscillators. Thanks to the relations (2.1) and (2.2) between Bessel functions and Hankel functions, the asymptotic formulae (2.3) and (2.4) of the Hankel functions, and the Taylor expansions, the considered integral (1.1) can be transformed into the tractable transforms. Then the two integrals on the interval $[0, +\infty )$ can be obtained by converting the original integration path to the complex plane. Finally, the regular or generalized Gauss–Laguerre quadrature rules can be used for calculating the two resulting integrals. In particular, we establish a series of new quadrature rules for this transform and carry out rigorous analysis, including the cases that the oscillator g(x) has zeros and stationary points. Furthermore, compared with the modified Filon-type method, the established method can achieve the higher accuracy and the decay rate of the error is faster under the given conditions.