Balanced-Norm and Energy-Norm Error Analyses for a Backward Euler/FEM Solving a Singularly Perturbed Parabolic Reaction-Diffusion Problem

Abstract

In the derivation of error bounds, uniformly in the singular perturbation parameter $\varepsilon$, for finite element methods (FEMs) applied to elliptic singularly perturbed linear reaction-diffusion problems, the usual energy norm is unsatisfactory since it is essentially no stronger than the $L^2$ norm. Consequently various researchers have analysed errors in FEM solutions, uniformly in $\varepsilon$, using balanced norms whose $H^1$ component is weighted correctly to maintain its influence. But the derivation of energy and balanced-norm error bounds for FEM solutions of singularly perturbed reaction-diffusion problems is confined almost entirely to steady-state elliptic problems — little has been proved for time-dependent parabolic singularly perturbed problems. The present paper addresses this gap in the literature: the backward Euler method in time, combined with a bilinear FEM on a spatial Shishkin mesh, is applied to solve a parabolic singularly perturbed reaction-diffusion problem, and energy-norm and balanced-norm error estimates, which are uniform in the singular perturbation parameter $\varepsilon$, are derived — these results are stronger than any previous results of the same type. Furthermore, numerical experiments demonstrate the sharpness of our error bounds.

1 Introduction

The numerical solution of elliptic singularly perturbed linear reaction-diffusion problems by finite element methods (FEMs) has been extensively researched; see [14, 20, 22]. In particular, the FEM solution of such problems using Shishkin meshes on the unit square in ${\mathbb {R}}^2$ has been well understood for some time; for example, an optimal-order energy-norm error analysis that is uniform in the singular perturbation parameter $\varepsilon$ is given in [16]. But although the energy norm $H^1_e$ (an $\varepsilon$-weighted $H^1$ norm — see Sect. 5) seems a natural choice for FEM error analysis, it was pointed out in [13] that it is scaled incorrectly when the problem is singularly perturbed: typically, its $H^1$ component of the error is dominated by its $L^2$ component, so an energy-norm error bound is in practice only an $L^2$ error bound.

As a consequence, in the last 10 years several papers (see [3, 7, 8, 13, 17,18,19] and their references) have given more sophisticated FEM analyses for elliptic singularly perturbed reaction-diffusion problems, deriving error bounds (uniformly in the singular perturbation parameter) in balanced norms where each component ($H^1$ and $L^2$) of the error has the same order of magnitude for typical solutions. (In Sect. 6 we shall define a balanced norm $\Vert \cdot \Vert _{Bal}$ that fits the problem that we study here.)

Despite these successes with the elliptic singularly perturbed linear reaction-diffusion problem, FEM energy-norm analysis of the corresponding time-dependent parabolic problem has lagged behind. To get a sense of the difficulty that arises in the parabolic problem, consider the error analysis of a semidiscretisation of the classical heat equation $u_t -\Delta u = f$ when it is discretised only in space using a standard FEM. In [23, Theorem 1.2] the $L^\infty (L^2)$ error of this method is analysed, and one sees easily that the same argument will work in the singularly perturbed case $u_t -\varepsilon ^2 \Delta u = f$, where $0<\varepsilon \ll 1$ (of course then one has to choose a suitable spatial mesh, such as a Shishkin mesh, to obtain a satisfactory result). A related argument in [23, Theorem 1.3] bounds the $L^\infty (H^1)$ error for the heat equation semidiscretisation — but if one attempts to apply this argument to the singularly perturbed problem to obtain a bound in $H^1_e$, the final error estimate is unsatisfactory because it contains a multiplicative factor $\varepsilon ^{-1}$.

The only papers we know of that give $H^1_e$ error estimates for a FEM applied in space to a singularly perturbed parabolic problem are [5, 10], who consider a convection-diffusion problem. One can modify their analyses by setting the convection term equal to zero to address the reaction-diffusion problem $u_t -\varepsilon ^2 \Delta u + bu= f$, but the bound obtained is only in $L^2(H^1_e)$ instead of the stronger $L^\infty (H^1_e)$ norm. Moreover, as we pointed out earlier, the $\varepsilon$-weighting in the $H^1_e$ norm is unbalanced (i.e., too strong) in the sense of Sect. 6. We do not know of any $L^\infty (H^1_e)$ norm error analysis for a FEM in space for this singularly perturbed problem, nor are we aware of a balanced $L^p(H^1)$ norm error bound for any $p> 1$. (Indeed, the only balanced-norm result appears to be the balanced $L^1(H^1)$ error bound in the preprint [1], which appeared after our paper was submitted for publication, and which unlike our paper uses a discontinuous Galerkin time discretisation.)

The current paper will fill both these gaps in the literature. It presents $L^\infty (H^1_e)$ and $L^\infty (\Vert \cdot \Vert _{Bal})$ error bounds when a spatial FEM is used to solve a parabolic singularly perturbed reaction-diffusion problem. The derivation of these error bounds requires, as one would expect, the introduction of some novel techniques.

We shall consider a singularly perturbed parabolic PDE where the spatial domain $\Omega$ is the unit square in ${\mathbb {R}}^2$. The corresponding steady-state problem has been extensively studied; see [14, 20, 22]. Any typical solution of this class of parabolic problems exhibits boundary layers on all sides of $\Omega$ at all positive times. To solve the problem numerically, we use a uniform mesh in time with backward Euler differencing, and in space a piecewise bilinear FEM on a Shishkin mesh (as is usually done in the steady-state case).

The numerical method is not particularly original, but our error analysis of it is very new — it differs substantially from previous error analyses of singularly perturbed parabolic reaction-diffusion problems. For example, Lemmas 3.1 and 3.2 for the backward Euler scheme are inspired by work on fractional-derivative parabolic problems; these inequalities have the advantage of simplicity but their usefulness in a singularly perturbed context has not previously been recognised. In contrast, the analysis in [1] depends on much deeper results from [6] for the discontinuous Galerkin time discretisation.

Our analysis leads to a $L^\infty (H^1_e)$ error bound in Theorem 5.4, and a $L^\infty (\Vert \cdot \Vert _{Bal})$ error bound in Theorem 6.4, both of which are novel — no analogous results have previously appeared in the literature for any numerical method that uses a FEM in space to solve this parabolic problem — and are of optimal order, as our numerical experiments will show.

The paper is structured as follows. In Sect. 2 we describe the singularly perturbed initial-boundary value problem that we study and the boundary layer behaviour of typical solutions. Some properties of the backward Euler scheme are derived in Sect. 3. The full numerical method (backward Euler in time on a uniform temporal mesh; piecewise bilinear FEM in space on a spatial Shishkin mesh) for solving our initial–boundary value problem is defined in Sect. 4. The energy-norm and balanced-norm error analyses for this method are carried out in Sects. 5 and 6 respectively. Finally, numerical experiments in Sect. 7 confirm the sharpness of our theoretical results.

Notation. We use $\Vert \cdot \Vert$ and $\langle \cdot , \cdot \rangle$ for the norm and inner product in $L^2(\Omega )$, while $\Vert \cdot \Vert _k$ and $\vert \cdot \vert _k$ denote the Sobolev norm and seminorm on $H^k(\Omega )$ for $k=1,2$. The generic constant C is independent of the singular perturbation parameter $\varepsilon$ and of the mesh, so that throughout our analysis any dependence on $\varepsilon$ is stated explicitly.

2 Statement of the Problem

Consider the parabolic singularly perturbed problem

$$\begin{aligned} \frac{\partial u}{\partial t}(x,t) - \varepsilon ^2\Delta u(x,t) + b(x)u(x,t)=f(x,t)\ \text {for} \ (x,t)\in Q:=\Omega \times (0,T], \end{aligned}$$

(2.1)

where $\Omega = (0,1)^2$ and T is a positive constant, with initial condition $u(x,0)=u_0(x)$ for $x= (x_1,x_2)\in \Omega$, and boundary conditions $u(x,t) =0$ for $(x,t)\in \partial \Omega \times (0,T]$. We assume that $u_0 \in C({{\bar{\Omega }}})$ where ${{\bar{\Omega }}} := [0,1]^2$, with $u_0(x)=0$ for $x\in \partial \Omega$. We also assume that f and b are smooth functions (more precise hypotheses will be given later), and without loss of generality we take $b>\beta ^2$ on ${{\bar{\Omega }}}$, where $\beta >0$ is a constant — this can always be achieved by a change of variable of the form $u(x,t)=e^{k t}v(x,t)$ for some suitable constant k.

Error bounds for our numerical method will be derived in two distinct norms: the energy norm of Sect. 5 and the balanced norm of Sect. 6. In these analyses, Sect. 6 requires more regularity of the solution u than Sect. 5.

Set ${{\bar{Q}}} := {{\bar{\Omega }}}\times [0,T]$. We use the Hölder spaces $C^{\beta ,\beta /2}({\bar{Q}})$, with $\beta >0$, that are standard in the analysis of parabolic PDEs. Let $\sigma \in (0,1)$ be arbitrary but fixed. From [12, pp. 319, 320] (see also [2, Section 2] and [21, Section 5.2]), sufficient conditions for $u \in C^{k+\sigma ,(k+\sigma )/2}({\bar{Q}})$ with $k=5$ (needed in Sect. 5) and $k=6$ (needed in Sect. 6) are that $f\in C^{k-2+\sigma ,(k-2+\sigma )/2}({\bar{Q}})$, $b\in C^{k-2+\sigma }({{\bar{\Omega }}})$, and $u_0\in C^{k+\sigma }({{\bar{\Omega }}})$, and that the following compatibility conditions are satisfied: setting ${{\mathcal {L}}}_\varepsilon w := - \varepsilon ^2\Delta w + bw$, for all $x\in \partial \Omega$ one has

$$\begin{aligned}&u_0(x) =0, \end{aligned}$$

(2.2a)

$$\begin{aligned}&-{{\mathcal {L}}}_\varepsilon u_0(x) + f(x,0) =0, \end{aligned}$$

(2.2b)

$$\begin{aligned}&({{\mathcal {L}}}_\varepsilon )^2 u_0(x) -{{\mathcal {L}}}_\varepsilon f(x,0) + \frac{\partial f}{\partial t}(x,0) =0, \end{aligned}$$

(2.2c)

$$\begin{aligned}&-({{\mathcal {L}}}_\varepsilon )^3 u_0(x) + ({{\mathcal {L}}}_\varepsilon )^2 f(x,0) -{{\mathcal {L}}}_\varepsilon \frac{\partial f}{\partial t}(x,0) + \frac{\partial ^2 f}{\partial t^2}(x,0) =0, \end{aligned}$$

(2.2d)

where (2.2a)–(2.2c) are required when $k=5$ and (2.2a)–(2.2d) are required when $k=6$.

Then from [2, Section 2] and [21, Section 5.2], the solution u can be decomposed as $u = U + \sum _{i = 1}^4 v_i + \sum _{i = 1}^4 w_i$, where U is a smooth component, the $v_i$ ($i = 1, 2, 3, 4$) are edge boundary layer functions associated with the four sides of the unit square and the $w_i$ ($i = 1, 2, 3, 4$) are corner layer terms. (This terminology is standard in this research area, although the corner layers are located not at the corners of ${\bar{Q}}$ but along the 4 line segments $(x_1, x_2,t)$ with $(x_1, x_2)$ a corner of ${{\bar{\Omega }}}$ and $0<t\le T$; a similar statement can be made for the edge layers.) Furthermore, these components satisfy the following bounds for all $(x,t)\in Q$ and $k_1+k_2+2k_t\le k$: there exists a constant $C>0$ such that

$$\begin{aligned} \left| \frac{\partial ^{k_1+k_2+k_t} U(x,t)}{\partial x_1^{k_1}\partial x_2^{k_2}\partial t^{k_t}}\right|&\le C, \end{aligned}$$

(2.3a)

$$\begin{aligned} \left| \frac{\partial ^{k_1+k_2+k_t} v_1(x,t)}{\partial x_1^{k_1}\partial x_2^{k_2}\partial t^{k_t}}\right|&\le C\varepsilon ^{-k_1}e^{-\beta x_1/\varepsilon }, \end{aligned}$$

(2.3b)

$$\begin{aligned} \left| \frac{\partial ^{k_1+k_2+k_t} w_1(x,t)}{\partial x_1^{k_1}\partial x_2^{k_2}\partial t^{k_t}}\right|&\le C\varepsilon ^{-k_1-k_2}\min \left\{ e^{-\beta x_1/\varepsilon },\, e^{-\beta x_2/\varepsilon }\right\} , \end{aligned}$$

(2.3c)

with analogous bounds for the other layer terms.

3 Stability of the Backward Euler Scheme

Throughout the paper, we use the uniform temporal mesh $\{t_m := m\tau \}_{m = 0}^M$ where M is a positive integer and $\tau = T/M$. Let $\delta _t$ denote the standard backward Euler operator defined by $\delta _t V^m = \left( V^m-V^{m-1}\right) /\tau$ for each mesh function $\{V^m\}_{m = 0}^M$.

The following lemma is related to [11, Theorem 2.1], which is a stability result for a discretisation of a Caputo fractional derivative.

Lemma 3.1

• (i) Suppose that the mesh function $\{V^m\}_{m = 0}^M$ satisfies $V^0=0$ and $\left| \delta _t V^m\right| \le K$ for $m=1,2,\dots , M$, where $K\ge 0$ is some quantity that is independent of m. Then $\vert V^m\vert \le K m\tau$ for $m=0,1,..., M$.

• (ii) The conclusion of part (i) still holds if the hypothesis $\left| \delta _t V^m\right| \le K$ is replaced by $\delta _t \vert V^m\vert \le K$.

Proof

Part (i): For $m = 1,...,M$, from $\left| \delta _t V^m\right| \le K$ we get $\left| V^m\right| \le \left| V^{m-1}\right| + K\tau$. An easy induction argument using $V^0 = 0$ then gives $\vert V^m\vert \le K m\tau$, as desired.

Part (ii): Like [11, Theorem 2.1], define the mesh function $\{W^m\}_{m = 0}^M$ by $W^0=0$ and $\delta _t W^m = \max \left\{ 0, \delta _t \vert V^m\vert \right\}$ for $m=1,2,\dots , M$. Then $0 \le \vert V^m\vert \le W^m$ for all m since $\delta _t$ is associated with an M-matrix, and the result follows from applying Part (i) to $W^m$. $\square$

The backward Euler scheme also enjoys the following properties (a related inequality for the L1 discretisation of the Caputo fractional derivative is proved in [9, Lemma 4.3]).

Lemma 3.2

Let $v^m\in L^2(\Omega )$ for $m = 0,1,\dots ,M$. Then

$$\begin{aligned} \left\langle \delta _t v^m, v^m\right\rangle \ge \left( \delta _t\left\| v^m\right\| \right) \left\| v^m\right\| \quad \text {and}\quad \left\langle \delta _t v^m, v^m\right\rangle \ge \frac{1}{2}\delta _t\left( \left\| v^m\right\| ^2\right) \end{aligned}$$

for each m.

Proof

The definition of $\delta _t v^m$ and a Cauchy-Schwarz inequality give

$$\begin{aligned} \tau \left\langle \delta _t v^m, v^m\right\rangle = \left\langle v^m - v^{m-1}, v^m\right\rangle \ge \left\| v^m\right\| ^2 - \left\| v^{m-1}\right\| \left\| v^m\right\| = \tau \left( \delta _t \left\| v^m\right\| \right) \Vert v^m\Vert , \end{aligned}$$

which proves the first inequality. For the second inequality, we have similarly

$$\begin{aligned} 2 \tau \left\langle \delta _t v^m, v^m\right\rangle&\ge 2\left\| v^m\right\| ^2 - 2 \left\| v^{m-1}\right\| \left\| v^m\right\| \\&\ge 2\left\| v^m\right\| ^2 - \left\| v^{m-1}\right\| ^2 - \left\| v^m\right\| ^2 = \tau \delta _t\left( \left\| v^m\right\| ^2\right) . \end{aligned}$$

$\square$

In Sect. 5 the first inequality of Lemma 3.2 will be used to bound the $L^2(\Omega )$ norm of the error, while the second inequality will bound its $H^1(\Omega )$ seminorm.

4 The Numerical Method

To discretise (2.1) we use the backward Euler scheme in time, and in space a bilinear FEM on a Shishkin mesh (to deal with the boundary layers in the solution). We now define the Shishkin mesh and the FEM space.

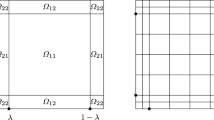
Let N be an even positive integer. Let $\lambda$ be a mesh transition parameter that specifies where the piecewsise-uniform mesh changes from coarse to fine: it is defined by $\lambda = \min \left\{ 1/4,\ 2 \varepsilon \beta ^{-1} \ln N\right\}$. Without loss of generality one can assume that $\varepsilon$ is so small that $\lambda = 2 \varepsilon \beta ^{-1} \ln N$. Divide each of the intervals $[0,\lambda ]$ and $[1-\lambda , 1]$ into N/4 equidistant subintervals and divide $[\lambda , 1-\lambda ]$ into N/2 equidistant subintervals. This gives a 1D Shishkin mesh that is coarse on $[\lambda ,1-\lambda ]$ and fine elsewhere in [0, 1]. Then take a tensor product of two 1D Shishkin meshes to construct the 2D Shishkin mesh on $\Omega$; Fig. 1 displays an example of this mesh for the case $N=8$. (See [22] for further discussion of Shishkin meshes.) Finally, let $V_{h0}\subset H_0^1(\Omega )$ be the piecewise bilinear finite element space defined on the Shishkin mesh $\Omega _h$.

Fig. 1

Shishkin mesh for reaction-diffusion

For any suitable function g, set $g^m(x) = g(x,t_m)$, $\partial g^m(x)/\partial t = \left[ \partial g(x,t)/\partial t\right] \big \vert _{t = t_m}$ and $\delta _t g^m(x) = \left[ g(x,t_m)-g(x,t_{m-1})\right] /\tau$.

Define the $L^2(\Omega )$ projector $P_h: L^2(\Omega )\rightarrow V_{h0}$ by $\langle P_hw, v_h\rangle = \langle w,v_h\rangle$ for all $v_h\in V_{h0}$. Clearly $\Vert P_hw\Vert \le \Vert w\Vert$ for all $w\in L^2(\Omega )$.

Define the Ritz projector ${{\mathcal {R}}}_h: H^1_0(\Omega )\rightarrow V_{h0}$ by

$$\begin{aligned} \varepsilon ^2\left\langle \nabla {{\mathcal {R}}}_h v, \nabla w_h \right\rangle + \left\langle b {{\mathcal {R}}}_h v,w_h\right\rangle = \varepsilon ^2\left\langle \nabla v, \nabla w_h \right\rangle + \left\langle b v, w_h\right\rangle \end{aligned}$$

for all $w_h\in V_{h0}$.

Define the discrete Laplacian $\Delta _h: V_{h0}\rightarrow V_{h0}$ by $\langle \Delta _h v_h, w_h\rangle = - \langle \nabla v_h,\nabla w_h\rangle$ for all $v_h,w_h \in V_{h0}$.

Our numerical method for solving (2.1) is: for $m=1,\ldots ,M$, find $u^m_h := u^m_h(\cdot , t_m) \in V_{h0}$ satisfying

$$\begin{aligned} \left\langle \delta _t u_h^m, v_h\right\rangle + \varepsilon ^2\left\langle \nabla u_h^m,\nabla v_h\right\rangle + \left\langle b u_h^m, v_h\right\rangle = \left\langle f^m,v_h\right\rangle \ \forall v_h\in V_{h0}, \end{aligned}$$

(4.1)

with $u_h^0 := {{\mathcal {R}}}_h u^0$. One can write (4.1) as

$$\begin{aligned} \left\langle \delta _t u_h^m, v_h\right\rangle - \varepsilon ^2\left\langle \Delta _h u_h^m, v_h\right\rangle + \left\langle P_h \left( b u_h^m\right) , v_h\right\rangle = \left\langle P_h f^m,v_h\right\rangle \ \forall v_h\in V_{h0}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \delta _t u_h^m - \varepsilon ^2\Delta _h u_h^m + P_h \left( b u_h^m\right) = P_h f^m, \end{aligned}$$

(4.2)

since each of these terms lies in $V_{h0}$.

5 Energy Norm Error Analysis

We begin our error analysis with some preliminary estimates involving ${{\mathcal {R}}}_h$.

For $i=0,1,2$, set

$$\begin{aligned} \rho _i(x,t) := \frac{\partial ^i \left[ {{\mathcal {R}}}_h u(x,t) - u(x,t)\right] }{\partial t^i} = \left[ {{\mathcal {R}}}_h \left( \frac{\partial ^i u}{\partial t^i}\right) \right] (x,t) - \frac{\partial ^i u(x,t)}{\partial t^i} \end{aligned}$$

(5.1)

since ${{\mathcal {R}}}_h$ acts only in the spatial variables. Also, set $\rho _i^m(x)=\rho _i(x,t_m)$.

Lemma 5.1

Assume that the derivative bounds (2.3) hold true for $k=4$. Then there exist constants C such that for $i=0,1$ and all $t\in (0,T]$, one has

$$\begin{aligned} \varepsilon \left| \rho _i(\cdot , t)\right| _1 + \left\| \rho _i(\cdot , t)\right\|&\le C\left( \varepsilon ^{1/2}N^{-1}\ln N + N^{-2}\right) \end{aligned}$$

(5.2)

and

$$\begin{aligned} \varepsilon ^{1/2}\left| \rho _i(\cdot ,t)\right| _1 + \left\| \rho _i(\cdot ,t)\right\|&\le CN^{-1}\ln N. \end{aligned}$$

(5.3)

If the derivative bounds (2.3) hold true for $k=6$, then (5.2) and (5.3) are also true when $i=2$.

Proof

From its definition, ${{\mathcal {R}}}_h u(\cdot , t)$ is the Galerkin solution of the steady-state problem got by deleting $\partial u/\partial t$ from (2.1) and taking $f= f(\cdot , t)$. Hence in the case $i=0$, one gets (5.2) from an inspection of the proof of [16, Theorem 3.1], while (5.3) follows from the proof of [7, Theorem 2.6]; note that both of these arguments use the bounds (2.3) only for $k_1+k_2\le 2$ and $k_t=0$.

The case $i=1$ is proved in a similar way, replacing u by $\partial u/\partial t$ and using (5.1) and (2.3) for $k_1+k_2\le 2$ and $k_t=1$; and if the derivative bounds (2.3) hold true for $k=6$, then the same argument applied to $\partial ^2 u/\partial t^2$ with $k_1+k_2\le 2$ and $k_t=2$ proves the case $i=2$. $\square$

For $m=1,2,\dots , M$, set $r_1^m := \left( \delta _t - \partial /\partial t\right) {{\mathcal {R}}}_h u^m$.

Lemma 5.2

Assume that the derivative bounds (2.3) hold true for $k=5$. Then there exists a constant C such that $\left\| r_1^m\right\| + \varepsilon \left| r_1^m\right| _1 \le CM^{-1}$ for $m = 1,...,M$.

Proof

The definition of ${{\mathcal {R}}}_h$ implies that for $t\in (0,T]$ one has

$$\begin{aligned} \Vert (\partial /\partial t)^2 {{\mathcal {R}}}_h u(\cdot , t)\Vert + \varepsilon \vert (\partial /\partial t)^2{{\mathcal {R}}}_h u(\cdot , t)\vert _1&= \Vert {{\mathcal {R}}}_h (\partial /\partial t)^2 u(\cdot , t)\Vert + \varepsilon \vert {{\mathcal {R}}}_h (\partial /\partial t)^2u(\cdot , t)\vert _1 \\&\le \Vert (\partial /\partial t)^2 u(\cdot , t)\Vert + \varepsilon \vert (\partial /\partial t)^2 u(\cdot , t)\vert _1 \\&\le C, \end{aligned}$$

where we used $k=5$ in (2.3) to derive the final inequality. The result follows. $\square$

Set $e_h^m:={{\mathcal {R}}}_hu^m-u_h^m$ and

$$\begin{aligned} r^m := \rho ^m_1 + r^m_1 = \frac{\partial \left[ {{\mathcal {R}}}_h u^m - u^m\right] }{\partial t} + \left( \delta _t - \partial /\partial t\right) {{\mathcal {R}}}_h u^m = \delta _t {{\mathcal {R}}}_h u^m - \frac{\partial u^m}{\partial t}. \end{aligned}$$

In the next lemma, we derive some preliminary bounds on $e_h^m(x)$.

Lemma 5.3

There exist constants C such that for $m = 1,...,M$ one has

$$\begin{aligned} \max _{m = 1,...,M}\left\| e_h^m\right\| \le C \max _{m = 1,...,M}\Vert r^m\Vert \end{aligned}$$

(5.4)

and

$$\begin{aligned} \varepsilon \max _{m = 1,...,M}\left| e_h^m \right| _1 \le C \max _{m = 1,...,M}\Vert r^m\Vert . \end{aligned}$$

(5.5)

Proof

The definition of $e_h^m$ and (4.2) give

$$\begin{aligned} \delta _t e_h^m - \varepsilon ^2 \Delta _h e_h^m + P_h \left( b e_h^m\right) = \delta _t {{\mathcal {R}}}_h u^m - \varepsilon ^2 \Delta _h {{\mathcal {R}}}_h u^m + P_h \left( b {{\mathcal {R}}}_h u^m\right) -P_h f^m. \end{aligned}$$

(5.6)

Take $v=u^m$ in the definition of ${{\mathcal {R}}}_h$, then recall the definitions of $\Delta _h$ and $P_h$ to get

$$\begin{aligned} \left\langle -\varepsilon ^2\Delta _h {{\mathcal {R}}}_h u^m + P_h \left( b{{\mathcal {R}}}_h u^m\right) , w_h \right\rangle&=\left\langle -\varepsilon ^2\Delta u^m + b u^m, w_h \right\rangle \\&= \left\langle -\frac{\partial u^m}{\partial t} + f^m, w_h \right\rangle \end{aligned}$$

using (2.1), for all $w_h\in V_{h0}$. Thus $-\varepsilon ^2\Delta _h {{\mathcal {R}}}_h u^m + P_h \left( b{{\mathcal {R}}}_h u^m\right) = P_h\left( -\frac{\partial u^m}{\partial t} + f^m \right)$. Hence (5.6) simplifies to

$$\begin{aligned} \delta _t e_h^m - \varepsilon ^2 \Delta _h e_h^m + P_h \left( b e_h^m\right) = \delta _t {{\mathcal {R}}}_h u^m - P_h\left( \frac{\partial u^m}{\partial t}\right) = P_hr^m. \end{aligned}$$

(5.7)

Invoking the first inequality of Lemma 3.2, we have

$$\begin{aligned} \left( \delta _t\left\| e_h^m\right\| \right) \left\| e_h^m\right\|&\le \left\langle \delta _t e_h^m, e_h^m\right\rangle \\&\le \left\langle \delta _t e_h^m, e_h^m\right\rangle + \varepsilon ^2\left\langle \nabla e_h^m,\nabla e_h^m\right\rangle + \left\langle b e_h^m,e_h^m\right\rangle \\&= \left\langle \delta _t e_h^m, e_h^m\right\rangle - \varepsilon ^2\left\langle \Delta _h e_h^m, e_h^m\right\rangle + \left\langle P_h \left( b e_h^m\right) ,e_h^m\right\rangle \\&= \left\langle P_h r^m, e_h^m\right\rangle \\&\le \Vert P_h r^m\Vert \, \Vert e_h^m\Vert , \end{aligned}$$

where we used (5.7). Thus, either $\Vert e_h^m\Vert =0$ or $\delta _t\left\| e_h^m\right\| \le \Vert P_h r^m\Vert \le \max _{m = 1,...,M}\Vert r^m\Vert$. Now Lemma 3.1 yields (5.4), since one can start its inductive proof at each value of m for which $\Vert e_h^m\Vert =0$ (note that $\Vert e_h^0\Vert =0$).

Invoking the second inequality of Lemma 3.2, we obtain

$$\begin{aligned} \left\| \delta _t e_h^m\right\| ^2 + \frac{1}{2}\varepsilon ^2 \delta _t\left( \left\| \nabla e_h^m\right\| ^2\right)&\le \left\langle \delta _t e_h^m, \delta _t e_h^m\right\rangle + \varepsilon ^2\left\langle \nabla e_h^m, \delta _t\nabla e_h^m\right\rangle \\&= \left\langle \delta _t e_h^m, \delta _t e_h^m\right\rangle - \varepsilon ^2\left\langle \Delta _h e_h^m, \delta _t e_h^m\right\rangle \\&= \left\langle P_h r^m, \delta _t e_h^m\right\rangle - \left\langle P_h \left( b e_h^m\right) ,\delta _t e_h^m\right\rangle \\&\le \frac{1}{2}\left( \Vert P_h r^m\Vert ^2 + \Vert \delta _t e_h^m\Vert ^2 + \Vert P_h \left( b e_h^m\right) \Vert ^2 + \Vert \delta _t e_h^m\Vert ^2 \right) , \end{aligned}$$

where we again used (5.7). Hence

$$\begin{aligned} \varepsilon ^2 \delta _t\left( \left\| \nabla e_h^m\right\| ^2\right)&\le \Vert P_h r^m\Vert ^2 + \Vert P_h \left( b e_h^m\right) \Vert ^2\\&\le C\left( \max _{m = 1,...,M} \Vert r^m\Vert \right) ^2, \end{aligned}$$

by (5.4). Then Lemma 3.1 gives us

$$\begin{aligned} \left( \varepsilon \left\| \nabla e_h^m\right\| \right) ^2 \le C m \tau \left( \max _{m = 1,...,M} \Vert r^m\Vert \right) ^2 \le C\left( \max _{m = 1,...,M} \Vert r^m\Vert \right) ^2, \end{aligned}$$

which is (5.5). $\square$

For any function $w\in H^1(\Omega )$, define its energy norm $\Vert w\Vert _{1,e}$ by

$$\begin{aligned} \Vert w\Vert _{1,e} = \left\{ \varepsilon ^2 \vert w\vert _1^2 + \Vert w\Vert ^2 \right\} ^{1/2} \end{aligned}$$

This norm was referred to as the $H_e^1$ norm in Sect. 1.

We now derive a $L^\infty (H_e^1)$ error bound for our method.

Theorem 5.4

(Energy norm error bound) Assume that the derivative bounds (2.3) hold true for $k=5$. Then there exists a constant C such that the solution u of (2.1) and the solution $u_h^m$ of (4.1) satisfy

$$\begin{aligned} {\max _{m = 1,...,M} \Vert u^m-u^m_h\Vert _{1,e} \le } C \left( \varepsilon ^{1/2}N^{-1}\ln N + N^{-2}+ M^{-1}\right) . \end{aligned}$$

Proof

By Lemma 5.3, Lemma 5.2, and (5.2), one has the energy norm error estimate

$$\begin{aligned} {\max _{m = 1,...,M} \Vert e_h^m\Vert _{1,e}}&\le C \max _{m = 1,...,M} \Vert r^m\Vert \\&\le C \left( \max _{m = 1,...,M} \Vert \rho _1^m\Vert + \max _{m = 1,...,M} \Vert r_1^m\Vert \right) \\&\le C \left( \varepsilon ^{1/2}N^{-1}\ln N + N^{-2}+ M^{-1}\right) . \end{aligned}$$

But $u-u_h^m = e_h^m - {\rho ^m_0}$, so we can combine the above estimate and the bound (5.2) of Lemma 5.1 for ${\rho ^m_0}$ to finish the proof. $\square$

6 Balanced Norm Error Analysis

In this section we use the derivative bounds (2.3) with $k=6$.

As we pointed out in Sect. 1, the energy norm of Sect. 5 is weaker than it looks — for solutions of typical singularly perturbed problems, it is dominated by its $L^2$ component. Thus we now derive an error bound in a balanced norm where the $\varepsilon$-dependent weighting of the $H^1$ component is such that the $H^1$ and $L^2$ components of the error have similar orders of magnitude. This result will be proved under the additional assumption that the reaction term coefficient b is a positive constant.

Remark 6.1

To extend our balanced-norm analysis analysis to variable b(x) seems not to be straightforward, essentially because the $L^2(\Omega )$ projector $P_h$ is not $H^1(\Omega )$-stable on a Shishkin mesh (this follows from [4, p.527]).

First, we sharpen the result of Lemma 5.2 under a stronger hypothesis on the derivative bounds (2.3).

Lemma 6.2

Assume that the derivative bounds (2.3) hold true for $k=6$. Then

$$\begin{aligned} \left\| r_1^m\right\| + \varepsilon ^{1/2}\left| r_1^m\right| _1 \le CM^{-1}\ \text { for }m = 1,...,M. \end{aligned}$$

Proof

From (2.3) with $k=6$, one sees that $\Vert (\partial /\partial t)^2 u(\cdot , t)\Vert +\varepsilon ^{1/2}\vert (\partial /\partial t)^2 u(\cdot , t)\vert _1\le C$ for all $t\in (0,T]$. This inequality, Lemma 5.1 with $i=2$, and a triangle inequality yield the desired result. $\square$

Lemma 6.3

There exists a constant C such that

$$\begin{aligned} \max _{m = 1,...,M} \left| e_h^m \right| _1 \le C\left( \max _{m = 1,...,M} \vert P_h \rho _1^m\vert _1 + \varepsilon ^{-1/2} M^{-1}\right) . \end{aligned}$$

(6.1)

Proof

From Lemma 3.2 and b constant it follows that

$$\begin{aligned} \left[ \delta _t\left\| \nabla e_h^m\right\| \right] \left\| \nabla e_h^m\right\|&\le \left\langle \delta _t \nabla e_h^m, \nabla e_h^m\right\rangle \\&\le \left\langle \delta _t e_h^m, -\Delta _h e_h^m\right\rangle - \varepsilon ^2\left\langle \Delta _h e_h^m, -\Delta _h e_h^m\right\rangle + \left\langle b \nabla e_h^m,\nabla e_h^m\right\rangle \\&= \left\langle \delta _t e_h^m, -\Delta _h e_h^m\right\rangle - \varepsilon ^2\left\langle \Delta _h e_h^m, -\Delta _h e_h^m\right\rangle + \left\langle b e_h^m,-\Delta _h e_h^m\right\rangle \\&= \left\langle P_h r^m, -\Delta _h e_h^m\right\rangle \\&\le \Vert \nabla P_h r^m\Vert \, \Vert \nabla e_h^m\Vert , \end{aligned}$$

where we used (5.7). If $\Vert \nabla e_h^m\Vert =0$ we are done; thus we assume that $\Vert \nabla e_h^m\Vert \ne 0$ and deduce that

$$\begin{aligned} \delta _t \left| e_h^m \right| _1 \le \vert P_h r^m\vert _1 \le \vert P_h \rho _1^m\vert _1+\vert P_h r_1^m\vert _1 \le \max _{m = 1,...,M}\vert P_h \rho _1^m\vert _1 + C\varepsilon ^{-1/2} M^{-1}, \end{aligned}$$

by Lemma 6.2 and $P_hr_1^m = r_1^m$. Now an appeal to Lemma 3.1 gives (6.1). $\square$

From the discussion in [13] and the bounds (2.3), one sees that the norm

$$\begin{aligned} \Vert w\Vert _{Bal} := \left\{ \varepsilon \vert w\vert _1^2 + \Vert w\Vert ^2 \right\} ^{1/2}\ \forall w\in H^1(\Omega ) \end{aligned}$$

defines a balanced norm for the class of problems that we are studying. The next result is an error bound for our numerical method in $L^\infty (\Vert \cdot \Vert _{Bal})$. Note that, unlike Theorem 5.4, the bound does not contain a factor that vanishes as $\varepsilon \rightarrow 0$ (for fixed N); this is precisely because of the balanced nature of the result.

Theorem 6.4

(Balanced norm error bound) Assume that the derivative bounds (2.3) hold true for $k=6$. Recall that u is the solution of (2.1) and $u_h^m$ is the solution of (4.1). Then there exists a constant C such that

$$\begin{aligned} \max _{m = 1,...,M} {\Vert u^m-u^m_h\Vert _{Bal}} \le C \left( N^{-1}\left( \ln N\right) ^{3/2} + M^{-1} \right) . \end{aligned}$$

Proof

From (5.1) we have

$$\begin{aligned} \left| P_h \rho _1^m(\cdot )\right| _1&= \left| {{\mathcal {R}}}_h \left[ \partial u^m(\cdot )/\partial t\right] - P_h \left[ \partial u^m(\cdot )/\partial t\right] \right| _1 \nonumber \\&\le \left| {{\mathcal {R}}}_h \left[ \partial u^m(\cdot )/\partial t\right] - \left[ \partial u^m(\cdot )/\partial t\right] \right| _1 + \left| \left[ \partial u^m(\cdot )/\partial t\right] - P_h \left[ \partial u^m(\cdot )/\partial t\right] \right| _1 \nonumber \\&\le \left| \rho _1^m\right| _1 + C \varepsilon ^{-1/2} N^{-1} \left( \ln N\right) ^{3/2}, \end{aligned}$$

(6.2)

by [19, (13)] applied to the function $\partial u/\partial t$, since the spatial derivative bounds for $\partial u/\partial t$ in (2.3) are the same as for the elliptic problem studied in [19].

Observe that $\Vert w\Vert _{Bal}$ is equivalent to $\varepsilon ^{1/2} \left| w\right| _1 + \left\| w\right\|$ for all $w\in H^1(\Omega )$. Then Lemma 6.3 and inequality (5.4) in Lemma 5.3 yield

$$\begin{aligned} \max _{m = 1,...,M} { \Vert e_h^m\Vert _{Bal}}&\le C\varepsilon ^{1/2}\left( \max _{m = 1,...,M} \vert P_h \rho _1^m\vert _1 + \varepsilon ^{-1/2}M^{-1}\right) + \max _{m = 1,...,M} \Vert r^m\Vert \\&\le C \left( \max _{m = 1,...,M} \varepsilon ^{1/2}\vert P_h \rho _1^m\vert _1 + M^{-1}\right) \\ {}&\quad + \max _{m = 1,...,M} \Vert \rho _1^m\Vert + \max _{m = 1,...,M} \Vert r_1^m\Vert , \end{aligned}$$

since $r^m = \rho _1^m+r_1^m$. Hence

$$\begin{aligned} \max _{m = 1,...,M} { \Vert e_h^m\Vert _{Bal}} \le C \left( N^{-1}\left( \ln N\right) ^{3/2} + M^{-1} \right) \end{aligned}$$

by (6.2), inequality (5.3) of Lemma 5.1, and Lemma 5.2. As $u^m-u^m_h = e_h^m - \rho _0^m$, the desired result now follows from Lemma 5.1 and a triangle inequality. $\square$

7 Numerical Results

Our numerical experiments will use the same test problem as [15, Example 1]. That is, we take $b = 1$ and $T = 1$, and choose the exact solution

$$\begin{aligned} u(x,y,t) = (1-e^{-t}) \left( \cos \frac{\pi x}{2}-\frac{e^{-x/\varepsilon }-e^{-1/\varepsilon }}{1-e^{-1/\varepsilon }}\right) \left( 1-y-\frac{e^{-y/\varepsilon }-e^{-1/\varepsilon }}{1-e^{-1/\varepsilon }}\right) . \end{aligned}$$

Then f is chosen so that (2.1) is satisfied, and we take $u_0(x,y) = u(x,y,0) \equiv 0$. The derivatives of u have exactly the form of the bounds (2.3), so it is a valid solution on which to test our theory. Unlike in (2.1), the function f depends on $\varepsilon$, but in a harmless way — one can verify easily that our error analysis is unaffected by this deviation from the form of (2.1).

Numerical errors will be measured in the energy norm and balanced norm that were used in Theorems 5.4 and 6.4 respectively to bound the error in the computed solution.

We concentrate first on the spatial error, since this is where the effect of the boundary layers is felt. In Tables 1 (energy-norm errors) and 2 (balanced-norm errors) we take $(N,M) = (16, 64), (32,182), (64,512), (128,1449)$, i.e., $M\approx N^{3/2}$ in each case, so that the spatial component of the error should dominate the total error. To see the rates of convergence more easily, we graph these energy-norm and balanced-norm errors in Figs. 2 and 3 respectively, where we take $\varepsilon =10^{-2}$ so that each figure encompasses the regimes $N \ll \varepsilon ^{-1}, N \approx \varepsilon ^{-1}, N \gg \varepsilon ^{-1}$.

Theorem 5.4 predicts an energy-norm error of $O( \varepsilon ^{1/2}N^{-1}\ln N + N^{-3/2})$; Table 1 and Fig. 2 agree with this. In particular, in Fig. 2 where $\varepsilon = 10^{-2}$, the convergence of the energy-norm error is $O(N^{-1}\ln N)$, while when $\varepsilon =10^{-8} \ll N^{-1}$ in Table 1, then the energy-norm error is $O(N^{-3/2})$.

Theorem 6.4 predicts balanced-norm errors that are $O(N^{-1}(\ln N)^{3/2})$, and this agrees with the numerical results in Table 2 and Fig. 3 (these errors may be $O(N^{-1}\ln N)$, which is slightly better). Note that for each fixed N in Table 2 the balanced-norm errors are essentially independent of $\varepsilon$ when $\varepsilon$ is small, as our theory predicts.

Of course the errors in the balanced norm are larger than those in the energy norm; compare Tables 1 and 2.

Table 1 Energy-norm errors and convergence rates

Table 2 Balanced-norm errors and convergence rates

Fig. 2

log-log graph of the energy-norm error when $\varepsilon = 10^{-2}$

Fig. 3

log-log graph of the balanced-norm error when $\varepsilon = 10^{-2}$

Next, we consider the temporal error by taking $(N,M) = (16,8), (32,14), (64,23), (128,39)$, i.e., $M \approx N^{3/4}$, so that the temporal error dominates the total error. Now Theorems 5.4 and 6.4 predict both the energy-norm error and balanced-norm error to be $O(N^{-3/4})$. Tables 3 and 4 evidently agree with this prediction.

Table 3 Energy-norm errors and convergence rates

Table 4 Balanced-norm errors and convergence rates