1 Introduction

The aim of this paper is to present the formulation and analysis of exponential integration when applied to the nonlinear Schrödinger equation (NLS) with periodic boundary conditions (see [16, 17])

$$\begin{aligned} \left\{ \begin{aligned}&\mathrm {i}u_{t}(t,x)=-{\frac{1}{\varepsilon }}\triangle u (t,x)+\lambda |u(t,x)|^{2}u(t,x),\ \ (t,x)\in [0,T]\times [-\pi ,\pi ]^d,\\&u(0,x)=u^0(x),\ \ \ \ \ \ x\in [-\pi ,\pi ]^d, \end{aligned}\right. \end{aligned}$$
(1.1)

where \(\lambda \) is a positive or negative parameter which leads to focusing or defocusing NLS, respectively. We note here that the methods and analysis presented in this paper are available for these both cases of \(\lambda \). The \(\varepsilon \) in (1.1) is a decisive parameter which determines the scaling of the solution. In this paper, we consider two different regimes: the normal regime \(\varepsilon =1\) and the semiclassical regime \(0 < \varepsilon \ll 1\) which means that the solution u(t, x) is highly oscillatory with respect to the time variable. More specifically, the operator \(e^{ \text{ i }t\triangle /\varepsilon }\) is periodic with respect to t and the (minimal) period is \({\mathcal {O}}(\varepsilon )\). Thus on any finite time interval, the number of oscillations tends to infinity as the parameter \(\varepsilon \) tends to zero, which renders the NLS highly oscillatory with respect to t for \(0 < \varepsilon \ll 1\). It is known that the solution of this equation (1.1) exactly conserves the following energy

$$\begin{aligned} H[u,{\bar{u}}]=\frac{1}{2(2 \pi )^d}\int _{[-\pi ,\pi ]^d}\Big ({\frac{1}{\varepsilon }} |\nabla u|^2 +\frac{1}{2}\lambda |u|^4\Big )dx, \end{aligned}$$
(1.2)

where \(|\cdot |\) denotes the Euclidean norm. Apart from this, the solution also has the conservations of the momentum

$$\begin{aligned} K[u,{\bar{u}}]=\text{ i }\frac{1}{(2 \pi )^d}\int _{[-\pi ,\pi ]^d}(u \nabla {\bar{u}}-{\bar{u}}\nabla u)dx, \end{aligned}$$
(1.3)

and of the density or mass

$$\begin{aligned} m[u,{\bar{u}}]=\text{ i }\frac{1}{(2 \pi )^d}\int _{[-\pi ,\pi ]^d}|u|^2dx. \end{aligned}$$
(1.4)

For the linear Schrödinger equation, its solution exactly conserves the actions

$$\begin{aligned} I_j(u,{\bar{u}})= \frac{1}{2}\left| u_j\right| ^2,\qquad j\in {\mathbb {Z}}^d, \end{aligned}$$
(1.5)

where \(u_j\) is defined by \(u(t,x)=\sum \limits _{j\in {\mathbb {Z}}^d}u_j(t)e^{\text{ i }(j\cdot x)}\) with \(j\cdot x=j_1x_1+\cdots +j_dx_d\). For nonlinear equation (1.1), it has been shown that these actions are approximately conserved over long times under conditions of small initial data and non-resonance (see [29, 30]). In this paper, only cubic Schrödinger equation with \(x \in [-\pi ,\pi ]^d\) is considered for brevity, although all our ideas, algorithms and analysis can be easily extended to the solutions of other NLS.

As is known, NLS often arises in a wide range of applications such as in fiber optics, physics, quantum transport and other applied sciences, and we refer the reader to [23, 40, 43]. In order to effectively solve NLS, various numerical methods have been developed and researched in recent decades. With regard to some related methods of this topic, we refer the reader to exponential-type integrators (see, e.g. [5, 7, 8, 12, 14, 19, 21, 52]), splitting methods (see, e.g. [1, 9, 17, 22, 30, 45, 50]), multi-symplectic methods (see, e.g. [5]), Fourier integrators (see, e.g. [24, 42, 47]), waveform relaxation algorithms (see, e.g. [27]) and other effective methods (see, e.g. [2, 3, 6, 31, 38, 41]).

In the last two decades, structure-preserving algorithms of Hamiltonian partial differential equations (PDEs) have also been received much attention and we refer to [10, 35, 38, 58]. Amongst the typical subjects of structure-preserving algorithms are energy-preserving (EP) schemes (see, e.g. [20, 26, 32, 39, 46, 49, 53, 54]). One important property of EP methods is that they can exactly preserve the energy of the considered system. On the other hand, long-time conservation properties of different methods when applied to Hamiltonian systems have been researched in many research publications (see, e.g. [19, 25, 29, 30, 34, 35]). All the long-time analyses can be achieved by using the technique of modulated Fourier expansions, which was developed by Hairer and Lubich in [33].

With regard to the existing researches on these two topics for Schrödinger equations, we have comments as follows:

  1. (a)

    Concerning EP methods for NLS, although the average vector field method (see [15]) and Hamiltonian Boundary Value Methods (see [11]) were considered, exponential EP methods have not been studied well for Schrödinger equations in the literature. Recently, the authors in [55] derived a kind of exponential collocation methods, but the energy conservation only holds under some special conditions. Exponential structure-preserving Runge-Kutta methods have been studied in [10] for first-order ODEs and the methods are shown to exactly preserve conformal symplecticity and decay (or growth) rates in linear and quadratic invariants. However, energy-preserving exponential Runge-Kutta methods have not been considered there. Exponential EP integrators as well as their convergence have not been established rigorously for NLS.

  2. (b)

    For the long time analysis of numerical methods applied to NLS, there have also been many publications, and we refer the reader to [19, 28,29,30]. Unfortunately, however, all the methods described in these publications are not EP methods. Too little attention has been paid to the long term analysis of EP methods in other qualitative aspects for solving NLS in the literature.

The above facts motivate this paper and the main contributions will be made as follows:

  1. (A)

    By using the idea of continuous-stage methods, we formulate a kind of exponential integration. This formulation will provide novel energy-preserving methods and this will be discussed in detail in Sect. 2.

  2. (B)

    For the obtained EP methods, we analyze their optimal convergence for the first time. We prove by using the averaging technique [17], that some schemes exhibit improved error bounds for highly oscillatory NLS (Sect. 3).

  3. (C)

    It is also shown that these EP integrators have near conservations of actions, momentum and density over long times by using modulated Fourier expansions (Sect. 4).

After these steps, a novel kind of exponential integration with energy preservation, optimal convergence and long time near conservations of actions, momentum and density is obtained. All the theoretical results presented in this paper will be supported numerically by a numerical experiment carried out in Sect. 5. The last section concerns some applications of the integrators and some issues which will be studied further.

2 Energy-Preserving Exponential Integrators

In order to derive energy-preserving exponential integrators, we consider the simple but classical way: Duhamel formulation of the equation and the discretization of the integral, which has been used in many publications (see, e.g. [3, 8, 10, 12, 14, 19, 21, 36, 44, 47]). Although this formulation is not new, the obtained methods will have some advantages and we will make some important notes in Remark 1 below.

Rewrite the NLS (1.1) as

$$\begin{aligned} \begin{aligned}&\frac{\partial u }{\partial t}(t,x)=\text{ i }{\mathcal {A}}u(t,x)+ f(u(t,x)), \ \ \ \ u(0,x)=u^0(x), \end{aligned} \end{aligned}$$
(2.1)

where \({\mathcal {A}}\) is the differential operator defined by \( ({\mathcal {A}}u)(t,x)= {\frac{1}{\varepsilon }}\triangle u(t,x)\) and \(f(u)=- \text{ i }\lambda |u|^{2}u\). The Duhamel principle of this system gives

$$\begin{aligned} \begin{aligned} u(t_n+h,x)=e^{ \text{ i }h {\mathcal {A}}}u(t_n,x)+ h \int _{0}^1 e^{(1-\xi )\text{ i }h {\mathcal {A}}}f(u(t_n+\xi h,x))d\xi \end{aligned} \end{aligned}$$
(2.2)

with the time stepsize h and \(t_n=nh\). Then we define the operator-argument functions \(\varphi _j\) by

$$\begin{aligned} \varphi _0(\text{ i }t{\mathcal {A}}):=e^{\text{ i }t {\mathcal {A}}},\ \ \varphi _j(\text{ i }t{\mathcal {A}}):=\int _{0}^{1} e^{\text{ i }(1-\xi )t {\mathcal {A}}}\frac{\xi ^{j-1}}{(j-1)!}\mathrm{d}\xi ,\quad j=1,2,\dots . \end{aligned}$$
(2.3)

We deal with the integral appearing in (2.2) by the idea of continuous-stage methods and define the novel integrators as follows.

Definition 1

(Exponential time integrators.) For solving the NLS (1.1), a continuous-stage exponential time integrator is defined for \(0\le \tau \le 1\) and \(n=0,1,\ldots \) as follows:

$$\begin{aligned} \begin{aligned} u^{n+\tau }(x)&=\varPhi ^{\tau h}(u^{n}(x)):=C_{\tau }({\mathcal {V}})u^n(x)+ h \int _{0}^{1}A_{\tau ,\sigma }({\mathcal {V}})f(u^{n+\sigma }(x))d\sigma , \end{aligned} \end{aligned}$$
(2.4)

where \({\mathcal {V}}=\text{ i }h{\mathcal {A}}\), \(C_{\tau }({\mathcal {V}})\) and \(A_{\tau ,\sigma }({\mathcal {V}})\) are bounded operator-argument functions and \(C_{\tau }({\mathcal {V}})\) is required to satisfy \(C_{c_{j}}({\mathcal {V}})= e^{c_{j}{\mathcal {V}}}\ \text{ for }\ j=0, 1,\ldots , s\) with the fitting nodes \(c_{j}\) and \(s\ge 1\). It is required that \(c_0=0\) and \(c_{s}=1\). The numerical solution after one time stepsize h is obtained by letting \(\tau =1\) in (2.4).

Remark 1

Although this exponential time integrator is formulated by the Duhamel formulation and the discretization of the integral, which is a simple and classical way, it is important to note that this scheme has the following advantages.

  • At the first sight, for a p-th order exponential integrator, it will produce errors of order \({\mathcal {O}}\big (\frac{h^p}{\varepsilon ^p}\big )\) when it is used to solving (1.1) with a time step size h. However, for the scheme (2.4) presented above, we will show that some obtained methods exhibit improved error bounds such as \({\mathcal {O}}\big (\frac{h^2}{\varepsilon }\big )\) or \({\mathcal {O}}\big (\frac{h^3}{\varepsilon ^2}\big )\).

  • We have noticed that some novel methods with improved or uniform accuracy have been presented (see, e.g. [3, 16, 17, 42, 47]). These methods have good even better convergence result than the methods given in this paper. However, it is noted that these methods do not have energy, actions, momentum and density conservations. Based on the scheme (2.4), we will obtain some exponential integrators with energy preservation and improved error bounds. We will also show that this scheme (2.4) can provide methods with near conservations of actions, momentum and density over long times. In other words, the scheme (2.4) can produce some practical methods with three properties simultaneously: energy preservation, improved error bounds and near conservations of actions, momentum and density.

For the integrator (2.4), its energy conservation property is shown as follows.

Theorem 1

(Energy-preserving conditions.) Let \({\mathcal {K}}=hJ{\mathcal {M}}\) with \( {\mathcal {M}}=\left( \begin{array}{cc} {\mathcal {A}} &{} 0 \\ 0 &{} {\mathcal {A}} \\ \end{array} \right) \) and \(J=\left( \begin{array}{cc} 0 &{} -1 \\ 1 &{} 0 \\ \end{array} \right) \). If the coefficients of the scheme (2.4) satisfy

$$\begin{aligned} \left\{ \begin{aligned}&A_{0,\sigma }({\mathcal {K}})={\mathbf {0}},\\&(e^{{\mathcal {K}}})^\intercal {\mathcal {M}} A_{1,\tau }({\mathcal {K}}) {\mathcal {K}}+(C'_{\tau }({\mathcal {K}}))^\intercal {\mathcal {M}}={\mathbf {0}},\\&{\mathcal {K}}^\intercal (A_{1,\tau }({\mathcal {K}}))^\intercal {\mathcal {M}} A_{1,\sigma }({\mathcal {K}}) {\mathcal {K}}+{\mathcal {M}}A'_{\tau ,\sigma }({\mathcal {K}}) {\mathcal {K}} +({\mathcal {M}} A'_{\sigma ,\tau } ({\mathcal {K}}) {\mathcal {K}})^\intercal ={\mathbf {0}},\\ \end{aligned}\right. \end{aligned}$$
(2.5)

with \( C_{\tau }^{'}({\mathcal {K}})=\frac{d}{\mathrm{d}\tau }C_{\tau }({\mathcal {K}})\) and \( A'_{\tau ,\sigma }({\mathcal {K}})=\frac{\partial }{\partial \tau }A_{\tau ,\sigma }({\mathcal {K}}),\) then the integrator (2.4) exactly preserves the energy (1.2), i.e., \(H[u^{n+1},{\bar{u}}^{n+1}]=H[u^{n},{\bar{u}}^{n}]\) for \( n=0,1,\ldots .\)

Proof

By letting \(u = p + \text{ i }q,\) we rewrite the equation (1.1) as a infinite-dimensional real Hamiltonian system

$$\begin{aligned} \begin{aligned} \frac{\partial y }{\partial t}=J{\mathcal {M}}y+J\nabla _y U(y)\ \ \ \ y_0(x)= \left( \begin{array}{c} \text{ Re }(u_0(x)) \\ \text{ Im }(u_0(x)) \\ \end{array} \right) , \end{aligned} \end{aligned}$$
(2.6)

where \(y=\left( \begin{array}{c} p \\ q \\ \end{array} \right) \) and \(U(y)=-\frac{\lambda }{4}(p^2+q^2)^2 .\) The energy of this system accordingly becomes

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}(p,q) =\frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d}\Big ( p {\mathcal {A}}p+q {\mathcal {A}}q-\frac{\lambda }{2}(p^2+q^2)^2 \Big )dx.\\ \end{aligned} \end{aligned}$$
(2.7)

Our continuous-stage exponential integrator (2.4) applying to (2.6) gives

$$\begin{aligned} \left\{ \begin{aligned} Y^{n+\tau }(x)&=C_{\tau }({\mathcal {K}})y^n(x)+ h \int _{0}^{1}A_{\tau ,\sigma }({\mathcal {K}})g(Y^{n+\sigma }(x))d\sigma ,\ \ 0\le \tau \le 1,\\ y^{n+1}(x)&=e^{{\mathcal {K}}}y^n(x)+h \displaystyle \int _{0}^{1}A_{1,\tau }({\mathcal {K}}) g(Y^{n+\tau }(x))d\tau ,\\ \end{aligned}\right. \end{aligned}$$
(2.8)

where \(g(y)=J\nabla _y U(y).\)

Inserting the numerical scheme (2.8) into (2.7) yields

$$\begin{aligned} \begin{aligned} {\mathcal {H}}[y^{n+1} ] =&\frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d}\Big \{\frac{1}{2}(y^n)^\intercal {\mathcal {M}} y^n +(y^n)^\intercal (e^{{\mathcal {K}}})^\intercal {\mathcal {M}}\int _{0}^{1}A_{1,\tau }({\mathcal {K}}) {\mathcal {K}} {\tilde{g}}(Y^{n+\tau })d\tau \\&+\frac{1}{2} \int _{0}^{1}\big (A_{1,\tau }({\mathcal {K}}) {\mathcal {K}} {\tilde{g}}(Y^{n+\tau })\big )^\intercal d\tau {\mathcal {M}}\int _{0}^{1}A_{1,\tau }({\mathcal {K}}) {\mathcal {K}} {\tilde{g}}(Y^{n+\tau })d\tau +U(y^{n+1})\Big \}dx, \end{aligned} \end{aligned}$$
(2.9)

where \({\tilde{g}}={\mathcal {M}}^{-1}\nabla _y U(y)\) and we have used the result \( (e^{{\mathcal {K}}})^\intercal {\mathcal {M}}e^{{\mathcal {K}}}={\mathcal {M}}\) (see [44]). It follows from the first condition of (2.5) that \(Y^{n}=y^n\) and \( Y^{n+1}=y^{n+1}.\) Then one arrives at

$$\begin{aligned} \begin{aligned}&U(y^{n+1})-U(y^{n}) =\int _{0}^1 \big (\nabla _y U(Y^{n+\tau })\big )^\intercal dY^{n+\tau }\\&\quad = \int _{0}^1 \big (\nabla _y U(Y^{n+\tau })\big )^\intercal d\Big (C_{\tau }({\mathcal {K}})y^n+ h \int _{0}^{1}A_{\tau ,\sigma }({\mathcal {K}})g(Y^{n+\sigma })d\sigma \Big )\\&\quad =(y^n)^\intercal \int _{0}^1 (C'_{\tau }({\mathcal {K}}))^\intercal {\mathcal {M}} {\tilde{g}}(Y^{n+\tau })d\tau + \int _{0}^{1} \int _{0}^{1} \big ({\tilde{g}}(Y^{n+\tau })\big )^\intercal {\mathcal {M}} A'_{\tau ,\sigma }({\mathcal {K}}){\mathcal {K}}{\tilde{g}}(Y^{n+\sigma })d\tau d\sigma . \end{aligned} \end{aligned}$$

Therefore, using the above results and the second condition of (2.5), we obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {H}}[y^{n+1} ]-{\mathcal {H}}[y^{n} ]\\&\quad =\frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d}\frac{1}{2}\int _{0}^{1} \int _{0}^{1} \big ({\tilde{g}}(Y^{n+\tau })\big )^\intercal \Big \{({\mathcal {K}})^\intercal (A_{1,\tau }({\mathcal {K}}))^\intercal {\mathcal {M}} A_{1,\sigma }({\mathcal {K}}) {\mathcal {K}}+2{\mathcal {M}}A'_{\tau ,\sigma }({\mathcal {K}}) {\mathcal {K}}\Big \}\\&\qquad {\tilde{g}}(Y^{n+\sigma })d\tau d\sigma dx\\&\quad =\frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d}\frac{1}{2}\int _{0}^{1} \int _{0}^{1} \big ({\tilde{g}}(Y^{n+\sigma })\big )^\intercal \Big \{({\mathcal {K}})^\intercal (A_{1,\sigma }({\mathcal {K}}))^\intercal {\mathcal {M}} A_{1,\tau }({\mathcal {K}}) {\mathcal {K}}+2{\mathcal {M}}A'_{\sigma ,\tau }({\mathcal {K}}) {\mathcal {K}}\Big \}\\&\qquad {\tilde{g}}(Y^{n+\tau }) d\sigma d\tau dx\\&\quad = \frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d}\frac{1}{2}\int _{0}^{1} \int _{0}^{1} \big ({\tilde{g}}(Y^{n+\tau })\big )^\intercal \Big \{({\mathcal {K}})^\intercal (A_{1,\tau }({\mathcal {K}}))^\intercal {\mathcal {M}} A_{1,\sigma }({\mathcal {K}}) {\mathcal {K}} +(2{\mathcal {M}}A'_{\sigma ,\tau }({\mathcal {K}}) {\mathcal {K}})^\intercal \Big \}\\&\qquad {\tilde{g}}(Y^{n+\sigma }) d\tau d\sigma dx. \end{aligned} \end{aligned}$$

It is clear from the third equality of (2.5) that

$$\begin{aligned} \begin{aligned} 2({\mathcal {H}}[y^{n+1} ]-{\mathcal {H}}[y^{n} ]) =&\frac{-1}{2(2 \pi )^d}\int _{{\mathbf {T}}^d} \int _{0}^{1} \int _{0}^{1} \big ({\tilde{g}}(Y^{n+\tau })\big )^\intercal \Big \{({\mathcal {K}})^\intercal (A_{1,\tau }({\mathcal {K}}))^\intercal {\mathcal {M}} A_{1,\sigma }({\mathcal {K}}) {\mathcal {K}}\\&+{\mathcal {M}}A'_{\sigma ,\tau }({\mathcal {K}}) {\mathcal {K}}+({\mathcal {M}}A'_{\sigma ,\tau }({\mathcal {K}}) {\mathcal {K}})^\intercal \Big \} {\tilde{g}}(Y^{n+\sigma }) d\tau d\sigma dx\\=&0. \end{aligned} \end{aligned}$$

The proof is completed. \(\square \)

In what follows, we present three practical energy-preserving algorithms based on the scheme (2.4) and on the conditions (2.5) of energy preservation. The coefficients are obtained by solving the conditions (2.5) and we omit the details of calculations for brevity.

Algorithm 1

(Energy-preserving algorithm 1.) For the integrator given in Definition 1, consider \(s=1\) and define a practical method (2.4) with the coefficients

$$\begin{aligned} C_{\tau }({\mathcal {V}})= (1-\tau )I+ \tau e^{{\mathcal {V}}},\ A_{\tau ,\sigma }({\mathcal {V}})=\tau \varphi _1({\mathcal {V}}). \end{aligned}$$

We shall refer to this integrator by EP1.

Algorithm 2

(Energy-preserving algorithm 2.) We choose \(s=2\) and the coefficients of (2.4) are given by

$$\begin{aligned} \begin{array}{ll}&C_{\tau }({\mathcal {V}})= \frac{(\tau -1)(\tau -m)}{m} I+\frac{\tau (\tau -1)}{m(m-1)}e^{m{\mathcal {V}}}+\frac{\tau (m-\tau )}{m-1} e^{{\mathcal {V}}},\ A_{\tau ,\sigma }({\mathcal {V}})=\sum \limits _{l=1}^2\sum \limits _{n=1}^2a_{ln} ({\mathcal {V}})\tau ^l\sigma ^{n-1}, \end{array} \end{aligned}$$

where m is a parameter required that \(m\ne 0,1\), and

$$\begin{aligned} \begin{array}{ll} &{}a_{11}({\mathcal {V}})= \frac{1+m}{m(1-m)}\varphi _1(m{\mathcal {V}})+\frac{m+1}{m-1}\varphi _1({\mathcal {V}}) +\frac{1}{1-m}\varphi _1((1-m){\mathcal {V}}),\\ &{}a_{22}({\mathcal {V}})= \frac{2}{m(1-m)}\big (\varphi _1(m{\mathcal {V}})-\varphi _1({\mathcal {V}})+\varphi _1((1-m) {\mathcal {V}})\big ),\\ &{}a_{21}({\mathcal {V}})=(1+1/m)\varphi _1({\mathcal {V}})-1/m\varphi _1((1-m){\mathcal {V}}) -a_{11}({\mathcal {V}}),\\ &{}a_{12}({\mathcal {V}})=-2/m(\varphi _1({\mathcal {V}})-\varphi _1((1-m){\mathcal {V}})) -a_{22}({\mathcal {V}}). \end{array} \end{aligned}$$

As an example of this method, we choose \(m=1/2\) and denoted it by EP2.

Algorithm 3

(Energy-preserving algorithm 3.) As another example, we choose \(s=3\) and

$$\begin{aligned} \begin{aligned} C_{\tau }({\mathcal {V}})=&\sum \limits _{k=0}^3l_k(\tau )e^{c_k{\mathcal {V}}}, \ A_{\tau ,\sigma }({\mathcal {V}})=\sum \limits _{l=1}^3\sum \limits _{n=1}^3a_{ln} ({\mathcal {V}})\tau ^l\sigma ^{n-1}, \end{aligned} \end{aligned}$$

where \(l_j(\tau )=\prod _{k\ne j}\frac{\tau -c_k}{c_j-c_k}\) for \(j=0,\ldots ,3\) and

$$\begin{aligned} \begin{aligned} a_{jj}({\mathcal {V}}) =&-\big (c_1C_{j0}C_{j1}\varphi _{1,c_1}+c_2C_{j0}C_{j2}\varphi _{1,c_2}+(c_2-c_1)C_{j1}C_{j2}\varphi _{1,c_2-c_1}\\&+C_{j0}C_{j3}\varphi _{1,1}+(1-c_1)C_{j1}C_{j3}\varphi _{1,1-c_1}\\ {}&+(1-c_2)C_{j2}C_{j3}\varphi _{1,1-c_2}\big )/j,\ j=1,2,3,\\ a_{j+1,1}({\mathcal {V}}) =&-\big (c_1C_{j1}C_{00}\varphi _{1,c_1}+c_2C_{j2}C_{00}\varphi _{1,c_2}+(c_2-c_1)C_{j2}C_{01}\varphi _{1,c_2-c_1}\\&+C_{j3}C_{00}\varphi _{1,1}+(1-c_1)C_{j3}C_{01}\varphi _{1,1-c_1}\\ {}&+(1-c_2)C_{j3}C_{02}\varphi _{1,1-c_2}\big )/j,\ j=1,2,\\ a_{1,j+1}({\mathcal {V}}) =&-\big (c_1C_{j0}C_{01}\varphi _{1,c_1}+c_2C_{j0}C_{02}\varphi _{1,c_2}+(c_2-c_1)C_{j1}C_{02}\varphi _{1,c_2-c_1}\\&+C_{j0}C_{03}\varphi _{1,1}+(1-c_1)C_{j1}C_{03}\varphi _{1,1-c_1}\\ {}&+(1-c_2)C_{j2}C_{03}\varphi _{1,1-c_2}\big )/j,\ j=1,2,\\ a_{32}({\mathcal {V}}) =&-\big (c_1C_{21}C_{10}\varphi _{1,c_1}+c_2C_{22}C_{10}\varphi _{1,c_2}+(c_2-c_1)C_{22}C_{11}\varphi _{1,c_2-c_1}\\&+C_{23}C_{10}\varphi _{1,1}+(1-c_1)C_{23}C_{11}\varphi _{1,1-c_1}+(1-c_2)C_{23}C_{12}\varphi _{1,1-c_2}\big ),\\ a_{23}({\mathcal {V}}) =&-\big (c_1C_{20}C_{11}\varphi _{1,c_1}+c_2C_{20}C_{12}\varphi _{1,c_2}+(c_2-c_1)C_{21}C_{12}\varphi _{1,c_2-c_1}\\&+C_{20}C_{13}\varphi _{1,1}+(1-c_1)C_{21}C_{13}\varphi _{1,1-c_1}+(1-c_2)C_{22}C_{13}\varphi _{1,1-c_2}\big ). \end{aligned} \end{aligned}$$

Here we choose \(c_1= 1/3,\ c_2= \frac{1}{18}(14+(71-9\sqrt{58})^{\frac{1}{3}} +(71+9\sqrt{58})^{\frac{1}{3}} )\) and use the notations

$$\begin{aligned} \begin{array}{ll} \varphi _{1,1}=\varphi _1({\mathcal {V}}),\ &{}\varphi _{1,c_1}=\varphi _1(c_1{\mathcal {V}}),\qquad \qquad \ \varphi _{1,c_2}=\varphi _1(c_2{\mathcal {V}}),\\ \varphi _{1,1-c_1}=\varphi _1((1-c_1){\mathcal {V}}),\ &{}\varphi _{1,1-c_2}=\varphi _1((1-c_2){\mathcal {V}}),\ \ \ \varphi _{1,c_2-c_1}=\varphi _1((c_2-c_1){\mathcal {V}}),\\ C_{00} = \frac{c_1 + c_2 + c_1c_2}{-c_1c_2},\ &{}C_{01} = \frac{c_2}{(-1 + c_1) c_1 (c_1 - c_2)},\quad \ \ C_{02} =\frac{-c_1}{(c_1 - c_2) (-1 + c_2) c_2)}, \\ C_{10} = \frac{2 (1 + c_1 + c_2)}{c_1 c_2},\ &{}C_{11} = \frac{2(1 + c_2)}{(-c_1 + c_1^2) (-c_1 + c_2)},\ \ \ \ C_{12} =\frac{2 (1 + c_1)}{(c_1 - c_2) (-1 + c_2) c_2},\\ C_{20} =\frac{ -3}{c_1 c_2},\ &{}C_{21} = \frac{3}{(-1 + c_1) c_1 (c_1 - c_2)},\ \ \ \ \ C_{22} =\frac{-3}{(c_1 - c_2) (-1 + c_2) c_2)}. \end{array} \end{aligned}$$

We shall refer to this semi-discrete integrator by EP3.

The presented three algorithms EP1-EP3 are obtained by considering the conditions (2.5) of energy preservation and this shows that all of them are energy-preserving schemes. It is noted that some more energy-preserving schemes can be derived from other value of s and (2.5) and we omit them for brevity. The main observation of the paper is that some of these energy-preserving algorithms show optimal error bound and good near conservations of density, momentum and actions over long times. All of these observations will be illustrated by numerical experiments in Sect. 5. The next two sections are respectively devoted to the optimal convergence and long time conservations in density, momentum and actions.

3 Optimal Convergence

In this section, we analyze the convergence of the presented three schemes EP1-EP3.

3.1 Notations and Auxiliary Results

In this part, we present some auxiliary results which will be used in the analysis.

For the exact solution to (1.1), we require the following assumption.

Assumption 1

It is assumed that the initial value \(u^0(x)\) is chosen in \(H^{\alpha }\) with the sufficiently large exponent \(\alpha > 0\). Then the exact solution to (1.1) is sufficiently regular.

In the analysis of convergence, we will reparametrize the time variable t as

$$\begin{aligned} \kappa :=t/\varepsilon . \end{aligned}$$
(3.1)

By letting

$$\begin{aligned} w(\kappa ,x):=u(t,x), \end{aligned}$$
(3.2)

it is obtained that

$$\begin{aligned} w_{\kappa }(\kappa ,x)=\frac{\partial }{\partial \kappa } u(t,x)=\varepsilon u_t(t,x). \end{aligned}$$

Thus in this section, we consider the following equivalent long-term NLS ([17])

$$\begin{aligned} \left\{ \begin{aligned}&\mathrm {i}w_{\kappa }(\kappa ,x)=-\triangle w (\kappa ,x)+\varepsilon \lambda |w(\kappa ,x)|^{2}w(\kappa ,x),\ \ (\kappa ,x)\in [0,T/\varepsilon ]\times [-\pi ,\pi ]^d,\\&w(0,x)=w^0(x):=u^0(x),\ \ \ \ \ \ x\in [-\pi ,\pi ]^d, \end{aligned}\right. \end{aligned}$$
(3.3)

which helps to zoom-in to see the different scales between \(\varepsilon \) and time step, and to see the averaging effect which will be used in the proof of the convergence. The solution of (3.3) satisfies the following properties.

Theorem 2

(See [13].) For any \(\varepsilon > 0\) and \(w^0 \in H^{\alpha }\), there exists a constant \(T > 0\) such that, the long-term NLS (3.3) has a unique solution which satisfies

$$\begin{aligned} w\in C^0([0,T/\varepsilon ];H^{\alpha })\bigcap C^1([0,T/\varepsilon ];H^{\alpha -2}) \end{aligned}$$

and

$$\begin{aligned} \left\| w(\kappa ,\cdot )\right\| _{H^{\alpha }}\le K \left\| w^0\right\| _{H^{\alpha }}\ \text{ for } \text{ any }\ \kappa \in [0,T/\varepsilon ], \end{aligned}$$

where \(\alpha > d/2+2\) and \(K > 1\).

Proposition 1

(See [17].) Let \(f(w)=- \text{ i }\lambda |w|^{2}w\) and the following two estimates hold for this function.

  • For the function \(f(w) \in C^{\infty }: H^{\alpha }\rightarrow H^{\alpha }\), there exists a constant \(M > 0\) such that for all \((w, v) \in H^{\alpha }\times H^{\alpha }\), it has the estimates

    $$\begin{aligned} \left\| f(w)\right\| _{H^{\alpha }}\le M,\ \ \left\| f'(w)(v)\right\| _{H^{\alpha }}\le M \left\| v\right\| _{H^{\alpha }}. \end{aligned}$$

    Moreover, similar estimates for higher derivatives also hold. If \(\alpha \) is changed into \(\alpha -2>0\), all the results are still true.

  • The function has the Lipschitz estimate

    $$\begin{aligned} \left\| f(w)-f(v)\right\| _{H^{\beta }}\le L \left\| u-v\right\| _{H^{\beta }},\ \ (w,v)\in H^{\alpha -2}\times H^{\alpha -2}, \end{aligned}$$

    where \(\beta \in [0, \alpha - 2]\) and \(L > 0\) is a constant.

Proposition 2

(See [21].) Denote by \(\varphi \) a bounded function (bounded by \(C\ge 0\)) from \(\text{ i }{\mathbb {R}}\) to \({\mathbb {C}}\) and then the operator-argument function \(\varphi (\text{ i } t \varDelta )\) is bounded by

$$\begin{aligned} \left\| \varphi (\text{ i } t \varDelta )\right\| _{H^{\alpha }\hookrightarrow H^{\alpha }}\le C \end{aligned}$$

for all \(t >0\) and \(\alpha \ge 0\). For example, the estimate \(\left\| e^{\text{ i }t \varDelta }\right\| _{H^{\alpha }\hookrightarrow H^{\alpha }}=1\) holds.

3.2 Main Result

We first note that for the long term NLS (3.3), the evolution operator \(e^{\text{ i }t\varDelta } \) is periodic with period \(T_0\) ([17]). For simplicity, it is assumed that \(T_0 = 1\) in this section since this can be achieved by a simple rescaling of time. For simplicity of notations, we shall denote

$$\begin{aligned} A\lesssim B \end{aligned}$$

for \(A\le CB\) with a generic constant \(C>0\) independent of n or the time step size or \(\varepsilon \) but depends on T and the constants appeared in Theorem 2 and Propositions 1-2. We use the abbreviation \(w(\kappa )\) instead of \(w(\kappa ,x)\) for brevity. For solving the long term NLS (3.3), the exponential time integrator becomes

$$\begin{aligned} \begin{aligned} w^{n+\tau }(x)&=\varPhi ^{\tau \delta \kappa }(w^{n}(x)):=C_{\tau }({\mathcal {W}})w^n(x)+ \varepsilon \delta \kappa \int _{0}^{1}A_{\tau ,\sigma }({\mathcal {W}})f(w^{n+\sigma }(x))d\sigma , \end{aligned} \end{aligned}$$
(3.4)

where \(0\le \tau \le 1,\) \(\delta \kappa :=\kappa _{n+1}-\kappa _n\) is the time step size and \({\mathcal {W}}=\text{ i }\delta \kappa \varDelta \). Then EP1-EP3 for solving (3.3) can also be obtained by considering Algorithms 1–3, respectively. The optimal convergence of these algorithms is given by the following theorem.

Theorem 3

(Optimal convergence of algorithms for the long term system.) There exists a constant \(N_0>0\) independent of \(\varepsilon \), such that for any time step \(\delta \kappa =\frac{T_0}{N}\) with any integer \(N\ge N_0\), the EP1-EP3 for solving the long term system (3.3) have the following error bounds for both regimes \(\varepsilon \):

$$\begin{aligned} \begin{aligned}&\text{ EP1 }:\ \ \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -4}} \lesssim \delta \kappa ^2,\\&\text{ EP2 }:\ \ \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -6}} \lesssim \varepsilon \delta \kappa ^2+ \delta \kappa ^3,\\&\text{ EP3 }:\ \ \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -8}} \lesssim \varepsilon \delta \kappa ^3+ \delta \kappa ^4, \end{aligned} \end{aligned}$$
(3.5)

where \(n\delta \kappa \le \frac{T}{\varepsilon }\). In this section, \(\alpha \) is required to satisfy \(\alpha > d/2+2\) and further to make the estimates be considered in non-negative Sobolev spaces. When \(\varepsilon =1\), the above results of EP2 and EP3 can be given in the \(H^{\alpha -4}\)-norm and \(H^{\alpha -6}\)-norm, respectively.

Remark 2

Similarly to [17, 57], the time step \(\delta \kappa =\frac{T_0}{N}\) with some integer N is only a technique condition for rigorous proof and we only need \(\delta \kappa \lesssim 1\) in practice, which will be shown numerically in Sect. 5.

Before we present the proof of Theorem 3, some remarks are given here. By the relation (3.2) and by directly comparing (2.4) and (3.4), it is clear that for \(h=\varepsilon \delta \kappa \) and for all \(n\ge 0\),

$$\begin{aligned} u(t_n,x)=w(\kappa _n,x),\quad u^n(x)=w^{n}(x). \end{aligned}$$

Therefore, the convergence of EP1-EP3 in the original scaling (1.1) is equivalently presented as follows.

Corollary 1

(Optimal convergence of algorithms for the original system.) For the methods EP1-EP3 with a time step size \(h\lesssim \varepsilon \) applied to the original system (1.1), their error bounds are given by

$$\begin{aligned} \begin{aligned}&\text{ EP1 }:\ \ \left\| (\varPhi ^{ h})^n(u^0)-u(t_n)\right\| _{H^{\alpha -4}} \lesssim \frac{h^2}{\varepsilon ^2},\\&\text{ EP2 }:\ \ \left\| (\varPhi ^{ h})^n(u^0)-u(t_n)\right\| _{H^{\alpha -6}} \lesssim \frac{h^2}{\varepsilon }+ \frac{h^3}{\varepsilon ^3},\\&\text{ EP3 }:\ \ \left\| (\varPhi ^{ h})^n(u^0)-u(t_n)\right\| _{H^{\alpha -8}} \lesssim \frac{h^3}{\varepsilon ^2}+ \frac{h^4}{\varepsilon ^4}, \end{aligned} \end{aligned}$$
(3.6)

where \(nh \le T\). The results of EP2 and EP3 can be respectively given in the \(H^{\alpha -4}\)-norm and \(H^{\alpha -6}\)-norm when \(\varepsilon =1\).

3.3 Proof of Theorem 3

In the light of Proposition  2, it is obtained that the coefficients of integrators EP1-EP3 are bounded as \(\left\| C_{\kappa }({\mathcal {W}})\right\| _{H^{\alpha }\hookrightarrow H^{\alpha }}\le 1\) and \( \left\| A_{\tau ,\sigma }({\mathcal {W}})\right\| _{H^{\alpha }\hookrightarrow H^{\alpha }}\le C_A,\) where the constant \(C_{A}\) is independent of \(\left\| {\mathcal {W}}\right\| _{H^{\alpha }\hookrightarrow H^{\alpha }}\). For simplicity, the proof will be given only for EP2 because with little modifications it can be adapted to EP1 and EP3. We begin with the local errors and stability of EP2, whose proofs are given in the Appendix.

Lemma 1

(Local errors.) For the local errors

$$\begin{aligned} \begin{aligned} \delta ^{n+\tau }&:=\varPhi ^{\tau \delta \kappa }(w(\kappa _n))-w(\kappa _{n}+\tau \delta \kappa ),\ \ \text{ for }\ \ 0<\tau <1,\\ \delta ^{n+1}&:=\varPhi ^{ \delta \kappa }(w(\kappa _n))-w(\kappa _{n+1}), \end{aligned} \end{aligned}$$

there exits \(\widehat{\delta \kappa }_0>0\) independent of \(\varepsilon \) such that for any \(0<\delta \kappa <\widehat{\delta \kappa }_0\), the following bounds hold for EP2

$$\begin{aligned} \begin{aligned}&\Vert \delta ^{n+\tau }\Vert _{H^{\alpha -2}}\lesssim \delta \kappa ,\qquad \ \Vert \delta ^{n+\tau }\Vert _{H^{\alpha -4}}\lesssim \delta \kappa ^2, \quad \text{ for }\ \ 0<\tau <1, \\&\Vert \delta ^{n+1}\Vert _{H^{\alpha -2}}\lesssim \varepsilon \delta \kappa ^2, \ \ \ \ \Vert \delta ^{n+1}\Vert _{H^{\alpha -4}}\lesssim \varepsilon \delta \kappa ^3. \end{aligned} \end{aligned}$$

Lemma 2

(Stability.) Consider the abbreviations \(R=2K\left\| w^0\right\| _{H^{\alpha }}, \ {\mathcal {H}}^s_R=\{w\in H^{s},\ \left\| w\right\| _{H^{s}}\le R\}.\) For the numerical solution \(\varPhi ^{\tau \delta \kappa }\) of EP2 applied to \(v, w \in {\mathcal {H}}^{\alpha -2}_{3R/4}\), there exist \(\varepsilon _0>0\) and \(\delta \kappa _0>0\) independent of \(\varepsilon \) such that for any \(0<\varepsilon <\varepsilon _0\) and \(0<\delta \kappa <\delta \kappa _0\), it holds that \(\varPhi ^{\tau \delta \kappa }(v),\varPhi ^{\tau \delta \kappa }(w)\in {\mathcal {H}}^{\alpha -2}_{R}\) and

$$\begin{aligned} \begin{aligned}&\Vert \varPhi ^{\tau \delta \kappa }(v)-\varPhi ^{\tau \delta \kappa }(w)\Vert _{H^{\beta }}\le e^{\varepsilon \tau \delta \kappa L C_A}\Vert v-w\Vert _{H^{\beta }},\ \ 0\le \tau \le 1,\\&\Vert (\varPhi ^{ \delta \kappa }(v)-e^{\text{ i }\delta \kappa \triangle }v)-(\varPhi ^{ \delta \kappa }(w)-e^{\text{ i }\delta \kappa \triangle }w)\Vert _{H^{\beta }}\le \varepsilon \delta \kappa L C_A e^{\varepsilon \tau \delta \kappa L C_A}\Vert v-w\Vert _{H^{\beta }}, \end{aligned} \end{aligned}$$
(3.7)

where \(\beta \in [0, \alpha -2]\).

We are now in a position to prove Theorem 3.

Proof

Boundedness of the method. The stated local errors and stability imply

$$\begin{aligned} \begin{aligned}&\left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -2}}\\&\quad =\left\| \sum _{l=1}^{n}\big ((\varPhi ^{\delta \kappa })^{n-l}\varPhi ^{\delta \kappa }(w(\kappa _{l-1})) -(\varPhi ^{\delta \kappa })^{n-l}(w(\kappa _{l}))\big )\right\| _{H^{\alpha -2}}\\&\quad \le \sum _{l=1}^{n} e^{\varepsilon (n-l) \delta \kappa L C_A}\left\| \delta ^l \right\| _{H^{\alpha -2}}\le C \varepsilon \delta \kappa ^2 \sum _{l=1}^{n} e^{\varepsilon (n-l) \delta \kappa L C_A}\le {\tilde{C}} \frac{e^{LTC_A}-1}{ L } \delta \kappa .\\ \end{aligned} \end{aligned}$$

Therefore, there exists \(\widetilde{\delta \kappa }_0>0\) independent of \(\varepsilon \) such that \(0<\delta \kappa <\widetilde{\delta \kappa }_0\), the time-discrete solutions satisfy \((\varPhi ^{ \delta \kappa })^n(w^0) \in {\mathcal {H}}^{\alpha -2}_{3R/4}\), where \(w(\kappa _n) \in {\mathcal {H}}^{\alpha -2}_{R/2}\) has been used here. Using a stability estimate with respect to the \(H^{\alpha -4}\)-norm and considering the local error result in this norm yields

$$\begin{aligned} \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -4}} \le {\tilde{C}} \frac{e^{LTC_A}-1}{ L } \delta \kappa ^2. \end{aligned}$$

Refined local error. For the method (2.4), we expand the nonlinear function f at \(C_{\xi }w(\kappa _n)\) and then get

$$\begin{aligned} \begin{aligned} \varPhi ^{ \delta \kappa }(w(\kappa _n)) =&e^{\text{ i }\delta \kappa \triangle }w(\kappa _n)+ \varepsilon \delta \kappa \int _{0}^{1}A_{1,\xi } f(C_{\xi }w(\kappa _n)) d\xi \\&+ \varepsilon ^2 \delta \kappa ^2 \int _{0}^1 \int _{0}^1 A_{1,\xi } A_{\xi ,\sigma } f'(C_{\xi }w(\kappa _n)) f(\varPhi ^{\sigma \delta \kappa }(w(\kappa _n))) d\xi d\sigma \\&+ \varepsilon ^3 \delta \kappa ^3 \int _{0}^1 \int _{0}^1(1-\zeta ) A_{1,\xi } f''\Big (C_{\xi }w(\kappa _n)\Big . \\&\Big .+\zeta \varepsilon \delta \kappa \int _{0}^1 A_{\xi ,\sigma } f(\varPhi ^{\sigma \delta \kappa }(w(\kappa _n)))d\sigma \Big )\\&\quad \Big (\int _{0}^1 A_{\xi ,\sigma } f(\varPhi ^{\sigma \delta \kappa }(w(\kappa _n)))d\sigma \Big )^2 d\xi d\zeta \\ =&e^{\text{ i }\delta \kappa \triangle }w(\kappa _n)+ \varepsilon \delta \kappa \int _{0}^{1}A_{1,\xi } f(C_{\xi }w(\kappa _n)) d\xi \\&+ \varepsilon ^2 \delta \kappa ^2 \int _{0}^1 \int _{0}^1 A_{1,\xi } A_{\xi ,\sigma } f'(C_{\xi }w(\kappa _n)) f(C_{\sigma }w(\kappa _n)) d\xi d\sigma + \varepsilon ^3 \delta \kappa ^3\varXi _{\varPhi }, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \varXi _{\varPhi } =&\int _{0}^1 \int _{0}^1 \int _{0}^1 A_{1,\xi } A_{\xi ,\sigma } f'\big (C_{\xi }w(\kappa _n)) f'(C_{\sigma }w(\kappa _n)+\zeta (\varPhi ^{\sigma \delta \kappa }(w(\kappa _n))-C_{\sigma }w(\kappa _n))\big ) \\&\quad \Big (\int _{0}^1 A_{\sigma ,\varsigma } f(\varPhi ^{\varsigma \delta \kappa }(w(\kappa _n)))d\varsigma \Big ) d \zeta d\xi d\sigma \\&+ \int _{0}^1 \int _{0}^1(1-\zeta ) A_{1,\xi } f''\Big (C_{\xi }w(\kappa _n)\\&+\zeta \varepsilon \delta \kappa \int _{0}^1 A_{\xi ,\sigma } f(\varPhi ^{\sigma \delta \kappa }(w(\kappa _n)))d\sigma \Big )\\&\quad \Big (\int _{0}^1 A_{\xi ,\sigma } f(\varPhi ^{\sigma \delta \kappa }(w(\kappa _n)))d\sigma \Big )^2 d\xi d\zeta . \end{aligned} \end{aligned}$$

For the exact solution (2.2), similarly we obtain its expansion as

$$\begin{aligned} \begin{aligned} w(\kappa _{n+1})=\,&e^{\text{ i }\delta \kappa \triangle }w(\kappa _n)+ \varepsilon \delta \kappa \int _{0}^1 e^{(1-\xi )\text{ i }\delta \kappa \triangle }f(e^{\text{ i }\xi \delta \kappa \triangle } w(\kappa _n))d\xi + \varepsilon ^3 \delta \kappa ^3 \varXi _{w}\\&+\varepsilon ^2 \delta \kappa ^2 \int _{0}^1 \int _{0}^1 \xi e^{(1-\xi )\text{ i }\delta \kappa \triangle }f'(e^{\text{ i }\xi \delta \kappa \triangle } w(\kappa _n)) e^{(1-\sigma )\text{ i }\xi \delta \kappa \triangle }f(e^{ \text{ i }\sigma \delta \kappa \triangle } w(\kappa _n)) d\xi d \sigma , \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} \varXi _{w} =&\int _{0}^1 \int _{0}^1\int _{0}^1 e^{(1-\xi ) \text{ i }\delta \kappa \triangle } e^{(1-\sigma )\xi \text{ i }\delta \kappa \triangle } f'(e^{\xi \text{ i }\delta \kappa \triangle } w(\kappa _n)) f'\big ( e^{ \text{ i }\sigma \delta \kappa \triangle } w(\kappa _n) \\&+\zeta (w(\kappa _n+\sigma \delta \kappa -e^{ \text{ i }\sigma \delta \kappa \triangle } w(\kappa _n))\big )\Big (\int _{0}^1 e^{(1-\varsigma )\text{ i }\sigma \delta \kappa \triangle } f(w(\kappa _n+\varsigma \delta \kappa ))d\varsigma \Big ) d \zeta d\xi d\sigma \\&+ \int _{0}^1 \int _{0}^1(1-\zeta ) e^{(1-\xi )\text{ i }\delta \kappa \triangle } f''\Big (e^{\xi \text{ i }\delta \kappa \triangle }w(\kappa _n)\Big .\\&\quad \Big .+\zeta \varepsilon \delta \kappa \int _{0}^1 e^{(1-\sigma )\text{ i }\xi \delta \kappa \triangle } f(w(\kappa _n+\sigma \delta \kappa ))d\sigma \Big )\\&\quad \Big (\int _{0}^1 e^{(1-\sigma )\text{ i }\xi \delta \kappa \triangle } f(w(\kappa _n+\sigma \delta \kappa ))d\sigma \Big )^2 d\xi d\zeta . \end{aligned} \end{aligned}$$

Then the local error \(\delta ^{n+1}\) can be refined as

$$\begin{aligned} \delta ^{n+1}=\varepsilon \delta \kappa \varPsi (\kappa _n)+\varepsilon ^2 \delta \kappa ^2 \varUpsilon (\kappa _n), \end{aligned}$$
(3.8)

where

$$\begin{aligned} \begin{aligned} \varPsi (\kappa _n)=&\int _{0}^{1}A_{1,\xi } f(C_{\xi }w(\kappa _n)) d\xi -\int _{0}^1 e^{(1-\xi ) \text{ i }\delta \kappa \triangle }f(e^{ \xi \text{ i }\delta \kappa \triangle } w(\kappa _n))d\xi ,\\ \varUpsilon (\kappa _n)=&\int _{0}^1 \int _{0}^1 A_{1,\xi } A_{\xi ,\sigma } f'(C_{\xi }w(\kappa _n)) f(C_{\sigma }w(\kappa _n)) d\xi d\sigma \\&-\int _{0}^1 \int _{0}^1 \xi e^{(1-\xi ) \text{ i }\delta \kappa \triangle }f'(e^{ \xi \text{ i }\delta \kappa \triangle } w(\kappa _n)) e^{(1-\sigma )\xi \text{ i }\delta \kappa \triangle }f(e^{\text{ i }\sigma \delta \kappa \triangle } w(\kappa _n)) d\xi d \sigma \\&+ \varepsilon \delta \kappa \varXi _{\varPhi }- \varepsilon \delta \kappa \varXi _{w}. \end{aligned} \end{aligned}$$

Concerning the previous local errors given in Lemma 1, one has

$$\begin{aligned} \Vert \varPsi (\kappa _n)\Vert _{H^{\alpha -4}}\lesssim \delta \kappa ^2,\quad \ \Vert \varUpsilon (\kappa _n)\Vert _{H^{\alpha -4}}\lesssim \delta \kappa . \end{aligned}$$

Refined convergence over one period. In this part, we consider convergence over one period, that is \(n\delta \kappa =T_0=1\). For the global error

$$\begin{aligned} \begin{aligned} (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)&=\sum _{l=1}^{n}\big ((\varPhi ^{\delta \kappa })^{n-l} \varPhi ^{\delta \kappa }(w(\kappa _{l-1}))-(\varPhi ^{\delta \kappa })^{n-l}(w(\kappa _{l}))\big ), \end{aligned} \end{aligned}$$

we introduce \(\varTheta ^{\delta \kappa }_{n-l}:=(\varPhi ^{\delta \kappa })^{n-l}-e^{\text{ i }(n-l) \delta \kappa \triangle }\) and then rewrite it as

$$\begin{aligned} \begin{aligned} (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)&=\underbrace{\sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \delta ^{l}}_{{\mathbb {E}}_1}+\underbrace{\sum _{l=1}^{n} \big (\varTheta ^{\delta \kappa }_{n-l}(\varPhi ^{\delta \kappa }(w(\kappa _{l-1}))) -\varTheta ^{\delta \kappa }_{n-l}(w(\kappa _{l}))\big )}_{{\mathbb {E}}_2}. \end{aligned} \end{aligned}$$
(3.9)

For the part \({\mathbb {E}}_2\), we first estimate

$$\begin{aligned} \begin{aligned} \left\| \varTheta ^{\delta \kappa }_{l}v-\varTheta ^{\delta \kappa }_{l}w\right\| _{H^{\beta }}&= \left\| (\varPhi ^{\delta \kappa })^{l}v-e^{\text{ i }l \delta \kappa \triangle }v-(\varPhi ^{\delta \kappa })^{l}w+e^{\text{ i }l \delta \kappa \triangle }w\right\| _{H^{\beta }}\\&\le \sum _{k=1}^l\left\| \varTheta ^{\delta \kappa }_{1} (\varPhi ^{\delta \kappa })^{k-1}v-\varTheta ^{\delta \kappa }_{1} (\varPhi ^{\delta \kappa })^{k-1}w\right\| _{H^{\beta }} \\&\le \varepsilon \delta \kappa L C_A e^{\varepsilon \tau \delta \kappa L C_A}\sum _{k=1}^l \left\| (\varPhi ^{\delta \kappa })^{k-1}v-(\varPhi ^{\delta \kappa })^{k-1}w\right\| _{H^{\beta }}\\&\le \varepsilon \delta \kappa L C_A e^{\varepsilon \tau \delta \kappa L C_A}\sum _{k=1}^l e^{\varepsilon (k-1) \delta \kappa L C_A} \left\| v-w\right\| _{H^{\beta }}\\&\le \varepsilon L C_A T_0 e^{\varepsilon L C_A T_0} \left\| v-w\right\| _{H^{\beta }}. \end{aligned} \end{aligned}$$

Then the following bound holds

$$\begin{aligned} \begin{aligned} \left\| {\mathbb {E}}_2\right\| _{H^{\alpha -4}}\le \varepsilon L C_A T_0 e^{\varepsilon L C_A T_0}\sum _{l=1}^{n} \left\| \delta ^{l}\right\| _{H^{\alpha -4}} \lesssim \varepsilon ^2 \delta \kappa ^2. \end{aligned} \end{aligned}$$
(3.10)

For the part \({\mathbb {E}}_1\), we use the refined local error (3.8) and then have

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_1=\sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \varepsilon \delta \kappa \varPsi (\kappa _{l-1})+\sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle }\varepsilon ^2 \delta \kappa ^2 \varUpsilon (\kappa _{l-1}). \end{aligned} \end{aligned}$$
(3.11)

According to (3.9)-(3.11) and the following bound

$$\begin{aligned} \begin{aligned} \left\| \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle }\varepsilon ^2 \delta \kappa ^2 \varUpsilon (\kappa _{l-1})\right\| _{H^{\alpha -4}} \le \varepsilon ^2 \delta \kappa ^3 \sum _{l=1}^{n} \left\| e^{\text{ i }(n-l) \delta \kappa \triangle } \right\| _{H^{\alpha -4}} \lesssim \varepsilon ^2 \delta \kappa ^2, \end{aligned} \end{aligned}$$

the global error is bounded by

$$\begin{aligned} \begin{aligned} \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -4}} \lesssim \varepsilon \delta \kappa \left\| \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \varPsi (\kappa _{l-1}) \right\| _{H^{\alpha -4}}+ \varepsilon ^2 \delta \kappa ^2. \end{aligned} \end{aligned}$$
(3.12)

In what follows, we derive the optimal bound for \(\varepsilon \delta \kappa \left\| \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \varPsi (\kappa _{l-1}) \right\| _{H^{\alpha -4}}\), which satisfies

$$\begin{aligned} \begin{aligned}&\varepsilon \delta \kappa \left\| \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \varPsi (\kappa _{l-1}) \right\| _{H^{\alpha -4}}\\&\quad \lesssim \varepsilon \delta \kappa \Vert \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \int _{0}^{1}A_{1,\xi } f(C_{\xi }e^{\text{ i }(l-1) \delta \kappa \triangle } w_0) d\xi \\&\qquad -\varepsilon \sum _{l=1}^{n}e^{\text{ i }(n-l+1) \delta \kappa \triangle } \int _{0}^{\delta \kappa } e^{- \text{ i }\xi \triangle }f(e^{ \text{ i }\xi \triangle } e^{\text{ i }(l-1) \delta \kappa \triangle } w_0 )d\xi \Vert _{H^{\alpha -4}}+ \varepsilon ^2 \delta \kappa ^2\\&\quad \lesssim \left\| \varepsilon \delta \kappa \sum _{l=1}^{n}e^{-\text{ i }l \delta \kappa \triangle } \int _{0}^{1}A_{1,\xi } f(C_{\xi }e^{\text{ i }(l-1) \delta \kappa \triangle } w_0) d\xi - \varepsilon \int _{0}^1 e^{- \text{ i }\xi \triangle }f(e^{ \text{ i }\xi \triangle } w_0 )d\xi \right\| _{H^{\alpha -4}} \\&\qquad + \varepsilon ^2 \delta \kappa ^2. \end{aligned} \end{aligned}$$

Here we used the result \(\left\| w(\kappa _{l-1})-e^{\text{ i }(l-1) \delta \kappa \triangle } w_0\right\| _{H^{\alpha -4}}\lesssim \varepsilon .\) We first consider Fourier expansion \(F_{\xi }(w)=\sum _{k\in {\mathbb {Z}}}e^{\text{ i }2 k \pi \xi }{\hat{F}}_{k}(w)\) of \(F_{\xi }(w):=e^{-\text{ i }\xi \triangle }f(e^{\text{ i }\xi \triangle } w)\), which yields that \(\int _{0}^1 e^{- \text{ i }\xi \triangle }f(e^{ \text{ i }\xi \triangle } w_0 )d\xi ={\hat{F}}_{0}(w_0).\) Then let

$$\begin{aligned} G_{l\delta \kappa }(w)= e^{-\text{ i }l \delta \kappa \triangle } \int _{0}^{1}A_{1,\xi } f(C_{\xi }e^{\text{ i }l \delta \kappa \triangle } w) d\xi \end{aligned}$$

and the Fourier expansion of \(G_{l\delta \kappa }(w)\) is given by \(G_{l\delta \kappa }(w)=\sum _{k\in {\mathbb {Z}}}e^{\text{ i }2 k \pi l\delta \kappa }{\hat{G}}_{k}(w).\) Therefore, it is obtained that

$$\begin{aligned} \begin{aligned}&\varepsilon \delta \kappa \sum _{l=1}^{n}e^{-\text{ i }l \delta \kappa \triangle } \int _{0}^{1}A_{1,\xi } f(C_{\xi }e^{\text{ i }(l-1) \delta \kappa \triangle } w_0) d\xi \\&\quad =\varepsilon \delta \kappa e^{-\text{ i }\delta \kappa \triangle } \sum _{l=0}^{n-1}\sum _{k\in {\mathbb {Z}}}e^{\text{ i }2 k \pi l\delta \kappa }{\hat{G}}_{k}(w)\\&\quad =\varepsilon e^{-\text{ i }\delta \kappa \triangle } \sum _{k\in {\mathbb {Z}}}\Big (\frac{1}{n} \sum _{l=0}^{n-1}e^{\text{ i }2 k \pi l\delta \kappa }{\hat{G}}_{k}(w)\Big ) =\varepsilon e^{-\text{ i }\delta \kappa \triangle } \sum _{k\in {\mathbb {Z}}} {\hat{G}}_{nk}(w). \end{aligned} \end{aligned}$$

Based on the above results, it follows that

$$\begin{aligned} \begin{aligned}&\varepsilon \delta \kappa \left\| \sum _{l=1}^{n}e^{\text{ i }(n-l) \delta \kappa \triangle } \varPsi (\kappa _{l-1}) \right\| _{H^{\alpha -6}}\\&\quad \lesssim \varepsilon \left\| {\hat{F}}_{0}(w_0)- e^{-\text{ i }\delta \kappa \triangle } {\hat{G}}_{0}(w) \right\| _{H^{\alpha -6}}+\varepsilon \left\| \sum _{k\in {\mathbb {Z}}^{*}} {\hat{G}}_{nk}(w)\right\| _{H^{\alpha -6}}+ \varepsilon ^2 \delta \kappa ^2\\&\quad \lesssim \varepsilon \left\| \int _{0}^{1}e^{ - \text{ i }\xi \triangle }f(e^{ \text{ i }\xi \triangle } w_0)d \xi - \int _{0}^{1}e^{ - \text{ i }\xi \triangle }\Big [ e^{-\text{ i }\delta \kappa \triangle } \int _{0}^{1}A_{1,\xi } f(C_{\xi }e^{\text{ i }\xi \triangle } w_0) d\xi \Big ] d \xi \right\| _{H^{\alpha -6}}\\&\qquad +\varepsilon \delta \kappa ^3+ \varepsilon ^2 \delta \kappa ^2 \lesssim \varepsilon \delta \kappa ^3+\varepsilon \delta \kappa ^3+ \varepsilon ^2 \delta \kappa ^2. \end{aligned} \end{aligned}$$
(3.13)

Here Lemma A.1 of [17] and the results \(A_{1,\xi }\) and \(C_{\xi }\) of EP2 are used to obtain the last two inequalities, respectively. Finally, combining (3.12) with (3.13), we obtain the global error over one period

$$\begin{aligned} \begin{aligned} \left\| (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\right\| _{H^{\alpha -6}} \lesssim \varepsilon \delta \kappa ^3+ \varepsilon ^2 \delta \kappa ^2,\ \ n\delta \kappa =T_0. \end{aligned} \end{aligned}$$
(3.14)

Refined global error.

For \(n\delta \kappa \le T/\varepsilon \), the global error of EP2 given in (3.5) can be derived by considering (3.14) and by using the same way presented in Sect. 5 of [17].

The whole proof is complete. \(\square \)

Remark 3

It is noted that for EP1, the estimate of (3.13) is only \(\varepsilon \delta \kappa ^2\). Therefore, EP1 does not have optimal convergence.

4 Long time Conservations in Actions, Momentum and Density

In this section, we turn back to the methods applied to the original system (1.1) and study their long time conservations in actions, momentum and density.

4.1 Preliminaries

In order to make the analysis be succinct, we choose \(\lambda =1\). For our integrator (2.4), spectral semi-discretisation (see [18, 19, 29, 30, 48]) with the points \(x_k=\frac{\pi }{M}k,\ k\in {\mathcal {M}}\) is used in space, where \({\mathcal {M}}=\{-M,\ldots ,M-1\}^d\) and 2M presents the number of internal discretisation points in space. Then the fully discrete scheme of (2.4) is

$$\begin{aligned} \begin{aligned} u^{n+\tau }&=C_{\tau }(V)u^n+ h \int _{0}^{1}A_{\tau ,\sigma }(V)f(u^{n+\sigma })d\sigma ,\ \ 0\le \tau \le 1, \end{aligned} \end{aligned}$$
(4.1)

where \(V=\text{ i }h \varOmega \), \(\varOmega =-\text{ diag }((\omega _j)_{j\in {\mathcal {M}}})\) and \(f(u)=-\text{ i }{\mathcal {Q}}(\left| u\right| ^2u)\)Footnote 1. Here, \( \omega _j= \frac{1}{\varepsilon }\left| j\right| ^2=\frac{1}{\varepsilon } (j_1^2+\cdots +j_d^2)\) for \(j=(j_1,\ldots ,j_d)\in {\mathcal {M}}\) are the eigenvalues of the linear part of (1.1) after spectral semi-discretisation in space, and the notation \({\mathcal {Q}}(v)\) denotes the trigonometric interpolation of a periodic function \(v=\sum \limits _{j\in {\mathbb {Z}}^d}v_je^{\text{ i }(j\cdot x)}\) in the collocation points, i.e., \({\mathcal {Q}}(v)=\sum \limits _{j\in {\mathcal {M}}}\big (\sum \limits _{l\in {\mathbb {Z}}^d}v_{j+2Ml}\big )\mathrm {e}^{\mathrm {i}(j\cdot x)}.\)

The following notations are needed in this section which have been used in [19, 29, 30]. For a sequence \(k = (k_j)_{j\in {\mathcal {M}}}\) of integers \(k_j\) and the sequence \(\omega = (\omega _j)_{j\in {\mathcal {M}}},\) denote

$$\begin{aligned} \left\| k\right\| =\sum \limits _{j\in {\mathcal {M}}}|k_j|, \ k\cdot \omega =\sum \limits _{j\in {\mathcal {M}}}k_j\omega _j, \ \omega ^{\sigma |k|}=\varPi _{j\in {\mathcal {M}}} \omega _j^{\sigma |k_j|} \end{aligned}$$

for a real \(\sigma \). Denote by \(\langle j\rangle \) the unit coordinate vector \((0, \ldots , 0, 1, 0, \ldots ,0)^{\intercal }\) with the only entry 1 at the |j|-th position.

4.2 Result of Near-Conservation Properties

Theorem 4

(Long time near-conservations.) Consider the small initial data

$$\begin{aligned} \left\| u^0\right\| _{H^s}\le {\tilde{\epsilon }} \ll 1, \ \ \text{ for } \text{ some }\ s\ge 0, \end{aligned}$$
(4.2)

and define the set

$$\begin{aligned} {\mathcal {R}}_{{\tilde{\epsilon }},M,h}=\Big \{(j, k):j=j(k),\ k\ne \langle j\rangle ,\ \left| \sin \big (\frac{1}{2}h(\omega _j-k \cdot \omega )\big )\right| \le \frac{1}{2}{\tilde{\epsilon }}^{1/2}h,\ \left\| k\right\| \le 2N+2\Big \}, \nonumber \\ \end{aligned}$$
(4.3)

where \(j(k):=\sum \limits _{l\in {\mathcal {M}}}k_ll \ \text{ mod }\ 2M\in {\mathcal {M}}=\{-M,\ldots ,M-1\}^d. \) For the near-resonant indices (j, k) in \({\mathcal {R}}_{{\tilde{\epsilon }},M,h}\), they are required such that

$$\begin{aligned} \sup _{(j, k)\in {\mathcal {R}}_{{\tilde{\epsilon }},M,h}} \frac{\left| \omega _j\right| ^{s-\frac{d+1}{2}}}{\omega ^{(s-\frac{d+1}{2}) |k|}}{\tilde{\epsilon }}^{\left\| k\right\| +1}\le {\tilde{C}} {\tilde{\epsilon }}^{2N+4} \end{aligned}$$
(4.4)

with a constant \({\tilde{C}}\) independent of \({\tilde{\epsilon }}\). For given \(N\ge 1\) and \(s \ge d + 1\), the numerical solution \(u^n\) of EP1 has the following conservations of density, momentum and actions, respectively

$$\begin{aligned} \begin{aligned}&\frac{|m[u^{n},{\bar{u}}^{n}]-m[u^{0},{\bar{u}}^{0}]|}{{\tilde{\epsilon }}^2} \le C {\tilde{\epsilon }}^{\frac{3}{2}},\\&\sum \limits _{r=1}^d\frac{|K_r[u^{n},{\bar{u}}^{n}]-K_r[u^{0},{\bar{u}}^{0}]|}{{\tilde{\epsilon }}^2} \le C {\tilde{\epsilon }}^{\frac{3}{2}},\\&\sum \limits _{j\in {\mathcal {M}}}|\omega _j|^{s}\frac{|I_j(u^{n},{\bar{u}}^{n})-I_j(u^{0},{\bar{u}}^{0})|}{{\tilde{\epsilon }}^2} \le C {\tilde{\epsilon }}^{\frac{3}{2}}, \end{aligned} \end{aligned}$$

where \(0\le t_n=nh\le {\tilde{\epsilon }}^{-N}\) and the constant C depends on \({\tilde{C}}\), \(\max _{j\in {\mathcal {M}}}\big \{ \frac{1}{\left| \cos (\frac{1}{2}h \omega _j)\right| }\big \}\), N, s and the dimension d but is independent of n, the size of the initial value \({\tilde{\epsilon }}\), the regime of the solution \(\varepsilon \), and the discretisation parameters M and h. Here \(K_r\) is referred to the rth component of K. For the schemes EP1-EP2, if the midpoint rule is used to the integral appearing in these methods, the above near conservations still hold.

Remark 4

We remark that the method EP3 does not have such near conservations and the reason will be explained at the end of this section.

Remark 5

It is noted that the authors in [19, 28, 30] analysed the long-time behaviour of exponential integrators, splitting integrators and split-step Fourier method for Schrödinger equations. However, those methods cannot preserve the energy (2.7) exactly. We remark that Theorem 4 shows that our energy-preserving integrators also have a near conservation of actions, momentum and density over long times.

Remark 6

Although the actions are not the invariants of NLS, the schemes EP1-EP2 will be shown to have long time near conservation of this quantity. This property is the same as that of momentum and density. Moreover, in the proof of this theorem, the long-time near-conservation of actions implies the long-time near-conservation of density and of momentum. Therefore, the quantity of actions is considered and analysed in this paper. Besides, the results of Theorem 4 cannot be extended for arbitrary initial date since large initial data case usually leads to large bounds of the coefficient functions in the modulation Fourier expansion, which prevents the derivation of long time near conservations.

4.3 The Proof of Theorem 4

The proof makes use of a modulated Fourier expansion [19, 29, 30, 54] in time of the numerical solution. We will use the following expansion

$$\begin{aligned} \begin{aligned}&{\tilde{u}}(t,x)= \sum \limits _{\left\| k\right\| \le K}z^{k}({\tilde{\epsilon }} t,x) \mathrm {e}^{-\mathrm {i}(k \cdot \omega ) t}= \sum \limits _{\left\| k\right\| \le K}\sum \limits _{j\in {\mathcal {M}}}z_j^{k}({\tilde{\epsilon }} t) \mathrm {e}^{\mathrm {i}(j \cdot x)} \mathrm {e}^{-\mathrm {i}(k \cdot \omega ) t} \end{aligned} \end{aligned}$$
(4.5)

to describe the numerical solution \(u^n\) at time \(t_n = nh\) after n time steps, where the functions \(z^{k}\) are termed the modulation functions which evolve on a slow time-scale \({\tilde{\tau }} = {\tilde{\epsilon }} t.\) Following [19], these functions can be assumed to be single spatial waves: \( z^{k}({\tilde{\epsilon }} t,x)=z_{j(k)}^{k}({\tilde{\epsilon }} t) \mathrm {e}^{\mathrm {i}(j(k) \cdot x)}, \) i.e., their Fourier coefficients \(z_j^{k}\) vanish for \(j\ne j(k)\) with \(j(k)=\sum \limits _{l\in {\mathcal {M}}}k_ll \ \text{ mod }\ 2M\in {\mathcal {M}}\).

It is noted that as a standard approach to the study of long-time behavior of numerical methods, modulated Fourier expansion is also used in the analysis of [19, 29, 30, 54, 56]. However, in this paper, there are novel modifications adapted to our integrators, which come from the implicitness of the integrator and the integral appearing in the integrator. We present the main differences in the proof. For the similar derivations as those of [19, 29, 30], we skip them in the analysis for brevity.

4.3.1 Modulation Equations

Lemma 3

(Modulation equations.) Define

$$\begin{aligned} \begin{aligned} L^{k}:&=(L^{k}_2)^{-1} L^{k}_1,\\ L_1^{k}:&=\mathrm {e}^{-\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{{\tilde{\epsilon }} hD}-2\cos (h\varOmega )+\mathrm {e}^{\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{-{\tilde{\epsilon }} hD},\\ L_2^{k}:&=\varphi _1(\text{ i }h \varOmega )\mathrm {e}^{-\frac{1}{2}\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{\frac{1}{2}{\tilde{\epsilon }} hD}-\varphi _1(-\text{ i }h \varOmega )\mathrm {e}^{\frac{1}{2}\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{-\frac{1}{2}{\tilde{\epsilon }} hD},\\ \end{aligned} \end{aligned}$$

where D is the differential operator (see [35]). The modulation equations for the coefficients \( z_j^{k}\) appearing in (4.5) are given by

$$\begin{aligned} \begin{aligned} L^{k} z_j^{k}({\tilde{\epsilon }} t)= -\text{ i }h \sum \limits _{k^1+k^2-k^3=k }\int _{0}^{1}w^{k^1}_{j(k^1)}({\tilde{\epsilon }} t,\sigma )w^{k^2}_{j(k^2)}({\tilde{\epsilon }} t,\sigma )\overline{w^{k^3}_{j(k^3)}}({\tilde{\epsilon }} t,\sigma )d\sigma , \end{aligned} \end{aligned}$$
(4.6)

where

$$\begin{aligned} w^{k}_{j(k)}({\tilde{\epsilon }} t,\sigma )=L^{k}_3(\sigma )z_{j(k)}^{k}({\tilde{\epsilon }} t) \end{aligned}$$
(4.7)

with

$$\begin{aligned} L_3^{k}(\sigma ):= (1-\sigma )\mathrm {e}^{\frac{1}{2}\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{- \frac{h}{2}{\tilde{\epsilon }} D} +\sigma \mathrm {e}^{-\frac{1}{2}\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{ \frac{h}{2}{\tilde{\epsilon }} D}. \end{aligned}$$

The initial condition for modulation equations is given by

$$\begin{aligned} u_j^0= \sum \limits _{k} z_{j(k)}^{k}(0). \end{aligned}$$
(4.8)

The proof of this lemma is given in the Appendix.

4.3.2 Some Skipped Points of the Proof

Then the following key points can be considered one by one.

  • An iterative construction of the functions is achieved by considering reverse Picard iteration.

  • A more convenient rescaling is presented.

  • The nonlinear terms are estimated and the size of the iterated modulation functions is shown.

  • The bound of the defect \(d^k\) is derived.

  • The size of the numerical solution and the difference of the numerical solution and its modulated Fourier expansion are derived.

We do not present the details for these points since they can be derived by similar arguments as in [19, 29, 30].

4.3.3 Almost Invariants Close to the Actions

In what follows, we show an invariant of the modulation system and its relationship with the actions.

Proposition 3

(Almost invariant.) There exits \({\tilde{\epsilon }} {\mathcal {J}}_{\langle j\rangle }({\tilde{\tau }})\) such that

$$\begin{aligned} \sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s} \left| \frac{d}{d {\tilde{\tau }}} {\mathcal {J}}_{\langle j\rangle }({\tilde{\tau }})\right| \le Ch{\tilde{\epsilon }}^{N+3}, \end{aligned}$$

where \({\tilde{\tau }}\le 1\) and C depends on \(\max _{j\in {\mathcal {M}}}\big \{ \frac{1}{\left| \cos (\frac{1}{2}h \omega _j)\right| }\big \}\). Moreover, it is true that

$$\begin{aligned} {\mathcal {J}}_{\langle j\rangle }({\tilde{\tau }})= \frac{1}{2} \left| z_{j}^{\langle j\rangle }({\tilde{\tau }})\right| ^2+{\mathcal {O}}\Big (h {\tilde{\epsilon }}^2\Big ). \end{aligned}$$

Proof

Let

$$\begin{aligned} {\mathcal {U}}({\mathbf {w}})= \sum \limits _{k^1+k^2-k^3-k^4=0 }\frac{1}{(2\pi )^d}\int _{[-\pi ,\pi ]^d}\int _{0}^{1}w^{k^1}w^{k^2} \overline{w^{k^3}}\overline{w^{k^4}}d\sigma dx. \end{aligned}$$

From the above analysis, we can write the defect formula \(d^{k}\) as

$$\begin{aligned} \begin{aligned}&{\tilde{L}}^{k} z^{k}=-\text{ i }h \sum \limits _{k^1+k^2-k^3=k }\int _{0}^{1}w^{k^1}_{j(k^1)}w^{k^2}_{j(k^2)}\overline{w^{k^3}_{j(k^3)}}d\sigma + d^{k}. \end{aligned} \end{aligned}$$
(4.9)

Here we use \({\tilde{L}}^{k}\) to denote the truncation of the operator \(L^{k}\) after the \({\tilde{\epsilon }}^N\) term. The transformation \(w^{k}\rightarrow \mathrm {e}^{\mathrm {i}(k \cdot \mu ) \theta } w^{k}\) for real sequences \(\mu = (\mu _l)_{l\ge 0}\) and \(\theta \in {\mathbb {R}}\) and the choice of \(k=\langle j\rangle \) leaves \({\mathcal {U}}\) invariant

$$\begin{aligned} \begin{aligned}&0=h\frac{d}{d\theta }\mid _{\theta =0} {\mathcal {U}}\Big ((\mathrm {e}^{\mathrm {i}(\langle j\rangle \cdot \mu ) \theta } w^{\langle j\rangle })_{\langle j\rangle }\Big ) \\&\quad = -4h \text{ Re }\Big (\sum \limits _{j} \mathrm {i}(\langle j\rangle \cdot \mu ) \overline{ w_{j}^{\langle j\rangle }} \sum \limits _{k^1+k^2-k^3=\langle j\rangle }\int _{0}^{1}w^{k^1}_{j(k^1)}w^{k^2}_{j(k^2)}\overline{w^{k^3}_{j(k^3)}}d\sigma \Big )\\&\quad = 4 \text{ Re }\Big (\sum \limits _{j} (\langle j\rangle \cdot \mu ) \overline{w_{j}^{\langle j\rangle }}\big ({\tilde{L}}^{\langle j\rangle } z^{\langle j\rangle }_j-d^{\langle j\rangle }_j\big )\Big )\\&\quad = 4 \text{ Re }\Big (\sum \limits _{j} (\langle j\rangle \cdot \mu ) \overline{L_3^{\langle j\rangle }(\sigma )z_{j}^{\langle j\rangle }}\big ({\tilde{L}}^{\langle j\rangle } z^{\langle j\rangle }_j-d^{\langle j\rangle }_j\big )\Big ). \end{aligned} \end{aligned}$$

Since the right-hand side is independent of \(\sigma \), we choose \(\sigma =1/2\) in the following analysis. With the above formula, we have

$$\begin{aligned} \begin{aligned} 4 \text{ Re } \sum \limits _{j} (\langle j\rangle \cdot \mu ) \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} {\tilde{L}}^{\langle j\rangle } z^{\langle j\rangle }_j=4 \text{ Re } \sum \limits _{j} (\langle j\rangle \cdot \mu ) \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} d^{\langle j\rangle }_j. \end{aligned} \end{aligned}$$
(4.10)

By the expansions of \(L_3^{\langle j\rangle }(1/2)\) and \({\tilde{L}}^{\langle j\rangle }\) and the “magic formulas" on p. 508 of [35], it is known that the left-hand side of (4.10) is a total derivative of function \({\tilde{\epsilon }} {\mathcal {J}}_{\mu }({\tilde{\tau }})\). Therefore (4.10) is identical to

$$\begin{aligned} {\tilde{\epsilon }}\frac{d}{d {\tilde{\tau }}} {\mathcal {J}}_{\mu }=4 \text{ Re } \sum \limits _{j} (\langle j\rangle \cdot \mu ) \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} d^{\langle j\rangle }_j. \end{aligned}$$

Considering the special case of \(\mu =\frac{\mathrm {sinc}(\frac{1}{2}h \omega _j)}{\cos (\frac{1}{2}h \omega _j)}\langle j\rangle \) and for the first result, it needs to prove that

$$\begin{aligned} \sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s}\left| \frac{\mathrm {sinc}(\frac{1}{2}h \omega _j)}{\cos (\frac{1}{2}h \omega _j)}\right| \left| \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} d^{\langle j\rangle }_j\right| \le Ch{\tilde{\epsilon }}^{N+4}. \end{aligned}$$

By the property of \(L_3\), we have

$$\begin{aligned} \sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s} \left| \frac{\mathrm {sinc}(\frac{1}{2}h \omega _j)}{\cos (\frac{1}{2}h \omega _j)}\right| \left| \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} d^{\langle j\rangle }_j\right| \le C\sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s} \left| z_{j}^{\langle j\rangle }\right| \left| {\dot{h}}^{\langle j\rangle }_j \right| . \end{aligned}$$

Here we decompose \(d_j^{k}\) into four parts: \(\big [d_j^{k}\big ]=\big [e_j^{k}+f_j^{k}+g_j^{k}+{\dot{h}}_j^{k}\big ],\) where \([e_j^{k}]=0\) for \((j, k)\in {\mathcal {L}}_{{\tilde{\epsilon }},M,h}:=\{(j, k):j=j(k),\ k\ne \langle j\rangle ,\ (j, k)\notin {\mathcal {R}}_{{\tilde{\epsilon }},M,h},\ \left\| k\right\| \le K\},\) \([f_j^{k}]=0\) for non-near resonant indices \((j, k)\in {\mathcal {R}}_{{\tilde{\epsilon }},M,h}\), \([{\dot{h}}_j^{k}]=0\) for \( k\ne \langle j\rangle \), and \([g_j^{k}]=0\) for \( \left\| k\right\| \le K\). The size of \(\dot{{\mathbf {h}}}({\tilde{\tau }})\) can be estimated as follows. For all \(l\ge 0\) and for \(0\le {\tilde{\tau }}={\tilde{\epsilon }} t\le 1\), it is true that \( |||\dot{{\mathbf {h}}}({\tilde{\tau }})|||_s\le C {\tilde{\epsilon }}^{\frac{p+4}{2}}h,\) where \(|||{\mathbf {z}}|||_s^2:=\sum \limits _{j}\left| \omega _j\right| ^s \big (\sum \limits _{k}\left| z_j^{k}\right| \big )^2\). Taking advantage of Cauchy-Schwarz inequality, one gets

$$\begin{aligned} \begin{aligned}&\sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s}\left| \frac{\mathrm {sinc}(\frac{1}{2}h \omega _j)}{\cos (\frac{1}{2}h \omega _j)}\right| \left| \overline{L_3^{\langle j\rangle }(1/2)z_{j}^{\langle j\rangle }} d^{\langle j\rangle }_j\right| \\&\quad \le C \sqrt{\sum \limits _{j\in {\mathcal {M}}}\big (\left| \omega _j\right| ^{\frac{s}{2}}\big )^2 \left| z_{j}^{\langle j\rangle }\right| ^2} \sqrt{\sum \limits _{j\in {\mathcal {M}}}\big (\left| \omega _j\right| ^{\frac{s}{2}}\big )^2 \left| {\dot{h}}^{\langle j\rangle }_j \right| ^2}\\&\quad \le C\sqrt{{\tilde{\epsilon }}^2}\sqrt{h^2{\tilde{\epsilon }}^{p+4}}= Ch {\tilde{\epsilon }}^{\frac{p}{2}+3}= Ch {\tilde{\epsilon }}^{\frac{L}{2}+3}. \end{aligned} \end{aligned}$$

The first statement is immediately obtained by considering \(L= 2N+2\).

Then, using the Taylor expansions of \(L_3^{\langle j\rangle }(1/2)\) and \(L^{\langle j\rangle }\) and the “magic formulas” on p. 508 of [35] gives the construction of \( {\mathcal {J}}_{\langle j\rangle }\). \(\square \)

After obtaining the almost invariant, its relationship with the actions is derived below.

Proposition 4

(The relationship between the almost invariant and the actions.) It is true that \(\sum \limits _{j\in {\mathcal {M}}}\left| \omega _j\right| ^{s} \left| {\mathcal {J}}_{\langle j\rangle }({\tilde{\tau }})-I_j(u^n, \overline{u^n})\right| \le C{\tilde{\epsilon }}^{\frac{7}{2}},\) where \({\tilde{\tau }}\le 1\).

Proof

This result can be obtained by following the proof of Proposition 6 given in [29]. \(\square \)

4.3.4 Near-Conservation of Density, Momentum and Actions

According to the analysis stated above, we consider the interface between the modulated Fourier expansions and extend it from short to long time intervals in the same way used in Sects. 4.10-4.11 of [19]. Then the near conservation of actions given in Theorem 4 is obtained. Meanwhile, it follows from the results presented in Sect. 6.4 of [30] and Sect. 4.11 of [19] that the long-time near-conservation of actions implies the long-time near-conservation of density and of momentum. Therefore, the other statements of Theorem 4 are proved.

This concludes the proof of Theorem 4 for the integrator EP1.

4.3.5 Proof for EP2

Consider the one-point quadrature formula with \(({\tilde{c}}_1,{\tilde{d}}_1)\) and then the scheme of (4.1) becomes

$$\begin{aligned} \begin{aligned} u^{n+1}&=e^{V}u^n+h {\tilde{d}}_1A_{1,{\tilde{c}}_1}(V) f\Big (C_{{\tilde{c}}_1}(V)u^n+A_{{\tilde{c}}_1,{\tilde{c}}_1}(V) A^{-1}_{1,{\tilde{c}}_1}(V)(u^{n+1}-e^{V}u^n) \Big ). \end{aligned} \end{aligned}$$
(4.11)

In terms of this formula, we can derive the modulation equations for the modulation functions \(z_j^{k}\) as \(L^{k} z_j^{k}({\tilde{\epsilon }} t)= -\text{ i }h \sum \limits _{k^1+k^2-k^3=k } z^{k^1}_{j(k^1)}({\tilde{\epsilon }} t)z^{k^2}_{j(k^2)}({\tilde{\epsilon }} t)\overline{z^{k^3}_{j(k^3)}}({\tilde{\epsilon }} t)\) by defining

$$\begin{aligned} \begin{aligned} L^{k}:&=\big (A_{{\tilde{c}}_1,{\tilde{c}}_1} A^{-1}_{1,{\tilde{c}}_1}(\mathrm {e}^{-\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{{\tilde{\epsilon }} hD}- \mathrm {e}^{\text{ i }h\varOmega })+C_{{\tilde{c}}_1}\big )^{-1}(\mathrm {e}^{-\mathrm {i}(k \cdot \omega ) h}\mathrm {e}^{{\tilde{\epsilon }} hD}- \mathrm {e}^{\text{ i }h\varOmega }) ({\tilde{d}}_1B_{{\tilde{c}}_1})^{-1}.\end{aligned} \end{aligned}$$

It can be seen that this formula has more concise expression than that of EP1. Then by modifying the nonlinearity and concerning the property of \(L^{k}\), the analysis given above can be changed accordingly for EP2.

Remark 7

It is noted that the scheme (4.11) has been analysed in [19]. Under an assumption on the coefficient functions of exponential integrator, long term conservations have been derived there. However, for the coefficients \(A_{{\tilde{c}}_1,{\tilde{c}}_1}(V)\) and \( A_{1,{\tilde{c}}_1}(V)\) of EP2, they do not satisfy that assumption required in [19]. Thus the part 4.2 of the proof given in [19] cannot be used for EP2. Therefor we consider the above approach to proving the result. On the other side, the operator \(L^{k}\) determined by EP3 does not have similar property as (6.1). Therefore, there is no invariant of the modulation system and the near conservations are not true for EP3.

5 Numerical Experiment

Table 1 Properties of the methods
Full size table

For the algorithms presented in this paper, their properties are summarized in Table 1. In order to show their advantages, we choose the second-order explicit exponential integrator which is termed pseudo steady-state approximation which was given in [51] (denoted by EEI) and the fourth-order explicit exponential Runge–Kutta method which was given in [37] (denoted by EEI4). Meanwhile, we present a mass-preserving (but not erengy-preserving) exponential integrator

$$\begin{aligned} \begin{aligned} U^{n+\tau }(x)&=C_{\tau }({\mathcal {V}})u^n(x)+ h \int _{0}^{1}A_{\tau ,\sigma }({\mathcal {V}})f(U^{n+\sigma }(x))d\sigma ,\ \ 0\le \tau \le 1,\\ u^{n+1}(x)&=e^{{\mathcal {V}}}u^n(x)+h \displaystyle \int _{0}^{1}B_{\tau }({\mathcal {V}}) f(U^{n+\tau }(x))d\tau ,\\ \end{aligned} \end{aligned}$$

with the coefficients \( C_{\tau }({\mathcal {V}})= e^{\tau {\mathcal {V}}}, \ B_{\tau }({\mathcal {V}})= e^{(1-\tau ){\mathcal {V}}}\) and \( A_{\tau ,\sigma }({\mathcal {V}})=(\frac{1}{2}+(\tau -\sigma ))e^{(\tau -\sigma ){\mathcal {V}}}\). It is easy to check that this integrator is mass-preserving and we refer to it as MP. As a numerical experiment, we consider the problem with \(d=1\) and \(\lambda =-2\) and the pseudospectral method with 64 points. In the practical computations, we apply the three-point Gauss-Legendre’s rule to the integral in (2.4) and use a fixed-point iteration with the error tolerance \(10^{-16}\) and the maximum number 100 for each iteration. In order to show the obtained methods behave well for different initial and boundary conditions, we will use various conditions in the experiment.

5.1 Energy conservation

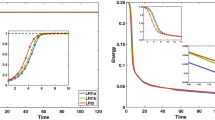
The initial value is given by \(u^0(x)= 0.5\text{ i }+ 0.025 \cos (\mu x)\) and the periodic boundary condition is \(u(t,0)=u(t,L)\). We consider \(L =4\sqrt{2}\pi \) and integrate this problem on [0, 100] with \(h=1/100\) for different \(\varepsilon \). The conservation of discretised energy is shown in Fig. 1. From these results, it can be seen clearly that the EP integrators EP1-EP3 preserve the energy with a very good accuracy, which supports the results of Theorem 1.

Fig. 1
figure 1

The relative error of discrete energy \(ERR=\frac{\left| H[u^n,{\bar{u}}^n]-H[u(0),{\bar{u}}(0)]\right| }{\left| H[u(0),{\bar{u}}(0)]\right| }\) against \(t=nh\)

Full size image

5.2 Convergence

For the convergence, in order to numerically test the results of Theorem 3, we apply the methods to solve the long term problem (3.3) with the time stepsize \(\delta \kappa \). Following [17], \(u^0(x)\) is chosen as \(u^0(x)=\cos (x)+\sin (x)\) and the boundary condition is \(u(t,0)=u(t,2\pi )\). The long term NLS (3.3) is solved in \([0,T/\varepsilon ]\) with \(T=1\) and \(\delta \kappa = 1/2^{i}\) for \(i=1,\ldots ,6\). The global errors of our methods measured in \(L^2\) and \(H^1\) for different \(\varepsilon \) are presented in Fig. 2. For comparison, the errors of EEI and MP are also displayed in Fig. 2. It follows that EP1 only has the global error \({\mathcal {O}}(\delta \kappa ^2)\) while EP2 has the error bound \({\mathcal {O}}(\varepsilon \delta \kappa ^2)\) and EP3 shows \({\mathcal {O}}(\varepsilon \delta \kappa ^3)\). This agrees with the results of Theorem  3. It seems here that EP3 has a better convergence than \({\mathcal {O}}(\varepsilon \delta \kappa ^3)\). But after presenting the errors for \(\varepsilon =1\) in Fig. 3, it can be observed that EP3 still shows a third-order convergence. Moreover, it follows from the results that MP behaves similarly to EP3 and its convergence can be derived by using the same arguments presented in this paper.

5.3 Near-Conservations in Other Aspects

In order to show the near conservations in other aspects, small initial value is required. Following [19, 30], we change the initial value into \(u^0(x)=0.1\big (\frac{x}{\pi }-1\big )^3\big (\frac{x}{\pi }+1\big )^2+\text{ i }\times 0.1\big (\frac{x}{\pi }-1\big )^3\big (\frac{x}{\pi }+1\big )^3\) and consider the periodic boundary condition \(u(t,-\pi )=u(t,\pi )\). The problem is solved on [0, 10000] with \(h=\frac{1}{100}\) and the relative errors of density and momentum are shown in Figs. 4, 5, respectivelyFootnote 2 . It can be observed clearly from these results that the density and momentum are conserved well by EP1-EP2 but not by EP3 over long terms, which supports the results stated in Theorem 4.

Fig. 2
figure 2

The global error \(err= (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\) of the long term problem (3.3) for \(n= \frac{1}{\epsilon \delta \kappa }\) measured in \(L^2\) (left) and \(H^1\) (right) against the stepsize

Full size image

Based on the numerical results, we can draw the following observations.

  1. (1)

    The energy-preserving methods EP1-EP3 preserve the energy with a very good accuracy for both regimes of \(\varepsilon \), which is much better than the existed exponential integrators EEI, EEI4 and MP (see Fig. 1).

  2. (2)

    For the highly oscillatory regime, the integrators EP2-EP3 and MP show improved error bounds while EP1 and EEI do not have the optimal convergence (see Fig. 2). For the regime \(\varepsilon =1\), EP1-EP3 show the normal global errors (see Fig. 3).

  3. (3)

    The MP method preserves the density and momentum well. The integrators EP1-EP2 have the long term near conservations in the density, momentum and action but the methods EP3, EEI and EEI4 do not show such long time behaviour (see Figs. 4, 5).

Fig. 3
figure 3

The global error \(err= (\varPhi ^{ \delta \kappa })^n(w^0)-w(\kappa _n)\) of the long term problem (3.3) for \(n= \frac{1}{\delta \kappa }\) measured in \(L^2\) (left) and \(H^1\) (right) against the stepsize

Full size image
Fig. 4
figure 4

The relative error of density \(ERR=\frac{\left| m[u^n,{\bar{u}}^n]-m[u(0),{\bar{u}}(0)]\right| }{\left| m[u(0),{\bar{u}}(0)]\right| }\) against \(t=nh\)

Full size image
Fig. 5
figure 5

The relative error of momentum \(ERR=\frac{\left| K[u^n,{\bar{u}}^n]-K[u(0),{\bar{u}}(0)]\right| }{\left| K[u(0),{\bar{u}}(0)]\right| }\) against \(t=nh\)

Full size image

6 Applications and Future Issues

This is a preliminary research on the long-time behaviour of energy-preserving exponential integrators and it is noted that the algorithms can be extended to the numerical solutions of the following equations (see Table 2) by replacing \(\text{ i }{\mathcal {A}}\) and f in (2.1) with the new ones.

Table 2 Some systems which the presented methods can be applied
Full size table

We also note that there are some issues which can be further considered.

  • The extensions of the methods as well as their analysis in this paper to the logarithmic Schrödinger equation ([4]) and time-dependent Schrödinger equation in semiclassical scaling ([43]) will be researched in future.

  • The long term analysis of other kinds of energy-preserving integrators in other PDEs such as Vlasov-Poisson system ([26, 46]) and Maxwell equations will also be considered.

  • Another issue for future exploration is the analysis of parareal algorithms of Schrödinger equations.