On the Backward Error Incurred by the Compact Rational Krylov Linearization

Abstract

One of the most successful methods for solving a polynomial (PEP) or rational eigenvalue problem (REP) is to recast it, by linearization, as an equivalent but larger generalized eigenvalue problem which can be solved by standard eigensolvers. In this work, we investigate the backward errors of the computed eigenpairs incurred by the application of the well-received compact rational Krylov (CORK) linearization. Our treatment is unified for the PEPs or REPs expressed in various commonly used bases, including Taylor, Newton, Lagrange, orthogonal, and rational basis functions. We construct one-sided factorizations that relate the eigenpairs of the CORK linearization and those of the PEPs or REPs. With these factorizations, we establish upper bounds for the backward error of an approximate eigenpair of the PEPs or REPs relative to the backward error of the corresponding eigenpair of the CORK linearization. These bounds suggest a scaling strategy to improve the accuracy of the computed eigenpairs. We show, by numerical experiments, that the actual backward errors can be successfully reduced by scaling and the errors, before and after scaling, are both well predicted by the bounds.

1 Introduction

Given a matrix-valued function $F(\lambda )$ : $\varOmega \subseteq \mathbb {C} \mapsto \mathbb {C}^{n\times n}$, the nonlinear eigenvalue problem (NEP) is to find eigenvalues $\lambda \in \varOmega$ and nonzero right eigenvectors x and left eigenvectors y so that

$$\begin{aligned} F(\lambda )x = 0 \quad \text{ and } \quad y^*F(\lambda ) = 0. \end{aligned}$$

(1)

In this article, we confine our discussion to regular NEPs, namely, those where $\det F(\lambda )$ is not identically zero on $\varOmega$.

One of the most widely-adopted numerical methods for solving such nonlinear eigenvalue problems is linearization, where the nonlinear eigenvalue problem (1) is first approximated by a proxy polynomial eigenvalue problem (PEP) or rational eigenvalue problem (REP)

$$\begin{aligned} F(\lambda ) \approx R_m(\lambda ) = D_0 b_0(\lambda ) + D_1 b_1(\lambda ) + \cdots + D_m b_m(\lambda ), \end{aligned}$$

(2)

where $D_j\in \mathbb {C}^{n\times n}$ are constant coefficient matrices,¹ before (2) is further reformulated as a generalized eigenvalue problem to which standard eigensolvers can be applied. In the rest of this paper, we will slightly abuse the notations by also denoting an eigenvalue, the associated right, and the associated left eigenvectors of $R_m(\lambda )$ by $\lambda$, x, and y, respectively. Here, $b_j(\lambda )$’s are polynomial basis functions of various kinds or rational basis functions [12, 22] and satisfy recurrence relations as follows.

• When $R_m(\lambda )$ is a degree m truncated Taylor series expansion of $F(\lambda )$ at $\lambda = \sigma$, $b_j(\lambda )$’s satisfy a two-term recurrence relation

  $$\begin{aligned} b_{j+1}(\lambda ) = \frac{\lambda -\sigma }{\beta _{j+1}}b_{j}(\lambda ), \end{aligned}$$

  with $b_0(\lambda ) = 1/\beta _{0}$, where $\beta _j$ are nonzero scaling constants.

• When $R_m(\lambda )$ is a Newton interpolant with nodes $\sigma _0, \sigma _1, \ldots , \sigma _m$, $b_j(\lambda )$’s satisfy a two-term recurrence relation

  $$\begin{aligned} b_{j+1}(\lambda ) = \frac{\lambda -\sigma _j}{\beta _{j+1}}b_{j}(\lambda ), \end{aligned}$$

  (3)

  with $b_0(\lambda ) = 1/\beta _{0}$.

• When $b_j(\lambda )$’s are the Lagrange cardinal polynomials, that is,

  $$\begin{aligned} b_{j}(\lambda ) = \frac{1}{\beta _j} \prod _{\begin{array}{c} i=0\\ i\ne j \end{array}}^m(\lambda -\sigma _i), \end{aligned}$$

  defined by the interpolation nodes $\sigma _0, \sigma _1, \ldots , \sigma _m$, $R_m(\lambda )$ becomes a Lagrange interpolant and the cardinal polynomials also satisfy a two-term recurrence relation

  $$\begin{aligned} \beta _j(\lambda -\sigma _j)b_j(\lambda ) = \beta _{j+1}(\lambda -\sigma _{j+1})b_{j+1}(\lambda ). \end{aligned}$$

• $R_m(\lambda )$ becomes a series of orthogonal polynomials when $b_j(\lambda )$’s are orthogonal polynomials defined by a three-term recurrence relation

  $$\begin{aligned} b_{j+1}(\lambda ) = \frac{\lambda b_j(\lambda ) + \alpha _j b_j(\lambda ) + \gamma _j b_{j-1}(\lambda )}{\beta _{j+1}} \end{aligned}$$

  (4)

  for $j \geqslant 0$ with $b_{-1}(\lambda ) = 0$ and $b_0(\lambda ) = 1/\beta _0$.

• Given interpolation nodes $\{\sigma _j\}_{j=0}^m \in \varOmega \subset \mathbb {C}$ and nonzero poles $\{\xi _j\}_{j=0}^m \subset \overline{\mathbb {C}} \setminus \varOmega$, the recurrence relation

  $$\begin{aligned} b_{j+1}(\lambda ) = \frac{\lambda -\sigma _j}{\beta _{j+1}(1-\lambda /\xi _{j+1})}b_j(\lambda ) \quad \text{ with } b_0(\lambda ) = \frac{1}{\beta _0} \end{aligned}$$

  (5)

  leads $R_m(\lambda )$ to become a rational approximation.

If the first $m+1$ basis functions are collected in a column vector $b(\lambda ) = [b_0(\lambda ),$ $b_1(\lambda ), \ldots , b_m(\lambda )]^T$, the recurrence relationships above can be written in a unified form

$$\begin{aligned} \lambda b^T(\lambda ) {K_m} = b^T(\lambda ){H_m}, \end{aligned}$$

(6)

where ${K_m}, {H_m} \in \mathbb {C}^{(m+1)\times m}$ can be readily derived for each basis.

Infinitely many different linearizations can be constructed such that they share the same eigenstructure with the PEP or REP, in the sense that such a linearization has the same eigenvalues as the PEP or REP and the eigenvectors of the PEP or REP can be easily obtained from those of the linearization. The most commonly used linearizations include the companion [10] and arrowhead [1] linearizations. In the last decade, as a generalization of the NLEIGS method [13] the compact rational Krylov (CORK) linearization [22] has been proposed and has attracted much attention since it has a unified and simple structure that covers many well-established linearizations, e.g., the companion linearization. It also enjoys the absence of spurious eigenvalues that one may see in other linearizations, e.g., the arrowhead linearization, and, therefore, has a smaller dimension. Moreover, the Kronecker structures in the CORK linearization (see (7) below) allow speedup in the solution of linear systems arising in the shift-and-invert step in Krylov subspace methods [22].

Specifically, the CORK linearization is an $mn\times mn$ pencil given by

$$\begin{aligned} \mathbf{L} _m(\lambda ) = \mathbf{A} _m - \lambda \mathbf{B} _m, \end{aligned}$$

where

$$\begin{aligned} \mathbf{A} _m = \begin{bmatrix} \underline{A_0~ A_1~ \cdots ~ A_{m-1}}\\ H_{m-1}^T\otimes I_n \end{bmatrix} \quad \text{ and }\quad \mathbf{B} _m = \begin{bmatrix} \underline{B_0~ B_1~ \cdots ~B_{m-1}}\\ K_{m-1}^T\otimes I_n \end{bmatrix}. \end{aligned}$$

(7)

Here, the horizontal lines are used to separate the top block rows from the lower parts which are Kronecker-structured. The $n \times n$ matrices $\{A_j\}_{j=0}^{m-1}$ and $\{B_j\}_{j=0}^{m-1}$ are obtained by rewriting $R_m(\lambda )$ in (2) as

$$\begin{aligned} g(\lambda )R_m(\lambda ) = \sum _{j=0}^{m-1}b_j(\lambda )(A_j-\lambda B_j), \end{aligned}$$

(8)

where $g(\lambda ) = \lambda - \sigma _m$ and $g(\lambda ) = 1- \lambda /\xi _m$ for the Lagrange and rational cases, respectively, and $g(\lambda ) = 1$ for all other bases. For a summary of $A_j$ and $B_j$ in various bases, see [22, Table 1]. We spell out $\mathbf {A}_m$ and $\mathbf {B}_m$ in Table 1 to facilitate the discussion in the rest of this article.

Table 1 $\mathbf {A_m}$ and $\mathbf {B_m}$ for various bases. For the Lagrange basis, $\theta _j = \beta _j/\beta _{j+1}$

The last few decades have witnessed the success of linearization in the solution of PEPs and REPs. The study has been focused on the linearization of PEPs represented in the monomial basis, see, for example, [2, 8, 16, 19]. A key question to answer is how accurate an approximate eigenpair of the PEPs or REPs is when it is found by recovering from that of the linearization, since a little error in the latter may lead to a much larger error in the former. In a pioneering work [14], some upper bounds are constructed for the backward error of an approximate eigenpair of the the PEPs expressed in the monomial basis relative to that of the corresponding approximate eigenpair of certain companion linearizations. These bounds are shown to be able to identify the circumstances under which the linearizations do or do not lead to larger backward errors. However, the PEPs expressed in non-monomial bases have been proposed due to the advantages offered by the non-monomial basis functions [1, 7] and the study of the accuracy of the eigenpairs obtained via linearization with the non-monomial basis functions are largely missing in the literature. The only investigation, so far, on the backward error associated to the PEPs in non-monomial bases is [17] which addresses the backward errors of the approximate eigenpairs incurred in the arrowhead linearization of the PEPs in the Lagrange basis. This paper aims at filling this gap.

A few preprocessing techniques have been proposed for the PEPs to gain improved accuracy, including the weighted balancing method in [4], the tropical scaling method due to [9], and the simple scaling method in [14], all of which deal with the monomial basis. So far, the only attempt to precondition the PEPs in a non-monomial basis is the work in [17], who proposed a two-sided balancing strategy based on block diagonal similarity transformations to improve the accuracy of an approximate eigenpair of the PEPs given in the Lagrange basis. Following a careful backward error analysis, we propose a diagonal scaling approach in this paper for the CORK linearization corresponding to PEPs expressed in various common non-monomial bases and our approach is shown to be effective in improving the accuracy of the computed eigenpairs.

Our discussion of the backward errors is based on the local backward error analysis first suggested in [14], for which we derive the one-sided factorization which are not found before for the aforementioned bases. This is the key to our analysis. We also note that the backward error analysis based on the global analysis framework [18] are, in general, not suitable for our work, since it was derived only for the right eigenpairs and the upper bounds obtained there can hardly help us develop a scaling strategy.

After introducing a few key definitions at the beginning of Sect. 2, we give the one-sided factorizations for the CORK linearization associated with the aforementioned basis functions. Based on these one-sided factorizations, we develop the bounds for the backward error of a computed eigenpair of $R_m(\lambda )$ relative to that of the corresponding eigenpair of the CORK linearization. To improve accuracy, we discuss the scaling strategy in Sect. 3, which is justified by the improved error bounds. We verify the bounds and the idea of scaling in Sect. 4 with a few numerical experiments and conclude in Sect. 5 with a couple of remarks.

2 Backward Errors

In this section, we relate the backward error of an approximate eigenpair of $R_m(\lambda )$ to that of the linearization $\mathbf {L}_m(\lambda )$ and further bound the former in terms of the latter. These bounds will help identify the cases where the eigenpairs of $R_m(\lambda )$ can be computed accurately via its CORK linearization in the backward error sense.

2.1 Definitions

We first include the definition of the normwise backward error of an approximate eigenpair of the rational function $R_m({\lambda })$ expressed in the aforementioned bases $b_j(\lambda )$. This definition is extended from the definition for the monomial basis given in [14]. The case of the basis $\{b_j(\lambda )\}$ being the Lagrange polynomials is discussed in, for example, [17] for the arrowhead linearization.

The normwise backward error of an approximate right eigenpair $(\lambda , x)$ of $R_m(\lambda )$, where $\lambda$ is finite, is defined by

$$\begin{aligned} \eta _{R_m}(\lambda , x) = \text {min}\left\{ \epsilon : (R_m(\lambda )+\varDelta R_m(\lambda ))x = 0, \Vert \varDelta D_j\Vert _2\leqslant \epsilon \Vert D_j\Vert _2, 0\leqslant j \leqslant m \right\} , \end{aligned}$$

where $\varDelta R_m(\lambda ) = \sum _{j=0}^{m}\varDelta D_j b_j(\lambda )$. Similarly, for an approximate left eigenpair $(\lambda , y^*)$ of $R_m(\lambda )$, the normwise backward error is defined by

$$\begin{aligned} \eta _{R_m}(\lambda , y^*) = \text {min}\left\{ \epsilon : y^*(R_m(\lambda )+\varDelta R_m(\lambda )) = 0, \Vert \varDelta D_j\Vert _2\leqslant \epsilon \Vert D_j\Vert _2, 0\leqslant j \leqslant m \right\} . \end{aligned}$$

Analogues can also be drawn from the monomial case [20] to obtain equivalent but explicit expressions for the backward errors of approximate eigenpairs $(\lambda , x)$ and $(\lambda , y^*)$ of $R_m(\lambda )$ in terms of the basis $\{b_j(\lambda )\}$

$$\begin{aligned} \eta _{R_m}(\lambda , x)= & {} \frac{\Vert R_m(\lambda )x\Vert _2}{(\sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|)\Vert x\Vert _2}, \nonumber \\ \eta _{R_m}(\lambda ,y^*)= & {} \frac{\Vert y^*R_m(\lambda )\Vert _2}{(\sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|)\Vert y\Vert _2}, \end{aligned}$$

(9)

and those of the approximate eigenpairs $(\lambda ,v)$ and $(\lambda ,w^*)$ of $\mathbf{L} _m(\lambda )$

$$\begin{aligned} \eta _\mathbf{L _m}(\lambda ,v)= & {} \frac{\Vert \mathbf{L} _m(\lambda )v\Vert _2}{(|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2)\Vert v\Vert _2}, \nonumber \\ \eta _\mathbf{L _m}(\lambda ,w^*)= & {} \frac{\Vert w^*\mathbf{L} _m(\lambda )\Vert _2}{(|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2)\Vert w\Vert _2}. \end{aligned}$$

(10)

2.2 One-sided Factorizations for CORK Linearization

The key to estimating the backward error of an approximate eigenpair of $R_m(\lambda )$ in terms of that of $\mathbf {L_m}(\lambda )$ is to find an appropriate one-sided factorization that relates $R_m(\lambda )$ and $\mathbf {L_m}(\lambda )$. Specifically, the first m equations in (6), when combined with (8), lead to

$$\begin{aligned} \mathbf {L}_m(\lambda ) H(\lambda ) =g(\lambda )e_1 \otimes R_m(\lambda ), \end{aligned}$$

(11)

where $e_1\in \mathbb {C}^{m\times 1}$ is the first unit vector and

$$\begin{aligned} H(\lambda ) = b(\lambda ) \otimes I_n = \begin{bmatrix} b_0(\lambda ) \\ b_1(\lambda ) \\ \vdots \\ b_{m-1}(\lambda ) \end{bmatrix} \otimes I_n \in \mathbb {C}^{mn\times n}, \end{aligned}$$

where the notation $b(\lambda )$ is reused here and in the rest of this paper to denote the same vector in (6) but with the last entry $b_m(\lambda )$ dropped. Note that this right-sided factorization is valid for any of the bases mentioned in Sect. 1.

We also need the left-sided factorization

$$\begin{aligned} G(\lambda ) \mathbf {L}_m(\lambda ) = e_1^T\otimes (g(\lambda ) R_m(\lambda )), \end{aligned}$$

(12)

where $G(\lambda )\in \mathbb {C}^{n\times mn}$. Unlike $H(\lambda )$, $G(\lambda )$ does not have a uniform expression valid for all the aforementioned bases. We now give $G(\lambda )$ below for each basis and to the best of our knowledge this is the first time it is constructed for these bases.

Taylor basis:

Newton Basis:

Orthogonal basis: To construct $G(\lambda )$ in the case of orthogonal basis, we define a new sequence of orthogonal polynomials $b^{(k)}_j(\lambda )$ that are associated with $b_j(\lambda )$ given in (4) by

$$\begin{aligned} b^{(k)}_{j+1}(\lambda ) = \frac{\lambda b^{(k)}_j(\lambda )+\alpha _{j+k} b^{(k)}_j(\lambda ) + \gamma _{j+k} b^{(k)}_{j-1}(\lambda )}{\beta _{j+k+1}}, \end{aligned}$$

(13)

where $b^{(k)}_{j}(\lambda ) \equiv 0$ for $j<0$ and $b^{(k)}_0(\lambda ) = 1$. When $k = 0$, $b^{(k)}_j(\lambda )$ reduces to the original orthogonal polynomials defined in (4).² We have not seen any discussion in the literature about the orthogonal polynomials defined by (13) and will simply call them the shifted orthogonal polynomials generated by the original orthogonal sequence or the shifted orthogonal polynomials for short, since they are defined by a subset of the same recurrence coefficients but with indices shifted by k. The Chebyshev polynomial of the first kind (known as Chebyshev T) and the second kind (known as Chebyshev U or as ultraspherical or Gegenbauer polynomial $C^{(1)}$) serve as the simplest example. If we let $b_j(\lambda ) = T_j(\lambda )$, where $T_j(\lambda )$ is the jth Chebyshev polynomial of the first kind, the new orthogonal sequence $b^{(1)}_j(\lambda ) = U_j(\lambda )$, i.e., the Chebyshev polynomial of the second kind, and the recurrence coefficients in (4) are

$$\begin{aligned} \begin{array}{ll} \begin{aligned} \alpha _k &{}= 0 \text{ for } \text{ all } k, \\ \beta _k &{}= \left\{ \begin{array}{ll} 1, &{} k = 1,\\ 1/2, &{} k \in \mathbb {Z}^{\geqslant 2}, \end{array} \right. \\ \gamma _k &{}= \left\{ \begin{array}{ll} 0, &{} k = 0,\\ -1/2, &{} k \in \mathbb {Z}^+. \end{array} \right. \end{aligned} \end{array} \end{aligned}$$

It can be verified by induction (see Appendix A) that for the orthogonal basis

$$\begin{aligned} G(\lambda )= & {} \left[ \begin{matrix}I_n,&-\frac{1}{\beta _1}\mathop {\sum }\limits _{j=1}^{m} b^{(1)}_{j-1}(\lambda ) D_j,&-\frac{1}{\beta _2}\mathop {\sum }\limits _{j=2}^{m} b^{(2)}_{j-2}(\lambda )D_j, \dots , \end{matrix}\right. \nonumber \\&\left. \begin{matrix} -\frac{1}{\beta _{k-1}}\mathop {\sum }\limits _{j=k-1}^{m} b^{(k-1)}_{j-(k-1)}(\lambda ) D_j,&\dots ,&-\frac{1}{\beta _{m-2}}\mathop {\sum }\limits _{j = m-2}^{m} b^{(m-2)}_{j-(m-2)}(\lambda )D_j, \end{matrix}\right. \nonumber \\&\left. \begin{matrix} -\frac{1}{\beta _{m-1}}\mathop {\sum }\limits _{j = m-1}^{m} b^{(m-1)}_{j-(m-1)}(\lambda )D_j \end{matrix} \right] . \end{aligned}$$

(14)

In practice, the most commonly used orthogonal polynomials for the purpose of function approximation are the Chebyshev polynomials, for which

$$\begin{aligned} G(\lambda )= & {} \left[ I_n, \ -\mathop {\sum }\limits _{j=1}^{m} U_{j-1}(\lambda ) D_j, \ -2\mathop {\sum }\limits _{j=2}^{m} U_{j-2}(\lambda )D_j, \dots , \ -2\mathop {\sum }\limits _{j=k-1}^{m} U_{j-(k-1)}(\lambda ) D_j,\ \dots ,\right. \\&\quad \left. -2\mathop {\sum }\limits _{j = m-2}^{m} U_{j-(m-2)}(\lambda )D_j, \ -2\mathop {\sum }\limits _{j = m-1}^m U_{j-(m-1)}(\lambda )D_j \right] . \end{aligned}$$

Lagrange basis:

Rational basis:

What is remarkable is the striking similarity shared by these $G(\lambda )$’s despite of basis functions. This enables us to develop bounds for the backward error ratios in a rather unified fashion in Theorems 2 and 3.

The following theorem serves as a generalization of its monomial counterpart given in [11] by associating the eigensystem of $R_m(\lambda )$ and that of $\mathbf {L}_m(\lambda )$ when the one-sided factorizations (11) and (12) hold.

Theorem 1

Let $R_m(\lambda )$ and $\mathbf {L}_m(\lambda )$ be matrix functions of dimensions $n \times n$ and $mn \times mn$, respectively. Assume that (11) and (12) hold at $\lambda \in \mathbb {C}$ with $g(\lambda ) \ne 0$ and $b(\lambda ) \ne 0$.

• (i) If v is a right eigenvector of $\mathbf {L}_m(\lambda )$ with eigenvalue $\lambda$, then $(g(\lambda )e_1^T\otimes I_n)v$ is a right eigenvector of $R_m(\lambda )$ with eigenvalue $\lambda$;

• (ii) if $w^*$ is a left eigenvector of $\mathbf {L}_m(\lambda )$ with eigenvalue $\lambda$, then $w^*(g(\lambda )e_1 \otimes I_n)$ is a left eigenvector of $R_m(\lambda )$ with eigenvalue $\lambda$ provided that it is nonzero.

Proof

Based on the relations (11) and (12), we have

$$\begin{aligned} G(\lambda ) \mathbf {L}_m(\lambda )v&= e_1^T\otimes (g(\lambda ) R_m(\lambda ))v= R_m(\lambda )(g(\lambda )e_1^T\otimes I_n)v, \end{aligned}$$

(15)

$$\begin{aligned} w^*\mathbf {L}_m(\lambda ) H(\lambda )&=w^*(g(\lambda )e_1 \otimes R_m(\lambda ))= w^*(g(\lambda )e_1\otimes I_n)R_m(\lambda ). \end{aligned}$$

(16)

$\square$

Now we are in the position to investigate the backward error incurred by the CORK linearization using (15) and (16).

2.3 The Bounds for Backward Error Ratios

Now we have all the ingredients for bounding the backward error of an eigenpair of $R_m(\lambda )$. The following theorem gives bounds for the backward error ratios $\eta _{R_m}(\lambda , x)/\eta _\mathbf{L _m}(\lambda ,v)$ and $\eta _{R_m}(\lambda , y^*)/\eta _\mathbf{L _m}(\lambda ,w^*)$.

Theorem 2

Let $(\lambda , x)$ and $(\lambda , y^*)$ be approximate right and left eigenpairs of $R_m(\lambda )$ respectively and $(\lambda , v)$ and $(\lambda , w^*)$ be the corresponding approximate right and left eigenpairs of $\mathbf{L} _m(\lambda )$. If $|b_0(\lambda )|=1$, the bound for the ratio of $\eta _{R_m}(\lambda , x)$ to $\eta _\mathbf{L _m}(\lambda ,v)$ is given by

$$\begin{aligned} \frac{\eta _{R_m}(\lambda , x)}{\eta _\mathbf{L _m}(\lambda ,v)} \leqslant \frac{|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2}{|g(\lambda )|\left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{G_U(\lambda )\Vert v\Vert _2}{\Vert x\Vert _2}, \end{aligned}$$

(17)

where

$$\begin{aligned} G_U(\lambda ) = \displaystyle \sqrt{m}\max \left( 1, \tilde{G}_U(\lambda ) \right) \end{aligned}$$

(18)

and

with

The bound for the backward error of a left eigenpair $(\lambda , y^*)$ relative to that of $(\lambda , w^*)$ is given by

$$\begin{aligned} \frac{\eta _{R_m}(\lambda , y^*)}{\eta _\mathbf{L _m}(\lambda ,w^*)} \leqslant \frac{|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2}{|g(\lambda )| \left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{H_U(\lambda )\Vert w\Vert _2}{\Vert y\Vert _2}, \end{aligned}$$

(21)

where

$$\begin{aligned} H_U(\lambda ) = \sqrt{m}\mathop {\max }\limits _{j=0:m-1}\left( |b_j(\lambda )|\right) . \end{aligned}$$

(22)

Proof

From (16) and (15), we have

$$\begin{aligned} \Vert R_m(\lambda )x\Vert _2&\leqslant \frac{1}{|g(\lambda )|}\Vert G(\lambda )\Vert _2\Vert \mathbf {L}_m(\lambda )v\Vert _2,\\ \Vert y^*R_m(\lambda )\Vert _2&\leqslant \frac{1}{|g(\lambda )|}\Vert H(\lambda )\Vert _2\Vert w^*\mathbf {L}_m(\lambda )\Vert _2, \end{aligned}$$

which, along with (9) and (2.1), give

$$\begin{aligned} \frac{\eta _{R_m}(\lambda , x)}{\eta _\mathbf{L _m}(\lambda ,v)}&\leqslant \frac{|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2}{|g(\lambda )| \left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{\Vert G(\lambda )\Vert _2\Vert v\Vert _2}{\Vert x\Vert _2}, \nonumber \\ \frac{\eta _{R_m}(\lambda , y^*)}{\eta _\mathbf{L _m}(\lambda ,w^*)}&\leqslant \frac{|\lambda |\Vert \mathbf{B} _m\Vert _2+\Vert \mathbf{A} _m\Vert _2}{|g(\lambda )| \left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{\Vert H(\lambda )\Vert _2\Vert w\Vert _2}{\Vert y\Vert _2}. \end{aligned}$$

(23)

By Lemma 3.5 in [14] we have

$$\begin{aligned} \Vert H(\lambda )\Vert _2 = \Vert b(\lambda )\otimes I_n\Vert _2 \leqslant H_U(\lambda ), \end{aligned}$$

which substituted into (23) leads to (21).

For the rational basis,

$$\begin{aligned} \Vert G(\lambda )\Vert _2 \leqslant \sqrt{m} ~ \max \left( 1, \mathop {\max }\limits _{j=0:m-2}\frac{1}{|\lambda -\sigma _j||b_j(\lambda )|} \times \mathop {\sum }\limits _{j=1}^{m}|b_j(\lambda )|\Vert D_j\Vert _2 \right) , \end{aligned}$$

which can be further relaxed to obtain the upper bound $G_U(\lambda )$ given by (18), (19b), and (20b). $G_U(\lambda )$ for all other bases except the orthogonal one can be derived analogously.

In the case of the orthogonal basis,

$$\begin{aligned} \Vert G(\lambda )\Vert _2 \leqslant \sqrt{m} \max \left( 1, \mathop {\max }\limits _{j=1:m-1}\frac{1}{|\beta _j|}\times \mathop {\sum }\limits _{j=1}^{m}\left( \mathop {\max }\limits _{i=1:m-1}\left| b_{j-1}^{(i)}(\lambda )\right| \right) \Vert D_j\Vert _2 \right) \leqslant G_U(\lambda ), \end{aligned}$$

which leads to (18) and (19a). $\square$

In particular, we furnish the following corollary which gives the bound for $\eta _{R_m}(\lambda , x)$ $/\eta _\mathbf{L _m}(\lambda ,v)$ when $b_j(\lambda )$ are Chebyshev polynomials $T_j(\lambda )$ for that is the most commonly used orthogonal basis in practice.

Corollary 1

Let $(\lambda , x)$ and $(\lambda , v)$ be approximate right eigenpairs of $R_m(\lambda )$ and $\mathbf{L} _m(\lambda )$, respectively. If $\{b_j(\lambda )\}_{j = 0}^{m-1}$ is the Chebyshev basis, the bound for the backward error ratio $\eta _{R_m}(\lambda , x)/\eta _\mathbf{L _m}(\lambda ,v)$ is given by (17) with

$$\begin{aligned} G_U(\lambda ) = \sqrt{m} \max \left( 1, m(m+1)\mathop {\max }\limits _{j=1:m}\Vert D_j\Vert _2\right) . \end{aligned}$$

Proof

Since $|U_j(\lambda )|\leqslant j+1$,

$$\begin{aligned} \Vert G(\lambda )\Vert _2 \leqslant \sqrt{m}~ \max \left( 1, 2\mathop {\sum }\limits _{j = 1}^{m} \left| U_{j-1}(\lambda )\right| \times \mathop {\max }\limits _{j=1:m}\Vert D_j\Vert _2 \right) \leqslant G_U(\lambda ). \end{aligned}$$

$\square$

3 Scaling the Linearization

It is ideal if the ratios $\eta _{R_m}(\lambda , x)/\eta _\mathbf{L _m}(\lambda ,v)$ and $\eta _{R_m}(\lambda , y^*)$ $/\eta _\mathbf{L _m}(\lambda ,w^*)$ are roughly 1. When this is the case, an eigenpair of $R_m(\lambda )$ would have accuracy comparable to that of the linearization. In practice, however, the ratios $\eta _{R_m}(\lambda , x)/\eta _\mathbf{L _m}(\lambda ,v)$ and $\eta _{R_m}(\lambda , y^*)$ $/\eta _\mathbf{L _m}(\lambda ,w^*)$ are often much larger than 1 and certain scaling techniques are employed to precondition the linearization so that the backward errors can be reduced. Based on the bounds derived in the last section, we now develop a simple diagonal scaling approach for the CORK linearization formed from PEPs and REPs expressed in any of the aforementioned bases. To see how it works, we let

$$\begin{aligned} S = \begin{bmatrix} 1 &{} &{} &{} \\ &{} s &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} s \end{bmatrix}\otimes I_n \in \mathbb {C}^{mn \times mn}, \end{aligned}$$

where $s = \mathop {\max }\limits _{j=1:m}(\Vert D_j\Vert _2)$. By (16) and (15), we have

$$\begin{aligned} \widehat{w}^* \widehat{\mathbf {L}}_m(\lambda ) H(\lambda )&= y^*R_m(\lambda ), \\ \widehat{G}(\lambda )\widehat{\mathbf {L}}_m(\lambda )v&= R_m(\lambda )x, \end{aligned}$$

where $\widehat{G}(\lambda ) = G(\lambda )S^{-1}$, $\widehat{\mathbf {L}}_m(\lambda ) = S\mathbf {L}_m(\lambda )$, $x = (g(\lambda )e_1^T\otimes I_n)v$, $y^*=w^*(g(\lambda )e_1 \otimes I_n)$ and $\widehat{w}^* = w^*S^{-1}$. Now we restate Theorem 2 with $G(\lambda )$, $\mathbf {L}_m(\lambda )$, and $w^*$ replaced by their hatted counterparts. The proof is omitted as it is similar to that of Theorem 2.

Theorem 3

The backward error $\eta _{R_m}(\lambda ,x)$ of an approximate right eigenpair $(\lambda ,x)$ of $R_m(\lambda )$ relative to the backward error $\eta _{R_m}(\lambda ,v)$ of the corresponding approximate eigenpair $(\lambda ,v)$ of $\widehat{\mathbf {L}}_m(\lambda )$ can be bounded by

$$\begin{aligned} \frac{\eta _{R_m}(\lambda , x)}{\eta _{\widehat{\mathbf {L}}_m}(\lambda ,v)} \leqslant \frac{(|\lambda |\Vert \widehat{\mathbf {B}}_m\Vert _2+\Vert \widehat{\mathbf {A}}_m\Vert _2)}{|g(\lambda )|\left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{G_S(\lambda )\Vert v\Vert _2}{\Vert x\Vert _2}, \end{aligned}$$

(24)

where $\widehat{\mathbf {A}}_m = S\mathbf {A}_m$, $\widehat{\mathbf {B}}_m = S\mathbf {B}_m$,

$$\begin{aligned} G_S(\lambda ) = \displaystyle \sqrt{m}\max \left( 1, \tilde{G}_S(\lambda ) \right) \end{aligned}$$

and

$$\begin{aligned} \tilde{G}_S(\lambda )=\left\{ \begin{array}{ll} \displaystyle \mathop {\max }\limits _{j=1:m-1}\frac{1}{|\beta _j|}\times \mathop {\sum }\limits _{j=1}^{m}\mathop {\max }\limits _{i=1:m-1}\left| b_{j-1}^{(i)}(\lambda )\right| ,&{}\text {orthogonal}, \\ \displaystyle Q(\lambda )\times \mathop {\sum }\limits _{j=1}^{m}|b_j(\lambda )|,&{}\text {all other bases}. \end{array}\right. \end{aligned}$$

Here, $Q(\lambda )$ is given in (20).

The backward error ratio ${\eta _{R_m}(\lambda , y^*)}/{\eta _{\widehat{\mathbf {L}}_m}(\lambda ,\widehat{w}^*)}$ of an approximate left eigenpair $(\lambda ,y^*)$ of $R_m(\lambda )$ can be bounded by

$$\begin{aligned} \frac{\eta _{R_m}(\lambda , y^*)}{\eta _{\widehat{\mathbf {L}}_m}(\lambda ,\widehat{w}^*)} \leqslant \frac{|\lambda |\Vert \widehat{\mathbf {B}}_m\Vert _2 +\Vert \widehat{\mathbf {A}}_m\Vert _2}{|g(\lambda )|\left( \sum _{j=0}^{m}\Vert D_j\Vert _2|b_j(\lambda )|\right) } \frac{H_U(\lambda )\Vert \widehat{w}\Vert _2}{\Vert y\Vert _2}, \end{aligned}$$

(25)

where $H_U(\lambda )$ is given by (22).

Remark 1

For the Chebyshev basis, the bound ${\eta _{R_m}(\lambda , x)}/{\eta _{\widehat{\mathbf {L}}_m}(\lambda ,v)}$ for the backward error ratio of a right eigenpair is similar to that given in Corollary 1 but with $G_U(\lambda )$ replaced by $G_S(\lambda ) = \sqrt{m}\, \text {max}\left( 1, m(m+1)\right)$.

Let us now compare the ratios given by Theorems 2 and 3. For the backward error ratio of a right eigenpair, we consider the case with $\tilde{G}_U(\lambda ) > 1$, which is very common in practice. The quantities $\Vert \mathbf{A} _m\Vert _2$, $\Vert \mathbf{B} _m\Vert _2$, and $G_U(\lambda )$ in (17) now become $\Vert \widehat{\mathbf {A}}_m\Vert _2$, $\Vert \widehat{\mathbf {B}}_m\Vert _2$, and $G_S(\lambda )$ in (24) respectively. If we bound $\Vert \mathbf{A} _m\Vert _2$, $\Vert \mathbf{B} _m\Vert _2$, $\Vert \widehat{\mathbf {A}}_m\Vert _2$, and $\Vert \widehat{\mathbf {B}}_m\Vert _2$ from above, we have

$$\begin{aligned} \begin{array}{l} \begin{aligned} \Vert \mathbf{A} _m\Vert _2 &{} \leqslant \sqrt{2}\max \left( \sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert A_j\Vert _2, \Vert H_{m-1}\Vert _2 \right) , \\ \Vert \mathbf{B} _m\Vert _2 &{} \leqslant \sqrt{2}\max \left( \sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert B_j\Vert _2, \Vert K_{m-1}\Vert _2 \right) , \end{aligned} \end{array} \end{aligned}$$

whereas

$$\begin{aligned} \begin{array}{l} \begin{aligned} \Vert \widehat{\mathbf {A}}_m\Vert _2 &{} \leqslant \sqrt{2}\max \left( \sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert A_j\Vert _2, s\Vert H_{m-1}\Vert _2 \right) , \\ \Vert \widehat{\mathbf {B}}_m\Vert _2 &{} \leqslant \sqrt{2}\max \left( \sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert B_j\Vert _2, s\Vert K_{m-1}\Vert _2 \right) . \end{aligned} \end{array} \end{aligned}$$

(26)

When $\sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert A_j\Vert _2$ and $\sqrt{m} \quad \mathop {\max }\limits _{j=0:m-1} \Vert B_j\Vert _2$ prevail in the $\max$ operators in (26), $\Vert \widehat{\mathbf {A}}_m\Vert _2$ and $\Vert \widehat{\mathbf {B}}_m\Vert _2$ stay the same after scaling, as we often see in practice (see Sect. 4). In case of $s\Vert H_{m-1}\Vert _2$ and $s\Vert K_{m-1}\Vert _2$ being dominant, $\Vert \widehat{\mathbf {A}}_m\Vert _2$ and $\Vert \widehat{\mathbf {B}}_m\Vert _2$ would be larger than $\Vert \mathbf{A} _m\Vert _2$ and $\Vert \mathbf{B} _m\Vert _2$, respectively, by a factor O(s) at most. On the other hand, the scaling reduces the norm of $G(\lambda )$ by a factor O(s) for sure, as can be seen from the upper bounds of $G_U(\lambda )$ and $G_S(\lambda )$

$$\begin{aligned} \begin{array}{l} \begin{aligned} G_U(\lambda ) &{} \leqslant \sqrt{m} \mathop {\sum }\limits _{j=0}^{m}|b_j(\lambda )|\max \left( 1, Q(\lambda )\times \mathop {\max }\limits _{j=1:m}\Vert D_j\Vert _2\right) , \\ G_S(\lambda ) &{} \leqslant \sqrt{m} \mathop {\sum }\limits _{j=0}^{m}|b_j(\lambda )|\max \bigg (1, Q(\lambda )\bigg ). \end{aligned} \end{array} \end{aligned}$$

With $\Vert \mathbf{A} _m\Vert _2$ and $\Vert \mathbf{B} _m\Vert _2$ unchanged or amplified by a factor which can be canceled out by the reduction in $G_U(\lambda )$, the bound for the backward error ratio ${\eta _{R_m}(\lambda , x)}/{\eta _{\widehat{\mathbf {L}}_m}(\lambda ,v)}$ is usually reduced, as we hope. In the meantime, the term ${\Vert w\Vert _2}/{\Vert y\Vert _2}$ in (21) is replaced by ${\Vert \widehat{w}\Vert _2}/{\Vert y\Vert _2}$, which is smaller than ${\Vert w\Vert _2}/{\Vert y\Vert _2}$ when $s > 1$. Since it is also very common in practice that $s > 1$, scaling also reduces the bound of the backward error ratio for left eigenpairs. As the bounds for the ratios reduced for both left and right eigenpairs, we expect to see improved accuracy using the CORK linearization when it is equipped with scaling.

4 Experimental Results

In this section, we test the bounds for the backward errors of the approximate eigenpairs of $R_m(\lambda )$ computed via the CORK linearization $\mathbf {L}_m(\lambda )$ and the scaled one $\widehat{\mathbf {L}}_m(\lambda )$ and the effectiveness of the scaling approach. In our experiments, the eigenpairs of the linearizations are computed using Matlab’s eig function with the eigenvectors of $R_m(\lambda )$ recovered by Theorem 1. The backward errors of the computed eigenpairs of $R_m(\lambda )$, $\mathbf {L}_m(\lambda )$, and $\widehat{\mathbf {L}}_m(\lambda )$ are obtained using (9) and (2.1), while the upper bounds for the ratios of the backward errors are calculated using (17), (21), (24), and (25).

4.1 Newton Basis

Our first test problem is the quadratic eigenvalue problem from a linearly damped mass-spring system [20], drawn from the collection of nonlinear eigenvalue problems NLEVP [5]

$$\begin{aligned} F(\lambda )x = (\lambda ^2 A_2 + \lambda A_1 + A_0)x=0, \end{aligned}$$

where the $20\times 20$ matrices are $A_0 = 5T$, $A_1 = 10T$, $A_2 = I$, and

$$\begin{aligned} T =\begin{bmatrix} 3 &{} -1 &{} &{} \\ -1 &{} \ddots &{} \ddots &{} \\ &{} \ddots &{} \ddots &{} -1 \\ &{} &{} -1 &{} 3 \end{bmatrix}. \end{aligned}$$

Table 2 The spring problem: norms of the relevant quantities. The entries corresponding to the scaled $\Vert \mathbf {A}_m\Vert _2$ and $\Vert \mathbf {B}_m\Vert _2$ are $\Vert \widehat{\mathbf {A}}_m\Vert _2$ and $\Vert \widehat{\mathbf {B}}_m\Vert _2$, respectively. Note the reduction in $\max G_U(\lambda )$ and $\max \Vert w\Vert _2/\Vert y\Vert _2$

Fig.\kern-4pt 1

The spring problem: actual backward error ratios $\eta _{R_{m}}(\lambda , y^{*})/\eta _{\mathbf{L}_{m}} (\lambda , w^{*})$ and $\eta _{R_{m}}(\lambda , x)/\eta _{\mathbf {L}_m}(\lambda , v)$ and their bounds

Fig.\kern-4pt 2

The spring problem: backward errors of the computed eigenpairs, before and after scaling

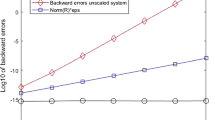
We interpolate $F(\lambda )$ at the nodes $\{-50,-25,0\}$ using the Newton basis (3) where $\beta _j = 1$ for $j = 0, 1, 2$. By the discussion in Sect. 3, we expect that the scaling reduces $G_U(\lambda )$ and $\Vert w\Vert _2/\Vert y\Vert _2$ while it keeps other quantities in the bounds relatively unchanged and this is confirmed by Table 2. The largest $G_U(\lambda )$ and $\Vert w\Vert _2/\Vert y\Vert _2$ for all the eigenvalues are reduced by a factor of $10^{2}$ and $10^1$, respectively. These reductions lead us to expect smaller bounds for the ratios $\eta _{R_m}(\lambda , x)/\eta _\mathbf{L _m}(\lambda ,v)$ and $\eta _{R_m}(\lambda , y^*)/\eta _\mathbf{L _m}(\lambda ,w^*)$. In Fig. 1, we display the bounds on these ratios for both the unscaled and the scaled linearizations, along with the actual ratios. The actual ratios are well predicted by the bounds. The reduced ratios in Fig. 1 further suggest improved accuracy and this is indeed what we see in Fig. 2, where we show the backward errors, with and without scaling. Scaling reduces the actual backward error ratios by 1 to 3 orders of magnitude.

4.2 Taylor Basis

Our second test problem is a PEP of degree 10 with randomly generated coefficient matrices

$$\begin{aligned} F(\lambda ) = \sum _{k = 0}^{10} D_k \lambda ^k, \end{aligned}$$

(27)

where the norms of the coefficient matrices $D_k\in \mathbb {R}^{100 \times 100}$ are listed in Table 3. This example is featured by the fact that the norms vary by orders with $\Vert D_0\Vert _2 \gg \Vert D_k\Vert _2$ for $k > 0$.

Table 3 The 10-degree problem: norms of the coefficient matrices

To perform the numerical experiment, we re-express (27) as a standard Taylor series about the origin. The effect of scaling is again reflected by the significant reduction of $G_U(\lambda )$ and $\Vert w\Vert _2/\Vert y\Vert _2$ in Table 4. Figure 3 clearly shows the improved accuracy brought about by scaling, where the backward errors are reduced approximately down to $O(10^{-14})$.

Table 4 The 10-degree problem: norms of the relevant quantities

Fig.\kern-4pt 3

The 10-degree problem: backward errors of the computed eigenpairs, before and after scaling

4.3 Orthogonal Basis

In the third example, we move to the CORK linearization when a PEP is represented in the orthogonal basis. Specifically, we choose $b_j(\lambda )$ to be the Chebyshev polynomial of the first kind $T_j(\lambda )$ and test on the quadratic eigenvalue problem arising in the spatial stability analysis of the Orr-Sommerfeld equation [21] which we, again, borrow from the collection of nonlinear eigenvalue problems [5]:

$$\begin{aligned} \left[ \left( \frac{d^2}{dz^2}-\lambda ^2\right) ^2 -iR \left\{ (\lambda U - \omega )\left( \frac{d^2}{dz^2}-\lambda ^2\right) -\lambda U^{''}\right\} \right] \phi = 0. \end{aligned}$$

The choice of Chebyshev polynomials amounts to having $\beta _1 = 1$, $\beta _2 = 1/2$, $\beta _3 = 1/2$, $\gamma _1 = \gamma _2 = -1/2$, and $\alpha _0 = \alpha _1 = \alpha _2 = 0$. We sample the polynomial at Chebyshev points of the second kind, that is $\sigma _j = \cos (j\pi /4), j = 0,1,\dots , 4$, in the interval $[-1,1]$ and the coefficient matrices $D_j$ are computed using Chebfun [6].

Table 5 The orr$_{-}$sommerfeld problem: norms of the relevant quantities

As shown in Table 5, scaling brings $\max G_U(\lambda )$ and $\max \Vert w\Vert _2/\Vert y\Vert _2$ down by $O(10^{10})$ while other key quantities are kept on the original order and this matches the reduction of the actual backward error ratios in Fig. 4. Figure 5 shows the backward errors are bought down to machine precision or below.

Fig.\kern-4pt 4

The orr$_{-}$sommerfeld problem: actual backward error ratios $\eta _{R_{m}}(\lambda , y^{*})/\eta _{\mathbf{L}_{m}} (\lambda , w^{*})$ and $\eta _{R_{m}}(\lambda , x)/\eta _{\mathbf {L}_{m}}(\lambda , v)$ and their bounds

Fig.\kern-4pt 5

The orr$_{-}$sommerfeld problem: backward errors of $R_m(\lambda )$ of the computed eigenpairs, before and after scaling

4.4 Lagrange Basis

This example is similar to the second one but now with the Lagrange basis, particularly with complex interpolation nodes. The matrix pencil $F(\lambda )= \sum _{k = 0}^{16}D_k \lambda ^k$ is of degree 16 with the coefficient matrices $D_k\in \mathbb {R}^{200 \times 200}$ randomly determined. Table 6 gives the norms of the coefficient matrices, which vary widely between $O(10^{-1})$ to $O(10^8)$ with $\Vert D_3\Vert _2$ and $\Vert D_5\Vert _2$ being the largest ones. We interpolate $F(\lambda )$ using Lagrange interpolant with the interpolation nodes shown in Fig. 6 by plus signs.

Table 6 The 16-degree problem: norms of the coefficient matrices

Fig.\kern-4pt 6

The 16-degree problem: interpolation nodes ($+$) and locations of the eigenvalues ($\circ$)

Table 7 shows that the largest $G_U(\lambda )$ and $\Vert w\Vert _2/\Vert y\Vert _2$ are successfully reduced by $10^8$ and $10^9$, respectively, due to the scaling, while the changes in other quantities are relatively negligible, which implies the significant reductions of the backward errors. Figure 7 confirms the effectiveness of scaling as the backward errors of the approximate eigenpairs of $R_m(\lambda )$ are brought down to about machine precision, despite of the high degree of this problem and the extreme discrepancies in the magnitude of the coefficient matrices. The location of the eigenvalues computed with scaling are plotted in Fig. 6 as circles.

Table 7 The 16-degree problem: norms of the relevant quantities with the Lagrange basis

Fig.\kern-4pt 7

The 16-degree problem: backward errors of computed eigenpairs, before and after scaling

4.5 Rational Basis

We test the rational basis using the railtrack$_{-}$rep problem which is a rational eigenvalue problem arising from the study of the vibration of rail tracks [15]:

$$\begin{aligned} F(\lambda )x = \left( \lambda A^T + B + \lambda ^{-1}A\right) x = 0, \end{aligned}$$

where A and B are $1005\times 1005$ complex matrices and $B = B^T$ is complex symmetric. In this example, we are particularly interested in eigenvalues with modulus between 3 and 10. In fact, $F(\lambda )$ can be recast in the rational basis as

$$\begin{aligned} F(\lambda ) \approx R_2(\lambda ) = b_0(\lambda )D_0 + b_1(\lambda )D_1 + b_2(\lambda )D_2, \end{aligned}$$

where $b_j(\lambda )$’s are given by (5). The pole locations $\xi _1 = 1$ and $\xi _2 = \infty$ and the parameters $\beta _0 = 1$, $\beta _1 = 0.78$, and $\beta _2 = 9.2$ are all found by using the RK Toolbox [3].

Table 8 The railtrack$_{-}$rep problem: norms of the relevant quantities

As seen from Table 8, the magnitudes of $\max G_U(\lambda )$ and $\max \Vert w\Vert _2/\Vert y\Vert _2$ fall down by orders of $10^{11}$ and $10^{7}$, respectively. The reduction of the error ratios is displayed in Fig. 8, where we see the ratios are made roughly $10^6$ times smaller by scaling for both the left and the right eigenpairs. The actual backward errors are brought down from somewhere between $10^{-10}$ and $10^{-8}$ to the level of machine precision, as shown in Fig. 9.

Fig.\kern-4pt 8

The railtrack$_{-}$rep problem: actual backward error ratios $\eta _{R_{m}}(\lambda , y^{*})/\eta _{\mathbf{L}_{m}} (\lambda , w^{*})$ and $\eta _{R_{m}}(\lambda , x)/\eta _{\mathbf {L}_{m}}(\lambda , v)$ and their bounds

Fig.\kern-4pt 9

The railtrack$_{-}$rep problem: backward errors of $R_m(\lambda )$ of computed eigenpairs, before and after scaling

5 Closing Remarks

In this work, we have performed a backward error analysis for the PEPs and REPs solved by the CORK linearization, which has not been seen in the literature. This investigation has made two novel contributions. The first is that we established upper bounds for the ratios of the backward errors of approximate eigenpairs of $R_m(\lambda )$ to those of the CORK linearization based on the one-sided factorization which are newly constructed and our treatment is given in a unified framework for all commonly-used bases. The second is a simple scaling approach, suggested by these bounds. Our analysis and this scaling approach are backed up by the numerical experiments in the last section which show an overall effectiveness and efficacy for reducing the backward errors.

A Proof of (14)

We now show that $G(\lambda )$ given by (14) satisfies (12) with $\mathbf{L} _m(\lambda )$ corresponding to the orthogonal basis and $g(\lambda ) = 1$. To simplify the notation, we drop the argument $\lambda$ of the basis function $b_j^{(k)}(\lambda )$ in the rest of this proof.

We shall concentrate on showing that the product of $G(\lambda )$ and the kth column of $\mathbf{L} _m(\lambda )$ is kth column of $e_1^T\otimes R_m(\lambda )$, that is

$$\begin{aligned} D_{k-1} - \sum _{j=k-1}^m b_{j-(k-1)}^{(k-1)} D_j + \frac{\lambda + \alpha _{k-1}}{\beta _k}\sum _{j=k}^m b_{j-k}^{(k)} D_j + \frac{\gamma _k}{\beta _{k+1}}\sum _{j = k+1}^m b_{j-(k+1)}^{(k+1)} D_j = 0, \end{aligned}$$

(28)

which is true if

$$\begin{aligned}&b_{0}^{(k-1)} = 1, \end{aligned}$$

(29a)

$$\begin{aligned}&\frac{\lambda +\alpha _{k-1}}{\beta _k} b_{j-k}^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_{j-(k+1)}^{(k+1)} = b_{j-(k-1)}^{(k-1)}, \quad k \leqslant j \leqslant m, \end{aligned}$$

(29b)

both hold.

Equation (29a) is given by the definition of the orthogonal basis. We now show (29b) by induction.

For $j = k$, (29b) reads

$$\begin{aligned} \frac{\lambda +\alpha _{k-1}}{\beta _k} b_0^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_{-1}^{(k+1)} = b_1^{(k-1)}, \end{aligned}$$

which reduces to

$$\begin{aligned} \frac{\lambda +\alpha _{k-1}}{\beta _k} b_0^{(k-1)} = b_1^{(k-1)}, \end{aligned}$$

(30)

since $b_{-1}^{(k+1)} = 0$ and $b_0^{(k)} = b_0^{(k-1)} = 1$. Equation (30) is the recurrence relation (13) with 0 and $k-1$ in place of j and k, respectively.

For $j = k+1$, (29b) becomes

$$\begin{aligned} \frac{\lambda +\alpha _{k-1}}{\beta _k} b_1^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_0^{(k+1)} = b_2^{(k-1)}. \end{aligned}$$

(31)

To show (31), we substitute $b_1^{(k)} = \frac{\lambda + \alpha _k}{\beta _{k+1}}b_0^{(k)}$ into to have

$$\begin{aligned} \frac{\lambda + \alpha _k}{\beta _{k+1}}\left( \frac{\lambda + \alpha _{k-1}}{\beta _k} b_0^{(k-1)}\right) + \frac{\gamma _k}{\beta _{k+1}}b_0^{(k-1)} = b_2^{(k-1)}, \end{aligned}$$

where $b_0^{(k-1)} = b_0^{(k)} = b_0^{(k+1)} = 1$ is used. Since the terms in the parentheses, by the recurrence relation, are just $b_1^{(k-1)}$, the task is boiled down to verify

$$\begin{aligned} \frac{\lambda + \alpha _k}{\beta _{k+1}}b_1^{(k-1)} + \frac{\gamma _k}{\beta _{k+1}}b_0^{(k-1)} = b_2^{(k-1)}. \end{aligned}$$

This is, again, a variant of the recurrence relation of (13).

Now suppose that (29b) and

$$\begin{aligned} \frac{\lambda +\alpha _{k-1}}{\beta _k} b_{j+1-k}^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_{j+1-(k+1)}^{(k+1)} = b_{j+1-(k-1)}^{(k-1)} \end{aligned}$$

(32)

both hold for any $k-1 \leqslant j \leqslant m-2$. By the recurrence relation (13), we have

$$\begin{aligned} (\lambda +\alpha _{j+1}) b^{(k-1)}_{j-k+2} + \gamma _{j+1} b^{(k-1)}_{j-k+1} = \beta _{j+2}b^{(k-1)}_{j-k+3}, \end{aligned}$$

where we now substitute (29b) and (32) for $b_{j-(k-1)}^{(k-1)}$ and $b_{j+1-(k-1)}^{(k-1)}$ respectively to have

$$\begin{aligned} \left( \frac{\lambda +\alpha _{k-1}}{\beta _k} b_{j-k+2}^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_{j-k+1}^{(k+1)}\right) \beta _{j+2} = b_{j-k+3}^{(k-1)}\beta _{j+2}, \end{aligned}$$

(33)

where we have used two variants of the recurrence relation

$$\begin{aligned} (\lambda +\alpha _{j+1}) b^{(k)}_{j-k+1} + \gamma _{j+1} b^{(k)}_{j-k}&= \beta _{j+2}b^{(k)}_{j-k+2}, \\ (\lambda +\alpha _{j+1}) b^{(k+1)}_{j-k} + \gamma _{j+1} b^{(k+1)}_{j-k-1}&= \beta _{j+2}b^{(k+1)}_{j-k+1}. \end{aligned}$$

Dropping $\beta _{j+2}$’s in (33) yields

$$\begin{aligned} \frac{\lambda +\alpha _{k-1}}{\beta _k} b_{j+2-k}^{(k)} + \frac{\gamma _k}{\beta _{k+1}} b_{j+2-(k+1)}^{(k+1)} = b_{j+2-(k-1)}^{(k-1)}. \end{aligned}$$

This, by induction, shows (29b), which, along with (29a), verifies (28).

The proofs for the first and the last two columns of $G(\lambda )\mathbf{L} _m(\lambda )$ are essentially the same, though the structures of $\mathbf{L} _m(\lambda )$ for these columns are slightly different from that of a general kth column.