A Fully Discrete Mixed Finite Element Method for the Stochastic Cahn–Hilliard Equation with Gradient-Type Multiplicative Noise

Abstract

This paper develops and analyzes a fully discrete mixed finite element method for the stochastic Cahn–Hilliard equation with gradient-type multiplicative noise that is white in time and correlated in space. The stochastic Cahn–Hilliard equation is formally derived as a phase field formulation of the stochastically perturbed Hele–Shaw flow. The main result of this paper is to prove strong convergence with optimal rates for the proposed mixed finite element method. To overcome the difficulty caused by the low regularity in time of the solution to the stochastic Cahn–Hilliard equation, the Hölder continuity in time with respect to various norms for the stochastic PDE solution is established, and it plays a crucial role in the error analysis. Numerical experiments are also provided to validate the theoretical results and to study the impact of noise on the Hele–Shaw flow as well as the interplay of the geometric evolution and gradient-type noise.

1 Introduction

We consider the following stochastic Cahn–Hilliard (SCH) problem:

$$\begin{aligned} du= & {} \Bigl [ - \Delta \Big (\epsilon \Delta u - \frac{1}{\epsilon } f(u) \Big ) \Bigr ] dt + \delta \nabla u \cdot X \circ dW_t \quad \text {in} \ {\mathcal {D}}_T:= {\mathcal {D}}\times (0,T], \end{aligned}$$

(1.1)

$$\begin{aligned} \frac{\partial u}{\partial n}= & {} \frac{\partial }{\partial n} \Big (\epsilon \Delta u - \frac{1}{\epsilon } f(u)\Big ) = 0 \quad \text {in} \ \partial {\mathcal {D}}_T:=\partial {\mathcal {D}}\times (0,T], \end{aligned}$$

(1.2)

$$\begin{aligned} u= & {} u_0 \quad \text {in} \ {\mathcal {D}}\times \{ 0 \}, \end{aligned}$$

(1.3)

where ${\mathcal {D}}\subset {\mathbb {R}}^d$ ($d = 2, 3$) is a bounded domain, n stands for the unit outward normal to $\partial {\mathcal {D}}$, and $T>0$ and $\delta >0$ are fixed numbers. $W_t$ denotes a standard real-valued Wiener process on a given filtered probability space $(\Omega , {\mathcal {F}}, \{ {\mathcal {F}}_t: t \ge 0 \}, {\mathbb {P}})$, “$\circ$” refers to the Stratonovich interpretation of the stochastic integral. $X: {\mathbb {R}}^d \longrightarrow {\mathbb {R}}^d$ is a smooth divergence-free vector field defined on ${\mathcal {D}}$ satisfying $X \cdot n = 0$ on $\partial {\mathcal {D}}$.

Moreover, $f=F'$, the derivative of a smooth double equal well potential F taking its global minimum zero at $\pm 1$. In this paper we focus on the following quartic potential density function:

$$\begin{aligned} F(u) = \frac{1}{4} (u^2 - 1)^2. \end{aligned}$$

(1.4)

We note that the Stratonovich SPDE (1.1) can be equivalently rewritten as the following Itô SPDE:

$$\begin{aligned} du = \left[ - \Delta \Big (\epsilon \Delta u - \frac{1}{\epsilon } f(u) \Big ) + \frac{\delta ^2}{2} \text {div} (B \nabla u) \right] dt + \delta \nabla u \cdot X dW_t, \end{aligned}$$

(1.5)

where $B = X \otimes X \in {\mathbb {R}}^{d \times d}$ with $B_{ij} = X_i X_j$ ($i,j = 1, \ldots , d$).

By introducing the so-called chemical potential $w:= -\epsilon \Delta u + \frac{1}{\epsilon } f(u)$, the above primal formulation of the SCH problem can be rewritten as the following mixed formulation:

$$\begin{aligned} du= & {} \Bigl [ \Delta w + \frac{\delta ^2}{2} \text {div} (B \nabla u) \Bigr ] dt + \delta \nabla u \cdot X d W_t \qquad \text {in} \ {\mathcal {D}}_T, \end{aligned}$$

(1.6)

$$\begin{aligned} w= & {} -\epsilon \Delta u + \frac{1}{\epsilon } f(u) \qquad \text {in} \ {\mathcal {D}}_T, \end{aligned}$$

(1.7)

$$\begin{aligned} \frac{\partial u}{\partial n}= & {} \frac{\partial w}{\partial n} = 0 \qquad \text {on} \ \partial {\mathcal {D}}_T, \end{aligned}$$

(1.8)

$$\begin{aligned} u= & {} u_0 \qquad \text {on} \ {\mathcal {D}}\times \{ 0 \}, \end{aligned}$$

(1.9)

which will be used to develop fully discrete finite element numerical methods in this paper.

The deterministic Cahn–Hilliard equation (i.e., $\delta = 0$) was originally introduced in [7] to describe complicated phase separation and coarsening phenomena in a melted alloy that is quenched to a temperature at which only two different concentration phases can exist stably. In the equation, u represents the concentration of one of two metallic components of the alloy mixture, the small parameter $\epsilon > 0$ is called the interaction length. Note that in (1.6)–(1.7), t is the fast time representing $\frac{t}{\epsilon }$ in the original Cahn–Hilliard formulation. The existence of bistable states suggests that nonconvex energy is associated with the equation (cf. [2, 7, 11]). The Cahn–Hilliard equation is well-known also because it closely relates to a celebrated moving interface problem, namely the Hele–Shaw (or Mullins–Sekerka) problem/flow. It was proved in [2, 37] that, as $\epsilon \searrow 0$, the chemical potential $w := -\epsilon \Delta u + \epsilon ^{-1} f(u)$ tends to a limit, which, together with a free boundary $\Gamma := \cup _{0 \le t \le T} (\Gamma _t \times \{t\})$, satisfies the following Hele–Shaw (or Mullins–Sekerka) problem:

$$\begin{aligned} \Delta w&= 0 \qquad&\text {in} \ {\mathcal {D}}{\setminus } \Gamma _t, \ t \in \quad (0,T], \end{aligned}$$

(1.10)

$$\begin{aligned} \frac{\partial w}{\partial n}&=0 \qquad&\text {on} \ \partial {\mathcal {D}}, \ t \in \quad (0,T], \end{aligned}$$

(1.11)

$$\begin{aligned} w&= \sigma \kappa \qquad&\text {on} \ \Gamma _t, \ t \in \quad (0,T], \end{aligned}$$

(1.12)

$$\begin{aligned} V_n&= \frac{1}{2} \left[ \frac{\partial w}{\partial n} \right] _{\Gamma _t} \qquad&\text {on} \ \Gamma _t, \ t \in \quad (0,T], \end{aligned}$$

(1.13)

$$\begin{aligned} \Gamma _0&= \Gamma _{00} \qquad&\text {on}\quad \ t=0, \end{aligned}$$

(1.14)

where $\sigma = \int _{-1}^1 \sqrt{\frac{F(s)}{2}} \, ds$, $\kappa$ and $V_n$ are the mean curvature and the outward normal velocity of the interface $\Gamma _t$, n is the unit outward normal to either $\partial {\mathcal {D}}$ or $\Gamma _t$, $\left[ \frac{\partial w}{\partial n} \right] _{\Gamma _t} := \frac{\partial w^+}{\partial n} - \frac{\partial w^-}{\partial n}$, and $w^+$ and $w^-$ are respectively the restriction of w in the exterior and interior of $\Gamma _t$ in ${\mathcal {D}}$. More details about the justification of the limit can be found in [2, 8, 40] and its numerical approximations in [13,14,15, 29, 41] and in [11].

In applications of the Hele–Shaw flow, uncertainty may arise and come from various sources such as thermal fluctuation, impurities of the materials and the intrinsic instabilities of the deterministic evolutions. Therefore, the evolution of the flow/interface under influence of noise is of great importance in applications, it is necessary and interesting to consider stochastic effects, and to study the impact of noise on its phase field models and solutions, especially on their long time behaviors. This then leads to considering the stochastic phase field models. However, how to incorporate noises correctly into phase field models is often a delicate issue.

In this paper, we consider the following stochastically perturbed Hale–Shaw flow:

$$\begin{aligned} V_n = \frac{1}{2} \left[ \frac{\partial w}{\partial n} \right] _{\Gamma _t} + \delta {\mathop {W}\limits ^{\circ }}_t X \cdot n, \end{aligned}$$

(1.15)

where a white-in-time noise multiplied by a smooth spatial coefficient function X is added to the normal velocity of the interface $\Gamma _t$, and the parameter $\delta > 0$ represents the noise intensity. By an heuristic argument (see [39] and [11] for an analogous argument), we can formally show that equation (1.1) is a phase field formulation of the above stochastic Hele-Shaw flow.

It should be noted that there is another stochastic Cahn–Hilliard equation, called Cahn–Hilliard–Cook (CHC) equation, which has been extensively studied in the literature, see [5, 10, 34] for PDE analysis and [19, 25, 26, 28] and the references therein for its numerical approximations. However, the noise in the CHC equation is additive and the parameter $\epsilon =1$ in those works. Hence, there may have no connection between the CHC equation and the above stochastic Hele–Shaw flow. We also note that numerical approximations of various stochastic versions of the following Allen–Cahn equation:

$$ u_t=\Delta u -\frac{1}{\varepsilon ^2} f(u), $$

which is a closely related to the Cahn–Hilliard equation, have been extensively investigated in the literature [17, 21, 23, 24, 30, 32]. Most of those works focused on either additive noise or function-type multiplicative noise. Recently, finite element approximations of the stochastic Allen–Cahn (SAC) equation with gradient-type multiplicative noise had been carried out by the authors in [16]. This SAC equation was derived as and partially proved to be a phase field formulation of the stochastic mean curvature flow (cf. [22, 39, 42]).

The goal of this paper is to extend the work of [16] to the stochastic Cahn–Hilliard problem (1.1)–(1.3). Specifically, we shall develop and analyze a fully discrete mixed finite element method for this problem, and establish strong convergence with rates for the proposed mixed finite element method, under similar assumptions as those given in [16]. We note that the divergence-free property of X plays a key role in our analysis, which guarantees the sample-wise mass conservation for the strong solution to problem (1.1)–(1.3) and the discrete solution to problem (3.1)–(3.2). As such, the inverse discrete Laplace operator (see (3.6)) defined in the deterministic case can be employed directly in the error analysis. Another key ingredient for the error analysis is the Hölder continuity estimates for the strong solution. To the best of our knowledge, numerical analysis has yet been done for the stochastic Cahn–Hilliard equation with gradient-type multiplicative noise in the literature.

The rest of the paper is organized as follows. In Sect. 2, we define the weak formulation for problem (1.1)–(1.3) and derive several Hölder continuity estimates for the strong solution of the SPDE problem. In Sect. 3, a fully discretized mixed finite element method is formulated and properties of the discrete inverse Laplacian operator are presented, which will be utilized to establish the well-posedness and stability of the discrete method, and to prove the strong convergence with rates in Sect. 4. In Sect. 5, we report several numerical experiments to validate our theoretical results and to examine the interplay of the geometric parameter $\epsilon$ and the noise intensity $\delta$. Finally, a short conclusion is provided in Sect. 6.

Throughout this paper we shall use C to denote a generic positive constant independent of the parameters $\epsilon$, $\delta$, space and time mesh sizes h and $\tau$, which can take different values at different occurrences.

2 Preliminaries

Standard functional space and function notation in [1] and [6] will be adopted in this paper. In particular, $H^k({\mathcal {D}})$ for $k \ge 0$ denotes the Sobolev space of order k, $(\cdot , \cdot )$ and $\Vert \cdot \Vert _{L^2({\mathcal {D}})}$ denote the standard inner product and norm of $L^2({\mathcal {D}})$.

In this section, we shall establish several technical lemmas about Hölder continuity estimates for the strong solution of problem (1.1)–(1.3) that play a key role in error analysis in Sect. 4. These estimates play the role of the time derivatives of the solution in the deterministic case.

First, we define the weak formulation for problem (1.1)–(1.3), based on the mixed formulation (1.6)–(1.9), as follows: Seeking an ${\mathcal {F}}_{t}$-adapted and $H^1({\mathcal {D}})\times H^1({\mathcal {D}})$-valued process $(u(\cdot ,t), w(\cdot ,t))$ such that there hold ${\mathbb {P}}$-almost surely

$$\begin{aligned} (u(t),\phi )_{}&= (u_0,\phi )_{} - \int _0^t (\nabla w(s), \nabla \phi )_{} \, ds - \frac{\delta ^2}{2} \int _0^t (\nabla u(s) \cdot X, \nabla \phi \cdot X)_{} \, ds \nonumber \\&\quad + \delta \int _0^t (\nabla u(s) \cdot X d W_s, \phi )_{} \qquad \forall \, \phi \in H^1({\mathcal {D}}) \quad \forall \, t \in (0,T], \end{aligned}$$

(2.1)

$$\begin{aligned} (w(t), \varphi )_{}&= \epsilon (\nabla u(t), \nabla \varphi )_{} + \frac{1}{\epsilon } \left( f(u(t)), \varphi \right) _{} \qquad \forall \, \varphi \in H^1({\mathcal {D}}) \quad \forall \, t \in (0,T]. \end{aligned}$$

(2.2)

Let

$$\begin{aligned} J(v) := \int _D \Big ( \frac{\epsilon }{2} |\nabla v|^2 + \frac{1}{\epsilon } F(v) \Big ) \, dx \end{aligned}$$

denote the Cahn–Hilliard energy functional. We now state an uniform estimate for the expectation of the p-th moment energy. Since its proof is similar to that for [16, Lemma 2.1], we omit it to save space.

Lemma 1

Let (u, w) be the solution to problem (1.6)–(1.9). We have for any $p > 1$

$$\begin{aligned} \sup _{t \in [0,T]} {\mathbb {E}}\left[ {J(u(t))^p} \right] + {\mathbb {E}}\left[ {\int _0^t p J(u(s))^{p-1} \Vert \nabla w(s) \Vert ^2_{L^2({\mathcal {D}})} \, ds} \right] \le C J(u_0)^p. \end{aligned}$$

(2.3)

Next, we derive a Hölder continuity estimate in time of the solution function u with respect to the spatial $H^1$-seminorm.

Lemma 2

Let (u, w) be the solution to problem (1.6)–(1.9) and assume u is sufficiently regular in the spatial variable. Then for any $t, s \in [0,T]$ with $t<s$, we have

$$\begin{aligned} {\mathbb {E}}\left[ {\Vert \nabla (u(s)-u(t))\Vert _{L^2({\mathcal {D}})}^2} \right] + \epsilon {\mathbb {E}}\left[ {\int _t^s\Vert \nabla \Delta (u(\zeta )-u(t))\Vert _{L^2({\mathcal {D}})}^2d\zeta } \right] \le C_1(s-t), \end{aligned}$$

where

$$\begin{aligned} C_1 = C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert \nabla \Delta u(\zeta )\Vert _{L^2({\mathcal {D}})}^2} \right] + C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^2({\mathcal {D}})}^6} \right] . \end{aligned}$$

Proof

Apply Itô’s formula to $\Psi (u^{}(s)):=||\nabla u^{}(s)-\nabla u^{}(t)||_{L^2({\mathcal {D}})}^2$, and notice that

$$\begin{aligned} \Psi ^{\prime }(u^{})(v)&=2\int _{{\mathcal {D}}} (\nabla u^{}(s)-\nabla u^{}(t))\cdot \nabla v(s)dx, \end{aligned}$$

(2.4)

$$\begin{aligned} \Psi ^{\prime \prime }(u^{})(m,v)&=2\int _{{\mathcal {D}}} \nabla m(s) \cdot \nabla v(s)dx, \end{aligned}$$

(2.5)

then we have

$$\begin{aligned}&\Vert \nabla (u(s)-u(t))\Vert _{L^2({\mathcal {D}})}^2\nonumber \\&\quad =2\int _{t}^s\bigl (\nabla (u(\zeta )-u(t)),\nabla (- \Delta (\epsilon \Delta u(\zeta ) - \frac{1}{\epsilon } f(u(\zeta )) )\nonumber \\&\quad \quad + \frac{\delta ^2}{2} \text {div}(B\nabla u(\zeta )))\bigr )d\zeta +2\int _{t}^s\bigl (\nabla (u(\zeta )-u(t)),\nabla (\delta \nabla u(\zeta )\cdot X d{W}_{\zeta })\bigr )\nonumber \\&\quad \quad +\delta ^2\int _{t}^s(\nabla (\nabla u(\zeta )\cdot X),\nabla (\nabla u(\zeta )\cdot X))d\zeta . \end{aligned}$$

(2.6)

Then we obtain

$$\begin{aligned} \Vert \nabla (u(s)-u(t))\Vert _{L^2({\mathcal {D}})}^2&=2\int _{t}^s\bigl (\nabla \Delta (u(\zeta )-u(t)),- \epsilon \nabla \Delta (u(\zeta ) - u(t))\bigr )d\zeta \nonumber \\&\quad -\,2\int _{t}^s\bigl (\nabla \Delta (u(\zeta )-u(t)),\epsilon \nabla \Delta u(t)\bigr )d\zeta \nonumber \\&\quad +\,2\int _{t}^s\bigl (\nabla \Delta (u(\zeta )-u(t)),\frac{1}{\epsilon } \nabla f(u(\zeta ))\bigr )d\zeta \nonumber \\&\quad -\,\delta ^2\int _t^s\bigl (\Delta (u(\zeta )-u(t)),B:D^2u(\zeta )+\nabla u(\zeta )\cdot \text {div}(B)\bigr )d\zeta \nonumber \\&\quad +\,2\int _{t}^s\bigl (\nabla (u(\zeta )-u(t)),\nabla (\delta \nabla u(\zeta )\cdot Xd{W}_{\zeta })\bigr )\nonumber \\&\quad +\,\delta ^2\int _{t}^s\int _{{\mathcal {D}}}|D^2 u(\zeta )X+(\nabla X)^T\nabla u(\zeta )|^2dxd\zeta . \end{aligned}$$

(2.7)

Taking the expectation on both sides of (2.7) and using the Young’s inequality, we get

$$\begin{aligned}&{\mathbb {E}}\left[ {\Vert \nabla (u(s)-u(t))\Vert _{L^2({\mathcal {D}})}^2} \right] + 2\epsilon {\mathbb {E}}\left[ {\int _t^s\Vert \nabla \Delta (u(\zeta )-u(t))\Vert _{L^2({\mathcal {D}})}^2d\zeta } \right] \nonumber \\&\quad \le \epsilon {\mathbb {E}}\left[ {\int _t^s\Vert \nabla \Delta (u(\zeta )-u(t))\Vert _{L^2({\mathcal {D}})}^2d\zeta } \right] +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert \nabla \Delta u(\zeta )\Vert _{L^2({\mathcal {D}})}^2} \right] (s-t)\nonumber \\&\qquad +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^2({\mathcal {D}})}^6} \right] (s-t)+C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert \nabla u(\zeta )\Vert _{L^2({\mathcal {D}})}^2} \right] (s-t)\nonumber \\&\qquad +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^2({\mathcal {D}})}^2} \right] (s-t), \end{aligned}$$

(2.8)

where the embedding theorem from $H^1({\mathcal {D}})$ to $L^{6}({\mathcal {D}})$ is used in estimating the nonlinear term.

The last two terms on the right-hand side of (2.8) can be incorporated into the third term, then the theorem is proved. $\square$

It turns out we also need to control the chemical potential w to handle the nonlinear terms in the error analysis. The following lemma establishes a Hölder continuity estimate in time for w with respect to the spatial $H^1$-seminorm.

Lemma 3

Let (u, w) be the solution to problem (1.6)–(1.9) which is assumed to be sufficiently regular in the spatial variable. Then for any $t, s \in [0,T]$ with $t<s$, we have

$$\begin{aligned} {\mathbb {E}}\left[ {\Vert \nabla w(s)-\nabla w(t)\Vert _{L^2({\mathcal {D}})}^2} \right] \le C_2(s-t), \end{aligned}$$

where

$$\begin{aligned} C_2 = C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^7({\mathcal {D}})}^2} \right] + C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^6({\mathcal {D}})}^6} \right] . \end{aligned}$$

Proof

Define $g(u(s)) := g_1(u(s))+g_2(u(s))$, where

$$\begin{aligned} g_1(u(s))&:= \Vert \epsilon \nabla \Delta u(s)-\epsilon \nabla \Delta u(t)\Vert _{L^2({\mathcal {D}})}^2, \\ g_2(u(s))&:= \Vert \frac{1}{\epsilon }\nabla f(u(s))-\frac{1}{\epsilon }\nabla f(u(t))\Vert _{L^2({\mathcal {D}})}^2. \end{aligned}$$

Notice that

$$\begin{aligned} g_1^{\prime }(u^{})(v)&=2\epsilon ^2\int _{{\mathcal {D}}}(\nabla \Delta u^{}(s)-\nabla \Delta u^{}(t)) \cdot \nabla \Delta v(s)dx, \end{aligned}$$

(2.9)

$$\begin{aligned} g_1^{\prime \prime }(u^{})(m,v)&=2\epsilon ^2\int _{{\mathcal {D}}}\nabla \Delta m(s) \cdot \nabla \Delta v(s)dx, \end{aligned}$$

(2.10)

and

$$\begin{aligned} g_2^{\prime }(u^{})(v)&=\frac{2}{\epsilon ^2}\int _{{\mathcal {D}}}\bigl [3u^2(s)\nabla u(s)-\nabla u(s)-\nabla f(u(t))\bigr ] \nonumber \\&\quad \cdot \, \bigl [6u(s)v(s)\nabla u(s)+3u^2(s)\nabla v(s)-\nabla v(s)\bigr ]dx, \end{aligned}$$

(2.11)

$$\begin{aligned} g_2^{\prime \prime }(u^{})(m,v)&=\frac{2}{\epsilon ^2}\int _{{\mathcal {D}}}\bigl [3u^2(s)\nabla u(s)-\nabla u(s)-\nabla f(u(t))\bigr ] \nonumber \\&\quad \cdot \, \bigl [6m(s)v(s)\nabla u(s)+6u(s)v(s)\nabla m(s)+6u(s)m(s)\nabla v(s)\bigr ]dx \nonumber \\&\quad +\,\frac{2}{\epsilon ^2}\int _{{\mathcal {D}}}\bigl [6u(s)v(s)\nabla u(s)+3u^2(s)\nabla v(s)-\nabla v(s)\bigr ]\nonumber \\&\quad \cdot \, \bigl [3u^2(s)\nabla m(s)+6u(s)m(s)\nabla u(s)-\nabla m(s)\bigr ] dx. \end{aligned}$$

(2.12)

Applying Itô’s formula to $g(w(s)) := \Vert \nabla w(s)-\nabla w(t)\Vert _{L^2({\mathcal {D}})}^2$, then we have

$$\begin{aligned}&\Vert \nabla w(s) -\nabla w(t)\Vert _{L^2({\mathcal {D}})}^2 \nonumber \\&\quad =2\epsilon ^2\int _{t}^s\bigl (\nabla \Delta (u(\zeta )-u(t)),\nabla \Delta M_1(\zeta )\bigr )d\zeta \nonumber \\&\qquad +2\epsilon ^2\int _{t}^s\bigl (\nabla \Delta (u(\zeta )-u(t)),\nabla \Delta M_2(\zeta )\bigr )d{W}_{\zeta }+\epsilon ^2\int _{t}^s \int _{{\mathcal {D}}} \nabla \Delta M_2(\zeta ) \nonumber \\&\qquad \cdot \nabla \Delta M_2(\zeta ) dx d\zeta +\frac{2}{\epsilon ^2}\int _{t}^s\int _{{\mathcal {D}}}\bigl [3u^2(\zeta )\nabla u(\zeta )-\nabla u(\zeta )-\nabla f(u(t))\bigr ] \nonumber \\&\qquad \cdot \bigl [6u(\zeta )M_1(\zeta )\nabla u(\zeta )+3u^2(\zeta )\nabla M_1(\zeta )-\nabla M_1(\zeta )\bigr ]dx d\zeta \nonumber \\&\qquad +\frac{2}{\epsilon ^2}\int _{t}^s\int _{{\mathcal {D}}}\bigl [3u^2(\zeta )\nabla u(\zeta )-\nabla u(\zeta )-\nabla f(u(t))\bigr ]\nonumber \\&\qquad \cdot \bigl [6u(\zeta )M_2(\zeta ) \nabla u(\zeta )+3u^2(\zeta )\nabla M_2(\zeta ) -\nabla M_2(\zeta ) \bigr ]dxdW_{\zeta }\nonumber \\&\qquad +\frac{\delta ^2}{\epsilon ^2}\int _{t}^s\int _{{\mathcal {D}}}\bigl [3u^2(\zeta )\nabla u(\zeta )-\nabla u(\zeta )-\nabla f(u(t))\bigr ]\nonumber \\&\qquad \cdot \bigl [6M_2^2(\zeta )\nabla u(\zeta )+6u(\zeta )M_2(\zeta )\nabla M_2(\zeta )+6u(\zeta )M_2(\zeta )\nabla M_2(\zeta )\bigr ]dxd\zeta \nonumber \\&\qquad +\frac{\delta ^2}{\epsilon ^2}\int _{t}^s\int _{{\mathcal {D}}}\bigl [6u(\zeta )M_2(\zeta )\nabla u(\zeta )+3u^2(\zeta )\nabla M_2(\zeta )-\nabla M_2(\zeta )\bigr ]\nonumber \\&\qquad \cdot \bigl [3u^2(\zeta )\nabla M_2(\zeta )+6u(\zeta )M_2(\zeta )\nabla u(\zeta )-\nabla M_2(\zeta )\bigr ] dx d\zeta , \end{aligned}$$

(2.13)

where

$$\begin{aligned} M_1(\zeta )&:=- \Delta \Big (\epsilon \Delta u(\zeta ) - \frac{1}{\epsilon } f(u(\zeta )) \Big ) + \frac{\delta ^2}{2} \text {div}(B\nabla u(\zeta )), \\ M_2(\zeta )&:=\delta \nabla u(\zeta )\cdot X. \end{aligned}$$

Taking the expectation on both sides of (2.13), and using the Young’s inequality and the embedding theorem, we get

$$\begin{aligned}&\Vert \nabla w(s) -\nabla w(t)\Vert _{L^2({\mathcal {D}})}^2 \end{aligned}$$

(2.14)

$$\begin{aligned}&\le \bigg \{C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^3({\mathcal {D}})}^2} \right] +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^7({\mathcal {D}})}^2} \right] + C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^6({\mathcal {D}})}^6} \right] \nonumber \\&\quad +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^4({\mathcal {D}})}^2} \right] +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^5({\mathcal {D}})}^2} \right] \nonumber \\&\quad +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^2({\mathcal {D}})}^2} \right] +C\sup _{t\le \zeta \le s}{\mathbb {E}}\left[ {|u(\zeta )|_{H^1({\mathcal {D}})}^2} \right] \bigg \}(s-t). \end{aligned}$$

(2.15)

The terms with lower moments can be absorbed into term $C\sup \limits _{t\le \zeta \le s}{\mathbb {E}}\left[ {\Vert u(\zeta )\Vert _{H^6({\mathcal {D}})}^6} \right]$ using the Young’s inequality, then the theorem is proved. $\square$

3 Formulation of mixed finite element method

In this section we define our mixed finite element method for (2.1)–(2.2) and introduce several auxiliary operators that will be used in Sect. 4.

Let $t_n = n \tau$ ($n = 0, 1, \ldots , N$) be a uniform partition of [0, T] with $\tau = T/N$ and ${\mathcal {T}}_h$ be a quasi-uniform triangulation of ${\mathcal {D}}$. Let $V_h$ be the finite element space given by

$$\begin{aligned} V_h := \{ v_h \in H^1({\mathcal {D}}): v_h|_K \in {\mathcal {P}}_1(K) \quad \forall \, K \in {\mathcal {T}}_h \}, \end{aligned}$$

where ${\mathcal {P}}_1(K)$ denotes the space of polynomials of degree one on $K \in {\mathcal {T}}_h$. Our fully discrete mixed finite element methods for (2.1)–(2.2) is defined as seeking ${\mathcal {F}}_{t_n}$-adapted and $V_h \times V_h$-valued process $\{ (u_h^n, w_h^n) \}$ ($n = 1, \dots , N$) such that ${\mathbb {P}}$-almost surely

$$\begin{aligned} (u^{n+1}_h,\eta _h)_{}&= (u^n_h,\eta _h)_{} - \tau (\nabla w^{n+1}_h, \nabla \eta _h)_{} - \tau \frac{\delta ^2}{2} (\nabla u^{n+1}_h \cdot X, \nabla \eta _h \cdot X)_{} \nonumber \\&\quad + \delta (\nabla u^n_h \cdot X {\bar{\Delta }} W_{n+1}, \eta _h)_{} \quad \forall \, \eta _h \in V_h, \end{aligned}$$

(3.1)

$$\begin{aligned} (w^{n+1}_h, v_h)_{}&= \epsilon (\nabla u^{n+1}_h, \nabla v_h)_{} + \frac{1}{\epsilon } \left( f^{n+1}, v_h \right) _{} \quad \forall \, v_h \in V_h, \end{aligned}$$

(3.2)

where ${\bar{\Delta }}$ denotes the difference operator, ${\bar{\Delta }} W_{n+1} := W_{t_{n+1}} - W_{t_n} \sim {\mathcal {N}}(0, \tau )$ and $f^{n+1} := (u^{n+1}_h)^3 - u^{n+1}_h$. The initial values $(u^0_h, w^0_h)$ are chosen by solving

$$\begin{aligned} (u^0_h, v_h)&= (u_0, v_h) \quad \forall \, v_h \in V_h, \\ (w^0_h, v_h)&= \epsilon (\nabla u^0_h, \nabla v_h) + \frac{1}{\epsilon } ((u^0_h)^3 - u^0_h, v_h) \quad \forall \, v_h \in V_h. \end{aligned}$$

Note that $u^0_h = P_h u_0$ where $P_h: L^2({\mathcal {D}}) \longrightarrow V_h$ is the standard $L^2$-projection operator satisfying the following error estimates [6, 9]

$$\begin{aligned}&\Vert v - P_h v \Vert _{L^2({\mathcal {D}})} + h \Vert \nabla (v - P_h v) \Vert _{L^2({\mathcal {D}})} \le C h^2 \Vert v\Vert _{H^2({\mathcal {D}})}, \end{aligned}$$

(3.3)

$$\begin{aligned}&\Vert v - P_h v \Vert _{L^{\infty }({\mathcal {D}})} \le C h^{2-d/2} \Vert v\Vert _{H^2({\mathcal {D}})} \end{aligned}$$

(3.4)

for all $v \in H^2({\mathcal {D}})$. Furthermore, the divergence-free property of X and its boundary condition imply that $(\nabla u^n_h \cdot X {\bar{\Delta }} W_{n+1}, 1) = (\text {div} (u^n_h X) {\bar{\Delta }} W_{n+1}, 1) = 0$. By taking $\eta _h = 1$ in (3.1), we observe that the numerical solution function $u^n_h$ satisfies the sample-wise mass conservation property, i.e., $(u^n_h, 1) = (u_0,1)$ almost surely for all $n = 1, \ldots , N$.

Let $\mathring{V}_h$ be the subspace of $V_h$ with zero mean, i.e.,

$$\begin{aligned} \mathring{V}_h := \bigl \{ v_h \in V_h:\, (v_h, 1)= 0 \bigr \}. \end{aligned}$$

(3.5)

We introduce the inverse discrete Laplace operator $\Delta _h^{-1}: \mathring{V}_h \rightarrow \mathring{V}_h$ as follows: given $\zeta \in \mathring{V}_h$, define $\Delta _h^{-1}\zeta \in \mathring{V}_h$ such that

$$\begin{aligned} \bigl ( \nabla (-\Delta _h^{-1}\zeta ),\nabla v_h \bigr ) = \bigl ( \zeta , v_h \bigr ) \quad \forall \, v_h\in V_h. \end{aligned}$$

(3.6)

For any $\zeta , \Phi \in \mathring{V}_h$, we can define the discrete $H^{-1}$ inner product by

$$\begin{aligned} (\zeta ,\Phi )_{-1,h}:= \bigl (\nabla (-\Delta _h^{-1}\zeta ),\nabla (-\Delta _h^{-1}\Phi ) \bigr ) =\bigl (\zeta ,-\Delta _h^{-1}\Phi \bigr )=\bigl (-\Delta _h^{-1}\zeta ,\Phi \bigr ). \end{aligned}$$

(3.7)

The induced mesh-dependent $H^{-1}$ norm is given by

$$\begin{aligned} \Vert \zeta \Vert _{-1,h}:=\sqrt{(\zeta ,\zeta )_{-1,h}} =\mathop {\sup }_{\Phi \in \mathring{V}_h}\limits \frac{(\zeta ,\Phi )}{|\Phi |_{H^1({\mathcal {D}})}}. \end{aligned}$$

(3.8)

The following properties can be easily verified [3]:

$$\begin{aligned} |(\zeta ,\Phi )| \Vert \zeta \Vert _{-1,h} |\Phi |_{H^1({\mathcal {D}})}&\quad \forall \,\zeta \in \mathring{V}_h, \ \Phi \in \mathring{V}_h, \end{aligned}$$

(3.9)

$$\begin{aligned} \Vert \zeta \Vert _{-1,h} \le C\Vert \zeta \Vert _{L^2({\mathcal {D}})}&\quad \forall \,\zeta \in \mathring{V}_h, \end{aligned}$$

(3.10)

and, if ${\mathcal {T}}_h$ is quasi-uniform, we further have

$$\begin{aligned} \Vert \zeta \Vert _{L^2({\mathcal {D}})}\le C h^{-1}\Vert \zeta \Vert _{-1,h}\quad \forall \,\zeta \in \mathring{V}_h. \end{aligned}$$

(3.11)

Setting ${\hat{u}}^n_h = u^n_h - {\bar{u}}_0$ and ${\hat{w}}^n_h = w^n - {\bar{w}}^n_h$, where ${\bar{v}} = |{\mathcal {D}}|^{-1} (v, 1)$, we can equivalently formulate (3.1)–(3.2) as: seeking ${\mathcal {F}}_{t_n}$-adapted and $\mathring{V}_h \times \mathring{V}_h$-valued process $\{ ({\hat{u}}_h^n, {\hat{w}}_h^n) \}$ ($n = 1, \dots , N$) such that ${\mathbb {P}}$-almost surely

$$\begin{aligned} ({\hat{u}}^{n+1}_h,\eta _h)_{}&= ({\hat{u}}^n_h,\eta _h)_{} - \tau \bigl (\nabla {\hat{w}}^{n+1}_h, \nabla \eta _h\bigr ) - \tau \frac{\delta ^2}{2} \bigl (\nabla {\hat{u}}^{n+1}_h \cdot X, \nabla \eta _h \cdot X \bigr ) \nonumber \\&\quad + \delta \bigl (\nabla {\hat{u}}^n_h \cdot X {\bar{\Delta }} W_{n+1}, \eta _h \bigr ) \quad \forall \, \eta _h \in \mathring{V}_h, \end{aligned}$$

(3.12)

$$\begin{aligned} ({\hat{w}}^{n+1}_h, v_h)_{}&= \epsilon \bigl (\nabla {\hat{u}}^{n+1}_h, \nabla v_h \bigr ) + \frac{1}{\epsilon } \bigl ( {\hat{f}}^{n+1}, v_h \bigr ) \quad \forall \, v_h \in \mathring{V}_h, \end{aligned}$$

(3.13)

where ${\hat{f}}^{n+1} = ({\hat{u}}^{n+1}_h + {\bar{u}}_0)^3 - ({\hat{u}}^{n+1}_h + {\bar{u}}_0)$.

The next theorem establishes the well-posedness for the proposed numerical method.

Theorem 1

The scheme (3.1)–(3.2) (or (3.12)–(3.13)) is uniquely solvable, provided that the following mesh constraint is satisfied

$$\begin{aligned} \tau \le C (\epsilon ^{-3} + \epsilon ^{-1} \delta ^4)^{-1}. \end{aligned}$$

(3.14)

Proof

For any $v_h \in \mathring{V}_h$, let $\eta _h = - \Delta ^{-1}_h v_h \in \mathring{V}_h$ in (3.12), we have

$$\begin{aligned} \left( {\hat{u}}^{n+1}_h, - \Delta ^{-1}_h v_h\right)&= \left( {\hat{u}}^n_h, - \Delta ^{-1}_h v_h\right) - \tau \left( \nabla {\hat{w}}^{n+1}_h, \nabla (- \Delta ^{-1}_h v_h)\right) \nonumber \\&\quad - \tau \frac{\delta ^2}{2} \bigl (\nabla {\hat{u}}^{n+1}_h \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X\bigr ) \nonumber \\&\quad + \delta \bigl (\nabla {\hat{u}}^n_h \cdot X {\bar{\Delta }} W_{n+1}, - \Delta ^{-1}_h v_h \bigr ). \end{aligned}$$

(3.15)

By (3.7), (3.13) and integration by parts, we can rewrite (3.15) as

$$\begin{aligned}&\left( {\hat{u}}^{n+1}_h, v_h\right) _{-1,h} + \tau \epsilon \left( \nabla {\hat{u}}^{n+1}_h, \nabla v_h\right) + \frac{\tau }{\epsilon } \left( ({\hat{u}}^{n+1}_h + {\bar{u}}_0)^3, v_h \right) - \frac{\tau }{\epsilon } ({\hat{u}}^{n+1}_h, v_h) \nonumber \\&\quad + \tau \frac{\delta ^2}{2} \left( \nabla {\hat{u}}^{n+1}_h \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X \right) - \left( {\hat{u}}^n_h, v_h\right) _{-1,h} \nonumber \\&\quad - \delta \bigl ({\hat{u}}^n_h X, \nabla (- \Delta ^{-1}_h v_h) \bigr ) {\bar{\Delta }} W_{n+1} = 0 \quad \forall \, v_h \in \mathring{V}_h. \end{aligned}$$

(3.16)

Now we define $B: \mathring{V}_h \longrightarrow \mathring{V}_h$ by

$$\begin{aligned} (B(z), v_h)_{-1,h}&= (z, v_h)_{-1,h} + \tau \epsilon (\nabla z, \nabla v_h) + \frac{\tau }{\epsilon } \left( (z + {\bar{u}}_0)^3, v_h \right) \nonumber \\&\quad - \frac{\tau }{\epsilon } (z, v_h) + \tau \frac{\delta ^2}{2} \left( \nabla z \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X\right) - \left( {\hat{u}}^n_h, v_h\right) _{-1,h} \nonumber \\&\quad - \delta \bigl ({\hat{u}}^n_h X, \nabla (- \Delta ^{-1}_h v_h) \bigr ) {\bar{\Delta }} W_{n+1} \quad \forall \, z, v_h \in \mathring{V}_h. \end{aligned}$$

(3.17)

For any $v_h \in \mathring{V}_h$, we have

$$\begin{aligned} (B(v_h), v_h)_{-1,h}&= \Vert v_h \Vert _{-1,h}^2 + \tau \epsilon \Vert \nabla v_h \Vert _{L^2({\mathcal {D}})}^2 + \frac{\tau }{\epsilon } \left( (v_h + {\bar{u}}_0)^3, v_h \right) \nonumber \\&\quad - \frac{\tau }{\epsilon } \Vert v_h \Vert ^2_{L^2({\mathcal {D}})} + \tau \frac{\delta ^2}{2} \bigl (\nabla v_h \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X \bigr ) \nonumber \\&\quad - ({\hat{u}}^n_h, v_h)_{-1,h} - \delta \bigl ({\hat{u}}^n_h X, \nabla (- \Delta ^{-1}_h v_h) \bigr ) {\bar{\Delta }} W_{n+1}. \end{aligned}$$

(3.18)

Notice that

$$\begin{aligned} \frac{\tau }{\epsilon } \left( (v_h + {\bar{u}}_0)^3, v_h \right)&= \frac{\tau }{\epsilon } \left( v_h^3 + 3 v_h^2 {\bar{u}}_0 + 3 v_h {\bar{u}}_0^2 + {\bar{u}}^3_0, v_h \right) \nonumber \\&= \frac{\tau }{\epsilon } \Vert v_h \Vert ^4_{L^4({\mathcal {D}})} + \frac{3 \tau {\bar{u}}_0}{\epsilon } \Vert v_h \Vert ^3_{L^3({\mathcal {D}})} + \frac{3 \tau {\bar{u}}_0^2}{\epsilon } \Vert v_h \Vert ^2_{L^2({\mathcal {D}})} \nonumber \\&\ge \frac{3 \tau {\bar{u}}_0^2}{4 \epsilon } \Vert v_h \Vert ^2_{L^2({\mathcal {D}})}, \end{aligned}$$

(3.19)

where we had used

$$\frac{3 \tau {\bar{u}}_0}{\epsilon } \Vert v_h \Vert ^3_{L^3({\mathcal {D}})} \ge - \frac{\tau }{\epsilon } \Vert v_h \Vert _{L^4({\mathcal {D}})}^4 - \frac{9 \tau {\bar{u}}_0^2}{4 \epsilon } \Vert v_h \Vert _{L^2({\mathcal {D}})}^2$$

to obtain the last inequality. Moreover, we have

$$\begin{aligned} - \frac{\tau }{\epsilon } \Vert v_h \Vert ^2_{L^2({\mathcal {D}})} \ge - \frac{C \tau }{\epsilon ^3} \Vert v_h \Vert _{-1,h}^2 - \frac{\tau \epsilon }{4} \Vert \nabla v_h \Vert _{L^2({\mathcal {D}})}^2 \end{aligned}$$

(3.20)

by (3.9), and

$$\begin{aligned} \tau \frac{\delta ^2}{2} (\nabla v_h \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X)&\ge - \frac{\tau \epsilon }{4} \Vert \nabla v_h \Vert _{L^2({\mathcal {D}})}^2 - \frac{C \tau \delta ^4}{\epsilon } \Vert v_h \Vert ^2_{-1,h}, \end{aligned}$$

(3.21)

$$\begin{aligned} - \delta \bigl ({\hat{u}}^n_h X, \nabla (- \Delta ^{-1}_h v_h) \bigr ) {\bar{\Delta }} W_{n+1}&\ge - C({\bar{\Delta }} W_{n+1}) \Vert {\hat{u}}^n_h \Vert _{L^2({\mathcal {D}})} \Vert v_h \Vert _{-1,h} \end{aligned}$$

(3.22)

by the Cauchy–Schwarz inequality, where $C({\bar{\Delta }} W_{n+1})$ depends on ${\bar{\Delta }} W_{n+1}$. Combining (3.18)–(3.22) yields

$$\begin{aligned} (B(v_h), v_h)_{-1,h}&\ge \Bigl \{ \bigl [ 1 - C \tau \left( \epsilon ^{-3} + \delta ^4 \epsilon ^{-1} \right) \bigr ] \Vert v_h \Vert _{-1,h} - \Vert {\hat{u}}^n_h \Vert _{-1,h} \nonumber \\&\quad - C({\bar{\Delta }} W_{n+1}) \Vert {\hat{u}}^n_h \Vert _{L^2({\mathcal {D}})} \Bigr \} \Vert v_h \Vert _{-1,h} + \frac{\tau \epsilon }{2} \Vert \nabla v_h \Vert _{L^2({\mathcal {D}})}^2. \end{aligned}$$

(3.23)

Hence we have

$$\begin{aligned}&(B(v_h), v_h)_{-1,h} \ge 0 \quad \forall \, v_h \in \mathring{V}_h, \end{aligned}$$

(3.24)

$$\begin{aligned}&\Vert v_h \Vert _{-1,h} = C \Vert {\hat{u}}^n_h \Vert _{-1,h} + C({\bar{\Delta }} W_{n+1}) \Vert {\hat{u}}^n_h \Vert _{L^2({\mathcal {D}})}, \end{aligned}$$

(3.25)

provided that the mesh constraint (3.14) holds. It follows from Brouwer’s fixed point theorem [20, 38] that there exists ${\hat{u}}^{n+1}_h \in \mathring{V}_h$ such that

$$\begin{aligned} B({\hat{u}}^{n+1}_h) = 0, \quad \Vert {\hat{u}}^{n+1}_h \Vert _{-1,h} \le C \Vert {\hat{u}}^n_h \Vert _{-1,h} + C({\bar{\Delta }} W_{n+1}) \Vert {\hat{u}}^n_h \Vert _{L^2({\mathcal {D}})}, \end{aligned}$$

(3.26)

which also implies the existence of the solution to (3.16). This ${\hat{u}}^{n+1}_h$ together with ${\hat{w}}^{n+1}_h$ determined by (3.13) solves (3.12)–(3.13).

Next, it suffices to establish the uniqueness of the solution to (3.16). Assume ${\hat{u}}^{n+1}_{h,1}$ and ${\hat{u}}^{n+1}_{h,2}$ are two solutions to (3.16). Denote $U^{n+1}_h = {\hat{u}}^{n+1}_{h,1} - {\hat{u}}^{n+1}_{h,2}$, we have

$$\begin{aligned}&(U^{n+1}_h, v_h)_{-1,h} + \tau \epsilon (\nabla U^{n+1}_h, \nabla v_h) + \frac{\tau }{\epsilon } \Bigl ( ({\hat{u}}^{n+1}_{h,1} + {\bar{u}}_0)^3 - ({\hat{u}}^{n+1}_{h,2} + {\bar{u}}_0)^3, v_h \Bigr ) \nonumber \\&\quad - \frac{\tau }{\epsilon } (U^{n+1}_h, v_h) + \tau \frac{\delta ^2}{2} (\nabla U^{n+1}_h \cdot X, \nabla (- \Delta ^{-1}_h v_h) \cdot X) = 0 \quad \forall \, v_h \in \mathring{V}_h. \end{aligned}$$

(3.27)

Taking $v_h = U^{n+1}_h$ in (3.27), using the fact that

$$\begin{aligned} \frac{\tau }{\epsilon } \Bigl ( ({\hat{u}}^{n+1}_{h,1} + {\bar{u}}_0)^3 - ({\hat{u}}^{n+1}_{h,2} + {\bar{u}}_0)^3, U^{n+1}_h \Bigr ) \ge 0, \end{aligned}$$

(3.28)

and the similar estimates to (3.20) and (3.21), we obtain

$$\begin{aligned} \left[ 1 - C \tau \left( \epsilon ^{-3} + \delta ^4 \epsilon ^{-1} \right) \right] \Vert U^{n+1}_h \Vert ^2_{-1,h} + \frac{\tau \epsilon }{2} \Vert \nabla U^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})} \le 0. \end{aligned}$$

(3.29)

Therefore, under the mesh constraint (3.14), we conclude that $U^{n+1}_h = 0$. This completes the proof. $\square$

Remark 1

Whenever $\delta = 0$, the scheme (3.1)–(3.2) reduces to a fully implicit scheme (cf. [13,14,15] and the references therein). In this case (3.14) becomes $\tau \le C \epsilon ^3$, which is consistent with the mesh constraint for the fully implicit scheme in the deterministic case. For the stochastic case (i.e., $\delta > 0$), the mesh constraint (3.14) depends on the noise intensity $\delta$. In particular, if $\delta \gg \epsilon ^{-1/2}$, we need stronger mesh constraint in terms of $\epsilon$ for the time step size $\tau$.

Next theorem derives an a priori estimates for $u^n_h$.

Theorem 2

Let $(u^n_h, w^n_h) \in V_h \times V_h$ be the unique solution of (3.1)–(3.2) and suppose the mesh constraint (3.14) is satisfied, there holds

$$\begin{aligned} \sup _{0 \le n \le N} {\mathbb {E}}\left[ {\Vert u^n_h \Vert _{-1,h}^2} \right] + {\mathbb {E}}\left[ {\sum _{n=1}^N \tau \Vert \nabla u^n_h \Vert _{L^2({\mathcal {D}})}^2} \right] \le C(\delta , \epsilon ^{-1}). \end{aligned}$$

(3.30)

Proof

It suffices to prove the estimates for the solution to (3.12)–(3.13). Taking $\eta _h = - \Delta ^{-1}_h {\hat{u}}^{n+1}_h$ in (3.12) and $v_h = {\hat{u}}^{n+1}_h$ in (3.13), we have

$$\begin{aligned}&({\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h, - \Delta ^{-1}_h {\hat{u}}^{n+1}_h) + \tau \epsilon \Vert \nabla {\hat{u}}^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})} \nonumber \\&\quad = - \tau \frac{\delta ^2}{2} \left( \nabla {\hat{u}}^{n+1}_h \cdot X, \nabla \left( - \Delta ^{-1}_h {\hat{u}}^{n+1}_h\right) \cdot X \right) \nonumber \\&\quad \quad + \delta \left( \nabla {\hat{u}}^n_h \cdot X {\bar{\Delta }} W_{n+1}, - \Delta ^{-1}_h {\hat{u}}^{n+1}_h\right) - \frac{\tau }{\epsilon } \left( {\hat{f}}^{n+1}, {\hat{u}}^{n+1}_h \right) . \end{aligned}$$

(3.31)

Notice that

$$\begin{aligned} \left( {\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h, - \Delta ^{-1}_h {\hat{u}}^{n+1}_h \right) = \frac{1}{2} \Vert {\hat{u}}^{n+1}_h \Vert ^2_{-1,h} - \frac{1}{2} \Vert {\hat{u}}^{n}_h \Vert ^2_{-1,h} + \frac{1}{2} \Vert {\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h \Vert ^2_{-1,h}, \end{aligned}$$

(3.32)

and the right-hand side of (3.31) can be estimated as follows:

$$\begin{aligned}&- \tau \frac{\delta ^2}{2}s \left( \nabla {\hat{u}}^{n+1}_h \cdot X, \nabla \left( - \Delta ^{-1}_h {\hat{u}}^{n+1}_h \right) \cdot X \right) \nonumber \\&\quad \le \frac{C \delta ^4 \tau }{\epsilon } \Vert {\hat{u}}^{n+1}_h \Vert ^2_{-1,h} + \frac{\epsilon \tau }{16} \Vert \nabla {\hat{u}}^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})}, \end{aligned}$$

(3.33)

and

$$\begin{aligned}&\delta \left( \nabla {\hat{u}}^n_h \cdot X {\bar{\Delta }} W_{n+1}, - \Delta ^{-1}_h {\hat{u}}^{n+1}_h \right) \nonumber \\&\quad = - \delta \left( {\hat{u}}^n_h X {\bar{\Delta }} W_{n+1}, \nabla (- \Delta ^{-1}_h ({\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h) ) \right) - \delta \bigl ({\hat{u}}^n_h X {\bar{\Delta }} W_{n+1}, \nabla (- \Delta ^{-1}_h {\hat{u}}^n_h) \bigr ) \nonumber \\&\quad \le C \delta ^2 \Vert {\hat{u}}^n_h \Vert ^2_{L^2({\mathcal {D}})} ({\bar{\Delta }} W_{n+1})^2 + \frac{1}{2} \Vert {\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h \Vert ^2_{-1,h} \nonumber \\&\qquad - \delta \bigl ({\hat{u}}^n_h X {\bar{\Delta }} W_{n+1}, \nabla (- \Delta ^{-1}_h {\hat{u}}^n_h) \bigr ) \nonumber \\&\quad \le \frac{\epsilon }{16} \Vert \nabla {\hat{u}}^{n}_h \Vert ^2_{L^2({\mathcal {D}})} ({\bar{\Delta }} W_{n+1})^2 + \frac{C \delta ^4}{\epsilon } \Vert {\hat{u}}^{n}_h \Vert ^2_{-1,h} ({\bar{\Delta }} W_{n+1})^2 + \frac{1}{2} \Vert {\hat{u}}^{n+1}_h - {\hat{u}}^{n}_h \Vert ^2_{-1,h} \nonumber \\&\qquad - \delta \bigl ({\hat{u}}^n_h X {\bar{\Delta }} W_{n+1}, \nabla (- \Delta ^{-1}_h {\hat{u}}^n_h) \bigr ) \end{aligned}$$

(3.34)

by integration by parts and (3.9). Moreover, it follows from (3.9) that

$$\begin{aligned} - \frac{\tau }{\epsilon } \bigl ( {\hat{f}}^{n+1}, {\hat{u}}^{n+1}_h \bigr )&\le - \frac{\tau }{2 \epsilon } \Vert {\hat{u}}^{n+1}_h \Vert ^4_{L^4({\mathcal {D}})} - \frac{3 \tau }{\epsilon } {\bar{u}}_0^2 \Vert {\hat{u}}^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})} + \frac{C \tau }{\epsilon } \Vert {\hat{u}}^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})} \nonumber \\&\le \frac{\epsilon \tau }{16} \Vert \nabla {\hat{u}}^{n+1}_h \Vert ^2_{L^2({\mathcal {D}})} + \frac{C \tau }{\epsilon ^3} \Vert {\hat{u}}^{n+1}_h \Vert ^2_{-1,h}. \end{aligned}$$

(3.35)

Taking the expectation on both sides of (3.31), summing over $n = 0, 1, \ldots , \ell -1$ with $1 \le \ell \le N$, using (3.32)–(3.35) and the fact that

$$\begin{aligned} {\mathbb {E}}\left[ {\delta ({\hat{u}}^n_h X {\bar{\Delta }} W_{n+1}, \nabla (- \Delta ^{-1}_h {\hat{u}}^n_h))} \right] = 0, \end{aligned}$$

we get

$$\begin{aligned}&\Bigl [ \frac{1}{2} - C \tau \left( \epsilon ^{-3} + \delta ^4 \epsilon ^{-1} \right) \Bigr ] {\mathbb {E}}\left[ {\Vert {\hat{u}}^{\ell }_h \Vert ^2_{-1,h}} \right] + \frac{\epsilon }{16} {\mathbb {E}}\left[ {\sum _{n = 1}^\ell \tau \Vert \nabla {\hat{u}}^{n}_h \Vert ^2_{L^2({\mathcal {D}})}} \right] \nonumber \\&\quad \le C (\delta ^4 \epsilon ^{-1} + \epsilon ^{-3}) \tau \sum _{n=1}^{\ell -1} {\mathbb {E}}\left[ {\Vert {\hat{u}}^n_h \Vert ^2_{-1,h}} \right] + \frac{1}{2} {\mathbb {E}}\left[ {\Vert u^0_h \Vert ^2_{-1,h}} \right] + \frac{\epsilon \tau }{16} {\mathbb {E}}\left[ {\Vert \nabla {\hat{u}}^0_h \Vert ^2_{L^2({\mathcal {D}})}} \right] . \end{aligned}$$

(3.36)

Finally, (3.30) follows from (3.14) and applying the discrete Gronwall inequality to (3.36). The proof is complete. $\square$

4 Strong convergence analysis

The goal of this section is to establish the strong convergence with rates for the fully discrete mixed finite element method defined in the previous section. To the end, we introduce for $n=0,1,2,\ldots ,N$,

$$\begin{aligned}&E^n = u(t_n) - u_h^n := \Theta ^n+\Phi ^n,\\&\Theta ^n := u(t_n) - P_hu(t_n),\qquad \Phi ^n := P_hu(t_n)-u_h^n,\\&G^n = w(t_n) - w_h^n := \Lambda ^n+\Psi ^n,\\&\Lambda ^n := w(t_n) - P_hw(t_n),\qquad \Psi ^n := P_hw(t_n)-w_h^n. \end{aligned}$$

With the help of Hölder continuity estimates derived in Sect. 2, we are able to prove strong convergence with rates for $E^n$, which is stated in the following theorem.

Theorem 3

Under the mesh constraint (3.14), there holds

$$\begin{aligned} \sup _{0 \le n \le N} {\mathbb {E}}\left[ {\Vert E^n \Vert ^2_{-1,h}} \right] + {\mathbb {E}}\left[ {\sum _{n = 1}^N \tau \Vert \nabla E^n \Vert ^2_{L^2({\mathcal {D}})}} \right] \le C(T, \epsilon ^{-1}, \delta ) \left( \tau + h^2 \right) . \end{aligned}$$

(4.1)

Proof

Subtracting (3.1)–(3.2) from (2.1)–(2.2) after substituting 0 by $t_n$, and t by $t_{n+1}$, we get ${\mathbb {P}}$-almost surely

$$\begin{aligned} (E^{n+1},\eta _h)_{}&= (E^n,\eta _h)_{} - \int _{t_n}^{t_{n+1}} (\nabla w(s)-\nabla w_h^{n+1}, \nabla \eta _h)_{} \, ds \nonumber \\&\quad - \frac{\delta ^2}{2} \int _{t_n}^{t_{n+1}} \big ( (\nabla u(s)-\nabla u_h^{n+1}) \cdot X, \nabla \eta _h \cdot X \big )_{} \, ds \nonumber \\&\quad + \delta \int _{t_n}^{t_{n+1}} \big ( (\nabla u(s)-\nabla u_h^n) \cdot X, \eta _h \big )_{} d W_s \quad \forall \, \eta _h \in V_h, \end{aligned}$$

(4.2)

$$\begin{aligned} (G^{n+1}, v_h)_{}&= \epsilon (\nabla E^{n+1}, \nabla v_h)_{} + \frac{1}{\epsilon } \big ( f(u(t_{n+1})) - f^{n+1}, v_h \big )_{} \quad \forall \, v_h \in V_h. \end{aligned}$$

(4.3)

Since $\Phi ^{n+1}(\omega ) \in \mathring{V}_h$, setting $\eta _h = - \Delta ^{-1}_h \Phi ^{n+1} (\omega )$ in (4.2) and $v_h = \tau \Phi ^{n+1}(\omega )$ in (4.3), it follows from the definition of $\Delta ^{-1}_h$ (cf. (3.6)) that

$$\begin{aligned}&(\Phi ^{n+1} - \Phi ^n, \Phi ^{n+1})_{-1,h} \nonumber \\&\quad = (\Theta ^{n+1} - \Theta ^n, \Delta ^{-1}_h \Phi ^{n+1}) - \tau (\Lambda ^{n+1}, \Phi ^{n+1}) \nonumber \\&\qquad - \tau (\Psi ^{n+1}, \Phi ^{n+1}) + \int _{t_n}^{t_{n+1}} (\nabla w(s) - \nabla w(t_{n+1}), \nabla \Delta ^{-1}_h \Phi ^{n+1}) \, ds \nonumber \\&\qquad + \frac{\delta ^2}{2} \int _{t_n}^{t_{n+1}} (\nabla (\Theta ^{n+1} + \Phi ^{n+1}) \cdot X, \nabla \Delta ^{-1}_h \Phi ^{n+1} \cdot X) \, ds \nonumber \\&\qquad + \frac{\delta ^2}{2} \int _{t_n}^{t_{n+1}} ( \nabla (u(s) - u(t_{n+1}) \cdot X ), \nabla \Delta ^{-1}_h \Phi ^{n+1} \cdot X) \, ds \nonumber \\&\quad \quad - \delta \int _{t_n}^{t_{n+1}} (\nabla (\Theta ^n + \Phi ^n) \cdot X, \Delta ^{-1}_h \Phi ^{n+1}) \, d W_s \nonumber \\&\quad \quad - \delta \int _{t_n}^{t_{n+1}} (\nabla (u(s) - u(t_n)) \cdot X, \Delta ^{-1}_h \Phi ^{n+1}) \, d W_s, \end{aligned}$$

(4.4)

$$\begin{aligned}&\tau (\Lambda ^{n+1} + \Psi ^{n+1}, \Phi ^{n+1}) \nonumber \\&\quad = \epsilon \tau (\nabla \Theta ^{n+1}, \nabla \Phi ^{n+1}) + \epsilon \tau (\nabla \Phi ^{n+1}, \nabla \Phi ^{n+1}) \nonumber \\&\quad \quad + \tau \frac{1}{\epsilon } \big ( f(u(t_{n+1})) - f^{n+1}, \Phi ^{n+1} \big ). \end{aligned}$$

(4.5)

Combining (4.4) and (4.5), and taking expectation on both sides, we have

$$\begin{aligned} {\mathbb {E}}&\left[ (\Phi ^{n+1} - \Phi ^n, \Phi ^{n+1})_{-1,h} \right] + \epsilon \tau {\mathbb {E}}\left[ (\nabla \Phi ^{n+1}, \nabla \Phi ^{n+1}) \right] \nonumber \\&\quad = {\mathbb {E}}\left[ (\Theta ^{n+1} - \Theta ^n, \Delta ^{-1}_h \Phi ^{n+1}) \right] \nonumber \\&\quad \quad - \epsilon \tau {\mathbb {E}}\left[ (\nabla \Theta ^{n+1}, \nabla \Phi ^{n+1}) \right] - \tau \frac{1}{\epsilon } {\mathbb {E}}\left[ \big ( f(u(t_{n+1})) - f^{n+1}, \Phi ^{n+1} \big ) \right] \nonumber \\&\qquad + {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} (\nabla w(s) - \nabla w(t_{n+1}), \nabla \Delta ^{-1}_h \Phi ^{n+1}) \, ds \right] \nonumber \\&\qquad + \frac{\delta ^2}{2} {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} (\nabla (\Theta ^{n+1} + \Phi ^{n+1}) \cdot X, \nabla \Delta ^{-1}_h \Phi ^{n+1} \cdot X) \, ds \right] \nonumber \\&\qquad + \frac{\delta ^2}{2} {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} ( \nabla (u(s) - u(t_{n+1})) \cdot X , \nabla \Delta ^{-1}_h \Phi ^{n+1} \cdot X) \, ds \right] \nonumber \\&\qquad - \delta {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} (\nabla (\Theta ^n + \Phi ^n) \cdot X, \Delta ^{-1}_h \Phi ^{n+1}) \, d W_s \right] \nonumber \\&\qquad - \delta {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} (\nabla (u(s) - u(t_n)) \cdot X, \Delta ^{-1}_h \Phi ^{n+1}) \, d W_s \right] \nonumber \\&\quad := \sum _{i = 1}^8 T_i. \end{aligned}$$

(4.6)

The left-hand side of (4.6) can be rewritten as

$$\begin{aligned} {\mathbb {E}}&\left[ (\Phi ^{n+1} - \Phi ^n, \Phi ^{n+1})_{-1,h} \right] + \epsilon \tau {\mathbb {E}}\left[ (\nabla \Phi ^{n+1}, \nabla \Phi ^{n+1}) \right] \nonumber \\&\quad = \frac{1}{2} \left( {\mathbb {E}}\left[ \Vert \Phi ^{n+1} \Vert _{-1,h}^2 \right] - {\mathbb {E}}\left[ \Vert \Phi ^n \Vert _{-1,h}^2 \right] \right) + \frac{1}{2} {\mathbb {E}}\left[ \Vert \Phi ^{n+1} - \Phi ^n \Vert _{-1,h}^2 \right] \nonumber \\&\quad \quad + \epsilon \tau {\mathbb {E}}\left[ \Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] . \end{aligned}$$

(4.7)

Now we estimate the right-hand side of (4.6). Since $P_h$ is the $L^2$-projection operator, we have

$$\begin{aligned} T_1 = 0. \end{aligned}$$

(4.8)

For the second term on the right-hand side of (4.6), we have by (3.3) that

$$\begin{aligned} T_2&\le \frac{\epsilon }{2} \tau {\mathbb {E}}\left[ \Vert \nabla \Theta ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] + \frac{\epsilon }{2} \tau {\mathbb {E}}\left[ \Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] \nonumber \\&\le \frac{\epsilon }{2} \tau h^2 {\mathbb {E}}\left[ |u(t_{n+1})|^2_{H^2({\mathcal {D}})} \right] + \frac{\epsilon }{2} \tau {\mathbb {E}}\left[ \Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] . \end{aligned}$$

(4.9)

For the third term on the right-hand side of (4.6), we observe that

$$\begin{aligned} T_3&= - \tau \frac{1}{\epsilon } {\mathbb {E}}\left[ \big ( f(u(t_{n+1})) - f(P_h(u(t_{n+1}))), \Phi ^{n+1} \big ) \right] \nonumber \\&\quad - \tau \frac{1}{\epsilon } {\mathbb {E}}\left[ \big ( f(P_h(u(t_{n+1}))) - f^{n+1}, \Phi ^{n+1} \big ) \right] . \end{aligned}$$

(4.10)

First of all, we have

$$\begin{aligned} - \tau \frac{1}{\epsilon } {\mathbb {E}}\left[ \big ( f(P_h(u(t_{n+1}))) - f^{n+1}, \Phi ^{n+1} \big ) \right] \le \tau \frac{1}{\epsilon } {\mathbb {E}}\left[ \Vert \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] \end{aligned}$$

(4.11)

by the monotonicity property of the nonlinearity. Secondly, we can estimate the first term on the right-hand side of (4.10) by

$$\begin{aligned}&- \frac{\tau }{\epsilon } {\mathbb {E}}\left[ \bigl ( f(u(t_{n+1}) - f(P_h u(t_{n+1})), \Phi ^{n+1} \bigr ) \right] \nonumber \\&\quad = - \frac{\tau }{\epsilon } {\mathbb {E}}\left[ \bigl ( \Theta ^{n+1} (u(t_{n+1})^2+u(t_{n+1})P_h u(t_{n+1})+P_h u(t_{n+1})^2-1),\Phi ^{n+1} \bigr ) \right] \nonumber \\&\quad \le \frac{\tau }{4 \epsilon } {\mathbb {E}}\Bigl [ \Vert u(t_{n+1})^2+u(t_{n+1})P_h u(t_{n+1})+P_h u(t_{n+1})^2-1\Vert _{L^{\infty }({\mathcal {D}})}^2 \nonumber \\&\qquad \times \Vert \Theta ^{n+1}\Vert ^2_{L^2({\mathcal {D}})} \Bigr ] + {\mathbb {E}}\left[ \Vert \Phi ^{n+1}\Vert ^2_{L^2({\mathcal {D}})} \right] \nonumber \\&\quad \le \frac{C \tau }{4 \epsilon } \Bigl ( {\mathbb {E}}\left[ \Vert P_h u(t_{n+1})\Vert _{L^\infty ({\mathcal {D}})}^{6} +\Vert u(t_{n+1})\Vert _{L^\infty ({\mathcal {D}})}^{6}+|D|^{3} \right] \Bigr )^{\frac{2}{3}} \nonumber \\&\qquad \times \Bigl ( {\mathbb {E}}\left[ \Vert \Theta ^{n+1}\Vert ^{6}_{L^2({\mathcal {D}})} \right] \Bigr )^{\frac{1}{3}} + \frac{\tau }{\epsilon } {\mathbb {E}}\left[ \Vert \Phi ^{n+1}\Vert ^2_{L^2({\mathcal {D}})} \right] \nonumber \\&\quad \le \frac{C \tau }{4 \epsilon } \left( {\mathbb {E}}\left[ \Vert \Theta ^{n+1}\Vert ^{6}_{L^2({\mathcal {D}})} \right] \right) ^{\frac{1}{3}} + \frac{\tau }{\epsilon } {\mathbb {E}}\left[ \Vert \Phi ^{n+1}\Vert ^2_{L^2({\mathcal {D}})} \right] , \end{aligned}$$

(4.12)

where we had applied (3.4). Combining (4.10)–(4.12), (3.3) and (3.9), we obtain

$$\begin{aligned} T_3&\le \frac{C\tau }{\epsilon ^3} {\mathbb {E}}\left[ \Vert \Phi ^{n+1}\Vert _{-1,h}^2 \right] + \frac{\epsilon \tau }{4} {\mathbb {E}}\left[ \Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] + \frac{C \tau }{\epsilon } \left( {\mathbb {E}}\left[ \Vert \Theta ^{n+1}\Vert ^{6}_{L^2({\mathcal {D}})} \right] \right) ^{\frac{1}{3}} \nonumber \\&\le \frac{C\tau }{\epsilon ^3} {\mathbb {E}}\left[ \Vert \Phi ^{n+1}\Vert _{-1,h}^2 \right] + \frac{\epsilon \tau }{4} {\mathbb {E}}\left[ \Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \right] \nonumber \\&\quad + \frac{C \tau h^4}{\epsilon } \left( {\mathbb {E}}\left[ | u(t_{n+1}) |_{H^2({\mathcal {D}})}^{6} \right] \right) ^{\frac{1}{3}}. \end{aligned}$$

(4.13)

For the fourth term on the right-hand side of (4.6), we have

$$\begin{aligned} T_4&\le {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} 2 \Vert \nabla w(s) - \nabla w(t_{n+1}) \Vert ^2_{L^2({\mathcal {D}})} + \frac{1}{8} \Vert \nabla \Delta ^{-1}_h \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})} \, ds \right] \nonumber \\&\le C \tau ^2 + \frac{1}{8} \tau {\mathbb {E}}\left[ \Vert \Phi ^{n+1} \Vert _{-1,h}^2 \right] \end{aligned}$$

(4.14)

by the Hölder continuity for $\nabla w$ (cf. Lemma 3). Similarly, we have

$$\begin{aligned} T_6&\le C \delta ^2 \tau ^2 + \frac{1}{8} \tau {\mathbb {E}}\left[ {\Vert \Phi ^{n+1} \Vert _{-1,h}^2} \right] \end{aligned}$$

(4.15)

by the Hölder continuity for $\nabla u$ (cf. Lemma 2).

For the fifth term on the right-hand side of (4.6), we have

$$\begin{aligned} T_5&\le C \delta ^4 \tau h^2 + \frac{\epsilon \tau }{8} {\mathbb {E}}\left[ {\Vert \nabla \Phi ^{n+1} \Vert ^2_{L^2({\mathcal {D}})}} \right] + \left( \frac{1}{8} + \frac{C \delta ^4}{\epsilon } \right) \tau {\mathbb {E}}\left[ {\Vert \Phi ^{n+1} \Vert _{-1,h}^2} \right] . \end{aligned}$$

(4.16)

For the seventh term on the right-hand side of (4.6), we have by the integration by parts, the martingale property, the Itô isometry and (3.9) that

$$\begin{aligned} T_7&= - \delta {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} \big ( (\Theta ^n + \Phi ^n) X, \nabla \Delta ^{-1}_h (\Phi ^{n+1} - \Phi ^n)\big ) \, d W_s \right] \nonumber \\&\le C \delta ^2 \tau h^4 {\mathbb {E}}\left[ {\Vert u(t_n) \Vert ^2_{H^2({\mathcal {D}})}} \right] + C \delta ^2 \tau {\mathbb {E}}\left[ {\Vert \Phi ^n X \Vert ^2_{L^2({\mathcal {D}})}} \right] \nonumber \\&\quad + \frac{1}{4} {\mathbb {E}}\left[ {\Vert \Phi ^{n+1} - \Phi ^n \Vert _{-1,h}^2} \right] \nonumber \\&\le C \delta ^2 \tau h^4 {\mathbb {E}}\left[ {\Vert u(t_n) \Vert ^2_{H^2({\mathcal {D}})}} \right] + \frac{1}{4} {\mathbb {E}}\left[ {\Vert \Phi ^{n+1} - \Phi ^n \Vert _{-1,h}^2} \right] \nonumber \\&\quad + \frac{\epsilon \tau }{16} {\mathbb {E}}\left[ {\Vert \nabla \Phi ^n \Vert ^2_{L^2({\mathcal {D}})}} \right] + \frac{C \delta ^4 \tau }{\epsilon } {\mathbb {E}}\left[ {\Vert \Phi ^n \Vert ^2_{-1,h}} \right] .5 \end{aligned}$$

(4.17)

Similarly, we have

$$\begin{aligned} T_8= & {} - \delta {\mathbb {E}}\left[ \int _{t_n}^{t_{n+1}} \big ( \nabla (u(s) - u(t_n)) \cdot X, \Delta ^{-1}_h (\Phi ^{n+1} - \Phi ^n) \big ) \, d W_s \right] \nonumber \\\le & {} C \delta ^2 \tau ^2 + \frac{1}{4} {\mathbb {E}}\left[ {\Vert \Phi ^{n+1} - \Phi ^n \Vert _{-1,h}^2} \right] , \end{aligned}$$

(4.18)

where we have used Lemma 2 and the following Poincaré’s inequality:

$$\begin{aligned} \Vert \Delta ^{-1}_h (\Phi ^{n+1} - \Phi ^n) \big ) \Vert ^2_{L^2({\mathcal {D}})} \le C \Vert \nabla \Delta ^{-1}_h (\Phi ^{n+1} - \Phi ^n) \big ) \Vert ^2_{L^2({\mathcal {D}})} = C \Vert \Phi ^{n+1} - \Phi ^n \Vert ^2_{-1,h}. \end{aligned}$$

Combining (4.6)–(4.9) and (4.13)–(4.18), summing over $n = 0, 1, \ldots , \ell -1$ with $1 \le \ell \le N$, we have

$$\begin{aligned}&\left( \frac{1}{8} - \frac{C \tau }{\epsilon ^3} - \frac{C \delta ^4 \tau }{\epsilon } \right) {\mathbb {E}}\left[ {\Vert \Phi ^\ell \Vert ^2_{-1,h}} \right] + \frac{\epsilon }{16} {\mathbb {E}}\left[ {\tau \sum _{n = 1}^\ell \Vert \nabla \Phi ^n \Vert ^2_{L^2({\mathcal {D}})}} \right] \nonumber \\&\quad \le \frac{1}{2} {\mathbb {E}}\left[ {\Vert \Phi ^0 \Vert ^2_{-1,h}} \right] + \frac{\epsilon }{16} \tau {\mathbb {E}}\left[ {\Vert \nabla \Phi ^0 \Vert ^2_{L^2({\mathcal {D}})}} \right] \nonumber \\&\qquad + C(\epsilon ^{-1}, \delta ) T (\tau + h^2 + h^4) \nonumber \\&\qquad + C \left( 1 + \frac{1}{\epsilon ^3} + \frac{\delta ^4}{\epsilon } \right) \tau \sum _{n=1}^{\ell -1} {\mathbb {E}}\left[ {\Vert \Phi ^n \Vert ^2_{-1,h}} \right] . \end{aligned}$$

(4.19)

Therefore, under the mesh constraint (3.14), we have by the discrete Gronwall inequality that

$$\begin{aligned}&{\mathbb {E}}\left[ {\Vert \Phi ^\ell \Vert ^2_{-1,h}} \right] + {\mathbb {E}}\left[ {\tau \sum _{n = 1}^\ell \Vert \nabla \Phi ^n \Vert ^2_{L^2({\mathcal {D}})}} \right] \nonumber \\&\quad \le C \Bigl ( {\mathbb {E}}\left[ {\Vert \Phi ^0 \Vert ^2_{-1,h}} \right] + \frac{\epsilon }{16} \tau {\mathbb {E}}\left[ {\Vert \nabla \Phi ^0 \Vert ^2_{L^2({\mathcal {D}})}} \right] + \tau + h^2 \Bigr ) e^{CT(1 + \epsilon ^{-3} + \delta ^4 \epsilon ^{-1})}. \end{aligned}$$

(4.20)

Finally, the estimate (4.1) follows from (4.20), (3.14), the triangle inequality, and the fact that $\Phi ^0 = 0$. The proof is complete. $\square$

Remark 2

The error estimates in Theorem 3 is sub-optimal with respect to h in the $\Vert \cdot \Vert _{-1,h}$-seminorm, this is essentially due to the existence of the gradient-type noise (see the estimates of $T_5$ and $T_7$ in the proof), hence, the estimate is sharp in general. Numerical results in Sect. 5 indeed confirm the sub-optimal convergence whenever the noise is relatively large. However, the error is optimal with respect to h in the $H^1$-seminorm which is also confirmed by the numerical experiments.

Remark 3

Because the discrete Gronwall inequality was employed near the end of the proof, the error estimate in Theorem 3 depends on $\frac{1}{\epsilon }$ exponentially. We note that a polynomial order dependence on $\frac{1}{\epsilon }$ of the errors was achieved in the deterministic case [13,14,15] by using a PDE spectrum estimate result, however, such a spectrum estimate is yet proved to hold in the stochastic setting.

5 Numerical experiments

In this section, we report several numerical examples to check the performance of the proposed fully discrete mixed finite element method and numerically study the impact of noise on the evolution of the solution and the stochastic Hele-Shaw flow.

We consider the SPDE (1.6)–(1.9) on the square domain ${\mathcal {D}}= [-1, 1]^2$ and choose

$$\begin{aligned} X = \varphi (r) [x_2, -x_1]^T, \qquad \varphi (r) = {\left\{ \begin{array}{ll} e^{-\frac{0.001}{0.64 - r^2}}, &{} \text {if } \ r < 0.8, \\ 0, &{} \text {if } \ r \ge 0.8, \end{array}\right. } \end{aligned}$$

where $r = |x|$. It is clear that $\text {div} X = 0$ in ${\mathcal {D}}$ and $X \cdot n = 0$ on $\partial {\mathcal {D}}$.

Let $N_h = \text {dim} V_h$ and $\{ \psi _i \}_{i=1}^{N_h}$ be the nodal basis of $V_h$. Denote by $\mathbf{u}^{n+1}$ (resp., $\mathbf{w}^{n+1}$) the coefficient vector of the discrete solution $u^{n+1}_h = \sum _{i = 0}^{N_h} u^{n+1}_i \psi _i$ (resp., $w^{n+1}_h = \sum _{i = 0}^{N_h} w^{n+1}_i \psi _i$) at time $t_{n+1} = (n+1) \tau$, $n=0,\ldots , N-1$. Then (3.1)–(3.2) are equivalent to

$$\begin{aligned} \left[ {\mathbf{M}} + \tau \frac{\delta ^2}{2} {\mathbf{A_X}} \right] {\mathbf{u}^{n+1}} + \tau \mathbf{A} \mathbf{w}^{n+1}&= \mathbf{M} \mathbf{u}^{n} + \delta {\bar{\Delta }} {\mathbf{W}_{n+1}} \mathbf{C_X} \mathbf{u}^n, \end{aligned}$$

(5.1)

$$\begin{aligned} \mathbf{M} \mathbf{w}^{n+1} - \epsilon \mathbf{A} \mathbf{u}^{n+1}&= \frac{1}{\epsilon } \mathbf{N} (\mathbf{u}^{n+1}), \end{aligned}$$

(5.2)

where $\mathbf{M}$ and $\mathbf{A}$ denote respectively the mass and stiffness matrices, $\mathbf{A}_{\mathbf{X}}$ is the weighted stiffness matrix with $(\mathbf{A_X} )_{ij} = (\nabla \psi _j \cdot X, \nabla \psi _i \cdot X)$, ${\mathbf{N}} ({\mathbf{u}^{n+1}})$ is the nonlinear contribution corresponding to the nonlinear term $(f^{n+1}, v_h)$, $({\mathbf{C}_{\mathbf{X}}})_{ij} = (\nabla \psi _j\cdot X, \psi _i)$ and $\mathbf{W}$ is the discrete Brownian motion with increments ${\bar{\Delta }} {\mathbf{W}_{n+1}} = {\mathbf{W}_{n+1}} - {\mathbf{W}_n}$.

In all our tests, we use the Brownian motion generated by using step size $\tau _{\text {ref}} = 5 \times 10^{-5}$ and compute at least $M = 1000$ Monte Carlo realizations. The first test concerns a smooth initial function, aiming to verify the rates of convergence of the proposed method with respect to the temporal mesh size $\tau$ and the spatial mesh size h. The second and third tests are designed to investigate the influence of the noise intensity $\delta$ and the parameter $\epsilon$ on the stochastic evolutions for two different non-smooth initial functions.

5.1 Test 1

In this test we check the rates of convergence of the method (3.1)–(3.2) with a smooth initial function

$$\begin{aligned} u_0(x) = x_1^2 (1-x_1)^2 x_2^2 (1-x_2^2). \end{aligned}$$

We examine the errors $\sup _{0 \le n \le N} {\mathbb {E}}\left[ {\Vert E^n \Vert ^2_{L^2({\mathcal {D}})}} \right]$ and ${\mathbb {E}}\left[ {\sum _{n = 1}^N \tau \Vert \nabla E^n \Vert ^2_{L^2({\mathcal {D}})}} \right]$, where $E^n = u(t_n) - u^n_h$. Since the exact solution is unknown, we approximate the errors by

$$\begin{aligned}&{\mathbb {E}}\left[ {\Vert E^n \Vert ^2_{L^2({\mathcal {D}})}} \right] \approx \frac{1}{M} \sum _{n=1}^M \Vert u^n_{h} - u^n_{\text {ref}} \Vert ^2_{L^2({\mathcal {D}})}, \\&{\mathbb {E}}\left[ {\Vert \nabla E^n \Vert ^2_{L^2({\mathcal {D}})}} \right] \approx \frac{1}{M} \sum _{n=1}^M \Vert \nabla (u^n_{h} - u^n_{\text {ref}}) \Vert ^2_{L^2({\mathcal {D}})}. \end{aligned}$$

Here $u^n_{\text {ref}}$ refers to a reference solution, which will be specified later. For simplicity, we use $L^{\infty }(L^2)$ (resp., $L^2(H^1)$) to denote the norm (resp., seminorm) corresponding to the square root of the approximating errors $\sup _{0 \le n \le N} {\mathbb {E}}\left[ {\Vert E^n \Vert ^2_{L^2({\mathcal {D}})}} \right]$ (resp., ${\mathbb {E}}\left[ {\sum _{n = 1}^N \tau \Vert \nabla E^n \Vert ^2_{L^2({\mathcal {D}})}} \right]$).

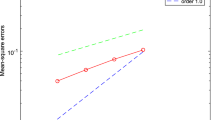
In Table 1, we first examine the convergence rates in the time discretization by varying $\tau$ with the fixed parameters $\epsilon = 0.1$, $\delta = 5$ and $h = 2/2^6$. For each $\tau$, the reference solution $u^n_{\text {ref}}$ is chosen to be the numerical solution with the time step size $\tau /2$ (i.e., we approximate the error by comparing the numerical solutions in two consecutive time discretizations). We observe the half order convergence rate for the $L^2(H^1)$-error as predicted in Theorem 3. Note that the $L^{\infty }(L^2)$ error estimate is not available in Theorem 3, however it still provides us useful information about the accuracy of the numerical method.

Table 1 Test 1: Temporal errors and convergence rates with $\epsilon = 0.1$, $\delta = 5$

Next we investigate convergence in the space discretization by varying h with the fixed parameters $\epsilon = 0.1$, $\delta = 25$ and $\tau = 5 \times 10^{-5}$. For each h, the reference solution $u^n_{\text {ref}}$ is chosen to be the numerical solution with the space size h/2. Since $\delta$ is relatively large, we compute $M = 10^4$ realizations. From Table 2, we see that the $L^2(H^1)$-error converges with order 1 which is consistent with the theoretical estimate of Theorem 3. Also, the $L^{\infty }(L^2)$-error converges with order less than 2, indicating a sub-optimal convergence in the lower order norm as predicted by Theorem 3.

Table 2 Test 1: Spatial errors and convergence rates with $\epsilon = 0.1$, $\delta = 25$

5.2 Test 2

In this test, we take the initial function to be

$$\begin{aligned} u_0(x) = \tanh \left( \frac{d_0(x)}{\sqrt{2} \epsilon } \right) , \end{aligned}$$

where $d_0(x)$ represents the signed distance function to the ellipse

$$\begin{aligned} \frac{x_1^2}{0.36} + \frac{x_2^2}{0.04} = 1. \end{aligned}$$

First, we investigate the evolution of the zero-level set with respect to the noise intensity $\delta$ with fixed $\epsilon = 0.01$. Figure 1 plots snapshots at several time points of the zero-level set of ${\bar{u}}_h$ for $\delta = 1, 5, 10$, where

$$\begin{aligned} {\bar{u}}_h = \frac{1}{M} \sum _{i=1}^{M} u_h (\omega _i). \end{aligned}$$

We observe that when the noise is relatively small ($\delta = 1$), the zero-level set is close to the deterministic interface ($\delta = 0$). However, for relatively large noises ($\delta = 5, 10$), the zero-level sets rotate and evolve faster.

Fig. 1

Test 2: Snapshots of the zero-level set of ${\bar{u}}_h$ at several time points with $\delta =1, 5, 10$ and $\epsilon = 0.01$

Next, we fix $\delta = 1$ and study the influence of the parameter $\epsilon$ on the evolution of the numerical interfaces. In Fig. 2, snapshots at four fixed time points of the zero-level set of ${\bar{u}}_h$ are depicted for three different $\epsilon = 0.01, 0.015, 0.04$. Numerical results suggest the convergence of the numerical interface to the stochastic Hele-Shaw flow as $\epsilon \rightarrow 0$ at each of four time points. In addition, the numerical interface evolves faster in time for larger $\epsilon$.

Fig. 2

Test 2: Snapshots of the zero-level set of ${\bar{u}}_h$ at several time points with $\epsilon =0.01, 0.015, 0.04$ and $\delta = 1$

Notice that in Figs. 1 and 2, we only plot the evolutions on the subdomain $[-0.6,0.6]^2$ for a better resolution.

In Fig. 3, we plot the change of the expected value of the discrete energy

$$\begin{aligned} {\mathbb {E}}\left[ {J(u^n_h)} \right] \approx \frac{1}{M} \sum _{i=1}^m J(u^n_h(\omega _i)) \end{aligned}$$

in time with fixed $\epsilon = 0.01$. It indicates that the decay property still holds for $\delta = 1, 5, 10$.

Fig. 3

Test 2: Decay of the expectation of numerical energy with $\epsilon = 0.01$

5.3 Test 3

In this test, we consider the case with

$$\begin{aligned} u_0(x) = \tanh \left( \frac{d_0(x)}{\sqrt{2} \epsilon } \right) , \end{aligned}$$

where $d_0(x) = \min \{d_1(x), d_2(x)\}$, and $d_1(x)$ and $d_2(x)$ denotes respectively the signed distance function to the ellipses

$$\begin{aligned} \frac{(x_1+0.2)^2}{0.15^2} + \frac{x_2^2}{0.45^2} = 1 \quad \text {and} \quad \frac{(x_1-0.2)^2}{0.15^2} + \frac{x_2^2}{0.45^2} = 1. \end{aligned}$$

In Fig. 4, we depict snapshots at several time points of the zero-level set of ${\bar{u}}_h$ for $\delta = 1, 5, 10$ with fixed parameter $\epsilon = 0.01$. For all cases, the two separated zero-level sets eventually merge and evolve to a circular shape. For larger noise intensity ($\delta = 5, 10$), the two interfaces merge faster and develop two concentric interfaces where the outer interface evolves to a circular shape and the inner interface shrinks and eventually vanishes.

Fig. 4

Test 3: Snapshots of the zero-level set of ${\bar{u}}_h$ at several time points with $\delta =1, 5, 10$ and $\epsilon = 0.01$

Next, we plot a few snapshots of the zero-level set of ${\bar{u}}_h$ for $\epsilon = 0.01, 0.015, 0.04$ with fixed $\delta = 1$ in Fig. 5. Again, the numerical interface evolves faster in time for larger $\epsilon$, and the numerical interfaces stay close for $\epsilon = 0.01$ and $\epsilon = 0.015$.

Fig. 5

Test 3: Snapshots of the zero-level set of ${\bar{u}}_h$ at several time points with $\epsilon =0.01, 0.015, 0.04$ and $\delta = 1$

The decay of the expected value of the discrete energy is shown in Fig. 6, where we consider three noise intensity levels $\delta = 1, 5, 10$ with fixed $\epsilon = 0.01$.

Fig. 6

Test 3: Decay of the expectation of numerical energy with $\epsilon = 0.01$

6 Conclusion

In this paper we studied a stochastic Cahn–Hilliard equation with gradient-type multiplicative noise, which is motivated by and proposed as a phase field model for the stochastically perturbed Hele-Shaw flow. We proposed a fully discrete mixed finite element method for solving the stochastic Cahn–Hilliard equation, and established its well-posedness and the $\Vert \cdot \Vert _{-1,h}$-norm stability of the numerical solution. Strong convergence with optimal rates were also proved with the help of various Hölder continuity estimates in time for the strong solution of the stochastic Cahn-Hillard equation.

Similar to [16], the energy-stability of the numerical solution is expected although a rigorous proof is yet be obtained. Such a stability is observed from our numerical experiments. It would be interesting to consider more general cases such as the diffusion operator depending on $\nabla u$ nonlinearly and the noise intensity $\delta$ depending on $\epsilon$ polynomially. It is also possible to extend the work of this paper to other types of fully discrete numerical methods (such as DG methods) for the stochastic Cahn–Hilliard equation. Furthermore, a performance comparison between different numerical methods should be interesting, which we intend to study in a future work.