A Characteristic-Featured Shock Wave Indicator for Conservation Laws Based on Training an Artificial Neuron

Abstract

In this work, we use exact solutions of one-dimensional Burgers equation to train an artificial neuron as a shock wave detector. The expression of the artificial neuron detector is then modified into a practical form to reflect admissible jump of eigenvalues. We show the working mechanism of the practical form is consistent with compressing or intersecting of characteristic curves. In addition, we prove there is indeed a discontinuity inside the cell detected by the practical form, and smooth extrema and large gradient regions are never marked. As a result, we apply the practical form to numerical schemes as a shock wave indicator with its easy extension to multi-dimensional conservation laws. Numerical results are present to demonstrate the robustness of the present indicator under Runge–Kutta Discontinuous Galerkin framework, its performance is generally compared to TVB-based indicators more efficiently and accurately. To treat the initial inadmissible jumps, including linear contact discontinuities and those evolving into rarefaction waves, a preliminary strategy of combining a traditional indicator in the beginning with the present indicator is suggested. We believe the present indicator can be applied to unstructured mesh in the future.

1 Introduction

At present, high order high resolution schemes, such as Discontinuous Galerkin (DG) [3,4,5,6,7], have been widely applied in numerical simulation of hyperbolic conservation laws. Since even under smooth initial conditions, solutions to conservation laws can develop discontinuities in a finite time [8], spurious oscillations occur in the regions of discontinuities when such high order schemes are applied. There are two steps in handling spurious oscillations. The first one is to detect cells where the solution loses regularity (troubled-cells), the other is to use correction techniques to eliminate spurious oscillations for the troubled-cells. There are several correction techniques in literature, such as artificial limiting [5, 6, 36], reconstruction techniques [13, 24, 26, 27, 31] and artificial viscosity [14, 15, 34]. Those correction techniques often lead to inefficiencies of numerical simulation and even deterioration of accuracy. In other word, the accuracy and regularity of numerical solution depend largely on effectiveness of the troubled-cell indicator applied. For example, the popular DG methods usually use minmod function [12] to detect troubled-cells, and simultaneously apply it as a limiter to eliminate oscillations, that is $\widetilde{u}_{i}^{(mod)}=minmod(\widetilde{u}_{i},\Delta _{+}u_{i}^{(0)},\Delta _{-}u_{i}^{(0)})=$

$$\begin{aligned} \left\{ \begin{array}{lr} s\cdot min\big \{ \widetilde{u}_{i},\Delta _{+}u_{i}^{(0)},\Delta _{-}u_{i}^{(0)} \big \} \quad if\; sign\big (\widetilde{u}_{i}\big )=sign\big (\Delta _{+}u_{i}^{(0)}\big )=sign\big (\Delta _{-}u_{i}^{(0)}\big )=s &{}\\ 0 \qquad otherwise, \end{array} \right. \end{aligned}$$

where $u_{i}^{(0)}$ is the $0^{th}$ moment degree of freedom(dof), and $\widetilde{u}_{i}$ is the interface collection of higher moment dofs. As one can observe, cells near extrema are indicated as troubled-cells with a minmod limiter. This leads to decreasing of scheme accuracy. In order to preserve high order of the schemes, Total Variation Bounded (TVB) limiter [6] are more popular, that is $\widetilde{u}_{i}^{(mod)}=$$\left\{ \begin{array}{ll} \widetilde{u}_{i} &{}\quad if\; |\widetilde{u}_{i}|\le M h^{2} \\ minmod(\widetilde{u}_{i},\Delta _{+}u_{i}^{(0)},\Delta _{-}u_{i}^{(0)}) &{} \quad otherwise \end{array} \right.$ However, the parameter M was found to depend heavily on problems and has a considerable impact on numerical solutions. In [25], Qiu and Shu shared performance of various TVB limiters under different selection of M. To improve efficiency, several procedure such as Weighted Essential Non-Oscillating (WENO) based reconstruction [27], KXRCF shock indicator [16] were proposed to improve the effectiveness of troubled-cell indication. Those indicators or procedure mentioned above mainly detect troubled-cells from aspects of numerical oscillations.

Recently, Ray and Hesthaven proposed artificial neural networks to implement troubled-cell indication under RKDG frameworks [28, 29]. They obtained a multi-layer perceptron (MLP) troubled-cell indicator. Numerical results presented in their paper demonstrated the MLP indicator performs generally better than TVB-based indicator. In this work, we employ exact solutions of the Burgers equation to train a concise artificial neuron (AN) with only one linear hidden layer for shock wave detecting, fortunately obtain a convergent AN detector, and it can be modified into a practical form to reflect admissible jump of eigenvalues. The advantage of the practical form is threefold: (a) it has a concise expression involving only cell-averages; (b) it is explicable, and can theoretically guarantee the only detection of discontinuities caused by characteristic curves compressing or intersecting; (c) it can handily be extended to multi-dimensional conservation laws.

The rest of the paper is structured as follows. In Sect. 2, we briefly summarize the theory of characteristic curves for one-dimensional scalar and system conservation laws. In Sect. 3, we illustrate the complete training process of the shock detector and give the expression of the trained AN detector. In Sect. 4, we modify the AN detector into a practical form and use the practical form to analyze its working mechanism. The practical form is then applied as a shock wave indicator and extended to system conservation laws. RKDG frameworks are briefly introduced in Sect. 5 and we show how TVB-based indicators and present indicator detect troubled-cells under RKDG frameworks. Several numerical results are presented in Sect. 6 to demonstrate the capability of the present shock wave indicator, as compared to TVB indicators. We make a few concluding remarks in Sect. 7.

2 Preliminaries of Hyperbolic Conservation Laws

2.1 One-Dimensional Scalar Conservation Laws

The one-dimensional scalar conservation law with an initial condition is given by

$$\begin{aligned} \left\{ \begin{array}{lr} \frac{\partial u}{\partial t}+\frac{\partial f(u)}{\partial x}=0 &{}\\ &{}\\ u(x,0)=u_{0}(x). \end{array} \right. \end{aligned}$$

(2.1)

For Eq. (2.1), we summarize the following useful conclusions without proof. Please refer to [2, 35] for more details.

Lemma 2.1

Assuming the initial value function $u(x,0)=u_0 (x)$ is smooth, and denoting $\lambda (u)=f'(u)$, then we have following properties for Eq. (2.1):

• (1) The characteristic curves in Eq. (2.1) are straight lines with the form of $x=x_0+\lambda (u_0 (x_0))t$, and the slope of characteristic curve is $\lambda (u)=f'(u)$. The solution remains unchanged along each characteristic curve.

• (2) The solution can be obtained by solving $``u''$ in the following implicit function $u=u_0 (x-\lambda (u)t)$.

• (3) The solution can evolve into discontinuities even under a smooth initial condition due to the intersection of characteristic lines.

• (4) Across the discontinuity, the solution satisfies the Rankine–Hugoniot jump relation $s[u]=[f]$, where $s=\frac{dx_{s}(t)}{dt}$ represents the speed of the discontinuity and [u] represents the jump value of variable u when across the discontinuity.

It is necessary to deal with non-smooth initial conditions. For the Riemann problem of Eq. (2.1), we list some properties of solution without proof.

Lemma 2.2

The Riemann problem for one-dimensional scalar conservation laws is given as follows,

$$\begin{aligned} \left\{ \begin{array}{lr} \frac{\partial u}{\partial t}+\frac{\partial f(u)}{\partial x}=0 &{}\\ u(x,0)=\left\{ \begin{array}{lr} u_{l} \qquad if \; x<0 &{}\\ u_{r} \qquad if \; x\ge 0. \end{array} \right. \end{array} \right. \end{aligned}$$

(2.2)

We can conclude that, if f(u) is convex,

• (1) If $\lambda (u_{l})>\lambda (u_{r})$, characteristic curves of two constant regions intersect, and the solution evolves into a discontinuity.

• (2) If $\lambda (u_{l})<\lambda (u_{r})$, characteristic curves of two constant regions diverge, and the solution evolves into a centered rarefaction wave connecting two constant regions.

2.2 One-Dimensional System Conservation Laws

One-dimensional system conservation laws with an initial condition are given by

$$\begin{aligned} \left\{ \begin{array}{lr} \frac{\partial \mathbf{U} }{\partial t}+\frac{\partial \mathbf{F} (\mathbf{U} )}{\partial x}=0 &{}\\ &{}\\ \mathbf{U} (x,0)=\mathbf{U} _{0}(x). \end{array} \right. \end{aligned}$$

(2.3)

Assuming $\mathbf{U} \in \mathbb {R}^{m}$, denoting $\mathbf{A} (\mathbf{U} )=\frac{\partial \mathbf{F} }{\partial \mathbf{U} }$, system (2.3) is called hyperbolic if matrix $\mathbf{A} (\mathbf{U} )$ can be diagonalized, $\mathbf{A} =\mathbf{R} \Lambda \mathbf{R} ^{-1}$ with real eigenvalues, here, $\Lambda = diag(\lambda _{1},\lambda _{2},...,\lambda _{m})$ is the eigenvalue matrix, and $\mathbf{R} =(\mathbf{R} _{1},\mathbf{R} _{2},...,\mathbf{R} _{m})$ is the corresponding right eigenvector matrix. Each eigenvalue $\lambda _{i}$ of $\mathbf{A} (\mathbf{U} )$ defines a characteristic field $\lambda _{i}$-field, if $\nabla \lambda _{i}(\mathbf{U} )\cdot \mathbf{R} _{i}(\mathbf{U} ) \ne 0$, the $\lambda _{i}$-field is genuinely nonlinear; if $\nabla \lambda _{i}(\mathbf{U} ) \cdot \mathbf{R} _{i}(\mathbf{U} ) = 0$, the $\lambda _{i}$-field is linearly degenerated.

We summarize some useful conclusions without proof. More details can be found in [35].

Lemma 2.3

The solution, $\mathbf{U} (x,t)$ , holds following properties:

• (1) The i-characteristic curves in system (2.3) are locally straight lines with the form of $x=x_{0}+\lambda _{i}(\mathbf{U} _{0}(x_{0}))\cdot t$, and the slope of i-characteristic curve is the i-eigenvalue $\lambda _{i}$.

• (2) The solution can evolve into discontinuities even under a smooth initial condition due to the intersection of a certain i-characteristic curves.

• (3) Across the discontinuity, the solution $\mathbf{U}$ satisfies the Rankine-Hugoniot jump relation, $s[\mathbf{U} ]=[\mathbf{F} ]$, where $s= \frac{dx_{s}(t)}{dt}$ represents the speed of the discontinuity and $[\mathbf{U} ]$ represents the jump value of $\mathbf{U}$ across the discontinuity.

In this work, we pay attention to the Euler equation, the Riemann problem for the Euler equation is given as follows,

$$\begin{aligned} \left\{ \begin{array}{lr} \frac{\partial }{\partial t} \begin{bmatrix} \rho \\ \rho u \\ E \end{bmatrix} +\frac{\partial }{\partial x} \begin{bmatrix} \rho u \\ p+ \rho u^{2} \\ (E+p) \rho \end{bmatrix} =0 &{}\\ &{}\\ (\rho _{0},u_{0},p_{0})^{T}(x)= \left\{ \begin{array}{lr} (\rho _{l},u_{l},p_{l})^{T} \qquad if \; x<0 &{}\\ (\rho _{r},u_{r},p_{r})^{T} \qquad if \; x\ge 0, \end{array} \right. \end{array} \right. \end{aligned}$$

(2.4)

where $\rho , u, p$ represent the fluid density, velocity, and pressure, respectively. The quantity E is the total energy per unit volume, which is given as $E=\rho (e+\frac{u^{2}}{2})$, where e is the specific internal energy given by a caloric equation of state, $e=e(\rho , p)$. We choose the equation of state for ideal gas given by $e=\frac{p}{(\gamma -1)\rho }$, with $\gamma =C_{p}/C_{V}$ denoting the ratio of specific heats. We set $\gamma =1.4$ for all the test cases in this work.

Again we summarize some useful conclusions for system (2.4) as follows.

Lemma 2.4

The solution holds the following properties:

• (1) Based on properties in Lemma 2.3, the solution can be divided into 4 constant regions by 3 $\lambda _{i}$-characteristic fields as shown in Fig. 1.

  • $\lambda _{1}=u-a$, $\lambda _{1}$-field is genuinely nonlinear, area I and area II are separated by 1-elementary wave (shock wave or centered rarefaction wave), where u is the fluid velocity and $a=\sqrt{\frac{\gamma p}{\rho }}$ represents the sound speed.

  • $\lambda _{2}=u$, $\lambda _{2}$-field is linearly degenerated, area II and area III are separated by 2-contact discontinuity, the pressure p and velocity u keep unchanged across the $\lambda _{2}$-field, the density $\rho$ allows a jump across the $\lambda _{2}$-field.

  • $\lambda _{3}=u+a$, $\lambda _{3}$-field is genuinely nonlinear, area III and area IV are separated by 3-elementary wave (shock wave or centered rarefaction wave).

• (2) According to (1) and Lemma 2.3(2), we can give a criterion of discontinuity for system (2.4) as follows,

  $$\begin{aligned}&u_{l}-a_{l}>u_{r}-a_{r}, \end{aligned}$$

  (2.5a)
  $$\begin{aligned}&u_{l}+a_{l}>u_{r}+a_{r}. \end{aligned}$$

  (2.5b)

Fig. 1

In the 1-D Euler equations, the space is devided into 4 constant regions by 3 characteristic fields

The inequality Eq. (2.5a) indicates the solution includes either a 1-shock wave or a 2-contact discontinuity or both. The inequality Eq. (2.5b) indicates the solution consists of either a 3-shock wave or a 2-contact discontinuity or both.

Remark Although the indicator to be developed is for shock wave detecting in this work, the Lemma 2.4(2) implies that the shock wave indicator is also capable of detecting contact discontinuities as shown in Sect. 4.

In Sect. 4, we will analyze mechanism of the shock wave detector is consistent with compressing or intersecting of characteristic curves mentioned in this section.

3 An Artificial Neuron for Shock Wave Indicating

In this section, our target is to explore an approximation of unknown function which can reflect the characteristics of shock wave discontinuities. Since we have no prior information about the intrinsic features of the indicator, an Artificial Neural Network (ANN) [11] becomes a suitable method to learn these undiscovered features. Generally, an ANN is designed to imitate the learning procedure of the complex biological network. With the rapid development of computing technology, ANNs have gradually evolved into more matured deep neural networks (DNNs) [30]. Except for an input layer and an output layer, the structure of an ANN consists of at least one hidden layer. The nodes of ANN are fully connected linearly, which means that each node in one layer connects with a certain weight to every node in the neighboring layer. For approximating a complex nonlinear function, the neurons adopt nonlinear activation function. Among the activation functions, Rectified Linear Units (ReLU) function [19] ($ReLU(x)=max(0,x)$) is popularly used in hidden layers, logistic sigmoid function [23] ($sigmoid(x)=\frac{1}{1+e^{-x}}$) is often used as the activation function of output layer. After an ANN is built, a large amount of tagged data is acquired to train the weights in ANN, the weights are acceptable if the output of ANN and the label of data are close enough under the measure of a certain loss function [21]. Cross entropy function [20] is often selected as the loss function.

In this work, to analyze the working mechanism easily, we initially build an artificial neuron (an ANN with only one linear hidden layer) as a shock wave indicator in conservation laws, and train weights via TensorFlow [1]. The complete training process for the AN model includes generating the training and validation sets, selecting the neuron structure, and training weights using error back propagation algorithm [22]. In this section, we will illustrate the whole process of generating the training and validation data set in detail. The process includes selecting training cases, setting the input stencil of the data, and setting the label for each data.

3.1 Training and Validation Set

3.1.1 Selection of Training Cases

We provide several functions as initial conditions to include shock wave discontinuities with various scales of jump values in the one-dimensional nondimensionalized Burgers equation, so that we can obtain a complete data set as well as possible. Notice for the Burgers equation, contact discontinuities are not included in the data set.

• Case-1:$f(u)=\frac{u^{2}}{2}, u(x,0)=sin(\pi x)+0.5$. $\quad x\in [0,2]$

• Case-2:$f(u)=\frac{u^{2}}{2}, u(x,0)=\left\{ \begin{array}{lr} u_{l} \qquad if \; x<0 &{}\\ u_{r} \qquad if \; x\ge 0 .\end{array} \right.$

Solutions to Case-1 consist of smooth extrema, smooth large gradient and discontinuities, we can use Newton Iteration method to solve “u” in nonlinear implicit equation $u=u_0(x-ut)$ mentioned in Sect. 2. Solutions to Case-2 include a centered rarefaction wave or a shock wave with different selections of $u_{l},u_{r}$.

3.1.2 Input Stencil for Training Data

Since the shock wave detector in this work is to detect discontinuities from perspective of characteristic curve rather than from the features of spurious oscillations, we only select the cell-average of the solution $\bar{u}_{e}$ and cell-size h as the input for training. For the Burgers equation (where $f(u)=\frac{u^{2}}{2}$), the input stencil is $[\bar{u}_{e-2},\;\bar{u}_{e-1},\;\bar{u}_{e},\;\bar{u}_{e+1},\;\bar{u}_{e+2},\; h]$, where $\bar{u}_{e}=\frac{1}{\Delta _{e}}\int _{I_{e}}u(x,t_{n})dx$ is the cell-average of the exact solution.

3.1.3 Labels for Each Data

Given a cell $I_{e}$ and its input information $[\bar{u}_{e-2},\;\bar{u}_{e-1},\;\bar{u}_{e},\;\bar{u}_{e+1},\;\bar{u}_{e+2},\; h]$, we label $I_{e}$ as a troubled-cell if a discontinuity of exact solution exists inside $I_{e}$, the label is set to 1. Otherwise, the label is set to 0 to represent $I_{e}$ is a good cell.

Based on the process mentioned in Sect. 3.1, the algorithm to generate the training and validation set for the Burgers equation is given as follows.

$\mathbf{Notice}$

• (1) The reason we choose 5-cell-stencil is a balance for accuracy and compactness. 3-cell-stencil might not be enough to capture the trend of the solution in cell-averages, and multi-cell-stencil might increase the computational cost greatly and lose the compactness of the scheme as well. To do so, we can largely maintain the local compactness if applied to DG scheme.

• (2) Although the obtained detector is applied under DG scheme in this work, it can be applied to high-order finite difference or finite volume schemes.

• (3) Contact discontinuities are not included in data set. Theoretically, contact discontinuities might not be detected by the resulting model for the scalar conservation law.

• (4) The amount of data labeled $``0''$ should be almost equal to that labeled $``1''$ in order to ensure unbiased data set.

3.2 Parameters in AN Training

In this part, we seek a suitable AN for constructing a shock wave detector and suitable conditions for AN training. Only one linear hidden layer with 6 neurons lies in the AN, and is connected with the input layer linearly, the sigmoid activation function is used in the output layer. The structure is given as follows (Fig. 2):

Fig. 2

The AN structure

The weight vectors in AN to be determined include weights $\mathbf{W}$ and biases $\mathbf{B}$. Here, with $\mathbf{W} _{1}\in \mathbb {R}^{6\times 6},\mathbf{W} _{2}\in \mathbb {R}^{6\times 1}$ and with $\mathbf{b} _{1}\in \mathbb {R}^{6}, \mathbf{b} _{2}\in \mathbb {R}^{1}$.

Following the Algorithm 3.1 in Sect. 3.1, we generate the training and validation data set with 1600 amounts of supervised data including 400 from Case-1, 1200 from Case-2.

Next, the AN is trained under following conditions. The weight parameters in AN are initialized based on a normal distribution. We use stochastic gradient descent (SGD) method for optimizing with a mini-batch size of 16. The learning algorithm converges fast and it takes only few minutes.

3.3 Training Weights Results

The convergent AN result is given as follows,

$$\begin{aligned} out_{e}=\frac{1}{1+e^{-(3.86\bar{u}_{e-2}+13.44\bar{u}_{e-1} +0.17\bar{u}_{e}-11.88\bar{u}_{e+1}-5.68\bar{u}_{e+2}-9.60h-4.22)}}. \end{aligned}$$

(3.1)

For the Burgers equation, the primitive variable u is precisely the characteristic variable $\lambda (u)$. Thus, using the exact solution as input is equivalent to using the exact eigenvalue (slope of characteristic curve) as input for the Burgers equation. In order to illustrate the mechanism of the expression (3.1) from the perspective of characteristic curves, we use the characteristic variable $\lambda (u)$ for subsequent analysis in Sect. 4.

In the next section, we will show that expression (3.1) implies the information of shock wave discontinuities.

4 The Shock Wave Indicator and Its Working Mechanism

In this section, we shall analyze the working mechanism of expression (3.1) obtained in Sect. 3 so that it can be used generally to numerical simulation of conservation laws. Before analysis, we firstly give two definitions.

Definition 4.1

For cell-average of u inside $I_{e}$ and its neighbor cells $\bar{u}_{e-1}, \bar{u}_{e},\bar{u}_{e+1}$, we call $\bar{u}_{L}=\sum _{i=0}^{1}w^{i}_{L}\bar{u}_{e-i}$ is a type of left-side weighted average of variable u in $I_{e}$ reconstructed by $\bar{u}_{e-1},\bar{u}_{e}$ if $w^{i}_{L}>0$ and $\sum _{i=0}^{1}w^{i}_{L}=1$; we call $\bar{u}_{R}=\sum _{i=0}^{1}w^{i}_{R}\bar{u}_{e+i}$ is a type of right-side weighted average of variable u in $I_{e}$ reconstructed by $\bar{u}_{e},\bar{u}_{e+1}$ if $w^{i}_{R}>0$ and $\sum _{i=0}^{1}w^{i}_{R}=1$. $w^{i}_{L},w^{i}_{R}$ are called weight coefficient.

In Sect. 4.2, we will show some properties of $\bar{u}_{L}$ and $\bar{u}_{R}$.

Definition 4.2

If a certain eigenvalue $\lambda (u)$ (slope of characteristic curve) has a jump somewhere, and this jump leads to characteristic curve compressing or intersecting, we call this jump of $\lambda (u)$ is $\mathbf{admissible}$. Otherwise, this jump is called $\mathbf{inadmissible}$.

Definition 4.2 is well-defined in the physical sense. According to the Lemma 2.1 and Lemma 2.3(2), the compressing or intersecting of characteristic curves leads to the solution evolving into a discontinuity, this discontinuity is admissible in weak solution, while the divergence of characteristic curves leads to the solution evolving into a rarefaction wave.

Remark The inadmissible jumps include linear contact discontinuities, across which the characteritic curves are parallel, and those initial jumps, which evolve into rarefaction waves.

In this section, we will construct a shock wave indicator in numerical simulation of conservation laws based on the AN model (3.1), and analyze its working mechanism based on the assumption “step-size h is sufficiently small” and Definitions 4.1, 4.2. This section consists of three subsections. In Sect. 4.1 we modify expression (3.1) into a more practical form for shock wave detecting. In Sect. 4.2, we apply the detector to numerical schemes as a shock wave indicator, and analyze its working mechanism. The indicator is extended to system conservation laws in Sect. 4.3 by directly applying it to each genuinely nonlinear characteristic field.

4.1 The Shock Wave Indicator

In order to make the output of artificial neuron model campact and explicable, we are going to modify the initial indicator (3.1) into a practical form on the assumption of small mesh cell and ignoring certain small terms. The results are presented in the following two lemmas.

Lemma 4.3

Under the assumption that the discontinuity only locates on $I_e$, if the space step-size h is sufficiently small, the form (3.1) can be approximately modified as the form of

$$\begin{aligned} out_{e}\approx \frac{1}{1+e^{-(W_{L}\bar{\lambda }_{L} -W_{R}\bar{\lambda }_{R})+M_{1}h+M_{2}}}:=out'_e. \end{aligned}$$

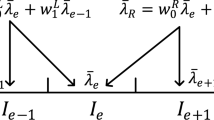
Here, $\bar{\lambda }_{L}=w_L^0\lambda (\bar{u}_e)+w_L^1\lambda (\bar{u}_{e-1})$ and $\bar{\lambda }_{R}=w_R^0\lambda (\bar{u}_e)+w_R^1\lambda (\bar{u}_{e+1})$ are the left and right side weighted averages of eigenvalue $\lambda (u)$ respectively, and $W,M_{1},M_{2}$ are constant.

Proof

Based on the assumption and Taylor expansion, we have $|\bar{u}_{e-2}-\bar{u}_{e-1}|=O(h),\;|\bar{u}_{e+2}-\bar{u}_{e+1}|=O(h)$, thus we have

$$\begin{aligned} \begin{aligned}&\frac{3.86\lambda (\bar{u}_{e-2})+13.44\lambda (\bar{u}_{e-1})+0.17\lambda (\bar{u}_{e})}{W_{L}}\approx \frac{17.30\lambda (\bar{u}_{e-1})+0.17\lambda (\bar{u}_{e})}{W_{L}}=:\bar{\lambda }_{L}, \\&\frac{0\lambda (\bar{u}_{e})+11.88\lambda (\bar{u}_{e+1})+5.68\lambda (\bar{u}_{e+2})}{W_{R}}\approx \frac{0\lambda (\bar{u}_{e})+17.56\lambda (\bar{u}_{e+1})}{W_{R}}=:\bar{\lambda }_{R}. \end{aligned} \end{aligned}$$

(4.1)

As a result, the expression (3.1) can be approximately rewritten as

$$\begin{aligned} out_{e}\overset{(4.1)}{\approx } \frac{1}{1+e^{-(W_{L}\bar{\lambda }_{L}-W_{R} \bar{\lambda }_{R})+M_{1}h+M_{2}}}=:out'_e, \end{aligned}$$

(4.2)

where $W_{L}=3.86+13.44+0.17=17.47$, $W_{R}=0+11.88+5.68=17.56, M_1=9.60, M_2=4.22$, and $\bar{\lambda }_{L},\;\bar{\lambda }_{R}$ are left and right side weighted averages of eigenvalue $\lambda (u)$ defined in (4.1) presented as

$$\begin{aligned} \begin{aligned}&\bar{\lambda }_{L}=w_L^0\lambda (\bar{u}_e) +w_L^1\lambda (\bar{u}_{e-1})=0.01\lambda (\bar{u}_e)+0.99\lambda (\bar{u}_{e-1})\\&\bar{\lambda }_{R}=w_R^0\lambda (\bar{u}_e) +w_R^1\lambda (\bar{u}_{e+1})=0.0\lambda (\bar{u}_e)+1.0\lambda (\bar{u}_{e+1}). \end{aligned} \end{aligned}$$

(4.3)

$\square$

One may note that $W_L\approx W_R$ in (4.2), we find the expression above $out'_e$ can be further modified into a more practical form, which is convenient for mechanism analyzing. Specifically, replacing $W_L,W_R$ by a constant number of $W=17.5$ and ignoring the impacts of small terms $\Delta W_L:=W_L-W$, $\Delta W_R:=W_R-W$, we have the following lemma.

Lemma 4.4

If ignoring the relatively small difference of weight coefficients

$O(\Delta W_L)$ and $O(\Delta W_R)$, the form (4.2) can be approximately modified into the following practical form of

$$\begin{aligned} out'_{e}\approx \frac{1}{1+e^{-W(\bar{\lambda }_{L} -\bar{\lambda }_{R})+M_{1}h+M_{2}}}:=\widetilde{out}_e. \end{aligned}$$

Here, $\bar{\lambda }_{L}$ and $\bar{\lambda }_{R}$ are the left and right side weighted averages of eigenvalue $\lambda (u)$ defined in (4.3), and $W=17.5,M_{1}=9.60,M_{2}=4.22$ remain constant.

Proof

Based on the assumption, we have

$$\begin{aligned} \begin{aligned} W_L\bar{\lambda }_{L}-W_R\bar{\lambda }_{R}&=W(\bar{\lambda }_{L}-\bar{\lambda }_{R})+\Delta W_L \bar{\lambda }_{L}+\Delta W_R \bar{\lambda }_{R}\\&=W(\bar{\lambda }_{L}-\bar{\lambda }_{R})+O(\Delta W_L)+ O(\Delta W_R)+O(h), \end{aligned} \end{aligned}$$

(4.4)

with $W=17.5$, $\Delta W_L=-0.03$ and $\Delta W_R=0.06$.

Although $\Delta W_L, \Delta W_R$ does not scale with h, we regard these as respectively small terms due to $\frac{\Delta W_L}{W},\frac{\Delta W_R}{W}\sim 1e-3\ll 1$ and in addition drop the term $O(\Delta W_L)+ O(\Delta W_R)$ in (4.4) so that the expression (4.4) is convenient to be explicable.

As a result, the expression (3.1) can be further approximately modified as

$$\begin{aligned} out_{e}\overset{(4.1)}{\approx }out'_e\overset{(4.4)}{\approx }\frac{1}{1+e^{-W(\bar{\lambda }_{L} -\bar{\lambda }_{R})+M_{1}h+M_{2}}}=:\widetilde{out}_{e}. \end{aligned}$$

(4.5)

$\square$

Thus, according to the Lemmas 4.3 and 4.4, the indicator (3.1) can be approximately rewritten as the concise and universal form of

$$\begin{aligned} \widetilde{out}_{e}=\frac{1}{1+e^{-W(\bar{\lambda }_{L} -\bar{\lambda }_{R})+M_{1}h+M_{2}}}. \end{aligned}$$

(4.6)

Note that the approximation made in (4.1) is to recover the “local” property of DG scheme, the approximation made in (4.4) is for the convenience of using characteristic compressing to analyze the working mechanism of (4.6). With the above modifications, we are able to discover the properties of the practical form (4.6) when applied to be a shock wave indicator in the next subsection.

4.2 Working Mechanism of the Shock Wave Indicator

In this subsection we will prove the practical form (4.6) can be used to detect shock wave discontinuities in numerical simulation of conservation laws.

We give the following assumption for discontinuity indicating in numerical simulation.

Assumption 4.1

Assuming h is sufficiently small, we consider the O(1) jump between $\bar{u}_{L}$ and $\bar{u}_{R}$ is a discontinuity in numerical simulation of variable “u”, where $\bar{u}_{L}$ and $\bar{u}_{R}$ are side weighted averages of u defined in Definition 4.1.

All analysis below is done under the Assumption 4.1.

By denoting the local region $I_{E}=\bigcup _{i=e-1}^{e+1}I_{i}$, we obtain the following lemma to explain the role $\bar{\lambda }_{L}$ and $\bar{\lambda }_{R}$ playing in numerical simulation of conservation laws.

Lemma 4.5

If the solution in region $I_{E}$ is differentiable, $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|\le M_{e}h \sim O(h)$. If there exists a discontinuity in $I_{e}$, $\bar{\lambda }_{L}$ and $\bar{\lambda }_{R}$ satisfy $\bar{\lambda }_{R}-\bar{\lambda }_{L}=C[\lambda (u)]+O(h)\sim O(1)$, where $C<1$ and depends on the weight coefficients $w^{0}_{L},w^{0}_{R}$. Specially, if $w^{0}_{L},w^{0}_{R}\rightarrow 0$, $\bar{\lambda }_{R}-\bar{\lambda }_{L}\rightarrow [\lambda (u)]+O(h)$, where $[\lambda (u)]$ represents jump of a certain eigenvalue.

Proof

(1) If solution u is differentiable in region $I_{E}$, denoting $\bar{\lambda }_e=\lambda (\bar{u}_e)$, by Taylor expansion we can conclude $\bar{\lambda }_{L}=\bar{\lambda }_{e-1}+w^{0}_{L}(\bar{\lambda }_{e}-\bar{\lambda }_{e-1})=\bar{\lambda }_{e-1}+w^{0}_{L}\lambda '(\xi _{1})O(h)=\bar{\lambda }_{e-1}+O(h)$, similarly $\bar{\lambda }_{R}=\bar{\lambda }_{e+1}+O(h)$. Then $\bar{\lambda }_{L}$ and $\bar{\lambda }_{R}$ satisfy $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|\le M_{e}h \sim O(h)$.

(2) If the solution consists of a discontinuity inside $I_{e}$, $\bar{\lambda }_{R}-\bar{\lambda }_{L}= w^{0}_{R}\bar{\lambda }_{e}+ (1-w^{0}_{R})\bar{\lambda }_{e+1} - w^{0}_{L}\bar{\lambda }_{e}-(1-w^{0}_{L})\bar{\lambda }_{e-1}= (1-w^{0}_{L}-w^{0}_{R})(\bar{\lambda }_{e+1}-\bar{\lambda }_{e-1}) +w^{0}_{L}(\bar{\lambda }_{e+1}-\bar{\lambda }_{e})+w^{0}_{R}(\bar{\lambda }_{e} -\bar{\lambda }_{e-1})+O(h)\overset{\triangle }{=}w_1(\bar{\lambda }_{e+1} -\bar{\lambda }_{e-1})+w_2(\bar{\lambda }_{e+1}-\bar{\lambda }_{e}) +w_3(\bar{\lambda }_{e}-\bar{\lambda }_{e-1})$ with $w_1+w_2+w_3=1$.

Note that on the left side of the discontinuity located in $I_e$, we have $\lambda (u(x))= \bar{\lambda }_{e-1}+O(h)$. Similarly, on the right side of the discontinuity we have $\lambda (u(x))= \bar{\lambda }_{e+1}+O(h)$. Thus, we have

$$\begin{aligned} \bar{\lambda }_{e+1}-\bar{\lambda }_{e-1}=[\lambda (u)]+O(h). \end{aligned}$$

(4.7)

Futhermore, we can always find a $0\le \mu \le 1$ which only depends on the cell-size h and the location of the discontinuity in $I_e$, such that

$$\begin{aligned} \bar{\lambda }_e=\mu \bar{\lambda }_{e-1}+(1-\mu )\bar{\lambda }_{e+1}+O(h). \end{aligned}$$

(4.8)

Using (4.7) and (4.8), we have

$\bar{\lambda }_{e+1}-\bar{\lambda }_{e}=\mu [\lambda (u(x))]+O(h),\quad \bar{\lambda }_{e}-\bar{\lambda }_{e-1}=(1-\mu )[\lambda (u(x))]+O(h)$.

Therefore, $\bar{\lambda }_{R}-\bar{\lambda }_{L}=C[\lambda (u)]+O(h)\sim O(1)$, where $C=w_1+\mu w_2 +(1-\mu ) w_3<1$. Specially, if $w^{0}_{L},w^{0}_{R}\rightarrow 0$, $C\rightarrow 1$, we can obtain $\bar{\lambda }_{R}-\bar{\lambda }_{L}\rightarrow [\lambda (u)]+O(h)$. $\square$

The following lemma show a relationship between $\widetilde{out}_{e}$ and $\bar{\lambda }_{L}-\bar{\lambda }_{R}$.

Lemma 4.6

In $I_{e}$,

(1) $\widetilde{out}_{e}< 0.0145\ll 0.5\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R}<0 \quad or \quad |\bar{\lambda }_{L}-\bar{\lambda }_{R}|\sim \frac{1.0e-3}{W}+O(h)$.

(2) $\widetilde{out}_{e}\ge 0.5\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R}\ge 0 \quad and \quad \bar{\lambda }_{L}-\bar{\lambda }_{R}\ge \frac{M_{1}h+M_{2}}{W}\sim O(1)$, and $\widetilde{out}_{e}\rightarrow 1\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R} \rightarrow +\infty$.

Proof

According to (4.6), we can derive,

$$\begin{aligned} \widetilde{out}_{e}\ge s \Longleftrightarrow e^{-W(\bar{\lambda }_{L}-\bar{\lambda }_{R})+M_{1}h+M_{2}} \le \frac{1}{s}-1 \Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R}\ge C_{0}. \end{aligned}$$

(4.9)

Here, s is a number belonging to (0, 1], and $C_{0}=\frac{1}{W}(M_{1}h+M_{2}-ln(\frac{1}{s}-1))$.

(1) If $\bar{\lambda }_{L}-\bar{\lambda }_{R}<0$, $\widetilde{out}_{e}<\frac{1}{1+e^{M_{1}h+M_{2}}}\approx 0.0145\ll 0.5$.

If $\bar{\lambda }_{L}-\bar{\lambda }_{R}>0$ and $\bar{\lambda }_{L}-\bar{\lambda }_{R}\sim \frac{1.0e-3}{W}+O(h)$, $\widetilde{out}_{e}\approx 0.0145\ll 0.5$.

Conversely, if $\widetilde{out}_{e} < 0.0145$, $\bar{\lambda }_{L}, \bar{\lambda }_{R}$ should satisfy $\bar{\lambda }_{L}-\bar{\lambda }_{R}<0$ or $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|\sim \frac{1.0e-3}{W}+O(h)$.

(2) Denoting $s=0.5$ in (4.9), we can obtain $C_{0}=\frac{M_{2}}{W}+O(h)\sim O(1)$. Therefore, $\bar{\lambda }_{L}-\bar{\lambda }_{R}\ge \frac{M_{1}h+M_{2}}{W}\sim O(1) \Longleftrightarrow \widetilde{out}_{e}\ge 0.5$.

As $\widetilde{out}_{e}$ increases from 0.5 to 1, $\bar{\lambda }_{L}-\bar{\lambda }_{R}$ also increases from $\frac{M_{1}h+M_{2}}{W}$ to $+\infty$. Therefore, $\widetilde{out}_{e}\rightarrow 1\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R} \rightarrow +\infty$. $\square$

Remark In numerical simulation, h is generally much larger than $\frac{1.0e-3}{W}\sim 10^{-5}$, therefore we can assume $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|\sim \frac{1.0e-3}{W}+O(h)$ in Lemma 4.6 is equivalent to $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|\sim O(h)$ in subsequent analysis.

Theorem 4.7

The output of (4.6) in $I_{e}$$\widetilde{out}_{e}$ satisfies $\widetilde{out}_{e}<0.0145\ll 0.5$ if $I_{e}$ is a cell near a smooth extrema or an inadmissible large-gradient/jump.

Proof

(1) For a smooth extrema. If $I_{e}$ is a cell near a smooth extrema, under the smooth assumption, the derivative of u at the extreme point is 0, then we can obtain $|\bar{\lambda }_{L}-\bar{\lambda }_{R}|<d_{0}|\lambda '(\xi )u'(\eta )|h<D_{0}h^{2}$ by Taylor expansion. Immediately by Lemma 4.6, $\widetilde{out}_{e}=\frac{1}{1+e^{M_{2}+O(h)}}\approx 0.0145 \ll 0.5$.

(2) For a inadmissible large gradient/jump. If $I_{e}$ is a cell near an inadmissible large-gradient/jump, $\bar{\lambda }_{L}-\bar{\lambda }_{R}<0$ by Definition 4.2, immediately we can obtain directly $\widetilde{out}_{e}\ll 0.5$ by Lemma 4.6. $\square$

Therefore, the indicator (4.6) can never indicate cells near a smooth extrema or an inadmissible large-gradient/jump as troubled-cells.

In theory, a solution discontinuity occurs only inside one cell. In numerical simulation, due to numerical dissipation, a discontinuity might span a few cells of the numerical solution. Therefore, these cells will be detected as the troubled-cells by the indicator (4.6), due to their O(1) magnitude admissible jump value of $\lambda (u)$.

Theorem 4.8

In the numerical simulation of system (2.1), a discontinuity of numerical solution caused by compressing of characteristic curves exists indeed inside $I_{e}$ if $\widetilde{out}_{e}\ge 0.5$.

Proof

As one can obtain in Lemma 4.6, $\widetilde{out}_{e}\ge 0.5\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R}\ge \frac{M_{1}h+M_{2}}{W}\sim O(1)$. By the Definition 4.2 there exists an admissible jump value of $\lambda (u)$ and the admissible jump value has a magnitude of O(1). Under the Assumption 4.1 there exists an occurrence of characteristic curves intersection inside $I_{e}$, consequently a discontinuity of numerical solution exists indeed inside $I_{e}$.

Therefore, $\widetilde{out}_{e}\ge 0.5\Longleftrightarrow \bar{\lambda }_{L}-\bar{\lambda }_{R}\ge \frac{M_{1}h+M_{2}}{W}\sim O(1)\Longrightarrow$ a discontinuity of numerical solution occurs inside $I_{e}$. $\square$

Remark

• (1) Since $I_{e}$ is detected as a troubled-cell if $\widetilde{out}_{e}\ge 0.5$, this correspondingly results in $\bar{\lambda }_{L}-\bar{\lambda }_{R}\ge 0.241+0.549h$. Therefore, if the jump strength of the discontinuity is less than 0.241, the present indicator would not treat it.

• (2) The scalar indicator (4.6) would not detect the initial inadmissible jumps (such as the initial linear contact discontinuities and those evolving into rarefaction waves). As a remedy, we suggest a simple strategy to treat the initial inadmissible jumps as for the 1-2-3 case to be given in the section of numerical simulation.

Next, we will extend the indicator (4.6) to one-dimensional system conservation laws.

4.3 Extension to System Conservation Laws

For system (2.3), according to Lemma 2.3(2), the solution can evolve into shock waves due to the intersection of a certain i-characteristic curves in genuinely nonlinear characteristic field, therefore, we only consider the eigenvalues in genuinely nonlinear characteristic field. By the Entropy Condition which is shown in [35], the intersection of a certain i-characteristic curves implies $\lambda ^{-}_{i}>\lambda ^{+}_{i}$, where $\lambda ^{\pm }_{i}=lim_{\epsilon \rightarrow 0^{+}}\lambda _{i}(u(x\pm \epsilon ))$.

For system conservation laws, we do not need to retrain the shock wave indicator, and can directly apply the indicator (4.6) to each genuinely nonlinear $\lambda _{i}$-characteristic field. Following the idea, we can extend indicator (4.6) to system conservation laws by two steps, the first one is to calculate the outputs of indicator (4.6) for each eigenvalue $\lambda _{i}$; the other is to select the maximum outputs among them.

The expression of indicator for the system is then given as follows,

$$\begin{aligned} \widehat{out}_{e}=max_{i}\{\widetilde{out}_{e}(\bar{\Lambda }_{i},h)\}. \end{aligned}$$

(4.10)

Here, $\bar{\Lambda }_{i}=(\bar{\lambda }_{i,e-1},\bar{\lambda }_{i,e},\bar{\lambda }_{i,e+1})$, $\widetilde{out}_{e}(\bar{\Lambda }_{i},h)$ is defined by the expression (4.6).

Lemma 4.9

For the 1-D Euler equations, the indicator (4.10) becomes

$$\begin{aligned} \widehat{out}_{e}=max\{\widetilde{out}_{e}(\bar{\mathbf{u }} -\bar{\mathbf{a }},h);\;\widetilde{out}_{e}(\bar{\mathbf{u }} +\bar{\mathbf{a }},h)\}. \end{aligned}$$

(4.11)

Here, $\bar{\mathbf{u }}\pm \bar{\mathbf{a }}=(\bar{u}_{e-1}\pm \bar{a}_{e-1},\bar{u}_{e}\pm \bar{a}_{e},\bar{u}_{e+1}\pm \bar{a}_{e+1})$.

For system (2.3), indicator (4.10) possesses similar indicating properties as indicator (4.6). Therefore, we give the following two conclusions without proof.

Theorem 4.10

The output of (4.10) in $I_{e}$ satisfies $\widehat{out}_{e}\ll 0.5$ if $I_{e}$ is a cell near a smooth extrema or an inadmissible large-gradient/jump.

Theorem 4.11

A discontinuity with admissible eigenvalue jump value exists indeed inside the $I_{e}$ if $\widehat{out}_{e}\ge 0.5$ .

Corollary 4.12

For the Euler equations, a shock wave discontinuity or a contact discontinuity exists indeed inside the $I_{e}$ if $\widehat{out}_{e}\ge 0.5$.

Proof

According to the Lemma 2.4, an admissible jump occurs to one of the non-linear eigenvalues if there is a shock wave. In addition, across the 2-contact discontinuity, $u,\;p$ remain unchanged while $\rho$ has a jump, leading to a jump occurrence for the sound speed a and the satisfaction of either $u_l-a_l>u_r-a_r$ or $u_l+a_l>u_r+a_r$ across the contact discontinuity. As a result, additionally there is always an admissible jump occurring to the 1- or 3- eigenvalue when across the 2-contact discontinuity. According to Theorem 4.8, if $\widehat{out}_{e}\ge 0.5$ , a shock wave discontinuity or a contact discontinuity exists inside the $I_e$. $\square$

Remark The Lemma 4.9 and Corollary 4.12 imply that besides the shock wave discontinuities, the present indicator (4.11) is able to detect the 2-contact discontinuities, althought the 2-characteristic is never be traced. The present indicator maintains the mathematical property shown in Lemma 2.4.

5 Runge–Kutta Discontinuous Galerkin (RKDG) Framework

In this section we take system (2.1) as an example to review the RKDG framework, and the indicator (4.6) will be applied to RKDG framework compared to TVB-based indicator.

To approximate the solution of system (2.1), the computational domain [a, b] is discretized into N non-overlapping cells, $[a,b]=\bigcup _{e=1}^{N}I_{e}, I_{e}=[x_{e-\frac{1}{2}},x_{e+\frac{1}{2}}]$, where $a=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N+\frac{1}{2}}=b$, $x_{e}$ is the center of $I_{e}$, h is the cell-size of each cell. The approximate solution $u_{h}$ is an element in the space of broken polynomials $V_{h}^{k}=\{ u\in L^{2}[a,b]:u|_{I_{e}}\in P^{k}(I_{e}) \}$, where $P^{k}(I_{e})$ is the space of polynomials with degree $d \le k$ in the cell $I_{e}$. In each $I_{e}$, the approximate solution $u_{h}$ can be represented by $u_{h}=\sum _{i=0}^{k}u_{e}^{(i)}(t)\cdot \phi _{e,i}(x)$, where $\{\phi _{e,i}(x)\}_{i}$ is a basis of $P^{k}(I_{e})$. The semi-discrete DG scheme can be formulated as follow,

$$\begin{aligned} \left( \int _{e}\phi _{e,i}\phi _{e,i}dx\right) \cdot \frac{d}{dt}u_{e}^{(i)}=\int _{e}f(u_{h}) \frac{d\phi _{e,i}}{dx}dx-\left[ \widehat{f}_{e+\frac{1}{2}}(u)\cdot \phi _{e,i}\left( x_{e+\frac{1}{2}}^{-}\right) -\widehat{f}_{e-\frac{1}{2}}(u)\cdot \phi _{e,i}\left( x_{e-\frac{1}{2}}^{+}\right) \right] \end{aligned}$$

(5.1)

Here, $\widehat{f}_{e+\frac{1}{2}}(u)=\frac{1}{2}[f(u_{e+\frac{1}{2}}^{-})+f(u_{e+\frac{1}{2}}^{+})-\alpha (u_{e+\frac{1}{2}}^{+}-u_{e+\frac{1}{2}}^{-})]$ is the Local-Lax Friedrichs numerical flux and $u(x^{\pm })=lim_{\epsilon \rightarrow 0^{+}}u(x\pm \epsilon )$. We use SSP-RK3 [10] scheme to discretize time derivative.

To suppress oscillations across the discontinuities, we use TVB limiters to correct the high order dofs of polynomial inside $I_{e}$, TVB-based indicators uses the 3-cell stencil to detect the troubled-cells. The process for TVB limiting technique and the present indicator based limiting technique are given as Algorithms 5.1 and 5.2,

Next section, we will test numerical cases under the framework of RKDG to compare the behaviors of the present indicators and the TVB-based indicators.

6 Numerical Results

We now demonstrate the capability of the present indicators (4.6) and (4.10) when applied to RKDG framework. We compare the performance of the indicators (4.6) and (4.10) with that of the TVB-based indicators. The notation TVB-1, TVB-2, TVB-3 are used to refer to the TVB limiter with the parameter $\hbox {M}=10$, $\hbox {M}=100$, and $\hbox {M}=1000$, respectively.

6.1 The 1-D Burgers Equation

6.1.1 Compound Wave Case

The initial condition for this test is a composition of smooth and discontinuous data [28], expressed as

$$\begin{aligned} u_{0}(x)= \left\{ \begin{array}{ll} sin(\pi x)&{}\quad if \; |x|\ge 1 \\ 3 &{}\quad if \; -1<x\le -0.5 \\ 1 &{}\quad if \; -0.5<x\le 0 \\ 3 &{}\quad if \quad 0<x\le 0.5 \\ 2 &{}\quad if \quad 0.5<x\le 1, \end{array} \right. \end{aligned}$$

on the domain $[-4,4]$ with periodic boundary conditions, the solution is simulated until time $T=0.4$. As the solution evolves, alternating shock and rarefaction waves begin to develop. We test this testcase under $N=200$ and $N=800$ cells to assess the behaviour of the present indicator under different cell-size.

Outputs (s) of the present indicator (4.6) at $T=0.4$ are shown in Figs. 3 and 4a. The results with various indicators on a mesh with $N=200$ cells and under DG(p4) framework are shown in Fig. 5a, b. The solution with TVB-3 indicator suffers from oscillations near the shock waves because some of the shock waves are not detected. The solution with the present indicator is similar to that with TVB-2 indicator, and is superior to that with TVB-1 indicator. We also show the time-history of the troubled-cell indication with 200 cells as shown in Fig. 6a–d, except that there is no indication for initial inadmissible discontinuities, the present indicator has a similar performance to the TVB-1 indicator. With $N=800$ cells under DG(p3) framework, as shown in Fig. 7, the TVB-3 indicator performs best among the TVB indicators, TVB-1 and TVB-2 indicators work worse than that with $N=200$ cells, this implies that the performance of TVB-based indicators is much related to the cell size. On the other hand, the present indicator works consistently.

Fig. 3

The Compound wave problem for the Burgers equation, the output (s) of the present indicator in each cells at $\hbox {T}=0.4$ with 200 cells

Fig. 4

Solutions of the Compound wave problem for the Burgers equation with various indicators at $T=0.4$ under RKDG(p4) framework with 800 cells

Fig. 5

Solutions of the Compound wave problem for the Burgers equation with various indicators at $\hbox {T}=0.4$ under RKDG(p4) framework with 200 cells

Fig. 6

The time-history of flagged troubled-cells of the compound wave problem for the Burgers equation with 200 cells

Fig. 7

The time-history of flagged troubled-cells of the compound wave problem for the Burgers equation with 800 cells

6.2 Buckley–Leverett Case

In order to demonstrate the performance of various indicators for non-convex flux, we consider the Buckley–Leverett case with the flux function

$$\begin{aligned} f(u)=\frac{u^{2}}{u^{2}+0.5(1-u)^{2}}, \end{aligned}$$

where u represents the water saturation in a mixture of oil and water [18]. We consider the initial condition

$$\begin{aligned} u_{0}(x)= \left\{ \begin{array}{ll} 0.95&{} \quad if \; x\le 0.5 \\ 0.1&{} \quad \; if \; x>0.5, \end{array} \right. \end{aligned}$$

on the domain [0, 1.5], which evolves into a compound wave consisting of a shock wave and a rarefaction wave. The numerical solutions are evaluated at time $T = 0.4$, on a mesh with $N = 150$ and open boundary conditions and under DG(p3) framework. The output (s) of the present indicator is shown in Fig. 8. Solutions of Buckley–Leverett case with various indicators are compared in Fig. 9a, b, as one can observe, the solutions with the present indicator are superior to those obtained with TVB-3 indicator which are superior to those obtained by TVB-1 and TVB-2 indicators. The time-history of flagged troubled-cells with various indicators are also compared in Fig. 10a–d, the present indicator detects the zones more regularly, and flags no cells near the rarefaction wave compared to TVB-1 and TVB-2 indicators which flag much more cells near the rarefaction wave. Note that the discontinuity appearing in this case is a contact discontinuity due to non-convex flux, the present indicator works well for this case because its mechanism of detecting troubled cell is via compressing of characteristic curves, although we never train the indictor with data set of non-convex flux.

Fig. 8

The Buckley–Leverett case, the output (s) of the present indicator in each cell at $T=0.4$ with 150 cells

Fig. 9

Solutions of the Buckley–Leverett case with various indicators at $T=0.4$ under RKDG(p3) framework with 150 cells

Fig. 10

The time-history of flagged troubled-cells of the Buckley–Leverett case with 150 cells

6.3 The 1-D Euler Equations

We consider the one-dimensional Euler equations to demonstrate the performance of the indicator (4.10) in system conservation laws.

6.3.1 Sod Test

This problem describes a mild shock tube test proposed by Sod [33], whose initial condition is given by

$$\begin{aligned} (\rho _{0},u_{0},p_{0})(x)= \left\{ \begin{array}{ll} (1,\;0,\;1) &{}\quad if \; x<0 \\ (0.125,\;0,\;0.1) &{}\quad if \; x\ge 0, \end{array} \right. \quad x\in [-5,5]. \end{aligned}$$

The solution is simulated on a mesh with $N=500$ cells and under DG(p3) framework, until the time $T=2$. TVB-3 is unable to produce correct results due to loss of positivity of density and TVB-2 leads to highly oscillatory results. The solutions with TVB-1 and the present indicator have similar simulations and eliminate the spurious oscillations near the 3-shock wave at $x=3.5$, as shown in Fig. 11b. Output (s) in each cell of the present indicator (4.10) at $\hbox {T}=2$ are shown in Fig. 12. The time-history of the troubled-cells is shown in Fig. 13, we can observe the present indicator marks less troubled-cells near the 3-shock wave than TVB-1 indicator. It should be pointed out that the present indictor with 0.5 as a threshold, passes over the admissible jump of contact discontinuity because its output is less than 0.5, as shown in Fig. 11b.

Fig. 11

Solutions (density) of the Sod test for the Euler equations with various indicators at $\hbox {T}=2$ under RKDG(p3) framework with 500 cells

Fig. 12

The Sod test for the Euler equations, the output (s) of the present indicator in each cell at $\hbox {T}=2$ with 500 cells

Fig. 13

The time-history of flagged troubled-cells of the Sod test for the Euler equations with 500 cells

6.3.2 Lax Test

We consider the Lax shock tube problem [17], whose initial condition is given by

$$\begin{aligned} (\rho _{0},u_{0},p_{0})(x)= \left\{ \begin{array}{ll} (0.445,\;0.698,\;3.528) &{}\quad if \; x<0 \\ (0.5,\;0,\;0.571) &{}\quad \; x\ge 0, \end{array} \right. \quad x\in [-5,5]. \end{aligned}$$

The solution is simulated on a mesh with $N=200$ cells and under DG(p3) framework, until the time $T=1.3$. TVB-3 is unable to produce correct results due to loss of positivity of density. The solutions with TVB-1, TVB-2 and present indicators are similar, as shown in Fig. 14. Output (s) of the present indicator (4.10) in each cell at $T=1.3$ is shown at Fig. 15. The time-history of the troubled-cells is shown in Fig. 16a–c, we can observe the present indicator marks similar regions as TVB-1 indicator near the 3-shock wave and marks contact discontinuity regions well.

Fig. 14

Solutions (density) of the Lax test for the Euler equations with various indicators at $\hbox {T}=1.3$ under RKDG(p3) framework with 200 cells

Fig. 15

The Lax test for the Euler equations, the output (s) of the present indicator in each cell at $\hbox {T}=1.3$ with 200 cells

Fig. 16

The time-history of flagged troubled-cells of the Lax test for the Euler equations with 200 cells

6.3.3 Left Half of the Blast-Wave

We consider a severe test case, describing the left of the blast-wave problem [37], the initial condition is given by

$$\begin{aligned} (\rho _{0},u_{0},p_{0})(x)= \left\{ \begin{array}{ll} (1,\;0,\;1000) &{}\quad if \; x<0.5 \\ (1,\;0,\;0.01) &{}\quad if \; x\ge 0.5, \end{array} \right. \quad x\in [0,1]. \end{aligned}$$

the solution is simulated on a mesh with $N=400$ cells and under DG(p3) framework, until the time $T=0.012$. Output s of the present indicator at $T=0.012$ is shown in (Fig. 17). As shown in Fig. 18, the results obtained by the present indicator (4.10) hold the best simulation of the wave peak compared to that obtained by TVB indicators. The time-history of the troubled-cells is shown in Fig. 19a–d, we can observe the present indicator marks much less cells than TVB-1 and TVB-2 and TVB-3, specially marked thinner zones of wave peak.

Fig. 17

The Left half of the blast-wave test for the Euler equations, the output (s) of the present indicator in each cell at $\hbox {T}=0.012$ with 400 cells

Fig. 18

Solutions (density) of the Left half of the blast-wave test for the Euler equations with various indicators at $\hbox {T}=0.012$ under RKDG(p3) framework with 400 cells

Fig. 19

The time-history of flagged troubled-cells of the Left half of the blast-wave test for the Euler equations with 400 cells

6.3.4 Shu–Osher Problem

This case proposed in [32], describes the interaction of a right moving shock with an oscillatory smooth wave. The initial condition is given as follows:

$$\begin{aligned} (\rho _{0},u_{0},p_{0})(x)= \left\{ \begin{array}{ll} (3.857143,\;2.629369,\;10.33333) &{}\quad if \; x<-4 \\ (1+0.2sin(5x),\;0,\;1) &{}\quad if \; x\ge -4, \end{array} \right. \quad x\in [-5,5]. \end{aligned}$$

The solution is simulated on a mesh with $N=400$ cells, until the time $T=1.8$. Various indicators are applied to this case under DG(p3) framework. Output s of the present indicator at $T=1.8$ is shown in (Fig. 20). Numerical results in Fig. 21 show that TVB-3 gives the most accurate simulations in the smooth high-frequency region, with slight oscillations. The simulations obtained by TVB-2 and the present indicators have a similar performance and are superior to that obtained by TVB-1 indicator. The Fig. 22 also shows the present indicator flags thinner regions than TVB-2.

Fig. 20

The Shu–Osher problem for the Euler equations, the output (s) of the present indicator in each cell at $\hbox {T}=1.8$ with 400 cells

Fig. 21

Solutions (density) of the Shu–Osher problem for the Euler equations with various indicators at $\hbox {T}=1.8$ under RKDG(p3) framework with 400 cells

Fig. 22

The time-history of flagged troubled-cells of the Shu–Osher problem for the Euler equations with 400 cells

6.3.5 1-2-3 Test

We consider the Riemann problem given by the following initial condition

$$\begin{aligned} (\rho _{0},u_{0},p_{0})(x)= \left\{ \begin{array}{ll} (7,\;-1,\;0.2) &{}\quad if \; x<0 \\ (7,\;1,\;0.2) &{}\quad if \; x\ge 0, \end{array} \right. \quad x\in [-1,1]. \end{aligned}$$

The solution is simulated on a mesh with $N=200$ cells and under DG(p3) framework, until the time $T=0.6$. The solution consists of two rarefaction waves pulling away from each other. This test case has an initial inadmissible discontinuity and the present indicator neglects it. As a result, numerical oscillations occur at the beginning, leading to the code broken down due to the loss of positivity of pressure and density. Here we give a simple strategy to solve this trouble. That is to combine a conventional indicator with the present indicator for the first few time steps, and then shift to the present indicator solely. The comparison of the solutions with the combined indicator and TVB-based indicators are shown in Fig. 23 (TVB-3 does not work out for this case). The solution with the combined indicator is slightly superior to solutions with the TVB-based indicators. We can observe the combined indicator marks no cells after the first few time steps, while the TVB-based indicators still flag part of rarefaction waves as troubled-cells, as shown in Fig. 24.

Fig. 23

Solutions (density) of the 1-2-3 test for the Euler equations with various indicators at $\hbox {T}=0.4$ under RKDG(p3) framework with 200 cells

Fig. 24

The time-history of flagged troubled-cells of the 1-2-3 test for the Euler equations with 200 cells

Fig. 25

Solutions (density) of the shock–vortex interaction case for the 2-D Euler equations with various indicators with $480\times 480$ cells at $\hbox {T}=0.2$ under RKDG(p2) framework

Fig. 26

troubled-cells flagged by various indicators in the shock–vortex interaction case for 2-D Euler equations with $480\times 480$ cells at $\hbox {T}T=0.2$ under RKDG(p2) framework

Fig. 27

Solutions (density) of the shock–vortex interaction case for the 2-D Euler equations with various indicators with $480\times 480$ cells at $\hbox {T}T=0.35$ under RKDG(p2) framework

Fig. 28

troubled-cells flagged by various indicators in the shock–vortex interaction case for 2-D Euler equations with $480\times 480$ cells at $\hbox {T}=0.35$ under RKDG(p2) framework

Fig. 29

Solutions (density) of the Double Mach reflection case for the 2-D Euler equations with various indicators with $400\times 100$ cells at $\hbox {T}=0.2$ under RKDG(p2) framework

Fig. 30

troubled-cells flagged by various indicators in the Double Mach reflection problem for 2-D Euler equations with $400\times 100$ cells at T = 0.2 under RKDG(p2) framework

Fig. 31

Solutions (density) of the Double Mach reflection case for the 2-D Euler equations with various indicators with $960\times 240$ cells at $\hbox {T}=0.2$ under RKDG(p2) framework

Fig. 32

troubled-cells flagged by various indicators in the Double Mach reflection problem for 2-D Euler equations with $960\times 240$ cells at $T=0.2$ under RKDG(p2) framework

The next two cases are to demonstrate the performance of the indicator (4.6) and (4.10) for multi-dimensional conservation laws. The present indicators (4.6) and (4.10) can be extended to multi-dimensional conservation laws by applying them to characteristic fields in different directions.

6.4 The 2-D Euler Equations

6.4.1 Shock–Vortex Interaction

This problem consists of interaction of a left-moving shock wave with a right-moving vortex [9]. The initial shock discontinuity on the domain $[0,1]\times [0,1]$ is given by

$$\begin{aligned} \mathbf{U} _0(x)= \left\{ \begin{array}{ll} \mathbf{U} _L &{}\quad if \; x<0.5 \\ \mathbf{U} _R &{}\quad if \; x\ge 0.5, \end{array} \right. \end{aligned}$$

where the left state is given by $(\rho _L,\;u_L,\;v_L,\;p_L)=(1,\sqrt{\gamma },0,1)$ while the right state is given by

$$\begin{aligned} \begin{aligned} p_R = 1.3,\qquad \rho _R=\rho _L\left( \frac{\gamma -1+(\gamma +1)p_R}{\gamma +1+(\gamma -1)p_R}\right) , \\ u_R = \sqrt{\gamma }+\sqrt{2}\left( \frac{1-p_R}{\sqrt{\gamma -1+(\gamma +1)p_R}}\right) ,\qquad v_R = 0. \end{aligned} \end{aligned}$$

The left state $\mathbf{U} _L$ is superposed onto an isentropic vortex described by the following perturbations in the velocity, temperature and physical entropy respectively

$$\begin{aligned} \begin{aligned} \delta u = \theta \frac{(y-y_c)}{r_c}exp(\beta (1-r^2)),\quad \delta v=-\theta \frac{(x-x_c)}{r_c}exp(\beta (1-r^2)) \\ \delta _T = -\frac{\gamma -1}{4\beta \gamma }\theta ^2 exp(2\beta (1-r^2)),\qquad \delta s = 0. \end{aligned} \end{aligned}$$

where $r^2 =((x-x_c)^2+(y-y_c)^2)/r_c^2$. The various parameters of the perturbation are chosen as $\theta =0.3,r_c=0.05,\beta = 0.204 and (x_c,\;y_c)=(0.25,0.5)$. The domain is discretized by $480\times 480$ structured grid with inflow boundary conditions applied on the left/right and reflective boundary conditions on the top/bottom. The simulation is under RKDG(p2) framework and till a final time T = 0.35. The solution and flagged troubled cells at different time instances are shown in Figs. 25, 26, 27 and 28. Note that the present indicator marked only the moving shock wave and never marked regions near the vortex, which might explain that solution with the present indicator preserves the vortex structure more precisely than that with TVB-3 indicator.

6.4.2 Double Mach Reflection Test

This problem is originally from [37], the computational domain for this problem is $[0,4]\times [0,1]$. The reflecting wall lies at the bottom, starting from $x=\frac{1}{6}$. Initially a right-moving Mach 10 shock wave is positioned at $x=\frac{1}{6},y=0$ and make a $60^{\circ }$ angle with the x-axis. For the bottom boundary, the exact post-shock condition is imposed for the part from $x=0$ to $x=\frac{1}{6}$ and a reflective boundary condition is used for the rest. At the top boundary, the flow values are set to describe the exact motion of a Mach 10 shock. We compute the solution up to $T = 0.2$ and plot only the simulation results on $400\times 100$ cells and $960\times 240$ cells under RKDG(p2) framework, all the figures are shown with 23 equally spaced density contours from 1.5 to 22.7.

The results for this problem show an excellent performance of the present indicator. Simulations by various TVB indicators have a better performance with the increased parameter M in the TVB indicator, we only compare the simulations by the present indicator with that by the TVB-3 indicator. Solutions (density) have a significant improvement with the present indicator near bottom boundary as shown in Figs. 29 and 31. The flagged troubled-cells detected by various indicators are compared in Figs. 30 and 32, we can observe the flagged regions detected by the present indicator are almost the discontinuity position of the solution, which are much more accurate than the TVB-3 indicator, and the flagged cells are significantly reduced compared to TVB-3 indicator, which might explain the significant improvement near bottom boundary under $960\times 240$ cells. The results with KXRCF shock indicator are presented in Figs. 29, 30, 31 and 32.(c), it shows the KXRCF indicator has similar behaviors with $400\times 100$ cells and marked extra cells at the bottom boundary with $960\times 240$ cells as compared to the present indicator.

7 Conclusion

In this work, we proposed a novel shock wave indicator that can be applied to various numerical schemes such as the RKDG scheme. The present indicator was obtained initially by training an AN, then modified and extended to multi-dimensional conservation laws.

The present indicator is concise, explicable and generalizable. We proved the present indicator can identify and detect the troubled-cells where exist solution discontinuities caused by compressing or intersecting of the characteristic curves, smooth extrema and inadmissible large gradient regions cannot be flagged by the present indicator. Several numerical results in this work demonstrated that the present indicator can improve the indicating efficiency, leading to a reduced computational cost and more accurate numerical results.

Because the present indicator detect troubled-cells by capturing the compressing or intersecting of characteristic curves, theoretically it might not detect the initial inadmissible discontinuities. One way to treat the initial inadmissible discontinuities is to follow the approach done for the 1-2-3 case in this work, the other way is to generate related data into database and deepen the neural network as presented in [28, 29], but the resultant indicator might be difficult to be explicable. In addition, we believe that the present indicator can be extended to unstructured mesh.