Hybrid High-Order Methods for the Elliptic Obstacle Problem

Abstract

Hybrid High-Order methods are introduced and analyzed for the elliptic obstacle problem in two and three space dimensions. The methods are formulated in terms of face unknowns which are polynomials of degree $k=0$ or $k=1$ and in terms of cell unknowns which are polynomials of degree $l=0$. The discrete obstacle constraints are enforced on the cell unknowns. Higher polynomial degrees are not considered owing to the modest regularity of the exact solution. A priori error estimates of optimal order, that is, up to the expected regularity of the exact solution, are shown. Specifically, for $k=1$, the method employs a local quadratic reconstruction operator and achieves an energy-error estimate of order $h^{\frac{3}{2}-\epsilon }$, $\epsilon >0$. To our knowledge, this result fills a gap in the literature for the quadratic approximation of the three-dimensional obstacle problem. Numerical experiments in two and three space dimensions illustrate the theoretical results.

1 Introduction

Hybrid High-Order (HHO) methods have been introduced for linear elasticity in [20] and linear diffusion in [22]. HHO methods have been extended to other linear PDEs, such as advection–diffusion [23], Stokes [24], and elliptic interface problems [12], and to nonlinear PDEs, such as Leray–Lions operators [18], steady incompressible Navier–Stokes equations [21], nonlinear elasticity with infinitesimal deformations [6], hyperelasticity with finite deformations [1], and plasticity with small deformations [2]. Lowest-order HHO methods are closely related to the hybrid finite volume method [26] and the mimetic finite difference methods [9, 10, 35], see also the unifying viewpoints in [5, 25]. HHO methods have been bridged in [17] to the hybridizable discontinuous Galerkin methods [16] and to the nonconforming virtual element methods [4].

HHO methods employ face unknowns which are polynomials of arbitrary order $k\ge 0$ on each mesh face and cell unknowns which are polynomials of order $l\ge 0$, with $l\in \{k,k\pm 1\}$, in each mesh cell. The cell unknowns can be eliminated locally by static condensation leading to a global transmission problem posed solely in terms of the face unknowns. For this reason, HHO methods are also termed discontinuous skeletal methods. The formulation of HHO methods relies on a local reconstruction operator of order $(k+1)$ in each mesh cell and a local stabilization operator which weakly enforces a matching between the face unknowns and the trace of the cell unknowns. HHO methods offer various assets: they support polyhedral meshes, lead to local conservation principles, are robust in various regimes, are computationally efficient owing to the above local elimination procedure, and lend themselves to generic programming software (see [15] and https://github.com/wareHHOuse/diskpp).

In this work, we devise and analyze a HHO method to approximate the solution of the elliptic obstacle problem in two and three space dimensions. We consider the polynomial degrees $k\in \{0,1\}$ for the face unknowns and the polynomial degree $l=0$ for the cell unknowns, and the obstacle constraint is enforced on the cell unknowns. Higher polynomial degrees are not considered owing to the modest regularity that is expected for the exact solution. Our main result is Theorem 1 below where we establish an energy-error estimate of order $h^r$, with h the mesh-size, $r=1$ if $k=0$ and $r=\frac{3}{2}-\epsilon$, $\epsilon >0$, if $k=1$, where these convergence rates optimally match the assumed regularity of the exact solution. Note that in the absence of contact and for a smooth enough solution, the present methods classically delivers a rate $h^2$ if $k=1$, even if piecewise constant cell functions are used. Thus, the above rate reflects the nonlinear nature of the problem. The salient point in Theorem 1 is the case where $k=1$, since we are able to reach the best convergence rate matching the expected regularity of the exact solution even in 3D. As the literature review below reveals, the present HHO method thus fills a gap for the quadratic approximation of the three-dimensional obstacle problem. We emphasize that the HHO methodology is instrumental in achieving this result, since the local reconstruction operator produces quadratic polynomials in each mesh cell if $k=1$, whereas the constraint is enforced on the cell unknowns and not on the reconstruction. Let us also stress that the proposed HHO method is particularly attractive from a computational viewpoint, since the discrete obstacle constraints are enforced on the cell unknowns which are constant in each mesh cell. Hence, well-established solvers like active-set methods [33] can be readily used.

Let us put our work in perspective with the literature. The elliptic obstacle problem relies on firm mathematical foundations and appears in many engineering applications; see, among others, the textbooks [29, 31, 34, 38]. The numerical analysis of the two-dimensional elliptic obstacle problem using finite elements was pioneered in the 1970s in [8, 28]. In [28], a linear finite element method was proposed and analyzed with discrete obstacle constraints enforced at the vertices of the triangulation, whereas in [8], a quadratic finite element method was proposed and analyzed with discrete obstacle constraints enforced at the edge midpoints of the triangulation. The assumption in [8] on the finiteness of the free boundary length was relaxed in [41]. More recently in [40], linear and quadratic discontinuous Galerkin (DG) methods were proposed and analyzed for the elliptic obstacle problem and a frictional contact problem. These methods are designed by enforcing the discrete obstacle constraints at the vertices and the edge midpoints of the triangulation, similarly to the case of conforming linear and quadratic finite elements, respectively. The classical Crouzeix–Raviart nonconforming method was first studied in [42] with the regularity assumption on the exact solution that $u\in W^{s,p}(\varOmega )$ with $s<2+1/p$ and $1<p<\infty$. A refined analysis for the nonconforming method with minimal regularity assumptions is presented in [13] by constructing a novel conforming companion to the nonconforming discrete solution. Mimetic finite difference methods which support general polyhedral meshes were studied in [3]. Mixed and stabilized mixed methods, where both the solution and the Lagrange multiplier are approximated, were analyzed in [32]. Let us emphasize that the analysis in the above articles for the obstacle problem is restricted to two-dimensional problems. The design and analysis of linear conforming finite element methods in three dimensions can be performed similarly to the two-dimensional case. However, the design of a three-dimensional quadratic finite element method that achieves optimal convergence rates (up to the regularity of the exact solution) is not similar to the two-dimensional case. Recently, in [30], a quadratic finite element method enriched with element-wise bubbles was proposed and analyzed for the three-dimensional elliptic obstacle problem. However the analysis assumes higher regularity, that is, $u\in H^3$ piecewise in the contact and non-contact regions. The above literature review shows that a gap still remains concerning the quadratic approximation of the three-dimensional elliptic obstacle problem.

This article is organized as follows. In Sect. 2, we present the model problem. In Sect. 3, we introduce the HHO discretization; we also derive the discrete elliptic obstacle problem and establish its well-posedness. In Sect. 4, we prove our main result, namely an energy-error estimate of order h for $k=0$ and of order $h^{\frac{3}{2}-\epsilon }$, $\epsilon >0$, for $k=1$. Finally, in Sect. 5, we present numerical results on two- and three-dimensional test cases to illustrate our error estimate.

2 Model Problem

Let $D\subset {\mathbb R}^d$ with $d\in \{2,3\}$ be an open subset with a Lipschitz boundary $\partial D$. Let $H^m(D)$ denote the standard $L^2$-based Sobolev space of order $m\ge 0$, and let $\gamma : H^1(D)\rightarrow H^{\frac{1}{2}}(\partial D)$ denote the well-known surjective trace map. More generally, for any subset $G\subseteq D$ (which is typically D or its boundary, a mesh cell or its boundary, or a mesh face), we denote the norm and semi-norm on the standard Sobolev space $W^{s,p}(G)$ by $\Vert \cdot \Vert _{W^{s,p}(G)}$ and $|\cdot |_{W^{s,p}(G)}$, where $s\ge 0$ is the order of the derivative and $1\le p\le \infty$ is the exponent in the integration (with the appropriate Lebesgue measure depending on the dimension of G). For simplicity, we denote $\Vert \cdot \Vert _{L^2(G)}$ by $\Vert \cdot \Vert _G$ and the $L^2(G)$-inner product by $(\cdot ,\cdot )_G$; the same notation is used for vector-valued functions.

We consider the elliptic obstacle problem posed in D with a non-homogeneous Dirichlet condition on $\partial D$. The data are the load function $f\in L^2(D)$, the Dirichlet value $g\in H^{\frac{1}{2}}(\partial D)$, and the obstacle function $\chi \in H^1(D)\cap C^0(\overline{D})$ such that $\chi \le g$ a.e. on $\partial D$. Define the set

$$\begin{aligned} {\mathcal K}:=\{v\in H^1(D) {\;|\;}v\ge \chi \text { a.e. in } D \text { and } \gamma (v)=g\}. \end{aligned}$$

(1)

Define the bilinear form $a:H^1(D)\times H^1(D)\rightarrow {\mathbb R}$ and the linear form $\ell : H^1(D)\rightarrow {\mathbb R}$, respectively, by

$$\begin{aligned} a(w,v)=(\nabla w,\nabla v)_D\quad \text {and}\quad \ell (v)=(f,v)_D. \end{aligned}$$

(2)

The model problem consists of finding $u\in {\mathcal K}$ such that

$$\begin{aligned} a(u,v-u) \ge \ell (v-u) \qquad \forall v\in {\mathcal K}, \end{aligned}$$

(3)

or, equivalently, of minimizing the functional $J(v):=\frac{1}{2}a(v,v)-\ell (v)$ over ${\mathcal K}$. Owing to the following Browder–Stampacchia Lemma (see [11, 34]), we infer that the model problem (3) is well-posed.

Lemma 1

(Browder–Stampacchia) Let H be a real Hilbert space with norm $\Vert \cdot \Vert _H$ and let $H'$ denote the dual space of H. Let a be a bilinear form on $H\times H$ satisfying

$$\begin{aligned} a(v,v)\ge \alpha \Vert v\Vert _H^2\quad \text {and}\quad |a(w,v)|\le \xi \Vert w\Vert _H\Vert v\Vert _H\quad \text {for all } w,v\in H, \end{aligned}$$

(4)

for some positive constants $\alpha$ and $\xi$. Let ${\mathcal K}$ be a nonempty, closed, convex subset of H and let $\ell \in H'$. Then there exists a unique $u\in {\mathcal K}$ such that $a(u,v-u)\ge \ell (v-u)$ for all $v\in {\mathcal K}$.

In what follows, we make some (reasonable) additional smoothness assumptions on the exact solution. Specifically, we assume that for all $1<p<\infty$ and all $s<2+\frac{1}{p}$, $u\in W^{s,p}(D)$, and that the following complementarity conditions hold true with $\lambda := -\varDelta u-f$,

$$\begin{aligned} \lambda&\ge 0 \,\,\text { a.e. in } D, \end{aligned}$$

(5a)

$$\begin{aligned} \lambda&=0 \,\,\text { in the interior of the set } \{x\in D: u(x)>\chi (x)\}, \end{aligned}$$

(5b)

$$\begin{aligned} (u-\chi )\lambda&=0\,\, \text { a.e. in } D. \end{aligned}$$

(5c)

The above assumptions are reasonable once invoking the elliptic regularity theory for obstacle problems if the problem data satisfies additional smoothness assumptions. In particular, if $\chi \in H^2(D)$ and g is the trace of a $H^2(D)$ function, then $u\in H^2(D)$ and the above complementarity conditions hold true [34]. Moreover, if $f\in L^\infty (D)\cap BV(D)$, $g,\chi \in C^{3}(\overline{D})$ with $g\ge \chi$ on $\partial D$, and if the boundary $\partial D$ is sufficiently smooth, then $u\in W^{s,p}(D)$ as stated above [7, 8, 34, 41]. In the present work, we are going to assume that the domain D is a polygon (if $d=2$) or a polyhedron (if $d=3$) so that it can be meshed exactly with cells having straight edges or planar faces, respectively, and we are going to assume that the above smoothness assumptions on the exact solution still hold true.

3 Discretization by the Hybrid High-Order Method

In this section, we present the setting for the HHO discretization of the elliptic obstacle problem introduced in the previous section.

3.1 Discrete Setting

We consider a sequence of refined meshes $({\mathcal T}_h)_{h>0}$ where the parameter h denotes the mesh-size and goes to zero during the refinement process. For all $h>0$, we assume that the mesh ${\mathcal T}_h$ covers D exactly and consists of a finite collection of non-empty disjoint open polyhedral cells T such that $\overline{D}=\bigcup _{T\in {\mathcal T}_h} \overline{T}$ and $h=\max _{T\in {\mathcal T}_h} h_T$, where $h_T$ is the diameter of T. The present HHO methods can be deployed on meshes having non-matching interfaces and cells of polyhedral shape with planar faces. A closed subset F of $\overline{D}$ is defined to be a mesh face if it is a subset of an affine hyperplane $H_F$ with positive $(d-1)$-dimensional Hausdorff measure and if either of the following two statements holds true: (i) There exist $T_1(F)$ and $T_2(F)$ in ${\mathcal T}_h$ such that $F= \partial T_1(F)\cap \partial T_2(F) \cap H_F$; in this case, the face F is called an internal face; (ii) There exists $T(F)\in {\mathcal T}_h$ such that $F= \partial T(F)\cap \partial D \cap H_F$; in this case, the face F is called a boundary face. The collection of all the internal (resp., boundary) faces is denoted by ${\mathcal F}_h^{\mathrm{i}}$ (resp., ${\mathcal F}_h^{\mathrm{b}}$), and we let ${\mathcal F}_h:={\mathcal F}_h^{\mathrm{i}}\cup {\mathcal F}_h^{\mathrm{b}}$. Let $h_F$ denote the diameter of $F\in {\mathcal F}_h$. For each $T\in {\mathcal T}_h$, the set ${\mathcal F}_T:=\{F\in {\mathcal F}_h {\;|\;}F\subset \partial T\}$ denotes the collection of all faces contained in $\partial T$, ${\varvec{n}}_T$ the unit outward normal to T, and we set ${\varvec{n}}_{TF}:={\varvec{n}}_{T|F}$ for all $F\in {\mathcal F}_T$. Following [20, Def. 1], we assume that the mesh sequence $({\mathcal T}_h)_{h>0}$ is shape-regular in the sense that, for all $h>0$, ${\mathcal T}_h$ admits a matching simplicial submesh ${\mathfrak T}_h$ (i.e., every cell and face of ${\mathfrak T}_h$ is a subset of a cell and a face of ${\mathcal T}_h$, respectively) so that the mesh sequence $({\mathfrak T}_h)_{h>0}$ is shape-regular in the usual sense and all the cells and faces of ${\mathfrak T}_h$ have uniformly comparable diameter to the cell and face of ${\mathcal T}_h$ to which they belong. For a shape-regular mesh sequence $({\mathcal T}_h)_{h>0}$, the maximum number of faces of a mesh cell is uniformly bounded (see [19, Lemma 1.41]), i.e., there is a positive integer $N_\partial$, uniform with respect to h, such that

$$\begin{aligned} \max _{T\in {\mathcal T}_h}\text {card}({{\mathcal F}_T})\le N_\partial \qquad \forall h>0. \end{aligned}$$

(6)

Moreover, the following discrete trace inequality holds true, where ${\mathbb P}^r(T)$ is the linear space of polynomials of degree at most $r\ge 0$ on T, see [19, Lemma 1.46]:

$$\begin{aligned} \Vert q\Vert _F\le C_\mathrm{tr} h_F^{-\frac{1}{2}} \Vert q\Vert _{T} \quad \forall T\in {\mathcal T}_h,\; \forall F\in {\mathcal F}_T,\; \forall q\in {\mathbb P}^r(T), \end{aligned}$$

(7)

where $C_\mathrm{tr}$ depends on the mesh regularity and the polynomial degree r but is uniform with respect to h. Henceforth, we use the notation C for a positive generic constant whose value can change at each occurrence but is independent of the mesh cell $T\in {\mathcal T}_h$ and of h. The value of C can depend on the shape-regularity of the mesh sequence and on the underlying polynomial degree.

3.2 Local Reconstruction and Stabilization Operators

Let the face polynomial degree $k\in \{0,1\}$ be fixed. For all $T\in {\mathcal T}_h$, we define the local discrete space

$$\begin{aligned} {\hat{U}}^k_{T}:= {\mathbb P}^0(T)\times {\mathbb P}^k({\mathcal F}_T), \end{aligned}$$

(8)

where is composed of piecewise polynomials of degree at most k on the faces composing the boundary of T. We represent a generic element ${\hat{v}}_T \in {\hat{U}}^k_{T}$ by ${\hat{v}}_T=(v_T,v_{\partial T})$ with $v_T\in {\mathbb P}^0(T)$ and $v_{\partial T}\in {\mathbb P}^k({\mathcal F}_T)$. For all $T\in {\mathcal T}_h$, we define the local reconstruction operator $R_T^{k+1}: {\hat{U}}^k_T\rightarrow {\mathbb P}^{k+1}(T)$ so that, for all ${\hat{v}}_T = (v_T,v_{\partial T})\in {\hat{U}}^k_{T}$,

$$\begin{aligned} \left( \nabla R_T^{k+1}({\hat{v}}_T),\nabla w\right) _T&=(\nabla v_T,\nabla w)_T+(v_{\partial T}-v_T,\nabla w\cdot {\varvec{n}}_{T})_{\partial T}, \end{aligned}$$

(9a)

$$\begin{aligned} \left( R_T^{k+1}({\hat{v}}_T),1\right) _T&= (v_T,1)_T, \end{aligned}$$

(9b)

where (9a) is enforced for all $w\in {\mathbb P}^{k+1}(T)$. The volume term on the right-hand side of (9a) is zero since $v_T$ is constant; we keep this term for the sake of consistency with the general setting from [20, 22]. Let $\pi _T^0$ be the $L^2$-projection onto ${\mathbb P}^0(T)$ and let $\pi _{\partial T}^k$ be the $L^2$-projection onto ${\mathbb P}^k({\mathcal F}_T)$. We define the local stabilization operator $S_{\partial T}^k : {\hat{U}}_T^k \rightarrow {\mathbb P}^k({\mathcal F}_T)$ such that, for all ${\hat{v}}_T=(v_T,v_{\partial T}) \in {\hat{U}}_T^k$, we have

$$\begin{aligned} S_{\partial T}^k({\hat{v}}_T) := \pi _{\partial T}^k\left( v_{\partial T}- R_T^{k+1}({\hat{v}}_T) \right) - \left( \pi _T^0\big (v_T - R_T^{k+1}({\hat{v}}_T) \big )\right) _{|_{\partial T}}. \end{aligned}$$

(10)

Finally, the discrete counterpart of the local exact bilinear form $(\nabla w,\nabla v)_T$ is the local discrete bilinear form $a_T: {\hat{U}}_T^k\times {\hat{U}}_T^k\rightarrow {\mathbb R}$ defined by

$$\begin{aligned} a_T({\hat{w}}_T,{\hat{v}}_T):= & {} \left( \nabla R_T^{k+1}({\hat{w}}_T),\nabla R_T^{k+1}({\hat{v}}_T)\right) _T \nonumber \\&+ \left( \eta _{\partial T} S_{\partial T}^k({\hat{w}}_T),S_{\partial T}^k({\hat{v}}_T)\right) _{\partial T}, \end{aligned}$$

(11)

with the piecewise constant weight $\eta _{\partial T}$ defined on $\partial T$ such that $\eta _{\partial T|F}=h_F^{-1}$ for all $F\in {\mathcal F}_T$.

Let us briefly outline the stability and approximation properties associated with the above operators. We equip the discrete space ${\hat{U}}_T^k$ with the following seminorm:

$$\begin{aligned} |{\hat{v}}_T|_{{\hat{U}}_T^k} := \left\| \eta _{\partial T}^{\frac{1}{2}}(v_{\partial T}-v_T)\right\| _{\partial T}, \qquad \forall {\hat{v}}_T = (v_T,v_{\partial T})\in {\hat{U}}^k_{T}. \end{aligned}$$

(12)

Observe that $|{\hat{v}}_T|_{{\hat{U}}_T^k}=0$ implies that $v_{\partial T}$ is constant on $\partial T$ and equal to $v_T$.

Lemma 2

(Stability) There exist positive constants $C_1$ and $C_2$, uniform with respect to T and h, such that, for all ${\hat{v}}_T\in {\hat{U}}_T^k$,

$$\begin{aligned} C_1|{\hat{v}}_T|_{{\hat{U}}_T^k}^2 \le a_T({\hat{v}}_T,{\hat{v}}_T) \le C_2 |{\hat{v}}_T|_{{\hat{U}}_T^k}^2. \end{aligned}$$

(13)

Proof

The proof follows that of [22, Lemma 4]. We briefly sketch it for completeness since we are dealing here with different polynomial degrees for the face and the cell unknowns. Let ${\hat{v}}_T\in {\hat{U}}_T^k$. Invoking the triangle inequality, the regularity of the mesh sequence, the $L^2$-stability of $\pi _{\partial T}^k$, and the approximation properties of $\pi _T^0$, we infer that

$$\begin{aligned} |{\hat{v}}_T|_{{\hat{U}}_T^k}&\le \left\| \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{v}}_T)\right\| _{\partial T} + \left\| \eta _{\partial T}^{\frac{1}{2}}\pi _{\partial T}^k\left( R_T^{k+1}({\hat{v}}_T)-\pi _T^0\left( R_T^{k+1}({\hat{v}}_T)\right) \right) \right\| _{\partial T}\\&\le \left\| \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{v}}_T)\right\| _{\partial T} + Ch_T^{-1} \left\| R_T^{k+1}({\hat{v}}_T)-\pi _T^0\left( R_T^{k+1}({\hat{v}}_T)\right) \right\| _T \\&\le \left\| \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{v}}_T)\right\| _{\partial T} + C'\left\| \nabla R_T^{k+1}({\hat{v}}_T)\right\| _T, \end{aligned}$$

which proves the leftmost bound in (13). Concerning the rightmost bound, we first observe that the definition (9a) of $R_T^{k+1}({\hat{v}}_T)$ combined with the Cauchy–Schwarz inequality and the trace inequality (7) readily imply that

$$\begin{aligned} \left\| \nabla R_T^{k+1}({\hat{v}}_T)\right\| _T\le C |{\hat{v}}_T|_{{\hat{U}}_T^k}. \end{aligned}$$

Moreover, invoking the same arguments as above implies that

$$\begin{aligned} \left\| \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{v}}_T)\right\| _{\partial T}&\le |{\hat{v}}_T|_{{\hat{U}}_T^k} + \left\| \eta _{\partial T}^{\frac{1}{2}}\pi _{\partial T}^k\left( R_T^{k+1}({\hat{v}}_T)-\pi _T^0\left( R_T^{k+1}({\hat{v}}_T)\right) \right) \right\| _{\partial T}\\&\le |{\hat{v}}_T|_{{\hat{U}}_T^k} + C'\left\| \nabla R_T^{k+1}({\hat{v}}_T)\right\| _T, \end{aligned}$$

and since we have already proved that $\Vert \nabla R_T^{k+1}({\hat{v}}_T)\Vert _T\le C |{\hat{v}}_T|_{{\hat{U}}_T^k}$, this concludes the proof. $\square$

We define the local reduction operator ${\hat{I}}_T^k : H^1(T)\rightarrow {\hat{U}}_T^k$ such that, for all $v\in H^1(T)$,

$$\begin{aligned} {\hat{I}}_T^k (v):=\left( \pi _T^0(v),\pi _{\partial T}^k(v)\right) \in {\hat{U}}_T^k. \end{aligned}$$

(14)

Then, $R_T^{k+1} \circ {\hat{I}}_T^k : H^1(T) \rightarrow {\mathbb P}^{k+1}(T)$ acts as an approximation operator.

Lemma 3

(Approximation) Let $s\ge 0$ and set $t:=\min (k,s)$. There is C, uniform with respect to T and h, so that, for any $v\in H^{s+2}(T)$, the following holds true:

$$\begin{aligned}&\left\| v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right\| _T+h_T^{\frac{1}{2}}\left\| v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right\| _{\partial T} +h_T\left\| \nabla \left( v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right) \right\| _T \nonumber \\&\quad +h_T^{\frac{3}{2}}\left\| \nabla \left( v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right) \right\| _{\partial T} \le C h_T^{t+2}|v|_{H^{t+2}(T)}. \end{aligned}$$

(15)

Moreover, we have

$$\begin{aligned} \left\| \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k\left( {\hat{I}}_T^k(v)\right) \right\| _{\partial T} \le C h_T^{t+1}|v|_{H^{t+2}(T)}. \end{aligned}$$

(16)

Proof

The proof of (15) is similar to [22, Lemma 3] (up to minor adaptations due to the different polynomial degrees for the face and the cell unknowns). The key observation is that $(\nabla (v- R^k_T({\hat{I}}_T^k (v))),\nabla w)_T =0$ for all $w\in {\mathbb P}^{k+1}(T)$, so that $\Vert \nabla (v- R^k_T{\hat{I}}_T^k (v)))\Vert _T=\inf _{w\in {\mathbb P}^{k+1}(T)}\Vert \nabla (v-w)\Vert _T$. Concerning (16), we have

$$\begin{aligned} S_{\partial T}^k\left( {\hat{I}}_T^k(v)\right) = \pi _{\partial T}^k\left( v-R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) -\pi _T^0\left( v-R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) _{|\partial T}. \end{aligned}$$

Therefore, proceeding as in [22, Eq. (45)], we use the triangle inequality, the stability of the $L^2$-projectors, that $\eta _{\partial T}$ is piecewise constant, and the regularity of the mesh sequence to infer that

$$\begin{aligned}&\left\| \eta _{\partial T}^{\frac{1}{2}}S_{\partial T}^k\left( {\hat{I}}_T^k(v)\right) \right\| _{\partial T} \\&\quad \le \left\| \eta _{\partial T}^{\frac{1}{2}}\pi _{\partial T}^k\left( v\!-\!R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) \right\| _{\partial T}+\left\| \eta _{\partial T}^{\frac{1}{2}}\pi _T^0\left( v\!-\!R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) \right\| _{\partial T}\\&\quad \le \left\| \eta _{\partial T}^{\frac{1}{2}}\left( v-R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) \right\| _{\partial T} + C h_T^{-1} \left\| \pi _T^0\left( v-R_T^{k+1}\left( {\hat{I}}_T^k(v)\right) \right) \right\| _T\\&\quad \le C'h_T^{-1}\left( h_T^{\frac{1}{2}}\left\| v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right\| _{\partial T}+\left\| v-R_T^{k+1}\left( {\hat{I}}_T^k (v)\right) \right\| _T\right) , \end{aligned}$$

and we conclude by invoking (15). $\square$

3.3 Discrete Elliptic Obstacle Problem

The global discrete space is defined by

$$\begin{aligned} {\hat{U}}_h^k:=\left( \prod _{T\in {\mathcal T}_h} {\mathbb P}^0(T)\right) \times \left( \prod _{F\in {\mathcal F}_h} {\mathbb P}^k(F)\right) . \end{aligned}$$

(17)

We use the notation ${\hat{v}}_h=\big ((v_T)_{T\in {\mathcal T}_h}, (v_F)_{F\in {\mathcal F}_h}\big )$ to denote a generic element ${\hat{v}}_h\in {\hat{U}}_h^k$. For all $T\in {\mathcal T}_h$, we denote by ${\hat{v}}_T=(v_T,(v_F)_{F\in {\mathcal F}_T})\in {\hat{U}}_T^k$ the components of ${\hat{v}}_h$ attached to the mesh cell T and the faces composing its boundary. We define the global reduction operator ${\hat{I}}_h^k : H^1(D)\rightarrow {\hat{U}}_h^k$ such that, for all $v\in H^1(D)$,

$$\begin{aligned} {\hat{I}}_h^k(v):=\left( \left( \pi _T^0(v)\right) _{T\in {\mathcal T}_h},\left( \pi _{F}^k(v)\right) _{F\in {\mathcal F}_h}\right) . \end{aligned}$$

(18)

Note that ${\hat{I}}_h^k(v)$ is well-defined since v is single-valued at all the internal faces of the mesh.

The global discrete bilinear form $a_h$ on ${\hat{U}}_h^k\times {\hat{U}}_h^k$ is defined by

$$\begin{aligned} a_h({\hat{w}}_h,{\hat{v}}_h):= \sum _{T\in {\mathcal T}_h} a_T({\hat{w}}_T,{\hat{v}}_T) + \sum _{F\in {\mathcal F}_h^{\mathrm{b}}} a_F^{\mathrm{b}}\left( {\hat{w}}_{T(F)},{\hat{v}}_{T(F)}\right) , \end{aligned}$$

(19)

with the Nitsche-type boundary penalty bilinear form [36] such that

$$\begin{aligned} a_F^{\mathrm{b}}\left( {\hat{w}}_{T(F)},{\hat{v}}_{T(F)}\right)&:= -\left( \nabla R_{T(F)}^{k+1}\left( {\hat{w}}_{T(F)}\right) \cdot {\varvec{n}}_D,v_F\right) _F-\left( w_F,\nabla R_{T(F)}^{k+1}\left( {\hat{v}}_{T(F)}\right) \cdot {\varvec{n}}_D\right) _F \nonumber \\&\quad +\varsigma h_F^{-1}(w_F,v_F)_F, \end{aligned}$$

(20)

where $\varsigma >0$ is the boundary penalty parameter, ${\varvec{n}}_D$ is the unit outward normal to D, and where we recall that T(F) is the unique mesh cell such that $F = \partial T(F) \cap \partial D \cap H_F$ for every boundary face $F\in {\mathcal F}_h^{\mathrm{b}}$ supported in the hyperplane $H_F$ (see Sect. 3.1). The linear form $\ell _h$ on ${\hat{U}}_h^k$ is defined by

$$\begin{aligned} \ell _h({\hat{v}}_h):=\sum _{T\in {\mathcal T}_h} (f,v_T)_T+\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) , \end{aligned}$$

(21)

with

$$\begin{aligned} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) := -\left( g,\nabla R_{T(F)}^{k+1}\left( {\hat{v}}_{T(F)}\right) \cdot {\varvec{n}}_D\right) _F+\varsigma h_F^{-1}(g,v_F)_F. \end{aligned}$$

(22)

We refer the reader to [14] for HHO methods combined with Nitsche’s boundary penalty method applied to Dirichlet and nonlinear Signorini boundary conditions.

Remark 1

(Dirichlet boundary conditions) Alternatively, one can also enforce Dirichlet boundary conditions strongly by setting the discrete unknowns attached to the boundary faces of the mesh equal to the $L^2$-projection of the Dirichlet data onto $\mathbb {P}^k_{d-1}(F)$ for all $F\in {\mathcal F}_h^{\mathrm{b}}$ and zeroing out the discrete test functions attached to the boundary faces of the mesh. In this case, the contribution of $a_F^{\mathrm{b}}$ is dropped from the right-hand side of (19) and that of $\ell _F^{\mathrm{b}}$ is dropped from the right-hand side of (21).

The discrete admissible set $\hat{\mathcal K}_h^k$ is defined by

$$\begin{aligned} \hat{\mathcal K}_h^k:=\left\{ {\hat{v}}_h\in {\hat{U}}_h^k {\;|\;}(v_T,1)_T \ge (\chi ,1)_T, \; \forall T\in {\mathcal T}_h \right\} . \end{aligned}$$

(23)

Notice that the constraint is enforced on the cell unknowns. The discrete elliptic obstacle problem consists of finding ${\hat{u}}_h\in \hat{\mathcal K}_h^k$ such that

$$\begin{aligned} a_h({\hat{u}}_h,{\hat{v}}_h-{\hat{u}}_h)\ge \ell _h({\hat{v}}_h-{\hat{u}}_h) \qquad \forall {\hat{v}}_h\in \hat{\mathcal K}_h^k. \end{aligned}$$

(24)

Equivalently, ${\hat{u}}_h$ minimizes over $\hat{\mathcal K}_h^k$ the discrete functional $\frac{1}{2}a_h({\hat{v}}_h,{\hat{v}}_h)-\ell _h({\hat{v}}_h)$. In order to establish the well-posedness of the discrete problem (24), we study the coercivity and boundedness of the discrete bilinear form $a_h$ on ${\hat{U}}_h^k\times {\hat{U}}_h^k$. To this purpose, we equip the space ${\hat{U}}_h^k$ with the following norm:

$$\begin{aligned} \Vert {\hat{v}}_h\Vert _{{\hat{U}}_h^k}^2 := \sum _{T\in {\mathcal T}_h} |{\hat{v}}_T|_{{\hat{U}}_T^k}^2 + \sum _{F\in {\mathcal F}_h^{\mathrm{b}}} h_F^{-1} \Vert v_F\Vert _F^2. \end{aligned}$$

(25)

Lemma 4

(Coercivity and boundedness) Assume that the boundary penalty parameter is such that $\varsigma > \frac{1}{4} N_\partial C_\mathrm{tr}^2$, where $N_\partial$ is defined by (6) and $C_\mathrm{tr}$ by (7). Then, there exists two positive constants $\alpha$ and $\xi$, uniform with respect to h, such that, for all ${\hat{v}}_h,{\hat{w}}_h \in {\hat{U}}_h^k$,

$$\begin{aligned} a_h({\hat{v}}_h,{\hat{v}}_h)&\ge \alpha \Vert {\hat{v}}_h\Vert _{{\hat{U}}_h^k}^2, \end{aligned}$$

(26a)

$$\begin{aligned} |a_h({\hat{v}}_h,{\hat{v}}_h)|&\le \xi \Vert {\hat{w}}_h\Vert _{{\hat{U}}_h^k} \Vert {\hat{w}}_h\Vert _{{\hat{U}}_h^k}. \end{aligned}$$

(26b)

Proof

The coercivity property (26a) follows from the left bound in (13) and classical techniques for Nitsche’s boundary penalty method, see, for example, [19, Lemma 4.12] in the context of discontinuous Galerkin methods and [23, Lemma 7] in the context of HHO methods. The boundedness property (26b) follows from the Cauchy–Schwarz inequality, the right bound in (13), and by invoking the discrete trace inequality (7) to bound the first two terms composing $a_h^{\mathrm{b}}$. $\square$

Corollary 1

(Well-posedness) Assume that $\varsigma > \frac{1}{4} N_\partial C_\mathrm{tr}^2$. There exists a unique ${\hat{u}}_h\in \hat{\mathcal K}_h^k$ solving the discrete elliptic obstacle problem (24).

Proof

The discrete admissible set $\hat{\mathcal K}_h^k$ is nonempty since ${\hat{I}}_h^k(u) \in \hat{\mathcal K}_h^k$. Moreover, $\hat{\mathcal K}_h^k$ is a closed convex subset of ${\hat{U}}_h^k$. We can then invoke the Browder–Stampacchia lemma together with coercivity and boundedness (see Lemma 4) to conclude. $\square$

4 Error Analysis

In this section, we state and prove our main result, that is, an energy-error estimate for the HHO method with $k\in \{0,1\}$. The estimate is optimal up to the regularity of the exact solution if $k=1$, whereas if $k=0$, the estimate is still optimal concerning the differentiability index of the exact solution, but requires a somewhat stronger assumption on the integrability index since we essentially require that $u\in W^{2,p}(D)$ with p large enough instead of just $u\in H^2(D)$ (see also Remark 2 below).

Theorem 1

(Energy-error estimate) Let u be the exact solution solving (3) and let ${\hat{u}}_h$ be the discrete solution solving (24). Let ${\hat{I}}_h^k$ be the global reduction operator defined by (18). If $k=1$, let $\epsilon \in (0,\frac{1}{2}]$, set $r=\frac{3}{2}-\epsilon$, and assume that $u\in H^{1+r}(D)=H^{\frac{5}{2}-\epsilon }(D)$, $(u-\chi ) \in W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)$ with $p=\frac{2(d-1)}{\epsilon }\in (1,\infty )$, and $\lambda :=-f-\varDelta u \in W^{1-\epsilon ,1}(D)$. If $k=0$, set $r=1$, let $\tau \in (0,1)$, and assume that $u\in H^{1+r}(D)=H^{2}(D)$, $(u-\chi ) \in W^{2,p}(D)$ with $p=\frac{d}{\tau }\in (1,\infty )$, and $\lambda :=-f-\varDelta u \in W^{\tau ,1}(D)$. Then, there is C, uniform with respect to h, such that the following holds true:

$$\begin{aligned} \left\| {\hat{I}}_h^k(u)-{\hat{u}}_h\right\| _{{\hat{U}}_h^k}\le C\big (|u|_{H^{1+r}(D)}+\varPhi _{u,\lambda }\big ) h^{r}, \end{aligned}$$

(27)

where

$$\begin{aligned} \varPhi _{u,\lambda } = {\left\{ \begin{array}{ll} \Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)}^{\frac{1}{2}} |\lambda |_{W^{1-\epsilon ,1}(D)}^{\frac{1}{2}}&{}\quad \text {if }k=1, \\ \Vert u-\chi \Vert _{W^{2,p}(D)}^{\frac{1}{2}}|\lambda |_{W^{\tau ,1}(D)}^{\frac{1}{2}}&{}\quad \text {if } k=0. \end{array}\right. } \end{aligned}$$

(28)

Moreover, we also have

$$\begin{aligned}&\left( \sum _{T\in {\mathcal T}_h}\left\| \nabla (u-R_T^{k+1}({\hat{u}}_T))\right\| _T^2+\sum _{F\in {\mathcal F}_h^{\mathrm{b}}}h_F^{-1}\Vert u-u_F\Vert _F^2 \right) ^{\frac{1}{2}} \nonumber \\&\quad \le C\big (|u|_{H^{1+r}(D)}+\varPhi _{u,\lambda }\big ) h^{r}. \end{aligned}$$

(29)

Proof

Let us set ${\hat{v}}_h:={\hat{I}}_h^k(u)-{\hat{u}}_h \in {\hat{U}}_h^k$. Using the discrete coercivity property (26a) and the discrete variational inequality (24) together with ${\hat{I}}_h^k(u)\in \hat{\mathcal K}_h^k$, we find that

$$\begin{aligned} \alpha \left\| {\hat{I}}_h^k(u)-{\hat{u}}_h\right\| _{{\hat{U}}_h^k}^2&\le a_h\left( {\hat{I}}_h^k(u)-{\hat{u}}_h,{\hat{I}}_h^k(u)-{\hat{u}}_h\right) \\&\le a_h\left( {\hat{I}}_h^k(u),{\hat{I}}_h^k(u)-{\hat{u}}_h\right) -\ell _h\left( {\hat{I}}_h^k(u)-{\hat{u}}_h\right) \\&= a_h\left( {\hat{I}}_h^k(u),{\hat{v}}_h\right) -\ell _h({\hat{v}}_h)\\&=a_h\left( {\hat{I}}_h^k(u),{\hat{v}}_h\right) +\sum _{T\in {\mathcal T}_h}(\varDelta u,v_T)_T-\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) \\&\quad +\sum _{T\in {\mathcal T}_h}\left( \lambda ,\pi _T^0(u)-u_T\right) _T, \end{aligned}$$

where we used $\lambda = -f-\varDelta u$ and that the cell component of ${\hat{v}}_h$ attached to $T\in {\mathcal T}_h$ is $v_T=\pi _T^0(u)-u_T$. Let us define ${\mathcal T}_h^\mathrm{n}:=\{T\in {\mathcal T}_h {\;|\;}u>\chi \text { on } T\}$ (collecting the non-contact cells), ${\mathcal T}_h^\mathrm{c}:=\{T\in {\mathcal T}_h {\;|\;}u\equiv \chi \text { on } T\}$ (collecting the contact cells), and ${\mathcal T}_h^\mathrm{f}:={\mathcal T}_h {\setminus } ({\mathcal T}_h^\mathrm{n}\cup {\mathcal T}_h^\mathrm{c})$ (collecting the free-boundary cells). Note that $\lambda \equiv 0$ on any $T\in {\mathcal T}_h^\mathrm{n}$ owing to (5b). Therefore, we have

$$\begin{aligned} \sum _{T\in {\mathcal T}_h} \left( \lambda ,\pi _T^0(u)-u_T\right) _T&=\sum _{T\in {\mathcal T}_h^\mathrm{c}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T+\sum _{T\in {\mathcal T}_h^\mathrm{f}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T. \end{aligned}$$

Moreover, for all $T\in {\mathcal T}_h^\mathrm{c}$, we have $\pi _T^0(u)=\pi _T^0(\chi )$, and hence

$$\begin{aligned} \left( \lambda ,\pi _T^0(u)-u_T\right) _T=\left( \lambda ,\pi _T^0(\chi )-u_T\right) _T\le 0, \end{aligned}$$

recalling that $u_T\ge \pi _T^0(\chi )$ since ${\hat{u}}_h\in \hat{\mathcal K}_h^k$ and that $\lambda \ge 0$ on D owing to (5a). As a result, we have

$$\begin{aligned} \alpha \left\| {\hat{I}}_h^k(u)-{\hat{u}}_h\right\| _{{\hat{U}}_h^k}^2&\le a_h\left( {\hat{I}}_h^k(u),{\hat{v}}_h\right) +\sum _{T\in {\mathcal T}_h}(\varDelta u,v_T)_T-\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) \\&\quad +\sum _{T\in {\mathcal T}_h^\mathrm{f}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T. \end{aligned}$$

The first three terms on the right hand side are estimated in Lemma 5 below, and the last term is estimated in Lemma 6 below. This readily lead to  (27). Finally, the bound (29) follows from (27) by invoking the rightmost bound in (13), the triangle inequality, and the bound (15) on $\nabla (u-R_T^{k+1}({\hat{I}}_T^k(u)))$ with $s=t=\frac{1}{2}-\epsilon \ge 0$ if $k=1$ and $s=t=0$ if $k=0$. $\square$

Remark 2

(Regularity for $k=0$) The regularity requirement $u\in W^{2,p}(D)$ with $p=\frac{d}{\tau }$ introduced in Theorem 1 for $k=0$ can be reduced to $u\in H^2(D)$ provided one uses a HHO method with cell unknowns of degree one on simplicial meshes and one enforces the obstacle constraint on the cell unknowns with respect to the linear Lagrange interpolate of the obstacle function. Details are omitted for brevity.

Lemma 5

(Consistency error on differential operator) Let r be as in Theorem 1 and assume that the exact solution u is in $H^{1+r}(\varOmega )$. There is C, uniform with respect to h, such that the following holds true for all ${\hat{v}}_h\in {\hat{U}}_h^k$:

$$\begin{aligned} \left| a_h\left( {\hat{I}}_h^k(u),{\hat{v}}_h\right) +\sum _{T\in {\mathcal T}_h}(\varDelta u,v_T)_T-\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) \right| \le C h^{r}|u|_{H^{1+r}(\varOmega )}\Vert {\hat{v}}_h\Vert _{{\hat{U}}_h^k}. \end{aligned}$$

Proof

The proof follows along the lines of [23, Sect. 6.2]; we sketch it for completeness. Re-organizing the various terms, we have

$$\begin{aligned} a_h\left( {\hat{I}}_h^k(u),{\hat{v}}_h\right) +\sum _{T\in {\mathcal T}_h}(\varDelta u,v_T)_T-\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} \ell _F^{\mathrm{b}}\left( {\hat{v}}_{T(F)}\right) = A_1+A_2+A_3, \end{aligned}$$

where

$$\begin{aligned} A_1&=\sum _{T\in {\mathcal T}_h} \left( \nabla R_T^{k+1}\left( {\hat{I}}_T^k(u)\right) ,\nabla R_T^{k+1}({\hat{v}}_T)\right) _T+(\varDelta u,v_T)_T\\&\quad -\sum _{F\in {\mathcal F}_h^{\mathrm{b}}}\left( \nabla R_{T(F)}^{k+1}\left( {\hat{I}}_{T(F)}^k(u)\right) \cdot {\varvec{n}}_D,v_F\right) _F,\\ A_2&=\sum _{T\in {\mathcal T}_h} \left( \eta _{\partial T} S_{\partial T}^k\left( {\hat{I}}_T^k(u)\right) ,S_{\partial T}^k({\hat{v}}_T)\right) _{\partial T},\\ A_3&=\sum _{F\in {\mathcal F}_h^{\mathrm{b}}} -\left( \pi _F^k(u)-g,\nabla R_{T(F)}^{k+1}\left( {\hat{v}}_{T(F)}\right) \cdot {\varvec{n}}_D\right) _F+\varsigma h_F^{-1}\left( \pi _F^k(u)-g,v_F\right) _F. \end{aligned}$$

Using the definition of $R_T^{k+1}$, integrating by parts the term $(\varDelta u,v_T)_T$, and since the normal component of $\nabla u$ is single-valued across the mesh internal faces, we infer that

$$\begin{aligned} A_1&= \sum _{T\in {\mathcal T}_h} \left( \nabla \left( u-R_T^{k+1}\left( {\hat{I}}_T^k(u)\right) \right) \cdot {\varvec{n}}_T,v_{\partial T}-v_{T}\right) _{\partial T} \\&\quad + \sum _{F\in {\mathcal F}_h^{\mathrm{b}}}\left( \nabla \left( u-R_{T(F)}^{k+1}\left( {\hat{I}}_{T(F)}^k(u)\right) \right) \cdot {\varvec{n}}_D,v_F\right) _{F}. \end{aligned}$$

We can now use the bound (15) on $(u-R_T^{k+1}({\hat{I}}_T^k(u)))$ where we set $s=r-1$ so that $t=\min (k,s)=s=r-1$ whether $k=1$ or $k=0$. Using the Cauchy–Schwarz inequality and the definition of the $\Vert \cdot \Vert _{{\hat{U}}_h^k}$-norm, we then obtain that $|A_1| \le C h^{r}|u|_{H^{1+r}(\varOmega )}\Vert {\hat{v}}_h\Vert _{{\hat{U}}_h^k}$. Furthermore, since $\Vert \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{v}}_T)\Vert _{\partial T}\le C|{\hat{v}}_T|_{{\hat{U}}_T^k}$ for all $T\in {\mathcal T}_h$, the Cauchy–Schwarz inequality and the bound (16) on $\Vert \eta _{\partial T}^{\frac{1}{2}} S_{\partial T}^k({\hat{I}}_T^k(u))\Vert _{\partial T}$ imply that $|A_2|\le C h^{r}|u|_{H^{1+r}(\varOmega )}\Vert {\hat{v}}_h\Vert _{{\hat{U}}_h^k}$. Finally, since $\nabla R_{T(F)}^{k+1}({\hat{v}}_{T(F)})\cdot {\varvec{n}}_D$ and $v_F$ are polynomials of order at most k on F, we have $A_3=0$. $\square$

Lemma 6

(Consistency error on Lagrange multiplier) Let p and $\varPhi _{u,\lambda }$ be as in Theorem 1. There is C, uniform with respect to h, such that the following holds true:

$$\begin{aligned} \sum _{T\in {\mathcal T}_h^\mathrm{f}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T \le C\varPhi _{u,\lambda } h^{r}. \end{aligned}$$

Proof

Let $T\in {\mathcal T}_h^\mathrm{f}$. Since (5c) implies that $(\lambda ,u-\chi )_T=0$, we infer that

$$\begin{aligned} \left( \lambda ,\pi _T^0(u)-u_T\right) _T=\left( \lambda ,\pi _T^0(u)-u+\chi -\pi _T^0(\chi )+\pi _T^0(\chi )-u_T\right) _T. \end{aligned}$$

Since $(\lambda , \pi _T^0(\chi )-u_T)_T\le 0$, we obtain

$$\begin{aligned} \left( \lambda ,\pi _T^0(u)-u_T\right) _T&\le \big (\lambda ,\pi _T^0(u-\chi )-(u-\chi )\big )_T \nonumber \\&=\big (\lambda -\pi _T^0(\lambda ),\pi _T^0(u-\chi )-(u-\chi )\big )_T \nonumber \\&\le \left\| \lambda -\pi _T^0(\lambda )\right\| _{L^1(T)}\left\| (u-\chi )-\pi _T^0(u-\chi )\right\| _{L^\infty (T)}. \end{aligned}$$

(30)

(1) The case $k=1$. The approximation properties of $\pi _T^0$ imply that

$$\begin{aligned} \left\| \lambda -\pi _T^0(\lambda )\right\| _{L^1(T)}&\le C h_T^{1-\epsilon }|\lambda |_{W^{1-\epsilon ,1}(T)}. \end{aligned}$$

(31)

Furthermore, we also have

$$\begin{aligned} \left\| (u-\chi )-\pi _T^0(u-\chi )\right\| _{L^\infty (T)}&\le C h_T | u-\chi |_{W^{1,\infty }(T)}. \end{aligned}$$

(32)

The definition of p implies that $\alpha :=1-\frac{d-1}{p}-\frac{\epsilon }{2}=1-\epsilon >0$. Moreover, by assumption, we have $(u-\chi )\in W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)$, so that $\nabla (u-\chi )\in W^{s,p}(D;{\mathbb R}^d)$ with $s:=1+\frac{1}{p}-\frac{\epsilon }{2}$. Since $1-\frac{d}{sp} \ge 1-\epsilon = \alpha$ as can be verified by a direct calculation using that $\epsilon \in (0,\frac{1}{2}]$ (actually $\frac{d}{sp}=\epsilon$ if $d=2$), the Sobolev Embedding Theorem implies that $\nabla (u-\chi )\in C^{0,\alpha }(\overline{D})$. Since $T\in {\mathcal T}_h^\mathrm{f}$, there is a point $x^*\in T$ such that $\nabla (u-\chi )(x^*)=0$ [39] and hence, for any $x\in T$, we have

$$\begin{aligned} |\nabla (u-\chi )(x)|&\le C |x-x^*|^\alpha \Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)} \\&\le C h_T^\alpha \;\Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} | u-\chi |_{W^{1,\infty }(T)} \le C h_T^\alpha \Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)}. \end{aligned}$$

(33)

Using (33) in (32), we obtain

$$\begin{aligned} \left\| (u-\chi )-\pi _T^0(u-\chi )\right\| _{L^\infty (T)}&\le C h_T^{1+\alpha } \Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)}. \end{aligned}$$

(34)

Substituting (31) and (34) in (30) and summing over all $T\in {\mathcal T}_h^\mathrm{f}$, we find that

$$\begin{aligned} \sum _{T\in {\mathcal T}_h^\mathrm{f}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T&\le C h^{2+\alpha -\epsilon }\Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)} \sum _{T\in {\mathcal T}_h^\mathrm{f}}|\lambda |_{W^{1-\epsilon ,1}(T)}\\&\le Ch^{3-2\epsilon } \Vert u-\chi \Vert _{W^{2+\frac{1}{p}-\frac{\epsilon }{2},p}(D)}|\lambda |_{W^{1-\epsilon ,1}(D)} = Ch^{3-2\epsilon } \varPhi _{u,\lambda }^2, \end{aligned}$$

since $2+\alpha -\epsilon =3-\frac{d-1}{p}-\frac{3\epsilon }{2} = 3-2\epsilon$ and where we used the definition (28) of $\varPhi _{u,\lambda }$ for $k=1$. This completes the proof for $k=1$.

(2) The case $k=0$. Using the approximation properties of $\pi _T^0$, we have

$$\begin{aligned} \left\| \lambda -\pi _T^0(\lambda )\right\| _{L^1(T)}&\le C h_T^{\tau } |\lambda |_{W^{\tau ,1}(T)}, \end{aligned}$$

(35)

and we also have

$$\begin{aligned} \left\| (u-\chi )-\pi _T^0(u-\chi )\right\| _{L^\infty (T)}&\le C h_T | u-\chi |_{W^{1,\infty }(T)}. \end{aligned}$$

Since $\tau \in (0,1)$ and $p=\frac{d}{\tau }$, we have $\gamma :=1-\frac{d}{p}=1-\tau >0$. Moreover, by assumption, we have $(u-\chi )\in W^{2,p}(D)$. Then, the Sobolev Embedding Theorem implies that $\nabla (u-\chi )\in C^{0,\gamma }(\overline{D})$. Proceeding as above for $k=1$, we infer that

$$\begin{aligned} \left\| (u-\chi )-\pi _T^0(u-\chi )\right\| _{L^\infty (T)}&\le C h_T^{1+\gamma } \Vert u-\chi \Vert _{W^{2,p}(D)}. \end{aligned}$$

(36)

Using (35) and (36) in (30) and summing over all $T\in {\mathcal T}_h^\mathrm{f}$, we find that

$$\begin{aligned} \sum _{T\in {\mathcal T}_h^\mathrm{f}}\left( \lambda ,\pi _T^0(u)-u_T\right) _T&\le C h^{1+\gamma +\tau }\Vert u-\chi \Vert _{W^{2,p}(D)} \sum _{T\in {\mathcal T}_h^\mathrm{f}} |\lambda |_{W^{\tau ,1}(T)}\\&\le C h^2 \Vert u-\chi \Vert _{W^{2,p}(D)}|\lambda |_{W^{\tau ,1}(D)} = Ch^2 \varPhi _{u,\lambda }^2, \end{aligned}$$

since $1+\gamma +\tau =2-\frac{d}{p}+\tau = 2$ and where we used the definition (28) of $\varPhi _{u,\lambda }$ for $k=0$. This completes the proof for $k=0$. $\square$

5 Numerical Experiments

In this section, we briefly review some implementation aspects of the present HHO method applied to elliptic obstacle problems, and we illustrate the above theoretical results on two- and three-dimensional test cases from [37].

5.1 Implementation Aspects

We consider Dirichlet boundary conditions enforced strongly and enforced via Nitsche’s method. Implementing Dirichlet conditions strongly leads to a linear system with slightly less degrees of freedom at a cost of a sligtly more complex assembly procedure, whereas Nitsche’s method allows one to avoid manipulating the global matrix in order to remove the rows/columns corresponding to the Dirichlet faces. In the case where strong boundary conditions are used, the standard HHO matrix associated with the bilinear form

$$\begin{aligned} a_h({\hat{w}}_h,{\hat{v}}_h)=\sum _{T\in {\mathcal T}_h} a_T({\hat{w}}_T,{\hat{v}}_T) \end{aligned}$$

(37)

is denoted ${\varvec{A}}\in \mathbb {R}^{N_h^k \times N_h^k}$ with $N_h^k:=|{\mathcal T}_h|+{k+d-1 \atopwithdelims ()d-1}|{\mathcal F}_h^{\mathrm{i}}|$ (recall that the cell unknowns are constant in each mesh cell), and the load vector associated with the linear form $\ell _h({\hat{v}}_h)=\sum _{T\in {\mathcal T}_h} (f,v_T)_T$ is denoted ${\varvec{b}} \in \mathbb {R}^{N_h^k}$. For any vector ${\varvec{\alpha }}\in \mathbb {R}^{N_h^k}$, we denote $\alpha _T\in \mathbb {R}$ its components attached to the mesh cell $T\in {\mathcal T}_h$ and $(\alpha _{F,n})_{0\le n<{k+d-1 \atopwithdelims ()d-1}}$ its components attached to the internal face $F\in {\mathcal F}_h^{\mathrm{i}}$ of the mesh.

The numerical solution of the discrete elliptic obstacle problem (24) is based on the primal-dual active set method (see [33]). Let $m\ge 0$ be the iteration counter. For all $m\ge 0$, we are looking for the solution vector ${\varvec{\alpha }}^m\in \mathbb {R}^{N_h^k}$ and the Lagrange multiplier vector ${\varvec{\beta }}^m\in \mathbb {R}^{N_h^k}$ (note that ${\varvec{\beta }}^m$ is actually a discrete counterpart of the function $-\lambda$ considered in the previous section). Since the constraint is enforced on the cell unknowns, the components of ${\varvec{\beta }}$ attached to the internal faces of the mesh are always zero. Moreover, since the cell unknowns are constant in each mesh cell, the primal-dual active set method leads to a partition of the mesh cells into active and inactive ones; specifically, we consider the subsets $\mathcal {T}_A^m := \{T\in \mathcal {T}_h \;|\; \beta ^m_{T} + c(\alpha ^m_T - \gamma _T) < 0\}$ and $\mathcal {T}_I^m := \mathcal {T}{\setminus } \mathcal {T}_A^m$, where $c>0$ is a numerical weighting parameter and $\gamma _T = \frac{1}{|T|}\int _T \chi$ for all $T\in \mathcal {T}_h$. For all $m\ge 1$, given the pair $({\varvec{\alpha }}^{m-1},{\varvec{\beta }}^{m-1})\in \mathbb {R}^{N_h^k} \times \mathbb {R}^{N_h^k}$ and the resulting partition $(\mathcal {T}_A^{m-1},\mathcal {T}_I^{m-1})$ of ${\mathcal T}_h$, we solve the following (nonsymmetric) linear system:

$$\begin{aligned} \left\{ \begin{array}{ll} {\varvec{A}}{\varvec{\alpha }}^m + {\varvec{\beta }}^m = {\varvec{b}} &{}\\ \alpha ^m_{T} = \gamma _{T} &{}\quad \forall T\in \mathcal {T}_A^{m-1},\\ \beta ^m_{T} = 0,&{}\quad \forall T\in \mathcal {T}_I^{m-1}. \end{array} \right. \end{aligned}$$

(38)

The iteration is started with ${\varvec{\alpha }}^0 = {\varvec{0}}$, $\beta ^0_T = -1$ for all $T\in {\mathcal T}_h$, and the stopping criterion is $\Vert \alpha ^{m+1} - \alpha ^{m}\Vert _{\ell ^2(\mathbb {R}^{N_h^k})} < 10^{-6}$. The weighting parameter is set to $c=1$. The above linear system is solved using the PARDISO direct linear solver included in the Intel MKL library. For further insight into the implementation of HHO methods, the reader is referred to [15]. The open-source template library DiSk++ is available at https://github.com/wareHHOuse/diskpp (see tag papers/obstacle).

Fig. 1

Isocontours of the 2D exact solution obtained on one of the hexagonal meshes

5.2 2D and 3D Test Cases

In 2D, we consider the square domain $\varOmega = (-1,1)^2$ and the obstacle function $\chi = 0$. We prescribe a contact radius $r_0 = 0.7$ and, setting $r^2 = x^2 + y^2$, we take the load function

$$\begin{aligned} f(x,y) := {\left\{ \begin{array}{ll} -4\left( 4r^2 - 2r_0^2\right) &{}\quad \text {if } r > r_0, \\ -8r_0^2\left( 1 - r^2 + r_0^2\right) &{} \quad \text {if } r \le r_0. \end{array}\right. } \end{aligned}$$

(39)

It can be shown that the exact solution solving (3) is $u(x,y) = \max (r^2 - r_0^2, 0)^2$. Isocontours of the exact solution obtained using one of the hexagonal meshes from our tests are displayed in Fig. 1. In 3D, we consider the cubic domain $\varOmega = (0,1)^3$ and the obstacle function $\chi = 0$. We prescribe again a contact radius $r_0 = 0.7$ and, setting $r^2 = x^2 + y^2 + z^2$, we take the load function

$$\begin{aligned} f(x,y,z) := {\left\{ \begin{array}{ll} -4\left( 5r^2 - 3r_0^2\right) &{}\quad \text {if } r > r_0, \\ -8r_0^2\left( 1 - r^2 + r_0^2\right) &{}\quad \text {if } r \le r_0, \end{array}\right. } \end{aligned}$$

(40)

so that the exact solution solving (3) is $u(x,y,z) = \max (r^2 - r_0^2, 0)^2$.

Table 1 Errors and convergence rates on triangular meshes, with both strong and Nitsche-based boundary conditions

Table 2 Errors and convergence rates on square Cartesian meshes, with both strong and Nitsche-based boundary conditions

Table 3 Errors and convergence rates on hexagonal meshes, with both strong and Nitsche-based boundary conditions

Table 4 Errors and convergence rates on tetrahedral meshes, with both strong and Nitsche-based boundary conditions

Table 5 Errors and convergence rates on cubic Cartesian meshes, with both strong and Nitsche-based boundary conditions

Table 6 Errors and convergence rates on hexagonal-based-prismatic meshes, with both strong and Nitsche-based boundary conditions

Fig. 2

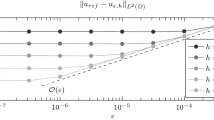
Summary of the convergence results for the 2D (top) and 3D (bottom) test cases, with both strong (left) and Nitsche-based boundary conditions (right). The mesh size is on the horizontal axis, and the energy error on the vertical axis. Solid lines (green color) show the results for $k=0$, and dashed lines (red color) for $k=1$ (Color figure online)

The computations are run on six types of mesh sequences. In 2D, we consider triangular, square Cartesian, and hexagonal mesh sequences, whereas in 3D, we consider tetrahedral, cubic Cartesian, and hexagonal-based-prismatic mesh sequences (this last mesh sequence corresponds to the set “F” of the FVCA6 benchmark [27]). Each mesh sequence is generated by successive uniform refinements from an initial coarse mesh; for the meshes involving hexagons, the process is performed on an underlying simplicial mesh and the hexagons are then created by agglomeration. The energy errors and convergence orders are reported in Tables 1, 2 and 3 for triangular, square Cartesian, hexagonal mesh sequences (2D) and in Tables 4, 5 and 6 for tetrahedral, cubic Cartesian, and hexagonal-based-prismatic mesh sequences (3D). A summary of the results is presented in Fig. 2. In all cases, we observe that the reported results match the theoretical predictions from the analysis. Moreover, there is practically no difference in terms of error when strong or Nitsche-based boundary conditions are used. In the latter case, we used the value $\varsigma =100$ for the penalty parameter (there is no appreciable difference in the errors between $\varsigma = 50$ and $\varsigma = 100$).