1 Introduction

The advent of exascale computing presents a disruptive shift in computer architectures. With the end of Moore’s law, applications can no longer rely on improving clock frequencies to further computational capabilities. The continued gains in computational performance are rather obtained through increasing core counts, which have been growing at exponential rates over the past decade and are forecasted to continue this trend in the near future with an exascale simulation expected to manage billions of concurrent threads [38]. On the “Stampede” series of NSF flagship supercomputing clusters at the Texas Advanced Computing Center, this has represented an over fourfold increase in the number of cores per node, going from 16 cores per node on Stampede1 to 68 cores per node on Stampede2.

This growth of concurrency makes application performance increasingly sensitive to synchronization mechanisms common in current parallelization strategies such as bulk-synchronous message passing or fork-join parallelism. Task-based parallelism has been noted as an attractive alternative programming model for handling power-constrained design choices including complex memory hierarchies, node heterogeneity, and asynchrony [1]. Fundamentally, task-based parallelism expresses an algorithm as a directed acyclic graph where the vertices are the application’s tasks and the edges represent data-dependencies between tasks. By allowing tasks to be scheduled as soon as their dependencies have been satisfied, task-based parallelism naturally gives rise to behaviors such as work stealing and message latency hiding. There has been extensive work on developing task-based programming models, creating a diverse ecosystem of software packages, e.g. Chapel [4, 13], Charm++ [36], HPX [29, 35], Legion [6], StarPU [2], and OpenMP starting with Version 3.0 [49].

The aim of this paper is to examine the performance of HPX versus a MPI parallelization. HPX is a standards-oriented C++ runtime system, which emphasizes the use of lightweight threads and algorithm dependent synchronization to utilize the concurrency exposed by these new architectures. HPX has been demonstrated to be highly scalable, scaling out to hundreds of thousands of cores for computational astrophysics simulations [28].

The motivating application for this work is the numerical simulation of large-scale coastal ocean physics, in particular, the modeling of hurricane storm surges. One of the leading simulation codes in this area is the Advanced Circulation (ADCIRC) model, developed by a large collaborative team including some of the co-authors [11, 17,18,19, 32, 33, 43, 52]. ADCIRC is a Galerkin finite element based model that uses continuous, piecewise linear basis functions defined on unstructured triangular meshes. The model has been parallelized using MPI and has been shown to scale well to a few thousand processors for large-scale problems [51]. While ADCIRC is now an operational model within the National Oceanographic and Atmospheric Administration’s Hurricane Surge On-Demand Forecast System (HSOFS), its performance on future computational architectures is dependent on potentially restructuring the algorithms and software used within the model. Furthermore, ADCIRC provides a low-order approximation and does not have special stabilization for advection-dominated flows, thus requiring a substantial amount of mesh resolution. Extending it to higher-order or substantially modifying the algorithms within the current structure of the code is a challenging task.

With this in mind, our group has also been investigating the use of discontinuous Galerkin (DG) methods for the shallow water equations [12, 39, 41, 42, 44,45,46,47, 53, 54], focusing on the Runge–Kutta DG method as described in [14]. We have shown that this model can also be applied to hurricane storm surge [16]. DG methods have potential advantages over the standard continuous Galerkin methods used in ADCIRC, including local mass conservation, ability to dynamically adapt the solution in both spatial resolution and polynomial order (hp-adaptivity), and potential for more efficient distributed memory parallelism [40]. While DG methods for the shallow water equations have not yet achieved widespread operational use, recent results have shown that for solving a physically realistic coastal application at comparable accuracies, the DG model outperformed ADCIRC in terms of efficiency by a speed-up of 2.3 and when omitting eddy viscosity, a speed-up of 3.9 [9]. In this paper, we will focus on the DG method applied to the shallow water equations and examine its parallel performance using both HPX and MPI. Based on the knowledge gained, we plan to extend this work to include additional physics necessary for modeling hurricane storm surge; however, in this paper we will focus on a simple test problem that captures the basic algorithm needed for any DG approximation of a shallow water system. One can expect that our results would extend to the application of Runge–Kutta DG methods for general conservation laws.

2 High Performance ParalleX

As computer architectures adapt to meet the design requirements of an exascale system, one of the most disruptive features of the proposed chips is the deluge of concurrency. Applications need to be able to expose increasingly fine grain parallelism to fully utilize these modern architectures. HPX is a C++ runtime system that is designed to take advantage of this concurrency using a task-based approach.

To motivate the design of HPX, we begin with the issues that HPX attempts to address. The Ste||ar groupFootnote 1 has coined the term S.L.O.W. to describe behaviors of multithreaded applications that hinder performance. The four components of S.L.O.W. are:

  1. 1.

    Starvation: cores idling due to insufficient parallelism exposed by the application,

  2. 2.

    Latency: delays induced by waiting on dependencies, e.g. waiting on messages which are sent through a cluster’s interconnect,

  3. 3.

    Overhead: additional work performed for a multithreaded application which is unnecessary in a sequential implementation,

  4. 4.

    Waiting for contention resolution: delays associated with the accessing of shared resources between threads.

In addition, HPX provides an elegant programming model based on and extending the C++ concurrency technical specification. Rather than forcing application developers to write efficient multithreaded code, which can lead to difficult to debug race conditions, HPX interfaces with the application at a task-dependency graph based level, taking care of issues such as scheduling. This guards application developers from common multithread-related pitfalls, and in doing so, increases developer productivity.

The HPX runtime system can be categorized into five major components described in the following subsections. A diagram of these components is displayed in Fig. 1.

Fig. 1
figure 1

Software stack diagram of the five major HPX components

Full size image

2.1 Local Control Objects

As mentioned previously, the application interfaces with HPX at the level of the application’s task dependency graph. The basic abstraction used in HPX is futurization. The completion of any given function returning a type T can be represented by a future, e.g.

figure a

When this function is invoked, an HPX-thread is created, which the HPX runtime will schedule and execute. Once the function has been executed, the return value can be retrieved. Upon which, the future is said to have returned.

While futures are used to represent the vertices of the application’s task-dependency graph, local control objects (LCOs) define the directed edges. One commonly used LCO is the then construct. As a member function of hpx::future, hpx::future::then accepts a function object as its argument, which will be executed upon the returning of the given future. The return type is itself a future, corresponding to the completion of the task being passed in hpx::future::then’s argument. The then construct allows the result of one function to be used in the evaluation of the continuation without having to explicitly wait for the first future to have returned.

Additional LCOs include hpx::when_all and hpx::when_any. These LCOs accept a collection of futures as arguments, and return a future, which will be returned either when one or all of the argument futures have returned, respectively. An example use case for hpx::when_all would be for a stencil-like kernel. We would like to evaluate the next timestep only after both the internal work and messages have been processed. hpx::when_all provides the means to represent this dependency relationship. For a full list of LCOs, we refer the reader to the HPX documentation [35].

Lastly, the task dependency graph can be forked using shared futures or nested parallelism. Since futures are simply C++ objects, the HPX runtime is able to handle nested parallelism simply by instantiating several futures at once. This approach suffices in the case that we begin with one task, and would like to parallelize the evaluation of several sub-tasks nested within the given task. However, in general, we rely on hpx::shared_future. One important aspect of hpx::future is that once the future has returned, the future’s data descopes and becomes inaccessible. In order to support multiple dependents, HPX has introduced the hpx::shared_future. For a given shared future, HPX manages the lifetime of the contents of the future in a manner akin to std::shared_ptr, descoping the data only after all the dependents have retrieved the shared future’s content. Thus, several then continuations may be attached to the same shared future, or the shared future may be passed to several LCOs. A pictorial overview of these LCOs is shown in Fig. 2.

Fig. 2
figure 2

Visual representation of how LCOs can be used to generate a task dependency graph in HPX. a Shows the input task x and the follow-up task, y. Using the then continuation once x has returned, y will be scheduled. b Shows \(\{x_i\}\) input tasks and one output task, y. Using the hpx::when_all construct, when all futures associated with \(\{x_i\}\) have returned, y may be executed. c Shows the input task x with dependents \(\{y_i\}\). Once the shared future x has returned, any \(y_i\) may be evaluated. The HPX runtime manages the lifetime of the shared future associated with the output of x, ensuring that the return value of x will remain available for each of the \(y_i\)

Full size image

2.2 Threading Subsystem

Once the task dependency graph has been created, the HPX runtime must execute the tasks, return the futures, and satisfy the dependencies. In doing so, HPX is particularly careful to avoid the pitfalls outlined by S.L.O.W.. Given the large overheads associated with spawning and joining operating system threads (OS threads), HPX provides lightweight HPX-threads that execute the tasks associated with the futures created by the application. The scheduler is implemented using an M : N hybrid scheduler [30]. Furthermore, the scheduler has been optimized for rapid context switching of HPX threads. This context switching plays a significant role in mitigating the effects of thread contention and network latencies. If a thread is unable to make progress, the scheduler is able to efficiently switch out the HPX thread and execute a different HPX thread. Ideally, after that thread has finished, the impediment of the original thread’s progress will have been resolved, and the application can resume without the core ever idling. This example illustrates one of HPX’s design principles: rather than relying on improving interconnect technologies to lower latencies, latencies are hidden by doing useful work until the required dependencies have arrived.

2.3 Active Global Address Space

While the threading subsystem operates within a single private address space, HPX extends its programming model to distributed runs via an active global address space (AGAS). Global address spaces attempt to emulate the ease of programming on a single node, while still maintaining tight control over data locality necessary for writing a performant distributed code. Two well-known global address space models are UPC [22] and Co-Array Fortran [48]. While global address space models like UPC’s partitioned global address space (PGAS) are more data-centric, e.g. by exposing pointers to memory addresses on different nodes, HPX approaches global address spaces in a more object-oriented manner.

AGAS consists of a collection of private address spaces, called localities. Each locality will run its own instance of the threading subsystem, scheduling threads with locally available resources. In practice, localities are typically chosen to be nodes or non-uniform memory access (NUMA) domains. The basic addressable unit in AGAS is the component. Components encapsulate the objects the user would like to remotely access. To interact with a component, the user must go through a smart-pointer-like wrapper class called a client. The client can not only manage the component’s lifetime via the “Resource acquisition is initialization” (RAII) idiom, but also exposes remotely invokable member functions. Clients can either reside on the same or different locality as their associated component. When a remote locality executes a client member function, HPX will send an active message to the locality where the component is located, execute the function there, and return the result to the client. By interfacing with components through clients, AGAS provides equivalent local and distributed semantics, simplifying the programming of distributed applications.

The key difference between AGAS and other global address space models is its native support for component migration. HPX’s AGAS layer allows the developer to relocate components to different localities during runtime. With all component functions being invoked through the client interface, HPX is able to ensure that the component functions invoked through the client will be executed on the correct localities, guaranteeing the application’s correctness. This functionality can be used to accelerate applications via dynamic load balancing. However, since component migration potentially requires sending large quantities of data through the interconnect, and the load profile is application dependent, HPX requires the application to manage component relocation.

Furthermore, the AGAS does not absolve the programmer of knowledge of where data is located. Since communicating across localities is a relatively expensive operation, the developer is still obliged to minimize this traffic. However, the AGAS guarantees that the task graph will be correctly executed in light of a dynamic distribution of the components across multiple localities.

2.4 Parcel Transport Layer

The parcel transport layer is the abstraction through which HPX sends messages. For this paper, we rely exclusively on the MPI parcelport, which sends messages using MPI_Isend and MPI_Irecv [30]. However, for optimal interconnect performance, HPX would be able to utilize vendor specific APIs. Note that the implementation of these vendor-specific parcelports through the OpenFabrics Interfaces API [27] are the subject of ongoing work.

2.5 Performance Counter Framework

The last major component of HPX is the performance counter framework. The increase in complexity of both computing architectures and applications has led to challenges in efficiently profiling performance. HPX integrates the process of profiling into the runtime, providing a lightweight mechanism for monitoring application behavior. These counters can not only inspect HPX-related quantities, such as the number of active AGAS components or the length of thread queues, but also provide hooks to hardware counters via PAPI [8] to directly measure low-level performance features such as memory bandwidth usage and cache misses [26]. With the performance counter framework integrated natively into the HPX runtime system, counters can readily be evaluated by the application, enabling optimizations such as autotuning.

3 Application: The Two-Dimensional Shallow Water Equations

The prediction of hurricane storm surge involves solving physics-based models that determine the effect of wind stresses pushing water onto land and the restorative effects of gravity and bottom friction. These flows typically occur in regimes where the shallow water approximation is valid [21, 46]. Taking the hydrostatic and Boussinesq approximations, the governing equations can be written as

$$\begin{aligned} \partial _t \zeta + \nabla \cdot {\mathbf {q}}&= 0,\\ \partial _t q_x + \nabla \cdot ( {\mathbf {u}}q_x) + \partial _x g(\zeta ^2/2 + \zeta b)&= g \zeta \partial _x b + S_1,\\ \partial _t q_y + \nabla \cdot ( {\mathbf {u}}q_y) + \partial _y g( \zeta ^2/2 + \zeta b)&= g \zeta \partial _y b + S_2, \end{aligned}$$

where:

  • \(\zeta \) is the water surface height above the mean geoid,

  • b is the bathymetry of the sea floor with the convention that downwards from the mean geoid is positive,

  • \(H = \zeta + b\) is the water column height,

  • \(\mathbf {u} =\left[ u \, , \, v\right] ^T\) is the depth-averaged velocity of the water,

  • \(\mathbf {q} = H \mathbf {u} = \left[ q_x \, , \, q_y \right] ^T\) is the velocity integrated over the water column height.

Additionally, g is the acceleration due to gravity, and \(S_1\) and \(S_2\) are source terms that introduce additional forcing associated with relevant physical phenomena, e.g. bottom friction, Coriolis forces, wind stresses, etc.

3.1 The Discontinuous Galerkin Finite Element Method

The discontinuous Galerkin (DG) kernel originally proposed by Reed and Hill [50] has achieved widespread popularity due to its stability and high-order convergence properties. For an overview on the method, we refer the reader to [15, 31] and references therein. For brevity, we forgo rigorous derivation of the algorithm, but rather aim to provide the salient features of the algorithm to facilitate discussion of the parallelization strategies.

We can rewrite the shallow water equations in conservation form

$$\begin{aligned} \partial _t {\mathfrak {U}} + \nabla \cdot \mathbf {F}(t,\mathbf {x}, {\mathfrak {U}}) = S(t,\mathbf {x},{\mathfrak {U}}), \end{aligned}$$
(1)

where

$$\begin{aligned} {\mathfrak {U}} = \begin{pmatrix}\zeta \\ q_x \\ q_y \end{pmatrix}, \quad \mathbf {F} = \begin{pmatrix}q_x &{}&{} q_y \\ u^2H + g(\zeta ^2/2 + \zeta b) &{}&{} uv H \\ uv H &{}&{} v^2 H + g ( \zeta ^2 /2 + \zeta b) \end{pmatrix}. \end{aligned}$$

Let \(\varOmega \) be the domain over which we would like to solve Eq. (1), and consider a mesh discretization \(\varOmega ^h = \cup _e^{n_{el}} \varOmega _e^h\) of the domain \(\varOmega \), where \(n_{el}\) denotes the number of elements in the mesh.

We define the discretized solution space, \({\mathcal {W}}^h\) as the set of functions such that for each state variable the restriction to any element \(\varOmega _e^h\) is a polynomial of degree p. Note that we enforce no continuity between element boundaries. Let \(\langle f , g\rangle _{\varGamma } = \int _{\varGamma } fg \,\mathrm {d}x\) denote the \(L^2\) inner product over a set \(\varGamma \). The discontinuous Galerkin formulation then approximates the solution by projecting \({\mathfrak {U}}\) onto \({\mathcal {W}}^h\) and enforcing Eq. (1) in the weak sense over \({\mathcal {W}}^h\), i.e.

$$\begin{aligned} \langle \partial _t \mathbf {U} + \nabla \cdot F(t,\mathbf {x},\mathbf {U}) - S(t,\mathbf {x}, \mathbf {U}) , \mathbf {w}\rangle _{\varOmega ^h} = 0 \end{aligned}$$

for all \(\mathbf {w} \in {\mathcal {W}}^h\), where \(\mathbf {U} \in {\mathcal {W}}^h\) denotes the projected solution. Due to the discontinuities between elements in both trial and test spaces, particular attention must be given to the flux integral, \(\langle \nabla \cdot F(t,\mathbf {x},\mathbf {U}) , \mathbf {w}\rangle _{\varOmega ^h}\), which is not well-defined between elements even in a distributional sense. For evaluation, we define this term as

$$\begin{aligned} \langle \nabla \cdot F(t,\mathbf {x},\mathbf {U}) , \mathbf {w}\rangle _{\varOmega ^h} \equiv \sum _{e=1}^{n_{el}} \left( \langle \widehat{\mathbf {F} \cdot \mathbf {n}} , \mathbf {w}\rangle _{\partial \varOmega _e} - \langle F(t,\mathbf {x},\mathbf {U}) , \nabla \mathbf {w}\rangle _{\varOmega _e} \right) , \end{aligned}$$

where the boundary integral’s integrand is replaced with a numerical flux \(\widehat{\mathbf {F} \cdot \mathbf {n}}(\mathbf {U}^{int}, \mathbf {U}^{ext}) \mathbf {w}^{int}\). To parse this term, let \(\mathbf {U}^{int}\) and \(\mathbf {w}^{int}\) denote the value of \(\mathbf {U}\) and \(\mathbf {w}\) at the boundary taking the limit from the interior of \(\varOmega ^h_e\), and let \(\mathbf {U}^{ext}\) denote the value of \(\mathbf {U}\) at the boundary by taking the limit from the interior of the neighboring element. For elements along the boundary of the mesh, the boundary conditions are enforced by setting \(\mathbf {U}^{ext}\) to the prescribed values. For the numerical flux, \(\widehat{\mathbf {F}\cdot \mathbf {n}}\), we use the local Lax–Friedrichs flux,

$$\begin{aligned} \widehat{\mathbf {F} \cdot \mathbf {n}}(\mathbf {U}^{int}, \mathbf {U}^{ext}) = \frac{1}{2} \left( {\mathbf {F}}(\mathbf {U}^{int}) + {\mathbf {F}}(\mathbf {U}^{ext}) + |\varLambda | (\mathbf {U}^{ext} - \mathbf {U}^{int}) \right) \cdot {\mathbf {n}}, \end{aligned}$$

where \({\mathbf {n}}\) is the unit normal pointing from \(\varOmega ^h_e\) outward, and \(|\varLambda |\) denotes the magnitude of the largest eigenvalue of \(\nabla _u {\mathbf {F}} \cdot \mathbf {n}\) at \(\mathbf {U}^{int}\) or \(\mathbf {U}^{ext}\).

Since the indicator functions over each element are members of \({\mathcal {W}}^h\), consider the set \(B_e\) for a given element \(\varOmega _e\),

$$\begin{aligned} B_e = \left\{ p {\mathbf {1}}_{\varOmega _e} \, : \, p \in \bigoplus _{d=1}^3 {\mathcal {P}}^p(\varOmega ^h)\right\} \subset {\mathcal {W}}^h, \end{aligned}$$

where \({\mathcal {P}}^p(\varGamma )\) is the set of polynomials of degree p on \(\varGamma \), and \({\mathbf {1}}_{\varGamma }\) is the indicator function over \(\varGamma \), i.e. \({\mathbf {1}}_{\varGamma }(x)\) is 1 if \(x \in \varGamma \) and 0 if \(x \not \in \varGamma \). Since \(\{B_e\}_{e=1}^{n_{el}}\) spans \({\mathcal {W}}^h\), the discontinuous Galerkin method can be alternatively formulated as

$$\begin{aligned} \partial _t \langle \mathbf {U} , \mathbf {w} \rangle _{\varOmega ^h_e} = \langle \mathbf {F} , \nabla \mathbf {w} \rangle _{\varOmega ^h_e} - \langle \widehat{\mathbf {F}\cdot \mathbf {n}} , \mathbf {w} \rangle _{\partial \varOmega ^h_e} + \langle \mathbf {S} , \mathbf {w} \rangle _{\varOmega ^h_e} \end{aligned}$$
(2)

for all \(\mathbf {w} \in \bigoplus _{d=1}^3 {\mathcal {P}}^p(\varOmega _e^h)\) and for all \(e = 1, \ldots , n_{el}\).

In order to convey more clearly the implementation of such a kernel in practice, consider the element \(\varOmega _e^h\). For simplicity of notation for the remainder of the subsection we drop all element-related subscripts, e. Over this element, we can represent our solution using a basis, \(\{ \varphi _i\}_{i=1}^{n_{dof}}\). Then we can let our solution be represented as

$$\begin{aligned} \mathbf {U}(t,x) = \sum _{i=1}^{n_{dof}} \tilde{\mathbf {U}}_i(t) \varphi _i(x), \end{aligned}$$

where \(\tilde{\mathbf {U}}\) are the basis-dependent coefficients describing \(\mathbf {U}\). Following the notation of Warbuton [23], it is possible to break down Eq. (2) into a set of kernels as

$$\begin{aligned} \partial _t \tilde{\mathbf {U}}_i = \sum _{j=1}^{n_{dof}} {\mathcal {M}}_{ij}^{-1}\left( \underbrace{\langle \mathbf {F} , \nabla \varphi _j \rangle _{\varOmega ^h_e}}_{{\mathcal {V}}_{j}} + \underbrace{\langle \mathbf {S} , \varphi _j \rangle _{\varOmega ^h_e}}_{{\mathcal {S}}_{j}} - \underbrace{\langle \widehat{\mathbf {F}\cdot \mathbf {n}} , \varphi _j \rangle _{\partial \varOmega ^h_e}}_{{\mathcal {I}}_{j}} \right) , \end{aligned}$$
(3)

where \({\mathcal {M}}_{ij} = \langle \varphi _i , \varphi _j \rangle _{\varOmega ^h_e}\) denotes the local mass matrix. Here we define the following kernels:

  • \({\mathcal {V}}\): The volume kernel,

  • \({\mathcal {S}}\): The source kernel,

  • \({\mathcal {I}}\): The interface kernel.

To discretize in time, we use the strong stability preserving Runge–Kutta methods [24]. Letting

$$\begin{aligned} {\mathcal {L}}^h \left( \tilde{\mathbf {U}}\right) = {\mathcal {M}}^{-1}\left( {\mathcal {V}}\left( \tilde{\mathbf {U}}\right) + {\mathcal {S}}\left( \tilde{\mathbf {U}}\right) - {\mathcal {I}}\left( \tilde{\mathbf {U}}\right) \right) , \end{aligned}$$

we can define the timestepping method, for computing the i-th stage as

$$\begin{aligned} \tilde{\mathbf {U}}^{(i)} = \sum _{k=0}^{i-1} \alpha _{ik} \tilde{\mathbf {U}}^{(k)} + \beta _{ik} \varDelta t {\mathcal {L}}^h\left( \tilde{\mathbf {U}}^{(k)}\right) , \end{aligned}$$

where \(\tilde{\mathbf {U}}^{(k)}\) denotes the basis coefficients at the k-th Runge–Kutta stage. We denote the operator, which maps \(\left\{ \tilde{\mathbf {U}}^{(k)},\,{\mathcal {V}}\left( \tilde{\mathbf {U}}^{(k)}\right) ,\,{\mathcal {S}}\left( \tilde{\mathbf {U}}^{(k)}\right) ,\,{\mathcal {I}}\left( \tilde{\mathbf {U}}^{(k)}\right) \right\} _{k=0}^{i-1}\) to \(\tilde{\mathbf {U}}^{(i)}\) as the update kernel, \({\mathcal {U}}\).

3.2 Parallelization Strategies

In order to parallelize the DG method, we observe that the evaluation of one Runge–Kutta stage of an element solely depends on the information of the element and its edge-wise neighbors for the previous Runge–Kutta stages. With the intent of parallelization, the DG method can be thought of as a stencil code with an unstructured communication pattern.

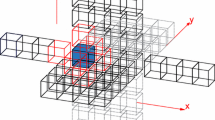
We assume that our computing environment can be modeled via a Candidate type architecture. Beyond ensuring that each CPU has access to sufficient work, the candidate type architecture approximation allows us to optimize communication patterns taking into account the difference in intra- and inter-node message latencies. The mesh partitioning is thus broken into 2 phases. An overview of the mesh partitioning strategy is shown in Fig. 3.

Fig. 3
figure 3

Overview of the mesh partitioning strategy. The first partitioning phase assigns elements to submeshes, forming our submesh partition. These submeshes are then assigned to localities, balancing the compute load across nodes

Full size image

In both partitioning phases, we aim to balance the compute load between partitions while minimizing the communication. Since the computational complexity of all kernels is \({\mathcal {O}}(n_{el})\), the number of elements can be used as a proxy for the computational load. Additionally, we assume that the communication is minimized when the number of edge cuts is minimized. All partitioning is performed using the METIS_PartGraphKway function from the METIS library [37].

The first partitioning phase decomposes the mesh into submeshes. For HPX, these submeshes define the granularity of parallelism exposed to the runtime, and ultimately determine the task dependency graph. For MPI, these submeshes correspond to the data assigned to individual MPI ranks. The graph partitioned in this phase uses the mesh’s elements as the graph’s vertices and places edges between edge-wise connected elements.

The second phase of the graph partitioning assigns submeshes to localities. Since the communication between submeshes is predicated by their shared interface, we can construct a graph from the submeshes of the previous partition. To balance the load, we weight the vertices of this second graph according to the number of elements associated with the relevant submesh, and weight the edges by the number of edge-cuts performed on the element-level graph between two submeshes. For both parallelization strategies, this second partitioning ensures that submeshes which communicate frequently with one another are more likely to be assigned to the same locality.

Beyond balancing the computational load, we include two DG specific optimizations from [3]:

  1. 1.

    Reduction of message sizes, by only sending state variables evaluated at quadrature points along shared interfaces. This reduces message sizes from \({\mathcal {O}}(p^2)\) to \({\mathcal {O}}(p)\) per shared interface, where p is the polynomial order of the DG discretization,

  2. 2.

    Hiding message latencies by first sending messages and then computing internal work before waiting for the messages to arrive.

Each Runge–Kutta stage update is broken into two steps as shown in Algorithms 1 and 2. We denote edges whose neighboring elements are assigned to the same submesh as internal interfaces, and edges whose neighboring elements are located on different submeshes as shared interfaces. Based on the data dependencies, the interface kernel can be evaluated for the internal interfaces as soon as SUBMESH_UPDATE_B of the previous timestep has returned, and thus these evaluations are used to hide send latencies. However, for the shared interfaces, the interface kernel relies on neighboring data, and therefore can only be evaluated once the messages from neighboring submeshes have arrived. These optimizations are applied to both our HPX and MPI implementations. Nevertheless there remain implementation specific details.

figure b
figure c

3.2.1 HPX Parallelization

For the HPX implementation, each locality maintains a vector of submeshes. The number of elements per submesh determines the grain size of parallelism. In selecting the grain size, one must balance two factors. If the grain size is too fine, task overheads will dominate the execution time. On the other hand, if the grain size is too large, we risk exposing insufficient parallelism and performance may suffer due to resource starvation. Due to discrete effects, the grain size is modulated in practice through an oversubscription factor, which is defined as the number of submeshes per core on a locality.

For a given submesh, the evaluation of Algorithms 1 and 2 are futurized, and the futures are chained together via hpx::future::then continuations. Furthermore, in Algorithm 1, rather than explicitly waiting for all messages to have been processed, we return a future that will return once all messages have been received and sent.

The use of futurization provides the key advantage of ceding control back to the runtime without unnecessarily suspending the OS thread. While the HPX runtime will internally monitor and process the messages associated with the given submesh, if available, the HPX scheduler will schedule other submesh updates whose dependencies have been satisfied on that OS thread. Thus, even though the locality is waiting for certain messages to arrive before the given submesh update can be completed, the HPX runtime is nonetheless able to use that core to execute tasks associated with other submeshes. Once all the message-related futures have returned, the continuation of the submesh update will be scheduled, and ideally, the application will have progressed without letting cores idle.

3.2.2 MPI Parallelization

The MPI implementation assigns one MPI rank to each core. These ranks communicate with one another via persistent, non-blocking, point-to-point routines. The messages are waited upon using an MPI_Waitall with the MPI requests of the local sends and receives as arguments. In the case that the messages have not arrived at the time the MPI_Waitall is called, the core will wait on these messages, halting local application progress.

One advantage of this approach is that—similar to HPX—each submesh waits solely on the messages of its neighbors. In doing so, we avoid one of the pitfalls of fork-join parallelism. To ensure application correctness, threads must be synchronized before leaving the fork-join parallel region. With increasing core counts on future architectures, the performance of a fork-join programming model is limited by Amdahl’s law. While using MPI to perform shared memory message passing introduces some unnecessary overhead, the fundamental programming model bypasses this limitation of a fork-join approach.

Lastly, although the send latency is partially hidden by completing internal work before waiting on the messages to arrive, the latency hiding capability of the MPI implementation is limited by the size of the submesh assigned to the MPI rank. With increasing concurrency on future architectures, this MPI parallelization’s latency hiding technique will become less efficient.

4 Results

4.1 Experimental Configuration

Table 1 Hardware specifications of the Knights Landing architecture on Stampede2
Full size table

To assess the advantages of using an HPX over MPI parallelization, we perform strong and weak scaling studies on the Intel Knights Landing (KNL) architecture—a many-core architecture with 68 cores per node. A detailed description of the KNL architecture is provided in Table 1. The software configuration and workflow used to generate the subsequent results are detailed in Appendix A.

As the intent of this paper is not to present high-order methods for hurricane storm surge modeling, but rather a performance comparison of parallelization strategies, we restrict ourselves to solving the 1D inlet problem from [41]. Consider the rectangular domain defined as the Cartesian product \((x_1,x_2)\times (y_1,y_2)\) with \(x_1 = 0\,{\mathrm {km}},\, x_2= 90\,{\mathrm {km}},\, y_1 = 0\,{\mathrm {km}},\,y_2 = 45\,{\mathrm {km}}\). Additionally, the acceleration due to gravity is set to \(g=9.81\,{\mathrm {m}}/{\mathrm {s}}^2\), and the bathymetry is constant with depth \(H_0=3\,{\mathrm {m}}\). For the boundary conditions, let the superscripts ex/in correspond to the exterior and interior values at the boundary, respectively. Across the boundary \((x_1,y_1)-(x_1,y_2)\), we force a tidal boundary condition, i.e.

$$\begin{aligned} \zeta ^{ex} = A \cos \left( \varOmega t + \eta \right) \quad \text {and} \quad \mathbf {q}^{ex} = \mathbf {q}^{in}, \end{aligned}$$

where \(A = 0.3\,{\mathrm {m}}\), \(\varOmega = 1.405\cdot 10^{-4}\, {\mathrm {rad}}/{\mathrm {s}}\), and \(\eta =3\pi /2\,{\mathrm {rad}}\). At the remaining boundaries, we enforce a land boundary, i.e.

$$\begin{aligned} \zeta ^{ex} = \zeta ^{in} \quad \text {and} \quad \mathbf {q}^{ex} \cdot \mathbf {n} = - \mathbf {q}^{in} \cdot \mathbf {n} \quad \text {and} \quad \mathbf {q}^{ex} \cdot \varvec{\tau } = \mathbf {q}^{in} \cdot \varvec{\tau }, \end{aligned}$$

where \(\mathbf {n}\) corresponds to the normal of the boundary, and \(\varvec{\tau }\) is the tangent along the boundary.

Each mesh will be a triangulation of the domain \((x_1,\,x_2) \times (y_1,y_2)\). For each simulation, we generate the mesh by partitioning the domain into an \(2 N \times N\) Cartesian grid. Each rectangle is then halved along opposite vertices to form a triangular mesh. All simulations are run using a quadratic Dubiner basis [20]. To avoid the CFL condition-related challenges associated with the various levels of mesh refinement, we select a RKSSP-(2,2) timestepping scheme for the temporal discretization and fix \(\varDelta t=0.05\,{\mathrm {s}}\) with the end-time, \(t_{end}=150\,{\mathrm {s}}\).

We exclude initialization from our time measurements, reporting only time spent evaluating Runge–Kutta stages. For the time measurements, we use the high_resolution_clock from the STL chrono library. The termination of the timings is enforced via a global barrier. For the MPI parallelization, this is achieved by placing an MPI_Barrier call after the computation and stopping the timing once MPI rank 0 exits the barrier. For the HPX parallelization, we explicitly wait for all localities to have have finished their computations via an hpx::wait_all call, similarly achieving a global synchronization of the application’s progress.

In the following sections, we perform strong and weak scaling studies. The execution time for a given run is denoted as , where

  • y is the type of experiment, with s and w used to indicate strong and weak scaling runs, respectively,

  • x is the parallelization strategy: either HPX or MPI,

  • n is the number of nodes used for that run.

For the strong scaling study we consider a \(1448 \times 724 \times 2\) element mesh and observe the speed-ups obtained by increasing the number of nodes. For a given number of nodes, the mesh is partitioned into two submeshes per core in the case of HPX and one submesh per core for the MPI parallelization. Thus, the communication overhead and task dependency graph grow with the number of cores. In order to compare the performance of the two approaches to one another, we evaluate the parallel efficiency, which we define as

where is the strong scaling execution time using the parallelization strategy x—HPX or MPI—with n nodes, C is the number of cores per node, and \(T^*\) corresponds to the serial execution time. We remark that the serial implementation’s performance is strongly affected by the random memory access pattern associated with the unstructured mesh. To mitigate these effects, the serial execution time \(T^*\) is obtained by running the HPX parallelization with one thread while still partitioning the mesh into 136 submeshes. This overdecomposition of the mesh effectively acts as a cache blocking mechanism. For reference, the naive serial implementation ran for \(122{,}000\,{\mathrm {s}}\), and the single-threaded HPX version took \(91{,}000\,{\mathrm {s}}\). These execution times are based on the average of 10 runs, with the standard deviation being below \(0.5\%\) for both cases.

The weak scaling study is done by assigning \(1024 \times 512 \times 2\) elements to each node, and then observing the behavior as the number of nodes increases. When the node count does not permit assigning precisely this element count to each node, the nearest number of subdivisions of the domain is chosen to ensure that elements scale linearly with the number of cores, e.g. for two nodes, a mesh with \(1448 \times 724\times 2\) elements was used. For the weak scaling, we use a metric of how many elements are updated by one Runge–Kutta stage per unit time. This is can be thought of as an application specific means of measuring throughput. We begin by analyzing the performance of the partitioning approach outlined in Sect. 3.2. For the remainder of the paper, we refer to this strategy as the 2-phase partitioning strategy. Thereafter, we present comparison results between HPX and MPI parallelizations.

4.2 Vectorization

One of the key aspects of achieving performance on modern CPU architectures is the ability to effectively utilize SIMD registers. With the KNL’s AVX-512 instruction set architecture extension, vectorization potentially allows for a speed-up of 8\(\times \) for double precision arithmetic. Achieving this speed-up however is hampered by how quickly data can be provided to the processor, and how well the compiler vectorizes the code. Vectorization in the context of DG methods for shallow water flows has been extensively studied in [10]. The method presented therein relies on transforming the code via loop inversion in a way that the compiler is able to generate the optimized binaries. This approach however suffers from maintainability issues that have prevented adoption in the main branch of the code base. For the results presented here, we have utilized the Blaze linear algebra library [34]. This library provides vector and matrix abstractions and combines them with expression templates for efficient evaluation without generating temporary variables. Internally, Blaze either implements vectorized versions of these basic linear algebra operations, or offloads the calls to a BLAS implementation, e.g. Intel’s Math Kernel Library (MKL). Although the vectorization achieved by this approach is nearly identical to that in [10], it is the authors’ opinion that code generated via this approach is more maintainable and readable.

Lastly, we remark that for the chosen test cases, the kernel remains memory bandwidth bound. In particular, gathering elements’ Gauss point values at the boundaries and scattering the flux values back to the elements during the interface kernel, \({\mathcal {I}}\), generates random access patterns. Reordering local element indices to minimize element-interface connectivity matrix bandwidth would alleviate some of these issues. However, this remains an issue that we will address in a later work.

4.3 Partitioner Performance

To begin, we benchmark the 2-phase partitioning strategy against a standard flat partitioning strategy. The flat partitioning strategy consists of using METIS to partition the mesh into submeshes, and then assigning submeshes to localities in a round robin manner.

Fig. 4
figure 4

Strong scaling comparison of flat and 2-phase partitioning approaches for MPI and HPX on the Knights Landing (KNL) architecture. Each data point was simulated ten times with no data being omitted

Full size image
Fig. 5
figure 5

Weak scaling comparison of flat and 2-phase partitioning approaches for MPI and HPX on the Knights Landing (KNL) architecture. Each data point was simulated ten times with the median value being reported here. The ideal line is the ideal weak scaling based on a serial simulation

Full size image

The strong scaling results for the two partitioning approaches are shown in Fig. 4, and the weak scaling results are shown in Fig. 5. Each configuration for the strong and weak scaling studies has been run ten times. For the strong scaling studies, the execution times varied considerably, and have thus been depicted via standard box-and-whisker plots with the whiskers extending up to 1.5 times the inter-quartile range from the relevant quartile.

For the MPI parallelization, the strong scaling results are shown in Fig. 4a and the weak scaling results are shown in Fig. 5a. These scaling results show the flat partitioning approach outperforming the 2-phase partitioning approach by approximately a factor of two. This discrepancy in performance is due the fact that METIS does not strictly satisfy partitioning constraints. In the second phase of the 2-phase partitioning, the number of submeshes assigned to each locality is not strictly equal to the number of cores. Thus, there exist MPI ranks which are assigned two submeshes, while other ranks are assigned none. Since there is no mechanism for work stealing between MPI ranks, the 2-phase approach doubles the length of the critical path of the task executions, causing the observed slow down. This slowdown for the 2-phase partitioning strategy is most clearly observed at 128 nodes for the weak scaling study where is 0.50. This aspect of METIS has been extensively studied in [5]. Nevertheless, it is worth noting that the flat partitioning approach proves to be highly scalable with the median parallel efficiency decreasing 2.5% between 1 node and 64 nodes for the strong scaling study, and for the weak scaling study, .

In contrast, the partitioning results for HPX show the 2-phase approach significantly outperforming the flat partitioning approach. For the strong scaling results shown in Fig. 4b, the 2-phase partitioning strategy is able to achieve comparable parallel efficiencies to the flat approach with as few as an eighth of the elements per submesh that the flat approach requires. Specifically, on the KNL nodes, we observe that using 2 nodes and a flat partitioning scheme we obtain a parallel efficiency of 23.6%, on the other hand, using the 2-phase approach we are able to scale out to 16 nodes, with a parallel efficiency of 19.1%. Similar to the MPI parallelization, the 2-phase partitioner assigns non-uniform numbers of submeshes to each locality. However, since the submeshes are assigned according to their approximate computational load, the partitioner nevertheless balances the load, and aggressive work stealing by the HPX scheduler and over-subscription of submeshes ensure that cores are given sufficient work. While the flat partitioning ensures that numbers of submeshes assigned to each node is constant, the increase of inter-node communication strongly affects HPX’s performance. HPX channels, which manage inter-component communication are able to optimize out overheads such as serializing messages when messages are sent to components on the same locality. For HPX, the key aspect to obtaining good performance is keeping the ratio of useful work to HPX overhead high. With the 2-phase partitioning, we find that we are able to maintain significantly improved performance over the flat partitioning scheme by minimizing this communication overhead. For the weak scaling comparison of the two partitioners shown in Fig. 5b, the 2-phase approach outperforms the flat partitioning approach by a factor of 3.30 at 128 nodes.

5 Comparison of HPX Versus MPI

We now directly compare the performance of the two parallelization approaches. In order to ensure a fair comparison, we consider the MPI and HPX parallelizations with their respective best partitioning schemes, i.e. comparing MPI runs using the flat partitioning approach and HPX runs using the 2-phase approach.

5.1 Single Node Performance Comparison

We begin by considering the weak scaling one node 1d inlet problem. The mesh contains 1,048,576 elements. To limit generated profiling data, we run this problem for a reduced time period of \(t_{end} = 10{\mathrm {s}}\). To profile the simulation, we use Intel’s VTune Amplifier 2018 Update 2. To add profiler support to our application code, HPX is compiled with VTune Amplifier support [35], and all binaries are compiled with debugging symbols. Otherwise, we make no modifications to the application configuration outlined in Appendix A. We additionally modify the I_MPI_FABRICS environment variable to shm.

Ignoring initialization and finalization, the MPI simulation takes \(67.9\,{\mathrm {s}}\), and the HPX simulation takes \(55.2\,{\mathrm {s}}\). Both timings are within 2% of the unprofiled runtimes. The HPX parallelization provides a speed-up of 1.23 over the MPI implementation. To help explain this performance difference, we used VTune to determine how much time the respective runs were spending in each module, i.e. the application code, libraries, and kernel calls. These results are presented in Fig. 6 and the timings are shown in Table 2. The dgswemv2 module refers to the application code. Modules hpx, mkl, mpi, and jemalloc refer to time spent in these respective libraries. Lastly, vmlinux refers to time spent in the Linux kernel.

The speed-up of the HPX parallelization versus the MPI parallelization can be attributed to two main factors: firstly, the application runs 6% faster with the HPX parallelization. Due to the overdecomposition of the mesh, the HPX parallelization uses submeshes half the size of the MPI parallelization. We suspect that the performance difference arises due to better cache behavior for the smaller submeshes. This performance difference in the evaluation speed of the RK update kernels accounts for 22.6% of the overall performance difference between the MPI and HPX parallelizations. The second factor is the difference spent evaluating Linux kernel functions and accounts for 67.4% of the performance difference. Using a bottom-up profile, the 5 most expensive functions are evaluated in the kernel for the MPI parallelization are in order: native_queued_spin_lock_slowpath, get_page_from_freelist, clear_page_c_e, handle_mm_fault, and page_fault. These functions suggest that the flat MPI parallelization generates large numbers of page faults. This overhead is not present in the HPX parallelization. These two factors account 90% of the performance discrepancy in the two approaches. Lastly, we remark that there is some imbalance, but it appears to only modestly impact application performance. The MPI implementation spends 3.9% of the time in the MPI module, including MPI_Wait calls. This is fairly small and partially offset by HPX runtime overhead. Thus, the performance discrepancy is caused by overhead generated by the MPI runtime, and not poor load balance or time spent waiting on messages to arrive.

Fig. 6
figure 6

Module composition of the discontinuous Galerkin method of HPX and MPI parallelizations

Full size image
Table 2 Time spent in modules for single node analysis for HPX and MPI parallelization
Full size table
Fig. 7
figure 7

Strong scaling results comparing the performance of HPX to MPI for up to 64 KNL nodes on Stampede2. For both machines, each simulation was run 10 times with no data being excluded

Full size image

5.2 Strong and Weak Scaling Studies

While the HPX parallelization outperforms the MPI parallelization in the single node analysis, the strong and weak scaling studies presented in this section explore the impact of task granularity and increased network communication.

The strong scaling results for the two approaches are shown in Fig. 7. For a single node run, HPX achieves a median parallel efficiency of 85.7%, and MPI achieves a parallel efficiency of 63.5%. This corresponds to a speed-up of 1.35 for the HPX parallelization relative to the MPI parallelization. We suspect that the MPI parallelization is incurring similar performance overheads to those noted in the previous section.

As we scale up in processor number, eventually the HPX task overhead begins to dominate the amount of useful work being performed, and the MPI implementation outperforms HPX. Furthermore, the scheduler’s aggressive work stealing leads to factors such as false sharing further degrading performance. It is not a question of if HPX will be slower than MPI, but rather at which point. On the KNL nodes, this point occurs around the task granularity associated with 4 nodes.

To understand the performance profile of HPX’s overhead, we look at the relation between the average task size versus the average overhead using HPX’s performance counters. The average task size, \(t_{avg}\) is computed as

$$\begin{aligned} t_{avg} = \frac{ \sum t_{app}}{n_t}, \end{aligned}$$

and the average task overhead, \(t_o\) is computed as

$$\begin{aligned} t_o = \frac{\sum t_{thread}- \sum t_{app}}{n_t}, \end{aligned}$$

where \(\sum t_{app}\) is defined as the amount of time spent executing application tasks, \(\sum t_{thread}\) is defined as the total execution time of all HPX threads, and \(n_t\) is the number of application threads. Both the average task size and the average task overhead are reported in units of time. The average task size is evaluated using the /threads/time/average counter and the average task overhead is evaluated using the /threads/time/average-overhead counter. For further details on the counters, we refer the reader to [25]. Table 3 and Fig. 8 show the composition of the thread execution times for the strong scaling results. Each run is done once, with the timings being thrown out if significant deviation from the median parallel efficiency reported in Fig. 7 was observed. For these results, the largest observed deviation was 1.1% from the median reported in the strong scaling runs reported in Fig. 7. The node configurations at which MPI outperforms HPX coincide with the task overheads comprising significant portions of the thread execution times.

Table 3 HPX thread execution composition for strong scaling runs on Knights Landing (KNL) architecture on Stampede2
Full size table
Fig. 8
figure 8

Comparison of the task overhead versus the the task size for strong scaling runs for KNL nodes on Stampede2

Full size image
Fig. 9
figure 9

Weak scaling study comparing the speed of the application to the number of nodes ranging from 1 to 128 nodes for each node type. The application speed, element updates per second is defined to be the number times any element is advanced by one Runge–Kutta stage per second. The results shown are based on the median of 10 runs

Full size image

Although the results presented here were obtained from a DG kernel for the shallow water equations, the impact of the HPX overhead can be determined by the task granularities. As such, the regimes in which HPX runs efficiently can be generalized to arbitrary stencil-type kernels. As a rule of thumb, for the KNL nodes, we recommend not scaling beyond the grain size observed at 4 nodes, which corresponds to an average task size, \(t_{avg}\) of \(3.6\,{\mathrm {ms}}\). At this granularity, HPX performs similarly to MPI. This task granularity is consistent with the results reported in [25].

For this weak scaling experiment, the task granularity is well within the regime where the HPX overhead constitutes a small fraction of the execution time. The results are shown in Fig. 9. The weak scaling results show HPX outperforming MPI across the entire set of nodes in consideration. Similar to the single node analysis and strong scaling study, HPX outperforms MPI at low node counts with on one node and decreases to 1.14 on two nodes once HPX sends messages over the interconnect. This speed-up of HPX versus MPI is maintained as we scale out to 128 nodes, with . These speed-ups underpin the conclusion of the previous sections that the key driver of HPX performance is the proper balancing of task overheads with useful work. By performing a weak scaling study, we are effectively fixing the scheduling overhead, and observe that HPX scales very well with equaling 0.86.

6 Conclusion

The massive increase in concurrency on future computer architectures necessitates the development of new programming models to efficiently utilize these architectures. In this paper, we compared the performance of an HPX versus MPI implementation of an unstructured grid DG finite element code for the shallow water equations.

Scaling results were presented for the Knights Landing processors on TACC’s Stampede2. Results indicate that with a sufficiently large task size HPX is able to outperform the MPI application by a factor of approximately 1.2 with the speed-up being attributed to lower runtime overhead. However, strong HPX performance is contingent upon the task granularities remaining above a machine dependent size. For tasks with durations shorter than this machine prescribed size, overheads will dominate the execution time. For these runs, we found that MPI outperformed HPX. When considering adopting an HPX-based parallelization, the question should be “Is this performance critical task granularity sufficiently fine for my use case?” If answered in the affirmative, we believe that HPX presents a significant improvement over traditional parallelization strategies.

One of the major benefits that remains unaddressed in this paper is the ability of HPX to efficiently execute irregular applications. Whereas the kernels evaluated in this paper are load balanced statically, there exists a large class of kernels whose task size varies at run time, e.g. adaptive mesh refinement algorithms and local timestepping. These approaches are more efficient theoretically, however, statically load balanced implementations achieve a fraction of the theoretical speed-up due to resource starvation. HPX’s aggressive on-node work stealing as well as task migration support should allow for more efficient implementations of these algorithms. These are topics of future work. Another application specifically related to the simulation of hurricane storm surge is load imbalance generated between the computational cost difference between wet and dry regions of the mesh. Validating the algorithms presented in [7] using HPX is another subject of ongoing work.

While this work has focused exclusively on the Knights Landing architecture, performance portability is another area of interest. The upcoming NERSC machine, Perlmutter, and the next TACC machine, Frontera, will both utilize manycore architectures similar to the Knights Landing architecture. While the task sizes that balance HPX overhead with application throughput will change, we expect that the results presented here should largely generalize to these CPU-based architectures. Targeting accelerator-based clusters with task-based programming models requires significantly more work, but is a topic of active development. HPX has support for evaluating CUDA and OpenCL kernels on GPUs. This approach allows HPX to utilize GPUs. However, HPX is not presently using task-based parallelism on the device itself. The viability of task-based approaches on GPUs will need to navigate the trade-offs between increased asynchrony and performance.

Ultimately, applications will require new programming models to efficiently utilize exascale machines. While the results in this paper are limited in scope, we believe they are indicative of the substantial utility of a task-based approach for the next generation of computer architectures. The observed performance benefits of HPX stem from a fundamental change in the parallelization paradigm. We remark that both MPI and OpenMP are actively changing their programming models as well. In the 3.0 standard, MPI has adopted many new features such as RDMAs and shared memory operations, while OpenMP has moved from a fork-join based parallelism model to adopting task-based parallelism and adding pragmas for SIMD support. These are features that are being broadly adopted across the high performance computing community. HPX represents one solution that incorporates these concepts in a succinct and C++ standards-oriented framework, that allows developers to productively parallelize their applications.