A Finite Element/Operator-Splitting Method for the Numerical Solution of the Two Dimensional Elliptic Monge–Ampère Equation

Abstract

We discuss in this article a novel method for the numerical solution of the two-dimensional elliptic Monge–Ampère equation. Our methodology relies on the combination of a time-discretization by operator-splitting with a mixed finite element based space approximation where one employs the same finite-dimensional spaces to approximate the unknown function and its three second order derivatives. A key ingredient of our approach is the reformulation of the Monge–Ampère equation as a nonlinear elliptic equation in divergence form, involving the cofactor matrix of the Hessian of the unknown function. With the above elliptic equation we associate an initial value problem that we discretize by operator-splitting. To enforce the pointwise positivity of the approximate Hessian we employ a hard thresholding based projection method. As shown by our numerical experiments, the resulting methodology is robust and can handle a large variety of triangulations ranging from uniform on rectangles to unstructured on domains with curved boundaries. For those cases where the solution is smooth and isotropic enough, we suggest also a two-stage method to improve the computational efficiency, the second stage being reminiscent of a Newton-like method. The methodology discussed in this article is able to handle domains with curved boundaries and unstructured meshes, using piecewise affine continuous approximations, while preserving optimal, or nearly optimal, convergence orders for the approximation error.

1 Introduction

Let $\varOmega$ be a bounded domain of $\mathbb {R}^2$. The Dirichlet problem for the canonical Monge–Ampère equation reads as

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u=f \text{ in } \varOmega ,\\ u=g \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(1)

${\mathbf {D}}^2u$ being the Hessian matrix of u, that is $\displaystyle {\mathbf {D}}^2u= \begin{pmatrix} \frac{\partial ^2 u}{\partial x_1^2} &{} \frac{\partial ^2 u}{\partial x_1 \partial x_2}\\ \frac{\partial ^2 u}{\partial x_1 \partial x_2} &{} \frac{\partial ^2 u}{\partial x_2^2} \end{pmatrix},$ the functions f and g being given. If $f>0$, problem (1) is a prototypical fully nonlinear elliptic boundary value problem. The existence and regularity properties of the solutions to fully nonlinear elliptic problems have been discussed in [2, 10, 25], a particular attention being given to the canonical Monge–Ampère equation in [31]. As shown in, e.g., [3, 9, 18, 24, 35], the Monge–Ampère equation has a wide range of applications, differential geometry, optimal transportation, physics and mechanics among them.

Starting with [39] various numerical methods have been developed for the numerical solution of fully nonlinear elliptic boundary problems, problem (1) being the most investigated by far. The fast multiplication of these methods during the last decade has made keeping track of all of them an almost impossible task. Several of them have been reported in [18], but a visit to Google Scholar has become a must to have a more complete view. Focusing on those approaches with which we have some familiarity, we will classify them roughly into two families. The methods of the first family treat a finite difference or finite element approximation of the equation under consideration (possibly coupled to a regularization procedure as done in [19, 20]; see also [18]); such methods, and the iterative solution of the resulting discrete problems, are discussed in, e.g., [1, 4,5,6, 22, 23, 34, 43]. Another approach is to reformulate the nonlinear elliptic problem as an optimization one; this can be done via least-squares or via the introduction of a well-chosen augmented Lagrangian algorithm. Such optimization based methods are discussed in e.g. [8, 11,12,13,14,15,16, 28,29,30, 35].

The method discussed in this article concerns problem (1) specifically. It relies on: (i) An equivalent divergence formulation of (1). (ii) An initial value problem associated with a mixed variant of the above divergence formulation. (iii) The time discretization by operator-splitting of the above initial value problem. (iv) An eigenvalue projection algorithm to enforce the pointwise positive semi-definiteness of the approximate Hessian at each time step. (v) A mixed finite element implementation of the above methodology. Also for those problems where the solution of (1) is sufficiently smooth and isotropic, we propose a two-stage strategy to speed up the convergence: during the first stage, the dynamical system (flow) we consider is associated with $\partial u/\partial t$, while during the second stage we use $\partial (Su)/\partial t$, S being a well-chosen elliptic operator, giving to this second stage a Newton-like flavor.

As reported in, e.g., various chapters of [30] (see also the references therein), operator-splitting methods have a long history for providing efficient solution methods for a large variety of problems modeled by partial differential equations and inequalities. Fully nonlinear elliptic equations are no exceptions: To the best of our knowledge, the first publication making use of an operator-splitting method for the solution of a fully nonlinear elliptic problem is the celebrated article [3] by J.D. Benamou and Y. Brenier on the solution of the Monge–Kantorovich optimal mass transfer problem by the alternating direction method of multipliers (ADMM), a particular operator-splitting method. The solution of (1) by another ADMM algorithm is discussed in [11, 13, 14, 16, 29, 30]. The numerical solution of the Monge–Ampère equation for domains with a curved boundary is one of the objectives of this article. Actually, one discussed in [6, 21, 32, 33] efficient methods to achieve that goal. In particular, the methods in [21, 32] are (among other things) mesh-free variants of the wide stencil finite difference methods developed by A. Oberman and his collaborators (see, e.g., [22, 38] and the references therein). Solution methods for the Monge–Ampère equation on two and three-dimensional domains with curved boundaries are discussed also in [7, 8]. Albeit relying on continuous piecewise affine approximations, like the methods in this article, the methods discussed in [7, 8] are more complicated to implement, and less robust and flexible than the quite simple and modular ones described in the following sections.

This article is organized as follows: In Sect. 2, we reformulate (1) as an elliptic problem in divergence form with which we associate an initial value problem whose time-discretization, by operator-splitting, is discussed in Sect. 3. The finite element implementation of the above operator-splitting method is discussed in Sect. 4. The two-stage strategy we mentioned above is discussed in Sect. 5. In Sect. 6 we present the results of numerical experiments. These results validate the methodology discussed in the preceding sections, including the two-stage strategy described in Sect. 5; they also show that problem (1) is solvable on domains with curved boundaries, using piecewise affine approximations associated with unstructured triangulations.

The main goal of this article was to access the possibility of solving a large variety of test problems, some of them quite singular, using continuous piecewise affine finite element approximations, associated with possibly unstructured meshes on domains with a curved boundary, while preserving good accuracy properties. The results of the many numerical experiments we have performed are promising and suggest further investigations and applications: among them, accelerating the convergence of our algorithm being an important objective, the two-stage method introduced in Sect. 5 (a Newton-like method) being just a first step in that direction. Actually, preliminary promising results suggest that the methodology introduced in the present article can be generalized to three dimensional problems, obstacle problems for the Monge–Ampère operator (like those discussed in [42]) and to the Gaussian curvature equation $\det {\mathbf {D}}^2u=K(1+|\nabla u|^2)^{1+d/2}$, with $d=2$ or 3, K (the given curvature) being a positive function.

2 A Divergence Formulation of Problem (1) and an Associated Initial Value Problem

Let us denote by $\mathrm {cof}({\mathbf {D}}^2u)$ the matrix-valued function $\begin{pmatrix} \frac{\partial ^2 u}{\partial x_2^2} &{} -\frac{\partial ^2 u}{\partial x_1 \partial x_2}\\ -\frac{\partial ^2 u}{\partial x_1 \partial x_2} &{} \frac{\partial ^2 u}{\partial x_1^2} \end{pmatrix}$. One can easily show that problem (1) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} -\nabla \cdot \left( \mathrm {cof}\left( {\mathbf {D}}^2u\right) \nabla u \right) +2f=0 \text{ in } \varOmega ,\\ u=g \text{ on } \partial \varOmega . \end{array}\right. } \end{aligned}$$

(2)

Similarly, one can also easily show that (2) characterizes formally u as being either a minimizer or a maximizer of the functional I over the space $V_g$ where

$$\begin{aligned} I(v)=\int _{\varOmega } \left( \mathrm {cof}\left( {\mathbf {D}}^2v\right) \right) \nabla v \cdot \nabla v \, dx+6\int _{\varOmega } fv dx \text{ and } V_g=\{v|v \text{ smooth },v=g \text{ on } \partial \varOmega \}. \end{aligned}$$

Assume that u is solution of (1), (2). Since the symmetric matrix-valued functions ${\mathbf {D}}^2u$ and $\mathrm {cof}({\mathbf {D}}^2u)$ are either point-wise positive definite or negative definite in the neighborhood of u, one can easily show that functional I is either convex or concave in the neighborhood of u, justifying using a well-initialized descent type method to compute the solutions of (1), (2); this can be achieved via the time integration of an initial value problem associated with (2). To partly overcome the nonlinear coupling between u and its second order derivatives we introduce a matrix-valued function ${\mathbf {p}}$ verifying the linear relation ${\mathbf {p}}= {\mathbf {D}}^2u$. Problem (2) is clearly equivalent to the following system of partial differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} -\nabla \cdot \left( \mathrm {cof}({\mathbf {p}})\nabla u\right) +2f=0 \text{ in } \varOmega ,\\ u=g \text{ on } \partial \varOmega , \end{array}\right. }\\ {\mathbf {p}}-{\mathbf {D}}^2u={\mathbf {0}}. \end{array}\right. } \end{aligned}$$

(3)

To handle those situations where $\inf _{x\in \varOmega } f(x)=0$, or for the solution of obstacle problems for the Monge–Ampère operator (as those considered in [42]), we found that one is on the safe side if one considers the following variant of (3), obtained by regularization:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} -\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+\mathrm {cof}({\mathbf {p}})\right) \nabla u\right] +2f=0 \text{ in } \varOmega ,\\ u=g \text{ on } \partial \varOmega , \end{array}\right. }\\ {\mathbf {p}}-{\mathbf {D}}^2u={\mathbf {0}}, \end{array}\right. } \end{aligned}$$

(4)

$\varepsilon$ being a small positive number (of the order of $h^2$ in practice, h being the space discretization step). In order to solve (4), we associate with it the following initial value problem (flow in the dynamical system terminology):

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}-\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+\mathrm {cof}({\mathbf {p}})\right) \nabla u\right] +2f=0 \text{ in } \varOmega \times (0,+\infty ),\\ u=g \text{ on } \partial \varOmega \times (0,+\infty ), \end{array}\right. }\\ \frac{\partial {\mathbf {p}}}{\partial t}+\gamma \left( {\mathbf {p}}-{\mathbf {D}}^2u\right) = {\mathbf {0}} \text{ in } \varOmega \times (0,+\infty ),\\ u(0)=u_0,\ {\mathbf {p}}(0)={\mathbf {p}}_0, \end{array}\right. } \end{aligned}$$

(5)

with $\gamma$ a positive constant [above and below, $\phi (t)$ denotes the function $x\rightarrow \phi (x,t)$].

Before discussing (in Sect. 3) the time discretization of problem (5), we will address two important issues, namely: (i) The choice of $\gamma$, and (ii) the choice of $u_0$ and ${\mathbf {p}}_0$. Concerning $\gamma$, the idea is to pick a value so that ${\mathbf {p}}(t)$ evolves in time roughly like u(t). Taking advantage of the fact that ${\mathbf {p}}$ and $\mathrm {cof}({\mathbf {p}})$ have the same eigenvalues, we suggest taking

$$\begin{aligned} \gamma = \beta \lambda _0\left( \varepsilon +\sqrt{\alpha }\right) , \end{aligned}$$

where $\lambda _0$ is the smallest eigenvalue of operator $-\nabla ^2$ in $H_0^1(\varOmega )$, $\alpha$ is the lower bound of function f, and $\beta$ is a constant of the order of 1. Assuming that we are looking for the convex solutions of (1), several possibilities (not exclusive of each other) do exist in order to force this convexity property. The simplest one is a proper choice of $u_0$ and ${\mathbf {p}}_0$ in (5). Following the discussion in [28, 29], we suggest taking for $u_0$ the solution of the following Poisson problem

$$\begin{aligned} \nabla ^2u_0=2\lambda \sqrt{f} \text{ in } \varOmega , u_0=g \text{ on } \partial \varOmega , \end{aligned}$$

(6)

with $\lambda (>0)$ of the order of 1. Concerning ${\mathbf {p}}_0$, an obvious choice is ${\mathbf {p}}_0={\mathbf {D}}^2u_0$, a simpler alternative being ${\mathbf {p}}_0=\lambda \sqrt{f} \, {\mathbf {I}}$.

Remark 1

A natural variant of (5) is obtained by replacing $\frac{\partial u}{\partial t}$ by $-\frac{\partial }{\partial t} \nabla ^2 u$. We did not pursue in that direction for two main reasons: (i) $\frac{\partial u}{\partial t}$ is much better suited than $-\frac{\partial }{\partial t}\nabla ^2 u$ for the numerical solution of obstacle problems for the Monge–Ampère operator (like those discussed in [42]), and (ii) the numerical experiments we performed showed that the the two-stage method discussed in Sect. 5 is as fast and, in general, more robust than the methodology based on $-\frac{\partial }{\partial t} \nabla ^2 u$.

3 On the Time Discretization of System (5) by Operator-Splitting

The structure of system (5) suggests using operator-splitting for its time-discretization. Among the many possible operator-splitting schemes (see, e.g., [30] for further information on operator-splitting methods) we advocate the particular Lie scheme described below, where $\varDelta t (> 0)$ is a time-discretization step and $t^n=n\varDelta t$:

$$\begin{aligned} u^0=u_0 \, ,\, {\mathbf {p}}^0={\mathbf {p}}_0. \end{aligned}$$

(7)

For $n\ge 0$, $\left\{ u^n,{\mathbf {p}}^n\right\} \rightarrow \left\{ u^{n+1/2},{\mathbf {p}}^{n+1/2}\right\} \rightarrow \left\{ u^{n+1},{\mathbf {p}}^{n+1}\right\}$ as follows

Fractional Step 1: Solve

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}-\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+\mathrm {cof}\left( {\mathbf {p}}^n\right) \right) \nabla u\right] + 2f=0 \text{ in } \varOmega \times \left( t^n,t^{n+1}\right) ,\\ u=g \text{ on } \partial \varOmega \times \left( t^n,t^{n+1}\right) , \end{array}\right. }\\ \frac{\partial {\mathbf {p}}}{\partial t}={\mathbf {0}} \text{ in } \varOmega \times \left( t^n,t^{n+1}\right) ,\\ u\left( t^n\right) =u^n,\, \, {\mathbf {p}}\left( t^n\right) ={\mathbf {p}}^n, \end{array}\right. } \end{aligned}$$

(8)

and set $u^{n+1/2}=u(t^{n+1}) \, ,\, {\mathbf {p}}^{n+1/2}={\mathbf {p}}^n.$

Fractional Step 2: Solve

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=0 \text{ in } \varOmega \times \left( t^n,t^{n+1}\right) ,\\ \frac{\partial {\mathbf {p}}}{\partial t}+\gamma {\mathbf {p}}=\gamma {\mathbf {D}}^2 u^{n+1/2} \text{ in } \varOmega \times \left( t^n,t^{n+1}\right) ,\\ u\left( t^n\right) =u^{n+1/2},\,\, {\mathbf {p}}\left( t^n\right) ={\mathbf {p}}^{n+1/2}, \end{array}\right. } \end{aligned}$$

(9)

and set

$$\begin{aligned} u^{n+1}=u^{n+1/2}, {\mathbf {p}}^{n+1}=P_+\left[ {\mathbf {p}}\left( t^{n+1}\right) \right] , \end{aligned}$$

(10)

where in (10), $P_+$ denotes a projection operator (to be defined in Sect. 4.5) on the convex cone of the symmetric positive semi-definite $2\times 2$ matrices, the projection being done pointwise. Scheme (7)–(10) is first-order accurate at most, and semi-constructive since we still have to solve the sub-initial value problems (8) and (9). There is no difficulty with (9) since it has a closed form solution. To time-discretize (8), we advocate just taking one step of the backward Euler scheme. The resulting scheme (of the Markchuk–Yanenko type) reads as follows (using a more compact notation):

$$\begin{aligned} u^0=u_0,\,\, {\mathbf {p}}^0={\mathbf {p}}_0. \end{aligned}$$

(11)

For $n\ge 0$, $\left\{ u^n,{\mathbf {p}}^n\right\} \rightarrow \left\{ u^{n+1},{\mathbf {p}}^{n+1}\right\}$ as follows

$$\begin{aligned}&{\left\{ \begin{array}{ll} \frac{u^{n+1}-u^n}{\varDelta t}-\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+ \mathrm {cof}\left( {\mathbf {p}}^n\right) \right) \nabla u^{n+1}\right] +2f=0 \text{ in } \varOmega ,\\ u^{n+1}=g \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(12)

$$\begin{aligned}&{\mathbf {p}}^{n+1}=P_+\left[ e^{-\gamma \varDelta t}{\mathbf {p}}^n+ \left( 1-e^{-\gamma \varDelta t}\right) {\mathbf {D}}^2 u^{n+1}\right] . \end{aligned}$$

(13)

If the matrix-valued function ${\mathbf {p}}^n$ is positive semi-definite, then (12) is a formally well-posed elliptic boundary value problem.

4 On the Finite Element Implementation of the Operator-Splitting Scheme

4.1 Synopsis

The equivalent divergence formulations (2) and (3) of problem (1) strongly suggest employing space approximations based on variational principles. To achieve such a goal, we are going to use finite element spaces consisting of functions which are globally continuous and piecewise affine on triangulations of $\varOmega$. As in, e.g., [8, 29] (see also the references therein), we are going to use a mixed finite element method, relying basically on the same finite dimensional spaces to approximate u, its three second order derivatives, and the entries of the matrix-valued function ${\mathbf {p}}$.

4.2 The Basic Finite Element Spaces

We follow the presentations in [8, 14, 26, 29]: Assuming that $\varOmega$ is a polygonal domain of $\mathbb {R}^2$ (or has been approximated by such a domain), we introduce a family $({\mathcal {T}}_h)_h$ of triangulations of $\varOmega$, like the ones in Fig. 1; usually, one denotes by h the length of the largest edge(s) of ${\mathcal {T}}_h$.

Fig. 1

Four meshes for two different domains used in the numerical experiments. a A regular mesh on the unit square. b A (highly) symmetric mesh on the unit square. c An isotropic unstructured mesh on the unit square. d An isotropic unstructured mesh on a half-unit disk

The first finite element space we introduce is the finite dimensional space $V_h$ defined by

$$\begin{aligned} V_h=\left\{ v|v\in C^0\left( {\bar{\varOmega }}\right) ,v|_T\in P_1,\forall T\in {\mathcal {T}}_h\right\} , \end{aligned}$$

(14)

where $P_1$ is the space of the polynomials of two variables of degree $\le 1$. Let us denote by $\varSigma _h$ the set of the vertices of the triangles of ${\mathcal {T}}_h$; we have then $\varSigma _h=\left\{ Q_j\right\} _{j=1}^{N_h}$. Next, we associate with each vertex $Q_j$ the (shape) function $w_j$, uniquely defined by:

$$\begin{aligned} w_j\in V_h, w_j(Q_j)=1, w_j(Q_k)=0,\forall k=1,\ldots ,N_h, k\ne j. \end{aligned}$$

The set ${\mathcal {B}}_h=\left\{ w_j\right\} _{j=1}^{N_h}$ is a vector basis of the space $V_h$; it verifies $v=\sum _{j=1}^{N_h} v(Q_j)w_j,\forall v\in V_h ,$ implying that dim $V_h=N_h$. We observe that the support of the basis function $w_j$ is the union of those triangles of ${\mathcal {T}}_h$ which have $Q_j$ as a common vertex.

Assuming that $g\in C^0(\partial \varOmega )$, we define $V_{gh}$, an affine subspace of $V_h$, by

$V_{gh}=\left\{ v|v\in V_h, v(Q_j)=g(Q_j),\forall Q_j\in \varSigma _h\cap \partial \varOmega \right\} .$ Note that if $g=0$, then $V_{gh}=V_{0h}$, where $V_{0h}=\left\{ v|v\in V_h, v=0 \text{ on } \partial \varOmega \right\} \left( =V_h\cap H_0^1(\varOmega )\right) .$

In Sect. 4.3 below, we are going to address the approximation of $\partial ^2u/\partial x_1^2$, $\partial ^2u/\partial x_2^2$ and $\partial ^2u/\partial x_1\partial x_2$, an important issue indeed.

4.3 Finite Element Approximation of the Three Second Order Derivatives

Unlike the collocation methods discussed in [7, 8, 29], the values taken on $\partial \varOmega$ by the discrete second order derivatives affect the approximate solutions. From that point of view, enforcing (as done in [7, 8, 29]) these discrete derivatives to vanish on $\partial \varOmega$ leads to large approximation errors on the solutions of problem (12), a consequence of the poor approximation of $\mathrm {cof}({\mathbf {p}}^n)$ in the neighborhood of $\partial \varOmega$. To overcome this difficulty, several approaches are available. We will focus on two of them. The starting point of the first one is to observe that the Divergence Theorem implies:

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall i,j=1,2,\forall v\in H^2(\varOmega ),\\ \int _{\varOmega }\frac{\partial ^2 v}{\partial x_i \partial x_j} w dx=-\frac{1}{2}\int _{\varOmega }\left[ \frac{\partial v}{\partial x_i} \frac{\partial w}{\partial x_j}+\frac{\partial v}{\partial x_j} \frac{\partial w}{\partial x_i}\right] dx\\ \forall w\in H^1_0(\varOmega ). \end{array}\right. } \end{aligned}$$

(15)

This suggests approximating $\frac{\partial ^2 v}{\partial x_i \partial x_j}$ by $D_{ijh}^2(v)$ verifying

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall i,j=1,2,\forall v\in V_h, D^2_{ijh}(v)\in V_h\\ \int _{\varOmega }D^2_{ijh}(v) w dx=-\frac{1}{2}\int _{\varOmega }\left[ \frac{\partial v}{\partial x_i} \frac{\partial w}{\partial x_j}+\frac{\partial v}{\partial x_j} \frac{\partial w}{\partial x_i}\right] dx\\ \forall w\in V_{0h}. \end{array}\right. } \end{aligned}$$

(16)

The finite dimensional problem (16) being undetermined, additional relations are required in order to force solution uniqueness. We suggest imposing (approximately)

$$\begin{aligned} \frac{\partial }{\partial {\mathbf {n}}} D^2_{ijh}(v)=0 \text{ on } \partial \varOmega . \end{aligned}$$

(17)

Among the various options available to impose (17), the one we selected reads as

$$\begin{aligned} \int _{\omega _k}\nabla D^2_{ijh}(v)\cdot \nabla w_k dx=0, \forall k=N_{0h}+1,\dots ,N_h, \end{aligned}$$

(18)

where in (18): (i) $N_{0h}=\dim V_{0h}$. (ii) $\{Q_k\}_{k=N_{0h}+1}^{N_h}=\varSigma _h\cap \partial \varOmega ,\varSigma _h= \{Q_k\}_{k=1}^{N_h}$ being the set of the vertices of ${\mathcal {T}}_h$. (iii) $w_k$ is the basis (shape) function of $V_h$ associated with $Q_k$. (iv) $\omega _k= \text{ support } \text{ of } w_k$ is the union of those triangles of ${\mathcal {T}}_h$ which have $Q_k$ as a common vertex; $|\omega _k|$ will denote the area of $\omega _k$.

The rationale behind (18) is easy to understand: we have (Green’s formula)

$$\begin{aligned} \int _{\partial \omega _k\cap \partial \varOmega } \frac{\partial \psi }{\partial {\mathbf {n}}} w_kd(\partial \varOmega )=\int _{\omega _k}\nabla ^2\psi w_k dx+\int _{\omega _k} \nabla \psi \cdot \nabla w_k dx, \forall \psi \in H^2(\varOmega ). \end{aligned}$$

(19)

Suppose now that $\psi$ is harmonic (that is $\nabla ^2\psi =0$), then relation (19) reduces to

$$\begin{aligned} \int _{\partial \omega _k\cap \partial \varOmega }\frac{\partial \psi }{\partial {\mathbf {n}}}w_k d(\partial \varOmega )=\int _{\omega _k} \nabla \psi \cdot \nabla w_k dx. \end{aligned}$$

(20)

Albeit the function $D^2_{ijh}(v)$ is piecewise harmonic only (being piecewise affine), we used (20) to impose (17), explaining where (18) comes from. It is clear that replacing the above homogeneous Neumann boundary condition by (18) is a typical example of variational crime (in the sense of [44]). The numerical experiment results reported in Sect. 6 will validate a regularized variant of the approach we just described, based essentially on relations (16) and (18). Indeed, numerical experiments performed with (16), (18) show that the quality of the approximation deteriorates as $h\rightarrow 0$, unless $\varOmega$ is a rectangle and that one uses regular triangulations like the one shown in Fig. 1a. To overcome the above difficulty, we advocate (inspired by [7, 8, 29]) the simple (Tychonoff) regularization procedure where one replaces system (16), (18) by:

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall i,j=1,2,\forall v\in V_h, D^2_{ijh}(v)\in V_h,\\ C\sum \nolimits _{T\in {\mathcal {T}}^k_h}|T|\int _T \nabla D^2_{ijh}(v)\cdot \nabla w_k dx+\int _{\omega _k}D^2_{ijh}(v) w_k dx\\ \qquad =-\frac{1}{2}\int _{\omega _k}\left[ \frac{\partial v}{\partial x_i} \frac{\partial w_k}{\partial x_j}+\frac{\partial v}{\partial x_j} \frac{\partial w_k}{\partial x_i}\right] dx, \forall k=1,\dots ,N_{0h},\\ \int _{\omega _k} \nabla D^2_{ijh}(v)\cdot \nabla w_k dx=0, \forall k=N_{0h}+1,\dots ,N_h, \end{array}\right. } \end{aligned}$$

(21)

where in (21), C is a positive constant of the order of 1, ${\mathcal {T}}^k_h$ being the set of those triangles of ${\mathcal {T}}_h$ which have $Q_k$ as a common vertex.

Remark 2

Suppose that one uses the trapezoidal rule to approximate the $L^2(\varOmega )$-inner products in (21), then the above system reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall i,j=1,2,\forall v\in V_h, D^2_{ijh}(v)\in V_h,\\ C\sum \nolimits _{T\in {\mathcal {T}}^k_h}|T|\int _T \nabla D^2_{ijh}(v)\cdot \nabla w_k dx+ \frac{|\omega _k|}{3}D^2_{ijh}(Q_k)\\ \quad =-\frac{1}{2}\int _{\omega _k}\left[ \frac{\partial v}{\partial x_i} \frac{\partial w_k}{\partial x_j}+\frac{\partial v}{\partial x_j} \frac{\partial w_k}{\partial x_i}\right] dx, \forall k=1,\dots ,N_{0h},\\ \int _{\omega _k} \nabla D^2_{ijh}(v)\cdot \nabla w_k dx=0, \forall k=N_{0h}+1,\dots ,N_h. \end{array}\right. } \end{aligned}$$

(22)

System (22) being simpler than system (21) from a matrix point of view, it is the one we have used for those computations relying on (18). The practical use of (22) to define discrete second order derivatives requires this finite dimensional variational problem to be well-posed. We will prove it is true in the particular case where ${\mathcal {T}}_h$ being isotropic one replaces (22) by

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall i,j=1,2,\forall v\in V_h, D^2_{ijh}(v)\in V_h,\\ Ch^2\int _{\omega _k} \nabla D^2_{ijh}(v)\cdot \nabla w_k dx+ \frac{|\omega _k|}{3}D^2_{ijh}(v)(Q_k)\\ \quad =-\frac{1}{2}\int _{\omega _k}\left[ \frac{\partial v}{\partial x_i} \frac{\partial w_k}{\partial x_j}+\frac{\partial v}{\partial x_j} \frac{\partial w_k}{\partial x_i}\right] dx, \forall k=1,\dots ,N_{0h},\\ \int _{\omega _k} \nabla D^2_{ijh}(v)\cdot \nabla w_k dx=0, \forall k=N_{0h}+1,\dots ,N_h. \end{array}\right. } \end{aligned}$$

(23)

Theorem 1

Suppose that in (23), the function v is given in $V_h$. Then the associated linear system providing $D^2_{ijh}(v)$ has a unique solution.

Proof

The proof is very simple once we introduce the space $M_h(\subset V_h)$ defined by

$$\begin{aligned} M_h=\left\{ \mu \in V_h, \mu =\sum _{k=N_{0h}+1}^{N_h} \mu _k w_k, (\mu _k)_{k=N_{0h}+1}^{N_h} \in \mathbb {R}^{N_h-N_{0h}}\right\} . \end{aligned}$$

(24)

We clearly have

$$\begin{aligned} V_h=V_{0h}\oplus M_h \text{ and } \mu \in M_h \Leftrightarrow \mu |_T =0, \forall T\in {\mathcal {T}}_h \text{ such } \text{ that } \partial T\cap \partial \varOmega =\varnothing . \end{aligned}$$

(25)

Next, we denote by $(\cdot ,\cdot )_{0h}$ the inner-product over $V_h$ defined by

$$\begin{aligned} (v,w)_{0h}=\frac{1}{3}\sum _{k=1}^{N_h} |\omega _k|v(Q_k)w(Q_k), \end{aligned}$$

(26)

where $(Q_k)_{k=1}^{N_h}=\varSigma _h$. We have then $V_{0h}^{\perp }=M_h$ for the inner product defined by (26).

In order to prove that (23) is well-posed, it is sufficient to show that

$$\begin{aligned} {\left\{ \begin{array}{ll} p\in V_h,\\ Ch^2\int _{\omega _k} \nabla p\cdot \nabla w_k dx +\frac{|\omega _k|}{3}p(Q_k)=0,\forall k=1,\dots ,N_{0h},\\ \int _{\omega _k} \nabla p\cdot \nabla w_k dx=0, \forall k=N_{0h}+1,\dots ,N_h, \end{array}\right. } \Rightarrow p=0. \end{aligned}$$

(27)

The variational system in the left part of (27) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} p\in V_h,\\ Ch^2\int _{\varOmega } \nabla p\cdot \nabla v dx +(p,v)_{0h}=0,\forall v\in V_{0h},\\ \int _{\varOmega } \nabla p\cdot \nabla \mu dx=0, \forall \mu \in M_h. \end{array}\right. } \end{aligned}$$

(28)

It follows from (25) that $p=p_0+p_1$ with $p_0\in V_{0h}$ and $p_1\in M_h$, the above decomposition being unique. We have $(p_0,p_1)_{0h}=0$ and [from (28)] $\int _{\varOmega } \nabla p\cdot \nabla p_1 dx=0$. Taking $v=p_0$ in (28), the above two relations imply

$$\begin{aligned} Ch^2\int _{\varOmega }|\nabla p|^2 dx+ (p_0,p_0)_{0h}=0. \end{aligned}$$

(29)

It follows from (29) that $p_0=0$ and $\nabla p=\nabla (p_0+p_1)=\nabla p_1=0$. Function $p_1$ is thus a constant, but since $p_1(Q_k)=0, \forall k=1,\dots ,N_{0h}$, this constant is 0, implying $p=p_0+p_1=0$. $\square$

Remark 3

We recall that h is the length of the largest edge(s) of ${\mathcal {T}}_h$. Denote by $h_{\mathrm {min}}$ the length of the smallest edge(s) of ${\mathcal {T}}_h$. If the ratio $h/h_{\mathrm {min}}\approx 1$ (a situation we already considered in Remark 2), then one can advantageously replace the term $C\sum _{T\in {\mathcal {T}}_h^k}|T| \int _T \nabla D_{ijh}^2(v) \cdot \nabla w_k dx$ in (22) by the following simpler one $\varepsilon _1 \int _{\omega _k} \nabla D_{ijh}^2(v) \cdot \nabla w_k dx$, with $\varepsilon _1$ a positive parameter of the order of $h^2$.

Remark 4

Suppose that $\varOmega =(0,1)^2$ and that the triangulation ${\mathcal {T}}_h$ is of the same type as the one in Fig. 1a. Suppose also that $h=\frac{1}{I+1}$, I being an integer greater than 1. In this particular case, we have $\varSigma _h=\{Q_{ij}|Q_{ij}=(ih,jh), 0\le i,j \le I+1\}$ and $\sum _{0h}=\{ Q_{ij}| Q_{ij}=(ih,jh), 1\le i,j \le I\}$, implying that $N_h=(I+2)^2$ and $N_{0h}=I^2$. Suppose that $C=0$ in (22) or (23), then if $1\le i,j \le I$, the relations giving $D_{klh}^2(v)(Q_{ij})(1\le k,l \le 2)$ reduce to simple finite difference formulas, exact for the polynomials of degree $\le 2$. These formulas can be found in [29] pages 390 and 391. $\square$

Although proving good convergence results, particularly if problem (1) has a smooth solution, the variational crime at the basis of relations (22) and (23) was leaving us uncomfortable. When using models (4), (5) to solve the Monge–Ampère equation (1), one can expect increased robustness (possibly at the expense of accuracy) if one uses smooth approximation of ${\mathbf {p}}$. Suppose that $\psi \in H^2(\varOmega )$ and consider (with $\varepsilon >0$) the following well-posed elliptic linear variational problem

$$\begin{aligned} {\left\{ \begin{array}{ll} p_{ij}^{\varepsilon }\in H_0^1(\varOmega ),\\ \varepsilon \int _{\varOmega } \nabla p_{ij}^{\varepsilon } \cdot \nabla \phi dx+ \int _{\varOmega } p_{ij}^{\varepsilon }\phi dx= -\frac{1}{2} \displaystyle \int _{\varOmega } \left[ \frac{\partial \psi }{\partial x_i}\frac{\partial \phi }{\partial x_j} + \frac{\partial \psi }{\partial x_j} \frac{\partial \phi }{\partial x_i} \right] dx, \forall \phi \in H_0^1(\varOmega ). \end{array}\right. } \end{aligned}$$

(30)

Function $p_{ij}^{\varepsilon }$ verifies

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} p_{ij}^{\varepsilon }=\frac{\partial ^2 \psi }{\partial x_i \partial x_j} \text{ in } L^2(\varOmega ), \end{aligned}$$

(31)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varepsilon \nabla ^2 p_{ij}^{\varepsilon }+ p_{ij}^{\varepsilon } = \frac{\partial ^2 \psi }{\partial x_i \partial x_j} \text{ in } \varOmega ,\\ p_{ij}^{\varepsilon }=0 \text{ on } \partial \varOmega \end{array}\right. } \end{aligned}$$

(32)

(in the sense of distributions). From the convexity of $\varOmega$, it follows from (32) that $p_{ij}^{\varepsilon }\in H_0^1(\varOmega ) \cap H^2(\varOmega )\left( \subset C^0({\bar{\varOmega }})\right)$. Discrete variants of the above regularization method were applied in [7, 8] to the solution of the Monge–Ampère equation in dimensions two and three. The numerical results reported in [7, 8] show that the least-squares collocation method discussed there has no problem to accommodate the boundary condition $p_{ij}^{\varepsilon }=0$ on $\partial \varOmega$, unlike the divergence formulation (2) of the Monge–Ampère equation we employ in this article. In order to overcome this difficulty, we suggest introducing a correcting step, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varepsilon \nabla ^2 {\tilde{p}}_{ij}^{\varepsilon }+ {\tilde{p}}_{ij}^{\varepsilon }= p_{ij}^{\varepsilon } \text{ in } \varOmega ,\\ \frac{\partial {\tilde{p}}_{ij}^{\varepsilon }}{\partial {\mathbf {n}}}=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(33)

whose variational formulation reads as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\tilde{p}}_{ij}^{\varepsilon }\in H^1(\varOmega ),\\ \varepsilon \int _{\varOmega } \nabla {\tilde{p}}_{ij}^{\varepsilon } \cdot \nabla \phi dx + \int _{\varOmega } {\tilde{p}}_{ij}^{\varepsilon } \phi dx=\int _{\varOmega } p_{ij}^{\varepsilon } \phi dx, \forall \phi \in H^1(\varOmega ). \end{array}\right. } \end{aligned}$$

(34)

Function ${\tilde{p}}_{ij}^{\varepsilon }$ verifies $\lim _{\varepsilon \rightarrow 0} {\tilde{p}}_{ij}^{\varepsilon }= \frac{\partial ^2 \psi }{\partial x_i \partial x_j}$ in $L^2(\varOmega )$, and ${\tilde{p}}_{ij}^{\varepsilon } \in H^4(\varOmega )$. These properties are at the foundation of our second approach concerning the approximation of the second order derivatives. Suppose that $v\in V_h$; one proceeds as follows to compute the discrete analogue $D^2_{ijh}(v)$ of $\frac{\partial ^2 v}{\partial x_i \partial x_j} (1\le i,j \le 2)$:

Solve:

$$\begin{aligned} {\left\{ \begin{array}{ll} p_{ij}\in V_{0h},\\ C\sum _{T\in {\mathcal {T}}_h^k} |T| \int _T \nabla p_{ij} \cdot \nabla w_k dx +\frac{|\omega _k|}{3}p_{ij}(Q_k)= -\frac{1}{2} \displaystyle \int _{\omega _k} \left[ \frac{\partial v}{\partial x_i} \frac{\partial w_k}{\partial x_j} + \frac{\partial v}{\partial x_j} \frac{\partial w_k}{\partial x_i}\right] dx,\\ \forall k=1,\dots ,N_{0h}, \end{array}\right. } \end{aligned}$$

(35)

and then

$$\begin{aligned} {\left\{ \begin{array}{ll} D_{ijh}^2(v) \in V_h,\\ C\sum _{T\in {\mathcal {T}}_h^k} |T| \int _T \nabla D_{ijh}^2(v) \cdot \nabla w_k dx +\frac{|\omega _k|}{3}D_{ijh}^2(v)(Q_k)= \frac{|\omega _k|}{3}p_{ij}(Q_k),\\ \forall k=1,\dots ,N_{h}, \end{array}\right. } \end{aligned}$$

(36)

C being of the order of 1. Anticipating on the numerical results reported in Sect. 6, we would like to mention the following facts concerning the two approaches we presented concerning the approximation of the second order derivatives: Although resting on more solid mathematical foundations the second approach is less accurate than the first one if the Monge–Ampère problem under consideration has smooth enough solutions. However, the second approach is more robust in the sense it can handle non-smooth situations more easily than the first one [typical examples in that direction being provided by problems (1) where f is not a function, but a positive measure (a Dirac’s one for example)].

Remark 3 still applies for the approximation of the second order derivatives defined by relations (35), (36).

Remark 5

When implementing the double regularization approach associated with relations (32), (33), it makes sense (and is even tempting) to replace $\varepsilon$ in (32) [resp. (33)] by $\eta _1$ of the order of $h^{2+\gamma }$ (resp., $\eta _2$ of the order of $h^{2-\gamma }$) with $\gamma (>0)$ not too large. Numerical experiments done with $\gamma =1/4, 1/3$ and 1 / 2 showed that for some test problems the introduction of a positive $\gamma$ may improve convergence. However since we found examples where it has the opposite effect, we decided to stay with $\gamma =0$.

4.4 Finite Element Implementation of the Operator-Splitting Scheme (11)–(13)

Let us recall that the set $\varSigma _{0h}$ of the vertices of ${\mathcal {T}}_h$ interior to $\varOmega$ has been ordered so that $\varSigma _{0h}=\left\{ Q_k\right\} _{k=1}^{N_{0h}}$ and $\varSigma _h=\varSigma _{0h}\cup \{Q_k\}_{k=N_{0h}+1}^{N_h}$. In the sequel, we will denote by ${\mathbf {Q}}_h$ the space $\{{\mathbf {q}}|{\mathbf {q}}\in (V_h)^{2\times 2},{\mathbf {q}}={\mathbf {q}}^T\}$.

4.4.1 Implementation of Scheme (11)–(13)

A fully discrete analogue of scheme (11)–(13) reads as

$$\begin{aligned} u^0=u_{0h}\left( \in V_{gh}\right) , {\mathbf {p}}^0={\mathbf {p}}_{0h} \left( \in {\mathbf {Q}}_h \right) . \end{aligned}$$

(37)

For $n\ge 0, \left\{ u^n,{\mathbf {p}}^n \right\} \rightarrow \left\{ u^{n+1},{\mathbf {p}}^{n+1} \right\}$ as follows:

Solve

$$\begin{aligned} {\left\{ \begin{array}{ll} u^{n+1}\in V_{gh},\\ \int _{\varOmega } u^{n+1}vdx+ \varDelta t\int _{\varOmega }\left( \varepsilon {\mathbf {I}}+\mathrm {cof}\left( {\mathbf {p}}^n\right) \right) \nabla u^{n+1} \cdot \nabla vdx \\ \quad = \int _{\varOmega } u^n vdx-2\varDelta t \int _{\varOmega } f_h vdx, \forall v\in V_{0h}, \end{array}\right. } \end{aligned}$$

(38)

and compute ${\mathbf {p}}^{n+1}$ via

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall k=1,\dots ,N_h, \text{ one } \text{ has } {\mathbf {p}}^{n+\frac{1}{2}}(Q_k)=e^{-\gamma \varDelta t}{\mathbf {p}}^n(Q_k)\\ \quad +\left( 1-e^{-\gamma \varDelta t}\right) \begin{pmatrix} D_{11h}^2\left( u^{n+1}\right) (Q_k) &{} D_{12h}^2\left( u^{n+1}\right) (Q_k)\\ D_{12h}^2\left( u^{n+1}\right) (Q_k) &{} D_{22h}^2\left( u^{n+1}\right) (Q_k) \end{pmatrix},\\ {\mathbf {p}}^{n+1}(Q_k)=P_+\left[ {\mathbf {p}}^{n+1/2}(Q_k)\right] , \end{array}\right. } \end{aligned}$$

(39)

where in (38), $f_h(>0)$ is a continuous approximation of f, and where in (39), the discrete second order derivatives of $u^{n+1}$ are computed using the methods discussed in Sect. 4.3, operator $P_+$ being defined in Sect. 4.5. The initialization of scheme (37)–(39) and the solution of the discrete variational problem (38) will be discussed in Sects. 4.4.2 and 4.4.3, respectively.

4.4.2 Initialization of Scheme (37)–(39)

Our starting point will be problem (6) defining $u_0$. The most natural discrete analogue of problem (6) is given by

$$\begin{aligned} u_{0h}\in V_{gh},\int _{\varOmega } \nabla u_{0h} \cdot \nabla vdx=-2\lambda \int _{\varOmega } \sqrt{f_h} vdx, \forall v \in V_{0h}. \end{aligned}$$

(40)

From a practical point of view, we advocate using the trapezoidal rule to compute (approximately) the integral $\int _{\varOmega } \sqrt{f_h} vdx$. We obtain then (using notation from previous sections):

$$\begin{aligned} \int _{\varOmega } \sqrt{f_h} vdx\approx \frac{1}{3} \varSigma _{j=1}^{N_{0h}}|\omega _j|\sqrt{f_h(Q_j)}v(Q_j). \end{aligned}$$

(41)

If $\varOmega$ is a rectangle and the triangulation we employ is of the Fig. 1a type, we advocate using finite differences and a fast Poisson solver to compute $u_{0h}$ from (6). The solution of (40) for more general domains and/or triangulations ${\mathcal {T}}_h$ will be (briefly) discussed in Sect. 4.4.3. Once $u_{0h}$ has been computed, we use the methods discussed in Sect. 4.3 to define ${\mathbf {p}}_{0h}$ by

$$\begin{aligned} {\mathbf {p}}_{0h}=\sum _{k=1}^{N_h} P_+\left[ \begin{pmatrix} D^2_{11h}(u_{0h}) &{} D^2_{12h}(u_{0h}) \\ D^2_{12h}(u_{0h}) &{} D^2_{22h}(u_{0h}) \end{pmatrix} (Q_k)\right] w_k. \end{aligned}$$

(42)

An alternative to (42) is to define ${\mathbf {p}}_{0h}$ by ${\mathbf {p}}_{0h}=\lambda \sum _{k=1}^{N_h} \sqrt{f_h(Q_k)}{\mathbf {I}}$, a discrete analogue of ${\mathbf {p}}_0=\lambda \sqrt{f}{\mathbf {I}}$.

4.4.3 On the Solution of Problems (38) and Related Linear Variational Problems

What follows is fairly classical (see, for example Appendix 1 of [26] and Chapter 5 of [27], and the references therein). Problems (38) and (40) are particular cases of the following finite dimensional linear variational problem (of the Dirichlet type):

$$\begin{aligned} \psi \in V_{gh},a\int _{\varOmega } \psi \phi dx+\int _{\varOmega } {\mathbf {M}}\nabla \psi \cdot \nabla \phi dx= \int _{\varOmega }f^*\phi dx,\forall \phi \in V_{0h}, \end{aligned}$$

(43)

where in (43), a is a non-negative constant, ${\mathbf {M}}$ is a piecewise affine uniformly positive definite symmetric matrix-valued function, $f^*$ being a given continuous function. From the positivity of ${\mathbf {M}}$, problem (43) has a unique solution. We will return on the matrix ${\mathbf {M}}$ positivity issue in Sect. 4.5.

Using the trapezoidal rule to approximate the first and third integrals in (43), the above problem takes the following formulation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi \in V_{gh},\forall \phi \in V_{0h}, \frac{a}{3}\sum _{l=1}^{N_{0h}}\left| \omega _l\right| \psi (Q_l) \phi (Q_l)\\ \quad +\int _{\varOmega }{\mathbf {M}}\nabla \psi \cdot \nabla \phi dx =\frac{1}{3}\sum _{l=1}^{N_{0h}} \left| \omega _l\right| f^*(Q_l)\phi (Q_l). \end{array}\right. } \end{aligned}$$

(44)

Since the set $\{w_k\}_{k=1}^{N_{0h}}$ is a vector basis of $V_{0h}$, and $\psi =\sum _{l=1}^{N_{0h}}\psi (Q_l)+\sum _{l=N_{0h}+1}^{N_h} g(Q_l)$, it follows from (44) that the vector $\{\psi (Q_k)\}_{k=1}^{N_{0h}}$ is clearly the solution of the following [equivalent to (44)] linear system [where $\psi _k$ denotes $\psi (Q_k)$]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{a}{3}\left| \omega _k \right| \psi _k+\sum _{l=1}^{N_{0h}}\left( \int _{\omega _k\cap \omega _l} {\mathbf {M}}\nabla w_k\cdot \nabla w_l dx\right) \psi _l\\ \quad =\frac{1}{3}\left| \omega _k \right| f^*(Q_k)-\sum _{l=N_{0h}+1}^{N_h}\left( \int _{\omega _k\cap \omega _l} {\mathbf {M}}\nabla w_k\cdot \nabla w_l dx\right) g(Q_l),\\ k=1,\ldots ,N_{0h}. \end{array}\right. } \end{aligned}$$

(45)

Since, in practice, h is small compared to the diameter of $\varOmega$, the matrix associated with the linear system (45) is sparse. Moreover, this matrix is symmetric positive definite, these properties following from the uniform positivity of the symmetric matrix-valued function ${\mathbf {M}}$. One can solve thus the linear system (45) by a sparse Cholesky solver, or a diagonally preconditioned conjugate gradient algorithm. An user friendly alternative is to use one of those MATLAB (or other library) programs which decides by itself which linear solver is the more appropriate to the linear system under consideration. Matrix ${\mathbf {M}}$ (resp., vector $\nabla w_k$) being piecewise affine (resp., piecewise constant) the various integrals in (45) can be computed exactly by the trapezoidal rule.

The above comments concerning problems (38) and (40) apply also to the linear problems (22), (23) and (35), (36) we used in Sect. 4.3 to compute the discrete second order partial derivatives.

4.5 Enforcing the Local Positive Semi-definiteness of ${\mathbf {p}}$ by Eigenvalue Projection

In relations (10), (13), (39) and (42) we made use of $P_+$ a (kind of) projection operator mapping the space of the $2\times 2$ symmetric real matrices onto the convex cone of the $2\times 2$ positive semi-definite symmetric real matrices. Suppose that ${\mathbf {A}}$ is a $2\times 2$ symmetric real matrix. From the symmetry of ${\mathbf {A}}$ there exists a $2\times 2$ orthogonal matrix ${\mathbf {S}}$ such that ${\mathbf {A}}={\mathbf {S}}{\varvec{\Lambda }} \mathbf{S}^{-1}$ with ${{\varvec{\Lambda }}}= \begin{pmatrix} \lambda _1 &{} 0\\ 0 &{} \lambda _2 \end{pmatrix}$, $\lambda _1$ and $\lambda _2$ being the two eigenvalues of matrix ${\mathbf {A}}$. Operator $P_+$ is defined by $P_+({\mathbf {A}})={\mathbf {S}} \begin{pmatrix} \lambda _1^+ &{} 0\\ 0 &{} \lambda _2^+ \end{pmatrix}{\mathbf {S}}^{-1}$, with $\lambda _i^+=\max (0,\lambda _i),\forall i=1,2.$

5 A Two-Stage Convergence Acceleration Strategy

In this section, we propose a simple strategy to speed up the convergence to steady states of scheme (11)–(13). Instead of (5), we consider the following initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} -\frac{\partial \left( \nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+{\mathbf {M}}\right) \nabla u\right] \right) }{\partial \tau }-\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+\mathrm {cof}({\mathbf {p}})\right) \nabla u\right] +2f=0 \text{ in } \varOmega \times (0,+\infty ),\\ u=g \text{ on } \partial \varOmega \times (0,+\infty ), \end{array}\right. }\\ \frac{\partial {\mathbf {p}}}{\partial \tau }+\gamma \left( {\mathbf {p}}-{\mathbf {D}}^2u\right) = {\mathbf {0}} \text{ in } \varOmega \times (0,+\infty ),\\ u(0)=u_1,\ {\mathbf {p}}(0)={\mathbf {p}}_1, \end{array}\right. } \end{aligned}$$

(46)

where $\tau$ is (as is t) an artificial time. In (46), ${\mathbf {M}}$ is a time independent matrix-valued function, which is supposed to be reasonably close to $\mathrm {cof}({\mathbf {D}}^2u)$, u being the convex solution of problem (1) (assuming that such a solution does exist). Scheme (11)–(13) can be easily modified to accommodate (46): we just have to replace $\frac{u^{n+1}-u^n}{\varDelta t}$ in (12) by

$$\begin{aligned} -\nabla \cdot \left[ \left( \varepsilon {\mathbf {I}}+{\mathbf {M}}\right) \nabla \left( \frac{u^{n+1}-u^n}{\varDelta \tau }\right) \right] . \end{aligned}$$

Compared to (12), the above preconditioning allows the use of a larger time step $\varDelta \tau$, typically of the order of 1 if $\gamma \approx 1$, and $u_1$ and ${\mathbf {p}}_1$ are well-chosen. If convergence takes place, we expect that $\lim _{n\rightarrow +\infty } u^n=u$. To guarantee convergence, a proper choice of $\{u_1,{\mathbf {p}}_1\}$ is in order: a simple way to achieve that goal is to proceed as follows:

• (i) Start iterating with scheme (11)–(13) for a small value of $\varDelta t$, then stop time-stepping after a sufficiently (but not too) large number of time steps, denoting by $\{u_1,{\mathbf {p}}_1\}$ the pair produced by scheme (11)–(13) (further details will be given in Sect. 6).

• (ii) Take for ${\mathbf {M}}$ the matrix-valued function $\mathrm {cof}({\mathbf {D}}^2u_1)$, and using $\{u_1,{\mathbf {p}}_1\}$ as initializer, switch until convergence to the variant of scheme (11)–(13) associated with the initial value-problem (46).

The reader will notice the Newton-like flavor of the above two-stage strategy. Its convergence is discussed in the PhD dissertation of the second author. It is shown in particular that if ${\mathbf {M}}$ is close to $\mathrm {cof}({\mathbf {D}}^2u)$, where u is solution to problem (1), large values of $\varDelta \tau$ can be used, leading to fast convergence properties.

6 Numerical Experiments

6.1 Generalities

In this section we will apply the computational methods discussed in Sects. 3–5, to the numerical solution of test problems, some of them without smooth solutions or no solution at all. The associated domains $\varOmega$ will be the unit square $(0,1)^2$ (as expected), and the disk of radius 1 / 2, centered at (1 / 2, 1 / 2). In Fig. 1a, b, c, d, we visualized finite element triangulations of these two domains. The mesh in Fig. 1a will be called a regular mesh, while the mesh on Fig. 1b will be called a symmetric mesh (it has five symmetries, while the mesh in Fig. 1a has three symmetries ‘only’). We will say that the meshes in Fig. 1c, d are unstructured, although they are quite isotropic.

We use DistMesh [40] to generate the meshes shown in Fig. 1c, d. As expected (from the experiments reported in [8]), of all the triangulations we tested, those as the one in Fig.  1a are the only ones not requiring a regularization of the discrete second order derivatives in relation (22) or (23) to produce accurate results, when applied to the solution of test problems with smooth solutions. However, for poorly smooth or non-smooth problems, regularization improves significantly the performances of our methods, even for meshes of Fig. 1a type.

One of our goals with the first two test problems we are going to consider was to test the performances of the original one-stage algorithm (11)–(13) (actually of a finite element variant of it), and compare them with those of the two-stage algorithm discussed in Sect. 5. In all of our tests, without specification, we use $C=1$ in (23), (35) and (36). We took $\varepsilon =h^2,\beta =1/4$ and $\varDelta t=2h^2$ in the discrete analogue of algorithm (11)–(13). In the first stage of the two-stage algorithm we used $\Vert {\mathbf {D}}^2u^n-{\mathbf {p}}^n\Vert <1$ as the criterion to switch to stage 2 (above, we defined the matrix-function norm $\Vert \cdot \Vert$ by

$$\begin{aligned} \Vert {\mathbf {S}}\Vert ^2=\frac{1}{3}\sum ^{N_h}_{k=1}|\omega _k|\Vert {\mathbf {S}}(Q_k)\Vert ^2, \, \forall {\mathbf {S}}\in {\mathbf {Q}}_h, \end{aligned}$$

the matrix norm of ${\mathbf {S}}(Q_k)$ being the Fröbenius one). In stage 2, we used $\varDelta \tau =8h$ and took, typically, $\Vert u^{n+1}-u^n\Vert _2<10^{-7}$, as stopping criterion ($\Vert \cdot \Vert _2$ being a trapezoidal rule based approximation of the canonical $L_2$-norm). When using only the discrete analog of scheme (11)–(13) we used a stopping criterion like the one used for stage 2, but with a smaller tolerance ($h^3$ seems to be a reasonable choice), in order to compensate that $\varDelta t(=2h^2)$ is quite small.

Remark 6

A smaller stopping criterion can be used for stage 2, but this is not necessary since (as visible on Fig. 2) the $L_2$ and $L_{\infty }$ distances to the exact solution do not decrease anymore past some value of n; this appears clearly on Fig. 2b, c, d.

Fig. 2

(Test problem (47), $\alpha =1$): graphs of the computed solutions obtained via the two-stage strategy with relations (23) and related convergence behavior for: a a unit square regular mesh ($h=1/80$), b a unit square symmetric mesh ($h=1/80$), c a unit square unstructured mesh ($h=1/80$), d a half unit disk triangulation ($h=1/80$)

6.2 A Polynomial Example

The first test problem we consider reads as

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=256 \text{ in } \varOmega ,\\ u(x_1,x_2)=8\left[ \alpha \left( x_1-\frac{1}{2}\right) ^2+\frac{1}{\alpha }\left( x_2-\frac{1}{2}\right) ^2\right] -1, \forall (x_1,x_2)\in \partial \varOmega , \end{array}\right. } \end{aligned}$$

(47)

with $\alpha \ge 1$, $\varOmega$ being either the unit square $(0,1)^2$ or the disk of radius 1/2 centered at (1 / 2, 1 / 2). Clearly, the exact convex solution of problem (47) is given by

$$\begin{aligned} u(x_1,x_2)=8\left[ \alpha \left( x_1-\frac{1}{2}\right) ^2+\frac{1}{\alpha }\left( x_2-\frac{1}{2}\right) ^2\right] -1, \forall (x_1,x_2)\in \partial \varOmega . \end{aligned}$$

The first problem (47) we considered was the one associated with $\alpha =1$, corresponding clearly to an isotropic solution. On Table 1, we have reported some of the results we obtained when applying the two-stage algorithm to the solution of problem (47), the second order derivatives being approximated by (23). For various values of h we have shown: (i) The number of iterations (time steps) necessary to achieve convergence. (ii) The value of $\Vert u^{n+1}-u^n\Vert _2$ at convergence. (iii) The $L_2$ and $L_{\infty }$ approximation errors and the associated convergence rates (roughly of the order of two, which is generically optimal for the continuous piecewise affine approximations of the solution of a second order elliptic problem). In addition, we have reported on the $8\mathrm{th}$ column of Table 1, a discrete $L_2$-norm of the gradient of the function $u^{n_c}-u$ where $n_c$ denotes the number of time steps necessary to achieve convergence ($n_c$ can be found in the second column of Table 1). For all tests with $h=1/160$, we set $\varepsilon =h$ and the stopping criterion $\Vert {\mathbf {D}}^2u^n-{\mathbf {p}}^n\Vert <10$ for stage-one and stopping criterion $\Vert u^{n+1}-u^n\Vert _2<10^{-8}$ for stage-two.

Table 1 (Test problem (47), $\alpha =1$): (i) number of iterations needed for the convergence of the two-stage algorithm. (ii) Approximation errors and convergence rates for the solution and its gradient. (a) Regular meshes of the unit square. (b) Symmetric meshes of the unit square. (c) Unstructured isotropic meshes of the unit square. (d) Unstructured isotropic meshes of the half-unit disk. Relations (23) have been used to approximate the second order derivatives. (In (a), $h=\varDelta x_1=\varDelta x_2$)

Actually, further explanations are in order: indeed, we defined $\Vert \nabla (u^{n_c}-u)\Vert _2$ by

$$\begin{aligned} \left\| \nabla \left( u^{n_c}-u\right) \right\| _2=\sqrt{\frac{1}{3} \sum _{k=1}^{N_h} |\omega _k| |\nabla _h u^{n_c}(Q_k)-\nabla u(Q_k)|^2} \end{aligned}$$

with

$$\begin{aligned} \nabla _h u^{n_c}(Q_k)=\frac{1}{|\omega _k|}\sum _{T\in {\mathcal {T}}_h} |T| \left( \nabla u^{n_c}\right) |_T, \end{aligned}$$

${\mathcal {T}}_h^k$ being, as in Sect. 4.3, the set of those triangles of ${\mathcal {T}}_h$ which have $Q_k$ as a common vertex. The (classical) averaging procedure associated with the definition of $\nabla _h u^{n_c}(Q_k)$ acts as a low pass filter, explaining the higher than one convergence rates reported in the $9^{th}$ column of Table 1. Let us define by $A_{Tq}, q=1,2$ and 3, the three vertices of triangle T; defining $\Vert \nabla (u^{n_c}-u)\Vert _2$ by

$$\begin{aligned} \left\| \nabla \left( u^{n_c}-u\right) \right\| _2=\sqrt{\frac{1}{3} \sum _{T\in {\mathcal {T}}_h} |T| \sum _{q=1}^3 \bigg |\nabla u^{n_c}|_T-\nabla u\left( A_{Tq}\right) \bigg |^2} \end{aligned}$$

would lead to rates of convergence equal to one for the gradient approximation.

Table 2 is the variant of Table 1 associated with the second order derivative approximations defined by relations (35) and (36). The results reported in Table 2 suggest faster convergence of the iterative method, but lower orders of convergence for the approximation errors as $h\rightarrow 0$. Since our method converges faster and the second order derivatives are smoother with relations (35) and (36), a very small stopping criterion is not necessary. Here we use $\Vert {\mathbf {D}}^2u^n-{\mathbf {p}}^n\Vert <10$ for stage-one and $\Vert u^{n+1}-u^n\Vert _2<10^{-4}$ for stage-two.

Table 2 (Test problem (47), $\alpha =1$): (i) number of iterations needed for the convergence of the two-stage algorithm. (ii) Approximation errors and convergence rates for the solution and its gradient. (a) Regular meshes of the unit square. (b) Symmetric meshes of the unit square. (c) Unstructured isotropic meshes of the unit square. (d) Unstructured isotropic meshes of the half-unit disk. Relations (35) and (36) have been used to approximate the second order derivatives. (In (a), $h=\varDelta x_1=\varDelta x_2$)

On Fig. 2, we have visualized the approximate solutions produced by the two-stage algorithm, the discrete second order derivatives being defined by relations (23). We clearly see that the $L_2$ and $L_{\infty }$ approximation errors reach a plateau for n large enough, implying that the actual approximation errors have been reached.

In Table 3, we have reported the CPU time necessary for the two-stage algorithm to solve problem (47), with $\alpha =1$, for the same types of meshes and space discretization steps that in Table 1, relations (23) being used to approximate the second order derivatives.

Table 3 (Test problem (47), $\alpha =1$): CPU times for the two-stage algorithm with regularization (23) and the four types of meshes shown in Fig. 1, the values of h being those in Table 1. (a) Unit square regular meshes. (b) Unit square symmetric meshes. (c) Unit square isotropic unstructured meshes. (d) Half-unit disk isotropic unstructured meshes

Remark 7

We would like to emphasize that the main goals of this article were: (i) Investigate the possibility of solving the Dirichlet problem for the Mong–Ampère equation using continuous piecewise affine finite element approximations, well-suited to domain with curved boundaries. (ii) Use a simple operator-splitting based method, to solve the discrete Monge–Ampère problems. Privileging simplicity versus sophistication, our goal was not at this stage to develop fast solution methods, although the two-stage algorithm (a Newton-like method) is a step in that direction. There is no doubt that CPU times can be improved by using dedicated linear solvers more efficient than the more general ones picked by MATLAB, with the user out the loop. $\square$

In Table 4 we have compared the results obtained by the discrete analogue of algorithm (11)–(13) and by its two-stage variant, the meshes being like those in Fig. 1(a) (regular) and (b) (symmetric). These results show the significantly faster convergence of the two-stage algorithm, and the higher accuracy obtained with the regular mesh. We have visualized on Fig. 3 the results of Table 4; the plateaus reached by the $L_2$ and $L_{\infty }$ approximation errors as n increases appear clearly on this figure.

Table 4 (Test problem (47), $\alpha =1$): comparison between the discrete analogue of the one-stage algorithm (11)–(13) and its two-stage variant. These comparisons have been done for Fig. 1a (regular) and b (symmetric) types of meshes: (i) one-stage algorithm and regular mesh. (ii) two-stage algorithm and regular mesh. (iii) one-stage algorithm and symmetric mesh. (iv) two-stage algorithm and symmetric mesh. Relations (23) have been used to approximate the second order derivatives. In (i) and (ii), $h=\varDelta x_1=\varDelta x_2$

Fig. 3

(Test problem (47), $\alpha =1$): convergence histories of the $L_2$ and $L_{\infty }$ approximation errors: a regular mesh for $h(=\varDelta x_1=\varDelta x_2)=1/80$. b Symmetric mesh for $h=1/80$. Relations (23) have been used to approximate the second order derivatives. We observe that the various errors reach a plateau for n sufficiently large

Suppose that one takes $\varepsilon =0$ in the discrete analogue of (12), $C=0$ in (23), and uses a mesh of Fig. 1a type to solve the discrete Monge–Ampère problem. The solution of problem (47) being a polynomial function of degree 2, it follows from Remark 4 that the relations giving the discrete second order derivatives are exact at the vertices of ${\mathcal {T}}_h$ interior to $\varOmega$. Since $\frac{\partial }{\partial {\mathbf {n}}}{\mathbf {D}}^2u=0$ on $\partial \varOmega$, one expects to reach machine precision for a sufficiently large number of time steps. The results visualized in Fig. 4 show that this prediction is verified. These results have been obtained using the one-stage algorithm with $\varDelta t=h^2$, h being equal to 1/40; they show indeed that both the $L_2$ and $L_{\infty }$ approximation errors converge to 0 with machine precision.

Fig. 4

(Test problem (47), $\alpha =1$): histories of the $L_2$ and $L_{\infty }$ approximation errors for the one-stage algorithm with $\varepsilon =0$ in (12), $C=0$ in (23), and $\varDelta t=h^2$ (regular mesh on the unit square, $h=1/40$)

Increasing $\alpha$ in (47) increases, as expected, the anisotropy of the solution to the problem. A consequence of this phenomenon is that beyond $\alpha =5$ there is no gain at using the two-stage algorithm, as shown by the numerical comparisons we performed. This appears clearly on Fig. 5 where we have visualized the convergence histories of the one-stage and two-stage algorithms, when applied to the solution of problem (47) with $\alpha =5$.

Fig. 5

(Test problem (47), $\alpha =5$): histories of the $L_2$ and $L_{\infty }$ approximation errors for the one-stage and two-stage algorithms. a Regular mesh on the unit square with $h=1/40$. b Symmetric mesh with $h=1/40$. Relations (23) have been used to approximate the second order derivatives. For the two-stage algorithm we used $\gamma =1$ and $\varDelta \tau =8h$ in the discrete analogue of (46)

6.3 A Smooth Exponential Example

In this section, we consider the following Monge–Ampère problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=64\left( 1+2r^2\right) e^{2r^2} \text{ in } \varOmega ,\\ u=4e^{r^2}-\frac{9}{2}, \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(48)

with $r=\sqrt{(x_1-1/2)^2+(x_2-1/2)^2}$, $\varOmega$ being either the unit square $(0,1)^2$ or the open disk of radius 1/2 centered at (1 / 2, 1 / 2). We recall that if function $\phi$ is radial with respect to (1 / 2, 1 / 2), then $\det {\mathbf {D}}^2 \phi =\frac{\phi '\phi ''}{r}$, implying that the function u defined by $u=\left. \left( 4e^{r^2}-\frac{9}{2} \right) \right| _{{\bar{\varOmega }}}$ is an exact convex solution to problem (48). We have reported on Table 5: (i) The number of iterations needed to have convergence of the two-stage algorithm, using $\Vert u^{n+1}-u^n\Vert _2\le 10^{-7}$ as stopping criterion, and (ii) various approximation errors. These results were obtained with $\varepsilon =h^2$, the discrete second order derivatives being defined by (23). The orders of convergence of the approximation errors are not optimal but significantly higher than 1, the symmetric meshes having-as expected-the lowest orders of convergence. It is worth noticing that the unstructured isotropic meshes used on the disk give orders of convergence almost as good as those produced by the symmetric meshes on the unit square. For all tests with $h=1/160$, we set $\varepsilon =h$ and the stopping criterion $\Vert {\mathbf {D}}^2u^n-{\mathbf {p}}^n\Vert <10$ for stage-one and stopping criterion $\Vert u^{n+1}-u^n\Vert _2<10^{-8}$ for stage-two.

Table 5 [Test problem (48)]: (i) number of iterations necessary for the convergence of the two-stage algorithm. (ii) Approximation errors and convergence rates for the solution and its gradient. (a) Regular meshes of the unit square. (b) Symmetric meshes of the unit square. (c) Unstructured isotropic meshes of the unit square. (d) Unstructured isotropic meshes of the half-unit disk. Relations (23) have been used to approximate the second order derivatives. (In (a), $h=\varDelta x_1=\varDelta x_2$)

In Fig. 6 we have compared the convergence histories of the one-stage and two-stage algorithms, when applied to the solution of problem (48). The comments we did, in Sect. 6.2, about Fig. 3 (concerning the solution of problem (47) with $\alpha =1$) still apply here.

Fig. 6

[Test problem (48)]: convergence histories of the $L_2$ and $L_{\infty }$ approximation errors: a regular mesh for $h=1/40$. b Symmetric mesh for $h=1/40$. We observe that the various errors reach a plateau for n sufficiently large. Relations (23) have been used to approximate the second order derivatives. (In a$h=\varDelta x_1=\varDelta x_2$)

In Table 6, we have reported the CPU time necessary for the two-stage algorithm to solve problem (48), for the same types of meshes and space discretization steps than in Table 5, relation (23) being used to approximate the second order derivatives.

Table 6 [Test problem (48)]: CPU times for the two-stage algorithm and the four types of meshes shown in Fig. 1, the values of h being those in Table 5. (a) Unit square regular meshes. (b) Unit square symmetric meshes. (c) Unit square unstructured meshes. (d) Half-unit disk unstructured meshes

In Table 7, we have compared the results obtained by the discrete analogue of algorithm (11)–(13) and by its two-stage variant, the meshes being like those in Fig. 1a, b with relations (23). These results show the significantly faster convergence of the two-stage algorithm. The above results, combined with those reported in Sect. 6.2, strongly suggest that for problems with smooth isotropic solutions the two-stage algorithm is clearly faster than the one-stage one.

Table 7 [Test problem (48)]: comparison between discrete analogue of the one-stage algorithm (11)–(13) and its two-stage variant. These comparisons have been done for meshes as in Fig. 1a (regular) and b (symmetric): (i) one-stage algorithm and regular mesh. (ii) two-stage algorithm and regular mesh. (iii) one-stage algorithm and symmetric mesh. (iv) two-stage algorithm and symmetric mesh. Relations (23) have been used to approximate the second order derivatives. In (i) and (ii), $h=\varDelta x_1=\varDelta x_2$

Finally, we have reported in Table 8, various convergence results obtained when combining the two-stage algorithm with the approximation of the second order derivatives defined by (35), (36). We use stopping criterion $\Vert {\mathbf {D}}^2u^n-{\mathbf {p}}^n\Vert <10$ for stage-one and $\Vert u^{n+1}-u^n\Vert _2<10^{-4}$ for stage-two, the same criterions as those for Table 2. Comparing with the results in Table 5 the following conclusions can be drawn: (i) The algorithms based on approximation (35), (36) of the second order derivatives are (roughly) twice faster than those based on approximation (23). (ii) Approximation (23) leads to higher orders of accuracy for the approximation errors. Further numerical experiments will show that for most non-smooth problems, the algorithms relying on (35), (36) are faster and more accurate than those based on (23).

Table 8 [Test problem (48)]: (i) number of iterations necessary for the convergence of the two-stage algorithm. (ii) Approximation errors and convergence rates for the solution and its gradient. (a) Regular meshes of the unit square. (b) Symmetric meshes of the unit square. (c) Unstructured isotropic meshes of the unit square. (d) Unstructured isotropic meshes of the half-unit disk. Relations (35) and (36) have been used to approximate the second order derivatives. (In (a), $h=\varDelta x_1=\varDelta x_2$)

6.4 A Popular Monge–Ampère Problem Without Classical Solution

The test problems we considered in Sects. 6.2 and 6.3 had exact, strictly convex classical solutions belonging to $C^{\infty }({\bar{\varOmega }})$. Our goal in this section is to investigate the ability of our methodology at handling a ’pathological’ (nevertheless very popular) Monge–Ampère problem, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=1 \text{ in } \varOmega , \\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(49)

with $\varOmega =(0,1)^2$. Problem (49) (introduced in [11], to the best of our knowledge) is pathological since, despite the simplicity of its data (making it the Monge–Ampère analogue of the Dirichlet problem $-\nabla ^2 u=1$ in $\varOmega ,u=0$ on $\partial \varOmega , \varOmega$ still being the unit square), this problem does not have smooth classical solutions. The non-existence of smooth solutions to problem (49) is very simple to prove (see, e.g., [14] for details), the difficulty stemming, from the non-strict convexity of $\varOmega$ (and from the corners of $\varOmega$). The non-existence of classical solutions does not prevent problem (49) to have generalized solutions, viscosity solutions for example. Actually, the approximation of the viscosity solutions to problem (49), and their computation, has been thoroughly investigated in, e.g., [4, 38]; this is fortunate since it will allow qualitative and quantitative comparisons. The computational method we used to solve problem (49) relies on the one-stage algorithm combined with the approximation (35), (36) of the second order derivatives, the other combinations being slower and less accurate. Using $\Vert u^{n+1}-u^n\Vert _2\le 10^{-8}$ as stopping criterion, we obtained the results reported and visualized on Table 9 and Figs. 7 and 8 [in Table 9(a) $h=\varDelta x_1=\varDelta x_2$, while in Table (b) and (c), h denotes the length of the mesh largest edge(s)].

Table 9 [Test problem (49)]: (i) second column—number of iterations of the one-stage algorithm necessary to achieve convergence (approximation (35), (36) of second order derivatives). (ii) Fourth and fifth columns: Discrete $L_2$-norms of the consistency gap ${\mathbf {D}}^2_h (u_h)-{\mathbf {p}}_h$. (iii) Minimal values of the computed solutions. (a) Regular meshes of the unit square. (b) Symmetric meshes of the unit square. (c) Isotropic unstructured meshes of the unit square. (In (a), $h=\varDelta x_1=\varDelta x_2$)

Fig. 7

[Test problem (49)]: graphs and contours of the computed solutions, using the one-stage algorithm and relations (35), (36) to approximate the second order derivatives. a Regular mesh with $h=1/120$. b Symmetric mesh with $h=1/120$. c Unstructured isotropic mesh with $h=1/120$. (In a$h=\varDelta x_1=\varDelta x_2$)

As $h\rightarrow 0$, the results from Table 9 and graphs of Figs. 7 and 8 indicate the convergence of the approximate computed solutions to a convex function whose minimal value is close to − 0.183. The three types of meshes we employed share these convergence properties. The graphs in Fig. 7 are qualitatively close to graphs reported in the literature (in references [4, 38], for example). Making quantitative comparisons is more difficult. Indeed the minimal values reached by the solutions computed in [4] Section 5.3 on a $141\times 141$ grid (the finest one used in [4]) range from 0.2621 to 0.3024. Since the test problem considered in [4] was

$$\begin{aligned} \det {\mathbf {D}}^2u=1 \text{ in } {\tilde{\varOmega }}, u=1 \text{ on } \partial {\tilde{\varOmega }}, \end{aligned}$$

Fig. 8

[Test problem (49)]: graphs of the restrictions of the computed solutions to: a the line $x_1=1/2$ and b the line $x_1=x_2$, for $h=1/20,1/40,1/80,$ and 1 / 120 (one-stage algorithm using regular meshes, and approximations (35), (36) of the second order derivatives). a, b Suggest the uniform convergence of the approximate solutions to a strictly convex generalized solution of problem (49)

with ${\tilde{\varOmega }}=(-1,1)^2$, corrections are needed (subtract 1 and divide by 4), leading to the range [− 0.184475, − 0.17315] which contains definitely all the values reported in the $6\mathrm{th}$ column of Table 9 (which is gratifying in itself). Actually, there is more: Indeed, one can assume reasonably that in Table 8 of [4] the most accurate approximation of the actual minimal value is 0.2695. Two reasons for that statement are that: (i) The value 0.2695 has been obtained with the finer mesh ($141\times 141$) and wider stencil (33 points) used in [4], and (ii) it has been proved (see, e.g., [22]) that the associated method guarantees convergence to a viscosity solution. After correction of the value 0.2695, one obtains − 0.182625, which is pretty close to the value − 0.1831 reported in Table 9(a) for $h=1/120$.

Remark 8

The above comparisons with the results in [4] suggest that our methodology produces approximate solutions converging to viscosity solutions if one uses (35), (36) to approximate the second order derivatives. Albeit we do not know how to prove this convergence result, it is not completely surprising since our method solves the regularized Mong–Ampère equation

$$\begin{aligned} -\frac{\varepsilon }{2} \nabla ^2 u-\det {\mathbf {D}}^2u=-1 \text{ in } \varOmega , u=0 \text{ on } \partial \varOmega , \end{aligned}$$

with $\varepsilon \approx h^2$ after space discretization.

We mentioned above that the non-strict convexity of $(0,1)^2$ was explaining the non-existence of smooth solutions to problem (49). In order to investigate the influence of boundary corners we considered the following variant of problem (49)

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=1 \text{ in } \varOmega , \\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(50)

where $\varOmega$ is the (eye-shape) strictly convex domain defined by

$$\begin{aligned} \varOmega =\{\{x_1,x_2\}|-x_1(1-x_1)<x_2<x_1(1-x_1),0<x_1<1\}, \end{aligned}$$

and visualized in Fig. 9 (where we have also visualized one of the triangulations we employed). We have reported on Table 10 and Figs. 10 and 11 numerical results obtained by the one-stage algorithm, using approximations (35), (36) of the second order derivatives, the stopping criterion still being $\Vert u^{n+1}-u^n\Vert _2<10^{-8}$. Comparing Tables 9 and 10 shows several qualitative similarities, namely: (i) The number of iterations necessary to achieve convergence of the one-stage algorithm is a fast increasing function of 1 / h. (ii) The discrete $L^2$-norm of the consistency gap ${\mathbf {D}}^2_h (u_h)-{\mathbf {p}}_h$ increases with 1/h. These results suggest the non-existence of a smooth convex solution to problem (50). We could have anticipated this result. Suppose indeed that u is a convex solution to (50) belonging to $C^1({\bar{\varOmega }})$: it follows then from the boundary conditions that

$$\begin{aligned} \nabla u(0,0)\cdot {{{\tau }}}_+=0, \nabla u(0,0)\cdot {{{\tau }}}_-=0, \end{aligned}$$

(51)

Fig. 9

[Test problem (50)]: a triangulation of the eye-shape domain ($h=1/40$)

Table 10 [Test problem (50)]: (i) second column—number of iterations of the one-stage algorithm necessary to achieve convergence (approximations (35), (36) of the second order derivatives). (ii) Fourth and fifth columns: Discrete $L_2$-norms of the consistency gap ${\mathbf {D}}^2_h(u_h)-{\mathbf {p}}_h$. (iii) Minimal values of the computed solutions

where the unit vectors ${{{\tau }}}_+(=(1/\sqrt{2},1/\sqrt{2}))$ and $\tau _-(=(1/\sqrt{2},-1/\sqrt{2}))$ are tangent at (0, 0) at the upper and lower parts of $\partial \varOmega$, respectively. Relations (51) imply $\nabla u(0,0)={\mathbf {0}}$. Similarly, one can show that $\nabla u(1,0)={\mathbf {0}}$. The function u being convex and differentiable on the convex set ${\bar{\varOmega }}$, and vanishing on $\partial \varOmega$, the relation $\nabla u(0,0)={\mathbf {0}}$ implies that $u=0$ on ${\bar{\varOmega }}$, which implies in turn that $\det {\mathbf {D}}^2u=0$ in $\varOmega$, contradicting (50).

Figures 10 and 11 suggest uniform convergence to a strictly convex function as $h\rightarrow 0$ , the gradient of this solution being infinite on $\partial \varOmega \backslash \left\{ \{0,0\},\{1,0\}\right\}$.

Fig. 10

[Test problem (50)]: graph and contours of the computed approximate solution ($h=1/80$)

Fig. 11

[Test problem (50)]: graphs of the computed approximate solutions restricted to the lines $x_2=0$ (left), and $x_1=1/2$ (right) ($h=1/20, 1/40, 1/80, 1/120$)

6.5 Test Problems with Singular Functions f

This subsection is dedicated to Monge–Ampère-Dirichlet problems, where function f in (1) is singular (in the sense that $\sup _{x\in \varOmega } f(x)=+\infty$). In that direction, the first problem we consider is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=\frac{1}{r} \text{ in } \varOmega ,\\ u=\frac{2\sqrt{2}}{3}r^{3/2} \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(52)

where $\varOmega =(-1,1)^2$ and $r=\sqrt{(x_1-1)^2+(x_2-1)^2}$, implying that function f blows up at the corner (1, 1). The strictly convex function u defined by

$$\begin{aligned} u(x_1,x_2)=\frac{2\sqrt{2}}{3}r^{3/2}, \forall (x_1,x_2)\in {\bar{\varOmega }}, \end{aligned}$$

is an exact solution to problem (52). Very clearly, $u\notin C^2({\bar{\varOmega }})$. On the other hand, one can easily verify that $u\in C^1({\bar{\varOmega }})\cap W^{2,s}(\varOmega ), \forall s\in [1,4)$, making problem (52) an ’almost’ smooth one. To solve problem (52), we used the finite element analogue of the one-stage algorithm (11)–(13) with $\varepsilon =2h^2$, the triangulations we employed being regular (as in Fig. 1a), or symmetric (as in Fig. 1b). We used relations (23) to approximate the second order derivatives with $C=2$. We took $\Vert u^{n+1}-u^n\Vert _2<10^{-5}$ as stopping criterion. For this test problem, h denotes the space discretization step $\varDelta x_1(=\varDelta x_2)$.

We have visualized on Fig. 12 (resp., Fig. 13) the graph of the computed approximate solution, and the convergence histories of the residual $\Vert u^{n+1}-u^n\Vert _2$ and of the $L_2$ and $L_{\infty }$ norms of the approximation error, Fig. 12 (resp., Fig. 13) being associated with the $h=1/64$ regular (resp., $h=1/64$ symmetric) triangulation.

Fig. 12

[Test problem (52)]: graphs of the computed approximate solution and convergence histories (regular triangulation with $h=1/64$)

Fig. 13

[Test problem (52)]: graphs of the computed solution and convergence histories (symmetric triangulation with $h=1/64$)

In Table 11(a), we have reported results obtained on regular meshes by the method detailed above, namely number of iterations necessary to achieve convergence and related approximation errors for various values of h. For comparison purpose, we have reported in Table 11(b) the related results obtained in [43] on identical meshes by two solution methods, both relying on those wide-stencil finite difference methods discussed in [22]. Comparing Table 11(a) and (b) shows that (for this test problem at least) the method we employed to solve problem (52) is significantly more accurate than the two methods discussed in [43] (however, for this test problem and for the same meshes, they are less accurate and much slower than the least-square/relaxation method discussed in [8]).

Table 11 [Test problem (52)]: number of iterations necessary to achieve convergence and associated approximation errors on regular meshes for various mesh sizes. (a) Results obtained by the methodology discussed in the current article. (b) Results obtained by the two methods discussed in [43] (M1 and M2 are the numbers of iterations needed by the two methods discussed in [43] to achieve convergence)

Remark 9

The methods discussed in [43] rely on accelerated gradient type algorithms à la Nesteroy ([36, 45]) whose convergence rate is $O(1/n^2)$, n denoting the number of iterations. Actually, the two methods discussed in [43] are also cascadic (in the sense that a first approximate solution is computed on a coarse mesh, and then interpolated on a mesh twice finer, in order to initialize an iterative method). Motivated by [36, 43] (and by suggestions of our colleague X.C. Tai) we applied the so-called Nesterov method (introduced by Polyak in [41]) to speed up the convergence of the algorithms considered in the present article. The improvement it brings to these algorithms are marginal (if any). A possible explanation is that our algorithms rely on implicit/explicit schemes, unlike the algorithms in [43], all related to fully explicit schemes. $\square$

The second problem we consider in this subsection is another classical test problem. It is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u=\frac{R^2}{(R^2-r^2)^2} \text{ in } \varOmega ,\\ u=-\sqrt{R^2-r^2} \text{ on } \partial \varOmega . \end{array}\right. } \end{aligned}$$

(53)

where $\varOmega \!=\!(0,1)^2, R\!\ge \!1/\sqrt{2}$, and $r\!=\!\sqrt{(x_1-1/2)^2\!+\!(x_2\!-\!1/2)^2}$. The function u defined by

$$\begin{aligned} u(x_1,x_2)=-\sqrt{R^2-r^2}, \forall (x_1,x_2)\in {\bar{\varOmega }}, \end{aligned}$$

is a strictly convex solution to problem (53), its graph being a part of the sphere of radius R centered at (1/2,1/2,0). The above function u belongs to $C^{\infty }({\bar{\varOmega }})$ if $R>1/\sqrt{2}$. On the other hand, $u\in C^0({\bar{\varOmega }}) \cap W^{1,s}(\varOmega ), s\in [1,4),$ if $R=1/\sqrt{2}$, the vector-valued function $\nabla u$ being singular at the four corners of ${\bar{\varOmega }}$. Function u reaches its minimal value $(-R)$ at (1/2,1/2). We tested our methodology on the two particular cases of problem (53) associated with $R=\sqrt{2}$ (a smooth case) and $R=1/\sqrt{2}$ (a non-smooth case). For both values of R we used: (i) Regular triangulations (like the one in Fig. 1a, with $h(=\varDelta x_1=\varDelta x_2)$ taking the values 1/20, 1/40 and 1/80, and (ii) the fully discrete analogue of the one-stage algorithm (11)–(13) with $\varepsilon =h^2$. The results in Table 12(a) [resp., Table 12(b)] have been obtained using approximation (23) [resp., (35), (36)] of the second derivatives, the stopping criterion being $\Vert u^{n+1}-u^n\Vert _2<10^{-10}$ (resp., $<10^{-8}$). These results show that the method relying on (23) is second order accurate, while the other one is first order accurate. We observe also that in Table 12(a) [resp., Table 12(b)] the minimal value of the computed solutions decreases (resp., increases) with h, the convergence to the exact value ($-\sqrt{2}(=-\,1.41421\dots )$, here) being much faster for the first method. From the smoothness of the $R=\sqrt{2}$ solution, the results reported just above were expected, including the clear superiority of the relation (23) based method (Table 12).

Table 12 (Test problem (53) with $R=\sqrt{2}$): number of iterations needed for the convergence of the one-stage algorithm, minimal value of the computed solutions, and associated $L_2$ and $L_{\infty }$ norms of the approximation errors. (a) Approximations (23) of the second order derivatives. (b) Approximations (35), (36) of the second order derivatives. We used regular triangulations (with $h=\varDelta x_1=\varDelta x_2$), as the one in Fig. 1a, to obtain these results. We recall that the minimal value of the exact solution is $-\sqrt{2}(=-\,0.141421\dots )$

Taking $R=1/\sqrt{2}$ in (53) makes this problem non-smooth (and therefore more challenging) since $\nabla u$ is singular at the four corners of ${\bar{\varOmega }}$. Taking $\Vert u^{n+1}-u^n\Vert _2<10^{-8}$ as stopping criterion, we obtained the results reported in Table 13(a) and (b).

Table 13 (Test problem (53) with $R=1/\sqrt{2}$): number of iterations needed for the convergence of the one-stage algorithm, minimal value of the computed solutions, and associated $L_2$ and $L_{\infty }$ norms of the approximation errors. (a) Approximations (23) of the second derivatives. (b) Approximations (35), (36) of the second derivatives. We used regular triangulations (with $h=\varDelta x_1=\varDelta x_2$), as the one in Fig. 1a, to obtain these results. We recall that the minimal value of the exact solution is $-1/\sqrt{2}(=-\,0.707106\dots )$

Comparing Table 13(a) and (b) suggest the following: (i) The two one-stage methods we employed, relying on either (23) or (35), (36) behave similarly as long as iterative properties are concerned. (ii) The first method produces better approximation errors for the values of h considered here, particularly for the discrete $L_2$ approximation error. Actually, the convergence rates reported in the last column of Table 13(a) are close to those reported in Section 5.4 of [4], for a closely related problem. (iii) We observe that in Table 13(a) [resp., Table 13(b)] the minimal value of the computed solutions decreases (resp., increases) with h . We observed a similar behavior in Table 12. As we already mentioned, the numerical solution of problem (53) with $R=1/\sqrt{2}$ is discussed in [4]; it is discussed also in [22, 37].

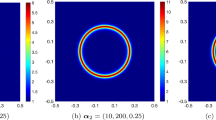
The two graphs in Fig. 14 are quite similar and show very clearly the singular behavior of $\nabla u$ close to the four corners of ${\bar{\varOmega }}$.

Fig. 14

(Test problem (53) with $R=1/\sqrt{2}$): graphs of the approximate solutions computed on a regular mesh with $h=1/80$. a Approximations (23) of the second order derivatives. b Approximations (35), (36) of the second order derivatives

Table 14 [Test problem (54)]: (i) number of iterations needed for the convergence of the one-stage algorithm. (ii) Approximations errors and orders of convergence. (a) Approximation (23) of the second order derivatives. (b) Approximations (35), (36) of the second order derivatives

Fig. 15

[Test problem (54)]: a, b graphs and contours of the approximate solution computed using approximations (23) of the second order derivatives ($h=1/160)$. c, d Graphs and contours of the approximate solution computed using approximations (35), (36) of the second order derivatives ($h=1/160$). e, f Graphs of the restrictions of the computed approximate solutions to the diameter $x_1=1/2$, for $h=1/20,1/40,1/80$ and 1/160 [e approximations (23), f approximations (35), (36)]

The next problem with a spherical solution we consider is the following variant of problem (53):

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u=\frac{4}{\left( 1-4r^2\right) ^2} \text{ in } \varOmega ,\\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(54)

where $\varOmega \!=\!\{\{x_1,x_2\},(x_1\!-\!1/2)^2+(x_2-1/2)^2<1/4\}$ and $r\!=\!\sqrt{(x_1-1/2)^2\!+\!(x_2-1/2)^2}$. The function u defined by

$$\begin{aligned} u(x_1,x_2)=-\frac{1}{2}\sqrt{1-4r^2} \text{ on } {\bar{\varOmega }} \end{aligned}$$

is a strictly convex solution to problem (54), taking its minimal value − 1/2 at (1/2,1/2). We can easily show that $u\in C^0({\bar{\varOmega }})\cap W^{1,s}(\varOmega ), \forall s\in [1,2)$.

Problem (54) is significantly ’more non-smooth’ than problem (53) since $|\nabla u|$ is infinite on the whole boundary of ${\bar{\varOmega }}$, making (54) a good test problem to investigate the robustness of our methodology. In order to solve problem (54) we used: (i) Isotropic unstructured finite element meshes like the one in Fig. 1d. (ii) The one-stage algorithm with $\varepsilon =h^2$. (iii) The approximations of the second order derivatives defined by (23) and (35), (36). (iv) $\Vert u^{n+1}-u^n\Vert _2<10^{-5}$ as stopping criterion. The results reported in Table 14(a) and (b) show that the two approaches we are considering are very close to each other as long as the number of iterations is concerned. On the other hand, these results show that the second method is more accurate than the first one. We obtain a clear-cut confirmation of the superiority of the second method by comparing Fig. 15e , f where we visualized, for various values of h, the graphs of the restrictions of the computed approximate solutions to the diameter $x_1=1/2$. Figure 15a–d (obtained with $h=1/160$) provide additional details.

Remark 10

When applied to the solution of problems (53) and (54), the two-stage algorithm (described in Sect. 5) does not decrease the number of iterations needed for convergence, when compared to the one-stage algorithm (11)–(13). This disappointing (but not surprising) property follows from the non-smoothness of the solution to both problems. To check again that solution smoothness enhances the speed of convergence of the two-stage algorithm we are going to consider another test problem with a spherical solution, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u=\frac{2}{\left( 2-r^2\right) ^2} \text{ in } \varOmega ,\\ u=-\sqrt{2-r^2} \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(55)

where $\varOmega \!=\!\{\{x_1,x_2\},(x_1-1/2)^2+(x_2-1/2)^2<1/4\}$ and $r\!=\!\sqrt{(x_1-1/2)^2+(x_2-1/2)^2}$. The function u defined by

$$\begin{aligned} u(x_1,x_2)=-\sqrt{2-r^2} \text{ on } {\bar{\varOmega }} \end{aligned}$$

is a strictly convex solution to problem (55), verifying $u\in C^{\infty }({\bar{\varOmega }})$. Applying the two-stage algorithm combined with unstructured isotropic triangulations, like those in Fig. 1d, leads to the results reported in Table 15 and visualized in Fig. 16 (we used $\Vert u^{n+1}-u^n\Vert _2<10^{-7}$ as topping criterion).

Fig. 16

[Test problem (55)]: graphs of the computed approximate solutions and variations with n of the residual and of the $L_2$ and $L_{\infty }$ norms of the approximation errors (two-stage algorithm and isotropic unstructured triangulation of the disk ${\bar{\varOmega }}$ with $h=1/80$). a, b Approximations (23) of the second order derivatives. c, d Approximations (35), (36) of the second order derivatives

Table 15 [Test problem (55)]: performances of the two-stage algorithm on a family of isotropic unstructured meshes. (a) Approximations (23) of the second order derivatives. (b) Approximations (35), (36) of the second order derivatives. The minimal value of the exact solution is $-\sqrt{2}(=-\,1.41421\dots )$

Table 15 shows that the two-stage approach we tested behave quite similarly as long as the number of iterations is concerned. On the other hand Table 15 shows that for this smooth test problem, the method based on (23) provides approximation errors ’almost’ two orders of magnitude smaller than the one based on (35), (36).

Figure 16 shows that, in practice, the final values of the approximation error norms are reached much more quickly, when using relations (35), (36) to approximate the second order derivatives, than when using (23). $\square$

To conclude this sub-section, dedicated to test problems with singular functions f, we are going to consider a test problem, which seems to be new in this context, namely:

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=f \text{ in } \varOmega ,\\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(56)

with $\varOmega =(0,1)^2$ and f defined by

$$\begin{aligned} f(x_1,x_2)=\frac{1-(1-2x_1)^2(1-2x_2)^2}{16x_1(1-x_1)x_2(1-x_2)}, \forall (x_1,x_2)\in \varOmega . \end{aligned}$$

The strictly convex function u defined by

$$\begin{aligned} u(x_1,x_2)=-\sqrt{x_1(1-x_1)x_2(1-x_2)}, \forall (x_1,x_2)\in {\bar{\varOmega }}, \end{aligned}$$

is solution to problem (56). We clearly have $u\in C^0({\bar{\varOmega }})\cap W^{1,s}(\varOmega ), \forall s\in [1,2)$, with $\nabla u$ singular on the whole boundary of $\varOmega$. Combining the one-stage algorithm with regular triangulations, we obtained the results reported in Table 16 and visualized in Fig. 17. These results show the clear superiority, in terms of accuracy, of the approach based on approximations (35), (36) of the second order derivatives. Actually, comparing Fig. 17f, h shows that the method based on (35), (36) has better convexity conservation properties than the method based on (23). We used $\Vert u^{n+1}-u^n\Vert _2<10^{-6}$ (resp. $10^{-7}$) as stopping criterion for $h=1/20, 1/40$ and 1/80 (resp., 1/160).

Fig. 17

[Test problem (56)]: a, b, c, d graphs and contours of the approximate solution obtained by the one-stage algorithm on a regular mesh with $h(=\varDelta x_1=\varDelta x_2)=1/80$. e, g Graphs of the restrictions of the computed approximate solutions to the line $x_1=1/2$. f, h Graphs of the restrictions of the computed approximate solutions to the line $x_1=x_2$. The results visualized on a, b and e, f (resp., c, d and g, h) have been obtained using relations (23) [resp., (35), (36)] to approximate the second order derivatives

Table 16 [Test problem (56)]: performance of the one-stage algorithm combined with regular triangulations: (a) Approximations (23) of the second order derivatives. (b) Approximations (35), (36) of the second order derivatives. The minimal value of the exact solution is − 0.25, showing the clear superiority of the second approach

Problem (56) deserves becoming a classical test problem for Monge–Ampère–Dirichlet solvers: Future will tell.

6.6 Test Problems with a Positive Measure as Right-Hand Side

Test problems where, in (1), f is a Dirac measure (possibly multiplied by some positive constant) are classical nowadays. Our goal in this section is to return to such test problems, and then to go one step further by considering situations where measure f is of the form

$$\begin{aligned} v\rightarrow \int _{\gamma } vd\gamma , \end{aligned}$$

$\gamma$ being a curve contained in $\varOmega$. We consider first the test problem defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u=\pi \delta _{(1/2,1/2)} \text{ in } \varOmega ,\\ u=r \text{ on } \partial \varOmega \end{array}\right. } \end{aligned}$$

(57)

where in (57): $\varOmega$ is either the square $(0,1)^2$ or the open disk of radius 1/2 centered at (1/2,1/2), $r=\sqrt{(x_1-1/2)^2+(x_2-1/2)^2}$, and $\delta _{(1/2,1/2)}$ is the Dirac measure at (1/2,1/2). The function u defined by $u=r|_{{\bar{\varOmega }}}$ is an exact convex solution to problem (57), belonging to $W^{1,\infty }(\varOmega )$.

In order to apply our methodology to the numerical solution of problem (57) we approximated (as in [8]) the measure $\pi \delta _{(1/2,1/2)}$ by the $C^{\infty }$ strictly positive function $f_{\eta }^1$ defined by

$$\begin{aligned} f_{\eta }^1(x_1,x_2)=\frac{\eta ^2}{\left[ \eta ^2+(x_1-1/2)^2+(x_2-1/2)^2\right] ^2}, \end{aligned}$$

(58)

with $\eta$ a small positive number having the dimension of a distance. In [8], good results were obtained using $\eta =h$. On the other hand, a ’good’ function $h\rightarrow \eta (h)$ seems more difficult to identify for the methodology we use in the present article. Assuming that (with obvious notation) the relation $\lim _{\eta \rightarrow 0}\lim _{h\rightarrow 0} u_h^{\eta }=u$ holds, we fixed $\eta$ and computed the associated approximate solution for various values of h, leading to the results reported and visualized in Tables 17, 18 and Figs. 18, 19. These results have been obtained using: (i) The one-stage algorithm with $\Vert u^{n+1}-u^n\Vert _2<10^{-8}$ as stopping criterion. (ii) Regular (resp., unstructured isotropic) triangulations of the unit square (resp., half unit disk). (iii) Approximations (35), (36) of the second order derivatives. Actually, we have also reported and visualized on those tables and figures, results obtained using the function $f_{\rho }^2$ defined, with $\rho >0$, by

$$\begin{aligned} f_{\rho }^2(x_1,x_2)=\frac{3}{\rho ^3}\max \left( 0, \rho -\sqrt{(x_1-1/2)^2+(x_2-1/2)^2}\right) +h, \end{aligned}$$

(59)

as approximation of the measure $\pi \delta _{(1/2,1/2)}$.

Table 17 (Test problem (57) for the unit square). For $h=1/20,1/40$ and 1 / 80: (i) number of iterations needed for convergence of the one-stage algorithm and associated residuals. (ii) Minimal value of the computed approximate solutions. (iii) Discrete $L_2$ and $L_{\infty }$ norms of the approximation errors and associated rates of convergence. Table (a) [resp., (b)] reports results associated with the approximation (58) [resp., (59)] of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$ (resp., $\rho =1/16$). The minimal value of the exact solution is 0

Table 18 (Test problem (57) for the half unit disk). For $h=1/20, 1/40$ and 1/80: (i) number of iterations needed for convergence of the one-stage algorithm and associated residuals. (ii) Minimal value of the computed approximate solutions. (iii) Discrete $L_2$ and $L_{\infty }$ norms of the approximation errors and associated rates of convergence. Table (a) [resp., (b)] reports results associated with the approximation (58) [resp., (59)] of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$ (resp., $\rho =1/16$). The minimal value of the exact solution is 0

Fig. 18

(Test problem (57) for the unit square): a, b, c (resp., d, e, f) are associated with the approximation (58) with $\eta =10^{-3/2}$ (resp., (59) with $\rho =1/16$) of the measure $\pi \delta _{(1/2,1/2)}$. a, d Graphs of the computed solutions for $h=1/80$. b, e Graphs of the restrictions of the computed solution to the line $x_1=1/2$ for $h=1/20,1/40$ and 1/80. c, f Graphs of the restrictions of the computed solution to the line $x_1=x_2$ for $h=1/20,1/40$ and 1/80. The minimal value of the exact solution is 0

Fig. 19

(Test problem (57) for the half-unit disk): a graph of the computed approximate solution obtained for $h=1/80$ by the one-stage algorithm, using the approximation (58) of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$. b Graphs of the restrictions of the computed approximate solutions to the diameter $x_1=1/2$, for $h=1/20,1/40$ and 1/80 (approximation (58) of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$). c Graphs of the restrictions of the computed approximate solutions to the diameter $x_1=1/2$, for $h=1/20,1/40$ and 1 / 80 (approximation (59) of the measure $\pi \delta _{(1/2,1/2)}$ with $\rho =1/16$). The minimal value of the exact solution is 0

Remark 11

If $\varOmega$ is a square, the solution of problem (57) (or closely related ones) has been addressed in various publications ([4, 8, 22, 23] among others), by a variety of computational methods, some of them particularly fast like the ones discussed in [23]. On the other hand, solving (57) on a disk using piecewise affine approximations is a more challenging issue; it has been addressed in particular in [8], using finite element approximations closely related (but not identical) to those discussed in Sect. 4. $\square$

We define as follows the last problem involving a Dirac measure we consider in this article:

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=2\delta _{(1/2,1/2)} \text{ in } \varOmega ,\\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(60)

where in (60), $\varOmega$ is the square $(0,1)^2$ and $\delta _{(1/2,1/2)}$ is the Dirac measure at (1/2,1/2). It follows from [17] that the function u defined by

$$\begin{aligned} u(x_1,x_2)=-\min \left( x_1, (1-x_1), x_2, (1-x_2)\right) , \forall (x_1,x_2)\in {\bar{\varOmega }} \end{aligned}$$

is an exact convex solution to problem (60), belonging to $W^{1,\infty }(\varOmega )$. Its minimal value is clearly − 0.5. In order to solve problem (60), we proceeded as follows: (i) For $h=1/20,1/40$ and 1/80, we used regular triangulations like the one in Fig. 1a. (ii) Employed the one-stage algorithm, using $\Vert u^{n+1}-u^n\Vert _2<10^{-6}$ or $10^{-8}$ as stopping criterion. (iii) Approximated the second order derivatives using relations (35), (36). (iv) Approximated the measure $2\delta _{(1/2,1/2)}$ by $\frac{2}{\pi } f_{\eta }^1$ (resp. $\frac{2}{\pi }f_{\rho }^2$), with $\eta =10^{-3/2}$ in (58) [resp., $\rho =1/16$ in (59)]. The results we obtained have been reported and visualized in Table 19 and Fig. 20.

Table 19 [Test problem (60)]. For $h=1/20,1/40$ and 1/80: (i) number of iterations needed for convergence of the one-stage algorithm and associated residuals. (ii) Minimal value of the computed approximate solutions. (iii) Discrete $L_2$ and $L_{\infty }$ norms of the approximation errors and associated rates of convergence. Table (a) [resp., (b)] reports results associated with the approximation (58) [resp., (59)] of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$ (resp., $\rho =1/16$). The minimal value of the exact solution is − 0.5

Fig. 20

[Test problem (60)] a, d graphs of the computed approximate solution obtained for $h=1/80$ by the one-stage algorithm. b, e Graphs of the restrictions of the computed approximate solutions to the line $x_1=1/2$, for $h=1/20,1/40$ and 1/80. c, f Graphs of the restrictions of the computed approximate solutions to the line $x_1=x_2$, for $h=1/20,1/40$ and 1/80. a, b, c (resp., d, e, f) correspond to the approximation (58) [resp., (59)] of the measure $\pi \delta _{(1/2,1/2)}$ with $\eta =10^{-3/2}$ (reps., $\rho =1/16$). The minimal value of the exact solution is − 0.5

Table 19 and Fig. 20 support the assumption $\lim _{\eta \rightarrow 0}\lim _{h\rightarrow 0} u_h^{\eta }=\lim _{\eta \rightarrow 0}\lim _{h\rightarrow 0}u_h^{\rho }=u$, but they show also that a critical issue needing to be addressed is identifying how to pick $\eta$ and $\rho$ as functions of h, in order to improve the convergence of the approximate solutions when $h\rightarrow 0$; we intend to investigate this issue.

To conclude this section dedicated to the numerical solution of problem (1), when f is a positive measure, we consider the following Monge–Ampère problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=f \text{ in } \varOmega ,\\ u=0 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(61)

where in (62): (i) $\varOmega =(0,1)^2$, and (ii) f is the positive measure defined by

$$\begin{aligned} \langle f,\phi \rangle =\int _{\gamma }\phi d\gamma , \forall \phi \in H_0^1(\varOmega ), \end{aligned}$$

(62)

the ’curve’ $\gamma$ being the cross defined by

$$\begin{aligned} \gamma =\{(x_1,x_2), 0<x_1<1, x_2=1/2\} \cup \{(x_1,x_2), x_1=1/2, 0<x_2<1\}. \end{aligned}$$

In order to apply to the solution of problem (61) the methodology discussed in Sects. 2–5, we approximate the above measure f by $f_{\eta }$, a strictly positive $C^{\infty }$ function defined by

$$\begin{aligned} f_{\eta }(x_1,x_2)=\eta ^2 \left[ \frac{1}{\left( \eta ^2+|x_1-1/2|^2\right) ^{3/2}}+\frac{1}{\left( \eta ^2+|x_2-1/2|^2\right) ^{3/2}}\right] , \forall (x_1,x_2)\in {\bar{\varOmega }}, \end{aligned}$$

(63)

with $\eta >0$. We can easily prove that $\lim _{\eta \rightarrow 0} f_{\eta }=f$ in the sense of distributions. The parameter $\eta$ having the dimension of a distance, we used $\eta =h$ when applying the methodology discussed in Sects. 2–5 to the solution of

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2 u_{\eta }=f_{\eta } \text{ in } \varOmega ,\\ u_{\eta }=0 \text{ on } \partial \varOmega . \end{array}\right. } \end{aligned}$$

(64)

The results reported and visualized in Table 20 and Fig. 21 have been obtain using: (i) Regular triangulations of $\varOmega$ for $h=1/20,1/40$ and 1/80 (here, $h=\varDelta x_1=\varDelta x_2$). (ii) The one-stage algorithm with $\Vert u^{n+1}-u^n\Vert <10^{-8}$ as stopping criterion. (iii) The approximations (35), (36) of the second order derivatives.

Table 20 [Test problem (61)]. For $h=1/20,1/40$ and 1/80: (i) Number of iterations needed for the convergence of the one-stage algorithm, and related residuals. (ii) Minimum values of the computed approximate solutions. We used $\eta =h$ in (63) when approximating the measure f by the function $f_{\eta }$

Fig. 21

[Test problem (61)]. a, b Graph and contours of the computed approximate solution for $h=1/80$. c Graph of the restrictions of the computed approximate solutions to the line $x_1=1/2$, for $h=1/20,1/40$ and 1/80. d Graphs of the restrictions of the computed approximate solutions to the line $x_1=x_2$, for $h=1/20,1/40$ and 1/80

From Fig. 21, we observe the convexity of the computed approximate solutions. Figure 21 suggests also a fast uniform convergence to a convex solution of problem (61) the choice $\eta =h$ works ’beautifully’.

Table 21 [Test problem (65)]. For $h=1/20,1/40, 1/80$ and 1/160: (i) Number of iterations needed for the convergence of the one-stage algorithm, and associated residuals. (ii) Minimum values of the computed approximate solutions. (iii) $L_2$ and $L_{\infty }$ norms of the approximation errors and related convergence rates. (a) $\eta =0$. (b) $\eta =h$. (c) $\eta =h^2$. The minimal value of the exact solution is 0

6.7 A Kind of Obstacle Problem

The last test problem we will consider in this article is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \det {\mathbf {D}}^2u=\max \left( 1-\frac{0.2}{r},0\right) \text{ in } \varOmega ,\\ u=\frac{1}{2}(\max (r-0.2,0))^2 \text{ on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(65)

where in (65), $\varOmega =(0,1)^2$ and $r=\sqrt{(x-1/2)^2+(_2-1/2)^2}$. Problem (65) was suggested to us by one of the anonymous referees of this article; its solution has been addressed in, e.g., [22, 37]. The function u defined by

$$\begin{aligned} u(x_1,x_2)=\frac{1}{2} \left( \max \left( \sqrt{(x_1-1/2)^2+(x_2-1/2)^2}-0.2,0\right) \right) ^2, \forall (x_1,x_2)\in {\bar{\varOmega }}, \end{aligned}$$

is the exact convex solution to problem (65); we clearly have $u\in C^1({\bar{\varOmega }})$. Since the function u vanishes in the open disk of radius 0.2 centered at (1/2,1/2), $\det {\mathbf {D}}^2 u$ shares the same property, making the elliptic problem (65) degenerated. In order to facilitate the solution of problem (65), we approximated the function $\max (1-\frac{0.2}{r},0)$ by $\max (1-\frac{0.2}{r},\eta )$, $\eta$ being a small non-negative parameter converging to 0 with h. We have reported in Table 21 and Fig. 22, numerical results associated with $\eta =0,\eta =h$ and $\eta =h^2$. These results have been obtained using: (i) Regular triangulations with $h(=\varDelta x_1=\varDelta x_2)=1/20, 1/40, 1/80$ and 1/160. (ii) The one-stage algorithm, the stopping criterion being $\Vert u^{n+1}-u^n\Vert _2<tol$ with $10^{-10}\le tol\le 10^{-7}$. (iii) Approximations (23) of the second order derivatives.

Fig. 22

[Test problem (65)]. Graphs of the computed approximate solutions for $h=1/80$: a$\eta =h$. b$\eta =h^2$. At first glance, the two graphs are identical

From an accuracy point of view, the results obtained for $\eta =h$ [Table 21(b)] match those reported in [22, 37], obtained using more sophisticated approximations. Moreover, Table 21(c) shows that taking $\eta =h^2$ increases accuracy by (roughly) one order of magnitude, the price to pay for this improvement being a much larger number of iterations in order to achieve the convergence of the one-stage algorithm.

Remark 12

We used the word obstacle in the title of this section. To justify this terminology, observe that, in (65), one can replace the equation

$$\begin{aligned} \det {\mathbf {D}}^2u=\max \left( 1-\frac{0.2}{r},0\right) \end{aligned}$$

by

$$\begin{aligned} \det {\mathbf {D}}^2 u=\left( 1-\frac{0.2}{r} \right) \chi _{(u>0)}, \end{aligned}$$

(66)

where $\chi _{(u>0)}$ is the characteristic function of the set $\{x\in \varOmega , u(x)>0\}$. One encounters equations similar to (66) in [42], a publication dedicated to obstacle problems for the Monge–Ampère operator $\phi \rightarrow \det {\mathbf {D}}^2\phi$. The obstacle associated with problem (65) is clearly the plane $x_3=0$.

7 Conclusion

In this article, we have developed a relatively easy to implement finite element and operator-splitting based methodology for the numerical solution of the Monge–Ampère equation. The related methods have performed well for various types of triangulations (structured and unstructured) and can handle curved boundaries quite easily since they rely on continuous piecewise affine approximations. We introduced also a Newton-like two-stage variant of our methodology, which accelerates significantly the convergence if the problem under consideration has a smooth convex solution. Our future investigations (some of them quite advanced) will include looking at techniques to further accelerate the convergence of our iterative procedures, and the solution of three-dimensional and obstacle problems for the Monge–Ampère operator $\phi \rightarrow \det {\mathbf {D}}^2\phi$.