Globally Divergence-Free Discontinuous Galerkin Methods for Ideal Magnetohydrodynamic Equations

Abstract

Ideal magnetohydrodynamic (MHD) equations are widely used in many areas in physics and engineering, and these equations have a divergence-free constraint on the magnetic field. In this paper, we propose high order globally divergence-free numerical methods to solve the ideal MHD equations. The algorithms are based on discontinuous Galerkin methods in space. The induction equation is discretized separately to approximate the normal components of the magnetic field on elements interfaces, and to extract additional information about the magnetic field when higher order accuracy is desired. This is then followed by an element by element reconstruction to obtain the globally divergence-free magnetic field. In time, strong-stability-preserving Runge–Kutta methods are applied. In consideration of accuracy and stability of the methods, a careful investigation is carried out, both numerically and analytically, to study the choices of the numerical fluxes associated with the electric field at element interfaces and vertices. The resulting methods are local and the approximated magnetic fields are globally divergence-free. Numerical examples are presented to demonstrate the accuracy and robustness of the methods.

1 Introduction

In this paper, we will develop globally divergence-free discontinuous Galerkin (DG) methods to numerically simulate ideal magnetohydrodynamic (MHD) equations. MHD equations model ionized plasmas under some simplified assumptions and are widely used for describing many problems in physics and engineering. The ideal MHD equations considered in this work can be written as a system of nonlinear hyperbolic conservation laws, in addition to a divergence-free constraint on the magnetic field. Even though the magnetic field in the exact solution satisfies the divergence-free condition as long as it does initially, insufficient preservation of this property numerically may lead to numerical instability or nonphysical features of approximated solutions [8, 9, 19, 37].

To handle the divergence-free constraint, various strategies have been developed in numerical modeling and mathematical analysis within divergence-cleaning or divergence-free algorithms. In [9], Brackbill and Barnes proposed a simple divergence correction technique based on Hodge decomposition. They projected the computed magnetic field into a divergence-free vector space by solving a Poisson equation and used the divergence-free magnetic field in the next time step. One widely used framework to achieve the preservation of the divergence, in some discrete or continuous sense, is “constrained transport”, introduced by Yee [40] in the context of the electromagnetism, and adapted by Evans and Hawley [19] to MHD simulations. This idea was further developed by many researchers within frameworks of finite difference, finite volume, and finite element methods, either upwind (also called Godunov) or central types, and with various accuracy [8, 17, 20, 26, 29]. Among the developments, there are exactly divergence-free numerical methods [1, 3, 26, 28, 29, 35]. Other approaches which attract different practitioners include Powell’s source term formulation [30] by adding source terms depending on $\nabla \cdot {\mathbf {B}}$, and generalized multiplier methods [18] with divergence cleaning technique.

In recent years, Li et al. [25,26,27, 38] developed divergence-free numerical methods for ideal MHD equations based on DG and central DG spatial discretizations. In [25], locally divergence-free DG methods were formulated, and they utilize divergence-free vector spaces inside each mesh element to approximate the magnetic field. In [26, 27], exactly divergence-free central DG methods were proposed for ideal MHD equations, and the methods can be of arbitrary accuracy. The discrete space to represent and to compute the magnetic field is a divergence-free subspace of the Brezzi–Douglas–Marini (BDM) finite element space [10], a well-established H(div)-conforming finite element space. DG method was first introduced in 1973 by Reed and Hill for linear neutron transport problems [33]. A major breakthrough was made by Cockburn et al. [13,14,15,16] to develop DG spatial discretizations for nonlinear hyperbolic conservation laws, coupled with high order Runge–Kutta methods in time. Exact or approximate Riemann solvers are used as numerical fluxes at element interfaces, and total variation bounded (TVB) nonlinear limiters [36] are applied in the presence of strong shocks to achieve non-oscillatory property. With their great flexibility in local approximations and geometry, local conservation, and high parallel efficiency, DG methods since then have been formulated and analyzed to various mathematical models, with broad applications in areas such as electromagnetism, gas dynamics, granular flow, plasma physics etc. One can refer to [22, 24, 34] for a more systematic description of the methods as well as their implementation and applications.

Our present work follows the development of exactly divergence-free central DG methods for ideal MHD equations in [26, 27], and it is related to the exactly divergence-free DG methods for the induction equation using multi-dimensional Riemann solvers [7]. On the one hand, the methods in [26, 27] achieve exactly divergence-free approximations for the magnetic field within a relatively simple formulation due to that the methods involve two copies of numerical solutions from two overlapping meshes, and no numerical fluxes are needed either on element interfaces or at mesh vertices. On the other hand, two copies of numerical solutions double the total number of unknowns and hence increase the computational complexity of the algorithms. In this work, we want to design exactly divergence-free DG methods that are defined on one mesh, which is structured, for ideal MHD equations in two dimensions. Similar as in central DG framework, our new methods will discretize the hydrodynamic variables, such as density, momentum, total energy using standard DG methods, while the equations evolving the magnetic fields, referred to as the induction equation, will be discretized differently by DG-type methods. More specifically, the normal components of the magnetic field along element edges will be updated first by DG methods defined on edges, and this is followed by an element-wise reconstruction to produce an exactly divergence-free magnetic field. For higher order accuracy, additional information will be computed for the magnetic field, and it will be used together with the normal components of the magnetic field to uniquely determine the reconstruction. It turns out that the entire algorithm to discretize the induction equation to obtain the magnetic field approximation can be equivalently reformulated to a form without any reconstruction. The magnetic fields will still be approximated by the exactly divergence-free H(div)-conforming BDM finite element functions as in [26, 27] (see Sect. 2.2 for comments on the use of general H(div)-conforming finite element spaces), and the new challenge comes from the need for numerical fluxes to approximate the electric field on element interfaces and at vertices.

It is known that the choices of numerical fluxes play an important role for the accuracy and stability of DG methods. To finalize our methods, we first identify two necessary conditions (see Theorem 3.1) on the numerical fluxes used in the different parts of the numerical methods, to ensure the reconstructed magnetic field is exactly divergence-free. We then adapt the proposed methods to a constant coefficient linear model, the induction equation with a given constant velocity field, and carry out both a numerical study and a Fourier analysis, to learn about the choices of numerical fluxes for the electric field especially at the mesh vertices, and their roles to the accuracy and numerical stability of the methods. Even though such study is only for a linear model for the magnetic field, the experience we have with it informs us how to choose numerical fluxes (see Sect. 4.3) for the proposed schemes to solve the full ideal MHD equations accurately and robustly. Our final choice of the electric field flux at mesh vertices is one type of multi-dimensional Riemann solver used in [7]. Our numerical tests in Sect. 4.1 imply that multi-dimensional Riemann solvers, when they introduce enough numerical dissipation, can make a good approximation to the electric field flux at vertices. Multi-dimensional Riemann solvers have been used within the WENO finite volume method frameworks in [4,5,6] to solve ideal MHD equations.

The rest of this paper is organized as follows. In Sect. 2, we describe the ideal MHD equations and introduce notations for meshes and discrete spaces. In Sect. 3, we present the proposed DG methods, and identify the conditions on the numerical fluxes to ensure the overall algorithms to be exactly divergence-free. In order to know what choices of numerical fluxes, especially for the electric field on element interfaces and at vertices, will render accurate and stable algorithms, in Sect. 4 we adapt the proposed methods to the induction equation and carry out numerical and analytical studies. In Sect. 5, nonlinear limiters are discussed, and the entire algorithm is also presented. Numerical examples are presented in Sect. 6 to illustrate the performance of the proposed methods, and this is followed by concluding remarks in Sect. 7.

2 MHD Equations, Notations and Discrete Spaces

2.1 MHD Equations

We consider the ideal MHD equations consisting of a set of nonlinear hyperbolic conservations laws

$$\begin{aligned}&\frac{\partial \rho }{\partial t}+ \nabla \cdot (\rho {\mathbf {u}}) =0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial (\rho {\mathbf {u}})}{\partial t}+ \nabla \cdot \left[ \rho {\mathbf {u}}{\mathbf {u}}^{\text {T}}+\left( p+\frac{1}{2}|{\mathbf {B}}|^2\right) {\mathbf {I}}- {\mathbf {B}}{\mathbf {B}}^{\text {T}}\right] =0, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial {\mathbf {B}}}{\partial t}- \nabla \times ({\mathbf {u}}\times {\mathbf {B}})=0, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial {\mathcal {E}}}{\partial t}+ \nabla \cdot \left[ \left( {\mathcal {E}}+p+\frac{1}{2}|{\mathbf {B}}|^2\right) {\mathbf {u}}-{\mathbf {B}}({\mathbf {u}}\cdot {\mathbf {B}})\right] =0, \end{aligned}$$

(4)

with a divergence-free constraint

$$\begin{aligned} \nabla \cdot {\mathbf {B}}=0. \end{aligned}$$

(5)

Here $\rho$ is the density, p is the hydrodynamic pressure, ${\mathbf {u}} = (u_x,u_y,u_z)^{\text {T}}$ is the velocity, and ${\mathbf {B}} = (B_x,B_y,B_z)^{\text {T}}$ is the magnetic field. The total energy is given by ${\mathcal {E}} = \frac{1}{2}\rho |{\mathbf {u}}|^2+\frac{1}{2}|{\mathbf {B}}|^2+\frac{p}{\gamma -1}$ with $\gamma$ as the ratio of the specific heats. The superscript $\text {T}$ denotes the vector transpose. ${\mathbf {I}}$ is the identity matrix, $\nabla \cdot$ is the divergence operator, and $\nabla \times$ is the curl operator. In two dimensions, all functions depend on the spatial variables x and y. Hence only $B_x$ and $B_y$ contribute to $\nabla \cdot {\mathbf {B}}$. The Eqs. (1)–(4) can be written as

$$\begin{aligned}&\frac{\partial {\mathbf {U}}}{\partial t} + \nabla \cdot {\mathbf {F}}({\mathbf {U}},\varvec{{\mathcal {B}}}) = 0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial \varvec{{\mathcal {B}}}}{\partial t} + {\widehat{\nabla }}\times E_z({\mathbf {U}},\varvec{{\mathcal {B}}}) = 0, \end{aligned}$$

(7)

where ${\mathbf {U}}=(\rho ,\rho u_x, \rho u_y, \rho u_z, B_z, {{\mathcal {E}}})^{\text {T}}$, $\varvec{{\mathcal {B}}}=(B_x,B_y)^{\text {T}}$, and ${\mathbf {F}}=(F_1,F_2)$ with

$$\begin{aligned} \begin{aligned} {F}_{1}({\mathbf {U}},{\varvec{{\mathcal {B}}}})&=\left( \rho u_x,\rho u_x^2+p+\frac{1}{2}|{\mathbf {B}}|^2-B_x^2,\rho u_xu_y-B_xB_y,\rho u_xu_z-B_xB_z,\right. \\&\qquad \left. u_xB_z-u_zB_x,u_x\left( {\mathcal {E}}+p+\frac{1}{2}|{\mathbf {B}}|^2\right) -B_x\left( {\mathbf {u}}\cdot {\mathbf {B}}\right) \right) ^{\text {T}},\\ \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} \begin{aligned} {F_{2}}({\mathbf {U}},{\varvec{{\mathcal {B}}}})&=\left( \rho u_y,\rho u_xu_y-B_xB_y,\rho u_y^2+p+\frac{1}{2}|{\mathbf {B}}|^2-B_y^2,\rho u_yu_z-B_yB_z,\right. \\&\qquad \left. u_yB_z-u_zB_y,u_y\left( {\mathcal {E}}+p+\frac{1}{2}|{\mathbf {B}}|^2\right) -B_y\left( {\mathbf {u}}\cdot {\mathbf {B}}\right) \right) ^{\text {T}}. \end{aligned} \end{aligned}$$

(9)

In addition, $E_z({\mathbf {u}},{\varvec{{\mathcal {B}}}})=u_yB_x-u_xB_y$ which is the z-component of the electric field ${\mathbf {E}}=-{\mathbf {u}}\times {\mathbf {B}}$, and ${\widehat{\nabla }}\times E_z=(\frac{\partial E_z}{\partial y},-\frac{\partial E_z}{\partial x})^{\text {T}}$ is the first two components of $\nabla \times (0,0,E_z)^{\text {T}}$. Without confusion, we will refer to ${\varvec{{\mathcal {B}}}}$ as the magnetic field.

2.2 Notations and Discrete Spaces

In this subsection, notations and discrete spaces for numerical schemes are introduced. We assume the computational domain is $\Omega =[x_{min},x_{max}]\times [y_{min},y_{max}] \subset$ ${\mathbb {R}}^d$ with $d=2$. Let $\{x_i\}_{i}$ and $\{y_j\}_{j}$ be the partitions of $[x_{min},x_{max}]$ and $[y_{min},y_{max}]$, respectively. We define $x_{i+\frac{1}{2}}=\frac{1}{2}(x_i+x_{i+1})$, $y_{j+\frac{1}{2}}=\frac{1}{2}(y_j+y_{j+1})$ and $I_{ij}=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]\times [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$ as an rectangle element with $(x_i,y_j)$ as the center. Let $\Delta x=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}$, $\Delta y=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}$, and let ${\mathcal {T}}_h=\bigcup \nolimits _{ij} I_{ij}$ be a partition of the domain $\Omega$.

The discrete spaces are defined over the mesh. For variable ${\mathbf {U}}$, we use the piecewise polynomial vector space

$$\begin{aligned} \varvec{{\mathcal {V}}}_h^k=\left\{ {\mathbf {v}}{:}\,{\mathbf {v}}|_K \in [P^k(K)]^{8-d}, \forall K \in {\mathcal {T}}_h\right\} , \end{aligned}$$

(10)

where $P^{k}(K)$ is the space of polynomials with the total degree at most k in K, and $[P^k(K)]^n$ is its vector version. For the magnetic field $\varvec{{\mathcal {B}}}$, we approximate it using globally (also called exactly) divergence-free polynomial functions, which are piecewise divergence-free with continuous normal components across element interfaces. This space is defined as

$$\begin{aligned} \begin{aligned} {\mathcal {M}}_h^k&=\left\{ {\mathbf {v}} \in H(\text {div}^0;\Omega ){:}\,{\mathbf {v}}|_K\in \varvec{{\mathcal {W}}}^k(K), \forall K\in {\mathcal {T}}_h\right\} \\&=\left\{ {\mathbf {v}}{:}\,{\mathbf {v}}|_K\in \varvec{{\mathcal {W}}}^k(K), \nabla \cdot {\mathbf {v}}|_K=0, \forall K \in {\mathcal {T}}_h,\right. \\&\qquad \left. \text {and the normal component of }{\mathbf {v}}\text { is continuous across each element interface}\right\} , \end{aligned} \end{aligned}$$

(11)

with $\varvec{{\mathcal {W}}}^k(K)$ defined as

$$\begin{aligned} \varvec{{\mathcal {W}}}^k(K)=[P^k(K)]^d\oplus \text {span} \left\{ {\widehat{\nabla }}\times (x^{k+1}y),{\widehat{\nabla }}\times (xy^{k+1})\right\} . \end{aligned}$$

(12)

${\mathcal {M}}_h^k$ is the divergence-free subspace of the H(div)-conforming Brezzi–Douglas–Marini (BDM) finite element space

$$\begin{aligned} \text {BDM}^k=\left\{ {\mathbf {v}}\in H(\text {div}){:}\,{\mathbf {v}}\mid _K \in \varvec{{\mathcal {W}}}^k(K), \forall K\in {\mathcal {T}}_h\right\} , \end{aligned}$$

(13)

and it has optimal accuracy to approximate functions in $H(\text {div}^{0})=\{ {\mathbf {v}}\in [L^2(\Omega )]^d{:}\,\nabla \cdot {\mathbf {v}}=0 \}$ [10]. As pointed out in [26], divergence-free subspaces of other H(div)-conforming finite element spaces, such as Brezzi–Douglas–Fortin–Marini (BDFM) [11] or Raviart–Thomas (RT) [32] finite element spaces can also be used to provide divergence-free approximations for the magnetic field by following the same framework proposed in the present paper. The BDM finite element space is chosen here as it is the smallest among these candidates to achieve the same order of accuracy in the $L^2$ norm.

3 Proposed Numerical Methods for Ideal MHD Equations

In this section, we will formulate the DG methods with a globally divergence-free magnetic field to solve the MHD equations (6)–(7). For simplicity, we use the forward Euler method as time discretization to present the schemes. For high order accuracy in time, strong-stability-preserving Runge–Kutta methods will be used [21]. Such time integrators can be expressed as convex combinations of the forward Euler method, and hence they preserve the globally divergence-free property of the magnetic field. To describe the proposed methods, we assume the numerical solutions at time $t=t_n$ are available, that is $({\mathbf {U}}_{h}^{n},{\varvec{{\mathcal {B}}}}_{h}^{n})\in \varvec{{\mathcal {V}}}_{h}^{k}\times {\mathcal {M}}_{h}^{k}$ with ${\varvec{{\mathcal {B}}}}_{h}^{n}=(B_{x,h}^{n},B_{y,h}^{n})^{\text {T}}$. We want to compute the numerical solutions at $t_{n+1}=t_{n}+\Delta t$, denoted as $({\mathbf {U}}_{h}^{n+1},{\varvec{{\mathcal {B}}}}_{h}^{n+1})\in \varvec{{\mathcal {V}}}_{h}^{k}\times {\mathcal {M}}_{h}^{k}$ with ${\varvec{{\mathcal {B}}}}_{h}^{n+1}=(B_{x,h}^{n+1},B_{y,h}^{n+1})^{\text {T}}$.

3.1 DG Methods to Update ${\mathbf {U}}_{h}^{n+1}$

We update the variable ${\mathbf {U}}_{h}^{n+1}$ by applying to (6) the standard DG method [16] as the spatial discretization and forward Euler method as the time discretization. That is, we look for ${\mathbf {U}}_h^{n+1}$ $\in$ $\varvec{{\mathcal {V}}}^k_h$, such that for any ${\mathbf {w}}$ $\in$ $\varvec{{\mathcal {V}}}^k_h$ and any element $I_{ij}$ $\in$ ${\mathcal {T}}_h$,

$$\begin{aligned} \begin{aligned}&\int _{I_{ij}}{\mathbf {U}}^{n+1}_h\cdot {\mathbf {w}}dxdy = \int _{I_{ij}}{\mathbf {U}}^{n}_h\cdot {\mathbf {w}}dxdy -\Delta t\left( \int _{\partial I_{ij}} \mathbf {H_{e,I_{ij}}}\left( {\mathbf {v}}^{int(I_{ij})},{\mathbf {v}}^{ext(I_{ij})};{\mathbf {n}}\right) \cdot {\mathbf {w}}ds\right. \\&\qquad \quad \left. -\,\int _{I_{ij}}{\mathbf {F}}({\mathbf {U}}_{h}^{n},{\varvec{{\mathcal {B}}}}_{h}^{n})\cdot \nabla {\mathbf {w}} dxdy\right) . \end{aligned} \end{aligned}$$

(14)

Here, $\mathbf {H_{e,I_{ij}}}({\mathbf {v}}^{int(I_{ij})},{\mathbf {v}}^{ext(I_{ij})};{\mathbf {n}})$ is the numerical flux to approximate ${\mathbf {F}}({\mathbf {U}},{\varvec{{\mathcal {B}}}}) \cdot {\mathbf {n}}$, and ${\mathbf {n}}=(n_1,n_2)^\text {T}$ is the outward normal vector of an edge e of the element $I_{ij}$. ${\mathbf {v}}$ is a symbol which denotes the variables $({\mathbf {U}}_{h}^{n},{\varvec{{\mathcal {B}}}}_{h}^{n})$, and ${\mathbf {v}}^{int(I_{ij})},{\mathbf {v}}^{ext(I_{ij})}$ are the limits of ${\mathbf {v}}$ from the interior and exterior of an element $I_{ij}$ along its edge e. In our simulation, we take the Lax–Friedrichs numerical flux

$$\begin{aligned} \mathbf {H_{e,I_{ij}}}({\mathbf {a}},{\mathbf {b}};{\mathbf {n}})=\frac{1}{2}\left( \mathbf {F(a)}\cdot {\mathbf {n}}+\mathbf {F(b)}\cdot {\mathbf {n}}-\alpha ({\mathbf {b}}-{\mathbf {a}})\right) , \end{aligned}$$

(15)

where $\alpha$ is an estimate of the maximal absolute eigenvalue of the Jacobian $\frac{\partial {\mathbf {F}}({\mathbf {U}},\varvec{{\mathcal {B}}})\cdot {\mathbf {n}}}{\partial ({\mathbf {U}},\varvec{{\mathcal {B}}})}$ in the neighborhood of the edge e.

3.2 DG Methods for Globally Divergence-Free Magnetic Field ${\varvec{{\mathcal {B}}}}$

In this subsection, we present DG methods for the induction equation (7) to generate a globally divergence-free approximation ${\varvec{{\mathcal {B}}}}_h^{n+1}=(B_{x,h}^{n+1},B_{y,h}^{n+1})^{\text {T}} \in {\mathcal {M}}_{h}^{k}$ for the magnetic field ${\varvec{{\mathcal {B}}}}$. It is known that a piecewise divergence-free vector field is globally divergence-free if its normal component is continuous on element interfaces. Therefore, we first approximate the normal component of the magnetic field $\varvec{{\mathcal {B}}}\cdot {\mathbf {n}}$ on element interfaces based on the DG methods (see Sect. 3.2.1). Then, an element by element reconstruction is used to reconstruct the globally divergence-free magnetic field (see Sect. 3.2.3). When $k\ge 2$, more information about the magnetic field is obtained by approximating the two-dimensional system (7) using a standard DG method that is less accurate (see Sect. 3.2.2). In Sect. 3.2.4, we will present a reformulation of the schemes, equivalent to that in Sects.  3.2.1–3.2.3 to update the magnetic field yet free of reconstruction. Throughout this subsection, $E_z$ in numerical schemes and its related numerical fluxes are from time $t_n$.

3.2.1 Approximation of ${\varvec{{\mathcal {B}}}}\cdot {\mathbf {n}}$ on the Element Interfaces

To get the continuous normal component $\varvec{{\mathcal {B}}}\cdot {\mathbf {n}}$ of the magnetic field, we formulate a DG-type scheme for magnetic field equations on the element interfaces. For the rectangular mesh, ${\varvec{{\mathcal {B}}}} \cdot {\mathbf {n}}$ is $B_{x,h}^{n+1}$ along y-direction edges with ${\mathbf {n}}=(1,0)^\text {T}$, and it is $B_{y,h}^{n+1}$ along the x-direction edges with ${\mathbf {n}}=(0,1)^\text {T}$.

To propose the DG method for Eq. (7) on the element interface, we consider the equation

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {B}}}\cdot {\mathbf {n}}}{\partial t} + {\widehat{\nabla }}\times E_z({\mathbf {U}},\varvec{{\mathcal {B}}})\cdot {\mathbf {n}}= 0. \end{aligned}$$

(16)

To this end, on a rectangular mesh, we need to consider two one-dimensional equations of the system (16)

$$\begin{aligned} \frac{\partial B_{x}}{\partial t}+\frac{\partial E_z}{\partial y} = 0, \end{aligned}$$

(17)

$$\begin{aligned} \frac{\partial B_{y}}{\partial t}-\frac{\partial E_z}{\partial x} = 0. \end{aligned}$$

(18)

We use the DG method as the spatial discretization and forward Euler method as the time discretization for Eqs. (17) and (18) on element interfaces. The method is as follows: look for $b_{ij}^{x}(y)\in P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$, such that for any $\varphi (y)$ $\in$ $P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$

$$\begin{aligned} \begin{aligned}&\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} b_{ij}^{x}(y)\varphi (y)dy=\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} B_{x}^{n}(x_{i+\frac{1}{2}},y)\varphi (y)dy \\&\quad -\,\Delta t \left( \widehat{E_z}(x_{i+\frac{1}{2}},y)\varphi (y)\Big |^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}} - \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\overline{E_z}(x_{i+\frac{1}{2}},y)\frac{\partial \varphi (y)}{\partial y}dy\right) , \\ \end{aligned} \end{aligned}$$

(19)

and look for $b_{ij}^{y}(x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$, such that for any $\varphi (x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$

$$\begin{aligned}&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} b_{ij}^{y}(x)\varphi (x)dx=\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} B_{y}^{n}(x,y_{j+\frac{1}{2}})\varphi (x)dx \nonumber \\&\quad -\,\Delta t \Bigg (\widehat{\widehat{-E_z}}(x,y_{j+\frac{1}{2}})\varphi (x)\Big |_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}- \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\overline{\overline{-E_z}}(x,y_{j+\frac{1}{2}})\frac{\partial \varphi (x)}{\partial x}dx\Bigg ). \end{aligned}$$

(20)

Here $b_{ij}^x$ and $b_{ij}^y$ denote the approximations of $B_x(x_{i+\frac{1}{2}},y)$ for $y\in$ $[y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$ and $B_y(x,y_{j+\frac{1}{2}})$ for $x\in$ $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ at time $t=$ $t_{n+1}$, respectively. $\widehat{E_z}$ and $\widehat{\widehat{-E_z}}$ are exact or approximate Riemann solvers to approximate the electric field flux $E_z$ at the vertices of a mesh element, while $\overline{E_z}$, $\overline{\overline{-E_z}}$ are exact or approximate Riemann solvers to approximate $E_z$ on the element interfaces, and their choices will be discussed in Theorem 3.1 and specified in Sect. 4.3. $\{b_{ij}^x\}_{ij}$ and $\{b_{ij}^y\}_{ij}$ will be used to reconstruct the globally divergence-free magnetic field.

3.2.2 Additional Information for the Magnetic Field ${\varvec{{\mathcal {B}}}}$: $\widetilde{\varvec{{\mathcal {B}}}}_h$ in Mesh Elements

When $k\geqslant 2$, $\{b_{ij}^{x}\}_{ij}$ and $\{b_{ij}^{y}\}_{ij}$ do not provide enough information to reconstruct a two-dimensional function in ${\mathcal {M}}_{h}^{k}$. For more information, a standard DG method with lower accuracy is applied to the two-dimensional system (7). For $k\geqslant 2$, we look for $\widetilde{\varvec{{\mathcal {B}}}}_h\in [P^{k-2}(I_{ij})]^2$ such that for any $\Phi \in [P^{k-2}(I_{ij})]^{2}$ with $\Phi =(\Phi _1,\Phi _2)^\text {T}$,

$$\begin{aligned} \begin{aligned}&\int _{I_{ij}}\varvec{\widetilde{{\mathcal {B}}}}_h\cdot \Phi dxdy= \int _{I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\cdot \Phi dxdy \\&\quad -\,\Delta t\Bigg ( \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j+\frac{1}{2}}})dx- \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j-\frac{1}{2}}})dx \\&\quad +\,\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i+\frac{1}{2}},y)dy - \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i-\frac{1}{2}},y)dy \\&\quad -\,\int _{I_{ij}}\left( E_z\frac{\partial \Phi _1}{\partial y}-E_z \frac{\partial \Phi _2}{\partial x} \right) dxdy\Bigg ). \\ \end{aligned} \end{aligned}$$

(21)

Here $\widetilde{E_z}$ is the numerical flux for $E_z=(0,E_z)^\text {T}\cdot {\mathbf {n}}$ with ${\mathbf {n}}=(0,1)^\text {T}$ along an x-direction edge, and $\widetilde{\widetilde{-\,E_z}}$ is the numerical flux for $-E_z=(-E_z,0)^\text {T}\cdot {\mathbf {n}}$ with ${\mathbf {n}}=(1,0)^\text {T}$ along a y-direction edge. Both $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ will be taken as the one-dimensional Lax–Friedrichs flux (15). It will be seen from Theorem 3.1 that the numerical fluxes $\overline{E_z}$ and $\overline{\overline{-E_z}}$ in (19)–(20) need to be related to $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ in order to ensure the globally divergence-free reconstruction, also see Sect. 4.3.

3.2.3 Reconstruct the Globally Divergence-Free Magnetic Field ${\varvec{{\mathcal {B}}}}_{h}^{n+1}$

Once we have $\{b_{ij}^{x}\}_{ij}$, $\{b_{ij}^{y}\}_{ij}$ on element interfaces from (19) and (20) as well as $\widetilde{{\varvec{{\mathcal {B}}}}}_{h}$ from (21), we will follow the idea of the BDM projection [10] (also see [26, 27]) to carry out an element-by-element reconstruction of a globally divergence-free magnetic field ${\varvec{{\mathcal {B}}}}_{h}^{n+1}$. Given an element $I_{ij}$, the reconstruction is to obtain $\varvec{{\mathcal {B}}}_h^{n+1}\mid _{I_{ij}}$ $\in$ $\varvec{{\mathcal {W}}}^k(I_{ij})$ on $I_{ij}$, such that $\varvec{{\mathcal {B}}}_h^{n+1}$ $=$ $(B_{x,h}^{n+1}, B_{y,h}^{n+1})^\text {T}$ satisfies

R1 :

$\displaystyle \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( B_{x,h}^{n+1}(x_{l+\frac{1}{2}},y)-b^{x}_{lj}(y)\right) \varphi (y) dy=0$ on the y-direction edge with $l=i-1,i$ and any $\varphi (y)\in P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$,

R2 :

$\displaystyle \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( B_{y,h}^{n+1}(x,y_{l+\frac{1}{2}})-b^{y}_{il}(x)\right) \varphi (x) dx=0$ on the x-direction edge with $l=j-1,j$ and any $\varphi (x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$,

R3 :

$\displaystyle \int _{I_{ij}}\left( \varvec{{\mathcal {B}}}_h^{n+1}(x,y)-{\widetilde{\varvec{{\mathcal {B}}}}}_h(x,y)\right) {\Phi }(x,y)dxdy=0$ for any $\Phi (x,y) \in [P^{k-2}(I_{ij})]^{2}$ when $k\ge 2$.

From the reconstruction, one can see that the normal component of the magnetic field $\varvec{{\mathcal {B}}}_h^{n+1}$, given by $\{b_{ij}^x\}_{ij}$ or $\{b_{ij}^y\}_{ij}$, is single-valued, and hence it is continuous on element interfaces. When $k \ge 2$, additional information is provided by $\widetilde{\varvec{{\mathcal {B}}}}_h$ via $L^2$ projection. In the next theorem, we will show that the reconstruction produces a globally divergence-free approximation for the magnetic field under some conditions for the numerical fluxes in schemes (19)–(21).

Theorem 3.1

Under the conditions that

• 1. the electric field flux approximations in (19)–(21) along the same edge satisfy

  $$\begin{aligned} \overline{E_z}=-(\widetilde{\widetilde{-E_z}}), \quad \overline{\overline{-E_z}}=-(\widetilde{E_z}), \end{aligned}$$

  (22)

• 2. and the electric field flux approximations in (19)–(20) at the same vertex is single-valued, satisfying

  $$\begin{aligned} \widehat{\widehat{-E_z}}=-\widehat{E_z}, \end{aligned}$$

  (23)

then for any k $\ge 0$, the reconstructed $\varvec{{\mathcal {B}}}_h^{n+1}(I_{ij})$ exists uniquely in $\varvec{{\mathcal {W}}}^k(I_{ij})$. In addition, $\nabla \cdot \varvec{{\mathcal {B}}}_h^{n+1}\mid _{I_{ij}}=0$.

Proof

One can follow the same proof as in [26] to show the unique existence of the reconstructed $\varvec{{\mathcal {B}}}_h^{n+1}(I_{ij}) \in \varvec{{\mathcal {W}}}^k(I_{ij})$. We here will only show the divergence-free property of $\varvec{{\mathcal {B}}}_h^{n+1}$.

For any $\omega \in P^{k-1}(I_{ij})$, from the reconstruction step R3 and equation (21), we have

$$\begin{aligned} \int _{I_{ij}}\varvec{\mathcal {B}}_h^{n+1}\nabla \omega dxdy=&\int _{I_{ij}}{\widetilde{\varvec{\mathcal {B}}}_h}\nabla \omega dxdy\nonumber \\ =&\int _{I_{ij}}\varvec{\mathcal {B}}_h^{n}\nabla \omega dxdy -\Delta t \left( \Theta _{inside}-\int _{I_{ij}}\left( E_z\frac{\partial ^{2}\omega }{\partial x\partial y}-E_z\frac{\partial ^{2}\omega }{\partial y\partial x}\right) dxdy\right) \nonumber \\ =&\int _{I_{ij}}\varvec{\mathcal {B}}_h^{n}\nabla \omega dxdy -\Delta t \Theta _{inside}, \end{aligned}$$

(24)

where

$$\begin{aligned} \Theta _{inside}=&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( \widetilde{E_z}\frac{\partial \omega }{\partial x}\right) (x,y_{j+\frac{1}{2}})dx -\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( \widetilde{E_z}\frac{\partial \omega }{\partial x} \right) (x,y_{j-\frac{1}{2}}) dx\\ +&\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \widetilde{\widetilde{-E_z}}\frac{\partial \omega }{\partial y}\right) (x_{i+\frac{1}{2}},y)dy -\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \widetilde{\widetilde{-E_z}}\frac{\partial \omega }{\partial y}\right) (x_{i-\frac{1}{2}},y) dy, \end{aligned}$$

and $\varvec{{\mathcal {B}}}_h^{n} \in {\mathcal {M}}_{h}^{k}$ is the globally divergence-free approximation of $\varvec{{\mathcal {B}}}$ at time $t_{n}$.

From the reconstruction steps R1 and R2, we have

$$\begin{aligned} \begin{aligned}&\int _{\partial I_{ij}}\varvec{{\mathcal {B}}}_h^{n+1}\cdot {\mathbf {n}} \omega ds=\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}b_{ij}^{y}(x)\omega (x,y_{j+\frac{1}{2}})dx -\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}b_{ij-1}^{y}(x)\omega (x,y_{j-\frac{1}{2}})dx \\&\quad +\,\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}b_{ij}^{x}(y)\omega (x_{i+\frac{1}{2}},y)dy -\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}b_{i-1j}^{x}(y)\omega (x_{i-\frac{1}{2}},y)dy. \end{aligned} \end{aligned}$$

(25)

With the schemes (19) and (20), we further get

$$\begin{aligned} \int _{\partial I_{ij}}\varvec{{\mathcal {B}}}_h^{n+1}\cdot {\mathbf {n}} \omega ds =\int _{\partial I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\cdot {\mathbf {n}} \omega ds+\Delta t( \Theta _{edge}-\Theta _{vertex}), \end{aligned}$$

(26)

with

$$\begin{aligned} \Theta _{edge}=&\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \overline{E_z} \frac{\partial \omega }{\partial y}\right) (x_{i+\frac{1}{2}},y)dy -\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( \overline{E_z} \frac{\partial \omega }{\partial y}\right) (x_{i-\frac{1}{2}},y)dy\\ +&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( \overline{\overline{-E_z}}\frac{\partial \omega }{\partial x}\right) (x,y_{j+\frac{1}{2}})dx -\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( \overline{\overline{-E_z}}\frac{\partial \omega }{\partial x}\right) (x,y_{j-\frac{1}{2}})dx, \end{aligned}$$

and

$$\begin{aligned} \Theta _{vertex}&=\Big (\widehat{E_z}\omega \Big )(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-\Big (\widehat{E_z}\omega \Big )\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}}\right) \\&\quad -\,\Big (\widehat{E_z}\omega \Big )(x_{i-\frac{1}{2}},y_{j+\frac{1}{2}})+\Big (\widehat{E_z}\omega \Big )\left( x_{i-\frac{1}{2}},y_{j-\frac{1}{2}}\right) \\&\quad +\,\Big (\widehat{\widehat{-E_z}}\omega \Big )(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-\Big (\widehat{\widehat{-E_z}}\omega \Big )\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}}\right) \\&\quad -\,\Big (\widehat{\widehat{-E_z}}\omega \Big )(x_{i+\frac{1}{2}},y_{j-\frac{1}{2}})+\Big (\widehat{\widehat{-E_z}}\omega \Big )\left( x_{i-\frac{1}{2}},y_{j-\frac{1}{2}}\right) . \end{aligned}$$

Under the condition in (23) that the electric field flux approximations at vertices are single-valued, we have $\Theta _{{ vertex}}=0$. Moreover, under the condition (22), we get $\Theta _{{ edge}}+\Theta _{{ inside}}=0$. Now we can apply Gauss theorem, utilize the relations in (24) and (26), and get

$$\begin{aligned}&\int _{I_{ij}}\nabla \cdot \varvec{{\mathcal {B}}}^{n+1}_h\omega dxdy=\int _{\partial I_{ij}}\varvec{{\mathcal {B}}}_h^{n+1}\cdot {\mathbf {n}}\omega ds-\int _{I_{ij}}\varvec{{\mathcal {B}}}_h^{n+1} \nabla \omega dxdy\nonumber \\&\quad =\int _{\partial I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\cdot {\mathbf {n}}\omega ds -\int _{I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\nabla \omega dxdy +\Delta t ( \Theta _{{ edge}}+ \Theta _{inside}-\Theta _{{ vertex}})\nonumber \\&\quad =\int _{I_{ij}}\nabla \cdot \varvec{{\mathcal {B}}}_h^{n}\omega dxdy+\Delta t (\Theta _{{ edge}}+ \Theta _{inside}-\Theta _{{ vertex}})=0. \end{aligned}$$

(27)

Here we have used the fact that $\nabla \cdot \varvec{{\mathcal {B}}}_{h}^{n}=0$ at time $t_{n}$. Finally, note that $\nabla \cdot \varvec{{\mathcal {B}}}_h^{n+1}\in P^{k-1}(I_{ij})$, by taking $\omega =\nabla \cdot \varvec{{\mathcal {B}}}_h^{n+1}$ in (27), we conclude $\nabla \cdot \varvec{{\mathcal {B}}}_h^{n+1}=0$. $\square$

Remark 3.2

Two conditions (22)–(23) are needed to ensure the exactly divergence-free reconstructions. The one in (23) that requires a single-valued electric field flux approximation at vertices has long been used for many constrained transport methods in various frameworks such as finite difference and finite volume methods, while the condition in (22) is needed only in finite element type of methods including DG methods. Both conditions can be avoided if central DG methods are used, see [26, 27].

3.2.4 Equivalent form of Numerical Schemes for ${\varvec{{\mathcal {B}}}}_h^{n+1}$: Without Reconstruction

From the reconstruction R1–R3 in Sect. 3.2.3, one can see that the normal components of ${\varvec{{\mathcal {B}}}}_h^{n+1}$ along the edges of an element are identical to $b_{ij}^{x}$ and $b_{ij}^{y}$ (at most up to a sign difference, or a shift in index i or j), and its $L^2$ projection onto $[P^{k-2}(I_{ij})]^{2}$ is identical to $\varvec{\widetilde{{\mathcal {B}}}}_h$. Therefore the schemes to compute the globally divergence-free ${\varvec{{\mathcal {B}}}}_h^{n+1}=(B_{x,h}^{n+1},B_{y,h}^{n+1})^{\text {T}} \in {\mathcal {M}}_{h}^{k}$ in Sects. 3.2.1–3.2.3 can be rewritten into an equivalent formulation as follows, without any reconstruction: look for ${\varvec{{\mathcal {B}}}}_h^{n+1}=(B_{x,h}^{n+1},B_{y,h}^{n+1})^{\text {T}}$ such that ${\varvec{{\mathcal {B}}}}_h^{n+1}|_{I_{ij}} \in \varvec{{\mathcal {W}}}^k(I_{ij})$ for any i, j, satisfying

$$\begin{aligned}&\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} B_{x,h}^{n+1}(x_{l+\frac{1}{2}}, y)\varphi (y)dy=\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} B_{x}^{n}(x_{l+\frac{1}{2}},y)\varphi (y)dy \nonumber \\&\quad -\,\Delta t \left( \widehat{E_z}(x_{l+\frac{1}{2}},y)\varphi (y)\Big |^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}} -\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\overline{E_z}(x_{l+\frac{1}{2}},y)\frac{\partial \varphi (y)}{\partial y}dy\right) \end{aligned}$$

(28)

for any $\varphi (y)\in P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$ and with $l=i-1, i$;

$$\begin{aligned}&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} B_{y,h}^{n+1}(x, y_{l+\frac{1}{2}} )\varphi (x)dx=\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} B_{y}^{n}(x,y_{l+\frac{1}{2}})\varphi (x)dx \nonumber \\&\quad -\,\Delta t \Bigg (\widehat{\widehat{-E_z}}(x,y_{l+\frac{1}{2}})\varphi (x)\Big |_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}-\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\overline{\overline{-E_z}}(x,y_{l+\frac{1}{2}})\frac{\partial \varphi (x)}{\partial x}dx\Bigg ) \end{aligned}$$

(29)

for any $\varphi (x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$ and with $l=j-1, j$; in addition,

$$\begin{aligned}&\int _{I_{ij}}{\varvec{{\mathcal {B}}}}_h^{n+1}\cdot \Phi dxdy= \int _{I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\Phi dxdy\nonumber \\&\quad -\,\Delta t\Bigg ( \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j+\frac{1}{2}}})dx- \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j-\frac{1}{2}}})dx\nonumber \\&\quad +\,\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i+\frac{1}{2}},y)dy - \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i-\frac{1}{2}},y)dy \nonumber \\&\quad -\,\int _{I_{ij}}\left( E_z\frac{\partial \Phi _1}{\partial y}-E_z \frac{\partial \Phi _2}{\partial x} \right) dxdy\Bigg ) \end{aligned}$$

(30)

for any $\Phi \in [P^{k-2}(I_{ij})]^{2}$ with $\Phi =(\Phi _1,\Phi _2)^\text {T}$. Again the numerical fluxes will satisfy the two conditions (22)–(23). Theorem 3.1 ensures that the resulting magnetic field ${\varvec{{\mathcal {B}}}}_h^{n+1}$ is in ${\mathcal {M}}_{h}^{k}$ and hence globally divergence-free. (One should refer to equations (5.4) and (5.6) in [10] for a more direct analysis.)

Even though the reformulation of the schemes in this subsection is more straightforward, in the presence of strong discontinuities in the solutions, nonlinear limiters need to be applied to all unknowns, including the magnetic field (see Sect. 5 and the numerical example of cloud–shock interaction in Sect. 6.2.5). When nonlinear limiters are needed for the magnetic field, it is more flexible to work with the schemes in the formulation as in Sect. 3.2.1–3.2.3, so the limiters are applied before the reconstruction or a revised reconstruction, in order to still have a globally divergence-free approximation for the magnetic field.

4 How to Choose Electric Field Flux Approximations?

Theorem 3.1 suggests that electric field flux approximations used in the different parts of the proposed schemes (19)–(21) need to be single-valued at vertices and share the same formulas on the element interfaces. Just as in standard DG methods, choices of numerical fluxes are crucial for accuracy and robustness of the schemes. In this section, we want to investigate numerically and analytically on the choices of the electric field flux approximations. To this end, we will focus on the following equation for the magnetic field

$$\begin{aligned} \frac{\partial \varvec{{\mathcal {B}}}}{\partial t} + {\widehat{\nabla }}\times E_z({\mathbf {U}},\varvec{{\mathcal {B}}})= 0. \end{aligned}$$

(31)

Here $E_z=u_yB_x-u_xB_y$, with a constant velocity field $(u_x,u_y)$ that is given. This system will be referred to as the induction equation. We will adapt the proposed schemes in Sect. 3.2 to the induction equation, and investigate numerically and analytically in next two subsections how different choices of electric field flux approximations affect accuracy and numerical stability. Based on such study, in Sect. 4.3 we will specify our choices of the numerical fluxes in the proposed schemes (19)–(21) to compute the magnetic field.

4.1 Numerical Study

Adapting from the proposed schemes (19)–(21) and following the two required conditions (22)–(23) in Theorem 3.1, we consider the following schemes for the induction equation on the element interfaces, that is: look for $b_{ij}^{x}(y)\in P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$, such that for any $\varphi (y) \in P^{k}([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}])$

$$\begin{aligned}&\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} b_{ij}^{x}(y)\varphi (y)dy =\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} B_{x}^{n}(x_{i+\frac{1}{2}},y)\varphi (y)dy - \Delta t \left( \widehat{E_z}(x_{i+\frac{1}{2}},y)\varphi (y)\Big |^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}} \right. \nonumber \\&\quad \left. +\,\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\widetilde{\widetilde{-E_z}} (x_{i+\frac{1}{2}},y)\frac{\partial \varphi (y)}{\partial y}dy\right) , \end{aligned}$$

(32)

and look for $b_{ij}^{y}(x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$, such that for any $\varphi (x)\in P^{k}([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])$

$$\begin{aligned}&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} b_{ij}^{y}(x)\varphi (x)dx=\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} B_{y}^{n}(x,y_{j+\frac{1}{2}})\varphi (x)dx- \Delta t \Bigg (-{\widehat{E_z}}(x,y_{j+\frac{1}{2}})\varphi (x)\Big |_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\nonumber \\&\quad +\,\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \widetilde{E_z} \left( x,y_{j+\frac{1}{2}}\right) \frac{\partial \varphi (x)}{\partial x}dx\Bigg ). \end{aligned}$$

(33)

Corresponding to (21), the induction equation is further discretized as a two-dimensional system when $k\ge 2$: look for $\widetilde{{\varvec{{\mathcal {B}}}}}_h\in [P^{k-2}(I_{ij})]^2$ such that for any $\Phi =(\Phi _1, \Phi _2)^2\in [P^{k-2}(I_{ij})]^2$,

$$\begin{aligned}&\int _{I_{ij}}\varvec{\widetilde{{\mathcal {B}}}}_h\cdot \Phi dxdy= \int _{I_{ij}}\varvec{{\mathcal {B}}}_h^{n}\cdot \Phi dxdy \nonumber \\&\quad -\,\Delta t\Bigg (\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j+\frac{1}{2}}})dx- \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\big (\widetilde{E_z}\Phi _1\big )(x,{y_{j-\frac{1}{2}}})dx \nonumber \\&\quad +\,\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i+\frac{1}{2}},y)dy - \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\big (\widetilde{\widetilde{-E_z}}\Phi _2\big )(x_{i-\frac{1}{2}},y)dy \nonumber \\&\quad -\,\int _{I_{ij}}\left( E_z\frac{\partial \Phi _1}{\partial y}-E_z \frac{\partial \Phi _2}{\partial x} \right) dxdy\Bigg ). \end{aligned}$$

(34)

Fig. 1

The notations of states around a vertex P, its neighboring elements, and the connected edges

To help with the presentation, we illustrate the notations of states around a vertex P, its neighboring elements, and the connected edges in Fig. 1. In (34), also in (32)–(33), $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ are taken as a one-dimensional Lax–Friedrichs flux. Namely, along an x-direction edge,

$$\begin{aligned} \widetilde{E_z} = \frac{E_z^{LD} + E_z^{LU}}{2} - \frac{\alpha _{y}}{2}\left( B_{x}^{LU}-B_{x}^{LD}\right) , \end{aligned}$$

(35)

and along a y-direction edge,

$$\begin{aligned} \widetilde{\widetilde{-E_z}} = \frac{\left( -E_z^{RD} - E_z^{LD}\right) }{2} - \frac{\alpha _{x}}{2}\left( B_{y}^{RD}-B_{y}^{LD}\right) . \end{aligned}$$

(36)

Here

$$\begin{aligned} \alpha _{x}=|u_x|,\quad \alpha _{y}=|u_y|, \end{aligned}$$

(37)

and they are the largest absolute-value of eigenvalues of the Jacobian $\frac{\partial (0,-E_z)^\text {T}}{\partial ({B_x},{B_y})^\text {T}}$ and $\frac{\partial (E_z,0)^\text {T}}{\partial ({B_x},{B_y})^\text {T}}$, respectively.

Just as in [3, 7, 8, 20], we use flux interpolations or approximate Riemann solvers to obtain the single-valued electric field flux $\widehat{E_z}$ at vertex P used in (32)–(33). Particularly, we take

$$\begin{aligned} \begin{aligned} \widehat{E_z}&=\frac{1}{4}\left( \frac{E_z^{LD}+E_z^{LU}}{2}-\frac{\beta }{2}(B_x^{LU}-B_x^{LD})\right) \\&\quad +\,\frac{1}{4}\left( \frac{E_z^{RD} +E_z^{RU}}{2}-\frac{\beta }{2}(B_x^{RU}-B_x^{RD})\right) \\&\quad +\,\frac{1}{4}\left( \frac{E_z^{LD}+E_z^{RD}}{2}+\frac{\alpha }{2}(B_y^{RD}-B_y^{LD})\right) \\&\quad +\,\frac{1}{4}\left( \frac{E_z^{LU}+E_z^{RU}}{2}+\frac{\alpha }{2}(B_y^{RU}-B_y^{LU})\right) \\&=\,\frac{1}{4}\Big (E_z^{LU}+E_z^{RU}+E_z^{LD}+E_z^{RD}\Big )\\&\quad -\,\frac{\beta }{4}\left( \frac{B_x^{LU}+B_x^{RU}}{2}-\frac{B_x^{LD}+B_x^{RD}}{2}\right) \\&\quad +\,\frac{\alpha }{4}\left( \frac{B_y^{RD}+B_y^{RU}}{2}-\frac{B_y^{LD}+B_y^{LU}}{2}\right) .\\ \end{aligned} \end{aligned}$$

(38)

Here $\alpha =\sigma \alpha _{x}$ and $\beta =\sigma \alpha _y$, with the constant $\sigma$ measures the amount of dissipation introduced by the numerical flux $\widehat{E_z}$, and $\alpha _x$, $\alpha _y$ from (37). When $\alpha =\alpha _x$, $\beta =\alpha _y$, $\widehat{E_z}$ is the arithmetic average of the one-dimensional Lax–Friedrichs flux, namely, an average with equal weight, 1 / 4, of the numerical fluxes in (35)–(36) from four edges connected to the vertex P. When $\alpha =1.2\alpha _x$ and $\beta =1.2\alpha _y$, $\widehat{E_z}$ turns out to be the multi-dimensional HLL Riemann solver restricted at the vertex P, while $\widehat{E_z}$ with $\alpha =2\alpha _x$ and $\beta =2\alpha _y$ is the multi-dimensional Lax–Friedrichs Riemann solver restricted at P. Both multi-dimensional Riemann solvers were used in [7].

Next we want to investigate numerically how the different choices of $\widehat{E_z}$ will affect the performance of the numerical schemes (32)–(34) for the induction equation. We consider the same example as in [39], with the initial condition

$$\begin{aligned} (B_{x},B_{y})=(-\sin (2\pi y), \sin (2\pi x)), \end{aligned}$$

and the constant velocity field is $(u_{x},u_ {y})=(1,1)$. Periodic boundary conditions are used. This example is computed on the domain $[0,1]\times [0,1]$ based on $P^{k}$ approximations with $k=0,1,2$. The third order TVD Runge–Kutta time discretization in (66) [21] is applied in time. The time step is determined as $\Delta t \le { CFL}/\left( \frac{|u_{x}|}{\Delta x}+\frac{|u_{y}|}{\Delta y}\right)$ where the Courant–Friedrichs–Lewy (CFL) number CFL is taken to be 0.5, 0.2, 0.1 for $k=0,1,2$, respectively. Table 1 shows the $L^{2}$ errors and orders of accuracy for the magnetic field component $B_x$ at $t=1.0$ and $t=10$, computed by the methods (32)–(34) with different choices of the numerical fluxes. More specifically, $\widehat{E_z}$ in (32)–(33) is evaluated as (38) with $\alpha =\sigma \alpha _x$ and $\beta =\sigma \alpha _y$, where $\alpha _x=\alpha _y=1$, and $\sigma =1$, 1.2, and 2. And $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ in (32)–(34) are from the one-dimensional Lax–Friedrichs flux (35)–(37). It is observed from Table 1 that when $\alpha =\alpha _x$, $\beta =\alpha _y$, the scheme is stable and first order accurate with $P^0$ approximation; With $P^1$ approximation, the scheme is only first order accurate which is suboptimal; while the scheme with $P^2$ approximation starts to be optimally accurate with third order accuracy and then shows instability over long time simulation. When $\alpha =1.2\alpha _x$ and $\beta =1.2\alpha _y$, the schemes have optimal accuracy with $P^{0}$ and $P^1$ approximations, yet with $P^2$ approximation the scheme becomes unstable at $t=10$. When $\alpha =2\alpha _x$ and $\beta =2\alpha _y$, the schemes have optimal accuracy and are stable over the time period we examine. Even though the results are not reported here, we have also tested the schemes with the central flux or upwind flux on the element interfaces for $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ and their arithmetic average for $\widehat{E_z}$ from the four edges connecting to a vertex. We have learned from the numerical experiments that if $\widehat{E_z}$ of the form (38) is used at vertices, it is important to have sufficient numerical dissipation. For instance, $\widehat{E_z}$ based on the multi-dimensional Lax–Friedrichs flux with $\alpha =2\alpha _x$ and $\beta =2\alpha _y$ leads to a stable scheme with optimal accuracy, yet $\widehat{E_z}$ based on either the one-dimensional Lax–Friedrichs flux with $\alpha =\alpha _x$ and $\beta =\alpha _y$, or the multi-dimensional HLL flux with $\alpha =1.2\alpha _x$ and $\beta =1.2\alpha _y$ leads to unstable schemes due to the insufficiency in numerical dissipation.

Table 1 Errors and convergence orders of $B_{x}$ for the induction equation, with the initial data $(B_{x},B_{y})=(-\sin (2\pi y), \sin (2\pi x))$ on the domain $\Omega =[0,1]\times [0,1]$ and at $t=1.0, 10.0$. The velocity field is $(u_{x},u_ {y})=(1,1)$

4.2 Fourier Analysis of the Scheme with $P^0$ Approximation

In this subsection, we will carry out the Fourier analysis for the scheme (32)–(33) with $P^0$ approximation. The goal is to further understand the role of the amount of the numerical dissipation in $\widehat{E_z}$ in the form of (38).

With the $P^0$ polynomial space, the scheme (32)–(33) becomes

$$\begin{aligned}&\int ^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}} b^x_{ij}(y)dy=\int ^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}}B_x^n(x_{i+\frac{1}{2}},y)dy -\,\Delta t\left( \widehat{E_z}(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-\widehat{E_z}(x_{i+\frac{1}{2}},y_{j-\frac{1}{2}})\right) ,\qquad \end{aligned}$$

(39)

$$\begin{aligned}&\int ^{x_{i+\frac{1}{2}}}_{x_{i-\frac{1}{2}}}b^y_{ij}(x)dx= \int ^{x_{i+\frac{1}{2}}}_{x_{i-\frac{1}{2}}}B_y^n(x,y_{j+\frac{1}{2}})dx +\,\Delta t \left( \widehat{E_z}(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-\widehat{E_z}(x_{i-\frac{1}{2}},y_{j+\frac{1}{2}})\right) ,\qquad \end{aligned}$$

(40)

and the electric field flux $\widehat{E_z}$ at the vertex $(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})$ is given by

$$\begin{aligned}&\widehat{E_z}\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) =\frac{1}{4}\left( E_z\mid _{I_{ij}}+E_z\mid _{I_{i+1j}}+E_z\mid _{I_{ij+1}}+E_z\mid _{I_{i+1j+1}}\right) \nonumber \\&\quad -\,\frac{\beta }{4}\left( \frac{B_x\mid _{I_{ij+1}}+B_x\mid _{I_{i+1j+1}}}{2}-\frac{B_x\mid _{I_{ij}}+B_x\mid _{I_{i+1j}}}{2}\right) \nonumber \\&\quad +\,\frac{\alpha }{4}\left( \frac{B_y\mid _{I_{i+1j}}+B_y\mid _{I_{i+1j+1}}}{2}-\frac{B_y\mid _{I_{ij}}+B_y\mid _{I_{ij+1}}}{2}\right) . \end{aligned}$$

(41)

We replace $E_z$ by $u_yB_x-u_xB_y$, and rewrite (41) into

$$\begin{aligned}&\widehat{E_z}\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) =\frac{2u_y-\beta }{8}\left( B_x\mid _{I_{ij+1}}+B_x\mid _{I_{i+1j+1}}\right) \nonumber \\&\quad +\,\frac{2u_y+\beta }{8}\left( B_x\mid _{I_{ij}}+B_x\mid _{I_{i+1j}}\right) -\frac{2u_x-\alpha }{8}\left( B_y\mid _{I_{i+1j}}+B_y\mid _{I_{i+1j+1}}\right) \nonumber \\&\quad -\,\frac{2u_x+\alpha }{8}\left( B_y\mid _{I_{ij}}+B_y\mid _{I_{ij+1}}\right) . \end{aligned}$$

(42)

Based on the divergence-free reconstruction procedure, we know $B_x\mid _{I_{ij}}=B_x\mid _{I_{i+1j}}=b^x_{ij}$ and $B_y\mid _{I_{ij}}=B_y\mid _{I_{ij+1}}=b^y_{ij}$. Therefore (41) is indeed

$$\begin{aligned} \widehat{E_z}\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}\right) =\frac{2u_y-\beta }{4}b^x_{ij+1}+\frac{2u_y+\beta }{4}b^x_{ij} -\frac{2u_x-\alpha }{4}b^y_{i+1j}-\frac{2u_x+\alpha }{4}b^y_{ij}, \end{aligned}$$

(43)

and our scheme (39)–(40) can be formulated more explicitly: look for $b^{x,n+1}_{ij}$ and $b^{y,n+1}_{ij}$ in ${{\mathbb {R}}}$, satisfying

$$\begin{aligned} \begin{aligned}&b^{x,n+1}_{ij}=b^{x,n}_{ij}-\frac{\Delta t}{\Delta y}\left( \frac{2u_y-\beta }{4}(b^{x,n}_{ij+1}-b^{x,n}_{ij})+\frac{2u_y+\beta }{4}(b^{x,n}_{ij}-b^{x,n}_{ij-1})\right) \\&\quad +\,\frac{\Delta t}{\Delta y}\left( \frac{2u_x-\alpha }{4}(b^{y,n}_{i+1j}-b^{y,n}_{i+1j-1})+\frac{2u_x+\alpha }{4}(b^{y,n}_{ij}-b^{y,n}_{ij-1})\right) ,\\ \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned} \begin{aligned}&b^{y,n+1}_{ij}=b^{y,n}_{ij}+\frac{\Delta t}{\Delta x}\left( \frac{2u_y-\beta }{4}(b^{x,n}_{ij+1}-b^{x,n}_{i-1j+1})+\frac{2u_y+\beta }{4}(b^{x,n}_{ij}-b^{x,n}_{i-1j})\right) \\&\quad -\,\frac{\Delta t}{\Delta x}\left( \frac{2u_x-\alpha }{4}(b^{y,n}_{i+1j}-b^{y,n}_{ij})+\frac{2u_x+\alpha }{4}(b^{y,n}_{ij}-b^{y,n}_{i-1j})\right) .\\ \end{aligned} \end{aligned}$$

(45)

Additionally, the divergence-free property of the numerical solution can be translated into the following relation, for any i, j, n,

$$\begin{aligned} \Delta y(b^{x,n}_{ij}-b^{x,n}_{i-1j})+\Delta x(b^{y,n}_{ij}-b^{y,n}_{ij-1})=0. \end{aligned}$$

(46)

The parameters $\alpha$ and $\beta$ in (41) are taken as

$$\begin{aligned} \alpha = \sigma |{u_x}|, \beta = \sigma |{u_y}|, \end{aligned}$$

(47)

and $\sigma$ is a constant that measures the amount of numerical dissipation introduced through the numerical flux $\widehat{E_z}$. In the next Theorem, we will study the role of this constant $\sigma$ to the numerical stability of the scheme. The stability condition for $\sigma =2$ was previously given in [7].

Theorem 4.1

The scheme (44)–(45) with (46)–(47) is stable under the following condition on the time step size $\Delta t$:

• 1. When $\sigma \le 2$,

  $$\begin{aligned} \Delta t \left( \frac{|u_x|}{\Delta x}+ \frac{|u_y|}{\Delta y}\right) \le \frac{\sigma }{2}; \end{aligned}$$

  (48)

• 2. when $\sigma >2$

  $$\begin{aligned} \Delta t\left( \frac{ |u_x|}{\Delta x}+ \frac{ |u_y|}{\Delta y}\right) \le \frac{2}{\sigma }. \end{aligned}$$

  (49)

And the maximum of the upper bound of both formulas is 1, that is, $\max _{\sigma \ge 0}(\frac{\sigma }{2}, \frac{2}{\sigma }) =1$, and it is attained at $\sigma =2$.

Proof

To carry out the Fourier analysis, let

$$\begin{aligned} (b^{x,n},b^{y,n})=({\widehat{b}}_x^{n},{\widehat{b}}_y^{n})e^{i(k_1x+k_2y)}, \end{aligned}$$

(50)

with $k_1$, $k_2$ being arbitrary integer. With (50), the Eq. (44) becomes

$$\begin{aligned} \begin{aligned} {\widehat{b}}^{n+1}_{x}&={\widehat{b}}^{n}_{x}-\frac{\Delta t}{\Delta y}\left( \frac{2u_y-\beta }{4}(e^{ik_2 \Delta y}-1)+\frac{2u_y+\beta }{4}(1-e^{-ik_2 \Delta y})\right) {\widehat{b}}^{n}_{x} \\&\quad +\,\frac{\Delta t}{\Delta y}\Bigg (\frac{2u_x-\alpha }{4}\left( e^{\frac{ik_1\Delta x}{2}+\frac{ik_2 \Delta y}{2}}-e^{\frac{ik_1\Delta x}{2}-\frac{ik_2 \Delta y}{2}}\right) \\&\quad +\,\frac{2u_x+\alpha }{4}\left( e^{-\frac{ik_1\Delta x}{2}+\frac{ik_2 \Delta y}{2}}-e^{\frac{-ik_1\Delta x}{2}-\frac{ik_2 \Delta y}{2}}\right) \Bigg ){\widehat{b}}^{n}_{y},\\ \end{aligned} \end{aligned}$$

(51)

and the divergence-free condition (46) becomes

$$\begin{aligned} \Delta y\left( e^{\frac{ik_1\Delta x}{2}}-e^{\frac{-ik_1\Delta x}{2}}\right) {{\hat{b}}}_x^n+\Delta x\left( e^{\frac{ik_2\Delta y}{2}}-e^{\frac{-ik_2\Delta y}{2}}\right) {{\hat{b}}}_y^n=0, \end{aligned}$$

i.e.

$$\begin{aligned} \Delta y\sin \left( \frac{k_1\Delta x}{2}\right) {{\hat{b}}}_x^n+\Delta x\sin \left( \frac{k_2\Delta y}{2}\right) {{\hat{b}}}_y^n=0. \end{aligned}$$

(52)

Combining (51) and (52), we get

$$\begin{aligned} {\widehat{b}}^{n+1}_{x}=Q{\widehat{b}}^{n}_{x}, \end{aligned}$$

(53)

where the amplification factor Q is

$$\begin{aligned} \begin{aligned} Q&=1-\frac{\Delta t}{\Delta y}\left( \frac{2u_y-\beta }{4}\left( e^{ik_2 \Delta y}-1\right) +\frac{2u_y+\beta }{4}\left( 1-e^{-ik_2 \Delta y}\right) \right) \\&\quad -\,\frac{\Delta t}{\Delta x}\left( \frac{2u_x-\alpha }{4}e^{\frac{ik_1\Delta x}{2}}+\frac{2u_x+\alpha }{4}e^{-\frac{ik_1\Delta x}{2}}\right) 2i\sin \left( \frac{k_1\Delta x}{2}\right) .\\ \end{aligned} \end{aligned}$$

(54)

One can easily check that (45) and the divergence-free relation (46) will lead to the same amplification factor Q. Without loss of generality, we assume $u_x\ge 0$, $u_y\ge 0$. Let $c_1=\frac{\Delta tu_x}{\Delta x}$ and $c_2=\frac{\Delta tu_y}{\Delta y}$, and with $\sigma$ defined in (47), we have

$$\begin{aligned} Q&=1-c_2\left( \frac{2-\sigma }{4}(e^{ik_2 \Delta y}-1)+\frac{2+\sigma }{4}(1-e^{-ik_2 \Delta y})\right) \nonumber \\&\quad -\,c_1\left( \frac{2-\sigma }{4}e^{\frac{ik_1\Delta x}{2}}+\frac{2+\sigma }{4}e^{-\frac{ik_1\Delta x}{2}}\right) 2i\sin \left( \frac{k_1\Delta x}{2}\right) \nonumber \\&=\,1-\frac{\sigma c_1}{2}\left( 1-\cos (k_1\Delta x)\right) -\frac{\sigma c_2}{2}\left( 1-\cos (k_2\Delta y)\right) \nonumber \\&\quad -i\left( c_1\sin (k_1\Delta x)+c_2\sin (k_2\Delta y)\right) . \end{aligned}$$

(55)

Next, we want to obtain the condition on the time step size to ensure $|Q|\le 1$. To this end,

$$\begin{aligned} |Q|^2=&\left( 1-\frac{\sigma c_1}{2}(1-\cos (k_1\Delta x))-\frac{\sigma c_2}{2}(1-\cos (k_2\Delta y))\right) ^2\nonumber \\&+\,\left( c_1\sin (k_1\Delta x)+c_2\sin (k_2\Delta y)\right) ^2\nonumber \\ =&1+\frac{\sigma ^2}{4}(c_1+c_2)^2+c_1^2+c_2^2-\sigma (c_1+c_2)\nonumber \\&+\,\frac{\sigma ^2}{4}(c_1\cos (k_1\Delta x)+c_2\cos (k_2\Delta y))^2-c_1^2\cos ^2(k_1\Delta x)-c_2^2\cos ^2(k_2\Delta y)\nonumber \\&+\,\left( \sigma c_1-\frac{\sigma ^2c_1^2}{2}-\frac{\sigma ^2}{2}c_1c_2\right) \cos (k_1\Delta x)+\left( \sigma c_2-\frac{\sigma ^2c_2^2}{2}-\frac{\sigma ^2}{2}c_1c_2\right) \cos (k_2\Delta y)\nonumber \\&+\,2c_1c_2\sin (k_1\Delta x)\sin (k_2\Delta y). \end{aligned}$$

(56)

To handle the last term in (56), we will use

$$\begin{aligned} \sin (k_1\Delta x)\sin (k_2\Delta y)= & {} \cos (k_1\Delta x-k_2\Delta y)-\cos (k_1\Delta x)\cos (k_2\Delta y)\nonumber \\\le & {} 1-\cos (k_1\Delta x)\cos (k_2\Delta y). \end{aligned}$$

Note that this inequality becomes an equality when $k_1\Delta x=k_2\Delta y+2\pi n$ for some $n\in {\mathbb {Z}}$. Now with $s=\cos (k_1\Delta x)\in [-\,1,1]$ and $t=\cos (k_2\Delta y)\in [-\,1,1]$, (56) turns to

$$\begin{aligned} |Q|^2&\le 1+\frac{\sigma ^2}{4}(c_1+c_2)^2+c_1^2+c_2^2-\sigma (c_1+c_2) +\frac{\sigma ^2}{4}(c_1s+c_2t)^2-c_1^2s^2-c_2^2t^2\nonumber \\&\quad +\,\frac{\sigma c_1}{2}(2-\sigma c_1-\sigma c_2)s+\frac{\sigma c_2}{2}(2-\sigma c_2-\sigma c_1)t+2c_1c_2-2c_1c_2st\nonumber \\&=1+\left( \frac{\sigma ^2}{4}+1\right) (c_1+c_2)^2+\left( \frac{\sigma ^2}{4}-1\right) (c_1s+c_2t)^2\nonumber \\&\quad -\,\sigma (c_1+c_2)+\sigma (c_1s+c_2t)-\frac{\sigma ^2}{2}(c_1+c_2)(c_1s+c_2t). \end{aligned}$$

(57)

We further set $A=c_1+c_2$ and $B=c_1s+c_2t$, and

$$\begin{aligned} |Q|^2&\le 1+\left( \frac{\sigma ^2}{4}+1\right) A^2+\left( \frac{\sigma ^2}{4}-1\right) B^2-\frac{\sigma ^2}{2}AB-\sigma (A-B)\\&=1+(A-B)\left( \left( \frac{\sigma ^2}{4}+1\right) A+\left( 1-\frac{\sigma ^2}{4}\right) B-\sigma \right) . \end{aligned}$$

From the definitions of A and B, we know $A-B=c_1(1-s)+c_2(1-t)$ $\ge 0$. Hence $|Q|^2\le 1$ if

$$\begin{aligned} \left( \frac{\sigma ^2}{4}+1\right) A+\left( 1-\frac{\sigma ^2}{4}\right) B-\sigma \le 0. \end{aligned}$$

(58)

There are two cases:

$\textsf {Case 1}$ When $\sigma \le 2$, we have $1-\frac{\sigma ^2}{4}\ge 0$. Therefore with $A\ge B$, it is sufficient to require

$$\begin{aligned} \left( \frac{\sigma ^2}{4}+1\right) A+\left( 1-\frac{\sigma ^2}{4}\right) A-\sigma \le 0, \end{aligned}$$

that is, $A\le \frac{\sigma }{2}$. This can not be further improved, since $A=B$ when $s=t=\cos (k_1\Delta x)=\cos (k_2\Delta y)=1$.

$\textsf {Case 2}$ When $\sigma > 2$, we have $1-\frac{\sigma ^2}{4}< 0$. Therefore with $A+B=c_1(1+s)+c_2(1+t)\ge 0$, it is sufficient to require

$$\begin{aligned} \left( \frac{\sigma ^2}{4}+1\right) A-\left( 1-\frac{\sigma ^2}{4}\right) A-\sigma \le 0, \end{aligned}$$

that is, $A\le \frac{2}{\sigma }$. Again, this can not be further improved, since $B=-A$ when $s=t=\cos (k_1\Delta x)=\cos (k_2\Delta y)=-1$.

In summary,

$$\begin{aligned} \Delta t \left( \frac{u_x}{\Delta x}+\frac{u_y}{\Delta y}\right) =A\le \left\{ \begin{array}{ll} \frac{\sigma }{2}, &{}\quad \hbox {if}\; \sigma \le 2, \\ \frac{2}{\sigma }, &{}\quad \hbox {if}\; \sigma > 2. \end{array} \right. \end{aligned}$$

(59)

Finally one can see the maximum of $\{\sigma /2, 2/\sigma \}$ is 1 when $\sigma =2$. $\square$

The theorem above implies that the scheme (44)–(45) with the multi-dimensional Lax–Friedrichs numerical flux for ${\widehat{E_z}}$, with $\alpha =2\alpha _x$ and $\beta =2\alpha _y$, has the largest stability region for our scheme with the $P^0$ approximation. This is also illustrated by Fig. 2, where comparison is given between the stability regions of the schemes with the multi-dimensional Lax–Friedrichs numerical flux ($\alpha =2\alpha _x$ and $\beta =2\alpha _y$) on the right, and one-dimensional Lax–Friedrichs numerical flux ($\alpha =\alpha _x$ and $\beta =\alpha _y$) on the left.

Fig. 2

The stability region of the scheme (32)–(33) for the $P^0$ approximation with $\widehat{E_z}$ in (38), and $\alpha =\sigma \alpha _x$ and $\beta =\sigma \alpha _y$. Here $c_1$ is $\frac{\Delta t |u_x|}{\Delta x}$, $c_2$ is $\frac{\Delta t |u_y|}{\Delta y}$. a $\sigma =1$, b $\sigma =2$

4.3 Our Choices of the Numerical Fluxes in (19)–(21)

Based on the numerical and theoretical studies in previous two subsections for the induction equation, the electric field flux approximations in our proposed schemes (19)–(21) to update the magnetic field in the full ideal MHD simulations will be chosen as follows.

• (1) They satisfy the two conditions in (22)–(23);

• (2) The singled-valued electric field flux $\widehat{E_z}$ at a vertex is determined by the average of the multi-dimensional Lax–Friedrichs numerical fluxes on four edges connecting to this vertex, given by (38) with $\alpha =2\alpha _x$ and $\beta =2\alpha _y$;

• (3) On an element interface, the standard one-dimensional Lax–Friedrichs numerical flux (35)–(36) will be applied for both $\widetilde{E_z}$ and $\widetilde{\widetilde{-E_z}}$ with parameters $\alpha _x$ and $\alpha _y$.

Both $\alpha _x$ and $\alpha _y$ in (2) and (3) represent the local speeds of the entire MHD system, and are taken as the largest absolute-value of eigenvalues of the Jacobian $\frac{\partial {\mathbf {F}}({\mathbf {U}},\varvec{{\mathcal {B}}})\cdot {\mathbf {n}}}{\partial ({\mathbf {U}},\varvec{{\mathcal {B}}})}$, with ${\mathbf {n}}=(0, 1)^{\text {T}}$, $(1, 0)^{\text {T}}$ respectively, in the neighborhood of the relevant edge. Note that these local speeds are different from that in (37) for the induction equation.

5 Nonlinear Limiter, a Revisit to the Reconstruction

In this section, we will discuss the use of nonlinear limiters to enhance numerical stability of the proposed schemes. Similar to high order DG methods for nonlinear hyperbolic conservation laws, nonlinear limiters are also needed for numerical stability of our methods. In this paper, the minmod total variation bounded (TVB) slope limiter in [16] is applied. This limiter involves a non-negative parameter M, and its value is often chosen for each example in actual implementation [14, 31]. This limiter can be applied to component-wise variables or in local characteristic fields with respect to the $7\times 7$-eigen system in [23].

Following the work in [26, 27] with globally divergence-free central DG methods, for non-smooth solutions, we first apply the limiter only to the hydrodynamic variables ${\mathbf {U}}_h$, not to $\varvec{{\mathcal {B}}}_h$, $\widetilde{\varvec{{\mathcal {B}}}}_h$ or $(b^x_{ij},b^y_{ij})$. This works well for the schemes with $P^1$ approximations, and when the discontinuities in the solutions are not strong.

It is known that central type schemes are in general more dissipative hence more stable than upwind type schemes. Therefore it is not unexpected that when our proposed DG methods are used to examples with strong shocks, it seems necessary to apply the nonlinear limiter to both ${\mathbf {U}}_h$ and the magnetic field ${\varvec{{\mathcal {B}}}}_h$ in order to effectively control numerical oscillations. One needs to be careful, though, about how to implement this without losing the globally divergence-free property of the computed magnetic field. A straightforward implementation will break the intrinsic relation between the data $\widetilde{\varvec{{\mathcal {B}}}}_h$ and $(b^x_{ij},b^y_{ij})$ used in the reconstruction (see the proof of Theorem 3.1). On the other hand, for the methods we will focus on in this paper with $P^1$ and $P^2$ approximations, an alternative but equivalent way was presented in [27] to reconstruct $I_{ij}$, look for $\varvec{{\mathcal {B}}}_h^{n+1} \in \varvec{{\mathcal {W}}}^k(I_{ij})$ such that

• 1. $B_x^{n+1}(x_{l+\frac{1}{2}},y)=b^x_{lj}(y)$ for $l=i-1,i$ and $y\in [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$,

• 2. $B_y^{n+1}(x,y_{l+\frac{1}{2}})=b^y_{il}(x)$ for $l=j-1,j$ and $x\in [x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$,

• 3. $\nabla \cdot \varvec{{\mathcal {B}}}_h^{n+1}|_{I_{ij}}=0$.

One can refer to [26] for the proof of the equivalency. An important feature of this equivalent reconstruction is that only the interface data $(b^x_{ij},b^y_{ij})$ is needed. Now when the nonlinear limiter needs to be applied to the magnetic field, the normal components of the magnetic field $\{b_{ij}^x\}_{ij}$, $\{b_{ij}^y\}_{ij}$ will be limited first (this will be discussed in details next), then the equivalent reconstruction given above will be used to obtain the globally divergence-free magnetic field based on the limited normal components of the magnetic field.

We here will use $k=2$ as an example to illustrate how to apply the minmod TVB limiter to $\{b^x_{ij}\}_{ij}$ and $\{b^y_{ij}\}_{ij}$. The quadratic polynomial $b^x_{ij}$ can be written as

$$\begin{aligned} b^x_{ij}(y)=\overline{b^x_{ij}}+c_yY+ c_{yy}\left( Y^2-\frac{1}{3}\right) , \end{aligned}$$

(60)

with $Y=\frac{y-y_j}{\Delta y/2}$, and $\overline{b^x_{ij}}$ is the edge average of $b^x_{ij}$, namely,

$$\begin{aligned} \overline{b^x_{ij}}=\frac{1}{\Delta y} \int ^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}}b^x_{ij}(y)dy. \end{aligned}$$

(61)

We compute $\widetilde{c_y}$ according to

$$\begin{aligned} \widetilde{c_y}={\widetilde{m}}\left( c_y,\Delta _+ \overline{b^x_{ij}},\Delta _- \overline{b^x_{ij}}\right) . \end{aligned}$$

(62)

Here $\Delta _+ \overline{b^x_{ij}}=\overline{b^x_{ij+1}}-\overline{b^x_{ij}}$, $\Delta _- \overline{b^x_{ij}}=\overline{b^x_{ij}}-\overline{b^x_{ij-1}}$, and the corrected minmod TVB function ${\widetilde{m}}$ is

$$\begin{aligned} {\widetilde{m}}(a_1, a_2, a_3) = \left\{ \begin{array}{ll} a_1, &{}\quad \text {if}\,\,|a_1|\le M(\Delta y)^{2};\\ m(a_1,a_2, a_3), &{} \quad \text {otherwise,}\\ \end{array} \right. \end{aligned}$$

(63)

with the minmod function m defined as

$$\begin{aligned} {m}(a_1, a_2, a_3)=\left\{ \begin{array}{lll} s \min \left( |a_1|, |a_2|, |a_3|\right) , &{}\quad \text {if}\,\,s=\text {sign}(a_1)=\text {sign}(a_2)=\text {sign}(a_3); \\ 0, &{}\quad \text {otherwise.}\\ \end{array} \right. \end{aligned}$$

(64)

If $\mid \widetilde{c_y}-c_y\mid > 10^{-6}$, we apply the limiter by setting $c_y=\widetilde{c_y}$ and $c_{yy}=0$ in (60). Otherwise, no modification is made to (60). The treatment for $b^y_{ij}$ is very similar. It is important to know that the limiter does not change the edge averages $\{b_{ij}^x\}_{ij}$ and $\{b_{ij}^{y}\}_{ij}$, hence a necessary compatible condition for the exactly divergence-free reconstruction, namely,

$$\begin{aligned} \int _{I_{ij}} \nabla \cdot \varvec{{\mathcal {B}}}_h^{n} dxdy= \Delta y\left( \overline{b^{x,n}_{ij}}-\overline{b^{x,n}_{i-1j}}\right) +\Delta x\left( \overline{b^{y,n}_{ij}}-\overline{b^{y,n}_{ij-1}}\right) =0 \end{aligned}$$

(65)

still holds.

Finally in Algorithm 1, we provide the flow chart of the proposed globally divergence-free methods when they are applied to ideal MHD equations. The time discretization is taken to be the forward Euler method.

6 Numerical Results

In this section, numerical examples are presented to illustrate the accuracy and stability of the proposed globally divergence-free methods with $P^1$ and $P^2$ approximations for the ideal MHD equations. They include two smooth examples and five non-smooth examples. In our simulations, uniform rectangular meshes with $N\times N$ elements are used. The initial numerical solution ${\mathbf {U}}_h\in \varvec{{\mathcal {V}}}_h^k$ is obtained through the $L^2$ projection, and ${\varvec{{\mathcal {B}}}}_h\in {{\mathcal {M}}}_h^k$ is by the BDM projection [10]. In time, a third order TVD Runge–Kutta method is applied [21]. That is, to solve $u_t=L(u, t)$, given the numerical solution $u^n$ at $t_n$, we compute $u^{n+1}$ at $t_{n+1}=t_n+\Delta t$ as follows,

$$\begin{aligned} u^{(1)}= & {} u^n + \Delta tL(u_n,t_n), \nonumber \\ u^{(2)}= & {} \frac{3}{4}u^n+\frac{1}{4}u^{(1)}+\frac{1}{4}\Delta tL\left( u^{(1)},t_n+\Delta t\right) , \nonumber \\ u^{n+1}= & {} \frac{1}{3}u^n+\frac{2}{3}u^{(2)}+\frac{2}{3}\Delta tL\left( u^{(2)},t_n+\frac{1}{2}\Delta t\right) . \end{aligned}$$

(66)

The time step is determined by

$$\begin{aligned} \Delta t=\frac{{{CFL}}}{\alpha _x/\Delta x + \alpha _y/\Delta y}, \end{aligned}$$

(67)

where $\alpha _x$ and $\alpha _y$ are the largest absolute eigenvalues of Jacobian $\frac{\partial F_1({\mathbf {U}},{\varvec{{\mathcal {B}}}})}{\partial ({\mathbf {U}},{\varvec{{\mathcal {B}}}})}$ and $\frac{\partial F_2({\mathbf {U}},{\varvec{{\mathcal {B}}}})}{\partial ({\mathbf {U}},{\varvec{{\mathcal {B}}}})}$, respectively. We take ${ CFL}=0.2$ for $k=1$ and ${ CFL}=0.1$ for $k=2$ similar as for the standard DG methods. The numerical fluxes in the schemes to update the magnetic field follow the strategies summarized in Sect. 4.3. The minmod TVB slope limiter is applied for non-smooth examples with $M=1$.

6.1 Smooth Examples

6.1.1 The Smooth Vortex Problem

The first example we consider is the smooth vortex example which was introduced in [2], and it models a smooth vortex propagating with speed (1, 1) in a two-dimensional domain. The initial condition is given by

$$\begin{aligned} (\rho ,u_x,u_y,u_z,B_x,B_y,B_z,p)=\left( 1,1+\delta u_x,1+\delta u_y,0,\delta B_x,\delta B_y,0,1+\delta p\right) , \end{aligned}$$

where

$$\begin{aligned}&(\delta u_x,\delta u_y)=\frac{\xi }{2\pi } {\widehat{\nabla }}\times \exp \{0.5(1-r^2)\},\quad (\delta B_x,\delta B_y)=\frac{\eta }{2\pi }{\widehat{\nabla }}\times \exp \{0.5(1-r^2)\},\\&\delta p=\frac{\eta ^2(1-r^2-\xi ^2)}{8\pi ^2} \exp (1-r^2). \end{aligned}$$

Here $r=\sqrt{x^2+y^2}$, $\xi =\eta =1$ and $\gamma =5/3$. The computational domain is taken as $[-\,10,10]\times [-\,10,10]$. Even though the problem is not-periodic, periodic boundary conditions are used in our simulation. This will introduce an error of size $O(10^{-22})$ which is negligible with respect to the resolution of the numerical solutions. In Table 2, $L^2$ errors and orders of accuracy are presented for the variables $\rho$, $u_x$, $B_x$ and pressure p at $t = 20$, right after one time period, by which the vortex returns to its initial location. The results show that our numerical schemes have $(k+1)$th order accuracy for $k=1,2$. For this smooth example, no nonlinear limiter is needed.

Table 2 $L^2$ errors and orders of accuracy of $\rho$, $u_{x}$, $B_x$ and p for smooth vortex problem at t = 20. The computational domain is $[-\,10,10]\times [-\,10,10]$

6.1.2 The Smooth Alfvén Wave

The second smooth example is the smooth Alfvén wave problem, which describes a circularly polarized Alfvén wave moving in the domain $\Omega =[0,1/\cos \alpha ]\times [0,1/\sin \alpha ]$ [28, 37]. Here, $\alpha$ represents the angle of the wave propagation with respect to x-axis, and it is set to be $\pi /4$. The same initial data as in [28] is taken

$$\begin{aligned} \rho= & {} 1, u_\Vert = 0, u_\perp = 0.1\sin (2\pi \beta ), u_z = 0.1\cos (2\pi \beta ), \\ B_\Vert= & {} 1, B_\perp = u_\perp , B_z = u_z, p = 0.1, \end{aligned}$$

where $\beta = x\cos \alpha +y\sin \alpha$. The subscripts $\Vert$ and $\perp$ denote the directions parallel and perpendicular to the wave propagation direction, respectively. Periodic boundary conditions are used and $\gamma =5/3$. The Alfvén wave travels at a constant Alfvén speed $B_\parallel /\sqrt{\rho }$ = 1. The solution returns to its initial configuration when time t is an integer. In Table 3, we present the $L^2$ errors and orders of accuracy for $u_x$, $u_z$, $B_x$ and p at time $t = 2$. From the results, we can see that the $P^k$ approximations with $k=1,2$ are $(k+1)$th order accurate, and they are optimal. No nonlinear limiter is applied.

Table 3 $L^2$ errors and orders of accuracy for $u_x,u_{z}$, p and $B_x$ for smooth Alfvén wave problem at $t=2$. The computational domain is $[0,\sqrt{2}]\times [0,\sqrt{2}]$

6.2 Non-smooth Examples

6.2.1 The Field Loop Advection

In this subsection, we consider the magnetic field loop advection problem originally introduced in [20]. The same initial data as in [27] is taken, with $(\rho , u_x, u_y, u_z, B_z, p) = (1,2,1,1,0,1)$, and $(B_x, B_y) = {\widehat{\nabla }} \times A_z$. Here $A_z$ is the z-component of the magnetic potential

$$\begin{aligned} A_z=\left\{ \begin{array}{ll} A_0(R-r) &{}\quad \hbox {if }\; r\le R, \\ 0 &{}\quad \hbox {if }\; r> R, \end{array} \right. \end{aligned}$$

with $A_0 = 10^{-3}$, $R = 0.3$ and $r = \sqrt{x^2+y^2}$. This problem is computed on the domain $[-\,1,1]\times [-\,0.5,0.5]$ with a $200\times 100$ mesh. Periodic boundary conditions are used and $\gamma = 5/3$.

In Fig. 3, we report the gray-scale images of the magnetic pressure $B_x^2+B_y^2$ (left) and the magnetic field lines (right) at time $t=0$, $t=2$ and $t=10$. With the globally divergence-free magnetic field, the magnetic field lines are plotted by contouring the z-component of the numerical magnetic potential $A_z$. The magnetic pressure is convected across the domain periodically, and this is confirmed by our numerical results based on $P^2$ approximation. The component-wise minmod TVB limiter is applied to ${\mathbf {U}}_h$ with the parameter $M=1$. There is no visible difference in the numerical results when the limiter is applied to the local characteristic fields. Overall our schemes capture the field loop well. From the images on the left in Fig. 3, one can observe numerical dissipation around the center and the boundary of the loop, similar to the observation in [20, 26, 27]. There is no obvious oscillations in our solutions even at later time $t=10$ unlike in some numerical results commented in [20, 28]. From the images on the right of Fig. 3, symmetry can be seen in the magnetic field lines, with some distortion at $t=10$ due to the accumulated numerical dissipation over long time simulation.

Fig. 3

The magnetic pressure $B_x^2+B_y^2$ (left) and magnetic field lines (right) of the field loop advection. $P^2$ approximation on $200\times 100$ mesh. The magnetic field lines are plotted with the same range. a Magnetic pressure at $t= 0$, b magnetic field lines at $t= 0$, c magnetic pressure at $t= 2$, d magnetic field lines at $t= 2$, e magnetic pressure at $t= 10$, f magnetic field lines at $t= 10$

Note that the initial data is discontinuous, and one needs to pay special attention to the initialization to ensure the magnetic field being divergence-free at $t=0$. For example, to apply the BDM projection to the initial magnetic field, one needs to compute the first order coefficient $B^0_x:=\frac{1}{\Delta x \Delta y} \displaystyle \int _{I_{ij}} B_x dxdy$ with $B_x=\partial A_z/\partial y$. If a numerical quadrature is applied without taking into account the discontinuity in $B_x$, then nonzero divergence will be introduced to the magnetic field approximation. Instead, we will evaluate $B_x^0$ as follows,

$$\begin{aligned} B^0_x=\frac{1}{\Delta x \Delta y} \int _{I_{ij}} \frac{\partial A_z}{\partial y} dxdy=\frac{1}{\Delta x \Delta y} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \left[ A_z(x,y_{j+\frac{1}{2}})-A_z(x,y_{j-\frac{1}{2}})\right] dx. \end{aligned}$$

(68)

Similarly, to evaluate $a_{0R}:= \frac{1}{\Delta y}\displaystyle \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}B_x(x_{i+\frac{1}{2}},y)dy$, we will follow

$$\begin{aligned} a_{0R}=\frac{1}{\Delta y}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \frac{\partial A_z}{\partial y}dy=\frac{1}{\Delta y}\left( A_z(x_{i+\frac{1}{2}},y_{j+\frac{1}{2}})-A_z(x_{i+\frac{1}{2}},y_{j-\frac{1}{2}})\right) . \end{aligned}$$

(69)

This will lead to an exactly divergence-free magnetic field approximation at $t=0$.

Fig. 4

Development of the density $\rho$ in Orszag–Tang vortex problem with $P^1$ approximation at $t=3,\,t=4$ on $192\times 192$ mesh. 15 equally spaced contours with ranges [1.144, 6.134], [1.179, 5.813] respectively. a $t=3$, b $t=4$

6.2.2 Orszag–Tang Vortex Problem

In this subsection, we test the Orszag–Tang vortex problem, whose solution involves the formation and interaction of multiple shocks as the nonlinear system evolves in time. The same initial date as in [25] is taken, namely,

$$\begin{aligned} \begin{aligned} \rho = \gamma ^2,\quad u_x = - \sin y,\quad u_y = \sin x,\quad u_z = 0,\\ B_x = -\sin y,\quad B_y = \sin 2x,\quad B_z = 0,\quad p = \gamma .\\ \end{aligned} \end{aligned}$$

This problem is computed on the domain $[0,2\pi ]\times [0,2\pi ]$ with a $192\times 192$ mesh based on $P^1$ and $P^2$ approximations. Periodic boundary conditions are used with $\gamma =5/3$. Figures 4 and 5 demonstrate the time evolutions of the density $\rho$ at times $t=3, 4$ with $P^1$ and $P^2$ approximations, respectively. The component-wise minmod TVB limiter is applied to ${\mathbf {U}}_h$ with the parameter $M=1$. The results show that our schemes work well for this problem and they are in good agreement with the results in literature [23, 25, 27].

Fig. 5

Development of the density $\rho$ in the Orszag–Tang vortex problem with $P^2$ approximation at $t=3$, $t=4$ on $192\times 192$ mesh. 15 equally spaced contours with ranges [1.122, 6.161], [1.127, 5.857], respectively. a $t=3$, b $t=4$

As observed in [23, 25, 29], different numerical methods can demonstrate different levels of stability for this example, (partially) depending on their ability to control the divergence error in the computed magnetic field. Standard numerical methods that work well for nonlinear hyperbolic conservation laws can show instability when simulating this example, if the divergence error is not sufficiently controlled. Our proposed exactly divergence-free DG methods display very good stability over long time simulation, for example the schemes with $P^1$ and $P^2$ approximations are stable up to $t=25$ (the maximum time we run) on the $192\times 192$ mesh when the minmod TVB limiter is applied in local characteristic fields. In addition to the divergence error, as indicated in [37] the choices of the limiters can also affect the numerical stability. When the component-wise minmod TVB limiter is applied, the simulation will break down at $t=7.4$ with the $P^2$ approximation. Again, the limiters are only applied to ${\mathbf {U}}_h$.

For this example, we further perform a convergence study for the methods with $P^2$ approximation. In Fig. 6, we plot the pressure p (left) at $y=1.99635$ and $t=2$, and the magnetic variable $B_x$ at $x=\pi$ and $t = 3$, computed with the $192\times 192$ (circle) and $384\times 384$ (line) meshes. With shocks developed in the solution, convergence is observed. The pressure lines and magnetic field lines are comparable to the results by the locally divergence-free DG methods in [25] and exactly divergence-free central DG methods in [26, 27]. As in [26, 27], there is no negative pressure produced throughout the simulation.

Fig. 6

The $P^2$ approximation for the Orszag–Tang vortex problem on $192\times 192$ (circle) and $384\times 384$ (solid line) meshes. a p with $y = 1.9635$ at $t = 2$, b $B_x$ with $x = \pi$ at $t = 3$

6.2.3 The Rotor Problem

In this subsection, a rotor problem is considered which was first documented in [8]. This problem describes a dense disk of fluid rapidly spinning in a light ambient fluid. To reduce the initial transition, a “taper” function is used to bridge these two areas. We take the same initial data as in [26, 37], that is,

$$\begin{aligned} (u_z, B_x, B_y, B_z, p) = \left( 0, 2.5/\sqrt{4\pi }, 0, 0, 0.5\right) , \end{aligned}$$

and

$$\begin{aligned} (\rho , u_x, u_y)=\left\{ \begin{array}{ll} \left( 10, -(y-0.5)/r_0,(x-0.5)/r_0\right) &{}\quad r< r_0 \\ \left( 1+9\lambda ,-\lambda (y-0.5)/r, \lambda (x-0.5)/r\right) &{}\quad r_0< r< r_1\\ (1,0,0) &{}\quad r> r_1 \end{array} \right. \end{aligned}$$

where $r=\sqrt{(x-0.5)^2+(y-0.5)^2}$, $r_0 = 0.1$, $r_1 = 0.115$ and $\lambda = (r_1-r)/(r_1-r_0)$. We simulate the problem in the domain $[0,1]\times [0,1]$. Periodic boundary conditions are used and $\gamma = 5/3$.

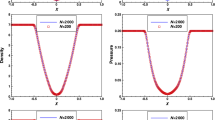
In Figs. 7 and 8, we present the results of density $\rho$, pressure p, the hydrodynamic Mach number $|{\mathbf {u}}|/c$ with the sound speed $c=\sqrt{\gamma p/\rho }$, and the magnetic pressure ${|{\mathbf {B}}|}^2/2$ at $t=0.295$, based on $P^1$ and $P^2$ approximations on the $200\times 200$ mesh. The minmod TVB limiter is applied in the characteristic fields and only to ${\mathbf {U}}_h$. Compared with the results in [25, 37], our methods also resolve this problem well. When divergence error is not sufficiently controlled in the magnetic field by some numerical methods, “distortion” can develop in Mach number [25, 37]. In Fig. 9, we zoom in the central part of the Mach number, and no “distortion” is observed.

Fig. 7

$P^1$ approximation for the rotor problem on the $200 \times 200$ mesh at $t = 0.295$. 15 equally spaced contours. a $\rho \in [0.507, 8.837]$, b $p \in [0.010, 0.774]$, c $|\mathbf{B}|^{2}/2 \in [0.012, 0.676]$, d $|\mathbf{u}| /c \in [0, 2.673]$

Fig. 8

$P^2$ approximation for the rotor problem on the $200 \times 200$ mesh at $t = 0.295$. 15 equally spaced contours. a $\rho \in [0.551, 9.910]$, b $p \in [0.008, 0.776]$, c $|\mathbf{B}|^{2}/2 \in [0.012, 0.847]$, d $|\mathbf{u}| /c \in [0, 3.033]$

Fig. 9

Zoom-in central part of Mach number $|{\mathbf {u}}|/c$ with $P^2$ approximation in the rotor problem at $t = 0.295$. 30 equally spaced contours with range [0.18, 3.12]. a $100\times 100$ mesh, b $200\times 200$ mesh, c $400\times 400$ mesh, d $600\times 600$ mesh

As in [26, 27], we examine the convergence of the methods with $P^2$ approximation. In Fig. 10, we present the Mach number with $x=0.413$ (left) and the magnetic field $B_x$ (right) with $x=0.25$ at $t=0.295$ on $400\times 400$ (circle) and $600\times 600$ (solid) meshes. Convergence of the method is observed, with the shocks being captured in the numerical solution. The cut lines in Fig. 10 are very close to the results in [26], and there is no significant oscillation in the solutions. In our simulation, negative pressure is not observed.

Fig. 10

The Mach number $|{\mathbf {u}}|/c$ and magnetic filed $B_x$ of the rotor problem with $P^2$ approximation at $t=0.295$ on $400\times 400$ (circle) and $600\times 600$ (solid line) meshes. a $|\mathbf{u}|/c$ with $x = 0.41$, b $B_x$ with $x = 0.25$

6.2.4 The Blast Problem

In this subsection, we consider the blast problem as in [8]. There are strong magnetosonic shocks in the solution. The initial condition is taken as

$$\begin{aligned} \left( \rho ,u_x,u_y,u_z,B_x,B_y,B_z,p\right) =\left\{ \begin{array}{ll} \left( 1,0,0,0,\frac{100}{\sqrt{4\pi }},0,0,1000\right) , &{}\quad r\le R, \\ \left( 1,0,0,0,\frac{100}{\sqrt{4\pi }},0,0,0.10\right) , &{}\quad r> R, \end{array} \right. \end{aligned}$$

with $r=\sqrt{x^2+y^2}$ and $R=0.1$. With this setup, the fluid pulse has very small plasma beta, namely, $\beta = \frac{p}{(B_x^2+B_y^2)/2} = 2.513E{-}04$, in the region outside the initial pressure pulse. We carry out the simulation in the domain $[-\,0.5,0.5]\times [-\,0.5,0.5]$ with a $200\times 200$ mesh. Outgoing boundary conditions are used and $\gamma =1.4$.

In Figs. 11 and 12, we report the numerical results at time $t=0.01$ based on $P^1$ and $P^2$ approximations for density $\rho$, pressure p, square of total velocity $u_x^2+u_y^2$, and the magnetic pressure $B_x^2+B_y^2$, respectively. As pointed out in [8, 26,27,28], this is a stringent problem to solve. In our simulation, negative pressure is observed near the shock front, similar as in many other methods when positivity preserving techniques are not applied to pressure [26,27,28]. In Fig. 13, we plot the negative part of pressure, $\min (0,p)$, based on the $P^1$ and $P^2$ approximations. The minimum of pressure in the $P^2$ approximation is $-\,16.295$, and it is more negative than $-\,4.369$, the minimum of the pressure in the $P^1$ approximation. These results are obtained when the component-wise minmod TVB limiter is applied only to ${\mathbf {U}}_h$.

Fig. 11

$P^1$ approximation for the blast problem on the $200\times 200$ mesh at $t=0.01$. 40 equally spaced contours are plotted. a $\rho \in [0.184,4.602]$, b $p\in [-\,4.369,259.297]$, c $u_x^2+u_y^2 \in [0,288.251]$, d $B_x^2+B_y^2\in [431.002,1186.060]$

Fig. 12

$P^2$ approximation for the blast problem on the $200\times 200$ mesh at $t=0.01$. 40 equally spaced contours are plotted. a $\rho \in [0.191,4.769]$, b $p\in [-\,16.397,256.291]$, c $u_x^2+u_y^2 \in [0,288.838]$, d $B_x^2+B_y^2\in [426.407,1236.830]$

Fig. 13

Negative part of the pressure, $\min (0,p)$, in the blast problem with $P^1$ and $P^2$ approximations at $t=0.01$ on the $200\times 200$ mesh. a $P^1$, b $P^2$

To further improve the numerical stability, we run the simulation by applying the minmod TVB limiter to both the hydrodynamic variables ${\mathbf {U}}_h$ and the normal component of the magnetic field $\{b^x_{ij}\}_{ij}$ and $\{b^y_{ij}\}_{ij}$ (see Sect. 5 for details of the limiter and the reconstruction). In Fig. 14, the results are shown for density $\rho$, pressure p, square of total velocity $u_x^2+u_y^2$, and the magnetic pressure $B_x^2+B_y^2$, respectively, at $t=0.01$ based on $P^2$ approximation. With the magnetic field being limited, the minimum of pressure is now $-\,7.347$ which is greatly improved, hence the schemes with all unknowns being limited are more robust.

Fig. 14

$P^2$ approximation for the blast problem on the $200\times 200$ mesh at $t=0.01$. Nonlinear limiter is applied to both ${\mathbf {U}}_h$ and $\{b^x_{ij}\}_{ij}$, $\{b^y_{ij}\}_{ij}$. 40 equally spaced contours are used. a $\rho \in [0.182,4.573]$, b $p\in [-\,7.347,254.906]$, c $u_x^2+u_y^2 \in [0,287.389]$, d $B_x^2+B_y^2\in [422.866,1188.86]$

Remark 6.1

Following Zhang and Shu’s important work in [41] to design positivity-preserving limiters for high order numerical methods, similar limiters were developed in [12] for DG and central DG methods to simulate ideal MHD equations. Locally divergence-free approximations can be easily used for the methods in [12] without affecting the positivity-preserving property of the overall algorithms. Unfortunately, such limiters can not be applied to the proposed methods in this paper, as they will destroy the globally divergence-free property of the numerical solutions.

6.2.5 The Cloud–Shock Interaction

The last example we consider is a cloud–shock interaction problem which involves strong MHD shocks interacting with a dense cloud. We take the same initial data as in [26, 27]. The computational domain, $\Omega =[0,2]\times [0,1]$, is divided into three regions initially: the post-shock region $\Omega _1 = \{(x,y){:}\,0\le x\le 1.2, 0\le y \le 1\}$, the pre-shock region $\Omega _2= \{(x,y){:}\,1.2\le x\le 2, 0\le y \le 1, \sqrt{(x-1.4)^2+(y-0.5)^2}\ge 0.18\}$ and the cloud region $\Omega _3=\{(x,y){:}\,\sqrt{(x-1.4)^2+(y-0.5)^2}<0.18\}$. The initial data in $\Omega _1$, $\Omega _2$ and $\Omega _3$ for $(\rho ,u_x,u_y,u_z,B_x,B_y,B_z,p)$ is given by ${\mathbf {U}}_1$, ${\mathbf {U}}_2$ and ${\mathbf {U}}_3$, respectively, with

$$\begin{aligned} {\mathbf {U}}_1&=\left( 3.88968,0,0,-\,0.05234,1,0,3.9353,14.2641\right) , \\ {\mathbf {U}}_2&=\left( 1,-\,3.3156,0,0,1,0,1,0.04\right) , \\ {\mathbf {U}}_3&=\left( 5,-\,3.3156,0,0,1,0,1,0.04\right) . \end{aligned}$$

The cloud in the region $\Omega _3$ is five times denser than its surrounding. Outgoing boundary conditions are used and $\gamma =5/3$. We run the simulation up to $t=0.6$.

In Fig. 15, we show the gray-scale images of the $P^1$ approximations for density $\rho$, pressure p and magnetic field component $B_x$, $B_y$ on the $600\times 300$ mesh. The white area represents relatively larger value. The numerical results are fairly close to those by exactly divergence-free central DG methods in [26, 27]. The minmod TVB limiter is implemented in the local characteristic fields and is only applied to ${\mathbf {U}}_h$.

Fig. 15

$P^1$ approximation of the cloud–shock interaction problem at $t = 0.6$ on the $600\times 300$ mesh. a $\rho \in [1.804,11.638]$, b $p \in [6.295,15.567]$, c $B_x \in [-\,3.073,4.355]$, d $B_y \in [-\,3.299,3.265]$

Fig. 16

$P^2$ approximation of the cloud–shock interaction problem at $t = 0.6$ on the $600\times 300$ mesh. a $\rho \in [1.777,11.655]$, b $p \in [1.028,16.734]$, c $B_x \in [-\,2.922,4.472]$, d $B_y \in [-\,3.027,2.961]$

In Fig. 16, gray-scale images of $P^2$ approximations are shown for density $\rho$, pressure p and magnetic field component $B_x$, $B_y$ on the $600\times 300$ mesh. In Fig. 17, we further plot the cut lines of density $\rho$ based on $P^2$ approximation with $y=0.6$ and $x=1.0$ on the $600\times 300$ and $800\times 400$ meshes. The convergence of the methods is confirmed. With $P^2$ approximation, it is not sufficient to just apply the nonlinear limiter to ${\mathbf {U}}_h$ for numerical stability. And the results presented here are obtained when the limiter is applied to both ${\mathbf {U}}_h$ and $\{b^x_{ij}\}_{ij}$, $\{b^y_{ij}\}_{ij}$. In order to see the necessity to limit the magnetic field is related to the strength of the discontinuity, we also simulate a similar clock–shock interaction example, with the cloud in region $\Omega _3$ two times denser than its surrounding at $t=0$. As expected, our methods are stable for this modified example when the limiter is applied only to ${\mathbf {U}}_h$. The numerical results are not included here.

Fig. 17

The $P^2$ approximation of $\rho$ in the cloud–shock interaction problem at $t = 0.6$ on $600\times 300$ (circle) and $800\times 400$ (solid) meshes. a $y=0.6$, b $x=1.0$

7 Concluding Remarks

In this paper, we propose second and third order globally divergence-free discontinuous Galerkin methods for ideal MHD equations on structured meshes in two dimensions. The main technical aspect is on the choices of numerical fluxes used in the different parts of the algorithms. Analysis is presented to identify conditions on numerical fluxes to ensure the exactly divergence-free property of the approximated magnetic field. A careful numerical and analytical study was carried out to find good choices of numerical fluxes for the accuracy and numerical stability of the methods. A set of smooth and non-smooth numerical examples are presented to illustrate the performance of the proposed methods. Our future efforts will include the extension of the methods to high order accuracy, three dimensions, and unstructured meshes.