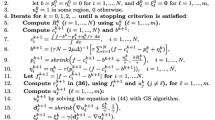Image Segmentation Using the Cahn–Hilliard Equation

Abstract

In this paper, we propose a novel model for image segmentation by using the Cahn–Hilliard equation. An interesting feature of this model lies in its ability of interpolating missing contours along wide gaps in order to form meaningful object boundaries, which is often achieved by curvature dependent models in the literature. To solve the associated equation, we employ a recently developed technique, that is, the tailored-finite-point method, which helps preserve sharp jumps and thus helps locate segmentation contours more exactly. Numerical experiments are presented to demonstrate the effectiveness of the proposed model and its features. In addition, analytical results on the existence and uniqueness of the associated equation are also provided.

1 Introduction and Motivations

Image segmentation is a fundamental problem in image processing and computer vision. It aims to partition a given image into regions in order to recognize different objects, and it has a wide range of applications in medical imaging, object detection, video surveillance, and so on. During the last three decades, many different approaches have been proposed to deal with this problem. These methods include clustering methods, graph partitioning methods, statistics based methods, partial differential equation (PDE) based methods, and variational methods. In this work, we mainly focus on PDE/variational methods.

For those PDE/variational methods, a typical method for image segmentation is to evolve active contours or snakes such that these contours could reside on object boundaries [4, 9]. The classical snake and active model was proposed by Kass, Witkin, and Terzopoulos [9], where the active contours are driven to desired boundaries by internal forces such as regularity and external one from the inhomogeneous distribution of image intensity. Later on, Caseslles, Kimmel, and Sapiro proposed using geodesic active contours for image segmentation [3].

Instead of using curve evolution, there are also lots of region-based image segmentation models in the literature. One of the most famous variational models for this problem is due to Mumford and Shah [10]. They treated the given image as a function and searched for its piecewise smooth approximation by minimizing some designed functional, and as a result, object boundaries can be defined as the transition between adjacent patches of the approximation function. In fact, besides for image segmentation, the Mumford–Shah’s model has led to many variants with applications in almost all research topics in image processing, such as image denoising, inpainting, and registration. The well-known Chan–Vese model [4] can be regarded as a special case of the Mumford–Shah’s model, and it seeks for a binary image to approximate the given image using level set function [12].

Even though they differ in the forms, the above segmentation models are all grey intensity based, that is, their outputs mainly rely on grey intensity values of the given images. However, due to the nature of real images, objects may not be well defined by the intensity values. Specifically, some parts of objects could be occluded by other ones or even missing. For instance, in medical images, target organs could be blended with other ones or tissues. As a result, those intensity based models might not successfully segment those meaning objects. To fix this problem, many segmentation models that incorporate prior shapes have been developed [5]. Another possible way is to impose effective regularity condition on those active contours. Recently, in [1, 19], the authors proposed variational segmentation models by using Euler’s elastica as the regularization of active contours. These models are able to integrate missing or broken parts to form complete meaningful objects, and they are more suited to capture objects with tiny but elongated structures than the Chan–Vese model.

In fact, ever since Mumford’s seminar work on segmentation with depth [11], Euler’s elastica has been broadly used in the development of variational models in mathematical imaging [1, 15, 19]. For instance, in [14], Chan, Kang, and Shen applied Euler’s elastica as an interpolator for the inpainting problem. Their model is able to connect relatively large gaps that cannot be fulfilled by using the total variation based regularizer. While these high-order models could effectively accomplish many imaging tasks in image inpainting, denoising, and segmentation, they are notoriously intractable both analytically and numerically, since the associated Euler–Lagrange equations are highly nonlinear and of fourth-order. Therefore, when compared with other lower order variational models, such as the well-known Rudin–Osher–Fatemi model [13], these curvature dependent models could achieve more at the expense of paying much more computational effort.

In this work, we plan to develop a novel segmentation model that takes advantage of the favorable features of high-order PDEs and is also more easily handled than those Euler’s elastica based models. Specifically, we propose using the Cahn–Hilliard equation together with intensity fitting terms for the purpose of image segmentation. This idea mainly originated from the attributes of the Cahn–Hilliard equation, which describes the process of phase separation of a binary fluid. While the Cahn–Hilliard equation is still of fourth-order, however, when compared with those Euler–Lagrange equations associated with Euler’s elastica based functionals, its highest order term is linear, which significantly reduces the difficulty of developing effective numerical schemes and also makes the analysis of such models possible. In fact, the Cahn–Hilliard equation has also been utilized in the field of image processing [2, 6]. In [2], Bertozzi, Esedoglu, and Gillette proposed using the Cahn–Hilliard equation for the binary image inpainting, and in [6], multi-phase inpainting for grey images, and so on.

Different from the numerical schemes used in Esedoglu’s paper [2], in this paper, we intend to apply a novel numerical scheme, that is, the tailored finite point method (TFPM) to solve the equation of our proposed model. The TFPM was originally proposed by Han, Huang, and Kellogg for solving a singular perturbation problem in order to resolve boundary/interior layers [7]. Its salient feature lies in its ability of preserving sharp transitions, since the schemes incorporate local information of the exact solutions of the related problems. Recently, in [18], we have applied this technique for solving the Rician denoising and deblurring model proposed by Getreuer, Tong, and Vese, and the improvement of the PSNR values can be observed when the obtained numerical results are compared with those using traditional finite difference schemes.

As a summary, the main contribution of this paper lies in the following two aspects:

• We propose a novel segmentation model that makes use of the Cahn–Hilliard equation and also provide the analytical study of the proposed model, including its existence and uniqueness of the associated equation.

• We apply the TFPM technique to solve the proposed model.

The outline of our paper is as follows. We first describe the proposed model that makes use of the Cahn–Hilliard equation in Sect. 2, and then discuss the well-posedness of this model in Sect. 3. In Sect. 4, we provide the details of applying TFPM for solving the resulting equation of this model. Numerical experiments are presented in Sect. 5 to demonstrate the features of the proposed model as well as the effectiveness of the numerical schemes, which is followed by a conclusion in Sect. 6.

2 The Modified Cahn–Hilliard Model

Suppose f is the given image, u is the corresponding recovered image. In what following, we would like to consider the following Cahn–Hilliard type equation for image segmentation:

$$\begin{aligned} u_t=-\Delta \Big (\epsilon _1 \Delta u-{\frac{2}{\epsilon _1}} W'(u)\Big )- \left[ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 \right] \frac{\epsilon _3}{\pi \left[ \epsilon _3^2 + (u-\frac{1}{2})^2\right] }, \qquad \end{aligned}$$

(2.1)

where $\epsilon _1$, $\epsilon _3$, $\lambda _1$, $\lambda _2 > 0$, u satisfies $\frac{\partial u}{\partial n}=\frac{\partial \Delta u}{\partial n}=0$ on $\partial \Omega$, the double-well function $W(u)=u^2(u-1)^2$, and $c_1$, $c_2$ are two constants that could be assigned using some strategy. For instance, we can set $c_1=1$ and $c_2=0$ initially, if the image function f is rescaled in the range [0, 1], and with these values of $c_1$, $c_2$, we can solve Equation (2.1) to steady state, and then update them using the following formula:

$$\begin{aligned} c_1= & {} \frac{\int _{\Omega } \left[ \frac{1}{2}+\frac{1}{\pi }\arctan \left( \frac{u-\frac{1}{2}}{\epsilon _3}\right) \right] f dx}{\int _{\Omega } \left[ \frac{1}{2}+\frac{1}{\pi }\arctan \left( \frac{u-\frac{1}{2}}{\epsilon _3}\right) \right] dx}, \\ c_2= & {} \frac{\int _{\Omega } \left[ \frac{1}{2}-\frac{1}{\pi }\arctan \left( \frac{u-\frac{1}{2}}{\epsilon _3}\right) \right] f dx}{\int _{\Omega } \left[ \frac{1}{2}-\frac{1}{\pi }\arctan \left( \frac{u-\frac{1}{2}}{\epsilon _3}\right) \right] dx}, \end{aligned}$$

and with this new values of $c_1$, $c_2$, we again solve Eq. (2.1) to steady state, and keep this process until $c_1$, $c_2$ converge.

Equation (2.1) is not a gradient flow for an energy. Indeed, the first term on the right-hand side of (2.1) is the gradient descent with respect to the $\bar{H}^{-1}$ inner product [16] of the following energy:

$$\begin{aligned} E_1(u)=\int _{\Omega }\Big (\frac{\epsilon _1}{2}|\nabla u|^2+\frac{2}{\epsilon _1}W(u)\Big )dx, \end{aligned}$$

(2.2)

which satisfies

$$\begin{aligned}\begin{array}{llllll} \displaystyle \frac{d}{dt}E_1(u) &{} = \displaystyle \frac{d}{dt}\int _{\Omega }\Big (\frac{\epsilon _1}{2}|\nabla u|^2+\frac{1}{\epsilon _1}W(u)\Big )dx \\ &{} = -\displaystyle \int _{\Omega }|\nabla w|^2 dx \le 0, \end{array}\end{aligned}$$

where $w=-\epsilon _1 \Delta u +\frac{1}{\epsilon _1} W'(u)$.

The second term in the right-hand side of (2.1) is the gradient descent with respect to the $L^2$ inner product of the following energy:

$$\begin{aligned} \begin{array}{llllll} E_2(u)&{}=\displaystyle \lambda _1 \int _{\Omega }(f-c_1)^2 H_{\epsilon _3}\left( u-\frac{1}{2}\right) dx\\ &{}\quad \displaystyle +\, \lambda _2 \int _{\Omega }(f-c_2)^2 \left[ 1-H_{\epsilon _3}\left( u-\frac{1}{2}\right) \right] dx, \end{array} \end{aligned}$$

(2.3)

where, as in [4],

$$\begin{aligned} H_{\epsilon _3}(z)=\frac{1}{2}\left( 1+\frac{2}{\pi }\arctan \left( \frac{z}{\epsilon _3}\right) \right) , \end{aligned}$$

is a $\mathbf {C}^{\infty }$ regularization of the Heaviside function H given by

$$\begin{aligned} H(z)=\left\{ \begin{array}{llll} 1, &{} \text {if} &{} z \ge 0,\\ 0, &{} \text {if} &{} z < 0, \end{array}\right. \end{aligned}$$

and the one-dimensional Dirac measure $\delta _0=\frac{d}{dz}H(z)$ can be approximated by $\delta _{\epsilon _3}=H'_{\epsilon _3}$, where

$$\begin{aligned} \delta _{\epsilon _3}(z)=\frac{\epsilon _3}{\pi \left( \epsilon _3^2+z^2\right) }. \end{aligned}$$

The above model (Eq. (2.1)) can be extended for the segmentation of color images. For a color image, f consists of three channels, that is $f=(f(1),f(2),f(3))$. Then $c_1$ and $c_2$ are defined as vectors with three elements

$$\begin{aligned} c_1(i)=\frac{\int _{\Omega } H_{\epsilon _3}\left( u-\frac{1}{2}\right) f(i) dx}{\int _{\Omega } H_{\epsilon _3}\left( u-\frac{1}{2}\right) dx}, \quad c_2(i)=\frac{\int _{\Omega } \left[ 1-H_{\epsilon _3}\left( u-\frac{1}{2}\right) \right] f(i) dx}{\int _{\Omega } \left[ 1-H_{\epsilon _3}\left( u-\frac{1}{2}\right) \right] dx},\quad i=1,2,3. \end{aligned}$$

Then for the segmentation of color images, our model can be expressed as follows:

$$\begin{aligned} u_t= & {} -\Delta \Big (\epsilon _1 \Delta u-\frac{2}{\epsilon _1} W'(u)\Big )\nonumber \\&\quad - \sum _{i=1}^{3}\left[ \lambda _1 (f(i)-c_1(i))^2 - \lambda _2 (f(i)-c_2(i))^2 \right] \frac{\epsilon _3}{\pi [\epsilon _3^2 + \left( u-\frac{1}{2}\right) ^2]}, \end{aligned}$$

(2.4)

with the boundary condition $\frac{\partial u}{\partial n}=\frac{\partial \Delta u}{\partial n}=0$ on $\partial \Omega$.

Moreover, our model can also be adapted to multi-phase segmentation. In what follows, we only consider the case of four phases. For this, as in [17], we only need two segmentation functions. Then we can write the energy $E_2$ for four phases as follows:

$$\begin{aligned} \begin{array}{llllll} E_2(u)&{}=\displaystyle \int _{\Omega }(f-c_{11})^2 H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) dx\\ &{}\quad \displaystyle + \int _{\Omega }(f-c_{10})^2 H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) dx\\ &{}\quad \displaystyle + \int _{\Omega }(f-c_{01})^2 \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) dx\\ &{}\quad \displaystyle + \int _{\Omega }(f-c_{00})^2 \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) dx, \end{array} \end{aligned}$$

(2.5)

where $c = (c_{11}, c_{10}, c_{01}, c_{00})$ is a constant vector, $u= (u_1, u_2)$, and

$$\begin{aligned} c_{11}= & {} \frac{\int _{\Omega } \left[ H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right] f dx}{\int _{\Omega }\left[ H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right] dx}, \\ c_{10}= & {} \frac{\int _{\Omega } \left[ H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) \right] f dx}{\int _{\Omega }\left[ H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) \right] dx}, \\ c_{01}= & {} \frac{\int _{\Omega } \left[ \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right] f dx}{\int _{\Omega }\left[ \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right] dx}, \\ c_{00}= & {} \frac{\int _{\Omega } \left[ \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) \right] f dx}{\int _{\Omega }\left[ \left( 1-H_{\epsilon _3}\left( u_1-\frac{1}{2}\right) \right) \left( 1-H_{\epsilon _3}\left( u_2-\frac{1}{2}\right) \right) \right] dx}. \end{aligned}$$

Therefore, we propose the following model for the four-phase segmentation:

$$\begin{aligned} \begin{aligned} \frac{\partial u_1}{\partial t}&=-\Delta \Big (\epsilon _1 \Delta u_1-\frac{2}{\epsilon _1} W'(u_1)\Big )\\&\quad - \sum _{i=1}^{3} \left[ (f(i)-c_{11}(i))^2 - (f(i)-c_{01}(i))^2\right] H_{\epsilon _3}(u_2-\frac{1}{2})\delta _{\epsilon _3}(u_1-\frac{1}{2})\\&\quad - \sum _{i=1}^{3}\left[ (f(i)-c_{10}(i))^2 - (f(i)-c_{00}(i))^2\right] \Big (1-H_{\epsilon _3}(u_2-\frac{1}{2})\Big ) \delta _{\epsilon _3}(u_1-\frac{1}{2}),\\ \frac{\partial u_2}{\partial t}&=-\Delta \Big (\epsilon _1 \Delta u_2-\frac{2}{\epsilon _1} W'(u_2)\Big )\\&\quad - \sum _{i=1}^{3} \left[ (f(i)-c_{11}(i))^2 - (f(i)-c_{10}(i))^2\right] H_{\epsilon _3}(u_1-\frac{1}{2})\delta _{\epsilon _3}(u_2-\frac{1}{2})\\&\quad - \sum _{i=1}^{3}\left[ (f(i)-c_{01}(i))^2 - (f(i)-c_{00}(i))^2\right] \Big (1-H_{\epsilon _3}(u_1-\frac{1}{2})\Big ) \delta _{\epsilon _3}(u_2-\frac{1}{2}), \end{aligned} \end{aligned}$$

with the boundary conditions $\frac{\partial u_{i}}{\partial n}=\frac{\partial \Delta u_{i}}{\partial n}=0$, $i=1,2$ on $\partial \Omega$. Certainly, it is easy to extend our idea to general multi-phase segmentation.

3 Existence of Weak Solutions of the Modified Cahn–Hilliard Equation

Based on the definitions of H, $\delta$, we can rewrite our model (2.1) as follows

$$\begin{aligned} u_t=-\Delta \left( \epsilon _1 \Delta u-\frac{2}{\epsilon _1} W'(u)\right) - \delta _{\epsilon _3}\left( u-\frac{1}{2}\right) [ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ]. \end{aligned}$$

(3.1)

We define a weak solution of the evolution Eq. (3.1), $\forall v \in \mathbf {V}$,

$$\begin{aligned} \frac{d}{dt}<u,v> +<\epsilon _1 \Delta u, \Delta v> -<\frac{2}{\epsilon _1} W'(u), \Delta v> = <-\delta _{\epsilon _3}[ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ], v>, \end{aligned}$$

(3.2)

where

$$\begin{aligned} \mathbf {V}=\left\{ \phi \in H^2(\Omega )\ \Big |\ \frac{\partial \phi }{\partial \vec {n}}=\frac{\partial \Delta \phi }{\partial \vec {n}}=0 \quad \text{ on } \quad \partial \Omega \right\} . \end{aligned}$$

Firstly, we give a priori bound for the $\mathbf {L}^2$ norm of the solution u, which is uniform in time. In fact, the proof for the following energy estimate is similar to lemma 4.2 in the article [2].

Lemma 3.1

Given a weak solution as described above, there exist constants $c(\epsilon _3, \lambda _2, f)>0$ and $\theta >0$ so that

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega } u^2 dx \le c(\epsilon _3, \lambda _2, f)-\theta \int _{\Omega } u^2 dx, \end{aligned}$$

(3.3)

for all $t\ge 0$.

Proof

Multiply Eq. (3.1) by u, and integrate on $\Omega$,

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega } u^2 dx= & {} -\epsilon _1\int _{\Omega }(\Delta u)^2 dx -\frac{2}{\epsilon _1}\int _{\Omega }W''(u)|\nabla u|^2 dx\\&\quad -\int _{\Omega } [\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2]\delta _{\epsilon _3} u dx. \end{aligned}$$

Using the fact $W''(u)\ge \gamma u^2 - C$ for all u, for some constants $\gamma$ and C, then

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega } u^2 dx\le & {} -\epsilon _1\int _{\Omega }(\Delta u)^2 dx -\frac{2\gamma }{\epsilon _1}\int _{\Omega }u^2|\nabla u|^2 dx +\frac{2C}{\epsilon _1}\int _{\Omega }|\nabla u|^2 dx\\&\quad -\int _{\Omega } [\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2]\delta _{\epsilon _3} u dx. \end{aligned}$$

First, estimating the last term of the inequality above as follows: Note $\tilde{C_1}=\frac{\lambda _1}{\pi }(f-c_1)^2+\frac{1}{2} \ge \frac{1}{2}$ and $\tilde{C_2}=\frac{\lambda _2}{\pi }(f-c_2)^2+\frac{1}{2} \ge \frac{1}{2}$. As $0\le u \le 1$,

$$\begin{aligned} \int _{\Omega } \tilde{C_2}\frac{\epsilon _3 u}{\epsilon _3^2+(u-\frac{1}{2})^2} dx \le \int _{\Omega } \tilde{C_2}\frac{1}{\epsilon _3} dx \equiv c(\epsilon _3, \lambda _2, f); \end{aligned}$$

and

$$\begin{aligned} \int _{\Omega } \tilde{C_1}\frac{\epsilon _3 u}{\epsilon _3^2+(u-\frac{1}{2})^2} dx \ge \epsilon _3 \int _{\Omega }\frac{\frac{1}{2}u}{\epsilon _3^2+(u-\frac{1}{2})^2} dx \ge \epsilon _3 \int _{\Omega }\frac{\frac{1}{2}u^2}{\epsilon _3^2+\frac{1}{4}} dx \equiv \tilde{C}\int _{\Omega } u^2 dx. \end{aligned}$$

Then

$$\begin{aligned} \int _{\Omega }(-\tilde{C_1}+ \tilde{C_2})\frac{\epsilon _3 u}{\epsilon _3^2+(u-\frac{1}{2})^2} dx \le c(\epsilon _3, \lambda _2, f) - \tilde{C}\int _{\Omega } u^2 dx. \end{aligned}$$

We refer to a standard interpolation inequality

$$\begin{aligned} \int _{\Omega } |\nabla u|^2 dx \le \delta \int _{\Omega } (\Delta u)^2 dx +\frac{1}{\delta } \int _{\Omega } u^2 dx, \end{aligned}$$

and put everything together,

$$\begin{aligned} \begin{array}{lll} \displaystyle \frac{1}{2}\frac{d}{dt}\int _{\Omega } u^2 dx &{} \le -\epsilon _1\int _{\Omega }(\Delta u)^2 dx -\frac{2\gamma }{\epsilon _1}\int _{\Omega }u^2|\nabla u|^2 dx +\frac{2C \delta }{\epsilon _1}\int _{\Omega }|\Delta u|^2 dx \\ &{}\quad \displaystyle +\frac{2C}{\epsilon _1 \delta }\int _{\Omega }u^2 dx +c(\epsilon _3, \lambda _2, f) - \tilde{C}\int _{\Omega } u^2 dx. \end{array}\end{aligned}$$

(3.4)

To satisfy the conditions $\frac{2 C \delta }{\epsilon _1} < \epsilon _1$ and $\frac{2C}{\epsilon _1 \delta } < \tilde{C}= \frac{\epsilon _3}{2\epsilon _3^2+\frac{1}{2}}$, take $\frac{C (4\epsilon _3+1)}{\epsilon _1 \epsilon _3}< \delta < \frac{\epsilon _1^2}{2C}$. With this choice, we have the following inequality:

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega } u^2 dx \le c(\epsilon _3, \lambda _2, f) - \theta \int _{\Omega } u^2 dx, \end{aligned}$$

where $\theta >0$. Thus the differential form of Gronwall’s inequality yields the estimate

$$\begin{aligned} \int _{\Omega } u^2 dx \le e^{-\theta t}\left[ \int _{\Omega }u_0^2 dx +ct\right] \le c(\epsilon _3, \lambda _2, f)t+\Vert u_0\Vert _{\mathbf {L}^2(\Omega )}^2 \end{aligned}$$

Returning to inequality (3.4) once more, we integrate from 0 to T and employ the inequality above to find

$$\begin{aligned} \max \limits _{0\le t \le T} \Vert u\Vert _{\mathbf {L}^2(\Omega )}^2 + \Vert u\Vert _{\mathbf {L}^2(0,T;H_0^2(\Omega ))}^2 \le c(\epsilon _3, \lambda _2, f)T+ \tilde{C} \Vert u_0\Vert _{\mathbf {L}^2(\Omega )}^2. \end{aligned}$$

(3.5)

$\square$

Theorem 3.2

(Existence of weak solution) There exists a weak solution of (3.1).

Proof

Step 1: Galerkin approximation.

Taking $\{w_k\}_{k=1}^{\infty }$ to be the complete set of appropriately normalized eigenfunctions for $L=-\Delta$ in $H^2(\Omega )$, $\{w_k\}_{k=1}^{\infty }$ is an orthogonal basis of $H^2(\Omega )$; $\{w_k\}_{k=1}^{\infty }$ is also an orthonormal basis of $L^2(\Omega )$. For each positive integer m, we look for a function $u_m$ of the form:

$$\begin{aligned} u_m=\sum _{k=1}^{m}d_m^k(t)w_k, \end{aligned}$$

(3.6)

where $d_m^k(0)=(u_0,w_k)$, and $u_m$ satisfies

$$\begin{aligned} \left( \frac{d u_m}{d t},w_k\right) +(\epsilon _1 \Delta u_m, \Delta w_k)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta w_k\right) {=}(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],w_k). \end{aligned}$$

(3.7)

Since $\{w_k\}_{k=1}^{\infty }$ is an orthonormal basis and $W'(u)$ is linearized, we have

$$\begin{aligned} \left( \frac{d u_m}{d t},w_k\right)= & {} \frac{d}{d t}d_m^k(t), \\ B[u_m,w_k;t]:= & {} (\epsilon _1 \Delta u_m, \Delta w_k)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta w_k\right) =\Sigma _{l=1}^{m} e^{kl}(t)d_m^l(t), \end{aligned}$$

for $e^{kl}(t):=B[w_l,w_k;t]$, $(k,l=1,\ldots , m)$. Note $f^k(t):=(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],w_k)$. Then the relation (3.7) is also equivalent to

$$\begin{aligned} \frac{d}{d t}d_m^k(t)+\Sigma _{l=1}^{m} e^{kl}(t)d_m^l(t)= & {} f^k(t) \quad (k=1,\ldots ,m), \end{aligned}$$

(3.8)

$$\begin{aligned} d_m^k(0)= & {} (u_0,w_k). \end{aligned}$$

(3.9)

According to Picard existence theory, there exists a unique absolutely continuous function $d_m(t)=(d_m^1(t),\ldots ,d_m^m(t))$ satisfying (3.8) and (3.9) for a.e. $0\le t \le T$.

Step 2: Energy estimates.

Multiply Eq. (3.7) by $d_m^k(t)$, sum for $k=1,\ldots ,m$,

$$\begin{aligned}&\left( \frac{d u_m}{d t},u_m\right) +(\epsilon _1 \Delta u_m, \Delta u_m)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta u_m\right) \\&\quad =(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],u_m). \end{aligned}$$

According to Lemma 3.1, we have

$$\begin{aligned} \max \limits _{0\le t \le T} \Vert u_m\Vert _{\mathbf {L}^2(\Omega )}^2 + \Vert u_m\Vert _{\mathbf {L}^2(0,T;H_0^2(\Omega ))}^2 \le c(\epsilon _3, \lambda _2, f)T+ \tilde{C} \Vert u_0\Vert _{\mathbf {L}^2(\Omega )}^2. \end{aligned}$$

Fix any $v \in \mathbf {V}$ with $\Vert v\Vert _{H^2(\Omega )}\le 1$, and write $v=v^1+v^2$, where $v^1 \in \text {span}\{w_k\}_{k=0}^{\infty }$, $(v^2,w_k)=0$. Since the functions $\{w_k\}_{k=0}^{\infty }$ are orthogonal in $H^2(\Omega )$, $\Vert v^1\Vert _{H^2(\Omega )}\le \Vert v\Vert _{H^2(\Omega )}\le 1$. Then we deduce that

$$\begin{aligned} (u_m',v^1)+(\epsilon _1 \Delta u_m, \Delta v^1)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta v^1\right)= & {} (-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v^1). \\ <u_m',v>= & {} (u_m',v)=(u_m',v^1), \end{aligned}$$

consequently,

$$\begin{aligned} \max \limits _{0\le t \le T} \Vert u_m\Vert _{\mathbf {L}^2(\Omega )}^2 {+} \Vert u_m\Vert _{\mathbf {L}^2(0,T;H_0^2(\Omega ))}^2 {+}\Vert u'_m\Vert _{\mathbf {L}^2(0,T;H^{-2}(\Omega ))}^2 \le c(\epsilon _3, \lambda _2, f)T+ \tilde{C} \Vert u_0\Vert _{\mathbf {L}^2(\Omega )}^2. \end{aligned}$$

Step 3: Existence.

According to the energy estimates, we see that $\{u_m\}_{m=1}^{\infty }$ is bounded in $L^2(0,T;H_0^2(\Omega ))$, $\{u_m'\}_{m=1}^{\infty }$ is bounded in $L^2(0,T;H^{-2}(\Omega ))$. By weak compactness, there exists $\{{u_m}_l\}_{l=1}^{\infty } \subset \{u_m\}_{m=1}^{\infty }$ and a function $u \in L^2(0,T;H_0^2(\Omega ))$ with $u' \in L^2(0,T;H^{-2}(\Omega ))$, such that

$$\begin{aligned}\begin{array}{llll} &{} {u_m}_l \rightharpoonup u &{} \text {weakly }\quad \text { in}&{} L^2(0,T;H_0^2(\Omega )),\\ &{} {u_m'}_l \rightharpoonup u' &{} \text {weakly }\quad \text { in} &{} L^2(0,T;H^{-2}(\Omega )). \end{array}\end{aligned}$$

Next fix N, and $v_N \in C^1([0,T]; V)$ with the following form

$$\begin{aligned} v_N=\Sigma _{k=1}^{N}d^k(t)w_k. \end{aligned}$$

Choosing $m\ge N$, multiply (3.7) by $d^k(t)$, sum $k=1,\ldots ,N$, and then integrate with respect to t,

$$\begin{aligned}&\int _0^T (u_m',v_N)+(\epsilon _1 \Delta u_m, \Delta v_N)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta v_N\right) dt \\&\quad = \int _0^T(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v_N)dt. \end{aligned}$$

Letting $m=m_l$, $l\rightarrow \infty$,

$$\begin{aligned}&\int _0^T (u',v_N)+(\epsilon _1 \Delta u, \Delta v_N)-\left( \frac{2}{\epsilon _1} w'(u),\Delta v_N\right) dt\\&\quad = \int _0^T\Big (-\delta _{\epsilon _3}\Big [\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2\Big ],v_N\Big )dt. \end{aligned}$$

As $C^1([0,T];H_0^2(\Omega ))$ is dense in $L^2([0,T];H_0^2(\Omega ))$, then $\forall v \in L^2([0,T];H_0^2(\Omega ))$, we have

$$\begin{aligned}&\int _0^T (u',v)+(\epsilon _1 \Delta u, \Delta v)-\left( \frac{2}{\epsilon _1} w'(u),\Delta v\right) dt\\&\quad = \int _0^T(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v)dt. \end{aligned}$$

Hence, $(u',v)+(\epsilon _1 \Delta u, \Delta v)-(\frac{2}{\epsilon _1} w'(u),\Delta v)=(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v)$, $\forall v \in V, \text {a.e.} 0\le t \le T$. In order to prove $u(0)=u_0$, first we note that

$$\begin{aligned}&\int _0^T (-v',u)+(\epsilon _1 \Delta u, \Delta v)-\left( \frac{2}{\epsilon _1} w'(u),\Delta v\right) dt \\&\quad = \int _0^T(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v)dt+(u(0),v(0)), \end{aligned}$$

for each $v \in C^1([0,T];H_0^2(\Omega ))$ with $v(T)=0$. Similarly, we have

$$\begin{aligned}&\int _0^T (-v',u_m)+(\epsilon _1 \Delta u_m, \Delta v)-\left( \frac{2}{\epsilon _1} w'(u_m),\Delta v\right) dt \\&\quad = \int _0^T(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v)dt+(u_m(0),v(0)). \end{aligned}$$

Letting $m=m_l$ and $l\rightarrow \infty$,

$$\begin{aligned}&\int _0^T (-v',u)+(\epsilon _1 \Delta u, \Delta v)-\left( \frac{2}{\epsilon _1} w'(u),\Delta v\right) dt \\&\quad = \int _0^T(-\delta _{\epsilon _3}[\lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2],v)dt+(u_0,v(0)). \end{aligned}$$

As v(0) is arbitrary, we deduced $u(0)=u_0$. $\square$

Theorem 3.3

(Uniqueness of weak solutions) A weak solution of (3.1) is unique.

Proof

Assuming $u_1$ and $u_2$ are solutions to this Eq. (3.1), we have

$$\begin{aligned}\begin{aligned}&<u'_1-u'_2,v> +<\epsilon _1 \Delta (u_1-u_2), \Delta v> -<\frac{2}{\epsilon _1} \big (W'(u_1)-W'(u_2)\big ), \Delta v> \\&\quad =<-\left( \delta _{\epsilon _3}(u_1-\frac{1}{2})-\delta _{\epsilon _3}(u_2-\frac{1}{2})\right) [ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ], v>. \end{aligned}\end{aligned}$$

Note $w=u_1-u_2$, $w(0)=0$, and $v=w$,

$$\begin{aligned}\begin{aligned}&<w',w> +<\epsilon _1 \Delta w, \Delta w> +<\frac{2}{\epsilon _1} \big (12(u_1+u_2-1)\big )w \nabla w, \nabla w> \\&\quad = <-\frac{\epsilon _3}{\pi }[ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ]\frac{u_1+u_2-1}{[\epsilon _3^2+(u_1-\frac{1}{2})^2][\epsilon _3^2+(u_2-\frac{1}{2})^2]}w, w>. \end{aligned}\end{aligned}$$

Integrate with respect to t, and consider the energy estimate,

$$\begin{aligned}\begin{aligned}&\frac{1}{2}\Vert w\Vert _{L^2(\Omega )}^2+\epsilon _1\Vert \Delta w\Vert _{L^2(0,T;L^2(\Omega ))}^2+\int _0^T \int _{\Omega }\frac{24}{\epsilon _1}w^2|\nabla w|^2+\frac{24(2u_2-1)}{\epsilon _1}w|\nabla w|^2 dxdt \\&\quad \le C\int _0^T\int _{\Omega } w^2 dxdt. \end{aligned}\end{aligned}$$

By the interpolation inequality, we have

$$\begin{aligned}\begin{aligned} \displaystyle \int _0^T \int _{\Omega }\frac{24(2u_2-1)}{\epsilon _1}w|\nabla w|^2 dxdt&\ge \displaystyle \int _0^T \int _{\Omega }\frac{-24}{\epsilon _1}|\nabla w|^2 dxdt\\&\ge \displaystyle \int _0^T \int _{\Omega }\frac{-24}{\epsilon _1}(\delta |\Delta w|^2+\frac{1}{\delta }|w|^2)dxdt. \end{aligned}\end{aligned}$$

Choosing $\delta \le \frac{\epsilon _1^2}{24}$, $\int _{\Omega } w^2 dx \le C \int _0^T\int _{\Omega }w^2 dxdt$. By Gronwall’s lemma, $w\equiv 0$, that is $u_1\equiv u_2$. $\square$

4 Tailored Finite Point Method (TFPM)

Firstly, we will show how TFPM could be applied to solve the non-equilibrium radiation diffusion equations. Let’s consider the following nonlinear parabolic problem in 1D case [8]:

$$\begin{aligned}\begin{array}{lll} &{} \frac{\partial u}{\partial t}-\frac{\partial }{\partial x}(a(x,u)\frac{\partial u}{\partial x})+c(x,u)u=f(x,t), &{}\forall x\in [0,1], t>0;\\ &{} u|_{x=0,1}=0, &{} t>0;\\ &{} u|_{t=0}=u_0(x), &{} x \in [0,1], \end{array}\end{aligned}$$

where $a(x,u)\ge a_0>0$, $c(x,u)\ge -c_0$, $c_0\ge 0$ and f(x, t) are given functions. Assuming that $h=N^{-1}$ be the mesh size, $x_j=jh$, $0\le j \le N$ and $t_n=n\tau$, $0\le n \le M$. We first integrate the equation on a small volume $[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]\times [t_n, t_{n+1}]$:

$$\begin{aligned} \int _{t_n}^{t_{n+1}}\int _{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}}\left( \frac{\partial u}{\partial t}-\frac{\partial }{\partial x}\Big (a(x,u)\frac{\partial u}{\partial x}\Big )+c(x,u)u\right) dxdt=\int _{t_n}^{t_{n+1}}\int _{x_{j-\frac{1}{2}}}^{x_{j+\frac{1}{2}}} f(x,t)dxdt, \end{aligned}$$

then we use a trapezoid rule in time and a mid-point rule in space to get

$$\begin{aligned}&\frac{u_j^{n+1}-u_j^n}{\tau }-\frac{a_{j+\frac{1}{2}}^{n+1}u_{x,j+\frac{1}{2}}^{n+1}+ a_{j+\frac{1}{2}}^{n}u_{x,j+\frac{1}{2}}^{n}}{2h}\\&\qquad +\,\frac{a_{j-\frac{1}{2}}^{n+1}u_{x,j-\frac{1}{2}}^{n+1}+ a_{j-\frac{1}{2}}^{n}u_{x,j-\frac{1}{2}}^{n}}{2h} +\frac{c_j^{n+1}u_j^{n+1}+c_j^n u_j^n}{2} \\&\quad = \frac{f_j^{n+1}+f_j^n}{2}, \end{aligned}$$

where $a_{j+\frac{1}{2}}^{n+1}=a(x_{j+\frac{1}{2}},u_{j+\frac{1}{2}}^{n+1})$. The remaining is the discretization of the first order derivative of u on each cell center. If we approximate them by a central difference scheme such as

$$\begin{aligned} u_{x,j+\frac{1}{2}}=\frac{u_{j+1}-u_j}{h}, \end{aligned}$$

we will get the classical finite volume scheme. But it might not be a suitable approximation when there exist some boundary/interior layers and a relatively large mesh size has to be used. Here we use some special basis functions to interpolate the function u on each cell $[x_j, x_{j+1}]$, and thus approximate the first-order derivative of u at the cell center using the interpolation function. The basis functions are chosen based on the properties of the reduced equation. For example, if we approximate $\frac{\partial u}{\partial t}$, a(x, u), c(x, u), f(x, t) on the cell $[x_j, x_{j+1}]$ by some cell average constants $v_{j+\frac{1}{2}}$, $a_{j+\frac{1}{2}}$, $c_{j+\frac{1}{2}}$, $f_{j+\frac{1}{2}}$, where

$$\begin{aligned} a_{j+\frac{1}{2}}=\frac{1}{h}\int _{x_j}^{x_{j+1}} a(x,\bar{u}(x))dx, \quad \text {with} \quad \bar{u}(x)=u_j+\frac{u_{j+1}-u_j}{h}(x-x_j), \end{aligned}$$

then the reduced equation on the cell $[x_j, x_{j+1}]$ is

$$\begin{aligned} -a_{j+\frac{1}{2}}\frac{d^2 u}{d x^2}+c_{j+\frac{1}{2}} u= & {} f_{j+\frac{1}{2}}-v_{j+\frac{1}{2}}. \end{aligned}$$

(4.1)

The solution of the reduced equation satisfies

$$\begin{aligned} u(x)\in \frac{f_{j+\frac{1}{2}}-v_{j+\frac{1}{2}}}{{c}_{j+\frac{1}{2}}}+span\{e^{\lambda x}, e^{-\lambda x}\} \quad \text {with} \quad \lambda = \sqrt{\frac{c_{j+\frac{1}{2}}}{a_{j+\frac{1}{2}}}}. \end{aligned}$$

Then we get

$$\begin{aligned} u_{x,j+\frac{1}{2}}=\lambda \frac{u_{j+1}-u_j}{e^{\frac{\lambda h}{2}}-e^{-\frac{\lambda h}{2}}}, \end{aligned}$$

holds for all the functions $u \in span\{1,e^{\lambda x}, e^{-\lambda x}\}$, and therefore we obtain the following tailored finite point scheme for Eq. (4.1):

$$\begin{aligned} -\alpha _{j-1}^{n+1}u_{j-1}^{n+1}+\alpha _j^{n+1}u_j^{n+1}-\alpha _{j+1}^{n+1}u_{j+1}^{n+1}=\beta ^n, \end{aligned}$$

where the coefficients are

$$\begin{aligned}\begin{aligned}&\alpha _j^{n+1}=\frac{1}{\tau }+\alpha _{j-1}^{n+1}+\alpha _{j+1}^{n+1}+\frac{c_j^{n+1}}{2},\\&\alpha _{j\pm 1}^{n+1}=\lambda _{\pm }\frac{a_{j\pm \frac{1}{2}}^{n+1}}{2h\Big (e^{\frac{\lambda _{\pm }h}{2}}-e^{-\frac{\lambda _{\pm }h}{2}}\Big )}, \quad \text {with} \quad \lambda _{\pm }=\sqrt{\frac{c_{j\pm \frac{1}{2}}}{a_{j\pm \frac{1}{2}}}},\\&\beta ^n = \alpha _{j-1}^n u_{j-1}^n+\left( \frac{1}{\tau }-\alpha _{j-1}^n-\alpha _{j+1}^n-\frac{c_j^n}{2}\right) u_j^n+\alpha _{j+1}^n u_{j+1}^n+\frac{f_j^{n+1}+f_j^n}{2}. \end{aligned}\end{aligned}$$

In the following, we propose using the TFPM method to solve the steady state of the modified Cahn–Hilliard equation (2.1). Let $v=\epsilon _1 \Delta u-\frac{2}{\epsilon _1} W'(u)$, then the steady state of the Eq. (2.1) is equivalent to the following equations:

$$\begin{aligned} \begin{aligned}&v=\epsilon _1 \Delta u-\frac{2}{\epsilon _1} W'(u);\\&0=-\Delta v - [ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ] \frac{\epsilon _3}{\pi [\epsilon _3^2 + (u-\frac{1}{2})^2]}. \end{aligned}\end{aligned}$$

(4.2)

For convenience, we convert the above equations into two coupled second-order parabolic equations:

$$\begin{aligned} \begin{aligned} u_t&=\epsilon _1 \Delta u-\frac{2}{\epsilon _1} W'(u)-v;\\&\quad -v_t=-\Delta v - [ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ] \frac{\epsilon _3}{\pi [\epsilon _3^2 + (u-\frac{1}{2})^2]}, \end{aligned}\end{aligned}$$

(4.3)

where u and v satisfy $\frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0$. For the first equation, we linearize $W'(u)$ as follows:

$$\begin{aligned} W'(u)=4u^3-6u^2+2u=(4u^2+2)u-6u^2, \end{aligned}$$

(4.4)

where $4u^2+2$ and $-6u^2$ can be seen as slice constants. Then we use TFPM [8] for the first equation in (4.3) as we describe at the begin of this section. For example, we can use the trapezoid rule which results in a second order accuracy in time (usually called the Crank–Nicolson method), and get

$$\begin{aligned} \frac{u_{ij}^{n+1}-u_{ij}^n}{\tau }= & {} \epsilon _1 \left[ \frac{u_{x,i+\frac{1}{2},j}^n - u_{x,i-\frac{1}{2},j}^n}{2h}+ \frac{u_{x,i+\frac{1}{2},j}^{n+1} - u_{x,i-\frac{1}{2},j}^{n+1}}{2h}\right] \nonumber \\&\quad +\,\epsilon _1 \left[ \frac{ u_{y,i,j+\frac{1}{2}}^n - u_{y,i,j-\frac{1}{2}}^n}{2h}+ \frac{ u_{y,i,j+\frac{1}{2}}^{n+1} - u_{y,i,j-\frac{1}{2}}^{n+1}}{2h}\right] \nonumber \\&\quad -\, \frac{2}{\epsilon _1}W'\left( \frac{ u_{ij}^n+u_{ij}^{n+1} }{2}\right) - v_{ij}^n. \end{aligned}$$

(4.5)

In order to capture some boundary and/or interior layers, we select some special basis functions to interpolate the function u. For example, if we approximate $\frac{\partial u}{\partial t}$ on cell $[x_i, x_{i+1}]\times [y_j, y_{j+1}]$ by some constants $z_{i+\frac{1}{2},j+\frac{1}{2}}$, then the solution of the reduced equation satisfies

$$\begin{aligned} u(x,y)\in \frac{\frac{12}{\epsilon _1}(u_{ij}^n)^2-v_{i,j}^n-z_{i+\frac{1}{2},j+\frac{1}{2}}}{\frac{4(2(u_{ij}^n)^2+1)}{\epsilon _1}}+span\{e^{\xi x},e^{-\xi x},e^{\xi y},e^{-\xi y}\}, \end{aligned}$$

where

$$\begin{aligned} \xi =\frac{2\sqrt{2(u_{ij}^n)^2+1}}{\epsilon _1 }. \end{aligned}$$

As discussed above, one can easily get

$$\begin{aligned} u_{x,i+\frac{1}{2},j}=\xi \frac{u_{i+1,j}-u_{ij}}{e^{\frac{\xi h}{2}}-e^{-\frac{\xi h}{2}}}; u_{y,i,j+\frac{1}{2}}=\xi \frac{u_{i,j+1}-u_{ij}}{e^{\frac{\xi h}{2}}-e^{-\frac{\xi h}{2}}}. \end{aligned}$$

Then the tailored finite point scheme for the parabolic equation of u reads

$$\begin{aligned}&\left( 1+\frac{2\tau }{\epsilon _1}\left( 2(u_{ij}^n)^2+1\right) \right) u_{ij}^{n+1}\nonumber \\&\qquad -\,\frac{\epsilon _1 \tau \xi }{2h\left( e^{\frac{\xi h}{2}}-e^{-\frac{\xi h}{2}}\right) } (u_{i+1,j}^{n+1}+u_{i-1,j}^{n+1}+u_{i,j+1}^{n+1}+u_{i,j-1}^{n+1}-4 u_{ij}^{n+1})\nonumber \\&\quad = \left( 1-\frac{2\tau }{\epsilon _1}\left( 2\left( u_{i,j}^n\right) ^2+1\right) \right) u_{ij}^{n}\nonumber \\&\qquad +\,\frac{\epsilon _1 \tau \xi }{2h\left( e^{\frac{\xi h}{2}}-e^{-\frac{\xi h}{2}}\right) }\left( u_{i+1,j}^n+u_{i-1,j}^n+u_{i,j+1}^n+u_{i,j-1}^n-4 u_{ij}^n\right) \nonumber \\&\qquad +\,\frac{12 \tau }{\epsilon _1}\left( u_{ij}^n\right) ^2-\tau v_{ij}^n, \end{aligned}$$

(4.6)

which can be solved by BiCGSTAB. For the second equation in (4.3), using the Crank–Nicolson scheme directly, we obtain

$$\begin{aligned} \frac{v_{ij}^{n+1}-v_{ij}^n}{\tau }=\frac{\Delta _h v_{ij}^{n+1}+\Delta _h v_{ij}^{n}}{2}+[ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ] \frac{\epsilon _3}{\pi [\epsilon _3^2 + (u-\frac{1}{2})^2]}, \end{aligned}$$

that is

$$\begin{aligned} \begin{aligned}&\displaystyle \left( 1+\frac{2 \tau }{h^2}\right) v_{ij}^{n+1}-\frac{\tau }{2h^2} \left( v_{i+1,j}^{n+1}+v_{i-1,j}^{n+1}+v_{i,j+1}^{n+1}+v_{i,j-1}^{n+1}\right) = \left( 1-\frac{2 \tau }{h^2}\right) v_{ij}^{n}\\&\quad \displaystyle +\frac{\tau }{2h^2}\left( v_{i+1,j}^n+v_{i-1,j}^n+v_{i,j+1}^n+v_{i,j-1}^n\right) \\&\quad +\tau [ \lambda _1 (f-c_1)^2 - \lambda _2 (f-c_2)^2 ] \frac{\epsilon _3}{\pi [\epsilon _3^2 + (u-\frac{1}{2})^2]}, \end{aligned}\end{aligned}$$

(4.7)

which can also be solved by BiCGSTAB. Of course, we can also use the traditional finite difference method to solve equations (4.3), which is denoted as FDM for convenience in the following.

Fig. 1

The image corrupted by the Gaussian noise with $\sigma =0.20$, the segmented image using our model (TFPM), and the plot of $c_1, c_2$ versus iteration

Fig. 2

The segmented image using our model, the energy, relative error in $u^k$, which are shown in $\log$-scale in the figures and the slices at the same location for the image

Fig. 3

The initial image “Tiger” (a), the segmented images and the contours using our model CH (b, c), respectively

Fig. 4

The segmented images and the contours using the Chan–Vese model with different values of the fidelity parameters. We set $\lambda _1=5, \lambda _2=4.5$ in the Chan–Vese model for plots (a, b); $\lambda _1=0.8, \lambda _2=1$ for plots (c, d); and $\lambda _1=0.5, \lambda _2=0.5$ for plots (e, f). One can see that the tail part cannot be captured for each case

Fig. 5

The initial image “Vessel” (a), the segmented images and the contours using our model CH (b, c), respectively

Fig. 6

The segmented images and the contours using the Chan–Vese model with different values of the fidelity parameters. We set $\lambda _1=5, \lambda _2=4.5$ in the Chan–Vese model for plots (a, b); $\lambda _1=1, \lambda _2=1.2$ for plots (c, d); and $\lambda _1=0.5, \lambda _2=0.5$ for plots (e, f). One can see that there exist lots of fine vessels cannot be captured for each case

Fig. 7

A real color image and the segmentation using our model

Fig. 8

The real image “Flowers” (a), the initial contours of $u_1$ and $u_2$ (b), and the segmentation result by using our model (c)

5 Numerical Experiments

In this section, we present some experimental results by applying the proposed numerical methods for our modified Cahn–Hilliard model on various synthetic and real images. For all the numerical experiments, we use the following stopping criterion:

$$\begin{aligned} \frac{\Vert u^{k}-u^{k-1}\Vert _2}{\Vert u^{k-1}\Vert _2}< \text {tol}, \end{aligned}$$

where $\text {tol}=1E-5$, $\Vert \cdot \Vert _{2}$ is the $L^{2}$-norm on $\Omega$, and k refers to the iteration number.

Before presenting the numerical results, we first discuss the parameters used in our experiments. Note that in our proposed model (c.f. Eq. (2.1)), there are four parameters: $\epsilon _1$, $\epsilon _3$ and $\lambda _1$, $\lambda _2$. The parameter $\epsilon _1$ mainly determines the evolution of u. To help connect the broken parts of objects, one needs to choose relatively large values of these two parameters in order to encourage the propagation of those regions in which u is close to 1. However, large values of $\epsilon _1$ lead to much wide transition layers, which surely blurs the desired segmentation boundary. To fix this problem, in our experiments, we take two stages: we first set $\epsilon _1$ to be some relatively large values, and once the steady state of u by solving Eq. (2.1) is achieved, we replace them by small values and resume the iterative process until a new steady state is arrived. Based on the feature of the Cahn–Hilliard equation, the small value of $\epsilon _1$ gives rise to thin transition layers, which helps locate the goal segmentation boundary.

The parameter $\epsilon _3$ controls how closely the function $H_{\epsilon _{3}}(x)$ approximates the Heaviside function H(x). In the experiments, we fix $\epsilon _3=0.1$. As for the fitting term coefficients $\lambda _1$ and $\lambda _2$, generally, $\lambda _2=1$ and $\lambda _1$ is around 1.

Note that we need to solve time-dependent equations for our model, the initial values of u and v have to be set up. In our experiments, we choose the initial value of u by using a threshold value. Precisely, for a given image f whose values are scaled in the interval [0, 1], we first set up a threshold $f_{0}\in (0,1)$, and then assign the initial u to be 1 in the region $\{f\ge f_0\}$ and 0 in the complement region. And the initial value of v could be calculated accordingly by using $v=\epsilon _1 \Delta u - \frac{2}{\epsilon _1}W'(u)$.

We first consider a synthetic image with different geometric shapes as shown in Fig. 1. This image is contaminated by the Gaussian noise with zero mean and standard deviation $\sigma =0.2$. In this experiment, we use $\lambda _1=1.1$, while $\epsilon _1=5$ for the first stage, and $\epsilon _1=0.01$ for the second stage. We present the initial segmentation (the initial u), the one after the first stage, and the one after the second stage, that is, the final segmentation in Fig. 1. From these plots, one can see that the proposed model is able to segment all those objects inside the image regardless of the strongly noisy background. Moreover, Fig. 1 also shows that the intensity averages $c_1$ and $c_2$ could arrive at their steady states around 100 iterations, which indicates the efficiency of the proposed method.

To further illustrate the merits of using the TFPM based scheme, in Fig. 2, we compare its performance with the one using conventional finite difference methods (FDM) for solving Eq. (2.1). For this, the evolutions of energy, relative error of u, and the area of $u>0.5$ (segmented region) versus iterations for the two methods are presented. The plots indicate that the energy and relative error of u drop faster for the TFPM than for the FDM, and thus the final segmentation can also be attained more quickly by using the TFPM scheme than the FDM.

In Figs. 3 and 4, we then consider a real image with a tiger walking in a lake. In this experiment, we use $\epsilon _1=80$ for the first stage, $\epsilon _1=0.01$ for the second stage, and $\lambda _1=0.65$. The goal of segmentation is to capture the complete boundary of the tiger. Note that there are many stripes on its body and tail, and standard intensity based segmentation models, such as the Chan–Vese model [4], could segment these stripes as individual objects, which can be observed in Fig. 4a–f. More importantly, those conventional methods fail to segment the tail part, since there exist relatively large gaps along the tail. To see this, in Fig. 4, we present the results of the Chan–Vese model by using several different groups of values of the fidelity parameters $\lambda _1$ and $\lambda _2$ (see [4] for details), and observe that by choosing these parameters in a wide range, the Chan–Vese model cannot capture the tiger’s tail as complete as our model. To interpolate those large gaps in segmentation, in [19], the authors proposed using Euler’s elastica as the regularization term for active contours, and the tail part can be largely recovered. However, in that work, one has to minimize a curvature dependent functional, which is challenging and also expensive numerically. In contrast, our proposed model is more tractable and involves much less computational cost, in other words, by using the Cahn–Hilliard equation, our model is able to achieve the goal of restoring boundaries along relatively large gaps as those curvature dependent models, and but at a much lower cost, as shown in Fig. 3b, c.

In Fig. 5, we apply our model for a medical image with tubular vessels in an inhomogeneous background. In this experiment, we use $\epsilon _1=4$ for the first stage, $\epsilon _1=0.01$ for the second stage, and $\lambda _1=0.85$. For this example, one again sees that our model successfully capture the meaningful elongated vessels by connecting those broken parts automatically, as shown in Fig. 5b, c. However, as an intensity based segmentation model, the Chan–Vese model can only segment out those white regions, leaving those broken but meaningful parts separated. To illustrate this, we also test different fidelity parameters of the Chan–Vese model and present the associated results in Fig. 6. These experiments again show that the proposed model can produce visually better segmentation results than the Chan–Vese model for some images.

In Fig. 7, we present the result of color image segmentation by applying our model (Eq. (2.4)). As for the grey image segmentation, the initial value of u is determined by a threshold. Precisely, for a given color image f, each channel f(i), $i=1,2,3$, is first rescaled to be in [0, 1], then we set up a threshold $f_{0}\in (0,1)$, and assign the initial u to be 1 in the region $\cap _{i=1}^{3}\{f(i)\ge f_0\}$ and 0 in the complement region. The plots show that our segmentation model is applicable for color images.

In Fig. 8, we apply our model for a real image “Flowers”, which presents four different phases: the blue sky, the yellow petals, the red petals, and the flower rods. As [17], the initial values of the two segmentation functions $u_{1}$ and $u_{2}$ are given by circles as shown in Fig. 8b. Once the final steady state of $u_1$ and $u_2$ is obtained, one can identify the four phases by the disjoint sets: $\{u_1 \ge \frac{1}{2}, u_2 \ge \frac{1}{2}\}$, $\{u_1 \ge \frac{1}{2}, u_2 < \frac{1}{2}\}$, $\{u_1 < \frac{1}{2}, u_2 \ge \frac{1}{2}\}$, $\{u_1< \frac{1}{2}, u_2 < \frac{1}{2}\}$. This experiment demonstrates that our model is also successful in dealing with multiphase segmentation.

6 Conclusions

In this work, we develop a new image segmentation model by incorporating the Cahn–Hilliard equation into the process of segmentation. Besides effectively segmenting objects from noisy background just like those conventional segmentation models, such as the Chan–Vese model, the proposed model is also able to automatically restore those missing contours along wide gaps, which is often achieved by curvature dependent models in the literature. As the Cahn–Hilliard equation presents in a relatively simpler form than those fourth-order Euler–Lagrange equations originated from curvature based models, the proposed model is more tractable both numerically and analytically. To efficiently solve the associated equation as well as preserve its features, we develop numerical schemes using the technique of TFPM [7]. The well-posedness analysis of the proposed model is also provided.