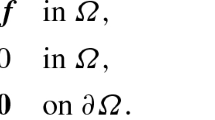Supercloseness of Primal-Dual Galerkin Approximations for Second Order Elliptic Problems

Abstract

We show that two widely used Galerkin formulations for second-order elliptic problems provide approximations which are actually superclose, that is, their difference converges faster than the corresponding errors. In the framework of linear elasticity, the two formulations correspond to using either the stiffness tensor or its inverse the compliance tensor. We find sufficient conditions, for a wide class of methods (including mixed and discontinuous Galerkin methods), which guarantee a supercloseness result. For example, for the HDG$_{k}$ method using polynomial approximations of degree ${k>0}$, we find that the difference of approximate fluxes superconverges with order ${k+2}$ and that the difference of the scalar approximations superconverges with order ${k+3}$. We provide numerical results verifying our theoretical results.

1 Introduction

We show that approximate solutions given by two Galerkin formulations for the model second-order elliptic problem

$$\begin{aligned} -\nabla \cdot (\mathrm {a}\nabla u)&=f \,\,\quad \mathrm {in }\, \Omega , \end{aligned}$$

(1a)

$$\begin{aligned} u&={u_{D}} \quad \mathrm { on }\,\partial \Omega _{D}, \end{aligned}$$

(1b)

$$\begin{aligned} -\mathrm {a}\nabla u\cdot \varvec{n}&=\mathsf {q}_{N} \quad \mathrm { on }\, \partial \Omega _{N}, \end{aligned}$$

(1c)

where $\mathrm {a}= \mathrm {a}(x)$ is a bounded, symmetric and uniformly positive-definite $d\times d$ matrix-valued function in ${\Omega }$, with inverse $\mathrm {c}(x)$, $f\in L^{2}(\Omega )$, $u_{D}\in H^{1/2}(\partial \Omega _{D})$ and $\textsf {q}_{N}\in H^{1/2}(\partial \Omega _{N})$, can be superclose, that is, the difference converges faster than the corresponding errors.

These Galerkin formulations differ only in the use of the tensor $\mathrm {a}$ or its inverse $\mathrm {c}$ in their formulations. Indeed, the formulations are based on the following equivalent rewritings of our model problem:

Thus, they differ only in the way the second equation is discretized. We observe that, when the tensors $\mathrm {a}$ and $\mathrm {c}$ are constant on the mesh, there is no difference between the corresponding Galerkin approximations. In the general case, we find sufficient conditions on the definition of the Galerkin methods which guarantee that their approximations are superclose.

The first formulation seems to be natural when mixed-like methods are defined. In contrast, in most cases, the tensor $\mathrm {a}$ is the natural data of the model which might be difficult or computationally expensive to actually invert. This is not only true for the simple model problem we are considering here but for more involved elliptic problems like the equations of linear elasticity where $\mathrm {a}$ corresponds to the stiffness tensor and $\mathrm {c}$ to the so-called compliance tensor. For the second-order elliptic problem under consideration, Galerkin formulations using the first set of equations have been used to define mixed methods [4] and have also been used for the original introduction of the hybridizable discontinuous Galerkin (HDG) methods [11]; see also the HDG methods for linear elasticity in [15]. On the other hand, there are many methods whose formulation is based on the second set of equations. For instance, in [1] the authors develop a so-called expandedmixed finite element method and give a finite difference interpretation. The HDG methods based on this set of equations are fully discussed in [7], where it is noted that they come directly from the the HDG methods for linear elasticity proposed in [21]. We also highlight that, as pointed out above, in the nonlinear case or when the tensor $\mathrm {a}$ can not be easily inverted, the second formulation becomes more relevant, see for example the HDG methods for the p-Laplacian equations [14] and the HDG methods for the equations of nonlinear elasticity [20]. Let us end by pointing out that the so-called Hybrid High-Order method, for diffusion [17, 18] and for elasticity, [16], uses a primal formulation which does use the tensor a. And yet, it can be re-interpreted as an HDG method using the first formulation, see [8]. Roughly speaking, this happens because the space of fluxes depends on the tensor a in a suitable manner.

In this paper, we want to address the question of how different are the numerical approximations based on the forms ($\hbox {A}_1$) and ($\hbox {A}_2$). To do that, we first prove estimates for the difference of the approximations to the negative gradient variable $\varvec{g}$ and the flux variable $\varvec{q}$ by a classical energy argument. Then we prove an estimate for the difference of the approximations to the the scalar variable u by using a standard duality argument and by using a non-standard approximation result. In particular, for the HDG method using polynomial approximations of degree $k>0$ for all the variables, we obtain that the difference of the approximations of the negative gradient and the flux variable converge with an order of $k+2$, and the scalar variable with an order of $k+3$, where k is the polynomial degree associated to the local finite element space. This is, in general, 1 and 2 degrees extra than the convergence of each numerical approximation. A practical consequence of these results is that using one or the other formulation is essentially immaterial.

The remainder of the paper is structured as follows. In Sect. 2, we introduce, the general properties satisfied by the finite element approximations based on the Eqs. ($\hbox {A}_1$) and ($\hbox {A}_2$). We then state and discuss our supercloseness result, Theorem 1; we prove it in Sect. 3. In Sect. 4, we present numerical experiments validating our theoretical findings. We end in Sect. 5 with some concluding remarks.

2 The Finite Element Approximations and Their Supercloseness Properties

In this section, we state and discuss our main results. We begin by introducing the Galerkin methods we consider. We then state our main results, that is, the supercloseness properties between their approximations.

2.1 The Numerical Schemes

Notation

In order to define the discrete primal-dual formulations we first introduce some notation. Let $\mathcal {T}_h= \{K\}$ be a conforming partition of $\overline{\Omega }$ into elements K, and let $\mathcal {F}_h= \{F \in \partial K: K\in \mathcal {T}_h\}$ be the set of all the faces (d ${=}\,$3) or edges (d ${=}\,$2) F of the partition. We assume that $\mathcal {T}_h$ satisfies standard finite element assumptions, see [5] and [6]. The numerical methods that we will introduce next seek for a finite element approximation to the vector fields $\varvec{g}$ and $\varvec{q}$, and the scalar field u. These numerical approximations will be defined on the following discontinuous piecewise polynomial spaces:

$$\begin{aligned} \varvec{V}_h&= \{\varvec{v}\in [L^2(\Omega )]^d: \varvec{v}|_{K}\in \varvec{V}(K), \forall K\in \mathcal {T}_h\},\\ W_h&= \{w\in L^2(\Omega ): w|_{K}\in W(K), \forall K\in \mathcal {T}_h\}, \end{aligned}$$

where $\varvec{V}(K)$ and W(K) are local spaces, each one contained in a polynomial space.

In addition, we are using the following standard notation:

$$\begin{aligned} ( \varvec{\sigma }, \varvec{v})_{\mathcal {T}_h}&=\sum _{K\in \mathcal {T}_h}\int _{K} \varvec{\sigma }(x)\cdot \varvec{v}(x) dx, \quad ( \zeta , w)_{\mathcal {T}_h}=\sum _{K\in \mathcal {T}_h}\int _{K} \zeta (x) w(x) dx, \\ \langle \zeta , w\rangle _{\partial \mathcal {T}_h}&=\sum _{K\in \mathcal {T}_h}\int _{\partial K} \zeta (s) w(s) ds. \end{aligned}$$

The Formulations Next, we define the different formulations satisfied by the finite element approximations we are considering. Note that although the methods are assumed to satisfy the equations of each formulation, they are not necessarily defined by them.

The first formulation is based on the Eq. ($\hbox {A}_1$): The approximation $(\varvec{g}_{h}^{1},\varvec{q}_{h}^{1},u_{h}^{1})\in \varvec{V}_h\times \varvec{V}_h\times {W_{h}}$ satisfies

$$\begin{aligned} ( \varvec{g}_{h}^{1}, \varvec{v})_{\mathcal {T}_h}-( u_{h}^{1}, \nabla \cdot \varvec{v})_{\mathcal {T}_h}+\langle \widehat{u}_{h}^{1}, \varvec{v}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}&=\,0, \quad \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(2a)

$$\begin{aligned} ( \mathrm {c}\varvec{q}_{h}^1-\varvec{g}_{h}^{1}, \varvec{v})_{\mathcal {T}_h}&=\,0,\quad \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(2b)

$$\begin{aligned} -( \varvec{q}_{h}^1, \nabla w)_{\mathcal {T}_h} + \langle \widehat{\varvec{q}}_{h}^1\cdot \varvec{n}, w\rangle _{\partial \mathcal {T}_h} =\,&( f, w)_{\mathcal {T}_h},\,\forall w\in {W_{h}}. \end{aligned}$$

(2c)

The second formulation is based on the equations ($\hbox {A}_2$): The approximation $(\varvec{g}_{h}^{2},\varvec{q}_{h}^{2},u_{h}^{2})\in \varvec{V}_h\times \varvec{V}_h\times W_{h}$ satisfies

$$\begin{aligned} ( \varvec{g}_{h}^{2}, \varvec{v})_{\mathcal {T}_h}-( u_{h}^{2}, \nabla \cdot \varvec{v})_{\mathcal {T}_h}+\langle \widehat{u}_{h}^{2}, \varvec{v}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}&=\,0, \qquad \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(3a)

$$\begin{aligned} ( \varvec{q}_{h}^2-\mathrm {a}\varvec{g}_h^{2}, \varvec{v})_{\mathcal {T}_h}&=\,0, \qquad \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(3b)

$$\begin{aligned} -( \varvec{q}_{h}^2, \nabla w)_{\mathcal {T}_h} + \langle \widehat{\varvec{q}}_{h}^2\cdot \varvec{n}, w\rangle _{\partial \mathcal {T}_h} =\,&( f, w)_{\mathcal {T}_h},\quad \forall w\in W_{h}. \end{aligned}$$

(3c)

Note that to complete the definition of the numerical methods, additional information about the local spaces and the numerical traces $\widehat{u}_{h}^{i}$ and $\widehat{\varvec{q}}_{h}^{i}\cdot \varvec{n}$ is required, for $i=1,2$. To obtain our results, only very general conditions need to be imposed which we gather in the assumptions we display next. We first introduce an auxiliary dual problem and its Galerkin approximation by form ($\hbox {A}_1$) needed for the estimates by the scalar approximations.

The Auxiliary Dual Problem To prove the estimates for the scalar variable of Theorem 1, we use a duality argument. So, we need to introduce the following dual problem

$$\begin{aligned} \mathrm {c}\varvec{\psi }+\nabla \varphi&=\varvec{0} \quad \mathrm{in }\, \Omega , \end{aligned}$$

(4a)

$$\begin{aligned} \nabla \cdot \varvec{\psi }&=\theta \quad \mathrm{in }\, \Omega , \end{aligned}$$

(4b)

$$\begin{aligned} \varphi&=0\quad \mathrm{on }\, \partial \Omega _{D}, \end{aligned}$$

(4c)

$$\begin{aligned} \varvec{\psi }\cdot \varvec{n}&=0\quad \mathrm{on }\, \partial \Omega _{N}. \end{aligned}$$

(4d)

and the approximation $(\varvec{\psi }_{h},\varphi _{h})\in \varvec{V}_h\times {W_{h}}$ of (4) satisfying Eq. (2), that is,

$$\begin{aligned} ( \mathrm {c}\varvec{\psi }_{h}, \varvec{v})_{\mathcal {T}_h}-( \varphi _{h}, \nabla \cdot \varvec{v})_{\mathcal {T}_h}+\langle \widehat{\varphi }_{h}, \varvec{v}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}&=\,0 \quad \quad \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(5a)

$$\begin{aligned} -( \varvec{\psi }_{h}, \nabla w)_{\mathcal {T}_h} + \langle \widehat{\varvec{\psi }}_{h}\cdot \varvec{n}, w\rangle _{\partial \mathcal {T}_h} =&\,( \theta , w)_{\mathcal {T}_h}\quad \forall w\in W_h. \end{aligned}$$

(5b)

Assumption

We make the following assumptions on

• (A) the local space $\varvec{V}(K)$, $K\in \mathcal {T}_h$:

  • (i) $\bar{\mathrm {a}}|_{K} (\varvec{g}_{h}^{1}-\varvec{g}_{h}^{2})|_{K} \in \varvec{V}(K)$, where $\bar{\mathrm {a}}|_{K}$ is the average of tensor $\mathrm {a}$ on K.

  • (ii) $\bar{\mathrm {c}}|_{K} (\varvec{q}_{h}^{1}-\varvec{q}_{h}^{2})|_{K} \in \varvec{V}(K)$, where $\bar{\mathrm {c}}|_{K}$ is the average of tensor $\mathrm {c}$ on K.

  • (iii) $\bar{\mathrm {a}}|_{K} \varvec{v}|_{K}, \bar{\mathrm {c}}|_{K} \varvec{v}|_{K}\in \varvec{V}(K)\quad \mathrm{for\, all} \quad \varvec{v}\in \varvec{V}(K).$

• (B) the numerical traces

  • (i) Single-valuedness: $\widehat{u}_{h}$ and $\widehat{\varvec{q}}_{h}\cdot \varvec{n}$ are single valued on $\mathcal {F}_{h}$.

  • (ii) Non-negativity: $\langle \widehat{u}_{h}-u_{h}, (\varvec{q}_{h}-\widehat{\varvec{q}}_{h})\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}\ge 0.$

  • (iii) Cancellation: $\langle u_{h}-\widehat{u}_{h}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} + \langle \varphi _{h}-\widehat{\varphi }_{h}, (\varvec{q}_{h}-\widehat{\varvec{q}}_{h})\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} = 0.$

• (C) the approximation properties the flux:

  • (i) $\varvec{V}(K) \supset [\mathcal {P}^{0}(K)]^d$,

  • (ii) $\Vert \varvec{q}-\varvec{q}^{1}_{h}\Vert _{L^2{{(\mathcal {T}_h)}}}\le {C_{a}} h^\alpha \Vert u\Vert _{H^2(\mathcal {T}_h)}\quad \mathrm{for\, some }\alpha \in (0,1].$

• (D) the elliptic regularity of the dual problem:

  $$\begin{aligned} \Vert \varphi \Vert _{H^{2}(\Omega )} + \Vert \varvec{\psi }\Vert _{H^{1}(\Omega ;\mathrm {c})} \le C \Vert \theta \Vert _{L^{2}(\Omega )}, \end{aligned}$$

  where the norm $\Vert \cdot \Vert _{H^{1}(\Omega ;\mathrm {c})}$ is the $H^{1}$-norm weighted with $\mathrm {c}^{1/2}$. See Sect. 2.2. This inequality is satisfied, for example, if the domain $\Omega$ is convex and either $\partial \Omega _{D}$ or $\partial \Omega _{N}$ vanishes.

Example

The main examples of methods satisfying the above weak formulations are the hybridized version of the Raviart–Thomas (RT) [19] and Brezzi–Douglas–Marini (BDM) [3] mixed methods, the Discontinuous Galerkin (DG) methods and the so-called hybridizable Discontinuous Galerkin (HDG) [9] methods. In Table 1, we display the choices of the local spaces $\varvec{V}(K)$, W(K). For the hybridized version of the mixed methods and for the HDG methods, $\widehat{u}_{h}$ is an additional unknown. This is why we also describe the space M(F) to which the restriction of $\widehat{u}_{h}$ to the face F belongs. Next, we briefly discuss the satisfaction of the assumptions (A), (B) and (C) by these methods.

Table 1 Local spaces of some mixed and DG methods

2.1.1 The Local Vector Spaces: Assumption (A)

For the DG and HDG$_{k}$ methods, we see that assumption (Aiii), and hence assumptions (Ai) and (Aii), are satisfied. Assumption (Aiii) is satisfied by the BDM$_{k}$ method for simplexes, but not for squares (or cubes). The RT$_{k}$ method does not satisfy condition (Aiii) neither; it does not satisfy condition (Aii) though. See Table 2.

2.1.2 The Numerical Traces: Assumption (B)

For the DG methods, the numerical traces $\widehat{u}_{h}$ and $\widehat{\varvec{q}}_{h}$ are explicitly defined in terms of the original unknowns of the problem, ${u_{h}}$ and $\varvec{q}_{h}$. To describe them, let us recall the standard DG notation for the averages and jumps on the interior faces

The numerical traces are then defined on each $F\in \mathcal {F}_h\backslash \partial \Omega$ by:

for $i=1,2$, where the auxiliary parameters $C_{11}$, $\varvec{C}_{12}$ and $C_{22}$ might depend on x. On the boundary faces we imposed the boundary conditions of the problems by

$$\begin{aligned} \widehat{\varvec{q}}_{h}^{i}\cdot \varvec{n}:=\left\{ \begin{array}{ll} \varvec{q}_{h}^{i}\cdot \varvec{n}+ C_{11}(u_{h}^{i}-u_D)\quad &{} \mathrm{on }\, \partial \Omega _{D}, \\ \textsf {q}_{N}\quad &{}\mathrm{on }\, \partial \Omega _{N}, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \widehat{u}_{h}^{i}:=\left\{ \begin{array}{ll} u_D\quad &{} \mathrm{on }\, \partial \Omega _{D}, \\ u_{h}^{i}+C_{22}(\varvec{q}_{h}^{i}\cdot \varvec{n}-\textsf {q}_{N})\quad &{}\mathrm{on }\, \partial \Omega _{N}, \end{array} \right. \end{aligned}$$

for $i=1,2$. In this way, the DG methods always satisfy assumptions (Bi) and (Biii). They satisfy (Bii) when $C_{11}$ and $C_{22}$ are nonnegative.

For the particular case

we have

on all interior faces, and it turns out that we can write

$$\begin{aligned} \widehat{\varvec{q}}_{h}\cdot \varvec{n}^\pm = \varvec{q}_{h}^\pm \cdot \varvec{n}^\pm +\tau ^\pm (u_{h}^\pm -\widehat{u}_{h}). \end{aligned}$$

We thus obtain an HDG method, see [7, 11]. For general HDG methods and the hybridized version of the mixed methods, the scalar numerical trace is a single-valued, new unknown on $\mathcal {F}_h\backslash \partial \Omega _{D}$; on $\widehat{u}_h=u_D$ on $\partial \Omega _D$ though. The numerical trace of the flux is defined as a linear combination of the other unknowns with a stabilization function $\tau$; for the mixed methods, $\tau =0$. Specifically, we have

$$\begin{aligned} \widehat{\varvec{q}}_{h}^{i}=\varvec{q}_{h}^{i}+\tau (u_{h}^{i}-\widehat{u}_{h}^{i})\varvec{n}\quad \mathrm{on } \quad \mathcal {F}_h, \quad \end{aligned}$$

for $i=1,2$. To ensure the satisfaction of assumption (Bi), the methods impose the condition

$$\begin{aligned} \langle \widehat{\varvec{q}}_{h}\cdot \varvec{n}, m\rangle _{\partial \mathcal {T}_h} = \langle \textsf {q}_{N}, m\rangle _{\partial \mathcal {T}_h},\quad \forall m \in M_{h}. \end{aligned}$$

(6)

where $M_{h} := \{m: m|_{F}\in M(F), \forall F\in \mathcal {F}_h\}$. Finally, when the stabilization function $\tau (\cdot )$ is just a multiplication operator, that is, $\tau (\mu ):=\tau {\cdot } \mu$, the assumption (Biii) is satisfied and the assumption (Bii) are satisfied if $\tau \ge 0$. See Table 2.

Table 2 Assumptions (A) and (B)

2.1.3 The Approximation of the Flux: Assumption (C)

In Table 3, we display several cases in which assumptions (C) are satisfied.

We only consider the cases for which condition (Aii) is also satisfied.

Table 3 Assumptions (C) for vector spaces satisfying (Aii)

2.2 Supercloseness of the Approximations

To state our results, we use the following notation.

We define the Sobolev space $X(\mathcal {T}_h) = \prod _{K\in \mathcal {T}_h} X(K)$, for any Sobolev space X, and its norm

$$\begin{aligned} \Vert \mu \Vert _{X(\mathcal {T}_h)}^{2} := \sum _{K\in \mathcal {T}_h} \Vert \mu \Vert _{X(K)}^{2},\quad \forall \mu \in X(\mathcal {T}_h). \end{aligned}$$

Finally, for $\varvec{v}\in [L^2(\mathcal {T}_h)]^{d}$ we define the norm weighted with a tensor $\mathrm {c}$ by

$$\begin{aligned} \Vert \varvec{v}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}^{2}:=( \mathrm {c}\varvec{v}, \varvec{v})_{\mathcal {T}_h}. \end{aligned}$$

We let u be the solution of problem (1) and set $\varvec{g}:=-\nabla u$ and $\varvec{q}:=\mathrm {a}\varvec{g}$. We also let $(\varvec{g}_{h}^{1},\varvec{q}_{h}^{1},u_{h}^1)$ and $(\varvec{g}_{h}^{2},\varvec{q}_{h}^{2},u_{h}^{2})$ be numerical approximations satisfying (2) and (3), respectively. for some estimates, we are going to use the following elliptic regularity inequality: Now we are ready to state the supercloseness properties of the approximations satisfying (2) and (3). Its proof is provided in the next section.

Theorem 1

Suppose that the assumption (B) on the numerical traces hold. Then

$$\begin{aligned} \Vert \varvec{g}_{h}^{1}-\varvec{g}_{h}^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {a})}&\,\le \ \Vert \mathrm {c}^{\frac{1}{2}}(\mathrm {a}-\bar{\mathrm {a}})\mathrm {c}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)} (\Vert \varvec{q}-\varvec{q}_{h}^1\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\nonumber \\&\quad + \Vert \varvec{g}-\varvec{g}_{h}^1\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})})\quad {if \,\mathrm{(Ai)}\,holds,} \\ \Vert \varvec{q}_{h}^{1}-\varvec{q}_{h}^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}&\,\le \Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)} (\Vert \varvec{q}-\varvec{q}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\nonumber \\&\quad + \Vert \varvec{g}-\varvec{g}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})})\quad {if \,\mathrm{(Aii)}\,holds,} \end{aligned}$$

Suppose now that assumptions (B) and (C) on the approximation of the flux of the first method hold. Then, if the elliptic regularity inequality of assumption (D) holds,

$$\begin{aligned} \Vert u_{h}^{1}-u_{h}^{2}\Vert _{L^2(\mathcal {T}_h)}&\le {C_{1}} h^\alpha (\Vert \varvec{q}-\varvec{q}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})}). \end{aligned}$$

Moreover, if assumption (Aiii) holds and if $[\mathcal {P}^1(K)]^{d}\subseteq \varvec{V}(K)$,

$$\begin{aligned} \Vert u_{h}^{1}-u_{h}^{2}\Vert _{L^2(\mathcal {T}_h)}&\le {C_{2}} h^{1+\alpha } (\Vert \varvec{q}-\varvec{q}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})}). \end{aligned}$$

The constants ${C_{1}}$ and ${C_{2}}$ are independent of h and the solution. The constant ${C_{1}}$ depends on $\Vert \mathrm {c}\Vert _{W^{1,\infty }(\mathcal {T}_h)}$ whereas the constant ${C_{2}}$ depends on $\Vert \mathrm {c}\Vert _{W^{2,\infty }(\mathcal {T}_h)}$.

Theorem 2

Assume that, for some positive constant $\kappa$, we have

$$\begin{aligned} \max \left\{ \Vert \mathrm {c}^{1/2}(\mathrm {a}-\bar{\mathrm {a}})\mathrm {c}^{1/2}\Vert _{L^{\infty }(K)}, \Vert \mathrm {a}^{1/2}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{1/2}\Vert _{L^{\infty }(K)}\right\} \le \kappa < 1 \quad \forall K\in \mathcal {T}_h, \end{aligned}$$

and set

$$\begin{aligned} \Upsilon _{h}:=\min _{i=1,2}\{\Vert \varvec{q}-\varvec{q}_{h}^i\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} +\Vert \varvec{g}-\varvec{g}_{h}^i\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})}\}. \end{aligned}$$

Then, the estimates of Theorem 1 become

We summarize the application of this result to the numerical methods described in our examples in Table 4. There, we assume that the extra assumption of Theorem 2 holds.

Table 4 Orders of convergence in h

A few remarks are in order. First, note that, when using simplexes, it is known that the first formulation of the HDG$_k$ method with $\tau$ of order one, converges with order $k+1$ in all the approximations; see [12]. Theorem 1 states the the second formulation and the first one are superclose in the sense that the order of convergence of the difference of their approximations converge with order $k+2$, for the vector-valued approximations, and with order $k+3$, for the scalar approximation when $\mathrm {c}\in W^{2,\infty }(\mathcal {T}_h)$.

Note also that, regardless of the actual shape of the elements, when the values of the stabilization function $\tau ^{\pm 1}$, respectively, $(h\tau )^{\pm 1}$, are of order one, respectively, the order of convergence of the difference of their approximations converge with an additional half an order, respectively, a full order, for the vector-valued approximations, and with three half orders, respectively two full orders, for the scalar approximation whenever $\mathrm {c}\in W^{2,\infty }(\mathcal {T}_h)$. This also applies to the DG$_k$ methods.

Concerning the mixed methods, similar results are obtained for the BDM$_k$ method. Interestingly enough, although the convergence of the method is of order k for the scalar approximations, their difference is of order $k+3$. On the other hand, since the assumption (Ai) is not satisfied for the RT$_k$ method, we see that the approximate fluxes, but not the approximate gradients, are superclose. Moreover, the scalar approximations are superclose with an extra power in h, but not two, like to the DG methods or three for the BDM$_{k}$ method.

The numerical results presented in Sect. 4 confirm that all the results in the above table are sharp.

To end this section, we note that, besides the supercloseness result, Theorem 1 implies that the approximation properties of one scheme can be deduced for those of the other. In particular, if either approximate solution converges, then the other approximate solution converges too, and converges with the same rate.

3 Proofs

Here, we provide detailed proofs of our main result, Theorem 1.

3.1 The Error Equations

We begin by obtaining the error equations. Let $(\varvec{g}_{h}^{1},\varvec{q}_{h}^{1},u_{h}^{1})$ and $(\varvec{g}_{h}^{2},\varvec{q}_{h}^{2},u_{h}^{2})$ be functions satisfying (2) and (3), respectively. Then, if we set

$$\begin{aligned} \varvec{e}_{\varvec{g}} := \varvec{g}_{h}^{1}-\varvec{g}_{h}^{2}, \varvec{e}_{\varvec{q}}:= \varvec{q}_{h}^{1}-\varvec{q}_{h}^{2}, e_{u} := u_{h}^{1}-u_{h}^{2}, \varvec{e}_{\widehat{\varvec{q}}} := \widehat{\varvec{q}}_{h}^{1}-\widehat{\varvec{q}}_{h}^{2}, e_{\widehat{u}} := \widehat{u}_{h}^{1}-\widehat{u}_{h}^{2}, \end{aligned}$$

we have, subtracting Eq. (3) from Eq. (2), that

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{v})_{\mathcal {T}_h}-( e_{u}, \nabla \cdot \varvec{v})_{\mathcal {T}_h}+\langle e_{\widehat{u}}, \varvec{v}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}&= 0 \quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(7a)

$$\begin{aligned} ( \mathrm {c}\varvec{q}_{h}^1-\varvec{g}_{h}^1, \varvec{v})_{\mathcal {T}_h} =( \varvec{q}_{h}^2-\mathrm {a}\varvec{g}_{h}^2, \varvec{v})_{\mathcal {T}_h}&=0\quad \forall \varvec{v}\in \varvec{V}_h, \end{aligned}$$

(7b)

$$\begin{aligned} -( \varvec{e}_{\varvec{q}}, \nabla w)_{\mathcal {T}_h} + \langle \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}, w\rangle _{\partial \mathcal {T}_h}&=0\quad \forall w\in {W_{h}}. \end{aligned}$$

(7c)

3.2 Proof of Estimates of the Difference for the Vector Unknowns

Here, we prove the estimates for the difference of the approximations to the gradient and to the flux of Theorem 1. To do that, we proceed by using a variation on the classic energy argument.

Step 1: The energy argument Taking $\varvec{v}:= \varvec{e}_{\varvec{q}}\in \varvec{V}_h$ in the first error Eq. (7a), $w:=e_u\in W_h$ in the third error Eq. (7c), and adding the resulting equations, we get

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}-( e_{u}, \nabla \cdot \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}+\langle e_{\widehat{u}}, \varvec{e}_{\varvec{q}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} -( \varvec{e}_{\varvec{q}}, \nabla e_{u})_{\mathcal {T}_h} + \langle \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}, e_{u}\rangle _{\partial \mathcal {T}_h}=0. \end{aligned}$$

After integrating by parts, and after adding and subtracting the term $\langle e_{\widehat{u}}, \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}$, we get

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h} + \langle e_{\widehat{u}}-e_{u}, (\varvec{e}_{\varvec{q}}-\varvec{e}_{\widehat{\varvec{q}}})\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}=0. \end{aligned}$$

where we have used the fact that $\langle e_{\widehat{u}}, \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}=0$ since the numerical traces are single-valued by (Bi), $e_{\widehat{u}}=0$ on $\partial \Omega _D$ and $e_{\widehat{\varvec{q}}}\cdot \varvec{n}=0$ on $\partial \Omega _N$. Then, by the positivity property (Bii), we obtain

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h} \le 0. \end{aligned}$$

Step 2: The estimate of the difference in the gradient By the second of the equations in (7b),

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}= ( \varvec{e}_{\varvec{g}}, \varvec{q}^{1}_h-\varvec{q}^2_{h})_{\mathcal {T}_h} =( \varvec{e}_{\varvec{g}}, \varvec{q}^1_h-\mathrm {a}\varvec{g}^2_h)_{\mathcal {T}_h} =\Vert \varvec{e}_{\varvec{g}}\Vert ^2_{L^{2}(\mathcal {T}_h;\mathrm {a})}+( \varvec{q}_{h}^1-\mathrm {a}\varvec{g}_{h}^1, \varvec{e}_{\varvec{g}})_{\mathcal {T}_h}, \end{aligned}$$

and, by the last inequality of Step 1,

$$\begin{aligned} \Vert \varvec{e}_{\varvec{g}}\Vert ^2_{L^2(\mathcal {T}_h;\mathrm {a})} \le&-( \varvec{q}_{h}^1-\mathrm {a}\varvec{g}_{h}^{1}, \varvec{e}_{\varvec{g}})_{\mathcal {T}_h}\\ =&-( \mathrm {c}\varvec{q}_{h}^{1}-\varvec{g}_{h}^{1}, \mathrm {a}\varvec{e}_{\varvec{g}})_{\mathcal {T}_h}\\ =&-( \mathrm {c}\varvec{q}_{h}^{1}-\varvec{g}_{h}^{1}, (\mathrm {a}-\bar{\mathrm {a}}) \varvec{e}_{\varvec{g}})_{\mathcal {T}_h}, \end{aligned}$$

since $( \mathrm {c}\varvec{q}_{h}^{1} - \varvec{g}_{h}^{1}, \bar{\mathrm {a}} \varvec{e}_{\varvec{g}})_{\mathcal {T}_h} = 0$. This holds because, by assumption (Ai), $\bar{\mathrm {a}} \varvec{e}_{\varvec{g}}\in \varvec{V}_h$, and so we can use the first of the equations in (7b) with $\varvec{v}:= \bar{\mathrm {a}} \varvec{e}_{\varvec{g}}$. Thus,

$$\begin{aligned} \Vert \varvec{e}_{\varvec{g}}\Vert ^2_{L^2(\mathcal {T}_h;\mathrm {a})}&\le -( \mathrm {c}\varvec{q}_{h}^{1}-\mathrm {c}\varvec{q}, \left( \mathrm {a}-\bar{\mathrm {a}}\right) \varvec{e}_{\varvec{g}})_{\mathcal {T}_h}-( \varvec{g}-\varvec{g}_{h}^{1}, \left( \mathrm {a}-\bar{\mathrm {a}}\right) \varvec{e}_{\varvec{g}})_{\mathcal {T}_h}\\&\le \left( \Vert \varvec{q}-\varvec{q}_{h}^{1}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^{1}\Vert _{L^2(\mathcal {T}_h;\mathrm {a})}\right) \Vert \mathrm {c}^{\frac{1}{2}}(\mathrm {a}-\bar{\mathrm {a}})\mathrm {c}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)} \Vert \varvec{e}_{\varvec{g}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})}, \end{aligned}$$

and we get our estimate

$$\begin{aligned} \Vert \varvec{e}_{\varvec{g}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})}\le \left( \Vert \varvec{q}-\varvec{q}_{h}^{1}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^{1}\Vert _{L^2(\mathcal {T}_h;\mathrm {a})}\right) \Vert \mathrm {c}^{\frac{1}{2}}(\mathrm {a}-\bar{\mathrm {a}})\mathrm {c}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)}. \end{aligned}$$

Step 3: The estimate of the difference in the flux By the first of the Eq. (7b) with $\varvec{v}:=\varvec{e}_{\varvec{q}}$,

$$\begin{aligned} ( \varvec{e}_{\varvec{g}}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}=&( \varvec{g}_{h}^1-\varvec{g}_{h}^{2}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}= ( \mathrm {c}\varvec{q}_{h}^1-\varvec{g}_{h}^{2}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}\nonumber \\ =&\, \Vert \varvec{e}_{\varvec{q}}\Vert ^2_{L^2(\mathcal {T}_h;\mathrm {c})}+( \mathrm {c}\varvec{q}_{h}^2-\varvec{g}_{h}^{2}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}, \end{aligned}$$

and by the last inequality of Step 1, we get

$$\begin{aligned} \Vert \varvec{e}_{\varvec{q}}\Vert ^2_{L^2(\mathcal {T}_h;\mathrm {c})} \le&-( \mathrm {c}\varvec{q}_{h}^2-\varvec{g}_{h}^{2}, \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}\\ =&-( \varvec{q}_{h}^2-\mathrm {a}\varvec{g}_{h}^{2}, \mathrm {c}\varvec{e}_{\varvec{q}})_{\mathcal {T}_h}\\ =&-( \varvec{q}_{h}^2-\mathrm {a}\varvec{g}_{h}^{2}, (\mathrm {c}-\bar{\mathrm {c}}) \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}, \end{aligned}$$

since $( \varvec{q}_{h}^{2} - \mathrm {a}\varvec{g}_{h}^{2}, \bar{\mathrm {c}} \varvec{e}_{\varvec{q}})_{\mathcal {T}_h} = 0$. Indeed, by assumption (Aii), $\bar{\mathrm {c}} \varvec{e}_{\varvec{q}}\in \varvec{V}_h$, and we can take $\varvec{v}:=\bar{\mathrm {c}} \varvec{e}_{\varvec{q}}$ in the second of the equations in (7b). Thus,

$$\begin{aligned} \Vert \varvec{e}_{\varvec{q}}\Vert ^2_{L^2(\mathcal {T}_h;\mathrm {c})} \le&-( \varvec{q}_{h}^2-\varvec{q}, (\mathrm {c}-\bar{\mathrm {c}}) \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}- ( \mathrm {a}(\varvec{g}-\varvec{g}_{h}^{2}), (\mathrm {c}-\bar{\mathrm {c}}) \varvec{e}_{\varvec{q}})_{\mathcal {T}_h}\\ \le&\left( \Vert \varvec{q}-\varvec{q}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})} \right) \Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)} \ \Vert \varvec{e}_{\varvec{q}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}, \end{aligned}$$

and we obtain our first estimate

$$\begin{aligned} \Vert \varvec{e}_{\varvec{q}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\le \left( \Vert \varvec{q}-\varvec{q}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} + \Vert \varvec{g}-\varvec{g}_{h}^2\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})} \right) \Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)}. \end{aligned}$$

This completes the proof of the estimates of the difference in the vector unknowns.

3.3 Proof of the Estimates of the Difference for the Scalar Variable

Step 1: An identity for the difference Taking $w := e_{u}\in W_h$ in the second equation of the approximation to the dual solution, (5b), we get

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&= -( \nabla e_{u}, \varvec{\psi }_h)_{\mathcal {T}_h}+ \langle \widehat{\varvec{\psi }}_{h}\cdot \varvec{n}, e_{u}\rangle _{\partial \mathcal {T}_h}\\&= ( e_{u}, \nabla \cdot \varvec{\psi }_h)_{\mathcal {T}_h}+ \langle (\widehat{\varvec{\psi }}_{h}-\varvec{\psi }_h)\cdot \varvec{n}, e_{u}\rangle _{\partial \mathcal {T}_h}\\&= ( \varvec{e}_{\varvec{g}}, \varvec{\psi }_h)_{\mathcal {T}_h}+\langle e_{\widehat{u}}, \varvec{\psi }_h\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}+ \langle (\widehat{\varvec{\psi }}_{h}-\varvec{\psi }_h)\cdot \varvec{n}, e_{u}\rangle _{\partial \mathcal {T}_h} \end{aligned}$$

by the error Eq. (7a) with $\varvec{v}:=\varvec{\psi }_{h}\in \varvec{V}_{h}$. Since $\langle \widehat{\varvec{\psi }}_{h}\cdot \varvec{n}, e_{\widehat{u}}\rangle _{\partial \mathcal {T}_h}=0$ because of the single-valuedness of the numerical traces, assumption (Bi) and the fact that $e_{\widehat{u}}=0$ on $\partial \Omega _{D}$ and $\widehat{\varvec{\psi }}_{h}\cdot \varvec{n}=0$ on $\partial \Omega _{N}$, we obtain

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&= ( \varvec{e}_{\varvec{g}}, \varvec{\psi }_h)_{\mathcal {T}_h}+\langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}\\&= ( \mathrm {c}\varvec{q}_{h}^{1}-\varvec{g}_h^{2}, \varvec{\psi }_h)_{\mathcal {T}_h}+\langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}, \end{aligned}$$

by the first of the Eq. (7b) with $\varvec{v}:=\varvec{\psi }_h\in \varvec{V}_h$. Finally,

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&= ( \mathrm {c}\varvec{e}_{\varvec{q}}, \varvec{\psi }_h)_{\mathcal {T}_h} +( \mathrm {c}\varvec{q}_h^{2}-\varvec{g}_h^{2}, \varvec{\psi }_h)_{\mathcal {T}_h}+\langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}\\&=( \mathrm {c}\varvec{q}_h^{2}-\varvec{g}_h^{2}, \varvec{\psi }_h)_{\mathcal {T}_h}, \end{aligned}$$

because the term $\Theta _h:=( \mathrm {c}\varvec{e}_{\varvec{q}}, \varvec{\psi }_h)_{\mathcal {T}_h}+ \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}$ is equal to zero.

Let us prove this claim. We have

$$\begin{aligned} \Theta _h&= ( \varvec{e}_{\varvec{q}}, \mathrm {c}\varvec{\psi }_h)_{\mathcal {T}_h} + \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}\\&= ( \nabla \cdot \varvec{e}_{\varvec{q}}, \varphi _h)_{\mathcal {T}_h}-\langle \widehat{\varphi }_h, \varvec{e}_{\varvec{q}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} + \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} \end{aligned}$$

by the Eq. (5a) with $\varvec{v}:=\varvec{e}_{\varvec{q}}$. Integrating by parts, we get

$$\begin{aligned} \Theta _h&= -( \varvec{e}_{\varvec{q}}, \nabla \varphi _h)_{\mathcal {T}_h}+\langle \varphi _h-\widehat{\varphi }_h, \varvec{e}_{\varvec{q}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} + \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}\\&= -\langle \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}, \varphi _h\rangle _{\partial \mathcal {T}_h}+\langle \varphi _h-\widehat{\varphi }_h, \varvec{e}_{\varvec{q}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} + \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}, \end{aligned}$$

by Eq. (7c) with $w:=\varphi _h$. Finally,

$$\begin{aligned} \Theta _h&= -\langle \varvec{e}_{\widehat{\varvec{q}}}\cdot \varvec{n}, \varphi _h-\widehat{\varphi }_h\rangle _{\partial \mathcal {T}_h}+\langle \varphi _h-\widehat{\varphi }_h, \varvec{e}_{\varvec{q}}\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h} + \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}&\quad&\\&=\langle (\varvec{e}_{\varvec{q}}-\varvec{e}_{\widehat{\varvec{q}}})\cdot \varvec{n}, \varphi _h-\widehat{\varphi }_h\rangle _{\partial \mathcal {T}_h}+ \langle e_{u}-e_{\widehat{u}}, (\widehat{\varvec{\psi }}_h-\varvec{\psi }_h)\cdot \varvec{n}\rangle _{\partial \mathcal {T}_h}.&\quad&\\&=0, \end{aligned}$$

by the cancellation property of the traces, assumption (Biii).

Step 2: The first estimate To obtain our first estimate, we first note that

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&=( \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}, \mathrm {c}\varvec{\psi }_h)_{\mathcal {T}_h} \\&=( \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}, \mathrm {c}(\varvec{\psi }_h-\varvec{\psi }))_{\mathcal {T}_h} + ( \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}, \mathrm {c}\varvec{\psi })_{\mathcal {T}_h} \\&=( \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}, \mathrm {c}(\varvec{\psi }_h-\varvec{\psi }))_{\mathcal {T}_h} + ( \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}, (I-P_{\varvec{V}_h}) (\mathrm {c}\varvec{\psi }))_{\mathcal {T}_h}, \end{aligned}$$

by the second of the equations in (7b) with $\varvec{v}:=P_{\varvec{V}_h}(\mathrm {c}\varvec{\psi })$, where $P_{\varvec{V}_h}$ is the $L^2$-projection into $\varvec{V}_h$. Then we easily get that

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&\le \Vert \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} ( \Vert \varvec{\psi }_h-\varvec{\psi }\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}+\Vert (I-P_{\varvec{V}_h}) (\mathrm {c}\varvec{\psi })\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}) \\&\le \Vert \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} C h^\alpha \Vert \varvec{\psi }\Vert _{H^1(\mathcal {T}_h;\mathrm {c})}, \end{aligned}$$

by assumption (Cii) and the approximation properties of $P_{\varvec{V}_{h}}$ in combination with assumption (Ci). The result now follows from the estimates of the errors in the vector unknowns and the elliptic regularity inequality.

Fig. 1

Initial unstructured triangulation

Table 5 Errors and estimated orders of convergence using RT$_{k}$ on an unstructured triangulation

Table 6 Errors and estimated orders of convergence using BDM$_k$ on an unstructured triangulation

Table 7 Errors and estimated orders of convergence using DG$_k$, with $C_{11} = 1$, $\varvec{C}_{12} = [1,1]^{t}$, $C_{22} = 1$ on an unstructured triangulation

Table 8 Errors and estimated orders of convergence using HDG$_{k}$, with stabilization parameter $\tau = 1$, using unstructured triangular meshes (top) and uniform Cartesian meshes (bottom)

Step 3: An auxiliary non-standard, approximation result The improved estimate of the error in the scalar unkown is more delicate to prove. To prove it, we are going to use the following simple but non-standard auxiliary result.

Lemma 3.1

Assume that $\mathcal {P}^{1}(K)\subseteq \varvec{V}(K)$. Then, the following estimate holds

$$\begin{aligned} \Vert (I-P_{\varvec{V}_h})\left( (\mathrm {c}-\bar{\mathrm {c}}) \varvec{\psi }\right) \Vert _{L^{2}(K;\mathrm {a})}\le C h^{2} \Vert \mathrm {a}\Vert ^{1/2}_{L^{\infty }(K)} \Vert \mathrm {c}\Vert _{W^{2,\infty }(K)}\Vert \varvec{\psi }\Vert _{H^{1}(K)}. \end{aligned}$$

Proof

Since $\mathcal {P}^{1}(K)\subseteq \varvec{V}(K)$, we have that $(I-{P}_{\varvec{V}_h})\mathcal {P}^{1}(K)=\{\varvec{0}\}$, and so

$$\begin{aligned} \Vert (I-P_{\varvec{V}_h})\left( (\mathrm {c}-\bar{\mathrm {c}}) \varvec{\psi }\right) \Vert _{L^2(K;\mathrm {a})} \le \Vert \mathrm {a}\Vert ^{1/2}_{L^{\infty }(K)} \inf _{\varvec{v}\in \mathcal {P}^{1}(K)} \Vert (\mathrm {c}-\bar{\mathrm {c}})\,\varvec{\psi }- \varvec{v}\Vert _{L^2(K)}. \end{aligned}$$

To estimate the right-hand side, we need a variation of Taylor’s expansion which would not use second-order derivatives of $\varvec{\psi }$ (otherwise we would not be able to use the elliptic regularity inequality), but only those of $\mathrm {c}$. In the one-dimensional case, such variation is the following identity:

$$\begin{aligned} f(s)g(s) =&\; (f(0)+sf'(0))g(0)+ \int _{0}^{s} [f(z)g'(z)+(s-z)(f''(z)g(z)+f'(z)g'(z)){]} d z. \end{aligned}$$

Using this identity (with $f:=(\mathrm {c}-\bar{\mathrm {c}})_{ij}$ and $g:=\varvec{\psi }_{j}$, $i,j=1,...,d$) and bounding each of the resulting terms using approximations in $\mathcal {P}^{1}(K)$, we easily get the following estimate for star-shaped, uniformly regular elements:

$$\begin{aligned} \inf _{\varvec{v}\in \mathcal {P}^{1}(K)} \Vert (\mathrm {c}-\bar{\mathrm {c}}) \varvec{\psi }- \varvec{v}\Vert _{L^2(K)} \le&C\,h^2\Vert \mathrm {c}\Vert _{W^{2,\infty }}\Vert \varvec{\psi }\Vert _{H^{1}(K)}. \end{aligned}$$

This completes the proof. $\square$

Step 4: The improved estimate We are now ready to prove the last estimate. Since assumption (Aiii) holds, we have that $\bar{\mathrm {c}}\varvec{\psi }_{h}\in \varvec{V}_{h}$, and we can take $\varvec{v}:=\bar{\mathrm {c}}\varvec{\psi }_{h}$ in the second of the Eq. (7b) to get that

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h}&=( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, \mathrm {c}\varvec{\psi }_{h})_{\mathcal {T}_h}\\&=( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, (\mathrm {c}-\bar{\mathrm {c}})\varvec{\psi }_{h})_{\mathcal {T}_h}\\&=( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, (\mathrm {c}-\bar{\mathrm {c}})\varvec{\psi })_{\mathcal {T}_h}+( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, (\mathrm {c}-\bar{\mathrm {c}})(\varvec{\psi }_{h}-\varvec{\psi }))_{\mathcal {T}_h},\\&=( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, (I-P_{\varvec{V}_h})\left( (\mathrm {c}-\bar{\mathrm {c}})\varvec{\psi }\right) )_{\mathcal {T}_h}+( \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_{h}^{2}, (\mathrm {c}-\bar{\mathrm {c}})(\varvec{\psi }_{h}-\varvec{\psi }))_{\mathcal {T}_h}, \end{aligned}$$

by the second of the Eq. (7b) with $\varvec{v}:=P_{\varvec{V}_h}\left( (\mathrm {c}-\bar{\mathrm {c}})\varvec{\psi }\right)$. Then,

$$\begin{aligned} ( e_{u}, \theta )_{\mathcal {T}_h} \le&\, \Vert \varvec{q}_{h}^{2}-\mathrm {a}\varvec{g}_h^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} (\Vert (I-P_{\varvec{V}_h})\left( (\mathrm {c}-\bar{\mathrm {c}})\varvec{\psi }\right) \Vert _{L^2(\mathcal {T}_h;\mathrm {a})}\\&+ \Vert \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^\infty (\mathcal {T}_h)}\Vert \varvec{\psi }-\varvec{\psi }_h\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}\\ \le&\, \Vert \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})} C h^2 \Vert \mathrm {a}\Vert ^{1/2}_{L^{\infty }(\mathcal {T}_h)} \Vert \mathrm {c}\Vert _{W^{2,\infty }(\mathcal {T}_h)}\Vert \varvec{\psi }\Vert _{H^{1}(\mathcal {T}_h)}\\&+ \Vert \varvec{q}_h^{2}-\mathrm {a}\varvec{g}_h^{2}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^\infty (\mathcal {T}_h)} C h^\alpha \Vert \varvec{\psi }\Vert _{H^1(\mathcal {T}_h)}, \end{aligned}$$

by Lemma 3.1 and by assumption (Cii). The improved estimate now follows by using the elliptic regularity inequality.

It remains to show the last statement of Theorem 1.

3.4 Proof of Theorem 2

Using the triangle inequality in the estimate of the error in the flux, we get

But by Step 2 of the estimates of the vector unknowns, we can obtain that

$$\begin{aligned} \Vert \varvec{e}_{\varvec{g}}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}&\le \Vert \varvec{q}_{h}^2-\mathrm {a}\varvec{g}_{h}^{2}\Vert _{L^2(\mathcal {T}_h;\mathrm {c})}, \end{aligned}$$

without having to use Asssumption (Ai). As a consequence, we readily get that

$$\begin{aligned} \Vert \varvec{e}_{\varvec{q}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\le C \left( \Vert \varvec{q}-\varvec{q}_{h}^1\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} +\Vert \varvec{g}-\varvec{g}_{h}^1\Vert _{L^{2}(\mathcal {T}_h;\mathrm {a})} \right) \Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)}, \end{aligned}$$

where $C:= 2/(1-\Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)}\le 2/(1-\kappa )$ by our assumption. We can then write that

$$\begin{aligned} \Vert \varvec{e}_{\varvec{q}}\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})}\le \frac{2}{1-\kappa } \Vert \mathrm {a}^{\frac{1}{2}}(\mathrm {c}-\bar{\mathrm {c}})\mathrm {a}^{\frac{1}{2}}\Vert _{L^{\infty }(\mathcal {T}_h)}\,\min _{i=1,2}\{\Vert \varvec{q}-\varvec{q}_{h}^i\Vert _{L^{2}(\mathcal {T}_h;\mathrm {c})} +\Vert \varvec{g}-\varvec{g}_{h}^i\Vert _{L^{2} (\mathcal {T}_h;\mathrm {a})} \}. \end{aligned}$$

The other estimates follow in a similar manner.

This completes the Proof of Theorem 2.

4 Numerical Experiments

We present numerical experiments devised to corroborate our theoretical results on supercloseness. To do that, we take $\Omega := (0,1)^{2}$, $\partial \Omega _{D} = \partial \Omega$, and set f and ${u_{D}}$ such that the exact solution of our model problem with

$$\begin{aligned} \mathrm {a}(x) = \left( \begin{array}{cc} {x_{1}}+{x_{2}}+1&{}-x_{2}\\ {-x_{2}} &{}\quad 2x_{1}+{x_2+1} \end{array}\right) , \end{aligned}$$

is $u=\sin (2\pi x_1)\sin (2\pi x_2)$. We consider an initial unstructured triangulation (see Fig. 1) and we estimate the orders of convergence as we refine uniformly, indexing the meshes with a mesh parameter $h_{l}$, for $l=1,2,3,4,5$. We do this piecewise polynomial approximations of degree $k =1 2, 3, 4$; we also take $k=0$ for the RT$_k$, DG$_k$ and HDG$_{k}$methods).

The results for the RT$_{k}$, BDM$_{k}$, DG$_{k}$ (with parameters $C_{11} = 1.0$, $C_{22} =1.0$ and $\varvec{C}_{12} = [1.0,1.0]^{t}$) and HDG$_{k}$ method (with $\tau =1.0$) are displayed on the Tables 5, 6, 7 and 8, respectively. In all cases, we observe the supercloseness orders predicted by Theorem 1 and displayed in Table 4. It is interesting to see that for the RT$_k$ method, the difference of the approximations of the flux shows one order of convergence more than the for difference of the approximations of the gradient, which reflects the fact that for the RT$_k$ method assumption (Bii) is satisfied but assumption (Bi) is not satisfied. This difference in the convergence properties of the approximate fluxes and gradients does not appear in the BDM$_{k}$ method as this method satisfies both assumptions.

For uniform meshes of squares of size h, we estimate the orders of convergence as we refine the mesh by taking $h=2^{-l}$, for $l=1,2,3,4,5$. The results for the HDG$_{k}$ method, with $\tau =1.0$, are displayed in the bottom of Table 8. Again, we do observe the same orders of supercloseness as the ones predicted by Theorem 1 and displayed in Table 4.

5 Extensions and Concluding Remarks

We have proved the supercloseness property of two Galerkin formulations for second-order elliptic problems. Our analysis holds for a wide class of mixed finite element methods, as for instance the Raviart–Thomas [19] and Brezzi–Douglas–Marini [3] elements, discontinuous Galerkin methods, and hybridizable discontinuous Galerkin methods [11].

Although we have not treated the interior penalty (IP) method [2], it is easy to get even stronger results by using slight modifications to our approach. Indeed, even though our theory does not apply directly, since the definition of the numerical traces does not necessarily satisfy assumptions B (ii) and B (iii), it is not difficult to show, for the first two formulations of the IP method, that difference of the approximations converge with order $k+3$, $k+3$ and $k+2$ for the scalar, the gradient and the flux approximations, respectively. Even more, it is a simple exercise to see that, if the tensor $\mathrm {a}$ is piecewise linear then the IP schemes give the same approximation for the scalar and gradient variables.

We believe that it is reasonable to expect that similar results hold for the corresponding formulations and numerical methods for linear elasticity.