Interior Penalty Discontinuous Galerkin Methods for Second Order Linear Non-divergence Form Elliptic PDEs

Abstract

This paper develops interior penalty discontinuous Galerkin (IP-DG) methods to approximate $W^{2,p}$ strong solutions of second order linear elliptic partial differential equations (PDEs) in non-divergence form with continuous coefficients. The proposed IP-DG methods are closely related to the IP-DG methods for advection-diffusion equations, and they are easy to implement on existing standard IP-DG software platforms. It is proved that the proposed IP-DG methods have unique solutions and converge with optimal rate to the $W^{2,p}$ strong solution in a discrete $W^{2,p}$-norm. The crux of the analysis is to establish a DG discrete counterpart of the Calderon–Zygmund estimate and to adapt a freezing coefficient technique used for the PDE analysis at the discrete level. To obtain such a crucial estimate, we need to establish broken $W^{1,p}$-norm error estimates for IP-DG approximations of constant coefficient elliptic PDEs, which is also of independent interest. Numerical experiments are provided to gauge the performance of the proposed IP-DG methods and to validate the theoretical convergence results.

1 Introduction

In this paper we develop interior penalty discontinuous Galerkin methods for approximating the $W^{2,p}$ strong solution to the following second order linear elliptic PDE in non-divergence form:

where $\Omega \subset \mathbb {R}^n$ is an open, bounded domain with boundary $\partial \Omega$, $f\in L^p(\Omega )$ with $1< p<\infty$, and $A\in [C^0(\overline{\Omega })]^{n\times n}$ is positive definite in $\overline{\Omega }$.

Non-divergence form elliptic PDEs arrive naturally from many applications such as stochastic optimal control and game theory [12]; they are also encountered in the linearization of fully nonlinear PDEs such as Monge–Ampère-type equations [4]. If A is differentiable, then it is easy to check that equation (1.1a) can be rewritten as a diffusion-convection equation with A as the diffusion coefficient and $\nabla \cdot A$ as the convection coefficient. However, if $A\in \left[ C^0(\overline{\Omega })\right] ^{n\times n}$, then this formulation is not possible since $\nabla \cdot A$ does not exist as a function, but rather only as a measure. We recall that in the literature there are three well-established PDE theories for non-divergence form elliptic PDEs depending on the smoothness of A and f (as well as the smoothness of the boundary $\partial \Omega$ which we assume sufficiently smooth here to ease the presentation). The first theory is the classical solution (or Schauder’s) theory [13, Chapter 6] which seeks solutions in the Hölder space $C^{2,\alpha }(\overline{\Omega })$ for $0<\alpha <1$ when $A\in [C^\alpha (\overline{\Omega })]^{n\times n}$ and $f\in C^\alpha (\overline{\Omega })$. The second one is the $W^{2,p}$ (strong) solution theory [13, Chapter 9] which seeks solutions in the Sobolev space $W^{2,p}(\Omega )$ for $1<p<\infty$ that satisfy the PDE almost everywhere in $\Omega$ under the assumptions that $A\in [C^0(\overline{\Omega })]^{n\times n}$ and $f\in L^p(\Omega )$. If the coefficient matrix satisfies the Cordes condition and if the domain is convex, then the notion of strong solutions may be extended to the case $A\in [L^\infty (\Omega )]^{n\times n}$ [16, 26]. The third one is the viscosity (weak) solution theory [7] which seeks solutions in $C^0(\Omega )$ (or even in $B(\Omega )$, the space of bounded functions in $\Omega$) that satisfy the PDE in the viscosity sense under the assumptions that $A\in [L^\infty (\Omega )]^{n\times n}$ and $f\in L^\infty (\Omega )$. We note that all the three solution concepts and PDE theories are non-variational; this is a main difference between divergence form PDEs [13, Chapter 8] and non-divergence form PDEs. We also note that in the case of the viscosity solution theory, the uniqueness and regularity of solutions had been the main focus of the study for second order non-divergence form PDEs (see [7, 17, 23, 26] and the references therein).

In contrast to the advances of the PDE analysis, almost no progress on numerical methods and numerical analysis was achieved until very recently for second order elliptic PDEs in non-divergence form with non-differentiable coefficient matrix A (cf. [8, 10, 15, 18, 20, 26, 28]). The main difficulty is caused by the non-divergence structure of the PDEs which prevents any straightforward application of Galerkin-type numerical methodologies such as finite element methods, discontinuous Galerkin methods and spectral methods. Moreover, the non-variational nature of the strong and viscosity solution concepts make convergence analysis and/or error estimates of any convergent numerical methods very delicate and difficult. Nonstandard numerical techniques are often required to do the job (cf. [10, 18, 20, 26, 28]).

The primary goal of this paper is to develop convergent interior penalty discontinuous Galerkin (IP-DG) methods for approximating the $W^{2,p}$ strong solution of problem (1.1) under the assumption that $A\in \left[ C^0(\overline{\Omega })\right] ^{n\times n}$ and its solution satisfies the Calderon–Zygmund estimate [13, Chapter 9]. The reason for developing IP-DG methods is twofold. First, we intend to take advantage of some of the features of DG methods such as simplicity and ease of computation, and flexibility of mesh and ease for adaptivity, to design better numerical methods for problem (1.1a)–(1.1b). Second, we intend to develop new numerical analysis techniques and machineries for non-divergence form PDEs. It is expected that the DG convergence analysis is more involved because of the difficulty caused by the non-conformity of the DG finite element space and by their complicate mesh-dependent bilinear forms. The crux of the analysis of this paper is to establish a discrete Calderon-Zygmund estimate for the proposed IP-DG methods and to adapt a freezing coefficient technique used in the PDE analysis at the discrete level. Moreover, in order to prove the desired discrete Calderon-Zygmund estimate, we need to establish the $W^{1,p}_h$ stability and error estimates for the IP-DG approximations of constant coefficient elliptic PDEs. Such estimates seem to be new and have independent interest.

The remainder of this paper is organized as follows. In Sect. 2 we provide the notation and a collection of preliminary estimates, in particular, some properties of DG functions are either cited or proved. Section 3 analyzes the IP-DG methods for constant coefficient elliptic PDEs. The $W^{1,p}_h$ stability and error estimates are derived, which in turn lead to global $W^{2,p}_h$ stability estimates. The latter estimate can be regarded as a discrete Calderon–Zygmund estimate for the proposed IP-DG methods. To the best of our knowledge, such an estimate is new and of independent interest. Sect. 4 is devoted to the formulation, stability and convergence analysis and error estimate for the proposed IP-DG methods. Here, using the continuity of the coefficient matrix A, the freezing coefficient technique is adapted to establish local stability (or a left-side inf-sup condition) for the IP-DG discrete operators, which together with a covering argument leads to a global Gärding-type inequality for the formal adjoint operators of the IP-DG operators. Next, using a duality argument we obtain a global left-side inf-sup condition for the IP-DG discrete operators. Finally, by employing another duality argument, we derive the desired discrete Calderon-Zygmund estimate for the DG discrete operators. Once this stability estimate is shown, well-posedness and convergence of the IP-DG methods follow easily. In Section 5 we present a number of numerical experiments to verify our theoretical results and to gauge the performance of the proposed IP-DG methods, even for the case $A\in \left[ L^\infty (\overline{\Omega })\right] ^{n\times n}$ which is not covered by our convergence theory.

This paper is a condensed version of [11] where one can find the detailed proofs of those lemmas which are omitted here due to page limitation.

2 Preliminary Results

2.1 Notation

Let $\Omega$ be an open and bounded domain in $\mathbb {R}^n$. For a subdomain D of $\Omega$ with boundary $\partial D$, let $L^p(D)$ and $W^{s,p}(D)$ for $s\ge 0$ and $1\le p\le \infty$ denote the standard Lebesgue and Sobolev spaces respectively, and $W_0^{1,p}(D)$ be the closure of $C_c^{\infty }(D)$ in $W^{1,p}(D)$. Let $(\cdot ,\cdot )_D$ be the $L^2$ inner product on D and $(\cdot ,\cdot ):=(\cdot ,\cdot )_{\Omega }$. To improve the readability of the paper, we adopt the convention that $a\lesssim b$ stands for $a\le Cb$ for some $C>0$ which does not depend on any discretization parameters.

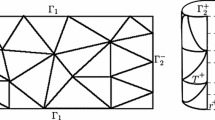
Let $\mathcal {T}_h$ be a shape-regular and conforming triangulation of $\Omega$. Let $\mathcal {E}_h^I$ and $\mathcal {E}_h^B$ denote respectively the sets of all interior and boundary edges/faces of $\mathcal {T}_h$, and set $\mathcal {E}_h:=\mathcal {E}_h^I\cup \mathcal {E}_h^B$. We introduce the broken Sobolev spaces

For any interior edge/face $e = \partial T^+ \cap \partial T^-\in \mathcal {E}_h^I$ we define the jump and average of a scalar or vector valued function v as $[v]\big |_{e} := v^+ - v^-,\{v\}\big |_{e} := \frac{1}{2}\left( v^+ + v^-\right)$, where $v^{\pm }=v|_{T^\pm }$. On a boundary edge/face $e\in \mathcal {E}_h^B$ with $e = \partial T^+\cap \partial \Omega$, we set $[v]\big |_{e} =\{v\}\big |_e = v^+$.

For any $e\in \mathcal {E}_h^I$ we use $\nu _e$ to denote the unit outward normal vector pointing in the direction of the element with the smaller global index. For $e\in \mathcal {E}_h^B$ we set $\nu _e$ to be the outward normal to $\partial \Omega$ restricted to e. The standard DG finite element space is defined as

$$\begin{aligned} V_h&:= \Bigl \{v_h\in W^{2,p}(\mathcal {T}_h);\, v_h\big |_T\in \mathbb {P}_k(T) \quad \forall T\in \mathcal {T}_h\Bigr \}, \end{aligned}$$

where $\mathbb {P}_k(T)$ denotes the set of all polynomials of degree less than or equal to k on T. We also introduce for any $D\subset \Omega$

$$\begin{aligned} V_h(D) := \Bigl \{v\in V_h;\, v\big |_{\Omega \setminus \overline{D}} \equiv 0 \Bigr \}. \end{aligned}$$

Note that $V_h(D)$ is nontrivial provided that there exists an inscribed ball B with radius $r\ge h$ such that $B\subset D$. We also adopt the convention $V_h(\Omega ) = V_h$.

For each $e\in \mathcal {E}_h$, let $\gamma _e>0$ be constant on e. We define the following mesh-dependent norms on $W^{2,p}_h(D)$ and $W_h^{1,p}(D)$:

$$\begin{aligned} \Vert v\Vert _{W^{2,p}_h(D)}&:= \Vert D^2_hv\Vert _{L^p(D)} + \Bigl (\sum _{e\in \mathcal {E}_h^I}h_e^{1-p} \big \Vert |[\nabla v]| \big \Vert _{L^p(e\cap \bar{D})}^p\Bigr )^\frac{1}{p} \end{aligned}$$

(2.1)

$$\begin{aligned}&\qquad +\Bigl (\sum _{e\in \mathcal {E}_h}\gamma _e^ph_e^{1-2p}\Vert [v]\Vert _{L^p(e\cap \bar{D})}^p\Bigr )^\frac{1}{p}, \nonumber \\ \Vert v\Vert _{W_h^{1,p}(D)}&:= \Vert \nabla _h v\Vert _{L^p(D)} + \Bigl (\sum _{e\in \mathcal {E}_h}\gamma _e^p h_e^{1-p}\Vert [v]\Vert _{L^p(e\cap \bar{D})}^p\Bigr )^\frac{1}{p} \\&\qquad +\Bigl (\sum _{e\in \mathcal {E}_h} h_e \Vert \{\nabla v\}\Vert _{L^p(e\cap \bar{D})}^p\Bigr )^\frac{1}{p}, \nonumber \end{aligned}$$

(2.2)

where $\nabla _h v$ and $D_h^2v$ denote the piecewise gradient and Hessian of v.

In addition, we define the discrete $W_h^{-2,p}$-norm and $W_h^{-1,p}$-norm as follows:

$$\begin{aligned} \Vert q\Vert _{W_h^{-2,p}(D)}&:= \sup _{0\ne v_h\in V_h}\frac{(q,v_h)_D}{\Vert v_h\Vert _{W_h^{2,p^\prime }(D)}}, \end{aligned}$$

(2.3)

$$\begin{aligned} \Vert q\Vert _{W_h^{-1,p}(D)}&:= \sup _{0\ne v\in W_h^{1,p'}(D)}\frac{(q,v)_D}{\Vert v\Vert _{W_h^{1,p^\prime }(D)}}, \end{aligned}$$

(2.4)

where $\frac{1}{p} +\frac{1}{p^\prime }=1$. Finally, for any domain $D\subseteq \Omega$ and any $w\in L^p_h(D)$, we introduce the following mesh-dependent semi-norm

$$\begin{aligned} \Vert w\Vert _{L^p_h(D)}:= \sup _{0\ne v_h\in V_h(D)} \frac{\bigl (w, v_h \bigr )_D}{\Vert v_h\Vert _{L^{p^\prime }(D)}}. \end{aligned}$$

(2.5)

It can be proved that (cf. [10])

$$\begin{aligned} \Vert w_h\Vert _{L^p(\Omega )} \lesssim \Vert w_h\Vert _{L^p_h(\Omega )}\qquad \forall w_h\in V_h. \end{aligned}$$

(2.6)

2.2 Properties of the DG Space $V_h$

In this subsection we collect some technical lemmas that cover the basic properties of functions in the DG space $V_h$. These facts will be used many times in the later sections. We first state the standard trace inequalities for broken Sobolev functions, a proof of this lemma can be found in [3].

Lemma 2.1

For any $T\in \mathcal {T}_h$ and $1<p<\infty$, there holds

$$\begin{aligned} \Vert v\Vert _{L^p(\partial T)}^p\lesssim \Bigl (h_T^{p-1}\Vert \nabla v\Vert _{L^p(T)}^p+h_T^{-1}\Vert v\Vert _{L^p(T)}^p\Bigr ) \quad \forall v\in W^{1,p}(T). \end{aligned}$$

(2.7)

Therefore by scaling we have

$$\begin{aligned} \sum _{e\in \mathcal {E}_h^I}h_e\Vert v\Vert _{L^p(e\cap \overline{D})}^p \lesssim {\left\{ \begin{array}{ll} \Vert v\Vert _{L^p(D)}^p &{}\quad \forall v\in V_h(D), \\ \Vert v\Vert _{L^p(D)}^p +h^p\Vert \nabla v\Vert _{L^p(D)}^p &{}\quad \forall v\in W^{2,p}(\mathcal {T}_h); v\big |_{\Omega \setminus D}=0. \end{array}\right. } \end{aligned}$$

(2.8)

Next, we state two inverse inequalities between the mesh-dependent norms defined above. We refer to [11] for their proofs.

Lemma 2.2

For any $v_h\in V_h$, $D\subseteq \Omega$, there hold for $1<p <\infty$

$$\begin{aligned} \Vert v_h\Vert _{W^{2,p}_h(D)}&\lesssim h^{-1}\Vert v_h\Vert _{W_h^{1,p}(D_h)}, \end{aligned}$$

(2.9)

$$\begin{aligned} \Vert v_h\Vert _{L^p(D)}&\lesssim h^{-1}\Vert v_h\Vert _{W_h^{-1,p}(D)}, \end{aligned}$$

(2.10)

where $D_h = \{x\in \Omega ;\,{\text {dist}}(x,D)\le h\}$.

The following lemma shows that the broken Sobolev norms are controlled by their corresponding Sobolev norms.

Lemma 2.3

For any $1<p<\infty$ there holds the following inequality:

$$\begin{aligned} \Vert \varphi \Vert _{W_h^{2,p}(\Omega )}&\le \Vert \varphi \Vert _{W^{2,p}(\Omega )} \quad \forall \varphi \in W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega ). \end{aligned}$$

Proof

Since the inequality holds for all $\varphi \in C^{\infty }(\Omega )\cap W^{1,p}_0(\Omega )$ and it can be extended to all $\varphi \in W^{2,p}(\Omega )\cap W^{1,p}_0(\Omega )$ by a density argument. $\square$

The next lemma establishes a Poincaré–Friedrichs’ inequality for DG functions. Again, we omit the proof to save space and refer the reader to [11] for its proof.

Lemma 2.4

Let $D\subset \Omega$ such that $V_h(D)\ne \{0\}$ and $\mathrm{diam}(D)\ge h$. Then for any $v_h\in V_h(D)$ there hold the following inequalities:

$$\begin{aligned} \Vert v_h\Vert _{L^{p}(D)}&\lesssim \mathrm{diam}(D)\Vert v_h\Vert _{W_h^{1,p}(D)} , \end{aligned}$$

(2.11)

$$\begin{aligned} \Vert v_h\Vert _{W_h^{1,p}(D)}&\lesssim \mathrm{diam}(D) \Vert v_h\Vert _{W_h^{2,p}(D)} . \end{aligned}$$

(2.12)

The last lemma of this section establishes some local super approximation estimates for the DG nodal interpolation in various discrete norms. The proof of the lemma is standard (cf. [19]); it can be given in [11].

Lemma 2.5

Let ${I}_h:C^0(\mathcal {T}_h):=\Pi _{T\in \mathcal {T}_h} C^0(\overline{T}) \rightarrow V_h$ denote the nodal interpolation operator, and $\eta \in C^{\infty }(\Omega )$ with $|\eta |_{W^{j,\infty }(\Omega )}\lesssim d^{-j}$ for $0\le j\le k$. Then for any $v_h\in V_h$ and $D\subseteq \Omega$ we have

$$\begin{aligned} \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{L^p(D)}&\lesssim \frac{h}{d}\Vert v_h\Vert _{L^p(D_h)}, \end{aligned}$$

(2.13)

$$\begin{aligned} h\Vert \nabla _h(\eta v_h-{I}_h(\eta v_h))\Vert _{L^p(D)}&\lesssim \frac{h}{d}\Vert v_h\Vert _{L^p(D_h)}, \end{aligned}$$

(2.14)

$$\begin{aligned} h^2\Vert D_h^2(\eta v_h-{I}_h(\eta v_h))\Vert _{L^p(D)}&\lesssim \frac{h}{d}\Vert v_h\Vert _{L^p(D_h)}, \end{aligned}$$

(2.15)

$$\begin{aligned} \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{W_h^{2,p}(D)}&\lesssim \frac{1}{d^2}\left( \Vert v_h\Vert _{L^p(D_h)} +\Vert \nabla _h v_h\Vert _{L^p(D_h)}\right) , \end{aligned}$$

(2.16)

where $D_h$ is the same as in Lemma 2.2. Moreover, there holds

$$\begin{aligned} \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{W_h^{2,p}(D)} \lesssim \dfrac{h}{d^3}\Vert v_h\Vert _{W_h^{2,p}(D_h)} \end{aligned}$$

(2.17)

if the polynomial degree k is greater than or equal to two.

3 DG Discrete $W^{1,p}$ and Calderon–Zygmund Estimates for PDEs with Constant Coefficients

In this section we consider the constant coefficient case, that is, $A(x)\equiv A_0\in \mathbb {R}^{n\times n}$ on $\Omega$. We define three interior-penalty discontinuous Galerkin discretizations $\mathcal {L}_{0,h}^{\varepsilon }$ to the PDE operator $\mathcal {L}$ and extend their domains to the broken Sobolev space $W^{2,p}(\mathcal {T}_h)$. Our goal in this subsection is to prove global stability estimates for $\mathcal {L}_{0,h}^{\varepsilon }$ which will be crucially used in the next section. The final global stability estimate given in Theorem 3.6 can be regarded as a DG discrete Calderon–Zygmund estimate for $\mathcal {L}_{0,h}^{\varepsilon }$.

Let $A_0$ be a constant, positive-definite matrix in $\mathbb {R}^{n\times n}$ and define

$$\begin{aligned} \mathcal {L}_0 w:=-A_0:D^2w=-\nabla \cdot (A_0\nabla w). \end{aligned}$$

(3.1)

From this we gather the standard PDE weak form:

$$\begin{aligned} a_0(w,v):=\int _{\Omega }A_0\nabla w\cdot \nabla v{\text {d}}\!{x} \quad \forall w,v\in H_0^1(\Omega ). \end{aligned}$$

(3.2)

The Lax-Milgram theorem [3] yields the existence and boundedness of $\mathcal {L}_0^{-1}:H^{-1}(\Omega )\rightarrow H_0^1(\Omega )$. Moreover if $\partial \Omega \in C^{1,1}$ we have from Calderon-Zygmund theory [13] that $\mathcal {L}_0^{-1}:L^p(\Omega )\rightarrow W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega )$ exists and

$$\begin{aligned} \Vert \mathcal {L}_{0}^{-1}\varphi \Vert _{W^{2,p}(\Omega )}\lesssim \Vert \varphi \Vert _{L^p(\Omega )} \qquad \forall \varphi \in L^p(\Omega ), \end{aligned}$$

and therefore

$$\begin{aligned} \Vert w\Vert _{W^{2,p}(\Omega )}\lesssim \Vert \mathcal {L}_0 w\Vert _{L^p(\Omega )} \quad \forall w\in W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega ). \end{aligned}$$

Define $\mathcal {L}_{0,h}^{\varepsilon }:V_h\rightarrow V_h$ by

$$\begin{aligned} \bigl (\mathcal {L}_{0,h}^{\varepsilon }w_h&,v_h\bigr ) := a_{0,h}^{\varepsilon }(w_h,v_h) \quad \forall v_h,w_h\in V_h, \end{aligned}$$

(3.3)

where the IP-DG bilinear form is defined by

$$\begin{aligned} a_{0,h}(w_h,v_h) :=&\int _\Omega A_0\nabla _h w_h \cdot \nabla _h v_h {\text {d}}\!{x}- \sum _{e\in \mathcal {E}_h}\int _e \{ A_0\nabla w_h\cdot \nu _{e}\} [v_h] {\text {d}}\!{S} \nonumber \\&-\varepsilon \sum _{e\in \mathcal {E}_h}\int _e \{A_0\nabla v_h\cdot \nu _{e}\}[w_h]{\text {d}}\!{S}+\sum _{e\in \mathcal {E}_h}\int _e \frac{\gamma _e}{h_e}[w_h][v_h] {\text {d}}\!{S}, \end{aligned}$$

(3.4)

and $\gamma _e>0$ is a penalization parameter. The parameter choices $\varepsilon \in \{ 1,0, -1\}$ give respectively the SIP-DG, IIP- DG, and NIP-DG formulations. For the sake of clarity and readability we shall assume for the rest of the paper that $\varepsilon$ may be either 1, 0, or $-1$ unless otherwise stated.

We recall the following well-known DG integration by parts formula:

$$\begin{aligned} \int _{\Omega }\tau \cdot \nabla _h v {\text {d}}\!{x}= -\int _{\Omega }&(\nabla _h\cdot \tau )v{\text {d}}\!{x} +\sum _{e\in \mathcal {E}_h^I}\int _e [\tau \cdot \nu _{e}]\{v\} {\text {d}}\!{S} +\sum _{e\in \mathcal {E}_h}\int _e\{\tau \cdot \nu _{e}\}[v]{\text {d}}\!{S}, \end{aligned}$$

(3.5)

which holds for any piecewise scalar-valued function v and vector-valued function $\tau$. Applying (3.5) to the first term on the right-hand side of (3.4) yields

$$\begin{aligned} a_{0,h}^{\varepsilon }(w_h,v_h) =&-\int _{\Omega }(A_0:D_h^2w_h)v_h {\text {d}}\!{x} + \sum _{e\in \mathcal {E}_h^I}\int _e [ A_0\nabla w_h\cdot \nu _{e}] \{v_h\} {\text {d}}\!{S} \nonumber \\&-\varepsilon \sum _{e\in \mathcal {E}_h}\int _e \{A_0\nabla v_h\cdot \nu _{e}\}[w_h]{\text {d}}\!{S}+\sum _{e\in \mathcal {E}_h}\int _e \frac{\gamma _e}{h_e}[w_h][v_h] {\text {d}}\!{S} \end{aligned}$$

(3.6)

for any $w_h,v_h\in V_h$. By Hölder’s inequality, it is easy to check that the above new form of $a_{0,h}^{\varepsilon }(\cdot ,\cdot )$ is also well-defined on $W^{2,p}(\mathcal {T}_h)\times W^{2,p'}(\mathcal {T}_h)$ with $\frac{1}{p}+\frac{1}{p'}=1$. As a result, this new form enables us to extend the domain of $a_{0,h}^{\varepsilon }(\cdot ,\cdot )$ to $W^{2,p}(\mathcal {T}_h)\times W^{2,p'}(\mathcal {T}_h)$ and $\mathcal {L}^\varepsilon _{0,h}: W^{2,p}(\mathcal {T}_h)\rightarrow (W^{2,p}(\mathcal {T}_h))^*$.

3.1 DG Discrete $W^{1,p}$ Error Estimates

From the standard IP-DG theory [22], there exists $\gamma ^* = \gamma ^*(\Vert A_0\Vert _{L^\infty (\Omega )}, \mathcal {T}_h)>0$ depending only on the shape regularity of the mesh and on $\Vert A_0\Vert _{L^\infty (\Omega )}$ such that $\mathcal {L}_{0,h}^{\varepsilon }$ is invertible on $V_h$ provided $\gamma _e\ge \gamma ^*$; in the non–symmetric case $\varepsilon =-1$, $\gamma _*$ can be any positive number. Moreover, if $w\in W^{2,2}(\mathcal {T}_h)\cap H^1_0(\Omega )$ and $w_h\in V_h$ satisfy

$$\begin{aligned} a^\varepsilon _{0,h}(w-w_h,v_h)=0\quad \forall v_h\in V_h, \end{aligned}$$

(3.7)

then the quasi-optimal error estimate

$$\begin{aligned} \Vert w-w_h\Vert _{W^{1,2}_h(\Omega )}\lesssim \inf _{v_h\in V_h} \Vert w-v_h\Vert _{W^{1,2}_h(\Omega )} \end{aligned}$$

(3.8)

is satisfied. The goal of this subsection is to generalize this result to general exponent $p\in (1,\infty )$ for the SIP-DG method. In particular, we have

Theorem 3.1

Suppose $w\in W^{2,p}(\Omega )\cap W^{1,p}_0(\Omega )\ (1<p<\infty )$ and $w_h\in V_h$ satisfy (3.7) with $\varepsilon =1$. Then there holds

$$\begin{aligned} \Vert w-w_h\Vert _{W^{1,p}_h(\Omega )}\lesssim h |\log h|^{t} \Vert w\Vert _{W^{2,p}(\Omega )}, \end{aligned}$$

(3.9)

where $t=(p+1)/p$ if $k=1$ and $t=0$ if $k\ge 2$.

To prove Theorem 3.1 we introduce some notation given in [5] (also see [25]). For given $z\in \overline{\Omega }$, we define the weight function $\sigma _z$ as

$$\begin{aligned} \sigma _z(x) = \frac{h}{|x-z|+h}. \end{aligned}$$

(3.10)

For $p\in [1,\infty )$, and $s\in \mathbb {R}$, we define the following weighted norms

$$\begin{aligned} \Vert v\Vert _{L^p(D),z,s}&= \left( \int _D \big |\sigma _z^s(x) v(x)\big |^p\, {\text {d}}\!{x}\right) ^{{1}/p},\nonumber \\ \Vert v\Vert _{W^{1,p}(D),z,s}&= \Vert v\Vert _{L^p(D),z,s} + \Vert \nabla _h v\Vert _{L^p(D),z,s},\nonumber \\ \Vert v\Vert _{W^{1,p}_h(D),z,s}&= \Vert v\Vert _{W^{1,p}(D),z,s} + \Big (\sum _{e\in \mathcal {E}_h} h_e^{1-p} \big \Vert \sigma ^s_z [v]\big \Vert _{L^p(e\cap \overline{D})}^p\Big )^{1/p}\nonumber \\&\qquad +\Big (\sum _{e\in \mathcal {E}_h} h_e \big \Vert \sigma _z^s \{\nabla _h v\}\big \Vert _{L^p(e\cap \overline{D})}^p\Big )^{1/p}. \end{aligned}$$

(3.11)

The weighted norms in the case $p=\infty$ are defined analogously.

The derivation of $W^{1,p}$ error estimates of DG approximations is based on the work [5], where localized pointwise estimates of DG approximations are obtained. There it was shown that if $w\in W^{2,\infty }(\Omega )$ and $w_h\in V_h$ satisfy (3.7) with $\varepsilon =1$, then

$$\begin{aligned} |\nabla (w-w_h)(z)|\lesssim \inf _{v_h\in V_h } \Vert w-v_h\Vert _{W^{1,\infty }_h(\Omega ),z,s}\quad 0\le s< k \end{aligned}$$

(3.12)

for all $z\in \overline{\Omega }$. Similar to pointwise estimates of finite element approximations (e.g., [3, 25]), the ingredients to prove (3.12) include duality arguments and DG approximation estimates of regularized Green functions in a weighted (discrete) $W^{1,1}$-norm. These results are rather technical and involve dyadic decompositions of $\Omega$, local DG error estimates, and Green function estimates.

Here, we follow a similar argument to derive $W^{1,p}$ estimates; the main difference being that we derive DG approximation estimates of regularized Green functions in a weighted (discrete) $W^{1,p'}$-norm with $1/p+1/p'=1$ (cf. Lemma 3.4). Using these estimates and applying similar arguments in [5, 25] yield the estimate

$$\begin{aligned} |\nabla (w-w_h)(z)|^p\lesssim h^{-n} \inf _{v_h\in V_h} \Vert w-v_h\Vert ^p_{W^{1,p}_h(\Omega ),z,s} \end{aligned}$$

for certain values of s. Integrating this expression with respect to z and applying Fubini’s theorem (cf. Lemma 3.2) then yields $L^p$ estimates of the piecewise gradient error.

Unfortunately, the strategy just described does not immediately give us estimates for the terms $h_e^{1-p}\Vert [w-w_h]\Vert ^p_{L^p(e)}$ appearing in the $W^{1,p}_h$-norm. To bypass this difficulty, we first use the trace inequality

$$\begin{aligned} \sum _{e\in \mathcal {E}_h} h_e^{1-p}\Vert [w-w_h]\Vert _{L^p(e)}^p \lesssim \Vert \nabla _h (w-w_h)\Vert ^p_{L^p(\Omega )}+ h^{-p}\Vert w-w_h\Vert ^p_{L^p(\Omega )}, \end{aligned}$$

and then derive estimates for $h^{-p} \Vert w-w_h\Vert ^p_{L^p(\Omega )}$. We note that the standard duality argument to derive $L^p$ estimates yields

$$\begin{aligned} \Vert w-w_h\Vert _{L^p(\Omega )}\lesssim h \Vert w-w_h\Vert _{W^{1,p}_h(\Omega )}, \end{aligned}$$

which is of little benefit. Rather, our strategy is to modify the arguments given in [5, Theorem 5.1] and estimate $|(w-w_h)(z)|$ in terms of $\inf _{v_h\in V_h} \Vert w-v_h\Vert _{W^{1,p}_h(\Omega ),z,s}$ (cf. Lemma 3.3), integrate the estimate with respect to z, and then apply Fubini’s theorem. We note that it is due to this term that the $|\log h|^t$ factor appears in Theorem 3.1.

To summarize, the derivation of $W^{1,p}$ error estimates of DG approximations consists of three main ingredients. The first result (Lemma 3.2) essentially follows from Fubini’s Theorem. The second result (Lemma 3.3) derives pointwise estimates of the error and is an extension of [5, Theorem 5.1] where the case $p=\infty$ is given. The third result (Lemma 3.4) gives DG error estimates of regularized Green functions and is a generalization of [5, Lemma 5.4] where the case $p^\prime =1$ is shown. The proofs of these results can be found in [11].

Lemma 3.2

Let $p\in [2,\infty )$ and $v\in L^p(\Omega )$. Let $z\in \Omega$ and $T_z\in \mathcal {T}_h$ such that $z\in T_z$. Then there holds

$$\begin{aligned} \int _\Omega \int _{T_z} |v(x)|^p {\text {d}}\!{x} {\text {d}}\!{z} \lesssim h^n \Vert v\Vert ^p_{L^p(\Omega )}. \end{aligned}$$

(3.13)

Moreover for any $s>n/p$ and $w\in W^{2,p}(\mathcal {T}_h)$, there holds

$$\begin{aligned} \int _\Omega \Vert v\Vert _{W^{1,p}_h(\Omega ),z,s}^p {\text {d}}\!{z}&\lesssim \frac{h^n}{ps-n} \big (\Vert \nabla _h v\Vert ^p_{L^{p}(\Omega )} +h^{-p}\Vert v\Vert ^p_{L^p(\Omega )}+h^p \Vert D^2_h v\Vert ^p_{L^p(\Omega )}\big ). \end{aligned}$$

(3.14)

If $s=n/p$, then we have

$$\begin{aligned} \int _\Omega \Vert v\Vert _{W^{1,p}_h(\Omega ),z,n/p}^p {\text {d}}\!{z}&\lesssim |\log h| {h^n} \big (\Vert \nabla _h v\Vert ^p_{L^{p}(\Omega )} +h^{-p}\Vert v\Vert ^p_{L^p(\Omega )}+h^p \Vert D^2_h v\Vert ^p_{L^p(\Omega )}\big ). \end{aligned}$$

(3.15)

Lemma 3.3

Let $w\in W^{2,p}(\mathcal {T}_h)\ (2\le p\le \infty )$ and $w_h\in V_h$ satisfy (3.7) with $\varepsilon =1$ Then for any $0\le s\le k-1+n/p$ and $z\in \overline{\Omega }$,

$$\begin{aligned} |(w-w_h)(z)|\lesssim h^{1-n/p} |\log h|^{\bar{s}(p)} \inf _{v_h\in V_h} \Vert w-v_h\Vert _{W^{1,p}_h(\Omega ),z,s}, \end{aligned}$$

where $\bar{s}(p) = 1$ if $k = s+1-n/p$ and $\bar{s}(p) = 0$ for $k>s+1-n/p$.

Lemma 3.4

Let z and $T_z$ be as in Lemma 3.2. For arbitrary $\varphi \in C^{\infty }_0(T_z)$, with $\Vert \varphi \Vert _{W^{1,2}(T_z)}=1$, we extend $\varphi$ to $\Omega$ by zero, and let $\hat{g}_z$ be the solution to

Let $\hat{g}_{z,h}\in V_h$ satisfy the discrete adjoint problem

$$\begin{aligned} a_{0,h}(v_h,\hat{g}_{z,h}) =h^{-n/2-1}\int _\Omega (\partial \varphi /\partial x_i) v_h\, {\text {d}}\!{x}\quad \forall v_h\in V_h, \end{aligned}$$

where we have dropped the superscript of the bilinear form for notational simplicity. Let $p\in [2,\infty ],\ p^\prime \in [1,2]$ such that $1/p+1/p^\prime = 1$. Then for any $0\le s\le k+n/p$ there holds

$$\begin{aligned} \Vert \hat{g}_z-\hat{g}_{z,h}\Vert _{W^{1,p^\prime }_h(\Omega ),z,-s}&\lesssim |\log h|^{\bar{\bar{s}}(p)} h^{-n/p}, \end{aligned}$$

where $\bar{\bar{s}}(p) = 1$ if $s = k+n/p$ and $\bar{\bar{s}}(p)=0$ otherwise.

Lemma 3.5

There holds, for $p^\prime \in [2,\infty )$,

$$\begin{aligned} \Vert v_h\Vert _{W^{1,p^\prime }_h(\Omega )}\lesssim |\log h|^{t'} \sup _{0\ne z_h\in V_h} \frac{a_{0,h}(v_h,z_h)}{\Vert z_h\Vert _{W^{1,p}_h(\Omega )}}\quad \forall v_h\in V_h, \end{aligned}$$

where $p\in (1,2]$ satisfies $1/p+1/p^\prime = 1$ and $t' = (p'+1)/p'$ if $k=1$ and $t'=0$ if $k\ge 2$.

3.1.1 Proof of Theorem 3.1 for p ${\ge 2}$

We now prove Theorem 3.1 in the case $p\in [2,\infty )$. To this end, let $z\in \Omega$ and $T_z\in \mathcal {T}_h$ such that $z\in T_z$. Using an inverse estimate, (2.10), and the triangle inequality we obtain

$$\begin{aligned} |\partial w_h(z)/\partial x_i|&\lesssim h^{-n/2}\Vert \partial w_h/\partial x_i\Vert _{L^2(T_z)} \nonumber \\&\lesssim h^{-n/2-1}\Vert \partial w_h/\partial x_i\Vert _{W^{-1,2}(T_z)}\nonumber \\&\lesssim h^{-n/2-1}\Bigl (\Vert \partial (w-w_h)/\partial x_i\Vert _{W^{-1,2}(T_z)} +\Vert \partial w/\partial x_i\Vert _{W^{-1,2}(T_z)}\Bigr ). \end{aligned}$$

(3.17)

Note that, by the Poincaré-Friedrichs and Hölder inequalities,

$$\begin{aligned} \Vert \partial w/\partial x_i\Vert _{W^{-1,2}(T_z)}&= \mathop {\sup _{\varphi \in C^\infty _0(T_z)}}_{\Vert \varphi \Vert _{W^{1,2}(T_z)}=1} (\partial w/\partial x_i,\varphi )_{T_z}\\&\lesssim \mathop {\sup _{\varphi \in C^\infty _0(T_z)}}_{\Vert \varphi \Vert _{W^{1,2}(T_z)}=1} |T_z|^{\frac{p-2}{2p}} \Vert \partial w/\partial x_i\Vert _{L^p(T_z)} \Vert \varphi \Vert _{L^2(T_z)}\\&\lesssim |T_z|^{\frac{p-2}{2p}} \mathrm{diam}(T_z) \Vert \partial w/\partial x_i\Vert _{L^p(T_z)} \lesssim h^{1+n/2-n/p}\Vert \partial w/\partial x_i\Vert _{L^p(T_z)}. \end{aligned}$$

Inserting this estimate into (3.17) yields

$$\begin{aligned} |\partial w_h(z)/\partial x_i|&\nonumber \lesssim h^{-n/p} \Vert \partial w/\partial x_i\Vert _{L^p(T_z)}+h^{-n/2-1}\Vert \partial (w-w_h)/\partial x_i\Vert _{W^{-1,2}(T_z)}. \end{aligned}$$

Replacing w by $w-v_h$ and $w_h$ by $w_h-v_h$ for some $v_h\in V_h$ in the argument above, we conclude

$$\begin{aligned} |\partial (w_h-v_h)(z)/\partial x_i|&\lesssim h^{-n/p} \Vert \partial (w-v_h)/\partial x_i\Vert _{L^p(T_z)}\nonumber \\&\quad +h^{-n/2-1}\Vert \partial (w-w_h)/\partial x_i\Vert _{W^{-1,2}(T_z)}. \end{aligned}$$

(3.18)

Let $\varphi$, $\hat{g}_z$ and $\hat{g}_{z,h}$ be as in Lemma 3.4. Setting $\hat{e}_z = \hat{g}_z-\hat{g}_{z,h}$, we have for arbitrary $v_h\in V_h$

$$\begin{aligned}&h^{-n/2-1} \int _{T_z}(w-w_h)\partial \varphi /\partial x_i\, dx = a_{0,h}(w-v_h,\hat{e}_z)\nonumber \\&\quad \lesssim \Vert w-v_h\Vert _{W_h^{1,p}(\Omega ),z,s} \Vert \hat{e}_z\Vert _{W^{1,p^\prime }_h(\Omega ),z,-s} \lesssim \Vert w-v_h\Vert _{W_h^{1,p}(\Omega ),z,s} |\log h|^{\bar{\bar{s}}(p)} h^{-n/p}, \end{aligned}$$

where $\bar{\bar{s}}(p)$ is defined in Lemma 3.4.

Applying this last estimate into (3.18) yields

$$\begin{aligned} |\nabla (w_h-v_h)(z)|&\lesssim h^{-n/p} \Vert \nabla (w-v_h)\Vert _{L^p(T_z)}\nonumber \\&\qquad +h^{-n/p} |\log h|^{\bar{\bar{s}}(p)}\Vert w-v_h\Vert _{W^{1,p}_h(\Omega ),z,s}. \end{aligned}$$

(3.19)

Raising (3.19) by the power p and integrating over $\Omega$ with respect to z, we conclude

$$\begin{aligned} \Vert \nabla _h (w_h-v_h)\Vert _{L^p(\Omega )}&\lesssim \left( h^{-n}\int _\Omega \Vert \nabla _h (w-v_h)\Vert _{L^p(T_z)}^p\, {\text {d}}\!{z}\right) ^{1/p}\\&\qquad \nonumber +\left( h^{-n} |\log h|^{\bar{\bar{s}}(p)p}\int _\Omega \Vert w-v_h\Vert ^p_{W^{1,p}_h(\Omega ),z,s}\, {\text {d}}\!{z}\right) ^{1/p}. \end{aligned}$$

Next, we choose s such that $n/p<s<k+n/p$. Then ${\bar{\bar{s}}(p)}=0$, and by (3.13)–(3.14)

$$\begin{aligned} \Vert \nabla _h (w_h-v_h)\Vert ^p_{L^p(\Omega )}&\lesssim \Vert \nabla _h(w{-}v_h)\Vert ^p_{L^{p}(\Omega )}+ h^{-p} \Vert w{-}v_h\Vert _{L^p(\Omega )}^p {+} h^p \Vert D^2_h(w-v_h)\Vert _{L^p(\Omega )}^p, \end{aligned}$$

and thus by the triangle inequality and taking $v_h = I_h w$, the nodal interpolant of w,

$$\begin{aligned} \Vert \nabla _h (w-w_h)\Vert _{L^p(\Omega )}\lesssim h \Vert w\Vert _{W^{2,p}(\Omega )}. \end{aligned}$$

(3.20)

Next we bound the jumps $\Vert [w-w_h]\Vert _{L^p(e)}$. First, by the trace inequalities stated in Lemma 2.1 we have

$$\begin{aligned} \sum _{e\in \mathcal {E}_h} h_e^{1-p} \Vert [w-w_h]\Vert _{L^p(e)}^p \lesssim C \Big (\Vert \nabla _h (w-w_h)\Vert _{L^p(\Omega )}^p+h^{-p}\Vert w-w_h\Vert _{L^p(\Omega )}^p\Big ). \end{aligned}$$

(3.21)

By Lemma 3.3 we have for any $z\in \overline{\Omega }$ and $v_h\in V_h$,

$$\begin{aligned} |(w-w_h)(z)|^p\lesssim h^{p-n} |\log h|^{p \bar{s}(p)} \Vert w-v_h\Vert ^p_{W^{1,p}_h(\Omega ),z,s}, \end{aligned}$$

where $\bar{s}(p) = 1$ if $k = s+1-n/p$ and $\bar{s}(p) = 0$ for $k>s+1-n/p$. Integrating this expression with respect to z yields

$$\begin{aligned} \Vert w-w_h\Vert _{L^p(\Omega )}^p\lesssim h^{p-n} |\log h|^{p \bar{s}(p)} \int _\Omega \Vert w-v_h\Vert ^p_{W^{1,p}_h(\Omega ),z,s}{\text {d}}\!{z}. \end{aligned}$$

(3.22)

If $k=1$, then we set $s = n/p$, so that $\bar{s}(p) = 1$, and by (3.15) with $v_h = I_h w$,

$$\begin{aligned} \Vert w-w_h\Vert _{L^p(\Omega )}^p&\lesssim h^{p-n} |\log h|^p \int _\Omega \Vert w-v_h\Vert ^p_{W^{1,p}_h(\Omega ),z,n/p}{\text {d}}\!{z}\\&\nonumber \lesssim h^{2p} |\log h|^{p+1} \Vert w\Vert _{W^{2,p}(\Omega )}^p. \end{aligned}$$

(3.23)

On the other hand, if $k\ge 2$, then we choose s such that $n/p<s<k-1+n/p$. Then $\bar{s}(p)=0$, and by (3.22) and (3.14),

$$\begin{aligned} \Vert w-w_h\Vert ^p_{L^p(\Omega )}&\lesssim h^{2p} \Vert w\Vert _{W^{2,p}(\Omega )}^p. \end{aligned}$$

(3.24)

Combining (3.21) with (3.20), (3.23) and (3.24) then yields,

$$\begin{aligned} \sum _{e\in \mathcal {E}_h} h_e^{1-p} \Vert [w-w_h]\Vert _{L^p(e)}^p\lesssim |\log h|^{p+1} h^p \Vert w\Vert ^p_{W^{2,p}(\Omega )}. \end{aligned}$$

(3.25)

Finally combining (3.20), (3.25) and applying standard scaling arguments yields (3.9). This completes the proof of Theorem 3.1 in the case $p\ge 2$. $\square$

3.1.2 Proof of Theorem 3.1 for ${ 1<}{ p}{<2}$

Next we prove Theorem 3.1 for $1<p<2$. To this end, for $w_h\in V_h$ and $w\in W^{2,p}(\Omega )\cap W^{1,p}_0(\Omega )$ satisfying (3.7), let $v_h\in V_h$ be the unique solution to

$$\begin{aligned} a_{0,h}(v_h,z_h) = \int _{\Omega } |\nabla _h w_h|^{p-2} \nabla _h w_h\cdot \nabla _h z_h{\text {d}}\!{x} +\sum _{e\in \mathcal {E}_h} h_e^{1-p} \int _e |[w_h]|^{p-2} [w_h][z_h]{\text {d}}\!{S} \end{aligned}$$

for all $z_h\in V_h$. Setting $z_h = w_h$ and using a scaling argument yields

$$\begin{aligned} \Vert w_h\Vert _{W^{1,p}_h(\Omega )}^p \lesssim a_{0,h}(v_h,w_h). \end{aligned}$$

Moreover, Lemma 3.5 and Hölder’s inequality gets

$$\begin{aligned} \Vert v_h\Vert _{W^{1,p^\prime }_h(\Omega )}\lesssim |\log h|^{t'} \Vert w_h\Vert _{W^{1,p}_h(\Omega )}^{p-1}. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert w_h\Vert _{W^{1,p}_h(\Omega )}&= \frac{\Vert w_h\Vert ^p_{W^{1,p}_h(\Omega )}}{\Vert w_h\Vert ^{p-1}_{W^{1,p}_h(\Omega )}} \lesssim |\log h|^{t'} \frac{a_{0,h}(v_h,w_h)}{\Vert v_h\Vert _{W^{1,p^\prime }_h(\Omega )}} \lesssim |\log h|^{t'}\Vert w\Vert _{W^{1,p}_h(\Omega )}. \end{aligned}$$

Standard arguments then show that this estimate implies

$$\begin{aligned} \Vert w-w_h\Vert _{W^{1,p}_h(\Omega )} \lesssim |\log h|^{t'} h\Vert w\Vert _{W^{2,p}(\Omega )}\quad 1<p<2. \end{aligned}$$

(3.26)

This completes the proof of Theorem 3.1 upon noting that $t' = (p'+1)/p' = (2p-1)/p\le (p+1)/p =t$ for $p\in (1,2]$. $\square$

3.2 DG Discrete Calderon–Zygmund Estimates for PDEs with Constant Coefficients

The goal of this subsection is to establish a stability result for the operator $\mathcal {L}_{0,h}^{\varepsilon }$ in the $W_h^{2,p}$-norm, which is a discrete counterpart of (3.3). Such an estimate can be regarded as a DG discrete Calderon-Zygmund estimate for $\mathcal {L}_{0,h}^{\varepsilon }$.

Theorem 3.6

• (i) For $\varepsilon =1$ and $1< p< \infty$ we have

  $$\begin{aligned} \Vert w_h\Vert _{W_h^{2,p}(\Omega )}\lesssim |\log h|^t \Vert \mathcal {L}^\varepsilon _{0,h} w_h\Vert _{L^p(\Omega )} \qquad \forall w_h\in V_h, \end{aligned}$$

  (3.27)

  where $t = (p+1)/p$ if $k=1$ and $t=0$ if $k\ge 2$.

• (ii) (3.27) also holds with $t=0$ for $\varepsilon \in \{1,0,-1\}$ and $p=2$.

Proof

• (i) We observe that (3.27) is equivalent to showing

  $$\begin{aligned} \Vert (\mathcal {L}_{0,h}^{\varepsilon })^{-1}\varphi _h\Vert _{W_h^{2,p}(\Omega )}\lesssim { |\log h|^t} \Vert \varphi _h\Vert _{L^p(\Omega )} \quad \forall \varphi _h\in V_h. \end{aligned}$$

  (3.28)

  For any $\varphi _h\in V_h$, let $w:=\mathcal {L}_0^{-1}\varphi _h\in W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega )$ and $w_h:=(\mathcal {L}_{0,h}^{\varepsilon })^{-1}\varphi _h\in V_h$. Since $w\in W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega )$ we have

  $$\begin{aligned} a_{0,h}^{\varepsilon }(w,v_h)&= (\varphi _h,v_h) = a_{0,h}^{\varepsilon }(w_h,v_h)\quad \forall v_h\in V_h. \end{aligned}$$

  Thus $w_h$ is the IP-DG approximate solution to w. Applying Theorem 3.1 and the elliptic regularity estimate, we obtain

  $$\begin{aligned} \Vert w-w_h\Vert _{W^{1,p}_h(\Omega )}\lesssim |\log h|^t h \Vert w\Vert _{W^{2,p}(\Omega )}\lesssim |\log h|^t h\Vert \varphi _h\Vert _{L^p(\Omega )}. \end{aligned}$$

  (3.29)

  Moreover, by Lemma 2.3 and the Calderon–Zygmund estimate for $\mathcal {L}_0$ we have

  $$\begin{aligned} \Vert w\Vert _{W^{2,p}_h(\Omega )} \le \Vert w\Vert _{W^{2,p}(\Omega )} \lesssim \Vert \varphi _h\Vert _{L^p(\Omega )}. \end{aligned}$$

  (3.30)

  Denote by $I_h:C^0(\Omega )\rightarrow V_h$ the nodal interpolation operator onto $V_h$. By finite element interpolation theory [6] we have

  $$\begin{aligned} h^{-1} \Vert w-I_h w\Vert _{W^{1,p}_h(\Omega )}+ \Vert w-I_h w\Vert _{W^{2,p}_h(\Omega )}\lesssim \Vert w\Vert _{W^{2,p}(\Omega )}. \end{aligned}$$

  (3.31)

  Therefore by the triangle inequality, an inverse estimate, Lemma 2.3, (3.29), and (3.30), we obtain

  $$\begin{aligned} \Vert w_h\Vert _{W^{2,p}_h(\Omega )}&\le \Vert w- I_h w\Vert _{W^{2,p}_h(\Omega )} +\Vert I_h w-w_h\Vert _{W^{2,p}_h(\Omega )} +\Vert w\Vert _{W^{2,p}_h(\Omega )}\\&\lesssim h^{-1} \Vert I_h w-w_h\Vert _{W^{1,p}_h(\Omega )}+ \Vert \varphi _h\Vert _{L^p(\Omega )}\\&\le h^{-1}\big (\Vert w-w_h\Vert _{W^{1,p}_h(\Omega )}+\Vert w-I_h w\Vert _{W^{1,p}_h(\Omega )}\big ) + \Vert \varphi _h\Vert _{L^p(\Omega )}\\&\lesssim |\log h|^t \Vert \varphi _h\Vert _{L^p(\Omega )} = |\log h|^t \Vert \mathcal {L}_{0,h} w_h \Vert _{L^p(\Omega )}. \end{aligned}$$

• (ii) The proof of this part is exactly same as that of Part (i), the only difference is that now (3.8), instead of (3.9), should be called in the proof.$\square$

4 IP-DG Methods and Their Convergence Analysis

As mentioned in Sect. 1, our primary goal in this paper to develop convergent IP-DG methods for approximating the $W^{2,p}$ strong solution to the boundary value problem (1.1). We assume that Eq. (1.1a) is uniformly elliptic, precisely, we assume $A\in \left[ C^0(\overline{\Omega })\right] ^{n\times n}$ is positive definite, that is, there exist constants $\Lambda>\lambda >0$ such that

$$\begin{aligned} \lambda |\xi |^2\le A(x) \le \Lambda |\xi |^2 \quad \text { for all } \xi \in \mathbb {R}^n \text { and } x\in \overline{\Omega }. \end{aligned}$$

(4.1)

We also assume that the solution u satisfies the following Calderon–Zygmund estimate:

$$\begin{aligned} \Vert u\Vert _{W^{2,p}(\Omega )}\lesssim \Vert f\Vert _{L^p(\Omega )}. \end{aligned}$$

(4.2)

It is well-known [13, Chapter 9] that the above estimate holds for any $f\in L^{p}(\Omega )$ with $1< p <\infty$ if $\partial \Omega \in C^{1,1}$. Moreover, when $n,p=2$, (4.2) also holds if $\Omega$ is a convex domain [2, 21].

4.1 Formulation of IP-DG Methods

We follow the same recipe as in the constant coefficient case to build our IP-DG methods. To this end, we momentarily assume $A\in [C^1(\Omega )]^{n\times n}$, so that we can rewrite the PDE (1.1a) in divergence form as follows:

$$\begin{aligned} -\nabla \cdot (A\nabla u) + (\nabla \cdot A)\cdot \nabla u = f, \end{aligned}$$

(4.3)

where $\nabla \cdot A$ is defined row-wise. We then define the following (standard) IP-DG methods for problem (4.3) by seeking $u_h\in V_h$ such that

$$\begin{aligned}&\int _{\Omega } (A\nabla _h u_h)\cdot \nabla _h v_h {\text {d}}\!{x} + \int _{\Omega }((\nabla \cdot A)\cdot \nabla _h u_h)v_h {\text {d}}\!{x} \nonumber \\&\qquad -\sum _{e\in \mathcal {E}_h}\int _{e}\{ A\nabla u_h\cdot \nu _{e}\} [v_h] {\text {d}}\!{S}-\varepsilon \sum _{e\in \mathcal {E}_h}\int _{e}\{ A\nabla v_h\cdot \nu _{e}\} [u_h] {\text {d}}\!{S} \nonumber \\&\qquad +\sum _{e\in \mathcal {E}_h} \int _e \frac{\gamma _e}{h_e}[u_h][v_h]{\text {d}}\!{S} = \int _{\Omega } fv_h {\text {d}}\!{x}, \end{aligned}$$

(4.4)

where $\gamma _e\ge \gamma _*(\Vert A\Vert _{L^\infty (\Omega )},\mathcal {T}_h)>0$. We emphasize that $\gamma ^*$ is independent of the derivatives of A.

Now come back to our case in hand with $A\in [C^0(\Omega )]^{n\times n}$. Clearly, the term $\nabla \cdot A$ does not exist as a function (it is in fact a Radon measure), so the above formulation is not defined for the case we are considering. To overcome this difficulty, our idea is to apply the DG integration by parts formula (3.5) to the first term on the left-hand side of (4.4), yielding

$$\begin{aligned} a_h(w_h,v_h) :=&-\int _{\Omega }(A:D_h^2w_h)v_h {\text {d}}\!{x} + \sum _{e\in \mathcal {E}_h^I}\int _e [ A\nabla w_h\cdot \nu _{e}] \{v_h\} {\text {d}}\!{S} \nonumber \\&-\varepsilon \sum _{e\in \mathcal {E}_h}\int _{e}\{ A\nabla v_h\cdot \nu _{e}\} [w_h] {\text {d}}\!{S} +\sum _{e\in \mathcal {E}_h}\int _e \frac{\gamma _e}{h_e}[w_h][v_h] {\text {d}}\!{S}. \end{aligned}$$

(4.5)

No derivative of A appears in the above new form of $a_h^{\varepsilon }(\cdot ,\cdot )$; thus, it is well-defined on $V_h\times V_h$. This leads to the following definition.

Definition 4.1

Our IP-DG methods are defined by seeking $u_h\in V_h$ such that

$$\begin{aligned} a^\varepsilon _h(u_h,v_h) = (f,v_h) \quad \forall v_h\in V_h, \quad \varepsilon \in \{1,0,-1\}. \end{aligned}$$

(4.6)

When $\varepsilon =1$ we will refer to the method as “symmetrically induced” even though the bilinear form is not symmetric. Likewise, $\varepsilon =0$ and $\varepsilon =-1$ yields an “incompletely induced” and “non-symmetrically induced” method, respectively.

4.2 Stability Analysis

As in Section 3 we can define the IP-DG approximation $\mathcal {L}_h^{\varepsilon }$ of $\mathcal {L}$ on $V_h$ using the bilinear form $a^\varepsilon _h(\cdot ,\cdot )$; precisely, we define $\mathcal {L}^\varepsilon _h:V_h\rightarrow V_h$ by

$$\begin{aligned} \bigl (\mathcal {L}^\varepsilon _h w_h,v_h\bigr ):=a^\varepsilon _h(w_h,v_h) \quad \forall w_h,v_h\in V_h. \end{aligned}$$

(4.7)

Since we can extend the domain of $a_h^\varepsilon (\cdot ,\cdot )$ to $W^{2,p}(\mathcal {T}_h)\times W^{2,p'}(\mathcal {T}_h)$, then the domain and co-domain of $\mathcal {L}_h$ can be extended to the broken Sobolev spaces $W^{2,p}(\mathcal {T}_h)$ and $(W^{2,p'}(\mathcal {T}_h))^*$ respectively.

The goal of this subsection is to establish a DG discrete Calderon–Zygmund estimate similar to (3.27) for the operator $\mathcal {L}^\varepsilon _h$. To this end, our main idea is to mimic, at the discrete level, the “freezing the coefficients” technique and the covering argument found in Schauder theory and $W^{2,p}$ strong solution theory [13, Chapters 6 and 9]. Since A is continuous, we show that in a small ball $B_{\delta } (\subset \Omega )$ A behaves as if it were constant. This allows us to conclude that $\mathcal {L}^\varepsilon _h$ is locally very close to $\mathcal {L}^\varepsilon _{0,h}$ in the ball $B_{\delta }(x_0)$ for any $x_0\in \Omega$. By applying the above mentioned “freezing the coefficients” technique and covering argument to the formal adjoint of $\mathcal {L}^\varepsilon _h$, we are able to prove a global left-side inf-sup condition for $\mathcal {L}^\varepsilon _h$. Then by employing a duality argument, we derive the desired discrete Calderon–Zygmund estimate for $\mathcal {L}^\varepsilon _h$.

We now proceed to establish a few auxiliary lemmas which will be needed to show the desired estimate.

Lemma 4.1

For all $\delta >0$, there exists $R_{\delta }>0$ and $h_{\delta }>0$ such that for all $x_0\in \Omega$ and $A_0\equiv A(x_0)$

$$\begin{aligned} \Vert (\mathcal {L}_h^{\varepsilon }-\mathcal {L}_{0,h}^{\varepsilon })w\Vert _{L_h^p(B_{R_{\delta }}(x_0))} \lesssim \delta \Vert w\Vert _{W_h^{2,p}(B_{R_{\delta }}(x_0))} \quad \forall w\in W^{2,p}(\mathcal {T}_h),\,\forall h\le h_{\delta }. \end{aligned}$$

(4.8)

Here, $B_{R_{\delta }}(x_0):=\{x\in \Omega :\ |x-x_0|<R_{\delta }\}$ denotes the ball with center $x_0$ and radius $R_{\delta }$.

Proof

Since A is continuous on $\overline{\Omega }$, then it is uniformly continuous. Therefore, for every $\delta >0$ there exists $R_{\delta }>0$ such that if $x,y\in \Omega$ satisfies $|x-y|<R_{\delta }$, we have $|A(x)-A(y)|<\delta$. Consequently, for any $x_0\in \Omega$

$$\begin{aligned} \Vert A-A_0\Vert _{L^{\infty }(B_{R_{\delta }})}\le \delta , \end{aligned}$$

(4.9)

where we have used the shorthand notation $B_{R_{\delta }}:=B_{R_{\delta }}(x_0)$.

Set $h_{\delta }=\min \{h_0,\frac{R_{\delta }}{4}\}$ and let $0<h<h_{\delta }$, $w\in W^{2,p}(\mathcal {T}_h)$, and $v_h\in V_h(B_{R_{\delta }})$. Since $(\mathcal {L}_{0,h}^{\varepsilon }-\mathcal {L}_h^{\varepsilon })w\in W^{2,p}(\mathcal {T}_h)$, it follows from (3.6) and (4.5) that for every $v_h\in V_h(B_{R_{\delta }})$ we have

Dividing both sides by $\Vert v_h\Vert _{L^{p'}(B_{R_{\delta }})}$ yields the estimate. The proof is complete.$\square$

The next lemma shows that $\mathcal {L}^\varepsilon _h$ is locally a bounded operator on $W^{2,p}(\mathcal {T}_h)$. We omit its proof to save space and refer the reader to [11] for a detailed proof.

Lemma 4.2

For any $x_0\in \Omega$ and $R\ge h$, there holds

$$\begin{aligned} \Vert \mathcal {L}_h^{\varepsilon } w\Vert _{L_h^p(B_R(x_0))}\lesssim \Vert w\Vert _{W_h^{2,p}(B_{R}(x_0))}\qquad \forall w\in W^{2,p}(\mathcal {T}_h). \end{aligned}$$

(4.10)

Our last lemma establishes a left-side inf-sup condition for $\mathcal {L}_h^{\varepsilon }$. This estimate relies on the formal adjoint operator $\mathcal {L}_h^*:=(\mathcal {L}_h^{\varepsilon })^*$ and some techniques from [24].

Lemma 4.3

There exists an $h_0>0$ such that for all $h\le h_0$ and $k\ge 2$ we have

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(\Omega )}\lesssim \sup _{0\ne w_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } w_h,v_h)}{\Vert w_h\Vert _{W_h^{2,p}(\Omega )}} \qquad \forall v_h\in V_h, \end{aligned}$$

(4.11)

where $1<p<\infty$ if $\varepsilon =1$ and $p=2$ if $\varepsilon \in \{0,-1\}$.

Proof

Note that (4.11) is equivalent to

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(\Omega )}&\lesssim \sup _{0\ne w_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } w_h,v_h)}{\Vert w_h\Vert _{W_h^{2,p}(\Omega )}} = \sup _{0\ne w_h\in V_h}\frac{(\mathcal {L}_h^*v_h,w_h)}{\Vert w_h\Vert _{W_h^{2,p}(\Omega )}} = \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )} \end{aligned}$$

(4.12)

for all $v_h\in V_h$. We divide the remaining proof into three steps.

Step 1: Local estimates Let $x_0\in \Omega ,\ A_0 \equiv A(x_0)$, $\delta _0$, $h_{\delta _0}$, $R_{\delta _0}$, $R_1:=(1/3)R_{\delta _0}$, and $B_1:=B_{R_1}(x_0)$ be as in Lemma 4.1 with $\delta _0>0$ to be determined, and set $h\le h_{\delta _0}$.

By the elliptic regularity of $\mathcal {L}$, for any $v_h\in V_h(B_1)$, there exists $\varphi \in W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega )$ such that $\mathcal {L}\varphi = v_h|v_h|^{p-2}$ in $\Omega$ and satisfies the estimate

$$\begin{aligned} \Vert \varphi \Vert _{W^{2,p}(\Omega )} \lesssim \Vert v_h\Vert _{L^{p'}(\Omega )}^{p'-1} = \Vert v_h\Vert _{L^{p'}(B_1)}^{p'-1}. \end{aligned}$$

(4.13)

Since $\mathcal {L}_h^{\varepsilon }$ is consistent with $\mathcal {L}$ for any $\varphi _h\in V_h$ we have

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}&= \Vert v_h\Vert _{L^{p'}(\Omega )} = (\mathcal {L}\varphi ,v_h) = (\mathcal {L}_h^{\varepsilon }\varphi ,v_h) \nonumber \\&= (\mathcal {L}_h^*v_h,\varphi _h) + \big (\mathcal {L}_{0,h}^{\varepsilon }(\varphi -\varphi _h),v_h\big ) + \big ((\mathcal {L}_h^{\varepsilon }-\mathcal {L}_{0,h}^{\varepsilon })(\varphi -\varphi _h),v_h\big ). \end{aligned}$$

(4.14)

From the existence-uniqueness of the IP-DG scheme (3.4), there exists $\varphi _h\in V_h$ such that

$$\begin{aligned} \big (\mathcal {L}_{0,h}^{\varepsilon }(\varphi -\varphi _h),w_h\big ) = 0 \quad \forall w_h\in V_h. \end{aligned}$$

Combining Galerkin orthogonality, Theorem 3.6, and (4.13) gives us the solution estimate

$$\begin{aligned} \Vert \varphi _h\Vert _{W_h^{2,p}(\Omega )} \lesssim \Vert \mathcal {L}_{0,h}^{\varepsilon }\varphi _h\Vert _{L_h^p(\Omega )} = \Vert \mathcal {L}_{0,h}^{\varepsilon }\varphi \Vert _{L_h^p(\Omega )} \lesssim \Vert \varphi \Vert _{W^{2,p}(\Omega )} \lesssim \Vert v_h\Vert _{L^{p'}(B_1)}^{p'-1}. \end{aligned}$$

(4.15)

Using Lemma 4.1 and (4.13)–(4.15) we have

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}^{p'}&= (\mathcal {L}_h^*v_h,\varphi _h) + ((\mathcal {L}_h^{\varepsilon }-\mathcal {L}_{0,h}^{\varepsilon })(\varphi -\varphi _h),v_h) \\&\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}\Vert v_h\Vert _{L^{p'}(B_1)}^{p'-1}+ \delta _0\Vert v_h\Vert _{L^{p'}(B_1)}^{p'}. \end{aligned}$$

Taking $\delta _0$ sufficiently small to move the right hand term to the left side and dividing by $\Vert v_h\Vert _{L^{p'}(B_1)}^{p'-1}$ gives us the local estimate

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p}(B_1)}\quad \forall v_h\in V_h(B_1). \end{aligned}$$

(4.16)

Step 2: A Gärding type inequality by a covering argument Given $R_1$ from Step 1, let $R_2 = 2R_1$ and $R_3=3R_1$. Let $\eta \in C^3(\Omega )$ be a cutoff function satisfying

$$\begin{aligned} 0\le \eta \le 1, \quad \eta \big |_{B_1}=1, \quad \eta \big |_{\Omega \setminus B_2}=0, \quad |\eta |_{W^{m,\infty }(\Omega )}=O(R_1^{-m}). \end{aligned}$$

(4.17)

For any $v_h\in V_h$, we have by (4.16),

$$\begin{aligned}&\Vert v_h\Vert _{L^{p'}(B_1)} = \Vert \eta v_h\Vert _{L^{p'}(B_1)} \le \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{L^{p'}(B_1)}+ \Vert {I}_h(\eta v_h)\Vert _{L^{p'}(B_1)}\nonumber \\&\quad \lesssim \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{L^{p'}(B_1)}+ \Vert \mathcal {L}_h^*({I}_h(\eta v_h)-\eta v_h)\Vert _{W_h^{-2,p'}(B_1)} + \Vert \mathcal {L}_h^*(\eta v_h)\Vert _{W_h^{-2,p'}(B_1)}. \end{aligned}$$

(4.18)

We now bound the second term on the right hand side of (4.18). By the definition of $\Vert \cdot \Vert _{W_h^{-2,p}}$, Lemma 4.2 and (2.6), for any $w_h\in V_h$ we have

$$\begin{aligned} \Vert \mathcal {L}_h^*(&{I}_h(\eta v_h)-\eta v_h)\Vert _{W_h^{-2,p'}(B_1)} = \sup _{0\ne w_h\in V_h}\frac{(\mathcal {L}_h^*({I}_h(\eta v_h)-\eta v_h),w_h)}{\Vert w_h\Vert _{W_h^{2,p}(B_1)}} \nonumber \\&\le \sup _{w_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } w_h,{I}_h(\eta v_h)-\eta v_h)}{\Vert w_h\Vert _{W_h^{2,p}(B_1)}}\lesssim \sup _{w_h\in V_h}\frac{\Vert \mathcal {L}_h^{\varepsilon } w_h\Vert _{L_h^p(B_1)}\Vert {I}_h(\eta v_h)-\eta v_h)\Vert _{L^{p'}(B_1)}}{\Vert w_h\Vert _{W_h^{2,p}(B_1)}}\nonumber \\&\lesssim \sup _{w_h\in V_h}\frac{\Vert w_h\Vert _{W_h^{2,p}(B_1)}\Vert {I}_h(\eta v_h)-\eta v_h)\Vert _{L^{p'}(B_1)}}{\Vert w_h\Vert _{W_h^{2,p}(B_1)}} = \Vert {I}_h(\eta v_h)-\eta v_h\Vert _{L^{p'}(B_1)}. \end{aligned}$$

Thus (4.18) becomes

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}\lesssim \Vert \eta v_h-{I}_h(\eta v_h)\Vert _{L^{p'}(B_1)}+ \Vert \mathcal {L}_h^*(\eta v_h)\Vert _{W_h^{-2,p'}(B_1)}. \end{aligned}$$

(4.19)

Using Lemmas 2.2, 2.5, and 4.2 with (4.19) yields

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}&\lesssim \frac{h}{R_1}\Vert v_h\Vert _{L^{p'}(B_3)}+ \Vert \mathcal {L}_h^*(\eta v_h)\Vert _{W_h^{-2,p'}(B_3)}\nonumber \\&\lesssim \frac{1}{R_1}\Vert v_h\Vert _{W^{-1,p'}(B_3)}+ \Vert \mathcal {L}_h^*(\eta v_h)\Vert _{W_h^{-2,p'}(B_3)}. \end{aligned}$$

(4.20)

We now want to remove the cutoff function $\eta$ from the adjoint operator appearing in the right-hand side of (4.20). For $w_h\in V_h(B_3)$, we break up $\mathcal {L}_h^*( \eta v_h)$ as follows:

$$\begin{aligned}&(\mathcal {L}_h^*( \eta v_h),w_h) = (\mathcal {L}_h^{\varepsilon } w_h,\eta v_h) = (\mathcal {L}_h^{\varepsilon } w_h\eta ,v_h)+\bigg [(\mathcal {L}_h^{\varepsilon } w_h,\eta v_h)-(\mathcal {L}_h^{\varepsilon } w_h\eta , v_h)\bigg ] \nonumber \\&\quad = (\mathcal {L}_h^{\varepsilon } ({I}_h(w_h\eta )),v_h)+(\mathcal {L}_h^{\varepsilon } (w_h\eta -{I}_h(w_h\eta )),v_h) \nonumber \\&\qquad +\bigg [(\mathcal {L}_h^{\varepsilon } w_h,\eta v_h)-(\mathcal {L}_h^{\varepsilon } w_h\eta , v_h)\bigg ]=: I_1 + I_2 + I_3 \end{aligned}$$

(4.21)

We then seek to bound each I in order. To bound $I_1$, we will use the definition of $\Vert \cdot \Vert _{W_h^{-2,p}}$, the stability of ${I}_h$, and Lemma 2.4 to obtain

$$\begin{aligned} I_1&= (\mathcal {L}_h^*v_h, {I}_h(w_h\eta )) \lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}\Vert {I}_h(\eta w_h)\Vert _{W_h^{2,p}(B_3)}\nonumber \\&\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}\Vert \eta w_h\Vert _{W_h^{2,p}(B_3)} \lesssim \frac{1}{R_1^2}\Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}\Vert w_h\Vert _{W_h^{2,p}(B_3)}. \end{aligned}$$

(4.22)

For $I_2$ we use Lemmas 2.2, 2.5, 4.2 to get

$$\begin{aligned} I_2&= (\mathcal {L}_h^{\varepsilon } (w_h\eta -{I}_h(w_h\eta )),v_h) \lesssim \Vert w_h\eta -{I}_h(w_h\eta ) \Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)} \nonumber \\&\lesssim \frac{h}{R_1^3}\Vert w_h \Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)} \lesssim \frac{1}{R_1^3}\Vert w_h \Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{W^{-1,p'}(B_3)}. \end{aligned}$$

(4.23)

To bound $I_3$ we introduce the operator $\mathcal {L}_{0,h}^{\varepsilon }$ . For $e\in \mathcal {E}_h$ let $e_3:= e\cap B_3$, and define $\tilde{A} := A-A_0$. We then write

$$\begin{aligned} I_3&= (\mathcal {L}_h^{\varepsilon } w_h,\eta v_h)-(\mathcal {L}_h^{\varepsilon } w_h\eta , v_h) \nonumber \\&= (\mathcal {L}_{0,h}^{\varepsilon } w_h,\eta v_h)-(\mathcal {L}_{0,h}^{\varepsilon } w_h\eta , v_h) \nonumber \\&\quad \quad + \big [ (\mathcal {L}_h^{\varepsilon } w_h,\eta v_h)-(\mathcal {L}_h^{\varepsilon } w_h\eta , v_h) - (\mathcal {L}_{0,h}^{\varepsilon } w_h,\eta v_h)+(\mathcal {L}_{0,h}^{\varepsilon } w_h\eta , v_h)\big ] \nonumber \\&= -\int _{B_3} \left( w_h A_0:D^2\eta + (A_0+A_0^T)\nabla \eta \cdot \nabla _h w_h\right) v_h {\text {d}}\!{x} \nonumber \\&\quad -\varepsilon \sum _{e\in \mathcal {E}_h} \int _{e_3} (A_0 \nabla \eta \cdot \nu _{e})\{v_h\} [w_h]{\text {d}}\!{S}\nonumber \\&\quad -\int _{B_3} \left( w_h (\tilde{A}:D^2\eta + \left( \tilde{A}+\tilde{A}^T\right) \nabla \eta \cdot \nabla _h w_h\right) v_h {\text {d}}\!{x}\nonumber \\&\quad -\varepsilon \sum _{e\in \mathcal {E}_h} \int _{e_3} (\tilde{A} \nabla \eta \cdot \nu _{e})\{v_h\}[w_h]{\text {d}}\!{S} =: K_1 + K_2 + K_3 + K_4. \end{aligned}$$

(4.24)

We now must bound each $K_i$. To bound $K_1$ we use the definition of $\Vert \cdot \Vert _{W_h^{-1,p}(B_3)}$ and Lemma 2.2 to get

$$\begin{aligned} K_1&\lesssim \left( \Vert w_h A_0:D^2\eta \Vert _{W_h^{1,p}(B_3)}+ \Vert (A_0+A_0^T)\nabla \eta \cdot \nabla _h w_h\Vert _{W_h^{1,p}(B_3)}\right) \Vert v_h\Vert _{W_h^{-1,p'}(B_3)} \nonumber \\&\lesssim \frac{1}{R_1^3}\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{W_h^{-1,p'}(B_3)}. \end{aligned}$$

(4.25)

The bound of $K_2$ uses Lemmas 2.1, 2.4 to obtain

$$\begin{aligned} K_2&\lesssim \frac{1}{R_1}\left( \sum _{e\in \mathcal {E}_h}h_e^{1-2p}\Vert [w_h]\Vert _{L^p(e_3)}^p\right) ^{\frac{1}{p}}\left( \sum _{e\in \mathcal {E}_h}h_eh_e^{p'}\Vert \{v_h\}\Vert _{L^{p'}(e_3)}^{p'}\right) ^{\frac{1}{p'}}\nonumber \\&\lesssim \frac{1}{R_1}\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{W_h^{-1,p'}(B_3)}. \end{aligned}$$

(4.26)

We use similar techniques as (4.25), (4.26) and the fact that $\Vert \tilde{A}\Vert _{L^\infty (B_3)} \le \delta _0$ to get

$$\begin{aligned} K_3&\lesssim \left( \Vert w_h \tilde{A}:D^2\eta \Vert _{L^p(B_3)}+ \Vert (\tilde{A}+\tilde{A}^T)\nabla \eta \cdot \nabla _h w_h\Vert _{L^p(B_3)}\right) \Vert v_h\Vert _{L^{p'}(B_3)} \nonumber \\&\lesssim \delta _0\left( \frac{1}{R_1^2}\Vert w_h\Vert _{L^p(B_3)}+ \frac{1}{R_1}\Vert w_h\Vert _{W^{1,p}_h(B_3)}\right) \Vert v_h\Vert _{L^{p'}(B_3)} \nonumber \\&\lesssim \delta _0\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)}, \end{aligned}$$

(4.27)

where we have used Lemma 2.4 to derive the last inequality. Likewise, we find

$$\begin{aligned} K_4&\lesssim \frac{1}{R_1}\left( \sum _{e\in \mathcal {E}_h}h_e^{1-2p}\Vert [w_h]\Vert _{L^p(e_3)}^p\right) ^{\frac{1}{p}}\left( \sum _{e\in \mathcal {E}_h}h_eh_e^{p'}\Vert \{v_h\}\Vert _{L^{p'}(e_3)}^{p'}\right) ^{\frac{1}{p'}}\nonumber \\&\lesssim \delta _0\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)}, \end{aligned}$$

(4.28)

where we have used the inequality $h\le R_1$. Combining (4.24)–(4.28) we get

$$\begin{aligned} I_3 \lesssim \frac{1}{R_1^3}\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{W_h^{-1,p'}(B_3)} + \delta _0\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)}, \end{aligned}$$

(4.29)

and bringing together (4.21)–(4.23), and (4.29) gives us

$$\begin{aligned} (\mathcal {L}_h^*(\eta v_h),w_h)&\lesssim \frac{1}{R_1^3}\left( \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}+ \Vert v_h\Vert _{W_h^{-1,p'}(B_3)} \right) \Vert w_h\Vert _{W_h^{2,p}(B_3)} \end{aligned}$$

(4.30)

$$\begin{aligned}&\quad \quad + \delta _0\Vert w_h\Vert _{W_h^{2,p}(B_3)}\Vert v_h\Vert _{L^{p'}(B_3)}. \end{aligned}$$

(4.31)

By the definition of $\Vert \cdot \Vert _{W_h^{-2,p'}(B_3)}$ and (4.30) we get

$$\begin{aligned} \Vert \mathcal {L}_h^*(\eta w_h)\Vert _{W_h^{-2,p'}(B_3)}&\lesssim \frac{1}{R_1^3}\left( \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}+ \Vert v_h\Vert _{W_h^{-1,p'}(B_3)} \right) + \delta _0\Vert v_h\Vert _{L^{p'}(B_3)}. \end{aligned}$$

(4.32)

Using (4.20) and (4.32) gives us

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(B_1)}\lesssim \frac{1}{R_1^3}\left( \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(B_3)}+ \Vert v_h\Vert _{W_h^{-1,p'}(B_3)} \right) + \delta _0\Vert v_h\Vert _{L^{p'}(B_3)}. \end{aligned}$$

Since $\overline{\Omega }$ is compact, employing a covering argument (cf. [10, 13]) then yields

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(\Omega )}\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}+ \Vert v_h\Vert _{W_h^{-1,p'}(\Omega )} + \delta _0\Vert v_h\Vert _{L^{p'}(\Omega )}. \end{aligned}$$

Because $\delta _0$ is small, we can absorb the last term on the right-hand side to the left-hand side to arrive at the global estimate

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(\Omega )}\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}+ \Vert v_h\Vert _{W_h^{-1,p'}(\Omega )}, \end{aligned}$$

(4.33)

which is a Gärding-type inequality.

Step 3: Duality argument on the adjoint operator To control the last term in (4.33) we now use a duality argument for $\mathcal {L}_h^*$. This argument uses the regularity estimate of the original problem $\mathcal {L}$.

Define the set $X = \{g\in W^{1,p}_h(\Omega );\, \Vert g\Vert _{W_h^{1,p}(\Omega )} = 1\}$. By the discrete Poincaré inequality, with constant $C=C(p,\Omega )$, we have for all $g\in X$

$$\begin{aligned} \Vert g\Vert _{L^p(\Omega )} \le C\Vert g\Vert _{W_h^{1,p}(\Omega )} < \infty , \end{aligned}$$

since X is bounded in $W^{1,p}_h(\Omega )$. Thus, X is precompact in $L^{p}(\Omega )$ by Sobolev embedding. Next we define the set $W = \{\varphi := \mathcal {L}^{-1}g;\,g\in X\}$. Note that $\mathcal {L}^{-1}:L^p(\Omega )\rightarrow W^{2,p}(\Omega )\cap W_0^{1,p}(\Omega )\subset W^{2,p}(\mathcal {T}_h)$ is well defined by well-posedness of the PDE. Also since $\mathcal {L}^{-1}$ is linear and satisfies the estimate

$$\begin{aligned} \Vert \mathcal {L}^{-1} g\Vert _{W^{2,p}_h(\Omega )}=\Vert \varphi \Vert _{W_h^{2,p}(\Omega )} \le \Vert \varphi \Vert _{W^{2,p}(\Omega )} \lesssim \Vert g\Vert _{L^p(\Omega )}, \end{aligned}$$

it is bounded in $W^{2,p}(\mathcal {T}_h)$. Thus W is precompact in $W^{2,p}(\mathcal {T}_h)$. From [24, Lemma 5], for every $\tau >0$ there exists $h_*>0$ that only depends on $\tau$ and $\overline{W}$ such that for each $\varphi \in W$ and $0<h\le h_*$ there is a $\varphi _h\in V_h$ such that if $k\ge 2$ we have

$$\begin{aligned} \Vert \varphi -\varphi _h\Vert _{W_h^{2,p}(\Omega )} \le \tau . \end{aligned}$$

(4.34)

Note by the reverse triangle inequality and (4.34) we have

$$\begin{aligned} \Vert \varphi _h\Vert _{W_h^{2,p}(\Omega )}\le \Vert \varphi \Vert _{W_h^{2,p}(\Omega )} \lesssim \Vert g\Vert _{L^p(\Omega )} \le C \end{aligned}$$

and hence $\{\varphi _h\in V_h;\, |\varphi _h - \varphi |\le \tau \}$ is uniformly bounded in $\varphi$ and h. Let $g\in X$ and choose $\varphi _g=\mathcal {L}^{-1}g\in W$ which tells us that $\mathcal {L}\varphi _g=g$. Let $v_h\in V_h$ and $\varphi _h\in V_h$. By Lemma 4.2 and the definition of $\Vert \cdot \Vert _{W_h^{-2,p'}(\Omega )}$ we have

$$\begin{aligned} \int _{\Omega }v_h g{\text {d}}\!{x}&= (\mathcal {L}_h^{\varepsilon }\varphi _g,v_h) = (\mathcal {L}_h^{\varepsilon }\varphi _h,v_h) + (\mathcal {L}_h^{\varepsilon }(\varphi _g-\varphi _h),v_h) \\&\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}\Vert \varphi _h\Vert _{W_h^{2,p}(\Omega )} + \Vert \varphi _g-\varphi _h\Vert _{W_h^{2,p}(\Omega )}\Vert v_h\Vert _{L^{p'}(\Omega )}. \end{aligned}$$

Selecting $\varphi _h$ to satisfy (4.34) and taking the supremum on g gives us

$$\begin{aligned} \Vert v_h\Vert _{W^{-1,p}(\Omega )} \lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}\Vert \varphi _h\Vert _{W_h^{2,p}(\Omega )} + \tau \Vert v_h\Vert _{L^{p'}(\Omega )}. \end{aligned}$$

(4.35)

Combining (4.33) and (4.35) yields

$$\begin{aligned} \Vert v_h\Vert _{L^{p'}(\Omega )}\lesssim \Vert \mathcal {L}_h^*v_h\Vert _{W_h^{-2,p'}(\Omega )}+ \tau \Vert v_h\Vert _{L^{p'}(\Omega )}. \end{aligned}$$

(4.36)

By choosing $\tau$ sufficiently small to kick back the right-most term we have (4.12). This completes the proof upon taking $h_0 = \min \{h_{\delta _0},h_*\}$.$\square$

We are now ready to prove the global stability of the operator $\mathcal {L}_h^{\varepsilon }$.

Theorem 4.4

Suppose that $h\le h_0$ and $k\ge 2$. Then there holds the following stability estimate:

$$\begin{aligned} \Vert w_h\Vert _{W_h^{2,p}(\Omega )}\lesssim \Vert \mathcal {L}_h^{\varepsilon } w_h\Vert _{L_h^p(\Omega )} \quad \forall w_h\in V_h, \end{aligned}$$

(4.37)

where $1<p<\infty$ if $\varepsilon = 1$, and $p=2$ if $\varepsilon \in \{0,-1\}$.

Proof

For $w_h\in V_h$, consider the auxiliary problem of finding $q_h\in V_h$ such that

$$\begin{aligned} \bigl (v_h,\mathcal {L}_h^*q_h\bigr )&=\bigl (\mathcal {L}_h^{\varepsilon } v_h,q_h\bigr ) = \int _{\Omega } |D^2_h w_h|^{p-2}D^2_h w_h:D^2v_h {\text {d}}\!{x}\nonumber \\&\quad +\sum _{e\in \mathcal {E}_h^I} h_e^{1-p} \int _e { |[\nabla w_h]|^{p-2} [\nabla w_h]\cdot [\nabla v_h]}\, {\text {d}}\!{S}\nonumber \\&\quad +\sum _{e\in \mathcal {E}_h} h_e^{1-2p} \int _e |[w_h]|^{p-2} [w_h] [v_h]\, {\text {d}}\!{S} \quad \forall v_h\in V_h. \end{aligned}$$

(4.38)

Since $V_h$ is finite dimensional and the operator is linear, the existence is equivalent to the uniqueness. To show the uniqueness, let $q_h^{(1)}$ and $q_h^{(2)}$ both solve (4.38). Then by Lemma 4.3 we get

$$\begin{aligned} \Vert q_h^{(1)}-q_h^{(2)}\Vert _{L^{p'}(\Omega )} \lesssim \sup _{0\ne v_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } v_h,q_h^{(1)}-q_h^{(2)})}{\Vert v_h\Vert _{W^{2,p}_h(\Omega )}} =0. \end{aligned}$$

Hence, (4.38) has a unique solution $q_h\in V_h$. Also by Lemma 4.3 and Hölder’s inequality,

$$\begin{aligned} \Vert q_h\Vert _{L^{p^\prime }(\Omega )} \lesssim \sup _{0\ne v_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } v_h,q_h)}{\Vert v_h\Vert _{W^{2,p}_h(\Omega )}} \lesssim \Vert w_h\Vert _{W^{2,p}_h(\Omega )}^{p-1}. \end{aligned}$$

Consequently, we find

$$\begin{aligned} \Vert w_h\Vert _{W^{2,p}_h(\Omega )}^p&\lesssim (w_h,\mathcal {L}_h^* q_h) = (\mathcal {L}_h w_h,q_h) \lesssim \Vert \mathcal {L}_h w_h\Vert _{L^p_h(\Omega )} \Vert q_h\Vert _{L^{p'}(\Omega )} \\&\lesssim \Vert \mathcal {L}_h w_h\Vert _{L^p_h(\Omega )} \Vert w_h\Vert _{W^{2,p}_h(\Omega )}^{p-1}. \end{aligned}$$

Dividing by $\Vert w_h\Vert _{W^{2,p}_h(\Omega )}^{p-1}$ now yields the desired result.$\square$

4.3 Well-Posedness and Error Estimates

The goals of this subsection are to establish the well-posedness for the IP-DG scheme (4.6) and to derive the optimal order error estimates in $W^{2,p}_h$-norm for the IP-DG solutions.

Theorem 4.5

Under the assumptions of Lemma 4.3, the IP-DG scheme (4.6) has a unique solution $u_h\in V_h$ such that

$$\begin{aligned} \Vert u_h\Vert _{W_h^{2,p}(\Omega )}\lesssim \Vert f\Vert _{L^p(\Omega )}. \end{aligned}$$

(4.39)

Proof

Since (4.6) is equivalent to a linear system, hence it suffices to prove the uniqueness. To show the uniqueness, we first prove (4.39).

Let $u_h\in V_h$ be a solution of (4.6), then from (4.37) and the definition of $\Vert \cdot \Vert _{L_h^p(\Omega )}$ we have

$$\begin{aligned} \Vert u_h\Vert _{W_h^{2,p}(\Omega )}\lesssim \Vert \mathcal {L}_h^{\varepsilon } u_h\Vert _{L_h^p(\Omega )} = \sup _{v_h\in V_h}\frac{(\mathcal {L}_h^{\varepsilon } u_h,v_h)}{\Vert v_h\Vert _{L^{p'}(\Omega )}} = \sup _{v_h\in V_h}\frac{(f,v_h)}{\Vert v_h\Vert _{L^{p'}(\Omega )}} \le \Vert f\Vert _{L^p(\Omega )}. \end{aligned}$$

Hence, (4.39) holds.

Suppose that $u_h^1,u_h^2\in V_h$ solve (4.6). Let $\tilde{u}_h = u_h^1-u_h^2$. Then by (4.39) we have

$$\begin{aligned} \Vert \tilde{u}_h \Vert _{W_h^{2,p}(\Omega )} \le \Vert 0\Vert _{L^p(\Omega )} = 0. \end{aligned}$$

Since $\tilde{u}_h \in V_h$ with $\Vert \tilde{u}_h \Vert _{W_h^{2,p}(\Omega )}=0$ we conclude that $\tilde{u}_h\in C^{1}(\Omega )$, $\tilde{u}_h\big |_{\partial \Omega }=0$, and $D_h^2\tilde{u}_h =0$ in $\Omega$. The only way this can happen is if $\tilde{u}_h =0$. Thus, the IP-DG solution must be unique. The proof is complete.$\square$

Next we show a Céa-type lemma for the IP-DG scheme, which immediately deduces the optimal order error estimates in the $W_h^{2,p}$-norm.

Theorem 4.6

Suppose that $h\le h_0$ and $k\ge 2$. Let $u\in W^{2,p}\cap W_0^{1,p}(\Omega )$ be the solution of problem (1.1) and $u_h\in V_h$ solve (4.6). Then

$$\begin{aligned} \Vert u-u_h\Vert _{W_h^{2,p}(\Omega )}\lesssim \inf _{w_h\in V_h}\Vert u-w_h\Vert _{W_h^{2,p}(\Omega )}. \end{aligned}$$

(4.40)

Moreover, if $u\in W^{s,p}(\Omega )$ for some $s\ge 2$, we have

$$\begin{aligned} \Vert u-u_h\Vert _{W_h^{2,p}(\Omega )}\lesssim h^{r-2}\Vert u\Vert _{W^{r,p}(\Omega )}, \quad r = \min \{s,k+1\}. \end{aligned}$$

(4.41)

Proof

By the consistency of $\mathcal {L}_h^{\varepsilon }$ we have the following Galerkin orthogonality:

$$\begin{aligned} \bigl (\mathcal {L}_h^{\varepsilon }(u-u_h),v_h \bigr ) = 0 \quad \forall v_h\in V_h. \end{aligned}$$

(4.42)

Let $w_h\in V_h$, Theorem 4.4, Lemma 4.2, (4.42), and the definition of $\Vert \cdot \Vert _{L_h^p(\Omega )}$ yield

$$\begin{aligned}&\Vert u_h-w_h\Vert _{W_h^{2,p}(\Omega )} \lesssim \Vert \mathcal {L}_h^{\varepsilon }(u_h-w_h)\Vert _{L_h^p(\Omega )} = \sup _{0\ne v_h\in V_h} \frac{(\mathcal {L}_h^{\varepsilon }(u_h-w_h),v_h)}{\Vert v_h\Vert _{L^{p'}(\Omega )}} \nonumber \\&\quad = \sup _{0\ne v_h\in V_h} \frac{(\mathcal {L}_h^{\varepsilon }(u-w_h),v_h)}{\Vert v_h\Vert _{L^{p'}(\Omega )}} = \Vert \mathcal {L}_h^{\varepsilon }(u-w_h)\Vert _{L_h^p(\Omega )} \lesssim \Vert u-w_h\Vert _{W_h^{2,p}(\Omega )}. \end{aligned}$$

(4.43)

Thus by (4.43) and the triangle inequality we get

$$\begin{aligned} \Vert u-u_h\Vert _{W_h^{2,p}(\Omega )} \le \Vert u-w_h\Vert _{W_h^{2,p}(\Omega )} + \Vert u_h-w_h\Vert _{W_h^{2,p}(\Omega )} \lesssim \Vert u-w_h\Vert _{W_h^{2,p}(\Omega )}. \end{aligned}$$

(4.44)

Taking the infimum on both sides over all $w_h\in V_h$ yields (4.40). Finally, (4.41) follows from taking $w_h = I_hu$ and using the finite element interpolation theory [3]. The proof is complete.$\square$

5 Numerical Experiments

In this section we present a number of 2-D numerical tests to verify our error estimate and to gauge the performance of our IP-DG methods. In particular, we shall compare our IP-DG methods to the related conforming finite element counterpart developed in [10]. Moreover, we shall also perform numerical tests which are not covered by our convergence theory, this includes the cases when the coefficient matrix is either discontinuous or degenerate.

5.1 Hölder Continuous Coefficient

For this test we take A as the following Hölder continuous matrix-valued function:

$$\begin{aligned} A(x) = \left[ \begin{array}{c c} |x|^{1/2}+1 &{} -|x|^{1/2} \\ -|x|^{1/2} &{} 5|x|^{1/2}+1 \end{array} \right] , \quad x\in \mathbb {R}^2. \end{aligned}$$

Let $\Omega =(-1/2,1/2)^2$ and choose f such that the exact solution is given by

$$\begin{aligned} u(x_1,x_2) = \sin (2\pi x_1)\sin (2\pi x_2)\exp (x_1\cos (x_2)), \end{aligned}$$

which has zero trace on the boundary.

Figure 1 shows the errors in the $L^2(\Omega ), W_h^{1,2}(\Omega ),$ and $W_h^{2,2}(\Omega )$ norms of both the symmetrically and incompletely induced methods. The convergence rates observed for the symmetrically induced method are

$$\begin{aligned} \Vert u-u_h\Vert _{L^2(\Omega )}&= \mathcal {O}(h^{k+1})\quad \text { for all } k,\\ \Vert \nabla _h(u-u_h)\Vert _{L^2(\Omega )}&= \mathcal {O}(h^{k}) \quad \text { for all } k, \\ \Vert D_h^2(u-u_h)\Vert _{L^2(\Omega )}&= \mathcal {O}(h^{k-1})\quad \text { for } k = 2,3. \end{aligned}$$

As expected, these convergence rates are optimal. However, for the incompletely induced method we find that the rate of convergence in the $L^2$-norm is sub-optimal for even degree polynomials and optimal with all other norms and degrees. This is expected since the incomplete scheme is sub-optimal even for smooth A [22].

Fig. 1

The $L^2$ (top), piecewise $H^1$ (middle), and piecewise $H^2$ (bottom) errors for both the symmetrically (left) and incompletely (right) induced schemes with polynomial degree $k=1,2,3$. $\gamma _e\equiv 100$ is used as the penalty parameter

Fig. 2

The piecewise $H^1$ (top) and piecewise $H^2$ (bottom) errors for both the symmetrically (left) and incompletely (right) induced schemes with polynomial degree $k=1,2,3$. $\gamma _e\equiv 1000$ is used as the penalty parameter

Fig. 3

The $L^2$ (top) and piecewise $H^1$ (bottom) errors for both the symmetrically (left) and incompletely (right) induced schemes with polynomial degree $k=1,2,3$. $\gamma _e\equiv 100$ is used as the penalty parameter

5.2 Uniformly Continuous Coefficients

In this test we take $\Omega =(0,1/2)^2$ and let

$$\begin{aligned} A(x) = \left[ \begin{array}{c c} -\dfrac{5}{\log (|x|)}+15 &{} 1 \\ 1 &{} -\dfrac{1}{\log (|x|)}+3 \end{array} \right] . \end{aligned}$$

f is chosen such that $u(x) = |x|^{7/4}$ is the exact solution. From [10] we see that the expected convergence rates are

$$\begin{aligned} \Vert \nabla _h(u-u_h)\Vert _{L^2(\Omega )}&= \mathcal {O}(h^{\min \{k,7/4-\delta \}})\quad \text { for all } k, \\ \Vert D_h^2(u-u_h)\Vert _{L^2(\Omega )}&= \mathcal {O}(h^{\min \{k,7/4-\delta \}-1})\quad \text { for } k = 2,3 \end{aligned}$$

for any $\delta >0$.

Figure 2 gives the computed results for both the symmetrically and incompletely induced schemes which match exactly the expected rates of convergence.

5.3 Degenerate Coefficients

In this test we take $\Omega =(0,1)^2$ and the matrix

$$\begin{aligned} A(x) = \frac{16}{9}\left[ \begin{array}{c c} x_1^{2/3} &{} -x_1^{1/3}x_2^{1/3} \\ -x_1^{1/3}x_2^{1/3} &{} x_2^{2/3} \end{array} \right] . \end{aligned}$$

$f=0$ and the exact solution $u(x) = x_1^{4/3}-x_2^{4/3}$. For an explanation for this example we refer to [10]. Note that $\det (A)=0$ for every $x\in \Omega$ so this PDE is degenerate everywhere and is outside the case considered in this paper. We also observe that $u\in W^{m,p}(\Omega )$ provided $(4-3m)p>-1$.

Figure 3 shows the $L^2$ and piecewise $H^1$ errors for both the symmetrically and incompletely induced methods. The numerical results suggest the following rates of convergence:

$$\begin{aligned} \Vert u-u_h\Vert _{L^2(\Omega )} = \mathcal {O}(h^{4/3}),\qquad \Vert \nabla _h(u-u_h)\Vert _{L^2(\Omega )} = \mathcal {O}(h^{5/6}) \end{aligned}$$

for $k=1,2,3$. These rates are consistent with the results of the related conforming finite element method given in [10].

5.4 $L^{\infty }$ Cordès Coefficients

Our next test is taken from [26, 28] where a different DG method and a weak Galerkin method were used to solve this problem. Let $\Omega =[-1,1]^2$ and

$$\begin{aligned} A(x) = \frac{16}{9}\left[ \begin{array}{c c} 2 &{} x_1 x_2/|x_1 x_2| \\ x_1 x_2/|x_1 x_2| &{} 2 \end{array} \right] . \end{aligned}$$

f is chosen so that the exact solution is $u(x) = x_1 x_2 \bigl (1-e^{1-|x_1|}\bigr )\bigl (1-e^{1-|x_2|}\bigr )$. Notice that the matrix A is discontinuous across the $x_1$-axis and $x_2$-axis, and it satisfies the Cordès condition. While our convergence theory does not apply to this example, we still compute the numerical solution on a uniform triangulation that has edges on all discontinuities of A. Due to its inconsistent behavior we list the $L^2$ error and convergence rates in Table 1. The following $H^1$ semi-norm rates are observed:

$$\begin{aligned} \Vert \nabla _h (u-u_h)\Vert _{L^2(\Omega )} = \mathcal {O}(h^{k})\quad \text{ for } k=1,2,3. \end{aligned}$$

Table 1 The $L^2$ errors and rates for the symmetrically induced method