Linearized Conservative Finite Element Methods for the Nernst–Planck–Poisson Equations

Abstract

The aim of this paper is to present and study new linearized conservative schemes with finite element approximations for the Nernst–Planck–Poisson equations. For the linearized backward Euler FEM, an optimal $L^2$ error estimate is provided almost unconditionally (i.e., when the mesh size h and time step $\tau$ are less than a small constant). Global mass conservation and electric energy decay of the schemes are also proved. Extension to second-order time discretizations is given. Numerical results in both two- and three-dimensional spaces are provided to confirm our theoretical analysis and show the optimal convergence, unconditional stability, global mass conservation and electric energy decay properties of the proposed schemes.

1 Introduction

In this paper, we study linearized conservative finite element methods for the Nernst–Planck–Poisson (NPP) equations

$$\begin{aligned}&\frac{\partial p}{\partial t} - \Delta p - \nabla \cdot (p \nabla \psi )= 0, \end{aligned}$$

(1.1)

$$\begin{aligned}&\frac{\partial n}{\partial t} - \Delta n + \nabla \cdot (n \nabla \psi )= 0, \end{aligned}$$

(1.2)

$$\begin{aligned}&- \Delta \psi = p-n, \end{aligned}$$

(1.3)

for ${\varvec{x}} \in \Omega$ and $t \in [0,T]$, where $\Omega$ is a bounded domain in $\mathbb {R}^d$, $d=2,3$. The boundary and initial conditions are defined by

$$\begin{aligned} \frac{\partial p}{\partial \mathbf {n}}= & {} 0, \quad \frac{\partial n}{\partial \mathbf {n}}=0, \quad \frac{\partial \psi }{\partial \mathbf {n}}=0, \quad \text {for }{\varvec{x}} \in \partial \Omega , t \in [0,T], \end{aligned}$$

(1.4)

$$\begin{aligned} p({\varvec{x}},0)= & {} p_0({\varvec{x}}), \quad n({\varvec{x}},0)=n_0({\varvec{x}}), \quad \text {for }{\varvec{x}} \in \Omega , \end{aligned}$$

(1.5)

where $\mathbf {n}$ is the unit outward normal vector on the domain boundary. In the NPP system (1.1)–(1.5), the first two unknowns p and n are the concentrations of the positively and negatively charged particles, respectively. The third unknown $\psi$ is the electric potential generated by the heterogeneous distribution of the positively and negatively charged particles. Subject to the homogeneous boundary condition (1.4), the existence of solutions to NPP equations require the following initial electroneutrality condition

$$\begin{aligned} \int _{\Omega } \, (p({\varvec{x}},0) - n({\varvec{x}},0)) \, \mathrm {d}{\varvec{x}} = 0. \end{aligned}$$

Since $\psi$ is unique up to a constant, here we only consider the zero mean value solution $\psi$ which satisfies $(\psi , 1)=0$, where $(\cdot , \cdot )$ denotes the standard $L^2$ inner product.

The NPP equations have been widely used in the study of transport of charged particles in biological membrane channels [17, 30, 31], semiconductors [4, 5, 10] and electrokinetic flows [26]. Theoretical analyses of the NPP equations can be found in [10, 20, 26]. The global existence and uniqueness of the solutions to the NPP system was proved in [10]. Numerical methods and analyses for the NPP system have been extensively studied, see [6, 9, 11, 14,15,16,17,18,19, 22, 25, 27, 31]. On the regular domain, there are several excellent works with finite difference discretizations, see [9, 11, 16, 19]. For the one-dimensional NPP equations, Flavell et al. [9] studied a nonlinear finite difference scheme with the mass conservation and total free energy (also called entropy in [22]) decay properties. Positivity of the numerical solutions in [9] can be achieved under the mesh ratio constriction $\tau < C h^2$, where $\tau$ and h are the time step and grid size, respectively. For more general geometries, finite element method (FEM) is much more attractive [3, 29]. In [22], Prohl and Markus proposed two nonlinear schemes, which preserve electric energy decay and entropy decay properties, respectively. Fixed point inner iterations were used at each time step for these schemes and convergence of the numerical solutions was also proved in [22]. Later, numerical methods for the NPP system (1.1)–(1.5) coupled with Navier–Stokes equations were investigated in [23]. Recently, Sun et al. [27] analyzed a fully nonlinear Crank–Nicolson FEM for the NPP equations, where a Picard’s linearization is used in the inner iteration. A sub-optimal error estimate was obtained in [27]. However, a mesh ratio restriction $\tau ^2 \le h^{\frac{d}{2}}$ (d is the dimension) is needed in their proof due to the use of inverse inequality and mathematical induction argument (see formula (5.10) in [27]).

For nonlinear parabolic problems, it is well known that linearized schemes which only need to solve a linear system at each time step are much more efficient, e.g., see [13, 28]. It should be remarked that all the schemes in [9, 22, 27] are nonlinear, where the motivation for using implicit schemes is to preserve most of the properties of the NPP system. The strong coupling of the concentrations p and n with the electric potential $\psi$ in the NPP system (1.1)–(1.5) poses a significant challenge for the design of linearized schemes which preserve mass conservation and energy decay. Furthermore, the analysis of linearized schemes is more difficult compared with the nonlinear ones. Working in this direction, He and Pan proposed a linearized finite difference scheme in [11], which preserves the mass conservation and electric energy decay. However, convergence rate and electric energy decay properties of the scheme were shown only numerically. No error analysis was done in [11].

In this paper, we propose and analyze linearized conservative FEMs for the NPP system (1.1)–(1.5). The proposed method is linear so that one only need to solve a linear system at each time step. Our main contributions are twofold. Firstly, for a linearized backward Euler FEM, an optimal $L^2$ error estimate of $O(\tau +h^{r+1})$ is proved almost unconditionally (i.e., no mesh ratio restriction condition is needed). Secondly and more importantly, although linearization is used, our schemes still preserve mass conservation and electric energy decay properties, which are crucial features of the NPP system (1.1)–(1.5).

The rest of this paper is organized as follows. In Sect. 2, we present a linearized backward Euler FEM, the main results on error estimate and two conservative properties (global mass conservation and electric energy conservation) of the proposed scheme. In Sect. 3, we prove an optimal $L^2$ error estimate without any restriction on mesh ratio between the time step $\tau$ and the mesh size h and the two conservative properties. In Sect. 4, we provide two second-order linearized schemes with Crank–Nicolson and BDF2 discretizations, respectively. Numerical examples for both two- and three-dimensional models are given in Sect. 5 to confirm our theoretical analyses and the efficiency of the proposed methods. Conclusions and discussions are given in the final section.

2 A Linearized Backward Euler FEM and Main Results

Before presenting the schemes, we clarify some conventional notations. For integer $k \ge 0$ and $1 \le p \le \infty$, let $W^{k,p}(\Omega )$ be the Sobolev space with the norm

$$\begin{aligned} \Vert u \Vert _{W^{k,p}}=\left\{ \begin{array}{ll} \biggl (\displaystyle \sum _{|\beta |\le k}\int _\Omega |D^\beta u|^p\,\mathrm{d}{\varvec{x}}\biggl )^\frac{1}{p}, &{}\quad \text {for }1 \le p < \infty , \\ \displaystyle \sum _{|\beta | \le k}\mathrm{ess\,sup}_{\Omega }|D^{\beta } u|, &{}\quad \text {for }p=\infty , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} D^\beta =\frac{\partial ^{|\beta |}}{\partial x_1^{\beta _1}\cdots \partial x_d^{\beta _d}}, \end{aligned}$$

for the multi-index $\beta =(\beta _1,\ldots ,\beta _d)$, $\beta _1\ge 0$, $\ldots$, $\beta _d\ge 0$, and $|\beta |=\beta _1+\cdots +\beta _d$. When $p=2$ we also note $H^k(\Omega ) := W^{k,2}(\Omega )$.

Then the weak solution (see also [10, 26]) to the NPP system (1.1)–(1.5) is to find $p, n, \psi \in L^2(0,T; H^1(\Omega ))$ with $\frac{\partial p}{\partial t}, \frac{\partial n}{\partial t} \in L^2(0,T; H^{-1}(\Omega ))$ and $(\psi ,1)=0$, such that

$$\begin{aligned}&\left( \frac{\partial p}{\partial t}, \xi _p \right) + (\nabla p, \nabla \xi _p) + (p \nabla \psi , \nabla \xi _p)= 0 , \quad \forall \, \xi _p \in H^1(\Omega ), \end{aligned}$$

(2.1)

$$\begin{aligned}&\left( \frac{\partial n}{\partial t}, \xi _n \right) + (\nabla n, \nabla \xi _n) - (n \nabla \psi , \nabla \xi _n) = 0, \quad \forall \, \xi _n \in H^1(\Omega ), \end{aligned}$$

(2.2)

$$\begin{aligned}&(\nabla \psi , \nabla \xi _\psi ) = (p-n, \xi _\psi ), \quad \forall \, \xi _\psi \in H^1(\Omega ), \end{aligned}$$

(2.3)

for a.e. $t \in (0,T]$ and $p({\varvec{x}},0)=p_0({\varvec{x}})$ and $n({\varvec{x}},0)=n_0({\varvec{x}})$.

To introduce the FEM, we simply assume that $\Omega$ is a convex polygon (or polyhedron). Let ${\mathcal {T}}_{h}$ be a quasi-uniform partition of $\Omega$ with $\Omega = \cup _{e} \Omega _{e}$, we denote the mesh size by $h=\max _{\Omega _{e} \in {\mathcal {T}}_{h}} \{ \mathrm {diam} \Omega _{e}\}$. For a given partition ${\mathcal {T}}_{h}$, we denote ${{V}_{h}}^{r}$ be the r-th order finite element subspaces of ${H}^{1}(\Omega )$. Let $\{t_j \}_{j=0}^J$ be a uniform partition in the time direction with $t_j = j \tau$, $T = J \tau$ and denote

$$\begin{aligned} u^j = u(x,t_j). \end{aligned}$$

For any sequence of functions $\{ u^j \}_{j=0}^{J}$, we define

$$\begin{aligned} D_\tau u^{j+1} = \frac{u^{j+1}-u^j}{\tau }, \quad \text {for }j=0, 1, \ldots , J-1. \end{aligned}$$

Now we are ready to introduce the linearized backward Euler scheme with Galerkin finite element approximations for the NPP equations (1.1)–(1.5). For $j=0,1,\ldots ,J-1$, find $(P_h^{j+1}$, $N_h^{j+1}, \Psi _h^{j+1}) \in [V^r_h]^3$, with $(\Psi _h^{j+1} \, ,1) = 0$, such that $\forall \ (\xi _p, \xi _n, \xi _\psi ) \in [V^r_h]^3$

$$\begin{aligned}&(D_\tau P_h^{j+1}, \xi _p) + (\nabla {P}_h^{j+1}, \nabla \xi _p) + ({P}_h^{j} \nabla {\Psi }_h^{j+1}, \nabla \xi _p) = 0, \end{aligned}$$

(2.4)

$$\begin{aligned}&(D_\tau N_h^{j+1}, \xi _n) + (\nabla {N}_h^{j+1},\nabla \xi _n) - ({N}_h^{j} \nabla {\Psi }_h^{j+1},\nabla \xi _n) = 0, \end{aligned}$$

(2.5)

$$\begin{aligned}&(\nabla \Psi _h^{j+1}, \nabla \xi _\psi ) = (P_h^{j+1}-N_h^{j+1},\xi _\psi ). \end{aligned}$$

(2.6)

At the initial step, we take $P_h^0 = R_h p^0$, $N_h^0 = R_h n^0$, where $R_h$ is a Ritz projector defined in (3.1)–(3.3).

In the above scheme, we have used standard linearizations $({P}_h^{j} \nabla {\Psi }_h^{j+1}, \, \nabla \xi _p)$ for $({p}\nabla {\psi }, \, \nabla \xi _p)$ and $({N}_h^{j} \nabla {\Psi }_h^{j+1}, \, \nabla \xi _n)$ for $({n}\nabla {\psi }, \, \nabla \xi _n)$, respectively. In fact, the above FEM equations (2.4)–(2.6) can be written in matrix form as

$$\begin{aligned} \left[ \begin{array}{ccc} \frac{1}{\tau } \, {\mathsf {M}} + {\mathsf {K}} &{}\quad {0} &{}\quad {{\mathsf {K}}}( P_h^{j} ) \\ {0} &{}\quad \frac{1}{\tau } \, {\mathsf {M}} + {\mathsf {K}} &{}\quad -{{\mathsf {K}}}( N_h^{j} ) \\ -{{\mathsf {M}}} &{}\quad {{\mathsf {M}}} &{}\quad {\mathsf {K}} \end{array} \right] \left[ \begin{array}{c} P_h^{j+1} \\ N_h^{j+1} \\ \Psi _h^{j+1} \end{array} \right] \, = \, {\varvec{F}}^j \end{aligned}$$

with $(\Psi _h^{j+1},1)=0$. In terms of basis functions $\{\phi \}_{i=1}^{N_h}$, the matrices ${\mathsf {M}}$ and ${\mathsf {K}}$ are generated by

$$\begin{aligned} \begin{array}{lll} {\mathsf {M}}_{ij}=(\phi _j,\phi _i), \quad &{}&{} {\mathsf {K}}_{ij}=(\nabla \phi _j,\nabla \phi _i)\, \nonumber \\ {{\mathsf {K}}}( P_h^{j_0} )_{ij}=(P_h^{j_0} \nabla \phi _j,\nabla \phi _i), &{}&{} -{{\mathsf {K}}}( N_h^{j_0} )_{ij}=-(N_h^{j_0} \nabla \phi _j,\nabla \phi _i)\,. \end{array} \end{aligned}$$

We shall note that the FEM equation (2.6) of $\Psi _h^{j+1}$ is a pure Neumann problem. As we focus on analyses of the numerical methods for NPP system in this paper, we refer to the seminal paper [2] for a detailed discussion of FEMs for pure Neumann problems.

In the rest part of this paper, if r-th order Lagrange FEM is used, we assume that the exact solution of the NPP equations (1.1)–(1.5) exists and satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \Vert p\Vert _{L^\infty (0,T;H^{r+1})} +\Vert p_t\Vert _{L^\infty (0,T;H^{r+1})}+\Vert p_{tt}\Vert _{L^2(0,T;H^{1})} \le C, \\ \Vert n\Vert _{L^\infty (0,T;H^{r+1})} +\Vert n_t\Vert _{L^\infty (0,T;H^{r+1})}+\Vert n_{tt}\Vert _{L^2(0,T;H^{1})} \le C, \\ \Vert \psi \Vert _{L^\infty (0,T;H^{r+1})} +\Vert \psi _t\Vert _{L^\infty (0,T;H^{r+1})}+\Vert \psi _{tt}\Vert _{L^2(0,T;H^{1})} \le C. \end{array} \right. \end{aligned}$$

(2.7)

It should be noted that the above regularity assumption might be not optimal. In this paper, we only emphasize on the analyses of numerical methods.

We present our main results on error estimate in the following theorem.

Theorem 2.1

Suppose that the NPP system (1.1)–(1.5) has a unique solution $(p, n, \psi )$ satisfying (2.7). Then the linearized backward Euler finite element system (2.4)–(2.6) admits a unique solution $(P^{j}_h, \, N^{j}_h, \, \Psi ^{j}_h)$, for $j=1, \ldots , J$, and there exist two positive constants $\tau _0$ and $h_0$ such that when $\tau < \tau _0$ and $h \le h_0$

$$\begin{aligned} \max _{0 \le j \le J} \, \, \left( \, \, \Vert P^j_h - p^j\Vert _{L^2} +\Vert N^j_h - n^j\Vert _{L^2} +\Vert \Psi ^{j}_h -\psi ^{j}\Vert _{L^2} \, \, \right) \le C_0(\tau + h^{r+1}) , \end{aligned}$$

(2.8)

where $C_0$ is a positive constant, independent of j, h and $\tau$.

Corollary 2.1

The linearized backward Euler FEM (2.4)–(2.6) fulfills two important physical properties of the NPP system. They are:

(i):

Global Mass Conservation: The FEM solutions $\{P_h^j\}_{j=0}^J$ and $\{N_h^j\}_{j=0}^J$ satisfy

$$\begin{aligned} \int _{\Omega } P_h^j \mathrm {d}{\varvec{x}} = M_{p}, \quad \int _{\Omega } N_h^j \mathrm {d}{\varvec{x}} = M_{n}, \end{aligned}$$

(2.9)

where $M_p = \int _{\Omega }p_0 \mathrm {d}{\varvec{x}}$ and $M_n = \int _{\Omega } n_0 \mathrm {d}{\varvec{x}}$ denote the total masses of positively and negatively charged particles, respectively.

(ii):

Electric Energy Decay: If we define a discrete electric energy by

$$\begin{aligned} {\mathcal {E}}^j = \frac{1}{2} \left\| \nabla \Psi _h^j \right\| _{L^2}^2, \end{aligned}$$

then the FEM solutions $\{(P_h^j, N_h^j, \Psi _h^j)\}_{j=0}^J$ satisfy a discrete energy law

$$\begin{aligned} {\mathcal {E}}^{j+1}&+ \frac{1}{2} \left\| \nabla \Psi _h^{j+1}- \nabla \Psi _h^j \right\| _{L^2}^2 \nonumber \\&+ \tau \left( \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \int _{\Omega }({P}_h^{j}+{N}_h^{j}) \left| \nabla {\Psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \right) = {\mathcal {E}}^j \end{aligned}$$

(2.10)

for $j=0$, 1, $\ldots$, $J-1$. Furthermore, we will show that

$$\begin{aligned} {\mathcal {E}}^{j+1} \le {\mathcal {E}}^j, \quad \text {for }j=0, 1, \ldots , J-1, \end{aligned}$$

(2.11)

when $\tau$ and h are smaller that a constant, see Sect. 3.

For simplicity, through out this paper, we denote by C a generic positive constant and by $\epsilon$ a generic small positive constant, which are independent of j, h, $\tau$ and $C_0$ in the above theorem.

3 Proof of the Main Results

In this section we prove the results in Theorem 2.1 and Corollary 2.1 for the linearized backward Euler FEM (2.4)–(2.6). We provide in Sect. 3.1 an optimal $L^2$ error estimate. In Sect. 3.2, we prove the global mass conservation and electric energy decay properties of the proposed scheme.

We define $R_{h}$ to be the following Ritz projection operator: For given $t \in [0,T]$, find $(R_{h}p, R_{h}n, R_{h}\psi ) \in [V_h^r]^3$ with $(R_{h}\psi , 1)=0$, such that $\forall \ (\xi _p, \xi _n, \xi _{\psi }) \in [V_h^r]^3$

$$\begin{aligned}&\left( \nabla ( R_{h}p - p ), \nabla \xi _p \right) +\left( p\nabla ( R_{h}\psi - \psi ), \nabla \xi _p \right) + (R_{h}p- p, \xi _p ) = 0, \end{aligned}$$

(3.1)

$$\begin{aligned}&\left( \nabla ( R_{h}n - n ), \nabla \xi _n \right) -\left( n\nabla ( R_{h}\psi - \psi ), \nabla \xi _n \right) + (R_{h}n- n, \xi _n ) = 0, \end{aligned}$$

(3.2)

$$\begin{aligned}&\left( \nabla ( R_{h}\psi - \psi ), \nabla \xi _{\psi } \right) - (R_{h}p- p, \xi _{\psi } ) + (R_{h}n- n, \xi _{\psi } ) = 0. \end{aligned}$$

(3.3)

We define the projection error by

$$\begin{aligned}&\theta _{p} = R_{h}p - p, \quad \theta _{n} = R_{h}n - n, \quad \theta _{\psi } = R_{h} \psi - \psi . \end{aligned}$$

Then, by standard finite element theory and the regularity assumption (2.7), we have

$$\begin{aligned} {\Vert \theta _{p} \Vert }_{L^{2}} + h {\Vert \theta _{p} \Vert }_{H^{1}}\le & {} C h^{r+1}, \end{aligned}$$

(3.4)

$$\begin{aligned} {\Vert \theta _{n} \Vert }_{L^{2}} + h {\Vert \theta _{n} \Vert }_{H^{1}}\le & {} C h^{r+1}, \end{aligned}$$

(3.5)

$$\begin{aligned} {\Vert \theta _{\psi } \Vert }_{L^{2}} + h {\Vert \theta _{\psi } \Vert }_{H^{1}}\le & {} C h^{r+1}, \end{aligned}$$

(3.6)

$$\begin{aligned} {\Vert (\theta _{p})_{t} \Vert }_{L^{2}} + h {\Vert (\theta _{p})_{t} \Vert }_{H^{1}}\le & {} C h^{r+1}, \end{aligned}$$

(3.7)

$$\begin{aligned} {\Vert (\theta _{n})_{t} \Vert }_{L^{2}} + h {\Vert (\theta _{n})_{t} \Vert }_{H^{1}}\le & {} C h^{r+1}. \end{aligned}$$

(3.8)

With the projection error estimates (3.4)–(3.8), we only need to analyze the following error functions

$$\begin{aligned}&e_{p}^j = P_h^j - R_{h}p^j, \quad e_{n}^j = N_h^j - R_{h}n^j, \quad e_{\psi }^j = \Psi _h^j - R_{h}\psi ^j,\quad \text {for }j=0, 1, \ldots , J. \end{aligned}$$

(3.9)

We present the estimate for the error functions $\{(e_p^{j}, e_n^{j}, e_{\psi }^{j} )\}_{j=0}^J$ in Sect. 3.1.

We present the Gagliardo–Nirenberg inequality, discrete Gronwall’s inequality and a regularity theory of elliptic equations in the following three lemmas which will be frequently used in our proofs.

Lemma 3.1

Gagliardo–Nirenberg inequality (see [21]): Let u be a function defined on $\Omega$ and $\partial ^{s} u$ be any partial derivative of u of order s, then

$$\begin{aligned} \Vert \partial ^{j} u\Vert _{L^p} \le C \Vert \partial ^{m} u\Vert _{L^r}^{a} \, \Vert u\Vert _{L^q}^{1-a} + C \Vert u\Vert _{L^q}, \end{aligned}$$

for $0 \le j < m$ and $\frac{j}{m} \le a \le 1$ with

$$\begin{aligned} \frac{1}{p} = \frac{j}{d} + a \left( \frac{1}{r} - \frac{m}{d}\right) +(1-a) \frac{1}{q} \, , \end{aligned}$$

except $1< r < \infty$ and $m-j-\frac{d}{r}$ is a non-negative integer, in which case the above estimate holds only for $\frac{j}{m} \le a < 1$.

Lemma 3.2

Discrete Gronwall’s inequality [12] : Let $\tau$, B and $a_{k}$, $b_{k}$, $c_{k}$, $\gamma _{k}$, for integers $k \ge 0$, be non-negative numbers such that

$$\begin{aligned} a_j + \tau \sum _{k=0}^j b_{k} \le \tau \sum _{k=0}^j \gamma _{k} a_{k} + \tau \sum _{k=0}^j c_{k} + B \, , \quad \mathrm {for } \quad j \ge 0 \, , \end{aligned}$$

suppose that $\tau \gamma _{k} < 1$, for all k, and set $\sigma _{k}=(1-\tau \gamma _{k})^{-1}$. Then

$$\begin{aligned} a_j + \tau \sum _{k=0}^j b_{k} \le \exp \left( \tau \sum _{k=0}^j \gamma _{k} \sigma _{k}\right) \left( \tau \sum _{k=0}^j c_{k} + B \right) \, , \quad \mathrm {for } \quad j \ge 0 \, . \end{aligned}$$

Lemma 3.3

Suppose that $\Omega \in \mathbb {R}^3$ be a bounded and smooth domain and $u \in H^k(\Omega )$ is a solution of

$$\begin{aligned} -\Delta u = f, \quad {\varvec{x}} \in \Omega ,\quad \frac{\partial u }{\partial \mathbf {n}}=0, \quad {\varvec{x}} \in \partial \Omega , \end{aligned}$$

where $(f,1)=0$. Then the following estimate holds for $1< p < \infty$

$$\begin{aligned} \Vert u \Vert _{W^{2,p}} \le C \Vert f \Vert _{L^{p}}\, . \end{aligned}$$

We refer to [7, 8] for the detailed proof of the above lemma.

3.1 Proof of Theorem 2.1

Proof

Since the coefficient matrices for $P_h^{j}$, $N_h^{j}$ and $\Psi _h^{j}$ are invertible. It is clear that the FEM system admits a unique solution.

Here we prove that the following inequality holds for $j=0$, 1, $\ldots$, $J-1$

$$\begin{aligned} \Vert e_p^{j+1} \Vert _{L^2}^2 + \Vert e_n^{j+1} \Vert _{L^2}^2 + \sum _{m=0}^{j} \left( \Vert e_p^{m+1} \Vert _{H^1}^2 + \Vert e_n^{m+1} \Vert _{H^1}^2 \right) \le \frac{C_0}{2} (\tau ^2 + h^{2r+2}) \end{aligned}$$

(3.10)

by mathematical induction. We assume that (3.10) holds for $j \le k-1$. We shall find a constant $C_0$, which is independent of $\tau$ and h such that (3.10) hold for $j \le k$.

By the weak formulation (2.1)–(2.3) and the Ritz projection (3.1)–(3.3), we have

$$\begin{aligned}&(D_\tau p^{j+1}, \xi _p) + (\nabla {R}_h p^{j+1}, \nabla \xi _p) + ({p}^{j} \nabla R_h{\psi }^{j+1}, \nabla \xi _p) = {\mathcal {R}}_p^{j+1}(\xi _p), \quad \forall \, \xi _p \in V_h^r, \end{aligned}$$

(3.11)

$$\begin{aligned}&(D_\tau n^{j+1}, \xi _n) + (\nabla {R}_h n^{j+1},\nabla \xi _n) - ({n}^{j} \nabla R_h{\psi }^{j+1}, \nabla \xi _n) = {\mathcal {R}}_n^{j+1}(\xi _n), \quad \forall \, \xi _n \in V_h^r, \end{aligned}$$

(3.12)

$$\begin{aligned}&(\nabla R_h\psi ^{j+1},\nabla \xi _\psi ) = (R_h p^{j+1}-R_h n^{j+1}, \xi _\psi ), \quad \forall \, \xi _\psi \in V_h^r, \end{aligned}$$

(3.13)

where the two truncation terms are defined by

$$\begin{aligned} {\mathcal {R}}_p^{j+1} (\xi _p) = \big (D_\tau p^{j+1} - \frac{\partial p}{\partial t}\Big |_{t_{j+1}}, \xi _p\big ) + \big (({p}^{j}-{p}^{j+1}) \nabla {\psi }^{j+1}, \nabla \xi _p\big )-\big (\theta ^{j+1}_{p},\xi _p\big ), \end{aligned}$$

and

$$\begin{aligned} {\mathcal {R}}_n^{j+1} (\xi _n) = \big (D_\tau n^{j+1} - \frac{\partial n}{\partial t}\Big |_{t_{j+1}}, \xi _n\big ) - \big (({n}^{j}-{n}^{j+1}) \nabla {\psi }^{j+1}, \nabla \xi _n\big )-\big (\theta ^{j+1}_{n},\xi _n\big ). \end{aligned}$$

From (3.11)–(3.12) and the FEM system (2.4)–(2.5), the error equations satisfy

$$\begin{aligned} (D_{\tau }{e_p^{j+1}}, \, \xi _p) + (\nabla {e}_p^{j+1}, \, \nabla \xi _p)= & {} -(D_\tau \theta _p^{j+1}, \, \xi _p) - ({P}_h^{j} \nabla {\Psi }_h^{j+1} - {p}^{j} \nabla R_h{\psi }^{j+1}, \, \nabla \xi _p) \nonumber \\&- {\mathcal {R}}_p^{j+1} (\xi _p), \quad \forall \, \xi _p \in V_h^r, \end{aligned}$$

(3.14)

$$\begin{aligned} (D_{\tau }{e_n^{j+1}}, \, \xi _n) + (\nabla {e}_n^{j+1}, \, \nabla \xi _n)= & {} -(D_\tau \theta _n^{j+1}, \, \xi _n) + ({N}_h^{j} \nabla {\Psi }_h^{j+1} - {n}^{j} \nabla R_h{\psi }^{j+1}, \, \nabla \xi _p) \nonumber \\&- {\mathcal {R}}_n^{j+1} (\xi _n), \quad \forall \, \xi _n \in V_h^r, \end{aligned}$$

(3.15)

$$\begin{aligned} (\nabla {e}_{\psi }^{j+1}, \, \nabla \xi _{\psi })= & {} (e_p^{j+1}-e_n^{j+1}, \, \nabla \xi _{\psi }) , \quad \forall \, \xi _{\psi } \in V_h^r. \end{aligned}$$

(3.16)

By taking $\xi _p = {e}_p^{j+1}$ in (3.14) and $\xi _n = {e}_n^{j+1}$ in (3.15), respectively, we have

$$\begin{aligned}&\frac{1}{2}D_\tau \big (\Vert {e}_p^{j+1}\Vert _{L^2}^2+\Vert {e}_n^{j+1}\Vert _{L^2}^2\big ) + \left( \Vert \nabla {e}_p^{j+1}\Vert _{L^2}^2 + \Vert \nabla {e}_n^{j+1}\Vert _{L^2}^2 \right) \nonumber \\&\quad \le -( D_\tau \theta _p^{j+1}, \, {e}_p^{j+1}) -( D_\tau \theta _n^{j+1}, \, {e}_n^{j+1}) - {\mathcal {R}}_p^{j+1} ({e}_p^{j+1}) - {\mathcal {R}}_n^{j+1} ({e}_n^{j+1}) \nonumber \\&\quad - ({P}_h^{j} \nabla {\Psi }_h^{j+1} - {p}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_p^{j+1}) + ({N}_h^{j} \nabla {\Psi }_h^{j+1} - {n}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_n^{j+1}) \end{aligned}$$

(3.17)

By the projection error estimates (3.4)–(3.8) and the regularity assumption (2.7), it is easy to see that

$$\begin{aligned}&-( D_\tau \theta _p^{j+1}, \, {e}_p^{j+1}) \le C \Vert {e}_p^{j+1}\Vert _{L^2}^2 + Ch^{2r+2} \,, \end{aligned}$$

(3.18)

$$\begin{aligned}&\quad -( D_\tau \theta _n^{j+1}, \, {e}_n^{j+1}) \le C \Vert {e}_n^{j+1}\Vert _{L^2}^2 + Ch^{2r+2} \,, \end{aligned}$$

(3.19)

$$\begin{aligned}&\quad -{\mathcal {R}}_p^{j+1} ({e}_p^{j+1}) \le C\Vert {e}_n^{j+1} \Vert _{L^2}^2+\epsilon \Vert \nabla {e}_p^{j+1} \Vert _{L^2}^2 + \epsilon ^{-1} C \tau ^2+Ch^{2r+2} \, , \end{aligned}$$

(3.20)

$$\begin{aligned}&\quad -{\mathcal {R}}_n^{j+1} ({e}_n^{j+1}) \le C\Vert {e}_n^{j+1} \Vert _{L^2}^2+\epsilon \Vert \nabla {e}_n^{j+1} \Vert _{L^2}^2 + \epsilon ^{-1} C \tau ^2+Ch^{2r+2} \, . \end{aligned}$$

(3.21)

Taking $\xi _{\psi }=e_{\psi }^{j+1}$ in (3.16) gives

$$\begin{aligned} \Vert \nabla e_{\psi }^{j+1}\Vert _{L^2} \le C(\Vert {e}_p^{j+1}\Vert _{L^2}+\Vert {e}_n^{j+1}\Vert _{L^2}) \,. \end{aligned}$$

(3.22)

Moreover, it is easy to see that the FEM equation (2.6) for ${\Psi }_h^{j+1}$ can be interpreted as the FEM solution to the following Poisson equation

$$\begin{aligned} - \Delta \varphi = {P}_h^{j+1} - {N}_h^{j+1} \, , \end{aligned}$$

(3.23)

with homogeneous Neumann boundary condition. From $W^{1,p}$-estimate of the FEMs [3, 24], we have

$$\begin{aligned} \Vert \Psi _h^{j+1} \Vert _{W^{1,\infty }} \le C \Vert \varphi \Vert _{W^{1,\infty }} \le C \Vert \varphi \Vert _{W^{2,4}} \le C \Vert {P}_h^{j+1} - {N}_h^{j+1}\Vert _{L^4} \, , \end{aligned}$$

(3.24)

where we have used the Gagliardo–Nirenberg inequality in Lemma 3.1 and the regularity estimate for elliptic equations in Lemma 3.3.

Now we turn to estimate the two nonlinear terms $- ({P}_h^{j} \nabla {\Psi }_h^{j+1} - {p}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_p^{j+1})$ and $({N}_h^{j} \nabla {\Psi }_h^{j+1} - {n}^{j} \nabla R_h{\psi }^{j+1}, \nabla {e}_n^{j+1})$. By noting (3.22) and (3.24), we have

$$\begin{aligned}&- ({P}_h^{j} \nabla {\Psi }_h^{j+1} - {p}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_p^{j+1}) \nonumber \\&\quad = - ((e_{p}^{j}+\theta _{p}^{j}) \nabla {\Psi }_h^{j+1} \,, \nabla {e}_p^{j+1}) - ({p}^{j} \nabla e_{\psi }^{j+1} \,, \nabla {e}_p^{j+1}) \nonumber \\&\quad \le \Vert e_{p}^{j}+\theta _{p}^{j}\Vert _{L^2} \Vert \nabla {\Psi }_h^{j+1}\Vert _{L^{\infty }} \Vert \nabla {e}_p^{j+1}\Vert _{L^2} + C\Vert \nabla e_{\psi }^{j+1}\Vert _{L^2} \Vert \nabla {e}_p^{j+1}\Vert _{L^2} \nonumber \\&\quad \le \Vert e_{p}^{j}+\theta _{p}^{j}\Vert _{L^2} \Vert P_h^{j+1} - N_h^{j+1}\Vert _{L^4} \Vert \nabla {e}_p^{j+1}\Vert _{L^2} + C(\Vert e_{p}^{j+1}\Vert _{L^2}+\Vert e_{n}^{j+1}\Vert _{L^2}) \Vert \nabla {e}_p^{j+1}\Vert _{L^2} \nonumber \\&\quad \le (\Vert e_{p}^{j}\Vert _{L^2} + Ch^{r+1}) (\Vert e_p^{j+1}\Vert _{L^4} + \Vert e_n^{j+1}\Vert _{L^4}) \Vert \nabla {e}_p^{j+1}\Vert _{L^2} \nonumber \\&\qquad + \epsilon \Vert \nabla {e}_p^{j+1}\Vert _{L^2}^2 + \epsilon ^{-1} C (\Vert e_{p}^{j+1}\Vert _{L^2}^2 + \Vert e_{n}^{j+1}\Vert _{L^2}^2 + \Vert e_{p}^{j}\Vert _{L^2}^2 + h^{2r+2}) \nonumber \\&\quad \le \Vert e_{p}^{j}\Vert _{L^2} (\Vert e_p^{j+1}\Vert _{L^4} + \Vert e_n^{j+1}\Vert _{L^4}) \Vert \nabla {e}_p^{j+1}\Vert _{L^2} \nonumber \\&\qquad + \epsilon (\Vert \nabla {e}_p^{j+1}\Vert _{L^2}^2 + \Vert \nabla {e}_n^{j+1}\Vert _{L^2}^2 ) + \epsilon ^{-1} C (\Vert e_{p}^{j+1}\Vert _{L^2}^2 + \Vert e_{n}^{j+1}\Vert _{L^2}^2 + \Vert e_{p}^{j}\Vert _{L^2}^2 + h^{2r+2}), \nonumber \\ \end{aligned}$$

(3.25)

where we shall require that $Ch^{r+1} \le \epsilon$. By the induction assumption that (3.10) hold for $j \le k-1$, we have

$$\begin{aligned}&\Vert e_{p}^{j}\Vert _{L^2} (\Vert e_p^{j+1}\Vert _{L^4} + \Vert e_n^{j+1}\Vert _{L^4}) \Vert \nabla {e}_p^{j+1}\Vert _{L^2} \nonumber \\&\quad \le C \sqrt{\frac{C_0}{2}(\tau ^2 + h^{2r+2})} (\Vert e_{p}^{j+1}\Vert _{H^1}+\Vert e_{n}^{j+1}\Vert _{H^1}) \Vert {e}_p^{j+1}\Vert _{H^1} \nonumber \\&\quad \le \epsilon (\Vert e_{p}^{j+1}\Vert _{H^1}^2 + \Vert e_{n}^{j+1}\Vert _{H^1}^2) \quad \text {for }j \le k \, , \end{aligned}$$

(3.26)

where $\tau$ and h satisfy that $C \sqrt{\frac{C_0}{2}(\tau ^2 + h^{2r+2})} \le \epsilon$. Substituting (3.26) into (3.25) yields

$$\begin{aligned}&- ({P}_h^{j} \nabla {\Psi }_h^{j+1} - {p}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_p^{j+1}) \nonumber \\&\quad \le \epsilon (\Vert e_{p}^{j+1}\Vert _{H^1}^2 + \Vert e_{n}^{j+1}\Vert _{H^1}^2) + \epsilon ^{-1} C (\Vert e_{p}^{j+1}\Vert _{L^2}^2 + \Vert e_{n}^{j+1}\Vert _{L^2}^2 + \Vert e_{p}^{j}\Vert _{L^2}^2 + h^{2r+2}). \end{aligned}$$

(3.27)

Similarly, we can derive an estimate for $({N}_h^{j} \nabla {\Psi }_h^{j+1} - {n}^{j} \nabla R_h{\psi }^{j+1} \,, \nabla {e}_n^{j+1})$ as below

$$\begin{aligned}&\left( {N}_h^{j} \nabla {\Psi }_h^{j+1} - {n}^{j} \nabla R_h{\psi }^{j+1}, \nabla {e}_n^{j+1}\right) \nonumber \\&\quad \le \epsilon \left( \Vert e_{p}^{j+1}\Vert _{H^1}^2 + \Vert e_{n}^{j+1}\Vert _{H^1}^2\right) + \epsilon ^{-1} C \left( \Vert e_{p}^{j+1}\Vert _{L^2}^2 + \Vert e_{n}^{j+1}\Vert _{L^2}^2 + \Vert e_{n}^{j}\Vert _{L^2}^2 + h^{2r+2}\right) . \end{aligned}$$

(3.28)

Finally, substituting estimates (3.18)–(3.21), (3.27), and (3.28) into (3.17), we arrive at

$$\begin{aligned}&\frac{1}{2}D_\tau \left( \Vert {e}_p^{j+1}\Vert _{L^2}^2+\Vert {e}_n^{j+1}\Vert _{L^2}^2\right) + \left( \Vert \nabla {e}_p^{j+1}\Vert _{L^2}^2 + \Vert \nabla {e}_n^{j+1}\Vert _{L^2}^2 \right) \\&\quad \le \epsilon \left( \Vert e_{p}^{j+1}\Vert _{H^1}^2 + \Vert e_{n}^{j+1}\Vert _{H^1}^2\right) \\&\qquad + \epsilon ^{-1}C \left( \Vert {e}_p^{j+1}\Vert _{L^2}^2 + \Vert {e}_n^{j+1}\Vert _{L^2}^2 + \Vert {e}_p^{j}\Vert _{L^2}^2 + \Vert {e}_n^{j}\Vert _{L^2}^2 + \tau ^2 + h^{2r+2}\right) . \end{aligned}$$

Then, we chose a small $\epsilon$ and sum up the last inequality for the index $j=0$, 1, $\ldots$, k to derive that

$$\begin{aligned}&\Vert e_p^{j+1} \Vert _{L^2}^2 + \Vert e_n^{j+1} \Vert _{L^2}^2 + \tau \sum _{m=0}^{j} \left( \Vert e_p^{m+1} \Vert _{H^1}^2 + \Vert e_n^{m+1} \Vert _{H^1}^2 \right) \\&\quad \le \tau C\sum _{m=0}^{j} \left( \Vert e_p^{j+1} \Vert _{L^2}^2 + \Vert e_n^{j+1} \Vert _{L^2}^2 \right) + C \left( \tau ^2 + h^{2r+2}\right) \,. \end{aligned}$$

By the discrete Gronwall’s lemma, when $C \tau \le \frac{1}{2}$, we have

$$\begin{aligned}&\Vert e_p^{j+1} \Vert _{L^2}^2 + \Vert e_n^{j+1} \Vert _{L^2}^2 + \tau \sum _{m=0}^{j+1} \left( \Vert e_p^{m+1} \Vert _{H^1}^2 + \Vert e_n^{m+1} \Vert _{H^1}^2 \right) \nonumber \\&\quad \le C\exp \left( \frac{TC}{ 1- C\tau }\right) \left( \tau ^2 + h^{2r+2}\right) \nonumber \\&\quad \le C\exp (2{TC}) \left( \tau ^2 + h^{2r+2}\right) \,. \end{aligned}$$

(3.29)

Thus, (3.10) holds for $j = k$, if we take $C_0 \ge 2C\exp (2{TC})$. We complete the induction.

Theorem (2.1) is proved by combining (3.10), the projection error estimates (3.4)–(3.8) and (3.22). $\square$

3.2 Proof of Corollary 2.1

Proof

We will first discuss the global mass conservation property of the proposed linearized backward Euler FEM (2.4)–(2.6). By setting the test functions $(\xi _p, \xi _n, \xi _\psi ) = (1,1,0)$, the FEM equation (2.4)–(2.6) gives

$$\begin{aligned} (D_\tau P_h^{j+1}, \, 1)= 0 , \quad (D_\tau N_h^{j+1}, \, 1)= 0 , \end{aligned}$$

(3.30)

which directly indicates the global mass conservation equality (2.9).

We now turn to (2.10) which shows the electric energy decay property of the proposed scheme. We recall that ${\mathcal {E}}^j = \frac{1}{2} \Vert \nabla \Psi _h^j \Vert _{L^2}^2$. Taking $D_{\tau }$ to (2.6) yields

$$\begin{aligned}&(D_{\tau } \nabla \Psi _h^{j+1}, \, \nabla \xi _\psi ) = (D_{\tau }(P_h^{j+1}-N_h^{j+1}), \, \xi _\psi ), \end{aligned}$$

(3.31)

then taking $\xi _\psi =\Psi _h^{j+1}$ into (3.31) further gives

$$\begin{aligned}&{\mathcal {E}}^{j+1} + \frac{1}{2} \left\| \nabla \Psi _h^{j+1}- \nabla \Psi _h^j \right\| _{L^2}^2 -{\mathcal {E}}^{j} \\&\quad = \tau (D_{\tau }(P_h^{j+1}-N_h^{j+1}), \, \Psi _h^{j+1}) \\&\quad = -\tau (\nabla {P}_h^{j+1} - \nabla {N}_h^{j+1}, \, \nabla \Psi _h^{j+1}) - \tau \int _{\Omega }({P}_h^{j}+{N}_h^{j}) \left| \nabla {\psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \\&\quad = - \tau \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 - \tau \int _{\Omega }({P}_h^{j}+{N}_h^{j}) \left| \nabla {\psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}}. \end{aligned}$$

Therefore, (2.10) is proved.

At last, we show ${\mathcal {E}}^{j+1} \le {\mathcal {E}}^{j}$. By the error estimate in Theorem (2.1) and requiring that $C\sqrt{C_0}(\tau + h^{r+1}) \le \frac{1}{2}$, we have

$$\begin{aligned}&\left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \int _{\Omega }({P}_h^{j}+{N}_h^{j}) \left| \nabla {\Psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \nonumber \\&\quad = \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \left\| \sqrt{p^{j}+{n}^{j}} \nabla {\Psi }_h^{j+1} \right\| _{L^2}^2 \nonumber \\&\qquad + \int _{\Omega }({P}_h^{j}-p^{j}+{N}_h^{j}-{n}^{j}) \left| \nabla {\Psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \nonumber \\&\quad \ge \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \left\| \sqrt{p^{j}+{n}^{j}} \nabla {\Psi }_h^{j+1} \right\| _{L^2}^2 \nonumber \\&\qquad - (\Vert p^{j}-{P}_h^{j}\Vert _{L^2}+\Vert n^{j}-{N}_h^{j}\Vert _{L^2}) \left\| \nabla {\Psi }_h^{j+1} \right\| _{L^6}^2 \nonumber \\&\quad \ge \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \left\| \sqrt{p^{j}+{n}^{j}} \nabla {\Psi }_h^{j+1} \right\| _{L^2}^2 \nonumber \\&\qquad - C\sqrt{C_0}(\tau + h^{r+1}) \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 \nonumber \\&\quad \ge \frac{1}{2} \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}^2 + \left\| \sqrt{p^{j}+{n}^{j}} \nabla {\Psi }_h^{j+1} \right\| _{L^2}^2 \nonumber \\&\quad \ge 0 \end{aligned}$$

(3.32)

where we have used the following result from (3.23) and Lemma 3.3

$$\begin{aligned} \left\| \nabla {\Psi }_h^{j+1} \right\| _{L^6} \le C \left\| \nabla {\varphi }^{j+1} \right\| _{L^6} \le C \left\| {\varphi }^{j+1} \right\| _{H^2} \le C \left\| {P}_h^{j+1} - {N}_h^{j+1}\right\| _{L^2}. \end{aligned}$$

We proved (2.11). $\square$

4 Extension to Second-order Time discretizations: Crank–Nicolson and BDF2 FEMs

In this section, we provide two linearized second-order time discretizations for the NPP equations (1.1)–(1.5). The first scheme is Crank–Nicolson based and the second one is a backward differential formula (BDF2) type scheme. The two time discretizations are both second-order. As before, linearizations are used for the nonlinear terms and at each time step, one only needs to solve a linear system. An unconditionally optimal $L^2$-norm error estimate of $O(\tau ^2 + h^{r+1})$ can be proved by similar analysis in Sect. 3. Thus, the proof is omitted here. We note that these two schemes are mass preserving and hold an electric energy decay property.

4.1 A Linearized Crank–Nicolson FEM

Besides notations from Sect. 2, we shall also define

$$\begin{aligned} {\overline{u}}^{j+1} = \frac{u^{j+1}+u^j}{2}, \quad {\widehat{u}}^{j+1} = \frac{3u^{j}-u^{j-1}}{2}, \end{aligned}$$

for any sequence of functions $\{ u^j \}_{j=0}^J$.

We introduce a linearized Crank–Nicolson FEM for the NPP equations (1.1)–(1.5) as below. For $j=1,2,\ldots ,J$, find $(P_h^{j+1}$, $N_h^{j+1}, \Psi _h^{j+1}) \in [V_h]^3$, with $(\Psi _h^{j+1} \, ,1) = 0$, such that $\forall \ (\xi _p, \xi _n, \xi _\psi ) \in [V_h]^3$

$$\begin{aligned}&\Big (D_{\tau } P_h^{j+1}, \xi _p \Big ) + \Big (\nabla \overline{{P}}_h^{j+1}, \nabla \xi _p \Big ) + \Big ({\widehat{P}}_h^{j+1} \nabla {\overline{\Psi }}_h^{j+1}, \nabla \xi _p \Big ) = 0 , \end{aligned}$$

(4.1)

$$\begin{aligned}&\Big (D_{\tau } N_h^{j+1},\xi _n \Big ) + \Big (\nabla {\overline{N}}_h^{j+1},\nabla \xi _n \Big ) - \Big ({\widehat{N}}_h^{j+1} \nabla {\overline{\Psi }}_h^{j+1},\nabla \xi _n \Big ) = 0, \end{aligned}$$

(4.2)

$$\begin{aligned}&\Big (\nabla \Psi _h^{j+1},\nabla \xi _\psi \Big ) = \left( P_h^{j+1}-N_h^{j+1},\xi _\psi \right) , \end{aligned}$$

(4.3)

where $(P_h^{1}$, $N_h^{1}, \Psi _h^{1})$ is provided by the backward Euler FEM (2.4)–(2.6).

Corollary 4.1

The linearized Crank–Nicolson FEM (4.1)–(4.3) holds for the following two properties:

(i):

Global Mass Conservation: The FEM solutions $\{P_h^j\}_{j=0}^J$ and $\{N_h^j\}_{j=0}^J$ satisfy

$$\begin{aligned} \int _{\Omega } P_h^j \mathrm {d}{\varvec{x}} = M_{p}, \quad \int _{\Omega } N_h^j \mathrm {d}{\varvec{x}} = M_{n}, \end{aligned}$$

(4.4)

where $M_p$ and $M_n$ denote the total masses of positively and negatively charged particles, respectively.

(ii):

Electric Energy Decay: For the FEM solution $\{(P_h^j, N_h^j, \Psi _h^j)\}_{j=0}^J$ , if we define a discrete electric energy by

$$\begin{aligned} {\mathcal {E}}^j = \frac{1}{2} \left\| \nabla \Psi _h^j \right\| _{L^2}^2, \end{aligned}$$

then a discrete energy law holds for $j=1,2,\ldots ,J-1$

$$\begin{aligned} {\mathcal {E}}^{j+1} + \tau \left( \left\| {\overline{P}}_h^{j+1} - {\overline{N}}_h^{j+1} \right\| _{L^2}^2 + \int _{\Omega }( ({\widehat{P}}_h^{j+1}+{\widehat{N}}_h^{j+1}) \left| \nabla {\overline{\Psi }}_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \right) = {\mathcal {E}}^j. \end{aligned}$$

(4.5)

4.2 A Linearized BDF2 FEM Scheme

BDF schemes are popular methods for solving stiff ordinary differential equations, which have also been widely used in the numerical solutions of partial differential equations, e.g., see [29]. Below is a linearized BDF2 FEM for the NPP equations (1.1)–(1.5).

For $j=1,2,\ldots ,J$, find $(P_h^{j+1}$, $N_h^{j+1}, \Psi _h^{j+1}) \in [V_h]^3$, with $(\Psi _h^{j+1},1) = 0$, such that $\forall (\xi _p, \xi _n, \xi _\psi ) \in [V_h]^3$

$$\begin{aligned}&\Big (\frac{3P_h^{j+1} - 4P_h^{j} + P_h^{j-1}}{2 \tau } , \, \xi _p \Big ) + \Big (\nabla {P}_h^{j+1}, \, \nabla \xi _p \Big ) + \Big ({\widetilde{P}}_h^{j+1} \nabla {\Psi }_h^{j+1}, \, \nabla \xi _p \Big ) = 0 \, , \end{aligned}$$

(4.6)

$$\begin{aligned}&\Big (\frac{3 N_h^{j+1} - 4 N_h^{j} + N_h^{j-1}}{2 \tau } , \, \xi _n \Big ) + \Big (\nabla {N}_h^{j+1}, \, \nabla \xi _n \Big ) - \Big ({\widetilde{N}}_h^{j+1} \nabla {\Psi }_h^{j+1}, \, \nabla \xi _n \Big ) = 0 \, , \end{aligned}$$

(4.7)

$$\begin{aligned}&\Big ( \nabla \Psi _h^{j+1}, \, \nabla \xi _\psi \Big ) = \left( P_h^{j+1}-N_h^{j+1}, \, \xi _\psi \right) , \end{aligned}$$

(4.8)

where we have used the standard extrapolation ${\widetilde{P}}_h^{j+1} = 2 {P}_h^{j} - {P}_h^{j-1}$ and ${\widetilde{N}}_h^{j+1} = 2 {N}_h^{j} - {N}_h^{j-1}$. Here $(P_h^{1}$, $N_h^{1}, \Psi _h^{1})$ can be also provided by the linearized backward Euler FEM (2.4)–(2.6).

Corollary 4.2

The linearized BDF2 FEM (4.6)–(4.8) hold the following two properties

(i):

Global Mass Conservation: The FEM solutions $\{P_h^j\}_{j=0}^J$ and $\{N_h^j\}_{j=0}^J$ of the linearized BDF2 FEM (4.6)–(4.8) satisfy

$$\begin{aligned} \int _{\Omega } P_h^j \mathrm {d}{\varvec{x}} = M_{p}, \quad \int _{\Omega } N_h^j \mathrm {d}{\varvec{x}} = M_{n}, \end{aligned}$$

(4.9)

where $M_p$ and $M_n$ denote the total masses of positively and negatively charged particles, respectively.

(i):

Electric Energy Decay: For the FEM solutions $\{(P_h^j, N_h^j, \Psi _h^j)\}_{j=0}^J$ , if we define a discrete electric energy by

$$\begin{aligned} {\mathcal {E}}^{j+1} = \frac{1}{4} \left( \left\| \nabla \Psi _h^{j+1} \right\| _{L^2}^2 +\left\| 2\nabla \Psi _h^{j} - \nabla \Psi _h^{j-1} \right\| _{L^2}^2 \right) , \quad \hbox {for} j=1 , \ldots , J-1, \end{aligned}$$

then a discrete energy law holds

$$\begin{aligned}&{\mathcal {E}}^{j+1} + \frac{1}{4} \left\| \nabla (\Psi _h^{j+1} -2\Psi _h^{j} + \Psi _h^{j-1})\right\| _{L^2}^2 \nonumber \\&\qquad + \tau \left( \left\| {P}_h^{j+1} - {N}_h^{j+1} \right\| _{L^2}^2 + \int _{\Omega }( ({\widetilde{P}}_h^{j+1}+{\widetilde{N}}_h^{j+1}) \left| \nabla {\psi }_h^{j+1}\right| ^2 \mathrm {d}{\varvec{x}} \right) = {\mathcal {E}}^{j} \, . \end{aligned}$$

(4.10)

5 Numerical Results

In this section, we provide some numerical examples in both two and three dimensional spaces to confirm our theoretical analyses. The computations are performed with free software FEniCS [1].

5.1 Two-dimensional Numerical Results

Example 5.1

We rewrite the NPP equations (2.4)–(2.5) as follow

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial p}{\partial t} - \Delta p - \nabla \cdot (p \nabla \psi )= f_1, \\ \frac{\partial n}{\partial t} - \Delta n + \nabla \cdot (n \nabla \psi )= f_2, \\ - \Delta \psi = p-n. \end{array} \right. \end{aligned}$$

(5.1)

We test the linearized backward Euler FEM (2.4)–(2.6) on the unit square $\Omega = (0,1)^2$. A uniform triangular partition with $M+1$ nodes in each direction is used. An illustration with $M=8$ is shown in Fig. 1. Here we can see that $h=\frac{\sqrt{2}}{M}$.

Fig. 1

A uniform triangulation on the unit square with $M=8$

In our computations, we take

$$\begin{aligned} \left\{ \begin{array}{l} p = 2 \pi ^2 \exp (t) \cos (\pi x) \cos (\pi y) \\ n = 4 \pi ^2 t^3 \cos (2 \pi x) \\ \psi = \exp (t) \cos (\pi x) \cos (\pi y) - t^3 \cos (2 \pi x) \end{array} \right. \end{aligned}$$

to be the exact solution to (5.1). Correspondingly, the right-hand side function $f_1$ and $f_2$ are determined by the above exact solution. We set the final time $T=1.0$.

To confirm our error estimate in Theorem 2.1, we choose $\tau = \frac{1}{M^{r+1}}$ for the r-th order FE method, where $r=1,2,$ and 3. From Theorem 2.1, we have $(r+1)$-th order convergence for the $L^2$-norm errors. We present the $L^2$-norm errors in Table 1. From Table 1, it is easy to see that the convergence rate for the linearized backward Euler FEM (2.4)–(2.6) is optimal.

Table 1 $L^2$-norm errors for the linearized backward Euler FEM (2.4)–(2.6) on the unit square. (Example 5.1)

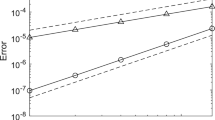
To show the unconditional convergence of the proposed scheme, we use a linear element method to solve (5.1) with three different time steps $\tau =0.1$, 0.05, 0.01 on gradually refined meshes with $M= 2^{k+2}$, $k=1, 2,\ldots ,5$. The $L^2$-norm errors are plot in Fig. 2. From Fig. 2, we can see that for a fixed $\tau$, when refining the mesh gradually, the $L^2$-norm errors asymptotically converge to a small constant, i.e., the temporal error which is $O(\tau )$. Thus, it is clear that the linearized backward Euler FEM is unconditionally convergent (stable) and no mesh ratio restriction is needed in the computation.

Fig. 2

$L^2$-norm errors of the linearized backward Euler FEM (2.4)–(2.6) on the unit square. (Example 5.1)

Example 5.2

In this example, we test the performance of the linearized Crank–Nicolson FEM (4.1)–(4.3) and the linearized BDF2 FEM (4.6)–(4.8). We use the two methods to solve (5.1) with the same exact solution in Example 5.1. As both schemes are three-step, we compute the first step numerical solutions $(P_h^{1}$, $N_h^{1}, \Psi _h^{1})$ by the backward Euler FEM (2.4)–(2.6). We set $\tau = \frac{1}{M}$, $\frac{1}{M^{3/2}}$, and $\frac{1}{M^2}$ for the linear, quadratic, and cubic FEMs, respectively. In this example, we also set the final time $T=1$. The $L^2$-norm errors of the numerical solutions for these two methods are $O(\tau ^2 + h^{r+1})$. We present the $L^2$-norm errors for the linearized Crank–Nicolson FEM (4.1)–(4.3) in Table 2 and the linearized BDF2 FEM (4.6)–(4.8) in Table 3, respectively. Table 2 and 3 show clearly that the $L^2$-norm errors of the linearized Crank–Nicolson FEM (4.1)–(4.3) and the linearized BDF2 FEM (4.6)–(4.8) are optimal.

Table 2 $L^2$-norm errors for the linearized Crank–Nicolson FEM (4.1)–(4.3) on the unit square. (Example 5.2)

Table 3 $L^2$-norm errors for the BDF2 FEM (4.6)–(4.8) on the unit square. (Example 5.2)

To show the unconditional convergence of these two second-order methods, we use the two schemes with a linear element method to solve (5.1) with three different time steps $\tau =0.1$, 0.05, 0.01 on gradually refined meshes with $M= 2^{k+3}$, $k=1,2,\ldots ,5$. The $L^2$-norm errors are shown in Fig. 3 and 4.

From Figs. 3 and 4, we can see that for a fixed $\tau$, when refining the mesh gradually, the $L^2$-norm errors converge to a small constant of $O(\tau ^2)$, which shows clearly that the proposed two second-order schemes are unconditionally convergent (stable).

Fig. 3

$L^2$-norm errors of the linearized Crank–Nicolson FEM (4.1)–(4.3).(Example 5.2)

Fig. 4

$L^2$-norm errors of the linearized BDF2 FEM (4.6)–(4.8).(Example 5.2)

Example 5.3

This example is taken from [22], where Prohl and Schmuck used a nonlinear FEM to solve the NPP equations. For comparison, we test the performance of the linearized backward Euler FEM (2.4)–(2.6) with the same settings in [22].

In our computations, we set the initial values

$$\begin{aligned} p_0= & {} \left\{ \begin{array}{rl} 1, &{} (0,1)^2\backslash \left\{ (0,0.75)\times (0,1) \cup (0.75,1)\times (0, \frac{11}{20}) \right\} , \\ 10^{-6}, &{} \text {else}, \end{array} \right. \\ n_0= & {} \left\{ \begin{array}{rl} 1, &{} (0,1)^2\backslash \left\{ (0,0.75)\times (0,1) \cup (0.75,1)\times (\frac{9}{20},1) \right\} , \\ 10^{-6}, &{} \text {else}. \end{array} \right. \end{aligned}$$

A quadratic element method with $M={32}$ and $\tau = 10^{-3}$ is used. In Fig. 5, We show the snapshots of the numerical solutions $P_h$, $N_h$, and $\Psi _h$ at time $T = 0.002$, 0.02, and 0.1. The plots in Fig. 5 agree well with results in [22].

Fig. 5

Snapshots of $P_h$, $N_h$ and $\Psi _h$ at time $T = 0.002$, 0.02, and 0.1. The linearized backward Euler FEM (2.4)–(2.6) with a linear element method with $M={32}$ and $\tau = 10^{-3}$ is used. (Example 5.3)

In addition, Corollary 2.1 tells that the linearized backward Euler FEM (2.4)–(2.6) admits global mass conservation and electric energy decay properties. We plot the global masses $\{(P_h^j,1)\}_{j=0}^J$ and $\{(N_h^j,1)\}_{j=0}^J$ and the electric energy ${\mathcal {E}}^j = \frac{1}{2} \Vert \nabla \Psi _h^j \Vert _{L^2}^2$ in Fig. 6. From Fig. 6, it is easy to see the mass conservation of $P_h$ and $N_h$ and the decreasing of the electric energy ${\mathcal {E}}(t)$ as time evolves.

Fig. 6

The evolution of global masses and electric energy computed by linearized backward Euler FEM (2.4)–(2.6) with a quadratic element method on the mesh with $M=32$ and $\tau =10^{-3}$. (Example 5.3)

5.2 Three-dimensional Numerical Results

In this subsection, we provide numerical results in three dimensional space.

Example 5.4

In this example, We test the performance of the linearized backward Euler FEM (2.4)–(2.6) on the unit cube $\Omega = (0,1)^{3}$. A uniform tetrahedral partition with $M+1$ nodes is used in each direction, where the mesh size $h = \frac{\sqrt{3}}{M}$.

In our computations, we take

$$\begin{aligned} \left\{ \begin{array}{l} p = 3 \pi ^2 \exp (-t) \cos (\pi x) \cos (\pi y) \cos (\pi z) \\ n = \pi ^2 t^3 \cos (\pi z) \\ \psi = \exp (-t) \cos (\pi x) \cos (\pi y) \cos (\pi z) - t^3 \cos (\pi z) \end{array} \right. \end{aligned}$$

to be the exact solution to (5.1).

Correspondingly, the right-hand side function $f_1$ and $f_2$ are determined by the above exact solution. We set the final time $T=1$. To confirm the error estimate in Theorem 2.1, we choose $\tau = \frac{1}{M^{r+1}}$ for the r-th order Lagrange FEM with $r = 1$ and 2. Therefore, from Theorem 2.1 we have $(r+1)$-th order convergence for the $L^2$-norm errors. We present in Table 4 the $L^2$-norm errors of the numerical solutions. From Table 4, it is clear that the convergence rate of the linearized backward Euler FEM (2.4)–(2.6) is optimal.

Table 4 $L^2$-norm errors for the linearize backward Euler FEM (2.4)–(2.6) on the unit cube. (Example 5.4)

To show the unconditional convergence of the linearized backward Euler FEM (2.4)–(2.6) in three-dimensional space, we use a linear element to solve (5.1) with three different time steps $\tau =0.1$, 0.05, 0.01 on gradually refined meshes with $M= 10$, 20, 40, 60. The $L^2$-norm errors are plot in Fig. 7. Similar to the two-dimensional case, we can see that when refining the mesh gradually, for a fixed $\tau$ the $L^2$-norm errors asymptotically converge to a small constant, i.e., the temporal error which is $O(\tau )$. Figure 7 shows clearly that the linearized backward Euler FEM is unconditionally convergent in three-dimensional space.

Fig. 7

$L^2$-norm errors of the linearized backward Euler FEM (2.4)–(2.6) on the unit cube.(Example 5.4)

Example 5.5

In the final example, we test the performances of the linearized Crank–Nicolson FEM (4.1)–(4.3) and the BDF2 FEM (4.6)–(4.6) in three-dimensional space. We use these two methods to solve (5.1) with the same exact solution in Example 5.4.

In our computation we set $\tau = \frac{1}{M^{{(r+1)}/{2}}}$ for the r-th order Lagrange FEM, where $r = 1$ and 2. Therefore, we have the $(r+1)$-th order convergence for the the $L^2$-norm errors. We present the $L^2$-norm errors for the Crank–Nicolson FEM (4.1)–(4.3) in Table 5 and the $L^2$-norm errors for the BDF2 FEM (4.6)–(4.8) in Table 6, respectively. It is easy to see that the convergence rates of these two methods are optimal in three-dimensional space.

Table 5 $L^2$-norm errors for the Crank–Nicolson FEM (4.1)–(4.3) on the unit cube. (Example 5.5)

Table 6 $L^2$-norm errors for the BDF2 FEM (4.6)–(4.8) on the unit cube. (Example 5.5)

6 Conclusions and Discussions

We have presented linearized conservative FEMs for the NPP equations. For a linearized backward Euler FEM, an optimal error estimate is proved almost unconditionally (i.e., we only require that $\tau$ and h are smaller than a constant). Global mass conservation and electric energy decay properties of the scheme are also proved. Numerical results for both two- and three-dimensional problems confirm our theoretical analyses and show clearly the efficiency and unconditional stability of the proposed schemes. The schemes proposed in this paper can be extended to the multi-ions. The technique presented in this paper can be applied to analyze higher order time discretizations for other nonlinear parabolic equations.

Finally, we point out that the current schemes have no evidence to satisfy the total free energy (entropy) decay property. Constructing the linearized FEM for the NPP equations which can satisfy total free energy decay property will be our future work.