Nonlinear Advection–Diffusion–Reaction Phenomena Involved in the Evolution and Pumping of Oil in Open Sea: Modeling, Numerical Simulation and Validation Considering the Prestige and Oleg Naydenov Oil Spill Cases

Abstract

The main goal of this article is to improve upon a previous model used to simulate the evolution of oil spots in the open sea and the effect of a skimmer ship pumping oil out from the spots. The concentration of the pollutant is subject to the effects of wind and sea currents, diffusion, and the pumping action of a skimmer (i.e., cleaning) ship that follows a pre-assigned trajectory. This implies that the mathematical model is of the advection–diffusion–reaction type. A drawback of our previous model was that diffusion was propagating with infinite velocity; in this article, we use an improved model relying on a nonlinear diffusion term, implying that diffusion propagates with finite velocity. To reduce numerical diffusion when approximating the advection part of the model, we consider second order discretization schemes with nonlinear flux limiters. We consider also absorbing boundary conditions to insure accurate results near the boundary. To reduce CPU time we use an operator-splitting scheme for the time discretization. Finally, we also introduce the modeling of coastlines and dynamic sources of pollutant. The novel approach we advocate in this article is validated by comparing our numerical results with real life measurements from the Oleg Naydenov and the Prestige oil spills, which took place in Spain in 2015 and 2002, respectively.

1 Introduction

Oil spill contamination in open sea has been at the origin of some of the worst environmental disasters in history (see [27, 35]). The ecological and economical impact of such hazards are generally important and should be controlled as quickly as possible. For instance in 1989, the Exxon Valdez tanker sank near Alaska, spilling more than 10 million gallons of crude oil [29]. It was estimated that more than 50 % of the sea birds and otters of the area were killed. The cost of depolluting the contaminated zone has been estimated to US$ 287 million.

One of the major cleaning techniques [14] for these hazards is the use of skimmer ships [6]. Those ships use various pumps distributed along its waterline to suck the oil from the surface of the water directly into storage units. Those vessels move inside the oil spots to clean them as quickly as possible.

In previous works, we have been interested in improving this process. To do so, we first introduce a numerical model to simulate the effect the skimmer ship on the evolution of the oil spill [2]. This model, based on a first order finite volume approximation of an advection–diffusion–reaction equation [15, 19], took into consideration: the motion of oil spots resulting from the combined effects of diffusion and of transport by wind and sea currents, and also the physical phenomena associated with the action of the pumping ship, assuming that it follows a pre-assigned trajectory. In a second article [16], we have designed the trajectory of a skimmer ship in order to maximize the amount of recovered oil in open sea or near coastline. Finally, we have validated our approach by considering numerical experiments based on real oil spill data [17]. Actually, the model and methodology we used in these previous studies require various modifications and improvements, such as:

• Use a diffusion model leading to diffusion propagating at finite speed.

• Reduce the numerical diffusion resulting from the discretization of the advection term in the model.

• Reduce the computational complexity.

• Use boundary conditions with better absorbing properties.

• Modeling of coastlines.

• Consider dynamic sources of pollutant.

These various issues will be addressed in this article. We introduce in particular a nonlinear diffusion term to obtain a diffusion propagating at finite speed. Next, we discuss an absorbing boundary condition [3, 12, 23], to handle those situations when the oil is exiting the computational domain. Then, to reduce numerical diffusion, we use second order numerical schemes for the discretization of the advection terms of the model. Finally, we discuss the use of splitting and un-split schemes and their impact on the computational complexity.

To validate this new methodology, we compare the numerical results with measurements from the Prestige [25] and the Oleg Naydenov [21, 24] oil spill hazards, which occurred in Spain in 2002 and 2015, respectively.

The content of this article is as follows: In Sect. 2, we present the old and new mathematical models we consider to simulate the motion of the oil spots and the action of the pumping ship. In Sect. 3, we discuss the numerical methods considered for these simulations. Finally, in Sect. 4, we describe the numerical experiments and discuss their results, including comparisons with measurements from the two real life disasters mentioned above.

2 Mathematical Models

2.1 Generalities

We consider a spatial domain ${\varOmega }\subset (x_{\mathrm {min}},x_{\mathrm {max}}) \times (y_{\mathrm {min}},y_{\mathrm {max}}) \subset \mathrm {\mathbb {R}}^{2}$, large enough to ensure that the pollutant will stay in ${\varOmega }$ during the corresponding fixed time interval (0, T). We denote by $\partial {\varOmega }_{o}$ the boundary of ${\varOmega }$ in the open sea and by $\partial {\varOmega }_{c}$ the boundary in the coast (land domains are not included in ${\varOmega }$).

We assume that the density of the pollutant is smaller than the one of the sea water (so that it remains at the top); we assume also that the layer-thickness of the pollutant is a known constant that we will denote by h [27]. We denote by c(x, t) the pollutant superficial concentration, measured as the volume of pollutant per surface area at $\{x, t\} \in {\varOmega }\times (0, T)$. We assume that the evolution of c is governed by five main effects, namely:

• The diffusion of the pollutant.

• The wind induced transport.

• The sea current induced transport.

• The transport and sink resulting from the pumping.

• The spill of oil due to a source of pollutant.

Moreover, we assume that the pumping ship and the source of pollutant follow trajectories $\gamma$ and $\zeta \in C^0([0,T],\mathbb {R}^2)$, respectively, such that $\gamma (t)$ and $\zeta (t) \in {\varOmega },$ for all $t \in [0,T]$.

From a practical point of view, a skimmer ship is composed of multiple pumps, cleaning the water along the vessel waterline. For simplicity (as in the numerical experiments discussed in Sect. 4), we neglect the length of the ship compared to the size of ${\varOmega }$. We suppose also that there is only one pump, which is a circle of radius $R_p$, pumping the fluid with velocity Q in the radial direction. Finally, the source of pollutant is taken as a circle of radius $R_s$, spilling an amount of oil S(t) per unit of time.

2.2 The Previous Model

In [2], a simple model, assuming linear diffusion and homogeneous boundary conditions was considered. More precisely, we proposed the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{lll} &{}\displaystyle \dfrac{\partial c}{\partial t}-\varvec{\nabla } \cdot \mathbf {d} \varvec{\nabla } c +\varvec{\nabla } \cdot c \; \mathbf {(w+s)} + \varvec{\nabla } \cdot c \; \mathbf {p} =\\ &{}\quad -\,\displaystyle \dfrac{2Q}{R_p}\;c \displaystyle \chi _{B(\gamma (t),R_p)}, \quad \hbox {in } {\varOmega }\times (0, T), \\ &{}c = 0, \quad \qquad \qquad \qquad \qquad \hbox {on } \partial {\varOmega }\times (0, T), \\ &{}c(0) = c_0, \end{array} \right. \end{aligned}$$

(1)

where:

• c(t) denotes the function $x \rightarrow c(x,t)$.

• $B(\gamma (t),R_p)$ is the ball of center $\gamma (t)$ and radius $R_p$.

• $\mathbf {p}(\xi ,t) = \left\{ \begin{array}{ll} \displaystyle Q R_p \dfrac{\overrightarrow{\gamma (t)\xi }}{\left( \Vert \overrightarrow{\gamma (t)\xi }\Vert _2\right) ^2}, &{}\quad \hbox {if } \xi \in {\varOmega }\backslash B(\gamma (t),R_p),\\ 0, &{}\quad \hbox {if } \xi \in B(\gamma (t),R_p), \end{array} \right.$ see details in [2].

• $\chi _{B(\gamma (t),R_p)}(\xi ) = \left\{ \begin{array}{ll} 0, &{}\quad \hbox {if } \xi \in {\varOmega }\backslash B(\gamma (t),R_p),\\ 1, &{}\quad \hbox {if } \xi \in B(\gamma (t),R_p). \end{array} \right.$

• The function $c_0$ is the initial superficial concentration; we assume that $c_0$ has a compact support in ${\varOmega }$.

• $\mathbf {d}= \left( \begin{array}{cc} d_{1} &{} 0 \\ 0 &{} d_{2} \end{array} \right)$, $d_1, d_2$ (both > 0) being the diffusion coefficients in the west–east and south–north directions.

• $\mathbf {w}=[w_1,w_2]$ is the horizontal component of the wind velocity multiplied by a suitable drag factor and $\mathbf {s}=[s_1,s_2]$ is the surface velocity of the sea.

2.3 An Improved Model

Six important drawbacks of the model described in Section 2.2 are: (i) the diffusion propagates at infinite speed, (ii) if the advection terms in (1) are discretized using a first order up-winding scheme, artificial diffusion is generated, (iii) the combined effects of the wind and sea velocities on the oil spots can be larger than the effect of the wind or sea alone, (iv) coastlines were omitted, (v) source of pollutant were not considered, (v) the Dirichlet boundary condition ($c = 0$) makes sense only as long as the pollutant does not reach the boundary of ${\varOmega }$ (or if only small quantities reach that boundary).

In this article, we have improved the model developed in [2] (namely the model given by (1)). To do so, we have : (i) replaced the linear diffusion term by a ${ nonlinear}$ one, (ii) replaced the boundary condition $c = 0$ on $\partial {\varOmega }\times (0, T)$ by one with better $absorbing properties$, (iii) included the possibility of considering coastline, (iv) included a dynamic source of contaminant, and (v) using a more realistic transport term. The new model is the following

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \dfrac{\partial c}{\partial t}-\varvec{\nabla } \cdot \dfrac{c^{\kappa }}{c^{\kappa }_\mathrm{ref}} \mathbf {d} \varvec{\nabla } c +{{\varvec{\nabla } \cdot c \; \mathbf {o} }} &{}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \varvec{\nabla } \cdot c \; \mathbf {p}_\mathrm{tol} = -\displaystyle \dfrac{2Q}{R_p}\;c \;\;\displaystyle \chi _{B(\gamma (t),R_p)},&{} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\; \;\; + { {\dfrac{S}{2 \pi R_S} \chi _{B(\zeta (t),R_s)}}}, &{} \hbox {in } {\varOmega }\times (0, T), \\ L \dfrac{\partial c}{\partial t} + \Big [ -(\mathbf {w}+\mathbf {s} +\mathbf {p}_\mathrm{tol}) c + \dfrac{c^{\kappa }}{c^{\kappa }_\mathrm{ref}} \mathbf {d} \varvec{\nabla } c\Big ] \cdot \mathbf {n}=0 , &{}\hbox {on } \partial {\varOmega }_o \times (0, T), \\ \Big ( \dfrac{c^{\kappa }}{c^{\kappa }_\mathrm{ref}} \mathbf {d} \varvec{\nabla } c\Big ) \cdot \mathbf {n}=0 , &{}\hbox {on } \partial {\varOmega }_{c} \times (0, T), \\ c(0) = c_0,&{} \end{array} \right. \end{aligned}$$

(2)

where:

• $\mathbf {p}_\mathrm{tol}(\xi ,t) = \displaystyle \max \Big ( \dfrac{\Vert \mathbf {p}(\xi ,t)\Vert _2-\mathrm{tol}}{Q-\mathrm{tol}},0 \Big ) \cdot \mathbf {p}(\xi ,t)$ is a corrected approximation of the velocity pump. This expression means that (i) the effect of the velocity field $\mathbf {p}$ on oil particles is neglected (i.e., $\mathbf {p}_\mathrm{tol}=0$) when $\Vert \mathbf {p}(\xi ,t)\Vert _2<$tol, for which the pump velocity is considered negligible regarding the diffusion coefficients; (ii) $\mathbf {p}_\mathrm{tol}(\xi ,t)=\mathbf {p}(\xi ,t)$, when $\Vert \overrightarrow{\gamma (t)\xi }\Vert _2 \le R_p$; and (iii) $\mathbf {p}_\mathrm{tol}(\xi ,t)<\mathbf {p}(\xi ,t)$ and $\mathbf {p}_\mathrm{tol}(\xi ,t)$ is a smooth function, when $\Vert \overrightarrow{\gamma (t)\xi }\Vert _2 > R_p$.

• $c_\mathrm{ref}$ is a reference pollutant concentration (here, $c_\mathrm{ref}=1$), and $\kappa > 0$ (typical values of $\kappa$ being 1, 2 and 3).

• L is a length, characteristic of the size of the domain ${\varOmega }$, typically the diameter of ${\varOmega }$ $\left( \hbox {that is}~ L = \sqrt{(x_{\mathrm {max}}-x_{\mathrm {min}})^2+(y_{\mathrm {max}}-y_{\mathrm {min}})^2} \right) .$

• $\mathbf {o}=[\min (s_1+w_1,\max (s_1,w_1)),\min (s_2+w_2,\max (s_2,w_2))]$.

In order to solve (2), we introduce in the next section, a numerical model that includes (a) second order schemes with linear and nonlinear limiters for the discretization of the advective terms, and (b) a time discretization by operator splitting to treat separately the diffusion-sea-wind and the pumping.

3 Numerical Methods

In Sect. 3.1 we present the numerical schemes used to solve numerically (2). Then, in Sect. 3.2, we describe the splitting technique used to improve the computational efficiency of the algorithm.

3.1 Approximation of Problems (1) and (2)

In order to introduce the notations used in this work, in Appendix we recall the basis of the piecewise linear Finite Volume scheme with limiters in the 1D case with constant velocity [10, 18]. In the following, we develop a 2D version of scheme (26) with non constant velocities.

The Finite Volume method is well-suited to the space-time discretization of problem (1). For simplicity, we assume the spatial domain ${\varOmega }=(x_{1,\mathrm {min}}, x_{1,\mathrm {max}}) \times (x_{2,\mathrm {min}},x_{2,\mathrm {max}})$. Given two positive integers I and J, we divide ${\varOmega }$ into IJ control volumes ${\varOmega }_{i,j}$. More precisely, for $i=1, \ldots , I$, $j = 1,\ldots , J$, we define ${\varOmega }_{i,j}$ by

$$\begin{aligned} {\varOmega }_{i,j}= & {} (x_{1, \min } + (i-1) \Delta x_1,x_{1, \min } + i \Delta x_1 ) \nonumber \\&\times (x_{2, \min } + (j-1) \Delta x_2, x_{2, \min } + j {\Delta x_2}), \end{aligned}$$

(3)

with $\Delta x_{1} = \displaystyle \dfrac{x_{1, \max } - x_{1, \min }}{I}$, $\Delta x_{2} = \dfrac{x_{2, \max } - x_{2, \min }}{J}$.

For simplicity, we will present only a fully explicit scheme, of the forward Euler type, for the time discretization of problem (1); constructing implicit or semi-implicit variants of the scheme to be described below is pretty easy.

The time step at the n-th step of the scheme is given by

$$\begin{aligned} \Delta t^{n}= \dfrac{ \mathcal {C} \Delta x_1 \Delta x_2}{\Delta x_1 (\overline{V}^n_1+d_1)+ \Delta x_2 (\overline{V}^n_2+d_2)+2 \pi Q}, \end{aligned}$$

(4)

where $\mathcal {C} \in [0,1]$ is a constant ($\mathcal {C}=1$, typically, for explicit schemes), $\overline{V}^n_1= \max _{(i = 1, \ldots , I+1; j=1, \ldots , J)} V^n_{1,i-\frac{1}{2},j}$ and $\overline{V}^n_2= \max _{(i = 1, \ldots , I; j=1, \ldots , J+1)} V^n_{2,i,j -\frac{1}{2}}$, with $V^n_{1,i-1/2,j}$ and $V^n_{2,i,j-1/2}$ defined below. We point out that $\Delta t^{n}$ is defined by considering a condition similar to the Courant–Friedrichs–Lewy (CFL) [8]. The role of such a condition is to ensure that the flow due to the advection, diffusion and reaction processes cannot make a particle in the boundary of one grid element to travel to the opposite grid element in less that one time step.

We note that for an implicit time discretization scheme, there is no limitation on the time step as long as stability is concerned; of course accuracy requires small time steps.

Let $C^0_{i,j} = c_0 (\xi _{i,j})$ with $\xi _{i,j}$ being the center of cell ${\varOmega }_{i,j}$. On each cell ${\varOmega }_{i,j}$, for $i = 1, \ldots , I$ and $j=1, \ldots , J$ at time step n we compute $C^{n+1}_{i,j} = C^{n+1} (\xi _{i,j})$ as follows.

For the diffusion term in (2), we consider the discretization scheme:

$$\begin{aligned} \mathcal {D}(i,j,n)= & {} 2 \Delta t^{n} \left( \dfrac{C^{n}_{i,j}}{c_\mathrm{ref}} \right) ^{\kappa } \left( \dfrac{d_1}{(\Delta x_1)^2} + \dfrac{d_2}{(\Delta x_2)^2}\right) C^n_{i,j} \nonumber \\&-\, \dfrac{d_1 \Delta t^{n}}{(\Delta x_1)^2} \left( \left( \dfrac{C^{n}_{i+1,j}}{c_\mathrm{ref}} \right) ^{\kappa } C^n_{i+1,j} + \left( \dfrac{C^{n}_{i-1,j}}{c_\mathrm{ref}} \right) ^{\kappa } C^n_{i-1,j}\right) \nonumber \\&-\, \dfrac{d_2 \Delta t^{n}}{(\Delta x_2)^2}\left( \left( \dfrac{C^{n}_{i,j+1}}{c_\mathrm{ref}} \right) ^{\kappa } C^n_{i,j+1}+ \left( \dfrac{C^{n}_{i,j-1}}{c_\mathrm{ref}} \right) ^{\kappa } C^n_{i,j-1}\right) \end{aligned}$$

(5)

For the transport term, we consider the scheme with limiters described below.

$$\begin{aligned} \mathcal {A}_{\mathbf {V}}^{+}(1,i,j,n)= & {} \big [ \sigma ^{+}_{1,i,j,n} + \phi (q_{1,i,j,n}) \vartheta (\sigma ^{+}_{1,i,j,n})\big ] C^{n}_{i,j}\\&-\, \big [ \sigma ^{+}_{1,i-1,j,n}+\big (\phi (q_{1,i,j,n}) \vartheta (\sigma ^{+}_{1,i,j,n})\\&+\, \phi (q_{1,i-1,j,n}) \vartheta (\sigma ^{+}_{1,i-1,j,n}) \big )\big ] C^{n}_{i-1,j}\\&+\, \big [ \phi (q_{1,i-1,j,n}) \vartheta (\sigma ^{+}_{1,i-1,j,n}) \big ] C^{n}_{i-2,j}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {A}_{\mathbf {V}}^{-}(1,i,j,n)= & {} \big [ \sigma ^{-}_{1,i,j,n} + \phi (r_{1,i,j,n}) \vartheta (\sigma ^{-}_{1,i,j,n})\big ] C^{n}_{i,j}\\&-\, \big [ \sigma ^{-}_{1,i+1,j,n}+\big (\phi (r_{1,i,j,n}) \vartheta (\sigma ^{-}_{1,i,j,n}) \\&+\, \phi (r_{1,i+1,j,n}) \vartheta (\sigma ^{-}_{1,i+1,j,n}) \big ) \big ] C^{n}_{i+1,j}\\&+\, \big [ \phi (r_{1,i+1,j,n}) \vartheta (\sigma ^{-}_{1,i+1,j,n}) \big ] C^{n}_{i+2,j}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {A}_{\mathbf {V}}^{+}(2,i,j,n)= & {} \big [ \sigma ^{+}_{2,i,j,n} + \phi (q_{2,i,j,n}) \vartheta (\sigma ^{+}_{2,i,j,n})\big ] C^{n}_{i,j}\\&-\, \big [ \sigma ^{+}_{2,i,j-1,n}+\big (\phi (q_{2,i,j,n}) \vartheta (\sigma ^{+}_{2,i,j,n}) \\&+\, \phi (q_{2,i,j-1,n}) \vartheta (\sigma ^{+}_{2,i,j-1,n}) \big ) \big ] C^{n}_{i,j-1}\\&+\, \big [ \phi (q_{2,i,j-1,n}) \vartheta (\sigma ^{+}_{2,i,j-1,n}) \big ] C^{n}_{i,j-2}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {A}_{\mathbf {V}}^{-}(2,i,j,n)= & {} \big [ \sigma ^{-}_{2,i,j,n} + \phi (r_{2,i,j,n}) \vartheta (\sigma ^{-}_{2,i,j,n})\big ] C^{n}_{i,j}\\&-\, \big [ \sigma ^{-}_{2,i,j+1,n}+\big (\phi (r_{2,i,j,n}) \vartheta (\sigma ^{-}_{2,i,j,n}) \\&+ \, \phi (r_{2,i,j+1,n}) \vartheta (\sigma ^{-}_{2,i,j+1,n}) \big ) \big ] C^{n}_{i,j+1}\\&+ \,\big [ \phi (r_{2,i,j+1,n}) \vartheta (\sigma ^{-}_{2,i,j+1,n}) \big ] C^{n}_{i,j+2}, \end{aligned}$$

where

• $\vartheta (a)=\dfrac{a}{2}(1-a);$

• $\sigma ^{+}_{1,i,j,n}= (\max (0, V^n_{1,i,j-\frac{1}{2}})\Delta t^{n})/\Delta x_1;$

• $\sigma ^{-}_{1,i,j,n}= (|\min (0, V^n_{1,i,j-\frac{1}{2}}) | \Delta t^{n})/\Delta x_1;$

• $\sigma ^{+}_{2,i,j,n}= (\max (0, V^n_{2,i-\frac{1}{2},j})\Delta t^{n})/\Delta x_2;$

• $\sigma ^{-}_{2,i,j,n}= (|\min (0, V^n_{2,i-\frac{1}{2},j}) | \Delta t^{n})/\Delta x_2;$

• $q_{1,i,j,n}= \dfrac{ C^{n}_{i+1,j}-C^{n}_{i,j}}{C^{n}_{i,j}-C^{n}_{i-1,j}};$

• $q_{2,i,j,n}= \dfrac{ C^{n}_{i,j+1}-C^{n}_{i,j}}{C^{n}_{i,j}-C^{n}_{i,j-1}};$

• $r_{k,i,j,n}= \dfrac{1}{q_{k,i,j,n}}, \hbox {with k}=1,2;$

• $V_{1,i,j-\frac{1}{2}}^{n} = V_1 ((x_{1, \min } + i\Delta x_1, x_{2, \min } + (j-\dfrac{1}{2}) \Delta x_2),\sum _{i=1}^n \Delta t^i);$

• $V_{2,i-\frac{1}{2}, j}^{n}= V_2 ((x_{1, \min } + (i-\dfrac{1}{2})\Delta x_1, x_{2, \min } + j \Delta x_2),\sum _{i=1}^n \Delta t^i).$

• $\mathbf {V}(x,t)=(V_1(x,t),V_2(x,t)) = \mathbf {w} (x,t) + \mathbf {s} (x,t) + \mathbf {p}_\mathrm{tol} (x,t)$, is the velocity field with $x \in {\varOmega }$ and $t \in [0,T]$.

Then, we denote

$$\begin{aligned} \mathcal {A}_{\mathbf {V}}(i,j,n)=\mathcal {A}_{\mathbf {V}}^{+}(1,i,j,n)+ \mathcal {A}_{\mathbf {V}}^{-}(1,i,j,n)+\mathcal {A}_{\mathbf {V}}^{+}(2,i,j,n) +\mathcal {A}_{\mathbf {V}}^{-}(2,i,j,n) \end{aligned}$$

For the (kind of) reaction term associated with the pumping process, we have the following scheme:

$$\begin{aligned} \mathcal {R}(i,j,n)= \Delta t^{n} \left( \dfrac{2 \pi R_p Q}{\Delta x_1 \Delta x_2} C^n_{i_p, j_p} \chi ^{p,n}_{i,j} - \dfrac{ S^n}{\Delta x_1 \Delta x_2} \chi ^{s,n}_{i,j}\right) , \end{aligned}$$

(6)

where ${\varOmega }_{i_{p,n},j_{p,n}}$ is the cell containing $\gamma _p (n \Delta t)$, $\chi ^{p,n}_{i,j} = 0$ if $\{i,j\} \not = \{i_{p,n},$ $j_{p,n}\}$, $\chi _{i,j}^{p,n} = 1$ if $\{i,j\} = \{i_{p,n}, j_{p,n}\}$, ${\varOmega }_{i_{s,n},j_{s,n}}$ is the cell containing $\zeta (n \Delta t)$, $\chi ^{s,n}_{i,j} = 0$ if $\{i,j\} \not = \{i_{s,n},$ $j_{s,n}\}$ and $\chi _{i,j}^{s,n} = 1$ if $\{i,j\} = \{i_{s,n}, j_{s,n}\}$.

Thus, the complete discretized scheme proposed for system (1) is:

$$\begin{aligned} C^n_{i,j}= C^{n-1}_{i,j}-\mathcal {D}(i,j,n-1)- \mathcal {A}_{\mathbf {V}}(i,j,n-1) -\mathcal {R}(i,j,n-1). \end{aligned}$$

(7)

This scheme is completed by the following discrete version of the boundary conditions (assuming $\partial {\varOmega }=\partial {\varOmega }_o$) of system (2).

for $i=1,\ldots ,I$ and $j=1,\ldots ,J$, we have

$$\begin{aligned} C^n_{I+1,j}= & {} \dfrac{\Delta t^{n}}{L}\bigg [ \bigg ( \dfrac{L}{\Delta t^{n}}+\min \left( 0,V^{n-1}_{1,I,j-\frac{1}{2}}\right) \bigg ) C^{n-1}_{I+1,j} \\&+\,\max \left( 0,V^{n-1}_{1,I,j-\frac{1}{2}}\right) C^{n-1}_{I,j} \\&- \, \Big (\dfrac{C^{n-1}_{I+1,j}+C^{n-1}_{I,j}}{2 c_\mathrm{ref} }\Big )^{\kappa } \dfrac{d_1}{\Delta x_1} \Big (C^{n-1}_{I+1,j}- C^{n-1}_{I,j} \Big ) \bigg ], \\ C^n_{0,j}= & {} \dfrac{\Delta t^{n}}{L}\bigg [ \bigg ( \dfrac{L}{\Delta t^{n}}+\max \left( 0,V^{n-1}_{1,0,j-\frac{1}{2}}\right) \bigg ) C^{n-1}_{0,j} \\&+\,\min \left( 0,V^{n-1}_{1,0,j-\frac{1}{2}}\right) C^{n-1}_{1,j} \\&- \,\Big (\dfrac{C^{n-1}_{0,j}+C^{n-1}_{1,j}}{2 c_\mathrm{ref} }\Big )^{\kappa } \dfrac{d_1}{\Delta x_1} \Big (C^{n-1}_{1,j}- C^{n-1}_{0,j} \Big ) \bigg ], \\ C^n_{i,J+1}= & {} \dfrac{\Delta t^{n}}{L}\bigg [ \bigg ( \dfrac{L}{\Delta t^{n}}+\min \left( 0,V^{n-1}_{2,i-\frac{1}{2},J}\right) \bigg ) C^{n-1}_{i,J+1} \\&+\,\max \left( 0,V^{n-1}_{2,i-\frac{1}{2},J}\right) C^{n-1}_{i,J} \\&- \, \Big (\dfrac{C^{n-1}_{i,J+1}+C^{n-1}_{i,J}}{2 c_\mathrm{ref} }\Big )^{\kappa } \dfrac{d_2}{\Delta x_2} \Big (C^{n-1}_{i,J+1}- C^{n-1}_{i,J} \Big ) \bigg ],\\ C^n_{i,0}= & {} \dfrac{\Delta t^{n}}{L}\bigg [ \bigg ( \dfrac{L}{\Delta t^{n}}+\max \left( 0,V^{n-1}_{2,i-\frac{1}{2},0}\right) \bigg ) C^{n-1}_{i,0} \\&+\,\min \left( 0,V^{n-1}_{2,i-\frac{1}{2},0}\right) C^{n-1}_{i,1} \\&- \, \Big (\dfrac{C^{n-1}_{i,0}+C^{n-1}_{i,0}}{2 c_\mathrm{ref} }\Big )^{\kappa } \dfrac{d_2}{\Delta x_2} \Big (C^{n-1}_{i,1}- C^{n-1}_{i,0} \Big ) \bigg ]. \end{aligned}$$

Remark 1

In Sect. 3.1, we are assuming, for the sake of simplicity, that $\partial {\varOmega }=\partial {\varOmega }_o$. The discretization scheme for the boundary conditions in $\partial {\varOmega }_s$ can be easily recovered (e.g., see [15]). The presentation of the general case (i.e., including $\partial {\varOmega }_o$ and $\partial {\varOmega }_s$) would require a large amount of storage. Therefore, it is omitted in this document and only the discretization of the new absorbing condition in (2) is detailed.

We note that if in scheme (7) we take

• $\phi (r)=0$ we obtain the first order upwind scheme,

• $\phi (r)=\dfrac{1}{2}(1+r)$ we obtain the Fromm scheme,

• $\phi (r)=1$ we obtain the Lax–Wendroff scheme,

• $\phi (r)=r$ we obtain the Beam–Warming scheme,

• $\phi (r)=$ minmod(1, r) we obtain the minmod scheme,

• $\phi (r)=\max (0,\min (1,2r),\min (2,r))$ we obtain the superbee scheme,

• $\phi (r)=\max (0,\min ((1+r)/2,2,r))$ we recover the monotonized central scheme,

• $\phi (r)=(r+|r|)/(1+|r|)$ we recover the Van Leer scheme,

• $\phi (r)=(r^2+r)/(r^2+1)$ we recover the Van Albada 1 scheme.

3.2 An Alternative Splitting Scheme

If an explicit scheme is used to treat the advection part of the mathematical model given by (1), the numerical model discussed in Sect. 3.1 is computationally quite expensive. In order to reduce the computational time we propose to consider a splitting technique.

Basically, the velocity field can be divided in two main components:

• the first one is the sea and wind currents $\mathbf {w} (x,t) + \mathbf {s} (x,t)$,

• the second one is the advection generated by the pump $\mathbf {p}_\mathrm{tol} (x,t)$.

As shown in the numerical experiments presented in the next section, the velocity $\mathbf {p}_\mathrm{tol}$ is much higher than $\mathbf {w} + \mathbf {s}$ generating small time steps due to the CFL condition. However, the effect of the pumping process is quite limited in space.

Thus, in order to reduce the computational effort we propose to split our scheme in those two velocities components. More precisely, to compute the solution from time $t^{n-1}$ up to time $t^{n}$ we first consider the intermediate step that handle the evolution of the solution $C^{n-1}_{i,j}$ considering only the effect of the wind and sea currents and diffusion from time $t^{n-1}$ up to $t^{n}$:

$$\begin{aligned} {{\tilde{C}}}^{n}_{i,j}= C^{n-1}_{i,j}-\mathcal {D}(i,j,n-1)-\mathcal {A}_{\mathbf {V}}(i,j,n-1), \end{aligned}$$

(8)

with $\Delta t^{n}=\dfrac{ \mathcal {C} \Delta x_1 \Delta x_2}{\Delta x_1 (\overline{V}^n_1+d_1)+ \Delta x_2 (\overline{V}^n_2+d_2)}$ and $\mathbf {V}=\mathbf {w}+ \mathbf {s}$.

Then, starting from the intermediate solution ${{\tilde{C}}}^{n}_{i,j}$, we compute the evolution of the general solution from time $t^{n-1}$ up to $t^{n}$ by considering only the effect of the pump.

To do so, we consider the smallest square domain, denoted by $\mathcal {S}(t)$, containing $B(\gamma (t),R_\mathrm{tol})$, the ball of center $\gamma (t)$ and radius $R_\mathrm{tol}$ in which $\mathbf {p}_\mathrm{tol}>0$.

Next, we use the following scheme

$$\begin{aligned} \bar{C}^{n_p}_{i,j}= \bar{C}^{n_p-1}_{i,j}-\mathcal {A}_{\mathbf {\mathbf {p}_\mathrm{tol}}}(i,j,n_p-1)-\mathcal {R}(i,j,n_p-1), \hbox {in } \mathcal {S}^{n_p}, \end{aligned}$$

(9)

where $n_p=1,\ldots ,n_p^{\max }$, $\bar{C}^{0}_{i,j}={{\tilde{C}}}^{n}_{i,j}$, $\mathcal {S}^{n_p}=\mathcal {S}(t^{n-1}+n_p\Delta t^{p_\mathrm{tol}})$, $\mathbf {p}_\mathrm{tol}=(p_\mathrm{tol,1}$ $,p_\mathrm{tol,2})$, $\Delta t^{p_\mathrm{tol}}=\dfrac{ \mathcal {C} \Delta x_1 \Delta x_2}{\Delta x_1 p_{tol,1}+ \Delta x_2 p_\mathrm{tol,2}+2\pi Q}$, $n_p^{\max }=$ceil($\dfrac{t^{n}-t^{n-1}}{\Delta t^{p_\mathrm{tol}}}$), ceil($\xi$) rounds $\xi$ upwards to the nearest integer.

Finally,

$$\begin{aligned} C^{n}_{i,j}=C^{n_p^{\max }}_{i,j}. \end{aligned}$$

4 Numerical Experiments

Here, in this Sect. 4.1, we will check the efficiency of the computational methods discussed in Sect. 3. It will be done by performing a variety of numerical experiments, all related to real life situations. Also the results obtained from models (1) and (2) will be compared. Then in Sect. 4.2, to validate our model, we reproduce the evolution of two real oil spills that took place near Spain: the Prestige and the Oleg Naydenov hazards in 2002 and 2015, respectively.

Remark 2

Anticipating on the results to be presented in Sect. 4.1.1, we would like to note that in order to obtain numerical results as accurate as possible, only fully explicit schemes are considered there, avoiding those additional errors produced by the solution of the linear systems associated with implicit schemes. Moreover, after performing various additional experiments (not presented here) relying on implicit or hybrid implicit–explicit schemes, we observed that the time steps $\Delta t^n$ required to obtain an accuracy comparable to the accuracy of the explicit scheme were much smaller than $\Delta t^n$ (from the explicit scheme CFL stability condition), another reason for favoring explicit schemes.

4.1 Comparison of Different Schemes of the Model

4.1.1 The Pollution Scenario Considered for the Numerical Simulations

We have considered numerical experiments and model parameters based on real data. More precisely, the initial shape and characteristics of the oil spill and the wind and sea currents are based on the Prestige hazard [25]. This event was caused by the sinking of an oil tanker in 2002 near the coast of the Spanish province of Galicia. Around $6.3 \times 10^4$ tons of oil were spilled on the open sea (at 200 km from the nearest coast).

The domain ${\varOmega }$ is defined by $x_{1,\mathrm {min}}=0$, $x_{1,\mathrm {max}}=8 \times 10^4$ m, $x_{2,\mathrm {min}}=0$ and $x_{2,\mathrm {max}}=8 \times 10^4$ m. The characteristic length L occurring in the boundary conditions of model (2) is given by $L=11.3 \times 10^4$ m.

The simulation time is equal to one day, $T=86{,}400$ s.

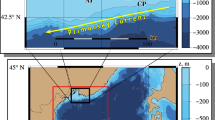
The diffusion coefficient of the oil in sea water is set to $d_1=d_2=0.5$ m s$^{-1}$ [26]. The oil density is 870 kg m$^{-3}$ [9] and its average thickness is 2 $\times 10^{-4}$ m [30]. The tolerance value is tol= 0.05 m s$^{-1}$. The initial position of the oil spill in ${\varOmega }$, presented in Fig. 1, is given by

$$\begin{aligned} c(\xi ,0)=\chi _{E(17{,}000,49{,}000,4700,10{,}000)}(\xi )+ \chi _{E(22{,}000,38{,}000,7000,13{,}000)}(\xi ), \end{aligned}$$

(10)

where $\xi =(\xi _1,\xi _2) \in {\varOmega }$ and $\chi _{E(a,b,c,d)}(\xi )=1$ if $(\xi _1-a)^2/c+(\xi _2-b)^2/d \le 1$ and 0 elsewhere.

Fig. 1

Position of the pollutant spot at time $t=0$. The initial (X) and final (o) positions and the trajectory (–) of the skimmer ship are also shown (in gray)

The wind plus sea velocity field $\mathbf {V}(x,t)=(V_1(x,t),V_2(x,t))=\mathbf {s}(x,t)+\mathbf {w}(x,t)$, expressed in m s$^{-1}$, is inspired from observations provided by [1, 7]. It is defined by

$$\begin{aligned} V_1(x,t)= & {} \dfrac{2}{9}-\dfrac{1}{9}\sin \left( \dfrac{\pi \Delta t}{172{,}800} \right) +\dfrac{x_{1}}{540{,}000} \nonumber \\ V_2(x,t)= & {} \left( \dfrac{1}{5}-\dfrac{1}{10}\cos (\dfrac{\pi \Delta t}{172{,}800})\right) \dfrac{2}{3}\sin \left( \pi (\dfrac{1}{2}+\dfrac{ x_{2}}{60{,}000})\right) , \end{aligned}$$

(11)

for $t \in [0,T]$ and $x=(x_1,x_2) \in {\varOmega }$.

The skimmer ship characteristics are based on the A-Whale Super Tanker Vessel [34]. This ship was used during the BP Deepwater Horizon oil spill in the Gulf of Mexico hazard in 2010. The pump parameters are $Q = 6.5$ m s$^{-1}$ and $R_p= 113$ m. The pumping ship follows the trajectory described in Fig. 1 which is generated by cubic spline interpolation trough the points (17,000,52,000) a time $t=0$ s, (23,000, 38,000) at $t=28{,}200$ s, (33,000, 47,500) at time $t=56{,}400$ s and (25,000, 41,000) at $t=84{,}600$ s.

4.1.2 Linear Versus Nonlinear Diffusion Models

Our goal in this section is to compare the results obtained from the linear diffusion model (1) and the nonlinear diffusion model (2).

To do so, we performed four numerical experiments. In each one we considered a spatial discretization mesh using $(I,J)=(100,$ 100). The time discretization scheme was explicit (to avoid -see Remark 2- the numerical errors produced by the solution of linear systems); the time step was set at $\Delta t=864$ s (considered small enough to produce accurate results [2]).

In the first experiment, denoted by Diff lin, we solved numerically the linear diffusion problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \dfrac{\partial c}{\partial t}-\varvec{\nabla } \cdot \mathbf {d}\varvec{\nabla } c = 0,&{}\quad \hbox {in } {\varOmega }\times (0, T), \\ \dfrac{\partial c}{\partial t} + \dfrac{\mathbf {d} \partial c}{L \partial \mathbf {n}}=0, &{}\quad \hbox {on } \partial {\varOmega }\times (0, T), \\ c = c_0,&{}\quad \hbox {in } {\varOmega }\times \{ 0 \}, \end{array} \right. \end{aligned}$$

(12)

with the parameters provided in Sect. 4.1.1.

In the second, third and fourth experiments, denoted by Diff nl $\varvec{\kappa }$ with $\kappa = 1, 2$ and 3, we solved numerically the nonlinear diffusion problem

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \dfrac{\partial c}{\partial t}- \varvec{\nabla } \cdot \dfrac{c^{\kappa }}{c^{\kappa }_\mathrm{ref}} \mathbf {d} \varvec{\nabla } c = 0,&{}\quad \hbox {in } {\varOmega }\times (0, T), \\ \dfrac{\partial c}{\partial t} + \dfrac{c^{\kappa }}{c^{\kappa }_\mathrm{ref}} \dfrac{\mathbf {d} \partial c}{L \partial \mathbf {n}}=0, &{}\quad \hbox {on } \partial {\varOmega }\times (0, T), \\ c = c_0,&{}\quad \hbox {in } {\varOmega }\times \{ 0 \}, \end{array} \right. \end{aligned}$$

(13)

with the parameters provided in Sect. 4.1.1 and $c_\mathrm{ref}=1$.

In each of these experiments, we are interested in computing

• CPUT: The CPU time needed to solve numerically the initial value problems (12) and (13).

• LOSS: The numerical mass loss in percentage of the oil concentration between the initial and final times. It is computed as:

  $$\begin{aligned} 100\left( \sum \limits _{i,j=1}^{I,J} C^N_{i,j} \Big /\sum \limits _{i,j=1}^{I,J} C^0_{i,j}\right) , \end{aligned}$$

  (14)

  where N is the value of n associated with the last time step of the numerical scheme (that is $N = \dfrac{T}{\Delta t}$). This quantity measures the conservation property of our numerical scheme.

• NFV $_\mathrm{\delta }$: The number of volume elements filled with an oil concentration greater than $\delta$ (a nonnegative real number suitably small). NFV $_\mathrm{\delta }$ is a measure of the effect on the polluted spots expansion due to the diffusion velocity and artificial diffusion of the schemes under consideration.

In Table 1, we present the results obtained when performing the experiments Diff lin, Diff nl1, Diff nl2 and Diff nl3. Regarding the NFV $_\mathrm{\delta }$ values, choosing in this case $\delta =0$, we see that the final concentration for the linear diffusion model reaches the boundary of the whole domain ${\varOmega }$. This is due to the infinite speed of propagation of linear diffusion. When using the nonlinear schemes this value is reduced by 90 % compared to the linear one and do not reach this boundary. Furthermore, as expected, the larger is $\kappa$ the lower is the expansion of the oil spots due to diffusion effects (velocity and artificial). This can be seen on Fig. 2, where the final concentration distribution and zero-contours generated by the nonlinear diffusion models are depicted. As a consequence, the numerical mass loss values of the nonlinear schemes are null. Moreover, the CPU time resulting from the linear model is four times larger than the one taken by the nonlinear ones.

Those results show the efficiency of the nonlinear scheme in controlling the undesired effects of the linear diffusion. The choice of $\kappa$ is an important issue (and also a complicated one, since $\kappa$ varies with the crude oil under consideration), however we failed at finding numerical values of this parameter in the open literature (it is likely that oil companies have quantitative information about $\kappa$, but they do not tell). From now on, we will use the nonlinear scheme with $\kappa =1$.

Table 1 Results obtained for the experiments presented in Sect. 4.1.2: CPUT, LOSS and NFV $_{0}$ values of the different types of diffusion

Fig. 2

Distribution of the final oil concentration and zero-concentration contours, generated by the nonlinear diffusion models Diff nl1, Diff nl2 and Diff nl3

4.1.3 Comparison of the Computational Methods

Now, we compare the performances of the different advection schemes presented in Sect. 1. We consider the advection equation:

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle \dfrac{\partial c}{\partial t} +\varvec{\nabla } \cdot c \; (\mathbf {w} + \mathbf {s}) = 0,&{}\quad \hbox {in } {\varOmega }\times (0, T), \\ c = c_0,&{}\quad \hbox {in } {\varOmega }\times \{ 0 \}, \end{array} \right. \end{aligned}$$

(15)

with the parameters provided in Sect. 4.1.1. Here, we assume that the support of the initial condition is compact and strictly inside our domain of integration, and that the support of the solution at time t does not reach the boundary either.

We perform various numerical experiments corresponding to the following nine numerical schemes for the numerical solution of (15): Adv DC (Donor Cell), Adv BW (Beam and Warming), Adv LW (Lax–Wendroff), Adv FR (Fromm), Adv MM (Min–Mod), Adv SB (Super Bee), Adv MC (monotonized central), Adv VL (Van Leer) and Adv VA (Van Albada).

In all those experiments we consider $(I,J)=(100,$ 100) and an explicit time discretization scheme with $\Delta t=864$ s (lower than the 1-CFL condition time step $\approx$ 2000 s). For each one, we compute the CPUT, LOSS, NFV $_\mathrm{\delta }$ values as defined in Sect. 4.1.1 and 4.1.2. In this case $\delta =10^{-8}$, which is a value small enough to measure the artificial diffusion of the considered schemes. Moreover, we also check the apparition of negative values or concentration provoked by the non monotonicity of a scheme by defining NVC=0 if the concentration at each time step is non negative and 1 otherwise).

In Table 2, we show the obtained results. We observe that the CPU times are of the same order but the faster one is the Donor Cell linear scheme. However, the artificial diffusion of this scheme produces the higher NFV $_{10^{-8}}$ value. This spot expansion measure is reduced when considering second order schemes. When regarding the linear second order schemes (i.e., BW, LW and FR), we observe the occurrence of unwanted negative concentration values and a higher LOSS value due to the numerical oscillations generated by those schemes (i.e., non monotonicity). This can be also observed in Fig. 3, where the final concentration distributions of the oil and their $10^{-8}$-contours obtained by Adv DC, Adv FR and Adv SB (chosen as representative cases) are depicted. We observe that the shape of the spot generated with $\mathbf Adv DC$ is more diffuse than with second order schemes. However, regarding the contours, we observe the oscillations produced by the linear second order model Adv FR. The solution produced with the nonlinear second order model Adv SB clearly shows that this kind of scheme controls artificial diffusion and monotonicity. Thus, the nonlinear second order schemes should be preferred. Among them, the Super Bee (SB) exhibits the lowest spot expansion value and will be used for the next experiments presented here.

Fig. 3

Distribution of the final oil concentration and $10^{-8}$-concentration contours (dotted line), generated by the advection models Adv DC (top-left), Adv FR (top-right) and Adv SB (bottom)

Table 2 Results obtained for the experiments presented in Sect. 4.1.3: CPUT, LOSS, NVC and $\mathbf NFV _{10^{-8}}$ values of the different schemes for the advection

4.1.4 Dirichlet Versus Absorbing Boundary Condition

In this section we discuss the advantage of using an absorbing boundary condition, instead of a Dirichlet one, to better simulate those cases where the oil spot crosses the boundary of the computational domain.

To do so, we introduce ${\varOmega }_h=[0,4 \times 10^4] \times [0,8 \times 10^4]$ m, representing half of the domain ${\varOmega }$ in the $x_1$-direction, and we solve the initial value problems (1) and (2) on ${\varOmega }_h$, without pumping (i.e. $Q=0$), the other parameters being those provided in Sect. 4.1.1. The resulting solutions are denoted by ADDH (Advection–Diffusion Dirichlet condition Half domain) and ADAH (Advection–Diffusion Absorbing condition Half domain), respectively. We observe that in these cases, the oil spot crosses the right boundary of ${\varOmega }_h$.

We compare previous solutions obtained on ${\varOmega }_h$ with the solution of problem (2), computed in the whole domain ${\varOmega }$ without pumping (i.e. $Q=0$), the other parameters being like those provided in Sect. 4.1.1. The solution is denoted by ADAF (Advection–Diffusion Absorbing condition Full domain). Here, the oil spot does not reach the boundary of ${\varOmega }$; the related solution can be considered as a reference solution.

The three initial value problems associated with ADDH, ADAH and ADAF were solved taking (I, J)=(100,100), $\kappa = 1$ in the nonlinear diffusion term, and using the nonlinear Super Bee scheme to treat the advection; no splitting was employed. Once these simulations were performed, we computed the differences between these solutions near the right boundary of ${\varOmega }_h$; to be more precise, we computed

$$\begin{aligned} \mathbf{EAA }=\int _{38 \mathrm{km}}^{40 \mathrm{km}} \int _{0 \mathrm{km}}^{80 \mathrm{km}} | \mathbf{ADAF }-\mathbf{ADAH } | \hbox {d}x_1 \hbox {d}x_2 \end{aligned}$$

(16)

and

$$\begin{aligned} \mathbf{EDI }=\int _{38 \mathrm{km}}^{40 \mathrm{km}} \int _{0 \mathrm{km}}^{80 \mathrm{km}} | \mathbf{ADAF } - \mathbf{ADDH } | \hbox {d}x_1 \hbox {d}x_2, \end{aligned}$$

(17)

respectively.

We obtained EAA $=1.1\times 10^6$ kg and EDI $=2.9\times 10^6$ kg, implying that the difference associated with the absorbing boundary condition is-approximately-three times smaller than the one for the Dirichlet condition. This improvement appears clearly on Fig. 4 where some contours of the ADDH, ADAH and ADAF solutions have been visualized; we observe that the ADAH contours fit better the ADAF contours than the ADDH ones.

From these results it appears that the absorbing boundary condition that we use produces a better approximation of the physical solution close to the boundary of the computational domain, than the Dirichlet’s one.

Fig. 4

Some contours of the oil concentration distribution generated by the ADAF (solid lines), ADAH (dashed lines) and ADDH (dotted lines) numerical models introduced in Sect. 4.1.4. Upper domain $(2 \times 10^4,4 \times 10^4) \times (2.5 \times 10^4,6 \times 10^4)$ m. Lower near boundary domain $(3.9 \times 10^4,4 \times 10^4) \times (4.6 \times 10^4,4.8 \times 10^4)$ m

4.1.5 Splitting Versus Un-split Schemes

Finally, we want to verify if it is advantageous to use splitting schemes. In order to achieve that goal, we performed the following numerical experiments, taking into account the results presented in Sects. 4.1.2 and 4.1.3:

• ADR DC: Solution of problem (1), using the linear first order donor-cell scheme to treat the advection, no splitting being used.

• ADR SB: Solution of problem (2) with $\kappa =1$ in the nonlinear diffusion term, using the nonlinear second order Super Bee scheme to treat the advection, no splitting being used.

• ADR SB-S: Solution of problem (2) with $\kappa =1$ in the nonlinear diffusion term, using the nonlinear second order Super Bee scheme to treat the advection. This time, the operator-splitting method described in Sect. 3.2 was used.

Table 3 Results from the experiments described in Sect. 4.1.5: values of PPUM, CPUT, LOCV and NFV $_{10^{-8}}$ for the three models and four meshes which have been considered

These numerical experiments were performed using four different meshes, namely (I, J)=(50, 50), (100,100), (150,150) and (200,200), the associated 1-CFL condition giving 500, 125, 56 and 31 s, respectively, for the maximal value of $\Delta {t^n}$.

For each experiment, we computed the values of CPUT and NFV $_{10^{-8}}$ (both defined in Sect. 4.1.3). Actually, we also computed:

• PPUM: The percentage of pumped oil at the end of the simulation with respect to its initial quantity.

• LOCV: The percentage of remaining oil at the end of the simulation with respect to its initial quantity plus the PPUM value. It measures the conservation property of our numerical models.

Results are presented in Table 3. They show the same behavior for the four grids we considered. The NFV $_{10^{-8}}$ values of the ADR SB and ADR SB-S models are of the same order and between twice and three times smaller than ADR DC. In addition, employing splitting allows us to drastically reduce the CPU time in comparison to the other two models. Also, the LOCV values of ADR SB and ADR SB-S are lower than the ADR DC ones. Thus, ADR SB-S provides major improvements with respect to ADR SB. This can also be noted on Fig. 5, where the final pollutant concentration and the $10^{-8}$-contour obtained by those three models are presented. Models ADR SB and ADR SB-S clearly exhibit similar behavior whereas the linear model ADR DC is more diffusive.

Fig. 5

Distribution of the final oil concentration and $10^{-8}$-concentration contours (..), generated by the advection models ADR DC (top), ADR SB (middle) and ADR SB-S (bottom). The initial position (X), the final position (o) and trajectory (–) of the pump are also shown

4.2 Validation of the Model with Real Cases

In this section, we aim to validate model (2) by comparing its solutions to real observations from two hazards that took place near Spain: The Prestige and the Oleg Naydenov cases in 2002 and 2015, respectively.

To do so, and regarding the results presented in Sect. 4.1, we have considered the following numerical schemes and parameters to compute a numerical approximation of the model solutions:

• We use a 100 $\times$ 100 spatial mesh and a time step of 1 hour (satisfying condition (4) with $\mathcal {C}=1$) [2].

• Since for the considered hazards and dates no cleaning processes with skimmer ships were applied, we set $Q=0$.

• The diffusion coefficient d is set to 0.5 (m s$^{-1}$) [2, 9].

• For the numerical schemes, we have used Super Bee, non linear diffusion with $\kappa =1$ and the absorbing boundary condition.

• No initial pollution in the domain is considered (i.e., $c_0=0$).

• The velocity fields $\mathbf {w}$ and $\mathbf {s}$ are estimated by considering historical discrete data provided by Mercator Ocean (http://www.mercator-ocean.fr)) and completed by 2D spline interpolation to be able to obtain values at points with no data. The considered drag factor for the wind velocities is 0.022 [2].

In next sections, we present the results obtained for each case.

4.2.1 Prestige Case

On November 13th, 2002, the ’Prestige’ ship starts to spill oil in open sea near the Galician coasts, Spain [29]. Authorities decided to send the ship far from the Spanish coasts. The ship sank in the Atlantic Ocean the 19th of November, 2002. Around 10 million gallons of crude oil were spilled, polluting thousands of kilometers of coastline in Spain, France and Portugal [4]. This spill is considered the largest environmental disaster in the history of both Spain and Portugal and the cost of this hazard was evaluated to more than 770 million euros [23].

We simulate the oil concentration evolution of this event from the beginning, on the 13th of November 2002, to the 17th of November 2002 (date of the only available clear satellite image of the situation, before the Prestige ship broke up). Considering this time interval, we use the following model parameters:

• ${\varOmega }\subset [-12.5,-7.5]\times [42,44.5]$ (in longitude–latitude coordinate system) which is assumed to be large enough to avoid the oil concentration leaving this domain during the considered time interval. Domain ${\varOmega }$ and the considered Spanish coastline are showed in Fig. 6.

• The trajectory followed by the Prestige ship was taken from the literature [7, 25].

• To our knowledge, the exact amount of oil S spilled by the Prestige ship into the ocean remains unknown [1, 7, 25]. It is only known that around 54.000 tons of oil were spilled into the sea before the Prestige ship broke on the 19th of November 2002. Thus, we have used the value of $S(t)=22$ (kg.s$^{-1}$), $\forall t$.

Taking into consideration those values, we present in Fig. 6 the solution given by our numerical model on the 17th of November 2002. In the same figure, we also show the satellite image taken by the Envisat ASAR satellite (European Spatial Agency: https://earth.esa.int) on the same date. We can observe graphical similarities between both images regarding the general behavior of the oil spill shape. This seems to indicate that our model predicts a reasonable evolution of the oil concentration of the Prestige case. However, this figure also illustrates some of the limitations of our model due to the omission of complex physical effects of the sea currents on the oil spill. For instance, our model does not allow to predict the splitting of the main oil spot in two branches.

Fig. 6

Left Satellite image of the Prestige oil spill situation taken by the Envisat ASAR satellite (European Spatial Agency) on November 17th, 2002. Right oil concentration simulated by model (2), with the parameters introduced in Sect. 4.2, for the same date. The coastline is represented in green (Color figure online)

4.2.2 Oleg Naydenov

The ship ’Oleg Naydenov’ sank near the Canary Islands coasts, Spain, on April 14th, 2015. The tanks of this ship were filled with around 1400 tons of oil. This oil spilled into the sea with flow estimated between [5,10] liters per hour (see [24]). During several weeks, this oil spill provoked the pollution of the ’Gran Canaria’ Island with several oil spots reaching its coastline (see [21]).

We consider model (2) and we simulate the oil concentration evolution from the beginning of this hazard on 14th to 21th of April, 2015 (date for which a satellite image is available). We use the following model parameters:

• ${\varOmega }\subset [-18,-13]\times [24,29.5]$ (in longitude–latitude coordinate system) which is assumed to be large enough to avoid the oil concentration leaving this domain during the considered time interval. Domain ${\varOmega }$ and the considered coastline are showed in Fig. 7. In addition, another computational domain focusing on the main part of the oil spill, denoted by ${\varOmega }_{z}\subset [-17,-15] \times [26,29]$, is also considered in order to give a more precise representation of the contamination in the most affected areas.

• The position of the ship is (−15.5,27.5) (in longitude–latitude coordinate system). We assume that the tanks of the ship were filled with 1400 tons of oil. The oil spill started on April 14th, 2015 with around 7.5 litters of pollutant per hour being spilled into the sea until reaching 1400 tons. Thus, we set $S(t)=0.08639 (\hbox {kg\,s}^{-1}), t \in [0,1.63 \times 10^{6}]$ (s).

Fig. 7

Computational domain ${\varOmega }$ considered for the numerical experiments presented in Sect. 4.2.2. The land is presented in green. The position of the Oleg Naydenov ship is represented by a blue star (Color figure online)

Fig. 8

Left NASA satellite image presenting the Oleg Naydenov oil spill situation at April 21th, 2015. The zone of interest is inside the red square. The ship position is represented by a blue circle and the oil spill with a black line. Right oil concentration simulated by the model presented in this work for the same date, considering the computational domain ${\varOmega }_{z}$. The coastline is represented in green and the position of the Oleg Naydenov ship by a blue star (Color figure online)

Taking into consideration those values, we present in Fig. 8 the solution given by our numerical model on April 21th, 2015 and the satellite image taken by a NASA satellite on the same date (http://www.nasa.gov/topics/earth/features/oilspill/). Again, we can observe that both images present similarities regarding the main behavior of the oil spill shape. In this case, we can also observe some limitations of our model, which predicts a smooth movement of the oil spill whereas the real oil spill has a meander shape (due to sea current vortexes present in this area and not considered in our numerical simulations by our model).

Fig. 9

Oleg Naydenov oil concentration simulated by the model, considering the computational domains left ${\varOmega }$ and right ${\varOmega }_{z}$ for the following dates: top April 27, 2015, middle April 29, 2015 and bottom May 1, 2015. The coastline is also represented in green. The position of the Oleg Naydenov ship is represented by a blue star (Color figure online)

We point out that, by using this model, on May 27th, 2015 we published a forecast of the possible oil spill evolution [20], which matched most of the real observations performed during this hazard [5, 11, 13]. We present in Fig. 9 the solutions given by our numerical model for the following dates: April 27th, April 29th and May 1th, 2015. We can observe, on April 29th, 2015, that the oil spill is close to south-western coasts of ’Gran Canaria’ Island with a risk of high contamination on this date. Then, the main oil spot is moving to the West and reach around May 1th, 2015 an area near the south coasts of the ’Tenerife’ Island. Eastern Canary Islands seem to be safe from pollution. We observe that reduced oil concentration (in light grey) reaches the south of the computational domain and may produce a contamination in open sea.

On April 30th, 2015 several oil spots were observed near the western coasts of ’Gran Canaria’ and were cleaned by authorities [5]. On May 2nd, 2015 additional small oil spots reached various southern and south-western beaches of ’Gran Canaria’, in areas highlighted by the model [13]. Finally, it has been reported (see, e.g., [11]) that the main part of the oil spill moved toward the south and disaggregated on the sea. Those observations seem to indicate that our model provides good results for the simulation of the evolution of oil spills.

5 Conclusions

In this article we have presented an improved version of the model discussed in [2, 16, 17], for simulating the evolution of oil spots in the open sea, taking into account: wind, sea currents and the effect of a skimmer ship used for the oil cleaning by pumping. Our objectives were to better control the artificial diffusivity, the velocity of the diffusion propagation, and the behavior of the computed solution at the boundary of the computational domain.

To achieve the goals listed above, we have: (i) Introduced a nonlinear diffusion term leading to diffusion effects propagating at finite velocity. (ii) Used second order accurate time discretization schemes with nonlinear limiters to treat the advection; these schemes have little artificial diffusion and good monotonicity conservation properties. (iii) Used an absorbing boundary condition to improve (with respect to the Dirichlet boundary condition) the behavior of the computed solutions near the boundary of the computational domain, particularly when the drifting oil spot crosses this boundary. (iv) Reduced the computational time required for the simulations, by using an operator-splitting method. (v) Considered the modeling of coastlines. (vi) Included dynamic sources of pollutant.

To verify the efficiency of the approach based on model (2), by comparison to the initial approach, based on model (1), and thoroughly discussed in [2] and [16], we have performed a large variety of numerical experiments based on realistic parameters.

First, we observed that the nonlinear diffusion model (2) leads to a diffusion propagating at finite velocity, unlike the diffusion associated with model (1). Furthermore, the computational time is smaller.

Secondly, we compared various linear and nonlinear second order accurate finite difference schemes to treat the advection terms in (2). The best results were obtained using a second order scheme based on the Super-Bee nonlinear limiter, a scheme producing very little artificial diffusion, when applied to model (2).

Thirdly, the introduction in (2) of boundary conditions, with good absorbing properties, on the boundary of the computational domain, produce a simulation method which creates little disturbance when the oil spot comes near the above boundary, and even crosses it: a behavior very different from the one which is observed if one prescribes a homogeneous Dirichlet condition at the boundary of the computational domain.

Finally, we have validated our approach by comparing the results given by the model with real observation from the the 2002 Prestige and 2015 Oleg Naydenov hazards (which took place on the coasts of Spain). We have observed that the general behavior of the simulated oil spills is similar to the real observed ones. Some minor discrepancies were also observed, highlighting the limitations of this model due to the omission of some physical effects.

As illustrated in [16] and [17], this model could be applied for optimizing skimmer ships trajectories in order to maximize the amount of recovered oil in open sea or near coastline.

Appendix: Review of the Piecewise Linear Schemes and of the Limiters

Suppose that we want to approximate the solution of the following 1-D equation

$$\begin{aligned} \begin{array}{rl} \dfrac{\partial c}{\partial t} + \dfrac{\partial (vc)}{\partial x}=0&\hbox {in } {\varTheta }\times ( 0,T ). \end{array} \end{aligned}$$

(18)

Here c is the concentration, v is the velocity and ${\varTheta }=[\underline{{\varTheta }},\overline{{\varTheta }}]$, where $\underline{{\varTheta }}$ and $\overline{{\varTheta }}$ belong both to $\mathbb {R}$, and are, respectively, the lower and upper boundaries of the interval ${\varTheta }$. Next, interval ${\varTheta }$ is decomposed into I finite volume cells (intervals here), that we denote by ${\varTheta }_i=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$. For simplicity of notation, we assume first that $v>0$ is constant and that the lengths of the intervals ${\varTheta }_i$ are all the same, and equal to $\Delta x$.

One way to obtain such an approximation is, for instance, to assume that in each finite volume ${\varTheta }_i$, with $i=1,\ldots ,I$, the concentration c is constant throughout the volume. This simplification allows to generate first order numerical schemes, such as the upwind scheme used in [2]. However, it was observed that this scheme produces a high level of artificial diffusion. To address this issue, it would be better to assume that the concentration within each volume ${\varTheta }_i$ is an affine function of the position (see [32]).

In this case, in ${\varTheta }_i$ at time $t_n$ the concentration can be linearly approximated by:

$$\begin{aligned} c(x,t_n)=c^n_i+\sigma _i^n (x-x_i) \hbox {, for } x \in {\varTheta }_i, \end{aligned}$$

(19)

where $x_i$ is the center of ${\varTheta }_i$, $c^n_i=c(x_i,t_n)$ and $\sigma _i^n$ is the slope of the linear approximation. We note that $\sigma _i^n$ can be defined in several ways. For instance

• $\sigma _i^n=\dfrac{c^{n}_{i+1}- c^{n}_{i-1}}{2\Delta x}$, in this case we obtain the Fromm method.

• $\sigma _i^n=\dfrac{c^{n}_{i}- c^{n}_{i-1}}{\Delta x}$, in this case we obtain the Beam–Warming method.

• $\sigma _i^n=\dfrac{c^{n}_{i+1}- c^{n}_{i}}{\Delta x}$, in this case we obtain the Lax–Wendroff method.

For these three cases, $c^n_i$ is equal to the average of $c(x,t_n)$ over ${\varTheta }_i$.

At the boundary $x_{i-\frac{1}{2}}$, the flux $f_{i-\frac{1}{2}}(t)$, with t in the time interval $[t_n,$ $t_{n+1}]$, is:

$$\begin{aligned} f_{i-\frac{1}{2}}(t)= & {} v c(x_{i-\frac{1}{2}},t)=v c(x_{i-\frac{1}{2}}-v(t-t_n),t_n)\\= & {} v c^n_{i-1}+ v \sigma _{i-1}^n \left( \frac{1}{2}\Delta x - v(t-t_n) \right) . \end{aligned}$$

At the boundary $x_{i+\frac{1}{2}}$, the flux $f_{i+\frac{1}{2}}(t)$, with t in the time interval $[t_n,$ $t_{n+1}]$, is:

$$\begin{aligned} f_{i+\frac{1}{2}}(t)= & {} v c(x_{i+\frac{1}{2}},t)=v c(x_{i+\frac{1}{2}}-v(t-t_n),t_n)\\= & {} v c^n_{i}+ v \sigma _{i}^n \left( \frac{1}{2}\Delta x - v(t-t_n) \right) . \end{aligned}$$

Thus, on the time interval $[t_n, t_{n+1}]$ the variation of concentration over the volume ${\varTheta }_i$ is given by

$$\begin{aligned} \dfrac{c^{n+1}_i-c^n_i}{\Delta t}=\dfrac{f^{n+\frac{1}{2}}_{i-\frac{1}{2}}-f^{n+\frac{1}{2}}_{i+\frac{1}{2}}}{\Delta x}, \end{aligned}$$

where $f^{n+\frac{1}{2}}_{i\pm \frac{1}{2}}=\dfrac{1}{\Delta t} {\int }_{t_n}^{t_{n+1}} f_{i\pm \frac{1}{2}}(t) \mathrm {d} t$ denotes the flux average during the time interval $[t_{n},t_{n+1}]$ which is similar to the flux at $\dfrac{t_{n+1}+t_{n}}{2}$.

Considering that

$$\begin{aligned} f^{n+\frac{1}{2}}_{i-\frac{1}{2}}-f^{n+\frac{1}{2}}_{i+\frac{1}{2}} = v (c^n_{i-1}-c^n_{i})+ \dfrac{1}{2}v( \sigma _{i-1}^n - \sigma _{i}^n) ( \Delta x - v\Delta t ), \end{aligned}$$

we obtain the following space-time discretization scheme:

$$\begin{aligned} c^{n+1}_i=c^n_i+\dfrac{\Delta t}{\Delta x} \left( v (c^n_{i-1}-c^n_{i})+ \dfrac{1}{2}v( \sigma _{i-1}^n - \sigma _{i}^n) ( \Delta x - v\Delta t ) \right) \end{aligned}$$

(20)

Now, we generalize scheme (20) to the case of non constant velocities $v: {\varTheta }\rightarrow \mathbb {R}$.

In this case

$$\begin{aligned} f^{n-\frac{1}{2}}_{i-\frac{1}{2}}= & {} \dfrac{1}{2}v_{i-\frac{1}{2}} \left[ (1+\beta _{i-\frac{1}{2}})c_{i-1}^n+(1-\beta _{i-\frac{1}{2}})c_{i}^n\right] \nonumber \\&+\, \dfrac{1}{4}|v_{i-\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i-\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \Delta x \left[ (1+\beta _{i-\frac{1}{2}})\sigma _{i-1}^n+(1-\beta _{i-\frac{1}{2}})\sigma _{i}^n\right] , \end{aligned}$$

(21)

and

$$\begin{aligned} f^{n+\frac{1}{2}}_{i+\frac{1}{2}}= & {} \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}})c_{i}^n+(1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \nonumber \\&+\, \dfrac{1}{4}|v_{i+\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i+\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \Delta x \left[ (1+\beta _{i+\frac{1}{2}})\sigma _{i}^n+(1-\beta _{i+\frac{1}{2}})\sigma _{i+1}^n\right] , \end{aligned}$$

(22)

where $\beta _{i\pm \frac{1}{2}}=1$ if $v_{i\pm \frac{1}{2}}\ge 0$ or $=-1$ if $v_{i\pm \frac{1}{2}}<0$.

Thus, scheme (20) becomes:

$$\begin{aligned} c^{n+1}_i= & {} c^n_i+\dfrac{\Delta t}{\Delta x} \left( \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}})c_{i}^n+ (1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \right. \nonumber \\&+\, \dfrac{1}{4}|v_{i-\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i-\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \Delta x \left[ (1+ \beta _{i-\frac{1}{2}}) \sigma _{i-1}^n+(1-\beta _{i-\frac{1}{2}})\sigma _{i}^n\right] \nonumber \\&-\, \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}}) c_{i}^n+(1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \nonumber \\&\left. -\,\dfrac{1}{4}|v_{i+\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i+\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \Delta x \left[ (1+ \beta _{i+\frac{1}{2}}) \sigma _{i}^n+(1-\beta _{i+\frac{1}{2}})\sigma _{i+1}^n\right] \right) . \end{aligned}$$

(23)

The previous scheme (23) is known to be conservative but not necessarily monotonous [10, 18]. This non-monotonicity may produce numerical solutions with unrealistic oscillations. These oscillations are due to the high variation of the concentration slopes $\sigma _i ^n$ near jumps of the concentration. A way to measure these oscillations is to use the concept of Total Variation (TV) defined as

$$\begin{aligned} TV\left( \{c^n_i\}_{i=1}^I\right) =\sum _{i=1}^I |c^n_{i}-c^n_{i-1}|. \end{aligned}$$

We are interested in creating numerical schemes with the property of Total Variation Diminishing (TVD), that is $TV(\{c^n_i\}_{i=1}^I)\ge TV(\{c^{n+1}_i\}_{i=1}^I)$. That property ensures that the scheme will not develop oscillations. Thus, we now introduce a variation of the scheme (23) that guarantee TVD.

To do so, we introduce the concept of flux limiters. In (21), we replace $\Delta x \left[ (1+\beta _{i-\frac{1}{2}}) \sigma _{i-1}^n +(1-\beta _{i-\frac{1}{2}})\sigma _{i}^n\right] \hbox { by } \phi (r_{i-\frac{1}{2}}^n)(c_i^n-c_{i-1}^n),$ and we obtain

$$\begin{aligned} f^{n-\frac{1}{2}}_{i-\frac{1}{2}}= & {} \dfrac{1}{2}v_{i-\frac{1}{2}} \left[ (1+\beta _{i-\frac{1}{2}})c_{i-1}^n+(1-\beta _{i-\frac{1}{2}})c_{i}^n\right] \nonumber \\&+\, \dfrac{1}{4}|v_{i-\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i-\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \phi (r_{i-\frac{1}{2}}^n)(c_i^n-c_{i-1}^n), \end{aligned}$$

(24)

where $\phi (r)$ is called flux limiter and $r_{i-\frac{1}{2}}^n=\dfrac{c_{i-1}^n-c_{i-2}^n}{c_i^n-c_{i-1}^n}$ if $v_{i-\frac{1}{2}}\ge 0$ or $=\dfrac{c_{i+1}^n-c_{i}^n}{c_i^n-c_{i-1}^n}$ if $v_{i-\frac{1}{2}}<0$. In a similar way we can rewrite

$$\begin{aligned} f^{n+\frac{1}{2}}_{i+\frac{1}{2}}= & {} \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}})c_{i}^n+(1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \nonumber \\&+\, \dfrac{1}{4}|v_{i+\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i+\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \phi (r_{i+\frac{1}{2}}^n)(c_{i+1}^n-c_{i}^n), \end{aligned}$$

(25)

where $r_{i-\frac{1}{2}}^n=\dfrac{c_{i}^n-c_{i-1}^n}{c_{i+1}^n-c_{i}^n}$ if $v_{i+\frac{1}{2}}\ge 0$ or $=\dfrac{c_{i+2}^n-c_{i+1}^n}{c_{i+1}^n-c_{i}^n}$ if $v_{i+\frac{1}{2}}<0$.

Then, scheme (23) can be rewritten as

$$\begin{aligned} c^{n+1}_i= & {} c^n_i+\dfrac{\Delta t}{\Delta x} \left( \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}}) c_{i}^n+(1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \right. \nonumber \\&+ \,\dfrac{1}{4}|v_{i-\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i-\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \phi (r_{i-\frac{1}{2}}^n)(c_i^n-c_{i-1}^n) \nonumber \\&-\, \dfrac{1}{2}v_{i+\frac{1}{2}} \left[ (1+\beta _{i+\frac{1}{2}}) c_{i}^n+(1-\beta _{i+\frac{1}{2}})c_{i+1}^n\right] \nonumber \\&\left. -\, \dfrac{1}{4}|v_{i+\frac{1}{2}}|\left( 1-\left| \dfrac{v_{i+\frac{1}{2}}\Delta t}{\Delta x}\right| \right) \phi (r_{i+\frac{1}{2}}^n)(c_{i+1}^n-c_{i}^n) \right) . \end{aligned}$$

(26)

We note that if in scheme (26) we take:

• $\phi (r)=0$, we recover the first order upwind scheme (a scheme producing a high level of artificial diffusion).

• $\phi (r)=\dfrac{1}{2}(1+r)$, we recover the Fromm scheme.

• $\phi (r)=1$, we recover the Lax–Wendroff scheme.

• $\phi (r)=r$, we recover the Beam–Warming scheme.

The first scheme is first order accurate and TVD. The second, third and fourth schemes are second order accurate, but non-TVD.

Let us consider the following nonlinear flux limiters:

• $\phi (r)=$minmod(1, r), we obtain the minmod scheme [28].

• $\phi (r)=\max (0,\min (1,2r),\min (2,r))$, we obtain the superbee scheme [28].

• $\phi (r)=\max (0,\min ((1+r)/2,2,r))$, we recover the monotonized central scheme [33].

• $\phi (r)=(r+|r|)/(1+|r|)$, we recover the Van Leer scheme [32].

• $\phi (r)=(r^2+r)/(r^2+1)$, we recover the Van Albada 1 scheme [31].

The five above schemes are TVD.