Application of a Multi-dimensional Limiting Process to Central-Upwind Schemes for Solving Hyperbolic Systems of Conservation Laws

Abstract

In this paper, we study semi-discrete central-upwind difference schemes with a modified multi-dimensional limiting process (MLP) to solve two-dimensional hyperbolic systems of conservation laws. In general, high-order central difference schemes for conservation laws involve no Riemann solvers or characteristic decompositions but have a tendency to smear linear discontinuities. To overcome this drawback of central-upwind schemes, we use a MLP that uses multi-dimensional information for slope limitation to control the oscillations across discontinuities for multi-dimensional applications. Some numerical results are provided to demonstrate the performance of the proposed scheme.

1 Introduction

In this study, we consider the central-upwind difference schemes [13, 14] with multi-dimensional limiting functions [4, 10, 11, 32] to solve the two-dimensional (2D) hyperbolic conservation law

$$\begin{aligned} \begin{aligned}&u_t + f(u)_x + g(u)_y = 0, \quad x \in {\mathbb {R}},\quad t\ge 0, \\&u(x,y,0) = u_0(x,y), \end{aligned} \end{aligned}$$

(1.1)

with proper boundary conditions. This equation is of practical importance with applications ranging from a variety of physical phenomena to mathematical financial modeling. Since solutions of the hyperbolic PDEs (1.1) may develop steep gradients, shock waves, and contact discontinuities in finite time, it is often impossible to find the analytic solution; hence robust shock-capturing schemes that do not create spurious oscillations are required. The development of stable, accurate, and effective numerical schemes for solving conservation laws (1.1) requires analyses of a variety of physical phenomena as well as achievement of a qualitative understanding of the behavior of their solutions. Over the past several decades, various numerical schemes have been proposed to solve such equations (1.1).

The most popular numerical methods for hyperbolic systems of conservation laws are the upwind schemes proposed by Godunov [6] and extended to second-order accuracy by van Leer [16]. An alternative to the Godunov-type upwind scheme is the Lax-Friedrichs (LxF) central difference scheme introduced by Lax and Fridrichs in [3, 15], in which no Riemann solvers or characteristic decompositions are involved. This has the advantage of simplicity compared with the first-order upwind scheme of Godunov [6]; however, the LxF scheme, yields a large numerical dissipation, which leads to a poor resolution of shock discontinuities and rarefaction waves. In order to reduce numerical dissipation, Nessyahu and Tadmor proposed a second-order extension of the LxF scheme (referred to as the NT scheme) in [24], based on a staggered form of the LxF scheme. The NT scheme replaces the first-order piecewise constant solution with van Leer’s MUSCL-type piecewise-linear solution to construct a second-order approximation that avoids oscillations at discontinuities and achieves a sharp and accurate shock capture. The NT scheme retains the simplicity of the Riemann-free LxF framework and avoids the disadvantage of the excessive first-order dissipation of the LxF scheme. In 2000, Kurganov and Tadmor [14] proposed the CU-KT scheme, which contains modifications to the NT scheme with a smaller amount of numerical viscosity than that in the original NT scheme. The second-order KT schemes with a semidiscrete formulation were based on integration over Riemann fans of variable sizes and the use of more precise information regarding the local propagation speeds. Extensions to multidimensional problems were introduced in [9].

Later, a generalization of the CU-KT schemes was proposed by Kurganov et al. [13], who utilized one-sided local speeds of propagation (referred to as the CU-KNP scheme). The numerical flux of the KT scheme used only the maximum wave speed, whereas the CU-KNP scheme used both the maximal and minimal wave speeds to reduce the numerical viscosity. Higher-than-second-order schemes were by Liu and Osher [21] based on non-oscillatory third-order reconstruction and Liu and Tadmor [23] with staggered evolution of the reconstructed cell averages. High-order essentially non-oscillatory (ENO) [7] and weighted ENO (WENO) [8, 22] reconstructions were combined with central schemes by Bianco et al. [1]. Modifications of the central schemes of Bianco, Puppo, and Russo [1] were introduced in [17] as a central WENO reconstruction. Other central schemes with WENO are presented in [18, 25], and extensions to multi-dimensional problems can be found in [19, 20]. The higher-order reconstructions of central schemes yielded decreasing numerical dissipations and greater resolution of shocks, rarefactions, and other spontaneous evolution of large-gradient phenomena, which were almost as sharp as those of comparable higher-order upwind schemes.

Most numerical schemes for hyperbolic conservation laws have been developed on the basis of one-dimensional (1D) flow physics, so that extension of 2D flows is straightforward by dimensional splitting. Although this approach allows the rigorous analysis of numerical schemes, 1D limiters may fail to achieve a good shock resolution if the shock is located in a direction diagonal to the computational grid. These numerical schemes lead to insufficient or excessive numerical dissipation because of the essential limitations of accurate and efficient calculations for multi-dimensional flows. Over the last two decades, there has been research toward controlling numerical oscillation and designing multi-dimensional limiter functions [2, 28, 30]. In successive studies, Kim and Kim extended the 1D monotonic condition to 2D flow and proposed a multi-dimensional limiting process (MLP) for the 2D compressible Euler equation [11]. They proposed an MLP in the same article that used multi-dimensional information for slope limitation to control oscillations across discontinuities for multi-dimensional applications. Later, improved MLP limiters were devised [4, 10, 12, 32] and they could be efficiently implemented in three-dimensional space. The main focus of the MLP methods is to eliminate excessive numerical dissipation and upgrade solution accuracy by predicting the physical distributions of flow variables in multi-space dimensions.

In this present paper, we study a multi-dimensional limiting process introduced by Yoon et al. [32] and derive a central scheme that incorporates a modification of the MLP. Since the CU-KNP scheme has low computational effort and high numerical stability, the combination of both approaches hold the potential for good monotone shock-capturing capabilities and good convergence behavior at a relatively low computational cost. Certain improvements in comparison to CU-KNP [13] shall be provided and a modified CU-KNP scheme (referred to as CU-MLP) shall be presented. We see that this modification yields better results than the original CU-KNP schemes. Some numerical experiments are conducted to demonstrate the performance of the proposed scheme.

The outline of this paper is designed as follows. In Sect. 2, we present reviews of central-upwind schemes. After a brief description of MLP limiters suggested by Yoon et al. [32] in Sect. 3, we introduce a modified MLP limiter along with the construction of a central-upwind scheme in Sect. 4. Finally, the concluding numerical results are provided in Sect. 5 to illustrate the advantages of the proposed scheme.

2 Review of the Central-Upwind Schemes in 2-D

In this section, the semi-discrete central-upwind scheme for 2D compressible flow that was suggested by Kurganov at el. [13] is briefly reviewed. We consider hyperbolic conservation laws in 2D space as

$$\begin{aligned} \begin{aligned}&u_t + f(u)_x + g(u)_y = 0. \end{aligned} \end{aligned}$$

(2.1)

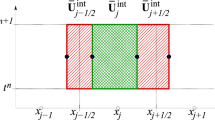
Central-upwind schemes can be easily implemented knowing only the physical flux functions and extremal eigenvalues of the flux Jacobian associated with a hyperbolic system of conservation laws. We discretize the conservation laws using a Cartesian grid with uniform spacing $\Delta x (=x_i - x_{i-1})$ and $\Delta y (=y_j - y_{j-1})$, and the intermediate points $x_{j \pm \frac{1}{2}} = x_{i} \pm \frac{\Delta x}{2}$ and $y_{j \pm \frac{1}{2}} = y_{j} \pm \frac{\Delta y}{2}$. We define the cell averages based on spatial cells $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] \times [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$,

$$\begin{aligned} \bar{u}^n_{ij} = \frac{1}{\Delta x \Delta y} \int ^{x_{i+\frac{1}{2}}}_{x_{i-\frac{1}{2}}} \int ^{y_{j+\frac{1}{2}}}_{y_{j-\frac{1}{2}}} u(x,y,t^n)dydx. \end{aligned}$$

(2.2)

To advance the computation to the next time level at $t=t^{n+1}$, we reconstruct a piecewise linear polynomial, $\tilde{u}(x,y,t^n)$, of the form

$$\begin{aligned} \tilde{u}(x,y,t^n) = \sum _{i,j} \left[ \bar{u}^n_{ij}+(u_x)^n_{ij}(x-x_i)+(u_y)^n_{ij}(y-y_j) \right] \chi _{ij}(x,y) \end{aligned}$$

(2.3)

where

$$\begin{aligned} ({u_x})^n_{ij}= & {} \frac{1}{\Delta x}{} \mathbf{minmod} \left( \alpha \Delta {\bar{u}_{i+1/2,j}}, \frac{1}{2} (\Delta {\bar{u}_{i+1/2,j}} + \Delta {\bar{u}_{i-1/2,j}}), \alpha \Delta {\bar{u}_{i-1/2,j}} \right) , \\ ({u_y})^n_{ij}= & {} \frac{1}{\Delta y}{} \mathbf{minmod} \left( \alpha \Delta {\bar{u}_{i,j+1/2}}, \frac{1}{2} (\Delta {\bar{u}_{i,j+1/2}} + \Delta {\bar{u}_{i,j-1/2}}), \alpha \Delta {\bar{u}_{i,j-1/2}} \right) , \end{aligned}$$

with $\alpha \in [1,2]$ and $\Delta \bar{u}_{i+1/2,j} = \bar{u}_{i+1,j} -\bar{u}_{ij}$. Here, $\chi _{ij}(x,y)$ represents the characteristic functions of the corresponding interval, $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] \times [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$, and the multivariable minmod function is defined by

$$\begin{aligned} \mathbf{minmod}(x_1,x_2, \ldots ) = \left\{ \begin{array}{l@{\quad }l} \min \{x_i\} &{} \hbox {if }x_{i} > 0\hbox { for all} ~ i, \\ \max \{x_i\} &{} \hbox {if }x_{i} < 0\hbox { for all} ~ i, \\ 0 &{} \hbox {otherwise}. \end{array} \right. \end{aligned}$$

The piecewise linear interpolant, $\tilde{u}$, may have discontinuities along the lines $x=x_{i \pm \frac{1}{2}}$ and $y=y_{j \pm \frac{1}{2}}$ which propagate with different right- and left-going local wave speeds. To compute the corresponding local wave speeds, one may use

$$\begin{aligned} \begin{aligned} a^+_{i+\frac{1}{2},j}&= \max \left[ \lambda _N \left( \frac{\partial f}{\partial u}\left( u^L_{i+\frac{1}{2},j}\right) \right) , \lambda _N \left( \frac{\partial f}{\partial u}\left( u^R_{i+\frac{1}{2},j}\right) \right) , 0 \right] , \\ a^-_{i+\frac{1}{2},j}&= \min \, \left[ ~\lambda _1 \left( \frac{\partial f}{\partial u}\left( u^L_{i+\frac{1}{2},j}\right) \right) , ~\lambda _1 \left( \frac{\partial f}{\partial u}\left( u^R_{i+\frac{1}{2},j}\right) \right) , 0 \right] , \\ b^+_{i,j+\frac{1}{2}}&= \max \left[ \lambda _N \left( \frac{\partial g}{\partial u}\left( u^L_{i,j+\frac{1}{2}}\right) \right) , \lambda _N \left( \frac{\partial g}{\partial u}\left( u^R_{i,j+\frac{1}{2}}\right) \right) , 0 \right] , \\ b^-_{i,j+\frac{1}{2}}&= \min \, \left[ ~\lambda _1 \left( \frac{\partial g}{\partial u}\left( u^L_{i,j+\frac{1}{2}}\right) \right) , ~\lambda _1 \left( \frac{\partial g}{\partial u}\left( u^R_{i,j+\frac{1}{2}}\right) \right) , 0 \right] , \end{aligned} \end{aligned}$$

(2.4)

where $\lambda _N$ and $\lambda _1$ denote the largest and the smallest eigenvalues of the Jacobians $\frac{\partial f}{\partial u}$ and $\frac{\partial g}{\partial u}$, respectively. The point values of the piecewise linear reconstruction (2.1) are given by :

$$\begin{aligned} \begin{aligned} u^{L}_{i+\frac{1}{2},j}&= \bar{u}_{ij} + 0.5 (u_x)^n_{ij} \Delta x, \\ u^{R}_{i+\frac{1}{2},j}&= \bar{u}_{i+1,j} - 0.5 (u_x)^n_{i+1,j} \Delta x, \\ u^{L}_{i,j+\frac{1}{2}}&= \bar{u}_{ij} + 0.5 (u_y)^n_{ij} \Delta y, \\ u^{R}_{i,j+\frac{1}{2}}&= \bar{u}_{i,j+1} - 0.5 (u_y)^n_{i,j+1} \Delta y. \end{aligned} \end{aligned}$$

(2.5)

The 2D semi-discrete schemes can be written in the conservation form:

$$\begin{aligned} \frac{d}{dt}{u}_{ij}= & {} - \frac{\hat{f}_{i+\frac{1}{2},j}(t) - \hat{f}_{i-\frac{1}{2},j}(t)}{\Delta x} - \frac{\hat{g}_{i,j+\frac{1}{2}}(t) - \hat{g}_{i,j-\frac{1}{2}}(t)}{\Delta y} \end{aligned}$$

(2.6)

where the numerical flux functions are

$$\begin{aligned} \begin{aligned} \hat{f}_{i+\frac{1}{2},j}(t)&= \frac{a^+_{i+\frac{1}{2},j} f\left( u^L_{i+\frac{1}{2},j}\right) - a^-_{i+\frac{1}{2},j} f\left( u^R_{i+\frac{1}{2},j}\right) }{a^+_{i+\frac{1}{2},j} -a^-_{i+\frac{1}{2},j}} + \frac{a^+_{i+\frac{1}{2},j} a^-_{i+\frac{1}{2},j}}{a^+_{i+\frac{1}{2},j} -a^-_{i+\frac{1}{2},j}} \left[ u^R_{i+\frac{1}{2},j}- u^L_{i+\frac{1}{2},j} \right] ,\\ \hat{g}_{i,j+\frac{1}{2}}(t)&= \frac{b^+_{i,j+\frac{1}{2}} g\left( u^L_{i,j+\frac{1}{2}}\right) - b^-_{i,j+\frac{1}{2}} g\left( u^R_{i,j+\frac{1}{2}}\right) }{b^+_{i,j+\frac{1}{2}} -b^-_{i,j+\frac{1}{2}}} +\frac{b^+_{i,j+\frac{1}{2}} b^-_{i,j+\frac{1}{2}}}{b^+_{i,j+\frac{1}{2}} -b^-_{i,j+\frac{1}{2}}} \left[ u^R_{i,j+\frac{1}{2}}- u^L_{i,j+1/2} \right] . \end{aligned} \end{aligned}$$

(2.7)

We have presented above the CU-KNP semi-discrete approximation of the spatial discretization for systems of conservation laws. For the time discretization, we can employ several methods for solving the ordinary differential equation(ODE):

$$\begin{aligned} u_t = \mathcal {L}(u,t). \end{aligned}$$

Here, we have used a 3rd-order TVD Runge-Kutta type discretization for time stepping to solve the ODE [27]:

$$\begin{aligned} \begin{aligned} u^{(1)}&= u^n + \Delta t {\mathcal {L}}( u^n), \\ u^{(2)}&= \frac{3}{4} u^n + \frac{1}{4} u^{(1)} + \frac{1}{4} \Delta t {\mathcal {L}}( u^{(1)}), \\ u^{n+1}&= \frac{1}{3} u^{n} + \frac{2}{3}u^{(2)} + \frac{2}{3} \Delta t {\mathcal {L}}(u^{(2)}). \end{aligned} \end{aligned}$$

(2.8)

3 Multidimensional Limiting Process

In this section, we describe the basic concept of the MLP limiter in 2D space [32]. Generally, most numerical methods of 2D or three-dimensional hyperbolic conservation laws are obtained through dimensional splitting. This approach is an efficient computational methods; however it is insufficient for controlling oscillations near a shock discontinuity and may fail to achieve a good shock resolution if the shock is a located in a direction diagonal to the computational grid in multi-dimensional space. When the TVD concept is extended to multi-dimensional flow by dimensional splitting, it cannot be guaranteed monotonic solutions. In this respect, it needs to be modified or extended with appropriate consideration to control the oscillation in a multi-dimensional space situation. To overcome this drawback, MLP was proposed by Kim et al. [11] and Yoon et al. [32] to reinforce oscillation control in multi-dimensional flow. MLP is referred to as a conventional second order limiter like superbee or minmod, but includes diagonal volume information. Before introducing the MLP, we consider the cell-interface value, u, with a symmetric MUSCL-type TVD limiter:

$$\begin{aligned} \begin{aligned} u^{L}_{i+1/2, j}&= \phantom {-} \bar{u}_{ij} + 0.5 \phi (r^{L}_{x}) \Delta \bar{u}_{i-1/2,j},\\ u^{R}_{i+1/2, j}&= \bar{u}_{i+1, j} - 0.5 \phi (r^{R}_{x}) \Delta \bar{u}_{i+3/2, j},\\ \end{aligned} \end{aligned}$$

(3.1)

with $\displaystyle {\Delta \bar{u}_{i-1/2,j} = \bar{u}_{ij} -\bar{u}_{i-1, j}}$, $\displaystyle {r_x^L = \frac{\Delta \bar{u}_{i+1/2,j} }{\Delta \bar{u}_{i-1/2,j}}}$, and $\displaystyle {r_x^R = \frac{\Delta \bar{u}_{i+1/2,j} }{\Delta \bar{u}_{i+3/2,j}}}$. Here, $\phi (r)$ is a limiting function and satisfies the symmetric condition $\phi (r) = r\phi (1/r)$, so that we can obtain

$$\begin{aligned} u^{R}_{i-1/2, j}&=\bar{u}_{ij} - 0.5 \phi (r_x^L) \Delta \bar{u}_{i-1/2, j}. \end{aligned}$$

The cell interface values of Eq. (3.1) may be interpreted as a first-order upwind representation plus an additional anti-diffusive term.

The Sweby’s TVD zone [29] of a 1D limiting condition is given by

$$\begin{aligned} 0 \le \phi (r) \le \min (2r, 2). \end{aligned}$$

(3.2)

Since the extension of (3.2) by dimensional splitting is insufficient to prevent oscillations in multi-dimensional flow, it needs to be modified and extended with appropriate consideration of the multidimensional situation. The MLP needs to obtain a monotonic solution in multi-dimensional space and satisfy the discrete maximum principle:

$$\begin{aligned} \bar{u}^{{\text {min}}}_{nbd} \le u \le \bar{u}^{{\text {max}}}_{nbd}, \end{aligned}$$

(3.3)

where u is the estimated value at a vertex point, and $\bar{u}^{{\text {min}}}_{nbd}$ and $\bar{u}^{{\text {max}}}_{nbd}$ are the minimum and maximum values, respectively, among the neighboring cell-averaged values sharing the vertex. The vertex point values are then expressed in terms of cell-averaged values and variations within a cell. A physical property at each vertex is then estimated by summing the monotonic variations along each coordinate direction, and the MLP condition of (3.3) is applied. To obtain the TVD regions of multi-dimensional space, a detailed analysis is performed using one-dimensional limiter functions. We have

$$\begin{aligned} 0 \le \phi (r) \le \min (\alpha r, \alpha ). \end{aligned}$$

(3.4)

$\alpha$ is the multi-dimensional restriction coefficient that determines the baseline variable limiting region. From (3.2) to (3.4), one can see that the MLP limiting region is determined depending on local multi-dimensional flow physics, while TVD provides a fixed limiting region. For practical reasons, the range of $\alpha$ is in [0, 2]. Because of $\phi (r)=0$ for $r<0$, the limiter switches to first-order accuracy if r becomes negative. This is the case for any extreme point.

For the third- and higher-order reconstructions, Kim et al. [11] used the local slope $\beta$ and a filtering of the unlimited values by the MLP conditions of (3.3) and (3.4). They, also introduced the MLP function $\phi (r_x)$ in the x-direction as

$$\begin{aligned} \phi ^{L(R)}(r_x) = \max \left( 0,\min \left( \alpha _x, \alpha _x r_x, \beta _x^{L(R)}\right) \right) . \end{aligned}$$

(3.5)

Finally we summarized the MLP methods proposed by [32] for 2D compressible flow. The cell-interface value of u is obtained as follows:

$$\begin{aligned} \begin{aligned} u^{L}_{i+1/2, j}&= \bar{u}_{ij} + 0.5 \phi ^L \left( \left( r^{L}_{x} \right) _{ij}\right) \Delta \bar{u}_{i-1/2,j},\\ u^{R}_{i-1/2, j}&= \bar{u}_{ij} - 0.5 \phi ^R \left( \left( r^{R}_{x}\right) _{ij} \right) \Delta \bar{u}_{i+1/2, j},\\ \end{aligned} \end{aligned}$$

(3.6)

where the MLP limiter functions, $\phi (\cdot )$, are shown as

$$\begin{aligned} \begin{aligned} \phi ^L \left( \left( r^{L}_{x} \right) _{ij}\right)&= \max \left( 0, \min (\alpha _x)_{ij},(\alpha _x)_{ij} \left( r^{L}_{x}\right) _{ij}, \left( \beta ^L_x\right) _{ij} \right) , \\ \phi ^R \left( \left( r^{R}_{x}\right) _{ij} \right)&= \max \left( 0, \min (\alpha _x)_{ij},(\alpha _x)_{ij} \left( r^{R}_{x}\right) _{ij}, \left( \beta ^R_x\right) _{ij} \right) ,\\ \end{aligned} \end{aligned}$$

(3.7)

where $\left( \alpha ^L_x\right) _{ij} = (\alpha _x)_{ij}$, $\left( \alpha ^R_x\right) _{ij} = (\alpha _x)_{ij}$, $\displaystyle {\left( r^{L}_{x}\right) _{ij} = (r_{x})_{ij}}$, and $\displaystyle {\left( r^{R}_{x}\right) _{ij} = {1}/{(r_{x})_{ij}}}.$ The $(\alpha _x)_{ij}$ is defined by

$$\begin{aligned} (\alpha _x)_{ij} = \Biggl |\frac{2\max \{ 1, (r_x)_{ij} \}}{\{ 1+(r_{xy})_{ij} \} \Delta \bar{u}_{i+1/2,j}} \Biggr | \min \left[ \Biggl |\bar{u}^{\max }_{\kappa _x, \kappa _y} - \bar{u}_{ij}\Biggr |, \Biggl |\bar{u}^{\min }_{\kappa '_x, \kappa '_y} - \bar{u}_{ij}\Biggr |\right] , \end{aligned}$$

(3.8)

where $\displaystyle {(r_x)_{ij} = \frac{\Delta \bar{u}_{i+1/2, j}}{\Delta \bar{u}_{i-1/2, j}} }$, $\displaystyle {(r_{xy})_{ij} = \frac{ \Delta \bar{u}^y_{i,j+\kappa _y/2}}{ \Delta \bar{u}^x_{i+\kappa _x/2,j}} }$ and

$$\begin{aligned} \begin{aligned} \bar{u}^{{\text {min}}}_{\kappa _x', \kappa _y'}&= \min (\bar{u}_{ij}, \bar{u}_{i+\kappa _x',j}, \bar{u}_{i,j+\kappa _y'} , \bar{u}_{i+\kappa _x', j+\kappa _y'}) ,\\ \bar{u}^{{\text {max}}}_{\kappa _x, \kappa _y}&= \max (\bar{u}_{ij}, \bar{u}_{i+\kappa _x,j}, \bar{u}_{i,j+\kappa _y} , \bar{u}_{i+\kappa _x, j+\kappa _y}). \end{aligned} \end{aligned}$$

(3.9)

Here, the cell-averaged values $\Delta \bar{u}^x_{i+\kappa _x/2,j}$ and $\Delta \bar{u}^y_{i,j+\kappa _y/2}$ are expressed as

$$\begin{aligned} \begin{aligned} \Delta \bar{u}^x_{i+\kappa _x/2,j}&= {u}^*_{i+\kappa _x/2,j} - \bar{u}_{ij}, \\ \Delta \bar{u}^y_{i,j+\kappa _y/2}&= {u}^*_{i,j+\kappa _y/2} - \bar{u}_{ij}, \end{aligned} \end{aligned}$$

(3.10)

where ${u}^*_{i+\kappa _x/2,j}$ and ${u}^*_{i,j+\kappa _y/2}$ are temporary cell-interface values at $(i+\kappa _x/2,j)$ and $(i,j+\kappa _y/2)$, respectively. For the computational efficiency,

$$\begin{aligned} r_{xy} \approx \biggl | \dfrac{\bar{u}_{i,j+1} - \bar{u}_{i,j-1}}{\bar{u}_{i+1,j} - \bar{u}_{i-1,j}}\biggr | \end{aligned}$$

is a reasonable choice and $(\beta ^L_x)_{ij}$ and $(\beta ^R_x)_{i+1,j}$ are determined by the third- or fifth-order polynomial interpolations given in Table 1. Numerical fluxes in the y-direction can be obtained similarly.

Table 1 Convergence order

4 Central-Upwind with Modified MLP

In the MUSCL-type linear reconstruction, local extrema occur at the vertex, and thus, only the vertex value is limited by the MLP condition. By considering all the neighboring cells sharing a vertex, the range of the multi-dimensional slope limiter can be obtained. From the basic premise of the MLP, the limiting condition in multi-dimensional space is satisfied by

$$\begin{aligned} \bar{u}^{\min }_{\kappa _x,\kappa _y} \le u_{i+\kappa _x/2,j+\kappa _y/2} \le \bar{u}^{\max }_{\kappa _x,\kappa _y}, \end{aligned}$$

(4.1)

where $u_{i+\kappa _x/2,j+\kappa _y/2}$ is a vertex point value. Indeed, the limiting condition, (4.1), is applied to the four vertex points $(i+\kappa _x/2, j+\kappa _y/2), \kappa _x,\kappa _y = \pm 1$. $\bar{u}^{\min }_{\kappa _x,\kappa _y}$ and $\bar{u}^{\max }_{\kappa _x,\kappa _y}$ are, respectively, the minimum and maximum cell-averaged values around the vertex point $(i+\kappa _x/2, j+\kappa _y/2)$. The vertex point value is calculated by the cell-averaged value and variations within a cell:

$$\begin{aligned} u_{i+\kappa _x/2 , j+\kappa _y/2} = \bar{u}_{ij}+ \Delta u^x_{i+\kappa _x/2,j} + \Delta u^y_{i,j+\kappa _y/2}. \end{aligned}$$

(4.2)

The variations (3.10) combined with MLP condition (3.4) can be defined by

$$\begin{aligned} \begin{aligned} \Delta u^x_{i+\kappa _x/2,j}&= 0.5\kappa _x\phi (r_{x})\Delta \bar{u}_{i-1/2,j},\\ \Delta u^y_{i,j+\kappa _y/2}&= 0.5\kappa _y\phi (r_{y})\Delta \bar{u}_{i,j-1/2}. \end{aligned} \end{aligned}$$

(4.3)

Using variations and employing the TVD-MUSCL limiting, we obtain (4.4) from (4.2),

$$\begin{aligned} u_{i+\kappa _x/2 , j+\kappa _y/2} = \bar{u}_{ij} + 0.5\kappa _x\phi (r_{x})\Delta \bar{u}_{i-1/2,j} + 0.5\kappa _y\phi (r_{y})\Delta \bar{u}_{i,j-1/2}. \end{aligned}$$

(4.4)

Since the vertex point values of (4.4) do not satisfy the limiting condition of (4.1) at all vertex points, we need to restrict the range of the limiter function $\phi$ for the TVD regions. In the limiter function in (4.4) and (3.5), if the parameters $\alpha _{x}$ and $\alpha _{y}$, respectively, are taken as 2, the 1D TVD property could be satisfied; however, it is not guaranteed that the TVD property in 2D space would be satisfied (see Fig.1). As a result, to control $\phi (r_x)$ and $\phi (r_y)$ to satisfy the multi-dimensional limiting condition of the MLP, we have to suitably determine the parameters $\alpha _{x}$ and $\alpha _{y}$. In [32], Yoon et al. introduced the single values of parameters $\alpha _{x}$ and $\alpha _{y}$. Later, Gerlinger suggested the different parameter values for both coordinate directions in [4] to satisfy the maximum property (4.1), to avoid local extrema at the corner points of a volume, and to prevent excessive numerical dissipation. The parameters $\alpha _{x}$ and $\alpha _{y}$, however, are smaller than those required by the MLP condition, and the numerical results are more dissipative than necessary near discontinuities. In contrast to previous parameters, the maximized $\alpha _{x}$ and $\alpha _{y}$ are introduced here to reduce the dissipation near discontinuities by modifying the limiting condition.

Fig. 1

Main concept of the MLP: in general, applying 1D TVD-limiting with dimensional splitting doesn’t guarantee the TVD property along the diagonal direction. a Initial profile. b TVD-limiting along the x-direction. c TVD-limiting along the y-direction. d TVD-limiting along the xy-direction. e Appropriate choices of $\alpha _{x}, \alpha _{y}$ to satisfy the maximum principle

For the variable-limiting regions, it is necessary to select appropriate values of the parameters $\alpha$ and $\beta$ in the limiter function to prevent overestimating the features that disturb TVD. For the purpose of computational efficiency in choosing the $\alpha _{x}$ and $\alpha _{y}$, we attempt to lessen the corresponding computational effort through the use of several propositions.

Proposition 4.1

Whenever $r_{xy} < 0$ in (3.8), (4.1) is satisfied automatically.

Proof

Without loss of generality, we may assume that

$$\begin{aligned} \Delta u^{x}_{i+\kappa _x/2,j} > 0 ~~ {\text {and}} ~~ \Delta u^{y}_{i,j+\kappa _y/2} \le 0. \end{aligned}$$

Then we have

$$\begin{aligned} \bar{u}_{ij} + \Delta u^{y}_{i,j+\kappa _y/2}&\le u_{i+\kappa _x/2, j+\kappa _y/2} \\&= \bar{u}_{ij}+\Delta u^{x}_{i+\kappa _x/2,j}+\Delta u^{y}_{i,j+\kappa _y/2}\\&\le \bar{u}_{ij}+\Delta u^{x}_{i+\kappa _x/2,j}. \end{aligned}$$

Since the variations $\Delta u^{x}_{i+\kappa _x/2,j}, \Delta u^{y}_{i,j+\kappa _y/2}$ are derived by the 1D TVD limiter,

$$\begin{aligned}&\bar{u}_{i,j+\kappa _y} \le \bar{u}_{ij} + \Delta u^{y}_{i,j+\kappa _y/2},\\&\bar{u}_{ij} + \Delta u^{x}_{i+\kappa _x/2,j} \le \bar{u}_{i+\kappa _x,j}. \end{aligned}$$

Therefore,

$$\begin{aligned} \bar{u}^{\min }_{\kappa _x,\kappa _y} \le \bar{u}_{i,j+\kappa _y} \le u_{i+\kappa _x/2,j+\kappa _y/2} \le \bar{u}_{i+\kappa _x,j} \le \bar{u}^{\max }_{\kappa _x,\kappa _y}. \end{aligned}$$

$\square$

Proposition 4.2

When $\Delta u^{x}_{i+\kappa _x/2,j} > 0 \; (\le 0)\; and \; \Delta u^{y}_{i,j+\kappa _y/2} > 0 \; (\le 0)$ (i.e., max(min) vertex), the left(right) inequality in (4.1) is satisfied.

Proof

$$\begin{aligned} \bar{u}^{\min }_{\kappa _x,\kappa _y} \le \bar{u}_{ij} \le \bar{u}_{ij} + \Delta u^{x}_{i+\kappa _x/2,j} + \Delta u^{y}_{i,j+\kappa _y/2} = u_{i+\kappa _x/2,j+\kappa _y/2}. \end{aligned}$$

$\square$

Since vertex point values other than the maximum and minimum satisfy (4.1), it is enough to show the following:

$$\begin{aligned} \begin{aligned}&u_{i+\kappa _x/2, j+\kappa _y/2} \le \max (\bar{u}_{i,j},\bar{u}_{i+\kappa _x,j}, \bar{u}_{i,j+\kappa _y}, \bar{u}_{i+\kappa _x,j+\kappa _y} )\\&\qquad \quad {\text {when}} \quad \, u_{i+\kappa _x/2,j+\kappa _y/2} \quad \, {\text {is a maximum vertex}}, \end{aligned} \end{aligned}$$

(4.5)

$$\begin{aligned} \begin{aligned}&\min (\bar{u}_{i,j},\bar{u}_{i+\kappa _x',j}, \bar{u}_{i,j+\kappa _y'}, \bar{u}_{i+\kappa _x',j+\kappa _y'} ) \quad \le u_{i+\kappa _x'/2, j+\kappa _y'/2} \\&\qquad \qquad {\text {when}} \quad u_{i+\kappa _x'/2,j+\kappa _y'/2} \quad {\text {is a minimum vertex}}, \end{aligned} \end{aligned}$$

(4.6)

for (4.4) and Yoon et al. computed parameters $\alpha _{x}, \alpha _{y}$ satisfying (4.5) and (4.6) in [32].

We now introduce the relieved maximum property to a simple modification of the original maximum property to control the contributions of the MLP parameters $\alpha _{x}$ and $\alpha _{y}$, which require the MLP condition and reduce the dissipation near discontinuities. We construct the new MLP parameters from the relieved maximum property,

$$\begin{aligned} \bar{u}_{ij} - c \le u_{i+\kappa _x/2, j+\kappa _y/2} \le \bar{u}_{ij} + c \end{aligned}$$

(4.7)

with $c = \frac{1}{2}(\bar{u}^{\max }_{\kappa _x,\kappa _y} - \bar{u}^{\min }_{\kappa '_x,\kappa '_y})$. In order to determine the parameters $\alpha _{x}$ and $\alpha _{y}$ that satisfy (4.7), we have the following equation using (4.4):

$$\begin{aligned} \bar{u}_{ij} - c \le \bar{u}_{ij}+ \Delta u^x_{i+\kappa _x/2,j} + \Delta u^y_{i,j+\kappa _y/2} \le \bar{u}_{ij} + c. \end{aligned}$$

(4.8)

We obtain

$$\begin{aligned} \Biggl |(1+r_{xy}) \Delta u^{x}_{i+\kappa _x/2,j}\Biggr | \le c \end{aligned}$$

(4.9)

with $r_{xy} = \dfrac{\Delta u^{y}_{i,j+\kappa _y/2}}{\Delta u^{x}_{i+\kappa _x/2,j}}$. We now assume that $u_{i+\kappa _x, j+\kappa _y}$ is the maximum vertex, $r_{xy} > 0$ and $\Delta u^{x}_{i+\kappa _x/2,j} > 0$. By the definition of the deviation term, we have

$$\begin{aligned} \left| \dfrac{\kappa _x}{2}\phi (r_{x}) \Delta \bar{u}_{i-1/2,j}\right| \le \dfrac{c}{1+r_{xy}} \end{aligned}$$

and

$$\begin{aligned} \max (0, \min (\alpha _{x}, \alpha _{x} r_{x})) \le \dfrac{2 c}{\kappa _x (1+r_{xy})\Delta \bar{u}_{i-1/2,j}} . \end{aligned}$$

We may assume that $r^{L}_{x} > 0$, so we have

$$\begin{aligned} \alpha _{x}\min (1, r^{L}_{x}) \le \left| \dfrac{2 c}{\kappa _x(1+r_{xy})\Delta \bar{u}_{i-1/2,j}}\right| . \end{aligned}$$

Thus we obtain

$$\begin{aligned} \begin{aligned} \alpha _{x}&\le \left| \dfrac{2 c\max \left( 1,1/ r_x^L\right) }{(1+r_{xy})\Delta \bar{u}_{i-1/2,j}}\right| \\&= \left| \dfrac{2 c\max \left( 1,1/ r_x^L\right) r_x^L}{(1+r_{xy})\Delta \bar{u}_{i-1/2,j} r_x^L}\right| \\&=\Biggl | \dfrac{2 c \max \left( 1, r^{L}_{x}\right) }{(1+r_{xy}) \Delta \bar{u}_{i+1/2,j}}\Biggl | \end{aligned} \end{aligned}$$

(4.10)

with $c = \frac{1}{2}(\bar{u}^{\max }_{\kappa _x,\kappa _y} -\bar{u}^{\min }_{\kappa '_x,\kappa '_y})$. In the case where $u_{i+\kappa _x/2, j+\kappa _y/2}$ is a minimum, by the symmetry of (4.9), it is easy to check whether (4.10) is derived. It is a simple observation that $u_{i-\kappa _x/2, j-\kappa _y/2}$ is a minimum if $u_{i+\kappa _x/2,j+\kappa _y/2}$ is a maximum facilitate vertex. Choosing the maximum $\alpha _{x}$, finally, we have

$$\begin{aligned} \alpha _{x} = \left| \dfrac{\left( \bar{u}^{\max }_{ \kappa _x, \kappa _y} - \bar{u}^{\min }_{-\kappa _x,-\kappa _y}\right) \max \left( 1,r^{L}_{x}\right) }{(1+r_{xy}) \Delta \bar{u}_{i+1/2,j}} \right| . \end{aligned}$$

To summarize the overall process, the formulae used to implement CU-MLP are presented as the following Algorithm 1:

5 Numerical Results

In this section, we present numerical results of the central-upwind scheme with a modified MLP limiter. We examine the numerical performance of the proposed scheme. The numerical presentation of this section starts with the solution of the 2-dimensional advection equation, followed by the solution of burgers’ equation and 2D Euler system of equations with Riemann initial-value problems. First, we apply our schemes to the scalar 2 D advection equation with appropriate initial conditions to test the propagation of arbitrary initial profiles containing jump discontinuities and corner points.

5.1 Linear Advection Equation

We apply the CU-MLP schemes to the scalar advection equation with a discontinuous initial condition to compare the behavior of the proposed schemes at discontinuities. We consider the follow the linear advection equation,

$$\begin{aligned} q_t+q_x+q_y =0, \qquad (x,y) \in [0,1] \times [0,1], \end{aligned}$$

(5.1)

with the initial condition,

$$\begin{aligned} q(x,y,0)=q_0(x,y)=\left\{ \begin{array}{l@{\quad }l} 1, &{} (x,y) \in Q \\ 0.1, &{}(x,y) \in Q^c \end{array} \right. \end{aligned}$$

(5.2)

where $Q = [0.25,0.75] \times [0.25,0.75]$. We solve the Eq. (5.1) up to $t=2$ to investigate the stability and the amount of smearing at discontinuities of the proposed scheme. The computational results are shown in Fig. 2. We can see that discontinuities smear less for CU-MLP than for CU-KNP.

Fig. 2

CU-KNP (a, c) and CU-MLP (b, d) with $\Delta x= \Delta y= 1/100$ at $t = 4$

5.2 Burger’s Equation

We approximate solutions to the inviscid Burgers’ equation

$$\begin{aligned} q_t+\left( \dfrac{q^2}{2}\right) _x+\left( \dfrac{q^2}{2}\right) _y=0, \qquad (x,y) \in [0,1] \times [0,1], \end{aligned}$$

(5.3)

with the initial condition where $Q = [0.1,0.6] \times [0.1,0.6]$. Figure 3 shows the solutions at time t = 2. The CU-KNP schemes smear the shock slightly more than the proposed CU-MLP schemes.

Fig. 3

2D Burgers’ CU-KNP (left) and CU-MLP(right) with $\Delta x= \Delta y= 1/100$ at $t = 4$

5.3 2D Euler System of Equations for Compressible Flow

In this subsection, we test the proposed scheme by applying to 2D compressible Euler systems of the below form:

$$\begin{aligned} q_t + f(q)_x + g(q)_y = 0, \end{aligned}$$

(5.4)

where

$$\begin{aligned}&q = (\rho , \rho u, \rho v, E)^T, \\&f(q) = (\rho u, \rho u^2 +p, \rho uv, u(E+p))^T,\\&g(q) = (\rho v, \rho vu, \rho v^2+p, v(E+p))^T,\\&p = (\gamma -1) \left( E -\frac{1}{2} \rho (u^2+v^2) \right) . \end{aligned}$$

Here, $\rho , u, v, p$, and E are the density, components of velocity in the x and y coordinate directions, pressure and total energy, respectively. q is the vector of conservative variables, f(q) the x-wise-flux component, and g(q) the y-wise-flux component.

Example 5.1

(2D Problem for 2D Euler-four-shocks) We consider numerical solutions of the 2D Riemann problems originally defined in [26]. This problem is solved on a square domain given by $[0,1] \times [0,1]$, which is divided into four quadrants by lines $x=0.8$ and $y=0.8$. We take the initial condition to be constant states in each of the four quadrants and compute this initial data up to time $t=0.8$. The Riemann problems are defined by initial constant states in each quadrant:

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (1.5, 0, 0, 1.5) &{}\,\,\, {\text {if }}\,0.8\le x\le 1, 0.8\le y\le 1, \\ (0.5323, 1.206, 0, 0.3)&{}\,\,\, {\text {if }}\,0\le x< 0.8, 0.8\le y\le 1, \\ (0.138, 1.206, 1.206, 0.029) &{}\,\,\, {\text {if }}\,0\le x < 0.8, 0\le y < 0.8,\\ (0.5323, 0, 1.206, 0.3)&{}\,\,\, {\text {if }}\,0.8 <x\le 1, 0 \le y< 0.8. \end{array}\right. } \end{aligned}$$

We set the gas constant to $\gamma = 1.4$. To the best of our knowledge, the exact solution has not yet been elucidated for this 2D problem. We compare the numerical performance of the CU-KNP scheme with that of the proposed scheme in Fig. 4. An examination of the results reveals that the proposed scheme displays a better resolution of the structure than that appearing in the CU-KNP scheme.

Fig. 4

2D Problem for 2D Euler-four-shock. a CU-KNP and b CU-MLP with $\Delta x= \Delta y= 1/400$ and c CU-KNP and d CU-MLP with $\Delta x= \Delta y= 1/800$ at $t = 0.8$

Example 5.2

(Two-dimensional Rayleigh–Taylor instability) Taylor instability in 2D incompressible fluids occurs on an interface between two fluids of different densities, where the lighter fluid is pushing the heavier fluid. Several experimental investigations of this phenomenon have been reported extensively in the literature (e.g. [5] and [33]). This problem is solved on a computational domain given by $[0,0.25] \times [0,1]$, with the following initial conditions:

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (2, 0, -0.025 a \cos (8 \pi x) , 2y+1) &{}\,\,\, {\text {if }}\, 0 \le y < 0.5, \\ \left( 1, 0, -0.025 a \cos (8 \pi x) , y+\frac{3}{2}\right) &{}\,\,\, {\text {if }}\, 0.5 \le y < 1. \end{array}\right. } \end{aligned}$$

Here, $a = \sqrt{\gamma p/\rho }$ and $\gamma = 5/3$ are the speed of sound and the ratio of specific heats, respectively. Adding $\rho$ and $\rho v$ to the right-hand sides of the third and fourth equations, respectively, allows modeling of the gravitational effect. Reflective boundary conditions are applied to the left and right boundaries, and

$$\begin{aligned} (\rho , u , v, p) = {\left\{ \begin{array}{ll} (2, 0, 0, 2.5) &{}\,\,\, {\text {top boundary}}, \\ (1, 0, 0, 1 )&{}\,\,\, {\text {bottom boundary}}. \end{array}\right. } \end{aligned}$$

The simulation time is $t=1.95$. From the density contours with $\Delta x = \Delta y = 1/480$ plotted in Fig. 5, it can be seen that the proposed scheme obtains more complex structures than the CU-KNP schemes.

Fig. 5

Density profiles of Rayleigh–Taylor instability. a CU-KNP and b CU-MLP with $\Delta x= \Delta y= 1/240$ and c CU-KNP and d CU-MLP with $\Delta x= \Delta y= 1/480$ at $t = 1.95$

Fig. 6

Density profiles of the Double-Mach reflection of a strong shock [31] at $t = 0.2$ with $\Delta x = \Delta y = 1/480$ (top CU-KNP, bottom CU-MLP)

Example 5.3

(Double-Mach reflection of a strong shock) The considered test case is the two-dimensional Double-Mach reflection of a shock-off of an oblique surface, which is also a very popular test case for high resolution schemes [31]. The whole computational domain is given by $[0, 4] \times [0, 1]$, with equally spaced grid points. Initially, a right-moving shock with Mach number 10 is located at the bottom of the computational domain of the x-axis at $x = \frac{1}{6}$, inclined at a $60^{\circ }$ angle with respect to the x-axis. A reflective boundary condition is applied along the bottom wall, and the top boundary of the problem is set to describe the exact motion of the Mach 10 shock. See [31] for a detailed description of this problem. We display the results in the $[0, 3] \times [0, 1]$ domain, as is customary. Figure 6 shows the details at the Mach stem of the density variable at the final time, $t=0.2$, with $\gamma = 1.4$ and $\Delta x = \Delta y = 1/480$. We can clearly see that the proposed scheme resolves the instabilities around the Mach stem.

Fig. 7

Contour plots of density profile of a Mach 3 wind tunnel with a step at $t = 4$ with $\Delta x = \Delta y = 1/240$ (top CU-KNP, bottom CU-MLP)

Example 5.4

(A Mach 3 wind tunnel with a step) This 2D model problem was first presented by Woodward and Collella [31]. This test begins with uniform Mach 3 flow in a wind tunnel that spans a domain of $[0,3] \times [0,1]$. A forward-facing step is located at (0.6, 0.2). Inflow boundary conditions are applied at the left boundary, where the flow enters the wind tunnel at a right-going Mach 3 with a density of 1.4 and a pressure of unity. Reflective boundary conditions are applied along the walls of the tunnel. Inflow and outflow boundary conditions are applied at the left and right boundaries, respectively. The simulation is run until a time of 4, and the ratio of specific heats is given by 1.4. For the treatment of the singularity at the corner of the step, we adopt the same technique used in [31]. The results of the proposed scheme are compared with those obtained by the central-upwind scheme with a KNP flux function. We solve it with $\Delta x = \Delta y = 1/240$. We display the density profiles obtained by these two schemes in Fig. 7.

6 Conclusion

In this paper, a central-upwind methods with a modified multi-dimensional limiting process (CU-MLP) has been introduced for the approximate solutions of 2D hyperbolic conservation laws. Even though central-upwind schemes have the advantage of simplicity while being Riemann-free with second order accuracy they have slighter larger dissipations than second-order upwind schemes. To overcome this drawback, we apply the MLP limiter to the central-upwind scheme and obtain excellent performances in all test cases. Compared to the original MLP parameter, $\alpha$, the modified MLP parameter for central-upwind methods sharply resolves discontinuities while maintaining its non-oscillatory performance. The improvement is attributed to the ability of the proposed scheme to detect complicated solution structures.