Recovery-Based Error Estimator for the Discontinuous Galerkin Method for Nonlinear Scalar Conservation Laws in One Space Dimension

Abstract

In this paper, we propose and analyze a robust recovery-based error estimator for the original discontinuous Galerkin method for nonlinear scalar conservation laws in one space dimension. The proposed a posteriori error estimator of the recovery-type is easy to implement, computationally simple, asymptotically exact, and is useful in adaptive computations. We use recent results (Meng et al. in SIAM J Numer Anal 50:2336–2356, 2012) to prove that, for smooth solutions, our a posteriori error estimates at a fixed time converge to the true spatial errors in the $L^2$-norm under mesh refinement. The order of convergence is proved to be $p + 1$, when $p$-degree piecewise polynomials with $p\ge 1$ are used. We further prove that the global effectivity index converges to unity at $\mathcal {O}(h)$ rate. Our proofs are valid for arbitrary regular meshes using $P^p$ polynomials with $p\ge 1$, under the condition that $|f'(u)|$ possesses a uniform positive lower bound, where $f(u)$ is the nonlinear flux function. We provide several numerical examples to support our theoretical results, to show the effectiveness of our recovery-based a posteriori error estimates, and to demonstrate that our results hold true for nonlinear conservation laws with general flux functions. These experiments indicate that the restriction on $f(u)$ is artificial.

1 Introduction

In this paper, we propose and analyze a robust recovery-type a posteriori error estimator based on a derivative recovery technique for the discontinuous Galerkin (DG) method applied to the classical nonlinear scalar conservation law in one space dimension

$$\begin{aligned} u_{t} + \left( f(u)\right) _{x}=g(x,t),\quad x\in [a,b],\ t \in [0,T], \end{aligned}$$

(1.1a)

subject to the initial condition

$$\begin{aligned} u(x,0) =u_0(x), \quad x \in [a,b], \end{aligned}$$

(1.1b)

and appropriate boundary conditions described below. Here, $g(x,t)$ and $u_0(x)$ are smooth functions possessing all the necessary derivatives. The unknown function $u$ is some scalar conserved quantity and $f(u)$ is a nonlinear flux function. In our analysis, we assume that $f(u)$ is a smooth function with respect to the variable $u$. We also assume that $|f'(u)|$ has a uniform positive lower bound, i.e., either $0<\delta \le f'(u(x,t))$ or $f'(u(x,t))\le - \delta < 0,\ \forall \ (x,t)\in [a,b]\times [0,T]$, where $\delta$ is a positive constant. We will consider both the periodic boundary condition $u(a, t) = u(b, t)$ and the Dirichlet boundary condition on the inflow boundary which depends on the sign of $f'(u)$. If $f'(u)>0$, then we complete (1.1a) and (1.1b) with

$$\begin{aligned} u(a,t) = h(t), \quad t \in [0,T], \end{aligned}$$

(1.1c)

and if $f'(u)<0$, we complete (1.1a) and (1.1b) with

$$\begin{aligned} u(b,t) = g(t), \quad t \in [0,T]. \end{aligned}$$

(1.1d)

We refer the reader to [27] and the references therein for a more detailed description of related theoretical results including stability analysis, a priori error estimates, and superconvergence error analysis of the semi-discrete DG methods for conservation laws (1.1).

The DG method considered here is a class of finite element methods using completely discontinuous piecewise polynomials for the numerical solution and the test functions. DG method combines many attractive features of the classical finite element and finite volume methods. It is a powerful tool for approximating some differential equations which model problems in physics, especially in fluid dynamics or electrodynamics. Comparing with the standard finite element method, the DG method has a compact formulation, i.e., the solution within each element is weakly connected to neighboring elements. The DG method was initially introduced by Reed and Hill in 1973 as a technique to solve neutron transport problems [29]. Lesaint and Raviart [25] presented the first numerical analysis of the method for a linear advection equation. Since then, DG methods have been used to solve ordinary differential equations [5, 20, 24, 25], hyperbolic [1–5, 9–11, 15, 18, 21, 23, 27, 28, 34] and diffusion and convection-diffusion [13–15, 19] partial differential equations, just to mention a few citations. The proceedings of Cockburn et al. [17] an Shu [32] contain a more complete and current survey of the DG method and its applications. In particular, Meng et al. [27] analyzed the DG method applied to (1.1). They proved a priori optimal error estimates and a superconvergence result toward a particular projection of the exact solution. The results in the present paper depend heavily on the results from [27].

A posteriori error estimates play an essential role in assessing the reliability of numerical solutions and in developing efficient adaptive algorithms. A posteriori error estimates are traditionally used to guide adaptive enrichment by $h$- and $p$-refinement and to provide a measure of solution reliability. Typically, a posteriori error estimators employ the known numerical solution to derive estimates of the actual solution errors. There are several error concepts available in the literature including (i) residual-type estimators that rely on the appropriate evaluation of the residual in a dual norm, (ii) hierarchical type estimators where the error equation is solved locally using higher order elements, (iii) error estimators that are based on local averaging; the so-called goal oriented dual weighted approach where information about the error is extracted from the solution of the dual problem, and (iv) functional type error majorants that provide guaranteed sharp upper bounds for the error. For an introduction to the subject of a posteriori error estimation see the monograph of Ainsworth and Oden [6]. The a posteriori error estimation of finite element approximations of elliptic, parabolic, and hyperbolic problems has reached some state of maturity as documented by the monographs [6, 12, 22, 33] and the references therein. However, a posteriori error estimation is much less developed for DG methods applied to hyperbolic problems. Recently, the author [10] presented and analyzed implicit residual-based a posteriori error estimates for a DG formulation applied to nonlinear scalar conservation laws in one space dimension. We used the superconvergence result of Meng et al. [27] to prove that the DG discretization error estimates converge to the true spatial errors under mesh refinement at $\mathcal {O}(h^{p+3/2})$ rate. Finally, we proved that the global effectivity index in the $L^2$-norm converges to unity.

A posteriori error estimators for finite element are classified mainly into two families [6]: residual-type error estimators and recovery-based error estimators. Although the a posteriori implicit residual-type estimators have been the most commonly used techniques to provide bounds of the error of the finite element method, the recovery-based estimates, based on the ideas of Zienkiewicz and Zhu [35] and, in particular,those based on the superconvergent patch recovery technique [36, 37], are often preferred by practitioners due to their simple implementation and robustness [7, 8].

Here, we propose a posteriori error estimator based on derivatives recovery. Recovery-based error estimators have been studied in [26] and the references therein. A much researched recovery-based error estimator was proposed by Zienkiewicz and Zhu [35], who suggested to post-process the discontinuous gradient in terms of some interpolation functions. The underlying idea is to post-process the gradient and to find an estimate for the true error by comparing the post-processed gradient and the nonpost-processed gradient of the approximation. A posteriori error estimators of the recovery-type possess a number of attractive features for the engineering community, because they are easy to implement, computationally simple, asymptotically exact, and produce quite accurate estimators on fine meshes. From a practical point of view, recovery-based error estimators are efficient compared to other implicit residual-based a posteriori error estimates. Several recovery-type a posteriori error estimators are known for elliptic problems. However, to author’s knowledge, no recovery-type a posteriori error estimator for DG methods applied to first-order hyperbolic problems is available in the literature.

In this paper, we propose and analyze a new recovery-based a posteriori error estimator for the DG method applied to one-dimensional nonlinear conservation laws. The proposed estimator of the recovery-type is easy to implement, computationally simple, and is asymptotically exact. We use recent results given in [27] to prove that these error estimates converge to the true spatial errors at $\mathcal {O}(h^{p+1})$ rate. We also prove that the global effectivity indices in the $L^2$-norm converge to unity at $\mathcal {O}(h)$ rate. To the best knowledge of the author, this is the first recovery-based error estimator for the DG method applied to nonlinear scalar conservation laws. As in [27], our proofs are valid for any regular meshes and using piecewise polynomials of degree $p\ge 1$, provided that $|f'(u)|$ is lower bounded uniformly by a positive constant. The proof of the general case involves several technical difficulties and will be investigated in the future. For general flux functions, we expect that similar results of Meng et al. [27] (see Theorem 2.1) will be needed.

This paper is organized as follows: In Sect. 2 we recall the semi-discrete DG method for solving (1.1) and we introduce some notation and definitions. We also present few preliminary results, which will be needed in our a posteriori error analysis. In Sect. 3, we present our error estimation procedures and prove that they converge to the true errors under mesh refinement in $L^2$-norm. In Sect. 4, we present several numerical examples to validate our theoretical results. We conclude and discuss our results in Sect. 5.

2 The Semi-Discrete DG Scheme

To obtain the semi-discrete DG scheme for (1.1), we first divide $\Omega =[a,b]$ into $N$ intervals $I_i = [x_{i-1},x_{i}],\ i=1,\ldots ,N$, where $a=x_0 < x_1 < \cdots < x_N=b.$ The length of each $I_i$ is denoted by $h_i = x_{i}-x_{i-1}$. We denote $h= \max \limits _{1 \le i \le N} h_i$ and $h_{min}= \min \limits _{1 \le i \le N} h_i$ as the length of the largest and smallest interval. In this paper, we consider regular meshes, that is $h\le K h_{min},$ where $K\ge 1$ is a constant during mesh refinement. If $K= 1$, then the mesh is uniformly distributed. Throughout this paper, $v\big |_{i}$ denotes the value of the function $v=v(x,t)$ at $x=x_i.$ We also define $v^{-}\big |_i$ and $v^{+}\big |_i$ to be the left limit and the right limit of the function $v$ at the discontinuity point $x_i$, i.e.,

$$\begin{aligned} v^{-}\big |_i =v(x_i^{-},t) = \lim \limits _{s\rightarrow 0^{-}} v(x_i+s,t),\qquad v^{+}\big |_i =v(x_i^{+},t) = \lim \limits _{s\rightarrow 0^{+}} v(x_i+s,t). \end{aligned}$$

Let us multiply (1.1a) by test a function $v$, integrate over $I_i$, and use integration by parts to write

$$\begin{aligned} \int _{I_i}u_{t} v \ dx - \int _{I_i}f(u) v_x \ dx +f(u)v^-\big |_{i}-f(u)v^+\big |_{i-1}=\int _{I_i}gv \ dx. \end{aligned}$$

(2.1)

Define the piecewise polynomial space $V_h^p$ as the space of polynomials of degree up to $p$ in $I_i$, i.e.,

$$\begin{aligned} V_h^p = \{v: \ v|_{I_i}\in P^p(I_i),\ i=1,\ldots ,N \}, \end{aligned}$$

where $P^p(I_i)$ is the space of polynomials of degree at most $p$ on $I_i$. Note that polynomials in the space $V_h^p$ are allowed to have discontinuities across element boundaries.

Next, we approximate the exact solution $u(.,t)$ by piecewise polynomial $u_h(.,t)\in V_h^p$. The semi-discrete DG method consists of finding $u_h \in V_h^p$ such that, $\forall \ v\in V_h^p$ and $\forall \ i=1,\ldots ,N$,

$$\begin{aligned} \int _{I_i}(u_h)_{t} v \ dx - \int _{I_i}f(u_h) v_x \ dx +\hat{f}v^-\big |_{i}-\hat{f}v^+\big |_{i-1}=\int _{I_i}gv \ dx, \end{aligned}$$

(2.2a)

where, the numerical flux $\hat{f}|_{i}$ is a single-valued function defined at the nodes and in general depends on the values of $u_h$ from both sides i.e., $\hat{f}|_{i}=\hat{f}(u_h^-,u_h^+)|_{i}$. The initial condition $u_h(x,0)=P_h^-u(x,0)\in V_h^p$ is obtained using a special projection of the exact initial condition $u(x,0)=u_0(x)$. The projection $P_h^-$ is defined in (2.3). In order to complete the definition of the scheme we need to select $\hat{f}$ on the boundaries of $I_i$. In this paper, we choose the upwind flux which depends on $f'(u)$. If $f'(u)>0$, the numerical flux associated with the Dirichlet boundary condition, $u(a,t)=h(t)$, can be taken as

$$\begin{aligned} \hat{f}\big |_0=f(u(a,t))= f(h(t)), \quad \hat{f}\big |_i=f(u_h^{-})\big |_i, \ i=1,\ldots ,N. \end{aligned}$$

(2.2b)

and if $f'(u)<0$, the numerical flux associated with the boundary condition, $u(b,t)=g(t)$, can be taken as

$$\begin{aligned} \hat{f}\big |_i= f(u_h^{+})\big |_i, \ i=0,\ldots ,N-1, \quad \hat{f}\big |_i= f(u(b,t))=f(g(t)). \end{aligned}$$

(2.2c)

Remark 2.1

Even though the proofs of our results are given using the numerical flux (2.2b), the same results can be proved using the numerical flux (2.2c), with only minor modifications.

Remark 2.2

We shall consider here only the Dirichlet boundary conditions. This assumption is for simplicity only and not essential. If other boundary conditions are chosen, the numerical flux $\hat{f}$ can be easily designed. For instance, in the case $f'(u)>0$, the numerical flux associated with the periodic boundary condition, $u(a,t)=u(b,t)$, can be taken as

$$\begin{aligned} \hat{f}\big |_i= \left\{ \begin{array}{ll} f(u_h^{-})\big |_N, &{} \quad i=0,\\ f(u_h^{-})\big |_i, &{} \quad i=1,\ldots ,N, \end{array} \right. \end{aligned}$$

(2.2d)

and if $f'(u)<0$, we take

$$\begin{aligned} \hat{f}\big |_i= \left\{ \begin{array}{ll} f(u_h^{+})\big |_i, &{} \quad i=0,\ldots ,N-1,\\ f(u_h^{+})\big |_0, &{} \quad i=N. \end{array} \right. \end{aligned}$$

(2.2e)

2.1 Discretization in Time

Expressing $u_h(.,t),\ x\in I_i$ as a linear combination of orthogonal basis $L_{k,i}(x),\ k=0,\ldots ,p$, where $L_{k,i}$ denotes the $k$th-degree Legendre polynomial on $I_i$, i.e., $u_h=\sum _{k=0}^pc_{k,i}(t)L_{k,i}(x),\ x\in I_i$, and choosing the test functions $v=L_{j,i}(x),\ j=0,\ldots ,p$, we obtain a system of ordinary differential equations which can be solved for the coefficients $\mathbf {c}_i=[c_{0,i},\ldots ,c_{p,i}]^t$. In what follows we assume that the system is integrated exactly. In practice, the system can be solved using e.g., the classical fourth-order Runge–Kutta method. A time step is chosen so that temporal errors are small relative to spatial errors. We do not discuss the influence of the time discretization error in this paper.

2.2 Norms

We begin by defining some norms that will be used throughout the paper. We define the standard $L^2$-norm of an integrable function $u=u(x,t)$ on the interval $I_i=[x_{i-1},x_{i}]$ and at a fixed time $t$ as $\left\| u(\cdot ,t)\right\| _{0,I_i}=(\int _{I_i}u^2(x,t)dx)^{1/2}$. Let $H^s(I_i)$, where $s= 0,1,\ldots$, denote the standard Sobolev space of square integrable functions on $I_i$ with all derivatives $\partial _x^k u=\frac{\partial ^ku}{\partial x^k}, \ k=0,1,\ldots ,s$ being square integrable on $I_i$ and equipped with the norm $\left\| u(\cdot ,t)\right\| _{s,I_i} = \left( \sum _{k=0}^s \left\| \partial _x^ku(\cdot ,t)\right\| _{0,I_i}^2\right) ^{1/2}.$ The $H^s(I_i)$-seminorm of $u$ on $I_i$ is given by $\left| u(\cdot ,t)\right| _{s,I_i}= \left\| \partial _x^su(\cdot ,t)\right\| _{0,I_i}$. We also define the norm and seminorm on the whole computational domain $\Omega$ as follows:

$$\begin{aligned} \left\| u(\cdot ,t)\right\| _{s,\Omega } = \left( \sum _{i=1}^{N} \left\| u\right\| _{s,I_i}^2\right) ^{1/2},\quad \left| u(\cdot ,t)\right| _{s,\Omega } = \left( \sum _{i=1}^{N} \left| u(\cdot ,t)\right| _{s,I_i}^2\right) ^{1/2}. \end{aligned}$$

For convenience, we use $\left\| u\right\| _{I_i}$, $\left\| u\right\|$, $\left\| u\right\| _{s,I_i}$, and $\left\| u\right\| _s$ to denote $\left\| u(\cdot ,t)\right\| _{0,I_i}$, $\left\| u(\cdot ,t)\right\| _{0,\Omega }$, $\left\| u(\cdot ,t)\right\| _{s,I_i}$, and $\left\| u(\cdot ,t)\right\| _{s,\Omega }$, respectively.

2.3 Projections

For $p\ge 1$, we will consider two special projection operators, $P_h^\pm$, which are defined as follows [15]: For any smooth function $u$, $P_h^{\pm } u\in V_h^p$ and the restrictions of $P_h^-u$ and $P_h^+u$ to $I_i$ are the unique polynomials in $P^p(I_i)$ satisfying the conditions

$$\begin{aligned}&\int _{I_i} \left( P_h^- u - u\right) v dx =0, \ \forall \ v \in P^{p-1}(I_i),\quad \text {and}\quad \left( P_h^- u-u\right) ^- \big |_{i}= 0,\end{aligned}$$

(2.3)

$$\begin{aligned}&\int _{I_i} \left( P_h^+ u - u\right) v dx =0, \ \forall \ v \in P^{p-1}(I_i),\quad \text {and}\quad \left( P_h^+ u-u\right) ^+\big |_{i-1}= 0. \end{aligned}$$

(2.4)

These special projections were used in the error estimates of the DG methods to derive optimal $L^2$ error bounds as well as superconvergence in the literature, e.g., in [15]. In our analysis, we need the following well-known results. Their proofs can be found in [16]. For any $u\in H^{p+1}(I_i)$ with $i=1,\cdots ,N$, there exists a constant $C$ independent of the mesh size $h$ such that

$$\begin{aligned} \left\| u-P_h^\pm u\right\| +h\left\| (u-P_h^\pm u)_x\right\| \le Ch^{p+1}\left| u\right| _{p+1,\Omega }. \end{aligned}$$

(2.5)

Moreover, we recall the inverse properties of the finite element space $V_h^p$ that will be used in our error analysis [27]: For any $v \in V_h^p$, there exists a positive constant $C$ independent of $v$ and $h$, such that

$$\begin{aligned} \left\| v_x\right\|\le & {} C h^{-1} \left\| v\right\| ,\quad \left\| v\right\| _{\infty } \le C h^{-1/2} \left\| v\right\| ,\quad \left( \sum _{i=1}^N\left( v^2\left( x_{i}^+\right) +v^2\left( x_{i}^-\right) \right) \right) ^{1/2}\nonumber \\\le & {} C h^{-1/2} \left\| v\right\| . \end{aligned}$$

(2.6)

From now on, the notation $C,\ C_1,\ C_2,\ c,\$ etc. will be used to denote positive constants that are independent of $h$, but which may depend upon the exact smooth solution of (1.1a) and its derivatives. Furthermore, all the constants will be generic, i.e., they may represent different constant quantities in different occurrences.

We also need a special projection $P_h^*$ which is defined element by element as follows: If $f'(u)$ is positive, we take $P_h^*=P_h^-$; otherwise, we use $P_h^*=P_h^+$. Throughout this paper, $e=u-u_h$ denotes the error between the exact solution of (1.1a) and the numerical solutions defined in (2.2). Let the projection error be defined as $\epsilon =u-P_h^*u$ and the error between the numerical solution and the projection of the exact solution be defined as $\bar{e}=P_h^*u-u_h.$ We note that, in the case $f'(u)>0$, $\epsilon =u-P_h^-u$ and $\bar{e}=P_h^-u-u_h$. Similarly, in the case $f'(u)<0$, $\epsilon =u-P_h^+u$ and $\bar{e}=P_h^+u-u_h$. We note that the true error can be split as $e=(u-P_h^*u)+(P_h^*u-u_h)=\epsilon +\bar{e}.$

2.4 Preliminaries Results

Here, we will only consider the case $0<\delta \le f'(u(x,t)),\ \forall \ (x,t)\in [a,b]\times [0,T]$, where $\delta$ is a positive constant. In this case $\epsilon =u-P_h^-u$ and $\bar{e}=P_h^-u-u_h$. We note that the other case $f'(u(x,t))\le - \delta < 0$ can be handled in a very similar way and hence we omit it; see [27] for more details.

Recently, Meng et al. [27] analyzed the same DG scheme for solving the nonlinear conservation laws. They selected the initial condition as $u_h(x,0)=P_h^-u(x,0)$ and proved a priori error estimates and a superconvergence result toward $P_h^-u$. For the sake of completeness, we summarize their results in the next theorem.

Theorem 2.1

Let $u$ be the exact solution of (1.1), which is assumed to be sufficiently smooth with bounded derivatives $i.e.,$ $\left\| u\right\| _{p+1,\Omega }$, $\left\| u_t\right\| _{p+1,\Omega }$, and $\left\| u_{tt}\right\| _{p+1,\Omega }$ are bounded uniformly for any $t\in [0,T]$. We further assume that $f(u)\in C^3(\mathbb {R})$ with $0<\delta \le f'(u(x,t)),\ \forall \ (x,t)\in \Omega \times [0,T]$, where $\delta$ is a positive constant. Let $p \ge 1$ and $u_h$ is the solution of (2.2a) with the numerical flux (2.2b) and subject to the approximated initial condition $u_h(x,0)=P_h^-u(x,0)$, then there exists a positive constant $C$ depends on the exact solution $u$, the final time $T$, and the maximum of $|f^{(m)}|$ ($m = 1, 2, 3$), but is independent of $h$, such that $\forall \ t\in [0,T]$,

$$\begin{aligned} \left\| e \right\|\le & {} C\ h^{p+1},\end{aligned}$$

(2.7a)

$$\begin{aligned} \left\| e_t \right\|\le & {} C\ h^{p+1},\end{aligned}$$

(2.7b)

$$\begin{aligned} \left\| \bar{e}\right\|\le & {} C\ h^{p+3/2}. \end{aligned}$$

(2.7c)

Proof

These results have been proved in [27]. More precisely, (2.7c) is proved in its Theorem 3.2, (2.7a) is proved in its Corollary 3.5, and (2.7b) is proved in its Lemma 3.7.

Corollary 2.1

Under the assumptions of Theorem 2.1, there exists a constant $C>0$ such that

$$\begin{aligned}&\left\| \bar{e}_x \right\| \le C h^{p+1/2},\end{aligned}$$

(2.8)

$$\begin{aligned}&\left\| e_x \right\| \le C h^{p}. \end{aligned}$$

(2.9)

Proof

We apply the inverse inequality and the estimate (2.7c) to get

$$\begin{aligned} \left\| \bar{e}_x \right\| \le C_1 h^{-1} \left\| \bar{e}\right\| \le C_1 h^{-1} C_2\ h^{p+3/2}=C \ h^{p+1/2}. \end{aligned}$$

(2.10)

Next, using the fact that $e_x=\bar{e}_x+\epsilon _x$, applying the triangle inequality, the projection result (2.5), and the estimate (2.10), we obtain

$$\begin{aligned} \left\| e_x \right\| \le \left\| \bar{e}_x \right\| +\left\| \epsilon _x \right\| \le C_1 h^{p+1/2}+ C_2 h^{p}\le C h^{p}, \end{aligned}$$

which establishes (2.9).

Remark 2.3

We note that the estimate (2.8) is not optimal. An improved result $\left\| \bar{e}_x \right\| \le C h^{p+1}$ can be easily obtained as follows: Let us define $\bar{e}= r_i+\frac{x-\bar{x}_i}{h_i}\mathbb {S}_i$ on each $I_i$, where $r_i =\bar{e}(\bar{x}_i,t)$ is a constant and $\mathbb {S}_i(\cdot ,t)\in P^{p-1}(I_i)$ with $\bar{x}_i=(x_{i-1}+x_{i})/2$. We further define the piecewise polynomial $\mathbb {S}$ whose restriction on $I_i$ is $\mathbb {S}_i$. In [27], the authors have shown the following estimates

$$\begin{aligned} \left\| \bar{e}_x\right\| \le Ch^{-1} \left\| \mathbb {S}\right\| ,\quad \left\| \mathbb {S}\right\| \le Ch \left\| e_t\right\| +C h^{p+2}. \end{aligned}$$

(2.11)

More precisely, the second estimate is proved in its Lemma 3.6 and the first estimate can be obtained by using $\bar{e}_x= \frac{x-\bar{x}_i}{h_i}(\mathbb {S}_i)_x+\frac{1}{h_i}\mathbb {S}_i$ and applying the inverse property.

Combining the estimates in (2.11) and using (2.7b), we obtain the improved estimate $\left\| \bar{e}_x \right\| \le C h^{p+1}$.

3 A Posteriori Error Estimation

A posteriori error estimates play a critical role in adaptive methods for solving hyperbolic conservation laws. In this section, we propose a robust recovery-based a posteriori error estimator for the DG method for nonlinear scalar conservation laws (1.1) and prove its asymptotic exactness under mesh refinement. We first present a superconvergence result for the approximation of the convection derivative using a derivative recovery formula where the order is $p+1$ which is one order higher that the optimal error estimate.

3.1 An Element-by-Element Postprocessing of the Derivative in the Direction of the Flow

Here, we postprocess the numerical solution $u_h$ to get a superconvergent approximation of $(f(u))_x$.

Let $g_h\in V_h^p$ be an approximation of the source function $g$ obtained using the special projection $P_h^-$ into $V_h^p$ i.e., $g_h=P_h^-g$. Then we define the recovered derivative $R_h((f(u))_x)$ by

$$\begin{aligned} R_h((f(u))_x)=g_h-(u_h)_t, \end{aligned}$$

(3.1)

which is an approximation to $(f(u))_x$ obtained by a postprocessing of $u_h$. Next, we state and prove the error estimate between $R_h((f(u))_x)$ and $(f(u))_x$ which is the key ingredient in proving the convergence of our a posteriori error estimate under mesh refinement.

Theorem 3.1

Assume that the conditions of Theorem 2.1 are satisfied. Let $R_h((f(u))_x)$ be the recovered derivative defined by (3.1), then we have the following superconvergence result

$$\begin{aligned} \left\| (f(u))_x -R_h((f(u))_x)\right\| \le C h^{p+1}. \end{aligned}$$

(3.2)

Proof

Adding and subtracting $g$ to $R_h((f(u))_x)$ and using $g=u_t+(f(u))_x$ by (1.1a), we get

$$\begin{aligned} R_h((f(u))_x) =g_h-g+g-(u_h)_t =g_h-g+u_t+(f(u))_x-(u_h)_t =g_h-g+(f(u))_x+ e_t. \end{aligned}$$

Next, we take the $L^2$-norm, we apply the triangle inequality, and we use the projection result (2.5) and the estimate (2.7b) to get

$$\begin{aligned} \left\| (f(u))_x-R_h((f(u))_x)\right\|= & {} \left\| g-g_h-e_t\right\| \le \left\| g-g_h\right\| +\left\| e_t\right\| \\\le & {} C_1h^{p+1}+C_2h^{p+1} \le C h^{p+1}, \end{aligned}$$

which completes the proof of the theorem.

Remark 3.1

The choice $g_h\in V_h^p$ is not unique. In fact, all results in this paper remain true if we choose $g_h$ such that $\left\| g-g_h\right\| =\mathcal {O}(h^{p+1})$. In particular, if we use the standard $L^2$ projection of $g$ instead of $P _h^- g$, then we obtain similar results.

Remark 3.2

Obviously the estimate (3.2) is superconvergent since $\left\| (f(u))_x -(f(u_h))_x\right\|$ is one order lower than that of $\left\| e\right\|$ which is $p+1$ [by (2.7a)]. To show this, we apply the classical Taylor formula with integral remainder to write

$$\begin{aligned} f(u)-f(u_h)=R_0\ (u-u_h)=R_0\ e,\quad \text {where} \ R_0=\int _0^1f'(u+s(u_h-u))ds. \end{aligned}$$

Thus,

$$\begin{aligned} \left\| (f(u))_x -(f(u_h))_x\right\| =\left\| (R_0)_x e+R_0 e_x\right\| \le \left\| (R_0)_x\right\| \left\| e\right\| +\left\| R_0\right\| \left\| e_x\right\| \end{aligned}$$

(3.3)

Using the smoothness of $f$, we have $|R_0|\le \int _0^1|f'(u+s(u_h-u))|ds\le \int _0^1C_1ds=C_1$, where $C_1=\max _{x\in [a,b],\ t\in [0,T]}|f'(u(x,t))|$. Similarly, using the fact that $(R_0)_x=\int _0^1(u_x-se_x)f''(u+s(u_h-u))ds$ and the smoothness of $u$ and $f$, we obtain

$$\begin{aligned} \big |(R_0)_x\big |\le & {} \int _0^1\big |u_x-se_x\big | \big |f''(u+s(u_h-u))\big |ds \le \int _0^1\left( C_2+C_3\big |e_x\big |\right) C_4ds\nonumber \\\le & {} C_5+C_6 \left\| e_x\right\| \le C_7, \end{aligned}$$

where we used (2.9). Consequently,

$$\begin{aligned} \left\| R_0\right\| \le C_1(b-a)^{1/2}=C_8,\quad \left\| (R_0)_x\right\| \le C_7(b-a)^{1/2}=C_9. \end{aligned}$$

(3.4)

Combining (3.3) and (3.4) and using the estimates (2.7a) and (2.9)yields

$$\begin{aligned} \left\| (f(u))_x -(f(u_h))_x\right\| \le C h^p. \end{aligned}$$

(3.5)

In the next section we use the recovered derivative $R_h((f(u))_x)$ to develop an a posteriori error estimator.

3.2 Recovery-Based a Posteriori Error Estimators

The main results of this section are stated in the following theorem. In particular, we prove that the a posteriori error estimates $\left\| r_h(u_h)\right\|$ converge to the true spatial errors $\left\| (f(u))_x-(f(u_h))_x\right\|$ at $\mathcal {O}(h^{p+1})$ rate. Moreover, we prove an asymptotic result of our a posteriori error estimator.

Theorem 3.2

Suppose that the assumptions of Theorem 2.1 are satisfied. Let $r_h(u_h)$ be the approximated local residual defined by

$$\begin{aligned} r_h(u_h)=g_h-(f(u_h))_x-(u_h)_t =R_h((f(u))_x)-(f(u_h))_x,\quad \! x \in I_i,\ i=1,\ldots , N,\ t\in [0,T], \end{aligned}$$

(3.6)

then there exists a positive constant $C$ independent of $h$ such that

$$\begin{aligned} \left\| (f(u))_x-(f(u_h))_x -r_h(u_h)\right\| \le C h^{p+1},\quad t\in [0,T]. \end{aligned}$$

(3.7)

As a consequence,

$$\begin{aligned} \bigg |\left\| (f(u))_x-(f(u_h))_x\right\| -\left\| r_h(u_h)\right\| \bigg | \le C h^{p+1}. \end{aligned}$$

(3.8)

Furthermore, if there exists a constant $C=C(u)>0$ independent of $h$ such that

$$\begin{aligned} \left\| e_x\right\| \ge C h^{p}, \end{aligned}$$

(3.9)

then, at a fixed time $t$, the global effectivity index in the $L^2$ norm which is defined as $\Theta (t)=\frac{\left\| r_h(u_h)\right\| }{\left\| (f(u))_x -(f(u_h))_x\right\| }$ and is used to appraise the accuracy of the error estimate, converges to unity at $\mathcal {O}(h)$ rate $i.e.,$

$$\begin{aligned} \Theta (t)= 1 + \mathcal {O}(h),\quad t\in [0,T]. \end{aligned}$$

(3.10)

Proof

Using the estimate (3.2), we obtain

$$\begin{aligned} \left\| (f(u))_x-(f(u_h))_x -r_h(u_h)\right\|= & {} \left\| (f(u))_x-((f(u_h))_x +r_h(u_h))\right\| \\ \quad= & {} \left\| (f(u))_x- R_h((f(u))_x)\right\| \le C h^{p+1}, \end{aligned}$$

which completes the proof of (3.7)

Next, we will prove (3.8). For convenience, we let $r(u)=(f(u))_x-(f(u_h))_x$. Using the reverse triangle inequality $\big |||v||-||w||\big |\le ||v-w||$ with $v=r(u)$ and $w=r_h(u_h)$ and applying the estimate (3.7), we obtain

$$\begin{aligned} \big |\left\| r(u)\right\| -\left\| r_h(u_h)\right\| \big | \le \left\| r(u)-r_h(u_h)\right\| \le C h^{p+1}, \end{aligned}$$

which completes the proof of (3.8).

In order to show (3.10), we use the triangle inequality to have

$$\begin{aligned} \big |\left\| r_h(u_h)\right\| - \left\| r(u)\right\| \big | \le \left\| r(u) -r_h(u_h)\right\| , \end{aligned}$$

which, after dividing by $\left\| r(u)\right\|$, yields

$$\begin{aligned} \bigg |\frac{\left\| r_h(u_h)\right\| }{\left\| r(u)\right\| }-1\bigg | \le \frac{\left\| r(u) -r_h(u_h)\right\| }{\left\| r(u)\right\| }. \end{aligned}$$

(3.11)

Next, we need to derive a lower bound for $\left\| r(u)\right\|$. Applying the first-order Taylor expansion with respect to the variable $u$, we write

$$\begin{aligned} r(u)= & {} (f(u)-f(u_h))_x=(R_0 (u-u_h))_x=(R_0\ e)_x\\= & {} (R_0)_xe+R_0e_x,\ \text {where} \ R_0=\int _0^1f'(u+s(u_h-u))ds. \end{aligned}$$

Using the smoothness of $f$ and the fact that $0<\delta \le f'(u(x,t)),\ \forall \ (x,t)\in [a,b]\times [0,T]$, where $\delta$ a positive constant, we get

$$\begin{aligned} \delta |e_x|\le |R_0e_x|=|r(u)-(R_0)_xe|\le |r(u)|+|(R_0)_x||e|\le |r(u)|+C_1|e|, \end{aligned}$$

where we used (3.4). Squaring both sides, using the inequality $(u+v)^2\le 2u^2+2v^2$, and integrating over the domain $[a,b]$, we obtain

$$\begin{aligned} \delta ^2 \left\| e_x\right\| ^2\le 2\left\| r(u)\right\| ^2+2C_1^2\left\| e\right\| ^2. \end{aligned}$$

Applying the inverse estimate (3.9) and the estimates (2.7a) and (2.9), we arrive at

$$\begin{aligned} C_1 h^{2p}\le \left\| r(u)\right\| ^2+C_2h^{2p+2}. \end{aligned}$$

Using the inequality $\sqrt{a+b}\le \sqrt{a}+\sqrt{b}$, we obtain

$$\begin{aligned} C_3 h^{p}\le \left\| r(u)\right\| +C_4h^{p+1}. \end{aligned}$$

Thus, for small $h$, we have

$$\begin{aligned} \left\| r(u)\right\| \ge C_3 h^{p}-C_4h^{p+1}\ge C_5h^p. \end{aligned}$$

(3.12)

Using the estimates (3.7) and (3.12), we get

$$\begin{aligned} \frac{\left\| r(u) -r_h(u_h)\right\| }{\left\| r(u)\right\| } \le \frac{C_1\ h^{p+1}}{C_5\ h^{p}}\le C\ h. \end{aligned}$$

(3.13)

Combining (3.11) and (3.13), we arrive at

$$\begin{aligned} \bigg |\frac{\left\| r_h(u_h)\right\| }{\left\| r(u)\right\| }-1\bigg | \le C\ h. \end{aligned}$$

Therefore, $\frac{\left\| r_h(u_h)\right\| }{\left\| r(u)\right\| }=1+\mathcal {O}(h)$, which establishes (3.10). $\square$

In the previous theorem, we proved that the a posteriori error estimates $\left\| r_h(u_h)\right\|$ converge to the true spatial errors $\left\| (f(u))_x-(f(u_h))_x\right\|$ at $\mathcal {O}(h^{p+1})$ rate. We also proved that the global effectivity index in the $L^2$-norm converges to unity at $\mathcal {O}(h)$ rate.

Remark 3.3

The assumption (3.9) implies that terms of order $\mathcal {O}(h^{p})$ are present in the error. If this were not the case, the error estimate $r_h(u_h)$ might not be such a good approximation of the error $(f(u))_x-(f(u_h))_x$. Even though the proof of (3.10) is valid under the assumption (3.9), our computational results given in the next section suggest that the global effectivity index in the $L^2$-norm converge to unity at $\mathcal {O}(h^2)$ rate. Thus, the proposed error estimation technique is an excellent measure of the error.

We note that the a priori estimate (2.9) is optimal in the sense that the exponent of $h$ is the largest possible. In fact, one may show that provided that the $p$th-order derivatives of the exact solution $u$ do not vanish identically over the domain ($u\not \in V_h^p$), then an inverse estimate of the form (3.9) is valid [6, 30, 31] for some positive constant $C$ which depends on $u$ but not on $h$. Combining (2.9) with (3.9), we show that $(u_h)_x$ approximates $u_x$ to $\mathcal {O}(h^{p})$ in the $L^2$ norm.

Remark 3.4

The performance of an error estimator is commonly measured by the effectivity index which is the ratio of the estimated error to the actual error. In particular, we say that the error estimator is asymptotically exact if the effectivity index approaches unity as the mesh size goes to zero. Thus, (3.10) indicated that our a posteriori error estimator is asymptotically exact.

Remark 3.5

We note that $r_h(u_h)$ is a computable quantity since it only depends on the numerical solution $u_h$ and the source term $g$. It provides an asymptotically exact a posteriori estimator on the error $\left\| (f(u))_x-(f(u_h))_x\right\|$. We would like to emphasize that our DG error estimate of recovery type for the convection derivative approximation is computationally simple which make it useful in adaptive computations. Finally, we would like to mention that our estimator is more accurate than the classical residual error estimator since the later requires solving a finite element formulation.

4 Numerical Examples

In this section, we present several numerical examples to validate our theoretical results. The initial condition is determined by $u_h(x,0)=P_h^*u(x,0)$, where the projection $P_h^*$ is defined element by element as follows: Let $\bar{x}_{i}=(x_{i}+x_{i-1})/2$ denote the center of each subinterval $I_i$. If $f'(u(\bar{x}_{i},0))$ is positive, then on $I_i$, we take $P_h^*=P_h^-$; otherwise, we take $P_h^*=P_h^+$. Temporal integration is performed by the fourth-order classical explicit Runge–Kutta method. A time step $\Delta t$ is chosen so that temporal errors are small relative to spatial errors. In all numerical experiments, the numerical order of convergence $\alpha$ is computed as follows:

$$\begin{aligned} \alpha =\frac{\ln \left( ||e^{N_1}||/||e^{N_2}||\right) }{\ln (N_2/N_1)}, \end{aligned}$$

where $e^{N_1}$ and $e^{N_2}$ denote the errors using $N_1$ and $N_2$ elements, respectively.

Let $\rho$, $\Theta$, and $\delta \Theta$ be defined as

$$\begin{aligned} \rho (t)\!=\!||(f(u))_x-R_h((f(u))_x)||, \quad \! \Theta (t)= \frac{\left\| r_h(u_h)\right\| }{\left\| (f(u))_x-(f(u_h))_x\right\| }, \!\quad \delta \Theta (t)= \big |\Theta (t) -1 \big |. \end{aligned}$$

Example 4.1

We consider the following nonlinear problem subject to the Dirichlet boundary condition

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}+(u^3+u)_{x}=-(2+3\cos ^2(x+t))\sin (x+t),\quad x \in [0,2\pi ], \ t\in [0,1],\\ u(x,0)=\cos (x),\quad x \in [0,2\pi ],\\ u(0,t)=\cos (t), \quad t\in [0,1]. \end{array} \right. \end{aligned}$$

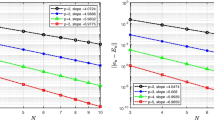
The exact solution is given by $u(x,t)=\cos (x+t).$ Note that $f'(u)=3u^2 + 1\ge 1 \ge \delta > 0$. Since $f'(u)=3u^2+1>0$, we take the numerical flux (2.2b). We solve this problem using the DG method on uniform meshes having $N = 5, 10, \ldots ,80$ elements and using the spaces $P^p$ with $p=0-4$. The results shown in Table 1 indicate that the derivative recovery formula $R_h((f(u))_x)$ at $t=1$ is $\mathcal {O}(h^{p+1})$ superconvergent approximation to the derivative $(f(u))_x$. These results show that the order of convergence given by Theorem 3.1 is optimal. This is in full agreement with the theory. In Table 2 we present the true $L^2$ errors and the global effectivity indices at time $t=1$. We observe that $\Theta$ is near unity and converge to one under $h$-refinement. Numerical results further indicate that the effectivity indices stay close to unity for all times and converge under $h$-refinement. These results are not included to save space. Thus, our a posteriori error estimates are asymptotically exact. Finally, the errors $\delta \Theta$ and their orders of convergence shown in Table 3 suggest that the convergence rate for $\delta \Theta$ is $\mathcal {O}(h^2)$ except for $p = 0$ which is due to the fact that the results in Theorem 2.1 hold under the assumption $p\ge 1$. We note that the observed numerical convergence rate is higher than theoretical rate established in (3.10) which is proved to be $\mathcal {O}(h)$.

Table 1 $\rho =||(f(u))_x-R_h((f(u))_x)||$ and their orders of convergence at $t=1$ for Example 4.1 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Table 2 $L^2$-norm of the true errors and global effectivity indices $\Theta$ at $t = 1$ for Example 4.1 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Table 3 $\delta \Theta$ and their orders of convergence at $t = 1$ for Example 4.1 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Example 4.2

In this example, we solve the following problem

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}+(u^3)_{x}=-(1+3\cos ^2(x+t))\sin (x+t),\quad x \in [0,2\pi ], \ t\in [0,1],\\ u(x,0)=\cos (x),\quad x \in [0,2\pi ],\\ u(-1,t)=\cos (t), \quad t\in [0,1]. \end{array}\right. \end{aligned}$$

The exact solution is given by $u(x,t)=\cos (x+t).$ Since $f'(u)=3u^2\ge 0$, we can still use the upwind fluxes. We solve this problem using the same parameters and meshes as for Example 4.1. We present the errors $||(f(u))_x-R_h((f(u))_x)||$ and their orders of convergence at $t=1$ in Table 4. These results indicate that the derivative recovery formula $R_h((f(u))_x)$ at $t=1$ is $\mathcal {O}(h^{p+1})$ superconvergent approximation to the derivative $(f(u))_x$. We note that the order of convergence given by Theorem 3.1 is optimal. The true $L^2$ errors and the global effectivity indices shown in Table 5 indicate that our a posteriori error estimates are asymptotically exact under mesh refinement. The results shown in Table 6 indicate that the convergence rate at $t=1$ for $\delta \theta$ is $\mathcal {O}(h^{2})$ which is higher than the theoretical rate proved in Theorem 3.2. Even though the assumption $0<\delta \le f'(u(x,t)),\ \forall \ (x,t)\in [0,2\pi ]\times [0,T]$ does not always hold true, the same results are observed.

Table 4 $\rho =||(f(u))_x-R_h((f(u))_x)||$ and their orders of convergence at $t=1$ for Example 4.2 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Table 5 $L^2$-norm of the true errors and global effectivity indices $\Theta$ at $t = 1$ for Example 4.2 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Table 6 $\delta \Theta$ and their orders of convergence at $t = 1$ for Example 4.2 on uniform meshes having $N = 5, 10, \ldots ,80$ elements using $p = 0{-}4$

Example 4.3

In this example, we test our theoretical results using the flux function $f(u)=u^2/2$

$$\begin{aligned} \left\{ \begin{array}{l} u_{t}+(u^2/2)_{x}=-(1+\cos (x+t))\sin (x+t),\quad x \in [0,2\pi ], \ t\in [0,1],\\ u(x,0)=\cos (x),\quad x \in [0,2\pi ],\\ u(-1,t)=\cos (t), \quad t\in [0,1]. \end{array}\right. \end{aligned}$$

The exact solution is given by $u(x,t)=\cos (x+t).$ In this case, since $f'(u)=u$ which changes sign in the computational domain, we use the Godunov flux, which is an upwind flux. The initial condition, $u_h(x,0)$, is taken as $u_h(x,0)=P_h^*u(x,0)$, where the projection $P_h^*$ is defined element by element as follows: If $u(\bar{x}_{i},t)$, where $\bar{x}_{i}=(x_{i-1}+x_{i})/2$, is positive, then on $I_i$, we choose $P_h^-$; otherwise, we choose $P_h^+$. We solve this problem using the DG method on uniform meshes having $N = 5, 10, \ldots ,80$ elements and using the space $P^p$ with $p=0-4$. The $L^2$ errors $||(f(u))_x-R_h((f(u))_x)||$ and their orders of convergence at $t=1$ shown Table 7 suggest $\mathcal {O}(h^{p+1})$ convergence rate which is in full agreement with the theory. In Table 8, we present the true $L^2$ errors and the global effectivity indices at time $t=1$. We observe that $\Theta$ is near unity and converge to one under $h$-refinement. Numerical results further indicate that the effectivity indices stay close to unity for all times and converge under $h$-refinement. We also used with general flux functions such as $f(u)=e^u$ and observed similar results. These results are not included to save space.

Table 7 $\rho =||(f(u))_x-R_h((f(u))_x)||$ and their orders of convergence at $t=1$ for Example 4.3 on uniform meshes having $N = 5, 10, \cdots ,80$ elements using $p = 0{-}4$

Table 8 $L^2$-norm of the true errors and global effectivity indices $\Theta$ at $t = 1$ for Example 4.3 on uniform meshes having $N = 5, 10, \cdots ,80$ elements using $p = 0{-}4$

5 Concluding Remarks

In this paper, we proposed and analyzed a robust recovery-based a posteriori error estimator for the DG method for nonlinear scalar conservation laws in one space dimension. The proposed estimator is easy to implement, computationally simple, and is asymptotically exact. Furthermore, it is useful in adaptive computations. We first proved that the a posteriori error estimates at a fixed time converge to the true spatial errors in the $L^2$-norm at $\mathcal {O}(h^{p+1})$ rate, when $p$-degree piecewise polynomials with $p\ge 1$ are used. Then we proved that the global effectivity index converges to unity at $\mathcal {O}(h)$ rate. Our proofs are valid for arbitrary regular meshes using $P^p$ polynomials with $p\ge 1$, under the condition that nonlinear flux function, $f'(u)$ possesses a uniform positive lower bound. As in [27], our numerical experiments demonstrate that the results in this paper hold true for nonlinear conservation laws with general flux functions, indicating that the restriction on $f(u)$ is artificial. The generalization of our proofs to nonlinear equations with general flux functions involves several technical difficulties and will be investigated in the future. For general flux functions, we expect that similar superconvergence results of Meng et al. [27] will be needed. We are currently investigating the superconvergence properties of the DG methods applied to two-dimensional conservation laws on rectangular and triangular meshes.