Strong Stability Preserving General Linear Methods

Abstract

We investigate the strong stability preserving (SSP) general linear methods with two and three external stages and $s$ internal stages. We also describe the construction of starting procedures for these methods. Examples of SSP methods are derived of order $p=2, p=3$, and $p=4$ with $2\le s\le 10$ stages, which have larger effective Courant–Friedrichs–Levy coefficients than the class of two-step Runge–Kutta methods introduced by Jackiewicz and Tracogna, whose SSP properties were analyzes recently by Ketcheson, Gottlieb, and MacDonald, and the class of multistep multistage methods investigated by Constantinescu and Sandu. Numerical examples illustrate that the class of methods derived in this paper achieve the expected order of accuracy and do not produce spurious oscillations for discretizations of hyperbolic conservation laws, when combined with appropriate discretizations in spatial variables.

1 Introduction

Consider the initial-value problem for a system of ordinary differential equations (ODEs)

$$\begin{aligned} \left\{ \begin{array}{ll} y'(t)=f\left( t,y(t)\right) , &{} \quad t\in [t_0,t_{ end }], \\ y(t_0)=y_0, &{}\quad \end{array}\right. \end{aligned}$$

(1.1)

where the function $f:{\mathbb R}\times {\mathbb R}^m\rightarrow {\mathbb R}^m$ is assumed to be sufficiently smooth. In many applications such systems arise from semidiscretization of the spatial derivatives in the partial differential equations (PDEs) of mathematical physics.

We assume that the discretization of (1.1) by the forward Euler method

$$\begin{aligned} y_n=y_{n-1}+h\,f(t_{n-1},y_{n-1}), \end{aligned}$$

(1.2)

$n=1,2,\ldots ,N, Nh=t_{ end }-t_0, t_n=t_0+nh$, is monotone or contractive. This means that the following inequality holds

$$\begin{aligned} \Vert y_n\Vert \le \Vert y_{n-1}\Vert , \end{aligned}$$

(1.3)

$n=1,2,\ldots ,N$, in some norm or semi-norm $\Vert \cdot \Vert$, for a suitably restricted time step determined by the condition

$$\begin{aligned} h\le h_{ FE }. \end{aligned}$$

(1.4)

It is then of interest to construct higher order numerical methods for (1.1), which preserve the monotonicity property (1.3), under the perhaps modified restriction on the time step of the form

$$\begin{aligned} h\le \mathcal {C}\cdot h_{ FE }. \end{aligned}$$

(1.5)

Numerical schemes for (1.1) that preserve the monotonicity condition (1.3) under the modified restriction (1.5) are called strong stability preserving (SSP) methods and the constant $\mathcal {C}\ge 0$ in (1.5) is called SSP coefficient.

Consider the explicit Runge–Kutta (RK) method with $s$ stages for (1.1)

$$\begin{aligned} \left\{ \begin{array}{ll} Y_i^{[n]}=y_{n-1}+h\sum \nolimits _{j=1}^{i-1}a_{ij}\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) , &{}\quad i=1,2,\ldots ,s, \\ y_n=y_{n-1}+h\sum \nolimits _{j=1}^sb_j\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) ,&{} \end{array}\right. \end{aligned}$$

(1.6)

$n=1,2,\ldots ,N$, where $Y_i^{[n]}$ are approximations to $y(t_{n-1}+c_ih), i=1,2,\ldots ,s$, and $y_n$ is an approximation to $y(t_n)$. This method is specified by the abscissa vector $\mathbf {c}=[c_1,\ldots ,c_s]^T\in {\mathbb R}^s$, the coefficient matrix $\mathbf {A}=[a_{ij}\in {\mathbb R}^{s\times s}$, and the vector of weights $\mathbf {b}=[b_1,\ldots ,b_s]^T\in {\mathbb R}^s$.

The search for SSP RK methods (1.6) is facilitated by a clever representation of these methods as convex combinations of Euler steps. This so-called Shu–Osher representation, which was first proposed in [53], has the form

$$\begin{aligned} \left\{ \begin{array}{ll} Y_1^{[n]}=y_{n-1},&{} \\ Y_i^{[n]}=\sum \nolimits _{j=1}^{i-1} \left( \alpha _{ij}Y_j^{[n]}+h\beta _{ij}\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) \right) , &{}\quad i=2,3,\ldots ,s, \\ y_n=\sum \nolimits _{j=1}^s\left( \alpha _{s+1,j}Y_j^{[n]}+h\beta _{s+1,j} \,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) \right) ,&{} \end{array}\right. \end{aligned}$$

(1.7)

$n=1,2,\ldots ,N$, where $\alpha _{ij}$ are scalars such that

$$\begin{aligned} \sum _{j=1}^{i-1}\alpha _{ij}=1, \quad i=2,3,\ldots ,s+1, \end{aligned}$$

and the coefficients $\beta _{ij}$ are given by

$$\begin{aligned} \left\{ \begin{array}{ll} \beta _{ij}=a_{ij}-\sum \nolimits _{k=j+1}^{i-1}\alpha _{ik}a_{kj}, &{}\quad i=2,3,\ldots ,s, \ j=1,2,\ldots ,i-1, \\ \beta _{s+1,j}=b_j-\sum \nolimits _{k=j+1}^s\alpha _{s+1,k}a_{kj}, &{}\quad j=1,2,\ldots ,s. \end{array} \right. \end{aligned}$$

The Shu–Osher representation (1.7) leads to the following

Theorem 1

[26, 53] Assume that the forward Euler method (1.2) applied to (1.1) is strongly stable, i.e., the inequality (1.3) holds under the time step restriction (1.4). Assume also that $\alpha _{ij}\ge 0$ and $\beta _{ij}\ge 0$. Then the solution $\{y_n\}$ obtained by the RK method (1.6) or (1.7) satisfies the strong stability bound

$$\begin{aligned} \Vert y_n\Vert \le \Vert y_{n-1}\Vert , \end{aligned}$$

$n=1,2,\ldots ,N$, under the time step restriction (1.5) with SSP coefficient $\mathcal {C}=\mathcal {C}(\alpha ,\beta )$ given by

$$\begin{aligned} \mathcal {C}(\alpha ,\beta )=\min \bigg \{\frac{\alpha _{ij}}{\beta _{ij}}: \quad i=2,3,\ldots ,s, \quad j=1,2,\ldots ,i-1\bigg \}. \end{aligned}$$

It was observed in [26] that it is also possible to characterize SSP methods if some of the coefficients $\beta _{ij}$ are negative. This characterization is based on the convex combinations of forward Euler steps and down winded (or backward in time) Euler steps, and the resulting methods satisfy $\Vert y_n\Vert \le \Vert y_{n-1}\Vert$ under the step size restriction (1.5) with a modified SSP coefficient $\mathcal {C}=\mathcal {C}(\alpha ,\beta )$ given by

$$\begin{aligned} \mathcal {C}(\alpha ,\beta )=\min \bigg \{\frac{\alpha _{ij}}{|\beta _{ij}|}:\quad i=2,3,\ldots ,s, \quad j=1,2,\ldots ,i-1\bigg \}. \end{aligned}$$

SSP RK and linear multistep methods (LMMs) have been studied by Shu and Osher [53], Gottlieb et al. [28], Spiteri and Ruuth [56], Hundsdorfer et al. [35], Gottlieb [24], Hundsdorfer and Ruuth [34], Ruuth and Hundsdorfer [50], Gottlieb and Ruuth [27], Gottlieb et al. [25, 26], Higueras [31–33] and Ferracina and Spijker [20–23]. SSP two-step Runge–Kutta (TSRK) methods [40, 42] were investigated by Ketcheson et al. [45]. Constantinescu and Sandu [19] generalized Shu–Osher representation to a class of multistep multistage schemes, which form a special subclass of GLMs. They also constructed some optimal SSP methods in this class by solving a constrained optimization problem, where the objective function for the SSP coefficient $\mathcal {C}$ depend on the parameters of Shu–Osher representation of these methods.

SSP general linear methods (GLMs) were investigated by Spijker in his seminal paper [55]. In this paper we will employ these results to construct new classes of SSP GLMs up to the order $p=4$ and stage order $1\le q\le 4$. In the context of ODEs coming from discretization of PDEs, order $p=4$ is usually considered to be sufficiently high. Moreover this is consistent with [18] where multistep multiderivative methods up to order $p=4$ only were investigated.

The organization of this paper is as follows. In Sect. 2 we review a theory of monotonicity of special representation of GLMs which was obtained by Spijker [55]. In Sect. 3 we apply this theory to the class of GLMs of the form introduced by Burrage and Butcher [7] and further investigated in [6, 8, 10, 11, 29, 30, 40, 57]. In particular, we will reformulate the expression for SSP coefficient $\mathcal {C}$, and the criterion for SSP GLMs obtained by Spijker [55] in terms of the coefficient matrices $\mathbf {A}, \mathbf {U}, \mathbf {B}$, and $\mathbf {V}$ of GLMs. In Sect. 4 we will use this criterion to search for SSP GLMs with two and three external stages up to the order $p=4$ and stage order $1\le q\le 4$. This search is based on the solution of the constrained minimization problem, where the objective function depends on the SSP coefficient of the method, and the nonlinear inequality constrains depend on the unknown parameters of the methods. In Sect. 5 we describe the construction of starting procedures for SSP GLMs constructed Sect. 4. In Sect. 6 we present some results of numerical experiments with the new SSP schemes. Finally, in Sect. 7 some concluding remarks are given and plans for future research are briefly outlined.

2 Monotonicity Theory for GLMs

Following Spijker [55] we consider the formulation of GLMs, for numerical solution of (1.1), of the form

$$\begin{aligned} \left\{ \begin{array}{ll} Y_i^{[n]}=h\sum \nolimits _{j=1}^mt_{ij}\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) +\sum \nolimits _{j=1}^{\ell }s_{ij}y_j^{[n-1]}, &{}\quad i=1,2,\ldots ,m, \\ y_i^{[n]}=Y_{m-\ell +i}^{[n]}, &{}\quad i=1,2,\ldots ,\ell , \end{array} \right. \end{aligned}$$

(2.1)

$n=1,2,\ldots ,N$, where $1\le \ell \le m$. Here, $Y_i^{[n]}, i=1,2,\ldots ,m$, are internal approximations or stages, which are used to compute the external approximations $y_i^{[n]}, i=1,2,\ldots ,\ell$, which propagate from step to step. This method is specified by the abscissa vector $\mathbf {c}=[c_1,\ldots ,c_m]^T\in {\mathbb R}^m$, and the coefficient matrices $\mathbf {T}=[t_{ij}]\in {\mathbb R}^{m\times m}$ and $\mathbf {S}=[s_{ij}]\in {\mathbb R}^{m\times \ell }$. Different representations of (2.1) are discussed by Butcher [8, 10, 11], Hairer et al. [29], Hairer and Wanner [30], and Jackiewicz [40]. Observe that the RK method (1.6) can be written as GLM (2.1) with $m=s+1, \ell =1$, and

$$\begin{aligned} \mathbf {T}=\left[ \begin{array}{c|c} \mathbf {A} &{} \mathbf {0} \\ \hline \mathbf {b}^T &{} 0 \end{array} \right] \in {\mathbb R}^{(s+1)\times (s+1)}, \quad \mathbf {S}=\left[ \begin{array}{c} \mathbf {e} \\ \hline 1 \end{array} \right] \in {\mathbb R}^{s+1}, \end{aligned}$$

where $\mathbf {e}=[1,\ldots ,1]^T\in {\mathbb R}^s$.

As in [55] we shall assume that the parameters $s_{ij}$ of the coefficient matrix $\mathbf {S}$ satisfy the condition

$$\begin{aligned} \sum _{j=1}^{\ell }s_{ij}=1, \quad i=1,2,\ldots ,m. \end{aligned}$$

(2.2)

Observe that this assumption is automatically satisfied for the RK methods (1.6) and for the class of GLMs considered in Sect. 3. Moreover, as observed by Spijker [55], this condition is no essential restriction on the method (2.1) since any preconsistent GLMs can be transformed into an equivalent GLM satisfying (2.2). We refer to Butcher [10, 11] and Jackiewicz [40] for the transformations of GLMs.

Denote by $\mathbf {I}$ the identity matrix of dimension $m$, and let $[\mathbf {S}\, | \, \gamma \mathbf {T}], \gamma \in {\mathbb R}$, stand for the $m\times (\ell +m)$ matrix whose first $\ell$ columns equal to those of $\mathbf {S}$ and the last $m$ columns equal to those of $\gamma \mathbf {T}$. Then following Spijker [55], we consider the condition

$$\begin{aligned} \det (\mathbf {I}+\gamma \mathbf {T})\ne 0 \quad \hbox {and} \quad (\mathbf {I}+\gamma \mathbf {T})^{-1}[\mathbf {S}\, | \, \gamma \mathbf {T}]\ge 0, \end{aligned}$$

(2.3)

where the inequality in (2.3) should be interpreted componentwise. Then the essence of the fundamental result obtained by Spijker [55] is that the SSP coefficient $\mathcal {C}=\mathcal {C}(\mathbf {S},\mathbf {T})$ of the GLM (2.1) is given by

$$\begin{aligned} \mathcal {C}=\mathcal {C}(\mathbf {S},\mathbf {T}) =\sup \Big \{\gamma \in {\mathbb R}: \ \gamma \quad \hbox {satisfies} \quad (2.3)\Big \}. \end{aligned}$$

(2.4)

This coefficient can be computed, similarly to [45], by the solution to the constrained minimization problem

$$\begin{aligned} \begin{array}{l} \min \limits _{\gamma ,\mathbf {c},\mathbf {S},\mathbf {T}} -\gamma , \\ \hbox {subject to} \ \ \left\{ \begin{array}{l} (\mathbf {I}+\gamma \mathbf {T})^{-1}[\mathbf {S}\, | \, \gamma \mathbf {T}]\ge 0, \\ \varPhi _{p,q}(\mathbf {c},\mathbf {S},\mathbf {T})=0, \end{array} \right. \\ \end{array} \end{aligned}$$

(2.5)

where the nonlinear equality constrains $\varPhi _{p,q}(\mathbf {c},\mathbf {S},\mathbf {T})=0$ represent the order conditions to achieve order $p$ and stage order $q$. This process will be discussed in more detail in Sect. 4 for specific examples of GLMs (2.1). In particular, solving the minimization problem (2.5) for the forward Euler method (1.2), for which $m=1, \ell =1$, and

$$\begin{aligned} \mathbf {T}=\left[ \begin{array}{c|c} 0 &{} 0 \\ \hline 1 &{} 0 \end{array} \right] \in {\mathbb R}^{2\times 2}, \quad \mathbf {S}=\left[ \begin{array}{c} 1 \\ \hline 1 \end{array} \right] \in {\mathbb R}^2, \end{aligned}$$

and the inequality constrains take the form

$$\begin{aligned} (\mathbf {I}+\gamma \mathbf {T})^{-1}[\mathbf {S}\, | \, \gamma \mathbf {T}] =\left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 1-\gamma &{} \gamma &{} 0 \end{array} \right] \ge 0, \end{aligned}$$

we obtain $\mathcal {C}=\mathcal {C}(\mathbf {S},\mathbf {T})=1$, as should be the case.

3 Construction of SSP GLMs

In this section we consider the class of GLMs investigated by Burrage and Butcher [7]. On the uniform grid $t_n=t_0+nh, n=0,1,\ldots ,N, Nh=t_{ end }-t_0$, these methods take the form

$$\begin{aligned} \left\{ \begin{array}{ll} Y_i^{[n]}=h\sum \nolimits _{j=1}^sa_{ij}\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) +\sum \nolimits _{j=1}^ru_{ij}y_j^{[n-1]}, &{}\quad i=1,2,\ldots ,s, \\ y_i^{[n]}=h\sum \nolimits _{j=1}^sb_{ij}\,f\left( t_{n-1}+c_jh,Y_j^{[n]}\right) +\sum \nolimits _{j=1}^rv_{ij}y_j^{[n-1]}, &{}\quad i=1,2,\ldots ,r, \end{array} \right. \end{aligned}$$

(3.1)

$n=1,2,\ldots ,N$. Here, the internal approximations or stages approximate the solution $y$ to (1.1) at the points $t_{n-1}+c_ih$, i.e.,

$$\begin{aligned} Y_i^{[n]}=y(t_{n-1}+c_ih)+O(h^{q+1}), \quad i=1,2,\ldots ,s, \end{aligned}$$

(3.2)

and the external approximations $y_i^{[n]}$ approximate the linear combinations of the scaled derivatives of the solution, i.e.,

$$\begin{aligned} y_i^{[n]}=\sum _{k=0}^pq_{ik}h^ky^{(k)}(t_n)+O(h^{p+1}), \quad i=1,2,\ldots ,r. \end{aligned}$$

(3.3)

These method are specified by the abscissa vector $\mathbf {c}=[c_1,\ldots ,c_s]^T\in {\mathbb R}^s$, four coefficient matrices $\mathbf {A}=[a_{ij}]\in {\mathbb R}^{s\times s}, \mathbf {U}=[u_{ij}]\in {\mathbb R}^{s\times r}, \mathbf {B}=[b_{ij}]\in {\mathbb R}^{r\times s}, \mathbf {V}=[v_{ij}]\in {\mathbb R}^{r\times r}$, the vectors $\mathbf {q}_i=[q_{1,i},\ldots ,q_{r,i}]^T\in {\mathbb R}^r, i=0,1,\ldots ,p$, and four integers: the order of the method $p$, the stage order $q$, the number of external approximations $r$, and the number of internal approximations or stages $s$.

In what follows we will restrict our attention to GLMs (3.1) with $s$ internal stages and $r=2$ external stages of order $p$ and stage order $1\le q\le p$. Moreover, we shall assume that the matrix $\mathbf {A}$ is strictly lower triangular, i.e.,

$$\begin{aligned} \mathbf {A}=\left[ \begin{array}{ccccc} 0 &{}\quad &{}\quad &{}\quad &{}\quad \\ a_{2,1} &{}\quad 0 &{}\quad &{}\quad &{}\quad \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad &{}\quad \\ a_{s-1,1} &{}\quad \ddots &{}\quad \ddots &{}\quad 0 &{}\quad \\ a_{s,1} &{}\quad a_{s,2} &{}\quad \cdots &{}\quad a_{s,s-1} &{}\quad 0 \end{array} \right] \in {\mathbb R}^{s\times s}, \end{aligned}$$

and the matrix $\mathbf {U}$ has the form

$$\begin{aligned} \mathbf {U}=\left[ \begin{array}{c} \mathbf {u}_1 \\ \vdots \\ \mathbf {u}_s \end{array} \right] \in {\mathbb R}^{s\times 2}, \quad \mathbf {u}_i=\left[ \begin{array}{cc} u_{i,1}&u_{i,2} \end{array} \right] \in {\mathbb R}^2, \quad u_{i,1}+u_{i,2}=1, \end{aligned}$$

$i=1,2,\ldots ,s$. We shall also assume that the matrix $\mathbf {V}$ is a rank one matrix of the following form $\mathbf {V}=\mathbf {e}\mathbf {v}^T$, where $\mathbf {e}=[1,1]^T\in {\mathbb R}^2, \mathbf {v}=[v_1,v_2]^T\in {\mathbb R}^r$, and $\mathbf {v}^T\mathbf {e}=1$. Then it follows that $\mathbf {V}$ is power bounded, and as a result the method (3.1) is zero-stable, compare [40]. In order to get methods with higher $\mathcal {C}_\mathrm{eff}$ coefficients we will also consider methods having $\hbox {rank}(\mathbf {V})=2$. In this case the matrix $\mathbf {V}$ will assume the form

$$\begin{aligned} \mathbf {V}=\left[ \begin{array}{cc} v_1 &{}\quad 1-v_1 \\ v_2 &{}\quad 1-v_2 \end{array} \right] , \end{aligned}$$

and its power boundedness will be ensured by the condition $|v_1-v_2|<1$.

Algebraic analysis of order of GLMs (3.1) was developed in the monographs by Butcher [8, 10, 11], see also [57]. Order conditions for these formulas are also discussed in the monograph [29] using the approach proposed by Skeel [54] for fixed-stepsize methods. Jackiewicz and Vermiglio [41] and Cardone et al. [17] derived order conditions for (3.1) using a generalization of the approach proposed by Albrecht [1–5] for RK and composite integration methods. Put

$$\begin{aligned} \left\{ \begin{array}{l} \gamma _0=\mathbf {e}-\mathbf {U}\mathbf {q}_0, \\ \gamma _k=\frac{\mathbf {c}^k}{k!}-\frac{\mathbf {A}\mathbf {c}^{k-1}}{(k-1)!}-\mathbf {U}\mathbf {q}_k, \quad k=1,2,\ldots ,p, \end{array} \right. \end{aligned}$$

(3.4)

and

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{\gamma }_0=\mathbf {q}_0-\mathbf {V}\mathbf {q}_0, \\ \widehat{\gamma }_k=\sum \nolimits _{l=0}^k\frac{\mathbf {q}_l}{(k-l)!} -\frac{\mathbf {B}\mathbf {c}^{k-1}}{(k-1)!}-\mathbf {V}\mathbf {q}_k, \quad k=1,2,\ldots ,p, \end{array} \right. \end{aligned}$$

(3.5)

where $\mathbf {e}=[1,\ldots ,1]^T\in {\mathbb R}^s, \mathbf {c}^i:=[c_1^i,\ldots ,c_s^i]^T$. It will be always assumed that $\mathbf {q}_0=\mathbf {e}=[1,\ldots ,1]^T\in {\mathbb R}^r$, so that the stage preconsistency condition $\gamma _0=0$, or $\mathbf {U}\mathbf {q}_0=\mathbf {e}$, and the preconsistency condition $\widetilde{\gamma }_0=0$, or $\mathbf {V}\mathbf {q}_0=\mathbf {q}_0$, are automatically satisfied. Moreover, we will always assume that the GLMs (3.1) has stage order at least one, i.e., $\gamma _1=0$, or $\mathbf {A}\mathbf {e}+\mathbf {U}\mathbf {q}_1=\mathbf {c}$, compare (3.4).

Assuming that the starting vector $y^{[0]}$ satisfies the condition

$$\begin{aligned} y^{[0]}=\mathbf {q}_0y(t_0)+h\mathbf {q}_1y'(t_0)+\cdots +h^p\mathbf {q}_py^{(p)}(t_0)+O(h^{p+1}), \end{aligned}$$

(3.6)

the order conditions for GLMs (3.1) up to the order $p=4$ derived in [17] take the form listed in Table 1, where

$$\begin{aligned} g_1(t)=\frac{\partial f}{\partial y}\Big (t,y(t)\Big ), \quad \mathbf {\Gamma }_{\mathbf {c}}=\hbox {diag}(c_1,\ldots ,c_s), \end{aligned}$$

and when there is a couple of conditions separated by ‘or’, the first condition refer to order $p$ methods, while the second condition refers to methods with order greater than $p$. In this table we have also listed the recursive differentials used in Albrecht approach to the derivation of order conditions.

Table 1 Recursive differentials and order conditions for $p\le 4$

The methods (3.1) can be written as GLMs of the form (2.1) with $m=s+r, \ell =r$, and the matrices $\mathbf {T}$ and $\mathbf {S}$ defined by

$$\begin{aligned} \mathbf {T}=\left[ \begin{array}{c|c} \mathbf {A} &{} \mathbf {0} \\ \hline \mathbf {B} &{} \mathbf {0} \end{array} \right] \in {\mathbb R}^{(s+r)\times (s+r)}, \quad \mathbf {S}=\left[ \begin{array}{c} \mathbf {U} \\ \hline \mathbf {V} \end{array} \right] \in {\mathbb R}^{(s+r)\times r}. \end{aligned}$$

Observe that it follows from the assumptions on the form of $\mathbf {U}$ and $\mathbf {V}$, that the condition (2.2) on the coefficients $s_{ij}$ of the matrix $\mathbf {S}$ is automatically satisfied.

We can reformulate the condition (2.3), and the characterization of SSP coefficient $\mathcal {C}=\mathcal {C}(\mathbf {S},\mathbf {T})$ of GLM (2.1) given by (2.4), in terms of the abscissa vector $\mathbf {c}$, and the coefficient matrices $\mathbf {A}, \mathbf {U}, \mathbf {B}$, and $\mathbf {V}$ of GLMs (3.1). We have

$$\begin{aligned} \mathbf {I}+\gamma \mathbf {T} =\left[ \begin{array}{c|c} \mathbf {I}+\gamma \mathbf {A} &{} \mathbf {0} \\ \hline \gamma \mathbf {B} &{} \mathbf {I} \end{array} \right] , \end{aligned}$$

and it follows that $\det (\mathbf {I}+\gamma \mathbf {T})\ne 0$ if and only if $\det (\mathbf {I}+\gamma \mathbf {A})\ne 0$. Since $\mathbf {A}$ is strictly lower triangular we have $\det (\mathbf {I}+\gamma \mathbf {A})\ne 0$,

$$\begin{aligned} \left[ \begin{array}{c|c} \mathbf {I}+\gamma \mathbf {A} &{} \mathbf {0} \\ \hline \gamma \mathbf {B} &{} \mathbf {I} \end{array} \right] ^{-1}=\left[ \begin{array}{c|c} (\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {0} \\ \hline -\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {I} \end{array} \right] , \end{aligned}$$

and it follows that

$$\begin{aligned} (\mathbf {I}+\gamma \mathbf {T})^{-1}[\mathbf {S}\, | \, \gamma \mathbf {T}]&= \left[ \begin{array}{c|c} (\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {0} \\ \hline -\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {I} \end{array} \right] \left[ \begin{array}{c|c|c} \mathbf {U} &{} \gamma \mathbf {A} &{} \mathbf {0} \\ \hline \mathbf {V} &{} \gamma \mathbf {B} &{} \mathbf {0} \end{array} \right] \\&= \left[ \begin{array}{c|c|c} (\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U} &{} (\mathbf {I}+\gamma \mathbf {A})^{-1}\gamma \mathbf {A} &{} \mathbf {0} \\ \hline \mathbf {V}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U} &{} \gamma \mathbf {B}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\gamma \mathbf {A} &{} \mathbf {0} \end{array} \right] . \end{aligned}$$

We have

$$\begin{aligned} (\mathbf {I}+\gamma \mathbf {A})^{-1}\gamma \mathbf {A}=(\mathbf {I}+\gamma \mathbf {A})^{-1}(\mathbf {I}+\gamma \mathbf {A}-\mathbf {I}) =\mathbf {I}-(\mathbf {I}+\gamma \mathbf {A})^{-1}, \end{aligned}$$

and

$$\begin{aligned}&\gamma \mathbf {B}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\gamma \mathbf {A} =\gamma \mathbf {B}\left( \mathbf {I}-(\mathbf {I}+\gamma \mathbf {A})^{-1}\gamma \mathbf {A}\right) \\&\quad =\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}(\mathbf {I}+\gamma \mathbf {A}-\gamma \mathbf {A}) =\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}, \end{aligned}$$

which leads to

$$\begin{aligned} (\mathbf {I}+\gamma \mathbf {T})^{-1}[\mathbf {S}\, | \, \gamma \mathbf {T}]= \left[ \begin{array}{c|c|c} (\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U} &{} \mathbf {I}-(\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {0} \\ \hline \mathbf {V}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U} &{} \gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1} &{} \mathbf {0} \end{array} \right] . \end{aligned}$$

Hence, it follows that the condition (2.3) is equivalent to

$$\begin{aligned} \begin{array}{c} (\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U}\ge 0, \quad \mathbf {I}-(\mathbf {I}+\gamma \mathbf {A})^{-1}\ge 0, \\ \mathbf {V}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U}\ge 0, \quad \gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\ge 0, \end{array} \end{aligned}$$

(3.7)

and the characterization of the SSP coefficient (2.4) for GLMs (3.1) can be reformulated as

$$\begin{aligned} \mathcal {C}=\mathcal {C}(\mathbf {c},\mathbf {A},\mathbf {U},\mathbf {B},\mathbf {V}) =\sup \Big \{\gamma \in {\mathbb R}: \ \gamma \ \hbox {satisfies} \ (3.7)\Big \}. \end{aligned}$$

(3.8)

4 Examples of SSP GLMs

In this section we will use the characterization (3.8) of the SSP coefficient $\mathcal {C}(\mathbf {c},\mathbf {A},\mathbf {U},\mathbf {B},\mathbf {V})$ of GLMs (3.1) to search for new methods, for which this coefficient is as large as possible. We will systematically investigate the cases of GLMs of order $2\le p\le 4$, stage order $1\le q\le p$, number of external stages $r=2$ or $r=3$ , and the number of internal stages $2\le s\le 10$.

When applied to nonstiff systems of differential equations methods of high stage order are not necessarily more accurate than methods of stage order $q=1$ or $q=2$. This was also observed in the numerical experiments reported in Sect. 6, where the methods of high stage order achieve similar accuracy as methods of stage order $q=1$ or $q=2$. However, methods of high stage order are usually more accurate for mildly stiff and stiff systems than the methods of low stage order because they do not suffer from order reduction phenomenon [8, 10, 11, 30] (compare Sect. 6). Moreover, methods of high stage order allow accurate, efficient, and robust local error estimation, and computation of continuous extensions of uniform order $p$. They also allow construction of methods with step-control stability and methods with inherent Runge–Kutta stability. These and related issues are discussed in [12–16, 38, 39] and the monograph [40]. Furthermore, efficient and reliable step changing strategies for GLMs, based on the so-called rescale and modify strategy, were proposed by Butcher and Jackiewicz and are discussed in [14] and the monograph [38].

Similarly to [45], consider the minimization problem

$$\begin{aligned} \begin{array}{ll} &{} \min \limits _{\gamma ,\mathbf {c},\mathbf {A},\mathbf {U},\mathbf {B},\mathbf {V},\mathbf {q}_1,\ldots ,\mathbf {q}_p} -\gamma , \\ \hbox {subject to} \ \ &{} \left\{ \begin{array}{l} (\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U}\ge 0, \\ \mathbf {I}-(\mathbf {I}+\gamma \mathbf {A})^{-1}\ge 0,\\ \mathbf {V}-\gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\mathbf {U}\ge 0, \\ \gamma \mathbf {B}(\mathbf {I}+\gamma \mathbf {A})^{-1}\ge 0, \\ \varPhi _{p,q}(\mathbf {c},\mathbf {A},\mathbf {U},\mathbf {B},\mathbf {V},\mathbf {q}_1,\ldots ,\mathbf {q}_p)=0, \end{array} \right. \\ \end{array} \end{aligned}$$

(4.1)

where $\varPhi _{p,q}$ represents the order conditions up the the order $p$ and stage order conditions up to the stage order $q\le p$. For methods of order $p=2$ the optimization problem (4.1) was analytically solved using the Minimize command in $\hbox {Mathematica}^{\circledR }$, while for methods of order $p\ge 3$ it was numerically solved using the $\hbox {MATLAB}^{\circledR }$ function fmincon choosing the sequential quadratic programming (‘sqp’) algorithm. In the latter case we ran an extensively numerical search using random starting points. The solution of this minimization problem (4.1), leads to specific SSP GLMs (3.1) with SSP coefficient $\mathcal {C}$. To compare methods with different number of stages $s$ we also define, as in [19] and [45], the effective CFL coefficient by the normalization

$$\begin{aligned} \mathcal {C}_\mathrm{eff}=\frac{\mathcal {C}}{s}. \end{aligned}$$

4.1 Methods with Two External Stages

The $\mathcal {C}_\mathrm{eff}$ coefficients for methods with two external stages are listed in Tables 2, 3 and 4, using the notation $\hbox {GLM}pqr$, where $p$ is the order of the method, $q$ is the stage order, and where $r$ now stands for the rank of the coefficient matrix $\mathbf {V}$. For comparison, in these tables we have also listed $\mathcal {C}_\mathrm{eff}$ coefficients for SSP TSRK methods investigated by Ketcheson et al. [45], and multistep multistage methods investigated by Constantinescu and Sandu [19]. These multistep multiderivative methods are denoted by $\hbox {MM}pq$, where $p$ is the order and $q$ is the stage order of the method.

Table 2 $\mathcal {C}_\mathrm{eff}$ for $\hbox {GLM}pqr$ with order $p=2$, stage order $q=1,2$ and $r=\hbox {rank}(\mathbf {V})=1,2, \mathcal {C}_\mathrm{eff}$ for TSRK methods of order $p=2$, with $s$ internal stages, $2\le s\le 10$ and $\mathcal {C}_\mathrm{eff}$ for $\hbox {MM}pq$ methods of order $p=2$, stage order $q=1,2$, with $k=2$ steps and $\overline{s}$ stages, $2\le \overline{s}\le 4$

Table 3 $\mathcal {C}_\mathrm{eff}$ for $\hbox {GLM}pqr$ with order $p=3$, stage order $q=1,2,3$ and $r=\hbox {rank}(\mathbf {V})=1,2, \mathcal {C}_\mathrm{eff}$ for TSRK methods of order $p=3$, with $s$ internal stages, $2\le s\le 10$ and $\mathcal {C}_\mathrm{eff}$ for $\hbox {MM}pq$ methods of order $p=3$, stage order $q=1,2,3$, with $k=2$ steps and $\overline{s}$ stages, $2\le \overline{s}\le 4$

Table 4 $\mathcal {C}_\mathrm{eff}$ for $\hbox {GLM}pqr$ with order $p=4$, stage order $q=1,2,3$ and $r=\hbox {rank}(\mathbf {V})=1,2, \mathcal {C}_\mathrm{eff}$ for TSRK methods of order $p=4$, with $s$ internal stages, $3\le s\le 10$ and $\mathcal {C}_\mathrm{eff}$ for $\hbox {MM}pq$ methods of order $p=4$, stage order $q=1,2,3$, with $k=2$ steps and $\overline{s}$ stages, $2\le \overline{s}\le 4$

We can see that GLMs (3.1) of order $p=2$ stage order $q=1$ have larger $\mathcal {C}_\mathrm{eff}$ coefficients than the optimal TSRK methods of order $p=2$ investigated by Ketcheson et al. [45]. These $\mathcal {C}_\mathrm{eff}$ coefficients for TSRK methods are equal to the threshold factors $(R_{s,k,p})$ of a class of GLMs investigated by Ketcheson [44] (compare with Table 1 in [44]). For $2\le s\le 4$ these coefficients are also equal to $\mathcal {C}_\mathrm{eff}$ coefficients of multistep multistage methods investigated by Constantinescu and Sandu [19]. We can also see that GLMs (3.1) of order $p=2$, stage order $q=2$, and $\hbox {rank}(\mathbf {V})=2$ have lager $\mathcal {C}_\mathrm{eff}$ coefficients than TSRK methods and, for $2\le s\le 4$, than $\hbox {MM}22$ methods. For GLMs (3.1) of order $p=2$, stage order $q=2$, and $\hbox {rank}(\mathbf {V})=1$ these coefficients are somewhat smaller than $\mathcal {C}_\mathrm{eff}$ coefficients for TSRK methods, but they are still larger, for $2\le s\le 4$, than $\mathcal {C}_\mathrm{eff}$ coefficients for $\hbox {MM}22$ methods. It follows from Table 3 that GLMs (3.1) with $p=3, q=1$, and $\hbox {rank}(\mathbf {V})=1$ have, for $s=2$ and $8\le s\le 10$, larger $\mathcal {C}_\mathrm{eff}$ coefficients than the optimal TSRK methods investigated by Ketcheson et al. [45], but smaller than the threshold factors $(R_{s,k,p})$ of a class of GLMs investigated by Ketcheson [44] for $s\ge 3$ (compare again with Table $1$ in [44]). These coefficients are also smaller, for $2\le s\le 4$, than the $\mathcal {C}_\mathrm{eff}$ coefficients for MM$31$ methods. For GLMs (3.1) with $p=3, q=1$ and $\hbox {rank}(\mathbf {V})=2 \mathcal {C}_\mathrm{eff}$ coefficients are larger than the $\mathcal {C}_\mathrm{eff}$ coefficients for TSRK methods and, for $2\le s\le 4$, than for $\hbox {MM}31$ methods. It follows from Table 4 that GLMs (3.1) with $p=4, q=1$, and $\hbox {rank}(\mathbf {V})=1$ have, for $6\le s\le 10$, larger $\mathcal {C}_\mathrm{eff}$ coefficients than optimal TSRK methods investigated in [45] but smaller than the threshold factors ($R_{s,k,p}$) of a class of GLMs investigated in [44] (compare with Table 1 in [44]). These coefficients are also smaller, for $3\le s\le 4$, than the $\mathcal {C}_\mathrm{eff}$ coefficinets of MM$41$ methods. We can also see that GLMs (3.1) with $p=4, q=1$ or $q=2$, and $\hbox {rank}(\mathbf {V})=2$ have larger $\mathcal {C}_\mathrm{eff}$ coefficients than MM$41$ or MM$42$ methods. The SSP coefficients of GLMs of stage order $q>1$ are smaller than the SSP coefficients of TSRK methods, but they have the advantage of higher stage order. Relaxing the requirement on the rank of $\mathbf {V}$ leads always to methods with larger $\mathcal {C}_\mathrm{eff}$ coefficients. Moreover, the GLMs (3.1) have quite large regions $\mathcal {A}$ of absolute stability. The scaled regions of absolute stability, obtained by multiplying the points on the boundary by $p/s$, where $p$ is the order of the method and $s$ the number of stages, are plotted in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. For comparison we have also plotted on these figures by thick line the stability regions of RK methods of the same order. The same coordinate axes are used for methods of order $p=2$ and stage order $q=1$ or $q=2$; order $p=3$ and stage order $q=1, q=2$, or $q=3$; and order $p=4$ and stage order $q=1, q=2$, or $q=3$.

Fig. 1

Stability region of RK method with $p=s=2$ (thick line) and scaled stability regions of SSP GLMs of order $p=2$ and stage order $q=1$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $2$ to $10$

Fig. 2

Stability region of RK method with $p=s=2$ (thick line) and scaled stability regions of SSP GLMs of order $p=2$ and stage order $q=2$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $2$ to $10$

Fig. 3

Stability region of RK method with $p=s=3$ (thick line) and scaled stability regions of SSP GLMs of order $p=3$ and stage order $q=1$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $2$ to $10$

Fig. 4

Stability region of RK method with $p=s=3$ (thick line) and scaled stability regions of SSP GLMs of order $p=3$ and stage order $q=2$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $2$ to $10$

Fig. 5

Stability region of RK method with $p=s=3$ (thick line) and scaled stability regions of SSP GLMs of order $p=3$ and stage order $q=3$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $3$ to $10$

Fig. 6

Stability region of RK method with $p=s=4$ (thick line) and scaled stability regions of SSP GLMs of order $p=4$ and stage order $q=1$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $3$ to $10$

Fig. 7

Stability region of RK method with $p=s=4$ (thick line) and scaled stability regions of SSP GLMs of order $p=4$ and stage order $q=2$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $3$ to $10$

Fig. 8

Stability region of RK method with $p=s=4$ (thick line) and scaled stability regions of SSP GLMs of order $p=4$ and stage order $q=3$ with $s$ stages (thin lines). These regions increase in size as $s$ ranges from $3$ to $10$

In the case $p=2$ and $q=1$ the minimization problem (4.1) can be solved exactly, and the resulting $s$-stage methods have the following coefficients:

$$\begin{aligned} \mathbf {c}&= \left[ \begin{array}{cccc} c_s-(s-1) a&\ldots&c_s-a&c_s \end{array} \right] ^T,\\ \left[ \begin{array}{c|c} \mathbf {A} &{} \mathbf {U} \\ \hline \mathbf {B} &{} \mathbf {V} \end{array} \right]&= \left[ \begin{array}{ccccc|cc} 0 &{} 0 &{} 0 &{} \ldots &{} 0 &{} 1 &{} 0 \\ a &{} 0 &{} 0 &{} \ldots &{} 0 &{} 1 &{} 0 \\ a &{} a &{} 0 &{} \ldots &{} 0 &{} 1 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots \\ a &{} a &{} a &{} \ldots &{} 0 &{} 1 &{} 0 \\ \hline b &{} b &{} b &{} \ldots &{} b &{} v &{} 1-v \\ 0 &{} 0 &{} 0 &{} \ldots &{} 0 &{} v &{} 1-v \\ \end{array} \right] ,\\ \mathbf {q_0}&= \left[ \begin{array}{cc} 1 &{} 1 \\ \end{array} \right] ^T, \quad \mathbf {q_1}= \left[ \begin{array}{cc} c_s-(s-1)a \ &{} c_s-(s-1)a + \frac{sb-1}{v-1} \\ \end{array} \right] ^T,\\ \mathbf {q_2}&= \left[ \begin{array}{cc} q_{1,2}&q_{1,2} + \frac{2 (bs-1) c_s - a (s-1) (bs-2) -1 }{2 (v-1)} \end{array} \right] ^T. \end{aligned}$$

For this method

$$\begin{aligned} a=\frac{1}{\gamma }, \quad b=\frac{3-a (s-1)}{2 s} \quad \hbox {and} \quad v=\frac{2}{3-a(s-1)}, \end{aligned}$$

where

$$\begin{aligned} \gamma =\mathcal {C}=\frac{5s-3+2\sqrt{4s^2-3s}}{9}. \end{aligned}$$

Observe that for optimal SSP RK methods of order 2 with $s$ stages we have $\mathcal {C}=s-1$ [26], and for optimal SSP TSRK methods of order 2 with $s$ stages we have $\mathcal {C}=\sqrt{s(s-1)}$ [45]. The effective SSP coefficients $\mathcal {C}_\mathrm{eff}$ for these methods satisfy the relation

$$\begin{aligned} \frac{s-1}{s} < \sqrt{\frac{s-1}{s}} < \frac{5s-3+2\sqrt{4s^2-3s}}{9s}, \quad s\ge 2 \end{aligned}$$

and they all tend to one as $s\rightarrow \infty$.

We conclude this section by listing the coefficients of some of the GLMs which will be used in our numerical experiments in Sect. 6. To simplify the implementation aspects we consider GLMs such that $q_{1,i}=0, i=0,1,\ldots ,p$, so that $y_1^{[n]}$ approximates directly $y(t_n)$ and no special finishing procedure is needed. The coefficients of GLMs of order $p=2,3,4$, stage order $q=1$, with $s=p$ stages are listed below.

1. GLM of order $p=s=2$ and stage order $q=1$:

$$\begin{aligned} \mathbf c&= \left[ \begin{array}{c} 0.3650467037271516 \\ 1 \end{array} \right] , \quad \mathbf A =\left[ \begin{array}{cc} 0 &{}\quad 0 \\ 0.7043404725156382 &{}\quad 0 \end{array} \right] ,\\ \mathbf U&= \left[ \begin{array}{cc} 0 &{}\quad 1 \\ 0.1900775312702241 &{}\quad 0.8099224687297759 \end{array} \right] ,\\ \mathbf B&= \left[ \begin{array}{cc} 0.3508928386155310 &{}\quad 0.4332425042681505 \\ 0.5142476411512765 &{}\quad 0.6349344054595566 \end{array} \right] ,\\ \mathbf v&= \left[ \begin{array}{cc} 0.4086656449371389&\quad 0.5913343550628611 \end{array} \right] ^T,\\ \mathbf {q}_0&= \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] , \ \mathbf {q}_1=\left[ \begin{array}{c} 0 \\ 0.3650467037271516 \end{array} \right] , \quad \mathbf {q}_2=\left[ \begin{array}{c} 0 \\ -0.1037226703320720 \end{array} \right] . \end{aligned}$$

For this method $\mathcal {C}_\mathrm{eff}=0.575$.

2. GLM of order $p=s=3$ and stage order $q=1$:

$$\begin{aligned} \mathbf c&= \left[ \begin{array}{ccc} 0.0684518223468909&\quad 0.9&\quad 1 \end{array} \right] ^T,\\ \mathbf A&= \left[ \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0.8306711524589209 &{}\quad 0 &{}\quad 0 \\ 0.4776457731022248 &{}\quad 0.4824893165972064 &{}\quad 0 \end{array} \right] ,\\ \mathbf U&= \left[ \begin{array}{cc} 0.5606899042304484 &{}\quad 0.4393100957695516 \\ 0.5550613320633171 &{}\quad 0.4449386679366829 \\ 0.7441549843152873 &{}\quad 0.2558450156847127 \end{array} \right] ,\\ \mathbf B&= \left[ \begin{array}{ccc} 0.5370363792990961 &{}\quad 0.1529221010600519 &{}\quad 0.2659459898471803 \\ 0.2951312505427116 &{}\quad 0.2981240144887791 &{}\quad 0.5184658435950905 \end{array} \right] ,\\ \mathbf v&= \left[ \begin{array}{cc} 0.7170037151312315&\quad 0.2829962848687685 \end{array} \right] ^T,\\ \mathbf {q}_0&= \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] , \quad \mathbf {q}_1=\left[ \begin{array}{c} 0 \\ 0.1558166384202529 \end{array} \right] ,\\ \mathbf {q}_2&= \left[ \begin{array}{c} 0 \\ 0.2108260905150779 \end{array} \right] , \quad \mathbf {q}_3=\left[ \begin{array}{c} 0 \\ -0.1042344495356952 \end{array} \right] . \end{aligned}$$

For this method $\mathcal {C}_\mathrm{eff}=0.397$.

3. GLM of order $p=s=4$ and stage order $q=1$:

$$\begin{aligned} \mathbf c&= \left[ \begin{array}{cccc} 0.4676018664273567&\quad 0.5676018664273567&\quad 0.6676018664273566&\quad 1 \end{array} \right] ^T,\\ \mathbf A&= \left[ \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0.3673596196753279 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0.1720505432778199 &{}\quad 0.4017691394372760 &{}\quad 0 &{}\quad 0 \\ 0.0899387057827172 &{}\quad 0.2100231463150690 &{}\quad 0.4484381257008554 &{}\quad 0 \end{array} \right] ,\\ \mathbf U&= \left[ \begin{array}{cc} 0.1224498945564486 &{}\quad 0.8775501054435514 \\ 0.6242046549256117 &{}\quad 0.3757953450743883 \\ 0.8239986383411790 &{}\quad 0.1760013616588210 \\ 0.5278213329229676 &{}\quad 0.4721786670770324 \end{array} \right] ,\\ \mathbf B&= \left[ \begin{array}{cccc} 0.2331192407258031 &{}0.1409247474047351 &{}0.3009003088461573 &{}0.1073705564586502 \\ 0.1338392960126851 &{}0.1813062195702598 &{}0.3871221944272032 &{}0.6128963374789214 \end{array} \!\right] \!,\\ \mathbf v&= \left[ \begin{array}{cc} 0.5914695020769672&\quad 0.4085304979230328 \end{array} \right] ^T,\\ \mathbf {q}_0&= \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] , \quad \mathbf {q}_1=\left[ \begin{array}{c} 0 \\ 0.5328491940537238 \end{array} \right] , \quad \mathbf {q}_2=\left[ \begin{array}{c} 0 \\ 0.0067355902309170 \end{array} \right] ,\\ \mathbf {q}_3&= \left[ \begin{array}{c} 0 \\ -0.0055320508775149 \end{array} \right] , \quad \mathbf {q}_4=\left[ \begin{array}{c} 0 \\ 0.0014251362856992 \end{array} \right] . \end{aligned}$$

For this method $\mathcal {C}_\mathrm{eff}=0.291$.

It is worth remarking that the coefficients listed here are computed using double precision accuracy and they are reported with 16 digits. Specifically, we used the $\hbox {MATLAB}^{\circledR }$ function fmincon setting the absolute and relative tolerances both equal to $10\varepsilon _M$, where $\varepsilon _M$ here stands for the machine epsilon. For the reported methods, we verified that the inequality constraints in (4.1) are satisfied, and the maximum residua for the equality constraints in (4.1) are smaller than $3\varepsilon _M$. A technique similar to the one used in [37] can be used when more accurate coefficients are needed, for example for implementation in an extended precision environment.

4.2 Methods with Three External Stages

The higher value of $\mathcal {C}_\mathrm{eff}$ coefficients obtained for the cases with $\hbox {rank}(\mathbf {V})=2$ suggests that good values of $\mathcal {C}_\mathrm{eff}$ can be also obtained considering methods having $r=3$ (three external stages) and $\hbox {rank}(\mathbf {V})=3$. The results of such investigation are listed in Tables 5 and 6. For comparison, in these tables we have again listed $\mathcal {C}_\mathrm{eff}$ coefficients for SSP TSRK methods investigated by Ketcheson et al. [45], and multistep multistage methods investigate by Constantinescu and Sandu [19].

Table 5 $\mathcal {C}_\mathrm{eff}$ for $\hbox {GLM}pqr$ with order $p=3$, stage order $q=1,2, r=\hbox {rank}(\mathbf {V})=3, \mathcal {C}_\mathrm{eff}$ for TSRK methods of order $p=3$, with $s$ internal stages, $2\le s\le 10$ and $\mathcal {C}_\mathrm{eff}$ for $\hbox {MM}pq$ methods of order $p=3$, stage order $q=1,2,3$, with $k=3$ steps and $\overline{s}$ stages, $2\le \overline{s}\le 4$

Table 6 $\mathcal {C}_\mathrm{eff}$ for $\hbox {GLM}pqr$ with order $p=4$, stage order $q=1,2,3, r=rank(\mathbf {V})=3, \mathcal {C}_\mathrm{eff}$ for TSRK methods of order $p=4$, with $s$ internal stages, $3\le s\le 10$ and $\mathcal {C}_\mathrm{eff}$ for $\hbox {MM}pq$ methods of order $p=4$, stage order $q=1,2,3$, with $k=3$ steps and $\overline{s}$ stages, $3\le \overline{s}\le 4$

5 Construction of Starting Procedures

In this section we describe the construction of starting procedures for GLMs (3.1) of order $p$ and stage order $q\le p$, which are defined by the abscissa vector $\mathbf {c}=[c_1,\ldots ,c_s]^T\in {\mathbb R}^s$, the coefficient matrices

$$\begin{aligned} \left[ \begin{array}{c|c} \mathbf {A} &{} \mathbf {U} \\ \hline \mathbf {B} &{} \mathbf {V} \end{array} \right] =\left[ \begin{array}{cccc|cc} 0 &{} &{} &{} &{} u_{1,1} &{} u_{1,2} \\ a_{2,1} &{} 0 &{} &{} &{} u_{2,1} &{} u_{2,2} \\ \vdots &{} \vdots &{} \ddots &{} &{} \vdots &{} \vdots \\ a_{s,1} &{} a_{s,2} &{} \cdots &{} 0 &{} u_{s,1} &{} u_{s,2} \\ \hline b_{1,1} &{} b_{1,2} &{} \cdots &{} b_{1,s} &{} v_1 &{} v_2 \\ b_{2,1} &{} b_{2,2} &{} \cdots &{} b_{2,s} &{} v_1 &{} v_2 \end{array} \right] , \end{aligned}$$

and the vectors

$$\begin{aligned} \mathbf {q}_0=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right] , \quad \mathbf {q}_1=\left[ \begin{array}{c} q_{1,1} \\ q_{2,1} \end{array} \right] , \quad \ldots , \quad \mathbf {q}_p=\left[ \begin{array}{c} q_{1,p} \\ q_{2,p} \end{array} \right] . \end{aligned}$$

This method requires the starting vector $y^{[0]}$ which satisfies the relation (3.6). The computation of such a vector can be achieved by associating with each component $y_i^{[0]}, i=1,2$, a starting procedure $S_i$ in the form of a generalized explicit RK method

$$\begin{aligned} \begin{array}{c|c} \mathbf {c}^{(i)} &{} \mathbf {A}^{(i)} \\ \hline b_0^{(i)} &{} {\mathbf {b}^{(i)}}^T \end{array}=\begin{array}{c|cccc} c_1^{(i)}=0 &{} 0 &{} &{} &{} \\ c_2^{(i)} &{} a_{2,1}^{(i)} &{} 0 &{} &{} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \\ c_{s_i}^{(i)} &{} a_{s_i,1}^{(i)} &{} a_{s_i,2}^{(i)} &{} \cdots &{} 0 \\ \hline b_0^{(i)} &{} b_1^{(i)} &{} b_2^{(i)} &{} \cdots &{} b_{s_i}^{(i)} \end{array}, \end{aligned}$$

(5.1)

with $s_i$ stages, $i=1,2$. The order conditions for these starting procedures can be derived in a similar way as order conditions for RK methods. Denote by $T_k$ the set of rooted trees of order less than or equal to $k$ [8, 10, 11]. For easy reference the trees up to the order four and the functions $\rho (t)$—the order of $t, \alpha (t)$—the number of ways of labeling $t, \sigma (t)$—the symmetry of $t$, and $\gamma (t)$ - the density of $t$, are listed in Table 7. In this table we have also listed the elementary differentials $F(t)$ and elementary weights $\varPhi (t)$ corresponding to $t\in T_k$, and $\mathbf {\Gamma }_{\mathbf {c}^{(i)}}$ stands for $\hbox {diag}(c_1^{(i)},\ldots ,c_{s_i}^{(i)})$. We refer to [8, 10, 11] for the definitions of these functions and the definition of $F(t)$ and $\varPhi (t)$.

Table 7 Trees $t\in T_{k}, 1\le k\le 4$, the functions $\rho (t), \alpha (t), \sigma (t), \gamma (t)$, elementary differentials $F(t)$ and elementary weights $\varPhi (t)$ corresponding to $t$

Expanding the solution $y(t_1)$ to (1.1) into Taylor series around $t_0$ we obtain

$$\begin{aligned} y(t_1)=y_0+hy'(t_0)+\frac{h^2}{2!}y''(t_0)+\cdots +\frac{h^p}{p!}y^{(p)}(t_0)+O(h^{p+1}). \end{aligned}$$

(5.2)

Similarly, expanding into Taylor series around $t_0$ the numerical solution defined by the continuous extension of the RK method (1.6)

$$\begin{aligned} \begin{array}{ll} Y_i(t)=y_0+(t-t_0)\sum \limits _{j=1}^{i-1}a_{ij}f\left( t_0+c_j(t-t_0),Y_j(t)\right) , &{} i=1,2,\ldots ,s, \\ \widetilde{y}(t)=y_0+(t-t_0)\sum \limits _{j=1}^sb_jf\left( t_0+c_j(t-t_0),Y_j(t)\right) , \end{array} \end{aligned}$$

$t\in [t_0,t_1]$, leads to

$$\begin{aligned} \widetilde{y}(t_1)=y_0+h\widetilde{y}'(t_0)+\frac{h^2}{2!}\widetilde{y}''(t_0) +\cdots +\frac{h^p}{p!}\widetilde{y}^{(p)}(t_0)+O(h^{p+1}). \end{aligned}$$

(5.3)

We can obtain order conditions for RK method (1.6) comparing (5.2) and (5.3). It is known [8, 10, 11] that the derivatives of the exact solution $y$ and numerical solution $\widetilde{y}$ can be written as

$$\begin{aligned} y^{(k)}(t_0)=\sum _{t\in T_k}\alpha (t)F(t)(y_0), \end{aligned}$$

and

$$\begin{aligned} \widetilde{y}^{(k)}(t_0)=\sum _{t\in T_k}\alpha (t)\gamma (t)\varPhi (t)F(t)(y_0), \end{aligned}$$

$k=1,2,\ldots ,p$. Hence, the RK method (1.6) has order $p$ if and only if

$$\begin{aligned} \widetilde{y}^{(k)}(t_0)=y^{(k)}(t_0), \quad 1\le k\le p, \end{aligned}$$

which, taking into account that $k=\rho (t)$, leads to the well known order conditions

$$\begin{aligned} \varPhi (t)=\frac{1}{\gamma (t)}, \quad \rho (t)\le p. \end{aligned}$$

To obtain order conditions for starting procedures $S_i$ defined by (5.1) we have to compare (5.3) with the expansions

$$\begin{aligned} y_i^{[0]}=q_{i,0}y_0+hq_{i,1}y'(t_0)+h^2q_{i,2}y''(t_0) +\cdots +h^pq_{i,p}y^{(p)}(t_0)+O(h^{p+1}), \end{aligned}$$

(5.4)

$i=1,2$. Since $q_{i,0}=1$ this implies that $b_0^{(i)}=1$, and

$$\begin{aligned} \widetilde{y}^{(k)}(t_0)=k!q_{i,k}y^{(k)}(t_0), \quad k=1,2,\ldots ,p. \end{aligned}$$

Hence, it follows that the order conditions for starting procedures $S_i$ take the form

$$\begin{aligned} \varPhi (t)=\frac{\rho (t)!q_{i,\rho (t)}}{\gamma (t)}, \quad \rho (t)\le p, \quad i=1,2. \end{aligned}$$

(5.5)

The starting procedures (5.1) can be written as GLM of the form (2.1) with $m_i=s_i+1, \ell =1$, and the matrices $\mathbf {T}^{(i)}$ and $\mathbf {S}^{(i)}$ given by

$$\begin{aligned} \mathbf {T}^{(i)}=\left[ \begin{array}{c|c} \mathbf {A}^{(i)} &{} \mathbf {0} \\ \hline {\mathbf {b}^{(i)}}^T &{} 0 \end{array} \right] \in {\mathbb R}^{(s_i+1)\times (s_i+1)}, \quad \mathbf {S}^{(i)}=\left[ \begin{array}{c} \mathbf {e} \\ \hline 1 \end{array} \right] \in {\mathbb R}^{s_i+1}, \end{aligned}$$

$i=1,2$.

We conclude this section by listing coefficients of starting procedures for the second stage of GLMs presented at the end of Sect. 4. We will write $\mathbf {c}, \mathbf {A}, b_0$, and $\mathbf {b}$ instead of $\mathbf {c}^{(2)}, \mathbf {A}^{(2)}, b_0^{(2)}$, and $\mathbf {b}^{(2)}$.

1. Starting procedure for GLM of order $p=s=2$ and stage order $q=1$:

$$\begin{aligned} \begin{array}{c|c} \mathbf {c} &{} \mathbf {A} \\ \hline b_0 &{} \mathbf {b}^T \end{array}=\begin{array}{c|cc} 0 &{} 0 &{} 0 \\ 0.2812093945309069 &{} 0.2812093945309069 &{} 0 \\ \hline 1 &{} 0.7338916724562181 &{} -0.3688449687290664 \end{array}. \end{aligned}$$

2. Starting procedure for GLM of order $p=s=3$ and stage order $q=1$:

$$\begin{aligned} \mathbf {c}&= \left[ \begin{array}{ccc} 0&\quad 0.7335162159189944&\quad 2.251072404473931 \end{array} \right] ^T,\\ \mathbf {A}&= \left[ \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0.7335162159189944 &{}\quad 0 &{}\quad 0 \\ 0.9141884855975350 &{}\quad 1.3368839188763961 &{}\quad 0 \end{array} \right] ,\\ b_0&= 1, \quad \mathbf {b}=\left[ \begin{array}{c} -0.3515107644351690 \\ 0.6136211845789465 \\ -0.1062937817235246 \end{array} \right] ^T. \end{aligned}$$

3. Starting procedure for GLM of order $p=s=4$ and stage order $q=1$:

$$\begin{aligned} \mathbf {c}&= \left[ \begin{array}{cccc} 0&\quad -0.0484369237260314&\quad 2.251072404473931&\quad -0.3753454798145245 \end{array} \right] ^T,\\ \mathbf {A}&= \left[ \! \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -0.0484369237260314 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 6.8617545996333957 &{}\quad -7.7088758801318322 &{}\quad 0 &{}\quad 0 \\ -2.7818048469195342 &{}\quad 2.6107806659149184 &{}\quad -0.2043212988099087 &{}\quad 0 \end{array} \!\right] \!,\\ b_0&= 1, \quad \mathbf {b}=\left[ \begin{array}{c} 0.3400007423942334 \\ 0.2240113419846398 \\ -0.0124829643367784 \\ -0.0186799259883710 \end{array} \right] . \end{aligned}$$

6 Numerical Experiments

To verify order of convergence of the methods derived in this paper we will use the test problem from [19, 52]

$$\begin{aligned} \frac{\partial y(x,t)}{\partial t}=-\frac{\partial y(x,t)}{\partial x} +\frac{t-x}{(1+t)^2}, \quad 0\le x\le 1, \quad 0\le t\le 1, \end{aligned}$$

(6.1)

with initial condition $y(x,0)=1+x, 0\le x\le 1$, and left boundary condition $y(0,t)= 1/(1+t), 0\le t\le 1$. The exact solution to this problem is

$$\begin{aligned} y(x,t)=\frac{1+x}{1+t}, \quad 0\le x\le 1, \quad 0\le t\le 1. \end{aligned}$$

This solution is linear in space and, as observed in [19] we can use first-order upwind discretization in space variable $x$ without introducing discretization errors.

It is the worth remarking that, from (3.3), the external stages of the GLMs (3.1) approximate a linear combination of the solution and its derivatives at grid points. So, usually, a finishing procedure is needed to recover an approximation for $y(t_{ end })$. This can be achieved by using information coming from one or two previous steps. This finishing procedure is a suitable linear combination of external stages, and does not involve any additional evaluation of the function $f$.

We have plotted on Figs. 9, 10 and 11 in double logarithmic scale the norm of global error at the end point $t_f$ of the interval of integration versus stepsize $h$ for methods of order $p=2, p=3, p=4$, and stage order $q=1$. We can see that all methods achieve the expected order of convergence. The convergence graphs for methods of order $p=2$ and stage order $q=2$, of order $p=3$ and stage order $q=2$ or $q=3$, and of order $p=4$ and stage order $q=2$ or $q=3$ also confirm the expected order of convergence. These graphs are not reproduced here. We have also presented in Table 8 the norm of the error at the end of the interval of integration and the observed order of convergence for GLMs with $p=s=2, p=s=3, p=s=4$, and $q=1$. The results for methods with larges number of stages $s$ and higher stage order $q$ are similar to those presented in Table 8 and are not reproduced here.

Fig. 9

Order verification for GLMs of order $p=2$ and stage order $q=1$ with $2\le s\le 10$ stages

Fig. 10

Order verification for GLMs of order $p=3$ and stage order $q=1$ with $2\le s\le 10$ stages

Fig. 11

Order verification for GLMs of order $p=4$ and stage order $q=1$ with $2\le s\le 10$ stages

Table 8 Accuracy test for problem (6.1) for the SSP GLM methods with $p=s=2, p=s=3, p=s=4$, and $q=1$

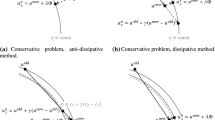
In order to further validate the order preservation for high stage order SSP GLM methods we report in Figs. 12 and 13 the results of numerical tests that point out that the constructed high order stages SSP GLM methods preserve the theoretical order of convergence $p$, while low stage order SSP RK methods suffer from the well known order reduction phenomenon. Specifically, following Constantinescu and Sandu [19], we considered problem (6.1) and pointed out that, when the spatial and temporal grids are refined simultaneously, SSPRK(3, 3) method [24] and SSPRK(5, 4) method [26, 48, 56] only achieve order $p=2$, while GLM of order $p=3$, stage order $q=3$ and $s=3$ internal stages, preserves the expected order $p=3$ (see Fig. 13).

Fig. 12

Order preservation for SSP GLM of order $p=3$, stage order $q=3$ and $s=3$ internal stages, and for SSPRK(3, 3) and SSPRK(5, 4) on problem (6.1) when only the temporal grid is refined

Fig. 13

Order preservation for SSP GLM of order $p=3$ and stage order $q=3$ (top figure) and order reduction phenomenon for SSPRK(3, 3) and SSPRK(5, 4) (bottom figure) on problem (6.1) when spatial and temporal grids are refined simultaneously

For the sake of completeness, it is worth to remark that when the space grid is maintained fixed—the ODE problem is fixed—then the expected order is preserved from all the considered Runge–Kutta and general linear methods (see Fig. 12). The order reduction phenomenon for RK methods reported in Fig. 13 is due to naive implementation of a time-dependent Dirichlet boundary condition. This phenomenon has been deeply analyzed in the literature and for linear hyperbolic equations it can be reduced or avoided by a suitable transformation or differentiation of the boundary conditions as shown in [18, 36, 51, 52].

To verify monotonicity properties of GLMs constructed in this paper we consider, following Constantinescu and Sandu [19] and Ketcheson et al. [46], the inviscid Burgers equation

$$\begin{aligned} \frac{\partial y(x,t)}{\partial t} +\frac{\partial }{\partial x}\bigg (\frac{1}{2}y^2(x,t)\bigg )=0, \quad 0\le x\le 2, \quad 0\le t\le t_f, \end{aligned}$$

(6.2)

with discontinuous initial condition

$$\begin{aligned} y(x,0)=\left\{ \begin{array}{ll} 0, &{}\quad 0\le x<0.5 \quad \hbox {or} \quad 1<x\le 2,\\ 1, &{}\quad 0.5\le x\le 1, \end{array} \right. \end{aligned}$$

and periodic boundary conditions

$$\begin{aligned} y(0,t)=y(1,t), \quad 0 \le t\le t_f. \end{aligned}$$

The space derivative in (6.2) was discretized by the conservative upwind approximation of the first order

$$\begin{aligned} y^2(x_i,t)\approx \frac{y^2(x_i,t)-y^2(x_{i-1},t)}{\varDelta x}, \end{aligned}$$

$i=1,2,\ldots ,N$, where $x_i=i\varDelta x, i=0,1,\ldots ,N, N\varDelta x=2$. The resulting system of ordinary differential equations corresponding to $N=100$ spatial points was then solved on the time interval $[0,0.5]$. We have found experimentally that the Euler method for this problem is SSP for $h\le h_{ FE }\approx 0.0167$ and the GLM with $p=2, q=1$, and $s=2$ is SSP if the time step $h$ satisfies the theoretical bound $h\le 1.48\, h_{ FE }$, compare with Table 2. However, the observed restriction on the time step $h$ is somewhat less stringent and given by $h\le 1.58\, h_{ FE }$. The results reported on Fig. 14 correspond to the time step $h=1.43\, h_{ FE }=0.0238$.

Fig. 14

Numerical approximations at $t_f=0.5$ to the discretization of Burgers equation with $N=100$, obtained by SSP GLM of order $p=2$ and stage order $q=1$, and by DIMSIM of order $p=2$ and stage order $q=2$ which is not SSP. These results correspond to $h=0.0238$

The numerical approximation obtained by the SSP GLM of order $p=2$ and stage order $q=1$ listed at the end of Sect. 4 with starting procedure given at the end of Sect. 5 is presented on the top graph of Fig. 14. We have also plotted the numerical approximation obtained by DIMSIM of order $p=2$ and stage order $q=2$ from [9] (see also [40]) which is not SSP, that is its SSP coefficient is $\mathcal {C}_\mathrm{eff}=0$. We can see that the SSP GLM exhibits smooth behavior, and that there are spurious oscillations generated by DIMSIM. Similar behavior of numerical approximations was observed for SSP GLM of order $p=3$ and $p=4$ listed at the end of Sect. 4 applied to the discretization of (6.2) with starting procedures listed in Sect. 5, and for DIMSIMs of order $p=3$ and $p=4$ and stage order $q=3$ and $q=4$ from [40].

Following Ferracina and Spijker [23] and Ketcheson et al. [45, 46] we consider also the Buckley–Leverett equation

$$\begin{aligned} \frac{\partial y(x,t)}{\partial t} +\frac{\partial }{\partial x}\Big (\varPhi \left( y(x,t)\right) \Big )=0, \quad 0\le x\le 1, \quad 0\le t\le t_f, \end{aligned}$$

(6.3)

with

$$\begin{aligned} \varPhi (y)=\frac{y^2}{y^2+a(1-y)^2}. \end{aligned}$$

This equation models a two-phase flow through the porous media, see for example [49]. We take $a=1/3$ and assume the discontinuous initial condition

$$\begin{aligned} y(x,0)=\left\{ \begin{array}{ll} 0, &{}\quad 0\le x\le 0.5, \\ 0.5, &{}\quad 0.5< x\le 1, \end{array} \right. \end{aligned}$$

and periodic boundary conditions

$$\begin{aligned} y(0,t)=y(1,t), \quad 0\le t\le t_f. \end{aligned}$$

As in [23] the Eq. (6.3) was approximated by the system of ordinary differential equations of the form

$$\begin{aligned} y'_i(t)=\frac{\varPhi \left( y_{i-\frac{1}{2}}(t)\right) -\varPhi \left( y_{i+\frac{1}{2}}(t)\right) }{\varDelta x}, \end{aligned}$$

(6.4)

where $y_i(t)\approx y(x_i,t), x_i=i\varDelta x, i=0,1,\ldots ,N, N\varDelta x=1$. We define

$$\begin{aligned} y_{j+\frac{1}{2}}(t)=y_j(t)+\frac{1}{2}\phi \left( \theta _j(t)\right) \left( y_{j+1}(t)-y_j(t)\right) , \end{aligned}$$

where $\phi (\theta )$ is a limiter function, due to Koren [36, 47], which is defined by

$$\begin{aligned} \phi (\theta )=\max \Big \{0,\min \Big \{2,\frac{2}{3}+\frac{1}{3}\theta ,2\theta \Big \}\Big \}, \end{aligned}$$

and

$$\begin{aligned} \theta _j(t)=\left\{ \begin{array}{ll} 0, &{}\quad j=0, \\ \frac{y_j(t)-y_{j-1}(t)}{y_{j+1}(t)-y_j(t)}, &{}\quad j=1,2,\ldots ,N. \end{array} \right. \end{aligned}$$

We semi-discretize the problem (6.3) using $N=100$ spatial points and, as in [23, 45, 46], we integrate the resulting system of ordinary differential equations (6.4) on the interval $[0,1/8]$. For this problem Euler method is SSP for $h\le h_{ FE }=0.0025$ [23, 45, 46], and the GLM with $p=2, q=1$, and $s=2$ is SSP if the time step $h$ satisfies the theoretical bound $h\le 1.48\, h_{ FE }$, compare again with Table 2. However, the observed restriction on the time step $h$ is less stringent and given by $h\le 2.17\, h_{ FE }$. Similar behavior was observed by Ketcheson et al. [45] in the context of TSRK methods, where they reported larger values of observed SSP coefficients $\mathcal {C}$ than those obtained by the solution of the minimization problem to compute optimal values of $\mathcal {C}$. The results reported on Fig. 15 correspond to the time step $h=2\, h_{ FE }=0.005$.

Fig. 15

Numerical approximations at $t_f=1/8$ to the discretization of the Buckley–Leverett equation with $N=100$, obtained by SSP GLM of order $p=2$ and stage order $q=1$, and by DIMSIM of order $p=2$ and stage order $q=2$ which is not SSP. These results correspond to $h=0.005$

The numerical approximation obtained by the SSP GLM of order $p=2$ and stage order $q=1$ listed at the end of Sect. 4 with starting procedure given at the end of Sect. 5 is presented on the top graph of Fig. 15. We have also plotted the numerical approximation obtained by DIMSIM of order $p=2$ and stage order $q=2$ from [9] (see also [40]) which is not SSP, that is its SSP coefficient is $\mathcal {C}_\mathrm{eff}=0$. We can observe that, similarly as in the previous example, the SSP GLM exhibits smooth behavior, and that there are spurious oscillations generated by DIMSIM. As before, similar behavior of numerical approximations was observed for SSP GLM of order $p=3$ and $p=4$ and stage order $q=1$ listed at the end of Sect. 4 applied to the discretization of (6.2) with starting procedures listed in Sect. 5, and for DIMSIMs of order $p=3$ and $p=4$ and stage order $q=3$ and $q=4$ from [40]. There is extensive numerical evidence that GLMs derived in this paper combined with starting procedures listed in Sect. 5 preserve SSP of the overall numerical processes.

7 Concluding Remarks

We have used the monotonicity theory of GLMs developed by Spijker [55] to construct SSP methods with two and three external stages and $s$ internal stages for differential systems. We also derived order conditions for starting procedures for GLMs investigated in this paper. Examples of methods are provided of order $p=2$ and stage order $q=1$ or $q=2$, order $p=3$ and stage order $q=1, q=2$, or $q=3$, and of order $p=4$ and stage order $q=1, q=2$, or $q=3$. Examples of starting procedures for these methods are also provided. Many methods derived in this paper have larger effective Courant–Friedrichs–Levy coefficients $\mathcal {C}_\mathrm{eff}$ than the class of TSRK methods introduced by Jackiewicz and Tracogna [42], whose SSP properties were analyzed recently by Ketheson et al. [45]. Numerical examples illustrate that all methods derived in this paper achieve the expected order of accuracy. Moreover, under appropriate stepsize restrictions, these methods combined with appropriate spatial discretization, do not produce spurious oscillations when applied to semidiscretizations of hyperbolic conservation laws.

Future work will address the construction of implicit SSP GLMs and explicit SSP GLMs of high order, and the efficient implementation of these methods for semidiscretizations in space variables of partial differential equations.