1 Introduction

Conceptual Density Functional Theory (noted C-DFT) is defined as the theory of chemical reactivity aimed to extract chemical concepts from the DFT [1,2,3,4]. This formalism constitutes a paradigm for understanding chemical reactivity and selectivity in chemistry. Its foundation was established in 1978 by R. G. Parr and coworkers [5], through the identification of the Lagrange multiplier \(\mu \) with the electronic chemical potential. Among several reactivity descriptors, local reactivity descriptors have allowed to explain reactivity and selectivity in a variety of chemical reactions. A problem that arises has to do with the use of Fukui functions [3] and also dual descriptor [6,7,8,9,10,11,12] to compare local reactivities among different molecular systems. These are local reactivity descriptors defined in the framework of the canonical ensemble, thus meaning that N, the number of electrons and \(\upsilon (\textbf{r})\), the external potential, are the natural variables that allow defining to all descriptors. In the grand canonical ensemble, the natural variables are the electronic chemical potential, \(\mu \), and the same external potential \(\upsilon (\textbf{r})\).

On the one hand, we can readily obtain working formulae for the first four global reactivity descriptors [electronic chemical potential \(\mu \), chemical hardness \(\eta \), hyper-hardness \(\gamma \), and second order hyper-hardness \(\gamma ^{(2)}]\) through the finite difference approximation (FDA):

$$\begin{aligned} \mu [N,\upsilon (\textbf{r})] \equiv \left( \frac{\partial E}{\partial N}\right) _{\upsilon (\textbf{r})}= & {} -\frac{1}{2}\left( I_1+A_1\right) \end{aligned}$$
(1)
$$\begin{aligned} \eta [N,\upsilon (\textbf{r})] \equiv \left( \frac{\partial ^2E}{\partial N^2}\right) _{\upsilon (\textbf{r})}= & {} I_1-A_1\end{aligned}$$
(2)
$$\begin{aligned} \gamma [N,\upsilon (\textbf{r})]\equiv \left( \frac{\partial ^3E}{\partial N^3}\right) _{\upsilon (\textbf{r})}= & {} -\frac{1}{2}\left( I_1+A_1-I_2-A_2\right) \nonumber \\= & {} -\mu -\frac{1}{2}\left( I_2+A_2\right) \end{aligned}$$
(3)
$$\begin{aligned} \gamma ^{(2)}[N,\upsilon (\textbf{r})]\equiv \left( \frac{\partial ^4E}{\partial N^4}\right) _{\upsilon (\textbf{r})}= & {} I_2-A_2-3(I_1-A_1)\nonumber \\= & {} I_2-A_2-3\eta \end{aligned}$$
(4)

The parameters \(I_1\), \(A_1\), \(I_2\), and \(A_2\) are the first vertical ionization potential, the first vertical electron affinity, the second vertical ionization potential and the second vertical electron affinity, respectively. We can recover these experimental parameters from photoelectronic spectroscopy or computed through quantum chemical calculations.

On the other hand, we can deduce local reactivity descriptors from electron density. Working formulae for getting the first two local reactivity descriptors, after the electron density \(\left[ \rho _{_{N}}(\textbf{r})\right] \), meaning Fukui functions \(\left[ f^{+}(\textbf{r})\right. \), \({\overline{f}}(\textbf{r})\), and \(f^{-}(\textbf{r})\) where \({\overline{f}}(\textbf{r})\) is a mere arithmetic average between \(f^{+}(\textbf{r})\) and \(\left. f^{-}(\textbf{r})\right] \) and second order Fukui function or dual descriptor \(\left[ f^{(2)}(\textbf{r})\right] \), are also obtained by means of the FDA method:

$$\begin{aligned}{} & {} \rho [N,\upsilon (\textbf{r});\textbf{r}]\equiv \rho _{_{N}}(\textbf{r}) = \langle \psi | {\hat{\rho }}(\textbf{r})|\psi \rangle \end{aligned}$$
(5)
$$\begin{aligned}{} & {} f[N,\upsilon (\textbf{r});\textbf{r}]=f(\textbf{r})\equiv \left( \frac{\partial \rho _{_{N}}(\textbf{r})}{\partial N}\right) _{\upsilon (\textbf{r})} = \left\{ \begin{array}{lll} \frac{\rho _{_{N+\textrm{p}}}(\textbf{r}) -\rho _{_{N}}(\textbf{r})}{\textrm{p}}&{} = &{} f^{+}(\textbf{r})\\ \frac{\textrm{q}\cdot \rho _{_{N+\textrm{p}}}(\textbf{r}) +(\textrm{p}-\textrm{q})\cdot \rho _{_{N}}(\textbf{r}) -\textrm{p}\cdot \rho _{_{N-\textrm{q}}}(\textbf{r})}{2\mathrm {p\cdot q}} &{} = &{} {\overline{f}}(\textbf{r})\\ \frac{\rho _{_{N}}(\textbf{r}) -\rho _{_{N-\textrm{q}}}(\textbf{r})}{\textrm{q}}&{} = &{} f^{-}(\textbf{r})\\ \end{array} \right. \end{aligned}$$
(6)
$$\begin{aligned}{} & {} f^{(2)}[N,\upsilon (\textbf{r});\textbf{r}]=f^{(2)}(\textbf{r})\equiv \left( \frac{\partial ^2\rho _{_{N}}(\textbf{r})}{\partial N^2}\right) _{\upsilon (\textbf{r})} = \frac{\textrm{q}\cdot \rho _{_{N+\textrm{p}}}(\textbf{r}) -(\mathrm {p+q})\cdot \rho _{_{N}}(\textbf{r}) +\textrm{p}\cdot \rho _{_{N-\textrm{q}}}(\textbf{r})}{\mathrm {p\cdot q}}\nonumber \\ \end{aligned}$$
(7)

where \(\psi \) is the wave function and \({\hat{\rho }}(\textbf{r})\) the electron density operator in the Eq. (5). As observed, the Fukui functions given by Eq. (6) and dual descriptor defined by Eq. (7), are written in their most generalized form according to the methodology reported for closed-shell molecular systems [11] where \(\rho _{_{N+\textrm{p}}}({\textbf{r}})\) is the electron density of the molecular system bearing \(N+\textrm{p}\) electrons; \(\rho ({\textbf{r}})_{_{N}}\) is the electron density of the original molecular system bearing N electrons and \(\rho _{_{N-\textrm{q}}}({\textbf{r}})\) is the electron density of the molecular system bearing \(N-\textrm{q}\) electrons, where p and q correspond to the degree of degeneracy of LUMO and HOMO, respectively.

Quantum chemical calculations must include the correct definition of spin-multiplicity during the three-system single point calculations involving electron density, so leading to \(\textrm{p}+1\), 1, and \(\textrm{q}+1\) spin-multiplicities for the molecular systems bearing \(N+\textrm{p}\), N and \(N-\textrm{q}\) electrons, respectively. The second order Fukui function or dual descriptor, \(f^{(2)}({\textbf{r}})\), including LUMO and HOMO (quasi-) degeneracies [10], has been implemented in the Multiwfn software [11, 13]. However, even proposing that they are functions of N by the use of notations such as \([N,\upsilon (\textbf{r})]\) and \([N,\upsilon (\textbf{r});\textbf{r}]\) for global and local descriptors, respectively, there are no analytic functions explicitly showing a dependence upon N. So that analytical formulae depending on N are not available.

Even so, we could give some steps to evidence that LS [3] and LHS [14,15,16,17,18,19,20,21,22,23], respectively, are more appropriate local reactivity descriptors than FF and DD through their working formulae.

The local softness and local hyper-softness have demonstrated to be useful for making comparisons of local reactivities among a variety of molecular systems. This feature is due to the presence of the global softness, which allows to scale the Fukui function according to the size of the system under study.

Hence, unlike the local softness and the local hyper-softness, the Fukui function and the dual descriptor cannot be used to compare local reactivities because we could consider them as sub-intensive properties, thus meaning the more number of electrons, the less significant the FF and DD are. This feature is a consequence of the normalization condition, since as FF (and DD) must integrate to one (to zero), all possible values between 0 and 1 for FF (and all possible values from \(-1\) to 1 for DD) are scattered in a bigger molecular volume when N increases.

2 Analysis of local softness and local hyper-softness

The energy is related with the number of electrons as follows [1]:

$$\begin{aligned} E(N)= & {} aN^2+bN+c \end{aligned}$$
(8)

Where a, b,  and c are adjustment parameters having a similar role as the Van der Waals equation for each gas. Then, we can infer that total electronic energy present a quadratic dependence on the number of electrons while the external potential is kept constant. But this classic assumption just allows to compute up to the molecular hardness. To compute the hyper-hardness, a new polynomic function in terms of N is required. Such a minimal function is one of third order (or cubic):

$$\begin{aligned} E(N)= & {} aN^3+bN^2+cN+d \end{aligned}$$
(9)

From equations (1), (2), an (3), coefficients in Eq. (9) a, b, and c could be computed and d can be defined as \(d=0\) thus implying that \(\gamma ^{(2)}=0\):

$$\begin{aligned} E(N)= & {} \frac{\gamma }{6}N^3+\frac{1}{2}\left( \eta - \gamma \,N_0\right) N^2+\left( \mu -\eta \,N_0+\frac{\gamma }{2}\,N_0 ^2\right) N \end{aligned}$$
(10)

where \(N_0\) is the number of electrons of the system under study, while N is any number of electrons \(N=N_0\); or \(N=N_0+1\), or \(N=N_0-1\), and so on.

But there is simpler method to evidence that LS and LHS are more appropriate local functions than FF and DD, respectively. In agreement with bibliography [1, 24] values of \(I_1\), \(I_2\), \(A_1\), and \(A_2\) are usually less than \(1\,hartree\). Normally for atoms, \(0<I_1<1\) and \(I_2\approx 1\) or \(0<I_2<2\); and \(0<A_1<1\) and \(-1<A_2<1\). For molecules, we could assume similar order relations; we resorted to a couple of molecules as examples in the last section of the present work to evidence these relations.

Along with energy, the electron density \(\rho _{_{N}}(\textbf{r})\) is another essential parameter that characterizes a molecular system. Alike density of mass, we can also assume the electron density is an intensive property, so by applying that ansatz, the following sequence of expressions are obtained until second order of partial derivative with respect to N:

$$\begin{aligned}{} & {} \rho _{_{N}}(\textbf{r})\equiv \rho [N,\upsilon (\textbf{r});\textbf{r}] \Longrightarrow \rho [\lambda \,N,\lambda \upsilon (\textbf{r});\textbf{r}] = \lambda ^0\,\rho \,[N,\upsilon (\textbf{r});\textbf{r}] \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \left( \frac{\partial \rho _{_{N}}(\textbf{r})}{\partial N}\right) _{\upsilon (\textbf{r})}\equiv f[N,\upsilon (\textbf{r});\textbf{r}] \Longrightarrow f[\lambda \,N,\lambda \upsilon (\textbf{r});\textbf{r}] = \lambda ^{-1}\,f[N,\upsilon (\textbf{r});\textbf{r}] \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \left( \frac{\partial ^2\rho _{_{N}}(\textbf{r})}{\partial N^2}\right) _{\upsilon (\textbf{r})}\equiv f^{(2)}[N,\upsilon (\textbf{r});\textbf{r}] \Longrightarrow f^{(2)}[\lambda \,N,\lambda \upsilon (\textbf{r});\textbf{r}] = \lambda ^{-2}\,f^{(2)}[N,\upsilon (\textbf{r});\textbf{r}] \nonumber \\ \end{aligned}$$
(13)

The Eq. (12) is supported by the work performed by Chattaraj et al. [25] and Pacios et al. [26, 27] who developed a gradient approximation for the Fukui function:

$$\begin{aligned} f(\textbf{r})=\frac{\rho (\textbf{r})}{N}\left\{ 1+\alpha \,\Phi \left( \textbf{r},\rho (\textbf{r}),\nabla \rho (\textbf{r}),\nabla ^2\rho (\textbf{r}),\cdots \right) \right\} \end{aligned}$$
(14)

Following the same idea, we can extend this development for the dual descriptor. So, when written in terms of a similar expansion, it leads to Eq. (13):

$$\begin{aligned} f^{(2)}(\textbf{r})=\frac{\rho (\textbf{r})}{N^2}\left\{ 1+\beta \,\Psi \left( \textbf{r},\rho (\textbf{r}),\nabla \rho (\textbf{r}),\nabla ^2\rho (\textbf{r}),\cdots \right) \right\} \end{aligned}$$
(15)

From Eqs. (12) and (13) we can also infer that Fukui function and dual descriptor are functions of degree –1 and –2, respectively, thus being supported by equations (14) and (15). That means they are not extensive neither intensive properties; they are sub-intensive properties, thus implying that the lobes representing these functions in the real space become less and less important as the system’s size increases. The dual descriptor (DD) offers the advantage of revealing nucleophilic and electrophilic regions on molecules in just one picture. However it is affected worse than the Fukui function (FF) as the system’s size increases because it is a sub-intensive property of degree \(-2\), it means that to perform a comparison of local reactivities among different molecules could lead to wrong conclusions. Neither the FF nor the DD are suitable to determine local reactivities among molecules with the aim of comparing them. To remedy this undesirable behavior on both functions, replacements of the Fukui function \(f(\textbf{r})\) with the local softness \(s(\textbf{r})\), and the dual descriptor \(f^{(2)}(\textbf{r})\) with the local hyper-softness \(s^{(2)}(\textbf{r})\) [14,15,16,17,18,19,20,21,22,23] have become a common practice. We will demonstrate the conceptual support for these replacements.

Since that \(\eta =\left( \frac{\partial ^2E}{\partial N^2}\right) _{\upsilon (\textbf{r})}=\left( \frac{\partial \mu }{\partial N}\right) _{\upsilon (\textbf{r})}\), we know that the local softness depends on the Fukui function and the molecular hardness as follows:

$$\begin{aligned} s(\textbf{r})=\left( \frac{\partial \rho _{_{N}}(\textbf{r})}{\partial \mu }\right) _{\upsilon (\textbf{r})}=\left( \frac{\partial \rho _{_{N}}(\textbf{r})}{\partial \,N}\right) _{\upsilon (\textbf{r})} \left( \frac{\partial \,N}{\partial \mu }\right) _{\upsilon (\textbf{r})}=\frac{f(\textbf{r})}{\eta }=f(\textbf{r})\cdot S \end{aligned}$$
(16)

Usually \(A_1< I_1\), then \(| I_1-A_1|=I_1-A_1\). Besides the following inequalities hold for all atoms and most of molecules:

$$\begin{aligned} 0<&I_1&<1\\ 0<&A_1&<1 \end{aligned}$$

which can be written as:

$$\begin{aligned} 0<&I_1&<1\\ -1<&- A_1&<0 \end{aligned}$$

After adding these inequalities, we lead to:

$$\begin{aligned} -1<&I_1 - A_1&<1 \nonumber \\&| I_1 - A_1 |&<1 \nonumber \\&I_1-A_1&<1 \nonumber \\&\left( I_1-A_1\right) ^{-1}&>1 \end{aligned}$$
(17)

The resulting inequality (17) is the reciprocal of the working formula of molecular hardness as shown in Eq. (2). Such a reciprocal corresponds to the global softness, \(S=\left( I_1-A_1\right) ^{-1}\), which satisfies the inequality \(S>1\) in atomic units. From such an inequality, we can prove that \(s(\textbf{r})>f(\textbf{r})\) under the assumption \(f(\textbf{r})>0\). The working equation to get the Fukui function \(f(\textbf{r})\) can be given by any of the three that define the Fukui function in Eq. (6): \( f^{+}(\textbf{r})\), \({\overline{f}}(\textbf{r})\), or \( f^{-}(\textbf{r})\) which \(0<f^{+}(\textbf{r})<1\), \(0<f^{-}(\textbf{r})<1\), and \(0<{\overline{f}}(\textbf{r})<1\), then:

$$\begin{aligned} S> & {} 1\,\,\,\,/\,\cdot \,f(\textbf{r})\\ f(\textbf{r})\cdot S> & {} f(\textbf{r})\\ s(\textbf{r})> & {} f(\textbf{r}) \end{aligned}$$

Then, the local softness (LS) is a greater scalar field than the Fukui function (FF) because the LS corresponds to the FF scaled by the factor S, the global softness, which tends to be greater than 1 thus helping to quantify the local reactivity in agreement with the molecular size.

Similarly, from the definition of local hyper-softness, its working formula is obtained to be analyzed in the same way:

$$\begin{aligned} s^{(2)}(\textbf{r})= & {} \left( \frac{\partial ^2\rho _{_{N}}(\textbf{r})}{\partial \mu ^2}\right) _{\upsilon (\textbf{r})}=\left( \frac{\partial \,s(\textbf{r})}{\partial \mu }\right) _{\upsilon (\textbf{r})} =\left( \frac{\partial s(\textbf{r})}{\partial \,N}\right) _{\upsilon (\textbf{r})} \left( \frac{\partial \,N}{\partial \mu }\right) _{\upsilon (\textbf{r})}\nonumber \\= & {} \frac{f^{(2)}(\textbf{r})}{\eta ^2} - \frac{\gamma \,f(\textbf{r})}{\eta ^3}\nonumber \\= & {} S^2\cdot f^{(2)}(\textbf{r}) - \gamma \cdot S^3\cdot f(\textbf{r}) \end{aligned}$$
(18)

We can start from the following inequalities:

$$\begin{aligned} 0<&A_1&<1 \\ -1<&A_2&< 0 \end{aligned}$$

where, for the sake of simplicity, we chose \(-1<A_2<0\) instead of \(-1<A_2<1\), thus leading to:

$$\begin{aligned} 0<&A_1&<1 \\ 0<&-A_2&< 1 \end{aligned}$$

After adding these inequalities, it leads to:

$$\begin{aligned} 0<&A_1 - A_2&<2 \end{aligned}$$
(19)

On the other hand, we can resort to the following inequalities:

$$\begin{aligned} 0<&I_1&<1 \\ 0<&I_2&< 2 \end{aligned}$$

We write them as follows:

$$\begin{aligned} 0<&I_1&<1 \\ -2<&-I_2&< 0 \end{aligned}$$

After adding these inequalities, it leads to:

$$\begin{aligned} -2<&I_1 - I_2&<1 \end{aligned}$$

which can be replaced with this inequality:

$$\begin{aligned} -2<&I_1 - I_2&<2 \\&| I_1 - I_2|&<2 \end{aligned}$$

Since \(I_2>I_1\) always, then:

$$\begin{aligned} 0<&I_2 - I_1&< 2 \end{aligned}$$
(20)

The inequality (20) can be written as:

$$\begin{aligned} -2<&I_1 - I_2&< 0 \end{aligned}$$
(21)

Now we can add inequalities (19) and (21) to get the following result:

$$\begin{aligned} -2<&I_1 - I_2 +A_1 - A_2&< 2 \nonumber \\&| I_1 - I_2 +A_1 - A_2 |&< 2/\,\cdot \frac{1}{2} \nonumber \\ \frac{1}{2}&| I_1 - I_2 +A_1 - A_2 |&< 1 \end{aligned}$$
(22)

The term of the inequality (22) corresponds to the absolute value of \(\gamma \) given by the working formula (3), and that means it is a small value without mattering its algebraic sign; in the Eq. (18) the second term becomes negligible because of the smallness of \(\gamma \) that helps to cancel the effect of \(S^3\) as we will prove in the next paragraph.

We know that:

$$\begin{aligned} A_2<&0&< I_2 \end{aligned}$$

and since \(|I_2|>|A_2|\), then :

$$\begin{aligned} 0<&I_2 +A_2&/\,\cdot 3\,\\ 0<&3I_2 +3A_2&\\ 0<&3I_2 +3A_2&/\,+3I_1\,\\ 3I_1 <&3I_1+ 3I_2 +3A_2&\end{aligned}$$

This inequality can be replaced with:

$$\begin{aligned} 3I_1<&10I_1+ 10I_2 +10A_2&/\,\cdot \frac{1}{10}\,\\ \frac{3}{10}I_1 <&I_1+ I_2 +A_2&\end{aligned}$$

We can assume that \(\frac{I_1}{10}\approx A_1\), then this inequality can be replaced with:

$$\begin{aligned}{} & {} 3A_1< I_1+ I_2 +A_2 \nonumber \\{} & {} 3A_1<I_1+ I_2 +A_2 /\,-A_2\,\nonumber \\{} & {} 3A_1 -A_2< I_1+ I_2 /\,-2A_1\,\nonumber \\{} & {} A_1 -A_2< I_1+ I_2-2A_1/\,-I_2\,\nonumber \\{} & {} -I_2+A_1 -A_2< I_1-2A_1/\,+I_1\,\nonumber \\{} & {} I_1-I_2+A_1 -A_2< 2I_1-2A_1/\cdot \frac{1}{2}\,\nonumber \\{} & {} \frac{1}{2}\left( I_1-I_2+A_1 -A_2\right)< I_1-A_1/\cdot \left( I_1-A_1\right) ^{-3}\,\nonumber \\{} & {} \frac{1}{2}\left( I_1-I_2+A_1 -A_2\right) \cdot \left( I_1-A_1\right) ^{-3}< \left( I_1-A_1\right) ^{-2} \end{aligned}$$
(23)

According to working equations (2) and (3), the inequality (23) is:

$$\begin{aligned} \frac{1}{2}\gamma \cdot \eta ^{-3}< & {} \eta ^{-2} \nonumber \\ \frac{1}{2}\gamma \cdot \,S^{3}< & {} S^{2} \nonumber \\ \frac{1}{2}\gamma \cdot \,S^{3}< & {} S^{2} \,\,\,\,\,\,/\cdot |f^{(2)}(\textbf{r})| \nonumber \\ |f^{(2)}(\textbf{r})|\cdot \frac{1}{2}\gamma \cdot \,S^{3}< & {} |f^{(2)}(\textbf{r})|\cdot S^{2} \end{aligned}$$
(24)

Again, we know that the working formula to get the Fukui function \(f(\textbf{r})\) can be given by any of the three working equations that define the Fukui function as indicated in Eq. (6). Since:

\( |f^{(2)}(\textbf{r})|<1\),

\( 0<f^{+}(\textbf{r})<1\),

\( 0<f^{-}(\textbf{r})<1\), and

\( 0<{\overline{f}}(\textbf{r})<1\),

we can replace \( |f^{(2)}(\textbf{r})|<1\) with \(f^{+}(\textbf{r})\), \(f^{-}(\textbf{r})\), or \({\overline{f}}(\textbf{r})\) in the left-hand side of inequality (24):

$$\begin{aligned} f(\textbf{r})\cdot \frac{1}{2}\gamma \cdot \,S^{3}< & {} |f^{(2)}(\textbf{r})|\cdot S^{2} \end{aligned}$$
(25)

The inequality (25) reveals that it does not matter whether the positive or negative phase of the dual descriptor predominates because in the working formula of the local hyper-softness given in Eq. (18), the \(S^2\cdot f^{(2)}(\textbf{r})\) term will be more important than \(\gamma \cdot S^3\cdot f(\textbf{r})\), thus supporting the approximation \(s^{(2)}(\textbf{r})\approx \,S^2\cdot f^{(2)}(\textbf{r})\). In other words, it will be usual that \(|S^2\cdot f^{(2)}(\textbf{r})|>|\gamma \cdot S^3\cdot f(\textbf{r})|\).

This is the reason why the term \(\gamma \cdot S^3\cdot f(\textbf{r})\) in the Eq. (18) is neglected when compared against \(S^2\cdot f^{(2)}(\textbf{r})\): The \(S^2\) coefficient increases \(f^{(2)}(\textbf{r})\) while the \(\gamma \cdot S^3\) coefficient decreases \(f(\textbf{r})\). Then, the use of the approximation \(s^{(2)}(\textbf{r})\approx \,S^2\cdot f^{(2)}(\textbf{r})\) should be sufficient accurate to obtain the local hyper-softness. Nevertheless, computing both components, \(S^2\cdot f^{(2)}(\textbf{r})\) and \(\gamma \cdot S^3\cdot f(\textbf{r})\), should be a good practice on any molecular system in order to check that \(s^{(2)}(\textbf{r})\approx \,S^2\cdot f^{(2)}(\textbf{r})\) is sufficient to describe local reactivity; in case of finding the opposite situation, then \(s^{(2)}(\textbf{r})\) should be computed by means of its complete working formula \(S^2\cdot f^{(2)}(\textbf{r})-\gamma \cdot S^3\cdot f(\textbf{r})\) instead of using \(S^2\cdot f^{(2)}(\textbf{r})\). For the sake of simplicity, the averaged versions of the Fukui function \({\overline{f}}(\textbf{r})=0.5\{f^{+}(\textbf{r})+f^{-}(\textbf{r})\}\) and the local softness \({\overline{s}}(\textbf{r})=0.5\{s^{+}(\textbf{r})+s^{-}(\textbf{r})\}\) can be simply represented by \(f(\textbf{r})\) and \(s(\textbf{r})\), respectively.

Equations (12) and (13) indicate that these functions are sub-intensive. Once we use the global softness or the squared global softness as coefficients, the local softness and the local hyper-softness arise, respectively. The sub-intensive characteristic tends to be diminished or suppressed on these two functions.

Taking into account a different perspective, thus meaning from the point of view of atomic orbitals for atoms, and without loss of generality, we can resort to the local softness and the Fukui function for 1s atomic orbital provided by Ordon, Zaklika, Hładyszowsli, and Komorowski [28, 29] thus allowing to generate analytic expressions for all these functions. We will demonstrate that LS is a scaled size function. We can infer a similar feature of LHS.

$$\begin{aligned} f(\textbf{r})= & {} (3\,\pi )^{-1}Z^5r^2\,e^{-2Zr} \end{aligned}$$
(26)
$$\begin{aligned} s(\textbf{r})= & {} 8Z^3r^4\,e^{-2Zr} \end{aligned}$$
(27)

Comparison by quotient between Eq. (27) and Eq. (26) lead us to:

$$\begin{aligned} \frac{s(\textbf{r})}{f(\textbf{r})}= & {} \frac{8Z^3r^4\,e^{-2Zr}}{(3\,\pi )^{-1}Z^5r^2\,e^{-2Zr}}=\frac{24\pi \,r^2}{Z^2} \end{aligned}$$
(28)

Since \(r>0\), from Eq. (28) we can infer again that \(s(\textbf{r})>f(\textbf{r})\), but under the constraints \(r>Z\cdot \left( 24\,\pi \right) ^{-\frac{1}{2}}\). This means that LS for the 1s orbital scales quadratically, thus allowing to understand that it keeps consistency as the molecular’s size increases. This evidence justifies the common practice to replace Fukui function \(f(\textbf{r})\) with local softness \(s(\textbf{r})\) and dual descriptor \(f^{(2)}(\textbf{r})\) with local hyper-softness \(s^{(2)}(\textbf{r})\) [14,15,16,17,18,19,20,21,22,23] respectively.

3 A brief example illustrating the exposed analysis: fullerenes \(\hbox {C}_{20}\) and \(\hbox {C}_{60}\)

\(\hbox {C}_{20}\) is the smallest possible known fullerene, while \(\hbox {C}_{60}\) is the most famous fullerene. Structurally, they are similar; they differ on their sizes. \(\hbox {C}_{20}\) and \(\hbox {C}_{60}\) were geometrically optimized at the \(\omega \)B97X-D/6-311+G(d) level of theory. The density functional was selected according the criterium exposed in the respective bibliography [30], but instead of using the Def2TZVP basis set, we employed the 6-311+G(d) basis set.

Table 1 Vertical ionization energies (\(I_1\), and \(I_2\)) and vertical electron affinities (\(A_1\), and \(A_2\))
Full size table
Table 2 Some global reactivity descriptors from Conceptual DFT: Electronic chemical potential \(\mu \), molecular hardness \(\eta \), global softness S, molecular hyperhardness \(\gamma \) and \(S^3\gamma \)
Full size table

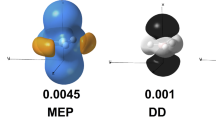
The molecular electrostatic potential (MEP, \(V(\textbf{r})\)) given by Fig. 1 indicates these carbon clusters present a predominance of protons over electrons, where \(\hbox {C}_{20}\) exhibits a sort of slight predominance of electrons on certain regions located in the equatorial positions, while \(\hbox {C}_{60}\) tends to show a sort of spherical reactivity. In both structures the presence of more than one type of carbon–carbon bond is evidenced. We shall notice that some local reactivity descriptors coming from the Conceptual DFT are more able to reveal such differences in carbon–carbon bonds.

Figures 2 and 3 show us isovalues of local softnesses and Fukui functions. We notice that Fukui functions require smaller isovalues. But to visualize the local softness, smaller values of isosurfaces are not mandatory due to inclusion of the global softness as a coefficient of the respective Fukui function. Even so, these descriptors show one phase that sometimes makes to detect regions having a legitime nucleophilic and electrophilic behavior harder.

Figures 4 and 5 the advantage when using a biphasic scalar field like any of both functions, DD or LHS, since certain regions present a nucleophilic and electrophilic behavior as evidenced. These two descriptors show us that \(\hbox {C}_{60}\) presents two types of carbon-carbon bonds as experimentally revealed, while the same couple of local reactivity descriptors indicate that \(\hbox {C}_{20}\) exhibits three types of carbon-carbon bonds. In addition, we can check that to visualize LHS, it does not require too much small values of isosurfaces due to the scale coefficient given by the squared global softness (\(S^2\)) as indicated in the Eq. (18).

To end this analysis, we can notice through Figs. 6 and 7 that \(S^2\cdot f^{(2)}(\textbf{r})\) is a very good approximation to get the \(s^{(2)}(\textbf{r})\) since its second component \(\gamma \cdot S^3\cdot f(\textbf{r})\) is negligible as demonstrated in the present article.

Fig. 1
figure 1

Molecular electrostatic potential, \(V(\textbf{r})\), of \(\hbox {C}_{20}\) and \(\hbox {C}_{60}\). All values are expressed in atomic units (hartree/e). Positive phase is blue-colored and negative phase is red-colored (Color figure online)

Full size image
Fig. 2
figure 2

Local softness (LS), \(s(\textbf{r})\) (nucleophilic, electrophilic and averaged versions), and Fukui function (FF), \(f(\textbf{r})\) (nucleophilic, electrophilic and averaged versions) of \(\hbox {C}_{60}\). Their values are given in atomic units: LS is measured in \(e^2\cdot \,hartree^{-1}\cdot \,bohr^{-3}\) and FF in \(bohr^{-3}\). These local reactivity descriptors have generally positive values because they are monophasic scalar fields so that any isosurface has just one color. In this work we have used the cyan-colored positive monophase. However, because the working formulae are based on arithmetic differences between electron densities, there could be certain regions presenting negative values which are given as yellow-colored lobes (Color figure online)

Full size image
Fig. 3
figure 3

Local softness (LS), \(s(\textbf{r})\) (nucleophilic, electrophilic and averaged versions), and Fukui function (FF), \(f(\textbf{r})\) (nucleophilic, electrophilic and averaged versions) of \(\hbox {C}_{20}\). Their values are given in atomic units: LS is measured in \(e^2\cdot \,hartree^{-1}\cdot \,bohr^{-3}\) and FF in \(bohr^{-3}\). These local reactivity descriptors have generally positive values because they are monophasic scalar fields so that any isosurface has just one color. In this work we have used the cyan-colored positive monophase. However, because the working formulae are based on arithmetic differences between electron densities, there could be certain regions presenting negative values which are given as yellow-colored lobes (Color figure online)

Full size image
Fig. 4
figure 4

Dual descriptor (DD), \(f^{(2)}(\textbf{r})\), and local hyper-softness (LHS), \(s^{(2)}(\textbf{r})\), of \(\hbox {C}_{60}\). Alike MEP, these local reactivity descriptors are biphasic scalar fields, so that the positive phase of DD is represented in dark color and the negative phase is represented in white color; the positive phase of LHS is given in light-green color and the negative phase, in purple color. Their values are given in atomic units: LHS is measured in \(e^3\cdot \,hartree^{-2}\cdot \,bohr^{-3}\) and DD in \(e^{-1}bohr^{-3}\) (Color figure online)

Full size image
Fig. 5
figure 5

Dual descriptor (DD), \(f^{(2)}(\textbf{r})\) and local hyper-softness (LHS), \(s^{(2)}(\textbf{r})\) of \(\hbox {C}_{20}\). Alike MEP, these local reactivity descriptors are biphasic scalar fields, so that the positive phase of DD is represented in dark color and the negative phase is represented in white color; the positive phase of LHS is given in light-green color and the negative phase, in purple color. Their values are given in atomic units: LHS is measured in \(e^3\cdot \,hartree^{-2}\cdot \,bohr^{-3}\) and DD in \(e^{-1}bohr^{-3}\) (Color figure online)

Full size image
Fig. 6
figure 6

The local hyper-softness, \(s^{(2)}(\textbf{r})\), and its components \(S^2\cdot f^{(2)}(\textbf{r})\) and \(\gamma \cdot S^3\cdot f(\textbf{r})\) of \(\hbox {C}_{60}\) (Color figure online)

Full size image
Fig. 7
figure 7

The local hyper-softness, \(s^{(2)}(\textbf{r})\), and its components \(S^2\cdot f^{(2)}(\textbf{r})\) and \(\gamma \cdot S^3\cdot f(\textbf{r})\) of \(\hbox {C}_{20}\)

Full size image

4 Conclusion

The study exposed in the present work allows one to consider as a priority the use of the local softness or local hyper-softness descriptors rather than the Fukui function and dual descriptor for making comparisons of local reactivities among molecules of different types and sizes.

Usually, the Fukui function or dual descriptor are employed to reveal the most intrinsically susceptible sites on a molecule to undergo nucleophilic and electrophilic attacks to lead a possible formation/breaking of a covalent bond. They are not suitable functions to compare local reactivities among molecules. The analysis makes no sense when performing a comparison among different molecules since lobes of Fukui function or dual descriptor become less significant as the molecules’ size increases. A family of compounds would allow us to make comparisons of local reactivities by means of the Fukui function or dual descriptor, but the molecular systems must have similar sizes; that is not the general case.

With the use of \(s(\textbf{r})\) and \(s^{(2)}(\textbf{r})\) we have sufficient certainty that we are carrying out a more appropriate analysis since these two local reactivity descriptors are not affected by differences in size of the systems as demonstrated in the present work.

Furthermore, \(s^{(2)}(\textbf{r})\) offers the advantage of being a biphasic scalar field as the dual descriptor or the molecular electrostatic potential, thus revealing the regions that legitimately have nucleophilic and eletrophilic behavior and in agreement with the molecular size.

This feature leads us to visualize easier isosurface values at different orders of magnitude.