1 Introduction

The development of strategies to describe and understand the reactivity of chemical species is one of the most important tasks and active research fields in chemistry. In recent decades, approaches based on properties determined by the electronic structure of atoms and molecules have gained popularity due to their usefulness, broad applicability and theoretical rigor. Examples of these models are frontier-orbital theory (FOT) [1, 2], quantum chemical topology (QCT) [3,4,5] and the chemical reactivity theory based on density functional theory (CR-DFT) [6,7,8,9,10,11,12,13,14].

In particular, the CR-DFT framework establishes that the chemical reactivity of species can be analyzed through a set of response functions known as reactivity indicators, which quantify the response of an isolated chemical species to an infinitesimal external perturbation [6,7,8,9,10,11,12,13,14]. For example, in cases where chemical reactions are driven by charge transfer, the chemical reactivity of the reacting species can be analyzed through the electronic chemical potential, \( \mu \) [15, 16] and the chemical hardness, \( \eta \) [17,18,19,20,21,22], defined as the first- and second-order responses of the electronic energy E with respect to variations in the number of electrons N, respectively,

$$ \mu = \left( {\frac{\partial E}{\partial N}} \right)_{{\nu \left( {\mathbf{r}} \right)}} , $$
(1)

and

$$ \eta = \left( {\frac{{\partial^{2} E}}{{\partial N^{2} }}} \right)_{{\nu \left( {\mathbf{r}} \right)}} , $$
(2)

where \( v\,({\mathbf{r}}) \) is the external potential generated by the nuclei. In analogy with the chemical potential defined in classical thermodynamics, the direction of charge transfer in a particular chemical reaction can be inferred through the electronic chemical potential of the reacting species, i.e., charge is transferred from the species with the higher value of \( \mu \) to the species with the lower value of \( \mu \) [6]. The chemical potential is therefore useful to distinguish an electron acceptor from an electron donor in a given chemical process and is thus an electronegativity indicator [15, 16, 23,24,25]. In the context of the Lewis theory of acids and bases [26], the electronic chemical potential is useful to differentiate between acids (ac) and bases (bs) in an acid–base reaction, i.e., \( \mu_{\text{ac}} < \mu_{\text{bs}} \). Acid–base reactions are also known to be governed by the hard and soft properties of the corresponding reacting species. Hard acids prefer to bind to hard bases, while soft acids prefer to bind to soft bases: This statement is known as the hard and soft acids and bases (HSAB) principle [17,18,19,20,21,22]. From the CR-DFT perspective, hard species (hd) are characterized by high values of the \( \eta \) descriptor (Eq. 2), while soft species (sf) display low values, i.e., \( \eta_{\text{hd}} > \eta_{\text{sf}} \).

Furthermore, the CR-DFT framework provides useful tools to analyze regioselectivity features of the reacting chemical species, specifically by formulating response coefficients associated with changes on the electron density due to an infinitesimal change in the number of electrons. In this context, the Fukui function [27,28,29] and the dual descriptor [30, 31] are defined as,

$$ f\left( {\mathbf{r}} \right) = \left( {\frac{{\partial \rho \left( {\mathbf{r}} \right)}}{\partial N}} \right)_{{\nu \left( {\mathbf{r}} \right)}} , $$
(3)

and

$$ \Delta f\left( {\mathbf{r}} \right) = \left( {\frac{{\partial^{2} \rho \left( {\mathbf{r}} \right)}}{{\partial N^{2} }}} \right)_{{\nu \left( {\mathbf{r}} \right)}} , $$
(4)

respectively. The Fukui function is the density variation that minimizes the energy change that results from adding or removing an electron. Therefore, the Fukui function identifies regions where the exchange of electrons is energetically most favored [29]. The dual descriptor in turn indicates the electrophilicity/nucleophilicity balance of a particular molecular site. A molecular region with \( \Delta f\left( {\mathbf{r}} \right) > 0 \) is known as a nucleophilic site, while if \( \Delta f\left( {\mathbf{r}} \right) < 0 \), it is defined as an electrophilic one. A region with \( \Delta f\left( {\mathbf{r}} \right) = 0 \) but a large value of the Fukui function displays amphiphilic features, and thus, it can both accept and donate electrons.

In recent reports, we have pointed out that more and deeper insights about the chemical reactivity of species can be inferred by extending the CR-DFT to temperature-dependent situations using the grand canonical ensemble [32,33,34,35,36,37,38,39,40,41,42,43]. Through this approach, we have been able not only to analyze current reactivity descriptors beyond the zero temperature limit, but also to develop new reactivity indexes that allow one to obtain a more complete description of the reactivity of some chemical systems [37, 38, 40].

In the present work, we will present first a simplified perspective of the procedure based on the ratio of two fluctuations, used to develop, in the temperature-dependent case, the local counterpart of a global response function and the linear (non-local) counterpart of a local response function [44,45,46,47]. Then, in order to assess the applicability of these new tools in the description of the reactivity properties of chemical species, we will present a systematic analysis of four different types of organic chemistry reactions, namely acid–base reactions, aliphatic nucleophilic substitutions, aromatic electrophilic substitutions and Markovnikov additions, using reactivity indicators that were obtained through the temperature-dependent approach (\( \tau \)-CRT).

2 Theoretical development

The mathematical framework of \( \tau \)-CRT is the grand canonical potential (GCP), \( \varOmega \), expressed as a unique functional of the equilibrium electron density \( \bar{\rho }\left( {\mathbf{r}} \right) \) [6, 48, 49],

$$ \varOmega \left[ {\bar{\rho }\left( {\mathbf{r}} \right)} \right] = E\left[ {\bar{\rho }\left( {\mathbf{r}} \right)} \right] - \mu_{\text{Bath}} N\left[ {\bar{\rho }\left( {\mathbf{r}} \right)} \right] - \beta^{ - 1} S_{\text{T}} \left[ {\bar{\rho }\left( {\mathbf{r}} \right)} \right], $$
(5)

where \( \mu_{\text{Bath}} \) is the chemical potential of the reservoir, \( \beta = 1/k_{\text{B}} T \), \( k_{\text{B}} \) is Boltzmann’s constant and T is the temperature. The average density functional corresponding to the quantum mechanical observable O is expressed as \( O\left[ {\bar{\rho }\left( {\mathbf{r}} \right)} \right] \equiv \left\langle O \right\rangle \) (see Ref. [6]).

As in the formulation of CR-DFT at zero temperature, a \( \tau \)-CRT reactivity descriptor is defined as a response coefficient, the difference is that in this case one has to consider the “grand canonical” average quantities, like the average electronic energy \( \left\langle E \right\rangle \) [33], the average electron density \( \left\langle {\bar{\rho }\left( {\mathbf{r}} \right)} \right\rangle \) [34] and the average electronic entropy \( \left\langle {S_{T} } \right\rangle \) [35], together with the average number of electrons \( \left\langle N \right\rangle \), in addition to the basic variables of a grand canonical ensemble, namely the chemical potential of the reservoir, \( \mu_{\text{Bath}} \), the external potential and the temperature. However, it is important to note that from all the set of response coefficients defined in the GCP framework, only those expressed as ratios of the thermal fluctuations between the average properties show meaningful and practical working formulas [37, 40].

In this context, the fluctuations ratio strategy has provided a new set of chemical reactivity descriptors, some of them correspond to the temperature-dependent expression of those already defined in the zero temperature limit, while some others are a consequence of the present approach. In the next section, we present the definition and the practical working formula of these descriptors while their detailed derivation can be found in Refs. [37, 38, 41].

2.1 Local counterpart of a global reactivity descriptor

If one considers the temperature-dependent expressions for the response coefficients described in the previous section, which correspond to derivatives of the energy and the electronic density with respect to the number of electrons, one must take into account that if the temperature and the external potential are kept constant, any variation in \( \mu_{\text{Bath}} \) modifies the equilibrium value of \( \left\langle N \right\rangle \),

$$ \left( {\frac{\partial \left\langle N \right\rangle }{{\partial \mu_{\text{Bath}} }}} \right)_{{T,\nu \left( {\mathbf{r}} \right)}} = \sigma_{NN} = \beta \left[ {\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle } \right], $$
(6)

More generally, for the average value of a global property (independent of the position within the molecule) denoted as \( \left\langle P \right\rangle \), then [33]

$$ \left( {\frac{\partial \left\langle P \right\rangle }{{\partial \mu_{\text{Bath}} }}} \right)_{{T,\nu \left( {\mathbf{r}} \right)}} = \sigma_{NP} = \beta \left[ {\left\langle {NP} \right\rangle - \left\langle N \right\rangle \left\langle P \right\rangle } \right]. $$
(7)

In general, \( \sigma_{XY} = \beta \left[ {\left\langle {XY} \right\rangle - \left\langle X \right\rangle \left\langle Y \right\rangle } \right] \) corresponds to the thermal fluctuations between the average property \( \left\langle X \right\rangle \) and the average property \( \left\langle Y \right\rangle \). The response function given by Eq. (6) is commonly denominated thermodynamic softness, S [50,51,52,53].

Consider now the response of \( \left\langle P \right\rangle \) to a change in \( \left\langle N \right\rangle \),

$$ R_{e} = \left( {\frac{\partial \left\langle P \right\rangle }{\partial \left\langle N \right\rangle }} \right)_{{T,\nu \left( {\mathbf{r}} \right)}} = \left( {\frac{\partial \left\langle P \right\rangle }{{\partial \mu_{\text{Bath}} }}} \right)_{{T,\nu \left( {\mathbf{r}} \right)}} \left( {\frac{{\partial \mu_{\text{Bath}} }}{\partial \left\langle N \right\rangle }} \right)_{{T,\nu \left( {\mathbf{r}} \right)}} , $$
(8)

where the subscript e is used to indicate that these \( \tau \)-CRT descriptors are exclusively related to electronic charge transfer processes. These special sets of reactivity indexes are known as electronic indicators [33, 34, 40]. Substituting Eqs. (6) and (7) in Eq. (8), one finds that

$$ R_{e} = \frac{{\sigma_{NP} }}{{\sigma_{NN} }} = \frac{{\left\langle {NP} \right\rangle - \left\langle N \right\rangle \left\langle P \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }}, $$
(9)

which corresponds to an expression of the reactivity index as a ratio of thermal fluctuations.

For any temperature value consistent with traditional chemistry conditions, any electronic indicator defined in terms of Eq. (9), for a chemical species with an integer number of electrons \( N_{0} \), can be determined through the three-ground-state ensemble model composed by the systems with \( N_{0} - 1 \), \( N_{0} \) and \( N_{0} + 1 \) electrons in their ground state, using the following schemes [33, 34, 40],

$$ R_{e} = \left\{ {\begin{array}{*{20}l} {R_{e}^{ - } = \left[\kern-0.15em\left[ {N_{0} ,P_{{N_{0} - 1}} } \right]\kern-0.15em\right]} \hfill & {{\text{for}}\;\omega < 0} \hfill \\ {R_{e}^{ + } = \left[\kern-0.15em\left[ {N_{0} ,P_{{N_{0} + 1}} } \right]\kern-0.15em\right]} \hfill & {{\text{for}}\;\omega > 0} \hfill \\ {R_{e}^{0} = \frac{{\left[\kern-0.15em\left[ {N_{0} ,P_{{N_{0} - 1}} } \right]\kern-0.15em\right] + \left[\kern-0.15em\left[ {N_{0} ,P_{{N_{0} + 1}} } \right]\kern-0.15em\right]}}{2}} \hfill & {{\text{for}}\;\omega = 0} \hfill \\ \end{array} } \right. $$
(10)

where \( \omega = \left\langle N \right\rangle - N_{0} \) is the fractional part of the average number of electrons,

$$ \left[\kern-0.15em\left[ {N_{0} ,P_{M} } \right]\kern-0.15em\right] = (N_{0} - {M} )(P_{N_{0}} - P_{M} ), $$
(11)

and \( P_{M} \) is the ground-state value of the property for the system with M electrons. Thus, using Eqs. (10) and (11) in Eq. (9) one can derive the temperature-dependent expression for the global response function \( R_{e} \) within the three-ground-state ensemble model.

Now, let us consider within the \( \tau \)-CRT framework, the local counterpart associated with the global descriptor \( R_{e} \), which will be denoted as \( R_{e} ({\mathbf{r}}) \). Since one can expect that the local counterpart will correspond to the distribution of the global indicator at the different positions within the molecule [54, 55], one may impose the constraint,

$$ R_{e} = \int {R_{e} ({\mathbf{r}}){\mathrm{d}}{\mathbf{r}}} $$
(12)

Although the selection of \( R_{e} ({\mathbf{r}}) \) is not strictly unique, because one may consider different functions that integrate to the same number, we have shown that for every global descriptor \( R_{e} \), there exists only one local \( R_{e} ({\mathbf{r}}) \) that fulfills Eq. (12), and that simultaneously is written as the ratio of two fluctuating properties [as Eq. (9) establishes] [37, 40]. Thus, in order to satisfy Eq. (12), it is important to recall that

$$ \left\langle N \right\rangle = \int {\left\langle {\rho ({\mathbf{r}})} \right\rangle {\mathrm{d}}{\mathbf{r}}} , $$
(13)

which corresponds to the variational constraint in the grand potential density functional Euler–Lagrange equations, and therefore, it is unique and fundamental [6, 48, 49]. From a conceptual viewpoint, as it was previously mentioned, any variation on \( \mu_{\text{Bath}} \) perturbs the equilibrium value of \( \left\langle N \right\rangle \), and of the fluctuations between \( \left\langle N \right\rangle \) and the remainder of the GC average properties. In this context, and in view of Eq. (13), it seems natural to consider that the local counterpart of \( \left\langle N \right\rangle \) is \( \left\langle {\rho ({\mathbf{r}})} \right\rangle \), and that through this identification one can provide a local or even a linear (non-local) nature to any of these fluctuations. To corroborate this statement, recall the hierarchal structure for the softness family of descriptors [34, 50, 51, 56],

$$ S = \int {s\left( {\mathbf{r}} \right){\mathrm{d}}{\mathbf{r}}} = \iint {s\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right){\mathrm{d}}{\mathbf{r}}^{\prime } \;}{\mathrm{d}}{\mathbf{r}}, $$
(14)

with,

$$ s\left( {\mathbf{r}} \right) = \sigma_{{N\rho \left( {\mathbf{r}} \right)}} = \beta \left[ {\left\langle {N\rho \left( {\mathbf{r}} \right)} \right\rangle - \left\langle N \right\rangle \left\langle {\rho \left( {\mathbf{r}} \right)} \right\rangle } \right] $$
(15)

and

$$ s\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) = \sigma_{{\rho \left( {{\mathbf{r}}^{\prime } } \right)\rho \left( {\mathbf{r}} \right)}} = \beta \left[ {\left\langle {\rho \left( {\mathbf{r}} \right)\rho \left( {{\mathbf{r}}^{\prime } } \right)} \right\rangle - \left\langle {\rho \left( {\mathbf{r}} \right)} \right\rangle \left\langle {\rho \left( {{\mathbf{r}}^{\prime } } \right)} \right\rangle } \right]. $$
(16)

That is, replacing N by \( \rho ({\mathbf{r}}) \) in the expression for the global softness S (Eq. 6) one is led to the local softness \( s\left( {\mathbf{r}} \right) \) (Eq. 15), and replacing N by \( \rho ({\mathbf{r}}^{\prime } ) \), in Eq. (15) one is led to the softness kernel (Eq. 16). The local softness corresponds to a distribution of the global softness at the different positions within the molecule, while the softness kernel \( s\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) \) indicates how the softness properties of a given molecular fragment depend on the softness properties of a second fragment.

Thus, according to this procedure the local counterpart of \( R_{e} \) may be obtained by replacing N by \( \rho ({\mathbf{r}}) \) in the numerator of Eq. (9), that is

$$ R_{e} ({\mathbf{r}}) = \frac{{\sigma_{{\rho ({\mathbf{r}})P}} }}{{\sigma_{NN} }} = \frac{{\left\langle {\rho ({\mathbf{r}})\,P} \right\rangle - \left\langle {\rho ({\mathbf{r}})} \right\rangle \left\langle P \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }}, $$
(17)

which satisfies the constraint given by Eq. (12).

As a direct consequence of this strategy, any electronic reactivity descriptor has a local counterpart with an explicit dependence on the average number of electrons, and therefore, higher-order \( \tau \)-CRT reactivity response functions can be defined therefrom. Recently, we have shown that meaningful nth order reactivity response functions are obtained by performing n successive partial derivatives at both sides of Eq. (12), with respect to the number of electrons [37, 38, 40],

$$ \left( {\frac{{\partial^{n} R_{e} }}{{\partial \left\langle N \right\rangle^{n} }}} \right) = \int {\left( {\frac{{\partial^{n} R_{e} \left( {\mathbf{r}} \right)}}{{\partial \left\langle N \right\rangle^{n} }}} \right)d{\mathbf{r}}} . $$
(18)

Now let us apply the general procedure just described to the case when the global property \( \left\langle P \right\rangle \) is the total electronic energy \( \left\langle E \right\rangle \). Then, according to Eq. (9), \( R_{e} \) is the temperature-dependent definition of the electronic chemical potential expressed in Eq. (1), that is

$$ \mu_{e} = \frac{{\sigma_{NE} }}{{\sigma_{NN} }} = \frac{{\left\langle {NE} \right\rangle - \left\langle N \right\rangle \left\langle E \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }}, $$
(19)

and the local counterpart, according to Eq. (17), will be given by [37]

$$ \mu_{e} \left( {\mathbf{r}} \right) = \frac{{\sigma_{{\rho \left( {\mathbf{r}} \right)E}} }}{{\sigma_{NN} }} = \frac{{\left\langle {\rho \left( {\mathbf{r}} \right)E} \right\rangle - \left\langle {\rho \left( {\mathbf{r}} \right)} \right\rangle \left\langle E \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }}, $$
(20)

which fulfills the constraint

$$ \mu_{e} = \int {\mu_{e} ({\mathbf{r}}){\text{d}}{\mathbf{r}}} . $$
(21)

Applying Eqs. (10) and (11) to Eq. (20) one can obtain the temperature-dependent expression for the local chemical potential. In particular, in the limit when \( T \to 0 \) one finds that

$$ \mu_{e} \left( {\mathbf{r}} \right) = \left\{ {\begin{array}{*{20}l} {\mu_{e}^{ - } \left( {\mathbf{r}} \right) = - If_{e}^{ - } ({\mathbf{r}})} \hfill & {{\text{for}}\;\omega < 0} \hfill \\ {\mu_{e}^{ + } \left( {\mathbf{r}} \right) = - A \, f_{e}^{ + } ({\mathbf{r}})} \hfill & {{\text{for}}\;\omega > 0} \hfill \\ {\mu_{e}^{0} \left( {\mathbf{r}} \right) = - \tfrac{1}{2}\left( {If_{e}^{ - } ({\mathbf{r}}) + Af_{e}^{ + } ({\mathbf{r}})} \right)} \hfill & {{\text{for}}\;\omega = 0} \hfill \\ \end{array} } \right., $$
(22)

where I and A are the first ionization potential and the electron affinity, while \( f_{e}^{ - } ({\mathbf{r}}) \) and \( f_{e}^{ + } ({\mathbf{r}}) \) are the left and right Fukui functions of the chemical species with \( N_{0} \) electrons, respectively.

An important feature of \( \mu_{e} \left( {\mathbf{r}} \right) \) is that, unlike the Fukui function \( f_{e} ({\mathbf{r}}) \) or the global chemical potential \( \mu_{e} \), it is a proper indicator to compare acid–base reactivity features of molecular fragments belonging to different chemical systems, even if they are not structurally related. Therefore, the local chemical potential is a more convenient quantity to analyze the acid–base behavior of different chemical substrates at the local level, even if they do not share the same functional groups. The quantity \( If_{e}^{ - } ({\mathbf{r}}) \) is approximately related to the local ionization energy [57, 58], which has been shown to provide a good description of the preferred sites within a molecule for an electrophilic attack [59,60,61]. Similarly, the quantity \( Af_{e}^{ + } ({\mathbf{r}}) \) is approximately related to the local electron affinity energy, which is a local indicator used to identify the sites for a nucleophilic attack [62,63,64]. Note also that the quantity \( (If_{e}^{ - } ({\mathbf{r}}) + Af_{e}^{ + } ({\mathbf{r}}))/2 \) corresponds to the local counterpart of Mulliken’s global electronegativity.

Applying Eq. (18) (with \( n = 1 \)) to Eq. (21), the electronic chemical hardness \( \eta_{e} = \left( {{{\partial \mu_{e} } \mathord{\left/ {\vphantom {{\partial \mu_{e} } {\partial \left\langle N \right\rangle }}} \right. \kern-0pt} {\partial \left\langle N \right\rangle }}} \right)_{{T,\upsilon \left( {\mathbf{r}} \right)}} \) and its corresponding local counterpart \( \eta_{e} \left( {\mathbf{r}} \right) = \left( {{{\partial \mu_{e} \left( {\mathbf{r}} \right)} \mathord{\left/ {\vphantom {{\partial \mu_{e} \left( {\mathbf{r}} \right)} {\partial \left\langle N \right\rangle }}} \right. \kern-0pt} {\partial \left\langle N \right\rangle }}} \right)_{{T,\upsilon \left( {\mathbf{r}} \right)}} \), are found, through this approach, to be related through the expression

$$ \eta_{e} = \int {\eta_{e} \left( {\mathbf{r}} \right){\text{d}}{\mathbf{r}}} $$
(23)

In the low-temperature regime (any temperature value of chemical interest), and in the limit when \( T \to 0 \), Eq. (23) can be expressed as follows [37],

$$ I - A = \int {\left[ {\left( {If^{ - } \left( {\mathbf{r}} \right) - Af^{ + } \left( {\mathbf{r}} \right)} \right) + \frac{\omega }{2}\left( {f^{ + } \left( {\mathbf{r}} \right) - f^{ - } \left( {\mathbf{r}} \right)} \right)\left( {I - A} \right)} \right]{\text{d}}{\mathbf{r}}} . $$
(24)

The quantity at the left-hand side of Eq. (24) is known as the Parr and Pearson hardness [19], \( \eta_{\text{PP}} = I - A \), while the integrand at the right corresponds to the temperature-dependent expression for the local hardness, that is,

$$ \eta_{\tau } \left( {\mathbf{r}} \right) = \eta_{\text{PP}} \left( {\mathbf{r}} \right) + \frac{\omega }{2}\eta_{\text{PP}}\Delta f\left( {\mathbf{r}} \right), $$
(25)

with,

$$ \eta_{\text{PP}} \left( {\mathbf{r}} \right) = If^{ - } \left( {\mathbf{r}} \right) - Af^{ + } \left( {\mathbf{r}} \right), $$
(26)

and

$$ \Delta f\left( {\mathbf{r}} \right) = f^{ + } \left( {\mathbf{r}} \right) - f^{ - } \left( {\mathbf{r}} \right), $$
(27)

corresponds to the expression for the dual descriptor, Eq. (4), that results from a smooth quadratic interpolation of the electronic density between the systems with \( N_{0} - 1 \), \( N_{0} \) and \( N_{0} + 1 \) electrons. In the limiting case in which (almost) a full electron is transferred (\( \left| \omega \right| \to 1 \)), in analogy to Eq. (22), Eq. (25) can be expressed as follows,

$$ \eta_{\tau } \left( {\mathbf{r}} \right) = \left\{ {\begin{array}{*{20}l} {\eta_{\text{pp}} \left( {\mathbf{r}} \right) - \tfrac{1}{2}\eta_{\text{pp}}\Delta f\left( {\mathbf{r}} \right)} \hfill & {{\text{for}}\;\omega = - 1} \hfill \\ {\eta_{\text{pp}} \left( {\mathbf{r}} \right) + \tfrac{1}{2}\eta_{\text{pp}}\Delta f\left( {\mathbf{r}} \right)} \hfill & {{\text{for}}\;\omega = + 1} \hfill \\ {\eta_{\text{pp}} \left( {\mathbf{r}} \right)} \hfill & {{\text{for}}\;\omega = 0} \hfill \\ \end{array} } \right.. $$
(28)

It is important to note that the local hardness given by Eq. (26) was first proposed, intuitively, by Meneses et al. [65, 66], and it was recently derived together with the additional terms that appear in Eq. (28), through an approach based on the chain rule for functional derivatives [44, 47]. Both expressions have been successfully used as local reactivity indicators, and both share the same advantages of the local chemical potential of Eq. (22) in the sense that because they are given in terms of a global property multiplied by the appropriate Fukui function they allow one to compare equivalent sites in different chemical environments.

2.2 Non-local counterpart of a local reactivity descriptor

The procedure just followed is related to the case in which \( \left\langle P \right\rangle \) corresponds to a global property. When the property depends on the position within the molecule, \( \left\langle {P_{e}^{\text{Local}} ({\mathbf{r}})} \right\rangle \), one can follow the same procedure, except that result is now a non-local reactivity indicator that depends simultaneously on two points within the molecule (that is, the local counterpart of \( \left\langle {R_{e}^{Local} ({\mathbf{r}})} \right\rangle \) will have the form \( \left\langle {R_{e}^{Local} ({\mathbf{r}},{\mathbf{r}}')} \right\rangle \)). The expressions in this case will be exactly equal to the ones just derived with \( \left\langle P \right\rangle \) replaced by \( \left\langle {P_{e}^{\text{Local}} ({\mathbf{r}})} \right\rangle \), \( \left\langle {R_{e}^{{}} } \right\rangle \) replaced by \( \left\langle {R_{e}^{\text{Local}} ({\mathbf{r}})} \right\rangle \) and \( \left\langle {R_{e}^{{}} ({\mathbf{r}})} \right\rangle \) replaced by \( \left\langle {R_{e}^{\text{Local}} ({\mathbf{r}},{\mathbf{r}}^{\prime } )} \right\rangle \).

Thus, let us consider the case when the local property \( \left\langle {P_{e}^{\text{Local}} ({\mathbf{r}})} \right\rangle \) is the total electronic density \( \left\langle {\rho ({\mathbf{r}})} \right\rangle \). Then, according to Eq. (9), \( \left\langle {R_{e}^{\text{Local}} ({\mathbf{r}})} \right\rangle \) is the temperature-dependent definition of the electronic Fukui function expressed in Eq. (3), that is

$$ f_{e} \left( {\mathbf{r}} \right) = \frac{{\sigma_{{\rho \left( {\mathbf{r}} \right)N}} }}{{\sigma_{NN} }} = \frac{{\left\langle {\rho \left( {\mathbf{r}} \right)N} \right\rangle - \left\langle {\rho \left( {\mathbf{r}} \right)} \right\rangle \left\langle N \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }} $$
(29)

and the non-local counterpart, according to the local version of Eq. (17) is given by the Fukui kernel [38, 40]

$$ f_{e} \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) = \frac{{\sigma_{{\rho \left( {\mathbf{r}} \right)\rho \left( {{\mathbf{r}}^{\prime } } \right)}} }}{{\sigma_{NN} }} = \frac{{\left\langle {\rho \left( {\mathbf{r}} \right)\rho \left( {{\mathbf{r}}^{\prime } } \right)} \right\rangle - \left\langle {\rho \left( {\mathbf{r}} \right)} \right\rangle \left\langle {\rho \left( {{\mathbf{r}}^{\prime } } \right)} \right\rangle }}{{\left\langle {NN} \right\rangle - \left\langle N \right\rangle \left\langle N \right\rangle }}. $$
(30)

For every pair of points defined in the molecular space, the corresponding Fukui kernel constitutes the proportionality factor between the softness kernel value (Eq. 16) computed at these points, and the thermodynamic (global) softness defined in Eq. (6).

Applying the local version of Eqs. (10) and (11) to Eq. (30), one can obtain the temperature-dependent expression for the Fukui kernel. In particular, in the limit when \( T \to 0 \) one finds that

$$ f_{e} \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) = \left\{ {\begin{array}{*{20}l} {f^{ - } \left( {\mathbf{r}} \right)f^{ - } \left( {{\mathbf{r}}^{\prime } } \right)} \hfill & {{\text{for}}\;\omega < 0} \hfill \\ {f^{ + } \left( {\mathbf{r}} \right)f^{ + } \left( {{\mathbf{r}}^{\prime } } \right)} \hfill & {{\text{for}}\;\omega > 0} \hfill \\ {\frac{1}{2}\left( {f^{ - } \left( {\mathbf{r}} \right)f^{ - } \left( {\mathbf{r}} \right) + f^{ + } \left( {\mathbf{r}} \right)f^{ + } \left( {{\mathbf{r}}^{\prime } } \right)} \right)} \hfill & {{\text{for}}\;\omega = 0} \hfill \\ \end{array} } \right. $$
(31)

Note that the calculation of the Fukui kernel only requires knowledge of the one-sided Fukui functions, which were already needed to determine the finite-temperature Fukui function (Eq. 29). Given the nearsightedness nature of the softness kernel (Eq. 16) [67,68,69,70], the Fukui kernel can be used as a bond reactivity/stability indicator in its condensed-to-atoms form [40]. Following the same procedure that led to the local hardness, one can make use of the local version of Eq. (18), with \( n = 1 \), to define an electronic dual descriptor kernel, \( \Delta f_{e} \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) \), which fulfills the following constraint,

$$ \Delta f_{e} \left( {\mathbf{r}} \right) = \int {\Delta f_{e} \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right){\text{d}}{\mathbf{r}}^{\prime } } $$
(32)

At \( T = 0 \), and up to temperatures of chemical interest, Eq. (32) can be expressed as follows [38, 40],

$$ \Delta f_{e} \left( {\mathbf{r}} \right) = \int {\left[ {\Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) + \frac{\omega }{2}\Delta f\left( {\mathbf{r}} \right)\Delta f\left( {{\mathbf{r}}^{\prime } } \right)} \right]{\text{d}}{\mathbf{r}}^{\prime } } , $$
(33)

where

$$ \Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) = f^{ + } \left( {\mathbf{r}} \right)f^{ + } \left( {{\mathbf{r}}^{\prime } } \right) - f^{ - } \left( {\mathbf{r}} \right)f^{ - } \left( {{\mathbf{r}}^{\prime } } \right), $$
(34)

while \( \Delta f\left( {\mathbf{r}} \right) \) is given by Eq. (27). Thus, the integrand in Eq. (33) may be identified with the temperature-dependent dual descriptor kernel,

$$ \Delta f_{\tau } \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) =\Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) + \frac{\omega }{2}\Delta f\left( {\mathbf{r}} \right)\Delta f\left( {{\mathbf{r}}^{\prime } } \right) $$
(35)

In analogy to Eq. (28), in the limiting case in which (almost) a full electron is transferred (\( \left| \omega \right| \to 1 \)), Eq. (35) adopts the form,

$$ \Delta f_{\tau } \left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) = \left\{ {\begin{array}{*{20}l} {\Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) - \tfrac{1}{2}\Delta f\left( {\mathbf{r}} \right)\Delta f\left( {{\mathbf{r}}^{\prime } } \right)} \hfill & {{\text{for}}\;\omega = - 1} \hfill \\ {\Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right) + \tfrac{1}{2}\Delta f\left( {\mathbf{r}} \right)\Delta f\left( {{\mathbf{r}}^{\prime } } \right)} \hfill & {{\text{for}}\;\omega = + 1} \hfill \\ {\Delta f\left( {{\mathbf{r}},{\mathbf{r}}^{\prime } } \right)} \hfill & {{\text{for}}\;\omega = 0} \hfill \\ \end{array} } \right. $$
(36)

As the (condensed) local dual descriptor does for an atom, the τ-dual descriptor kernel indicates the balance between the electrophilic and nucleophilic features of a given chemical bond. A negative value indicates a bond with electrophilic features, and a positive value indicates a bond with nucleophilic features, while if the kernel between two atoms is equal to zero, the corresponding chemical bond does not show a preference for accepting or donating electrons.

3 Computational details

For every molecule considered in this work, a geometry optimization of the \( N_{0} \)-electron system was performed with the Gaussian program [71], using the PBE0 functional [72,73,74], and the 6-311G** basis set [75, 76], using default thresholds for SCF and geometry optimizations, as well as default grids for numerical integrations.

To simplify the presentation and interpretation of the data, we will use the condensed-to-atom representation for the local descriptors and for the reactivity kernels. Although there is some ambiguity that is normally associated with atom-condensed reactivity indicators [77], in the present work we have used the response-of-molecular-fragment approach, because it allows one to determine them from atomic charges of the atoms in the molecule. The latter were calculated using the Hirshfeld (or stockholder) partitioning method [78, 79]. As noted by Roy et al. [80], Hirshfeld partitioning also has favorable practical properties for condensed reactivity indicators, and it is one of the few population analysis methods where the response-of-molecular-fragment and fragment-of-molecular-response approaches give identical results. We use the frontier molecular orbital approximation to the reactivity indicators, and so the density of the highest occupied molecular orbital (HOMO) is used to compute \( f_{k}^{ - } = f_{k}^{\text{H}} \) and the density of the lowest unoccupied molecular orbital (LUMO) is used to compute \( f_{k}^{ + } = f_{k}^{\text{L}} \) [77], using a developmental version 4.3 of deMon2k [81]. The deMon2k calculations used the same optimized geometry, functional and basis set as those of the Gaussian calculations, together with an auxiliary basis GEN-A2*, to perform a Hirshfeld population analysis that led, basically, to the same results obtained in the Gaussian code, but that additionally calculates \( f_{k}^{\text{H}} \) and \( f_{k}^{\text{L}} \). In Table 1, one can find the low-temperature expressions for the different reactivity indicators considered in this work, within the frontier-orbital approximation.

Table 1 Condensed-to-atoms formulas for the global, local and linear \( \tau \)-CRT descriptors in the zero temperature limit described in this study within the frontier-orbital approximation
Full size table

4 Applications to selected organic chemistry reactions

In this section, we present the results and the analysis of the reactivity features of four prototypical and paradigmatic types of chemical reactions, using the frontier orbitals and the condensed-to-atoms representation of the global, local and linear \( \tau \)-CRT descriptors (Table 1).

4.1 Brønsted acid–base reactions: phenols, carboxylic acids and anilines

As a first example, we analyzed a set of protonation reactions constituted by 17 phenols, 17 carboxylic acids and 17 aniline derivatives, using our acid–base local reactivity descriptor, the local chemical potential. Condensed-to-atoms values for the “electrophilic” local chemical potential “\( \mu_{k}^{ - } \)” were computed for the proper protonation sites of each family of compounds, that is, on the (deprotonated) acidic oxygen atom for phenols and carboxylic acids and on the nitrogen atom in the amino moiety for anilines. Note that since we are using “\( \mu_{k}^{ - } \)” in our analysis, we are evaluating the ability of the phenolic, carboxylic or amino moieties to attach an electron deficient species, as a free proton. The obtained results were directly compared with experimental pKa values available in the literature [82, 83]. Figure 1a displays the corresponding \( \mu_{k}^{ - } = \varepsilon^{\text{H}} f_{k}^{\text{H}} \) versus pKa correlation profile, and, for comparison purposes, in Fig. 1b, we are also reporting the \( \mu_{{}}^{ - } = \varepsilon^{\text{H}} \) versus pKa profile. The two cases are for the 51 compounds considered in our statistical analysis. The numerical data for each molecule are available in the Supporting Information.

Fig. 1
figure 1

Correlation profiles between experimental pKa values of phenol (red), carboxylic acid (green) and aniline (purple) derivatives, with the corresponding. a Condensed-to-atom values for the local chemical potential at the protonation site and b global chemical potential, in atomic units

Full size image

As mentioned before, unlike the electronic chemical potential (a global property), the local chemical potential is a more convenient descriptor to analyze the acid–base reactivity features of chemical species at the local level, particularly when they do not share the same functional reactive groups. This statement is corroborated by the correlation profiles shown in Fig. 1a, b. Only the condensed-to-atoms values corresponding to the electrophilic local chemical potential display a similar trend than experimental data (Fig. 1a). As can be seen in Fig. 1b, the global chemical potential \( \left( {\mu_{e}^{ - } = \varepsilon_{\text{HOMO}} } \right) \) is a more suitable quantity to classify and analyze the acid–base reactivity features of the species per family of functional group. The aniline derivatives have the lowest \( \varepsilon^{\text{H}} \) values, followed by the carboxylic acids and phenols as \( \varepsilon^{\text{H}} \) increases.

It is pertinent to note that when the aniline derivatives are discarded in the \( \mu_{k}^{ - } = \varepsilon^{\text{H}} f_{k}^{\text{H}} \) versus pKa statistical analysis, the corresponding determination coefficient is considerably enhanced to \( R^{2} = 0.96 \). Recent theoretical studies have pointed out that a dynamical description of explicit solute–solvent interactions is required in order to perform reliable pKa predictions for amines [84].

4.2 Nucleophilic aliphatic substitution (SN2)

A nucleophilic aliphatic substitution SN2 is characterized by a nucleophile with a lone pair that attacks an alkyl carbon center initially attached to a leaving group (LG) [85, 86]. The nucleophile binds the carbon center while the leaving group is commonly released carrying a lone pair, often as a negative ion (which can be stabilized by the solvent and/or a counterion). The SN2 reaction occurs in a concerted fashion, in a one-step reaction with the addition of the nucleophile and the elimination of the leaving group occurring simultaneously. The stability of the leaving group (after the departure) is important for the thermodynamic favorability of a SN2 reaction. In polar non-protic media where leaving groups do not exhibit hydrogen bonds with solvent molecules, experimental evidence suggests the following hierarchy for the leaving groups,

$$ {\text{I}} > {\text{Br}} > {\text{Cl}} > > {\text{F}} > {\text{NH}}_{2} \approx {\text{OH}}, $$
(37)

which indicates that iodide alkyl derivatives are the most prone species to participate in a SN2 reaction, while the amino and the hydroxyl derivatives are often considered inert. It is worth to remark that unlike the remaining halides, the fluorine derivatives do not commonly behave as good substrates in a SN2 process, presumably due to the poor stability of the fluoride anion. Another relevant aspect for the spontaneity of a SN2 reaction is the degree/length of the alkyl chains attached to the electrophilic carbon atom. A primary alkane is the most reactive, which is often attributed to steric hindrance.

Since the leaving group departs carrying an electrons pair and the whole process is carried out in one step, one may establish that the release of such group from the substrate molecule to the reaction media must occur due to an electronic flux from the nucleophile toward the LG, through the carbon–LG bond. The whole process will be thus influenced by the following reactivity properties of the isolated substrate molecule (a) the polarizability of the carbon atom since the local electronic distribution of this moiety must be easily modified in order to initiate the electronic flux toward the LG; (b) the electrophilicity/nucleophilicity balance of the C–LG bond, because if such bond will serve as an electronic channel, it must be able to accept the electronic charge coming from the nucleophile, so that this charge will be now available for the LG before its departure; (c) the C–LG bond stability, since a strong bond will not favor the departure of the LG; and (d) the electronegativity of the LG inside the substrate, because the more electronegative the leaving group is relative to the substrate, the easier it takes the electrons from the C–LG bond.

The analysis performed above is now presented in terms of the \( \tau \)-CRT descriptors. To do so, recall the close relationship between the polarizability and the hardness properties of molecular species [21, 87]. One may expect that, at the local level, a carbon center with low hardness will be more polarizable and it thus favors the electron transfer from the nucleophile toward the LG. In Fig. 2a, we present the dependence of the condensed-to-atoms local hardness values at the carbon center (\( \eta_{C}^{0} \)) for several iodine, bromine, chlorine, fluorine, amino and hydroxide linear alkyl derivatives, with respect to the alkyl chain length (a total of 36 chemical species were analyzed). At first instance, note that our local hardness descriptor indicates that the “less” hard carbon atom is in fact the most reactive one, that is, the carbon center bonded to the iodine halide (see Supporting Information). The next hard species (in increasing order) are the carbon center belonging to the bromide derivatives, followed by the fluorine and amino derivatives while the hydroxyl followed by the chlorine species have the hardest carbon centers. This tendency closely resembles the experimental trend in Eq. (37) and suggests that the low reactivity of the chlorine alkyl derivatives can be in part attributed to the low polarizability (high local hardness value) of its corresponding carbon center. Likewise, it can be also observed that, except for the fluorine derivatives, the \( \eta_{\text{C}}^{0} \) values are almost independent to the chain length in all cases.

Fig. 2
figure 2

Dependence of the condensed-to-atom values corresponding to a local hardness at the Carbon center \( \left( {\eta_{\text{C}}^{0} } \right) \), b Fukui kernel at the C–LG bond \( \left( {f_{\text{C,LG}}^{0} } \right) \) and c local chemical potential at the LG atom \( \left( {\mu_{\text{LG}}^{0} } \right) \), with the alkyl chain length (in atomic units). In Fig. 2b red and purple markers are used to indicate electrophilic and nucleophilic C–LG bonds, respectively

Full size image

To analyze the reactivity as well as, the electrophilicity/nucelophilicity balance of the C–LG bond we used the corresponding condensed-to-atoms Fukui \( \left( {f_{\text{C,LG}}^{0} } \right) \) and dual descriptor \( \left( {\Delta f_{\text{C,LG}}^{0} } \right) \) kernels, respectively. Figure 2b displays the \( f_{\text{C,LG}}^{0} \) dependence with the alkyl chain length for the set of 36 chemical compounds under consideration. Red markers are used to indicate the electrophilic bonds \( \left( {\Delta f_{\text{C,LG}}^{0} < 0} \right) \), able to accept electronic charge from the nucleophile, while purple markers are used to indicate nucleophilic bonds \( \left( {\Delta f_{\text{C,LG}}^{0} > 0} \right) \), which prefer to donate electronic charge. As expected, the C–LG bonds with a net electrophilic character are those corresponding to the most reactive halides, the alkyl iodide, bromide and chloride compounds. One the contrary, the less reactive fluorine, amino and hydroxyl derivatives display a nucleophilic nature, indicating that such bonds are not prone to receiving electrons from the nucleophile. As can be observed, the alkyl chain length does not modify the electrophilicity/nucelophilicity character of the C–LG bonds for the species considered here. Inspecting now the \( f_{\text{C,LG}}^{0} \) values, one can corroborate that the bond reactivity trend predicted by our Fukui kernel descriptor, condensed in the indicated bonds, is in full agreement with experimental observations, the highest reactive bonds (highest \( f_{\text{C,LG}}^{0} \) value) corresponds to the most reactive halides. In contrast with the dual kernel, the Fukui kernel depends on the alkyl chain length. As the chain increases, the C–LG bond reactivity decreases. This is in agreement with experimental knowledge, the chain length decreases the SN2 reactivity of a substrate, as was recently discussed [88]. Interestingly, our results suggest that this effect cannot be exclusively attributed to steric hindrance, because there is an additional electronic effect that also contributes.

Finally, we used our local electronegativity indicator, the condensed local chemical potential, to inspect the local electronegativity properties of the LG’s belonging to the SN2 substrates under consideration. Figure 2c displays the corresponding \( \mu_{{\text{LG}}}^{0} \) vs alkyl chain length profile. The most electronegative (lower value of the local chemical potential) leaving groups are those considered as the most stable as isolated species in the literature [85], thus favoring the SN2 process. Note that as in the case for the Fukui kernel for the C–LG bonds, the local chemical potential results exactly reproduce the experimental reactivity trend for leaving groups, that is, \( \mu_{{\text{I}}}^{0} < \mu_{{\text{Br}}}^{0} < \mu_{\text{Cl}}^{0} < < \mu_{{\text{F}}}^{0} < \mu_{{\text{OH}}}^{0} < \mu_{{{\text{NH}}_{ 2} }}^{0} \). As it can be observed, the local chemical potential is a quantity that depends on the chain length. This dependence is more pronounced for the fluorine derivatives than for the other descriptors under consideration, indicating that the reactivity of these compounds will quickly decay as the chain length increases due to the decreased local electronegativity of the fluorine atom.

4.3 Markovnikov additions

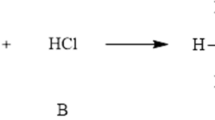
Markovnikov’s rule for the electrophilic addition of hydrogen halides (H-A) across a carbon–carbon double bond asserts that the hydrogen atom will rather prefer to bind the carbon atom with the highest number of hydrogen atoms attached to it, while the halide will attach the carbon bonded with fewer hydrogens [85, 89]. In a previous report we have shown that the zero temperature “version” of our local hardness descriptor accurately predicts Markovnikov’s addition rule for a select set of substituted ethenes. The hard hydrogen in the H-A species binds to the hardest carbon atom, suggesting that Markovnikov’s rule may be a consequence of the HSAB principle at the local level [44]. In this work we want to go one step further and use our \( \tau \)-CRT descriptors to quantitatively describe the reactivity of the same set of substituted ethylenes in the context of Markovnikov´s rule. To do so, we compared local hardness and local chemical potential condensed-to-atom values, at the C1 and at the C2 carbon atoms belonging to the C1 = C2 double bond, with reaction (\( E_{\text{r}} \)) and activation (\( E_{\text{act}} \)) energies calculated for the electrophilic addition of hydrogen chloride (HCl) to each of the ethylene derivatives considered by us in our previous report. Ab initio data were taken from Ref. [66]. In our analysis we labeled C1 to the carbon attached to more hydrogen atoms, in all cases. Figure 3a displays the correlation profile between the local hardness ratio \( {{\eta_{\text{C2}}^{ - } } \mathord{\left/ {\vphantom {{\eta_{\text{C2}}^{ - } } {\eta_{\text{C1}}^{ - } }}} \right. \kern-0pt} {\eta_{\text{C1}}^{ - } }} \) and the reaction energy ratio \( {{E_{{{\text{r\_C2}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{r\_C2}}}} } {E_{{{\text{r\_C1}}}} }}} \right. \kern-0pt} {E_{{{\text{r\_C1}}}} }} \) where \( E_{{{\text{r\_C1}}}} \) and \( E_{{{\text{r\_C2}}}} \) are the reaction energies corresponding to the hydrogen addition to C1 (Markovnikov addition) and C2 (anti-Markovnikov addition) carbon atoms, respectively. Figure 3b displays the correlation profile between the local chemical potential condensed at the C1 carbon atom \( \left( {\mu_{\text{C1}}^{0} } \right) \) and the activation energy corresponding to the Markovnikov addition \( E_{{{\text{act}}\_{\text{C1}}}} \) (numerical data can be found in the Supporting Information).

Fig. 3
figure 3

Correlation profile between a the local hardness ratio \( {{\eta_{\text{C2}}^{ - } } \mathord{\left/ {\vphantom {{\eta_{\text{C2}}^{ - } } {\eta_{\text{C1}}^{ - } }}} \right. \kern-0pt} {\eta_{\text{C1}}^{ - } }} \) and the reaction energy ratio \( {{E_{{{\text{r\_C2}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{r\_C2}}}} } {E_{{{\text{r\_C1}}}} }}} \right. \kern-0pt} {E_{{{\text{r\_C1}}}} }} \), and b the local chemical potential condensed at the C1 carbon atom \( \left( {\mu_{\text{C1}}^{0} } \right) \) and the activation energy corresponding to the Markovnikov addition \( E_{{{\text{act\_C1}}}} \)

Full size image

The regression parameters displayed in Fig. 3a indicate that the local hardness descriptor discriminates between the molecular sites most energetically susceptible to hard–hard and soft–soft interactions; this reinforces our former statement that Markovnikov’s rule is a consequence of the HSAB principle. The correlation between the local chemical potential condensed at the C1 atoms and the corresponding \( E_{{{\text{act}}\_{\text{C1}}}} \) (Fig. 3b) suggest in turn that the determining step of the Markovnikov’s addition may be governed by electron transfer to the carbon atom with the most hydrogen substituents.

4.4 Electrophilic aromatic substitutions (AEAr)

In the electrophilic aromatic substitution a substituent (generally a hydrogen atom) attached to a benzene ring is replaced by a strong electrophile. This reaction proceeds by the formation of a sigma-complex intermediate, which is characterized by a non-aromatic six membered ring with five sp2-hybridized carbon atoms and one sp3-hybridized carbon atom, forming sigma bonds with both the attacking electrophile and the departing substituent. The formation of the sigma-complex is generally the rate-limiting step for electrophilic aromatic substitution reactions [85, 90].

We performed a \( \tau \)-CRT analysis of ortho/para selectivity ratios for different AEAr reactions, namely, chlorination [91, 92], bromination [91], nitration [93, 94], mercuration [95], and protonation [96, 97] of a set of benzene derivatives (bromine, chlorine, fluorine, iodine, methoxy, methyl, nitro, and hydroxy). A statistical analysis was performed using the experimental data available in the literature. A total of 20 AEAr reactions were analyzed (numerical data can be found in the Supporting Information). We found two different patterns, one in which the experimental ortho/para selectivity ratios correlate with the corresponding ortho/para electrophilic local chemical potential ratios, that is \( \mu_{\text{ortho}}^{ - } /\mu_{\text{para}}^{ - } \) (Fig. 4a), and one in which the experimental ortho/para selectivity ratios correlate with the local electrophilic hardness values condensed at the para position, \( \eta_{\text{para}}^{ - } \) (Fig. 4b). Figure 4a shows that the substitution at the ortho position is favored by the acid–base interaction between the electrophile and the corresponding carbon atom: increasing the basicity of this carbon increases the amount of the ortho adduct. Figure 4b shows that the para derivative will prevail when the local hardness values of the carbon at this position is bigger than the hardness at the ortho position, indicating that the para adduct is favored by the HSAB principle (at the local level). These patterns suggest that the regioselectivity in AEAr reactions may be determined by the (local) acid–base and hard-soft properties of ortho/para carbons. If the carbon atom at ortho is harder than the carbon atom at para, the ortho/para ratio will increase with the basicity of the ortho carbon atom. Conversely, when the carbon atom at para is harder than the carbon atom at ortho, the amount of the para adduct will increase with the hardness of the para carbon.

Fig. 4
figure 4

Correlation profiles between experimental AEAr ortho/para selectivity ratios and a condensed \( {{\mu_{\text{ortho}}^{ - } } \mathord{\left/ {\vphantom {{\mu_{\text{ortho}}^{ - } } {\mu_{\text{para}}^{ - } }}} \right. \kern-0pt} {\mu_{\text{para}}^{ - } }} \) local chemical potentials ratios, b condensed \( \eta_{\text{para}}^{ - } \) values

Full size image

5 Conclusions

The temperature-dependent formalism of CR-DFT, denominated as \( \tau \)-CRT, based on the grand canonical ensemble, is known to provide a useful framework for defining zero temperature response functions, and these response functions are known to be useful for studying chemical reactivity [43]. In this work we simplified the procedure used to develop, in the temperature-dependent case, the local counterparts of global indicators, and the non-local counterparts of local indicators. Reactivity indicators then emerge as ratios-of-fluctuations.

We have tested the performance of these \( \tau \)-CRT indexes for 113 reactions of various types, including acid–base reactions, aliphatic nucleophilic substitutions, aromatic electrophilic substitutions, and Markovnikov additions. In all cases we were able to find quantitative correlations between the \( \tau \)-CRT descriptors and reference experimental/computational data, showing that the information contained in these indicators is closely related to the reactivity of the chemical species here considered. Moreover, we were able to identify the most relevant chemical interactions for each type of chemical process and which molecular fragment(s) controlled the reactivity preferences.

In general, our study indicates that \( \tau \)-CRT descriptors are reliable and useful quantities for scrutinizing chemical reactions. Besides their ability to reveal chemical information about different sites within a molecule, their inclusion of a global factor that characterizes the reactivity of the molecule as a whole allows one to perform comparative studies of chemical processes across a set of substrates including structurally different reactive moieties. Thus, they can be used to reveal chemical reactivity trends of different systems with substantial differences in their size, making them particularly useful to identify the way reactivity features vary across a set of substrates due to systematic changes in the reactivity of their substituent functional groups.