Two mathematical models for dissolved oxygen in a lake—CMMSE-16

Abstract

In this paper two mathematical models for handling water pollution are introduced. In the first one we assume that algae and fungi are in competition for resources that come from wastewater, while in the second one we introduce explicitly the equation of nutrients. Both algae and fungi need dissolved oxygen (DO) for their biological process of growth. But there is a difference, indeed algae produce it too and in a higher quantity than the one they use. For the first model it is shown that if the coexistence equilibrium exists, it is stable without additional conditions. If the competition rate between algae and fungi is not high for a chosen set of parameters the stability of the coexistence equilibrium is reached even without an external constant input of DO in the system. For the second model we have found the matching equilibrium points with the ones of the first model, furthermore other two equilibria are found.

1 Introduction

Algae are important in a lake, as they can improve the quality of the aquatic ecosystem, growing under right conditions such as adequate nutrients (mostly phosphorus, but nitrogen is important too). The nutrients that are present in the wastewater can derive from agricultural and/or industrial discharges. Fungi can be used for biodegradation of organic pollutant in a waterbody, because the grow using the nutrients obtained from the biodegradation, [1]. Some mathematical models in the literature study the behaviour of algae biomass in a waterbody in the presence of organic pollutants, [4, 5]. In [2, 3] the case of fungi has been addressed. In this paper we want to investigate the situation in which both algae and fungi are present in the same waterbody, assuming that they compete for the resources coming from the pollutants.

In this paper we introduce two mathematical systems modeling the algae and fungi behaviour in a waterbody. The waterbody considered could be nutrient-rich waters, like municipal wastewater or some industrial effluents. Both algae and fungi can feed on these wastes and therefore purify the water, while also producing a biomass suitable for biofuels production.

In the next Section we present the first model and in Sect. 3 its qualitative analysis. Sect. 4 contains the extended model in which also nutrients are present, its qualitative behaviour is examined in Sect. 5. These two models are compared in Sect. 6 and a final discussion concludes the paper.

2 The first mathematical model

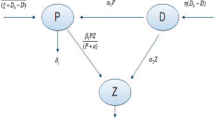
In the first model we assume that algae and fungi are in competition for food, since both share the same resources. Further, fungi as well as algae need dissolved oxygen (DO) to thrive but we assume that the algae’s production and input of DO into the system is much larger than their own use for their growth.

The model consists of three equations that describe the time evolution of the algae population, the fungi population and the DO respectively. The model, in which all the parameters are nonnegative, reads:

$$\begin{aligned} \frac{dA}{dt}= & {} r_AA-a_AA-b_AA^2-cAF \nonumber \\ \frac{dF}{dt}= & {} \dfrac{hOF}{k+k_O O}-a_FF-b_F F^2-cAF \nonumber \\ \frac{dO}{dt}= & {} q_O+gA-a_OO-f\dfrac{hOF}{k+k_OO}. \end{aligned}$$

(1)

In the first equation algae grow at a constant rate $r_A$ and are washed out at a constant rate $a_A$. We assume that algae are in competition among themselves at a constant rate $b_A$ and also experience interspecific competition with fungi at rate c.

In the second equation the fungi’s growth depends on the presence of DO. They are washed out at rate $a_F$. The intraspecific competition occurs at rate $b_F$ while c denotes the rate of the interspecific competition with the algae population.

The third equation shows the evolution in time of DO. We assume that it is supplied from external sources at rate $q_O$, but a part of it comes from the algae own production at rate g. We take further into account its washing out, at rate $a_O$ and its depletion due to its assumption by fungi at rate $f \geqslant 1$.

3 The qualitative analysis of the model

To find the equilibrium points of the model, we need to solve the equilibrium equations, i.e. the system obtained by setting the right hand side of (1) to zero, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} A(r_A-a_A-b_AA-cF)=0 \\ F \left( \dfrac{hO}{k+k_O O}-a_F-b_F F-cA \right) =0 \\ q_O+gA-a_OO-f\dfrac{hOF}{k+k_OO}=0. \end{array}\right. } \end{aligned}$$

(2)

Further, for the stability analysis, we need to calculate the Jacobian matrix J of system (1), given by

$$\begin{aligned} \left[ \begin{array}{ccc} r_A-a_A-2b_AA-cF &{} -cA &{} 0 \\ -cF &{} -a_F-2b_FF-cA+\dfrac{hO}{k+k_OO} &{} \dfrac{hkF}{(k+k_OO)^2} \\ g &{} -\dfrac{fhO}{k+k_OO}&{} -a_O- \dfrac{fhkF}{(k+k_OO)^2} \end{array} \right] .\nonumber \\ \end{aligned}$$

(3)

Solving (2) we obtain the analytic expression of three equilibrium points. In addition, we prove that two other equilibria exist. We also show that all these points are conditionally locally asymptotically stable, while the coexistence equilibrium is stable if it is feasible.

Proposition 3.1

The trivial equilibrium point, $E_0=(0,0,0)$, exists if

$$\begin{aligned} q_O=0. \end{aligned}$$

(4)

Furthermore, it is stable if the following condition holds:

$$\begin{aligned} r_A<a_A. \end{aligned}$$

(5)

Proof

For $A=F=O=0$ in the system (2) we get that $E_0$ exists if $q_O=0$. The characteristic polynomial associated to the matrix (3) evaluated at $E_0$ is

$$\begin{aligned} \det (J-\mu )=(r_A-a_A-\mu )(-a_F-\mu )(-a_O-\mu )=0. \end{aligned}$$

To have the stability of $E_0$ all the eigenvalues should be negative thus the condition (5) must hold. $\square$

Proposition 3.2

The fungi-and-algae-free point $E_1=\left( 0,0,q_Oa_O^{-1}\right)$ exists always. It is stable if the following conditions hold:

$$\begin{aligned} r_A<a_A \quad \text{ and } \quad \dfrac{hq_O}{ka_O+k_Oq_O}<a_F . \end{aligned}$$

(6)

Proof

In fact for $A=F=0$ in (2) from the last equation we get $O=q_Oa_O^{-1}$. While the characteristic polynomial associated to $E_1$ is

$$\begin{aligned} \det (J-\mu )=(r_A-a_A-\mu )(-a_O-\mu ) \left( \dfrac{hq_O}{ka_O+k_Oq_O}-a_F-\mu \right) =0. \end{aligned}$$

To have all the eigenvalues negative the conditions (6) must hold. $\square$

In Fig. 1 one can see that for a chosen set of parameters the equilibrium $E_1$ is stably achieved.

Fig. 1

The equilibrium $E_1$ is stably achieved with the parameter values $r_A=10.1273$, $a_A=16.93072$, $b_A=11.7382$, $c=19.3012$, $h=1.61592$, $k=0.454245$, $k_O=5.87845$, $a_F=2.55798$, $b_F=0.0344478$, $q_O=2$, $g=3.63317$, $a_O=5.41771$, $f=1$

Proposition 3.3

The fungi-free equilibrium

$$\begin{aligned} E_2=\left( \dfrac{r_A-a_A}{b_A},0,\dfrac{q_Ob_A+g(r_A-a_A)}{b_Aa_O} \right) \end{aligned}$$

is feasible if

$$\begin{aligned} r_A>a_A \end{aligned}$$

(7)

and it is stable if

$$\begin{aligned} \dfrac{hO_2}{k+k_OO_2}<a_F+cA_2 \end{aligned}$$

(8)

holds.

Proof

From the first equilibrium equation of (2) in which we set $F=0$ it follows

$$\begin{aligned} A=\dfrac{r_A-a_A}{b_A} . \end{aligned}$$

Thus for the nonnegativity of the algae population, (7) must hold. From the third equation instead we get the equilibrium value of the oxygen.

$$\begin{aligned} O=\dfrac{q_Ob_A+g(r_A-a_A)}{b_Aa_O}. \end{aligned}$$

The characteristic polynomial associated to $E_1$ is once again easily obtained,

$$\begin{aligned} \det (J-\mu )=(-r_A+a_A-\mu )(-a_O-\mu )\left( \dfrac{hO_2}{k+k_OO_2}-a_F-cA_2-\mu \right) =0, \end{aligned}$$

as well as its eigenvalues

$$\begin{aligned} \mu _1= & {} -r_a+a_A<0 \\ \mu _2= & {} -a_O<0\\ \mu _3= & {} \dfrac{hO_2}{k+k_OO_2}-a_F-cA_2 \\ \end{aligned}$$

Requiring $\mu _3<0$ we find the condition (8). $\square$

In Fig. 2 we show that for a chosen set of parameters the stability of the fungi-free equilibrium, $E_2$, is attained.

Fig. 2

The equilibrium $E_2$ is stable for the parameter values $r_A=8.90096$, $a_A=4.14886$, $b_A=1.62848$, $c=0.0691916$, $h=11.8402$, $k=1.92602$, $k_O=16.7554$, $a_F=18.7713$, $b_F=15.4976$, $q_O=69.5303$, $g=13.847$, $a_O=19.037$, $f=1$

Proposition 3.4

The algae-free point is in fact a set of multiple equilibria, namely $(0,F_3,O_3)$, $(0,F_4,O_4)$ and $(0,F_5,O_5)$. Of them, only one is feasible, if

$$\begin{aligned} O>\dfrac{a_Fk}{h-a_Fk_O} , \end{aligned}$$

(9)

and it is stable if

$$\begin{aligned} r_A<a_A+cF_3. \end{aligned}$$

(10)

Proof

Part 1: Existence

For $A=0$ the system (2) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} A=0 \\ \dfrac{hO}{k+k_O O}-a_F-b_F F=0 \\ q_O-a_OO-f\dfrac{hOF}{k+k_OO}=0. \end{array}\right. } \end{aligned}$$

(11)

Solving the second equation with respect to F we get

$$\begin{aligned} F=\dfrac{O(h-a_Fk_O)-a_Fk}{b_F(k+k_OO)}. \end{aligned}$$

(12)

Condition (9) arises by requiring the positivity of the expression (12). Note that the opposite case, obtained when $h-a_Fk_O<0$,

$$\begin{aligned} O<\dfrac{a_Fk}{h-a_Fk_O}, \end{aligned}$$

cannot arise, because $O<0$ would then follow, which is impossible because the oxygen must be a nonnegative quantity.

Substituting the expression (12) for F into the third equation of the system (11) we obtain the following third degree equation in O

$$\begin{aligned} aO^3+bO^2+cO+d=0, \end{aligned}$$

(13)

with

$$\begin{aligned} a= & {} -a_Ob_Fk_O^2 <0 \\ b= & {} q_Ob_Fk_O^2-2a_Ob_Fkk_O-fh^2+fha_Fk_O \\ c= & {} 2 q_Ob_Fkk_O-a_Ob_Fk^2+fha_Fk \\ d= & {} q_Ob_Fk^2 >0. \end{aligned}$$

Since $a<0$ and $d>0$ by Descartes’ rule of signs the third degree polynomial (13) in O has at least one positive root. We are able to show that there is exactly one such root. In Table 1 the only four possible cases are summarized.

Table 1 The four possible cases for the signs of the coefficients of the third degree equation (13)

The first case is impossible, in fact assuming that $b>0$ and $c<0$ we find

$$\begin{aligned} a_Ob_Fk+\dfrac{fh^2}{k_O}<q_Ob_Fk_O-a_Ob_Fk+fha_F<-q_Ob_Fk_O. \end{aligned}$$

But this is a contradiction, because the term in the middle should be less than a negative term (on the right) and greater than a positive one (on the left side).

Thus there is only one positive equilibrium, with $O_3$

$$\begin{aligned} E_3= \left( 0,\dfrac{O_3(h-a_Fk_O)-a_Fk}{b_F(k+k_OO_3)}, O_3\right) \end{aligned}$$

with $O_3$ the real positive root of (13) satisfying (9).

Part 2: Stability

To study the stability of the equilibrium point we evaluate the Jacobian matrix (3) at $E_3$. The resulting characteristic polynomial $\det (J-\mu )$ explicitly becomes

$$\begin{aligned}&(r_A-a_A-cF_3-\mu ) \left\{ \mu ^2+ \left( a_F+2b_FF_3+a_O+\dfrac{fhkF_3}{(k+k_OO_3)^2}\right. \right. \\&\quad \left. \left. -\dfrac{hO_3}{k+k_OO_3} \right) \mu +\left( a_O+\dfrac{fhkF_3}{(k+k_OO_3)^2} \right) (a_F+2b_FF_3)-\dfrac{a_OhO_3}{k+k_OO_3} \right\} =0. \end{aligned}$$

The eigenvalue $\mu _1=r_A-a_A-cF_3$ is negative if (10) holds, while the roots of the quadratic polynomial in $\mu$ are negative with no further conditions. It turns out that both coefficients of the terms of the two lowest degrees in $\mu$ are positive, so that the Routh–Hurwitz conditions are unconditionally satisfied. In fact, substituting $F_3$, (12), for the coefficient of $\mu$ we get

$$\begin{aligned}&\left( a_F+\dfrac{2hO_3}{k+k_OO_3}-\dfrac{2(O_3a_Fk_O+a_Fk)}{k+k_OO_3}+a_O +\dfrac{fhkF_3}{(k+k_OO_3)^2}-\dfrac{hO_3}{k+k_OO_3} \right) \\&=\left( a_F+\dfrac{hO_3}{k+k_OO_3}-2a_F+a_O+\dfrac{fhkF_3}{(k+k_OO_3)^2} \right) \\&=\dfrac{O_3(h-a_Fk_O)-a_Fk}{b_F(k+k_OO_3)}+a_O+\dfrac{fhkF_3}{(k+k_OO_3)^2} =F_3+a_O+\dfrac{fhkF_3}{(k+k_OO_3)^2} >0. \end{aligned}$$

Similarly, for the constant term, by dividing by $a_O$, denoting by H a positive quantity, we have:

$$\begin{aligned} a_F+2b_FF_3-\dfrac{hO_3}{k+k_OO_3} +H >0. \end{aligned}$$

$\square$

Figure 3 shows that for a chosen set of parameters the algae-free equilibrium, $E_3$, is stably achieved.

Fig. 3

The equilibrium $E_3$ is stabile for the parameters $r_A=4.85571$, $a_A=13.2729$, $b_A=11.6077$, $c=12.7024$, $h=11.4803$, $k=2.3815$, $k_O=1.11246$, $a_F=1.40551$, $b_F=1.95987$, $q_O=65.3973$, $g=16.7907$, $a_O=15.374$, $f=1$

For the coexistence equilibrium point we have the following result

Proposition 3.5

There exists at least one feasible coexistence equilibrium $E_4=(A^*,F^*,O^*)$ if the following three conditions hold:

$$\begin{aligned} \delta =b_Fb_A-c^2>0, \quad r_A-a_A-b_AA^*>0, \quad (a_Fc+b_F)(k+k_OO^*)(r_A-a_A)>chO^* \end{aligned}$$

(14)

and whenever it exists, it is stable.

Proof

To find the conditions for the existence of the coexistence equilibrium point from the first equation of the system (2) we get

$$\begin{aligned} F=\dfrac{r_A-a_A-b_AA}{c} \end{aligned}$$

and substitute it into the remaining two equations. We solve these two equations with respect to A and we match the resulting expressions

$$\begin{aligned} A= & {} \dfrac{(a_Fc+b_F)(r_A-a_A)(k+k_OO)-chO}{(k+k_OO)(b_Fb_A-c^2)}\\= & {} \dfrac{fhO(r_A-a_A)+c(a_OO-q_O)(k+k_OO)}{cg(k+k_OO)+fhb_AO}. \end{aligned}$$

Thus, we now have the following cubic polynomial in O:

$$\begin{aligned} a_1O^3+b_1O^2+c_1O+d_1=0, \end{aligned}$$

(15)

with

$$\begin{aligned} a_1= & {} -a_Ok_O^2\delta \\ b_1= & {} k_O(fhc+b_Fk_Og)(r_A-a_A)+k_O(k_Oq_O-2a_Ok)\delta \\&+(a_Fk_O-h)(fhb_A+ck_Og) \\ c_1= & {} k(fhc+2b_Fk_Og)(r_A-a_A)+k(2k_Oq_O-a_Ok)\delta \\&+chg(2a_Fk_O-h)+a_Fkhb_A \\ d_1= & {} a_Fck^2g+k^2q_O\delta +b_Fk^2g(r_A-a_A). \end{aligned}$$

For $\delta =b_Fb_A-c^2>0$, it follows $a_1<0$ and $d_1>0$. Thus the polynomial (15) by the Descartes’ rule of signs has at least one positive root $O^*$. For the feasibility of the equilibrium we need to have $F^*>0$ and $A^*>0$, providing thus the second and the third conditions in (14).

To study the stability, the characteristic polynomial of (3) evaluated at $E_4$ gives the cubic equation

$$\begin{aligned} \det (J-\mu )= & {} \mu ^3+R\mu ^2+ S\mu +P =0 \end{aligned}$$

with

$$\begin{aligned} R= & {} b_AA^*+a_O+b_FF^*+\dfrac{fhkF^*}{(k+k_OO^*)^2}>0 \\ S= & {} A^*F^*\delta +b_Fa_OF^*+\dfrac{fhkF^*(b_AA^*+b_FF^*)}{(k+k_OO^*)^2} +\dfrac{h^2kF^*O^*}{(k+k_OO^*)^3}>0 \\ P= & {} \delta \left( a_OA^*F^*+\dfrac{fhk{F^*}^2A^*}{(k+k_OO^*)^2}\right) +\dfrac{b_AA^*h^2kF^*O^*}{(k+k_OO^*)^3}+\dfrac{cghkA^*F^*}{(k+k_OO^*)^2} >0 . \end{aligned}$$

For $\delta =b_Fb_A-c^2>0$, which holds by feasibility, the three eigenvalues are negative. Thus $E_4$ is stable whenever it is feasible. $\square$

In Fig. 4 we show that the coexistence equilibrium is stable for a selected set of parameter values.

In Table 2 we summarize the feasibility and stability conditions for the five equilibrium points of model (1).

In Fig. 5 for a chosen set of parameters and using the same initial conditions, but changing the value of $q_O$, the constant input of DO in the system, the stable coexistence equilibrium, $E_4$, is obtained, left frame, while in the right frame instead $E_2$ is found. Thus, starting from the coexistence equilibrium, by decreasing the rate $q_O$ at which oxygen is supplied into the system, the fungi-free equilibrium is obtained.

Fig. 4

Two possible configurations for the equilibrium $E_4$, $q_O=0$ and $q_O=1$. It is stable in the following cases. Left: $q_O=0$, the point (1.20, 0.30, 0.55) is achieved for the parameters $r_A=1$, $a_A=0.001$, $b_A=0.8$, $c=0.1224$, $h=1.1$, $k=1$, $k_O=1$, $a_F=0.001$, $b_F=0.8$, $g=.1$, $a_O=0.001$, $f=1$. Right: $q_O=1$, the point (1.08, 1.08, 10.15) is obtained for the same parameters as before but changing the value of $q_O$

Table 2 The feasibility and stability conditions for the five equilibrium points of model (1)

Fig. 5

Left frame: the equilibrium $E_4$ is stable for $q_O=30$; $r_A=19.6445$, $a_A=1.73234$, $b_A=11.5828$, $c=3.34324$, $h=16.676$, $k=12.4305$, $k_O=0.517493$, $a_F=3.04963$, $b_F=1.3597$, $g=11.5323$, $f=0.835718$, $a_O=5.42261$ Right frame: the equilibrium $E_2$ at the stability for the same parameters as before and $q_O=20$

4 The mathematical model with nutrients

In this section we consider another model in which the nutrients N are explicitly taken into account as a dependent dynamic variable. The model reads:

$$\begin{aligned} \frac{dA}{dt}= & {} g(N)A -e_AA-m_AA^2 \nonumber \\ \frac{dF}{dt}= & {} k(N,O)F-e_FF-m_F F^2 \nonumber \\ \frac{dN}{dt}= & {} q_N-r g(N)A-sk(N,O)F-e_NN \nonumber \\ \frac{dO}{dt}= & {} q_O+g_AA-e_OO-c_Ok(N,O)F \end{aligned}$$

(16)

with

$$\begin{aligned} g(N)=\dfrac{h_A N}{k_A+k_N N} \quad \text{ and } \quad k(N,O)=\dfrac{k_1 NO}{k_2+k_3N+k_4O+k_3k_4NO}. \end{aligned}$$

Note that in (16) the growth rate of A is assumed to depend directly on N. This fact is expressed using a Monod equation, i.e. the function g(N). The growth of F depends on both N and O, thus it is expressed by a product of two Monod equations in N and O respectively, giving the function k(N, O). All the parameters are nonnegative, and furthermore we assume $r,s,c_O \ge 1$.

5 The qualitative analysis of the second model

To find the equilibrium points of the model, we need to solve the equilibrium equations of (16), thus the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} A\left[ g(N)-e_A-m_AA \right] =0 \\ F\left[ k(N,O)-e_F-m_F F\right] =0\\ q_N-r g(N)A-sk(N,O)F-e_NN =0\\ q_O+g_AA-e_OO-c_Ok(N,O)F=0 \end{array}\right. } \end{aligned}$$

(17)

Further, for the stability analysis, we need to calculate the Jacobian matrix of the system (1)

$$\begin{aligned} \widetilde{J} = \left[ \begin{array}{cccc} \widetilde{J}_{1,1} &{} 0 &{}\widetilde{J}_{1,3}&{} 0 \\ 0 &{} k(N,O)-e_F-2m_FF &{} \dfrac{dk(N,O)}{dN}F &{} \dfrac{dk(N,O)}{dO}F \\ \dfrac{rh_AN}{k_A+k_NN} &{} -sk(N,O)&{} J_{3,3} &{} -s\dfrac{dk(N,O)}{dO}F \\ g_A &{} -c_O k(N,O) &{} -c_O \dfrac{dk(N,O)}{dN}F &{} \widetilde{J}_{4,4} \end{array} \right] , \end{aligned}$$

(18)

with

$$\begin{aligned} \widetilde{J}_{1,1}= & {} \dfrac{h_AN}{k_A+k_NN}-e_A-2m_AA, \quad \widetilde{J}_{1,3}=\dfrac{h_A(k_A+k_NN)A-k_Nh_ANA}{(k_A+k_NN)^2}, \\ \widetilde{J}_{3,3}= & {} -\dfrac{rh_A A \left( k_A+k_NN-k_NN\right) }{(k_A+k_NN)^2} -s\dfrac{dk(N,O)}{dN}F \quad \widetilde{J}_{4,4}=-e_O-c_O\dfrac{dk(N,O)}{dO}F \end{aligned}$$

Here

$$\begin{aligned} \dfrac{dk(N,O)}{dN}, \quad \dfrac{dk(N,O)}{dO} \end{aligned}$$

are the derivatives of k(N, O) with respect to N and O respectively.

Solving the equilibrium equations we obtain the analytic expressions of four equilibrium points. In addition, we prove that three other equilibria exist. We also show that all these points are conditionally locally asymptotically stable.

Proposition 5.1

The trivial equilibrium point, $\tilde{E}_0=(0,0,0,0)$, exists if

$$\begin{aligned} q_O=q_N=0. \end{aligned}$$

(19)

Furthermore, if it exists, it is stable.

Proof

For $A=F=N=O=0$ in the system (17) we obtain that $\tilde{E}_0$ exists if $q_O=q_N=0$. The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_0$ is

$$\begin{aligned} \det (\widetilde{J}-\mu )=(e_A+\mu )(e_F+\mu )(e_N+\mu )(e_O+\mu )=0. \end{aligned}$$

All the eigenvalues are negative thus $\tilde{E}_0$ is stable if it exists. $\square$

In Fig. 6 we show that for a chosen set of parameters the stability of $\tilde{E}_0$ is attained.

Fig. 6

The equilibrium $\tilde{E}_0$ is stable for the parameter values $h_A=1.26987$, $k_A=9.13376$, $k_N=6.32359$, $e_A=0.975404$, $m_A=2.78498$, $k_1=5.46882$, $k_2=9.57507$, $k_3=9.64889$, $k_4=1.57613$, $e_F=9.70593$, $m_F=9.57167$, $q_N=0$, $r=1.41886$, $s=4.21761$, $e_N=4.85376$, $q_O=0$, $g_A=8.0028$, $e_O=9.15736$, $c_O=7.92207$

Proposition 5.2

The algae-fungi-and-oxygen-free point, namely $\tilde{E}_1=(0,0,q_Ne_N^{-1}, 0)$, exists if

$$\begin{aligned} q_O=0. \end{aligned}$$

(20)

Furthermore, it is stable if the following condition holds:

$$\begin{aligned} e_Aq_Nk_N+e_Ae_Nk_A-h_Aq_N>0. \end{aligned}$$

(21)

Proof

For $A=F=O=0$ in the system (17) we get that $\tilde{E}_1$ exists if $q_O=0$. The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_1$ is

$$\begin{aligned} \det (\widetilde{J}-\mu ) =\left( e_A-\dfrac{h_Aq_N}{q_Nk_N+e_Nk_A}+\mu \right) (e_F+\mu )(e_N+\mu )(e_O+\mu )=0. \end{aligned}$$

To have the stability of $\tilde{E}_1$ the condition (21) must hold. $\square$

Figure 7 shows that for a chosen set of parameters the stability of $\tilde{E}_1$ is attained.

Fig. 7

The equilibrium $\tilde{E}_0$ is stable for the same parameter values as for Fig. 6 and $q_N=45.2896$

Proposition 5.3

The algae-fungi-and-nutrient-free point, namely $\tilde{E}_2=(0,0,0,q_O e_O^{-1})$, exists if

$$\begin{aligned} q_N=0. \end{aligned}$$

(22)

Furthermore, if it exists it is stable.

Proof

For $A=F=N=0$ in the system (17) we get that $\tilde{E}_2$ exists if $q_N=0$. The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_2$ is

$$\begin{aligned} \det (\widetilde{J}-\mu )=(e_A+\mu )(e_F+\mu )(e_N+\mu )(e_O+\mu )=0. \end{aligned}$$

For stability all the eigenvalues must be negative thus $\tilde{E}_2$ is stable if it exists. $\square$

Figure 8 shows the stable equilibrium $\tilde{E}_2$ achieved for a chosen set of parameters.

Fig. 8

The equilibrium $\tilde{E}_2$ is stable for the same parameter values as for Fig. 6 and $q_O=40.7362$

Proposition 5.4

The algae-and-fungi-free point, $\tilde{E}_3=(0,0,q_Ne_N^{-1},q_Oe_O^{-1})$, exists always. Furthermore, it is stable if the following conditions hold

$$\begin{aligned} e_Aq_Nk_N+e_Ae_Nk_A-h_Aq_N>0 \end{aligned}$$

(23)

and

$$\begin{aligned} \dfrac{k_1q_Nq_O}{q_Nq_Ok_3k_4+e_Oq_Nk_3+e_Nq_Ok_4+e_Ne_Ok_2} < e_F. \end{aligned}$$

(24)

Proof

For $A=F=0$ in the system (17) we get that $\tilde{E}_3$ exists always. The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_2$ is

$$\begin{aligned} \det (\widetilde{J}-\mu )= & {} \left( e_F-\dfrac{k-1q_Nq_O}{q_Nq_Ok_3k_4+e_Oq_Nk_3+e_Nq_Ok_4+e_Ne_Ok_2} +\mu \right) \\&\times \left( e_A-\dfrac{h_Aq_N}{q_Nk_N+e_Nk_A} +\mu \right) (e_N+\mu )(e_O+\mu )=0. \end{aligned}$$

To have all the eigenvalues negative (23) and (24) must hold, thus $\tilde{E}_3$ is stable. $\square$

In Fig. 9 we show that for a chosen set of parameters the stable equilibrium $\tilde{E}_3$ is attained.

Fig. 9

The equilibrium $\tilde{E}_3$ is stable for the same parameter values as for Fig. 6 and $q_N=45.2896$, $q_O=40.7362$

Proposition 5.5

The fungi-free point is in fact a set of multiple equilibria, namely $(A_4,0,N_4,O_4)$, $(A_5,0,N_5,O_5)$ and $(A_6,0,N_6,O_6)$. Of them, only one is feasible, if

$$\begin{aligned} \dfrac{h_AN}{k_A+k_NN}>e_A \end{aligned}$$

(25)

and it is stable if

$$\begin{aligned} N_4O_4e_Fk_3k_4-N_4O_4k_1+N_4e_Fk_3+O_4e_Fk_4+e_Fk_2>0 \end{aligned}$$

(26)

and

$$\begin{aligned} B_1>0 \quad \text{ and } \quad C_1>0 \end{aligned}$$

(27)

hold, with $B_1$ and $C_1$ as below.

Proof

Part 1: Existence

For $F=0$ the system (17) becomes,

$$\begin{aligned} {\left\{ \begin{array}{ll} A\left[ g(N)-e_A-m_AA\right] =0 \\ q_N-r g(N)A-e_NN =0\\ q_O+g_AA-e_OO=0 \\ F=0 \end{array}\right. } \end{aligned}$$

(28)

Solving the third equation of (28) with respect to O we find

$$\begin{aligned} O=\dfrac{q_O+g_AA}{e_O} >0, \end{aligned}$$

(29)

and from the first equation we obtain A,

$$\begin{aligned} A=\dfrac{g(N)-e_A}{m_A}. \end{aligned}$$

(30)

For the feasibility of $\tilde{E}_4$ we need to ask the positivity of (30), thus condition (25) must hold. Substituting the expression of A previously found into the second equation of the system (28), a third degree polynomial in N is obtained,

$$\begin{aligned} a_2N^3+b_2N^2+c_2N+d_2=0, \end{aligned}$$

(31)

with

$$\begin{aligned} a_2= & {} k_N^2m_Ae_N >0 \\ b_2= & {} 2k_Ak_Nm_Ae_N+rh_A^2-k_N^2m_Aq_N-re_Ah_Ak_N \\ c_2= & {} k_A^2m_Ae_N-2k_Ak_Nm_Aq_N-re_Ah_Ak_A \\ d_2= & {} -k_A^2m_Aq_N<0. \end{aligned}$$

Since $a_2>0$ and $d_2<0$ by Descartes’ rule of signs the third degree polynomial (31) in N has at least one positive root. We will show below that there is exactly one such root. In Table 3 the only four possible cases are summarized.

Table 3 The four possible cases for the signs of the coefficients of the third degree equation (31)

The third case is impossible, in fact assuming that $b_2<0$ and $c_2>0$ we find

$$\begin{aligned} b_2=k_N(k_Am_Ae_N+k_Am_Ae_N-k_Nm_Aq_N-re_Ah_A)+rh_A^2<0. \end{aligned}$$

Let us set

$$\begin{aligned} Q=k_Am_Ae_N-k_Nm_Aq_N-re_Ah_A<-\dfrac{rh_A^2}{k_N}-k_Am_Ae_N<0 \end{aligned}$$

thus

$$\begin{aligned} c_2=k_A(Q-k_Nm_Aq_N)<0. \end{aligned}$$

But this is a contradiction with the assumption $c_2>0$.

Thus there is only one positive equilibrium

$$\begin{aligned} \tilde{E}_4=\left( \dfrac{g(N_4)-e_A}{m_A},0,N_4,\dfrac{q_O+g_AA_4}{e_O}\right) , \end{aligned}$$

where $N_4$ is the real positive root of (31).

Part 2: Stability

The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_4$ is

$$\begin{aligned} \det (\widetilde{J}-\mu )= & {} \left( \dfrac{N_4O_4e_Fk_3k_4-N_4O_4k_1+N_4e_Fk_3+O_4e_Fk_4+e_Fk_2}{N_4O_4k_3k_4+N_4k_3+O_4k_4+k_2}+\mu \right) \\&\times (e_O+\mu ) (A_1 \mu ^2 +B_1 \mu +C_1) =0, \end{aligned}$$

with

$$\begin{aligned} A_1= & {} N_4^2k_N^2+2N_4k_Ak_N+k_A^2 >0, \\ B_1= & {} 2AN_4^2k_N^2m_A+4AN_4k_Ak_Nm_A+N_4^2(e_Ak_N^2+e_Nk_N^2)+Ah_Ak_Ar+2Ak_A^2m_A+ \\&-N_4^2h_Ak_N+2N_4(e_Ak_Ak_N+e_Nk_Ak_N)-N_4h_Ak_A+e_Ak_A^2+e_Nk_A^2 \\ C_1= & {} 2AN_4^2e_Nk_N^2m_A+2A^2h_Ak_Am_Ar+4AN_4e_Nk_Ak_Nm_A+N_4^2e_Ae_Nk_N^2+ \\&+ Ae_Ah_Ak_Ar+2Ae_Nk_A^2m_A\\&-N_4^2e_Nh_Ak_N+2N_4e_Ae_Nk_Ak_N-N_4e_Nh_Ak_A+e_Ae_Nk_A^2. \end{aligned}$$

To have all the eigenvalues negative (26) and (27) must hold, thus $\tilde{E}_4$ is stable. $\square$

In Fig. 10 we show that for a chosen set of parameters the stability of $\tilde{E}_4$ is attained.

Fig. 10

The equilibrium $\tilde{E}_4$ is stable for the set of parameter values $h_A=7.04047$, $k_A=4.42305$, $k_N=0.195776$, $e_A=3.30858$, $m_A=4.24309$, $k_1=2.7027$, $k_2=1.97054$, $k_3=8.21721$, $k_4=4.29921$, $e_F=8.87771$, $m_F=3.91183$, $q_N=34.1708$, $r=8.08514$, $s=7.55077$, $e_N=7.69114$, $q_O=19.7354$, $g_A=3.96792$, $e_O=3.77396$, $c_O=2.16019$

Proposition 5.6

There exist at least one feasible algae-free point,

$$\begin{aligned} \tilde{E}_5=\left( 0, \dfrac{k(N_5,O_5)-e_F}{m_F} ,N_5,\dfrac{e_Nc_ON_5-q_Nc_O+q_Os}{e_Os} \right) , \end{aligned}$$

if

$$\begin{aligned} k(N_5,O_5)-e_F>0, \quad e_Nc_ON_5-q_Nc_O+q_Os>0, \quad f_3<0. \end{aligned}$$

(32)

where $f_3$ is given below in (40). Furthermore, it is stable if the following condition holds:

$$\begin{aligned} e_Ak_NN_5+e_Ak_A-h_AN_5>0, \end{aligned}$$

(33)

and the Routh–Hurwitz criteria hold

$$\begin{aligned} \dfrac{B_2}{A_2}>0, \quad \dfrac{C_2}{A_2}>0, \quad \dfrac{B_2C_2}{A_2^2}>\dfrac{D_2}{A_2}. \end{aligned}$$

(34)

Proof

Part 1: Existence

For $A=0$ the system (17) becomes,

$$\begin{aligned} {\left\{ \begin{array}{ll} F\left[ k(N,O)-e_F-m_FF\right] =0 \\ q_N-sk(N,O)F-e_NN =0\\ q_O-e_OO-c_Ok(N,O)F=0 \\ A=0 \end{array}\right. } \end{aligned}$$

(35)

We solve the first equation of (35) with respect to F, and we get

$$\begin{aligned} F=\dfrac{k(N,O)-e_F}{m_F}. \end{aligned}$$

(36)

Solving the second and the third equations of (35) with respect to F and equating them we find an expression in O

$$\begin{aligned} F=\dfrac{q_N-e_NN}{sk(N,O)}=\dfrac{q_O-e_OO}{c_Ok(N,O)}, \end{aligned}$$

(37)

and from (37) we get O,

$$\begin{aligned} O=\dfrac{e_Nc_ON-q_Nc_O+q_Os}{e_Os}. \end{aligned}$$

(38)

Substituting (36) into the third equation of (35) we get a fifth degree polinomial in N

$$\begin{aligned} a_3N^5+b_3N^4+c_3N^3+d_3N^2+e_3N+f_3=0, \end{aligned}$$

(39)

with

$$\begin{aligned} a_3= & {} c_O^2e_N^3k_3^2k_4^2m_F>0 \nonumber \\ f_3= & {} -m_Fq_N\left[ c_Ok_4q_N(c_Ok_4q_N-2e_Ok_2s-2k_4q_Os)+(e_Ok_2s+k_4q_Os)^2\right] ,\qquad \end{aligned}$$

(40)

and $b_3$, $c_3$, $d_3$ and $e_3$ are defined in Appendix A. Since $a_3>0$, to have at least one positive root of (39) $f_3$ must be negative.

Part 2: Stability

The characteristic polynomial associated to the matrix (18) evaluated at $\tilde{E}_5$ is

$$\begin{aligned} \det (\widetilde{J}-\mu )= & {} (A_2 \mu ^3 +B_2 \mu ^2 +C_2 \mu +D_2)\left( \dfrac{e_Ak_NN+e_Ak_A-h_AN}{k_NN+k_A}+\mu \right) =0. \end{aligned}$$

Requiring the negativity of all the eigenvalues, conditions (33) and (34) must hold. $\square$

In Fig. 11 we show that for a chosen set of parameters $\tilde{E}_5$ is stably attained.

Fig. 11

The equilibrium $\tilde{E}_5$ is stable for the set of parameter values $h_A=0.647781$, $k_A=4.86608$, $k_N=9.93558$, $e_A=3.89696$, $m_A=7.01721$, $k_1=2.14784$, $k_2=4.99448$, $k_3=0.556305$, $k_4=0.354883$, $e_F=4.89305$, $m_F=2.94844$, $q_N=40.5671$, $r=3.15619$, $s=7.82938$, $e_N=0.648179$, $q_O=15$ ,$g_A=7.00175$, $e_O=1.80741$, $c_O=0.243628$

Numerically, the coexistence equilibrium point, $\tilde{E}_6=(A_6,F_6,N_6,O_6)$ exists for a chosen set of parameters. From the first and the second equations of system (35) we obtain the analytical expressions for A and O, as functions of N and F,

$$\begin{aligned} A=\dfrac{h_AN-e_Ak_NN-e_Ak_A}{k_Am_A+m_Ak_NN} \end{aligned}$$

(41)

and

$$\begin{aligned} O=\dfrac{e_Fk_2+e_Fk_3N+m_Fk_2F+m_Fk_3NF}{k_1N-e_Fk_4-e_Fk_3k_4N-m_Fk_4F-m_Fk_3k_4NF}. \end{aligned}$$

(42)

For the feasibility of the coexistence equilibrium we must have $A>0$ and $O>0$.

Substituting A and O from (41) and (42) respectively, into the third and fourth equations of (35) we get two expressions in F and N, say H(F, N) and G(F, N). In Fig. 12 we plot the intersection point between the two expressions.

Fig. 12

The intersection point between the two isoclines, H(F, N) (black) and G(F, N) (red), depending of F and N (Color figure online)

The characteristic polynomial associated to $\tilde{E}_6$ is:

$$\begin{aligned} \tilde{A} \mu ^4+\tilde{B} \mu ^3+\tilde{C}\mu ^2 +\tilde{D} \mu + \tilde{E}=0, \end{aligned}$$

where $\tilde{A}$, $\tilde{B}$, $\tilde{C}$, $\tilde{D}$ and $\tilde{E}$ are expressions depending on the parameters of the system. If the Routh–Hurwitz conditions hold $\tilde{E}_6$ is stable.

In Fig. 13 we show that for a chosen set of parameters $\tilde{E}_6$ is stably attained. For $q_O=47.7051$, $\tilde{E}_6=(2.7090, 0.2036, 5.8428, 8.2499)$ while for $q_O=0$, $\tilde{E}_6=(2.7090, 0.1861, 5.8428, 1.6889)$. From Fig. 13, if there is no external input of oxygen into the system only the oxygen population is affected.

Fig. 13

The equilibrium $\tilde{E}_6$ is stable for the set of parameter values $h_A=5.40106$, $k_A=3.1111$, $k_N=0.712346$, $e_A=1.8198$, $m_A=0.929889$, $k_1=4.63489$, $k_2=0.0933251$, $k_3=9.15026$, $k_4=6.42742$, $e_F=0.0141906$, $m_F=0.303853$, $q_N=27.1407$, $r=1.27266$, $s=0.0864769$, $e_N=2.0847$, $g_A=4.54966$, $e_O=7.2708$, $c_O=3.54116$; On the left: $q_O=47.7051$; On the right: $q_O=0$

In Table 4 we summarize the feasibility and stability conditions for the seven equilibrium points of model (16).

Table 4 The feasibility and stability conditions for the five equilibrium points of model (16)

6 Comparison between the models without and with nutrients

In Table 5 we summarize the equilibrium points of the models (1) and (16).

Table 5 Summary of the equilibrium points of the models (1) and (16)

For each fixed point of (1) we find a corresponding equilibrium of (16). In addition, the mathematical system with nutrients explicitly modeled has two more equilibria. From the above summarizing Tables 2 and 4 we observe the differences between the conditions needed for the feasibility and stability of the various equilibria.

In both cases the ecosystem may collapse, but while it is enough not to feed oxygen and nutrients into system (16) to achieve this status, as $\tilde{E}_0$ is unconditionally stable, for (1) even disrupting the inflow of oxygen, harldly thinkable in view of the fact that some will always enter into the waterbody from the atmosphere, to obtain the stability of this outcome a further condition must hold (5). Thus in this case it is possible to avoid the system’s collapse if the algae reproduction rate $r_A$ exceeeds their mortality rate $a_A$. On the other hand, if we consider also nutrients in the system, a similar situation can be obtained in (16) with no algae, nor fungi nor oxygen, if condition (21) holds. In such case, to avoid collapse, the parameters appearing in the response function g(N) should be suitably tuned together with the nutrients input flow rate $q_N$.

This very same condition (21) together with (24) ensures the stability of the algae-and-fungi-free equilibrium $\tilde{E}_3$ in (16). In the simpler model (1) less involved conditions must hold for the corresponding situation, i.e. the point $E_1$, namely giving lower bounds on the fungi and algae mortality rates.

Instead there is a second equilibrium in (16) giving this very same outcome, $\tilde{E}_2$. It is achieved if the nutrients supply stops, and in such case it is unconditionally stable. Evidently, this is a considerable difference among the two models. Whether nutrients are taken into account or not appears to have a substantial effect on the ecosystem behaviour.

To obtain the fungi-free situation, equilibrium $E_2$ in (1), the growth rate of algae should be greater than the mortality rate for feasibility (7), while for its stability the fungi mortality rate should be high enough (8), although in this condition the algae level also helps in satisfying it. For the corresponding equilibrium in (16), $\tilde{E}_4$, the feasibility condition imposes restrictions on the response function g(N), for stability the conditions are much more involved, see (26) and (27).

The feasibility condition of the algae-free point $E_3$ relies on a high enough level of the oxygen in the first model, while in the second one, equilibrium $\tilde{E}_5$, it depends on both oxygen and the nutrients and further also on a high level of nutrients, see (32). It therefore may give a more relaxed condition. In other words, nutrients may help to deplete the algae. Stability of this outcome in (1) is obtained if the algae reproduction rate is bounded above by their mortality augmented by a quantity that depends on the fungi equilibrium level. Thus even in a highly reproducing environment, a suitable quantity of fungi may avoid eutrophization of the waters. It is very hard to assess the meaning of the corresponding stability conditions in the model (16) in view of the fact that they are quite involved, (33), (34).

The coexistence equilibrium $E_4$ of the model (1) is always stable if it exists while for the model (16) the existence of $\tilde{E}_6$ is shown numerically and for its stability the Routh–Hurwitz conditions must hold. For both $E_4$ and $\tilde{E}_6$ we have made numerical simulations with two fixed set of parameters varying only the input of oxygen $q_O$. The results are quite interesting. For the equilibrium $E_4$ changing $q_O$ from 0 to 1 leads to a significant increase in the DO concentration and in the fungi biomass, respectively, see Fig. 4. For $\tilde{E}_6$ changing $q_O$ from 0 to 47.7051 only the concentration of DO will increase while A, F and N will remain at the same value, see Fig. 13.

7 Conclusions

A three dimensional, nonlinear mathematical model has been introduced and analysed. In addition to the trivial equilibrium, four additional equilibrium points have been found. Their stability was been completely analysed. For a chosen set of parameters with the same initial conditions we get the stability of the coexistence equilibrium, $E_4$, both in the absence, $q_O=0$, and with full, $q_O=1$, external oxygen supply, Fig. 4. Thus the constant input of DO is not necessarily needed if the parameters are chosen appropriately, to have a viable system. In fact algae contribution of DO to the system is enough for the fungi utilization. The simulations of Fig. 5 instead show that the DO concentration should not drop below a critical threshold, because in such situation the fungi may disappear. Such a loss would be detrimental for the ecosystem.

One of the hypothesis of the model is the competition for food between algae and fungi, but in an indirect way the results indicate that algae help the fungi growth by producing DO.

Also a four dimensional, nonlinear mathematical model has been analysed. The model was built starting from (1) in which the equation of nutrients was introduced explicitly.

Seven equilibrium points were found among which three of them exist if no external input of oxygen and/or nutrient is considered, one of them exist always and three other need feasibility conditions. For six of them we found the analytical expression or we proved their existence analytically, while for the coexistence equilibrium we used numerical methods. For the equilibrium stability we found that two of them are stable without conditions and the remaining ones are locally conditionally stable.

As for the system (1) in Fig. 13 one can see that the coexistence equilibrium $\tilde{E}_6$ can be reached even without constant input of oxygen from the external environment, thus the algae population helps indirectly the fungi population.

Appendix A

$$\begin{aligned} {b_3}= & {} -3\,{{c_O}}^{2}{{e_N}}^{2}{{k_3}}^{2}{{k_4}}^{2}{m_F}\, {q_N}+2\,{c_O}\,{{e_N}}^{2}{{k_3}}^{2}{{k_4}}^{2}{m_F}\,{q_O}\,s -{{c_O}}^{2}{e_F}\,{{e_N}}^{2}{k_1}\,{k_3}\,{k_4}\,s + \nonumber \\&+2\,{{c_O}}^{2}{{e_N}}^{3}{k_3}\,{{k_4}}^{2}{m_F}+2\,{c_O}\,{{e_N}}^{2}{e_O}\,{{k_3}}^{2}{k_4}\,{m_F}\,s+{{c_O}}^{2}{{e_N}}^{2}{{k_1}}^{2}s \end{aligned}$$

(43)

$$\begin{aligned} {c_3}= & {} 3\,{{c_O}}^{2}{e_N}\,{{k_3}}^{2}{{k_4}}^{2}{m_F}\,{{q_N}}^{2} -4\,{c_O}\,{e_N}\,{{k_3}}^{2}{{k_4}}^{2}{m_F}\,{q_N}\,{q_O}\,s +{e_N}\,{{k_3}}^{2}{{k_4}}^{2}{m_F}\,{{q_O}}^{2}{s}^{2}+ \nonumber \\&+2\,{{c_O}}^{2}{e_F}\,{e_N}\,{k_1}\,{k_3}\,{k_4}\,{q_N}\,s -6\,{{c_O}}^{2}{{e_N}}^{2}{k_3}\,{{k_4}}^{2}{m_F}\,{q_N}-2\,{c_O}\,{e_F}\,{e_N}\,{k_1}\,{k_3}\,{k_4}\,{q_O}\,{s}^{2}+ \nonumber \\&+2\,{c_O}\,{{e_N}}^{2}{e_O}\,{k_2}\,{k_3}\,{k_4}\,{m_F}\,s+4\,{c_O}\,{{e_N}}^{2}{k_3}\,{{k_4}}^{2}{m_F}\,{q_O}\,s-4\,{c_O}\,{e_N}\,{e_O}\,{{k_3}}^{2}{k_4}\,{m_F}\,{q_N}\,s+ \nonumber \\&+2\,{e_N}\,{e_O}\,{{k_3}}^{2}{k_4}\,{m_F}\,{q_O}\,{s}^{2}-{{c_O}}^{2}{e_F}\,{{e_N}}^{2}{k_1}\,{k_4}\,s +{{c_O}}^{2}{{e_N}}^{3}{{k_4}}^{2}{m_F}-{c_O}\,{e_F}\,{e_N}\,{e_O}\,{k_1}\,{k_3}\,{s}^{2}+\nonumber \\&+2\,{c_O}\,{{e_N}}^{2}{e_O}\,{k_3}\,{k_4}\,{m_F}\,s+{e_N}\,{{e_O}}^{2}{{k_3}}^{2}{m_F}\,{s}^{2}-2\,{{c_O}}^{2}{e_N}\,{{k_1}}^{2}{q_N}\,s+2\,{c_O}\,{e_N}\,{{k_1}}^{2}{q_O}\,{s}^{2} \end{aligned}$$

(44)

$$\begin{aligned} {d_3}= & {} -{{cO}}^{2}{{k3}}^{2}{{k4}}^{2}{mF}\,{{qN}}^{3} +2\,{cO}\,{{k3}}^{2}{{k4}}^{2}{mF}\,{{qN}}^{2}{qO}\,s-{{k3}}^{2}{{k4}}^{2}{mF}\,{qN}\,{{qO}}^{2}{s}^{2}- \nonumber \\&+ {{cO}}^{2}{eF}\,{k1}\,{k3}\,{k4}\,{{qN}}^{2}s+ 6\,{{cO}}^{2}{eN}\,{k3}\,{{k4}}^{2}{mF}\,{{qN}}^{2} \ \ +2\,{cO}\,{eF}\,{k1}\,{k3}\,{k4}\,{qN}\,{qO}\,{s}^{2}- \nonumber \\&+ 4\,{cO}\,{eN}\,{eO}\,{k2}\,{k3}\,{k4}\,{mF}\,{qN}\,s-8\,{cO}\,{eN}\,{k3}\,{{k4}}^{2}{mF}\,{qN}\,{qO}\,s +2\,{cO}\,{eO}\,{{k3}}^{2}{k4}\,{mF}\,{{qN}}^{2}s- \nonumber \\&+ {eF}\,{k1}\,{k3}\,{k4}\,{{qO}}^{2}{s}^{3}+2\,{eN}\,{eO}\,{k2}\,{k3}\,{k4}\,{mF}\,{qO}\,{s}^{2}+2\,{eN}\,{k3}\,{{k4}}^{2}{mF}\,{{qO}}^{2}{s}^{2}- \nonumber \\&+ 2\,{eO}\,{{k3}}^{2}{k4}\,{mF}\,{qN}\,{qO}\,{s}^{2} +2\,{{cO}}^{2}{eF}\,{eN}\,{k1}\,{k4}\,{qN}\,s-3\,{{cO}}^{2}{{eN}}^{2}{{k4}}^{2}{mF}\,{qN}- \nonumber \\&+ {cO}\,{eF}\,{eN}\,{eO}\,{k1}\,{k2}\,{s}^{2}- 2\,{cO}\,{eF}\,{eN}\,{k1}\,{k4}\,{qO}\,{s}^{2}+{cO}\,{eF}\,{eO}\,{k1}\,{k3}\,{qN}\,{s}^{2}+ \nonumber \\&+ 2\,{cO}\,{{eN}}^{2}{eO}\,{k2}\,{k4}\,{mF}\,s+2\,{cO}\,{{eN}}^{2}{{k4}}^{2}{mF}\,{qO}\,s-4\,{cO}\,{eN}\,{eO}\,{k3}\,{k4}\,{mF}\,{qN}\,s- \nonumber \\&+{eF}\,{eO}\,{k1}\,{k3}\,{qO}\,{s}^{3}+2\,{eN}\,{{eO}}^{2}{k2}\,{k3}\,{mF}\,{s}^{2}+2\,{eN}\,{eO}\,{k3}\,{k4}\,{mF}\,{qO}\,{s}^{2}- \nonumber \\&+{{eO}}^{2}{{k3}}^{2}{mF}\,{qN}\,{s}^{2}+{{cO}}^{2}{{k1}}^{2}{{qN}}^{2}s -2\,{cO}\,{{k1}}^{2}{qN}\,{qO}\,{s}^{2}+{{k1}}^{2}{{qO}}^{2}{s}^{3} \end{aligned}$$

(45)

$$\begin{aligned} {e_3}= & {} -2\,{{cO}}^{2}{k3}\,{{k4}}^{2}{mF}\,{{qN}}^{3} +2\,{cO}\,{eO}\,{k2}\,{k3}\,{k4}\,{mF}\,{{qN}}^{2}s+4\,{cO}\,{k3}\,{{k4}}^{2}{mF}\,{{qN}}^{2}{qO}\,s- \nonumber \\&+ 2\,{eO}\,{k2}\,{k3}\,{k4}\,{mF}\,{qN}\,{qO}\,{s}^{2}-2\,{k3}\,{{k4}}^{2}{mF}\,{qN}\,{{qO}}^{2}{s}^{2}-{{cO}}^{2}{eF}\,{k1}\,{k4}\,{{qN}}^{2}s \nonumber + \\&+ 3\,{{cO}}^{2}{eN}\,{{k4}}^{2}{mF}\,{{qN}}^{2}+{cO}\,{eF}\,{eO}\,{k1}\,{k2}\,{qN}\,{s}^{2}+2\,{cO}\,{eF}\,{k1}\,{k4}\,{qN}\,{qO}\,{s}^{2}- \nonumber \\&+ 4\,{cO}\,{eN}\,{eO}\,{k2}\,{k4}\,{mF}\,{qN}\,s-4\,{cO}\,{eN}\,{{k4}}^{2}{mF}\,{qN}\,{qO}\,s+2\,{cO}\,{eO}\,{k3}\,{k4}\,{mF}\,{{qN}}^{2}s- \nonumber \\&+{eF}\,{eO}\,{k1}\,{k2}\,{qO}\,{s}^{3}-{eF}\,{k1}\,{k4}\,{{qO}}^{2}{s}^{3}+{eN}\,{{eO}}^{2}{{k2}}^{2}{mF}\,{s}^{2}+ \nonumber \\&+2\,{eN}\,{eO}\,{k2}\,{k4}\,{mF}\,{qO}\,{s}^{2}+{eN}\,{{k4}}^{2}{mF}\,{{qO}}^{2}{s}^{2} -2\,{{eO}}^{2}{k2}\,{k3}\,{mF}\,{qN}\,{s}^{2}- \nonumber \\&+2\,{eO}\,{k3}\,{k4}\,{mF}\,{qN}\,{qO}\,{s}^{2} \end{aligned}$$

(46)