1 Introduction

After the discovery of carbon nanotubes (CNTs) three decades ago [1], extensive studies have been carried out due to their remarkable properties and indispensable role in shaping the modes of futuristic technologies [2]. The dynamic character of CNTs depends strongly on their geometrical structure and physical properties. Collective electronic excitation and surface mode propagation in various settings have been fascinating to understand the transport and interactions properties of CNTs [3]. That’s why, there have been a great deal of interest in theoretical [4,5,6,7,8,9], and experimental [10,11,12] investigations of localized collective oscillations, surface plasmons, acoustic modes and instabilities in single- and multi-walled CNTs. In carbon nanotubes, plasma oscillations with wavelength comparable to electron skin depth are effected by Fermi degeneracy of electrons. Earlier studies of collective excitations utilized different theoretical models like classical hydrodynamics [13] and quantum dielectric response method by random phase approximation [14, 15]. The role of quantum effects like electrons tunneling and statistical pressure is found significant in self-consistent quantum hydrodynamics using the mean-field approach [16,17,18,19,20,21,22]. The excited modes in CNTs and their dispersion properties help in determining the parameters and scales to control electronic and energy transport properties of CNTs.

The characteristics of propagating modes depend upon the nature of CNTs which can be metallic or semiconducting owing to their energy gaps, radii and geometric angles. Mowbray et al. have found the significant role of quantum corrections to fluid modeling of propagating quasiacoustic plasmons [23]. In CNTs, the electron and ion components can be considered as two-species quantum plasma in which both the species can oscillate under the influence of low frequency perturbations. This was considered by Wei and Wang [24] to study the quantum ion-acoustic waves in single-walled CNTs. The assumption of low frequency or long wavelength \(\lambda \gg \lambda _{\mathrm{TF}}\) (Thomas–Fermi length) is valid when the resolvable length scale is several times larger than the average inter-electron distance.

By assuming the cylindrical geometry of single-walled CNTs with surfaces populated by electron-ion-dust plasma, low frequency oscillations on ion and dust time scales have been studied. In dust-ion acoustic wave oscillations in CNTs, it is shown that the increasing dust charge density increases the phase velocity of the wave as compared to the conventional ion-acoustic wave in a plasma [25]. Under the similar conditions, low frequency dust-ion acoustic wave oscillations in multi-walled CNTs [26] and dust acoustic wave oscillations in single-walled CNTs [27] have been studied. The modes frequencies have shown strong influence of the presence of dust and the change of density balance.

In different physical processes like nanoscale engineering and plasma treatment of metallic or semiconducting nanotubes, deposition of metastable charged ion clusters and/or metallic nanoparticles takes place as a covering on single-walled CNTs [28,29,30]. The space charge effect varies appreciably over large distances in charged CNTs as compared to average inter-particle separation. This was considered by Shukla [31] in plasma-assisted CNTs taking charging of the CNTs by electric field emission [32, 33] into account. Excitation of low frequency dispersive oscillations was studied by considering the CNTs as charged dust rods surrounded by ions and electrons. In a similar setting, Shukla and Morfill [34] have considered degenerate electron-hole plasma in CNTs including the surrounding of non-degenerate ions and nanoparticles. The authors have investigated the excitation of low frequency modes due to species collective interactions using the quantum fluid equations and assuming a three-dimensional form of quantum statistical pressure law for electrons and holes. Stable electrostatic excitations in degenerate electron-hole plasmas have also been studied earlier [36, 36, 37].

In metallic CNTs, electron-hole excitation takes place at the surface of CNTs due to the crossover of valence band and conduction band by thermal effects at equilibrium [38]. Hence, geometrical constraint of the CNTs should be taken into account with a 2D form of Fermi energy for reasonably correct explanation of stable and unstable perturbations. It is also worth noting that the exchange interactions were not considered in the model of Ref. [34] which give rise to an additional force on electrons and holes. Exchange-correlation force was included in quantum hydrodynamics by Manfredi et al. [39] with an inspiration by the density functional theory (DFT). It should be stressed here that the inclusion of exchange and correlation effects in quantum hydrodynamics is of phenomenological nature which provides a simple way to include many-particle effects, but limited in scope for flawless application to dynamical problems. The fermion exchange and correlation effects have been proved significant in quantum plasmas [40, 41] and single-walled CNTs [42, 43]. To investigate the low frequency (as compared to ion plasma frequency) electrostatic oscillations and instability threshold of a non-thermal wave in the present work, a charged single-walled CNT is regarded as a long cylindrical shell of radius a surrounded by charged nanoparticles, thereby constituting a plasma of degenerate electrons and holes, and non-degenerate ions and nanoparticles. The 2D geometry of the tubule is taken into account to obtain the dispersion equation and discuss the effects of electron and hole exchange interaction, ion axial drift and hole mass by applying quantum hydrodynamics equations. The species concentration for a typical system is considered for numerical study and illustration of the wave dispersion. In organizing the paper, we have described the mathematical model in Sect. 2, analyzed waves and stability condition in Sect. 3, discussed the results numerically in Sect. 4, and concluded the study in Sect. 5

2 Mathematical Formulation

In a simple representation, let us consider a single-walled CNT as a cylindrical shell surrounded by degenerate electrons and holes, non-degenerate ions and charged nanoparticles. The quasi-neutrality condition requires that the equilibrium number density should satisfy

$$\begin{aligned} q_i n_{i0}+q_h n_{h0} + q_e n_{e0}+q_d n_{d0}=0, \end{aligned}$$
(1)

where subscript ’0’ refers to the unperturbed state, \(q_e (q_h) = -e (e)\) with e the elementary charge, \(q_i = Z_i e\) is the ion charge state, and \(q_d = Z_d e (-Z_d e)\) for positively (negatively) charged nanoparticles (dust). For degenerate electrons and holes, we can write the set of continuity and momentum balance equations

$$\begin{aligned} \frac{\partial n_{j}}{\partial t}+\varvec{\nabla }\cdot (n_j{\mathbf {v}} _{j})=0, \end{aligned}$$
(2)

and

$$\begin{aligned} m_{j}\left[ \frac{\partial }{\partial t}+ \mathbf{v}_j \cdot \nabla \right] \mathbf{v}_j =- q_j \varvec{\nabla }\Phi -\varvec{\nabla }W_{j}+\varvec{\nabla }V_{Bj} + e \varvec{\nabla } V_{xj}, \end{aligned}$$
(3)

where \(m_{j}\) is the species (\(j=e,h\)) effective mass, \(\mathbf{v}_{j}\) the species fluid velocity and \(\hbar\) the Planck’s constant divided by \(2\pi .\) We assume cylindrical coordinates by defining \(\mathbf{x}= \left\{ a,\phi ,z\right\}\) for an arbitrary point on the surface of nanotube with \(r=a\) and \(\varvec{\nabla }=\varvec{\hat{e}}_{z}\left( \partial /\partial z\right) +\varvec{\hat{e}}_{\phi }a^{-1}\left( \partial /\partial \phi \right)\). Furthermore, \(\Phi \left( {\mathbf {x}},t\right)\) is the self-consistent electrostatic potential, \(W_{j}=\left( \pi {\hbar }^{2}/m_{j}\right) n_{j}\) is the Fermi energy, and \(V_{Bj}=(\hbar ^2 / 2m_{j})\varvec{\nabla } (1/\sqrt{n_j}) \bigtriangleup \sqrt{n_j}\) is the quantum Bohm potential (also known as von Weizsäcker correction) arising due to quantum diffraction effects representing the quantum pressure. The last term in Eq. (3) includes the gradient of species exchange potential [44] given by

$$\begin{aligned} V_{xj}= \frac{2 \pi e}{\epsilon k_{Fj}}n_j, \end{aligned}$$
(4)

where \(\epsilon\) is the relative dielectric constant of the system, and \(k_{Fj} = (2 \pi n_{j0})^{1/2}\) is the magnitude of Fermi wavevector. It is noted that contribution of the exchange interaction is increased by the correlation potential [45]. The dynamics of heavy species (\(s=i,d\)) can be described by the fluid equations

$$\begin{aligned} \frac{\partial n_s}{\partial t} + \nabla \cdot (n_s{\mathbf {v}}_{s}) = 0, \end{aligned}$$
(5)
$$\begin{aligned} m_s \left[ \frac{\partial }{\partial t}+ \mathbf{v}_s \cdot \nabla \right] \mathbf{v}_s =- q_s\varvec{\nabla }\Phi , \end{aligned}$$
(6)

where \(m_s\) is the species mass. The self-consistent electrostatic potential \(\Phi _{1}(\mathbf{x},t)\) is given by

$$\begin{aligned} \Phi (\mathbf{x},t)=\int {{\mathrm{d}}^2 \mathbf{x}}^{\prime } \frac{q_{i}n_{i}(\mathbf{x }^{\prime },t)+e n_h (\mathbf{x } ^{\prime },t)-en_e (\mathbf{x }^{\prime },t)+q_{d}n_d (\mathbf{x }^{\prime },t)}{\mid \mathbf{x }-\mathbf{x }^{\prime } \mid }, \end{aligned}$$
(7)

where \(d^2 \mathbf{x^{\prime }}=a\,d \phi ^{\prime }\, dz^{\prime }\). For cylindrical geometry, the Coulomb potential \(1/\mid \mathbf{x }-\mathbf{x }^{\prime } \mid\) can be expressed as [24]

$$\begin{aligned} \Phi ({\mathbf {x}},t)&=\sum _{m=-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{{\mathrm{d}}k}{(2\pi )^{2}}g(a,k,m)\int {\mathrm{d}} \mathbf{x}^{\prime } [ q_{i}n_{i}(\mathbf{x }^{\prime },t)+q_{d}n_{d}(\mathbf{x }^{\prime },t) \nonumber \\&\quad +en_{h}(\mathbf{x }^{\prime },t)-en_e (\mathbf{x }^{\prime },t)e^{ik(z-z^{\prime })+im(\phi -\phi ^{\prime })} ], \end{aligned}$$
(8)

where m is azimuthal quantum number, k is the longitudinal (axial) wave number, \(g(a,k,m)=4\pi I_{m}(ka)K_{m}(ka)\), while \(I_{m}\) and \(K_{m}\) are the cylindrical Bessel functions order m.

3 Linearized Wave Analysis

Let us consider the first-order perturbations and linearize the set of Eqs. (2)–(3) and (5)–(7). For small inertial force of electrons and holes in the limit \(m_{j}/m_s \ll 1\), the l.h.s. of Eq. (3) vanishes under the low frequency limit. Then, one can write for the density perturbation \(n_{j1} (\ll n_{j0})\) from Eq. (3) as

$$\begin{aligned} q_j\nabla \Phi = - \left( \frac{\pi \hbar ^2}{ m_{j}} -\frac{\hbar ^2}{4 m_{j} n_{j0}} \nabla ^2 - \frac{2 \pi e^2}{\epsilon k_{Fj}} \right) n_{j1} \cdot \end{aligned}$$
(9)

The space charge electric field couples the electrons and holes with the heavier species (ions and charged nanoparticles). Equations (5)–(7) on linearizing reduce to

$$\begin{aligned} \frac{\partial n_{s1}}{\partial t} + n_{s0}\nabla \cdot {\mathbf {v}}_{s1} = 0, \end{aligned}$$
(10)
$$\begin{aligned} m_s \frac{\partial \mathbf{v}_{s1}}{\partial t}+ q_s\varvec{\nabla }\Phi _1=0, \end{aligned}$$
(11)

and

$$\begin{aligned} \Phi _1 (\mathbf{x},t)=\int {{\mathrm{d}}^2 \mathbf{x}}^{\prime } \frac{q_{i}n_{i1}(\mathbf{x }^{\prime },t)+e n_{h1} (\mathbf{x } ^{\prime },t)-en_{e1} (\mathbf{x }^{\prime },t)+q_d n_{d1} (\mathbf{x }^{\prime },t)}{\mid \mathbf{x }-\mathbf{x }^{\prime } \mid }\cdot \end{aligned}$$
(12)

Using the expansion of the Coulomb potential (8), we apply the Fourier transform

$$\begin{aligned} F(a,\phi ,z,t) =\sum _{m=-\infty }^{\infty } \int _{-\infty }^{\infty }\frac{{\mathrm{d}}k}{(2\pi )^2} \int \frac{{\mathrm{d}} \omega }{(2\pi )} \times F(a,m,k,\omega ) e^{ik(z-z^{\prime })+im(\phi - \phi ^{\prime }) -i\omega t}, \end{aligned}$$
(13)

where \(F (a,\phi ,z,t)\) denotes any of the abovementioned perturbed quantities. Then, the Fourier transformed perturbed densities and potential obtained from Eqs. (9)–(12) result in

$$\begin{aligned} n_{e1}(a,k,m)= & {} \frac{4em_{e}n_{e0} \Phi _1 (a,k,m)}{\left[ \hbar ^2 \left( k_m^2 + 2k_{Fe}^2\right) -4m_{e}^2 v_{xe}^2\right] }, \end{aligned}$$
(14)
$$\begin{aligned} n_{h1}(a,k,m)= & {} - \frac{4em_{h}n_{h0} \Phi _1 (a,k,m)}{\left[ \hbar ^2 \left( k_m^2 + 2k_{Fh}^2 \right) -4m_{h}^2 v_{xh}^2\right] }, \end{aligned}$$
(15)
$$\begin{aligned} n_{i1}(a,k,m)= & {} \frac{q_i k_m ^2 n_{i0} \Phi _1 (a,k,m)}{\omega ^2 m_i}, \end{aligned}$$
(16)
$$\begin{aligned} n_{d1}(a,k,m)= & {} \frac{q_d k_m ^2 n_{d0} \Phi _1 (a,k,m)}{\omega ^2 m_d}, \end{aligned}$$
(17)

and

$$\begin{aligned} \Phi _1 (a,k,m)= a g(a,k,m)\left[ q_i n_{i1} (a,k,m)+en_{h1} (a,k,m)-en_{e1} (a,k,m)+q_d n_{d1} (a,k,m)\right] , \end{aligned}$$
(18)

where \(v_{xj} = (2 \pi e^2 n_{j0}/\epsilon k_{Fj})^{1/2}\) and \(k_m^2=\left( k^2+m^2/a^2\right)\). Equations (14)–(18) lead to the dispersion relation

$$\begin{aligned} \omega ^2 = \frac{k_m^2 a^2 (\omega _{pi}^2 + \omega _{pd}^2)}{\frac{4 \pi }{g(a,k,m)} + 4a^2 \sum \limits _{j=e,h}(\frac{m_{j}^2 \omega _{pj}^2}{\hbar ^2\left( k_m^2+2 k_{Fj}^2\right) -4m_{j}^2 v_{xj}^2})} \end{aligned}$$
(19)

where the species plasma frequencies are defined by \(\omega _{pj}^2=4\pi n_{j0} e^2/a m_j\), \(\omega _{pi}^2=4\pi n_{i0}Z_{i}^{2}e^{2}/a m_{i}\), and \(\omega _{pd}^2=4\pi n_d Z_d^2 e^2 /a m_d\). The dispersion relation shows a significant effect of exchange interaction and system’s geometry. Curvature effects diminishes for large a corresponding to \(k_{Fj}a \gg 1\).

For analysis, let us consider the modified Bessel functions \(I_{m}(x)\) and \(K_{m}(x)\) in the long wavelength limit \(ka\rightarrow 0.\) In this case, \(I_{m}(x)\longrightarrow a_{m}x^{m}\), \(K_{m}(x)\longrightarrow b_{m}x^{-m}\) (for \(m \ne 0\)) for \(x\longrightarrow 0\) with \(a_{m}=2^{-m}/\Gamma \left( m+1\right)\), \(b_{m}=2^{m-1}/\Gamma \left( m\right)\) and \(K_{0}(x)\longrightarrow \ln \left( 1.123/x\right) .\) In this situation, it is seen that \(\omega =0\) for \(m=0\), whereas for \(m\ne 0,\) the dispersion relation reduces to

$$\begin{aligned} \omega ^2 = \frac{m^2 (\omega _{pi}^2 + \omega _{pd}^2)}{4\left[ \frac{m}{2} + a^2 \sum \limits _{j=e,h}\left( \frac{m_{j}^2 \omega _{pj}^2}{\hbar ^2\left( k_m^2+2 k_{Fj}^2\right) -4m_{j}^2 v_{xj}^2}\right) \right] }\cdot \end{aligned}$$
(20)

In the asymptotic case, we can set \(I_{m}(x)=\exp \left( x\right) /\sqrt{2\pi x}\) and \(K_{m}(x)=\left( \sqrt{\pi /2x}\right) \exp \left( - x\right)\) as \(x\longrightarrow \infty .\) This is pertinent to the limit \(k a\longrightarrow \infty\) which yields

$$\begin{aligned} \omega ^2 = \frac{k_m^2 a^2 (\omega _{pi}^2 + \omega _{pd}^2)}{4\left[ \frac{k a}{2} + a^2 \sum \limits _{j=e,h}\left( \frac{m_{j}^2 \omega _{pj}^2}{\hbar ^2\left( k_m^2+2 k_{Fj}^2\right) -4m_{j}^2 v_{xj}^2}\right) \right] }\cdot \end{aligned}$$
(21)

In both the cases above, it is evident that the quantum effects due to Fermi degeneracy of electrons and holes and many-particle effect of exchange interaction in 2D geometry have significant role on wave dispersion. We have considered the first-order perturbations of plasma parameters for equilibrium charge neutrality condition (1). In some situations, mode excitation in CNTs is accompanied by various drift effects like velocity drift of change carriers in the presence of high field streaming [46] or flow induced currents and voltages [47]. A small perturbation in the presence of species streaming can lead to unstable modes. For a scenario of electron-hole plasma system surrounded by ions and charged nanoparticles (dust) on the nanotube surface, the ion density perturbation produces electric field which eventually gives rise to ion plasma excitation. Let us consider a simple case when ions have an equilibrium axial drift \(v_0\) against the nanoparticles caused by dc electric field. In this case, a non-thermal wave excitation can take place. A streaming term appears in the ion fluid equations which can be included simply by replacing \(\omega\) by \(\omega - k v_0\) in Eq. (16). The resulting dispersion relation from Eq. (18) becomes

$$\begin{aligned} 1 = \frac{g(a,k,m) k_m^2 a^2}{4 \pi \left\{ 1 + \frac{g(a,k,m) a^2}{\pi } \sum \limits _{j=e,h} \left( \frac{m_{j}^2 \omega _{pj}^2}{\hbar ^2\left( k_m^2+2 k_{Fj}^2\right) -4m_{j}^2 v_{xj}^2}\right) \right\} } \left[ \frac{\omega _{pi}^2}{(\omega - k v_0)^2} + \frac{\omega _{pd}^2}{\omega ^2} \right] \cdot \end{aligned}$$
(22)

For threshold value to determine the possibility of an instability, let us consider \(\omega = k v_0 + \Delta\) which yields

$$\begin{aligned} k v_0 = \sqrt{\frac{g}{\pi }} \frac{k_m a \omega _{pd}}{2 (1+ Q_{j})^{1/2}}, \end{aligned}$$
(23)

and

$$\begin{aligned} \Delta ^3 = \left( \frac{\omega _{pi}^2}{2 \omega _{pd}^2} \right) (k v_0)^3, \end{aligned}$$
(24)

where

$$\begin{aligned} Q_{j}= \frac{g(a,k,m) a^2}{\pi } \sum \limits _{j=e,h} \left( \frac{m_{j}^2 \omega _{pj}^2}{\hbar ^2\left( k_m^2+2 k_{Fj}^2\right) -4m_{j}^2 v_{xj}^2}\right) \cdot \end{aligned}$$
(25)

One can observe that a solution of Eq. (24) above

$$\begin{aligned} \Delta = \frac{(1+i \sqrt{3})}{2^{4/3}} \left( \frac{\omega _{pi}}{ \omega _{pd}} \right) ^{2/3} k v_0 , \end{aligned}$$
(26)

is unstable leading to the growth rate

$$\begin{aligned} \gamma = \sqrt{\frac{3 g (a,k,m)}{\pi }} \frac{k_m a}{2^{7/2} (1+Q_{j})^{1/2}} \Omega _{id}, \end{aligned}$$
(27)

where \(\Omega _{id}= \omega _{pi}^{2/3} \omega _{pd}^{1/3}\) is the contribution of ion and dust plasma oscillations. The growth rate \(\gamma\) is influenced by the nanotube parameters and fermionic character of electrons and holes.

4 Numerical Results and Discussion

Let us analyze the dispersion relation (19) numerically for species density, and characteristic parameters of electrons and holes. In many situations [48,49,50,51,52], the presence of heavy charged species (ions, ion clusters, nanostructures, etc.) surrounding the CNTs is inevitable. The ions and charged nanoparticles influence the dynamics of electrons and holes of the tubule which change of density balance and wave potential affecting the transport and dispersion properties of the plasma system [53]. Similar situation is also seen in encapsulation of heavy ions in nanotubes, their laser-mediated engineering, and self-organization phenomena [54]. The space charged effect created by heavy positive or negative species surrounding the charged nanotubes can be described in a self-consistent way.

There are variety of types and sizes or electronic structures of carbon nanotubes and typical ones vary in diameter from 1 to several nanometers. For a metallic carbon tubule, we can estimate the 2D electron density by \(n_e = n_C \nu\) where \(\nu\) is the number of conduction electrons released per carbon (C) atom, and the density of carbon atoms \({n_C} = 0.38{{\AA}^{ - 2}}\) [55]. The electron Fermi wavevector is deduced by \(k_{Fe} = \sqrt{2 \pi n_e}\) which amounts to \(3.5 \times 10^8 \,\text {cm}^{-1}\). Low frequency or long wavelength modes are observed in the metallic carbon nanotubes usually with slightly different electron and hole effective masses, \(m_h/m_e \ge 1\), and similar electron and hole concentrations. For quasi-neutral case, the wave phase velocity should be much smaller than the electron Fermi velocity. For qualitative analysis of dispersion effects, we assume singly charged ions and negatively charged dust particles with typical 2D atomic density of graphite sheet \(38\,\, \text {nm}^{-2}\) with surface electron density approximated by \(4 \times 38\,\, \text {nm}^{-2}\) [8, 24]. Various hole to electron effective mass ratios \(m_h/m_e\) are considered with \(a k_{Fj} \gg 1\) taking care of the charge neutrality condition [56].

Fig. 1
figure 1

(Color online). The wave frequency \(\omega\) normalized by the ion plasma frequency (\(\omega _{pi}\)) is plotted versus \(k a_B\) for various values of azimuthal quantum number m where \(a=16 a_B\)

Full size image

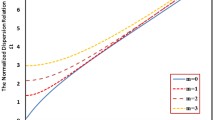
Figure 1 shows the behavior of low frequency (as compared to ion plasma frequency) sound mode against \(k a_B\) for different angular mode numbers, \(m=0,2,4,6\) and 8 where \(a=16 a_B\) with \(a_B\) the Bohr radius. The exchange effects of electrons and holes are included for \(m_h/m_e =3\), where \(m_e\) is assumed to be the bare electron mass. The wave frequency is normalized by the ion plasma frequency \(\omega _{pi}\simeq 1.44 \times 10^{13} \,\,\text {rad/s}\). The electron plasma frequency is \(\omega _{pe}\simeq 6.67 \times 10^{15} \,\,\text {rad/s}\), which is slightly smaller for relatively massive holes. In real numbers, the wave frequency is in terahertz (THz) range (\(\sim 10^{12}\,\,\text {rad/s}\)) which appears to be an order of magnitude lower than the ion plasma frequency. It is seen that the wave frequency increases with m showing an asymptotic behavior in the short wavelength regime. The trend of the frequency curves shows agreement with the hydrodynamic behavior of collective oscillations [8, 23]. THz sound modes in graphene and carbon nanotubes have also been studied using other approaches like Boltzmann transport equation to investigate landau damping [57] and elastic-beam models to predict critical frequencies for coaxial and noncoaxial waves [4].

Fig. 2
figure 2

(Color online). The normalized wave frequency \(\omega /\omega _{pi}\) versus \(k a_B\) showing the effect of exchange interaction on wave dispersion where \(a=16 a_B\), \(m=0\) (red lines) and \(m=2\) (green lines). The solid curves show that the frequency of the wave reduces in the case of nonzero exchange term

Full size image

Many-particle effect of exchange interaction on dispersion relation is illustrated in Fig. 2. In the presence of exchange force, it is found that the wave frequency decreases. For the same electron to hole mass ratio, two cases were considered with \(m=0\) and \(m=2\). The curve separation with and without exchange interaction increases for larger k and more significant at smaller k for nonzero m. The influence of the radii on low frequency oscillations against the dimensionless parameter \(k a_B\) is shown in Fig. 3. The behavior of the curves for \(m=0\) (upper panel) and \(m=2\) (lower panel) is almost similar at higher frequencies. For smaller radii, the frequency is higher and rate of increase of frequency with k is larger. It is evident that the role of nanotube radii on wave dispersion is very important in long wavelength limit and change of frequency for larger k is almost linear. The tubule radius is measured in the units of \(a_B\) which is larger than \(10 \,a_B\) in most of the cases in literature.

Fig. 3
figure 3

(Color online). The dispersion relation is plotted for various values of radii a with \(m=0\) (upper panel) and \(m=2\) (lower panel). Increase in the radii is expressed in terms of the Bohr radius \(a_B\). The wave frequency goes on reducing with a

Full size image

Figure 4 shows the wave frequency for different electron to hole mass ratios. The hole effective mass is larger than the electron effective mass which influences the wave dynamics due to different values of parameters like Fermi energy, Fermi momentum, etc., of holes and electrons. In Fig. 4a (upper panel) for \(m=0\) and 4b (lower panel) for \(m=2\), \(m_h\) is considered either equal to \(m_e\) or 3, 6, and 9 times of \(m_e\). For heavier holes, the wave frequency is very small and dispersion effects are weak. The difference of electron and hole mass does not influence the exchange potential which is independent of species mass. The presence of heavy holes in an electron-hole plasma is a signature of the low frequency modes with frequency falling in the acoustic range [55].

Fig. 4
figure 4

(Color online). Effect of hole mass on the wave dispersion for \(m=0\) (upper panel) and \(m=2\) (lower panel) where \(a=16 a_B\). Increase in the hole mass reduces the frequency which can lead to static approximation of heavy-hole case with \(m_h/m_e \gg 1\)

Full size image

In the presence of equilibrium ion axial drift, the electrostatic wave produced in a non-thermal process exhibits an unstable solution with growth rate given by Eq. (27) which is illustrated in Fig. 5. For \(a=16a_B\) and \(m_h=3m_e\), the growing modes \(m=0, 2\) and 4 are plotted which show saturation for higher wave number. A possible reason of the instability and growth can be identified as transfer of energy to the plasma wave which has been identified previously as a mechanism of the drift velocity thresholds for plasma wave instabilities in cylindrical nanotubes [58].

Fig. 5
figure 5

(Color online). The unstable mode corresponding to \(\Delta\) given in Eq. (26) is plotted for nonzero ion streaming velocity. The normalized growth rate \(\gamma /\omega _{pi}\) for different m values is shown which displays the curves saturation for large wave number where \(a=16 a_B\)

Full size image

In experimental observations on nanotubes and other nanostructures, acoustic modes in GHz and THz frequency range have been identified using various approaches. The studies include THz dispersion properties of super-aligned multi-walled carbon nanotubes [59], acoustic phonon scattering in carbon nanotubes [60], acoustic properties of carbon nanotubes and their interplay with coherent transport [61], acoustic phonon absorption in degenerate carbon nanotubes [62], and so on. In the present work, electrostatic oscillations on time scales defined by ion plasma frequency are considered for \(k\ll k_{\mathrm{Fe}}\) including exchange force in the spirit of DFT, and an equation of state for degenerate fermions. Our main purpose here is to show qualitative properties of low frequency wave on ion time scale which falls in the THz range. The approach subsumes the linearized quantum hydrodynamics invoked earlier [24, 31] in a general way for electrons and holes to elucidate the contributions of exchange interaction, quantum Bohm potential and Fermi degeneracy on low frequency stable and unstable acoustic modes.

It is worth mentioning that collective oscillations are more pronounced for decreasing electron effective mass and increasing mobility. The electron and hole densities and characteristic (Fermi) velocities in graphene based structures can be effectively varied by the gate voltage [63]. In the linearized quantum hydrodynamics formulation of degenerate electron-hole plasma in the presence of massive species here, influence of an external potential on the wave dynamics is not considered. If a gate voltage is applied to the nanotube, one has to take into account various implications on steady-state and dynamic electron and hole transport properties due to dependence of carrier mobility and density on chemical potentials and various scattering phenomena. This has been pointed out in collective THz excitations and sound modes in an electron-hole plasma in gated graphene heterostructures and nanotubes [64, 65]. Extension of the present study for propagating and damping modes in degenerate electron-hole plasma with nonzero gate voltage will be considered in our future work.

5 Conclusion

To conclude, we have studied the low frequency electrostatic oscillations in single-walled CNTs including exchange interactions. The changed single-walled CNT is modeled as a long cylindrical shell which is surrounded by uniform distribution of degenerate electrons and holes as well as non-degenerate ions and nanoparticles (dust). Variation of space charge effect over large distance relevant to ions and nanoparticles scale lengths is considered including fermionic character of electrons and holes. The important role of electrons and holes exchange interaction is emphasized and its influence is discussed in 2D geometry. The dispersion properties of THz frequency acoustic waves for various angular mode numbers and radii of the tubules are discussed with illustrations using typical parameters. In the case of heavy holes, the frequency of the wave goes on decreasing to low values with very weak dispersion. As a special case, ions axial drift at equilibrium is considered which may be caused by a dc electric field and excites an electrostatic wave non-thermally giving an unstable solution. The unstable solution leads to a growing mode possibly due to transfer of energy to the plasma. The low frequency oscillations owing to species collective motion can be useful to determine the wave propagation range and damping properties, like those in typical electron-hole plasmas in CNTs [56], and to study the nanoparticle charging phenomena in a dense plasma [34].