Peculiarities of Spherically Symmetric Counterflow

Abstract

Thermal counterflow in superfluid $^4$He (He II) was studied numerically using the vortex filament model in a spherically symmetric geometry (as resulting from a point heat source). It is found that for the range of temperatures and velocities studied, turbulent tangle of the quantised vortices develops only for sufficiently low temperatures, hinting at the existence of a critical temperature, and only for velocities bounded from above (and presumably from below). A velocity–temperature phase diagram is presented. A simple physical model is proposed that qualitatively explains both observations.

1 Introduction

Unique properties of superfluid $^4$He (He II) allow for a construction of a spherically symmetric flow simply using a point heat source. He II flows as if composed of two interpenetrating fluids [1]—the normal and the superfluid component, each with its own temperature-dependent density ($\rho _{\text {n,s}}$, with the total density of He II $\rho = \rho _\mathrm{s} + \rho _\mathrm{n}$) and velocity field ($\mathbf {v}_\text {n, s}$). Normal fluid behaves approximately classically, possessing viscosity and entropy. The superfluid component is inviscid and carries no entropy, and additionally, its vorticity is quantised with quantum of circulation $\kappa \approx 9.997 \times 10^{-4}$ cm$^{-2}$/s. The vortices in the superfluid component exist as singly quantised thin topological defects (quantised vortices). The turbulence in He II, quantum turbulence [2], takes the form of a dense tangle of quantised vortices in the superfluid component coexisting with possible turbulence of more classical nature in the normal component.

The most studied form of quantum turbulence in He II, counterflow, involves oppositely oriented flows of the normal and superfluid component with relative counterflow velocity$v_{{\text {ns}}}$, typically in a rectilinear channel [3, 4]. Above (temperature- and geometry-dependent) critical counterflow velocity [5], a tangle of quantised vortices develops [3]. The tangle can be created for all temperatures, and its density increases with temperature for fixed counterflow velocity [6]. Note that the vortex tangle in rectilinear counterflow is always slightly anisotropic [7]. A point heat source in an unbounded He II bath, on the other hand, results in spherically symmetric counterflow. As in channel-bound thermal counterflow, the heater generates entropy at rate $\dot{Q}/T$ which is carried away by the normal fluid. This outflux is balanced by the influx of the superfluid component. Assuming spherical symmetry of the flow fields and the heater placed at the origin, the radial velocity $v_{{\text {n}}}$ of the normal fluid through a shell of radius r is

$$\begin{aligned} v_{{\text {n}}}4\pi r^2 \rho S = \frac{\dot{Q}}{T}, \end{aligned}$$

(1)

where S is the entropy per unit mass. The superfluid velocity is given by the standard counterflow condition $\rho _\mathrm{s}v_{{\text {s}}}= \rho _\mathrm{n}v_{{\text {n}}}$. In the following, the strength of the flow will be identified by the radial counterflow velocity at 5 mm distance from the origin, denoted $v_{{\text {ns}}}^\text {5mm}$.

Such flow might be experimentally constructed using a miniature resistive heater suspended on thin lead wires or using a magnetically levitated sphere of a suitable material heated, e.g., by laser irradiation. Turbulence generated by such flow may serve as an ideal case of isotropic turbulence due to the absence of a globally preferred direction which is always present in channel flows. Localised turbulence thus generated might also be a useful model case for the study of the effects of the inhomogeneous distribution of vorticity in quantum turbulence and the associated large-scale tangle dynamics [4].

The present work attempts to characterise the basic properties of the vortex tangle in spherical counterflow. Behaviour of quantised vortices in such flow is studied using numerical simulations of the vortex filament model [8]. A striking contrast with the rectilinear case is found in two aspects: turbulence does not develop at temperatures higher than roughly 1.45 K and the velocities, where the turbulence does occur, also appear to be bounded from above.

2 Computational Setup

The simulations are implemented using the vortex filament model pioneered by Schwarz [9] with the full non-local Biot–Savart interaction included [7]. The vortices are represented as thin lines $\mathbf {s}(\xi )$ parameterised in terms of their arc length $\xi$. The superfluid velocity at point $\mathbf {r}$ (not on any vortex) is given by the Biot–Savart integral

$$\begin{aligned} \mathbf {v}_\mathrm{s}(\mathbf {r}) = \frac{\kappa }{4\pi }\int \frac{{\text {d}}\mathbf {s} \times (\mathbf {r} - \mathbf {s})}{|\mathbf {s} - \mathbf {r}|^3}, \end{aligned}$$

(2)

where integration runs through all vortices in the system. The equation of motion for the vortex is

$$\begin{aligned} \dot{\mathbf {s}} = \mathbf {v}'_\mathrm{s}(\mathbf {s}) + \alpha \mathbf {s}'\times (\mathbf {v}_\mathrm{n} - \mathbf {v}'_\mathrm{s}) - \alpha '\mathbf {s}'\times [\mathbf {s}'\times (\mathbf {v}_\mathrm{n} - \mathbf {v}'_\mathrm{s})], \end{aligned}$$

(3)

where $\mathbf {s}'$ is the local tangent of the line ($\partial \mathbf {s}(\xi )/\partial \xi$) and $\mathbf {v}'_\mathrm{s}$ denotes the standard de-singularisation of the Biot–Savart integral (2) by splitting into local and non-local contributions [9]. The differentials of $\mathbf {s}$ are calculated using fourth-order finite differences, and time stepping is accomplished with fourth- order Runge–Kutta scheme. The distances between the discretisation points of the lines are maintained between $10^{-3}$ and $2\times 10^{-3}$ cm (for a subset of runs, the results were also checked with discretisation distances between 2 and 4 $\times 10^{-3}$ cm). The time step used was approximately $6.4\times$$10^{-4}$, $10^{-5}$ or $10^{-6}$ s for $v_{{\text {ns}}}^\text {5mm}=$ 0.1, 1 or 10 mm/s, respectively (corresponding to temperature-dependent dissipated power of approximately 4, 40 and 400 mW at the maximum; the possibility of localised boiling is outside the scope of the present work).

The spherical flow (1) has a singularity at the origin which is removed using an exponential cutoff as

$$\begin{aligned} v_{{\text {ns}}}= \frac{v_0}{4\pi r^2}\mathrm{e}^{-(r_\text {cutoff}/r)^2}, \end{aligned}$$

(4)

where $v_0$ is the adjustable strength and $r_\text {cutoff} = 200$$\upmu$m in all runs. Additional cutoff is necessary to remove nearly parallel vortex loops that cluster in large quantities (such that they render the calculation unfeasible) near the origin. These vortices are tightly packed near the cutoff region around the origin. Thus, when a vortex loop is fully enclosed by a shell of radius $r^\mathrm{O} = 150$$\upmu$m centred on the origin, it is removed from the simulation. This removal can be thought of as analogous to annihilation of the vortices on the solid surface that would be present in an experimental realisation.

3 Development and Sustainability of the Turbulent Tangle

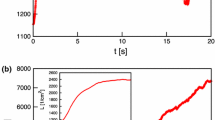
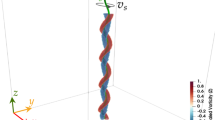
As the initial condition (see an example in Fig. 1a), random loops of total length about 5 cm are placed near the origin. The loops are oriented isotropically and have radii uniformly distributed between 50 $\upmu$m and 1 mm, and their centres are placed in a cube of 1 mm side centred on the origin with uniform distribution. The loops that are not perfectly concentric with the origin are deformed such that part of them points towards the flow source. A straight vortex parallel with the local counterflow velocity is unstable [10], and Kelvin waves of large amplitude are quickly excited (see Fig. 1b), whose initial wavelength in the simulation is most likely affected by the discretisation length. The time evolution of total vortex length $\mathcal {L}= \int {\text {d}}\xi$ for a particular velocity is shown in Fig. 2 for the case of $v_{{\text {ns}}}^\text {5mm}= 0.1$ mm/s. As the evolution progresses, the Kelvin waves from different vortices either interact and create a turbulent tangle near the origin or the vortices are pulled towards the origin and annihilate (Fig. 1c, d, respectively).

Fig. 1

Example of the tangle evolution. a The initial condition; b large-amplitude Kelvin waves induced by the spherical flow; c turbulent tangle at 1.3 K (evolved for $t\approx 0.29$ s); d vortices at 2.1 K shortly before complete annihilation ($t\approx 1.5$ ms). All panels show a $1\times 1\times 1$ mm region. The initial condition a is the same for c and d. The velocity is $v_{{\text {ns}}}^\text {5mm}= 1$ mm/s (Color figure online)

The time in Fig. 2 is normalised by the “fall time” $t_\text {fall}$, the time a superfluid Lagrangian particle would take to fall to the origin from a given distance r. The particle would move towards the origin with the local superfluid velocity, i.e., ${\text {d}}{r}/{\text {d}}{t} = -v_{{\text {ns}}}(r)\rho _\mathrm{n}/\rho$, where $v_{{\text {ns}}}(r)$ is given by Eq. (4) (neglecting the exponential cutoff). Integrating from a given initial position r to $r=0$ yields

$$\begin{aligned} t_\text {fall}(r,T) = \frac{4\pi r^3}{3v_0}\frac{\rho }{\rho _\mathrm{n}}. \end{aligned}$$

(5)

For the normalisation fall time in Fig. 2, $r_0 = 1$ mm is chosen, as this distance is comparable to the initial distance of the vortices from the origin. From Fig. 2, it is clear that when the tangle annihilates, the annihilation takes place at timescale comparable to $t_\text {fall}$. Similar behaviour is observed for other velocities.

Fig. 2

Time evolution of the total vortex line density at several different temperatures for the case of $v_{{\text {ns}}}^\text {5mm}= 0.1$ mm/s. Results obtained from four different (random) initial conditions are shown for every temperature. The time is compensated by the “fall time” from $r=$1 mm given by Eq. (5) (Color figure online)

The tangle evolution was calculated for a range of temperatures and three different $v_{{\text {ns}}}^\text {5mm}$—0.1, 1 and 10 mm/s. A “phase diagram” showing where the turbulence does or does not develop is shown in Fig. 3. No stable turbulence is observed for temperatures higher than 1.45 K, and this temperature appears to decrease with increasing velocity. No stable turbulence was observed for the 10 mm/s case. Note that for the turbulent cases, the simulation did not reach a proper steady state. This is due to a large number of vortices created which make calculating further evolution of the tangle computationally very costly. The qualitative difference in behaviour, however, is clear. The situation presented in Fig. 3 is reminiscent of the critical temperature for the transition to turbulence observed in $^3$He–B by Finne et al. [11]. In $^3$He–B, the critical temperature for turbulence is the consequence of temperature dependence of the mutual friction, which acts to damp Kelvin waves propagating along the vortices. In the present work, the apparent critical temperature is likely the consequence of the compression of the vortex tangle by the inward-facing superflow, as will be shown now.

Fig. 3

Phase diagram of the development of sustained turbulence. The velocity on the y-axis shows $v_{{\text {ns}}}^\text {5mm}$—the counterflow velocity on the 5 mm shell around origin. The size of the points is proportional to the total length of the vortices; the outer radius (red) is proportional to $\bar{\mathcal {L}}_f + \sigma _\mathcal {L}$ and the inner (blue) to $\bar{\mathcal {L}}_f - \sigma _\mathcal {L}$ where $\mathcal {L}_f$ is the total vortex length at the end of simulation run, $\bar{\mathcal {L}}_f$ is the average of $\mathcal {L}_f$ for different runs and $\sigma _\mathcal {L}$ is the associated standard deviation. The existence of sustained turbulence appears to be bounded by both velocity and temperature. For the 10 mm/s case at 1.3 K and 1.35 K, one simulation run in the ensemble experienced a (presumably) transient tangle of high density (Color figure online)

In order for a stable tangle to develop, a sustainable mechanism (one that does not depend on the existence of the large seed vortices) of increase of vortex length must exist. One such mechanism might be the escape of vortex loops from the tangle, which subsequently expand and slow down. The vortex loop expands until it is so slow such that it is pulled back towards the tangle. Obviously, outward-propagating and expanding loops are crucial for this mechanism; therefore, the sizes and positions of such vortex rings in the field of the spherical counterflow are now determined.

Assuming the ring and flow source geometry as in Fig. 4, the motion of the vortex ring is determined by $\dot{\mathbf {s}} = \mathbf {v}^\mathrm{R}_\mathrm{s} + \mathbf {v}_\mathrm{s}^\mathrm{O} + \alpha \mathbf {s}'\times (\mathbf {v}_\mathrm{n} - \mathbf {v}_\mathrm{s})$, where $\mathbf {v}^\mathrm{R}_\mathrm{s}$ is the self-induced velocity of the ring oriented along the x-direction, with magnitude given by [10]

$$\begin{aligned} v^\mathrm{R}_\mathrm{s} = \frac{\kappa }{4\pi R}\left[ \log \left( \frac{8R}{a}\right) - 0.5\right] , \end{aligned}$$

(6)

with $a \approx 10^{-10}$ m denoting the vortex core parameter. The second term is the inward-facing spherical superflow of magnitude $v_\mathrm{s}^\mathrm{O} = v_{{\text {ns}}}\rho _\mathrm{n}/\rho _\mathrm{s}$. The last term is the mutual friction, with $\mathbf {v}_\mathrm{n}$ and $\mathbf {v}_\mathrm{s}$ standing for the total normal and superfluid velocities. The resulting configurations of d and R where the ring is outward-propagating ($\dot{s}_x > 0$) and expanding ($\dot{s}_y > 0$ for the special point in Fig. 4) are shown in Fig. 5. The number of possible configurations clearly decreases as the temperature increases. With increasing velocity, the favourable ring geometries shift to greater distances d which fit the initial condition more poorly. The rings that are too large or too close to the origin are being pulled towards the origin and/or are shrinking. Rings that are too small, on the other hand, have large enough self-induced velocity to escape the flow completely.

Fig. 4

Sketch of the assumed ring geometry in Fig. 5. The self-induced ring velocity is parallel with the line connecting the origin and the ring centre and faces outward. The velocity of the points on the vortex is a combination of three effects: the self-induced velocity $v^\mathrm{R}$, the spherical flow field $v^\mathrm{O}$ and the mutual friction (Color figure online)

Fig. 5

Possible configurations (indicated by the filled regions) of outward-propagating and expanding vortex rings for different temperatures and counterflow velocities. The admissible regions shrink with increasing temperature. For increasing velocities, the favourable configurations shift away from the configuration of the initial condition (i.e., $d \le$ 2 mm) (Color figure online)

4 Conclusions

Spherically symmetric thermal counterflow in He II provides an interesting vantage point for the study of the effect mutual friction has on the development and structure of quantum turbulence. Evolution of a few seed vortex loops in the vicinity of a point heat source was studied using the vortex filament model. It was found that the spherical flow field is very effective at inducing large-amplitude Kelvin waves on the vortices due to the instability present for vortices oriented parallel with the local counterflow velocity. Moreover, it was found that for the velocities studied, sustained turbulent tangle does not develop for sufficiently high temperatures and, counterintuitively, for sufficiently high velocities. A simple physical model explaining these findings is proposed, postulating that at least in the initial stages of the tangle development, outward-propagating and expanding vortex loops are crucial for the development of the tangle.