Study of Dissipative Losses in AC-Biased Mo/Au Bilayer Transition-Edge Sensors

Abstract

We are developing kilo-pixel arrays of transition-edge sensors (TESs) for the X-ray Integral Field Unit on ESA’s Athena observatory. Previous measurements of AC-biased Mo/Au TESs have highlighted a frequency-dependent loss mechanism that results in broader transitions and worse spectral performance compared to the same devices measured under DC bias. In order to better understand the nature of this loss, we are now studying TES pixels in different geometric configurations. We present measurements on devices of different sizes and with different metal features used for noise mitigation and X-ray absorption. Our results show how the loss mechanism is strongly dependent upon the amount of metal in close proximity to the sensor and can be attributed to induced eddy current coupling to these features. We present a finite element model that successfully reproduces the magnitude and geometry dependence of the losses. Using this model, we present mitigation strategies that should reduce the losses to an acceptable level.

1 Introduction

We are developing X-ray microcalorimeter arrays using Mo/Au transition-edge sensors (TES) for the Athena X-ray Integral Field Unit (X-IFU) [1]. This instrument will have a hexagonal microcalorimeter array consisting $\sim 4000$ pixels, read out using frequency-division multiplexing (FDM). This instrument will be designed to achieve an energy resolution of $<2.5\,\mathrm {eV}$ for X-rays with energies in the range of 0.2–7$\,\mathrm {keV}$, and $E/\delta E$ of 2800 up to $12\,\mathrm {keV}$ [2]. TESs developed at NASA/GSFC have historically been designed and optimized for readout schemes that assume a DC current will be used to bias the TES in the superconducting to normal transition. However, for FDM, the devices will be AC biased in the range of 1–5$\,\mathrm {MHz}$.

Previous measurements of AC-biased Mo/Au TESs have shown a frequency-dependent dissipative loss associated with the TES [3], which is not apparent in DC-biased measurements. This dissipation changes the R(T) surface for the TES in a way that is similar to adding a series resistance to the original R(T) seen under DC bias. The size of the additional resistance can be a significant fraction of the ideal operating resistance (up to 10% of the normal state resistance). Consequently, the resistive transition can be significantly broadened compared to the equivalent DC transitions. Since the device energy resolution is highly dependent upon its transition shape, the reduced sensitivity degrades the energy resolution, particularly at higher frequencies.

In this paper, we present measurements of AC losses for TESs in different geometric configurations. These are designed specifically to study the nature of the loss mechanism (Sect. 3). We also present a finite element model (FEM) that is used to simulate the losses that we compare to the measurements (Sect. 4). Finally, we examine possible mitigation strategies for reducing the losses to an acceptable level.

2 Experimental Setup

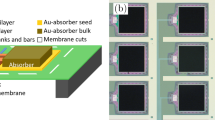
We measured AC losses and transition properties for various TES geometries. Figure 1 shows the different TES geometries recently investigated that we discuss here. The square Mo/Au bilayer is electrically connected with Nb leads. Au banks are placed along the edges of the TES perpendicular to the leads. For devices with stripes, Au stripes are placed parallel to the leads to make the meandering current path to reduce the unexplained excess noise [4, 5]. These devices have no stripes, one stripe, three stripes, and five stripes; all of these devices have contact stems between the TES and absorber that consist of two small circular “dots,” as shown. In addition, there is T-stem device that has a “T”-shaped contact stem. The absorber is a bilayer of Bi and Au with a thickness of $\sim 4$ and $\sim 1.5\,\upmu \hbox {m}$, and the size is $240\,\upmu \hbox {m}$ for all the devices.

Fig. 1

Various TES geometries measured under AC bias. The top row shows the view from side, and the bottom row shows the view from above. Mo/Au bilayers are shown in orange, Nb leads in red, Au banks and strips in orange, Au stems in yellow, and Bi/Au absorbers in pink. Back-etched membranes are shown in gray. The sizes of TESs are 50, 100, 120, and $140\,\upmu \hbox {m}$. The pixels are arranged on a $250\,\upmu \hbox {m}$ pitch in a $8\times 8$ array. The sizes of absorbers are all $240\,\upmu \hbox {m}$ (Color figure online)

We measured four different TES sizes: 50, 100, 120, and $140\,\upmu \hbox {m}$. We also measured TESs with different sheet resistances. The sheet resistances are $\sim 16$, $\sim 28$, and $\sim 37\,\mathrm {m}{\Omega /\Box }$, referred to as regular z, high $z_1$, and high $z_2$, respectively, in this paper. One final variation was to compare pixels that had a TES only to ones that had a TES, stems, and an absorber.

Fig. 2

Schematic for AC-bias setup at the 55 mK cryogenic stage (only showing a single channel circuitry for the LC filter, the transformer, and the TES). The dash-line boxes in the diagram represent the TES chip, the transformer chip, the LC filter chip, the summing chip, the first-SQUID chip, and the second-SQUID chip

Figure 2 shows the 55 mK cryogenic stage setup schematic. The setup consists of the TES chip, a transformer chip, an LC filter chip, a current-summing chip, and a two-staged SQUID. The LC filter chip was fabricated at SRON [6]. The AC bias is applied to the TES via a two-stage voltage division circuit that consists of a $100\,\mathrm {m}{\Omega }$ resistive shunt followed by a capacitive voltage divider. The ratio of $C_\mathrm{bias}/C\sim 10$ is kept constant but the absolute values are varied for each channel to tune the resonant frequency. The resonant frequency of the circuit is then well approximated by $f\sim 1/2\pi \sqrt{L_\mathrm{tot}(C+C_\mathrm{bias})}$, where $L_\mathrm{tot}$ is the total circuit inductance including the filter inductance $L=400\,\mathrm {nH}$ and any additional circuit parasitics ($\sim 10$–$20\,\mathrm {nH}$). The LC chip had six measurable channels, and the resonance frequencies are 1.4, 1.6, 2.0, 2.6, 3.5, and $4.3\,\mathrm {MHz}$. The exact value of the resonant frequency can vary slightly ($\sim 10\,\mathrm {kHz}$) due to variations in the wire bond length. The TESs were connected to the LC filter chip via the 1:5 transformer chip with the coupling constant of $k=0.87$. The low operating resistances of the NASA/GSFC Mo/Au TESs ($R \sim 1\,\mathrm {m}{\Omega }$) necessitate transformer coupling to boost the effective sensor resistance by the square of the transformer turns ratio. The LC filter chip was then connected to the two-staged SQUID via the current-summing chip. The two-summing SQUID was fabricated at VTT [7]. For AC-bias demultiplexing, we used the digital readout electronics that was developed at SRON.

3 Measurement Results

For AC loss measurements, we swept the AC-bias frequency through each resonance frequency while keeping the AC-bias amplitude very small so that the output from the SQUID stayed within a linear region. For each resonance profile, we fit a series RLC resonance model to obtain an equivalent series resistance $R_\mathrm{loss}$ at the TES side of the transformer as a loss figure of merit. We first measured a loss from the shunt resistor and any additional circuit parasitics by shorting the TES inputs on the transformer chip for each resonance. We then measured a loss with a TES and subtracted the loss without the TES from this measurement to determine losses due to the TES.

Figure 3 shows the losses $R_\mathrm{loss}$ for each size of TESs as determined by the resonance width. The losses for the TESs with absorbers are clearly frequency dependent. The number of stripes does not cause a significant difference in the losses, although T-stem TESs tend to have slightly larger losses. As for the regular-z TESs, the losses for $50\,\upmu \hbox {m}$ TESs are smaller than the losses for 100 and $140\,\upmu \hbox {m}$ TESs. The difference due to the sheet resistances can be seen in $50\,\upmu \hbox {m}$ TESs, and the results show larger losses for high-$z_1$ TESs. However, the AC-bias currents used in these measurements are so low that under DC bias, with the same nominal Joule power heating, the TESs would remain in the superconducting state, and therefore it is difficult to imagine that the TES impedance itself is causing the difference in the loss. The most significant difference in the losses is due to absorbers. The losses for TESs without absorbers are 3–10 times smaller than the losses for TESs with absorbers. These results indicate that the most likely largest source of the losses is due to dissipation in normal metal components of the pixels, such as in the absorbers.

The most plausible explanation for these losses is eddy current heating. A bias signal of order a few MHz will produce eddy currents. The eddy currents then dissipate energy as heat in normal metals. This dissipation alters the transition shape in a way similar to if there was a series resistance within the TES. This is particularly apparent low in the transition as the dissipated heat becomes comparable to the heat generated by the TES. The difference in the frequency dependence for regular and high impedance devices is considered to be due to the difference in the electrical conductivity of the absorber normal metal. The absorber is a bilayer of bismuth and gold, with the dominant electrical conductivity coming from the gold. In theory, the eddy current heating is proportional to the conductivity of the metal and therefore a higher purity gold layer for better thermal conductance ironically causes higher loss under AC bias.

Fig. 3

Measured AC losses as equivalent series resistances for various sizes of TES: $50\,\upmu \hbox {m}$ (top left), $100\,\upmu \hbox {m}$ (top right), $120\,\upmu \hbox {m}$ (bottom left), and $140\,\upmu \hbox {m}$ (bottom right). The color represents the sheet resistances. The filled markers represent TESs with absorbers, and the unfilled markers represent TESs without absorbers (Color figure online)

We also measured the different TES I–V characteristics at various bath temperatures and calculated the TES R-T. The top plots in Fig. 4 show, from left to right, the R-T curves for regular-z $50\,\upmu \hbox {m}$ stripeless TESs with absorbers, regular-z $50\,\upmu \hbox {m}$ stripeless TESs without absorbers, and high-$z_1$ $50\,\upmu \hbox {m}$ stripeless TESs with absorbers at various bias frequencies. From these R-T curves, we calculated $\alpha$ ($=d\log R/d\log T$), which are shown in the bottom of the figure. The oscillations seen in both R-T and $\alpha$ are due to weak-link effects [8,9,10].

Fig. 4

Measured R-T and $\alpha$. The R-T curves were derived from I-V measurements. From left to right, regular-z $50\,\upmu \hbox {m}$ stripeless with absorber, regular-z $50\,\upmu \hbox {m}$ stripeless without absorber, and high-$z_2$ $100\,\upmu \hbox {m}$ three-stripe with absorber (Color figure online)

Fig. 5

(Left) Averaged $\alpha$ over $R/R_\mathrm{normal}=20$–30% for regular-z and high-$z_1$ $50\,\upmu \hbox {m}$ stripeless TESs as a function of bias frequency. The dashed lines show the fittings; $\alpha =40.3\times (f/1\,\mathrm {MHz})^{-0.77}$ for regular z, and $\alpha =59.1\times (f/1\,\mathrm {MHz})^{-0.78}$ for high $z_1$. (Right) The ratio of the averaged $\alpha$ over $R/R_\mathrm{normal}=20$–30% under AC bias to the same under DC bias as a function of the loss normalized by the TES normal resistance. The dashed line shows the fitting; $\overline{\alpha _\mathrm{AC}}/\overline{\alpha _\mathrm{AC}}=88\%\times (R_\mathrm{loss}/R_\mathrm{normal}/1\%)^{-0.61}$ (Color figure online)

We calculated the average $\alpha$ over $R/R_\mathrm{normal}=20$–30%, which the nominal TES operating point under AC bias is within, for regular-z and high-$z_1$ $50\,\upmu \hbox {m}$ stripeless TESs. The left plot in Fig. 5 shows the average $\alpha$ as a function of bias frequency. The $\alpha$ decreases as the bias frequency increases, and the frequency dependence of the $\alpha$ to the frequency is approximately $\alpha \propto f^{-0.8}$ for both regular z and high $z_1$ TESs. If we normalize the average $\alpha$ under AC bias ($\overline{\alpha _\mathrm{AC}}$) by the average $\alpha$ under DC bias ($\overline{\alpha _\mathrm{DC}}$), and the loss by the TES normal resistance, the results from both regular z and high $z_1$ reasonably agree (right plot in Fig. 5). The fitting result shows the dependence of $\overline{\alpha _\mathrm{AC}}/\overline{\alpha _\mathrm{DC}}$ to $R_\mathrm{loss}/R_\mathrm{normal}$ is $\overline{\alpha _\mathrm{AC}}/\overline{\alpha _\mathrm{DC}}=88\%\times (R_\mathrm{loss}/R_\mathrm{norma l}/1\%)^{-0.61}$. In the small-signal limit, the energy resolution becomes approximately proportional to $\alpha ^{-1/2}$, and if we extrapolate the fitting, the energy resolution degradation can be kept less than 1% when $R_\mathrm{loss}/R_\mathrm{normal}<0.8\%$.

Fig. 6

Simulated $\alpha$ using the two-fluid model for no loss, a loss of 5% of $R_\mathrm{normal}$, and a loss of 10% of $R_\mathrm{normal}$ (Color figure online)

We have simulated the effect of the AC loss on $\alpha$ using the two-fluid model [11]. The TES model parameters used in the simulation are $T_\mathrm{c}=90\,\mathrm {mK}$, $T_\mathrm{bath}=55\,\mathrm {mK}$, $R_\mathrm{normal}=9.3\,\mathrm {m}{\Omega }$, $R_\mathrm{shunt}=0.2\,\mathrm {m}{\Omega }$, $G=115\,\mathrm {pW/K}$, and $C=0.8\,\mathrm {pJ/K}$. Figure 6 shows the simulated $\alpha$ for TESs with no AC loss, a loss of 5% of $R_\mathrm{normal}$, and a loss of 10% of $R_\mathrm{normal}$. The loss at $4\,\mathrm {MHz}$ for the $50\,\upmu \hbox {m}$ stripeless TES is roughly 4–5%, so the $4\,\mathrm {MHz}$ $\alpha$ in the left bottom plot of Fig. 4 can be compared with the 5%-$R_\mathrm{normal}$ simulation result. Although the scale of degradation is smaller in the simulation, the trend of degradation is fairly comparable with the measurement result.

4 FEM Simulation on Dissipative Losses

We performed electromagnetic simulations on the dissipative loss using finite element modeling with COMSOL Multiphysics. The left plot in Fig. 7 shows the TES model and the volumetric loss density at the absorber for a $50\,\upmu \hbox {m}$ stripeless TES. The absorber of the simulation model is a $4\,\upmu \hbox {m}$ single Au layer. The electrical conductivity of the Au layer was set to $2.5\times 10^8\,\mathrm {S/m}$, so that the simulated loss became comparable to the measurement results. The skin depth of the gold is more than $10\,\upmu \hbox {m}$ at this frequency range and electrical conductivity, and thus the skin effect does not play a significant role. The right plot in the same figure shows the simulated total losses for various bias frequencies along with the measured losses. The simulated $R_\mathrm{loss}$ in the plot was calculated by integrating the volumetric loss density for all the components in the model to obtain the total loss in power and then dividing that by the square of the bias current used in the simulation. The total loss, however, is mostly dominated by the loss at the absorber, and for the $50\,\upmu \hbox {m}$ stripeless TES case, $\sim 90$% of the total loss is due to the loss at the absorber. The simulation shows that the loss is proportional to the square of the bias frequency as eddy current heating predicts, and this frequency dependence reasonably matches with the measurement results.

Fig. 7

Simulated AC loss (volumetric loss density) in absorber for $50\,\upmu \hbox {m}$ stripeless TES (left) and the simulated total AC loss as a function of bias frequency along with the measurement results (right) (Color figure online)

Fig. 8

Simulated AC loss as a function of the distance L between the edge of the TES and the microstrip wire splitting point (left) and the simulated AC loss as a function of the distance H from the TES to the absorber (right) both for $50\,\upmu \hbox {m}$ TES biased in $5\,\mathrm {MHz}$ (Color figure online)

According to the simulation results, the most dominant source of the magnetic field that causes eddy current heating is the non-microstrip region of the bias lead wiring. One possible mitigation to the dissipation is to minimize the length of non-microstrip wire. The left plot in Fig. 8 shows the simulated $R_\mathrm{loss}$ as a function of the distance L between the TES edge and the microstrip wire splitting point for a $50\,\upmu \hbox {m}$ stripeless TES. The current distance between the bias lead and the $50\,\upmu \hbox {m}$ TES is roughly $80\,\upmu \hbox {m}$. We are now developing new TESs with various distances of L to determine the effect of this distance to the loss. In principle, this distance can be minimized down to the edge of membrane, and for $50\,\upmu \hbox {m}$ TESs, it can be down to $\sim 50\,\upmu \hbox {m}$, which makes the loss 20% smaller.

Another possible mitigation is to make the vertical distance from the wire to the absorber as far as possible. The right plot in Fig. 8 shows the simulated $R_\mathrm{loss}$ as a function of the vertical distance H from the TES to the absorber for the same type TES. The current vertical distance is 2–3$\,\upmu \hbox {m}$, and our next generation of TES arrays will have this distance larger than $7\,\upmu \hbox {m}$, which would decrease the loss by a factor of 2 smaller.

Moreover, we are also making thinner TESs to make the TES normal resistance larger. As we discussed in Sect. 3, increasing the TES normal resistance reduces the effect of the loss. Our goal for the sheet resistance is $50\,\mathrm {m}{\Omega /\Box }$, and this would make the TES normal resistance $\sim 3$ times larger than the regular-z TESs. This also means that the $R_\mathrm{loss}/R_\mathrm{normal}$ becomes smaller by a factor of 3.

The combination of these mitigations has the potential to reduce the $R_\mathrm{loss}/R_\mathrm{normal}$ by a factor of $\sim 8$. This will make the current $R_\mathrm{loss}/R_\mathrm{normal}\sim 5\%@5\,\mathrm {MHz}$ for regular-z $50\,\upmu \hbox {m}$ stripeless TESs reduced down to $\sim 0.6\%$. With this small loss ratio, the degradation to the energy resolution will be less than 1%.

5 Summary

We measured AC losses for various TES devices and found that the AC loss is frequency dependent and depends on the amount of the normal metal used in TES, which implied that the loss is due to eddy current heating. We have seen the transition becomes broadened and $\alpha$ becomes smaller due to the AC loss as the bias frequency increases in both actual measurements and two-fluid model simulations. We have also reproduced the AC loss using finite element modeling and found that the dominant source of the eddy current heating is the non-microstrip wire. From simulation results, we identified possible routes to make the effect of the AC loss negligible by reducing the loss approximately by a factor of 8.