Electronic Structure of Vortices Pinned by Columnar Defects in $p_x {\pm }{i}{p_{y}}$ Superconductors

Abstract

Insulating columnar inclusions in a type II chiral $p_x \pm i p_y$ superconductor are shown to affect essentially the electronic structure of pinned vortices, and, as a consequence, the scanning tunneling microscopy (STM) patterns and the microwave response in the vortex phase. The structure of the anomalous spectral branch analyzed within the Bogolubov–de Gennes theory is found to depend strongly on the mutual orientation of the angular momenta of the center of mass and the relative motion of two electrons in the Cooper pair. This dependence reveals itself in the nontrivial behavior of the Hall part of the microwave response and difference of the STM patterns for opposite magnetic field orientations.

1 Introduction

The experimental search for superconducting compounds with unconventional order parameters remains a “hot topic” in the condensed matter community during the recent decades. Such activity is certainly accompanied by a lot of theoretical works aimed to suggest reliable tests probing the gap anisotropy at the Fermi surface. These tests are usually based either on the presence of gap nodes at the Fermi surface or on the order parameter peculiar phase structure in the momentum space. The latter group of suggestions is especially effective for the detection of the so-called chiral superconductivity which could be realized, e.g., in $\mathrm {Sr}_2\mathrm {Ru}\mathrm {O}_4$ [1–3] or heavy-fermions compounds [4, 5]. The Cooper pairs in such superconductors presumably have an internal orbital momentum with a projection $l_z = \pm 1$ on the crystal anisotropy axis. Such a superconducting state breaks the time reversal symmetry as it was observed experimentally [1–3]. Although the compounds listed above are good candidates for p-wave conductivity [6], this type of pairing has not been unambiguously identified in any real material, which increases the importance of various suggestions to detect the p-wave superconductivity.

The nontrivial phase structure of the gap in the momentum space can reveal itself in the presence of an external magnetic field which introduces vortex lines in the superconducting sample. The resulting inhomogeneous superconducting state can reveal many unusual magnetic and transport properties originated from the interplay between the nonzero vorticities in both the momentum and coordinate spaces. This interplay is known to be responsible for the specific structure of quasiparticle subgap states inside the vortex cores investigated, e.g., in Ref. [7, 8]. Unfortunately, the key difference in the quasiparticle spectra of the vortex core states from the ones obtained within the standard Caroli–de Gennes–Matricon (CdGM) solution appears only beyond the quasiclassical consideration. Namely, the anisotropic gap structure can shift the quasiparticle energy quantization rules causing the changes in the minigap value. Taking the simplest gap in the form $p_x \pm i p_y$, we can get a complete suppression of the minigap [7, 8]. The resulting zero energy mode appears to be extremely robust to the perturbations such as the ones caused by scattering centers, etc. [7, 8]. However, the interlevel energy distance inside the cores appears to be pretty small: $\sim \Delta _0^2/E_\mathrm{F}$, where $\Delta _0$ is the superconducting gap magnitude and $E_\mathrm{F}$ is the Fermi energy. The observation of these discrete levels assumes, thus, the use of the experimental techniques with a high energy resolution. The existing scanning tunneling microscopy (STM)/scanning tunneling spectroscopy (STS) data, for instance, cannot provide the reliable evidence for the minigap existence.

In this paper, we suggest an alternative way to detect the chiral superconductivity in the vortex state by studying the distinctive features of the vortex electronic structure in the presence of rather large columnar defects parallel to the applied magnetic field so that the vortex line is pinned over the entire length. Such defects can be created artificially by proton or heavy ion irradiation, by normal particles and nanorods inclusion and by introducing arrays of submicrometer holes. The quasiparticle spectrum in the vortex trapped by the columnar defect was studied in the Refs. [9] and [10] for the simplest case of conventional s-wave superconductor. It was shown that the defect leads to a significant minigap increase up to the values of the order $\Delta _0$. One can expect that for unconventional superconductors, the physical picture of the defect influence on the vortex states can become much more complicated and spectacular since in this case the subgap states bound to the defects or the sample surface can appear even without any vortices [11, 12]. These edge states should interact with the vortex-bound states, thus changing the resulting spectrum significantly. The hybridization of these quasiparticle modes has been studied previously for a particular case of a mesoscopic disk trapping a singly quantized vortex [13, 14]. It was shown that the vortex and antivortex spectra differ qualitatively due to the interplay between the internal vorticity in the momentum space and the vorticity in the coordinate space associated with the vortex.

Besides its fundamental interest, the problem of pinned vortex spectrum in type II superconductors with anisotropic gap is particularly important for understanding the nature of dissipation in such compounds. Indeed, vortex pinning affects the vortex motion and, thus, strongly modifies the superconductor transport properties in the flux flow regime. The microscopic consideration of pinned vortex matter should become important, of course, either at low temperatures well below the critical temperature $T_c$ or for defect dimensions smaller than the coherence length $\xi$ (see discussion in Refs. [15–19]). The opposite limits corresponding to the temperature range close to the critical temperature or large defects can be perfectly described within phenomenological approaches [20–25].

Fig. 1

Quasiparticle specular reflection at the defect surface. Here s and b are the coordinates chosen along and perpendicular to the classical trajectory

In this paper, we do not consider, of course, the full problem of collective pinning which can be resolved only taking account of the vortex–vortex interaction [26]. Instead we focus on the consideration of the individual pinned vortex and study the modification of the local density of states (LDOS) pattern and microwave response caused by the columnar defect. We calculate these quantities on the basis of the quasiparticle spectrum analysis for a pinned vortex. Assuming the columnar defect to have the form of an insulating cylinder of a finite radius $R <\xi$ (see Fig. 1), we study the transformation of the anomalous energy branches originated from the normal reflection at the defect boundary. Let us elucidate the key point of our work and start from a qualitative discussion of the spectrum transformation. We analyze the spectrum within the one-dimensional quasiclassical quantum mechanics of the electrons and holes propagating along the classical trajectories. Each trajectory is defined by an impact parameter b and a trajectory orientation angle $\theta _k$. We assume the reflection to be specular and the trajectory experiencing the break at the defect consists of two rays with the same impact parameters and different $\theta _k$ values satisfying the Snellius law. According to the general theory [27], the quasiparticle spectrum at each trajectory is determined by the order parameter phase difference $\delta \varphi$ at the ends of the trajectory. This phase difference has two contributions arising from the vorticities in the coordinate and momentum spaces: $\delta \varphi = \delta \varphi _{r}+\delta \varphi _{k}$. The first term $\delta \varphi _{r} = \mp 2 \arcsin (b / R)$ originates from the vortex phase in the coordinate space and the signs $-$ and $+$ correspond to opposite vorticities. The second term results from the order parameter phase circulation in the momentum space and for the simplest choice of the chiral p-wave gap function $\Delta \propto e^{i \theta _k}$ this contribution takes the form: $\delta \varphi _{k} = -2\arcsin (b / R) - \pi$. Using the standard expression $\epsilon _J(b) = -\Delta _0 \cos (\delta \varphi / 2) \mathop {\mathrm {sign}}[\sin (\delta \varphi / 2)]$ for the subgap quasiparticle energy level in a single mode Josephson junction [27] we find: $\epsilon _J(b) = - 2 \Delta _0$ $\mathop {\mathrm {sign}}\left( 1-2b^2/R^2\right) b / R \sqrt{1 - b^2/R^2}$ and $\epsilon _J(b) = 0$ for the coinciding and opposite vorticities in the coordinate and the momentum spaces, respectively. Let us denote these vortices as $N_+$ vortex and $N_-$ vortex, correspondingly. The above result illustrates the qualitative difference between the chiral and conventional superconductors. For the latter case, the total phase difference $\delta \varphi$ is completely determined by $\delta \varphi _r$ and, thus, the change of the vorticity sign cannot change the energy levels.

The quasiparticles with large impact parameters $|b| > R$ do not experience the reflection at the defect surface, so the spectrum in this case should be the same as the CdGM spectrum. Provided this crossover occurs at small $b\ll \xi$ we get $\epsilon _{CdGM}(b) \approx \Delta _0 b / \xi$ while in the large $b\gtrsim \xi$ limit the spectrum saturates at the gap value [28]. The above reasoning cannot give this crossover to the CdGM branch because the Doppler shift associated with the superfluid velocity has been omitted. One can expect that in the limit $R\ll \xi$ and $b<R$, this Doppler shift contribution cannot exceed the value of the CdGM energy $\sim \Delta _0 b/\xi$. Thus, for $N_-$ vortices, the spectrum should only slightly deviate from the Fermi level being close to the CdGM solution. In the case of $N_+$ vortices, the Doppler shift correction is small comparing to the term $-2\Delta _0 b/R$ introduced above. The negative sign in the latter expression results in the important spectrum peculiarity: the inversion of the anomalous branch slope for the $N_+$ vortex pinned by the defect comparing to the slope for a free vortex. Note that this inversion effect has been overlooked in numerical calculations presented in Ref. [29]. The change in the slope sign can cause rather drastic changes in the measurable characteristics. In particular, according to the spectral flow theory [30], it is the behavior of the anomalous branch which determines the high-frequency conductivity and Kerr effect. The qualitative behavior of the Kerr angle dependence on the magnetic field is discussed.

The rest of the paper is organized as follows. In Sect. 2, the basic equations used for the spectrum calculation are introduced. In Sect.  3, we find the quasiparticle spectrum for a single-quantum vortex trapped by a columnar defect. Section 4 is devoted to the analysis of the local density of states (DOS). In the next Sect. 5, we discuss the defect influence on the high-frequency field response.

2 Model

We consider a columnar defect as an insulator cylinder of the radius R. The magnetic field $\mathbf B$ is parallel to the cylinder axis z, and the vortex axis coincides with the cylinder axis. Thus, the system is invariant with respect to the translations along the z-axis and the rotations around it. For simplicity, we restrict ourselves with a two-dimensional case and consider a motion of quasiparticles only in the (x, y) plane. The excitation spectrum can be obtained from the Bogolubov–de Gennes equations (BdG) written for a two-component quasiparticle wave function $\psi (\mathbf {r}) = (u,\;v)$:

$$\begin{aligned} -\frac{\hbar ^2}{2m}\left( \nabla ^2 + k_\mathrm{F}^2\right) \tau _3 \psi + \left( \widehat{\Delta }(\mathbf {r}) \tau _+ + h.c.\right) \psi = \epsilon \psi \ , \end{aligned}$$

(1)

where $\tau _\pm = (\tau _1 \pm i \tau _2) / 2$, $\tau _1$, $\tau _2$, and $\tau _3$ are the Pauli matrices in the Nambu space, $\hbar k_\mathrm{F}$ is the Fermi momentum, and $\widehat{\Delta }$ is the superconducting gap operator. Considering an extreme type II superconductor with a large London penetration depth $\lambda \gg \xi$, we neglect the vector potential of the magnetic field $A_\theta \approx B r / 2$ because its contribution to the superfluid velocity $A/\varPhi _0 \propto r/\lambda ^2$ is small compared to the gradient of the order parameter phase $\propto 1/r$ [31]. Here r and $\theta$ are the polar coordinates and $\varPhi _0$ is the magnetic flux quantum. We assume that the quasiparticle wavefunction does not penetrate the defect and imply the zero boundary conditions at the defect surface:

$$\begin{aligned} \psi (R, \theta ) = 0 \ . \end{aligned}$$

(2)

2.1 Quasiclassical Approach

The superconducting gap $\widehat{\Delta }$ varies at the spatial scale $\xi$ which is much greater than the atomic scale $k_\mathrm{F}^{-1}$ in all known superconductors. Hence one can solve the system (1) within the quasiclassical approximation. We follow the approach described in Refs. [9, 30] and introduce the momentum representation:

$$\begin{aligned} \psi (\mathbf r) = \int \frac{d^2k}{(2\pi )^2} e^{i\mathbf {kr}}\psi (\mathbf k) \ , \end{aligned}$$

(3)

where $\mathbf k = k (\cos \theta _k, \sin \theta _k) = k \mathbf {k}_0$. The unit vector $\mathbf k_0$ which depends on the angle $\theta _k$ determines the trajectory direction in the (x, y) plane. We assume that the solutions of the Eq. (1) correspond to the absolute momentum values close to $\hbar k_\mathrm{F}$: $k = k_\mathrm{F} + q$ ($q \ll k_\mathrm{F}$). Using the Fourier transformation

$$\begin{aligned} \psi (\mathbf k) = \frac{1}{k_\mathrm{F}} \int \limits _{-\infty }^{+\infty } \mathrm{d}s\;e^{i(k_\mathrm{F} - k) s}g(s, \theta _k), \end{aligned}$$

(4)

one can finally express the wavefunction in the coordinate space $\psi (\mathbf r)$ through the function $g(s, \theta _k)$:

$$\begin{aligned} \psi (r, \theta ) = \int \limits _0^{2\pi } e^{i k_\mathrm{F} r \cos (\theta _k - \theta )} g \left[ r \cos (\theta _k - \theta ), \theta _k\right] \; \frac{\mathrm{d}\theta _k}{2\pi } \ . \end{aligned}$$

(5)

To obtain the quasiclassical equation along the quasiparticle trajectory, we introduce an angular eikonal:

$$\begin{aligned} g(s,\theta _k) = e^{i S(\theta _k)} \overline{\psi }(s, \theta _k) \ , \end{aligned}$$

(6)

assuming $\overline{\psi }$ to be a slowly varying function of $\theta _k$. Quasiparticles propagating along the trajectories are characterized by the angular momentum $\mu$:

$$\begin{aligned} \mu = -k_\mathrm{F} b = \frac{\partial S}{\partial \theta _k} \ . \end{aligned}$$

(7)

Here we introduce the impact parameter b which determines the classical trajectory along with the $\theta _k$ angle. The angular momentum is conserved due to the axial symmetry of the system.

Substituting (5) and (6) into (1), one can obtain the equation for $\overline{\psi }$ at the classical trajectory (see Fig. 1):

$$\begin{aligned} -i\hbar v_\mathrm{F} \tau _3 \frac{\partial \overline{\psi }}{\partial s} + \left( \tau _+ \overline{\Delta }(\mathbf r, \theta _k) + h.c. \right) \overline{\psi }= \epsilon \overline{\psi }\ , \end{aligned}$$

(8)

where $m v_\mathrm{F} = \hbar k_\mathrm{F}$, $\overline{\Delta }$ is the quasiclassical form of the gap operator, and s is a coordinate along the classical trajectory. The transition from the (s, b) coordinates (see Fig. 1) to the usual cartesian (x, y) coordinates can be performed as follows:

$$\begin{aligned} x = s \cos \theta _k - b \sin \theta _k,~ y = s \sin \theta _k + b \cos \theta _k \ . \end{aligned}$$

(9)

Further consideration requires an explicit expression of the gap operator $\widehat{\Delta }$.

In the homogeneous case, the gap operator for the superconductors with spin-triplet coupling is determined by a momentum-dependent vector $\mathbf d$ [32]:

$$\begin{aligned} \widehat{\Delta }(\mathbf k)= & {} -i\sigma _y (\mathbf d(\mathbf k), \mathbf \sigma ) \nonumber \\= & {} \begin{pmatrix} -d_x(\mathbf k) - i d_y(\mathbf k) &{} d_z(\mathbf k)\\ d_z(\mathbf k) &{} d_x(\mathbf k) - i d_y(\mathbf k)\\ \end{pmatrix} \ . \end{aligned}$$

(10)

We consider a superconductor with $d_x = d_y = 0$ and $d_z \propto \hat{k}_x + i \hat{k}_y,~ \hat{k}_x - i \hat{k}_y$. Such an order parameter possibly describes a superconducting state in $\mathrm {Sr_2RuO_4}$ [33] and heavy-fermion compounds [34]. Separating the spin dependence and generalizing the operator for the inhomogeneous case, we get the following expression for $\Delta$:

$$\begin{aligned} \widehat{\Delta }= \frac{\Delta _0}{2 k_\mathrm{F}}\left( \left\{ \eta _+(\mathbf r),\;-i\partial _+ \right\} + \left\{ \eta _-(\mathbf r),\;-i\partial _- \right\} \right) \ , \end{aligned}$$

(11)

where $\Delta _0$ is a gap magnitude, $\eta _\pm (\mathbf r)$ are the coordinate-depending order parameters, which describe the Cooper pairs with the opposite angular momenta directions, $\{a, b\} = ab + ba$ is an anticommutator and $\partial _\pm = \partial /\partial x \pm i \partial / \partial y$. Two degenerate ground states are described by the following order parameters: $\eta _+ = 1$, $\eta _- = 0$ and $\eta _- = 1$, $\eta _+ = 0$. In a general inhomogeneous case, both order parameters are nonzero, while usually far from the topological defects, one of them is suppressed. The areas where only one order parameter is nonzero are called chiral domains.

One can find the quasiclassical form of $\widehat{\Delta }$, neglecting the terms of the order of $(k_\mathrm{F} \xi )^{-1}$:

$$\begin{aligned} \overline{\Delta }(\mathbf r, \theta _k) = \Delta _0 \left( \eta _+(\mathbf r) e^{i \theta _k} + \eta _-(\mathbf r) e^{-i \theta _k}\right) \ . \end{aligned}$$

(12)

Hence the Eq. (8) takes the following form:

$$\begin{aligned} -i \xi \tau _3 \frac{\partial \overline{\psi }}{\partial s} + \left( D(\mathbf r, \theta _k) \tau _+ + h.c.\right) \overline{\psi }= \varepsilon \overline{\psi }\ , \end{aligned}$$

(13)

where $\xi = \hbar v_\mathrm{F} / \Delta _0$ is the coherence length and $D(\mathbf r, \theta _k) = \eta _+(\mathbf r)\exp (i \theta _k) + \eta _-(\mathbf r) \exp (-i \theta _k)$, $\varepsilon = \epsilon / \Delta _0$.

The axially symmetric vortex solutions are described by the following order parameters [35, 36]:

$$\begin{aligned} \eta _\pm (\mathbf r) = f_\pm ^{(m)}(r)e^{i(m \mp 1)\theta } \ , \end{aligned}$$

(14)

where m is the sum of the winding numbers in the coordinate and the momentum spaces. One of the functions $f_\pm$ saturates at unity at large $r \gg \xi$ and another one vanishes far from the core. The magnetic flux carried by the vortex is determined by the winding number of the dominating order parameter component, i.e., it is equal to $m + 1$ flux quanta for a vortex trapped in the $\eta _-$ domain and $m - 1$ flux quanta for a vortex in the $\eta _+$ domain. Using (9) and (14), we find the order parameter profile at the classical trajectory:

$$\begin{aligned} D_b(s, \theta _k) = e^{i m \theta _k} \sum f_\pm ^{(m)}\left( \sqrt{s^2 + b^2}\right) \left( \frac{s + ib}{\sqrt{s^2 + b^2}} \right) ^{m \mp 1} \ . \end{aligned}$$

(15)

We can separate the $\theta _k$ dependence, introducing a new function:

$$\begin{aligned} \overline{\psi }= e^{i (m \tau _3/2)\theta _k} \widetilde{\psi }\end{aligned}$$

(16)

and the Eq. (13) becomes

$$\begin{aligned} -i \xi \tau _3 \frac{\partial \widetilde{\psi }}{\partial s} + \left( \widetilde{D}_b(s) \tau _+ + h.c.\right) \widetilde{\psi }= \varepsilon \widetilde{\psi }, \end{aligned}$$

(17)

where $\widetilde{D}_b(s) = \exp (-im\theta _k) D_b(s, \theta _k)$. For definiteness, we consider the $\eta _+$ domain, thus, the values $m = 2$ and $m = 0$ correspond to $N_+$ and $N_-$ vortices, respectively.

The true quasiparticle wavefunction $\psi (k, \theta _k)$ must be, of course, a single-valued function of $\theta _k$. This requirement imposes a certain quantization rule: the value of $\mu + m / 2$ must be an integer number. Since m is even for the singly quantized vortex, the angular momentum $\mu$ is an integer (cf. Ref. [7, 8]). It means that defect does not change the quantization rule and does not shift the zero energy level.

In this paper, we do not solve the gap equation self-consistently restricting ourselves to the consideration of several model profiles of the radial dependence of the gap function. Such consideration is justified by the fact that the main factor affecting the quasiparticle energy branches comes from the order parameter phase difference at the ends of the classical trajectories and the Doppler shift caused by the superfluid velocity. We claim that the qualitative behavior of the spectral branches is only weakly influenced by the specific shape of the profile of the order parameter absolute value. In order to check this statement, we compared subgap spectra for two different model profiles of the order parameters. In the first one, we assumed the order parameters to behave similarly to the free vortices:

$$\begin{aligned} f_+ = \frac{r}{\sqrt{r^2 + \xi ^2}},~f_- = 0 \ . \end{aligned}$$

(18)

The second model form assumes the order parameter suppression near the defects or the sample surface [37, 38]:

$$\begin{aligned} f_+ = \tanh \left( \frac{r - R}{\xi }\right) ,~f_- = 0 \ , \end{aligned}$$

(19)

where $r>R$. As we expected, the qualitative behavior of the subgap spectral branches appears to be robust to the changes in the order parameter profile.

2.2 Boundary Conditions

Now we need to rewrite the boundary condition (2) imposed on the quasiparticle wavefunction in the quasiclassical form. Using the expressions (5) and (16), we obtain

$$\begin{aligned} \int \limits _0^{2\pi } e^{i k_\mathrm{F} R \cos \alpha + i \mu \alpha } e^{i m \tau _3 \alpha / 2}\widetilde{\psi }\left( R \cos \alpha \right) \; \mathrm{d}\theta _k = 0 \end{aligned}$$

(20)

Supposing the argument of the first exponent to vary rather fast we can use the stationary phase method in order to evaluate the integral. The stationary phase points are given by the equation $\sin \alpha = \mu / k_\mathrm{F} R = -b/ R$. This equation has no solutions if the impact parameter is greater than the defect radius. It means that the integral (20) is negligible and no boundary conditions are required because the trajectory does not hit the defect. In the opposite case $|b|<R$, there are two stationary angles $\alpha _1 = -\arcsin (b/R)$ and $\alpha _2 = \pi - \alpha _1$ that correspond to the incident and specularly reflected classical trajectories. The sum of the two contributions provides the boundary condition:

$$\begin{aligned} e^{i\varphi _0}\widetilde{\psi }(s_0) = e^{-i \varphi _0}\widetilde{\psi }(-s_0) \ , \end{aligned}$$

(21)

where $s_0 = \sqrt{R^2 - b^2}$ and

$$\begin{aligned} \varphi _0 = k_\mathrm{F} s_0 + (\mu + m \tau _3 / 2) (\alpha _1 - \alpha _2)/2 + \pi / 4 \ . \end{aligned}$$

3 Excitation Spectrum

3.1 Large Impact Parameters $|b| > R$

In this case, the trajectory does not hit the defect and does not experience any reflection, thus, the spectrum should be similar to the standard CdGM solution [28].

Here we find spectrum and wave functions considering the imaginary part of $\widetilde{D}$ as a perturbation [39, 40]. Neglecting the corresponding part in (17), we find

$$\begin{aligned} -i \xi \tau _3 \frac{\partial \widetilde{\psi }}{\partial s} + \tau _1 Re \widetilde{D}_b(s) \widetilde{\psi }= \varepsilon \widetilde{\psi }\ . \end{aligned}$$

(22)

This equation has a zero eigenvalue with the following eigenfunction:

$$\begin{aligned} \widetilde{\psi }_{b} = \frac{1}{\sqrt{2I_b}} \left( \begin{array}{l}i\\ 1\end{array}\right) e^{-K_b(s)} \ , \end{aligned}$$

(23)

where

$$\begin{aligned} K_b(s) = \frac{1}{\xi } \int \limits _0^s Re \widetilde{D}_b(s')\;\mathrm{d}s',~ I_b = \int \limits _{-\infty }^{+\infty } e^{-2K_b(s)}\;\mathrm{d}s \ . \end{aligned}$$

The first-order perturbation theory yields the following excitation spectrum:

$$\begin{aligned} \varepsilon _b = \frac{1}{I_b}\int \limits _{-\infty }^{+\infty } Im \widetilde{D}_b(s) e^{-2K_b(s)}\;\mathrm{d}s \ . \end{aligned}$$

(24)

3.2 Small Impact Parameters $|b| < R$

In this case, the quasiparticle experiences reflection from the cylinder surface which modifies the spectrum. In order to solve the Eq. (17), we have to take into account the boundary conditions (21), so we introduce the function:

$$\begin{aligned} \varPsi (s) = \left\{ \begin{array}{l} e^{+i\varphi _0}\widetilde{\psi }(s), \quad s > 0\\ e^{-i\varphi _0}\widetilde{\psi }(s), \quad s < 0\\ \end{array}\right. \end{aligned}$$

(25)

Due to the boundary condition (21), $\varPsi (s_0) = \varPsi (-s_0)$. The new function satisfies the following equation:

$$\begin{aligned} -i\xi \tau _3 \frac{\partial \varPsi }{\partial s} + \left( \tau _+ G_b(s) + h.c.\right) \varPsi = \varepsilon \varPsi \ , \end{aligned}$$

(26)

where $G_b(s) = e^{i \phi \mathop {\mathrm {sign}}s} \widetilde{D}_b(s)$ and $\phi = m(\alpha _1 - \alpha _2) / 2$. The Eq. (26) is similar to a quasiclassical equation describing a Josephson junction: the order parameter is constant if $s \rightarrow \pm \infty$. Assuming such step-like form of the order parameter along the trajectory, we find the energy [27]:

$$\begin{aligned} \varepsilon = \chi \cos (\phi + \pi /2) = -\chi \sin \phi \ , \end{aligned}$$

(27)

where $\chi = \mathop {\mathrm {sign}}\left( \cos \phi \right)$. The energy depends only on the order parameter phase difference on the trajectory ends. The additional phase difference $\pi$ arises from the order parameter symmetry property $G_b(s) = -G_b^*(s)$. The above approximate solution can be, of course, improved if we take account of the Doppler shift of quasiparticle energy caused by the superflow around the core. Such improvement is particularly important for the case of $N_-$ vortex when the expression (27) yields $\varepsilon = 0$ for all impact parameters and, thus, does not allow to get the correct slope of the anomalous spectral branch.

We can apply the perturbation theory used above in order to obtain a more precise solution. First we neglect the imaginary part of G and obtain the wave functions corresponding to the zero energy $\varepsilon = 0$:

$$\begin{aligned} \varPsi _b(s) = \frac{1}{\sqrt{2 I_b}} \left( \begin{array}{l} i\chi \\ 1\end{array}\right) e^{-K_b(s)},~s > s_0 \ , \end{aligned}$$

(28)

where

$$\begin{aligned} K_b(s) = \frac{\chi }{\xi }\int \limits _{s_0}^s Re G_b(s')\;\mathrm{d}s',~ I_b(s) = 2 \int \limits _{s_0}^{+\infty } e^{-2K_b(s)}\;\mathrm{d}s \ . \end{aligned}$$

The eigenfunction is even, $\varPsi _b(s) = \varPsi _b(-s)$. This localized solution can be used as a zero-order approximation for the wave function. Within the first-order perturbation theory, we find the spectrum:

$$\begin{aligned} \varepsilon _b = \frac{2 \chi }{I_b} \int \limits _{s_0}^{+\infty } Im G_b(s) e^{-2K_b(s)}\; \mathrm{d}s \ . \end{aligned}$$

(29)

The behavior of the subgap spectral branches found within this perturbation procedure is illustrated in Fig. 2a, b for $N_+$ and $N_-$ vortices, respectively. To verify the approximate solution, we have also solved the quasiclassical equations (17) numerically. Hereafter we show the results for a model form of the order parameters given by the expression (19). The difference between the spectrum for this profile and the profile defined by the expression (18) results in a minor change of the slope of the spectral branches. The results of numerical calculations shown in Fig. 2 demonstrate a good coincidence with the ones obtained using the perturbation approach except the energies close to the superconducting gap $\Delta _0$. The failure of the perturbation procedure for the $N_+$ vortex arises from the divergence of the wave function (28) localization radius at the points $\mu = \pm k_\mathrm{F} R / \sqrt{2}$. At these points, the analytical solution marked as blue-dashed lines experiences a break which is shown in Fig. 2a by blue- dotted lines. The sharpness of the features at the points $\mu = \pm k_\mathrm{F} R$ is an artifact of the quasiclassical approach. These peculiarities should be slightly smoothed out at the scale of $\mu \sim 1$ if one takes the diffraction effects into account.

Fig. 2

Quasiparticle spectrum for two vortex types found from the solution of the quasiclassical Eq. (17). The numerical solution is shown by the solid red lines, the dashed blue lines correspond to the results of perturbation theory, the black dotted line is the CdGM branch. The defect radius is $R = 0.4\xi$, $(k_\mathrm{F} \xi )^{-1} = 0.06$, $\mu = -k_\mathrm{F} b$. The blue vertical dotted lines in the panel (a) correspond to the values $\mu =\pm k_\mathrm{F} R/\sqrt{2}$ (Color figure online)

The spectrum of the $N_-$ vortex does not differ qualitatively from the CdGM solution (see Fig. 2b). In this vortex, the order parameter vorticity in $\mathbf r$-space is compensated by its chirality in $\mathbf k$-space and the phase difference at the ends of every classical trajectory is always equal to $\pi$. All the changes result from the order parameter suppression at the scale of $\xi$ near the defect. Thus, we see that this suppression does not cause any qualitative changes in the spectrum.

In opposite, for the $N_+$ vortex, the phase difference at the ends of classical trajectory causes a significant spectrum modification even for small impact parameters (see Fig. 2a). As a result, the subgap spectrum consists of three branches. Within the perturbation approach, these branches reveal themselves in the spectrum discontinuity at the points $b = \pm R / \sqrt{2}$, where perturbation theory is not applicable. One can observe this energy discontinuity even in the simplified expression (27) where $\chi$ changes sign at the points $b = \pm R / \sqrt{2}$. There are two branches which transform into the CdGM-like branch at large $|b| > R$ and approach the superconducting gap at small b. The similar spectral branches have been observed earlier in the spectrum of a pinned vortex in a s-wave superconductor [9]. In addition to these branches, there is an almost linear branch that goes through the origin with the slope inversed with respect to the CdGM solution (cf. the introductory section). We propose that this branch corresponds to the edge states bound to the surface of the unconventional superconductor. The spectrum of these surface states can be easily found within the quasiclassical approach solving the Eq. (26) with $D = \exp (i \theta _k)$ which corresponds to the homogeneous chiral domain. Performing the same calculations as we had done for a vortex, we obtain the following spectrum:

$$\begin{aligned} \varepsilon _b = \left\{ \begin{array}{ll} -\frac{b}{R},~&{}\quad |b| < R\\ -\mathop {\mathrm {sign}}b,~&{}\quad |b| > R \end{array}\right. \ . \end{aligned}$$

(30)

Fig. 3

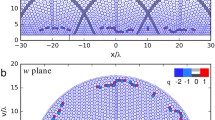
Comparison of the subgap spectral branches (red lines) in the $N_+$ vortex with the ones found in Ref. [29] from numerical simulations on the basis of BdG theory (blue-dashed lines) (Color figure online)

Note that this simple form of the spectrum does not take into account the order parameter suppression at the defect surface. The improved description accounting for this suppression results in a slight modification of the spectral branch slope. This quasiparticle spectrum is close to the anomalous spectrum branch in Fig. 2a, so we can claim that this branch corresponds to the surface states. The spectrum of quasiparticles in the $N_-$ vortex does not contain the branch of the edge states and, thus, the $N_-$ vortex suppresses the edge states on not very large defects $R \lesssim \xi$. In the opposite limit $R \gg \xi$, we can expect that the spectra of quasiparticles for both vortices are similar to the spectra of the defect, because the superfluid velocity decays as 1 / r and the major contribution to the quasiparticle energy arises from the internal chirality of the superconductor.

The anomalous branch with the inverse slope has been overlooked by the authors of Ref. [29]. The results of their numerical calculations are shown in Fig. 3. Note that at large angular momenta, the spectrum found in Ref. [29] transforms into the CdGM solution as expected. Our solution shows the similar behavior at large momenta but the spectrum is shifted because of the suppression of the order parameter.

The spectrum is certainly sensitive to the type of the quasiparticle reflection at the defect boundary. We have shown that the reflection of the trajectories is specular in the quasiclassical limit $k_\mathrm{F} R \gg 1$ for a cylindrical defect. Assuming the defect to be smooth on the atomic length scale, one can expect this reflection to remain specular for an arbitrary defect shape. However, the reflection is no more specular if the defect surface is rough on the atomic length scale. The deviations from the specular reflection can cause the coupling of the trajectories with different impact parameters and, thus, result in the broadening of the spectral branches for $\mu < k_\mathrm{F} R$.

4 Local Density of States

As a next step, we turn to the calculations of the LDOS which can be probed, e.g., in the STM/STS studies. The measurable quantity in these experiments is the local differential conductance:

$$\begin{aligned} \frac{\mathrm{d}I/\mathrm{d}V}{(\mathrm{d}I/\mathrm{d}V)_N} = \int \limits _{-\infty }^{+\infty } \frac{N(\mathbf r, \epsilon )}{N_0} \frac{\partial f(\epsilon - eV)}{\partial V}\;\mathrm{d}\epsilon \ , \end{aligned}$$

(31)

where V is the voltage, $(\mathrm{d}I/\mathrm{d}V)_N$ is the junction conductance in the normal state, N is the LDOS in the superconductor, $N_0$ is the normal state DOS, and $f(\epsilon ) = \left[ 1 + \exp (\epsilon /T)\right] ^{-1}$ is the Fermi function. Within the quasiclassical approach, the local DOS is determined as follows:

$$\begin{aligned} N(\mathbf r, \epsilon ) = \frac{1}{2\pi } \int k_\mathrm{F} \left| u_{b}(\mathbf r)\right| ^2 \delta \left( \epsilon - \epsilon _{b}\right) \;\mathrm{d}b \ . \end{aligned}$$

(32)

Substituting (32) into (31), we obtain

$$\begin{aligned} \frac{\mathrm{d}I/\mathrm{d}V}{(\mathrm{d}I/\mathrm{d}V)_N} = k_\mathrm{F} \int \limits _{-\infty }^{+\infty } \frac{|u_b(\mathbf r)|^2}{N_0} \frac{\partial f(\epsilon _b - eV)}{\partial V}\;\mathrm{d}b \ . \end{aligned}$$

(33)

The local DOS and the differential conductance are both expressed through the electron-like wave function $u_{b}(\mathbf r)$ corresponding to the energy $\epsilon _{b}$. We use the expressions (5), (6), and (16) in order to restore $u_b(r)$. If $k_\mathrm{F} r \gg 1$, it can be evaluated using the stationary phase method. In this limit, the wave function is determined by the quasiclassical wave functions at two classical trajectories passing through the point $(r,\theta )$:

$$\begin{aligned} u_{b}(r, \theta ) = \frac{e^{i \mu \theta + i m \theta / 2}}{\sqrt{2\pi i k_\mathrm{F} r}} \sum \limits _{j=1,2} e^{i \varphi _j} \frac{\widetilde{\psi }_{u,b}\left( r \cos \beta _j\right) }{\sqrt{\cos \beta _j}} \ , \end{aligned}$$

(34)

where $\varphi _j = k_\mathrm{F} \cos \beta _j + i (\mu + m/2) \beta _j$, $\beta _1 = -\arcsin b/R$, $\beta _2 = \pi - \beta _1$. Neglecting the part oscillating at the atomic length scale and applying the normalization condition, we obtain

$$\begin{aligned} \left| u_{b}(r)\right| ^2 = \frac{\exp \left[ -2K_b\left( \sqrt{r^2 - b^2}\right) \right] }{\pi I_b \sqrt{r^2 - b^2}} \end{aligned}$$

(35)

Fig. 4

The local differential conductance vs the voltage V and the distance from the vortex axis r for different vortex types. Here we put $R = 0.4\xi$ and $T = 0.02 \Delta _0$ (Color figure online)

The local conductance is shown in Fig. 4 for different types of vortices. The conductance profile for the $N_-$ vortex (Fig. 4b) reveals the typical CdGM behavior for $r>R$ [41]. This conclusion is no more valid if we consider $N_+$ vortex where the large slope of the inversed anomalous branch causes changes in the LDOS pattern (Fig. 4a) at low voltage near the defect. The local conductance distribution in this case is similar to the one for a pinned vortex in the s-wave superconductor [9].

5 High-Frequency Conductivity

Besides the STM/STS studies, there exists another efficient method for experimental investigation of quasiparticle subgap spectrum based on the measurements of the conductivity tensor at finite frequencies. In the classical limit, the interaction of the quasiparticles with the high-frequency field can be described using the following Hamiltonian:

$$\begin{aligned} H(\mu , \theta ) = \epsilon (\mu ) + \hbar \mathbf {k_\mathrm{F}} \mathbf {v_s} \ , \end{aligned}$$

(36)

where $\epsilon (\mu )$ is the energy of the anomalous spectral branch and $\mathbf {v_s} = -e/ (mc) \mathbf A$ is the superfluid velocity induced by the electromagnetic field. Taking a circularly polarized field $\mathbf {v_s}$ with frequency $\varOmega$, finally we obtain the following Hamiltonian:

$$\begin{aligned} H(\mu , \theta ) = \epsilon (\mu ) - \frac{2 e \hbar k_\mathrm{F}}{mc} Re \left( A_\pm e^{\pm i \theta - i \varOmega t}\right) \ , \end{aligned}$$

(37)

where the sign “+” or “$-$” denotes the circular polarization orientation and $A_\pm$ is the complex magnitude, i.e., the total magnetic potential is $\mathbf A =Re\left( e^{-i\varOmega t} A_\pm (\mathbf x_0 \pm i \mathbf y_0)\right)$. In order to find the conductivity, one should solve the Boltzmann equation written for the quasiparticle distribution function $f(\theta , \mu , t)$ :

$$\begin{aligned} \frac{\partial f}{\partial t} + \frac{1}{\hbar }\left( \frac{\partial H}{\partial \mu } \frac{\partial f}{\partial \theta } - \frac{\partial H}{\partial \theta } \frac{\partial f}{\partial \mu }\right) = - \nu \left( f - f_0\right) , \end{aligned}$$

(38)

where $f_0 (\mu )$ is the equilibrium distribution function and $\nu$ is the quasiparticle relaxation rate. This equation can be solved within the perturbational approach, so that the total distribution function is represented as a sum $f = f_0 + f_1$, where $f_1$ is the first-order perturbation term:

$$\begin{aligned} f_1(\theta , \mu , t) = 2 Re \frac{\mp i e k_\mathrm{F} E_\pm }{m \varOmega \left( \varOmega \mp \omega - i \nu \right) } \frac{\partial f_0}{\partial \mu } e^{\pm i \theta - i \varOmega t} . \end{aligned}$$

(39)

Here $\hbar \omega = \partial \epsilon / \partial \mu$ and $E_\pm = i \varOmega /c A_\pm$ are the electric field complex magnitudes. Let us find the current for the zero-temperature case:

$$\begin{aligned} j_\pm = \frac{e^2 k_\mathrm{F}}{2 m \varOmega \left( i \varOmega \mp i \omega _0 + \nu \right) } E_\pm \ , \end{aligned}$$

(40)

where $\hbar \omega _0 = \partial \epsilon / \partial \mu |_{\mu = 0}$. One can easily obtain the Ohmic and Hall conductivities from the Eq. (40):

$$\begin{aligned} \sigma _O = \frac{e^2 k_\mathrm{F}}{2 m \varOmega } \frac{\nu + i\varOmega }{\left( \nu + i \varOmega \right) ^2 + \omega _0^2}\end{aligned}$$

(41)

$$\begin{aligned} \sigma _H = -\frac{e^2 k_\mathrm{F}}{2 m \varOmega } \frac{\omega _0}{\left( \nu + i \varOmega \right) ^2 + \omega _0^2} \end{aligned}$$

(42)

Thus, one can see that the sign and the value of the Hall conductivity are strongly determined by the slope of the anomalous spectral branch at the Fermi level. Certainly, the above picture for the $N_+$ vortex is valid for rather low frequencies $\varOmega <\Delta _0 R/\xi$, i.e., when the rf field cannot induce the transitions to the levels at the broken CdGM branch in Fig. 3.

The Hall conductivity can be probed experimentally, in particular, by the polar Kerr effect measurements [3]. In order to verify the above results, we propose to measure the Kerr angle dependence on the external magnetic field parallel to the z axis. The total Kerr angle is determined by three contributions which come from the quasiparticle transitions between the energy levels in free vortices, pure defects, and pinned vortices, respectively. For the case of zero field, the Kerr angle is determined only by the density of defects. An external magnetic field produces $N_+$ or $N_-$ vortices depending on the field orientation which may be pinned by the columnar defects. Indeed, the exact amount of pinned and free vortices depends on the sample geometry and the distribution of the defects. For simplicity, we assume that the free vortices appear only after all the defects are occupied by vortices. Such vortex distribution may be implemented experimentally in conditions of the field cooled measurements.

Consider a magnetic field creating $N_+$ vortices in the sample. While the field is low enough so that all vortices are pinned, the Kerr angle appears to be constant because the slope of the anomalous branch of a pinned $N_+$ vortex almost coincides with the slope of the edge modes branch. With the increasing magnetic field, the free vortices enter the sample and the Kerr angle decreases because the free and pinned vortex contributions into the Hall conductivity have different signs. Finally, the Kerr angle changes its sign in high enough magnetic fields.

The Kerr angle behavior changes drastically if one inverts the direction of the external magnetic field. Low field produces pinned $N_-$ vortices whose contribution to the Hall conductivity has the same sign as the contribution of the pure defects but has a smaller absolute value. Thus, the Kerr angle should decrease with the field increase until all defects become occupied by $N_-$ vortices. Further increase of the field introduces free $N_-$ vortices into the sample which increases total Hall conductivity of the sample and, thus, the Kerr angle, so its dependence on the magnetic field appears to be nonmonotonic. Such a nontrivial behavior of the Kerr angle dependence on the external magnetic field can be helpful for unambiguous detection of $p_x \pm i p_y$ in real compounds.

6 Summary

We have calculated the subgap excitation spectrum of quasiparticles for vortex lines pinned by columnar defects in chiral p wave superconductors. The spectrum is shown to depend strongly on the orientation of the magnetic field with respect to the internal angular momentum (chirality) of the Cooper pairs. If the magnetic field produces flux lines with the vorticity opposite to this internal angular momentum, the quasiparticle spectra in pinned vortices are only slightly disturbed by the presence of defects. In the case of coinciding signs of vorticity and chirality, the subgap spectra in pinned vortex cores appear to be strongly different from the ones for free vortices: the anomalous branch at small impact parameters changes its slope resulting in the change in the LDOS pattern and contribution of the quasiparticles into the Ohmic and Hall conductivities at finite frequencies. Experiments which probe these quantities, i.e., STM/STS and polar Kerr effect measurements, can be useful for probing the gap symmetry in $\mathrm {Sr_2RuO_4}$.

Note in conclusion that the above results can be also of interest in the context of recent experiments studying $^3\mathrm {He}$ in aerogel-like nafen strands [42]. The nafen strands act like columnar pinning centers in superconductor and $^3\mathrm {He}$ has a p-wave pairing symmetry, though, with a more complicated order parameter than considered in the present work.

Recently, we were aware about new results [43] of Boris Shapiro and his group regarding quasiparticle spectrum calculations based on the full BdG equations. These results appeared to be in very good accordance with the quasiclassical results presented in this paper.