Parallel machine scheduling with position-dependent processing times and deteriorating maintenance activities

Abstract

Maintenance and production exert reciprocal influence in practical manufacturing applications. However, decisions regarding production scheduling and maintenance planning are often made separately, leading to frequent conflicts between production and maintenance plans. This paper investigates an integrated production scheduling and maintenance planning problem for a parallel machine system, considering both deteriorating jobs and deteriorating maintenance activities. Additionally, the problem features constraints on the number of available maintenance activities due to maintenance budget limitations. The objective is to determine the optimal scheduling and maintenance plan that minimizes the makespan. To tackle this complex problem, we initially delve into the special case where jobs and maintenance activities are already assigned to machines. In our endeavor to minimize the makespan for each machine, we uncover some crucial structural properties and present a polynomial-time algorithm. Subsequently, we develop a hybrid algorithm that combines Whale Optimization Algorithm and Variable Neighborhood Search (WOA–VNS) to address the assignment challenge encompassing jobs and maintenance activities within the parallel machine environment. A series of rigorous comparative experiments are conducted to assess the effectiveness of the proposed algorithm. The results conclusively demonstrate the superior performance of the WOA–VNS algorithm over the WOA, VNS, ABC, and ACO algorithms in addressing the presented problem.

1 Introduction

Production scheduling plays a critical role in modern manufacturing, contributing to enhanced efficiency, cost reduction, meeting customer demands, and ensuring the smooth operation of production processes [1]. Extensive research efforts in production scheduling have yielded significant contributions. Nevertheless, existing research still exhibits certain limitations. Firstly, most production scheduling studies assume that job processing times are constant and known in advance. However, in actual manufacturing scenarios, the efficiency of machines can gradually decline as they operate, leading to an increase in job processing times. This phenomenon is widely recognized as the deteriorating effect [2]. Secondly, most production scheduling studies assume that machines are perpetually available for job processing, such as [3,4,5]. In reality, machines require preventive maintenance, rendering them temporarily unusable for production purposes [6, 7]. Consequently, there has been a notable surge in research interest in recent years focusing on integrated production scheduling and maintenance planning (IPSMP), with a particular emphasis on addressing the challenges posed by the deteriorating effect.

The initial studies on IPSMP with deteriorating effect were conducted in the context of a single machine. Wu and Lee [8] investigated a single machine scheduling problem that incorporates linearly deteriorating jobs and an unavailability period caused by maintenance, with the primary aim of minimizing the makespan. They successfully demonstrated that the problem they tackled could be solved using the 0–1 integer programming technique. Subsequently, Ji et al. [9] extended the work by Wu and Lee [8] and conclusively established that the problem under examination is NP-hard. Furthermore, they introduced an optimal approximation algorithm to address this challenging scheduling problem. Low et al. [10] conducted a research study akin to that of Wu and Lee [8]. But in their problem formulation, the deteriorating effect of the machine began to re-accumulate after maintenance. Building on this novel aspect, Low et al. [10] conducted an extensive analysis and successfully demonstrated that the problem they investigated is likewise NP-hard, and they also put forward several heuristic algorithms based on bin packing concepts.

Different from those studies with predetermined maintenance schedules, Lodree and Geiger [11] considered a flexible rate-modifying activity when investigating the single machine scheduling problem with a deteriorating effect. Their objective is to determine an integrated schedule for both jobs and the RMA that minimizes the makespan. In a related vein, Sun and Geng [12] also explored the single machine scheduling problem with deteriorating effects and a rate-modifying activity. They proved that the problem is polynomial time solvable whether the optimization goal is to minimize the maximum completion time or to minimize the sum of the total completion time. Rustogi and Strusevich [13] further presented a single machine scheduling problem with general position-based processing time and multiple rate-modifying activities. In this intricate problem, decision-makers were tasked with not only determining the job sequence but also strategically deciding the optimal number of maintenance activities to insert into the schedule. Zhang et al. [14] also discussed the single-machine scheduling problem with deteriorating effect and multiple maintenance activities. But in their study, the duration of a maintenance activity is considered as a non-decreasing function of the continuous running time of the machine. Subsequently, some researchers expanded the IPSMP problem with deteriorating effects into more complex parallel machine environments. Lu et al. [15] introduced a parallel machine scheduling problem featuring maintenance deterioration, with the primary aim of minimizing the makespan. In their problem formulation, each machine was mandated to undergo one mandatory maintenance activity. Zhang et al. [16] conducted a similar research study to that of Lu et al. [15], but their objective was to minimize the sum of completion times. Lee et al. [17] introduced a unique dimension to the parallel machine scheduling problem by considering job processing times as position-dependent. Additionally, their problem formulation allowed for at most one maintenance activity for each machine. The overarching goal of minimizing total earliness and tardiness costs. Da et al. [18] investigated a parallel machine scheduling problem with deteriorating jobs and flexible maintenance strategy, in which the actual processing time of a job depends on the effective age and the processing rate of the machine. Their two goals are to minimize the preventive maintenance mean cost rate and total completion time. Woo and Kim [19] delved into a parallel machine scheduling problem with deterioration effect and multiple maintenance activities, in which the actual processing time of job is time-dependent. Their research aimed at jointly determining the assignment of jobs to machines and the sequence of jobs and maintenance activities on each machine, all with the overarching goal of minimizing makespan.

Table 1 Main characteristics of previous works and current work

Following the exhaustive examination of the existing literature, several significant observations come to light: (i) The majority of prior studies have generally overlooked the deterioration of maintenance activity. However, in actual production scenarios, delaying maintenance can lead to deteriorating machine conditions, resulting in longer maintenance duration. (ii) Many previous studies assumed the presence of only one maintenance activity per machine during the planning period. However, practical production environments frequently involve multiple maintenance activities. Embracing this aspect is imperative to ensure that scheduling models better reflect the complexities found in real-life production settings. (iii) When considering deteriorating effects, time-based processing time has received considerable attention, whereas position-based processing time has not been subject to equivalent scrutiny.

Therefore, in this paper, we investigate a new IPSMP problem, in which position-dependent processing times and multiple deteriorating maintenance activities are simultaneously considered. In addition, given the constraints of maintenance budget, the number of available maintenance activities in the problem is limited. The objective is to minimize the makespan by concurrently determining the allocation of jobs and maintenance activities to machines and establishing a joint sequence for both jobs and maintenance activities on each machine. Table 1 provides the comparison of previous studies and ours. To the best of our knowledge, the proposed problem has not been investigated in the literature.

The main contributions of this research are as follows:

(1) This paper investigates an IPSMP problem for a parallel machine system, in which both deteriorating jobs and deteriorating maintenance activities are considered.

(2) In the special case where jobs and maintenance activities are already allocated to each machine, we uncover several critical structural properties and present a polynomial-time algorithm aimed at minimizing the makespan for each machine.

(3) To solve the assignment of jobs and maintenance activities in parallel machine environment, we propose a hybrid algorithm that combines Whale Optimization Algorithm and Variable Neighborhood Search (WOA–VNS).

The remainder of this paper is organized as follows. Section 2 describes the studied problem. Section 3 analyzes the sequencing problem of jobs and maintenance activities on a given machine, and presents a polynomial time algorithm. Section 4 develops a hybrid WOA–VNS algorithm. Section 5 discusses the validity of the developed WOA–VNS through rigorous comparison experiments. Section 6 concludes this research.

2 Problem description

The notations used in this paper and their definitions are presented as follows.

Notions	Definitions
$n$	Total number of jobs
$m$	Total number of machines
$M_{l}$	The machine $l$,$\ l = 1,\ldots ,m$.
$k_{\max }$	Number of available maintenance activities, $m \le k_{\max } \le n$
$k_{l}$	The number of maintenance activities performed on $M_{l}$
$J_{j}$	The job $j$,$\ j = 1,\ldots ,n$.
$p_{j}$	Normal processing time of $J_{j}$,$j = 1,\ldots ,n$
$p_{j}^{A}$	Actual processing time of $J_{j}$
$n_{l}$	The number of jobs processed on $M_{l}$, where$\sum _{l = 1}^{m}n_{l} = n$.
$G_{{i}{l}}$	The $i^{th}$ group of jobs processed on $M_{l}$, $i = 1,\ldots ,k_{l}$.
$n_{{i}{l}}$	The number of jobs in $G_{{i}{l}}$, where$\sum _{i = 1}^{k_{l}}n_{{i}{l}} = n_{l}$
$P_{{i}{l}}$	The processing time of$\ G_{{i}{l}}$, where$P_{{i}{l}} = \sum _{J_{j} \in G_{{i}{l}}\ }^{}p_{j}^{A}$
$\alpha$	The normal duration of a maintenance activity
$\beta$	The deteriorating maintenance factor, $\beta \ge 0$
${{m}{a}}_{{i}{l}}$	The actual duration of the $i^{th}$ maintenance activity on $M_{l}$
$C_{\max }$	The makespan

The problem is described as follows. There are $n$ independent jobs to be processed on $m$ identical parallel machines. All of the jobs are available at time zero, and no preemption is allowed. Each machine can only process one job at a time, and the processing of each job cannot be interrupted. As the machine operates, its condition deteriorates, ultimately causing a gradual increase in the actual processing time of jobs. Hence, implementing maintenance becomes imperative to minimize actual production time. The maintenance is assumed to be perfect, ensuring the machine is restored to an “as good as new” condition. It is also presumed that all machines are initially new. To maintain this assumption in subsequent planning phase, a mandatory maintenance activity is executed immediately after the machine completes its final job. Throughout the planning horizon, the number of available maintenance activities is restricted due to the budget constraints. We use $k_{\max }$ ($m \le k_{\max } \le n$) to represent the total number of available maintenance activities and $k_{l}$ to indicate the number of maintenance activities assigned to $M_{l}$. Noting that, $k_{l}$ includes the final mandatory maintenance activity on $M_{l}$. Figure 1 is an illustrative diagram of the described problem. We designate the set of jobs between any two adjacent maintenance activities or prior to the first maintenance activity as a group. Hence, a schedule on machine $M_{l}$ can be represented by$\ \pi (M_{l}) = (G_{1\,l},{MA}_{1\,l},\ G_{2\,l},\ {MA}_{1\,l},\ldots ,G_{k_{l},l},{MA}_{k_{l},l})$, where $G_{{il}}$ represents the $i^{th}$ group on $\ M_{l}$.

Fig. 1

Schematic diagram of the proposed problem

According to Öztürkoğlu [20], the actual processing time of $J_{j}$ can be formulated as:

$$\begin{aligned} p_{j}^{A} = {(1 + \theta )}^{r - 1}p_{j} \end{aligned}$$

(1)

where $p_{j}$ is the normal processing time of $J_{j}$, $r$ represents the position of $J_{j}$ within its corresponding group, and $\theta$ ($\ \ge 0$) is the deteriorating rate of the machine.

Additionally, the duration of a maintenance activity is also deteriorating. Following Yang [21], the actual duration of the $i^{th}$ maintenance activity on $M_{l}$ can be formulated as:

$$\begin{aligned} ma_{il} = \alpha + \beta P_{il} \end{aligned}$$

(2)

where $\alpha$ is the basic duration of a maintenance activity, $\beta$ is the maintenance deteriorating factor, and $P_{il}$ represent represent the actual processing time of $G_{il}$.

The objective is to is to determine a combined schedule for both jobs and maintenance activities that minimizes the makespan. Using the three-filed notation scheme [22], the studied problem can be denoted as $\ {P}{m}\ |p_{j}^{A} = {(1 + \theta )}^{r - 1}p_{j},\ \ m \le MA \le k_{\max }|C_{\max }$, where${\ MA}$ represents the number of maintenance activities actually performed.

3 Special case study

To address our problem, two crucial decisions need to be made: first, allocating jobs and maintenance activities to machines, and second, organizing the sequence for jobs and maintenance activities on each machine. Given the complexity of this problem, our initial focus will be on the special case where jobs and maintenance activities are already assigned to each machine.

With the known count of maintenance activities on each machine, the problem on a given single machine can be denoted as$\ 1\ |p_{j}^{A} = \left( 1 + \theta \right) ^{r - 1}p_{j},\ \ MA = k_{l}|C_{\max }$. To address this problem, we establish essential structural properties and then introduce a heuristic method in this section.

Lemma 1

For the problem ${1\ |}{p}_{{j}}^{{A}}{=}\left( {1 + \theta } \right) ^{{r - 1}}{p}_{{j}}{,\ \ MA =}{k}_{{l}}{|}{C}_{{\max }}$, exchanging the positions of any two groups does not alter the makespan.

Proof

For any given schedule$\ \pi$, the makespan on machine $M_{l}$ can be calculated as:

$$\begin{aligned} \begin{aligned} C_{\max }\left( M_{l},\pi \right)&= \sum _{i = 1}^{k_{l}}P_{{il}} + \sum _{i = 1}^{k_{l}}{ma}_{{il}} = \sum _{i = 1}^{k_{l}}P_{{il}} + \sum _{i = 1}^{k_{l}}\left( \alpha + \beta P_{{il}} \right) \\&= k_{l}\alpha + \left( 1 + \beta \right) \sum _{i = 1}^{k_{l}}P_{{il}} \\&= \ k_{l}\alpha + \left( 1 + \beta \right) \sum _{i = 1}^{k_{l}}\left( \sum _{J_{j} \in G_{{il}}\ }^{}p_{j}^{A}\right) \end{aligned} \end{aligned}$$

(3)

According to the above equation, it’s evident that the makespan solely relies on the grouping result and the job sequence within each group. Changing the order of groups doesn’t impact the total job processing time or the overall duration of maintenance activities. Thus, Lemma 1 is proved. $\square$

Lemma 2

For the problem ${1\ |}{p}_{{j}}^{{A}}{=}\left( {1 + \theta } \right) ^{{r - 1}}{p}_{{j}}{,\ \ MA =}{k}_{{l}}{|}{C}_{{\max }}$, if there exists an optimal schedule, the number of jobs within each group cannot exceed ${\lceil }\frac{{n}_{{l}}}{{k}_{{l}}}{\rceil }$.

Proof

Suppose there exists an optimal schedule$\ \pi$ in which there is a group $G_{{xl}}$ containing$\ \varphi \ (\varphi \ge \big \lceil \frac{n_{l}}{k_{l}} \big \rceil + 1)$ jobs. Then there must be a group $G_{{yl}}$ containing fewer jobs than$\ \big \lceil \frac{n_{l}}{k_{l}} \big \rceil$. Denote the number of jobs in the group $G_{{yl}}$ as$\ \delta \ (\delta < \big \lceil \frac{n_{l}}{k_{l}} \big \rceil )$.Let $J_{a}$ represent the last job in the group $G_{{xl}}$, with a normal processing time of $p_{a}$. Move $J_{a}$ to the last position of the group$\ G_{{yl}}$ to obtain a new schedule$\ \pi ^{*}$. According to Lemma 1, the difference in makespan between the schedule$\ \pi$ and$\ \pi ^{*}$is:

$$\begin{aligned} \begin{aligned}&C_{\max }\left( M_{l}, \pi \right) - C_{\max }\left( M_{l}, \pi ^{*} \right) \ \\&\quad = P_{{xl}}\left( \pi \right) - P_{{xl}}\left( \pi ^{*} \right) + P_{{yl}}\left( \pi \right) - P_{{yl}}\left( \pi ^{*} \right) \\&\qquad + {ma}_{{xl}}\left( \pi \right) - {ma}_{{xl}}\left( \pi ^{*} \right) + {ma}_{{yl}}\left( \pi \right) - {ma}_{{yl}}\left( \pi ^{*} \right) \\&\quad = \left( 1 + \theta \right) ^{\varphi - 1}p_{a} - \left( 1 + \theta \right) ^{\delta }p_{a} + \beta \left( 1 + \theta \right) ^{\varphi - 1}p_{a} - \beta \left( 1 + \theta \right) ^{\delta }p_{a} \\&\quad = \left( 1 + \beta \right) \left[\left( 1 + \theta \right) ^{\varphi - 1} - \left( 1 + \theta \right) ^{\delta } \right]p_{a} \end{aligned} \end{aligned}$$

(4)

As $\varphi - 1 \ge \delta$, it follows that $C_{\max }\left( \pi \right) - C_{\max }\left( \pi ^{*} \right) \ge 0$. This indicates that relocating job $J_{a}$leads to a shorter makespan. Hence, $\pi$ cannot be the optimal schedule. With this, the proof of Lemma 2 is completed. $\square$

Lemma 2 sets an upper limit for the number of jobs within a group but doesn’t ascertain the exact count of jobs in each group. For example, if there are 10 jobs and 3 maintenance activities to be scheduled, the possible grouping results could be $\left\{ n_{1\,l} = 4,n_{2\,l} = 3,n_{3\,l} = 3\ \right\}$ and$\ \left\{ n_{1\,l} = 4,n_{2\,l} = 4,n_{3\,l} = 2 \right\}$, as indicated by Lemma 2. To address this uncertainty regarding the number of jobs in each group, Lemma 3 is introduced.

Lemma 3

For the problem ${1\ |}{p}_{{j}}^{{A}}{=}\left( {1 + \theta } \right) ^{{r - 1}}{p}_{{j}}{,\ \ MA =}{k}_{{l}}{|}{C}_{{\max }}$, if there exists an optimal schedule, the number of jobs within a group cannot be less than $\big \lfloor \frac{{n}_{{l}}}{{k}_{{l}}} \big \rfloor$.

Proof

Here are two cases.

Case 1: $n_{l}\ {mod}\ k_{l}\ = 0$

In this case, the number of jobs in each group is $\big \lfloor \frac{n_{l}}{k_{l}} \big \rfloor$, where$\big \lfloor \frac{n_{l}}{k_{l}} \big \rfloor = \big \lceil \frac{n_{l}}{k_{l}} \big \rceil$.

Case 2: $n_{l}\ {mod}\ k_{l}\ \ne 0$

Suppose there exists an optimal schedule$\ \pi$ in which there is a group $G_{{xl}}$ containing $\varphi \ (\varphi < \big \lfloor \frac{n_{l}}{k_{l}} \big \rfloor )$ jobs. Then there must be more than one group containing $\big \lceil \frac{n_{l}}{k_{l}} \big \rceil$ jobs. Randomly choose a group containing $\big \lceil \frac{n_{l}}{k_{l}} \big \rceil$ jobs and denote this group as $G_{{yl}}$. Let $J_{a}$ represent the last job in the group $G_{{yl}}$, with a normal processing time of $p_{a}$. Move $J_{a}$ to the last position of the group $G_{{xl}}$ to obtain a new schedule $\pi ^{*}$. Then the difference in makespan between the schedule $\pi$ and $\pi ^{*}$ is:

$$\begin{aligned} \begin{aligned}&C_{\max }\left( M_{l}, \pi \right) - C_{\max }\left( M_{l}, \pi ^{*} \right) \ \\&\quad = P_{{xl}}\left( \pi \right) - P_{{xl}}\left( \pi ^{*} \right) + P_{{yl}}\left( \pi \right) - P_{{yl}}\left( \pi ^{*} \right) \\&\qquad + {ma}_{{xl}}\left( \pi \right) - {ma}_{{xl}}\left( \pi ^{*} \right) + {ma}_{{yl}}\left( \pi \right) - {ma}_{{yl}}\left( \pi ^{*} \right) \\&\quad = \left( 1 + \theta \right) ^{\big \lceil \frac{n_{l}}{k_{l}} \big \rceil - 1}p_{a} - \left( 1 + \theta \right) ^{\varphi }p_{a} + \beta \left( 1 + \theta \right) ^{\big \lceil \frac{n_{l}}{k_{l}} \big \rceil - 1}p_{a} - \beta \left( 1 + \theta \right) ^{\varphi }p_{a} \\&\quad = \left( 1 + \beta \right) \left[\left( 1 + \theta \right) ^{\big \lceil \frac{n_{l}}{k_{l}} \big \rceil - 1} - \left( 1 + \theta \right) ^{\varphi } \right]p_{a} \end{aligned} \end{aligned}$$

(5)

As $\varphi < \big \lfloor \frac{n_{l}}{k_{l}} \big \rfloor = \big \lceil \frac{n_{l}}{k_{l}} \big \rceil - 1$, it follows that $C_{\max }\left( \pi \right) - C_{\max }\left( \pi ^{*} \right) > 0$. This indicates that relocating job $J_{a}$leads to a shorter makespan. Therefore, $\pi$ cannot be the optimal schedule.

Combining case 1 and case 2, we complete the proof of lemma 3. $\square$

Lemma 4

Given two sequences of positive numbers, ${X}$ and ${Y}$, the sum of products of their corresponding elements $\sum _{}^{}{{X}_{{i}}{Y}_{{i}}}$ is minimized when the two sequences are monotonic in the opposite sense.

Proof

See in Hardy et al. [23]. $\square$

Lemma 5

For the problem ${1\ |}{p}_{{j}}^{{A}}{=}\left( {1 + \theta } \right) ^{{r - 1}}{p}_{{j}}{,\ \ MA =}{k}_{{l}}{|}{C}_{{\max }}$, if there exists an optimal schedule, the jobs within a group should be processed in non-increasing order of their normal processing times.

Proof

Suppose that the job sequence in the group $G_{{il}}$ is $s = \{ J_{1},J_{2},\ldots ,J_{n_{{il}}}\}$, and the normal processing time of each job is $p_{j} = \{ p_{1},p_{2},\ldots ,p_{n_{{il}}}\}$, then the processing time of the group $G_{{il}}$ and the duration of the closely-following maintenance activity is:

$$\begin{aligned} P_{{il}} + {ma}_{{il}} = P_{{il}} + \alpha + \beta P_{{il}} = \alpha + (1 + \beta )\sum _{\sigma = 1}^{n_{{il}}}{p_{\sigma }{(1 + \theta )}^{\sigma - 1}} \end{aligned}$$

(6)

Clearly, ${(1 + \theta )}^{\sigma - 1}$ increases with $\sigma ,\$ where $\sigma = 1,2,\ldots ,\ n_{{il}}$. Therefore, $P_{{il}} + {ma}_{{il}}$ is minimized when $p_{\sigma } = \{ p_{1},p_{2},\ldots ,p_{n_{{il}}}\}$ is sequenced in non-increasing order, as per Lemma 4. Thus, the proof of Lemma 5 is completed.

Utilizing the established lemmas, a polynomial time algorithm is developed to solve the single machine problem $1\ |p_{j}^{A} = \left( 1 + \theta \right) ^{r - 1}p_{j},\ \ MA = k_{l}|C_{\max }$. The pseudo-code for the proposed polynomial-time algorithm are outlined in Algorithm I. Noting that, $k_{l}$ includes the last mandatory maintenance activity on $M_{l}$. $\square$

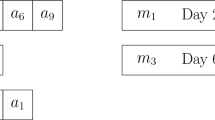
To provide a more intuitive understanding of Algorithm I, we present an example with 10 jobs and 3 maintenance activities (including the last mandatory maintenance activity). Let’s consider a job set $J = \{ J_{1},J_{2},\ldots ,J_{10}\}$ to be processed on the machine$\ M_{l}$, with the job set following the condition$\ p_{1} \ge p_{2} \ge \cdots \ge p_{10}$. Based on Algorithm I, the scheduling result is depicted in Fig. 2.

Fig. 2

An example to illustrate Algorithm I

Theorem 1

Algorithm I is optimal for solving the single machine problem ${1\ |}{p}_{{j}}^{{A}}{=}\left( {1 + \theta } \right) ^{{r - 1}}{p}_{{j}}{,\ \ MA =}{k}_{{l}}{|}{C}_{{\max }}$.

Proof

Denote the schedule generated by the Algorithm I as $\pi ^{opt}$. Evidently, schedule $\pi ^{opt}$ satisfies Lemmas 2 and 3. Now, let’s shift our focus to the makespan of schedule $\pi ^{opt}$. The makespan of schedule $\pi ^{opt}$ can be calculated as follows:

$$\begin{aligned} \begin{aligned}&C_{max}\left( M_{l},\pi ^{opt} \right) = k_{l}\alpha + \left( 1 + \beta \right) \sum _{i = 1}^{k_{l}}\left( \sum _{J_{j} \in G_{{il}}\ }^{}p_{j}^{A} \right) \\&\quad = k_{l}\alpha + \left( 1 + \beta \right) \bigg [ p_{1} + \cdots + p_{k_{l}} + p_{k_{l} + 1}\left( 1 + \theta \right) + \cdots + p_{{2k}_{l}}\left( 1 + \theta \right) \\&\qquad + p_{{2k}_{l} + 1}\left( 1 + \theta \right) ^{2} + \cdots + p_{{3k}_{l}}\left( 1 + \theta \right) ^{2} + p_{{3k}_{l} + 1}\left( 1 + \theta \right) ^{3} \\&\qquad + \cdots + p_{{4k}_{l}}\left( 1 + \theta \right) ^{3} + \cdots + p_{n_{l}}\left( 1 + \theta \right) ^{\big \lceil \frac{n_{l}}{k_{l}} \big \rceil - 1} \bigg ]\\&\quad = k_{l}\alpha + \left( 1 + \beta \right) \sum \limits _{x=1}^{n_{l}} p_{x} (1+\theta )^{\big \lceil \frac{x}{k_{l}} \big \rceil - 1} \end{aligned} \end{aligned}$$

(7)

Since the two sequences,$\left\{ p_{x} \right\}$ and $\left\{ (1+\theta )^{\big \lceil \frac{x}{k_{l}} \big \rceil - 1}\right\}$, demonstrate opposite monotonicity, the makespan is minimized, as per Lemma 4. Therefore, the proposed Algorithm I is optimal for solving the single machine problem. $\square$

4 WOA–VNS algorithm

In Sect. 3, we delve into the special case where jobs and maintenance activities are pre-assigned to each machine. To solve the joint sequencing of jobs and maintenance activities on each machine, we present a polynomial time algorithm which is proxved to be optimal. In this section, our focus will be on the allocation of parts and maintenance activities within the parallel machine environment. Without accounting for the deteriorating effects and maintenance activities, the investigated parallel problem can be simplified to the problem $\ {Pm}||C_{\max }$, which has been proved to be NP-hard by Sethi [24]. Therefore, the proposed problem is at least NP-hard, and it is difficult to address it with an accurate algorithm. Consequently, to solve the proposed problem within a reasonable time, a hybrid algorithm that combines Whale Optimization Algorithm and Variable Neighborhood Search (WOA–VNS) is developed. More specific information about the WOA–VNS algorithm is detailed below.

4.1 Encoding method

Due to the mandatory maintenance required after each machine completes its final job, the actual number of assignable maintenance activities becomes $k_{max} - m$. It’s worth noting that, when the time spent on maintenance exceeds the reduction in processing time for jobs, the maintenance activity no longer remains beneficial. This implies that an optimal allocation plan doesn’t necessarily require utilizing all available maintenance activities to their fullest extent. Consequently, the following one-dimensional vector is proposed to represent the solution to the addressed problem.

$$\begin{aligned} \vec {X} = \left( x_{1},x_{2},\ldots ,x_{n},x_{n + 1},\ldots ,x_{n + k_{max} - m} \right) ,\ x_{i} \in (0,1] \end{aligned}$$

In the vector $\vec {X}$, the first $n$ elements represent the assignment results for each job, and the last $k_{max} - m$ elements represent the allocation results for each maintenance activity. For the first $n$ elements, if$\text {\ x}_{i}$ falls within the interval$\ (\frac{k - 1}{M},\frac{k}{M}]$, where $k = 1,\ldots ,M$, then job $i$ is assigned to the machine$\ M_{k}$. For the last $kmax - m$ elements, if$\text {\ x}_{i}$ falls within the interval$\ (\frac{k}{M + 1},\frac{k + 1}{M + 1}]$, where $k = 1,\ldots ,M$, then the corresponding maintenance activity is assigned to the machine$\ M_{k}$. It is worth noting that if $x_{i}$ falls within the interval $(0,\frac{1}{M + 1}]$, the corresponding maintenance activity will not be assigned to any machine. This encoding permits maintenance activities to remain unassigned, ensuring the potential for discovering a balanced maintenance solution when maintenance resources are excessive. Figure 3 provides a more visual representation of this encoding method with an example involving 10 jobs, 3 machines, and 4 available maintenance activities (excluding the final mandatory maintenance activity on each machine).

Fig. 3

An example to illustrate the encoding method

4.2 The standard WOA

The Whale Optimization Algorithm (WOA) was introduced by Mirjalili and Lewis [25] in 2016, drawing inspiration from the hunting behavior of humpback whales. Since the WOA was developed, it has been widely used in various fields, such as feature selection, clustering, image classification, and scheduling optimization, due to its straightforward iterative approach and rapid convergence. The primary steps of the WOA are outlined as follows.

(1) Encircling prey

Since the exact location of the target prey is unknown in advance, the WOA algorithm operates under the assumption that the current optimal individual is the target prey. Subsequently, candidate whales update their positions in the direction of this presumed prey. This behavior can be described as follows:

$$\begin{aligned} \vec {D}= & {} \left| C* \vec {X^{*}}\left( t \right) - \vec {X}\left( t \right) \right| \ \end{aligned}$$

(8)

$$\begin{aligned} \vec {X}\left( t + 1 \right)= & {} \vec {X^{*}}\left( t \right) - A * \vec {D} \end{aligned}$$

(9)

where $\vec {X^{*}}$ is the current optimal individual, $t$ is the current iteration, $A$ and $C$ and are coefficient values, and $\big |\big |$ signifies taking the absolute value of each element within the vector.

The calculation formulas for and are as follows:

$$\begin{aligned} A= & {} 2a * r - a\ \end{aligned}$$

(10)

$$\begin{aligned} C= & {} 2*r\ \end{aligned}$$

(11)

$$\begin{aligned} a= & {} 2*\left( 1-\frac{t}{{T_{max}}} \right) \ \end{aligned}$$

(12)

where $T_{max}$ is the maximum number of iterations, and $r$ is a random value in [0,1]

(2) Bubble-net attacking (Exploitation)

While swimming around the prey, whales employ two mechanisms to update their positions: the shrinkage mechanism and the spiral mechanism. The shrinkage mechanism is accomplished by establishing the coefficient value within the range of [-1,1] while linearly decreasing the value of throughout the iterations. The spiral mechanism can be represented by the following formula.

$$\begin{aligned} \vec {D^{'}}= & {} \left| \vec {X^{*}}\left( t \right) - \vec {X}\left( t \right) \right| \end{aligned}$$

(13)

$$\begin{aligned} \vec {X}\left( t+1 \right)= & {} \vec {X^{*}} + \vec {D^{'}}*e^{{bl}}*\cos \left( 2\pi l \right) \end{aligned}$$

(14)

Because two mechanisms are used simultaneously, the entire model can be described as follows.

$$\begin{aligned} \vec {X}(t+1)=\left\{ \begin{array}{ll} \vec {X^{*}}(t)-A*\vec {D}, &{}\quad {if}\; p{i} <0.5\\ \vec {D^{'}}*e^{{bl}}*\cos \left( 2\pi l \right) , &{}\quad {if}\; p{i} \ge 0.5\\ \end{array}\right. \end{aligned}$$

(15)

where $p_{i}$ is a random value in [0,1].

(3) Search for prey

Over the course of iteration, when $\left| A \right| >1$, the whales update their position according to the randomly selected whale $\vec {X_{rand}}$. This mechanism motivates the whales to venture away from the current best solution, actively seeking potentially superior prey. This behavior can be expressed as follows.

$$\begin{aligned}{} & {} \vec {D} = \left| C * \vec {X_{rand}} - \vec {X}(t) \right| \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \vec {X}(t+1)= \vec {X_{rand}} -A*\vec {D} \end{aligned}$$

(17)

4.3 Hybrid WOA–VNS

Despite the widespread adoption of the WOA algorithm across diverse applications, certain researchers have highlighted its potential challenges in effectively exploring extensive search spaces. This becomes especially pertinent when tackling intricate, large-scale problems [26,27,28]. To address these concerns, a VNS algorithm [29] is specifically developed and integrated into the standard WOA framework, aimed at augmenting its search capabilities.

As known, the key to success for VNS is the neighborhood structure it applies. Given the distinctive encoding method in this paper, classic local search operators may not be efficient. Consequently, a novel local search operator is designed, tailored to the specific characteristics of the encoding method utilized herein. The devised local search operator initiates by generating a random integer $\tau$ within the range of $(1,n + k_{max} - m)$. It subsequently determines whether to alter the job assignment or the maintenance activity assignment based on the generated integer. Algorithm II delineates the procedure steps of the designed local search operator.

Employing the tailored local search operator, a VNS algorithm is further developed and integrated into the WOA algorithm. Within each iteration, the VNS takes the optimal solution found by WOA as its initial solution, progressively refining it through iterations using the local search operator. Algorithm III illustrates the comprehensive process of the WOA–VNS algorithm, where lines 21 to 29 delineate the implementation steps of the designed VNS algorithm.

5 Computational experiment

To evaluate the efficacy of our algorithm, we conduct a comparative analysis between the proposed WOA–VNS algorithm and several benchmarks, including the Gurobi solver, along with four other intelligent algorithms: the standard WOA algorithm [25], the VNS algorithm [30], the ant colony optimization (ACO) algorithm [31], and the artificial bee colony (ABC) algorithm [32]. These selected intelligent algorithms, except for the WOA algorithm, have been enhanced and demonstrated strong performance in solving similar parallel machine problems. For fair comparisons, the proposed Algorithm I is utilized in all of these algorithms to solve the single machine problem. Moreover, identical initial solutions are used for all algorithms on each problem instance. All algorithms are implemented in Python and executed on a computer with an Intel(R) Core (TM) i7-7770 CPU @3.60 GHz, 8GB RAM, and a Windows 10 operating system. Further details of the computational experiments are elaborated below.

5.1 Test instances and parameter settings

To ensure the robustness of the results, various scales of test instances are generated. Each instance is denoted as, where represents the number of jobs, represents the number of machines, and represents the actual number of assignable maintenance activities. Every algorithm utilizes a population size set at 10, with the termination condition set to reach 100 iterations. Each algorithm undergoes 10 executions for every test instance. For fair comparisons,the suggested parameters for the standard WOA algorithm [25], the VNS algorithm [30], ACO [31], and ABC [32] are employed. Table 2 details the parameters and their levels for the addressed problem.

Table 2 Experimental factors and their levels

5.2 Comparison with Gurobi solver

This subsection employs both the Gurobi solver and WOA–VNS on various small-scale problem instances, offering a comparative analysis of their operational outcomes. Before employing the Gurobi solver, establishing the mathematical model for the addressed problem is crucial. Given that single-machine problems can be solved by Algorithm I, our primary objective revolves around determining the allocation of jobs and maintenance activities. Therefore, the following decision variables are defined:

$$\begin{aligned} x_{[i][j]}= & {} \left\{ \begin{array}{ll} 1, &{}\quad {job}\ i\ {is}\ {asigned}\ {to}\ M_{j} \\ 0, &{}\quad {otherwise} \end{array}\right. \\ y_{[k][j]}= & {} \left\{ \begin{array}{ll} 1, &{}\quad {the} \ k^{th} \ {maintenance} \ {activity} \ {is} \ {asigned}\ {to}\ M_{j} \ \\ 0, &{}\quad {otherwise} \end{array}\right. \end{aligned}$$

Further, the mathematical model of the simplified problem can be represented as follows:

$$\begin{aligned}&Min \quad \max _{l=1\longrightarrow m } \left\{ C_{max}(M_{l},\pi ^{opt}) \right\} \\&s.t.\left\{ \begin{array}{c} \mathop {\sum }\nolimits _{j=1}^{m}x_{[i][j]}=1\\ \mathop {\sum }\nolimits _{j=1}^{m}y_{[k][j]}\le 1\\ x_{[i][j]}= \left\{ 0,1 \right\} \\ y_{[k][j]}= \left\{ 0,1 \right\} \end{array}\right. \end{aligned}$$

where $i=1,\ldots , n$, $j=1,\ldots , m$, and $k=1,\ldots , k_{max}-m$.

In the aforementioned model, the first constraint signifies that a job can only be allocated to a single machine, and all jobs must be assigned. The subsequent constraint specifies that a maintenance activity can be assigned to only one machine or remain unassigned to any machine. For any given feasible assignment plan, the optimal sequence of jobs and maintenance activities on each machine can be determined by Algorithm I, and the corresponding makespan on each machine ($C_{max}(M_{l},\pi ^{opt})$) can be calculated according to formula 7.

To solve the aforementioned model using the Gurobi solver, a maximum runtime of 1800s is set. Table 3 displays the results of the Gurobi solver and the proposed WOA–VNS for solving problems of different scales. The final column indicates the difference in outcomes between the WOA–VNS algorithm and the Gurobi solver, also known as the GAP. Examining Table 3, it’s evident that the WOA–VNS algorithm significantly outperforms the Gurobi solver in terms of solution time. Furthermore, as the scale reaches (50, 4, 6), the Gurobi solver fails to yield a feasible solution within the designated time limit. Additionally, for all test instances, the difference (GAP) between the outcomes of the WOA–VNS algorithm and the Gurobi solver remains under 4%. Therefore, it can be inferred that the proposed WOA–VNS is effective in solving the given problem.

Table 3 Results generated by WOA–VNS and Gurobi solver

5.3 Comparison with other algorithms

In this subsection, the proposed WOA–VNS algorithm is further compared with other intelligent algorithms, namely WOA [25], VNS [30], ACO [31], and ABC [32]. To assess the advantages of the WOA–VNS algorithm over others, Friedman tests are conducted. These tests formulate a null hypothesis assuming that the distributions of solutions produced by WOA, VNS, ABC, ACO, and WOA–VNS are identical. By analyzing the solutions, the tests calculate the asymptotic significance. If the asymptotic significance is less than 0.05, the null hypothesis is rejected; otherwise, it is accepted. Table 4 summarizes the results of the Friedman test, with the asymptotic significant values above 0.05 indicated in bold. The table indicates that among the 21 test instances, there are significant differences in the solutions obtained by these algorithms in 19 test instances, excluding instances (150, 3, 8) and (200, 6, 12).

Table 4 Summary of Hypothesis Test

In addition to hypothesis tests, the Friedman tests also yield the mean ranks of WOA, VNS, ABC, ACO, and WOA–VNS. In the pursuit of minimizing the objective function, a lower mean rank indicates that the results obtained by a specific algorithm are closer to the optimal solution. Figure 4 vividly portrays the mean ranks of each algorithm across various problem instances. Remarkably, the WOA–VNS algorithm consistently attains the lowest mean rank for each test instance. This consistent pattern underscores the superiority of the proposed WOA–VNS algorithm over others, consistently delivering outstanding results.

Fig. 4

Mean ranks of each algorithm for different problem instances

To emphasize the superiority of WOA–VNS over other algorithms, the relative percentage deviations (RPD) analysis is also performed. The RPD is expressed as follows:

$$\begin{aligned} RPD = \frac{Z_{A} - Z_{B}}{Z_{B}} \end{aligned}$$

where $Z_{A}$ is the result obtained by a given algorithm for an instance and $Z_{B}$ is the best result obtained by all selected algorithms for the same instance. Table 5 displays the RPD results of the maximum (Max), minimum (Min), average (AVE), and standard deviation (SD) of each algorithm for different problem instances. The better results are bold.

As shown in Table 5, in terms of minimum (Min) results, the WOA–VNS algorithm outperforms other selected algorithms in 17 out of 21 test problem instances. Additionally, when assessing the maximum (Max) and average (AVE) results, the WOA–VNS algorithm demonstrates superiority over the comparison algorithms across all test instances. Regarding standard deviation (SD), the WOA–VNS algorithm consistently delivers the best results, except for the specific problem instance (250, 6, 15). Therefore, it can be confidently concluded that the proposed WOA–VNS algorithm is both more efficient and stable compared to other selected algorithms in effectively addressing the presented problem.

Table 5 RPD results

Fig. 5

Convergence curves for different problem instances

Furthermore, Fig. 5 displays the convergence curves of these algorithms. Each point on the curve represents the average fitness of all individuals in each generation. Particularly noteworthy is that even when the iterations reach 80, the WOA–VNS algorithm exhibits a continuous decline, indicating ongoing improvement. This observation strongly suggests that the hybrid WOA–VNS algorithm effectively mitigates the original WOA algorithm’s tendency to converge towards local optima, significantly addressing this limitation.

6 Conclusion

In this paper, we investigate a joint production scheduling and maintenance planning problem in the parallel machine system, and the objective to minimize the makespan. Both deteriorating jobs and deteriorating maintenance activities are considered in our model. Considering the complexity of this problem, we initiate our study by focusing on a special case wherein the assignments of jobs and the number of maintenance activities allocated to each machine are predetermined. To tackle this challenge on a single-machine level, we introduce a heuristic approach that capitalizes on essential structural properties. Subsequently, we extend our investigation to address the assignment problem encompassing jobs and maintenance activities within the parallel machine environment, and develop a hybrid WOA–VNS algorithm. Computational experiments results unveil the superior performance of the WOA–VNS algorithm, which excels in both search capability and stability when compared to the WOA, VNS, ABC, and ACO algorithms.

Similar to numerous existing studies, our paper assumes a constant processing rate for the machines. However, in actual production settings, the equipment’s rate is often adjustable. Future research endeavors can delve into the integration of controllable machining speeds to offer a more comprehensive analysis. Furthermore, our study does not encompass the consideration of potential random equipment failures. This omission represents another promising avenue for advancing research in this field, as it introduces an added layer of complexity and realism to the problem.