On tackling reverse convex constraints for non-overlapping of unequal circles

Abstract

We study the unequal circle-circle non-overlapping constraints, a form of reverse convex constraints that often arise in optimization models for cutting and packing applications. The feasible region induced by the intersection of circle-circle non-overlapping constraints is highly non-convex, and standard approaches to construct convex relaxations for spatial branch-and-bound global optimization of such models typically yield unsatisfactory loose relaxations. Consequently, solving such non-convex models to guaranteed optimality remains extremely challenging even for the state-of-the-art codes. In this paper, we apply a purpose-built branching scheme on non-overlapping constraints and utilize strengthened intersection cuts and various feasibility-based tightening techniques to further tighten the model relaxation. We embed these techniques into a branch-and-bound code and test them on two variants of circle packing problems. Our computational studies on a suite of 75 benchmark instances yielded, for the first time in the open literature, a total of 54 provably optimal solutions, and it was demonstrated to be competitive over the use of the state-of-the-art general-purpose global optimization solvers.

1 Introduction

The circle-circle non-overlapping constraint is imposed to guarantee that two circles (generally of different radius) do not overlap, which can be achieved by requiring that their centers are sufficiently far in terms of Euclidean distance. In particular, the constraint has the mathematical form

$$\begin{aligned} \left( a_i - a_j\right) ^2 + \left( b_i - b_j\right) ^2 \ge \left( r_i + r_j\right) ^2, \end{aligned}$$

(1)

where $\left( a_i, b_i\right)$ and $\left( a_j, b_j\right)$ represent the coordinates of the centers of two circles i and j, while $r_i$ and $r_j$ denote their corresponding radii, respectively.

Studying this type of constraint has both theoretical and practical interest. From a theoretical perspective, mathematical models with non-overlapping constraints usually have a highly non-convex solution space whose convexification towards a tight relaxation still poses a tremendous challenge for the global optimization community; solving these models to guaranteed optimality remains extremely hard, even for the state-of-the-art solvers. From a practical point of view, circle-circle non-overlapping constraints often appear in many models for cutting and packing applications, and efforts to solve them more efficiently can add significant value to industry.

The first and foremost, archetypal family of problems of interest are the circle packing problems. These come in many variants, such as packing identical circles into a rectangular container with the objective of minimizing the container’s area [14], or identifying the minimal radius of a circle within which other circles can simultaneously be placed [27], among others. Related applications include container loading, cyclinder packing and wireless communication network layout, to name but a few [11]. Another related cutting and packing application is the irregular shape nesting problem, in which one seeks a feasible configuration for a given set of irregular shapes within a rectangular sheet of a fixed width such that no overlap among these shapes exists and the sheet length is minimized. This problem often appears when carving out of metal rolls parts for automobiles, airplanes and other machinery, as well as when cutting leather and fabrics for apparel and upholstery applications. The work of [17] proposed to enforce no overlap between any two irregular shapes by imposing that circles inscribed within one shape do not overlap with circles inscribed within another one, resulting in an optimization model with non-convex quadratic constraints. Using this approach, the authors obtained for the first time optimal nesting solutions to a four polygon problem, using off-the-shelf global optimization solvers to tackle the non-convex quadratically constrained models. Focusing on the circle-inscribing approach for nesting problems, [34] proposed a novel branching scheme on circle-circle non-overlapping constraints and demonstrated the ability to find global optimal nestings to benchmark instances with five polygons, as well as solutions to instances with up to seven polygons under fixed rotation. Both the circle packing problem and the irregular shape nesting problem have been studied extensively, with most of the focus being on the development of heuristics to obtain large-scale packings [4, 20]. While heuristic methods are practically valuable for the generation of feasible solutions, they cannot rigorously quantify the optimality gap, and therefore provide no guarantees regarding how much value is left on the table by the packings produced. Arguably, the exact solution of optimization models with non-overlapping constraints is of great practical importance.

Mathematical models with circle-circle non-overlapping constraints fall into the quadratically constrained quadratic programming (QCQP) class, which is currently a very active research area in global optimization. Generally speaking, there are two approaches for convexifying QCQPs, namely semi-definite programming (SDP) relaxation and multi-term polyhedral relaxation with reformulation-linearization techniques [7]. The polyhedral approach calls for approximating the convex hull of the non-convex feasible solution space via linear inequalities, while the SDP method is to characterize the convex hull via semi-definite cones. Interested readers are referred to [5] for details. Although the SDP relaxation is usually tighter than the polyhedral one, optimizing an SDP problem is generally computationally less efficient than a linear one. Therefore, general-purpose global solvers [24, 32, 33] commonly rely on polyhedral relaxations to address QCQPs. Despite many recent advances in global optimization solvers, however, optimizing models with non-overlapping constraints is still incredibly challenging. Our computational studies on circle packing instances (Section 5) also show that general-purpose global solvers could only solve instances of up to 10 circles to guaranteed optimality.

At the same time, there exist only a handful of attempts in the open literature to address such models in a customized approach. The work of [18] considered the problem of packing a fixed number of identical circles into a given square with the objective of maximizing the circle radius. The authors conducted a theoretical comparison of several convexification techniques on non-overlapping constraints, including polyhedral and semi-definite relaxations, and assessed their strength theoretically. They pessimistically concluded that the current state-of-the-art bounding techniques within general-purpose global optimization algorithms are only effective for small-size instances (e.g., with up to 10 or so circles). In contrast, several tailored exact algorithms, utilizing interval arithmetic-based branch-and-bound methods, have been shown to be effective at solving to optimality instances of packing an excess of 30 identical circles in the unit square [14]. More specifically, the authors of [19] incorporated into a rectangular branch-and-bound approach optimality conditions satisfied by at least one optimal solution, solving instances of up to 39 circles to optimality. In addtion, [22] and [30] proposed methods for eliminating large sets of suboptimal points of the equivalent point packing problem. In [23], the authors employed interval arithmetic to expedite the branch-and-bound algorithm, while the work of [21] presented geometric results concerning the structural properties of such problems of packing circles in the unit square. Finally, for more general settings, the work of [26] proposed to approximate the quadratic function in the left-hand side of a non-overlapping constraint via piecewise linear functions. This approach necessitates the introduction of binary variables to represent the latter, resulting in a mixed-integer linear programming model, and thus might become impractical as the approximation accuracy increases.

This paper presents an extension of the branching strategy on non-overlapping constraints previously developed in [34]. The main idea is rooted in the geometric interpretation of a circle-circle non-overlapping constraint. More specifically, the constraint (1) dictates that any feasible point in the transformed variable space $\left( a_i - a_j\right)$–$\left( b_i - b_j\right)$ should lie outside (or exactly on) the circumference of the circle that has a center with coordinates $\left( 0, 0\right)$ and has a radius of $r_i + r_j$. Unlike a traditional, general-purpose spatial branch-and-bound based solver, which must generically handle each non-convex constraint by relaxing it individually into its convex relaxation and tighten that relaxation via branching on the domains of the problem’s variables, our perspective is to split the feasible, non-convex domain imposed by non-overlapping constraints and enforce feasibility in a more direct fashion. This approach is also clearly distinct from the aforementioned works on identical circles packing [19, 21,22,23, 30], since those utilize branching on variable intervals.

More specifically, we will follow an approach that branches on the domain of constraint, rather than the domain of variables. Additionally, we observe that the non-overlapping constraint imposes a reverse convex region [15]. It is well-known that reverse convex constraints can induce intersection cuts [6, 15], which are also called concavity cuts [16] in the global optimization community. These cuts are computationally cheap to generate, and they can be utilized to strengthen the model relaxation. In order to further tighten the model relaxation, we also propose three feasibility-based tightening techniques. The distinct contributions of our work can be summarized as follows.

• We develop a customized branch-and-bound (BB) approach for solving problems with unequal circle-circle non-overlapping constraints.

• We apply a generalized version of the intersection cut formula from the seminal paper of [6], as well as propose three types of feasibility-based tightening techniques, to strengthen the BB node relaxations.

• We conduct a comprehensive computational study based on two popular variants of the circle packing problem to demonstrate that our approach achieves superior performance over the use of various state-of-the-art general-purpose global optimization solvers.

The remainder of the paper is organized as follows. In Sect. 2, we provide a concise description of an optimization model with non-convexities that stem from the presence of non-overlapping constraints. In Sect. 3, we discuss how to construct a suitable linear relaxation of such a model that we can use as the basis of our BB algorithm, followed by a presentation of the complete algorithmic procedure. In Sect. 4, we discuss strengthening techniques, including strengthened intersection cuts and feasibility-based tightening. Section 5 presents results on the algorithm’s computational performance as well as a comprehensive comparison against the use of five different state-of-the-art global optimization solvers. Finally, we conclude our paper with some remarks in Sect. 6.

2 Problem definition

In this work, we focus on the following problem (2).

$$\begin{aligned} \begin{aligned}&\underset{x \in \mathbb {R}^n}{\text {minimize}}&c^\top x \\&\text {subject to}&f_k(x) \le 0&\forall \, k \in \mathcal {K} \\&&x_i^2 + x_j^2 \ge \rho _{ij}^2&\forall \left( i, j\right) \in \mathcal {M} \\&&x^L \le x \le x^U, \end{aligned} \end{aligned}$$

(2)

where $f_k(x) : \mathbb {R}^n \mapsto \mathbb {R}$ denotes a convex function, for each applicable index $k \in \mathcal {K}$, while $x_i^2 + x_j^2 \ge \rho _{ij}^2$ represents a circle-circle non-overlapping constraint, for each applicable ordered pair $\left( i, j\right) \in \mathcal {M}$.¹ Without loss of generality, we assume $x_i^L \le x_i^U$, for all $i \in \left\{ 1, 2,..., n\right\}$, where these variable bounds are not necessarily finite; that is, we allow for $x_i^L \rightarrow -\infty$ and/or $x_i^U \rightarrow +\infty$.

Since non-overlapping constraints induce a non-convex solution space, problem (2) is a global optimization problem. In this work, we aim to develop exact, custom-built methods for solving this problem to provable global optimality. We remark that this paper focuses on the case where $\rho _{ij}$ are generally different from each other, i.e., we are interested in packing unequal, a.k.a. non-identical, circles. Of course, the methodologies developed herein can still be applied with instances featuring identical circles, though in that case the use of specialized algorithms for packing identical circles is advisable for better overall tractability. We also remark that this paper is dedicated to the case where $\rho _{ij}$ are constant. The setting where $\rho _{ij}$ become variables (presumably to be penalized in the objective) constitutes an interesting generalization, and whereas some of the ideas contemplated in this paper, such as the purpose-designed branching scheme and the use of intersection cuts, would be straightforward to adapt, other aspects, such as the feasibility-based tightening techniques, would require further exploration as future work.

3 Solution approach

Our approach is based on the construction of a branch-and-bound tree where linear programming (LP) relaxations are solved at each node. Specifically, the convex domain defined by $f_k(x) \le 0$ in (2) is outer-approximated by linear inequalities. The main challenge arises from the non-convexities introduced by the non-overlapping constraints, $x_i^2 + x_j^2 \ge \rho _{ij}^2$, which we address in the remainder of this section.

3.1 Customized model relaxation

Here, we shall discuss how a suitable linear relaxation is constructed as the basis of the BB search algorithm. First, we adopt the branching scheme from our previous work [34], applied on a non-overlapping constraint from the set $\left( i, j\right) \in \mathcal {M}$. Let $\bar{x}$ represent the current optimal solution of the LP relaxation at some BB node, and let $D_{ij}$ denote a disk that is centered at the origin $\left( 0, 0\right)$ and has a radius of $\rho _{ij}$.. Furthermore, let $\theta _{ij}$ be the angle between the positive $x_i$-axis and the point given by the coordinates $\left( \bar{x}_i, \bar{x}_j\right)$, and let $\left[ \theta _{ij}^L, \theta _{ij}^U\right]$ represent its feasible interval, which is originally equal to $\left( 0, 2\pi \right)$.

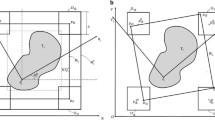
In the $x_i$–$x_j$ space, the non-overlapping constraint requires that all feasible points project either outside or exactly on the circumference of disk $D_{ij}$ (Fig. 1a). Initially, dropping this constraint from consideration results in a convex relaxation that is defined by the full space (Fig. 1b). Feasibility of the non-convex constraint can be then be gradually enforced by branching on the implicit domain of variable $\theta _{ij}$ variable, and by tightening the relaxation in the $x_i$–$x_j$ space, as follows.

Let X denote a solution of the relaxed problem with coordinates $\left( \bar{x}_i, \bar{x}_j\right)$ such that it violates the original constraint. Using this solution as a guide, we can split the circumference of $D_{ij}$ into three parts (each representing an arc of angle $2\pi /3$ radians), and we can define a set of three linear constraints (corresponding to one secant and two boundary lines) to form the convex relaxation of the original non-overlapping constraint in each of the three resulting subdomains. As long as they are properly oriented with respect to X (Fig. 1c), it can be guaranteed that all of the three subdomains exclude the parent solution.

In subsequent violations of the same constraint $\left( i, j\right) \in \mathcal {M}$, one could further dissect the applicable $\theta _{ij}$ interval into two parts. Again, as long as the solution X is used as the guide to define the branching point, one can guarantee that this parent solution is excluded from both resulting subdomains, defining a proper branching strategy to be employed in the course of the BB search process. In particular, one can analytically identify a point N on the circumference of disk $D_{ij}$ such that the Euclidean distances between X and two resulting secant lines are equal, in the hope of producing a more balanced BB tree. Let $\theta _{ij}^*$ denote the angle in radians between the positive $x_i$-axis and the point N, then the resulting proposed split is $\left[ \theta _{ij}^L, \theta _{ij}^*\right]$ and $\left[ \theta _{ij}^*, \theta _{ij}^U\right]$ (Fig. 1d).

We highlight that the aforementioned branching scheme proceeds from the perspective of splitting the space induced by the non-convex non-overlapping constraints, which distinguishes our work from the classic idea of branching on each variable’s interval. By using the novel scheme, we enforce non-convex constraint feasibility in a direct manner, which is essential in global optimization, yet difficult to achieve in general-purpose global optimization codes for all but the simplest constraint functional forms.

Fig. 1

The non-overlapping constraint and its dynamically tightened relaxation (adapted from [34])

Given the above relaxation strategy, Eqs.(3)–(7) constitute a relaxed LP formulation to be solved at each node of our BB search process.

$$\begin{aligned}&\underset{x \in \mathbb {R}^n}{\text {minimize}}&c^\top x \end{aligned}$$

(3)

$$\begin{aligned}&\text {subject to}&f_k(\tilde{x}) + \nabla f_k(\tilde{x})^\top (x - \tilde{x}) \le 0&\forall \, \tilde{x} \in \mathcal {H}_k, \forall \, k \in \mathcal {K} \end{aligned}$$

(4)

$$\begin{aligned}&&\alpha _{ij\ell } x_i + \beta _{ij\ell } x_j \ge \gamma _{ij\ell }&\forall \, \ell \in \{1, 2, 3\}, \forall \, (i, j) \in \tilde{\mathcal {M}} \end{aligned}$$

(5)

$$\begin{aligned}&&\phi ^\top _t x \ge \xi _t&\forall \, t \in \mathcal {T} \end{aligned}$$

(6)

$$\begin{aligned}&&x^L \le x \le x^U&\end{aligned}$$

(7)

In the above formulation, constraints (4) constitute outer-approximation inequalities for $f_k(x) \le 0, k \in \mathcal {K}$, where $\tilde{x}$ are the points of linearization, noting that such outer-approximation is superfluous for any affine $f_k(x)$. The parameters $\alpha _{ij\ell }$, $\beta _{ij\ell }$ and $\gamma _{ij\ell }$ in constraints (5) are suitably chosen in each case to define the linear inequalities that relax the original non-overlapping constraints discussed above, while the set $\tilde{\mathcal {M}} \subseteq \mathcal {M}$ denotes the set of circle pairs for which the corresponding $\theta _{ij}$ interval has been branched at least once. Constraints (6) generically denote strengthening cuts that we shall discuss in Sect. 4, while variable bounds are provided in constraints (7).

Note how, after a branch is applied, the parent node relaxation is tightened by adding elements to the set $\tilde{\mathcal {M}}$, when a new circle pair is branched upon for the first time, or by updating the coefficients $\alpha /\beta /\gamma$, when the circle pair is branched upon further. The relaxation is also tightened by appending and/or updating the set of strengthening cuts $\mathcal {T}$, while the outer-approximation sets $\mathcal {H}_k$ are also expanded as appropriate (see details later).

3.2 The branch-and-bound algorithm

We shall now focus on the implementation of the customized BB algorithm. At the root node, the set $\mathcal {H}_k$ is initialized with points $w x^L + \left( 1 - w\right) x^U$, where $w \in \{0.25, 0.5, 0.75\}$, while the sets $\tilde{\mathcal {M}}$ and $\mathcal {T}$ begin as empty sets. All of them will be dynamically expanded and updated as the algorithm proceeds.

After solving the LP relaxation (3)–(7) at each node, we check whether each of the convex constraints (set $\mathcal {K}$) as well as each of the non-overlapping constraints (set $\mathcal {M}$) are satisfied within some predefined tolerance $\varepsilon$ (we use $\varepsilon = 10^{-5}$) at the current LP solution $\bar{x}$.² We first focus on the convex constraints, and if $f_k(\bar{x}) > \varepsilon$ for some $k \in K$, we add an outer-approximation cut by setting $\mathcal {H}_k \leftarrow \mathcal {H}_k \cup \{\bar{x}\}$. Note that, at each iteration, we only add such cuts for the (up to) 5 most violated convex constraints k. If any outer-approximation cuts are added, we resolve the LP relaxation; otherwise, we proceed with checking the feasibility of the non-overlapping constraints, as follows. For each non-overlapping constraint $x_i^2 + x_i^2 \ge \rho _{ij}^2$, $\left( i,j\right) \in \mathcal {M}$, we define $V_{ij} := \rho _{ij} - \sqrt{\bar{x}_i^2 + \bar{x}_j^2}$, and we consider this constraint to be violated, if $V_{ij} > \varepsilon$. If no violated non-overlapping constraints exist, then a feasible solution $\bar{x}$ has been obtained; this solution is considered as a possible new incumbent, and the node is fathomed. However, if at least one non-overlapping constraint is violated, the node must be either tightened or branched, eliminating the current LP solution in either case.

Deferring the discussion of tightening techniques to Sect. 4, we now focus on our branching strategy, namely how we choose which implicit $\theta _{ij}$ variable (element of set $\mathcal {M} : \left\{ V_{ij} > \varepsilon \right\}$) to branch upon. Recalling that further branching of a previously branched $\theta _{ij}$ variable produces fewer child nodes in the BB tree than the initial branching (two versus three subdomains), the violation of currently unbranched non-overlapping constraints is first discounted by a factor of $\tau ^{unbr}$ (we use $\tau ^{unbr} = 0.7$); that is, $V_{ij} \leftarrow \left( 1- \tau ^{unbr}\right) V_{ij}$, for all $\left( i,j\right) \in \mathcal {M} \setminus \tilde{\mathcal {M}}$. We then choose to branch on the implicit $\theta _{ij}$ variable that corresponds to the highest violation after such modifications. Note that, according to the earlier discussion, the branching is implemented either as updating existing left-hand side coefficients or by adding new constraints, depending on whether $\left( i,j\right) \in \tilde{\mathcal {M}}$ or not.

4 Strengthening techniques

We consider two types of relaxation strengthening techniques, namely intersection cuts and feasibility-based tightening. Even though intersection cuts [6] are well-known for their use in integer programming, their applicability goes much beyond that area, being generic tools to deal with non-convexities that may stem from either integrality or continuous nonlinear constraints. However, to the best of our knowledge, only a few works in the literature to date have attempted to apply these techniques in the context of continuous nonlinear optimization. In this work, we propose to utilize strengthened intersection cuts to tighten our LP relaxations. Additionally, various feasibility-based tightening techniques are also introduced.

4.1 Intersection cuts

The idea of intersection cuts was originally proposed in [6] to construct valid cuts for integer programming. It has gradually received more and more attention in other areas such as reverse convex programming [15], bilevel optimization [13], polynomial programming [10], and factorable MINLP [28], among others. To the best of our knowledge, the literature always considers the case where variables are bounded from below by zero, while the more general case where variables are bounded from below and/or above by arbitrary values has been ignored. The challenge comes from the fact that, at the LP optimal solution, some non-basic variable might be at its upper bound, or some non-basic variable might be at its lower bound yet that bound not being 0. In such cases, the intersection cut formula from the seminal paper [6] is not immediately valid. Whereas this can be easily dealt with by explicitly adding to the model variable-bounding constraints (thus forcing all non-basic variables at an optimal LP solution to be slack variables), it is generally much more common and useful for general-purpose global optimization solvers to separate variable bounds from other constraints and to handle them separately. To this end, we present in Sect. 4.1.1 a complete derivation of intersection cuts for more general cases where variable bounds might be arbitrary numbers. Afterwards, in Sect. 4.1.3, we consider a strengthening method to further tighten these cuts.

4.1.1 Generating intersection cuts

Consider the following problem:

$$\begin{aligned} \begin{aligned}&\underset{x \in \mathbb {R}^n}{\text {minimize}}&c^\top x \\&\text {subject to}&x \in \mathcal {P} \cap \mathcal {Q}, \end{aligned} \end{aligned}$$

(8)

where $\mathcal {P} := \left\{ x \in \mathbb {R}^n: Ax \le b; \, x^L \le x \le x^U\right\}$,³ with $A \in \mathbb {R}^{m \times n}$ and $b \in \mathbb {R}^m$, while $\mathcal {Q}$ represents a “complicating” set. In this work, we consider

$$\begin{aligned} \mathcal {Q} := \left\{ x \in \mathbb {R}^n: x_i^2 + x_j^2 \ge \rho _{ij}^2, \, \forall \, (i, j) \in \mathcal {M} \right\} . \end{aligned}$$

Initially, we relax the feasible region by only considering $x \in \mathcal {P}$, and we introduce slack variables $s \in \mathbb {R}^m_{\ge 0}$ to obtain a linear program in standard form.

Let $t := \left( x, s\right)$ denote all variables, for convenience. Assume that the linear program is feasible and that its objective function is bounded; then, it can be solved via the simplex algorithm. Let $\bar{t}= \left( \bar{x}, \bar{s}\right)$ represent the current LP optimal solution. Without loss of generality, we assume that $\bar{x} \notin \mathcal {Q}$, since otherwise problem (8) has been solved. We assume that we are given a closed convex set $\mathcal {S}$ whose interior contains $\bar{x}$ but no feasible point; that is, $\bar{x} \in int(\mathcal {S})$ and $int(\mathcal {S}) \cap (\mathcal {P} \cap \mathcal {Q}) = \emptyset$. In the following, we shall discuss how to generate a valid intersection cut to eliminate $\bar{x}$ using $\mathcal {S}$ for the case where structural variables x might be bounded from below and/or above.

Let $\mathcal {I}$ represent the index set of structural variables x. Let $\mathcal {B}$ and $\mathcal {N}$ denote the index sets associated with the basic and non-basic variables, respectively. Furthermore, let $\mathcal {N}^L$ denote the set of non-basic variables that are currently at their lower bounds and $\mathcal {N}^U := \mathcal {N} \setminus \mathcal {N}^L$ represent the set of non-basic variables at their upper bounds. Note that both structural and slack variables might be non-basic. We focus on the structural variables and, for each non-basic such variable $x_i$, $i \in \mathcal {I} \cap \mathcal {N}$, we add a trivial relation, setting $x_i$ to itself. The modified simplex tableau is demonstrated in (9), where non-basic variable $t_j$ might correspond to either a structural (i.e., $x_k$, for some k) or a slack (i.e., $s_k$, for some k) variable.

$$\begin{aligned} \begin{aligned}&x_i = \bar{x}_{i}- & {} \sum _{j \in \mathcal {N}^L}^{} \bar{a}_{ij} (t_j - t_j^L)+ & {} \sum _{j \in \mathcal {N}^U}^{} \bar{a}_{ij} (t_j^U - t_j)&\forall \, i \in \mathcal {I} \cap \mathcal {B} \\&x_i = \bar{x}_{i}- & {} (-1) (x_i - x_i^L)&&\forall \, i \in \mathcal {I} \cap \mathcal {N}^L \\&x_i = \bar{x}_{i}&+ & {} (-1)(x_i^U - x_i)&\forall \, i \in \mathcal {I} \cap \mathcal {N}^U \end{aligned} \end{aligned}$$

(9)

For convenience, tableau (9) can also be represented in vector form, where $\bar{a}_{j}$ are suitably defined vectors:

$$\begin{aligned} x = \bar{x} - \sum _{j \in \mathcal {N}^L}^{} \bar{a}_{j} (t_j - t_j^L) + \sum _{j \in \mathcal {N}^U}^{} \bar{a}_{j} (t_j^U - t_j). \end{aligned}$$

(10)

Associated with the simplex tableau (10) is a conic relaxation of $\mathcal {P}$, called the LP-cone, whose apex is $\bar{x}$ and whose facets are defined by n hyperplanes that form the basis of $\bar{x}$. Thus, the LP-cone has n extreme rays, each formed by an extreme direction $r^j$ emanating from the apex $\bar{x}$, where $r^j = - \bar{a}_j$ if $j \in \mathcal {N}^L$, or $r^j = \bar{a}_j$ if $j \in \mathcal {N}^U$. Following the extreme ray $\bar{x} + \lambda _j r^j$ (where $\lambda _j \ge 0$), we seek its intersecting point with the boundary of the set $\mathcal {S}.$ More specifically, for each extreme ray $\bar{x} + \lambda _j r^j$, $j \in \mathcal {N}$, we seek to solve

$$\begin{aligned} \lambda _j^* := \underset{\lambda _j \ge 0}{\text {maximize}} \left\{ \lambda _j: \bar{x} + \lambda _j r^j \in \mathcal {S} \right\} . \end{aligned}$$

(11)

Since $\bar{x} \in int(\mathcal {S})$, problem (11) is always feasible (e.g., $\lambda _j = 0$ is a feasible solution). If $r^j$ is a recessive direction of $\mathcal {S}$ (i.e., $r^j \in rec(\mathcal {S})$, where $rec(\mathcal {S})$ denotes the recession cone of $\mathcal {S}$), there is no intersection point between the extreme ray $\bar{x}+\lambda _jr^j$ and the boundary of the set $\mathcal {S}$. Thus, in this case, the objective in (11) is unbounded from above and we set $\lambda _j^* = +\infty$. Otherwise, we obtain a unique solution $\lambda _j^*$ and the intersection point is $\bar{x}+\lambda _j^*r^j$.

Let $\mathcal {N}^1:= \left\{ j \in \mathcal {N}: r^j \in rec(\mathcal {S}) \right\}$ and $\mathcal {N}^2:= \mathcal {N} \setminus \mathcal {N}^1$ for convenience. The intersection cut that cuts off $\bar{x}$ is defined to be the halfspace whose boundary contains each intersection point $\bar{x} + \lambda _j^* r^j$, $j \in \mathcal {N}^2$ and which is parallel to each extreme direction $r^j$, $j \in \mathcal {N}^1$ (Fig. 2). The validity of intersection cuts is intuitive from a geometric perspective. Thus, we skip its proof and instead focus on the derivation of the intersection cut formula.

Fig. 2

Generation of intersection cuts

Proposition 1

The intersection cut can be represented in non-basic space (e.g., using non-basic variables $t_j$) as follows:

$$\begin{aligned} \sum _{j \in \mathcal {N}^L}^{} \frac{t_j - t_j^L}{\lambda _j^*} + \sum _{j \in \mathcal {N}^U}^{} \frac{t_j^U - t_j}{\lambda _j^*} \ge 1. \end{aligned}$$

(12)

Proof

We only need to prove that this halfspace passes through all intersection points $\bar{x} + \lambda _j^* r^j$, $j \in \mathcal {N}^2$ and that it is parallel to extreme directions $r^j$, $j \in \mathcal {N}^1$. We consider the following two cases.

• If $j \in \mathcal {N}^2$, the intersection point $\bar{x} + \lambda _j^* r^j$ is obtained via moving from $\bar{x}$ along the direction $r^j$ by a distance of $\lambda _j^*$. If $j \in \mathcal {N}^2 \cap \mathcal {N}^L$, in the non-basic space we have $t_j = t_j^L + \lambda _j^* \cdot 1$, and the other non-basic variables $t_{j^\prime }$ ($j^\prime \in \mathcal {N} \setminus \left\{ j\right\}$) will remain at their lower or upper bounds at this intersection point. Therefore,

  $$\begin{aligned} \sum _{j^\prime \in \mathcal {N}^L}^{} \frac{t_{j^\prime } - t_{j^\prime }^L}{\lambda _{j^\prime }^*} + \sum _{j^\prime \in \mathcal {N}^U}^{} \frac{t_{j^\prime }^U - t_{j^\prime }}{\lambda _{j^\prime }^*} = \frac{t_j^L + \lambda _j^* - t_j^L}{\lambda _j^*} = 1. \end{aligned}$$

  In other words, the intersection cut passes through the intersection point $\bar{x} + \lambda _j^* r^j$. This also applies in the case $j \in \mathcal {N}^2 \cap \mathcal {N}^U$.

• If $j \in \mathcal {N}^1$, we only need to prove that the intersection cut is parallel to $r^j$. Moving along the direction $r^j$ from the point $\bar{x}$, if $j \in \mathcal {N}^1 \cap \mathcal {N}^L$, we have $t_j = t_j^L + \lambda \cdot 1$ (where $\lambda \ge 0$), and the other non-basic variables $t_{j^\prime }$ ($j^\prime \in \mathcal {N} \setminus \left\{ j\right\}$) will remain unchanged. Therefore,

  $$\begin{aligned} \sum _{j^\prime \in \mathcal {N}^L}^{} \frac{t_{j^\prime } - t_{j^\prime }^L}{\lambda _{j^\prime }^*} + \sum _{j^\prime \in \mathcal {N}^U}^{} \frac{t_{j^\prime }^U - t_{j^\prime }}{\lambda _{j^\prime }^*} = \frac{t_j^L + \lambda - t_j^L}{\lambda _j^*} = \frac{\lambda }{+\infty } = 0. \end{aligned}$$

  The parallel relationship is proved. This also applies in the case $j \in \mathcal {N}^1 \cap \mathcal {N}^U$. $\square$

As mentioned in [6], $\lambda _j^*$ should be approximated from below for numerical validity. Readers are referred to that work for further details, with the observation however that the intersection cut formula (12) is more generic than the one presented in [6], reducing to the latter when structural variables x are only bounded from below by zero.

Note that, given a mathematical model, one has to identify a suitable set $\mathcal {S}$ to derive valid intersection cuts. We highlight that such a convex set $\mathcal {S}$ generally exists, if some constraint in the model imposes a reverse convex region. In fact, from problem (11), one can infer that deeper cuts will be produced from larger sets $\mathcal {S}$ whose boundary intersects with extreme rays at intersections points further away from the apex, $\bar{x}$.

4.1.2 Generating intersection cuts for non-overlapping constraints

In our context, we can easily identify a valid sets $\mathcal {S}$ for generating intersection cuts. Considering the fact that the non-overlapping constraint $x_i^2 + x_j^2 \ge \rho _{ij}^2$ represents a reverse convex region [15], we can define $\mathcal {S}_{ij} := \{x \in \mathbb {R}^n: x_i^2 + x_j^2 \le \rho _{ij}^2 \}$ (Fig. 3a) such that $\bar{x} \in int(\mathcal {S}_{ij})$. Furthermore, recalling that enlarging the set whenever possible leads to stronger cuts, we can enlarge $S_{ij}$ using the following formula (Fig. 3b) when $\theta _{ij}^U - \theta _{ij}^L < 2 \pi$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{ij} \leftarrow \mathcal {S}_{ij} \cup \left\{ x \in \mathbb {R}^n \left| \begin{aligned}&\cos (\theta ) x_i + \sin (\theta ) x_j \le \rho _{ij}, \;\;\; \forall \, \theta \in \{\theta _{ij}^{L}, \theta _{ij}^{U} \} \\&\cos (\frac{\theta _{ij}^{L} + \theta _{ij}^{U}}{2} ) x_i + \sin (\frac{\theta _{ij}^{L} + \theta _{ij}^{U}}{2}) x_j \le \rho _{ij} \cos (\frac{\theta _{ij}^{U} - \theta _{ij}^{L} }{2}) \end{aligned} \right. \right\} . \end{aligned} \end{aligned}$$

(13)

The enlarged set $\mathcal {S}_{ij}$ remains convex and does not contain any feasible solution in its interior; therefore, intersection cuts generated from $\mathcal {S}_{ij}$ will be valid. We highlight that enlarging the convex set and generating stronger intersection cuts becomes possible due to the chosen scheme to branch upon non-overlapping constraints.

In our implementation, we define $\mathcal {S}_{ij}$ for every $\left( i, j\right) \in \mathcal {M}$. When $\theta _{ij}^U - \theta _{ij}^L < 2 \pi$, we use the enlarged version (13). We use these sets to generate intersection cuts for which the corresponding non-overlapping constraint is violated, but only the best 5 cuts with Euclidean distances from $\bar{x}$ larger than tolerance $\delta = 10^{-2}$ are added to the model. Furthermore, whenever $\theta _{ij}^L$ or $\theta _{ij}^U$ is updated due to branching or tightening, we always enlarge the set $\mathcal {S}_{ij}$ and attempt to compute new $\lambda _j^*$ values from (12) towards strengthening the related intersection cuts that have already been generated.

Fig. 3

Valid convex sets $\mathcal {S}_{ij}$ for generating intersection cuts

4.1.3 Strengthening intersection cuts

Figure  4 demonstrates a simple case where the intersection cut (blue solid line) generated from Sect. 4.1.1 can be further tightened. The generated intersection cut passes through an intersection point and is parallel to the extreme direction $r^j$ (since $r^j \in rec(\mathcal {S})$). In this case, we can identify another cut $\widehat{IC}$ (red solid line), which also passes through the same intersection point, but which is parallel to some other recessive direction $\widehat{r} \in rec(\mathcal {S})$. Apparently, $\widehat{IC}$ is a valid cut that dominates IC.

Fig. 4

Strengthened intersection cuts

The validity of $\widehat{IC}$ deduces from the fact that, by convexity of $\mathcal {S}$, any point satisfying IC but not $\widehat{IC}$ lies within the interior of $\mathcal {S}$ and is thus outside $\mathcal {P} \cap \mathcal {Q}$. The stronger cut $\widehat{IC}$ can be regarded as a halfspace that passes through the existing intersection point and a new one residing at the negative part of the extreme ray $\bar{x} + \lambda r^j$ (where $\lambda \ge 0$). In order to maintain the validity of the new intersection cut, as the work of [10] suggested, one has to guarantee that $\widehat{r}: = (\bar{x} + \lambda _{j^\prime }^* r^{j^\prime }) - (\bar{x} + \lambda _j r^j)$, the direction from the new intersection point, $(\bar{x} + \lambda _j r^j)$, to every intersection point, $(\bar{x} + \lambda _{j^\prime }^* r^{j^\prime })$, is a recessive direction of $\mathcal {S}$ (i.e., $\widehat{r} \in rec(\mathcal {S})$) for every $j^\prime \in \mathcal {N}^2$. It is clear from (12) that increasing $\lambda _j$ while $\lambda _j \le 0$ leads to a stronger cut. Thus, for each extreme direction $r^j, j \in \mathcal {N}^1$, we define the following problem:

$$\begin{aligned} \lambda _j^* := \underset{\lambda _j \le 0}{\text {maximize}} \left\{ \lambda _j: \lambda _{j^\prime }^* r^{j^\prime } - \lambda _j r^j \in rec(\mathcal {S}), \forall \, j^\prime \in \mathcal {N}^2 \right\} . \end{aligned}$$

(14)

If problem (14) is infeasible, we set $\lambda _j^* = -\infty$; otherwise, a unique solution $\lambda _j^*$ is obtained, resulting in a new intersection point $(\bar{x} + \lambda _j^* r^j)$. With this, we arrive at Proposition 2.

Proposition 2

The intersection cut defined by (12) and using $\lambda _j^*$ from (11), for $j \in \mathcal {N}^2$, and $\lambda _j^*$ from (14), for $j \in \mathcal {N}^1$, is valid.

Given a convex set $\mathcal {S}$, the problem (14) is in general hard to solve because no closed-form formula for $rec(\mathcal {S})$ is available. However, in our context, the recession cone $rec(\mathcal {S}_{ij})$ can be easily identified. More specifically, we distinguish three cases:

• (i) when $\theta _{ij}^U - \theta _{ij}^L > \pi$, the projection of $\mathcal {S}_{ij}$ onto the $x_i$–$x_j$ space is a bounded area, and hence its recession cone is

  $$\begin{aligned} rec(\mathcal {S}_{ij}) = \left\{ x \in \mathbb {R}^n: x_i = 0, \,x_j = 0\right\} , \end{aligned}$$

  projecting to a singleton on the $x_i$–$x_j$ space;

• (ii) when $\theta _{ij}^U - \theta _{ij}^L = \pi$, the recession cone becomes

  $$\begin{aligned} rec(\mathcal {S}_{ij}) = \left\{ x \in \mathbb {R}^n: x_i = -\lambda \sin (\theta _{ij}^L), \,x_j = \lambda \cos (\theta _{ij}^L), \, \forall \, \lambda \ge 0 \right\} , \end{aligned}$$

  projecting to a ray on the $x_i$–$x_j$ space;

• (iii) when $\theta _{ij}^U - \theta _{ij}^L < \pi$, it is easy to show that

  $$\begin{aligned} rec(\mathcal {S}_{ij})&= rec \left( \left\{ x \in \mathbb {R}^n: \cos (\theta ) x_i + \sin (\theta ) x_j \le \rho _{ij}, \forall \, \theta \in \{\theta _{ij}^{L}, \theta _{ij}^{U} \} \right\} \right) \nonumber \\&= \left\{ x \in \mathbb {R}^n: \cos (\theta )x_i + \sin (\theta ) x_j \le 0, \forall \, \theta \in \left\{ \theta _{ij}^L, \theta _{ij}^U \right\} \right\} . \end{aligned}$$

  (15)

We remark that, when case (i) applies, the problem (14) is almost always infeasible, due to insufficient degrees of freedom. Furthermore, case (ii) is unlikely to be relevant in the context of double-precision arithmetic, due to inability to detect that $\theta _{ij}^U - \theta _{ij}^L$ equals $\pi$ exactly, and hence, we did not consider this case in our implementation. It is only under case (iii) that the closed-form formula (15) can be plugged into (14) and a value for $\lambda _j^*$ be analytically identified for every $j \in \mathcal {N}^1$. Therefore, in our implementation, we generate intersection cuts using Proposition 1 in cases (i) and (ii), and we attempt to generate a strengthened version of such cuts using Proposition 2 only in case (iii).

4.2 Feasibility-based tightening

Feasibility-based tightening is a common technique in global optimization to reduce variable bounds, and it is usually implemented via interval arithmetic [25]. In our context, since explicit structural variable domains are not branched upon, the interval arithmetic technique would not tighten variable bounds effectively. Considering that our strategy is to branch on the feasible intervals of implicit variables $\theta _{ij}$, our feasibility-based tightening approach will instead focus on reducing the domains for these variables.

From a geometric perspective, the non-overlapping constraint, $x_i^2 + x_j^2 \ge \rho _{ij}^2$, requires the solution’s projection on the $x_i$–$x_j$ space to lie either outside or exactly on the circumference of disk $D_{ij}$ (Fig. 1). Let $FR_{ij}$ denote the feasible region of the $x_i$–$x_j$ space. At the root node of the BB tree, we have $FR_{ij} = conv\left( \left\{ (x_i, x_j): x_i^L \le x_i \le x_i^U, x_j^L \le x_j \le x_j^U \right\} \setminus int(D_{ij})\right)$, and this region gradually reduces due to branching or tightening. We emphasize that the feasible spaces $FR_{ij}$, $\left( i, j\right) \in \mathcal {M}$ are not explicitly enforced in the relaxation model, (3)–(7), because they are generally implied by other constraints. We also note that $FR_{ij}$ is always a bounded polyhedron (assuming that valid lower and upper bounds for $x_i$, $i \in \{1, 2, \ldots n\}$, can be extracted or deduced), and that this region might correspond to a reduced interval $\left[ \theta _{ij}^L, \theta _{ij}^U\right]$ for the implied variable $\theta _{ij}$. To that end, in our implementation, we attach our description of $FR_{ij}$ to the BB node as important information to be used for tightening the $\theta _{ij}$ intervals, as follows.

Assume that the projection of the current LP solution $\bar{x}$ lies in the interior of $D_{ij}$, i.e., $X \in FR_{ij} \cap int(D_{ij})$. Whenever $FR_{ij}$ is reduced due to some tightening technique, we can revisit the geometric meaning of the non-overlapping constraint and obtain $FR_{ij} \leftarrow conv\left( FR_{ij} \setminus int(D_{ij})\right)$ (Fig. 5). From that, we can infer possibly tighter $\left[ \theta _{ij}^L, \theta _{ij}^U\right]$ bounds, and whenever the latter are indeed tightened, we first update the relaxations for its corresponding non-overlapping constraint and then check whether X is cut off by the halfspace formed by the new secant line. Next, we discuss three opportunities to reducing $FR_{ij}$.

Fig. 5

Feasibility-based tightening

4.2.1 Generating concave envelopes

Let us begin by defining $h(x_i, x_j) := x_i^2 + x_j^2$, where $(x_i, x_j) \in FR_{ij}$. We seek the concave envelope, i.e., the tightest possible over-estimator, of $h(x_i, x_j)$ over its domain $FR_{ij}$, which we shall denote as $conc_{FR_{ij}} h(x_i, x_j)$. It is clear that the function $h(x_i, x_j)$ has a vertex polyhedral concave envelope over the bounded polyhedral domain $FR_{ij}$ [31]; therefore, its concave envelope coincides with the concave envelope of its restriction to the vertices of $FR_{ij}$ and consists of finitely many hyperplanes.⁴

As a result, we obtain the following constraints that are valid for our relaxation:

$$\begin{aligned} conc_{FR_{ij}} h(x_i, x_j) \ge \rho _{ij}^2. \end{aligned}$$

(16)

We remark that constraints (16) are not directly added to the relaxation model, (3)–(7), rather used to reduce $FR_{ij}$. More specifically, $FR_{ij} \leftarrow FR_{ij} \cap \Big \{(x_i, x_j): conc_{FR_{ij}} h(x_i, x_j) \ge \rho _{ij}^2 \Big \}$. If $FR_{ij}$ is indeed reduced in this manner, we then attempt to apply feasibility-based tightening as described in the preamble of this section to further tighten $FR_{ij}$. Note that this process can be applied recursively, since a smaller polytope $FR_{ij}$ will induce a tighter over-estimator for $h(x_i, x_j)$, which might in turn further reduce $FR_{ij}$.

4.2.2 Calculating Minkowski sums

Another typical feasibility-based tightening technique in global optimization is bound propagation [25]. Adapting this idea into our context, we propose to apply domain propagation. For example, in the context of packing three circles i, j and k, one usually seeks to enforce non-overlapping constraints in a pairwise sense. In this case, any feasible point $(a_i - a_j, b_i - b_j)$ satisfying the non-overlapping constraint $(a_i - a_j)^2 + (b_i - b_j)^2 \ge (r_i + r_j)^2$ must correspond to a point $(a_i - a_k, b_i - b_k)$ in the domain $FR_{ik}$ as well as to a point $(a_k - a_j, b_k - b_j)$ in the domain $FR_{kj}$. This results from the simple observation that

$$\begin{aligned} (a_i - a_j, b_i - b_j) = (a_i - a_k, b_i - b_k) + (a_k - a_j, b_k - b_j). \end{aligned}$$

(17)

Consequently, one can calculate the Minkowski sum of $FR_{ik}$ and $FR_{kj}$ to tighten $FR_{ij}$; that is, $FR_{ij} \leftarrow FR_{ij} \cap \left( FR_{ik} \oplus FR_{kj}\right)$. If $FR_{ij}$ is indeed reduced, the feasibility-based tightening $FR_{ij} \leftarrow conv\left( FR_{ij} \setminus int(D_{ij})\right)$ will be considered. Note that the Minkowski sum of two polytopes with $n_1$ and $n_2$ vertices, respectively, can be computed in $O(n_1 + n_2)$ time [9]; thus, the proposed procedure is computationally efficient.

4.2.3 Solving LPs

We can also refine feasible region $FR_{ij}$ by using the projection of the feasible region of the relaxation model, (3)–(7), onto the $x_i$–$x_j$ space. Considering that computing the exact projection is not practical, we choose to outer-approximate it via linear inequalities defined in the $x_i$–$x_j$ space. More specifically, one can solve an LP with the objective of minimizing some linear function, e.g., $\mu x_i + \nu x_j$, and with constraints (4)–(7), where $\mu$ and $\nu$ are properly chosen coefficients. Let $\sigma$ be its optimal value, thus $\mu x_i + \nu x_j \ge \sigma$ is a valid inequality to characterize the projection area and can be used to refine $FR_{ij}$; that is, $FR_{ij} \leftarrow FR_{ij} \cap \left\{ (x_i, x_j): \mu x_i + \nu x_j \ge \sigma \right\}$. If $FR_{ij}$ is successfully reduced in this manner, we then apply feasibility-based tightening as before.

In our context, we apply the above process for two separate objective functions, namely those that are parallel to the two linear boundaries of $FR_{ij}$ that neighbor the secant line. These were specifically chosen due to their potential to immediately tighten the secant line, which might thus help to eliminate the current LP solution, $\bar{x}$.

4.3 Implementation details

We note the following details about our implementation.

• With regards to the protocol via which we employ the various tightening techniques, we note the following. We first apply intersection cuts, followed by calculating Mikowski sums, and finally by solving LPs. Tightening from concave envelopes is swiftly applied as soon as $FR_{ij}$ is tightened during the latter two steps, and whenever $\bar{x}$ is cut off, we skip the subsequent routines and turn our attention to resolving the LP relaxation (3)–(7).

• Since the intersection cuts are formulated in non-basic space, and since we do not have access to non-basic slack variables when enforcing a constraint in the LP solver, we first convert it to the structural space. After this step, we apply some presolve reductions to mitigate numerical difficulties [3]. In particular, we first scale the coefficients in a cut such that their largest absolute value is 1.0, and we then perform proper reductions on small coefficients (e.g., less than $10^{-4}$) while maintaining the cut’s validity.

• In order to alleviate tapering off from using intersection cuts, we stop the separation if the gap is decreased by less than $0.01\%$ a total of 3 times.

• Outer-approximation and intersection cuts are removed from the LP model (3)–(7), if they are not active for the past 50 LP-solving rounds. We note that removed intersection cuts are still stored in the cut pool and will be strengthened when the corresponding convex sets are enlarged, in the hope that they might be added back to the set $\mathcal {T}$ if violated at some future point.

• Whenever $FR_{ij}$ is reduced at some BB node, we recursively call this routine to further reduce the feasible region, and this continues until the reduction in area of $FR_{ij}$ is less than $1\%$. Moreover, whenever the area of $FR_{ij}$ is reduced by at least $5\%$, we attempt to apply domain propagation to tighten relevant domains. However, since solving LPs can add up to the overall computational time, we only consider the 10 pairs $(i, j) \in \mathcal {M}$ with the largest violation values, $V_{ij}$.

5 Computational studies

In this section, we test our customized branch-and-bound approach and compare its performance against the state-of-the-art general purpose global optimization solvers, namely ANTIGONE 1.1 [24], BARON 19.7.13 [32], COUENNE 0.5 [8], LINDOGLOBAL 12.0 and SCIP 6.0 [2, 33]. Our algorithm was implemented in C++ and the LP relaxation models were solved via CPLEX Optimization Studio 12.8.0 through the C application programming interface. Global solvers were called within the GAMS 28.2.0 environment. The absolute optimality tolerance was set to be $10^{-4}$. All computational experiments were conducted on a single thread of an Intel Xeon CPU E5-2689 v4 @ 3.10GHz with 32GB of RAM.

5.1 Circle packing

5.1.1 Problem definitions

Let $\mathcal {C} = \left\{ 1, 2, 3 \ldots \right\}$ denote a set of circles. For each circle $i \in \mathcal {C}$, let $r_i$ denote its radius. Without loss of generality, we assume a circle ordering such that $r_i \ge r_j$, when $i < j$, for all $i, j \in \mathcal {C}$. We aim to identify a feasible configuration of these circles within (i) a larger circle, and (ii) a sheet of fixed width W, such that no circles overlap and the size of the circle (radius R) or the sheet (length L) is minimized. We refer to these settings as packing circles into a circle and packing circles into a rectangle, respectively. The latter is often also referred to in the literature as the circular open dimension problem (CODP).

Fig. 6

Two variants of circle packing problems

5.1.2 Mathematical modeling

Let $(a_i, b_i)$ denote the final coordinates for the center of circle $i \in C$. Assuming that the center of the containing circle is fixed to the point (0, 0), the problem of packing circles into a circle can be formulated as the non-convex model (18)–(21).

$$\begin{aligned}&\underset{a_i, b_i, R}{\text {minimize}}&R&\end{aligned}$$

(18)

$$\begin{aligned}&\text {subject to}&a_i^2 + b_i^2 \le \left( R - r_i\right) ^2&\forall \, i \in \mathcal {C} \end{aligned}$$

(19)

$$\begin{aligned}&&\left( a_i - a_j\right) ^2 + \left( b_i - b_j\right) ^2 \ge \left( r_i + r_j\right) ^2&\forall \, (i, j) \in \mathcal {C} \times \mathcal {C}: i < j \end{aligned}$$

(20)

$$\begin{aligned}&&R \ge \underset{i \in \mathcal {C}}{\text {max}} \left\{ r_i \right\}&\end{aligned}$$

(21)

Constraints (19) enforce that all circles lie within the circular container, constraints (20) guarantee that there is no overlap among the circles, while constraint (21) specifies the applicable lower bound on the containing circle’s radius. Additionally, as also pointed out in [27], two types of symmetry-breaking constraints can be added to the above model:

• i. Identical circles: When two circles i and j, $i < j$, are identical (i.e., $r_i = r_j$), then $a_i \le a_j$ breaks this symmetry. In our implementation, we equivalently enforce this by tightening $\left[ \theta _{ij}^L, \theta _{ij}^U \right] = \left[ \pi /2, 3\pi /2\right]$ at the root node.

• ii. Rotational symmetry and reflection: Rotational symmetry arises due to the fact that an equivalent packing solution can always be obtained via rotating the entire configuration by any angle; hence, one can enforce that $a_1 \le 0$ and $b_1 = 0$. Furthermore, the reflection of a feasible configuration through the horizontal axis results in an equivalent solution; hence, one can further impose $b_2 \ge 0$.

The mathematical formulation for packing circles into a rectangle is similar. Assuming that the bottom left corner of the rectangle is fixed to the point (0, 0), the non-convex model (22)–(25) applies.

$$\begin{aligned}&\underset{a_i, b_i, L}{\text {minimize}}&L&\end{aligned}$$

(22)

$$\begin{aligned}&\text {subject to}&r_i \le a_i \le L - r_i&\forall \, i \in \mathcal {C} \end{aligned}$$

(23)

$$\begin{aligned}&&r_i \le b_i \le W - r_i&\forall \, i \in \mathcal {C} \end{aligned}$$

(24)

$$\begin{aligned}&&\left( a_i - a_j\right) ^2 + \left( b_i - b_j\right) ^2 \ge \left( r_i + r_j\right) ^2&\forall \, (i, j) \in \mathcal {C} \times \mathcal {C}: i < j \end{aligned}$$

(25)

In this case, applicable constraints to break symmetry from reflection are: (i) $a_1 \le L/2$, and (ii) $b_1 \le W/2$.

5.1.3 Benchmark instances

In order to evaluate the performance of our approach, we consider instances of packing circles into a circle from [1]. Each instance is defined by two numbers, p and N, and the size of circles to be packed in every instance is defined by $r_i = i^p$, where $i = 1, 2, \ldots N$. We consider $N \in \{5, 6, \ldots , 11\}$ and $p \in \{-2/3, -1/2, -1/5, +1/2, +1\}$; thus, in total we have 35 instances of difference sizes.

For packing circles into a rectangle, we generate a suite of instances using data from the thirty-circle example in [29]. We consider $N \in \{6, 7, \ldots , 10\}$, and using the first N circles in each case, we generate all possible packing instances with $N-1$ circles. Therefore, we generate a total of 40 instances, namely 6 five-circle, 7 six-circle, 8 seven-circle, 9 eight-circle and 10 nine-circle instances. The rectangle width W is chosen to be 9.5, as per the literature reference [29].

5.2 Computational results

The goals of our computational study are to (i) assess the effect of strengthened intersection cuts and feasibility-based tightening on the BB tree, and (ii) conduct a comprehensive comparison between our proposed algorithm and state-of-the-art global solvers. These two goals are covered in Sects. 5.2.1 and 5.2.2, respectively. To ensure a fair comparison, all algorithms (including the global solvers) were initialized with heuristic solutions, which were obtained after running BARON heuristics with a time limit of 1 hour.

5.2.1 Effect of node relaxation tightening

We first analyze the effect of using strengthened intersection cuts on the branch-and-bound algorithm. We then enable our feasibility-based tightening techniques and assess the additional tractability gains from doing so. Overall, we consider three versions of our algorithm: (i) the rudimentary branch-and-bound algorithm (denoted by “BB”); (ii) “BB” enhanced with strengthened intersection cuts (denoted by “BB+SIC”); (iii) “BB+SIC” enhanced with feasibility-based tightening (denoted by “BB+SIC+FBT”). For each version, we adopt the best-bound first search node selection strategy during the branch-and-bound process.

Tables 1 and 2 present the computational results for packing circles into a circle and a rectangle, respectively. The first two columns in these tables list the input size (number of circles) and the number of instances of a given input size, for a respective total of 35 and 40 instances, as described above. The tables also present the number of instances that were solved to provable optimality within a given time limit of 1 hour, as well as the geometric means of solution time and number of branch-and-bound nodes explored; for the remaining instances for which optimality could not be proven, we present the average residual gap, defined as $(UB - LB) / UB$, at the time limit.

Table 1 Effect of strengthened intersection cuts and feasibility-based tightening on solving instances of packing circles into a circle

Table 2 Effect of strengthened intersection cuts and feasibility-based tightening on solving instances of packing circles into a rectangle

Table 1 shows that BB could solve 20 out of 35 instances optimally, while both BB+SIC and BB+SIC+FBT solved 23 and 26 of them to optimality, respectively, including one of the largest instances featuring the packing of eleven circles. Putting aside the fact that it allowed us to solve three more instances within the allotted time limit, the addition of strengthened intersection cuts resulted in a noticeable improvement in average solution times, number of nodes explored and residual gaps (when applicable). The BB+SIC+FBT version performed even better in terms of these metrics, especially for instances of larger input size, such as instances with ten or eleven circles.

Turning our attention to Table 2, we observe that all three variants can easily address instances featuring up to seven circles. The BB+SIC improved upon the baseline approach in terms of being able to prove optimality within the allotted time limit for a number of the eight-circle instances, with the BB+SIC+FBT approach solving the majority of them while also demonstrating a noticeable reduction in the average solution time to do so. Instances with nine circles remained elusive to all methods, with a significant average residual gap above $15\%$; for this problem size category, enabling feasibility-based tightening did not seem to improve the results already obtained via the use of only intersection cuts.

Considering all instances across both datasets, we conclude that the utilization of both strengthened intersection cuts and feasibility-based tightening has an overall positive impact on performance of the algorithm. Therefore, we adopt approach BB+SIC+FBT during the comparative study that follows.

5.2.2 Comparison with global optimization solvers

In order to evaluate the competitiveness of our proposed approach against general-purpose global optimization solvers, we solve every benchmark instance independently with each of five state-of-the-art solvers, namely ANTIGONE, BARON, COUENNE, LINDOGLOBAL and SCIP, imposing the same time limit of 1 hour. The consolidated results are presented in Tables 3 and 4, using similar format as before, while the detailed results are presented in Tables 5 and 6.

Table 3 Computational results for global solvers on solving instances of packing circles into a circle

Table 4 Computational results for global solvers on solving instances of packing circles into a rectangle

Table 5 Detailed results for packing circles into a circle

Table 6 Detailed results for packing circles into a rectangle

Considering all five global solvers, BARON performs the best in terms of number of solved instances and solution time. The smallest average residual gaps for unsolved instances were obtained by SCIP, though possibly this results from aggressive branching, rather than from tight relaxations constructed at its branch-and-bound nodes. This is corroborated by the observation that the number of branch-and-bound nodes in SCIP runs was significantly larger than in other solvers. Processing a large branch-and-bound tree takes more time, which might explain why SCIP could only solve fewer instances to guaranteed optimality within the time limit, performing generally worse than the other four global solvers.

More specifically, for the problem of packing circles in a circle, BARON was able to prove optimality in 21 out of 35 instances, with the largest solvable input size being a single nine-circle instance. In contrast, our proposed algorithm (Table 1) could in addition solve a handful of nine-circle, ten-circle and eleven-circle instances, pushing the state-of-the-art in terms of what is considered solvable for this class of packing problems. Furthermore, the solution time of our approach is generally much less than that of the global optimization solvers. Turning our attention to the application of packing circles into a rectangle, BARON again performs the best among the five general-purpose global solvers, being able to solve to confirmed optimality 29 out of 40 instances. While our algorithm (Table 2) solved 28 instances with comparable solution time, it achieved a much smaller average residual gaps for the remaining instances. Notably, across both problem datasets, our proposed approach was able to close the gap in a total of 6 instances for which none of the global optimization solvers was able to prove optimality. The competitiveness of our approach against these solvers can also be inferred from rigorous performance profiles [12], which we present in Fig. 7.

Fig. 7

Performance profiles across all benchmark instances of each problem variant. In both graphs, “This work” refers to the performance of our proposed algorithm using strengthened intersection cuts and feasibility-based tightening (BB+SIC+FBT). For each curve, the value at $t = 0$ provides the fraction of benchmark instances for which the corresponding solver/algorithm is fastest, while the limiting value at $t \rightarrow \infty$ provides the fraction of instances that could be solved within the time limit of 1 hour

6 Conclusions

In this work, we focused on a class of reverse convex constraints called circle-circle non-overlapping constraints, which are popular in many cutting and packing optimization models. Adapting a custom-built branch-and-bound algorithm that we had previously developed to address irregular shape nesting problems [34], we proposed strengthened intersection cuts and various feasibility-based tightening techniques to expedite the search based on direct branching upon the set of non-overlapping constraints. To this end, we first generalized the intersection cut formula from the seminal paper of [6] to more generic cases where variables can be bounded by arbitrary values, and used the fact that a non-overlapping constraint represents a reverse convex domain to incorporate such intersection cuts into our relaxations. In addition, we proposed feasibility-based tightening techniques that differ from the ones commonly used in global optimization, in the sense that we sought to reduce the feasible domain enforced by non-overlapping constraints directly, rather than rely on domain reduction from variable bounds. Our extensive computational studies on 75 instances for unequal circle packing elucidated the effectiveness of tightening the relaxations in terms of speeding up the branch-and-bound process, and showcased that the purposed-build search approach performs favorably as compared to using state-of-the-art, yet general-purpose global optimization solvers.

Despite these advances, however, there remains a considerable gap between our ability to globally optimize instances that solely feature identical circles and those involving non-identical circles as well. Indeed, how to adapt many of the techniques utilized in specialized solvers for the former setting, such as employing optimality-based cuts to tighten the relaxations, in the case of unequal circle packing and general shape nesting constitute interesting avenues for future research.