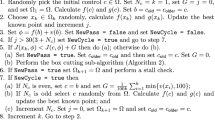Oscars-ii: an algorithm for bound constrained global optimization

Abstract

An adaptation of the oscars algorithm for bound constrained global optimization is presented, and numerically tested. The algorithm is a stochastic direct search method, and has low overheads which are constant per sample point. Some sample points are drawn randomly in the feasible region from time to time, ensuring global convergence almost surely under mild conditions. Additional sample points are preferentially placed near previous good sample points to improve the rate of convergence. Connections with partitioning strategies are explored for oscars and the new method, showing these methods have a reduced risk of sample point redundancy. Numerical testing shows that the method is viable in practice, and is substantially faster than oscars in 4 or more dimensions. Comparison with other methods shows good performance in moderately high dimensions. A power law test for identifying and avoiding proper local minima is presented and shown to give modest improvement.

1 Introduction

This paper looks at the bound constrained global optimization problem

$$\begin{aligned} \min _{x \in \Omega } f(x) \end{aligned}$$

(1)

where $\Omega \subset {\mathbb {R}}^n$ is the box shaped feasible region aligned with the coordinate axes. The objective function f(x) is assumed to be ‘black-box’ in the sense that, if provided with a point x, it will return f(x) and no other information. The feasible region $\Omega$ is defined by simple bounds via

$$\begin{aligned} \Omega = \left\{ x \in {\mathbb {R}}^n : L_i \le x_i \le U_i \;\;\; \forall i = 1,2,\ldots ,n \right\} . \end{aligned}$$

The upper ($U_i$) and lower ($L_i$) bounds on each element $x_i$ of x are necessarily finite, where $x_i$ is the $i^{\mathrm{th}}$ element of x, etc. It is assumed that $L_i < U_i$ for all $i = 1,\ldots ,n$, without loss of generality.

This problem has been the subject of a plethora of approaches in many different papers, a selection of which can be found in [8, 10, 15, 19, 31, 32] and the references therein. In spite of its apparently simple form, there are many different variations on this problem, and each in turn has many different ways it can be addressed. Variations include the the dimension n of the problem, the level of differentiability of the objective function f, the number of derivatives which are available to the algorithm, and the cost of calculating function values, and derivatives, where applicable. Additionally, finding one global minimizer might suffice, or all global minimizers might be required. The latter is closely related to approximating a near optimal level set [13].

A very simple method for solving (1) is Pure Random Search (prs), which calculates f at N random points in $\Omega$ and returns the lowest as an estimate of a global minimizer. This method has very low overheads, does not require derivatives, and can be shown to converge almost surely. Nevertheless it is seldom used as it is intolerably slow in practice.

An obvious strategy for improving prs is to sample preferentially in areas where the objective appears to be relatively low. An example of this is Accelerated Random Search (ars) [3] which uniformly samples in box shaped sub-regions of $\Omega$. A finite sequence of successively smaller boxes containing the current best known point are polled until either a new best point is found, or the sequence is exhausted. The first box in each such sequence is always $\Omega$. Each subsequent box is formed by taking a scaled version of $\Omega$, translating it so that it is centred on the best known point, and intersecting it with the feasible region. If an improving point is found, a new sequence is constructed centred on the new best point. Otherwise, if the sequence of boxes is exhausted without locating a new best point, that sequence of boxes is repeatedly re-used until a new best point is found or the algorithm halts. A version of ars with an exponential rate of convergence is described in [27]. However this result applies only when close to the global minimizer, and the tendency of ars to sample largely in the vicinity of the best known point can mean locating a neighbourhood of the global optimizer might not happen quickly.

The way the sequence of sampling boxes is formed for ars is very simple, but can have undesirable properties at times. For instance, let ars generate a non-improving sample point s with the best known point being b. Since a point better than b has not been found, the next sampling box is a subset of its predecessor. If s is far from b, s will not be part of the new sampling box. However points on the opposite side of b to s will also be excluded from the new sampling box, and s provides no evidence that these points are worse than b. Moreover, if s is sufficiently near b, ars will retain the area around s where f is known to be worse.

A more sophisticated approach [25] is to shrink the sampling box along one coordinate axis only, so that s lies outside the new box, but b does not. More precisely, one face of the box is moved inwards to lie between s and b, and the remaining $2n-1$ faces are left in their original positions. The face that is shifted is the one orthogonal to the largest component of $s-b$. This forms the nub of the One Side Cut Accelerated Random Search (oscars) algorithm [25].

An important feature of the way oscars shrinks the polling box at each iteration is that every face which is closer to b than to s remains unmoved. Clearly $f(s) \ge f(b)$ does not constitute evidence that points on the opposite side of b to s are also higher than b. In fact, if the sample box is sufficiently small, and f is $C^1$, then f will be approximately linear on the sample box. In this case $f(s) \ge f(b)$ provides weak evidence that points on the opposite side of b to s are likely to be better. This is in stark contrast to ars which moves all faces inwards towards b after a non-improving sample point has been generated.

Herein we present a variation on oscars. The first significant change is that the box can be cut by several hyperplanes aligned with different coordinate axes in the same iteration. Like oscars, each of these hyperplanes separates b from s. The purpose of this change is to reduce the number of iterations needed to generate a small box around the control point when n is large. The second change is that the lengths of the cycles are directly limited. A new examination of the ability of both algorithms to avoid redundancy in the sample points chosen is also presented. The new method is tested both with and without a power law test for identifying and avoiding suspected proper local minima.

Almost sure convergence is shown in exact arithmetic when f is bounded below, Lebesgue measurable, and lower semi-continuous over $\Omega$. If these conditions do not hold, the algorithm can be executed but no guarantees of convergence are established. In addition, connections with partitioning strategies, and the implications for the non-asymptotic convergence behaviour of these methods are explored.

Both oscars and the new method have low overheads which are constant per function evaluation. This is in contrast to methods such as direct [14] which store all function evaluations and have overheads per function evaluation which increase as the number of function evaluations already performed increases. This is especially advantageous on functions which are cheap to evaluate, as the low overheads allow many more function evaluations to be performed in the same length of time [25]. Methods with low overheads can also be usefully employed for minimizing surrogates on methods which select iterates by, for example, minimizing a radial basis function approximation of the objective [28].

Partitioning methods [1, 7, 17, 18, 22, 30] typically subdivide $\Omega$ into sub-regions which overlap only at their boundaries, and then calculate f at various sample points in each sub-region. The partition is then refined, or updated in some way to reflect the information gained from the sample points, and the process repeated as necessary. Adapting the partition from time to time allows areas found to be lower to be explored more heavily. One advantage of partitioning is that it reduces the risk of a sample point being placed unintentionally very close to a previous sample point, resulting in a wasted function evaluation. Generally speaking, the fewer sample points that are placed in each sub-region, the less the risk of wasted function evaluations. This requires that the partition be refined as the total number of sample points increases. Hence, for many of these methods the storage requirements and overheads per function evaluation tend to rise as the number of function evaluations increases. A number of methods, both stochastic [23] and deterministic [14] push this approach to its limit, by having one sample point per sub-region. These methods store and use all previous sample points when generating further sample points. Consequently as the number of iterations increases, the overheads per iterate of these methods climb steadily, and eventually dominate the cost of computing the objective function [25].

The general structure of the paper is as follows. The new algorithm is described in detail in the next section. Section 3 examines the convergence properties. Numerical results are presented and discussed in Sect. 4, and concluding remarks are in Sect. 5.

2 The oscars-ii algorithm

The structure of the algorithm consists of a series of alternating cycles, each of limited length. Each cycle is in turn made up of a finite number of passes. Loosely speaking, a pass is performed by constructing a sequence of nested sample boxes and drawing one sample point randomly from each box in turn. The act of drawing one sample point s randomly from one box, calculating f(s), and constructing the next sample box constitutes one iteration of the algorithm.

Each pass begins with a control point c where f(c) is known. The aim of a pass is to find a point which is better than the control point. If this aim is achieved, the pass is called successful, and ends immediately. Otherwise the pass ends unsuccessfully when, for example, the sample box is too small, or the cycle length limit is reached. If the pass ends successfully, the improving point becomes the new control point, and another pass is begun. If the pass ends unsuccessfully, then the cycle containing that pass also ends.

The cycles alternate in the sense that odd numbered cycles begin with a random control point, and even numbered cycles use the best known point as the initial control point. This is referred to as the sorc strategy, where sorc stands for ‘start odd cycles with a random control.’ The purpose of this is to avoid focusing effort too heavily in the vicinity of the current best known point.

At each iteration the algorithm uses a control point $c_k$ and a current sample box $\Omega _k$, where $c^{(k)} \in \Omega _k$, and $\Omega _k \subseteq \Omega$. The counter k is the iteration number, and it is attached either as a subscript, or as a superscript (k) on various quantities to refer to the values taken in iteration k. A superscript (k) is used on vector quantities where subscripts refer to individual elements of that vector. Iteration k’s sample box $\Omega _k$ is defined by the upper and lower bounds $u^{(k)}$ and $\ell ^{(k)}$ via

$$\begin{aligned} \Omega _k = \{ x \in \Omega : \ell ^{(k)} \le x \le u^{(k)} \}. \end{aligned}$$

A random sample point $x^{(k)} \in \Omega _k$ is chosen, and if $x^{(k)}$ is not a better point than $c^{(k)}$ (i.e. $f(x^{(k)}) \ge f(c^{(k)})$) the box $\Omega _k$ is shrunk, and the process repeated. This ‘sample and shrink’ continues until one of the following four reset conditions is met:

• (a) improving reset: An improving point is found. That is to say $f(x^{(k)}) < f(c^{(k)})$;

• (b) box size reset: The box $\Omega _k$ falls below a minimum size $h_{\mathrm{min}}$ as measured by the infinity norm of its main diagonal;

• (c) cycle length reset: The number of iterations j since the cycle began reaches the cycle length limit J(m), where m is the current cycle number; or

• (d) power law fit reset: A power law test indicates convergence to a proper local minimizer. This can only be used on odd numbered cycles.

Each of the above four outcomes is called a reset, and marks the completion of one pass of the method. If an improving reset occurs, the method sets the new control point $c^{(k+1)} = x^{(k)}$ and resets the new sampling box $\Omega _{k+1}$ to $\Omega$. All non-improving resets mark not only the end of a pass, but also the end of a cycle. The power law fit reset is optional, and the method is tested both with and without it.

The process of shrinking (or cutting) a box is as follows. Let c be the current control point, and let x be a sample point generated in the box $\Omega$. The component of the vector $x-c$ which has the largest magnitude is identified. Let this component be along the $i{\mathrm{th}}$ coordinate axis with magnitude M. A cut orthogonal to the $i{\mathrm{th}}$ axis is put through $\Omega _k$, where this cut passes through the point $(1-A)x + Ac$, where $0< A < 1$. The part of $\Omega _k$ that is retained is the part containing c. At this stage, this cut is exactly that used in the oscars algorithm. An illustration of this cut appears in Figure 3 of [26].

Oscars-ii also performs an additional cut for each other coordinate axis along which the component of $x-c$ is at least $\beta M$ in magnitude, where $0< \beta < 1$. This cut passes through the point $(1-\gamma _r A)x + \gamma _r Ac$ where $\gamma _r = |x_r-c_r|/M$ is the relative magnitude of the component along coordinate axis r. The factor $\gamma _r$ means the cut passes relatively closer to x for faces orthogonal to coordinate directions along which $x-c$ has smaller magnitude components.

Algorithm 1

oscars-ii  

• 1. Choose a random point $x^{(0)} \in \Omega$. Calculate $f_s = f_c=f_b = f(x^{(0)})$. Set $k=m=1$, set $b = c = x^{(0)}$, and set $u =U$ and $\ell = L$. Choose $A,\beta \in (0,1)$. Select $h_{\mathrm{min}} > 0$.

• 2. If stopping conditions hold, then exit. Set $j=0$. If $f_c < f_b$ set $b=c$ and $f_b=f_c$.

• 3. Randomly choose $x^{(k)}$ subject to $\ell \le x^{(k)} \le u$. Calculate $f^{(k)} = f(x^{(k)})$.

• 4. If $f^{(k)} < f_c$ then set $c = x^{(k)}$, set $f_c = f^{(k)}$, set $u = U$, set $\ell = L$, increment k, and go to step 2.

• 5. Set $M = \left\| x^{(k)}-c \right\| _{\infty }$ and set $\gamma _i = |x_i^{(k)}-c_i|/M$ for $i=1,\ldots ,n$.

• 6. For each $i \in 1,\ldots ,n$ perform the following steps:

  • (a) Calculate the cut position $K_i = (1-\gamma _i A)x^{(k)}_i + \gamma _i A c_i$.

  • (b) If $x_i^{(k)}-c_i \ge \beta M$, set $u_i = K_i$, otherwise if $x_i^{(k)}-c_i \le -\beta M$, set $\ell _i = K_i$.

• 7. Increment j and k. If $\Vert u-\ell \Vert _\infty \le h_\mathrm{min}$ or $j \ge J(m)$, go to the next step. Otherwise, if the power law test does not indicate convergence to a local minimizer, go to step 3.

• 8. Set $u=U$ and $\ell =L$. If $f_c < f_b$ set $b=c$ and $f_b=f_c$. Increment m.

• 9. If m is odd, randomly choose $c \in \Omega$ and set $f_c = f(c)$; otherwise set $c = b$ and $f_c = f_b$. Set $f_s = f_c$ and go to step 2.

Here $f_b$, $f_c$ and $f_s$ are the objective function values at the current best known point b, the current control point c, and the initial control point used at the beginning of the current cycle. The quantities c, b, $\ell$, and u are not explicitly indexed by k in the algorithm description, however the sequences of these quantities are needed to analyse the algorithm. To this end a superscript (k) is affixed to these quantities to identify the values they take in step 3 of iteration k. This yields the sequences of best known points $\{b^{(k)}\}_{k=1}^\infty$ and control points $\{c^{(k)}\}_{k=1}^\infty$. Subscripts on a vector refer to a specific element of that vector.

2.1 Cycles, passes, and iterations

Cycles and passes are made up of a number of consecutive iterations. Iterations are indexed by the iteration number k. Each iteration executes step 3 once, generating a random sample point $x^{(k)} \in \Omega _k$ and calculating $f^{(k)}$. One or more of the steps following step 3 are performed. The iteration ends when execution transfers back to either step 2 or step 3.

Each pass consists of a number of consecutive iterations (iterations $k+1$ to $k+p$ say). For these iterations to form a pass three conditions must hold:

• 1. Either $k=0$ or there is a reset in iteration k;

• 2. There is a reset in iteration $k+p$; and

• 3. There are no resets of any sort in iterations $k+1$ to $k+p-1$.

The situation for cycles is similar. If a cycle consists of iterations $k+1$ to $k+p$, then firstly either $k=0$ or there was a cycle ending reset in iteration k. Secondly, there must be a cycle ending reset in iteration $k+p$, with no cycle ending resets in iterations $k+1$ to $k+p-1$. In contrast to a pass, a cycle is permitted to have improving resets in iterations $k+1$ to $k+p-1$. Hence a cycle consists of one or more complete passes, whereas each pass is contained entirely within one cycle. Cycles are indexed by m, passes are not indexed.

2.2 The cycle length reset

The original oscars algorithm had only two reset mechanisms: an improving reset (a), and a box size reset (b). The inclusion of the cycle length reset means that at least m points are chosen randomly from $\Omega$ after $\sum _{i=1}^m J(i)$ iterations, which guarantees almost sure convergence to an essential global minimizer. The maximum cycle length J(m) is required to be a positive, strictly increasing function of the cycle counter m with the property that $J(m) \rightarrow \infty$ as $m \rightarrow \infty$. The optional power law reset operates similarly to the cycle length reset when the current cycle appears to be converging to a proper local minimizer.

The cycle length resets are used to improve the numerical performance of the algorithm by eliminating undesirable behaviour that can occasionally occur with the original oscars algorithm. This behaviour occurs most prominently on the Hartmann 6 problem. This behaviour can occur if the control point is near a stationary point which is not a global minimizer. In such a case oscars can generate a large number of passes, each of which ends in an improving reset. This means all of these passes belong to a single cycle. Each such improving reset yields a negligible improvement in the objective function f, and the improving iterate is only marginally different from the control point. Since all of this occurs in a single cycle, the sorc strategy is not invoked, and the search is strongly focused in the vicinity of the non-optimal stationary point. If the basin of the global minimizer(s) is distant from that stationary point, oscars will have only a very low chance of detecting it in each pass. Using a cycle reset curtails such cycles. The next odd numbered cycle will start with a randomly generated control point, and will usually have a much better chance of locating the distant basin more quickly.

2.3 The power law fit reset

Stopping rules based on power law distributions for near minimal values of f have been explored extensively [9, 11], including for local optima via the Kolmogorov–Smirnov test [24]. Herein we use these ideas to test for convergence to a proper local minimizer. If this convergence is detected, the current cycle is ended to prevent the method from wasting effort by refining a proper local minimizer to high accuracy. A record of the B best function values $\phi _1,\ldots ,\phi _B$ seen in the current cycle is kept, where these values are assumed to be in increasing order for simplicity. This data is used to estimate the lowest function value that cycle is likely to reach. If this value is significantly above the best known function value, the empirical cumulative distribution function (ecdf) of the data is compared against two relevant power law distributions using a Kolmogorov–Smirnov test. If either fit is accepted, the cycle halts.

The power law fit test automatically fails if less than B data values are held, or if $\phi _1 > f_s - \tau _{\mathrm{ks}}$ where $f_s$ is the value of f at the initial control point for that cycle. The latter ensures that f is not so nearly flat compared to the power law fit tolerance $\tau _{\mathrm{ks}}$ that the test would be misleading. The initial estimate of the lowest value the cycle is likely to reach is formed by assuming that the data are drawn randomly from a power law distribution of the form

$$\begin{aligned} \rho _\mathsf{cdf}(\phi ) = \left( \frac{\phi - \phi ^{\sharp }}{\phi _B-\phi ^{\sharp }} \right) ^{n} \end{aligned}$$

where $\phi ^{\sharp }$ is the lowest value for which the probability that $B-2$ points drawn randomly from this distribution will have at least a 1% chance of all lying in the interval $[\phi _1,\phi _B]$. If $\phi ^{\sharp } > f_b + 10\tau _{\mathrm{ks}}$, where $\tau _{\mathrm{ks}}$ is the power law fit tolerance in f, then Kolmogorov–Smirnov goodness of fit tests are performed at the 5% level against two power law distributions:

$$\begin{aligned} \rho _\mathsf{cdf}(\phi ) = \left( \frac{\phi - \phi _1^{\sharp }}{\phi _B-\phi _1^{\sharp }} \right) ^{n} \;\;\;\;\;\; \mathrm{and} \;\;\;\;\;\; \rho _\mathsf{cdf}(\phi ) = \left( \frac{\phi - \phi _2^{\sharp }}{\phi _B-\phi _2^{\sharp }} \right) ^{(n/2)} \end{aligned}$$

where $\phi _1^{\sharp }$ and $\phi _2^{\sharp }$ are calculated as per $\phi ^{\sharp }$, but with a 50% chance of $B-2$ random points lying in the interval $[\phi _1,\phi _B]$. If either power law is accepted by the goodness of fit test, the current cycle is ended. The first power law distributions includes many local minimizers of non-smooth locally Lipschitz functions, and the second includes local minimizers with positive definite Hessians when f is twice continuously differentiable [9].

The cost of this test can be significant, especially in low dimensions. This cost can be reduced by, say, performing this test only every $5^{\mathrm{th}}$ or $10^{\mathrm{th}}$ iteration, and automatically rejecting both power law fits in all other iterations. Even if the power law test is not used at all, the cycle length resets will limit the number of function evaluations wasted in accurately finding proper local minimizers, but to a lesser extent.

The difference between the algorithm with (hereafter oscars-ii(p)) and without (hereafter oscars-ii(n)) the power law test is slight. Algorithm 1 lists it with the power law test implemented. To remove it, the second sentence of step 7 is replaced with “Otherwise, go to step 3.” Recording the initial random control point’s function value $f_s$ in steps 1 and 9 is no longer needed, and can be removed.

2.4 Avoiding the neighbourhood of disinterest

Lower semi-continuity of f on $\Omega$ implies all level sets of the form $\{ x \in \Omega : f(x) \le \eta \}$ are closed. Hence, for all s such that $f(s) > f(c)$, there is a ‘neighbourhood of disinterest’ $N_s(f(c))$ centred on s such that $f(x) > f(c)$ for all $x \in N_s(f(c))$.

The main justification in [25] of the ‘one side cut’ method of shrinking the sampling box, is that in contrast to ars, it guaranteed that a neighbourhood of a failed sample point would not be resampled in the same pass. This reduces the risk of sampling in the neighbourhood of disinterest of a previous sample point in the same pass. This is now extended to sample points from different passes. Clearly the box cutting process can not be used directly to separate sample points from different paths. An alternative approach which guarantees separation of sample points is partitioning [1, 22, 30]. The essence of this tactic is simple: different sample points are drawn from different non-overlapping subsets of $\Omega$, reducing the risk that two points are extremely close to each other.

Herein we show that similar sampling boxes in different passes have a strong tendency to diverge from one another. A full analysis of the box cutting strategy is extremely messy due to the myriad of different cases that arise from the relative positions of the control and sample points, and so is not attempted.

For simplicity, we look at one step of each of two passes, where both passes have the same control point c and same sampling box $\Omega _c = \{ x \in \Omega : \ell \le x \le u\}$. Let the two sample points from the two passes be s and t. After cutting, let the new sample boxes be $\Omega _s$ and $\Omega _t$ respectively, and let $s_\mathsf{new}$ and $t_\mathsf{new}$ be the new sample points chosen randomly from $\Omega _s$ and $\Omega _t$. A measure $M_\mathrm{overlap}$ of the separation between $\Omega _s$ and $\Omega _t$ is the probability that both $s_\mathsf{new}$ and $t_\mathsf{new}$ will lie in $\Omega _s \cap \Omega _t$. For ars this probability is one.

For the original oscars algorithm [25] the situation is better. Without loss of generality, we assume that the dimensions have been ordered, and if necessary reversed, so that $c \le s$, and the components of $s-c$ are in decreasing order. Then oscars forms $\Omega _s$ by imposing an upper bound on $\Omega _c$, viz.

$$\begin{aligned} \Omega _s = \{ x \in \Omega _c : x_1 \le c_1 + (1-A)(s_1 - c_1) \}. \end{aligned}$$

Let C, S and T be the vectors of edge lengths of the boxes $\Omega _c$, $\Omega _s$ and $\Omega _t$. Hence $C = u - \ell$. When $\Omega _t$ is formed by imposing an upper or lower bound on $x_1$, the measure of overlap is

$$\begin{aligned} M_{\mathrm{overlap}} = \frac{\min (S_1,T_1)}{\max (S_1,T_1)} \;\;\;\; \text{ or } \;\;\;\; M_{\mathrm{overlap}} = \frac{(S_1 + T_1 - C_1 )^2}{S_1 T_1} \end{aligned}$$

respectively. The bound when only $\Omega _s$ is cut along $x_1$ can be found by setting $T_1 = C_1$ in either formula. If cuts are made orthogonal to more than one coordinate axis, the measure of overlap is simply the product of the measures for each dimension. Hence if a bound is imposed on $x_i$, $i \ne 1$ to form $\Omega _t$, then $M_{\mathrm{overlap}} = S_1 T_i (C_1 C_i)^{-1}$.

For oscars the risk of a large overlap is greatest when two passes impose the same type of bound (upper or lower) on the same variable. Since oscars can impose 2n different types of bounds when c is near the centre of $\Omega _c$, eventually some passes must impose the same type of bound on the same variable. However, this situation is much improved over that of ars.

For oscars-ii a similar analysis yields

$$\begin{aligned} M_{\mathrm{overlap}} = \left( \prod _{i \not \in I_{\mathrm{lower}}} \frac{\min (S_i,T_i)}{\max (S_i,T_i)} \right) \left( \prod _{i \in I_{\mathrm{lower}}} \frac{(S_i + T_i - C_i )^2}{S_i T_i} \right) \end{aligned}$$

where the index set $I_{\mathrm{lower}}$ contains the values of i for which a lower bound on $x_i$ is imposed when forming $\Omega _t$ from $\Omega _c$. Clearly oscars-ii will usually have a lower overlap than oscars. The number of different combinations of bounds oscars-ii can impose when c is near the centre of $\Omega _c$ is $3^{n}-1$. If c is a corner of $\Omega _c$, this falls to $2^{n}-1$, which is still well above that for oscars except when n is very small.

This observation is useful in choosing $\beta$. If the largest component (the $i{\mathrm{th}}$ say) of $t-c$ has magnitude M, then the other components of $t-c$ are uniformly distributed across the interval $[-M,M]$, assuming for simplicity that the boundary of $\Omega _c$ is remote and can be neglected. A choice of $\beta = 1/3$ gives a 1/3 probability that each coordinate direction (other than the $i{\mathrm{th}}$) will have a new upper bound, a new lower bound, or no new bound. Similar reasoning when c is a corner point of $\Omega _c$ suggests $\beta = 1/2$.

3 Convergence

oscars-ii uses only function values, and so can be executed even when the objective function is not smooth, or even discontinuous. We show oscars-ii almost surely finds the essential global minimum, which is defined as follows.

Definition 1

The essential global minimum $f^*_{\mathrm{egm}}$ of f over $\Omega$ is defined as

$$\begin{aligned} f^*_\mathsf{egm} = \sup \left\{ \phi : \mu \left( \{ x \in \Omega : f(x) < \phi \} \right) = 0 \right\} \end{aligned}$$

where $\mu (\cdot )$ denotes the Lebesgue measure in ${\mathbb {R}}^n$.

Points in the level set $\{x \in \Omega : f(x) \le f^*_\mathsf{egm} \}$ are referred to as essential global minimizers of f over $\Omega$. The following assumption guarantees the sequence $\{b^{(k)}\}_{k=1}^\infty$ of best known points converges almost surely to one or more essential global minimizers.

Assumption 2

  The objective function f is lower semi-continuous and bounded below on $\Omega$.

Theorem 3

Given Assumption 2, if oscars-ii is run forever in exact arithmetic, the sequence $\{b^{(k)}\}_{k=1}^\infty$ of best known points converges to one or more essential global minimizer(s), almost surely.

Proof

The feasible region $\Omega$ is closed and bounded, and thus compact. The absence of stopping conditions means $\{b^{(k)}\}$ is an infinite sequence. Since $\{b^{(k)}\} \subset \Omega$, this sequence must have limit points. Let $b_*$ be a point to which $\{b^{(k)}\}$ converges (possibly in subsequence) but is otherwise arbitrary.

The sequence of best function values $\{f(b_k)\}$ is monotonically decreasing and bounded below, so its limit $f_{\infty }$ exists. If $f_{\infty } > f^*_\mathsf{egm}$, then $\mu \left( \{ x \in \Omega : f(x) < f_{\infty } \} \right) > 0$. Now oscars-ii generates one random sample in $\Omega$ at the start of each cycle. Noting $k \le \sum _{i=1}^m J(i)$ it follows that $k \rightarrow \infty$ implies $m \rightarrow \infty$. The probability $P_m$ that a point with a lower function value than $f_{\infty }$ is located within m cycles has the lower bound

$$\begin{aligned} P_m = P\left( f(b^{(k)})< f_{\infty } \; \text{ after } \; m \; \text{ cycles } \right) \ge 1 - \left( 1 - \frac{ \mu \left( \{ x \in \Omega : f(x) < f_{\infty } \} \right) }{\mu (\Omega )} \right) ^m. \end{aligned}$$

Now $k \rightarrow \infty$ implies $m \rightarrow \infty$ which implies $P_m \rightarrow 1$ as $k \rightarrow \infty$. Hence $\lim _{k \rightarrow \infty } f(b^{(k)}) \le f^*_{\mathrm{egm}}$ almost surely. Finally, lower semi-continuity of f means

$$\begin{aligned} f\left( b_* \right) \le \lim _{k \rightarrow \infty } f(b^{(k)}) \le f^*_{\mathrm{egm}} \end{aligned}$$

and so $b_*$ is an essential global minimizer of f over $\Omega$ almost surely, as required. $\square$

In practice a weaker form of Assumption 2 is sufficent to prove this result: lower semi-continuity at the limits of $\{b^{(k)}\}$ is sufficient. Of course these limits are not known in advance.

4 Numerical results

Table 1 An overview of the performances of 5 methods on Test Set 1

Table 2 A comparison of four methods on Test Set 2, averaged over 30 runs. Columns marked ‘F’ list the number of runs which halted after reaching the function evaluation cap of 250,000

The new method is compared with the original oscars algorithm [25], with a variant of direct [14], and with two particle swarm methods [6, 16]. Test Set 1 consists of the 50 problems which form the main test set for oscars [25]. These problems are listed in Table 1 of [25], and can be found in [2, 20, 23, 25]. An extra 21 problems form Test Set 2, and are used to explore the algorithm’s behaviour in moderate dimensions and above, along with the Schoen family of test functions [29]. Test Set 2 is listed in Table 2, where problems 54, 57, 64, 66, and 71 are from [2]; problems 51, 55, 58, 67 and 68 are from [20]; problem 59 (with $\Omega = [-10,10]^n$) is from [4]; problem 56 is from [25] and problem 69 is from [12].

The remaining problems, and problems modified for use herein are listed below along with any bounds not listed elsewhere. These problems all have $f^* = 0$. Weka 2 is

$$\begin{aligned} f_{\mathrm{weka2}} = \sum _{i=1}^n x_i(1-x_i) + \sum _{i=1}^n \left( k_i \lfloor p_i x_i \rfloor \mod p_i \right) \;\;\;\;\;\;\;\;\; x \in [0,1]^n, \end{aligned}$$

where the floor function $\lfloor s \rfloor$ denotes the greatest integer not larger than s. The parameter values used by Weka 2 in n dimensions are the first n entries of the lists $p_i=2, 3, 5, 7, 11, 13, 17, 19$, 23, 29 and $k_i=1, 1, 2, 2, 5, 5, 7, 11, 13, 17$.

The Himmelblau ring problem is defined via the two dimensional Himmelblau function

$$\begin{aligned} H(x_1,x_2) = \left( x_1^2 + x_2 - 11\right) ^2 + \left( x_1 + x_2^2 - 7\right) ^2 \end{aligned}$$

which has four global minimizers at approximately (3, 2), $(3.5844,-1.8481)$, $(-2.8051,3.1313)$ and $(-3.7793,-3.2832)$. The Himmelblau ring function for n even is

$$\begin{aligned} f_{60} = \sum _{i=1}^{n/2} H(x_{2i-1},x_{2i}) + \sum _{i=2}^{n/2} \left( x_{2i-1} - x_{2i-3} \right) ^2 + \left( x_{2n-1} - x_1 \right) ^2 \;\;\;\;\;\;\;\;\; x \in [-5,5]^n. \end{aligned}$$

The first summation term alone has $2^n$ global minimizers and no local minimizers. The remaining terms are minimized when all odd numbered variables are identical. This means that the Himmelblau ring function has four global minimizers. There are another 2n local minimizers that are nearly global, and many other less deep local minimizers.

Dixon’s function is

$$\begin{aligned} f_{61} = (1-x_1)^2 + (1-x_n)^2 + \sum _{i=2}^n \left( x_{i-1}^2 - x_i \right) ^2 \;\;\;\;\;\;\;\;\; x \in [-2,2]^n. \end{aligned}$$

Dixon’s function is separable, indeed many test functions are partially or totally separable. To test the effect of loss of separability, Dixon’s function was reflected through the hyperplane orthogonal to $w = (1, 2, \ldots , n)$ which passes through the origin, with $\Omega$ held constant. This leaves the solution inside $\Omega$ but destroys any separability. Results for both forms of Dixon’s function are presented.

The modified Qing problem is to minimize

$$\begin{aligned} f_{63} = \sum _{i=1}^n \left( x_i^2 - i \right) ^2 \;\;\;\;\;\; \text{ subject } \text{ to } \;\;\;\;\;\; -1 \le x_i \le \sqrt{n} \;\;\;\;\;\; \forall i = 1,\ldots ,n \end{aligned}$$

where the bounds have been changed from $-50 \le x \le 50$ to $-1 \le x \le \sqrt{n}$. With the original bounds, $f_{63}$ has $2^n$ global minima at $(\pm 1, \pm \sqrt{2}, \ldots , \pm \sqrt{n})$, and no local minima. Restricting the feasible region eliminates all but two of these global minimizers, and yields $2^n-2$ local minimizers on the boundary of the feasible region. In spite of the feasible region being smaller, this makes the problem much harder.

A problem with similar characteristics to $f_{63}$ is the linked exponential function, which is

$$\begin{aligned} f_{65} = x_1^2 e^{x_1} + x_n^2 e^{x_n} + \sum _{i=1}^{n-1} e^{-x_{i+1}} \left( x_{i+1} + x_i - 1 \right) ^2 \;\;\;\;\;\;\;\;\; x \in [0,4]^n \end{aligned}$$

where n must be odd. The modified Bohachevsky 2 problem with $x \in [-50,50]^n$ is

$$\begin{aligned} f_{70} = \sum _{i=1}^n \nu _i x_i^2 + 0.3 \left( 1 - \prod _{i=1}^n \cos \left( \pi x_i (2+\nu _i) \right) \right) \;\;\;\;\;\; \text{ where } \;\;\;\;\;\; \nu _i = 1+\frac{i-1}{n-1} \;\;\; \forall i. \end{aligned}$$

4.1 The testing process

On all problems in all test sets except the Trigonometric function, the tolerance in f was set to $\tau = 10^{-3}$, and all runs halted immediately after locating a point with a function value less than $f^* + \tau$, where $f^*$ is the known optimal function value for the problem. For the Trigonometric function (with $n=5$, 10, and 30) $\tau = 10^{-5}$ was used in order to prevent termination at a local (but non-global) minimizer. Other parameter values were as follows: $A = 0.9$, $h_\mathsf{min} = 10^{-6}$ and $\beta = 1/3$. The cycle length limit J was chosen as $J(m) = 90 + 30m$. This choice was motivated by a rough estimate of 62 iterations as the length of an unsuccessful pass when $\Omega$ is the unit hypercube. Hence the $\kappa ^{\mathrm{th}}$ odd cycle is typically expected to make at least $\kappa + 1$ improving steps before being halted by a cycle length reset. The power law fit test used $\tau _{\mathrm{ks}} = 10^{-3}$ and $B = 100$.

The numerical experiments were performed in accordance with [5], with solution quality measured by a fixed target solve time: specifically the number of function evaluations needed to be within $\tau$ of the optimum. Reliability is assessed via the number of runs attaining an accuracy of $\tau$ before striking the function evaluation cap, and the efficiency is measured by the function evaluation count, which, in light of the low and constant per unit overheads, is a reasonable measure. The fixed target stopping condition is clearly only viable when the optimum is known in advance. If it is not, other stopping conditions must be used.

Data profiles are presented for the Schoen test functions. In each case computational effort is measured along the horizontal axis, and is simply the number of function evaluations N taken to reach the fixed target accuracy $\tau$. The vertical axis plots the number of functions requiring at most N function evaluations to solve, on average where appropriate.

Comparisons are made with the original oscars algorithm, with a variant of direct, and with two particle swarm methods. These last three are described now.

Two versions of the SPSO particle swarm were used, where SPSO is as described in [6] with $\max (5n,50)$ particles and the global best topology. The parameter values recommended by [16] were used. The two methods differed in their reset strategies. The first (pso-a) resets whenever all particles were within $10^{-5}$ of the global best known point, as measured by the infinity norm. This resetting retained the best known point, but placed all particles in random locations in $\Omega$ with zero initial velocities. The best known points for each particle were reset to their new random locations. Numerical testing showed that this resetting improved the performance of pso, reducing the number of fails on Test Set 1 by about 25%.

The second particle swarm method (pso-i) reset each particle individually whenever it was within a distance of $10^{-6}$ of the global best known point, and its velocity’s magnitude was at most $10^{-6}$, both measured using the infinity norm. Each reset particle was placed at a random point in $\Omega$ with zero initial velocity. Its best known position was reset to this new random location.

A slightly modified version of Direct is used herein and in [25] which we describe now. First, $\Omega$ is normalized to the unit hypercube. At each iteration direct has a list of boxes aligned with the coordinate axes, where f is known at the centre point of each box. Initially the list contains one box: $\Omega$. The size of each box is measured by the length of any main diagonal of the box, and the height of the box is equal to the value of f at the centre point of the box. At each iteration, each box which is either lower or larger than every other box is subdivided. Subdivision consists of cutting a box into three sub-boxes of identical size and shape. The two cuts are made using hyperplanes orthogonal to one coordinate axis along which the length of the uncut box is maximal. The centre point of the uncut box is also the centre of the middle sub-box, and so f does not have to be calculated there. The values f takes at the centres of the other two sub-boxes are calculated, which completes the subdivision. This process differs somewhat from the original algorithm in [14] in that all Pareto optimal (i.e. larger or lower) boxes are cut, whereas [14] subdivides only those on the efficient frontier. Numerical testing showed that there was little difference between the two in terms of function evaluations, but that the Pareto version took significantly less time.

Oscars-ii was tested extensively both with and without the power law fit test. In order to distinguish between them oscars-ii(p) will denote results generated with the power law test implemented, and oscars-ii(n) will mark results generated without the power law test.

4.2 Results and discussion for test sets 1 and 2

A comparison of both variants of oscars-ii with oscars, and the two particle swarm methods on Test Set 1 appears in Table 1. The testing regime from [25] is used, which forms ten run averages of the number of function evaluations needed to get within $\tau$ of $f^*$ for each problem, with the number of function evaluations capped at 50,000. If this cap is reached the run is classed as a fail and the number of function evaluations is set at the cap’s value. The first column in Table 1 lists the method used to generate the results. Columns 2–5 list the average function evaluations taken across all problems, the number of problems on which each method used the fewest function evaluations, the number of failed runs, and average normalized function evaluation counts. Columns 6–9 list the same quantities as columns 2–5, but for the subset of problems in Test Set 1 with dimension at least four. Function evaluation counts for each problem are normalized by dividing by the smallest of the average function counts of each method for that problem. Using the cap value on failed runs biases the figures in columns 2, 5, 6, and 9 in favour of methods with more fails. These results show that the two variants of oscars-ii are similar, with oscars and pso-i coming in third and fourth places respectively.

Test Set 2 looks at four algorithms over a range of problems in nine or more dimensions. For this test set the cap on the number of function evaluations was increased to 250,000. Results on this test set using 30 run averages on each problem are listed in Table 2. Results for oscars and pso-i are listed, along with those for the new method with and without the power law test. Bolded entries mark the best method on each problem.

The data in Table 2 shows that oscars-ii outperforms oscars by a significant margin, on average. Noting the runs which strike the cap are set to the cap’s value when evaluating the average function counts, the high number of times oscars struck the cap (168 from 630 runs) on Test Set 2 suggests the margin between the two methods could be significantly greater than the table suggests. The performance of pso-i is similar to oscars, with 175 fails.

Oscars-ii(p) and oscars-ii(n) used an average of 54,938 and 55,344 function evaluations per run respectively, where this average is across all 21 problems in Test Set 2. Considering these two methods in isolation, the average normalized function counts are 1.083 for oscars-ii(p) and 1.107 for oscars-ii(n) respectively.

In comparison to pso-i, all methods did particularly poorly on problem 59, which is unimodal, but non-smooth. This problem requires a method to follow a curved ‘V’ shaped valley to the solution. The ability of particle swarm methods to take uphill steps is very useful in navigating such valleys. On the other non-smooth problems (52, 53, and 56) pso-i did comparatively better than the other methods. This suggests non-smoothness causes more difficulty for an oscars type method than a particle swarm method. Oscars-ii largely has the approach of retaining a good control point until a better point is found. The only exception to this being at the start of odd iterations when the sorc strategy is applied. In contrast, particle swarm methods routinely move from a good point to a worse one, and this is a well known tactic for trying to deal with nonsmooth and ill conditioned valleys.

Pso-i also did very well on problem 67. This problem has a deep local minimizer on the opposite side of $\Omega$ to the global minimizer. If oscars-ii focuses on the deep local minimizer, it might take several cycles to locate the global minimizer on the far side of $\Omega$. In constrast, pso-i’s use of multiple particles seems to give it a better chance of spotting the global basin quickly. Problems 52 and 53 also have similar features, which partly explains oscars-ii’s comparatively poor performance on these problems.

Comparing pso-i against oscars-ii(n) alone, there are 10 problems where one method was at least 3 times as fast as the other. On eight of these 10 problems the faster method was oscars-ii(n), and the margin of oscars-ii(n) over pso-i is greater than it looks in Table 2. This is because oscars-ii(n) did not strike the function evaluation cap of 250,000 at all on those problems, whereas pso-i struck that cap 79 times. If the cap were removed, oscars-ii(n)’s results would be unchanged, but those of pso-i would be substantially worse.

Results for Test Set 2 were also generated for direct. Problems 70 and 71 were omitted as their solutions are at the centre of $\Omega$, which is the first point used by direct. It solved eight of the remaining 19 problems, and was the fastest of all methods on two: Dixon (nf = 2005) and modified Qing (nf = 30,667). Both of these problems are separable. It also solved the reflected Dixon problem, taking 165,631 function evaluations. Reflected Dixon is non-separable. The disparity between direct’s results on the two Dixon problems suggests that separability is advantageous for direct.

4.3 Results and discussion for the Schoen test set

Table 3 Results for oscars-ii(n) on sets of 100 Schoen test functions of the form (2) with a function evaluation cap of 250,000

Test functions from the Schoen class [29] used herein have the form

$$\begin{aligned} f(x) = \frac{ \sum _{i=1}^S \theta _i \prod _{j \ne i} \Vert x - z_j \Vert ^2 }{ \sum _{i=1}^S \prod _{j \ne i} \Vert x - z_j \Vert ^2 } \end{aligned}$$

(2)

where the indices in each product run from $j=1$ to S, excluding $j=i$. Each $z_i \in \Omega$ is a stationary point of f, and is chosen randomly from $\Omega$. The values $\theta _i$ give the heights of these stationary points, and are chosen randomly from a unit normal distribution, with one exception. After choosing all $\theta _i$ in this way, the lowest ($\theta ^*$ say) is reduced by $10^{-3}$, ensuring that any point with a function value less than $\theta ^*+10^{-3}$ is in the vicinity of the global minimizer. Let the point $z^*$ be the global minimizer of f. In general, f will have many other local minimizers, some of which will be other $z_i \ne z^*$, and others will lie on the boundary of $\Omega$.

The initial tests of oscars-ii on the Schoen test functions did not use the power law fit test. These initial tests used $10 \le n \le 60$ in steps of 10, and various numbers S of interpolation points; specifically $S \in \{15,30,60,90\}$. For each combination of S and n, 100 different Schoen functions were generated and minimized once each by oscars-ii(n). Each run was capped at 250,000 function evaluations. Runs which struck that cap were costed at the cap value, and recorded as fails. These results are listed in Table 3 and show that oscars-ii copes well with increasing dimension, provided the structure of f remains benign. Performance worsens with both increasing dimension, and increasing complexity in roughly equal measure, where the complexity here is measured by the number of interpolation points S. In almost all cases the standard deviation of the function evaluation cost exceeded its mean. This is because, on most runs, oscars-ii solves the problem using far fewer function evaluations than the mean. Rarely, it takes many more function evaluations than the mean, yielding a high standard deviation.

Fig. 1

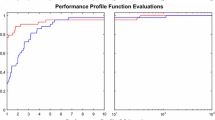
Data profile for six methods on 50 randomly generated 15 dimensional Schoen test functions with the number of interpolation points varying randomly from 15 to 50. Each test problem was solved 30 times by each stochastic method, and once by direct. The graph plots the number of problems (vertical axis) with an average solution cost not more than the function count given on the horizontal axis

Fig. 2

Data profile for five methods on 400 randomly generated 30 dimensional Schoen test functions with the number of interpolation points varying randomly from 15 to 50. Each test problem was solved once by each method. The graph plots the number of problems (vertical axis) which were solved using at most the number of function evaluations given on the horizontal axis

Fig. 3

Data profile for two methods on 100 randomly generated 60 dimensional Schoen test functions with 120 interpolation points. Each test problem was solved once by each method. The graph plots the number of problems (vertical axis) which were solved using at most the number of function evaluations given on the horizontal axis

This “usually quick, occasionally very slow” behaviour was also evident on problems in Test Sets 1 and 2. After some investigation it was found that the even numbered cycles were usually short and ended with a box size reset, whereas the odd numbered cycles were much longer. These odd cycles appeared to make fairly regular tiny reductions in f, with f significantly higher than the best known value. These tiny improvements yielded improving resets, allowing the cycle to continue until ended by a cycle length reset. The power law reset was included in an attempt to limit such behaviour.

The new method was compared against other algorithms using data profiles [5]. The first profile used 50 Schoen problems in 15 dimensions, where the number of interpolation points S for each problem was a randomly selected integer in the range $15 \le S \le 50$. Each test problem was solved 30 times by each of oscars, pso-a, pso-i, oscars-ii with and without the power law fit, and once by the deterministic method direct. All runs are capped at 50,000 function evaluations. The number of function evaluations N is the horizontal axis variable in Fig. 1, and the number of problems which, on average, take at most N function evaluations, is the vertical axis variable. The results show oscars-ii outperforms the other methods. Direct is initially a good performer, but lags as the number of required function evaluations increases. Both particle swarm methods are similar, with oscars having an edge.

The second profile appears in Fig. 2. Here 400 Schoen functions were generated with $n=30$ and S was a randomly selected integer in [15, 50]. Each test problem was solved once by each method, with a maximum function evaluation cap of 100,000 function evaluations. Figure 2 plots the number of problems solved after a given number of function evaluations against the number of function evaluations. Once again, both variants of oscars-ii are superior, and very similar to one another. Given that the number S of interpolation points is quite low, one would expect the particle swarm methods to perform well. However the results show they are outdone by the other methods.

The data profile for oscars in Fig. 2 has three distinct regions. The left most is a steep rise due to problems solved within the first two cycles. For the remaining problems these cycles continued until terminated by minimum box size resets. These cycles typically contain many improving resets which make negligible improving changes to the control point, and yield the central flat region of oscars’ profile. The right hand rise appears to be due to problems solved in the third and subsequent cycles. All odd numbered cycles have random initial control points. Hence at the start of each odd cycle oscars’ focus shifts to a different part of $\Omega$, enabling it to solve additional problems. The flat region in oscars’ profile is exactly what the extra cycle length resets in oscars-ii are designed to prevent.

The final profile is given in Fig. 3, and compares oscars-ii with and without the power law test in 60 dimensions with 120 interpolation points. In low dimensions the improvement from the power law test is most significant (see Table 1), and reduces somewhat with increasing dimension. Collectively, all results show the power law test makes a modest improvement, at the expense of an increase in overheads, and a more complex algorithm. This is due to one simple fact. If a single cycle is focused on a proper local minimizer for any significant length of time, it must be making occasional improving resets to avoid a cycle ending box size reset. The iterations following an improving reset explore $\Omega$ widely. The alternative of ending the cycle through a power law reset also does this, but to a greater degree. Clearly the former is able to compensate partially for the latter over the time scale governed by the cycle length reset J(m). The supposed independence of the algorithm’s behaviour with regard to the control point’s location can be tested more vigourously by using the best known point as the initial control point for all cycles, not just the even numbered ones. This leads to a marked deterioration in performance (far more so than for oscars [25]).

These data profiles and the results in Tables 2 and 3 show that oscars-ii is effective on problems of moderate ($10 \le n \le 20$) dimension and up to the bottom of high dimensional ($n \ge 50$) problems [21], provided the objective function is reasonably benign. As shown in [21], providing guarantees for random search methods on less benign functions in high dimensions is very hard.

5 Conclusion

A variation on the oscars algorithm for global optimization has been presented. The principal changes to oscars are that each sampling box can be shrunk simultaneously along several dimensions, and that the lengths of each cycle are initially kept short, and only slowly allowed to grow. A power law test for abandoning proper local minimizers was also tested. This test can be used with any algorithm in the accelerated random search class, and possibly with many other methods.

The new method was compared to direct and two particle swarm methods and was found to be superior on average. Numerical results also show that the new method outperforms oscars above three dimensions. The new algorithm has constant overheads per function evaluation. Additional analysis shows that both oscars and the new method have point separation properties similar to partition methods, in contrast to ars. This separation property enables oscars-ii to outperform oscars above three dimensions in spite of a box shrinkage rate similar to ars rather than oscars. Oscars-ii was compared with two particle swarm algorithms on Schoen test functions, and demonstrated a significant capability on reasonably benign problems of moderately high dimension.