1 Introduction

We consider the following quadratically constrained quadratic program (QCQP):

$$\begin{aligned} \begin{array}{lll} \underset{{\varvec{x}}\in \mathbb {R}^n}{\text {minimize}} &{}\quad {\varvec{x}}^\top Q_0{\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0 &{}\quad \\ \text {subject to} &{} \quad {\varvec{x}}^\top Q_i{\varvec{x}}+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i\le 0, &{}\quad i=1,\ldots ,m,\\ \end{array} \end{aligned}$$
(1)

where each \(Q_i\) is an \(n\times n\) symmetric matrix. \(Q_i=O\) means a linear function. We call a QCQP with m constraints m-QCQP. In the case \(Q_i\succeq O\) for every \(i=0,\ldots ,m\), (1) is a convex program. However, in general, positive semidefiniteness is not assumed, and (1) is NP-hard [23]. QCQPs are important in optimization theory and in practice.

QCQPs are fundamental nonlinear programming problems that appear in many applications such as max-cut problems [24] and binary quadratic optimizations. A standard approach for finding a global solution of (1) is the branch-and-bound (or cut) method, where a simple relaxation, e.g., a linear programming (LP) relaxation problem [2], is solved in each iteration. Audet et al. [5] proposed to introduce additional constraints, constructed using the reformulation linearization technique (RLT), to the relaxation problem. Lagrangian bounds, i.e., bounds computed by Lagrangian relaxation, have also been used in branch-and-bound methods in order to reduce the duality gap [22, 28, 30]. The branch-and-bound (or cut) algorithm yields a global solution by solving many relaxation subproblems, which restricts the size of QCQPs.

Another avenue of research has investigated tight relaxation problems for QCQPs. Among the many convex relaxation methods, a semidefinite program (SDP) relaxation is well known and have been extensively studied [11, 19, 29]. It is known that the an SDP relaxation can be viewed as the Lagrangian dual problem of the original QCQP. The SDP relaxation has been applied to various QCQPs that appear in combinatorial optimization problems [12, 13] as well as in signal processing and communications [19]. The SDP relaxation is powerful, and it gives the exact optimal value for 1-QCQP having only one constraint such as the trust region subproblem (TRS). Furthermore, recent studies such as [3] have proposed to add new valid inequalities (e.g., linear constraints for matrix variables using the original upper and lower bound constraints) to SDP relaxation problems. In particular, Zheng et al. [31, 32] proposed a decomposition–approximation scheme that generates an SDP relaxation at least as tight as the ordinary one. Jiang and Li [16] proposed second order cone constraints as valid inequalities for the ordinary SDP relaxation. Such methods aim at obtaining a better relaxed solution even if they take more time to solve than the ordinary SDP relaxation.

However, an SDP relaxation including additional valid inequalities increases the problem size, which leads to a longer computation time and often memory shortage errors for large-scale problems. Here, Kim and Kojima [17] proposed a second-order cone programming relaxation (SOCP relaxation), where valid second-order cone constraints derived from the positive semidefinite inequality are added to the LP relaxation. Burer et al. [9] proposed a “weaker but faster” method that uses a block matrix decomposition, compared to SDP relaxations. Such faster relaxation methods are useful for large-scale problems, and they can be repeatedly solved in, e.g., a branch-and-bound method.

In this paper, we propose a faster convex relaxation method that is not stronger than SDP relaxations if valid constraints are not considered. Our method solves the Lagrangian dual problem of the original QCQP by using a subgradient method, though the Lagrangian dual problem can be reformulated as an SDP and is solvable with the interior-point method. Indeed, there are various studies that propose to solve the Lagrangian dual problems for nonconvex problems, but most of them transform the dual problem into an SDP problem [6] or a more general cone problem [18]. Here, to resort to more easily solved problems, we divide the minimization of the objective function in the Lagrangian dual problem into two levels and iteratively solve the inner problem as a 1-QCQP, which can be solved exactly and efficiently. There are mainly two approaches to solving a 1-QCQP: one is based on eigenvalue computation, the other is on the SDP relaxation. In particular, Moré and Sorensen [20] proposed to iteratively solve a symmetric positive-definite linear system for TRS, while Adachi et al. [1] proposed an accurate and efficient method that solves only one generalized eigenvalue problem. In this paper, we propose a new relaxation method that can solve a 1-QCQP exactly and efficiently as a convex quadratic optimization problem. Furthermore, we prove that the convex quadratic problem constructs the convex hull of the feasible region of a 1-QCQP. Numerical experiments confirm that our convex quadratic relaxation method for solving 1-QCQPs is faster than SDP relaxations and eigenvalue methods. They also show that our method can quickly find a relaxed solution of an m-QCQP by iteratively solving a 1-QCQP with updated Lagrange multipliers. By adding valid constraints to our formulation, our method can sometimes find a better relaxed solution in a shorter computation time compared with the ordinary SDP relaxation. The relaxation technique can be embedded within a branch-and-bound framework to find a global optimum to the original m-QCQP.

The remainder of this paper is organized as follows. We introduce SDP relaxations and other related studies in Sect. 2. We describe our method and its some properties in Sects. 3 and 4. We present computational results in Sect. 5. We conclude the paper in Sect. 6. The Appendix contains proofs of the presented theorems in Sects. 3 and 4.

Throughout the paper, we denote matrices by using uppercase letters such as “Q”, vectors by using bold lowercase such as “\({\varvec{q}}\)” and scalars by using normal lower case such as “\(\gamma \)”. The notation \(A\succ B\) or \(A\succeq B\) implies that the matrix \(A-B\) is positive definite or semidefinite. \({\varvec{e}}\) means the all-one vector.

2 Existing SDP relaxation methods for m-QCQP

2.1 SDP relaxation

The Lagrangian dual problem of the original problem (1) is described as

$$\begin{aligned} \underset{{\varvec{\xi }}\ge {\varvec{0}}}{\text {max}} \qquad \phi ({\varvec{\xi }}). \end{aligned}$$
(2)

Here, \(\phi ({\varvec{\xi }})\) is an optimal value function defined by

$$\begin{aligned} \phi ({\varvec{\xi }})&:=\underset{{\varvec{x}}}{\text {min}}\left[ \;{\varvec{x}}^\top \left( Q_0+\sum _{i=1}^m\xi _i Q_i\right) {\varvec{x}}+2\left( {\varvec{q}}_0+\sum _{i=1}^m\xi _i {\varvec{q}}_i\right) ^\top {\varvec{x}}+\gamma _0+\sum _{i=1}^m\xi _i \gamma _i\right] , \end{aligned}$$
(3)
$$\begin{aligned}&\phantom {:}={\left\{ \begin{array}{ll} -{\varvec{q}}({\varvec{\xi }})^\top Q({\varvec{\xi }})^\dag {\varvec{q}}({\varvec{\xi }})+\gamma ({\varvec{\xi }}), &{} (\mathrm {if} \;Q({\varvec{\xi }})\succeq O),\\ -\infty , &{} (\mathrm {otherwise}), \end{array}\right. } \end{aligned}$$
(4)

where \(Q({\varvec{\xi }}):=Q_0+\sum _{i=1}^m\xi _i Q_i\), \({\varvec{q}}({\varvec{\xi }}):={\varvec{q}}_0+\sum _{i=1}^m\xi _i{\varvec{q}}_i\), \(\gamma ({\varvec{\xi }}):=\gamma _0+\sum _{i=1}^m\xi _i \gamma _i\) and “†” means the pseudo-inverse. Note that from (4), (2) is equivalent to

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{\xi }}\ge {\varvec{0}}}{\text {max}} &{}\quad \phi ({\varvec{\xi }})\\ \text {s.t.} &{} \quad Q_0+\sum _{i=1}^m\xi _i Q_i\succeq O. \end{array} \end{aligned}$$
(5)

By considering \(-{\varvec{q}}({\varvec{\xi }})^\top Q({\varvec{\xi }})^\dag {\varvec{q}}({\varvec{\xi }})+\gamma ({\varvec{\xi }})\) as a Schur complement of \(\begin{pmatrix}Q({\varvec{\xi }}) &{} {\varvec{q}}({\varvec{\xi }})\\ {\varvec{q}}({\varvec{\xi }})^\top &{} \gamma ({\varvec{\xi }})\end{pmatrix}\), we can equivalently rewrite the dual problem (5) as a semidefinite program (SDP)

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{\xi }}\ge {\varvec{0}},\tau }{\text {max}} &{} \quad \tau \\ \text {s.t.} &{}\quad \begin{pmatrix} Q({\varvec{\xi }}) &{} {\varvec{q}}({\varvec{\xi }})\\ {\varvec{q}}({\varvec{\xi }})^\top &{} \gamma ({\varvec{\xi }})-\tau \end{pmatrix}\succeq O, \end{array} \end{aligned}$$
(6)

which can be solved by using an interior-point method. It should be noted that the dual of (6) is

$$\begin{aligned} \begin{array}{lll} \underset{{\varvec{x}},X}{\text {min}} &{}\quad Q_0\cdot X+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0&{} \\ \text {s.t.} &{}\quad Q_i\cdot X+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i\le 0, &{}\quad i=1,\ldots ,m,\\ &{} \quad X\succeq {\varvec{x}}{\varvec{x}}^\top &{} \\ \end{array} \end{aligned}$$
(7)

and (6) and (7) are equivalent under the Primal/Dual Slater condition.

The SDP relaxation is a popular approach to find a relaxed solution of (1). Sturm and Zhang [27] proved that the SDP relaxation can always obtain the exact optimal value for a 1-QCQP. Goemans and Williamson showed an approximation bound given by the SDP relaxation for max-cut problems [13], and Goemans [12] applied the SDP relaxation to various combinatorial problems. Their numerical experiments show that the SDP relaxation can find a very tight relaxed solution for many kinds of problems. However, the SDP relaxation has disadvantages in both computation time and space complexity because of the matrix variable; it cannot deal with large-scale problems because of shortage of memory. Although polynomial time algorithms, such as an interior-point method, have been established, they often take a long time to solve an SDP relaxation problem in practice.

Remark 1

We propose a subgradient-based approach for (5) instead of applying the interior-point method to the equivalent SDP (6) or (7) in this paper. Efficiently applying the ordinary subgradient method to (5) is not straightforward. Indeed, after obtaining a subgradient vector of \(\phi ({\varvec{\xi }})\), we need to project the vector onto the the set \(\Lambda :=\{{\varvec{\xi }}: {\varvec{\xi }} \ge {\varvec{0}}, Q_0+\sum _{i=1}^m\xi _i Q_i\succeq O\}\). For the projection computation, we need to solve another SDP with similar matrix size to (7). This direct application of a subgradient method to (5) is not a good idea.

We will construct a subset of \(\Lambda \) such that the projection of a vector onto the set is easy and use the subset instead of \(\Lambda \). The proposed approach may give loser relaxation than the SDP relaxation to QCQPs, but our numerical experiments show that the proposed approach combined with the reformulation linearization technique (RLT) can be better than the SDP relaxation in terms of the tightness of the relaxation and computation time.

2.2 Stronger SDP relaxation using RLT

Anstreicher [3] used the reformulation linearization technique (RLT) to further strengthen the SDP relaxation; new constraints are added to the ordinary SDP relaxation and the range of the new variables \(X_{ij}\), \(\forall i,j\) is restricted. Here, one assumes the original problem (1) has box constraints, i.e., lower and upper bounds on each variable \(x_j\) (\(l_j\) and \(u_j\), respectively). Note as well that even if there are no box constraints, we may be able to compute \(l_j\) and \(u_j\) by using the original constraints if the feasible region is bounded. The inequality \(l_j\le x_j\le u_j\) (as a vector expression, \({\varvec{l}}\le {\varvec{x}}\le {\varvec{u}}\)) leads to

$$\begin{aligned} (x_i-u_i)(x_j-u_j)\ge 0&\iff x_ix_j-u_ix_j-u_jx_i+u_iu_j\ge 0, \end{aligned}$$
(8)
$$\begin{aligned} (x_i-u_i)(x_j-l_j)\le 0&\iff x_ix_j-u_ix_j-l_jx_i+u_il_j\le 0, \end{aligned}$$
(9)
$$\begin{aligned} (x_i-l_i)(x_j-l_j)\ge 0&\iff x_ix_j-l_ix_j-l_jx_i+l_il_j\ge 0, \end{aligned}$$
(10)

for \(i,j=1,\ldots ,n\). By replacing \(x_ix_j\) with \(X_{ij}\), we have

$$\begin{aligned} X_{ij}-u_ix_j-u_jx_i+u_iu_j&\ge 0, \end{aligned}$$
(11)
$$\begin{aligned} X_{ij}-u_ix_j-l_jx_i+u_il_j&\le 0, \end{aligned}$$
(12)
$$\begin{aligned} X_{ij}-l_ix_j-l_jx_i+l_il_j&\ge 0. \end{aligned}$$
(13)

(11)–(13) are linear inequalities that include matrix variables \(X_{ij}\). Therefore, by adding these constraints, we can get a stronger relaxation. The disadvantage of RLT is that it increases computation time because of the increased variables \(X_{ij}\) and additional constraints (11)–(13).

Many studies such as [16, 26, 31, 32] have aimed at strengthening the relaxation by adding valid inequalities other than (11)–(13). These methods give very tight bounds, but they tend to entail large amounts of computation time.

2.3 Weaker SDP relaxation method by block decomposition

Burer et al. [9] aims to solve a relaxed problem faster than SDP relaxations, although it is a weaker relaxation; as such, it shares a similar motivation as ours. First, [9] assumes that the original problem has [0,1] box constraints (i.e. \(\forall i;\; 0\le x_i\le 1\)) in order to avoid a situation in which the optimal value of a relaxation problem diverges. Then, by following [9], we can compute a block diagonal matrix \(D_i\) which satisfies \(Q_i+D_i\succeq O\) for the matrix \(Q_i\) appearing in the objective function or the constraints. By using \(D_i\), we transform a quadratic polynomial as follows,

$$\begin{aligned} {\varvec{x}}^\top Q_i{\varvec{x}}+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i=-{\varvec{x}}^\top D_i{\varvec{x}}+{\varvec{x}}^\top (Q_i+D_i){\varvec{x}}+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i \end{aligned}$$

and relax \({\varvec{x}}^\top D_i{\varvec{x}}\) to \(D_i\cdot X\) and \(X\succeq O\). As a whole, a relaxation problem is

$$\begin{aligned} \begin{array}{lll} \underset{{\varvec{x}},X}{\text {min}} &{}\quad -D_0\cdot X+{\varvec{x}}^\top (Q_0+D_0){\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0 &{} \\ \text {s.t.} &{}\quad -D_i\cdot X+{\varvec{x}}^\top (Q_i+D_i){\varvec{x}}+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i\le 0, &{}\quad i=1,\ldots ,m,\\ &{} \quad X_k \succeq {\varvec{x}}_k{\varvec{x}}_k^\top , &{}\quad k=1,\ldots ,r,\\ \end{array} \end{aligned}$$

where r denotes the number of blocks of \(D_i\) and \(X_k\) or \({\varvec{x}}_k\) denotes a partial matrix or vector in X or \({\varvec{x}}\) corresponding to each block of \(D_i\), \(\forall i\). Note that in a similar way as (12), we have new constraints \(X_{ii}\le x_i,\;i=1,\ldots ,m\) for the matrix variable X from the box constraints. Since we relax only the quadratic form for each block part, the matrix X only has block part components. Therefore, we can consider the positive semidefinite constraint only for the block parts: \(X_k\succeq {\varvec{x}}_k{\varvec{x}}_k^\top \). The number of variables related to the positive semidefinite constraint is reduced, which will shorten the computation time. We call this method Block-SDP and use it in the numerical experiments in Sect. 5.

In [9], it is proposed to divide \(D_i\) as evenly as possible, that is, by making the difference between the largest block size and the smallest block size at most one for a given r.

3 Proposed method

3.1 Assumptions

Before we explain our method, we will impose the following three assumptions.

Assumption 1

  1. (a)

    The feasible region of (1) has some interior points.

  2. (b)

    There exists at least one matrix \(Q_i\;(i=0,\ldots ,m)\) such that \(Q_i\succ O\).

  3. (c)

    An optimal solution of QCQP (1) can not be obtained by solving the following unconstrained optimization problem

    $$\begin{aligned} \underset{{\varvec{x}}}{\mathrm {min}} \qquad {\varvec{x}}^\top Q_0{\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0. \end{aligned}$$
    (14)

Assumption 1 (a) is the primal Slater condition, and (b) is a sufficient condition of the Dual Slater condition of the original QCQP.

3.2 The whole algorithm

We further transform the Lagrangian dual problem (2) into

$$\begin{aligned} \underset{{\varvec{\lambda }}\in \Lambda _{\mathrm {s}}}{\text {max}} \qquad \underset{\mu \ge 0}{\text {max}} \qquad \phi (\mu {\varvec{\lambda }}), \end{aligned}$$
(15)

where \(\Lambda _{\mathrm {s}}:=\{{\varvec{\lambda }}\ge {\varvec{0}}\mid \;{\varvec{e}}^\top {\varvec{\lambda }}=1\}\) is a simplex. Now we define \(\psi ({\varvec{\lambda }})\) as the optimal value of the inner optimization problem of (15) for a given \({\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\):

$$\begin{aligned} \psi ({\varvec{\lambda }}):= \qquad \underset{\mu \ge 0}{\text {max}} \qquad \phi (\mu {\varvec{\lambda }}). \end{aligned}$$
(16)

Note that (16) is the Lagrangian dual problem for the following 1-QCQP:

$$\begin{aligned} \begin{array}{lll} \psi ({\varvec{\lambda }})= &{}\quad \underset{{\varvec{x}}}{\text {min}} &{}\quad {\varvec{x}}^\top Q_0{\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0 \\ &{}\quad \text {s.t.} &{} \quad {\varvec{x}}^\top \left( \sum \limits _{i=1}^m\lambda _iQ_i\right) {\varvec{x}}+2\left( \sum \limits _{i=1}^m\lambda _i{\varvec{q}}_i\right) ^\top {\varvec{x}}+\sum \limits _{i=1}^m\lambda _i\gamma _i\le 0. \end{array} \end{aligned}$$
(17)

There is no duality gap between (16) and its Lagrangian dual (17), since [27] proves that the SDP formulation of (16) has the same optimal value as the 1-QCQP (17). We will show how to exactly and efficiently solve the 1-QCQP (17) in Sect. 4.1. The Lagrangian dual problem (2) can be written as

$$\begin{aligned} \underset{{\varvec{\lambda }}\in \Lambda _{\mathrm {s}}}{\text {max}} \qquad \psi ({\varvec{\lambda }}). \end{aligned}$$
(18)

Here, we propose an algorithm which iteratively solves (17) with updated \({\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\) for finding an optimal solution of the Lagrangian dual problem. \(\Lambda _{\mathrm {s}}\) is a convex set, and \(\psi ({\varvec{\lambda }})\) is a quasi-concave function, as shown in Sect. 3.3. Therefore, we will apply the standard gradient descent method to (18) for updating \({\varvec{\lambda }}\). The speed of convergence of gradient methods is slow in general especially near optimal solutions, and therefore, we will obtain a relaxed solution by using an appropriate termination criterion. Algorithm 1 summarizes the proposed method.

figure a

We divide the “max” for the Lagrange function into two levels and iteratively solve the inner problem, 1-QCQP, which computes \(\psi ({\varvec{\lambda }})\) with a given \({\varvec{\lambda }}\). Our method is not stronger than the ordinary SDP relaxation as discussed in Sect. 4. We also explain the details of our method (especially, the relationship between (\(\mathrm {P}_k\)) and (27) or (28)) later in Sect. 4.

3.3 Quasi-concavity of \(\psi ({\varvec{\lambda }})\)

Objective functions of Lagrangian dual problems are concave with respect to Lagrange multipliers (e.g. [7]). The function \(\phi (\mu {\varvec{\lambda }})\) with fixed \({\varvec{\lambda }}\) is hence concave with respect to \(\mu \), but \(\psi ({\varvec{\lambda }})\) is not necessarily concave for \({\varvec{\lambda }}\). However, we can prove that \(\psi ({\varvec{\lambda }})\) is a quasi-concave function and has some of the desirable properties that concave functions have.

Before we prove the quasi-concavity of \(\psi ({\varvec{\lambda }})\), we have to define the set \(\Lambda _+\),

$$\begin{aligned} \Lambda _+=\{{\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\mid \psi ({\varvec{\lambda }})>\phi ({\varvec{0}})\}, \end{aligned}$$
(19)

in order to explain the properties of \(\psi ({\varvec{\lambda }})\). Note that \(\phi ({\varvec{0}})\) is the optimal value of the unconstrained problem (14) and \(\psi ({\varvec{\lambda }})\ge \phi ({\varvec{0}})\) holds for all \({\varvec{\lambda }}\). We can also see that \(\Lambda _+\) is nonempty if and only if the SDP relaxation value is larger than \(\phi ({\varvec{0}})\), i.e., \(\mathrm {OPT}_\mathrm {SDP}>\phi ({\varvec{0}})\) holds. This is obvious from \(\mathrm {OPT}_\mathrm {SDP}=\max \{\psi ({\varvec{\lambda }})\mid {\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\}\) (see 18 and 19). In other words, \(\mathrm {OPT}_\mathrm {SDP}=\phi ({\varvec{0}})\) means that the SDP relaxation gives us an optimal solution of (14).

From the definition of \(\Lambda _+\), we see that an optimal solution of (16) for \({\varvec{\lambda }}\in \Lambda _+\), which we denote by \(\bar{\mu }_{{{\varvec{\lambda }}}}\), is a positive value. When \({\varvec{\lambda }}\notin \Lambda _+\) (i.e. \(\psi ({\varvec{\lambda }})=\phi ({\varvec{0}})\)), we can set \(\bar{\mu }_{{{\varvec{\lambda }}}}\) to zero without changing the optimal value and solution. By using such \(\bar{\mu }_{{{\varvec{\lambda }}}}\), we will identify (19) and

$$\begin{aligned} \Lambda _+=\{{\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\mid \bar{\mu }_{{{\varvec{\lambda }}}}>0\}. \end{aligned}$$
(20)

Now let us prove the quasi-concavity of \(\psi ({\varvec{\lambda }})\) and some other properties.

Theorem 1

Let \(\psi ({\varvec{\lambda }})\) be the optimal value of (16) and \((\bar{{\varvec{x}}}_{{{\varvec{\lambda }}}},\bar{\mu }_{{{\varvec{\lambda }}}})\) be its optimal solution. Then, the following (i)–(iv) hold.

  1. (i)

    The vector

    $$\begin{aligned} (\tilde{{\varvec{g}}}_{{{\varvec{\lambda }}}})_i=\bar{\mu }_{{{\varvec{\lambda }}}}\left( \bar{{\varvec{x}}}_{{{\varvec{\lambda }}}}^\top Q_i\bar{{\varvec{x}}}_{{{\varvec{\lambda }}}}+2{\varvec{q}}_i^\top \bar{{\varvec{x}}}_{{{\varvec{\lambda }}}}+\gamma _i\right) \end{aligned}$$
    (21)

    is a subgradient of \(\psi \) at \({\varvec{\lambda }}\), which is defined as a vector in the quasi-subdifferential (see e.g., [14, 15]):

    $$\begin{aligned} \partial \psi ({\varvec{\lambda }}):=\{{\varvec{s}}\mid {\varvec{s}}^\top ({\varvec{\nu }}-{\varvec{\lambda }})\ge 0,\;\;\;\forall {\varvec{\nu }};\;\psi ({\varvec{\nu }})>\psi ({\varvec{\lambda }})\}. \end{aligned}$$
    (22)
  2. (ii)

    \(\psi ({\varvec{\lambda }})\) is a quasi-concave function for \({\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\).

  3. (iii)

    \(\Lambda _+\) is a convex set.

  4. (iv)

    If \(\psi ({\varvec{\lambda }})\) has stationary points in \(\Lambda _+\), all of them are global optimal solutions of (18).

The proof is in the Appendix.

Note that the set of global solutions of \(\psi \) is convex because of the quasi-concavity of \(\psi ({\varvec{\lambda }})\). (iv) is similar to the property that concave functions have. Therefore, a simple subgradient method such as SLR works well. SLR is an algorithm for finding a stationary point in \(\Lambda _+\), which Theorem 1 (iv) proves to be a global optimal solution in \(\Lambda _s\).

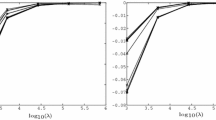
Figures 1 and 2 are images of \(\psi ({\varvec{\lambda }})\) for \(m=2\), where \({\varvec{\lambda }}\in \Lambda _{\mathrm {s}}\) is expressed by one variable \(\alpha \in [0,1]\) as \({\varvec{\lambda }}=(\alpha ,1-\alpha )^\top \). The vertical axis shows \(\psi ({\varvec{\lambda }})\), and the horizontal one shows \(\alpha \) for a randomly generated 2-QCQP. We can make sure that \(\psi ({\varvec{\lambda }})\) is a quasi-concave function from these figures and also that \(\psi \) is not always a concave function even over \(\Lambda _+\).

Fig. 1
figure 1

\(\psi ({\varvec{\lambda }})\) and \(\Lambda _+\) when \(Q_0\succeq O\)

Full size image
Fig. 2
figure 2

\(\psi ({\varvec{\lambda }})\) and \(\Lambda _+\) when \(Q_0\nsucceq O\)

Full size image

There are subgradient methods for maximizing a quasi-concave function. If the objective function satisfies some assumptions, the convergence of the algorithms is guaranteed. However, this may not be the case for the problem setting of (18). For example, in [14], \(\psi ({\varvec{\lambda }})\) must satisfy the Hölder condition of order \(p>0\) with modulus \(\mu >0\), that is,

$$\begin{aligned} \psi ({\varvec{\lambda }})-\psi _*\le \mu (\mathrm {dist}({\varvec{\lambda }},\Lambda ^*))^p,\;\;\;\;\forall {\varvec{\lambda }}\in \mathbb {R}^m, \end{aligned}$$

where \(\psi _*\) is the optimal value, \(\Lambda ^*\) is the set of optimal solutions and \(\mathrm {dist}({\varvec{y}},Y)\) denotes the Euclidean distance from a vector \({\varvec{y}}\) to a set Y. It is hard to check whether \(\psi ({\varvec{\lambda }})\) satisfies the Hölder condition. Ensuring the convergence of SLR seems difficult, but numerical experiments imply that SLR works well and often achieves the same optimal value as the SDP relaxation value.

4 Details of SLR

4.1 Subproblem of SLR: 1-QCQP

SLR needs to solve 1-QCQP \(\mathrm {(P_k)}\). Here, we describe a fast and exact solution method for a general 1-QCQP. First, we transform the original 1-QCQP by using a new variable t into the form:

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{x}},t}{\text {min}} &{}\quad t \\ \text {s.t.} &{}\quad {\varvec{x}}^\top Q_0{\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0\le t,\\ &{}\quad {\varvec{x}}^\top Q_{{{\varvec{\lambda }}}}{\varvec{x}}+2{\varvec{q}}_{{{\varvec{\lambda }}}}^\top {\varvec{x}}+\gamma _{{{\varvec{\lambda }}}}\le 0, \\ \end{array} \end{aligned}$$
(23)

where

$$\begin{aligned} Q_{{{\varvec{\lambda }}}}=\sum _{i=1}^m\lambda _i^{(k)}Q_i,\;\;{\varvec{q}}_{{{\varvec{\lambda }}}}=\sum _{i=1}^m\lambda _i^{(k)}{\varvec{q}}_i,\;\;\gamma _{{{\varvec{\lambda }}}}=\sum _{i=1}^m\lambda _i^{(k)}\gamma _i, \end{aligned}$$

in the SLR algorithm. Here, we assume that (23) satisfies the following Primal and Dual Slater conditions:

$$\begin{aligned} \begin{array}{lll} \text {(Primal}\;\text {Slater}\;\text {condition)} &{} \quad \exists {\varvec{x}}\in \mathbb {R}^n &{} \quad \mathrm {s.t.}\;\;{\varvec{x}}^\top Q_{{{\varvec{\lambda }}}}{\varvec{x}}+2{\varvec{q}}_{{{\varvec{\lambda }}}}^\top {\varvec{x}}+\gamma _{{{\varvec{\lambda }}}}< 0\\ \text {(Dual}\;\text {Slater}\;\text {condition)} &{} \quad \exists \sigma \ge 0&{}\quad \mathrm {s.t.}\;\;Q_0+\sigma Q_{{{\varvec{\lambda }}}}\succ O \end{array} \end{aligned}$$

Indeed, \(\mathrm {(P_k)}\) satisfies the Primal Slater condition because of Assumption 1 (a), and it also satisfies the Dual Slater condition because either \(Q_0\) or \(Q_{{{\varvec{\lambda }}}}\) is positive definite by the updating rule of \({\varvec{\lambda }}^{(k)}\) explained in the next subsection. Here, we define

$$\begin{aligned} S :&=\{\sigma \ge 0\mid Q_0+\sigma Q_{{{\varvec{\lambda }}}}\succeq O\}, \end{aligned}$$

which is a convex set of one dimension, that is, an interval. The Dual Slater condition implies that S is not a point, and therefore, \(\underline{\sigma }<\bar{\sigma }\) holds for

$$\begin{aligned} \bar{\sigma }:=\underset{\sigma \in S}{\sup }\;\sigma , \end{aligned}$$
(24)
$$\begin{aligned} \underline{\sigma }:=\underset{\sigma \in S}{\inf }\;\sigma . \end{aligned}$$
(25)

We set \(\bar{\sigma }=+\infty \) when \(Q_{{{\varvec{\lambda }}}} \succ O\) and \(\underline{\sigma }=0\) when \(Q_0\succeq O \). We construct the following relaxation problem of (23) using \(\bar{\sigma }\) and \(\underline{\sigma }\):

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{x}},t}{\text {min}} &{}\quad t \\ \text {s.t.} &{} \quad {\varvec{x}}^\top (Q_0+\underline{\sigma }Q_{{{\varvec{\lambda }}}}){\varvec{x}}+2({\varvec{q}}_0+\underline{\sigma }{\varvec{q}}_{{{\varvec{\lambda }}}})^\top {\varvec{x}}+\gamma _0+\underline{\sigma }\gamma _{{{\varvec{\lambda }}}}\le t, \\ &{} \quad {\varvec{x}}^\top (Q_0+\bar{\sigma }Q_{{{\varvec{\lambda }}}}){\varvec{x}}+2({\varvec{q}}_0+\bar{\sigma }{\varvec{q}}_{{{\varvec{\lambda }}}})^\top {\varvec{x}}+\gamma _0+\bar{\sigma }\gamma _{{{\varvec{\lambda }}}}\le t, \end{array} \end{aligned}$$
(26)

which will be shown to be equivalent to (23) later in Theorem 2. Note that in the SLR algorithm, we keep either \(Q_0\) or \(Q_{{{\varvec{\lambda }}}}\) positive semidefinite. When \(\underline{\sigma }=0\) (i.e., \(Q_0\succeq O\)), (26) is equivalent to the following relaxed problem:

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{x}},t}{\text {min}} &{}\quad t \\ \text {s.t.} &{}\quad {\varvec{x}}^\top Q_0{\varvec{x}}+2{\varvec{q}}_0^\top {\varvec{x}}+\gamma _0\le t, \\ &{}\quad {\varvec{x}}^\top (\hat{\sigma } Q_0+Q_{{{\varvec{\lambda }}}}){\varvec{x}}+2(\hat{\sigma }{\varvec{q}}_0+{\varvec{q}}_{{{\varvec{\lambda }}}})^\top {\varvec{x}}+(\hat{\sigma }\gamma _0+\gamma _{{{\varvec{\lambda }}}})\le \hat{\sigma } t, \\ \end{array} \end{aligned}$$
(27)

where \(\hat{\sigma }=1/\bar{\sigma }\), and \(\hat{\sigma }\) can be easily calculated. On the other hand, when \(\bar{\sigma }=+\infty \) (i.e., \(Q_{{{\varvec{\lambda }}}} \succ O\)), (26) is equivalent to

$$\begin{aligned} \begin{array}{ll} \underset{{\varvec{x}},t}{\mathrm {min}} &{}\quad t \\ \mathrm {s.t.} &{}\quad {\varvec{x}}^\top (Q_0+\underline{\sigma }Q_{{{\varvec{\lambda }}}}){\varvec{x}}+2({\varvec{q}}_0+\underline{\sigma }{\varvec{q}}_{{{\varvec{\lambda }}}})^\top {\varvec{x}}+\gamma _0+\underline{\sigma }\gamma _{{{\varvec{\lambda }}}}\le t, \\ &{}\quad {\varvec{x}}^\top Q_{{{\varvec{\lambda }}}}{\varvec{x}}+2{\varvec{q}}_{{{\varvec{\lambda }}}}^\top {\varvec{x}}+\gamma _{{{\varvec{\lambda }}}}\le 0.\\ \end{array} \end{aligned}$$
(28)

(28) can be viewed as dividing the second constraint of (26) by \(\bar{\sigma }\) and \(\bar{\sigma }\rightarrow \infty \).

The following theorem shows the equivalence of the proposed relaxation problem (26) and the original problem (23).

Theorem 2

Under the Primal and Dual Slater conditions, the feasible region \(\Delta _{\mathrm {rel}}\) of the proposed relaxation problem (26) is the convex hull of the feasible region \(\Delta \) of the original problem (23), i.e., \(\Delta _{\mathrm {rel}}=\mathrm {conv}(\Delta )\).

The proof is in the Appendix.

Theorem 2 implies that (26) gives an exact optimal solution of 1-QCQP (23) since the objective function is linear. The outline of the proof is as follows (see Fig. 3). We choose an arbitrary point \(({\varvec{x}}^*,t^*)\) in \(\Delta _{\mathrm {rel}}\) and show that there exists two points P and Q in \(\Delta \) which express \(({\varvec{x}}^*,t^*)\) as a convex combination of P and Q. We show in the Appendix how to obtain P and Q of \(\Delta \) for an arbitrary point \(({\varvec{x}}^*,t^*)\) in \(\Delta _{\mathrm {rel}}\). Using this technique, we can find an optimal solution of 1-QCQP (23). By comparison, SDP relaxations can not always find a feasible solution for the 1-QCQP (though it can obtain the optimal value).

Fig. 3
figure 3

Image of \(\Delta \) and \(\Delta _{\mathrm {rel}}\)

Full size image

(26) is a convex quadratic problem equivalent to 1-QCQP, which we will call CQ1. CQ1 can be constructed from a general 1-QCQP including the Trust Region Subproblem (TRS). The numerical experiments in Sect. 5 show that CQ1 can be solved by a convex quadratic optimization solver faster than by an efficient method for solving a TRS and the interior-point method, and hence, solving CQ1 as subproblems can speed up SLR.

Now let us explain how to calculate \(\hat{\sigma }\) or \(\underline{\sigma }\) using a positive definite matrix, i.e., for both cases when \(Q_0\succ O\) in (27) and \(Q_{{{\varvec{\lambda }}}}\succ O\) in (28). We calculate \(\hat{\sigma }\) in (27) when \(Q_0\succ O\) as follows. Let \(Q_0^{\frac{1}{2}}\) be the square root of the matrix \(Q_0\) and \(Q_0^{-\frac{1}{2}}\) be its inverse. Then, \(\hat{\sigma }\) can be calculated as

$$\begin{aligned} \hat{\sigma }=\left| \min \left\{ \sigma _{\mathrm {min}}\left( Q_0^{-\frac{1}{2}}Q_{{{\varvec{\lambda }}}}Q_0^{-\frac{1}{2}}\right) ,0\right\} \right| , \end{aligned}$$

where \(\sigma _{\mathrm {min}}(X)\) is the minimum eigenvalue of X, because

$$\begin{aligned} \sigma Q_0+Q_{{{\varvec{\lambda }}}}\succeq O&\iff Q_0^{-\frac{1}{2}}(\sigma Q_0+Q_{{{\varvec{\lambda }}}})Q_0^{-\frac{1}{2}}\succeq O\nonumber \\&\iff \sigma I+Q_0^{-\frac{1}{2}}Q_{{{\varvec{\lambda }}}}Q_0^{-\frac{1}{2}}\succeq O. \end{aligned}$$

Similarly, we can calculate \(\underline{\sigma }\) in (28) as

$$\begin{aligned} \underline{\sigma }=\left| \min \left\{ \sigma _{\mathrm {min}}\left( Q_{{{\varvec{\lambda }}}}^{-\frac{1}{2}}Q_0Q_{{{\varvec{\lambda }}}}^{-\frac{1}{2}}\right) ,0\right\} \right| , \end{aligned}$$

when \(Q_{{{\varvec{\lambda }}}}\succ O\).

4.2 Update rule of \({\varvec{\lambda }}\)

figure b

Now let us explain the update rule of \({\varvec{\lambda }}\), which is used in Step 3 of Algorithm 1. Algorithm 2 summarizes the procedure of updating \({\varvec{\lambda }}\). The whole algorithm, SLR, updates \({\varvec{\lambda }}^{(k)}\) and \({\varvec{x}}^{(k)}\) in each iteration \(k=1,2,\ldots \). In order for \(\mathrm {(P_k)}\) to have an optimal solution \({\varvec{x}}^{(k)}\), \({\varvec{\lambda }}^{(k)}\) needs to be set appropriately so as to satisfy \(Q_0+\mu \sum _{i=1}^m\lambda _i^{(k)} Q_i\succeq O\) for some \(\mu \ge 0\). If the input \(Q_0\) of the given problem satisfies \(Q_0 \succ O\), then \(Q_0+\mu \sum _{i=1}^m\lambda _i^{(k)} Q_i\succeq O\) holds with \(\mu = 0\), which makes \(\mathrm {(P_k)}\) bounded.

On the other hand, in the case of \(Q_0\nsucceq O\), the optimal value of \(\mathrm {(P_k)}\), \(\psi ({\varvec{\lambda }}^{(k)})\), possibly becomes \(-\infty \) with inappropriately chosen \({\varvec{\lambda }}^{(k)}\), and we can not find an optimal solution. In such case, we can not calculate \({\varvec{g}}^{(k)}\) in Step 1 of Algorithm 2 and the algorithm stops. To prevent this from happening, we use a subset \(\Lambda _+\) of \(\Lambda _s\) so that \(\psi ({\varvec{\lambda }}^{(k)})\) does not become \(-\infty \) and \(\Lambda _+\) does not change the optimum value of the Lagrangian dual problem (18). When \(Q_0\nsucc O\), \(\Lambda _+\) of (20) can be rewritten as

$$\begin{aligned} \Lambda _+=\left\{ {\varvec{\lambda }}\ge {\varvec{0}}\mid \; {\varvec{e}}^\top {\varvec{\lambda }}=1,\;\exists \mu \ge 0;\;Q_0+\mu \sum _{i=1}^m\lambda _i Q_i\succ O\right\} \end{aligned}$$

under Assumption 1 (b). \(\Lambda _+\) is the set of \({\varvec{\lambda }}\) for which \(\psi ({\varvec{\lambda }})>-\infty \). To exactly solve the problem (18), the projection computation in (29) should be done for the set \(\Lambda _+\) when \(Q_0 \nsucc O\). However, the projection computation can not be easily done because of the complicated condition on \(\mu \). Therefore, when \(Q_0\nsucc O\), we approximate \(\Lambda _+\) as

$$\begin{aligned} \Lambda '_+:=\left\{ {\varvec{\lambda }}\ge {\varvec{0}}\mid \; {\varvec{e}}^\top {\varvec{\lambda }}=1,\;\sum _{i=1}^m\lambda _i Q_i\succ O\right\} , \end{aligned}$$

and keep \({\varvec{\lambda }}^{(k)}\) in \(\Lambda '_+\) by Step 4. It can be easily confirmed that \(\Lambda '_+\) is a convex set. By replacing the feasible region \(\Lambda _s\) of (18) by \(\Lambda '_+\;(\subseteq \Lambda _+)\), the relaxation can be weaker and the optimal value is not necessarily equal to the SDP relaxation value. Thus, when \(Q_0\nsucc O\), SLR may be worse than it is when \(Q_0\succ O\).

Now we give details on some steps in Algorithm 2.

Step 1: Theorem 1 (i) shows that a subgradient vector of \(\psi ({\varvec{\lambda }})\) at \({\varvec{\lambda }}^{(k)}\) is

$$\begin{aligned} \tilde{{\varvec{g}}}_{{{\varvec{\lambda }}}^{(k)}}= \bar{\mu }_{{{\varvec{\lambda }}}^{(k)}} {\varvec{g}}^{(k)}, \end{aligned}$$

where \(g^{(k)}_i={{\varvec{x}}^{(k)}}^\top Q_i{\varvec{x}}^{(k)}+2{\varvec{q}}_i^\top {\varvec{x}}^{(k)}+\gamma _i\), \(\forall i\). At the kth iteration of the algorithm, we use \({\varvec{g}}^{(k)}\) as the subgradient vector of \(\psi ({\varvec{\lambda }})\) rather than \(\tilde{{\varvec{g}}}_{{{\varvec{\lambda }}}^{(k)}}\) for the following reasons. When \(\bar{\mu }_{{{\varvec{\lambda }}}^{(k)}}>0\), we can use \({\varvec{g}}^{(k)}\) as a subgradient vector of \(\psi ({\varvec{\lambda }})\) at \({\varvec{\lambda }}^{(k)}\). When \(\bar{\mu }_{{{\varvec{\lambda }}}^{(k)}}=0\) (i.e. \({\varvec{\lambda }}^{(k)}\notin \Lambda _+\)), \(Q_0\) should be positive semidefinite because of the constraint \(Q_0+\mu \sum _{i=1}^m\lambda _iQ_i\succeq O\), and the optimal value of (17) equals that of (14) (\(=\phi ({\varvec{0}})\)). In this case, \(\phi ({\varvec{0}})\) is the smallest possible value, but it is not the optimal one of the original problem (1) because an optimal solution of the unconstrained problem (14), \(\bar{{\varvec{x}}}\), is not in the feasible region of (1), from Assumption 1 (c). Therefore, when \(\bar{\mu }_{{{\varvec{\lambda }}}^{(k)}}=0\), the algorithm needs to move \({\varvec{\lambda }}^{(k)}\) toward \(\Lambda _+\); precisely, \({\varvec{\lambda }}^{(k)}\) is moved in the direction of \({\varvec{g}}^{(k)}\), although \(\tilde{{\varvec{g}}}_{{{\varvec{\lambda }}}^{(k)}}\) is the zero vector. It can be easily confirmed that by moving \({\varvec{\lambda }}^{(k)}\) sufficiently far in this direction, the left side of the constraint of (\(\mathrm {P}_k\)) becomes positive and \(\bar{{\varvec{x}}}\) moves out of the feasible region of \(\mathrm {(P_k)}\).

Step 2: We compute \({\varvec{\lambda }}^{(k+1)}\) with \({\varvec{g}}^{(k)}\) and h as in (29). We can easily compute the projection onto \(\Lambda _{\mathrm {s}}\) by using the method proposed by Chen and Ye [10]. Here, the condition: \(\exists \mu \ge 0;\;Q_0+\mu \sum _{i=1}^m\lambda _i Q_i\succ O\) in \(\Lambda _+\) is ignored in the projection operation, but when \(Q_0\succ O\), the resulting projected point \({\varvec{\lambda }}^{(k+1)}\) is in \(\Lambda _+\). On the other hand, when \(Q_0\nsucc O\), the vector \({\varvec{\lambda }}^{(k+1)}\) is not necessarily in \(\Lambda _+\) or \(\Lambda '_+\). In such a case, \({\varvec{\lambda }}^{(k+1)}\) is modified in Step 4 so as to belong to \(\Lambda '_+\). Step 4 is a heuristic step; it is needed to keep \({\varvec{\lambda }}\in \Lambda '_+\) when \(Q_0\nsucc O\).

Now let us explain how to choose the step size h. Gradient methods have various rules to determine an appropriate step size. Simple ones include a constant step size \(h=c\) or a diminishing step size (e.g. \(h=c/\sqrt{k}\)), where k is the number of iterations (e.g., see [8]). A more complicated one is the backtracking line search (e.g., see [4, 21]). Although the backtracking line search has been shown to perform well in many cases, we use a diminishing step size \(h=c/\sqrt{k}\) to save the computation time of SLR. The advantage of SLR is to efficiently find a relaxed solution, so we will choose a simple policy for the step size h.

Step 4: It is needed only when both conditions, \(Q_0\nsucc O\) and \(\sum _{i=1}^m\lambda ^{(k+1)}_iQ_i\nsucc O\), hold. We update the Lagrange multipliers corresponding to convex constraints, whose index set is defined as \(C:=\{i\mid 1\le i\le m,\;Q_i\succ O\}\). When \(Q_0\nsucc O\), Assumption 1 (b) assures that C is non-empty.

Remark 2

Remark 1 explains that a direct application of the subgradient method to the SDP (5) is not efficient because the projection computation onto the set \(\Lambda :=\{{\varvec{\xi }}: {\varvec{\xi }} \ge {\varvec{0}}, Q_0+\sum _{i=1}^m\xi _i Q_i\succeq O\}\) is not easy. As shown above, we can project a subgradient vector onto a simple set \(\Lambda ':=\{ {\varvec{\xi }}: {\varvec{\xi }} \ge {\varvec{0}}\}\) and modify the projected point so as to satisfy \(Q_0+\sum _{i=1}^m\xi _i Q_i\succeq O\). We tried some heuristic modifications in numerical experiments, but the resulting subgradient method with any of modifications does not converge properly.

Now we will discuss why the above subgradient method does not converge unlike our method.

When the concerned problem has \(Q_0\succ O\), the modification is not necessary for our method, while it is necessary for the subgradient method. Even for the case of \(Q_0\nsucc O\), the modification shown in Step 4 of Algorithm 2 is simple and \(\mu \) in \(\Lambda _+\) is appropriately determined by solving \((\mathrm {P}_k)\), which might give us a good approximation to the projection onto \(\Lambda _+\). On the other hand, the modification in the subgradient method for satisfying \(Q_0+\sum _{i=1}^m\xi _i Q_i\succeq O\) often drastically changes the projected vector because of \(Q_0\), which may be a reason of unstable performance.

4.3 Setting an initial solution

The number of iterations of SLR depends on how we choose an initial solution. In this section, we propose two strategies for choosing it. Note that at an optimal solution \({\varvec{\lambda }}\), all elements \(\lambda _i\) corresponding to convex constraints with \(Q_i\succ O\), \(i \in C\), are expected to have positive weights. Hence, we will give positive weights only for \(\lambda _i\), \(i \in C\) (if it exists).

Here, we assume that \((Q_i, {\varvec{q}}_i,\gamma _i)\) in each constraint is appropriately scaled by a positive scalar as follows. When the matrix \(Q_i\) has positive eigenvalues, \((Q_i, {\varvec{q}}_i,\gamma _i)\) is scaled so that the minimum positive eigenvalue of \(Q_i\) is equal to one. If \(Q_i\) has no positive eigenvalues, it is scaled such that the maximum negative eigenvalue is equal to \(-1\).

Equal weights rule The first approach is “equal” weights. It gives equal weights to \(\lambda ^{(0)}_i\) corresponding to \(Q_i\succ O\) or if there are no \(Q_i\succ O\) (which implies that \(Q_0\succ O\)), it gives equal weights to all \(\lambda ^{(0)}_i\).

More specifically, if the index set of convex constraints C is nonempty, we define \({\varvec{\lambda }}^{(0)}\) as

$$\begin{aligned} \lambda ^{(0)}_i={\left\{ \begin{array}{ll} \frac{1}{|C|}, &{} \text {if}~Q_i\succ O,\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(30)

If \(C=\emptyset \), we define \({\varvec{\lambda }}^{(0)}\) as

$$\begin{aligned} \lambda ^{(0)}_i=\frac{1}{m}, \quad i=1,\ldots ,m. \end{aligned}$$
(31)

Schur complement rule The second approach uses the idea of the Schur complement. Note that this rule only applies when there are some \(i\;(\ge 1)\) such that \(Q_i\succ O\). For the constraint with \(Q_i\succ O\), we have

$$\begin{aligned}&{\varvec{x}}^\top Q_i{\varvec{x}}+2{\varvec{q}}_i^\top {\varvec{x}}+\gamma _i\le 0\nonumber \\&\quad \iff ({\varvec{x}}+Q_i^{-1}{\varvec{q}})^\top Q_i({\varvec{x}}+Q_i^{-1}{\varvec{q}}_i)\le {\varvec{q}}_i^\top Q_i^{-1}{\varvec{q}}_i-\gamma _i. \end{aligned}$$

The right-hand side \(\eta _i:={\varvec{q}}_i^\top Q_i^{-1}{\varvec{q}}_i-\gamma _i\) can be considered the volume of the ellipsoid and the value \(-\eta _i\) can be viewed as the Schur complement of the block \(Q_i\) of \(\begin{pmatrix} \gamma _i &{} {\varvec{q}}_i^\top \\ {\varvec{q}}_i &{} Q_i\end{pmatrix}\). From Assumption 1 (a), the ellipsoid has positive volume and we have \(\eta _i>0\). Numerical experiments show that constraints having small positive \(\eta _i\) tend to become active in the SDP relaxation. Therefore, it seems reasonable to give large weights to the constraints whose \(-\eta _i \;(<0)\) are close to zero; that is, \(\frac{1}{|\eta _i|}\) are large. Here, we consider the following rule:

For \(i\in C\), calculate \(s_i:=1/|\eta _i|\). We define \({\varvec{\lambda }}^{(0)}\) as

$$\begin{aligned} \lambda ^{(0)}_i={\left\{ \begin{array}{ll} \frac{s_i}{\sum _{i=1}^ms_i} &{} \text {if}~Q_i\succ O,\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(32)

Although the Schur complement rule also has no theoretical guarantee, numerical experiments show their usefulness especially when \(Q_0\nsucc O\).

4.4 RQT constraints

We can find a better optimal value of the Lagrangian dual problem (2) by adding a redundant convex quadratic constraint constructed similarly to RLT (this is discussed in Sect. 2.2) to (1) when there are box constraints and by applying SLR to the resulting QCQP. Since (9) holds for \(1\le i=j\le n\), we have

$$\begin{aligned} x_i^2-(u_i+l_i)x_i+u_il_i\le 0, \qquad i=1,\ldots ,n. \end{aligned}$$
(33)

The summation of (33) for \(i=1,\ldots ,n\) leads to

$$\begin{aligned} {\varvec{x}}^\top {\varvec{x}}-({\varvec{u}}+{\varvec{l}})^\top {\varvec{x}}+{\varvec{u}}^\top {\varvec{l}}\le 0. \end{aligned}$$
(34)

We call this method the reformulation quadraticization technique (RQT). Since (34) is a convex quadratic constraint, it may be effective to make the SLR relaxation tighter. The numerical experiments in Sect. 5 show that by adding (34), we could get a tighter optimal value in some cases than SDP relaxations.

There are other ways of making new convex quadratic constraints. Furthermore, even nonconvex constraints (like (8) or (10)) are possibly effective for tightening SLR. However, in this study, we only considered (34) to save computation time.

5 Numerical experiments

We compared the performance of SLR, SDP relaxation (6), and Block-SDP shown in Sect. 2.3. We used MATLAB Ver. 8.4.0 (R2014b) for all the numerical experiments. We solved SDP relaxation and Block-SDP by using the interior-point method (SeDuMi 1.3 [25] with the tolerance \(10^{-8}\) (initial setting)). We solved 1-QCQP (27) and (28) in the SLR algorithm by using a convex quadratic optimization solver (CPLEX Ver. 12.5). We used a laptop computer with a 2.4 GHz CPU and 16GB RAM. In [9], there are no rules to decide the number of blocks r of Block-SDP. In our experiments, we tried several values of r and chose \(r:=0.05\times n\), which seemed to work well.

5.1 Performance of SLR for random m-QCQP

First, we checked the performance of SLR for random m-QCQP generated in the way of Zheng et al. [32]. In this subsection, we consider problems without box constraints; we compare SLR (or the subroutine of solving CQ1) and SDP relaxation. In Sect. 5.3, we consider problems including box constraints; we compare SLR, SDP relaxation, and Block-SDP.

5.1.1 Tolerance \(\epsilon \) and computation time

We now investigate computation time of SLR for given tolerance values \(\epsilon \). We randomly generated 30 instances of 10-QCQP, whose problem sizes were \(n=30\) and \(m=10\). Among the \(m=10\) constraints, there were five convex ones. The objective functions of all instances were strictly convex, i.e., \(Q_0\succ O\).

The relationship between the tolerance \(\epsilon \) and the computation time is shown in Fig. 4. The smaller \(\epsilon \) becomes, the longer the computation takes. In this setting, SLR could solve the 10-QCQP faster than SDP relaxation when \(\epsilon >10^{-4}\). Hence, we set \(\epsilon =10^{-4}\) in what follows.

Fig. 4
figure 4

Average computation time versus tolerance \(\epsilon \)

Full size image

5.1.2 Comparison of two initial-solution strategies

We compared the two strategies for choosing the initial solutions (30) (or (31)) and (32) and checked the results for \(Q_0\succ O\) and \(Q_0\nsucc O\). We only show results for \(Q_0\nsucc O\) because both initial-solution rules gave almost the same results when \(Q_0\succ O\). We randomly generated 30 instances for each setting, where \(n=100\) and \(m=10\), and varied the number of convex constraints from \(|C|=1\) to 9.

Note that SLR is not stronger than SDP relaxation and we do not know the exact optimal value of each random m-QCQP. Therefore, we checked the performance of SLR by comparing its value with the optimal value of SDP relaxation. Here, we used the error ratio defined as

$$\begin{aligned} \mathrm {Ratio}:=\left| \frac{\mathrm {OPT}_{\mathrm {SLR}}}{\mathrm {OPT}_{\mathrm {SDP relax}}}\right| . \end{aligned}$$

This indicator was used in all of the experiments described below. It is greater than or equal to one since SLR is not stronger than the ordinary SDP relaxation (6). The performance of SLR is said to be good when the ratio is close to one.

Figures 5a, b plot the number of iterations and the error ratio versus the number of convex constraints. When there is only one convex constraint, an optimal solution \({\varvec{\lambda }}\) for \(\psi ({\varvec{\lambda }})\) usually has only one positive element corresponding to the convex constraint and all the other elements are zero. In this case, SLR needs only a few iterations. When \(Q_0\nsucc O\), the Schur complement rule works well in terms of computation time and the error ratio as the number of convex constraints increases. On the basis of the above considerations, we decided to use the Schur complement rule in the remaining experiments.

Fig. 5
figure 5

Comparison of two initial-solution strategies. a Average number of iterations (\(Q_0\nsucc O\)). b Average error ratio (\(Q_0\nsucc O\))

Full size image

5.1.3 Computation time and error for the number of variables n and the number of constraints m

We checked the computation time of SLR by changing the number of variables n and the number of constraints m, respectively. In this experiment of Fig. 6a–d, n was varied from 25 to 5000, and we set \(m=15\), of which 8 constraints were convex. We generated 30 instances when \(n\le 250\), ten instances when \(250<n\le 1000\), and one instance when \(n\ge 2500\). In this experiment, we set \(\epsilon =1.0^{-3}\) because large problems take a very long time to solve.

In Fig. 6e, f, we checked the computation time of SLR by varying the number of constraints m. The number of constraints m was varied from 2 to 50, while the number of variables was fixed as \(n=100\). Half of the constraints (i.e. ceil(m / 2)) were convex. We generated 30 instances for each setting.

Fig. 6
figure 6

Computation time and error with varied number of variables n and Varied number of constraints m. a Average computation time for n (\(Q_0\succ O\)). b Average error ratio for n (\(Q_0\succ O\)). c Average computation time for n (\(Q_0\nsucc O\)). d Average error ratio for n (\(Q_0\nsucc O\)). e Average computation time for m (\(Q_0\succ O\)). f Average error ratio for m (\(Q_0\succ O\))

Full size image

Case 1 \(Q_0\succ O\). SLR performed well when \(Q_0\succ O\) (Fig. 6a, b). The computation time was almost one order of magnitude smaller than that of SDP relaxation, and the error ratio was less than 1.06. The relaxation precision suddenly deteriorated as the number of variables n increased, but there were many instances with smaller n which SLR could obtain the optimal value same as the SDP relaxation value. Furthermore, SLR was able to solve problems with \(n=5000\), while SDP relaxation could not because of out of memory issue. Regarding varied m, the error ratios were less than 1.0015, and the computation time was about one order of magnitude smaller than that of SDP relaxation.

Case 2 \(Q_0\nsucc O\). We replaced the objective function of each instance used in Case 1 by a nonconvex quadratic function and conducted the same experiments in each case. Figure 6c, d show the results for \(Q_0\nsucc O\). The error rate of SLR deteriorated compared to the case of \(Q_0\succ O\), but it was still faster than SDP relaxation and the error ratio was about 1.1. Note that we conducted only one experiment on \(n=2500,5000\) to shorten the time of the experiment. Although the numerical results of varied m are omitted to save space in the paper, the trends of time and error with respect to increased m were almost same to Fig. 6e, f except that the error ratio was about 1.06.

SLR tends to give smaller error rates for QCQPs with \(Q_0\succ O\) than for QCQPs with \(Q_0\nsucc O\). This may be because we do no need to approximate the feasible region \(\Lambda _+\) when \(Q_0\succ O\).

5.2 Performance of CQ1 for solving 1-QCQP

We checked the performance of CQ1; transforming 1-QCQP of \((\mathrm {P}_\mathrm {k})\) to the convex quadratic formulation (26) and solving it by the CPLEX solver. We compared CQ1, SDP relaxation, and an eigen-computation-based method for random 1-QCQPs. For a 1-QCQP with \(Q_1\succ O\), Adachi et al. [1] proposed an accurate and efficient method that solves a generalized eigenvalue problem only once. They called this method “GEP”. We ran their MATLAB code for solving a 1-QCQP with \(Q_1\succ O\). It should be noted that all of the methods can obtain the exact optimal value of 1-QCQP. The computation time was plotted versus n. As described in Sect. 5.1, we generated the 1-QCQP in the way of [32]. Figure 7a, b are double logarithmic charts of n and the average computation time of 30 instances. Figure 7a shows that CQ1 is about one order of magnitude faster than SDP relaxation for all n. Figure 7b shows that CQ1 is faster than GEP when n is large. Therefore, we see that solving a quadratic optimization problem with two convex constraints (26) by the CPLEX is a good strategy for solving 1-QCQP of \((\mathrm {P}_\mathrm {k})\) in Algorithm 1.

Fig. 7
figure 7

Comparison of three exact solution methods for 1-QCQP . a Average computation time (\(Q_0\succ O\)). b Average computation time (\(Q_1\succ O\))

Full size image

5.3 Strengthened SLR by additional constraints

From the performance of SLR shown in Sect. 5.1, we confirmed that SLR is a “weaker but faster” method than SDP relaxation. The numerical experiment in this subsection implies that SLR including the RQT constraint (34) can be “stronger and faster” than ordinary SDP relaxation: (6) and (7).

Fig. 8
figure 8

Effects of additional RQT constraint. a Average computation time for n and m. b Average error ratio for n and m. c Average computation time for n and m. d Average error ratio for n and m.

Full size image

We randomly generated problems with box constraints as follows: We varied n from 30 to 2000 and set \(m= \text{ floor }(0.08 n)\) or \(m=\text{ floor }(0.3n)\) including ceil(m / 2) convex constraints. We generated 30 instances when \(n\le 100\), ten instances when \(100<n \le 1000\) and one instance for the case of \(n=2000\). We added box constraints \(-1\le x_i\le 1\), \(\forall i\), to all the instances, which make it possible to generate additional constraints such as the RLT constraints (12) and the RQT constraint (34). The following results are only for the case in which the objective function is nonconvex because the RQT constraint affected the performance of our method by much.

The results for instances with smaller number of constraints \(m= \text{ floor }(0.08 n)\) are shown in Fig. 8a, b, while the results for instances with larger number of constraints \(m=\text{ floor }(0.3n)\) are shown in Fig. 8c, d. “SLR \(+\) RQT” indicates that SLR includes the RQT constraint (34). Block-SDP includes some RLT constraints (12) generated from the box constraints (see Sect.  2.3). On the other hand, SDP relaxation includes none of additional constraints.

In Fig. 8b, d, the ratio is less than one. This implies that SLR can get better optimal values than SDP relaxation by adding RQT constraints, i.e, SLR can be “stronger and faster” than SDP relaxation. If all RLT constraints are added to SDPs, the interior-point method for such SDPs will give the tighter relaxation than those three methods. However, the resulting SDPs grow larger than those of ordinary SDP relaxation, which will be a serious problem when solving them with the interior-point method. Indeed, the interior-point method could not solve ordinary SDP instances with \(n=10^3\) because of out of memory issue. Therefore, if we use the interior-point method for SDP relaxation of QCQPs, problem instances of QCQPs might be restricted to less than \(n=10^3\).

The performance of Block-SDP is highly influenced by the number of constraints m. When m is small (i.e., \(m= \text{ floor }(0.08 n)\)), Block-SDP performs closely to SLR+RQT in terms of computation time and error ratio. When \(m= \text{ floor }(0.3 n)\), Block-SDP finds very good relaxed solutions with almost the same computation time to the ordinary SDP relaxation. Block-SDP could solve \(n=10^3\) when \(m= \text{ floor }(0.08 n)\)Footnote 1 but could not solve instances of \(n=2000\) with both settings of m because of out of memory status.

5.4 Iterative application of SLR to max-cut problems

Max-cut problems [24] can be viewed as an application of 1-QCQP. A graph Laplacian matrix L can be obtained from a given undirected and weighted graph G. For the max-cut value for G, we solve the following \(\{-1,1\}\) integer program:

$$\begin{aligned} \underset{{\varvec{x}}}{\text {min}} ~~ {\varvec{x}}^\top L{\varvec{x}} ~~~ \text {s.t. } ~~ x_i \in \{-1,1\}, \quad i=1,\ldots ,n. \end{aligned}$$
(35)

We relax (35) into

$$\begin{aligned} \underset{{\varvec{x}}}{\text {min}} ~~ {\varvec{x}}^\top L{\varvec{x}} ~~~ \text {s.t.} ~~ -1\le x_i\le 1, \quad i=1,\ldots ,n, \end{aligned}$$

and then apply SDP relaxation and Block-SDP.

In SLR, the box constraints are replaced by the RQT constraint \({\varvec{x}}^\top {\varvec{x}}\le n\) because SLR needs at least one strictly convex constraint. Then the resulting problem is a 1-QCQP;

$$\begin{aligned} \underset{{\varvec{x}}}{\text {min}} ~~ {\varvec{x}}^\top L{\varvec{x}} ~~~ \text {s.t.} ~~ {\varvec{x}}^\top {\varvec{x}}\le n. \end{aligned}$$
(36)

Therefore, the SLR for (36) is the same approach to CQ1 which solves 1-QCQP \((\mathrm {P}_\mathrm {k})\). Here we identify CQ1 and SLR in this problem setting. Note that (36) can be regarded as a simple minimum eigenvalue problem. An optimal solution is an eigenvector corresponding to the minimum eigenvalue. However, our purpose is to check the computational result, and we use SLR for (36).

We solved max-cut instances from [24]. Many randomly generated instances are shown in [24], and the optimal values are known. The results are in Table 1. In this table, the “error” is defined as

$$\begin{aligned} \mathrm {Error}:=\left| \frac{\mathrm {OPT}_{\mathrm {method}}-\mathrm {OPT}}{\mathrm {OPT}}\right| , \end{aligned}$$

where \(\mathrm {OPT}_{\mathrm {method}}\) is the optimal value of each method and \(\mathrm {OPT}\) is the exact optimal value. In [24], the names of the instances indicate how they were generated as well as the number of variables. For example, “g05_80”, “80” means the number of variables, and “g05” means the density of edges and whether the weights of graph are all positive or include negative values. The details are given in [24] and there are ten instances for each kind of problem. In Table 1, “Time(s)” means the average time for ten instances, and the best methods among SDP relaxation, Block-SDP, and SLR in terms of either average computation time or average error are listed in bold.

Table 1 Time and error for max-cut
Full size table

Table 1 shows that SLR is “weaker” but “faster” than SDP relaxation. Block-SDP is weaker and even slower than SDP relaxation in these problem settings. SLR is much faster than SDP relaxation, so we could solve SLR many times with the time to solve an SDP by the interior-point method. Accordingly, we tried to strengthen SLR by iterating it with a certain rounding rule as follows. An optimal solution of SLR, \(\bar{{\varvec{x}}}\), satisfies \(\bar{{\varvec{x}}}^\top \bar{{\varvec{x}}}=n\) because the objective function is nonconvex. Consequently, there exists a component of \(\bar{{\varvec{x}}}\) whose absolute value is more than one (otherwise, all the components are \(\pm 1\), and \(\bar{{\varvec{x}}}\) is an exact optimal solution for (35)). Then, we fix such a component as \(\pm 1\) and solve a small problem recursively. Note that if the objective function becomes positive (semi)definite by fixing some of the components and there exists no \(x_i\) whose absolute value is more than one, we set the component which has the maximum absolute value of all the components to 1 or \(-1\). We perform this rounding until all the components are \(\pm 1\). Therefore, we have a feasible solution of the original problem (35) and obtain an upper bound of the original optimal value, while SDP relaxation, Block-SDP, and SLR find lower bounds. We call this rounding “Multiple SLR” and show the results in the right-most column of Table 1. The results indicate that Multiple SLR is still “faster” than SDP relaxation. Such a faster method is useful when we want to solve a problem repeatedly.

6 Conclusions

In this paper, we proposed SLR, a new, fast convex relaxation for QCQP. SLR is a method for solving the Lagrangian dual problem of a given QCQP. There have been various studies on constructing Lagrangian dual problems for nonconvex problems and reformulating them as semidefinite problems (SDPs). Instead of solving an SDP, our method divides the objective function of the Lagrangian dual problem into two levels and iteratively solves a 1-QCQP. We furthermore transform the 1-QCQP into a convex quadratic 1-QCQP called CQ1 whose feasible region forms the convex hull of the feasible region of the original 1-QCQP. Hence, we can obtain the exact optimal value of the 1-QCQP by solving CQ1. SDP relaxation can also solve the 1-QCQP exactly, but CQ1 is much faster. Numerical experiments confirmed this advantage of CQ1. CQ1 performed well for randomly generated 1-QCQP and max-cut problems.

In SLR, we successively solve a 1-QCQP with the Lagrange multiplier \({\varvec{\lambda }}\) updated using a gradient method. We proved that the objective function \(\psi ({\varvec{\lambda }})\) is quasi-concave and has the good property that all the stationary points in \(\Lambda _+\) are global optimal solutions, and thus, simple gradient methods work well. SLR is a faster relaxation compared with the interior-point method for SDP relaxation for large n and m. Furthermore, by adding a new valid RQT constraint, we could obtain even a better optimal value than SDP relaxation for some m-QCQP instances.

Our method can be regarded as a subgradient method that is applied to a quasi-concave problem induced from the Lagrangian dual of an m-QCQP. To ensure convergence, the quasi-concave problem must satisfy certain conditions, (e.g., the Hölder condition in [14]) but unfortunately, it is not easy to check whether our quasi-concave problem satisfies the Hölder condition. In the future, we would like to investigate the global convergence of our algorithm.

When the objective function is nonconvex, we need to approximate the feasible region \(\Lambda _+\) of the Lagrangian dual problem, and as a result, the SLR becomes worse in performance than that of solving m-QCQP with the convex objective function. We would like to improve the performance of SLR for instances having nonconvex objective functions.