Abstract
We deal with a constrained vector optimization problem between real linear spaces without assuming any topology and by considering an ordering defined through an improvement set E. We study E-optimal and weak E-optimal solutions and also proper E-optimal solutions in the senses of Benson and Henig. We relate these types of solutions and we characterize them through approximate solutions of scalar optimization problems via linear scalarizations and nearly E-subconvexlikeness assumptions. Moreover, in the particular case when the feasible set is defined by a cone-constraint, we obtain characterizations by means of Lagrange multiplier rules. The use of improvement sets allows us to unify and to extend several notions and results of the literature. Illustrative examples are also given.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the literature there exist a lot of papers and books dealing with optimization problems from an algebraic point of view (see, for instance, [5] and the references quoted in [2]). Adán and Novo introduced this research line in vector optimization studying these problems without using topological tools [1,2,3,4]. So, in these papers, the initial and final spaces of the optimization problems are not endowed with any topology. To overcome this fact, some algebraic counterparts of the main topological tools are introduced, which exploit their geometrical nature. Between them, let us underline the concept of vector closure (see [2]).
On the other hand, Chicco et al. [6], in the finite dimensional setting and via an improvement set \(E{\subset }{\mathbb {R}}^p\) (i.e., \(0\notin E\) and \(E+{\mathbb {R}}^p_+=E\), where \({\mathbb {R}}^p_+\) denotes the nonnegative orthant), defined the notion of E-optimal point—a kind of nondominated point with respect to the ordering set E—that encompasses the concepts of Pareto efficiency and weak Pareto efficiency. By definition, an improvement set can be considered as an approximation of the ordering cone that does not contain the point 0, and because of that this type of sets are useful to deal with approximate Pareto efficient points.
Later, this concept was studied by Gutiérrez et al. [9] in the framework of real locally convex Hausdorff topological linear spaces to unify several notions and results on exact and approximate efficient solutions of vector optimization problems. In [22], Xia et al. provided several characterizations of improvement sets via quasi interior, and in [18] Lalitha and Chatterjee established stability and scalarization results in vector optimization by using improvement sets. Notice that the nondominated solutions with respect to an improvement set are global solutions of the problem. In particular, under convexity assumptions, they can be characterized by \(\varepsilon \)-subgradients (see [10, 11])—recall that the \(\varepsilon \)-subdifferential of a convex function is a global concept provided that \(\varepsilon >0\) (see [13])—.
Essentially, an improvement set E in an arbitrary ordered linear space is a free disposal set (i.e., it coincides with its cone expansion \(E+K\), where K is the ordering cone). This kind of sets was introduced by Debreu [7] and they have been frequently used in mathematical economics and optimization. So, one can find in the literature several previous concepts very close to the notion of improvement set.
During the last years and motivated by the quoted contributions by Adán and Novo [1,2,3,4] and Chicco et al. [6], approximate solutions of vector optimization problems have been studied in the setting of linear spaces and via optimality concepts based on improvement sets (see, for instance, [16, 25,26,27]). In particular, by considering the so-called algebraic interior, the vector closure and different generalized convexity assumptions, several characterizations for weak and proper approximate solutions have been obtained through linear scalarizations and Lagrangian type optimality conditions.
This work is a new contribution in the same direction. It is structured as follows: in Sect. 2, the framework of the paper and some basic algebraic and geometric tools are recalled or stated. In Sect. 3, two new concepts of proper approximate efficient solution in the senses of Benson and Henig are introduced. They are based on certain classes of improvement sets, and it is proved that they encompass the more important exact and approximate Benson and Henig efficiency concepts of the literature. The relationships between them and also with respect to weak E-optimal solutions are derived. In Sects. 4 and 5, some characterizations of these three notions are provided by linear scalarizations in problems with abstract constraints, and by scalar Lagrangian optimality conditions in cone-constrained problems. At the end of Sect. 5 two illustrative examples show in detail the main results. Finally, in Sect. 6, the highlights of the paper are collected.
The obtained results extend and improve other results published in the last years, since they are obtained through very general concepts of efficient solution—recall that they are based on arbitrary improvement sets—and by assuming new and weaker generalized convexity hypotheses. These assumptions, called E-subconvexlikeness, relatively solid E-subconvexlikeness, generalized E-subconvexlikeness and relatively solid generalized E-subconvexlikeness, are suitable “approximate” extensions of well-known notions of cone subconvexlikeness and generalized cone subconvexlikeness (see [2] and the references therein). Moreover, let us underline that the Lagrangian optimality conditions are obtained as particular cases of the previous linear scalarizations. To the best of our knowledge, this approach is new in the setting of approximate efficiency.
2 Notations and preliminaries
Let Y be a real linear space and \(K{\subset } Y\) be a nonempty proper (\(\{0\}\ne K\ne Y\)) convex cone (we consider that \(0\in K\)). In the sequel, Y is assumed to be ordered through the following quasi order:
We denote \(K_0:=K\backslash \{0\}\). Moreover, we write \({\mathbb {R}}^p_+\) to refer the nonnegative orthant of \({\mathbb {R}}^p\) and \({\mathbb {R}}_+:={\mathbb {R}}^1_+\).
Given a nonempty set \(A{\subset }Y\), we denote by \({\mathop {\mathrm{cone}}\nolimits A}, {\mathop {\mathrm{co}}\nolimits A}\) and \({\mathop {\mathrm{span}}\nolimits A}\) the generated cone, the convex hull and the linear hull of A, respectively. A cone \(D{\subset } Y\) is said to be pointed iff \(D{\cap }(-D)=\{0\}\). The segment of extreme points \(a,b{\in } Y\) is denoted [a, b] (i.e., \([a,b]:=\mathop {\mathrm{co}}\nolimits \{a,b\}\)).
In order to avoid topological concepts we use algebraic counterparts. In particular, the so-called algebraic interior (or core), relative algebraic interior and vector closure of the set A (see [2]) are denoted, respectively, by \({\mathop {\mathrm{cor}}\nolimits A}, {\mathop {\mathrm{icr}}\nolimits A}\) and \({\mathop {\mathrm{vcl}}\nolimits A}\), i.e.,
When \(\mathop {\mathrm{cor}}\nolimits A \ne \emptyset \) (respectively, \(\mathop {\mathrm{icr}}\nolimits A\ne \emptyset \)) we say that A is solid (respectively, relatively solid). Clearly, if \(\mathop {\mathrm{cor}}\nolimits A\ne \emptyset \) then \(\mathop {\mathrm{cor}}\nolimits A=\mathop {\mathrm{icr}}\nolimits A\) since \(\mathop {\mathrm{span}}\nolimits (A-A)=Y\). Moreover, for each nonempty set \(B{\subset } Y\), the set \(A+B\) is solid whenever A is solid. The set A is called vectorially closed if \(A=\mathop {\mathrm{vcl}}\nolimits A\).
Let us observe that \({\mathop {\mathrm{vcl}}\nolimits A}{\subset } {\mathop {\mathrm{cl}}\nolimits A}\) (see [2, Proposition 1]), where \(\mathop {\mathrm{cl}}\nolimits A\) denotes the topological closure of A, whenever Y is endowed with a topology. Although the vector closure is an algebraic counterpart of the topological closure, they do not have the same properties. For example, in general \({\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{vcl}}\nolimits A}\ne {\mathop {\mathrm{vcl}}\nolimits A}\) (see [2, Example 2]) even if A is convex (see [5, Example I.2.4]). In particular, this last example shows that, in general, it is not possible to endow an arbitrary linear space with a locally convex topology in such a way that the vector closure of any convex set coincides with the topological one.
For the convenience of the reader, we provide the following three lemmas that will be used in this work. In the first one, we gather several basic properties related to the vector closure and the core of a set. The second lemma was stated in [2, Propositions 5 and 6] and the third one is directly deduced from the results given in [2, Sections 2 and 3]. Both of them show properties of the cone extension \(A+D\).
Lemma 2.1
Let \(A{\subset } Y\) be convex. Then \({\mathop {\mathrm{vcl}}\nolimits A}\) and \({\mathop {\mathrm{cor}}\nolimits A}\) are convex and \({\mathop {\mathrm{cor}}\nolimits \mathop {\mathrm{cor}}\nolimits A}={\mathop {\mathrm{cor}}\nolimits A}\). Moreover, for each nonempty set \(M{\subset } Y\) it follows that \({\mathop {\mathrm{vcl}}\nolimits {A}}+M{\subset } {\mathop {\mathrm{vcl}}\nolimits (A+M)}\) and if A is solid, then \({\mathop {\mathrm{cor}}\nolimits {A}}+M{\subset } {\mathop {\mathrm{cor}}\nolimits (A+M)}\).
Proof
For the first part, see [14, Lemma 1.9]. On the other hand, the inclusion \({\mathop {\mathrm{vcl}}\nolimits {A}}+M{\subset } {\mathop {\mathrm{vcl}}\nolimits (A+M)}\) is obvious. Then, let us only prove \({\mathop {\mathrm{cor}}\nolimits {A}}+M{\subset } {\mathop {\mathrm{cor}}\nolimits (A+M)}\).
Indeed, if \(a\in {\mathop {\mathrm{cor}}\nolimits A}\) and \(y\in M\), then for each \(v\in Y\) there exists \(t_0>0\) such that \([a,a+t_0v]{\subset } A\). Therefore,
and \(a+y\in \mathop {\mathrm{cor}}\nolimits (A+M)\). \(\square \)
Lemma 2.2
Let \(\emptyset \ne A{\subset } Y\) and let \(D{\subset } Y\) be a convex cone.
-
(i)
If D is solid, then \(\mathop {\mathrm{vcl}}\nolimits (A+D)=\mathop {\mathrm{vcl}}\nolimits (A +\mathop {\mathrm{cor}}\nolimits D)\).
-
(ii)
If D is solid, then
$$\begin{aligned} \mathop {\mathrm{cor}}\nolimits (A+D)=\mathop {\mathrm{cor}}\nolimits (A+\mathop {\mathrm{cor}}\nolimits D)=\mathop {\mathrm{cor}}\nolimits \mathop {\mathrm{vcl}}\nolimits (A+D)=\mathop {\mathrm{vcl}}\nolimits {A}+\mathop {\mathrm{cor}}\nolimits {D}=A+\mathop {\mathrm{cor}}\nolimits D. \end{aligned}$$ -
(iii)
\(\mathop {\mathrm{vcl}}\nolimits (\mathop {\mathrm{cone}}\nolimits A+ D)=\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (A+D)\).
Lemma 2.3
Let \(\emptyset \ne A{\subset } Y\) and let \(D{\subset } Y\) be a solid convex cone. If \(\mathop {\mathrm{vcl}}\nolimits (A+D)\) is convex, then \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (A+D)\) is convex.
Observe that if D is a solid convex cone, then from Lemmas 2.1 and 2.2(ii), we deduce that \(\mathop {\mathrm{cor}}\nolimits D\cup \{0\}\) is a convex cone, \(\mathop {\mathrm{cor}}\nolimits D+D=\mathop {\mathrm{cor}}\nolimits D\) and \(\mathop {\mathrm{cor}}\nolimits \mathop {\mathrm{cor}}\nolimits D=\mathop {\mathrm{cor}}\nolimits (\mathop {\mathrm{cor}}\nolimits D\cup \{0\})=\mathop {\mathrm{cor}}\nolimits D\).
The following lemma will be needed along the work.
Lemma 2.4
Let \(\emptyset \ne A,B{\subset } Y\) and suppose that B is solid and convex. Then,
Proof
Since \(A{\subset } \mathop {\mathrm{vcl}}\nolimits A\), implication \(\Longleftarrow \) is obvious. Reciprocally, suppose by contradiction that there exists \(y\in \mathop {\mathrm{vcl}}\nolimits A\cap \mathop {\mathrm{cor}}\nolimits B\). Since \(y\in \mathop {\mathrm{vcl}}\nolimits A\), there exist \((t_n){\subset } {\mathbb {R}}_{+}\backslash \{0\}\), \(t_n\downarrow 0\), and \(v\in Y\) such that \(y+t_n v\in A\), for all \(n\in \mathbb {N}\).
On the other hand, by Lemma 2.1 we have that \(y\in \mathop {\mathrm{cor}}\nolimits B=\mathop {\mathrm{cor}}\nolimits (\mathop {\mathrm{cor}}\nolimits B)\), and then there exists \(n_0\in \mathbb {N}\) such that \(y+t_n v\in \mathop {\mathrm{cor}}\nolimits B\), for all \(n\ge n_0\). Hence, \(y+t_nv\in A\cap \mathop {\mathrm{cor}}\nolimits B\), for all \(n\ge n_0\), obtaining a contradiction, and the proof is complete. \(\square \)
The algebraic dual of Y is denoted by \(Y'\). Moreover, the positive dual, and the strict positive dual of a nonempty set \(A{\subset } Y\) are defined, respectively, by
It is known that \(A^{+}\) is a vectorially closed convex cone and
The following separation theorem for vectorially closed convex cones is due to Adán and Novo [3, Theorem 2.2]. Let us observe that the hypothesis on the relative solidness of D assumed in [3, Theorem 2.2] can be removed as a consequence of [3, Proposition 2.3].
Theorem 2.5
Let M, D be two vectorially closed convex cones in Y such that M is relatively solid and \(D^+\) is solid. If \(M\cap D=\{0\}\), then there exists a linear functional \(\lambda \in Y'\backslash \{0\}\) such that \(\forall d\in D,\, m\in M, \lambda (d)\ge 0 \ge \lambda (m)\) and furthermore \(\forall d\in D_0, \lambda (d)>0\), i.e., \(\lambda \in D^{+s}\).
Note that assumption \(\mathop {\mathrm{cor}}\nolimits (D^+)\ne \emptyset \) in Theorem 2.5 implies that D is pointed whenever \(Y'\) separates points in Y (see [14, Lemmas 1.25 and 1.27]).
In this paper, we consider the following vector optimization problem:
where \(f:X\rightarrow Y\) (recall that Y is ordered by the relation \(\le _K\), see (2.1)), X is an arbitrary decision space and the feasible set \(S{\subset } X\) is nonempty. We say that (2.2) is a Pareto problem when \(Y={\mathbb {R}}^p\) and \(K={\mathbb {R}}^p_+\).
In many situations, the feasible set S is defined in terms of a cone-constraint as follows:
where \(g:X\rightarrow Z\), Z is a real linear space and \(M{\subset } Z\) is a solid vectorially closed convex cone. In this case we say that g satisfies the Slater constraint qualification if there exists a point \({\hat{x}}\in X\) such that \(g({\hat{x}})\in -\mathop {\mathrm{cor}}\nolimits M\).
The aim of this work is to introduce and study concepts of approximate optimal solution for problem (2.2), where the approximation error is stated by an improvement set \(E{\subset } Y\) with respect to K. Next we recall the definition of this kind of sets.
We say that a nonempty set \(E{\subset } Y\) is free disposal with respect to K (free disposal for short, see [7]) if \(E+K=E\).
Definition 2.6
A nonempty set \(E{\subset } Y\) is said to be an improvement set with respect to K (improvement set for short) if \(0\notin E\) and E is free disposal.
The class of improvement sets is very wide (see [9, Example 2.3]), and it will be denoted by \(\mathcal {I}_K\). See [6, 9] for more details on these sets.
Proposition 2.7
Suppose that \(E\in \mathcal {I}_K\). Then
-
(i)
\(\mathop {\mathrm{vcl}}\nolimits E\) is free disposal.
-
(ii)
If E is solid, then \(\mathop {\mathrm{cor}}\nolimits E\in \mathcal {I}_K\).
Proof
(i) We have just to check that \(\mathop {\mathrm{vcl}}\nolimits E+K{\subset } \mathop {\mathrm{vcl}}\nolimits E\), because the reciprocal inclusion is clear. Let \(y\in \mathop {\mathrm{vcl}}\nolimits E\) and \(k\in K\). Then there exist \(v\in Y\) and a sequence \((t_n){\subset }{\mathbb {R}}_+\backslash \{0\}\), \(t_n\downarrow 0\), such that \(y+t_nv\in E\) for all \(n\in \mathbb {N}\), and consequently
which proves that \(y+k\in \mathop {\mathrm{vcl}}\nolimits E\).
(ii) As a consequence of Lemma 2.1 one has
and hence \(\mathop {\mathrm{cor}}\nolimits E +K=\mathop {\mathrm{cor}}\nolimits E\). \(\square \)
The following lemma is also necessary.
Lemma 2.8
Let \(\emptyset \ne A{\subset } Y\) and \(K^{\prime }{\subset } Y\) be a proper, solid and convex cone such that \(K_0{\subset } \mathop {\mathrm{cor}}\nolimits K^{\prime }\). Then,
-
(i)
\(K_0+\mathop {\mathrm{cor}}\nolimits K^{\prime }=K+\mathop {\mathrm{cor}}\nolimits K^{\prime }=\mathop {\mathrm{cor}}\nolimits K^{\prime }\).
-
(ii)
\(\mathop {\mathrm{cor}}\nolimits K^{\prime }\subset \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })_0\).
-
(iii)
\(0\notin A+\mathop {\mathrm{cor}}\nolimits K^{\prime }\Longleftrightarrow (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })\cap (-K^{\prime })=\emptyset \Longleftrightarrow (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })\cap (-K)=\emptyset \).
-
(iv)
If \(0\notin A+\mathop {\mathrm{cor}}\nolimits K^{\prime }\), then \(A+\mathop {\mathrm{cor}}\nolimits K^{\prime }\in \mathcal {I}_K\cap \mathcal {I}_{K^{\prime }}\cap \mathcal {I}_{(\mathop {\mathrm{cor}}\nolimits K^{\prime })\cup \{0\}}\).
Proof
-
(i)
For each cone \(D{\subset } Y, D\ne \{0\}\), and for each solid convex cone \(M{\subset } Y\) we have that
$$\begin{aligned} D+\mathop {\mathrm{cor}}\nolimits {M}=D_0+\mathop {\mathrm{cor}}\nolimits {M}. \end{aligned}$$(2.4)Indeed, by Lemmas 2.1 and 2.2(ii) it follows that
$$\begin{aligned} D_0+\mathop {\mathrm{cor}}\nolimits {M}&\subset D+\mathop {\mathrm{cor}}\nolimits {M}{\subset }\mathop {\mathrm{vcl}}\nolimits {D_0}+\mathop {\mathrm{cor}}\nolimits {M}=\mathop {\mathrm{cor}}\nolimits (\mathop {\mathrm{vcl}}\nolimits {D_0}+M){\subset }\mathop {\mathrm{cor}}\nolimits \mathop {\mathrm{vcl}}\nolimits (D_0+M)\\&=D_0+\mathop {\mathrm{cor}}\nolimits {M}. \end{aligned}$$Then,
$$\begin{aligned} \mathop {\mathrm{cor}}\nolimits {K^{\prime }}{\subset } K+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}=K_0+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}{\subset } \mathop {\mathrm{cor}}\nolimits {K^{\prime }}+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}=\mathop {\mathrm{cor}}\nolimits {K^{\prime }} \end{aligned}$$and the proof of part (i) finishes.
-
(ii)
Let us suppose that \(A\ne \{0\}\), since the result is obvious otherwise. By (2.4) we have that
$$\begin{aligned} \mathop {\mathrm{cor}}\nolimits {K^{\prime }}{\subset } \mathop {\mathrm{cone}}\nolimits {A}+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}=(\mathop {\mathrm{cone}}\nolimits {A})_0+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}{\subset }\mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}) \end{aligned}$$and the result follows since \(0\notin \mathop {\mathrm{cor}}\nolimits {K^{\prime }}\).
-
(iii)
Since \(\mathop {\mathrm{cor}}\nolimits K^{\prime }+K^{\prime }=\mathop {\mathrm{cor}}\nolimits K^{\prime }\), it follows that
$$\begin{aligned} 0\notin A+\mathop {\mathrm{cor}}\nolimits K^{\prime }\Longleftrightarrow 0\notin (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })+K^{\prime }\Longleftrightarrow (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })\cap (-K^{\prime })=\emptyset . \end{aligned}$$In the same way, as by part (i) we have that \(\mathop {\mathrm{cor}}\nolimits K^{\prime }+K=\mathop {\mathrm{cor}}\nolimits K^{\prime }\), we deduce that
$$\begin{aligned} 0\notin A+\mathop {\mathrm{cor}}\nolimits K^{\prime }\Longleftrightarrow 0\notin (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })+K\Longleftrightarrow (A+\mathop {\mathrm{cor}}\nolimits K^{\prime })\cap (-K)=\emptyset . \end{aligned}$$ -
(iv)
It follows directly by part (i). \(\square \)
Let \(D{\subset } Y\) be a proper convex cone and \(N{\subset } X\) be a nonempty set. We recall that a mapping \(f:X\rightarrow Y\) is said to be D-convex on N iff N is convex and
(here X is a real linear space), and it is D-convexlike (respectively, D-subconvexlike, with D relatively solid) on N iff \(f(N)+D\) (respectively, \(f(N)+\mathop {\mathrm{icr}}\nolimits D\)) is convex. Moreover, we say that f is v-closely D-convexlike (respectively, v-nearly D-subconvexlike) on N iff \(\mathop {\mathrm{vcl}}\nolimits (f(N)+D)\) (respectively, \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(N)+D)\)) is convex.
In the following proposition we gather several relations between these generalized convexity notions.
Proposition 2.9
The following implications hold:
-
(i)
fD-convex on \(N \Rightarrow f D\)-convexlike on \(N \Rightarrow f\) v-closely D-convexlike on N.
-
(ii)
fD-convexlike on \(N \Rightarrow f\) v-nearly D-subconvexlike on N.
-
(iii)
If D is solid, fD-convexlike on N \(\Rightarrow f D\)-subconvexlike on \(N \Leftrightarrow f\) v-closely D-convexlike on \(N \Rightarrow f\) v-nearly D-subconvexlike on N.
Proof
Parts (i) and (ii) are easy to check. We prove part (iii). The first implication is clear. For the second necessary condition, if f is D-subconvexlike on N, then \(f(N)+\mathop {\mathrm{cor}}\nolimits D\) is convex and by Lemma 2.1 the set \(\mathop {\mathrm{vcl}}\nolimits (f(N)+\mathop {\mathrm{cor}}\nolimits D)\) is convex too. Moreover, observe that by Lemma 2.2(i) one has \(\mathop {\mathrm{vcl}}\nolimits (f(N)+D)=\mathop {\mathrm{vcl}}\nolimits (f(N)+\mathop {\mathrm{cor}}\nolimits D)\), and the conclusion follows.
Reciprocally, by Lemma 2.2(ii) we know that \(f(N)+\mathop {\mathrm{cor}}\nolimits D=\mathop {\mathrm{cor}}\nolimits \mathop {\mathrm{vcl}}\nolimits (f(N)+D)\), and since \(\mathop {\mathrm{vcl}}\nolimits (f(N)+D)\) is convex, by Lemma 2.1 we deduce that \(f(N)+\mathop {\mathrm{cor}}\nolimits D\) is convex too. Finally, suppose that \(\mathop {\mathrm{vcl}}\nolimits (f(N)+D)\) is convex. Then, by Lemma 2.3 we deduce that \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(N)+D)\) is convex, and the last implication is proved. \(\square \)
For a more complete study of these generalized convexity notions see, for instance, [2, Section 3].
Additionally, we consider the next notions of generalized convexity. The first one is an immediate translation of the nearly E-subconvexlikeness, introduced by Gutiérrez et al. [8, Definition 2.3] in the framework of topological linear spaces. The second and third concepts are new and they extend, respectively, the above concept of cone subconvexlikeness and the so-called generalized cone subconvexlikeness (see [2] and the references therein). Recall that if \(\mathop {\mathrm{icr}}\nolimits {K}\ne \emptyset \), then the mapping \(f:X\rightarrow Y\) is said to be generalized K-subconvexlike on a nonempty set \(N{\subset } X\) if the set \(\mathop {\mathrm{cone}}\nolimits {f(N)}+\mathop {\mathrm{icr}}\nolimits {K}\) is convex.
Definition 2.10
Let \(\emptyset \ne E{\subset } Y\). The mapping \(f:X \rightarrow Y\) is said to be v-nearly E-subconvexlike on a nonempty set \(N{\subset } X\) if \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(N)+E)\) is a convex set.
Definition 2.11
Let \(\emptyset \ne E{\subset } Y\) and suppose that K is relatively solid. The mapping \(f:X \rightarrow Y\) is said to be E-subconvexlike (respectively, generalized E-subconvexlike) on a nonempty set \(N{\subset } X\) (with respect to K) if \(f(N)+E+\mathop {\mathrm{icr}}\nolimits {K}\) (respectively, \(\mathop {\mathrm{cone}}\nolimits (f(N)+E)+\mathop {\mathrm{icr}}\nolimits {K}\)) is a convex set.
Remark 2.12
Consider that K is relatively solid. Since \(K+\mathop {\mathrm{icr}}\nolimits {K}=\mathop {\mathrm{icr}}\nolimits {K}\) (see [2]), then for all nonempty set \(A{\subset } Y\) it is easy to check that
Moreover, it is clear that \(\mathop {\mathrm{icr}}\nolimits {K}+\mathop {\mathrm{icr}}\nolimits {K}=\mathop {\mathrm{icr}}\nolimits {K}\). Therefore, the notions of E-subconvexlikeness and generalized E-subconvexlikeness reduce to the concepts of K-subconvexlikeness and generalized K-subconvexlikeness by taking \(E=K\) or \(E=\mathop {\mathrm{icr}}\nolimits {K}\).
Proposition 2.13
Let \(E{\subset } Y\) and \(N{\subset } X\) be two nonempty sets. We have the following implications:
-
(i)
f E-subconvexlike on N \(\Rightarrow \) f generalized E-subconvexlike on N.
-
(ii)
If \(E\in \mathcal {I}_K\), f generalized E-subconvexlike on N \(\Rightarrow \) f v-nearly E-subconvexlike on N.
-
(iii)
If K is solid and \(E\in \mathcal {I}_K\), f is generalized E-subconvexlike on N \(\Leftrightarrow \) f is v-nearly E-subconvexlike on N.
Proof
For part (i) see [2], and part (ii) is a direct consequence of Lemma 2.1 and [2, Propositions 5(iii) and 6(i)].
On the other hand, by [2, Propositions 5(iii) and 6(i),(iv)] we see that
and the sufficient condition of part (iii) follows by (2.6) and Lemma 2.1. \(\square \)
By Remark 2.12 we see that Proposition 2.13(iii) extends [25, Proposition 3.1].
In the following result we give sufficient conditions for the v-nearly E-subconvexlikeness of the mapping f. For each \(y\in Y\), \(f-y:X\rightarrow Y\) denotes the mapping \((f-y)(x)=f(x)-y\), for all \(x\in X\).
Theorem 2.14
Let \(\emptyset \ne E{\subset } Y\) be a convex free disposal set and \(N{\subset } X\) be a nonempty set.
-
(i)
If f is K-convexlike on N, then \(f-y\) is v-nearly E-subconvexlike on N, for all \(y\in Y\).
-
(ii)
If K is solid and f is v-closely K-convexlike on N, then \(f-y\) is v-nearly E-subconvexlike on N, for all \(y\in Y\).
Proof
(i) As \(f(N)+K\) and E are convex, one has \(f(N)+K+E=f(N)+E\) is convex. Hence, \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(N)-y+E)\) is convex for all \(y\in Y\).
(ii) By assumptions it is clear that \(f(N)-y+\mathop {\mathrm{cor}}\nolimits K+E\) is convex, and by Lemma 2.1 and Lemma 2.2(i) it follows that \(\mathop {\mathrm{vcl}}\nolimits (f(N)-y+ E+K)\) is convex. Thus, applying Lemma 2.3 the proof finishes. \(\square \)
Finally, given a scalar function \(h:X\rightarrow {\mathbb {R}}\) and \(\emptyset \ne S{\subset } X\), the set of \(\varepsilon \)-optimal (respectively, sharp \(\varepsilon \)-optimal) solutions with error \(\varepsilon \ge 0\) of the scalar optimization problem
is denoted by \(\mathop {\mathrm{argmin}}\nolimits _S(h,\varepsilon )\) (respectively, \(\mathop {\mathrm{argmin}}\nolimits _S^<(h,\varepsilon )\)), i.e.,
We denote \(\mathop {\mathrm{argmin}}\nolimits _Sh:=\mathop {\mathrm{argmin}}\nolimits _S(h,0)\), i.e., the set of exact minima of h on S.
Remark 2.15
It is clear that \(\mathop {\mathrm{argmin}}\nolimits _S(h,\varepsilon _1){\subset } \mathop {\mathrm{argmin}}\nolimits _S(h,\varepsilon _2)\) whenever \(0\le \varepsilon _1\le \varepsilon _2\).
For \(\lambda \in Y'\) and \(\emptyset \ne E{\subset } Y\), we denote \(\tau _E(\lambda )=\inf _{e\in E}\lambda (e)\). Let us observe that \(\lambda \in E^+\) if and only if \(\tau _E(\lambda )\ge 0\).
3 Optimality notions with improvement sets
From now on we assume that K is vectorially closed and \(E\in \mathcal {I}_K\). The E-optimality notion due to Chicco et al. (see [6, Definition 3.1]) was introduced for Pareto problems, and it was translated in [9] to problem (2.2) when Y is a topological linear space. Next we reformulate this approximate optimality notion when Y is a real linear space.
Definition 3.1
A point \(x_0\in S\) is said to be an E-optimal (respectively, weak E-optimal) solution of problem (2.2), denoted by \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E)\) (respectively, \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\)), if
Remark 3.2
(a) If \(\mathop {\mathrm{cor}}\nolimits E=\emptyset \) then \(\mathop {\mathrm{WOp}}\nolimits (f,S;E)=S\). Thus, in order to deal with nontrivial sets of weak E-optimal solutions, we assume that E is solid whenever this kind of solutions are considered.
On the other hand, observe that \(\mathop {\mathrm{WOp}}\nolimits (f,S;E)=\mathop {\mathrm{Op}}\nolimits (f,S;\mathop {\mathrm{cor}}\nolimits E)\). Moreover, if K is pointed, then \(K_0\in \mathcal {I}_K\) and it is clear that \(\mathop {\mathrm{Op}}\nolimits (f,S;K_0)\) is the set of (exact) minimal solutions of problem (2.2). In this case we denote \(\mathop {\mathrm{Op}}\nolimits (f,S):=\mathop {\mathrm{Op}}\nolimits (f,S;K_0)\).
(b) Since \(E \in \mathcal {I}_K\), it follows that
Moreover, since \(\mathop {\mathrm{cor}}\nolimits E\in \mathcal {I}_K\) (see Proposition 2.7(ii)) we have that
If additionally K is solid, then by Lemma 2.2(ii) we have \(\mathop {\mathrm{cor}}\nolimits E=E+\mathop {\mathrm{cor}}\nolimits K\) and
(c) By taking different sets \(E\in \mathcal {I}_K\), the notion of E-optimal solution reduces to well-known concepts of exact and approximate solution of problem (2.2), as it was shown in [9, Remark 4.2] in the setting of topological linear spaces. For example, we can take as E the sets \(Y\backslash (-K)\), \(K\cap (Y\backslash (-K))\) and \(\mathop {\mathrm{cor}}\nolimits K\), and then we obtain the set of ideal solutions, minimal solutions and weak efficient solutions, respectively.
Moreover, if K is pointed and we consider \(E=q+K_0\), with \(q\notin -K_0\), then \(E\in \mathcal {I}_K\) and the notion of E-optimality given in Definition 3.1 reduces to the first part of [16, Definition 3.1]. Analogously, if K is solid and we consider \(q\in Y\backslash (-\mathop {\mathrm{cor}}\nolimits {K})\), then \(E=q+\mathop {\mathrm{cor}}\nolimits {K}\in \mathcal {I}_K\) and \(x_0\in S\) is a weak E-optimal solution of (2.2) if and only if \((f(S)-f(x_0))\cap (-q-\mathop {\mathrm{cor}}\nolimits K)=\emptyset \), which is equivalent to \((f(S)-f(x_0)+q)\cap (-\mathop {\mathrm{cor}}\nolimits K)=\emptyset \). This is the second part of [16, Definition 3.1] and also the concept of q-weakly efficient point given in [25, Definition 2.4].
On the other hand, approximate proper efficiency notions for vector optimization problems defined on real linear spaces have been studied, for instance, by Zhou and Peng [25], Kiyani and Soleimani-damaneh [16] and Zhou et al. [26, 27]. In these papers, the authors focus overall on approximate proper efficiency concepts in the senses of Hurwicz, Benson and Henig.
Let us define
and for each \(E\in \overline{\mathcal {H}}\),
Motivated by the works cited above and [11], we introduce the following two definitions.
Definition 3.3
Let \(E\in \overline{\mathcal {H}}\). A point \(x_0\in S\) is said to be a Benson E-proper optimal solution of problem (2.2) if
We denote the set of all Benson E-proper optimal solutions of problem (2.2) by \(\mathop {\mathrm{Be}}\nolimits (f,S;E)\).
Definition 3.4
Let \(E\in \overline{\mathcal {H}}\). A point \(x_0\in S\) is said to be a Henig E-proper optimal solution of problem (2.2) if there exists \(K^{\prime }\in \mathcal {G}(E)\) such that \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K^{\prime })\).
The set of all Henig E-proper optimal solutions of problem (2.2) will be denoted by \(\mathop {\mathrm{He}}\nolimits (f,S;E)\).
Remark 3.5
(a) In Definition 3.4, observe that \(E+\mathop {\mathrm{cor}}\nolimits {K^{\prime }}\in \mathcal {I}_K\) (see Lemma 2.8(iv)) and \(\mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K^{\prime })=\mathop {\mathrm{WOp}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K^{\prime })\), since \(\mathop {\mathrm{cor}}\nolimits (E+\mathop {\mathrm{cor}}\nolimits K^{\prime })=E+\mathop {\mathrm{cor}}\nolimits K^{\prime }\) by Lemma 2.2(ii).
(b) From statement (3.3) we deduce that
Analogously, by Lemma 2.4 we know that \(E\cap (-\mathop {\mathrm{cor}}\nolimits K^{\prime })=\emptyset \Longrightarrow \mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits E\cap (-K_0)=\emptyset \). Because of that, we consider \(E\in \overline{\mathcal {H}}\) in Definitions 3.3 and 3.4.
(c) If K is not pointed, then \(\overline{\mathcal {H}}=\emptyset \). Indeed, take \(k\in K\cap (-K_0)\), and assume that there exists \(E\in \overline{\mathcal {H}}\). Choose a sequence \((r_n){\subset } {\mathbb {R}}_+\) such that \(r_n\uparrow +\infty \) and a fixed point \(e\in E\). Then \(e+r_n k\in E+K=E\), and therefore \(r_n^{-1}(e+r_n k)=k+r_n^{-1} e\in \mathop {\mathrm{cone}}\nolimits E\). As \(r_n^{-1}\downarrow 0\) it follows that \(k\in \mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits E\). As \(k\in -K_0\), we achieve a contradiction to the fact that \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits E\cap (-K_0)=\emptyset \).
Thus, when we consider Benson or Henig E-proper optimal solutions, we assume that K is pointed. In this case it is clear that \(K_0\in \overline{\mathcal {H}}\). Other sets belonging to the class \(\overline{\mathcal {H}}\) are \(\mathop {\mathrm{cor}}\nolimits {K}\) (respectively, \(\mathop {\mathrm{icr}}\nolimits {K}\)) whenever K is solid (respectively, relatively solid), \(q+K_0\), for all \(q\in K\), and \(q+K\), for all \(q\in Y\backslash (-K)\) whenever \(K^+\) is solid. Let us check this last statement (in a similar way one can prove that \(q+K_0\in \overline{\mathcal {H}}\), for all \(q\in Y\backslash (-K_0)\) whenever \(K^+\) is solid). It is easy to prove that \(E=q+K\in \mathcal {I}_K\). On the other hand, by applying Theorem 2.5 to \(M=\mathop {\mathrm{cone}}\nolimits (\{q\})\) and \(D=-K\) we deduce that there exists \(\lambda \in K^{+s}\) such that
Suppose that \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (q+K)\cap (-K_0)\ne \emptyset \) and consider \(z'\in \mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (q+K)\cap (-K_0)\). As \(\lambda \in K^{+s}\) then \(\lambda (z')<0\). Moreover, there exist \(v\in Y\) and sequences \((t_n),(\alpha _n){{\subset }}{\mathbb {R}}_+\), \(t_n\downarrow 0\), and \((k_n){\subset } K\) such that \(z'+t_nv=\alpha _n(q+k_n)\), for all n. Therefore, by (3.4) we have that
that is a contradiction. Thus, \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (q+K)\cap (-K_0)=\emptyset \) and \(q+K\in \overline{\mathcal {H}}\).
(d) It is not hard to check that for all nonempty set \(A{\subset } Y\),
Thus, when we choose \(E=K_0\), Definition 3.3 reduces to the concept of (exact) Benson proper efficiency considered by Adán and Novo [3, Definition 3.1]. Analogously, by Lemma 2.8(i) we deduce that Definition 3.4 encompasses the notion of (exact) proper efficiency in the sense of Henig via the set \(E=K_0\) (see [25, Definition 2.6 and Remark 2.3]). As a consequence we denote \(\mathop {\mathrm{Be}}\nolimits (f,S):=\mathop {\mathrm{Be}}\nolimits (f,S;K_0)\) and \(\mathop {\mathrm{He}}\nolimits (f;S):=\mathop {\mathrm{He}}\nolimits (f,S;K_0)\).
(e) By considering \(E=q+K_0\) and \(q\in K\) it follows that Definition 3.3 reduces to [16, Definition 3.2] and [25, Definition 2.5], and Definition 3.4 reduces to [25, Definition 2.6]. Moreover, if \(K^+\) is solid, then [16, Definition 3.2] and [25, Definition 2.5] can be generalized to vectors \(q\in Y\backslash (-K_0)\) by Definition 3.3 and the set \(E=q+K_0\).
In the following theorem we relate Benson E-proper optimal solutions to weak E-optimal solutions of problem (2.2).
Theorem 3.6
Let \(E\in \overline{\mathcal {H}}\). It follows that \(\mathop {\mathrm{Be}}\nolimits (f,S;E){\subset }\mathop {\mathrm{WOp}}\nolimits (f,S;E)\).
Proof
Let \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\). Then, \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\cap (-K_0)=\emptyset \), which in particular implies that
Suppose, reasoning by contradiction, that \(x_0\notin \mathop {\mathrm{WOp}}\nolimits (f,S;E)\). Then \((f(S)-f(x_0))\cap (-\mathop {\mathrm{cor}}\nolimits E)\ne \emptyset \). Hence, there exist \(x\in S\) and \(e\in \mathop {\mathrm{cor}}\nolimits E\) such that \(f(x)-f(x_0)=-e\). Fix an arbitrary point \(k\in K_0\). Since \(e\in \mathop {\mathrm{cor}}\nolimits E\) there exists \(t>0\) such that \(e-tk=:e'\in E\). Thus, \(f(x)-f(x_0)=-e'-tk\), i.e., \(f(x)+e'-f(x_0)=-tk\in -K_0\), which contradicts (3.7). \(\square \)
Remark 3.7
If \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\), we have in particular that \((f(S)-f(x_0))\cap (-E-K_0)=\emptyset \). Thus, \(\mathop {\mathrm{Be}}\nolimits (f,S;E){\subset } \mathop {\mathrm{Op}}\nolimits (f,S;E+K_0)\) (note that \(E+K_0\in \mathcal {I}_K\)).
However, the inclusion \(\mathop {\mathrm{Be}}\nolimits (f,S;E){\subset } \mathop {\mathrm{Op}}\nolimits (f,S;E)\) does not hold, in general, as it is shown in Example 3.15.
By taking into account Remark 3.7, it is clear that we can improve the conclusion of Theorem 3.6 if
which is equivalent to \(E=E+K_0\), since \(E\in \mathcal {I}_K\). Indeed, we obtain the following result.
Theorem 3.8
Let \(E\in \overline{\mathcal {H}}\). If (3.8) holds, then \(\mathop {\mathrm{Be}}\nolimits (f,S;E){\subset }\mathop {\mathrm{Op}}\nolimits (f,S;E)\).
Remark 3.9
Many usual sets \(E\in \overline{\mathcal {H}}\) satisfy property (3.8), for instance:
-
(a)
\(E:=K_0\), since \(K_0+K_0=K_0\).
-
(b)
\(E:=\mathop {\mathrm{cor}}\nolimits K\), whenever K is solid, since K is proper and by Lemma 2.2(ii) we know that
$$\begin{aligned} \mathop {\mathrm{cor}}\nolimits K=\mathop {\mathrm{cor}}\nolimits K_0=\mathop {\mathrm{cor}}\nolimits (K_0+K)=K_0+\mathop {\mathrm{cor}}\nolimits K. \end{aligned}$$ -
(c)
Let \(\emptyset \ne H{\subset } Y\) such that \(H+K_0\in \overline{\mathcal {H}}\). Then \(E:=H+K_0\) satisfies (3.8) since \((H+K_0)+K_0=H+K_0\). From part (a) and Theorem 3.8 we obtain the well-known inclusion \(\mathop {\mathrm{Be}}\nolimits (f,S){\subset } \mathop {\mathrm{Op}}\nolimits (f,S)\) (exact case). Finally, taking into account Remarks 3.5(c) and 3.9(c), observe that Theorem 3.8 reduces to [16, Proposition 3.3] when \(E=q+K_0\) and \(q\in K_0\).
With respect to the Henig E-proper optimal solutions of problem (2.2), from Definition 3.4 and Remark 3.5(a) we deduce that
In the following result, we establish equivalent formulations for this type of solutions. Let us define \(\mathcal {O}(E):=\{K^{\prime }\in \mathcal {G}(E): \mathop {\mathrm{cor}}\nolimits K^{\prime }=K^{\prime }_0\}\).
Theorem 3.10
Let \(E\in \overline{\mathcal {H}}\) and \(x_0\in S\). The following statements are equivalent:
-
(i)
\(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\).
-
(ii)
There exists \(K^{\prime }\in \mathcal {O}(E)\) such that \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K^{\prime })\).
-
(iii)
There exists \(K^{\prime }\in \mathcal {O}(E)\) such that
$$\begin{aligned} \mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\cap (-K^{\prime })=\{0\}. \end{aligned}$$(3.9)
Proof
(i) \(\Longrightarrow \) (ii). Since \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), there exists \(\overline{K}\in \mathcal {G}(E)\) such that \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits \overline{K})\). Then, the cone \(K^{\prime }:=\mathop {\mathrm{cor}}\nolimits \overline{K}\cup \{0\}\) satisfies the conditions given in part (ii).
(ii) \(\Longrightarrow \) (iii). Suppose that there exists \(K^{\prime }\in \mathcal {O}(E)\) such that \((f(S)-f(x_0))\cap (-E-\mathop {\mathrm{cor}}\nolimits K^{\prime })=\emptyset \). This is equivalent to \((f(S)+E-f(x_0))\cap (-\mathop {\mathrm{cor}}\nolimits K^{\prime })=\emptyset \), which implies that
Thus, by Lemma 2.4 applied to the sets \(\mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\) and \(\mathop {\mathrm{cor}}\nolimits (-K^{\prime })=-\mathop {\mathrm{cor}}\nolimits K^{\prime }\), we deduce that
which is equivalent to (3.9), since \(K^{\prime }_0=\mathop {\mathrm{cor}}\nolimits K^{\prime }\).
(iii) \(\Longrightarrow \) (i). If there exists \(K^{\prime }\in \mathcal {O}(E)\) such that (3.9) holds, we deduce in particular that \((f(S)+E-f(x_0))\cap (-\mathop {\mathrm{cor}}\nolimits K^{\prime })=\emptyset \), since \(K^{\prime }_0=\mathop {\mathrm{cor}}\nolimits K^{\prime }\), which clearly implies that \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K^{\prime })\), and then, \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), concluding the proof. \(\square \)
Remark 3.11
-
(a)
Observe that \(\mathcal {G}(E)=\emptyset \Leftrightarrow \mathcal {O}(E)=\emptyset \). The first implication is clear, since \(\mathcal {O}(E){\subset }\mathcal {G}(E)\). Reciprocally, suppose by contradiction that there exists \(\overline{K}\in \mathcal {G}(E)\). Then, the cone \(K^{\prime }:=\mathop {\mathrm{cor}}\nolimits \overline{K}\cup \{0\}\in \mathcal {O}(E)\) (see the proof of implication (i) \(\Longrightarrow \) (ii) in Theorem 3.10), and we reach the contradiction.
-
(b)
The cones \(K^{\prime }\in \mathcal {O}(E)\) are, in addition, pointed since \(K^{\prime }_0=\mathop {\mathrm{cor}}\nolimits {K^{\prime }}\) and \(K^{\prime }\) is proper.
-
(c)
Theorem 3.10 is the algebraic counterpart of [11, Theorem 3.3(a)-(c)], where similar equivalent statements are proved in the setting of topological linear spaces, by replacing the algebraic concepts with their topological counterparts (observe that condition \(E\in \mathcal {I}_K\) is not required in the proof of Theorem 3.10).
In the next theorem, we show that the set of Henig E-proper optimal solutions is included in the set of Benson E-proper optimal solutions. However, in general, the sets of Benson and Henig E-proper optimal solutions are different (see Example 5.16).
Theorem 3.12
Let \(E\in \overline{\mathcal {H}}\). It follows that \(\mathop {\mathrm{He}}\nolimits (f,S;E){\subset } \mathop {\mathrm{Be}}\nolimits (f,S;E)\).
Proof
Let \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\). By Theorem 3.10(iii) there exists \(K^{\prime }\in \mathcal {O}(E)\) such that \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\cap (-K^{\prime })=\{0\}\), which in particular implies that \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\cap (-K)=\{0\}\), since \(K{\subset } \mathop {\mathrm{cor}}\nolimits K^{\prime }\cup \{0\}=K^{\prime }\). Hence, \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\), and the proof is finished. \(\square \)
Remark 3.13
Theorem 3.12 reduces to [25, Proposition 2.1] by considering \(E=q+K_0\), \(q\in K\). Moreover, it encompasses [11, Theorem 4.7], which was stated in the topological framework.
From the results stated above, we obtain the following corollary.
Corollary 3.14
Let \(E\in \overline{\mathcal {H}}\). It follows that
Moreover, if E satisfies property (3.8), then
In the next example, we show that, in general, the set of Henig E-proper optimal solutions and, consequently, the set of Benson E-proper optimal solutions of problem (2.2) are not included in the set of E-optimal solutions.
Example 3.15
Consider the following data: \(X=Y={\mathbb {R}}^2, f=\textit{Id}, K={\mathbb {R}}_+^2, E=\{(x,y)\in {\mathbb {R}}_+^2: ~x+y\ge 1\}, S={\mathbb {R}}_+^2\) and \(x_0=(1,0)\). One has \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E){\subset }\mathop {\mathrm{Be}}\nolimits (f,S;E)\) but \(x_0\notin \mathop {\mathrm{Op}}\nolimits (f,S;E)\).
4 Weak E-optimality and linear scalarization
In this section we give necessary and sufficient conditions for weak E-optimal solutions of problem (2.2), with \(E\in \mathcal {I}_K\), through linear scalarization, i.e., in terms of approximate solutions of scalar optimization problems associated to (2.2), and under generalized convexity assumptions. Moreover, when the feasible set is given by a cone-constraint (see (2.3)), we also derive Lagrangian optimality conditions for this type of solutions.
In the following result we state necessary conditions for weak E-optimal solutions of problem (2.2) through linear scalarization.
Theorem 4.1
Let \(x_0\in S\). Assume that one of the following conditions holds:
-
(A1)
f is v-closely K-convexlike on S and E is a solid convex set.
-
(A2)
\(f-f(x_0)\) is v-nearly E-subconvexlike on S and K is solid. If \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\), then there exists \(\lambda \in E^+\backslash \{0\}\) such that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\).
Proof
As \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\), then by statements (3.1) and (3.2) it follows that
whenever K is solid for statement (4.2).
From assumption (A1), statement (4.1) and by applying Lemma 2.4 we derive that \(\mathop {\mathrm{vcl}}\nolimits (f(S)+K-f(x_0))\cap (-\mathop {\mathrm{cor}}\nolimits E)=\emptyset \).
As \(\mathop {\mathrm{vcl}}\nolimits (f(S)+K-f(x_0))\) is a convex set since f is v-closely K-convexlike on S, by the standard separation theorem (see, for instance, [14, Theorem 3.14]) there exist \(\lambda \in Y'\backslash \{0\}\) and \(\alpha \in {\mathbb {R}}\) such that
By taking \(x=x_0\) and \(k=0\) it results \(0\ge -\lambda (e)\) for all \(e\in E\), and so \(\lambda \in E^+\backslash \{0\}\). From (4.3), by taking \(k=0\), it follows that \(\lambda (e)\ge \lambda (f(x_0))-\lambda (f(x))\) for every \(e\in E,x\in S\), and so \(\tau _E(\lambda )\ge \lambda (f(x_0))-\lambda (f(x))\) for every \(x\in S\). In consequence, \(\lambda (f(x))\ge \lambda (f(x_0))-\tau _E(\lambda )\) for every \(x\in S\), i.e., \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\).
On the other hand, if (A2) holds, we proceed in a similar way. From (4.2), by taking into account that \(\mathop {\mathrm{cor}}\nolimits K\cup \{0\}\) is a cone and by Lemma 2.4 we derive that \([\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))]\cap (-\mathop {\mathrm{cor}}\nolimits K)=\emptyset \). As \(f-f(x_0)\) is v-nearly E-subconvexlike on S, the set \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\) is convex and we can apply the separation theorem, from which we see that there exists \(\lambda \in K^+\backslash \{0\}\) such that
In particular, if \(x=x_0\) we obtain \(\lambda (e)\ge 0\) for all \(e\in E\), and so \(\lambda \in E^+\). From (4.4) the conclusion follows. \(\square \)
Remark 4.2
(a) Conditions (A1) and (A2) are independent. By Theorem 2.14(ii) and Proposition 2.9(iii), if K is solid, E is convex and f is v-closely K-convexlike on S, then \(f-f(x_0)\) is v-nearly E-subconvexlike on S for each \(x_0\in S\). However, in general, \(\mathop {\mathrm{cor}}\nolimits K\) may be empty and \(\mathop {\mathrm{cor}}\nolimits E\) be nonempty. In the case that \(\mathop {\mathrm{cor}}\nolimits K\ne \emptyset \), (A2) is weaker than (A1).
(b) If K is solid and we choose \(E=q+\mathop {\mathrm{cor}}\nolimits {K}\) with \(q\in K\), then \(E\in \mathcal {I}_K\) and Theorem 4.1, under assumption (A2), reduces to [25, Theorem 5.1]. Let us observe that the authors use as generalized convexity condition that \(\mathop {\mathrm{cone}}\nolimits (f(S)-f(x_0)+q)+\mathop {\mathrm{cor}}\nolimits K\) is convex, which is equivalent to (A2). Indeed, let \(A:=f(S)-f(x_0)+q\). If \(\mathop {\mathrm{cone}}\nolimits (A)+\mathop {\mathrm{cor}}\nolimits K\) is convex, then by Lemma 2.1 and parts (i) and (iii) of Lemma 2.2 we see that assumption (A2) is satisfied.
Reciprocally, by applying parts (i) and (iii) of Lemma 2.2 to \(D=\mathop {\mathrm{cor}}\nolimits K\cup \{0\}\) and by (3.6) we see that
Therefore, by parts (i) and (ii) of Lemma 2.2 we deduce that
and so \(\mathop {\mathrm{cone}}\nolimits A+\mathop {\mathrm{cor}}\nolimits K\) is convex whenever assumption (A2) is fulfilled.
Moreover, observe that, in this case, \(\mathop {\mathrm{cor}}\nolimits E\ne \emptyset \) if and only if \(\mathop {\mathrm{cor}}\nolimits K\ne \emptyset \).
On the other hand, for the same set E and also under (A2), Theorem 4.1 reduces to [16, Theorem 4.3], where it is assumed that \(\mathop {\mathrm{cone}}\nolimits (f(S)-f(x_0)+q+K)\) is convex, which is a stronger condition than the v-nearly E-subconvexlikeness of \(f-f(x_0)\).
Next lemma is well-known and easy to prove.
Lemma 4.3
If \(\lambda \in Y'\), \(a\in \mathop {\mathrm{cor}}\nolimits A\) and \(\min _{y\in A} \lambda (y)=\lambda (a)\), then \(\lambda =0\).
In the next theorem we give sufficient conditions through linear scalarization for E-optimal and weak E-optimal solutions of problem (2.2).
Theorem 4.4
Let \(\lambda \in E^+\backslash \{0\}\). Then,
-
(i)
\(\mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda )){\subset }\mathop {\mathrm{WOp}}\nolimits (f,S;E)\).
-
(ii)
\(\mathop {\mathrm{argmin}}\nolimits ^<_S(\lambda \circ f,\tau _E(\lambda )){\subset }\mathop {\mathrm{Op}}\nolimits (f,S;E)\).
Proof
(i) Let \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\). Then,
Suppose that \(x_0\notin \mathop {\mathrm{WOp}}\nolimits (f,S;E)\). Then there exist \(\hat{x}\in S\) and \(\hat{e}\in \mathop {\mathrm{cor}}\nolimits E\) such that \(f(\hat{x})-f(x_0)=-\hat{e}\). By applying (4.5) to \(x=\hat{x}\) it results
i.e., \(\inf _{e\in E}\lambda (e)\ge \lambda (\hat{e})\), and so \(\min _{e\in E}\lambda (e)=\lambda (\hat{e})\). This implies by Lemma 4.3 that \(\lambda =0\), a contradiction.
(ii) Let \(x_0\in \mathop {\mathrm{argmin}}\nolimits ^<_S(\lambda \circ f,\tau _E(\lambda ))\). Then,
Suppose that \(x_0\notin \mathop {\mathrm{Op}}\nolimits (f,S;E)\). Then there exist \(\hat{x}\in S\backslash \{x_0\}\) and \(\hat{e}\in E\) such that \(f(\hat{x})-f(x_0)=-\hat{e}\). By applying (4.6) to \(x=\hat{x}\) it follows that
i.e., \(\inf _{e\in E}\lambda (e)>\lambda (\hat{e})\), which is a contradiction. \(\square \)
Remark 4.5
Theorem 4.4 reduces to [16, Theorem 4.2]. Indeed, in this last theorem it is assumed that \(\lambda \in K^+\backslash \{0\}\), \(q\in K\backslash \{0\}\) and \(\lambda (q)>0\). Thus, \(q\notin -K\) and so Theorem 4.4 encompasses this result via the improvement set \(E=q+K\).
As a consequence of Theorems 4.1 and 4.4, we obtain the following characterization for weak E-optimal solutions of problem (2.2) through linear scalarization and by assuming generalized convexity assumptions.
Corollary 4.6
If either (A1) holds, or (A2) is fulfilled for all \(x_0\in S\), then
Remark 4.7
(a) In the topological framework, Corollary 4.6 under assumption (A2) reduces to the vector-valued version of [24, Theorem 4.1], where additionally it is assumed that K is pointed. Analogously, under assumption (A1) Corollary 4.6 reduces to [9, Corollary 5.4].
(b) In particular, if K is solid and we choose \(E=\mathop {\mathrm{cor}}\nolimits K\), this corollary encompasses the following well-known result (see, for instance, [1, Theorem 2.3] or [2, Theorem 2]):
Now, we are going to derive Lagrangian optimality conditions for weak E-optimal solutions of problem (2.2) and S defined by a cone-constraint (see (2.3)). The mapping \((f,g):X\rightarrow Y\times Z\) is defined by \((f,g)(x)=(f(x),g(x))\). On the other hand, let us observe that \(E\times (M+z)\in \mathcal {I}_{K\times M}\) for all \(z\in Z\) whenever \(E\in \mathcal {I}_K\).
Lemma 4.8
The following implication holds:
Proof
Suppose by contradiction that there exists \(x\in X\) such that \((f,g)(x)-(f,g)(x_0)\in -\mathop {\mathrm{cor}}\nolimits (E\times (M+g(x_0)))\). It is clear that
and so \(f(x)-f(x_0)\in -\mathop {\mathrm{cor}}\nolimits E\) and \(g(x)\in -\mathop {\mathrm{cor}}\nolimits M\). Therefore, \(x\in S\) and we deduce that \(x_0\notin \mathrm {WOp}(f,S;E)\), which is a contradiction. \(\square \)
Theorem 4.9
Let \(x_0\in S\). Suppose that g satisfies the Slater constraint qualification and assume that one of the following conditions holds:
-
(B1)
(f, g) is v-closely \((K\times M)\)-convexlike on X and E is a solid convex set.
-
(B2)
\((f,g)-(f(x_0),0)\) is v-nearly \((E\times M)\)-subconvexlike on X and K is solid.
If \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\), then there exist \(\lambda \in E^+\backslash \{0\}\) and \(\mu \in M^+\) such that
Proof
Let \(x_0\in \mathrm {WOp}(f,S;E)\). By Lemma 4.8 we have that \(x_0\in \mathrm {WOp}((f,g),X;E\times (M+g(x_0)))\).
It is easy to check that \(E\times (M+g(x_0))\) is a solid convex set whenever E is a solid convex set, since M is assumed to be solid and convex, and \((f,g)-(f,g)(x_0)\) is v-nearly \(E\times (M+g(x_0))\)-subconvexlike on X whenever \((f,g)-(f(x_0),0)\) is v-nearly \((E\times M)\)-subconvexlike on X.
Therefore, Theorem 4.1 can be applied under assumption (A1) (respectively, (A2)) if hypothesis (B1) (respectively, (B2)) holds, and we deduce that there exists \(\xi \in (E\times (M+g(x_0)))^+\backslash \{0\}\) such that \(x_0\in \text{ argmin }_X(\xi \circ (f,g),\tau _{E\times (M+g(x_0))}(\xi ))\). Let us define \(\lambda \in Y'\) and \(\mu \in Z'\) as follows: \(\lambda (y):=\xi (y,0)\), for all \(y\in Y\), and \(\mu (z):=\xi (0,z)\), for all \(z\in Z\). Then \(\xi (y,z)=\lambda (y)+\mu (z)\), for all \(y\in Y\) and \(z\in Z\) and so
As M is a cone, it follows that \(\mu \in M^+\). In particular we have \(\mu (g(x_0))\le 0\), since \(x_0\in S\). By taking \(z=0\) in (4.9) we deduce that \(\lambda (y)\ge -\mu (g(x_0))\ge 0\), \(\forall \,y\in E\), and so \(\lambda \in E^+\) and \(\tau _E(\lambda )\ge -\mu (g(x_0))\).
On the other hand, \(\xi \circ (f,g)=\lambda \circ f+\mu \circ g\) and \(\tau _{E\times (M+g(x_0))}(\xi )=\tau _E(\lambda )+\mu (g(x_0))\). Thus,
Finally it follows that \(\lambda \ne 0\). Indeed, if \(\lambda =0\) then \(\mu \in M^+\backslash \{0\}\) and by (4.10) we see that \(\mu (g(x))\ge 0\), for all \(x\in X\). By the Slater constraint qualification there exists \(\hat{x}\in X\) such that \(g(\hat{x})\in -\mathop {\mathrm{cor}}\nolimits {M}\) and so \(\mu (g(\hat{x}))<0\), which is a contradiction. \(\square \)
Remark 4.10
(a) Analogously as it was shown in Remark 4.2(a), assumptions (B1) and (B2) are independent. However, if K is solid, then (B1) \(\Longrightarrow \) (B2).
(b) Theorem 4.9 encompasses the vector-valued version of [21, Theorem 5.1], which was stated in the setting of Banach spaces and by assuming that K is pointed. For it, consider assumption (B1) and \(E=q+K_0\), \(q\in K\). Let us observe that the approximation error in [21, Theorem 5.1] is \(\tau _E(\lambda )=\langle \lambda , q\rangle \), which is bigger than the precision \(\langle \lambda , q\rangle +\mu (g(x_0))\) obtained via Theorem 4.9.
In the following result we state a sufficient condition for E-optimal and weak E-optimal solutions of problem (2.2) with the feasible set S given by (2.3).
Theorem 4.11
Let \(x_0\in S\). If there exist \(\lambda \in E^+\backslash \{0\}\) and \(\mu \in M^+\) such that
then \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\) (respectively, \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E)\)).
Proof
First, assume that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _X(\lambda \circ f+\mu \circ g,\tau _E(\lambda )+\mu (g(x_0)))\). Then,
Therefore, for all \(x\in S\),
since \(-g(x)\in M\) and \(\mu \in M^+\). From here it follows that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f, \tau _E(\lambda ))\), and by Theorem 4.4(i) the conclusion is obtained.
The proof of the other part is similar by applying Theorem 4.4(ii). \(\square \)
From Theorems 4.9 and 4.11 we deduce the following characterization of weak E-optimal solutions of problem (2.2) through linear scalarization.
Corollary 4.12
Let \(x_0\in S\). Suppose that g satisfies the Slater constraint qualification and that either (B1) or (B2) is satisfied. Then, \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\) if and only if there exist \(\lambda \in E^+\backslash \{0\}\) and \(\mu \in M^+\) such that (4.7) and (4.8) are satisfied.
Remark 4.13
Given \(\lambda \in E^+\backslash \{0\}\) and \(\mu \in M^+\), we denote by \(L_{\lambda ,\mu }^E:X\rightarrow {\mathbb {R}}\) the well-known scalar Lagrangian \(\lambda \circ f+\mu \circ g\), i.e.,
and we define
Suppose that g satisfies the Slater constraint qualification and that either (B1) holds, or (B2) is satisfied for all \(x_0\in S\). Then, by Corollary 4.12 it is easy to check that
In the precision \(\tau _E(\lambda )+\mu (g(x_0))\) obtained in Theorem 4.9, both the improvement set and the constraint mapping take part. It is worth to note that this precision has allowed us to derive the characterization of weak E-optimal solutions of problem (2.2) given in Corollary 4.12.
In Example 5.17 we apply this characterization to obtain the weak E-optimal solutions of a particular vector optimization problem.
5 E-proper optimality and linear scalarization
In this section we are going to derive necessary and sufficient conditions through linear scalarization for Henig and Benson E-proper optimal solutions of problem (2.2) under generalized convexity hypotheses. We also study the particular case in which the feasible set is given by a cone-constraint (see (2.3)), obtaining in this case Lagrangian optimality conditions. Recall that K is assumed to be vectorially closed and pointed (see Remark 3.5(c)).
The necessary conditions are based on the next new generalized convexity concepts.
Definition 5.1
Let \(\emptyset \ne E{\subset } Y\) and assume that K is relatively solid. The mapping \(f:X\rightarrow Y\) is said to be relatively solid E-subconvexlike (respectively, relatively solid generalized E-subconvexlike) on a nonempty set \(N{\subset } X\) (with respect to K) if f is E-subconvexlike (respectively, generalized E-subconvexlike) on N (with respect to K) and \(f(N)+E+\mathop {\mathrm{icr}}\nolimits {K}\) (respectively, \(\mathop {\mathrm{cone}}\nolimits (f(N)+E)+\mathop {\mathrm{icr}}\nolimits {K}\)) is relatively solid.
Proposition 5.2
If f is relatively solid E-subconvexlike on N, then f is relatively solid generalized E-subconvexlike on N.
Proof
By Proposition 2.13(i) we have that f is generalized E-subconvexlike on N whenever f is E-subconvexlike on N. Then the result follows since for all nonempty set \(A{\subset } Y\) such that \(A+\mathop {\mathrm{icr}}\nolimits {K}\) is convex, the next statement is true:
Indeed, it is easy to check that \(D:=(\mathop {\mathrm{cone}}\nolimits {A}+\mathop {\mathrm{icr}}\nolimits {K})\cup \{0\}\) is a convex cone and \(\mathop {\mathrm{cone}}\nolimits {A}+\mathop {\mathrm{icr}}\nolimits {K}\) is relatively solid whenever D is relatively solid. Then the result is proved if D is relatively solid.
By [3, Proposition 2.3] we have that an arbitrary convex cone \(H{\subset } Y\) is relatively solid if and only if \(H^+\) is relatively solid. Therefore, we have to prove that \(D^+\) is relatively solid.
As \(A+\mathop {\mathrm{icr}}\nolimits {K}\) is convex and relatively solid, by [12, Lemma 5.3] we see that \(\mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})\) is a relatively solid convex cone, and so \(\mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\) is relatively solid. Let us check that \(D^+=\mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\), which finishes the proof.
Indeed, it is obvious that \(D^+{\subset } \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\). Reciprocally, let \(\xi \in \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\) and consider two arbitrary points \(y\in \mathop {\mathrm{cone}}\nolimits {A}\) and \(d\in \mathop {\mathrm{icr}}\nolimits {K}\). If \(y\ne 0\), then there exists \(\alpha >0\) and \(a\in A\) such that \(y=\alpha a\) and it follows that
since \(\xi \in \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\) and \(\alpha (a+(1/\alpha )d)\in \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})\). Now suppose that \(y=0\) and consider an arbitrary point \(\bar{a}\in A\). Then,
since \(\xi \in \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})^+\) and \((1/n)(\bar{a}+nd)\in \mathop {\mathrm{cone}}\nolimits (A+\mathop {\mathrm{icr}}\nolimits {K})\), for all n. Thus, \(\xi \in D^+\) and the proof finishes. \(\square \)
Remark 5.3
(a) If K is solid and \(E\in \mathcal {I}_K\), then f is relatively solid generalized E-subconvexlike on N if and only if f is v-nearly E-subconvexlike on N (see Proposition 2.13(iii)).
(b) The concept of relatively solid E-subconvexlike mapping is more general than the vector-valued version of the notion of relatively solid K-subconvexlike mapping introduced in [12, Definition 3.5]. To be precise, the first one reduces to the second one by taking \(E=\mathop {\mathrm{icr}}\nolimits {K}\), since \(\mathop {\mathrm{icr}}\nolimits {K}+\mathop {\mathrm{icr}}\nolimits {K}=\mathop {\mathrm{icr}}\nolimits {K}\).
Moreover, let us observe that \(\mathop {\mathrm{icr}}\nolimits {K}\in \mathcal {I}_K\) (in particular, \(0\notin \mathop {\mathrm{icr}}\nolimits {K}\) since K is assumed to be pointed).
In the following two results, we give necessary conditions for Benson and Henig E-proper optimal solutions of problem (2.2) by means of linear scalarization.
Theorem 5.4
Let \(x_0\in S\) and \(E\in \overline{\mathcal {H}}\). Suppose that \(K^+\) is solid, \(f-f(x_0)\) is relatively solid generalized E-subconvexlike on S. If \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\), then there exists \(\lambda \in K^{+s}\cap E^+\) such that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\).
Proof
As \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\) it follows that
As \(K^+\) is solid, by [3, Proposition 2.3] we deduce that K is relatively solid. Since \(f-f(x_0)\) is relatively solid generalized E-subconvexlike on S, we have that \(\mathop {\mathrm{cone}}\nolimits (f(S)-f(x_0)+E)+\mathop {\mathrm{icr}}\nolimits {K}\) is relatively solid and convex. Then, by [2, Propositions 3(iii),(iv) and 4(i)] we deduce that \(\mathop {\mathrm{vcl}}\nolimits (\mathop {\mathrm{cone}}\nolimits (f(S)-f(x_0)+E)+\mathop {\mathrm{icr}}\nolimits {K})\) is relatively solid, vectorially closed and convex. Moreover, by [2, Proposition 6(i)] and Lemma 2.2(iii) it follows that
and this set is a cone. Then, by applying Theorem 2.5 to statement (5.1) we deduce that there exists a linear functional \(\lambda \in K^{+s}\) such that
Hence, it is clear that
From here, we deduce that \(\lambda \in E^+\) (by choosing \(x=x_0\)). Moreover, (5.2) is equivalent to
which means that \(x_{0}\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _{E}(\lambda ))\), concluding the proof. \(\square \)
Remark 5.5
(a) By considering \(E=\mathop {\mathrm{icr}}\nolimits {K}\) we see that Theorem 5.4 encompasses the vector-valued version of [12, Theorem 5.4]. This conclusion follows by Remark 5.3(b), Proposition 5.2 and by observing that \(\text{ Be }(f,S)=\text{ Be }(f,S;\mathop {\mathrm{icr}}\nolimits {K})\), since for all nonempty set \(A{\subset } Y\) we have that (see [2, Proposition 6(i)], Lemma 2.2(iii) and (3.6))
Moreover, note that Theorem 5.4 is based on a convexity assumption more general than the convexity assumption used in [12, Theorem 5.4].
Analogously, Theorem 5.4 extends [3, Theorem 4.2] (see also [4]), where the v-nearly K-subconvexlikeness of \(f-f(x_0)\) is assumed.
(b) Let us suppose that \(K^+\) is solid and consider \(E=q+\mathop {\mathrm{icr}}\nolimits {K}\) with \(q\in Y\backslash (-K_0)\). By (5.3) and Remark 3.5(c) it is clear that \(E\in \overline{\mathcal {H}}\). Then, by applying Theorem 5.4 to this improvement set we obtain [16, Theorem 4.6]. In this case, the relatively solid generalized E-subconvexlikeness assumption states that the set \(\mathop {\mathrm{cone}}\nolimits (f(S)-f(x_0)+q)+\mathop {\mathrm{icr}}\nolimits {K}\) (see (2.5)) is relatively solid and convex.
Let us underline that the assumptions in [16, Theorem 4.6] are stronger than the ones of Theorem 5.4. In particular, observe that K is assumed to be solid and so the generalized convexity hypotheses of both results are equivalent (see Remark 5.3(a) and (5.3)).
(c) Theorem 5.4 is the algebraic counterpart of [8, Theorem 3.2] and [10, Theorem 2.9], which were stated in the topological setting.
Theorem 5.6
Let \(x_0\in S\) and \(E\in \overline{\mathcal {H}}\). Suppose that \(f-f(x_0)\) is v-nearly E-subconvexlike on S. If \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), then there exists \(\lambda \in K^{+s}\cap E^+\) such that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\).
Proof
By Theorem 3.10(iii) there exists \(K^{\prime }\in \mathcal {O}(E)\) such that
Then, since \(f-f(x_0)\) is v-nearly E-subconvexlike on S, the set \(\mathop {\mathrm{vcl}}\nolimits \mathop {\mathrm{cone}}\nolimits (f(S)+E-f(x_0))\) is convex and by [14, Theorem 3.14] there exists \(\lambda \in K^{\prime +}\backslash \{0\}\cap E^+\) such that (5.2) holds, which is equivalent to say that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\).
On the other hand, as \(\lambda \in K^{\prime +}\backslash \{0\}\) and \(K_0{\subset } \mathop {\mathrm{cor}}\nolimits K^{\prime }\), we deduce that \(\lambda \in K^{+s}\), and the proof is complete. \(\square \)
Remark 5.7
Theorem 5.6 is the algebraic counterpart of [11, Theorem 4.5], which was stated in the topological setting.
The next result provides a sufficient condition for Henig E-proper optimal solutions of problem (2.2) through linear scalarization.
Theorem 5.8
Let \(E\in \overline{\mathcal {H}}\). If there exists \(\lambda \in K^{+s}\cap E^+\) such that \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))\), then \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\).
Proof
Consider the cone
It is easy to see that \(K^{\prime }\) is proper, convex and solid, with \(\mathop {\mathrm{cor}}\nolimits K^{\prime }=K'\backslash \{0\}\) and \(K_0{\subset } \mathop {\mathrm{cor}}\nolimits K^{\prime }\). Moreover, since \(\lambda \in E^+\) it also follows that \(E\cap (-K'\backslash \{0\})=\emptyset \), so \(K'\in \mathcal {O}(E)\).
We have that \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K')\). Indeed, suppose on the contrary that there exist \(\bar{x}\in S\) and \(\bar{e}\in E\) such that
From here, we have
which contradicts the hypothesis. Thus, \(x_0\in \mathop {\mathrm{Op}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits K')\), which implies by definition that \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), as we want to prove. \(\square \)
Remark 5.9
Theorem 5.8 reduces to [25, Theorem 5.2] by taking \(E=q+K_0\), \(q\in K\) (see Remark 3.5(e)), and it is the algebraic counterpart of [11, Theorem 4.4].
As a direct consequence of Theorems 3.12, 5.4, 5.6 and 5.8 we obtain the next corollary. Part (iii) reduces to the vector-valued version of [12, Corollary 5.5] by considering \(E=\mathop {\mathrm{icr}}\nolimits {K}\) (see Remark 5.3(b)). Observe that the generalized convexity assumption of Corollary 5.10 with \(E=\mathop {\mathrm{icr}}\nolimits {K}\) is more general than the one considered in [12, Corollary 5.5].
Corollary 5.10
The following statements hold:
-
(i)
\(\displaystyle \bigcup _{\lambda \in K^{+s}\cap E^+}\mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda )){\subset }\mathop {\mathrm{He}}\nolimits (f,S;E){\subset }\mathop {\mathrm{Be}}\nolimits (f,S;E).\)
-
(ii)
Suppose that \(f-f(x_0)\) is v-nearly E-subconvexlike on S, for all \(x_0\in S\). Then,
$$\begin{aligned} \bigcup _{\lambda \in K^{+s}\cap E^+}\mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))=\mathop {\mathrm{He}}\nolimits (f,S;E). \end{aligned}$$ -
(iii)
Suppose that \(K^+\) is solid and \(f-f(x_0)\) is relatively solid generalized E-subconvexlike on S, for all \(x_0\in S\). Then,
$$\begin{aligned} \bigcup _{\lambda \in K^{+s}\cap E^+}\mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f,\tau _E(\lambda ))=\mathop {\mathrm{He}}\nolimits (f,S;E)=\mathop {\mathrm{Be}}\nolimits (f,S;E). \end{aligned}$$
Next, we study problem (2.2) with the feasible set given in (2.3) and we obtain the following Lagrangian results.
Theorem 5.11
Let \(x_0\in S\) and \(E\in \overline{\mathcal {H}}\). Suppose that \((f,g)-(f(x_0),0)\) is v-nearly \((E\times M)\)-subconvexlike on X and g satisfies the Slater constraint qualification. If \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), then there exist \(\lambda \in K^{+s}\cap E^+\) and \(\mu \in M^+\) such that
Proof
Let \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\). By Theorem 3.10 we deduce that there exists \(K'\in \mathcal {O}(E)\) such that \(x_0\in \mathop {\mathrm{WOp}}\nolimits (f,S;E+\mathop {\mathrm{cor}}\nolimits {K'})\). By Lemma 2.8(iv) we see that \(E':=E+\mathop {\mathrm{cor}}\nolimits {K'}\in \mathcal {I}_{K'}\). Let us check that \((f,g)-(f(x_0),0)\) is v-nearly \((E'\times M)\)-subconvexlike on X. Indeed, by the generalized convexity assumption we have that the cone \(\mathop {\mathrm{vcl}}\nolimits {\mathop {\mathrm{cone}}\nolimits ((f,g)(X)-(f(x_0),0)+E\times M})\) is convex, and so
is also convex, since \(K'\) and M are solid convex cones. By Lemma 2.2(ii) it is clear that
Therefore, \((f,g)-(f(x_0),0)\) is relatively solid generalized \((E'\times M)\)-subconvexlike on X (with respect to the cone \(K'\times M\) in \(Y\times Z\)) and by Remark 5.3(a) it follows that \((f,g)-(f(x_0),0)\) is v-nearly \((E'\times M)\)-subconvexlike on X.
By applying Theorem 4.9, we deduce that there exist \(\lambda \in E'^+\backslash \{0\}\) and \(\mu \in M^+\), such that
Let us check that \(\lambda \in K^{+s}\cap E^+\) and \(\tau _{E'}(\lambda )=\tau _{E}(\lambda )\), which finishes the proof. Indeed, as \(\lambda \in E'^+\backslash \{0\}\) it is clear that \(\lambda \in K'^+\backslash \{0\}\), since \(\mathop {\mathrm{cor}}\nolimits {K'}\cup \{0\}\) is a cone and \((\mathop {\mathrm{cor}}\nolimits {K'})^+=K'^+\). Thus, \(\lambda \in K^{+s}\), since \(K_0{\subset } \mathop {\mathrm{cor}}\nolimits {K'}\), and so \(\tau _E(\lambda )=\tau _{E'}(\lambda )\) and \(\lambda \in E^+\), since \(\tau _{E'}(\lambda )\ge 0\). \(\square \)
Theorem 5.12
Let \(x_0\in S\) and \(E\in \overline{\mathcal {H}}\). Assume that \(K^+\) is solid, \(f-f(x_0)\) is relatively solid generalized E-subconvexlike on S, \((f,g)-(f(x_0),0)\) is v-nearly \((E\times M)\)-subconvexlike on X and g satisfies the Slater constraint qualification. If \(x_0\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\), then there exist \(\lambda \in K^{+s}\cap E^+\) and \(\mu \in M^+\) such that (5.4) and (5.5) hold.
Proof
By applying successively Theorem 5.4 and Corollary 5.10(i) we have that \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\), and then the result follows by applying Theorem 5.11. \(\square \)
Theorem 5.13
Let \(x_0\in S\) and \(E\in \overline{\mathcal {H}}\). If there exist \(\lambda \in K^{+s}\cap E^+\) and \(\mu \in M^+\) such that (5.4) and (5.5) hold, then \(x_0\in \mathop {\mathrm{He}}\nolimits (f,S;E)\).
Proof
By hypothesis, \(\lambda (f(x))+\mu (g(x))+\tau _E(\lambda )+\mu (g(x_0))\ge \lambda (f(x_0))+\mu (g(x_0))\) for all \(x\in X\). Hence, for all \(x\in S\),
since \(g(x)\in -M\) and \(\mu \in M^+\). From here, \(x_0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f, \tau _E(\lambda ))\), and by Theorem 5.8 the conclusion is obtained.
Remark 5.14
In [8, Theorem 3.8] the authors obtained, in the topological setting and for a kind of approximate proper solutions in the sense of Benson, Lagrangian optimality conditions similar to these in Theorem 5.12. It is worth to note that the precision \(\tau _E(\lambda )+\mu (g(x_0))\) attained in Theorem 5.12 is better than the approximation error given in [8, Theorems 3.8], and this improvement let us just derive a characterization of Benson and Henig E-proper optimal solutions of problem (2.2) through scalar Lagrangian conditions (see Corollary 5.15 below).
From Theorems 3.12, 5.11, 5.12 and 5.13 we deduce the next corollary.
Corollary 5.15
Let \(E\in \overline{\mathcal {H}}\). The following holds:
-
(i)
\(\displaystyle {\mathop \bigcup _{\begin{array}{c} {\lambda \in K^{+s}\cap E^+}\\ {\mu \in M^+} \end{array}}}\Gamma _{\lambda ,\mu }^E{\subset }\mathop {\mathrm{He}}\nolimits (f,S;E){\subset }\mathop {\mathrm{Be}}\nolimits (f,S;E).\) Suppose that \((f,g)-(f(x_0),0)\) is v-nearly \((E\times M)\)-subconvexlike on X, for all \(x_0\in S\), and g satisfies the Slater constraint qualification.
-
(ii)
We have that
$$\begin{aligned} {\mathop \bigcup _{\begin{array}{c} {\lambda \in K^{+s}\cap E^+}\\ {\mu \in M^+} \end{array}}}\Gamma _{\lambda ,\mu }^E=\mathop {\mathrm{He}}\nolimits (f,S;E). \end{aligned}$$ -
(iii)
If additionally \(K^+\) is solid and \(f-f(x_0)\) is relatively solid generalized E-subconvexlike on S, for all \(x_0\in S\), then
$$\begin{aligned} {\mathop \bigcup _{\begin{array}{c} {\lambda \in K^{+s}\cap E^+}\\ {\mu \in M^+} \end{array}}}\Gamma _{\lambda ,\mu }^E=\mathop {\mathrm{He}}\nolimits (f,S;E)=\mathop {\mathrm{Be}}\nolimits (f,S;E). \end{aligned}$$
Next we illustrate the above results with an example in the setting of an infinite dimensional space, which furthermore shows that the sets \(\mathop {\mathrm{Be}}\nolimits (f,S;E)\) and \(\mathop {\mathrm{He}}\nolimits (f,S;E)\) are, in general, different.
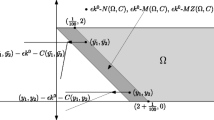
Example 5.16
Let \(Y={\mathbb {R}}^\mathbb {N}=\{(a_i)_{i\in \mathbb {N}} \}\) be the linear space of all sequences of real numbers and K the v-closed convex cone of nonnegative sequences, i.e.,
Consider the family \(e^n\in Y\), \(n\in \mathbb {N}\), defined by \(e^n=(\delta _{in})_{i\in \mathbb {N}}\), where \(\delta _{in}=1\) if \(i=n\) and \(\delta _{in}=0\) if \(i\ne n\).
(i) First, we prove that
Indeed, let \(\lambda \in K^+\), \(\beta _i:=\lambda (e^i)\ge 0\), \(a=(a_i)_{i\in \mathbb {N}}\in K\) and \(L=\lambda (a)\in {\mathbb {R}}_+\). One has \(a=\sum _{i=1}^n a_ie^i +\bar{a}^n\), for all n, where \(\bar{a}^n:=a-\sum _{i=1}^n a_ie^i\in K\). Then
and since \(\lambda (\bar{a}^n)\ge 0\), it follows that \(\sum _{i=1}^n a_i\beta _i\le L\) \(\forall n\), i.e., it is bounded. Therefore, the series of positive numbers \(\sum _{i=1}^\infty a_i\beta _i\) is convergent and consequently
This property implies that there exists \(i_0\) such that \(\beta _i=0\) \(\forall i>i_0\). Indeed, if for each \(n\in \mathbb {N}\) there exists \(i_n>i_0\) such that \(\beta _{i_n}>0\), then we select \(a_{i_n}=\beta _{i_n}^{-1}\) and \(a_i=i\) for \(i\ne i_n\). For this sequence, the subsequence \((a_{i_n})_{n\in \mathbb {N}}\) satisfies \(a_{i_n}\beta _{i_n}=1\) and this contradicts (5.6).
In consequence, we identify \(\lambda =(\beta _i)_{i\in \mathbb {N}}\).
(ii) Second, we prove that
Let \(\lambda \in Y'\) and define \(I_+:=\{i\in \mathbb {N}:~ \lambda (e^i)>0\}\) and \(I_-:=\{i\in \mathbb {N}:~ \lambda (e^i)<0\}\). The sets \(I_+\) and \(I_-\) are finite. Suppose that \(I_+\) is an infinite set. Then we consider the linear space \(Y_1=\mathbb {R}^{I_+}\) and its natural ordering cone \(K_1\) and we restrict \(\lambda \) to \(Y_1\) and so \(\lambda \in K_1^+\). Reasoning as above we conclude that only a finite numbers of \(\lambda (e^i)\), \(i\in I_+\), are non null, which is a contradiction. Similarly if we assume that \(I_-\) is an infinite set (we consider \(-\lambda \) instead of \(\lambda \)).
Let us observe that the map \(\lambda \in Y' \mapsto (\lambda (e^i))\in \mathcal {P}\) is an isomorphism of linear spaces.
(iii) \(K^{+s}=\emptyset \). Indeed, if \(\lambda \in K^{+s}\) then \(\lambda =(\lambda _i)_{i\in \mathbb {N}}\) and there exists \(i_0\) such that \(\lambda _i=0\) for all \(i>i_0\). Choosing \(e^{i_0+1}\in K\backslash \{0\}\) we have \(\lambda (e^{i_0+1})=0\), which is a contradiction.
(iv) Now we consider \(X=Y\), \(S=K\), \(f= Id \) and \(x_0=0\in S\). It is easy to check that \(0\in \mathop {\mathrm{Be}}\nolimits (f,S)\) since \(S=K\) is a pointed v-closed convex cone. However, \(0\notin \mathop {\mathrm{He}}\nolimits (f,S)\). Indeed, it is clear that \(f-f(x_0)\) is v-nearly K-subconvexlike on S. If we assume that \(0\in \mathop {\mathrm{He}}\nolimits (f,S)\), by Theorem 5.6 there exists \(\lambda \in K^{+s}\) such that \(0\in \mathop {\mathrm{argmin}}\nolimits _S(\lambda \circ f)\). But this is a contradiction since \(K^{+s}=\emptyset \).
Moreover, in this case,
The first left to right implication is clear by the definition of (exact) Henig proper optimal solution, and the second one is obvious. Moreover, if \(0\notin \mathop {\mathrm{He}}\nolimits (f,S)\), by Theorem 3.10 there does not exist \(K'\in \mathcal {O}(K_0)\) such that \(K\cap (-K')=\{0\}\). If \(\mathcal {O}(K_0)\ne \emptyset \) then there is \(K'\in \mathcal {O}(K_0)\) and by Remark 3.11(b) we know in particular that \(K'\) is pointed. Hence, \(K^{\prime }_0\cap (-K')=\emptyset \), which implies that \(K_0\cap (-K')=\emptyset \), since \(K_0{\subset }\mathop {\mathrm{cor}}\nolimits K'=K^{\prime }_0\), a contradiction. Finally, by Remark 3.11(a) we deduce that \(\mathcal {G}(K_0)=\emptyset \).
(v) It holds that \(\mathop {\mathrm{cor}}\nolimits (K^+)=\emptyset \). Indeed, suppose that \(b\in \mathop {\mathrm{cor}}\nolimits (K^+)\). Then for each \(v\in Y'\) there exists \(t_0>0\) such that \(b+tv\in K^+\) for all \(t\in [0,t_0]\). As \(b\in Y'\) there exists \(i_0\) such that \(b_i=0\) for all \(i>i_0\). Choose \(v=-e^{i_0+1}\). Then \(b+tv\notin K^+\) \(\forall t>0\) because the \((i_0+1)\)-th component is negative.
As a consequence, Theorem 5.4 is not applicable.
(vi) \(\mathop {\mathrm{cor}}\nolimits K=\emptyset \). Indeed, let \(a\in \mathop {\mathrm{cor}}\nolimits K\). If \(a_i=0\) for some i, then we choose \(v=-e^i\) and we have \(a+tv\notin K\) \(\forall t>0\). Hence we can assume that \(a_i>0\) for all i. Then we choose \(v=(-i a_i)_{i\in \mathbb {N}}\) and there does not exist \(t_0>0\) such that \(a+t_0v\in K\), since it should verify \(a_i+t_0(-ia_i)\ge 0\) for all i, or equivalently, \(t_0\le 1/i\) for all i, which is impossible.
(vii) Now we consider the space \(\mathcal {P}\) and its natural ordering cone \(D:=\{(y_i)_{i\in \mathbb {N}}\in \mathcal {P}:~ y_i\ge 0~\forall i\}\). One has \(\mathcal {P}'=Y\) (that is, the bidual of Y is itself), \(D^+=K\) but now \(D^{+s}=\{(a_i)_{i\in \mathbb {N}}\in Y:~ a_i>0~\forall i\}\). Let problem (2.2) be with \(f= Id :\mathcal {P}\rightarrow \mathcal {P}\), \(S_1=D\) and \(x_0=0\in S_1\). One has \(0\in \mathop {\mathrm{He}}\nolimits (f,S_1)\). Indeed, if we select \(\lambda =(1,1,1,\dots )\in D^{+s}\) it result that \(\lambda (y)\ge 0\) \(\forall y\in S_1\) and by Theorem 5.8 the result follows.
As a consequence, \(0\in \mathop {\mathrm{Be}}\nolimits (f,S_1)\) by Theorem 3.12.
Next, we provide an illustrative example in which we calculate the E-optimal, weak E-optimal and the Benson and Henig E-proper optimal solutions of a given problem.
Example 5.17
Consider problem (2.2) with the following data: \(X=Y=\mathbb {R}^2, Z=\mathbb {R}, f:\mathbb {R}^2\rightarrow \mathbb {R}^2\) is given by \(f(x,y)=(x,y), g:\mathbb {R}^2\rightarrow \mathbb {R}\) is given by \(g(x,y)=\varphi (x)-y\), where \(\varphi (x)=x^2\) if \(x\le 0\) and \(\varphi (x)=0\) if \(x>0, E=\{(x,y)\in \mathbb {R}^2:~y\ge 0,~x+y\ge 1\}, K=\mathbb {R}_+^2, M=\mathbb {R}_+\). We wish to obtain the weak E-optimal solutions, and the Benson and Henig E-proper optimal solutions.
It is clear that E is a convex improvement set with respect to \(\mathbb {R}_+^2\), \(E^+=\{(\lambda _1,\lambda _2)\in \mathbb {R}_+^2:~\lambda _2\ge \lambda _1\}\), (f, g) is \((\mathbb {R}_+^2\times \mathbb {R}_+)\)-convex on \(\mathbb {R}^2\), f is \(\mathbb {R}_+^2\)-convex on \(\mathbb {R}^2\) and g satisfies the Slater constraint qualification. Clearly, by Proposition 2.9, Theorem 2.14 and Remark 5.3(a), \((f,g)-(f(x_0),0)\) is v-nearly \(E\times M\)-subconvexlike on \(\mathbb {R}^2\) and \(f-f(x_0)\) is relatively solid v-nearly E-subconvexlike on S for all \(x_0\in S\).
Let \((a,b)\in S\) be a feasible point and suppose that \((a,b)\in \mathop {\mathrm{WOp}}\nolimits (f,S;E)\) or \((a,b)\in \mathop {\mathrm{Be}}\nolimits (f,S;E)\). We are going to apply Theorems 4.9 and 5.12. We have to find multipliers \(\lambda =(\lambda _1,\lambda _2)\in E^+\backslash \{0\}\) and \(\mu \ge 0\) satisfying the conclusions of the above theorems.
Condition (4.8) becomes
From here, it follows that \(\mu =\lambda _2\). Therefore, the above expression is equivalent to
We have that \(\lambda _2\ne 0\), because in the other case, since \(\lambda _2\ge \lambda _1\ge 0\) it would be \(\lambda _1=0\) and then \(\lambda =0\), which is a contradiction. For \(\lambda \in E^+\) one has \(\tau _E(\lambda )=\inf _{e\in E}\lambda (e)=\lambda _1\) (since the minimum is attained at \((1,0)\in E\)). In consequence, by dividing by \(\lambda _2\) in (5.7) we can assume that \(\lambda _2=1\) and \(0\le \lambda _1\le 1\). Thus, (5.7) is written as
and this expression can be divided into two parts:
As \(\lambda _1\ge 0\), equation (5.9) is equivalent to \((1-a)\lambda _1 -b\ge 0\), and this condition is deduced from (5.8) by choosing \(x=0\).
On the other hand, condition (5.4), i.e. \(\mu g(a,b)+\tau _E(\lambda )\ge 0\), reduces to \(\lambda _2(\varphi (a)-b)+\lambda _1\ge 0\), which (taking into account that we can assume \(\lambda _2=1\)) can be expressed in the following way
Inequality (5.11) is also a consequence of (5.9) by choosing \(x=a\), and inequality (5.10) is a consequence of (5.8) by choosing \(x=a\). The quadratic function
has the (global) minimum at the point \(x=-\lambda _1/2\le 0\), and the minimum is
So, condition (5.8) is satisfied if and only if \(-\frac{\lambda _1^2}{4}+(1-a)\lambda _1-b\ge 0\), i.e., if
The quadratic function \(\psi (\lambda _1):=\frac{\lambda _1^2}{4}+(a-1)\lambda _1+b\) has the (global) minimum at the point \(q_a:=2(1-a)\).
Case (i) \(q_a\ge 1\), that is, \(2(1-a)\ge 1\), or equivalently \(a\le 1/2\).
As \(\psi \) is strictly decreasing on [0, 1], there is a solution \(\lambda _1\in [0,1]\) satisfying (5.12) if
Hence if \(a\le 1/2\), \(b\le \frac{3}{4}-a\) and \((a,b)\in S\), we can take \(\lambda _1=1\), \(\lambda _2=1\).
Case (ii) \(0<q_a<1\), i.e., \(0<2(1-a)<1\), or equivalently \(1/2<a<1\).
The minimum of \(\psi \) is \(\psi (q_a)=\frac{4(1-a)^2}{4}+(a-1)\cdot 2(1-a)+b=b-(a-1)^2\), and so (5.12) is satisfied if and only if \(b-(a-1)^2\le 0\), that is, \(b\le (a-1)^2\). In this case, we can choose \(\lambda _1=q_a\) and \(\lambda _2=1\). Let us observe that \(0<\lambda _1<1\), and so \(\lambda =(\lambda _1,\lambda _2)\in K^{+s}\cap E^+\).
Case (iii) \(q_a\le 0\), i.e., \(a\ge 1\).
There is a solution of (5.12) with \(\lambda _1\in [0,1]\) and \(b\ge 0\) (remember that \((a,b)\in S\)) if and only if \(b=0\) and \( \lambda _1=0\), since \(\psi \) is strictly increasing on [0, 1] and \(\psi (0)=b\). Hence \(\lambda =(0,1)\in E^+\backslash K^{+s}\) satisfies (5.12).
Taking into account that the line \(b=3/4-a\), with \(a\le 1/2\), and the parabola \(b=a^2\) meet at \((-3/2,9/4)\), the above can be summarized as follows: for the points (a, b) that satisfy
there exist \(\lambda \in K^{+s}\cap E^+\) and \(\mu =1\in M^+\) satisfying the necessary conditions of Theorem 5.12. Moreover, it is easy to check that all these points (a, b) also satisfy the sufficient conditions of Corollary 5.15(iii) (the inequality above can be reverted). Therefore, \(\mathop {\mathrm{Be}}\nolimits (f,S;E)\) is the set of all points (a, b) satisfying (5.13). We know that they are also weak E-optimal points by Theorem 3.6. In addition, for the points
there exist \(\lambda =(0,1)\in E^+\) and \(\mu =1\in M^+\) satisfying the necessary conditions of Theorem 4.9. Moreover, it is easy to check that the points of (5.14) also satisfy the sufficient conditions of Theorem 4.11, and so they are weak E-optimal points too, and all of them (5.13)–(5.14) make the set \(\mathop {\mathrm{WOp}}\nolimits (f,S;E)\) up.
Finally, for the points (a, b) satisfying
there exists \(\lambda _1\ge 0\) such that \(\psi (\lambda _1)<0\), and so there exist \(\lambda \in E^+\) and \(\mu \in M^+\) satisfying the assumptions of Theorem 4.11 with strict inequality, i.e., \((a,b)\in \mathop {\mathrm{argmin}}\nolimits _X^<(\lambda \circ f+\mu \circ g,\tau _E(\lambda )+\mu (g(x_0)))\), and therefore \((a,b)\in \mathop {\mathrm{Op}}\nolimits (f,S;E)\). Let us note that the points (a, b) such that
are not E-optimal (this is proved by checking the definition), and so the set \(\mathop {\mathrm{Op}}\nolimits (f,S;E)\) is just defined by (5.15).
In the next figure, we have drawn the sets \(\mathop {\mathrm{Be}}\nolimits (f,S;E), \mathop {\mathrm{WOp}}\nolimits (f,S;E)\) and \(\mathop {\mathrm{Op}}\nolimits (f,S;E)\).

According to Corollary 5.15(iii), we have \(\mathop {\mathrm{He}}\nolimits (f,S;E)=\mathop {\mathrm{Be}}\nolimits (f,S;E)\).
Moreover, note that if we change E by \(E_1=\{(x,y)\in \mathbb {R}^2:~y\ge 0,~ x+y>1\}\), then \(\mathop {\mathrm{Op}}\nolimits (f,S;E_1)=\mathop {\mathrm{WOp}}\nolimits (f,S;E)\), \(\mathop {\mathrm{WOp}}\nolimits (f,S;E_1)=\mathop {\mathrm{WOp}}\nolimits (f,S;E)\) and \(\mathop {\mathrm{Be}}\nolimits (f,S;E_1)=\mathop {\mathrm{He}}\nolimits (f,S;E_1)=\mathop {\mathrm{Be}}\nolimits (f,S;E)\).
Remark 5.18
In several recent papers, constrained set-valued vector optimization problems as (2.3) are considered, i.e., f and g are assumed to be set-valued mappings and the feasible set S is given by \(S=\{x\in X:~g(x)\cap (-M)\ne \emptyset \}\). In this framework, different optimality conditions for approximate solutions are established under the assumption \(0\in g(x_0)\), see for example [23, Theorems 4.1 and 4.2], [24, Theorem 5.1], [26, Theorem 5.1] and [27, Theorem 3.1].
This assumption is very restrictive for dealing with approximate solutions. For instance, in Example 5.17, one can see that only the points in the boundary of the feasible set satisfy such condition. However, we have proved that there are many approximate solutions that do not satisfy it (see the figure above). For these points such results are not applicable even if \(E=q+K\) or \(E=K_0\).
6 Conclusions
In this paper, we study notions of approximate solution for optimization problems defined on real linear spaces without considering any topology, that is, just by using algebraic structures.
Specifically, we study approximate weak solutions and approximate proper solutions in the sense of Benson and Henig, where the error is determined by an improvement set E. This kind of sets frequently appears in the literature, because they are very used in economics and optimization.
We establish the relationships between these three types of solutions and we characterize them in terms of approximate solutions of associated scalar optimization problems, under generalized convexity assumptions. Moreover, when the feasible set is given by a cone-constraint, we also characterize these solutions by means of scalar Lagrangian optimality conditions.
Note that the scalarization techniques employed to characterize these solutions are linear. In a forthcoming paper, we are interested in obtaining other characterizations of approximate weak/efficient/proper solutions with respect to an improvement set. To carry this line out, the use of the approaches to derive optimality conditions due to Mordukhovich (see [20, Chapter 5]) or the so-called “smallest strictly monotonic functional” frequently used in mathematics (see [15, 19]) will be very interesting, as well as the comparison of the results obtained by means of these different techniques.
The results presented in this work extend to the algebraic setting several well-known results obtained in topological frameworks. On the other hand, in the literature the most usual notions of approximate efficiency and proper efficiency are defined in the Kutateladze sense (see [17]), i.e., by means of a vector. These concepts are particular cases of the corresponding notions introduced in this paper. Moreover, it is worth to underline that the use of a unique vector for measuring the error can cause in practice sets of approximate solutions that contains points too far from the efficient set. This fact was shown in [10, 11].
One more research line is to study conditions on the set E in the algebraic setting in order to avoid the above problem and to derive saddle point results for the solutions stated in this paper.
References
Adán, M., Novo, V.: Optimality conditions for vector optimization problems with generalized convexity in real linear spaces. Optimization 51(1), 73–91 (2002)
Adán, M., Novo, V.: Weak efficiency in vector optimization using a closure of algebraic type under cone-convexlikeness. Eur. J. Oper. Res. 149(3), 641–653 (2003)
Adán, M., Novo, V.: Proper efficiency in vector optimization on real linear spaces. J. Optim. Theory Appl. 121(3), 515–540 (2004)
Adán, M., Novo, V.: Proper efficiency in vector optimization on real linear spaces. Errata corrige. J. Optim. Theory Appl. 124(3), 751 (2005)
Bair, J., Fourneau, R.: Etude Géométrique des Espaces Vectoriels. Une Introduction. Lecture Notes in Mathematics 489. Springer, Berlin (1975)
Chicco, M., Mignanego, F., Pusillo, L., Tijs, S.: Vector optimization problems via improvement sets. J. Optim. Theory. Appl. 150(3), 516–529 (2011)
Debreu, G.: Theory of Value: An Axiomatic Analysis of Economic Equilibrium. Wiley, New York (1959)
Gutiérrez, C., Huerga, L., Novo, V.: Scalarization and saddle points of approximate proper solutions in nearly subconvexlike vector optimization problems. J. Math. Anal. Appl. 389(2), 1046–1058 (2012)
Gutiérrez, C., Jiménez, B., Novo, V.: Improvement sets and vector optimization. Eur. J. Oper. Res. 223(2), 304–311 (2012)
Gutiérrez, C., Huerga, L., Jiménez, B., Novo, V.: Proper approximate solutions and \(\varepsilon \)-subdifferentials in vector optimization: basic properties and limit behaviour. Nonlinear Anal. 79, 52–67 (2013)
Gutiérrez, C., Huerga, L., Jiménez, B., Novo, V.: Henig approximate proper efficiency and optimization problems with difference of vector mappings. J. Convex Anal. 23(3), 661–690 (2016)
Hernández, E., Jiménez, B., Novo, V.: Weak and proper efficiency in set-valued optimization on real linear spaces. J. Convex Anal. 14(2), 275–296 (2007)
Hiriart-Urruty, J.-B.: \(\varepsilon \)-Subdifferential calculus. In: Aubin, J.P., Vinter, R.B. (eds.) Convex Analysis and Optimization, Research Notes in Mathematics 57, pp. 43–92. Pitman, Boston (1982)
Jahn, J.: Vector Optimization. Theory, Applications, and Extensions. Springer, Berlin (2011)
Khan, A.A., Tammer, C., Zălinescu, C.: Set-Valued Optimization. An Introduction with Applications. Springer, Berlin (2015)
Kiyani, E., Soleimani-damaneh, M.: Approximate proper efficiency on real linear vector spaces. Pac. J. Optim. 10(4), 715–734 (2014)
Kutateladze, S.S.: Convex \(\varepsilon \)-programming. Sov. Math. Dokl. 20, 391–393 (1979)
Lalitha, C.S., Chatterjee, P.: Stability and scalarization in vector optimization using improvement sets. J. Optim. Theory Appl. 166(3), 825–843 (2015)
Luc, D.T.: Theory of Vector Optimization. Springer, Berlin (1989)
Mordukhovich, B.S.: Variational Analysis and Generalized Differentiation II. Applications. Springer, Berlin (2006)
Taa, A.: \(\varepsilon \)-Subdifferentials of set-valued maps and \(\varepsilon \)-weak Pareto optimality for multiobjective optimization. Math. Methods Oper. Res. 62(2), 187–209 (2005)
Xia, Y.M., Zhang, W.L., Zhao, K.Q.: Characterizations of improvement sets via quasi interior and applications in vector optimization. Optim. Lett. 10, 769–780 (2016)
Zhao, K.Q., Yang, X.M.: Characterizations of the E-Benson proper efficiency in vector optimization problems. Numer. Algebra Control Optim. 3(4), 643–653 (2013)
Zhao, K.Q., Yang, X.M., Peng, J.W.: Weak E-optimal solution in vector optimization. Taiwan. J. Math. 17(4), 1287–1302 (2013)
Zhou, Z.A., Peng, J.W.: Scalarization of set-valued optimization problems with generalized cone subconvexlikeness in real ordered linear spaces. J. Optim. Theory Appl. 154(3), 830–841 (2012)
Zhou, Z.A., Yang, X.M., Peng, J.W.: \(\varepsilon \)-Henig proper efficiency of set-valued optimization problems in real ordered linear spaces. Optim. Lett. 8(6), 1813–1827 (2014)
Zhou, Z.A., Yang, X.M., Peng, J.W.: \(\varepsilon \)-Optimality conditions of vector optimization problems with set-valued maps based on the algebraic interior in real linear spaces. Optim. Lett. 8(3), 1047–1061 (2014)
Acknowledgements
The authors are grateful to the anonymous referee and the Associated Editor for their useful suggestions and remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was partially supported by Ministerio de Economía y Competitividad (Spain) under Project MTM2015-68103-P (MINECO/FEDER).
Rights and permissions
About this article
Cite this article
Gutiérrez, C., Huerga, L., Jiménez, B. et al. Approximate solutions of vector optimization problems via improvement sets in real linear spaces. J Glob Optim 70, 875–901 (2018). https://doi.org/10.1007/s10898-017-0593-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-017-0593-y
Keywords
- Vector optimization
- Improvement set
- Approximate weak efficiency
- Approximate proper efficiency
- Nearly E-subconvexlikeness
- Linear scalarization
- Lagrange multipliers
- algebraic interior
- Vector closure