1 Introduction

Optimization in real-world problems is usually time consuming and computationally expensive in the evaluation of objective functions [1, 2]. Surrogate models are often useful to solve this difficulty. Surrogate models are constructed to promptly estimate the values of the objective functions at any point from sample points where real values of the objective functions are obtained by expensive computations. Therefore, it is important that accurate models can be constructed even with a small number of sample points.

The most common surrogate model is polynomial regression (PR) [3]. In construction of the PR model, users give the polynomial order arbitrarily and then compute the coefficients of each term in the polynomial fitting the sample points using the least-squares method. The accuracy of the PR model significantly depends on the polynomial order, which corresponds to the number of local maxima and/or minima in an objective function. However, it is not always possible to achieve sufficient accuracy by adjusting the order because the real shape of the objective function is usually not known. Generally, quadratic functions are employed to approximate the function locally in the real-world problems [4]. In this case, adequate optimization cannot be performed if the objective function has some local optima and too many sample points are required to obtain the global optimum. Furthermore, a Pareto dominance-based evolutionary multi-objective optimization algorithm explores large design space where diverse Pareto-optimal solutions exist. The surrogate models are also required to approximate large design space as accurately as possible. From this point of view, the local PR model with quadratic functions is not suitable for multi-objective problems.

To approximate complex functions, radial basis function (RBF) networks [5] and the Kriging model [6] are often used. Both of them can adapt well to complex functions because they approximate a function as a weighted superposition of basis functions such as Gaussian function. Thus, the model complexity can be controlled by changing the weight coefficients and variance of each basis function. Gaussian basis functions in the Kriging model have independently different variance values along each design variable direction to fit the complexity and scale while those of the RBF have the same values (Fig. 1). This anisotropy enhances the accuracy of the Kriging model. In addition, the Kriging model gives not only estimated function values but also approximation errors, which help users determine the locations of the additional sample points to improve the accuracy of the surrogate model. Jones et al. [7] have proposed the efficient global optimization (EGO) in which additional sample points are selected by maximizing the expected improvement (EI) value derived from the estimated function value and the approximation error. The EI value enables the Kriging model to efficiently explore the optimum as well as to improve the model accuracy.

Fig. 1
figure 1

Gaussian basis functions. a Radial basis function, b Kriging model

Full size image

It is desirable that one of these models approximates the function accurately. However, sometimes more complex models are needed. Hybrid methods that combine two surrogate models may be effective if the function consists of complex macro- and micro-trends [8, 9]. The universal Kriging model (PR+Kriging) [10] and the extended RBF (PR+RBF) [11] are typical hybrid methods. In contrast, Xiong et al. [12] proposed the non-stationary covariance based Kriging model whose variance values of each basis function vary depending on the location of the basis functions in the design space. This model showed good performance if the complexity of the objective function changes according to the location.

Some design variables can be correlated with each other in real-world problems, e.g., control points of spline curves and free-form deformation (FFD) [13]. Optimization with such design variables can express various configurations while the problem tends to become difficult to solve. However, only the PR model takes account of the correlation as the cross-terms among different variables though the PR model does not approximate the complex function accurately due to the reason described above.

In this study, we propose modified Kriging models suitable for the problems with correlated design variables by focusing on the anisotropy of Gaussian basis functions. It means finding out suitable coordinates in the design variable space, which represent significant trends in the objective function (Fig. 2a) and then defining the variance of basis functions along each coordinate in the transformed system (Fig. 2b). Suitable coordinates are identified using two criteria: one is based on likelihood derived by the Kriging model and the other uses estimated gradients of the objective function. The Kriging models with coordinate transformation based on likelihood (KCTL) and gradients (KCTG) and the ordinary Kriging (OK) model are applied to test functions and airfoil design problems to investigate the feature of the proposed models.

Fig. 2
figure 2

Extraction of suitable coordinates. a Objective function, b basis function

Full size image

2 Construction of Kriging models

The flowchart explaining EGO with KCTL, KCTG, and OK is summarized in Fig. 3. Initial sample points are generated uniformly in the design space using the Latin-hypercube sampling (LHS) method [14]. The Kriging models are constructed by interpolating these sample points. Construction of KCTG consists of three parts: construction of the Kriging model (OK) in the original coordinate system, coordinate transformation, and reconstruction of the Kriging model (KCTG) in the transformed coordinate system while OK and KCTL are constructed in a single part. An optimal solution is explored by the EGO framework, which explores the solution where the EI value becomes maximum by an optimizer such as evolutionary algorithm (the non-dominated sorting genetic algorithm II (NSGA-II) [15] is employed in our EGO system toward the application to multi-objective optimization in real-world problems) and adds it as an additional sample point. EGO is completed by iterating the procedure illustrated in Fig. 3 until a termination condition is satisfied. Generally, execution time and cost consumed for surrogate-based optimization are dominated by the function evaluation at sample points while those for surrogate model construction and optimal solution exploration on the model are ignorable. Hence, it can be said that better surrogate models should approximate functions more accurately with less sample points. The following present details of the Kriging models.

Fig. 3
figure 3

Flowchart of EGO with KCTL, KCTG, and OK

Full size image

2.1 Ordinary Kriging model

The Kriging model expresses the unknown function f(x) as

$$\begin{aligned} f(\mathbf{x})=\mu (\mathbf{x})+\varepsilon (\mathbf{x}), \end{aligned}$$
(1)

where x is an m-dimensional vector (m design variables), \(\mu \) (x) is a global model, and \(\varepsilon \) (x) represents a local deviation from the global model, which is defined as the Gaussian process following \(N(0, \sigma ^{2})\). The correlation between \(\varepsilon (\mathbf{x}^{i})\) and \(\varepsilon (\mathbf{x}^{j})\) is strongly related to the distance between the two corresponding points, \(\mathbf{x}^{i}\) and \(\mathbf{x}^{j}\). In the Kriging model, a specially weighted distance is used instead of the Euclidean distance because the latter weighs all design variables equally. The distance function between the points at \(\mathbf{x}^{i}\) and \(\mathbf{x}^{j}\) is expressed as

$$\begin{aligned} d(\mathbf{x}^{i},\mathbf{x}^{j})=\sum _{k=1}^m {\theta _k \left( {x_k^i -x_k^j } \right) ^{2}}, \end{aligned}$$
(2)

where \(\theta _{k}\,(0\le \theta _k <\infty )\) is the weight coefficient and the k-th element of an m-dimensional weight vector \({\varvec{\uptheta }}\). These weights give the Kriging model anisotropy and enhance its accuracy. The correlation between the points \(\mathbf{x}^{i}\) and \(\mathbf{x}^{j}\) is defined as

$$\begin{aligned} Corr\left( {\varepsilon (\mathbf{x}^{i}),\varepsilon (\mathbf{x}^{j})} \right) =\exp \left( {-d(\mathbf{x}^{i},\mathbf{x}^{j})} \right) . \end{aligned}$$
(3)

The Kriging predictor is

$$\begin{aligned} \hat{f}(\mathbf{x})=\hat{{\mu }}(\mathbf{x})+\mathbf{r}^{\mathrm{T}}{} \mathbf{R}^{-1}(\mathbf{f}-\hat{{\varvec{\upmu }}}), \end{aligned}$$
(4)

where \(\hat{{\mu }}(\mathbf{x})\) is the estimated value of \(\mu (\mathbf{x}), \mathbf{R}\) denotes the \(n\times n\) matrix whose (i, j) entry is \({\textit{Corr}}({\varepsilon (\mathbf{x}^{i}),\varepsilon (\mathbf{x}^{j})} )\), r is an n-dimensional vector whose i-th element is \({\textit{Corr}}({\varepsilon (\mathbf{x}),\varepsilon (\mathbf{x}^{i})} )\), and f and \(\hat{{\varvec{\upmu }}}\) denote as follows (n sample points):

$$\begin{aligned} \mathbf{f}=\left( {{\begin{array}{ccc} {f(\mathbf{x}^{1})}&{} \cdots &{} {f(\mathbf{x}^{n})} \\ \end{array} }} \right) ^{\mathrm{T}}, \end{aligned}$$
(5)
$$\begin{aligned} \hat{{\varvec{\upmu }}}=\left( {{\begin{array}{ccc} {\hat{{\mu }}(\mathbf{x}^{1})}&{} \cdots &{} {\hat{{\mu }}(\mathbf{x}^{n})} \\ \end{array} }} \right) ^{\mathrm{T}}. \end{aligned}$$
(6)

Thus, the unknown parameters in the Kriging model are \(\hat{{\sigma }}^{2}\) (estimated \(\sigma ^{2}), \hat{{\mu }}(\mathbf{x})\), and \({\varvec{\uptheta }}\), which are obtained by maximizing the following log-likelihood function:

$$\begin{aligned} Ln(\hat{{\mu }},\hat{{\sigma }}^{2},{{\varvec{\uptheta }} })= & {} -\frac{n}{2}\ln (2\pi )-\frac{n}{2}\ln (\hat{{\sigma }}^{2})-\frac{1}{2}\ln (\left| \mathbf{R} \right| )\nonumber \\&-\frac{1}{2\hat{{\sigma }}^{2}}(\mathbf{y}-\hat{{\varvec{\upmu }}})^{\mathrm{T}}{} \mathbf{R}^{-1}(\mathbf{y}-\hat{{\varvec{\upmu }}}). \end{aligned}$$
(7)

\(\hat{{\sigma }}^{2}\) is analytically determined through partial differentiation as

$$\begin{aligned} \hat{{\sigma }}^{2}=\frac{(\mathbf{f}-\hat{{\varvec{\upmu }}})^{\mathrm{T}}{} \mathbf{R}^{-1}(\mathbf{f}-\hat{{\varvec{\upmu }}})}{n}. \end{aligned}$$
(8)

The definition of \(\hat{{\mu }}(\mathbf{x})\) has some variations. The OK model, which is the most widely used Kriging model, assumes the global model to be a constant value as \(\hat{{\mu }}(\mathbf{x})=\hat{{\mu }}\). In this case, \(\hat{{\mu }}\) is also analytically determined as

$$\begin{aligned} \hat{{\mu }}(\mathbf{x})=\hat{{\mu }}=\frac{\mathbf{1}^{\mathrm{T}}{} \mathbf{R}^{-\mathbf{1}}{} \mathbf{f}}{\mathbf{1}^{\mathrm{T}}\mathbf{R}^{-\mathbf{1}}{} \mathbf{1}}, \end{aligned}$$
(9)

where 1 denotes an n-dimensional unit vector. Plugging in Eq. (8) for Eq. (7), the log-likelihood function becomes

$$\begin{aligned} Ln(\hat{{\mu }},\hat{{\sigma }}^{2},{{\varvec{\uptheta }} })=-\frac{n}{2}\left( {\ln (2\pi )+1} \right) -\frac{n}{2}\ln (\hat{{\sigma }}^{2})-\frac{1}{2}\ln (\left| \mathbf{R} \right| ). \end{aligned}$$
(10)

The first term can be ignored in the maximization because it has a constant value. Therefore, the log-likelihood maximization becomes an m-dimensional unconstrained non-linear optimization problem. In this study, a simple genetic algorithm is adopted to solve this problem.

2.2 Expected improvement

The accuracy of the function value predicted by the Kriging model depends largely on the distance from sample points. The closer point x is to the sample points, the more accurate the prediction, \(\hat{{f}}(\mathbf{x})\), becomes. This is expressed as:

$$\begin{aligned} s^{2}(\mathbf{x})=\hat{{\sigma }}^{2}\left( {\mathbf{1}-\mathbf{r}^{\mathrm{T}}{} \mathbf{R}^{-\mathbf{1}}{} \mathbf{r}+\frac{(1-\mathbf{1}^{\mathrm{T}}{} \mathbf{R}^{-\mathbf{1}}{} \mathbf{r})^{2}}{\mathbf{1}^{\mathrm{T}}\mathbf{R}^{-\mathbf{1}}{} \mathbf{1}}} \right) , \end{aligned}$$
(11)

where \(s^{2}\)(x) is the mean square error at point x, which indicates the uncertainty of the estimated value. Thus, estimated values in the Kriging model do not have deterministic values but follows the Gaussian distribution denoted by \(N(\hat{{f}}(\mathbf{x}),s^{2}(\mathbf{x}))\), from which the probability that the solution at point x may achieve a new global optimum can be calculated. The EI value, which corresponds to the expected value of the objective function improvement from the current optimal solution among the sample points, is also derived by using this probability. In f(x) minimization problem, the improvement value I(x) and the EI value, \(E\left( {I(\mathbf{x})} \right) \) of f(x) are expressed, respectively, as

$$\begin{aligned} I(\mathbf{x})= & {} \max ({f_{ref} -f,0} ), \end{aligned}$$
(12)
$$\begin{aligned} E({I(\mathbf{x})} )= & {} \int _{-\infty }^{f_{ref} } {(f_{ref} -f)\varphi (f)} df, \end{aligned}$$
(13)

where \(f_{ref}\) is the reference value of f and corresponds to the minimum value of f among the sample points in this study. \(\varphi \) is the probability density function denoted by \(N(\hat{{f}}(\mathbf{x}),s^{2}(\mathbf{x}))\) and represents uncertainty about f.

Special modification for EI has been proposed to enhance the constrained optimization [16]. A modified EI value is expressed by multiplying the probability satisfying the constraint to the conventional EI value. If the constraint function which should be approximated by the Kriging model is expressed as \(g(\mathbf{x})>c\), the modified EI (\(\hbox {E}_{\mathrm{c}}\hbox {I}\)) value is calculated as follows:

$$\begin{aligned} E_c \left( {I(\mathbf{x})} \right) =E\left( {I(\mathbf{x})} \right) \int _c^\infty {\varphi (g)} dg. \end{aligned}$$
(14)

2.3 Coordinate transformation based on likelihood function

An affine coordinate transformation is used in KCTL. Generally, such transformations are capable of rotation, scaling, translation, and shear mapping. However, scaling has the same effect as tuning the weight coefficient, \(\theta _{k}\) for each design variable in the Kriging model, and translation has no effect in the approximation of objective functions because design variables are normalized before constructing surrogate models. Only rotation is considered in KCTL because shear mapping violates the orthonormality of the design variables.

A rotation in multi-dimensional space is defined on each plane consisting of two arbitrary dimensions (design variables). In m-dimensional space, a rotation on all \({}_mC_2 ={m(m-1)}/2\) planes needs to be defined. For example, rotations in three-dimensional space are expressed as the product of three rotation matrices as follows.

$$\begin{aligned} \left[ {{\begin{array}{c} {y_1} \\ {y_2} \\ {y_3} \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{ccc} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\cos \phi _3 }&{}\quad {-\sin \phi _3 } \\ 0&{}\quad {\sin \phi _3 }&{}\quad {\cos \phi _3 } \\ \end{array} }} \right] \left[ {{\begin{array}{ccc} {\cos \phi _2 }&{} 0&{} {-\sin \phi _2 } \\ 0&{}\quad 1&{}\quad 0 \\ {\sin \phi _2 }&{}\quad 0&{}\quad {\cos \phi _2 } \\ \end{array} }} \right] \nonumber \\&\left[ {{\begin{array}{ccc} {\cos \phi _1 }&{}\quad {-\sin \phi _1 }&{}\quad 0 \\ {\sin \phi _1 }&{}\quad {\cos \phi _1 }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{c} {x_1} \\ {x_2} \\ {x_3} \\ \end{array} }} \right] . \end{aligned}$$
(15)

Note that the order of the rotational planes must be defined uniquely before the fact because the final coordinate transformation matrix changes with order even if the same rotation angles are applied to each rotational plane. KCTL is generated in the rotated coordinate system, \(\mathbf{y}=[y_1 ,\ldots ,y_m ]^{\mathrm{T}}\) instead of the original coordinate system, \(\mathbf{x}=[x_1 ,\ldots ,x_m ]^{\mathrm{T}}\).

Rotation angles in each plane are determined to maximize log-likelihood function in Eq. (10) which becomes a \(m(m + 1)/2\)-dimensional optimization problem with rotation angles, \(\phi _{\kappa }\) (\(0^{\circ }\le \phi _\kappa <90^{\circ } {\vert } \kappa = 1, \ldots , m(m - 1)/2)\) as variables besides \(\theta _{k}\) in the KCTL construction. \(\phi _{\kappa }\) from \(0^{\circ }\) to \(90^{\circ }\) is sufficient to arbitrarily define the rotated coordinate system because axes consisting of the plane where the rotation is conducted are orthogonal to each other. This optimization problem has a tendency to become extremely high-dimensional one (15-dimension when \(m = 5\), 55-dimension when \(m = 10\), and 120-dimension when \(m = 15\)). Thus, we adopt an artificial bee colony (ABC) algorithm [17], whose robustness to high-dimensional problems has already been confirmed [18], to solve this problem.

2.4 Coordinate transformation based on estimated gradients

To identify suitable coordinates and improve the approximation accuracy, gradients of the objective function to each design variable are employed in KCTG as is the case in the active subspace method [19]. First, the \(m\times m\) covariance matrix C, whose (k, l) entry is

$$\begin{aligned} C_{kl} =\frac{\partial \hat{{f}}}{\partial x_k}\frac{\partial \hat{{f}}}{\partial x_l}, \end{aligned}$$
(16)

is defined. The objective function estimated by the Kriging model, \(\hat{{f}}\) is used in this study whereas gradients of the real objective function are used in [19]. After the construction of OK in Fig. 3, the estimated gradients are calculated by differentiating Eq. (4) analytically as follows:

$$\begin{aligned} \frac{{{\partial \!\hat{f}}}(\mathbf{x})}{\partial x_k}=\left( {\frac{\partial \mathbf{r}}{\partial x_k }} \right) ^{\mathrm{T}}{} \mathbf{R}^{-1}(\mathbf{f}-\hat{\varvec{\upmu }}), \end{aligned}$$
(17)

where i-th element of \({\partial \mathbf{r}}/{\partial x_k }\) is

$$\begin{aligned} \left. {\frac{\partial \mathbf{r}}{\partial x_k }} \right| _i =-2\theta _k \left( {x_k -x_k^i } \right) \exp \left( {-\sum _{l=1}^m {\theta _l \left( {x_l^ -x_l^i } \right) ^{2}} } \right) . \end{aligned}$$
(18)

Using estimated gradients, neither the finite difference of the real objective function nor the adjoint computation [20] is needed; also the function evaluation costs are reduced immensely. Note that we can deal with the objective function as a black box function. This study calculates C at 100,000 points in the design space, which are randomly sampled using the Monte Carlo method, and averages them as \(\bar{\mathbf{C}}\). Second, an eigenvalue decomposition is performed on \(\bar{\mathbf{C}}\) as

$$\begin{aligned} \bar{\mathbf{C}}=\mathbf{W}\Lambda \mathbf{W}^{\mathrm{T}}, \end{aligned}$$
(19)

where \(\mathbf{W}=\left( {{\begin{array}{ccc} {\mathbf{w}_1 }&{} \cdots &{} {\mathbf{w}_m } \\ \end{array} }} \right) \) are the eigenvectors, which represent the suitable coordinates and \(\Lambda =\hbox {diag}\left( {{\begin{array}{ccc} {\lambda _1 }&{} \cdots &{} {\lambda _m } \\ \end{array} }} \right) \) is the eigenvalue matrix. Third, the design variable vector in the new coordinate system y is calculated from the original vector x as

$$\begin{aligned} \mathbf{y}=\mathbf{W}^{\mathrm{T}}{} \mathbf{x}. \end{aligned}$$
(20)

KCTG is constructed in the new coordinate system y in the same way as OK except its coordinate system.

3 Application to test functions

3.1 Test problem definition

KCTL, KCTG, and OK are applied to the following seven types (five of them are widely employed [7, 21,22,23]) of rotated and un-rotated (original) test functions with various dimensions:

Ellipsoid function:

$$\begin{aligned} f(\mathbf{x})=\sum _{i=1}^m {\left( {i\cdot y_i } \right) ^{2}} ; \end{aligned}$$
(21)

Rosenbrock function:

$$\begin{aligned} f(\mathbf{x})=\sum _{i=1}^{m-1} {\left( {\left( {1-y_i } \right) ^{2}+100\left( {y_{i+1} -y_i^2 } \right) ^{2}} \right) } ; \end{aligned}$$
(22)

Branin function:

$$\begin{aligned} f(x_1 ,x_2 )=\left( {y_2 -\frac{5.1}{4\pi ^{2}}y_1^2 +\frac{5}{\pi }y_1 -6} \right) ^{2}+10\left( {1-\frac{1}{8\pi }} \right) \cos y_1 +10; \end{aligned}$$
(23)

Translated Hartmann function (m = 3):

$$\begin{aligned} f(x_1 ,x_2 ,x_3 )=-\sum _{i=1}^4 {\alpha _i \exp \left[ {-\sum _{j=1}^3 {A_{ij} \left( {y_j -\left( {P_{ij} -0.5} \right) } \right) ^{2}} } \right] } , \end{aligned}$$
(24)

where \(\alpha =\left( {1.0,1.2,3.0,3.2} \right) ^{T}\)

$$\begin{aligned} A=\left[ {{\begin{array}{ccc} {3.0}&{}\quad {10}&{}\quad {30} \\ {0.1}&{}\quad {10}&{}\quad {35} \\ {3.0}&{}\quad {10}&{}\quad {30} \\ {0.1}&{}\quad {10}&{}\quad {35} \\ \end{array} }} \right] ,\;P=\left[ {{\begin{array}{ccc} {0.3689}&{}\quad {0.1170}&{}\quad {0.2673} \\ {0.4699}&{}\quad {0.4387}&{}\quad {0.7470} \\ {0.1091}&{}\quad {0.8732}&{}\quad {0.5547} \\ {0.0381}&{}\quad {0.5743}&{}\quad {0.8828} \\ \end{array} }} \right] ; \end{aligned}$$

Translated Hartmann function (\(m = 6\)):

$$\begin{aligned} f(x_1 ,x_2 ,x_3 ,x_4 ,x_5 ,x_6 )=-\sum _{i=1}^4 {\alpha _i \exp \left[ {-\sum _{j=1}^6 {A_{ij} \left( {y_j -\left( {P_{ij} -0.5} \right) } \right) ^{2}} } \right] } , \end{aligned}$$
(25)

where \(\alpha =\left( {1.0,1.2,3.0,3.2} \right) ^{T}\)

$$\begin{aligned} A= & {} \left[ {{\begin{array}{cccccc} {10}&{}\quad 3&{}\quad {17}&{}\quad {3.5}&{}\quad {1.7}&{}\quad 8 \\ {0.05}&{}\quad {10}&{}\quad {17}&{}\quad {0.1}&{}\quad 8&{}\quad {14} \\ 3&{}\quad {3.5}&{}\quad {1.7}&{}\quad {10}&{}\quad {17}&{}\quad 8 \\ {17}&{}\quad 8&{}\quad {0.05}&{}\quad {10}&{}\quad {0.1}&{}\quad {14} \\ \end{array} }} \right] \\ P= & {} \left[ {{\begin{array}{cccccc} {0.1312}&{}\quad {0.1696}&{}\quad {0.5569}&{}\quad {0.0124}&{}\quad {0.8283}&{}\quad {0.5886} \\ {0.2329}&{}\quad {0.4135}&{}\quad {0.8307}&{}\quad {0.3736}&{}\quad {0.1004}&{}\quad {0.9991} \\ {0.2348}&{}\quad {0.1451}&{}\quad {0.3522}&{}\quad {0.2883}&{}\quad {0.3047}&{}\quad {0.6650} \\ {0.4047}&{}\quad {0.8828}&{}\quad {0.8732}&{}\quad {0.5743}&{}\quad {0.1091}&{}\quad {0.0381} \\ \end{array} }} \right] . \end{aligned}$$

Sine function:

$$\begin{aligned} f(x_1 ,x_2 )=\sin \left( {2\pi y_1 } \right) \sin \left( {2\pi My_2 } \right) ; \end{aligned}$$
(26)

where M = 1, 2, 4

Parabolic function:

$$\begin{aligned} f(\mathbf{x})=y_1^2 ; \end{aligned}$$
(27)

The Hartmann functions are translated from the original domain [0, 1] to [−0.5, 0.5] because the functions are rotated around the origin of the coordinate system. All of them are minimization problems and functions of m design variables x (\(m = 2\) for the Branin function, the six-hump camel function, and the sine function and m = 3, 6 for the Hartmann functions) through intermediate variables y in the rotated coordinate system, as shown in Eq. (15) when \(m = 3\). All rotation angles are set to \(\phi _{i} = 30{^{\circ }}\) (\(i = 1, \ldots , m)\) when rotated functions are employed. Experimental conditions are summarized in Table 1, and the shapes of the original and rotated functions with m = 2 are shown in Fig. 4. Before comparing three models according to the EGO framework, they are compared at fixed numbers of sample points in the ranges described in Table 1. Sample points are generated by LHS and the number of samples depends on the non-linearity (dimension and order of polynomial) of test functions.

Subsequently, EGO with three models is conducted in multidimensional ellipsoid and Rosenbrock functions. Initial sample points are generated by LHS and additional sample points are employed one after another at the location where the EI value calculated by Eq. (13) becomes a maximum. The number of initial and additional samples is shown in Table 2. The numbers of population and generation in NSGA-II to maximize the EI value are 500 and 100, respectively. The EI value computed as a double-precision floating point number has the potential to become zero when test functions with low non-linearity are approximated with excessive numbers of sample points. If NSGA-II fails to find a candidate of an additional sample point due to this situation, NSGA-II maximizes mean square error defined by Eq. (11) and employs it as an additional sample points.

Table 1 Experimental conditions
Full size table

To compare the accuracy of the three models, the following root mean square error (RMSE) between the surrogate model and the real function is calculated at uniformly-distributed \(N\approx 10000\) validation points.

$$\begin{aligned} RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N {\left( {f(\mathbf{x}^{i})-\hat{{f}}(\mathbf{x}^{i})} \right) } ^{2}}. \end{aligned}$$
(28)

One hundred independent trials starting with different initial sample points are performed and the averaged RMSE is evaluated for comparison. The optimal solutions obtained by each model are also compared by averaged values in 100 trials when EGO is conducted.

Fig. 4
figure 4

Shapes of the two-dimensional test functions. a E2, b E2R, c R2, d R2R, e B2 and f B2R

Full size image

3.2 Results and discussion for test functions

3.2.1 Comparison between original and rotated test functions

E2, R2, B2, H3, H6, and their rotated versions are approximated by KCTL, KCTG, and OK to compare their model accuracy for rotated and un-rotated functions. Figure 5 show the averaged histories of RMSE. Table 3 summarizes statistics (mean, standard deviation, best, and worst) of RMSE in 100 trials when numbers of sample points are intermediate values between minimum and maximum presented in Table 1.

Table 2 Experimental conditions for EGO
Full size table

To begin, we focus on E2 and E2R which are the simplest functions in the test functions. KCTL achieves the lowest RMSE at any number of sample points in both functions because it can immediately identify the suitable coordinate system corresponding to the exact rotation angle. KCTG can also identify the suitable coordinate although KCTG and OK show comparable RMSEs in E2 and E2R. Both KCTL and KCTG can identify the suitable coordinate but only KCTL shows extremely high accuracy at 10 sample points in both functions even though OK is constructed with the exact coordinate system in E2. This is because only KCTL can tune the rotation angle to increase the likelihood function. The Kriging model approximates a function as a superposition of Gaussian functions whose centers correspond to the locations of sample points. Thus, slightly changing the rotation angle from the exact angle sometimes improves the model accuracy if a few sample points can be used.

In R2 and R2R, RMSE of KCTL decreases rapidly at around 15 sample points whereas KCTL cannot identify the suitable coordinate system with a few sample points. Note that KCTL should be employed with a sufficient number of initial sample points to guarantee its model accuracy. The rotation angles in KCTL correspond to the exact angles (\(0{^{\circ }}\) for R2 and \(30{^{\circ }}\) for R2R) when a sufficient number of sample points are employed. Additionally, transformed coordinate system of KCTG has converged toward \(0{^{\circ }}\) in R2 because R2 roughly symmetric about \(x_{1} = 0\), which leads the off-diagonal elements in \(\bar{\mathbf{C}}\) to zero. In approximation of R2R, it converges toward \(40{^{\circ }}\) which is slightly different from the exact rotation angle due to the asymmetric property of R2R and its large gradient around (\(x_{1}, x_{2}) = (1, -1)\). Nevertheless, KCTG has better coordinate system than OK and shows lower RMSE in Fig. 5d.

KCTL and KCTG can approximate B2R with the same accuracy as their approximation of B2: the histories of RMSE and the objective function value for B2 and B2R are virtually identical when more than 20 sample points are employed. It is applied to E2–E2R, R2–R2R, and H3–H3R as well. The coordinate transformation enables the Kriging models to approximate functions independent of the arbitrarily defined coordinate system (design variables). Thus, KCTL and KCTG are applicable to the optimization problems with design variables which do not correlate directly with the objective functions and have strong correlation among themselves (spline curves and FFD). High RMSEs of KCTG in B2 and B2R are derived from the misled coordinate system. B2 has three minimal points and two of them (left two in Fig. 4e) constitute a large valley along which KCTG makes the coordinate system rotate although the suitable coordinate system found by KCTL is the original one (\(x_{1}\) and \(x_{2})\). Additionally, KCTG and OK have the same RMSE in approximation of B2R because B2R also has this valley roughly along \(x_{2}\) axis.

The suitable coordinate systems of H3 and H3R correspond to their exact rotation angles because they consist of a superposition of four Gaussian functions. Therefore, RMSEs of KCTL and KCTG are lower than those of OK if sufficient sample points are employed.

Fig. 5
figure 5

Averaged histories of RMSE between original and rotated test functions. a E2, b E2R, c R2, d R2R, e B2, f B2R, g H3, h H3R, i H6 and j H6R

Full size image
Table 3 Statistics of RMSE for original and rotated test functions
Full size table

H6 and H6R should have the same trend as H3 and H6R. However KCTL has extremely high RMSE in these functions because of their high dimensionality which makes it difficult to find the suitable coordinate system; maximizing likelihood function becomes a 21-dimensional optimization problem in KCTL when \(m = 6\). This optimization itself is solved appropriately, but the likelihood function fails to lead KCTL to a suitable coordinate system in these cases. Instead of KCTL, KCTG should be employed to approximate the functions with more than five correlated design variables. KCTG shows the same trend as OK for not only H6 but also H6R, although KCTG is expected to show higher accuracy than OK in H6R. H3 and H3R have large gradients along the first design variable in all four Gaussian functions constructing them, as the first column has lowest values in each row of matrix A in Eq. (24). In contrast, the steepest directions of the four Gaussian functions constructing H6 and H6R are not the same [matrix A in Eq. (25)], which makes KCTG fail in finding a suitable coordinate system.

The statistics of RMSE are strongly correlated with mean values shown in Fig 5. KCTL mostly achieves the lowest statistics in the functions where KCTL has the lowest mean RMSE among three models (E2, E2R, R2, R2R, B2, and B2R). By contrast, KCTL has the highest values in most statistics in H6 and H6R where approximation accuracy of KCTL is poor.

3.2.2 Comparison among the sine functions with different wavelengths

Three methods are applied to the sine functions to investigate effects of wavelength difference between two directions because shorter wavelength with higher gradient means stronger contribution to an objective function. The averaged histories of RMSE for each function are shown in Fig. 6. Compared to OK, both KCTL and KCTG cannot improve approximation accuracy in S2R1 where wavelengths in two directions are the same. Obviously, KCTG is not suitable for this function because gradients along any directions are the same. On the other hand, KCTL frequently find out the suitable coordinates although its approximation accuracy is not improved. Figure 7 shows rotation angle histograms for S2R1 with 50 sample points. The histogram of KCTL has a peak around \(30{^{\circ }}\) while that of KCTG is uniformly distributed. Hence, KCTL can identify the suitable coordinates even though gradients have no trend along any directions. In S2R2 and S2R4, both KCTL and KCTG find out the suitable coordinates and accomplish better approximation accuracy than OK. Their accuracy improvement are emphasized as the wavelength difference becomes large.

Fig. 6
figure 6

Averaged histories of RMSE among the sine functions. a S2R1, b S2R2 and c S2R4

Full size image
Fig. 7
figure 7

Rotation angle histograms for S2R1 with 50 sample points. a KCTL and b KCTG

Full size image
Fig. 8
figure 8

Averaged histories of RMSE for multi-dimensional functions. a E3R, b E4R, c E5R, d E10R and e P10R

Full size image

3.2.3 Comparison among multi-dimensional functions

A multi-dimensional rotated ellipsoid and parabolic functions are employed to investigate the capability of KCTL and KCTG for relatively high-dimensional optimization problems. Figure 8 shows the averaged histories of RMSE. KCTL shows the best accuracy except for E10R. Note that KCTL successfully approximates objective functions with the number of effective correlated design variables no greater than five. Both E10R and P10R includes 10 design variables though KCTL behaves in different manners. E10R is a function of all translated design variables (10 effective variables) though P10R is a function of only \(y_{1}\) in the translated coordinate system.

KCTG is applicable to high-dimensional functions with many effective variables such as E10R. Comparing E5R and E10R, the difference in RMSE between KCTG and OK is clearer in E10R. KCTG is more suitable for real-world optimization problems with correlated design variables than KCTL. This is because spline curves and FFD usually include 10–300 control points as design variables [24, 25], and more than five variables may be effective even in the translated coordinate system.

3.2.4 Comparison in efficient global optimization

Multi-dimensional rotated ellipsoid and Rosenbrock functions are minimized by EGO with KCTL, KCTG, and OK to compare their exploration capability for rotated functions. Figure 9 shows the averaged histories of the objective function value of optimal solution in the sample points. KCTL shows the best performance in each optimization except for E10R. Thus, KCTL not only approximates objective functions more accurately but also optimizes them more efficiently when the number of correlated design variables is no greater than five.

KCTG also finds optimal solutions with less sample points than OK in most functions including E10R although the optimal solution obtained by OK sometimes exceeds that obtained by KCTG when all additional sample points are employed. KCTG finds the quasi-optimal solution around the exact optimal solution in the early stages of the EGO process. It prohibits KCTG from exploring the exact optimal solution to exploit another domain of the design space because EGO is based on two principles: exploration and exploitation.

Fig. 9
figure 9

Averaged histories of the objective function value. a E2R, b E3R, c E4R, d E5R, e E10R, f R2R, g R3R, h R4R and i R5R

Full size image

3.3 Application to an airfoil design problem

The results in Sect. 3 show that KCTG approximates the function accurately regardless of the coordinate system and the dimension and has an advantage in the optimization with correlated design variables. However, the test functions in Sect. 3 include simple ones and roughly symmetric ones. We must evaluate the practicality of KCTG through a real-world shape design optimization problem, which includes correlated design variables for shape representation such as the control points of spline curves. In Sect. 4, an airfoil design optimization is considered with KCTG and OK to investigate the effects of the coordinate transformation in a real-world problem.

3.4 Design problem definition

The objective function and the constraints in the airfoil design problem are defined as follows:

$$\begin{aligned}&\hbox {Maximize }L/D, \end{aligned}$$
(29)
$$\begin{aligned}&\hbox {subject to }C_m \ge -0.1535, \end{aligned}$$
(30)
$$\begin{aligned}&{t_{\max } }/c\ge 0.11, \end{aligned}$$
(31)

at the angle of attack \(\alpha = 4{^{\circ }}\) and the Reynolds number \(\hbox {Re}=5\times 10^{5}\). L / D and \(C_{m}\) denote the lift-drag ratio and the pitching moment coefficient, respectively. \(t_{\max }\) is the maximum thickness of the airfoil and c is the chord length. L / D and \(C_{m}\) at the sample points are evaluated by a subsonic flow solver “XFOIL” [26] which calculates incompressible viscous flow in this study. Hence, KCTG and OK are used to estimate these two values whereas \(t_{\max }/c\) is calculated directly by representing the airfoil. Generally, computational times for XFOIL are less than one second for one flow condition. This study employs XFOIL to achieve many independent trials of airfoil design optimization and evaluate statistics of the results properly. The constraint values in Eqs. (30) and (31) correspond to those of DAE31 airfoil whose L / D is 138.6.

The nine design variables correspond to the locations of nine control points for two non-uniform rational basis spline curves defining the airfoil thickness distribution and camber line in Fig. 10. The five red dots and four blue dots are the control points for thickness and camber, respectively; the red and blue bars show the ranges of each design variable. Only \(x_{3}\) has a relatively small range to help the maximum thickness meet the constraint in Eq. (31). Each range is shown as follows:

$$\begin{aligned}&0.02\le x_1 \le 0.04, \quad 0.05\le x_2 \le 0.09, \quad 0.12\le x_3 \le 0.13,\nonumber \\&0.09\le x_4 \le 0.13, \quad 0.00\le x_5 \le 0.04, \quad 0.02\le x_6 \le 0.06,\nonumber \\&0.02\le x_7 \le 0.06, \quad 0.02\le x_8 \le 0.06, \quad 0.00\le x_9 \le 0.04. \end{aligned}$$
(32)

Fifty initial sample points are generated by LHS and 150 additional sample points are employed one after another at the location where the \(\hbox {E}_\mathrm{c}\hbox {I}\) value calculated by Eq. (14) becomes a maximum. KCTG and OK are compared by optimal solutions obtained by EGO with each model and RMSE in Eq. (28) where validation points are generated by LHS and \(N = 10,000\). Seventy independent trials are performed and their averaged \(L/D, C_{m}\), and RMSE are evaluated. The numbers of population and generation in NSGA-II are 500 and 100, respectively, as for the case in Sect. 3.

Depending on the airfoil shape, the flow computation with XFOIL sometimes does not converge. An alternative initial sample point and validation point are randomly selected from the entire design space if convergence is not achieved. The same treatment is applied if an initial sample point and a validation point do not meet at least one of the constraints.

Fig. 10
figure 10

Design variables and their ranges

Full size image

3.5 Results and discussion for airfoil design problem

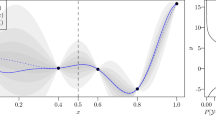
Figure 11 shows the averaged histories of RMSE for L / D and \(C_{m}\). KCTG reduces RMSE of L / D compared with that for OK at any number of sample points in EGO process. Therefore, it is shown that KCTG can approximate the function for a real-world problem using spline curves as design variables more accurately than OK. Regarding \(C_{m}\), OK has lower RMSE than KCTG although both models converge along similar trends with increasing sample points. From aerodynamic theory, \(C_{m}\) is regarded as a function that depends on the camber line and is not affected by the thickness, i.e., the effective number of design variables for \(C_{m}\) is almost 4. OK does not consider the correlation between camber and thickness, which enables OK to easily ignore the variables related with the thickness by decreasing the weight coefficients in Eq. (2). KCTG can also ignore these variables although the coordinate transformation may disturb it in an early stage of EGO.

Approximation accuracy is strongly related to the transformed coordinate system. Figure 12 shows eigenvalue proportions for each mode (eigenvector), which correspond to the squared gradients of the objective and constraint functions estimated by KCTG along each transformed coordinate. The estimated gradient of L / D is mostly occupied by the first and second modes whose eigenvalue proportions are about 95% in total whereas 95% is accomplished with the first three modes in \(C_{m}\). L / D has a suitable coordinate system representing the significant trend of the function and KCTG successfully identifies this coordinate system. In contrast, KCTG fails to find a suitable coordinate system in the approximation of \(C_{m}\), or \(C_{m}\) originally does not have such a suitable coordinate system. As a result, eigenvalue proportions are more widely dispersed in \(C_{m}\) than L / D, and KCTG and OK have comparable RMSEs. Additionally, Fig. 13 shows eigenvectors of the first three modes, which indicate design variables related to the airfoil’s camber line (\(x_{6}\)–\(x_{9})\) are dominant in both L / D and \(C_{m}\). \(C_{m}\) is also sensitive to the airfoil’s thickness at the trailing edge (\(x_{5})\) because the elements of the eigenvectors for \(x_{5}\) have large values in the second and third modes. This makes KCTG even more difficult to approximate \(C_{m}\).

Averaged histories of L / D and \(C_{m}\) at the optimal solution among feasible sample points are shown in Fig. 14. KCTG obtains better solutions than OK on average when the number of sample points is over 67. \(C_{m}\) values are comparable between two models. Therefore, it is suggested that KCTG has an advantage over OK not only in approximation accuracy but also in the ability to explore the optimal solution if design variables are correlated with each other.

Fig. 11
figure 11

Averaged histories of RMSE for airfoil design problem. a L / D and b \(C_m\)

Full size image
Fig. 12
figure 12

Eigenvalue proportion for each mode in KCTG. a L / D and b \(C_m\)

Full size image
Fig. 13
figure 13

Eigenvectors for each mode in KCTG. a L / D and b \(C_m\)

Full size image
Fig. 14
figure 14

Averaged histories of the objective function and constraint values at the optimal solution for airfoil design problem. a L / D and b \(C_m\)

Full size image

4 Conclusions

The Kriging models with coordinate transformation based on likelihood and gradients were proposed and validated in various test functions and an airfoil design problem with correlated design variables. A suitable coordinate system was identified by maximizing likelihood function or by finding the eigenvalues of the covariance matrix of the estimated objective function gradients along each design variables. Averaged RMSEs between surrogate models and the real objective function and the optimal solutions obtained by efficient global optimization were used to evaluate the practicality of the proposed methods.

In the application to test functions, the proposed methods approximated the entire function shape more accurately than the conventional method if design variables were correlated with each other and a sufficient number of sample points were employed. The proposed methods also showed greater comparative accuracy to the conventional method even if the correlation between design variables was not strong. The capability to explore the optimal solution was also better than the conventional method if the proposed method achieved higher approximation accuracy. Additionally, maximizing the likelihood function in the Kriging model was preferable in finding a suitable coordinate system for functions with correlated design variables although this method did not function well when the number of design variables was greater than five. The coordinate transformation based on estimated gradients was available for functions with more than five design variables. This method was more suited to real-world optimization problems with correlated design variables than the former because real-world problems usually include 10–1000 design variables.

Control points of the non-uniform rational basis spline curves defining an airfoil’s thickness distribution and camber line were employed as the correlated design variables in the airfoil design optimization. The latter proposed method approximated the objective function (lift–drag ratio) more accurately and found better solutions than the conventional method although the constraint function (pitching moment coefficient) was difficult to approximate by the proposed method. Therefore, the proposed method revealed usefulness in real-world optimization problem with correlated design variables.

In this study, optimization problems with up to ten design variables were adopted. The number is relatively smaller than the usual number of design variables in real-word optimization problems which use spline curves and free form deformation for shape definition. Moreover, these real-world problems tend to have more than two objective functions. Therefore, in the future, it is desirable that the proposed method is validated in the multi-objective optimization problems with more design variables.