The extended supporting hyperplane algorithm for convex mixed-integer nonlinear programming

Abstract

A new deterministic algorithm for solving convex mixed-integer nonlinear programming (MINLP) problems is presented in this paper: The extended supporting hyperplane (ESH) algorithm uses supporting hyperplanes to generate a tight overestimated polyhedral set of the feasible set defined by linear and nonlinear constraints. A sequence of linear or quadratic integer-relaxed subproblems are first solved to rapidly generate a tight linear relaxation of the original MINLP problem. After an initial overestimated set has been obtained the algorithm solves a sequence of mixed-integer linear programming or mixed-integer quadratic programming subproblems and refines the overestimated set by generating more supporting hyperplanes in each iteration. Compared to the extended cutting plane algorithm ESH generates a tighter overestimated set and unlike outer approximation the generation point for the supporting hyperplanes is found by a simple line search procedure. In this paper it is proven that the ESH algorithm converges to a global optimum for convex MINLP problems. The ESH algorithm is implemented as the supporting hyperplane optimization toolkit (SHOT) solver, and an extensive numerical comparison of its performance against other state-of-the-art MINLP solvers is presented.

1 Introduction

Mixed-integer nonlinear programming (MINLP) is a challenging field of optimization since the problem class can contain both continuous and discrete variables as well as linear and nonlinear functions. MINLP has received a great deal of interest both from the scientific and industrial communities due to its ability to accurately model complex systems. Even though the first algorithm for solving MINLP problems was presented as early as in the 1960s [7], general MINLP problems are still considered difficult and some classes of MINLP problems are even proven undecidable [14]. Here we will consider a subclass of MINLP problems where the feasible set is defined by linear and convex nonlinear constraints. Note that a MINLP problem is referred to as convex if the integer-relaxed problem is convex.

There are several versatile algorithms for solving convex MINLP problems, e.g., generalized Benders decomposition [13], outer approximation (OA) [8], branch-and-bound techniques using nonlinear programming (NLP) subsolvers [7, 17] and the extended cutting plane (ECP) algorithm [28]. However, solving convex MINLP problems efficiently is still a difficult task as shown in the solver comparisons later on. Some global solution techniques for nonconvex MINLP solve sequences of overestimated convex MINLP subproblems in order to find global optima of nonconvex problems [18–20]. For these global solution techniques the ability to efficiently solve convex MINLP problems is of paramount importance. A thorough review of deterministic global MINLP is given in [10]. Overall the ability to efficiently solve MINLP problems is of great importance, due to the huge amount of real-world applications with both economical and environmental impact.

In this paper, a new algorithm called the extended supporting hyperplane (ESH) algorithm for convex MINLP is presented. Like the ECP algorithm and OA, the method uses linearizations of the nonlinear functions to generate an overestimated set of the feasible domain. Unlike the ECP algorithm the linearizations form supporting hyperplanes to the feasible set, and should therefore generate tighter linear approximations. The linearization point is found by a simple line search procedure unlike OA, where the linearization point is obtained from an NLP subproblem. The ESH algorithm is described in detail in Sect. 2, where it is also proven convergent under mild assumptions.

To evaluate the performance of the ESH algorithm it has been implemented as a solver utilizing several of the subprojects in the open source Computational Infrastructure for Operations Research (COIN-OR) project. The solver implementation has been compared against several state-of-the-art deterministic MINLP solvers available in the General Algebraic Modeling System (GAMS). All problem instances classified as convex and containing at least one discrete variable in MINLP Library 2 (MINLPLib 2) were used in the comparison. MINLPLib 2 is a problem library containing a large variety of both theoretical and real-world optimization problems [22]. As of May 2015 the total number of instances in the library was 1359 and 333 of these are classified as convex and contain discrete variables. The following solvers were used in the comparison: AlphaECP, ANTIGONE, BARON, BONMIN, DICOPT, SBB and SCIP.

Since AlphaECP is based on the ECP algorithm, it creates a linear approximation of the original MINLP problem by solving a sequence of mixed-integer linear programming (MILP) problems and generating cutting planes in the solution point obtained. Additional features are also incorporated in the solver improving the convergence and ensuring global optimality for MINLP problems with both pseudoconvex objective function and pseudoconvex constraint functions [16, 29]; the solver has a pure convex strategy as well which was used in the comparison. Algorithms for coNTinuous/Integer Global Optimization of Nonlinear Equations (ANTIGONE) is a general optimization framework for nonconvex MINLP. It uses several reformulation techniques and a branch-and-cut global optimization algorithm [23]. BARON (Branch And Reduce Optimization Navigator) is another global solver for nonconvex MINLP. It combines a conventional branch-and-bound algorithm with a wide variety of range reduction tests [25]. Although ANTIGONE and BARON are solvers for nonconvex MINLP, they both have convexity identification procedures increasing the performance on convex problems. DICOPT (DIscrete and Continuous OPTimizer) is an MINLP solver based on OA and finds global optima to MINLP problems with convex objective functions and convex constraint functions. DICOPT generates iteratively improving linear approximations of the original problem and solves a sequence of MILP and NLP subproblems [15]. Simple Branch-and-Bound (SBB) implements a branch-and-bound algorithm and solves an NLP problem in each node [4]. SBB is a convex solver and cannot guarantee optimal solutions to nonconvex MINLP problems. Basic Open-source Nonlinear Mixed INteger programming (BONMIN) is an open source MINLP solver implementing branch-and-bound, branch-and-cut and outer approximation algorithms [3, 6]. Like DICOPT and SBB, BONMIN is a convex solver and can only guarantee optimal solutions to convex MINLP problems. Solving Constraint Integer Programs (SCIP) implements a spatial branch-and-bound algorithm and utilizes linear relaxations for the bounding step [6]. SCIP can handle nonconvex MINLP problems by implementing convex relaxations but the solver has a convex strategy as well.

The ESH algorithm is described in more detail in the next section, where a proof of convergence for convex MINLP problems and two illustrative examples are also provided. In Sect. 3 the solver implementation is briefly described and a numerical comparison with the MINLP solvers mentioned above is given in Sect. 4. Finally, some ideas for future work and conclusions are given in Sects. 5 and 6.

2 The ESH algorithm

The ESH algorithm is intended for solving convex MINLP problems of the type

where $x = [x_1,x_2,\ldots ,x_N]^T$ is a vector of continuous variables in a bounded set

$$\begin{aligned} X=\left\{ x \, \left| \, {\underline{x}_i}\le x_i \le {\overline{x}_i},\ i =1,\ldots ,N \right. \right\} \end{aligned}$$

(P-MINLP)

and the feasible set $L \cap C \cap Y$ is defined by

$$\begin{aligned} L= & {} \left\{ x \, \left| \, Ax\le a,\ Bx = b,\ x \in X\right. \right\} ,\nonumber \\ C= & {} \left\{ x \, \left| \, g_m(x) \le 0,\ m=1,\ldots ,M,\ x \in X\right. \right\} , \nonumber \\ Y= & {} \left\{ x \, \left| \ x_i \in {\mathbb {Z}},\ \forall i \in {I_{\mathbb {Z}}},\ x \in X\right. \right\} . \end{aligned}$$

(1)

X is a compact subset of an N-dimensional Euclidean space $X \subset {\mathbb {R}^{N}}$ restricted by the variable bounds. The sets L and C are defined by the regions satisfying the linear and nonlinear constraints respectively. The linear equalities and inequalities are defined by the matrices A and B together with the vectors a and b. In this paper, it is assumed that all of the constraint functions $g_m:{\mathbb {R}}^N \rightarrow {\mathbb {R}}$ are bounded, continuously differentiable and convex within X. If all the functions $g_m$ are convex it is obvious that the set C is convex since convex functions have convex level sets. If some variables $x_i$ in (P-MINLP) are restricted to integer values their corresponding indices are included in the index set ${I_{\mathbb {Z}}}\subset \left\{ 1,2,\ldots N\right\}$, and the set Y defines the space of all integer values of these variables. In case no discrete variables are present, (P-MINLP) is simply an NLP problem. Although the ESH algorithm is capable of handling convex NLP problems, it is intended for solving MINLP problems, and it is from now on assumed that some variables in (P-MINLP) are restricted to integer values. The objective function in (P-MINLP) is written in linear form and it is defined as $c^Tx$, where c is a vector of constants; nonlinear convex objective functions are further discussed in Sect. 2.7.

The ESH algorithm solves a sequence of linear programming (LP) and MILP subproblems where the convex set C is overestimated by a finite number of hyperplanes. The linear approximation of C is improved in each iteration by generating new supporting hyperplanes. In order to minimize the number of MILP subproblems required for solving the original MINLP problem, integer-relaxed MILP problems are solved. Supporting hyperplanes are rapidly generated from the integer-relaxed problems creating an initial linear overestimation of the set C. An interior point of the convex set C is required in order to find the generation point of the supporting hyperplanes and can, e.g., be found by solving a nonlinear minimax problem. The different steps and subproblems in the algorithm are summarized in Algorithm 1 and described in more detail in the following subsections.

2.1 The NLP step

In the ESH algorithm an interior point $x_\text {NLP}$ is first obtained by solving the following convex NLP problem

$$\begin{aligned} \text {find} \ x_\text {NLP} \in \mathop {\hbox {arg min}}\limits _{x \in X \cap L} F(x), \end{aligned}$$

(2)

where

$$\begin{aligned} F(x) := \max _{m} \left\{ g_m(x)\right\} \end{aligned}$$

(P-NLP)

using a suitable method. Note that $x_\text {NLP}$ is not necessarily a feasible solution to (P-MINLP). However, in this paper a point within the interior of C is referred to as an interior point. Observe that a valid interior point can also be obtained by minimizing F within X, which might be an easier problem and therefore favorable in some cases. Since F is defined as the pointwise maximum of all the nonlinear constraint functions $g_m$, it is convex if all $g_m$ are convex functions. Note that (P-NLP) may be a nonsmooth problem if $M > 1$ even if all functions $g_m$ are smooth. Therefore a standard gradient based method might fail to solve (P-NLP) and instead a nonsmooth approach, e.g., a bundle method, can be used [2]. A survey of nonsmooth bundle methods is given in [21].

However, since all the functions $g_m$ are convex, (P-NLP) can also be formulated as an equivalent smooth NLP problem by adding an auxiliary variable $x_{N+1}$ and defining the variable vector $y=[x_\text {NLP}, \ x_{N+1}]^T$. An interior point $x_\text {NLP}$ can then be obtained by solving the following smooth NLP problem

$$\begin{aligned} \text {find} \ y\in \mathop {\hbox {arg min}}\limits _{y \in X \cap L \cap C^*} x_{N+1}, \end{aligned}$$

(3)

where

$$\begin{aligned} C^*=\left\{ y \, \left| \ g_m(x) -x_{N+1} \le 0,\ m=1,\ldots ,M ,\ x \in X,\ x_{N+1} \in {\mathbb {R}}\right. \right\} . \end{aligned}$$

Note that the functions $g_m(x) -x_{N+1}$ are still convex and hence (P-NLP*) can be solved with any suitable convex NLP solver. Assuming that (P-MINLP) has a solution, there exist at least one point $x_\text {NLP} \in X \cap L\cap C^*$ such that $F(x_\text {NLP}) \le 0$. For the line search procedure it is required that the point $x_\text {NLP}$ is within the interior of the convex set C and not on the boundary, otherwise the line search can result in identical solutions in each iteration. Therefore it is from here on assumed that C has a nonempty interior and there exists a point $x_\text {NLP} \in X \cap L\cap C^*$ such that $F(x_\text {NLP}) < 0$, see Remark 1. Note that it is not necessary to solve the previously mentioned NLP problems to optimality as long as a feasible solution fulfilling $F(x_\text {NLP}) < 0$ is obtained.

2.2 The LP step

After the solution to (P-NLP) is obtained, a tight overestimated set $\varOmega _k$ of the convex set C can be generated by iteratively solving a sequence of simple LP problems and conducting line searches for the boundary of C. Initially the counter $k=1$, the set $\varOmega _0 = X \cap L$, and the following relaxation of (P-MINLP) only considering the variable bounds and linear constraints, is solved:

$$\begin{aligned} \text {find} \ x_{\text {LP}}^k \in \mathop {\hbox {arg min}}\limits _{x \in \varOmega _{k-1}} c^T x. \end{aligned}$$

(P-NLP*)

The set $\varOmega _0$ can also be defined simply as $\varOmega _0 = X$, which might simplify the solution of problem (P-LP). The linear constraints could then be ignored in the LP step or added to $\varOmega _k$ after some iterations. However, since the goal is to obtain a tight linear relaxation of the set C within $L \cap C$ it is usually favorable to immediately add the linear constraints to (P-LP). Assuming there exists a solution to (P-MINLP), then (P-LP) has to be feasible. If $F(x_{\text {LP}}^k) \le 0$, then the integer relaxation of (P-MINLP) is bounded only by the linear constraints and the LP step can be terminated. Otherwise, i.e., if $F(x_{\text {LP}}^k) > 0$, $F(x_\text {NLP})$ and $F(x_\text {LP}^k)$ have different signs and it is possible to update the set $\varOmega _k$ by generating new supporting hyperplanes through a line search procedure.

After solving (P-LP), a line search is performed between $x_\text {NLP}$ and $x_{\text {LP}}^k$, i.e., the equation

$$\begin{aligned} x^k = \lambda _k x_\text {NLP} + (1-\lambda _k) x_{\text {LP}}^k, \end{aligned}$$

(P-LP)

is used to find the value of $\lambda _k \in [0,1]$ such that $F(x^k) = 0$. Since F is a continuous function there exists a solution to Eq. (4) according to the intermediate value theorem and due to the convexity of F only one such solution exists. At the point $x^k$ supporting hyperplanes defined by

$$\begin{aligned} l_{k,m} = \nabla g_m \left( x^k\right) ^T \left( x-x^k\right) \le 0 \end{aligned}$$

(4)

are generated for all functions $g_m$ active at $x^k$ (functions such that $g_m(x^k)=F(x^k)$). The line search and supporting hyperplane generation are illustrated in Fig. 1. Note that all the gradients $\nabla g_m (x^k)$ of the active functions are valid subgradients of the functions F at the point $x^k$. The LP step generates at least one supporting hyperplane and at most M supporting hyperplanes in each iteration. Thus, the set $\varOmega _k$ is updated to

$$\begin{aligned} \varOmega _{k} = \left\{ x \, \left| \, l_{k,m}(x) \le 0 \quad \forall m: g_m\left( x^k\right) =0, \ x \in \varOmega _{k-1}\right. \right\} . \end{aligned}$$

(5)

The problem (P-LP) is solved repeatedly (increasing the counter k in the next iteration) until a maximum number of iterations has been reached, or until

$$\begin{aligned} F\left( x_{\text {LP}}^k\right) \le \varepsilon _{\text {LP}} \end{aligned}$$

(6)

where $\varepsilon _{\text {LP}}$ is a desired tolerance for the nonlinear constraints in the LP step.

Fig. 1

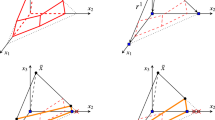
A sketch of the main principle of the ESH algorithm: a line search for the point $x^k$ such that $F(x^k) = 0$ is performed between the point obtained from the (MI)LP relaxation $x_{\text {(MI)LP}}$ and the interior point $x_{\text {NLP}}$. A supporting hyperplane $l_k$ is generated at the point $x^k$. (Color figure online)

In Sect. 2.6, it will be proved that the solution to the LP step converges to a point within the set C. Although the LP step actually solves an integer relaxation of (P-MINLP) with the supporting hyperplane method [26], the actual solution to the integer-relaxed problem is of little interest and can merely be used as a lower bound for the original problem. Instead, the goal is to obtain an initial overestimated set $\varOmega _k$ to reduce the number of MILP iterations required to solve the original problem.

2.3 The MILP step

Once a linear approximation of the nonlinear constraints has been obtained through the LP step the integer requirements in (P-MINLP) are also included. These are considered by solving MILP relaxations of (P-MINLP) in $\varOmega _k \cap Y$. The problems solved in this step are, thus, defined as

$$\begin{aligned} \text {find} \ x_{\text {MILP}}^k \in \mathop {\hbox {arg min}}\limits _{\varOmega _{k-1} \cap Y} c^T x. \end{aligned}$$

(7)

Similarly to the LP step, the termination criterion is defined as

$$\begin{aligned} F\left( x_{\text {MILP}}^k\right) \le \varepsilon _{\text {MILP}}, \end{aligned}$$

(P-MILP)

where $\varepsilon _{\text {MILP}}$ is a given tolerance for the nonlinear constraints, i.e., the maximum allowed violation of the nonlinear constraints. If the current solution $x_{\text {MILP}}^k$ does not fulfill the termination criterion, more supporting hyperplanes are generated and added to $\varOmega _k$ by the same procedure as in the LP step. After the new hyperplanes have been added to $\varOmega _k$ the iteration counter k is increased and (P-MILP) is resolved. The procedure is repeated until the termination criterion is fulfilled. If $F(x_{\text {MILP}}^k) \le \varepsilon _{\text {MILP}}$ then $x_{\text {MILP}}^k$ is an optimal solution to the original problem (P-MINLP) with the given tolerance $\varepsilon _{\text {MILP}}$, since it is an optimal solution within $\varOmega _{k-1} \cap Y$ which encloses the entire feasible set of (P-MINLP). In case the tolerance $\varepsilon _{\text {MILP}}=0$, then the ESH algorithm will generate a solution sequence which converges to a global optimum of (P-MINLP) as shown in Theorem 2. In Theorem 3, it is also proven that an arbitrary tolerance $\varepsilon _{\text {MILP}}>0$ is achieved after a finite number of iterations.

Note that it is not necessary to solve (P-MILP) to optimality in each iteration, although the final MILP iteration has to be solved to optimality to guarantee that the solution is an optimal solution of (P-MINLP). Intermediate MILP solutions to generate new supporting hyperplanes need only be feasible MILP solutions in $\varOmega _k \cap Y$ and not in $L \cap C\cap Y$. If the current nonoptimal solution satisfies the nonlinear constraints the MILP solver can continue without rebuilding the branch-and-bound tree, this strategy was presented in [29] and is discussed further in Sect. 3.2.

Next, a simple MINLP problem is solved with the ESH algorithm to exemplify the NLP, LP and MILP steps.

2.4 Example 1

The ESH algorithm is now applied to the following MINLP problem

(8)

The objective function and feasible set are shown in Fig. 2. The termination tolerances for the LP and MILP steps are set to $\varepsilon _\text {LP}=0.5$ and $\varepsilon _\text {MILP}=0.001$.

Fig. 2

Left the linear, nonlinear and integer constraints in problem (9). Right the feasible region, objective function and optimal solution. The objective function contours are indicated with light gray lines. (Color figure online)

2.4.1 The NLP step

First an interior point $x_\text {NLP}$ to be used as the end point for the line searches is needed. According to Sect. 2.1, it is defined as

$$\begin{aligned} x_\text {NLP} \in \mathop {\hbox {arg min}}\limits _{(x_1,x_2) \in L} F(x_1,x_2), \end{aligned}$$

(9)

where

Since the functions $g_1$ and $g_2$ are both convex, the NLP problem is reformulated into the following smooth NLP problem

(10)

The solution to problem (11) is $\mu =-3.72$ with $x_1=7.45$ and $x_2=8.54$, hence $x_\text {NLP} = (7.45,\ 8.54)$ and $F(x_\text {NLP})=-3.72$.

2.4.2 The LP step

After the interior point has been obtained, LP and MILP relaxations of the original MINLP problem are solved and new supporting hyperplanes are added iteratively to the reduced feasible set denoted by $\varOmega _k$ in the kth iteration.

Iteration 1 Initially the feasible region of the relaxations is the domain defined by the variable bounds and linear constraint, i.e., $\varOmega _0 = X \cap L$. A solution to the initial relaxed LP problem in the first ($k=1$) iteration is then obtained by

$$\begin{aligned} \text {find} \ \ x^{(1)}_\text {LP} \in \mathop {\hbox {arg min}}\limits _{x\in \varOmega _{0}} \ c^T x \quad \Longrightarrow \quad x^{(1)}_\text {LP}=(20.0,\ 20.0). \end{aligned}$$

Since $F\big (x^{(1)}_\text {LP}\big ) = 30,359 > \varepsilon _\text {LP} = 0.5$, the LP step continues. Now, a line search is performed between the points $x_\text {NLP}$ and $x^{(1)}_\text {LP}$, i.e., a value for $\lambda ^{(1)} \in [0,1]$ such that $F(x^{(1)})= 0$, where $x^{(1)} = \lambda ^{(1)} x_\text {NLP} + (1-\lambda ^{(1)}) x^{(1)}_\text {LP}$, is sought. Using Eq. (5), the supporting hyperplane

$$\begin{aligned} l_1(x) = 3.26 x_1 +0.313 x_2-33.9 \end{aligned}$$

is generated in $x^{(1)} = (9.40,\ 10.3)$ and added to $\varOmega _1 = \left\{ x | l_1(x) \le 0,\ x \in \varOmega _0\right\}$.

Iteration 2 After this the new tighter LP relaxation is solved:

$$\begin{aligned} \text {find} \ \ x^{(2)}_\text {LP} \in \mathop {\hbox {arg min}}\limits _{x \in \varOmega _{1}} \ c^T x \quad \Longrightarrow \quad x^{(2)}_\text {LP}=(8.47,\ 20.0). \end{aligned}$$

The maximal constraint value $F\big (x^{(2)}_\text {LP}\big ) = 14.93 > \varepsilon _\text {LP} = 0.5$. A line search between the points $x_\text {NLP}$ and $x^{(2)}_\text {LP}$ gives the point $x^{(2)} = (7.83,\ 12.8)$ on the boundary of C, and in this point the supporting hyperplane

$$\begin{aligned} l_2(x) = 0.332 x_1 +1.30 x_2-19.2 \end{aligned}$$

is generated and added to $\varOmega _2 = \left\{ x | l_2(x) \le 0,\ x \in \varOmega _1\right\}$.

Iterations 3 and 4 The same procedure is repeated resulting in the two supporting hyperplanes

$$\begin{aligned} l_3(x) = 1.66 x_1 +0.951 x_2-26.2 \quad \text { and } \quad l_4(x) = 1.16x_1 + 0.962x_2 - 22.6. \end{aligned}$$

Since $F(x^{(4)}_\text {LP}) = 0.23 < \varepsilon _\text {LP} = 0.5$, the LP step is terminated and the integer restrictions are included in the next iteration.

2.4.3 The MILP step

Iterations 5 and 6 The variable $x_2$ is now required to be integer-valued, i.e., MILP problems are solved. The solution in iteration 5 is $x^{(5)}_\text {MILP} = (8.91,\ 12)$ with $F\big (x^{(5)}_\text {MILP}\big ) = 0.004 > \varepsilon _\text {MILP} = 0.001$ and the supporting hyperplane

$$\begin{aligned} l_5(x) = 1.55x_1 + 0.986x_2 - 25.7 \end{aligned}$$

is added in the fifth iteration. The next iteration yields the solution $x^{(6)}_\text {MILP} = (8.90,\ 12)$ with $F\big (x^{(6)}_\text {MILP}\big ) = 4 \cdot 10^{-6}$, which fulfills the termination criterion given by $\varepsilon _\text {MILP}$.

The solution to problem (9) is thus $(8.90362,\ 12)$ with the objective value $-20.9036$. The iteration results are given in Table 1 and the LP and MILP relaxations are illustrated in Fig. 3. It can be noted that it requires 17 iterations, i.e., 17 MILP problems solved to optimality, for the ECP algorithm to solve problem (9) with the same tolerance requirement, compared to four LP and two MILP problems for the ESH algorithm. An illustration of the cutting planes added with the ECP algorithm is given in Fig. 4. Finally a comparison of the solution times of some different convex MINLP solvers is provided in Table 2. The solution times were obtained using GAMS 24.4.1.

Table 1 The solution progress in the different iterations when solving problem (9) with the ESH algorithm

Table 2 Comparison of the solution times of solving problem (9) using different convex MINLP solvers

Fig. 3

The feasible regions, line searches performed and supporting hyperplanes generated in each iteration when solving Example 1 with the ESH algorithm. The interior point is represented by the white point, the solutions to the subproblems by the black points, the points given by the line searches by the red points and the optimal solution to the MINLP problem by the green point. (Color figure online)

Fig. 4

The cutting planes generated at the black points in iterations 1–17 when solving problem (9) using the ECP algorithm. The green point indicates the optimal solution. (Color figure online)

2.5 Example 2

For MINLP problems where the relaxed MILP problem is not bounded by linear constraints and variable bounds are excessive or poorly defined the ESH method should have a clear advantage over both the ECP algorithm and OA. In such problems the MILP solutions might be far from the feasible set making cutting planes inefficient and causing a large number of the NLP problems in OA to become infeasible, as demonstrated by the following example:

(11)

The problem was solved with the ESH algorithm, AlphaECP and DICOPT and the result is shown in Table 3. When considering the problem size, it is clear that both AlphaECP and DICOPT fails to solve the problem efficiently.

Table 3 Comparison of the solution times of solving problem (12) using ESH, AlphaECP and DICOPT. DICOPT failed to find the optimal solution in 180 s

2.6 Proof of convergence

In this section, it is proven that the ESH algorithm either converges to a global optimum of (P-MINLP) in a finite number of iterations or generates a sequence which converges to a global optimum. Furthermore it is shown that the problem (P-MINLP) can be solved with the ESH algorithm to an arbitrary positive tolerance for the nonlinear constraints in a finite number of iterations. Although the convergence proof for the MILP step also applies to the LP step it will not be dealt with specifically; the convergence of the ESH algorithm is independent of the LP step and the LP step will terminate after k iterations due to the termination criterion of the LP step. The convergence proof for the ESH algorithm has some similarities with the one for the ECP method, cf. [9, 28]. However, since the supporting hyperplanes are not generated at $x_{\text {MILP}}^k$ the convergence proof for the ECP method does not apply to the ESH algorithm.

In order to prove the convergence it is assumed that all MILP subproblems are solved to optimality. It is also assumed that there exists a solution $x_{\text {NLP}}$ to (P-NLP) such that $F(x_{\text {NLP}})< 0$, the special case with $F(x_{\text {NLP}})=0$ is discussed further in Remark 1. Since all the functions $g_m$ are convex, both the max function F and the set C are also convex. Due to the convexity, the supporting hyperplanes defined by Eq. (5) are all valid underestimators of the function F and hence the set $\varOmega _k$ overestimates the convex set C. Because more supporting hyperplanes are added in each iteration, the algorithm creates a sequence of overestimated sets $\varOmega$ with the property

$$\begin{aligned} L \cap C \cap Y \subset L \cap C \subset \varOmega _k \subset \varOmega _{k-1} \subset \cdots \subset \varOmega _0 \subseteq X. \end{aligned}$$

(12)

Theorem 1

If the ESH algorithm stops after a finite number of K iterations and the last solution $x_{\text {MILP}}^K$ fulfills all the constraints in the original problem (P-MINLP), the solution is also an optimal solution to the original problem.

Proof

Since the ESH algorithm stops at iteration K, $x_{\text {MILP}}^K$ is an optimal solution to (P-MILP) and $x_{\text {MILP}}^K$ gives the optimal value to the objective function of (P-MINLP) within $\varOmega _K \cap Y$. From Eq. (13) it is clear that $\varOmega _K \cap Y$ also includes the entire feasible set defined by $L \cap C \cap Y$. Since $x_{\text {MILP}}^K$ also satisfies the nonlinear constraints, it is also within the feasible set, ${{i.e., }}x_{\text {MILP}}^K \in L \cap C \cap Y$. Because $x_{\text {MILP}}^K$ minimizes the objective function within $\varOmega _K \cap Y$, which includes the entire feasible set, and $x_{\text {MILP}}^K \in L \cap C \cap Y$, it is also an optimal solution to (P-MINLP). $\square$

In Theorem 2 it is proven that the ESH algorithm generates a sequence of solution points converging to a global optimum, however, the proof requires some intermediate results given by Lemmas 1–4.

Lemma 1

If the current solution $x_{\text {MILP}}^k \not \in L \cap C$, then it is excluded from the set $\varOmega _{k+1}$ by the supporting hyperplanes added in iteration k.

Proof

Since $x_{\text {MILP}}^k \not \in L \cap C$ a line search between $x_{\text {MILP}}^k$ and $x_{\text {NLP}}$ for the boundary of the feasible set is conducted, which gives the point $x_k$. At least one supporting hyperplane is generated at $x^k$, with the equation

$$\begin{aligned} \nabla g_m \left( x^k\right) ^T \left( x-x^k\right) \le 0, \end{aligned}$$

(13)

where $\nabla g_m (x^k)$ is the gradient of a function active at $x^k$ (a function such that $g_m(x^k)=F(x^k)$). Since F is a convex function the subgradient definition states that

$$\begin{aligned} F\left( x_{\text {NLP}}\right) \ge F\left( x^k\right) +\xi _F \left( x^k\right) ^T\left( x_{\text {NLP}}-x^k\right) , \end{aligned}$$

(14)

where $\xi _F (x^k)$ is a subgradient of F at $x^k$, see [2, 24]. Because $F(x^k)=0$ and $F(x_{\text {NLP}})<0$, rewriting Eq. (15) gives

$$\begin{aligned} \xi _F \left( x^k\right) ^T\left( x_{\text {NLP}}-x^k\right) <0. \end{aligned}$$

(15)

Note that inequality (16) applies for all subgradients of F at $x^k$, including $\nabla g_m (x^k)$, and therefore

$$\begin{aligned} \nabla g_m \left( x^k\right) ^T \left( x_{\text {NLP}}-x^k\right) <0. \end{aligned}$$

(16)

Using the fact that the vector $\left( x_{\text {NLP}}-x^k\right) =-a\left( x_{\text {MILP}}^k-x^k\right)$, where a is a positive scalar (see Fig. 1), Eq. (17) can be rewritten as

$$\begin{aligned} \nabla g_m \left( x^k\right) ^T \left( x_{\text {MILP}}^k-x^k\right) >0 \end{aligned}$$

(17)

and thereby it is clear that $x_{\text {MILP}}^k$ is excluded from $\varOmega _{k+1}$ by the supporting hyperplanes defined by Eq. (14). $\square$

Next it is shown that if the ESH algorithm does not stop in a finite number of iterations, the sequence of solution points contains at least one convergent subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$, where

$$\begin{aligned} \left\{ k_1,k_2,\ldots \right\} \subseteq \left\{ 1,2,\ldots \right\} \quad \text {and }\quad \big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty \subseteq \big \{x_{\text {MILP}}^{k}\big \}_{k=1}^\infty . \end{aligned}$$

Since the subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ is convergent there exists a limit $\lim _{i \rightarrow \infty } x_{\text {MILP}}^{k_i}=\tilde{x}$. In Lemmas 3 and 4, it is shown that $\tilde{x}$ is not only within the feasible set of (P-MINLP) but also an optimal solution to (P-MINLP).

Lemma 2

If the ESH algorithm does not stop in a finite number of iterations it generates at least one convergent subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$.

Proof

Because the algorithm has not terminated, none of the solutions to (P-MILP) are within the feasible set, i.e., $x_{\text {MILP}}^{k} \not \in L \cap C \cap Y$ for all $k=1,2,\ldots$ in the solution sequence. Therefore all the points in the sequence $\big \{x_{\text {MILP}}^{k}\big \}_{k=1}^\infty$ will be distinct due to Lemma 1. Since $\big \{x_{\text {MILP}}^{k}\big \}_{k=1}^\infty$ contains an infinite number of different points, all within the compact set X, according to the Bolzano–Weierstrass theorem the sequence therefore contains at least one convergent subsequence. $\square$

Lemma 3

The limit $\tilde{x}$ of any convergent subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ generated by the ESH algorithm belongs to the feasible set of (P-MINLP).

Proof

In Lemma 1 we showed that the supporting hyperplanes added in iteration k excludes the current solution $x_{\text {MILP}}^{k}$ from the new set $\varOmega _{k+1}$. Choosing two points $x_{\text {MILP}}^{k_{j+1}}$ and $x_{\text {MILP}}^{k_j}$ from the sequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ gives

$$\begin{aligned} \nabla g_m \left( x^{k_j}\right) ^T \left( x_{\text {MILP}}^{k_{j+1}} - x^{k_j}\right) \le 0 \le \nabla g_m \left( x^{k_j}\right) ^T \left( x_{\text {MILP}}^{k_j} - x^{k_j}\right) , \end{aligned}$$

(18)

where $x^{k_j}$ is the point given by the line search between $x_{\text {MILP}}^{k_j}$ and $x_{\text {NLP}}$. According to previous notation $\nabla g_m (x^{k_j})$ is a gradient of a function active at $x^{k_j}$. Note that from Eq. (16) it is clear that Eq. (19) holds for all gradients of the functions active at $x^{k_j}$. Adding $g_m (x^{k_j})^T x^{k_j}$ to each side of the inequality (19) renders

$$\begin{aligned} \nabla g_m \left( x^{k_j}\right) ^T x_{\text {MILP}}^{k_{j+1}} \le \nabla g_m \left( x^{k_j}\right) ^Tx^{k_j} \le \nabla g_m \left( x^{k_j}\right) ^T x_{\text {MILP}}^{k_j}. \end{aligned}$$

The point $x^{k_j}$, given by the line search, can also be written as $x^{k_j} = \lambda _{k_j} x_\text {NLP} + (1-\lambda _{k_j}) x_{\text {MILP}}^{k_j}$, and therefore

$$\begin{aligned} \nabla g_m (x^{k_j})^Tx_{\text {MILP}}^{k_{j+1}} \le \nabla g_m (x^{k_j})^T\left( \lambda _{k_j} x_\text {NLP} + (1-\lambda _{k_j}) x_{\text {MILP}}^{k_j}\right) \le \nabla g_m (x^{k_j})^T x_{\text {MILP}}^{k_j}. \end{aligned}$$

(19)

Since $\lim _{j \rightarrow \infty }x_{\text {MILP}}^{k_j}=\tilde{x}$ and $x_{\text {MILP}}^k \not = x_{\text {NLP}}$ for each point in the sequence $\big \{x_{\text {MILP}}^{k}\big \}_{k=1}^\infty$, it is true that $\lim _{j \rightarrow \infty } \lambda _{k_j}=0$ from Eq. (20) according to the sandwich theorem. Since $F(x_{\text {NLP}})<0$ and all functions $g_m$ are convex, $x^{k_j}$ cannot be a local minimum of $g_m$ and therefore the gradient used in Eq. (20) cannot be a zero vector in any iteration. Because $\lim _{j \rightarrow \infty } \lambda _{k_j}=0$, $F(\tilde{x})=0$ is obtained, and therefore $\tilde{x}\in C$. Since each solution to (P-MILP) is within $L \cap Y$ and $\tilde{x}\in C$, the limit point $\tilde{x}$ will be within the feasible set of (P-MINLP) i.e., $\tilde{x}\in L \cap C \cap Y$. $\square$

Lemma 4

The limit point of a convergent subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ is a global minimum of (P-MINLP).

Proof

Because each set $\varOmega _k$ overestimates the feasible set of (P-MINLP), $c^Tx_{\text {MILP}}^{k_i}$ gives a lower bound on the optimal value of the objective function. Due to relation (13), the sequence $\big \{c^Tx_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ is nondecreasing and since the objective function is continuous we get $\lim _{i \rightarrow \infty } c^Tx_{\text {MILP}}^{k_i}=c^T\tilde{x}$. Lemma 3 showed that the limit point $\tilde{x}$ will be within the feasible set of (P-MINLP) and because it is a minimizer of the objective function within a set enclosing the entire feasible set, it is also an optimal solution to (P-MINLP). $\square$

Lemma 2 states that there exists at least one convergent subsequence and there might actually exist several such subsequences. Because Lemmas 3 and 4 applies to all convergent subsequences generated by the MILP step, any limit point of such a sequence will be a global optimum. Now the convergence results can be summarized in the next theorem.

Theorem 2

The ESH algorithm either finds a global optimum of (P-MINLP) in a finite number of iterations or generates a sequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ converging to a global optimum.

Proof

Suppose the algorithm stops in a finite number of iterations and $\varepsilon _{\text {MILP}}=0$. Then the last iteration satisfies all constraints and according to Theorem 1 it is a global optimum of (P-MINLP). In case the algorithm does not stop in a finite number of iterations, it generates a sequence converging to a global optimum of (P-MINLP) according to Lemmas 2 and 4. $\square$

Next, consider the case when the tolerance $\varepsilon _{\text {MILP}}> 0$. Note, that $\varepsilon _{\text {MILP}}$ does not correspond to a specific optimality gap for the objective function, it is merely a bound on the maximum violation of the nonlinear constraints $g_m(x) \le 0$.

Theorem 3

For any given tolerance $\varepsilon _{\text {MILP}}>0$, the ESH algorithm finds, in a finite number of iterations, a point x such that $F(x)< \varepsilon _{\text {MILP}}$.

Proof

Assume the ESH algorithm does not terminate after a finite number of iterations. According to Lemmas 2 and 4 the algorithm then generates a convergent subsequence $\big \{x_{\text {MILP}}^{k_i}\big \}_{i=1}^\infty$ and the limit of this sequence $\tilde{x}$ is an optimal solution to (P-MINLP). Furthermore Lemma 3 states that $\tilde{x} \in C$, and therefore $F(\tilde{x}) \le 0$. Since F is a continuous function,

$$\begin{aligned} \exists \ \delta >0: \quad \left| F(x)-F(\tilde{x})\right| < \varepsilon _{\text {MILP}} \quad \forall x: \ \left| \left| x_{\text {MILP}}^{k_i}-\tilde{x}\right| \right| _2< \delta . \end{aligned}$$

Because $\{x_{\text {MILP}}^{k_i}\}_{i=1}^\infty$ is a convergent sequence

$$\begin{aligned} \exists \ N \in {\mathbb {Z}}_+: \quad \left| \left| x_{\text {MILP}}^{k_i}-\tilde{x}\right| \right| _2< \delta \quad \forall i>N. \end{aligned}$$

The solution $x_{\text {MILP}}^{k_i}$ then satisfies the nonlinear constraints within the given tolerance, i.e., $F(x_{\text {MILP}}^{k_i})<\varepsilon _{\text {MILP}}$. Hence the tolerance $\varepsilon _{\text {MILP}}$ is achieved in a finite number of N iterations.

$\square$

Remark 1

So far it has been assumed that the set C has a nonempty interior and there exists a point $x_\text {NLP}$ such that $F(x_\text {NLP})<0$. However, even if $F(x_\text {NLP})=0$, it is still possible to solve the MINLP problem to an arbitrary tolerance $\varepsilon _\text {MILP}>0$ with the ESH algorithm. The nonlinear constraints are relaxed by $g_m(x) - \frac{\varepsilon _\text {MILP}}{2}\le 0$ and an overestimated set of C is defined as $\hat{C}=\left\{ x \, \left| \, g_m(x) - \frac{\varepsilon _\text {MILP}}{2} \le 0,\ m=1,\ldots ,M,\ x \in X\right. \right\}$. In case the original MINLP problem is feasible, the overestimated set $\hat{C}$ has an nonempty interior and an interior point of the set can be found by solving an NLP problem as described Sect. 2.1. As proven earlier, an MINLP problem with the relaxed nonlinear constraints can be solved with the ESH algorithm to the tolerance $\frac{\varepsilon _\text {MILP}}{2}$ in a finite number of iterations. The original MINLP problem can therefore be solved to an arbitrary tolerance $\varepsilon _\text {MILP}>0$ within a finite number of iterations by relaxing the nonlinear constraints.

2.7 Instances with nonlinear objective function and quadratic functions

So far in this paper it has been assumed that the objective function is linear in the original MINLP problem. However, a MINLP problem with a nonlinear objective function f can easily be transformed into one with a linear objective function by adding an auxiliary variable $x_{N+1}$ and the nonlinear constraint $f(x) - x_{N+1} \le 0$. The new linear objective is then to minimize the auxiliary variable $x_{N+1}$. In case the objective function f is convex the new nonlinear constraint will also be convex. Furthermore, to guarantee convergence the function f has to be continuously differentiable and bounded on X.

Since many MILP solvers, e.g., CPLEX, Gurobi and CBC, are able to directly handle a quadratic objective function efficiently it is not necessary to transform it into a nonlinear constraint. This has the advantage that each subproblem then utilizes the real objective function instead of a linear approximation. The original problem (P-MINLP) can in this case be written as

$$\begin{aligned} \text {find} \ x^*\in \mathop {\hbox {arg min}}\limits _{x \in L \cap C \cap Y}\ x^TQ\ x+c^T x, \end{aligned}$$

(20)

where Q is a positive semidefinite real matrix. In this case the subproblems discussed in previous sections are solved as mixed-integer quadratic programming (MIQP) problems.

Note that all the proofs given in the Sect. 2.6 also applies for a quadratic objective function. Additionally, if the subsolver can handle quadratic constraints it is possible to directly incorporate them in the set L and define the set C only by the remaining nonlinear constraints. The quadratic constraints are then handled in the same manner as the linear constraints and the proofs given in the previous section still applies. Incorporating the quadratic constraints in the set L gives a tighter overestimated set and could hence reduce the number of iterations needed to solve the MINLP problem.

3 SHOT: a solver implementation of the ESH algorithm

In this section, the supporting hyperplane optimization toolkit (SHOT) solver for convex MINLP is introduced. SHOT is an implementation of the ESH algorithm in C++ together with heuristics for obtaining primal solutions. The solver utilizes several subprojects of the COIN-OR initiative, such as the optimization services (OS) library [12] together with its XML-based optimization services instance language (OSiL) [11] for problem file input. The goal is to release SHOT as an open source solver part of COIN-OR.

3.1 Interior point strategy

In the solver implementation, the interior point used for the line searches is obtained by solving the smooth minimax problem in (P-NLP*), in practice this is done by calling on the NLP solver Ipopt [27].

3.2 Solution of subproblems

In SHOT, the subsolvers CPLEX, Gurobi and CBC can be used to find solutions to LP and MILP subproblems. Since problems where discrete variables are relaxed are much easier to solve than the corresponding MILP problem, it is possible to instead solve LP relaxations of the MILP subproblems. In this way it is possible to find a tight linear approximation by supporting hyperplanes much faster. However, in problems where the discrete nature of the variables has a significant impact on the solution found in the subproblems, the supporting hyperplanes generated in the LP step may give a poor relaxation of the feasible set of the original problem. The LP solution also always provides a dual bound on the value of the objective value. The standard LP relaxation strategy is to initially solve LP problems until some criterion has been fulfilled and after this only solve MILP problems. In the current version of SHOT, the LP step is terminated whenever a maximum constraint violation tolerance $\varepsilon _{\text {LP}}$ is reached [cf. Eq. (7)], the change in objective function value $c^T \left( x_\text {LP}^{k+1} - x_\text {LP}^{k} \right)$ is less than a specified tolerance, or a maximum number of LP iterations $K_\text {LP}$ has been reached.

All the MILP subproblems do not need to be solved to optimality; however, to obtain a dual bound, i.e., a lower bound on the objective value for the original MINLP problem, the MILP solution must be optimal. In the GAMS implementation of the ECP algorithm, i.e., AlphaECP, this is done by initially using a large value for the relative objective gap tolerance in the MILP subsolver. In SHOT however, the solution limit parameter of the subsolver is used as described in [29]. This setting determines the maximal number of integer-feasible solutions to find before terminating the MILP solver in each iteration. In many cases this reduces the solution time required significantly as several MILP subproblems can be solved utilizing a warm start and no extra time is spent on proving the optimality of intermediate solutions. Initially the solution limit can be set to one, i.e., the MILP solver is interrupted as soon as it finds the first integer-feasible solution. The solution limit is then increased whenever the maximal constraint violation for the returned solution is less than a user-set parameter or when a maximal number of MILP iterations have used the same solution limit. The solution limit can be increased without the solver needing to rebuild the branch-and-bound tree if no new linear constraints have been added to the model, so supporting hyperplanes are not added in iterations where the solution limit is updated but instead added in the next possible iteration.

If the MINLP problem has a quadratic objective function it can be directly handled by the subsolver as mentioned in Sect. 2.7, i.e., a sequence of QP or MIQP problems are solved instead of LP or MILP problems. This can greatly reduce the time needed to solve the original problem. In the case of a problem instance with a quadratic objective function subject to only linear constraints, only one call to the subsolver is needed to find the solution.

3.3 Line search and supporting hyperplane generation

Many MILP solvers, including CPLEX, Gurobi and CBC, are capable of returning a pool of feasible solutions to a problem in addition to the optimal solution. In the current version of SHOT, the maximal solution pool size is a user-determined setting. Supporting hyperplanes can be directly generated in points on the boundary of the nonlinear feasible region, and points on the exterior can be utilized as end points for the line searches. By adding more then one hyperplane in each iteration, the performance can in many cases be increased since less iterations are required. However, each individual MILP problem will be computationally more demanding so there is a definite trade-off for larger problem instances.

As mentioned before, it is possible to add hyperplanes for all the active constraint functions, or in practice the one with the greatest function value since line searches do not give exact values for the root. In SHOT the line search procedure utilizes quadratic interpolation as well as inverse cubic interpolations [1]. The line search always gives an interval in which the actual root lies and the length of this interval is dependent on the tolerance used for terminating the line search. Therefore, to obtain the optimal solution with a high level of accuracy requires that the line searches are conducted with a high precision. To guarantee that feasible solutions are not cut off by the added supporting hyperplanes due to the numerical accuracy of the line search, in practice cutting planes are added according to the formula

$$\begin{aligned} l_{k,m} = g_m\left( x^k\right) + \nabla g_m \left( x^k\right) ^T \left( x-x^k\right) \le 0 \end{aligned}$$

(P-MINLP*)

instead of according to Eq. (5) where $g_m(x^k)=0$. In practice the constant value $g_m(x^k)$ is often very small but due to numerical accuracy it might not be identical to zero.

3.4 Primal bound strategies

Dual solutions to the MINLP problem are given by optimal solutions to the LP, QP, MILP or MIQP subproblems. However, in order to calculate a duality gap for the objective function, primal solutions to the MINLP problem are also required. These solutions can be obtained from the solution pool the MILP solver returns if the solutions are feasible also for the nonlinear constraints, i.e., belongs to the set $L\cap C \cap Y$. A strategy specifically designed to find primal solutions is to solve continuous NLP relaxations of the MINLP problem, where the discrete variables are fixed to their values obtained when solving the current MILP problem. In SHOT this strategy is executed when a time limit or number of iterations since the last NLP call has been reached. These intermediate problems are solved using Ipopt. If the solution found is feasible for problem (P-MINLP) it provides a primal bound. In addition to being used for calculating an objective duality gap, the obtained primal solutions can also be used as starting points for the MILP solver, thus providing upper cut off values on the objective function.

3.5 Termination criteria

In addition to a user-set maximal number of iterations and time limit, the termination criteria used in SHOT is whenever all nonlinear constraints are fulfilled to an $\varepsilon$-tolerance

$$\begin{aligned} F\left( x_{\text {MILP}}^k\right) \le \varepsilon _{\text {MILP}}, \end{aligned}$$

(21)

or absolute or relative duality gap tolerances for the objective have been reached. If the current lower bound (dual) on the objective value is DB and the best known integer solution objective value (primal) is PB, then these termination criterions are given by

$$\begin{aligned} \left| \text {DB} - \text {PB}\right| \le \varepsilon _{\text {abs}} \qquad \text {and} \qquad \frac{\left| \text {DB}- \text {PB} \right| }{10^{-10} +|\text {PB}|} \le \varepsilon _{\text {rel}}. \end{aligned}$$

(22)

Note that for a minimization problem of type (9), all solutions to subproblems give lower bounds on the original objective function value as long as they are solved to optimality.

4 Numerical comparisons

To benchmark the performance of SHOT it has been tested on all 333 convex problems containing discrete variables in MINLPLib 2 [22]. The number of variables varies from 3 to 107 223 with the mean 999 and the largest number of discrete variables in any of the problems is 1500. The absolute $\varepsilon _\text {abs}$ and relative $\varepsilon _\text {rel}$ termination tolerances were both set at 0.001 and the constraint tolerance $\varepsilon _\text {MILP} = 10^{-5}$. The maximal number of LP iterations $K_\text {LP}$ was set at 300 and $\varepsilon _\text {LP} = 0.001$. A maximal solution pool limit of ten was used for the MILP solver. In case of a quadratic objective function, these were directly passed on to the MILP solver, but quadratic constraints were treated as general nonlinear. The total time limit per problem was set at 900 s. Ipopt 3.11.7 was used for solving the NLP problems and CPLEX 12.6.1 for the LP, QP, MILP and MIQP subproblems. The Linux based 64 bit computer used for all comparisons had an Intel Xeon 3.6 GHz processor with four physical cores and a total of eight logical cores. The amount of system memory was 32 GB.

SHOT was compared to some other MINLP solvers available in GAMS 24.4.1: AlphaECP, ANTIGONE, BARON, BONMINH, DICOPT, SBB and SCIP. DICOPT and SBB are convex solvers and convex solver strategies were activated for AlphaECP and SCIP. In BONMIN the B-Hyb strategy was used as it is recommended for convex problems. ANTIGONE and BARON are nonconvex solvers, but can identify convexities in many problems. Default settings were used for all solvers except for increasing the maximum number of threads to 8 and setting the iteration limit and other similar stopping criteria to prevent termination before optimality. The absolute and relative termination tolerances for all solvers were set at 0.001. CPLEX and CONOPT were used as the default MILP and NLP subsolvers. The data from the solver runs were processed with PAVER [5], a tool for analysis and visualization of benchmark data for optimization solvers. Even with the 900 s time limit, running the comparison took close to 150 h.

In Fig. 5 the termination status for the different solvers in the benchmark are shown, e.g., it is shown how many problems are terminated normally within 900 s. The solvers with the fewest timeouts are SHOT 13, BARON 18 and AlphaECP 41. Performance profiles are provided in Figs. 6 and 7 where the number of problems solved with respect to time by the different solvers are shown; in the two figures the number of instances with an objective duality gap of 1 % and primal bound gap of 1 % are shown respectively.

Fig. 5

The termination reason for the solvers. Note that a the solution can be optimal even though a limit (e.g., time) has been reached, the solver has simply not proven optimality. Similarly, depending on the solver, normal completion does not automatically guarantee that the optimal solution has been found only that some termination criteria has been met

Fig. 6

A performance profile of solving the 333 convex MINLP instances as described in Sect. 4. The number of problem instances in the graph corresponds to those where the gap between the dual and primal bounds returned were $\le$1 %. Note that the time is linear in the time interval [0, 10] and logarithmic in [10, 900]. The shaded area indicates the difference between the virtual best and virtual worst solvers, i.e., selecting the fastest or slowest solver for each problem individually. From the plot it can be obtained that by a smart solver selection, 282 of the problems can be solved to within an objective gap of 1 % within 10 s and 324 problems in 900 s; SHOT solved 262 problems in 10 s and 317 problems in 900 s to the required tolerance. (Color figure online)

Fig. 7

A performance profile illustrating the number of problem instances of the 242 with reported optimal solutions in MINLPLib 2, that were solved to within 1 % of the optimal solution. Note that the time is linear in the time interval [0, 10] and logarithmic in [10, 900]. The shaded area indicates the difference between the virtual best and virtual worst solvers, i.e., selecting the fastest or slowest solver for each instance. From the plot it can be obtained that by a smart solver selection 230 of the problems can be solved to within 1 % of the optimal solution within 10 s and 242 problems in 900 s. SHOT solved 221 problems to a primal gap less then 1 % in 10 s and 241 problems in 900 s. (Color figure online)

The results from this test set indicates that SHOT is on par with, and in many cases surpasses, the state-of-the-art solvers in this field both when regarding performance and solution quality. SHOT, SCIP, BARON and DICOPT are all effective for many problems with low solution times; however, the performance of DICOPT levels off after a few seconds. When it comes to the quality of the solution given, SHOT is very good as can be seen in Fig. 8, where the number of problems solved to objective duality gaps of 1 and 0.1 %, are shown. Note that the relative gap termination tolerance was set at 0.1 % and the absolute gap tolerance at 0.001. For this test set SHOT is also the most efficient solver for obtaining both tight primal and dual bounds, as can be seen in Fig. 9. Note that, out of the 333 convex instances in MINLPLib2 only 242 instances have verified optimal solutions in the library. Out of these 242 instances with known solutions in MINLPLib2, SHOT manages to obtain a primal bound gap of $<$1 % for 241 instances and obtains a dual bound gap of $<$1 % for all these 242 instances within 900 s.

Fig. 8

The number of problems solved to objective duality gaps of 1 % (left) and 0.1 % (right)

Fig. 9

The number of problem instances with primal (left) and dual (right) bound gaps $\le$1 % as calculated by PAVER for the 242 problems with reported optimal solution available in MINLPLib 2

As a comment on the results of the two nonconvex solvers without a specific convex strategy, the difference in performance between ANTIGONE and BARON may partly be due to the former not being able to identify the convexity of some constraints, thus triggering unnecessary reformulations for convexifying the problems. Also, regarding the performance of SBB it can be noted that the solver has not been updated since 2002. In addition, SBB does not utilize the possibility of parallelization whereas the main computational work in SHOT is performed in the MILP subsolver, i.e., CPLEX, which utilizes multiple cores of the processor very well in many cases. Directly using a quadratic objective function, instead of transforming it into a nonlinear constraint, was beneficial for SHOT. In many cases it was significantly faster to use the quadratic objective compared to rewriting it into a nonlinear constraint. Both AlphaECP and DICOPT could take advantage of directly utilizing a quadratic objective function in their mixed-integer subproblems. However, at the moment neither one of the solvers has this functionality.

5 Future work

Even though the ESH algorithm is clearly defined, there are some uncertain details regarding the solver implementation which can affect its efficiency. First the choice of interior point might affect the performance of the solver and this will be investigated further. As described earlier the interior point is obtained by solving a minimax problem, which ideally gives a point close to the center of the convex set C. However, in some cases the distance to the geometric center of the set can be quite large. Choosing an interior point close to an optimal solution to the original problem should be favorable, since supporting hyperplanes would then be generated close to an optimal solution in an early stage. Unfortunately this is not possible since an optimal solution is not known in advance, although it would be possible to approximate the solution point by an optimal solution of an integer relaxation of the original problem.

It would also be possible to generate more supporting hyperplanes in each iteration. For example, it is possible to generate supporting hyperplanes for all nonlinear constraints violated at the MILP solution $x_{\text {MILP}}^{k}$, since all these violated constraints may not be active at the point given by the line search. Additional supporting hyperplanes could improve the linear relaxation, although they would also increase the size of the MILP subproblems. It should therefore be investigated how to best utilize these additional supporting hyperplanes. It could also be possible to use some cut-removal strategies to reduce the size of the MILP problems, cf. [4].

6 Conclusions

The ESH algorithm for convex MINLP was presented in this paper. It is a solution method based on solving a sequence of linear overestimations of the nonlinear feasible set to obtain a global solution to the MINLP problem. Although it shares some similarities with the ECP algorithm, there are several differences, the main one being that supporting hyperplanes are used instead of cutting planes to exclude earlier solutions and improve the linear relaxation. The supporting hyperplanes often provide a tighter relaxation of the convex nonlinear feasible set. In the numerical comparison SHOT, an implementation of the ESH algorithm, proved to be on par with other state-of-the-art MINLP solvers. In this benchmark, SHOT was even the most efficient solver when considering the solution times and the number of instances solved. Finally, the numerical comparison showed that efficiently solving large-scale convex MINLP problems is still a nontrivial task, further motivating the development of convex MINLP solvers.