Construction of Multi-solitons for a Generalized Derivative Nonlinear Schrödinger Equation

Abstract

We consider a derivative nonlinear Schrödinger equation with general nonlinearlity:

$$\begin{aligned} i\partial _tu+\partial _x^2u+i|u|^{2\sigma }\partial _xu=0, \end{aligned}$$

In Tang and Xu (J Differ Equ 264(6):4094–4135, 2018), the authors prove the stability of two solitary waves in energy space for $\sigma \in (1,2)$. As a consequence, there exists a solution of the above equation which is close arbitrary to sum of two solitons in energy space when $\sigma \in (1,2)$. Our goal in this paper is proving the existence of multi-solitons in energy space for $\sigma \geqslant \frac{3}{2}$. Our proofs proceed by fixed point arguments around the desired profile, using Strichartz estimates.

1 Introduction

In this paper, we consider the following generalized derivative nonlinear Schrödinger equation:

$$\begin{aligned} i\partial _tu+\partial _x^2u+i|u|^{2\sigma }\partial _xu=0, \end{aligned}$$

(1.1)

where $\sigma \in \mathbb {R}^{+}$ is a given constant and $u:\mathbb R_t\times \mathbb R_x\rightarrow \mathbb C$.

The Eq. (1.1) was studied in many works. In the special case $\sigma =1$, local well-posedness, global well posedness, stability of solitary waves and stability of multi-solitons have been investigated. In [15], Ozawa gave a sufficient condition for global well posedness of (1.1) in the energy space by using a Gauge transformation to remove the derivative terms. In [2], Colin–Ohta showed that the equation has a two parameters family of solitary waves and proved the stability of these particular solutions by using variational methods. In [8], Kwon-Wu gave a result on stability of solitary waves when the parameters are at the threshold between existence and non-existence. In [11], Le Coz–Wu proved stability of multi-solitons in the energy space under some conditions on the parameters of the composing solitons.

In the general case, the local well-posedness and global well- posedness of (1.1) was studied in [6] when the initial data is in the Sobolev space $H_0^1(\Omega )$, where $\Omega$ is any unbounded interval of $\mathbb {R}$. In this work, Hayashi-Ozawa used an approximation argument. In [16], Santos proved the local well-posedness for small size initial data in weighted Sobolev spaces. The arguments used in this work follow parabolic regularization approach introduced by Kato [7].

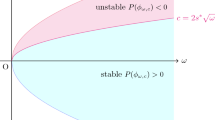
The Eq. (1.1) has a two parameters family of solitons. The stability of the solitons has attracted the attention of many researchers. In [12], by using the abstract theory of Grillakis–Shatah–Strauss [3, 4], Liu–Simpson–Sulem proved that in the case $\sigma \geqslant 2$, the solitons of (1.1) are orbitally unstable; in the case $0<\sigma <1$, they are orbitally stable and in the case $\sigma \in (1,2)$ they are orbitally stable if $c<2z_0\sqrt{\omega }$ and orbitally unstable if $c>2z_0\sqrt{\omega }$ for some constant $z_0 \in (0,1)$. In the critical case $c=2z_0\sqrt{\omega }$, Guo–Ning–Wu [5] proved that solitons are always orbitally unstable. In [1], Bai–Wu–Xue proved that when $\sigma \geqslant \frac{3}{2}$, the solution is global and scattering when the initial data small in $H^s(\mathbb {R})$, $\frac{1}{2}\leqslant s\leqslant 1$. Moreover, the authors showed that when $\sigma <2$, the scattering may not occur even under smallness conditions on the initial data. Therefore, in this model, the exponent $\sigma \geqslant 2$ is optimal for small data scattering. In [17], in the case $\sigma \in (1,2)$, Tang and Xu proved the stability of the sum of two solitary waves in the energy space provided that solitons are stables i.e $c<2z_0\sqrt{\omega }$, using perturbation arguments, modulational analysis and an energy argument as in [13, 14].

In this paper, we show the existence of multi-solitons in energy space in the case $\sigma \geqslant \frac{3}{2}$. Before stating the main result, we give some preliminaries on multi-solitons of (1.1).

As mentioned in [12], the Eq. (1.1) admits a two-parameters family of solitary waves solutions given by

$$\begin{aligned} \psi _{\omega ,c}(t,x)=\varphi _{\omega ,c}(x-ct)\exp \left( i\left( \omega t+\frac{c}{2}(x-ct)-\frac{1}{2\sigma +2}\int _{-\infty }^{x-ct}\varphi _{\omega ,c}^{2\sigma }(\eta )\,d\eta \right) \right) ,\nonumber \\ \end{aligned}$$

(1.2)

where $\omega >\frac{c^2}{4}$ and

$$\begin{aligned} \varphi _{\omega ,c}^{2\sigma }(y)=\frac{(\sigma +1)(4\omega -c^2)}{2\sqrt{\omega }\left( \cosh (\sigma \sqrt{4\omega -c^2}y)-\frac{c}{2\sqrt{\omega }}\right) }. \end{aligned}$$

(1.3)

The profile $\varphi _{\omega ,c}$ is a positive solution of

$$\begin{aligned} -\partial _y^2\varphi _{\omega ,c}+\left( \omega -\frac{c^2}{4}\right) \varphi _{\omega ,c}+\frac{c}{2}|\varphi _{\omega ,c}|^{2\sigma }\varphi _{\omega ,c}-\frac{2\sigma +1}{(2\sigma +2)^2}|\varphi _{\omega ,c}|^{4\sigma }\varphi _{\omega ,c}=0. \end{aligned}$$

(1.4)

Define

$$\begin{aligned} \phi _{\omega ,c}(y)=\varphi _{\omega ,c}(y)e^{i\theta _{\omega ,c}(y)}, \end{aligned}$$

(1.5)

where

$$\begin{aligned} \theta _{\omega ,c}(y)=\frac{c}{2}y-\frac{1}{2\sigma +2}\int _{-\infty }^y\varphi _{\omega ,c}^{2\sigma }(\eta )\, d\eta . \end{aligned}$$

(1.6)

Clearly, we have

$$\begin{aligned} \psi _{\omega ,c}(t,x)=e^{i\omega t}\phi _{\omega ,c}(x-ct). \end{aligned}$$

(1.7)

and $\phi _{\omega ,c}$ solves

$$\begin{aligned} -\partial _y^2\phi _{\omega ,c}+\omega \phi _{\omega ,c}+ic\partial _y\phi _{\omega ,c}-i|\phi _{\omega ,c}|^{2\sigma }\partial _y\phi _{\omega ,c}=0, \quad y\in \mathbb {R}. \end{aligned}$$

(1.8)

Let $K\in \mathbb {N}$, $K \geqslant 2$. For each $1 \leqslant j \leqslant K$, let $(\omega _j,c_j,\theta _j) \in \mathbb {R}^3$ be parameters such that $\omega _j>\frac{c_j^2}{4}$. Define, for each $j=1,\ldots ,K$

$$\begin{aligned} R_j(t,x)=e^{i\theta _j}\psi _{\omega _j,c_j}(t,x) \end{aligned}$$

and define the multi-soliton profile by

$$\begin{aligned} R=\sum _{j=1}^{K}R_j. \end{aligned}$$

(1.9)

For convenience, define $h_j=\sqrt{4\omega _j-c_j^2}$, for each $j=1,\ldots ,K$. Our main result is the following.

Theorem 1.1

Let $\sigma \geqslant \frac{3}{2}$, $K\in \mathbb {N}$, $K\geqslant 2$ and for each $1\leqslant j\leqslant K$, $(\theta _j,\omega _j,c_j)$ be a sequence of parameters such that $\theta _j\in \mathbb {R}$, $c_j\ne c_k$, for $j\ne k$. The multi-soliton profile R is given as in (1.9). There exists a certain positive constant $C_*$ such that if the parameters $(\omega _j,c_j)$ satisfy

$$\begin{aligned}{} & {} C_*\left( \left( 1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)}\right) \left( 1+\Vert R\Vert _{L^{\infty }H^1}^2 \right) \left( 1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}\right) \right) \nonumber \\{} & {} \quad \leqslant v_{*}=\inf _{j\ne k}h_j|c_j-c_k|, \end{aligned}$$

(1.10)

then there exists a solution u of (1.1) such that

$$\begin{aligned} \Vert u-R\Vert _{H^1} \leqslant Ce^{-\lambda t}, \quad \forall t\geqslant T_0, \end{aligned}$$

for positive constants $C,T_0$ depending only on the parameters $\omega _1,\ldots ,\omega _K,c_1,\ldots ,c_K$ and $\lambda =\frac{1}{16}v_{*}$.

Remark 1.2

The condition $\sigma \geqslant \frac{3}{2}$ is used to prove the existence of solution $\eta$ of (2.14) by using contraction mapping theorem.

The condition (1.10) is an implicit condition on the parameters. Below, we show that for large, negative and enough separated velocities, the condition (1.10) holds.

Remark 1.3

We prove that there exist parameters $(\omega _j,c_j,\theta _j)$ for $1 \leqslant j\leqslant K$ such at the condition (1.10) is satisfied for any prescribed $h_j$ and ratio $c_1:c_2:\cdot \cdot \cdot :c_K$ between negative $c_j$. Let $M>0$, $h_j>0$, $d_j<0$, for each $1\leqslant j\leqslant K$. We chose $(c_j,\omega _j)=\left( Md_j,\frac{1}{4}(h_j^2+M^2d_j^2)\right)$. We verify that this choice satisfies the condition (1.10) for M large enough. Indeed, we see that $c_j<0$ and $h_j \ll |c_j|$ for M large enough. We have

$$\begin{aligned} \varphi ^{2\sigma }_{\omega _j,c_j}&\approx \frac{h_j^2}{2\sqrt{\omega _j}\left( \cosh (\sigma h_j y)-\frac{c_j}{2\sqrt{\omega _j}}\right) }\\ \partial _x\varphi _{\omega _j,c_j}&\approx \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{2\sigma }}\frac{-\sinh (\sigma h_j y)}{\left( \cosh (\sigma h_j y)-\frac{c_j}{2\sqrt{\omega _j}}\right) ^{1+\frac{1}{2\sigma }}}. \end{aligned}$$

Using $|\sinh (x)| \leqslant |\cosh (x)|$ for all $x\in \mathbb {R}$ we have

$$\begin{aligned} |\partial _x\varphi _{\omega _j,c_j}| \leqslant \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{2\sigma }}\frac{1}{(\cosh (\sigma h_j y)-\frac{c_j}{2\sqrt{\omega _j}})^{\frac{1}{2\sigma }}}\lesssim |\varphi _{\omega _j,c_j}|. \end{aligned}$$

Thus,

$$\begin{aligned} \Vert R_j\Vert _{L^{\infty }L^{\infty }}&=\Vert \varphi _{\omega _j,c_j}\Vert _{L^{\infty }}\lesssim \root 2\sigma \of {\frac{h_j^2}{|c_j|}} \ll 1\\ \Vert \partial _xR_j\Vert _{L^{\infty }L^{\infty }}&=\Vert \partial _x\phi _{\omega _j,c_j}\Vert _{L^{\infty }}\\&\lesssim \Vert \partial _x\varphi _{\omega _j,c_j}\Vert _{L^{\infty }}+\left\Vert \frac{c_j}{2}\varphi _{\omega _j,c_j}-\frac{1}{2\sigma +2}\varphi _{\omega _j,c_j}^{2\sigma +1}\right\Vert _{L^{\infty }}\\&\lesssim \Vert \varphi _{\omega _j,c_j}\Vert _{L^{\infty }}+|c_j|\Vert \varphi _{\omega _j,c_j}\Vert _{L^{\infty }}\\&\lesssim \root 2\sigma \of {\frac{h_j^2}{|c_j|}}+|c_j|\root 2\sigma \of {\frac{h_j^2}{|c_j|}}. \end{aligned}$$

Hence,

$$\begin{aligned} \Vert R\Vert _{L^{\infty }L^{\infty }}&\lesssim \sum _{j}\root 2\sigma \of {\frac{h_j^2}{|c_j|}} \lesssim 1\\ \Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}&\lesssim \sum _j \left( \root 2\sigma \of {\frac{h_j^2}{|c_j|}}+|c_j|\root 2\sigma \of {\frac{h_j^2}{|c_j|}}\right) . \end{aligned}$$

Furthermore,

$$\begin{aligned} \Vert R_j\Vert _{L^{\infty }H^1}^2&=\Vert R_j\Vert _{L^{\infty }L^2}^2+\Vert \partial _xR_j\Vert ^2_{L^{\infty }L^2}=\Vert \varphi _{\omega _j,c_j}\Vert _{L^2}^2+\Vert \partial _x\varphi _{\omega _j,c_j}\Vert _{L^2}^2\\&\lesssim \Vert \varphi _{\omega _j,c_j}\Vert _{L^2}^2 \lesssim \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{\sigma }}\left\Vert \frac{1}{\cosh (\sigma h_j y)^{\frac{1}{2\sigma }}}\right\Vert ^2_{L^2}\lesssim \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{\sigma }}\Vert e^{-\frac{h_j}{2}|y|}\Vert ^2_{L^2}\\&\approx \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{\sigma }} \frac{1}{h_j}\lesssim h_j^{\frac{1}{\sigma }}h_j^{-1}=h_j^{\frac{1}{\sigma }-1}, \end{aligned}$$

where we use $h_j \leqslant 2\sqrt{\omega _j}$. Thus,

$$\begin{aligned} \Vert R\Vert _{L^{\infty }H^1}^2&\lesssim \sum _jh_j^{\frac{1}{\sigma }-1}. \end{aligned}$$

The condition (1.10) satisfies if the following estimate holds:

$$\begin{aligned} C_*\left( \left( 1+\sum _jh_j^{\frac{1}{\sigma }-1}\right) \left( 1+\sum _j \left( \root 2\sigma \of {\frac{h_j^2}{|c_j|}}+|c_j|\root 2\sigma \of {\frac{h_j^2}{|c_j|}}\right) \right) \right) \leqslant \inf _{j\ne k}h_j|c_j-c_k|. \end{aligned}$$

(1.11)

We see that the left hand side of (1.11) is order $M^{1-\frac{1}{2\sigma }}$ and the right hand side of (1.11) is order $M^1$. Hence, the condition (1.10) satisfies if we choose M large enough.

Remark 1.4

The exponent $\sigma = 2$ is the borderline for the existence of stable solitons. Since the example given in Remark 1.3 chooses all $c_j$ negative, by the work of Liu-Simpson-Sulem [12], solitons are stable for $\sigma < 2$ and unstable for $\sigma \geqslant 2$. This shows that in Theorem 1.1, we can construct multi-solitons from stable solitons or unstable solitons.

Our strategy of the proof of Theorem 1.1 is as follows. First, we define $\varphi ,\psi$ based on u in such a way that $\varphi$ and $\psi$ satisfy a system of nonlinear Schrödinger equations without derivatives (see (2.3)). Let R be a multi-soliton profile which satisfies the assumptions of Theorem 1.1. Then R solves (1.1) up to a small perturbation. Let (h, k) be defined in a similar way as $(\varphi ,\psi )$ but replace u by R. We see that (h, k) solves (2.3) up to small perturbations. Setting $\tilde{\varphi }=\varphi -h$ and $\tilde{\psi }=\psi -k$, we see that if u solves (1.1) then $(\tilde{\varphi },\tilde{\psi })$ solves a system and a relation between $\tilde{\varphi }$ and $\tilde{\psi }$ holds and vice versa. By using the Banach fixed point theorem, we prove that there exists a solution $(\tilde{\varphi },\tilde{\psi })$ of this system which decays exponentially in time on $H^1(\mathbb {R})$ for t large. Combining with the assumption (1.10), we can prove a relation between $\tilde{\varphi }$ and $\tilde{\psi }$. Thus, we easily obtain the solution u of (1.1) satisfying the desired property.

This paper is organized as follows. In Sect. 2, we prove the existence of multi-solitons for the Eq. (1.1). In Sect. 3, we prove some technical results which are used in the proof of the main result Theorem 1.1. More precisely, we prove the exponential decay of perturbations in the equations of h, k (Lemma 3.1) and the existence of decaying solutions for the system of equations of $\tilde{\varphi },\tilde{\psi }$ (Lemma 3.8).

Before proving the main result, we introduce some notation used in this paper.

Notation

• (1) We denote the Schrödinger operator as follows

  $$\begin{aligned} L=i\partial _t+\partial ^2_x. \end{aligned}$$

• (2) Given a time $t\in \mathbb {R}$, the Strichartz space $S([t,\infty ))$ is defined via the norm

  $$\begin{aligned} \Vert u\Vert _{S([t,\infty ))}=\sup _{(q,r) \text { admissible }}\Vert u\Vert _{L^q_t L^r_x([t,\infty )\times \mathbb {R})}. \end{aligned}$$

  We denote the dual space by $N[t,\infty )=S([t,\infty ))^{*}$. Hence for any (q, r) admissible pair we have

  $$\begin{aligned} \Vert u\Vert _{N([t,\infty ))}\leqslant \Vert u\Vert _{L^{q'}_tL^{r'}_x([t,\infty )\times \mathbb {R})}. \end{aligned}$$

• (3) For $a,b \in \mathbb {R}^2$, we denote $|(a,b)|=|a|+|b|$.

• (4) Let $a,b>0$. We denote $a\lesssim b$ if a is smaller than b up to multiplication by a positive constant and denote $a \lesssim _c b$ if a is smaller than b up to multiplication by a positive constant depending on c. Moreover, we denote $a \approx b$ if a equals to b up to multiplication by a positive constant.

2 Proof of the Main Result

In this section we give the proof of Theorem 1.1. We use the Banach fixed point theorem and Strichartz estimates. We divide our proof in three steps. Step 1. Preliminary analysis. Let $u \in C(I,H^1(\mathbb {R}))$ be a $H^1(\mathbb {R})$ solution of (1.1) on I. Consider the following transform:

$$\begin{aligned} \varphi (t,x)&=\exp (i\Lambda )u(t,x), \end{aligned}$$

(2.1)

$$\begin{aligned} \psi&= \exp (i\Lambda )\partial _xu=\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi , \end{aligned}$$

(2.2)

where

$$\begin{aligned} \Lambda =\frac{1}{2}\int _{-\infty }^x|u(t,y)|^{2\sigma }\,dy. \end{aligned}$$

As in [6, section 4], using $|u|=|\varphi |$ and , we have

Thus, using $|u|=|\varphi |$ and , we have

Since u solves (1.1), we have

As in [6, section 4], we have

Thus, if u solves (1.1) then $(\varphi ,\psi )$ solves

(2.3)

For convenience, we define

(2.4)

(2.5)

Let R be the multi-soliton profile satisfying the assumption of Theorem 1.1. Define h, k by

$$\begin{aligned} h(t,x)&=\exp \left( \frac{i}{2}\int _{-\infty }^x|R(t,x)|^{2\sigma }\,dy\right) R(t,x),\\ k&=\partial _xh-\frac{i}{2}|h|^{2\sigma }h. \end{aligned}$$

Since $R_j$ solves (1.1) for each $1\leqslant j\leqslant K$, we have

$$\begin{aligned} LR+i|R|^{2\sigma }R_x=-\sum _{j}i|R_j|^{2\sigma }R_{jx}+i|R|^{2\sigma }R_x. \end{aligned}$$

(2.6)

By Lemma 3.1 for $t \gg T_0$ large enough we have

$$\begin{aligned} \left\Vert -\sum _{j}i|R_j|^{2\sigma }R_{jx}+i|R|^{2\sigma }R_x\right\Vert _{H^2}&\leqslant e^{-\lambda t}. \end{aligned}$$

(2.7)

Thus, we rewrite (2.6) as follows:

$$\begin{aligned} LR+i|R|^{2\sigma }R_x=e^{-\lambda t}\Omega , \end{aligned}$$

(2.8)

where

$$\begin{aligned} \Omega =e^{\lambda t}(-\sum _{j}i|R_j|^{2\sigma }R_{jx}+i|R|^{2\sigma }R_x). \end{aligned}$$

(2.9)

By an elementary calculation, we have

(2.10)

where

(2.11)

(2.12)

Since $\Omega$ is uniformly bounded in time in $H^2(\mathbb {R})$, we see that m, n are uniformly bounded in time in $H^1(\mathbb {R})$. Let $\tilde{\varphi }=\varphi -h$ and $\tilde{\psi }=\psi -k$. Then $(\tilde{\varphi },\tilde{\psi })$ solves:

$$\begin{aligned} {\left\{ \begin{array}{ll} L\tilde{\varphi }=P(\varphi ,\psi )-P(h,k)-e^{-\lambda t}m(t,x),\\ L\tilde{\psi }=Q(\varphi ,\psi )-Q(h,k)-e^{-\lambda t}n(t,x). \end{array}\right. } \end{aligned}$$

(2.13)

Set $\eta =(\tilde{\varphi },\tilde{\psi })$, $W=(h,k)$ and $f(\varphi ,\psi )=(P(\varphi ,\psi ),Q(\varphi ,\psi ))$ and $-H=e^{-\lambda t}(m,n)$. We will find in Step 2 a solutions of (2.13) in Duhamel form:

$$\begin{aligned} \eta (t)=i\int _t^{\infty }S(t-s)[f(W+\eta )-f(W)+H](s)\,ds, \end{aligned}$$

(2.14)

where S(t) denote the Schrödinger group. Moreover, since $\psi =\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi$, we will prove in Step 3

$$\begin{aligned} \tilde{\psi }=\partial _x\tilde{\varphi }-\frac{i}{2}(|\tilde{\varphi }+h|^{2\sigma }(\tilde{\varphi }+h)-|h|^{2\sigma }h). \end{aligned}$$

(2.15)

Step 2 Existence of a solution of the system From Lemma 3.8, there exists $T_{*} \gg 1$ such that for $T_0 \geqslant T_{*}$ there exists a unique solution $\eta$ of (2.13) defined on $[T_0,\infty )$ such that

$$\begin{aligned} \Vert \eta \Vert _X:=\sup _{t>T_0}\left( e^{\lambda t}\Vert \eta \Vert _{S([t,\infty )) \times S([t,\infty ))}+e^{\lambda t}\Vert \partial _x\eta \Vert _{S([t,\infty ))\times S([t,\infty ))} \right) \leqslant 1. \end{aligned}$$

(2.16)

Thus, for all $t \geqslant T_0$, we have

$$\begin{aligned} \Vert \tilde{\varphi }\Vert _{H^1}+\Vert \tilde{\psi }\Vert _{H^1}\lesssim e^{-\lambda t}. \end{aligned}$$

(2.17)

Step 3 Existence of a multi-soliton train We first prove that the solution $\eta =(\tilde{\varphi },\tilde{\psi })$ of (2.13) satisfies the relation (2.15). Set $\varphi =\tilde{\varphi }+h$, $\psi =\tilde{\psi }+k$ and $v=\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi$ and $\tilde{v}=v-k$. Since $(\tilde{\varphi },\tilde{\psi })$ solves (2.13) and (h, k) solves (2.10), we have $(\varphi ,\psi )$ solves (2.3). Furthermore,

$$\begin{aligned} Lv&=\partial _xL\varphi -\frac{i}{2}L(|\varphi |^{2\sigma }\varphi ). \end{aligned}$$

(2.18)

Moreover,

$$\begin{aligned}&L(|\varphi |^{2\sigma }\varphi )\\&=(i\partial _t+\partial _x^2)(\varphi ^{\sigma +1}\overline{\varphi }^{\sigma })=i\partial _t(\varphi ^{\sigma +1}\overline{\varphi }^{\sigma })+\partial _x^2(\varphi ^{\sigma +1}\overline{\varphi }^{\sigma })\\&=i(\sigma +1)|\varphi |^{2\sigma }\partial _t\varphi +i\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\partial _t\overline{\varphi }\\&\quad +\partial _x((\sigma +1)|\varphi |^{2\sigma }\partial _x\varphi +\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\partial _x\overline{\varphi })\\&=i(\sigma +1)|\varphi |^{2\sigma }\partial _t\varphi +i\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\partial _t\overline{\varphi }+(\sigma +1)\left[ \partial _x^2\varphi |\varphi |^{2\sigma }+\partial _x\varphi \partial _x(|\varphi |^{2\sigma })\right] \\&\quad +\sigma \left[ \partial _x^2\overline{\varphi }|\varphi |^{2(\sigma -1)}\varphi ^2+(\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi +(\sigma -1)|\varphi |^{2(\sigma -2)}\varphi ^3(\partial _x\overline{\varphi })^2\right] \\&=(\sigma +1)|\varphi |^{2\sigma }(i\partial _t\varphi +\partial _x^2\varphi )+\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(i\partial _t\overline{\varphi }+\partial _x^2\overline{\varphi })+(\sigma +1)\partial _x\varphi \partial _x(|\varphi |^{2\sigma })\\&\quad +\sigma (\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi +\sigma (\sigma -1)(\partial _x\overline{\varphi })^2|\varphi |^{2(\sigma -2)}\varphi ^3\\&=(\sigma +1)|\varphi |^{2\sigma }L\varphi +\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(-\overline{L\varphi }+2\partial _x^2\overline{\varphi })+(\sigma +1)\partial _x\varphi \partial _x(|\varphi |^{2\sigma })\\&\quad +\sigma (\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi +\sigma (\sigma -1)(\partial _x\overline{\varphi })^2|\varphi |^{2(\sigma -2)}\varphi ^3. \end{aligned}$$

Combining with (2.18) and using (2.3), we have

$$\begin{aligned} Lv&=\partial _xL\varphi -\frac{i}{2}L(|\varphi |^{2\sigma }\varphi )\\&=\partial _xL\varphi -\frac{i}{2}\left[ (\sigma +1)|\varphi |^{2\sigma }L\varphi +\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(-\overline{L\varphi }+2\partial _x^2\overline{\varphi })\right. \\&\quad \left. +(\sigma +1)\partial _x\varphi \partial _x(|\varphi |^{2\sigma })+\sigma (\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi +\sigma (\sigma -1)(\partial _x\overline{\varphi })^2|\varphi |^{2(\sigma -2)}\varphi ^3\right] \\&=\partial _x(P(\varphi ,\psi )-P(\varphi ,v))+\partial _xP(\varphi ,v)-\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }\left( P(\varphi ,\psi )-P(\varphi ,v)\right) \\&\quad -\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }P(\varphi ,v)+\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(\overline{P(\varphi ,\psi )}-\overline{P(\varphi ,v)})\\&\quad +\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\overline{P(\varphi ,v)}-i\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\partial _x^2\overline{\varphi }\\&\quad -\frac{i}{2}\left[ (\sigma +1)\partial _x\varphi \partial _x(|\varphi |^{2\sigma })+\sigma (\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi \right. \\&\quad \left. +\sigma (\sigma -1)(\partial _x\overline{\varphi })^2|\varphi |^{2(\sigma -2)}\varphi ^3\right] \\&=\partial _x(P(\varphi ,\psi )-P(\varphi ,v))-\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }\left( P(\varphi ,\psi )-P(\varphi ,v)\right) \\&\quad +\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(\overline{P(\varphi ,\psi )}-\overline{P(\varphi ,v)})+G(\varphi ,v), \end{aligned}$$

where $G(\varphi ,v)$ contains the remaining ingredients and $G(\varphi ,v)$ only depends on $\varphi$ and v:

$$\begin{aligned}&G(\varphi ,v)\nonumber \\&=\partial _xP(\varphi ,v)-\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }P(\varphi ,v)+\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\overline{P(\varphi ,v)}\nonumber \\&\quad -i\sigma |\varphi |^{2(\sigma -1)}\varphi ^2\partial _x^2\overline{\varphi }-\frac{i}{2}\left[ (\sigma +1)\partial _x\varphi \partial _x(|\varphi |^{2\sigma })+\sigma (\sigma +1)|\partial _x\varphi |^2|\varphi |^{2(\sigma -1)}\varphi \right. \nonumber \\&\quad \left. +\sigma (\sigma -1)(\partial _x\overline{\varphi })^2|\varphi |^{2(\sigma -2)}\varphi ^3\right] . \end{aligned}$$

(2.19)

As the calculations of $L\psi$ in the step 1, noting that the role of v is similar to the role of $\psi$ in the process of calculation, we have $G(\varphi ,v)=Q(\varphi ,v)$ (see Lemma 3.7 for a detailed proof). Hence,

$$\begin{aligned} L\psi -Lv&=Q(\varphi ,\psi )-Q(\varphi ,v)-\partial _x(P(\varphi ,\psi )-P(\varphi ,v))\\&\quad +\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }\left( P(\varphi ,\psi )-P(\varphi ,v)\right) \\&\quad -\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(\overline{P(\varphi ,\psi )}-\overline{P(\varphi ,v)}). \end{aligned}$$

Thus,

$$\begin{aligned} L\tilde{\psi }-L\tilde{v}&=L\psi -Lv\nonumber \\&=Q(\varphi ,\tilde{\psi }+k)-Q(\varphi ,\tilde{v}+k)-\partial _x(P(\varphi ,\tilde{\psi }+k)-P(\varphi ,\tilde{v}+k)\nonumber \\&\quad +\frac{i}{2}(\sigma +1)|\varphi |^{2\sigma }(P(\varphi ,\tilde{\psi }+k)-P(\varphi ,\tilde{v}+k))\nonumber \\&\quad -\frac{i}{2}\sigma |\varphi |^{2(\sigma -1)}\varphi ^2(\overline{P(\varphi ,\tilde{\psi }+k)}-\overline{P(\varphi ,\tilde{v}+k)}). \end{aligned}$$

(2.20)

Multiplying both side of (2.20) by $\overline{{\tilde{\psi }}-\tilde{v}}$, taking imaginary part and integrating over space with integration by parts we obtain

(2.21)

(2.22)

(2.23)

(2.24)

We denote by A, B, C, D the terms (2.21), (2.22), (2.23) and (2.24) respectively. First, we try to estimate A, B, C, D in term of R. We have

(2.25)

where,

$$\begin{aligned} K_1:&=\Vert \varphi \Vert ^{2\sigma -1}_{L^{\infty }}\Vert \tilde{\psi }+\tilde{v}+2k\Vert _{L^{\infty }}+\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+k)^2\Vert _{L^1}\\&\quad +\Vert \tilde{v}+k\Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^2}. \end{aligned}$$

Furthermore,

(2.26)

By using integration by parts for the second term of (2.26) and using Hölder inequality we have

(2.27)

(2.28)

where

$$\begin{aligned} K_2:{} & {} =\Vert \partial _x(|\varphi |^{2(\sigma -1)}\varphi ^2)\Vert _{L^{\infty }}+\Vert \partial _x\varphi \Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }\\{} & {} \quad +\tilde{v}+2k)\Vert _{L^2}+\Vert \varphi ^{2\sigma -1}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^{\infty }}. \end{aligned}$$

Using (2.4), we have

(2.29)

where

$$\begin{aligned} K_3:=\Vert \varphi ^{4\sigma }\Vert _{L^{\infty }}+\Vert \varphi ^{2\sigma +1}\Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^2}. \end{aligned}$$

Now, we give an estimate for D. We have

(2.30)

Combining (2.25), (2.27), (2.29) and (2.30), we have

$$\begin{aligned} \left| \partial _t\Vert \tilde{\psi }-\tilde{v}\Vert ^2_{L^2}\right|&\lesssim \Vert \tilde{\psi }-\tilde{v}\Vert ^2_{L^2}(K_1+K_2+K_3). \end{aligned}$$

Using the Grönwall inequality, we have for any $t<N<\infty$,

$$\begin{aligned} \Vert \tilde{\psi }(t)-\tilde{v}(t)\Vert ^2_{L^2}&\lesssim \Vert \tilde{\psi }(N)-\tilde{v}(N)\Vert ^2_{L^2}\exp \left( \int _t^N (K_1+K_2+K_3)\,ds\right) \nonumber \\&\leqslant e^{-2\lambda N}\exp \left( \int _t^N (K_1+K_2+K_3)\,ds\right) . \end{aligned}$$

(2.31)

The second inequality is by (2.17). Now, we try to estimate $K_1+K_2+K_3$ in term of R. When we have this kind of estimate, we will use the assumption (1.10) to obtain that $\tilde{\psi }=\tilde{v}$. We have

$$\begin{aligned}&\int _t^N(K_1+K_2+K_3)\,ds\nonumber \\&=\int _t^N \Vert \varphi \Vert ^{2\sigma -1}_{L^{\infty }}\Vert \tilde{\psi }+\tilde{v}+2k\Vert _{L^{\infty }}+\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+k)^2\Vert _{L^1}\nonumber \\&\quad +\Vert \tilde{v}+k\Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^2}\,ds \end{aligned}$$

(2.32)

$$\begin{aligned}&\quad +\int _t^N\Vert \partial _x(|\varphi |^{2(\sigma -1)}\varphi ^2)\Vert _{L^{\infty }}+\Vert \partial _x\varphi \Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^2}\nonumber \\&\quad +\Vert \varphi ^{2\sigma -1}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^{\infty }}\,ds \end{aligned}$$

(2.33)

$$\begin{aligned}&\quad +\int _t^N\Vert \varphi ^{4\sigma }\Vert _{L^{\infty }}+\Vert \varphi ^{2\sigma +1}\Vert _{L^2}\Vert \varphi ^{2(\sigma -1)}(\tilde{\psi }+\tilde{v}+2k)\Vert _{L^2}\,ds. \end{aligned}$$

(2.34)

Using (2.16) and (2.17), we have

$$\begin{aligned}&\Vert \varphi \Vert _{L^{\infty }}\leqslant \Vert \tilde{\varphi }\Vert _{L^{\infty }}+\Vert h\Vert _{L^{\infty }}\lesssim 1+\Vert h\Vert _{L^{\infty }} \end{aligned}$$

(2.35)

$$\begin{aligned}&\Vert \varphi \Vert _{L^2}\leqslant \Vert \tilde{\varphi }\Vert _{L^2}+\Vert h\Vert _{L^2}\lesssim 1+\Vert h\Vert _{L^2} \end{aligned}$$

(2.36)

$$\begin{aligned}&\Vert \psi \Vert _{L^{\infty }}\lesssim 1 \end{aligned}$$

(2.37)

We denote by $Z_1,Z_2,Z_3$ the terms (2.32), (2.33) and (2.34) respectively. Using (2.35), (2.36), (2.37), (2.16) and (2.17), for $N \gg t$, we have

$$\begin{aligned} |Z_1|&\lesssim \Vert \varphi \Vert ^3_{L^4(t,N)L^{\infty }}\Vert \varphi \Vert ^{2(\sigma -2)}_{L^{\infty }L^{\infty }}\Vert \tilde{\psi }+\tilde{v}+2k\Vert _{L^4(t,N)L^{\infty }}\\&\quad +(N-t)\Vert \varphi \Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }}(\Vert \tilde{\psi }\Vert _{L^{\infty }L^2}+\Vert k\Vert _{L^{\infty }L^2})^2\\&\quad +\Vert \tilde{v}+k\Vert _{L^{\frac{4}{3}}(t,N)L^2}\Vert \varphi \Vert _{L^{\infty }L^2}\Vert \varphi \Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }}(\Vert \tilde{\psi }+\tilde{v}\Vert _{L^4(t,N)L^{\infty }}+\Vert k\Vert _{L^4(t,N)L^{\infty }})\\&\lesssim (N-t)^{\frac{3}{4}}\Vert \varphi \Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }}(1+\Vert k\Vert _{L^{\infty }L^{\infty }}(N-t)^{\frac{1}{4}})\\&\quad +(N-t)(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert k\Vert ^2_{L^{\infty }L^2})\\&\quad +(N-t)^{\frac{3}{4}}(1+\Vert k\Vert _{L^{\infty }L^2})(1+\Vert h\Vert _{L^{\infty }L^2})(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+(N-t)^{\frac{1}{4}}\Vert k\Vert _{L^{\infty }L^{\infty }})\\&\lesssim (N-t)\Vert k\Vert _{L^{\infty }L^{\infty }}(1+\Vert h\Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }})+(N-t)(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert k\Vert ^2_{L^{\infty }L^2})\\&\quad +(N-t)\Vert k\Vert _{L^{\infty }L^{\infty }}(1+\Vert k\Vert _{L^{\infty }L^2})(1+\Vert h\Vert _{L^{\infty }L^2})(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})\\&:=(N-t)W_1(h,k). \end{aligned}$$

Similarly, for $N\gg t$, we have

$$\begin{aligned} |Z_2|&\lesssim \Vert \partial _x\varphi \varphi ^{2\sigma -1}\Vert _{L^1(t,N)L^{\infty }}+(N-t)\Vert \partial _x\varphi \Vert _{L^{\infty }(t,N)L^2}\Vert \varphi \Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }}\Vert \tilde{\psi }+\tilde{v}+k\Vert _{L^{\infty }(t,N)L^2}\\&\quad +(N-t)^{\frac{3}{4}}\Vert \varphi \Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }}(\Vert \tilde{\psi }+\tilde{v}\Vert _{L^4(t,N)L^{\infty }}+\Vert k\Vert _{L^4(t,N)L^{\infty }})\\&\lesssim (N-t)^{\frac{3}{4}}(\Vert \partial _x{\tilde{\varphi }}\Vert _{L^4(t,N)L^{\infty }}+\Vert \partial _xh\Vert _{L^4(t,N)L^{\infty }})\Vert \varphi \Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }}\\&\quad +(N-t)(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert k\Vert _{L^{\infty }L^2})\\&\quad +(N-t)^{\frac{3}{4}}(1+\Vert h\Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }})(1+(N-t)^{\frac{1}{4}}\Vert k\Vert _{L^{\infty }L^{\infty }})\\&\lesssim (N-t)\Vert \partial _xh\Vert _{L^{\infty }L^{\infty }}(1+\Vert h\Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }})+ (N-t)(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert k\Vert _{L^{\infty }L^2})\\&\quad +(N-t)\Vert k\Vert _{L^{\infty }L^{\infty }}(1+\Vert h\Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }})\\&:=(N-t)W_2(h,k), \end{aligned}$$

and

$$\begin{aligned} |Z_3|&\lesssim (N-t)(\Vert \tilde{\varphi }\Vert _{L^{\infty }L^{\infty }}+\Vert h\Vert _{L^{\infty }L^{\infty }})^{4\sigma }\\&\quad +(N-t)\Vert \varphi \Vert _{L^{\infty }L^2}\Vert \varphi \Vert ^{2\sigma }_{L^{\infty }L^{\infty }}\Vert \varphi \Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }}(\Vert \tilde{\psi }+\tilde{v}\Vert _{L^{\infty }L^2}+\Vert k\Vert _{L^{\infty }L^2}) \\&\lesssim (N-t)(1+\Vert h\Vert ^{4\sigma }_{L^{\infty }L^{\infty }})+(N-t)(1+\Vert h\Vert _{L^{\infty }L^2})(1+\Vert h\Vert ^{4\sigma -2}_{L^{\infty }L^{\infty }})(1+\Vert k\Vert _{L^{\infty }L^2})\\&:=(N-t)W_3(h,k). \end{aligned}$$

Hence, from (2.31), we have

$$\begin{aligned} \Vert \tilde{\psi }(t)-\tilde{v}(t)\Vert _{L^2}^2&\lesssim e^{-2\lambda N}\exp \left( \int _t^N(K_1+K_2+K_3)\,ds\right) \nonumber \\&\lesssim e^{-2\lambda N}\exp ((N-t)(W_1(h,k)+W_2(h,k)+W_3(h,k))) \end{aligned}$$

(2.38)

The above estimate is not enough explicit. As said above, we would like to estimate the right hand side of (2.38) in terms of R. Noting that $|h|=|R|$ and $|k|=|\partial _xR|$, we have

$$\begin{aligned} W_1(h,k)&=\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert R\Vert ^{2\sigma -1}_{L^{\infty }L^{\infty }})+(1+\Vert R\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert \partial _xR\Vert ^2_{L^{\infty }L^2})\\&\quad +\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})(1+\Vert R\Vert _{L^{\infty }L^2})(1+\Vert R\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }}) \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})\left[ \Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert R\Vert _{L^{\infty }L^{\infty }})+(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})\right. \\&\quad \left. +\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})(1+\Vert R\Vert _{L^{\infty }L^2})\right] \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})\times \\&\quad \times \left[ \Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert R\Vert _{L^{\infty }H^1})+(1+\Vert R\Vert _{L^{\infty }H^1}^2)+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}(1+\Vert R\Vert _{L^{\infty }H^1}^2)\right] \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)(1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}). \end{aligned}$$

Similarly, by noting that $|\partial _xh|\leqslant |k|+|h|^{2\sigma +1}$, we have

$$\begin{aligned} W_2(h,k)&\lesssim (\Vert k\Vert _{L^{\infty }L^{\infty }}+\Vert h\Vert ^{2\sigma +1}_{L^{\infty }L^{\infty }})(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert h\Vert _{L^{\infty }L^{\infty }})\\&\quad +(1+\Vert h\Vert ^{2(\sigma -1)})(1+\Vert k\Vert _{L^{\infty }L^2})+\Vert k\Vert _{L^{\infty }L^{\infty }}(1+\Vert h\Vert ^{2(\sigma -1)}_{L^{\infty }L^{\infty }})(1+\Vert h\Vert _{L^{\infty }L^{\infty }})\\&\lesssim (1+\Vert h\Vert ^{2(\sigma -1)})\times \\&\quad \times \left[ (\Vert k\Vert _{L^{\infty }L^{\infty }}+\Vert h\Vert ^{2\sigma +1}_{L^{\infty }L^{\infty }})(1+\Vert h\Vert _{L^{\infty }L^{\infty }})\right. \nonumber \\&\quad \left. +(1+\Vert k\Vert _{L^{\infty }L^2})+\Vert k\Vert _{L^{\infty }L^{\infty }}(1+\Vert h\Vert _{L^{\infty }L^{\infty }})\right] \\&\lesssim (1+\Vert h\Vert ^{2(\sigma -1)})\times \\&\quad \times \left[ (1+\Vert h\Vert _{L^{\infty }L^{\infty }})(\Vert k\Vert _{L^{\infty }L^{\infty }}+\Vert h\Vert ^{2\sigma +1}_{L^{\infty }L^{\infty }})+(1+\Vert k\Vert _{L^{\infty }L^2})\right] \\&=(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})\times \\&\quad \times \left[ (1+\Vert R\Vert _{L^{\infty }L^{\infty }})(\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1})+(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})\right] \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1})(1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1})\\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)(1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}), \end{aligned}$$

and

$$\begin{aligned} W_3(h,k)&=(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{4\sigma })+(1+\Vert R\Vert _{L^{\infty }L^2})(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{4\sigma -2})(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})\\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{4\sigma -2})\left[ (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^2)+(1+\Vert R\Vert _{L^{\infty }L^2})(1+\Vert \partial _xR\Vert _{L^{\infty }L^2})\right] \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{4\sigma -2})(1+\Vert R\Vert _{L^{\infty }H^1}^2). \end{aligned}$$

Combining the above estimates, we have

$$\begin{aligned}&W_1(h,k)+W_2(h,k)+W_3(h,k)\\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)\left( 1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}\right) \\&\quad +(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{4\sigma -2})\left( 1+\Vert R\Vert _{L^{\infty }H^1}^2\right) \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)\left( 1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}\right) \\&\quad +(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma })\left( 1+\Vert R\Vert _{L^{\infty }H^1}^2\right) \\&\lesssim (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)\left( 1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}\right) . \end{aligned}$$

Thus, there exists a positive constant $C_0$ such that

$$\begin{aligned}&W_1(h,k)+W_2(h,k)+W_3(h,k)\\&\leqslant C_0\left( (1+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2(\sigma -1)})(1+\Vert R\Vert _{L^{\infty }H^1}^2)\left( 1+\Vert \partial _xR\Vert _{L^{\infty }L^{\infty }}+\Vert R\Vert _{L^{\infty }L^{\infty }}^{2\sigma +1}\right) \right) . \end{aligned}$$

Note that the constant $C_0$ in the right side is independent of parameters $\omega _j,c_j$. Let $C_*=16C_0$. Using the assumption (1.10), we have

$$\begin{aligned} W_1(h,k)+W_2(h,k)+W_3(h,k) \leqslant \frac{v_*}{16}=\lambda , \end{aligned}$$

for t large enough. Thus, by (2.38), we have

$$\begin{aligned} \Vert \tilde{\psi }(t)-\tilde{v}(t)\Vert ^2_{L^2}\leqslant e^{-2\lambda N+(N-t)\lambda }, \end{aligned}$$

for t large enough. Letting $N \rightarrow \infty$ in the above estimate, we obtain

$$\begin{aligned} \Vert \tilde{\psi }(t)-\tilde{v}\Vert _{L^2}^2=0, \end{aligned}$$

for all t large enough. This implies that

$$\begin{aligned} \tilde{\psi }=\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi -k, \end{aligned}$$

(2.39)

which is equivalent to (2.15) and then

$$\begin{aligned} \psi =\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi . \end{aligned}$$

(2.40)

Moreover, since $(\tilde{\psi },\tilde{\varphi })$ solves (2.13) we have $(\psi ,\varphi )$ solves (2.3). Combining with (2.40), if we set

$$\begin{aligned} u=\exp \left( -\frac{i}{2}\int _{-\infty }^x|\varphi |^{2\sigma }\,dy\right) \varphi \end{aligned}$$

(2.41)

then u solves (1.1) by Lemma 3.6. Furthermore, by Lemma 3.6, we have

$$\begin{aligned} \Vert u-R\Vert _{H^1}&=\left\Vert \exp \left( -\frac{i}{2}|\varphi |^{2\sigma }\,dy\right) \varphi -\exp \left( \frac{i}{2}|h|^{2\sigma }\,dy\right) h\right\Vert _{H^1}\\&\lesssim C(\Vert \varphi \Vert _{H^1},\Vert h\Vert _{H^1}) \Vert \varphi -h\Vert _{H^1}\lesssim \Vert \tilde{\varphi }\Vert _{H^1}\lesssim e^{-\lambda t}, \end{aligned}$$

Thus for t large enough, we have

$$\begin{aligned} \Vert u-R\Vert _{H^1} \leqslant Ce^{-\lambda t}, \end{aligned}$$

(2.42)

for $\lambda =\frac{1}{16}v_{*}$ and $C=C(\omega _1,\ldots ,\omega _K,c_1,\ldots ,c_K)$. This completes the proof of Theorem 1.1.

3 Some Technical Lemmas

3.1 Properties of Solitons

In this section, we give the proof of (2.7). We have the following result.

Lemma 3.1

Let $\lambda =\frac{1}{16}v_{*}$, where $v_{*}$ is defined by (1.10). There exist $C>0$ and such that for $t>0$ large enough, the estimate (2.7) uniformly holds in time.

Proof

First, we need some estimates on the profile. We have

$$\begin{aligned} |R_j(t,x)|&=|\psi _{\omega _j,c_j}(t,x)|=|\phi _{\omega _j,c_j}(x-c_jt)|=|\varphi _{\omega _j,c_j}(x-c_jt)|\\&\approx \left( \frac{4\omega _j-c_j^2}{2\sqrt{\omega _j}\left( \cosh (\sigma h_j (x-c_jt))-\frac{c_j}{2\sqrt{\omega _j}}\right) }\right) ^{\frac{1}{2\sigma }}\\&\lesssim \left( \frac{4\omega _j-c_j^2}{2\sqrt{\omega _j}\left( \cosh (\sigma h_j(x-c_jt))-\frac{|c_j|}{2\sqrt{\omega _j}}\cosh (\sigma h_j(x-c_jt))\right) }\right) ^{\frac{1}{2\sigma }}\\&\lesssim \left( \frac{4\omega _j-c_j^2}{(2\sqrt{\omega _j}-|c_j|)\cosh (\sigma h_j(x-c_jt))}\right) ^{\frac{1}{2\sigma }}\lesssim \left( \frac{2\sqrt{\omega _j}+|c_j|}{\cosh (\sigma h_j (x-c_jt))}\right) ^{\frac{1}{2\sigma }}\\&\lesssim _{\omega _j,|c_j|} e^{-\frac{h_j}{2}|x-c_jt|}, \end{aligned}$$

Furthermore,

$$\begin{aligned} \partial _x\varphi _{\omega _j,c_j}(y)&\approx \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{2\sigma }}\frac{-\sinh (\sigma h_jy)}{\left( \cosh (\sigma h_j y)-\frac{c_j}{\sqrt{\omega _j}}\right) ^{1+\frac{1}{2\sigma }}}. \end{aligned}$$

Thus,

$$\begin{aligned} |\partial _x\varphi _{\omega _j,c_j}(y)|&\lesssim \left( \frac{h_j^2}{2\sqrt{\omega _j}}\right) ^{\frac{1}{2\sigma }}\frac{|\sinh (\sigma h_j y)|}{\left( 1-\frac{|c_j|}{\sqrt{\omega _j}}\right) ^{1+\frac{1}{2\sigma }} \cosh (\sigma h_j y)^{1+\frac{1}{2\sigma }}}\\&\lesssim _{\omega _j,|c_j|}\frac{1}{\cosh (\sigma h_jy)^{\frac{1}{2\sigma }}} \lesssim _{\omega _j,|c_j|} e^{-\frac{h_j}{2}|y|}, \end{aligned}$$

Using the above estimates, we have

$$\begin{aligned} |\partial _xR_j(t,x)|&=|\partial _x\psi _{\omega _j,c_j}(t,x)|=|\partial _x\phi _{\omega _j,c_j}(x-c_jt)|\\&=|\partial _x\varphi _{\omega _j,c_j}(x-c_jt)+i\varphi _{\omega _j,c_j}(x-c_jt)\partial _x\theta _{\omega _j,c_j}(x-c_jt)|\\&\lesssim |\partial _x\varphi _{\omega _j,c_j}(x-c_jt)|+|\varphi _{\omega _j,c_j}(x-c_jt)||\partial _x\theta _{\omega _j,c_j}(x-c_jt)|\\&\lesssim _{\omega _j,|c_j|} |\partial _x\varphi _{\omega _j,c_j}(x-c_jt)|+e^{\frac{-h_j}{2}|x-c_jt|}\\&\lesssim _{\omega _j,|c_j|} e^{-\frac{h_j}{2}|x-c_jt|}. \end{aligned}$$

By similar arguments, we have

$$\begin{aligned} |\partial _x^2R_j(t,x)|+|\partial _x^3R_j(t,x)|&\lesssim _{\omega _j,|c_j|}e^{\frac{-h_j}{2}|x-c_jt|}, \end{aligned}$$

For convenience, we set

$$\begin{aligned}&\chi =-i|R|^{2\sigma }\partial _xR+i\Sigma _{j}|R_j|^{2\sigma }\partial _xR_{j},\\&f(R,\overline{R},\partial _xR)= i|R|^{2\sigma }\partial _xR,\\&g(R,\overline{R},\partial _xR,\partial _x\overline{R},\partial _x^2R)=i\partial _x(|R|^{2\sigma }\partial _xR),\\&r(R,\partial _xR,\ldots ,\partial _x^3R,\partial _x\overline{R},\partial _x^2\overline{R})=i\partial _x^2(|R|^{2\sigma }\partial _xR). \end{aligned}$$

Fix $t>0$, for each $x\in \mathbb {R}$, choose $m=m(x)\in \left\{ 1,2,\ldots ,K\right\}$ so that

$$\begin{aligned} |x-c_mt|=\min _{j}|x-c_jt|. \end{aligned}$$

For $j \ne m$ we have

$$\begin{aligned} |x-c_jt|\geqslant \frac{1}{2}(|x-c_jt|+|x-c_mt|)\geqslant \frac{1}{2}|c_jt-c_mt|=\frac{t}{2}|c_j-c_m|. \end{aligned}$$

Thus, we have

$$\begin{aligned}&|(R-R_m)(t,x)|+|\partial _x(R-R_m)(t,x)|+|\partial _x^2(R-R_m)(t,x)|+|\partial _x^3(R-R_m)(t,x)|\\&\leqslant \sum _{j\ne m}(|R_j(t,x)|+|\partial _xR_j(t,x)|+|\partial _x^2R_j(t,x)|+|\partial _x^3R_j(t,x)|)\\&\lesssim _{\omega _1,\ldots ,\omega _K,|c_1|,\ldots ,|c_K|}\delta _m(t,x):=\sum _{j\ne m}e^{\frac{-h_j}{2}|x-c_jt|}. \end{aligned}$$

Recall that

$$\begin{aligned} v_{*}=\inf _{j\ne k}h_j|c_j-c_k|. \end{aligned}$$

We have

$$\begin{aligned}&|(R-R_m)(t,x)|+|\partial _x(R-R_m)(t,x)|+|\partial _x^2(R-R_m)(t,x)|+|\partial _x^3(R-R_m)(t,x)| \\&\quad \lesssim \delta _m(t,x)\\&\quad \lesssim e^{-\frac{1}{4}v_{*}t}. \end{aligned}$$

We see that f, g, r are polynomials in R, $\partial _xR$, $\partial _x^2R$, $\partial _x^3R$, $\partial _x\overline{R}$ and $\partial _x^2\overline{R}$. Denote

$$\begin{aligned} A=\sup _{|u|+|\partial _xu|+|\partial _x^2u|+|\partial _x^3u| \leqslant \sum _j\Vert R_j\Vert _{H^4}}(|df|+|dg|+|dr|). \end{aligned}$$

We have

$$\begin{aligned}&|\chi |+|\partial _x\chi |+|\partial _x^2\chi |\\&\leqslant |f(R,\overline{R}, \partial _xR)-f_{R_m,\partial _x\overline{R}_m, R_m}|+|g(R,\overline{R},\partial _xR,..)-g(R_m,\overline{R}_m,\partial _xR_m,..)|\\&\quad +|r(R,\partial _xR,\ldots ,\partial _x^3R,\overline{R},..)-r(R_m,\partial _xR_m,\ldots ,\partial _x^3R_m,\overline{R}_m,..)|\\&\quad +\Sigma _{j\ne m}(f(R_j,\overline{R}_j,\partial _xR_j)+g(R_j,\partial _xR_j,\partial _x^2R_j,\overline{R}_j,\partial _x\overline{R}_j)+r(R_j,\ldots ,\partial _x^3R_j,\overline{R}_j,\ldots ,\partial _x^2\overline{R}_j))\\&\lesssim A(|R-R_m|+|\partial _x(R-R_m)|+|\partial _x^2(R-R_m)|+|\partial _x^3(R-R_m)|)\\&\quad +A\Sigma _{j\ne m}(|R_j|+|\partial _xR_j|+|\partial _x^2R_j|+|\partial _x^3R_j|)\\&\lesssim 2A\Sigma _{j\ne m} (|R_j|+|\partial _xR_j|+|\partial _x^2R_j|+|\partial _x^3R_j|)\\&\lesssim 2A \delta _m(t,x). \end{aligned}$$

In particular,

$$\begin{aligned} \Vert \chi \Vert _{W^{2,\infty }} \lesssim e^{-\frac{1}{4}v_{*}t}. \end{aligned}$$

(3.1)

Moreover,

$$\begin{aligned} \Vert \chi \Vert _{W^{2,1}}&\lesssim \Sigma _j (\Vert |R_j|^{2\sigma }\partial _xR_j\Vert _{L^1}+\Vert \partial _x(|R_j|^{2\sigma }\partial _xR_j)\Vert _{L^1}+\Vert \partial _x^2(|R_j|^{2\sigma }\partial _xR_j)\Vert _{L^1})\\&\lesssim \Sigma _j (\Vert R_j\Vert _{H^1}^(2\sigma +1)+\Vert R_j\Vert _{H^2}^{2\sigma +1}+\Vert R_j\Vert _{H^3}^{2\sigma +1})<\infty . \end{aligned}$$

Thus, using Hölder inequality we obtain

$$\begin{aligned} \Vert \chi \Vert _{H^2}&\lesssim _{\omega _1,\ldots ,\omega _K,|c_1|,\ldots ,|c_K|} e^{-\frac{1}{8}v_{*}t}. \end{aligned}$$

It follows that if $t \gg \max \{\omega _1,\ldots ,\omega _K,|c_1|,\ldots ,|c_K|\}$ is large enough then

$$\begin{aligned} \Vert \chi \Vert _{H^2} \leqslant e^{-\frac{1}{16}v_{*}t}=e^{-\lambda t}. \end{aligned}$$

This implies the desired result. $\square$

3.2 Some Useful Estimates

Lemma 3.2

Fix $\alpha ,\beta \in \mathbb {R}$ with $\alpha +\beta >0$. We have

$$\begin{aligned} \left| (w+z)^{\alpha }(\overline{w}+\overline{z})^{\beta }-w^{\alpha }\overline{w}^{\beta }\right| \lesssim |z|^{\alpha +\beta }+|z||w|^{\alpha +\beta -1}. \end{aligned}$$

(3.2)

Proof

We may assume that $w\ne 0$. We may assume $w=1$ be replacing z by $\frac{z}{w}$. Let

$$\begin{aligned} f(t)=(1+tz)^{\alpha }(1+t\overline{z})^{\beta }. \end{aligned}$$

It suffices to show

$$\begin{aligned} |f(1)-f(0)| \lesssim |z|^{\alpha +\beta }+|z|. \end{aligned}$$

(3.3)

When $|z|\geqslant \frac{1}{2}$, we have $|f(1)-f(0)| \lesssim |z|^{\alpha +\beta }$. When $|z|<\frac{1}{2}$, we have $f(1)-f(0)=f'(t)$ for some $t\in (0,1)$ by mean value theorem, but $\sup _{0<t<1}|f'(t)|\lesssim |z|$. This shows (3.3) and hence (3.2). $\square$

As a consequence of (3.2), we have the following result.

Lemma 3.3

Fix $\alpha >0$. We have

$$\begin{aligned} \left| |w+z|^{\alpha }-|w|^{\alpha }\right| \lesssim |z|^{\alpha }+|z||w|^{\alpha -1}. \end{aligned}$$

(3.4)

Proof

Using (3.2) for $\alpha =\beta$, we obtain (3.4). $\square$

Lemma 3.4

Let $w_1,w_2,\eta _1,\eta _2\in \mathbb {C}$ and $\sigma \geqslant \frac{3}{2}$. Define

Then

$$\begin{aligned} |J(\eta _1,\eta _2)-J(0,0)| \lesssim |\eta |(|\eta |^{2\sigma -1}+|W|^{2\sigma -1}), \end{aligned}$$

where $|\eta |=|\eta _1|+|\eta _2|$ and $|W|=|w_1|+|w_2|$.

Proof

We have

$$\begin{aligned} |J(\eta _1,\eta _2)-J(0,0)| \leqslant |J(\eta _1,\eta _2)-J(\eta _1,0)|+|J(\eta _1,0)-J(0,0)|. \end{aligned}$$

Moreover,

$$\begin{aligned}&|J(\eta _1,\eta _2)-J(\eta _1,0)|\lesssim |w_1+\eta _1|^{2(\sigma -1)}|(w_2+\eta _2)^2-w_2^2|\\&\quad \lesssim |w_1+\eta _1|^{2(\sigma -1)} |\eta _2|(|\eta _2|+|w_2|)\\&\quad \lesssim (|W|+|\eta |)^{2\sigma -1}|\eta |\\&\quad \lesssim (|W|^{2\sigma -1}+|\eta |^{2\sigma -1})|\eta |. \end{aligned}$$

Thus, it suffices to check the other term. Rewrite

$$\begin{aligned} J(\eta _1,0)&=\frac{1}{2i}|w_1+\eta _1|^{2(\sigma -2)}\left[ w_2^2(\overline{w}_1+\overline{\eta }_1)^2-\overline{w}_2^2(w_1+\eta _1)^2\right] \\&=\frac{w_2^2}{2i}(w_1+\eta _1)^{\sigma -2}(\overline{w}_1+\overline{\eta }_1)^{\sigma }-\frac{\overline{w}_2^2}{2i}(w_1+\eta _1)^{\sigma }(\overline{w}_1+\overline{\eta }_1)^{\sigma -2}. \end{aligned}$$

By (3.2),

$$\begin{aligned} |J(\eta _1,0)-J(0,0)|&\lesssim |w_2|^2(|\eta _1|^{2\sigma -2}+|\eta _1||w_1|^{2\sigma -3})\\&\lesssim |W|^2|\eta |(|W|^{2\sigma -3}+|\eta |^{2\sigma -3})\\&\lesssim |\eta |(|\eta |^{2\sigma -1}+|W|^{2\sigma -1}), \end{aligned}$$

where in the second estimate, the term $|\eta _1|^{2\sigma -2}$ is superlinear provided $\sigma \geqslant \frac{3}{2}$ and in the last estimate, we use the Cauchy inequality $|W|^2|\eta |^{2\sigma -3} \lesssim |W|^{2\sigma -1}+|\eta |^{2\sigma -1}$ provided $\sigma \geqslant \frac{3}{2}$. This implies the desired result. $\square$

Lemma 3.5

Let $w,\eta \in \mathbb {C}$ and $\sigma \geqslant 1$. We have

$$\begin{aligned}{} & {} |\partial _x(|w+\eta |^{2(\sigma -1)}(w+\eta )^2-|w|^{2(\sigma -1)}w^2)|\lesssim |\partial _x\eta |(|w|^{2\sigma -1}+|\eta |^{2\sigma -1})\\{} & {} \quad +|\partial _xw||\eta |(|\eta |^{2\sigma -2} +|w|^{2\sigma -2}). \end{aligned}$$

Proof

We have

$$\begin{aligned}&|\partial _x(|w+\eta |^{2(\sigma -1)}(w+\eta )^2-|w|^{2(\sigma -1)}w^2)|\\&= |\partial _x((w+\eta )^{\sigma +1}(\overline{w}+\overline{\eta })^{\sigma -1}-w^{\sigma +1}\overline{w}^{\sigma -1})|\\&\lesssim |(\sigma +1)(\partial _xw+\partial _x\eta )(w+\eta )^{\sigma }(\overline{w}+\overline{\eta })^{\sigma -1}-(\sigma +1)\partial _xw w^{\sigma }\overline{w}^{\sigma -1}|\\&\quad +|(\sigma -1)(w+\eta )^{\sigma +1}(\partial _x\overline{w}+\partial _x\overline{\eta })(\overline{w}+\overline{\eta })^{\sigma -2}-(\sigma -1)w^{\sigma +1}\partial _x\overline{w}\overline{w}^{\sigma -2}|. \end{aligned}$$

We only need to treat the first term. The second term is similar. Using $\sigma \geqslant \frac{3}{2}$ and (3.2), we have

$$\begin{aligned}&|(\sigma +1)(\partial _xw+\partial _x\eta )(w+\eta )^{\sigma }(\overline{w}+\overline{\eta })^{\sigma -1}-(\sigma +1)\partial _xw w^{\sigma }\overline{w}^{\sigma -1}|\\&\lesssim |\partial _x\eta ||w+\eta |^{2\sigma -1}+|\partial _xw||(w+\eta )^{\sigma }(\overline{w}+\overline{\eta })^{\sigma -1}-w^{\sigma }\overline{w}^{\sigma -1}|\\&\lesssim |\partial _x\eta |(|w|^{2\sigma -1}+|\eta |^{2\sigma -1})+|\partial _xw|(|\eta |^{2\sigma -1}+|\eta ||w|^{2\sigma -2})\\&=|\partial _x\eta |(|w|^{2\sigma -1}+|\eta |^{2\sigma -1})+|\partial _xw||\eta |(|\eta |^{2\sigma -2}+|w|^{2\sigma -2}). \end{aligned}$$

$\square$

Lemma 3.6

Let u be defined as in (2.41). Then u is a solution of (1.1) on $(T_0,\infty )$. Moreover,

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(T_0,\infty ;H^1(\mathbb {R}))} \lesssim \Vert \varphi \Vert _{L^{\infty }(T_0,\infty ;H^1(\mathbb {R}))}+\Vert \varphi \Vert ^{2\sigma +1}_{L^{\infty }(T_0,\infty ;H^1(\mathbb {R}))}, \end{aligned}$$

(3.5)

and

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(T_0,\infty ;H^1(\mathbb {R}))}\lesssim 1. \end{aligned}$$

(3.6)

Proof

Since $\psi =\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi$ and $(\varphi ,\psi )$ solves (2.3), we have

$$\begin{aligned} L\varphi =P(\varphi ,\psi )=P\left( \varphi ,\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi \right) . \end{aligned}$$

(3.7)

We recall that

$$\begin{aligned} u=\exp \left( \frac{-i}{2}\int _{-\infty }^x|\varphi |^{2\sigma }\,dy\right) \varphi . \end{aligned}$$

(3.8)

Using (3.7) and (3.8), we may prove that u is a solution of (1.1).

Since (3.8), for each $t>0$,

$$\begin{aligned} \Vert u(t)\Vert _{L^2(\mathbb {R})}&=\Vert \varphi (t)\Vert _{L^2(\mathbb {R})}\\ \Vert \partial _xu(t)\Vert _{L^2}&\leqslant \Vert \partial _x\varphi (t)\Vert _{L^2(\mathbb {R})}+\frac{1}{2}\Vert |\varphi |^{2\sigma +1}\Vert _{L^2(\mathbb {R})}\\&\lesssim \Vert \varphi (t)\Vert _{H^1(\mathbb {R})}+\Vert \varphi (t)\Vert _{H^1(\mathbb {R})}^{2\sigma +1}. \end{aligned}$$

This implies (3.5).

Moreover, using (2.17), we have, for all $t\geqslant T_0$,

$$\begin{aligned}&\Vert \varphi (t)\Vert _{H^1(\mathbb {R})}\\&\leqslant \Vert \tilde{\varphi }(t)\Vert _{H^1(\mathbb {R})}+\Vert h\Vert _{L^{\infty }(\mathbb {R},H^1(R))}\\&\lesssim e^{-\lambda T_0}+\Vert R\Vert _{L^{\infty }(\mathbb {R},H^1(R))}+\Vert R\Vert ^{2\sigma +1}_{L^{\infty }(\mathbb {R},H^1(R))}\\&\lesssim 1. \end{aligned}$$

Combining with (3.5), we obtain (3.6). This completes the proof. $\square$

3.3 Proof $G(\varphi ,v)=Q(\varphi ,v)$

Let $G(\varphi ,v)$ be defined as in (2.19) and Q be defined as in (2.5). Then we have the following result.

Lemma 3.7

Let $v=\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi$. Then the following equality holds:

$$\begin{aligned} G(\varphi ,v)=Q(\varphi ,v). \end{aligned}$$

Proof

We have

The term contains in the expression of $G(\varphi ,v)$ is the following.

which equals to the term contains in the expression of $Q(\varphi ,v)$. We only need to check the equality of the remaining terms. The remaining terms of $G(\varphi ,v)$ is the following.

(3.9)

(3.10)

Noting that and $v=\partial _x\varphi -\frac{i}{2}|\varphi |^{2\sigma }\varphi$, we have

Moreover, using we have

Combining the above expressions we obtain

This is exactly the remaining terms of $Q(\varphi ,v)$. Thus, $G(\varphi ,v)=Q(\varphi ,v)$. $\square$

3.4 Existence of a Solution of the System

In this section, using similar arguments as in [9, 10], we prove the existence of a solution of (2.13). For convenience, we recall the equation:

$$\begin{aligned} \eta (t)=i\int _t^{\infty }S(t-s)[f(W+\eta )-f(W)+H](s)\,ds, \end{aligned}$$

(3.11)

where

$$\begin{aligned} W&=(h,k),\\ H&=e^{-\lambda t}(m,n),\\ f(\varphi ,\psi )&=(P(\varphi ,\psi ),Q(\varphi ,\psi )). \end{aligned}$$

We have the following lemma.

Lemma 3.8

Let $H=H(t,x):[0,\infty )\times \mathbb {R}\rightarrow \mathbb {C}^2$, $W=W(t,x):[0,\infty )\times \mathbb {R}\rightarrow \mathbb {C}^2$ be given vector functions which satisfy for some $C_1>0$, $C_2>0$, $\lambda >0$, $T_0 \geqslant 0$:

$$\begin{aligned}&\Vert W(t)\Vert _{L^{\infty }(\mathbb {R})\times L^{\infty }(\mathbb {R})}+e^{\lambda t}\Vert H(t)\Vert _{L^2(\mathbb {R}) \times L^2(\mathbb {R})} \leqslant C_1, \quad \forall t \geqslant T_0, \end{aligned}$$

(3.12)

$$\begin{aligned}&\Vert \partial W(t)\Vert _{L^2(\mathbb {R}) \times L^2(\mathbb {R})}+\Vert \partial W(t)\Vert _{L^{\infty }(\mathbb {R}) \times L^{\infty }(\mathbb {R})}+e^{\lambda t}\Vert \partial H(t)\Vert _{L^2(\mathbb {R}) \times L^2(\mathbb {R})} \leqslant C_2, \quad \forall t \geqslant T_0. \end{aligned}$$

(3.13)

Consider Eq. (3.11). There exists a constant $\lambda _{*}$ independent of $C_2$ such that if $\lambda \geqslant \lambda _{*}$ then there exists a unique solution $\eta$ of (3.11) on $[T_0,\infty ) \times \mathbb {R}$ satisfying

$$\begin{aligned} e^{\lambda t}\Vert \eta \Vert _{S([t,\infty )) \times S([t,\infty ))}+e^{\lambda t}\Vert \partial \eta \Vert _{S([t,\infty )) \times S([t,\infty ))} \leqslant 1, \quad \forall t \geqslant T_0. \end{aligned}$$

Proof

We rewrite (3.11) by $\eta =\Phi \eta$. We show that, for $\lambda$ large enough, $\Phi$ is a contraction map in the following ball

$$\begin{aligned} B=\left\{ \eta :\Vert \eta \Vert _X:=\sup _{t>T_0} \left( e^{\lambda t}\Vert \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}+e^{\lambda t}\Vert \partial _x\eta \Vert _{S([t,\infty ))\times S([t,\infty ))}\right) \leqslant 1\right\} . \end{aligned}$$

We will use condition $\lambda \gg 1$ in the proof without specifying it.

Step 1. Proof $\Phi$ maps B into B

Let $t \geqslant T_0$, $\eta =(\eta _1,\eta _2) \in B$, $W=(w_1,w_2)$ and $H=(h_1,h_2)$. By Strichartz estimates, we have

$$\begin{aligned} \Vert \Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}&\lesssim \Vert f(W+\eta )-f(W)\Vert _{N([t,\infty ))\times N([t,\infty ))}, \end{aligned}$$

(3.14)

$$\begin{aligned}&\quad +\Vert H\Vert _{L^1_{\tau }L^2_x([t,\infty ))\times L^1_{\tau }L^2_x([t,\infty ))}. \end{aligned}$$

(3.15)

For (3.15), using (3.12), we have

$$\begin{aligned} \Vert H\Vert _{L^1_{\tau }L^2_x([t,\infty ))\times L^1_{\tau }L^2_x([t,\infty ))}&=\Vert h_1\Vert _{L^1_{\tau }L^2_x([t,\infty ))}+\Vert h_2\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\nonumber \\&\lesssim \int _t^{\infty }e^{-\lambda \tau }\,d\tau \leqslant \frac{1}{\lambda }e^{-\lambda t}<\frac{1}{10}e^{-\lambda t}. \end{aligned}$$

(3.16)

For (3.14), we have

(3.17)

(3.18)

Using the assumption $\sigma \geqslant \frac{3}{2}$ and the inequality (3.4), we have

$$\begin{aligned}&\text { the term }(3.17) \\&\lesssim \left| ||w_1+\eta _1|^{2(\sigma -1)}-|w_1|^{2(\sigma -1)}||w_1+\eta _1|^2|w_2+\eta _2|\right| \\&\quad +\left| |w_1|^{2(\sigma -1)}|(w_1+\eta _1)^2-w_1^2||w_2+\eta _2|\right| +\left| |w_1|^{2(\sigma -1)}|w_1|^2|\eta _2|\right| \\&\lesssim (|\eta _1|^{2(\sigma -1)}+|\eta _1||w_1|^{2(\sigma -1)-1})(|W|+|\eta |)^3\\&\quad +|w_1|^{2(\sigma -1)}(|w_1||\eta _1|+|\eta _1|^2)|w_2+\eta _2|+|w_1|^{2\sigma }|\eta _2|\\&\lesssim (|\eta |^{2(\sigma -1)}+|\eta ||W|^{2(\sigma -1)-1})(|W|^3+|\eta |^3)\\&\quad +|W|^{2(\sigma -1)}(|W||\eta |+|\eta |^2)(|W|+|\eta |)+|W|^{2\sigma }|\eta |\\&\lesssim |\eta |(|\eta |^{2\sigma -3}+|W|^{2\sigma -3})(|\eta |^3+|W|^3)+|\eta ||W|^{2(\sigma -1)}(|W|^2+|\eta |^2)+|W|^{2\sigma }|\eta |\\&\lesssim |\eta |(|\eta |^{2\sigma }+|W|^{2\sigma })+|\eta ||W|^{2\sigma }+|\eta |^3|W|^{2(\sigma -1)}+|W|^{2\sigma }|\eta |\\&\lesssim |\eta |^{2\sigma +1}+|\eta ||W|^{2\sigma }. \end{aligned}$$

Moreover, using Lemma 3.4, we have

$$\begin{aligned}&\text { the term }(3.18)\\&\lesssim |\eta _1|\int _{-\infty }^x|w_1+\eta _1|^{2(\sigma -2)}|w_2+\eta _2|^2|w_1+\eta _1|^2\,dy\\&\quad +|w_1|\int _{-\infty }^x J(\eta _1,\eta _2)-J(0,0)dy\\&\lesssim |\eta |\int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\, dy+|W|\int _{-\infty }^x|\eta |(|W|^{2\sigma -1}+|\eta |^{2\sigma -1})\,dy\\&= |\eta |\int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\,dy+|W|\int _{-\infty }^x|\eta ||W|^{2\sigma -1}+|\eta |^{2\sigma }\,dy. \end{aligned}$$

Thus, we obtain

$$\begin{aligned}&|P(W+\eta )-P(W)|\\&\quad \lesssim |\eta |^{2\sigma +1}+|\eta ||W|^{2\sigma }+|\eta |\int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\,dy+|W|\int _{-\infty }^x|\eta ||W|^{2\sigma -1}+|\eta |^{2\sigma }\,dy. \end{aligned}$$

Similarly,

$$\begin{aligned}&|Q(W+\eta )-Q(W)|\\&\lesssim |\eta |^{2\sigma +1}+|\eta ||W|^{2\sigma }+|\eta |\int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\,dy+|W|\int _{-\infty }^x|\eta ||W|^{2\sigma -1}+|\eta |^{2\sigma }\,dy. \end{aligned}$$

Hence, using $\sigma \geqslant \frac{3}{2}$, we have:

$$\begin{aligned}&\Vert f(W+\eta )-f(W)\Vert _{N([t,\infty ))\times N([t,\infty ))}\\&\lesssim \Vert P(W+\eta )-P(W)\Vert _{L^1_{\tau }L^2_x([t,\infty ))}+\Vert Q(W+\eta )-Q(W)\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\lesssim \Vert |\eta |^{2\sigma +1}\Vert _{L^1_{\tau }L^2_x([t,\infty ))}+\Vert |\eta |\int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\,dy\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\quad +\Vert |W|\int _{-\infty }^x|\eta ||W|^{2\sigma -1}+|\eta |^{2\sigma }\,dy\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\lesssim \Vert |\eta |\Vert _{L^{\infty }L^2_x([t,\infty ))} \Vert |\eta |\Vert ^4_{L^4_{\tau }L^{\infty }_x([t,\infty ))}\\&\quad +\Vert |\eta |\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\left\Vert \int _{-\infty }^x|W|^{2\sigma }+|\eta |^{2\sigma }\,dy\right\Vert _{L^{\infty }_{\tau }L^{\infty }_x([t,\infty ))}\\&\quad +\Vert |W|\Vert _{L^{\infty }_{\tau }L^2_x([t,\infty ))}\Vert \int _{-\infty }^x|\eta ||W|^{2\sigma -1}+|\eta |^{2\sigma }\,dy\Vert _{L^1_{\tau }L^{\infty }_x([t,\infty ))}\\&\lesssim e^{-5\lambda t}+ \Vert |\eta |\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\Vert |W|^{2\sigma }+|\eta |^{2\sigma }\Vert _{L^{\infty }_{\tau }L^1_x}\\&\quad +\Vert W\Vert _{L^{\infty }_tL^2_x}\Vert \eta \Vert _{L^1_{\tau }L^2_x([t,\infty ))}\Vert |W|^{2\sigma -1}+|\eta |^{2\sigma -1}\Vert _{L^{\infty }_{\tau }L^2_x([t,\infty ))}\\&\lesssim e^{-5\lambda t}+ \Vert |\eta |\Vert _{L^1_{\tau }L^2_x([t,\infty ))}=e^{-5\lambda t}+\int _{t}^{\infty }e^{-\lambda \tau }d\tau \\&\lesssim e^{-5\lambda t}+\frac{1}{\lambda }e^{-\lambda t}<\frac{1}{10}e^{-\lambda t}, \end{aligned}$$

Combining with (3.16) and (3.14), (3.15) we obtain

$$\begin{aligned} \Vert \Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))} <\frac{1}{5}e^{-\lambda t}. \end{aligned}$$

(3.19)

We have

$$\begin{aligned} \Vert \partial _x\Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}&\lesssim \Vert \partial _x(f(W+\eta )-f(W))\Vert _{N([t,\infty ))\times N([t,\infty ))} \end{aligned}$$

(3.20)

$$\begin{aligned}&\quad +\Vert \partial _xH\Vert _{L^1_{\tau }L^2_x([t,\infty ))\times L^1_{\tau }L^2_x([t,\infty ))} . \end{aligned}$$

(3.21)

For (3.21), using (3.13) we have

$$\begin{aligned} \Vert \partial _xH\Vert _{L^1_{\tau }L^2_x([t,\infty ))\times L^1_{\tau }L^2_x([t,\infty ))}\lesssim \int _t^{\infty } e^{-\lambda \tau }\,d\tau =\frac{1}{\lambda }e^{-\lambda t}<\frac{1}{10} e^{-\lambda t}, \end{aligned}$$

(3.22)

For (3.20), we have

$$\begin{aligned} \Vert \partial _x(f(W+\eta )-f(W))\Vert _{N([t,\infty ))\times N([t,\infty ))}&=\Vert \partial _x(P(W+\eta )-P(W))\Vert _{N([t,\infty ))}\\&\quad +\Vert \partial _x(Q(W+\eta )-Q(W))\Vert _{N([t,\infty ))}. \end{aligned}$$

Furthermore,

(3.23)

(3.24)

(3.25)

For (3.23), using Lemma 3.5 and (3.2) we have

$$\begin{aligned}&\text { the term }(3.23)\\&\lesssim |\partial _x(|w_1+\eta _1|^{2(\sigma -1)}(w_1+\eta _1)^2-|w_1|^{2(\sigma -1)}w_1^2)\overline{w}_2|\\&\quad +|\eta _2|(|\partial _xW|+|\partial _x\eta |)(|W|^{2\sigma -1}+|\eta |^{2\sigma -1})\\&\quad +|(|w_1+\eta _1|^{2(\sigma -1)}(w_1+\eta _1)^2-|w_1|^{2(\sigma -1)}w_1^2)\partial _x\overline{w}_2|\\&\quad +|\partial _x\eta _2|(|W|^{2\sigma }+|\eta |^{2\sigma })\\&\lesssim |\partial _x\eta _1|(|w_1|^{2\sigma -1}+|\eta _1|^{2\sigma -1})+|\partial _xw_1||\eta _1|(|\eta _1|^{2\sigma -2}+|w_1|^{2\sigma -2})\\&\quad + |\eta _2|(|\partial _xW|+|\partial _x\eta |)(|W|^{2\sigma -1}+|\eta |^{2\sigma -1})\\&\quad +|\partial _xw_2|(|\eta _1|^{2\sigma }+|\eta _1||w_1|^{2\sigma -1})\\&\quad +|\partial _x\eta _2|(|W|^{2\sigma }+|\eta |^{2\sigma }). \end{aligned}$$

Thus,

$$\begin{aligned} \Vert \text {the term } (3.23)\Vert _{L^1_{\tau }L^2_x([t,\infty ))}&\lesssim \Vert |\eta |+|\partial \eta |\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\lesssim \frac{1}{\lambda }e^{-\lambda t}<\frac{1}{10}e^{-\lambda t}. \end{aligned}$$

For (3.24), using the inequality (3.4), we have

For (3.25), using the inequality (3.4), we have

$$\begin{aligned}&\Vert \text {the term }(3.25)\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\lesssim \Vert |\eta |(|W|^{2\sigma }+|\eta |^{2\sigma })\Vert _{L^1_{\tau }L^2_x([t,\infty ))}+\Vert |W|(J(\eta _1,\eta _2)-J(0,0))\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\lesssim \Vert |\eta |(|W|^{2\sigma }+|\eta |^{2\sigma })\Vert _{L^1_{\tau }L^2_x([t,\infty ))}+\Vert |\eta ||W|(|W|^{2\sigma -1}+|\eta |^{2\sigma -1})\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\lesssim \Vert |\eta |\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\\&\leqslant \int _t^{\infty }e^{-\lambda \tau }\,d\tau \lesssim \frac{1}{\lambda }e^{-\lambda t}<\frac{1}{10}e^{-\lambda t}, \end{aligned}$$

Combining the above estimates, we obtain

$$\begin{aligned}&\Vert \partial _x(P(W+\eta )-P(W))\Vert _{N([t,\infty ))} \nonumber \\&\leqslant \Vert \partial _x(P(W+\eta )-P(W))\Vert _{L^1_{\tau }L^2_x([t,\infty ))}\leqslant \frac{3}{10}e^{-\lambda t}, \end{aligned}$$

(3.26)

Similarly,

$$\begin{aligned} \Vert \partial _x(Q(W+\eta )-Q(W))\Vert _{N([t,\infty ))}&\leqslant \frac{3}{10}e^{-\lambda t}, \end{aligned}$$

(3.27)

Combining the estimates (3.20), (3.21), (3.22), (3.26) and (3.27), we have

$$\begin{aligned} \Vert \partial _x\Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}\leqslant \frac{7}{10}e^{-\lambda t}. \end{aligned}$$

(3.28)

Combining (3.19) with (3.28), we obtain

$$\begin{aligned} \Vert \Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}+\Vert \partial _x\Phi \eta \Vert _{S([t,\infty ))\times S([t,\infty ))}\leqslant \frac{9}{10}e^{-\lambda t}, \end{aligned}$$

(3.29)

Thus, for $\lambda$ large enough

$$\begin{aligned} \Vert \Phi \eta \Vert _X <1. \end{aligned}$$

This implies that $\Phi$ maps B into B.

Step 2. $\Phi$ is a contraction map on B

By using (3.12), (3.13) and a similar estimate of (3.29), we can show that, for any $\eta \in B$ and $\kappa \in B$ we have

$$\begin{aligned} \Vert \Phi \eta -\Phi \kappa \Vert _X\leqslant \frac{1}{2}\Vert \eta -\kappa \Vert _X. \end{aligned}$$

for $\lambda$ large enough. From Banach fixed point theorem, there exists a unique solution in B of (3.11) and thus a solution of (2.13). This completes the proof of Lemma 3.8. $\square$