Abstract
We establish the equivalence of various admissibility properties for an evolution family and its associated evolution semigroups on several Banach spaces. As an application, we describe how these results can give further relations between hyperbolicity for evolution families and evolution semigroups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Admissibility Properties
Our main aim is to discuss the correspondence between the notions of admissibility for evolution families and their evolution semigroups. It turns out that using appropriate spaces for each of them these notions become equivalent. We consider spaces of bounded continuous functions, continuous functions with bounded exponential growth, and integrable functions. In particular, the equivalence between the notions of admissibility for evolution families and evolution semigroups leads to several new criteria of hyperbolicity for the original evolution family as a perturbation of an autonomous linear dynamics even if the original dynamics is nonautonomous.
We start by recalling the concept of admissibility, which essentially goes back to Perron in [17]. More precisely, he showed that if the equation
with A(t) varying continuously with \(t\ge 0\), has a bounded solution on \({\mathbb {R}}^n\) for any bounded continuous function \(f:{\mathbb {R}}^+_0\rightarrow {\mathbb {R}}^n\), then any bounded solution of the linear equation \(x'=A(t)x\) tends to zero when time approaches \(+\infty \). Related results for discrete time were first obtained by Li in [12]. For some early contributions we refer to the books by Massera and Schäffer [15] (see also [14]) and by Dalec\('\)kiĭ and Kreĭn [8]. Related results for discrete time were obtained by Coffman and Schäffer in [7]. See also [11] for some early results in infinite-dimension. For detailed lists of references, we refer to [1, 6].
More generally, we can consider different spaces in which we look for the perturbations and for the solutions. Consider an evolution family U(t, s), for \(t\ge s\), composed of linear maps on a Banach space X. These can be obtained from a linear equation \(x'=A(t)x\) for some linear operators A(t) varying continuously with t and possibly unbounded. We say that a pair of Banach spaces (C, D) is admissible if for each \(f \in C\) there exists a unique \(x \in D\) satisfying
It is this notion of admissibly that we consider in various situations, and in particular for the pairs of spaces
where C(X), \(C_0(X)\) and \(L^p(X)\) are sets of functions \(u:{\mathbb {R}}\rightarrow X\): the set of bounded continuous functions, the set of continuous functions vanishing at infinity, and the set of measurable functions whose pth power is integrable (identified if they are equal almost everywhere).
We continue by recalling the notion of evolution semigroup. Again, let U(t, s) be an evolution family on a Banach space X. We define an evolution semigroup \(S_t\) on each appropriate space of functions \(u:{\mathbb {R}}\rightarrow X\) by
for all \(t\ge 0\) and \(s\in {\mathbb {R}}\). We emphasize that the evolution semigroup gives rise to an autonomous dynamics even if the original dynamics is nonautonomous, although at the expense of considering an infinite-dimensional space even when X is finite-dimensional.
1.2 Motivation and Advantages of our Work
Sometimes, evolution semigroups allow giving simpler proofs of known results, by first passing some problem at the level of the evolution family U(t, s) and its perturbations to the level of the evolution semigroup. Another less immediate application is that passing to the evolution semigroup we transform not only the original dynamics but also its properties into corresponding ones at the semigroup level. Sometimes this is quite helpful in finding right nonautonomous notions, in some appropriate sense. A major example of such a correspondence is the study of hyperbolicity and its various variations that goes back to Mather in [16]. Today the theory of semigroups is an important tool in the theory of differential equations (see for example [9, 19]).
A main motivation for our work is that it is in general simpler to verify an admissibility property for an autonomous dynamics, sometimes even on an infinite-dimensional space. This causes that it is convenient to have characterizations of admissibility in terms of an autonomous dynamics. There is however another motivation that is equally important. In order to explain it, we recall that often admissibility and hyperbolicity are well related (see [1, 6] and the references therein). There are however quite general types of hyperbolicity that are much harder to relate to admissibility properties, such as tempered hyperbolicity for a cocycle with nonzero Lyapunov exponents that occurs naturally in the context of smooth ergodic theory (see [2, 5]).
On the other hand, one should expect such admissibility properties to play an important role in discussing for example shadowing or Ulam stability properties in the context of smooth ergodic theory, particularly its nonautonomous version. Part of the problem seems to be what are the right or at least reasonable nonautonomous notions that should correspond to the usual autonomous properties. Thus, one can expect that the autonomous admissibility notions considered in our paper and some appropriate modifications play a relevant role in discussing nonautonomous versions of some results of smooth ergodic theory, with the advantage that some important parts of the theory have been extended successfully to infinite-dimensional spaces such as Oseledets’ multiplicative ergodic theorem and certain applications to invariant manifold theory (see [4, 13]).
Coming back to the motivation for our work, it follows from the former discussion that it is of interest to obtain autonomous characterizations of admissibility properties without involving hyperbolicity and indeed the main advantage of our work is that we give direct streamlined proofs of the equivalence of the notions of admissibility for evolution families and their evolution semigroups. It turns out that this requires some new nontrivial elements, of which the most delicate is the construction of appropriate functions at the level of evolution semigroups that somehow correspond to given functions at the level of evolutions families.
1.3 Brief Description of our Results
As already noted above, the main aim of our paper is to transfer in a faithful manner the admissibility properties mentioned above such as for the pairs in (2) to equivalent admissibility properties at the level of evolution semigroups. There are two main reasons why this is nontrivial:
-
1.
One cannot know a priori what are the right Banach spaces on which one should consider the evolution semigroup. Indeed, if we consider for example a larger space for the perturbations, then we may need to reduce the space on which we look for the solutions so that these are unique and so that the admissibility property holds.
-
2.
It is in general difficult to deduce equivalent properties, since while at the level of evolution semigroups there is plenty information, although often perhaps too much that somehow needs to be localized, at the level of the evolution family it needs instead to be globalized, often with a quite different approach as is the case in our work.
As an illustration of our results, we formulate a particular case of Theorem 4 for continuous functions. For simplicity we write \(D_0(X)=C_0(C_0(X))\).
Theorem 1
Let U(t, s) be an evolution family composed of linear maps on X such that \(\Vert U(t,s) \Vert \le \kappa e^{\alpha (t-s)}\) for all \(t\ge s\) and some \(\kappa ,\alpha >0\). Then the following properties are equivalent:
-
1.
For each \(f \in C_0(X)\) there exists a unique \(x \in C_0(X)\) satisfying (1);
-
2.
For each \(F \in D_0(X)\) there exists a unique \(u \in D_0(X)\) such that
$$\begin{aligned} u(t)=S_{t-s} u(s) +\int _s^t S_{t-\tau } F(\tau ) \, d \tau \quad \mathrm{{for }} \,t\ge s. \end{aligned}$$
We emphasize that a major problem is to identify the space \(D_0(X)\) in the second property that ensures the equivalence of the two properties. More generally, we shall consider families of norms \(\Vert \cdot \Vert _t\), for \(t\in {\mathbb {R}}\), and we shall consider spaces C(X), \(C_0(X)\) and \(L^p(X)\) defined in terms of these norms. This essentially corresponds to consider the nonuniform exponential behavior that is ubiquitous in smooth ergodic theory.
It turns out that these admissibility properties are also related to the hyperbolicity of the original evolution family as well as of the associated evolutions semigroups. As an application, we shall also explore this relation, by giving further relations between hyperbolicity for evolution families and evolution semigroups (see Sect. 7).
We note that some results could be obtained using hyperbolicity. Namely, Theorem 4 is an immediate consequence of Theorem 7 in [3] together with the equivalence of the corresponding admissibility and hyperbolicity properties. On the other hand, for a family of norms \(\Vert \cdot \Vert _t=\Vert \cdot \Vert \) independent of t our characterizations of admissibility can be obtained as consequences of former results in the area (see [6] for details building on work in [10]). Nevertheless, our proofs are new. Our main interest is precisely to characterize admissibility without using hyperbolicity. Incidentally, a family of norms \(\Vert \cdot \Vert _t=\Vert \cdot \Vert \) essentially amounts to consider uniform hyperbolicity, while for nonuniform hyperbolicity it is convenient to consider other norms (see [2] for a detailed description building on the multiplicative ergodic theorem).
2 Basic Notions
Let  be the set of all continuous maps \(T :X \rightarrow X\) on a Banach space \(X=(X,\Vert \cdot \Vert )\) and write
be the set of all continuous maps \(T :X \rightarrow X\) on a Banach space \(X=(X,\Vert \cdot \Vert )\) and write
An evolution family on X is a family  of maps in
of maps in  such that:
such that:
-
1.
\(V(t,t)=\mathrm{Id}\) and \(V (t,s) V(s,r)=V(t,r)\) for \(t,s,r \in {\mathbb {R}}\) with \(t\ge s\ge r\);
-
2.
The map \((t,s) \mapsto V(t,s)(x)\) is continuous on \(\Pi \) for each \(x \in X\).
For simplicity of the notation, we shall write \(V(t,s)(x)=V(t,s)x\). When all maps V(t, s) are linear, we shall also say that  is a linear evolution family.
is a linear evolution family.
A semigroup on a Banach space Y is a family  of maps in
of maps in  (the set of all continuous maps \(T :Y \rightarrow Y\)) such that
(the set of all continuous maps \(T :Y \rightarrow Y\)) such that
A semigroup  on Y is called a \(C_0\) semigroup or a strongly continuous semigroup on Y if
on Y is called a \(C_0\) semigroup or a strongly continuous semigroup on Y if
To each evolution family  on X we associate semigroups
on X we associate semigroups  on certain Banach spaces \(Y_X\) composed of functions \(u :{\mathbb {R}}\rightarrow X\). Namely, we define
on certain Banach spaces \(Y_X\) composed of functions \(u :{\mathbb {R}}\rightarrow X\). Namely, we define
provided that
One can easily verify that property (3) holds. The semigroup  is called the evolution semigroup of
is called the evolution semigroup of  on \(Y_X\).
on \(Y_X\).
3 Evolution Families
In this section we introduce a family of evolution families that later on are used to study an admissibility property.
Let  be a linear evolution family on a Banach space X. Given a locally integrable function \(f :{\mathbb {R}}\rightarrow X\), for each pair \((s,x_s) \in {\mathbb {R}}\times X\) we define a function \(x :[s,+\infty ) \rightarrow X\) by
be a linear evolution family on a Banach space X. Given a locally integrable function \(f :{\mathbb {R}}\rightarrow X\), for each pair \((s,x_s) \in {\mathbb {R}}\times X\) we define a function \(x :[s,+\infty ) \rightarrow X\) by
for \(t\ge s\) (note that x is well defined because the integrand is continuous). We shall write it in the form \(x(t)=V(t,s)x_s\), for \(t\ge s\), and we consider the family of maps  .
.
Theorem 2
 is an evolution family on X.
is an evolution family on X.
Proof
For \(t=s\) we have \(x(t)=x_t\) and so \(V(t,t)=\mathrm{Id}\). Moreover, for any \(t,s,r \in {\mathbb {R}}\) with \(t\ge s\ge r\) we have
which establishes the first property in the notion of an evolution family. For the second property, we note that
for all \((t,s), ({\bar{t}}, {\bar{s}}) \in \Pi \) and \(x \in X\). We must show that
Since  is an evolution family, we already know that
is an evolution family, we already know that
So it suffices to show that the difference of integrals in (5) converges to zero when \((t,s) \rightarrow ({\bar{t}}, {\bar{s}})\). Assume that
In view of the second property in the notion of an evolution family and the uniform boundedness principle, we have
Now we consider the functions
which satisfy
Since f is locally integrable, it follows from Lebesgue’s dominated convergence theorem that
when \((t,s) \rightarrow ({\bar{t}}, {\bar{s}})\). Therefore, the map \((t,s) \mapsto V(t,s)x\) is continuous on \(\Pi \) for each \(x \in X\) and so  is an evolution family on X. \(\square \)
is an evolution family on X. \(\square \)
We say that Eq. (4) generates the evolution family  .
.
Now let \(\Vert \cdot \Vert _t\), for \(t \in {\mathbb {R}}\), be a family of norms on the Banach space X with the map \(t \mapsto \Vert x \Vert _t\) continuous for each \(x \in X\) such that
for some continuous function \(R :{\mathbb {R}}\rightarrow {\mathbb {R}}^+\). We say that the linear evolution family  is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\) if there exist \(\alpha , \kappa >0\) such that
is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\) if there exist \(\alpha , \kappa >0\) such that
The following result is a straightforward consequence of identity (4).
Proposition 1
If the evolution family  is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\), then the evolution family
is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\), then the evolution family  satisfies
satisfies
for all \(t\ge s\) and \(x,y \in X\).
4 Admissibility I: Continuous Functions
In this section and in the following two we show how to transfer a certain admissibility property from evolution families to evolution semigroups and vice-versa. Here we consider evolution semigroups defined on a space of continuous functions.
4.1 Evolution Semigroups
We consider evolution semigroups on some appropriate Banach spaces. Let C(X) be the set of all continuous functions \(x :{\mathbb {R}}\rightarrow X\) such that
We note that C(X) is a Banach space when endowed with the norm \(\Vert \cdot \Vert _C\). Let \(C_0(X) \subset C(X)\) be the closed subspace of all functions \(x \in C(X)\) with
Using the evolution family  generated by Eq. (4) for a given function \(f \in C(X)\), we define an operator \(T_t :C(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
generated by Eq. (4) for a given function \(f \in C(X)\), we define an operator \(T_t :C(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
Note that the maps \(T_t\) need not be linear.
Proposition 2
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties hold:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties hold:
-
1.
For each \(f \in C(X)\) we have
$$\begin{aligned} T_t(C(X))\subset C(X) \quad \text {for each }t \ge 0; \end{aligned}$$ -
2.
For each \(f \in C_0(X)\) we have
$$\begin{aligned} T_t(C_0(X)) \subset C_0(X) \quad \text {for each }t \ge 0. \end{aligned}$$
Proof
Take \(f,u \in C(X)\). Given \(t\ge 0\) and \(s,\sigma \in {\mathbb {R}}\), we have
In view of (6) and (7) we obtain
when \(s \rightarrow \sigma \) (recall that the functions R and u are continuous). Finally, using the second property in the notion of an evolution family, it follows from (8) and (9) that
when \(s \rightarrow \sigma \). Moreover, we have
and so \(T_t u \in C(X)\).
Now take \(f,u \in C_0(X)\). By property 1, we already know that \(T_t u \in C(X)\). Moreover,
when \(|s |\rightarrow \infty \) and so \(T_t u \in C_0(X)\). This completes the proof of the proposition. \(\square \)
The semigroup  is thus the evolution semigroup of
is thus the evolution semigroup of  on C(X) and also on the closed subspace \(C_0(X)\).
on C(X) and also on the closed subspace \(C_0(X)\).
4.2 Admissibility
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then  generates an evolution semigroup
generates an evolution semigroup  on C(X) defined by
on C(X) defined by
By Proposition 2 with \(f=0\) in (4), indeed \(S_t(C(X)) \subset C(X)\) for all \(t \ge 0\).
Moreover, let D(X) be the set of all continuous functions \(v :{\mathbb {R}}\rightarrow C(X)\) such that
We note that D(X) is a Banach space when endowed with the norm \(\Vert \cdot \Vert _D\). We also consider the closed subspace \(D_0(X) \subset D(X)\) of all continuous functions \(v :{\mathbb {R}}\rightarrow C_0(X)\) such that
Note that
The following theorem is our main result.
Theorem 3
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
-
1.
For each \(f \in C_0(X)\) there exists a unique \(x \in C(X)\) such that
$$\begin{aligned} x(t)=U(t,s)x(s) +\int _s^t U(t,\tau ) f(\tau ) \, d \tau \quad \text {for all }(t,s) \in \Pi ; \end{aligned}$$(10) -
2.
For each \(F \in D_0(X)\) there exists a unique \(u \in D(X)\) such that
$$\begin{aligned} u(t)=S_{t-s} u(s) +\int _s^t S_{t-\tau } F(\tau ) \, d \tau \quad \text {for all }(t,s) \in \Pi . \end{aligned}$$(11)
Proof
We first prove an auxiliary result.
Lemma 1
Given \(F, u \in D(X)\), Eq. (11) holds if and only if
with \(t\ge s\), where \(f_k(t)=F(t-k)(t)\).
Proof of the lemma
For simplicity of the notation we shall write \(u(t) =u_t\). First assume that Eq. (11) holds, that is,
By the definition of \(S_t\) we have
Taking \(\tau =t-k\) and \(\sigma =s-k\), we obtain
Now assume that property (12) holds. Proceeding as in (13) and again by the definition of \(S_t\), we have
Taking \(k=t-\tau \), this equality can be rewritten as
Finally, taking \(s=\sigma +t-\tau \), we conclude that
that is,
as we wanted to show.\(\square \)
We proceed with the proof of the theorem. We prove both implications separately.
\((1 \Rightarrow 2)\). Take \(F \in D_0(X)\). For each \(k \in {\mathbb {R}}\) we define a map \(f_k :{\mathbb {R}}\rightarrow X\) by
We show that \(f_k \in C_0(X)\). Note that
Since the maps \(t \mapsto F(t-k)\) and \(F(s-k)\) are continuous, letting \(t \rightarrow s\) in (15), we find that \(f_k(t) \rightarrow f_k(s)\) and so \(f_k\) is continuous. Moreover,
since \(F \in D_0(X)\), and so \(f_k \in C_0(X)\). By property 1, there exists a unique solution \(x_k \in C(X)\) of Eq. (10) with \(f=f_k\), for each \(k \in {\mathbb {R}}\). We shall use these functions to construct a solution of Eq. (11).
We continue to write \(u(t)=u_t\) for each function \(u :{\mathbb {R}}\rightarrow C(X)\). By Lemma 1, if \(u\in D(X)\) is a solution of Eq. (11), then \(t \mapsto u_{t-k}(t)\) is a solution of Eq. (10) with \(f=f_k\), for each \(k \in {\mathbb {R}}\). So, necessarily, \(u_{t-k}(t)=x_k(t)\) for all \(t,k \in {\mathbb {R}}\), that is, \(u_t(s)=x_{s-t}(s)\) for all \(t,s \in {\mathbb {R}}\). In particular, this implies that (11) has at most one solution \(u \in D(X)\). This leads us to define
We show below that \(u \in D(X)\). Then it follows from Lemma 1 that u is a solution of Eq. (11) and as noted above it is automatically unique.
Now let R be the linear operator defined by \(Rx=f\) on the domain composed of the functions \(x \in C(X)\) for which there exists \(f \in C_0(X)\) satisfying (10). We show that R is a well-defined closed operator. To show that R is well-defined, take \(g \in C_0(X)\) such that
for all \((t,s) \in \Pi \). Then
for all \((t,s) \in \Pi \) with \(t \ne s\). Since \(f,g \in C_0(X)\), one can show that the function
is continuous. For completeness we give the argument. Take \({\bar{\tau }}\in {\mathbb {R}}\) and write \(h=f-g\). We have
whenever \((t,\tau ),(t,{\bar{\tau }}) \in \Pi \). Now assume that \(\tau ,{\bar{\tau }}\in [s-\delta , t]\) for some \(\delta >0\). In view of the second property in the notion of an evolution family and the uniform boundedness principle, we have
Therefore,
and so, letting \(\tau \rightarrow {\bar{\tau }}\) we conclude that the map \((t,\tau ) \mapsto U(t,\tau ) h(\tau )\) is continuous. Hence, letting \(s \nearrow t\), we find that \(f(t)=g(t)\) for all \(t \in {\mathbb {R}}\). This shows that the operator R is well defined.
To show that R is closed, let \((x^\ell )_{\ell \in {\mathbb {N}}}\) be a sequence in the domain of R converging to \(x \in C(X)\) such that \(f^\ell =Rx^\ell \) converges to \(f \in C_0(X)\). Then
for all \((t,s) \in \Pi \). We have
where
in view of the uniform boundedness principle. Thus, letting \(\ell \rightarrow \infty \) in (17) we find that
for all \((t,s) \in \Pi \). This shows that \(Rx =f\) and so x is in the domain of R. Hence, the operator R is closed. By the closed graph theorem, R is bounded. Moreover, by property 1 the operator R is onto and invertible. It follows from the open mapping theorem that it has a bounded inverse.
Now we show that \(u \in D(X)\). First we prove that \(u_t \in C(X)\) for each \(t \in {\mathbb {R}}\). Note that
Letting \(s \rightarrow {\bar{s}}\), the second term on the right-hand side tends to zero. For the first term we note that
We have
and thus,
Since \(F \in D_0(X)\), the map \(\tau \mapsto F(\tau )\) is uniformly continuous and so, letting \(s \rightarrow {\bar{s}}\) the right-hand side of (21) tends to zero. Hence, it follows from (20) that \(x_{s-t} \rightarrow x_{{\bar{s}}-t}\) in C(X) when \(s \rightarrow {\bar{s}}\). By (19) we conclude that \(u_t\) is continuous. Moreover,
and
which shows that
and so \(u_t \in C(X)\). Finally, since
we obtain
Hence, it follows from (21) and the uniform continuity of the map \(\tau \mapsto F(\tau )\) that \(u_t \rightarrow u_\tau \) in C(X) when \(t \rightarrow \tau \). Therefore, the map \(t \mapsto u_t\) is continuous and so \(u \in D(X)\).
\((2 \Rightarrow 1)\). Take \(f \in C_0(X)\) and define a function \(F :{\mathbb {R}}\rightarrow C_0(X)\) by
We show that \(F \in D_0(X)\). Note first that
and so
For \(t \in [\tau -\delta ,\tau +\delta ]\) we have
and so, letting \(t \rightarrow \tau \) we find that \(F(t) \rightarrow F(\tau )\) in C(X). Moreover, we have
Given \(\epsilon >0\), take \(\rho >0\) such that \(\Vert f(s) \Vert _s<\epsilon \) whenever \(|s|\ge \rho \). Then
when \(|t|\rightarrow \infty \). It follows from the arbitrariness of \(\epsilon \) that \(F\in D_0(X)\).
By property 2, there exists a unique \(u \in D(X)\) satisfying (11). In view of Lemma 1, for each \(k\in {\mathbb {R}}\) the function \(x_k(t)=u_{t-k}(t)\) satisfies Eq. (10) with f replaced by
Note that \(y_k=(1+k^2)x_k\) satisfies Eq. (10) for each \(k\in {\mathbb {R}}\). Before proceeding, we show that \(x_k\) is continuous. We have
Therefore, letting \(t\rightarrow s\) we conclude that \(x_k(t)\rightarrow x_k(s)\) since \(u\in D(X)\). Moreover,
We also show that \(y_k\) is independent of k. Otherwise, take distinct \(p,q\in {\mathbb {R}}\) with \(y_p\ne y_q\). We define a function \(v:{\mathbb {R}}\rightarrow C(X)\) by
One can show as in (23) that \(v\in D(X)\). Then \(v_{t-k}(t)=y_p(t)/(1+k^2)\) satisfies Eq. (12) for all k and so by Lemma 1, v is a solution of Eq. (11). But in view of property 2, we must have \(v=u\), which is impossible since then
and so \(y_q=y_p\). This contradiction shows that \(y:=y_k\), which is a solution of Eq. (10), is independent of k. To show that Eq. (10) has a unique solution, assume that z was a different solution. As before, we define a function \(w\in D(X)\) by
Similarly, \(w_{t-k}(t)=z(t)/(1+k^2)\) satisfies Eq. (12) for all k and so by Lemma 1, w is a solution of Eq. (11). But then both \(u,w\in D(X)\) are solutions of Eq. (11), which by hypothesis has a single solution. This contradiction shows that indeed Eq. (10) has a unique solution.
This concludes the proof of the theorem. \(\square \)
5 Admissibility II: Exponential Growth
In this section we transfer a certain admissibility property from evolution families to evolution semigroups and vice-versa on spaces of continuous functions with at most exponential growth with a given exponential rate.
5.1 Evolution Semigroups
Given \(c\ge 0\), consider the set \(E^c(X)\) of all continuous functions \(x :{\mathbb {R}}\rightarrow X\) such that the function \(x_c :{\mathbb {R}}\rightarrow X\) defined by \(x_c(t)=e^{-c|t|}x(t)\) for \(t\in {\mathbb {R}}\) is in \(C_0(X)\). We note that \(E^c(X)\) is a Banach space when endowed with the norm
Using the evolution family  generated by Eq. (4) for a given function \(f \in E^c(X)\), we define an operator \(T_t :E^c(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
generated by Eq. (4) for a given function \(f \in E^c(X)\), we define an operator \(T_t :E^c(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
Proposition 3
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(c\ge 0\) and \(f \in E^c(X)\) we have
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(c\ge 0\) and \(f \in E^c(X)\) we have
Proof
Take \(f,u \in E^c(X)\). It follows as in the proof of Proposition 3 that the function \(T_t u\) is continuous for each \(t\ge 0\). Moreover, we have
when \(|s |\rightarrow \infty \) and so \(T_t u \in E^c(X)\). \(\square \)
The semigroup  is thus the evolution semigroup of
is thus the evolution semigroup of  on \(E^c(X)\).
on \(E^c(X)\).
5.2 Admissibility
As a preparation for the result relating the admissibility properties we first establish a version of Theorem 3 in which we consider the same spaces for the perturbations and for the solutions. This corresponds to consider \(c=0\) and so the space \(E^c(X)=C_0(X)\).
Theorem 4
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
-
1.
For each \(f \in C_0(X)\) there exists a unique \(x \in C_0(X)\) satisfying (10);
-
2.
For each \(F \in D_0(X)\) there exists a unique \(u \in D_0(X)\) satisfying (11).
Proof
We prove both implications separately.
\((1 \Rightarrow 2)\). Take \(F \in D_0(X)\) and consider again the maps \(f_k \in C_0(X)\) defined by (14) for each \(k \in {\mathbb {R}}\). By property 1, there exists a unique solution \(x_k \in C_0(X)\) of Eq. (10) with \(f=f_k\). Again we consider the function \(u_t(s)=x_{s-t}(s)\) as in (16). We shall show that \(u \in D_0(X)\). As in the proof of Theorem 3, u is a solution of Eq. (11) and it is then the unique solution in \(D_0(X)\).
We already know from the proof of Theorem 3 that \(u \in D(X)\) and so it remains only to verify that \(u_t\in C_0(X)\) for each \(t\in {\mathbb {R}}\) and that
We first show that
Since
for each \(\epsilon >0\) there exists \(T>0\) such that
For each \(t\in [-T,T]\) we take an open interval \(I_t\) centered at t and \(s_t>0\) such that
Since \([-T,T]\) is compact, it has a finite cover by intervals \(I_{t_i}\) with \(i=1,\ldots ,n\) and we let \(S=\max _{1\le i\le n}S_{t_i}<\infty \). Then
In particular, this implies that \(\Vert f_k\Vert _C<\epsilon \) for any sufficiently large integer |k| since the line \(\{(t-k,t):t\in {\mathbb {R}}\}\) is then outside \([-T,T]\times [-S,S]\). Property (24) follows now readily from the arbitrariness of \(\epsilon \).
Let \(R_0\) be the linear operator defined by \(R_0x=f\) on the domain composed of the functions \(x \in C_0(X)\) for which there exists \(f \in C_0(X)\) satisfying (10). One can show as in the proof of Theorem 3 that \(R_0\) has a bounded inverse. Then
in view of (24) and so \(u_t\in C_0(X)\) for each \(t\in {\mathbb {R}}\). Finally, we show that
Since \(\Vert x_k\Vert _C\le \Vert R_0^{-1}\Vert \cdot \Vert f_k\Vert _C\), it follows from (24) that for each \(\epsilon >0\) there exists \(K>0\) such that
On the other hand, we already showed in the proof of Theorem 3 that the map \(k\mapsto x_k\) is continuous, which follows from (21) together with the uniform continuity of the map \(\tau \mapsto F(\tau )\). Since \(x_k \in C_0(X)\), for each \(k\in [-K,K]\) there exist an open interval \(J_k\) centered at k and \(s_k>0\) such that
Since \([-K,K]\) is compact, one can proceed as above to find \(S>0\) such that
In particular, this implies that \(\sup _{s\in {\mathbb {R}}}\Vert x_{s-t}(s)\Vert _s<\epsilon \) for any sufficiently large |t| since the line \(\{(s-t,s):t\in {\mathbb {R}}\}\) is then outside \([-K,K]\times [-S,S]\). Property (26) follows now from the arbitrariness of \(\epsilon \) and so \(u \in D_0(X)\).
\((2 \Rightarrow 1)\). Take \(f \in C_0(X)\) and consider the function \(F \in D_0(X)\) defined by (22). By property 2, there exists a unique \(u \in D_0(X)\) satisfying (11). We know from the proof of Theorem 3 that the function \(x(t)=(1+k^2)u_{t-k}(t)\) is independent of k and that it is the unique solution of Eq. (10) in C(X). It remains to verify that \(x\in C_0(X)\).
In the proof of the implication \((1 \Rightarrow 2)\) we showed that given \(F\in D_0(X)\) and \(\epsilon >0\), there exist \(T,S>0\) such that property (25) holds. Since \(u\in D_0(X)\), given \(\epsilon >0\), there exist \(T,S>0\) such that
Also as before, this implies that \(\sup _{t\in {\mathbb {R}}}\Vert u_{t-k}(t)\Vert _s<\epsilon \) for any sufficiently large |k|. It thus follows from the arbitrariness of \(\epsilon \) that \(x(t)\rightarrow 0\) when \(|t|\rightarrow \infty \) and so \(x\in C_0(X)\). This completes the proof of the theorem. \(\square \)
Using this result we are able to consider the space \(E^c(X)\) for an arbitrary constant \(c\ge 0\). Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Given \(c\ge 0\), the evolution family
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Given \(c\ge 0\), the evolution family  generates an evolution semigroup
generates an evolution semigroup  on \(E^c(X)\) defined by
on \(E^c(X)\) defined by
By Proposition 3 with \(f=0\) in (4), indeed \(S_t(E^c(X)) \subset E^c(X)\) for all \(t \ge 0\). Moreover, let \(F^c(X)\) be the set of all continuous functions \(v :{\mathbb {R}}\rightarrow E^c(X)\) such that
We note that \(F^c(X)\) is a Banach space when endowed with the norm
In other words, \(F^c(X)=C_0(E^c(X))\).
Theorem 5
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(c\ge 0\) the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(c\ge 0\) the following properties are equivalent:
-
1.
For each \(f \in E^c(X)\) there exists a unique \(x \in E^c(X)\) satisfying (10);
-
2.
For each \(F \in F^c(X)\) there exists a unique \(u \in F^c(X)\) satisfying (11).
Proof
Take \(f,x \in E^c(X)\). We consider the functions \(f_c,x_c\in C_0(X)\) defined by
for \(t\in {\mathbb {R}}\). Note that property (10) holds if and only if
where
Therefore, property 1 holds if and only if for each \(f \in E^c(X)\) there exists a unique \(x \in E^c(X)\) satisfying (27).
Notice that the evolution family formed by the linear operators \(U_c(t,s)\) for \((t,s)\in \Pi \) and a given \(c\ge 0\) is also exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Since the maps \(f\mapsto f_c\) and \(x\mapsto x_c\) are bijections from \(E^c(X)\) onto \(C_0(X)\), it follows from Theorem 4 that property 1 holds if and only if for each \(F \in D_0(X)\) there exists a unique \(u \in D_0(X)\) satisfying
where
We have
that is,
Letting \(u_c(s)=\gamma (u(s))\) we have
and so property (28) is equivalent to
where
Since the maps \(F\mapsto F_c\) and \(u\mapsto u_c\) are bijections from \(D_0(X)\) onto \(F^c(X)\), it follows from (29) that property 1 holds if and only if property 2 holds. \(\square \)
6 Admissibility III: Integrable Functions
In this section we show once more how to transfer a certain admissibility property from evolution families to evolution semigroups and vice-versa. Here we consider evolution semigroups defined on a \(L^p\) space.
6.1 Evolution Semigroups
For each \(p\in [1,+\infty )\), let \(L^p(X)\) be the set of all (Bochner) measurable functions \(x :{\mathbb {R}}\rightarrow X\) such that
identified almost everywhere with respect to the Lebesgue measure. We note that \({L^p}(X)\) is a Banach space when endowed with the norm \(\Vert \cdot \Vert _{L^p}\). Using the evolution family  generated by Eq. (4) for a given function \(f \in {L^p}(X)\), we define an operator \(T_t :{L^p}(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
generated by Eq. (4) for a given function \(f \in {L^p}(X)\), we define an operator \(T_t :{L^p}(X)\rightarrow X^{{\mathbb {R}}}\) for each \(t\ge 0\) by
again identifying the functions almost everywhere.
Proposition 4
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(f \in {L^r}(X)\) with \(1\le r\le p<\infty \), we have
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then for each \(f \in {L^r}(X)\) with \(1\le r\le p<\infty \), we have
Proof
Take \(u\in L^p(X)\). By Minkowski’s inequality we have
and so
First assume that \(r=p\). For \(p=1\) we obtain
On the other hand, for \(p>1\) and \(q\in (1,+\infty )\) such that \(1/p+1/q=1\), it follows from Hölder’s inequality that
and again by (30) we obtain
This shows that \(T_t u \in L^p(X)\) when \(r=p\).
Now assume that \(r<p\) and take \(\sigma \in (1,+\infty )\) such that \(1/r+1/\sigma =1\). It follows from Hölder’s inequality that
and so
Hence, it follows from (30) that
which shows that \(T_t u \in L^p(X)\) when \(r<p\). \(\square \)
The semigroup  is thus the evolution semigroup of
is thus the evolution semigroup of  on \(L^p(X)\) for each \(p\in [1,+\infty )\).
on \(L^p(X)\) for each \(p\in [1,+\infty )\).
6.2 Admissibility
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then  generates an evolution semigroup
generates an evolution semigroup  on \(L^p(X)\) defined by
on \(L^p(X)\) defined by
By Proposition 4 with \(f=0\) in (4), indeed \(S_t(L^p(X)) \subset L^p(X)\) for all \(t \ge 0\).
Moreover, for each \(p\in [1,+\infty )\) let \(M^p(X)=L^p(L^p(X))\) be the set of all (Bochner) measurable functions \(v :{\mathbb {R}}\rightarrow L^p(X)\) such that
identified almost everywhere with respect to the Lebesgue measure. We note that \(M^p(X)\) is a Banach space when endowed with the norm \(\Vert \cdot \Vert _{M^p}\).
Theorem 6
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
-
1.
For each \(f \in L^p(X)\) there exists a unique \(x \in L^p(X)\) satisfying (10);
-
2.
For each \(F \in M^p(X)\) there exists a unique \(u \in M^p(X)\) satisfying (11).
Proof
We note that the statement in Lemma 1 also holds for \(F\in M^p(X)\) and \(u \in M^p(X)\). We proceed with the proof of the theorem.
\((1 \Rightarrow 2)\). Take \(F \in M^p(X)\). For each \(k \in {\mathbb {R}}\) we define a map \(f_k :{\mathbb {R}}\rightarrow X\) by (14). We have
and so \(f_k \in L^p(X)\) for almost all \(k\in {\mathbb {R}}\). By property 1, there exists a unique solution \(x_k\in L^p(X)\) of Eq. (10) with \(f=f_k\), for almost all \(k\in {\mathbb {R}}\). Writing \(u(t)=u_t\) for each function \(u :{\mathbb {R}}\rightarrow L^p(X)\), we define
We show below that \(u \in M^p(X)\). Then it follows from Lemma 1 that u is a solution of Eq. (11) and as in the proof of Theorem 3 it is automatically unique.
Let R be the linear operator defined by \(Rx=f\) on the domain composed of the functions \(x \in L^p(X)\) for which there exists \(f \in L^p(X)\) satisfying (10). As in the proof of Theorem 3, we show that R is a well-defined closed operator. To show that R is well-defined, take \(g \in L^p(X)\) such that
for all \((t,s) \in \Pi \). Then
for all \((t,s) \in \Pi \) with \(t \ne s\). Since the integrand is locally integrable (which follows from Hölder’s inequality), letting \(s \nearrow t\) it follows from the Lebesgue differentiation theorem that \(f(t)=g(t)\) for almost every \(t \in {\mathbb {R}}\). This shows that the operator R is well defined.
To show that R is closed, let \((x^\ell )_{\ell \in {\mathbb {N}}}\) be a sequence in the domain of R converging to \(x \in L^p(X)\) such that \(f^\ell =Rx^\ell \) converges to \(f \in L^p(X)\). Then property (17) holds for all \((t,s) \in \Pi \). We have
with d as in (18) and with \(q\in (1,+\infty ]\) such that \(1/p+1/q=1\) (when \(p=1\) we make the convention that \((t-s)^{1/q}=1\)). Thus, letting \(\ell \rightarrow \infty \) in (17) we find that
for all \((t,s) \in \Pi \). This shows that \(Rx =f\) and so x is in the domain of R. Hence, the operator R is closed and by property, it has a bounded inverse.
Now we show that \(u \in M^p(X)\). We have
Since
it follows from (31) that
and so \(u \in M^p(X)\).
\((2 \Rightarrow 1)\). Take \(f \in L^p(X)\) and define a function \(F :{\mathbb {R}}\rightarrow L^p(X)\) by
Note that \(F \in M^p(X)\). Indeed,
for some constant \(c_p>0\) that depends only on p. By property 2, there exists a unique \(u \in M^p(X)\) satisfying (11). By Lemma 1, for each \(k\in {\mathbb {R}}\) the function
satisfies Eq. (10) with f replaced by
Proceeding as in (32), we obtain
and so \(x_k\in L^p(X)\) for almost all \(k\in {\mathbb {R}}\). One can then show in a similar manner to that in the proof of Theorem 3 that \(x(t)=(1+k^2)x_k(t)\) is the same for all k in a full measure set and that it is the unique solution of Eq. (10) in \(L^p(X)\). This concludes the proof of the theorem.
\(\square \)
7 Hyperbolicity
In this section we consider the relation between the notions of admissibility and hyperbolicity, and how the former results can give further relations between hyperbolicity for evolution families and evolution semigroups.
We continue to consider a family of norms \(\Vert \cdot \Vert _t\), for \(t \in {\mathbb {R}}\), on a Banach space X. We say that an evolution family  of linear maps on X is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\) if:
of linear maps on X is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\) if:
-
1.
There exist projections \(P_t :X \rightarrow X\), for \(t \in {\mathbb {R}}\), such that
$$\begin{aligned} P_t U(t,s)=U(t,s) P_s \end{aligned}$$and, writing \(Q_s =\mathrm{Id}-P_s\), the map
$$\begin{aligned} U(t,s)|_{{{\,\mathrm{Im}\,}}Q_s}:{{\,\mathrm{Im}\,}}Q_s \rightarrow {{\,\mathrm{Im}\,}}Q_t, \end{aligned}$$is onto and invertible for each \(t \ge s\);
-
2.
There exist constants \(\lambda , N>0\) such that
$$\begin{aligned} \Vert U(t,s)P_s x\Vert _t \le N e^{-\lambda (t-s)} \Vert x \Vert _s \end{aligned}$$and
$$\begin{aligned} \Vert {\bar{U}}(s,t)Q_t x\Vert _s \le N e^{-\lambda (t-s)} \Vert x \Vert _t \end{aligned}$$for \(t \ge s\) and \(x \in X\), where \({\bar{U}}(s,t)=(U(t,s)|_{{{\,\mathrm{Im}\,}}Q_s})^{-1}\).
The following statement relates admissibility and hyperbolicity in various situations (among many other equivalent properties considered in the area).
Proposition 5
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
-
1.
The evolution family
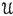 is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\);
is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\); -
2.
For each \(f \in C_0(X)\) there exists a unique \(x \in C_0(X)\) satisfying (10);
-
3.
For each \(f \in L^p(X)\) there exists a unique \(x \in L^p(X)\) satisfying (10);
-
4.
There exists \(d>0\) such that for each \(c\in [0,d)\) and \(f \in E^c(X)\) there exists a unique \(x \in E^c(X)\) satisfying (10).
These results can be obtained for example as in [10] replacing the family of norms \(\Vert \cdot \Vert _t=\Vert \cdot \Vert \), for \(t \in {\mathbb {R}}\), by an arbitrary family. This essentially corresponds to consider the nonuniform exponential behavior that is ubiquitous in smooth ergodic theory.
The following result is a simple consequence of the former Theorems 4, 5 and 6 together with Proposition 5.
Theorem 7
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then the following properties are equivalent:
-
1.
The evolution family
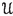 is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\);
is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\); -
2.
For each \(F \in D_0(X)\) there exists a unique \(u \in D_0(X)\) satisfying (11);
-
3.
For each \(F \in M^p(X)\) there exists a unique \(u \in M^p(X)\) satisfying (11);
-
4.
There exists \(d>0\) such that for each \(c\in [0,d)\) and \(F \in F^c(X)\) there exists a unique \(u \in F^c(X)\) satisfying (11).
One can also establish relations with the hyperbolicity of the evolution semigroup on various Banach spaces. We recall that a semigroup  of linear maps on a Banach space Y is said to be hyperbolic if:
of linear maps on a Banach space Y is said to be hyperbolic if:
-
1.
There exists a projection \(P :Y \rightarrow Y\) such that \(P T_t=T_t P\) and, writing \(Q=\mathrm{Id}-P\), the map
$$\begin{aligned} T_t |_{{{\,\mathrm{Im}\,}}Q} :{{\,\mathrm{Im}\,}}Q \rightarrow {{\,\mathrm{Im}\,}}Q, \end{aligned}$$is onto and invertible for each \(t \ge 0\);
-
2.
There exist constants \(\lambda ,N > 0\) such that
$$\begin{aligned} \Vert T_t P\Vert \le N e^{-\lambda t} \quad \text {and}\quad \Vert {\bar{T}}_t Q\Vert \le N e^{-\lambda t} \end{aligned}$$for \(t \ge 0\), where \({\bar{T}}_t =(T_t |_{{{\,\mathrm{Im}\,}}Q})^{-1}\).
The equivalence of the notions of hyperbolicity for an evolution family  and its evolution semigroup
and its evolution semigroup  on \(C_0(X)\) and on \(L^p(X)\) lead to further equivalences to the former admissibility properties (see [6, 18]). In particular, we have the following result.
on \(C_0(X)\) and on \(L^p(X)\) lead to further equivalences to the former admissibility properties (see [6, 18]). In particular, we have the following result.
Theorem 8
Let  be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then
be a linear evolution family that is exponentially bounded with respect to the norms \(\Vert \cdot \Vert _t\). Then  is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\) if and only if there exists \(d>0\) such that the semigroup defined by
is hyperbolic with respect to the norms \(\Vert \cdot \Vert _t\) if and only if there exists \(d>0\) such that the semigroup defined by
for \(t\ge 0\), \(r \in {\mathbb {R}}\) and \(v \in C_0(X)\) is hyperbolic on \(C_0(X)\) for each \(c\in [0,d)\).
References
Barreira, L., Dragičević, D., Valls, C.: Admissibility and Hyperbolicity. SpringerBriefs in Mathematics. Springer, Cham (2018)
Barreira, L., Pesin, Y.: Nonuniform Hyperbolicity, Encyclopedia of Mathematics and Its Applications, vol. 115. Cambridge University Press, Cambridge (2007)
Barreira, L., Popescu, L.H., Valls, C.: Nonuniform exponential behavior via evolution semigroups. Mathematika 66, 15–38 (2020)
Blumenthal, A.: A volume-based approach to the multiplicative ergodic theorem on Banach spaces. Discrete Contin. Dyn. Syst. 36, 2377–2403 (2016)
Bonatti, C., Díaz, L., Viana, M.: Dynamics Beyond Uniform Hyperbolicity, Encyclopaedia of Mathematical Sciences, vol. 102. Mathematical Physics III. Springer-Verlag, Berlin (2005)
Chicone, C., Latushkin, Yu.: Evolution Semigroups in Dynamical Systems and Differential Equations, Mathematical Surveys and Monographs, vol. 70. American Mathematical Society, Providence (1999)
Coffman, C., Schäffer, J.: Dichotomies for linear difference equations. Math. Ann. 172, 139–166 (1967)
Dalec’kiĭ, Ju., Kreĭn, M.: Stability of Solutions of Differential Equations in Banach Space, Translations of Mathematical Monographs, vol. 43. American Mathematical Society, Providence (1974)
Engel, K., Nagel, R.: One-Parameter Semigroups for Evolution Equations. Springer-Verlag, New York (2000)
Latushkin, Y., Randolph, T., Schnaubelt, R.: Exponential dichotomy and mild solutions of nonautonomous equations in Banach spaces. J. Dyn. Differ. Equ. 10, 489–510 (1998)
Levitan, B., Zhikov, V.: Almost Periodic Functions and Differential Equations. Cambridge University Press, Cambridge (1982)
Li, T.: Die stabilitätsfrage bei differenzengleichungen. Acta Math. 63, 99–141 (1934)
Mañé, R.: Lyapounov exponents and stable manifolds for compact transformations. In Geometric Dynamics (Rio de Janeiro, 1981), Lecture Notes in Mathematics, vol. 1007, pp. 522–577. Springer (1983)
Massera, J., Schäffer, J.: Linear differential equations and functional analysis, I. Ann. Math. 2(67), 517–573 (1958)
Massera, J., Schäffer, J.: Linear Differential Equations and Function Spaces, Pure and Applied Mathematics, vol. 21. Academic Press, New York (1966)
Mather, J.: Characterization of Anosov diffeomorphisms. Ned. Akad. Wet. Proc. Ser. A 71, 479–483 (1968)
Perron, O.: Die stabilitätsfrage bei differentialgleichungen. Math. Z. 32, 703–728 (1930)
Räbiger, F., Schnaubelt, R.: The spectral mapping theorem for evolution semigroups on spaces of vector-valued functions. Semigroup Forum 52, 225–239 (1996)
Sell, G., You, Y.: Dynamics of Evolutionary Equations, Applied Mathematical Sciences, vol. 143. Springer-Verlag, New York (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Partially supported by FCT/Portugal through UID/MAT/04459/2019.
Rights and permissions
About this article
Cite this article
Barreira, L., Valls, C. Admissibility via Evolution Semigroups. J Dyn Diff Equat 36, 595–618 (2024). https://doi.org/10.1007/s10884-021-10126-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-021-10126-x



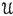 is hyperbolic with respect to the norms
is hyperbolic with respect to the norms 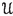 is hyperbolic with respect to the norms
is hyperbolic with respect to the norms