On the Qualitative Behavior of a Class of Generalized Liénard Planar Systems

Abstract

We study the problem of existence/nonexistence of limit cycles for a class of Liénard generalized differential systems in which, differently from the most investigated case, the function F depends not only on x but also on the y-variable. In this framework, some new results are presented, starting from a case study which, actually, already exhibits the most significant properties. In particular, the so-called “superlinear case” presents some new phenomena of escaping orbits which will be discussed in detail.

1 Introduction

In this paper we study the qualitative behavior of the trajectories of a planar system of the form

Such a system can be viewed as a generalization of the classical planar system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = y - \mathtt{F}(x)\\ \dot{y} = - x, \end{array}\right. } \end{aligned}$$

(1.1)

with $\mathtt{F}(x):= \int _{0}^x f(u)\,du,$ introduced by Liénard in the pioneering work [26] in 1928 for the study of the equation

$$\begin{aligned} \ddot{x} + f(x)\dot{x} + x = 0. \end{aligned}$$

Although there is an enormous literature concerning (1.1) and its generalizations as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = y - \mathtt{F}(x)\\ \dot{y} = - g(x) \end{array}\right. } \end{aligned}$$

(1.2)

with

$$\begin{aligned} g(0) = 0, \quad g(x)x > 0 \;\; \text {for }\; x\not =0, \end{aligned}$$

(see the monographs [14, 24, 34, 44, 47], as well as the articles [8, 15, 16, 25, 27, 29, 36,37,38,39,40] and the quotations therein) or

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = h(y) - \mathtt{F}(x)\\ \dot{y} = - g(x) \end{array}\right. } \end{aligned}$$

(1.3)

with the additional assumption

$$\begin{aligned} h(0) = 0, \quad h(y)y > 0 \;\; \text {for }\; y\not =0, \end{aligned}$$

(see the monographs [44, 47] as well as the articles [1, 2, 13, 19,20,21,22, 42, 43, 45, 46] and the references therein), as far as we know, no systematic study has been performed for (S). This because the classical assumptions on $\mathtt{F}, g, h$ guarantee that the origin is the unique equilibrium point and the trajectories move clockwise around it in the plane. For equation (S), additional conditions on F(x, y) would be required in order to obtain a similar behavior. Moreover, the problem of possible blow-up in finite forward time of the solutions should be considered. On the other hand, the presence of a term of the form F(x, y) in the first equation gives some more flexibility, if one looks for examples of rich dynamics, for instance, exhibiting a prescribed number of limit cycles. Previous contributions on the study of system (S) can be found in the work of Cartwright and Swinnerton-Dyer [6, 7] concerning the boundedness of the solutions of non-autonomous equations of the form

$$\begin{aligned} \dot{x} = g_1(y) - \varepsilon F(x,y,t), \quad \dot{y} = - g_2(x) \end{aligned}$$

and, for the autonomous case, in [3, 32], concerning the uniqueness of limit cycles (see also [30], where a special case of (S),  with peculiar assumptions, was considered) and in [31], dealing with a $\phi$-Laplacian Liénard equation which, studied in the phase-plane, leads to a system of the form (S) with x and y inverted.

The plan of the paper is the following.

In Sect. 2 we discuss some basic facts of equation (S) related to the use of the energy of the associated Duffing equations as a Lyapunov function. Moreover, we present a first result of multiple limit cycles which shows the above mentioned flexibility in the use of the function F(x, y).

The other sections are focused on the study of the case

$$\begin{aligned} F(x,y)= \lambda B(y)A(x) \end{aligned}$$

where A(x) satisfies the standard assumptions on $\mathtt{F}(x)$ in the classical case.

In particular, In Sect. 3, a case study is analyzed for the choice

$$\begin{aligned} B(y)= |y|^p, \quad A(x)= x^3-x, \end{aligned}$$

which already exhibits the mean features of this problem that, as far as we know, have not been investigated before.

Section 4 presents the main results, namely a theorem of existence/nonexistence of limit cycles for system (S) (see Theorem 6) as well as results about existence and uniqueness (see Theorem 4 and Theorem 5).

2 Preliminary Results

Throughout the paper the following assumptions are made on system

We suppose that $F: {\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ and $g:{\mathbb {R}} \rightarrow {\mathbb {R}}$ are locally Lipschitz continuous functions, in order to guarantee the uniqueness of the solutions for the associated initial value problems. We also assume

$$\begin{aligned} g(0) = 0, \; g(x)x > 0 \;\; \text {for }\; x\not =0 \end{aligned}$$

and

$$\begin{aligned} F_0(y):= y-F(0,y), \; \text {vanishes only at } y= 0, \end{aligned}$$

therefore the origin is the only singular point of (S). When $F\equiv 0,$ our system reduces to the classical Duffing one, namely

It is well known (cf. [14, 24]) that system (D) has the Hamiltonian structure

$$\begin{aligned} \dot{x} = \frac{\partial H}{\partial y}(x,y), \quad \dot{x} = -\frac{\partial H}{\partial x}(x,y) \end{aligned}$$

with

$$\begin{aligned} H(x,y) = \frac{1}{2} y^2 + G(x), \quad \text { for } \; G(x) =\int _{0}^x g(u)\,du \end{aligned}$$

and the origin is a global center if and only if $G(x) \rightarrow +\infty$ as $|x|\rightarrow +\infty .$ Taking the energy H as a Lyapunov function for system (S),  we obtain, for its time-derivative along the trajectories, the expression

$$\begin{aligned} \dot{H}(x,y) = - g(x) F(x,y), \end{aligned}$$

(2.1)

which generalizes the classical one for system (1.2). Therefore, the orbits of (S) enter the ones of (D) which are the level lines of H,  when $g(x) F(x,y) > 0,$ while they exit when this product is negative. In view of this property and in the light of the classical Poincaré example (see [29, §3.3]), a first result giving examples of a prescribed number of periodic solutions is the following.

Proposition 1

Assume $G(x)\rightarrow +\infty$ as $|x|\rightarrow +\infty .$ Then, for

$$\begin{aligned} F(x,y):= x\,\prod _{k=1}^{n}\left( \tfrac{1}{2} y^2 + G(x) - k\right) , \end{aligned}$$

system (S) has exactly n limit cycles which become arbitrarily large as n grows. Conversely, if $G(x)\not \rightarrow +\infty$ as $|x|\rightarrow +\infty ,$ given any energy level E with $0< E < \min \{G(-\infty ),G(+\infty )\},$ then, for

$$\begin{aligned} F(x,y):= x\,\prod _{k=1}^{n}\left( \tfrac{1}{2} y^2 + G(x) - \tfrac{E}{k}\right) , \end{aligned}$$

system (S) has exactly n limit cycles which become arbitrarily close to the origin as n grows.

Proof

The proof is straightforward using the above mentioned properties of the orbits following from (2.1). $\square$

A similar construction has been recently proposed in [5] for the relativistic and the curvature generalized Liénard equations

$$\begin{aligned} \frac{d}{dt}\frac{\dot{x}}{\sqrt{1{\mp } \dot{x}^2}} + f(x,\dot{x}) + g(x) = 0. \end{aligned}$$

Clearly, it is also possible to produce an arbitrarily large number of small limit cycles approaching the origin even when $G(x)\rightarrow +\infty$ as $|x|\rightarrow +\infty .$ In this case we can start from any positive energy level E. As a side remark, we observe that this result shows the flexibility of working with systems like (S),  because analogous results of non-perturbative nature (like those referring to small-amplitude limit cycles) are very hard to obtain for the classical Liénard systems (see [44, §7]).

At this point, following again (2.1) we assume at first the following conditions.

There exist $\alpha< 0 <\beta$ such that

$$\begin{aligned}&g(x)F(x,y) <0,\quad \textit{for } \; x\in \,]\alpha ,\beta [ \; \textit{and } \; x\not =0 \; \textit{ and for all } y\not =0. \\&g(x)F(x,y) >0,\quad \textit{for } \; x\not \in [\alpha ,\beta ] \; \textit{ and for all } y\not =0. \end{aligned}$$

These assumptions fit with with the classical conditions considered in the Liénard systems. Moreover, we also assume

$$\begin{aligned} G(x)\rightarrow +\infty \;\; \text { as }\; |x|\rightarrow +\infty . \end{aligned}$$

As a consequence, the origin is a source and outside the strip $[\alpha ,\beta ]\times {\mathbb {R}},$ trajectories of system (S) are guided by those of system (D). Hence, as in the classical case, the problem is that of controlling the orbits in the strip. However, the phase-portrait in the strip is now more complicated due to the possible presence of two phenomena, namely:

(a):

the existence of several branches of the vertical isocline, that is the set $y = F(x,y),$

(b):

the existence of blow-up solutions, given by possible superlinear terms in y.

In order to control the above defined situations, we focus our attention to the case of

$$\begin{aligned} F(x,y)= A(x)B(y), \end{aligned}$$

with A such that

There exist $\alpha , \beta$ with $\alpha< 0 < \beta$ such that A(x) is strictly increasing for $x \le \alpha$ and $x \ge \beta$ and, moreover, $A(\alpha ) = A(\beta ) = 0$ with $A(x)x < 0$ for $x\in \,]\alpha ,\beta [$, $x\not = 0.$

For the function B assume that

$$\begin{aligned} B(y) > 0,\; \forall \, y\not =0. \end{aligned}$$

We observe again that such choice seems natural, because, when $B\equiv 1,$ the obtained Liénard system presents a nonlinearity with a typical cubic-shaped curve, which is common in most papers and is crucial in order to prove uniqueness of the limit cycle (see [14, 17, 18, 24, 32, 39,40,41] and the references quoted therein). On the other hand, the assumptions on B(y) allow to consider power-like nonlinearities as $B(y) = |y|^p.$ This will be our starting point and will be treated in the next section.

3 A Case Study

In this section we focus our attention on the equation

with $\lambda > 0$ and $p > 0.$

Here we are mainly interested in the case $p\ge 1.$ This, because for $0< p < 1,$ $|y|^p$ is sublinear and therefore the geometry is not very far from the classical one. Moreover, the equation of the vertical isocline may be split in a simple way, namely the x-axis and a graph of the function $y=\tilde{F}(x),$ so that the situation is similar to the one of the classical case and the problem can be treated in a similar way.

We shall discuss separately the two cases study $p=1$ and $p>1.$

3.1 The case $p=1.$

We start with an analysis of the system for $p=1.$ In this case, for simplicity, we write $(H_{\lambda }) = (H_{1,\lambda }).$ System $(H_{\lambda })$ can be split as two systems of the form

and

Both systems have an Hamiltonian structure, with Hamiltonians

$$\begin{aligned} {\mathcal {E}}^+_{\lambda }(x,y):= \frac{1}{2}y^2 + \varPhi ^+_{\lambda }(x), \; \text {on } y\ge 0, \quad {\mathcal {E}}^-_{\lambda }(x,y):= \frac{1}{2}y^2 + \varPhi ^-_{\lambda }(x), \; \text {on } y\le 0, \end{aligned}$$

where

$$\begin{aligned} \frac{d}{dx}\left( \varPhi ^{\pm }_{\lambda }(x)\right) = \frac{x}{1 {\mp }\lambda (x^2-1)x}\,. \end{aligned}$$

Using the fact that $\max \{(x^2-1)x: \, -1\le x\le 0\}= 2/(3\sqrt{3}),$ we find that for $\lambda > 0,$ the equation $\lambda (x^2-1)x -1=0$ has a unique zero if and only if $0< \lambda < \lambda ^* := 3\sqrt{3}/2.$ In this case, we denote by $x=a_{\lambda }$ such unique solution, with $a_{\lambda } > 1.$ Hence we have that $\varPhi ^+_{\lambda }$ is well defined on $(-\infty ,a_{\lambda }[$ and, without loss of generality, we can take, among all the primitives of $\frac{x}{1 -\lambda (x^2-1)x}$ as $\varPhi ^+_{\lambda }$ the one such that $\varPhi ^+_{\lambda }(0)=0.$ Figure 1a shows the typical graph of $\varPhi ^+_{\lambda }(x)$ on $(-\infty ,a_{\lambda }[$ for $0< \lambda < \lambda ^*.$

If we use for the function $\varPhi ^-_{\lambda }$ the same convention that $\varPhi ^-_{\lambda }(0) = 0,$ we find that

$$\begin{aligned} \varPhi ^-_{\lambda }(x) = \varPhi ^+_{\lambda }(-x), \quad \forall \, x > - a_{\lambda } \end{aligned}$$

(3.1)

where $- a_{\lambda } < - 1$ is the unique real root of $1 +\lambda (x^2-1)x.$ Figure 1b shows the above symmetry.

Fig. 1

The functions $\varPhi ^{\pm }_{\lambda }$ are the primitives of $\frac{x}{1 {\mp }\lambda (x^2-1)x}$ with $\varPhi ^{\pm }_{\lambda }(0)=0.$ The graphs are produced using [48]

With reference to the graph of $\varPhi ^+_{\lambda }$ we can describe the dynamics of system $(H^+_{\lambda })$ for $0<\lambda < \lambda ^*.$ Let $c_{\lambda }:= \varPhi ^+_{\lambda }(-\infty ).$ For every energy level c with $0< c < c_{\lambda },$ the energy level line

$$\begin{aligned} {\mathcal {E}}^+_{\lambda }(x,y) = \frac{1}{2}y^2 + \varPhi ^+_{\lambda }(x) = c, \end{aligned}$$

is a closed curve in the phase-plane (x, y) which is also a periodic orbit of the system $(H^+_{\lambda })$, considered as a differential system defined on the whole plane. This orbit intersects the x-axis on two points $u^{\pm }(\lambda ,c)$ where

$$\begin{aligned} u^{-}(\lambda ,c)< 0 < u^{+}(\lambda ,c), \quad \text {with }\; \; \varPhi ^+_{\lambda }(u^{\pm }(\lambda ,c))=c. \end{aligned}$$

On the other hand, for $c\ge c_{\lambda },$ the energy level line ${\mathcal {E}}^+_{\lambda }(x,y) = c$ is an unbounded curve, symmetric with respect to the x-axis which, restricted to $y \ge 0,$ is the graph of a function with an asymptote at $y=\sqrt{2(c-c_{\lambda })},$ increasing on $(-\infty ,0]$ and decreasing on $[0,u^{+}(\lambda ,c)],$ where

$$\begin{aligned} 0< u^{+}(\lambda ,c) < a_{\lambda }, \quad \text {with }\; \; \varPhi ^+_{\lambda }(u^{+}(\lambda ,c))=c. \end{aligned}$$

Analogously, with reference to the graph of $\varPhi ^-_{\lambda }$ we can describe the dynamics of system $(H^-_{\lambda })$ for $0<\lambda < \lambda ^+.$ Let $d_{\lambda }:= \varPhi ^-_{\lambda }(+\infty ).$ By symmetry, we know that $d_{\lambda } = c_{\lambda }.$ For every energy level d with $0< d < d_{\lambda },$ the energy level line

$$\begin{aligned} {\mathcal {E}}^-_{\lambda }(x,y) = \frac{1}{2}y^2 + \varPhi ^-_{\lambda }(x) = d, \end{aligned}$$

is a closed curve in the phase-plane (x, y) which is also a periodic orbit of the system $(H^-_{\lambda })$, considered as a differential system defined on the whole plane. This orbit intersects the x-axis on two points $v^{\pm }(\lambda ,d)$ where

$$\begin{aligned} v^{-}(\lambda ,d)< 0 < v^{-}(\lambda ,d), \quad \text {with }\; \; \varPhi ^-_{\lambda }(v^{\pm }(\lambda ,d))=d. \end{aligned}$$

On the other hand, for $d\ge d_{\lambda },$ the energy level line ${\mathcal {E}}^-_{\lambda }(x,y) = d$ is an unbounded curve, symmetric with respect to the x-axis which, restricted to $y \le 0,$ is the graph of a function with an asymptote at $y=\sqrt{2(d-d_{\lambda })},$ increasing on $[0,+\infty )$ and decreasing on $[v^{-}(\lambda ,d),0],$ where

$$\begin{aligned} -a_{\lambda }< v^{-}(\lambda ,d) <0, \quad \text {with }\; \; \varPhi ^-_{\lambda }(v^{-}(\lambda ,d))=d. \end{aligned}$$

Now, to get the global dynamics of $(H_{\lambda })$, we can glue the orbits of $(H^+_{\lambda })$ on the upper half-plane with those of $(H^-_{\lambda })$ on the lower half-plane.

Let us consider system $(H_{\lambda })$ for $0< \lambda < \lambda ^*.$ Without loss of generality, we can assume to start from an initial point $P_0:=(x_0,y_0)$ with $y_0 > 0.$ First of all, we observe that if $x_0 = a_{\lambda }$ then $\dot{x} = 0$ and $\dot{y} = \text {constant} = -x_0 < 0,$ so that the trajectory hits the x-axis in finite time. For convenience, we suppose now that $y_0> 0$ is sufficiently large and $x_0\not = a_{\lambda }$. It is easy to check that in this situation, the trajectory moves fast close to the vertical line $x=a_{\lambda }$ and then goes down to the x-axis almost parallel to the line $x=a_{\lambda }$. Thus, we can suppose that we enter in the lower half-plane from a point of the x-axis $P_1:=(x_1,0)$ with $x_1$ close to $a_{\lambda }.$ Let now $d_1:= \varPhi ^-_{\lambda }(x_1).$ We have $0< d_1 < d_{\lambda }$ and now we follow in the lower half-plane the lower part of the closed orbit of energy $d_1$ of system $(H^-_{\lambda })$ which intersects the x-axis at two points $(v^{\pm }(\lambda ,d_1),0)$ with $v^{-}(\lambda ,d_1)< 0 < v^{+}(\lambda ,d_1) = x_1.$ Thus, setting $x_2:= v^{-}(\lambda ,d_1)$ we get a new point $P_2:=(x_2,0)$ on the orbit of $(H_{\lambda })$ where the x-axis is hit again. From $P_2$ we continue with the orbit path of $(H^+_{\lambda })$ which is the upper-half of a closed orbit which hits again the x-axis at a point $P_3:=(x_3,0)$ with $x_3= u^+(\lambda ,c)$ for $c:= \varPhi ^+_{\lambda }(x_2).$ Continuing in this manner, by induction, we obtain a sequence of points $P_i=(x_i,0)$ on the x-axis with $x_1> x_3> x_5, \dots > 0$ and $x_2< x_4< \dots < 0$ which shows that the semi-orbit $\gamma ^+(P_0)$ is winding. Since we already know that the orbits unwind from the origin, we conclude, in virtue of the Poincaré-Bendixson theorem, that the orbit $\gamma ^+(P_0)$ tends to a limit cycle $\varGamma .$ The intersection of the limit cycle $\varGamma$ with the x-axis is made by two symmetric points $P^-=(-\bar{x},0)$ and $P^+:=(\bar{x},0)$ with $P^+$ being the limit of the subsequence $(P_k)_k$ for k odd and $P^-$ the limit of the subsequence $(P_k)_k$ for k even. The uniqueness of the limit cycle can be deduced by the fact that the graphs of $\varPhi ^+_{\lambda }$ and $\varPhi ^-_{\lambda }$ intersect at a unique point for $x>0$ (and a unique symmetric one for $x < 0$).

We observe that the above analytical argument works only in the case $p=1$ because only in this case we can exploit the symmetry and the Hamiltonian structure for the two phase-portraits which are glued together. In order to overcome this difficulty, we present now a different and more general argument to prove the existence and the uniqueness of a limit cycle which can be extended to more general situations. This approach was actually already present in the above mentioned work of Liénard [26] and then by Levinson and Smith [25], and Sansone [33]. Such approach was also treated in [3, 17, 18, 32, 40, 41]. The idea is to observe that the integral of the time-derivative $\dot{H}$ (cf. (2.1)) along a closed trajectory must be zero and then to show that this can happen only once. A detailed proof for $F(x,y) = \mathtt{F}(x)$ may be found in [41].

Here we give a sketch of the proof, because the argument is similar.

At first we observe that, from (2.1), we have $\dot{H}= - \lambda |y|(x^2-1)x^2$ and therefore the energy function H is increasing inside the strip $]-1,1[\,\times {\mathbb {R}}$ and hence, due to the symmetry property of system $(H_{\lambda }),$ all the limit cycles must intersects the vertical lines $x=-1$ and $x=1.$ Assume (by contradiction) that there are two limit cycles $\varGamma _1$ and $\varGamma _2$ (with $\varGamma _1$ in the internal region of $\varGamma _2$) and compute the line integrals $\oint _{\varGamma _i} - g(x(t))F(x(t),y(t))\,dt$ for $i=1,2.$ Splitting these integrals along the orbit paths inside and outside the strip $]-1,1[\,\times {\mathbb {R}},$ we observe the following:

• (1) Inside the strip, the integral takes the form

  $$\begin{aligned} \int \dot{H}dt= & {} \int - g(x(t))F(x(t),y(t))\,dt = \int _{-1}^{1}\frac{-\lambda (x^2-1)x^2}{1- \lambda (x^2-1)x}\,dx, \; \text {for} \; y > 0 \\ \int \dot{H}dt= & {} \int - g(x(t))F(x(t),y(t))\,dt = \int _{1}^{-1}\frac{\lambda (x^2-1)x^2}{1+ \lambda (x^2-1)x}\,dx, \; \text {for} \; y < 0. \end{aligned}$$

  Notice that the denominators in the above integrals do not vanish for $0< \lambda < \lambda ^*= 3\sqrt{3}/2.$

  As y does not appear in the integrals, the variation of energy in the strip is the same for both limit cycles.

• (2) outside the strip, the integral takes the form

  $$\begin{aligned} \int \dot{H}dt= \int - g(x(t))F(x(t),y(t))\,dt = \int F(x,y)\,dy = \int \lambda |y|(x^2-1)x \,dy. \end{aligned}$$

  Now one must take into account the intervals of integration, in the y-variable, which are different for the two limit cycles. However, we observe that, since the function $x^3-x$ is monotone increasing for $|x|\ge 1$ (positive for $x > 1$ and negative for $x <1$), we can follows step by step the proof in [41, Section 2] and, in virtue of the clockwise orientation of the limit cycles, we find that the contribution to the energy along the external limit cycle is less than the contribution in the internal one.

As a final balance, we get that

$$\begin{aligned} 0= \oint _{\varGamma _2} - g(x(t))F(x(t))\,dt < \oint _{\varGamma _1} - g(x(t))F(x(t))\,dt = 0 \end{aligned}$$

which is a contradiction and shows also that the unique limit cycle is stable (Figs. 2 and 3).

Fig. 2

From the phase-portrait of $(H_{\lambda }),$ the symmetry between $(H^+_{\lambda })$ for $y\ge 0$ and $(H^-_{\lambda })$ for $y\le 0$ appears evident. The simulation corresponds to the case $\lambda =1$. The graph is produced using [49]

Fig. 3

The figure represents the dynamics for system $(H_1),$ in the phase-plane (panel left) and for component x(t) in the time variable (panel right). The graphs are produced using [48]

Summarizing this discussion, we have obtained the following result.

Theorem 1

The system

has a unique limit cycle for $0< \lambda < \lambda ^*=3\sqrt{3}/2,$ while, for $\lambda > \lambda ^*$ there are no limit cycles.

Remark 1

Following the dynamics for $\lambda \nearrow \lambda ^*$ we can say that, at this value, the limit cycle collapses at $\pm \infty$ in a vertical strip. In this light we produce simulations for $\lambda = 2< \lambda ^* < \lambda =3$ (see Fig. 4 below). Therefore, this result can be viewed as a bifurcation from infinity in the strip $]-1,1[$ and this clearly does not appear in the classical case of the Van der Pol equation. $\square$

Fig. 4

The figures represent the dynamics for system $(H_{1,\lambda }),$ for $\lambda$ less than and $\lambda$ greater than the critical value $\lambda ^*.$ The graphs are produced using [49]

3.2 The Case $p>1.$

We consider now system $(H_{p,\lambda })$ for $p>1.$ In order to understand the dynamical behavior of such class of systems, we deal, at first, with the particular case

since the other systems exhibit the same dynamical features. Now, the vertical isocline will play a crucial role. It is given by the union of the x-axis with the graph of

$$\begin{aligned} y = \frac{1}{\lambda (x^3- x)}. \end{aligned}$$

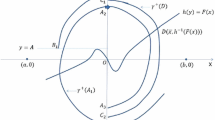
Standard phase-plane arguments show that the trajectories, as before, are symmetric with respect to the origin and the directions of the vector field are the following (see Fig. 5).

The symmetric regions

$$\begin{aligned} {\mathcal {V}}_1:= & {} \left\{ (x,y): -1< x<0,\, y> \tfrac{1}{\lambda (x^3- x)}\right\} \\ {\mathcal {V}}_2:= & {} \left\{ (x,y): 0< x<1, \, y <\tfrac{1}{\lambda (x^3- x)}\right\} \end{aligned}$$

are positively invariant and play a crucial role because all the trajectories entering such regions become unbounded in the y-component. Notice that, however, there is no blow-up in forward time and the solutions entering $V_1$ or $V_2$ are defined on ${\mathbb {R}}^+.$ Indeed, if $(x(t),y(t))\in V_i$ (for $i=1,2$), for $t\ge 0,$ then $|x(t)|\le 1$ and hence, from the second equation in system $(H_{p,\lambda })$ we have $|y'(t)|\le 1.$

Unboundedness in backward time occur also in the negatively invariant regions

$$\begin{aligned} {\mathcal {W}}_1:= & {} \left\{ (x,y): x> 1,\, y> \tfrac{1}{\lambda (x^3- x)}\right\} \\ {\mathcal {W}}_2:= & {} \left\{ (x,y): x< -1, \, y <\tfrac{1}{\lambda (x^3- x)}\right\} \end{aligned}$$

(see Fig. 5), but this latter fact does not involve extra difficulties (and sometimes it may help) in the search of the limit cycle.

Fig. 5

The infinite-isocline and the zero-isocline for system $(H_{2,1}),$ with the direction of the vector field. The graph is produced using [48]

An inspection of the vector field in a neighborhood of the origin and observing also that $\dot{H}(x,y) = - \lambda y^2 x^2 (x^2-1) > 0$ for $0< |x| <1$ and $y\not =0,$ shows that the origin is a source and therefore small orbits are unwinding. However, for $\lambda > 0$ large, all these orbits will enter the positively invariant regions $V_1$ or $V_2$ and ultimately will be unbounded, so that there are no limit cycles (the precise details and estimates justifying our assertion on the nonexistence of limit cycles are given in Step 1 of the proof of Theorem 2, below). On the other hand, for $\lambda$ small enough, the are trajectories exiting the negatively invariant region $W_1$ that reach the negative y-axis, without entering the “forbidden region” $V_1$. Such trajectories eventually intersect the x-axis at some $x < 0$. Due to the symmetry of the system, any such trajectory is bounded above in the upper plane by a symmetric one and therefore is winding. As usual, the Poincaré-Bendixson theorem guarantees the existence of at least a limit cycle. The fact that this behavior of the orbits is possible for $\lambda$ is small, as well the fact that the trajectories become unbounded for $\lambda$ large, is granted by the fact that the infinite isoclines in the strip $]-1,1[\times {\mathbb {R}}$ monotonically move with respect to the parameter $\lambda$ (see Fig. 6).

Fig. 6

The movement of the infinite-isocline when $\lambda$ varies. The graph represent (from the external to the internal ones) three different isoclines for $\lambda =1,2,3$ and show the monotonicity. The graphs are produced using [48]

In view of the above discussion, now we are in position to establish the following result.

Theorem 2

There is $\lambda ^*_2> 0$ such that for every $\lambda \in \,]0,\lambda ^*_2[$ system $(H_{2,\lambda })$ has a limit cycle, while for $\lambda >\lambda ^*_2$ all the nontrivial trajectories are ultimately unbounded.

Proof

In the introductory part preceding the statement of the theorem, we have already described the qualitative analysis leading to the strategy of the proof. We provide now the technical estimates which justify our previous assertions. To this end, we split the proof in three steps.

Step 1. Nonexistence of limit cycles for $\lambda$ large. Considering the previously introduced energy function $H(x,y) = \tfrac{1}{2}\bigl (y^2 + x^2)$ associated to the (linear) autonomous Duffing equation $\dot{x}=y,$ $\dot{y}=-x,$ we find that

$$\begin{aligned} \dot{H}(x,y)= - \lambda y^2(x^2-1)x^2. \end{aligned}$$

Hence $\dot{H}(x,y)\ge 0,$ with $\nabla H(x,y)\not =0$ on all the points of the circumference $H(x,y)=1/2.$ This implies that the disc $D:=\{(x,y): H(x,y)\le 1/2\}$ (the closed disc of center the origin and radius one) is a negatively invariant region for the dynamical system associated with $(H_{2,\lambda })$ (for each $\lambda > 0$). Hence the Lyapunov–LaSalle theory (cf. [23]) guarantees that for each initial point $P_0\in D$ the negative semi-orbit $\gamma ^-(P_0)$ tends to the origin (for $t\rightarrow -\infty ).$ In other words the disc D is contained in the region of repulsivity of the origin.

Now, it is sufficient to take $\lambda > 0$ sufficiently large so that at least one of the regions ${\mathcal {V}}_1$ or ${\mathcal {V}}_2$ (in our case both the regions, by the symmetry of the system) intersects the disc D (see Fig. 7 for an illustration of this fact). Clearly, if we take any initial point $P_0\in D\cap {\mathcal {V}}$ (with ${\mathcal {V}}= {\mathcal {V}}_1$ or ${\mathcal {V}} = {\mathcal {V}}_2$), we have that the orbit $\gamma (P_0)$ tends to the origin in the negative time, while its positive semi-orbit enters ${\mathcal {V}}$ and is unbounded in the future. By construction, the orbit $\gamma (P_0)$ prevents the possibility of the existence of a closed orbit (which should surround the origin). At this point the Boincaré-Bendixson theory implies that all the nontrivial positive trajectories must be unbounded. In this manner we have proved that there exists $\check{\lambda } > 0$ such that for each $\lambda > \check{\lambda }$ all the nontrivial trajectories are ultimately unbounded.

Fig. 7

Taking $\lambda > 0$ sufficiently large we move down the “forbidden” region ${\mathcal {V}}_1$ and up the symmetric one ${\mathcal {V}}_2$ (in dark) until they cross the disc D. The graph is produced using [48]

Step 2. Existence of limit cycles for $\lambda$ small. Let

$$\begin{aligned} x_m:= -\frac{1}{\sqrt{3}},\quad y_m:= \frac{3\sqrt{3}}{2} \end{aligned}$$

be the coordinates of the minimum point of $1/(x^3-x)$ on the interval $]-1,0[\,.$ Consider also the line

$$\begin{aligned} y = \frac{1}{2\lambda (x^3-x)}, \quad \text {for }\; -1< x < 0 \end{aligned}$$

which is below the region ${\mathcal {V}}_1$ and has $y_m/2\lambda$ as a minimum value. By construction, we have that

$$\begin{aligned} \dot{x} = y - \lambda y^2(x^3-x) \ge y/2, \;\; \forall \,(x,y): \, -1< x< 0,\,\, 0 < y \le \frac{1}{2\lambda (x^3-x)}. \end{aligned}$$

(3.2)

Consider the initial point

$$\begin{aligned} P_0=(-1,y_0), \quad \text {with }\; y_0 = \frac{y_m}{2\lambda } - 2. \end{aligned}$$

Clearly $y_0 > 0$ for $\lambda$ small, namely, $0< \lambda < y_m/4.$

The slope of the trajectory departing from $P_0$ satisfies the relation

$$\begin{aligned} 0 \le \frac{d y}{dx} \le - \frac{2x}{y},\quad \forall \, (x,y)\in {\mathcal {R}}:= [-1,0]\times [y_0,y_0+2], \end{aligned}$$

hence, an elementary and standard estimate shows that the positive trajectory departing from $P_0$ remains in the region ${\mathcal {R}}$ and crosses the y-axis at some point $P_1=(y_1,0)$ with $y_0< y_1 < y_0 +2.$ Consider now the point $P_2=(x_1,y_1)$ of intersection of the horizontal line $y=y_1$ with the boundary of the region ${\mathcal {W}}_1\,,$ given by the equation $y=1/(\lambda (x^3-x))$ for $x>1$ and observe that the segment $\overline{P_1P_2}$ is crossed by the vector field from the exterior to the interior, as $\dot{x}\ge 0$ and $\dot{y}< 0$ (for $x>0$).

Consider now the negative semi-orbit departing from $P_0$ and let $C(P_0)$ be the circumference of center the origin and passing through $P_0$ of equation

$$\begin{aligned} x^2 + y^2 = 1 + y_0^2 = 1 + \left( \frac{y_m}{2\lambda } - 2\right) ^2. \end{aligned}$$

Since $\dot{H}(x,y) \le 0$ for all $x\le -1,$ we have that the region outside the circumference $C(P_0)$ in the half-plane $x\le -1$ is negatively invariant is for the dynamical system associated with $(H_{2,\lambda })$ (for each $\lambda > 0$), with respect to the open set $x< -1.$ Now we are in position to consider the following

Claim For $\lambda > 0$ sufficiently small the circumference $C(P_0)$ crosses the curve $y = \frac{1}{\lambda (x^3-x)}$ for $x < -1.$

We observe that we look for an intersection point in the third quadrant, therefore we study the system

$$\begin{aligned} {\left\{ \begin{array}{ll} y = - \sqrt{1 + (\frac{y_m}{2\lambda } - 2)^2 - x^2}\\ y = \frac{1}{\lambda (x^3-x)} \end{array}\right. } \end{aligned}$$

(3.3)

looking for a solution x in the domain

$$\begin{aligned} - \sqrt{1 + \bigl (\frac{y_m}{2\lambda } - 2\bigr )^2}< x < -1. \end{aligned}$$

Clearly, from system (3.3) we get the equation

$$\begin{aligned} f(x,\lambda ) = -1,\quad \text {for }\; f(x,\lambda ):= (x^3 -x)\sqrt{\bigl (\frac{y_m}{2} - 2\lambda \bigr )^2 - \lambda ^2(x^2-1)}. \end{aligned}$$

Such equation has always solutions in the desired range for $\lambda$ sufficiently small. It is enough to observe that

$$\begin{aligned} \lim _{x\rightarrow -1^-} f(x,\lambda ) = 0 > -1 \end{aligned}$$

and then take a suitable (large in absolute value) $\tilde{x} < -1$ such that $\eta :=(\tilde{x}^3 -\tilde{x})y_m/2 < -1$ and observe that

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+} f(\tilde{x},\lambda ) = \eta < -1 \end{aligned}$$

and therefore the claim is proved.

The claim we have just proved guarantees that the negative semi-trajectory departing from $P_0$ crosses the line $y = 1/(\lambda (x^3-x))$ at some point with $P_{-1} = (x_{-1},y_{-1})$ with $x_{-1} < -1$ and $y_{-1} < 0.$

To conclude the proof, we just repeat symmetrically the same construction starting from the point $Q_0=(1,-y_0)$ and obtain the corresponding (and symmetric) points $Q_1\,,$ $Q_2$ and $Q_{-1}\,.$ In this manner, we have determine a piecewise smooth Jordan curve $\varUpsilon$ defined as follows: from $P_{-1}$ to $P_{0}$ and from $P_0$ to $P_{1}$ along an orbit-path of the trajectory through $P_0\,,$ next, the segment $\overline{P_{1}P_{2}}\,,$ then the arc of curve $y=1/(\lambda (x^3-1))$ for $x > 1$ from $P_2$ to $Q_{-1}$ and, finally, the symmetric orbit-path from $Q_{-1}$ to $Q_{1}$ (passing through $Q_{0}$), the segment $\overline{Q_{1}Q_{2}}$ and the arc of curve $y=1/(\lambda (x^3-1))$ for $x < -1$ from $Q_2$ to $P_{-1}\,.$ The curve $\varUpsilon$ is the boundary of a positively invariant region containing the origin as the unique equilibrium point, which is also a source. Therefore, the Poincaré-Bendixson theorem guarantees the existence of at least a limit cycle bounded by $\varUpsilon .$ In this manner we have proved that there exists $\hat{\lambda } > 0$ such that, for each $0<\lambda < \hat{\lambda },$ system $(H_{2,\lambda })$ has at least a limit cycle. Figure 8 illustrates the geometry involved in the proof of Step 2.

Fig. 8

Taking $\lambda > 0$ sufficiently small we move up the “forbidden” region ${\mathcal {V}}_1$ and down the symmetric one ${\mathcal {V}}_2$ (in dark) and an invariant region bounded by ${\mathcal {W}}_1$ and ${\mathcal {W}}_1$ can be constructed. The graph is produced using [48]

Step 3. The existence of $\lambda _2^*.$ This last assertion follows by defining

$$\begin{aligned} \lambda _{2}^{*}:= \sup \{k > 0: (H_{2,\lambda })\; \text {has a bounded nontrivial orbit}\, \forall \, \lambda :\, 0<\lambda < k\} \end{aligned}$$

and observing that if for a certain $\lambda _1$ all the solutions of $(H_{2,\lambda })$ are unbounded, then the same holds for any $\lambda _2 > \lambda _1\,.$ This because the unbounded solutions of $(H_{2,\lambda })$ either eventually enter in the regions ${\mathcal {V}}_1$ and ${\mathcal {V}}_2$ or they correspond to the separatrices contained, respectively in $]-1,0[$ and in ]0, 1[ and very close (below/above) to these regions. Now, increasing $\lambda$ has the effect of moving down the region ${\mathcal {V}}_1$ and up the region ${\mathcal {V}}_2$ (and the corresponding separatrices). This in turn implies that all the obits which were escaping to infinity for $\lambda _1$ are also escaping to infinity for $\lambda _2\,.$ This completes the proof of our result. $\square$

As a comment to this lengthy proof, we observe that we choose to describe in detail all the steps, because the same argument will work in the general case and this will avoid tedious computations in the proof of Theorem 6, where the geometry is exactly the same except for the symmetry (Figs. 9 and 11.).

Remark 2

As before, we observe that for $\lambda \nearrow \lambda ^*_2$ the limit cycle collapses at $\pm \infty$ in the vertical strip $]-1,1[\times {\mathbb {R}}$. $\square$

Remark 3

The same argument, with minor changes, allows to extend the result of Theorem 2 to system $(H_{p,\lambda })$ for every $p> 1.$ In this case, we find a constant $\lambda ^*_p$ such that the system has a limit cycle if and only if $0< \lambda < \lambda ^*_p.$ The same result applies also to more general functions A(x) (see also Theorem 6). Example 2, considered at the end of the article, shows the applicability of our approach to other situations. $\square$

Fig. 9

Planar dynamics for system $(H_{2,2}).$ It is evident that the trajectories are unwinding from the origin and ultimately become unbounded entering the regions $V_1$ or $V_2$. The graph is produced using [49]

Fig. 10

The figures represent the dynamics for system $(H_{2,\lambda }).$ Numerical simulations suggest that the critical value of the parameter $\lambda ^*_2$ satisfies the bound $1.474<\lambda ^* < 1.475.$ The graphs are produced using [48]

Fig. 11

The figures represent the behavior of the components x(t) (left panel) and y(t) (right panel) for system $(H_{2,\lambda })$ with $\lambda =1.475$ as in the right panel of Fig. 10. The graphs are produced using [48]

The problem of the uniqueness of the limit cycle

We conclude our analysis by discussing the problem of the uniqueness of the limit cycle for $p >1.$ Although there is a numerical evidence of the uniqueness, unfortunately, the previous proof does not work. It is interesting to point out the issues even because this will give a proof for the case $0<p<1.$

Let $p > 1$. As before, a computation of $\dot{H}= - \lambda |y|^p(x^2-1)x^2$ and the symmetry property of system $(H_{p,\lambda }),$ show that the origin is a source and all the limit cycles must intersects the vertical lines $x=-1$ and $x=1.$ Again, assume (by contradiction) that there are two limit cycles $\varGamma _1$ and $\varGamma _2$ (with $\varGamma _1$ in the internal region of $\varGamma _2$) and compute the line integrals $\oint _{\varGamma _i} - g(x(t))F(x(t))\,dt$ for $i=1,2.$ Splitting these integrals along the orbit paths inside and outside the strip $]-1,1[\,\times {\mathbb {R}},$ we observe, in the same way, the following:

$\diamond$:

Outside the strip, the integral takes the form

$$\begin{aligned} \begin{array}{lll} \int \dot{H}dt&{}=&{} \int - g(x(t))F(x(t),y(t))\,dt = \int F(x,y)\,dy \\ &{}=&{} \int \lambda |y|^p(x^2-1)x\,dy. \end{array} \end{aligned}$$

(3.4)

Arguing as before, we find that the contribution to the energy along the external limit cycle is less than the contribution of the internal one. This is true not only for $p>1,$ but for every $p>0.$

$\diamond$:

Inside the strip, the integral takes the form

$$\begin{aligned} \begin{array}{lll} \int \dot{H}dt&{}=&{} \int - g(x(t))F(x(t),y(t))\,dt = \int _{-1}^{1}\frac{-\lambda |y|^{p}(x^2-1)x^2}{y- \lambda |y|^{p}(x^2-1)x}\,dx \\ &{}=&{} \int _{-1}^{1}\frac{-\lambda y^{p-1}(x^2-1)x^2}{1- \lambda y^{p-1}(x^2-1)x}\,dx, \; \text {for} \;\; y > 0 \end{array} \end{aligned}$$

(3.5)

$$\begin{aligned} \begin{array}{lll} \int \dot{H}dt &{}=&{} \int - g(x(t))F(x(t),y(t))\,dt = \int _{1}^{-1}\frac{-\lambda |y|^{p}(x^2-1)x^2}{y- \lambda |y|^{p}(x^2-1)x}\,dx \\ &{}=&{} \int _{1}^{-1}\frac{\lambda |y|^{p-1}(x^2-1)x^2}{1+ \lambda |y|^{p-1}(x^2-1)x}\,dx, \; \text {for} \;\; y < 0. \end{array} \end{aligned}$$

(3.6)

Clearly, a limit cycle cannot intersect the vertical isocline and enter in the “forbidden” regions that before were indicated by $V_1$ and $V_2$ for $p=2$. Hence, for $0< \lambda < \lambda ^*_p$, the denominators in the above integrals do not vanish. Let us consider the first of the above integrals and write it as

$$\begin{aligned} \int _{-1}^{1}\frac{-\lambda (x^2-1)x^2}{y^{1-p} - \lambda (x^2-1)x}\,dx \end{aligned}$$

(3.7)

(for the second integral the situation is symmetric and so we do not repeat the discussion). However, now a problem appears, because, as one can see, for $p >1$ the integrand is increasing with respect to y. This means that in the strip $]-1,1[\times {\mathbb {R}}^+$, the part of the outer limit cycle gains more energy than the part of the inner limit cycle. This does not allow to repeat the above proof and show that the complete integral along the outer limit cycle is less than the integral along the inner one. This is also evident from the numerical simulations, where we see that in the strip the limit cycles tend to have an arbitrary large amplitude and the function H(x, y) is actually the square of the distance from the origin.

3.3 The case $0< p <1.$

At first we notice that even if in this case B(y),  and therefore F(x, y),  is not locally Lipschitz continuous at $y=0,$ nevertheless there is still uniqueness of the trajectories. Indeed, near the origin (which could be the only point in which the uniqueness might fail) standard phase inspection shows that trajectories are clockwise and the origin is a source.

Concerning the existence of limit cycles, we stress that the proof for the case $p>1$ does not work because a crucial point in that case was the fact there were trajectories coming from the negatively invariant regions $W_1$ and $W_2$ and such regions are not present in this case. To overcome this question, we use a different (still geometrical) approach.

From $(H_{p,\lambda })$ we consider the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = |y|^p(|y|^{1-p}\mathrm{sign}(y) - (x^2-1)x)\\ |y|^p\dot{y} = -|y|^p x \end{array}\right. } \end{aligned}$$

(3.8)

which, via the change of variables

$$\begin{aligned} w= \frac{1}{p+1}|y|^{p}y,\quad y= (p+1)^{\frac{1}{p+1}}w^{\frac{1}{p+1}}\mathrm{sign}(w), \end{aligned}$$

(3.9)

takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = L(w)(h(w) - (x^2-1)x)\\ \dot{w} = -L(w)x \end{array}\right. } \end{aligned}$$

(3.10)

where

$$\begin{aligned} L(w):=(p+1)^{\frac{p}{p+1}}|w|^{\frac{p}{p+1}},\quad \text {and }\; h(w):=(p+1)^{\frac{1-p}{p+1}}|w|^{\frac{1-p}{p+1}}\mathrm{sign}(w). \end{aligned}$$

It is worth to note that this change of variables is not smooth at $w=0.$ However, being the origin a source, this is not a problem and the uniqueness of the solutions is always granted (the uniqueness also follows from more general results in [12] regarding differential equations with even a discontinuous right-hand side, provided that the vector field presents a surface of discontinuity which is crossed transversally, as is in our case). Finally, from (3.10), we consider the associated system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = h(w) - (x^2-1)x\\ \dot{w} = -x \end{array}\right. } \end{aligned}$$

(3.11)

It is well known (see, for instance, [2]) that such a system has at least a limit cycle. As the slopes for (3.10) and (3.11) are the same, due to the fact that the factor L(w) simplifies, the two systems have the same phase-portrait. However, this argument fails at the x-line, where $L(w)=0.$ Indeed, one may observe that (3.10) as $w=0$ as a whole line of critical points. But this is not a problem if we compare the two system for $w>0$ (that is $y>0$) and $w<0$ (that is $y<0$) respectively. More in detail, let $\varGamma$ be a limit cycle of system (3.11). We split $\varGamma$ in two arcs, $\varGamma ^+$ for $w>0$ and $\varGamma ^-$ for $w<0,$ ignoring the two points where $\varGamma$ intersects the x-axis. Clearly, the same arcs $\varGamma ^{\pm }$ are orbits of system (3.10). At this point we apply on these arcs the transformation $(x,w)\rightarrow (x,y)$ considered in (3.9), obtaining two new arcs $\varGamma _1^{\pm }$ which are orbits of system (3.8). Cancelling $|y|^p$ in the second equation of (3.8), we are back to system $(H_{p,\lambda }).$ Finally, we glue the closures of $\varGamma _1^+$ and $\varGamma _1^-$ (in a smooth way due to the fact that the vector field on the x-axis is vertical), obtaining the desired limit cycle for $(H_{p,\lambda }).$

Let us consider now the problem of the uniqueness of the limit cycle. We just observe that the previous computation, which was failing or the case $p>1,$ now works for $0< p <1.$ Indeed, the integral (3.7) in decreasing in the strip $[-1,1]$ (and a symmetric argument works for $y<0$). Hence, the computations produced for (3.4)-(3.5)-(3.6) can be repeated and we have the following result.

Theorem 3

For every $\lambda > 0$ and $0<p<1,$ system $(H_{p,\lambda })$ has exactly one limit cycle.

A comment to Theorem 3 is given by the following Fig. 12 concerning the case $p=1/2$ and $\lambda =2.$

Fig. 12

Uniqueness of the limit cycle for $(H_{p,\lambda })$ in the case $p=1/2$ and $\lambda =2$, as above proved

4 The General Case

As in the previous section, we consider the case

$$\begin{aligned} F(x,y) = \lambda A(x)B(y), \quad \lambda >0, \end{aligned}$$

where $A, B: {\mathbb {R}}\rightarrow {\mathbb {R}}$ satisfy analogous assumptions to those of Sect. 2, namely:

(A0):

There exist $\alpha , \beta$ with $\alpha< 0 < \beta$ such that $A(\alpha ) = A(\beta ) = A(0)=0$ with $A(x)x < 0$ for $x\in \,]\alpha ,\beta [$, $x\not = 0$ and, moreover,

$$\begin{aligned} \lim _{x\rightarrow -\infty }A(x) = -\infty , \quad \lim _{x\rightarrow +\infty }A(x) = +\infty \end{aligned}$$

(B0):

$B(y) > 0,\; \forall \, y\not =0.$

System (S) takes the form

with

and A, B, g satisfying regularity conditions in order that the uniqueness of the solutions for the initial value problems is guaranteed.

In the light of the previous section, we consider two cases for the function B(y),  namely, the sublinear case and the superlinear one.

The sublinear case: $B(y)/y\rightarrow 0$ for $y\rightarrow \pm \infty$

As already discussed, if B(y) is not locally Lipschitz continuous at $y=0,$ this is not a problem because the origin is a source in virtue of the sign of A(x) in a neighborhood of $x=0.$ As before, we replace system (S1) with

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = B(y)(\frac{y}{B(y)} - \lambda A(x))\\ B(y)\dot{y} = - B(y)g(x) \end{array}\right. } \end{aligned}$$

(4.1)

Next we introduce the function

$$\begin{aligned} {\mathcal {B}}(y):= \int _{0}^y B(s)\,ds \end{aligned}$$

which is strictly monotone increasing and we assume that

Thus we can consider the change of variable

$$\begin{aligned} w:={\mathcal {B}}(y),\quad y:= {\mathcal {B}}^{-1}(w) \end{aligned}$$

and transform system (4.1) to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = L(w)(h(w) - \lambda A(x))\\ \dot{w} = - L(w)g(x) \end{array}\right. } \end{aligned}$$

(4.2)

with

$$\begin{aligned} L(w):=B({\mathcal {B}}^{-1})(w),\quad h(w):= \frac{{\mathcal {B}}^{-1}(w)}{L(w)}\,. \end{aligned}$$

The orbit-paths of (4.2) for $w\not =0$ (that is $y\not =0$) are the same of those of

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = h(w) - \lambda A(x)\\ \dot{w} = - g(x). \end{array}\right. } \end{aligned}$$

(4.3)

Observe that the sublinear condition implies that $h(w)\rightarrow \pm \infty$ for $w\rightarrow \pm \infty .$ Hence, in order to enter in the setting of the existence result in [19, 42] (see also [46] for a survey on this topic) for system (4.3), we just need to assume that

At this point we can replicate the argument for $(H_{p,\lambda })$ with $0<p<1$ and get the existence of at least a limit cycle for the original system. Thus we have the following result.

Theorem 4

Assume (g10) as well as (A0),  (B0),  (B1),  (B2). Then, for every $\lambda > 0$ system (S1) has at least a limit cycle.

Example 1 provides an explicit application of Theorem 4, namely for

$$\begin{aligned} B(y)= \tfrac{2}{\pi }\arctan (|y|^{1/2} + y^2), \quad A(x)= (x^2 - x -1)x \end{aligned}$$

and $g(x)=x^3,$ so that (g0) holds. Observe that, in this case, all the assumptions (A0),  (B0),  (B1),  (B2) are satisfied.

Example 1

To show an example of applicability of Theorem 4 we consider the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = y - \lambda \tfrac{2}{\pi }\arctan (|y|^{1/2} + y^2)(x^2 - x -1)x\\ \dot{y} = - x^3. \end{array}\right. } \end{aligned}$$

Figure 13 illustrates the associated dynamics for $\lambda =1.$ $\square$

Fig. 13

The figure represents the dynamics for system (S1),  in the phase-plane (panel left) and for component x(t) in the time variable (panel right). This example concerns the sublinear case with $B(y)=\tfrac{2}{\pi }\arctan (|y|^{1/2} + y^2),$ $A(x)=(x^2 - x -1)x$ and $g(x)=x^3.$ The simulation suggests the uniqueness of the limit cycle, but in order to rigorously prove this fact, one should first check the validity of the property $(\mathscr {S})$ introduced below. The graphs are produced using [48]

As discussed in [9, 20, 22, 46] the topic concerning the uniqueness of the limit cycle is more delicate. We show how our argument developed in Sect. 3 for system $(H_{p,\lambda })$ can be affectively applied to our situation as well. We recall that the problem of the uniqueness of the limit cycle for the classical Liénard equation (1.2) has been studied in [40, 41], by considering the following classical property:

which we referred to R. Conti [10] in [41]. It is worth to note, and it is a pleasure, that Professor Roberto Conti was the thesis advisor of the first author, and was a mentor and a guide for both authors when they were moving their first steps in this fascinating mathematical field area.

As remarked in [46, p.1192], this crossing condition (implicitly used in the proof of the result in [20], further corrected in [22] and [46]) is crucial also for the proof of the uniqueness of the limit cycles for (4.3) or, equivalently, (1.3), otherwise some counterexamples can be constructed. In this setting we present the following result.

Theorem 5

Assume (g10) and that there exist $\alpha , \beta$ with $\alpha< 0 < \beta$ such that $A(\alpha ) = A(\beta ) = A(0)=0$ such that $A(x)x < 0$ for $x\in \,]\alpha ,\beta [$, with A(x) is strictly increasing for $x \le \alpha$ and $x \ge \beta .$ Assume that B(y) satisfies (B0) and (B2). Then system (S1) has at most one limit cycle provided that $(\mathscr {S})$ holds.

Proof

By property $(\mathscr {S})$ all the possible limit cycles cross the strip $[\alpha ,\beta ]\times {\mathbb {R}}.$

Assume (by contradiction) that there are two limit cycles $\varGamma _1$ and $\varGamma _2$ (with $\varGamma _1$ in the internal region of $\varGamma _2$) and compute the line integrals

$$\begin{aligned} \oint _{\varGamma _i} - g(x(t))F(x(t),y(t))\,dt \end{aligned}$$

for $i=1,2.$ Splitting these integrals along the orbit paths inside and outside the strip $[\alpha ,\beta ]\times {\mathbb {R}},$ we obtain:

Outside the strip, the integrals (3.4) take the form

$$\begin{aligned} \int \dot{H}dt= \int - g(x(t))F(x(t),y(t))\,dt = \int F(x,y)\,dy = \lambda \int B(y)A(x)\,dy. \end{aligned}$$

Since the function A(x) is monotone increasing and is positive for $x > \beta$ and negative for $x <\alpha ,$ we find that the contribution to the energy along the external limit cycle is less than the contribution in the internal one.

Inside the strip the integrals (3.5) and (3.6), become, respectively

$$\begin{aligned} \int \dot{H}dt= & {} \int - g(x(t))F(x(t),y(t))\,dt = -\lambda \int _{\alpha }^{\beta }\frac{B(y)A(x)}{y- \lambda B(y)A(x)}\,dx \\= & {} -\lambda \int _{\alpha }^{\beta }\frac{A(x)}{\frac{y}{B(y)}- \lambda A(x)}\,dx, \; \text {for} \;\; y > 0 \end{aligned}$$

and

$$\begin{aligned} \int \dot{H}dt= & {} \int - g(x(t))F(x(t),y(t))\,dt = -\lambda \int _{\beta }^{\alpha }\frac{B(y)A(x)}{y- \lambda B(y)A(x)}\,dx \\= & {} \lambda \int _{\alpha }^{\beta }\frac{A(x)}{\frac{y}{B(y)}- \lambda A(x)}\,dx, \; \text {for} \;\; y < 0. \end{aligned}$$

Now, using the assumption (B2) we find again that the contribution to the energy along the external limit cycle is less than the contribution in the internal one. In conclusion we get that

$$\begin{aligned} 0= \oint _{\varGamma _2} - g(x(t))F(x(t))\,dt < \oint _{\varGamma _1} - g(x(t))F(x(t))\,dt = 0 \end{aligned}$$

which is a contradiction. $\square$

In our case, in order to fulfill the implicit assumption $(\mathscr {S})$, we need some symmetry properties which, for example are satisfied if B(y) is even and A(x) and g(x) are odd. If these additional assumptions hold, combining Theorem 4 and Theorem 5 we get that:

System (S1) has exactly one limit cycle which is asymptotically stable.

Remark 4

One may argue that assuming the above mentioned symmetry conditions one can get directly the uniqueness of the limit cycle from the auxiliary system (4.3). This because the results on the number of limit cycles for (4.3) transfer to our case via the change of variables considered in the proof of Theorem 4. This argument is correct. However, we observe that our uniqueness result can be applied to situations where the above quoted existence results for (4.3) are not applicable. This occurs, for instance, when the growth conditions for F(x) or G(x) at infinity are not satisfied. On the other hand, limit cycles may in principle exist and Theorem 5 gives the uniqueness. A result related to Theorem 4 was previously obtained in [32, Theorem 1], for the study of a system of the form (S1) in the sublinear case. This also shows the effectiveness of the method of energy integration introduced in the pioneering work of Liénard and developed by several authors since then. $\square$

The superlinear case: $y/B(y)\rightarrow 0$ for $y\rightarrow \pm \infty$

This case is more intriguing, due to the presence of new branches of the infinite isocline as it was shown in Figs. 5 and 6 and now the parameter $\lambda > 0$ will play a crucial role. As far as we know, this interesting phenomenon has never been investigated in this context before.

From now on, besides (B0) and (g0), we suppose that (A0) holds with the function A(x) having exactly three zeros $\alpha<0 < \beta ,$ so that we assume the following

(A1):

There exist $\alpha , \beta$ with $\alpha< 0 < \beta$ such that $A(\alpha ) = A(\beta ) = A(0)=0$ with $A(x)x < 0$ for $x\in \,]\alpha ,\beta [$, $x\not = 0$ and $A(x)x > 0$ for $x\notin \,[\alpha ,\beta ].$ Moreover,

$$\begin{aligned} \lim _{x\rightarrow -\infty }A(x) = -\infty , \quad \lim _{x\rightarrow +\infty }A(x) = +\infty . \end{aligned}$$

Observe again that this assumption is common for the classical Liénard equation (1.2).

Moreover, assume that

Under the above assumption, the map $\eta (y):= B(y)/y$ is an increasing bijection of the real line with $\eta (0)=0$ and therefore the vertical isocline is given by the union of the x-axis with the graph of

$$\begin{aligned} y = \kappa _{\lambda }(x):=\eta ^{-1}\left( \frac{1}{\lambda A(x)} \right) . \end{aligned}$$

This graph, in view of the hypotheses on A(x),  exhibits a behavior similar to the one of the case study with $p>1,$ depicted in Fig. 5.

As in Sect. 3 (cf. Fig. 5), we can define the positively invariant regions

$$\begin{aligned} {\mathcal {V}}_1= & {} {\mathcal {V}}_1^{\lambda }:= \{(x,y): \alpha< x<0,\, y > \kappa _{\lambda }(x)\}, \\ {\mathcal {V}}_2= & {} {\mathcal {V}}_2^{\lambda }:= \{(x,y): 0< x<\beta , \, y <\kappa _{\lambda }(x)\}. \end{aligned}$$

Analogously, we introduce the negatively invariant regions

$$\begin{aligned} {\mathcal {W}}_1= & {} {\mathcal {W}}_1^{\lambda }:= \{(x,y): x> \beta ,\, y> \kappa _{\lambda }(x)\} \\ {\mathcal {W}}_2= & {} {\mathcal {W}}_2^{\lambda }:= \{(x,y): x< \alpha , \, y <\kappa _{\lambda }(x)\}. \end{aligned}$$

By the properties of A(x) and $\eta ^{-1}$ (which, in turns, depends on the behavior of B(y)/y in (B3)), we have that $\kappa _{\lambda }: {\mathbb {R}}\setminus \{\alpha ,0,\beta \}\rightarrow {\mathbb {R}}$ is a continuous function such that $\kappa _{\lambda }(x)< 0$ for $x < \alpha$ and $0< x < \beta ,$ $\kappa _{\lambda }(x)>0$ for $\alpha< x < 0$ and $x > \beta$ and $\eta (x)\rightarrow 0$ for $x\rightarrow \pm \infty .$ Moreover, $\kappa _{\lambda }\rightarrow \pm \infty$ as $x\rightarrow \alpha ^{\pm },$ as $x\rightarrow 0^{{\mp }}$ and $x\rightarrow \beta ^{\pm }.$

Our next and final result is an extension of Theorem 2 which was proved for the “case study” $(H_{2,\lambda })$ to general systems of the form (S1). For the proof of our previous theorem we used the fact that $B(y)= |y|^p$, for $p>1$ (even if only the case $p=2$ was discussed in detail). In Theorem 2 we considered a special form of odd A(x),  namely $A(x)=x^3-x$ and $g(x)=x.$ In the general superlinear case studied in this section we try to avoid as possible any condition of symmetry. However, checking the proof of Step 2 in Theorem 2 one realizes that the crucial fact in the proof of the intersection of the circumference $C(P_0)$ with the curve which is the boundary of the region ${\mathcal {W}}_2$ involves a comparison between the 1/A(x) on $]-1,0[$ with A(x) on $(-\infty ,-1[\,.$ Now, there two terms are transformed through the function $\eta ^{-1},$ hence a condition relating the behavior of $\eta ^{-1}$ at $-\infty$ with $\eta ^{-1}$ at $+\infty$ will be required. Accordingly, we assume the following condition.

Condition (RV) is strongly related to the usual assumption considered in the theory of Karamata’s Regularly Varying Functions. Classical regularly varying function usually involve a limit of the form $f(\sigma s)/f(s)$ and appear in different areas of interest such as real analysis, probability theory and asymptotic theory for ODEs (see the books [28, 35] and the references therein).

In this framework the following main existence result holds.

Theorem 6

Assume (g0) as well as (A1),  (B0),  (B3) and (RV). There is $\varLambda ^*> 0$ such that for every $\lambda \in \,]0,\varLambda ^*[$ system (S2) has a limit cycle, while for $\lambda >\varLambda ^*$ all the nontrivial trajectories are ultimately unbounded.

Proof

The proof follows the same argument already described in detail along the proof of the “case study” Theorem 2. Therefore, we will concentrate only on the small modifications which are needed in the present case.

Let $x_M\in \,]\alpha ,0[$ be a point of maximum for A(x) in the interval $]\alpha ,0[$ and, respectively, let $x_m\in \,]0,\beta [$ be a point of minimum for A(x) in the interval $]0,\beta [\,.$ Having in mind the graph of $\kappa _{\lambda }$ we define

$$\begin{aligned} \mu _{\lambda }:= & {} \kappa _{\lambda }(x_M)= \eta ^{-1}\left( \frac{1}{\lambda A(x_M)} \right) = \min \{\kappa _{\lambda }(x): \alpha< x< 0\}, \\ \nu _{\lambda }:= & {} \kappa _{\lambda }(x_m)= \eta ^{-1}\left( \frac{1}{\lambda A(x_m)} \right) = \max \{\kappa _{\lambda }(x): 0< x < \beta \}, \end{aligned}$$

with $\mu _{\lambda }> 0 > \nu _{\lambda }.$ Note that $\mu _{\lambda }, -\nu _{\lambda } \rightarrow +\infty$ as $\lambda \rightarrow 0^+$ and $\mu _{\lambda }, \nu _{\lambda } \rightarrow 0$ as $\lambda \rightarrow +\infty .$

Step 1. Nonexistence of limit cycles for $\lambda$ large. We consider the energy function $H(x,y)= \tfrac{1}{2} y^2 + G(x)$ associated to the Duffing equation (D) and, according to (2.1) we have

$$\begin{aligned} \dot{H}(x,y) = -\lambda B(y)A(x)g(x). \end{aligned}$$

Consider now the region

$$\begin{aligned} {\mathcal {D}}:=\{(x,y): \, H(x,y)\le c_0\}, \quad \text {with }\; c_0=\min \{G(\alpha ),G(\beta )\}. \end{aligned}$$

The set ${\mathcal {D}}$ is negatively invariant and for each $P_0\in {\mathcal {D}}$ it holds that $\gamma ^-(P_0)$ tends to the origin. Using the fact that $\mu _{\lambda }, \nu _{\lambda } \rightarrow 0$ as $\lambda \rightarrow +\infty ,$ we can determine a value of $\lambda$ such that for all the larger values a region ${\mathcal {V}}$ (with ${\mathcal {V}}= {\mathcal {V}}_1$ or ${\mathcal {V}}= {\mathcal {V}}_2$) intersects ${\mathcal {D}}$ (a situation completely similar to that depicted in Fig. 7). Taking $P_0\in {\mathcal {V}}\cap {\mathcal {D}}$ we find that the orbit $\gamma (P_0)$ tends to the origin in negative time and is unbounded. This prevents the possibility of having limit cycles. In this manner we have proved that there exists $\check{\lambda } > 0$ such that for each $\lambda > \check{\lambda }$ all the nontrivial trajectories are ultimately unbounded.

Step 2. Existence of limit cycles for $\lambda$ small. First of all, we introduce the line

$$\begin{aligned} y = \eta ^{-1}\left( \frac{1}{2\lambda A(x)}\right) , \quad \text {for }\; \alpha< x < 0 \end{aligned}$$

which is below the region ${\mathcal {V}}_1$ and has $\displaystyle {v_{M,\lambda }:=\eta ^{-1}\left( \frac{1}{2\lambda A(x_M)} \right) }$ as a minimum value. By construction, we have that

$$\begin{aligned} \dot{x} = y - \lambda B(y)A(x) \ge y/2, \;\; \forall \, (x,y): \, \alpha< x< 0,\,\, 0 < y \le \frac{1}{2\lambda A(x)}, \end{aligned}$$

which is the analogue of (3.2).

Consider the initial point

$$\begin{aligned} P_0=(\alpha ,y_0), \quad \text {with }\; y_0 = v_{M,\lambda } - K, \end{aligned}$$

with $K>\sqrt{2G(\alpha )}$ a fixed constant. Clearly $y_0 > 0$ for $\lambda$ small, as $v_{M,\lambda }\nearrow +\infty$ as $\lambda \rightarrow 0^+.$

The slope of the trajectory departing from $P_0$ satisfies the relation

$$\begin{aligned} 0 \le \frac{d y}{dx} \le - \frac{2g(x)}{y},\quad \forall \, (x,y)\in {\mathcal {R}}:= [\alpha ,0]\times [y_0,y_0+K], \end{aligned}$$

so that $y(x)^2 - y_0^2 \le 2G(\alpha ) - 2G(x) \le 2G(\alpha )$ and then

$$\begin{aligned} y(x)\le \bigl (y_0^2 + 2G(\alpha )\bigr )^{1/2}\le y_0 + \sqrt{2G(\alpha )} \end{aligned}$$

as long as (x, y(x)) remains in the rectangle. Hence, the above a priori estimate shows that the positive trajectory departing from $P_0$ remains in the region ${\mathcal {R}}$ and crosses the y-axis at some point $P_1=(y_1,0)$ with $y_0< y_1 < y_0 +K.$ Consider now the point $P_2=(x_1,y_1)$ of intersection of the horizontal line $y=y_1$ with the boundary of the region ${\mathcal {W}}_1\,,$ given by the equation $y=\kappa _{\lambda }(x)$ for $x>\beta$ and observe that the segment $\overline{P_1P_2}$ is crossed by the vector field from the exterior to the interior, as $\dot{x}\ge 0$ and $\dot{y}< 0$ (for $x>0$).

Considering now the negative semi-orbit $\gamma ^-(P_0)$ departing from $P_0$ we have that such a trajectory remains in the region outside the level line

$$\begin{aligned} H(x,y) = \frac{1}{2}y^2 + G(x) = \frac{1}{2}y_0^2 + G(\alpha ) \end{aligned}$$

as long as $x < \alpha .$

We claim that $\gamma ^-(P_0)$ crosses the negatively invariant region ${\mathcal {W}}_2$ for $\lambda > 0$ sufficiently small. To this end, it is sufficient to show that the system

$$\begin{aligned} {\left\{ \begin{array}{ll} y = - \sqrt{2(G(\alpha ) - G(x)) + \bigl (\eta ^{-1}\bigl (\tfrac{1}{2\lambda A(x_M)}\bigr )-K \bigr )^2}\\ y = \eta ^{-1}\bigl (\tfrac{1}{\lambda A(x)} \bigr ) \end{array}\right. } \end{aligned}$$

(which is the analogue of (3.3) to our situation) has solution x in the domain

$$\begin{aligned} G_{l}^{-1}\left( G(\alpha ) + \tfrac{1}{2} \bigl (\eta ^{-1}\bigl (\tfrac{1}{2\lambda A(x_M)}\bigr )-K \bigr )^2\right)< x < \alpha , \end{aligned}$$

where $G_{l}^{-1}$ is the inverse of G restricted on the negative real numbers. From the above system we get the equation

$$\begin{aligned} f(x,\lambda ) = -1,\quad \text {for }\; f(x,\lambda ):= \frac{\sqrt{2(G(\alpha ) - G(x)) + \bigl (\eta ^{-1}\bigl (\tfrac{1}{2\lambda A(x_M)}\bigr )-K \bigr )^2}}{\eta ^{-1}\bigl (\tfrac{1}{\lambda A(x)} \bigr )}\,. \end{aligned}$$

To prove that this equation has solutions in the desired range for $\lambda$ sufficiently small, we proceed as follows.

$$\begin{aligned} \lim _{x\rightarrow -1^-} f(x,\lambda ) = 0 > -1, \end{aligned}$$

because $\kappa _{\lambda }(x)= {\eta ^{-1}\bigl (\tfrac{1}{\lambda A(x)} \bigr )} \rightarrow -\infty$ as $x\rightarrow \alpha ^-.$ On the other hand, for any fixed $\tilde{x} < \alpha$ we have that

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+} f(\tilde{x},\lambda ) = \lim _{\lambda \rightarrow 0^+} \frac{\eta ^{-1}\bigl (\tfrac{1}{2\lambda A(x_M)}\bigr )}{\eta ^{-1}\bigl (\tfrac{1}{\lambda A(\tilde{x})} \bigr )}. \end{aligned}$$

Using condition (RV) with $s:= 1/(\lambda |A(\tilde{x})|)$ and $\sigma := |A(\tilde{x})|/2A(x_M),$ we obtain that

$$\begin{aligned} \lim _{\lambda \rightarrow 0^+} f(\tilde{x},\lambda ) = \eta :=- \bigl (\,|A(\tilde{x})|/2A(x_M)\bigr )^2 \end{aligned}$$

and observe that we can have $\eta <-1$ if we take $\tilde{x}< \alpha$ sufficiently negative (using also the fact that $|A(x)|\rightarrow +\infty$ for $x\rightarrow \pm \infty$).

Therefore the existence of an intersection point $P_{-1}$ of $\gamma ^{-}(P_0)$ with the boundary of ${\mathcal {W}}_2$ is guaranteed. From now on, we proceed in a complete symmetrical manner to determine points $Q_{-1},Q_{0},Q_{1}$ and $Q_{2}$ starting from a point $Q_0 = (\beta ,z_0)$ above the region ${\mathcal {V}}_2$ and, like in the proof of Theorem 2, we arrive at the construction of a Jordan curve $\varUpsilon$ which is the boundary of a positively invariant region surrounding the origin and bounding a limit cycle. In this manner we have proved that there exists $\hat{\lambda } > 0$ such that, for each $0<\lambda < \hat{\lambda },$ system (S2) has a limit cycle.

We skip the discussion concerning Step 3 because the geometry of (S2) in the strip $\alpha< x < \beta$ is the same as that of $(H_{2,\lambda })$ in $-1<x<1.$ This concludes the proof of our theorem. $\square$

Example 2 provides an explicit application of Theorem 6, namely for

$$\begin{aligned} B(y)= (\tanh (y^2+y+1))y^2, \quad A(x)= (x^2 - 2x- 3)x. \end{aligned}$$

and $g(x)=x,$ so that (g0) holds. Observe that, in this case, all the assumptions (A1),  (B0),  (B3) are satisfied and also (RV) holds.

Example 2

To show an example of applicability of Theorem 6 we consider the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x} = y - \lambda (\tanh (y^2+y+1))y^2 (x^2 - 2x- 3)x\\ \dot{y} = - x. \end{array}\right. } \end{aligned}$$

Figures 14, 15, 16 illustrate, respectively, the associated dynamics for $\lambda =0.0522$ (existence of a limit cycle) and for $\lambda =0.0523$ (escape of all the nontrivial orbits). Clearly, this is just a numerical simulation which shows the above phenomenon which is proved analytically. Precise estimates from above and below on $\varLambda ^*$ are in any case obtained within the limits of the numerical approximations. $\square$

Fig. 14

The figure represents the dynamics for system (S1),  in the phase-plane (panel left) and for component x(t) in the time variable (panel right). This example concerns the superlinear case with $B(y)=(\tanh (y^2+y+1))y^2,$ $A(x)=(x^2 - 2x- 3)x$ and $g(x)=x.$ The simulation suggests that for these parameters the limit cycle is unique. In the phase-plane we also have plotted part of the infinite-isocline near the trajectories. The limit cycle is possible because “fortunately” the trajectories avoid (it is narrow escape !) the regions ${\mathcal {V}}_1$ and ${\mathcal {V}}_2$. The graphs are produced using [48]

Fig. 15

The figure represents the dynamics for system (S1),  in the phase-plane (panel left) and for component x(t) in the time variable (panel right). This example concerns the superlinear case with $B(y)=(\tanh (y^2+y+1))y^2,$ $A(x)=(x^2 - 2x- 3)x$ and $g(x)=x.$ In this case there is no limit cycle because all the nontrivial solutions enter eventually the regions the regions ${\mathcal {V}}_1$ and ${\mathcal {V}}_2$. In the phase-plane we also have plotted part of the infinite-isocline near the trajectories. The graphs are produced using [48]

The “escape effect” exhibited by a single orbit in Fig. 15 is even more dramatically illustrated considering the whole set of trajectories in Fig. 16.

Fig. 16

Planar dynamics for system (S1). It is evident that the trajectories are unwinding from the origin and eventually become unbounded entering the regions ${\mathcal {V}}_1$ or ${\mathcal {V}}_2$. Our simulation shows that a large region around the origin (excluding (0, 0)) is attracted to ${\mathcal {V}}_2$. The graph is produced using [49] for the same value of the parameter $\lambda = 0.0523$ as in Fig. 15 and the same functions B(y),  A(x) and g(x)

Another approach to prove the existence of limit cycles for $\lambda \in ]0,\varLambda ^*[$ is based on a classical bifurcation technique, dating back to Poincaré (according to Lefschetz [24, pp. 314–320]) and Liénard to prove the existence of limit cycles bifurcating form a periodic orbit of a center when a parameter multiplying the nonlinear terms is small. This method was successfully applied by Duff and Levinson [11] (see also [34]) to produce multiple limit cycles bifurcating from circular orbits of the harmonic oscillator and represents a very useful technique to construct specific examples of multiplicity results for Liénard or Rayleigh equations. We refer also to [4, Remark 2.4] for another application of this method. Due to space limitations, we do not enter into these details, however we think that it is interesting to mention the fact that this averaging approach provides an independent proof for the existence of limit cycles.