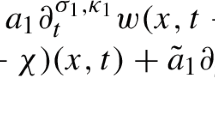Existence of Attractors for a Nonlinear Timoshenko System with Delay

Abstract

This paper deals with Timoshenko’s classic model for beams vibrations. Regarding the linear model of Timoshenko, there are several known results on exponential decay, controllability and numerical approximation, but there are few results that deal with the nonlinear case or even the linear case with delay type damping. In this paper, we will establish the existence of global and exponential attractors for a semilinear Timoshenko system with delay in the rotation angle equation and a friction-type damping in the transverse displacement equation. Since the damping acts on the two equations of the system, we should not assume the well-known velocity equality.

1 Introduction

In 1921 Stephen Timoshenko [1] described a model of beams which takes into account the effects of shear deformation on transverse vibrations. The model is based on D’Alembert’s principle for the equilibrium dynamics [2], from which the following coupled equations of evolution

$$\begin{aligned} \rho A\varphi _{tt}-S_{x}= & {} 0, \end{aligned}$$

(1.1)

$$\begin{aligned} \rho I\psi _{tt}-M_{x}+S= & {} 0, \end{aligned}$$

(1.2)

with $S=k'AG(\varphi _{x}+\psi )$ denoting the transverse shear force and $M=E \psi _{x}$ the moment of flexion. The functions $\varphi$ and $\psi$ denote the vertical displacement of the beam centerline and the rotation of the vertical filament in the beam. The positive constants $\rho$, A, I, E, G, $k'$ denote, respectively, the mass density of the material, the cross-sectional area, the moment of inertia of the cross section, the Young’s modulus, the stiffness modulus and the shear factor. The Tymoshenko system is usually studied in coupled form

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x= & {} 0, \end{aligned}$$

(1.3)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )= & {} 0, \end{aligned}$$

(1.4)

where $\rho _1=\rho A$, $\kappa =k'AG$, $\rho _2=\rho I$ and $b=EI$, but can also be represented in the decoupled form [3],

$$\begin{aligned} \frac{\rho _1 \rho _2}{\kappa }\varphi _{tttt}+\rho _1\varphi _{tt}-b\bigg (\frac{\rho _1 }{\kappa }+\frac{\rho _2}{b}\bigg )\varphi _{xxtt} +b\varphi _{xxxx}=0, \end{aligned}$$

(1.5)

eliminating the variable $\psi$ in both equations. It is important to note that in the (1.3)–(1.4) the curvature effects, vertical displacement, shear deformation and rotational inertia are present.

One of the first works to study the stabilization of the Timoshenko system belongs to Kim and Renardy [4]. They considered the Eqs. (1.3)–(1.4) with boundary conditions

$$\begin{aligned} \varphi (0,t)=\psi (0,t)= & {} 0, \end{aligned}$$

(1.6)

$$\begin{aligned} \kappa \big (\varphi _x(L,t)+\psi (L,t)\big )+\alpha \varphi _{t}(L,t)= & {} 0, \end{aligned}$$

(1.7)

$$\begin{aligned} b\psi _{x}(L,t)+\beta \psi _{t}(L,t)= & {} 0, \end{aligned}$$

(1.8)

and showed that the system can be uniformly stabilized by means of control (1.6) in the boundary. In addition, a numerical study on the spectrum is presented. On the other hand, in the case of internal control, Soufyane [5] considered the system of Tymoshenko

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x= & {} 0 \quad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.9)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+b(x)\psi _t= & {} 0 \quad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.10)

with the variable coefficient satisfying the relation $0<b_{0}\le b(x)\le b_{1}$ and homogeneous Dirichlet boundary conditions. He proved that the system decays exponentially if and only if the equality between the velocities

$$\begin{aligned} \frac{\kappa }{\rho _1}=\frac{b}{\rho _2}, \end{aligned}$$

(1.11)

is satisfied. In [6], Soufyane and Wehbe considered again the same system, but with damping located satisfying $0<{\bar{b}}\le b(x)$ in $[b_{0},b_{1}]\subset [0,L]$ and once again proved that the equality relationship between velocities is a necessary and sufficient condition to establish the exponential decay of the system. In [7], Rivera and Racke have proven a similar result to that of Soufyane [5], where the damping function $b(x)\in L^{\infty }(0,L)$ can change signal, but must satisfy the conditions ${\bar{a}}=(1/L)\int _{0}^{L}b(x)dx>0$ and $||a-{\bar{a}}||_{L^{2}}\,<\epsilon$ with $\epsilon$ small enough. Since then, several studies have emerged considering damping in a single equation, among them we can cite [8,9,10], in all of them, the relationship was used (1.11).

Many researchers [11,12,13,14,15,16] have studied the asymptotic behavior of the Timoshenko system under the action of several dissipative mechanisms. Among them, we highlight the dynamics of systems with a time delay [17, 18], quite widespread in the 1970s. The effects of time lag are in many cases a source of instability, however for some systems, the presence of delay may have a stabilizing effect. For example, in the wave equation the time delay in the feedback term (internal or at the boundary) can destabilize the system, depending on the weight of each term [19, 20]. In this context, Said-Houari and Laskri [21] studied the stability of the system

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x= & {} 0 \quad \text{ in }\quad (0,1)\times (0,\infty ), \end{aligned}$$

(1.12)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+\mu _1\psi _t+\mu _2\psi _t(\cdot ,t-\tau )= & {} 0 \quad \text{ in }\quad (0,1)\times (0,\infty ).\nonumber \\ \end{aligned}$$

(1.13)

They have proved that if $\mu _2\le \mu _1$ and the relationship (1.11) is satisfied, then the system is exponentially stable. On the other hand, Feng and Yang [22] based on [21] obtained the existence of global attractors with finite fractal dimension as well as the existence of exponential attractor for the following nonlinear system of Timoshenko with delay

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x= & {} h \quad \text{ in }\quad (0,1)\times (0,\infty ),\end{aligned}$$

(1.14)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+\mu _1\psi _t+\mu _2\psi _t(\cdot ,t-\tau )+f(\psi )= & {} g \quad \text{ in }\quad (0,1)\times (0,\infty ),\nonumber \\ \end{aligned}$$

(1.15)

under the hypothesis $\mu _2\le \mu _1$ and (1.11), where $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ satisfies

$$\begin{aligned} |f(x)-f(y)|\le k_0(|x|^\theta +|y|^\theta )|x-y|,\quad \forall x,y\in {\mathbb {R}}, \end{aligned}$$

(1.16)

with $k_0,\theta >0$ and

$$\begin{aligned} -k_1\le {\hat{f}}(x)\le f(x)x,\quad \forall x\in {\mathbb {R}},\quad {\hat{f}}(y)=\int _0^yf(s)ds, \quad \text{ for } \text{ some } \quad k_1>0. \end{aligned}$$

(1.17)

In [23] Fatori et al. studied the following nonlinear Timoshenko system

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x+f_1(\varphi ,\psi )+\varphi _t= & {} h_1 \quad \text{ in }\quad (0,1)\times (0,\infty ), \end{aligned}$$

(1.18)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+f_2(\varphi ,\psi )+\psi _t= & {} h_2 \quad \text{ in }\quad (0,1)\times (0,\infty ), \end{aligned}$$

(1.19)

where $f_1$ and $f_2$ are nonlinear source terms representing the elastic foundation and $h_1$, $h_2$ are external forces. They obtained the existence of global and exponential attractor and without assuming the well-known equal wave speeds condition (1.11).

There are also works that consider localized nonlinear damping. For example, in [24] Guesmia and Messaoudi studied the system

$$\begin{aligned}&\rho _1\varphi _{tt}-\kappa _{1}(\varphi _x+\psi )_x=0 \quad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.20)

$$\begin{aligned}&\rho _2\psi _{tt}-\kappa _{2}\psi _{xx}+\int _{0}^{t}g(t-\tau )\big (a(x)\psi _{x}(\tau )\big )_{x}d\tau +\kappa _{1}(\varphi _x+\psi )+b(x)h(\psi _{t})=0\nonumber \\&\qquad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.21)

with Dirichlet boundary conditions and initial data where a, b, g and h are specific functions and $\rho _1, \rho _2, \kappa _{1}, \kappa _{2}$ and L are given positive constants. They establish a general stability estimate using the multiplier method and some properties of convex functions. Without imposing any growth condition on h at the origin, they showed that the energy of the system is bounded above by a quantity, depending on g and h, which tends to zero as time goes to infinity. In [25] Cavalcanti et al. considered the system

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x+\alpha _1(x)g_{1}(\varphi _t)= & {} 0 \quad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.22)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+\alpha _2(x)g_{2}(\psi _t)= & {} 0 \quad \text{ in }\quad (0,L)\times (0,\infty ), \end{aligned}$$

(1.23)

where the functions $\alpha _1$ and $\alpha _2$ are supposed to be smooth and nonnegative, while the nonlinear functions $g_1$ and $g_2$ are continuous, monotone increasing, and zero at the origin. Using a method introduced in Daloutli et al. [26], they proved that the damping placed on an arbitrarily small support, unquantitized at the origin and without assuming equal speeds of propagation of waves, leads to uniform decay rates (asymptotic in time) for the energy function.

A common point in both localized damping papers is that they do not take into account the presence of external forces or the action of nonlinear source terms. According to Malatkar [27], nonlinear terms arise in a system whenever there are products of dependent variables and their derivatives in equations of motion, boundary conditions, and / or constitutive laws, and whenever there is any kind of discontinuity or jump in the system. In the literature (e.g. [28,29,30]) we find various types of nonlinearities, such as damping nonlinearities, geometric nonlinearities (caused by large deformations) and others.

In [31], Zhong and Guo, studied a Timoshenko beam systems, taking into account various nonlinear effects. But precisely, they considered Hooke’s law and the nonlinear relations given by

$$\begin{aligned} \varepsilon:= & {} u_{x}+\frac{1}{2}w_{x}^{2}, \ \ \kappa :=\frac{\theta _x}{\sqrt{1+w_{x}^{2}}}\approx \theta _x\bigg (1-\frac{1}{2}w_{x}^{2}+\frac{3}{8}w_{x}^{4}\bigg ) \ \ \text{ and } \nonumber \\ \gamma:= & {} \tan ^{-1} w_{x}-\theta \approx w_{x}-\frac{1}{3}w_{x}^{3}-\theta , \end{aligned}$$

(1.24)

where $u, w, \theta , \varepsilon , \kappa$ and $\gamma$ represent the axial displacement, the deflection, the cross-section rotation, the membrane strain, the bending curvature, and the shear strain, respectively. Keeping in mind the Lagrangian function $L=K-U$, with

$$\begin{aligned} K:=\frac{1}{2}\int _{0}^{L}\rho Aw_{t}^{2}dx+\frac{1}{2}\int _{0}^{L}\rho I \theta _{t}^{2}dx \quad \text{ and } \quad U:=\frac{1}{2}\int _{0}^{L}\bigg (EA\varepsilon ^{2}+EI\kappa ^{2}+k GA\gamma ^{2}\bigg )dx,\nonumber \\ \end{aligned}$$

(1.25)

and applying the Hamilton Principle

$$\begin{aligned} \delta \int _{t_{1}}^{t_{2}}L\,dt=0, \end{aligned}$$

(1.26)

the authors obtained the Timoshenko system given by

$$\begin{aligned} \rho Aw_{tt}-kGA(w_{x}-\theta )_{x}+f_{1}(w,\theta )= & {} 0, \end{aligned}$$

(1.27)

$$\begin{aligned} \rho I\theta _{tt}-EI\theta _{xx}-kGA(w_{x}-\theta )+f_{2}(w,\theta )= & {} 0, \end{aligned}$$

(1.28)

with nonlinear source terms

$$\begin{aligned} f_{1}(w,\theta ):= & {} EI\frac{\partial }{\partial x}\Big [\theta _{x}^{2}(w_{x}-2w_{x}^{2})\Big ] +\frac{1}{3}kGA\frac{\partial }{\partial x}\Big [w_{x}^{3}+3(w_{x}-\theta )w_{x}^{2}\Big ], \end{aligned}$$

(1.29)

$$\begin{aligned} f_{2}(w,\theta ):= & {} EI\frac{\partial }{\partial x}\Big [(w_{x}^{2}-w_{x}^{4})\theta _{x}^{2}\Big ] +\frac{1}{3}kGAw_{x}^{3}. \end{aligned}$$

(1.30)

The interesting thing about studying such models is that many physical phenomena such as jumps, saturation, subharmonic, superharmonic, combination resonances, self-excited oscillations, modal interactions and chaos are present only in nonlinear systems. In fact, no physical system is strictly linear and linear constraints are only applied to very small amplitude vibrations [27]. Therefore, to accurately study and understand the dynamic behavior of structural systems under general loading conditions, it is essential that we consider more general source terms $f_{i}(\cdot , \cdot )$ $(i=1,2)$, given due to its intrinsic mathematical properties.

In this paper we consider the following nonlinear Timoshenko system with delay term

$$\begin{aligned}&\rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x+f_1(\varphi ,\psi )+\varphi _t=h_1 \quad \text {in}\quad (0,1)\times (0,\infty ), \end{aligned}$$

(1.31)

$$\begin{aligned}&\rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+f_2(\varphi ,\psi )+\mu _1\psi _t+\mu _2\psi _t(\cdot ,t-\tau )=h_2\nonumber \\&\quad \quad \text {in}\quad (0,1)\times (0,\infty ), \end{aligned}$$

(1.32)

where, $\varphi =\varphi (x,t)$ and $\psi =\psi (x,t)$, represent the transverse displacement and the is the rotation angle of the filament of beam, respectively. Positive constants $\rho _1$, $\rho _2$, $\kappa$ and b represent physical properties of the beam material and $\tau$ is time delay. The functions $f_1(\varphi ,\psi )$ and $f_2(\varphi ,\psi )$ are nonlinear source terms, whereas $h_1$ and $h_2$ represent external forces. This system is subjected to the following initial conditions

$$\begin{aligned} \varphi (x,0)=\varphi _0(x), \ \varphi _t(x,0)=\varphi _1(x), \ \psi (x,0)=\psi _0(x),\ \psi _{t} (x,0) = \psi _{1}(x),\quad x\in (0,1),\nonumber \\ \end{aligned}$$

(1.33)

and boundary conditions

$$\begin{aligned} \varphi (0,t)=\varphi (1,t)=\psi (0,t)=\psi (1,t)=0, \quad t\ge 0. \end{aligned}$$

(1.34)

We believe that this work is the first to study the dynamics of attractors in the system (1.31)–(1.34) and our main results refer to the existence of global and exponential attractors without the need for equality (1.11) between speeds.

The plan of this paper is as follows: In Sect. 2, we present our assumptions and state the results on existence and global well-posedness to the system (1.31)–(1.34). In Sect. 3 we consider the corresponding dynamical system and state our main result concerning long-time dynamics and without assuming the equal wave speeds condition. Finally, Sect. 4 is dedicated to prove the existence of exponential attractor with finite fractal dimension in the generalized space.

2 Well-Posedness

In order to obtain the well-posedness of the problem (1.31)–(1.34), consider the following change of variable as found in [21, 32],

$$\begin{aligned} z(x,y,t)=\psi _t(x,t-\tau y)&\text {in}&(0,1)\times (0,1)\times (0,\infty ), \end{aligned}$$

(2.1)

so we have readily

$$\begin{aligned} \tau z_t(x,y,t)+z_y(x,y,t)=0&\text {in}&(0,1)\times (0,1)\times (0,\infty ). \end{aligned}$$

(2.2)

Therefore, the system (1.31)–(1.34) takes the following form

$$\begin{aligned} \rho _1\varphi _{tt}-\kappa (\varphi _x+\psi )_x+f_1(\varphi ,\psi )+\varphi _t= & {} h_1 \quad \text {in}\quad (0,1)\times (0,\infty ), \end{aligned}$$

(2.3)

$$\begin{aligned} \rho _2\psi _{tt}-b\psi _{xx}+\kappa (\varphi _x+\psi )+f_2(\varphi ,\psi )+\mu _1\psi _t+\mu _2 z(x,1,t)= & {} h_2 \quad \text {in}\quad (0,1)\times (0,\infty ), \end{aligned}$$

(2.4)

$$\begin{aligned} \tau z_t(x,y,t)+z_y(x,y,t)= & {} 0 \ \, \text {in}\quad (0,1)\times (0,1)\times (0,\infty ),\nonumber \\ \end{aligned}$$

(2.5)

with initial conditions

$$\begin{aligned}&\varphi (x,0)=\varphi _0(x), \ \varphi _t(x,0)=\varphi _1(x), \ \psi (x,0)=\psi _0(x), \ \psi _t(x,0)=\psi _1(x), \quad x\in (0,1),\nonumber \\ \end{aligned}$$

(2.6)

$$\begin{aligned}&z(x,y,0)=f_0(x,-\tau y), \quad (x,y)\in (0,1)\times (0,1), \end{aligned}$$

(2.7)

and boundary conditions

$$\begin{aligned}&\varphi (0,t)=\varphi (1,t)=\psi (0,t)=\psi (1,t)=0, \quad t > 0, \end{aligned}$$

(2.8)

$$\begin{aligned}&z(x,0,t)=\psi _t(x,t),\quad x\in (0,1), \quad t>0. \end{aligned}$$

(2.9)

From now on, we will use notation $z_1$ to represent z when $y=1$. In this way, we can write the system (2.3)–(2.9) in the form of an abstract nonlinear initial value problem in the unknown $U(t)=(\varphi (t),\varphi _t(t),\psi (t),\psi _t(t),z_1(t))^T$

$$\begin{aligned}&U_t(t)=\mathcal {A}U(t)+\mathcal {F}(U(t)), \quad t>0, \end{aligned}$$

(2.10)

$$\begin{aligned}&U(0)=U_0 \in \mathcal {H}, \end{aligned}$$

(2.11)

where $U_0=(\varphi _0,\varphi _1,\psi _0,\psi _1,f_0(\cdot ,-\tau ))$, $\mathcal {A}:D(\mathcal {A})\subset \mathcal {H}\rightarrow \mathcal {H}$ is the linear operator and $\mathcal {F}:\mathcal {H}\rightarrow \mathcal {H}$ given by

$$\begin{aligned}&\mathcal {A}W=\left( \begin{array}{c} u\\ \frac{\kappa }{\rho _1}(\varphi _x+\psi )_x-\frac{1}{\rho _1}u \\ v \\ \frac{b}{\rho _2}\psi _{xx}-\frac{\kappa }{\rho _2}(\varphi _x+\psi )-\frac{\mu _1}{\rho _2}v -\frac{\mu _2}{\rho _2}z_1\\ -\frac{1}{\tau }z_y \end{array}\right) \quad \text{ and }\nonumber \\&\quad \mathcal {F}(W)=\left( \begin{array}{c} 0 \\ \frac{1}{\rho _1}[h_1-f_1(\varphi ,\psi )] \\ 0 \\ \frac{1}{\rho _2}[h_2-f_2(\varphi ,\psi )] \\ 0 \end{array}\right) , \end{aligned}$$

(2.12)

with domain

$$\begin{aligned} D(\mathcal {A}):=\Big \{W=(\varphi ,u,\psi ,v,z)\in {\mathscr {H}}; \ v=z(\cdot ,0) \ \ \text{ in } \ (0,1)\Big \}, \end{aligned}$$

(2.13)

where

$$\begin{aligned} {\mathscr {H}}:= & {} (H^2(0,1)\cap H_0^1(0,1))\times H_0^1(0,1)\times (H^2(0,1)\cap H_0^1(0,1))\times H_0^1(0,1)\nonumber \\&\times L^2(0,1;H_0^1(0,1)). \end{aligned}$$

(2.14)

The energy space is given by

$$\begin{aligned} \mathcal {H}:=H_0^1(0,1)\times L^2(0,1)\times H_0^1(0,1)\times L^2(0,1)\times L^2\big ((0,1)\times (0,1)\big ). \end{aligned}$$

(2.15)

We consider $\xi$ a positive constat satisfying

$$\begin{aligned} \tau \mu _2\le \xi \le \tau (2\mu _1-\mu _2). \end{aligned}$$

(2.16)

We define in $\mathcal {H}$ the following inner produto and norm

$$\begin{aligned} \Big (W,{\hat{W}}\Big )_{\mathcal {H}}= & {} \rho _1(u,{\hat{u}})+\rho _2(v,{\hat{v}})+b(\psi _x,{\hat{\psi }}_x)+\kappa (\varphi _x+\psi , {\hat{\varphi }}_x+{\hat{\psi }}) \nonumber \\&+\xi \int _0^1\int _0^1z(x,y){\hat{z}}(x,y)dxdy, \end{aligned}$$

(2.17)

$$\begin{aligned} \Vert W\Vert _{\mathcal {H}}^{2}= & {} \rho _1\Vert u\Vert _2^2+\rho _2\Vert v\Vert _2^2+b\Vert \psi _x\Vert _2^2+\kappa \Vert \varphi _x+\psi \Vert _2^2+\xi \int _0^1\int _0^1z^2(x,y)dxdy,\nonumber \\ \end{aligned}$$

(2.18)

for any $W=(\varphi ,u,\psi ,v,z)$ and ${\hat{W}}=({\hat{\varphi }},{\hat{u}},{\hat{\psi }},{\hat{v}},{\hat{z}})$ in $\mathcal {H}$, where $(\cdot ,\cdot )$ and $\Vert \cdot \Vert _2$ are inner product and norm in $L^2(0,1)$, respectively.

2.1 Existence and Uniqueness

The question of the existence and uniqueness of the solution of problem (2.11) will be considered in this subsection. Firstly, let us remember the following concepts:

• A function $U:[0,T)\rightarrow \mathcal {H}$, with $T>0$, is a strong solution of (2.11), if U is continuous on [0, T), continuously differentiable on (0, T), with $U(t)\in D(\mathcal {A})$ for all $t\in (0,T)$ and satisfies (2.11) on [0, T) almost everywhere.

• A function $U\in C([0,T),\mathcal {H})$, $T>0$, satisfying the integral equation

  $$\begin{aligned} U(t)=e^{\mathcal {A}t}U_0+\int _0^te^{\mathcal {A}(t-s)}\mathcal {F}(U(s))ds, \ \ t\in [0,T), \end{aligned}$$

  (2.19)

  is called a mild solution of initial value problem (2.11).

In order to obtain well-posedness, consider the following assumptions on $f_i$ and $h_i$ for $i=1,2$.

(A1):

$h_i\in L^2(0,1)$;

(A2):

$f_i:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ is locally Lipschitz continuous on each of its arguments, namely, there exist a constant $\gamma _i\ge 1$ and a continuous function $\sigma _i:{\mathbb {R}}\rightarrow {\mathbb {R}}_+$ such that

$$\begin{aligned} |f_i(s_1,r)-f_i(s_2,r)|\le & {} \sigma _i(|r|)(1+|s_1|^{\gamma _i}+|s_2|^{\gamma _i})|s_1-s_2|, \end{aligned}$$

(2.20)

$$\begin{aligned} |f_i(s,r_1)-f_i(s,r_2)|\le & {} \sigma _i(|s|)(1+|r_1|^{\gamma _i}+|r_2|^{\gamma _i})|r_1-r_2|, \end{aligned}$$

(2.21)

for every $(s_j,r)$, $(s,r_j)\in {\mathbb {R}}^2$, $j=1,2$;

(A3):

There is a function $F:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} \frac{\partial F}{\partial s}(s,\cdot )=f_1(s,\cdot )\quad \text {and}\quad \frac{\partial F}{\partial r}(\cdot ,r)=f_2(\cdot ,r), \end{aligned}$$

(2.22)

and

$$\begin{aligned}&F(s,r)\ge -\theta _2-\alpha _1|r|^2-\theta _1|s|^2, \quad \forall (s,r)\in {\mathbb {R}}^2, \end{aligned}$$

(2.23)

$$\begin{aligned}&F(s,r)\le f_1(s,r)s+f_2(s,r)r+\theta _1|s|^2+\alpha _1|r|^2+\theta _2,\quad \forall (s,r)\in {\mathbb {R}}^2, \end{aligned}$$

(2.24)

where $\theta _i$ and $\alpha _i$, with $i=1,2$, are constants satisfying

$$\begin{aligned} 0\le \theta _1\le \min \bigg \{\frac{\kappa }{8},\frac{b}{16}\bigg \}, \quad 0\le \alpha _1\le \frac{b}{4} \quad \text {and} \quad \theta _2,\alpha _2\ge 0. \end{aligned}$$

(2.25)

Remark 2.1

A simple example of $f_{i}(s,r)$ $(i=1,2)$ is given by

$$\begin{aligned} f_{1}(s,r)= & {} 4(s+r)^{3}-2(s+r)+2c_{1}sr^{2} \quad \text{ and }\nonumber \\ f_{2}(s,r)= & {} 4(s+r)^{3}-2(s+r)+2c_{1}s^{2}r, \quad c_{1}>0, \end{aligned}$$

(2.26)

the primitive function is

$$\begin{aligned} F(s,r)=|s+r|^{4}-|s+r|^{2}+c_{1}|sr|^{2}. \end{aligned}$$

(2.27)

Lemma 2.1

Assume that $\mu _2\le \mu _1$, then the operator $\mathcal {A}:D(\mathcal {A})\subset \mathcal {H}\rightarrow \mathcal {H}$ defined in (2.12) is a infinitesimal generator of a $C_0$-semigroup of contractions in $\mathcal {H}$.

Proof

Following [21] it not so difficult to prove that $R(I-\mathcal {A})=\mathcal {H}$, where $R(I-\mathcal {A})$ stands for range of the operator $I-\mathcal {A}$, and that $\mathcal {A}$ is dissipative operator in $\mathcal {H}$, namely, for all $W=(\varphi ,u,\psi ,v,z)\in D(\mathcal {A})$,

$$\begin{aligned} (\mathcal {A}W,W)_{\mathcal {H}}\le -\Vert u\Vert _2^2-\bigg (\mu _1-\frac{\mu _2}{2}-\frac{\xi }{2\tau }\bigg )\Vert v\Vert _2^2 -\bigg (\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert z_1\Vert _2^2. \end{aligned}$$

(2.28)

From (2.16), we have

$$\begin{aligned} \mu _1-\frac{\mu _2}{2}-\frac{\xi }{2\tau }\ge 0 \quad \text{ and } \quad \frac{\xi }{2\tau }-\frac{\mu _2}{2}\ge 0, \end{aligned}$$

(2.29)

which implies

$$\begin{aligned} (\mathcal {A}W,W)_{\mathcal {H}}\le -\Vert u\Vert _2^2-\bigg (\mu _1-\frac{\mu _2}{2}-\frac{\xi }{2\tau }\bigg )\Vert v\Vert _2^2 -\bigg (\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert z_1\Vert _2^2 \ \ \le 0. \end{aligned}$$

(2.30)

Therefore, from Lumer–Phillips Theorem, $\mathcal {A}$ is the infinitesimal generator of a $C_0$-semigroup of contractions on $\mathcal {H}$. $\square$

It is opportune now to define the functional energy E(t) of a solution $U=(\varphi ,\varphi _t,\psi ,\psi _t,z)$ by the expression

$$\begin{aligned} E(t):= & {} \displaystyle \frac{\rho _1}{2}\Vert \varphi _t\Vert _2^2+\frac{\rho _2}{2}\Vert \psi _t\Vert _2^2+\frac{b}{2}\Vert \psi _x\Vert _2^2+ \frac{\kappa }{2}\Vert \varphi _x+\psi \Vert _2^2+\frac{\xi }{2} \int _0^1\int _0^1z^2(x,y,t)dxdy \nonumber \\&+\int _0^1F(\varphi ,\psi )dx-\int _0^1h_1\varphi dx-\int _0^1h_2\psi dx,\quad \forall t\ge 0. \end{aligned}$$

(2.31)

The prove of the following Lemma can be found in [23].

Lemma 2.2

Suppose that (A1) and (A2) are valid, then $\mathcal {F}:\mathcal {H}\rightarrow \mathcal {H}$ defined in (2.12) is locally Lipschitz continuous operator.

Lemma 2.3

Assume that $\mu _2\le \mu _1$, then energy functional E(t) is non-increasing, more precisely, for any strong solution $U=(\varphi ,\varphi _t,\psi ,\psi _t,z)$ of (2.11), we have

$$\begin{aligned} \frac{d}{dt}E(t)\le -\Vert \varphi _t\Vert _2^2-\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert \psi _t\Vert _2^2 -\bigg (\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert z_1\Vert _2^2\le 0, \quad \forall t\ge 0.\nonumber \\ \end{aligned}$$

(2.32)

Also, there exists a constant $K_{E_1}=K_{E_1}\Big (\Vert h_1\Vert _2,\Vert h_2\Vert _2\Big )>0$ such that

$$\begin{aligned} E(t)\ge \frac{1}{4}\Vert U(t)\Vert _{\mathcal {H}}^2-K_{E_1},\quad \forall t\ge 0. \end{aligned}$$

(2.33)

Proof

Multiplying (2.3) by $\varphi _t$ and (2.4) $\psi _t$, integrating over [0, 1] with respect to x and applying Young’s inequality we obtain

$$\begin{aligned}&\frac{d}{dt}\bigg \{\frac{\rho _1}{2}\Vert \varphi _t\Vert _2^2+\frac{\rho _2}{2}\Vert \psi _t\Vert _2^2+\frac{b}{2}\Vert \psi _x\Vert _2^2\nonumber \\&\quad + \frac{\kappa }{2}\Vert \varphi _x+\psi \Vert _2^2+\int _0^1F(\varphi ,\psi )dx-\int _0^1(h_1\varphi +h_2\psi )dx\bigg \}\le -\Vert \varphi _t\Vert _2^2 \nonumber \\&\quad -\bigg (\mu _1-\frac{\mu _2}{2}\bigg )\Vert \psi _t\Vert _2^2+ \frac{\mu _2}{2}\Vert z_1\Vert _2^2. \end{aligned}$$

(2.34)

Multiplying (2.5) by $\frac{\xi }{\tau }z$ and integrating in $[0,1]\times [0,1]$ with respect to x and y, respectively, we have

$$\begin{aligned} \frac{\xi }{2}\frac{d}{dt}\int _0^1\int _0^1z^2(x,y,t)dydx= & {} -\frac{\xi }{2\tau }\int _0^1\int _0^1\frac{\partial }{\partial y}z^2(x,y,t)dydx \nonumber \\= & {} \frac{\xi }{2\tau }\int _0^1(z^2(x,0,t)-z^2(x,1,t))dx. \end{aligned}$$

(2.35)

Combining (2.34) and (2.35), we get (2.32).

In the other hand, it follows from (2.31) and (2.18)

$$\begin{aligned} E(t)=\frac{1}{2}\Vert U(t)\Vert _{\mathcal {H}}+\int _0^1F(\varphi ,\psi )dx-\int _0^1h_1\varphi dx-\int _0^1h_2\psi dx. \end{aligned}$$

(2.36)

From (2.23) and by using Poincaré’s inequality

$$\begin{aligned} \int _0^1F(\varphi ,\psi )dx\ge & {} -\theta _2-\alpha _1\Vert \psi \Vert _2^2-\theta _1\Vert \varphi \Vert _2^2 \ge -\theta _2-\alpha _1\Vert \psi _x\Vert _2^2-\theta _1\Vert \varphi _x\Vert _2^2 \nonumber \\\ge & {} -\theta _2-\alpha _1\Vert \psi _x\Vert _2^2-\theta _1\Vert \varphi _x+\psi \Vert _2^2-\theta _1\Vert \psi _x\Vert _2^2 \nonumber \\\ge & {} -\theta _2-(\alpha _1+2\theta _1)\Vert \psi _x\Vert _2^2-2\theta _1\Vert \varphi _x+\psi \Vert _2^2. \end{aligned}$$

(2.37)

Applying the Holder’s, Poincaré’s and Young’s inequalities we have

$$\begin{aligned} \int _0^1h_1\varphi dx\le & {} \Vert h_1\Vert _2\Vert \varphi _x\Vert _2 \le \Vert h_1\Vert _2\Vert \varphi _x+\psi \Vert _2+\Vert h_1\Vert _2\Vert \psi \Vert _2\nonumber \\\le & {} \Vert h_1\Vert _2\Vert \varphi _x+\psi \Vert _2+\Vert h_1\Vert _2\Vert \psi \Vert _2 \nonumber \\\le & {} \frac{1}{\kappa }\Vert h_1\Vert _2^2+\frac{\kappa }{4}\Vert \varphi _x+\psi \Vert _2^2+\frac{4}{b}\Vert h_1\Vert _2^2+\frac{b}{16}\Vert \psi _x\Vert _2^2, \end{aligned}$$

(2.38)

and

$$\begin{aligned} \int _0^1h_2\psi dx\le & {} \frac{4}{b}\Vert h_2\Vert _2^2+\frac{b}{16}\Vert \psi _x\Vert _2^2. \end{aligned}$$

(2.39)

Combining (2.36), (2.37), (2.38) and (2.39), we arrive

$$\begin{aligned}&\frac{1}{2}\Vert U(t)\Vert -\underbrace{\bigg [\theta _2+\bigg (\frac{1}{\kappa }+\frac{4}{b}\bigg )\Vert h_1\Vert _2^2+\frac{4}{b}\Vert h_2\Vert _2^2\bigg ]}_{2K_{E_1}}\nonumber \\&\quad \le E(t)+\frac{b}{2}\Vert \psi _x\Vert _2^2+\frac{\kappa }{2}\Vert \varphi _x+\psi \Vert _2^2\le 2E(t), \end{aligned}$$

(2.40)

proving thus (2.33) which completes the prove of the Lemma 2.3. $\square$

Theorem 2.2

(Local and Global Solution) Suppose that $\mu _2\le \mu _1$, (A1) and (A2) holds, we have:

(i):

If $U_0\in \mathcal {H}$, then there exists $T_{\text {max}}>0$ such that (2.11) has a unique mild solution $U:[0,T_{\text {max}})\rightarrow \mathcal {H}$. In addition, if $U_0\in D(\mathcal {A})$, then the mild solution is strong solution;

(ii):

The solution U(t) is globally bounded in $\mathcal {H}$ and thus $T_{\text {max}}=+\infty$;

(iii):

If $U_1$ and $U_2$ are two mild solutions of problem (2.11), then there exists a positive constant $C_{E_1}=C_{E_1}(U_1(0),U_2(0))$ such that

$$\begin{aligned} \Vert U_1(t)-U_2(t)\Vert _{\mathcal {H}}\le e^{C_{E_1} t}\Vert U_1(0)-U_2(0)\Vert _{\mathcal {H}},\quad \forall t\in [0,T_{\text {max}}). \end{aligned}$$

(2.41)

Proof

(i) The result follows from Lemmas 2.1, 2.2 and of [33, Chap. 6, Theorems 1.4 and 1.5].

(ii) From (2.32), we have

$$\begin{aligned} E(t)\le & {} E(0),\quad \forall t>0, \end{aligned}$$

(2.42)

and combining with (2.33), we obtain

$$\begin{aligned} \frac{1}{4}\Vert U(t)\Vert _{\mathcal {H}}^2\le & {} E(0)+K_{E_1},\quad \forall t\ge 0, \end{aligned}$$

(2.43)

and together with [33, Chap. 6, Theorems 1.4] results $T_{\text {max}}=+\infty$.

(iii) Since $U_1$ and $U_2$ are mild solutions of (2.11), we have

$$\begin{aligned} \Big \Vert U_1(t)-U_2(t)\Big \Vert _{\mathcal {H}}=\bigg \Vert e^{\mathcal {A}t}(U_1(0)-U_2(0))-\int _0^te^{\mathcal {A}(t-s)}(\mathcal {F}(U_1(s))-\mathcal {F} (U_2(s)))ds\bigg \Vert _{\mathcal {H}}.\nonumber \\ \end{aligned}$$

(2.44)

Being $e^{\mathcal {A}t}$ a semigroup of contractions, we have

$$\begin{aligned} \Big \Vert U_1(t)-U_2(t)\Big \Vert _{\mathcal {H}}\le \Big \Vert U_1(0)-U_2(0)\Big \Vert _{\mathcal {H}}+\int _0^t\Big \Vert \mathcal {F}(U_1(s))-\mathcal {F} (U_2(s))\Big \Vert _{\mathcal {H}}ds. \end{aligned}$$

(2.45)

From Lemma 2.2 and (2.43), there exists a positive constant $C_{E_1}$ such that, for any $T>0$

$$\begin{aligned} \Big \Vert U_1(t)-U_2(t)\Big \Vert _{\mathcal {H}}\le & {} \Big \Vert U_1(0)-U_2(0)\Big \Vert _{\mathcal {H}}\nonumber \\&+C_{E_1}\int _0^t\Big \Vert U_1(s)- U_2(s)\Big \Vert _{\mathcal {H}}ds,\quad \forall t\in [0,T_{\text {max}}). \end{aligned}$$

(2.46)

Applying the Gronwall’s inequality we get (2.41). This completes the proof of Theorem 2.2. $\square$

Remark 2.3

It is worth emphasizing that being $D(\mathcal {A})$ dense in $\mathcal {H}$, then for every $U_0\in \mathcal {H}$ and its respective mild solution $U:[0,\infty )\rightarrow \mathcal {H}$, it is possible to obtain a sequence $(U_0^n)$ in $D(\mathcal {A})$ with $U_0^n\rightarrow U_0$ and a sequence $U^n\in C([0,+\infty );\mathcal {H})$ where $U^n$ is a strong solution of

$$\begin{aligned}&\frac{d}{dt}U^n(t)=\mathcal {A}U^n(t)+\mathcal {F}\big (U^n(t)\big ), \quad t>0, \end{aligned}$$

(2.47)

$$\begin{aligned}&U^n(0)=U_0^n, \end{aligned}$$

(2.48)

with

$$\begin{aligned} U^n\rightarrow U \quad \text{ in } \quad C([0,T]; \mathcal {H}), \ \forall \, T>0. \end{aligned}$$

(2.49)

This means that the regularity for the solutions obtained in Theorem 2.2 are sufficient to justify the calculations that will be performed in this work.

3 Long-Time Dynamics

We can from the Theorem 2.2 and Lemma 2.3 defining the dynamical system $(\mathcal {H},S(t))$, associated with the problem (2.11), where $\mathcal {H}$ was defined in (2.15) and S(t) is the semigroup (evolution operator) given by

$$\begin{aligned}&S(t)U_0=U(t),\quad \forall t\ge 0, \end{aligned}$$

(3.1)

$$\begin{aligned}&U_0=(\varphi _0,\varphi _1,\psi _0,\psi _1,f_0)\in \mathcal {H}, \end{aligned}$$

(3.2)

where U(t) is the mild solution of (2.11) with initial condition $U_0$.

Key concepts as well as main results related to dynamical systems can be found, among others, in [34,35,36,37,38,39,40].

3.1 Some Concepts and Results Related to Dynamical Systems

In this subsection, we will outline some concepts and results related to dynamical systems that will be important for this work. In the sequence, H will represent a generic Banach space and $\mathcal {S}(t)$ a strongly continuous evolution operator.

A dynamical system $(H,\mathcal {S}(t))$ is said asymptotically smooth if for any bounded set ${\mathscr {D}}\subset H$, such that $\mathcal {S}(t){\mathscr {D}}\subset {\mathscr {D}}$ for all $t>0$, there exists a compact set ${\mathscr {K}}\subset \overline{{\mathscr {D}}}$, where $\overline{{\mathscr {D}}}$ is the closure of ${\mathscr {D}}$, such that

$$\begin{aligned} \lim _{t\rightarrow +\infty }d_H(\mathcal {S}(t){\mathscr {D}},{\mathscr {K}})=0, \end{aligned}$$

(3.3)

where $d_H$ denotes the Hausdorff semi-distance between sets in H, that is

$$\begin{aligned} d_H(A,B)=\sup _{a\in A}\inf _{b\in B}\Vert a-b\Vert _H \quad \text {for sets}\ A, B \subset H. \end{aligned}$$

An closed and bounded set ${\mathscr {A}}\subset H$ is called a global attractor for $(H,\mathcal {S}(t))$ if ${\mathscr {A}}$ is an invariante set, that is $\mathcal {S}(t){\mathscr {A}}={\mathscr {A}}$, for all $t\ge 0$ and ${\mathscr {A}}$ is uniformly attracting, that is, for every bounded set ${\mathscr {D}}\subset H$, we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }d_H(\mathcal {S}(t){\mathscr {D}},{\mathscr {A}})=0. \end{aligned}$$

(3.4)

An closed and bounded set ${\mathfrak {A}}_{\text {min}}\subset H$ is called a global minimal attractor for $(H,\mathcal {S}(t))$ if ${\mathfrak {A}}_{\text {min}}$ is positively invariant, that is, $\mathcal {S}(t){\mathfrak {A}}_{\text {min}}\subseteq {\mathfrak {A}}_{\text {min}}$ for all $t\ge 0$ and ${\mathfrak {A}}_{\text {min}}$ attracts every point of H, that is,

$$\begin{aligned} \lim _{t\rightarrow +\infty }d_H(\mathcal {S}(t)U_0,{\mathfrak {A}}_{\text {min}})=0,\quad \forall U_0\in H, \end{aligned}$$

(3.5)

and ${\mathfrak {A}}_{\text {min}}$ is minimal, that is, ${\mathfrak {A}}_{\text {min}}$ has no proper subsets satisfying these two properties.

Let ${\mathscr {N}}$ be the sets of stationary points of $(H,\mathcal {S}(t))$, that is,

$$\begin{aligned} {\mathscr {N}}:=\Big \{h \in H; \ \mathcal {S}(t)h=h, \ \forall t \ge 0\Big \}, \end{aligned}$$

(3.6)

an unstable manifold emanating from ${\mathscr {N}}$, represented by ${\mathscr {M}}^u({\mathscr {N}})$, is the set of all $h\in H$ such that there is a full trajectory $\gamma =\{u(t); \ t \in {\mathbb {R}}\}$ satisfying

$$\begin{aligned} u(0)=h\quad \text {and}\quad \lim _{t\rightarrow -\infty }\text {dist}_H (u(t),{\mathscr {N}})=0. \end{aligned}$$

(3.7)

It is clear that ${\mathscr {M}}^u({\mathscr {N}})$ is an invariant set for $(H,\mathcal {S}(t))$ and if ${\mathscr {A}}\subset H$ is global attractor for $(H,\mathcal {S}(t))$, then ${\mathscr {M}}^u({\mathscr {N}})\subset {\mathscr {A}}$ (cf. [34, 37]).

The dynamical system $(H,\mathcal {S}(t))$ is called gradient, if there exists a strict Lyapunov function on H, that is, there exists a continuous function $\Phi$ such that $t\mapsto \Phi (\mathcal {S}(t)y)$ is non-increasing for any $y\in H$, and if $\Phi (\mathcal {S}(t)y_0)=\Phi (y_0)$ for all $t>0$ and some $y_0\in H$, then $y_0$ is a stationary point of $(H,\mathcal {S}(t))$.

The fractal dimension of a compact set M in H is defined by

$$\begin{aligned} \text {dim}_f^HM:=\lim _{\varepsilon \rightarrow 0}\sup \frac{\ln n(M,\varepsilon )}{\ln (1/\varepsilon )}, \end{aligned}$$

(3.8)

where $n(M,\varepsilon )$ is the minimal number of closed balls of radius $\varepsilon$ which covers M.

An compact set ${\mathfrak {A}}_{\text {exp}}\subset H$ is called a exponential attractor for $(H,\mathcal {S}(t))$ if ${\mathfrak {A}}_{\text {exp}}$ is a positively invariant set with finite fractal dimension in H and for any bounded set ${\mathscr {D}}\subset H$ there exist $t_{{\mathscr {D}}}, C_{{\mathscr {D}}}, \gamma _{{\mathscr {D}}}>0$ such that

$$\begin{aligned} d_H(\mathcal {S}(t){{\mathscr {D}}},{\mathfrak {A}}_{\text {exp}})\le C_{{{\mathscr {D}}}} e^{-\gamma _{{{\mathscr {D}}}}(t-t_{{{\mathscr {D}}}})},\quad \forall t\ge t_{{{\mathscr {D}}}}. \end{aligned}$$

The proof of the following theorem can be found in [37] p. 360.

Theorem 3.1

Let $(H,\mathcal {S}(t))$ be a gradient and asymptotically smooth dynamical system. Assume that the Lyapunov function $\Phi (y)$ of $(H,\mathcal {S}(t))$ is bounded from above on any bounded subset of H and the set $\Phi _R=\{y; \ \Phi (y) \le R\}$ is bounded for every R. If the set ${\mathscr {N}}$ of stationary points of $(H,\mathcal {S}(t))$ is bounded, then $(H,\mathcal {S}(t))$ possesses a compact global attractor ${\mathscr {A}}={\mathscr {M}}^u({\mathscr {N}})$.

Let X, Y and Z be reflexives Banach spaces with X compactly embedded in Y. We consider the space $H=X\times Y\times Z$, with norm

$$\begin{aligned} \Vert h\Vert _H^2:=\Vert \pi _0\Vert _X^2+\Vert \pi _1\Vert _Y^2+\Vert \eta _0\Vert _Z^2,\quad h=(\pi _0,\pi _1,\eta _0)\in H, \end{aligned}$$

(3.9)

and the dynamical system $(H,\mathcal {S}(t))$ given by an evolution operator

$$\begin{aligned} \mathcal {S}(t)h_0=(\pi (t),\pi _t(t),\eta (t))\quad t\ge 0,\quad h_0=(\pi (0),\pi _t(0),\eta (0))\in H, \end{aligned}$$

(3.10)

where the functions $\pi (t)$ and $\eta (t)$ possess the properties

$$\begin{aligned} \pi \in C({\mathbb {R}}_+,X)\cap C^1({\mathbb {R}}_+,Y),\quad \eta \in C({\mathbb {R}}_+,Z). \end{aligned}$$

(3.11)

The dynamical system $(H,\mathcal {S}(t))$ is called quasi-stable on a set ${\mathscr {B}}\subset H$ if there exist a compact seminorm $\eta _X(\cdot )$ on the space X and nonnegative scalar functions a(t), b(t) and c(t) on ${\mathbb {R}}_+$ such that

Q(S1):

a(t) and c(t) are locally bounded on $[0,\infty )$;

Q(S2):

$b(t)\in L^1({\mathbb {R}}_+)$ possesses the property

$$\begin{aligned} \lim _{t\rightarrow \infty }b(t)=0; \end{aligned}$$

(3.12)

Q(S3):

for every $h_1,h_2\in {\mathscr {B}}$ and $t>0$ the following relations

$$\begin{aligned} \Vert \mathcal {S}(t)h_1-\mathcal {S}(t)h_2\Vert _{H}^2\le & {} a(t)\Vert h_1-h_2\Vert _{H}^2 \end{aligned}$$

(3.13)

and

$$\begin{aligned} \Vert \mathcal {S}(t)h_1-\mathcal {S}(t)h_2\Vert _{H}^2\le & {} b(t)\Vert h_1-h_2\Vert _{H}^2+c(t)\sup _{0\le s\le t}[\eta _X(\pi ^1(s)-\pi ^2(s))]^2\nonumber \\ \end{aligned}$$

(3.14)

hold. Here we denote $\mathcal {S}(t)h_i=(\pi ^i(t),\pi _t^i(t),\eta ^i(t))$, $i=1,2$.

The following two results can be found in [37, Chapter 7], show us how strong the property of quasi-stability is for a dynamical system. The first, relates the quasi-stability to the asymptotically smooth and the second relates the quasi-stability to the fractal dimension of an attractor.

Theorem 3.2

Let $(H,\mathcal {S}(t))$ be a dynamical system with the evolution operator of the form (3.10). Assume that $(H,\mathcal {S}(t))$ is quasi-stable over bounded forward invariant set ${\mathscr {B}}\subset H$. Then, $(H,\mathcal {S}(t))$ is asymptotically smooth.

Theorem 3.3

Suppose $(H,\mathcal {S}(t))$ be a dynamical system with the evolution operator of the form (3.10). Assume that $(H,\mathcal {S}(t))$ possesses a compact global attractor ${\mathscr {A}}$ and is quasi-stable on ${\mathscr {A}}$. Then the fractal dimension of ${\mathscr {A}}$ is finite.

3.2 Existence of Global Attractor

In this subsection, we will study the existence of global attractor for the dynamic system $(\mathcal {H},S(t))$ defined in (3.2), we will often refer to the inequality $\mu _2\le \mu _1$ associated with (2.16).

Lemma 3.1

If $\mu _2\le \mu _1$, then the dynamical system $(\mathcal {H},S(t))$ is gradient, that is, there exists a strict Lyapunov function $\Phi$ defined in $\mathcal {H}$. In addition,

(a):

$\Phi$ is bounded from above on any bounded subset of $\mathcal {H}$;

(b):

For all $R>0$, the set $\Phi _R=\{W_0\in \mathcal {H}; \ \Phi (W_0)\le R\}$ is bounded.

Proof

Let us consider the functional energy defined in (2.31) as the Lyapunov function, that is, $\Phi \equiv E$. Thus, given $U_0=(\varphi _0,\varphi _1,\psi _0,\psi _1,f_0)\in \mathcal {H}$, it follows from the Lemma (2.3) that the function $t\mapsto \Phi (S(t)U_0)$ is non-increasing and

$$\begin{aligned}&\Phi (S(t)U_0)+\int _0^t\bigg [\Vert \varphi _t\Vert _2^2+\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert \psi _t\Vert _2^2 +\bigg (\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert z(1)\Vert _2^2\bigg ]ds\nonumber \\&\quad \le \Phi (U_0),\quad \forall t\ge 0, \end{aligned}$$

(3.15)

with

$$\begin{aligned} \mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}>0\quad \text {and}\quad \frac{\xi }{2\tau }-\frac{\mu _2}{2}>0. \end{aligned}$$

(3.16)

If $\Phi (S(t)U_0)=\Phi (U_0)$ for all $t\ge 0$ then, from (3.15), we have

$$\begin{aligned} \varphi _t(t)=\psi _t(t)= z(1,t)=0, \ \ \text {a.e. in} \ \ (0,1), \ \ \forall t\ge 0, \end{aligned}$$

(3.17)

which implies

$$\begin{aligned} \varphi (t)=\varphi _0, \ \psi (t)=\psi _0 \ \ \text {and} \ \ z(\cdot ,1,t)=0\quad \forall t\ge 0. \end{aligned}$$

(3.18)

This gives us $U(t)=S(t)U_0=(\varphi _0,0,\psi _0,0,0)$ for all $t\ge 0$, that is, $U_0$ is a stationary point of $(\mathcal {H},S(t))$, thus proving that $\Phi$ is a strict Lyapunov function of $(\mathcal {H},S(t))$ and therefore, the dynamical system is gradient.

It is easy to see from (3.15) that $\Phi$ is bounded from above on bounded subsets of $\mathcal {H}$, which proves (a). Given $W_0\in \Phi _R$, consider W(t) the mild solution corresponding to $W_0$, from the inequalities (2.33) and (3.15) we have

$$\begin{aligned} \Vert W(t)\Vert _{\mathcal {H}}\le 4\Phi (S(t)W_0)+4K_{E_1}\le 4\Phi (W_0)+4K_{E_1},\quad t\ge 0, \end{aligned}$$

(3.19)

for $t=0$, we obtain

$$\begin{aligned} \Vert W_0\Vert _{\mathcal {H}}\le 4R+4K_{E_1}, \end{aligned}$$

(3.20)

showing thus $\Phi _R$ is a bounded set of $\mathcal {H}$, which proves (b) and completes the proof of the Lemma 3.1. $\square$

Lemma 3.2

The set of stationary points $\mathcal {N}$ of the dynamical system $(\mathcal {H},S(t))$ is bounded.

Proof

Based on the Lemma 3.1, the set $\mathcal {N}$ is given by

$$\begin{aligned} \mathcal {N}=\Big \{U=(\varphi ,0,\psi ,0,0)\in \mathcal {H}; \ \mathcal {A}U+\mathcal {F}(U)=0\Big \}. \end{aligned}$$

(3.21)

Therefore, $\varphi$ and $\psi$ must satisfy

$$\begin{aligned} -\kappa (\varphi _x+\psi )_x+f_1(\varphi ,\psi )= & {} h_1 \quad \text{ in }\quad (0,1), \end{aligned}$$

(3.22)

$$\begin{aligned} -b\psi _{xx}+\kappa (\varphi _x+\psi )+f_2(\varphi ,\psi )= & {} h_2 \quad \text{ in }\quad (0,1). \end{aligned}$$

(3.23)

Multiplying (3.22) by $\varphi$ and (3.23) by $\psi$, integrating over (0, 1) and adding the results, we obtain

$$\begin{aligned} \Vert \varphi _x+\psi \Vert _2^2+b\Vert \psi _x\Vert _2^2+\int _0^1[f_1(\varphi ,\psi )\varphi +f_2(\varphi ,\psi )\psi ]dx= \int _0^1[h_1\varphi +h_2\psi ]dx.\nonumber \\ \end{aligned}$$

(3.24)

From (2.23) and (2.24), we have

$$\begin{aligned}&\int _0^1[f_1(\varphi ,\psi )\varphi +f_2(\varphi ,\psi )\psi ]dx\nonumber \\&\quad \ge -2\theta _2-2\theta _1\Vert \varphi \Vert _2^2-\alpha _1\Vert \psi \Vert _2^2 \ge -2\theta _2-2\theta _1\Vert \varphi _x\Vert _2^2-\alpha _1\Vert \psi _x\Vert _2^2 \nonumber \\&\quad \ge -2\theta _2-2\theta _1\Vert \varphi _x+\psi \Vert _2^2-(\alpha _1+2\theta _1)\Vert \psi _x\Vert _2^2. \end{aligned}$$

(3.25)

By Hölder’s and Poincaré’s inequalities, we have

$$\begin{aligned} \int _0^1[h_1\varphi +h_2\psi ]dx\le & {} \Vert h_1\Vert _2\Vert \varphi \Vert _2+\Vert h_2\Vert _2\Vert \psi \Vert _2 \le \Vert h_1\Vert _2\Vert \varphi _x\Vert _2+\Vert h_2\Vert _2\Vert \psi _x\Vert _2 \nonumber \\\le & {} \frac{\kappa }{2}\Vert \varphi _x+\psi \Vert _2^2+\frac{b}{2}\Vert \psi _x\Vert _2^2+\bigg (\frac{1}{2\kappa }+\frac{1}{b}\bigg )\Vert h_1\Vert _2^2+\frac{1}{b}\Vert h_2\Vert _2^2.\nonumber \\ \end{aligned}$$

(3.26)

From (3.24)–(3.26) we obtain

$$\begin{aligned} \frac{1}{4}\Vert U\Vert _{\mathcal {H}}^2=\frac{\kappa }{8}\Vert \varphi _x+\psi \Vert _2^2+\frac{b}{8}\Vert \psi _x\Vert _2^2\le \bigg (\frac{1}{2\kappa }+\frac{1}{b}\bigg )\Vert h_1\Vert _2^2+\frac{1}{b}\Vert h_2\Vert _2^2, \end{aligned}$$

(3.27)

showing that $\mathcal {N}$ is bounded in $\mathcal {H}$, this completes the proof of the Lemma 3.2. $\square$

Lemma 3.3

Suppose that $\mu _2\le \mu _1$ and (A1)–(A3) are valid. For every set bounded ${\mathscr {B}}\subset \mathcal {H}$, there are positive constants $\gamma$, $\vartheta$ and $C_{{\mathscr {B}}}$, with $C_{{\mathscr {B}}}$ depending on ${\mathscr {B}}$, such that

$$\begin{aligned}&\Vert S(t)U_1-S(t)U_2\Vert _{\mathcal {H}}^2\le \vartheta e^{-\gamma t}\Vert U_1-U_2\Vert _{\mathcal {H}}^2\nonumber \\&\quad +C_{{\mathscr {B}}}\int _0^te^{-\gamma (t-s)}\Big [\Vert u(s)\Vert _2^2+\Vert v(s)\Vert _2^2\Big ]ds, \quad t\ge 0, \end{aligned}$$

(3.28)

for any $U_i=(\varphi _0^i,\varphi _1^i,\psi _0^i,\psi _1^i,f_0^i)\in {\mathscr {B}}$, where $S(t)U_i=(\varphi ^i(t),\varphi ^i_t(t),\psi ^i(t),\psi ^i_t(t),z_1^i(t))$ is mild solution of (2.11) to $i= 1,2$, $u=\varphi ^1-\varphi ^2$ and $v=\psi ^1-\psi ^2$.

Proof

Consider the representation $U(t)=S(t)U_1-S(t)U_2=(u(t),u_t(t),v(t),v_t(t),w(t))$, $t\ge 0$, where $w=z_1^1-z_1^2$. Thus U(t), in the sense of mild solution, solves the following system

$$\begin{aligned}&\rho _1u_{tt}-\kappa (u_x+v)_x+f_1(\varphi ^1,\psi ^1)-f_1(\varphi ^2,\psi ^2)+u_t=0 \quad \text {in} \quad (0,1)\times (0,\infty ), \end{aligned}$$

(3.29)

$$\begin{aligned}&\rho _2v_{tt}-bv_{xx}+\kappa (u_x+v)+f_2(\varphi ^1,\psi ^1)-f_2(\varphi ^2,\psi ^2)+\mu _1v_t+\mu _2 w(\cdot ,1,\cdot )\nonumber \\&\quad =0 \quad \text {in} \quad (0,1)\times (0,\infty ), \end{aligned}$$

(3.30)

$$\begin{aligned}&\tau w_t(x,y,t)+w_y(x,y,t)=0 \quad \text {in} \quad (0,1)\times (0,1)\times (0,\infty ). \end{aligned}$$

(3.31)

Multiplying (3.29) by $u_t$ and (3.30) by $v_t$, integrating with respect to x in [0, 1] and adding the results, we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\bigg (\rho _1\Vert u_t\Vert _2^2+\rho _2\Vert v_t\Vert _2^2+\kappa \Vert u_x+v\Vert _2^2\bigg )= & {} -\int _0^1(\Delta f_1)u_tdx-\int _0^1(\Delta f_2)v_tdx \nonumber \\&-\Vert u_t\Vert _2^2-\mu _1\Vert v_t\Vert _2^2-\mu _2\int _0^1w(x,1,t)v_tdx,\nonumber \\ \end{aligned}$$

(3.32)

where

$$\begin{aligned} \Delta f_i= & {} f_i(\varphi ^1,\psi ^1)-f_i(\varphi ^2,\psi ^2) =[f_i(\varphi ^1,\psi ^1)-f_i(\varphi ^1,\psi ^2)]\nonumber \\&+[f_i(\varphi ^1,\psi ^2)-f_i(\varphi ^2,\psi ^2)]. \end{aligned}$$

(3.33)

Multiplying (3.31) by $\frac{\xi }{\tau }w$ and integrating with respect to x and y in $[0,1]\times [0,1]$ we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _0^1\int _0^1 \xi w^2(x,y,t)dydx= & {} -\frac{\xi }{2\tau }\int _0^1\int _0^1\frac{\partial }{\partial y} w^2(x,y,t)dydx\nonumber \\= & {} -\frac{\xi }{2\tau }\int _0^1 w^2(x,y,t)|_{y=0}^{y=1}dx \nonumber \\= & {} \frac{\xi }{2\tau }\Vert u_t\Vert _2^2-\frac{\xi }{2\tau }\int _0^1w^2(x,1,t)dx. \end{aligned}$$

(3.34)

Adding (3.32) and (3.34), we get

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\bigg (\rho _1\Vert u_t\Vert _2^2+\rho _2\Vert v_t\Vert _2^2+b\Vert v_x\Vert _2^2+\kappa \Vert u_x+v\Vert _2^2+ \xi \int _0^1\int _0^1 w^2(x,y,t)dydx\bigg )\nonumber \\&\quad = -\int _0^1(\Delta f_1)u_tdx \nonumber \\&\qquad -\int _0^1(\Delta f_2)v_tdx -\Vert u_t\Vert _2^2-\bigg (\mu _1-\frac{\xi }{2\tau }\bigg )\Vert v_t\Vert _2^2-\mu _2\int _0^1w(x,1,t)v_tdx\nonumber \\&\qquad -\frac{\xi }{2\tau }\int _0^1w^2(x,1,t)dx. \end{aligned}$$

(3.35)

Considering now the functional ${\mathscr {L}}$ given by

$$\begin{aligned} {\mathscr {L}}(t)&:=\rho _1\Vert u_t\Vert _2^2+\rho _2\Vert v_t\Vert _2^2+b\Vert v_x\Vert _2^2+\kappa \Vert u_x\nonumber \\&\quad +v\Vert _2^2+ \xi \int _0^1\int _0^1 w^2(x,y,t)dydx\equiv \Vert U(t)\Vert _{\mathcal {H}}^2. \end{aligned}$$

(3.36)

Let’s now estimate the right side of (3.35). Since ${\mathscr {B}}$ is bounded, it follows from (2.32)–(2.33) the existence of a constant $K_{{\mathscr {B}}_1}$ depending on ${\mathscr {B}}$ such that

$$\begin{aligned} \Vert S(t)U_1\Vert _{\mathcal {H}}, \ \Vert S(t)U_2\Vert _{\mathcal {H}}\le K_{{\mathscr {B}}_1}, \ \forall t\ge 0. \end{aligned}$$

(3.37)

Since $\sigma _i$ is continuous and $H_0^1(0,1)\hookrightarrow L^\infty (0,1)$, there exists a constant $K_{{\mathscr {B}}_2}>0$ depending on ${\mathscr {B}}$ such that

$$\begin{aligned} \sigma _i(|\varphi ^j|), \ \sigma _i(|\psi ^j|)\le K_{{\mathscr {B}}_2} \quad \text {a.e in} \quad (0,1)\times (0,\infty ), \quad i,j=1,2. \end{aligned}$$

(3.38)

From (2.20)–(2.21), (3.37), (3.38) and Hölder’s inequality we obtain

$$\begin{aligned} \bigg |\int _0^1(\Delta f_1)u_tdx\bigg |\le & {} \int _0^1\sigma _1(|\varphi ^1(t)|)(1+|\psi ^1(t)|^{\gamma _1}+|\psi ^2(t)|^{\gamma _1})|v(t)||u_t(t)|dx \nonumber \\&+ \int _0^1\sigma _1(|\psi ^2(t)|)(1+|\varphi ^1(t)|^{\gamma _1}+|\varphi ^2(t)|^{\gamma _1})|u(t)||u_t(t)|dx \nonumber \\\le & {} K_{{\mathscr {B}}_2}(1+\Vert \psi ^1(t)\Vert _{\infty }^{\gamma _1}+\Vert \psi ^2(t)\Vert _{\infty }^{\gamma _1})\int _0^1|v(t)||u_t(t)|dx \nonumber \\&+ K_{{\mathscr {B}}_2}(1+\Vert \varphi ^1(t)\Vert _{\infty }^{\gamma _1}+\Vert \varphi ^2(t)\Vert _{\infty }^{\gamma _1})\int _0^1|u(t)||u_t(t)|dx \nonumber \\\le & {} K_{{\mathscr {B}}_3}\Vert v(t)\Vert _2\Vert u_t(t)\Vert _2+K_{{\mathscr {B}}_3}\Vert u(t)\Vert _2\Vert u_t(t)\Vert _2, \end{aligned}$$

(3.39)

for some constant $K_{{\mathscr {B}}_3}$ depending on ${\mathscr {B}}$. Applying Young’s inequality with $\varepsilon =\frac{\alpha _1}{4}$, there exists a constant $K_{{\mathscr {B}}_4}>0$ such that

$$\begin{aligned} \bigg |\int _0^1(\Delta f_1)u_t(t)dx\bigg | \le K_{{\mathscr {B}}_4}(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)+\frac{\alpha _1}{2}\Vert u_t(t)\Vert _2^2. \end{aligned}$$

(3.40)

In a similar way we can obtain a constant $K_{{\mathscr {B}}_5}>0$ depending on ${\mathscr {B}}$ such that

$$\begin{aligned} \bigg |\int _0^1(\Delta f_2)v_t(t)dx\bigg | \le K_{{\mathscr {B}}_5}(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)+\frac{\alpha _2}{2}\Vert v_t(t)\Vert _2^2. \end{aligned}$$

(3.41)

From Young’s inequality, we have

$$\begin{aligned} \mu _2\int _0^1w(x,1,t)v_tdx\le \frac{\mu _2}{2}\Vert v_t(t)\Vert _2^2+\frac{\mu _2}{2}\int _0^1w^2(x,1,t)dx. \end{aligned}$$

(3.42)

Combining (3.40)–(3.42), we arrive at

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\mathcal {L}(t)\le & {} K_{{\mathscr {B}}_6}(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)-\bigg (1-\frac{\alpha _1}{2}\bigg )\Vert u_t(t)\Vert _2^2 \nonumber \\&-\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}-\frac{\alpha _2}{2}\bigg )\Vert v_t\Vert _2^2 -\bigg (\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\int _0^1w^2(x,1,t)dx.\nonumber \\ \end{aligned}$$

(3.43)

where $K_{{\mathscr {B}}_6}=K_{{\mathscr {B}}_4}+K_{{\mathscr {B}}_5}$. Considering now

$$\begin{aligned} \alpha _1=1\quad \text {and}\quad \alpha _2=\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}>0, \end{aligned}$$

(3.44)

we obtain

$$\begin{aligned} \frac{d}{dt}\mathcal {L}(t)\le & {} 2K_{{\mathscr {B}}_6}(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)-\Vert u_t(t)\Vert _2^2 \nonumber \\&-\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )\Vert v_t\Vert _2^2 -\bigg (\frac{\xi }{\tau }-\mu _2\bigg )\int _0^1w^2(x,1,t)dx. \end{aligned}$$

(3.45)

We now define the following functional

$$\begin{aligned} \mathcal {I}(t):=N\mathcal {L}(t)+\mathcal {J}(t)+\mathcal {K}(t)+M\mathcal {P}(t), \end{aligned}$$

(3.46)

where N and M are positive constants to be chosen a posteriori and

$$\begin{aligned} \mathcal {J}(t):= & {} \rho _1\int _0^1u_t(t)u(t)dx,\ \ \mathcal {K}(t):=\rho _2\int _0^1v_t(t)v(t)dx \ \ \text{ and }\ \ \mathcal {P}(t)\nonumber \\:= & {} \tau \int _0^1\int _0^1e^{-2\tau y}w^2(x,y,t)dydx. \end{aligned}$$

(3.47)

It is not difficult to check that there exists a constant $C_{\mathcal {I}_1}>0$ such that

$$\begin{aligned} |\mathcal {I}(t)-N\mathcal {L}(t)|\le C_{\mathcal {I}_1}\mathcal {L}(t), \quad \forall t\ge 0. \end{aligned}$$

(3.48)

Therefore, for N large enough, we obtain positive constants $C_{\mathcal {I}_2}$ and $C_{\mathcal {I}_3}$ such that

$$\begin{aligned} C_{\mathcal {I}_2}\mathcal {L}(t)\le \mathcal {I}(t)\le C_{\mathcal {I}_3}\mathcal {L}(t), \quad \forall t\ge 0. \end{aligned}$$

(3.49)

We will now show that there are positive constants $N_1$ and $N_{{\mathscr {B}}}$, with $N_{{\mathscr {B}}}$ depending on ${\mathscr {B}}$, such that

$$\begin{aligned} \frac{d}{dt}\mathcal {I}(t)+N_1\mathcal {L}(t)\le N_{{\mathscr {B}}}(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2), \quad \forall t>0. \end{aligned}$$

(3.50)

In fact, deriving $\mathcal {J}$, we have

$$\begin{aligned} \frac{d}{dt}\mathcal {J}(t)= & {} \rho _1\int _0^1u_t^2dx+\rho _1\int _0^1u_{tt}udx =\rho _1\Vert u_t\Vert _2^2+\int _0^1[\kappa (u_x+v)_x-\Delta f_1-u_t]udx \nonumber \\= & {} \rho _1\Vert u_t\Vert _2^2-\kappa \int _0^1(u_x+v)u_xdx-\int _0^1(\Delta f_1)udx-\int _0^1u_tudx. \end{aligned}$$

(3.51)

Deriving now $\mathcal {K}$, we obtain

$$\begin{aligned} \frac{d}{dt}\mathcal {K}(t)= & {} \rho _2\int _0^1v_t^2dx+\rho _2\int _0^1v_{tt}vdx \nonumber \\= & {} \rho _2\Vert v_t\Vert _2^2+\int _0^1\Big [bv_{xx}-\kappa (u_x+v)-\Delta f_2-\mu _1v_t-\mu _2w(x,1,t)\Big ]vdx \nonumber \\= & {} \rho _2\Vert v_t\Vert _2^2-b\Vert v_x\Vert _2^2-\kappa \int _0^1(u_x+v)vdx-\int _0^1(\Delta f_2)vdx \nonumber \\- & {} \mu _1\int _0^1v_tvdx-\mu _2\int _0^1w(x,1,t)vdx. \end{aligned}$$

(3.52)

From (3.51)–(3.52), we arrived at

$$\begin{aligned} \frac{d}{dt}\Big (\mathcal {J}(t)+\mathcal {K}(t)\Big )= & {} \rho _1\Vert u_t\Vert _2^2+\rho _2\Vert v_t\Vert _2^2-b\Vert v_x\Vert _2^2-\kappa \Vert u_x+v\Vert _2^2\nonumber \\&-\int _0^1\Big [(\Delta f_1)u+(\Delta f_2)v\Big ]dx \nonumber \\&-\int _0^1(u_tu+\mu _1v_tv)dx-\mu _2\int _0^1w(x,1,t)vdx. \end{aligned}$$

(3.53)

By analogous arguments to (3.39), we can conclude the existence of a constant $K_{{\mathscr {B}}_7}>0$ depending on ${\mathscr {B}}$, such that

$$\begin{aligned} \int _0^1\Big ((\Delta f_1)u+(\Delta f_2)v\Big )dx\le K_{{\mathscr {B}}_7}\Big (\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2\Big ). \end{aligned}$$

(3.54)

By using the Young’s and Poincaré’s inequalities, we have

$$\begin{aligned} \bigg |\int _0^1[u_tu+\mu _1v_tv]dx\bigg |\le & {} \int _0^1|u_tu|dx+\mu _1\int _0^1|v_tv|dx \le \Vert u_t\Vert _2\Vert u_x\Vert _2+\mu _1\Vert v_t\Vert _2\Vert v_x\Vert _2 \nonumber \\\le & {} \Vert u_t\Vert _2\Vert u_x+v\Vert _2+\Vert u_t\Vert _2\Vert v_x\Vert _2+\mu _1\Vert v_t\Vert _2\Vert v_x\Vert _2 \nonumber \\\le & {} \frac{b}{3}\Vert v_x(t)\Vert _2^2+\frac{\kappa }{2}\Vert u_x+v\Vert _2^2+\bigg (\frac{1}{2\kappa }+\frac{3}{2b}\bigg )\Vert u_t\Vert _2^2 +\frac{3\mu _1^2}{2b}\Vert v_t\Vert _2^2,\nonumber \\ \end{aligned}$$

(3.55)

and

$$\begin{aligned} \mu _2\int _0^1w(x,1,t)vdx\le \frac{b}{6}\Vert v_x\Vert _2^2+\frac{3\mu _2^2}{2b}\int _0^1w^2(x,1,t)dx. \end{aligned}$$

(3.56)

From (3.52)–(3.56) we obtain

$$\begin{aligned} \frac{d}{dt}[\mathcal {J}(t)+\mathcal {K}(t)]\le & {} \bigg (\frac{1}{2\kappa }+\frac{3}{2b}+\rho _1\bigg )\Vert u_t\Vert _2^2+ \bigg (\rho _2+\frac{3\mu _1^2}{2b}\bigg )\Vert v_t\Vert _2^2-\frac{b}{2}\Vert v_x\Vert _2^2 \nonumber \\&-\frac{\kappa }{2}\Vert u_x+v\Vert _2^2+ K_{{\mathscr {B}}_7}\Big (\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2\Big )+ \frac{3\mu _2^2}{2b}\int _0^1w^2(x,1,t)dx.\nonumber \\ \end{aligned}$$

(3.57)

Deriving $\mathcal {P}$, we have

$$\begin{aligned} \frac{d}{dt}\mathcal {P}(t)= & {} 2\tau \int _0^1\int _0^1e^{-2\tau y}w(x,y,t)w_t(x,y,t)dx\nonumber \\= & {} -2\int _0^1\int _0^1e^{-2\tau y}w(x,y,t)w_y(x,y,t)dx \nonumber \\= & {} -\int _0^1\int _0^1e^{-2\tau y}\frac{\partial }{\partial y}w^2(x,y,t)dx =-\int _0^1\bigg [e^{-2\tau y}w^2(x,y,t)\bigg ]_{y=0}^{y=1}dx\nonumber \\&-2\tau \int _0^1\int _0^1e^{-2\tau y}w^2(x,y,t)dx \nonumber \\= & {} \int _0^1w^2(x,0,t)dx-\int _0^1w^2(x,1,t)dx-2\tau \int _0^1\int _0^1e^{-2\tau y}w^2(x,y,t)dx \nonumber \\= & {} \Vert v_t(t)\Vert _2^2-\int _0^1w^2(x,1,t)dx-2\tau \int _0^1\int _0^1e^{-2\tau y}w^2(x,y,t)dx. \end{aligned}$$

(3.58)

Therefore, combining (3.46), (3.57) and (3.58) arrived at

$$\begin{aligned} \frac{d}{dt}\mathcal {I}(t)\le & {} \big (2NK_{{\mathscr {B}}_6}+K_{{\mathscr {B}}_7}\big )(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)-\bigg (N-\frac{1}{2\kappa }-\frac{3}{2b}- \rho _1\bigg )\Vert u_t(t)\Vert _2^2 \nonumber \\&-\bigg [N\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )-\bigg (\rho _2+\frac{3\mu _1^2}{2b}\bigg )-M \bigg ]\Vert v_t\Vert _2^2 \nonumber \\&-\bigg [N\bigg (\frac{\xi }{\tau }-\mu _2\bigg )-\frac{3\mu _2^2}{2b}+M\bigg ]\int _0^1w^2(x,1,t)dx-\frac{b}{2} \Vert v_x\Vert _2^2- \frac{\kappa }{2}\Vert u_x+v\Vert _2^2 \nonumber \\&-2M\tau e^{-2\tau }\int _0^1\int _0^1w^2(x,y,t)dx. \end{aligned}$$

(3.59)

On the other hand,

$$\begin{aligned}&N_1{\mathscr {L}}(t)=\rho _1N_1\Vert u_t\Vert _2^2+\rho _2N_1\Vert v_t\Vert _2^2+bN_1\Vert v_x\Vert _2^2+\kappa N_1\Vert u_x+v\Vert _2^2\nonumber \\&\quad + \xi N_1\int _0^1\int _0^1 w^2(x,y,t)dydx. \end{aligned}$$

(3.60)

Accordingly,

$$\begin{aligned}&\frac{d}{dt}\mathcal {I}(t)+N_1{\mathscr {L}}(t)\nonumber \\&\quad \le \big (2NK_{{\mathscr {B}}_6}+K_{{\mathscr {B}}_7}\big )(\Vert u(t)\Vert _2^2+\Vert v(t)\Vert _2^2)-\bigg (N-\frac{1}{2\kappa }-\frac{3}{2b}- \rho _1-\rho _1 N_1\bigg )\Vert u_t(t)\Vert _2^2 \nonumber \\&\qquad -\bigg [N\bigg (\mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}\bigg )-\bigg (\rho _2+\frac{3\mu _1^2}{2b}\bigg )-M -\rho _2 N_1\bigg ]\Vert v_t\Vert _2^2 \nonumber \\&\qquad -\bigg [N\bigg (\frac{\xi }{\tau }-\mu _2\bigg )-\frac{3\mu _2^2}{2b}+M\bigg ]\int _0^1w^2(x,1,t)dx-\bigg (\frac{b}{2} -bN_1\bigg )\Vert v_x\Vert _2^2 \nonumber \\&\qquad -\bigg (\frac{\kappa }{2}-\kappa N_1\bigg )\Vert u_x+v\Vert _2^2 -\bigg (2M\tau e^{-2\tau }-\xi N_1\bigg )\int _0^1\int _0^1w^2(x,y,t)dx. \end{aligned}$$

(3.61)

We must first consider $0<N_1<1/2$ and after that $M>\xi N_1 e^{2\tau }/2\tau$. Once,

$$\begin{aligned} \mu _1-\frac{\xi }{2\tau }-\frac{\mu _2}{2}>0\quad \text {and}\quad \frac{\xi }{\tau }-\mu _2>0, \end{aligned}$$

(3.62)

just take $N>0$ large enough to get (3.50).

Finally, combining (3.49) and (3.50) and using Gronwall’s inequality, we arrived at

$$\begin{aligned} \mathcal {L}(t)\le \vartheta e^{-\gamma t} \mathcal {L}(0)+C_{{\mathscr {B}}}\int _0^te^{-\gamma (t-s)}\Big (\Vert u(s)\Vert _2^2+\Vert v(s)\Vert _2^2\Big )ds, \quad t>0. \end{aligned}$$

(3.63)

Recalling that

$$\begin{aligned} \mathcal {L}(t)=\Vert U(t)\Vert _{\mathcal {H}}^2=\Vert S(t)U_1-S(t)U_2\Vert _{\mathcal {H}}^2,\quad t\ge 0. \end{aligned}$$

(3.64)

The proof of Lemma 3.3 is complete. $\square$

Remark 3.4

Since the embedded $H_0^1(0,1)\times H_0^1(0,1)\hookrightarrow L^2(0,1)\times L^2(0,1)$ is compact, in order to obtain the quasi-stability for the dynamical system $(\mathcal {H},S(t))$, we will consider the isomorphism $\mathcal {H}\cong \widetilde{\mathcal {H}}$, where

$$\begin{aligned} \widetilde{\mathcal {H}}:=(H_0^1(0,1)\times H_0^1(0,1))\times (L^2(0,1)\times L^2(0,1))\times L^2((0,1)\times (0,1)). \end{aligned}$$

(3.65)

We will make the following identification

$$\begin{aligned} (\varphi ,u,\psi ,v,z)\in \mathcal {H}\Longleftrightarrow (\varphi ,\psi ,u,v,z)\in \widetilde{\mathcal {H}}. \end{aligned}$$

(3.66)

The inner product and norm in $\widetilde{\mathcal {H}}$ are the same as in (2.17)–(2.18). The trajectory of the solutions will be given by $(\varphi (t),\psi (t),\varphi _t(t),\psi _t(t),z_1(t))$. When there is no danger of confusion, we will write $\mathcal {H}$ instead of $\widetilde{\mathcal {H}}$.

Theorem 3.5

Suppose that $\mu _2\le \mu _1$ and (A1)–(A3) are valid. Then the dynamical system $(\mathcal {H},S(t))$ is quasi-stable on any bounded positively invariant subset of $\mathcal {H}$.

Proof

Let ${\mathscr {B}}\subset \mathcal {H}$ be a limited and positively invariant set of $(\mathcal {H},S(t))$ and consider $U_1, U_2\in {\mathscr {B}}$. As already mentioned, we denote to $i=1,2$

$$\begin{aligned} S(t)U_i=(\varphi ^i(t),\psi ^i(t),\varphi ^i_t(t),\psi ^i_t(t),z^i_1(t)),\quad \text {and}\quad (u,v)=(\varphi ^1-\varphi ^2,\psi ^1-\psi ^2).\nonumber \\ \end{aligned}$$

(3.67)

From the Theorem 2.2 (ii), we obtain $a(t)=e^{C_{E_1}t}> 0$ which is locally bounded in $[0,\infty )$. We also consider the seminorm $\eta (\cdot )$ in $X=H_0^1(0,1)\times H_0^1(0,1)$ given by

$$\begin{aligned} \eta (u,v)=\Vert u\Vert _2+\Vert v\Vert _2, \end{aligned}$$

(3.68)

which is compact in X, since the embedding $X\hookrightarrow L^2(0,1)\times L^2(0,1)$ is compact. It follows from Lemma 3.3 that

$$\begin{aligned} \Vert S(t)U_1-S(t)U_2\Vert _{H}^2\le b(t)\Vert U_1-U_2\Vert _{H}^2+c(t)\sup _{0\le s\le t}[\eta _X(u(s),v(s))]^2, \end{aligned}$$

(3.69)

where

$$\begin{aligned} b(t)=\vartheta e^{-\gamma t}\quad \text {and}\quad c(t)=C_{{\mathscr {B}}}\int _0^te^{-\gamma (t-s)}ds, \quad t\ge 0. \end{aligned}$$

(3.70)

Thus we have $b(t)\in L^1({\mathbb {R}}_+)$, with $\lim _{t\rightarrow \infty }b(t)=0$ and $c_{\infty }=\sup _{t\in {\mathbb {R}}_+}c(t)\le \frac{C_{{\mathscr {B}}}}{\gamma }<\infty$. Hence (QS1)–(QS3) are satisfied and the $(\mathcal {H},S(t))$ is quasi-stable over any positively invariant limited set and the Theorem 3.5 is proved. $\square$

Theorem 3.6

Suppose that $\mu _2\le \mu _1$ and (A1)–(A2) are valid. Then the dynamical system $(\mathcal {H},S(t))$ possesses a unique compact global attractor ${\mathfrak {A}}\subset \mathcal {H}$, with finite fractal dimension. Moreover, the global attractor ${\mathfrak {A}}$ is characterized by

$$\begin{aligned} {\mathfrak {A}}:={\mathscr {M}}^u(\mathcal {N}), \end{aligned}$$

(3.71)

where $\mathcal {N}$ is the set of stationary point of $(\mathcal {H},S(t))$ and ${\mathscr {M}}^u(\mathcal {N})$ is the unstable manifold of $\mathcal {N}$.

Proof

It follows from Lemma 3.1 and Theorems 3.3 and 3.5 that $(\mathcal {H},S(t))$ is gradient and asymptotically smooth. Thus, the result is readily established by properties (a) and (b) of Lemma 3.1, Theorems 3.1 and 3.3. $\square$

Corollary 3.1

Suppose that $\mu _1\le \mu _2$ and (A1)–(A3) are valid. Then every trajectory stabilizes to the set $\mathcal {N}$, namely, for any $U\in \mathcal {H}$ one has

$$\begin{aligned} \lim _{t\rightarrow +\infty }\text {dist}_{\mathcal {H}}(S(t)U,\mathcal {N})=0. \end{aligned}$$

In particular, there exists a global minimal attractor ${\mathfrak {A}}_{\text {min}}$ given by ${\mathfrak {A}}_{\text {min}}=\mathcal {N}$.

Proof

The result follows from Theorem 3.6 and [37, Theorem 7.5.10]. $\square$

4 Regularity and Exponential Attractors

Theorem 4.1

Suppose that $\mu _2\le \mu _1$ and assumptions (A1)–(A3) are valid. Then any full trajectory

$$\begin{aligned} \Big (\varphi (t),\psi (t),\varphi _t(t),\psi _t(t),z(t)\Big ) \quad \text{ in } \quad {\mathfrak {A}}, \end{aligned}$$

(4.1)

has further regularity

$$\begin{aligned} \Big (\varphi _t,\psi _{t},\varphi _{tt},\psi _{tt},z_{t}\Big )\in L^\infty ({\mathbb {R}},\mathcal H). \end{aligned}$$

(4.2)

Moreover, there exists $R>0$ such that

$$\begin{aligned}&\Vert (\varphi _t(t),\psi _t(t))\Vert _{(H_0^1(0,L))^2}^2+ \Vert (u_{tt}(t),\psi _{tt}(t))\Vert _{(L^2(0,L))^2}^2+\Vert z_{t}(t)\Vert _{L^2((0,1)\times (0,1))}^2\nonumber \\&\quad \le R,\quad \forall t\in {\mathbb {R}}. \end{aligned}$$

(4.3)

Proof

Since we have shown that $(\mathcal H,S(t))$ is quasi-stable on the global attractor ${\mathfrak {A}}$ with $c_\infty =\sup _{t\in {\mathbb {R}}^+}c(t)<\infty$, then the regularity properties (4.2) and (4.3) follows by [37, Theorem 7.9.8]. The proof is complete. $\square$

Theorem 4.2

Assume that $\mu _2\le \mu _1$ and (A1)–(A3) hold, then the dynamical system $(\mathcal {H},S(t))$ possesses a generalized exponential attractor representing ${\mathfrak {A}}_{\text {exp}}\subset \mathcal {H}$ with finite dimension in the extended space

$$\begin{aligned} \mathcal {H}_{-1}:=L^2(0,1)\times H^{-1}(0,1)\times L^2(0,1)\times H^{-1}(0,1)\times L^2((0,1)\times (0,1)), \end{aligned}$$

(4.4)

which is isomorphic to space $L^2(0,1)\times L^2(0,1)\times H^{-1}(0,1)\times H^{-1}(0,1)\times L^2((0,1)\times (0,1))$. In addition, from the interpolation theorem, for all $0<\delta < 1$ there exists a generalized fractal exponential attractor whose fractal dimension is finite in the extended space $\mathcal {H}_{-\delta }$, where

$$\begin{aligned} \mathcal {H}_0:=\mathcal {H},\quad \text {and}\quad \mathcal {H}\subset H_{-\delta }\subset \mathcal {H}_{-1}. \end{aligned}$$

(4.5)

Proof

Let $\Phi$ be the functional of Lyapunov considered in Lemma 3.1, let us take

$$\begin{aligned} {\mathfrak {B}}:=\{U;\ \Phi (U)\le R\}. \end{aligned}$$

(4.6)

It is clear that for R large enough, the set ${\mathfrak {B}}$ is absorbent and positively invariant, thus $(\mathcal {H},S(t))$ is quasi-stable on ${\mathfrak {B}}$. In another hand, for strong solutions U(t) with initial data $U_0\in {\mathfrak {B}}$, from (2.11) and the positive invariance of ${\mathfrak {B}}$, we get $C_{{\mathfrak {B}},T}>0$ such that for any $0\le t \le T$,

$$\begin{aligned} \Vert U_t(t)\Vert _{\mathcal {H}_{-1}} \le \Vert \mathcal A U(t)\Vert _{\mathcal {H}}+\Vert \mathcal F(U(t))\Vert _{\mathcal {H}}\le C_{{\mathfrak {B}},T}. \end{aligned}$$

(4.7)

Consequently,

$$\begin{aligned} \Vert S(t_1)U_0-S(t_2)U_0\Vert _{\mathcal {H}_{-1}}\le \int _{t_1}^{t_2}\Vert U_t(s)\Vert _{\mathcal {H}_{-1}}ds\le C_{{\mathfrak {B}}}|t_1-t_2|,\quad 0\le t_1\le t_2\le T.\nonumber \\ \end{aligned}$$

(4.8)

Therefore, the application $t\mapsto S(t)U_0$ is Hölder continuous on space extending $\mathcal {H}_{-1}$ with exponent $\delta =1$ for every $U_0\in {\mathfrak {B}}$. Thus, based on [37, Theorem 7.9.9] the system $(\mathcal {H},S(t))$ possesses a generalized exponential attractor with finite fractal dimension in generalized space $\widetilde{\mathcal {H}}_{-1}$.

Using an analogous argument to that found in [41, 42] we can show the existence of exponential attractor with finite fractal dimension in the generalized space $\mathcal {H}_{-\delta }$ with $\delta \in (0,1)$, thus concluding the proof of the Theorem 4.2. $\square$