Bifurcation Analysis for a Delayed Diffusive Logistic Population Model in the Advective Heterogeneous Environment

Abstract

In this paper, we investigate a delayed reaction–diffusion–advection equation, which models the population dynamics in the advective heterogeneous environment. The existence of the nonconstant positive steady state and associated Hopf bifurcation are obtained. A weighted inner product associated with the advection rate is introduced to compute the normal forms, which is the main difference between Hopf bifurcation for delayed reaction–diffusion–advection model and that for delayed reaction–diffusion model. Moreover, we find that the spatial scale and advection can affect Hopf bifurcation in the heterogenous environment.

1 Introduction

In recent decades, there are extensive works on the population dynamics in the advective environments. For example, the population may have a tendency towards better quality habitat, and Belgacem and Cosner [1] proposed the following model

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} =\nabla \cdot [d\nabla u-au\nabla m]+ u\left[ m(x)-u\right] ,&{}x\in \Omega ,\ t>0,\\ u(x,t)=0,&{} x\in \partial \Omega ,\ t>0,\\ \end{array}\right. } \end{aligned}$$

(1.1)

where a measures the tendency of the population to move up or down along the gradient of m(x). We refers to [4, 6, 10, 11, 31] and the references therein for results on this type of advection. Moreover, in streams and rivers, the unidirectional water flow always exists and can influence the population dynamics of the river species [30, 37,38,39]. Lou and Zhou [36] considered the following single species model,

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} =du_{xx}-\alpha u_x+ u\left( r-u\right) ,&{}0<x<L,\ t>0,\\ du_x(0,t)-\alpha u(0,t)=0,&{} t>0,\\ du_x(L,t)-\alpha u(L,t)=-b\alpha u(L,t), &{}t>0, \end{array}\right. } \end{aligned}$$

(1.2)

where u(x, t) denotes the population density at location x and time t, $d>0$ is the diffusion rate, $r>0$ represents the intrinsic growth rate, $x=0,L$ are the upstream end and downstream ends respectively, $\alpha$ accounts for the advection rate caused by the unidirectional water flow, and b measures the lose of the species at the downstream end. Equation (1.2) can also model the population dynamics of a species in a water column, where x runs from the top ($x=0$) to the bottom ($x=L$). Therefore, $\alpha$ may be positive or negative depending on whether the density of the species is heavier or lighter than the water [50]. If $b\rightarrow \infty$, the hostile boundary condition at the downstream is obtained, and Speirs and Gurney showed [42] that the species can persist only when the speed of the flow is slow and the stream is long. If $b=1$, the boundary condition is referred to as the free-flow boundary condition or the Danckwerts boundary condition, see [45] for detailed analysis on persistence. For more general case, Lou and Zhou [36] gave the necessary and sufficient condition for the persistence of the species with respect to b. We also refer to [33,34,35,36, 49,50,51,52] and the references therein for results on two competing species with this type of advection.

For reaction–diffusion equations without advection term, it is well-known that time delay can make the constant steady states or nonconstant steady states unstable, and spatial homogeneous or nonhomogeneous periodic solutions can occur through Hopf bifurcation, see [14, 16, 20, 24, 27, 32, 40] and the references therein. Especially, Busenberg and Huang [3] firstly studied the Hopf bifurcation near the nonconstant positive steady state, and they found that, for the following single population model,

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u(x,t)}{\partial t} =d\Delta u(x,t)+r u(x,t)\left( 1-u(x,t-\tau )\right) ,&{}x\in \Omega ,\ t>0,\\ u(x,t)=0,&{} x\in \partial \Omega ,\ t>0,\\ \end{array}\right. } \end{aligned}$$

(1.3)

time delay $\tau$ can induce Hopf bifurcation, see also [28, 43, 44, 47, 48] for some more general population models. We also refer to [8, 9, 21,22,23] for the Hopf bifurcation of models with the nonlocal delay effect and homogenous Dirichlet boundary conditions. A natural question is that whether delay can induce instability for reaction–diffusion–advection models. For model (1.1), considering the delay effect, Chen et al. [7] studied the following model

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} =\nabla \cdot [d\nabla u-au\nabla m]+ u\left( m(x)-u(x,t-\tau )\right) ,&{}x\in \Omega ,\ t>0,\\ u(x,t)=0,&{} x\in \partial \Omega ,\ t>0,\\ \end{array}\right. } \end{aligned}$$

(1.4)

and showed that Hopf bifurcation is more likely to occur when the advection rate increases.

In this paper, we mainly concern whether delay can induce Hopf bifurcation for model (1.2), and for simplicity we only consider the case of $b=0$. Actually, we investigate the following model for a single species in the advective heterogeneous enviroment

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t =du_{xx}-\alpha u_x+ u\left( m(x)-\int _0^LK(x,y)u(y,t-\tau )dy\right) ,&{}0<x<L,\ t>0,\\ du_x(0,t)-\alpha u(0,t)=0,\;du_x(L,t)-\alpha u(L,t)=0,&{} t>0,\\ \end{array}\right. } \end{aligned}$$

(1.5)

where parameters d, $\alpha$ and L have the same meanings as that in model (1.2), delay $\tau$ represents the maturation time, and intrinsic growth rate m(x) is spatially dependent and show the effect of the heterogenous environment. Here K(x, y) accounts for the nonlocality of the species. We remark that this kind of nonlocal effect is not induced by the time delay, and it represents the nonlocal interspecific competition of the species for resources. The individuals at different locations may compete for common resource or communicate either visually or by chemical means, see [2, 19] for the detailed biological explaination. Throughout the paper, unless otherwise specified, we assume that m(x) satisfies:

$\mathbf {(A_1)}$:

$m(x)\in L^\infty ((0,L))$, and $m(x)>0$ on (0, L),

and the following assumption is imposed on the kernel function K(x, y):

$(\mathbf {A_2})$:

either

$$\begin{aligned} K(x,y)=\delta (x-y), \end{aligned}$$

or

$$\begin{aligned} ~K(x,y)\in L^\infty ((0,L)\times (0,L)), \;\;K(x,y)\ge 0 \;\text {on}\;(0,L)\times (0,L), \end{aligned}$$

and $L_+:=\{(x,y)\in (0,L)\times (0,L):K(x,y)>0\}$ has positive Lebesgue measure.

For example, the following kernel function

$$\begin{aligned} K(x,y)={\left\{ \begin{array}{ll} 0,\;\;y>x\\ 1,\;\;0<y\le x\\ \end{array}\right. } \end{aligned}$$

(1.6)

satisfies assumption $(\mathbf {A_2})$, and was used to model the nonlocal competition of the phytoplankton for light [13, 29]. Moreover, if $K(x,y)=\delta (x-y)$, then

$$\begin{aligned} \int _0^LK(x,y)u(y,t-\tau )dy=u(x,t-\tau ), \end{aligned}$$

and there is no nonlocal effect.

For the case that advection $\alpha =0$ and $K(x,y)=\delta (x-y)$, Shi et al. [41] showed that delay can induce Hopf bifurcation for model (1.5). Our main results extend the results of [3, 41], and show that Hopf bifurcation can also occur at the nonconstant positive steady state when $\alpha \ne 0$. Moreover, we will show that if m(x) is spatially dependent, then the spatial scale and advection can affect Hopf bifurcation. For example, Hopf bifurcation can be more likely to occur when the advection rate increases or decreases for different types of m(x). This phenomenon is different from that for model (1.4), where Hopf bifurcation is more likely to occur when the advection rate increases. We point out that, since the boundary condition is different, the method and arguments in [8] should be modified to investigate this model.

Letting $\tilde{u}=e^{(-\alpha /d)x}u$, $\tilde{t}=d t$, denoting $\tilde{r}=1/d$, $\tilde{\alpha }=a/d$, $\tilde{\tau }=d\tau$, and dropping the tilde sign, model (1.5) can be transformed as the following equivalent model:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=e^{-\alpha x}\left( e^{\alpha x} u_x\right) _x+ r u\left( m(x)-\int _0^L K(x,y)e^{\alpha y}u(y,t-\tau )dy\right) ,\;\;x\in (0,L),\ t>0,\\ u_x(0,t)=u_x(L,t)=0,\;\;t>0.\\ \end{array}\right. } \end{aligned}$$

(1.7)

The initial value of model (1.7) is

$$\begin{aligned} u(x,s)=\eta (x,s)\ge 0,\;\;\;\; x\in (0,L),\ s\in [-\tau ,0], \end{aligned}$$

(1.8)

where $\eta \in C:=C([-\tau ,0],Y)$ and $Y=L^2((0,L))$. Note that $e^{-\alpha x}\frac{\partial }{\partial x}\left( e^{\alpha x} \frac{\partial }{\partial x}\right)$ generates an analytic semigroup T(t) on Y with the domain

$$\begin{aligned} \mathscr {D} \left( e^{-\alpha x}\frac{\partial }{\partial x}\left( e^{\alpha x} \frac{\partial }{\partial x}\right) \right) = \{\psi \in H^2((0,L)):\psi _x(0)=\psi _x(L)=0\}. \end{aligned}$$

(1.9)

Define $F:C\rightarrow Y$ by

$$\begin{aligned} F(\Psi )(x)=r \Psi (0)\left( m(x)-\int _0^LK(x,y)e^{\alpha y}\Psi (-\tau )(y)dy\right) . \end{aligned}$$

(1.10)

An easy calculation implies that F is locally Lipschitz continuous. Therefore, it follows from [46] that, for each $\Psi \in C$, there exists a maximum $t_{\Psi }>0$ such that model (1.7) has a unique solution $u_{\Psi }(t)$ existing on $[-\tau ,t_{\Psi })$. The following eigenvalue problem is crucial for our further investigation

$$\begin{aligned} {\left\{ \begin{array}{ll} -e^{-\alpha x}\left( e^{\alpha x}\phi _x\right) _x=\lambda m(x) \phi (x),\;\;x\in (0,L),\\ \phi _x(0)=\phi _x(L)=0. \end{array}\right. } \end{aligned}$$

(1.11)

We say that $\lambda$ is a principle eigenvalue if (1.11) has a positive solution. Denote by $\lambda _1$ the principal eigenvalue of problem (1.11), and let $\phi$ be the corresponding eigenfunction with respect to $\lambda _1$ such that $\phi (x)>0$. It follows from [36] that

$$\begin{aligned} \lambda _1=\inf _{0\ne \psi \in W^{1,2}}\displaystyle \frac{\int _0^L e^{\alpha x}\psi _x^2dx}{\int _0^Le^{\alpha x}m(x)\psi ^2dx}=0, \end{aligned}$$

(1.12)

$\phi$ is constant, and we choose $\phi \equiv 1$ for simplicity.

The rest of the paper is organized as follows. In Sect. 2, we show the existence of a nonconstant positive steady state through bifurcation theory, and the Hopf bifurcation near this nonconstant positive steady state is also investigated. In Sect. 3, we obtain the direction of the Hopf bifurcation and the stability of the bifurcating periodic orbits. In Sect. 4, the effect of spatial heterogeneity are obtained, and the spatial scale and advection can affect Hopf bifurcation in the heterogenous environment. Moreover, some numerical simulations are given to illustrate our theoretical results. Especially, Eq. (1.5) can model the population dynamics for a species in a water column with nonlocal competition for light. We numerically show that when advection rate $\alpha =0$, the density of the species concentrates on the top of the water column. However when $\alpha$ is large, the density of the species concentrates on the bottom of the water column.

For simplicity of the notations, as in [8], we also denote the spaces

$$\begin{aligned} X=\{\psi \in H^2((0,L)):\psi _x(0)=\psi _x(L)=0\}, \end{aligned}$$

$Y=L^2((0,L))$, $C=C([-\tau ,0],Y)$, and $\mathcal {C}=C([-1,0],Y)$ throughout the paper. Let the complexification of a linear space Z be $Z_\mathbb {C}:= Z\oplus iZ=\{x_1+ix_2|~x_1,x_2\in Z\}$, and define the domain of a linear operator T by $\mathscr {D}(T)$, the kernel of T by $\mathscr {N}(T)$, and the range of T by $\mathscr {R}(T)$. Moreover, for Hilbert space $Y_{\mathbb {C}}$, the standard inner product is $\langle u,v \rangle =\displaystyle \int _{0}^L \overline{u}(x) {v}(x) dx$.

2 Stability and Hopf Bifurcation

2.1 Positive Steady States and Eigenvalue Problem

Firstly, we show the existence of positive steady states of Eq. (1.7), which satisfy

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( e^{\alpha x}u_x\right) _x+r e^{\alpha x}u\left( m(x)-\int _0^LK(x,y)e^{\alpha y}u(y)dy\right) =0, &{} x\in (0,L),\\ u_x(0)=u_x(L)=0. \end{array}\right. } \end{aligned}$$

(2.1)

Denote

$$\begin{aligned} P_0:=\frac{\partial }{\partial x}\left( e^{\alpha x} \frac{\partial }{\partial x}\right) . \end{aligned}$$

(2.2)

Then

$$\begin{aligned} X = \mathscr {N}\left( P_0\right) \oplus X_1,\;\; Y = \mathscr {N}\left( P_0\right) \oplus Y_1, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \mathscr {N}\left( P_0\right)&=\text {span}\{\phi \}=\text {span}\{1\},\;\; X_1=\left\{ y\in X:\int _{0}^L y(x)dx=0\right\} ,\\ Y_1&=\mathscr {R}\left( P_0\right) =\left\{ y\in Y:\int _{0}^L y(x)dx=0\right\} . \end{aligned} \end{aligned}$$

(2.3)

By the arguments similar to Theorem A.2. of [5], we obtain the existence of positive steady states in the following.

Theorem 2.1

There exist $r_1>0$ and a continuously differentiable mapping $r\mapsto u_r$ from $[0,r_1]$ to X such that $u_r$ is a positive solution of Eq. (2.1) for $r\in (0,r_1]$, and $u_0=c_0$, where

$$\begin{aligned} c_0=\displaystyle \frac{\int _0^L m(x) e^{\alpha x}dx}{\int _0^L\int _0^L K(x,y) e^{\alpha x+\alpha y}dxdy}>0. \end{aligned}$$

(2.4)

Proof

It follows from assumptions $(\mathbf {A_1})$ and $(\mathbf {A_2})$ that $c_0>0$. Define $H: \mathbb {R}\times X_1\times \mathbb {R}\rightarrow Y$ by

$$\begin{aligned} H(c,w,r)=P_0w+re^{\alpha x}(c+w)\left( m(x)-\int _0^L K(x,y)e^{\alpha y}(c+w(y))dy\right) . \end{aligned}$$

Letting

$$\begin{aligned} u= c+w,\;\; c\in \mathbb {R},\;w\in X_1, \end{aligned}$$

(2.5)

and substituting it into Eq. (2.1), we see that (u, r) solves Eq. (2.1), where $u\in X$, $r>0$, if and only if $H(c,w,r)=0$ is solvable for some value of $c\in \mathbb {R}$, $w\in X_1$ and $r>0$. Note that $H(c,0,0)=0$ for any $c\in \mathbb {R}$. An easy calculation implies that

$$\begin{aligned} \begin{aligned} D_{(w,r)}H(c,w,r)[v,\sigma ]=&P_0v+rm(x)e^{\alpha x} v-re^{\alpha x}(c+w)\int _0^LK(x,y)e^{\alpha y}v(y)dy\\&-re^{\alpha x}v\int _0^L K(x,y)e^{\alpha y}(c+w(y))dy\\&+\sigma e^{\alpha x}(c+w)\left( m(x)-\int _0^LK(x,y)e^{\alpha y}(c+w(y))dy\right) . \end{aligned} \end{aligned}$$

Here $D_{(w,r)}H(c,w,r)$ is the Fréchet derivative of H(c, w, r) with respect to (w, r). Then,

$$\begin{aligned} D_{(w,r)}H(c,0,0)[v,\sigma ]=P_0 v+\sigma ce^{\alpha x}\left( m(x)-c\int _0^L K(x,y) e^{\alpha y}dy\right) . \end{aligned}$$

Since

$$\begin{aligned} -c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y) e^{\alpha y}dy\right) \in Y_1=\mathscr {R}\left( P_0\right) , \end{aligned}$$

there exists a unique $v^*\in X_1$ such that

$$\begin{aligned} P_0v^*=-c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y) e^{\alpha y}dy\right) , \end{aligned}$$

and consequently,

$$\begin{aligned} \mathscr {N}( D_{(w,r)}H(c_0,0,0))=\{(sv^*,s):s\in \mathbb {R}\}. \end{aligned}$$

A direct computation yields

$$\begin{aligned} D_cD_{(w,r)}H(c_0,0,0)[v^*,1]=m(x)e^{\alpha x}-2c_0 e^{\alpha x}\int _0^L K(x,y)e^{\alpha y}dy, \end{aligned}$$

where $D_cD_{(w,r)}H(c_0,0,0)$ is the Fréchet derivative of $D_{(w,r)}H(c,w,r)$ with respect to c at $(c_0,0,0)$. We claim that

$$\begin{aligned} D_cD_{(w,r)}H(c_0,0,0)[v^*,1]\not \in \mathscr {R}\left( D_{(w,r)}H(c_0,0,0)\right) . \end{aligned}$$

(2.6)

Suppose it is not true. Then, there exists $(\tilde{v},\tilde{\sigma })$ such that

$$\begin{aligned} \begin{aligned} D_{(w,r)}H(c_0,0,0)[\tilde{v},\tilde{\sigma }]&=P_0 \tilde{v}+\tilde{\sigma } c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y) e^{\alpha y}dy\right) \\&=m(x)e^{\alpha x}-2c_0 e^{\alpha x}\int _0^L K(x,y)e^{\alpha y}dy, \end{aligned} \end{aligned}$$

(2.7)

which implies that

$$\begin{aligned} m(x)e^{\alpha x}-2c_0 e^{\alpha x}\int _0^L K(x,y)e^{\alpha y}dy\in \mathscr {R}(P_0). \end{aligned}$$

This contradicts the fact that

$$\begin{aligned} \int _0^Lm(x)e^{\alpha x}dx-2c_0\int _0^L\int _0^LK(x,y)e^{\alpha x+\alpha y}dxdy=-\int _0^L m(x)e^{\alpha x}dx\ne 0. \end{aligned}$$

Therefore, Eq. (2.6) holds, and it follows from the Crandall–Rabinowitz bifurcation theorem [12] that the solutions of $H(c,w,r)=0$ near $(c_0,0,0)$ consist precisely by the curves $\{(c,0,0):c\in \mathbb {R}\}$ and

$$\begin{aligned} \{(c(s),w(s),r(s)): s\in (-\delta ,\delta )\}, \end{aligned}$$

where (c(s), w(s), r(s)) are continuously differentiable, $c(0)=c_0$, $w(0)=0$, $r(0)=0$, $w'(0)=v^*$, and $r'(0)=1$. Since $r'(0)=1>0$, r(s) has a inverse function s(r) for small s. Noticing that $c_0>0$, we see that there exists $r_1>0$ such that Eq. (2.1) has a positive solution $u_r=c(s(r))+w(s(r))$ for $r\in (0,r_1]$. Moreover,

$$\begin{aligned} u_0=c(s(0))+w(s(0))=c(0)+w(0)=c_0. \end{aligned}$$

This completes the proof. $\square$

Remark 2.2

It follows from the imbedding theorem that $u_r\in C^{1+\delta }([0,L])$ for some $\delta \in (0,1)$, and $\lim _{r\rightarrow 0} u_r=c_0$ in $C^{1+\delta }([0,L])$.

Then, we obtain the eigenvalue problem associated with $u_r$. The linearized equation of (1.7) at $u_r$ takes the following form

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \frac{\partial v}{\partial t} = e^{-\alpha x}P_0v+ r \left( m(x)-\int _0^L K(x,y) e^{\alpha y}u_r(y)dy\right) v\\ ~~~~-r u_r\int _0^L K(x,y)e^{\alpha y} v(y,t-\tau )dy,&{} x\in (0,L),\; t>0,\\ v_x(x,t)=0,&{}x=0,L,\; t>0. \end{array}\right. } \end{aligned}$$

(2.8)

Denote

$$\begin{aligned} \tilde{K}(r):= m(x)-\int _0^L K(x,y) e^{\alpha y}u_{r}(y)dy. \end{aligned}$$

(2.9)

From [46], we see that the solution semigroup of Eq. (2.8) has the infinitesimal generator $A_\tau (r)$ defined by

$$\begin{aligned} A_\tau (r) \Psi =\dot{\Psi }\end{aligned}$$

(2.10)

with the domain

$$\begin{aligned}\begin{aligned}&\mathscr {D}(A_\tau (r)) = \big \{\Psi \in C_\mathbb {C} \cap C^1_\mathbb {C}:\ \Psi (0)\in X_{\mathbb {C}},\dot{\Psi }(0) =e^{-\alpha x}P_0\Psi (0)+r\tilde{K}(r)\Psi (0)\\&\qquad -r u_r\int _0^L K(x,y)e^{\alpha y} \Psi (-\tau )(y)dy \big \}, \end{aligned}\end{aligned}$$

where $C^1_\mathbb {C}=C^1([-\tau ,0],Y_\mathbb {C})$, $P_0$ and $\tilde{K}(r)$ are defined as in Eqs. (2.2) and (2.9) respectively. Moreover, $\mu \in \mathbb {C}$ is an eigenvalue of $A_\tau (r)$, if and only if there exists $\psi (\ne 0)\in X_{\mathbb {C}}$ such that $\Delta (r,\mu ,\tau )\psi =0$, where

$$\begin{aligned} \begin{aligned}&\Delta (r,\mu ,\tau )\psi :=e^{-\alpha x}P_0\psi +r \tilde{K}(r)\psi -r u_r\int _0^L K(x,y)e^{\alpha y} \psi (y)dy e^{-\mu \tau }-\mu \psi . \end{aligned} \end{aligned}$$

(2.11)

Then $A_\tau (r)$ has a purely imaginary eigenvalue $\mu =i\nu \ (\nu >0)$ for some $\tau \ge 0$, if and only if

$$\begin{aligned} \begin{aligned}&P_0\psi +r e^{\alpha x}\tilde{K}(r)\psi -r u_re^{\alpha x}\int _0^L K(x,y)e^{\alpha y} \psi (y)dy e^{-i\theta }-i\nu e^{\alpha x}\psi =0 \end{aligned} \end{aligned}$$

(2.12)

is solvable for some value of $\nu >0$, $\theta \in [0,2\pi )$, and $\psi (\ne 0)\in X_{\mathbb {C}}$. The estimates for solutions of Eq. (2.11) can be derived as follows.

Lemma 2.3

Assume that $(\mu _r,\tau _r,\psi _r)$ solves $\Delta (r,\mu ,\tau )\psi =0$ with ${\mathcal Re}\mu _r,\tau _{r}\ge 0$ and $0\ne \psi _r \in X_{\mathbb {C}}$. Then $\left| \displaystyle \frac{\mu _r}{r}\right|$ is bounded for $r\in (0,r_1]$.

Proof

Noticing that $u_{r}$ is the principal eigenfunction of $P_0+re^{\alpha x}\tilde{K}(r)$ with principal eigenvalue 0, we have $\langle \psi , P_0\psi +re^{\alpha x}\tilde{K}(r)\psi \rangle \le 0$ for any $\psi \in X_{\mathbb {C}}$. Substituting $(\mu _r,\tau _r,\psi _r)$ into $\Delta (r,\mu ,\tau )\psi =0$, multiplying it by $e^{\alpha x}\overline{\psi }_r$, and integrating the result over (0, L), we have

$$\begin{aligned} \begin{aligned}&\langle \psi _{r}, P_0\psi _{r}+re^{\alpha x}\tilde{K}(r)\psi _{r}\rangle \\&\quad =r \int _0^L\int _0^L K(x,y)e^{\alpha x+\alpha y}u_r(x)\overline{\psi _{r}}(x)\psi _{r}(y)dxdye^{-\mu _r\tau _r}+\mu _{r}\int _0^L e^{\alpha x}|\psi _{r}|^2dx. \end{aligned} \end{aligned}$$

(2.13)

Since ${\mathcal Re}\mu _r,\tau _{r}\ge 0$, we see that

$$\begin{aligned} \begin{aligned} 0\le {\mathcal Re}(\mu _{r}/r)\le&\displaystyle \frac{1}{\int _0^L e^{\alpha x} |\psi _{r}|^2dx}{\mathcal Re}\left[ -\int _0^L\int _0^L K(x,y)e^{\alpha x+\alpha y}u_r(x)\overline{\psi _{r}}(x)\psi _{r}(y)dxdye^{-\mu _r\tau _r}\right] \\ \le&\Vert u_r\Vert _\infty \Vert K(x,y)\Vert _\infty \int _0^Le^{\alpha x}dx, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |\mathcal {I}m (\mu _{r}/r)|=&\displaystyle \frac{1}{\int _0^L e^{\alpha x}|\psi _{r}|^2dx}\left| \mathcal {I}m\left[ \int _0^L\int _0^L K(x,y)e^{\alpha x+\alpha y}u_r(x)\overline{\psi _{r}}(x)\psi _{r}(y)dxdye^{-\mu _r\tau _r}\right] \right| \\ \le&\Vert u_r\Vert _\infty \Vert K(x,y)\Vert _\infty \int _0^Le^{\alpha x}dx. \end{aligned} \end{aligned}$$

It follows from the continuity of $r\mapsto \Vert u_r\Vert _\infty$ that $\displaystyle \left| \frac{\mu _r}{r}\right|$ is bounded for $r\in (0,r_1]$. $\square$

The following result is similar to Lemma 2.3 of [3] and we omit the proof here.

Lemma 2.4

Assume that $z\in (X_1)_{\mathbb {C}}$. Then $| \langle P_0z,z\rangle |\ge \lambda _2\Vert z\Vert ^2_{Y_{\mathbb {C}}}$, where $\lambda _2$ is the second eigenvalue of operator $-P_0$.

For $r\in (0,r_1]$, ignoring a scalar factor, $\psi$ in Eq. (2.12) can be represented as

$$\begin{aligned} \begin{aligned}&\psi = \beta c_0+r z,\;\;\; z\in (X_1)_{\mathbb {C}},\; \; \beta \ge 0, \\&\Vert \psi \Vert ^2_{Y_{\mathbb {C}}}=\beta ^2 c_0^2L +r^2\Vert z\Vert ^2_{Y_{\mathbb {C}}}= c_0^2L, \end{aligned} \end{aligned}$$

(2.14)

where $c_0$ is defined as in Eq. (2.4). Then, substituting the first Equation of (2.14) and $\nu =rh$ into Eq. (2.12), we obtain that $(\nu ,\theta ,\psi )$ solves Eq. (2.12), where $\nu >0$, $\theta \in [0,2\pi )$ and $\psi \in X_{\mathbb {C}}(\Vert \psi \Vert ^2_{Y_{\mathbb {C}}}= c_0^2L)$, if and only if the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} g_1(z,\beta ,h,\theta ,r):=P_0z+e^{\alpha x}\tilde{K}(r) (\beta c_0+rz)-ihe^{\alpha x}(\beta c_0+rz)\\ ~~~~~~~~~~~~~~~~~~~-e^{\alpha x}u_r\int _0^L K(x,y)e^{\alpha y}(\beta c_0+rz(y))dy e^{-i\theta }=0\\ g_2(z,\beta ,r):=(\beta ^2-1)c_0^2L+r^2\Vert z\Vert ^2_{Y_{\mathbb {C}}}=0 \end{array}\right. } \end{aligned}$$

(2.15)

has a solution $(z,\beta ,h,\theta )$, where $z\in (X_1)_{\mathbb {C}}$, $\beta \ge 0$, $h>0$ and $\theta \in [0,2\pi )$. Define $G:(X_1)_{\mathbb {C}}\times \mathbb {R}^4\rightarrow Y_{\mathbb {C}}\times \mathbb {R}$ by $G=(g_1,g_2)$. Note that $u_0=c_0$, and we first show that $G(z,\beta ,h,\theta ,r)=0$ is uniquely solvable for $r=0$.

Lemma 2.5

The following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} G(z,\beta ,h,\theta ,0)=0\\ z\in (X_1)_{\mathbb {C}},\;h\ge 0,\;\beta \ge 0,\; \theta \in [0,2\pi ]\\ \end{array}\right. } \end{aligned}$$

(2.16)

has a unique solution $(z_{0},\beta _{0},h_{0},\theta _{0})$, where

$$\begin{aligned} \beta _{0}=1,\;\;\theta _{0}=\pi /2,\;\;h_{0}=\displaystyle \frac{\int _0^L m(x)e^{\alpha x}dx}{\int _0^L e^{\alpha x}dx}, \end{aligned}$$

(2.17)

and $z_{0}\in (X_1)_{\mathbb {C}}$ is the unique solution of

$$\begin{aligned} P_0 z=-c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y)e^{\alpha y}dy\right) -ic_0^2 e^{\alpha x}\int _0^L K(x,y)e^{\alpha y}dy+ih_0c_0 e^{\alpha x}. \end{aligned}$$

(2.18)

Proof

Obviously, $g_2(z,\beta ,0)=0$ if and only if $\beta =\beta _{0}=1$. Then, substituting $\beta =\beta _0$ into $g_1(z,\beta ,h,\theta ,0)=0$, we have

$$\begin{aligned} P_0z=-c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y)e^{\alpha y}dy\right) +c_0^2 e^{\alpha x}\int _0^L K(x,y)e^{\alpha y}dy e^{-i\theta }+ihc_0e^{\alpha x}. \end{aligned}$$

(2.19)

It follows from Eq. (2.4) that

$$\begin{aligned} c_0\int _0^L\int _0^L K(x,y) e^{\alpha x+\alpha y }dxdy=\int _0^L m(x)e^{\alpha x}dx. \end{aligned}$$

Then Eq. (2.19) has a solution $(z,h,\theta )$, where $z\in (X_1)_{\mathbb {C}}$, $h\ge 0$, $\theta \in [0,2\pi ]$, if and only if

$$\begin{aligned} {\left\{ \begin{array}{ll} c_0\int _0^L\int _0^L K(x,y) e^{\alpha x+\alpha y }dxdy\sin \theta =h\int _0^L e^{\alpha x}dx\\ \int _0^L K(x,y) e^{\alpha x+\alpha y}dxdy\cos \theta =0\\ \end{array}\right. } \end{aligned}$$

(2.20)

has a solution $(\theta ,h)$ with $h\ge 0$ and $\theta \in [0,2\pi ]$, which yields

$$\begin{aligned} \theta =\theta _{0}=\pi /2,\;\;h=h_{0}=\displaystyle \frac{\int _0^L m(x)e^{\alpha x}dx}{\int _0^L e^{\alpha x}dx}. \end{aligned}$$

(2.21)

Substituting $h=h_0$ and $\theta =\theta _0$ into Eq. (2.19), we see that the right side of Eq. (2.19) belongs to $\mathscr {R}\left( P_0\right)$, which implies that $z=z_0$. $\square$

Then, we show that $G(z,\beta ,h,\theta ,r)=0$ is also uniquely solvable for small r.

Theorem 2.6

There exist $r_2>0$ and a continuously differentiable mapping $r\mapsto (z_r,\beta _r,h_r,\theta _r)$ from $[0,r_2]$ to $(X_1)_{\mathbb {C}}\times \mathbb {R}^3$ such that $(z_r,\beta _r,h_r,\theta _r)$ is the unique solution of the following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} G(z,\beta ,h,\theta ,r)=0,\\ z\in (X_1)_{\mathbb {C}},\;h>0,\;\beta \ge 0, \;\theta \in [0,2\pi ),\\ \end{array}\right. } \end{aligned}$$

(2.22)

for $r\in [0,r_2]$.

Proof

Denote the Fréchet derivative of G with respect to $(z,\beta ,h,\theta )$ at $(z_{0},\beta _{0},h_{0},\theta _{0},0)$ by $T=(T_1,T_2):(X_1)_{\mathbb {C}}\times \mathbb {R}^3\mapsto Y_{\mathbb {C}}\times \mathbb {R}$. Then, a direct calculation leads to

$$\begin{aligned} \begin{aligned} T_1(\chi ,\kappa ,\epsilon ,\vartheta )=&P_0\chi +\kappa c_0 e^{\alpha x}\left[ m(x)-c_0\int _0^L K(x,y)e^{\alpha y}dy\right] +i\kappa c_0^2 e^{\alpha x}\int _0^LK(x,y)e^{\alpha y}dy\\&-ic_0h_0\kappa e^{\alpha x}+\vartheta c_0^2e^{\alpha x}\int _0^LK(x,y)e^{\alpha y}dy-i\epsilon c_0e^{\alpha x},\\ T_2(\kappa )=&2\kappa c_0^2L. \end{aligned} \end{aligned}$$

Obviously, T is a bijection from $(X_1)_{\mathbb {C}}\times \mathbb {R}^3$ to $Y_{\mathbb {C}}\times \mathbb {R}$. It follows from the implicit function theorem that there exist $r_2>0$ and a continuously differentiable mapping $r\mapsto (z_r,\beta _r,h_r,\theta _r)$ from $[0,r_2]$ to $X_{\mathbb {C}}\times \mathbb {R}^3$ such that $G(z_r,\beta _r,h_r,\theta _r,r)=0$. Now, we show the uniqueness, and only need to prove that if $z^r\in (X_1)_{\mathbb {C}}$, $\beta ^{r}\ge 0$, $h^{r}>0$, $\theta ^{r}\in [0,2\pi )$ satisfy $G(z^r,\beta ^r,h^r,\theta ^r,r)=0$, then $(z^r,\beta ^r,h^r,\theta ^r)\rightarrow (z_{0},\beta _0,h_0,\theta _0)$ as $r\rightarrow 0$ in $X_{\mathbb {C}}\times \mathbb {R}^3.$ From Lemma 2.3 and Eq. (2.15), we obtain that $\{h^r\}, \{\beta ^r\}$ and $\{\theta ^r\}$ are bounded for $r\in [0,r_1]$. Multiplying the first equation of (2.15) by $\overline{z^r}$, and integrating the result over (0, L), we obtain that there exist positive constants $M_1$ and $M_2$ such that $\lambda _2\Vert z^r\Vert ^2_{Y_{\mathbb {C}}}\le | \langle z^r,P_0z^r\rangle |\le M_1\Vert z^r\Vert _{Y_{\mathbb {C}}}+ M_2r\Vert z^r\Vert ^2_{Y_{\mathbb {C}}}$ for $r\in (0,r_2]$, where $\lambda _2$ is defined as in Lemma 2.4. Then, for sufficiently small $r_2$, $\{z^r\}$ is bounded in $Y_{\mathbb {C}}$ for $r\in [0,r_2]$. Note that $P_0:(X_1)_{\mathbb {C}}\rightarrow (Y_1)_{\mathbb {C}}$ has a bounded inverse $P_0^{-1}$. Then, $\{z^r\}$ is also bounded in $(X_1)_{\mathbb {C}}$, and $\{(z^r,\beta ^r,h^r,\theta ^r): r\in (0,r_2]\}$ is precompact in $Y_{\mathbb {C}}\times \mathbb {R}^3.$ Therefore, there exists a subsequence $\{(z^{r^n},\beta ^{r^n},h^{r^n},\theta ^{r^n})\}_{n=1}^\infty$ such that

$$\begin{aligned} (z^{r^n},\beta ^{r^n},h^{r^n},\theta ^{r^n}) \rightarrow (z^{0},\beta ^{0},h^{0},\theta ^{0})\;\;\text {in}\;\;Y_{\mathbb {C}}\times \mathbb {R}^3, \end{aligned}$$

and $r^n\rightarrow 0$ as $n\rightarrow \infty$. Taking the limit of the equation

$$\begin{aligned} P_0^{-1}g_1(z^{r^n},\beta ^{r^n},h^{r^n},\theta ^{r^n},r^n)=0 \end{aligned}$$

as $n\rightarrow \infty$, we see that

$$\begin{aligned} (z^{r^n},\beta ^{r^n},h^{r^n},\theta ^{r^n}) \rightarrow (z^{0},\beta ^{0},h^{0},\theta ^{0})\;\;\text {in}\;\;X_{\mathbb {C}}\times \mathbb {R}^3, \end{aligned}$$

as $n\rightarrow \infty$, and $(z^{0},r^{0},h^{0},\theta ^{0})$ is also a solution of Eq. (2.16), which leads to

$$\begin{aligned} (z^{0},r^{0},h^{0},\theta ^{0})=(z_{0},\beta _{0},h_{0},\theta _{0}). \end{aligned}$$

This completes the proof. $\square$

Finally, from Theorem 2.6, we derive the following result.

Theorem 2.7

For $r\in (0,r_2],$$(\nu ,\tau ,\psi )$ solves

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta (r,i\nu ,\tau )\psi =0,\\ \nu >0,\;\tau \ge 0,\;\psi (\ne 0) \in X_{\mathbb {C}},\\ \end{array}\right. } \end{aligned}$$

if and only if

$$\begin{aligned} \nu =\nu _r=rh_r,\;\psi = a\psi _r,\; \tau =\tau _{n}=\frac{\theta _r+2n\pi }{\nu _r},\;\; n=0,1,2,\cdots , \end{aligned}$$

(2.23)

where $\psi _r=\beta _rc_0+rz_r$, a is a nonzero constant, and $(z_r,\beta _r,h_r,\theta _r)$ is defined as in Theorem 2.6.

2.2 Distribution of the Eigenvalues and Hopf Bifurcation

In this subsection, we will show the distribution of the eigenvalues of $A_\tau (r)$ and the existence of the Hopf bifurcation for model (1.7). Throughout this subsection, unless otherwise specified, we always assume $r\in (0,r_2]$, and the value of $r_2$ may be chosen smaller than the one in Theorem 2.6, since further perturbation arguments are used. Firstly, we show the distribution of the eigenvalues of $A_\tau (r)$ for $\tau =0$.

Theorem 2.8

For $r\in (0,r_2],$ all the eigenvalues of $A_{\tau }(r)$ have negative real parts when $\tau =0$.

Proof

To the contrary, there exists a sequence $\{r^n\}_{n=1}^\infty$ such that $\displaystyle \lim _{n\rightarrow \infty }r^n=0$, and for $n\ge 1$, $r^n>0$, and corresponding eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} P_0\psi +r^ne^{\alpha x}\tilde{K}(r^n)\psi -r^ne^{\alpha x} u_{r^n}\int _0^L K(x,y)e^{\alpha y} \psi (y)dy=\mu e^{\alpha x}\psi ,\;\;x\in (0,L)\\ \psi _x(0)=\psi _x(L)=0 \end{array}\right. } \end{aligned}$$

(2.24)

has an eigenvalue $\mu _{r^n}$ with ${\mathcal Re}\mu _{r^n}\ge 0$, where $P_0$ and $\tilde{K}(r)$ are defined as in Eqs. (2.2) and (2.9) respectively. Ignoring a scalar factor, we assume that the associated eigenfunction $\psi _{r^n}$ with respect to $\mu _{r^n}$ satisfies $\Vert \psi _{r^n}\Vert ^2_{Y_{\mathbb {C}}}=c_0^2L$, and $\psi _{r^n}$ can be represented as $\psi _{r^n}=\beta _{r^n}c_0+r^nz_{r^n}$, where $\beta _{r^n}\ge 0$, $z_{r_n}\in (X_1)_{\mathbb {C}}$ and $c_0$ is defined as in Eq. (2.4). As in Sect. 2.1, $\mu _{r^n}$ can also be represented as $\mu _{r^n}=r^n h_{r^n}$, and it follows from Lemma 2.3 that $\left| h_{r^n}\right|$ is bounded for $r\in [0,r_2]$. Then, substituting $\psi =\psi _{r^n}=\beta _{r^n}c_0+r^nz_{r^n}$ and $\mu =r^n h_{r^n}$ into the first equation of Eq. (2.24), we see that $(z_{r^n},\beta _{r^n},h_{r^n})$ satisfies the following system

$$\begin{aligned} \begin{aligned}&H_1(z,\beta ,h,r_n): =P_0 z+e^{\alpha x}\tilde{K}(r^n)(\beta c_0+r^nz)\\&\quad -e^{\alpha x}u_{r^n}\int _0^L K(x,y)e^{\alpha y}[\beta c_0+r^nz(y)]dy-he^{\alpha x}(\beta c_0+r^nz)=0,\\&H_2(z,\beta ,r_n)=(\beta ^2-1)c_0^2L+(r^n)^2\Vert z\Vert ^2_{Y_{\mathbb {C}}}=0. \end{aligned} \end{aligned}$$

(2.25)

Using the arguments similar to Theorem 2.6, we see that $(z_{r^n},\beta _{r^n},h_{r^n})$ is bounded in $Y_{\mathbb {C}}\times \mathbb {R}\times \mathbb {C}$. Since the operator $P_0:(X_1)_{\mathbb {C}}\mapsto (Y_1)_{\mathbb {C}}$ has a bounded inverse $P_0^{-1}$, by applying $P_0^{-1}$ on

$$\begin{aligned} H_1(z_{r^n},\beta _{r^n},h_{r^n},r^n)=0, \end{aligned}$$

we find that $\{z_{r^n}\}_{n=1}^\infty$ is also bounded in $(X_1)_{\mathbb {C}}$, and consequently $\{(z_{r^n},\beta _{r^n},h_{r^n})\}_{n=1}^\infty$ is precompact in $Y_{\mathbb {C}}\times \mathbb {R}\times \mathbb {C}$. Therefore, there is a subsequence $\{(z_{r^{n_k}},\beta _{r^{n_k}},h_{r^{n_k}})\}_{k=1}^\infty$ convergent to $(z^{*},\beta ^{*},h^*)$ as $k\rightarrow \infty$ in the norm of $Y_{\mathbb {C}}\times \mathbb {R}\times \mathbb {C}$, where $\beta ^*=1$, $z^*\in Y_{\mathbb {C}}$ and $h^{*}\in \mathbb {C}$ with ${\mathcal Re}h^*\ge 0$. Taking the limit of the equation

$$\begin{aligned} P_0^{-1}H_1(z_{r^{n_k}},\beta _{r^{n_k}},h_{r^{n_k}})=0 \end{aligned}$$

as $k\rightarrow \infty$, we see that $z^*\in (X_1)_{\mathbb {C}}$ and $(z^*, \beta ^*,h^*)$ satisfies

$$\begin{aligned} \begin{aligned}&P_0z^*+c_0e^{\alpha x}\left( m(x)-c_0\int _0^L K(x,y)e^{\alpha y}dy\right) \\&-c_0^2e^{\alpha x}\int _0^LK(x,y)e^{\alpha y}dy-h^*c_0e^{\alpha x}=0. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} -c_0\int _0^L\int _0^L K(x,y) e^{\alpha x+\alpha y }dxdy=h^*\int _0^L e^{\alpha x}dx, \end{aligned}$$

which leads to $h^*<0$. This contradicts the fact that ${\mathcal Re}h^*\ge 0$. $\square$

Then, we show the distribution of the eigenvalues of $A_\tau (r)$ for $\tau >0$. As in [8], one needs to study the adjoint operator $\tilde{\Delta }(r,i\nu ,\tau )$ of $e^{\alpha x}\Delta (r,i\nu ,\tau )$, which takes the following form:

$$\begin{aligned} \tilde{\Delta }(r,i\nu ,\tau )\tilde{\psi }=P_0\tilde{\psi }+r e^{\alpha x}\tilde{K}(r)\psi -r e^{\alpha x}\int _0^L K(y,x)u_r(y)e^{\alpha y} \tilde{\psi }(y)dy e^{i\nu \tau }+i\nu e^{\alpha x}\tilde{\psi }. \end{aligned}$$

(2.26)

It follows that

$$\begin{aligned} \langle \tilde{\psi },e^{\alpha x}\Delta (r,i\nu ,\tau )\psi \rangle = \langle \tilde{\Delta }(r,i\nu ,\tau )\tilde{\psi },\psi \rangle , \end{aligned}$$

(2.27)

for any $\tilde{\psi }, \psi \in X_{\mathbb {C}}$, and

$$\begin{aligned} \sigma _p(e^{\alpha x}\Delta (r,i\nu ,\tau ))=\sigma _p(\tilde{\Delta }(r,i\nu ,\tau )). \end{aligned}$$

Now, we consider the corresponding adjoint equation

$$\begin{aligned} P_0\tilde{\psi }+re^{\alpha x}\tilde{K}(r)\tilde{\psi }-re^{\alpha x}\int _{0}^LK(y,x)e^{\alpha y}u_r(y)\tilde{\psi }(y)dy e^{i\tilde{\theta }}+i\tilde{\nu } e^{\alpha x}\tilde{\psi }=0,\;0\ne \tilde{\psi }\in X_{\mathbb {C}}. \end{aligned}$$

(2.28)

Note that if Eq. (2.28) is solvable for some value of $\tilde{\nu }>0$, $\tilde{\theta }\in [0,2\pi )$ and $\tilde{\psi }(\ne 0)\in X_{\mathbb {C}}$, then

$$\begin{aligned} \tilde{\Delta }(r,i\tilde{\nu },\tilde{\tau }_n)\tilde{\psi }=0,\;\; \text {where}\;\; \tilde{\tau }_n=\frac{\tilde{\theta }+2n\pi }{\tilde{\nu }},\;\; n=0,1,2,\cdots . \end{aligned}$$

Similarly, ignoring a scalar factor, $\tilde{\psi }$ in Eq. (2.28) can also be represented as

$$\begin{aligned} \begin{aligned}&\tilde{\psi }= \tilde{\beta } c_0+r \tilde{z},\;\; \tilde{z}\in (X_1)_{\mathbb {C}},\;\;\tilde{\beta }\ge 0, \\&\Vert \tilde{\psi }\Vert ^2_{Y_{\mathbb {C}}}=\tilde{\beta }^2 c_0^2L +r^2\Vert \tilde{z}\Vert ^2_{Y_{\mathbb {C}}}= c_0^2L, \end{aligned} \end{aligned}$$

(2.29)

where $c_0$ is defined as in Eq. (2.4). Then, substituting the first equation of (2.29) and $\tilde{\nu }=r\tilde{h}$ into Eq. (2.28), we obtain that $(\tilde{\nu },\tilde{\theta },\tilde{\psi })$ solves Eq. (2.28), where $\tilde{\nu }>0$, $\tilde{\theta }\in [0,2\pi )$ and $\tilde{\psi }\in X_{\mathbb {C}}(\Vert \tilde{\psi }\Vert ^2_{Y_{\mathbb {C}}}= c_0^2L)$, if and only if the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{g}_1(\tilde{z},\tilde{\beta },\tilde{h},\tilde{\theta },r):=P_0\tilde{z}+e^{\alpha x}\tilde{K}(r)(\tilde{\beta } c_0+r\tilde{z})+i\tilde{he}^{\alpha x}(\tilde{\beta } c_0+r\tilde{z})\\ ~~~~~~~~~~~~~~~~~~~-e^{\alpha x}\int _0^L K(y,x)e^{\alpha y}u_r(y)(\tilde{\beta } c_0+r\tilde{z}(y))dy e^{i\tilde{\theta }}=0\\ g_2(\tilde{z},\tilde{\beta },r):=(\tilde{\beta }^2-1)c_0^2L+r^2\Vert \tilde{z}\Vert ^2_{Y_{\mathbb {C}}}=0 \end{array}\right. } \end{aligned}$$

(2.30)

has a solution $(\tilde{z},\tilde{\beta },\tilde{h},\tilde{\theta })$, where $\tilde{z}\in (X_1)_{\mathbb {C}}$, $\tilde{\beta }\ge 0$, $\tilde{h}>0$, and $\tilde{\theta }\in [0,2\pi )$. Define $\tilde{G}:(X_1)_{\mathbb {C}}\times \mathbb {R}^4\rightarrow Y_{\mathbb {C}}\times \mathbb {R}$ by $\tilde{G}=(\tilde{g}_1,\tilde{g}_2)$. By the arguments similar to Lemma 2.5, we obtain that $G(\tilde{z},\tilde{\beta },\tilde{h},\tilde{\theta },0)=0$ is also uniquely solvable.

Lemma 2.9

The following equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{G}(\tilde{z},\tilde{\beta },\tilde{h},\tilde{\theta },0)=0\\ \tilde{z}\in (X_1)_{\mathbb {C}},\;\tilde{h}\ge 0,\;\tilde{\beta }\ge 0,\; \tilde{\theta }\in [0,2\pi ]\\ \end{array}\right. } \end{aligned}$$

(2.31)

has a unique solution $(\tilde{z}_{0},\tilde{\beta }_{0},\tilde{h}_{0},\tilde{\theta }_{0})$, where

$$\begin{aligned} \tilde{\beta }_{0}=1,\;\;\tilde{\theta }_{0}=\pi /2,\;\;\tilde{h}_{0}=h_0, \end{aligned}$$

(2.32)

and $\tilde{z}_{0}\in (X_1)_{\mathbb {C}}$ is the unique solution of

$$\begin{aligned} P_0 z=-c_0e^{\alpha x}\left[ m(x)-c_0\int _0^L K(x,y)e^{\alpha y}dy\right] +ic_0^2 e^{\alpha x}\int _0^L K(y,x)e^{\alpha y}dy-ic_0h_0 e^{\alpha x}. \end{aligned}$$

(2.33)

The following results can also be proved similarly as in Theorems 2.6 and 2.7.

Theorem 2.10

• (I) There exists a continuously differentiable mapping

  $$\begin{aligned} r\mapsto (\tilde{z}_r,\tilde{\beta }_r,\tilde{h}_r,\tilde{\theta }_r) \end{aligned}$$

  from $[0,r_2]$ to $(X_1)_{\mathbb {C}}\times \mathbb {R}^3$ such that $(\tilde{z}_r,\tilde{\beta }_r,\tilde{h}_r,\tilde{\theta }_r)$ is the unique solution of the following equation

  $$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{G}(\tilde{z},\tilde{\beta },\tilde{h},\tilde{\theta },r)=0,\\ \tilde{z}\in (X_1)_{\mathbb {C}},\;\tilde{h}>0,\;\tilde{\beta }\ge 0, \;\tilde{\theta }\in [0,2\pi ),\\ \end{array}\right. } \end{aligned}$$

  (2.34)

  for $r\in [0,r_2]$.

• (II) For $r\in [0,r_2]$, the eigenvalue problem

  $$\begin{aligned} \tilde{\Delta }(r,i\tilde{\nu },\tilde{\tau })\tilde{\psi }=0,\;\;\tilde{\nu }>0, \;\;\tilde{\tau }\ge 0,\;\; 0\ne \tilde{\psi } \in X_{\mathbb {C}} \end{aligned}$$

  has a solution $(\tilde{\nu },\tilde{\tau },\tilde{\psi })$ if and only if

  $$\begin{aligned} \tilde{\nu }=\tilde{\nu }_{r}=r\tilde{h}_r,\;\;\tilde{\psi }=a \tilde{\psi }_r,\;\; \tilde{\tau }=\tilde{\tau }_{n}=\frac{\tilde{\theta }_r+2n\pi }{\tilde{\nu }_r},\;\; n=0,1,2,\cdots ,\;\; \end{aligned}$$

  (2.35)

  where a is a nonzero constant, $\tilde{\psi }_r=\tilde{\beta }_rc_0+r\tilde{z}_r$, and $\tilde{z}_r,\tilde{\beta }_r,\tilde{h}_r,\tilde{\theta }_r$ are defined as in Part (I).

For later application, we give a remark on $(\tilde{h}_r,\tilde{\theta }_r,\tilde{\nu }_r)$.

Remark 2.11

By the arguments similar to Remark 2.8 of [8], we see that $h_{r}=\tilde{h}_{r}$, $\theta _{r}=\tilde{\theta }_{r}$, $\nu _r=\tilde{\nu }_r$ and $\tau _n=\tilde{\tau }_n$. Therefore, in the following, we will always use $(h_{r},\theta _{r}, \nu _{r},\tau _n)$ instead of the ones with tilde. Moreover, we remark that the corresponding solution $\psi _r$ of $\Delta (r,i\nu _{r},\tau _{n})\psi =0$ may be different from $\tilde{\psi }$.

Now, we show that $i\nu _r$ is simple.

Theorem 2.12

Assume that $r\in (0,r_2]$. Then $\mu =i\nu _r$ is a simple eigenvalue of $A_{\tau _{n}}(r)$ for $n=0,1,2,\cdots$, where $i\nu _r$ and $\tau _n$ are defined as in Theorem 2.7.

Proof

From Theorem 2.7, we obtain that $\mathscr {N}[A_{\tau _{n}} (r)-i\nu _r]=\text {Span}[e^{i\nu _r\theta }\psi _r]$, where $\theta \in [-\tau _n,0]$ and $\psi _r$ is defined as in Theorem 2.7. If $\phi _1\in \mathscr {N}[A_{\tau _{n}} (r)-i\nu _r]^2$, then

$$\begin{aligned}{}[A_{\tau _{n}} (r)-i\nu _r]\phi _1\in \mathscr {N}[A_{\tau _{n}}(r)-i\nu _r]= \text {Span}[e^{i\nu _r\theta }\psi _r], \end{aligned}$$

which implies that there exists a constant a such that

$$\begin{aligned}{}[A_{\tau _{n}} (r)-i\nu _r]\phi _1=ae^{i\nu _r\theta }\psi _r. \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned} \dot{\phi _1}(\theta )&=i\nu _r\phi _1(\theta )+ae^{i\nu _r\theta }\psi _r, \ \ \ \ \theta \in [-\tau _{n},0], \\ \dot{\phi _1}(0)&= e^{-\alpha x}P_0\phi _1(0)+r \tilde{K}(r)\phi _1(0)-r u_{r}\int _0^L K(x,y)e^{\alpha y}\phi _1(-\tau _n)(y)dy. \end{aligned} \end{aligned}$$

(2.36)

The first equation of Eq. (2.36) yields

$$\begin{aligned} \begin{aligned} \phi _1(\theta )&=\phi _1(0)e^{i\nu _r\theta }+a\theta e^{i\nu _r\theta }\psi _r,\\ \dot{\phi _1}(0)&=i\nu _r\phi _1(0)+a\psi _r. \end{aligned} \end{aligned}$$

(2.37)

Then, it follows from Eqs. (2.36) and (2.37) that

$$\begin{aligned} \begin{aligned}&e^{\alpha x}\Delta (r,i\nu _r,\tau _{n})\phi _1(0)\\&\quad =P_0\phi _1(0)-i\nu _r e^{\alpha x}\phi _1(0)+re^{\alpha x}\tilde{K}(r)\phi _1(0)-re^{-i\theta _r} e^{\alpha x}u_r\int _0^LK(x,y)e^{\alpha y}\phi _1(0)(y)dy\\&\quad =ae^{\alpha x}\left( \psi _{r}-re^{-i\theta _{r}}\tau _{n}u_r\int _0^L K(x,y)e^{\alpha y}\psi _{r}(y)dy\right) . \end{aligned}\end{aligned}$$

(2.38)

Multiplying the above equation by $\overline{\tilde{\psi }_r}(x)$ and integrating the result over (0, L), we see from Eq. (2.27) and Remark 2.11 that

$$\begin{aligned} \begin{aligned} 0&=\left\langle \tilde{\Delta }(r,i\tilde{\nu },\tilde{\tau }_{n})\tilde{\psi }_r,\phi _1(0)\right\rangle =\left\langle \tilde{\Delta }(r,i\nu ,\tau _{n})\tilde{\psi }_r,\phi _1(0)\right\rangle =\left\langle \tilde{\psi }_r,e^{\alpha x}\Delta (r,i\nu ,\tau _{n})\phi _1(0)\right\rangle \\&=a\left( \int _0^Le^{\alpha x}\overline{\tilde{\psi }_r}\psi _rdx-r\tau _{n}e^{-i\theta _r}\int _0^L\int _0^Lu_r(x) K(x,y) e^{\alpha x+\alpha y}\overline{\tilde{\psi }_r}(x)\psi _{r}(y) dxdy\right) \\&:=aS_{n}(r). \end{aligned} \end{aligned}$$

(2.39)

It follows from Theorems 2.6, 2.7 and 2.10 that $\theta _{r}\rightarrow \pi /2$, $r\tau _n\rightarrow \left( \displaystyle \frac{\pi }{2}+2n\pi \right) /h_0$, $\psi _r,\tilde{\psi }_r\rightarrow c_0$ in $X_{\mathbb {C}}$ as $r\rightarrow 0$. Therefore,

$$\begin{aligned} \lim _{r\rightarrow 0}S_n(r)=c_0^2\left[ 1+i\left( \frac{\pi }{2}+2n\pi \right) \right] \int _{0}^Le^{\alpha x}dx\ne 0, \end{aligned}$$

(2.40)

which yields $a=0$. Therefore,

$$\begin{aligned} \mathscr {N}[A_{\tau _{n}}(r)-i\nu _r]^j =\mathscr {N}[A_{\tau _{n}}(r)-i\nu _r],\;\;j= 2,3,\cdots ,\;\; n=0,1,2,\cdots , \end{aligned}$$

and $\mu =i\nu _r$ is a simple eigenvalue of $A_{\tau _{n}}$ for $n=0,1,2,\cdots .$$\square$

Noticing that $\mu =i\nu _{r}$ is a simple eigenvalue of $A_{\tau _{n}}$, from the implicit function theorem, we see that there are a neighborhood $O_{n}\times D_{n}\times H_{n}\subset \mathbb {R}\times \mathbb {C}\times X_{\mathbb {C}}$ of $(\tau _{n},i\nu _r,\psi _r)$ and a continuously differential function $(\mu (\tau ),\psi (\tau )):O_{n}\rightarrow D_{n}\times H_{n}$ such that $\mu (\tau _{n})=i\nu _r$, $\psi (\tau _{n})=\psi _r$, and for each $\tau \in O_{n}$, the only eigenvalue of $A_\tau (r)$ in $D_{n}$ is $\mu (\tau ),$ and

$$\begin{aligned} \begin{aligned}&e^{\alpha x}\Delta (r,\mu (\tau ),\tau )\psi (\tau )=P_0\psi (\tau )+re^{\alpha x}\tilde{K}(r)\psi (\tau )-\mu (\tau ) e^{\alpha x} \psi (\tau ) \\&\quad -ru_re^{\alpha x}\int _0^LK(x,y)e^{\alpha y}\psi (\tau )(y)dye^{-\mu (\tau )\tau }=0. \end{aligned} \end{aligned}$$

(2.41)

A direct calculation can lead to the transversality condition, and here we omit the proof.

Theorem 2.13

For $r\in (0,r_2]$, $\frac{d{\mathcal Re}[\mu (\tau _{n})]}{d\tau }>0$, $n=0,1,2,\cdots$.

Then, from Theorems 2.7, 2.8, 2.12 and 2.13, we obtain the distribution of eigenvalues of $A_\tau (r)$.

Theorem 2.14

For $r\in (0,r_2]$, the infinitesimal generator $A_\tau (r)$ has exactly $2(n+1)$ eigenvalues with positive real parts when $\tau \in (\tau _{n},\tau _{n+1}],\ n=0,1,2,\cdots .$

Finally, we obtain the stability of the positive steady state $u_{r}$, and the existence of the associated Hopf bifurcation.

Theorem 2.15

For $r\in (0,r_2]$, the positive steady state $u_r$ obtained in Theorem 2.1 is locally asymptotically stable when $\tau \in [0,\tau _{0})$, and unstable when $\tau \in (\tau _{0},\infty )$. Moreover, when $\tau =\tau _n$, $(n=0,1,2,\cdots )$, system (1.7) occurs Hopf bifurcation at the positive steady state $u_{r}$.

3 The Properties of the Hopf Bifurcation

In this section, we obtain the direction of the Hopf bifurcation of Eq. (1.7) and the stability of the bifurcating periodic solutions, the methods used are motivated by [15, 17, 18, 26]. Here, unless otherwise specified, we also assume $r\in (0,r_2]$ throughout this section, and the value of $r_2$ may be chosen smaller than the one in Sect. 2, since further perturbation arguments are also used. Letting $U(t)=u(\cdot ,t)-u_r$, $t=\tau \tilde{t}$, $\tau =\tau _n+\gamma$, and dropping the tilde sign, system (1.7) can be transformed as follows:

$$\begin{aligned} \displaystyle \frac{dU(t)}{dt}=\tau _n e^{-\alpha x}P_0 U(t)+\tau _nP_1U_t+J(U_t,\gamma ), \end{aligned}$$

(3.1)

where $U_t\in \mathcal {C}=C([-1,0],Y)$, $P_0$ is defined as in Eq. (2.2), and

$$\begin{aligned} \begin{aligned} P_1U_t&:=r\tilde{K}(r)U(t)-ru_r\int _0^L K(x,y) e^{\alpha y} U(t-1)(y)dy,\\ J(U_t,\gamma )&:=\gamma e^{-\alpha x}P_0U_t+\gamma P_1U_t-(\gamma +\tau _n)r U(t)\int _0^L K(x,y)e^{\alpha y}U(t-1)(y)dy.\\ \end{aligned} \end{aligned}$$

Then Eq. (3.1) occurs Hopf bifurcation near the zero equilibrium when $\gamma =0$. The linearized equation of (3.1) for $\gamma =0$ is

$$\begin{aligned} \displaystyle \frac{dU(t)}{dt}=\tau _n e^{-\alpha x}P_0U(t)+\tau _nP_1U_t. \end{aligned}$$

(3.2)

Denote by $\mathcal {A}_{\tau _n}$ the infinitesimal generator of the solution semigroup for Eq. (3.2). From [46], we have

$$\begin{aligned} \begin{aligned} \mathcal {A}_{\tau _n} \Psi =&\dot{\Psi },\\ \mathscr {D}(\mathcal {A}_{\tau _n})=&\Big \{\Psi \in \mathcal {C}_\mathbb {C} \cap \mathcal {C}^1_\mathbb {C}:\ \Psi (0)\in X_{\mathbb {C}},\dot{\Psi }(0)=\tau _n e^{-\alpha x}P_0 \Psi (0)+\tau _nP_1 U_t\Big \}, \end{aligned} \end{aligned}$$

where $\mathcal {C}^1_\mathbb {C}=C^1([-1,0],Y_\mathbb {C})$, and the abstract form of Eq. (3.1) is

$$\begin{aligned} \displaystyle \frac{dU_t}{dt}=\mathcal {A}_{\tau _n}U_t+X_0J(U_t,\gamma ), \end{aligned}$$

(3.3)

where

$$\begin{aligned} X_0(\theta )={\left\{ \begin{array}{ll}0, \;\;\; &{} \theta \in [-1,0),\\ I, \;\;\; &{}\theta =0.\\ \end{array}\right. } \end{aligned}$$

In order to compute the normal forms, we need to introduce a weighted inner product for $Y_{\mathbb {C}}$:

$$\begin{aligned} \langle u,v \rangle _1=\displaystyle \int _{0}^L e^{\alpha x}\overline{u}(x) {v}(x) dx\;\;\text { for }\;\;u,v\in Y_{\mathbb {C}}. \end{aligned}$$

Here the weight function is concerned with advection rate $\alpha$, $Y_{\mathbb {C}}$ is also a Hilbert space with this product, for $\alpha \ge 0$,

$$\begin{aligned} \langle v, v\rangle \le \langle v,v\rangle _1\le e^{\alpha L}\langle v, v\rangle , \end{aligned}$$

and for $\alpha <0$,

$$\begin{aligned} e^{\alpha L}\langle v, v\rangle \le \langle v,v\rangle _1\le \langle v, v\rangle . \end{aligned}$$

Following the methods of [17, 44], we introduce the formal duality $\langle \langle \cdot ,\cdot \rangle \rangle$ in $\mathcal {C}$ by

$$\begin{aligned} \langle \langle \tilde{\Psi },\Psi \rangle \rangle =\langle \tilde{\Psi }(0),\Psi (0)\rangle _1-r\tau _n\int _{-1}^0\left\langle \tilde{\Psi }(s+1), u_r\int _0^L K(\cdot ,y)e^{\alpha y}\Psi (s)(y)dy\right\rangle _1 ds, \end{aligned}$$

(3.4)

for $\Psi \in \mathcal {C}_{\mathbb {C}}$ and $\tilde{\Psi }\in \mathcal {C}_{\mathbb {C}}^*:= C([0,1],Y_{\mathbb {C}})$. As in [25], we can compute the formal adjoint operator $\mathcal {A}^*_{\tau _n}$ of $\mathcal {A}_{\tau _n}$ with respect to the formal duality. We remark that $\mathcal {A}^*_{\tau _n}$ is referred to as the formal adjoint operator of $\mathcal {A}_{\tau _n}$, if

$$\begin{aligned} \langle \langle \mathcal {A}^*_{\tau _n}\tilde{\Psi },\Psi \rangle \rangle =\langle \langle \tilde{\Psi },\mathcal {A}_{\tau _n}\Psi \rangle \rangle \end{aligned}$$

(3.5)

for any $\Psi \in \mathscr {D}(\mathcal {A}_{\tau _n})$ and $\tilde{\Psi }\in \mathscr {D}(\mathcal {A}^*_{\tau _n})$.

Lemma 3.1

The formal adjoint operator $\mathcal {A}^*_{\tau _n}$ of $\mathcal {A}_{\tau _n}$ is defined by

$$\begin{aligned} \mathcal {A}^*_{\tau _n}\tilde{\Psi }(s)=-\dot{\tilde{\Psi }}(s) \end{aligned}$$

with the domain

$$\begin{aligned}\begin{aligned} \mathscr {D}(\mathcal {A}^*_{\tau _n}) = \Big \{&\tilde{\Psi }\in \mathcal {C}^*_\mathbb {C} \cap (\mathcal {C}^*_\mathbb {C})^1:\tilde{\Psi }(0)\in X_\mathbb {C},-\dot{\tilde{\Psi }}(0)=\tau _n e^{-\alpha x}P_0\tilde{\Psi }(0)\\ {}&+r \tau _n\tilde{K}(r)\tilde{\Psi }(0)-r\tau _n \int _0^L K(y,x) e^{\alpha y} u_{r}(y)\tilde{\Psi }(1)(y) dy\Big \}, \end{aligned} \end{aligned}$$

where $(\mathcal {C}^*_\mathbb {C})^1=C^1([0,1],Y_\mathbb {C})$.

Proof

For $\Psi \in \mathscr {D}(\mathcal {A}_{\tau _n})$ and $\tilde{\Psi }\in \mathscr {D}(\mathcal {A}^*_{\tau _n})$,

$$\begin{aligned} \begin{aligned}&\langle \langle \tilde{\Psi },\mathcal {A}_{\tau _n}\Psi \rangle \rangle \\&\quad =\left\langle \tilde{\Psi }(0), (\mathcal {A}_{\tau _n}\Psi )(0)\right\rangle _1-r\tau _n\int _{-1}^0 \left\langle \tilde{\Psi }(s+1), u_r\int _0^L K(x,y)e^{\alpha y}\dot{\Psi }(s)(y)dy\right\rangle _1 ds\\&\quad =\left\langle \tilde{\Psi }(0),\tau _n e^{-\alpha x}P_0 \Psi (0)+\tau _nP_1\Psi \right\rangle _1\\&\qquad -r\tau _n\left[ \left\langle \tilde{\Psi }(s+1), u_r \int _0^L K(x,y) e^{\alpha y}\Psi (s)(y) dy\right\rangle _1\right] _{-1}^{0}\\&\qquad +r\tau _n\int _{-1}^0\left\langle \dot{\tilde{\Psi }}(s+1), u_r \int _0^L K(x,y)e^{\alpha y}\Psi (s)(y)dy\right\rangle _1 ds\\&\quad =\left\langle (\mathcal {A}^*_{\tau _n}\tilde{\Psi })(0),\Psi (0)\right\rangle _1 -r\tau _n\int _{-1}^0\left\langle -\dot{\tilde{\Psi }}(s+1), u_r \int _0^L K(x,y)e^{\alpha y}\Psi (s)(y)dy\right\rangle _1 ds\\&\quad =\langle \langle \mathcal {A}^*_{\tau _n}\tilde{\Psi },\Psi \rangle \rangle . \end{aligned} \end{aligned}$$

This completes the proof. $\square$

It follows from Theorem 2.14 that $\mathcal {A}_{\tau _n}$ has only one pair of simple purely imaginary eigenvalues $\pm i \nu _r\tau _n$, and the associated eigenfunction with respect to $i\nu _r\tau _n$ (respectively, $-i\nu _r\tau _n$) is $\psi _r e^{ i \nu _r\tau _n\theta }$ (respectively, $\overline{\psi _r} e^{-i\nu _r\tau _n\theta }$) for $\theta \in [-1,0]$, where $\psi _r$ is defined as in Theorem 2.7. Similarly, it follows from Theorem 2.10, Remark 2.11 and Lemma 3.1 that the operator $\mathcal {A}^*_{\tau _n}$ also has only one pair of simple purely imaginary eigenvalues $\pm i \nu _r\tau _n$, and the corresponding eigenfunction with respect to $-i\nu _r\tau _n$ (respectively, $i\nu _r\tau _n$) is $\tilde{\psi }_r(x) e^{i \nu _r\tau _n s}$ (respectively, $\overline{\tilde{\psi }_r}(x) e^{i \nu _r\tau _ns}$) for $s\in [0,1]$, where $\tilde{\psi }_r$ is defined in Theorem 2.10. From [46], we see that the center subspace of Eq. (3.1) is $P=\text {span}\{p(\theta ),\overline{p}(\theta )\}$, where $p(\theta )=\psi _r e^{ i \nu _r\tau _n\theta }$ is the eigenfunction of $\mathcal {A}_{\tau _n}$ with respect to $i\nu _r\tau _n$, and the formal adjoint subspace of P with respect to the bilinear form (3.4) is $P^*=\text {span}\{q(s),\overline{ q}(s)\}$, where $q(s)=\tilde{\psi }_r e^{ i \nu _r\tau _ns}$ is the eigenfunction of $\mathcal {A}^*_{\tau _n}$ with respect to $-i\nu _r\tau _n$. Denote $\Phi _I=(p(\theta ),\overline{p}(\theta ))$, $\Psi _I=\displaystyle \frac{1}{\overline{S_n}(r)}(q(s),\overline{q}(s))^{T}$, where $S_n(r)$ is defined as in Eq. (2.39), and then $\langle \langle \Psi _I,\Phi _I\rangle \rangle = I$, where I is the identity matrix in $\mathbb {R}^{2\times 2}$.

Note that formulas for the direction and stability of Hopf bifurcation are all relative to $\gamma =0$ only, let $\gamma =0$ in Eq. (3.1), and we obtain a center manifold as follows

$$\begin{aligned} w(z,\overline{z})=w_{20}(\theta )\displaystyle \frac{z^{2}}{2}+w_{11}(\theta )z\overline{z} +w_{02}(\theta )\displaystyle \frac{\overline{z}^{2}}{2}+O(|z|^3). \end{aligned}$$

(3.6)

The solution semi-flow of Eq. (3.1) on the center manifold is

$$\begin{aligned} U_t=\Phi _I(z(t),\overline{z}(t))^{T}+w(z(t),\overline{z}(t)), \end{aligned}$$

where z(t) satisfies

$$\begin{aligned} \begin{aligned} \dot{z}(t)&=\displaystyle \frac{d}{dt}\langle \langle q(s),U_t\rangle \rangle \\&= i\nu _r\tau _n z(t)+\displaystyle \frac{1}{S_n(r)}\left\langle q(0), J\left( \Phi _I(z(t),\overline{z}(t))^{T}+w(z(t),\overline{z}(t)),0\right) \right\rangle _1. \end{aligned} \end{aligned}$$

(3.7)

Denote

$$\begin{aligned} \begin{aligned} g(z,\overline{z})=&\displaystyle \frac{1}{S_n(r)}\left\langle q(0), J\left( \Phi _I(z(t),\overline{z}(t))^{T}+w(z(t),\overline{z}(t)), 0\right) \right\rangle _1\\=&\sum _{2\le i+j\le 3}\frac{g_{ij}}{i!j!}z^i \overline{z}^j+O(|z|^4). \end{aligned} \end{aligned}$$

(3.8)

As in [8], we derive

$$\begin{aligned} \begin{aligned} g_{20}=&-\displaystyle \frac{2r\tau _n}{S_n(r)}e^{-i\nu _r\tau _n}\int _0^L\int _0^L \overline{\tilde{\psi }_r}(x)\psi _r(x)K(x,y)e^{\alpha x+\alpha y}\psi _r(y)dxdy,\\ g_{11}=&-\displaystyle \frac{r\tau _n}{S_n(r)}e^{i\nu _r\tau _n}\int _0^L\int _0^L \overline{\tilde{\psi }_r}(x)\psi _r(x)K(x,y)e^{\alpha x+\alpha y} \overline{\psi _r}(y)dxdy\\&-\displaystyle \frac{r\tau _n}{S_n(r)}e^{-i\nu _r\tau _n}\int _0^L\int _0^L \overline{\tilde{\psi }_r}(x)\overline{\psi _r}(x)K(x,y)e^{\alpha x+\alpha y}\psi _r(y)dxdy,\\ g_{02}=&-\displaystyle \frac{2r\tau _n}{S_n(r)}e^{i\nu _r\tau _n}\int _0^L\int _0^L \overline{\tilde{\psi }_r}(x)\overline{\psi _r}(x)K(x,y)e^{\alpha x+\alpha y} \overline{\psi _r}(y)dxdy,\\ g_{21}=&-\displaystyle \frac{2r\tau _n}{S_n(r)}\int _0^L\int _0^L\overline{\tilde{\psi }_r}(x) \psi _r(x)K(x,y)e^{\alpha x+\alpha y}w_{11}(-1)(y)dxdy\\&-\displaystyle \frac{r\tau _n}{S_n(r)}\int _0^L\int _0^L\overline{\tilde{\psi }_r}(x) \overline{\psi _r}(x)K(x,y)e^{\alpha x+\alpha y}w_{20}(-1)(y)dxdy\\&-\displaystyle \frac{r\tau _n}{S_n(r)} e^{i\nu _r\tau _n}\int _0^L\int _0^L\overline{\tilde{\psi }_r}(x)w_{20}(0)(x) K(x,y)e^{\alpha x+\alpha y}\overline{\psi _r}(y)dxdy\\&-\displaystyle \frac{2r\tau _n}{S_n(r)}e^{-i\nu _r\tau _n}\int _0^L\int _0^L \overline{\tilde{\psi }_r}(x)w_{11}(0)(x)K(x,y)e^{\alpha x+\alpha y}\psi _r(y)dxdy, \end{aligned} \end{aligned}$$

(3.9)

where $w_{20}(\theta )$ and $w_{11}(\theta )$ are needed to be computed.

Note that $w(z(t),\overline{z}(t))$ satisfies

$$\begin{aligned} \begin{aligned} \dot{w}&=\mathcal {A}_{\tau _n}w+X_0J(\Phi _I(z,\overline{z})^{T}+w(z,\overline{z}),0)\\&\quad -\Phi _I\langle \langle \Psi _I,X_0J(\Phi _I(z,\overline{z})^{T}+w(z,\overline{z}),0) \rangle \rangle \\&=\mathcal {A}_{\tau _n}w+H_{20}\displaystyle \frac{z^2}{2}+H_{11}z\overline{z}+H_{02} \displaystyle \frac{\overline{z}^2}{2}+O(|z|^3), \end{aligned} \end{aligned}$$

(3.10)

where $H_{20}$, $H_{11}$ and $H_{02}$ satisfy

$$\begin{aligned} \begin{aligned}&X_0J(\Phi _I(z,\overline{z})^{T}+w(z,\overline{z}),0) -\Phi \langle \langle \Psi ,X_0J(\Phi _I(z,\overline{z})^{T}+w(z,\overline{z}),0) \rangle \rangle \\&\quad =H_{20}\displaystyle \frac{z^2}{2}+H_{11}z\overline{z}+H_{02}\displaystyle \frac{\overline{z}^2}{2} +O(|z|^3). \end{aligned}\end{aligned}$$

By using the chain rule, we see that w also satisfies

$$\begin{aligned} \dot{w}=\displaystyle \frac{\partial w(z,\overline{z})}{\partial z}\dot{z}+\displaystyle \frac{\partial w(z,\overline{z})}{\partial \overline{z}}\dot{\overline{z}}. \end{aligned}$$

Therefore,

$$\begin{aligned} {\left\{ \begin{array}{ll} (2i\nu _r\tau _n-\mathcal {A}_{\tau _n})w_{20}=H_{20},\\ -\mathcal {A}_{\tau _n}w_{11}=H_{11}.\\ \end{array}\right. } \end{aligned}$$

(3.11)

Note that for $\theta \in [-1,0)$,

$$\begin{aligned} \begin{aligned}&H_{20}(\theta )=-(g_{20}p(\theta )+\overline{g}_{02}\overline{p}(\theta )),\\&H_{11}(\theta )=-(g_{11}p(\theta )+\overline{g}_{11}\overline{p}(\theta )). \end{aligned} \end{aligned}$$

(3.12)

Then, from Eq. (3.11) and (3.12), $w_{20}$ and $w_{11}$ can be expressed as

$$\begin{aligned} w_{20}(\theta )=\displaystyle \frac{ig_{20}}{\nu _r\tau _n}p(\theta )+ \displaystyle \frac{i\overline{g}_{02}}{3\nu _r\tau _n} \overline{p}(\theta )+E_re^{2i\nu _r\tau _n\theta }, \end{aligned}$$

(3.13)

and

$$\begin{aligned} w_{11}(\theta )=-\displaystyle \frac{ig_{11}}{\nu _r\tau _n}p(\theta ) +\displaystyle \frac{i\overline{g}_{11}}{\nu _r\tau _n}\overline{p}(\theta )+F_r. \end{aligned}$$

(3.14)

Noticing that

$$\begin{aligned} H_{20}(0) =-\left( g_{20}p(0)+\overline{g}_{02}\overline{p}(0)\right) -2r\tau _n e^{-i\nu _r\tau _n}\psi _r\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy, \end{aligned}$$

we see from From Eqs. (3.10) and (3.11) with $\theta =0$ that $E_r$ satisfies

$$\begin{aligned}(2i\nu _r\tau _n-\mathcal {A}_{\tau _n}) E_re^{2i\nu _r\tau _n\theta }\bigg \vert _{\theta =0}=-2r\tau _ne^{-i\nu _r\tau _n} \psi _r\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy, \end{aligned}$$

that is,

$$\begin{aligned} \Delta (r,2i\nu _r,\tau _n)E_r=2r e^{-i\nu _r\tau _n}\psi _r\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy. \end{aligned}$$

(3.15)

From Corollary 2.7, we have that $2i\nu _r$ is not the eigenvalue of $A_{\tau _n}(r)$, and hence

$$\begin{aligned} E_r=2r e^{-i\nu _r\tau _n}\Delta (r,2i\nu _r,\tau _n)^{-1}\left( \psi _r\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy\right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{aligned} F_r&=r\Delta (r,0,\tau _n)^{-1}\left( e^{i\nu _r\tau _n}\psi _r\int _0^L K(x,y)e^{\alpha y}\overline{\psi _r}(y)dy\right) \\&\quad +r\Delta (r,0,\tau _n)^{-1}\left( e^{-i\nu _r\tau _n}\overline{\psi _r}\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy\right) . \end{aligned} \end{aligned}$$

(3.16)

Then, $E_r$ and $F_r$ can be derived in the following.

Lemma 3.2

For $r\in (0,r_2],$ let $E_r$ and $F_r$ be defined as in (3.15) and (3.16). Then

$$\begin{aligned} E_r=b_rc_0+\phi _r,\;\; \end{aligned}$$

(3.17)

where $c_0$ is defined as in Eq. (2.4), $\phi _r\in (X_1)_{\mathbb {C}}$, and $b_r$, $\phi _r$ satisfy

$$\begin{aligned} \lim _{r\rightarrow 0} b_r=\displaystyle \frac{2i}{2i-1},\;\;\lim _{r\rightarrow 0} \Vert \phi _r\Vert _{Y_{\mathbb {C}}}=0, \end{aligned}$$

and $\lim _{r\rightarrow 0} \Vert F_r\Vert _{Y_{\mathbb {C}}}=0$.

Proof

We only prove the estimate for $E_r$, and $F_r$ can be derived similarly. Substituting Eq. (3.17) in to Eq. (3.15), we have

$$\begin{aligned} \begin{aligned}\displaystyle \frac{1}{r}P_0\phi _r&=-e^{\alpha x}\tilde{K}(r)(b_rc_0+\phi _r)+ u_re^{\alpha x}\int _{0}^LK(x,y)e^{\alpha y}[b_r c_0+\phi _{r}(y)]dye^{-2i\nu _r\tau _n}\\&\qquad +2ih_re^{\alpha x}(b_rc_0+\phi _r)+2 e^{-i\nu _r\tau _n}\psi _re^{\alpha x}\int _0^L K(x,y)e^{\alpha y}\psi _r(y)dy,\end{aligned} \end{aligned}$$

(3.18)

where $h_r$ is defined as in Theorem 2.6. Integrating Eq. (3.18) over (0, L), and noticing that $|h_r|$, $\Vert u_r\Vert _\infty$ and $\Vert \psi _r\Vert _\infty$ are bounded for $r\in (0,r_2]$, we see that there exist constants $M_0,~M_1>0$ such that

$$\begin{aligned} |b_r|\le M_0\Vert \phi _{r}\Vert _{Y_\mathbb {C}}+M_1, \end{aligned}$$

(3.19)

for any $r\in (0,r_2]$. Multiplying Eq. (3.18) by $\overline{\phi }_r$, and integrating the result over (0, L), we see from Lemma 2.4 and Eq. (3.19) that there exist constants $M_2,~M_3>0$ such that

$$\begin{aligned} \lambda _2\Vert \phi _r\Vert ^2_{Y_{\mathbb {C}}}\le rM_2\Vert \phi _{r}\Vert ^2_{Y_\mathbb {C}}+rM_3\Vert \phi _{r}\Vert _{Y_\mathbb {C}}, \end{aligned}$$

for any $r\in (0,r_2]$, where $\lambda _2$ is defined as in Lemma 2.4. This leads to $\lim _{r\rightarrow 0} \Vert \phi _r\Vert _{Y_{\mathbb {C}}}=0$. Then, integrating Eq. (3.18) over (0, L), and taking the limit of the equation at both sides as $r\rightarrow 0$, we obtain

$$\begin{aligned} (2i-1)\left( \lim _{r\rightarrow 0}b_r\right) \int _0^L m(x)e^{\alpha x}dx=2i\int _0^Lm(x)e^{\alpha x}dx, \end{aligned}$$

which leads to $\lim _{r\rightarrow 0} b_r=\frac{2i}{2i-1}$. Similarly, we can prove that $\lim _{r\rightarrow 0} \Vert F_r\Vert _{Y_{\mathbb {C}}}=0$. $\square$

Therefore, by similar arguments similar to [8], one can also derive

$$\begin{aligned} \lim _{r\rightarrow 0}g_{11}=0\;\;\text {and}\;\;\lim _{r\rightarrow 0}\mathcal {R}e[g_{21}]<0. \end{aligned}$$

(3.20)

It follows from [26, 46] that $C_1(0)$ determines the direction and stability of bifurcating periodic orbits, where

$$\begin{aligned} C_1(0)=\dfrac{i}{2\nu _r\tau _n}\left( g_{11}g_{20}-2|g_{11}|^2 -\dfrac{|g_{02}|^2}{3}\right) +\dfrac{g_{21}}{2}. \end{aligned}$$

Then, Eq. (3.20) implies $\lim _{r\rightarrow 0}\mathcal {R}e[C_1(0)]<0$. Hence we have the following result.

Theorem 3.3

Assume that $r\in (0,r_2]$, where $0<r_2\ll 1$. Let $\{\tau _n(r)\}_{n=0}^\infty$ be the Hopf bifurcation points of Eq. (1.7) obtained in Theorem 2.15. Then, for each $n\in \mathbb {N} \cup \{0\}$, the direction of the Hopf bifurcation at $\tau =\tau _n$ is forward and the bifurcating periodic solutions from $\tau =\tau _0$ is orbitally asymptotically stable.

4 The Effect of Spatial Heterogeneity

In this section, we will consider the effect of spatial heterogeneity on Hopf bifurcation values. It follows from Lemma 2.5, Theorems 2.14 and 2.15 that the first Hopf bifurcation value $\tau _0$ of Eq. (1.7) depends on r, $\alpha$, L, and satisfies:

$$\begin{aligned} \begin{aligned} \tau _0(r,\alpha ,L)=&\frac{\theta _r(\alpha ,L)}{r h_r(\alpha ,L)},\;\;\lim _{r\rightarrow 0}\theta _r(\alpha ,L)=\displaystyle \frac{\pi }{2},\\ \lim _{r\rightarrow 0}h_r(\alpha ,L)=&h_{0}(\alpha ,L)=\displaystyle \frac{\int _0^L m(x)e^{\alpha x}dx}{\int _0^Le^{\alpha x}dx}. \end{aligned} \end{aligned}$$

(4.1)

If $m(x)\equiv m_0$, where $m_0$ is a positive constant, then

$$\begin{aligned} h_0(\alpha ,L)=m_0\; \;\text {and}\;\;\lim _{r\rightarrow 0} r\tau _0(r,\alpha ,L)=\displaystyle \frac{\pi }{2m_0} \end{aligned}$$

for any $\alpha \in (-\infty ,\infty )$ and $L>0$, and hence $\tau _0(r,\alpha ,L)\approx \displaystyle \frac{\pi }{2rm_0 }$ for small r. It seems that the value of $\tau _0(r,\alpha ,L)$ has no significant change as advection $\alpha$ or spatial scale L changes, when m(x) is spatially homogeneous.

Then we consider the case that m(x) is spatially heterogeneous. We find that Hopf bifurcation is more likely to occur as spatial scale L increases, if m(x) achieve its maximum at boundary $x=L$.

Proposition 4.1

Suppose that m(x) is non-constant, $m(L)=\max _{x\in [0,L]} m(x)$, $\alpha \in (-\infty , \infty )$, and $L_1>L_2>0$. Then there exists $\tilde{r}>0$, depending on $L_1$, $L_2$ and $\alpha$, such that $\tau _0(r,\alpha ,L_1)<\tau _0(r,\alpha , L_2)$ for $t\in (0,\tilde{r}]$.

Proof

Since

$$\begin{aligned} \displaystyle \frac{\partial h_0(\alpha ,L)}{\partial L}=\displaystyle \frac{e^{\alpha L}\int _0^L\left[ m(L)-m(x)\right] e^{\alpha x}dx}{\left( \int _0^L e^{\alpha x} dx\right) ^2}>0, \end{aligned}$$

we see that, for any fixed $\alpha \in (-\infty ,\infty )$, $h_0(\alpha , L)$ is strictly increasing for $L\in (0,\infty )$. Note that

$$\begin{aligned} \tau _0(r,\alpha ,L)=\frac{\theta _r(\alpha ,L)}{r h_r(\alpha ,L)}\;\;\text {and}\;\;\lim _{r\rightarrow 0}r\tau _0(r,\alpha ,L)=\displaystyle \frac{\pi }{2h_0(\alpha ,L)}. \end{aligned}$$

It follows that there exists $\tilde{r}>0$, depending on $L_1$, $L_2$ and $\alpha$, such that $\tau _0(r,\alpha ,L_1)<\tau _0(r,\alpha , L_2)$ for $t\in (0,\tilde{r}]$. $\square$

In the following we will choose different types of m(x) to show the effect of spatial heterogeneity.

Example 4.2

Choose

$$\begin{aligned} m(x)=x. \end{aligned}$$

(4.2)

In this case,

$$\begin{aligned} \begin{aligned} h(\alpha ,L)=&\displaystyle \frac{\alpha L e^{\alpha L}-e^{\alpha L}+1}{\alpha (e^{\alpha L}-1)},\;\;h_0(0,L)=\displaystyle \frac{L}{2},\\ \displaystyle \frac{\partial h_0(\alpha ,L)}{\partial a}=&\displaystyle \frac{\int _0^L x^2e^{\alpha x} dx\int _0^L e^{\alpha x}dx-\left( \int _{0}^L x e^{\alpha x}dx\right) ^2}{\left( \int _0^L e^{\alpha x}dx\right) ^2}>0,\\ \displaystyle \frac{\partial h_0(\alpha ,L)}{\partial L}=&\displaystyle \frac{e^{\alpha L}\left( e^{\alpha L}-\alpha L -1\right) }{\left( e^{\alpha L}-1\right) ^2}>0. \end{aligned} \end{aligned}$$

Consequently, if we choose

$$\begin{aligned} m(x)=m_0-x, \end{aligned}$$

(4.3)

where $m_0$ is a constant and $m_0>L$, then

$$\begin{aligned} \displaystyle \frac{\partial h_0(\alpha ,L)}{\partial a}<0,\;\;\displaystyle \frac{\partial h_0(\alpha ,L)}{\partial L}<0. \end{aligned}$$

Then we have the following two statements on the effect of advection $\alpha$.

• 1. Assume that $L\in (0,\infty )$, $m(x)=x$ and $\alpha _1>\alpha _2$. Then there exists $\tilde{r}>0$, depending on $\alpha _1$, $\alpha _2$ and L, such that $\tau _0(r,\alpha _1,L)<\tau _0(r,\alpha _2,L)$ for $r\in (0,\tilde{r}]$.

• 2. Assume that $L\in (0,\infty )$, $m(x)=m_0-x$, where $m_0>L$, and $\alpha _1>\alpha _2$. Then there exists $\tilde{r}>0$, depending on $\alpha _1$, $\alpha _2$ and L, such that $\tau _0(r,\alpha _1,L)>\tau _0(r,\alpha _2,L)$ for $r\in (0,\tilde{r}]$.

Therefore, Hopf bifurcation is more likely to occur when the advection rate increases (respectively, decreases) for $m(x)=x$ (respectively, $m(x)=m_0-x$, where $m_0>L$). Similarly, we have the following two statements on the effect of spatial scale L.

• 1. Assume that $\alpha \in (-\infty ,\infty )$, $m(x)=x$ and $L_1>L_2$. Then there exists $\tilde{r}>0$, depending on $L_1$, $L_2$ and $\alpha$, such that $\tau _0(r,\alpha ,L_1)<\tau _0(r,\alpha ,L_2)$ for $r\in (0,\tilde{r}]$.

• 2. Assume that $\alpha \in (-\infty ,\infty )$, $m(x)=m_0-x$, where $m_0>L$, and $L_1>L_2$. Then there exists $\tilde{r}>0$, depending on $L_1$, $L_2$ and $\alpha$, such that $\tau _0(r,\alpha ,L_1)>\tau _0(r,\alpha ,L_2)$ for $r\in (0,\tilde{r}]$.

Therefore, Hopf bifurcation is more likely to occur when spatial scale L increases (respectively, decreases) for $m(x)=x$ (respectively, $m(x)=m_0-x$, where $m_0>L$).

Example 4.3

Choose

$$\begin{aligned} m(x)=\sin \frac{\pi x}{L}. \end{aligned}$$

(4.4)

In this case,

$$\begin{aligned} h(\alpha ,L)=\displaystyle \frac{\pi \alpha L \left( e^{\alpha L}+1\right) }{\left( \pi ^2+\alpha ^2L^2\right) (e^{\alpha L}-1)},\;\;h_0(0,L)=\displaystyle \frac{2}{\pi }. \end{aligned}$$

Therefore, if $\alpha L>\pi$, then

$$\begin{aligned} \displaystyle \frac{\partial h_0(\alpha ,L)}{\partial a}<0\;\;\text {and}\;\;\displaystyle \frac{\partial h_0(\alpha ,L)}{\partial L}<0. \end{aligned}$$

Consequently, we have the following two statements on the effects of advection $\alpha$ and spatial scale L.

• 1. Assume that $\alpha _1>\alpha _2>\pi /L$. Then there exists $\tilde{r}>0$, depending on $\alpha _1$, $\alpha _2$ and L, such that $\tau _0(r,\alpha _1,L)>\tau _0(r,\alpha _2,L)$ for $r\in (0,\tilde{r}]$.

• 2. Assume that $L_1>L_2>\pi /\alpha$. Then there exists $\tilde{r}>0$, depending on $L_1$, $L_2$ and $\alpha$, such that $\tau _0(r,\alpha _1,L_1)>\tau _0(r,\alpha _2,L_2)$ for $r\in (0,\tilde{r}]$.

Therefore, Hopf bifurcation is more likely to occur when advection rate $\alpha >\pi /L$ decreases or spatial scale $L>\pi /\alpha$ decreases.

5 Numerical Simulations

Finally, some numerical simulations are given to support our obtained theoretical results in Sects. 2 and 3. For simplicity, we only give the numerical results when m(x) is spatially homogeneous. Firstly, we assume that kernel K(x, y) satisfies Eq. (1.6), and model (1.5) with this kernel takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} =du_{xx}-\alpha u_x+ ru\left( 1-\int _0^xu(y,t-\tau )dy\right) ,&{}0<x<L,\ t>0,\\ du_x(0,t)-\alpha u(0,t)=0,&{} t>0,\\ du_x(L,t)-\alpha u(L,t)=0, &{}t>0. \end{array}\right. } \end{aligned}$$

(5.1)

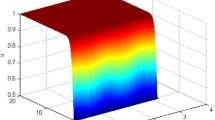
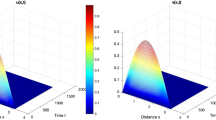
We see that when $\tau$ is small, the solution converges to a positive steady state, and when $\tau$ is large, Hopf bifurcation can occur and the solution converges to a positive periodic solution, see Fig. 1 for $\alpha =0$ and Fig. 2 for $\alpha =0.45$. In some sense, Eq. (5.1) can also model the population dynamics for a river species in a water column, where $x=0$ and $x=L$ represent the top and the bottom of the water column respectively, and the individuals at location x only compete with the ones in [0, x]. There are some examples of this type of nonlocal competition, such as the competition for the oxygen or the light [29]. Numerically, we find that when advection rate $\alpha =0$, the density of the species concentrates on the top of the water column, see Fig. 1. However, when $\alpha$ becomes large, the density of the species concentrates from the top to the bottom of the water column, see Figs. 1 and 2.

Fig. 1

Equation (5.1) occurs Hopf bifurcation with advection $\alpha =0$. Here $d=1$, $L=4\pi$ and $r=0.5$. (Left): $\tau =1$; (Right): $\tau =4$

Fig. 2

Equation (5.1) occurs Hopf bifurcation with advection $\alpha =0.45$. Here $d=1$, $L=4\pi$ and $r=0.5$. (Left): $\tau =1$; (Right): $\tau =4$

Then we consider the case that $K(x,y)=\delta (x-y)$, and model (1.5) with this kernel takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t} =du_{xx}-\alpha u_x+ ru\left( 1-u(x,t-\tau )\right) ,&{}0<x<L,\ t>0,\\ du_x(0,t)-\alpha u(0,t)=0,&{} t>0,\\ du_x(L,t)-\alpha u(L,t)=0, &{}t>0. \end{array}\right. } \end{aligned}$$

(5.2)

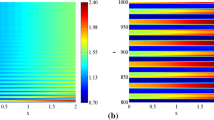
Similarly, we see that when $\tau$ is small, the solution converges to a positive steady state, and when $\tau$ is large, Hopf bifurcation can occur and the solution converges to a positive periodic solution, see Fig. 3 for $\alpha =0$ and Fig. 4 for $\alpha =0.2$. Moreover, the steady state and periodic solution are spatially homogeneous for $\alpha =0$ and spatially nonhomogeneous for $\alpha =0.2$.

Fig. 3

Equation (5.2) occurs Hopf bifurcation with advection $\alpha =0$. Here $d=1$, $L=4\pi$ and $r=0.5$. (Left): $\tau =1$; (Right): $\tau =4$

Fig. 4

Equation (5.2) occurs Hopf bifurcation with advection $\alpha =0.2$. Here $d=1$, $L=4\pi$ and $r=0.5$. (Left): $\tau =1$; (Right): $\tau =4$