Turing Instability and Turing–Hopf Bifurcation in Diffusive Schnakenberg Systems with Gene Expression Time Delay

Abstract

In this paper, we study the delayed reaction–diffusion Schnakenberg systems with Neumann boundary conditions. Sufficient and necessary conditions for the occurrence of Turing instability are obtained, and the existence of Turing, Hopf and Turing–Hopf bifurcation for the model are also established. Furthermore, for Turing–Hopf bifurcation, the explicit formula of the truncated normal form up to third order is derived. With the aid of these formulas, we determine the regions on two parameters plane, on which a pair of stable spatially inhomogeneous steady states and a pair of stable spatially inhomogeneous periodic solutions exist, respectively. The theoretical results not only reveals the joint effect of diffusion and delay on the patterns that the model can exhibit, but also explain the phenomenon that time delay may induce a failure of Turing instability, found by Gaffney and Monk (Bull Math Biol 68(1):99–130, 2006).

1 Introduction

The morphogen is an important concept in developmental biology, because it describes a mechanism by which the emission of a signal from one part of an embryo can determine location, differentiation and fate of many surrounding cells [10]. A reaction diffusion model with Schnakenberg kenetics [26], has been widely used to describe spatial distribution of morphogen, and to understand how various morphogens interact with cells and patterns. The Schnakenberg system is chosen as a simple exemplar, given it is representative of the behavior of many, though certainly not all, two species reaction diffusion systems [22]. Recently, it is argued in [6] that there is an evidence that time delay in gene expression due to transcription and translation plays an import role in dynamics of cellular systems. Therefore, a diffusive Schnakenberg system with time delay is proposed in [17], as follows:

$$\begin{aligned} \begin{array}{rll} u_t(x,t)=&{}\varepsilon d u_{xx}(x,t)+a-u(x,t)+u^2(x,t-\tau )v(x,t-\tau ), &{}x\in (0,1),t>0,\\ v_t(x,t)=&{}d v_{xx}(x,t)+b-u^2(x,t-\tau )v(x,t-\tau ), &{}x\in (0,1),t>0,\\ u_x(0,t)=&{}u_x(1,t)=v_x(0,t)=v_x(1,t)=0, \;\; &{}t\ge 0,\\ u(x,t)=&{}\phi (x,t)\ge 0, v(x,t)=\varphi (x,t)\ge 0,&{} (x,t)\in [0,1]\times [-\tau ,0], \end{array}\nonumber \\ \end{aligned}$$

(1.1)

where u(x, t) and v(x, t) are concentrations of activator and inhibitor at (x, t) respectively, and $a,b,d, \varepsilon$ are all positive constants.

For (1.1) with $\tau =0$, numerous studies have been done. As known to all, Turing’s theory shows that the diffusion could destabilize a stable steady state of reaction diffusion equation, and lead to nonuniform spatial patterns [12, 20, 23, 30]. Based on Turing bifurcation analysis, sufficient conditions for the occurrence of Turing instability of (1.1) is provided in [22, 36]. Hopf bifurcation problem of (1.1) with $\tau =0$ is also investigated in [19, 25, 34], by using an intermediate parameter depending on a and b. In addition, Turing–Hopf bifurcation is studied in [25], where the main idea is to show the existence of time-periodic solutions through Hopf bifurcation in the first place, and then to prove the Turing instability of the bifurcated periodic solution, showing the existence of spatially inhomogeneous time-periodic patterns. For more information on Turing–Hopf bifurcation for other specific models, we refer the readers to [2, 14, 18, 21, 28]. In [32], asymmetric spike patterns for (1.1) are constructed, and explicit conditions for the existence and stability of these asymmetric patterns are determined.

Due to the factor of time delay, Hopf bifurcation occurs frequently as delay may destabilize the steady state and induce a temporally periodic solution, see [3, 8, 9, 24, 29, 31, 35, 37]. When $\tau \ne 0$, the detailed stability and Hopf bifurcation analysis is performed for (1.1) in [36], showing the existence of spatially homogeneous periodic solutions. Aside from this, the authors also show in [36] that time delay could induce a failure of Turing instability, due to the Hopf bifurcation at the spatially inhomogeneous steady state (bifurcated from the constant steady states through Turing bifurcation).

In the present paper, we first carry out detailed analysis on Turing, Hopf and Turing–Hopf bifurcation for (1.1). Firstly, we obtain an critical curve in $(\varepsilon ,d)$-plane that separates Turing stable and instable regions. The curve is continuous and piecewise smooth, and the nonsmooth points corresponds to the critical values for Turing-Turing bifurcation. The results will provide the sufficient and necessary condition for the occurrence of Turing instability, extending most of the results in the literature [22] as the conditions established there are only necessary. Other than this, from the explicit expression of this curve, one can easily find the spatial inhomogeneous steady state in various profiles, depending on the wave number. This theoretically explains why the spatially inhomogeneous steady-states with high frequency in space are prone to coexist, when the diffusion rate is small and the size of spatial domain is fixed. Secondly, we prove that (1.1) will undergoes Hopf bifurcations as time delay $\tau$ passes through a sequence of critical values. Finally, much attention is paid on the interaction of diffusion rate and time delay. The techniques we used here is combining the center manifold theorem and normal form theory to study this codimension-two bifurcation directly, which is distinguished from the two methods that have been extensively used in the existing literature (the first method is to study the Hopf bifurcation at the spatially inhomogeneous steady state generated through Turing bifurcation, the other one is to examine the Turing instability of periodic solution arising from Hopf bifurcation). In [13], within the framework of [4, 5], we already derived a set of explicit formulas for calculating normal forms (up to third order) of Hopf-steady state bifurcation (including Turing–Hopf bifurcation) for a general delayed reaction diffusion equation with Neumann boundary condition. By employing these formulas, we obtain the normal forms of (1.1) when Turing–Hopf bifurcation occurs, where the coefficients in the normal form explicitly depend on the original parameter in the system. From the dynamics of unfolding of the normal form, we theoretically prove the existence of various spatiotemporal patterns for different parameter values, such as, a pair of spatially inhomogeneous steady state, a stable spatially homogeneous periodic orbit and two spatially inhomogeneous periodic orbits.

Turing–Hopf bifurcation for delayed reaction diffusion equation has been covered in [11, 15, 27, 33] and reference therein. The method employed here is different from the ones in the literature. It requires a great deal of symbolic manipulation, whereas, its advantages are also threefold: (1) From the bifurcation set for the unfolding of the normal form, one can specify what kind of spatiotemporal pattern the model can exhibit for any parameters near the critical bifurcation values; (2) One can also easily find the curves where periodic solution undergoes Turing bifurcation or spatially inhomogeneous steady state undergoes Hopf bifurcation. From this point of view, our approach can be regarded as an integration of the two methods mentioned above; (3) Through this codimension two bifurcation analysis, other complex patterns could be theoretically shown, such as spatially inhomogeneous quasi-periodic solutions (see the cases of VIa and VIIa in [7] or [16]), relying on the signs of the coefficients in the normal form.

The paper is organized as follows. In Sect. 2, by analyzing characteristic equations at the positive constant steady state, conditions for Turing instability, as well as Hopf bifurcation and Turing–Hopf bifurcation are established. In Sect. 3, applying the general formula of normal form for Hopf-steady state bifurcation in [13], explicit formulas for quadratic and cubic coefficients of normal forms at Turing–Hopf singularity are derived. In Sect. 4, for a certain set of parameter values, we use the unfolding of normal form to prove the existence of various spatiotemporal pattern, caused by Turing–Hopf bifurcation. Numerical simulations are also carried out to support the theoretical findings. We finish our study with conclusions in Sect. 5. Throughout the paper, ${{\mathbb {N}}}$ is the set of all positive integers, and ${{\mathbb {N}}}_0={{\mathbb {N}}}\cup \{0\}$ represents the set of all non-negative integers.

2 Turing and Hopf Bifurcation

In this section, Turing instability, Turing bifurcation and Hopf bifurcation for system (1.1) are investigated.

It is straightforward that the system (1.1) admits a unique positive constant steady state $E_*=(u_*,v_*)$, with

$$\begin{aligned} u_*=a+b,\;v_*=\frac{b}{(a+b)^2}. \end{aligned}$$

The linearized equation of system (1.1) at $E_*$ is given by

$$\begin{aligned} \begin{aligned} u_t(x,t)&=\varepsilon du_{xx}(x,t)-u(x,t)+2u_*v_*u(x,t-\tau )+u_*^2v(x,t-\tau ),&x\in (0,1),t>0,\\ v_t(x,t)&=d v_{xx}(x,t)-2u_*v_*u(x,t-\tau )-u_*^2v(x,t-\tau ),&x\in (0,1),t>0,\\ u_x(0,t)&=u_x(1,t)=v_x(0,t)=v_x(1,t)=0, \;\;&t\ge 0. \end{aligned}\nonumber \\ \end{aligned}$$

(2.1)

Let $\mu _k$, $k\in {\mathbb {N}}_0$ be the eigenvalues of $-\Delta$ with Neumann boundary condition in one dimensional spatial domain (0, 1). Then, $\mu _k=k^2\pi ^2$, and the characteristic equation of (2.1) is

$$\begin{aligned} D_k(\lambda ,\tau ,\varepsilon ):=\lambda ^2+p_k\lambda +r_k+(s_k\lambda +q_k)e^{-\lambda \tau }=0,\;k\in {\mathbb {N}}_0, \end{aligned}$$

(2.2)

where

$$\begin{aligned} \begin{aligned} p_k&\triangleq (\varepsilon +1)dk^2\pi ^2+1,\;&r_k&\triangleq \varepsilon d^2k^4\pi ^4+dk^2\pi ^2,\\ s_k&\triangleq u_*^2-2u_*v_*,\;&q_k&\triangleq (\varepsilon u_*^2-2u_*v_*)dk^2\pi ^2+u_*^2. \end{aligned} \end{aligned}$$

(2.3)

In particular, for $\tau =0$, (2.2) turns into

$$\begin{aligned} D_k(\lambda ,0,\varepsilon )=\lambda ^2+(p_k+s_k)\lambda +(r_k+q_k)=0,\;k\in {\mathbb {N}}_0. \end{aligned}$$

(2.4)

Denote $DET_k:= r_k+q_k$ and $TR_k:=-(p_k+s_k)$ for $k\in {\mathbb {N}}_0$. Then

$$\begin{aligned} \begin{array}{rl} DET_k=&{}\varepsilon d^2k^4\pi ^4+(\varepsilon u_*^2-2u_*v_*+1)dk^2\pi ^2+u_*^2,\\ TR_k=&{}-(\varepsilon +1)dk^2\pi ^2-1-u_*^2+2u_*v_*, \end{array} \end{aligned}$$

Throughout this paper, we assume

• $\mathbf{(N_0)}$$u_*^2>2u_*v_*-1>0$;

By $\mathbf{(N_0)}$, we know that all eigenvalues of (2.4) with $k=0$ have negative real parts. In the remaining parts, k-mode Turing (Hopf) bifurcation is referred to the corresponding k-th characteristic equation having a zero root (a pair of purely imaginary roots), and (m, n)-mode Turing–Hopf bifurcation is related to the fact that (2.2) with m and n have a zero root and a pair of purely imaginary roots, respectively.

2.1 Turing Bifurcation and Turing Instability

We first determine the feasible region on $(\varepsilon ,d)$-plane, on which Turing bifurcation curve may exist.

Lemma 2.1

For (1.1), the Turing bifurcation point $(\varepsilon ,d)$ always exist, and $(\varepsilon ,d)\in \{(\varepsilon ,d)\in {\mathbb {R}}_2^+, d>0, 0<\varepsilon <\varepsilon _B(d)\}:=S$, where

$$\begin{aligned} \varepsilon _B(d)=\left\{ \begin{array}{ll} \varepsilon _1\triangleq \frac{1}{u_*^2}(\sqrt{2u_*v_*}-1)^2, &{}{\mathrm {if}} ~~0<d\le d_0,\\ \varepsilon _2(d)\triangleq \frac{2u_*v_*-1}{\pi ^2d+u_*^2}, &{}{\mathrm {if}} ~~d\ge d_0. \end{array}\right. \end{aligned}$$

(2.5)

Proof

For $k\in {\mathbb {R}}^+$, $DET_k$ attains its minimum at $k_{min}^2\triangleq \frac{2u_*v_*-\varepsilon u_*^2-1}{2d\varepsilon \pi ^2}$. It then can be verified that $\min \limits _{k\in {\mathbb {R}}^+ } DET_k=u_*^2-\frac{(\varepsilon u_{*}^{2}-2u_*v_*+1)^2}{4\varepsilon } >0$ if and only if $\varepsilon >\varepsilon _1$. From $\mathbf{(N_0)}$, we have $TR_k<0$ for any $k\in {\mathbb {N}}_0$. Therefore, 0 can not be a zero of (2.4) for any $k\in {\mathbb {N}}_0$ as long as $\varepsilon >\varepsilon _1$.

When $\varepsilon <\varepsilon _2(d)$, we have $k_{min}>\frac{1}{\sqrt{2}}$. Consequently, there exists $(\varepsilon ,d)$, such that $\varepsilon <\varepsilon _2(d)$ and 0 is a root of (2.4) with such $(\varepsilon ,d)$ for some $k\in {\mathbb {N}}$. By $\sqrt{2u^*v^*}>1$, we know $\varepsilon _2(0)>\varepsilon _1$. Since $\varepsilon _2(d)$ is strictly decreasing in d. there is a unique $d=d_0\triangleq \frac{2u_*^2}{\pi ^2(\sqrt{2u_*v_*}-1)}$ such that $\varepsilon _2(d_0)=\varepsilon _1$, $\varepsilon _2(d)>\varepsilon _1$ for $d\in (0,d_0)$ and $\varepsilon _2(d)<\varepsilon _1$ for $d\in (d_0,+\infty )$. From the above discussion, we can conclude that the Turing bifurcation point $(\varepsilon ,d)\in S$. $\square$

For any $k\in {\mathbb {N}}$, define

$$\begin{aligned} \varepsilon _*(k,d)=\frac{(2u_*v_*-1)dk^2 \pi ^2-u_*^2}{dk^2\pi ^2(dk^2\pi ^2+u_*^2)}, \end{aligned}$$

(2.6)

for $d>d_k\triangleq \frac{u_*^2}{k^2\pi ^2(2u_*v_*-1)}$. Obviously, $DET_{k}=0$ whenever $\varepsilon =\varepsilon _*(k,d)$. Using a geometric argument, we have the following properties for $\varepsilon _*(k,d)$.

Lemma 2.2

Suppose that $\mathbf{(N_0)}$ holds. Then, we have

• (a) For any fixed $k\in {\mathbb {N}}$, $\varepsilon =\varepsilon _*(k,d)$ reaches its maximum $\varepsilon _1$ at $d=d_M(k)\triangleq \frac{u_*^2}{k^2\pi ^2(\sqrt{2u_*v_*}-1)}>d_k$, and $\varepsilon _*(k,d)$ is monotonically decreasing (increasing) in d, for $d>d_{M}(k)$ ($d_k<d<d_{M}(k)$).

• (b) For any $k\in {\mathbb {N}}$, the equation

  $$\begin{aligned} \varepsilon _*(k,d)=\varepsilon _*(k+1,d), d>0, \end{aligned}$$

  has a unique positive root $d_{k,k+1} ~\in (d_M(k+1),d_M(k))$ for d, which is given by

  $$\begin{aligned} d_{k,k+1}=\frac{u_*^2}{2\pi ^2(2u_*v_*-1)}\left[ \frac{1}{k^2}+ \frac{1}{(k+1)^2}+\sqrt{\left( \frac{1}{k^2}+ \frac{1}{(k+1)^2}\right) ^2+\frac{4(2u_*v_*-1)}{k^2(k+1)^2}} \right] .\nonumber \\ \end{aligned}$$

  (2.7)

  Moreover,

  $$\begin{aligned} \varepsilon _*(k,d)>\varepsilon _*(k+1,d)>\varepsilon _*(k+2,d)>\cdots , ~{\mathrm {for}}~d>d_{k,k+1}. \end{aligned}$$

  (2.8)

• (c) Let

  $$\begin{aligned} \varepsilon _*(d):=\varepsilon _*(k,d),~~~\text {for} ~d\in [d_{k,k+1},d_{k-1,k}),k\in {\mathbb {N}}. \end{aligned}$$

  (2.9)

  where $d_{0,1}:=+\infty$. Then, $\varepsilon _*(d)\le \varepsilon _B(d)$ for $0<d<+\infty$, and $\varepsilon _*(d)=\varepsilon _B(d)$ if and only if $d=d_M(k)$, $k\in {\mathbb {N}}$.

In Fig. 1, we plot the curves of $\varepsilon _*(k,d)$ for different k to illustrate the properties as presented in Lemma 2.2. We will show that the graph of $\varepsilon _*(d)$ is actually the critical curve of Turing instability.

Fig. 1

The graph of functions $\varepsilon =\varepsilon _1$, $\varepsilon =\varepsilon _2(d)$ and $\varepsilon =\varepsilon _*(k,d)$ for different k in $(d,\varepsilon )$ plane

Lemma 2.3

Assume that $\mathbf{(N_0)}$ holds. Then,

• (1) If $d\in (d_{k_1,k_1+1},d_{k_1-1,k_1})$ for some $k_1\in {\mathbb {N}}$ and $\varepsilon =\varepsilon _*(d)$, then 0 is a simple root of (2.2) with $k=k_1$, and all the other roots of (2.2) have strictly negative real parts for $\tau =0$. Furthermore, let $\lambda =\lambda (k_1,\tau ,\varepsilon )$ be the root of (2.2) with $k=k_1$ such that $\lambda (k_1,\tau ,\varepsilon _*(d))=0$, where $(\tau ,\varepsilon )\in [0,+\infty )\times (\varepsilon _*(d) -\delta ,\varepsilon _*(d)+\delta )$ for sufficiently small $\delta >0$. Then,

  $$\begin{aligned} \frac{{\mathrm {d }}D_{k_1}(\lambda ,\tau ,\varepsilon )}{{\mathrm {d}}\varepsilon }|_{\lambda =0,\varepsilon = \varepsilon _*(d)}< 0. \end{aligned}$$

  (2.10)

• (2) If $d=d_{k,k+1}$ and $\varepsilon =\varepsilon _*(d_{k,k+1})$, then 0 is a simple root of (2.2) for both k and $k+1$, $k\in {\mathbb {N}}$.

Proof

(1) Recall that $DET_{k}=0$ if and only if $\varepsilon =\varepsilon _*(k,d)$ for $k\in {\mathbb {N}}$. Then, for any $k\in {\mathbb {N}}$, $\lambda =0$ is always a root of (2.2) with such k when $\varepsilon =\varepsilon _*(k,d)$. By the definition of $\varepsilon _*(d)$ and $\varepsilon _*(k,d)$, we know that if $d\in (d_{k_1,k_1+1},d_{k_1-1,k_1})$ for some $k_1$ and $\varepsilon =\varepsilon _*(d)$, then $\lambda =0$ is a root of (2.2) with $k=k_1$. Furthermore, $\lambda =0$ is simple, since

$$\begin{aligned} \frac{{\mathrm {d }}D_{k_1}(\lambda ,\tau ,\varepsilon )}{{\mathrm {d}}\lambda }|_ {\lambda =0}=p_{k_1}+s_{k_1}-\tau q_{k_1}=-TR_{k_1}+\tau r_{k_1}>0. \end{aligned}$$

Note that the assumption $\mathbf{(N_0)}$ ensures $TR_k<0$, for all $k\in {\mathbb {N}}_0$, and $DET_k>0$ for $k\in {\mathbb {N}}, k\ne k_1$. Therefore, all the other roots of (2.2) for $\tau =0$ has strictly negative real parts when $\varepsilon =\varepsilon _*(d)$.

It remains to verify the (2.10). Differentiating (2.2) with respect to $\varepsilon$, we obtain

$$\begin{aligned} \frac{{\mathrm {d }}D_{k_1}(\lambda ,\tau ,\varepsilon )}{{\mathrm {d}}\varepsilon } |_{\lambda =0,\varepsilon =\varepsilon _*(d)}=(p_{k_1}+s_{k_1} -\tau q_{k_1})\frac{{\mathrm {d}}\lambda (k_1,\tau ,\varepsilon _*(d))}{{\mathrm {d}}\varepsilon }\,+\,d^2k_1^4\pi ^4+dk_1^2\pi ^2 u_*^2\,=\,0. \end{aligned}$$

Using $\mathbf (N_0)$ and $DET_{k_1}=0$ again, we have

$$\begin{aligned} p_{k_1}+s_{k_1}-\tau q_{k_1}=u_*^2-2u_*v_*+1+(\varepsilon _*(d)+1)dk_1^2 \pi ^2+\tau r_{k_1}>0. \end{aligned}$$

Thus,

$$\begin{aligned} \frac{{\mathrm {d}}\lambda (k_1,\tau ,\varepsilon _*)}{{\mathrm {d}}\varepsilon }=-\frac{d^2k_1^4\pi ^4+dk_1^2 \pi ^2u_*^2}{p_{k_1}+s_{k_1}-\tau q_{k_1}}<0,\ {\mathrm {for}} \ \tau \ge 0. \end{aligned}$$

This proves the first statement.

(2) By a similar argument as above, one can show the second assertion. $\square$

As a direct consequence of Lemma 2.3, we arrive at the following conclusion on the Turing bifurcation of (1.1).

Theorem 2.4

Assume that $\mathbf{(N_0)}$ holds. Then,

• (1) For $d>0$, if $\varepsilon >\varepsilon _*(d)$, then the constant steady state $(u_*,v_*)$ of system (1.1) is asymptotically stable for $\tau =0$, and if $0<\varepsilon <\varepsilon _*(d)$, then $(u_*,v_*)$ is unstable.

• (2) For $d\in (d_{k,k+1},d_{k-1,k})$, the system (1.1) will undergoes k-mode Turing bifurcation at $\varepsilon =\varepsilon _*(d)$, and the bifurcated inhomogeneous steady state near $(\varepsilon _*(d), u_*,v_*)$ can be parameterized as $(\varepsilon (s), u(s),v(s))$ for $s\in (-\delta ,\delta )$ with sufficiently small $\delta$, where

  $$\begin{aligned} \varepsilon (s)=\varepsilon _*(d)+s,~~~~ (u(s),v(s))=(u_*,v_*)+r(s)\cos (k_1 \pi x)(1,p_{k_1}). \end{aligned}$$

  and $p_{k_1}=\frac{1}{u_*^2}(1-2u_*v_*-d\varepsilon _* \mu _{k_1})$, $r(s)\ne 0$.

• (3) When $d=d_{k,k+1}$, $(k,k+1)$-mode Turing-Turing bifurcation occurs at $\varepsilon =\varepsilon _*(d_{k,k+1})$.

Remark 2.5

The graph of $\varepsilon =\varepsilon _*(d),~d >0$ is called the first Turing bifurcation curve in this context. From Lemma 2.2, we know it is continuous and piecewise smooth on $(0,+\infty )$, and the nonsmooth points of $\varepsilon _*(d)$ are exactly the Turing–Turinig bifurcation points $T_{k.k+1},k\in {\mathbb {N}}$, see Fig. 2. Since the expression of $\varepsilon _*(d)$ explicitly depends on wave number k and diffusion rate d as in (2.9), we can easily find stable spatial inhomogeneous patterns of (1.1) with arbitrary wave number, see the numerical simulations in Sect. 4. In addition, if $\varepsilon$ is fixed, then the diffusion coefficient d also has great impact on wave number k, and hence on the spatial patterns of (1.1)

Fig. 2

The first Turing bifurcation line $T: ~\varepsilon =\varepsilon _*(d),~d>0$, and Turing–Turing bifurcation point $T_{k,k+1},k=1,2,3,\ldots$

Remark 2.6

It is also remarked that $\varepsilon <\varepsilon _*(d)$ is the sharp condition for the occurrence of Turing instability for (1.1), i.e., $(u_*,v_*)$ is stable for $\varepsilon >\varepsilon _*(d)$, and will be destabilized through Turing bifurcation, as $\varepsilon$ decreasingly crosses $\varepsilon _*(d)$. This extends most of the existing results in the literature. For instance, it has been shown in [11] that Turing instability will not happen for $\varepsilon >\varepsilon _1$, where $\varepsilon _1$, defined in (2.5), is independent of d. In Theorem 2.4, we prove that the steady state $(u_*,v_*)$ is always stable for $\varepsilon >\varepsilon _*(d)$, which can be viewed an extension of the results in [11], since $\varepsilon _*(d)\le \varepsilon _B(d)\le \varepsilon _1$.

Remark 2.7

If $\varepsilon \in (\varepsilon _*(d_{{\tilde{k}},{\tilde{k}}+1}), \varepsilon _*(d_{{\tilde{k}}+1,{\tilde{k}}+2}))$ is fixed, for some ${\tilde{k}}\in {\mathbb {N}}$, from the graph of $\varepsilon _*(d)$, there exists a sequence of ${\tilde{d}}_i$, such that 0 is a root of (2.4) when $d={\tilde{d}}_i$, $i=1,2,\ldots 2{\tilde{k}}+1$, and ${\tilde{d}}_i>{\tilde{d}}_{j}$ if $j>i$. Let ${\tilde{\lambda }}(k_*,\tau ,d)$ be the root of (2.4) with some $k=k_*$ such that ${\tilde{\lambda }}(k_*,\tau ,{\tilde{d}}_i)=0$. Then, it can be verified that $\frac{d{\tilde{\lambda }}(k_*,\tau ,d)}{d}|_{d={\tilde{d}}_i}>0$ and $k_*=\frac{i+1}{2}$$\left( \frac{\partial \tilde{\lambda }(k_*,\tau ,d)}{\partial d}|_{d=\tilde{d}_i}<0 \,\,\text {and}\,\, k_*=\frac{i}{2}\right)$ for $i=1,3,5,\ldots ,2{\tilde{k}}+1$ ($i=2,4,6,\ldots ,2{\tilde{k}}$). This will implies the stability of $(u_*,v_*)$ interchanges repeatedly as d passes through ${\tilde{d}}_i$, and (1.1) has a spatially inhomogeneous steady state with wave number $\frac{i+1}{2}$ for $d\in ({\tilde{d}}_{i+1},{\tilde{d}}_i)$ and $i=1,3,5,\ldots ,2{\tilde{k}}+1$.

2.2 Hopf Bifurcation

Now, we will study the Hopf bifurcation of (1.1) in the case of $\varepsilon \ge \varepsilon _*(d),~d>0$. Suppose that $\lambda =\pm {\mathrm {i}}\omega _k$ with $\omega _k > 0$ are a pair of purely imaginary roots of (2.2). Then,

$$\begin{aligned} D_k({\mathrm {i}}\omega _k, \tau ,\varepsilon )= & {} r_k-\omega _k^2+q_k \cos (\omega _k \tau )+s_k\omega _k \sin (\omega _k \tau ) \nonumber \\&+{\mathrm {i}}[p_k\omega _k+s_k\omega _k \cos (\omega _k\tau )-q_k \sin (\omega _k \tau )]=0, \end{aligned}$$

for $k\in {\mathbb {N}}_0$. Separating the real and imaginary parts, we have

$$\begin{aligned} \begin{array}{rl} \cos (\omega _k \tau )&{}=\frac{q_k(\omega _k^2-r_k)-p_ks_k\omega _k^2}{s_k^2\omega _k^2+q_k^2} ,\\ \sin (\omega _k \tau )&{}=\frac{s_k\omega _k(\omega _k^2-r_k)+p_kq_k\omega _k}{s_k^2\omega _k^2+q_k^2} . \end{array} \end{aligned}$$

(2.11)

which yields

$$\begin{aligned} \omega _k^4+(p_k^2-s_k^2-2r_k)w_k^2+r_k^2-q_k^2=0. \end{aligned}$$

(2.12)

Define

$$\begin{aligned} \omega _k^{\pm }:=\frac{\sqrt{2}}{2}\bigg (s_k^2-p_k^2+2r_k\pm \sqrt{(s_k^2-p_k^2+2r_k)^2 -4(r_k^2-q_k^2)}\bigg )^{1/2}. \end{aligned}$$

(2.13)

Theorem 2.8

Assume that $\mathbf{(N_0)}$ holds and $\frac{2u_*v_*+1}{u_*^2}\ge \varepsilon \ge \varepsilon _*(d)$ for any $d>0$. For (2.12) with $k\in {\mathbb {N}}_0$, the following statements are valid.

• (1) When $0\le k<K^0$, $\omega _k^+$ is the unique positive root to (2.12), where

  $$\begin{aligned} K ^0:=\frac{1}{\sqrt{2\varepsilon d}\pi }\left[ (\varepsilon u_*^2-2u_*v_*-1)+\sqrt{(\varepsilon u_*^2-2u_*v_*-1)^2+4\varepsilon u_*^2}\right] ^{\frac{1}{2}}. \end{aligned}$$

  (2.14)

• (2) For $k\ge K^0$,

  • (a) if $(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)<1$, then (2.12) has no positive root;

  • (b) if $(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)\ge 1$ and $K^0\ge K^+$, where

    $$\begin{aligned} K ^{+}=\frac{1}{\pi \sqrt{(\varepsilon ^2+1) d}}\left( -\varepsilon +\sqrt{(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)- 1}\right) ^{1/2}, \end{aligned}$$

    (2.15)

    then (2.12) also has no positive root for $k\ge K^0$;

  • (c) if $(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)\ge 1$ and $K^0< K^+$, there is a $K_*\in (K^0,K^+)$, such that (2.12) has two positive roots $\omega _k^{\pm }$ for $k\in (K^0,K_*)$, a positive root $\omega _k^{+}$ for $k=K^0$ or $K_*$ and and has no positive root for $k>K_*$.

Proof

(1) Obviously, $r_k+q_k=DET_k\ge 0$. From $\varepsilon \le \frac{2u_*v_*+1}{u_*^2}$, we know $\varepsilon u_*^2-2u_*v_*-1\le 0$. Hence,

$$\begin{aligned} r_k-q_k=\varepsilon (dk^2\pi ^2)^2-(\varepsilon u_*^2-2u_*v_*-1)(dk^2\pi ^2)-u_*^2 \end{aligned}$$

is strictly increasing in $k\in {\mathbb {R}}^+$ and $r_k-q_k>r_0-q_0=-u_*^2$. For $K^0$ defined in (2.14), we have $r_{K^0}^2-q_{K^0}^2=0$. This implies

$$\begin{aligned} \begin{array}{rll} r_k^2-q_k^2<0, &{} {\mathrm {for}}&{} 0\le k<K^0,\\ r_k^2-q_k^2\ge 0, &{} {\mathrm {for}}&{} k\ge K^0, \end{array} \end{aligned}$$

and therefore, $\omega _k^+$ is the unique positive root to equation (2.12) for $0\le k<K^0$.

(2) If $(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)<1$, then $p_0^2-s_0^2-2r_0=-(u_*^2-2u_*v_*)^2+1>0$. Note that

$$\begin{aligned} p_k^2-s_k^2-2r_k=({\varepsilon }^2+1)d^2k^4\pi ^4+2\varepsilon dk^2\pi ^2-(u_*^2-2u_*v_*)^2+1. \end{aligned}$$

By the monotonicity of $p_k^2-s_k^2-2r_k$ with respect to k, it concludes that $p_k^2-s_k^2-2r_k>0$ for all $k\in {\mathbb {R}}^+$. If $(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)\ge 1$, then $K^+$ in (2.15) is well-defined, and is the unique nonnegative root of $p_k^2-s_k^2-2r_k=0$ with respect to k. Therefore, $p_k^2-s_k^2-2r_k>0$ for $k>K^+$ in this case. On the other hand, it follows form (1) that $r_k^2-q_k^2>0$ for $k>K^0$. Therefore, both $\omega _k^+$ and $\omega _k^-$ can not be positive under the assumptions of (a) or (b) in (2), which proves the first and second assertion.

For the case of $K^0<K^+$, let

$$\begin{aligned} \Delta (k):=(s_k^2-p_k^2+2r_k)^2 -4(r_k^2-q_k^2). \end{aligned}$$

Then, $\Delta (K^0)=(s_{K^0}^2-p_{K^0}^2+2r_{K^0})^2 >0$ and $\Delta (K^+)= -4(r_{K^+}^2-q_{K^+}^2)<0$. So there exist $K_*\in (K^0,K^+)$ such that $\Delta (K_*)=0$, and $\Delta (k)>0,~r_k^2-q_k^2>0$ for $k\in (K^0,K_*)$. Accordingly, equation (2.12) has two positive roots $\omega _k^{\pm }$ for $k\in (K^0,K_*)$. When $k=K^0$, $(s_{k}^2-p_{k}^2+2r_{k})^2 >0$ and $r_{k}^2-q_{k}^2=0$. Therefore, $\omega _{K^0}^{-}=0$ and $\omega _{K^0}^{+}$ is the unique positive root of (2.12). For $k=K_*$, from $\Delta (K_*)=0$ and $(s_{K_*}^2-p_{K_*}^2+2r_{K_*})^2>0$, we have $\omega _{K_*}^+=\omega _{K_*}^- >0$. This proves the third statement in (2). $\square$

Corollary 2.9

Suppose that $\mathbf{(N_0)}$ holds, and $\frac{2u_*v_*+1}{u_*^2}\ge \varepsilon \ge \varepsilon _*(d)$, for $d>0$. Let

$$\begin{aligned} K^*:=\left\{ \begin{array}{ll} K^0, &{} {\mathrm {for}} ~(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)<1\\ K^0, &{} {\mathrm {for}} ~(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)\ge 1~ {\mathrm {and}} ~K^0\ge K^+,\\ K_*, &{} {\mathrm {for}} ~(u_*^2-2u_*v_*)^2(\varepsilon ^2+1)\ge 1~ {\mathrm {and}} ~K^0< K^+, \end{array}\right. \end{aligned}$$

(2.16)

Then, equation (2.12) has at least a positive root $\omega _k^+$ for $0\le k<K^*$ and $k\in {\mathbb {N}}_0$.

Suppose that $\omega _k^+$ is a positive root of (2.12). Let $\tau _k$ be the root of (2.11) with $\omega _k=\omega _k^+$ in $(0,2\pi ]$. Then, we can define the critical values for $\tau$ by

$$\begin{aligned} \tau _k^{(j)}=\tau _k+\frac{2\pi j}{\omega _k^+},~j,k=0,1,2,\ldots , 0\le k<K^*. \end{aligned}$$

(2.17)

at which $\pm {\mathrm {i}}\omega _k^+$ are pure imaginary roots of (2.2). Denote by $\lambda (\tau )=\alpha (\tau )+{\mathrm {i}}\omega (\tau )$ the root of (2.2) near $\tau =\tau _k^{(j)}$ satisfying $\alpha (\tau _k^{(j)})=0, ~\omega (\tau _k^{(j)})=\omega _k^+$, for $k\in {\mathbb {N}}_0,~0\le k<K^*$. Then,

Theorem 2.10

Suppose that $\mathbf{(N_0)}$ holds, $\frac{2u_*v_*+1}{u_*^2}\ge \varepsilon \ge \varepsilon _*(d),~d>0$ and $0\le k<K^*$. Then,

$$\begin{aligned} \frac{{\mathrm {d}}\alpha (\tau )}{{\mathrm {d}}\tau }|_{\tau _k^{(j)}}>0. \end{aligned}$$

Proof

The proof is similar to the proof of Theorem 2.2 in [36], and hence omitted here. $\square$

Let $k_2\in [0,K^*)$ be an integer such that

$$\begin{aligned} \tau _{k_2}=\min _{k\in {\mathbb {N}}_0,k\in [0,K^*)}\tau _k. \end{aligned}$$

(2.18)

Theorem 2.11

Suppose that $\mathbf{(N_0)}$ holds, and $\frac{2u_*v_*+1}{u_*^2}\ge \varepsilon>\varepsilon _*(d),~d>0$. Then

• (1) The steady states $(u_*,v_*)$ of (1.1) is locally asymptotically stable for $\tau \in [0,\tau _{k_2})$. When $\tau =\tau _{k_2}$, $D_{k_2}(\lambda ,\tau ,\varepsilon )=0$ has a pair of pure imaginary roots for $\lambda$, with all other roots of (2.2) having strictly negative real parts for any $k\in {\mathbb {N}}_0$.

• (2) At $\tau =\tau _k^{(j)}$ with $0\le k<K^*$ and $j, k\in {\mathbb {N}}_0$, (1.1) undergoes k-mode Hopf bifurcation near $(u_*,v_*)$, and the bifurcating periodic solutions near $(\tau _k^{(j)}, u_*,v_*)$ can be parameterized as $(\tau (s), u(s),v(s))$, for $s\in (-\delta , 0)$ (or $s\in (0, \delta )$), where $\delta >0$ is sufficiently small,

  $$\begin{aligned} \tau (s)= & {} \tau _k^{(j)}+s,~~~ (u(s),v(s))=(u_*,v_*)+[r_1(s)(1,p_{k}^0)e^{\texttt {i}\tau _{k}\omega _{k}^+ \theta }\nonumber \\&+\,r_2(s)(1,\overline{p_{k}^0})e^{-\texttt {i}\tau _{k}\omega _{k}^+ \theta }]\cos (k \pi x) \end{aligned}$$

  for $-1\le \theta \le 0$, and $p_{k}^0=\frac{1}{u_*^2}(1-2u_*v_*e^{-{\mathrm {i}}\tau _{k}\omega _{k}^+} -d\varepsilon _*\mu _{k}+{\mathrm {i}}\omega _{k}^+)e^{{\mathrm {i}}\tau _{k}\omega _{k}^+}$, $r_1(s)~{\mathrm {or}}~r_2(s)\ne 0$.

Remark 2.12

If $\omega _k^-$ is also a positive root of (2.12), one can compute $\tau _k^-\in (0,2\pi ]$ such that $\tau _k^-$ is a root of (2.11) with $\omega _k=\omega _k^{-}$, and define

$$\begin{aligned} \tau _k^{(j-)}=\tau _k^-+\frac{2\pi j}{\omega _k^-},~j,k=0,1,2,\ldots , K^ 0\le k<K_*, \end{aligned}$$

(2.19)

The tranversality condition is now described as:

$$\begin{aligned} \frac{{\mathrm {d Re}}\lambda (\tau )}{{\mathrm {d}}\tau }|_{\tau _k^{(j-)}}<0. \end{aligned}$$

Therefore, $\tau _{k_2}<\mathop {min}\limits _{K^0\le s<K_*,s\in {\mathbb {N}}_0}\tau _s^-$. This implies $\tau _{k_2}$ is always the first Hopf bifurcation value no matter if $\omega _k^-$ exists or not.

3 Turing–Hopf Bifurcation

In this part, we will study the Turing Hopf bifurcation for (1.1), based on the conclusions of Turing bifurcation and Hopf bifurcation in previous section. It has been shown in Theorems 2.4 and 2.11 that Hopf-steady state bifurcation of (1.1) will never happen, in either case of $\tau >0$ and $d=0$ or $\tau =0$ and $d>0$. Using Theorems 2.4 and 2.11, one can easily prove the existence of Turing–Hopf bifurcation, induced by the joint effect of diffusion rate d and delay $\tau$.

Theorem 3.1

Suppose that $\mathbf{(N_0)}$ holds. Given $k_1\in {\mathbb {N}}$. Then, for $d\in (d_{k_1,k_1+1},d_{k_1-1,k_1})$, system (1.1) undergoes $(k_1,k_2)$-mode Turing–Hopf bifurcation near $(u_*,v_*)$ at $(\tau ,\varepsilon )=(\tau _{k_2},\varepsilon _*(d)): =(\tau _{k_2},\varepsilon _*)$, where $k_2$ is determined by (2.18).

For the purpose of determining the spatiotemporal patterns, which can be induced by Turing Hopf bifurcation, we shall derive the third-order normal forms of system (1.1) for $(k_1,k_2)$-mode Turing–Hopf bifurcation, with $(\tau ,\varepsilon )$ near the bifurcation point $(\tau _{k_2},\varepsilon _*)$. In order to use the formula, derived for the normal form of Hopf-steady state bifurcation in [13], we normalize the delay $\tau$ in system (1.1) by time-scaling $t\rightarrow t/\tau$, and translate $(u_*,v_*)$ into origin. Then, system (1.1) becomes

$$\begin{aligned} \begin{array}{rl} \frac{\partial u}{dt}=&{}\tau \big (\varepsilon du_{xx}+a-(u(t,x)+u_*)+(u(t-1,x)+u_*)^2(v(t-1,x)+v_*)\big ), \\ \frac{\partial v}{dt}=&{}\tau \big (d v_{xx}+b-(u(t-1,x)+u_*)^2(v(t-1,x)+v_*)\big ). \\ \end{array} \end{aligned}$$

(3.1)

The corresponding characteristic equations are now given by

$$\begin{aligned} \lambda ^2+\tau p_k(\varepsilon )\lambda +\tau ^2r_k(\varepsilon )+(\tau s_k\lambda +\tau ^2 q_k(\varepsilon ))e^{-\lambda }=0,\;k\in {\mathbb {N}}_0, \end{aligned}$$

(3.2)

Rewrite $\tau =\tau _{k_2}+\alpha _1, \varepsilon =\varepsilon _*+\alpha _2$, and let $U(t)=(u(t),v(t))$ Then, system (3.1) can be written as

$$\begin{aligned} \frac{d}{dt}U(t)= & {} L_0(U_t)+D_0\Delta U(t)+\frac{1}{2}L_1(\alpha )U_t+\frac{1}{2}D_1(\alpha )\Delta U(t)+\frac{1}{2!}Q(U_t,U_t)\nonumber \\&+\,\frac{1}{3!}C(U_t,U_t,U_t)+\cdots , \end{aligned}$$

(3.3)

where

$$\begin{aligned} D_0= & {} d\tau _{k_2} \left( \begin{array}{cc} \varepsilon _*&{}0\\ 0&{}1 \end{array}\right) ,~~ D_1(\alpha )=2d\left( \begin{array}{cc} \alpha _1\varepsilon _*+\alpha _2\tau _{k_2}&{}0\\ 0&{}\alpha _1 \end{array}\right) , \\ L_0\varphi= & {} \tau _{k_2}\left( \begin{array}{c} -\varphi ^{(1)}(0)+2u_*v_*\varphi ^{(1)}(-1)+u_*^2\varphi ^{(2)}(-1) \\ -(2u_*v_*\varphi ^{(1)}(-1)+u_*^2\varphi ^{(2)}(-1)) \end{array}\right) , \\ L_1(\alpha )\varphi= & {} 2\alpha _1\left( \begin{array}{c} -\varphi ^{(1)}(0)+2u_*v_*\varphi ^{(1)}(-1)+u_*^2\varphi ^{(2)}(-1) \\ -(2u_*v_*\varphi ^{(1)}(-1)+u_*^2\varphi ^{(2)}(-1)) \end{array}\right) , \\ Q(\varphi ,\varphi )= & {} 2\tau _{k_2}\varphi ^{(1)}(-1)[v_*\varphi ^{(1)}(-1)+2u_*\varphi ^{(2)}(-1)]\left( \begin{array}{c} 1\\ -1 \end{array}\right) , \\ C(\varphi ,\varphi ,\varphi )= & {} 3!\tau _{k_2}{\varphi ^{(1)}}^2(-1)\varphi ^{(2)}(-1)\left( \begin{array}{c} 1\\ -1 \end{array}\right) . \end{aligned}$$

with $\varphi =\left( \varphi ^{(1)}, \varphi ^{(2)}\right) ^T$. The phase space of (3.3) is chosen as ${\mathcal {C}}=C([-1,0];X)$, with $X=\left\{ (u,v):u,v\in W^{2,2}(\Omega ): u'(0)=u'(1)=v'(0)=v'(1)=0\; \right\}$. Thus, the symmetric multilinear forms Q and C can be written as

$$\begin{aligned} Q_{xy}= & {} 2\tau _{k_2}\{v_*x_1(-1)y_1(-1)+u_*(x_1(-1)y_2(-1)+x_2(-1)y_1(-1))\}\left( \begin{array}{c} 1\\ -1 \end{array}\right) ,\\ C_{xyz}= & {} 2\tau _{k_2}[x_1(-1)y_1(-1)z_2(-1)+x_1(-1)y_2(-1)z_1(-1)\\&+\,x_2(-1)y_1(-1)z_1(-1)]\left( \begin{array}{c} 1\\ -1 \end{array}\right) , \end{aligned}$$

for $x=\left( \begin{array}{c} x_1\\ x_2 \end{array}\right) , ~y=\left( \begin{array}{c} y_1\\ y_2 \end{array}\right) ,~z=\left( \begin{array}{c} z_1\\ z_2 \end{array}\right) .$

For $\alpha =(\alpha _1,\alpha _2)$ in a small neighbourhood of (0, 0), it follows from [13] that the normal forms of (3.3) for $\Omega =(0,l\pi )$ for any $l>0$, up to the third order, are

$$\begin{aligned} \begin{aligned} \dot{z}_1=\,&a_{1}(\alpha )z_1+a_{11}z_1^2+a_{23}z_2{\bar{z}}_2+a_{111}z_1^3+ a_{123}z_1z_2{\bar{z}}_2+h.o.t.,\\ \dot{z}_2=\,&{\mathrm {i}}\omega _0z_2+b_{2}(\alpha )z_2+b_{12}z_1z_2+b_{112}z_1^2z_2+ b_{223}z_2^2{\bar{z}}_2 + h.o.t. .\\ \dot{{\bar{z}}}_2=&-{\mathrm {i}}\omega _0{\bar{z}}_2+\overline{b_{2}(\alpha )}{\bar{z}}_2+\overline{b_{12}}z_1{\bar{z}}_2 +\overline{b_{112}}z_1^2{\bar{z}}_2+\overline{b_{223}}z_2{\bar{z}}_2^2+ h.o.t. , \end{aligned} \end{aligned}$$

(3.4)

In order to represent the explicit formula for the coefficients in (3.4), we introduce the following notations, see [13, (2.4),(2.6)–(2.9)] .

$$\begin{aligned} \begin{aligned} \phi _1(\theta )&\equiv \phi _1(0), \;\; \phi _2(\theta )=\phi _2(0)e^{{\mathrm {i}}\omega _0\theta },\\ \psi _1(s)&\equiv \psi _1(0), \;\; \psi _2(s)=\psi _2(0)e^{-{\mathrm {i}}\omega _0s} \end{aligned} \end{aligned}$$

(3.5)

for $\theta \in [-r,0],~s\in [0,r]$, where $\phi _1(0)$, $\psi _1(0)$, $\phi _2(0)$, $\psi _2(0)$ are determined by

$$\begin{aligned} \begin{aligned} \triangle _{k_1}(0)\phi _1(0)&=0, \;\; \psi _1(0)\triangle _{k_1}(0)=0,\\ \triangle _{k_2}(i\omega _0)\phi _2(0)&=0, \;\; \psi _2(0)\triangle _{k_2}(i\omega _0)=0,\\ (\psi _i,\phi _i)_{k_i}&=1,\;\; i=1,2. \end{aligned} \end{aligned}$$

(3.6)

Here, $\triangle _k(\cdot )$ and $(\cdot ,\cdot )_{k}$ are given by

$$\begin{aligned} \triangle _k(\lambda )= & {} \lambda I-\mu _k D_0-L_0(e^{\lambda \cdot }I), \end{aligned}$$

(3.7)

$$\begin{aligned} (\psi ,\ \varphi )_{k}= & {} \psi (0)\varphi (0)-\int ^0_{-r}\int ^\theta _0\psi (\xi -\theta ) {\mathrm {d}}\eta _{k}(\theta )\varphi (\xi ){\mathrm {d}}\xi ,\nonumber \\&\psi \in C^*\triangleq C([0,r];~ {\mathbb {C}}^{m*}),\ \varphi \in C, \end{aligned}$$

(3.8)

with $\mu _k=k^2/l^2$, $k\in {\mathbb {N}}_0$. And, $\eta _k\in BV([-r,0],{\mathbb {C}}^m)$ for $k\in {\mathbb {N}}_0$ satisfies

$$\begin{aligned} -\mu _kD_0 \psi (0)+L_0\psi = \int _{-r}^0 {\mathrm {d}}\eta _k(\theta )\psi (\theta ),\;\; ~\psi \in C\triangleq C([-r,0],\mathbb {C}^m). \end{aligned}$$

(3.9)

From [13], we have the following conclusion on the normal form (3.4), in the case of $k_2=0,~k_1\ne 0$ (which is referred to Turing–Hopf bifurcation of Hopf-pitchfork type).

Lemma 3.2

([13]) For $k_2=0,~k_1\ne 0$, the parameters $a_{1}(\alpha )$, $b_{2}(\alpha )$, $a_{11}$, $a_{23}$, $a_{111}$, $a_{123}$, $b_{12}$, $b_{112}$ and $b_{223}$ in (3.4) are given by

$$\begin{aligned} a_{1}(\alpha )= & {} \frac{1}{2}\psi _1 (0)(L_1(\alpha )\phi _1-\mu _{k_1}D_1(\alpha )\phi _1(0)),\nonumber \\ b_{2}(\alpha )= & {} \frac{1}{2}\psi _2 (0)(L_1(\alpha )\phi _2-\mu _{k_2}D_1(\alpha )\phi _2(0)),\nonumber \\ a_{11}= & {} a_{23}=b_{12}=0,\nonumber \\ a_{111}= & {} \frac{1}{4}\psi _1 (0)C_{\phi _1\phi _1\phi _1}+\frac{1}{\omega _0}\psi _1 (0){\mathrm {Re}}({\mathrm {i}}Q_{\phi _1\phi _2}\psi _2 (0))Q_{\phi _1\phi _1}{+}\psi _1 (0) Q_{\phi _1} \left( h_{200}^{0}{+}\frac{1}{\sqrt{2}}h_{200}^{2k_1}\right) ,\nonumber \\ a_{123}= & {} \psi _1 (0)C_{\phi _1\phi _2{\bar{\phi }}_2}+\frac{2}{\omega _0}\psi _1 (0){\mathrm {Re}}({\mathrm {i}}Q_{\phi _1\phi _2}\psi _2 (0))Q_{\phi _2{\bar{\phi }}_2}\nonumber \\&+\psi _1 (0) \left[ Q_{\phi _1} \left( h_{011}^{0}+\frac{1}{\sqrt{2}}h_{011}^{2k_1}\right) +Q_{\phi _2} h_{101}^{k_1} +Q_{{\bar{\phi }}_2} h_{110}^{k_1}\right] , \nonumber \\ b_{112}= & {} \frac{1}{2}\psi _2 (0)C_{\phi _1\phi _1\phi _2}+\frac{1}{2i\omega _0}\psi _2 (0)\{2Q_{\phi _1\phi _1}\psi _1 (0) Q_{\phi _1\phi _2} +[-Q_{\phi _2\phi _2}\psi _2 (0) \nonumber \\&+Q_{\phi _2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)]Q_{\phi _1\phi _1}\}+\psi _2 (0) \left( Q_{\phi _1} h_{110}^{k_1} +Q_{\phi _2} h_{200}^{0}\right) \nonumber \\ b_{223}= & {} \frac{1}{2}\psi _2 (0)C_{\phi _2\phi _2{\bar{\phi }}_2}+\frac{1}{4i\omega _0}\psi _2 (0)\left\{ \frac{2}{3}Q_{{\bar{\phi }}_2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)Q_{\phi _2\phi _2}+\left[ \phantom {b_{223}=\frac{1}{2}\psi _2 (0)C_{\phi _2\phi _2{\bar{\phi }}_2}+\frac{1}{4i\omega _0}\psi _2 (0)\left\{ \frac{2}{3}Q_{{\bar{\phi }}_2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)Q_{\phi _2\phi _2}+\left[ -2Q_{\phi _2\phi _2}\psi _2 (0) \right. \right. }-2Q_{\phi _2\phi _2}\psi _2 (0) \right. \right. \nonumber \\&\left. \left. +\,4Q_{\phi _2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)\right] Q_{\phi _2{\bar{\phi }}_2}\right\} +\psi _2 (0) (Q_{\phi _2} h_{011}^0+Q_{{\bar{\phi }}_2} h_{020}^0). \end{aligned}$$

(3.10)

where

$$\begin{aligned} h_{200}^0(\theta )= & {} -\frac{1}{2}\left[ \int _{-r}^0{\mathrm {d}}\eta _0(\theta )]^{-1}Q_{\phi _1\phi _1}+\frac{1}{2i\omega _0}(\phi _2(\theta )\psi _2(0)-{\bar{\phi }}_2(\theta ){\bar{\psi }}_2(0))\right] Q_{\phi _1\phi _1},\nonumber \\ h_{200}^{2k_1}(\theta )\equiv&-\frac{1}{2\sqrt{2}}\left[ \int _{-r}^0{\mathrm {d}}\eta _{2k_1}(\theta )\right] ^{-1}Q_{\phi _1\phi _1},\nonumber \\ h_{011}^0(\theta )= & {} -\left[ \int _{-r}^0{\mathrm {d}}\eta _0(\theta )]^{-1}Q_{\phi _2{\bar{\phi }}_2}+\frac{1}{i\omega _0}(\phi _2(\theta )\psi _2(0)-{\bar{\phi }}_2(\theta ){\bar{\psi }}_2(0))\right] Q_{\phi _2{\bar{\phi }}_2},\nonumber \\ h_{011}^{2k_1}(\theta )= & {} 0,\nonumber \\ h_{020}^0(\theta )= & {} \frac{1}{2}\left[ 2i\omega _0I-\int _{-r}^0e^{2i\omega _0\theta }{\mathrm {d}}\eta _{0}(\theta )\right] ^{-1}Q_{\phi _2\phi _2}e^{2i\omega _0\theta }-\frac{1}{2i\omega _0}\left[ \phantom {\left. +\frac{1}{3}{\bar{\phi }}_2(\theta ){\bar{\psi }}_2(0)\right] Q_{\phi _2\phi _2},} \phi _2(\theta )\psi _2(0)\right. \nonumber \\&\left. +\frac{1}{3}{\bar{\phi }}_2(\theta ){\bar{\psi }}_2(0)\right] Q_{\phi _2\phi _2},\nonumber \\ h_{110}^{k_1}(\theta )= & {} \left[ i\omega _0I-\int _{-r}^0e^{i\omega _0\theta }{\mathrm {d}}\eta _{k_1}(\theta )\right] ^{-1}Q_{\phi _1\phi _2}e^{i\omega _0\theta }-\frac{1}{i\omega _0}\phi _1(0)\psi _1(0)Q_{\phi _1\phi _2},\nonumber \\ h_{002}^0(\theta )= & {} \overline{h_{020}^0(\theta )},~~~h_{101}^{k_1}(\theta )=\overline{h_{110}^{k_1}(\theta )}, \end{aligned}$$

(3.11)

$\theta \in [-r,0]$. $\phi _1,\phi _2,\psi _1(0),\psi _2(0)$ and $\eta _k$ are denoted by (3.5), (3.6) and (3.9), respectively.

For (3.1), $m=2, ~r=1, ~l=1$. Now, we can see that it remains to compute $\phi _1,\phi _2,\psi _1(0),\psi _2(0)$ and $Q{\phi _i\phi _j}$, $C{\phi _i\phi _j\phi _l}$, for $i,j,l=1,2$. Note that $\omega _0=\tau _{k_2}\omega _{k_2}^+$ we have that

$$\begin{aligned} \phi _1(\theta ) =\left( \begin{array}{c} 1 \\ p_1^0 \end{array}\right) ,~~ \phi _2(\theta ) =\left( \begin{array}{c} 1 \\ p_2^0 \end{array}\right) e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ \theta },~~-1\le \theta \le 0 \end{aligned}$$

(3.12)

and

$$\begin{aligned} \psi _1(0 ) =\frac{1}{N_1}\left( 1 , q_1^0 \right) ,~~ \psi _2(0) =\frac{1}{N_2}\left( 1 , q_2^0 \right) , \end{aligned}$$

(3.13)

where

$$\begin{aligned} q_1^0= & {} -\frac{1}{2u_*v_*}(1-2u_*v_*-d\varepsilon _*\mu _{k_1}),\nonumber \\ p_1^0= & {} \frac{1}{u_*^2}(1-2u_*v_*-d\varepsilon _*\mu _{k_1}),\nonumber \\ q_2^0= & {} -\frac{1}{2u_*v_*}(1-2u_*v_*e^{-{\mathrm {i}}\tau _{k_2}\omega _{k_2}^+}-d\varepsilon _*\mu _{k_2}+{\mathrm {i}}\omega _{k_2}^+)e^{{\mathrm {i}}\tau _{k_2}\omega _{k_2}^+},\nonumber \\ p_2^0= & {} \frac{1}{u_*^2}(1-2u_*v_*e^{-{\mathrm {i}}\tau _{k_2}\omega _{k_2}^+}-d\varepsilon _*\mu _{k_2}+{\mathrm {i}}\omega _{k_2}^+)e^{{\mathrm {i}}\tau _{k_2}\omega _{k_2}^+},\nonumber \\ N_1= & {} 1+p_1^0q_1^0+\tau _{k_2} u_*(2v_*+u_*p_1^0)(1-q_1^0),\nonumber \\ N_2= & {} 1+p_2^0q_2^0+\tau _{k_2} u_*(2v_*+u_*p_2^0)(1-q_2^0)e^{-{\mathrm {i}}\tau _{k_2}\omega _{k_2}^+}. \end{aligned}$$

(3.14)

Therefore, the coefficient $a_1(\alpha )$ and $b_2(\alpha )$ in the normal form are

$$\begin{aligned} a_{1}(\alpha )= & {} \frac{1}{N_1}[-1+u_*(2v_*+u_*p_1^0)(1-q_1^0)-dk_1^2\pi ^2(\varepsilon _*+p_1^0q_1^0)]\alpha _1- \frac{1}{N_1}dk_1^2\pi ^2\tau _{k_2}\alpha _2,\nonumber \\ b_{2}(\alpha )= & {} \frac{1}{N_2}[-1+u_*(2v_*+u_*p_2^0)(1-q_2^0)e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+}-dk_2^2\pi ^2(\varepsilon _*+p_2^0q_2^0)]\alpha _1\nonumber \\&-\frac{1}{N_2}dk_2^2\pi ^2\tau _{k_2}\alpha _2. \end{aligned}$$

(3.15)

Furthermore,

$$\begin{aligned} \begin{aligned} Q_{\phi _1\phi _1}&= 2\tau _{k_2}(v_*+2u_*p_1^0)( 1,\ -1)^{T},\\ Q_{\phi _1\phi _2}&= 2\tau _{k_2}e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+ }[v_*+u_*(p_1^0+p_2^0)]( 1,\ -1)^{T},\\ Q_{\phi _1{\bar{\phi }}_2}&= 2\tau _{k_2}e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ }[v_*+u_*(p_1^0+\overline{p_2^0})]( 1,\ -1)^{T},\\ Q_{\phi _2\phi _2}&= 2\tau _{k_2}e^{-2\texttt {i}\tau _{k_2}\omega _{k_2}^+ }(v_*+2u_*p_2^0)( 1,\ -1)^{T},\\ Q_{\phi _2{\bar{\phi }}_2}&= 2\tau _{k_2}(v_*+u_*(p_2^0+\overline{p_2^0}))( 1,\ -1)^{T},\\ Q_{{\bar{\phi }}_2{\bar{\phi }}_2}&= 2\tau _{k_2}e^{2\texttt {i}\tau _{k_2}\omega _{k_2}^+ }(v_*+2u_*\overline{p_2^0})( 1,\ -1)^{T} \end{aligned} \end{aligned}$$

(3.16)

and

$$\begin{aligned} \begin{aligned} C_{\phi _1\phi _1\phi _1}&= 6\tau _{k_2}p_1^0( 1,\ -1)^{T},\\ C_{\phi _1\phi _2{\bar{\phi }}_2}&= 2\tau _{k_2}(p_1^0+p_2^0+\overline{p_2^0})]( 1,\ -1)^{T},\\ C_{\phi _1\phi _1\phi _2}&= 2\tau _{k_2}e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+ }(2p_1^0+p_2^0)( 1,\ -1)^{T},\\ C_{\phi _2\phi _2{\bar{\phi }}_2}&= 2\tau _{k_2} (2p_2^0+\overline{p_2^0}) e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+ }( 1,\ -1)^{T}. \end{aligned} \end{aligned}$$

(3.17)

Substituting (3.12), (3.13), (3.16) and (3.17) into (3.11), one can get

$$\begin{aligned} \begin{aligned} h_{200}^0(\theta )&=(v_*-2u_*p_1^0)\left[ \frac{1}{u_*^2}\left( \begin{array}{c} 0 \\ -1 \end{array}\right) +\frac{2}{\omega _{k_2}^+}\left( \begin{array}{c} {\mathrm {Re}}(\frac{1-q_2^0}{\texttt {i}N_2}e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ \theta }) \\ {\mathrm {Re}}(\frac{(1-q_2^0)p_2^0}{\texttt {i}N_2}e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ \theta }) \end{array}\right) \right] ,\\ h_{200}^{2k_1}(\theta )&=-\frac{1}{\sqrt{2}}(v_*+2u_*p_1^0)\frac{1}{q_{2k_1}(\varepsilon _*)+r_{2k_1}(\varepsilon _*)}\left( \begin{array}{c} -(2k_1)^2\pi ^2d \\ 1+(2k_1)^2\pi ^2d\varepsilon _* \end{array}\right) \\ h_{011}^0(\theta )&=2[v_*+u_*(p_2^0+\overline{p_2^0})]\left[ \frac{1}{u_*^2}\left( \begin{array}{c} 0 \\ -1 \end{array}\right) +\frac{2}{\omega _{k_2}^+}\left( \begin{array}{c} {\mathrm {Re}}(\frac{1-q_2^0}{\texttt {i}N_2}e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ \theta }) \\ {\mathrm {Re}}(\frac{(1-q_2^0)p_2^0}{\texttt {i}N_2}e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ \theta }) \end{array}\right) \right] ,\\ h_{011}^{2k_1}(\theta )&=0,\\ h_{020}^0(\theta )&=(v_*+2u_*p_1^0)\frac{e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ (\theta -2)}}{D_0(2\texttt {i}\omega _{k_2}^+,\tau _{k_2},\varepsilon _*)}\left( \begin{array}{c} 2\texttt {i}\omega _{k_2}^+ \\ -2\texttt {i}\omega _{k_2}^+ -1 \end{array}\right) \\&\quad -\frac{(v_*+2u_*p_1^0)}{\texttt {i}\omega _{k_2}^+}\left( e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+(\theta -2)}\frac{(1-q_2^0)}{N_2}\left( \begin{array}{c} 1 \\ p_2^0 \end{array}\right) +\frac{1}{3} e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+ (\theta +2)}\frac{(1-\overline{q_2^0})}{\overline{N_2}}\left( \begin{array}{c} 1 \\ \overline{p_2^0} \end{array}\right) \right) \\ h_{002}^0(\theta )&=\overline{h_{020}^0(\theta )},\\ h_{110}^{k_1}(\theta )&=2[v_*+u_*(p_1^0+p_2^0)]e^{\texttt {i}\tau _{k_2}\omega _{k_2}^+ (\theta -1)}\frac{1}{ D_{k_1}(\texttt {i}\omega _{k_2}^+,\tau _{k_2},\varepsilon _*)}\left( \begin{array}{c} \texttt {i}\omega _{k_2}^++d k_1^2\pi ^2 \\ -\texttt {i}\omega _{k_2}^+-\varepsilon _*d k_1^2\pi ^2-1 \end{array}\right) \\&\quad -2[v_*+u_*(p_1^0+p_2^0)]e^{-\texttt {i}\tau _{k_2}\omega _{k_2}^+}\frac{(1-q_1^0)}{\texttt {i}\omega _{k_2}^+N_1}\left( \begin{array}{c} 1 \\ p_1^0 \end{array}\right) ,\\ h_{101}^{k_1}(\theta )&=\overline{h_{110}^{k_1}(\theta )}. \end{aligned} \end{aligned}$$

(3.18)

which, together with (3.16), (3.17), (3.18) and (3.10), will yield all the other expressions of $a_{111}$, $a_{123}$, $b_{112}$ and $b_{223}$ in the normal form.

Theorem 3.3

Assume that $\mathbf{(N_0)}$ holds. Let $d\in (d_{k_1,k_1+1},d_{k_1-1,k_1})$ for some $k_1\ne 0$, and $k_2=0$. If $a_{111}\ne 0$, $a_{123}\ne 0$, ${\mathrm {Re}}b_{112}\ne 0$, ${\mathrm {Re}}b_{223} \ne 0$ and $a_{111}{\mathrm {Re}}b_{223}-a_{123}{\mathrm {Re}}b_{112}\ne 0$, then Turing–Hopf bifurcation of (1.1) is non-degenerate. Moreover, the cylindrical coordinate equation, associated with (3.4), is

$$\begin{aligned} \begin{array}{rlc} \dot{r}=&{} r(\varepsilon _1(\alpha )+r^2+b_0z^2),\\ \dot{z}=&{} z(\varepsilon _2(\alpha )+c_0r^2+d_0z^2), \end{array} \end{aligned}$$

(3.19)

where $\varepsilon _1(\alpha )={\mathrm {Re}}b_2(\alpha ) {\mathrm {sign}}({\mathrm {Re}}b_{223})$, $\varepsilon _2(\alpha )=a_1(\alpha ) {\mathrm {sign}}({\mathrm {Re}}b_{223})$ , $b_0= \frac{{\mathrm {Re}}b_{112}}{|a_{111}|} {\mathrm {sign}}({\mathrm {Re}}b_{223})$,  $c_0=\frac{a_{123}}{|{\mathrm {Re}}b_{223}|} {\mathrm {sign}}({\mathrm {Re}}b_{223})$ and $~d_0={\mathrm {sign}}(a_{111}{\mathrm {Re}}b_{223})$.

According to the standard theory on (3.19) in [7], we know that there are twelve distinct unfoldings for (3.19), depending on the signs of $b_0$, $c_0$, $d_0$ and $d_0-b_0c_0$, as presented in Table 1. In addition, each of these unfoldings will have different bifurcation scenario with respect to bifurcation parameters. With the aid of the dynamical behavior of (3.19), one can determine what kind of spatiotemporal patterns that (1.1) can exhibit as $(\tau ,\varepsilon )$ varies within a small neighbourhood of $(\tau _{k_2},\varepsilon _*)$. See [1] for the possible spatiotemporal patterns near the Turing–Hopf bifurcation point.

Table 1 The twelve unfoldings of (3.19), see [7]

4 Pattern Formation

In this section, we will illustrate how to use the results in Sects. 2 and 3 to show the existence of various spatiotemporal patterns for (1.1) with a certain set of fixed parameter values, such as, spatially inhomogeneous steady state (induced by Turing bifurcation), temporally periodical solutions with homogeneous or inhomogeneous spatial variables (through Hopf bifurcation), and other mixed patterns (caused by Turing–Hopf bifurcations).

Set $a=0.1,\ b=0.9.$ Then, it can be calculated that

$$\begin{aligned} (u_*,v_*)=(1,0.9), \varepsilon _1= 0.1167, d_0=0.5931, K^0=0.2721, \end{aligned}$$

Moreover, $\mathbf{(N_0)}$ is also satisfied. Given $k_1\in {\mathbb {N}}$, for $d\in (d_{k_1,k_1+1},~d_{k_1-1,k_1})$, we have

$$\begin{aligned} \varepsilon _*=\varepsilon _*(d)=\varepsilon _*(k_1,d)=\frac{4dk_1^2\pi ^2-5}{5dk_1^2\pi ^2(dk_1^2\pi ^2+1)}. \end{aligned}$$

From Theorem 2.4, $k_1$-mode Turing bifurcation of (1.1) will take place at $\varepsilon =\varepsilon _*$ for any fixed $d\in (d_{k_1,k_1+1},~d_{k_1-1,k_1})$.

4.1 (1, 0)-Mode Turing–Hopf Bifurcation

If we set $k_1=1$, then from (2.7), we have $d_{1,2}=0.1765$. Fix $d=0.5\in (d_{1,2},~+\infty )$. Then, $\varepsilon _*(0.5)=0.1007$, and 1-mode Turing bifurcation of (1.1) will occur at $\varepsilon _*(0.5)=0.1007$, see Fig. 3.

When $\varepsilon >0.1007$, according to (1) in Theorem 2.8, we assert that (2.12) has a unique positive root $\omega _k^+=0.9144$ when $0\le k<K^0$, and $k_2=0$. Therefore, the first critical value $\tau _*$ for the occurrence of Hopf bifurcation is $\tau _*=0.2171$. Thus, by Theorems 2.11 and 3.1, we can conclude that

Fig. 3

The line $d=0.5$ and $d=0.05$ intersect with Turing bifurcation line T at $\varepsilon _*(1,0.5)=0.1007$ and $\varepsilon _*(3,0.05)=0.1056$, respectively

Corollary 4.1

For parameters $a=0.1$, $b=0.9$ and $d=0.5$, we have

• (1) The equilibrium $(u_*,v_*)=(1,0.9)$ of system (1.1) with $\tau \in [0,0.2171)$ is asymptotically stable for $\varepsilon >0.1007$, and unstable for $0<\varepsilon <0.1007$.

• (2) System (1.1) undergoes (1, 0)-mode Turing–Hopf bifurcation near the constant steady states $(u_*,v_*)=(1,0.9)$ at $\tau =0.2171,\ \varepsilon =0.1007$.

Now, we compute the coefficients in the normal form associated with Turing Hopf bifurcation. From (2.3) and (3.14), we have

$$\begin{aligned} q_1^0= & {} 0.16837,~~q_2^0=0.55554-0.60759{\mathrm {i}}, ~~p_1^0=-0.30307,~~p_2^0=-0.99997 + 1.0937{\mathrm {i}}, \\ N_1= & {} 1.2192,~~N_2=1.0848 + 1.4353{\mathrm {i}}, \\ r_{k_2}= & {} 0,~~q_{k_2}=1,~~p_{k_2}=1, \\ r_{k_1}= & {} 7.3859,~~q_{k_1}=-7.3859,~~p_{k_1}=6.4359, \\ r_{2k_1}= & {} 58.9574,~~q_{2k_1}=-32.5438,~~p_{2k_1}=22.7260. \end{aligned}$$

By (3.18), we also obtain that

$$\begin{aligned}&h_{200}^0(0)= \left( \begin{array}{c} 0.0084241\\ -0.0079706 \end{array} \right) ,\quad h_{200}(-1)= \left( \begin{array}{c} -0.097808\\ 0.088523 \end{array}\right) ,\\&h_{200}^2(0)= h_{200}^2(-1)=\left( \begin{array}{c} 0.31035\\ -0.046975 \end{array} \right) , \\&h_{011}^0(0)= \left( \begin{array}{c} -0.031531\\ 0.029834 \end{array}\right) ,\quad h_{011}^0(-1)=\left( \begin{array}{c}0.36609\\ -0.33134) \end{array}\right) , \\&h_{020}^0(0)=\left( \begin{array}{c} 0.0020659 + 0.069984{\mathrm {i}}\\ -0.0021214 - 0.066282{\mathrm {i}} \end{array}\right) ,\quad h_{020}^0(-1)=\left( \begin{array}{c} -0.08515 - 0.80808{\mathrm {i}}\\ 0.082398 + 0.73077{\mathrm {i}} \end{array}\right) , \\&h_{110}^1(0)= \left( \begin{array}{c} -0.0043069 + 0.10203{\mathrm {i}}\\ 0.0073407 - 0.25347{\mathrm {i}} \end{array}\right) ,\quad h_{110}^1(-1)= \left( \begin{array}{c} 0.03495 -0.24323 {\mathrm {i}}\\ -0.048564 - 0.14565{\mathrm {i}} \end{array} \right) ,\\&h_{101}^1=\overline{h_{110}^1},\quad h_{002}^0=\overline{h_{020}^0},\quad h_{011}^2=0. \end{aligned}$$

Substituting these values into (3.10) and (3.15), we can get all the coefficients in normal form,

$$\begin{aligned} \begin{aligned}&a_1(\alpha )=-0.00018873\alpha _1-0.8787\alpha _2,\\&b_2(\alpha )=(0.07723 + 0.83252 {\mathrm {i}})\alpha _1,\\&a_{11}=a_{23}=b_{12}=0,\\&a_{111}= -0.1399,~~~~~~~b_{112}=-0.0906 + 0.0967{\mathrm {i}}, \\&a_{123}=-0.1966,~~~~~~~b_{223}= -0.1675 - 0.0489{\mathrm {i}}. \end{aligned} \end{aligned}$$

(4.1)

In addition, the coefficients in cylindrical coordinate equation (3.19) are

$$\begin{aligned} \begin{array}{c} \varepsilon _1(\alpha )=-0.07723 \alpha _1, \varepsilon _2(\alpha )=0.00018873\alpha _1+0.8787\alpha _2,\\ b_0=0.6476,~c_0=1.1737,~d_0=1,~d_0-b_0c_0=0.2399 \end{array} \end{aligned}$$

(4.2)

which implies the case of Ia in Table 1. Since ${\mathrm {sign}}({\mathrm {Re}}b_{223})=-1$, we know from [7] that the complete bifurcation set for (1.1) in $(\tau ,\varepsilon )$-plane should be the one, as shown in Fig. 4a. In Fig. 4a, the critical bifurcation lines are expressed by

$$\begin{aligned} \begin{array}{rlc} L_1:&{}\tau =\tau _*,~\varepsilon>\varepsilon _*,\\ L_2:&{}\varepsilon =\varepsilon _*-0.00021478(\tau -\tau _*),~\tau>\tau _*,\\ L_3:&{}\varepsilon =\varepsilon _*-0.1034(\tau -\tau _*),~\tau>\tau _*,\\ L_4:&{}\varepsilon =\varepsilon _*-0.1359(\tau -\tau _*),~\tau >\tau _*,\\ L_5:&{}\tau =\tau _*,~\varepsilon<\varepsilon _*,\\ L_6:&{}\varepsilon =\varepsilon _*-0.00021478(\tau -\tau _*),~\tau <\tau _*. \end{array} \end{aligned}$$

The regions divided by those lines are denoted by $D_i$, $i=1,2,\ldots ,6$, respectively. For instance, $D_1$ is the area enclosed by the lines $L_1$ and $L_6$ (but not including $L_1$ and $L_6$), i.e, $D_1=\{(\tau ,\varepsilon )\in {\mathbb {R}}^2: \varepsilon >\varepsilon _*-0.00021478(\tau -\tau _*), \tau <\tau _*\}$. For $(\tau ,\varepsilon )$ in different region $D_i$, $i=1,2,\cdots 6$, the dynamical behaviors of (3.19), with its coefficients given by (4.2), are shown in Fig. 4b.

Fig. 4

a The bifurcation set for (1.1) in $(\tau ,\varepsilon )$ plane and b phase portraits of (3.19) and (4.2), in the case of ${\mathrm {Ia}}$. Here, $a=0.1$, $b=0.9$, $d=0.5$

Theorem 4.2

For system (1.1) with $a=0.1$, $b=0.9$, $d=0.5$, there are six possible dynamics of (1.1) for $(\tau ,\varepsilon )$ sufficiently close to $(\tau _*,\varepsilon _*)$, depending on the region $D_i$ that $(\tau ,\varepsilon )$ lies in, $i=1,2,\ldots ,6$. More specifically,

• (1) The steady state $(u_*,v_*)$ is asymptotically stable for $(\tau ,\varepsilon )\in D_1$, and 0-mode Hopf bifurcation near $(u_*,v_*)$ occurs at $(\tau ,\varepsilon )\in L_1$.

• (2) For $(\tau ,\varepsilon )\in D_2$, $(u_*,v_*)$ becomes unstable and there exists a stable spatially homogeneous periodic orbit through Hopf bifurcation at $(u_*,v_*)$, as $(\tau ,\ \varepsilon )$ crosses $L_1$ from left-hand side. On the line $L_2$, 1-mode Turing bifurcation occurs near the unstable steady state $(u_*,v_*)$.

• (3) If $(\tau ,\varepsilon )\in D_3$, then there are two unstable spatially inhomogeneous steady states, which are bifurcated from the steady state $(u_*,v_*)$ on $L_2$, and the spatially homogeneous periodic solution still remains. Moreover, on the line $L_3$, 1-mode Turing bifurcation occurs near the spatially homogeneous periodic orbit.

• (4) In region $D_4$, (1.1) possesses two stable spatially inhomogeneous periodic orbit, bifurcated from unstable spatially homogeneous periodic solution on the line $L_3$. The linear parts of these two periodic solutions are

  $$\begin{aligned} E_*+\rho \phi _{2}(0)e^{{\mathrm {i}}\tau _*\omega _* t}+{\bar{\rho }}{\bar{\phi }}_{2}(0)e^{{\mathrm {-i}}\tau _* \omega _* t}\pm h\phi _{1}(0)\cos (\pi x), \end{aligned}$$

  where $\rho$ and h are constants. In addition, 0-mode Hopf bifurcations occur near the two stable inhomogeneous steady-states at $(\tau ,\varepsilon )\in L_4$. It is remarked that the two unstable inhomogeneous steady states in $D_3$ still persist for $(\tau ,\varepsilon )\in D_4$.

• (5) For $(\tau ,\varepsilon )\in D_5$, the two stable spatially inhomogeneous periodic orbits vanish (due to Hopf bifurcation on $L_4$), and there are two stable inhomogeneous steady-states for (1.1). Aside from these solutions, (1.1) also has another unstable spatially homogeneous periodic orbit, bifurcated through Hopf bifurcation at $(u_*,v_*)$ on the line $L_5$.

• (6) If $(\tau ,\varepsilon )\in D_6$, then $(u_*,v_*)$ is unstable, and two stable spatially inhomogeneous steady states will be bifurcated from $(u_*,v_*)$ at $L_6$. (The unstable spatially homogeneous periodic orbit disappears, due to the occurrence of Hopf bifurcation as $(\tau ,\varepsilon )$ passes through $L_5$).

where $\tau _*=0.2171$, $\varepsilon _*=0.1007$, $\omega _*=0.9144$ and $(u_*,v_*)=(1,0.9)$.

We carry out numerical simulations for (1.1), to detect its solution patterns for different choice of $(\tau ,\varepsilon )$, as stated in Theorem 4.2.

Fig. 5

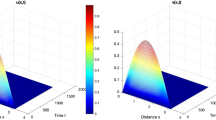
A solution of (1.1) tends to the steady state $(u_*,v_*)$ as $t\rightarrow \infty$ for $(\tau ,\varepsilon )\in D_1$. The initial functions are $(u(x,t),v(x,t))=(1+0.1\cos (\pi x), 1+0.1\cos (\pi x)$, for $(x,t)\in [0,1]\times [-0.1671,0]$. au(t, x) and bv(t, x)

Fig. 6

An asymptotically stable spatially homogeneous periodic orbit for (1.1) in the case of $(\tau ,\ \varepsilon )\in D_2$. The initial functions are the same as the ones for $(x,t)\in [0,1]\times [-0.2671,0]$ in Fig. 5. au(t, x) and bv(t, x)

Fig. 7

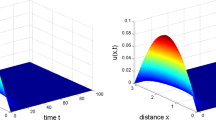
The coexistence of two stable spatially inhomogeneous periodic orbits of (1.1) for $(\tau ,\ \varepsilon )\in D_4$. au(t, x), bv(t, x), cu(t, x) and dv(t, x)

• (i) Let $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(-0.05,0.05)$. Then $(\tau ,\varepsilon )\in D_1$, and $(u_*,v_*)$ is asymptotically stable, see Fig. 5.

• (ii) Set $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(0.05,0.05)$. Then $(\tau ,\varepsilon )\in D_2$. From (2) of Theorem 4.2, one can observe an asymptotically stable spatially homogeneous periodic orbit for (1.1), see Fig. 6. Furthermore, if $(\tau ,\varepsilon )\in D_3$, there still exists an spatially homogeneous periodic orbit, which is consistent with the assertions (3) of Theorem 4.2.

• (iii) For $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(0.05,-0.0063)\in D_4$. If we assign two different initial functions for (1.1), i.e.,

  $$\begin{aligned} \begin{aligned} (u_1(x,t),u_2(x,t))&=(1-0.1\cos (\pi x), 1-0.1\cos (\pi x))\\ (u_2(x,t),u_2(x,t))&=(1+0.1\cos (\pi x), 1+0.1\cos (\pi x)) \end{aligned} \end{aligned}$$

  (4.3)

  for $(x,t)\in [0,1]\times [-0.2671,0]$, then it is found that the solutions with these two functions will approach distinct periodic orbits, indicating the co-existence of two spatially inhomogeneous periodic solutions, see Fig. 7.

• (iv) Choose $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(0.05,-0.03)\in D_5$. Then the solutions of (1.1), equipped with the following two initial functions:

  $$\begin{aligned} \begin{aligned} (u_1(x,t),u_2(x,t))&=(0.9, 1.1)\\ (u_2(x,t),u_2(x,t))&=(1+0.1\cos (\pi x), 1+0.1\cos (\pi x)) \end{aligned} \end{aligned}$$

  (4.4)

  for $(x,t)\in [0,1]\times [-0.2671,0]$, will converge to different steady states, as shown in Fig. 8. Similarly, for $(\tau , \varepsilon )\in D_6$, a pair of stable spatially inhomogeneous steady state solutions can be also simulated.

Fig. 8

For $(\tau ,\ \varepsilon )\in D_5$, two stable spatially inhomogeneous steady state solutions of (1.1) coexist au(t, x), bv(t, x), cu(t, x) and dv(t, x)

4.2 (3, 0)-Mode Turing–Hopf Bifurcation

In this part, we choose $k_1=3$ and $d=0.05$, and all the other parameters are the same as before. Then, $d_{3,4}=0.0255$, $d_{2,3}=0.0525$, $d\in (d_{3,4},~d_{2,3})$ and $\varepsilon _*=\varepsilon _*(3,0.05)=0.1056$. The system (1.1) will undergoes 3-mode Turing bifurcation at $\varepsilon _*$, see Fig. 3. Moreover, we have $k_2=0$, $\omega _k^+=0.9144$ and $\tau _*=0.2171$.

Corollary 4.3

For parameters $a=0.1,\ b=0.9,\ d=0.05$, we have that

• (1) The steady state $(u_*,v_*)$ is asymptotically stable for $\tau \in [0,0.2171)$ and $0.1056<\varepsilon <0.1079$, and unstable for $0.0600<\varepsilon <0.1056$.

• (2) System (1.1) undergoes (3, 0)-mode Turing–Hopf bifurcation near $(u_*,v_*)=(1,0.9)$ at $\tau =0.2171,\varepsilon =0.1056$.

For the parameters in (3.19), one can compute $\varepsilon _1(\alpha )=-0.07723 \alpha _1$, $\varepsilon _2(\alpha )=0.00018873\alpha _1+0.8787\alpha _2$, $b_0=0.6476,~c_0=1.1737,~d_0=1,~d_0-b_0c_0=0.2399$, ${\mathrm {sign}}({\mathrm {Re}}b_{223})=-1$. Therefore, the Case ${\mathrm {Ia}}$ in Table 1 holds again, and the critical bifurcation lines in Fig. 4a are now given by

$$\begin{aligned} \begin{array}{rlc} L_1:&{}\tau =\tau _*,~\varepsilon>\varepsilon _*,\\ L_2:&{}\varepsilon =\varepsilon _*+0.00020177(\tau -\tau _*),~\tau>\tau _*,\\ L_3:&{}\varepsilon =\varepsilon _*-0.1154(\tau -\tau _*),~\tau>\tau _*,\\ L_4:&{}\varepsilon =\varepsilon _*-0.1231(\tau -\tau _*),~\tau >\tau _*,\\ L_5:&{}\tau =\tau _*,~\varepsilon<\varepsilon _*,\\ L_6:&{}\varepsilon =\varepsilon _*+0.00020177(\tau -\tau _*),~\tau <\tau _*. \end{array} \end{aligned}$$

When $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(0.05,-0.0063)\in D_4$, it follows from Theorem 4.2 that two stable spatially inhomogeneous periodic solutions also coexist, However, the patterns are different from the ones in (iii), in that the solutions oscillate with respect to spatial variable x, see Fig. 9. If $(\tau ,\varepsilon )=(\tau _*,\varepsilon _*)+(0.05,-0.03)\in D_5$, then there are two stable inhomogeneous steady states, which is also periodic in x, for (1.1), see Fig. 10.

Fig. 9

For $(\tau ,\varepsilon )\in D_4$, two spatially inhomogeneous periodic orbits with different initial functions in (4.3) are plotted. au(t, x), bv(t, x), cu(t, x) and dv(t, x)

Fig. 10

Two stable spatially inhomogeneous steady states of (1.1), for $(\tau ,\ \varepsilon )\in D_5$. The initial functions are given by (4.4). au(t, x), bv(t, x), cu(t, x) and dv(t, x)

5 Conclusion

In this paper, we studied the Turing bifurcation(instability), Hopf bifurcation and Turing–Hopf bifurcation for a delayed reaction–diffusion Schnakenberg system, combining characteristic equation analysis, center manifold theorem and normal form theory. An explicit expression of $\varepsilon _*(d)$ for the first Turing bifurcation curve has been derived. The constant steady state $(u_*,v_*)$ is stable for $(\varepsilon ,d)$ on one side of this curve, while Turing instability occurs for $(\varepsilon ,d)$ on the other side. For $(\varepsilon ,d)$ in the Turing instability region, a pair of stable spatially inhomogeneous steady states are bifurcated from $(u_*,v_*)$. The first Turing bifurcation curve is continuous and piecewise smooth, and its non-smooth points correspond to the critical values at which (1.1) undergoes Turing-Turing bifurcation. Owing to the explicit expression of $\varepsilon _*(d)$, it is easy to find the spatially inhomogeneous steady state with arbitrary wave number. In addition, if we choose d as varying parameter for Turing bifurcation, then the phenomenon of stability switches of $(u_*,v_*)$ is observed, which will induce spatially inhomogeneous steady state with various wave number.

Under the condition for avoiding Turing instability, we studied the Hopf bifurcation near $(u_*,v_*)$, by using time delay $\tau$ as varying parameter. It turns out that only spatially homogeneous periodic solution will be bifurcated from $(u_*,v_*)$ for (1.1) with Neumann boundary condition, as $\tau$ crosses a sequence of critical values.

We further investigate the Turing–Hopf bifurcation to explore the joint effect of diffusion rate $\varepsilon$ and time delay $\tau$. For Turing–Hopf bifurcation, the truncated normal forms up to 3rd order has been derived in [13] for a general partial functional differential equations. Applying these formula to (1.1), we compute the normal form of the model in a special (but most interesting) case of $k_1\ne 0$ and $k_2=0$, when Turing–Hopf bifurcation occurs. Moreover, the coefficients in the normal form are expressed explicitly by the original parameters in the model. The complete bifurcation diagram for the derived normal form are given in [33], from which one can show (1.1) may have various spatiotemporal patterns as the $(\tau ,\varepsilon )$ are changed. In particular, we prove that two spatially inhomogeneous periodic solutions of (1.1) coexist, caused by the joint effect of $\varepsilon$ and $\tau$. Numerical simulations help us to detect all the spatiotemporal patterns as expected from theoretical analysis.

In [6], it is numerically observed that time delay could induce a failure of Turing instability. This phenomenon is later explained in [36] from Hopf bifurcation point of view. In Turing–Hopf bifurcation analysis, we have shown that the spatially inhomogeneous steady states, generated through Turing bifurcation, will lose its stability as delay $\tau$ varies, and spatially inhomogeneous periodic solutions are induced by Hopf bifurcation. This provides another interpretation of failure of Turing instability caused by delay.