An Explicit Periodic Solution of a Delay Differential Equation

Abstract

In this paper we prove that the following delay differential equation

$$\begin{aligned} \frac{d}{dt}x(t)=rx(t)\left( 1-\int _{0}^{1}x(t-s)ds\right) , \end{aligned}$$

has a periodic solution of period two for $r>\frac{\pi ^{2}}{2}$ (when the steady state, $x=1$, is unstable). In order to find the periodic solution, we study an integrable system of ordinary differential equations, following the idea by Kaplan and Yorke (J Math Anal Appl 48:317–324, 1974). The periodic solution is expressed in terms of the Jacobi elliptic functions.

1 Introduction

The delay differential equation

$$\begin{aligned} \frac{d}{dt}z(t)=f\left( z(t-1)\right) , \end{aligned}$$

(1.1)

where $f:\mathbb {R}\rightarrow \mathbb {R}$ is a continuous function, has been extensively studied in the literature. For a special case, $f(z)=r\left( 1-e^{z}\right) ,\ r>0,$ the Eq. (1.1) is referred to as Wright’s equation, named after the paper [35]. Jones investigated the existence of a periodic solution of Wright’s equation in [13, 14] by the fixed-point theorem. Nussbaum then established a general fixed-point theorem and study the existence of periodic solutions for a class of functional differential equations in [21, 22]. See also [12, 19, 31] and references therein for the recent progress by a computer assisted approach.

Assuming that f is an odd function, in the paper [15], Kaplan and Yorke constructed a periodic solution of the equation (1.1) via a Hamiltonian system of ordinary differential equations. The idea is used to investigate a periodic solution of the equation (1.1) with a particular nonlinear function f in [6] and for a system of differential equations with distributed delay in [1]. We refer the readers to the survey paper [34] and the references therein. See also Chapter XV of [5]. In this paper we follow the approach by Kaplan and Yorke [15]: we find a periodic solution of a differential equation with distributed delay, considering a system of ordinary differential equations.

The following mathematical model for a single species population is known as the Hutchinson equation and as a delayed logistic equation

$$\begin{aligned} \frac{d}{dt}x(t)=rx(t)\left( 1-x\left( t-1\right) \right) . \end{aligned}$$

(1.2)

The Eq. (1.2) can be derived from Wright’s equation by the transformation $z(t)=\ln x(t)$. Many extensions of the Hutchinson equation (1.2) have been investigated, see [7, 9, 28] and references therein. Nevertheless, the Hutchinson–Wright equation still poses mathematical challenges [12, 31].

In this paper we study the existence of a periodic solution of the following delay differential equation

$$\begin{aligned} \frac{d}{dt}x(t)=rx(t)\left( 1-\int _{0}^{1}x(t-s)ds\right) , \end{aligned}$$

(1.3)

where r is a positive parameter, $r>0$. The delay differential equation (1.3) can be seen as a variant of the Hutchinson–Wright equation (1.2). The author’s motivation to study (1.3) is that the equation appears as a limiting case of an infectious disease model with temporary immunity (see “Appendix B”). For the equation (1.3), the existence of periodic solutions does not seem to be well understood. The periodicity, which may explain the recurrent disease dynamics, is a trigger of this study. Differently from the discrete delay case, the distributed delay is an obstacle, when one tries to construct a suitable Poincare map to find a periodic solution, but see [16, 32, 33]. We also refer the readers to [7, 27, 28] and references therein for studies of logistic equations with distributed delay.

In this paper we prove the following theorem.

Theorem 1

Let $r>\frac{\pi ^{2}}{2}$. Then the delay differential equation (1.3) has a nontrivial periodic solution of period 2, i.e., $x(t)=x(t-2),\ t\in \mathbb {R}$, satisfying

$$\begin{aligned} x(t)x(t-1)=\text {Const},\ \int _{0}^{2}x(t-s)ds=2 \end{aligned}$$

for any $t\in \mathbb {R}$.

The existence of the periodic solution is proven, solving a corresponding ordinary differential equation, which turns out to be equivalent to the Duffing equation. The periodic solution, explicitly expressed in terms of the Jacobi elliptic functions, appears at $r=\frac{\pi ^{2}}{2}$, as the positive equilibrium ($x=1$) loses stability via Hopf bifurcation.

This paper is organized as follows. In Sect. 2, we first study stability of the positive equilibrium, applying the principle of linearized stability. We then derive a system of ordinary differential equations (2.5) that generates the solution of period 2 of the original delay differential equation (1.3). In Sect. 3, the system of ordinary differential equations (2.5) is reduced to a scalar differential equation (3.4) that turns out to be the Duffing equation. The equation is explicitly solved using the Jacobi elliptic functions. In Sect. 4, we consider an Eq. (4.7) to find a parameter such that the period of the solution becomes two.

2 Preliminary

For the delay differential equation (1.3) the natural phase space is $C\left( \left[ -1,0\right] ,\mathbb {R}\right)$ equipped with the supremum norm [5, 10]. For (1.3) we consider the following initial condition

$$\begin{aligned} x(\theta )=\phi \left( \theta \right) ,\ \theta \in \left[ -1,0\right] , \end{aligned}$$

where $\phi \in C\left( \left[ -1,0\right] ,\mathbb {R}\right)$ with $\phi (0)>0$. We are interested in the positive solution.

For the Eq. (1.3) it is easy to see that $x=1$ is the unique positive equilibrium. We have the following result for stability of the positive equilibrium (see also Theorem 4.1 of [24]).

Proposition 2

The positive equilibrium $x=1$ for the Eq. (1.3) is asymptotically stable for $0<r<\frac{\pi ^{2}}{2}$ and it is unstable for $r>\frac{\pi ^{2}}{2}$. Hopf bifurcation occurs at $r=\frac{\pi ^{2}}{2}$ and a periodic solution appears.

Proof

We deduce the following characteristic equation [5, 10]

$$\begin{aligned} \lambda =-r\int _{0}^{1}e^{-\lambda s}ds,\ \lambda \in \mathbb {C}. \end{aligned}$$

(2.1)

Let $\lambda =\mu +i\omega ,\ (\mu ,\omega \in \mathbb {R})$ to obtain the following two equations

$$\begin{aligned} \mu&=-r\int _{0}^{1}e^{-\mu s}\cos \left( \omega s\right) ds, \end{aligned}$$

(2.2a)

$$\begin{aligned} \omega&=r\int _{0}^{1}e^{-\mu s}\sin \left( \omega s\right) ds. \end{aligned}$$

(2.2b)

First one sees that if $\text {Re}\lambda >0$ then

$$\begin{aligned} \left| \lambda \right| =\sqrt{\mu ^{2}+\omega ^{2}}\le r \end{aligned}$$

(2.3)

Assume that there is a root in the right half complex plane (i.e., $\mu >0$) for sufficiently small $r>0$. One sees $\int _{0}^{1}e^{-\mu s}\cos \left( \omega s\right) ds>0$ from the estimation (2.3), thus, if $r>0$ is sufficiently small, from (2.2a) all roots of the characteristic equation (2.1) are in the left half complex plane.

Suppose now that for some $r>0$ purely imaginary roots exist. Substituting $\mu =0$ into the Eq. (2.2a), one sees that for $r=\frac{1}{2}\left( \left( 2n+1\right) \pi \right) ^{2}$ the characteristic equation (2.1) has purely imaginary roots $\lambda =\pm i\omega =\pm i\left( 2n+1\right) \pi$ for $n=0,1,2,\dots .$. We show that, for $n=0,1,2,\dots ,$ the purely imaginary roots $\lambda =\pm i\left( 2n+1\right) \pi$ cross the imaginary axis transversally from left to right as r increases in the neighborhood of $r=\frac{1}{2}\left( \left( 2n+1\right) \pi \right) ^{2}$. Applying the implicit function theorem to the equation (2.1), one has

$$\begin{aligned} \lambda ^{\prime }(r)\left( 1-r\int _{0}^{1}se^{-\lambda s}ds\right) +\int _{0}^{1}e^{-\lambda s}ds=0. \end{aligned}$$

One sees that

$$\begin{aligned} \int _{0}^{1}se^{-\lambda s}ds&=-\frac{e^{-\lambda }}{\lambda }+\frac{1}{\lambda }\int _{0}^{1}e^{-\lambda s}ds=-\frac{e^{-\lambda }}{\lambda }-\frac{1}{r},\\ \int _{0}^{1}e^{-\lambda s}ds&=-\frac{\lambda }{r}. \end{aligned}$$

Therefore, at $r=\frac{1}{2}\left( \left( 2n+1\right) \pi \right) ^{2}$ and $\lambda =i\omega =i\left( 2n+1\right) \pi$, it follows that

$$\begin{aligned} \lambda ^{\prime }\left( r\right) \left| _{r=\frac{1}{2}\left( \left( 2n+1\right) \pi \right) ^{2}}\right. =\frac{i\frac{\omega }{r}}{1+1+i\frac{r}{\omega }}\implies \text {Re}\lambda ^{\prime }(r)\left| _{r=\frac{1}{2}\left( \left( 2n+1\right) \pi \right) ^{2}}\right. =\frac{1}{4+\left( \frac{r}{\omega }\right) ^{2}}>0. \end{aligned}$$

From the Hopf bifurcation theorem (see Theorem 6.1 in [29]; see also Theorem 2.7 of Chapter X of [5]), we obtain the conclusion. $\square$

Thus a periodic solution of period 2 emerges at $r=\frac{\pi ^{2}}{2}$ and the positive equilibrium is unstable for $r>\frac{\pi ^{2}}{2}$.

Observe that, defining

$$\begin{aligned} y(t)=\int _{0}^{1}x(t-s)ds-1,\ t\ge 0, \end{aligned}$$

the delay differential equation (1.3) is equivalent to the following system of delay differential equations

$$\begin{aligned} \frac{d}{dt}x(t)&=-rx(t)y(t), \end{aligned}$$

(2.4a)

$$\begin{aligned} \frac{d}{dt}y(t)&=x(t)-x(t-1) \end{aligned}$$

(2.4b)

with the following initial condition

$$\begin{aligned} x(\theta )&=\phi \left( \theta \right) ,\ \theta \in \left[ -1,0\right] ,\\ y(0)&=\int _{0}^{1}\phi (-s)ds-1. \end{aligned}$$

Assume that for (1.3) there exists a periodic solution of period 2. Denote by $x^{*}(t)$ the periodic solution, i.e., $x^{*}(t)=x^{*}(t-2)$. Then we let

$$\begin{aligned} x_{1}(t)&=x^{*}(t),\ y_{1}(t)=\int _{0}^{1}x^{*}(t-s)ds-1,\\ x_{2}(t)&=x^{*}\left( t-1\right) ,\ y_{2}(t)=\int _{1}^{2}x^{*}(t-s)ds-1. \end{aligned}$$

We are interested in the positive periodic solution. The periodic solution satisfies the following system of ordinary differential equations

$$\begin{aligned} \frac{d}{dt}x_{1}(t)&=-rx_{1}(t)y_{1}(t), \end{aligned}$$

(2.5a)

$$\begin{aligned} \frac{d}{dt}y_{1}(t)&=x_{1}(t)-x_{2}(t), \end{aligned}$$

(2.5b)

$$\begin{aligned} \frac{d}{dt}x_{2}(t)&=-rx_{2}(t)y_{2}(t), \end{aligned}$$

(2.5c)

$$\begin{aligned} \frac{d}{dt}y_{2}(t)&=x_{2}(t)-x_{1}(t). \end{aligned}$$

(2.5d)

The initial condition is

$$\begin{aligned} x_{1}(0)&=a>0,\ x_{2}(0)=b>0, \end{aligned}$$

(2.6a)

$$\begin{aligned} y_{1}\left( 0\right)&=y_{2}\left( 0\right) =0, \end{aligned}$$

(2.6b)

where a and b will be determined later ($a=x^{*}(0)=x^{*}(2),\ b=x^{*}(-1)=x^{*}(1))$ in Sect. 4, so that $x_{1}(t)=x_{1}(t+2)$ holds.

From (2.5) one sees that

$$\begin{aligned} y_{1}(t)+y_{2}(t)&=0, \end{aligned}$$

(2.7a)

$$\begin{aligned} x_{1}(t)x_{2}(t)&=ab \end{aligned}$$

(2.7b)

hold for any $t\ge 0$ . Thus one sees that the periodic solution satisfies the following properties

$$\begin{aligned} \int _{0}^{2}x^{*}(t-s)ds=2,\ x^{*}(t)x^{*}(t-1)=\text {Const},\ t\in \mathbb {R}. \end{aligned}$$

(2.8)

3 Integrable Ordinary Differential Equations

The system (2.5) with (2.7) is reduced to the following system of ordinary differential equations

$$\begin{aligned} \frac{d}{dt}x(t)&=-rx(t)y(t), \end{aligned}$$

(3.1a)

$$\begin{aligned} \frac{d}{dt}y(t)&=x(t)-ab\frac{1}{x(t)}, \end{aligned}$$

(3.1b)

dropping the indices from $x_{1}$ and $y_{1}$ (cf. ()). The initial condition of (3.1) is

$$\begin{aligned} x(0)&=a, \end{aligned}$$

(3.2a)

$$\begin{aligned} y\left( 0\right)&=0 \end{aligned}$$

(3.2b)

(see (2.6)). We see that the system (3.1) has a conservative quantity.

Proposition 3

It holds that

$$\begin{aligned} x(t)+ab\frac{1}{x(t)}+\frac{r}{2}y^{2}(t)=a+b,\ t\in \mathbb {R} \end{aligned}$$

(3.3)

for the solution of the equation (3.1) with the initial condition (3.2).

Proof

Differentiating the left hand side of (3.3), we obtain

$$\begin{aligned}&\frac{d}{dt}\left( x(t)+ab\frac{1}{x(t)}+\frac{r}{2}y^{2}(t)\right) \\&\quad = \left( 1-ab\frac{1}{x^{2}(t)}\right) x'(t)+ry(t)y'(t)\\&\quad = \left( 1-ab\frac{1}{x^{2}(t)}\right) \left( -rx(t)y(t)\right) +ry(t)\left( x(t)-ab\frac{1}{x(t)}\right) \\&\quad = 0. \end{aligned}$$

From (3.2), it then follows that

$$\begin{aligned} x(t)+ab\frac{1}{x(t)}+\frac{r}{2}y^{2}(t)=x(0)+ab\frac{1}{x(0)}+\frac{r}{2}y^{2}(0)=a+b \end{aligned}$$

for $t\in \mathbb {R}$. $\square$

Differentiating the both sides of the Eq. (3.1b), we obtain

$$\begin{aligned} \frac{d^{2}}{dt^{2}}y(t)&=-\left( 1+ab\frac{1}{x^{2}(t)}\right) rx(t)y(t)\\&=-ry(t)\left( x(t)+ab\frac{1}{x(t)}\right) . \end{aligned}$$

Using the identity (3.3) in Proposition 3, we derive the Duffing equation:

$$\begin{aligned} \frac{d^{2}}{dt^{2}}y(t)=-ry(t)\left( a+b-\frac{r}{2}y^{2}(t)\right) \end{aligned}$$

(3.4)

with the following initial condition

$$\begin{aligned} y(0)&=0, \end{aligned}$$

(3.5a)

$$\begin{aligned} \frac{d}{dt}y(0)&=x(0)-ab\frac{1}{x(0)}=a-b. \end{aligned}$$

(3.5b)

Denote by $\text {sn}$ the Jacobi elliptic sine function [3, 20]. It is known that the solution of the Duffing equation (3.4) is given by

$$\begin{aligned} y(t)=\alpha \text {sn}(\beta t,k), \end{aligned}$$

(3.6)

where $\alpha ,\beta$ and k are functions of a and b defined by

$$\begin{aligned}&\alpha (a,b)=\sqrt{\frac{2}{r}}\left( \sqrt{a}-\sqrt{b}\right) ,\ \beta (a,b)=\sqrt{\frac{r}{2}}\left( \sqrt{a}+\sqrt{b}\right) , \end{aligned}$$

(3.7)

$$\begin{aligned}&k(a,b)=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}, \end{aligned}$$

(3.8)

In “Appendix A”, we give a brief introduction of the Jacobi elliptic functions and derivation of the solution (3.6). See also e.g. Chapter 4 in [18] and Chapter 2 in [26]. To simplify the notation, we occasionally drop (a, b) from $\alpha ,\ \beta$ and k.

We then obtain the explicit solution of the system (3.1) with the initial condition (3.2).

Proposition 4

The solution of the equations (3.1) with the initial condition (3.2) is expressed as

$$\begin{aligned} x(t)&=a\left( \frac{1-k}{\text {dn}(\beta t,k)-k\text {cn}(\beta t,k)}\right) ^{2}=a\left( \frac{\text {dn}(\beta t,k)+k\text {cn}(\beta t,k)}{1+k}\right) ^{2}, \end{aligned}$$

(3.9)

$$\begin{aligned} y(t)&=\alpha \text {sn}(\beta t,k), \end{aligned}$$

(3.10)

where $\alpha ,\beta$ and k are defined in (3.7) and (3.8).

Proof

Since (3.10) is given in (3.6), we show the equality in (3.9), integrating the equation (3.1a). We get

$$\begin{aligned} x(t)=ae^{-r\int _{0}^{t}y(s)ds}. \end{aligned}$$

Using (3.10) we compute

$$\begin{aligned} r\int _{0}^{t}y(s)ds&=r\alpha \int _{0}^{t}\text {sn}(\beta u,k)du\\&=\frac{r\alpha }{\beta k}\left[ \ln \left( \text {dn}(s,k)-k\text {cn}(s,k)\right) \right] _{0}^{\beta t}\\&=\frac{r\alpha }{\beta k}\ln \left( \frac{\text {dn}(\beta t,k)-k\text {cn}(\beta t,k)}{1-k}\right) . \end{aligned}$$

Note that $\frac{r\alpha }{\beta k}=2$ holds from the Definitions in (3.7) and (3.8). We then get

$$\begin{aligned} r\int _{0}^{t}y(s)ds=2\ln \left( \frac{\text {dn}(\beta t,k)-k\text {cn}(\beta t,k)}{1-k}\right) , \end{aligned}$$

from which the first equality in (3.9) follows.

Using the properties of the elliptic functions, it holds that

$$\begin{aligned} \left( \text {dn}-k\text {cn}\right) \left( \text {dn}+k\text {cn}\right) =\text {dn}^{2}-k^{2}\text {cn}^{2}=1-k^{2}. \end{aligned}$$

Therefore, we obtain the following equality

$$\begin{aligned} \left( \frac{1-k}{\text {dn}(\beta t,k)-k\text {cn}(\beta t,k)}\right) ^{2}=\left( \frac{\text {dn}(\beta t,k)+k\text {cn}(\beta t,k)}{1+k}\right) ^{2}. \end{aligned}$$

$\square$

4 Periodic Solution of Period 2

In this section we will determine a, the initial value for the x component of the system (3.1), so that, for the solution given in Proposition 4, the period is 2 and the integral constant becomes $-1$. The periodic solution finally solves the delay differential equation (1.3).

Let us introduce the complete elliptic integrals of the first kind and of the second kind [3, 20]. Those are respectively given as

$$\begin{aligned} K(k)&=\int _{0}^{\frac{\pi }{2}}\frac{1}{\sqrt{1-k^{2}\sin ^{2}\theta }}d\theta ,\\ E(k)&=\int _{0}^{\frac{\pi }{2}}\sqrt{1-k^{2}\sin ^{2}\theta }d\theta \end{aligned}$$

for $0\le k<1$. The Jacobi elliptic functions $\text {sn}$ and $\text {cn}$ are periodic functions with period 4K(k), i.e.,

$$\begin{aligned} \text {sn}\left( t,k\right) =\text {sn}\left( t+4K\left( k\right) ,k\right) ,\ \text {cn}\left( t,k\right) =\text {cn}\left( t+4K\left( k\right) ,k\right) ,\ t\in \mathbb {R} \end{aligned}$$

and $\text {dn}$ is periodic with period 2K(k). See also “Appendix A”.

In the following theorem we derive two conditions so that the period of the solution given in Proposition 4 is two.

Theorem 5

Assume that the following two conditions hold

$$\begin{aligned}&\sqrt{\frac{r}{2}}\left( \sqrt{a}+\sqrt{b}\right) =2K(k), \end{aligned}$$

(4.1)

$$\begin{aligned}&\left( \sqrt{a}+\sqrt{b}\right) \sqrt{\frac{2}{r}}E(k)-\sqrt{ab}=1. \end{aligned}$$

(4.2)

Then, for the solution of the equation (3.1) with the initial condition (3.2), it holds that

$$\begin{aligned} \left( x(t),y\left( t\right) \right) =\left( x(t+2),y(t+2)\right) \end{aligned}$$

(4.3)

and that

$$\begin{aligned} y(t)=\int _{t-1}^{t}x(s)ds-1 \end{aligned}$$

(4.4)

for any $t\in \mathbb {R}$.

Proof

From (4.1), we have $2\beta =4K(k)$. Since the Jacobi elliptic functions, $\text {sn},\ \text {cn}$ and $\text {dn}$ are periodic with period 4K(k), one has

$$\begin{aligned} \text {sn}\left( \beta t,k\right)&=\text {sn}(\beta \left( t+2\right) ,k),\\ \text {cn}\left( \beta t,k\right)&=\text {cn}(\beta \left( t+2\right) ,k),\\ \text {dn}\left( \beta t,k\right)&=\text {dn}(\beta \left( t+2\right) ,k). \end{aligned}$$

Then it is easy to see that (4.3) follows from (3.9) and (3.10). Next we show that (4.4) holds. From the symmetry of the Jacobi elliptic functions, we have

$$\begin{aligned} \text {cn}\left( \beta \left( t-1\right) ,k\right)&=-\text {cn}(\beta t,k),\\ \text {dn}\left( \beta \left( t-1\right) ,k\right)&=\text {dn}(\beta t,k). \end{aligned}$$

Thus from (3.9) we obtain

$$\begin{aligned} x(t-1)=a\left( \frac{\text {dn}(\beta \left( t-1\right) ,k)+k\text {cn}(\beta \left( t-1\right) ,k)}{1+k}\right) ^{2}=a\left( \frac{\text {dn}\left( \beta t,k\right) -k\text {cn}\left( \beta t,k\right) }{1+k}\right) ^{2} \end{aligned}$$

and $x(t)x(t-1)=a^{2}\left( \frac{1-k}{1+k}\right) ^{2}=ab$ follows. Then from (3.1b), for the solution of the equation (3.1), we have the following equality

$$\begin{aligned} \frac{d}{dt}y(t)=x(t)-x(t-1), \end{aligned}$$

implying that

$$\begin{aligned} y(t)=\int _{0}^{1}x(t-s)ds+\text {const}. \end{aligned}$$

(4.5)

From (4.1) (i.e., $2\beta =4K(k)$) and (3.10) we have

$$\begin{aligned} y(0)=y(1)=0. \end{aligned}$$

Now we show that

$$\begin{aligned} \int _{0}^{1}x(t)dt=\left( \sqrt{a}+\sqrt{b}\right) \sqrt{\frac{r}{2}}E(k)-\sqrt{ab}. \end{aligned}$$

(4.6)

Using the properties of the Jacobi elliptic functions [3], we compute

$$\begin{aligned} \left( \text {dn}+k\text {cn}\right) ^{2}&=\text {dn}^{2}+2k\text {dn}\text {cn}+k^{2}\text {cn}^{2}=k^{2}-1+2\text {dn}^{2}+2k\text {dn}\text {cn}. \end{aligned}$$

From the following computations

$$\begin{aligned} \int _{0}^{1}\text {dn}^{2}(\beta t,k)dt&=\frac{1}{\beta }\int _{0}^{2K(k)}\text {dn}^{2}(u,k)dt=\frac{2}{\beta }E(k),\\ \int _{0}^{1}\text {dn}(\beta t,k)\text {cn}(\beta t,k)dt&=0, \end{aligned}$$

one sees that

$$\begin{aligned} \int _{0}^{1}x(t)dt=a\frac{k^{2}-1+\frac{4}{\beta }E(k)}{\left( 1+k\right) ^{2}} \end{aligned}$$

by (3.9). Then we obtain (4.6) from (3.7) and (3.8). from the condition (4.2) the integral constant in (4.5) becomes $-1$, for the solution of the equation (3.1). $\square$

The conditions (4.1) and (4.2) ensure the existence of a periodic solution of period 2 for the system of ordinary differential equations (3.1), satisfying (4.4). The periodic solution obtained in Theorem 5 is also a periodic solution of the delay differential equation (1.3). Our remaining task is to interpret the conditions (4.1) and (4.2) in terms of the parameter r in the equation (1.3).

Eliminating a and b from the conditions (4.1) and (4.2), we obtain the following equality

$$\begin{aligned} r=L(k),\ 0\le k<1, \end{aligned}$$

(4.7)

where

$$\begin{aligned} L(k):=2K(k)\left( 2E(k)-K(k)\left( 1-k^{2}\right) \right) . \end{aligned}$$

For the derivation of (4.7), see the proof of Proposition 7 below. Now we show that the equation (4.7) has a unique root.

Lemma 6

The function L is a strictly increasing function with

$$\begin{aligned} L(0)=\frac{\pi ^{2}}{2}<\lim _{k\rightarrow 1-0}L(k)=\infty . \end{aligned}$$

Proof

From the definition of L, it is easy to see $L(0)=\frac{\pi ^{2}}{2}.$ By the straightforward calculation, we obtain

$$\begin{aligned}&\frac{d}{dk}\left( 2E(k)-K(k)\left( 1-k^{2}\right) \right) \\&\quad = \frac{2}{k}\left( E\left( k\right) -K\left( k\right) \right) -\frac{1}{k}\left( E\left( k\right) -\left( 1-k^{2}\right) K\left( k\right) \right) +2kK\left( k\right) \\&\quad = \frac{1}{k}\left( E\left( k\right) -\left( 1-k^{2}\right) K\left( k\right) \right) \\&\quad = \left( 1-k^{2}\right) K^{\prime }\left( k\right) \\&\quad > 0, \end{aligned}$$

noting that

$$\begin{aligned} K^{\prime }(k)&=\frac{1}{k}\left( \frac{E(k)}{1-k^{2}}-K(k)\right) .\\ E^{\prime }(k)&=\frac{1}{k}\left( E(k)-K(k)\right) , \end{aligned}$$

see e.g. P. 282 of [3]. Since it can be shown that

$$\begin{aligned} \lim _{k\rightarrow 1-0}K(k)(1-k^{2})=\lim _{k\rightarrow 1-0}\int _{0}^{\frac{\pi }{2}}\frac{1-k^{2}}{\sqrt{1-k^{2}\sin ^{2}\theta }}d\theta =0, \end{aligned}$$

L is a strictly increasing function with $\lim _{k\rightarrow 1-0}L(k)=\infty$. $\square$

Then, a and b are determined by the following proposition.

Proposition 7

There exist $a>0$ and $b>0$ such that the two conditions (4.1) and (4.2) in Theorem 5 hold if and only if $r>\frac{\pi ^{2}}{2}$. In particular, a and b are given as

$$\begin{aligned} \left[ \begin{array}{c} a\\ b \end{array}\right] =\frac{K(k)}{2E(k)-K(k)\left( 1-k^{2}\right) }\left[ \begin{array}{c} \left( 1+k\right) ^{2}\\ \left( 1-k\right) ^{2} \end{array}\right] =\frac{2K(k)^{2}}{r}\left[ \begin{array}{c} \left( 1+k\right) ^{2}\\ \left( 1-k\right) ^{2} \end{array}\right] , \end{aligned}$$

(4.8)

where $k=L^{-1}(r),\ r>\frac{\pi ^{2}}{2}$.

Proof

Consider $a>0$ and $b>0$ for the two equations (4.1) and (4.2). From the definition of k in (3.8) we have

$$\begin{aligned} \sqrt{b}=\frac{1-k}{1+k}\sqrt{a}. \end{aligned}$$

(4.9)

thus the two conditions (4.1) and (4.2) are expressed in terms of a and k, namely

$$\begin{aligned} \sqrt{a}=K(k)\left( 1+k\right) \sqrt{\frac{2}{r}}. \end{aligned}$$

(4.10)

Substituting (4.10) to (4.2), we arrive at the following equation

$$\begin{aligned} L(k)=r,\ 0\le k<1. \end{aligned}$$

From Lemma 6, for $r>\frac{\pi ^{2}}{2}$, we can find $k=L^{-1}\left( r\right) >0$. From (4.9) and (4.10), a and b can be computed as in (4.8). $\square$

Finally we obtain the following theorem.

Theorem 8

Let $r>\frac{\pi ^{2}}{2}$. Then the delay differential equation (1.3) has a periodic solution of period 2. The periodic solution is expressed as in (3.9), where a and b are determined in Proposition 7.

Denote by $x^{*}(t)$ the periodic solution of (1.3) with $x^{*}(0)=a$, which satisfies (2.8). It is easy to see that

$$\begin{aligned} \max _{t\in \left[ -1,1\right] }x^{*}(t)=x^{*}(0)=a,\ \min _{t\in \left[ -1,1\right] }x^{*}(t)=x^{*}(-1)=x^{*}(1)=b. \end{aligned}$$

Thus from (2.8) one sees that $x^{*}(t)x^{*}(t-1)=ab$ for $t\in \mathbb {R}$. From (4.8) it can be shown that $\lim _{r\rightarrow \infty }\left( a,b\right) =\left( \infty ,0\right)$, thus the amplitude of the periodic solution tends to $\infty$ as $r\rightarrow \infty$. We also note that

$$\begin{aligned} \lim _{r\rightarrow \infty }ab=0. \end{aligned}$$

Finally, from the symmetry of the Jacobi elliptic functions, it follows that

$$\begin{aligned} x^{*}(2n+s)=x^{*}(2n-s),\ n\in \mathbb {Z},\ s\in \mathbb {R}. \end{aligned}$$

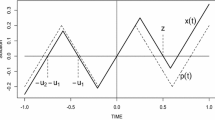
In Fig. 1, we plot a and b as functions of r. See Fig. 2 for the periodic solution for $r=5$ and $r=10$.

Fig. 1

Bifurcation of the equilibrium. The equilibrium $x=1$ is asymptotically stable for $r<\frac{\pi ^{2}}{2}$ and is unstable for $r>\frac{\pi ^{2}}{2}$. At $r=\frac{\pi ^{2}}{2}$ a Hopf bifurcation occurs and the periodic solution appears

Fig. 2

Time profile of the periodic solution for $r=5$ and $r=10$

5 Discussion

There have been many studies on the existence of periodic solutions of the delay differential equation (1.1), see [34] and references therein. Kaplan and Yorke show the existence of periodic solutions of period 4 for (1.1), assuming that f is an odd function, from a Hamiltonian system [15]. If f is not an odd function (e.g., $f\left( z\right) =r\left( 1-e^{z}\right)$ in the case of Wright’s equation), the existence of a solution of period 4 can not be expected, see [4, 23].

The equation (1.3), we study in this paper, is a Hutchinson–Wright equation having distributed delay, instead of discrete delay. The ansatz, $x^{*}\left( t\right) =x^{*}\left( t-2\right)$, derives the second order nonlinear ordinary differential equation (3.4), where the explicit solution is available in terms of the Jacobi elliptic functions. Finding a class of delay differential equations that have solutions with period 2 is our future work. One sees that, from the linear analysis (see Proposition 2), a period-2 solution emerges at the first Hopf bifurcation for a class of differential equations with distributed delay. Which class of nonlinear delay differential equations does allow the existence of period-2 solutions for a range of parameters?

The delay differential equation (1.3) is a special case of the following delay differential equation

$$\begin{aligned} \frac{d}{dt}x(t)=rx(t)\left( 1-\alpha x(t)-\int _{0}^{1}x(t-s)ds\right) , \end{aligned}$$

(5.1)

where $0\le \alpha <1$. The delay differential equation (5.1) arises from a mathematical model for disease transmission dynamics (see “Appendix B”). We wish to analyze the periodic solutions of (5.1) to explain disease transmission dynamics ([25]). However, differently from Wright’s equation, the estimation of the non-delay term, together with the distributed delay term, seems to be an obstacle, when one tries to construct a Poincare map to find a periodic solution (cf. [16, 32, 33]). Multiple periodic solutions seem to be possible for the SIRS model in “Appendix B” with the demographic turn-over [30]. See also [17] for multiple periodic solutions of a logistic equation.

Our study leads to open problems. Numerical simulations of the equation (1.3) suggest that the periodic solution of period 2 attracts many positive solutions. Uniqueness and stability of the solution of period 2 are open problems. It would be also interesting to discuss the periodic solution with respect to the kernel of distributed delay. To the author, it is not obvious if the periodic solution of period 2 of (1.3) is related to the periodic solution of Wright’s equation (as varying the uniform kernel of the distributed delay to a Dirac mass).

Appendices

Appendix A. Elliptic Functions

We briefly introduce the Jacobi elliptic functions. See [3] for detail. See also [20], where the Jacobi elliptic functions are defined as the solutions of a system of ordinary differential equations. We then show that the solution of the Duffing equation is expressed in terms of the Jacobi elliptic function.

The incomplete elliptic integrals of the first kind and second kind are respectively given as

$$\begin{aligned} F\left( \varphi ,k\right)&=\int _{0}^{\varphi }\frac{1}{\sqrt{1-k^{2}\sin ^{2}\theta }}d\theta ,\\ E\left( \varphi ,k\right)&=\int _{0}^{\varphi }\sqrt{1-k^{2}\sin ^{2}\theta }d\theta \end{aligned}$$

for $\varphi \in \mathbb {R}$ and $0\le k<1$. Here k is a parameter called the modulus. Then the complete elliptic integrals of the first kind and second kind introduced in Sect. 4 are

$$\begin{aligned} K(k):=F\left( \frac{\pi }{2},k\right) ,\ E(k):=E\left( \frac{\pi }{2},k\right) . \end{aligned}$$

The amplitude function $\text {am}$ is defined as the inverse function of the elliptic integral of the first kind, fixing the modulus k, i.e.,

$$\begin{aligned} \text {am}\left( F\left( \varphi ,k\right) ,k\right) =\varphi . \end{aligned}$$

Then the Jacobi elliptic functions $\text {sn},\text {cn}:\mathbb {R}\rightarrow \left[ -1,1\right]$ are respectively defined as

$$\begin{aligned} \text {sn}\left( t,k\right)&=\sin \left( \text {am}\left( t,k\right) \right) ,\\ \text {cn}\left( t,k\right)&=\cos \left( \text {am}\left( t,k\right) \right) . \end{aligned}$$

One then sees that the period of $\text {sn}$ and $\text {cn}$ is given as 4K(k). Then the Jacobi elliptic function $\text {dn}$ is defined by

$$\begin{aligned} \text {dn}\left( t,k\right) =\sqrt{1-k^{2}\text {sn}\left( t,k\right) }. \end{aligned}$$

The period of $\text {dn}$ is 2K(k).

The Duffing equation can be solved by the Jacobi elliptic function (see [3, 20]). Let us consider the following ordinary differential equation

$$\begin{aligned} \frac{d^{2}}{dt^{2}}y(t)&=-py(t)+qy(t)^{3} \end{aligned}$$

(A.1)

with initial condition

$$\begin{aligned} \frac{d}{dt}y(0)&=d, \end{aligned}$$

(A.2a)

$$\begin{aligned} y(0)&=0. \end{aligned}$$

(A.2b)

Here $p,\ q$ and d are assumed to be real. One obtains the equation (3.4) with the initial condition (3.5) from (A.1) with (A.2) by

$$\begin{aligned} p=r\left( a+b\right) ,\ q=\frac{r^{2}}{2},\ d=a-b. \end{aligned}$$

(A.3)

For (A.1) with the initial condition (A.2), we consider the following ansatz

$$\begin{aligned} y(t)=\alpha \text {sn}\left( \beta t,k\right) \end{aligned}$$

with $\alpha >0$ and $\beta >0$, noting that $\text {sn}$ is an odd function. Differentiating the Jacobi elliptic functions, we have

$$\begin{aligned} y^{\prime }(t)&=\alpha \beta \text {cn}\left( \beta t,k\right) \text {dn}\left( \beta t,k\right) ,\\ y^{\prime \prime }(t)&=-\alpha \beta ^{2}\text {sn}\left( \beta t,k\right) \left( \text {dn}^{2}\left( \beta t,k\right) +k^{2}\text {cn}^{2}\left( \beta t,k\right) \right) \\&=-\alpha \beta ^{2}\text {sn}\left( \beta t,k\right) \left( \left( 1+k^{2}\right) -2k^{2}\text {sn}^{2}\left( \beta t,k\right) \right) , \end{aligned}$$

thus

$$\begin{aligned} y^{\prime \prime }(t)=-\beta ^{2}y(t)\left( 1+k^{2}-2\frac{k^{2}}{\alpha ^{2}}y^{2}(t)\right) \end{aligned}$$

follows. We then obtain the following three equations

$$\begin{aligned} d&=\alpha \beta , \end{aligned}$$

(A.4a)

$$\begin{aligned} p&=\beta ^{2}\left( 1+k^{2}\right) , \end{aligned}$$

(A.4b)

$$\begin{aligned} q&=\frac{2\beta ^{2}k^{2}}{\alpha ^{2}}. \end{aligned}$$

(A.4c)

Let us now solve the Eq. (A.4) in terms of $\alpha ,\ \beta$ and k. One obtains

$$\begin{aligned} k^{2}-ck+1=0, \end{aligned}$$

(A.5)

where

$$\begin{aligned} c:=\frac{p}{d}\sqrt{\frac{2}{q}}. \end{aligned}$$

(A.6)

Since the equation (A.5) has a root in $\left[ 0,1\right)$ if and only if $2<c$, assume that $2<c$ holds. We then get

$$\begin{aligned} k=\frac{1}{2}\left( c-\sqrt{c^{2}-4}\right) \in \left[ 0,1\right) . \end{aligned}$$

Now it follows

$$\begin{aligned} \alpha =d\sqrt{\frac{1+k^{2}}{p}},\ \beta =\sqrt{\frac{p}{1+k^{2}}}. \end{aligned}$$

For the equation (3.4) with the initial condition (3.5), substituting (A.3) to (A.6), we obtain

$$\begin{aligned} c=2\left( \frac{a+b}{a-b}\right) >2. \end{aligned}$$

Then one can easily obtain $\alpha ,\ \beta$ and k as in (3.7) and (3.8).

Appendix B. An Epidemic Model with Temporary Immunity

The delay differential equation (1.3) can be related to an epidemic model that accounts for temporary immunity ([2, 8, 11, 30, 36]). Let us derive the delay differential equation (1.3) as a limiting case of the following SIRS type epidemic model with temporary immunity

$$\begin{aligned} \frac{d}{dt}S(t)&=-\beta S(t)I(t)+\gamma I(t-\tau ), \end{aligned}$$

(B.1a)

$$\begin{aligned} \frac{d}{dt}I(t)&=\beta S(t)I(t)-\gamma I(t), \end{aligned}$$

(B.1b)

$$\begin{aligned} \frac{d}{dt}R(t)&=\gamma I(t)-\gamma I(t-\tau ). \end{aligned}$$

(B.1c)

The model (B.1) is equivalent to the model studied in Section 3 of [11] (see (B.4) below) and is a special case of the model considered in [8]. As in [8, 11], ignoring birth and death of individuals, transitions of susceptible, infective and recovered populations are described. Here $S(t),\ I(t)$ and R(t) respectively denote the fraction of susceptible, infective and recovered populations at time t. The model (B.1) has three parameters: transmission coefficient $\beta >0$, the recovery rate $\gamma >0$ and the immune period $\tau >0$. See also [2, 30] for SIRS models with demographic turn-over.

The initial condition is given as follows

$$\begin{aligned} S(0)&=S_{0}>0,\\ I(s)&=\psi (s),\ s\in \left[ -\tau ,0\right] ,\\ R(0)&=\gamma \int _{0}^{\tau }\psi (-s)ds, \end{aligned}$$

where $\psi$ is a positive continuous function. We now require that

$$\begin{aligned} S_{0}+\psi (0)+\gamma \int _{0}^{\tau }\psi (-s)ds=1, \end{aligned}$$

so that

$$\begin{aligned} S(t)+I(t)+R(t)=1,\ t\ge 0 \end{aligned}$$

(B.2)

implying the constant total population. It also follows

$$\begin{aligned} R(t)=\gamma \int _{0}^{\tau }I(t-s)ds,\ t\ge 0. \end{aligned}$$

(B.3)

From (B.2) and (B.3) we get

$$\begin{aligned} S(t)=1-I(t)-\gamma \int _{0}^{\tau }I(t-s)ds. \end{aligned}$$

Then from (B.1b) we obtain the following scalar delay differential equation

$$\begin{aligned} \frac{d}{dt}I(t)=I(t)\left\{ \beta \left( 1-I(t)-\gamma \int _{0}^{\tau }I(t-s)ds\right) -\gamma \right\} . \end{aligned}$$

(B.4)

We let $x(t)=\frac{I(t)}{I_{e}},$ where $I_{e}$ is a nontrivial equilibrium of (B.4) given as

$$\begin{aligned} I_{e}=\frac{1-\frac{\gamma }{\beta }}{1+\gamma \tau }. \end{aligned}$$

It is assumed that $\beta >\gamma$ to ensure $I_{e}>0$. Considering a nondimensional time so that the immune period is 1, we obtain

$$\begin{aligned} \frac{d}{dt}x(t)=\left( \beta -\gamma \right) x(t)\left( 1-\frac{x(t)+\gamma \tau \int _{0}^{1}x(t-s)ds}{1+\gamma \tau }\right) . \end{aligned}$$

We now fix $r=\beta -\gamma$ and let $\gamma \tau \rightarrow \infty$ to formally obtain the equation (1.3). Local stability analysis for (B.4) can be found in [8, 11]. See also [25] for the application of the mathematical model to explain the periodic outbreak of a childhood disease.