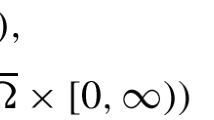A Note on the Convergence of Singularly Perturbed Second Order Potential-Type Equations

Abstract

In this paper we study the limit as $\varepsilon \rightarrow 0$ of the singularly perturbed second order equation $\varepsilon ^2 \ddot{u}_\varepsilon + \nabla _{\!x} V(t,u_\varepsilon (t))=0$, where V(t, x) is a potential. We assume that $u_0(t)$ is one of its equilibrium points such that $\nabla _{\!x}V(t,u_0(t))=0$ and $\nabla _{\!x}^2V(t,u_0(t))>0$. We find that, under suitable initial data, the solutions $u_\varepsilon$ converge uniformly to $u_0$, by imposing mild hypotheses on V. A counterexample shows that they cannot be weakened.

1 Introduction

A problem of interest in various areas of applied mathematics is to find stable equilibrium points for time-dependent energies. In a simplified setting, the problem is to find an evolution $t\rightarrow u(t)$ such that

$$\begin{aligned} \left\{ \begin{array}{l} \nabla _{\!x} V(t,u(t))=0, \\ \nabla _{\!x}^2 V(t,u(t)) > 0, \end{array}\right. \end{aligned}$$

(1.1)

where V(t, x) is a potential, $\nabla _{\!x}$ denotes the gradient with respect to x, and $\nabla _{\!x}^2$ the corresponding Hessian. This problem can be locally solved by means of the Implicit Function Theorem, which provides a smooth solution defined in a neighborhood of $t=0$.

Problem (1.1) has also been studied in finite dimension as the limit case of $\varepsilon$-gradient flows. A first general result was given by Zanini [15], where the author studies the system

$$\begin{aligned} \varepsilon \dot{u}_\varepsilon (t) + \nabla _{\!x} V(t,u_\varepsilon (t))=0. \end{aligned}$$

(1.2)

In [15] it is proved that the solutions $u_\varepsilon$ to (1.2) converge to a solution u to (1.1), obtained by connecting smooth branches of solutions to the equilibrium equation (1.1) through suitable heteroclinic solutions of the $\varepsilon$-gradient flows (1.2).

In [1] V. Agostiniani analysed the second order approximation with a dissipative term:

$$\begin{aligned} \varepsilon ^2 A\ddot{u}_\varepsilon (t)+\varepsilon B\dot{u}_\varepsilon (t) + \nabla _{\!x} V(t,u_\varepsilon (t))=0, \end{aligned}$$

(1.3)

where A and B are positive definite and symmetric matrices. It turns out that $(u_\varepsilon , \varepsilon B \dot{u}_\varepsilon ) \rightarrow (u,0)$, where u is piecewise continuous and satisfies (1.1). Moreover the behaviour of the system at jump times is described by trajectories connecting the states before and after the jumps; such trajectories are given by a suitable autonomous second order system related to A, B, and $\nabla _{\!x} V$.

We remark that studying the asymptotic behaviour of solutions, as $\varepsilon \rightarrow 0$, in systems of the form (1.3) with $A \ne 0$ and $B=0$ (vanishing inertia), or $A = 0$ and $B \ne 0$ (vanishing viscosity), or $A,B \ne 0$ (vanishing viscosity and inertia), may give a selection principle for quasistatic evolutions (namely those evolutions whose loading is assumed to be so slow that at every time the system is at equilibrium and internal oscillation can be neglected). This approach has been successfully adopted in various situations in the case of vanishing viscosity (cf. e.g. [3–7, 10, 11]) and in the case of vanishing viscosity and inertia (cf. e.g. [2, 9, 12–14]). We remark that in [2] viscosity can be neglected under suitable assumptions.

The above mentioned results [1, 15] require strong smoothness assumptions on V ($C^3$-regularity is required). The aim of the present paper is to weaken the assumptions under which second order perturbed problems converge to (1.1). More precisely, we consider a second order equation of the form (1.3) without the dissipative term $B\dot{u}_\varepsilon$. (Notice that in general, when $B>0$, it is easier to prove the convergence of solutions.) We therefore study the asymptotic behaviour of the solutions $u_\varepsilon$ of the problem

$$\begin{aligned} \varepsilon ^2 \ddot{u}_\varepsilon (t)+ \nabla _{\!x} V(t,u_\varepsilon (t))=0 \end{aligned}$$

(1.4)

to a continuous stable equilibrium $u_0$ of (1.1). Our main result is that the convergence $u_\varepsilon \rightarrow u_0$ still holds under some regularity and growth conditions on V that are weaker than those required in [1, 15]. Furthermore we provide a counterexample to that convergence when such assumptions do not hold.

More precisely we require continuity for V in both variables and we assume that $V(t,\cdot ) \in C^2$. We also suppose that there is a function $V_t(t,x)$ of class $C^1$-Carathéodory (i.e., $V_t(\cdot ,x)$ is measurable and $V_t(t,\cdot )$ is of class $C^1$) such that

$$\begin{aligned} V(t_2,x)-V(t_1,x)=\int _{t_1}^{t_2} V_t(t,x)\,\mathrm {d}t, \end{aligned}$$

for a.e. $t_1,t_2$. With some further boundedness conditions on V (listed in Sect. 2) we prove that $u_0(t)$ is absolutely continuous and we obtain the convergence result, see Theorem 3.3 in Sect. 3. Specifically, we find that solutions to (1.4) satisfy

$$\begin{aligned} u_\varepsilon \rightarrow u_0 \text{ uniformly } \text{ and } \varepsilon \Vert \dot{u}_\varepsilon -\dot{u}_0\Vert _{L^1} \rightarrow 0 \end{aligned}$$

(1.5)

as $\varepsilon \rightarrow 0$.

In Sect. 4 we show that, if we weaken the assumptions on V, we are not able to get (1.5). More precisely we provide a counterexample for a model case where the time-dependent energy is given by

$$\begin{aligned} V(t,x):= \frac{1}{2} |x-u_0(t)|^2. \end{aligned}$$

We remark that, when $u_0 \in W^{1,1}(0,T)$, then V in its turn satisfies the assumptions of Sect. 3. In this case, solutions $u_\varepsilon$ of (1.4) converge uniformly to $u_0$. On the other hand we show that, if $u_0$ is the Cantor–Vitali function, then (1.5) can not be satisfied (see Example 4.3). In fact we prove that no subsequences of solutions to (1.4) could converge to $u_0$ and that the continuous functions $u_0$ with this property are infinitely many (see Proposition 4.1, Remark 4.2).

This result thus shows a case in which the dynamic solutions do not converge to the expected (quasistatic) equilibrium. A similar phenomenon was observed in [8] where the authors give an example of non-convergence, in the context of a one-dimensional peeling test without viscosity: more precisely, their dynamic solutions converge to a limit that does not fulfill first order stability. Our non-convergence result in Sect. 4 can therefore be regarded as an example in which, in the absence of a damping viscous term, dynamic solutions do not converge to stable equilibria even in very simple situations.

2 Setting of the Problem

Let $V:\mathbb {R}{\times } \mathbb {R}^n \rightarrow \mathbb {R}$ be a continuous function such that $V(t,\cdot ) \in C^{2}(\mathbb {R}^n)$. It will play the role of a time-dependent energy. We assume that there exists a function $u_0 \in C^0([0,T];\mathbb {R}^n)$ such that the following properties are satisfied:

$$\begin{aligned}&\nabla _{\!x} V(t,u_0(t))=0, \,\, \text{ for } \text{ every } t \in [0,T], \end{aligned}$$

(2.1)

$$\begin{aligned}&\exists \,\alpha >0 :\nabla _{\!x}^2 V(t,u_0(t))\xi \cdot \xi \ge \alpha |\xi |^2, \text{ for } \text{ all } \xi \in \mathbb {R}^n. \end{aligned}$$

(2.2)

Furthermore, for a.e. $t \in [0,T]$ and for every $x \in \mathbb {R}^n$, we assume that there is a constant $A>0$ such that

$$\begin{aligned} |\nabla _{\!x} V(t,x)|,\,\,|\nabla _{\!x}^2 V(t,x)| \le A. \end{aligned}$$

(2.3)

We also assume that there exists a $C^1$-Carathéodory function $V_t:\mathbb {R}{\times } \mathbb {R}^n \rightarrow \mathbb {R}$, i.e., a Carathéodory function such that $V_t(t,\cdot ) \in C^1(\mathbb {R}^n)$, satisfying

$$\begin{aligned} V(t_2,x)-V(t_1,x)=\int _{t_1}^{t_2} V_t(t,x)\,\mathrm {d}t, \end{aligned}$$

(2.4)

for a.e. $t_1,t_2 \in \mathbb {R}$ and all $x \in \mathbb {R}^n$. Moreover, for every $R>0$, we require that there exists $a_R \in L^1(\mathbb {R})$ such that

$$\begin{aligned} |V_t(t,x)|,\,\,|\nabla _{\!x} V_t(t,x)| \le a_R(t), \end{aligned}$$

(2.5)

for a.e. $t \in \mathbb {R}$ and all $x \in B_R(0)$. We notice that, by condition (2.5), it is possible to prove that $\nabla _{\!x}V$ is continuous in both variables.

We consider, for fixed $\varepsilon >0$, the Cauchy problem

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon ^2\ddot{u}_\varepsilon + \nabla _{\!x} V(t,u_\varepsilon (t))=0, \\ u_\varepsilon (0)=u_\varepsilon ^0, \\ \dot{u}_\varepsilon (0)=v_\varepsilon ^0, \end{array} \right. \end{aligned}$$

(2.6)

where we assume that

$$\begin{aligned} u_\varepsilon ^0 \rightarrow u_0(0)=0 \text{ and } \varepsilon v_\varepsilon (0)\rightarrow 0. \end{aligned}$$

(2.7)

Global existence and uniqueness of the solutions $u_\varepsilon$ to (2.6) are consequences of standard theorems on ordinary differential equations thanks to the continuity of $\nabla _{\!x}V$ and to condition (2.3). Our goal is to study when convergence, as $\varepsilon \rightarrow 0$, of solutions $u_\varepsilon$ to (2.6) satisfying conditions (2.7) to $u_0$ is possible.

Using (2.3) and (2.5), we now study the dependence on x of the set of Lebesgue points for a function $t \mapsto f(t,x)$ which will then play the role of $V_t$ and $\nabla _{\!x} V_t$.

Lemma 2.1

Let $f:\mathbb {R}{\times } \mathbb {R}^n \rightarrow \mathbb {R}^m$ be a Carathéodory function such that, for every $R>0$, there exists $a_R \in L^1(\mathbb {R})$ with $f(t,x) \le a_R(t)$ for every $x \in B_R(0)$. Fix $x \in \mathbb {R}^n$, then for a.e. $t \in \mathbb {R}$

$$\begin{aligned} \lim _{y \rightarrow x} \lim _{h\rightarrow 0} \frac{1}{h} \int _t^{t+h}[ f(\tau ,y)-f(t,y)]\,\mathrm {d}\tau =0. \end{aligned}$$

Proof

Let $t \in \mathbb {R}$ be a right Lebesgue point for $\tau \mapsto f(\tau ,x)$, i.e.,

$$\begin{aligned} \lim _{h\rightarrow 0} \frac{1}{h} \int _t^{t+h}[ f(\tau ,x) - f(t,x)]\,\mathrm {d}\tau =0. \end{aligned}$$

Let $\delta >0$ and define

$$\begin{aligned} \omega _R^\delta (\tau ) := \sup _{\begin{array}{c} x,y \in B_R(0)\\ |x-y|<\delta \end{array}} |f(\tau ,x)-f(\tau ,y)|. \end{aligned}$$

(2.8)

By assumption we have that $\omega _R^\delta (\tau )\le 2 a_R(\tau )$; moreover $\omega _R^\delta$ is measurable because the supremum can be taken over all rational points and along a sequence $\delta =1/n$. Therefore $\omega _R^\delta (\cdot ) \in L^1(\mathbb {R})$.

If t is also a right Lebesgue point for $\tau \mapsto \omega _R^\delta (\tau )$ for every $\delta \in \mathbb {Q}, \delta > 0$ and $|x-y| < \delta$, then

$$\begin{aligned}&\lim _{h\rightarrow 0} \frac{1}{h} \int _t^{t+h}\left| f(\tau ,x) - f(t,x)- (f(\tau ,y)-f(t,y))\right| \,\mathrm {d}\tau \nonumber \\&\quad \le \,\, \lim _{h\rightarrow 0}\frac{1}{h} \int _t^{t+h} \left[ \omega _R^\delta (\tau )+\omega ^\delta _R(t)\right] \,\mathrm {d}\tau = 2\omega _R^\delta (t). \end{aligned}$$

(2.9)

Since $f(t,\cdot )$ is uniformly continuous in $\overline{B_R(0)}$, the last term in (2.9) tends to zero as $\delta \rightarrow 0$ for a.e. $t \in \mathbb {R}$. $\square$

Remark 2.2

Given any $u\in W^{1,1}(0,T;\mathbb {R}^n)$, we are now able to get a chain rule for a.e. $t \in [0,T]$, by differentiating $z(t):= V(t,u(t))$. Indeed, if t is a Lebesgue point for $\tau \mapsto V_t(\tau ,u(t))$, by (2.4) we have

$$\begin{aligned} \frac{z(t+h)-z(t)}{h}&= \frac{V(t+h,u(t+h))-V(t,u(t+h))}{h} + \frac{V(t,u(t+h))-V(t,u(t))}{h}\nonumber \\&= \frac{1}{h} \int _t^{t+h} V_t(\tau , u(t+h))\,\mathrm {d}\tau + \nabla _{\!x} V(t,\xi )\frac{u(t+h)-u(t)}{h}, \end{aligned}$$

(2.10)

for some point $\xi$ belonging to the segment $[u(t),u(t+h)]$, thanks to the Mean Value Theorem. We now re-write the first summand of (2.10) in the following form:

$$\begin{aligned}&\frac{1}{h} \int _t^{t+h} V_t(\tau ,u(t+h))\,\mathrm {d}\tau \nonumber \\&\quad =\frac{1}{h} \int _t^{t+h}\left[ V_t(\tau ,u(t+h))- V_t(t,u(t+h))\right] \! \,\mathrm {d}\tau + V_t(t,u(t+h). \end{aligned}$$

(2.11)

In view of Lemma 2.1, the integral in (2.11) tends to zero, for a.e. $t \in [0,T]$ as $h \rightarrow 0$: this is done by a diagonal argument using the fact that $u(t+h) \rightarrow u(t)$, because u is an absolutely continuous function. Moreover, by continuity of $V_t(t,u(\cdot ))$, the second summand in (2.11) tends to $V_t(t,u(t))$. Therefore, as $h \rightarrow 0$ in (2.10), we get

$$\begin{aligned} \frac{\,\mathrm {d}}{\,\mathrm {d}t} V(t,u(t)) = \dot{z}(t) = V_t(t,u(t)) + \nabla _{\!x} V(t,u(t))\dot{u}(t), \end{aligned}$$

(2.12)

for a.e. $t \in [0,T]$, because $\nabla _{\!x} V(t,\cdot )$ is continuous.

We now argue similarly for $\nabla _{\!x} V(t,u(t))$ and get a chain rule again. Since $V_t(t,\cdot ) \in C^1(\mathbb {R}^n)$ for a.e. t and condition (2.5) holds, by an application of the Dominated Convergence Theorem, we have that

$$\begin{aligned} \nabla _{\!x} V(t_2,x) - \nabla _{\!x} V(t_1,x) = \int _{t_1}^{t_2} \nabla _{\!x} V_t(t,x) \,\mathrm {d}t. \end{aligned}$$

(2.13)

Therefore,

$$\begin{aligned}&\frac{\nabla _{\!x} V(t+h, u(t+h)) - \nabla _{\!x} V(t,u(t))}{h} \nonumber \\&\quad = \frac{\nabla _{\!x} V(t+h,u(t+h)) - \nabla _{\!x} V(t,u(t+h))}{h} + \frac{\nabla _{\!x} V(t,u(t+h))-\nabla _{\!x} V(t,u(t))}{h} \nonumber \\&\quad = \frac{1}{h} \int _t^{t+h}\nabla _{\!x} V_t(\tau ,u(t+h))\,\mathrm {d}\tau + \frac{\nabla _{\!x} V(t,u(t+h))-\nabla _{\!x} V(t,u(t))}{h}. \end{aligned}$$

(2.14)

Since $\nabla _{\!x} V_t(t,\cdot )$ is continuous and $\nabla _{\!x} V_t(\cdot ,x)$ is measurable (indeed, it can be obtained as the limit along a sequence of measurable difference quotients), then $\nabla _{\!x} V_t$ is a Carathéodory function controlled by an integrable function $a_R(t)$. Arguing as before and recalling that $V(t,\cdot ) \in C^2(\mathbb {R}^n)$, we have that for a.e. $t \in [0,T]$

$$\begin{aligned} \lim _{h \rightarrow 0} \frac{\nabla _{\!x} V(t+h, u(t+h)) - \nabla _{\!x} V(t,u(t))}{h} = \nabla _{\!x} V_t(t,u(t)) + \nabla _{\!x}^2 V(t,u(t))\dot{u}(t). \end{aligned}$$

In particular, since $\nabla _{\!x} V(t,u_0(t))=0$, we have

$$\begin{aligned} \nabla _{\!x} V_t(t,u_0(t)) + \nabla _{\!x}^2 V(t,u_0(t))\dot{u_0}(t) = 0. \end{aligned}$$

(2.15)

We are now in the position to state the following result which will enable us to restrict to the case of absolutely continuous functions throughout the sequel.

Proposition 2.3

Let $V:\mathbb {R}{\times } \mathbb {R}^n \rightarrow \mathbb {R}$ be a continuous function which satisfies $V(t,\cdot ) \in C^{2}(\mathbb {R}^n)$ for a.e. $t \in \mathbb {R}$. Let $V_t$ fulfill conditions (2.4) and (2.5), and let $u_0:[0,T] \rightarrow \mathbb {R}^n\,\,$ be a continuous function such that there exists $\alpha >0:$

$$\begin{aligned} \nabla _{\!x}^2 V(t,u_0(t))\xi \cdot \xi \ge \alpha |\xi |^2, \end{aligned}$$

(2.16)

for every $\xi \in \mathbb {R}^n$ and for a.e. $t \in [0,T]$. Then, $u_0$ is absolutely continuous in [0, T].

Proof

We want to show that, if $\varepsilon$ is small enough, there exists $\delta >0$ such that, for a.e. $t_1,t_2 \in [0,T]$ with $|t_1-t_2|<\delta$, there exists $M_\varepsilon >0$ and an integrable function g such that

$$\begin{aligned} |u_0(t_2)-u_0(t_1)| \le M_\varepsilon \int _{t_1}^{t_2} g(t)\,\mathrm {d}t. \end{aligned}$$

(2.17)

We know that

$$\begin{aligned} 0&=\nabla _{\!x} V(t_2,u_0(t_2))-\nabla _{\!x} V(t_1,u_0(t_1)) \\&= \nabla _{\!x} V(t_2,u_0(t_2))-\nabla _{\!x} V(t_1,u_0(t_2))+ \nabla _{\!x} V(t_1,u_0(t_2))-\nabla _{\!x} V(t_1,u_0(t_1)) \\&= \nabla _{\!x} V(t_2,u_0(t_2))-\nabla _{\!x} V(t_1,u_0(t_2)) + \nabla _{\!x}^2 V(t_1,y)(u_0(t_2)-u_0(t_1)), \end{aligned}$$

where y is in the segment $[u_0(t_1),u_0(t_2)]$. Therefore we have

$$\begin{aligned} u_0(t_2)-u_0(t_1)=-\nabla _{\!x}^2 V(t_1,y)^{-1}[\nabla _{\!x} V(t_2,u_0(t_2))-\nabla _{\!x} V(t_1,u_0(t_2))]. \end{aligned}$$

(2.18)

Since $\nabla _{\!x}^2 V(t_1,\cdot )$ is continuous and satisfies the coercivity assumption (2.16), we can find $\varepsilon >0$ such that, if $y \in B_\varepsilon (u_0(t_1))$ then

$$\begin{aligned} \nabla _{\!x}^2 V(t_1,y)\xi \cdot \xi \ge \frac{\alpha }{2} |\xi |^2. \end{aligned}$$

We can thus invert $\nabla _{\!x}^2 V(t_1,\cdot )$ in a neighborhood of $u_0(t_1)$. Let $\lambda _y$ be the minimum eigenvalue of $\nabla _{\!x}^2 V(t_1,y)$. Therefore we can control the norm of $\nabla _{\!x}^2 V(t_1,y)^{-1}$ with $1/\lambda _y$. If $v_y$ is an eigenvector of $\nabla _{\!x}^2 V(t_1,y)$ with eigenvalue $\lambda _y$, then we have

$$\begin{aligned} \lambda _y |v_y|^2 = \nabla _{\!x}^2 V(t_1,y)v_y \cdot v_y \ge \frac{\alpha }{2} |v_y|^2, \end{aligned}$$

from which we deduce that $\lambda _y \ge \frac{\alpha }{2}$ and therefore

$$\begin{aligned} \Vert \nabla _{\!x}^2 V(t_1,y)^{-1}\Vert \le \frac{2}{\alpha }. \end{aligned}$$

(2.19)

We can now plug (2.19) in (2.18) and, arguing as in (2.13) of the previous Remark, we get

$$\begin{aligned} |u_0(t_2)-u_0(t_1)|\le \frac{2}{\alpha } \int _{t_1}^{t_2} |\nabla _{\!x} V_t(t,u_0(t_2))|\,\mathrm {d}t \le \frac{2}{\alpha }\int _{t_1}^{t_2} a_R(t)\,\mathrm {d}t \end{aligned}$$

and we have thus obtained (2.17). $\square$

3 Convergence of Solutions

This section is devoted to the study of the convergence for solutions $u_\varepsilon$ of problem (2.6). We will show that $u_\varepsilon$ uniformly converges to $u_0$, which is the equilibrium for the potential V introduced in the previous section, provided initial conditions (2.7) are satisfied.

We recall here the standard Gronwall lemma which will be used as a main tool in the proof of the convergence.

Lemma 3.1

(Gronwall) Let $\varphi \in L^\infty (\mathbb {R}), \varphi (t)\ge 0$ for a.e. $t \in \mathbb {R}$ and $a \in L^1(\mathbb {R}), a(t)\ge 0$ for a.e. $t \in \mathbb {R}$. We assume that there exists a constant $C>0$ such that

$$\begin{aligned} \varphi (t) \le \int _0^t a(s)\varphi (s)\,\mathrm {d}s + C, \text{ for } \text{ a.e. } t \in \mathbb {R}. \end{aligned}$$

Then,

$$\begin{aligned} \varphi (t)\le C \exp \left( \int _0^t a(s) \,\mathrm {d}s\right) \!, \text{ for } \text{ a.e. } t \in \mathbb {R}. \end{aligned}$$

Remark 3.2

From now on assume that there exists $\psi :[0,+\infty ) \rightarrow \mathbb {R}$ such that

$$\begin{aligned} \lim _{t \rightarrow +\infty } \psi (t) = +\infty \text{ and } V(t,x) \ge \psi (|x|), \end{aligned}$$

(3.1)

for all $t \in [0,T]$ and $x \in \mathbb {R}^n$, and there exist $a(\cdot ), b(\cdot ) \in L^1(0,T)$ such that

$$\begin{aligned} V_t(t,x) \le a(t) + b(t)V(t,x), \end{aligned}$$

(3.2)

for a.e. $t \in [0,T]$ and for all $x \in \mathbb {R}^n$. Then it is easy to deduce uniform boundedness for the sequence $\{u_\varepsilon \}$, by applying Lemma 3.1 to the following energy estimate:

$$\begin{aligned} V(t,u_\varepsilon (t)) \le \Vert a\Vert _{L^1(0,T)} + \int _0^T b(t) V(t,u_\varepsilon (t))\,\mathrm {d}t. \end{aligned}$$

We remark that conditions (3.1) and (3.2), which are standard in this context, are not necessary for establishing our result if we already know that the sequence $\{u_\varepsilon \}$ is uniformly bounded.

We are now in the position to state the main result of this section.

Theorem 3.3

Let V be a function fulfilling the assumptions of Proposition 2.3 and let $u_0 \in C^0([0,T];\mathbb {R}^n)$ be such that $\nabla _{\!x}V(t,u_0(t))=0$ for every $t \in [0,T]$. Assume also that conditions (3.1) and (3.2) are satisfied and that $\nabla _{\!x}^2 V(t,x)$ and $\nabla _{\!x} V_t(t,x)$ are locally equi-Lipschitz in x, uniformly in t, i.e.  for every $x \in \mathbb {R}^n$ there exists $\delta >0$ and constants $C_1,C_2>0$ (which may depend on x), such that, for every $|h| < \delta$

$$\begin{aligned} \begin{array}{l} |\nabla _{\!x}^2 V(t,x+h)-\nabla _{\!x}^2 V(t,x)| \le C_1|h|,\\ |\nabla _{\!x} V_t(t,x+h)-\nabla _{\!x} V_t(t,x)| \le C_2|h|, \end{array} \end{aligned}$$

(3.3)

for a.e. $t \in [0,T]$. Let $u_\varepsilon$ be a solution of the Cauchy problem

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon ^2\ddot{u}_\varepsilon + \nabla _{\!x} V(t,u_\varepsilon (t))=0, \\ u_\varepsilon (0)=u_\varepsilon ^0, \\ \dot{u}_\varepsilon (0)=v_\varepsilon ^0, \end{array} \right. \end{aligned}$$

(3.4)

where the initial data $u_\varepsilon ^0$ and $v_\varepsilon ^0$ are such that

$$\begin{aligned} u_\varepsilon ^0 \rightarrow u_0(0)=0 \text{ and } \varepsilon v_\varepsilon ^0\rightarrow 0. \end{aligned}$$

(3.5)

Then, $u_\varepsilon \rightarrow u_0$ uniformly in [0, T] and $\varepsilon \Vert \dot{u}_\varepsilon -\dot{u}_0\Vert _{L^1} \rightarrow 0$, as $\varepsilon \rightarrow 0$.

Proof

We fix a sequence $\varepsilon _j \rightarrow 0$ and we prove convergence for $u_{\varepsilon _j}$: this will show convergence for the whole family $\{u_\varepsilon \}$ to $u_0$, by the arbitrariness of $\varepsilon _j$. However we will keep writing just $u_\varepsilon$ for the sake of simplicity of notation.

By Proposition 2.3, we have that $u_0 \in W^{1,1}(0,T;\mathbb {R}^n)$. Since $C^2([0,T];\mathbb {R}^n)$ is dense in $W^{1,1}(0,T;\mathbb {R}^n)$, for every $k \in \mathbb {N}$ there exists a sequence $\{u_0^k\}\subset C^2([0,T];\mathbb {R}^n)$ such that

$$\begin{aligned} \Vert u_0-u_0^k\Vert _{W^{1,1}} < \frac{1}{k}. \end{aligned}$$

(3.6)

A suitable choice of k will take place in due course. However, we can already notice that, since $W^{1,1}(0,T;\mathbb {R}^n) \subset C^0([0,T];\mathbb {R}^n)$, then $u_0^k$ uniformly converges to $u_0$ in [0, T] and therefore they are all contained in a compact set containing $\{u_0(t), t \in [0,T]\}$.

We now introduce a surrogate of energy estimate, multiplying the equation in (3.4) by $\dot{u}_\varepsilon (t)-\dot{u}_0^k(t)$. After an integration we get

$$\begin{aligned}&\frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (t)-\dot{u}_0^k(t)|^2+V(t,u_\varepsilon (t))\nonumber \\&\quad = \frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (0)-\dot{u}_0^k(0)|^2+V(0,u_\varepsilon (0))- \int _0^t\varepsilon ^2\ddot{u}_0^k(s)(\dot{u}_\varepsilon (s)-\dot{u}_0^k(s))\,\mathrm {d}s\nonumber \\&\qquad +\int _0^t \left[ V_t(s,u_\varepsilon (s))+\nabla _{\!x} V(s,u_\varepsilon (s))\dot{u}_0^k(s)\right] \,\mathrm {d}s \end{aligned}$$

(3.7)

Our aim is thus to infer some lower and upper bounds for (3.7) in order to get, by Lemma 3.1, convergence of $u_\varepsilon -u_0^k$ and then deduce convergence to $u_0$. It is thus convenient to consider the following “shifted” potential $\tilde{V}$ defined as

$$\begin{aligned} \tilde{V}(t,x):=V(t,x)-V(t,u_0^k(t)). \end{aligned}$$

(3.8)

Since $u_0^k$ is of class $C^2$, then all regularity assumptions on V are inherited by $\tilde{V}$. We have, in particular, that

$$\begin{aligned} \tilde{V}_t(t,x) = V_t(t,x) - V_t(t,u_0^k(t)) - \nabla _{\!x}V(t,u_0^k(t))\dot{u}_0^k(t). \end{aligned}$$

(3.9)

Moreover it is easy to show that

$$\begin{aligned} \nabla _{\!x}\tilde{V}(t,u_0(t))=0, \,\,\forall t \in [0,T]. \end{aligned}$$

(3.10)

We also notice that (3.7) is equivalent to

$$\begin{aligned}&\frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (t)-\dot{u}_0^k(t)|^2+\tilde{V}(t,u_\varepsilon (t))\nonumber \\&\quad = \frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (0)-\dot{u}_0^k(0)|^2+\tilde{V}(0,u_\varepsilon (0)) -\int _0^t\varepsilon ^2\ddot{u}_0^k(s)(\dot{u}_\varepsilon (s)-\dot{u}_0^k(s))\,\mathrm {d}s\,\,\nonumber \\&\qquad +\int _0^t \tilde{V}_t(s,u_\varepsilon (s))+\nabla _{\!x} \tilde{V}(s,u_\varepsilon (s))\dot{u}_0^k(s)\,\mathrm {d}s. \end{aligned}$$

(3.11)

We set $A_\varepsilon {:=} \frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (0)-\dot{u}_0^k(0)|^2+\tilde{V}(0,u_\varepsilon (0))$, which tends to 0 as $\varepsilon \rightarrow 0$, by the initial conditions (3.5) and because $u_0^k \rightarrow u_0$ uniformly in [0, T].

We now subdivide the proof into parts obtaining estimates which will then be used in the final Gronwall argument.

Lower Estimate. We look for a lower bound for the summand $\tilde{V}(t,u_\varepsilon )$ in the left hand side of (3.11). We have that, by first order expansion, there exists y in the segment [0, x] such that

$$\begin{aligned} V(t,x+u_0(t))&=V(t,u_0(t))+\nabla _{\!x} V(t,u_0(t))x+\nabla _{\!x}^2 V(t,y)x\cdot x\nonumber \\&=V(t,u_0(t))+\nabla _{\!x}^2 V(t,y)x\cdot x, \end{aligned}$$

(3.12)

because $\nabla _{\!x}V(t,u_0(t))=0$ for every $t \in [0,T]$. We now compute twice (3.12), once for $x=u_\varepsilon (t)-u_0(t)$ and once for $x=u_0^k(t)-u_0(t)$, and then we make the difference between the two results. Therefore, for suitable $y_1$ between $u_0(t)$ and $u_\varepsilon (t)$, and $y_2$ between $u_0(t)$ and $u_0^k(t)$, we have

$$\begin{aligned} \tilde{V}(t,u_\varepsilon (t))&=\nabla _{\!x}^2 V(t,y_1)(u_\varepsilon (t)-u_0(t))\cdot (u_\varepsilon (t)-u_0(t)) \nonumber \\&\quad -\nabla _{\!x}^2 V(t,y_2)(u_0^k(t)-u_0(t))\cdot (u_0^k(t)-u_0(t)). \end{aligned}$$

(3.13)

By a continuity argument and the coercivity assumption for $\nabla _{\!x}^2 V$ (2.16) we can find $\delta >0$ such that, if $|z|<\delta$, then

$$\begin{aligned} \nabla _{\!x}^2 V(t,z+u_0(t))\xi \cdot \xi \ge \frac{\alpha }{2}|\xi |^2. \end{aligned}$$

We apply this estimate in the first summand of the right hand side of (3.13), while for the other one we use boundedness of $\nabla _{\!x}^2 V(t,\cdot )$. We thus get

$$\begin{aligned} \tilde{V}(t,u_\varepsilon (t))\ge \frac{\alpha }{2} |u_\varepsilon (t)-u_0(t)|^2-c |u_0^k(t)-u_0(t)|^2, \end{aligned}$$

(3.14)

for a suitable $c>0$, provided that

$$\begin{aligned} |u_\varepsilon (t)-u_0(t)|<\delta \,\, \text{ for } \text{ every } \,t \in [0,T]\, \text{ and } \text{ for } \, \varepsilon \,\text{ small } \text{ enough. } \end{aligned}$$

(3.15)

For the moment we assume that this bound holds and postpone its proof to the end.

Since

$$\begin{aligned} \frac{\alpha }{4}|u_\varepsilon (t)-u_0^k(t)|^2\le \frac{\alpha }{2}|u_\varepsilon (t)-u_0(t)|^2+\frac{\alpha }{2}|u_0(t)-u_0^k(t)|^2, \end{aligned}$$

we deduce, from (3.14), that

$$\begin{aligned} \tilde{V}(t,u_\varepsilon (t))\ge \frac{\alpha }{4}|u_\varepsilon (t)-u_0^k(t)|^2-(c+\frac{\alpha }{2})|u_0^k(t)-u_0(t)|^2, \end{aligned}$$

(3.16)

where the last summand on the right hand side of (3.16) is small by the uniform convergence of $u_0^k$ to $u_0$.

Upper Estimate.   We now switch our attention to the estimate on the right hand side of (3.11), which we now re-write in the following way:

$$\begin{aligned}&A_\varepsilon -\int _0^t\varepsilon ^2\ddot{u}_0^k(s)(\dot{u}_\varepsilon (s)-\dot{u}_0^k(s))\,\mathrm {d}s +\int _0^t \left[ \tilde{V}_t(s,u_\varepsilon (s))+\nabla _{\!x} \tilde{V}(s,u_\varepsilon (s))\dot{u}_0^k(s)\right] \,\mathrm {d}s \\&\quad =: A_\varepsilon -A_1 + A_2. \end{aligned}$$

Estimate of A1. We first apply the Cauchy inequality and obtain

$$\begin{aligned} |A_1|=\left| \int _0^t\varepsilon ^2\ddot{u}_0^k(\dot{u}_\varepsilon -\dot{u}_0^k) \,\mathrm {d}s \right| \le \frac{\varepsilon ^2}{2}\int _0^t|\ddot{u}_0^k|^2 \,\mathrm {d}s+\frac{\varepsilon ^2}{2}\int _0^t|\dot{u}_\varepsilon -\dot{u}_0^k |^2\,\mathrm {d}s \end{aligned}$$

(3.17)

The second summand in (3.17) will enter the final estimate via the Gronwall lemma, while for the first one we argue in the following way. We have no information about how big $\Vert \ddot{u}_0^k\Vert _{L^2(0,T)}$ is, nevertheless we can find, for every $k \in \mathbb {N}$, an $\varepsilon >0$ such that

$$\begin{aligned} \Vert \ddot{u}_0^k\Vert ^2_{L^2(0,T)}\le \frac{1}{\varepsilon }. \end{aligned}$$

(3.18)

Then, we can invert the function which associates $\varepsilon$ to k and get $k(\varepsilon )\rightarrow \infty$ as $\varepsilon \rightarrow 0$, though this convergence may be very slow. This is done by recalling that $\varepsilon =\varepsilon _j$ and then defining

$$\begin{aligned} k(\varepsilon _j):= \min \left\{ k \in \mathbb {N}: \Vert \ddot{u}_0^k\Vert ^2_{L^2(0,T)} > \frac{1}{\varepsilon _j}\right\} -1. \end{aligned}$$

From now on we will keep writing k intending $k(\varepsilon _j)$ with this peculiar construction and we have, combining (3.17) with (3.18),

$$\begin{aligned} |A_1| \le A_1^\varepsilon + \frac{\varepsilon ^2}{2}\int _0^t|\dot{u}_\varepsilon -\dot{u}_0^k |^2\,\mathrm {d}s, \end{aligned}$$

(3.19)

where $A_1^\varepsilon \rightarrow 0$ as $\varepsilon \rightarrow 0$.

Estimate of A2. By using a variable x which will play the role of $u_\varepsilon (t)-u_0^k(t)$, we have that, for a.e. $t \in [0,T]$,

$$\begin{aligned}&|\tilde{V}_t(t,x+u_0^k)+\nabla _{\!x}\tilde{V}(t,x+u_0^k)\dot{u}_0^k| \nonumber \\&\quad \le |\tilde{V}_t(t,x+u_0^k)-\tilde{V}_t(t,x+u_0)|+|\nabla _{\!x}\tilde{V}(t,x+u_0^k)\dot{u}_0^k-\nabla _{\!x}\tilde{V}(t,x+u_0^k)\dot{u}_0|\nonumber \\&\qquad +|\nabla _{\!x}\tilde{V}(t,x+u_0^k)\dot{u}_0-\nabla _{\!x}\tilde{V}(t,x+u_0)\dot{u}_0|+|\tilde{V}_t(t,x+u_0)+\nabla _{\!x}\tilde{V}(t,x+u_0)\dot{u}_0|. \end{aligned}$$

(3.20)

The first three summands on the right are easy to deal with, by using Lipschitz and boundedness assumptions. They are estimated, independently of x, by

$$\begin{aligned} C(1+|\dot{u}_0|)(|u_0^k-u_0|+|\dot{u}_0^k-\dot{u}_0|). \end{aligned}$$

As for the fourth summand, we call

$$\begin{aligned} f(x):=\tilde{V}_t(t,x+u_0)+\nabla _{\!x}\tilde{V}(t,x+u_0)\dot{u}_0. \end{aligned}$$

If we set $g(x):=f(x)-\nabla f(0) x$, then there exists y in the segment [0, x] such that $g(x)-g(0)=\nabla g(y)x$. Therefore we have, for a.e. $t \in [0,T]$,

$$\begin{aligned}&\tilde{V}_t(t,x+u_0)+\nabla _{\!x}\tilde{V}(t,x+u_0)\cdot \dot{u}_0-\tilde{V}_t(t,u_0)\nonumber \\&\qquad -\nabla _{\!x}\tilde{V}(t,u_0)\cdot \dot{u}_0-\nabla _{\!x}\tilde{V}_t(t,u_0)\cdot x-\nabla _{\!x}^2\tilde{V}(t,u_0)\dot{u}_0\cdot x\nonumber \\&\quad \le \left| \nabla _{\!x}\tilde{V}_t(t,y+u_0)+\nabla _{\!x}^2\tilde{V}(t,y+u_0)\dot{u}_0-\nabla _{\!x}\tilde{V}_t(t,u_0)-\nabla _{\!x}^2\tilde{V}(t,u_0)\dot{u}_0 \right| |x|\nonumber \\&\quad \le c(1+ |\dot{u}_0|)|y||x| \nonumber \\&\quad \le c|x|^2(1+|\dot{u}_0|), \end{aligned}$$

(3.21)

since $\nabla _{\!x}\tilde{V}_t$ and $\nabla _{\!x}^2\tilde{V}$ are locally equi-Lipschitz in x uniformly in t, by condition (3.3), and the constant $c >0$ is independent of $x=u_\varepsilon - u_0^k$ because the functions $u_\varepsilon$ are bounded in $\varepsilon$ as we pointed out in Remark 3.2. Moreover, by (3.9),

$$\begin{aligned} |\tilde{V}_t(t,u_0)|&= |V_t(t,u_0)-V_t(t,u_0^k)-\nabla _{\!x} V(t,u_0^k)\cdot \dot{u}_0^k| \nonumber \\&\le |V_t(t,u_0)-V_t(t,u_0^k)|+|\nabla _{\!x} V(t,u_0)\cdot \dot{u}_0^k- \nabla _{\!x} V(t,u_0^k)\cdot \dot{u}_0^k|\nonumber \\&\le C|u_0-u_0^k|(1+|\dot{u}_0^k|), \end{aligned}$$

(3.22)

for a.e. $t \in [0,T]$. As in (2.15), we have that for a.e. $t \in [0,T]$,

$$\begin{aligned} \nabla _{\!x} \tilde{V}_t(t,u_0(t))+\nabla _{\!x}^2 \tilde{V}(t,u_0(t))\dot{u}_0(t)=0. \end{aligned}$$

(3.23)

Therefore, plugging (3.10), (3.21), (3.22), and (3.23) in (3.20), we get

$$\begin{aligned}&|\tilde{V}_t(t,x+u_0^k)+\nabla _{\!x}\tilde{V}(t,x+u_0^k)\cdot \dot{u}_0^k|\nonumber \\&\quad \le c_1(1+|\dot{u}_0|)(|u_0^k-u_0|+|\dot{u}_0^k-\dot{u}_0|)+ c_2|x|^2(1+|\dot{u}_0|)+c_3|u_0-u_0^k|(1+|\dot{u}_0^k|), \end{aligned}$$

(3.24)

for a.e. $t \in [0,T]$, where $c_1, c_2$, and $c_3 > 0$. We may therefore compute (3.24) with $x=u_\varepsilon (t)-u_0^k(t)$ and, if we integrate between 0 and t, we find that

$$\begin{aligned} c_1\int _0^t (1+|\dot{u}_0|)(|u_0^k-u_0|+|\dot{u}_0^k-\dot{u}_0|)\,\mathrm {d}s \rightarrow 0, \end{aligned}$$

as $k \rightarrow \infty$ by $W^{1,1}$-convergence of $u_0^k$ to $u_0$. Also

$$\begin{aligned} c_3\int _0^t |u_0-u_0^k|(1+|\dot{u}_0^k|)\,\mathrm {d}s \rightarrow 0, \end{aligned}$$

as $k \rightarrow \infty$ using this time the uniform convergence of $u_0^k$ to $u_0$ and the fact that $\dot{u}^k_0 \in L^1(0,T)$. Therefore the second integral in (3.11) is estimated by

$$\begin{aligned} c_2\int _0^t |u_\varepsilon -u_0^k|^2(1+|\dot{u}_0|)\,\mathrm {d}s + A_k, \end{aligned}$$

(3.25)

where $A_k \rightarrow 0$ as $k \rightarrow \infty$.

Gronwall Argument.   We are now able to get, by the previous estimates, the conclusion of the proof. We set

$$\begin{aligned} B_\varepsilon :=A_\varepsilon + A_1^\varepsilon + A_{k(\varepsilon )} + \left( c+ \frac{\alpha }{2}\right) |u_0^{k(\varepsilon )}(t)-u_0(t)|^2 , \end{aligned}$$

which tends to zero as $\varepsilon \rightarrow 0$, and we plug (3.16), (3.17), (3.18), and (3.25) into (3.11). We therefore have, for every $t \in [0,T]$,

$$\begin{aligned}&\frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (t)-\dot{u}_0^k(t)|^2+\frac{\alpha }{4}|u_\varepsilon (t)-u_0^k(t)|^2\nonumber \\&\quad \le B_\varepsilon + \frac{\varepsilon ^2}{2}\int _0^t|\dot{u}_\varepsilon -\dot{u}_0^k |^2 +c_2\int _0^t |u_\varepsilon -u_0^k|^2(1+|\dot{u}_0|). \end{aligned}$$

(3.26)

With some further manipulations we are in position to apply Lemma 3.1. Therefore, there exists $C>0$ such that

$$\begin{aligned} \frac{\varepsilon ^2}{2}|\dot{u}_\varepsilon (t)-\dot{u}_0^k(t)|^2+\frac{\alpha }{4}|u_\varepsilon (t)-u_0^k(t)|^2 \le B_\varepsilon \exp \left( C\int _0^t (1+|\dot{u}_0(s)|)\,\mathrm {d}s\right) . \end{aligned}$$

(3.27)

Since $u_0 \in W^{1,1}(0,T)$, we have that the right hand side of (3.27) tends to zero as $\varepsilon \rightarrow 0$, for every $t \in [0,T]$. In particular, since $|u_\varepsilon (t)-u_0(t)|\le |u_\varepsilon (t)-u_0^k(t)|+|u_0^k(t)-u_0(t)|$, we obtain that $u_\varepsilon (t) \rightarrow u_0(t)$ uniformly in [0, T] as $\varepsilon \rightarrow 0$. We also have

$$\begin{aligned} \varepsilon \Vert \dot{u}_\varepsilon -\dot{u}_0\Vert _{L^1(0,T)}&\le \varepsilon \Vert \dot{u}_\varepsilon -\dot{u}_0^k\Vert _{L^1(0,T)} + \varepsilon \Vert \dot{u}_0^k-\dot{u}_0\Vert _{L^1(0,T)} \\&\le \varepsilon ^2 T \int _0^T|\dot{u}_\varepsilon -\dot{u}_0^k|^2 + \varepsilon \Vert \dot{u}_0^k-\dot{u}_0\Vert _{L^1(0,T)}, \end{aligned}$$

from which we deduce

$$\begin{aligned} \varepsilon \Vert \dot{u}_\varepsilon -\dot{u}_0\Vert _{L^1} \rightarrow 0, \end{aligned}$$

as $\varepsilon \rightarrow 0$, because $\Vert \dot{u}_0^k-\dot{u}_0\Vert _{L^1(0,T)}$ is bounded.

Proof of (3.15)

In order to conclude we only need to prove that $|u_\varepsilon (t)-u_0(t)| < \delta$, for every $t \in [0,T]$ and for $\varepsilon$ small enough. We can define, for every $\varepsilon >0$

$$\begin{aligned} t_\varepsilon =\inf \{t\in [0,T] :|u_\varepsilon (t)-u_0(t)|>\delta \}, \end{aligned}$$

with the convention that $\inf \emptyset = T$. Notice that the continuity of $u_\varepsilon (\cdot )-u_0(\cdot )$ and the initial condition $u_\varepsilon (0)\rightarrow u_0(0)$ as $\varepsilon \rightarrow 0$, implies that $t_\varepsilon >0$. We thus have that (3.15) is satisfied for every $t \in [0,t_\varepsilon )$. We now assume, by contradiction, that $t_\varepsilon < T$. Then, with the previous Gronwall argument, we can find $\bar{\varepsilon }$ so small such that $|u_\varepsilon (t)-u_0(t)|<\frac{\delta }{2}$ for every $\varepsilon \in (0,\bar{\varepsilon })$ and $t \in [0,t_\varepsilon ]$. However this contradicts the continuity of $u_\varepsilon -u_0$ in $t=t_\varepsilon$. Therefore $t_\varepsilon = T$ and this concludes the proof of the theorem. $\square$

4 Counterexample

In the previous section we proved that, under certain assumptions on V, the solutions $u_\varepsilon$ of problems (3.4) converge in $W^{1,1}(0,T)$ to $u_0$, whenever $u_0$ is continuous and the initial conditions (3.5) are satisfied. We now prove that assumptions on V can not be further relaxed in order to get the same result.

Let us consider the sample case

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon ^2 \ddot{u}_\varepsilon +u_\varepsilon -u_0=0, \\ u_\varepsilon (0)=u_\varepsilon ^0, \\ {u}_\varepsilon (0)=v_\varepsilon ^0, \end{array} \right. \end{aligned}$$

(4.1)

where we assume that $u_\varepsilon ^0 \rightarrow u_0(0)=0$ and $\varepsilon v_\varepsilon ^0\rightarrow 0$ as $\varepsilon \rightarrow 0$. In this case the potential V is given by

$$\begin{aligned} V(t,x):=\frac{1}{2}|x-u_0(t)|^2. \end{aligned}$$

We have that $\nabla _{\!x} V(t,u_0(t))=0$ for every t and $\nabla _{\!x}^2V(t,u_0(t))$ is the identity matrix. We notice that, if we only assume continuity of $u_0$, then a chain rule similar to (2.12) can not be established. We can, nevertheless, find an explicit solution of (4.1) with standard methods of ordinary differential equations:

$$\begin{aligned} u_\varepsilon (t)=\left( -\frac{1}{\varepsilon }\int _0^t u_0(s)\sin \tfrac{s}{\varepsilon }\,\mathrm {d}s+u_\varepsilon ^0\right) \cos \tfrac{t}{\varepsilon }+\left( \frac{1}{\varepsilon }\int _0^t u_0(s)\cos \tfrac{s}{\varepsilon }\,\mathrm {d}s+\varepsilon v_\varepsilon ^0\right) \sin \tfrac{t}{\varepsilon }. \end{aligned}$$

(4.2)

If we assume that $u_0 \in W^{1,1}(0,T)$, then assumption of Theorem 3.3 are satisfied and therefore $u_\varepsilon \rightarrow u_0$ uniformly for every $t \in [0,T]$ and that $\varepsilon \dot{u}_\varepsilon \rightarrow 0$ for a.e. $t \in \mathbb {R}$. This result can be equivalently obtained by direct computation through the explicit formula (4.2). We may remark the fact that, in the presence of a dissipative term as in [1], the convergence of the solutions to the approximated problems is satisfied with weaker assumptions on the initial conditions. More precisely if the equation is

$$\begin{aligned} \varepsilon ^2 \ddot{u}_\varepsilon +\varepsilon \dot{u}_\varepsilon +u_\varepsilon -u_0=0, \end{aligned}$$

then it is sufficient to assume only that

$$\begin{aligned} u_\varepsilon ^0 e^{-\frac{1}{2\varepsilon }} \rightarrow 0 \text{ and } \varepsilon v_\varepsilon ^0 e^{-\frac{1}{2\varepsilon }} \rightarrow 0 \text{ as } \varepsilon \rightarrow 0. \end{aligned}$$

We now show that convergence for the problem (4.1) fails if we only assume that $u_0$ is continuous. This gives a counterexample to the convergence result of Theorem 3.3 when the regularity assumptions on V are not satisfied. Indeed, there is at least a continuous function that can not be approximated by solutions to second order perturbed problems, as we show in the next proposition; we will exhibit one of these functions in Example 4.3. Furthermore in $W^{1,1}$ there is a dense set of $C^0_0$ functions with this property (see Remark 4.2).

Proposition 4.1

There exists $u_0 \in C^0_0([0,T])$ such that the functions $u_\varepsilon$, defined in (4.2), do not converge uniformly to $u_0$ as $\varepsilon \rightarrow 0$.

Proof

We argue by contradiction. Assume that for every $u_0 \in C^0_0([0,T])$ $u_\varepsilon$ uniformly converges to $u_0$ as $\varepsilon \rightarrow 0$. Without loss of generality we can assume that $T\ge 1$ and we show that the convergence fails at $t=1$. Let us fix $\varepsilon _k \rightarrow 0$. Then we have, from (4.2),

$$\begin{aligned} u_{\varepsilon _k}(1)=-\frac{1}{\varepsilon _k}\int _0^1 u_0(s)\left[ \sin \tfrac{s}{\varepsilon _k}\cos \tfrac{1}{\varepsilon _k}-\cos \tfrac{s}{\varepsilon _k}\sin \tfrac{1}{\varepsilon _k}\right] \,\mathrm {d}s+u_{\varepsilon _k}^0\cos \tfrac{1}{\varepsilon _k} + \varepsilon _k v_{\varepsilon _k}^0\sin \tfrac{1}{\varepsilon _k}. \end{aligned}$$

Since $u_{\varepsilon _k}^0,\varepsilon _k v_{\varepsilon _k}^0 \rightarrow 0$ by assumption, we have convergence of $u_\varepsilon (1)$ to $u_0(1)$ if and only if the operator $F_{\varepsilon _k}:C^0_0([0,T])\rightarrow \mathbb {R}$, defined as

$$\begin{aligned} F_{\varepsilon _k}(u_0):=-\frac{1}{\varepsilon _k}\int _0^1 u_0(s) \left[ \sin \tfrac{s}{\varepsilon _k}\cos \tfrac{1}{\varepsilon _k}-\cos \tfrac{s}{\varepsilon _k}\sin \tfrac{1}{\varepsilon _k}\right] \,\mathrm {d}s, \end{aligned}$$

converges. We thus have pointwise convergence of $F_{\varepsilon _k}$ to $F_0$ defined by $F_0(u_0)=u_0(1)$. By the Banach–Steinhaus Theorem this implies uniform equiboundedness. On the other hand we notice that

$$\begin{aligned} F_{\varepsilon _k}(u_0)=\int _0^1 u_0(s)\,\mathrm {d}\mu _{\varepsilon _k}(s), \end{aligned}$$

where $\,\mathrm {d}\mu _{\varepsilon _k}(s)=-\frac{1}{\varepsilon _k}[\sin \tfrac{s}{\varepsilon _k}\cos \tfrac{1}{\varepsilon _k}-\cos \tfrac{s}{\varepsilon _k}\sin \tfrac{1}{\varepsilon _k}]\,\mathrm {d}s$. However

$$\begin{aligned} \sup _k|\mu _{\varepsilon _k}|(0,1)=\sup _k \left( \frac{1}{\varepsilon _k}\int _0^1 |\sin \tfrac{s-1}{\varepsilon _k}|\,\mathrm {d}s\right) =\sup _k\int _{-\tfrac{1}{\varepsilon _k}}^0 |\sin \tau |\,\mathrm {d}\tau = +\infty \end{aligned}$$

which contradicts the uniform equiboundedness. $\square$

Remark 4.2

The Banach–Steinhaus Theorem also implies that the set

$$\begin{aligned} R:=\{u_0 \in C_0^0([0,T]):\sup _\varepsilon |F_\varepsilon (u_0)|=+\infty \} \end{aligned}$$

is dense. Therefore there are indeed infinitely many functions for which $u_\varepsilon$ can not converge to $u_0$.

Example 4.3

We now give an explicit example of a continuous function that is not approximated by solutions to second order perturbed problems. We consider as $u_0$ the Cantor–Vitali function $\hat{u} :[0,1] \rightarrow [0,1]$. Plugging $u_0=\hat{u}$ into (4.2) and through integration by parts, we get

$$\begin{aligned} u_\varepsilon (t)=\hat{u}(t)-\cos \tfrac{t}{\varepsilon }\int _0^t \cos \tfrac{s}{\varepsilon }\,\mathrm {d}\mu (s) - \sin \tfrac{t}{\varepsilon }\int _0^t \sin \tfrac{s}{\varepsilon }\,\mathrm {d}\mu (s) + u_\varepsilon ^0 \cos \tfrac{t}{\varepsilon } + \varepsilon v_\varepsilon ^0 \sin \tfrac{t}{\varepsilon }, \end{aligned}$$

(4.3)

where $\mu$ is intended to be the distributional derivative of $u_0$. We now choose $\varepsilon _k=\frac{1}{2k\pi }$ and remark that

$$\begin{aligned} \int \cos (2k\pi s)\,\mathrm {d}\mu (s) = \int e^{-i 2k\pi s}\,\mathrm {d}\mu (s), \end{aligned}$$

where $\hat{u}$ and $\mu$ have been extended to $\mathbb {R}$ by setting $\hat{u}=0$ in the complement of [0, 1]. By using the well-known expression for the Fourier Transform of the Cantor measure we can compute (4.3) in $t=1$ and get

$$\begin{aligned} u_{\varepsilon _k}(1)=\hat{u}(1)+u_{\varepsilon _k}^0-\int _0^1 \cos (2k\pi s)\,\mathrm {d}\mu (s)=\hat{u}(1)+u_{\varepsilon _k}^0 - (-1)^k\prod _{h=1}^{\infty } \cos \tfrac{2k\pi }{3^h}. \end{aligned}$$

Since $u_{\varepsilon _k}^0 \rightarrow 0$ by the assumptions on the initial conditions, we focus our attention on the term

$$\begin{aligned} (-1)^k \prod _{h=1}^{\infty } \cos \tfrac{2k\pi }{3^h}= (-1)^k f(2k\pi ), \end{aligned}$$

where we have defined $f:[0,+\infty )\rightarrow [-1,1]$ by

$$\begin{aligned} f(x)=\prod _{h=1}^{\infty } \cos \tfrac{x}{3^h}. \end{aligned}$$

We now prove that there exists a sequence $k_n$ such that $(-1)^{k_n}f(2k_n\pi )$ does not converge to 0.

By the definition f satisfies

$$\begin{aligned} f(3x)=f(x)\cos (x). \end{aligned}$$

In particular this implies

$$\begin{aligned} f(6\pi )=f(3\cdot 2\pi )=f(2\pi ). \end{aligned}$$

Inductively one gets

$$\begin{aligned} f(3^n\cdot 2\pi )=f(2\pi ) \end{aligned}$$

and similarly

$$\begin{aligned} f(2\cdot 3^n \cdot 2\pi ) = f(4 \pi ). \end{aligned}$$

Therefore we choose as $k_n$ the sequence

$$\begin{aligned} \{3,\, 2\cdot 3,\, 3^2,\, 2 \cdot 3^2, \ldots , 3^n,\, 2 \cdot 3^n, \ldots \}. \end{aligned}$$

Along this sequence $(-1)^{k_n}f(2k_n\pi )$ tends to $-f(2\pi )$ for the odd indeces and to $f(4\pi )$ for the odd indexes and to $f(4 \pi )$ for the even ones. We now prove that $f(2\pi )$ and $f(4\pi )$ are real numbers with the same sign. This implies that $(-1)^{k_n}f(2k_n\pi )$ does not converge and therefore $u_{\varepsilon _k}(1)$ does not converge to $\hat{u}(1)$.

We have that (using the convention that $\log 0 = - \infty$)

$$\begin{aligned} \log f(x) = \sum _{h=1}^\infty \log \left| \cos \tfrac{x}{3^h}\right| \ge -\sum _{h=1}^\infty \tfrac{x^2}{3^{2h}}, \end{aligned}$$

if $y \in (0,1)$, because in this interval

$$\begin{aligned} \log |\cos y | = \log \cos y \ge \frac{\cos y -1 }{\cos y}. \end{aligned}$$

Moreover

$$\begin{aligned} 1 - \frac{1}{\cos y} \ge - x^2 \iff \cos y(1 + y^2) \ge 1, \end{aligned}$$

which is verified in (0, 1) using the fact that $\cos y \ge 1 - \frac{y^2}{2}$. Since $\frac{2\pi }{3^h}$ and $\frac{4\pi }{3^h}$ are in the interval (0, 1) for h large enough, then $f(2\pi )$ and $f(4\pi )$ are controlled by the geometric series and therefore $f(2\pi ),f(4\pi ) \ne 0$. This is enough in order to prove that along the sequences $k_{2n}$ or $k_{2n+1}$ convergence of $u_{\varepsilon _{k_n}}(1)$ to $\hat{u}(1)$ is not satisfied. Moreover we notice that $f(2\pi )$ and $f(4\pi )$ have the same sign because $\cos \tfrac{2\pi }{3}=\cos \tfrac{4\pi }{3}=-\tfrac{1}{2}$, while $\cos \big (\frac{2\pi }{3^n}\big ) \ge 0$ for every $n \ge 3$. Therefore we have found more than we claimed, since $u_{\varepsilon _{k_n}}(1)$ does not converge at all.

We have thus shown an explicit example in which convergence of (4.2) to a particular continuous function $u_0$ fails.