From Random Poincaré Maps to Stochastic Mixed-Mode-Oscillation Patterns

Abstract

We quantify the effect of Gaussian white noise on fast–slow dynamical systems with one fast and two slow variables, which display mixed-mode oscillations owing to the presence of a folded-node singularity. The stochastic system can be described by a continuous-space, discrete-time Markov chain, recording the returns of sample paths to a Poincaré section. We provide estimates on the kernel of this Markov chain, depending on the system parameters and the noise intensity. These results yield predictions on the observed random mixed-mode oscillation patterns. Our analysis shows that there is an intricate interplay between the number of small-amplitude oscillations and the global return mechanism. In combination with a local saturation phenomenon near the folded node, this interplay can modify the number of small-amplitude oscillations after a large-amplitude oscillation. Finally, sufficient conditions are derived which determine when the noise increases the number of small-amplitude oscillations and when it decreases this number.

1 Introduction

Oscillation patterns with large variations in amplitude occur frequently in dynamical systems, differential equations and their applications. A class of particular interest are mixed-mode oscillations (MMOs) which are patterns consisting of alternating structures of small-amplitude and large-amplitude oscillations. Typical applications arise from chemical systems such as the Belousov–Zhabotinskii reaction [47], the peroxidase–oxidase reaction [25] and autocatalytic reactions [71] as well as from neuroscience, e.g. stellate cells [28], Hodgkin–Huxley-type neurons [73] and pituitary cells [80]. A remarkable number of models for these phenomena lead to differential equations with multiple timescales see e.g. [27, 40, 66, 84]. Frequently, it suffices to consider two timescales and study fast–slow ordinary differential equations (ODEs) which already provide many generic mechanisms leading to MMOs. For a detailed review of the topic we refer to the survey [26], the special issue [23], and references therein. The basic idea is that a local mechanism induces the small-amplitude oscillations (SAOs) while a global return mechanism leads to large-amplitude oscillations (LAOs). In this introduction, we shall just outline the main ideas; the precise development of our set-up and results starts in Sect. 2.

For a deterministic trajectory, we can symbolically write an MMO as a sequence

$$\begin{aligned} \cdots L_{j-1}^{s_{j-1}} L_j^{s_j} L_{j+1}^{s_{j+1}}\cdots \end{aligned}$$

(1.1)

where $L_{j}^{s_{j}}$ denotes $L_{j}$ LAOs followed by $s_{j}$ SAOs, etc. For example, a periodic solution alternating between $2$ SAOs and 1 LAO would be $\cdots 1^21^21^2\cdots$ or simply $1^2$ with the periodicity understood. A prototypical mechanism to generate SAOs are folded-node singularities [24] which are generic in three-dimensional ODEs with one fast and two slow variables [7, 77]. For the global return mechanism, one frequently encounters a relaxation-type structure induced by a cubic (or S-shaped) fast-variable nullcline, also called the critical manifold, which was studied extensively already in the context of van der Pol-type oscillators; see e.g. [20, 24, 35, 51] and the references therein. Non-degenerate folds, folded-node singularities and S-shaped critical manifolds form the basic deterministic building blocks for the work in this paper. However, let us mention already here that the stochastic techniques we develop in this paper could potentially be adapted to other cases such as singular Hopf bifurcation and folded saddle-nodes [38, 58], bursting oscillations [30, 48], tourbillon structures [26, 81], and other global return mechanisms [40, 61]. Although it is certainly of high interest to study all these cases, it seems to us that the combination of folded singularities and relaxation oscillations is a natural first step as both components are basic elements which occur in a large variety of different models [26].

While in some experiments, remarkably clear MMO patterns have been observed [42, 47], in many other cases the SAOs in the patterns appear noisy [28, 65]. Weak noise acting on a dynamical system is known to induce a variety of phenomena, ranging from small fluctuations around deterministic solutions to large excursions in phase space, as shown, e.g., in stochastic resonance [12, 34, 64] and transitions near tipping points [4, 60, 74]. In the context of oscillatory patterns, the effect of noise on MMO patterns in low-dimensional prototypical models has been studied, for instance, in [43, 52, 62, 69, 76, 87], using numerical simulations, bifurcation theory and asymptotic descriptions of the Fokker–Planck equation.

This work concerns the effect of noise on fast–slow differential equations with one fast and two slow variables, containing a folded-node singularity and an S-shaped critical manifold responsible for the global return mechanism. The resulting stochastic differential equations (SDEs) show a subtle interplay between noise, local and global dynamics, which requires a careful analysis of the behaviour of stochastic sample paths. Our approach builds upon our earlier work [17] which in turn was based upon a pathwise approach to fast–slow SDEs [14, 15].

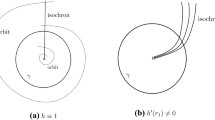
Our main focus is the derivation of estimates for the Poincaré (or return) map of the stochastic system, for a conveniently chosen two-dimensional section $\Sigma$. Deterministic return maps in the presence of folded-node singularities have been analyzed, e.g., in [37, 54]. Although the two-dimensional Poincaré map is invertible, the strong contraction near attracting critical manifolds implies that it is close to a one-dimensional, usually non-invertible map. Figure 1a shows an example of such a one-dimensional deterministic return map $z_n\mapsto z_{n+1}$. The apparent discontinuities are in fact points where the map’s graph displays very narrow dips, due to the presence of so-called canard orbits. Canards are particular solutions of the system staying close to both the attracting and repelling parts of the critical manifold [7, 10, 11], which separate the phase space into sectors of rotation characterized by different numbers of SAOs [24].

Fig. 1

$z$-Coordinate of the first-return map on the section $\Sigma _1$ for the Koper model (7.1). Parameter values are $k = -10$, $\lambda = -7.6$, $\epsilon _2=0.7$, $\epsilon _1=0.01$, with noise intensities a $\sigma =\sigma ^{\prime }=0$, b $\sigma =\sigma ^{\prime }=2\cdot 10^{-7}$, c $\sigma =\sigma ^{\prime }=2\cdot 10^{-5}$, and d $\sigma =\sigma ^{\prime }=2\cdot 10^{-3}$. The horizontal and vertical lines mark the location of canards

The concept of return maps has been extended to stochastic systems, see for instance [18, 44, 85]. This requires some care, because the rapid fluctuations of stochastic sample paths prevent one from using their very first return to $\Sigma$ to define the map. Instead, one has to consider the first return after a suitably defined, sufficiently large excursion in phase space has taken place. With these precautions, successive intersections $X_0, X_1, X_2, \dots$ of sample paths with $\Sigma$ define a continuous-space, discrete-time Markov chain. The distribution of $X_{n+1}$ is obtained from the distribution of $X_n$ via integration with respect to a transition kernel $K$. Under suitable regularity assumptions [6], the theory of harmonic measures ensures that the kernel $K$ admits a smooth density $k$, so that the evolution of $X_n$ is specified by an integral equation, namely

$$\begin{aligned} \mathbb {P}\bigl \{ X_{n+1}\in A \mid X_n = x \bigr \} = \int _A k(x,y) {{\mathrm{d}}}\!y =: K(x,A) \end{aligned}$$

(1.2)

holds for all Borel sets $A\subset \Sigma$; see for instance [16, Sects. 5.2 and 5.3]. The main aim of the present work is to provide estimates on the kernel $K$. Part of the mathematical challenge is due to the fact that the deterministic flow is not a gradient flow, and thus the stochastic system is irreversible.

Figure 1b–d shows simulated stochastic return maps for increasing noise intensity. For each value of $z_n$, the red points indicate the value of $z_{n+1}$ for $10$ different realizations of the noise. The deterministic return map is plotted in blue for comparison. Several interesting phenomena can be observed:

• 1. The size of fluctuations increases with the noise intensity;

• 2. Orbits in sectors with a small number of SAOs (inner sectors) are less affected by noise than those in sectors with a large number of SAOs (outer sectors);

• 3. There is a saturation effect, in the sense that for large enough SAO numbers, the typical value of the stochastic return map and its spreading become independent of the sector;

• 4. The saturation effect sets in earlier for larger noise intensities.

While the first phenomenon is not surprising, the other observed features are remarkable, and can lead to non-intuitive effects. In the example shown in Fig. 1, the deterministic map has a stable fixed point in the 11th sector, so that the deterministic system will display a stable MMO pattern $1^{11}$. For sufficiently strong noise, the stochastic system will asymptotically operate in the 12th sector, with occasional transitions to neighbouring sectors such as sectors 11 and 13. Hence, the noise shifts the global return to a higher rotation sector. However, two more noise-induced effects may also affect the number of observed SAOs. First, the noise may alter the number of SAOs for orbits starting in a given sector, by causing earlier escapes away from the critical manifold. Second, it may produce fluctuations large enough to mask small oscillations. All these effects must be quantified and compared to determine which oscillatory pattern we expect to observe.

The estimates on the kernel we provide in this work yield quantitative information on the above phenomena. In particular, we obtain estimates on the typical size of fluctuations as a function of noise intensity and sector number, and on the onset of the saturation phenomenon. These results complement those already obtained in [17] on the size of fluctuations near a folded-node singularity.

The structure of this article is the following: After introducing the deterministic set-up in Sect. 2, we provide first estimates on noise-induced fluctuations in Sect. 3. Sections 4 and 5 extend the analysis to a neighbourhood of the regular fold and of the folded node, respectively. Section 6 combines all the local estimates to provide quantitative results on the kernel. The main results are:

• Theorem 6.1 (Global return map) quantifies the effect of noise during the global return phase;

• Theorem 6.2 (Local map for inner sectors) provides estimates on noise-induced fluctuations for orbits starting near a folded node in sectors with small SAO number; together with Theorem 6.1 it yields bounds on the size of fluctuations of the Poincaré map in all inner sectors;

• Theorem 6.4 (Local map for outer sectors) gives similar estimates for orbits starting in sectors with a large SAO number; in particular, it proves the saturation effect.

A short discussion of the consequences of these results on the observed MMO patterns is given in Sect. 6.3. Finally, Sect. 7 illustrates these results with numerical simulations for the Koper model.

Fig. 2

A singularly perturbed Markov chain

The results obtained here are a first step towards the understanding of stochastic MMOs, that calls for further work. In particular, it would be desirable to obtain a more precise description of the possible MMO patterns. Let us mention two possible ways to achieve this:

• 1. Singularly perturbed Markov chains: Consider the ideal case where the sectors of rotation form a Markov partition, meaning that the image of each sector is entirely contained in a sector. Then the dynamics can be described by a topological Markov chain between sectors, see Fig. 2. Such a chain will in general not be irreducible, for instance, for the chain shown in Fig. 2, state 3 is an absorbing state. In the presence of noise, however, new transitions between sectors appear, typically yielding an irreducible chain. In this sense, the chain for the stochastic system is a singular perturbation of its deterministic limit. For weak, non-vanishing noise, transitions between all states may become possible, but transition times diverge as the noise intensity goes to zero. Methods allowing to determine transition rates in singularly perturbed Markov chains for small positive noise have been developed, for instance, in [5, 41, 75, 86].

• 2. Metastable transitions between periodic orbits: Consider a situation where the deterministic system admits several stable periodic orbits, each corresponding to an MMO pattern. Weak noise will induce rare transitions between these orbits. The theory of large deviations [33] provides a way to estimate the exponential asymptotics of transition rates (Arrhenius’ law [3]), via a variational problem. In the reversible case, Kramers’ law [31, 53] provides a more precise expression for transition rates, which are related to exponentially small eigenvalues of the diffusion’s infinitesimal generator, see for instance [21, 22], and [13] for a recent review. For irreversible systems, such precise expressions for transition rates are not available. However, the spectral-theoretic approach may still yield useful information, as in similar irreversible problems involving random Poincaré maps [16, 18].

Notations

We write $\left| \cdot \right|$ to denote the absolute value and $\left\| \cdot \right\|$ for the Euclidean norm. For $x\in \mathbb {R}$ we write $\lceil x\rceil$ for the smallest integer not less than $x$. Furthermore, for $a,b\in \mathbb {R}$ we use $a\wedge b:=\min \{a,b\}$ and $a\vee b:=\max \{a,b\}$. Regarding asymptotics, we use ${\mathcal {O}}(\cdot )$ in the usual way, i.e., we write $f(x)={\mathcal {O}}(g(x))$ as $x\rightarrow x^*$ if and only if $\limsup _{x\rightarrow x^*} \bigl |f(x)/g(x)\bigr | <\infty$. The shorthand $f(x)\asymp g(x)$ is used whenever $f(x)={\mathcal {O}}(g(x))$ and $g(x)={\mathcal {O}}(f(x))$ hold simultaneously. Furthermore, by $f(x)\ll g(x)$ we indicate that $\lim _{x\rightarrow x^*} \bigl |f(x)/g(x)\bigr | =0$. Vectors are assumed to be column vectors and $v^{{\mathrm {T}}}$ denotes the transpose of a vector $v$.

2 Mixed-Mode Oscillations: The Setup

In this section, we shall outline a typical setup for deterministic mixed-mode oscillations based upon three-dimensional fast–slow systems of the form

(2.1)

where $(x,y,z)\in \mathbb {R}^3$ and $0<\epsilon \ll 1$ is a small parameter. Throughout, we shall make the following assumption:

• (A0) The functions $f,g_1,g_2:\mathbb {R}^4\rightarrow \mathbb {R}$ are of class $C^3$.

In particular, (A0) implies that on a fixed compact set there exist uniform bounds on $f,g_1,g_2$. We remark that the system (2.1) is allowed to depend smoothly upon further system parameters $\mu \in \mathbb {R}^p$ although we do not indicate this dependence in the notation. The critical set of (2.1) is

$$\begin{aligned} C_0=\{(x,y,z)\in \mathbb {R}^3:f(x,y,z;0)=0\}. \end{aligned}$$

(2.2)

Motivated by several applications, such as the Hodgkin–Huxley model [45, 73], the Koper model [51, 59], the forced van der Pol equation [36, 79] and the Rössler model [72], we will assume that the geometric structure of the critical set is an S-shaped smooth manifold; see also Fig. 3. More precisely, this assumption can be stated as follows:

• (A1) Suppose $C_0$ is a smooth manifold composed of five smooth submanifolds,

  $$\begin{aligned} C_0=C^{a-}_0\cup L^-\cup C^{r}_0 \cup L^+ \cup C^{a+}_0, \end{aligned}$$

  (2.3)

  where the two-dimensional submanifolds $C^{a\pm }_0$ are normally hyperbolic attracting, while the two-dimensional submanifold $C^r_0$ is normally hyperbolic repelling, i.e.,

  $$\begin{aligned} \frac{\partial f}{\partial x}(p;0)<0\ \ \forall p\in C^{a\pm }_0 \quad \text {and}\quad \frac{\partial f}{\partial x}(p;0)>0\ \ \forall p\in C^{r}_0, \end{aligned}$$

  (2.4)

  and $L^\pm$ are one-dimensional smooth fold curves consisting of generic fold points

  $$\begin{aligned} f(p;0)&= 0, \quad \frac{\partial f}{\partial x}(p;0)=0, \quad \frac{\partial ^2 f}{\partial x^2}(p;0)\ne 0, \quad \begin{pmatrix} \partial _y f(p;0) \\ \partial _z f(p;0) \end{pmatrix} \ne \begin{pmatrix} 0\\ 0\\ \end{pmatrix} \nonumber \\&\forall p\in L^\pm . \end{aligned}$$

  (2.5)

  Without loss of generality we assume from now on that $\partial _y f(p;0)\ne 0$ for all $p\in L^\pm$.

Fenichel theory [32] shows that for $\epsilon >0$, the critical submanifolds $C^{a\pm }_0$ and $C^{r}_0$ perturb to invariant manifolds $C^{a\pm }_\epsilon$ and $C^{r}_\epsilon$, which are $\epsilon$-close to $C^{a\pm }_0$ and $C^{r}_0$ in points bounded away from the fold curves $L^\pm$.

Setting $\epsilon =0$ in (2.1) leads to the slow subsystem

$$\begin{aligned} 0&= f(x,y,z;0),\nonumber \\ \dot{y}&= g_1(x,y,z;0),\nonumber \\ \dot{z}&= g_2(x,y,z;0), \end{aligned}$$

(2.6)

which is solved by the so-called slow flow. Differentiating $f$ implicitly with respect to $s$ yields

$$\begin{aligned} \frac{\partial f}{\partial x}\dot{x} =-\frac{\partial f}{\partial y}\dot{y} -\frac{\partial f}{\partial z}\dot{z} =-\frac{\partial f}{\partial y}g_1- \frac{\partial f}{\partial z}g_2 \end{aligned}$$

(2.7)

for the slow flow, so that the slow subsystem (2.6) can be written as

$$\begin{aligned} \frac{\partial f}{\partial x}~\dot{x}&=-\frac{\partial f}{\partial y}g_1 -\frac{\partial f}{\partial z}g_{2},\nonumber \\ \dot{z}&= g_2, \end{aligned}$$

(2.8)

where it is understood that all functions are evaluated at points $(x,y,z;\epsilon )=(p;0)$ with $p\in C_0$. One may use that (2.8) can locally be written as a closed system by applying the implicit-function theorem to express $C_0$ as a graph, e.g. $y=h(x,z)$, near the fold as $\frac{\partial f}{\partial y}\ne 0$.

Observe that (2.8) is singular on the fold curves as $\frac{\partial f}{\partial x}=0$ on $L^\pm$. The desingularized slow subsystem is obtained by multiplying the right-hand side of (2.8) by $\frac{\partial f}{\partial x}$ and applying a rescaling of time. It reads

$$\begin{aligned} \dot{x}&= -\frac{\partial f}{\partial y}g_1-\frac{\partial f}{\partial z}g_2,\nonumber \\ \dot{z}&= \frac{\partial f}{\partial x}g_2. \end{aligned}$$

(2.9)

We make the following further assumptions:

• (A2) Suppose all fold points on $L^-$ satisfy the normal switching condition [67, 78]

  $$\begin{aligned} \begin{pmatrix} \frac{\partial f}{\partial y} (p;0) \\ \frac{\partial f}{\partial z} (p;0)\\ \end{pmatrix}\cdot \begin{pmatrix} g_1(p;0) \\ g_2(p;0)\\ \end{pmatrix}\ne 0 \qquad \forall p\in L^-. \end{aligned}$$

  (2.10)

  Furthermore, assume that the projections of $L^\pm$ along the $x$-coordinate onto $C^{a\mp }_0$, which are also called the drop curves, are transverse to the slow flow.

• (A3) Assume that the normal switching condition fails only at a unique singularity $p^*\in L^+$ and $p^*$ is a node equilibrium point of (2.9); in this case, $p^*$ is called a folded node (or folded-node singularity) [9, 77].

Let us stress that the above geometric assumptions (A1)–(A3), as well as several further assumptions to follow, provide a convenient framework but that the deterministic and stochastic techniques we present here apply to a much wider range of multiscale systems displaying oscillatory patterns.

On the fast timescale $t=s/\epsilon$ the limit $\epsilon \rightarrow 0$ of (2.1) leads to the fast subsystem

$$\begin{aligned} \tfrac{{{\mathrm{d}}}\!x}{{{\mathrm{d}}}\!t}&=x^{\prime } = f(x,y,z;0),\nonumber \\ \tfrac{{{\mathrm{d}}}\!y}{{{\mathrm{d}}}\!t}&=y^{\prime } = 0,\nonumber \\ \tfrac{{{\mathrm{d}}}\!z}{{{\mathrm{d}}}\!t}&=z^{\prime } = 0, \end{aligned}$$

(2.11)

which is solved by the fast flow. It is helpful to decompose the singular limit flows and their perturbations into several parts; see Fig. 3 for an illustration. In particular, we consider the sections of the form

$$\begin{aligned} \Sigma _i&:=\{(x,y,z)\in \mathbb {R}^3:x=x_i,y\in [y_{i,a},y_{i,b}],z\in [z_{i,a},z_{i,b}]\}, \qquad i\in \{2,5\},\nonumber \\ \Sigma _i&:=\{(x,y,z)\in \mathbb {R}^3:y=y_i,x\in [x_{i,a},x_{i,b}],z\in [z_{i,a},z_{i,b}]\}, \qquad i\in \{1,3,4,6\}, \end{aligned}$$

(2.12)

for $x_{i,a}<x_{i,b}$, $y_{i,a}<y_{i,b}$, $z_{i,a}<z_{i,b}$ suitably chosen to capture the return map. For an appropriate choice of the constants $x_i$ and $y_i$ (see below or consider the approach in [59]), there are well-defined maps from $\Sigma _i$ to $\Sigma _j$.

• (A4) The geometry of the flow-induced maps and sections is as shown in Fig. 3.

In particular, Assumption (A4) implies that there is an ${\mathcal {O}}(1)$ transition time on the slow timescale from $\Sigma _3$ to $\Sigma _4$ as well as from $\Sigma _6$ to $\Sigma _1$. (A4) incorporates that there is an ${\mathcal {O}}(1)$ spatial separation between each pair of fold/drop curves and it guarantees there is an ${\mathcal {O}}(1)$ transition time on the fast timescale from $\Sigma _2$ to $\Sigma _3$ as well as from $\Sigma _5$ to $\Sigma _6$. Furthermore, we exclude the case of a singular Hopf bifurcation [38, 39], where an equilibrium of the full system (2.1) may occur in the neighbourhood of a folded node.

There are four distinct important parts of the flow to analyze:

• (I) the flow near the folded node $\Sigma _1\rightarrow \Sigma _2$,

• (II) the fast segment $\Sigma _2\rightarrow \Sigma _3$,

• (III) the slow-flow region $\Sigma _{3}\rightarrow \Sigma _4$ near $C_\epsilon ^{a-}$, and

• (IV) the non-degenerate fold via $\Sigma _4\rightarrow \Sigma _5$.

The map $\Sigma _5\rightarrow \Sigma _6$ can be covered by the same techniques as $\Sigma _2\rightarrow \Sigma _3$, and $\Sigma _6\rightarrow \Sigma _1$ is similar to $\Sigma _3\rightarrow \Sigma _4$.

The geometry of flow maps and the possible generation mechanisms for mixed-mode oscillations under the assumptions (A0)–(A4) are well-known; see for example [24, 26]. A main idea is that twisting of the slow manifolds $C_{\epsilon }^{a+}$ and $C_\epsilon ^r$ near a folded node generates SAOs and the global return mechanism via the S-shaped critical manifold induces the LAOs. Fixed points of a full return map, say $\Sigma _1\rightarrow \Sigma _1$, correspond to MMOs with a certain pattern

$$\begin{aligned} \cdots L_{k}^{s_{k}} L_{k+1}^{s_{k+1}}\cdots L_{k+l}^{s_{k+l}} L_{k+1}^{s_{k+1}}\cdots \end{aligned}$$

(2.13)

The main question we address in this paper is how noise influences the patterns (2.13). We are going to split the analysis into two main parts. In Sect. 3 we provide basic estimates and consider the global part of the return map. Sections 4–5 address local dynamics in the regions near the regular fold and the folded node.

3 The Stochastic System

3.1 Estimating Stochastic Deviations

As a stochastic extension to (2.1) we consider the fast–slow SDE

$$\begin{aligned} {{\mathrm{d}}}\!x_s&= \frac{1}{\epsilon } f(x_s,y_s,z_s){{\mathrm{d}}}\!s + \frac{\sigma }{\sqrt{\epsilon }} F(x_s,y_s,z_s){{\mathrm{d}}}\!W_s, \nonumber \\ {{\mathrm{d}}}\!y_s&= g_1(x_s,y_s,z_s){{\mathrm{d}}}\!s + \sigma ^{\prime } G_1(x_s,y_s,z_s){{\mathrm{d}}}\!W_s,\nonumber \\ {{\mathrm{d}}}\!z_s&= g_2(x_s,y_s,z_s){{\mathrm{d}}}\!s + \sigma ^{\prime } G_2(x_s,y_s,z_s){{\mathrm{d}}}\!W_s, \end{aligned}$$

(3.1)

where $(W_s)_{s\geqslant 0}$ is a $k$-dimensional standard Brownian motion on a probability space $(\Omega ,\mathcal {F},\mathbb {P})$. The maps

$$\begin{aligned} F(x,y,z)\in \mathbb {R}^{1\times k}, \qquad G(x,y,z)= \begin{pmatrix} G_1(x,y,z) \\ G_2(x,y,z) \end{pmatrix} \in \mathbb {R}^{2\times k} \end{aligned}$$

(3.2)

may depend on $\epsilon$, and are assumed to be $C^1$ and to satisfy the usual bounded-growth condition guaranteing existence of a unique strong solution of (3.1). We shall adopt the shorthand notation to write just $(x,y,z)$ instead of $(x,y,z;\epsilon )$.

We will assume that the diffusion coefficients satisfy the following uniform ellipticity assumption:

• (A5) Let

  $$\begin{aligned} D(x,y,z) = \begin{pmatrix} FF^{{\mathrm {T}}} (x,y,z) &{}\quad FG^{{\mathrm {T}}} (x,y,z)\\ GF^{{\mathrm {T}}} (x,y,z)&{}\quad GG^{{\mathrm {T}}} (x,y,z) \end{pmatrix} \in \mathbb {R}^{3\times 3} \end{aligned}$$

  (3.3)

  be the diffusion matrix. There exist constants $c_+ \geqslant c_- > 0$ such that

  $$\begin{aligned} c_- \left\| \xi \right\| ^2 \leqslant \langle \xi , D(x,y,z)\xi \rangle \leqslant c_+ \left\| \xi \right\| ^2 \qquad \forall \xi \in \mathbb {R}^3\quad \forall (x,y,z)^{{\mathrm {T}}}\in \mathbb {R}^3. \end{aligned}$$

  (3.4)

Remark 3.1

In fact, most of our results remain valid under a weaker hypoellipticity assumption (cf. [6, p. 175]—this weaker condition is needed for the random Poincaré map to have a smooth density). The only result that requires the lower bound in (3.4) is Theorem 6.4, which relies on the early-escape result [17, Theorem 6.4]. See [46] for recent work under weaker assumptions.

Finally we make the following assumption on the noise intensities:

• (A6) Assume $0<\sigma =\sigma (\epsilon )\ll 1$ and $0<\sigma ^{\prime }=\sigma ^{\prime }(\epsilon )\ll 1$.

In fact, in the course of the analysis, we will encounter more restrictive conditions of the form $\sigma = {\mathcal {O}}(\epsilon ^\alpha )$, $\sigma ^{\prime } = {\mathcal {O}}(\epsilon ^\beta )$ with $\alpha , \beta >0$. The most stringent of these conditions will be needed for the analysis near the folded node, and requires $\sigma , \sigma ^{\prime } = {\mathcal {O}}(\epsilon ^{3/4})$.

The main goal is to establish bounds on the noise-induced deviation from a deterministic solution. In [15, Theorem 5.1.18], rather precise bounds for the deviation near normally hyperbolic critical manifolds are derived. We want to adapt these to the other phases of motion. As it turns out, the leading-order effect of noise occurs near the folded-node singularity. Therefore, it will be sufficient to determine the order of magnitude of noise-induced deviations during other phases of the dynamics, as a function of $\sigma , \sigma ^{\prime }$ and $\epsilon$.

We fix a deterministic reference solution $(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ and set

$$\begin{aligned} \xi _s=x_s-x^{\det }_s,\qquad \eta _s= \begin{pmatrix} y_s\\ z_s \end{pmatrix} - \begin{pmatrix} y^{\det }_s\\ z^{\det }_s \end{pmatrix}, \qquad \zeta _s= \begin{pmatrix} \xi _s\\ \eta _s \end{pmatrix}. \end{aligned}$$

(3.5)

As initial condition we choose $(\xi _0,\eta _0)=(0,0)$ as it corresponds to $(x^{\det }_0,y^{\det }_0,z^{\det }_0)$. Substituting in (3.1) and Taylor-expanding, we obtain a system of the form

$$\begin{aligned} {{\mathrm{d}}}\!\zeta _s = \frac{1}{\epsilon } {\mathcal {A}}(s)\zeta _s\, {{\mathrm{d}}}\!s + \begin{pmatrix} \frac{\sigma }{\sqrt{\epsilon }} {\mathcal {F}}(\zeta _s,s) \\ \sigma ^{\prime } {\mathcal {G}}(\zeta _s,s) \end{pmatrix} {{\mathrm{d}}}\!W_s + \begin{pmatrix} \frac{1}{\epsilon } b_\xi (\zeta _s,s) \\ b_\eta (\zeta _s,s) \end{pmatrix} {{\mathrm{d}}}\!s, \end{aligned}$$

(3.6)

where

$$\begin{aligned} {\mathcal {A}}(s)\in \mathbb {R}^{3\times 3}, \qquad {\mathcal {F}}(\zeta _s,s),\ b_\xi (\zeta _s,s)\in \mathbb {R}, \qquad {\mathcal {G}}(\zeta _s,s),\ b_\eta (\zeta _s,s)\in \mathbb {R}^2. \end{aligned}$$

(3.7)

The nonlinear terms $b_{\xi }$ and $b_{\eta }$ satisfy $b_\cdot (\zeta _s,s) = {\mathcal {O}}(\left\| \zeta \right\| ^2)$ as $\left\| \zeta \right\| \rightarrow 0$. The matrix ${\mathcal {A}}(s)$ of the system linearized around the deterministic solution has the structure

$$\begin{aligned} {\mathcal {A}}(s) = \begin{pmatrix} a(s) &{}\quad c_1(s) \\ \epsilon c_2(s) &{}\quad \epsilon B(s) \end{pmatrix}, \end{aligned}$$

(3.8)

where $a(s)=\frac{\partial f}{\partial x}(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ and so on, so that in particular $c_1(s)\in \mathbb {R}^{1\times 2}$, $c_2(s)\in \mathbb {R}^{2\times 1}$ and $B(s)\in \mathbb {R}^{2\times 2}$. Let

$$\begin{aligned} U(s,r) = \begin{pmatrix} U_{\xi \xi }(s,r) &{}\quad U_{\xi \eta }(s,r) \\ U_{\eta \xi }(s,r) &{}\quad U_{\eta \eta }(s,r) \end{pmatrix} \end{aligned}$$

(3.9)

denote the principal solution of the linear system $\epsilon \dot{\zeta }= {\mathcal {A}}(s)\zeta$. Then the solution of (3.6) can be written in the form

$$\begin{aligned} \xi _s&= \frac{\sigma }{\sqrt{\epsilon }} \int _0^s U_{\xi \xi }(s,r) {\mathcal {F}}(\zeta _r,r) {{\mathrm{d}}}\!W_r + \sigma ^{\prime } \int _0^s U_{\xi \eta }(s,r) {\mathcal {G}}(\zeta _r,r) {{\mathrm{d}}}\!W_r \nonumber \\&\quad + \frac{1}{\epsilon } \int _0^s U_{\xi \xi }(s,r) b_\xi (\zeta _r,r) {{\mathrm{d}}}\!r + \int _0^s U_{\xi \eta }(s,r) b_\eta (\zeta _r,r) {{\mathrm{d}}}\!r, \end{aligned}$$

(3.10)

and

$$\begin{aligned} \eta _s&= \frac{\sigma }{\sqrt{\epsilon }} \int _0^s U_{\eta \xi }(s,r) {\mathcal {F}}(\zeta _r,r) {{\mathrm{d}}}\!W_r + \sigma ^{\prime } \int _0^s U_{\eta \eta }(s,r) {\mathcal {G}}(\zeta _r,r) {{\mathrm{d}}}\!W_r \nonumber \\&\quad + \frac{1}{\epsilon } \int _0^s U_{\eta \xi }(s,r) b_\xi (\zeta _r,r) {{\mathrm{d}}}\!r + \int _0^s U_{\eta \eta }(s,r) b_\eta (\zeta _r,r) {{\mathrm{d}}}\!r. \end{aligned}$$

(3.11)

In both equations, we expect the stochastic integrals to give the leading contribution to the fluctuations. They can be estimated by the Bernstein-type inequality Lemma 8.2. The magnitude of the other integrals can then be shown to be smaller, using a direct estimate which is valid as long as the system does not exit from the region where the nonlinear terms are negligible; see e.g. [17, p. 4826] or [14, Theorem 2.4].

In order to carry out this program, we need estimates on the elements of the principal solution $U$. Note that the $\xi$-components are in principle larger than the $\eta$-components, but this is compensated by the fact that $x^{\det }_s$ spends most of the time in the vicinity of stable critical manifolds. The following ODEs will play an important rôle:

$$\begin{aligned} \epsilon \dot{p}_1&= c_1(s) + a(s) p_1 - \epsilon p_1 B(s) - \epsilon p_1 c_2(s) p_1, \nonumber \\ \epsilon \dot{p}_2&= c_2(s) - a(s) p_2 + \epsilon B(s) p_2 - \epsilon p_2 c_1(s) p_2. \end{aligned}$$

(3.12)

Here $p_1(s)\in \mathbb {R}^{1\times 2}$ and $p_2(s)\in \mathbb {R}^{2\times 1}$. If $a(s)$ is bounded away from 0, standard singular perturbation theory implies that these ODEs admit solutions $p_1(s)$ and $p_2(s)$ of order 1 (and in fact $p_1(s)$ close to $-a(s)^{-1}c_1(s)$). If $a(s)$ approaches 0 or changes sign, this need no longer be the case, but there may still be solutions such that $\epsilon |p_1(s) p_2(s)|$ remains small.

Lemma 3.2

Assume $s-r\leqslant {\mathcal {O}}(1)$ and that the ODEs (3.12) admit solutions such that $\epsilon |p_1(u) p_2(u)|$ is bounded for $u\in [r,s]$ by a function $\rho (\epsilon )$ satisfying $\lim _{\epsilon \rightarrow 0}\rho (\epsilon )=0$. Let $\alpha (s,r)=\int _r^s a(u){{\mathrm{d}}}\!u$. Then for sufficiently small $\epsilon$,

$$\begin{aligned} U_{\xi \xi }(s,r)&= \bigl [{{\mathrm{e}}}^{(\alpha (s,r)+{\mathcal {O}}(\epsilon ))/\epsilon } - \epsilon ~ p_1(s)Vp_2(r)\bigr ](1+{\mathcal {O}}(\rho )) , \nonumber \\ U_{\xi \eta }(s,r)&= \bigl [-{{\mathrm{e}}}^{(\alpha (s,r)+{\mathcal {O}}(\epsilon ))/\epsilon }p_1(r) + p_1(s)V\bigr ](1+{\mathcal {O}}(\rho )) , \nonumber \\ U_{\eta \xi }(s,r)&= \epsilon \bigl [{{\mathrm{e}}}^{(\alpha (s,r)+{\mathcal {O}}(\epsilon ))/\epsilon }p_2(s) -Vp_2(r)\bigr ](1+{\mathcal {O}}(\rho )) , \nonumber \\ U_{\eta \eta }(s,r)&= \bigl [V - \epsilon {{\mathrm{e}}}^{(\alpha (s,r)+{\mathcal {O}}(\epsilon ))/\epsilon } p_2(s)p_1(r)\bigr ](1+{\mathcal {O}}(\rho )) , \end{aligned}$$

(3.13)

where $V=V(s,r)$ is the principal solution of the system

$$\begin{aligned} \dot{\eta }= \left[ B(s)+c_2(s)p_1(s)\right] \eta . \end{aligned}$$

(3.14)

Proof

Consider the matrix

$$\begin{aligned} S(s) = \begin{pmatrix} 1 &{}\quad p_1(s) \\ \epsilon p_2(s) &{}\quad {1\!\!1} \end{pmatrix}. \end{aligned}$$

(3.15)

Then the equations (3.12) imply

$$\begin{aligned} \epsilon \dot{S} = {\mathcal {A}}S - S D \quad \text {with}\quad D(s)=\begin{pmatrix} d_1(s) &{}\quad 0\\ 0 &{}\quad \epsilon D_2(s) \end{pmatrix}, \end{aligned}$$

(3.16)

where the blocks $d_1(s)\in \mathbb {R}$ and $\epsilon D_2(s)\in \mathbb {R}^{2\times 2}$ are given by

$$\begin{aligned} d_1(s)&= a(s) + \epsilon c_1(s) p_2(s), \nonumber \\ \epsilon D_2(s)&= \epsilon B(s) + \epsilon c_2(s) p_1(s). \end{aligned}$$

(3.17)

Consider now the variable $\zeta _1=S(s)^{-1}\zeta$. If $\epsilon \dot{\zeta }={\mathcal {A}}(s)\zeta$, then (3.16) implies

$$\begin{aligned} \epsilon \dot{\zeta }_1 = D(s) \zeta _1. \end{aligned}$$

(3.18)

The principal solution of this equation is block-diagonal, with blocks ${{\mathrm{e}}}^{\frac{1}{\epsilon }\int _r^s d_1(u){{\mathrm{d}}}\!u}$ and $V(s,r)$, where $V$ is the principal solution of $\dot{\eta }=D_2(s)\eta$. The principal solution of the original equation is then given by

$$\begin{aligned} U(s,r) = S(s) \begin{pmatrix} {{\mathrm{e}}}^{\frac{1}{\epsilon }\int _r^s d_1(u){{\mathrm{d}}}\!u} &{}\quad 0 \\ 0 &{}\quad V(s,r) \end{pmatrix} S(r)^{-1}. \end{aligned}$$

(3.19)

Furthermore, we have

$$\begin{aligned} S(s)^{-1} = \begin{pmatrix} 1 &{}\quad -p_1(s) \\ -\epsilon p_2(s) &{}\quad {1\!\!1} \end{pmatrix} \begin{pmatrix} [1-\epsilon p_1(s)p_2(s)]^{-1} &{}\quad 0 \\ 0 &{}\quad [{1\!\!1} -\epsilon p_2(s)p_1(s)]^{-1} \end{pmatrix}. \end{aligned}$$

(3.20)

Computing the matrix product in (3.19) yields the result. Note that more precise expressions for the matrix elements can be obtained if needed. $\square$

To describe the size of fluctuations, for given $h,h_1>0$ we introduce stopping times

$$\begin{aligned} \tau _\xi&= \inf \bigl \{s>0 :|\xi _s|> h \bigr \}, \nonumber \\ \tau _\eta&= \inf \bigl \{s>0 :\left\| \eta _s\right\| > h_1 \bigr \}. \end{aligned}$$

(3.21)

Proposition 3.3

Suppose the assumptions of Lemma 3.2 are satisfied with $p_{1}$, $p_{2}$ bounded uniformly in $\epsilon$. Given a finite time horizon $T$ of order 1 on the slow timescale, there exist constants $\kappa , h_0>0$ such that whenever $h,h_1\leqslant h_0$, $h_1^2\leqslant h_0h$ and $h^2\leqslant h_0h_1$,

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\xi \wedge \tau _\eta < s \bigr \} \leqslant \biggl \lceil \frac{s}{\epsilon }\biggr \rceil \left( {{\mathrm{e}}}^{-\kappa h^2/\sigma ^2} + {{\mathrm{e}}}^{-\kappa h^2/(\sigma ^{\prime })^2} + {{\mathrm{e}}}^{-\kappa h_1^2/(\sigma ^{\prime })^2} + {{\mathrm{e}}}^{-\kappa h_1^2/(\epsilon \sigma ^2)}\right) \end{aligned}$$

(3.22)

holds for all $s\leqslant T$.

Proof

Denote by $\xi ^i_s$, $i=0,1,2,3$, the four terms on the right-hand side of (3.10). We will start by estimating $\xi ^{0}_{s}$ and $\xi ^{1}_{s}$. Since $p_{1}$, $p_{2}$ are assumed to be bounded, we may choose $\rho (\epsilon )$ of order $\epsilon$ in (3.13), and $U_{\eta \xi }$ is of order $\epsilon$, while the other elements of $U$ are of order 1 at most.

By Lemma 8.2 and the bounds on $U_{\xi \xi }$ and $U_{\xi \eta }$, there exists a constant $M>0$ such that

$$\begin{aligned} \mathbb {P}\biggl \{ \sup _{0\leqslant r\leqslant s} |\xi ^0_r| > h \biggr \} \leqslant \biggl \lceil \frac{s}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h^2/(M\sigma ^2)} \quad \text {and}\quad \mathbb {P}\biggl \{ \sup _{0\leqslant r\leqslant s} |\xi ^1_r| > h \biggr \} \leqslant \biggl \lceil \frac{s}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h^2/(M(\sigma ^{\prime })^2)}. \end{aligned}$$

(3.23)

Indeed, to estimate $\xi ^{0}_{s}$ we first use that on any short time interval $s\in [s_{1},s_{2}]$ with $|s_{2}-s_{1}|\leqslant \epsilon$, the stochastic process $\xi ^{0}_{s}= U_{\xi \xi }(s,s_{2})\mathcal {M}_{s}$ is close to the martingale $\mathcal {M}_{s}$, defined by

$$\begin{aligned} {\mathcal {M}}_{s} = \frac{\sigma }{\sqrt{\epsilon }} \int _{0}^{s} U_{\xi \xi }(s_{2},r){\mathcal {F}}(\zeta _r,r){{\mathrm{d}}}\!r, \end{aligned}$$

(3.24)

since $|U_{\xi \xi }(s,s_{2})|$ remains of order 1 on these time intervals. First using (3.13) and (A0) and then our choice of $\rho$ and Lemma 8.1, we see that the martingale’s variance is bounded by

$$\begin{aligned} \frac{\sigma ^{2}}{{\epsilon }}\int _0^s \left| U_{\xi \xi }(s_{2},r) ({\mathcal {F}}{\mathcal {F}}^{{\mathrm {T}}})(\zeta _r,r)U_{\xi \xi }^{{\mathrm {T}}}(s_{2},r)\right| {{\mathrm{d}}}\!r \leqslant \widetilde{M} \frac{\sigma ^2}{\epsilon } \int _0^s \left[ {{\mathrm{e}}}^{(2\alpha (s,r)+{\mathcal {O}}(\epsilon ))/\epsilon }+\rho ^{2} \left\| V\right\| ^{2}\right] {{\mathrm{d}}}\!r \end{aligned}$$

(3.25)

for some positive constant $\widetilde{M}$. Thus the variance is at most of order $\sigma ^{2}$ for all $s\in [s_{1}, s_{2}]$. Now the first inequality in (3.23) follows immediately from the Bernstein-type estimate Lemma 8.2. The prefactor in (3.23) simply counts the number of intervals $[s_{1},s_{2}]$ needed to cover $[0,s]$, see e.g. [15, Proposition 3.15] for a detailed proof in a simpler, one-dimensional setting. The second inequality in (3.23) is shown similarly.

Furthermore, we have $|\xi ^2_s|+|\xi ^3_s|\leqslant M^{\prime }(h^2+h_1^2)$ for a constant $M^{\prime }>0$ and $s\leqslant \tau _\xi \wedge \tau _\eta$. From this, together with Gronwall’s lemma, we deduce that there exists a constant $M>0$ such that

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\xi < s\wedge \tau _\eta \bigr \} \leqslant \biggl \lceil \frac{s}{\epsilon }\biggr \rceil \exp \biggl \{ - \frac{[h - M^{\prime }(h^2+h_1^2)]^2}{M\sigma ^2}\biggr \} + \biggl \lceil \frac{s}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h^2/(M(\sigma ^{\prime })^2)}. \end{aligned}$$

(3.26)

In a similar way, we find

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\eta < s\wedge \tau _\xi \bigr \} \leqslant \biggl \lceil \frac{s}{\epsilon }\biggr \rceil \exp \biggl \{ - \frac{[h_1 - M^{\prime }(h^2+h_1^2)]^2}{M(\sigma ^{\prime })^2}\biggr \} + \biggl \lceil \frac{s}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h_1^2/(M\epsilon \sigma ^2)}. \end{aligned}$$

(3.27)

Choosing $h_0$ small enough, we can ensure that the terms $M^{\prime }(h^2+h_1^2)$ are negligible, and the result follows by taking the sum of the last two estimates. $\square$

The size of typical fluctuations is given by the values of $h,h_1$ for which the probability (3.22) starts getting small, namely $h\gg \sigma \vee \sigma ^{\prime }$ and $h_1\gg \sigma ^{\prime }\vee \sigma \sqrt{\epsilon }$. We conclude that fluctuations have size $\sigma + \sigma ^{\prime }$ in the fast direction, and $\sigma ^{\prime }+\sigma \sqrt{\epsilon }$ in the slow direction. Note that for simplicity we ignore the logarithmic contribution arising from the prefactor $\lceil s/\epsilon \rceil$.

We now want to estimate the noise-induced spreading for the Poincaré map, starting on the section $\Sigma _2$ after the folded node, and arriving on the section $\Sigma _1$ before the folded node. As described in Sect. 2 we decompose the map into several maps, see Fig. 3, and estimate the spreading for each map separately. This means that we fix an initial condition on each section, and estimate the deviation of the stochastic sample paths from the deterministic solution when it first hits the next section.

Fig. 3

Sketch illustrating the definition of the different sections. The horizontal coordinate is $x$, the vertical one is $y$, and $z$ points out of the plane

3.2 The Fast Segments

The fast segments are given by $\Sigma _2 \rightarrow \Sigma _3$ and $\Sigma _5 \rightarrow \Sigma _6$. By Assumption (A4) there exists a slow time $T_{0}$ of order $\epsilon$ in which the deterministic solution starting on $\Sigma _2$ reaches a neighbourhood of order 1 of the stable critical manifold. In this neighbourhood, the linearization $a(s)=\frac{\partial f}{\partial x}(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ is negative and of order 1. To reach an $\epsilon$-neighbourhood of the critical manifold, an additional slow time $T_1$ of order $\epsilon |\log \epsilon |$ is required. By the drop-curve transversality assumption (A2) and using (A4), it takes another slow time $T_2$ of at most order 1 to reach the section $\Sigma _3$. For $T:=T_{0} +T_1+T_2$ we thus have

$$\begin{aligned} a(s) \leqslant {\left\{ \begin{array}{ll} a_1 &{} \text {for all s} \\ -a_2 &{} \text {for }c_1\epsilon \leqslant s \leqslant T \end{array}\right. } \end{aligned}$$

(3.28)

for some positive constants $a_1,a_2,c_1$. This implies that whenever $T\geqslant s>r\geqslant 0$,

$$\begin{aligned} \alpha (s,r) \leqslant c_2 \epsilon \end{aligned}$$

(3.29)

for a constant $c_2$, and furthermore $\alpha (s,r)$ is negative as soon as $s$ is larger than a constant times $\epsilon$.

Consider now the equations (3.12) for $p_1$ and $p_2$. We will show that $p_{1}$ remains bounded on $[0,T]$ and that there exists a particular solution $p_{2}$ which also remains bounded on $[0,T]$. For $p_1$, we proceed in two steps:

• For $0\leqslant s\leqslant c_1\epsilon$, $p_1(s)$ can grow at most by an amount of order 1.

• For $c_1\epsilon < s \leqslant T$, since $a(s)$ is negative, we can use standard singular perturbation theory to show that $p_1(s)$ remains of order 1, and in fact approaches $c_1(s)/|a(s)|$.

For $p_2(s)$, we change the direction of time and consider the equation

$$\begin{aligned} \dot{p}_2 = -c_2(T-s) + a(T-s) p_2 - \epsilon B(T-s) p_2 + \epsilon p_2 c_1(T-s) p_2. \end{aligned}$$

(3.30)

We know that $a(T-s)$ is negative, bounded away from 0, except for a time interval of length $c_1\epsilon$ near $T$. Thus we conclude that there exists a particular solution which remains bounded, of order 1, on the whole time interval. Therefore Lemma 3.2 shows that $U_{\xi \xi }$, $U_{\xi \eta }$ and $U_{\eta \eta }$ remain bounded (in norm), of order 1, and that $U_{\eta \xi }$ remains of order $\epsilon$ for $0\leqslant r<s\leqslant T$. As a consequence, we can apply Proposition 3.3 as is, with the result that on the section $\Sigma _3$,

• the spreading in the fast direction is of order $\sigma + \sigma ^{\prime }$,

• the spreading in the slow $z$-direction is of order $\sigma ^{\prime } + \sigma \sqrt{\epsilon }$.

3.3 The Slow Segments

The slow segments are given by $\Sigma _3\rightarrow \Sigma _4$ and $\Sigma _6\rightarrow \Sigma _1$. The analysis of the previous subsection can actually be extended to these segments, because $a(t)$ is always negative, bounded away from 0. The conclusions on typical spreading are the same:

• the spreading in the fast direction is of order $\sigma + \sigma ^{\prime }$,

• the spreading in the slow $z$-direction is of order $\sigma ^{\prime } + \sigma \sqrt{\epsilon }$.

Note that [15, Theorem 5.1.18] provides a more precise description of the dynamics, by constructing more precise covariance tubes. The qualitative conclusion on typical spreading is the same as above.

4 The Regular Fold

4.1 Approach

The regular fold corresponds to the transition $\Sigma _4\rightarrow \Sigma _5$. We again fix a deterministic solution, now starting on $\Sigma _4$. We choose the origin of the coordinate system on the regular fold $L^-$ and the origin of time in such a way that at time $s=0$, $(y^{\det }_0,z^{\det }_0)=(0,0)$.

Recall from the deterministic analysis (see e.g. [55, 68] for the two-dimensional and [67, 78] for the three-dimensional case) that, given $s_0<0$ of order 1,

• for $s_0 \leqslant s \leqslant -\epsilon ^{2/3}$, the distance of $x^{\det }_s$ to the critical manifold grows like $\epsilon /|s|^{1/2}$;

• there exists a $c_1>0$ such that $x^{\det }_s\asymp \epsilon ^{1/3}$ for $-\epsilon ^{2/3} \leqslant s \leqslant c_1\epsilon ^{2/3}$;

• there exists a $c_2>0$ such that $x^{\det }_s$ reaches order 1 before time $c_2\epsilon ^{2/3}$.

In this section, we consider the transition $\Sigma _4\rightarrow \Sigma ^{\prime }_4$, where $\Sigma ^{\prime }_4$ is a section on which $y=c_1\epsilon ^{2/3}$. In this region, the linearization $a(s)=\frac{\partial f}{\partial x}(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ satisfies

$$\begin{aligned} a(s) \asymp - (|s|^{1/2} + \epsilon ^{1/3}). \end{aligned}$$

(4.1)

Lemma 4.1

There are solutions of the equations (3.12) satisfying

$$\begin{aligned} {\left\| p_1(s)\right\| }, \left\| p_2(s)\right\| = {\mathcal {O}}\biggl ( \frac{1}{|a(s)|} \biggr ) = {\mathcal {O}}\biggl ( \frac{1}{|s|^{1/2} + \epsilon ^{1/3}} \biggr ) \qquad \text {for }s_0\leqslant s \leqslant c_1\epsilon ^{2/3}. \end{aligned}$$

(4.2)

Proof

For $p_1(s)$, we first consider the equation $\epsilon \dot{p}_1 = a(s)p_1+c_1(s)$, whose solution we know behaves as above, see Lemma 8.1 (or [15, pp. 87–88]). Regular perturbation theory allows us to extend the estimate to the full equation for $p_1$. In the case of $p_2$, we change the direction of time, and thus consider an equation similar to the equation for $p_1$ on an interval $[-c_1\epsilon ^{2/3},-s_0]$. The above bound can be obtained, e.g., by scaling space by $\epsilon ^{1/3}$ and time by $\epsilon ^{2/3}$ on $[-c_1\epsilon ^{2/3},\epsilon ^{2/3}]$, and using integration by parts on the remaining time interval.   $\square$

Corollary 4.2

For all $s_0\leqslant r\leqslant s\leqslant c_1\epsilon ^{2/3}$, the principal solution $U(s,r)$ satisfies

$$\begin{aligned} |U_{\xi \xi }(s,r)|&= {\mathcal {O}}\biggl ( {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } +\frac{\epsilon }{(|s|^{1/2}+\epsilon ^{1/3})(|r|^{1/2}+\epsilon ^{1/3})}\biggr ),\end{aligned}$$

(4.3)

$$\begin{aligned} \left\| U_{\xi \eta }(s,r)\right\|&= {\mathcal {O}}\biggl ( \frac{{{\mathrm{e}}}^{\alpha (s,r)/\epsilon }}{|r|^{1/2}+\epsilon ^{1/3}} + \frac{1}{|s|^{1/2}+\epsilon ^{1/3}}\biggr ),\end{aligned}$$

(4.4)

$$\begin{aligned} \left\| U_{\eta \xi }(s,r)\right\|&= {\mathcal {O}}\biggl ( \epsilon \biggl [ \frac{{{\mathrm{e}}}^{\alpha (s,r)/\epsilon }}{|s|^{1/2}+\epsilon ^{1/3}} + \frac{1}{|r|^{1/2}+\epsilon ^{1/3}}\biggr ]\biggr ), \end{aligned}$$

(4.5)

$$\begin{aligned} \left\| U_{\eta \eta }(s,r)\right\|&= {\mathcal {O}}(1). \end{aligned}$$

(4.6)

Proof

We can apply Lemma 3.2, since $\epsilon |p_1(s)p_2(s)|={\mathcal {O}}(\epsilon ^{1/3})$. Recall that the matrix $V$ occurring in (3.13) is the principal solution of $\dot{\eta } = D_2(s)\eta$, where

$$\begin{aligned} D_2(s) = B(s) + c_2(s)p_1(s) = {\mathcal {O}}(|a(s)|^{-1}). \end{aligned}$$

(4.7)

It follows that

$$\begin{aligned} \frac{\hbox {d}}{{{\mathrm{d}}}\!s} \left\| \eta _s\right\| ^2 = 2(\eta _1\dot{\eta }_1 + \eta _2\dot{\eta }_2) \leqslant \frac{M}{|a(s)|}\left\| \eta _s\right\| ^2 \end{aligned}$$

(4.8)

for some constant $M>0$, so that Gronwall’s Lemma implies

$$\begin{aligned} \left\| \eta _s\right\| ^2 \leqslant \left\| \eta _{s_0}\right\| ^2 \exp \biggl \{ \int _{s_0}^s \frac{M}{|a(u)|}{{\mathrm{d}}}\!u\biggr \}. \end{aligned}$$

(4.9)

A direct computation using (4.1) shows that for $s\leqslant c_{1}\epsilon ^{2/3}$ the integral has order 1, and thus the principal solution $V$ has order 1 as well. Then the result follows from Lemma 3.2. $\square$

Proposition 4.3

There exist constants $\kappa , h_0>0$ such that whenever $h\leqslant h_0\epsilon ^{1/3}$, $h_1\leqslant h_0$, $h^2\leqslant h_0h_1$ and $h_1^2\leqslant h_0h\epsilon ^{1/3}$,

$$\begin{aligned}&\mathbb {P}\bigl \{\tau _\xi \wedge \tau _\eta < c_1\epsilon ^{2/3} \bigr \} \nonumber \\&\quad \leqslant \biggl \lceil \frac{1}{\epsilon }\biggr \rceil \left( {{\mathrm{e}}}^{-\kappa h^2/(\sigma ^2\epsilon ^{-1/3})} + {{\mathrm{e}}}^{-\kappa h^2/((\sigma ^{\prime })^2\epsilon ^{-2/3})} + {{\mathrm{e}}}^{-\kappa h_1^2/(\sigma ^{\prime })^2} + {{\mathrm{e}}}^{-\kappa h_1^2/(\epsilon |\log \epsilon |\sigma ^2)}\right) . \end{aligned}$$

(4.10)

Proof

Estimate (4.3) and Lemma 8.1 imply

$$\begin{aligned} \frac{1}{\epsilon }\int _{s_0}^s U_{\xi \xi }(s,r)^2 {{\mathrm{d}}}\!r ={\mathcal {O}}\biggl ( \frac{1}{|s|^{1/2} + \epsilon ^{1/3}}\biggr ) \leqslant {\mathcal {O}}\left( \epsilon ^{-1/3}\right) \end{aligned}$$

(4.11)

for $s_0+{\mathcal {O}}(1)\leqslant s\leqslant c_1\epsilon ^{2/3}$. Indeed, the term ${{\mathrm{e}}}^{\alpha (s,r)/\epsilon }$ yields a contribution of this order, while the second term in (4.3) gives a contribution of order $\epsilon |\log \epsilon |/(|s|^{1/2} + \epsilon ^{1/3})$, which is smaller. Next, we estimate

$$\begin{aligned} \int _{s_0}^s \left\| U_{\xi \eta }(s,r)\right\| ^2 {{\mathrm{d}}}\!r ={\mathcal {O}}\biggl (\frac{1}{|s| + \epsilon ^{2/3}}\biggr ) \leqslant {\mathcal {O}}\left( \epsilon ^{-2/3}\right) , \end{aligned}$$

(4.12)

where the main contribution now comes from the second term in (4.4). We also obtain

$$\begin{aligned} \frac{1}{\epsilon }\int _{s_0}^s \left\| U_{\eta \xi }(s,r)\right\| ^2 {{\mathrm{d}}}\!r ={\mathcal {O}}\bigl ( \epsilon |\log \epsilon |\bigr ), \end{aligned}$$

(4.13)

where the main contribution comes from the second term in (4.5). Finally

$$\begin{aligned} \int _{s_0}^s \left\| U_{\eta \eta }(s,r)\right\| ^2 {{\mathrm{d}}}\!r = {\mathcal {O}}(1). \end{aligned}$$

(4.14)

Similarly, we obtain the estimates

$$\begin{aligned} \frac{1}{\epsilon }\int _{s_0}^s |U_{\xi \xi }(s,r)| {{\mathrm{d}}}\!r&={\mathcal {O}}\biggl ( \frac{1}{|s|^{1/2} + \epsilon ^{1/3}}\biggr ),\nonumber \\ \int _{s_0}^s \left\| U_{\xi \eta }(s,r)\right\| {{\mathrm{d}}}\!r&={\mathcal {O}}\biggl ( \frac{1}{|s|^{1/2} + \epsilon ^{1/3}}\biggr ),\nonumber \\ \frac{1}{\epsilon }\int _{s_0}^s \left\| U_{\eta \xi }(s,r)\right\| {{\mathrm{d}}}\!r&={\mathcal {O}}(1), \nonumber \\ \int _{s_0}^s \left\| U_{\eta \eta }(s,r)\right\| {{\mathrm{d}}}\!r&= {\mathcal {O}}(1). \end{aligned}$$

(4.15)

We can now adapt the proof of Proposition 3.3 to the present situation. Recall the definitions of $\tau _\xi , \tau _\eta$ from (3.21). We denote again by $\xi ^i_s$, $i=0,1,2,3$, the four terms on the right-hand side of (3.10). Let $T=c_1\epsilon ^{2/3}$. The Bernstein-type estimate Lemma 8.2 and (4.11) yield

$$\begin{aligned} \mathbb {P}\biggl \{ \sup _{s_0\leqslant r\leqslant T} |\xi ^0_r| > h \biggr \} \leqslant \biggl \lceil \frac{1}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h^2/(M\sigma ^2\epsilon ^{-1/3})}, \end{aligned}$$

(4.16)

and similarly

$$\begin{aligned} \mathbb {P}\biggl \{ \sup _{s_0\leqslant r\leqslant T} |\xi ^1_r| > h \biggr \} \leqslant \biggl \lceil \frac{1}{\epsilon }\biggr \rceil {{\mathrm{e}}}^{-h^2/(M(\sigma ^{\prime })^2\epsilon ^{-2/3})}. \end{aligned}$$

(4.17)

Furthermore, using (4.15) we obtain $|\xi ^2_s|+|\xi ^3_s|\leqslant M^{\prime }\epsilon ^{-1/3}(h^2+h_1^2)$ for $s\leqslant \tau _\xi \wedge \tau _\eta$. From this we can deduce

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\xi < T\wedge \tau _\eta \bigr \} \leqslant \biggl \lceil \frac{1}{\epsilon }\biggr \rceil \biggl ( \exp \biggl \{ - \frac{[h - M^{\prime }\epsilon ^{-1/3}(h^2+h_1^2)]^2}{M\sigma ^2\epsilon ^{-1/3}}\biggr \} + {{\mathrm{e}}}^{-h^2/(M(\sigma ^{\prime })^2\epsilon ^{-2/3})} \biggr ).\quad \end{aligned}$$

(4.18)

In a similar way, we get

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\eta < T\wedge \tau _\xi \bigr \} \leqslant \biggl \lceil \frac{1}{\epsilon }\biggr \rceil \biggl ( \exp \biggl \{ - \frac{[h_1 - M^{\prime }(h^2+h_1^2)]^2}{M\sigma ^2\epsilon |\log \epsilon |}\biggr \} + {{\mathrm{e}}}^{-h_1^2/(M(\sigma ^{\prime })^2)} \biggr ). \end{aligned}$$

(4.19)

This concludes the proof. $\square$

The condition $h_1^2\leqslant h_0h\epsilon ^{1/3}$ together with $h\leqslant h_{0}\epsilon ^{1/3}$ imposes that we can take $h_1$ at most of order $\epsilon ^{1/3}$. For the typical spreadings, we obtain

• in the fast direction:

  $$\begin{aligned} \frac{\sigma }{\epsilon ^{1/6}} + \frac{\sigma ^{\prime }}{\epsilon ^{1/3}}, \end{aligned}$$

  (4.20)

• in the slow direction:

  $$\begin{aligned} \sigma ^{\prime } + \sigma \sqrt{\epsilon |\log \epsilon |}. \end{aligned}$$

  (4.21)

For the bound (4.10) to be useful, we need the spreading in the fast direction to be small compared to $\epsilon ^{1/3}$, because of the condition on $h$. This yields the conditions

$$\begin{aligned} \sigma \ll \epsilon ^{1/2}, \qquad \sigma ^{\prime } \ll \epsilon ^{2/3}. \end{aligned}$$

(4.22)

The term $\sigma /\epsilon ^{1/6}$ of the $x$-spreading and the condition $\sigma \ll \epsilon ^{1/2}$ are expected, because they already occur when there is no noise acting on the slow variables (see [15, Sect. 3.3]). The term $\sigma ^{\prime }/\epsilon ^{1/3}$ and the condition $\sigma ^{\prime } \ll \epsilon ^{2/3}$ are due to the coupling with the slow variables.

Remark 4.4

By using sharper estimates on the size of the linear terms $\xi ^0_r$ and $\xi ^1_r$ (cf. Remark 8.3), one can in fact show that the typical spreading in the $x$-direction grows like

$$\begin{aligned} \frac{\sigma }{|s|^{1/4}+\epsilon ^{1/6}} + \frac{\sigma ^{\prime }}{|s|^{1/2}+\epsilon ^{1/3}}. \end{aligned}$$

(4.23)

4.2 Normal Form

Before analysing the behaviour during the jump, we make a preliminary transformation to normal form near the fold. Recall that $t=s/\epsilon$ denotes the fast timescale.

Proposition 4.5

Near a regular fold on $L^-$ satisfying the assumptions (A1)–(A2) there exists a smooth change of coordinates such that (3.1) is locally given by

$$\begin{aligned} {{\mathrm{d}}}\!x_t&= \bigl [y_t+x_t^2+{\mathcal {O}}(z_t,{\left\| (x_t,y_t)^{{\mathrm {T}}}\right\| }^3\!,\epsilon ,\sigma ^2)\bigr ]{{\mathrm{d}}}\!t +\sigma \widehat{F}_1(x_t,y_t,z_t) {{\mathrm{d}}}\!W_t \nonumber \\&+\, \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{F}_2(x_t,y_t,z_t) {{\mathrm{d}}}\!W_t,\nonumber \\ {{\mathrm{d}}}\!y_t&= \epsilon \hat{g}_1(x_t,y_t,z_t;\epsilon ,\sigma ^{\prime }){{\mathrm{d}}}\!t + \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{G}_1(x_t,y_t,z_t) {{\mathrm{d}}}\!W_t,\nonumber \\ {{\mathrm{d}}}\!z_t&= \epsilon \hat{g}_2(x_t,y_t,z_t;\epsilon ){{\mathrm{d}}}\!t + \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{G}_2(x_t,y_t,z_t){{\mathrm{d}}}\!W_t, \end{aligned}$$

(4.24)

where $\hat{g}_1 = g_1 + {\mathcal {O}}((\sigma ^{\prime })^2)$ and

$$\begin{aligned} \hat{g}_1(0,0,0;0,0) = 1, \qquad \hat{g}_2(0,0,0;0) = 0. \end{aligned}$$

(4.25)

Proof

The result is a stochastic analogue of the transformation result for deterministic systems. We extend the proof presented by Szmolyan and Wechselberger in [78, pp. 73–74] and [82, pp. 8–10] to the stochastic case.

First, we may use a translation of coordinates so that the neighbourhood of $L^-$ is chosen with center $(0,0,0)\in L^-$. From the normal switching condition Assumption (A2) we may assume without loss of generality that $g_1(0,0,0;0)\ne 0$; indeed, if $g_1(0,0,0;0)=0$ then $g_2(0,0,0;0)\ne 0$ and we may exchange the names of the two slow variables. Next, define a coordinate change

$$\begin{aligned} z=:\bar{z}+\gamma y \quad \text {with}\quad \gamma =\frac{g_2(0,0,0;0)}{g_1(0,0,0;0)}\not =0. \end{aligned}$$

(4.26)

This yields

$$\begin{aligned} {{\mathrm{d}}}\!\bar{z}_t = {{\mathrm{d}}}\!z_t-\gamma {{\mathrm{d}}}\!y_t =&\ \epsilon \bigl [g_2(x,y,\bar{z}+\gamma y;\epsilon )-\gamma g_1(x,y,\bar{z}+\gamma y;\epsilon )\bigr ]{{\mathrm{d}}}\!t\nonumber \\&+\,\sigma ^{\prime }\sqrt{\epsilon }\bigl [G_1(x,y,\bar{z}+\gamma y;\epsilon )-\gamma G_2(x,y,\bar{z}+\gamma y;\epsilon )\bigr ]{{\mathrm{d}}}\!W_t. \end{aligned}$$

(4.27)

Introducing new maps $\bar{g}_2=g_2-\gamma g_1$ and $\bar{G}_2=G_1-\gamma G_2$ and then dropping all the overbars from the notation yields a stochastic fast–slow system of the form (3.1) which now satisfies

$$\begin{aligned} g_1(0,0,0;0)\ne 0\qquad \text {and}\qquad g_2(0,0,0;0)=0. \end{aligned}$$

(4.28)

The next step is to rectify the fold curve. By the implicit-function theorem there exists a parametrization of $L^-$ by $(\xi (z),\eta (z),z)$ for $z\in {\mathcal {I}}\subset \mathbb {R}$ where ${\mathcal {I}}$ is a suitable interval. The transformation

$$\begin{aligned} (x,y,z)=(\bar{x}+\xi (z),\bar{y}+\eta (z),\bar{z}) \end{aligned}$$

(4.29)

rectifies the fold curve in new coordinates $(\bar{x},\bar{y},\bar{z})$, in the sense that $\bar{f}(0,0,\bar{z})=0$. Itô’s formula shows

$$\begin{aligned} {{\mathrm{d}}}\!\bar{x}_t&= \bigl [\bar{f}(\bar{x}_t,\bar{y}_t,\bar{z}_t)+ {\mathcal {O}}(\epsilon (\sigma ^{\prime })^2)\bigr ]{{\mathrm{d}}}\!t +\bigl [\sigma \bar{F}(\bar{x}_t,\bar{y}_t,\bar{z}_t)- \sigma ^{\prime }\sqrt{\epsilon }(\partial _z\xi ) \bar{G}_2(\bar{x}_t,\bar{y}_t,\bar{z}_t)\bigr ]{{\mathrm{d}}}\!W_t \nonumber \\ {{\mathrm{d}}}\!\bar{y}_t&= \bigl [\epsilon \bar{g}_1(\bar{x}_t,\bar{y}_t,\bar{z}_t)+ {\mathcal {O}}(\epsilon (\sigma ^{\prime })^2)\bigr ]{{\mathrm{d}}}\!t +\sigma ^{\prime }\sqrt{\epsilon }\bigl [\bar{G}_1(\bar{x}_t,\bar{y}_t,\bar{z}_t) -(\partial _z\eta )\bar{G}_2 (\bar{x}_t,\bar{y}_t,\bar{z}_t)\bigr ]{{\mathrm{d}}}\!W_t, \end{aligned}$$

(4.30)

where $\bar{f}(\bar{x},\bar{y},\bar{z}) = a\bar{y} + b\bar{x}^2 + c\bar{x}\bar{y} + d\bar{y}^2 + {\mathcal {O}}(z,\left\| (\bar{x},\bar{y})^{{\mathrm {T}}}\right\| ^3)$. By a scaling of $\bar{x}, \bar{y}$ and time, we can achieve that $a=b=1$ and $\bar{g}_1(0,0,0)=1$.

The final step is a normal-form transformation $\hat{x}=\bar{x}-\frac{1}{2} c\bar{x}^2 - d\bar{x}\bar{y}$, which eliminates the terms of order $\bar{x}\bar{y}$ and $\bar{y}^2$ in the drift term of ${{\mathrm{d}}}\!\bar{x}_t$. Applying again Itôs formula yields the result. $\square$

Remark 4.6

It is possible to further simplify the drift term, in such a way that for $\epsilon =0$ and $\sigma =0=\sigma ^{\prime }$, $g_1(x,y,z)=g(z)+g_{11}(x,y,z)$ where $g_{11}(0,0,z)=0$ and $g_2(0,0,z)=0$, see [82, pp. 9–10] and [78, p. 73]. However, this introduces a diffusion term of order $\sigma$ in ${{\mathrm{d}}}\!y_t$, which we want to avoid.

4.3 Neighbourhood and Escape

We determine now the size of fluctuations during the “jump phase” of sample paths starting on $\Sigma ^{\prime }_4$, until they hit the section $\Sigma _5$ which is located at a distance of order 1 in the $x$-direction from the fold.

Before giving a rigorous estimate, we briefly recall some well-known deterministic asymptotics as they are going to motivate several choices in the analysis of the stochastic dynamics.

The lowest-order approximation for the deterministic dynamics near the planar fold is

$$\begin{aligned} \epsilon \frac{{{\mathrm{d}}}\!x}{{{\mathrm{d}}}\!y} = y + x^2, \end{aligned}$$

(4.31)

which is just the classical Ricatti equation; see [68, pp. 68–72] or [57, p. 100]. Setting $y=\epsilon ^{2/3}\theta$ and $x=\epsilon ^{1/3}\tilde{x}$ removes $\epsilon$ and yields

$$\begin{aligned} \frac{{{\mathrm{d}}}\!\tilde{x}}{{{\mathrm{d}}}\!\theta } = \theta + \tilde{x}^2 \end{aligned}$$

(4.32)

as the system of first approximation [2, p. 175] which also appears as the key asymptotic problem in the blow-up analysis [55, p. 293] of the non-degenerate fold. It is known [68, pp. 68–72] that there exists an orbit $\theta (\tilde{x})$ of (4.32) with

$$\begin{aligned} \theta (\tilde{x})&= -\tilde{x}^2-\frac{1}{2\tilde{x}}+{\mathcal {O}}\left( \frac{1}{\tilde{x}^4}\right) \qquad \text {as }x\rightarrow -\infty ,\end{aligned}$$

(4.33)

$$\begin{aligned} \theta (\tilde{x})&= \theta ^*-\frac{1}{\tilde{x}}+{\mathcal {O}}\left( \frac{1}{\tilde{x}^3}\right) \qquad \text {as }x\rightarrow \infty , \end{aligned}$$

(4.34)

which is the extension of the attracting slow manifold through the fold region; the constant $\theta ^*$ is the horizontal asymptote which can be expressed as the zero of suitable Bessel functions. However, if we look at the variational equation of (4.32) around $\theta (\tilde{x})$ to leading order it follows that

$$\begin{aligned} \frac{{{\mathrm{d}}}\!\xi }{{{\mathrm{d}}}\!\theta }=2\,\frac{1}{\theta ^*-\theta }\xi ,\qquad \text {as } \tilde{x}\rightarrow \infty \ \text {(or }\theta \rightarrow \theta ^*). \end{aligned}$$

(4.35)

The solution is given by

$$\begin{aligned} \xi (\theta )\cong \frac{1}{(\theta ^*-\theta )^2}\xi (\theta _0). \end{aligned}$$

(4.36)

This growth of the linearization in the fast direction turns out to be too fast to apply directly the same method to control stochastic sample paths as in the previous cases. However, we do not need such a precise control of fluctuations in the fast direction. It is sufficient to show that sample paths are likely to stay in a tube around the deterministic solution, with some specific extension in the slow directions $y$ and $z$. To do so, we will compare the random process with different deterministic solutions on successive time intervals $[\theta _n,\theta _{n+1}]$ during which fluctuations in the fast direction remain bounded (cf. Fig. 4). The expression (4.36) shows that a possible choice are geometrically accumulating $\theta _n$ of the form $\theta _n = \theta ^* - 2^{-n}$. During the interval $[\theta _n,\theta _{n+1}]$, the deterministic solution $x(\theta )$ moves by a distance of order $\epsilon ^{1/3}(2^{n+1}-2^n)=\epsilon ^{1/3}2^n$. For $x(\theta )$ to reach order 1, we need to choose $n$ of order $|\log \epsilon |$.

Fig. 4

Geometry of sections near the regular fold

To make the last idea rigorous, we write the system (4.24) on the timescale $\theta =\epsilon ^{1/3}t=\epsilon ^{-2/3}s$ as

$$\begin{aligned} {{\mathrm{d}}}\!x_\theta&= \frac{1}{\epsilon ^{1/3}} \hat{f}(x_\theta ,y_\theta ,z_\theta ){{\mathrm{d}}}\!\theta + \frac{\sigma }{\epsilon ^{1/6}} \widehat{F}_1(x_\theta ,y_\theta ,z_\theta ) {{\mathrm{d}}}\!W_\theta + \sigma ^{\prime }\epsilon ^{1/3} \widehat{F}_2(x_\theta ,y_\theta ,z_\theta ) {{\mathrm{d}}}\!W_\theta ,\nonumber \\ {{\mathrm{d}}}\!y_\theta&= \epsilon ^{2/3} \hat{g}_1(x_\theta ,y_\theta ,z_\theta ;\epsilon ,\sigma ^{\prime }){{\mathrm{d}}}\!\theta + \sigma ^{\prime }\epsilon ^{1/3} \widehat{G}_1(x_\theta ,y_\theta ,z_\theta ) {{\mathrm{d}}}\!W_\theta ,\nonumber \\ {{\mathrm{d}}}\!z_\theta&= \epsilon ^{2/3} \hat{g}_2(x_\theta ,y_\theta ,z_\theta ;\epsilon ){{\mathrm{d}}}\!\theta + \sigma ^{\prime }\epsilon ^{1/3} \widehat{G}_2(x_\theta ,y_\theta ,z_\theta ){{\mathrm{d}}}\!W_\theta , \end{aligned}$$

(4.37)

where $\hat{f}(x,y,z) = y+x^2+{\mathcal {O}}(z,\left\| (x,y)^{{\mathrm {T}}}\right\| ^3\!,\epsilon ,\sigma ^2)$. Given $\delta >0$ of order 1, there exists a $\delta _0$ of order 1 such that by restricting the analysis to a cube of size $\delta _0$, we may assume that $|\hat{g}_1-1| < \delta$ and $|\hat{g}_2| < \delta$.

For convenience, we set $\Sigma ^*_0 = \{(x_0,y_0,z_0)\} \subset \Sigma ^{\prime }_4$, where we recall that the initial condition satisfies $x_0\asymp -\epsilon ^{1/3}$, $y_0=c_1\epsilon ^{2/3}$ for some $c_{1}>0$, and that we may assume $|z_0|\ll \epsilon ^{2/3}$. For $n\geqslant 1$ and $\epsilon >0$ such that $\epsilon ^{1/3}2^n<\delta _0$, we introduce sets

$$\begin{aligned} \Sigma ^*_n = \left\{ (x,y,z) :x=\epsilon ^{1/3}2^n, (y,z)\in D_n \right\} , \end{aligned}$$

(4.38)

see Fig. 4. The sets $D_n$ are defined inductively as follows:

$$\begin{aligned} D_1=(y_1-c_2\epsilon ^{2/3},y_1+c_2\epsilon ^{2/3}) \times (-c_2\epsilon ^{2/3},c_2\epsilon ^{2/3}), \end{aligned}$$

(4.39)

where $y_1$ is such that $(2\epsilon ^{1/3},y_1,z_1)$ belongs to the deterministic orbit starting in $(x_0,y_0,z_0)$, and $c_2<c_1$ is a sufficiently small constant. Given $D_{n}$, the next set $D_{n+1}$ is chosen as the $c_2\epsilon ^{2/3}2^{-n/2}$-neighbourhood of the image of $D_n$ under the deterministic Poincaré map from $\Sigma ^*_n$ to $\Sigma ^*_{n+1}$. It is not difficult to show that for sufficiently small $\delta$ and $c_2$, the time needed for the deterministic flow to go from $\Sigma ^*_n$ to $\Sigma ^*_{n+1}$ is of order $\theta ={\mathcal {O}}(2^{-n})$. During this time, $y$ and $z$ vary by ${\mathcal {O}}(\epsilon ^{2/3}2^{-n})$ at most, and thus

$$\begin{aligned} {{\mathrm{diam}}}(D_{n+1}) \leqslant {{\mathrm{diam}}}(D_n) + {\mathcal {O}}(\epsilon ^{2/3}2^{-n/2}). \end{aligned}$$

(4.40)

The geometric decay in $2^{-n/2}$ shows that the diameter of the $D_n$ has a uniform bound of order $\epsilon ^{2/3}$. In fact, by taking $\delta$ small, we can make the extension of $D_n$ in the $z$-direction small.

We return to the stochastic system (4.37). Fix $n$. For an initial condition $(x_n,y_n,z_n)\in \Sigma ^*_n$, we denote by $(x^{\det }_\theta ,y^{\det }_\theta ,z^{\det }_\theta )$ and $(x_\theta , y_\theta , z_\theta )$ the deterministic and stochastic solutions starting in $(x_n,y_n,z_n)$. We write $\mathbb {P}^{(x_n,y_n,z_n)}$ whenever we wish to stress the initial condition.

Consider the stopping times

$$\begin{aligned} \tau _{n+1}&= \inf \{ \theta :(x_\theta , y_\theta , z_\theta )\in \Sigma ^*_{n+1} \}, \nonumber \\ \tau ^{\det }_{n+1}={}\tau ^{\det }&= \inf \{ \theta :(x^{\det }_\theta , y^{\det }_\theta , z^{\det }_\theta )\in \Sigma ^*_{n+1} \}, \nonumber \\ \tau _\xi = \tau ^{(n)}_\xi (h)&= \inf \{ \theta :|x_\theta -x^{\det }_\theta | > h 2^{-n/2} \} , \nonumber \\ \tau _\eta = \tau ^{(n)}_\eta (h_1)&= \inf \{ \theta :\Vert (y_\theta ,z_\theta ) - (y^{\det }_\theta ,z^{\det }_\theta )\Vert > h_1 2^{-n/2} \}. \end{aligned}$$

(4.41)

We first establish that sample paths are likely to go from $\Sigma ^*_n$ to $\Sigma ^*_{n+1}$ in a time of order $\theta ={\mathcal {O}}(2^{-n})$, as in the deterministic case.

Lemma 4.7

There exist $h_0, c,c_{2}, \kappa >0$, not depending on $n$, such that for all initial conditions $(x_n,y_n,z_n)\in \Sigma ^*_n$ and $h\leqslant h_0\epsilon ^{1/3}$, $h_1\leqslant c_2\epsilon ^{2/3}$,

$$\begin{aligned} \mathbb {P}^{(x_n,y_n,z_n)}\bigl \{ \tau _{n+1}\wedge \tau ^{(n)}_\xi (h)\wedge \tau ^{(n)}_\eta (h_1) > c2^{-n} \bigr \} \leqslant \exp \biggl \{ -\kappa \frac{2^{3n}\epsilon }{\sigma ^2+(\sigma ^{\prime })^2\epsilon } \biggr \}. \end{aligned}$$

(4.42)

Proof

First note that $\tau _{n+1}>c 2^{-n}$ implies that either $x$ does not reach the level $\epsilon ^{1/3}2^{n+1}$ before time $c2^{-n}$ or that $x$ does reach $\epsilon ^{1/3}2^{n+1}$ at a stopping time $\tau ^{x}_{n+1}\leqslant c2^{-n}$ while $(y_{\tau ^{x}_{n+1}},z_{\tau ^{x}_{n+1}})\not \in D_{n+1}$.

Let us estimate the probability that $\tau ^{x}_{n+1}> c2^{-n}$. Note that $h_0$ and $c_2$ can be chosen sufficiently small to guarantee that $\hat{f}\geqslant \epsilon ^{2/3}2^{2n-2}$ for all times $\theta \leqslant \tau _\xi \wedge \tau _\eta$. From the representation

$$\begin{aligned} x_{c2^{-n}} = \epsilon ^{1/3} 2^n + \frac{1}{\epsilon ^{1/3}} \int _0^{c2^{-n}} \hat{f} {{\mathrm{d}}}\!\theta + \frac{\sigma }{\epsilon ^{1/6}} \int _0^{c2^{-n}} \widehat{F}_1 {{\mathrm{d}}}\!W_\theta + \sigma ^{\prime }\epsilon ^{1/3} \int _0^{c2^{-n}} \widehat{F}_2 {{\mathrm{d}}}\!W_\theta \quad \end{aligned}$$

(4.43)

we find that

$$\begin{aligned}&\mathbb {P}\{ x_{c2^{-n}} < \epsilon ^{1/3} 2^{n+1}, \tau _\xi \wedge \tau _\eta > c2^{-n} \} \nonumber \\&\quad \leqslant \mathbb {P}\biggl \{ \frac{\sigma }{\epsilon ^{1/6}} \int _0^{c2^{-n}} \widehat{F}_1 {{\mathrm{d}}}\!W_\theta + \sigma ^{\prime }\epsilon ^{1/3} \int _0^{c2^{-n}} \widehat{F}_2 {{\mathrm{d}}}\!W_\theta < -\left( \frac{1}{4}c-1\right) \epsilon ^{1/3} 2^n \biggr \} \nonumber \\&\quad \leqslant \exp \biggl \{ - \frac{(\frac{1}{4}c-1)^2 \epsilon ^{2/3} 2^{2n}}{Mc2^{-n} [\sigma ^2\epsilon ^{-1/3}+(\sigma ^{\prime })^2\epsilon ^{2/3}]}\biggr \} \end{aligned}$$

(4.44)

for some constant $M>0$, provided $c>4$. In the last line, we used the fact that if $M_t=\int _{0}^{t}F(s,\cdot ){{\mathrm{d}}}\!W_{t}$ with integrand $F(s,\omega )$ bounded in absolute value by a constant $K$, then Novikov’s condition [49, pp. 198–199] is satisfied and thus

$$\begin{aligned} Z_t = \exp \biggl \{ \gamma M_t - \frac{\gamma ^2}{2}\int _0^t F(s,\omega )^2{{\mathrm{d}}}\!s\biggr \} \end{aligned}$$

(4.45)

is a martingale for any $\gamma >0$. It follows that for $h>0$,

$$\begin{aligned} \mathbb {P}\bigl \{ M_t > h \bigr \} \leqslant \mathbb {P}\bigl \{ Z_t > {{\mathrm{e}}}^{\gamma h - \gamma ^2 K^{2}t/2}\bigr \} \leqslant {{\mathrm{e}}}^{-\gamma h + \gamma ^2 K^{2}t/2} \mathbb {E}\{Z_t\} = {{\mathrm{e}}}^{-\gamma h + \gamma ^2 K^{2}t/2}, \end{aligned}$$

(4.46)

where we used Markov’s inequality and the fact that a martingale has constant expectation.

Thus we obtained a bound on the probability of $x$ not reaching $\epsilon ^{1/3}2^{n+1}$ despite of $\xi$ and $\eta$ remaining small. It remains to consider the case $(y_{\tau ^{x}_{n+1}},z_{\tau ^{x}_{n+1}})\not \in D_{n+1}$ for $\tau ^{x}_{n+1}\leqslant c2^{-n}$.

By (4.37), the lower bound on $\hat{f}$ and the fact that $x^{\det }_{\tau ^{\det }}=\epsilon ^{1/3}2^{n+1}=x_{\tau ^{x}_{n+1}}$, we see that on the set $\Omega ^{\prime }=\{\omega \in \Omega :\tau ^{\det }\vee \tau ^{x}_{n+1}(\omega ) \leqslant \tau _\xi (\omega ) \wedge \tau _\eta (\omega )\}$,

$$\begin{aligned} \nonumber |y^{\det }_{\tau ^{x}_{n+1}} - y^{\det }_{\tau ^{\det }}|&\leqslant \textit{const }\epsilon ^{2/3} |\tau ^{x}_{n+1} - \tau ^{\det }| \leqslant \frac{\textit{const }\epsilon ^{2/3}}{\epsilon ^{1/3}2^{2n-2}} |x^{\det }_{\tau ^{x}_{n+1}} - x^{\det }_{\tau ^{\det }}| \\&\leqslant {\mathcal {O}}(\epsilon ^{1/3} h 2^{-5n/2}) \leqslant {\mathcal {O}}(h_{0}\epsilon ^{2/3}2^{-5n/2}) \end{aligned}$$

(4.47)

and $|y_{\tau ^{x}_{n+1}} - y^{\det }_{\tau ^{x}_{n+1}}| \leqslant h_1 2^{-n/2} =c_2\epsilon ^{2/3}2^{-n/2}$. Similar estimates hold for the $z$-coordinate. Since $(y^{\det }_{\tau ^{\det }},z^{\det }_{\tau ^{\det }})$ belongs to the image of $D_n$ under the deterministic Poincaré map, we conclude that $(y_{\tau ^{x}_{n+1}},z_{\tau ^{x}_{n+1}})$ belongs to an $\epsilon ^{2/3}2^{-n/2}$-neighbourhood of this image. Thus $\tau ^{x}_{n+1}=\tau _{n+1}$ on $\Omega ^{\prime }$. Choosing $c$ large enough to guarantee $\tau ^{\det } \leqslant c2^{-n}$ concludes the proof. $\square$

The next result gives a bound on fluctuations of sample paths, up to time $c2^{-n}$.

Lemma 4.8

There exist $M, h_0>0$ such that for all initial conditions $(x_n,y_n,z_n)\in \Sigma ^*_n$ and all $h, h_1>0$ satisfying $h\leqslant h_0\epsilon ^{1/3}2^{5n/2}$, $h_1\leqslant h_0\epsilon ^{-1/3}2^{7n/2}$, $h^2\leqslant h_0\epsilon ^{-1/3}2^{7n/2}h_1$ and $h_1^2\leqslant h_0\epsilon ^{1/3}2^{5n/2}h$,

$$\begin{aligned}&\mathbb {P}^{(x_n,y_n,z_n)}\bigl \{ \tau ^{(n)}_\xi (h)\wedge \tau ^{(n)}_\eta (h_1) < c2^{-n} \bigr \} \nonumber \\&\quad \leqslant \exp \biggl \{ -\frac{h^2}{M(\sigma ^2+(\sigma ^{\prime })^2\epsilon )\epsilon ^{-1/3}} \biggr \} + \exp \biggl \{ -\frac{h^2}{M(\sigma ^{\prime })^22^{-2n}} \biggr \} \nonumber \\&\qquad +\, \exp \biggl \{ -\frac{h_1^2}{M(\sigma ^2+(\sigma ^{\prime })^2\epsilon )\epsilon 2^{-2n}} \biggr \} + \exp \biggl \{ -\frac{h_1^2}{M(\sigma ^{\prime })^2\epsilon ^{2/3}} \biggr \} . \end{aligned}$$

(4.48)

Proof

The proof is similar to the proof of Proposition 4.3. First note that the linearization $a(\theta )=\partial _x\hat{f}(x^{\det }_\theta ,y^{\det }_\theta ,z^{\det }_\theta )$ has order $x^{\det }_\theta$, satisfying $x^{\det }_\theta \leqslant \textit{const }\epsilon ^{1/3}2^{k+1}$ for $\theta \leqslant \tau ^{\det }_{k+1}$ for any $k$. Since $\tau ^{\det }_{k+1} \asymp 2^{-k}$ for all $k$, $x^{\det }_\theta$ remains of order $\epsilon ^{1/3}2^n$ for all $\theta \leqslant c2^{-n}$. Thus $a(\theta )={\mathcal {O}}(\epsilon ^{1/3}2^{n})$ for all $\theta \leqslant c2^{-n}$, which implies

$$\begin{aligned} \alpha (\theta ,\phi ) = \int _\phi ^\theta a(u){{\mathrm{d}}}\!u \leqslant {\mathcal {O}}(\tau ^{\det } \epsilon ^{1/3}2^{n}) \leqslant {\mathcal {O}}(2^{-n} \epsilon ^{1/3}2^{n}) = {\mathcal {O}}(\epsilon ^{1/3})\; \end{aligned}$$

(4.49)

for all $0\leqslant \phi \leqslant \theta \leqslant c2^{-n}$.

Using this, one shows that the analogue of (3.12) admits solutions $p_1(\theta ), p_2(\theta ) = {\mathcal {O}}(\epsilon ^{-1/3}2^{-n})$, so that by Lemma 3.2,

$$\begin{aligned}&U_{\xi \xi }(\theta ,\phi ) = {\mathcal {O}}(1), \, \qquad \qquad \quad \ \, U_{\xi \eta }(\theta ,\phi ) = {\mathcal {O}}(\epsilon ^{-1/3}2^{-n}), \,\nonumber \\&U_{\eta \xi }(\theta ,\phi ) = {\mathcal {O}}(\epsilon ^{2/3}2^{-n}), \, \qquad U_{\eta \eta }(\theta ,\phi ) = {\mathcal {O}}(1), \end{aligned}$$

(4.50)

for $0\leqslant \phi \leqslant \theta \leqslant c2^{-n}$. It follows from computations similar to those yielding (4.18) that

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\xi < c2^{-n}\wedge \tau _\eta \bigr \} \leqslant \exp \biggl \{ - \frac{[h-M\epsilon ^{-1/3}2^{-5n/2}(h^2+h_1^2)]^2}{M(\sigma ^2+(\sigma ^{\prime })^2\epsilon )\epsilon ^{-1/3}} \biggr \} + {{\mathrm{e}}}^{-h^2/(M(\sigma ^{\prime })^22^{-2n})}. \end{aligned}$$

(4.51)

Since we are working on rather short time intervals, we can approximate the stochastic integral by the same Gaussian martingale on the whole time interval. Thus there is no subexponential prefactor of the type $\lceil \cdot \rceil$.

In a similar way, using the fact that $\epsilon ^{1/3}\leqslant \delta _{0}{2^{-n}}$, we get

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _\eta < c2^{-n}\wedge \tau _\xi \bigr \} \leqslant \exp \biggl \{ - \frac{[h_1-M\epsilon ^{1/3}2^{-7n/2}(h^2+h_1^2)]^2}{M(\sigma ^2+(\sigma ^{\prime })^2\epsilon )\epsilon 2^{-2n}} \biggr \} + {{\mathrm{e}}}^{-h_1^2/(M(\sigma ^{\prime })^2\epsilon ^{2/3})}.\quad \end{aligned}$$

(4.52)

The conditions on $h, h_1$ guarantee that the terms in $(h^2+h_1^2)$ are negligible. $\square$

The conditions on $h$ and $h_1$ are illustrated in Fig. 5.

Fig. 5

The shaded area is the set of $(h_1,h)$ satisfying the conditions given in Lemma 4.8 (if $h_0=1$ and $n=0$). Lemma 4.7 requires in addition that $h_1\leqslant \epsilon ^{2/3}$.

Putting the preceeding two results together, we obtain the following estimate on the spreading of sample paths when they hit $\Sigma _5$.

Proposition 4.9

Denote by $(y^*,z^*)$ the point where the deterministic solution starting in $(x_0,y_0,z_0)\in \Sigma ^{\prime }_4$ first hits $\Sigma _5 = \{ x=\delta _0 \}$. Then there exist $C, \kappa , h_0>0$ such that for any $h_1$ satisfying $h_1\leqslant h_0\epsilon ^{2/3}$, the stochastic sample path starting in $(x_0,y_0,z_0)$ first hits $\Sigma _5$ at time $\tau =\tau _{\Sigma _5}$ at a point $(\delta _0, y_{\tau }, z_{\tau })$ such that

$$\begin{aligned} \mathbb {P}\left\{ \left\| (y_{\tau }, z_{\tau }) - (y^*,z^*)\right\| > h_1 \right\}&\leqslant C|\log \epsilon | \left[ \exp \biggl \{ -\frac{\kappa h_1^2}{\sigma ^2\epsilon + (\sigma ^{\prime })^2\epsilon ^{1/3}}\biggr \}\right. \nonumber \\&\left. \qquad \qquad \qquad +\, \exp \biggl \{ -\frac{\kappa \epsilon }{\sigma ^2 + (\sigma ^{\prime })^2\epsilon }\biggr \} \right] . \end{aligned}$$

(4.53)

Proof

Let $N$ be the largest integer such that $\epsilon ^{1/3}2^N\leqslant \delta _0$, and $\tau ^{(n)}=\tau ^{(n)}_\xi (h)\wedge \tau ^{(n)}_\eta (h_1/2)$ for $n=1,\dots ,N$, where $h=h_0(\epsilon ^{1/3}\wedge \epsilon ^{-1/6}h_1^2)$ is taken as large as possible, cf. Fig. 5.

If $\tau _{h_1}$ denotes the first time the stochastic sample path leaves a tube of size $h_1$ around the deterministic solution, the left-hand side of (4.53) can be bounded above by $\mathbb {P}\{ \tau _{h_1} < \tau _{\Sigma _5}\}$. Since

$$\begin{aligned} \bigcap _{n=1}^N \bigl \{ \tau _{n+1} \leqslant c2^{-n}\wedge \tau ^{(n)} \bigr \} \subset \biggl \{ \tau _{\Sigma _5} \leqslant \sum _{n=1}^N c2^{-n} \wedge \tau _{h_1} \biggr \}, \end{aligned}$$

(4.54)

we have the bound

$$\begin{aligned} \mathbb {P}\bigl \{ \tau _{h_1} < \tau _{\Sigma _5} \bigr \} \leqslant \mathbb {P}\biggl \{ \tau _{h_1}\wedge \sum _{n=1}^N c2^{-n} < \tau _{\Sigma _5} \biggr \} \leqslant \sum _{n=1}^N \mathbb {P}\bigl \{ \tau _{n+1} > c2^{-n}\wedge \tau ^{(n)} \bigr \}. \end{aligned}$$

(4.55)

Each term of the sum is bounded by $\mathbb {P}\{\tau _{n+1}\wedge \tau ^{(n)}>c2^{-n}\} +\mathbb {P}\{\tau ^{(n)}<c2^{-n}\wedge \tau _{n+1}\}$, so that the result follows from the last two lemmas. By distinguishing the cases $h_1\geqslant \epsilon$ and $h_1\leqslant \epsilon$, one checks that our choice of $h$ implies that the terms in $h^2$ are negligible, compared to at least one of the two summands on the right-hand side of (4.53). $\square$

This result implies that the spreading in the $y$- and $z$-directions on $\Sigma _5$, for a given initial condition on $\Sigma ^{\prime }_4$, is of order

$$\begin{aligned} \sigma \sqrt{\epsilon } + \sigma ^{\prime }\epsilon ^{1/6}. \end{aligned}$$

(4.56)

5 The Folded Node

In this section we analyze the transition $\Sigma _1\rightarrow \Sigma _2$ of sample paths in a neighbourhood of the folded-node point $p^*$. For convenience, we translate the origin of the coordinate system to $p^*$. We will decompose the transition into three parts, by introducing further sections $\Sigma _1^{\prime } = \{x=\delta \sqrt{\epsilon }\,\}$ and $\Sigma _1^{\prime \prime } = \{x=-\delta \sqrt{\epsilon }\,\}$, where $\delta$ is a small constant of order 1. The transitions $\Sigma _1\rightarrow \Sigma _1^{\prime }$, $\Sigma _1^{\prime }\rightarrow \Sigma _1^{\prime \prime }$, and $\Sigma _1^{\prime \prime }\rightarrow \Sigma _2$ are analyzed, respectively, in Sect. 5.2, in Sects. 5.3 and 5.4, and in Sect. 5.5.

5.1 Normal Form

We start by making a preliminary transformation to normal form near the folded node point $p^*$. Recall once again that $t=s/\epsilon$ denotes the fast timescale.

Proposition 5.1

Near a folded-node point $p^*\in L^+$ satisfying the assumptions (A1) and (A3), there exist a smooth change of coordinates and a random time change such that (3.1) is locally given by

$$\begin{aligned} {{\mathrm{d}}}\!x_t&= \hat{f}(x_{t},y_{t},z_{t};\epsilon ,\sigma ,\sigma ^{\prime }) {{\mathrm{d}}}\!t + \bigl [\sigma \widehat{F}_1(x_t,y_t,z_t) + \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{F}_2(x_t,y_t,z_t) \bigr ]{{\mathrm{d}}}\!W_t,\nonumber \\ {{\mathrm{d}}}\!y_t&= \epsilon \hat{g}_1(x_t,y_t,z_t;\epsilon ,\sigma ^{\prime }){{\mathrm{d}}}\!t + \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{G}_1(x_t,y_t,z_t) {{\mathrm{d}}}\!W_t,\nonumber \\ {{\mathrm{d}}}\!z_t&= \frac{1}{2} \epsilon \mu {{\mathrm{d}}}\!t + \sigma ^{\prime }\sqrt{\epsilon }\, \widehat{G}_2(x_t,y_t,z_t){{\mathrm{d}}}\!W_t, \end{aligned}$$

(5.1)

where $\mu \in (0,1)$ is the ratio of weak and strong eigenvalues at the folded node (see also [17, p. 4793] or [24, p. 48]), and

$$\begin{aligned} \hat{f}(x,y,z;\epsilon ,\sigma ,\sigma ^{\prime })&= y-x^2+{\mathcal {O}}\left( \left\| (x,y,z)^{{\mathrm {T}}}\right\| ^3\!,\epsilon \left\| (x,y,z)^{{\mathrm {T}}}\right\| , \sigma ^2,(\sigma ^{\prime })^2\epsilon \right) , \nonumber \\ \hat{g}_1(x,y,z;\epsilon ,\sigma ^{\prime })&= -(\mu +1)x - z + {\mathcal {O}}(y,(x+z)^2,\epsilon ,(\sigma ^{\prime })^2), \end{aligned}$$

(5.2)

while the diffusion matrices $\widehat{F}_1, \widehat{F}_2, \widehat{G}_1, \widehat{G}_2$ all remain of order 1.

Proof

The result is again a stochastic analogue of the transformation result for deterministic systems, see [82, pp. 8–10], as well as [83].

We start by translating the origin of the coordinate system to the folded-node point $p^*$. Note that the failure of the normal-switching condition (A2) implies that the vectors $(\frac{\partial f}{\partial y} ,\frac{\partial f}{\partial z})(0)$ and $g(0)$ are orthogonal. We may thus rotate coordinates in such a way that $g_1(0)=0$ and $\frac{\partial f}{\partial z}(0)=0$. This rotation does not change the order of magnitude of the diffusion coefficients $\sigma ^{\prime }\sqrt{\epsilon }\,G_1$ and $\sigma ^{\prime }\sqrt{\epsilon }\,G_2$.

Calculating the linearization of the desingularized slow flow (2.9) and using Assumption (A1), we see that $g_2(0)\ne 0$, since otherwise $p^{*}=0$ would not be a node for (2.9) as required by Assumption (A3). We can thus carry out locally a random time change given by

$$\begin{aligned} {{\mathrm{d}}}\!\tilde{t} = \frac{g_2(x_t,y_t,z_t)}{g_2(0,0,0)} {{\mathrm{d}}}\!t. \end{aligned}$$

(5.3)

Lemma 8.4 in Appendix 1 shows that this time change yields a system in which all drift coefficients have been multiplied by $g_2(0,0,0)/g_2(x,y,z)$, and all diffusion coefficients have been multiplied by $[g_2(0,0,0)/g_2(x,y,z)]^{1/2}$. We may thus assume that $g_2(x,y,z)$ is constant and equal to $g_2(0,0,0)$ in (3.1).

The remainder of the proof is similar to the proof of Proposition 4.5. A transformation $x=\bar{x}+\xi (z)$, $y=\bar{y} + \eta (z)$ rectifies the fold curve, i.e. $f(\xi (z),\eta (z),z)=0$ and $\frac{\partial f}{\partial x}(\xi (z),\eta (z),z)=0$ in a neighbourhood of $z=0$, and thus

$$\begin{aligned} \bar{f}(\bar{x},\bar{y},z) = a\bar{y} + b\bar{x}^2 + c\bar{x}\bar{y} + d\bar{y}^2 + e\bar{y}z + k\epsilon + {\mathcal {O}}(\left\| (\bar{x},\bar{y},z)\right\| ^3,\epsilon z, (\sigma ^{\prime })^2\epsilon ). \end{aligned}$$

(5.4)

The standard form of $f$ and $g_1$ can then be achieved by combining a translation of $x$ by ${\mathcal {O}}(\epsilon )$, a scaling of space and a near-identity transformation $\hat{x} = \bar{x} - \frac{1}{2} c \bar{x}^2 - d \bar{x}\bar{y} - e \bar{x}z$ (cf. [82, pp. 9–10]). These transformations do not change the order of the diffusion coefficients for $y$ and $z$. $\square$

5.2 Approach

In this section, we consider solutions of the normal form (5.1), starting at a fast time $s_0\asymp -1$ on $\Sigma _1$, as long as $x\geqslant {\mathcal {O}}(\sqrt{\epsilon }\,)$. We fix a deterministic solution $(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ which is sufficiently close to the strong canard to display SAOs when approaching the folded-node point $p^*$. From the deterministic analysis we know that

$$\begin{aligned} a(s) = \partial _x f(x^{\det }_s,y^{\det }_s,z^{\det }_s) = -2x^{\det }_s = cs + {\mathcal {O}}(s^2) \qquad \text {for }s_0\leqslant s\leqslant -\sqrt{\epsilon }, \end{aligned}$$

(5.5)

where $c$ is a constant of order 1. Scaling time if necessary, we may assume that $c=1$.

The linearization of the deterministic system at $(x^{\det }_s,y^{\det }_s,z^{\det }_s)$ has the form $\epsilon \dot{\zeta }= {\mathcal {A}}(s)\zeta$, where

$$\begin{aligned} {\mathcal {A}}(s) = \begin{pmatrix} A(s) &{}\quad c_1(s) \\ 0 &{}\quad 0 \end{pmatrix}, \qquad A(s) = \begin{pmatrix} 2a(s) &{} 1 + {\mathcal {O}}(s^2) \\ -\epsilon (1+\mu ) + {\mathcal {O}}(\epsilon s) &{} {\mathcal {O}}(\epsilon ) \end{pmatrix}, \end{aligned}$$

(5.6)

and $c_1(s) = (1+{\mathcal {O}}(s^2),{\mathcal {O}}(\epsilon ))^{{\mathrm {T}}}$. We have used the fact that $s^2 \geqslant \epsilon$ to simplify the expression of the error terms.

For $s\leqslant -\sqrt{\epsilon }$, the eigenvalues of $A(s)$ behave like $s$ and $\epsilon /|s|$. This implies that while for $s\asymp -1$, the variable $x$ is faster than both $y$ and $z$, $\dot{x}$ and $\dot{y}$ become of comparable order $1/\sqrt{\epsilon }$ as $s$ approaches $-\sqrt{\epsilon }$. This is the well-known effect that one may extend the normally hyperbolic theory slightly near fold points from $x\asymp 1$ up to a neighbourhood with $x\asymp \sqrt{\epsilon }$, see [24, pp. 48–49]. Instead of blocking $y$ and $z$ as in (3.5), we write

$$\begin{aligned} \xi _s = \begin{pmatrix} x_s \\ y_s \end{pmatrix} - \begin{pmatrix} x^{\det }_s \\ y^{\det }_s \end{pmatrix}, \qquad \eta _s = z_s - z^{\det }_s, \qquad \zeta _s = \begin{pmatrix} \xi _s\\ \eta _s\end{pmatrix}, \end{aligned}$$

(5.7)

since $\dot{x}$ and $\dot{y}$ eventually become comparable. Then $\zeta _s$ obeys a system of the form

$$\begin{aligned} {{\mathrm{d}}}\!\zeta _s = \frac{1}{\epsilon } {\mathcal {A}}(s)\zeta _s {{\mathrm{d}}}\!s + \begin{pmatrix} \frac{\sigma }{\sqrt{\epsilon }} {\mathcal {F}}_1(\zeta _s,s) + \sigma ^{\prime } {\mathcal {F}}_2(\zeta _s,s) \\ \sigma ^{\prime } {\mathcal {G}}_1(\zeta _s,s) \\ \sigma ^{\prime } {\mathcal {G}}_2(\zeta _s,s) \end{pmatrix} {{\mathrm{d}}}\!W_s + \begin{pmatrix} \frac{1}{\epsilon } b_x(\zeta _s,s) \\ b_y(\zeta _s,s) \\ 0 \end{pmatrix} {{\mathrm{d}}}\!s. \end{aligned}$$

(5.8)

The principal solution of $\epsilon \dot{\zeta }= {\mathcal {A}}(s)\zeta$ has the block structure

$$\begin{aligned} U(s,r) = \begin{pmatrix} V(s,r) &{}\quad \displaystyle \frac{1}{\epsilon }\int _s^r V(s,u) c_1(u) {{\mathrm{d}}}\!u \\ 0 &{}\quad 1 \end{pmatrix}, \end{aligned}$$

(5.9)

where $V(s,r)$ denotes the principal solution of $\epsilon \dot{\xi }= A(s)\xi$.

Lemma 5.2

For $s_0 \leqslant r \leqslant s \leqslant -\sqrt{\epsilon }$, the matrix elements of $V(s,r)$ satisfy

$$\begin{aligned} V_{xx}(s,r)&= {\mathcal {O}}\biggl ( \frac{\left| a(r)\right| ^{1+\mu }}{\left| a(s)\right| ^{1+\mu }} {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } \biggr ), \nonumber \\ V_{xy}(s,r)&= {\mathcal {O}}\biggl ( \frac{\left| a(r)\right| ^{\mu }}{\left| a(s)\right| ^{1+\mu }} {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } + \frac{\left| a(s)\right| ^{\mu }}{\left| a(r)\right| ^{1+\mu }} \biggr ), \nonumber \\ V_{yx}(s,r)&= {\mathcal {O}}\biggl ( \epsilon \, \frac{\left| a(r)\right| ^{1+\mu }}{\left| a(s)\right| ^{2+\mu }} {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } + \epsilon \, \frac{\left| a(s)\right| ^{1+\mu }}{\left| a(r)\right| ^{2+\mu }} \biggr ), \nonumber \\ V_{yy}(s,r)&= {\mathcal {O}}\biggl ( \frac{\left| a(s)\right| ^{1+\mu }}{\left| a(r)\right| ^{1+\mu }} + \epsilon \, \frac{\left| a(r)\right| ^{\mu }}{\left| a(s)\right| ^{2+\mu }} {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } \biggr ), \end{aligned}$$

(5.10)

where

$$\begin{aligned} \alpha (s,r) = \int _r^s {{\mathrm{Tr}}}A(u) {{\mathrm{d}}}\!u = (s^2 - r^2) + {\mathcal {O}}((s-r)(s^2 + r^2)). \end{aligned}$$

(5.11)

In the particular case where $A(s)= \bigl ( \begin{matrix} 2s &{} 1 \\ -\epsilon (1+\mu ) &{} 0 \end{matrix}\bigr )$, the equation $\epsilon \dot{\xi }= A(s)\xi$ for $\xi _{s}=(\xi _{1,s},\xi _{2,s})^{{\mathrm {T}}}$ is equivalent to a Weber equation

$$\begin{aligned} \epsilon \frac{{{\mathrm{d}}}\!^2\xi _1}{{{\mathrm{d}}}\!s^2} -2s \frac{{{\mathrm{d}}}\!\xi _1}{{{\mathrm{d}}}\!s}+(\mu -1)\xi _1=0, \end{aligned}$$

(5.12)

and the estimates (5.10) follow directly from the asymptotics of parabolic cylinder functions [1, p. 689]; see also [77, p. 449]. In Appendix 2, we provide a proof of Lemma 5.2 valid in the general case, which does not rely on these asymptotics. With the above estimates, we obtain the following result on the size of fluctuations during the approach phase.

Proposition 5.3

Define the stopping times

$$\begin{aligned} \tau _{\xi ,1}&= \inf \{s>s_0:|\xi _{1,s}|>h\}, \nonumber \\ \tau _{\xi ,2}&= \inf \{s>s_0:|\xi _{2,s}|>h_1\}, \nonumber \\ \tau _{\eta }&= \inf \{s>s_0:|\eta _s|>h_2\}. \end{aligned}$$

(5.13)

There exist constants $\kappa , h_0 > 0$ such that for all $s_0 \leqslant s \leqslant -\sqrt{\epsilon }$, and all $h, h_1, h_2>0$ satisfying $h^2 + h_1^2 + h_2^2 \leqslant h_0|s|h$ and $h^2 + h_1^2 + h_2^2 \leqslant h_0h_1$,

(5.14)

Proof

The proof is similar to the proof of Proposition 4.3, so we omit the details. Let us just remark that when evaluating the elements in (5.9), one encounters integrals of the form

$$\begin{aligned} \int _{s_0}^s \frac{\left| s\right| ^\mu }{\left| u\right| ^{1+\mu }} {{\mathrm{d}}}\!u = \frac{1-y^\mu }{\mu } = \left| \log y\right| \frac{1-{{\mathrm{e}}}^{-\mu \left| \log y\right| }}{\mu \left| \log y\right| } \end{aligned}$$

(5.15)

where $y=\left| s\right| /\left| s_0\right|$. The fraction on the right-hand side being bounded, the integral is bounded by a constant times $\left| \log (\left| s\right| /\left| s_0\right| )\right|$. $\square$

Under the condition $\sigma , \sigma ^{\prime } = {\mathcal {O}}(\epsilon ^{3/4})$, we obtain the typical spreadings

• $(\sigma +\sigma ^{\prime })\left| s\right| ^{-1/2}$ in the $x$-direction, which reaches order $(\sigma +\sigma ^{\prime })\epsilon ^{-1/4}$ for $s\asymp -\sqrt{\epsilon }$,

• $\sigma \epsilon ^{1/2}\left| s\right| ^{-1/2} + \sigma ^{\prime }\left| s\right| ^{1/2}$ in the $y$-direction, which reaches order $(\sigma +\sigma ^{\prime })\epsilon ^{1/4}$ for $s\asymp -\sqrt{\epsilon }$,

• and $\sigma ^{\prime }$ in the $z$-direction.

Note carefully that the integrals in (5.15) become unbounded when $s\rightarrow 0$ as $\mu \in (0,1)$ so we cannot use the same methods to control sample paths closer to the folded node.

5.3 Neighbourhood: Deterministic Dynamics

In this section we briefly describe the behaviour of solutions of the normal form (5.1) in the deterministic case $\sigma =\sigma ^{\prime }=0$. Recall that standard results (see [77, Sect. 4], [26, Theorem 2.3] and the foundational work [7, 8]) imply the existence of two primary canards and $k_\mu$ secondary canards [83] where

$$\begin{aligned} 2k_\mu + 1 < \mu ^{-1} < 2k_\mu + 3 , \end{aligned}$$

(5.16)

and each canard lies in $C_\epsilon ^r\cap C^{a+}_\epsilon$. One strategy to prove the existence of canards, as first suggested for the planar case in [29], is to look for transversal intersections of $C_\epsilon ^r$ and $C^{a+}_\epsilon$ by extending the manifolds via the blow-up method [77] into a region near the folded node where the blow-up reduces to the scaling (or zoom-in) transformation

$$\begin{aligned} x = \sqrt{\epsilon }\, \bar{x},\quad y = \epsilon \, \bar{y},\quad z = \sqrt{\epsilon }\, \bar{z}. \end{aligned}$$

(5.17)

The scaling (5.17) transforms the deterministic version of the normal form (5.1) to

$$\begin{aligned} \mu \frac{{{\mathrm{d}}}\!\bar{x}}{{{\mathrm{d}}}\!\bar{z}}&= 2\bar{y} - 2\bar{x}^2 + {\mathcal {O}}(\sqrt{\epsilon }\,),\nonumber \\ \mu \frac{{{\mathrm{d}}}\!\bar{y}}{{{\mathrm{d}}}\!\bar{z}}&= -2(1+\mu )\bar{x} - 2\bar{z} + {\mathcal {O}}(\sqrt{\epsilon }\,). \end{aligned}$$

(5.18)

We consider henceforth the dynamics for $\epsilon =0$, as results can be extended to small positive $\epsilon$ by regular perturbation theory. Note that the system is symmetric under the transformation

$$\begin{aligned} (\bar{x}, \bar{y}, \bar{z}) \mapsto (-\bar{x}, \bar{y}, -\bar{z}). \end{aligned}$$

(5.19)

The normal form admits a particular solution $\gamma ^{w}$ given by

$$\begin{aligned} \bar{x} = - \bar{z}, \qquad \bar{y} = \bar{z}^2 - \frac{\mu }{2}, \end{aligned}$$

(5.20)

which is called the singular weak canard (there is also a singular strong canard, given by $\bar{x} = - \bar{z}/\mu$, $\bar{y} = (\bar{z}/\mu )^2 - 1/2$). Generic solutions twist a certain number of times around the weak canard, see Fig. 6 for an illustration. One possibility to prove the persistence of the weak and strong canards as well as secondary canards is to analyse the zeros of the variational Weber equation as shown in [77]. To also obtain estimates on individual non-canard orbits, our aim is to determine the map from an initial condition $P_0=(\delta , \bar{y}_0, \bar{z}_0) \in \Sigma _1^{\prime }$, close to the attracting slow manifold, to the first-hitting point $P_1=(-\delta , \bar{y}_1, \bar{z}_1) \in \Sigma _1^{\prime \prime }$. The key tool will be suitable coordinate transformations; we note that although the method only provides a small refinement of previous results, it has the advantage of being quite explicit so we choose to record the results here. We will proceed in three steps, see Fig. 7:

• (S1) Estimate the coordinates of $P^{\prime }=(0,\bar{y}^{\prime },\bar{z}^{\prime })$, the first-hitting point of $\{\bar{x}=0\}$.

• (S2) Use an averaging-type transformation to describe the rotations of this orbit around the weak canard, until the last-hitting point $P^{\prime \prime }=(0,\bar{y}^{\prime \prime },\bar{z}^{\prime \prime })$ of $\{\bar{x}=0\}$.

• (S3) Determine the map from $P^{\prime \prime }$ to $P_1$.

Fig. 6

Sketch of the geometry of the orbits near the folded-node singularity

Fig. 7

The map from $\Sigma ^{\prime }_1$ to $\Sigma ^{\prime \prime }_1$ is decomposed into three phases

For Steps (S1) and (S3), it is useful to introduce the rectified coordinate $\eta = \bar{y} - \bar{x}^2 + (1+\mu )/2$. The normal form (with $\epsilon =0$) in rectified coordinates then reads

$$\begin{aligned} \mu \frac{{{\mathrm{d}}}\!\bar{x}}{{{\mathrm{d}}}\!\bar{z}}&= 2\eta - (1+\mu ),\nonumber \\ \mu \frac{{{\mathrm{d}}}\!\eta }{{{\mathrm{d}}}\!\bar{z}}&= -4\bar{x}\eta - 2\bar{z}. \end{aligned}$$

(5.21)

Lemma 5.4

Fix constants $0<\beta <\alpha \leqslant 1$ and $0<L\leqslant \sqrt{(\alpha -\beta )|\log \mu |/2}$. Then for $\mu >0$ small enough the orbit of (5.21) passing through a point $(\bar{x},\eta ,\bar{z})=(0,\eta _*,\bar{z}_*)$ with $|\eta _*|\leqslant \mu ^\alpha$ and $|\bar{z}_*|\leqslant \mu ^\beta$ is given by

$$\begin{aligned} \eta (\bar{x})&= {{\mathrm{e}}}^{2\bar{x}^2} \biggl [ \eta _* + \bar{z}_*\int _0^{2\bar{x}}{{\mathrm{e}}}^{-u^2/2}{{\mathrm{d}}}\!u + {\mathcal {O}}(\mu )\biggr ] \bigl [ 1+{\mathcal {O}}(\mu ^\beta L^2)\bigr ] , \nonumber \\ \bar{z}(\bar{x})&= \bar{z}_* + \mu \bar{x} \bigl [ 1+{\mathcal {O}}(\mu ^\beta ) \bigr ], \end{aligned}$$

(5.22)

for all $\bar{x} \in [-L,L]$.

Proof

For $\eta ={\mathcal {O}}(\mu ^\beta )$ the equations (5.21) can be rewritten in the form

$$\begin{aligned} \frac{{{\mathrm{d}}}\!\bar{z}}{{{\mathrm{d}}}\!\bar{x}}&= \mu [1+{\mathcal {O}}(\mu ^\beta )],\nonumber \\ \frac{{{\mathrm{d}}}\!\eta }{{{\mathrm{d}}}\!\bar{x}}&= a(\bar{x})\eta + 2\bar{z}[1+{\mathcal {O}}(\mu ^\beta )], \end{aligned}$$

(5.23)

where $a(\bar{x}) = 4\bar{x}[1+{\mathcal {O}}(\mu ^\beta )]$. Integrating the first equation yields the expression for $\bar{z}(\bar{x})$. To obtain the expression for $\eta (\bar{x})$, observe that $\exp (\int _0^{\bar{x}}a(y){{\mathrm{d}}}\!y) = {{\mathrm{e}}}^{2\bar{x}^2}[1+{\mathcal {O}}(\mu ^\beta L^2)]$ and solve the equation for $\eta$ by variation of the constant. $\square$

From this result we immediately see that the map from $P_0$ to $P^{\prime }$ is given by

$$\begin{aligned} \eta ^{\prime }&= {{\mathrm{e}}}^{-2\delta ^2} \eta _0 [1+{\mathcal {O}}(\delta ^2\mu ^\beta )] - \bar{z}_0\int _0^{2\delta }{{\mathrm{e}}}^{-u^2/2}{{\mathrm{d}}}\!u + {\mathcal {O}}(\mu ), \nonumber \\ \bar{z}^{\prime }&= \bar{z}_0 + {\mathcal {O}}(\delta \mu ), \end{aligned}$$

(5.24)

provided $\eta _0, \bar{z}_0 = {\mathcal {O}}(\mu ^\beta )$ for some $\beta \in (0,1)$. Similarly, the map from $P^{\prime \prime }$ to $P_1$ is given by

$$\begin{aligned} \eta _1&= {{\mathrm{e}}}^{2\delta ^2} \biggl [\eta ^{\prime \prime } - \bar{z}^{\prime \prime }\int _{-2\delta }^0{{\mathrm{e}}}^{-u^2/2}{{\mathrm{d}}}\!u + {\mathcal {O}}(\mu )\biggr ][1+{\mathcal {O}}(\delta ^2\mu ^\beta )], \nonumber \\ \bar{z}_1&= \bar{z}^{\prime \prime } + {\mathcal {O}}(\delta \mu ), \end{aligned}$$

(5.25)

provided $\eta ^{\prime \prime }={\mathcal {O}}(\mu ^\alpha )$ and $\bar{z}^{\prime \prime }={\mathcal {O}}(\mu ^\beta )$ for some choice of $0<\beta <\alpha \leqslant 1$. In addition, Lemma 5.4 shows that for sufficiently small $\bar{z}$, the distance at $\bar{x}=0$ between the invariant manifolds $C^{a+}_\epsilon$ and $C^r_\epsilon$ has order $\bar{z}$. This follows from the fact that orbits in $C^{a+}_\epsilon$ should be such that $\eta (\bar{x})$ is close to 0 for large positive $\bar{x}$, while orbits in $C^r_\epsilon$ should be such that $\eta (\bar{x})$ is close to 0 for large negative $\bar{x}$.

We now turn to Step (S2), estimating the map from $P^{\prime }$ to $P^{\prime \prime }$. The difference $u$ between a general solution of (5.18) and the weak canard $\gamma ^w$ satisfies the variational equation

$$\begin{aligned} \nonumber \mu \frac{{{\mathrm{d}}}\!u_1}{{{\mathrm{d}}}\!\bar{z}}&= 4\bar{z} u_1 + 2 u_2 - 2u_1^2 ,\\ \mu \frac{{{\mathrm{d}}}\!u_2}{{{\mathrm{d}}}\!\bar{z}}&= -2(1+\mu )u_1. \end{aligned}$$

(5.26)

Consider the variable

$$\begin{aligned} K := \biggl [ 1+\frac{2}{1+\mu }(u_2-u_1^2) \biggr ] {{\mathrm{e}}}^{-2u_2/(1+\mu )}, \end{aligned}$$

(5.27)

which is a first integral of the system when $\bar{z}=0$. In fact, $K$ is just a version of the classical first integral near planar degenerate folded singularities (cf. [56, Lemma 3.3; Figure 3.2], [54, Figure 5],  [69, Figure 2]). Although $K$ is not a first integral for arbitrary $\bar{z}$ it turns out that the variable $K$ is still very useful for obtaining explicit control over the oscillations near the folded node. A short computation yields

$$\begin{aligned} \mu \frac{{{\mathrm{d}}}\!K}{{{\mathrm{d}}}\!\bar{z}} = -\frac{16 \bar{z}}{1+\mu } u_1^2 {{\mathrm{e}}}^{-2u_2/(1+\mu )}. \end{aligned}$$

(5.28)

In [17, Section D.2] we provided an averaging result valid in a small neighbourhood of the weak canard (for the stochastic case). The following result extends this to the larger domain $\{K>0\}$.

Proposition 5.5

(Averaged system) Set $\rho (K) = (1-K)(1+|\log K|^{3/2})$. For $\bar{z}$ in a neighbourhood of 0 and $K>0$, there exist a variable $\bar{K}= K + {\mathcal {O}}(\left| \bar{z}\right| \rho (K))$, an angular variable $\varphi$, a function $\bar{g}$ and constants $c_\pm >0$ such that

$$\begin{aligned} \frac{c_-}{1+|\log K|^{1/2}} \leqslant \mu \frac{{{\mathrm{d}}}\!\varphi }{{{\mathrm{d}}}\!\bar{z}} \leqslant c_+ (1+|\log K|^{1/2}) \end{aligned}$$

(5.29)

for $K\geqslant {\mathcal {O}}(\left| \bar{z}\right| )$ and

$$\begin{aligned} \frac{{{\mathrm{d}}}\!\bar{K}}{{{\mathrm{d}}}\!\varphi } = \bar{z} \bar{g}(\bar{K},\bar{z}) + {\mathcal {O}}\Bigl ( (\mu +\bar{z}^2) \rho (\bar{K})\Bigr ), \end{aligned}$$

(5.30)

where $c_-(1-\bar{K}) \leqslant -\bar{g}(\bar{K},\bar{z}) \leqslant c_+(1-\bar{K})$.

We give the proof in Appendix 3.

The averaged equation (5.30) is similar to the equation describing dynamic pitchfork or Hopf bifurcations, which display a bifurcation delay. Initially, i.e. when $\bar{z}=\bar{z}^{\prime }<0$, $\bar{K}$ has a value $\bar{K}_0>0$ of order $\bar{z}_0$. As long as $\bar{z}<0$, $\bar{K}$ will keep increasing, and thus get so close to 1 that a time of order $|\bar{z}^{\prime }|$ is needed, once $\bar{z}$ becomes positive, for $\bar{K}$ to decrease to the value $\bar{K}_0$ again. We set

$$\begin{aligned} \tau = \inf \{\bar{z}>0:\bar{K}= \bar{K}_0\}. \end{aligned}$$

(5.31)

Note that the error term in (5.30) is no longer negligible when $\left| \bar{z}\right|$ is of order $\mu$, but this only results in a shift of the delay by a quantity of order $\mu$, which will be negligible.

Corollary 5.6

Let $\rho _1 = (\mu + \bar{z}_0^2)|\log \bar{z}_0|^{3/2}$. We have

$$\begin{aligned} \tau = -\bar{z}^{\prime } + {\mathcal {O}}(\rho _1). \end{aligned}$$

(5.32)

Furthermore, the change in angle is given by $\varphi (\tau ) - \varphi (\bar{z}^{\prime }) = \phi (\bar{z}^{\prime })/\mu$, where $\phi$ is monotonically decreasing for $\bar{z}^{\prime }<0$ and satisfies

$$\begin{aligned} \frac{2c_-}{1+|\log \bar{z}_0|^{1/2}} \bigl [ |\bar{z}^{\prime }| + {\mathcal {O}}(\rho _1) \bigr ] \leqslant \phi (\bar{z}^{\prime }) \leqslant 2c_+ (1+|\log \bar{z}_0|^{1/2}) \bigl [ |\bar{z}^{\prime }| + {\mathcal {O}}(\rho _1) \bigr ]. \end{aligned}$$

(5.33)

Proof

Set $Q=1-\bar{K}$. As long as $\bar{z} \leqslant \tau$, we can bound $|\log \bar{K}|$ by $|\log \bar{z}_0|$ and write

$$\begin{aligned} \frac{{{\mathrm{d}}}\!Q}{{{\mathrm{d}}}\!\varphi } \leqslant Q \Bigl [ c_+ \bar{z} + {\mathcal {O}}\bigl ( Q(\mu +\bar{z}^2) |\log \bar{z}_0|^{3/2}\bigr )\Bigr ]. \end{aligned}$$

(5.34)

Using (5.29) we obtain

$$\begin{aligned} \frac{{{\mathrm{d}}}\!Q}{{{\mathrm{d}}}\!\bar{z}} \leqslant \frac{1}{\mu }Q \Bigl [ c_+^2 \bar{z} + {\mathcal {O}}\bigl ( Q(\mu +\bar{z}^2) |\log \bar{z}_0|^{3/2}\bigr )\Bigr ] \bigl [1+{\mathcal {O}}(|\log \bar{z}_0|^{1/2})\bigr ]. \end{aligned}$$

(5.35)

Integrating, we arrive at

$$\begin{aligned} Q(\bar{z}) \leqslant Q(\bar{z}^{\prime }) \exp \biggl \{ \frac{c_+^2}{2\mu } (\bar{z} - \bar{z}^{\prime }) \bigl [ \bar{z} + \bar{z}^{\prime } + {\mathcal {O}}(\rho _1)\bigr ] \bigl [1+{\mathcal {O}}(|\log \bar{z}_0|^{1/2})\bigr ] \biggr \}. \end{aligned}$$

(5.36)

This shows that $\tau \geqslant -\bar{z}^{\prime } + {\mathcal {O}}(\rho _1)$. Using the corresponding lower bounds, we also get $\tau \leqslant -\bar{z}^{\prime } - {\mathcal {O}}(\rho _1)$. This proves (5.32), and (5.33) follows by using (5.29) again. $\square$

We can now draw consequences on the Poincaré map from the last results. If

$$\begin{aligned} \phi (\bar{z}^{\prime }) = 2\pi n\mu , \qquad n\in \mathbb {N}, \end{aligned}$$

(5.37)

then the orbit will hit the plane $\{\bar{x}=0\}$ at $P^{\prime \prime }=P^{\prime }$, which is on (or very near) the repelling slow manifold $C^r_\epsilon$, cf. (5.24). Therefore (5.37) gives a condition on $\bar{z}^{\prime }$ (and thus on $\bar{z}_0$) for the orbit being a canard. If, on the other hand,

$$\begin{aligned} \phi (\bar{z}^{\prime }) = (2\pi n-\theta )\mu , \qquad 0 < \theta < 2\pi , \end{aligned}$$

(5.38)

the orbit will leave the set $\{\bar{K}>\bar{K}_0\}$ far from the repelling slow manifold $C^r_\epsilon$, see Fig. 7. One can then use Proposition 5.5 to estimate $\bar{z}^{\prime \prime }$, which is of the form $\bar{z}^{\prime \prime } = \tau + {\mathcal {O}}(\mu \theta )$. As $\theta$ increases from 0 to $2\pi$, $P^{\prime \prime }$ moves downwards until it approaches the continuation of the attracting slow manifold $C^{a+}_\epsilon$.

Once orbits have hit $\bar{x}=0$ at some point $P^{\prime \prime }$ below $P^{\prime }$, one can use (5.25) to follow their future evolution. Note in particular that the domain $\{\bar{x}<0, \eta <0\}$ is positively invariant, so that once orbits have reached this domain they will stay bounded away from the repelling slow manifold.

5.4 Neighbourhood: Stochastic Dynamics

We now consider the stochastic dynamics of sample paths starting on $\Sigma _1^{\prime }$ up to the first time they hit the section $\Sigma _1^{\prime \prime } = \{x=-\delta \sqrt{\epsilon }\,\}$. The first step is again to apply the scaling (or zoom-in)

$$\begin{aligned} x = \sqrt{\epsilon }\, \bar{x},\quad y = \epsilon \, \bar{y},\quad z = \sqrt{\epsilon }\, \bar{z},\quad \frac{1}{2} \mu \sqrt{\epsilon }\, t = \theta , \end{aligned}$$

(5.39)

which transforms the normal form (5.1) into

$$\begin{aligned} {{\mathrm{d}}}\!\bar{x}_\theta&= \frac{2}{\mu }\bigl [ \bar{y}_\theta - \bar{x}_\theta ^2 + {\mathcal {O}}(\sqrt{\epsilon }\,) \bigr ] {{\mathrm{d}}}\!\theta + \sqrt{\frac{2}{\mu }}\, \bigl [ \bar{\sigma } \widehat{F}_1(\bar{x}_\theta ,\bar{y}_\theta ,\bar{z}_\theta ) + \bar{\sigma }^{\prime }\sqrt{\epsilon }\, \widehat{F}_2(\bar{x}_\theta ,\bar{y}_\theta ,\bar{z}_\theta ) \bigr ] {{\mathrm{d}}}\!W_\theta ,\nonumber \\ {{\mathrm{d}}}\!\bar{y}_\theta&= \frac{2}{\mu }\bigl [ -(1+\mu )\bar{x}_\theta - \bar{z}_\theta + {\mathcal {O}}(\sqrt{\epsilon }\,) \bigr ] {{\mathrm{d}}}\!\theta + \sqrt{\frac{2}{\mu }}\, \bar{\sigma }^{\prime } \widehat{G}_1(\bar{x}_\theta ,\bar{y}_\theta ,\bar{z}_\theta ) {{\mathrm{d}}}\!W_\theta ,\nonumber \\ {{\mathrm{d}}}\!\bar{z}_\theta&= {{\mathrm{d}}}\!\theta + \sqrt{\frac{2}{\mu }}\, \bar{\sigma }^{\prime }\sqrt{\epsilon }\, \widehat{G}_2(\bar{x}_\theta ,\bar{y}_\theta ,\bar{z}_\theta ){{\mathrm{d}}}\!W_\theta , \end{aligned}$$

(5.40)

where

$$\begin{aligned} \bar{\sigma } = \epsilon ^{-3/4}\sigma \qquad \text {and}\qquad \bar{\sigma }^{\prime } = \epsilon ^{-3/4}\sigma ^{\prime }. \end{aligned}$$

(5.41)

The deviation $\zeta _\theta$ from the deterministic solution $(\bar{x}^{\det }_\theta ,\bar{y}^{\det }_\theta ,\bar{z}^{\det }_\theta )$, defined as in (5.7), satisfies a SDE of the form

$$\begin{aligned} {{\mathrm{d}}}\!\zeta _\theta = \frac{1}{\mu } {\mathcal {A}}(\theta )\zeta _\theta {{\mathrm{d}}}\!\theta + \frac{1}{\sqrt{\mu }} \begin{pmatrix} \bar{\sigma }{\mathcal {F}}_1(\zeta _\theta ,\theta ) + \bar{\sigma }^{\prime }\sqrt{\epsilon }\,{\mathcal {F}}_2(\zeta _\theta ,\theta ) \\ \bar{\sigma }^{\prime } {\mathcal {G}}_1(\zeta _\theta ,\theta ) \\ \bar{\sigma }^{\prime }\sqrt{\epsilon }\, {\mathcal {G}}_2(\zeta _\theta ,\theta ) \end{pmatrix} {{\mathrm{d}}}\!W_\theta + \frac{1}{\mu }\begin{pmatrix} b_x(\zeta _\theta ,\theta ) \\ \sqrt{\epsilon }\,b_y(\zeta _\theta ,\theta ) \\ 0 \end{pmatrix} {{\mathrm{d}}}\!\theta . \end{aligned}$$

(5.42)

The principal solution of $\mu \dot{\zeta }= {\mathcal {A}}(\theta )\zeta$ has a block structure similar to (5.9). Provided we take $\delta$ sufficiently small, the upper left block $A(\theta )$ has complex conjugated eigenvalues $a(\theta )\pm 2{{\mathrm{i}}}\omega (\theta )$, where

$$\begin{aligned} a(\theta ) = -2\bar{x}^{\det }_\theta + {\mathcal {O}}(\sqrt{\epsilon }\,), \qquad \omega (\theta ) = \sqrt{1 - (\bar{x}^{\det }_\theta )^2 + \mu } \, + {\mathcal {O}}(\sqrt{\epsilon }\,). \end{aligned}$$

(5.43)

By [17, Theorem 4.3], the principal solution $V(\theta ,\phi )$ of $\mu \dot{\xi }= A(\theta )\xi$ can be written in the form

$$\begin{aligned} V(\theta ,\theta _0) = {{\mathrm{e}}}^{\alpha (\theta ,\theta _0)/\mu } S(\theta ) \begin{pmatrix} \cos (\phi (\theta ,\theta _0)/\mu ) &{} \sin (\phi (\theta ,\theta _0)/\mu ) \\ -\sin (\phi (\theta ,\theta _0)/\mu ) &{} \cos (\phi (\theta ,\theta _0)/\mu ) \end{pmatrix} S(\theta _0)^{-1}, \end{aligned}$$

(5.44)

where

$$\begin{aligned} S(\theta ) = \frac{1}{\sqrt{\omega (\theta )}} \begin{pmatrix} - \theta + \omega (\theta ) &{} -\theta - \omega (\theta ) \\ 1 &{} 1 \end{pmatrix} + {\mathcal {O}}(\mu ), \end{aligned}$$

(5.45)

and

$$\begin{aligned} \alpha (\theta ,\theta _0) = \int _{\theta _0}^\theta a(\psi ){{\mathrm{d}}}\!\psi , \qquad \phi (\theta ,\theta _0) = \int _{\theta _0}^\theta 2\omega (\psi ){{\mathrm{d}}}\!\psi +{\mathcal {O}}(\mu ). \end{aligned}$$

(5.46)

The off-diagonal term in the principal solution of $\mu \dot{\zeta }= {\mathcal {A}}(\theta )\zeta$ has the form

$$\begin{aligned} U_{\xi \eta }(\theta ,\theta _0)&= \frac{1}{\mu } \int _{\theta _0}^\theta V(\theta ,\psi ) c_1(\psi ){{\mathrm{d}}}\!\psi \nonumber \\&= \frac{1}{\mu } \int _{\theta _0}^\theta {{\mathrm{e}}}^{\alpha (\theta ,\psi )/\mu } \biggl [ \cos \biggl ( \frac{\phi (\theta ,\psi )}{\mu }\biggr ) v_1 + \sin \biggl ( \frac{\phi (\theta ,\psi )}{\mu }\biggr ) v_2\biggr ]{{\mathrm{d}}}\!\psi \end{aligned}$$

(5.47)

for some vectors $v_1, v_2$. Using integration by parts and the fact that the eigenvalues $a\pm {{\mathrm{i}}}\omega$ are bounded away from 0, one shows that the elements of $U_{\xi \eta }$ are of order 1 at most. The next proposition then follows in the same way as before.

Proposition 5.7

Define stopping times

$$\begin{aligned} \tau _{\xi }&= \inf \{\theta >\theta _0:\left\| \xi _\theta \right\| >h\}, \nonumber \\ \tau _{\eta }&= \inf \{\theta >\theta _0:|\eta _\theta |>h_1\}. \end{aligned}$$

(5.48)

There exist constants $\kappa , h_0 > 0$ such that for all $\theta _0 \leqslant \theta \leqslant \sqrt{\mu }$, and all $0<h, h_1 \leqslant \sqrt{\mu }$,

$$\begin{aligned}&\mathbb {P}\bigl \{ \tau _\xi \wedge \tau _\eta > \theta \bigr \} \leqslant \biggl \lceil \frac{\theta -\theta _0}{\mu }\biggr \rceil \biggl (\exp \biggl \{ - \frac{\kappa [h-\mu ^{-1/2}(h^2+h_1^2)]^2}{(\bar{\sigma }^2+(\bar{\sigma }^{\prime })^2)\mu ^{-1/2}}\biggr \}\nonumber \\&\qquad \qquad +\, \exp \biggl \{\!- \frac{\kappa h^2}{(\bar{\sigma }^2\!+\!(\bar{\sigma }^{\prime })^2)\epsilon \mu ^{-1}(\theta \!-\theta _0)}\biggr \} \!+\! \exp \biggl \{ - \frac{\kappa h_1^2}{(\bar{\sigma }^{\prime })^2\epsilon \mu ^{-1}(\theta -\theta _0)}\biggr \} \biggr ). \qquad \end{aligned}$$

(5.49)

These estimates show that if the deterministic solution hits $\Sigma _1^{\prime \prime }$ at a point such that $\bar{z}\leqslant \sqrt{\mu }$, and provided $\epsilon (\theta -\theta _{0})\leqslant \sqrt{\mu }$ and $\bar{\sigma }+\bar{\sigma }^{\prime } \ll \mu ^{3/4}$, the typical spreadings are

$$\begin{aligned} \Delta \bar{y} \asymp (\bar{\sigma } + \bar{\sigma }^{\prime }) \biggl (\frac{1}{\mu ^{1/4}} + \frac{\epsilon ^{1/2}(\theta -\theta _0)^{1/2}}{\mu ^{1/2}}\biggr ) \qquad \text {and}\qquad \Delta \bar{z} \asymp \frac{\bar{\sigma }^{\prime }\epsilon ^{1/2}(\theta -\theta _0)^{1/2}}{\mu ^{1/2}}.\quad \end{aligned}$$

(5.50)

In particular, if $\theta -\theta _0\asymp \mu ^{1/2}$, going back to original variables we find that provided $\sigma +\sigma ^{\prime } \ll (\epsilon \mu )^{3/4}$, the typical spreadings on $\Sigma _1^{\prime \prime }$ are of order

• $(\sigma +\sigma ^{\prime })(\epsilon /\mu )^{1/4}$ in the $y$-direction,

• and $\sigma ^{\prime }(\epsilon /\mu )^{1/4}$ in the $z$-direction.

Remark 5.8

Theorem 6.2 in [17] provides a more precise description of the dynamics, in a slightly simpler setting (in particular without noise on the $z$-variable): it shows that sample paths concentrate in a “covariance tube” centred in the deterministic solution. The size of the tube is compatible with the above estimates on noise-induced spreading. Such a refined analysis is possible in the present setting as well, but it would require some more work, mainly in order to control the effect of the position-dependence of the noise term.

Remark 5.9

It is possible to extend Estimate (5.49) to slightly larger $\theta$, at the cost of replacing $\mu ^{-1/2}$ in the denominator by $\mu ^{-1/2}{{\mathrm{e}}}^{2c\theta ^2/\mu }$ for some $c>0$. This is due to the exponential growth of the variance for $\theta >\sqrt{\mu }$.

5.5 Escape

In this subsection, we fix an initial condition $(-\delta \sqrt{\epsilon },y_0,z_0) \in \Sigma _1^{\prime \prime }$, sufficiently close to the folded-node point $p^*$, and estimate the fluctuations of sample paths up to their first hitting of $\Sigma _2 = \{x=-\delta _0\}$.

Proposition 5.10

Denote by $(y^*,z^*)$ the point where the deterministic solution starting in $(x_0=-\delta \sqrt{\epsilon },y_0,z_0)\in \Sigma _1^{\prime \prime }$ first hits $\Sigma _2 = \{ x=-\delta _0 \}$. Assume $y_0 \leqslant x_0^2 - \epsilon (\frac{1+\mu }{2}+c_0)$ for a constant $c_0>0$, and $0\leqslant z_0\leqslant {\mathcal {O}}(\sqrt{\epsilon })$. For sufficiently small $\delta , \delta _0>0$, there exist $C, \kappa , h_0>0$ such that for all $h_1, h_2>0$ satisfying $h_1\leqslant h_0\epsilon$ and $h_2\leqslant h_0\sqrt{h_1}$, the stochastic sample path starting in $(x_0,y_0,z_0)$ first hits $\Sigma _2$ at time $\tau =\tau _{\Sigma _2}$ in a point $(-\delta _0, y_{\tau }, z_{\tau })$ such that

$$\begin{aligned}&\mathbb {P}^{(x_0,y_0,z_0)} \left\{ |y_{\tau } - y^*| > h_1 \text { or } |z_{\tau } - z^*| > h_2 \right\} \nonumber \\&\quad \leqslant C\left| {\log \epsilon }\right| \biggl ( \exp \biggl \{ -\frac{\kappa h_1^2}{(\sigma ^2 + (\sigma ^{\prime })^2)\sqrt{\epsilon }\,}\biggr \} + \exp \biggl \{ -\frac{\kappa h_2^2}{ (\sigma ^{\prime })^2\sqrt{\epsilon }\,}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon ^{3/2}}{\sigma ^2 + (\sigma ^{\prime })^2\epsilon }\biggr \} \biggr ).\nonumber \\ \end{aligned}$$

(5.51)

The result remains true uniformly in initial conditions $(x_0,y,z)$ such that $|y-y_0|\leqslant h_1$ and $|z-z_0|\leqslant h_2$.

Proof

The proof is basically the same as the proof of Proposition 4.9, so we will omit its details. We introduce sections $\Sigma ^*_n=\{x=-\delta \sqrt{\epsilon }\,2^n, (y,z)\in D_n\}$, where each $D_{n+1}$ is obtained by enlarging the image of $D_n$ under the deterministic flow by order $h_12^{-n/2}$ in the $y$-direction, and by order $h_22^{-n/2}$ in the $z$-direction. Choosing $D_1$ as a rectangle of size $2h_1\times 2h_2$ allows to deal with more general initial conditions. Let $\tau ^{(n)}$ denote the first-exit time from a block of dimensions $2h\times 2h_1\times 2h_2$ centred in a given deterministic solution.

Then the analogue of Lemma 4.7 reads

$$\begin{aligned} \mathbb {P}^{(x_n,y_n,z_n)}\bigl \{ \tau _{n+1}\wedge \tau ^{(n)} > c\delta 2^{-n}\mu \bigr \} \leqslant \exp \biggl \{ -\frac{\kappa \delta ^22^{3n}\epsilon ^{3/2}}{\sigma ^2+(\sigma ^{\prime })^2\epsilon } \biggr \}, \end{aligned}$$

(5.52)

while the equivalent of Lemma 4.8 is

$$\begin{aligned}&\mathbb {P}^{(x_n,y_n,z_n)}\bigl \{ \tau ^{(n)} < c\delta 2^{-n}\mu \bigr \} \nonumber \\&\quad \leqslant \exp \biggl \{ -\frac{\kappa h^2\sqrt{\epsilon }}{\delta [\sigma ^2\!+\!(\sigma ^{\prime })^22^{-2n}]} \biggr \} + \exp \biggl \{ -\frac{\kappa h_1^2}{\delta \sqrt{\epsilon }[\sigma ^2\delta ^22^{-2n}\!+\!(\sigma ^{\prime })^2]} \biggr \} + \exp \biggl \{ -\frac{\kappa h_2^2}{\delta (\sigma ^{\prime })^2\sqrt{\epsilon }} \biggr \}. \end{aligned}$$

(5.53)

The remainder of the proof is similar to the proof of Proposition 4.9, after redefining $\kappa$. $\square$

This result shows that if $\sigma +\sigma ^{\prime }\ll \epsilon ^{3/4}$, for a given initial condition on $\Sigma _1^{\prime \prime }$, the spreading in the $y$- and $z$-directions on $\Sigma _2$ is of order

$$\begin{aligned} (\sigma + \sigma ^{\prime })\epsilon ^{1/4} \qquad \text {and}\qquad \sigma ^{\prime }\epsilon ^{1/4}. \end{aligned}$$

(5.54)

6 From Noisy Returns to Markov Chains

In this section we combine the results from the last three sections to obtain estimates on the kernel $K$ of the random Poincaré map on $\Sigma _1$. Table 1 summarizes the results obtained so far. For each part of the dynamics, it shows the typical size of fluctuations when starting in a point on the previous section. Deviations will not necessarily add up because of the contraction during some phases of the motion.

Table 1 Summary of results on the size of fluctuations at the time of first hitting a section $\Sigma _j$, when starting from a specific point on $\Sigma _i$, under the assumption $\sigma +\sigma ^{\prime } \ll \epsilon ^{3/4}$, cf. Fig. 3

6.1 The Global Return Map

The following result describes the global return map $\Sigma _2\rightarrow \Sigma _1$.

Theorem 6.1

(Global return map) Fix $P_2=(x^*_2,y^*_2,z^*_2)\in \Sigma _2$. Assume the deterministic orbit starting in $P_2$ hits $\Sigma _1$ for the first time in $P_1=(x^*_1,y^*_1,z^*_1)$. Then there exist constants $h_0, \kappa , C >0$ such that for all $h\leqslant h_0$ and $h^2/h_0 \leqslant h_1 \leqslant h$, the stochastic sample path starting in $P_2$ hits $\Sigma _1$ for the first time in a point $(x_1,y^*_1,z_1)$ satisfying

$$\begin{aligned}&\mathbb {P}^{P_2} \bigl \{ |x_1 - x^*_1| > h \text { or } |z_1 - z^*_1| > h_1 \bigr \} \nonumber \\&\quad \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa h^2}{\sigma ^2 \!+\! (\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa h_1^2}{\sigma ^2\epsilon |\log \epsilon |\! +\! (\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon }{\sigma ^2 + (\sigma ^{\prime })^2\epsilon ^{-1/3}}\biggr \} \biggr ). \nonumber \\ \end{aligned}$$

(6.1)

Proof

Denote by $(x^*_i,y^*_i,z^*_i)$ the deterministic first-hitting point of section $\Sigma _i$, and by $(x_i,y_i,z_i)$ the corresponding random first-hitting point. We use similar notations for $\Sigma _4^{\prime }$. We will decompose the dynamics into three main steps, and introduce the events

$$\begin{aligned} \Omega _1(h,h_1)&= \bigl \{ |x_4^{\prime } - (x_4^{\prime })^*| \leqslant h, |z_4^{\prime } - (z_4^{\prime })^*| \leqslant h_1\bigr \}, \nonumber \\ \Omega _2(H_1)&= \bigl \{ \left\| (y_5,z_5) - (y^*_5,z^*_5)\right\| \leqslant H_1 \bigr \}. \end{aligned}$$

(6.2)

• Step 1: $\Sigma _2 \rightarrow \Sigma _3 \rightarrow \Sigma _4 \rightarrow \Sigma _4^{\prime }$. Propositions 3.3 and 4.3 can be applied simultaneously, because they are based on the same kind of estimates of the principal solution. This directly yields the bound

  $$\begin{aligned} \mathbb {P}^{P_2}\bigl (\Omega _1(h,h_1)^c\bigr ) \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa h^2}{\sigma ^2\epsilon ^{-1/3} + (\sigma ^{\prime })^2\epsilon ^{-2/3}}\biggr \} + \exp \biggl \{ -\frac{\kappa h_1^2}{\sigma ^2\epsilon |\log \epsilon | + (\sigma ^{\prime })^2}\biggr \}\biggr ) \end{aligned}$$

  (6.3)

  for some $C>0$, which is valid for all $h, h_1$ satisfying $h\leqslant h_0\epsilon ^{1/3}$, $h_1\leqslant h_0$, $h^2\leqslant h_0h_1$ and $h_1^2\leqslant h_0h\epsilon ^{1/3}$.

• Step 2: $\Sigma _4^{\prime } \rightarrow \Sigma _5$. The difference $\zeta _\theta$ between two deterministic solutions starting on $\Sigma _4^{\prime }$ satisfies a relation of the form

  $$\begin{aligned} \zeta _\theta = U(\theta ,\theta _0) \zeta _{\theta _0} + \int _{\theta _0}^\theta U(\theta ,\phi ) b(\zeta _\phi ,\phi ) {{\mathrm{d}}}\!\phi , \end{aligned}$$

  (6.4)

  where $b(\zeta ,\phi )$ is a nonlinear term. Using the estimates on the principal solution (cf. (4.50) in the proof of Lemma 4.8), one obtains that the deterministic orbit starting in $(\hat{x}_4,(y_4^{\prime })^*,\hat{z}_4)\in \Sigma _4^{\prime }$ hits $\Sigma _5$ at a point $(x^*_5,\hat{y}_5,\hat{z}_5)$ satisfying

  $$\begin{aligned} \left\| (\hat{y}_5,\hat{z}_5)-(y^*_5,z^*_5)\right\| \leqslant M\epsilon ^{2/3}|\hat{x}_4 - (x_4^{\prime })^*| + M|\hat{z}_4 - (z_4^{\prime })^*| \end{aligned}$$

  (6.5)

  for some constant $M>0$. Proposition 4.9 yields that for $H_1\leqslant h_0\epsilon ^{2/3}$,

  $$\begin{aligned}&\mathbb {P}^{P_2}\Bigl (\Omega _1(h,h_1) \cap \Omega _2(H_1)^c \Bigr ) \nonumber \\&\qquad \leqslant C|\log \epsilon |\biggl (\exp \biggl \{ -\frac{\kappa (H_1-M[\epsilon ^{2/3}h+h_1])^2}{\sigma ^2\epsilon + (\sigma ^{\prime })^2\epsilon ^{1/3}}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon }{\sigma ^2+(\sigma ^{\prime })^2\epsilon }\biggr \} \biggr ). \end{aligned}$$

  (6.6)

  We now choose $h_1 = H_1/(3M)$ and $h = \epsilon ^{1/3} \wedge H_1/(3M\epsilon ^{2/3})$. Distinguishing the cases $h = \epsilon ^{1/3}$ and $h = H_1/(3M\epsilon ^{2/3})$ when using (6.3), this yields

  $$\begin{aligned} \mathbb {P}^{P_2}\bigl (\Omega _2(H_1)^c\bigr ) \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa H_1^2}{\sigma ^2\epsilon |\log \epsilon | + (\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon }{\sigma ^2 + (\sigma ^{\prime })^2\epsilon ^{-1/3}}\biggr \}\biggr ), \end{aligned}$$

  (6.7)

  where $\kappa$ has been redefined.

• Step 3: $\Sigma _5 \rightarrow \Sigma _6 \rightarrow \Sigma _1$. A similar argument as above shows that two deterministic solutions starting at distance $H_1$ on $\Sigma _5$ hit $\Sigma _1$ at a distance of order $H_1$. The result then follows from Proposition 3.3 and (6.7), choosing $H_1=\epsilon ^{2/3}\wedge ch_1$ for a sufficiently small constant $c$.$\square$

This result is useful if $\sigma \ll \sqrt{\epsilon }$ and $\sigma ^{\prime }\ll \epsilon ^{2/3}$. It shows that stochastic sample paths are likely to hit $\Sigma _1$ at a distance of order $\sigma +\sigma ^{\prime }$ in the fast directions from the deterministic solution, and at a distance of order $\sigma \sqrt{\epsilon |\log \epsilon |}+\sigma ^{\prime }$ in the slow direction.

6.2 The Local Map

We know from the deterministic analysis (cf. (5.16)) that the section $\Sigma _1$ can be subdivided into $k_\mu \simeq 1/(2\mu )$ sectors of rotation. An orbit starting in the $k$ th sector makes $2k+1$ half-turns before hitting $\Sigma _2$. The width of the $k$ th sector has order $\epsilon ^{(1-\mu )/2}$, cf. [24]. The analysis of Sect. 5.3 shows that the images of these sectors on $\Sigma _1^{\prime }$ have a size of order $\mu \epsilon$.

Fig. 8

Inner (blue) and outer (green) canards. The shaded sets indicate the extension of typical fluctuations (Color figure online)

For the stochastic system, it will be relevant to distinguish (Fig. 8) between

• inner sectors, which are sectors with $k\leqslant {\mathcal {O}}(1/\sqrt{\mu })$; orbits starting in these sectors hit $\Sigma _1^{\prime \prime }$ for $z\leqslant {\mathcal {O}}(\sqrt{\epsilon \mu })$;

• outer sectors, which are sectors with $k>{\mathcal {O}}(1/\sqrt{\mu })$.

Theorem 6.2

(Local return map for inner sectors) Fix $P_0=(x^*_0,y^*_0,z^*_0)\in \Sigma _1$, and suppose that $P_0$ lies in an inner sector. Assume the deterministic orbit starting in $P_0$ hits $\Sigma _2$ for the first time in $P_2=(x^*_2,y^*_2,z^*_2)$. Further assume $\epsilon \leqslant \mu$. Then there exist constants $h_0, \kappa , C >0$ such that for all $h\leqslant h_0\epsilon \sqrt{\mu }$ and $h_2\leqslant h_0 (\sqrt{h_1}\wedge \sqrt{\epsilon \mu }\,)$, the stochastic sample path starting in $P_0$ hits $\Sigma _2$ for the first time in a point $(x^*_2,y_2,z_2)$ satisfying

$$\begin{aligned}&\mathbb {P}^{P_0} \bigl \{ |y_2 - y^*_2| > h_1 \text { or } |z_2 - z^*_2| > h_2 \bigr \} \nonumber \\&\quad \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa h_1^2\sqrt{\mu }}{(\sigma ^2 + (\sigma ^{\prime })^2)\sqrt{\epsilon }}\biggr \} + \exp \biggl \{ -\frac{\kappa h_2^2}{(\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon ^{3/2}}{\sigma ^2 + (\sigma ^{\prime })^2}\biggr \} \biggr ). \qquad \end{aligned}$$

(6.8)

Proof

We introduce the events

$$\begin{aligned} \Omega _1(h_1,h_2)&= \bigl \{ |y_1^{\prime } - (y_1^{\prime })^*| \leqslant h_1,|z_1^{\prime } - (z_1^{\prime })^*| \leqslant h_2\bigr \}, \nonumber \\ \Omega _2(H_1,H_2)&= \bigl \{ |y_1^{\prime \prime } - (y_1^{\prime \prime })^*| \leqslant H_1, |z_1^{\prime \prime } - (z_1^{\prime \prime })^*| \leqslant H_2\bigr \}, \end{aligned}$$

(6.9)

where $(y_1^{\prime },z_1^{\prime })$ and $(y_1^{\prime \prime },z_1^{\prime \prime })$ denote the first-hitting points of the stochastic path with $\Sigma _1^{\prime }$ and $\Sigma _1^{\prime \prime }$, and the starred quantities are the corresponding deterministic hitting points. Proposition 5.3 with $h$ of order $\sqrt{\epsilon }$ implies

$$\begin{aligned} \mathbb {P}^{P_0}(\Omega _1(h_1,h_2)^c) \!\leqslant \! \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa h_1^2}{(\sigma ^2 + (\sigma ^{\prime })^2)\sqrt{\epsilon }} \biggr \} + \exp \biggl \{ -\frac{\kappa h_2^2}{(\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon ^{3/2}}{\sigma ^2+(\sigma ^{\prime })^2}\biggr \} \biggr )\nonumber \\ \end{aligned}$$

(6.10)

for some $C>0$. Using this bound with $h_1$ of order $H_1$ and $h_2$ of order $H_1\wedge H_2$, together with Proposition 5.7 to estimate the probability of $\Omega _1\cap \Omega _2^c$ and the assumption $\epsilon \leqslant \mu$ yield

$$\begin{aligned} \mathbb {P}^{P_0}(\Omega _2(H_1,H_2)^c) \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa H_1^2\sqrt{\mu }}{(\sigma ^2\!+\!(\sigma ^{\prime })^2)\sqrt{\epsilon }} \biggr \} + \exp \biggl \{ -\frac{\kappa H_2^2}{(\sigma ^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon ^{3/2}}{\sigma ^2\!+\!(\sigma ^{\prime })^2}\biggr \} \biggr ).\nonumber \\ \end{aligned}$$

(6.11)

The result then follows from Proposition 5.10, taking $h_1=H_1$ and $h_2=H_2$. $\square$

This result is useful if $\sigma , \sigma ^{\prime }\ll (\epsilon \mu )^{3/4}$. It shows that stochastic sample paths are likely to hit $\Sigma _2$ at a distance of order $(\sigma +\sigma ^{\prime })(\epsilon /\mu )^{1/4}$ in the $y$-direction from the deterministic solution, and at a distance of order $\sigma ^{\prime }$ in the $z$-direction. Combining this with Theorem 6.1 on the global return map, we conclude that for initial conditions $P_0\in \Sigma _1$, starting in a inner sector, stochastic sample paths will return to $\Sigma _1$ in a neighbourhood of the deterministic solution, of width

• $\sigma +\sigma ^{\prime }$ in the fast $x$-direction,

• $\sigma \sqrt{\epsilon |\log \epsilon |} + \sigma ^{\prime }$ in the $z$-direction.

Remark 6.3

The limitation $k\leqslant {\mathcal {O}}(1/\sqrt{\mu })$ is due to the fact that Proposition 5.7 is formulated for $\theta \leqslant \sqrt{\mu }$. Using Remark 5.9, Theorem 6.2 can be extended to sectors $k=\sqrt{a|\log (\sigma +\sigma ^{\prime })|/\mu }$, which results in fluctuations of $y$ of order $(\sigma +\sigma ^{\prime })^{1-ca}(\epsilon /\mu )^{1/4}$. This does not affect the order of fluctuations in the $z$-direction as long as $a$ is small enough.

Fig. 9

Escape of sample paths starting in an outer sector from a neighbourhood of the weak canard $\gamma ^w$

Finally, we consider what happens to sample paths starting on $\Sigma _1$ in an outer sector.

Theorem 6.4

(Local return map for outer sectors) Fix $P_0=(x^*_0,y^*_0,z^*_0)\in \Sigma _1$, and assume $P_0$ lies in an outer sector $k$, with $k\geqslant k_0/\sqrt{\mu }$ for some $k_0>0$. If $k_0$ is large enough, there exist constants $\kappa ,C_0,C,\gamma >0$ such that the stochastic sample path starting in $P_0$ hits $\Sigma _2$ for the first time in a point $(x^*_2,y_2,z_2)$ satisfying

$$\begin{aligned} \mathbb {P}^{P_0} \bigl \{ z_2 \leqslant \sqrt{\epsilon \mu } \bigr \}&\leqslant \frac{C}{\epsilon } \exp \biggl \{ -\frac{\kappa \mu ^{1/2}\epsilon ^{3/2}}{\sigma ^2 + (\sigma ^{\prime })^2}\biggr \} , \end{aligned}$$

(6.12)

$$\begin{aligned} \mathbb {P}^{P_0} \bigl \{ z_2 \geqslant z \bigr \}&\leqslant C_0|\log \sigma |^\gamma \exp \biggl \{ -\frac{\kappa (z^2-\epsilon \mu )}{\epsilon \mu |\log (\sigma + \sigma ^{\prime })|}\biggr \} \qquad \forall z\geqslant \sqrt{\epsilon \mu }. \end{aligned}$$

(6.13)

Furthermore, there exist a constant $h_0>0$ and an interval $I$ of size of order $\epsilon$, independent of $k\geqslant k_0/\sqrt{\mu }$, such that

$$\begin{aligned} \mathbb {P}^{P_0} \bigl \{ {{\mathrm{dist}}}(y_2,I) > h_1 \bigr \} \leqslant \frac{C}{\epsilon } \biggl ( \exp \biggl \{ -\frac{\kappa h_1^2}{(\sigma ^2 + (\sigma ^{\prime })^2)\sqrt{\epsilon }}\biggr \} + \exp \biggl \{ -\frac{\kappa \epsilon ^{3/2}}{\sigma ^2 + (\sigma ^{\prime })^2\epsilon }\biggr \} \biggr ) \end{aligned}$$

(6.14)

holds for all $h_1\leqslant h_0\epsilon$.

Proof

We shall work in the zoomed-in coordinates $(\bar{x},\bar{y}, \bar{z})$, cf. (5.17). Fix a $K_0\in (0,1)$ and introduce a neighbourhood ${\mathcal {D}}$ of the weak canard $\gamma ^w$ given by

$$\begin{aligned} {\mathcal {D}}= \bigl \{ (\bar{x}, \bar{y}, \bar{z}) :K \geqslant K_0, \bar{z} \geqslant \sqrt{\mu } \bigr \} = {\mathcal {D}}_0 \times [\sqrt{\mu },\infty ), \end{aligned}$$

(6.15)

where $K$ is the first integral introduced in (5.27) (recall that $u_1$ and $u_2$ measure the deviation of $(\bar{x},\bar{y})$ from the weak canard)— see Fig. 9. The proof proceeds in four main steps:

• Step 1: Entering ${\mathcal {D}}$. From Theorem 4.4 in [17] describing the spacing of canards, we know that the deterministic solution starting in $P_0$ hits ${\mathcal {D}}$ in a point $P^*_0$ at a distance of order ${{\mathrm{e}}}^{-c(2k+1)^2\mu } < {{\mathrm{e}}}^{-4ck_0^2}$ from the weak canard. Taking $k_0$ sufficiently large, we may assume that $P^*_0$ is bounded away from the boundary $\partial {\mathcal {D}}_0$. Combining, as in the previous theorem, Proposition 5.3 and Proposition 5.7, we obtain that the stochastic sample path first hits ${\mathcal {D}}$ at a point $P_{\tau _z}$ such that

  $$\begin{aligned} \mathbb {P}^{P_0} \bigl \{ (\bar{x}_{\tau _z}, \bar{y}_{\tau _z}) \notin {\mathcal {D}}_0 \bigr \} \leqslant \frac{C}{\epsilon } \exp \biggl \{ -\frac{\kappa \mu ^{1/2}\epsilon ^{3/2}}{\sigma ^2 + (\sigma ^{\prime })^2}\biggr \}. \end{aligned}$$

  (6.16)

  This proves in particular (6.12).

• Step 2: Leaving ${\mathcal {D}}$. Theorem 6.4 in [17] estimates the probability of sample paths not leaving a neighbourhood of the weak canard. Because we worked in polar coordinates, the result only applied to a small neighbourhood of size proportional to $\sqrt{\bar{z}}$. However by using the coordinate $K$ instead of the distance to $\gamma ^w$, the same proof applies to the exit from ${\mathcal {D}}$. It suffices to realize that the nonlinear drift term $\beta$ in Equation (D.33) of [17] is replaced by a term of order $\bar{z}$ as a consequence of Proposition 5.5. We thus conclude that the sample path leaves ${\mathcal {D}}$ at a point $P_{\tau _{\mathcal {D}}}$ whose $\bar{z}$-coordinate satisfies

  $$\begin{aligned} \mathbb {P}^{P_0} \bigl \{ \bar{z}_{\tau _{\mathcal {D}}} \geqslant \bar{z} \bigr \} \leqslant C_0|\log \bar{\sigma }|^\gamma \exp \biggl \{ -\frac{\kappa (\bar{z}^2-\mu )}{\mu \log |\bar{\sigma } + \bar{\sigma }^{\prime }|}\biggr \} \qquad \forall \bar{z}\geqslant \sqrt{\mu } \end{aligned}$$

  (6.17)

  for some constants $C_0, \gamma >0$.

• Step 3: Transition from ${\mathcal {D}}$ to $\Sigma _1^{\prime \prime }$. Since $P_{\tau _{\mathcal {D}}}$ is at distance of order 1 from the weak canard, we know that the deterministic solutions starting in $P_{\tau _{\mathcal {D}}}$ will take a time of order $\mu$ to reach $\Sigma _1^{\prime \prime }$, in a point that we will denote $P_1^*=(\bar{x}^*_1,\bar{y}^*_1, \bar{z}^*_1)$. Let $P_1=(\bar{x}^*_1,\bar{y}_1, \bar{z}_1)$ denote the point where the stochastic sample path first hits $\Sigma _1^{\prime \prime }$. Starting from System (5.40) and applying the usual procedure, we obtain the estimate

  $$\begin{aligned}&\mathbb {P}^{P_{\tau _{\mathcal {D}}}} \bigl \{ |\bar{y}_1-\bar{y}^*_1| > \bar{h}_1 \text { or } |\bar{z}_1-\bar{z}^*_1| > \bar{h}_2 \bigr \} \nonumber \\&\quad \leqslant {C} \biggl ( \exp \biggl \{ -\frac{\kappa [\bar{h}_1 - M(\bar{h}_1^2+\bar{h}_2^2)]^2}{\bar{\sigma }^2+(\bar{\sigma }^{\prime })^2}\biggr \} + \exp \biggl \{ -\frac{\kappa \bar{h}_2^2}{(\bar{\sigma }^{\prime })^2\epsilon }\biggr \} \biggr ). \end{aligned}$$

  (6.18)

  Note that this implies fluctuations of size $\bar{\sigma }+\bar{\sigma }^{\prime }$ in the $\bar{y}$-direction, and of size $\bar{\sigma }^{\prime }\sqrt{\epsilon }$ in the $\bar{z}$-direction. Going back to original variables, this entails fluctuations of size $(\sigma +\sigma ^{\prime })\epsilon ^{1/4}$ in the $y$-direction, and $\sigma ^{\prime }\epsilon ^{1/4}$ in the $z$-direction. We also have to take into account the fact that we do not know the $(\bar{x},\bar{y})$-coordinates of $P_{\tau _{\mathcal {D}}}$. In fact all exit points on $\partial {\mathcal {D}}_0$ might have a comparable probability. Hence the coordinate $\bar{y}^*_1$ can vary in an interval $I_1$, which is the image of $\partial {\mathcal {D}}_0$ under the deterministic flow. It follows from (5.25) that $I_1$ has a size of order $\bar{z}^*_1$ in $\bar{y}$-coordinates.

• Step 4: Transition from $\Sigma _1^{\prime \prime }$ to $\Sigma _2$. If $P_1$ satisfied $y_1 \leqslant x_1^2 - \epsilon (\frac{1+\mu }{2}+c_0)$ for some $c_0>0$, or equivalently $\eta _1\leqslant -c_0$, we could directly apply Proposition 5.10 to estimate the fluctuations during the last transition step, which would remain of the same order as in Step 3. The estimate (5.25) shows that $P_1$ is too close to the repelling slow manifold $C^r_\epsilon$ to apply Proposition 5.10 directly. However, using (5.40), we obtain that the variable $\eta$ measuring the distance to $C^r_\epsilon$ satisfies an equation of the form

  $$\begin{aligned} {{\mathrm{d}}}\!\eta _\theta = \frac{2}{\mu } \Bigl [ -2\bar{x}_\theta \eta _\theta - \bar{z}_\theta + {\mathcal {O}}\bigl (\sqrt{\epsilon }(1+|\bar{x}_\theta |)\bigr )\Bigr ] {{\mathrm{d}}}\!\theta + \sqrt{\frac{2}{\mu }} \bigl [ \bar{\sigma } \widetilde{G}_1 + \bar{\sigma }^{\prime } \widetilde{G}_2\bigr ] {{\mathrm{d}}}\!W_\theta .\quad \end{aligned}$$

  (6.19)

  We have used that we may assume $\sigma , \sigma ^{\prime } \ll \sqrt{\epsilon }$ to simplify the error term (for larger noise intensities, the main results of the theorem become meaningless). Using the same approach as in [15, Sect. 3.2] or [17, Section D], one can show that $\eta _\theta$ is likely to leave $[-c_0,c_0]$ in a time $\theta$ of order $\mu \sqrt{|\log (\bar{\sigma }+\bar{\sigma }^{\prime })|}$. During this time interval, $\bar{x}_\theta$ decreases by an amount of order $\sqrt{|\log (\bar{\sigma }+\bar{\sigma }^{\prime })|}$. Either this exit takes place in the direction of negative $\eta$, and we can apply again Proposition 5.10. Or it takes place in the direction of positive $\eta$, and the sample path makes one more excursion towards $C_\epsilon ^{a+}$ (backward canard). In this case we have to use one more time the analysis of Step 3 before applying again Proposition 5.10. Finally, one can check that the deterministic flow maps the set of points where paths escape $\{-c_0\leqslant \eta \leqslant c_0\}$ to points in $\Sigma _2$ with a $y$-coordinate in an interval $I$ of size ${\mathcal {O}}(\epsilon )$.$\square$

The important point of Theorem 6.4 is that the bounds on the distribution of $(y_2,z_2)$ are independent of the starting sector number $k$, as soon as $k>k_0/\sqrt{\mu }$. Thus we observe a saturation effect, in the sense that the stochastic Poincaré map becomes independent of the initial condition—see Fig. 1. Combining the local result with Theorem 6.1, we see in particular that the size of fluctuations in the $z$-direction is at most of order

$$\begin{aligned} \sqrt{\epsilon \mu |\log (\sigma +\sigma ^{\prime })|} + \sigma \sqrt{\epsilon |\log \epsilon |} + \sigma ^{\prime }. \end{aligned}$$

(6.20)

Disregarding logarithms, we observe that unless $\mu <\sigma ^2\wedge ((\sigma ^{\prime })^{2}/\epsilon )$, the first term will be the dominating one. We conclude that in this regime, the noise-induced fluctuations in the $z$-direction are at most of order $\sqrt{\epsilon \mu |\log (\sigma +\sigma ^{\prime })|}$. However this bound is certainly not sharp, since it uses $z=\sqrt{\epsilon \mu }$ as lower bound of typical exits from a neighbourhood of the weak canard, which may underestimate typical exit times if the noise is weak.

6.3 Consequences for the MMO Patterns

As mentioned in the introduction, which MMO patterns will be observed depends on the following factors:

• 1. in which rotation sector, if any, the Poincaré map admits a fixed point;

• 2. how many SAOs the stochastic system performs when starting at that fixed point;

• 3. whether or not stochastic fluctuations mask the smallest oscillations.

Figure 10 gives a schematic view of the situation. Assume that the deterministic Poincaré map on the section $\Sigma _1$ is such that $z_{n+1}$ is a decreasing function of $z_n$ on average (that is, disregarding the dips caused by canards), as indicated by the blue dashed line. Here we assume that the $z$-axis is oriented in such a way that larger values of $z_n$ lead to more SAOs. When $z_n$ belongs to an inner sector, Theorems 6.1 and 6.2 apply, and show that stochastic sample paths are likely to return to $\Sigma _1$ in the green shaded set, that is, at a distance of order $\sigma \sqrt{\epsilon |\log \epsilon |}+\sigma ^{\prime }$ from the deterministic orbit. When $z_n$ belongs to an outer sector, however, the saturation effect sets in, meaning that stochastic sample paths tend to return to $\Sigma _1$ in the red shaded set, at a coordinate $z_{n+1}$ that no longer depends on the starting point.

Fig. 10

Sketch of the Poincaré map $z_n\mapsto z_{n+1}$ on the section $\Sigma _1$. The dashed blue line indicates the position of the deterministic map, disregarding the canards. $\Pi _1$ denotes the $z$-component of the map $\Sigma _1\rightarrow \Sigma _2$. The saturation effect sets in when $\Pi _1(z_n)$ reaches $\sqrt{\epsilon \mu }$ (Color figure online)

In order to quantify Point 1 listed above, we may consider that the average map $z_n\mapsto z_{n+1}$ induces a map $k_n\mapsto k_{n+1}$ between sectors of rotation given approximately by

$$\begin{aligned} \Pi (k) = {\left\{ \begin{array}{ll} \Pi ^{\det }(k) &{} \text {if }k < k^* \\ \Pi ^{\det }(k^*) &{} \text {if }k\geqslant k^*, \end{array}\right. } \end{aligned}$$

where $\Pi ^{\det }$ is the deterministic map, and $k^*$ is the number of the sector in which the saturation effect sets in. According to the discussion in the previous section (see in particular Remark 6.3), we have

$$\begin{aligned} {\mathcal {O}}(1/\sqrt{\mu }\,) \leqslant k^*(\mu ,\sigma ,\sigma ^{\prime }) \leqslant {\mathcal {O}}(\sqrt{|\log (\sigma +\sigma ^{\prime })|/\mu }\,). \end{aligned}$$

Assume that $\Pi ^{\det }$ is decreasing, and admits a unique fixed point $k^{\det }$. Then the map $\Pi$ admits a fixed point in the sector

$$\begin{aligned} \max \{k^{\det },\Pi ^{\det }(k^*)\}. \end{aligned}$$

Consider now Point 2, i.e., determine the number $n^{\text {stoch}}$ of SAOs associated with the fixed point. Recall that in the deterministic case, the system performs $n^{\det }=k^{\det }$ SAOs (this being the rounded value of the $2k^{\det }+1$ half-turns). If $k^{\det } < k^*$, we have $n^{\text {stoch}}=n^{\det }=k^{\det }$. Otherwise, the number of SAOs will be given by

$$\begin{aligned} n^{\text {stoch}} = \frac{1}{2}\bigl ( \Pi ^{\det }(k^*) + k^* \bigr ) \end{aligned}$$

because the system starts in the sector $\Pi ^{\det }(k^*)$, performs $\Pi ^{\det }(k^*)$ half-turns for $z<0$, and only $k^*$ half-turns for $z>0$ before escaping. Using the fact that $\Pi ^{\det }(k^{\det })=k^{\det }$, it is easy to see that

$$\begin{aligned} n^{\text {stoch}} > n^{\det } \quad \Leftrightarrow \quad \Pi ^{\det }(k^*) + k^* > \Pi ^{\det }(k^{\det })+ k^{\det }. \end{aligned}$$

(6.21)

In other words, the number of SAOs may increase in the presence of noise provided the map $k\mapsto \Pi ^{\det }(k) + k$ is decreasing.

Consider finally Point 3, namely whether the amplitude of SAOs may become so small as to be indistinguishable from random fluctuations due to the noise. In fact, this phenomenon has been analysed in [17, Sect. 6.3]. The results obtained there show that for orbits starting in the sector $k$, fluctuations start dominating the small oscillations near $z=0$ if

$$\begin{aligned} k^2 \mu \geqslant \log \biggl (\frac{\mu ^{1/4}\epsilon ^{3/4}}{\sigma }\biggr ), \end{aligned}$$

(6.22)

where we have already incorporated the zoom-out transformation, cf (5.41). First note that owing to our assumption $\sigma \ll (\epsilon \mu )^{3/4}$, the right-hand side of (6.22) will always be larger than 1. In the saturated regime, the left-hand side is bounded below by $(k^*)^2\mu$, and thus at least of order 1. However, $(k^*)^2\mu$ can be as large as order $|\log (\sigma +\sigma ^{\prime })| = \log (1/(\sigma +\sigma ^{\prime }))$. Thus whether or not the SAOs are masked by fluctutations depends crucially on where $k$ lies in the window of possible values: the SAOs will still be visible as long as $k$ is sufficiently close to $1/\sqrt{\mu }$.

It is important to note that one key component in the previous analysis is the “dynamical skeleton” provided by the global return map for the deterministic system. For example, if the global deterministic return map already generates a highly complicated multi-stable scenario with several possible MMO patterns, then the noise-induced effects can become even more complicated.

7 An Example: The Koper Model

In order to illustrate some of our results numerically, we consider the example of the Koper model [51]. Its deterministic version [59] is given by

$$\begin{aligned} \epsilon _1\dot{x}&= y-x^3+3x,\nonumber \\ \dot{y}&= kx-2(y+\lambda )+z,\nonumber \\ \dot{z}&= \epsilon _2(\lambda +y-z), \end{aligned}$$

(7.1)

with parameters $k$, $\lambda$, $\epsilon _1$, $\epsilon _2$. Note that there is a symmetry

$$\begin{aligned} (x,y,z,\lambda ,k)\mapsto (-x,-y-z,-\lambda ,k) \end{aligned}$$

(7.2)

so that we can restrict the parameter space. We shall assume that $0<\epsilon _1=:\epsilon \ll 1$ and $\epsilon _2=1$ so that (7.1) has the structure (2.1) and Assumption (A0) obviously holds. For a detailed bifurcation analysis we refer to [26, 59].

Of course, if $0<\epsilon _2\ll 1$ one may still simulate the three-scale system numerically, and it is even known via explicit asymptotic analysis which MMO patterns one expects to observe in certain classes of three-scale systems [54]. The first variant of the Koper model was a planar system due to Boissonade and De Kepper [19]. Koper [51] introduced the third variable and studied MMOs via numerical continuation. In fact, the system (7.1) has been suggested independently by various other research groups as a standard model for MMOs [24, 38, 50]. Therefore it certainly provides an excellent test case.

The critical manifold of (7.1) is given by $C_0=\{(x,y,z)\in \mathbb {R}^3:y=c(x)\}$ with $c(x):= x^3-3x$, and the two fold curves are $L^\pm =\{(x,y,z)\in \mathbb {R}^3:x=\pm 1,y=\mp 2\}$. This yields a decomposition

$$\begin{aligned} C_0=C^{a-}_0\cup L^- \cup C^r_0 \cup L^+ \cup C_0^{a+}, \end{aligned}$$

(7.3)

where $C_0^{a-}=C_0\cap \{x<-1\}$, $C^r=C_0\cap \{-1<x<1\}$ and $C_0^{a+}=C_0\cap \{1<x\}$ are normally hyperbolic. It is easy to verify that Assumption (A1) is satisfied.

The desingularized slow subsystem is of the form

$$\begin{aligned} \dot{x}&=kx-2(c(x)+\lambda )+z,\nonumber \\ \dot{z}&= (3x^2-3)(\lambda +c(x)-z). \end{aligned}$$

(7.4)

Note that in (7.4) the direction of time is reversed on $C_0^r$. The only folded equilibria are $(x,z)=(1,2\lambda -4-k)\in L^+$ and $(x,z)=(-1,2\lambda +4+k)\in L^-$. From the linearization of the slow subsystem

$$\begin{aligned} A^\pm =\begin{pmatrix} k &{}\quad 1 \\ 6(2+k\mp \lambda ) &{}\quad 0 \end{pmatrix} \end{aligned}$$

(7.5)

at the folded singularities one may determine the parameter values for which we have a folded node on $L^+$. It turns out that there exist parameter regimes where this is the case, and the only passages of deterministically stable MMO orbits near $L^-$ are via nondegenerate folds [26, 59]. Furthermore, the fast flow is transverse to the relevant drop curves in such a regime [26, 59]. From now on, we shall restrict our attention to this parameter regime so that Assumptions (A2)–(A4) are satisfied in a suitable compact absorbing set in phase space.

Since (7.1) is a phenomenological model, it is not immediate how to derive noise terms so we will just choose correlated additive noise as a first benchmark, setting

$$\begin{aligned} {{\mathrm{d}}}\!x_s&= \frac{1}{\epsilon }(y_{s}-x_{s}^3+3x_{s}){{\mathrm{d}}}\!s+\frac{\sigma }{\sqrt{\epsilon }} F{{\mathrm{d}}}\!W_s,\nonumber \\ {{\mathrm{d}}}\!y_s&= (kx_{s}-2(y_{s}+\lambda )+z_{s}){{\mathrm{d}}}\!s + \sigma ^{\prime } G_1{{\mathrm{d}}}\!W_s,\nonumber \\ {{\mathrm{d}}}\!z_s&= \epsilon _2(\lambda +y_{s}-z_{s}){{\mathrm{d}}}\!s + \sigma ^{\prime } G_2{{\mathrm{d}}}\!W_s, \end{aligned}$$

(7.6)

where the Brownian motion $(W_s)_{s}$ is assumed to be three-dimensional, and $\frac{\sigma }{\sqrt{\epsilon }} F$, $\sigma ^{\prime } G_1$, $\sigma ^{\prime } G_2$ may be viewed as rows of a constant matrix $M\in \mathbb {R}^{3\times 3}$. Figure 11 shows the basic geometry of the Koper model including two orbits computed for $(\epsilon ,k,\lambda )=(0.01,-10,-7)$. One of these orbits is deterministic ($\sigma =0=\sigma ^{\prime }$) and the other one shows a realization of a stochastic sample path computed for $\sigma =0.01=\sigma ^{\prime }$ and

$$\begin{aligned} M=\begin{pmatrix} F\\ G_1\\ G_2 \end{pmatrix} = \begin{pmatrix} 1.0 &{} 0.5 &{} 0.2\\ 0.5 &{} 1.0 &{} 0.3\\ 0.2 &{} 0.3 &{} 1.0 \end{pmatrix}. \end{aligned}$$

(7.7)

Note that the deterministic orbit exhibits an MMO of type $1^11^2$ while the stochastic sample path shows combinations of patterns of the form $1^0$, $1^1$ and $1^2$. Since we proved results about separate phases of the flow we investigate the estimates for each phase as summarized in Table 1.

Fig. 11

Basic structure of the dynamics for the Koper model (7.6). a Phase space with deterministic critical manifold $C_0$ (grey) and the two fold lines $L^\pm$ (blue). Two orbits are also shown, one for the deterministic system ($\sigma =0=\sigma ^{\prime }$, green) and one for the stochastic system ($\sigma =0.01=\sigma ^{\prime }$, black). For both, the parameter values are $\epsilon =0.01$, $k=-10$, $\lambda =-7$, and $M$ is given by (7.7). b Projection of the full system onto the $(x,z)$-plane. c Time series for the two orbits (Color figure online)

Figure 12 illustrates the map $\Sigma _2\rightarrow \Sigma _3$ which describes the fast flow towards the critical manifold $C_0^{a-}$. Several stochastic sample paths are compared with the deterministic solution. In Sect. 3.2 we derived the typical spreading of stochastic sample paths around their deterministic counterpart. It was shown that the typical spreading has an upper bound ${\mathcal {O}}(\sigma +\sigma ^{\prime })$ in the $x$-coordinate and ${\mathcal {O}}(\sigma ^{\prime }+\sigma \sqrt{\epsilon })$ in the $z$-coordinate. Since the typical spreading can be understood as standard deviation, cf. [15, Prop. 3.1.13], Fig. 12b confirms that the theoretical results indeed provide upper bounds (note the scaling on the axes and that $\sigma =0.01=\sigma ^{\prime }$).

Fig. 12

Computation of the transition map $\Sigma _2\rightarrow \Sigma _3$ where the sections (blue) have been defined by the conditions $x=0.5$ and $y=-1.8$ respectively. All paths have been started at $(x,y,z)=(0.5,-2.1,-8)$. There is one deterministic path (green) and 300 different realizations (black) for the stochastic case with $M$ given by (7.7) and $\sigma =0.1=\sigma ^{\prime }$. The relevant part of the critical manifold $C_0^{a+}$ (grey) is shown as well. a Phase space. b View of the landing points on the section $\Sigma _3$ where the landing point of the deterministic path is in the center of the green circle (Color figure online)

To investigate the scaling results further, we computed sample paths going from $\Sigma _2$ to $\Sigma _3$ numerically for a much wider range of noise values as shown in Fig. 13a. For the hitting point on $\Sigma _3$ we plotted the standard deviation of the hitting point’s distance to its deterministic counterpart for the $(x,z)$-coordinates in a $\log$–$\log$ plot for different noise levels with $\sigma =\sigma ^{\prime }$. The slope of 1 for both coordinates in Fig. 13a, b is expected from the upper bounds in Table 1. However, the overall spreading is smaller than expected since we have started the orbits in the vicinity of an attracting deterministic periodic orbit, cf. Fig. 11. Therefore, contraction transverse to the periodic orbit shrinks the stochastic neighbourhood more than the general upper-bound estimates predict. Similarly, we may also study the remaining phases of the flow which are analyzed in Fig. 13b, d. We observe not only the correct asymptotic decrease in size of the stochastic neighbourhood as $\sigma \rightarrow 0$, but also a larger spreading of sample paths near the folded node, see Fig. 13d. This is related to the mechanism that sample paths may jump only with high probability during certain parts of the SAOs after the folded node; this effect has already been discussed in detail in [17] with associated numerics in [17, Sect. 7] so we shall not detail it here.

Fig. 13

Dependence of the standard deviation of the distance between the stochastic and the deterministic transition maps on the noise intensity for an attracting deterministic periodic MMO during various phases of the flow. We have always fixed the matrix $M$ by (7.7), $\epsilon =0.01$ and $\sigma =\sigma ^{\prime }$. The results are shown on a $\log$–$\log$ scale with two directions out of $x$ (red), $y$ (blue) and $z$ (black). The standard deviation std has been computed from $100$ realizations of sample paths and the domain for the noise level was subdivided into $40$ points. a Transition map from $\Sigma _2\rightarrow \Sigma _3$ with $\Sigma _2=\{x=0.5\}$, $\Sigma _3=\{y=-1.8\}$ and $(x_0,y_0,z_0)=(0.5,-2.1,-8)$. b Transition map from $\Sigma _3\rightarrow \Sigma _4$ with $\Sigma _4=\{y=1.8\}$ and $(x_0,y_0,z_0)=(-2,-1.8,-8)$. c Transition map from $\Sigma _4\rightarrow \Sigma _5$ with $\Sigma _5=\{x=-0.5\}$ and $(x_0,y_0,z_0)=(-1.3,1.8,-7.8)$. d Transition map from $\Sigma _1\rightarrow \Sigma _2$ with $\Sigma _1=\{y=-1.8\}$ and $(x_0,y_0,z_0)=(1.3,-1.8,-7.7)$ (Color figure online)

Via the same strategy as in Fig. 13 one may also numerically investigate the dependence upon $\epsilon$. Fig. 14 shows the results for this computation. Again, the results are consistent with the derived upper bounds. Fig. 14a, b verifies that for the maps $\Sigma _2\rightarrow \Sigma _3$ and $\Sigma _3\rightarrow \Sigma _4$ the stochastic spreadings of order ${\mathcal {O}}(\sigma +\sigma ^{\prime })$ and ${\mathcal {O}}(\sigma \sqrt{\epsilon }+\sigma ^{\prime })$ are dominated by $\sigma ,\sigma ^{\prime }$ if the noise level is fixed. For the map $\Sigma _4\rightarrow \Sigma _5$ analyzed in Fig. 14c we expect from Table 1 that the spreading is dominated by a scaling ${\mathcal {O}}(\epsilon ^{1/6})$ since we have fixed $\sigma =0.01=\sigma ^{\prime }$ and $\epsilon ^{1/2}\ll \epsilon ^{1/6}$ as $\epsilon \rightarrow 0$. Inspection of Fig. 14c shows indeed a corresponding slope of approximately $1/6$. Figure 14d is also consistent with the expected scaling ${\mathcal {O}}(\epsilon ^{1/4})$ near the folded node for noise level and $\mu$ fixed. These results provide very good evidence that our theoretical estimates may also form a practical guideline to analyze the spreading due to noise.

Fig. 14

Dependence of the standard deviation of the distance between the stochastic and the deterministic transition maps on $\epsilon$ for an attracting deterministic periodic MMO during various phases of the flow. We have always fixed $\sigma =0.01=\sigma ^{\prime }$ and viewed $\epsilon$ as a parameter. Otherwise, the same conventions as in Fig. 13 apply

Of course, one may also consider the influence of noise on sample paths for global returns. Figure 1 shows the global return map $\Sigma _1\rightarrow \Sigma _1$. For this computation, in contrast to the previous computations in this section, we have chosen a regime with many secondary canards [17, 83]. Indeed, the parameter values have been fixed to $k=-10$, $\lambda =-7.6$ so that the folded node on $L^+$ is given by $(x,z)=(1,-9.2)$ with eigenvalues of the matrix $A$ from (7.5) given by $\rho _s<-1<\rho _w<0$. The eigenvalue ratio $\mu :=\rho _w/\rho _s$ is approximately given by $\mu \approx 0.0252$ so that [26, Thm. 2.3] implies that there are two primary and $19$ secondary canards. The deterministic return map has been analyzed numerically in [37, 59], and the structure of the different rotational sectors separated by canard orbits is well understood; see also [40]. However, Fig. 1 shows that the attracting deterministic periodic orbit corresponding to a fixed point of the return map, can shift due to noise, even to a higher sector of rotation. This effect can be seen directly from Theorem 6.4 above.

In summary, we may conclude that there is a highly non-trivial interplay between the number of SAOs, the global return map and the noise level (cf. also [17, Cor. 6.3]). As discussed already in Sect. 1, the natural next step is to consider the analysis of the discrete-time Markov chain on a finite state space of MMO patterns. The results in this paper and in [17] provide the necessary estimates for the kernel of the Markov chain and may form the starting point for future work.

Appendices

Appendix 1: Technical Lemmas

Lemma 8.1

(Scaling behaviour) Assume $a(s)\asymp -(|s|^{1/2}+\epsilon ^{1/3})$ for $-1\leqslant s\leqslant \epsilon ^{2/3}$, and define $\alpha (s,r) = \int _r^s a(u){{\mathrm{d}}}\!u$. Then for any $\nu \geqslant -1$,

$$\begin{aligned} \int _{s_0}^s {{\mathrm{e}}}^{\alpha (s,r)/\epsilon } |a(r)|^\nu {{\mathrm{d}}}\!r \asymp \epsilon |a(s)|^{2\nu -1} \end{aligned}$$

(8.1)

holds for $-1\leqslant s_0 \leqslant s_0+{\mathcal {O}}(\epsilon |\log \epsilon |) \leqslant s \leqslant \epsilon ^{2/3}$.

Lemma 8.2

(Bernstein-type inequality) Let $W^{(1)}_t, \dots , W^{(k)}_t$ be $k$ independent standard Brownian motions, and let $X_t$ be adapted to the filtration generated by the $W^{(j)}_t$. For measurable functions $g_{ij}$ and deterministic bounds $G_{i}$ satisfying almost surely

$$\begin{aligned} \sum _{j=1}^k g_{ij}(X_{s},s)^2 \leqslant G_i(s)^2, \qquad V_i(t) = \int _0^t G_i(s)^2 {{\mathrm{d}}}\!s < \infty , \end{aligned}$$

(8.2)

consider the $n$ martingales

$$\begin{aligned} M^{(i)}_t = \sum _{j=1}^k \int _0^t g_{ij}(X_s,s) {{\mathrm{d}}}\!W^{(j)}_s, \qquad i=1,\dots ,n. \end{aligned}$$

(8.3)

Then for any $h>0$ and any choice of $\gamma _1,\dots ,\gamma _n\in [0,1]$ such that $\gamma _1+\dots +\gamma _n=1$, one has

$$\begin{aligned} \mathbb {P}\biggl \{ \sup _{0\leqslant s\leqslant t} \left\| M_s\right\| \geqslant h \biggr \} \leqslant 2\sum _{i=1}^n \exp \biggl \{ -\frac{\gamma _i h^2}{2V_i(t)}\biggr \}. \end{aligned}$$

(8.4)

Proof

The left-hand side of (8.4) is bounded above by

$$\begin{aligned} \mathbb {P}\biggl \{ \sum _{i=1}^n \sup _{0\leqslant s\leqslant t} (M^{(i)}_s)^2 \geqslant h^2 \biggr \} \leqslant \sum _{i=1}^n \mathbb {P}\biggl \{ \sup _{0\leqslant s\leqslant t} (M^{(i)}_s)^2 \geqslant \gamma _i h^2 \biggr \}. \end{aligned}$$

(8.5)

Each term in this sum is bounded by $2{{\mathrm{e}}}^{-\gamma _i h^2/(2V_i(t))}$, cf. [17, Lemma D.8]. $\square$

Remark 8.3

It is possible to obtain sharper estimates of the form

$$\begin{aligned} \mathbb {P}\biggl \{ \sup _{0\leqslant s\leqslant t} \frac{\left\| M_s\right\| }{\left\| V(s)\right\| ^{1/2}}\geqslant h \biggr \} \leqslant C(t,\kappa ) {{\mathrm{e}}}^{-\kappa h^2/2\sigma ^2} \end{aligned}$$

(8.6)

for any $\kappa <1$, using a decomposition of $[0,t]$ in small intervals (see [15, Sect. 5.1.2]).

Lemma 8.4

(Random time change) Consider an $\mathbb {R}^n$-valued diffusion $(Y_t)_{t\geqslant 0}$ given by

$$\begin{aligned} {{\mathrm{d}}}\!Y_t = f(Y_t){{\mathrm{d}}}\!t + g(Y_t){{\mathrm{d}}}\!W_t, \end{aligned}$$

(8.7)

where $f:\mathbb {R}^n\rightarrow \mathbb {R}^n$ is such that the $n$ th component $f_{n}$ of $f$ satisfies $f_n(y)>0$ for all $y$. We further assume that $g:\mathbb {R}^n\rightarrow \mathbb {R}^{n\times k}$, and that $(W_t)_{t\geqslant 0}$ is a $k$-dimensional standard Brownian motion. Fix $\gamma >0$ and let

$$\begin{aligned} \beta (t,\omega ) = \gamma \int _0^t f_n(Y_s(\omega )){{\mathrm{d}}}\!s. \end{aligned}$$

(8.8)

Then $(Y_{\beta ^{-1}(t)})_{t\geqslant 0}$ is equal in distribution to $(X_t)_{t\geqslant 0}$, where $X_t$ satisfies $X_{0}=Y_{0}$ and

$$\begin{aligned} {{\mathrm{d}}}\!X_t = \frac{1}{\gamma f_n(X_t)}f(X_t){{\mathrm{d}}}\!t + \frac{1}{\sqrt{\gamma f_n(X_t)}}g(X_t){{\mathrm{d}}}\!W_t. \end{aligned}$$

(8.9)

If the condition $f_n(y)>0$ is only satisfied in a subset ${\mathcal {D}}$ of $\mathbb {R}^n$, then the result remains true for $0\leqslant t\leqslant \tau _{\mathcal {D}}= \inf \{s\geqslant 0:Y_s\not \in {\mathcal {D}}\}$.

Proof

Write ${{\mathrm{d}}}\!X_t = \tilde{f}(X_t){{\mathrm{d}}}\!t + \tilde{g}(X_t){{\mathrm{d}}}\!W_t$ for the SDE (8.9). The stochastic process $c(t,\omega ) = \gamma f_n(Y_t(\omega ))$ is adapted to the filtration $({\mathcal {F}}_t)_{t}$ of the Brownian motion. Since $t\mapsto \beta (t)$ is almost surely invertible, [70, Theorem 8.5.1,p. 154] implies that $(X_t)_{t}$ is equal in distribution to $(Y_{\beta ^{-1}(t)})_{t}$, with $Y_{t}$ is given by

$$\begin{aligned} {{\mathrm{d}}}\!Y_t = u(t,\omega ){{\mathrm{d}}}\!t + v(t,\omega ){{\mathrm{d}}}\!W_t, \end{aligned}$$

(8.10)

provided

$$\begin{aligned} u(t,\omega )&= c(t,\omega ) \tilde{f}(Y_t), \nonumber \\ vv^{{\mathrm {T}}}(t,\omega )&= c(t,\omega ) \tilde{g} \tilde{g}^{{\mathrm {T}}}(Y_t). \end{aligned}$$

(8.11)

Setting $u(t,\omega )=f(Y_t(\omega ))$ and $v(t,\omega )=g(Y_t(\omega ))$ this is clearly the case. To prove the last statement, it suffices to consider $Y_{t\wedge \tau _{\mathcal {D}}}$. $\square$

Appendix 2: Proof of Lemma 5.2

We would like to estimate the principal solution of $\epsilon \dot{\xi }= A(s)\xi$ for times $s\leqslant -\sqrt{\epsilon }$, where

$$\begin{aligned} A(s) = \begin{pmatrix} a_0(s) &{} d(s) \\ c(s) &{} \epsilon a_1(s) \end{pmatrix} = \begin{pmatrix} s + {\mathcal {O}}(s^2) &{} 1 + {\mathcal {O}}(s^2) \\ -\epsilon (1+\mu ) + {\mathcal {O}}(\epsilon s) &{} \epsilon {\mathcal {O}}(1) \end{pmatrix}. \end{aligned}$$

(9.1)

By changing $s$ into $-s$ and $\xi _2$ into $-\xi _2$, we can restrict the analysis to positive $s$. The proof of the lemma is close in spirit to the proof of [17, Theorem 4.3], and consists in a number of changes of variables bringing the system into diagonal form.

A first transformation

$$\begin{aligned} \xi = \exp \biggl \{\frac{1}{2\epsilon }\int _0^s {{\mathrm{Tr}}}A(u){{\mathrm{d}}}\!u\biggr \} \xi _1 =: {{\mathrm{e}}}^{\alpha (s)/2\epsilon } \xi _1 \end{aligned}$$

(9.2)

yields the system $\epsilon \dot{\xi }_1 = A_1(s)\xi _1$, where

$$\begin{aligned} A_1(s) = \begin{pmatrix} \frac{1}{2} a(s) &{} d(s) \\ c(s) &{} -\frac{1}{2} a(s) \end{pmatrix}, \qquad a(s) = a_0(s) - \epsilon a_1(s) = s + {\mathcal {O}}(s^2). \end{aligned}$$

(9.3)

Next we set $\xi _1 = S_1(s) \xi _2$, where

$$\begin{aligned} S_1(s) = \frac{1}{\sqrt{d(s)}} \begin{pmatrix} d(s) &{} 0 \\ -\frac{1}{2} a(s) + \frac{1}{2} \epsilon \frac{\dot{d}(s)}{d(s)} &{} 1 \end{pmatrix}, \end{aligned}$$

(9.4)

which yields $\epsilon \dot{\xi }_2 = A_2(s)\xi _2$, with

$$\begin{aligned} A_2(s) = \begin{pmatrix} 0 &{} 1 \\ h(s) &{} 0 \end{pmatrix}, \end{aligned}$$

(9.5)

and

$$\begin{aligned} h = \frac{a^2}{4} + cd + \epsilon \frac{\dot{a}}{2} - \epsilon \frac{a\dot{d}}{2d} + \frac{\epsilon ^2}{2}\frac{\ddot{d}}{d} + \frac{3}{4} \epsilon ^2 \frac{\dot{d}^2}{d^2} = \frac{a^2}{4} - \epsilon \biggl ( \frac{1}{2} + \mu \biggr ) + {\mathcal {O}}(\epsilon s). \end{aligned}$$

(9.6)

Note that this system is equivalent to $\epsilon ^2 \ddot{\xi }_{2,1} = h(s)\xi _{2,1}$, which reduces to Weber’s equation in the particular case $a(s)=s$. The next step is to set $\xi _2 = S_2(s) \xi _3$, where

$$\begin{aligned} S_2(s) = \frac{1}{\sqrt{2}} \begin{pmatrix} h(s)^{-1/4} &{}\quad -h(s)^{-1/4} \\ h(s)^{1/4} &{}\quad h(s)^{1/4} \end{pmatrix} \end{aligned}$$

(9.7)

is such that $S_2^{-1}A_2S_2$ is diagonal. This yields $\epsilon \dot{\xi }_3 = A_3(s)\xi _3$, with

$$\begin{aligned} A_3(s) = \begin{pmatrix} h(s)^{1/2} &{}\quad -\frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)} \\ -\frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)} &{}\quad -h(s)^{1/2} \end{pmatrix}. \end{aligned}$$

(9.8)

The last transformation $\xi _3 = S_3(s) \xi _4$ makes the system diagonal. This final transformation is given by

$$\begin{aligned} S_3(s) = \begin{pmatrix} 1 &{}\quad p_2(s) \\ p_1(s) &{}\quad 1 \end{pmatrix}, \end{aligned}$$

(9.9)

where $p_1$ and $p_2$ satisfy the ODEs

$$\begin{aligned} \epsilon \dot{p_1}&= -2h(s)^{1/2}p_1 + \frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)} (p_1^2 - 1), \end{aligned}$$

(9.10)

$$\begin{aligned} \epsilon \dot{p_2}&= 2h(s)^{1/2}p_2 + \frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)} (p_2^2 - 1). \end{aligned}$$

(9.11)

One can show that these ODEs admit solutions of order $\epsilon /s^2$. The resulting system has the form $\epsilon \dot{\xi }_4 = A_4(s)\xi _4$, where

$$\begin{aligned} A_4(s) = \begin{pmatrix} h(s)^{1/2} -\frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)}p_1(s) &{} 0 \\ 0 &{} -h(s)^{1/2} -\frac{\epsilon }{4}\frac{\dot{h}(s)}{h(s)} p_2(s) \end{pmatrix}, \end{aligned}$$

(9.12)

and the principal solution is thus of the form $V(s,r) = V(s)V(r)^{-1}$, where

$$\begin{aligned} V(s) = {{\mathrm{e}}}^{\alpha (s)/2\epsilon }S_1(s)S_2(s)S_3(s) \begin{pmatrix} {{\mathrm{e}}}^{\alpha _+(s)/\epsilon } &{} 0 \\ 0 &{} {{\mathrm{e}}}^{\alpha _-(s)/\epsilon } \end{pmatrix} \end{aligned}$$

(9.13)

with

$$\begin{aligned} \alpha _\pm (s) = \pm \int _{1}^s h(u)^{1/2}{{\mathrm{d}}}\!u + {\mathcal {O}}\biggl (\frac{\epsilon ^2}{s^2}\biggr ). \end{aligned}$$

(9.14)

Expanding $h(s)^{1/2}$ and using the fact that $\dot{a}(s)=1+{\mathcal {O}}(s)$, one obtains

$$\begin{aligned} {{\mathrm{e}}}^{\alpha _\pm (s)/\epsilon } \asymp a(s)^{\mp (1/2+\mu )} {{\mathrm{e}}}^{\pm \alpha (s)/2\epsilon }. \end{aligned}$$

(9.15)

The result follows by evaluating the matrix products in (9.13). $\square$

Appendix 3: Proof of Proposition 5.5

We shall use a parametrization of the level curves of $K$ for $K>0$ which was introduced in [18]. It is given by

$$\begin{aligned} u_1&= \sqrt{\frac{1+\mu }{2} |\log K|} \,\sin \varphi , \nonumber \\ u_2&= u_1^2 + \frac{1+\mu }{2} f\bigl ( X \bigr ), \qquad X := \sqrt{\frac{|\log K|}{2} } \cos \varphi , \end{aligned}$$

(10.1)

where $f(t)$ is the solution of

$$\begin{aligned} \log (1+f(t)) = f(t) - 2t^2 \end{aligned}$$

(10.2)

satisfying ${{\mathrm{sign}}}f(t) = {{\mathrm{sign}}}t$. It is easy to check (see [63, Sect. 5.2.1]) that

• $f(t) = 2t + {\mathcal {O}}(t^2)$ near $t=0$;

• $-1 + {{\mathrm{e}}}^{-1-2t^2} \leqslant f(t) \leqslant -1 + {{\mathrm{e}}}^{-1-2t^2} + {\mathcal {O}}(({{\mathrm{e}}}^{-1-2t^2})^2)$ for $t\leqslant 0$;

• $f(t) \leqslant 2t^2 + {\mathcal {O}}(t)$ for all $t\geqslant 0$.

Lemma 10.1

The variational equations (5.26) are equivalent to

$$\begin{aligned} \mu \frac{{{\mathrm{d}}}\!K}{{{\mathrm{d}}}\!\bar{z}}&= -8\bar{z} \frac{K|\log K|}{1+f(X)} \sin ^2\varphi , \nonumber \\ \mu \frac{{{\mathrm{d}}}\!\varphi }{{{\mathrm{d}}}\!\bar{z}}&= \frac{1}{X} \biggl [ \sqrt{1+\mu } f(X) - 4\bar{z} \sqrt{\frac{|\log K|}{2} } \sin \varphi \biggl ( \frac{\sin ^2\varphi }{1+f(X)}-1\biggr ) \biggr ]. \end{aligned}$$

(10.3)

Proof

The first equation is a direct consequence of (5.28), using the fact that ${{\mathrm{e}}}^{-f(X)}=K^{\cos ^2\varphi }/[1+f(X)]$. The second one is obtained by differentiating the first equation in (10.1) and solving for $\mu {{\mathrm{d}}}\!\varphi /{{\mathrm{d}}}\!\bar{z}$. $\square$

The first term on the right-hand side of $\mu {{\mathrm{d}}}\!\varphi /{{\mathrm{d}}}\!\bar{z}$ is of order $f(X)/X$, which varies between $1/|X|$ and $2|X|$. As for the second term, it is easy to see that it is negligible for $X\geqslant 0$. For $X<0$, setting $u=\sin \varphi$, we have $1+f(X)=K^{1-u^2}$. The function $u\mapsto u^3K^{u^2-1}$ has a maximal value $1/(K|\log K|^{3/2})$, reached when $u^2=3/(2|\log K|)$. This allows to bound the second term for $X<0$ and proves (5.29).

It follows immediately from (10.3) that we can write

$$\begin{aligned} \frac{{{\mathrm{d}}}\!K}{{{\mathrm{d}}}\!\varphi } = \bar{z} g(K,\varphi ,\bar{z}), \end{aligned}$$

(10.4)

where

$$\begin{aligned} g(K,\varphi ,\bar{z}) = -8 \frac{K|\log K|}{1+f(X)} \frac{X\sin ^2\varphi }{\sqrt{1+\mu }f(X) - 4\bar{z} R\sin \varphi \Bigl [\frac{\sin ^2\varphi }{(1+f(X))}-1\Bigr ]}, \end{aligned}$$

(10.5)

and we have set $R=\sqrt{|\log K|/2}$. Note that $\mu {{\mathrm{d}}}\!K/{{\mathrm{d}}}\!\bar{z}$ has order $(1-K)$ near $K=1$, and order $|\log K|$ near $K=0$, because $1+f(X)\geqslant {{\mathrm{e}}}^{-1} K$. This shows that

$$\begin{aligned} |g(K,\varphi ,\bar{z})| \leqslant {\mathcal {O}}((1-K)(1+|\log K|)^{3/2}) =: {\mathcal {O}}(\rho (K)). \end{aligned}$$

(10.6)

We now perform the averaging transformation

$$\begin{aligned} \bar{K}= K + \bar{z} w(K,\varphi ,\bar{z}), \end{aligned}$$

(10.7)

where

$$\begin{aligned} \frac{\partial }{\partial \varphi }w(K,\varphi ,\bar{z}) = -g(K,\varphi ,\bar{z}) + \bar{g}(K,\bar{z}), \qquad \bar{g}(K,\bar{z}) = \frac{1}{2\pi } \int _0^{2\pi } g(K,\varphi ,\bar{z}) {{\mathrm{d}}}\!\varphi .\quad \end{aligned}$$

(10.8)

This yields

$$\begin{aligned} \frac{{{\mathrm{d}}}\!\bar{K}}{{{\mathrm{d}}}\!\varphi } = \bar{z} \bar{g}(K,\bar{z}) + \bar{z} \frac{\partial w}{\partial K} \frac{{{\mathrm{d}}}\!K}{{{\mathrm{d}}}\!\varphi } + \biggl ( \bar{z} \frac{\partial w}{\partial \bar{z}} + w \biggr ) \frac{{{\mathrm{d}}}\!\bar{z}}{{{\mathrm{d}}}\!\varphi }. \end{aligned}$$

(10.9)

Recalling that ${{\mathrm{d}}}\!K/{{\mathrm{d}}}\!\varphi$ has order $\bar{z} g$ and ${{\mathrm{d}}}\!\bar{z}/{{\mathrm{d}}}\!\varphi$ has order $\mu |\log K|^{1/2}$, together with (10.6) allows to bound the last two terms.

Finally, we show that $c_-(1-K) \leqslant -\bar{g} \leqslant c_+(1-K)$ for $K\geqslant c\bar{z}$. The result will then follow by expressing $K$ in terms of $\bar{K}$ (note that $1-K$ and $1-\bar{K}$ are comparable for $K\geqslant c\bar{z}$). It will be sufficient to consider the behaviour of $\bar{g}$ near $K=1$ and near $K=0$. Near $K=1$ we have

$$\begin{aligned} g(K,\varphi ,\bar{z}) = -\frac{4(1-K)}{\sqrt{1+\mu }} \bigl [ 1+{\mathcal {O}}(1-K) + {\mathcal {O}}(\bar{z})\bigr ] \sin ^2\varphi , \end{aligned}$$

(10.10)

and $\sin ^2\varphi$ averages to $1/2$. Near $K=0$, the integral defining $\bar{g}$ is dominated by $\varphi$ near $\pi$. Performing the change of variables $u=2R\sin \varphi$, we obtain

$$\begin{aligned} \int _{\pi /2}^{3\pi /2} g(K,\varphi ,\bar{z}) {{\mathrm{d}}}\!\varphi&= -\frac{2{{\mathrm{e}}}}{\sqrt{1+\mu }} \int _{-2R}^{2R} u^2 {{\mathrm{e}}}^{-u^2/2} \biggl [ 1 + {\mathcal {O}}(K{{\mathrm{e}}}^{u^2/2}) + {\mathcal {O}}\biggl ( \frac{\bar{z}u^3}{KR^2}{{\mathrm{e}}}^{-u^2/2}\biggr ) \biggr ] \nonumber \\&= -\frac{2\sqrt{2\pi }{{\mathrm{e}}}}{\sqrt{1+\mu }} \Bigl [ 1 + {\mathcal {O}}(K|\log K|) + {\mathcal {O}}(\bar{z}/(K|\log K|)) \Bigr ], \end{aligned}$$

(10.11)

while the integral over $[-\pi /2,\pi /2]$ has order $K|\log K|$. $\square$