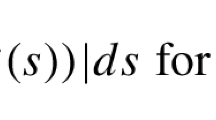Regularity of the Inertial Manifolds for Evolution Equations in Admissible Spaces and Finite-Dimensional Feedback Controllers

Abstract

Our main aims in this paper are to investigate the regularity of inertial manifolds for non-autonomous semi-linear evolution equations and to give an application of inertial manifolds to a feedback control problem. We first prove that the inertial manifolds are smooth if the nonlinear term is smooth. Then, using the theory of inertial manifolds for non-autonomous semi-linear evolution equations, we construct a feedback controller for a class of control problems for the one-dimensional reaction-diffusion equations with the Lipschitz coefficient of the nonlinear term which may depend on time and belong to an admissible space.

1 Introduction

Many phenomena in mechanics, physics, ecology, and so on can be described by partial differential equations. By choosing appropriate function spaces and linear operators, these partial differential equations can be rewritten into semi-linear evolution equations in an infinite-dimensional Banach space whose linear part is the generator of a continuous semigroup and the nonlinear term satisfies the Lipschitz condition.

We are particularly interested in the non-autonomous semi-linear evolution equations of the concise form $\frac {\mathrm {d}u}{\mathrm {d}t}+Au = f(u),$ where the operator A is in general an unbounded linear operator on a separable infinite-dimensional Hilbert space X and f is a nonlinear mapping. For such evolution equations, it is desirable to understand whether the asymptotic behavior is described essentially by a finite-dimensional structure. For example, many dissipative dynamical systems have global attractors of finite Hausdorff or fractal dimensions. An inertial manifold is a beautiful and ideal finite-dimensional structure to study asymptotic behavior of solutions to the evolution equations as time goes to infinity. The notion of inertial manifolds was introduced in 1985 by C. Foias, G.R. Sell, and R. Temam in [11] (see also [13])in an attempt to reduce the study of the asymptotic behavior of the system to a Lipschitz manifold of finite-dimension. An inertial manifold is a (at least Lipschitz) smooth finite-dimensional manifold of the phase space which is positively invariant, contain the global attractor and attracts exponentially all the solutions of the system. The feature of exponential attraction allows to apply the reduction principle to study the asymptotic behavior of the partial differential equation by determining the structures of its induced solutions belonging to these inertial manifolds, which turn out to be solutions to some induced ordinary differential equations due to the finite-dimensional structure of the manifold. In terms of fluid dynamics, R. Temam [38] once wrote that: “From the physical point of view an inertial manifold is an interaction law relating small and large eddies in a turbulent flow. In that application, the specification of an inertial manifold is equivalent to a modeling of turbulence”.

With a history of nearly 40 years, the field of inertial manifolds has been extensively studied and gained many achievements in both theoretical and applied aspects. First, the existence of inertial manifolds has been proved for several important classes of evolution equations (see, e.g., [3,4,5,6,7, 12, 14, 16, 18, 22, 23, 34, 35, 37] and the references therein). In order to overcome the technical conditions related to the spectral gap condition, some recent work (see, e.g., [2, 15, 20, 21, 42]) have been published that are based on special approaches. The concept of inertial manifolds is also generalized into many new types of manifolds that are more useful for application problems (see, e.g., [8,9,10, 27]). In general, the conditions for the existence of an inertial manifold are the spectral gap condition of the linear operator A and the global and uniform Lipschitz condition of the nonlinear term f. Roughly speaking, there should be a sufficiently large gap between two successive eigenvalues of A such that the uniform Lipschitz constant (of f ) can be bounded by the length of that gap multiplied by a fixed constant. In fact, in applications, the nonlinear term is usually only locally Lipschitz (i.e., Lipschitz in a neighborhood of a fixed point). However, in many circumstances, thanks to the existence of a global attractor, the nonlinear term can be truncated to contain the interesting part of the asymptotic dynamics of the system, in such a way that it becomes globally Lipschitz. Furthermore, for complicated evolutionary processes arising in natural sciences and technology, for example, partial differential equations in population ecology (the Fisher-Kolmogorov model describing the spread of an advantageous gene, predator-prey model with cross-diffusion, or competition model with cross-diffusion, see, e.g., J.D. Murray [24, 25]), the nonlinear part represents the source of material in many contexts where the Lipschitz coefficient may depend on time. Recenty, using Lyapunov-Perron method and the admissibility of function spaces, T.H. Nguyen [26] proved a more general condition on nonlinear part for the existence of inertial manifolds, that is, φ-Lipschitz condition, $\|f(t, x) - f(t, y)\| \leq \varphi (t) \left \|A^{\theta } (x-y)\right \|$, for φ being a real and positive function which belongs to an admissible space. Instead of requiring the upper bound for uniform Lipschitz coefficient, the upper bound is now required for $\|{\Lambda }_{1}\varphi \|_{\infty } := \sup _{t \in \mathbb {R}} {\int \limits }_{t-1}^{t}\varphi (\tau )\mathrm {d}\tau$. In the past few years, there have been some studies on the existence of inertial manifolds for evolution equations under such the φ-Lipschitz condition, which can be found in [1, 28, 40].

On aspect of application, we would like to emphasize applications of the inertial manifold theory to feedback control problems, such as, using inertial manifolds to stabilize semi-linear diffusion systems (see also [33, 36] and the references therein), for equations of nonlinear elasticity (see Y. You [41]), for reaction-diffusion equations (see R. Rosa and R. Temam [32], R. Rosa [30]), or for non-autonomous evolution equations by N. Koksch and S. Siegmund [19]. Among those applications, we are particularly interested in R. Rosa and R. Temam [32]. Consider the following semi-linear open-loop system

$$ \left\{ \begin{array}{ll} \frac{\mathrm{d}u}{\mathrm{d}t}+Au &= f(u)+Bg,\\ ~~~~~~~~~~~~y &= Cu, \end{array} \right. $$

(1.1)

where u is the state in an infinite-dimensional Hilbert space, y is the observation, g is the finite-dimensional control input, and B and C are bounded linear operators. R. Rosa and R. Temam [32] introduces a finite-dimensional feedback control for a open-loop problem of a scalar reaction-diffusion equation so that the closed-loop system behaves in a desired way given a priori by a finite-dimensional system. The finite-dimensional property and characteristics of the inertial manifolds are used to reduce the closed-loop system to a finite-dimensional system and that work concludes that the vector field of this finite-dimensional system is close in a weighted C¹-metric to some finite-dimensional vector field.

The purpose of the present paper is to extend the results by R. Rosa and R. Temam [31, 32] to the case of a class of non-autonomous closed-loop systems. Precisely, using the method in [31], we will show that the inertial manifolds obtained by in T.H. Nguyen [26, Theorem 3.5] are of class C¹ as long as the nonlinear term is of class C¹ with respect to the state of the evolutionary systems. Then, for a non-autonomous closed-loop system of a scalar reaction-diffusion equation in concrete settings, we will extend the results in R. Rosa and R. Temam [32] by applying the existence theorem of an inertial manifold for mild solutions to the non-autonomous evolution equations in admissible spaces, (see [26, Theorem 3.5]), and theorem of regularity has just proved, for that closed-loop system. Our method and techniques are based on the Lyapunov-Perron equation, fixed point argument, and the techniques of functional analysis combined with admissibility of function spaces. Our main results are contained in Theorems 2.7, 2.9, 3.2, and 3.3. Theorems 2.7 and 2.9 present the results of the regularity of inertial manifolds corresponding to the cases of the evolution equation in Banach and Hilbert space. The Theorem 3.2 describes the study of an infinite-dimensional control system through an inertial manifold of the corresponding closed-loop system. As a consequence of Theorem 3.2, Theorem 3.3 states the structurally stable (see, e.g., [17, 29, 39]) of dynamical systems.

This paper is organized as follows. In next section, Section 2, we recall the result T.H. Nguyen [26, Theorem 3.5] on the existence of inertial manifolds for evolution equations when the partial differential operator A is positive definite and self-adjoint with a discrete spectrum and Lipschitz coefficient of the nonlinear term depends on the time and belongs to some admissible spaces. After that, regularity of the inertial manifolds will be substantiated. We will show that if the nonlinear term is of class C¹ with respect to the state variable then those inertial manifolds are of class C¹. In Section 3, first subsection presents the settings and some assumptions for the open-loop system of a reaction-diffusion system. The desired dynamics of the infinite-dimensional control system under consideration will be described in the second subsection. We next recall some estimates for the input and output control operators of the system which is obtained by R. Rosa and R. Temam [32]. Finally, we study the closed-loop system and establishes the main result. We design a finite-dimensional feedback controller for a class of one-dimensional reaction-diffusion equations under some certain conditions.

2 Regularity of the Inertial Manifolds for Parabolic Evolution Equations in Admissible Spaces

In this section, we are concerned with the first-order regularity of the inertial manifolds for the mild solution to the semi-linear parabolic evolution equations in admissible spaces. First of all, we will recall some definitions and properties of admissible spaces and the existence conditions of an inertial manifold, which is the main result of the T.H. Nguyen [26]. We will then give a detailed proof of the regularity of the aforementioned inertial manifolds. Finally, as an addition, we will state a similar result for inertial manifolds for the evolution equations involving the sectorial operator, whose existence is recently proved in T.H. Nguyen and X.-Q. Bui [28, Theorem 3.5].

First of all, we recall some information about the function space, including the Banach function spaces and admissible spaces (see T.H. Nguyen [26] and references therein for more information on the matter).

Definition 2.1

Denote by ${\mathscr{B}}$ the Borel algebra and by λ the Lebesgue measure on $\mathbb {R}$. A vector space E of real-valued Borel-measurable functions on $\mathbb {R}$ (modulo λ-nullfunctions) is called a Banach function space (over $(\mathbb {R},{\mathscr{B}},\lambda )$) if

• (1) E is a Banach lattice with respect to the norm ∥⋅∥_E;

• (2) the characteristic functions χ_A belong to E for all $A\in {\mathscr{B}}$ of finite measure and $\sup _{t\in \mathbb {R}}\|\chi _{[t,t+1]}\|_{E}<\infty$, $\inf _{t\in \mathbb {R}}\|\chi _{[t,t+1]}\|_{E}>0$;

• (3) $E\hookrightarrow L_{1}, \text {loc}(\mathbb {R})$.

Definition 2.2

The Banach function space E is called admissible if it satisfies

• (1) there is a constant M ≥ 1 such that for every compact interval $[a,b]\subset \mathbb {R}$ we have

  $$ {{\int}_{a}^{b}}|\varphi(t)|dt\leq \frac{M(b-a)}{\|\chi_{[a,b]}\|_{E}}\|\varphi\|_{E}, \quad\text{ for all } \varphi \in E; $$

  (2.1)

• (2) for φ ∈ E the function ${\Lambda }_{1}\varphi (t)={\int \limits }_{t-1}^{t}\varphi (\tau )d\tau$ belongs to E;

• (3) the space E is $T_{\tau }^{+}$-invariant and $T_{\tau }^{-}$-invariant where $T_{\tau }^{+}$ and $T_{\tau }^{-}$ are defined, for $\tau \in \mathbb {R}$, by

  $$ \begin{array}{@{}rcl@{}} & T_{\tau}^{+}\varphi(t) := \varphi(t-\tau), \quad\text{ for }t\in\mathbb{R}, \end{array} $$

  (2.2)
  $$ \begin{array}{@{}rcl@{}} & T_{\tau}^{-}\varphi(t) := \varphi(t+\tau), \quad\text{ for }t\in\mathbb{R}. \end{array} $$

  (2.3)

  Moreover, there are constants N₁ and N₂ such that

  $$ \|T_{\tau}^{+}\|\leq N_{1} \quad\text{ and }\quad \|T_{\tau}^{-}\|\leq N_{2}, \quad\text{ for all }\tau\in\mathbb{R}. $$

Proposition 2.3

Let E be an admissible space. Let $\varphi \in L_{1}, \text {loc}(\mathbb {R})$ be such that φ ≥ 0 and Λ₁φ ∈ E, where ${\Lambda }_{1}\varphi (t) :={\int \limits }_{t-1}^{t}\varphi (\tau )d\tau .$ For σ > 0, functions ${\Lambda }^{\prime }_{\sigma }\varphi$ and ${\Lambda }^{\prime \prime }_{\sigma }\varphi$ are defined by

$$ {\Lambda}^{\prime}_{\sigma}\varphi(t) := \int\limits_{-\infty}^{t}e^{-\sigma(t-s)}\varphi(s)\mathrm{d}s, \quad {\Lambda}^{\prime\prime}_{\sigma}\varphi(t) := \int\limits_{t}^{\infty}e^{-\sigma(s-t)}\varphi(s)\mathrm{d}s. $$

Then, ${\Lambda }^{\prime }_{\sigma }\varphi$ and ${\Lambda }^{\prime \prime }_{\sigma }\varphi$ belong to E. In particular, if $\sup _{t\in \mathbb {R}}{\int \limits }_{t-1}^{t}\varphi (\tau )\mathrm {d}\tau <\infty ,$ then ${\Lambda }^{\prime }_{\sigma }\varphi$ and ${\Lambda }^{\prime \prime }_{\sigma }\varphi$ are bounded. Moreover, the following estimates hold:

$$ \|{\Lambda}^{\prime}_{\sigma}\varphi\|_{\infty}\leq\frac{N_{1}}{1-e^{-\sigma}}\|{\Lambda}_{1}\varphi\|_{\infty}, \quad \|{\Lambda}^{\prime\prime}_{\sigma}\varphi\|_{\infty}\leq\frac{N_{2}}{1-e^{-\sigma}}\|{\Lambda}_{1}\varphi\|_{\infty}, $$

where N₁ and N₂ are defined in Definition 2.2.

2.1 The Existence of Inertial Manifolds Revisited

Consider the evolution problem of the form

$$ \left \{ \begin{array}{cccc} \frac{\mathrm{d}u(t)}{\mathrm{d}t}+Au(t) &= f(t,u(t)), && \quad t>s,\\ ~~~~~~~~~~~~~u(s)&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!= u_{s}, && \quad s\in\mathbb{R}. \end{array} \right . $$

(2.4)

where A is a positive definite operator with discrete spectrum on an infinite-dimensional separable Hilbert space X (see Assumption (A) below) and $f \colon \mathbb {R} \times X_{\theta } \rightarrow X$ is a nonlinear mapping with $X_{\theta } := {\mathscr{D}} (A^{\theta })$ being the domain of the fractional power A^𝜃, for 0 ≤ 𝜃 < 1, equipped with the norm $\left \|A^{\theta } \cdot \right \|$ (the fractional power of A is computed using spectral resolution as in I.D. Chueshov [4, §1 – Chapter 2]).

In this case − A generates a strongly continuous semigroup (e^−tA)_t≥ 0 on the Hilbert space X. Instead of the evolution equation (2.4), we consider the integral equation

$$ u(t)=e^{-(t-s)A}u(s)+{\int\limits_{s}^{t}}e^{-(t-\xi)A}f(\xi,u(\xi)) \mathrm{d}\xi, \quad \text{ for a.e. } t\geq s. $$

(2.5)

By a solution of equation (2.5) we mean a strongly measurable function u(t) defined on an interval J with the values in X_𝜃 that satisfies (2.5) for t, s ∈ J. The solution u to equation (2.5) is called a mild solution of evolution equation (2.4).

To obtain the existence of an inertial manifold for equation (2.5), we need the following assumptions on the linear operator and the Lipschitz coefficient of the nonlinear term.

Assumption (A): :

Consider (X,∥⋅∥) is a separable Hilbert space. Let A be a positive definite operator with discrete spectrum in X. Suppose that {e_k} is an orthonormal basis of X such that

$$ \begin{array}{@{}rcl@{}} && Ae_{k}=\lambda_{k} e_{k}, \end{array} $$

(2.6)

$$ \begin{array}{@{}rcl@{}} && 0 < \lambda_{1} \leq \lambda_{2} \leq {\cdots} \lambda_{k} \leq \cdots, \quad \lambda_{k} \rightarrow \infty \text{ as } k \rightarrow \infty, \end{array} $$

(2.7)

and each λ_k with finite multiplicity.

Assumption (F): :

Let E be an admissible space on the whole line $\mathbb {R}$ andφ be a positive function belonging to E such that

$$ R(\varphi,\theta) :=\sup_{t\in\mathbb{R}} \left( {\int}_{t-1}^{t} \frac{\varphi(\tau)^{\frac{1+\theta}{2\theta}}}{(t-\tau)^{\frac{1+\theta}{2}}} \mathrm{d}\tau \right)^{\frac{2\theta}{1+\theta}} <\infty, \text{ where } 0<\theta<1. $$

(2.8)

In the case 𝜃 = 0 we do not need this assumption.

Assume that the function $f\colon \mathbb {R}\times X_{\theta }\rightarrow X$ isφ-Lipschitz, that is, f satisfies

• (1) $\|f(t,x)\|\leq \varphi (t)\left (1+\left \|A^{\theta }x\right \|\right )$, for all a.e. $t\in \mathbb {R}$ and for all x ∈ X_𝜃,

• (2) $\|f(t,x_{1})-f(t,x_{2})\|\leq \varphi (t)\left \|A^{\theta }(x_{1} - x_{2})\right \|$, for all a.e. $t\in \mathbb {R}$ and for all x₁, x₂ ∈ X_𝜃.

We assume further that the nonlinear term is of classC¹ with respect to the state,

$$ \|Df(t,u)-Df(t,v)\|_{\mathcal{L}(X_{\theta}, X)} \leq \varphi_{2} (t) \left \|A^{\theta} (u-v)\right \|^{\nu}, $$

(2.9)

here 0 < ν ≤ 1 andDf(t, u) denotes the derivative of f(t, u) with respect to u.

For brevity, we will write Lip_φ(f) = φ(t) to represent the function f satisfies the φ-Lipschitz condition as in the above definition.

Suppose that linear operator A satisfies Assumption (A) and let $f\colon \mathbb {R}\times X_{\theta }\rightarrow X$ be a φ-Lipschitz function for φ satisfies Assumption (F). Let λ_n and λ_n+ 1 be two successive and different eigenvalues with λ_n < λ_n+ 1. Consider P = P_n is the orthogonal projection onto the first n eigenvectors of the linear operator A. Set Q = Q_n = I − P_n, where I = I_X is the identity operator on the phase space X. Put

$$ \alpha:= \frac{\lambda_{n+1} - \lambda_{n}}{2}, \qquad \gamma := \frac{\lambda_{n+1} + \lambda_{n}}{2}, $$

(2.10)

and Green’s function by

$$ \mathcal{G}(t,\tau)= \left\{\begin{array}{ll} e^{-(t-\tau)A}Q, \quad & \text{ for } t>\tau,\\ -e^{-(t-\tau)A}P, \quad & \text{ for } t\leq \tau. \end{array}\right. $$

(2.11)

Proposition 2.4 (see G.R. Sell and Y. You 35)

For 𝜃 > 0 we have the following dichotomy estimates

$$ \begin{array}{@{}rcl@{}} \left \|e^{-tA}P\right \| & \leq& Me^{\lambda_{n} |t|}, \quad t\in\mathbb{R}\text{ and for some constant }M\geq 1, \end{array} $$

(2.12)

$$ \begin{array}{@{}rcl@{}} \left \|A^{\theta}e^{-tA}P\right \| & \leq& M\lambda_{n}^{\theta} e^{\lambda_{n}|t|}, \quad t\in\mathbb{R}, \end{array} $$

(2.13)

$$ \begin{array}{@{}rcl@{}} \left \|e^{-tA}(I-P) \right \| & \leq& Me^{-\lambda_{n+1} t}, \quad t\geq 0, \end{array} $$

(2.14)

$$ \begin{array}{@{}rcl@{}} \left \|A^{\theta}e^{-tA}(I-P)\right \| & \leq& M \left [ \left( \frac{\theta}{t}\right)^{\theta}+\lambda_{n+1}^{\theta} \right ] e^{-\lambda_{n+1} t}, \quad t>0. \end{array} $$

(2.15)

We then make precisely the notion of inertial manifolds in the following definition.

Definition 2.5

An inertial manifold of equation integral (2.5) is a collection of Lipschitz manifolds ${\mathscr{M}}=\big ({\mathscr{M}}_{t}\big )_{t\in \mathbb {R}}$ in X such that each ${\mathscr{M}}_{t}$ is the graph of a Lipschitz function ${\Phi }_{t}\colon P_{n}X \rightarrow (I-P_{n})X_{\theta },$ i.e.,

$$ \mathcal{M}_{t} =\left \{ x+{\Phi}_{t}x : x\in P_{n}X \right \}, \quad \text{ for }t\in \mathbb{R} $$

(2.16)

and the following conditions are satisfied:

• (1) The Lipschitz constants of Φ_t are independent of t, i.e., there exists a constant C independent of t such that

  $$ \left \|A^{\theta}({\Phi}_{t} x_{1}-{\Phi}_{t} x_{2})\right \| \leq C\left \|A^{\theta}(x_{1}-x_{2})\right \|, $$

  (2.17)

  for all $t\in \mathbb {R}$ and x₁, x₂ ∈ X_𝜃.

• (2) There exists γ > 0 such that to each $x_{0}\in {\mathscr{M}}_{t_{0}}$ there corresponds one and only one solution u(t) to (2.5) on $(-\infty ,t_{0}]$ satisfying that u(t₀) = x₀ and

  $$ \underset{t\leq t_{0}}{\text{esssup}} \left \|e^{-\gamma(t_{0}-t)}A^{\theta} u(t)\right \| <\infty. $$

  (2.18)

• (3) The collection $\big ({\mathscr{M}}_{t}\big )_{t\in \mathbb {R}}$ is positively invariant under (2.5), i.e., if a solution x(t), t ≥ s, to (2.5) satisfies $x_{s}\in {\mathscr{M}}_{s}$, then we have that $x(t)\in {\mathscr{M}}_{t}$ for t ≥ s.

• (4) The collection $\big ({\mathscr{M}}_{t}\big )_{t\in \mathbb {R}}$ exponentially attracts all the solutions to (2.5), i.e., for any solution u(⋅) of (2.5) and any fixed $s\in \mathbb {R}$, there is a positive constant H such that

  $$ \text{dist}_{X_{\theta}}(u(t),\mathcal{M}_{t}) \leq He^{-\gamma(t-s)}, \quad\text{ for }t\geq s, $$

  (2.19)

  where γ is the same constant as the one in (2.18), and $\text {dist}_{X_{\theta }}$ denotes the Hausdorff semi-distance generated by the norm in X_𝜃.

Assume that the inertial manifold for evolution equation (2.4) exists, the notion of the inertial manifold is closely related to the notion of the inertial form. If we rewrite the solution in the form u(t) = p(t) + q(t), where

$$ p(t)\in P_{n} u(t), \quad q(t)\in Q_{n} u(t) = (I-P_{n}) u(t) $$

then evolution equation (2.4) can be rewritten as a system of two differential equations

$$ \left \{ \begin{array}{ll} & \frac{\mathrm{d} p(t)}{\mathrm{d}t}+Ap(t) = P_{n} f(t,p(t)+q(t)), \\ & \frac{\mathrm{d} q(t)}{\mathrm{d}t}+Aq(t) = Q_{n} f(t,p(t)+q(t)) = (I-P_{n}) f(t, p(t)+q(t)), \\ & p\big|_{t=s}=p_{s} \equiv P_{n} u_{s} , \quad q\big|_{t=s}=q_{s} \equiv Q_{n} u_{s}. \end{array} \right . $$

(2.20)

To construct the desired inertial manifolds, we introduce the space

$$ \begin{array}{@{}rcl@{}} L_{\infty}^{\gamma, t_{0}, \theta} := \left \{ x \in C ((- \infty, t_{0}], X_{\theta}) : \underset{t \leq t_{0}}{\text{esssup}}~~e^{-\gamma(t_{0}-t)} \left \|A^{\theta} x(t)\right \| < \infty \right \}, \end{array} $$

(2.21)

which is a Banach space when endowed with the norm

$$ \|x\|_{\gamma, \theta, \infty} := \underset{t \leq t_{0}}{\text{esssup}}~~e^{-\gamma(t_{0}-t)} \left \|A^{\theta} x(t)\right \|. $$

(2.22)

For $x \in L_{\infty }^{\gamma , t_{0}, \theta }$ and y ∈ P_nX we consider the formal map

$$ \begin{array}{@{}rcl@{}} T (x, y) (t) = e^{-(t-t_{0}) A} Py + \int\limits_{-\infty}^{t_{0}} \mathcal{G} (t, s) f(s, x(s)) \mathrm{d}s. \end{array} $$

(2.23)

First, the form of the solutions to (2.5) which are rescaledly bounded on the half-line $(-\infty , t_{0}]$ is as follows: For any fixed $t_{0}\in \mathbb {R}$ let x(t), t ≤ t₀, be a solution to equation (2.5) such that x(t) ∈ X_𝜃 for t ≤ t₀ and $x \in L_{\infty }^{\gamma , t_{0}, \theta }$. Then, this solution x(t) can be rewritten in the form

$$ x(t)=e^{-(t-t_{0})A}p +\int\limits_{-\infty}^{t_{0}}\mathcal{G}(t,\tau)f(\tau, x(\tau))\mathrm{d}\tau, \quad \text{ for a.e. } t\leq t_{0}, $$

(2.24)

where p ∈ P_nX.

With this result, we can understand that, we have a mapping from P_nX to $L_{\infty }^{\gamma , t_{0}, \theta }$. For convenience in later proofs, the solution x(t) satisfies to the Lyapunov-Perron equation (2.24) can also be denoted by x(p)(t), or x(p, t).

Now, construction of an invariant manifold is based on a fixed point argument. A function $\mathbf {x} \in L_{\infty }^{\gamma , t_{0}, \theta }$ is a solution of evolution equation (2.4) if and only if x a fixed point of T. The idea then is to prove that the map T is well defined from $L_{\infty }^{\gamma , t_{0}, \theta } \times P_{n}X$, and is a strict contraction in $L_{\infty }^{\gamma , t_{0}, \theta }$, uniformly in P_nX. Hence, there will be a map $\mathbf {x} \colon P_{n}X \rightarrow L_{\infty }^{\gamma , t_{0}, \theta }$ such that T(x(y₀), y₀) = x(y₀), for all y₀ ∈ P_nX, with each x(y₀) solving (2.4).

We can then define a collection of surfaces $\big ({\mathscr{M}}_{t_{0}} \big )_{t_{0} \in \mathbb {R}}$ by

$$ \mathcal{M}_{t_{0}} := \left \{ y + {\Phi}_{t_{0}} y : y \in P_{n}X \right \}, $$

(2.25)

here ${\Phi }_{t_{0}} \colon P_{n}X \rightarrow Q_{n}X_{\theta }$ is defined by

$$ {\Phi}_{t_{0}} (y) = \int\limits_{-\infty}^{t_{0}} e^{-(t_{0} - s) A} Q_{n} f(s, \mathbf{x}(y)(s)) \mathrm{d}s = Q_{n} \mathbf{x}(y) (t_{0}), $$

(2.26)

Finally, we check that $\big ({\mathscr{M}}_{t}\big )_{t \in \mathbb {R}}$ is Lipschitz, invariant and has the asymptotic completeness property, so that $\big ({\mathscr{M}}_{t}\big )_{t \in \mathbb {R}}$ is the desired inertial manifold. We now fully state the main results about the existence of an inertial manifold for mild solutions to the semi-linear evolution equations is as follows.

Theorem 2.6 (see T.H. Nguyen [26, Theorem 3.5])

Let the operator A satisfying Assumption (A) and φ belongs to some admissible space E. Let f be φ-Lipschitz function such that the function φ satisfying Assumption (F). Suppose that there are two successive eigenvalues λ_n < λ_n+ 1 of linear operator A satisfying

$$ k_{\gamma} <1 \quad\text{ and }\quad \frac{k_{\gamma} M^{3} N_{2}\lambda_{n}^{2\theta}\|{\Lambda}_{1}\varphi\|_{\infty}}{(1-k_{\gamma} )(1-e^{-\alpha})} + k_{\gamma} <1, $$

(2.27)

where

$$ k_{\gamma} := \left\{\begin{array}{ll} \frac{M \left( \theta^{\theta} N_{1} +\lambda_{n+1}^{\theta}N_{1}+\lambda_{n}^{\theta}N_{2} \right)\|{\Lambda}_{1}\varphi\|_{\infty}}{1-e^{-\alpha}} + M \theta^{\theta} R(\varphi,\theta) \left( \frac{1-\theta}{\alpha(1+\theta)} \right)^{\frac{1-\theta}{1+\theta}} & \text{ if } 0<\theta<1, \\ \frac{M (N_{1}+N_{2})}{1-e^{-\alpha}} \|{\Lambda}_{1}\varphi\|_{\infty} & \text{ if }\theta=0. \end{array}\right. $$

(2.28)

Then, integral equation (2.5) has an inertial manifold.

2.2 Regularity of the Inertial Manifolds

We now show the main result of this section, namely that the inertial manifold given in Theorem 2.6 is of class C¹ as long as the nonlinear term is of class C¹ with respect to the state of system. Correctly, we will point out that the mapping ${\Phi }_{t} \colon P_{n} X \rightarrow Q_{n} X_{\theta }, y \mapsto {\Phi }_{t} (y)$ is of class C¹.

Theorem 2.7

If f(t,⋅) ∈ C¹(X_𝜃, X), then the inertial manifold given in Theorem 2.6 is of class C¹ and Φ_t satisfies the Sacker’s equation

$$ D {\Phi}_{t}(y) (- Ay + P_{n} f(t, y + {\Phi}_{t}(y)) + A {\Phi}_{t}(y)) = Q_{n} f (t, y + {\Phi}_{t}(y)), $$

(2.29)

for all y in the domain of Φ_t. Here, DΦ_t(y) is Fréchet differential with respect to y of y↦Φ_t(y).

Proof

The proof will be carried on in several steps.Step 1. A candidate for the differential. By the definition of inertial manifolds, we have ${\Phi }_{t_{0}}(y) = Q_{n} \mathbf {x}(y, t_{0})$ and

$$ \begin{array}{@{}rcl@{}} \mathbf{x}(y, t_{0}) & = e^{-(t-t_{0})A} y - \int\limits_{-\infty}^{t_{0}} e^{-(t-s)A} \mathcal{G} (t, s) f(s, \mathbf{x}(y, s)) \mathrm{d}s. \end{array} $$

(2.30)

We will look for the differential of Φ_t by first looking for the differential of x. Then, we just note that $D {\Phi }_{t_{0}} (y) = Q_{n} \partial _{y} \mathbf {x}(y, t_{0})$. By differentiating (2.30) formally with respect to y, we see that ∂_yx(y) is a fixed point of T^◇(⋅, y) where T^◇ is given by

$$ \begin{array}{@{}rcl@{}} T^{\diamondsuit} ({\Delta}, y)(t) & = e^{-(t-t_{0})A} y + \int\limits_{-\infty}^{t_{0}} \mathcal{G} (t, s) f(s, {\Delta}(s)) \mathrm{d}s. \end{array} $$

(2.31)

As for T, we must verify that the map T^◇ above is well defined and is a strict contraction in Δ, uniformly with respect to y; this in some appropriate function space.

Denote

$$ \begin{array}{@{}rcl@{}} L_{\infty, \diamondsuit}^{\gamma, t_{0}, \theta} \!:=\! \Bigg \{\! {\Delta} \in C ((- \infty, t_{0}], \mathcal{L} (P_{n}X, X)) : \sup_{t \leq t_{0}} e^{- \gamma (t_{0} - t)} \| {\Delta} (t) \|_{\mathcal{L} (P_{n}X, X)} \!<\! \infty \Bigg \}, \end{array} $$

(2.32)

endowed with the norm

$$ \|{\Delta}\|_{\gamma, \diamondsuit} := \sup_{t \leq t_{0}} e^{- \gamma (t_{0} - t)} \| {\Delta} (t) \|_{\mathcal{L} (P_{n}X, X)} . $$

(2.33)

Thanks to definition of a φ-Lipschitz function as in Assumption (F), we have

$$ \| Df(t, u) \|_{\mathcal{L} (X_{\theta}, X)} \leq \varphi (t), \quad \text{ for all } u \in X_{\theta}. $$

(2.34)

Using the admissibility of function spaces and the dichotomy estimates in (2.12)–(2.15), in a same way as in T.H. Nguyen [26] we can see that T^◇ is well defined as a function from $L_{\infty , \diamondsuit }^{\gamma , t_{0}, \theta } \times P_{n}X$ into $L_{\infty , \diamondsuit }^{\gamma , t_{0}, \theta }$ and is Lipschitz in Δ with Lipschitz constant k_γ.

Since k_γ < 1, we deduce that there exists a mapping ${\Delta } \colon P_{n}X \rightarrow L_{\infty , \diamondsuit }^{\gamma , t_{0}, \theta }$ such that

$$ T^{\diamondsuit} ({\Delta} (y), y) = {\Delta} (y) , \quad \text{ for all } y \in P_{n}X. $$

(2.35)

For simplicity, we set Δ(y)(t) = Δ(y, t), then Δ is our candidate for the differential of the mapping x.Step 2. The function Δ is continous. Fix y₀ ∈ P_nX and consider y ∈ P_nX close to y₀. Then proceeding as in T.H. Nguyen [26, Theorem 3.5] we will check that

$$ \| {\Delta}(y) - {\Delta} (y_{0}) \|_{\gamma, \diamondsuit} \leq \frac{1}{1- k_{\gamma}} \left \| T^{\diamondsuit} ({\Delta}(y_{0}), y) - T^{\diamondsuit} ({\Delta} (y_{0}), y_{0}) \right \|_{\gamma, \diamondsuit}. $$

(2.36)

Hence, for the continuity of Δ, we need

$$ \left \| T^{\diamondsuit} ({\Delta}(y_{0}), y) - T^{\diamondsuit} ({\Delta} (y_{0}), y_{0} ) \right \|_{\gamma, \diamondsuit} \rightarrow 0 \quad\text{ as } y \rightarrow y_{0}. $$

(2.37)

Take μ such that μ < γ, so that by Step 1 we have ${\Delta } (y_{0}) \in L_{\infty , \diamondsuit }^{\mu , t_{0}, \theta }$. Thus if we put

$$ N(s, y) = \| D f(s, \mathbf{x}(y_{0}, s)) - D f(s, \mathbf{x}(y, s)) \|_{\mathcal{L}(X_{\theta}, X)}, $$

(2.38)

we can write

$$ \begin{array}{@{}rcl@{}} && \left \| T^{\diamondsuit} ({\Delta}(y_{0}), y)(t) - T^{\diamondsuit} ({\Delta} (y_{0}), y_{0} )(t) \right \| \\ && \leq \| {\Delta}(y_{0}) \|_{\mu, \diamondsuit} M \int\limits_{- \infty }^{t} e^{- \lambda_{n+1}(t-s)} \left( \left( \frac{\theta}{t-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) N(s, y) e^{-\mu (s-t_{0})} \mathrm{d}s \\ && \quad + \| {\Delta}(y_{0}) \|_{\mu, \diamondsuit} M \lambda_{n}^{\theta} \int\limits_{t}^{t_{0}} e^{- \lambda_{n}(t-s)} N(s, y) e^{-\mu (s-t_{0})} \mathrm{d}s. \end{array} $$

Hence,

$$ \left \| T^{\diamondsuit} {\Delta}(y_{0}), y) - T^{\diamondsuit} {\Delta} (y_{0}), y_{0}) \right \|_{\gamma, \diamondsuit} \leq \left \{ \left( M\lambda_{n}^{\theta} + M \right) \| {\Delta}(y_{0}) \|_{\mu, \diamondsuit} \right \} \widetilde{N} (y), $$

where

$$ \begin{array}{@{}rcl@{}} \widetilde{N}(y) &:=& \sup_{t \leq t_{0}} \Bigg [ e^{(\gamma - \lambda_{n+1})(t-t_{0})} \int\limits_{- \infty}^{t} \left( \left( \frac{\theta}{t-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) e^{(\lambda_{n+1} - \mu)s} N(s, y) \mathrm{d}s \\ & &\qquad\quad+ e^{(\gamma - \lambda_{n})(t-t_{0})} \int\limits_{t}^{t_{0}} e^{(\lambda_{n} - \mu)s} N(s, y) \mathrm{d}s \Bigg ]. \end{array} $$

To prove that $\widetilde {N} (y) \rightarrow 0$ as $y \rightarrow y_{0}$, we argue by contradiction. Suppose that $\widetilde {N} (y_{j}) > \varepsilon$, for some ε > 0 and some sequence $\{y_{j}\}_{j \in \mathbb {N}}$ in P_nX with

$$ \|y_{j} - y_{0}\| \rightarrow \infty \quad \text{ as } j \rightarrow \infty. $$

Thus, there exists a sequence $\{t_{j}\}_{j \in \mathbb {N}}$, with t_j ≤ t₀, such that

$$ \begin{array}{@{}rcl@{}} && e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \int\limits_{- \infty}^{t_{j}} \left( \left( \frac{\theta}{t_{j}-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) e^{(\lambda_{n+1} - \mu)s} N(s, y_{j}) \mathrm{d}s + \\ && \quad + e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu)s} N(s, y_{j}) \mathrm{d}s \\ && \geq \varepsilon, \quad \text{ for all } j \in \mathbb{N}. \end{array} $$

(2.39)

But by (2.34), N = N(s, y) satisfies

$$ \| N(s, y) \|_{\mathcal{L} (P_{n}X, X)} \leq 2 \varphi (s), $$

(2.40)

so that the left-hand side (“L.H.S.” for short) of (2.39) is estimated as follows

$$ \begin{array}{@{}rcl@{}} & &\| \text{L.H.S. of} (2.39) \| \\ & &\leq 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \int\limits_{- \infty}^{t_{j}} \left( \left( \frac{\theta}{t_{j}-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) e^{(\lambda_{n+1} - \mu)s} \varphi (s) \mathrm{d}s \\ && \quad + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu)s} \varphi (s) \mathrm{d}s\\ &&= 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \left \{ \int\limits_{- \infty}^{t_{j}} \left( \frac{\theta}{t_{j}-s} \right)^{\theta} e^{(\lambda_{n+1} - \mu)s} \varphi (s) \mathrm{d}s + \int\limits_{- \infty}^{t_{j}} \lambda_{n+1}^{\theta} e^{(\lambda_{n+1} - \mu)s} \varphi (s) \mathrm{d}s \right \} \\ && \quad + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu)s} \varphi (s) \mathrm{d}s. \end{array} $$

Since t_j ≤ t₀, for all $j \in \mathbb {N}$, we can therefore write

$$ \begin{array}{@{}rcl@{}} && 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \left \{ \int\limits_{- \infty}^{t_{j}} \left( \frac{\theta}{t_{j}-s} \right)^{\theta} e^{(\lambda_{n+1} - \mu)s} \varphi (s) \mathrm{d}s + \int\limits_{- \infty}^{t_{j}} \lambda_{n+1}^{\theta} e^{(\lambda_{n+1} - \mu)s} \varphi (s) \mathrm{d}s \right \} \\ && \quad + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu)s} \varphi (s) \mathrm{d}s\\ & &\leq 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \times \\ && \quad \times \left \{ \int\limits_{- \infty}^{t_{j}} \left( \frac{\theta}{t_{j}-s} \right)^{\theta} e^{(\lambda_{n+1} - \mu)(s-t_{j})} \varphi (s) \mathrm{d}s + \int\limits_{- \infty}^{t_{j}} \lambda_{n+1}^{\theta} e^{(\lambda_{n+1} - \mu)(s-t_{j})} \varphi (s) \mathrm{d}s \right \} \\ && \quad + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu) (s-t_{j})} \varphi (s) \mathrm{d}s\\ && \leq 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \times \\ && \quad \times \left \{ \int\limits_{- \infty}^{t_{j}} \left( \frac{\theta}{t_{j}-s} \right)^{\theta} e^{(\lambda_{n+1} - \mu)(s-t_{j})} \varphi (s) \mathrm{d}s + \int\limits_{- \infty}^{t_{j}} \lambda_{n+1}^{\theta} e^{(\lambda_{n+1} - \mu)(s-t_{j})} \varphi (s) \mathrm{d}s \right \} \\ && \quad + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{t_{j}}^{t_{0}} e^{(\lambda_{n} - \mu) (s-t_{j})} \varphi (s) \mathrm{d}s\\ & &\leq 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \left \{ \frac{\theta^{\theta} N_{1} \|{\Lambda}_{1} \varphi\|_{\infty}}{1 - e^{(\lambda_{n+1} - \mu)}} + \theta^{\theta} R(\varphi,\theta) \left( \frac{1-\theta}{(\lambda_{n+1} - \mu)(1+\theta)}\right)^{\frac{1-\theta}{1+\theta}} \|{\Lambda}_{1} \varphi\|_{\infty} \right \} \\ && \quad + 2 e^{(\gamma - \lambda_{n+1})(t_{j}-t_{0})} \frac{\lambda_{n+1}^{\theta} N_{1}}{1 - e^{(\lambda_{n+1} - \mu)}} \|{\Lambda}_{1} \varphi\|_{\infty} + 2 e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \frac{\lambda_{n}^{\theta} N_{2}}{1 - e^{(\lambda_{n} - \mu)}} \|{\Lambda}_{1} \varphi\|_{\infty}\\ & &\leq 2 e^{(\gamma - \mu)(t_{j}-t_{0})} \Bigg \{ \frac{\theta^{\theta} N_{1} \|{\Lambda}_{1} \varphi\|_{\infty}}{1 - e^{(\lambda_{n+1} - \mu)}} + \theta^{\theta} R(\varphi,\theta) \left( \frac{1-\theta}{(\lambda_{n+1} - \mu)(1+\theta)}\right)^{\frac{1-\theta}{1+\theta}} \|{\Lambda}_{1} \varphi\|_{\infty} + \\ && \quad + \frac{\lambda_{n+1}^{\theta} N_{1}}{1 - e^{(\lambda_{n+1} - \mu)}} \|{\Lambda}_{1} \varphi\|_{\infty} + \frac{\lambda_{n}^{\theta} N_{2}}{1 - e^{(\lambda_{n} - \mu)}} \|{\Lambda}_{1} \varphi\|_{\infty} \Bigg \}. \end{array} $$

Therefore, in view of (2.39), t_j must be bounded from below since μ < γ, say

$$ -\infty < T \leq t_{j} \leq t_{0}, \quad \text{ for all } j \text{ and for some } T \leq t_{0}. $$

Then

$$ \begin{array}{@{}rcl@{}} \| {L.H.S. of (2.39)}\| & \leq& e^{(\gamma - \mu)(t_{j}-t_{0})} \int\limits_{- \infty}^{t_{j}} \left( \frac{\theta}{t_{j}-s} \right)^{\theta} e^{-(\lambda_{n+1} - \mu)(t_{j} - s)} N(s, y_{j}) \mathrm{d} s + \\ && \quad + \lambda_{n+1}^{\theta} e^{(\gamma - \lambda_{n+1})(T-t_{0})} \int\limits_{- \infty}^{t_{0}} e^{(\lambda_{n+1} - \mu)s} N(s, y_{j}) \mathrm{d}s \\ && \quad + e^{(\gamma - \lambda_{n})(t_{j}-t_{0})} \int\limits_{T}^{t_{0}} e^{(\lambda_{n} - \mu)s} N(s, y_{j}) \mathrm{d}s. \end{array} $$

Hence, by a change of variable in the first integral,

$$ \begin{array}{@{}rcl@{}} \| L.H.S. of (2.39)\| & \leq& \int\limits_{t_{0}}^{\infty} s^{- \theta} e^{-(\lambda_{n+1} - \mu)s} N(t_{j} - s, y_{j})\mathrm{d}s \\ && \quad + \lambda_{n+1}^{\theta} e^{(\gamma - \lambda_{n+1})(T-t_{0})} \int\limits_{- \infty}^{t_{0}} e^{(\lambda_{n+1} - \mu)s} N(s, y_{j}) \mathrm{d}s \\ && \quad + \int\limits_{T}^{t_{0}} e^{(\lambda_{n+1} - \mu)s} N(s, y_{j}) \mathrm{d}s. \end{array} $$

(2.41)

But, using T.H. Nguyen [26, Theorem 3.5] (in the proof of the main theorem) we have

$$ \begin{array}{@{}rcl@{}} && \| \mathbf{x}(y_{0}, t_{j} - s) - \mathbf{x}(y, t_{j} - s ) \| \\ & &\leq e^{- \gamma(t_{j} -s)} \|\mathbf{x}(y_{0}) - \mathbf{x}(y) \|_{\gamma, t_{0}, \theta} \\ & &\leq \frac{M\lambda_{n}^{\theta}}{1- k_{\gamma}} e^{- \gamma(T -s)} \left \| A^{\theta} (y_{j} - y_{0}) \right \| \rightarrow 0 \quad \text{ as } j \rightarrow \infty,\quad \text{pointwise in } s. \end{array} $$

Thus $N (t_{j} - s, y_{j}) \rightarrow 0$ as $j \rightarrow \infty$, pointwise in s ≥ t₀ as well as $N (s, y_{j}) \rightarrow 0.$ Then by the Lebesgue Dominated Convergence Theorem applied to the right-hand side of (2.41), we find that

$$ \| L.H.S. of (2.39)\| \rightarrow 0 \quad\text{ as } j \rightarrow \infty, $$

(2.42)

which contradicts (2.39).

Therefore, $\widetilde {N} (y) \rightarrow 0$ as $\|y-y_{0}\| \rightarrow 0$ and hence, Δ = Δ(y) is continuous as a function from P_nX into $L_{\infty , \diamondsuit }^{\gamma , t_{0}, \theta }$.Step 3.∂_yx(y) = Δ(y). Consider y, h ∈ P_nX. We have

$$ \begin{array}{@{}rcl@{}} && \mathbf{x}(y+h, t) - \mathbf{x}(y, t) - {\Delta} (y, t)h \\ & &= \int\limits_{- \infty}^{t} e^{-(t-s)A} Q_{n} \big [ f(s, \mathbf{x}(y + h, s)) - f(s, \mathbf{x}(y,s)) - D f (s, \mathbf{x}(y, s)) {\Delta} (y, s) h \big ] \mathrm{d}s + \\ && \quad + \int\limits_{t}^{t_{0}} e^{-(t-s)A} P_{n} \big [ f(s, \mathbf{x}(y + h,s)) - f(s, \mathbf{x}(y,s)) - D f (s, \mathbf{x}(y, s)) {\Delta} (y, s) h \big ] \mathrm{d}s.\\ \end{array} $$

(2.43)

Let

$$ \begin{array}{@{}rcl@{}} & &\rho (y,h,t) = \frac{\|\mathbf{x}(y + h, t) - \mathbf{x}(y,t) - {\Delta} (y, t)h\|}{\|h\|}, \quad \text{ for all } y, h \in P_{n}X \text{ and } t \leq t_{0}, \\ & &r(u, w) = \frac{\|f(t, u + w)- f(t, u) - D f(t, u)w\|}{\left \|A^{\theta} w\right \|}, \quad \text{ for all } u, w \in X_{\theta}, \end{array} $$

and

$$ \vartheta (y, h, t) = r \big(\mathbf{x}(y,t), \mathbf{x}(y+h, t) -\mathbf{x}(y, t) \big), \quad \text{ for all } y, h \in P_{n}X, \text{ for all } t \leq t_{0}. $$

Then, by adding and subtracting Df(s, x(y, s)(x(y + h, s) −x(y, s))) in the expression between brackets in (2.43), we can estimate ρ(y, h, t) by

$$ \begin{array}{@{}rcl@{}} && \rho (y, h, t) \\ & &\leq M \int\limits_{- \infty}^{t} e^{- \lambda_{n+1} (t-s)} \left( \left( \frac{\theta}{t-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) \vartheta (y,h,s) \frac{\|\mathbf{x}(y+h, s)-\mathbf{x}(y,s)\|}{\|h\|} \mathrm{d}s \\ && \quad + M \lambda_{n}^{\theta} \int\limits_{t}^{t_{0}} e^{- \lambda_{n}(t-s)} \vartheta(y,h,s) \frac{\|\mathbf{x}(y+h, s)- \mathbf{x}(y,s)\|}{\|h\|} \mathrm{d}s \\ && \quad + M \int\limits_{- \infty}^{t} e^{- \lambda_{n+1}(t-s)} \left( \left( \frac{\theta}{t-s} \right)^{\theta} + \lambda_{n+1}^{\theta} \right) \varphi (s) \rho(y, h, s) \mathrm{d}s \\ && \quad + M \lambda_{n}^{\theta} \int\limits_{t}^{t_{0}} e^{- \lambda_{n} (t-s)} \rho(y, h, s) \varphi (s) \mathrm{d}s. \end{array} $$

Let

$$ \begin{array}{@{}rcl@{}} \widetilde{\rho} (y, h) & = &\sup_{t \leq t_{0}} \left \{ e^{-\gamma(t_{0} - t)} \rho (y, h, t) \right \} \\ & =& \frac{\|\mathbf{x}(y+h, \cdot) - \mathbf{x}(y, \cdot) - {\Delta} (y, \cdot)h \|_{\gamma, \theta, \infty}}{\|h\|}, \quad \text{ for all } y, h \in P_{n}X. \end{array} $$

Hence, from the above inequality, we find

$$ \begin{array}{@{}rcl@{}} \widetilde{\rho} (y, h) & \leq& \widetilde{\vartheta} (y, h) + \widetilde{\rho} (y, h) \Bigg \{ \int\limits_{- \infty}^{t} e^{(\gamma - \lambda_{n+1})(t-s)} \left( \left( \frac{\theta}{t-s}\right)^{\theta} + \lambda_{n+1}^{\theta} \right) \varphi (s) \mathrm{d}s \\ && \quad + M \lambda_{n}^{\theta} \int\limits_{t}^{t_{0}} e^{(\gamma - \lambda_{n})(t-s)} \varphi (s) \mathrm{d}s \Bigg \} \\ & \leq& \widetilde{\vartheta} (y, h) + k_{\gamma} \widetilde{\rho} (y, h), \end{array} $$

where

$$ \begin{array}{@{}rcl@{}} && \widetilde{\vartheta} (y, h) \\ && := \sup_{t \leq t_{0}} \Bigg \{ M e^{-\gamma(t_{0} - t)} \times \\ && \quad \times \int\limits_{- \infty}^{t} \left( \left( \frac{\theta}{t-s}\right)^{\theta} + \lambda_{n+1}^{\theta} \right) e^{- \lambda_{n+1}(t-s)} \vartheta(y,h,s) \frac{\|\mathbf{x}(y+h,s) - \mathbf{x}(y,s)\|}{\|h\|} \mathrm{d}s \\ && \quad + M \lambda_{n}^{\theta} e^{-\gamma(t_{0} - t)} \int\limits_{t}^{t_{0}} e^{- \lambda_{n}(t-s)} \vartheta(y, h, s) \frac{\|\mathbf{x}(y+h,s) - \mathbf{x}(y, s)\|}{\|h\|} \mathrm{d}s \Bigg \}. \end{array} $$

Thus, since k_γ < 1, we obtain

$$ \widetilde{\rho}(y,h) \leq \frac{1}{1- k_{\gamma}} \widetilde{\vartheta}(y,h). $$

As we did for $\widetilde {N} = \widetilde {N}(y)$ in Step 2, one can prove that $\widetilde {\vartheta }(y,h) \rightarrow 0$ as $\|h\| \rightarrow 0$, this time using the fact that

$$ \frac{\|\mathbf{x}(y+h,s) - \mathbf{x}(y,s)\|}{\|h\|} \leq \frac{M \lambda_{n}^{\theta}}{1- k_{\mu} } e^{- \mu s}, $$

for some μ with μ < γ.

Therefore, $\widetilde {\rho }(y,h) \rightarrow 0$ as $\|h\| \rightarrow 0$, which shows that ∂_yx(y) = Δ(y).Step 4.${\Phi }_{t_{0}} \in C^{1} (P_{n}X, Q_{n}X_{\theta })$. It follows directly from Step 2 and Step 3 above since ${\Phi }_{t_{0}}(y) = Q_{n} \mathbf {x}(y, t_{0})$, hence

$$ \begin{array}{@{}rcl@{}} && \frac{ \left \| A^{\theta} \left( {\Phi}_{t_{0}} (y + h) - {\Phi}_{t_{0}}(y) - D{\Phi}_{t_{0}}(y) \right) \right \| }{\|h\|} \\ && = \frac{\left \| A^{\theta} \left( Q_{n} \mathbf{x}(y+h, t_{0}) - Q_{n} \mathbf{x}(y, t_{0}) - Q\partial_{y} \mathbf{x}(y, t_{0})h \right) \right \|}{\|h\|} \\ && = \rho (y, h, t_{0}) \leq \widetilde{\rho}(y, h) \rightarrow 0 \quad \text{ as } \|h\| \rightarrow 0, \text{ for all } y \in P_{n}X \end{array} $$

where ρ(y, h, t) and $\widetilde {\rho }(y, h)$ are as in Step 3.

The theorem is proved. □

2.3 Regularity of the Inertial Manifolds for Evolution Equations Involving Sectorial Operators

This subsection will briefly describes the regularity of inertial manifolds for which the assumptions used are more general than those in Section 2.2. More specifically, we state the regularity of the inertial manifold for evolution equations involving just a sectorial operator in a general Banach space, no longer self-adjoint on a Hilbert space, nor with a compact resolvent with a discrete spectrum.

We use the sectorial operator according to the following definition.

Definition 2.8

Let X be a Banach space. A closed and densely defined linear operator $B\colon X\supset {\mathscr{D}}(B)\rightarrow X$ is called a sectorial operator if there exist real numbers $\omega \in \mathbb {R}$, $\sigma \in \left (0,\frac {\pi }{2}\right )$ and M ≥ 1 such that

$$ \begin{array}{@{}rcl@{}} & &\rho(B)\supset {\Sigma}_{\sigma}(\omega):= \left \{ z\in\mathbb{C}: |\arg (z-\omega)| < \sigma+\frac\pi2, z\neq \omega \right \}, \end{array} $$

(2.44)

$$ \begin{array}{@{}rcl@{}} &&\|R(\lambda,B)\|\leq \frac{M}{|\lambda - \omega|}, \quad\text{ for all }\lambda\in {\Sigma}_{\sigma}(\omega). \end{array} $$

(2.45)

We only consider the class of sectorial operators satisfying the following conditions.

Assumption (SO) :

The linear operator A is a closed linear operator on a Banach space X such that− A is a sectorial operator and the spectrum σ(−A) of − A can be decomposed as

$$ \sigma(-A)=\sigma_{\mathrm{u}}(-A) \cup \sigma_{\mathrm{c}}(-A)\subset \mathbb{C}_{-} $$

withσ_c(−A) compact, and ω_u < ω_c < ω < 0, where

$$ \omega_{\mathrm{u}}:=\sup\{\text{Re}\lambda: \lambda\in\sigma_{\mathrm{u}}(-A)\}, \quad \omega_{\mathrm{c}}:=\inf\{\text{Re}\lambda: \lambda\in\sigma_{\mathrm{c}}(-A)\} $$

(2.46)

Sectorial operators that satisfy Assumption (SO) appear, for example, in ecological models. For example, in the paper T.H. Nguyen and X.-Q. Bui [28] we showed in detail that a competition model with cross-diffusion with the Neumann boundary condition contains such a sectorial operator.

Assumption (SO) allows us to choose real numbers κ and μ such that

$$ \omega_{\mathrm{u}}<\kappa <\mu <\omega_{\mathrm{c}}<0. $$

(2.47)

In this case, we will use the Riesz projection P corresponding to σ_c(−A) defined by the formula

$$ P=\frac{1}{2\pi i}\int\limits_{\ell^{+}}R(\lambda,-A)\mathrm{d}\lambda, $$

(2.48)

where ℓ⁺ is a closed regular curve contained in ρ(−A), surrounding σ_c(−A) and positively oriented.

Consider the evolution equation (2.4) with the linear part satisfying Assumption (SO) and the nonlinear term satisfying Assumption (F). Recently, T.H. Nguyen and X.-Q. Bui [28, Theorem 3.5] has established a sufficient condition for the existence of an inertial manifold which can be shortened, inertial manifolds exist if the following two conditions are satisfied: First, spectral gap μ − κ is sufficiently large, and secondly, the norm $\|{\Lambda }_{1}\varphi \|_{\infty }=\sup _{t\in \mathbb {R}}{\int \limits }_{t-1}^{t}\varphi (\tau )\mathrm {d}\tau$ is sufficiently small.

Similar to the proof of Theorem 2.7, we obtain the following result :

Theorem 2.9

Consider the evolution equation (2.4) under the conditions that the linear partial differential operator − A is a sectorial operator on the Banach space X, has a spectral gap satisfying Assumption (SO), and the nonlinear term satisfies a φ-Lipschitz condition for some φ satisfying (2.8) and satisfies Assumption (F). If f(t,⋅) is C¹, then the inertial manifolds given by T.H. Nguyen and X.-Q. Bui [28, Theorem 3.5] is of class C¹.

3 Finite-Dimensional Feedback Control via Inertial Manifold Theory

3.1 The Open-Loop System

We first start with the following nonlinear one-dimensional reaction-diffusion equation with zero Dirichlet boundary condition and distributed observation and control

$$ \left \{ \begin{array}{clcccc} \frac{\partial u(t,x)}{\partial t} & = {\Delta} u(t,x ) + f(t,u(t,x)) + \sum\limits_{i=1}^{I-1}g_{i}(t,y)\psi_{i}(x), && t > s, && 0< x < \pi, \\ y(t) & = (y_{i}(t))_{j=1}^{J-1} =(u(t,x_{j}))^{J-1}_{j=1}, && t \geq s, && \\ u(t,0) & = u(t,\pi) = 0, && t > s, && \\ u(s,x) & = u_{s}(x), && && 0 \leq x \leq \pi, \end{array} \right . $$

(3.1)

where u = u(t, x) is the state variable, for x ∈Ω := (0, π), y is the observation, g = (g_i)_i is the control, f is a nonlinear term, and $I, J \in \mathbb {N}$. The functions ψ_i are called the actuators and are assumed to lie in the Sobolev space ${H^{1}_{0}}({\Omega })$, while the points x_j are distinct points in Ω called the obervation points and assumed to increase with j. We further assume that we are given another set of points $\{\tilde {x}_{i}\}_{i=1}^{I}$, with

$$ 0=\tilde{x}_{0}<{\ldots} <\tilde{x}_{i}<\tilde{x}_{i+1}<{\ldots} <\tilde{x}_{I}=\pi, $$

and that ψ_i, for i = 1,…, I − 1, is given more precisely by

$$ \psi_{i}(x) =\left\{\begin{array}{ll} \frac{x-\tilde{x}_{i-1}}{\tilde{h}_{i}}, & \quad x \in [\tilde{x}_{i-1},\tilde{x}_{i}),\\ \frac{\tilde{x}_{i+1}-x}{\tilde{h}_{i+1}}, & \quad x \in [\tilde{x}_{i},\tilde{x}_{i+1}),\\ 0, & \quad \text{otherwise}, \end{array}\right. $$

(3.2)

where $\tilde {h}_{i}=\tilde {x}_{i}-\tilde {x}_{i-1}$. Set also

$$ h_{j}=x_{j}-x_{j-1}, \quad h =\max_{j}\{h_{j}\}, \quad \tilde{h}=\max_{i}\left \{\tilde{h}_{i}\right \}. $$

(3.3)

We consider this equation in the phase space $X= {H_{0}^{1}}({\Omega })$ endowed with the norm ∥u∥ = |Du|, for u ∈ X, where |⋅| denotes the usual L²-norm on Ω and Du denotes the derivative of u. We also denote by ((⋅,⋅)) and (⋅,⋅) the corresponding inner-products in X and L²(Ω), respectively. We consider the linear operator A := −Δ on the domain $D(A) := \left \{ u\in H^{2} ({\Omega }) \cap {H_{0}^{1}} ({\Omega }) : Au \in {H_{0}^{1}} ({\Omega }) \right \}$. We have that the linear operator A is a self-adjoint operator with eigenvalues given by $\{\lambda _{n} =n^{2}\}_{n\in \mathbb {N}}$ and eigenfunctions $\{e_{n} = {\sin \limits } (nx)\}_{n\in \mathbb {N}}$. Moreover, we have 𝜃 = 0, $X_{\theta } = {H_{0}^{1}}({\Omega })$, and the dichotomy constant in the Proposition 2.4 is M = 1, and constants in the Proposition 2.3 are N₁ = N₂ = 1.

Now, let Z₁ and Z₂ be two finite-dimensional Hilbert spaces satisfying $Z_{1} \simeq \mathbb {R}^{I-1},Z_{2} \simeq \mathbb {R}^{J-1}$ and endowed with the norms

$$ \begin{array}{@{}rcl@{}} \|g\|_{Z_{1}}^{2}&=&\sum\limits_{i=1}^{I-1} \left |\frac{g_{i}-g_{i-1}}{h_{i}}\right |^{2} \tilde{h}_{i}, \quad \text{ for } g \in Z_{1}, \end{array} $$

(3.4)

$$ \begin{array}{@{}rcl@{}} \|y\|^{2}_{Z_{2}}&=&\sum\limits_{j=1}^{J-1}\left |\frac{y_{j}-y_{j-1}}{h_{j}}\right |^{2} h_{j}, \quad \text{ for } y\in Z_{2}. \end{array} $$

(3.5)

We define two bounded linear operators

$$ \begin{array}{@{}rcl@{}} B \colon Z_{1} &\rightarrow& X \quad \text{ by } Bg=\sum\limits_{i=1}^{I-1}g_{i} \psi_{i} (x), \qquad~\quad\qquad\qquad \text{ for } g=(g_{i})_{i=1}^{I-1}\in Z_{1}, \end{array} $$

(3.6)

$$ \begin{array}{@{}rcl@{}} C \colon X &\rightarrow& Z_{2} \quad \text{ by } Cu=((Cu)_{j})_{j=1}^{J-1}=(u(x_{j}))_{j=1}^{J-1}, \quad \text{ for } u \in X. \end{array} $$

(3.7)

It is known in [32] that with a large number of properly located actuators and observation points, the operators B and C have respectively right and left inverses on appropriate spectral spaces of the operator A. The result is exactly stated as follows:

Lemma 3.1

For m and n are two arbitrary natural numbers, we have the following estimates for the operators B and C

$$ \begin{array}{@{}rcl@{}} \left \|(CP_{m} )^{-1}_{\ell}\right \|_{\mathcal{L}(Z_{2}, X)} &\leq& \sqrt{\frac{2}{1-2h^{2}\lambda_{m} }}, \end{array} $$

(3.8)

$$ \begin{array}{@{}rcl@{}} \left \|(P_{n} B)_{r}^{-1}\right \|_{\mathcal{L}(P_{n} X, Z_{1})} &\leq& \sqrt{\frac{1}{1-4\tilde{h}^{2}\lambda_{n}}}, \end{array} $$

(3.9)

where P_m, P_n denote the spectral projectors associated with the first m, n eigenvalues of A, respectively.

It is not very difficult to show that

$$ \|B\|_{\mathcal{L}(Z_{1}, X)}=1 \qquad \text{ and } \qquad \|C\|_{\mathcal{L}(X, Z_{2})}=1. $$

(3.10)

We can now rewrite the control problem (3.1) in the Sobolev space $X = {H_{0}^{1}} ({\Omega })$ in the form

$$ \left \{ \begin{array}{rl} \frac{\mathrm{d}u}{\mathrm{d}t}+Au & = f(t,u)+Bg,\\ y & = Cu. \end{array} \right . $$

(3.11)

In the next subsection, we will construct a feedback control g = g(t, y) as a function of both the time t and the observation y so that the closed-loop system behaves in a certain desired way.

3.2 The Finite-Dimensional Feedback Controller

Consider a nonlinear mapping $W \colon \mathbb {R} \times P_{n_{0}}X \rightarrow P_{n_{0}}X$ satisfying the following conditions

$$ \begin{array}{@{}rcl@{}} \|W(t, u)-W(t, v)\| & \leq \psi_{1} (t)\|u-v\|, \quad \text{ for all } u, v \in P_{n_{0}}X, \end{array} $$

(3.12)

$$ \begin{array}{@{}rcl@{}} \|DW(t, u)-DW(t, v)\|_{\mathcal{L}(X)} & \leq \psi_{2} (t)\|u-v\|^{\nu}, \quad \text{ for all } u, v \in P_{n_{0}}X, \end{array} $$

(3.13)

for some positive valued functions ψ_i(t), i = 1,2, belonging to an admissible space, for ν as in (2.9), and the finite-dimensional non-autonomous ordinary differential equation

$$ \frac{\mathrm{d}z(t)}{\mathrm{d}t}=W(t, z(t)), $$

(3.14)

where $n_{0} \in \mathbb {N}$ is fixed. We look forward that the desired dynamics for the system (3.11) will be determined by system (3.14). Consider m and n arbitrary such that

$$ m \geq n > n^{\ast}, $$

(3.15)

where $n^{\ast } \in \mathbb {N}$ such that Theorem 2.6 is satisfied. This means that Theorem 2.6 holds for $\lambda _{n^{\ast }}$ and $\lambda _{n^{\ast } + 1}$. Choose the x_j and the $\widetilde {x}_{i}$ such that

$$ \tilde{h} \leq \frac{\sqrt{3}}{4 \lambda_{n}^{1/2}} \quad \text{ and }\quad h \leq \frac{1}{2 \lambda_{m}^{1/2}}. $$

(3.16)

Then, it implies that

$$ \sqrt{\frac{1}{1-4 \tilde{h} \lambda_{n} }} \leq 2 \quad \text{ and }\quad \sqrt{\frac{2}{1-2h\lambda_{m} }} \leq 2. $$

(3.17)

We now construct a feedback control $g\colon \mathbb {R} \times Z_{2} \rightarrow Z_{1}$ as follows

$$ g(t, y) = (P_{n} B)_{r}^{-1} \left [ AP_{n_{0}}(CP_{m})_{\ell}^{-1}y + W\left( t, P_{n_{0}}(CP_{m})_{\ell}^{-1}y\right) - P_{n} f \left( t, (CP_{m})_{\ell}^{-1}y \right) \right ], $$

(3.18)

for all y ∈ Z₂ and $t \in \mathbb {R}$. Thanks to Lemma 3.1, we have g is a globally Lipschitz function with

$$ \begin{array}{@{}rcl@{}} \text{Lip}_{\varphi} (g)& \leq& \left \|(P_{n} B)_{r}^{-1}\right \|_{\mathcal{L}(P_{n} X, Z_{1})} \left \|(CP_{m})_{\ell}^{-1}\right \|_{\mathcal{L}(Z_{2}, X)} \left( \|AP_{n_{0}}\|_{\mathcal{L}(X)}+ \text{Lip}_{\varphi} (W) + \text{Lip}_{\varphi} (f)\right) \\ & \leq& \sqrt{\frac{1}{1-4\tilde{h} \lambda_{n} }} \sqrt{\frac{2}{1-2h\lambda_{m} }} \left( \lambda_{n_{0}} + \psi_{1} (t) + \varphi_{1} (t) \right) \\ & \leq& 4 \left( \lambda_{n_{0}} + \psi_{1} (t) + \varphi_{1} (t) \right). \end{array} $$

Thus

$$ \text{Lip}_{\varphi} (g) \leq \xi (t), \quad \text{ where } \xi (t) :=4\left( \lambda_{n_{0}}+\psi(t)+\varphi (t)\right), \text{ for all } t \in \mathbb{R}. $$

(3.19)

With g given by (3.18), (3.11) becomes in the closed-loop form

$$ \frac{\mathrm{d}u}{\mathrm{d}t}+Au=f(t, u)+Bg(t, Cu). $$

(3.20)

We shall also consider the following auxiliary evolution equation

$$ \frac{\mathrm{d}v}{\mathrm{d}t}+Av=P_{m} f(t, P_{m} v)+P_{m} Bg(t, CP_{m} v). $$

(3.21)

Note that the nonlinear term of both the equations above have Lipschitz coefficient less than or equal to η(t) := φ₁(t) + ξ(t), for $t \in \mathbb {R}$. We want that, under the suitable conditions, there will be inertial manifolds for evolution equations (3.20) and (3.21). Applying Theorem 2.6, with 𝜃 = 0, for the evolution equations (3.20) and (3.21), we obtain that, if n^∗ is large enough and the norm $\|{\Lambda }_{1} \eta \|_{\infty } = \sup _{t \in \mathbb {R}} {\int \limits }_{t-1}^{t} \eta (\tau ) \mathrm {d}\tau$ is sufficiently small, then there exist inertial manifolds ${\mathscr{M}} = \big ({\mathscr{M}}_{t}\big )_{t \in \mathbb {R}}$ and $\mathcal {N} = \big (\mathcal {N}_{t}\big )_{t \in \mathbb {R}}$, respectively for (3.20) and (3.21).

In more detail, the inertial manifold for the evolution equation (3.20) is

$$ \mathcal{M} = \big(\mathcal{M}_{t}\big)_{t \in \mathbb{R}}, \quad \text{ where } \mathcal{M}_{t}=\{p+{\Phi}_{t} (p): p\in P_{n}X\}, $$

(3.22)

here ${\Phi }_{t}\colon P_{n}X \rightarrow Q_{n}X,$ defined by ${\Phi }_{t_{0}} (p) := Q_{n} \mathbf {x}(p) (t_{0})$ where x(p) is the unique solution in $L_{\infty }^{\gamma , t_{0}, \theta }$ to the equation (2.5) satisfying that P_nx(p)(t₀) = p. Similarly,

$$ \mathcal{N} = \big(\mathcal{N}_{t}\big)_{t \in \mathbb{R}}, \quad \text{ where } \mathcal{N}_{t}=\{p+{\Psi}_{t} (p): p\in P_{n}X\}, \text{ here } {\Psi}_{t}\colon P_{n}X \rightarrow Q_{n}X $$

(3.23)

is the inertial manifold for the auxiliary evolution equation (3.21).

When the two evolution equations (3.20) and (3.21) have their inertial manifolds, the corresponding inertial forms on P_nX are

$$ \frac{\mathrm{d}p}{\mathrm{d}t}+Ap = P_{n} f(t, p+{\Phi}_{t} (p)) + P_{n} Bg(t, C(p+{\Phi}_{t} (p))), $$

(3.24)

and

$$ \frac{\mathrm{d} \rho}{\mathrm{d}t}+A \rho = P_{n} f(t, P_{m} (\rho +{\Psi}_{t} (\rho))) + P_{n} Bg(t, CP_{m} (\rho +{\Psi}_{t} (\rho))). $$

(3.25)

Note that

$$ \begin{array}{@{}rcl@{}} && \frac{\mathrm{d} \rho}{\mathrm{d}t}+A(P_{n} -P_{n_{0}})\rho \\ & &= - AP_{n_{0}}\rho + P_{n} f(t, P_{m} (\rho +{\Psi}_{t} (\rho))) \\ && \quad + P_{n} B(P_{n} B)_{r}^{-1} \Big [AP_{n_{0}}(CP_{m})_{\ell}^{-1}CP_{m} (\rho +{\Psi}_{t} (\rho)) \\ && \quad + W \Big(t, P_{n_{0}}(CP_{m})_{\ell}^{-1}CP_{m} (\rho +{\Psi}_{t} (\rho))\Big) - P_{n} f \Big(t, (CP_{m})_{\ell}^{-1}CP_{m} (\rho +{\Psi}_{t} (\rho)\Big ) \Big ] \\ &&= -AP_{n_{0}}\rho +P_{n} f\Big (t, P_{m} (\rho +{\Psi}_{t} (\rho ))\Big) + \\ && \Big[ AP_{n_{0}}P_{m} (\rho +{\Psi}_{t} (\rho)) + W \Big(t, P_{n_{0}}P_{m} (\rho +{\Psi}_{t} (\rho))\Big) - P_{n} f\Big(t, P_{m} (\rho +{\Psi}_{t} (\rho))\Big) \Big] \\ &&= W(t, P_{n_{0}}\rho). \end{array} $$

Thus, the inertial form for (3.21) reads

$$ \frac{\mathrm{d} \rho }{\mathrm{d}t}+A(P_{n} -P_{n_{0}})\rho =W(t, P_{n_{0}}\rho), $$

(3.26)

and can be split for ρ = ρ₁ + ρ₂, where $\rho _{1} \in P_{n_{0}}X$, $\rho _{2} \in (P_{n} -P_{n_{0}})X$ as

$$ \left \{ \begin{array}{rl} \frac{\mathrm{d} \rho_{1}}{\mathrm{d}t} & = W(t, \rho_{1}), \\ \frac{\mathrm{d} \rho_{2}}{\mathrm{d}t}+A(P_{n} -P_{n_{0}})\rho_{2} & = 0. \end{array} \right . $$

(3.27)

The system (3.27) above is now decoupled with

$$ \rho_{2} (t)=e^{-(t-s)A(P_{n} -P_{n_{0}})}\rho_{2}(s) = \mathcal{O}\left( e^{-(n_{0}+1)^{2}(t-s)}\right), \quad \text{ as } t \rightarrow \infty. $$

Hence, the long-time dynamics of the inertial form and, hence, of the auxiliary equation (3.21) is given by the system $\frac {\mathrm {d} \rho _{1}(t)}{\mathrm {d} t}= W(t, \rho _{1})$.

Concerning the inertial form (3.24), we can write it as

$$ \frac{\mathrm{d} p}{\mathrm{d}t} + A(P_{n} -P_{n_{0}})p = W(t, P_{n_{0}}p) + \varepsilon (t, p), $$

(3.28)

where ε(t, p) is regarded as an error term given by

$$ \begin{array}{@{}rcl@{}} \varepsilon (t, p) &=& P_{n} f(t, p +{\Phi}_{t} (p)) + P_{n} Bg(t, C(p+{\Phi}_{t} (p))) \\ &&\!\!\!\!\!\!\! - P_{n} f(t, p+P_{m} {\Psi}_{t} (p)) - P_{n} Bg(t, C(p+P_{m} {\Psi}_{t} (p))). \end{array} $$

Note that

$$ \begin{array}{@{}rcl@{}} \|\varepsilon (t, p)\| & \leq& \left( \varphi_{1} (t) + \xi (t)\right) \left \|{\Phi}_{t} (p)-P_{m} {\Psi}_{t} (p)\right \| \\ & =& \left( \varphi_{1} (t) + \xi (t)\right) \left \|{\Phi}_{t} (p) - {\Psi}_{t} (p)\right \|, \end{array} $$

(3.29)

where the equality follows because Ψ_t(p) already lies in P_mX, which is not difficult to see. Thus, Lip_φ(ε) = φ₁(t) + ξ(t) := η(t).

We expect that, for each $t \in \mathbb {R}$, the error term ε(t, p) and Dε(t, p) are small quantities in the sense that the norms ∥ε(t, p)∥ and $\|D \varepsilon (t, p)\|_{{\mathscr{L}} (P_{n}X)}$ converge to zero as m approaches infinity for each fixed t, where p ∈ P_nX and m, n as in (3.15). For convenience, we put

$$ F(t, u) := f(t, u) + Bg(t, Cu), \quad \text{ for } u \in X \text{ and } t\in\mathbb{R}. $$

For a fixed $t_{0} \in \mathbb {R}$, let us estimate $\left \|{\Phi }_{t_{0}} (p) - {\Psi }_{t_{0}} (p)\right \|$. We have ${\Phi }_{t_{0}} (p) = Q_{n} \mathbf {x}(p) (t_{0})$, ${\Psi }_{t_{0}} (p) = Q_{n} \tilde {\mathbf {x}} (p) (t_{0}),$ for t ≤ t₀, for the solution x(p) is defined as fixed point of the map T as in (2.23) with f replaced by F, and similar for $\tilde {\mathbf {x}} (p)$, $\tilde {\mathbf {x}} (p)$ is a fixed point of $\widetilde {T}$ as in (2.23) with f replaced by P_nF(s, P_nx(s)).

For the derivative of error term, $\|D\varepsilon (t, p)\|_{{\mathscr{L}} (P_{n}X)}$, we have

$$ \begin{array}{@{}rcl@{}} && D \varepsilon (t, p) \\ && = P_{n} D F(t, p + {\Phi}_{t}(p)) (I_{P_{n}X} + D {\Phi}_{t}(p)) - P_{n} D F(p + P_{n} {\Psi}_{t}(p)) (I_{P_{n}X} + P_{n} D {\Psi}_{t} (p)), \\ && = P_{n} \Big [ D F(t, p + {\Phi}_{t}(p)) - D F(t, p + {\Psi}_{t} (p)) \Big ] (I_{P_{n}X} + D {\Phi}_{t}(p)) \\ && \quad + P_{n} D F(t, p + {\Psi}_{t} (p)) \big (D {\Phi}_{t}(p) - D {\Psi}_{t} (p) \big). \end{array} $$

Hence

$$ \begin{array}{@{}rcl@{}} \|D \varepsilon (t, p)\|_{\mathcal{L} (P_{n}X)} & \leq& (1+\text{Lip}_{\varphi} ({\Phi}_{t})) \left \| D F (t, p + {\Phi}_{t}(p)) - D F (t, p+{\Psi}_{t}(p)) \right \|_{\mathcal{L} (X)} + \\ && \quad + \eta (t) \left \| D {\Phi}_{t}(p) - D_{t}{\Psi}_{t} (p) \right \|_{\mathcal{L}(P_{n}X, Q_{n}X)}. \end{array} $$

In the first term, the norm $\left \| D F (t, p + {\Phi }_{t}(p)) - D F (t, p+{\Psi }_{t}(p)) \right \|_{{\mathscr{L}} (X)},$ for each $t \in \mathbb {R}$, satisfies the estimate $O \left (\frac {1}{\lambda _{n}^{\nu /2}} \right )$ as $n \rightarrow \infty$.

In the second term, to estimate the norm $\left \| D {\Phi }_{t}(p) - D {\Psi }_{t}(p) \right \|_{{\mathscr{L}} (P_{n}X, X)},$ we use the fixed point technique. We have DΦ_t(p) = Q_n∂_px(p), and $D {\Psi }_{t} (p) = Q_{n} \partial _{p} \tilde {\mathbf {x}}(p)$ and consider the fixed points ∂_px(p) = T^◇(∂_px(p), p), and $\partial _{p} \tilde {\mathbf {x}} (p) = \widetilde {T}^{\diamondsuit } (\partial _{p} \tilde {\mathbf {x}} (p), p)$, where

$$ \begin{array}{@{}rcl@{}} T^{\diamondsuit} ({\Delta}, p) &=& e^{-(t-t_{0})A} p - \int\limits_{-\infty}^{t_{0}} e^{-(t-s)A} \mathcal{G}(t, s) D F (s, \mathbf{x}(p(s))) {\Delta} (s) \mathrm{d}s, \\ \widetilde{T}^{\diamondsuit} ({\Delta}, p) &=& e^{-(t-t_{0})A} p - \int\limits_{-\infty}^{t_{0}} e^{-(t-s)A} \mathcal{G}(t, s) D \widetilde{F} \left( s, \tilde{\mathbf{x}} (p (s))\right) {\Delta} (s) \mathrm{d}s, \end{array} $$

for ${\Delta } \in L_{\infty , \diamondsuit }^{\gamma , t_{0}, \theta }$.

By using dichotomy estimates and admissibility of function spaces we can obtain

$$ \begin{array}{@{}rcl@{}} && \|\varepsilon (t, p)\| \leq \frac{\eta (t)}{\lambda^{1/2}_{m}}(c_{1}+c_{2} \|p\|), \quad \text{ for all } p \in P_{n}X, \end{array} $$

(3.30)

$$ \begin{array}{@{}rcl@{}} && \|D \varepsilon (t, p)\|_{\mathcal{L} (P_{n}X)} \leq \eta (t) \left( \frac{c_{3}}{\lambda_{m}^{1/2}}+\frac{c_{4}}{\lambda_{m}^{\nu /2}} \right), \quad \text{ for all } p \in P_{n}X, \end{array} $$

(3.31)

where the c_i’s are constant such that

$$ \begin{array}{@{}rcl@{}} c_{i}&=&c_{i} \left( n_{0}, n, \|{\Lambda}_{1} \varphi\|_{\infty}, \|{\Lambda}_{1} \psi_{1}\|_{\infty} \right), \quad \text{ for } i=1, 2, 3, \\ c_{4}&=&c_{4} \left( n_{0}, n, \|{\Lambda}_{1} \varphi_{2}\|_{\infty}, \|{\Lambda}_{1} \psi_{2}\|_{\infty}, \nu \right). \end{array} $$

Thus for each $t \in \mathbb {R}$, we have $\|\varepsilon (t, p)\| \rightarrow 0$ and $\|D \varepsilon (t, p)\|_{{\mathscr{L}} (P_{n}X)} \rightarrow 0$ as $m \rightarrow \infty$.

We will summarize the above events in the following main results:

Theorem 3.2

Consider the open-loop system (3.1). Let a non-autonomous ordinary differential equation (3.14) be given with $n_{0} \in \mathbb {N}$ and W satisfying (3.12) and (3.13). Suppose that n^∗ is the natural number that the conditions in the Theorem 2.6 satisfied with $\lambda _{n^{\ast }}$ and $\lambda _{n^{\ast }+1}$, and conditions (3.15) and (3.16) hold.

If a feedback law g = g(t, y) is given by (3.18), then the closed-loop equation (3.20) has an inertial manifold whose inertial form (3.28) is close to (3.26), which has essentially the same dynamics as (3.14), in a weighted metric for the vector fields as estimated in (3.30) and (3.31).

Similar to the work R. Rosa and R. Temam [32], we state the following result about structural stability of the dynamical systems.

Theorem 3.3

Assume the hypotheses in Theorem 3.2 hold and the nonlinear funtion W satisfies condition, for some r₀ > 0,

$$ ((W(t, z), z)) \leq -\alpha \|z\|, \quad \text{ for all } \|z\| \geq r_{0}, \text{ and for some } \alpha >0, $$

and that the flow induced by $\frac {\mathrm {d}z}{\mathrm {d}t}=W(t, z)$ for z restricted to the ball

$$ B_{r_{0}}^{n_{0}} := \{z \in P_{n_{0}}X: \|z\| \leq r_{0}\} $$

is structurally stable.

If feedback law g = g(t, y) is given by (3.18) with m chosen large enough, then the long-time dynamics of the inertial form (3.28) of the closed-loop equation (3.20) is contained in the ball $B_{r_{0}}^{n}=\{p \in P_{n}X: \|p\| \leq r_{0}\}$ and the corresponding flow restricted to this ball $B_{r_{0}}^{n}$ is topologically equivalent to the flow given by 3.26, so that the dynamics of the closed-loop system is essentially that of $\frac {\mathrm {d}z}{\mathrm {d}t}=W(t, z)$.