The doubly metric dimensions of cactus graphs and block graphs

Abstract

Given a connected graph G, two vertices $u,v\in V(G)$ doubly resolve $x,y\in V(G)$ if $d_{G}(x,u)-d_{G}(y,u)\ne d_{G}(x,v)-d_{G}(y,v)$. The doubly metric dimension $\psi (G)$ of G is the cardinality of a minimum set of vertices that doubly resolves each pair of vertices from V(G). It is well known that deciding the doubly metric dimension of G is NP-hard. In this work we determine the exact values of doubly metric dimensions of unicyclic graphs which completes the known result. Furthermore, we give formulae for doubly metric dimensions of cactus graphs and block graphs.

1 Introduction

The concept of metric dimension of graphs, independently introduced by Harary and Melter (1976) and Slater (1975), has many real-life applications such as medicinal chemistry (Chartrand et al. 2000), robot navigation (Khuller et al. 1996) and sonar (Slater 1975). Garey and Johnson (1979) proved that determining the metric dimension of an arbitrary graph is NP-hard. Since then several concepts related to the metric dimension have also been naturally proposed. Chartrand et al. (2000) characterized all graphs of order n with metric dimension 1, $n-1$, or $n-2$, respectively. Sedlar and Škrekovski (2021) studied the metric dimension of graphs with edge-disjoint cycles where they raised an open problem of identifying the exact difference between the metric dimension and the edge metric dimension of unicyclic graphs. Recently, Sedlar and Škrekovski (2022) and Zhu et al. (2022) solved this problem in different ways. Readers can refer to Cáceres et al. (2007), Hernando et al. (2010), Jiang and Polyanskii (2019), Klavžar and Tavakoli (2020), Klavžar and Tavakoli (2021), Nie and Xu (2023b), Wei et al. (2022), Zhang and Gao (2020) for more results.

One of the most interesting and important problems in graph theory is calculating the doubly metric dimension of a graph. Cáceres et al. (2007) introduced the definition of a doubly resolving set in order to determine the metric dimension of the Cartesian product of graphs. Kratica et al. (2009) proved that determining the doubly metric dimension of an arbitrary graph is NP-hard and gave its integer linear programming formulation, which implies that it is meaningful to determine the doubly metric dimension of specific classes of graphs. Chen and Wang (2014) established a polynomial time algorithm to find minimum doubly resolving sets of unicyclic graphs. Subsequently, Lu et al. (2022) designed a linear time algorithm for the problem of cactus graphs and block graphs and showed that the problem of deciding minimum doubly resolving sets of cactus and block graphs can be solved in $O(|V|+|E|)$. A connection between doubly resolving set problem and the coin weighing problem was established by Lu et al. Lu and Ye (2022). Furthermore, related algorithms for computing the doubly metric dimension of a graph were also researched, such as approximation algorithm (Chen et al. 2016), IP-based swapping algorithm (Hertz 2020) and variable neighborhood search (Mladenović et al. 2012). For some results on the doubly metric dimensions of special graphs, please see (Čangalović et al. 2013) (prism graphs), Kratica et al. (2012a) (Hamming graphs) and Kratica et al. (2012b) (convex polytopes). We researched the doubly metric dimensions of cylinder graphs (Nie and Xu 2023a) and the corona product of graphs (Nie and Xu 2023c), the former extends the main result in Čangalović et al. (2013). Liu et al. studied the doubly metric dimensions of Cayley graphs (Liu and Zafari 2022) and layer sun graphs (Liu and Zafari 2020). Sultan et al. (2022) determined the exact values of the doubly metric dimensions of antiprism graphs and Möbius ladders, respectively. Recently, Jannesari obtained bounds on the doubly metric dimension of unicyclic graphs (Jannesari 2022) and characterized graphs with doubly metric dimension two (Jannesari 2023).

All graphs are finite, undirected and connected in this paper. Let $G=(V(G),E(G))$ with vertex set V(G) and edge set E(G). We denote by $P_{n}$, $C_{n}$, $K_{n}$ the path, the cycle and the complete graph of order n, respectively. For $u,v\in V(G)$, the distance $d_{G}(u,v)$ is the length of a shortest path between u and v, where the shortest $u-v$ path is called the $u-v$geodesic. The diameter of G is $diam(G)=\max \{d_{G}(u,v): u,v\in V(G)\}$. The interval $I_{G}(u,v)$ between u and v is defined as the set of vertices that lie on some $u-v$ geodesic, that is, $I_{G}(u,v)=\{x\in V(G): d_{G}(u,v)=d_{G}(u,x)+d_{G}(x,v)\}$. The degree of a vertex u, denoted by deg(u), is the cardinality of $N_{G}(u)$ where $N_{G}(u)=\{v\in V(G): uv\in E(G)\}$ is the neighbourhood of u. A pendant vertex of a graph G is a vertex with degree 1. L(G) is the set of all pendant vertices in G whose cardinality is denoted by $\ell (G)$. In cases where the graph G is not ambiguous, we will remove the subscript G from these symbols. The definitions of the metric dimension and the doubly metric dimension of a graph are as follows:

• A vertex $v\in V(G)$ resolves two vertices $x,y\in V(G)$ if $d(x,v)\ne d(y,v)$. The set $W\subseteq V(G)$ is a resolving set of G if each pair of vertices of G is resolved by some vertex in W. The minimum cardinality of resolving sets of G, denoted by $\beta (G)$, is the metric dimension of G.

• Two vertices $u,v\in V(G)$ doubly resolve two vertices $x,y\in V(G)$ if $d(x,u)-d(y,u)\ne d(x,v)-d(y,v)$. The set $W\subseteq V(G)$ is a doubly resolving set (or DR set for short) of G if each pair of vertices is doubly resolved by some pair of vertices in W. That is, the set W doubly resolves each pair of vertices from V(G). The doubly metric dimension (or DMD for short) of G, denoted by $\psi (G)$, is the minimum cardinality of DR sets.

From above, $\beta (G)\le \psi (G)$ holds for any connected graph G. We focus on the DMD of cactus graphs and block graphs in this paper. A maximal connected subgraph without a cut vertex is called a block of a graph. A cactus graph is a connected graph in which each block is a cycle or an edge. A cactus graph with exactly one cycle is a unicyclic graph. A block graph is a graph in which each block is a complete graph.

We say that $K_{1}$ and $K_{2}$ are trivial blocks and that blocks of order 3 in a graph are nontrivial blocks. Given a cactus or block graph G with some nontrivial block B, the set of cut vertices of G in B is denoted by $\Phi (B)$, whose cardinality is denoted by $\phi (B)$. For $W\subseteq V(G)$, we give below the concept of W-active introduced in Sedlar and Škrekovski (2021). A vertex $v_{i}\in V(B)$ is W-active if $V(T_{v_{i}}(B))\bigcap W\ne \emptyset$, where $T_{v_{i}}(B)$ is the component of $G-E(B)$ containing the vertex $v_{i}$. Let $A_{B}(W)$ be the set of W-active vertices in the nontrivial block B and $A(W)=\bigcup _{B\in \mathcal {B}}A_{B}(W)$ be the set of W-active vertices in G and a(W) be the cardinality of A(W) where the set $\mathcal {B}$ consists of all nontrivial blocks in G.

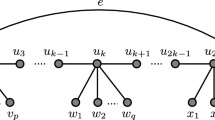
We use the cactus graph as an example to explain these concepts more clearly. For a cactus graph G with some cycle C, the component $T_{v_{i}}(C)$ is a tree when G is a unicyclic graph, and $T_{v_{i}}(C)$ may contain cycles when there are at least two cycles in G. Given a cactus graph G with two cycles $C^{1}$ and $C^{2}$ as shown in Fig. 1, it is clear that $T_{v_{4}}(C^{1})$, $T_{u_{3}}(C^{2})$ and $T_{u_{4}}(C^{2})$ are trees, while $T_{v_{2}}(C^{1})$ and $T_{u_{6}}(C^{2})$ contain a cycle. We can also obtain $\Phi (C^{1})=\{v_{2},v_{4}\}$ and $\Phi (C^{2})=\{u_{3},u_{4},u_{6}\}$. Set $W=\{w_{1},w_{4},w_{6}\}$. Then we have $A(W)=\{v_{2},v_{4},u_{3},u_{6}\}$ and $a(W)=4$.

Fig. 1

A cactus graph G with two cycles $C^{1}$ and $C^{2}$

In Sect. 2, we present some preliminary results to promote our main results. In Sect. 3, we determine the exact values of the DMD of unicyclic graphs. We show the formulae for DMD of cactus graphs and block graphs in Sects. 4 and 5, respectively.

2 Preliminaries

In this section, we present some preliminary results in order to promote our main results. For a connected graph G, a set $\Lambda \subseteq V(G)$ with cardinality $\alpha$ is an $\alpha$-maximum distance set if $\sum _{u,v\in \Lambda }d(u,v)=\max \{\sum _{x,y\in P}d(x,y):P\subseteq V(G),|P|=\alpha \}$. Clearly, two vertices $u,v\in V(G)$ form a 2-maximum distance set if $d(u,v)=diam(G)$.

Lemma 2.1

(Cáceres et al. 2007) Let $C_{n}$ be a cycle of order $n\ge 3$. Then

$$ \psi (C_{n})= {\left\{ \begin{array}{ll} 2 &{} n\ is\ odd;\\ 3 &{} n\ is\ even. \end{array}\right. }$$

Lemma 2.2

(Cáceres et al. 2007) Let $K_{n}$ be a complete graph of order $n>1$. Then

$$ \psi (K_{n})= {\left\{ \begin{array}{ll} 2 &{} n=2;\\ n-1 &{} n\ge 3. \end{array}\right. }$$

Lemma 2.3

(Cáceres et al. 2007) The set L(T) of leaves is the unique minimum DR set of a tree T.

Lemma 2.4

(Jannesari 2022; Nie and Xu 2023c) Let W be a DR set of a graph G. Then $L(G)\subseteq W$.

Lemma 2.5

(Nie and Xu 2023a) Let $C_{n}$ be an odd cycle. Then W is a minimum DR set of $C_{n}$ if and only if W is a 2-maximum distance set.

Lemma 2.6

For $u_{i},u_{j},u_{k}\in V(C_{n})$, we have $d(u_{i},u_{j})+d(u_{j},u_{k})+d(u_{i},u_{k})\le n$.

Proof

Assume, w.l.o.g., that $d(u_{i},u_{k})=\max \{d(u_{i},u_{j}),d(u_{j},u_{k}),d(u_{i},u_{k})\}$. Note that $d(u_{i},u_{k})\le \lfloor \frac{n}{2}\rfloor$. If $u_{j}\in I_{C_{n}}(u_{i},u_{k})$, then we have $d(u_{i},u_{j})+d(u_{j},u_{k})+d(u_{i},u_{k})=2d(u_{i},u_{k})\le n$. If $u_{j}\not \in I_{C_{n}}(u_{i},u_{k})$, then these three edge-disjoint geodesics $u_{i}-u_{k}$ geodesic, $u_{j}-u_{k}$ geodesic and $u_{i}-u_{j}$ geodesic form the cycle $C_{n}$, completing the proof. $\square$

Given a cycle $C_{n}$, we can assert that three vertices $u_{i},u_{j},u_{k}\in V(C_{n})$ form a 3-maximum distance set if $d(u_{i},u_{j})+d(u_{j},u_{k})+d(u_{i},u_{k})= n$ from Lemma 2.6. Let $\gamma = \min \{d(u_{i},u_{j})+d(u_{j},u_{k}),d(u_{j},u_{i})+d(u_{i},u_{k}),d(u_{i},u_{k})+d(u_{k},u_{j})\}$. Below we give a result for the 3-maximum distance set.

Lemma 2.7

Let $C_{n}$ be a cycle of order $n\ge 3$. Then $u_{i},u_{j},u_{k}\in V(C_{n})$ form a 3-maximum distance set if and only if $\gamma \ge \lceil \frac{n}{2}\rceil$.

Proof

Assume, w.l.o.g., that $\gamma =d(u_{i},u_{j})+d(u_{j},u_{k})$.

We first show the proof of necessity by negation. Assume that $\gamma <\lceil \frac{n}{2}\rceil$. We have $d(u_{i},u_{k})<\lceil \frac{n}{2}\rceil$, and then $d(u_{i},u_{j})+d(u_{j},u_{k})+d(u_{i},u_{k})<n$, which contradicts that $\{u_{i},u_{j},u_{k}\}$ is a 3-maximum distance set. We now turn to show the sufficiency. If $\gamma \ge \lceil \frac{n}{2}\rceil$, then we can directly derive that $d(u_{i},u_{j})+d(u_{j},u_{k})+d(u_{i},u_{k})=n$. Therefore, the result is proved. $\square$

Lemma 2.8

Let $C_{n}=u_{1}u_{2}\ldots u_{n}u_{1}$ be a cycle and let W be a DR set of $C_{n}$. Then

• (i) W contains a 3-maximum distance set for even n.

• (ii) W contains an $\alpha$-maximum distance set for odd n and $\alpha \in \{2,3\}$.

Proof

(i):

Note that $\psi (C_{n})=3$ for even n. We have $|W|\ge 3$. Assume, to the contrary, that there is no 3-maximum distance set in W. For any three vertices $u_{i},u_{j},u_{k}\in W$, assume that $\gamma =d(u_{i},u_{j})+d(u_{j},u_{k})<\frac{n}{2}$ by Lemma 2.7. There is a vertex $u_{k'}\in N(u_{k})\setminus I_{C_{n}}(u_{j},u_{k})$ such that $d(u_{k'},s)-d(u_{k},s)= d(u_{k'},t)-d(u_{k},t)=1$ for any pair of vertices $s,t\in W$, which leads to a contradiction.

(ii):

Note that $\psi (C_{n})=2$ for odd n. We assert $|W|\ge 2$. By Lemma 2.5, the result follows when $|W|=2$, and we only consider $|W|\ge 3$. To the contrary, assume that there is neither 2-maximum distance set nor 3-maximum distance set in W. For any three vertices $u_{i},u_{j},u_{k}\in W$, assume that $\gamma =d(u_{i},u_{j})+d(u_{j},u_{k})\le \lceil \frac{n}{2}\rceil -1=\lfloor \frac{n}{2}\rfloor$ by Lemma 2.7. This implies that $u_{j}\in I_{C_{n}}(u_{i},u_{k})$. Since there is no 2-maximum distance set, we have $d(u_{i},u_{j})+d(u_{j},u_{k})<\lfloor \frac{n}{2}\rfloor$. Hence, there is a vertex $u_{k'}\in N(u_{k})\setminus I_{C_{n}}(u_{j},u_{k})$ such that $d(u_{k'},s)-d(u_{k},s)= d(u_{k'},t)-d(u_{k},t)=1$ for any pair of vertices $s,t\in W$, a contradiction.

$\square$

Lemma 2.9

Let $C_{n}$ be a cycle and $W\subseteq V(C_{n})$. Then

• (i) W is a DR set for even n if and only if W contains a 3-maximum distance set.

• (ii) W is a DR set for odd n if and only if W contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$.

Proof

By Lemma 2.8, we just need to consider sufficiencies in both (i) and (ii). By Lemma 2.5, we only consider that W contains a 3-maximum distance set in (ii).

Let $C_{n}=u_{1}u_{2}\ldots u_{n}u_{1}$ with natural adjacency relations. We can fix a vertex $u_{1}\in W$. Let $\Lambda \subseteq W$ and $\Lambda =\{u_{1},u_{k},u_{\ell }\}$ be a 3-maximum distance set in $C_{n}$. By Lemma 2.7, assume that $\gamma =d(u_{1},u_{k})+d(u_{k},u_{\ell })\ge \lceil \frac{n}{2}\rceil$ and $1<k<\ell$. There are three edge-disjoint geodesics which are $u_{1}-u_{k}$ geodesic, $u_{k}-u_{\ell }$ geodesic and $u_{\ell }-u_{n+1}$ geodesic. For $x,y\in V(G)$, if they belong to the same geodesic, then we derive that two end vertices of the geodesic doubly resolve x and y. We only consider three cases: $x\in I_{C_{n}}(u_{1},u_{k})$ and $y\in I_{C_{n}}(u_{k},u_{\ell })$; $x\in I_{C_{n}}(u_{1},u_{k})$ and $y\in I_{C_{n}}(u_{\ell },u_{n+1})$; $x\in I_{C_{n}}(u_{k},u_{\ell })$ and $y\in I_{C_{n}}(u_{\ell },u_{n+1})$. Similarly, we only consider the cases $x\in I_{C_{n}}(u_{1},u_{k})$ and $y\in I_{C_{n}}(u_{k},u_{\ell })$ in both (i) and (ii).

(i):

Let $d(u_{k},u_{k'})=\frac{n}{2}$ for $u_{k'}\in V(C_{n})$. Then we have $\frac{n}{2}+1\le \ell <k'$. Suppose that $d(x,u_{k})\ge d(y,u_{k})$. We obtain $d(x,u_{k'})\le d(y,u_{k'})$. The distance between y and $u_{1}$ is

$$\begin{aligned} d(y,u_{1})=d(y,u_{k'})+d(u_{k'},u_{1})\ge d(x,u_{k'})+d(u_{k'},u_{1})>d(x,u_{1}) \end{aligned}$$

or $d(y,u_{1})=d(y,x)+d(x,u_{1})>d(x,u_{1})$. Hence, $u_{1}$ and $u_{k}$ doubly resolve x and y. Suppose that $d(x,u_{k})<d(y,u_{k})$. We assert $d(x,u_{k'})>d(y,u_{k'})$. We obtain

$$\begin{aligned} d(x,u_{\ell })=d(x,u_{k'})+d(u_{k'},u_{\ell })>d(y,u_{k'})+d(u_{k'},u_{\ell })>d(y,u_{\ell }) \end{aligned}$$

or $d(x,u_{\ell })=d(x,y)+d(y,u_{\ell })>d(y,u_{\ell })$. This means that $u_{k}$ and $u_{\ell }$ doubly resolve x and y, completing the proof of (i).

(ii):

Let $d(u_{k},u_{k'})=d(u_{k},u_{k''})=\lfloor \frac{n}{2}\rfloor$ where $k'=k+\lfloor \frac{n}{2}\rfloor$ and $k''=k+1+\lfloor \frac{n}{2}\rfloor$. Then we obtain $\lfloor \frac{n}{2}\rfloor +2\le \ell <k'$. Suppose that $d(x,u_{k})\ge d(y,u_{k})$. We have $d(x,u_{k''})<d(y,u_{k''})$. The distance between y and $u_{1}$ is

$$\begin{aligned} d(y,u_{1})=d(y,u_{k''})+d(u_{k''},u_{1})>d(x,u_{k''})+d(u_{k''},u_{1})>d(x,u_{1}) \end{aligned}$$

or $d(y,u_{1})=d(y,x)+d(x,u_{1})>d(x,u_{1})$. Then, $u_{1}$ and $u_{k}$ doubly resolve x and y. Suppose that $d(x,u_{k})<d(y,u_{k})$. We obtain $d(x,u_{k'})>d(y,u_{k'})$. We assert

$$\begin{aligned} d(x,u_{\ell })=d(x,u_{k'})+d(u_{k'},u_{\ell })>d(y,u_{k'})+d(u_{k'},u_{\ell })>d(y,u_{\ell }) \end{aligned}$$

or $d(x,u_{\ell })=d(x,y)+d(y,u_{\ell })>d(y,u_{\ell })$. This means that $u_{k}$ and $u_{\ell }$ doubly resolve x and y, ending the proof.

$\square$

3 Unicyclic graphs

Jannesari (2022) showed that $\psi (G)\in \{\ell (G),\ell (G)+1,\ell (G)+2\}$ for a unicyclic graph G which is not a cycle. We give the exact values of doubly metric dimensions of unicyclic graphs in this section.

Lemma 3.1

Let W be a DR set of a unicyclic graph G of order n with a cycle $C_{m}$. Then

• (i) A(W) contains a 3-maximum distance set for even m.

• (ii) A(W) contains an $\alpha$-maximum distance set for odd m and $\alpha \in \{2,3\}$.

Proof

(i):

Assume, to the contrary, that A(W) contains no 3-maximum distance set. Suppose that $|A(W)|=1$. Note that $u_{i}\in A(W)$ for $u_{i}\in W\bigcap V(C_{m})$. Set $A(W)=\{u_{k}\}$, then there exist $x,y\in V(C_{m})$ such that $d(x,u_{k})-d(y,u_{k})=d(x,s)-d(y,s)=d(x,t)-d(y,t)$ for any $s,t\in V(T_{u_{k}}(C_{m}))\bigcap W$, which contradicts the fact that W is a DR set of G. Suppose that $|A(W)|\ge 2$. By Lemma 2.9 (i), there exist $x,y\in V(C_{m})$ such that $d_{C_{m}}(x,u_{k})-d_{C_{m}}(y,u_{k})=d_{C_{m}}(x,u_{\ell })-d_{C_{m}}(y,u_{\ell })$ for any $u_{k},u_{\ell }\in A(W)$. Note that $d_{C_{m}}(x,u_{k})-d_{C_{m}}(y,u_{k})=d_{G}(x,s)-d_{G}(y,s)$ and $d_{C_{m}}(x,u_{\ell })-d_{C_{m}}(y,u_{\ell })=d_{G}(x,t)-d_{G}(y,t)$ for $s\in V(T_{u_{k}}(C_{m}))\bigcap W$ and $t\in V(T_{u_{\ell }}(C_{m}))\bigcap W$. Therefore, W can not doubly resolve x and y, a contradiction.

(ii):

Assume, to the contrary, that A(W) contains neither 2-maximum distance set nor 3-maximum distance set. Suppose that $|A(W)|=1$. Set $A(W)=\{u_{k}\}$, then there exist $x,y\in V(C_{m})$ satisfying $d(x,u_{k})-d(y,u_{k})=d(x,s)-d(y,s)=d(x,t)-d(y,t)$ for any $s,t\in W$, a contradiction. Suppose that $|A(W)|\ge 2$. By Lemma 2.9 (ii), A(W) is not a DR set of $C_{m}$. There exist $x,y\in V(C_{m})$ satisfying $d_{C_{m}}(x,u_{k})-d_{C_{m}}(y,u_{k})=d_{C_{m}}(x,u_{\ell })-d_{C_{m}}(y,u_{\ell })$ for any $u_{k},u_{\ell }\in A(W)$. Note that $d_{C_{m}}(x,u_{k})-d_{C_{m}}(y,u_{k})=d_{G}(x,s)-d_{G}(y,s)$ and $d_{C_{m}}(x,u_{\ell })-d_{C_{m}}(y,u_{\ell })=d_{G}(x,t)-d_{G}(y,t)$ for $s\in V(T_{u_{k}}(C_{m}))\bigcap W$ and $t\in V(T_{u_{\ell }}(C_{m}))\bigcap W$. Hence, we assert that W can not doubly resolve x and y, a contradiction.

$\square$

Lemma 3.2

Let G be a unicyclic graph of order n with an even cycle $C_{m}$. Then the set $W\subseteq V(G)$ is a DR set of G if and only if $L(G)\subseteq W$ and there is a 3-maximum distance set in A(W).

Proof

For a DR set W of G, we obtain that $L(G)\subseteq W$ and there is a 3-maximum distance set in A(W) from Lemmas 2.4 and 3.1 (i). The necessity holds.

We now show the sufficiency. Let $V(C_{m})=\{v_{1},v_{2},\ldots ,v_{m}\}$. The set $W\subseteq V(G)$ contains all pendant vertices of G and there is a 3-maximum distance set $\Lambda =\{v_{a},v_{b},v_{c}\}$ in A(W). For $x,y\in V(G)$, our goal is to show that W doubly resolves x and y.

For $x,y\in V(T_{v_{i}}(C_{m}))$, this means that $T_{v_{i}}(C_{m})$ is a subtree of G. Since $L(T_{v_{i}}(C_{m}))$ is the DR set of $T_{v_{i}}(C_{m})$ by Lemma 2.3, we derive that W doubly resolves x and y.

For $x,y\in V(C_{m})$, assume that $d(x,v_{a})-d(y,v_{a})\ne d(x,v_{b})-d(y,v_{b})$ for $v_{a},v_{b}\in A(W)$ by Lemma 2.9 (i) as there is a 3-maximum distance set $\{v_{a},v_{b},v_{c}\}$ in A(W). Since $d(x,s)-d(y,s)=d(x,v_{a})-d(y,v_{a})$ for $s\in V(T_{v_{a}}(C_{m}))\bigcap W$ and $d(x,t)-d(y,t)=d(x,v_{b})-d(y,v_{b})$ for $t\in V(T_{v_{b}}(C_{m}))\bigcap W$, we can assert that s and t doubly resolve x and y.

For $x\in V(T_{v_{i}}(C_{m}))\setminus \{v_{i}\}$ and $y\in V(T_{v_{j}}(C_{m}))\setminus \{v_{j}\}$, this means $v_{i},v_{j}\in A(W)$. There are two pendant vertices $s\in W\bigcap V(T_{v_{i}}(C_{m}))$ and $t\in W\bigcap V(T_{v_{j}}(C_{m}))$ such that $s,t\in W$ doubly resolve x and y.

For $x\in V(C_{m})$ and $y\in V(T_{v_{i}}(C_{m}))\setminus \{v_{i}\}$, there are two cases.

Suppose that $v_{i}\not \in \Lambda$. Set $v_{a}$ and $v_{b}$ doubly resolve x and $v_{i}$ for $v_{a},v_{b}\in \Lambda$ by Lemma 2.9 (i). As $v_{a}$ and $v_{b}$ are W-active, there exist two vertices $s\in V(T_{v_{a}}(C_{m}))\bigcap W$ and $t\in V(T_{v_{b}}(C_{m}))\bigcap W$ such that s and t doubly resolve x and $v_{i}$. Then we derive $d(x,s)-d(v_{i},s)-d(y,v_{i})\ne d(x,t)-d(v_{i},t)-d(y,v_{i})$, that is, s and t doubly resolve x and y.

Suppose that $v_{i}\in \Lambda$. There is a vertex $t\in W\bigcap L(T_{v_{i}}(C_{m}))$ satisfying $d(x,t)=d(x,y)+d(y,t)$, that is, $d(x,t)>d(y,t)$. Let $\{v_{i},v_{a},v_{b}\}$ be the 3-maximum distance set in A(W). If $d(x,v_{a})\le d(v_{i},v_{a})$, then

$$\begin{aligned} d(x,v_{a})&\le d(v_{i},v_{a})\\&<d(v_{i},v_{a})+d(y,v_{i})\\&=d(y,v_{a}). \end{aligned}$$

Note that $v_{a}$ is W-active. There is a vertex $s\in V(T_{v_{a}}(C_{m}))\bigcap W$ satisfying $d(x,s)<d(y,s)$. Thus, t and s doubly resolve x and y.

We now turn to consider $d(x,v_{a})> d(v_{i},v_{a})$. Let $d(v_{i},v_{i'})=\frac{m}{2}$ and $d(v_{a},v_{a'})=\frac{m}{2}$ for $v_{i'},v_{a'}\in V(C_{m})$. For $d(x,v_{a})> d(v_{i},v_{a})$, we obtain $d(x,v_{a'})<d(v_{i},v_{a'})$. We need to consider the following two cases $x\in I_{C_{m}}(v_{i},v_{b})$ and $x\in I_{C_{m}}(v_{a},v_{b})$ as illustrated in Figs. 2(a, b). Note that $v_{i},v_{a},v_{b}$ form a 3-maximum distance set. We have $v_{b}\in I_{C_{m}}(v_{i'},v_{a'})$. Suppose that $x\in I_{C_{m}}(v_{i},v_{b})$. Then $d(v_{i},v_{b})=d(v_{i},x)+d(x,v_{b})$ and $d(v_{i},v_{b})>d(x,v_{b})$, and so $d(y,v_{b})>d(x,v_{b})$. Since $v_{b}$ is W-active, there is a vertex $v\in V(T_{v_{b}}(C_{m}))\bigcap W$ with $d(y,v)>d(x,v)$. Hence, these two vertices $t,v\in W$ doubly resolve x and y. Suppose that $x\in I_{C_{m}}(v_{a},v_{b})$. We derive $d(y,v_{b})>d(x,v_{b})$ and

$$\begin{aligned} d(v_{i},v_{b})&=d(v_{i},v_{a'})+d(v_{a'},v_{b})\\&\quad>d(x,v_{a'})+d(v_{a'},v_{b})\\&\quad >d(x,v_{b}). \end{aligned}$$

Similarly, there is a vertex $v\in V(T_{v_{b}}(C_{m}))\bigcap W$ satisfying $d(y,v)>d(x,v)$. Therefore, these two vertices $t,v\in W$ doubly resolve x and y, ending the proof. $\square$

Fig. 2

The 3-maximum distance set $\{v_{i},v_{a},v_{b}\}$ in $V(C_{m})$

Lemma 3.3

Let G be a unicyclic graph of order n with an odd cycle $C_{m}$. Then $W\subseteq V(G)$ is a DR set of G if and only if $L(G)\subseteq W$ and there is an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in A(W).

Proof

For a DR set W of G, we assert that $L(G)\subseteq W$ and A(W) contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ from Lemmas 2.4 and 3.1 (ii).

We now show the sufficiency. Let $V(C_{m})=\{v_{1},v_{2},\ldots ,v_{m}\}$. We may assume that A(W) contains a 2-maximum distance set $\{v_{k},v_{\ell }\}$ or a 3-maximum distance set $\{v_{a},v_{b},v_{c}\}$. Similarly, we only consider that $L(G)\subseteq W$ and there is a 2-maximum distance set in A(W). We show that W doubly resolves $x,y\in V(G)$.

For $x,y\in V(T_{v_{i}}(C_{m}))$, we know that $T_{v_{i}}(C_{m})$ is a subtree of G. Note that $L(T_{v_{i}}(C_{m}))$ doubly resolves x and y by Lemma 2.3. We assert that W doubly resolves x and y.

For $x,y\in V(C_{m})$, we derive that $v_{k}$ and $v_{\ell }$ doubly resolve x and y by Lemma 2.9 (ii) since there is a 2-maximum distance set $\{v_{k},v_{\ell }\}$ in A(W). Note that $v_{k}$ and $v_{\ell }$ are W-active. There are two vertices $s\in V(T_{v_{k}}(C_{m}))\bigcap W$ and $t\in V(T_{v_{\ell }}(C_{m}))\bigcap W$ such that $s,t\in W$ doubly resolve x and y.

For $x\in V(T_{v_{i}}(C_{m}))\setminus \{v_{i}\}$ and $y\in V(T_{v_{j}}(C_{m}))\setminus \{v_{j}\}$, there also exist two vertices $s\in W\bigcap L(T_{v_{i}}(C_{m}))$ and $t\in W\bigcap L(T_{v_{j}}(C_{m}))$ such that these two vertices $s,t\in W$ doubly resolve x and y.

For $x\in V(C_{m})$ and $y\in V(T_{v_{i}}(C_{m}))\setminus \{v_{i}\}$, there are two cases.

Suppose that $v_{i}\not \in \{v_{k},v_{\ell }\}$. We assert that $v_{k}$ and $v_{\ell }$ doubly resolve x and $v_{i}$ by Lemma 2.9 (ii). For $s\in W\bigcap V(T_{v_{k}}(C_{m}))$ and $t\in W\bigcap V(T_{v_{\ell }}(C_{m}))$, we can also derive that $s,t\in W$ doubly resolve x and $v_{i}$. Hence, we have $d(x,s)-d(v_{i},s)-d(v_{i},y)\ne d(x,t)-d(v_{i},t)-d(v_{i},y)$ which means that $s,t\in W$ doubly resolve x and y.

Suppose that $v_{i}\in \{v_{k},v_{\ell }\}$. Let $\{v_{i},v_{k}\}$ be the 2-maximum distance set in A(W). Then $d(v_{i},v_{k})=\lfloor \frac{m}{2}\rfloor$. It is clear that

$$\begin{aligned} d(x,v_{k})&\le d(v_{i},v_{k})\\&<d(v_{i},v_{k})+d(y,v_{i})\\&=d(y,v_{k}). \end{aligned}$$

Since $v_{k}$ is W-active, there is a vertex $t\in V(T_{v_{k}}(C_{m}))\bigcap W$ with $d(x,t)<d(y,t)$. Note that there is a vertex $s\in W\bigcap L(T_{v_{i}}(C_{m}))$ with $d(x,s)=d(x,y)+d(y,s)$, that is, $d(x,s)>d(y,s)$. Then $s,t\in W$ doubly resolve x and y, completing the proof. $\square$

Given a unicyclic graph G with a cycle C, we have $\Phi (C)=\emptyset$ for $G\cong C$. We already know the doubly metric dimension of a cycle by Lemma 2.1. Below we only consider unicyclic graphs with $\phi (C)\ge 1$.

Definition 3.4

Let G be a unicyclic graph of order n and $G\not \cong C_{n}$. Then we can classify G into three families of graphs:

• (i) $\mathcal {G}_{1}$ is a family of unicyclic graphs in which each graph contains an even cycle $C_{m}$ with $\phi (C_{m})=1$.

• (ii) $\mathcal {G}_{2}$ is a family of unicyclic graphs in which each graph contains either an even cycle $C_{m}$ with $\phi (C_{m})\ge 2$ where $\Phi (C_{m})$ contains no 3-maximum distance set or an odd cycle $C_{m}$ with $\phi (C_{m})\ge 1$ where $\Phi (C_{m})$ contains no $\alpha$-maximum distance set for $\alpha \in \{2,3\}$.

• (iii) $\mathcal {G}_{3}$ is a family of unicyclic graphs in which each graph contains either an even cycle with $\phi (C_{m})\ge 3$ where $\Phi (C_{m})$ contains a 3-maximum distance set or an odd cycle $C_{m}$ with $\phi (C_{m})\ge 2$ where $\Phi (C_{m})$ contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$.

See Fig. 3 for some simple examples in Definition 3.4. In Fig. 3(a), the graph $G\in \mathcal {G}_{1}$ with $\Phi (C_{8})=\{v_{1}\}$ and $\phi (C_{8})=1$. In Fig. 3(b), the graph $G\in \mathcal {G}_{2}$ with $\Phi (C_{8})=\{v_{1},v_{3},v_{4}\}$ and $\phi (C_{8})=3$ where $\Phi (C_{8})$ is not a 3-maximum distance set. In Fig. 3(c), the graph $G\in \mathcal {G}_{2}$ with $\Phi (C_{7})=\{v_{1},v_{2},v_{3}\}$ and $\phi (C_{7})=3$ where $\Phi (C_{7})$ contains neither 2-maximum distance set nor 3-maximum distance set. In Fig. 3(d), the graph $G\in \mathcal {G}_{3}$ with $\Phi (C_{7})=\{v_{1},v_{4}\}$ and $\phi (C_{7})=2$ where $\Phi (C_{7})$ is a 2-maximum distance set. In Fig. 3(e), the graph $G\in \mathcal {G}_{3}$ with $\Phi (C_{8})=\{v_{1},v_{3},v_{6}\}$ and $\phi (C_{8})=3$ where $\Phi (C_{8})$ is a 3-maximum distance set.

Fig. 3

Five examples for Definition 3.4

Theorem 3.5

Let G be a unicyclic graph of order n and $G\not \cong C_{n}$. Then

$$ \psi (G)= {\left\{ \begin{array}{ll} \ell (G) &{} G\in \mathcal {G}_{3};\\ \ell (G)+1 &{} G\in \mathcal {G}_{2};\\ \ell (G)+2 &{} G\in \mathcal {G}_{1}. \end{array}\right. }$$

Proof

Let $C_{m}=v_{1}v_{2}\ldots v_{m}v_{1}$ with natural adjacency relation in G and let W be a minimum DR set of G. There are three cases in the following:

Suppose that $G\in \mathcal {G}_{1}$. We first show the lower bound. Note that $L(G)\subseteq W$ and $\Phi (C_{m})\subseteq A(W)$. Since $\phi (C_{m})=1$, we have $|W|\ge \ell (G)+2$ by Lemma 3.2. The upper bound is now shown. Let $v_{i}\in V(C_{m})$ be the only vertex with degree at least three. Since $m\ge 4$, we can choose two vertices $v_{j},v_{k} \in V(C_{m})$ such that $v_{i},v_{j},v_{k}$ form a 3-maximum distance set in $C_{m}$. Let $W'=L(G)\bigcup \{v_{j},v_{k}\}$. We can assert that $W'$ is a DR set of G with $\ell (G)+2$ vertices by Lemma 3.2.

Suppose that $G\in \mathcal {G}_{2}$.

We first assume that m is even. Note that there is no 3-maximum distance set in $\Phi (C_{m})$ and $\Phi (C_{m})\subseteq A(W)$. We assert $|W|\ge \ell (G)+1$ by Lemma 3.2. The upper bound is now shown. Let $v_{i},v_{j}\in \Phi (C_{m})$. Then we can select a vertex $v_{k}\in V(C_{m})$ to form a 3-maximum distance set with $v_{i}$ and $v_{j}$. Set $W'=L(G)\bigcup \{v_{k}\}$. Again, by Lemma 3.2, $W'$ is a DR set of G, and so $\psi (G)=\ell (G)+1$.

We now assume that m is odd. We have $|W|\ge \ell (G)+1$ for any minimum DR set W of G by Lemma 3.3. Let $v_{i}\in \Phi (C_{m})$ and $d(v_{i},v_{j})=\lfloor \frac{m}{2}\rfloor$ for $v_{j}\in V(C_{m})\setminus \Phi (C_{m})$. Then $v_{i}$ and $v_{j}$ form a 2-maximum distance set. Let $W'=L(G)\bigcup \{v_{j}\}$. Then $v_{i},v_{j}\in A(W')$ which means that $W'$ is a DR set of G by Lemma 3.3. Hence, $\psi (G)=\ell (G)+1$.

Suppose that $G\in \mathcal {G}_{3}$. We derive that $|W|\ge \ell (G)$ by Lemmas 3.2 and 3.3. We now show that $W'=L(G)$ doubly resolves any pair of vertices in V(G). Note that $A(W')=\Phi (C_{m})$. We assert that $W'$ is a DR set of G from Lemmas 3.2 and 3.3. Therefore, $\psi (G)=\ell (G)$. This completes the proof. $\square$

4 Cactus graphs

In this section we extend the result for unicyclic graphs of the previous to all cactus graphs. Let G be a cactus graph of order n. We assert that $\phi (C)\ge 1$ for any cycle C in $G\not \cong C_{n}$. Let $\ell _{1}$ and $\ell _{2}$ be the number of even cycles without 3-maximum distance set in $\Phi (C)$ and the number of odd cycles without $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in $\Phi (C)$ respectively, where there are $\ell _{3}$ even cycles with $\phi (C)=1$ in these $\ell _{1}$ even cycles. Below we give the formula for the DMD of cactus graphs.

Theorem 4.1

Let G be a cactus graph of order n and $G\ne C_{n}$. Then

$\psi (G)=\ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$.

When G is a tree or a unicyclic graph, we know the DMD of G by Lemmas 2.1 and 2.3, and Theorem 3.5. We only need to consider the doubly metric dimension of G with $p\ge 2$ cycles. We give two lemmas below which complete the proof of Theorem 4.1.

Lemma 4.2

Let G be a cactus graph of order n with $p\ge 2$ cycles. Then

$\psi (G)\ge \ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$.

Proof

Let W be a minimum DR set of G. We derive that $L(G)\subseteq W$ by Lemma 2.4 and W contains $\ell _{1}+\ell _{3}$ and $\ell _{2}$ vertices from these $\ell _{1}$ even cycles and $\ell _{2}$ odd cycles respectively such that A(W) contains a 3-maximum distance set in each even cycle and A(W) contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in each odd cycle. That is, $\psi (G)=|W|\ge \ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$. Otherwise, there are two cases:

Case 1. There is an even cycle $C^{r}$ such that $A_{C^{r}}(W)$ contains no 3-maximum distance set.

Suppose that $|A_{C^{r}}(W)|=1$. Set $A_{C^{r}}(W)=\{v_{k}\}$. Then there is only one W-active vertex in $C^{r}$. Hence, there always exist two vertices $v_{i}, v_{j}\in V(C^{r})$ satisfying $d(v_{i},v_{k})-d(v_{j},v_{k})=d(v_{i},s)-d(v_{j},s)=d(v_{i},t)-d(v_{j},t)$ for any $s,t\in V(T_{v_{k}}(C^{r}))\bigcap W$. This means that W can not doubly resolve $v_{i}$ and $v_{j}$, a contradiction.

Suppose that $|A_{C^{r}}(W)|\ge 2$. By Lemma 2.9 (i), there are two vertices $v_{i}, v_{j}\in V(C^{r})$ that are not doubly resolved by $A_{C^{r}}(W)$, that is, $d(v_{i},v_{k})-d(v_{j},v_{k})=d(v_{i},v_{\ell })-d(v_{j},v_{\ell })$ for any pair of vertices $v_{k},v_{\ell }\in A_{C^{r}}(W)$. Since $v_{k}$ and $v_{\ell }$ are W-active, we have $d(v_{i},v_{k})-d(v_{j},v_{k})= d(v_{i},s)-d(v_{j},s)$ and $d(v_{i},v_{\ell })-d(v_{j},v_{\ell })= d(v_{i},t)-d(v_{j},t)$ for $s\in V(T_{v_{k}}(C^{r}))\bigcap W$ and $t\in V(T_{v_{\ell }}(C^{r}))\bigcap W$. Hence, W can not doubly resolve $v_{i}$ and $v_{j}$, a contradiction.

Case 2. There is an odd cycle $C^{r}$ such that $A_{C^{r}}(W)$ contains neither 2-maximum distance set nor 3-maximum distance set.

There also exist two vertices $v_{i}, v_{j}\in V(C^{r})$ that are not doubly resolved by $A_{C^{r}}(W)$ from Lemma 2.9 (ii). The case is similar to Case 1, we can also obtain that W can not doubly resolve $v_{i}$ and $v_{j}$, again a contradiction.

Therefore, $\Psi (G)\ge \ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$ and the result follows. $\square$

Given a cactus graph G with $p\ge 2$ cycles, let $E_{C}(G)\subseteq E(G)$ be a set of edges which contains all edges of each cycle in G and $E_{C}(G)=E(C^{1})\bigcup \cdots \bigcup E(C^{p})$. The unicyclic subgraph $G^{i}$ is a component of $G\setminus (E_{C}(G)\setminus E(C^{i}))$ that contains the cycle $C^{i}$. Note that two distinct unicyclic subgraph $G^{i}$ and $G^{j}$ are not necessarily vertex-disjoint but $G=G^{1}\bigcup \cdots \bigcup G^{p}$. For a set $W\subseteq V(G)$, the set $W_{i}\subseteq V(G^{i})$ is formed by $W\bigcap V(G^{i})$ and $V(G^{i})\bigcap V(C^{\ell })$ for every $\ell \ne i$.

Proposition 4.3

Let $W\subseteq V(G)$ and $W_{i}\subseteq V(G^{i})$ in a cactus graph G of order n with $p\ge 2$ cycles. Then the following two conditions hold:

• (i) If $L(G)\subseteq W$, then $L(G^{i})\subseteq W_{i}$.

• (ii) If A(W) contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in each cycle of G, then $A(W_{i})$ contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in $C^{i}$.

Again see Fig. 1. The graph $G^{1}$ is induced by $V(C^{1})\bigcup \{w_{1},w_{2},w_{3},w_{4},w_{8},w_{9},u_{6}\}$, while the graph $G^{2}$ is induced by $V(C^{2})\bigcup \{w_{3},w_{4},w_{5},w_{6},w_{7},w_{9},w_{10},v_{2}\}$. Set $W=\{w_{1},w_{2},v_{1},w_{3},w_{4},w_{5},w_{6},w_{7}\}$. Then the set $A(W)=\{v_{1},v_{2},v_{4},u_{3},u_{4},u_{6}\}$. Note that $W_{1}=\{w_{1},w_{2},v_{1},w_{3},w_{4},u_{6}\}$ and $W_{2}=\{w_{3},w_{4},w_{5},w_{6},w_{7},v_{2}\}$. We find that $A(W_{1})=\{v_{1},v_{2},v_{4}\}$ is a 3-maximum distance set in $C^{1}$ and $A(W_{2})=\{u_{3},u_{4},u_{6}\}$ contains a 2-maximum distance set in $C^{2}$.

Lemma 4.4

Let G be a cactus graph of order n with $p\ge 2$ cycles. Then

$\psi (G)\le \ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$.

Proof

Let $W=L(G)\bigcup L_{1}\bigcup L_{2}$ where all vertices in $L_{1}$ and $L_{2}$ are picked from these $\ell _{1}$ even cycles and $\ell _{2}$ odd cycles respectively such that A(W) contains a 3-maximum distance set in each even cycle and A(W) contains an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in each odd cycle. Clearly, $L_{1}\bigcap L_{2}=\emptyset$, $|L_{1}|=\ell _{1}+\ell _{3}$ and $|L_{2}|=\ell _{2}$. Then $|W|=\ell (G)+\ell _{1}+\ell _{2}+\ell _{3}$. Our aim is to show that W doubly resolves $x,y\in V(G)$.

Case 1. $x,y\in V(G^{i})$.

From Proposition 4.3, the set $W_{i}$ contains all pendant vertices of $G^{i}$, $A(W_{i})$ contains a 3-maximum distance set in even cycle $C^{i}$ or an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in odd cycle $C^{i}$. From Lemmas 3.2 and 3.3, we can assert that $W_{i}$ is a DR set of $G^{i}$.

Assume that $s,t\in W_{i}$ doubly resolve x and y. If $s,t\in W\bigcap W_{i}$, then they also doubly resolve x and y for $s,t \in W$. If $s\in W\bigcap W_{i}$ and $t\in W_{i}\setminus W$, then $t\in V(G^{i})\bigcap V(C^{\ell })$ for $\ell \ne i$. Note that each cycle in G contains a 2-maximum distance set or a 3-maximum distance set of W-active vertices. There exists a vertex $t'\in W\setminus V(G^{i})$ such that $d(x,t')-d(y,t')=d(x,t)-d(y,t)$. Hence, $s,t'\in W$ doubly resolve x and y. For $s,t\in W_{i}\setminus W$, we can also obtain that W doubly resolves x and y.

Case 2. $x\in V(G^{i})$ and $y\in V(G^{j})$.

Let $V(C^{i})=\{u_{1},u_{2},\ldots ,u_{m}\}$ and $V(C^{j})=\{v_{1},v_{2},\ldots ,v_{m'}\}$. We consider $x\not \in V(G^{j})$ and $y\not \in V(G^{i})$, otherwise the case is equivalent to Case 1. Assume that $x\in V(T_{u_{k}}(C^{i}))$ and $y\in V(T_{v_{k}}(C^{j}))$. Set $P^{1}$ be a shortest $u_{1}-v_{1}$ path for $u_{1}\in V(C^{i})$ and $v_{1}\in V(C^{j})$ where $V(P^{1})\bigcap V(C^{i})=\{u_{1}\}$ and $V(P^{1})\bigcap V(C^{j})=\{v_{1}\}$. Then we consider the following two subcases.

Suppose that $y\ne v_{k}$. We now extend the unicyclic graph $G^{i}$ to a unicyclic graph $G^{i'}$ which contains x and y. Since $y\ne v_{k}$, there is a vertex $s\in L(G)\bigcap V(G^{j})$ or a W-active vertex $s\in V(G^{j})\bigcap V(C^{\ell })$. Let $P^{2}$ be a shortest $v_{1}-v_{k}$ path, $P^{3}$ be a shortest $v_{k}-s$ path where $y\in I_{G}(v_{k},s)$. To apply the properties of unicyclic graphs, we construct the unicyclic graph $G^{i'}=G^{i}\bigcup P^{1}\bigcup P^{2}\bigcup P^{3}$ which is an isometric subgraph of G. See, for example, Fig. 4, where the unicyclic graph $G^{i'}$ is constructed by dashed line. Let $W_{i'}=W_{i}\bigcup \{s\}$. Note that $L(G^{i'})\subseteq W_{i'}$ and $A(W_{i'})$ contains a 3-maximum distance set in even cycle $C^{i}$ or an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in odd cycle $C^{i}$. The set $W_{i'}$ is a doubly resolving set of $G^{i'}$ by Lemmas 3.2 and 3.3. The case is similar to Case 1, we can derive that W doubly resolves x and y since x and y belong to the same unicyclic graph $G^{i'}$.

Suppose that $y=v_{k}$. There always exists a W-active vertex $v_{j}\in V(C^{j})$ with $d(y,v_{j})\le d(v_{1},v_{j})$ as A(W) contains a 3-maximum distance set in even cycle $C^{j}$ or an $\alpha$-maximum distance set for $\alpha \in \{2,3\}$ in odd cycle $C^{j}$. That is, $d(y,v_{j})\le d(v_{1},v_{j})<d(v_{1},v_{j})+d(x,v_{1})=d(x,v_{j})$. If $x\ne u_{k}$, then there is a vertex $t\in L(G)\bigcap V(G^{i})$ or a W-active vertex $t\in V(G^{j})\bigcap V(C^{k})$ such that $d(x,t)<d(y,t)$. We derive that t and $v_{j}$ doubly resolve x and y. Hence, there is some pair of vertices in W to doubly resolve x and y as $v_{j}$ is W-active. If $x= u_{k}$, then there always exists a W-active vertex $u_{j}\in V(C^{i})$ satisfying $d(x,u_{j})\le d(u_{1},u_{j})$ in $C^{i}$. This means that $d(x,u_{j})\le d(u_{1},u_{j})<d(u_{1},u_{j})+d(y,u_{1})=d(y,u_{j})$. Hence, $v_{j},u_{j}\in A(W)$ doubly resolve x and y. We can also assert that W doubly resolves x and y, ending the proof. $\square$

Fig. 4

The unicyclic graph $G^{i'}$ with dashed line

5 Block graphs

Note that block as a graph has no cut vertex, but block in some graph may contain cut vertices of the graph. Given a block graph G of order n, let q(G) be the number of nontrivial blocks of G containing non-cut vertices in it and $\zeta (G)$ be the number of non-cut vertices of G in all nontrivial blocks of G. Below we determine the formula for the DMD of block graphs.

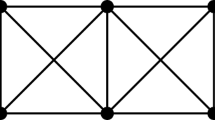
We give an example to illustrate the above two symbols more clearly, see Fig. 5. The block graph G contains three nontrivial blocks $K^{1}$, $K^{2}$ and $K^{3}$ with $V(K^{1})=\{v_{3},v_{4},v_{5},v_{6}\}$, $V(K^{2})=\{v_{7},v_{8},v_{9},v_{10}\}$ and $V(K^{3})=\{v_{10},v_{11},v_{12}\}$. Clearly, $K^{1}$ and $K^{2}$ are nontrivial blocks with non-cut vertices of G, $K^3$ is a nontrivial block without non-cut vertices of G, hence $q(G)=2$. Note that $L(G)=\{v_{1}, v_{2}, v_{13}, v_{14}\}$. Moreover, $v_{4},v_{5}$ and $v_{8},v_{9}$ form the sets of non-cut vertices of G in $K^{1}$ and $K^{2}$, respectively. Directly, we obtain that $\ell (G)=4$ and $\zeta (G)=4$. And we can routinely check that the set $W=\{v_{1}, v_{2}, v_{4},v_{8}, v_{13}, v_{14}\}$ doubly resolves G.

Fig. 5

The block graph G with three nontrivial blocks

We already know the doubly metric dimension of complete graphs by Lemma 2.2. Next we consider the block graphs $G\not \cong K_{n}$.

Lemma 5.1

Let $G\not \cong K_{n}$ be a block graph of order $n\ge 3$. If $W\subseteq V(G)$ is a DR set of G, then

• (i) $L(G)\subseteq W$.

• (ii) At most one non-cut vertex of G in each nontrivial block does not belong to W.

Proof

Note that $L(G)\subseteq W$ by Lemma 2.4. To the contrary, assume that there are two non-cut vertices $v_{i},v_{j}\in { V(G)\bigcap } (V(K^{q})\setminus W)$ for some nontrivial block $K^{q}$, then

$$d(v_{i},v_{k})-d(v_{j},v_{k})=0=d(v_{i},v_{p})-d(v_{j},v_{p})$$

for any pair of vertices $v_{k},v_{p}\in V(G)\setminus \{v_{i},v_{j}\}$, contradicting that W is a DR set of G. $\square$

Corollary 5.2

Let $G\not \cong K_{n}$ be a block graph of order $n\ge 3$. Then

$\psi (G)\ge \ell (G)+\zeta (G)-q(G)$.

Proof

From Lemma 5.1(i) and (ii), we obtain $\psi (G)\ge \ell (G)+\zeta (G)-q(G)$. $\square$

Lemma 5.3

Let $G\not \cong K_{n}$ be a block graph of order $n\ge 3$. Then

$\psi (G)\le \ell (G)+\zeta (G)-q(G)$.

Proof

Let $K^{i}$ be a nontrivial block in G, and let $W=L(G)\bigcup L^{*}(G)$ where $L^{*}(G)$ is the union of the set of non-cut vertices of G in each nontrivial block after removing one non-cut vertex of G from each nontrivial block. Then $|L^{*}(G)|=\zeta (G)-q(G)$. Note that all vertices of L(G) and $L^{*}(G)$ belong to trivial blocks and nontrivial blocks of G, respectively. Since $L(G)\bigcap L^{*}(G)= \emptyset$, we have $|W|=\ell (G)+\zeta (G)-q(G)$. Next we show that W is a DR set of G. Before doing it, we first prove the following claim. $\square$

Claim 1. $\Phi (K^{i})\subseteq A_{K^{i}}(W)$.

Proof of Claim 1

For any vertex $u\in \Phi (K^{i})$, recall that $T_{u}(K^{i})$ is the component of $G-E(K^{i})$ containing u. Then $T_{u}(K^{i})$ is still a block graph containing end blocks each of which has exactly one cut vertex of G. By its choice, W contains at least one vertex from each end block of G. That is, $V(T_{u}(K^{i}))\bigcap W\ne \emptyset$ for any vertex $u\in \Phi (K^{i})$. By the definition of W-active vertex, we derive $u\in A_{K^{i}}(W)$ and $\Phi (K^{i})\subseteq A_{K^{i}}(W)$. This completes the proof of Claim 1. $\square$

Note that $u\in W$ means $u\in A_{K^{i}}(W)$ for any vertex $u\in V(K^{i})$. By Claim 1 and $W=L(G)\bigcup L^{*}(G)$, we have $|V(K^{i})\setminus A_{K^{i}}(W)|\le 1$. We now turn to prove that W doubly resolves $x,y\in V(G)$. Next we only consider the cases of nontrivial blocks since the case of trivial blocks is similar and omitted here.

Case 1. $x,y\in V(K^{i})$.

Suppose that $x,y\in A_{K^{i}}(W)$. There are two vertices $s\in V(T_{x}(K^{i}))\bigcap W$ and $t\in V(T_{y}(K^{i}))\bigcap W$ satisfying $d(x,s)-d(y,s)=-1\ne 1=d(x,t)-d(y,t)$.

Suppose that $x\in A_{K^{i}}(W)$ and $y\not \in A_{K^{i}}(W)$. Note that $|V(K^{i})|\ge 3$. There are two vertices $s\in V(T_{x}(K^{i}))\bigcap W$ and $t\in V(T_{u_{i}}(K^{i}))\bigcap W$ satisfying $d(x,s)-d(y,s)=-1\ne 0=d(x,t)-d(y,t)$ for some $u_{i}\in V(K^{i})\setminus \{x,y\}$.

Case 2. $x\in V(K^{i})$ and $y\in V(K^{j})$ with $i\ne j$.

In this case we have $|V(K^{i})\setminus A_{K^{i}}(W)|\le 1$ and $|V(K^{j})\setminus A_{K^{j}}(W)|\le 1$. There are two vertices $u_{i}\in V(K^{i})\bigcap A_{K^{i}}(W)$ and $u_{j}\in V(K^{j})\bigcap A_{K^{j}}(W)$ such that $d(x,u_{i})-d(y,u_{i})< 0<d(x,u_{j})-d(y,u_{j})$. Hence, $s\in V(T_{u_{i}}(K^{i}))\bigcap W$ and $t\in V(T_{u_{j}}(K^{j}))\bigcap W$ doubly resolve x and y.

Therefore W is a DR set with $\ell (G)+\zeta (G)-q(G)$ vertices of G.

From Corollary 5.2 and Lemma 5.3, we obtain the result below.

Theorem 5.4

Let $G\not \cong K_{n}$ be a block graph of order $n\ge 3$. Then

$\psi (G)=\ell (G)+\zeta (G)-q(G)$.