Online scheduling of two-machine flowshop with lookahead and incompatible job families

Abstract

This paper considers online scheduling on two unit flowshop machines, which there exists unbounded parallel-batch scheduling with incompatible job families and lookahead intervals. The unit flowshop machine means that the processing time of any job on each machine is unit processing time. The objective is to minimize the maximum completion time. The lookahead model means that an online algorithm can foresee the information of all jobs arriving in time interval $(t,t+\beta ]$ at time t. There exist incompatible job families, that is, jobs belonging to different families cannot be processed in the same batch. In this paper, we address the lower bound of the proposed problem, and provide a best possible online algorithm of competitive ratio $1+\alpha _f$ for $0\le \beta <1$, where $\alpha _f$ is the positive root of the equation ${(f+1)} \alpha ^{2}+(\beta +2) \alpha +\beta -f=0$ and f is the number of incompatible job families which is known in advance.

1 Introduction

Scheduling theory is an important branch of combinatorial optimization. Under certain conditions, it reasonably allocates limited resources to complete tasks and achieve one or more objectives. In online over time scheduling problems (Say to online scheduling), the jobs information becomes known until they are arrived. In other word, the all characteristics (such as, arrival time, processing time, due date, and so on) of each job are unknown until its arrival time. For a minimization problem, the competitive ratio of an online algorithm A is defined as

$$\begin{aligned} \rho _{A}=\sup \limits _{\forall {I}}\displaystyle \frac{A(I)}{opt(I)}, \end{aligned}$$

where A(I) denotes the objective value of the schedule given by online algorithm A for job list I, and opt(I) denotes the objective value in an optimal off-line schedule for I. It is trivial for $\rho _{A}\ge 1$, and the online algorithm is the better algorithm if the ratio is smaller. Furthermore, we say that online algorithm A is an optimal algorithm if $\rho _A=1$, and A is also an off-line optimal algorithm. An online algorithm A is called best possible if there does not exist any online algorithm which its competitive ratio is less than that of A.

The parallel-batch scheduling problem is that at most b jobs are processed simultaneously as a batch with capacity b in the machine. The processing time of a batch is defined to be the maximum processing time of jobs in the batch. Furthermore, the jobs in a batch have a common starting time and a common completion time. There exist two versions about parallel-batch scheduling: unbounded model with $b=\infty$, and bounded model with $b<\infty$.

Many important results about online parallel-batch scheduling problems have been published. Such as, Zhang et al. (2001) provided the best possible online algorithm of competitive ratio $\displaystyle \frac{\sqrt{5}+1}{2}$ for problem $1|online, p-batch, b=\infty |C_{\max }$. Furthermore, the unbound model provided two online algorithm with a competitive ratio at most 2 is also studied. Liu and Lu (2021) studied online scheduling on an unbounded drop-line parallel batch machine with delivery times and limited restarts, given the lower bound and presented a best possible online algorithm. More recent papers could be founded in literature (Zhang et al. 2003; Tian et al. 2009; Li et al. 2012; Arman and Philip 2021; Chai et al. 2021; Fowler and Mönch 2022; Xia and Zhang 2022).

To be obtain a better competitive ratio, we will consider some semi-online models, i.e., adding the more information of jobs and machines. In this paper, we consider the semi-online models by using the function of lookahead, where lookahead means that an online algorithm can foresee the information of some future jobs. Lookahead problems have been comprehensively investigated in previous literature with different definitions (Keskinocak 1999; Zheng et al. 2008; Mandelbaum and Shabtay 2011; Jiao et al. 2019). Li et al. (2009) pointed that the lookahead model, denoted by $LK_\beta$, is defined by the length of processing time, i.e., algorithm A can foresee the jobs arrived in time interval $(t, t+\beta ]$ at time t.

Assume that there are f incompatible job families and each job belongs to a given family. Jobs from different families cannot be processed in the same batch because they may have different chemical properties, or they may need different operations. Hence, we must schedule the jobs into batches where each batch consists of jobs from the same family and the number of jobs in a batch does not exceed the capacity of the machine. Relevant results on off-line parallel-batch scheduling problems with incompatible job families, the readers may refer to (Fu et al. 2009; Yang and Li 2012; Li et al. 2019).

For problem $1|online, p-batch, b=\infty , f-family|C_{\max }$, when $f=1$, Zhang et al. (2001) provided a best possible online algorithm with a competitive ratio of $\displaystyle \frac{\sqrt{5}+1}{2}$. When $f=2$, Fu et al. (2009) proposed a best possible online $\displaystyle \frac{\sqrt{17}+3}{4}$ -competitive algorithm. Further, for general f, Fu et al. (2013) provided a best possible online algorithm with a competitive ratio of $1+\alpha _f$, where $\alpha _f$ is the positive root of the equation $f\alpha ^2+\alpha -f=0$, i.e., $\alpha _f=\displaystyle \frac{\sqrt{4f^2+1}-1}{2f}$. For the problem $1|online, p-batch, b =\infty , p_j=1, LK_\beta , families|C_{max}$, Li et al. (2014) gave that the lower bound of the problem and provided a best possible online algorithm with a competitive ratio of $1+\alpha _f$, where $\alpha _f$ is the positive root of the equation $f\alpha ^{2}+(1+\beta )\alpha +\beta -f=0$, $0\le \beta <1$.

In this paper, we extends the single machine online scheduling problem of f incompatible job families with lookahead interval into flowshop environment. The rest of the paper is organized as follows. In Section 2, we give the definition of unit flowshop machine and present the formally problem description. In Section 3, we prove the competitive ratio of any online algorithm for the scheduling model under study. In Section 4, we provide a best possible online algorithm to match the lower bound. In Section 5, the conclusion of this paper is given.

2 Problem description

In this section, we will give the definition of unit flowshop machine and present formally the problem description.

Definition 1

Unit flow shop machine (uf): The processing time of a job on each machine is unit processing time.

This paper will study unbounded parallel-batch online scheduling problem with f incompatible job families on two unit flowshop machine, in which our objective is to minimize the makespan with lookahead of the jobs arrival. Preemption or restart is not allowed and the value of f is known in advance. The processing time of each job on each machine is 1 and an arrival time $r_j$ is a nonnegative real number. $\beta$ denotes the lookahead length in the online setting. Then, at time t, an online algorithm can foresee the information of all the jobs arriving in time interval $(t,t+\beta ]$. Using the standard scheduling classification scheme of Lawler et al. (1993), the problem studied here is written as

$$\begin{aligned} F_2|online, p-batch, b =\infty , uf, LK_\beta , f-family|C_{max}(0\le \beta <1). \end{aligned}$$

Let jobs set $J =\{J_{1}, J_{2}, \cdots , J_{n}\}$, machines set $M =\{M_{1}, M_{2}\}$. The proposed scheduling problem can be normally narrated as follows:

• $p_{i, j}=1$ the normal processing time of job $J_j$ at machine $M_i$, $j=1, 2, \cdots , n$, $i=1, 2$.

• $r_{j}$ the arriving time of job $J_j$, $j=1, 2, \cdots , n$.

• $\beta$ length of lookahead interval.

• $\mathcal {F}_i$ the ith job family, $i=1, 2, \cdots , f$.

• $|\mathcal {F}_i|$ the number of batches of the ith job family. Here, $i=1, 2, \cdots , f$.

• $C_{\max }(\sigma )$ the maximum completion time of the online sequence $\sigma$ given by algorithm A for job instance L.

• $C_{\max }(\pi )$ the maximum completion time in an optimal off-line sequence $\pi$ for job instance L.

3 The lower bound

Let f be the number of incompatible job families, which is known in advance. Suppose that $\alpha _f=\displaystyle \frac{\sqrt{4f(f-\beta +1)+\beta ^2+4}-(2+\beta )}{2(f+1)}$ is the positive root of the equation ${(f+1)} \alpha ^{2}+(\beta +2) \alpha +\beta -f=0$ $(0\le \beta <1)$. Then $0<\alpha _f<1$ and $(f+1)\alpha _f=\displaystyle \frac{\sqrt{4f(f-\beta +1)+\beta ^2+4}-(2+\beta )}{2}$.

Theorem 1

For problem $F_2|online, p-batch, b =\infty , uf, LK_\beta , f-family|C_{max}$ $(0\le \beta <1)$, there does not exist online algorithm with a competitive ratio of less than $1+\alpha _f$.

Proof

Let $\epsilon$ be a sufficiently small positive number. We will take the adversary to generate the following job instance:

For any online algorithm A, at time 0, the adversary releases f jobs belonging to the f distinct job families, respectively. If no job has been started before or at a time t by A, we are informed that no jobs will arrive at the time interval $(t, t+\beta ]$. In the time interval $[0,(f+1)\cdot \alpha _f)$, whenever a job J is started by A at a time t, the adversary informs us at time $t+\epsilon$ that a new job $J^{\prime }$ from the same family as J will be released at time $t+\beta +\epsilon$. Furthermore, at time $(f+1)\cdot \alpha _f$, the adversary informs us that no jobs will arrive at any time $t\ge (f+1)\cdot \alpha _f+\beta$.

If no job is started before time $(f+1)\cdot \alpha _f$ in $\sigma$, then f jobs and all of them are released at time 0. Since the f jobs belong to f distinct job families, we have $C_{\max }(\sigma )\ge {(f+1)\cdot \alpha _f+f+1}=(f+1)\cdot (\alpha _f+1)$ and $C_{\max }(\pi )=f+1$. Consequently, ${C_{\max }(\sigma )}\ge (1+\alpha _f){C_{\max }(\pi )}$.

Next, we assume that at least one job is started before time $(f+1)\cdot \alpha _f$ in $\sigma$. Let $S^{\prime }<(f+1)\cdot \alpha _f$ be maximum so that some job is started at time $S^{\prime }$ in $\sigma$. Then the last job is released at time $S^{\prime }+\beta +\epsilon$. By the construction of the job instance, there are still f unprocessed jobs belonging to f distinct job families available at time $S^{\prime }+1$. Let $S\ge {S^{\prime }+1}$ be minimum so that some job is started at time S in $\sigma$. Then we have $S\ge {(f+1)\cdot \alpha _f}$ and $S^{\prime }\le {S-1}$. Consequently, we have

$$\begin{aligned} C_{\max }(\sigma ) \ge S+f+1 \ge \max \left\{ \left( 1+\alpha _{f}\right) (f+1), S^{\prime }+f+2\right\} . \end{aligned}$$

(1)

Assume that, in time interval $[0,S+1)$, the processed jobs in $\sigma$ are from k distinct families, say $\mathcal {F}_{1}, \mathcal {F}_{2}, \cdots , \mathcal {F}_{k}$. The other $f-k$ families are denoted by $\mathcal {F}_{k+1}, \mathcal {F}_{k+2}, \cdots , \mathcal {F}_{f}$. Then $|\mathcal {F}_i|\ge 2$ for $1\le {i}\le {k}$, and $|\mathcal {F}_i|=1$ for ${k+1}\le {i}\le {f}$. For each $\mathcal {F}_i$ with $1\le {i}\le {k}$, let $S_i$ be the last starting time of the jobs in $\mathcal {F}_i$ starting before time S. Suppose further that $S_1<S_2<\cdots <S_k$. Then $S_k=S$ and $S_{i+1}-S_i\ge 1$ for $1\le {i}\le {k-1}$. Note that the last arrival time of the jobs in family $\mathcal {F}_i$ with $1\le {i}\le {k}$, denoted by $R_i$, where $R_i=S_i+\beta +\epsilon$, and the arrival time of the jobs in family $\mathcal {F}_i$ with ${k+1}\le {i}\le {f}$ is 0. Thus we also have

$$\begin{aligned} R_{i+1}-R_{i}\ge 1 \ \ for \ \ 1\le {i}\le {k-1} \end{aligned}$$

(2)

Let $\varOmega =\max \left\{ R_{k}, f-1\right\} -k+1$. Then $\varOmega \ge R_{k}-k+1$. Define $S_{i}^{*}=\varOmega +i-1$ for $1 \le i \le k$, and $S_{i}^{*}=i-k-1$ for $k+1 \le i \le f$. From Eq. (2) and by the fact that $\varOmega \ge R_{k}-k+1$, we have

$$\begin{aligned} S_{i}^{*}\ge {R_{i}} \ \ for \ \ 1\le {i}\le {k} \end{aligned}$$

(3)

Since $\varOmega =\max \left\{ R_{k}, f-1\right\} -k+1 \ge f-k$, we have $S_{1}^{*}=\varOmega \ge f-k$. Let $\pi ^*$ be an off-line schedule of the jobs in the f job families in which each family $\mathcal {F}_i$, $1\le {i}\le {f}$, is scheduled as a single batch starting at time $S_{i}^{*}$ . Then the sequence of the processing batches in $\pi ^*$ is given by $(\mathcal {F}_{k+1}, \cdots , \mathcal {F}_{f}, \mathcal {F}_{1}, \cdots , \mathcal {F}_{k})$. Based on Eq. (3) and $S_{1}^{*}\ge {f-k}$, it can be verified that $\pi ^*$ is feasible and $C_{\max }(\pi ^*)=S_{k}^{*}+1+1=\varOmega +k+1=\max \{R_k,f-1\}+2$. Since $R_k=S^{\prime }+\beta +\epsilon$, we have

$$\begin{aligned} C_{\max }(\pi ) \le C_{\max }\left( \pi ^{*}\right) =\max \left\{ S^{\prime }+\beta +\epsilon +2, f+1\right\} . \end{aligned}$$

(4)

If $f+1\ge {S^{\prime }+\beta +\epsilon +2}$, from Eq. (1) and Eq. (4), we have ${C_{\max }(\sigma )}\ge {(f+1)\cdot (1+\alpha _{f})}$ and $C_{\max }(\pi )\le {f+1}$. Consequently, ${C_{\max }(\sigma )}\ge (1+\alpha _{f}){C_{\max }(\pi )}$.

If $f+1<{S^{\prime }+\beta +\epsilon +2}$, from Eq. (1) and Eq. (4), we have ${C_{\max }(\sigma )}\ge {S^{\prime }+f+2}$ and $C_{\max }(\pi )\le {S^{\prime }+\beta +\epsilon +2}$. From the fact $S^{\prime }<(f+1)\alpha _{f}$, we have

$$\begin{aligned} \begin{aligned} \displaystyle \frac{C_{\max }(\sigma )}{C_{\max }(\pi )}&\ge \displaystyle \frac{S^{\prime }+f+2}{S^{\prime }+\beta +\epsilon +2} \rightarrow \displaystyle \frac{S^{\prime }+f+2}{S^{\prime }+\beta +2} \\&= 1+\displaystyle \frac{f-\beta }{S^{\prime }+\beta +2}\\&> 1+\displaystyle \frac{f-\beta }{(f+1) \cdot \alpha _{f}+\beta +2}\\&= 1+\alpha _{f}. \end{aligned} \end{aligned}$$

as $\epsilon \rightarrow 0$, The result follows. $\square$

4 A best possible online algorithm

This section presents a best possible online algorithm $A_f(\beta )$, with a competitive ratio of $1+\alpha _f=1+\displaystyle \frac{\sqrt{4f(f-\beta +1)+\beta ^2+4}-(2+\beta )}{2(f+1)}$ for the proposed problem. We first give some important properties of the optimal off-line schedules by the job-exchanging argument. Let job $J_i$ be the last arriving job in family $\mathcal {F}_{i}$, $1\le {i}\le {f}$. We index the f job families by the early release date first ERD(Li et al. 2014) rule so that $r_1\le r_2\le \cdots \le r_f$.

Some notations and parameters that will be used in the algorithm are defined as follows.

• U(t) is the set of jobs available for processing at time t.

• $U_i(t)=U(t)\bigcap \mathcal {F}_{i}$ is the set of jobs from $\mathcal {F}_{i}$ available for processing at time t. $U_i(t)$ is called a waiting batch at time t if $U_i(t)\ne \emptyset$.

• $U(t,\beta )$ is the set of jobs arriving at the time interval $(t,t+\beta ]$.

• $N(t)=\{i: U_i(t)\ne \emptyset , U(t,\beta )=\emptyset \}$.

• $n(t)=|N(t)|$ denotes the number of waiting batches $U_i(t)$.

• $r_i(t)(1\le {i}\le {n(t)})$ is the last arrival time of jobs in $U_i(t)$ if $U_i(t)\ne \emptyset$.

• q(t) is the number of job families in $U(t)\bigcup {U(t,\beta )}$.

• $r_l$ the last arrival time of all jobs in the online sequence $\sigma$.

If there exists an idle time at one of machines and at least one waiting batch, then it will be the decision point of the algorithm. The following algorithm is described:

Algorithm $A_f(\beta )$

Step 0: Set $t =0$.

Step 1: If $U(t)=\emptyset$, reset t to be the minimum time moment such that U(t) is not empty.

Step 2: Determine q(t).

Step 2.1: If $t<(q(t)+1)\alpha _f$, then wait for the first time moment $t^*\in (t,(q(t)+1)\alpha _f]$ so that either $t^*=(q(t)+1)\alpha _f$ or a new job arrives at time $t^*+\beta$. Reset $t:=t^*$ and return to Step 2.

Step 2.2: Else, if $N(t) \ne \emptyset$, we normalize the n(t) waiting batches $U_i(t)$, $i\in {N(t)}$, at time t, say $U_1(t), \cdots , U_{n(t)}(t)$, so that $r_1(t)\le \cdots \le r_{n(t)}(t)$. Then start processing the waiting batch $U_1(t)$ at time t. Reset $t:=t+1$ and return to Step 1.

Step 2.3: Else, we wait for the first time moment $t_1$ such that either $t_1$ is the first arriving time in $(t,t+\beta ]$ or a new job will arrive at time $t_1+\beta$. Reset $t:=t_1$ and return to Step 2.

As it is an unbounded capacity model in this work, at each time there arrive more than one job from the same job family is equivalent to the case with one arrival job. Without loss of generality, we assume that at each arrival time, there is at most one job arriving from each job family. Let the last arrival time of the jobs be $r_l$. Based on algorithm $A_f(\beta )$, there will be a batch block (which is a set of batches processed consecutively), say $\mathcal {B}$, processed after time $r_l$ in schedule $\sigma$. The block $\mathcal {B}$ is composed by some batches $B_1, B_2, \cdots , B_k$ which belong to distinct families, $1\le {k}\le {f}$. We use $S_i$ and $C_i$ to denote the starting time and the completion time of each batch $B_i$, respectively. Furthermore, the k batches are indexed so that $S_1<\cdots <S_k$, thus $S_1\ge {r_l}$.

Apart from the k batches in $\mathcal {B}$, there may be other batches generated by algorithm $A_f(\beta )$. For a batch $B_i$ generated by algorithm $A_f(\beta )$, if $J_i$ is the latest arriving job in $B_i$, we call $J_i$ the critical job of $B_i$. Then

$$\begin{aligned} C_{\max }(\sigma )=S_1+k+1\ge {r_l+k+1}. \end{aligned}$$

(5)

The following three observations for schedule $\sigma$ are implied in the implementation of algorithm $A_f(\beta )$.

Observation 1

If $U_i(t)$ is a batch starting at time t in $A_f(\beta )$, then there is no job from $\mathcal {F}_i$ arriving in the interval $(t,t+\beta ]$.

Observation 2

If $U_i(t)$ is a batch starting at time t in $A_f(\beta )$, and there are h distinct families in $U(t)\bigcup {U(t,\beta )}$, then $t\ge (q(t)+1)\alpha _f$. Furthermore, if there is an idle time immediately preceding t, then $t=$ max $\{r_i(t),(q(t)+1)\alpha _f\}$.

Observation 3

If $J_x$ and $J_y$ are two critical jobs of two batches from distinct families with $C_x<C_y$, then $r_x<r_y$, that is, the jobs are batched and processed in ERD order.

Next, we will give a useful lemma to solve the following lemmas and theorem, in which it can be showed by the differential method.

Lemma 1

If a, b, c are positive, then $f(x)=\displaystyle \frac{x-a}{bx+c}$ is an increasing function.

Proof

For $f^{\prime }(x)=\displaystyle \frac{(bx+c)-b(x-a)}{(bx+c)^2}=\displaystyle \frac{c+ab}{(bx+c)^2}>0$, therefore, $f(x)=\displaystyle \frac{x-a}{bx+c}$ is an increasing function.

Lemma 2

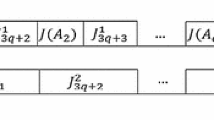
There exists an idle time immediately preceding time $S_1$ in $\sigma$ (see fig 1), then we have

$$\begin{aligned} C_{\max }(\sigma )\le (1+\alpha _f)C_{\max }(\pi ). \end{aligned}$$

Fig. 1

An idle time immediately preceding time $S_1$ in $\sigma$ picture

Proof

Since there exists an idle time before time moment $S_1$ in $\sigma$, by Observation 2, we have $S_1=\max \{r_l,(k+1)\alpha _f\}$.

If $S_1=(k+1)\alpha _f$, then we have $C_{\max }(\sigma )=S_1+k+1=(k+1)(1+\alpha _f)$. Since the jobs in $B_1, B_2, \cdots , B_k$ belong to distinct families, we have $C_{\max }(\pi )\ge {k+1}$ and $C_{\max }(\sigma )\le (1+\alpha _f)C_{\max }(\pi )$.

If $S_1=r_l>(k+1)\alpha _f$, then we claim that all critical jobs in block $\mathcal {B}$ arrive at time $S_1$. Otherwise, if some critical job in $\mathcal {B}$ arrive before $S_1$, then the corresponding batch in $\mathcal {B}$ should be started before time $S_1$ in $\sigma$, a contradiction. So, $C_{\max }(\sigma )=S_1+k+1=C_{\max }(\pi )$. The result follows. $\square$

Lemma 3

There exists no idle time immediately preceding time $S_1$ in $\sigma$ (see fig 2), then we have

$$\begin{aligned} C_{\max }(\sigma )\le (1+\alpha _f)C_{\max }(\pi ). \end{aligned}$$

Fig. 2

there exists no idle time immediately preceding time $S_1$ in $\sigma$ picture

Proof

Since there exists no idle time immediately preceding time $S_1$ in $\sigma$, $S_1$ is the completion time of some batch, say $B^{\prime }$, in $\sigma$. Then $S_1=S^{\prime }+1$, where $S^{\prime }$ is the starting time of batch $B^{\prime }$ in $\sigma$. It is easy to see that $S_1\ge {r_l}>S^{\prime }$.

We divide block $\mathcal {B}$ into two batch sets, say $\mathcal {B}_1$ and $\mathcal {B}_2$, such that the critical job of each batch in $\mathcal {B}_1$ arrives before or at time $S^{\prime }+\beta$ and the critical job of each batch in $\mathcal {B}_2$ arrives after time $S^{\prime }+\beta$. Suppose that $\mathcal {B}_1$ includes $k_1$ batches and $\mathcal {B}_2$ includes $k_2$ batches. Then $k_1+k_2=k$ and

$$\begin{aligned} C_{\max }(\sigma )=S^{\prime }+1+k+1=S^{\prime }+2+k_{1}+k_{2}. \end{aligned}$$

(6)

From Observation 1, batch $B^{\prime }$ belongs to distinct family with each batch (if any) in $\mathcal {B}_1$. Since $B^{\prime }$ and the batches (if any) in $\mathcal {B}_1$ are in $U(S^{\prime })\bigcup {U(S^{\prime }, \beta )}$, and there are at most $f-1$ distinct families in $\mathcal {B}_1$, by Observation 2, we have $k_1+1\le {f}$ and

$$\begin{aligned} S^{\prime }\ge {\alpha _f(k_1+2)}. \end{aligned}$$

(7)

If $r_l>S^{\prime }+\beta$, then $\mathcal {B}_2\ne \emptyset$, and $1\le {k_2}\le {f}$. Note that the critical jobs of the batches in $\mathcal {B}_2$ arrive after $S^{\prime }+\beta$, we have $C_{\max }(\pi )\ge {S^{\prime }+\beta +k_2+1}$. From Eq. (6), we have $C_{\max }(\sigma )-C_{\max }(\pi )\le {(S^{\prime }+2+k_{1}+k_{2})-(S^{\prime }+\beta +k_2+1)}=k_{1}+1-\beta$. It follows that

$$\begin{aligned} \begin{aligned} \displaystyle \frac{C_{\max }(\sigma )-C_{\max }(\pi )}{C_{\max }(\pi )}&\le \displaystyle \frac{k_{1}+1-\beta }{S^{\prime }+\beta +k_{2}+1} \\&\le \displaystyle \frac{k_{1}+1-\beta }{\alpha _{f} \cdot \left( k_{1}+2\right) +\beta +2} \\&\le \displaystyle \frac{f-\beta }{(f+1) \cdot \alpha _{f}+\beta +2}\\&=\alpha _{f}. \end{aligned} \end{aligned}$$

From Lemma 1 and $k_1+1\le {f}$. If $r_l\le {S^{\prime }+\beta }$, then $\mathcal {B}_2=\emptyset$ and $k=k_1$. Let $S_l(\pi )$ be the starting time of $J_l$ in the off-line optimal schedule $\pi$. We consider the following two cases.

(1):

$S_l(\pi )>{S^{\prime }+\beta }$. Then $C_{\max }(\pi )\ge {S_l(\pi )+1+1}>{S^{\prime }+\beta +2}$. From Eq. (6) and Eq. (7), we have

$$\begin{aligned} \begin{aligned} \displaystyle \frac{C_{\max }(\sigma )-C_{\max }(\pi )}{C_{\max }(\pi )}&\le \displaystyle \frac{k_1+1-\beta }{S^{\prime }+\beta +2} \\&\le \displaystyle \frac{k_1+1-\beta }{\alpha _{f} \cdot \left( k_1+2\right) +\beta +2} \\&\le \displaystyle \frac{f-\beta }{(f+1) \cdot \alpha _{f}+\beta +2}\\&=\alpha _{f}. \end{aligned} \end{aligned}$$

(2):

$S_l(\pi )\le {S^{\prime }+\beta }$. Note that $r_l$ is the largest arrival time of critical jobs in $\mathcal {B}$ and two batches in block $B^{\prime }\bigcup \mathcal {B}$ belong to two distinct families. Suppose that the critical job in $B^{\prime }$ is $J^{\prime }$ and the arrival time of $J^{\prime }$ is $r^{\prime }$. By Observation 3, we have $r^{\prime }\le {r_1}\le \cdots \le {r_k}$, where $r_i$ is the arrival time of the critical job in $B_i$ with $1\le {i}\le {k}$. By ERD rule, in $\pi$, the starting time of $J^{\prime }$ is not larger than $S_l(\pi )-k$. So, $r^{\prime }\le {S_l(\pi )-k}$. Since $S_l(\pi )\le {S^{\prime }+\beta }$, we further have

$$\begin{aligned} r^{\prime }\le {S_l(\pi )-k}\le (S^{\prime }-k)+\beta . \end{aligned}$$

(8)

We establish three claims in the following.

$\square$

Claim 1

There exists no idle time in $[r^{\prime }, S^{\prime }]$ in $\sigma$.

Since $r_l\le {S^{\prime }+\beta }$, there are $k+1$ distinct families in $U(S^{\prime })\bigcup {U(S^{\prime }, \beta )}$, so $r^{\prime }$ is the last arriving time of the jobs from the family of batch $B^{\prime }$. By the implementation of algorithm $A_f(\beta )$, if there exists an idle time in $[r^{\prime }, S^{\prime }]$, then the starting time of batch $B^{\prime }$ should be earlier than $S^{\prime }$, a contradiction. Claim 1 follows.

Claim 2

There exists no idle time in $[S^{\prime }-k, S^{\prime }]$ in $\sigma$.

If $r^{\prime }\le {S^{\prime }-k}$, then Claim 2 follows from Claim 1. Hence, if $r^{\prime }>{S^{\prime }-k}$,. then we have ${S^{\prime }-k}<r^{\prime }\le (S^{\prime }-k)+\beta$. We now only need to show that there exists no idle time in $[S^{\prime }-k, r^{\prime }]$. Otherwise, there is some batch starting in $(S^{\prime }-k, r^{\prime })\subseteq [S^{\prime }-k, (S^{\prime }-k)+\beta ]$, which is an interval of length at most $\beta <1$. This results an idle time in $[r^{\prime }, S^{\prime }]$ since the batches have the unit processing times, contradicting Claim 1. Claim 2 follows.

From Claim 2, we may suppose that the k batches consecutively scheduled in $[S^{\prime }-k, S^{\prime }]$ in $\sigma$ are $B^{(1)}, \cdots , B^{(k)}$ in this order and the arrival times of the critical jobs of these batches are $r^{(1)}, r^{(2)}, \cdots , r^{(k)}$, respectively. Then the starting time of $B^{(1)}$ is $S^{(1)}=S^{\prime }-k$. By ERD rule, we have $r^{(1)}\le {r^{(2)}}\le \cdots \le {r^{(k)}}\le {r^{\prime }}$. Furthermore, we have $r^{\prime }\le {S^{(1)}+\beta }$. By the implementation of the algorithm, we have the following Claim 3.

Claim 3

The batches $B^{(1)}, \cdots , B^{(k)}, B^{\prime }$ belong to distinct families and $S^{(1)}\ge {\alpha _f\cdot (k+2)}$.

Recall that $C_{\max }(\pi )\ge {S_l(\pi )+2}\ge {r_l+2}$. From Eq. (6), we have

$$\begin{aligned} {C_{\max }(\sigma )-C_{\max }(\pi )}\le {(S^{\prime }+2+k)-(S_l(\pi )+2)}=S^{\prime }+k-S_l(\pi )\le {k+1-\beta }, \end{aligned}$$

where the last inequality follows from the assumption that $S_l(\pi )\le {S^{\prime }+\beta }$. By Claim 3 and the fact that $k\ge 1>\beta$, we have $C_{\max }(\pi )\ge {r_l+2}>{S^{\prime }+2}=S^{(1)}+k+2\ge {\alpha _f\cdot (k+2)+\beta +2}$. Thus,

$$\begin{aligned} \displaystyle \frac{C_{\max }(\sigma )-C_{\max }(\pi )}{C_{\max }(\pi )} \le \displaystyle \frac{k+1-\beta }{\alpha _f\cdot (k+2)+\beta +2} \le \displaystyle \frac{f-\beta }{(f+1) \cdot \alpha _{f}+\beta +2}=\alpha _{f}. \end{aligned}$$

This completes the proof of Lemma 3.

From Theorem 1, Lemma 2 and Lemma 3, we conclude the following final result.

Theorem 2

For the problem $F_2|online, p-batch, b =\infty , uf, LK_\beta , f-family |C_{max}$ $(0\le \beta <1)$, algorithm $A_f(\beta )$ is a best possible online algorithm with a competitive ratio of $1+\alpha _f$ for $0\le \beta <1$, where $\alpha _f$ is the positive root of the equation ${(f+1)} \alpha ^{2}+(\beta +2) \alpha +\beta -f=0$ and f is the number of job families which is known in advance.

5 Conclusion

For problem $F_2|online, p-batch, b =\infty , uf, LK_\beta , f-family|C_{max}$ $(0\le \beta <1)$, there exists no online algorithm with a competitive ratio of less than $1+\alpha _f$. Meanwhile, we give a best possible online algorithm $A_f(\beta )$. Where $\alpha _f$ is the positive root of the equation ${(f+1)} \alpha ^{2}+(\beta +2) \alpha +\beta -f=0$ and f is the number of job families which is known in advance.

For future research we suggest several interesting topics as follows:

• The general version: The processing time of the job on each machine is arbitrary, the problem is worthy of being further studied;

• Extending our model to m flowshop machines;

• Extending our model to considering other classical scheduling objectives, e.g., $\sum C_j$, $\sum W_jC_j$;

• Extending our model to different machine environments, e.g., the open shop.