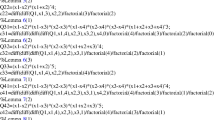Adjacent vertex distinguishing edge coloring of IC-planar graphs

Abstract

The adjacent vertex distinguishing edge coloring of a graph G is a proper edge coloring in which each pair of adjacent vertices is assigned different color sets. The smallest number of colors for which G has such a coloring is denoted by $\chi '_a(G)$. An important conjecture due to Zhang et al. (Appl Math Lett 15:623–626, 2002) asserts that $\chi '_a(G)\le \Delta (G)+2$ for any connected graph G with order at least 6. By applying the discharging method, we show that this conjecture is true for any IC-planar graph G with $\Delta (G)\ge 16$.

1 Introduction

Throughout this paper, we are only concerned with finite and simple graphs. For a plane graph G, let $V(G), E(G), F(G), \Delta (G)$ and $\delta (G)$ be the vertex set, edge set, face set, maximum degree and minimum degree of G, respectively. For an arbitrary $x\in V(G)\cup F(G)$, let $d_G(x)$ denote the degree of x in G. Let $N_G(v)$ denote the set of neighbors of a vertex v in G. A vertex v satisfying $d_G(v)=k$ ($d_G(v)\ge k$, $d_G(v)\le k$) is a k-vertex ($k^+$-vertex, $k^-$-vertex). The k-face and $k^+$-face are defined similarly. For each $v\in V(G)$, let $d_G^k(v)$ denote the number of k-vertices adjacent to v in G. We call a 3-vertex $v\in V(G)$ bad if $d_G^3(v)=1$ and good if $d_G^3(v)=0$. Let $d_G^{3b}(v)$ and $d_G^{3g}(v)$ denote the number of bad and good 3-vertices adjacent to v in G, respectively. A 3-face (or cycle) $v_1v_2v_3$ is called a $(k_1,k_2,k_3)$-face (or cycle) if $v_i$ is a $k_i$-vertex for all $1\le i\le 3$. A 3-cycle is bad if it is incident with two 3-vertices. Any undefined notation can refer to (Bondy and Murty 1976).

A proper k-edge coloring of a graph G is a mapping $\varphi :E(G)\rightarrow \{1,2,\ldots ,k\}$ such that $\varphi (e)\ne \varphi (e')$ for any two adjacent edges e and $e'$ of G. For any $v\in V(G)$, let $C_\varphi (v)=\{\varphi (uv)| uv \in E(G)\}$ be the color set of v with respect to $\varphi$. For two adjacent vertices u and v, we call u conflict with v respect to $\varphi$ if $C_\varphi (u)=C_\varphi (v)$. A proper k-edge coloring $\varphi$ is a k-adjacent vertex distinguishing edge coloring (k-avd-coloring for short) provided that $C_\varphi (u)\ne C_\varphi (v)$ for all $uv\in E(G)$. The adjacent vertex distinguishing edge chromatic index of G, denoted by $\chi '_a(G)$, is the smallest k such that G has a k-avd-coloring. A graph without isolated edges is normal. Clearly, only normal graph can have avd-colorings. Thus, for avd-coloring, we only consider normal graphs.

Zhang et al. (2002) first introduced the concept of avd-coloring and put forward the following conjecture.

Conjecture 1

Zhang et al. (2002) If G is a connected graph with order at least 6, then $\chi '_{{a}}(G)\le \Delta (G)+2$.

Conjecture 1 was determined by Balister et al. (2007) for bipartite graphs and graphs with maximum degree 3. Horňák et al. (2014) showed that Conjecture 1 holds for planar graphs with maximum degree at least 12. Bonamy et al. (2013) verified that $\chi '_{a}(G)\le \Delta (G)+1$ for any planar graph G with $\Delta (G)\ge 12$. Wang and Huang (2015) proved that $\chi '_{a}(G)\le \Delta (G)+1$ for any planar graph G with $\Delta (G)\ge 16$ and $\chi '_{a}(G)=\Delta (G)+1$ if and only if G contains two adjacent vertices of maximum degree.

A graph is 1-planar if it can be drawn in the plane such that each edge is crossed by at most one other edge. Albertson (2008) first introduced the definition of IC-planar graph. A graph is IC-planar if it admits a drawing in the plane where each edge is crossed at most once and no two crossings are incident with the same vertex. Clearly, each IC-planar graph is 1-planar. The associated plane graph $G^\times$ of a 1-planar graph G is a plane graph obtained by turning all crossings of G into new 4-vertices. A vertex $v\in V(G^\times )$ is false if v is not a vertex of G and real otherwise. A face is false if it is incident with at least one false vertex. Clearly, for an associated plane graph $G^\times$ of an IC-planar graph G, each real vertex in $G^\times$ is adjacent to at most one false vertex and incident with at most two false 3-faces in $G^\times$. In the following, we always assume that every IC-planar graph is drawn in a plane such that the number of crossings is as few as possible.

Lemma 1

Zhang and Wu (2011) Let G be a 1-plane graph and $G^\times$ be the associated plane graph of G. If $d_G(u)=3$ and v is a false vertex of $G^\times$, then either $uv\notin E(G^\times )$ or uv is not incident with two 3-faces.

In this paper, we will prove that Conjecture 1 is true for any IC-planar graph with maximum degree at least 16, which can be expressed more concisely as follows:

Theorem 1

Let G be an IC-planar graph, then $\chi '_{a}(G)\le \max \{\Delta (G)+2,18\}$.

2 The proof of Theorem 1

We will prove Theorem 1 by contradiction. Let G be a counterexample to Theorem 1 minimizing $|V(G)|+|E(G)|$. Clearly, G is a connected graph. Let $t_G=\max \{\Delta (G)+2,18\}$ and $C=\{1,2,\ldots ,t_G\}$. Then $\{1,2,\ldots ,18\}\subseteq C$. First we will prove the following claims.

Claim 1

There is no edge $uv\in E(G)$ with $d_G(u)=1$ and $d_G(v)\le 9$.

Proof

Assume, to the contrary, that G contains an edge uv with $d_G(u)=1$ and $d_G(v)\le 9$. We have ${d_G}(v)\ge 2$ because G is normal. Let $H=G-u$. If H contains only one edge, then we color this edge with 1 and color uv with 2 to obtain a $t_G$-avd-coloring of G, a contradiction. If H contains at least two edges, H has a $t_G$-avd-coloring $\varphi$ with the color set C by the minimality of G. Note that v has at most eight conflict vertices. Hence we can color uv with a color in $C\setminus {C_\varphi }(v)$ such that v does not conflict with its neighbors, which yields a $t_G$-avd-coloring of G, a contradiction. $\square$

Remark 1

Claim 1 implies that for an arbitrary $e\in E(G)$, $H=G-e$ is normal. Therefore $\chi '_a(H)\le t_G$ by the minimality of G.

Remark 2

In the following, if $d_G(v)=k$, set $N_G(v) := \{v_1,v_2,\ldots ,v_k\}$.

Claim 2

Let v be a k-vertex of G with $2\le k\le 6$, then ${d_G^{k}}(v)\le 1$.

Proof

Assume, to the contrary, that G contains a k-vertex v ($2\le k\le 6$) satisfying ${d_G^{k}}(v)\ge 2$. We prove the case that $k=6$ (the proof can be given similarly and simply for $2\le k\le 5$). Assume that $d_G(v_1)=d_G(v_2)=6$. Let $N_G(v_1)=\{v,w_1,w_2,w_3,w_4,w_5\}$. Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. Without loss of generality (W.l.o.g.), $\varphi (vv_i)=i-1$ for $2\le i\le 6$ and $\varphi (v_1w_i)=a_i$ for $1\le i\le 5$. We consider the next three cases.

Case 1: $3\le |\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|\le 5$. If $|\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|=5$, then we recolor $vv_2$ with a color in $C\setminus ({C_\varphi }(v)\cup {C_\varphi }(v_2))$ such that $v_2$ does not conflict with its neighbors. So we may assume that $3\le |\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|\le 4$. Hence we can color $vv_1$ with a color in $C\setminus ({C_\varphi }(v)\cup {C_\varphi }(v_1))$ such that v and $v_1$ do not conflict with their neighbors, which yields a $t_G$-avd-coloring of G, a contradiction.

Case 2: $1\le |\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|\le 2$. Set $|\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|=l$, then $1\le l\le 2$. W.l.o.g., $a_i=i$ for $1\le i\le l$ and $a_i=i-l+5$ for $l+1\le i\le 5$. Suppose that $vv_1$ cannot be colored without causing conflicts, say, $C_\varphi (v_i) = \{1,2,3,4,5,i-l+9\}$ for $2\le i\le 6$ and $C_\varphi (w_i) = \{1,6,7,8,16-7l,i-l+15\}$ for $1\le i\le l+3$. We recolor $vv_2$ with a color in $\{13,14,\ldots ,18\}$ such that $v_2$ does not conflict with its neighbors, then we color $vv_1$ with a color in $\{11,12\}$ such that $v_1$ does not conflict with its neighbors, which yields a $t_G$-avd-coloring of G, a contradiction.

Case 3: $|\{a_1,a_2,\ldots ,a_5\}\cap \{1,2,\ldots ,5\}|=0$. W.l.o.g., $a_i=i+5$ for $1\le i\le 5$. Suppose that $vv_1$ cannot be colored without causing conflicts, say, $C_\varphi (v_i)=\{1,2,3,4,5,i+9\}$ for $2\le i\le 6$ and $C_\varphi (w_i)=\{6,7,8,9,10,i+15\}$ for $1\le i\le 3$, or $C_\varphi (v_i) = \{1,2,3,4,5,i+9\}$ for $2\le i\le 5$ and $C_\varphi (w_i)=\{6,7,8,9,10,i+14\}$ for $1\le i\le 4$. If $C_\varphi (v_i)=\{1,2,3,4,5,i+9\}$ for $2\le i\le 6$ and $C_\varphi (w_i)=\{6,7,8,9,10,i+15\}$ for $1\le i\le 3$, then we recolor $vv_2$ with a color in $\{6,7,8,16,17,18\}$ such that $v_2$ does not conflict with its neighbors, and color $vv_1$ with a color in $\{12,13,14\}$ such that $v_1$ does not conflict with $w_4$ and $w_5$, which yields a $t_G$-avd-coloring of G, a contradiction. If $C_\varphi (v_i)=\{1,2,3,4,5,i+9\}$ for $2\le i\le 5$ and $C_\varphi (w_i)=\{6,7,8,9,10,i+14\}$ for $1\le i\le 4$, then we recolor $vv_2$ with a color in $\{6,7,8,9,10,18\}$ such that $v_2$ does not conflict with its neighbors, and color $vv_1$ with a color in $\{12,13,14\}$ such that v and $v_1$ do not conflict with their neighbors, which yields a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 3

There is no edge $vv_1\in E(G)$ with $2\le d_G(v_1)\le 6$ and $d_G(v_1)+1\le d_G(v)\le 9$.

Proof

Assume, to the contrary, that G contains an edge $vv_1$ with $2\le d_G(v_1)\le 6$ and $d_G(v_1)+1\le d_G(v)\le 9$. We prove the case that $d_G(v_1)=6$ and $d_G(v)=9$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le 9$ and $C_\varphi (v_1)\subseteq \{1,2,\ldots ,13\}$. By Claim 2, every 6-vertex has at most one conflict vertex. Suppose that $vv_1$ cannot be colored without causing conflicts, say, $C_\varphi (v_i)=\{1,2,\ldots ,8,i+12\}$ for $2\le i\le 5$ and $C_\varphi (v_1)=\{9,10,...,13\}$. Without considering the conflict of v, for any given integer i ($2\le i\le 5$), we select $\{b_i,d_i\}$ from $\{9,10,\ldots ,18\}\setminus \{i+12\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least two selected ways. Since i has four possibilities, we have at least $2\times 4=8$ ways such that $v_1$ does not conflict with its neighbors and v does not conflict with $v_2,v_3,v_4$ and $v_5$, while v has at most four conflict vertices other than $v_2,v_3,v_4$ and $v_5$. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 4

Let v be a k-vertex of G with $10\le k\le 11$, then ${d_G^{(16-k)^-}}(v)\le 1$.

Proof

Assume, to the contrary, that G contains a k-vertex v ($10\le k\le 11$) satisfying ${d_G^{(16-k)^-}}(v)\ge 2$. Suppose that $d_G(v_1)=d_G(v_2)=16-k$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le k$. Clearly, $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|\le 15-k$ for $1\le i\le 2$. By Claim 2, every $6^-$-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$, and $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|=15-k$ for $1\le i\le 2$, then we recolor $v_iw_i$ with a color in $\{2,3,\ldots ,9\}\setminus C_\varphi (w_i)$. Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{k,k+1,\ldots ,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least four available colors. (b): We select $\{b_1,b_2\}$ from $\{k,k+1,\ldots ,18\}$ to recolor $vv_2$ and color $vv_1$ such that $v_2$ and $v_1$ do not conflict with their neighbors. $\{b_1,b_2\}$ has at least $\frac{4\times 3}{2}=6$ selected ways. Hence we have at least $4+6=10$ ways, while v has at most $k-2\le 9$ conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 5

Let v be a 12-vertex of G, then ${d_G^{3^-}}(v)\le 1$.

Proof

Assume, to the contrary, that G contains a 12-vertex v satisfying ${d_G^{3^-}}(v)\ge 2$. Suppose that $d_G(v_1)=d_G(v_2)=3$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le 12$. Clearly, $|C_\varphi (v_i)\cap \{12,13,\ldots ,18\}|\le 2$ for $1\le i\le 2$. By Claim 2, each 3-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$ for $1\le i\le 2$, we assume that $\varphi (v_iw_i)\notin \{12,13,\ldots ,18\}$ (if $\varphi (v_iw_i)\in \{12,13,\ldots ,18\}$, then we recolor $v_iw_i$ with a color in $\{2,3,\ldots ,11\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{12,13,\ldots ,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least five available colors. (b): We select $\{b_1,b_2\}$ from $\{12,13,\ldots ,18\}$ to recolor $vv_2$ and color $vv_1$ such that $v_2$ and $v_1$ do not conflict with their neighbors. $\{b_1,b_2\}$ has at least $\frac{5\times 4}{2}=10$ selected ways. Hence we have at least $5+10=15$ ways, while v has at most ten conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 6

Let v be a k-vertex of G with $11\le k\le 12$, then ${d_G^{6^-}}(v)\le 3k-31$.

Proof

Assume, to the contrary, that G contains a k-vertex v ($11\le k\le 12$) satisfying ${d_G^{6^-}}(v)\ge 3k-30$. Suppose that $d_G(v_i)=6$ for $1\le i\le 3k-30$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le k$. Clearly, $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|\le 5$ for $1\le i\le 3k-30$. By Claim 2, each 6-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$, and $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|=5$ for $1\le i\le 3k-30$, then we recolor $v_iw_i$ with a color in $\{3k-30,3k-29,\ldots ,k-1\}\setminus C_\varphi (w_i)$. Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{k,k+1,\ldots ,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least $14-k$ available colors. (b): For any given integer i ($2\le i\le 3k-30$), we select $\{b_i,d_i\}$ from $\{k,k+1,\ldots ,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least $\frac{(14-k)\times (13-k)}{2}$ selected ways. Since i has $3k-31$ possibilities, we have at least $\frac{(14-k)\times (13-k)}{2}\times (3k-31)=17-k$ different coloring ways. Hence we have at least $14-k+17-k=31-2k$ ways, while v has at most $k-(3k-30)=30-2k$ conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 7

Let v be a k-vertex of G with $13\le k\le 14$, then the following statements hold.

(1) ${d_G^{2^-}}(v)\le k-12$;

(2) If ${d_G^{m^-}}(v)\ge 1$ for $m\le 18-k$, then ${d_G^{k}}(v)\ge (19-k-m){d_G^{{(19-k)}^-}}(v)+1$.

Proof

(1) Assume, to the contrary, that G contains a k-vertex v ($13\le k\le 14$) satisfying ${d_G^{2^-}}(v)\ge k-11$. Suppose that $d_G(v_i)=2$ for $1\le i\le k-11$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le k$. Clearly, $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|\le 1$ for $1\le i\le k-11$. By Claim 2, each 2-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$ for $1\le i\le k-11$, we assume that $\varphi (v_iw_i)\notin \{k,k+1,\ldots ,18\}$ (if $\varphi (v_iw_i)\in \{k,k+1,\ldots ,18\}$, then we recolor $v_iw_i$ with a color in $\{3,4,\ldots ,12\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{k,k+1,\ldots ,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least $18-k\ge 4$ available colors. (b): For any given integer i ($2\le i\le k-11$), we select $\{b_i,d_i\}$ from $\{k,k+1,\ldots ,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least $\frac{(18-k)(17-k)}{2}$ selected ways. Since i has $k-12$ possibilities, we have at least $\frac{(18-k)(17-k)}{2}\times (k-12)\ge 10$ different coloring ways. Hence we have at least $4+10=14$ ways, while v has at most eleven conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction.

(2) Assume, to the contrary, that there is a k-vertex $v\in V(G)$ ($13\le k\le 14$) and an integer m ($m\le 18-k$) satisfying ${d_G^{m^-}}(v)\ge 1$, where ${d_G^{k}}(v)\le (19-k-m){d_G^{{(19-k)}^-}}(v)$. Set ${d_G^{{(19-k)}^-}}(v)=l$. W.l.o.g., ${d_G}(v_1)=m$ and ${d_G}(v_i)\le 19-k$ for $1\le i\le l$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. Suppose that $\varphi (vv_i)=i-1$ for $2\le i\le k$. Clearly, $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|\le 18-k$ for $1\le i\le l$. By Claim 2, each $6^-$-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$, and $|C_\varphi (v_i)\cap \{k,k+1,\ldots ,18\}|= d_G(v_i)-1$ for $1\le i\le l$, then we recolor $v_iw_i$ with a color in $\{7,8,\ldots ,12\}\setminus C_\varphi (w_i)$. Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{k,k+1,\ldots ,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least $20-k-m$ available colors. (b): For any given integer i ($2\le i\le l$), we select $\{b_i,d_i\}$ from $\{k,k+1,\ldots ,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least $19-k-m$ selected ways. Since i has $l-1$ possibilities, we have at least $(19-k-m)(l-1)$ different coloring ways. Hence we have at least $(20-k-m)+(19-k-m)(l-1)=(19-k-m)l+1$ ways, while v has at most $(19-k-m)l$ conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 8

Let v be a 15-vertex of G, then the following statements hold.

(1) ${d_G^{2^-}}(v)\le 3$;

(2) If ${d_G^{2^-}}(v)\ge 1$, then ${d_G^{3^-}}(v)\le 4$;

(3) If ${d_G^{m^-}}(v)\ge 1$ for $m\le 3$, then ${d_G^{15}}(v)\ge (4-m){d_G^{4^-}}(v)+1$;

(4) If v is incident with a bad 3-cycle, then ${d_G^{15}}(v)\ge 9$.

Proof

(1) Assume, to the contrary, that G contains a 15-vertex v satisfying ${d_G^{2^-}}(v)\ge 4$. Suppose that $d_G(v_i)=2$ for $1\le i\le 4$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. Suppose that $\varphi (vv_i)=i-1$ for $2\le i\le 15$. Clearly, $|C_\varphi (v_i)\cap \{15,16,17,18\}|\le 1$ for $1\le i\le 4$. By Claim 2, each 2-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$ for $1\le i\le 4$, we assume that $\varphi (v_iw_i)\notin \{15,16,17,18\}$ (if $\varphi (v_iw_i)\in \{15,16,17,18\}$, then we recolor $v_iw_i$ with a color in $\{4,5,\ldots ,14\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{15,16,17,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least three available colors. (b): For any given integer i ($2\le i\le 4$), we select $\{b_i,d_i\}$ from $\{15,16,17,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least three selected ways. Since i has three possibilities, we have at least $3\times 3=9$ different coloring ways. Hence we have at least $3+9=12$ ways, while v has at most eleven conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction.

(2) Assume, to the contrary, that G contains a 15-vertex v satisfying ${d_G^{2^-}}(v)\ge 1$, where ${d_G^{3^-}}(v)\ge 5$. Suppose that ${d_G}(v_1)=2$ and ${d_G}(v_i)=3$ for $2\le i\le 5$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. W.l.o.g., $\varphi (vv_i)=i-1$ for $2\le i\le 15$. Clearly, $|C_\varphi (v_i)\cap \{15,16,17,18\}|\le 2$ for $1\le i\le 5$. By Claim 2, each $3^-$-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$ for $1\le i\le 5$, we assume that $\varphi (v_iw_i)\notin \{15,16,17,18\}$ (if $\varphi (v_iw_i)\in \{15,16,17,18\}$, then we recolor $v_iw_i$ with a color in $\{8,9,\ldots ,14\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{15,16,17,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least three available colors. (b): For any given integer i ($2\le i\le 5$), we select $\{b_i,d_i\}$ from $\{15,16,17,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least two selected ways. Since i has four possibilities, we have at least $2\times 4=8$ different coloring ways. Hence we have at least $3+8=11$ ways, while v has at most ten conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction.

(3) Assume, to the contrary, that there is a 15-vertex $v\in V(G)$ and an integer m ($m\le 3$) satisfying ${d_G^{m^-}}(v)\ge 1$, where ${d_G^{15}}(v)\le (4-m){d_G^{{4}^-}}(v)$. Set ${d_G^{{4}^-}}(v)=l$. Suppose that ${d_G}(v_1)=m$ and ${d_G}(v_i)\le 4$ for $1\le i\le l$ (the proof can be given similarly and simply for other cases). Let $H=G-vv_1$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. Suppose that $\varphi (vv_i)=i-1$ for $2\le i\le 15$. Clearly, $|C_\varphi (v_i)\cap \{15,16,17,18\}|\le 3$ for $1\le i\le l$. By Claim 2, each $4^-$-vertex has at most one conflict vertex. If $v_i$ has a conflict vertex $w_i$ for $1\le i\le l$, we assume that $\varphi (v_iw_i)\notin \{15,16,17,18\}$ (if $\varphi (v_iw_i)\in \{15,16,17,18\}$, then we recolor $v_iw_i$ with a color in $\{8,9,\ldots ,14\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following two types of proper colorings. (a): We color $vv_1$ with a color in $\{15,16,17,18\}$ such that $v_1$ does not conflict with its neighbors. There are at least $5-m$ available colors. (b): For any given integer i ($2\le i\le l$), we select $\{b_i,d_i\}$ from $\{15,16,17,18\}$ to recolor $vv_i$ and color $vv_1$ such that $v_i$ and $v_1$ do not conflict with their neighbors. $\{b_i,d_i\}$ has at least $4-m$ selected ways. Since i has $l-1$ possibilities, we have at least $(4-m)(l-1)$ different coloring ways. Hence we have at least $(5-m)+(4-m)(l-1)=(4-m)l+1$ ways, while v has at most $(4-m)l$ conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction.

(4) Assume, to the contrary, that there exists a 15-vertex $v\in V(G)$ incident with a bad 3-cycle $vv_1v_2$ ($d_G(v_1)=d_G(v_2)=3$), where ${d_G^{15}}(v)\le 8$. Let $w_i$ ($1\le i\le 2$) be the neighbor of $v_i$ other than $v, v_{3-i}$. Let $H=G-v_1v_2$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. By Claim 2, $v_i$ ($1\le i\le 2$) has exactly one conflict vertex. If $C_\varphi (v_1)\ne C_\varphi (v_2)$, then we color $v_1v_2$ with a color in $C\setminus (C_\varphi (v_1)\cup C_\varphi (v_2))$ to get a $t_G$-avd-coloring of G, a contradiction. If $C_\varphi (v_1)=C_\varphi (v_2)$, w.l.o.g., $\varphi (vv_1)=\varphi (v_2w_2)=1,\varphi (vv_2)=\varphi (v_1w_1)=2$ and $\varphi (vv_i)=i$ for $3\le i\le 15$. Without considering the conflict of v, we have the following two types of proper colorings. (a): For any given integer i ($1\le i\le 2$), we recolor $vv_i$ with an arbitrary color in $\{16,17,18\}$ and color $v_1v_2$ with 3. Since i has two possibilities, we have $3\times 2=6$ different coloring ways. (b): We select $\{b_1,b_2\}$ from $\{16,17,18\}$ to recolor $vv_1$ and $vv_2$, and color $v_1v_2$ with 3. $\{b_1,b_2\}$ has three selected ways. Hence we have $6+3=9$ ways, while v has at most eight conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 9

Let v be a k-vertex of G with $k\ge 14$, then v is incident with at most one bad 3-cycle.

Proof

Assume, to the contrary, that there exists a k-vertex $v\in V(G)$ ($k\ge 14$) incident with two bad 3-cycles $vv_1v_2,vv_3v_4$, where $d_G(v_i)=3$ for $1\le i\le 4$. Let $w_i$ be the neighbor of $v_i$ for $1\le i\le 4$. Let $H=G-v_1v_2$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. By Claim 2, each 3-vertex has at most one conflict vertex. If $C_\varphi (v_1)\ne C_\varphi (v_2)$, then we color $v_1v_2$ with an arbitrary color in $C\setminus (C_\varphi (v_1)\cup C_\varphi (v_2))$ to yield a $t_G$-avd-coloring of G, a contradiction. If $C_\varphi (v_1)=C_\varphi (v_2)$, w.l.o.g., $\varphi (vv_1)=\varphi (v_2w_2)=1,\varphi (vv_2)=\varphi (v_1w_1)=2$ and $\varphi (vv_i)=i$ for $3\le i\le k$. Note that $|\{\varphi (v_3w_3),\varphi (v_4w_4)\}\cap \{3,4\}|\le 1$, w.l.o.g., $\varphi (v_4w_4)\ne 3$. Clearly, $|\{\varphi (v_4w_4)\}\cap \{1,2\}|\le 1$, w.l.o.g., $\varphi (v_4w_4)\ne 1$. We first delete the color of $v_3v_4$, switch the colors of $vv_1$ and $vv_4$, then color $v_1v_2,v_3v_4$ properly to yield a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 10

Let v be a k-vertex of G with $k\ge 16$. If v is incident with a bad 3-cycle, then ${d_G^{k}}(v)\ge 2d_G^{4^-}(v)+1$.

Proof

Assume, to the contrary, that there exists a k-vertex $v\in V(G)$ ($k\ge 16$) incident with a bad 3-cycle $vv_1v_2$ ($d_G(v_1)=d_G(v_2)=3$), where $d_G^{k}(v)\le 2d_G^{4^-}(v)$. Let $w_i$ ($1\le i\le 2$) be the neighbor of $v_i$ other than $v,v_{3-i}$. Set $d_G^{4^-}(v)=m$. Suppose that $d_G(v_i)\le 4$ for $1\le i\le m$. Let $H=G-v_1v_2$, by Remark 1, H has a $t_G$-avd-coloring $\varphi$ with the color set C. By Claim 2, each $4^-$-vertex has at most one conflict vertex. If $C_\varphi (v_1)\ne C_\varphi (v_2)$, then we color $v_1v_2$ with an arbitrary color in $C\setminus (C_\varphi (v_1)\cup C_\varphi (v_2))$ to yield a $t_G$-avd-coloring of G, a contradiction. If $C_\varphi (v_1)=C_\varphi (v_2)$, w.l.o.g., $\varphi (vv_1)=\varphi (v_2w_2)=1,\varphi (vv_2)=\varphi (v_1w_1)=2$ and $\varphi (vv_i)=i$ for $3\le i\le k$. Clearly, $|C_\varphi (v_i)\cap \{1,2,k+1,k+2\}|\le 3$ for $1\le i\le m$. If $v_i$ has a conflict vertex $w_i$ for $3\le i\le m$, we assume that $\varphi (v_iw_i)\notin \{1,2,k+1,k+2\}$ (if $\varphi (v_iw_i)\in \{1,2,k+1,k+2\}$, then we recolor $v_iw_i$ with a color in $\{k-6,k-5,\ldots ,k\}\setminus (C_\varphi (v_i)\cup C_\varphi (w_i))$ to satisfy this condition). Without considering the conflict of v, we have the following three types of proper colorings. (a): For any given integer i ($1\le i\le 2$), we recolor $vv_i$ with an arbitrary color in $\{k+1,k+2\}$ and color $v_1v_2$ with 3. Since i has two possibilities, we have $2\times 2=4$ different coloring ways. (b): We recolor $vv_i$ with $k+i$ for $1\le i\le 2$ and color $v_1v_2$ with 3. (c): For any given integer i ($3\le i\le m$), we recolor $vv_i$ with $b_i$ in $\{1,2,k+1,k+2\}$ such that $v_i$ does not conflict with its neighbors. If $b_i\in \{1,2\}$, then we recolor $vv_{b_i}$ with $k+1$ or $k+2$ and color $v_1v_2$ with 3, so there are two coloring ways. If $b_i\in \{k+1,k+2\}$, then we recolor $vv_1$ or $vv_2$ with a color in $\{k+1,k+2\}\setminus \{b_i\}$ and color $v_1v_2$ with 3, so there are two ways. Since i has $m-2$ possibilities, we have $2(m-2)$ ways. Hence we have $4+1+2(m-2)=2m+1$ ways, while v has at most 2m conflict vertices. So we can obtain a $t_G$-avd-coloring of G, a contradiction. $\square$

Claim 11

Yan et al. (2012) Let v be a k-vertex of G with $k\ge 16$. If ${d_G^{2^-}}(v)\ge 1$, then ${d_G^{3^-}}(v)\le \left\lceil {\frac{k}{2}}\right\rceil -1$ and ${d_G^{k}}(v)\ge {d_G^{3^-}}(v)+1$.

Let H be one of the connected component of the graph which is obtained from G by deleting all $2^-$-vertices. By Claims 1, 3–5, 7–8, 11, the relation between $d_G(v)$ and $d_{H}(v)$ is as in Table 1.

Table 1 The relation between $d_G(v)$ and $d_{H}(v)$

By Table 1, we deduce that $\delta (H)\ge 3$, and for any $v\in V(H)$, we have $d_H^k(v)=d_G^k(v)$, where $3\le k\le 6$. Let $H^\times$ be the associated plane graph of H. By Claims 2–4, 11 and Table 1, every 3-face of $H^\times$ is one of the following types:

Type I: (3, 3, 4)-faces, (4, 4, 4)-faces;

Type II: $(3,3,10^+)$-faces, $(3,4,10^+)$-faces, $(4,4,9^+)$-faces, $(4,5,9^+)$-faces;

Type III: $(3,10^+,10^+)$-faces, (4, 5, 5)-faces, (4, 6, 6)-faces, $(4,6,9^+)$-faces, $(4,7^+,7^+)$-faces, $(5,5,9^+)$-faces, $(5,9^+,9^+)$-faces, $(6,6,9^+)$-faces, $(6,9^+,9^+)$-faces;

Type IV: $(7^+,7^+,7^+)$-faces.

Let $c_f$ be the false vertex incident with a false 3-face f, and $N_{\bar{f}}(c_f)$ be the set of neighbors of $c_f$ which are not incident with f. f is the corresponding face of the vertices in $N_{\bar{f}}(c_f)$. By Claims 2–3, v has at most one corresponding 3-face of Type I. A vertex v is of Type I if it has a corresponding 3-face of Type I. Let $n_i(v)$ be the number of 3-faces of Type i incident with v, $i\in \{{\mathrm{II,III,IV}}\}$. Let $n_{4^+}(v)$ be the number of $4^+$-faces incident with v in $H^\times$.

By Euler’s formula $|V(H^\times )|-|E(H^\times )|+|F(H^\times )|=2$, we have:

$$\begin{aligned} \sum \limits _{v\in V(H^\times )}{\left( {{d_{H^\times }}(v)-4}\right) }+\sum \limits _{f\in F({H^\times })}{\left( {{d_{H^\times }}(f)-4}\right) }=-8 \end{aligned}$$

Next, we will apply the discharging method to derive a contradiction. We define the initial charge function $w(x)=d_{H^\times }(x)-4$ for $x\in V({H^\times })\cup F({H^\times })$, and design discharging rules to redistribute charges. Let $w'$ be the new charge after the discharging process, then we will show that $w'(x)\ge 0$ for $x\in V({H^\times })\cup F({H^\times })$, which leads to a contradiction.

The discharging rules are defined as follows. In the following rules, the degree of a vertex refers to its degree in H.

R1: Each 3-face f of Type I gets ${\frac{1}{2}}$ from every $9^+$-vertex in $N_{\bar{f}}(c_f)$ (by Claims 2–3, f is false and $N_{\bar{f}}(c_f)$ consists of two $9^+$-vertices);

R2: Each 3-face of Type II gets 1 from its incident $9^+$-vertex;

R3: Each of $(5,9^+,9^+)$-faces and $(6,9^+,9^+)$-faces gets ${\frac{1}{2}}$ from every incident $9^+$-vertex, and each other 3-face of Type III gets ${\frac{1}{2}}$ from every incident $5^+$-vertex;

R4: Each 3-face of Type IV gets ${\frac{1}{3}}$ from every incident $7^+$-vertex;

R5: Each good 3-vertex gets ${\frac{1}{3}}$ from every adjacent $10^+$-vertex in H, and each bad 3-vertex gets ${\frac{1}{2}}$ from every adjacent $10^+$-vertex in H.

We first verify the new charge of $f\in F(H^\times )$.

$\bullet$ $d_{H^\times }(f)=3$. By R1–R4, $w'(f)\ge 0$.

$\bullet$ $d_{H^\times }(f)\ge 4$. The charge remains unchanged, $w'(f)=d_{H^\times }(f)-4\ge 0$.

Next, we verify the new charge of $v\in V(H^\times )$. For each real vertex $v\in V(H^\times )$, we have $d_{H^\times }(v)=d_G(v)-d_G^{2^-}(v)$.

$\bullet$ $d_{H^\times }(v)=3$. By Claims 2–4 and Table 1, $d_H^{9^-}(v)=d_H^3(v)\le 1$. If v is good, then $d_H^{10^+}(v)=3$, otherwise $d_H^{10^+}(v)=2$. By R5, $w'(v)\ge 3-4+\min \{\frac{1}{3}\times 3,\frac{1}{2}\times 2\}=0$.

$\bullet$ $d_{H^\times }(v)=4$. No rule applies to v, then $w'(v)=4-4=0$.

$\bullet$ $d_{H^\times }(v)=5$. By Claims 2–3 and Table 1, $d_H^{8^-}(v)=d_H^5(v)\le 1$. By R3, only (4, 5, 5)-faces and $(5,5,9^+)$-faces incident with v get charges from v. There are at most two such faces incident with v. By R3, $w'(v)\ge 5-4-\frac{1}{2}\times 2=0$.

$\bullet$ $d_{H^\times }(v)=6$. By Claims 2–3 and Table 1, $d_H^{8^-}(v)=d_H^6(v)\le 1$. By R3, only (4, 6, 6)-faces, $(4,6,9^+)$-faces and $(6,6,9^+)$-faces incident with v get charges from v. There are at most four such faces incident with v. By R3, $w'(v)\ge 6-4-\frac{1}{2}\times 4=0$.

$\bullet$ $7\le d_{H^\times }(v)\le 8$. By Claim 3 and Table 1, $d_H^{6^-}(v)=0$ and v is not of Type I. Thus we have $n_{\mathrm{III}}(v)\le 2$. By R3–R4, $w'(v)\ge d_{H^\times }(v)-4-\frac{1}{2}\times {2}-\frac{1}{3}\times {(d_{H^\times }(v)-2)}=\frac{2d_{H^\times }(v)-13}{3}>0$.

$\bullet$ $d_{H^\times }(v)=9$. We first give the following fact.

Fact 1

If $d_{H^\times }(v)=9$, then $d_H^{3}(v)=0$ and $d_H^{6^-}(v)\le 1$.

Proof

By Table 1, we have $d_G(v)\in \{9,10,16,17\}$. If $d_G(v)=9$, by Claim 3, $d_H^{6^-}(v)=0$. If $d_G(v)=10$, then $d_G^{2^-}(v)=1$. By Claim 4, $d_H^{6^-}(v)=0$. If $d_G(v)=k$ ($16\le k\le 17$), then $d_G^{2^-}(v)=k-9$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1=k-9$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)=0$ and $d_H^{6^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-9)-(k-8)\le 1$. $\square$

By Fact 1, if v is of Type I, then $n_{\mathrm{II}}(v)=0$, otherwise $n_{\mathrm{II}}(v)\le 1$. By R1–R4, $w'(v)\ge 9-4-\max \{\frac{1}{2}+\frac{1}{2}\times 9,1+\frac{1}{2}\times {8}\}=0$.

$\bullet$ $d_{H^\times }(v)=10$. We first give the following fact.

Fact 2

If $d_{H^\times }(v)=10$, then $d_H^{3}(v)\le 1$ and $d_H^{6^-}(v)\le 3$.

Proof

By Table 1, we have $d_G(v)\in \{10,11\}$ or $d_G(v)\ge 16$. If $d_G(v)=10$, by Claim 4, $d_H^{6^-}(v)\le 1$. If $d_G(v)=11$, then $d_G^{2^-}(v)=1$. By Claims 4 and 6, $d_G^{5^-}(v)\le 1$ and $d_G^{6^-}(v)\le 2$. Thus $d_H^{3^-}(v)=0$ and $d_H^{6^-}(v)\le 1$. If $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-10$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1\ge d_G^{2^-}(v)+1$. Thus $d_H^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-10)\le 1$ and $d_H^{6^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-10)-(k-9)\le 3$. $\square$

By Fact 2, if v is of Type I, then $n_{\mathrm{II}}(v)\le 1$ and $n_{\mathrm{III}}(v)\le 5$; otherwise we have either $n_{\mathrm{II}}(v)\le 1$, or $n_{\mathrm{II}}(v)=2$ and $n_{\mathrm{III}}(v)\le 4$. Noting that $d_H^{3}(v)\le 1$, by R1–R5, we have $w'(v)\ge 10-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 5+\frac{1}{3}\times 4,1+\frac{1}{2}\times 9,1\times 2+\frac{1}{2}\times {4}+\frac{1}{3}\times 4\}-\frac{1}{2}=0$.

$\bullet$ $d_{H^\times }(v)=11$. We first give the following fact.

Fact 3

If $d_{H^\times }(v)=11$, then $d_H^{3}(v)\le 2$ and $d_H^{6^-}(v)\le 5-d_H^{3}(v)$.

Proof

By Table 1, we have $d_G(v)\in \{11,12\}$ or $d_G(v)\ge 16$. If $d_G(v)=11$, by Claims 4 and 6, $d_H^{3^-}(v)\le 1$ and $d_H^{6^-}(v)\le 2$. If $d_G(v)=12$, then $d_G^{2^-}(v)=1$. By Claims 5–6, $d_G^{3^-}(v)\le 1$ and $d_G^{6^-}(v)\le 5$. Thus $d_H^{3}(v)=0$ and $d_H^{6^-}(v)\le 4$. If $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-11$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)=d_G^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-11)\le 2$ and $d_H^{6^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-11)-(k-10+d_G^{3}(v))\le 5-d_H^{3}(v)$. $\square$

- $d_H^{3}(v)\ne 0$. By Fact 3, if v is of Type I, then $n_{\mathrm{II}}(v)\le 1$ and $n_{\mathrm{III}}(v)\le 7$; otherwise we have either $n_{\mathrm{II}}(v)\le 1$ or $n_{\mathrm{II}}(v)=2$ and $n_{\mathrm{III}}(v)\le 6$. Noting that $d_H^{3}(v)\le 2$, by R1–R5, we have $w'(v)\ge 11-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 7+\frac{1}{3}\times 3,1+\frac{1}{2}\times 10,1\times 2+\frac{1}{2}\times 6+\frac{1}{3}\times 3\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)=0$. By Fact 3, if v is of Type I, then $n_{\mathrm{II}}(v)\le 2$, otherwise $n_{\mathrm{II}}(v)\le 3$. By R1–R4, $w'(v)\ge 11-4-\max \{\frac{1}{2}+1\times 2+\frac{1}{2}\times 9,1\times 3+\frac{1}{2}\times 8\}=0$.

$\bullet$ $d_{H^\times }(v)=12$. We first give the following fact.

Fact 4

If $d_{H^\times }(v)=12$, then either $d_H^{3}(v)\le 1$ and $d_H^{5^-}(v)\le 7-d_H^{3}(v)$, or $2\le d_H^{3}(v)\le 3$ and $d_H^{6^-}(v)\le 7-d_H^{3}(v)$.

Proof

By Table 1, we have $d_G(v)\ge 12$. (a): $d_G(v)=12$. By Claims 5–6, $d_H^{3}(v)\le 1$ and $d_H^{5^-}(v)\le 5$. So, in this case, Fact 4 holds. (b): $d_G(v)=k$ ($13\le k\le 14$). Then $d_G^{2^-}(v)=k-12>0$, by Claim 7(2), let $m=2$, we have $d_G^{{k}}(v)\ge (17-k)d_G^{{(19-k)}^-}(v)+1$. Noting that $d_G^{{(19-k)}^-}(v)+d_G^k(v)\le k$, we get that $d_H^{{(19-k)}^-}(v)=d_G^{{(19-k)}^-}(v)-d_G^{2^-}(v)\le \lfloor \frac{k-1}{18-k}\rfloor -(k-12)=1$. So, in this case, Fact 4 holds. (c): $d_G(v)=15$, then $d_G^{2^-}(v)=3$. By Claim 8(2), $d_H^{3}(v)=d_G^{3^-}(v)-d_G^{2^-}(v)\le 1$. By Claim 8(3), let $m=2$, we have $d_G^{15}(v)\ge 2d_G^{{4}^-}(v)+1$. Thus $d_H^{5^-}(v)\le d_G(v)-d_G^{2^-}(v)-d_G^{15}(v)\le 14-3d_G^{2^-}(v)=5$. So, in this case, Fact 4 holds. (d): $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-12$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)= d_G^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-12)\le 3$ and $d_H^{6^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-12)-(k-11+d_G^{3}(v))\le 7-d_H^{3}(v)$. So, in this case, Fact 4 holds. $\square$

- $d_H^{3}(v)=3$ and $d_H^{6^-}(v)\le 4$. If v is of Type I, by Lemma 1, we have $n_{\mathrm{II}}(v)\le 1$ and $n_{4^+}(v)\ge 1$; otherwise we have either $n_{\mathrm{II}}(v)\le 1$, or $n_{\mathrm{II}}(v)=2$ and $n_{\mathrm{III}}(v)\le 6$. By R1–R5, $w'(v)\ge 12-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 10,1+\frac{1}{2}\times {11},1\times 2+\frac{1}{2}\times 6+\frac{1}{3}\times 4\}-\frac{1}{2}\times 3=0$.

- $d_H^{3}(v)=2$ and $d_H^{6^-}(v)\le 5$. If v is of Type I, then either $n_{\mathrm{II}}(v)\le 1$, or $n_{\mathrm{II}}(v)=2$ and $n_{\mathrm{III}}(v)\le 6$; otherwise we have either $n_{\mathrm{II}}(v)\le 2$, or $n_{\mathrm{II}}(v)=3$ and $n_{\mathrm{III}}(v)\le 6$. By R1–R5, $w'(v)\ge 12-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 11,\frac{1}{2}+1\times 2+\frac{1}{2}\times 6+\frac{1}{3}\times 4,1\times 2+\frac{1}{2}\times 10,1\times 3+\frac{1}{2}\times 6+\frac{1}{3}\times 3\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)\le 1$. By Fact 4, if v is of Type I, then $n_{\mathrm{II}}(v)\le 3-d_H^{3}(v)$, otherwise $n_{\mathrm{II}}(v)\le 4-d_H^{3}(v)$. By R1–R5, $w'(v)\ge 12-4-\max \{\frac{1}{2}+1\times (3-d_H^{3}(v))+\frac{1}{2}\times (12-(3-d_H^{3}(v))),1\times (4-d_H^{3}(v))+\frac{1}{2}\times (12-(4-d_H^{3}(v)))\}-\frac{1}{2}d_H^{3}(v)=0$.

$\bullet$ $d_{H^\times }(v)=13$. We first give the following fact.

Fact 5

If $d_{H^\times }(v)=13$, then $d_H^{3}(v)\le 4$ and $d_H^{5^-}(v)\le 9-d_H^{3}(v)$. Furthermore, if $2\le d_H^{3}(v)\le 4$ and $d_H^{5^-}(v)\ge 7-d_H^{3}(v)$, then v is not incident with any bad 3-cycle.

Proof

By Table 1, we have $d_G(v)\ge 13$. (a): $d_G(v)=13$. If $d_G^3(v)\ge 1$, by Claim 7(2), $d_G^{13}(v)\ge 3d_G^{6^-}(v)+1$. Noting that $d_G^{6^-}(v)+d_G^{13}(v)\le 13$, we have $d_H^{5^-}(v)\le d_G^{6^-}(v)\le 3$. If $d_G^3(v)=0$ and $d_G^{5^-}(v)\ge 1$, by Claim 7(2), $d_G^{13}(v)\ge d_G^{5^-}(v)+1$. Noting that $d_G^{5^-}(v)+d_G^{13}(v)\le 13$, we have $d_H^{5^-}(v)\le d_G^{5^-}(v)\le 6$. So, in this case, Fact 5 holds. (b): $d_G(v)=14$, then $d_G^{2^-}(v)=1$. By Claim 7(2), let $m=2$, we have $d_G^{14}(v)\ge 3d_G^{{5}^-}(v)+1$. Noting that $d_G^{5^-}(v)+d_G^{14}(v)\le 14$, we get that $d_H^{5^-}(v)=d_G^{{5}^-}(v)-d_G^{2^-}(v)\le 3-1=2$. So, in this case, Fact 5 holds. (c): $d_G(v)=15$, then $d_G^{2^-}(v)=2$. By Claim 8(2), we have $d_H^{3}(v)=d_G^{3^-}(v)-d_G^{2^-}(v)\le 2$. By Claim 8(3), let $m=2$, we have $d_G^{15}(v)\ge 2d_G^{{4}^-}(v)+1$. Thus $d_H^{5^-}(v)\le d_G(v)-d_G^{2^-}(v)-d_G^{15}(v)\le 14-3d_G^{2^-}(v)-2d_G^{3}(v)=8-2d_H^{3}(v)$. So, in this case, Fact 5 holds. (d): $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-13$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)=d_G^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-13)\le 4$ and $d_H^{5^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-13)-(k-12+d_G^{3}(v))\le 9-d_H^{3}(v)$. Furthermore, suppose that $2\le d_H^{3}(v)\le 4$ and $d_H^{5^-}(v)\ge 7-d_H^{3}(v)$. Assume that v is incident with a bad 3-cycle, by Claim 10, $d_G^{k}(v)\ge 2d_G^{4^-}(v)+1$. Noting that $d_G^{2^-}(v)+d_H^{5^-}(v)+d_G^{k}(v)-k\le 0$, while $d_G^{2^-}(v)+d_H^{5^-}(v)+d_G^{k}(v)-k\ge k-13+ 7-d_H^{3}(v)+2(k-13) +2d_H^{3}(v)+1-k>2k-31>0$, a contradiction. So, in this case, Fact 5 holds. $\square$

- $d_H^{3}(v)=4$ and $d_H^{5^-}(v)\le 5$. By Fact 5, v is not incident with any bad 3-cycle. If v is of Type I, by Lemma 1, $n_{\mathrm{II}}(v)=0$, otherwise $n_{\mathrm{II}}(v)\le 1$. By R1–R5, $w'(v)\ge 13-4-\max \{\frac{1}{2}+\frac{1}{2}\times 13,1+\frac{1}{2}\times 12\}-\frac{1}{2}\times 4=0$.

- $d_H^{3}(v)=3$. By Fact 5, $d_H^{5^-}(v)=3$, or $4\le d_H^{5^-}(v)\le 6$ and v is not incident with any bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 1$, otherwise $n_{\mathrm{II}}(v)\le 2$. By R1–R5, $w'(v)\ge 13-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 12,1\times 2+\frac{1}{2}\times 11\}-\frac{1}{2}\times 3=0$.

- $d_H^{3}(v)=2$. By Fact 5, $d_H^{5^-}(v)\le 4$, or $5\le d_H^{5^-}(v)\le 7$ and v is not incident with any bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 2$, otherwise $n_{\mathrm{II}}(v)\le 3$. By R1–R5, $w'(v)\ge 13-4-\max \{\frac{1}{2}+1\times 2+\frac{1}{2}\times 11,1\times 3+\frac{1}{2}\times 10\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)\le 1$. By Fact 5, if v is of Type I, then $n_{\mathrm{II}}(v)\le 4-d_H^{3}(v)$, otherwise $n_{\mathrm{II}}(v)\le 5-d_H^{3}(v)$. By R1–R5, $w'(v)\ge 13-4-\max \{\frac{1}{2}+1\times (4-d_H^{3}(v))+\frac{1}{2}\times (13-(4-d_H^{3}(v))),1\times (5-d_H^{3}(v))+\frac{1}{2}\times (13-(5-d_H^{3}(v)))\}-\frac{1}{2}\times d_H^{3}(v)=0$.

$\bullet$ $d_{H^\times }(v)=14$. We first give the following fact.

Fact 6

If $d_{H^\times }(v)=14$, then either $d_H^{3}(v)=0$, or $1\le d_H^{3}(v)\le 5$ and $d_H^{5^-}(v)\le 11-d_H^{3}(v)$. Furthermore, if $d_H^{3}(v)\ge 4$ and $d_H^{5^-}(v)\ge 5$, or $2\le d_H^{3}(v)\le 3$ and $d_H^{5^-}(v)\ge 6$, then v is not incident with any bad 3-cycle.

Proof

By Table 1, we have $d_G(v)\ge 14$. (a): $d_G(v)=14$. If $d_G^3(v)\ge 1$, by Claim 7(2), $d_G^{14}(v)\ge 2d_G^{5^-}(v)+1$. Noting that $d_G^{5^-}(v)+d_G^{14}(v)\le 14$, we have $d_H^{5^-}(v)\le d_G^{5^-}(v)\le 4$. So, in this case, Fact 6 holds. (b): $d_G(v)=15$, then $d_G^{2^-}(v)=1$. By Claim 8(2), we have $d_H^{3}(v)=d_G^{3^-}(v)-d_G^{2^-}(v)\le 3$. By Claim 8(3), let $m=2$, we have $d_G^{15}(v)\ge 2d_G^{{4}^-}(v)+1$. Thus $d_H^{5^-}(v)\le d_G(v)-d_G^{2^-}(v)-d_G^{15}(v)\le 14-3d_G^{2^-}(v)-2d_G^{3}(v)-2d_G^{4}(v)\le 11-2d_H^{3}(v)$, which implies that $d_H^{3}(v)\le 3$. Furthermore, if $d_H^{5^-}(v)\ge 6$, by $d_G^{2^-}(v)+d_H^{5^-}(v)+d_G^{15}(v)\le 15$ and Claim 8(4), v is not incident with any bad 3-cycle. So, in this case, Fact 6 holds. (c): $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-14$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)=d_G^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-14)\le 5$ and $d_H^{5^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-14)-(k-13+d_G^{3}(v))\le 11-d_H^{3}(v)$. Furthermore, suppose that $d_H^{3}(v)\ge 4$ and $d_H^{5^-}(v)\ge 5$, or $2\le d_H^{3}(v)\le 3$ and $d_H^{5^-}(v)\ge 6$. Assume that v is incident with a bad 3-cycle, by Claim 10, $d_G^k(v)\ge 2d_G^{4^-}(v)+1$. Noting that $d_G^{2^-}(v)+d_H^{5^-}(v)+d_G^{k}(v)-k\le 0$, while $d_G^{2^-}(v)+d_H^{5^-}(v)+d_G^{k}(v)-k\ge d_G^{2^-}(v)+d_H^{5^-}(v)+2d_G^{4^-}(v)+1-k\ge 3d_G^{2^-}(v)+2d_H^{3}(v)+d_H^{5^-}(v)+1-k\ge 3(k-14)+\min \{2\times 4+5,2\times 2+6\}+1-k=2k-31>0$, a contradiction. So, in this case, Fact 6 holds. $\square$

By Fact 6, we consider the following cases.

- $d_H^{3}(v)=5$ and $d_H^{5^-}(v)\le 6$, or $d_H^{3}(v)=4$ and $5\le d_H^{5^-}(v)\le 7$. By Fact 6, v is not incident with any bad 3-cycle. If v is of Type I, by Lemma 1, we have $n_{\mathrm{II}}(v)\le 5-d_H^{3}(v)$, otherwise $n_{\mathrm{II}}(v)\le 6-d_H^{3}(v)$. By R1–R5, $w'(v)\ge 14-4-\max \{\frac{1}{2}+1\times (5-d_H^{3}(v))+\frac{1}{2}\times (14-(5-d_H^{3}(v))),1\times (6-d_H^{3}(v))+\frac{1}{2}\times (14-(6-d_H^{3}(v)))\}-\frac{1}{2}d_H^{3}(v)=0$.

- $d_H^{3}(v)=d_H^{5^-}(v)=4$. If v is of Type I, by Lemma 1, we have $n_{\mathrm{II}}(v)\le 1$, otherwise, by Claim 9, we have $n_{\mathrm{II}}(v)\le 2$. By R1–R5, $w'(v)\ge 14-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 13,1\times 2+\frac{1}{2}\times 12\}-\frac{1}{2}\times 4=0$.

- $2\le d_H^{3}(v)\le 3$ and $d_H^{5^-}(v)\le 5$, or $d_H^{3}(v)=3$ and $6\le d_H^{5^-}(v)\le 8$ and v is not incident with any bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 2$, otherwise $n_{\mathrm{II}}(v)\le 3$. Noting that $d_H^{3}(v)\le 3$, by R1–R5, we have $w'(v)\ge 14-4-\max \{\frac{1}{2}+1\times 2+\frac{1}{2}\times 12,1\times 3+\frac{1}{2}\times 11\}-\frac{1}{2}\times 3=0$.

- $d_H^{3}(v)=2$, $6\le d_H^{5^-}(v)\le 9$ and v is not incident with any bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 3$, otherwise $n_{\mathrm{II}}(v)\le 4$. By R1–R5, $w'(v)\ge 14-4-\max \{\frac{1}{2}+1\times 3+\frac{1}{2}\times 11,1\times 4+\frac{1}{2}\times 10\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)=1$ and $d_H^{5^-}(v)\le 10$. If v is of Type I, then $n_{\mathrm{II}}(v)\le 4$, otherwise $n_{\mathrm{II}}(v)\le 5$. By R1–R5, $w'(v)\ge 14-4-\max \{\frac{1}{2}+1\times 4+\frac{1}{2}\times 10,1\times 5+\frac{1}{2}\times 9\}-\frac{1}{2}=0$.

- $d_H^{3}(v)=0$. Then $n_{\mathrm{II}}(v)\le 5$, or $n_{\mathrm{II}}(v)=6$ and $n_{4^+}(v)\ge 1$, or $n_{\mathrm{II}}(v)=7$ and $n_{4^+}(v)\ge 5$ by Claims 2–3. By R1–R4, $w'(v)\ge 14-4-\frac{1}{2}-\max \{1\times 5+\frac{1}{2}\times 9,1\times 6+\frac{1}{2}\times 7,1\times 7+\frac{1}{2}\times 2\}=0$.

Remark 3

For any $15^+$-vertex $v\in V(H^\times )$, if v is not incident with any bad 3-cycle and $d_H^{3b}(v)\ge 2$, then $n_{4^+}(v)\ge 1$.

$\bullet$ $d_{H^\times }(v)=15$. We first give the following fact.

Fact 7

If $d_{H^\times }(v)=15$, then either $d_H^{3}(v)=0$, or $1\le d_H^{3}(v)\le 7$ and $d_H^{6^-}(v)\le 14-d_H^{3}(v)$. Furthermore, if $d_H^{3}(v)\ge 3$ and $d_H^{6^-}(v)\ge 7$, or $d_H^{3}(v)=2$ and $d_H^{6^-}(v)\ge 9$, then v is not incident with any bad 3-cycle.

Proof

By Table 1, we have $d_G(v)\ge 15$. (a): $d_G(v)=15$. If $d_G^{3}(v)\ge 1$, by Claim 8(3), let $m=3$, we have $d_G^{15}(v)\ge d_G^{4^-}(v)+1$. Noting that $d_H^{3}(v)\le d_G^{4^-}(v)\le d_G^{6^-}(v)\le d_G(v)-d_G^{15}(v)$, we have $d_H^{3}(v)\le 7$ and $d_H^{6^-}(v)\le 14-d_H^3(v)$. Furthermore, if $d_H^{6^-}(v)\ge 7$, by $d_G^{6^-}(v)+d_G^{15}(v)\le 15$ and Claim 8(4), v is not incident with any bad 3-cycle. So, in this case, Fact 7 holds. (b): $d_G(v)=k$ ($k\ge 16$), then $d_G^{2^-}(v)=k-15$. By Claim 11, $d_G^{3^-}(v)\le \lceil \frac{k}{2}\rceil -1$ and $d_G^k(v)\ge d_G^{3^-}(v)+1$. Thus $d_H^{3}(v)=d_G^{3}(v)\le \lceil \frac{k}{2}\rceil -1-(k-15)\le 6$ and $d_H^{6^-}(v)\le k-d_G^{2^-}(v)-d_G^{k}(v)\le k-(k-15)-(k-14+d_G^{3}(v))<14-d_H^{3}(v)$. Furthermore, suppose that $d_H^{3}(v)\ge 3$ and $d_H^{6^-}(v)\ge 7$, or $d_H^{3}(v)=2$ and $d_H^{6^-}(v)\ge 9$. Assume that v is incident with a bad 3-cycle, by Claim 10, $d_G^k(v)\ge 2d_G^{4^-}(v)+1$. Noting that $d_G^{2^-}(v)+d_H^{6^-}(v)+d_G^{k}(v)-k\le 0$, while $d_G^{2^-}(v)+d_H^{6^-}(v)+d_G^{k}(v)-k\ge d_G^{2^-}(v)+d_H^{6^-}(v)+2d_G^{4^-}(v)+1-k\ge 3d_G^{2^-}(v)+2d_H^{3}(v)+d_H^{6^-}(v)+1-k\ge 3(k-15)+\min \{2\times 3+7,2\times 2+9\}+1-k=2k-31>0$, a contradiction. So, in this case, Fact 7 holds.$\square$

By Fact 7, we consider the following cases.

- $d_H^{3}(v)=d_H^{6^-}(v)=7$, and v is not incident with any bad 3-cycle. If v is of Type I, by Lemma 1, we have $n_{\mathrm{II}}(v)=0$ and $n_{4^+}(v)\ge 1$; otherwise we have $n_{\mathrm{II}}(v)\le 1$ and either $d_H^{3b}(v)\le 1$ or $n_{4^+}(v)\ge 1$ by Remark 3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+\frac{1}{2}\times 14+\frac{1}{2}\times 7,1+\frac{1}{2}\times 14+\frac{1}{2}+\frac{1}{3}\times 6,1+\frac{1}{2}\times 13+\frac{1}{2}\times 7\}=0$.

- $d_H^{3}(v)=d_H^{6^-}(v)=6$. By Claim 9, v is incident with at most one bad 3-cycle. If v is of Type I, by Lemma 1, then $n_{\mathrm{II}}(v)\le 1$ and $n_{4^+}(v)\ge 1$; otherwise we have either $n_{\mathrm{II}}(v)\le 1$, or $n_{\mathrm{II}}(v)=2$ and $n_{\mathrm{III}}(v)\le 10$. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 13,1+\frac{1}{2}\times 14,1\times 2+\frac{1}{2}\times 10+\frac{1}{3}\times 3\}-\frac{1}{2}\times 6=0$.

- $d_H^{3}(v)=6$, $7\le d_H^{6^-}(v)\le 8$, and v is not incident with any bad 3-cycle. If v is of Type I, we have $n_{\mathrm{II}}(v)\le 1$ and either $d_H^{3b}(v)\le 1$ or $n_{4^+}(v)\ge 1$ by Remark 3; otherwise we have $n_{\mathrm{II}}(v)\le 2$ and either $d_H^{3b}(v)\le 1$ or $n_{4^+}(v)\ge 1$ by Remark 3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 14+\frac{1}{2}+\frac{1}{3}\times 5,\frac{1}{2}+1+\frac{1}{2}\times 13+\frac{1}{2}\times 6,1\times 2+\frac{1}{2}\times 13+\frac{1}{2}+\frac{1}{3}\times 5,1\times 2+\frac{1}{2}\times 12+\frac{1}{2}\times 6\}=0$.

- $d_H^{3}(v)=5$ and $d_H^{6^-}(v)\le 6$. By Claim 9, v is incident with at most one bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 1$, otherwise $n_{\mathrm{II}}(v)\le 2$. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 14,1\times 2+\frac{1}{2}\times 13\}-\frac{1}{2}\times 5=0$.

- $d_H^{3}(v)=5$, $7\le d_H^{6^-}(v)\le 9$, and v is not incident with any bad 3-cycle. If v is of Type I, then either $n_{\mathrm{II}}(v)\le 1$, or $n_{\mathrm{II}}(v)=2$ and $n_{4^+}(v)\ge 1$ by Claims 2–3; otherwise we have $n_{\mathrm{II}}(v)\le 3$ and either $d_H^{3b}(v)\le 1$ or $n_{4^+}(v)\ge 1$ by Remark 3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1+\frac{1}{2}\times 14+\frac{1}{2}\times 5,\frac{1}{2}+1\times 2+\frac{1}{2}\times 12+\frac{1}{2}\times 5,1\times 3+\frac{1}{2}\times 12+\frac{1}{2}+\frac{1}{3}\times 4,1\times 3+\frac{1}{2}\times 11+\frac{1}{2}\times 5\}=0$.

- $3\le d_H^{3}(v)\le 4$ and $d_H^{6^-}(v)\le 6$. By Claim 9, v is incident with at most one bad 3-cycle. If v is of Type I, then $n_{\mathrm{II}}(v)\le 2$, otherwise $n_{\mathrm{II}}(v)\le 3$. Noting that $d_H^{3}(v)\le 4$, by R1–R5, we have $w'(v)\ge 15-4-\max \{\frac{1}{2}+1\times 2+\frac{1}{2}\times 13,1\times 3+\frac{1}{2}\times 12\}-\frac{1}{2}\times 4=0$.

- $3\le d_H^{3}(v)\le 4$, $7\le d_H^{6^-}(v)\le 14-d_H^{3}(v)$, and v is not incident with any bad 3-cycle. If v is of Type I, then either $n_{\mathrm{II}}(v)\le 6-d_H^{3}(v)$, or $n_{\mathrm{II}}(v)=7-d_H^{3}(v)$ and $n_{4^+}(v)\ge 1$ by Claims 2–3; otherwise we have either $n_{\mathrm{II}}(v)\le 7-d_H^{3}(v)$, or $n_{\mathrm{II}}(v)=8-d_H^{3}(v)$ and $n_{4^+}(v)\ge 1$ by Claims 2–3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1\times (6-d_H^{3}(v))+\frac{1}{2}\times (15-(6-d_H^{3}(v))),\frac{1}{2}+1\times (7-d_H^{3}(v))+\frac{1}{2}\times (14-(7-d_H^{3}(v))),1\times (7-d_H^{3}(v))+\frac{1}{2}\times (15-(7-d_H^{3}(v))),1\times (8-d_H^{3}(v))+\frac{1}{2}\times (14-(8-d_H^{3}(v)))\}-\frac{1}{2}d_H^{3}(v)=0$.

- $d_H^{3}(v)=2$ and $d_H^{6^-}(v)\le 8$. If v is of Type I, then $n_{\mathrm{II}}(v)\le 4$, otherwise $n_{\mathrm{II}}(v)\le 5$. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1\times 4+\frac{1}{2}\times 11,1\times 5+\frac{1}{2}\times 10\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)=2$, $9\le d_H^{6^-}(v)\le 12$, and v is not incident with any bad 3-cycle. If v is of Type I, then either $n_{\mathrm{II}}(v)\le 4$, or $n_{\mathrm{II}}(v)=5$ and $n_{4^+}(v)\ge 1$ by Claims 2–3; otherwise we have either $n_{\mathrm{II}}(v)\le 5$, or $n_{\mathrm{II}}(v)=6$ and $n_{4^+}(v)\ge 1$ by Claims 2–3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1\times 4+\frac{1}{2}\times 11,\frac{1}{2}+1\times 5+\frac{1}{2}\times 9,1\times 5+\frac{1}{2}\times 10,1\times 6+\frac{1}{2}\times 8\}-\frac{1}{2}\times 2=0$.

- $d_H^{3}(v)\le 1$ and $d_H^{6^-}(v)\le 15-2d_H^{3}(v)$. If v is of Type I, then either $n_{\mathrm{II}}(v)\le 6-d_H^{3}(v)$, or $n_{\mathrm{II}}(v)=7-d_H^{3}(v)$ and $n_{4^+}(v)\ge 1$ by Claims 2–3; otherwise we have either $n_{\mathrm{II}}(v)\le 7-d_H^{3}(v)$, or $n_{\mathrm{II}}(v)=8-d_H^{3}(v)$ and $n_{4^+}(v)\ge 1$ by Claims 2–3. By R1–R5, $w'(v)\ge 15-4-\max \{\frac{1}{2}+1\times (6-d_H^{3}(v))+\frac{1}{2}\times (15-(6-d_H^{3}(v))),\frac{1}{2}+1\times (7-d_H^{3}(v))+\frac{1}{2}\times (14-(7-d_H^{3}(v))),1\times (7-d_H^{3}(v))+\frac{1}{2}\times (15-(7-d_H^{3}(v))),1\times (8-d_H^{3}(v))+\frac{1}{2}\times (14-(8-d_H^{3}(v)))\}-\frac{1}{2}d_H^{3}(v)=0$.

$\bullet$ $d_{H^\times }(v)=k$ ($k\ge 16$). By Claim 2 and Table 1, every $5^-$-vertex has at most one conflict vertex.

- $d_H^{3}(v)=0$. (a): $3n_{\mathrm{II}}(v)\le {k+5}$. By R1–R4, $w'(v)\ge k-4-\frac{1}{2}-1\times n_{\mathrm{II}}(v)-\frac{1}{2}\times (k-n_{\mathrm{II}}(v))\ge \frac{k-16}{3}\ge 0$. (b): $3n_{\mathrm{II}}(v)>{k+5}$. Note that a 3-face of Type II is incident with two $5^-$-vertices. If v is not adjacent to any false vertex, then $d_{H}^{9^+}(v)\le k-2n_{\mathrm{II}}(v)$ and $n_{4^+}(v)\ge n_{\mathrm{II}}(v)-d_{H}^{9^+}(v)$; otherwise we have $d_{H}^{9^+}(v)\le k-2n_{\mathrm{II}}(v)+2$ and $n_{4^+}(v)\ge n_{\mathrm{II}}(v)-d_{H}^{9^+}(v)-1$. Thus $n_{4^+}(v)\ge \min \{n_{\mathrm{II}}(v)-(k-2n_{\mathrm{II}}(v)),n_{\mathrm{II}}(v)-(k-2n_{\mathrm{II}}(v)+2)-1\}=3n_{\mathrm{II}}(v)-k-3$. By R1–R4, $w'(v)\ge k-4-\frac{1}{2}-1\times n_{\mathrm{II}}(v)-\frac{1}{2}\times (k-n_{\mathrm{II}}(v)-n_{4^+}(v))=\frac{1}{2}(k-n_{\mathrm{II}}(v)+n_{4^+}(v)-9)\ge \frac{1}{2}(k- n_{\mathrm{II}}(v)+(3n_{\mathrm{II}}(v)-k-3)-9)=n_{\mathrm{II}}(v)-6>\frac{k+5}{3}-6>0$.

- $d_H^{3}(v)\ge 1$ and v is incident with a bad 3-cycle. (a): If v is of Type I, then v is not incident with any $(4,5,16^+)$-face. By Lemma 1 and Claim 9, we have $n_{\mathrm{II}}(v)\le \frac{d_H^4(v)}{2}+1$. (b): If v is not of Type I. Noting that v is incident with at most two $(4,5,16^+)$-faces, we have $n_{\mathrm{II}}(v)\le \frac{d_H^4(v)}{2}+3$. By Claim 10, $d_H^3(v)+d_H^4(v)\le d_G^{4^-}(v)\le \frac{k-1}{3}$. By R1–R5, $w'(v)\ge k-4-\max \{\frac{1}{2}+1\times (\frac{d_H^4(v)}{2}+1)+\frac{1}{2}\times (k-\frac{d_H^4(v)}{2}-1),1\times (\frac{d_H^4(v)}{2}+3)+\frac{1}{2}\times (k-\frac{d_H^4(v)}{2}-3)\}-\frac{1}{2}d_H^3(v)=\frac{k}{2}-\frac{d_H^3(v)}{2}-\frac{d_H^4(v)}{4}-\frac{11}{2}\ge \frac{k-11}{2}-\frac{d_H^3(v)+d_H^4(v)}{2}\ge \frac{k-11}{2}-\frac{k-1}{6}=\frac{k-16}{3}\ge 0$.

- $d_H^{3}(v)\ge 1$ and v is not incident with any bad 3-cycle.

- - $n_{4^+}(v)=0$. Then $3n_{\mathrm{II}}(v)+2d_H^3(v)-4\le k$. By Remark 3, $d_H^{3b}(v)\le 1$. By R1–R5, $w'(v)\ge k-4-\frac{1}{2}-1\times n_{\mathrm{II}}(v)-\frac{1}{2}\times (k-n_{\mathrm{II}}(v))-(\frac{1}{2}+\frac{1}{3}(d_H^3(v)-1))=\frac{k}{2}-\frac{1}{6}(3n_{\mathrm{II}}(v)+2d_H^3(v))-\frac{14}{3}\ge \frac{k}{2}-\frac{k+4}{6}-\frac{14}{3}=\frac{k-16}{3}\ge 0$.

- - $n_{4^+}(v)\ge 1$ and $3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor \le k+4$. Note that v is not incident with any bad 3-cycle. If v is of Type I, $n_{4^+}(v)\ge \lceil \frac{d_H^{3b}(v)}{2}\rceil$; otherwise we have $n_{4^+}(v)\ge \lceil \frac{d_H^{3b}(v)}{2}\rceil -1$. By R1–R5, $w'(v)\ge k-4-\max \{\frac{1}{2}+1\times n_{\mathrm{II}}(v)+\frac{1}{2}\times (k-n_{ \mathrm {II}}(v)-\lceil \frac{d_H^{3b}(v)}{2}\rceil ),1\times n_{\mathrm{II}}(v)+\frac{1}{2}\times (k-n_{ \mathrm {II}}(v)-(\lceil \frac{d_H^{3b}(v)}{2}\rceil -1))\}-(\frac{1}{3}\times d_H^{3g}(v)+\frac{1}{2}\times d_H^{3b}(v))=\frac{k-9}{2}-\frac{n_{\mathrm{II}}(v)}{2}-\frac{d_H^{3g}(v)}{3}-\frac{d_H^{3b}(v)}{2}+\frac{1}{2}\lceil \frac{d_H^{3b}(v)}{2}\rceil =\frac{k-9}{2}-\frac{1}{6}(3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor )\ge \frac{k-9}{2}-\frac{k+4}{6}=\frac{2k-31}{6}>0$.

- - $n_{4^+}(v)\ge 1$ and $3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor \ge k+5$. Note that v is not incident with any bad 3-cycle. If v is of Type I, $n_{4^+}(v)\ge 3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor -(k+5)+\lceil \frac{d_H^{3b}(v)}{2}\rceil$; otherwise we have $n_{4^+}(v)\ge 3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor -(k+5)+(\lceil \frac{d_H^{3b}(v)}{2}\rceil -1)$. By R1–R5, $w'(v)\ge k-4-\max \{\frac{1}{2}+1\times n_{\mathrm{II}}(v)+\frac{1}{2}\times (k-n_\mathrm{{II}}(v)-(3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor -(k+5)+\lceil \frac{d_H^{3b}(v)}{2}\rceil )),1\times n_{\mathrm{II}}(v)+\frac{1}{2}\times (k-n_\mathrm{{II}}(v)-(3n_{\mathrm{II}}(v)+2d_H^{3g}(v)+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor -(k+5)+\lceil \frac{d_H^{3b}(v)}{2}\rceil -1))\}-(\frac{1}{3}\times d_H^{3g}(v)+\frac{1}{2}\times d_H^{3b}(v)) ={n_{\mathrm{II}}(v)}+\frac{2}{3}d_H^{3g}(v)+\frac{1}{2}\lceil \frac{d_H^{3b}(v)}{2}\rceil +\frac{3}{2}\lfloor \frac{d_H^{3b}(v)}{2}\rfloor -\frac{d_H^{3b}(v)}{2}-7=\frac{1}{3}(3{n_{\mathrm{II}}(v)}+2{d_H^{3g}(v)}+3\lfloor \frac{d_H^{3b}(v)}{2}\rfloor )-7\ge \frac{k+5}{3}-7\ge 0$.

In conclusion, the new charge of $x\in V({H^\times })\cup F({H^\times })$ is nonnegative, a contradiction. The proof of Theorem 1 is done.