A linear-time algorithm for weighted paired-domination on block graphs

Abstract

In a graph $G = (V,E)$, a set $S\subseteq V(G)$ is said to be a dominating set of G if every vertex not in S is adjacent to a vertex in S. Let G[S] denote the subgraph of G induced by a subset S of V(G). A dominating set S of G is called a paired-dominating set of G if the induced subgraph G[S] contains a perfect matching. Suppose that, for each $v \in V(G)$, we have a weight w(v) specifying the cost for adding v to S. The weighted paired-domination problem is to find a paired-dominating set S whose total weights $w(S) = \sum _{v \in S} {w(v)}$ is minimized. In this paper, we propose an $O(n+m)$-time algorithm for the weighted paired-domination problem on block graphs using dynamic programming, which strengthens the results in [Theoret Comput Sci 410(47–49):5063–5071, 2009] and [J Comb Optim 19(4):457–470, 2010]. Moreover, the algorithm can be completed in O(n) time if the block-cut-vertex structure of G is given.

1 Introduction

In a graph $G = (V,E)$, a set $S\subseteq V(G)$ is said to be a dominating set of G if every vertex not in S is adjacent to a vertex in S. Let G[S] denote the subgraph of G induced by a subset S of V(G). A dominating set S of G is called a paired-dominating set if the induced subgraph G[S] contains a perfect matching. The paired-domination problem involves finding a paired-dominating set S of G such that the cardinality of S is minimized. Suppose that, for each $v \in V(G)$, we have a weight w(v) specifying the cost for adding v to S. The weighted paired-domination problem is to find a paired-dominating set S whose total weights $w(S) = \sum _{v \in S} {w(v)}$ is minimized. Throughout this paper, we let $n = |V(G)|$ and $m = |E(G)|$.

The domination problem has been extensively studied in the area of algorithmic graph theory for several decades; see (Hedetniemi and Laskar 1990, 1991; Haynes et al. 1998b, a; Goddard and Henning 2013; Henning 2009; Chang 2013) for books and survey papers. It has many applications in the real world such as location problems, communication networks, and kernels of games (Haynes et al. 1998b). Depending on the requirements of different types of applications, there are several variants of the domination problem, such as the independent domination, connected domination, total domination, and perfect domination problems (Chang 2013; Goddard and Henning 2013; Henning 2009; Yen and Lee 1996). These problems are proved to be NP-complete and have polynomial-time algorithms on some special classes of graphs. In particular, Haynes and Slater (1998) introduced the concept of paired-domination motivated by security concerns. In a museum protection program, besides the requirement that each region has a guard in it or is in the protection range of some guard, the guards must be able to back each other up. Similarly, to ensure the stability of the power supply, we require that each power station has another power station as a backup.

The paired-domination number $\gamma _p(G)$ is the number of vertices in a smallest paired-dominating set for G. Haynes and Slater (1998) introduced the concept of paired-domination problem and showed that the problem of determining whether $\gamma _p(G) \le c$ is NP-complete for general graph G with positive integer c. In addition, they presented bounds on $\gamma _p(G)$ and results relating $\gamma _p(G)$ to other domination parameters, e.g., $\gamma (G) \le \gamma _t(G) \le \gamma _p(G)$. Recently, many studies have been made for this problem in proving NP-completeness, providing approximation algorithms, and finding polynomial-time algorithms on some special classes of graphs. Here, we only mention some related results. For more detailed information regarding this problem, please refer to Kang (2013). Chen et al. (2010) demonstrated that the paired-domination problem is also NP-complete on bipartite graphs, chordal graphs, and split graphs. In Chen et al. (2009a), Chen et al. proposed an approximation algorithm with ratio $\ln (2\Delta (G))+1$ for general graphs and showed that the problem is APX-complete, i.e., has no PTAS. Panda and Pradhan (2013b) strengthened the results in Chen et al. (2010) by showing that the problem is also NP-complete for perfect elimination bipartite graphs. Further, Henning and Pradhan (2020) gave algorithmic results of upper paired-domination problem. Lu et al. (2019) proved a sharp upper bound of 4n/7 for claw-free graphs.

Meanwhile, polynomial-time algorithms have been studied intensively on some special classes of graphs such as tree graphs (Qiao et al. 2003), weighted tree graphs (Chen et al. 2009a), inflated tree graphs (Kang et al. 2004), convex bipartite graphs (Hung 2012; Panda and Pradhan 2013a), permutation graphs (Cheng et al. 2009; Lappas et al. 2009, 2013), interval graphs (Chen et al. 2010), circular-arc graphs (Lin and Tu 2015), strongly chordal graphs (Chen et al. 2009b), strongly orderable graphs (Pradhan and Panda 2019), and distance-hereditary graphs (Lin et al. 2020). Especially, Chen et al. (2010) presented an $O(n+m)$-time algorithm for block graphs, a proper superfamily of tree graphs. In this paper, we propose an $O(n+m)$-time algorithm for the weighted paired-domination problem on block graphs, which strengthens the results in Chen et al. (2009a, 2010). Moreover, the algorithm can be completed in O(n) time if the block-cut-vertex structure of G is given. Notice that the block-cut-vertex structure of a block graph G can be constructed in $O(n+m)$ time by the depth first search algorithm (Aho et al. 1974).

Over the last few decades, several variants of the classic domination problem, such as total domination, perfect domination, and power domination have studied intensively in block graphs. These problems have been proved to have linear-time algorithms in block graphs (Chang 1989; Yeh and Chang 1998; Xu et al. 2006). Recently, some other important domination problems, such as double roman domination, perfect roman domination, semitotal domination, and secure domination also have significant results in block graphs (Argiroffo et al. 2020; Pradhan and Jha 2018; Banerjee et al. 2019, 2020; Henning et al. 2019). Hence, the results of this paper complete the role of paired-domination problem on block graphs.

The remainder of this paper is organized as follows. In Sect. 2, given the block-cut-vertex structure of a block graph G, we employ dynamic programming to present an $O(n+m)$-time algorithm for finding a minimum-weight paired-dominating set of G. In Sect. 3, the correctness proof and complexity analysis of the algorithm are provided. Section 4 contains some concluding remarks and future work.

2 The proposed algorithm for block graphs

In this section, given a weighted block graph G with the corresponding block-cut-vertex structure $G^*$, we propose an O(n)-time algorithm that determines a minimum-weight paired-dominating set of G using dynamic programming. Since a graph G containing isolated vertices has no paired-dominating set, we suppose that G is a connected graph with $n \ge 2$ in the rest of this paper. First, we introduce some preliminaries for block graphs.

Fig. 1

a A block graph G. b The corresponding block-cut-vertex graph $G^*$ for the block graph G in (a). In particular, Algorithm 1 considered the blocks of G in turn according to the ordering $B_1, B_2,\ldots , B_8$

For any connected graph G, a vertex $v\in V(G)$ is called a cut-vertex of G, if deleting v from G increases the number of connected components of G. A block is a maximal connected subgraph without a cut-vertex. A graph G is called a block graph, if every block in G is a complete graph. It is known (Chen et al. 2010) that block graphs are a proper superfamily of tree graphs and a proper subfamily of chordal graphs. Suppose G has blocks $B_1, B_2,\ldots ,B_x$ and cut vertices $c_1, c_2,\ldots ,c_y$. We define the block-cut-vertex graph $G^* = (V, E)$ of G, where

$$\begin{aligned} V(G^*)&= \{{B_1,B_2,\ldots ,B_x,c_1, c_2,\ldots ,c_y}\}; \text { and}\\ E(G^*)&= \{{(B_i,c_j) \mid c_j \in B_j, 1\le i \le x, 1\le j \le y }\}. \end{aligned}$$

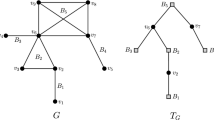
Consequently, the graph $G^*$ is a tree and the leaves in $G^*$ are precisely the blocks with exactly one cut-vertex in G. A block containing exactly one cut-vertex in G is called a pendant block. It should be noted that, by using the depth first search algorithm, one can recognize the block graphs and construct the block-cut-vertex graphs $G^*$, both in $O(n+m)$ time (Aho et al. 1974). Figure 1 shows an illustrative example, in which Fig. 1b depicts the corresponding block-cut-vertex graph $G^*$ for the block graph G in Fig. 1a. Clearly, G has 8 blocks $B_1, B_2,\ldots ,B_8$ and 6 cut vertices $c_1, c_2,\ldots ,c_6$. Moreover, the pendant blocks of G are $B_1, B_2, B_4$, $B_5$, and $B_7$.

2.1 The algorithm

Given a weighted block graph G with the corresponding block-cut-vertex structure $G^*$, we propose an O(n)-time algorithm to finding a minimum-weight paired-dominating set of G in this subsection. The neighborhood $N_G(v)$ of a vertex v is the set of all vertices adjacent to v in G; and the closed neighborhood $N_G[v] = \{{v}\} \cup N_G(v)$. For a set $S \subseteq V(G)$, we define $N_G[S] = \{{v \mid v \in N_G[u] \text { and } u \in S}\}$. Before describing the approach in detail, four kinds of dominating sets D(H, u), P(H, u), $P'(H, u)$, and ${\bar{P}}(H, u)$ are defined below, where H is a subgraph of G and $u \in V(H)$. The notations are introduced for the purpose of describing the recursive formulations in developing dynamic programming algorithms.

D(H, u) : :

A minimum-weight dominating set of H, $u\in D(H, u)$ and $H[D(H, u)-\{{u}\}]$ has a perfect matching.

P(H, u) : :

A minimum-weight paired-dominating set of H and $u\in P(H, u)$.

$P'(H, u) :$:

A minimum-weight paired-dominating set of H and $u \not \in P'(H, u)$.

${\bar{P}}(H, u) :$:

A minimum-weight paired-dominating set of $H-\{{u}\}$, and u is not dominated by ${\bar{P}}(H, u)$.

Clearly, either P(G, u) or $P'(G, u)$ is a minimum-weight paired-dominating set of G. For ease of subsequent discussion, D(H, u), P(H, u), $P'(H, u)$, and ${\bar{P}}(H, u)$ are called a $\kappa _1$-paired-dominating set, $\kappa _2$-paired-dominating set, $\kappa _3$-paired-dominating set, and $\kappa _4$-paired-dominating set of H with respect to u, respectively. Suppose that B is a block of H with $V(B) = \{{u_1, u_2,\ldots , u_k}\}$. For $1 \le i \le k$, we further suppose that $G_i$ is a maximal connected subgraph containing $u_i$ in $G[(V(H)\setminus V(B)) \cup \{{u_i}\}]$. If $i \not = j$, the following lemma shows that $G_i$ and $G_j$ are two subgraphs of H with disjoint vertex sets. Refer to Fig. 2 for an illustrative example.

Fig. 2

A weighted block graph $H = B \cup G_1 \cup G_2 \cup \ldots \cup G_k$

Lemma 1

For $1 \le i \not = j \le k$, $G_i$ and $G_j$ are two subgraphs of H with disjoint vertex sets.

Proof

Suppose to the contrary that $v \in V(G_i) \cap V(G_j)$. Then, there exist two paths $P_1 = (v,\ldots ,u_i)$ and $P_2 = (v,\ldots ,u_j)$ in $G_i$ and $G_j$, respectively. Since B is a block of H, $G[B \cup P_i \cup P_j]$ is a connected subgraph of H without a cut-vertex. This contradicts our assumption that B is a maximal connected subgraph without a cut-vertex. $\square$

Based on the above observation, we designed a dynamic programming algorithm to iteratively determine $D(H, u_1)$, $P(H, u_1)$, $P'(H, u_1)$, and ${\bar{P}}(H, u_1)$ in a bottom-up manner. One block is considered in each iteration of the loop. Notice that, during the determination, the block-cut-vertex structure $G^*$ can be exploited to get the corresponding blocks and cut vertices.

The algorithm first sets the current graph $G' = G$ and the set of processed blocks $W = \emptyset$. Meanwhile, it initially assigns $D(G[\{v\}],v ) = \{{v}\}$, $P(G[\{v\}],v ) = \bigtriangleup$, $P'(G[\{v\}],v ) = \bigtriangleup$ and ${{\bar{P}}}(G[\{v\}],v ) = \emptyset$ for each vertex $v \in V(G)$. Specially, we use $\bigtriangleup$ to denote the empty set with a weight of infinity, i.e., $\bigtriangleup = \emptyset$ and $w(\bigtriangleup ) = \infty$. Then, the algorithm iteratively processes block B with $V(B) = \{{u_1, u_2,\ldots , u_k}\}$ in the repeat loop. Suppose the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ are given and are stored in arrays corresponding to $u_i$ for $1 \le i \le k$. The algorithm determines the dominating sets $D(H, u_1)$, $P(H, u_1)$, $P'(H, u_1)$, and ${\bar{P}}(H, u_1)$; and records the results in arrays corresponding to vertex $u_1$. Moreover, the two graphs $G'$ and $G^*$ are modified to indicate that block B has been processed.

After the execution of the repeat loop, we have only one block left, i.e., the current graph $G'$ is a block and the corresponding block-cut-vertex structure $G^*$ is a vertex. With the information determined in the repeat loop, we now can find the two paired-dominating sets P(G, u) and $P'(G, u)$, where u is an arbitrary vertex in $G'$. Finally, the output S is selected from P(G, u) and $P'(G, u)$ based on the weights of the sets. The steps of the algorithm are detailed below.

2.2 An example

Consider the block graph G in Fig. 3 for an illustrative example. In the beginning, the algorithm sets the default values to each vertex v in G. Then, by the rules of removing blocks, one block is removed from $G'$ for each iteration of the repeat loop. The blocks in G are removed with respect to the ordering $B_1, B_2,\ldots , B_8$. Figure 3a depicts the case that block $B_1 = G[\{{v_{10},v_{14}}\}]$ is selected in the first iteration. One can see that $H = G[\{{v_{10},v_{14}}\}] \cup G[\{{v_{10}}\}] \cup G[\{{v_{14}}\}]$. Four dominating sets $D(H, v_{10}), P(H, v_{10}), P'(H, v_{10}), {{\bar{P}}}(H, v_{10})$ are recorded in vertex $v_{10}$ by the rules of determining and recording results in Steps (10) and (11), respectively. Please refer to Fig. 3b for the result of removing $v_{14}$ from $G'$.

Fig. 3

The intermediate execution steps of Algorithm 1. The blocks in G are removed with respect to the ordering $B_1, B_2,\ldots , B_8$

Similarly, Fig. 3c depicts the case that block $B_3 = G[\{{v_6,v_{10},v_{11}}\}]$ is selected in the third iteration with $H = G[\{{v_6,v_{10},v_{11}}\}] \cup G[\{{v_6}\}] \cup G[\{{v_{10},v_{14}}\}] \cup G[\{{v_{11},v_{15}}\}]$. Again, by the rules of determining and recording results, vertices $v_{10}$ and $v_{11}$ were removed from $G'$ and the corresponding results are recorded in vertex $v_6$. One can see Fig. 3d for an illustrative example. After removing blocks $B_1, B_2,\ldots , B_7$, we have exactly one block $B_8$ left in $G'$, i.e., $G^*$ now is a vertex, then the algorithm exits the repeat loop. In Step (15), the two dominating sets $P(G, v_1)$ and $P'(G, v_1)$ are determined by using a similar method of the arguments in Steps (10) and (11). Figure 3e illustrates the execution status of Step (15). Clearly, either $P(G, v_1)$ or $P'(G, v_1)$ is a minimum-weight paired-dominating set of G depending on which has the smaller total weight.

2.3 Correctness and complexity analysis

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ for $1 \le i \le k$, four dynamic programming procedures are proposed in Sects. 3.1–3.4, which can determine $D(H, u_1)$, $P(H, u_1)$, $P'(H, u_1)$, and ${\bar{P}}(H, u_1)$ in O(k) time, respectively. Clearly, the proposed procedures ensure the correctness of the algorithm. For the complexity analysis, suppose that G has blocks $B_1, B_2,\ldots ,B_x$. Since the dynamic programming procedures can be completed in O(k) time, Steps (10) and (15) can be implemented in $O(|V(B_1)|+ |V(B_2)|+\ldots +|V(B_x)|)$ time. Recall that all the vertices in $B_i$ are deleted from $G'$ except the cut vertex in each iteration of the repeat loop. This implies that $|V(B_1)|+ |V(B_2)|+\ldots +|V(B_x)| = n + (x -1)$.

Meanwhile, by using the depth-first search algorithm, one can determine a vertex ordering $u_1, u_2,\ldots , u_h$ of a h-vertices tree graph T in O(h) time such that $u_i$ is a leaf in $T[\{{u_1,u_2,\ldots ,u_i}\}]$ for $1 \le i \le h$. Therefore, with an O(x)-time preprocessing for $G^*$, it takes O(1) time to implement Step (7), for each iteration of the repeat loop. Since G has at most $n-1$ blocks, we have $x \le n - 1$. So, the repeat loop can be done in O(n) time. Further, the other steps can be done in O(n) time as well. Consequently, we obtain the main result of this paper.

Theorem 2

Given a weighted block graph G with corresponding block-cut-vertex structure $G^*$, a minimum-weight paired-dominating set of G can be determined by Algorithm 1 in O(n) time.

3 Finding $D(H, u_1)$, $P(H, u_1)$, $P'(H, u_1)$, and ${\bar{P}}(H, u_1)$

In this section, given dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, we propose O(k)-time dynamic programming procedures to determine $D(H, u_1)$, $P(H, u_1)$, $P'(H, u_1)$, and ${\bar{P}}(H, u_1)$, respectively, in Sects. 3.1–3.4. Before describing the procedures, some notations are introduced below. For a set S of sets of vertices, let F(S) denote the set with minimum weight in S. Let $S_i^*$ be the set of vertices such that $S_i^* = F(\{{D(G_i, u_i), P(G_i, u_i), P'(G_i, u_i), {{\bar{P}}}(G_i, u_i)}\})$ for $2 \le i \le k$. Further, three variables $\alpha$, $\beta$, and $\gamma$ are introduced. We use $\alpha$ to denote the index in $\{{2, 3, \ldots , k}\}$ such that $S_\alpha ^* \not = D(G_\alpha , u_\alpha )$ and $w(D(G_\alpha , u_\alpha )) - w(S_\alpha ^*)$ is minimized, and $\beta$ to denote the index in $\{{2, 3, \ldots , k}\}$ such that $S_\beta ^* = D(G_\beta , u_\beta )$ and $w(F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})) - w(S_\beta ^*)$ is minimized. Moreover, let $\gamma$ denote the number of $S_i^*$ such that $S_i^* = D(G_i, u_i)$, i.e., $\gamma = |\{{S_i^* \mid S_i^* =D(G_i, u_i) \text {~and~} 2 \le i \le k}\}|$.

3.1 Determination of $D(H, u_1)$

Notice that $D(H,u_1)$ is a minimum-weight dominating set of H over all sets S satisfying $u_1 \in S$, and $H[S-\{{u_1}\}]$ has a perfect matching. Hence, we have $D(G_1, u_1) \subseteq D(H,u_1)$. In order to obtain the other parts of $D(H,u_1)$, the procedure first constructs a dominating set $X = D(G_1,u_1) \cup S_2^* \cup S_3^* \cup \ldots \cup S_k^*$. In Lemma 3, we will show that if $\gamma$ is even, then $S = X$ is a $\kappa _1$-dominating set of H with respect to $u_1$. Otherwise, in order to satisfy the constraint that $H[S-\{{u_1}\}]$ contains a perfect matching, we can either replace one $S_i^* \not = D(G_i, u_i)$ with $D(G_i, u_i)$ or replace one $S_j^* = D(G_j, u_j)$ with $F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})$, where $2 \le i,j \le k$. For the former case, a dominating set $X^+ = (X - S_\alpha ^*) \cup D(G_\alpha , u_\alpha )$ is created. On the other hand, a dominating set $X^- = (X - S_\beta ^*) \cup F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})$ is built for the latter case. The output $S = F(\{{X^+, X^-}\})$ is selected from $X^+$ and $X^-$ based on the weights of the sets. Similarly, we will show that S is a $\kappa _1$-dominating set of H with respect to $u_1$ in this situation. The procedure is described in detail in the next page.

Lemma 3

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, Procedure 2 outputs a $\kappa _1$-paired-dominating set $D(H, u_1)$ in O(k) time.

Proof

It suffices to show that the output S is a minimum-weight dominating set of H subject to the constraint that $u_1 \in S$ and $H[S - \{{u_1}\}]$ has a perfect matching. By the definition of $D(H, u_1)$, we have $D(G_1, u_1) \subseteq D(H,u_1)$. Since $u_1 \in D(G_1, u_1)$ and B is a clique, all the three sets $X, X^+$ and $X^-$ are dominating sets of H. Thus, it remains to show that the weight w(S) of S is minimized subject to the constraint that $H[S - \{{u_1}\}]$ contains a perfect matching.

For $2 \le i \le k$, $G_i[D(G_i, u_i)- \{{u_i}\}]$, $G_i[P(G_i, u_i)]$, $G[P'(G_i, u_i)]$ and $G[{\bar{P}}(G_i, u_i)]$ all contain perfect matchings. Hence, if $\gamma$ is even, then $H[X-\{{u_1}\}]$ contains a perfect matching and the weight w(X) of X is minimized, as a consequence of the selections of $S_i^*$. Now we suppose that $\gamma$ is odd. To satisfy the constraint that $H[S-\{{u_1}\}]$ contains a perfect matching, we can replace one $S_i^* \not = D(G_i, u_i)$ with $D(G_i, u_i)$ or replace one $S_j^* = D(G_j, u_j)$ with $P(G_j, u_j), P'(G_j, u_j)$, or ${\bar{P}}(G_j, u_j)$, where $2 \le i,j \le k$. For the former case, a dominating set $X^+ = (X - S_\alpha ^*) \cup D(G_\alpha , u_\alpha )$ is created. On the other hand, a dominating set $X^- = (X - S_\beta ^*) \cup F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})$ is built for the latter case. One can verify that $S = F(\{{X^+, X^-}\})$ is a minimum-weight dominating set of H such that $H[S - \{{u_1}\}]$ contains a perfect matching in this situation.

Below we provide the analysis of running time. Let A be an array corresponding $u_1$. For $2 \le i \le k$, we use A[i] to denote the choice of vertices set for $S_i^*$, i.e., $A[i] = 1$ if $S_i^* = D(G_i, u_i),\ldots ,$ and $A[i] = 4$ if $S_i^* = {\bar{P}}(G_i, u_i)$. Meanwhile, variable c is used to denote the choice of vertices set for S, i.e., $c = 1$ if $S = X,\ldots ,$ and $c = 3$ if $S = X^-$. Further, we use variable w to denote the weight of S, i.e., $w = w(S)$. With the aid of above data structures and variables $\alpha , \beta$, and $\gamma$, one can verify that the the procedure can be done in O(k) time. $\square$

3.2 Determination of $P(H, u_1)$

Notice that $P(H,u_1)$ is a minimum-weight paired-dominating set of H over all sets S satisfying $u_1\in S$. Therefore, either $D(G_1,u_1)\subseteq P(H,u_1)$ or $P(G_1,u_1)\subseteq P(H,u_1)$ is a dominating set of $G_1$. In order to obtain $P(H,u_1)$, we construct six dominating sets $X, X^+$, $X^-$, $Y, Y^+$, and $Y^-$ of H. The dominating sets $X, X^+$ and $X^-$, which are the same as those described in Sect. 3.1, are created for the situation when $D(G_1,u_1)\subseteq P(H,u_1)$. Meanwhile, the dominating sets $Y, Y^+$ and $Y^-$ are built for the situation when $P(G_1,u_1)\subseteq P(H,u_1)$, where $Y = P(G_1,u_1)\cup S_2^* \cup S_3^* \cup \cdots \cup S_k^*$, $Y^+ = (Y-S_\alpha ^*) \cup D(G_\alpha , u_\alpha )$, and $Y^- = (Y-S_\beta ^*)\cup F(\{P(G_\beta , u_\beta ),P'(G_\beta , u_\beta ),{{\bar{P}}}(G_\beta , u_\beta )\})$.

If $\gamma$ is even, then the induced subgraphs $H[X^+], H[X^-]$ and H[Y] all contain perfect matchings. The output $S = F(\{{X^+, X^-,Y}\})$ is selected from $X^+, X^-$ and Y based on the weights of the sets. We will show that S is a $\kappa _2$-dominating set of H with respect to $u_1$. Similarly, if $\gamma$ is odd, then all the induced subgraphs $H[X], H[Y^+]$ and $H[Y^-]$ contain perfect matchings. And, we will show that the output $S = F(\{{X, Y^+,Y^-}\})$ is a $\kappa _2$-dominating set of H with respect to $u_1$ in this situation. The procedure is detailed below.

Lemma 4

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, Procedure 3 outputs a $\kappa _2$-paired-dominating set S of H with respect to $u_1$ in O(k) time.

Proof

By using a similar method of the arguments in Lemma 3, one can show that the procedure can be completed in O(k) time. To prove the correctness of the procedure, it suffices to show that the output S is a minimum-weight dominating set of H such that $u_1 \in S$ and H[S] contains a perfect matching. Further, since $v_1 \in D(G_1, u_1) \cap P(G_1, u_1)$ and B is a clique, $X, X^+, X^-, Y, Y^+$, and $Y^-$ are all dominating sets of H. Thus, it remains to show that the weight w(S) of S is minimized subject to the constraint that H[S] contains a perfect matching.

Notice that, for $2 \le i \le k$, both $G_i[D(G_i, u_i)- \{{u_i}\}]$ and $G_i[P(G_i, u_i)]$ contain perfect matchings and $u_i \not \in P'(G_i, u_i) \cup {\bar{P}}(G_i, u_i)$. We first consider the situation when $\gamma$ is even. For the case when $D(G_1,u_1)$ is a dominating set of $G_1$, in order to satisfy the constraint that H[X] contains a perfect matching with minimum cost, we can either replace $S_\alpha ^*$ with $D(G_\alpha ,u_\alpha )$ or replace $S_\beta ^*$ with $F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})$. Thus, $X^+$ and $X^-$ are the two potential candidates for S when $D(G_1,u_1)\subseteq P(H,u_1)$. For the case when $P(G_1,u_1)$ is a dominating set of $G_1$, H[Y] contains a perfect matching. We select $S = F(\{{X^+, X^-,Y}\})$ from $X^+$, $X^-$ and Y based on the weights of the sets. As a consequence of selections of $S_\alpha ^*$, $S_\beta ^*$, and $S_i^*$ for $2 \le i \le k$, one can verify that the output S is a minimum-weight dominating set of H such that H[S] contains a perfect matching. Further, using a similar method of the above arguments, one can show that the correctness also holds for the situation when $\gamma$ is odd. $\square$

3.3 Determination of $P'(H, u_1)$

Recall that $P'(H,u_1)$ is a minimum-weight paired-dominating set of H over all sets S satisfying $u_1 \not \in S$. Therefore, either $P'(G_1,u_1)\subseteq P'(H,u_1)$ or ${\bar{P}}(G_1,u_1)\subseteq P'(H,u_1)$ is a dominating set of $G_1$. For ease of subsequent discussion, we consider the two cases $P'(G_1,u_1)\subseteq P'(H,u_1)$ and ${\bar{P}}(G_1,u_1)\subseteq P'(H,u_1)$, respectively, in Sects. 3.3.1 and 3.3.2. More concretely, a paired-dominating set $Q_1$ is created for the former situation. Meanwhile, a paired-dominating set $Q_2$ is built for the latter situation. Clearly, $P'(H, u_1)$ can be selected from $Q_1$ and $Q_2$ based on the weights of the sets.

3.3.1 Finding $Q_1$

Below we present an O(k)-time procedure for finding $Q_1$. The procedure solves the problem by considering eight cases $C_1, C_2, \ldots , C_8$, all of which are dependent on the values of $S_i^*$ and $\gamma$. For $1 \le i \le 8$, the case $C_i = (c_1, c_2,c_3,c_4, c_5)$ is an ordered 5-tuple. If condition $D_j$ holds, then $c_j = 1$; and $c_j = 0$ otherwise, where $1 \le j \le 5$. Further, $c_j = ``*$” means “do not care”, i.e., condition $D_j$ is not a factor in this case. The five conditions $D_1,D_2,\ldots ,D_5$ are defined as follows:

$D_1$::

$S_i^* = P(G_i,u_i)$ for some $2 \le i \le k$.

$D_2$::

$\gamma$ is odd.

$D_3$::

$\gamma$ is equal to 1.

$D_4$::

$\gamma$ is equal to 0.

$D_5$::

$S_i^* = {\bar{P}}(G_i,u_i)$ for some $2 \le i \le k$.

Then, we define the cases $C_1 = (1,1,*,*,*)$, $C_2 = (1,0,*,*,*)$, $C_3 = (0,1,1,*,1)$, $C_4 = (0,1,1,*,0)$, $C_5 = (0,1,0,*,*)$, $C_6 = (0,0,*,1,1)$, $C_7 = (0,0,*,1,0)$, and $C_8 = (0,0,*,0,*)$. For example, case $C_1$ represents the situation when there exists an index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$ with $2 \le \ell \le k$ and $\gamma$ is an odd number. Further, case $C_7$ represents the situation when there exists no index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$, or $S_\ell ^* = {\bar{P}}(G_\ell ,u_\ell )$ and $r = 0$, i.e., $S_i^* = P'(G_i,u_i)$ for $2 \le i \le k$. Moreover, one can verify that all the possible combinations of the five conditions have been considered.

Next, some notations and paired-dominating sets are introduced. Let ${\alpha '}$ be the index in $\{{2, 3, \ldots , k}\} - \{{\alpha }\}$ such that $S_{\alpha '}^* \not = D(G_{\alpha '}, u_{\alpha '})$ and $w(D(G_{\alpha '}, u_{\alpha '})) - w(S_{\alpha '}^*)$ is minimized. Let $\delta$ be the index in $\{{2, 3, \ldots , k}\}$ such that $S_\delta ^* \not = P(G_\delta , u_\delta )$ and $w(P(G_\delta , u_\delta )) - w(S_\delta ^*)$ is minimized. Let $I = \{{i \mid S_i^* = {\bar{P}}(G_i, u_i) \text { and } 2 \le i \le k}\}$. We define the following paired-dominating sets of H, which are the potential candidates for $Q_1$.

$$\begin{aligned}&Z_1 = P'(G_1,u_1)\cup S_2^* \cup S_3^* \cup \ldots \cup S_k^*. \\&Z_1^+ = (Z_1-S_\alpha ^*) \cup D(G_\alpha ,u_\alpha ).\\&Z_1^- = (Z_1-S_\beta ^*)\cup F(\{P(G_\beta , u_\beta ),P'(G_\beta , u_\beta ),{{\bar{P}}}(G_\beta , u_\beta )\}).\\&T_1 = (Z_1-S_\delta ^*) \cup P(G_\delta , u_\delta ).\\&T_2 = (Z_1-S_\alpha ^*-S_{\alpha '}^*) \cup D(G_\alpha ,u_\alpha )\cup D(G_{\alpha '}, u_{\alpha '}).\\&T_3 = (Z_1-\cup _{i\in I}S_i^*)\cup (\cup _{i\in I}P'(G_i,u_i)).\\&T_4 = (Z_1-S_\beta ^*)\cup P(G_\beta ,u_\beta ).\\&T_5 = (Z_1-S_\beta ^*)\cup F(\{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta )\}).\\&T_6 = (Z_1-S_\beta ^*-S_\delta ^*)\cup F(\{P'(G_\beta ,u_\beta ), {{\bar{P}}}(G_\beta ,u_\beta )\}) \cup P(G_\delta ,u_\delta ).\\&T_7 = (Z_1-S_\beta ^*-S_\delta ^*) \cup {{\bar{P}}}(G_\beta ,u_\beta ) \cup P(G_\delta , u_\delta ).\\&T_8 = (Z_1-S_\beta ^* - \cup _{i\in I}S_i^*) \cup P'(G_\beta ,u_\beta ) \cup (\cup _{i\in I}P'(G_i,u_i)). \end{aligned}$$

As mentioned earlier, we solve the problem by considering the eight cases $C_1, C_2, \ldots , C_8$. The relations between the cases $C_1, C_2, \ldots , C_8$ and the dominating sets $Z_1$, $Z_1^+$, $Z_1^-$, $T_1, \ldots , T_8$ are detailed in Procedure 4. We will prove its correctness and analyze its running time in Lemma 5.

Lemma 5

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, Procedure 4 outputs a minimum-weight dominating set S of H such that $u_1 \not \in S$, H[S] has a perfect matching, and $P'(G_1,u_1)\subseteq S$. Moreover, the procedure can be completed in O(k) time.

Proof

By using a similar method of the arguments in Lemma 3, one can show that all the paired-dominating sets $Z_1$, $Z_1^+$, $Z_1^-$, $T_1, \ldots , T_8$ can be constructed in O(k) time. Hence, the procedure certainly runs in O(k) time. Further, one can verify that all the possible combinations of conditions $D_1, D_2, \ldots , D_5$ have been considered in cases $C_1, C_2, \ldots , C_8$. Hence, to prove the correctness of the procedure, it suffices to show that each step of the procedure is correct.

First, we consider cases $C_1$ and $C_2$. In both of these cases, there exists an index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$. Therefore, $Z_1, Z_1^+$, and $Z_1^-$ are dominating sets of H. It follows that, if $\gamma$ is even, then $Z_1$ is a minimum-weight dominating set of H such that $u_1 \not \in Z_1$ and $H[Z_1]$ has a perfect matching due to the selections of $S_i^*$ for $2 \le i \le k$. So, we have $S = Z_1$ for case $C_2$. On the other hand, if $\gamma$ is odd, then in order to satisfy the constraint that $H[Q_1]$ contains a perfect matching with minimum cost, we can either replace $S_\alpha ^*$ with $D(G_\alpha ,u_\alpha )$, or replace $S_\beta ^*$ with $F(\{{P(G_\beta , u_\beta ), P'(G_\beta , u_\beta ), {{\bar{P}}}(G_\beta , u_\beta )}\})$. This implies that we have $S = F(\{{Z_1^+, Z_1^-}\})$ for case $C_1$.

Next, we consider cases $C_3, C_4$, and $C_5$. Notice that in all three cases, there exists no index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$ and $\gamma$ is an odd number. Moreover, for any paired-dominating set $Q_1$ of H, we have either $S_i^* = P'(G_i,u_i)$ for $2 \le i \le k$ or $V(B) \cap V(Q_1) \not = \emptyset$, where $B = H[\{{u_1,u_2,\ldots ,u_k}\}]$. In case $C_3$, a paired-dominating set $T_8$ is created for the former. Meanwhile, paired-dominating sets $Z_1^+$, $T_4$, and $T_6$ are built for the latter. As a consequence of $\gamma = 1$, in order to ensure $H[Q_1]$ contains a perfect matching when $V(B) \cap V(Q_1) \not = \emptyset$, we replace $S_\alpha ^*$ with $D(G_\alpha ,u_\alpha )$ in $Z_1^+$, replace $S_\beta ^*$ with $P(G_\beta ,u_\beta )$ in $T_4$, and replace $S_\delta ^*$ and $S_\beta ^*$ with $P(G_\delta ,u_\delta )$ and $F(\{P'(G_\beta ,u_\beta ), {{\bar{P}}}(G_\beta ,u_\beta )\})$ in $T_6$, respectively. Under the premise of minimizing weight, one can verify that $Z_1^+$, $T_4$, and $T_6$ are exactly the three potential candidates for $Q_1$. In case $C_4$, we have $S_\beta ^* = D(G_\beta ,u_\beta )$ and $S_i^* = P'(G_i,u_i)$ for $2 \le i \le k$ and $i \not = \beta$. Using a similar method of the above arguments, one can show that $S = F(\{{Z_1^+, T_5, T_7}\})$ is true for case $C_4$. In case $C_5$, we have $\gamma \ge 3$. Therefore, for the same reasons as case $C_1$, we have $S = F(\{{Z_1^+, Z_1^-}\})$ for case $C_5$.

Finally, we consider cases $C_6, C_7$, and $C_8$. Notice that in all three cases, there exists no index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$ and $\gamma$ is an even number. In case $C_6$, we have either $S_i^* = P'(G_i,u_i)$ or $S_i^* = {\bar{P}}(G_i,u_i)$, where $1 \le i \le k$. To ensure $H[Q_1]$ contains a perfect matching, we replace $S_\delta ^*$ with $P(G_\delta ,u_\delta )$ in $T_1$, replace $S_\alpha ^*$ and $S_{\alpha '}^*$ with $D(G_\alpha ,u_\alpha )$ and $D(G_{\alpha '},u_{\alpha '})$ in $T_2$, and replace $S_i^*$ with $P'(G_i,u_i))$ for all $i \in I$ in $T_3$, respectively. Under the premise of minimizing the weight w(S), one can verify that $T_1$, $T_2$, and $T_3$ are exactly the three potential candidates for $Q_1$. Notice that, in case $C_7$, $S_i^* = P'(G_i,u_i)$ for $2 \le i \le k$. Further, $\gamma \ge 2$ is an even number in case $C_8$. Thus, in both of these cases, we have $S = Z_1$ for the same reasons as case $C_2$. $\square$

3.3.2 Finding $Q_2$

In the following, we present a procedure to finding the paired-dominating set $Q_2$. Similar to Procedure 4, the procedure solves the problem by considering six cases $C_9, C_{10}, \ldots , C_{14}$. For $9 \le i \le 14$, the case $C_i = (c_1, c_2,c_3,c_4)$ is an ordered 4-tuple. Further, the value of $c_j$ has the same definition as described in Sect. 3.3.1 for $1 \le j \le 4$. Then, we define $C_9 = (1,1,*,*)$, $C_{10} = (1,0,*,*)$, $C_{11} = (0,1,1,*)$, $C_{12} = (0,1,0,*)$, $C_{13} = (0,0,*,1)$, and $C_{14} = (0,0,*,0)$. Again, one can verify that all the possible combinations of the four conditions have been considered in cases $C_9, C_{10}, \ldots , C_{14}$. The paired-dominating sets $Z_2$, $Z_2^+$, $Z_2^-$, $T_9, \ldots , T_{12}$ of H are defined below, which are the potential candidates for $Q_2$.

$$\begin{aligned}&Z_2 = {\bar{P}}(G_1,u_1)\cup S_2^* \cup S_3^* \cup \ldots \cup S_k^*. \\&Z_2^+ = (Z_1-S_\alpha ^*) \cup D(G_\alpha ,u_\alpha ).\\&Z_2^- = (Z_1-S_\beta ^*)\cup F(\{P(G_\beta , u_\beta ),P'(G_\beta , u_\beta ),{{\bar{P}}}(G_\beta , u_\beta )\}).\\&T_9 = (Z_2-S_\delta ^*) \cup P(G_\delta , u_\delta ).\\&T_{10} = (Z_2-S_\alpha ^*-S_{\alpha '}^*) \cup D(G_\alpha ,u_\alpha )\cup D(G_{\alpha '}, u_{\alpha '}).\\&T_{11} = (Z_2-S_\beta ^*)\cup P(G_\beta ,u_\beta ).\\&T_{12} = (Z_2-S_\beta ^*-S_\delta ^*)\cup F(\{P'(G_\beta ,u_\beta ), {{\bar{P}}}(G_\beta ,u_\beta )\}) \cup P(G_\delta ,u_\delta ).\\ \end{aligned}$$

Moreover, the relations between the cases $C_9, C_{10}, \ldots , C_{14}$ and the paired-dominating sets $Z_2$, $Z_2^+$, $Z_2^-$, $T_9, \ldots , T_{12}$ are detailed in Procedure 5.

Lemma 6

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, Procedure 5 outputs a minimum-weight dominating set S of H such that $u_1 \not \in S$, H[S] has a perfect matching, and ${\bar{P}}(G_1,u_1)\subseteq S$. Moreover, the procedure can be completed in O(k) time.

Proof

By using a similar method of the arguments in Lemma 3, one can show that each step of the procedure can be completed in O(k) time. Therefore, the procedure runs in O(k) time. Further, one can verify that all the possible combinations of conditions $D_1, D_2, D_3$, and $D_4$ have been considered in cases $C_9, C_{10}, \ldots , C_{14}$. Hence, to prove the correctness of the procedure, it suffices to show that each step of the procedure is correct.

First, we consider cases $C_9$ and $C_{10}$. In both of these cases, there exists an index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$. Therefore, for the same reasons as cases $C_1$ and $C_2$ in Procedure 4, we have $S = F(\{{Z_2^+, Z_2^-}\})$ for case $C_9$ and $S = Z_2$ for case $C_{10}$, respectively. Next, we consider cases $C_{11}$, and $C_{12}$. Notice that in both cases, there exists no index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$ and $\gamma$ is an odd number. Since we have $r = 1$ in case $C_{11}$, in order to satisfy the constraint that $H[Q_2]$ contains a perfect matching with minimum cost, we replace $S_\alpha ^*$ with $D(G_\alpha ,u_\alpha )$ in $Z_2^+$, replace $S_\beta ^*$ with $P(G_\beta ,u_\beta )$ in $T_{11}$, and replace $S_\delta ^*$ and $S_\beta ^*$ with $P(G_\delta ,u_\delta )$ and $F(\{P'(G_\beta ,u_\beta ), {{\bar{P}}}(G_\beta ,u_\beta )\})$ in $T_{12}$, respectively. Under the premise of minimizing weight, one can verify that $Z_2^+$, $T_{11}$, and $T_{12}$ are exactly the three potential candidates for $Q_2$. In case $C_{12}$, we have $r \ge 3$. Therefore, for the same reasons as case $C_1$, we have $S = F(\{{Z_2^+, Z_2^-}\})$ for case $C_{12}$.

Finally, we consider cases $C_{13}$, and $C_{14}$. Notice that in both cases, there exists no index $\ell$ such that $S_\ell ^* = P(G_\ell ,u_\ell )$ and $\gamma$ is an even number. In case $C_{13}$, either $S_i^* = P'(G_i,u_i)$ or $S_i^* = {\bar{P}}(G_i,u_i)$ for $1 \le i \le k$. Therefore, to satisfy the constraint that $H[Q_2]$ contains a perfect matching, we replace $S_\delta ^*$ with $P(G_\delta ,u_\delta )$ in $T_9$, and replace $S_\alpha ^*$ and $S_{\alpha '}^*$ with $D(G_\alpha ,u_\alpha )$ and $D(G_{\alpha '},u_{\alpha '})$ in $T_{10}$, respectively. Again, under the premise of minimizing the weight, one can verify that $T_9$ and $T_{10}$ are exactly the two potential candidates for $Q_2$. Notice that, in case $C_{14}$, $r \ge 2$ is an even number. Thus, we have $S = Z_2$ for the same reasons as case $C_{2}$ in Procedure 4. $\square$

Combining Lemmas 5 and 6, we obtain the following result.

Lemma 7

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ for $1 \le i \le k$, a $\kappa _3$-paired-dominating set $P'(H, u_1)$ can be determined in O(k) time.

3.4 Determination of ${\bar{P}}(H, u_1)$

Remember that ${\bar{P}}(H,u_1)$ is a minimum-weight paired-dominating set of $H-\{{u_1}\}$ over all sets S satisfying $u_1 \not \in N[S]$. Hence, by the definition of ${\bar{P}}(H,u_1)$, the only composition is ${\bar{P}}(H, u_1) = {\bar{P}}(G_1,u_1)\cup P'(G_2,u_2)\cup \ldots \cup P'(G_k,u_k)$. This implies that, given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, a $\kappa _4$-paired-dominating set ${\bar{P}}(H, u_1)$ can be determined in O(k) time. Thus, we have the following result.

Lemma 8

Given the dominating sets $D(G_i, u_i)$, $P(G_i, u_i)$, $P'(G_i, u_i)$, and ${\bar{P}}(G_i, u_i)$ with $1 \le i \le k$, a $\kappa _4$-paired-dominating set ${\bar{P}}(H, u_1)$ can be determined in O(k) time.

4 Conclusion and future work

In this paper, we have presented an optimal algorithm for finding a paired-dominating set of a weighted block graph G. The algorithm uses dynamic programming to iteratively determine D(H, u), P(H, u), $P'(H, u)$, and ${\bar{P}}(H, u)$ in a bottom-up manner, where H is a subgraph of G and $u \in V(H)$ is a cut vertex of G. When the graph is given in an adjacency list representation, our algorithm runs in $O(n+m)$ time. Moreover, the algorithm can be completed in O(n) time if the block-cut-vertex structure of G is given.

Below we present some open problems related to the paired-domination problem. Recently, Lin et al. (2020) presented an $O(n^2)$-time algorithm for distance-hereditary graphs. Meanwhile, the complexity for circle graphs is still open. It is well known that the family of distance-hereditary graphs is a proper superfamily of the family of block graphs, and is a proper subfamily of the family of circle graphs. In addition, the problems of finding minimum independent, connected, and total dominating sets all have $O(n+m)$-time algorithms in distance-hereditary graphs and are proved to be NP-complete in circle graphs. Therefore, it is interesting to improve the results in Lin et al. (2020) to show that the paired-domination problem is also $O(n+m)$-time solvable in distance-hereditary graphs and remains NP-complete in circle graphs. Furthermore, many real-life problems can be represented by planar graphs, e.g., the museum protection problem. To transforming theory into reality, it would be desirable to show that the problem is NP-complete in planar graphs and design an approximation algorithm.