Discount allocation for cost minimization in online social networks

Abstract

We introduce the discount allocation problem to a new online social networks (OSNs) scenario where the nodes and the relationships between nodes are determined but the states of edges between nodes are unknown. We can know the states of all the edges centered on a node only when it becomes active. Different from most previous work on influence maximization discount allocation problem in OSNs, our goal is to minimize the discount cost that the marketer spends while ensuring at least Q customers who adopt the target product in the end in OSNs. We propose an online discount allocation policy to select seed users to spread the product information. The marketer initially selects one seed user to offer him a discount and observes whether he accepts the discount. If he accepts the discount, the marketer needs to observe how well this seed user contributes to the diffusion of product adoptions and how much discount he accepts. The remaining seeds are chosen based on the feedback of diffusion results obtained by all previous selected seeds. We propose two online discount allocation greedy algorithms under two different situations: uniform and non-uniform discounts allocation. We offer selected users discounts changing from the lowest to highest in the discount rate set until the users receive the discount and become seed users in non-uniform discount allocation situation, which saves the cost of firms comparing with the previous method that providing product to users for free. We present a theoretical analysis with bounded approximation ratios for the algorithms. Extensive experiments are conducted to evaluate the performance of the proposed online discount allocation algorithms on real-world online social networks datasets and the results demonstrate the effectiveness and efficiency of our methods.

1 Introduction

In recent years, online social networks (OSNs) have gained popularity at a rapid pace and become an important part in our daily lives. People use OSN sites such as Twitter, Microblog, Facebook, and LinkedIn not only to stay in touch with friends but also to generate, spread and share various social contents. OSNs enable government agencies to post news and events as well as ordinary people to post contents from their own perspectives and experience.

As an important application of OSNs, viral marketing has become a focus of attention by many firms. It is an effective marketing strategy based on person-to-person recommendation within an OSN (Jurvetson 2000). More and more firms promote their products through OSNs. We consider a problem that a firm has a new product they would like to advertise through OSNs. They want to offer some discounts to a set of initial users who will potentially introduce the new product to their friends. Only a limited number of users will get discounts because of the limited budget. So which set of initial users should be selected to provide the discount and whether they are willing to accept the discount to be active? How much discounts should be provided by the firm?

The above questions have been addressed in many studies researches (Domingos and Richardson 2001; Richardson and Domingos 2002). They formulate them as an optimal selection problem in which a good set of initial adopters, called seed users, is selected. A classical problem, called influence maximization (Kempe et al. 2003), is to maximize the influence spread, i.e., the number (or expected number) of users who finally adopt the target product under influence initiated by seed users. In this paper, we study a minimization problem, i.e., to use the minimal cost for seeds to reach a certain level of the influence spread. For seed user selection, we propose an online discount allocation method, i.e., choosing seed users based on the observation of the previous seeds propagation results until a certain level of the influence spread is achieved.

Most of existing research on influence maximization problem has strategies in three categories: zero-feedback model (Kempe et al. 2003), full-feedback model (Golovin and Krause 2011) and partial feedback model (Yuan and Tang 2016). The first one has to commit all the seed users at once in advance. The second one selects one seed or more seeds at a time and waits until the diffusion completes, then selects the next seed. The third one selects one seed or a batch of seeds and wait several slots but not the end of the propagating, which can balance the delay and performance tradeoff. Goyal et al. (2011) show that most zero-feedback models may over-predict the actual spread. This model has no delay but poorer performance. We focus on the full-feedback model in discount allocation problem in online social networks. Instead of selecting all seeds at once in the influence maximization problem, we use greedy discount allocation policy to select one node at a time and offer him a discount, then we observe his state and how he propagates through the social networks. Based on the historical observation, we adaptively select the next seed user.

Currently, many influence diffusion models have been proposed, two most commonly used classical models are Independent Cascade (IC) and Linear Threshold (LT) models, which are proposed by Kempe et al. (2003). They prove that the expected number of influenced users, called influence spread, is monotone and submodular. They also propose a greedy algorithm to maximize the influence spread in the network. The maximization of the influence spread, i.e., the influence maximization, is NP-hard under IC and LT models. Tong et al. (2019) and Wang et al. (2016) showed that in some networks, the influence maximization is NP-hard under IC model while polynomial-time solvable in LT model. In this work, we adopt the Independent Cascade (IC) model.

We summarize the main contributions in this paper as follows:

• We explore a new discount allocation scenario and use the online full-feedback setting to the discount allocation problem in the OSNs scenario. Then we divide the cascade into two stages: seed selection and information diffusion. Each selected initial user has to give feedback about whether he adopted the discount and the discount rate if he accepted the discount to become a seed. Each current decision depends on all the previous feedbacks and cascades.

• We introduce a new utility function which is to influence at least a certain number Q of people who adopt the product with the minimal cost in expectation, instead of maximizing the active users at the end of the diffusion process.

• We present two algorithms in uniform and non-uniform discount situations, respectively. In non-uniform discount allocation situation, we offer discount to selected users from lowest to highest in the discount rate set until the users become active, which saves the cost of firms comparing with the previous method that provides product to users for free.

• The performance guarantee is analyzed. An approximation ratio $\alpha ln(\frac{Q}{\beta })$ in uniform discount situation and an approximation ratio of the worst-case cost $\alpha (ln(\frac{Q}{\beta }+1))$ in non-uniform discount are got.

• We numerically validate the effectiveness of the proposed algorithm on real-world online social networks datasets.

The rest of this paper is organized as follows. In Sect. 2 we begin by recalling some existing work. We introduce the problem description and influence diffusion model and process in Sect. 3. In Sect. 4, we propose the online full-feedback policy and present the greedy algorithm under uniform discount and non-uniform discount conditions. We also give the theoretical proof of the algorithms in Sects. 5, and 6 presents the simulation results, while finally, the conclusion is presented in Sect. 7.

2 Related work

In this paper, we focus on using online discount allocation policy to get a minimum cost target with a certain number of market penetration of the product. Discount allocation of viral marketing in OSNs has been studied in many scenarios. Below we discuss recent related work on related topics.

Discount allocation in OSNsYang et al. (2016) study the problem that what discount should be offered to users so that the expected number of adopted users is maximized within a predefined budget. They develop a coordinate descent algorithm and an engineering technology in practice. They illustrate that compared to the traditional influence maximization methods, continuous influence maximization can improve influence spread significantly. Abebe et al. (2018) study how to make use of social influence when there is a risk of overexposure in viral marketing. They present a seeding cascade model that has benefits when reaching positive inclined customers and cost when reaching negative inclined customers. They show how it captures some qualitative phenomena related to overexposure. They provide a polynomial-time algorithm to optimally find a marketing strategy. Tang (2018) study the stochastic coupon probing problem in social networks. They adaptively offer coupons to some users and those users who accept the coupons will become seed users and then influence their friends. There are two constraints that have to be satisfied for a coupon probing policy that achieve the influence maximization: the set of coupons redeemed by users must meet inner constraints; the set of probed users must meet outer constraints. The proposed constant approximation policy for the stochastic coupon probing problem is suitable for any monotone submodular utility function. Yuan and Tang (2017) study the influence maximization discount allocation problem under both non-adaptive and adaptive policies. They provide a limited budget of B to a set of initial users, and the target is to maximize the active users who adopt the product. They propose a greedy algorithm with a constant approximation ratio. Han et al. (2018) study how to use influence propagation to optimize the ‘pure gravy’ of a marketing strategy. They consider that seed nodes only can be activated by the offered discounts probabilistically, and try to find discount allocation strategy to maximize the expected difference of revenue. They formulate this problem as a non-monotone and non-submodular optimization problem. A novel ‘surrogate optimization’ method and two randomized algorithms are presented. They prove the constant performance ratio for the proposed algorithms.

Feedback policy in OSNs Salha et al. (2018) introduce a myopic partial observation policy in the influence maximization problem. The proposed optimal algorithm guarantees to provide an $(1-1/e)$-approximation ratio under a variant of the IC model. Yuan and Tang (2016) also study the influence maximization problem under partial feedback model. They propose an $\alpha$-greedy policy to capture the trade-off between delay and performance by adjusting the value of $\alpha$. The algorithm guarantees a constant approximation ratio. Tong et al. (2017) consider the uncertainty of the diffusion process in real-world social networks because of high-speed data transmission and a large population of participants. They introduce a seeding strategy that seed nodes are only selected between spread rounds under the dynamic Independent Cascade model, this solution has a provable performance guarantee. An efficient heuristic algorithm is also provided for better scalability. Tang (2018) study the optimal social advertising problem from the platform’s perspective. Their goal is to maximize the expected revenue by finding the best ad sequence for each user. They integrate viral marketing into existing ad sequencing model and use zero-feedback and full-feedback ad sequencing policies to maximize the efficiency of viral marketing. Choi and Yi (2018) study the problem that detecting the source of diffused information by the means of querying individuals. Two paid queries are asked: whether the respondent is the source or not; if not, which neighbor spreads the information to the respondent. The assumption is that respondents may lie. They design two kinds of algorithms: full-feedback and zero-feedback, which correspond to whether we adaptively select the next respondents based on respondents’ previous answers. Their goal is to evaluate the budget to achieve the detection probability $1-\delta$, ${\forall }$ $0<\delta <1$. Dhamal (2018) focus on that selecting seed users in multiple phases based on the observed historical diffusion under IC model. They present a negative result but do not guarantee a better spread in more phases. They study the effect of diffusion in multiple phases on average and the standard deviation of the extent of diffusion, and how to reduce the uncertainty in diffusion with multiple phases. Singer (2016) survey the feedback based seeding methods for influence maximization. They discuss the algorithmic approaches, the friend paradox in random models and experiments on feedback based seeding. Han et al. (2018) study the adaptive Influence Maximization (IM) problem, which selects seed users in batches of size b. They use full feedback strategy that the i-th batch can be selected after they observe the influence results of the $(i-1)$th batch seed users. They propose two practical algorithms for $b=1$ with an approximation ratio $1-e^{(\xi -1)}$ and $b>1$ with $1-e^{(\xi -1+1/e)}$ approximation guarantee, where $\xi \in (0,1)$. Tong et al. (2020) present a time-constrained adaptive influence maximization problem. They provide a $\frac{e^2-2}{e-1}$ lower bound on the adaptive gap for the time-constrained case. The adaptive gap measures the ratio between full feedback and the zero-feedback.

3 Network model and problem formulation

3.1 The network model

In this model, the online social network is a directed graph G(V, E), where each vertex in V is a person, and E is the set of social ties. In this model, the nodes and edges in the graph are deterministic, the states of edges between nodes are unknown. We can know the states of all the edges centered on that node through activating it. Assuming that a marketer provides m discount rates $D=\{d_1,\ldots ,d_m\}$ to each user for a product and the marketer offers a user only one discount at a time. We assume the discount as the amount taken off from the original price which are integers in our problem. We denote $c_v=d_i$ as that we provide discount $d_i$ to user v. So in the graph, each user $v\in V$ has m choices for the discount rates but he only can accept one discount. We assume that each user v is independently associated with a discount adoption probability function $p_{vd_i}\in [0,1$], which models the probability that v accepts different discounts. Whether users would accept these discounts is uncertain. We assume that the adoption probability of any initial user is monotonically increasing with respect to discounts. So if $d_j\ge d_i$, $p_{vd_j}\ge p_{vd_i}$. The incoming neighbor set and the outgoing neighbor set of a node v are denoted as $N^-(v)$ and $N^+(v)$, respectively. Each edge $(u,v)\in E$ in the graph is associated with a probability $p_{uv}\in [0,1]$ indicating the probability that node u independently influences node v once u has been influenced. If u activates v, the edge is in ‘live’ state, if u does not activate v successfully, the edge is in ‘blocked’ state. Influence can then spread from user u to his outgoing neighbors and so on according to the same process.

3.2 Diffusion process

We compose the cascade into two phases: seeds selection phase and information diffusion phase.

In the seeds selection phase, we select some initial seed users to provide some discounts to each of them. After receiving these discounts, every user will decide whether to accept the discount or not. It is affected by factors such as users’ preference for the products or the discount rates and so on. A user can only accept one discount at a time. If a user has accepted a discount $d_i$, which means that any larger discount is also acceptable for him. If a user rejects the highest discount, he will reject all offered discounts. We use $\phi (v)$ to define the active state of a user v. If a user v accepts the discount to become a seed, its state is active, and $\phi (v)=1$, otherwise $\phi (v)=0$.

In the information diffusion phase, every initial user who becomes the seed then has to propagate the product information to her neighbors across the social network under the Independent Cascade (IC) model. Independent Cascade (IC) model: each active seed user has a single chance to influence his uninfluenced neighbors with given probabilities. Each newly influenced user also has a single chance to influence his uninfluenced outgoing neighbors in the next step. If a node v has multiple newly activated incoming neighbors, their influences are sequenced in an arbitrary order. The diffusion completes until there is no new user is influenced. The expected cascade of U denoted as I(U), is the expected number of users influenced by seed set U.

We select one seed at a time and wait until the diffusion completes before selecting the next seed. We define the state $\psi (uv)$ as the state of edge (u, v), if v is activated by one of its incoming active neighbor u and edge(u, v) is ‘live’, $\psi (uv)=1$, otherwise, edge (u, v) is ‘dead’, $\psi (uv)=0$. So we can see that activating u will reveal the status of edge (u, v) (i.e., the value of $\psi (uv)$).

3.3 Problem formulation

In the model, each user has two states: $\phi$ and $\psi$. We represent the user’s state $\left\langle \phi ,\psi \right\rangle$ as an online realization. In the full feedback model, every initial user needs to give feedback whether or not he adopted the discount. After activating u, we observe the set of out-edges from node u that become active or ‘live’. These active nodes are those who are successfully activated by node u. After each pick, our observations so far can be represented as an online partial realization. We use the notation $dom(\phi ,\psi )$ to refer to the domain of $\left\langle \phi ,\psi \right\rangle$ (i.e., the set of states observed in $\left\langle \phi ,\psi \right\rangle$ ). In the online seed selection policy, we choose the current user dynamically, it is up to the current state of observation $dom(\phi , \psi )$.

We define our online discount allocation strategy for picking users as a policy $\pi$($\left\langle \phi ,\psi \right\rangle )$, which is a function from a set of partial realization to current observation, specifying which user to probe in the next step under the known online partial realization and the resulting cascade. So we choose the next user to probe based on what seeds we have detected so far, whether they accept the discount or not, and their feedbacks about the network diffusions.

Let $\Phi$ and $\Psi$ denote a random realization of $\phi$ and $\psi$. We assume that there is a known prior probability distribution $p(\phi ):=P[\Phi =\phi ]$ (and $p(\psi ):=P[\Psi =\psi ]$ resp.) over online seeding realization (and online diffusion realization resp.). Given a online realization $\left\langle \phi ,\psi \right\rangle$, let $\pi (\phi , \psi )$ denote all users picked by policy $\pi$ under online realization $\left\langle \phi ,\psi \right\rangle$. $c(\pi )$ denotes the total amount of discounts that have been delivered by $\pi$ under $\left\langle \phi ,\psi \right\rangle$. The policy $\pi$ terminates (stops probing users) upon online observation $\left\langle \phi ,\psi \right\rangle$ until the resulting expected spread is above a given threshold.

We denote $S(\pi , \psi )\subseteq V$ as the seed node set that has been selected by $\pi$ under realization $\psi$. The expected cascade of a policy $\pi$ is defined as: $f(\pi )=\mathbb E[f(\pi ;\Phi ,\Psi )]$. Marketers want to get as many people as possible to buy the products at as low cost as possible. We specify a threshold Q of the expected cascade that we would like to obtain, and try to find the cheapest policy to achieve that spread goal. The policy $\pi$ is to minimize the expected cost of the marketer under all possible online realization, and at least Q is achieved. We define the expected total cost $c(\pi )= \mathbb E[c(\pi ; \Phi ,\Psi )]$ we would like. The problem we want to solve can be described as follows:

Online Minimal Cost Target Seed Selection Problem: Given a directed probabilistic network $G=(V, E)$, the spread threshold is $Q>0$, which is a certain fraction of the size of the OSNs. Find the optimal policy $\pi ^*$ that leads to the minimum cost, i.e., $\pi ^*=arg \min \{c(\pi ^*)|f(\pi ^*)\ge Q\}$.

Fig. 1

Illustration of a policy $\pi$

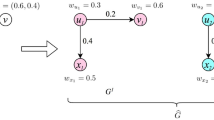
We use a toy social network in Fig. 1 to illustrate our online discount allocation policy $\pi$. There are six users $V=\{a,b,c,d,e,f\}$. The propagation probabilities are on the edges. The graph is unknown in advance, it can be partially revealed after some nodes being active. Our expected spread Q is 5. Possible discount set is $D=\{1,2\}$. Assume that we select node a as the first seed node and set $\pi (\emptyset )=a$, which means that we probe (a, 1) firstly, i.e. offering discount 1 to user a, and we observe the realization $\left\langle \phi ,\psi \right\rangle$ of user a, $\phi (a,1)$=1, i.e., a accepts the offer and become a seed; $\psi (ab)=0$, $\psi (ac)=1$, $\psi (cf)=1$, $\psi (ad)=1$, i.e. node c, f, d are influenced by seed a, b has not been influenced by a and e has not been influenced by d. In the graph, we use solid line (dotted line) represent a node successfully (resp. unsuccessfully) influences its outgoing neighbour nodes, that is to say, solid lines represent active edges and dotted lines represent inactive edges. After observing the state of edges of the active nodes, we can decide our policy in the next step: $\pi ({\left\langle a,1\right\rangle })=e$. Because in this graph, only nodes e and b are inactive. We firstly offer discount 1 to e. We observe that $\phi (e,1)=0$, it means that e does not accept the discount and he is still inactive. As $\pi ({\left\langle e,0\right\rangle })=b$. In the third step, we can probe user b with discount 1, b accepts the offer, i.e. $\phi (b,1)=1$. When b is active, he can not influence his neighbors since he does not have any outgoing neighbors, then the number of influenced users is 5 which achieved our threshold spread 5 and the cost is 2 eventually. But if we use the zero-feedback setting, we may choose nodes a and d as seed users in advance since these two nodes have the maximum outgoing neighbors, in which case we can only influence 4 nodes at most.

4 The online discount allocation greedy policy

Before presenting our algorithms, we introduce the definition of the conditional expected marginal benefit of a seed.

Definition 1

Given an online partial realization $\psi$ and a user v, the conditional expected marginal benefit of v conditioned on having observed $\psi$ is denoted $\varDelta (v|\psi )$ as

$$\begin{aligned} \begin{aligned} \varDelta (v|\psi ):=\mathbb E[f(dom(\psi )\cup {v})-f(dom(\psi )] \end{aligned} \end{aligned}$$

where the expectation is computed with respect to $p(\psi ):=[\Psi =\psi ]$.

In our seeds selection condition, $\varDelta (v|\psi )$ quantifies the expected amount of additional increment by adding a seed user to the seed set to propagate the product information, in expectation over the posterior distribution $p(\Psi ):=\mathbb {P}[\Psi ]$ of how many users he will influence if he becomes a seed.

Definition 2

Function f is online monotone with respect to distribution $p(\psi )$ if conditional expected marginal benefit of any seed is non-negative, i.e., for all $\psi$ with $\mathbb {P}[\Psi \sim \psi ]>0$ and all $v\in V$ we have

$$\begin{aligned} \begin{aligned} \varDelta (v|\psi )\ge 0 \end{aligned} \end{aligned}$$

Definition 3

A function f is online submodular with respect to distribution $p(\psi )$ if for all $\psi$, and $\psi ^\prime$ such that $\psi$ is a sub-realization of $\psi ^\prime$, and for all $v\in V\backslash dom(\psi ^\prime )$, we have

$$\begin{aligned} \begin{aligned} \varDelta (v|\psi )\ge \varDelta (v|\psi ^\prime ) \end{aligned} \end{aligned}$$

Assume $\pi _{ag}$ is the online greedy policy which selects the node $v\in V\backslash dom(\psi )$ with the largest expected marginal gain $\varDelta (v|\psi )$ under the given partial realization $\psi$, $\pi _{opt}$ is the online optimal policy. Golovin and Krause (2011) proved that, the expected spread function f under edge level full feedback is monotone and submodular w.r.t. $p(\psi )$, and also prove that $\pi _{ag}$ is an $(1-1/e)$- approximation of the adaptive optimal policy $\pi _{opt}$, $f_{avg}(\pi _{ag})\ge (1-1/e)f_{avg}(\pi _{opt})$.

4.1 Greedy policy under uniform discount

First, we focus on the case with uniform discount $c_v\equiv d$, $\forall v\in V$ in Algorithm 1. When the cost is uniform, we just need to select minimal number of seeds that can achieve the minimal sum cost while ensuring that a sufficient value $f\ge Q$ is obtained.

Given the observation of the current state $dom(\phi ,\psi )$. We use $\varDelta (v|\psi )$ to denote the expected marginal benefit of v in $V\backslash dom(\psi )$ where the condition is that v has been the seed. The greedy policy $\pi$ myopically probes the seed which can get the maximal expected marginal gain ($v^*=arg\ max_{v\in V\backslash dom(\psi )}\varDelta (v|\psi )$) at each iteration based on $dom(\phi ,\psi )$. If there are multiple users in an iteration at the same time to obtain the maximal expected marginal gain, we just need to randomly choose one. If $v^*$ accepts the discount, we remove $v^*$ from V in the following round and add $v^*$ to set S which is the selected seed set. Otherwise, if $v^*$ rejects the discount, we put $v^*$ aside and don’t consider it any more. We have to update the new diffusion realization when a new seed is selected and completes his spread. This process iterates until reaching the spread threshold of Q. Our online greedy algorithm under the uniform discount is as Algorithm 1.

4.2 Greedy policy under non-uniform discount

In Algorithm 2, we consider the case when the cost is not uniform, and assume that the discounts are sorted in ascending order: $\forall 0<i<j<|D|$: $d_i<d_j$. First, we probe user $v^*$ who has the largest ratio of conditional expected marginal benefit to cost ($v^*=arg\ max_{v\in V\backslash S}\varDelta (v|\psi )/d_i$) when offering him the lowest discount to each user. If there are multiple users in an iteration at the same time to obtain the maximal ratio of conditional expected marginal benefit to cost, we just randomly choose one. If he accepts this discount, we add $v^*$ to selected seed set S. Then updating the diffusion realization. If the influence can reach Q, we can terminate the selection of the seed. If $f<Q$, we have to go on selecting seeds. If $v^*$ rejects the discount $d_1$, we can increase the discount rate. If the maximal discount can not be accepted by $v^*$, we simply don’t consider it any more. The entire procedure will be repeated until function f obtains the value of Q.

5 Performance analysis

Theorem 1

When the discount is uniform and $c_v\equiv d$. Let $\beta >0$ be the spread shortfall for the online greedy discount allocation policy over its optimal discount allocation spread. The optimal discount allocation policy $\pi ^*$ achieves a target spread Q. The online greedy discount allocation policy $\pi$ which is an $\alpha$-approximate greedy policy and can achieve $Q-\beta$. Then we have the following relation between the cost of online greedy discount allocation policy $c_{avg}(\pi )$ and the cost of optimal discount allocation policy $c_{avg}(\pi ^*)$

$$\begin{aligned} \begin{aligned} c_{avg}(\pi )\le \alpha c_{avg}(\pi ^*)ln\left( \frac{Q}{\beta }\right) \end{aligned} \end{aligned}$$

Theorem 2

When the discount in non-uniform. Let $\beta >0$ be the spread shortfall for the online discount allocation greedy policy over its optimal discount allocation spread. Let $\pi ^*_{wc}$ be the optimal policy minimizing the worst-case cost $c_{wc}$ while guaranteeing the maximum possible expected spread $f(\pi ^*)=Q$. Let $\pi$ be an $\alpha$-approximate greedy policy, run until it achieves $f(\pi )\ge Q-\beta$. Then

$$\begin{aligned} \begin{aligned} c_{wc}(\pi )\le \alpha c_{wc}(\pi _{wc}^*)\left( ln\left( \frac{Q}{\beta }\right) +1\right) \end{aligned} \end{aligned}$$

Definition 4

A policy $\pi$ is an $\alpha$-approximate greedy policy if $\varDelta (v|\psi )>0$, $\exists v\in V$ under online partial realization $\psi$,

$$\begin{aligned} \begin{aligned} \pi (\psi )\in \left\{ v: \frac{\varDelta (v|\psi )}{c(v)}\right\} \ge \frac{1}{\alpha } \max \limits _{v^\prime }\left( \frac{\varDelta (v^\prime |\psi )}{c(v^\prime )}\right) \end{aligned} \end{aligned}$$

$\pi$ will terminate when observing a $\psi$ has a negative conditional expected marginal benefit, that is $\varDelta (v|\psi )\le 0$ for and $v\in V$. An $\alpha$-approximate greedy policy always obtains at least (1/$\alpha$) of the maximal possible ratio of conditional expected marginal benefit to cost. It terminates when no more benefits can be obtained in expectation.

Lemma 1

Suppose we have made online observations $\left\langle \phi ,\psi \right\rangle$. Let $\pi ^*$ be any policy. Then for online greedy monotone submodular f:

$$\begin{aligned} \begin{aligned} \varDelta (\pi ^*,\psi )\le c(\pi ^*|\psi )\max \limits _{v}\left( \frac{\varDelta (v|\psi )}{c(v)}\right) \end{aligned} \end{aligned}$$

Proof

Consider policy $\pi$ that attempts to select $v\in dom(\psi )$, terminating if $\Psi (v)\ne \psi (v)$, and then executing policy $\pi ^*$. $p_{vd_i}$ is the probability that v accept discount $d_i$ and become a seed when running $\pi$, the online partial realization $\psi ^\prime$ contains $\psi$ as a online subrealization. By submodularity it implies $\varDelta (v|\psi ^\prime )\le \varDelta (v|\psi )$. So the total contribution of v to $\varDelta (\pi ^*|\psi )$ is upper bounded by $p_{vd_i} \varDelta (v|\psi )$. By summing all $v\in V \backslash dom(\psi )$, we can get bound that

$$\begin{aligned} \begin{aligned} \varDelta (\pi ^*|\psi )\le \sum \limits _{v\in V\backslash dom(\psi )}p_{vd_i}\varDelta (v|\psi ) \end{aligned} \end{aligned}$$

For each $v\in V\backslash dom(\psi )$ contributes $p_{vd_i}c(v)$ cost to $c(\pi ^*|\psi )$. So we have,

$$\begin{aligned} \begin{aligned} \sum \limits _{v\in V\backslash dom(\psi )} p_{vd_i}c(v)\le c(\pi ^*|\psi ) \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \varDelta (\pi ^*|\psi )\le \sum \limits _{v\in V}p_{vd_i}\varDelta (v|\psi )&\le \sum \limits _{v\in V}p_{vd_i}c(v)\max \limits _{v\in V}\frac{\varDelta (v|\psi )}{c(v)}\\ {}&\le c(\pi ^*|\psi )\max \limits _{v\in V}\frac{\varDelta (v|\psi )}{c(v)} \end{aligned} \end{aligned}$$

$\square$

Theorem 3

Fix any $\alpha \ge 1$ and the discount that v accepts. Let $\pi ^*\in arg \max \limits _{\pi }f_{avg}(\pi _{[k]})$, where k is the number of selected seeds. If f is monotone and submodular with respect to the distribution $p(\psi )$, and $\pi$ is an $\alpha$-approximate greedy policy, then for all policy $\pi ^*$, and positive integers h and l, we have

$$\begin{aligned} \begin{aligned} f_{avg}(\pi _{[h]})> (1-e^{-h/{\alpha l }})f_{avg}(\pi _{[l]}^*) \end{aligned} \end{aligned}$$

Proof

The proof goes along the lines of the performance analysis is an extension analysis for the $\alpha$- approximate greedy algorithm. We assume without loss of generality that $\pi =\pi _{[h]}$ and $\pi ^*=\pi ^*_{[l]}$. Then for any $0<i<l$, we can derive that:

$$\begin{aligned} \begin{aligned} f_{avg}(\pi ^*)\le f_{avg}(\pi _{[i]})+\alpha l(f_{avg}(\pi _{[i+1]})-f_{avg}(\pi _{[i]})) \end{aligned} \end{aligned}$$

(1)

This inequation follows from the monotonicity of f and Lemma 1. From Lemma 1 we also can get that

$$\begin{aligned} \begin{aligned} \mathbb E[\varDelta (\pi ^*|\psi )]\le \mathbb E[c(\pi ^*|\psi )]\max \limits _{v}\left( \frac{\varDelta (v|\psi )}{c(v)}\right) , \end{aligned} \end{aligned}$$

Since $\pi ^*$ has the form $\pi _{[k]}$ and k is the number of selected seeds. We have $\mathbb E[c(\pi ^*|\psi )]\le l$ for all $\psi$. It follows that $\mathbb E[\varDelta (\pi ^*|\psi )]\le l\max \limits _{v}(\frac{\varDelta (v|\psi )}{c(v)})$. By the definition of an $\alpha$-approximate greedy policy, $\pi$ obtains at least $\frac{1}{\alpha } \max \limits _{v}(\frac{\varDelta (v|\psi )}{c(v)}) \ge \mathbb E[\varDelta (\pi ^*|\psi )]/\alpha l$ expected marginal benefit per unit cost in a step immediately following its observation of $\psi$.

Based on the monotonicity equivalence property in Golovin and Krause (2011), given two policies $\pi _1$ and $\pi _2$, $\pi _1 @ \pi _2$ defined as the policy that after running $\pi _1$ then running policy $\pi _2$ ignoring the information gathered during the running of $\pi _1$. We can get that $f_{avg}(\pi _1)\le f_{avg}(\pi _1@\pi _2)$

Then, for a random partial realization $\Psi$, we can get following inequality:

$$\begin{aligned} \begin{aligned} f_{avg}(\pi _{[i+1]})-f_{avg}(\pi _{[i]})&\ge \mathbb E\left[ \frac{1}{\alpha }\max \limits _{v}(\frac{\varDelta (v|\Psi )}{c(v)})\right] \\&\ge \mathbb E\left[ \frac{\mathbb E[\varDelta (\pi ^*|\Psi )]}{\alpha l}\right] \\&=\frac{f_{avg}(\pi _{[i]}@\pi ^*)-f_{avg}(\pi _{[i]})}{\alpha l} \end{aligned} \end{aligned}$$

Now define $\varDelta _i :=f_{avg}(\pi ^*)-f_{avg}(\pi _{[i]})$, so that in equation 1 implies $\varDelta _i\le \alpha l(\varDelta _i-\varDelta _{i+1})$, we can infer that $\varDelta _{i+1}\le (1-\frac{1}{\alpha l})\varDelta _i$ and hence $\varDelta _h\le (1-\frac{1}{\alpha l})^h\varDelta _0\le e^{-h/\alpha l}\varDelta _0$, where for the second inequality we used the fact that $1-x<e^{-x}$ for all $x>0$. Hence $f_{avg}(\pi ^*)-f_{avg}(\pi _{[h]})<e^{-h/\alpha l}(f_{avg}(\pi ^*)-f_{avg}(\pi _{[0]}))\le e^{-h/\alpha l}f_{avg}(\pi ^*)$ so $f_{avg}(\pi )>(1-e^{-h/\alpha l})f_{avg}(\pi ^*)$. $\square$

Proof of Theorem 2

Let $\beta >0$. Assume that l is the least seeds number that adaptive optimal policy $\pi ^*$ selected to achieve influence spread $f_{avg}(\pi ^*)\ge Q$. Then running adaptive greedy policy $\pi$ for h seeds, as $f_{avg}(\pi )\ge Q-\beta$, apply these two parameters to Theorem 3, we can get $h=\alpha l(lnQ/\beta )$. Let $l=c_{wc}(\pi ^*_{wc})$, and apply parameters h and l to Theorem 3 we can get the following inequation

$$\begin{aligned} \begin{aligned} f_{avg}(\pi _{[h]})\ge \left( 1-\frac{\beta }{Q}\right) f_{avg}(\pi _{[wc]}^*) \end{aligned} \end{aligned}$$

(2)

As $\pi ^*_{wc}$ can cover all the realization, $f_{avg}(\pi ^*_{wc})=\mathbb E[f(V(\pi , \psi ),\Psi )]=Q$. The inequation 2 can denote as $Q-f_{avg}(\pi _{[h]})\le \beta$. Since f is monotonicity, $f_{avg}(\pi _{[h]})\le f_{avg}(\pi _{[h\rightarrow ]})$, we can get that $Q-f_{avg}(\pi _{[h\rightarrow ]})\le \beta$, this can infer that $Q-f_{avg}{(\pi _{[h\rightarrow ]})}=0$, so $\pi _{[h\rightarrow ]}$ covers every realization. It is known that $\pi$ is an $\alpha$-approximate greedy policy and $\pi _{wc}^*$ covers all the online realizations at most l cost. From Lemma 1, we have:

$$\begin{aligned} \begin{aligned} \max \limits _{v\in V}\frac{\varDelta (v|\psi )}{c(v)}\ge \frac{\varDelta (\pi _{wc}^*|\psi )}{c(\pi ^*_{wc}|\psi )} \ge \frac{\varDelta (\pi ^*_{wc}|\psi )}{l} \end{aligned} \end{aligned}$$

(3)

We suppose that $\psi \in dom(\pi )$, we have $max_v\varDelta (v|\psi )\le \varDelta (\pi ^*_{wc}|\psi )$ as f is monotone submodular. Any user v with cost $c(v)>\alpha l$ also has $max_v\varDelta (v|\psi )/c(v)\le \varDelta (\pi ^*_{wc}|\psi )/\alpha l$, it can not be selected by any $\alpha$-approximate greedy policy after observing $\psi$ by inequation 3. The final user executed by $\pi _{[h\rightarrow ]}$ has cost at most $\alpha l$ for any realization. So that $\pi _{[h\rightarrow ]}$ has worst-case cost at most $h+\alpha l$, where $l=c_{wc}^*$. This completes the proof. $\square$

Proof of Theorem 1

When the cost $c_v=d$ for all seeds, the the number of seeds multiplies d equals the sum cost. So we conduct some algebraic manipulation in Theorem 3 to set $f_{avg}(\pi _{[h]})=Q-\beta$, $f_{avg}(\pi ^*_{[l]})=Q$, we can get the conclusion of Theorem 1. $\square$

6 Performance evaluation

In this section, we will show the simulation of our proposed algorithms. The preparation of the experiment will be discussed in Sect. 6.1 with the datasets and parameter settings.

6.1 Experimental setup

Datasets: In this paper, we have used two datasets from Opsahl (2013), Newman (2001). One of the dataset is a Forum Network which was collected from an online community very similar to the Facebook online social network. This dataset contained records of users activities in the forum. It is a collection of nodes and edges that depict the relationship among the 899 users. The other dataset is the Newmans scientific collaboration network which represents the co-authorship network based on preprints posted to Condensed Matter section of arXiv E-Print Archive between 1995 and 1999. This data represents the relationship among the co-authors.The details about the data is mentioned in the Table 1.

Table 1 Statistics of two datasets

Propagation Probability: In both the datasets, the file containing the information about the node relation is used to build the graphs. The influence probability is assigned as 1/N where N is the number of in-degree of a given node, this method is widely used in previous literatures (Wang et al. 2012; Tang et al. 2014; Yang et al. 2016). We use random numbers between 0 and 1 as the propagation probability threshold to find how many nodes are activated by each seed node. The generated random number is compared with the influence probabilities on the edges to count the number of nodes that can activate in each iteration. If the probability on the edge is greater than the random number it will influence its neighbor; otherwise, it can not influence its neighbor.

Adoption Probability: We use $x\in [0,1]$ to denote the percentage of the offered discount in the product price. The adoption probability $p_{v,x}$ of each node v for the discount rate x is set as: for the graph $G=(V,E)$, we randomly choose $85\%$ nodes of to assign $p_{v,x}=\root 3 \of {x}$, these users are sensitive to discount, and $10\%$ nodes to assign $p_{v,x}=x$, and $5\%$ nodes to assign $p_{v,x}=x^2$ as their seed probability function, which means that those users are insensitive to discount, this setting is also used in some previous literatures (Tang 2018).

Also, the random number between 0 and 1 is generated as the adoption probability threshold each time to determine if a node accepts the discount. If the probability of the node accepting the discount is greater than the random number it is assumed that it will accept the discount; otherwise, it will reject the discount.

6.2 Comparison method

Zero-feedback greedy method. It selects seed node set which has the largest expected influence at once in advance, and probes these nodes with discounts in increasing order. We should make sure that these selected seed users can spread a target influence value Q.

We use the Monte Carlo sampling to get the mean of the expected influence function f for our problem and the Zero-feedback greedy method as well as the $\pm 1$ standard deviation intervals over 100 runs of each node.

6.3 Result analysis

Fig. 2

Results with zero-feedback greedy method on dataset 1

Fig. 3

Results with online greedy method on dataset 1

Comparison with zero-feedback greedy method on dataset 1. This experiment is done on dataset 1 and the discount is uniform. In Fig. 2, we show the variation of the number of seeds selected by changing the value of Q with the zero-feedback greedy method. The five different curves are in different discounts changing from 100 to 500. We can see that the smaller the discount is, the more the seeds are needed. But when the value of Q is less than 200, the number of seed users required is the same, as we can find influential users easily since just a small influence is needed. As the spread threshold of Q increases, we need to find more influential seeds, so larger discount will be more attractive for these users to be active. We can see in Fig. 2, when the discount equals 100 and Q is over 200, it needs the most seeds in the five different discounts situations. When the discount equals 400 and 500, we can see the curves increase more slowly when the Q exceeds 400. It is because the larger discount can attract more high influential nodes, which can activate more nodes with fewer seed nodes. Although providing larger discount is more attractive, it can activate more influential seeds so that it just needs fewer seeds to reach the expected spread threshold Q, but it also has an obvious drawback of being expensive. We can calculate that when $D=100$ and $Q=600$, we need choose 70 seed nodes, it costs 7000, while when $D=500$ and $Q=600$, we need choose 25 seed nodes, it costs 12,500, which the cost is far greater than the uniform discount 100 situation, so bigger discount costs more.

In Fig. 3, we do the experiment in online greedy method, we also set the uniform discount in five different values. We can see from the lines that the tendency of change is the similar to Fig. 2, they are also monotone increasing and the larger discounts need a smaller number of seeds. We can see that when the discount is 100, we need more seed users but when we calculate the cost, we can find that it takes the least cost. The reason is the same with zero-feedback greedy method above.

From Figs. 2 and 3, we can see that every curve is a gradient rise. And the growth ratio is larger when the discount is smaller. Because when the discount is smaller, many influential users would not accept the discounts to become seeds, we need to find some less influential users to accept the discounts. It can also be noted that the lines of the algorithms clearly illustrate the phenomenon of diminishing marginal returns, empirically illustrating monotonicity and submodularity. Comparing Fig. 2 with 3, for a certain value of Q and the same discount offered, the online greedy method needs fewer seeds, because the online greedy algorithm can choose the next seed wisely based on real spread triggered by existing seeds. Although the larger discount can activate more influential users to become the seeds, it also needs a larger cost. On the contrary, the smaller discount needs to choose some less influential seeds but it saves the cost. So using a smaller discount, it can achieve our expected spread threshold Q and save cost at the same time.

Fig. 4

Results with online greedy method in non-uniform discount situation on dataset 1

Varying the discount rate set with proposed method. We do the experiment with the online greedy method in the non-uniform discount situation firstly, the results shows in Fig. 4. The number of discount changes from three kinds to seven kinds, and we can see from the changes of lines that when the discounts are a combination of $D=\{100,200,300\}$, it needs the most seeds, and greater the discount combination is, the fewer the seeds we will select. The reason is the same as the results in Figs. 2 and 3, because a greater discount is more attractive to the influential users. So for the combination $D=\{100\sim 700\}$, it selects the least number of seeds. But based on the experimental results, we know that it cost the least with the combination of $D=\{100,200,300\}$, but it cost the most as the high influential seed would like to accept larger discount. So the smaller discount combination can achieve larger spread with minimum cost.

Comparing Fig. 4 with Figs. 2 and 3, we can see that for a certain value Q, the non-uniform discount requires less seeds. Based on the experiment results in these three situations, non-uniform discount needs less cost than the uniform discount with the online greedy method as well as the uniform discount with the zero-feedback greedy method for the same Q. As in non-uniform cost, we have more discount choice, we would choose some high influential nodes who would accept low discounts.

Fig. 5

Results with online greedy method in uniform discount situation on dataset 2

In Fig. 5, we use a dataset 2 to continue our experiments with the online greedy method under the uniform discount situation. Because the dataset 2 is larger than dataset 1, and the indegree of every node is larger than dataset 1, too, the influence probabilities are smaller than that in dataset 1. We can observe the change of the lines in Fig. 5, for the same discount and Q, it needs more seeds than that in Fig. 3, as the influence of the seed is smaller than that of dataset 1. But in the larger dataset 2, we can still get the result which is got in the Fig.  3 with dataset 1 that the smallest discount 100 can save the most cost to get the spread threshold Q. So the results in 5 with dataset 2 are consistent with the results with dataset 1, which further confirms the correctness of the previous results .

Changes of running time with two proposed methods. The unit of the runtime is in seconds. The y-axis in Figs. 6 and 7 is the total runtime when the expected spread threshold Q increases from 100 to 800 in two different datasets with Online greedy uniform discount and non-uniform discount methods, respectively. In Fig. 6, we set the uniform discount as 100, 200, 300 to do different simulations in dataset 1 and dataset 2 respectively, we can observe that the running time decreases with the increasing of uniform discount when the spread threshold is the same, its because that when the discount increases, it is easier to find a seed users and more time saving. This results is verified in both dataset 1 and dataset 2. In non-uniform discount situation, we set discount combination as $D=\{100\sim 300\}$, $D=\{100\sim 500\}$, $D=\{100\sim 700\}$, the results in Fig. 7 show that when we increase the number of discount in the discount combination, the running time decreases, which is because the larger discount in the combination is easier to accept by a high influential seed node, this can save time to find a suitable seed node. This result is also shown in two different datasets. From the above results in Figs. 3 and 4, we know that it costs less when the uniform discount $D=100$ than that in other larger uniform discount and the non-uniform discount situation with the online greedy method. From Figs. 6 and 7, we can see that the uniform discount takes more running time when the dataset and spread threshold are same. Although the uniform discount with online greedy method saves more cost than the non-uniform discount with online greedy method, the non-uniform discount method is more time saving. Because when we choose a node with the maximal marginal gain, it may not accept the lower discount, and we can increase the discount as it has several discount choices in non-uniform discount method. The greater discount has a larger probability to be accepted by a user. It is more time saving than the uniform discount method as we have to find another seed again in the uniform situation once a node rejects a discount. And we also find that the dataset 2 need more time to reach the same expected spread threshold with the same method, which is easy to understand since dataset 2 has much more nodes than dataset 1.

Fig. 6

The runtime of different expected spread threshold Q with uniform discount method in two datasets

Fig. 7

The runtime of different expected spread threshold Q with non-uniform method in two datasets

Results on sampling graph from dataset 1. At last, we take samples from the dataset 1. The graphs are sampled to give various subsets of the original graph. For building the sample graph, a random number is generated and if the edge probability is less than the generated number, that edge will be removed from the original graph to give a resulting sample sub-graph. The Algorithm 1 is applied to each of the sample graphs to obtain the average results. We generate 100 sample graphs and iterate over all these sample graphs to obtain the results. Each time due to some random parameters in the algorithm, the solution is approximately the same thus the simulation converges. We observe that the trend of the lines in Fig. 8 are also in accordance with previous experimental results. When the uniform discount is 300, it needs to selects least seed users but cost the most to achieve the spread threshold Q.

Fig. 8

Results on sampling graph from dataset 1

From the above experimental results, we can get that the online greedy method is superior to the zero-feedback greedy method, and the lower uniform discount situation is more cost saving than the non-uniform discount situation. But the non-uniform discount situation is more time saving than the uniform discount situation.

7 Conclusion

We propose an online full-feedback setting model to solve the discount allocation problem in OSNs and divide the cascade into seed selection and information diffusion stages. Our goal is to minimize the cost that marketer spends while ensuring that the number of people who adopted the target product should not be less than a spread threshold of Q. We present two algorithms under uniform and non-uniform discount conditions and analyze the approximation ratios in these two situations. Finally, we use experiments on real-world OSNs to illustrate the empirical superiority of the proposed strategy.

In future, we intend to study a problem which evaluates a suitable discount for each seed but without using stochastic discount probing as used in this paper. We also want to study another problem that the marketer has multiple products to advertise at the same time and different products have their specific features which are suitable for user group with different needs. How should we allocate the budget to each product to achieve influence maximization or profit maximization.